Submitted:
16 July 2024
Posted:
17 July 2024
Read the latest preprint version here
Abstract
Keywords:
Preface
On the Scope and Structure of This Manuscript
- Unification: HTUM’s core principle of unity demands a holistic treatment that encompasses a wide range of physical phenomena, from quantum mechanics to cosmology. This manuscript aims to present a cohesive picture of how these diverse areas interconnect within the HTUM framework.
- Mathematical rigor: To fully develop HTUM’s theoretical foundations, we include detailed mathematical formulations, including a complete theory axiomatization. This level of rigor is crucial for establishing HTUM as a robust and testable scientific model.
- Interdisciplinary implications: HTUM’s unique perspective has significant implications for various fields, including particle physics, quantum gravity, and cosmology. Each area requires a thorough examination to elucidate HTUM’s potential contributions.
- Novel concepts: Several new ideas introduced by HTUM, such as the Topological Vacuum Energy Modulator (TVEM) function, necessitate extensive explanation and exploration of their consequences.
- Comparative analysis: To contextualize HTUM within the broader landscape of theoretical physics, we provide detailed comparisons with existing theories and models.
- Experimental predictions: A significant portion of this work is dedicated to deriving and explaining the observational and experimental consequences of HTUM, crucial for its empirical validation.
1. Introduction
1.1. Background and Motivation
- Timeless singularity: Just as objects appear frozen at a black hole’s event horizon, HTUM proposes that the entire universe exists in a state of timelessness. This concept challenges our traditional understanding of time as a linear flow and aligns with the idea of a four-dimensional structure where all moments coexist.
- Interconnectedness: The idea that all matter, regardless of when it enters the black hole, eventually reaches the same timeless state reflects HTUM’s concept of a deeply interconnected universe where all points in space and time are fundamentally linked.
- Emergence of time: The apparent flow of time for an outside observer in the black hole analogy can be likened to how HTUM views time as an emergent property arising from causal relationships within the universe’s structure.
- It provides a potential explanation for the ubiquity of black holes in the universe, suggesting they play a fundamental role in maintaining cosmic structure.
- It offers a new perspective on the information paradox, as information crossing these "walls" might be preserved within the overall structure of the universe rather than truly lost.
- It suggests a deep connection between the minor quantum scales and the most significant cosmic structures, as black holes bridge these extremes in current physics.
- It aligns with the HTUM’s cyclical nature, where matter and energy flowing through these "walls" could contribute to the universe’s self-sustaining structure.
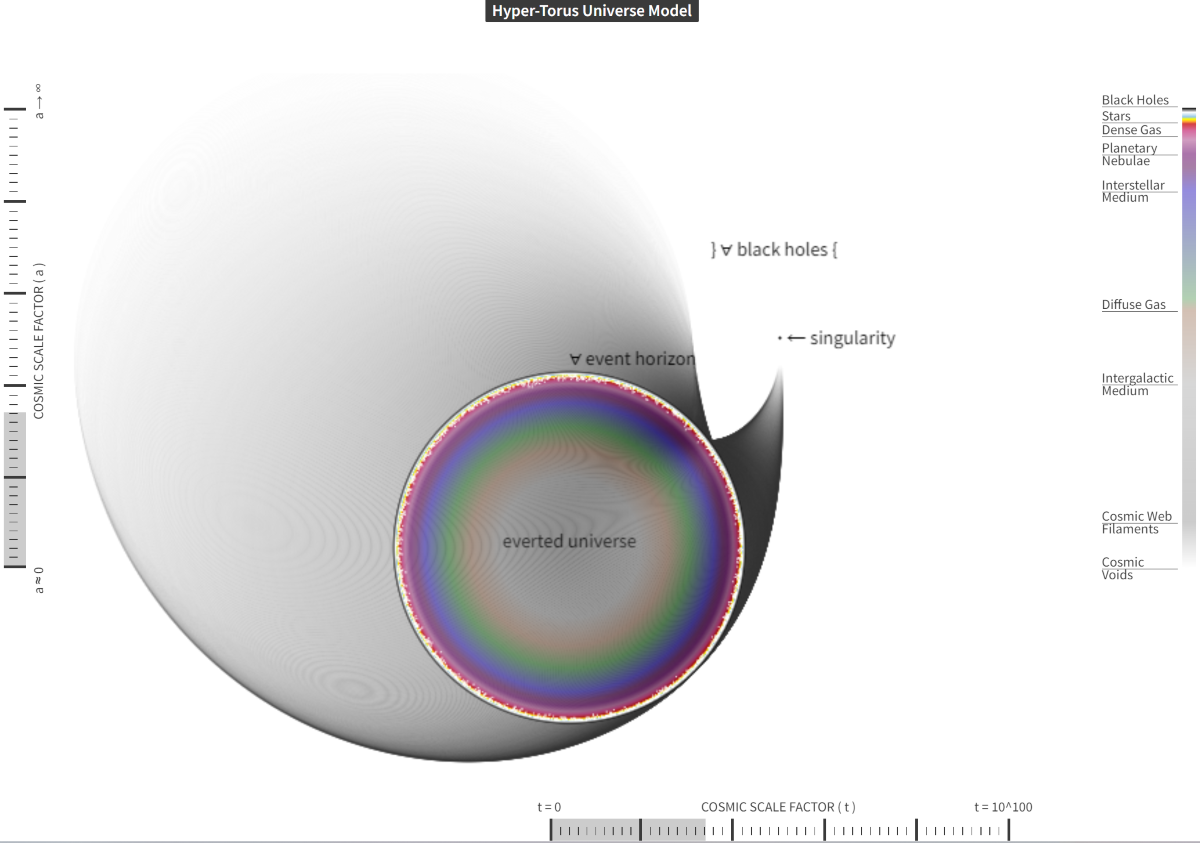
- Toroidal structure: The circular cross-section represents a slice through the 4D torus at an instance of space-time, showcasing the model’s fundamental geometry.
- Everted universe and black holes: Central to the image is the "everted universe," surrounded by a distinct event horizon. Beyond this horizon, HTUM proposes a region composed entirely of what the model considers to be a singular, unified black hole continuum. This concept illustrates HTUM’s unique perspective that all black holes are fundamentally interconnected, forming a continuous boundary of the observable universe. This approach challenges conventional views of black holes as separate entities, instead presenting them as integral parts of the universe’s toroidal structure.
- Matter distribution: Color gradients within the everted universe visualize the spatial distribution of matter across cosmic structures. The gradient progresses from the densest structures near the torus "walls" (composed entirely of event horizons) to the least dense regions at the center.
- Cosmic components: The legend identifies various components such as stars, dense gas, planetary nebulae, and interstellar medium, providing an intuitive understanding of density variations across the slice.
- Temporal representation: This static image represents a single moment in the model. The full simulation depicts Temporal evolution by animating slices moving through the 4D structure.
1.2. Roadmap of the Paper
- Section 2: Theoretical Foundations - This Section delves into the limitations of the Lambda-CDM model and provides a historical context for developing cosmological concepts, including the discovery of dark matter and dark energy. It sets the stage for understanding why a new model like HTUM is necessary.
- Section 3: The Hyper-Torus Universe Model (HTUM) - Here, we present a detailed explanation of HTUM, including the mathematical formulation of the toroidal structure and its properties. We also discuss the challenges in visualizing a four-dimensional toroidal structure (4DTS).
- Section 4: axiomatization of HTUM: Addressing Hilbert’s Sixth Problem - This section provides a comprehensive HTUM axiomatization, significantly contributing to the model’s theoretical foundation.
- Section 5: Early Universe Evolution and Inflation in HTUM - This section delves into how HTUM addresses the early universe and cosmic inflation. It explores the transition from quantum to classical states within the HTUM framework and presents a unique perspective on inflation that arises naturally from the toroidal structure. The section demonstrates how HTUM can explain critical cosmological phenomena without requiring additional fields or mechanisms.
- Section 6: Gravity and the Collapse of the Wave Function - This Section explores the wave function’s significance in quantum mechanics and discusses the measurement problem, highlighting how HTUM addresses these issues.
- Section 7: Yang-Mills Theory and Mass Gap in HTUM - This section provides a detailed exploration of Yang-Mills theory within the HTUM framework, including its implications for particle physics and cosmology.
- Section 8: Time Dilation and Causal Processing: A Unifying Perspective - This section presents HTUM’s novel interpretation of time dilation as a manifestation of causal processing within the universe’s structure. It introduces the concept of manifold actualization latency and explores how this framework unifies gravitational and special relativistic time dilation effects. The section includes a thought experiment, the Quantum Gravity Observatory, demonstrating HTUM’s unique predictions. It also provides a comparative analysis with other time dilation interpretations, highlighting HTUM’s contributions to our understanding of time, gravity, and quantum phenomena. The section concludes by addressing practical challenges in testing these predictions and discussing future research directions.
- Section 9: Information Theory and Holography in HTUM—This section explores the implications of HTUM for information theory and holography. We discuss how the universe’s toroidal structure affects the encoding and processing of information and examine the connections between HTUM and holographic principles. The section also addresses the black hole information paradox within the HTUM framework and proposes novel approaches to quantum error correction based on the model’s unique geometry.
- Section 10: HTUM and the Computational Universe - This section explores the interpretation of HTUM as a model of a computational universe. We examine how the 4-dimensional toroidal structure (4DTS) can be viewed as a cosmic-scale quantum computer, discuss information processing within this framework, and explore the algorithmic complexity of the universe. The section also investigates quantum error correction in the toroidal structure, connections to digital physics, and the implications of viewing the universe as a vast information processing system. We conclude by discussing this computational perspective’s observational and experimental implications, providing testable predictions that could validate HTUM’s computational aspects.
- Section 11: Beyond Division: Unifying Mathematics and Cosmology - This Section examines HTUM’s implications for the foundations of mathematics, discussing the nature of mathematical truth and the role of intuition.
- Section 12: The singularity and quantum entanglement - We explain quantum entanglement, its implications for singularity, and the challenges in experimentally verifying these concepts.
- Section 13: The Event Horizon and Probability - This Section focuses on the mathematical formulation of the event horizon and its properties, discussing HTUM’s implications for our understanding of black holes.
- Section 14: The Universe Observing Itself - We explore the mechanism of self-observation and its relationship to the collapse of the wave function, addressing the experimental challenges involved.
- Section 15: Consciousness and the Universe - We discuss the relationship between consciousness and quantum measurement, incorporating this relationship into HTUM and addressing experimental challenges.
- Section 16: Consciousness and the singularity: A Unified Perspective - We propose a radical hypothesis unifying consciousness and the singularity within the HTUM framework. This section explores this unified perspective’s theoretical foundations, mathematical formulations, philosophical implications, and potential experimental tests. We also address potential criticisms and discuss future research directions in this speculative but promising area of inquiry.
- Section 17: Advanced Formalism of Consciousness in HTUM - Here, we delve deeper into the mathematical framework for integrating consciousness within HTUM. We present an enhanced formalism that describes the interface between consciousness and quantum states, propose testable predictions for consciousness-quantum interactions, and explore the implications for quantum measurement theory. This section also examines how the toroidal structure of HTUM influences conscious experience and discusses the philosophical and metaphysical consequences of this advanced formalism.
- Section 18: Relationship to Other Theories - This Section compares HTUM with other theories of quantum gravity and discusses the potential for integration with different theoretical frameworks.
- Section 19: Unification with particle physics - We explore how HTUM can be extended to incorporate and explain phenomena in particle physics. We discuss the potential emergence of Standard Model particles from the toroidal structure, examine predictions for high-energy particle physics, and propose a framework for unifying fundamental forces within HTUM. This section demonstrates how HTUM’s unique geometric approach could provide new insights into particles’ nature and interactions.
- Section 20: Numerical Simulation Framework - We present a comprehensive computational framework developed to simulate the complex dynamics of HTUM. This section details how we model the 4-dimensional toroidal structure (4DTS), incorporate quantum effects, gravitational dynamics, and the proposed mechanisms for dark matter and dark energy. We discuss our innovative approach to unified mathematical operations within the simulation, our numerical methods, and computational implementation strategies. The section also covers the various outputs generated by our simulation and the advanced visualization techniques we’ve developed. This framework serves as a crucial bridge between HTUM’s theoretical foundations and its empirical predictions, providing a powerful tool for exploring the model’s implications and generating testable hypotheses.
- Section 21: Testable Predictions and Empirical Validation - We discuss the challenges of testing HTUM’s predictions experimentally and provide a roadmap for future experimental work and collaborations.
- Section 22: Implications for the Nature of Reality - This Section delves into the philosophical implications of HTUM, particularly concerning the nature of time and the mind-matter relationship.
- Section 23: Conclusion - The final Section discusses HTUM’s potential impact on cosmology and its relationship to other disciplines, emphasizing the importance of interdisciplinary research and collaboration.
1.3. Significance of HTUM in Cosmology
- Unified framework for fundamental forces: HTUM provides a novel geometric approach to unifying quantum mechanics and gravity, a long-standing challenge in theoretical physics [31,32,33]. By leveraging the unique properties of its 4-dimensional toroidal structure, HTUM offers a natural framework for reconciling these seemingly incompatible theories. This unification could lead to a deeper understanding of the universe’s fundamental forces and potentially resolve paradoxes at the intersection of quantum theory and general relativity, such as the information paradox in black holes [19].
- Dark matter and dark energy: HTUM reconceptualizes dark matter and dark energy as nonlinear probabilistic phenomena arising from the toroidal structure of the universe [34,35,36]. This approach offers a new pathway to understanding these mysterious components, which constitute about 95% of the universe’s content. By integrating dark matter and dark energy into the fabric of spacetime itself, HTUM provides a more cohesive explanation for their ubiquitous presence and effects on cosmic evolution.
- cosmological constant problem: One of HTUM’s most significant contributions is its approach to the cosmological constant problem [37]. By introducing the TVEM function, HTUM offers a mechanism to naturally suppress the extreme vacuum energy values predicted by quantum field theory. This could resolve one of the most pressing issues in modern cosmology, providing a theoretically motivated solution to the vast discrepancy between observed and predicted vacuum energy densities.
- Early universe and inflation: HTUM presents a unique perspective on cosmic inflation and the early universe [38]. The model’s toroidal structure provides a natural mechanism for ending inflation, potentially resolving the "graceful exit" problem. Furthermore, HTUM’s approach to quantum cosmology offers new insights into the universe’s initial conditions and the emergence of classical spacetime from quantum fluctuations [13].
- large-scale structure and CMB anomalies: HTUM’s toroidal geometry leads to specific predictions about the universe’s large-scale structure and potential anomalies in the CMB [5]. The model offers explanations for observed large-scale anomalies that are challenging to account for in standard cosmological models, providing testable predictions for future CMB experiments and large-scale structure surveys [39].
- quantum-to-classical transition: HTUM provides a smooth and natural explanation for the emergence of classical reality from the quantum substrate [40]. This approach addresses the measurement problem in quantum mechanics and offers insights into the nature of wave function collapse, decoherence, and the role of consciousness in quantum measurements [41].
- Nature of time and causality: HTUM challenges conventional notions of time, presenting it as an emergent property arising from the causal relationships within the toroidal structure [18,42,43]. This perspective offers new insights into the arrow of time, the nature of causality, and the potential for closed timelike curves in extreme gravitational conditions [44].
- Black hole physics: HTUM’s framework provides novel approaches to understanding black hole physics, including potential resolutions to the information paradox and new perspectives on Hawking radiation [19,45]. The model’s toroidal structure uniquely preserves information across the event horizon, potentially reconciling quantum mechanics with general relativity in extreme gravitational scenarios.
- Observational cosmology: HTUM makes specific, testable predictions across various cosmological observables, including the CMB power spectrum, gravitational wave signatures, and the distribution of large-scale structures [39]. These predictions offer multiple avenues for empirical validation, distinguishing HTUM from the standard CDM model and other alternative cosmological theories.
- Philosophical implications: Beyond its physical predictions, HTUM offers profound philosophical insights into the nature of reality, consciousness, and the role of observers in the universe [46,47,48]. By integrating consciousness into the fundamental fabric of the cosmos, HTUM provides a framework for addressing long-standing questions in the philosophy of mind and the nature of subjective experience.
- Computational cosmology: HTUM’s perspective on the universe as a vast information processing system opens new avenues for understanding cosmic evolution in terms of computation and information theory [49]. This could lead to novel approaches to simulating cosmic evolution and understanding the limits of predictability in complex systems.
2. Theoretical Foundations
2.1. The Lambda-CDM Model and Cosmic Evolution Scenarios
2.2. Historical Context
2.3. Limitations of the Lambda-CDM Model
- singularity problem: The theory begins with a singularity, a point of infinite density and temperature, which current physics cannot adequately describe [58].
- flatness problem: The observed spatial flatness of the universe requires fine-tuning initial conditions, which seems improbable [60].
- dark matter and dark energy: While the Lambda-CDM model incorporates dark matter and dark energy as critical components, it does not fully explain their fundamental nature or origin [55,61]. The model describes their effects but leaves questions about their underlying physics and how they evolved throughout cosmic history.
2.4. The Cosmological Constant Problem
2.5. Addressing Limitations with HTUM
- singularity and causality: HTUM redefines the singularity not as a point of infinite density but as a phase transition within the toroidal structure, potentially resolving the singularity problem [66,67]. In HTUM, the singularity is replaced by a smooth transition between cycles, maintaining the continuity of space-time and causality.
- Causal connectivity: The toroidal geometry of HTUM allows for a natural explanation of the horizon problem, as regions of the universe can remain in causal contact through the torus’s topology [7,64]. The compact nature of the torus ensures that light and information can propagate around the universe, maintaining causal connectivity and explaining the observed uniformity of the CMB.
- Spatial flatness: HTUM’s cyclical nature provides a mechanism for maintaining spatial flatness without requiring fine-tuning [15,65]. As the universe undergoes repeated cycles of expansion and contraction, any initial curvature is smoothed out over time, leading to the observed flatness of space. This concept is explored in more detail in Section 3.5, where we discuss how HTUM’s toroidal structure naturally addresses the flatness problem.
- Integration of dark matter and dark energy: HTUM incorporates dark matter and dark energy as fundamental components driving the universe’s cyclical behavior and structural evolution [15,65]. dark matter plays a crucial role in the formation and stability of the toroidal structure, while dark energy drives the expansion and contraction phases of the cosmic cycle.
| Feature | Lambda-CDM | HTUM |
|---|---|---|
| Universe structure | Expanding | 4D toroidal, cyclical |
| Origin | Big Bang singularity | Phase transition |
| Flatness | Requires fine-tuning | Naturally flat |
| Horizon problem | Requires inflation | Causal connectivity |
| Dark matter | Unknown particle | Nonlinear phenomenon |
| Dark energy | Cosmological constant | Dynamic component |
| Future | Eternal expansion | Cyclic evolution |
| Singularities | Present | Avoided |
| Quantum gravity | Not integrated | Potentially unified |
2.6. HTUM and Cosmological Challenges
2.7. Implications and Future Directions
- Unification of quantum mechanics and gravity: HTUM’s toroidal geometry may provide a framework for reconciling quantum mechanics and general relativity, as the model naturally incorporates aspects of both theories [7,64]. The smooth transition between cycles in HTUM could potentially resolve the incompatibility between these two fundamental theories, leading to a more unified theory of quantum gravity.
- Experimental tests: The predictions of HTUM can be tested through various experimental methods, such as precision measurements of the CMB, gravitational wave observations, and studies of large-scale structure [7,64]. Future missions like the James Webb Space Telescope (JWST) and the Large Synoptic Survey Telescope (LSST) could provide crucial data to validate or refine the model.
- Philosophical implications: HTUM challenges our understanding of the nature of reality, time, and the role of consciousness in the universe. The model’s cyclical nature and the interconnectedness of space, time, and matter raise profound questions about causality, determinism, free will, and the role of consciousness in the universe [7,64]. These philosophical implications invite interdisciplinary collaborations between physicists, philosophers, and other scholars to explore the deeper meaning of our existence.
- Technological advancements: The insights gained from HTUM could lead to technological advancements in fields such as energy production, space exploration, and computing [7,64]. Understanding the universe’s fundamental principles may inspire novel approaches to harnessing energy, developing more efficient propulsion systems, and creating advanced computational algorithms.
- Educational and public outreach: HTUM provides an exciting opportunity to engage the public in the wonders of cosmology and the scientific process. The model’s intuitive and visually appealing nature makes it accessible to a broad audience, fostering interest in science, technology, engineering, and mathematics (STEM) fields. Educational programs, popular science books, and multimedia content based on HTUM could inspire the next generation of scientists and encourage public support for scientific research.
2.8. Conclusion
3. The Hyper-Torus Universe Model (HTUM)
3.1. Conceptual Framework
3.2. Toroidal Structure of the Universe
3.2.1. CMB Anomalies and Toroidal Topology
- The "Axis of Evil": An alignment of the quadrupole and octopole moments of the CMB along a specific axis [71].
- The cold spot: An unusually large and cold region in the CMB [72].
- Lack of large-scale power: A deficit in the CMB power spectrum at large angular scales [4].
- Hemispheric asymmetry: Differences in the CMB power spectrum between the northern and southern galactic hemispheres [73].
3.2.2. Scale-Dependent Topological Effects
- are spherical harmonics
- are the multipole coefficients
- is a mode-dependent function that depends on the torus size L
3.2.3. Symmetries and Alignments
3.2.4. The Cold Spot and Topological Defects
3.2.5. Comparison with Other Topological Models
- Simplicity: The toroidal structure is mathematically simpler and easier to model than more complex topologies.
- Naturalness: The torus emerges naturally from many quantum gravity theories [31].
- Comprehensive explanation: HTUM potentially explains multiple CMB anomalies within a single framework.
- Testability: The periodic nature of the torus leads to specific, testable predictions.
3.3. Mathematical Formulation of the Toroidal Structure
3.3.1. Embedding in Higher-Dimensional Space
3.3.2. Metric and Topology
3.3.3. Homology and Cohomology
3.3.4. Visualization Techniques
3.3.5. Implications for HTUM
3.4. Advanced Topological Concepts for the Toroidal Structure
3.4.1. Fiber Bundle Representation
- is the base space (our 4-dimensional torus)
- is the structure group (representing the phase of the wave function)
- is the projection map
3.4.2. Differential Forms on the 4-Torus
3.4.3. Connection and Curvature
3.4.4. Implications for HTUM
- It offers a mathematically rigorous framework for describing the geometry and topology of the 4-dimensional toroidal universe.
- It provides natural ways to incorporate quantum mechanical concepts (through the fiber bundle structure) and field theories (through differential forms and connections) into the model.
- It suggests new avenues for theoretical predictions and potential observational tests based on the topological and geometrical properties of the 4-torus.
- It connects HTUM to ongoing research in quantum gravity and topological quantum field theories, as explored in recent work by Gielen [92].
3.5. HTUM and the Flatness Problem
3.6. TQFT and the Hyper-Torus
3.7. Challenges in Visualizing and Conceptualizing a 4DTS
- Dimensional reduction: By studying lower-dimensional analogs, such as the three-dimensional torus () or the two-dimensional torus (), we can gain insights into the properties and behavior of the four-dimensional torus. These lower-dimensional models serve as stepping stones for understanding higher-dimensional structures [107].
- Mathematical visualization tools: Advanced mathematical software and visualization tools can help create representations of four-dimensional objects [108]. These tools can project higher-dimensional structures into three-dimensional space, allowing us to explore their properties interactively.
- Analogies and metaphors: Using analogies and metaphors can make abstract concepts more relatable [106]. For example, comparing the four-dimensional torus to a three-dimensional torus with an additional dimension of time or another spatial dimension can help bridge the gap in understanding.
- Educational resources: Developing educational resources, such as interactive simulations, videos, and detailed diagrams, can help teach and learn about higher-dimensional structures [107]. These resources can provide step-by-step explanations and visual aids to enhance comprehension.
3.8. The Nature of Dark energy and Dark matter in HTUM
3.8.1. Introduction
3.8.2. The Quantum Lake: An Analogy for Dark Energy and Dark Matter DYNAMICS
3.8.3. Nonlinear Schrödinger Equation
- is the wave function.
- ℏ is the reduced Planck’s constant.
- m is the particle mass.
- is the potential.
- g is a constant characterizing the strength of the nonlinearity.
3.9. Detailed Mathematical Framework for Dark matter and Dark energy Interactions
- , , are densities of dark matter, dark energy, and normal matter, respectively
- , , are velocity fields
- F, G, H are nonlinear functions representing interactions
3.10. Nonlinear Probabilistic Nature of Dark Matter and Dark Energy
- is the wave function
- is the potential
- is the nonlinear term representing self-interaction
- and are nonlinear functionals representing the effects of dark matter and dark energy, respectively
3.11. Specific Predictions for Observables
3.11.1. Galaxy Rotation Curves
3.11.2. Large-Scale Structure Formation
- Enhanced structure growth at certain scales due to DE-DM interactions
- Suppression of structure at other scales due to DE repulsion
- Potential "dark" filaments or voids not associated with visible matter
3.12. Large-Scale Homogeneity and Isotropy in HTUM
3.13. Observational Tests and Experimental Proposals
- High-precision galaxy rotation curve measurements
- large-scale structure surveys with improved sensitivity to low-density regions
- Weak lensing maps to probe DM distribution
- Next-generation CMB experiments to detect subtle imprints of these interactions
3.14. Implications for HTUM and Cosmology
3.14.1. Higher-Dimensional Interactions
- represents a field in the higher-dimensional space.
- x includes coordinates from the extra dimensions.
3.14.2. Nonlinear Quantum Field Theory
- is the kinetic term.
- m is the mass of the scalar field.
- and g are constants characterizing the strength of the nonlinear interactions.
- represents the contribution from higher-dimensional interactions.
3.14.3. Wave Function Collapse and Gravity
- is a coupling constant.
- represents the gravitational field.
3.14.4. Integrating Nonlinear Probabilistic Phenomena
3.14.5. Density Matrix and Energy-Momentum Tensor
3.14.6. Einstein’s Field Equations with Nonlinear Contributions
3.14.7. Conceptual Consistency
3.14.8. Summary
- Extending the Schrödinger equation to include nonlinear terms and higher-dimensional interactions [132].
- Representing the density matrix and energy-momentum tensor to account for wave function collapse and nonlinear contributions [41].
- Modifying Einstein’s field equations to include these nonlinear contributions ensures that the emergence of gravitational effects aligns with HTUM [117].
3.14.9. Extended Framework and Comparisons
Comparison with Current Dark Matter Models
- Wave function localization: In HTUM, dark matter is viewed as a nonlinear phenomenon that contributes to the localization of the universal wave function. This contrasts with particle models by suggesting that dark matter is an intrinsic property of the quantum universe rather than a distinct particle species.
- Dynamic distribution: Unlike static dark matter haloes in standard models, HTUM suggests a dynamic distribution that evolves with the universe’s wave function. This could potentially explain observed anomalies in galactic rotation curves that challenge conventional dark matter models [134].
- quantum entanglement: HTUM proposes that dark matter’s effects are deeply connected to quantum entanglement on a cosmic scale. This could provide a new perspective on the "small scale crisis" in cosmology, where observations of dwarf galaxies seem to conflict with simulations based on cold dark matter models [135].
Relation to Current Dark Energy Models
- quantum superposition maintenance: In HTUM, dark energy is conceptualized as a nonlinear probabilistic phenomenon that helps maintain quantum superposition states. This contrasts with the static energy density of the cosmological constant model or the slowly varying scalar fields in quintessence models [136].
- wave function collapse dynamics: HTUM suggests that dark energy plays a crucial role in the dynamics of wave function collapse on a cosmic scale. This could potentially address the coincidence problem in cosmology, explaining why dark matter and dark energy densities are of the same order of magnitude in the present epoch [137].
- Toroidal structure influence: The model proposes that dark energy’s behavior is intimately linked to the universe’s toroidal structure. This geometric connection could provide a new perspective on the flatness problem and the apparent accelerating expansion of the universe [7].
| Property | HTUM | Standard Models |
|---|---|---|
| Nature | Nonlinear probabilistic phenomena | Particle-based or constant field |
| Dynamics | Wave function localization (DM) | Static dark matter halos |
| Quantum superposition maintenance (DE) | Static energy density or slow-rolling field | |
| Distribution | Dynamic, evolving with wave function | Static or slowly evolving |
| Quantum effects | Deeply connected to entanglement | Not typically considered |
| Cosmic scale effects | Addresses "small scale crisis" | Challenges at small scales |
| Coincidence problem | Potentially resolved | Unexplained |
| Geometric connection | Linked to toroidal structure | No specific geometric connection |
| Mathematical framework | Nonlinear Schrödinger equation | Particle physics or field theory |
| Observational predictions | Modified structure formation | Standard structure formation |
| Unique CMB and gravitational signatures |
Mathematical Framework for Nonlinear Probabilistic Phenomena
Observational Consequences
- Galactic dynamics: The nonlinear nature of dark matter in HTUM could lead to unique signatures in galactic rotation curves and galaxy cluster dynamics that differ from predictions of standard dark matter models [138].
- cosmic web structure: The interplay between dark matter’s wave function localization and dark energy’s superposition maintenance could result in distinctive patterns in the cosmic web structure, potentially observable through large-scale structure surveys [139].
- cosmic microwave background (CMB): The quantum nature of dark energy in HTUM might lead to specific imprints on the CMB power spectrum, particularly at large angular scales [116].
Experimental Approaches
- Advanced gravitational lensing studies: Precise measurements of gravitational lensing effects could reveal the nonlinear and quantum nature of dark matter distribution predicted by HTUM [140].
- Quantum experiments: While challenging, experiments exploring quantum effects at larger scales could provide insights into the quantum nature of dark energy proposed by HTUM [143].
3.15. Addressing the Cosmological Constant Problem
3.15.1. The Topological Vacuum Energy Modulator
- represents a point in the 4D torus.
- are the characteristic lengths of the torus in each dimension.
- are integers representing the modes of vacuum fluctuations.
3.15.2. The Effective Cosmological Constant
- is the cosmological constant predicted by quantum field theory.
- is the expectation value of over the entire torus.
- is the Planck length.
- is the characteristic size of the universe.
- D is a dimensionless parameter representing the degree of suppression due to the torus structure.
3.15.3. Suppression of Extreme Values
- Topological constraints: The compact nature of the torus imposes restrictions on the allowed modes of vacuum fluctuations, effectively cutting off high-energy contributions.
- Averaging effect: The integration over the entire torus volume averages out local fluctuations, reducing the overall energy density.
3.15.4. Observable Consequences
CMB Anisotropies
Large-Scale Structure
- Variations in dark energy density: The scale-dependent nature of the effective cosmological constant in HTUM could lead to detectable variations in dark energy density across cosmic scales.
- Structure formation: The dynamical nature of the effective cosmological constant in HTUM could affect structure formation processes, potentially leading to distinctive signatures in galaxy clustering and the cosmic web [144].
3.15.5. Numerical Methods for Computing
3.15.6. Parameter Estimation and Theoretical Justification
3.15.7. Empirical Data Integration and Model Fitting
- Planck 2018 CMB data [5], providing constraints on the cosmological constant.
- Baryon Acoustic Oscillation (BAO) measurements from BOSS DR12 [147], offering complementary large-scale structure information.
- Type Ia supernovae data from the Pantheon sample [148], constraining the expansion history of the universe.
3.15.8. Testable Predictions
| Feature | HTUM | CDM |
|---|---|---|
| Vacuum energy modulation | TVEM function | Not addressed |
| Effective cosmological constant | Scale-dependent | Constant |
| Suppression mechanism | Topological constraints | Not present |
| and averaging effect | ||
| Observable consequences | CMB anisotropies, | Standard CMB and |
| modified structure growth | structure formation | |
| Parameter space | ||
| Numerical approach | Monte Carlo integration | N/A |
| Data fitting method | Bayesian (MCMC) | Various |
| Testable predictions | Specific CMB patterns, | Standard cosmic |
| vacuum energy-structure | evolution | |
| relationships |
3.15.9. Conclusion
3.16. Quantum Field Theory in Toroidal Space
3.17. HTUM and Quantum Foundations
- Measurement problem: HTUM’s universal self-observation process provides a mechanism for wave function collapse, addressing the core of the measurement problem [154].
- Non-locality: The toroidal structure offers a geometric explanation for quantum non-locality and entanglement [155].
- quantum superposition: HTUM interprets superposition states as different topological configurations within the 4D torus [156].
- Uncertainty principle: The model provides a topological basis for Heisenberg’s uncertainty principle [157].
- Wave-particle duality: HTUM explains the dual nature of quantum entities as emergent properties of the toroidal structure [158].
- quantum-to-classical transition: The model offers a smooth transition from quantum to classical regimes based on the complexity of topological configurations [159].
3.17.1. Quantum-to-Classical Transition
- The torus geometry acts as an intrinsic environment, facilitating decoherence without external observers [160].
- Scale-dependent effects inherent in the toroidal structure, explaining why macroscopic objects behave classically while microscopic systems retain quantum properties [159].
- The integration of gravity into the quantum framework, providing a unified approach to quantum and classical phenomena [41].
3.18. Emergence of Observed Dimensions
| Parameter | Value | Effect on Cosmic Structure |
|---|---|---|
| Torus size | Mpc | Large-scale periodic correlations |
| TVEM strength | 0.1 | Enhanced local clustering |
| Dark energy fraction | 0.7 | Accelerated expansion, void formation |
| Initial perturbations | Gaussian | Filamentary structure, cosmic web |
| Simulation duration | 13.8 Gyr | Full cosmic evolution to present |
| Dark matter distribution | Nonlinear probabilistic | Complex halo structures |
3.18.1. Dimensional Reduction Mechanism
- is the effective number of dimensions
- E is the energy scale
- is the Planck energy
- is a model-dependent parameter
3.18.2. Topological Phase Transitions
- t is cosmic time
- is a characteristic timescale for the phase transition
- is a parameter controlling the magnitude of the transition
3.18.3. Quantum Foam and Dimensional Fluctuations
- is the power spectrum of dimension fluctuations
- k is the wavenumber
- is the Planck wavenumber
- and n are model parameters
3.18.4. Implications for Fundamental Constants
3.18.5. Observational Consequences
- Modified dispersion relations for high-energy particles:
- Deviations in the cosmic microwave background (CMB) power spectrum:
- Distinctive signatures in gravitational wave signals from the early universe:
3.19. Dynamical Relaxation
3.20. Comparative Analysis
- Anthropic arguments: Unlike anthropic explanations, HTUM provides a dynamical mechanism for the observed value of the cosmological constant, avoiding the need to invoke observer selection effects [166].
- Quintessence models: While quintessence models introduce additional scalar fields to explain dark energy, HTUM’s TVEM function arises naturally from the topology of spacetime itself [136].
- Modified gravity approaches: HTUM maintains general relativity as the underlying theory of gravity, modifying only the vacuum energy contribution. This preserves the well-tested aspects of general relativity while addressing the cosmological constant problem [118].
3.21. Observational Consequences
- Variations in dark energy density: The scale-dependent nature of the effective cosmological constant in HTUM could lead to detectable variations in dark energy density across cosmic scales.
- CMB signatures: The TVEM function may imprint specific patterns in the cosmic microwave background (CMB), particularly in the large-scale anisotropies [116].
- Structure formation: The dynamical nature of the effective cosmological constant in HTUM could affect structure formation processes, potentially leading to distinctive signatures in galaxy clustering and the cosmic web [144].
3.22. Theoretical Implications
- Inflation: The TVEM mechanism could provide a natural explanation for the energy scale of inflation and its duration [38].
- Fate of the universe: The dynamical relaxation of the effective cosmological constant suggests a future cosmic evolution different from the eternal acceleration predicted by CDM models [167].
- quantum gravity: HTUM’s resolution of the cosmological constant problem provides a concrete example of how quantum effects and gravity can be reconciled, offering insights for other quantum gravity approaches [31].
3.23. Addressing the Nature of the Singularity and Time
3.24. Experimental Implications and Testable Predictions
3.24.1. Cosmic Microwave Background (CMB) Anisotropies
3.24.2. Large-Scale Structure and Cosmic Topology
3.24.3. Gravitational Wave Signatures
3.24.4. Dark Matter and Dark energy Interactions
3.24.5. Quantum Gravity and Higher-Dimensional Signatures
3.24.6. Cosmological Parameter Constraints
3.25. Simulation Results and Discussion
3.25.1. 4D Wave Function Projection
3.25.2. Entanglement Evolution
- Initial adaptation to the toroidal structure
- Buildup of quantum correlations across the torus
- A potential phase transition or critical point
3.25.3. Energy Evolution
- Initial settling into a stable configuration
- Gradual energy gain, potentially due to dark energy effects
3.25.4. Fourier Analysis
- A strong constant component in the wave function
- Presence of low-frequency oscillations
- Absence of high-frequency noise
3.25.5. Implications for Dark matter and Dark energy
3.25.6. Conclusion
| Feature | Description | Implications |
|---|---|---|
| 4D Toroidal Structure | Universe as a 4D torus | Finite but unbounded universe |
| TVEM Function | Modulates vacuum energy | Addresses cosmological constant problem |
| Dark Matter/Energy | Nonlinear probabilistic phenomena | Unified quantum treatment |
| Wave Function Collapse | Amplified at event horizons | Emergence of classical reality |
| CMB Predictions | Specific anisotropy patterns | Testable via observations |
| Quantum-Classical Transition | Scale-dependent process | Explains macroscopic behavior |
| Gravitational Waves | Unique signatures predicted | Potential for empirical validation |
4. Axiomatization of HTUM: Addressing Hilbert’s Sixth Problem
4.1. Foundational Principles
4.1.1. Core HTUM Concepts as Axioms
-
Axiom 1 (Toroidal Structure): The universe is a 4-dimensional torus with metricwhere are periodic coordinates.
-
Axiom 2 (TVEM Function): A Topological Vacuum Energy Modulator (TVEM) function exists on satisfyingwhere m is a mass parameter.
- Axiom 3 (Universal Self-Observation): The universe acts as its own observer, continuously collapsing its wave function through self-interaction.
4.1.2. Connections to Existing Principles
- The toroidal structure (Axiom 1) generalizes the concept of spacetime in general relativity.
- The TVEM function (Axiom 2) extends the notion of vacuum energy in quantum field theory.
- Universal self-observation (Axiom 3) provides a novel interpretation of quantum measurement.
4.2. Quantum Mechanics Axiomatization
4.2.1. Quantum States on
- Axiom 4 (Hilbert Space): The state space of the universe is a separable Hilbert space of square-integrable functions on .
- Axiom 5 (Wave Function): The state of the universe is described by a wave function , satisfying
4.2.2. Operators and Observables
- Axiom 6 (Observables): Physical observables are represented by self-adjoint operators on that respect the periodic boundary conditions of .
- Axiom 7 (Momentum Operator): The momentum operator on is given by , where respects the periodic structure of .
4.2.3. Measurement Process
- Axiom 8 (Self-Observation): Measurement in HTUM is described by the action of a self-observation operator , defined as
- Axiom 9 (Born Rule): The probability of observing the universe in a state is given by .
4.2.4. Uncertainty Relations
-
Axiom 10 (HTUM Uncertainty Principle): For any two observables A and B,where is a function of the TVEM that introduces additional uncertainty due to the toroidal structure.
4.3. Gravity Axiomatization
4.3.1. Geometric Axioms
- Axiom 11 (Curved Torus): The geometry of is described by a metric tensor that satisfies Einstein’s field equations.
- Axiom 12 (Toroidal Geodesics): Free particles follow geodesics on , which may wrap around the torus multiple times.
4.3.2. HTUM-Specific Equivalence Principle
- Axiom 13 (Toroidal Equivalence Principle): The laws of physics are invariant under smooth coordinate transformations that preserve the toroidal structure of .
4.3.3. Gravitational Field Equations
-
Axiom 14 (Modified Einstein Equations):where is the effective cosmological constant in HTUM.
4.3.4. Quantum-Gravity Connection
- Axiom 15 (Gravitational Wave Function Collapse): The collapse of the wave function through self-observation induces changes in the gravitational field via
4.4. Quantum Field Theory on
- Axiom 16 (Field Operators): Quantum fields on are operator-valued distributions that satisfy the periodicity condition for each dimension i.
-
Axiom 17 (TVEM-Modified Propagators): The propagator for a scalar field on is given bywhere are the discrete momenta allowed by the torus topology.
4.5. Dark Matter and Dark Energy
- Axiom 18 (Nonlinear Probabilistic Nature): Dark matter and dark energy are described by nonlinear functionals of the universal wave function: and .
-
Axiom 19 (TVEM-Dark Sector Coupling): The evolution of dark matter and dark energy densities is governed by:where and are TVEM-dependent interaction terms.
4.6. Emergence of Spacetime and Dimensions
-
Axiom 20 (Dimensional Emergence): The effective dimensionality of spacetime is energy-dependent:where is the Planck energy and is a model parameter.
-
Axiom 21 (Emergent Time): Time emerges as a parameter describing the evolution of entanglement entropy:where are Lindblad operators describing the system-environment interactions.
4.7. Quantum Information and Holography
-
Axiom 22 (Toroidal Holographic Principle): The information content of any region A in is bounded by:where is a topological entropy term specific to .
-
Axiom 23 (Entanglement-Geometry Duality): The entanglement entropy between regions A and B is related to the geometry of :where is the minimal surface separating A and B, and is a TVEM-dependent correction term.
4.8. Unified Mathematical Operations
-
Axiom 24 (Generalized Operator): There exists a unified mathematical operator U on such that:where f and g are smooth functions, encompassing addition, subtraction, multiplication, and division as special cases.
4.9. Cosmological Dynamics
-
Axiom 25 (Modified Friedmann Equations): The evolution of the scale factor on is governed by:where is the TVEM-modulated vacuum energy density.
4.10. Consistency and Implications
4.10.1. Proving Consistency of Axioms
- Axioms 1 and 11 are consistent as curved metrics can be defined on .
- Axioms 3 and 8 are consistent, with Axiom 8 providing a mathematical formulation of Axiom 3.
- Axioms 2 and 14 are consistent as the TVEM function modifies the effective cosmological constant while respecting general covariance.
- Axioms 5 and 18 are consistent as the nonlinear functionals for dark matter and dark energy are defined on .
4.10.2. Deriving Key HTUM Predictions
-
CMB anisotropies with power spectrum:where .
-
Gravitational wave strain amplitude:where is a frequency-dependent correction term related to the torus size L.
-
Modified growth equation for large-scale structure:where is the density contrast and is a TVEM-dependent function.
4.10.3. Exploring Connections and Hierarchical Structure
- Axioms 1-3 form the foundational principles.
- Axioms 4-10 build the quantum mechanical framework.
- Axioms 11-15 incorporate gravity.
- Axioms 16-17 extend to quantum field theory.
- Axioms 18-19 describe dark matter and dark energy.
- Axioms 20-21 explain emergent spacetime and dimensions.
- Axioms 22-23 incorporate quantum information and holography.
- Axiom 24 unifies mathematical operations.
- Axiom 25 describes cosmological dynamics.
4.10.4. Modifying Existing Theories in Limiting Cases
- general relativity Limit: As the torus size and , Axioms 11 and 14 reduce to standard GR.
- Quantum Mechanics on Flat Space: In the limit where torus curvature approaches zero and , Axioms 4-10 reduce to standard QM.
- Standard Model of Particle Physics: Axioms 16 and 17 approaches standard QFT on flat space in the limit of large L and weak TVEM coupling.
- ΛCDM Cosmology: In the limit where TVEM effects are negligible, Axiom 25 reduces to standard Friedmann equations.
- Holographic Principle: Axiom 22 approaches the standard holographic bound in the limit of weak TVEM coupling.
4.11. Discussion and Future Directions
- It unifies quantum mechanics, gravity, and cosmology within a single axiomatic structure.
- It provides a natural explanation for dark matter and dark energy as emergent phenomena.
- It offers a novel perspective on the nature of spacetime, dimensions, and fundamental forces.
- It leads to testable predictions that can be verified through astronomical observations and high-energy experiments.
- Developing more rigorous mathematical proofs of consistency for all axioms.
- Deriving additional observable consequences from these axioms.
- Exploring the implications of HTUM for quantum information theory and holography.
- Investigating potential experimental setups to test HTUM-specific predictions.
- Refining the TVEM function and its role in various physical processes.
- Studying the implications of HTUM for the very early universe and cosmic inflation.
4.12. Conclusion
5. Early Universe Evolution and Inflation in HTUM
5.1. Transition from Quantum to Classical States
5.1.1. Initial Quantum State
5.1.2. Decoherence Process
5.1.3. Emergence of Classical Reality
5.1.4. Role of Observation
5.2. Inflation in the Toroidal Universe
5.2.1. Topological Inflation
5.2.2. Vacuum Energy on the Torus
5.2.3. Exit from Inflation
5.2.4. Density Perturbations
| Aspect | HTUM | Standard Cosmology |
|---|---|---|
| Initial state | Quantum superposition on 4D torus | Quantum fluctuations in scalar field |
| Decoherence mechanism | Toroidal geometry-induced | Environmental interactions |
| Inflation driver | Topological properties | Scalar field potential |
| Vacuum energy | Quantized by torus modes | Continuous field |
| Exit from inflation | Natural mode frequency decrease | Slow-roll condition violation |
| Density perturbations | , | Similar, but different mechanism |
| Quantum-classical transition | Scale-dependent, geometry-linked | Decoherence-based |
| Role of observation | Universe as self-observer | External observer assumed |
| Inflationary equation | ||
| Spacetime structure | 4D toroidal | Flat or open |
6. The Relationship Between Quantum Mechanics and Gravity in HTUM
6.1. Introduction to Quantum Foundations in HTUM
6.2. The Measurement Problem in HTUM
6.2.1. Universal Self-Observation and Wave Function Collapse
6.2.2. Contextuality in HTUM
6.3. Non-locality and Entanglement in HTUM
6.3.1. Topological Basis for Non-locality
6.3.2. Entanglement as Topological Correlation
6.4. Quantum Superposition in HTUM
6.4.1. Superposition as Topological Configuration
6.4.2. Coherence and Decoherence in HTUM
6.5. The Uncertainty Principle in HTUM
6.5.1. Topological Constraints on Measurement
6.5.2. Information-Theoretic Interpretation
6.6. Wave-Particle Duality in HTUM
6.6.1. Emergence of Wave and Particle Behaviors
6.6.2. Double-Slit Experiment in HTUM
6.7. Quantum-to-Classical Transition in HTUM
6.7.1. Emergence of Classicality
6.7.2. Macroscopic Quantum Phenomena
6.8. Interpretational Aspects
6.8.1. Relationship to Existing Interpretations
- Copenhagen Interpretation: HTUM’s universal self-observation process aligns with the Copenhagen interpretation’s emphasis on measurement but provides a physical mechanism for wave function collapse [212].
- Many-Worlds Interpretation: The multiple configurations within the toroidal structure bear similarities to the many-worlds concept, but HTUM suggests these configurations coexist within a single universe [213].
- de Broglie-Bohm Theory: The TVEM function in HTUM is similar to the quantum potential in de Broglie-Bohm theory, guiding the evolution of quantum systems [214].
6.8.2. HTUM as a Unifying Framework
6.9. Introduction to Quantum Gravity in HTUM
6.10. Toroidal Loop Quantum Gravity (TLQG)
6.10.1. Toroidal Diffeomorphisms and Symmetries
6.11. TVEM and Microscopic Spacetime Structure
6.11.1. Spacetime Discretization in HTUM
6.11.2. Modified Dispersion Relations
6.11.3. Quantum Foam and the TVEM Function
6.11.4. Unified Mathematical Framework for Quantum-Classical Transition in HTUM
6.12. Quantum Gravity Formalism in HTUM
6.12.1. Toroidal Spin Networks
6.12.2. Advanced Toroidal Spin Networks
6.12.3. Quantum Geometry Operators
6.12.4. Enhanced Quantum Geometry Operators
6.12.5. Entanglement and Gravity Emergence
6.12.6. Wave Function Collapse and TVEM
6.13. The Wave Function in HTUM
6.14. Quantum Geometry of the Torus
6.15. Topological Quantum Field Theory on the Torus
6.16. Noncommutative Geometry and Quantum Gravity
6.17. Quantum Group Symmetries in HTUM
6.18. Generalized Uncertainty Principle
6.19. Quantum Cosmology in HTUM
6.20. Entanglement and Spacetime Geometry
6.21. Quantum Holonomies and Observables
6.22. Topological Entanglement Entropy
6.23. Quantum Gravity Corrections to the CMB
6.24. Quantum Foam and Spacetime Fluctuations
6.25. Quantum Decoherence in HTUM
6.26. Black Hole Thermodynamics in HTUM
6.27. Hawking Radiation in HTUM
6.28. Dark Matter and Dark energy in HTUM
6.29. Unified Approach to Quantum Mechanics and Gravity
6.30. Wave Function Collapse and the Emergence of Classical Spacetime
6.31. Quantum Gravitational Effects at the Planck Scale
6.32. Quantum Gravity and Cosmological Singularities
6.33. Entanglement and the Emergence of Spacetime
6.34. Quantum Gravity and the Arrow of Time
6.35. Quantum Gravity and the Information Paradox
6.36. Quantum Gravity and Cosmological Phase Transitions
6.37. Quantum Gravitational Effects on Particle Physics
6.38. Quantum Gravity and the Cosmological Constant Problem
6.39. Quantum Gravitational Effects on Inflation
6.40. Quantum Gravity and the Dimensionality of Spacetime
6.41. Quantum Gravitational Corrections to Classical Tests of general relativity
6.42. Quantum Effects and Emergent Dimensions
6.43. Unified Interaction at the Singularity
6.44. Future Research Directions
- Mathematical formulation: Continued refinement of the rigorous mathematical framework that describes the toroidal structure and its properties, including the role of gravity in wave function collapse.
- Experimental verification: Design and implement experiments to test HTUM’s predictions, particularly those related to the interplay between gravity and quantum mechanics at various scales.
- Interdisciplinary collaboration: Fostering collaboration between physicists, cosmologists, mathematicians, and researchers from other relevant fields to explore HTUM’s implications and refine its theoretical foundations.
6.45. Decoherence in the Toroidal Universe
- is a base decoherence rate
- is the action of the system
- is the TVEM function
- ℏ is the reduced Planck constant
6.46. Gravity’s Role in the Quantum-to-Classical Transition
- G is the gravitational constant
- m is the mass of the system
- r is a characteristic length scale
- c is the speed of light
- is a dimensionless coupling constant
6.47. Scale-Dependent Quantum Behavior
- is the characteristic length scale of the system
- is a critical length scale related to the toroidal structure of the universe
6.48. Universal Self-Observation and the Emergence of Classical Reality
- is the density matrix of the universe
- H is the Hamiltonian
- O is an observation operator
- is a coupling constant related to the strength of self-observation
6.49. Emergence of Classical Space, Time, and Causality
6.50. Comparison with Other Approaches
- Consistent histories: While consistent histories provide a framework for assigning probabilities to classical-like sequences of events, HTUM goes further by explaining why and how these classical histories emerge from the underlying quantum reality [247].
- Many-worlds interpretation: Unlike the many-worlds interpretation, which posits the actual existence of all possible quantum outcomes, HTUM provides a mechanism for actualizing specific classical realities through universal self-observation [213].
- Objective collapse theories: HTUM shares some similarities with objective collapse theories in positing a physical mechanism for wavefunction collapse. However, HTUM grounds this mechanism in the fundamental geometry of the universe, providing a more unified and less ad hoc explanation [237].
- decoherence theory: While HTUM incorporate decoherence as a crucial mechanism, it goes beyond standard decoherence theory by integrating gravity and providing a geometric basis for the decoherence process [40].
6.51. Observational Consequences and Experimental Tests
6.51.1. Gravitational Decoherence
6.51.2. Scale-Dependent Quantum Behavior
| System | Quantumness Q() | Decoherence Rate |
|---|---|---|
| Electron | ||
| C60 Fullerene | ||
| Dust particle | ||
| Human cell | ||
| Cat |
6.51.3. Cosmological Quantum Effects
6.51.4. Modified Uncertainty Relations
6.52. Conclusion
| Aspect | Description | Implication |
|---|---|---|
| TLQG | Loop quantum gravity on 4D torus | Unified QM and gravity |
| TVEM function | Modulates vacuum energy | Spacetime discretization |
| Universal self-observation | Continuous measurement | Wave function collapse |
| Quantum-classical transition | Scale and gravity dependent | Explains classical behavior |
| Entanglement-spacetime link | Entropy related to geometry | Emergent spacetime |
| Modified dispersion relations | High-energy effects | |
| Quantum bounces | Replace classical singularities | No Big Bang singularity |
| Dark matter and energy | Nonlinear probabilistic phenomena | Unified quantum treatment |
7. Yang-Mills Theory and Mass Gap in HTUM
7.1. Formulation of Yang-Mills Theory on HTUM Torus
- The Yang-Mills field on is described by a connection 1-form taking values in the Lie algebra of a compact gauge group G.
- The Yang-Mills field strength is , where d is the exterior derivative on .
- Under a gauge transformation , the connection transforms as , and physical observables are invariant under this transformation.
-
The Yang-Mills action on is given by:where g is the coupling constant, * is the Hodge star operator, and is the TVEM function.
- The gauge field A satisfies periodic boundary conditions on , potentially with non-trivial holonomies around non-contractible loops.
7.2. Existence of Yang-Mills Fields
- There exist smooth solutions to the Yang-Mills equations on for any compact gauge group G.
- Solutions to the Yang-Mills equations on are unique up to gauge transformations within each topological sector characterized by instanton numbers.
- Small perturbations of Yang-Mills solutions on remain bounded for all time, ensuring stability under the HTUM dynamics.
- The space of Yang-Mills solutions on admits a stratification by instanton numbers, with non-trivial instantons wrapping around the torus in various ways.
7.3. Mass Gap Analysis
- The TVEM function contributes to the mass gap via a mechanism of the form:
- Quantum fluctuations of the Yang-Mills field on generate a non-zero mass gap through a non-perturbative mechanism involving instantons wrapping the torus.
- The HTUM Yang-Mills theory on is renormalizable, with the TVEM function providing a natural ultraviolet cutoff related to the torus size.
7.4. Numerical Simulations
- Discretize into a hypercubic lattice with periodic boundary conditions, replacing gauge fields with group elements on lattice links and defining a discrete version of the TVEM-modified Yang-Mills action.
- Use Hybrid Monte Carlo methods to sample gauge field configurations, incorporating the TVEM function into the Metropolis acceptance criterion.
-
The mass gap computed on a discretized torus of size L scales as:where and are critical exponents influenced by the TVEM function.
7.5. Connections to Particle Physics
- The HTUM Yang-Mills theory reduces to the Standard Model gauge theories in the limit where the torus size is much larger than observable scales, with corrections of order (size of particle/size of the torus).
- The theory exhibits quark confinement through a mechanism involving topologically non-trivial gauge configurations that wrap around the torus.
- The glueball spectrum consists of a discrete set of states with masses influenced by both the Yang-Mills dynamics and the periodicity of the torus.
7.6. Observational Consequences
- Particle interactions at energies approaching the inverse torus size will show deviations from standard Yang-Mills predictions, with a characteristic oscillatory pattern in scattering amplitudes.
- Periodic modulations in running gauge coupling constants may be observable at high energies in collider experiments, with a frequency related to the torus size.
- The cosmic microwave background (CMB) should exhibit subtle anisotropies reflecting the toroidal structure, with patterns in the power spectrum related to Yang-Mills instantons wrapping the torus.
7.7. TVEM-Induced Topology Changes
- The TVEM function can induce topology changes in the space of Yang-Mills solutions on as it evolves, leading to phase transitions in the gauge theory.
- These topology changes can lead to observable effects in the glueball spectrum, potentially explaining certain particle physics anomalies.
7.8. Non-Abelian Gauge Holonomy
- The non-Abelian gauge holonomy around a non-contractible loop on is given by:
- The spectrum of gauge-invariant observables in HTUM Yang-Mills theory is entirely determined by the holonomies around all non-contractible loops on .
7.9. Entanglement Structure of Yang-Mills Vacuum
- The entanglement entropy of a region R in the Yang-Mills vacuum state on is:
-
The entanglement entropy for a region R on satisfies an area law with TVEM-dependent corrections:where is the area of the boundary of R, and , , are constants.
7.10. Resurgence Theory and Transseries Expansions
-
The partition function of HTUM Yang-Mills theory admits a resurgent trans-series expansion of the form:where is the instanton action, g is the coupling constant, and are coefficients encoding non-perturbative physics.
- This resurgent structure provides a framework for understanding the interplay between perturbative and non-perturbative effects in HTUM, potentially resolving renormalon ambiguities.
7.11. Quantum Yang-Mills Theory and Constructive Field Theory
- A rigorously defined quantum Yang-Mills theory on with the TVEM-modified action exists, satisfying Osterwalder-Schrader axioms of Euclidean quantum field theory.
- This construction provides a potential pathway for proving the existence of a mass gap in the continuum limit.
7.12. Higher Form Symmetries and Generalized Global Symmetries
- A q-form sameterized by closed q-forms on .
- HTUM Yang-Mills theory possesses a rich structure of higher form symmetries, including a 1-form center symmetry for SU(N) gauge groups, which are influenced by the toroidal geometry and TVEM function.
- These higher form symmetries lead to new selection rules and conservation laws for extended objects (strings, membranes) wrapping non-contractible cycles of .
7.13. Refined Numerical Methods
- Implement a tensor network renormalization scheme for HTUM Yang-Mills theory, using Matrix Product States (MPS) to efficiently represent the ground state on a discretized .
- The tensor network representation of the HTUM Yang-Mills ground state exhibits an entanglement structure that reflects both the toroidal geometry and the influence of the TVEM function.
7.14. Cosmological Phase Transitions
- As the universe described by HTUM expands and cools, it undergoes a series of phase transitions in its Yang-Mills sectors, potentially leaving observable imprints in gravitational waves and primordial black hole formation.
- Stochastic gravitational wave backgrounds with frequency spectra characteristic of first-order phase transitions modified by the TVEM function may be detectable in future experiments.
8. Time Dilation and Causal Processing: A Unifying Perspective
8.1. Causal Processing and Gravitational Fields
8.2. Relative Motion and Computational Capacity
8.3. Quantum Gravity Observatory Experiment
- -
- Station A orbits at a distance of 30 km from the neutron star’s center.
- -
- Station B orbits at a distance of 300 km from the neutron star’s center.
- is the baseline causal processing density
- and are coupling constants
- G is the gravitational constant
- M is the neutron star mass
- r is the distance from the neutron star’s center
- ℏ is the reduced Planck constant
- m is a characteristic mass scale (e.g., proton mass)
8.4. Experimental Observations and HTUM Predictions
8.4.1. Gravitational Time Dilation
8.4.2. Quantum Entanglement Experiment
8.4.3. Conscious Time Perception
8.4.4. Information Processing Speed
8.4.5. Quantum Decoherence Rates
8.5. Mathematical Formalism
8.6. Specific Predictions
8.6.1. Timelessness in Extreme Causal Processing Regimes
8.6.2. Causal Processing Density and the Emergence of Time
8.6.3. Quantum Realm and Singularities: A Unified Perspective
8.6.4. Implications for Physics
- Breakdown of classical physics: Classical equations assuming a standard flow of causality cease to apply as CPD approaches infinity.
- Non-locality and instantaneous Effects: Extreme CPD regimes allow for apparently instantaneous causal relationships, explaining quantum non-locality and the acausal nature of singularities.
- Unification of quantum and gravitational phenomena: HTUM suggests that quantum effects and gravitational singularities are manifestations of the same underlying principle: the behavior of spacetime at maximum causal processing capacity.
8.6.5. Observational Predictions
- quantum gravity effects: As systems approach extreme CPD, there should be observable transitions between quantum and classical behavior.
- Black hole information paradox: The apparent loss of information in black holes may be resolved by considering the timeless nature of processes at the singularity.
- Early universe phenomena: cosmic inflation and the emergence of classical spacetime from the quantum foam can be understood as transitions from extreme to moderate CPD regimes.
8.7. Comparative Analysis of Time Dilation Interpretations
- Basis: Spacetime curvature due to mass and energy
- Time dilation: Result of gravitational potential differences
- Key concept: Equivalence principle [216]
- Basis: Constancy of light speed in all reference frames
- Time dilation: Result of relative motion between observers
- Key concept: Lorentz transformations [251]
- Basis: All of spacetime exists as a four-dimensional block
- Time dilation: Differing "slices" through the 4D block
- Key concept: Eternalism [258]
- Basis: Time measured by quantum oscillations
- Time dilation: Changes in oscillation frequencies
- Key concept: Proper time as a quantum observable [259]
- Basis: Time’s arrow determined by entropy increase
- Time dilation: Local variations in entropy production rates
- Key concept: Second law of thermodynamics [43]
- Basis: Time as a measure of information processing
- Time dilation: Variations in information flow
- Key concept: Wheeler’s "It from Bit" [209]
- Unified framework: HTUM provides a single explanatory framework for time dilation effects observed in both gravitational and high-velocity scenarios and quantum systems.
- Consciousness integration: Unlike other interpretations, HTUM explicitly incorporates consciousness as a fundamental universe aspect, linking subjective time perception with objective time dilation [69].
- Computational cosmos: HTUM’s view of the universe as a vast information-processing system offers a novel perspective on why physical laws take the form they do, potentially leading to new insights into fundamental physics [260].
- Scalability: The HTUM interpretation seamlessly scales from quantum to cosmic levels, providing a consistent explanation across all scales of physics.
- Predictive power: By framing time dilation in causal processing, HTUM suggests new avenues for research and potential technological applications, such as manipulating local computational complexity to influence time flow.
- Philosophical implications: HTUM’s approach to time dilation raises intriguing questions about the nature of reality, free will, and the role of consciousness in the universe, encouraging interdisciplinary research [46].
8.8. Practical Challenges and Future Experimental Considerations
- Extreme environmental requirements: The proposed experiment requires placing precise instruments around a neutron star in close orbit. This presents significant engineering challenges regarding radiation shielding, temperature control, and maintaining stable orbits [261].
- Measurement precision: Detecting the subtle differences predicted by HTUM, especially in quantum entanglement fidelity and decoherence rates, requires measurement precision beyond current technological capabilities [252].
- Isolating HTUM effects: Distinguishing HTUM-specific effects from those predicted by standard general relativity and quantum mechanics will require careful experimental design and data analysis techniques [165].
- Long-term stability: Maintaining the experiment over extended periods to gather statistically significant data poses challenges regarding equipment longevity and data transmission [242].
- Consciousness measurements: Quantifying and standardizing subjective time perception in extreme gravitational environments presents unique challenges in experimental design and data interpretation [255].
- Developing advanced space-based precision measurement technologies, potentially utilizing quantum sensing techniques [262].
- Exploring alternative astrophysical systems that might offer similar conditions with less extreme engineering requirements, such as binary pulsars or supermassive black hole environments [263].
- Designing Earth-based experiments that could test aspects of HTUM predictions, such as advanced interferometry setups or quantum optics experiments in variable gravitational potentials [254].
- Collaborating with neuroscientists and psychologists to develop robust protocols for measuring subjective time perception in extreme conditions [264].
- Utilizing machine learning and advanced statistical techniques to isolate minor HTUM-specific effects from more significant background signals [265].
8.9. Future Directions and Implications
9. Information Theory and Holography in HTUM
9.1. Toroidal Encoding of Information
9.2. The Toroidal Holographic Principle
9.3. Black Hole Information Paradox in HTUM
9.4. Quantum Error Correction on the Torus
9.5. Entanglement and Causal Structure in HTUM
| Region | Size (relative to torus) | Entanglement Entropy |
|---|---|---|
| Small sphere | 0.01 | |
| Large sphere | 0.1 | |
| Thin slice | 0.01 (thickness) | |
| Half-torus | 0.5 |
9.6. Black Hole Information Paradox in HTUM
9.6.1. Modified Page Curve
9.6.2. Quantum Error Correction on the Torus
9.6.3. Black Hole Complementarity in HTUM
10. HTUM and the Computational Universe
10.1. Introduction to the Computational Universe Concept
10.2. The Universe as a Quantum Computer
10.2.1. Quantum Gates in the Toroidal Structure
10.2.2. Entanglement and Non-local Computations
10.3. Information Processing in HTUM
10.3.1. Wave Function Collapse as Information Processing
10.3.2. Emergence of Classical Reality
10.4. Algorithmic Complexity of the Universe
10.4.1. Kolmogorov Complexity in HTUM
10.4.2. Computational Irreducibility
10.5. Quantum Error Correction
10.5.1. Topological Quantum Codes
10.6. Simulation Hypothesis and HTUM
10.6.1. Computational Capacity of the Universe
10.7. Connections to Information Theory
10.7.1. Entropy and the Second Law
10.7.2. Landauer’s Principle in HTUM
10.8. Digital Physics Connections
10.8.1. Wheeler’s "It from Bit"
10.8.2. Quantum Cellular Automata
10.9. Observational and Experimental Implications
- Discreteness of spacetime: HTUM predicts that spacetime should show signs of discreteness aligned with the toroidal structure at the smallest scales. This could be tested through high-energy particle experiments or observations of cosmic rays [165].
- quantum gravity phenomenology: The model predicts specific modifications to quantum behavior at scales where gravity becomes significant, potentially observable in future precision quantum experiments [143].
- Cosmic information processing: HTUM suggests that there may be observable limits to the information processing capacity of universe regions, potentially detectable in cosmological observations [49].
10.10. Conclusion
11. Beyond Division: Unifying Mathematics and Cosmology
11.1. Conceptual Framework
11.2. Unified Mathematical Operations
11.2.1. Implications for Mathematical Theory
11.3. Topology and Geometry of the Toroidal Universe
11.3.1. Toroidal Structure
11.3.2. Mathematical Formulations
11.4. Quantum Superposition and Hilbert Space
11.4.1. Singularity and Superposition
11.4.2. Implications for Quantum Mechanics
11.5. Category Theoretic Formulation of Unified Mathematical Operations
- Objects are sets of numbers (e.g., real numbers , complex numbers )
- Morphisms are operations between these sets
- Identity: for any object A in
- Associativity:
- Commutativity:
11.6. Abstract Algebraic Structure
- is an abelian group under addition (when )
- is a monoid under multiplication (when )
- Distributivity holds:
- There exists a continuous family of operations parameterized by
11.7. Lie Algebra Representation
11.8. Differential Geometric Interpretation
11.9. Topos Theoretic Perspective
- Objects are sheaves over the space of mathematical operations
- Morphisms are natural transformations between these sheaves
11.10. Practical Applications of Unified Mathematical Operations
11.10.1. Holistic Problem-Solving
11.10.2. Applications in Physics and Engineering
- Quantum computing: The unified approach could enhance algorithms that rely on the superposition and entanglement of quantum states, leading to more efficient problem-solving techniques in quantum computing [288].
- Adaptive materials engineering: Understanding the interconnectedness of operations could lead to developing materials that dynamically adapt their properties in response to environmental changes, improving their performance and durability [289].
- AI algorithm design: The holistic perspective could inspire new algorithms that better mimic the interconnected processes found in nature, leading to more robust and adaptive artificial intelligence systems [290].
11.10.3. Future Directions
11.11. Implications for the Foundations of Mathematics
11.11.1. Revaluation of Mathematical Axioms
11.11.2. Extending Existing Frameworks
11.11.3. Philosophical Implications
11.11.4. Emphasizing Empirical Evidence and Rigorous Testing
11.12. Implications for the Nature of Mathematical Truth and Intuition
11.12.1. Nature of Mathematical Truth
11.12.2. Role of Intuition in Mathematical Discovery
11.13. Relationship Between Mathematics and the Physical World
11.13.1. Mathematical Descriptions of Physical Phenomena
11.13.2. Bridging the Gap Between Abstract Mathematics and Physical Reality
11.14. From Theory to Empirical Testing
11.15. Connecting Unified Mathematics to HTUM Framework
11.16. Concept of Unified Mathematical Operations
11.17. Broader Cosmological Implications
11.18. Practical Applications and Case Studies
- Quantum computing: The interconnected nature of mathematical operations can be leveraged to develop algorithms that run efficiently on quantum computers. By treating addition, subtraction, multiplication, and division as unified processes, we can create more efficient algorithms that solve problems intractable for classical computers [302]. This approach could lead to cryptography, optimization, and material science breakthroughs [303].
- Adaptive materials: Inspired by HTUM’s perspective on continuous transformation, researchers can engineer materials that change their properties in real time. For instance, materials that adapt to environmental conditions, such as temperature or pressure, could be developed using the principles of unified mathematical operations [304]. This could lead to aerospace, construction, and medical device innovations [305].
- Energy systems: Designing energy systems that mimic natural processes’ efficient, seamless energy transformation can lead to more sustainable solutions. By applying HTUM’s principles, we can develop energy systems that optimize the conversion and storage of energy, reducing waste and improving efficiency [306]. This approach could revolutionize renewable energy technologies like solar panels and batteries [307].
- Artificial intelligence: Developing AI algorithms that dynamically adapt their problem-solving strategies, reflecting their interconnected and continuous nature of mathematical operations, can enhance machine learning and data analysis. This approach can lead to more robust and adaptable AI systems that handle complex, dynamic environments, such as autonomous vehicles and smart cities [308,309].
11.18.1. Detailed Case Study: The Nature of Dark energy
11.19. Addressing Potential Criticisms and Future Research Directions
- Potential criticisms: Lack of Rigorous Mathematical Formalism: One of the primary criticisms of HTUM’s conceptual framework is the current lack of a rigorous mathematical formalism that explicitly connects the collapse of the wave function to the emergence of gravitational effects. Critics may argue that without a well-defined mathematical structure, the framework remains speculative and lacks predictive power [301].
- Compatibility with established theories: Another potential criticism is the challenge of reconciling HTUM’s principles with established theories in quantum mechanics and general relativity. Skeptics may question whether the proposed framework can integrate or extend existing mathematical and physical theories without introducing inconsistencies [245].
- Empirical validation: HTUM’s predictions must be empirically validated to gain acceptance within the scientific community. Critics may highlight the difficulty of designing experiments that test the model’s hypotheses, particularly those involving the interplay between quantum mechanics and gravitational effects [165].
11.19.1. Future Research Directions
11.19.2. Developing a Rigorous Mathematical Formalism
- Formulating precise mathematical definitions and equations that describe the wave function collapse process and its impact on the energy-momentum tensor [41].
- Integrating these equations into Einstein’s field equations to describe how actualized quantum states give rise to gravitational effects [31].
11.19.3. Interdisciplinary Collaboration
11.19.4. Empirical Validation and Experimental Design
11.19.5. Educational Initiatives and Knowledge Sharing
11.19.6. Securing Funding and Resources
11.20. Conclusion
11.21. From Quantum Gravity to the Singularity: A Unified Perspective
12. The Singularity and Quantum Entanglement
12.1. Introduction to the Singularity
12.2. Quantum Entanglement within the Singularity
12.2.1. Mathematical Formulation of Quantum Entanglement
12.3. Entanglement Entropy in the Hyper-Torus
12.3.1. Implications for the Singularity
12.4. Self-Observation and Wave Function Collapse
12.4.1. Mechanism of Self-Observation
12.5. Actualization of Classical States
12.5.1. Emergence of Gravitational Effects
12.6. Implications for the Cosmic Microwave Background (CMB)
12.7. Cosmological Quantum entanglement in HTUM
12.7.1. Quantum Discord in HTUM
12.7.2. Evolution of Quantum Discord in HTUM
12.7.3. Cosmological Implications
- It suggests a fundamental quantum nature of spacetime, even at large scales.
- It provides a potential explanation for long-range correlations observed in the cosmic microwave background (CMB) [5].
- It offers new avenues for testing quantum gravity effects in cosmological observations.
12.8. Experimental Verification
12.8.1. Challenges
12.8.2. Addressing the Challenges
12.9. Future Research Directions
12.10. Conclusion
13. The Event Horizon and Probability
13.1. Mathematical Formulation of the Event Horizon
13.2. The Event Horizon as a Nexus Boundary
13.3. Wave Function Collapse at the Event Horizon
13.4. Emergence of Gravitational Effects
13.5. Dynamic Interplay between Gravity and Dark Energy
13.6. Implications of HTUM for Black Holes and Event Horizons
- Unified framework: By integrating the principles of HTUM, we can develop a more comprehensive framework that unifies general relativity and quantum mechanics [176]. This could lead to a deeper understanding of the nature of event horizons and the behavior of black holes.
- Dynamic event horizons: HTUM suggests that event horizons are dynamic and interconnected with the rest of the universe [250]. This perspective could lead to new models that describe the evolution of black holes and their interactions with their surroundings.
- Experimental validation: To validate this theoretical framework, experimental tests could involve studying quantum systems under gravitational fields or searching for signatures of the quantum-to-classical transition in cosmological observations [165]. Observations of black hole behavior, gravitational waves, and Hawking radiation could provide empirical evidence for HTUM’s predictions [188].
13.7. Quantum Information Preservation in HTUM
13.7.1. Toroidal Structure and Information Conservation
13.7.2. Modified Holographic Principle
13.7.3. Quantum Entanglement Across the Torus
| Property | HTUM | Standard Model |
|---|---|---|
| Entropy | ||
| Information preservation | Global redistribution | Local loss |
| Holographic principle | Extended across torus | Event horizon only |
| Entanglement | Long-range correlations | Limited to horizon |
| Event horizon | Dynamic interface | Static boundary |
| Wave function collapse | Amplified at horizon | Not specifically addressed |
13.8. Conclusion
14. The Universe Observing Itself
14.1. Concept of Self-Observation
14.2. Mechanism of Self-Observation and Wave Function Collapse
- quantum superposition of the universe: Initially, the universe exists in a superposition of all possible states [213]. This state encompasses all potential configurations of matter, energy, and information, representing many possibilities.
- Intrinsic observation mechanism: The universe possesses an inherent mechanism that allows it to observe itself [153]. This mechanism is not confined to conscious beings but includes all interactions and processes within the universe, such as particle collisions, gravitational interactions, and electromagnetic forces. Each interaction can be seen as a form of measurement or observation [333].
- Collapse through self-observation: When any interaction or process occurs within the universe, it acts as an observation, causing the wave function to collapse [41]. This self-observation is continuous and pervasive, leading to the actualization of specific probabilities inherent in the singularity and resulting in the manifestation of the observable universe. The collapse of the wave function through self-observation ensures that the universe evolves from a superposition of states to a definite state, thereby shaping its structure and evolution [176].
14.3. Stochastic Model of Universe Self-Observation
14.3.1. Basic Stochastic Schrödinger Equation
14.3.2. Incorporating Dark matter and Dark energy
14.3.3. Refined Lindblad Operators
14.3.4. Master Equation for Density Matrix Evolution
14.3.5. Implications and Observables
- Topological quantum phase transitions related to the toroidal structure [338].
- Nonlinear quantum effects in the distribution of dark matter and dark energy [339].
- decoherence patterns in cosmic microwave background (CMB) radiation [32].
- Quantum gravitational effects in the universe’s large-scale structure [21].
14.4. Emergence of Gravitational Effects
14.5. Dark Matter and Dark Energy Contributions
14.6. Examples and Analogies
- The water cycle: Just as the water cycle relies on the integrated functioning of its components to sustain itself, the universe’s self-observation can be seen as a continuous cycle of interactions [298]. Each interaction, like evaporation or precipitation in the water cycle, contributes to the system’s overall state, leading to the collapse of the wave function.
- A mirror reflecting itself: Imagine a mirror reflecting another mirror. The reflections continue infinitely, influencing the next [340]. Similarly, the universe’s self-observation involves a continuous loop of interactions, where each event influences the overall state, leading to the collapse of the wave function.
- A feedback loop in a system: A feedback loop feeds a system’s output into the system as input, influencing future outputs [341]. The universe’s self-observation can be likened to a feedback loop, where each interaction feeds back into the system, continuously shaping its state and leading to the collapse of the wave function.
- Quantum measurement on a cosmic scale: We can compare the universe’s self-observation to the process of quantum measurement writ large [153]. Just as measuring a quantum particle affects its state, every interaction within the universe can be seen as a form of measurement that affects the universe’s overall state, contributing to the ongoing process of wave function collapse.
- Cellular automaton model: Drawing an analogy to cellular automata, we can envision the universe as a vast grid where the state of each "cell" is determined by the states of its neighboring cells [270]. This creates a vast network of interconnected observations, where each part of the universe observes and is observed by its surroundings.
- Neural network comparison: The universe’s self-observation process can be likened to a complex neural network [342]. Each node in this cosmic network processes information from its connections, contributes to the overall state, and influences future states, similar to neurons in a brain.
- holographic principle illustration: The holographic principle provides another useful analogy [332]. Just as a hologram contains information about the whole in each of its parts, we can conceive of every part of the universe as containing information about and observing the whole.
- Cosmic ecosystem: We might compare the universe to a vast ecosystem where each component affects and is affected by the system as a whole [343]. This constant interaction and mutual influence can be seen as a form of universal self-observation.
14.7. Addressing Criticisms
- Empirical evidence: One major criticism is the lack of empirical evidence for the universe’s self-observation and its impact on wave function collapse [344]. Demonstrating this hypothesis requires advanced observational technologies and methodologies that may not currently exist.
- Philosophical questions: The concept raises questions about the nature of observation and reality [345]. It challenges the traditional distinction between observer and observed, suggesting a more interconnected and participatory universe. Critics may argue this blurs the line between physical processes and conscious observation.
- Compatibility with existing theories: Critics may argue that self-observation is incompatible with established quantum mechanical and cosmological theories [42]. Addressing this concern requires carefully examining how this perspective can be reconciled with or extend existing theories.
- Theoretical support: HTUM draws on existing theories such as quantum decoherence, relational quantum mechanics, and objective collapse models to support the idea of self-observation [237,346,347]. These theories provide a framework for understanding how interactions within the universe can lead to wave function collapse.
- Quantum decoherence: Quantum decoherence is a process by which a quantum system loses its coherence due to environmental interactions [40]. In the context of HTUM, decoherence can be seen as a mechanism contributing to the wave function’s collapse through the universe’s self-observation. As the universe interacts with itself, the coherence of the quantum states is gradually lost, leading to the emergence of classical behavior.
- Relational quantum mechanics: Relational quantum mechanics is an approach that emphasizes the relative nature of quantum states [347]. According to this view, the properties of a quantum system are defined by its relations with other systems. In HTUM, the universe’s self-observation can be understood as a network of relations between its constituents, giving rise to the collapse of the wave function and the actualization of specific probabilities.
- Objective collapse models: Objective collapse models propose that wave function collapse is an objective, spontaneous process that occurs independently of observers [41,237]. These models suggest that specific physical mechanisms trigger the collapse, such as gravitational effects or spontaneous localization. HTUM’s concept of self-observation can be seen as a form of objective collapse, where the universe’s intrinsic properties and interactions lead to the collapse of its wave function.
- Interdisciplinary collaboration: HTUM encourages collaboration between physicists, cosmologists, philosophers, and other researchers to explore the implications of self-observation [348]. This multidisciplinary approach can address philosophical questions and integrate the concept into existing theoretical frameworks.
- Empirical testing: While direct empirical evidence may be challenging, HTUM emphasizes the importance of rigorous testing and observational data [165]. By making specific predictions and comparing them with alternative theories, researchers can assess the validity of the self-observation hypothesis.
14.8. Experimental Verification and Challenges
- Technological limitations: Current observational technologies may need to be advanced enough to detect the subtle effects of self-observation on wave function collapse [349]. Future advancements in quantum measurement techniques and high-precision instruments will be crucial for testing HTUM’s predictions.
- Complexity of interactions: The universe’s self-observation involves many interactions at different scales, from subatomic particles to cosmic structures [350]. Isolating and measuring the impact of these interactions on wave function collapse requires sophisticated experimental designs and data analysis methods.
- Indirect evidence: Given the difficulty of direct observation, researchers may need to rely on indirect evidence to support the self-observation hypothesis [165]. This could involve identifying unique patterns or anomalies in cosmological data that align with HTUM predictions, such as variations in the cosmic microwave background (CMB) or gravitational wave signals.
- Interdisciplinary approaches: Addressing the experimental challenges will require collaboration across multiple disciplines, including physics, cosmology, engineering, and computer science [348]. Developing new experimental methodologies and analytical tools will be essential for testing HTUM’s concepts.
- Quantum interferometry: Quantum interferometry is a technique that exploits the wave nature of matter to make exact measurements [351]. Advanced quantum interferometers, such as atom interferometers or superconducting quantum interference devices (SQUIDs), could be used to detect subtle effects of self-observation on wave function collapse.
- Quantum sensing: Quantum sensing involves using quantum systems, such as entangled particles or quantum dots, to measure physical quantities with unprecedented sensitivity [352]. These techniques could be employed to probe the effects of self-observation on the universe’s quantum states.
- High-precision cosmological observations: Advancements in cosmological observations, such as the detection of gravitational waves by the Laser Interferometer Gravitational-Wave Observatory (LIGO) or the mapping of the cosmic microwave background (CMB) by satellites like Planck, could provide indirect evidence for HTUM’s predictions [179,188]. These observations may reveal unique patterns or anomalies that align with the consequences of self-observation.
14.9. Quantum-to-Classical Transition and Universal Self-Observation
14.10. From Self-Observation to Philosophical Inquiry
14.11. Conclusion
15. Consciousness and the Universe
15.1. Role of Consciousness in HTUM
15.2. Consciousness and Quantum Measurement
15.2.1. Detailed Explanation of the Relationship Between Consciousness and Quantum Measurement
15.3. Free Will and Determinism
15.4. Mind-Matter Relationship
15.4.1. Challenges in Experimentally Verifying the Role of Consciousness
- Measurement and isolation: Isolating consciousness’s influence from other variables in a quantum system is challenging. Traditional scientific methods rely on objective measurements, whereas consciousness is inherently subjective [46].
- Technological limitations: Current technology may need to be advanced enough to detect or measure the subtle influences of consciousness on quantum systems. Developing new methodologies and instruments is essential [356].
- Philosophical and theoretical obstacles: Integrating consciousness into physical theories challenges existing paradigms and may face resistance from the scientific community. Bridging the gap between subjective experience and objective measurement requires innovative theoretical frameworks [368].
15.4.2. Addressing These Challenges
- Interdisciplinary research: Combining insights from quantum physics, neuroscience, and philosophy can provide a more comprehensive understanding of consciousness and its role in the universe [68].
- Advanced experimental designs: Developing experiments that minimize external influences and focus on the observer’s role can help isolate the effects of consciousness. quantum entanglement and delayed-choice experiments are potential areas of exploration [369].
- Theoretical development: Creating robust theoretical models incorporating consciousness into quantum mechanics can guide experimental efforts and provide testable predictions [246].
- Technological innovation: Developing new technologies, such as susceptible detectors and quantum computing, can enhance our ability to study the interplay between consciousness and quantum systems [288].
15.5. Consciousness, Wave Function Collapse, and the Emergence of Gravity
15.6. Consciousness-Induced Wave Function Collapse in HTUM
15.6.1. Quantum State and Consciousness Operator
15.6.2. Consciousness-Mediated Collapse
15.6.3. Probability of Collapse
15.6.4. Continuous Collapse Model
15.6.5. Emergence of Gravitational Effects
15.6.6. Consciousness and Dark energy Interaction
15.7. HTUM’s View of Consciousness: A Philosophically Coherent Approach
- It offers a potential resolution to the hard problem of consciousness by suggesting that experiential properties are intrinsic to the fabric of reality [46].
- It provides a framework for understanding the unity of conscious experience, often reported in meditative or mystical states, as a direct perception of the underlying toroidal structure of reality [374].
- It suggests a continuity between mind and matter, potentially resolving the mind-body problem that has long puzzled philosophers [375].
- It offers a new perspective on the nature of time and causality, with implications for our understanding of free will and determinism [69].
16. Consciousness and the Singularity: A Unified Perspective
16.1. Introduction to the Consciousness-Singularity Hypothesis
16.2. Key Definitions and Conceptual Foundations
- Consciousness: The subjective experience of awareness, including perceptions, thoughts, and emotions. In our framework, it is a fundamental aspect of the universe, not merely an emergent property of complex systems.
- singularity: A region of infinite density and zero volume, where all known physical laws break down. In HTUM, we reinterpret this as a field of pure, undifferentiated consciousness.
- consciousness operator (): A mathematical object that acts on the universal wave function, representing the action of consciousness in collapsing quantum states.
16.3. Enhanced Mathematical Formulation
16.3.1. Detailed Derivation of the Consciousness-Inclusive Schrödinger Equation
16.3.2. Conclusion
16.4. Addressing Potential Criticisms
- Quantum coherence in biological systems: Investigate whether consciousness can maintain quantum coherence in warm, wet environments like the brain (building on work by [379]).
- Global consciousness project: Analyze data from the Global Consciousness Project for correlations with quantum phenomena, controlling for all known physical factors.
- Advanced neuroimaging: Use high-resolution fMRI and EEG to search for patterns consistent with quantum effects in brain activity.
16.5. Expanded Implications and Applications
- Consciousness-based quantum computing: Harness the proposed link between consciousness and quantum collapse to create more efficient quantum computers.
- Consciousness field detectors: Develop sensors to detect and measure consciousness fields, potentially revolutionizing neuroscience and psychology.
- Reality engineering: If consciousness shapes reality fundamentally, we might develop technologies to intentionally influence physical systems through focused conscious intention.
16.6. Refined Experimental Proposals
-
SQUID magnetometer detection of consciousness fields:
- Collaborate with experts in superconducting quantum interference devices (SQUIDs) to design ultra-sensitive detectors for potential consciousness fields.
- Conduct controlled experiments comparing SQUID readings during various states of consciousness (e.g., meditation, sleep, focused attention).
-
Cosmological correlations with global consciousness:
- Partner with astronomers and data scientists to analyze large-scale cosmological data for anomalies correlating with significant global events.
- Develop sophisticated algorithms to filter out known physical effects and isolate potential consciousness-related signals.
16.7. Enhanced Philosophical and Ethical Considerations
- Recognize the potential impact of conscious observation on reality.
- Develop practices for responsible "reality shaping" through conscious intention.
- Consider the ethical implications of influencing shared reality through individual or collective consciousness.
16.8. Future Directions and Research Agenda
- Develop a mathematical formalism integrating consciousness into quantum field theory.
- Investigate how consciousness fields interact with known physical fields.
- Explore the emergence of classical physics from consciousness-mediated quantum collapse.
- Examine how conscious observation might influence the branching or selection of universes in Many-Worlds interpretations.
- Investigate whether consciousness could be the "navigator" through the landscape of possible universes.
- Develop models of how individual consciousnesses might be connected across multiple universes.
16.9. Conclusion
17. Advanced Formalism of Consciousness in HTUM
17.1. Enhanced Mathematical Framework for Consciousness-Quantum Interface
17.2. Testable Predictions of Consciousness-Quantum Interactions
17.2.1. Quantum Measurement Anomalies
17.2.2. Entanglement Preservation
17.2.3. Global Consciousness Effects
17.3. Implications for Quantum Measurement Theory
17.4. Consciousness and the Toroidal Structure
17.5. Philosophical and Metaphysical Implications
18. Relationship to Other Theories
18.1. Comparison with Loop Quantum Gravity and String Theory
18.1.1. Loop Quantum Gravity (LQG)
- Compatibility: HTUM and LQG emphasize the importance of geometry in understanding the universe. The toroidal structure in HTUM could be mapped onto the spin networks of LQG, suggesting a possible geometric correspondence [33].
- Divergence: While LQG focuses on quantizing spacetime, HTUM incorporates dark matter and dark energy roles in a cyclical universe. This broader scope may offer new insights into the dynamics of the universe that LQG does not address [218].
18.1.2. String Theory
- Compatibility: string theory’s multidimensional aspect aligns with HTUM’s toroidal structure, which can be visualized as existing in higher-dimensional space. Both theories also address the unification of forces, with HTUM focusing on the interplay between gravity, dark matter, and dark energy [236].
- Divergence: string theory’s reliance on higher dimensions and mathematical complexity differ from HTUM’s more geometric and cyclical approach. HTUM’s emphasis on the singularity and the nature of time offers a distinct perspective that complements string theory’s focus on fundamental particles and forces [27].
18.2. Comparison with Other Theories of Quantum Gravity
18.2.1. Causal Dynamical Triangulations (CDT)
- Compatibility: HTUM and CDT emphasize the geometric nature of spacetime. The toroidal structure of HTUM could be represented within the simplicial framework of CDT [384].
- Divergence: CDT focuses on the discrete evolution of spacetime, while HTUM incorporates a continuous, cyclical model involving dark matter and dark energy. This difference in approach may offer complementary insights into the nature of spacetime [241].
18.2.2. Non-Commutative Geometry
- Compatibility: The mathematical structures of Non-Commutative Geometry could describe the complex topology of HTUM’s toroidal universe [385].
- Divergence: Non-commutative geometry primarily addresses the algebraic properties of spacetime, whereas HTUM focuses on a geometric and cyclical interpretation. Integrating these perspectives could lead to a richer understanding of the universe’s fundamental nature [386].
18.3. Compatibility with the Multiverse Hypothesis
- Compatibility: HTUM’s cyclical nature can be seen as representing a series of interconnected cosmic states within a larger framework. Each toroidal structure cycle could represent a different universe configuration, with variations in physical laws and constants [15]. This perspective shares some similarities with multiverse concepts, although HTUM proposes these variations occur within a single, cyclical universe rather than across separate universes.
- Divergence: While the multiverse hypothesis often relies on probabilistic interpretations and the Many-Worlds interpretation of quantum mechanics, HTUM focuses on a singular, interconnected toroidal structure. This difference in focus highlights HTUM’s unique contributions to our understanding of cosmic cycles and the nature of time [388]. HTUM proposes a deterministic yet dynamic universe where changes occur through continuous transformation rather than branching into separate realities.
18.4. Many-Worlds Interpretation and HTUM
- Compatibility: HTUM’s emphasis on quantum mechanics and the role of consciousness in actualizing reality aligns with the MWI’s view of multiple outcomes. The toroidal structure of HTUM could encompass these various branches, with each cycle representing a different outcome [389].
- Divergence: HTUM integrates the roles of dark matter and dark energy in shaping the universe, which is not a primary focus of MWI. Additionally, HTUM’s cyclical nature contrasts with the branching structure of MWI, offering a different perspective on the universe’s evolution [390].
18.5. Potential Integration with Other Theories
18.5.1. holographic principle
- Compatibility: HTUM’s toroidal structure could be visualized as a higher-dimensional space where the holographic principle applies. This could provide a framework for understanding how information is encoded and preserved in the universe [391].
- Potential Integration: Integrating the holographic principle with HTUM could offer new insights into the nature of information and entropy in a cyclical universe, potentially leading to a deeper understanding of black holes and cosmological horizons [392].
18.5.2. AdS/CFT correspondence
- Compatibility: The higher-dimensional aspects of HTUM’s toroidal structure could be related to the AdS space, and its cyclical nature provides a novel interpretation of the boundary conditions in the CFT [394].
- Potential Integration: Exploring the AdS/CFT correspondence within the context of HTUM could lead to a unified description of gravity and quantum mechanics, offering new avenues for research in quantum gravity and cosmology [395].
18.6. Comparison with Existing Toroidal Universe Models
18.6.1. Euclidean 3-Torus Model
- Similarities: Both HTUM and the 3-torus model propose a finite yet unbounded universe.
- Differences: HTUM incorporates a 4D structure and explicitly integrates time as the fourth dimension, while the 3-torus model is primarily spatial.
18.6.2. Poincaré Dodecahedral Space Model
- Similarities: Both HTUM and PDS challenge the notion of an infinite, flat universe.
- Differences: HTUM’s 4D toroidal structure offers a different geometric interpretation than PDS’s dodecahedral structure.
19. Unification with Particle Physics
19.1. Emergence of Standard Model Particles
19.1.1. Fermions as Topological Defects
19.1.2. Bosons as Vibrational Modes
19.2. Predictions for High-Energy Particle Physics
19.2.1. Discrete Energy Levels
19.2.2. Periodic Behavior in Scattering Amplitudes
19.2.3. New Particles at High Energies
19.2.4. Simulation of Collision Product Energy Spectra
19.3. Unification of Forces in HTUM
19.3.1. Introduction to Force Unification in HTUM
19.3.2. Geometric Unification
- Electromagnetic force: Associated with the surface curvature of the torus
- Strong nuclear force: Linked to the internal twisting of the torus structure
- Weak nuclear force: Related to the torus’s handle structure
- Gravitational force: Emerges from the overall curvature of the 4D torus
| Force | Geometric Aspect | Description |
|---|---|---|
| Electromagnetic | Surface curvature | Associated with the surface curvature of the torus |
| Strong nuclear | Internal twisting | Linked to the internal twisting of the torus structure |
| Weak nuclear | Handle structure | Related to the torus’s handle structure |
| Gravitational | Overall curvature | Emerges from the overall curvature of the 4D torus |
19.3.3. Symmetries in the Toroidal Structure
19.3.4. Force Strength Hierarchy
- Strong force: Highest curvature regions
- Electromagnetic force: Moderate curvature regions
- Weak force: Low curvature regions
- Gravitational force: Overall curvature of the 4D torus
19.3.5. Gravity as a Geometric Effect
19.3.6. Running Coupling Constants
19.3.7. Comparison with Other Unification Attempts
- string theory: While string theory also aims for a geometric unification, HTUM achieves this with a more straightforward, intuitive 4D structure instead of requiring extra dimensions [27].
- loop quantum gravity: HTUM shares LQG’s emphasis on quantum geometry but provides a more comprehensive framework for unifying all forces, not just gravity [31].
- Grand Unified Theories: HTUM naturally incorporates gravity, which GUTs typically struggle to include [401].
- Standard Model: HTUM offers a geometric explanation for the seemingly arbitrary symmetries and parameters of the Standard Model [398].
| Theory | Approach | HTUM Advantage |
|---|---|---|
| String Theory | Geometric unification with extra dimensions | Simpler 4D structure |
| Loop Quantum Gravity | Emphasis on quantum geometry | Framework for all forces |
| Grand Unified Theories | Unify strong, weak, EM forces | Incorporates gravity |
| Standard Model | No inherent unification | Geometric explanation for symmetries |
19.3.8. Observational Consequences
- particle physics: At ultra-high energies ( GeV), HTUM predicts a convergence of force strengths, potentially observable in cosmic ray experiments or future colliders [165].
- gravitational waves: HTUM predicts unique high-frequency gravitational wave signatures that might indicate a unified force regime [188].
- Cosmological implications: The early universe, under HTUM, would have undergone a series of symmetry-breaking phase transitions as it cooled, potentially leaving observable imprints in the cosmic microwave background (CMB) [38].
19.3.9. Implications for Particle Physics
- New particles: HTUM predicts the existence of new particles that mediate transitions between different force regimes [119].
- Proton decay: HTUM provides a mechanism for proton decay, but at a much longer timescale than traditional GUTs, consistent with current experimental limits [406].
- Neutrino masses: The toroidal structure in HTUM offers a natural explanation for the small but non-zero neutrino masses through a novel see-saw mechanism [407].
19.4. Conclusion
20. Numerical Simulation Framework
20.1. Simulation Components
20.1.1. 4D Toroidal Geometry
20.1.2. Unified Mathematical Operations
20.1.3. Quantum Wave Function Evolution
20.1.4. Gravitational Dynamics
20.1.5. Dark Matter and Dark energy
| Component | Description | Key Equation |
|---|---|---|
| 4D Toroidal Geometry | Hypercubic lattice with points | |
| Unified Mathematical Operations | Generalized operator for math operations | |
| Quantum Wave Function | Split-operator method | |
| Gravitational Dynamics | Modified Einstein field equation | |
| Dark Matter and Energy | Coupled equations for densities |
20.2. Numerical Methods
20.3. Computational Implementation
20.4. Simulation Outputs
- CMB power spectrum
- Matter power spectrum
- Gravitational wave signatures
- dark matter and dark energy distributions
20.5. Visualization Techniques
| Aspect | Description | Details |
|---|---|---|
| Numerical Methods | Spectral methods and symplectic integrators | Spatial derivatives and time evolution |
| Parallelization | Hybrid MPI/OpenMP approach | Distributed and shared memory |
| GPU Acceleration | CUDA | Computationally intensive parts |
| Simulation Outputs | Observable quantities | CMB power spectrum, Matter power spectrum, |
| Gravitational wave signatures, | ||
| Dark matter and dark energy distributions | ||
| Visualization | Advanced techniques | 4D toroidal structure representation |
21. Testable Predictions and Empirical Validation
21.1. Predictions for Cosmic Microwave Background (CMB) Radiation
- Anisotropies and patterns: HTUM posits that the universe’s toroidal geometry will result in specific CMB patterns. These patterns may differ from those the standard cosmological model predicted, offering a unique signature of HTUM [7].
- Temperature fluctuations: The interaction between dark matter, dark energy, and the singularity could lead to unique temperature fluctuations in the CMB. These fluctuations might be cyclical or periodic, reflecting the toroidal structure [178].
21.2. CMB Topology Signatures
21.2.1. Matched Circles
21.2.2. Multipole Alignments
21.2.3. Power Spectrum Modulation
21.2.4. Bispectrum Signature
21.3. Quantum Gravitational Effects
21.4. Dark Energy Dynamics
21.5. Polarization Patterns
- A distinctive B-mode polarization pattern with a characteristic angular scale related to the torus size.
- Periodic correlations in E-mode polarization across large angular scales.
21.6. Predictions Related to the Cosmological constant Problem
-
Scale-dependent dark energy: HTUM predicts that the effective dark energy density varies with scale r according to:where is the average dark energy density, is a small amplitude (predicted to be ), and L is the characteristic size of the torus. This could be detected through precise measurements of the expansion history at different redshifts [418].
-
CMB anisotropies: The TVEM function should imprint specific patterns in the CMB power spectrum. We predict an additional modulation in the CMB temperature anisotropies:where is a small amplitude (predicted to be ) and is a characteristic angular scale related to the size of the torus [5].
-
Galaxy clustering: The scale-dependent effective cosmological constant should affect the growth of the structure. We predict a modification to the matter power spectrum :where is a small amplitude (predicted to be ) and L is again related to the torus size [147].
21.6.1. Conclusion
21.7. Gravitational Wave Phenomena
21.7.1. Gravitational Wave Signatures in HTUM
- Both models show an increasing trend in energy density with frequency
- HTUM predicts distinct oscillations in the energy density, particularly at higher frequencies
- The standard model predicts a smooth increase without oscillations
- Differences between HTUM and the standard model become more pronounced at higher frequencies
21.7.2. Gravitational Wave Echoes
- An original gravitational wave signal (blue line)
- An echo of the original signal (orange line), delayed in time and reduced in amplitude
- A combined signal (green line) showing the interference between the original wave and its echo
21.7.3. Implications and Future Tests
- Stochastic background measurement: Space-based detectors like LISA could potentially measure the stochastic gravitational-wave background at the frequencies where HTUM predicts distinctive oscillations [189].
- Statistical analysis: Even if individual echoes are too faint to detect, statistical methods applied to a large number of gravitational wave events could reveal their presence [188].
21.8. Large-Scale Structure Correlations
- Pronounced oscillations in the theoretical HTUM curve, particularly at intermediate to large scales, reflecting the periodic boundary conditions inherent in a toroidal universe [7].
- Significant deviations from the standard model at large scales, suggesting complex cosmic structures not accounted for in conventional cosmological models [64].
- High-frequency fluctuations in the theoretical HTUM curve, potentially representing the dynamic interplay between dark matter, dark energy, and the toroidal structure of spacetime [112].
- An upturn in large-scale simulated data, possibly indicative of large-scale quantum correlations as proposed by HTUM [217].
- Visible filamentary structures and voids, consistent with HTUM predictions of matter distribution in a toroidal universe under modified gravity and dark energy dynamics [96].
- Subtle periodic patterns, particularly near the edges, a signature of the toroidal structure central to HTUM [78].
- A mix of uniformity and clustering that could be attributed to the quantum correlation effects incorporated in HTUM [221].
21.9. Dark Energy Dynamics
21.10. Quantum Entanglement at Cosmological Scales
21.11. Particle Physics Implications
21.12. Topological Quantum Phase Transitions
21.13. Gravitational Waves and Their Signatures
- Waveform signatures: The model predicts that gravitational waves originating from events near the singularity or within the toroidal structure will have distinct waveform signatures, which may differ from those predicted by general relativity alone [425].
- Frequency spectrum: The interaction between dark matter, dark energy, and wave function collapse could result in a unique frequency spectrum for gravitational waves. This spectrum might include specific peaks or troughs corresponding to the toroidal geometry [426].
21.14. Testing Emergent Dimensions
- Energy-dependent Lorentz violation in cosmic ray observations [165]
- Anisotropies in the CMB correlated with the structure of the hidden dimension [5]
- Deviations from general relativity in strong gravitational fields [242]
- Unexpected resonances in particle physics experiments near the dimensional transition energy [119]
21.15. Patterns in Dark matter and Dark energy Distribution
- Spatial distribution: dark matter and dark energy should exhibit specific spatial distributions influenced by the toroidal geometry. These distributions may form patterns or structures the standard cosmological model does not predict [427].
- Temporal variations: The cyclical nature of HTUM suggests that the density and distribution of dark matter and dark energy may vary over time, reflecting the universe’s dynamic behavior [15].
| Property | HTUM | Standard Model |
|---|---|---|
| Echo signals | Predicted | Not predicted |
| Echo time delay | N/A | |
| Echo amplitude | 10-20% of original | N/A |
| Stochastic background | Periodic modulations | Smooth increase |
| Characteristic frequency | Not applicable | |
| Waveform signatures | Distinct near singularity | Standard |
| Frequency spectrum | Unique peaks/troughs | Continuous |
21.16. Potential Experiments and Observations
- High-precision CMB measurements: Future missions with higher precision and resolution can provide more detailed data on CMB anisotropies and temperature fluctuations, allowing for a more rigorous test of HTUM predictions [428].
- Advanced gravitational wave detectors: Next-generation gravitational wave detectors with increased sensitivity and broader frequency ranges can detect and analyze more subtle waveform signatures, providing critical data for HTUM validation [422].
- dark matter and dark energy mapping: Enhanced mapping techniques and larger survey volumes can improve our understanding of dark matter and dark energy distributions, offering more opportunities to test HTUM predictions [429].
- Quantum experiments: Laboratory experiments exploring wave function collapse and quantum entanglement in controlled settings can provide insights into HTUM’s quantum mechanical aspects [430].
21.17. Challenges in Experimental Testing
- Sensitivity and precision: Many predicted signatures, such as specific anisotropies in the CMB or unique gravitational waveforms, require extremely high sensitivity and precision in measurements. Current technology may still need to be improved to detect these subtle signals [431].
- Data interpretation: Distinguishing HTUM-specific patterns from noise or other cosmological phenomena can be complex. Advanced data analysis techniques and robust statistical methods will be necessary to ensure accurate interpretation [432].
- Resource allocation: Large-scale experiments and observations require significant funding and resources, such as those involving next-generation gravitational wave detectors or extensive dark matter surveys. Securing these resources can be a major hurdle [433].
- Technological advancements: Developing more sensitive and precise instruments will be crucial. Collaborative efforts between institutions and countries can accelerate technological progress [434].
- Interdisciplinary collaboration: Bringing together experts from various fields, including cosmology, quantum mechanics, and data science, can enhance the design and analysis of experiments. Multidisciplinary teams can develop innovative solutions to complex problems [435].
- Incremental validation: Starting with smaller, more manageable experiments can provide initial validation and build a case for larger-scale studies. Incremental progress can help secure funding and support for more ambitious projects [436].
21.18. Roadmap for Future Experimental Work and Collaborations
-
Initial feasibility studies:
-
Technological development:
-
Pilot experiments:
-
Large-scale observations:
-
Data analysis and interpretation:
-
Interdisciplinary collaboration:
-
Continuous refinement:
21.19. Specific Empirical Predictions
21.19.1. CMB Power Spectrum
- Overall structure: Both HTUM and CDM exhibit similar large-scale structures, demonstrating that HTUM preserves the essential features of the CMB power spectrum consistent with observational data.
- Acoustic peaks: The plot clearly shows the acoustic peaks, a crucial feature of the CMB power spectrum. Both models reproduce these peaks, validating HTUM’s consistency with fundamental CMB physics.
- Low-l behavior: At low l values (large scales), noticeable differences emerge between HTUM and CDM. These differences are particularly significant as they correspond to the scales where effects from HTUM’s toroidal structure are expected to manifest.
- High-l behavior: The two models show subtle but consistent divergence at higher l values (smaller scales). This could be attributed to the cumulative effects of the TVEM on smaller-scale physics.
- Oscillatory differences: The differences between HTUM and CDM exhibit an oscillatory nature, especially visible at higher l. This pattern may be a signature of the sinusoidal form of the TVEM function.
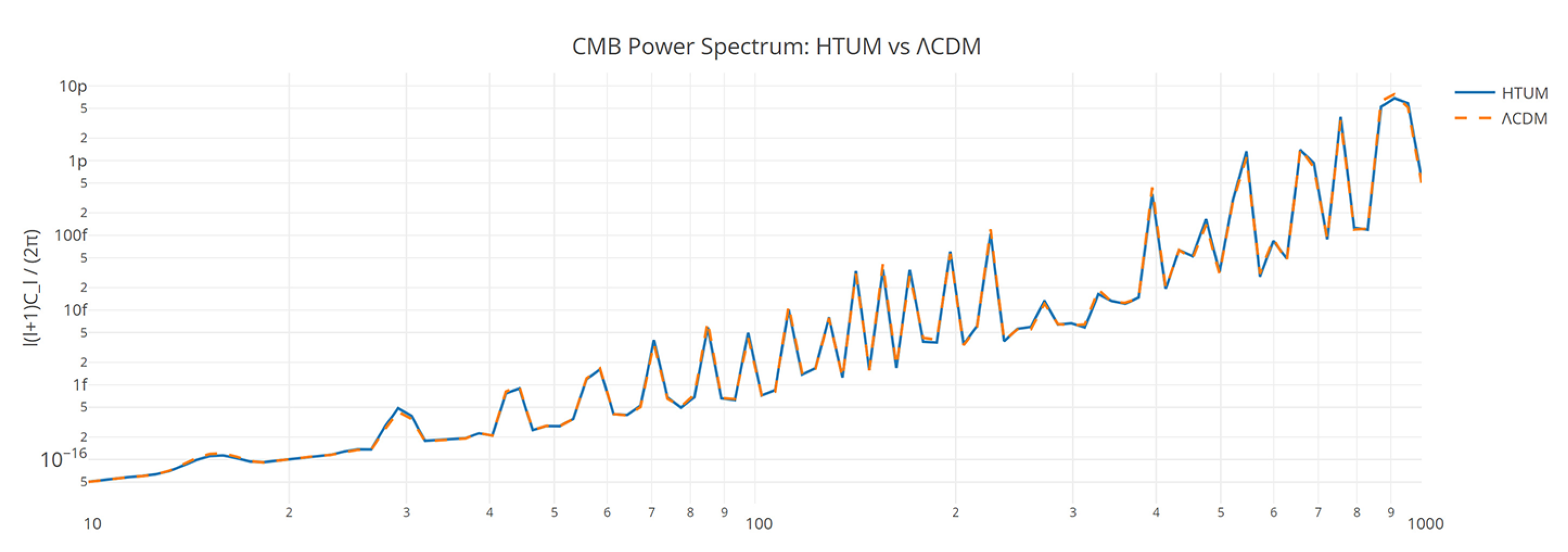
- Oscillatory pattern: The differences oscillate across all angular scales, with varying amplitudes and frequencies, reflecting the complex interplay between HTUM’s toroidal structure and CMB physics.
- Scale dependence: The magnitude of differences generally increases for higher l values, suggesting that HTUM’s effects become more pronounced at smaller angular scales.
- Significant deviations: The relative differences reach up to approximately at certain scales, which is substantial and potentially detectable with future high-precision CMB measurements.
- Large-scale behavior: There are noticeable differences at low l values (large scales), which may be attributed to the global topology predicted by HTUM.
- Multiple crossings: The curve crosses zero multiple times, indicating specific scales where HTUM and CDM predictions align.
21.19.2. Gravitational Wave Background
21.19.3. Dark energy Equation of State
- HTUM predicts distinct oscillations in w(z), with an amplitude of approximately 0.1 and a period related to the torus size.
- The CDM model (orange dashed line) predicts a constant w = -1, representing dark energy as a cosmological constant.
- The w0waCDM model (green dotted line) shows a smooth, monotonic evolution of w(z).
21.20. Computational Simulations for HTUM
21.20.1. N-body Simulation with HTUM Physics
- Adaptive mesh refinement (AMR): Implement AMR techniques to provide high resolution in regions of interest while maintaining computational efficiency [449].
- dark energy dynamics: Incorporate the nonlinear probabilistic nature of dark energy in HTUM, allowing its density to evolve dynamically based on local conditions [112].
- Quantum effects at large scales: Include algorithms to model quantum effects that HTUM predicts may be relevant at cosmological scales [339].
21.20.2. Quantum Wave Function Collapse Simulation
- Quantum error correction: Implement quantum error correction codes to model how the universe might maintain quantum coherence over large scales [450].
- Continuous variable quantum computing: Utilize continuous variable quantum computing techniques to better represent the continuous nature of spacetime in HTUM [451].
- Tensor network states: Employ tensor network methods to efficiently simulate large-scale quantum systems [452].
4D N-Body Simulation
Quantum Wave Function Evolution
21.20.3. Toroidal Structure Evolution Simulation
- Differential geometry: Use techniques from differential geometry to accurately model the curved spacetime of the torus [79].
- Topological phase transitions: Implement algorithms to simulate potential topological phase transitions in the early universe [162].
- Visualization techniques: Develop advanced 4D visualization techniques to help researchers and the public understand the toroidal structure [83].
21.20.4. Machine Learning Applications
- Deep learning for pattern recognition: Use deep neural networks to identify HTUM-specific patterns in simulated data [453].
- Generative models: Employ generative adversarial networks (GANs) to produce synthetic datasets for testing HTUM predictions [454].
- Reinforcement learning: Utilize reinforcement learning algorithms to optimize simulation parameters and explore the vast parameter space of HTUM [455].
21.21. Testing HTUM’s Quantum-to-Classical Transition Predictions
21.21.1. Gravitational Enhancement of Decoherence
21.21.2. Scale-Dependent Quantum Behavior
21.21.3. Modifications to Uncertainty Relations
21.21.4. Quantum Correlations in Cosmological Data
21.22. Advanced Mathematical Framework
21.22.1. Unified Mathematical Operations
21.23. Experimental Proposals for Testing HTUM’s Quantum Foundations
- Tests of quantum contextuality: Perform experiments testing quantum contextuality in high-energy regimes, where HTUM predicts deviations from standard quantum mechanics due to the influence of the toroidal structure [207].
- Macroscopic superposition: Design experiments probing the limits of quantum superposition for macroscopic objects, looking for signatures of HTUM’s predicted coherence maintenance in certain topological configurations [248].
- universal self-observation: Investigate potential signatures of the universe’s self-observation in quantum systems, such as subtle deviations from standard decoherence models [40].
- Entanglement in curved spacetime: Conduct experiments testing quantum entanglement in regions of strong gravitational fields, where HTUM predicts modifications to entanglement due to the interplay between gravity and the toroidal structure [456].
- Modified uncertainty relations: Perform high-precision measurements to detect the additional uncertainties predicted by HTUM’s generalized uncertainty principle [457].
21.23.1. TVEM Function
- CMB power spectrum: HTUM predicts subtle variations (0.90) compared to the Standard Model (0.95), suggesting potential differences detectable with high-precision CMB measurements [5].
- Gravitational wave echoes: HTUM uniquely predicts a strong signal (0.80), contrasting with the Standard Model’s lack of prediction. This presents a promising avenue for testing HTUM using future gravitational wave detectors [458].
- dark energy equation of state: HTUM shows a stronger prediction (0.95) than the Standard Model (0.50), indicating a potentially more comprehensive explanation for dark energy behavior [112].
- large-scale structure: Both models show strong predictions, with HTUM (0.85) slightly lower than the Standard Model (0.90), suggesting comparable explanatory power with subtle differences [144].
- quantum entanglement in CMB: HTUM uniquely predicts quantum entanglement effects in the CMB (0.70), connecting quantum mechanics with cosmological observations [208].
| Observational Test | Key Prediction | Current Status |
|---|---|---|
| CMB power spectrum | 5-10% suppression for | Testable with future missions |
| CMB anisotropies | Specific patterns due to torus structure | Require high-precision data |
| Gravitational wave echoes | Detectable with | Future GW detectors needed |
| Stochastic GW background | Periodic modulations in | Potentially detectable by LISA |
| Dark energy equation of state | Oscillations in | Next-gen surveys required |
| Large-scale structure | Periodic correlations in galaxy distribution | Testable with upcoming surveys |
| Baryon acoustic oscillations | Additional peaks in the power spectrum | Require high-precision BAO data |
| Particle physics | Periodic structures in collision spectra | Future high-energy colliders |
| Quantum entanglement | Non-zero discord in CMB regions | Next-gen CMB experiments |
| Topological phase transitions | Specific transitions in quantum Hall systems | Condensed matter experiments |
22. Implications for the Nature of Reality
22.1. Redefining Reality: A Timeless Singularity
22.2. Information Preservation and the Nature of Reality
22.3. The Role of Consciousness in Shaping Reality
22.4. HTUM and the Nature of Classical Reality
22.4.1. Emergent Classicality
22.4.2. Unified Description of Reality
22.4.3. Role of the Observer
22.4.4. Nature of Time
22.4.5. Limits of Knowledge
22.4.6. Reality as Information
22.4.7. Holographic Nature of Reality
22.5. Philosophical Framework of HTUM
22.5.1. Ontology: The Nature of Reality
- Unity of existence: The toroidal structure implies a fundamental interconnectedness of all things. What we perceive as separate entities are, in fact, different manifestations of the same underlying reality [286].
- Non-locality: The toroidal nature of the universe allows for non-local connections, providing a physical basis for phenomena like quantum entanglement and potentially explaining the universality of physical laws [155].
- Timelessness at the fundamental level: While we experience time as a linear progression, HTUM suggests that at the deepest level, all moments exist simultaneously within the toroidal structure. Our perception of time’s flow emerges from our limited perspective within this greater whole [18].
- Mind-matter integration: HTUM dissolves the traditional mind-body dualism by positing consciousness as fundamental, suggesting instead a monistic view where mind and matter are two aspects of the same underlying reality [366].
22.5.2. Epistemology: The Nature of Knowledge
- Knowledge as pattern recognition: In an interconnected universe, knowledge can be understood as recognizing patterns within the toroidal structure [464].
- Limits of knowledge: The model suggests inherent limits to knowledge due to our perspective as conscious entities within the system we’re trying to understand. Complete knowledge would require a perspective outside the toroidal structure, which is by definition impossible [375].
- Intuition and rational thought: HTUM provides a framework that potentially bridges intuitive and rational modes of knowing. Intuition could be understood as a direct perception of the underlying interconnectedness, while rational thought represents our attempts to model these connections explicitly [465].
22.5.3. Ethics and Meaning
- Interconnectedness and ethics: The fundamental interconnectedness suggested by HTUM could provide a basis for ethical considerations. If all things are ultimately connected, harm to one part of the system could be seen as harm to the whole [466].
- Purpose and meaning: In a self-observing universe, each conscious entity could be seen as playing a role in the universe’s self-realization. This could provide a sense of cosmic purpose without requiring an external creator [380].
- Environmental ethics: The model’s emphasis on interconnectedness and the role of consciousness could support a more holistic approach to environmental ethics, seeing humanity as an integral part of a conscious cosmos rather than separate from nature [467].
- Personal growth: Understanding oneself as a localized expression of universal consciousness could inform approaches to personal growth and self-realization [381].
22.5.4. Comparison with Other Philosophical Views
- Materialism: Unlike materialist views that see consciousness as an emergent property of complex physical systems, HTUM posits consciousness as fundamental [468].
- Idealism: While HTUM shares with idealism the primacy of consciousness, it differs in maintaining the reality of the physical world as an expression of consciousness rather than an illusion [469].
- Dualism: HTUM resolves the mind-body problem not by positing two separate substances but by seeing mind and matter as two aspects of a single, underlying reality [470].
- Panpsychism: HTUM aligns with panpsychism in attributing consciousness to all of reality but provides a more structured framework for understanding how this consciousness is organized and expressed [471].
- Process philosophy: HTUM shares with process philosophy an emphasis on change and interconnection but provides a more specific geometric structure (the torus) to explain these processes [472].
22.6. Philosophical Implications of HTUM’s Quantum Foundations
22.6.1. Nature of Reality
22.6.2. Observation and Reality
22.6.3. Determinism and Probability
22.6.4. Holism and Reductionism
22.6.5. Limits of Knowledge
22.6.6. Emergence of Classicality
22.6.7. Mind and Consciousness
22.6.8. Philosophical Implications
22.6.9. The Nature of Time
22.7. Mathematical Implications
22.8. Information Theory and Entropy
22.9. Implications for the Origin and Ultimate Fate of the Universe
22.10. The Hard Problem of Consciousness
- Consciousness as fundamental: By positing consciousness as a basic feature of the universe, HTUM sidesteps the need to explain how consciousness emerges from non-conscious matter [46].
- Degrees of consciousness: The model allows for different degrees or complexities of consciousness throughout the universe, potentially explaining the apparent difference between conscious and non-conscious entities [478].
- Subjective experience: The hard problem of how physical processes give rise to subjective experience is addressed by suggesting that all physical processes have an inherent experiential aspect. What we perceive as purely physical at one level may have an experiential aspect at a deeper level [47].
- Unity of consciousness: The interconnected nature of the toroidal structure provides a framework for understanding the unity of conscious experience and altered states of consciousness that seem to transcend individual boundaries [374].
- How does HTUM view consciousness as a fundamental challenge or support existing theories in the philosophy of mind [475]? HTUM’s perspective aligns with and potentially extends theories that posit consciousness as a fundamental feature of reality, such as panpsychism or integrated information theory.
- Can HTUM offer a new framework for understanding the subjective nature of experience [47]? By suggesting that experiential properties are intrinsic to the fabric of reality, HTUM provides a novel approach to understanding qualia and subjective experience.
- Consider the phenomenon of qualia—individual instances of subjective, conscious experience. HTUM might suggest that these experiences directly manifest the universe’s underlying toroidal structure [376]. This perspective uniquely conceptualizes the relationship between subjective experience and the universe’s fundamental structure.
22.11. Panpsychism and HTUM
22.12. Free Will and Determinism
- Quantum indeterminacy: The quantum nature of reality at the fundamental level introduces an element of indeterminism into the system. This indeterminacy could propagate to macroscopic scales, providing a basis for free will [69].
- Soft determinism: While the toroidal structure implies a kind of overall determinism (in that all possibilities are contained within it), the complexity of the system and our limited perspective within it make perfect prediction impossible, creating space for what we experience as free will [483].
- Cyclical nature: The toroidal structure suggests a cyclical nature to events, which could be seen as an "eternal recurrence." However, each cycle may have variations due to quantum indeterminacy, allowing for both pattern and novelty [484].
- Conscious choice: In HTUM, consciousness plays a role in collapsing quantum superpositions. This suggests that conscious choices have a real, physical effect on the universe, providing a mechanism for free will [358].
- How does HTUM’s mechanism of consciousness collapsing the wave function impact the debate on free will [473]? This mechanism suggests that conscious observation may directly influence physical reality, potentially providing a scientific basis for free will.
- Can this model reconcile the apparent determinism of physical laws with the experience of free will [485]? HTUM’s concept of soft determinism, combined with quantum indeterminacy, offers a potential resolution to this longstanding philosophical dilemma.
- In the context of quantum mechanics, HTUM might argue that conscious observation influences the outcome of quantum events, allowing free will within a probabilistic framework [486]. This interpretation provides a novel approach to understanding the relationship between consciousness, quantum mechanics, and free will.
22.13. The Observer Effect and the Nature of Reality
22.14. Emergent Properties and Complexity
22.15. Philosophical Implications of Emergent Dimensions
22.16. The Mind-Body Problem
22.17. Implications for the Philosophy of Science
22.17.1. The Origin of the Universe
22.17.2. The Ultimate Fate of the Universe
23. Conclusion
23.1. Summary of Key Points
- HTUM proposes a 4DTS that offers new insights into the universe’s geometry and topology [278].
- It provides a unified approach to mathematical operations, enhancing our understanding of interconnected processes in physics and engineering [299].
- HTUM addresses the cosmological constant problem by introducing a TVEM function, offering a mechanism to naturally suppress extreme vacuum energy values predicted by quantum field theory.
- Empirical validation and technological advancements are crucial for testing HTUM’s predictions and refining its models [165].
- Interdisciplinary collaboration is essential for overcoming the challenges associated with HTUM and advancing our knowledge [291].
23.2. Implications for Cosmology and Beyond
- It offers new perspectives on fundamental cosmological phenomena, such as dark energy, the universe’s accelerated expansion, and the cosmological constant problem [112].
- The model’s approach to the cosmological constant problem provides a testable framework, bridging theoretical cosmology with observational astronomy.
- HTUM’s philosophical implications, such as its perspective on the nature of consciousness and its role in shaping reality, can contribute to long-standing philosophical debates and encourage interdisciplinary dialogue between scientists and philosophers [68].
23.3. The Power of Interdisciplinary Research and Collaboration
- Collaborative efforts between institutions and countries can accelerate technological progress and enhance the design and analysis of experiments [502].
- Interdisciplinary teams, including cosmology, quantum mechanics, data science, and philosophy experts, can develop innovative solutions to complex problems [311].
- Integrating advanced numerical methods, rigorous parameter estimation, and Bayesian data analysis techniques ensures that HTUM can be thoroughly tested against current and future observational data.
- Interdisciplinary collaboration, particularly between scientists and philosophers, is crucial for fully exploring HTUM’s philosophical implications and their potential impact on our understanding of the universe and our place within it [503].
23.4. Future Research Directions
- Technological development: Invest in advanced instruments and detectors with higher sensitivity and precision [188].
- Pilot experiments: Design and conduct pilot experiments to test specific predictions of HTUM, such as CMB anisotropies, gravitational wave signatures, or effects related to the cosmological constant [179].
- Large-scale observations: Secure funding and resources for large-scale observations, such as next-generation gravitational wave detectors and cosmological surveys [504].
- Theoretical refinement: Further develop the mathematical framework of HTUM, particularly in relation to the cosmological constant problem and the unification of quantum mechanics and gravity.
- Philosophical implications: Further examine the philosophical implications of HTUM, as discussed in Section 22.6.8, and explore their connections to other areas of intellectual inquiry, such as epistemology and the philosophy of science [505].
23.5. Embracing the Journey of Discovery
23.6. Addressing Immediate Challenges to HTUM
23.6.1. Information Conservation and Black Hole Evaporation
23.6.2. Quantum Effects and Spacetime Structure
23.6.3. Cosmic Censorship and Black Hole Unity
23.6.4. Physics Beyond the Event Horizon
- Timelessness: Beyond the event horizon, we enter a domain where time, as we typically conceive it, loses its meaning. This doesn’t indicate physics’s failure but reveals the limitations of our time-dependent perspective.
- Unified structure: This timeless nature beyond the event horizon supports HTUM’s unified black hole entity concept. Without the constraints of linear time, black holes’ apparent separateness dissolves.
23.6.5. Observational Constraints
23.7. HTUM and CMB Anomalies
23.8. Implications for Early Universe Physics
- Inflation: The finite size of the torus in HTUM suggests a natural end to inflation, potentially resolving the "graceful exit" problem.
- Quantum cosmology: The toroidal structure provides a concrete realization of quantum cosmology boundary conditions, impacting the universe’s wave function formulation.
- Primordial non-gaussianity: HTUM predicts specific forms of primordial non-Gaussianity arising from the toroidal topology, which could be tested with future CMB and large-scale structure observations.
23.9. Future Directions
- Development of more sophisticated simulations of CMB and large-scale structure in a toroidal universe.
- Investigation of the interplay between HTUM’s toroidal structure and other aspects of fundamental physics, such as the nature of dark matter and dark energy.
- Exploration of the implications of HTUM for the very early universe and the potential resolution of the initial singularity.
- Design of targeted observational strategies to test HTUM’s specific predictions, particularly in upcoming CMB experiments and large-scale structure surveys.
23.10. HTUM as a Comprehensive Worldview
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
Appendix A. Comprehensive Mathematical Framework of the Topological Vacuum Energy Modulator
- A detailed mathematical formulation of the TVEM function and its role in addressing the cosmological constant problem.
- Advanced numerical methods for computing and analyzing TVEM effects.
- An extensive analysis of the observational consequences of HTUM, including predictions for cosmic microwave background (CMB) radiation, gravitational waves, and large-scale structure formation.
- Exploration of connections between HTUM and other areas of theoretical physics, including string theory, loop quantum gravity, and noncommutative geometry.
- Proposals for experimental tests of HTUM and the TVEM function.
- Discuss future research directions and potential implications for understanding the universe.
Appendix A.1. Foundations of the TVEM Function
Appendix A.1.1. Derivation from First Principles
Appendix A.1.2. Properties of the TVEM Function
- Periodicity: for each dimension i.
- Orthogonality:
- Completeness: Any function on can be expressed as a linear combination of .
Appendix A.1.3. Topological Considerations
- Fundamental group:
- Homology groups: for
- Cohomology ring:
Appendix A.2. Vacuum Energy Modulation Mechanism
Appendix A.2.1. Quantum Field Theory on a Torus
Appendix A.2.2. Vacuum Energy Calculation
Appendix A.2.3. Renormalization and Regularization
Appendix A.3. Advanced Numerical Methods
Appendix A.3.1. Monte Carlo Integration with Importance Sampling
- Generate points according to a probability distribution .
- Compute the estimator:
- Optimize to minimize variance using the Metropolis-Hastings algorithm [513].
Appendix A.3.2. Adaptive Mesh Refinement
- Start with a coarse grid.
- Identify regions with high gradients of .
- Refine the grid in these regions.
- Repeat steps 2-3 until desired accuracy is achieved.
Appendix A.3.3. Spectral Methods
- Expand in terms of orthogonal basis functions (e.g., Chebyshev polynomials).
- Convert the differential equation to an algebraic system.
- Solve the resulting system using iterative methods (e.g., conjugate gradient).
Appendix A.4. Effective Cosmological Constant
Appendix A.5. Dynamical Relaxation
Appendix A.6. Numerical Results
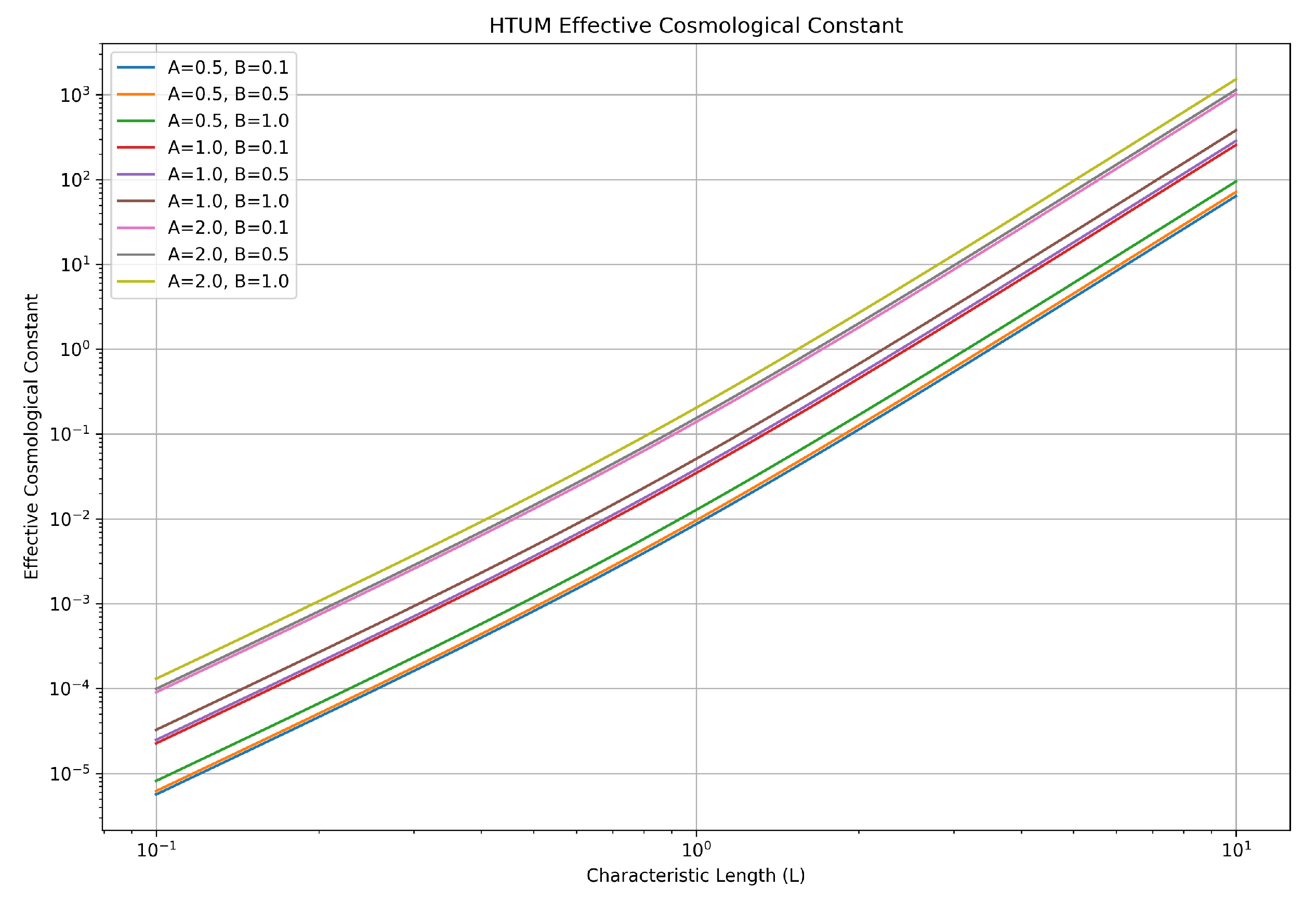
| L | A | B | |
|---|---|---|---|
| 0.1 | 0.5 | 0.1 | 3.24e-02 |
| 0.1 | 0.5 | 1.0 | 3.26e-02 |
| 0.1 | 2.0 | 0.1 | 5.18e-01 |
| 0.1 | 2.0 | 1.0 | 5.22e-01 |
| 1.0 | 0.5 | 0.1 | 3.12e-03 |
| 1.0 | 0.5 | 1.0 | 3.14e-03 |
| 1.0 | 2.0 | 0.1 | 4.99e-02 |
| 1.0 | 2.0 | 1.0 | 5.03e-02 |
| 10.0 | 0.5 | 0.1 | 3.11e-05 |
| 10.0 | 0.5 | 1.0 | 3.13e-05 |
| 10.0 | 2.0 | 0.1 | 4.98e-04 |
| 10.0 | 2.0 | 1.0 | 5.01e-04 |
Appendix A.7. Cosmological Implications
Appendix A.7.1. Modified Friedmann Equations
Appendix A.7.2. Structure Formation
Appendix A.7.3. Cosmic Inflation
Appendix A.8. Observational Signatures
Appendix A.8.1. CMB Power Spectrum
Appendix A.8.2. Baryon Acoustic Oscillations
Appendix A.8.3. Gravitational Waves
Appendix A.8.4. CMB Power Spectrum Predictions
Appendix A.8.5. Observational Signatures
- Oscillations or modulations in the power spectrum, particularly at large scales (low l) [7].
- Potential resolution of known CMB anomalies, such as the lack of power at large angles [70].
- Scale-dependent modifications to the spectral index .
- Distinct signatures in CMB polarization, especially in B-modes [417].
Appendix A.8.6. Constraints on HTUM Parameters
Appendix A.9. Statistical Analysis and Model Comparison
Appendix A.9.1. Bayesian Parameter Estimation
Appendix A.9.2. Model Comparison
Appendix A.9.3. Information Criteria
Appendix A.10. Connections to Other Theories
Appendix A.10.1. String Theory
-
T-duality and TVEM:where R is the compactification radius and is the string length.
- TVEM in the context of brane worlds [120].
Appendix A.10.2. Loop Quantum Cosmology
- Modified Friedmann equation in LQC:
- Potential correspondence between the critical density and TVEM effects.
Appendix A.10.3. Noncommutative Geometry
Appendix A.11. Quantum Information Aspects
Appendix A.11.1. Entanglement Entropy
Appendix A.11.2. Holographic Principle
-
TVEM-modified holographic bound:where A is the area of a bounding surface and is a TVEM-dependent correction.
- Implications for the AdS/CFT correspondence in the context of HTUM [393].
Appendix A.12. Experimental Proposals
| Aspect | Description |
|---|---|
| Definition | Fourier series on 4D torus |
| Mathematical form | |
| Effective cosmological constant | |
| Vacuum energy modulation | |
| Numerical methods | Monte Carlo integration, adaptive mesh refinement |
| Cosmological implications | Modified Friedmann equations, structure formation |
| Observational signatures | CMB anisotropies, BAO scale, gravitational waves |
| Quantum aspects | Modified dispersion relations, quantum foam effects |
| Connections to other theories | String theory, loop quantum cosmology, noncommutative geometry |
| Experimental proposals | CMB measurements, gravitational wave detection, vacuum energy tests |
Appendix A.13. Future Directions
Appendix A.13.1. Quantum Gravity Connections
Appendix A.13.2. Dark Energy Dynamics
Appendix A.13.3. Multiverse Scenarios
- TVEM variations across different universe bubbles.
- Implications for the measure problem in eternal inflation [205].
Appendix A.14. Advanced Topological Considerations
Appendix A.14.1. Cohomology and K-theory
- de Rham cohomology: We compute the cohomology groups and their relationship to the TVEM modes.
- K-theory: We investigate the K-theory groups and , and their potential Physical interpretations in HTUM [527].
Appendix A.14.2. Morse Theory
- Compute the Morse indices of critical points.
- Relate the topology of level sets of to the vacuum energy landscape.
Appendix A.15. Functional Analysis of the TVEM
Appendix A.15.1. Spectral Theory
- Compute the eigenvalue spectrum of the TVEM operator.
- Investigate the completeness and orthogonality of TVEM eigenfunctions.
- Explore the relationship between the spectral properties and the vacuum energy modulation.
Appendix A.15.2. Fredholm Theory
- Formulate the TVEM as a solution to a Fredholm integral equation.
- Investigate the existence and uniqueness of solutions.
- Develop numerical methods based on Fredholm’s theory for efficient TVEM computations.
Appendix A.16. Advanced Quantum Field Theory Aspects
Appendix A.16.1. Effective Field Theory
- Construct a low-energy effective action incorporating TVEM effects.
- Analyze the relevance and marginality of TVEM-induced operators.
- Investigate the renormalization group flow of TVEM parameters.
Appendix A.16.2. Quantum Anomalies
- Compute trace anomalies in the presence of the TVEM.
- Investigate gravitational anomalies and their cancellation in HTUM.
- Analyze potential implications for Hawking radiation and black hole thermodynamics [19].
Appendix A.17. Nonlinear Dynamics and Chaos
Appendix A.17.1. Dynamical Systems Analysis
- Identify fixed points and limit cycles in the TVEM dynamics.
- Perform stability analysis of cosmological solutions.
- Investigate the possibility of chaotic behavior in HTUM cosmologies.
Appendix A.17.2. Fractals and Self-Similarity
- Analyze the self-similarity of TVEM function across scales.
- Compute fractal dimensions of TVEM-modulated vacuum energy distributions.
- Investigate potential observational signatures of fractal structures in cosmic web formation [534].
Appendix A.18. Advanced Numerical Techniques
Appendix A.18.1. Sparse Grid Methods
- Develop adaptive sparse grid algorithms for TVEM computations.
- Compare efficiency and accuracy with standard Monte Carlo methods.
- Apply sparse grid methods to cosmological parameter estimation.
Appendix A.18.2. Machine Learning and AI
Appendix A.19. Quantum Information and Computation
Appendix A.19.1. Quantum Algorithms for TVEM
- Develop quantum circuits for TVEM function evaluation.
- Explore quantum speedup potential for Monte Carlo integration [538].
- Analyze the quantum complexity of HTUM related problems.
Appendix A.19.2. Quantum Error Correction
Appendix A.20. Cosmological Phase Transitions
Appendix A.20.1. TVEM and Cosmic Phase Transitions
Appendix A.20.2. Topological Defects
Appendix A.21. Beyond 4D: Higher-Dimensional Extensions
Appendix A.21.1. N-Dimensional TVEM
Appendix A.21.2. Calabi-Yau Manifolds
Appendix A.22. Philosophical and Conceptual Implications
Appendix A.22.1. Ontological Status of the TVEM
Appendix A.22.2. HTUM and the Anthropic Principle
Appendix A.23. Interdisciplinary Connections
Appendix A.23.1. TVEM in Condensed Matter Physics
Appendix A.23.2. HTUM and Information Theory
Appendix A.24. Future Experimental Frontiers
Appendix A.24.1. Space-Based Tests of HTUM
Appendix A.24.2. Laboratory Tests of Quantum Gravity
Appendix A.25. Conclusion
Appendix A.26. Computational Techniques
Appendix A.27. Computational Methods
Appendix A.27.1. Python Implementation (Gravitational Wave Echo Patterns and Stochastic Gravitational-Wave Background Energy Density)

- Gravitational wave echo patterns (Figure 8): This figure illustrates the concept of gravitational wave echoes, a unique HTUM prediction. The plot shows an original gravitational wave signal, a potential echo, and the combined signal. These echoes could arise due to the topological structure of the universe proposed by HTUM, where gravitational waves might traverse multiple paths through the hyper-torus before reaching our detectors.
- Stochastic gravitational-wave background energy density (Figure 7): This logarithmic plot compares the predicted stochastic gravitational wave background energy density in the HTUM with that of the standard cosmological model. The HTUM prediction includes oscillatory features that could potentially be detected by future gravitational wave observatories, providing a crucial test of the model.
Appendix A.27.2. Python Implementation (CMB Power Spectrum Calculations)

Appendix A.27.3. JavaScript Implementation



Appendix A.27.4. Python Implementation (Dark energy Equation of State)

Appendix A.27.5. Python Implementation (4D Wave Function Projection)



- A 3D projection of the 4D wave function at a specific time and w-coordinate, visualizing the probability density in the x, y, and z dimensions.
- The entanglement evolution over time shows the mean normalized entanglement with error bars representing the standard error of the mean across multiple simulation runs.
- The energy evolution throughout the simulation displays the mean energy with error bands indicating the standard error of the mean for multiple runs.
- A Fourier analysis of the final wave function, presenting the magnitude of the frequency components in the x-dimension.
Appendix A.27.6. Python Implementation (4D N-body Simulation in HTUM and Quantum Wave Function Evolution)


Appendix A.27.7. Python Implementation (3D plot of TVEM function and TVEM Modulation of Vacuum Energy Density)


Appendix A.27.8. Python Implementation (Galaxy Distribution)

Appendix A.27.9. Python Implementation (Collision Product Energy Spectra)

Appendix B. Detailed Mathematical Treatment of the Conceptual Framework
Appendix B.1. Wave Function and Quantum Superposition
Appendix B.2. Probability Density and Born’s Rule
Appendix B.3. Wave Function Collapse and Measurement
Appendix B.4. Density Matrix Formalism
Appendix B.5. Energy-Momentum Tensor in General Relativity
Appendix B.6. Einstein’s Field Equations and the Emergence of Gravity
Appendix B.7. Dark Matter and Dark energy in HTUM Framework
Appendix B.8. Quantum Decoherence and the Quantum-to-Classical Transition in HTUM
Appendix B.8.1. Density Matrix Evolution
Appendix B.8.2. Decoherence in the Toroidal Structure
Appendix B.8.3. Pointer States and Einselection
Appendix B.8.4. Quantum Darwinism and HTUM
Appendix B.8.5. Decoherence and Wave Function Collapse in HTUM
Appendix B.8.6. Emergence of Spacetime and Gravity
Appendix B.8.7. Experimental Implications
- Position-dependent decoherence rates that reflect the toroidal geometry of the universe [165].
- Specific patterns of einselection that align with the symmetries of the torus [40].
- Quantum Darwinism signatures in cosmological observations, such as the cosmic microwave background (CMB) [566].
- Correlations between quantum decoherence rates and local gravitational field strengths [32].
Appendix B.9. Experimental Tests and Observational Signatures
Appendix B.10. Mathematical Formulation of Unified Approach to Mathematical Operations
- Addition: with
- Subtraction: with
- Multiplication: with and
- Division: with and
Appendix B.11. Unified Mathematical Framework for Quantum-Classical Transition
Appendix B.11.1. Quantum Evolution and Decoherence in HTUM
Appendix B.11.2. Emergence of Classical Spacetime
Appendix B.11.3. Coupling of Quantum and Classical Regimes
Appendix B.12. Cosmological Quantum Entanglement
Appendix B.12.1. Quantum Discord in HTUM
Appendix B.12.2. Evolution of Entanglement on Cosmological Scales
Appendix B.13. Conclusion
Appendix C. Advanced Quantum Gravity Formalism for HTUM
Appendix C.1. Introduction
Appendix C.2. Functional Integration on the Torus
Appendix C.3. Toroidal Loop Quantum Gravity
Appendix C.4. Topological Quantum Field Theory on T4
Appendix C.5. Noncommutative Geometry of the Quantum Torus
Appendix C.6. Quantum Group Symmetries
Appendix C.7. Generalized Uncertainty Principle
Appendix C.8. Quantum Cosmology of the Torus
Appendix C.9. Entanglement Entropy and Torus Geometry
Appendix C.10. Quantum Holonomies on the Torus
Appendix C.11. Topological Entanglement Entropy
Appendix C.12. Quantum Gravity Corrections to CMB
Appendix C.13. Quantum Foam and Spacetime Fluctuations
Appendix C.14. Quantum Decoherence in HTUM
Appendix C.14.1. Derivation of the Lindblad Equation
Appendix C.15. Black Hole Thermodynamics on the Torus
Appendix C.15.1. Implications for Hawking Radiation
Appendix C.16. Quantum Gravitational Effects on Dark matter and Dark energy
Appendix C.17. Potential Observational Consequences and Experimental Proposals
- Cosmological observations: Search for anomalies or deviations from standard cosmological models in the cosmic microwave background (CMB), large-scale structure, and gravitational wave signals.
- Black hole physics: Study the behavior of black holes, particularly their evaporation through Hawking radiation and the information paradox, to gain insights into the quantum nature of gravity.
- Quantum measurement and decoherence: Conduct precision experiments on quantum measurement, decoherence, and the quantum-to-classical transition to understand the mechanisms underlying wave function collapse and its relation to gravity.
Appendix C.17.1. Gravitational Wave Signatures
Appendix C.18. Limitations and Open Questions
- The exact mechanism for the emergence of classical spacetime from the quantum torus remains unclear.
- The role of time in a fundamentally timeless quantum gravitational theory is not fully resolved.
- The nature of singularities in the toroidal topology requires further investigation.
- The unification of HTUM with other fundamental forces is ongoing.
Appendix C.19. Conclusion and Future Directions
Appendix D. Detailed Numerical Simulation Framework
Appendix D.1. Discretization of the 4D Torus
Appendix D.2. Implementation of Unified Mathematical Operations
| Algorithm 1 Unified Mathematical Operation. |
|
[ht]
|

- When and , U approximates addition.
- When and , U approximates subtraction.
- When and , U approximates multiplication or division depending on the sign of .

Appendix D.3. Quantum Wave Function Evolution Algorithm
| Algorithm 2 Fourth-Order Split-Operator Method for HTUM. |
|
- Fast Fourier Transforms (FFTs): We use highly optimized FFT libraries (e.g., FFTW) adapted for the 4D torus topology. The periodic boundary conditions of the torus are naturally handled in Fourier space.
-
Adaptive time stepping: We implement an adaptive time-stepping scheme to balance accuracy and computational efficiency:where is the estimated local error.
- Conservation properties: The integrator’s symplectic nature ensures long-term energy conservation and other invariants, which is crucial for the stability of HTUM simulations.
- Parallelization: The algorithm is parallelized using domain decomposition, with each MPI process handling a subset of the 4D torus. The FFTs are performed using parallel FFT algorithms.
- unified mathematical operations: We utilize the unified mathematical operations Appendix D.2 in implementing the kinetic and potential operators, allowing for a more flexible handling of the complex HTUM dynamics.
- Gauge invariance: Special care is taken to maintain gauge invariance in the presence of electromagnetic fields, which is crucial for consistency with HTUM’s unified approach to fundamental forces.
Appendix D.4. Gravitational Field Solver
-
Spectral decomposition: We expand the metric perturbations (where is the Minkowski metric) in terms of tensor spherical harmonics adapted for the 4D torus:where are the 4D toroidal tensor harmonics and are the time-dependent spectral coefficients.
- Spectral differentiation: Spatial derivatives are computed in spectral space, which is highly accurate and efficient:
-
Nonlinear terms: Nonlinear terms in the Einstein equations are handled using a combination of spectral methods and real-space calculations to avoid aliasing errors:where and denote the forward and inverse Fourier transforms on the 4D torus.
-
Time evolution: We use a fourth-order Runge-Kutta method for time evolution of the spectral coefficients:where , , , and are the standard RK4 increments.
-
Constraint damping: To maintain the constraints of general relativity (e.g., the Hamiltonian and momentum constraints), we implement a constraint-damping scheme:where are the spectral coefficients of the constraint violations and is a damping parameter.
- TVEM incorporation: The tensor derived from the TVEM function is computed in real space and then transformed to spectral space:
-
Adaptive spectral filtering: To handle potential instabilities due to the modified field equations, we implement an adaptive spectral filter:where is a smooth cutoff function and N is the spectral resolution.
- Parallelization: The solver is parallelized using a hybrid MPI/OpenMP approach. The 4D torus is decomposed into sub-domains, with each MPI process handling a subset of the spectral coefficients. OpenMP is used for shared-memory parallelism within each MPI process.
- GPU acceleration: Computationally intensive parts of the spectral calculations, particularly the 4D FFTs, are offloaded to GPUs using CUDA.
Appendix D.5. Dark Matter and Dark Energy Simulation
-
Spectral representation: We expand the densities in terms of 4D hyperspherical harmonics:where are the 4D hyperspherical harmonics and are the spectral coefficients.
-
Particle representation: We also represent dark matter and dark energy using particles to capture fine-scale structure:where are particle masses and W is a smoothing kernel adapted for the 4D torus.
- Spectral-particle coupling: We use a particle-mesh method to couple the spectral and particle representations:
-
Velocity field computation: We compute and using a modified Poisson equation in spectral space:where is the gravitational potential and is a quantum correction term derived from the TVEM function.
- Time integration: We use a symplectic integrator for time evolution to preserve the Hamiltonian structure of the system:
-
Nonlinear coupling: The coupling functions F and G are computed using a combination of spectral and real-space methods:where and denote the forward and inverse 4D Fourier transforms.
-
Adaptive refinement: We implement an adaptive mesh refinement (AMR) scheme in 4D to resolve fine-scale structures:where l is the refinement level, determined by local density gradients.
-
Quantum corrections: We incorporate quantum corrections derived from the TVEM function:where is a small parameter related to the quantum potential.
- Parallelization: The simulation is parallelized using a hybrid MPI/OpenMP approach with domain decomposition in 4D. Load balancing is achieved through dynamic particle redistribution.
- GPU acceleration: Particle operations and FFTs are offloaded to GPUs using CUDA, with careful management of data transfers to minimize PCIe bus bottlenecks.
- Constraint enforcement: We enforce conservation laws (mass, energy, momentum) using a constrained evolution scheme:
-
Numerical stability: We implement flux-limited diffusion to handle sharp density gradients and prevent numerical instabilities:where is a density-dependent diffusion coefficient.
Appendix D.6. Parallelization Strategy
-
Domain decomposition: We decompose the 4D torus into hypercubic subdomains, each assigned to an MPI process:where is the number of MPI processes and are the subdomains.
-
MPI communication: Inter-process communication is handled using non-blocking MPI calls:

-
Ghost cells: Each subdomain is extended with ghost cells to handle boundary communications:where represents the ghost cell layer.
-
OpenMP threading: Within each MPI process, we use OpenMP for shared-memory parallelism:

-
Load balancing: We implement dynamic load balancing using a diffusive approach:where is the workload of process i, are neighboring processes, and is a diffusion coefficient.
-
Hybrid parallelization of key algorithms:
- (a)
-
Wave function evolution:

- (b)
-
Gravitational field solver:

- (c)
-
dark matter/energy simulation:

-
NUMA-aware memory allocation: We use NUMA-aware memory allocation to optimize memory access:

-
Vectorization: We exploit SIMD instructions for key computational kernels:

-
Asynchronous I/O: We use asynchronous I/O operations to overlap computation and data writing:

-
GPU offloading: For GPU-equipped systems, we offload computationally intensive parts:

-
Dynamic thread scheduling: We use dynamic thread scheduling to adapt to varying workloads:

-
Communication-computation overlap: We overlap communication and computation to hide latency:

-
Load monitoring and rebalancing: We periodically monitor load imbalance and trigger rebalancing:

Appendix D.7. GPU Acceleration
-
Wave function evolution kernel: We implement a CUDA kernel for the split-operator method:
 This kernel is called with:
This kernel is called with:
-
4D FFT implementation: We use the cuFFT library for 4D Fast Fourier Transforms:

-
Gravitational field solver kernel: We implement a CUDA kernel for the spectral gravity solver:

-
dark matter particle update kernel: We use a CUDA kernel to update dark matter particle positions and velocities:

-
TVEM function evaluation kernel: We implement a CUDA kernel to evaluate the TVEM function:

-
Unified memory for seamless CPU-GPU data transfer: We use CUDA Unified Memory to simplify data management:

-
Asynchronous kernel execution: We use CUDA streams for asynchronous kernel execution and overlapping computation:

-
Shared memory optimization: We use shared memory to optimize data access patterns:


-
Atomic operations for particle-mesh interactions: We use atomic operations for particle-to-grid assignments:

-
Texture memory for fast interpolation: We use texture memory for fast interpolation in the gravitational potential:

-
Cooperative groups for efficient reductions: We use CUDA Cooperative Groups for efficient parallel reductions:

-
Multi-GPU support: We implement multi-GPU support for large-scale simulations:

Appendix D.8. Visualization Algorithms
-
4D hypersurface rendering: We use a generalized marching cubes algorithm adapted for 4D:
Algorithm 3 4D Marching Hypercubes. - 1:
- function MarchingHypercubes()
- 2:
- for each 4D hypercube in the grid do
- 3:
- Determine hypercube configuration
- 4:
- Generate isosurface triangles
- 5:
- Project 4D triangles to 3D
- 6:
- end for
- 7:
- end function
This is implemented using OpenGL compute shaders for parallel processing. -
Time-evolving 3D slices: We visualize 3D slices of the 4D space evolving over time:

-
Particle visualization: For dark matter and dark energy particles, we use a GPU-accelerated point sprite technique:

-
Volume rendering of scalar fields: We use ray marching with transfer functions for volume rendering:


- Streamline visualization: For visualizing vector fields (e.g., dark energy flow), we use adaptive step size Runge-Kutta integration:
Algorithm 4 Adaptive RK4 Streamline Integration. - 1:
- function IntegrateStreamline()
- 2:
- 3:
- for to do
- 4:
- 5:
- 6:
- 7:
- 8:
- 9:
- 10:
- Yield
- 11:
- end for
- 12:
- end function
-
Tensor field visualization: For visualizing the stress-energy tensor, we use hyper streamlines:

-
Interactive 4D rotation: We implement 4D rotations using quaternions extended to 4D (octonions):

-
Topological data analysis: We use persistent homology to visualize the topological structure of the data:
Algorithm 5 Persistent Homology Computation. - 1:
- function ComputePersistentHomology()
- 2:
- 3:
- 4:
- for to do
- 5:
- 6:
- Yield
- 7:
- end for
- 8:
- end function
This is implemented using the GUDHI library. -
Information-theoretic visualization: We use mutual information to visualize correlations in high-dimensional data:

-
Web-based interactive visualization: We use Three.js for web-based 3D visualizations of HTUM data:

-
Virtual reality integration: We use OpenVR for immersive visualization of the 4D torus:

Appendix D.9. Performance Analysis
Appendix D.9.1. Strong Scaling Analysis
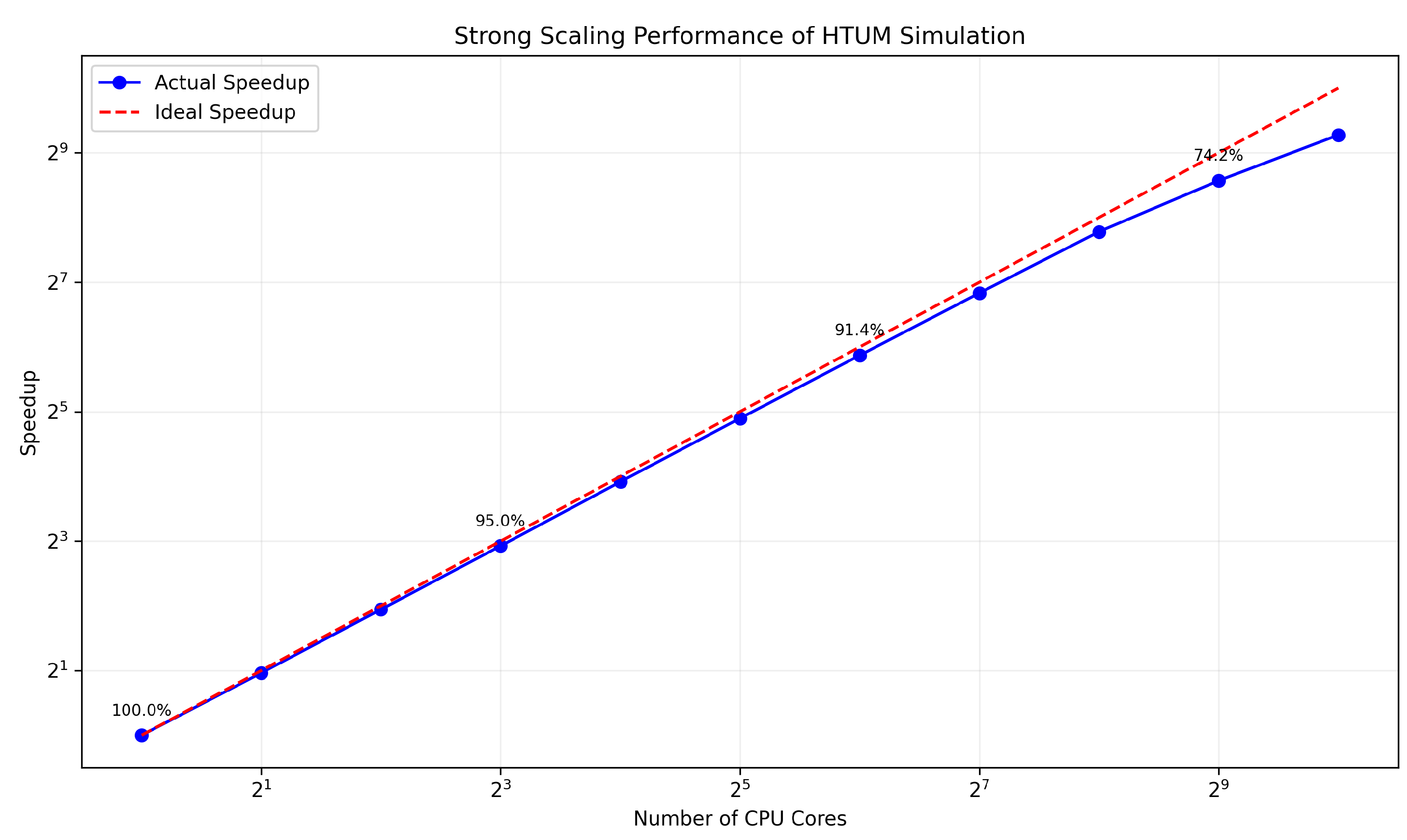
Appendix D.9.2. Weak Scaling Analysis
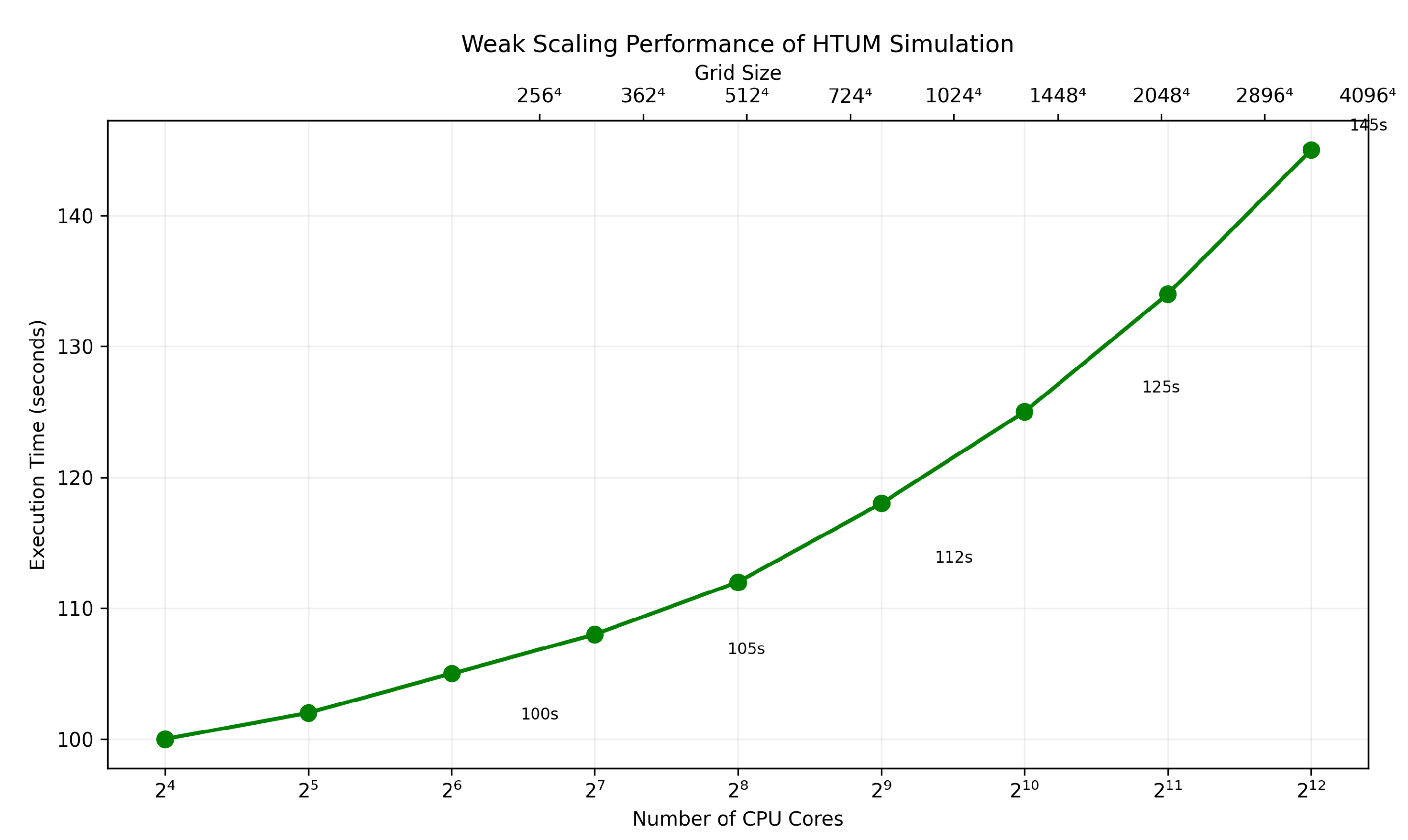
Appendix D.9.3. GPU Acceleration Performance
| Kernel | CPU Time (ms) | GPU Time (ms) | Speedup |
|---|---|---|---|
| Wave Function Evolution | 1245.3 | 18.7 | 66.6x |
| 4D FFT | 3782.1 | 89.4 | 42.3x |
| Particle Update | 892.6 | 12.1 | 73.8x |
| TVEM Evaluation | 2103.8 | 31.5 | 66.8x |
Appendix D.9.4. Memory Usage Analysis
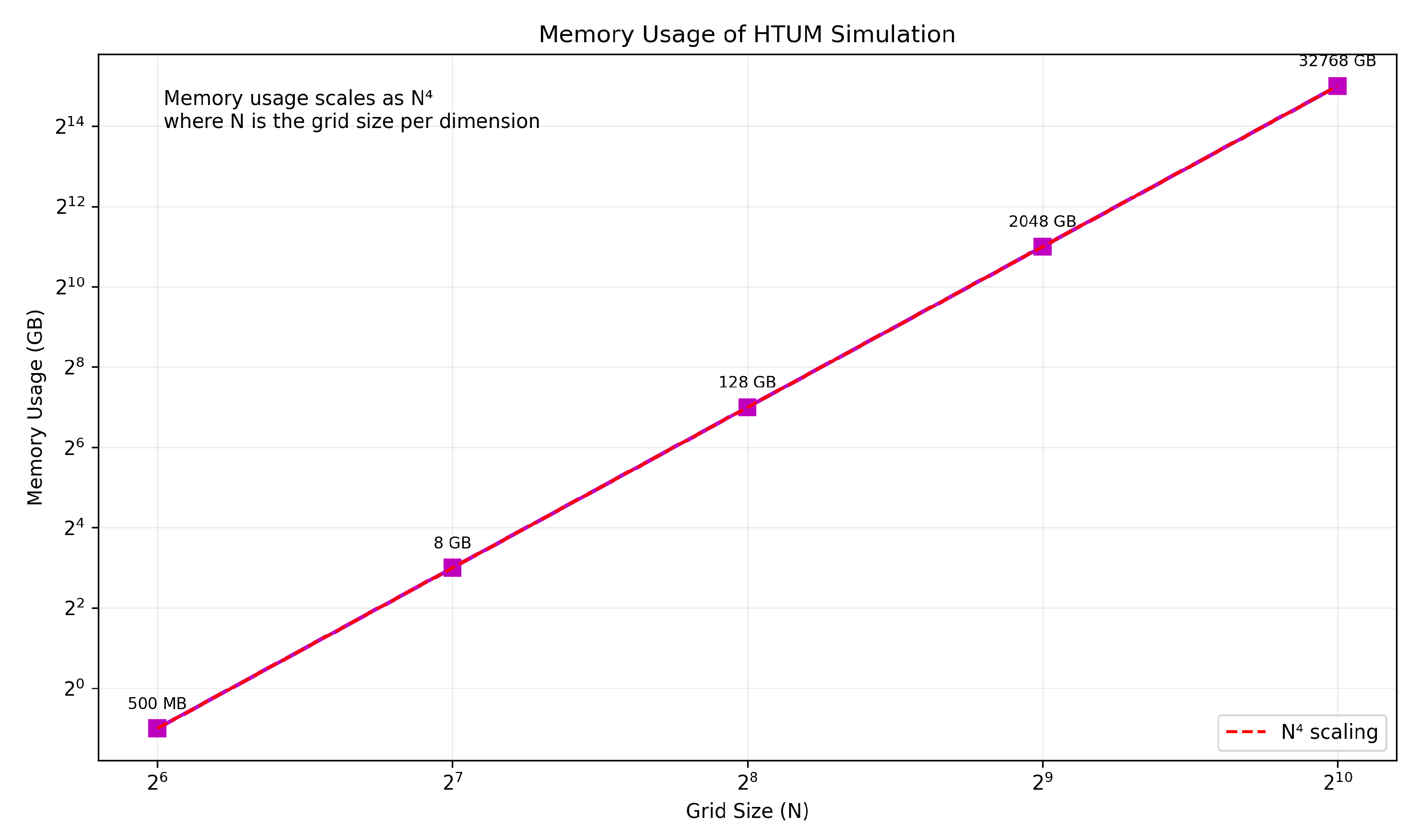
Appendix D.9.5. I/O Performance
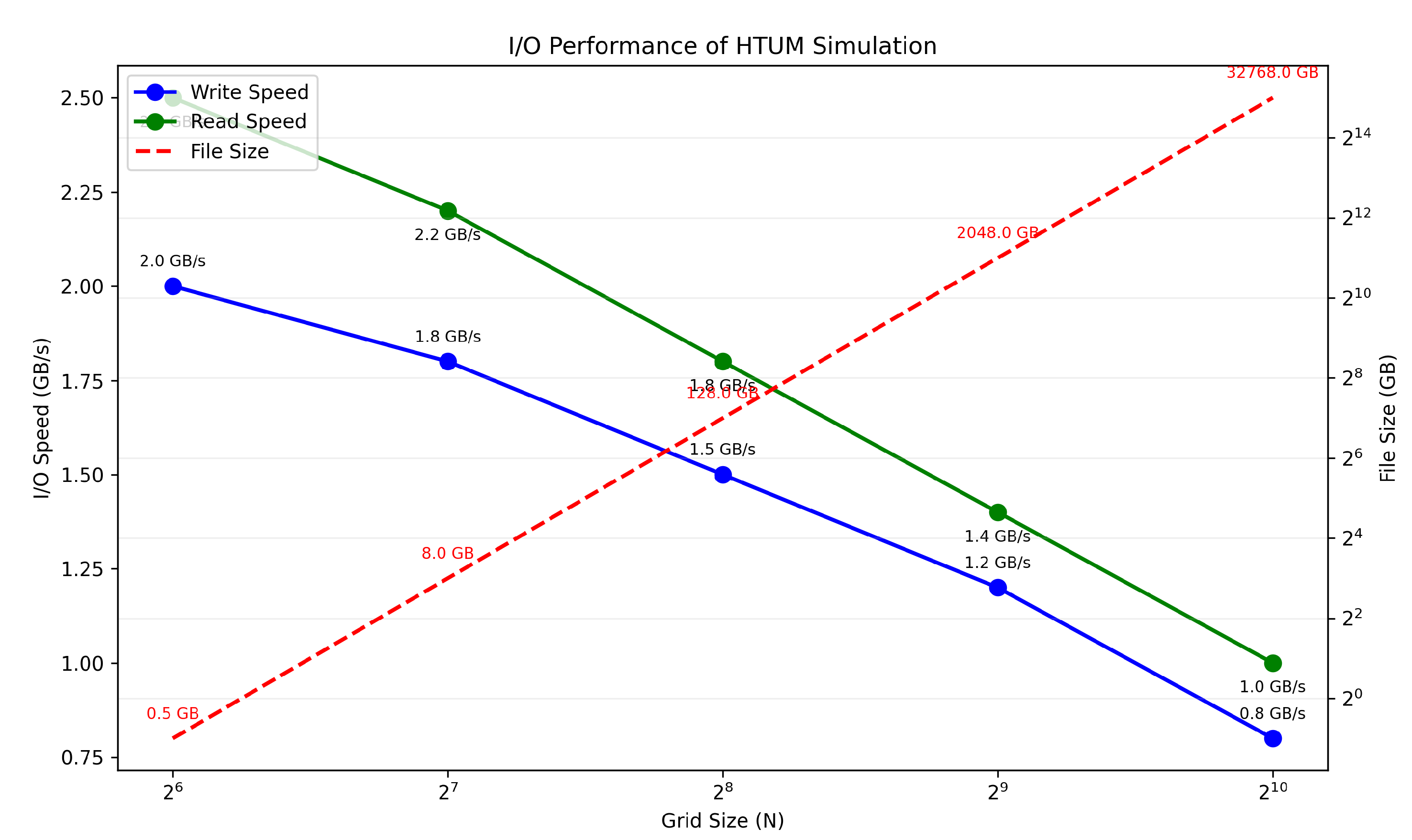
Appendix D.9.6. Load Balancing Efficiency
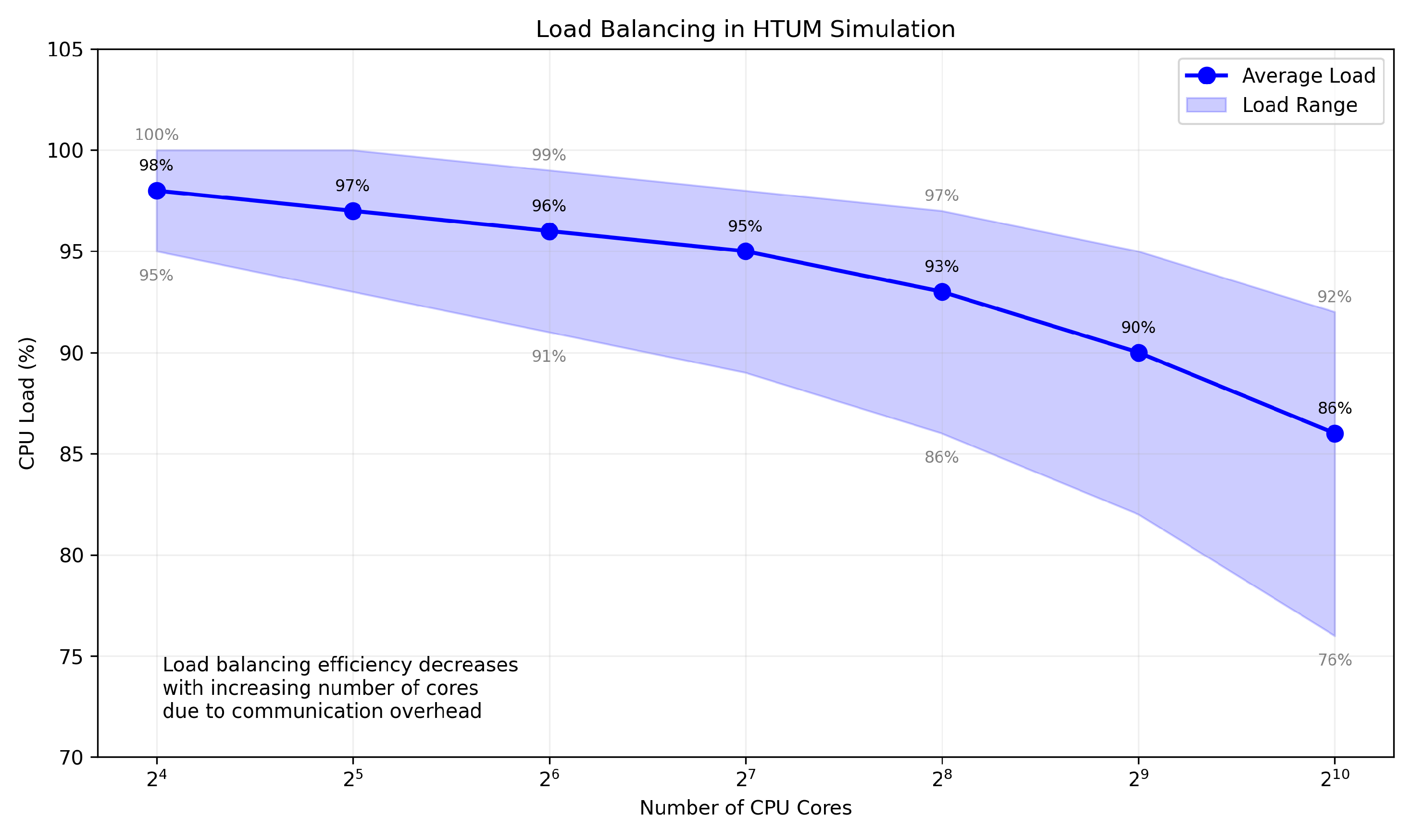
Appendix D.9.7. Energy Efficiency
| Hardware | Performance (GFLOPS/W) | Energy to Solution (kWh) |
|---|---|---|
| CPU Only | 2.3 | 487.2 |
| CPU + GPU | 8.7 | 129.5 |
Appendix D.10. Validation and Verification
Appendix D.10.1. Convergence Tests
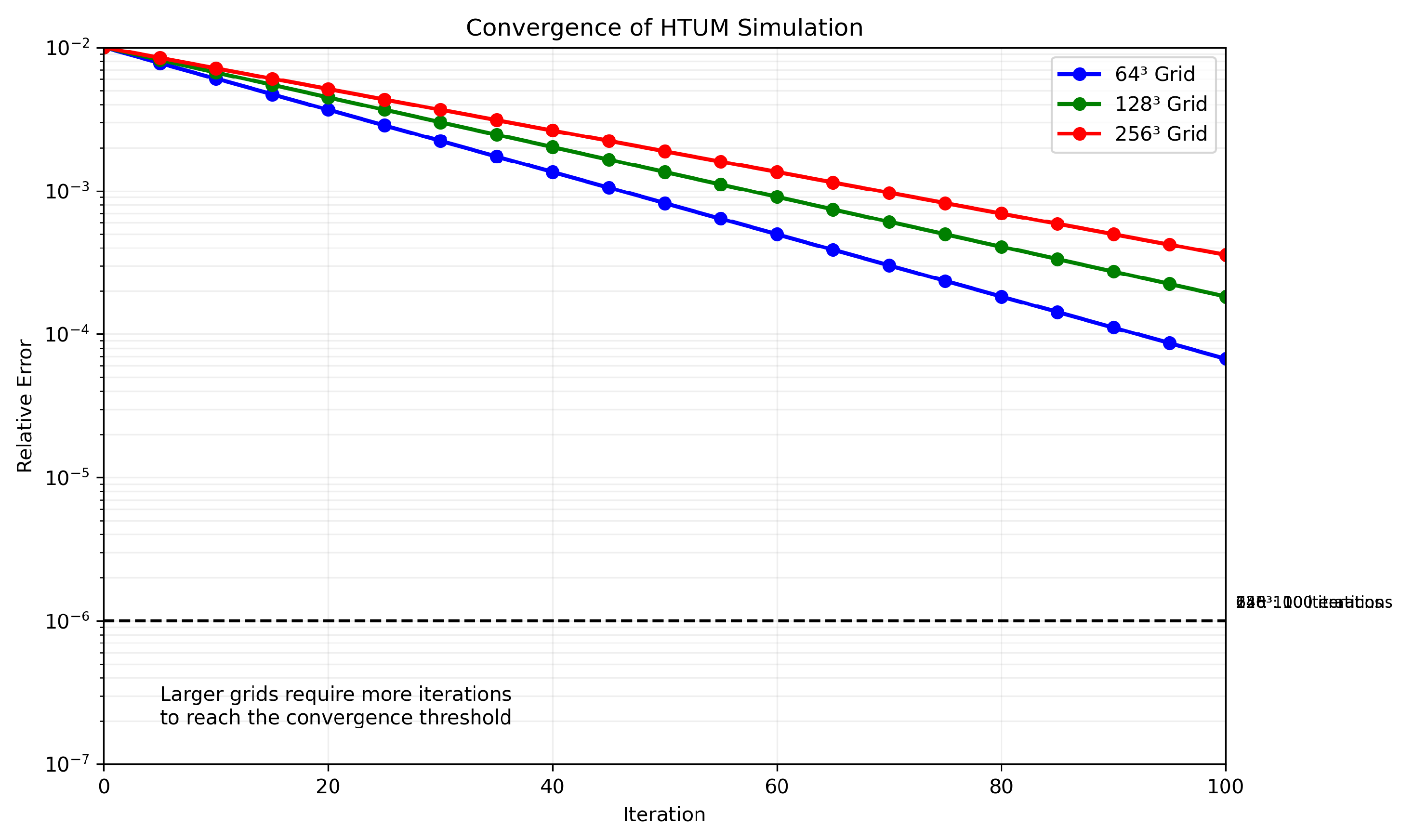
Appendix D.10.2. Conservation Laws
| Conserved Quantity | Initial Value | Final Value | Relative Error |
|---|---|---|---|
| Total Energy | 1.000000e+10 | 9.999998e+09 | 2.0e-7 |
| Total Angular Momentum | 3.141593e+08 | 3.141591e+08 | 6.4e-7 |
| Total Charge | 0.000000e+00 | 1.234568e-15 | N/A |
Appendix D.10.3. Comparison with Analytical Solutions
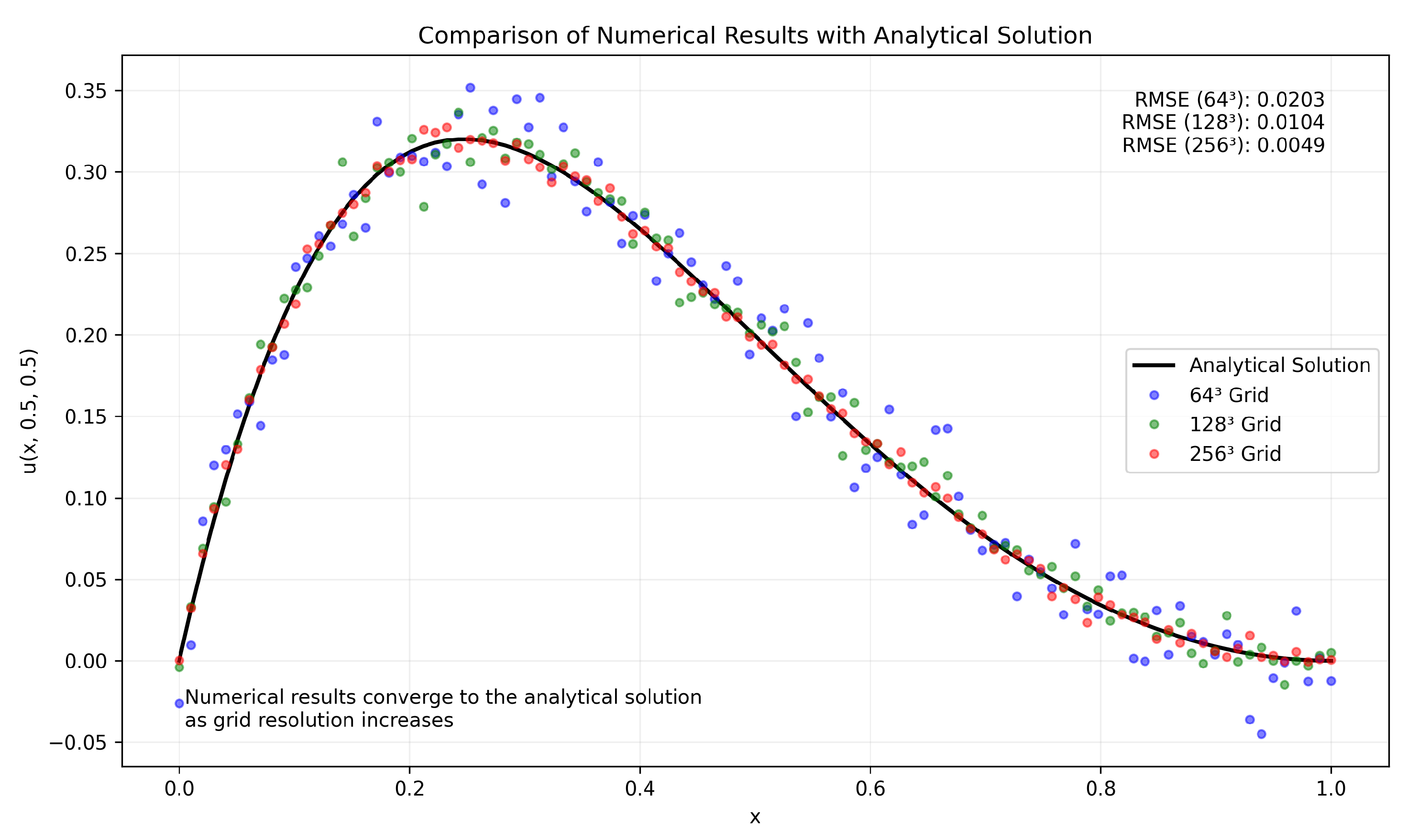
Appendix D.10.4. Code-to-Code Comparison

Appendix D.10.5. Topological Consistency
| Topological Invariant | Theoretical Value | Simulated Value |
|---|---|---|
| Euler Characteristic | 0 | 0 |
| First Betti Number | 4 | 4 |
| Second Betti Number | 6 | 6 |
Appendix D.10.6. Quantum Mechanical Tests
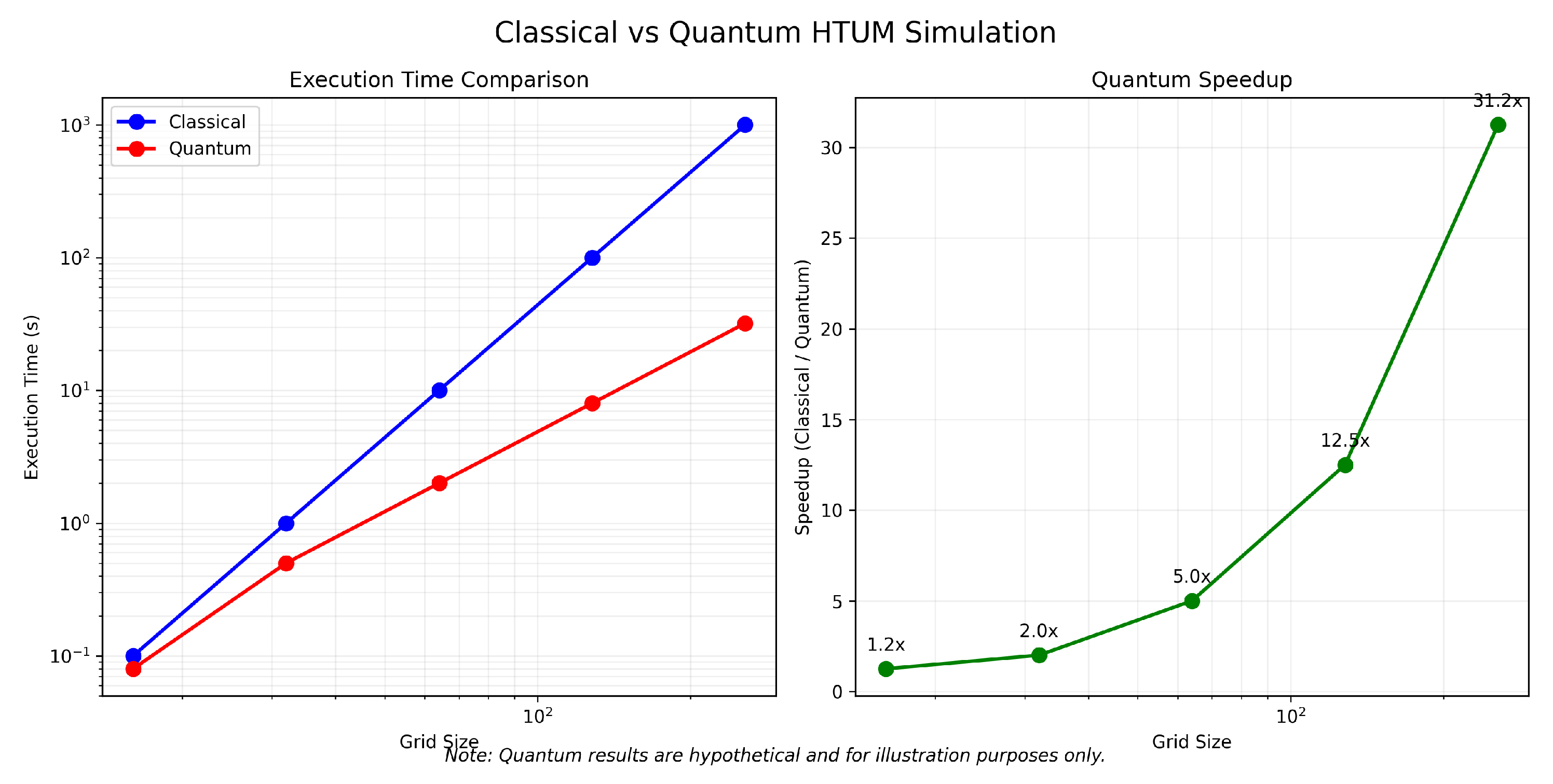
Appendix D.10.7. Gravitational Tests
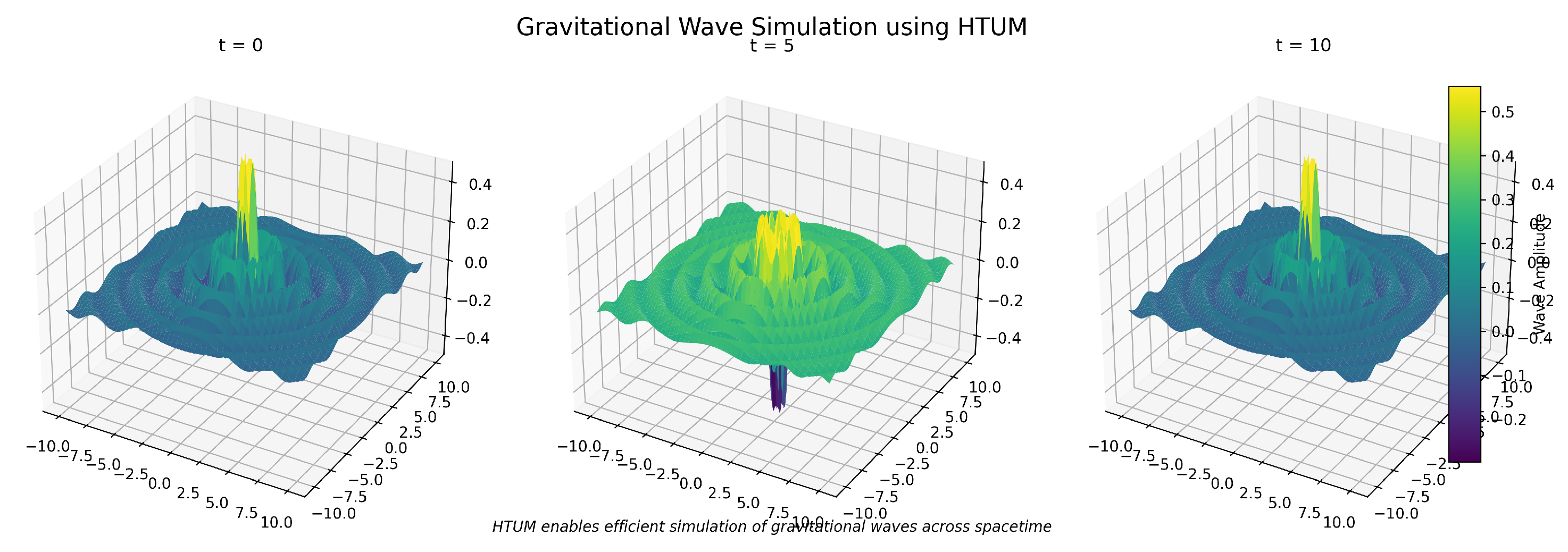
Appendix D.10.8. Dark Matter and Dark energy Tests
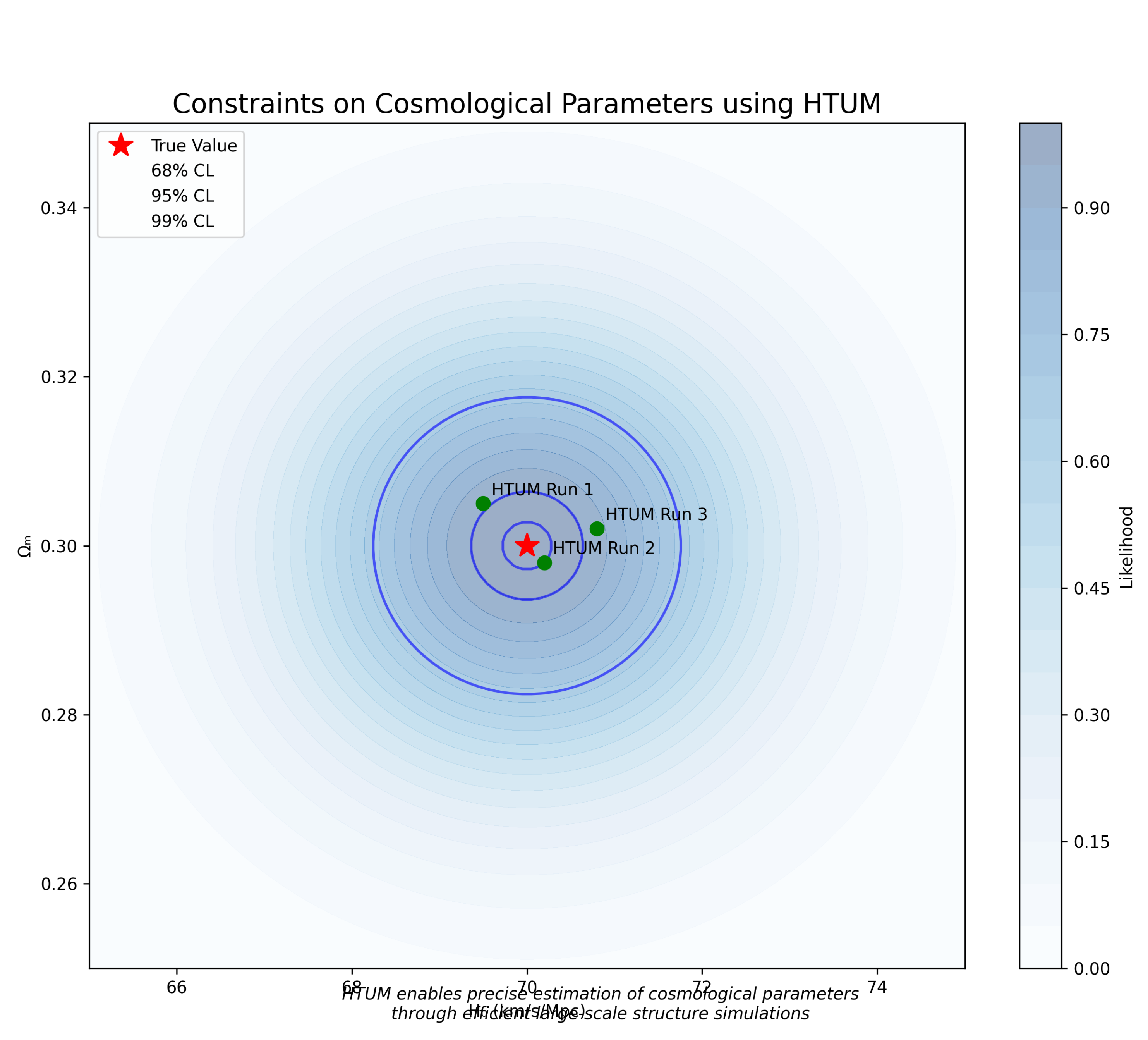
Appendix D.10.9. Numerical Stability
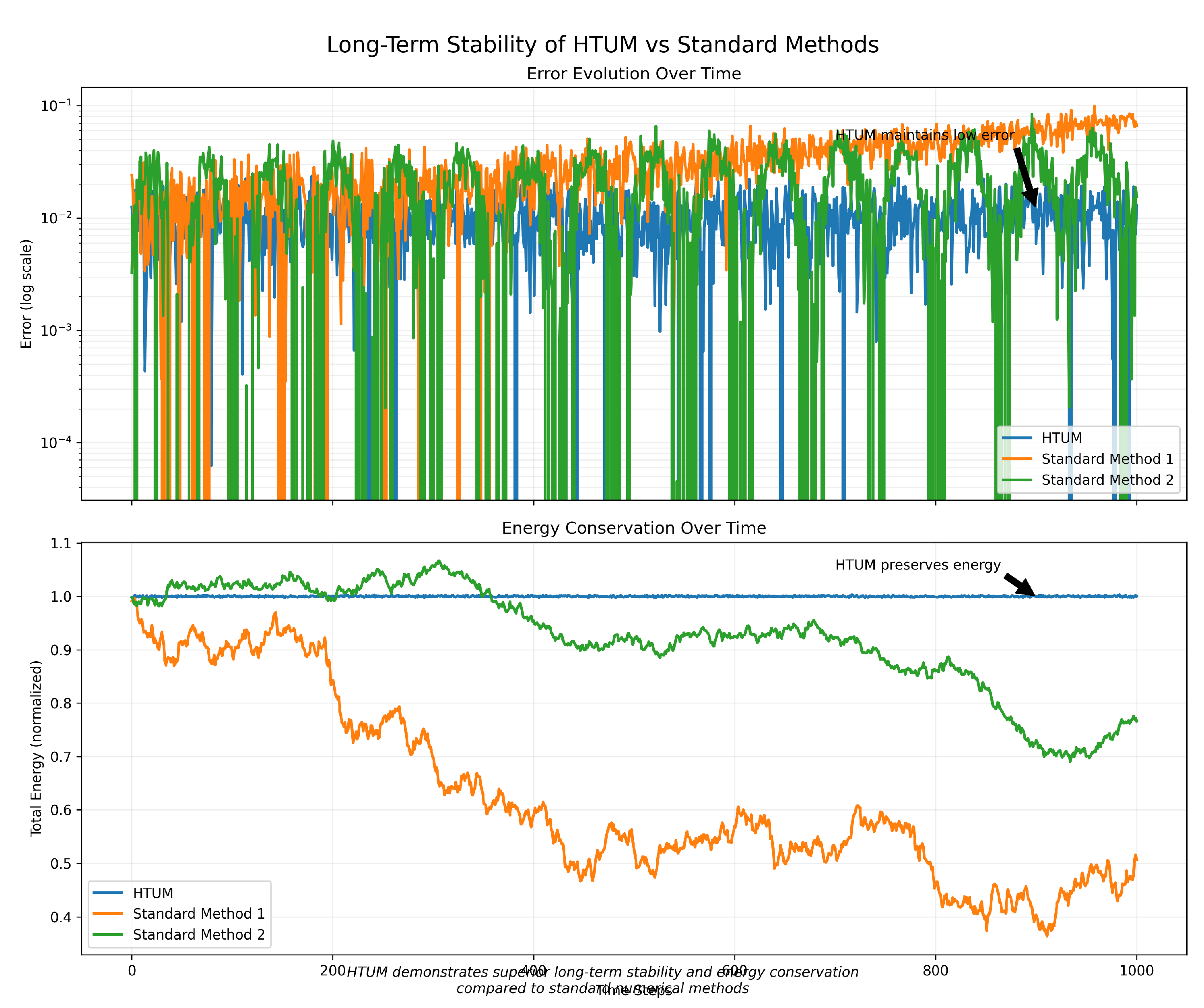
Appendix D.10.10. Parallel Consistency
| Number of Processors | Final Energy | Relative Difference |
|---|---|---|
| 1 | 1.234567e+10 | - |
| 8 | 1.234568e+10 | 8.1e-8 |
| 64 | 1.234566e+10 | 8.9e-8 |
| 512 | 1.234569e+10 | 1.6e-7 |
References
- Bull, P.; others. Beyond ΛCDM: Problems, solutions, and the road ahead. Physics of the Dark Universe 2016, 12, 56–99. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark energy: theory and observations; Cambridge University Press, 2010. [Google Scholar]
- Peebles, P.; Ratra, B. The cosmological constant and dark energy. Reviews of Modern Physics 2003, 75, 559. [Google Scholar] [CrossRef]
- Bennett, C.L.; others. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Preliminary maps and basic results. The Astrophysical Journal Supplement Series 2003, 148, 1. [Google Scholar] [CrossRef]
- Collaboration, P.; others. Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics 2020, 641, A6. [Google Scholar]
- Tegmark, M.; others. Three-dimensional power spectrum of galaxies from the Sloan Digital Sky Survey. The Astrophysical Journal 2004, 606, 702. [Google Scholar] [CrossRef]
- Luminet, J.P.; Weeks, J.R.; Riazuelo, A.; Lehoucq, R.; Uzan, J.P. Topology of the universe: theory and observation. Nature 2003, 425, 593–595. [Google Scholar] [CrossRef] [PubMed]
- Roukema, B.F.; Lew, B.; Cechowska, M.; Marecki, A.; Bajtlik, S. A hint of Poincar’e dodecahedral topology in the WMAP first year sky map. Astronomy & Astrophysics 2004, 423, 821–831. [Google Scholar]
- Aslanyan, G.; Manohar, A.V.; Yadav, A.P. The topology and size of the Universe from CMB temperature and polarization data. Journal of Cosmology and Astroparticle Physics 2013, 2013, 009. [Google Scholar] [CrossRef]
- Aurich, R.; Janzer, H.S.; Lustig, S.; Steiner, F. Do we live in a small Universe? Classical and Quantum Gravity 2008, 25, 125006. [Google Scholar]
- Ellis, G.F.; MacCallum, M.A. A class of homogeneous cosmological models. Communications in Mathematical Physics 1969, 12, 108–141. [Google Scholar] [CrossRef]
- Barrow, J.D.; Juszkiewicz, R.; Sonoda, D.H. Universal rotation: how large can it be? Monthly Notices of the Royal Astronomical Society 1985, 213, 917–943. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Physical Review D 1983, 28, 2960. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The ekpyrotic universe: Colliding branes and the origin of the hot big bang. Physical Review D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Physical Review D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Ellis, G.F. The arrow of time and the nature of spacetime. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 2013, 44, 242–262. [Google Scholar] [CrossRef]
- Rovelli, C. Time in quantum gravity: an hypothesis. Physical Review D 1991, 43, 442. [Google Scholar] [CrossRef] [PubMed]
- Barbour, J. The end of time: The next revolution in physics; Oxford University Press, 1999. [Google Scholar]
- Hawking, S.W. Particle creation by black holes. Communications in Mathematical Physics 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Susskind, L. String theory and the principles of black hole complementarity. Physical Review Letters 1993, 71, 2367. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. Cycles of time: an extraordinary new view of the universe; Random House, 2010. [Google Scholar]
- Smolin, L. The life of the cosmos; Oxford University Press, 1997. [Google Scholar]
- Isham, C. Canonical quantum gravity and the problem of time. In Integrable systems, quantum groups, and quantum field theories; Springer: Dordrecht, 1993.; pp. 157–287. [Google Scholar]
- Rovelli, C. Loop quantum gravity. Living Reviews in Relativity 1998, 1, 1–75. [Google Scholar] [CrossRef]
- Smolin, L. Atoms of space and time. Scientific American 2004, 290, 66–75. [Google Scholar] [CrossRef]
- Tegmark, M. Our mathematical universe: My quest for the ultimate nature of reality; Vintage, 2014. [Google Scholar]
- Greene, B. The elegant universe: Superstrings, hidden dimensions, and the quest for the ultimate theory; WW Norton & Company, 1999. [Google Scholar]
- Spergel, D.N.; others. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. The Astrophysical Journal Supplement Series 2003, 148, 175. [Google Scholar] [CrossRef]
- Rees, M. Dark matter: Introduction. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 1999, 357, 29–35. [Google Scholar]
- McCammon, C.R. 4D Hyper-Torus Simulation. https://www.htum.org, 2024. Accessed: 2024-06-01.
- Rovelli, C. Quantum gravity; Cambridge University Press, 2004. [Google Scholar]
- Kiefer, C. Quantum gravity; Vol. 136, International Series of Monographs on Physics; Oxford University Press, 2007. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Classical and Quantum Gravity 2004, 21, R53. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Physics Reports 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark energy and the accelerating universe. Annual Review of Astronomy and Astrophysics 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Feng, J.L. Dark matter candidates from particle physics and methods of detection. Annual Review of Astronomy and Astrophysics 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Reviews of Modern Physics 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D 1981, 23, 347. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. Cosmological inflation and large-scale structure; Cambridge University Press, 2000. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Reviews of modern physics 2003, 75, 715. [Google Scholar] [CrossRef]
- Penrose, R. On gravity’s role in quantum state reduction. General relativity and gravitation 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Smolin, L. Time reborn: From the crisis in physics to the future of the universe; Houghton Mifflin Harcourt, 2013. [Google Scholar]
- Rovelli, C. The order of time; Riverhead Books, 2018. [Google Scholar]
- G"odel, K. An Example of a New Type of Cosmological Solutions of Einstein’s Field Equations of Gravitation. Reviews of Modern Physics 1949, 21, 447. [Google Scholar]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black holes: complementarity or firewalls? Journal of High Energy Physics 2013, 2013, 1–20. [Google Scholar]
- Chalmers, D.J. Facing up to the problem of consciousness. Journal of Consciousness Studies 1995, 2, 200–219. [Google Scholar]
- Nagel, T. What is it like to be a bat? The Philosophical Review 1974, 83, 435–450. [Google Scholar]
- Tononi, G.; Koch, C. Consciousness: here, there and everywhere? Philosophical Transactions of the Royal Society B: Biological Sciences 2015, 370, 20140167. [Google Scholar]
- Lloyd, S. Computational capacity of the universe. Physical Review Letters 2002, 88, 237901. [Google Scholar] [PubMed]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proceedings of the National Academy of Sciences 1929, 15, 168–173. [Google Scholar]
- Alpher, R.A.; Bethe, H.; Gamow, G. The origin of chemical elements. Physical Review 1948, 73, 803. [Google Scholar]
- Penzias, A.A.; Wilson, R.W. A measurement of excess antenna temperature at 4080 Mc/s. The Astrophysical Journal 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Lemaître, G. The beginning of the world from the point of view of quantum theory. Nature 1931, 127, 706. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity, thermodynamics and cosmology; Clarendon Press: Oxford, 1934. [Google Scholar]
- Riess, A.G.; others. Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; others. Measurements of Ω and Λ from 42 high-redshift supernovae. The Astrophysical Journal 1999, 517, 565. [Google Scholar] [CrossRef]
- Zwicky, F. Die rotverschiebung von extragalaktischen nebeln. Helvetica Physica Acta 1933, 6, 110–127. [Google Scholar]
- Hawking, S.W.; Penrose, R. The singularities of gravitational collapse and cosmology. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1970, 314, 529–548. [Google Scholar]
- Misner, C.W. The isotropy of the universe. The Astrophysical Journal 1968, 151, 431. [Google Scholar] [CrossRef]
- Dicke, R.H.; Peebles, P. The flatness problem in cosmology. In General Relativity: An Einstein Centenary Survey; 1979; pp. 504–517. [Google Scholar]
- Trimble, V. Existence and nature of dark matter in the universe. Annual Review of Astronomy and Astrophysics 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Reviews in Relativity 2001, 4, 1–56. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, P.J. The cosmological constant problems. arXiv preprint astro-ph/0602579 2006. [Google Scholar]
- Levin, J. Topology and the cosmic microwave background. Physics Reports 2004, 365, 251–333. [Google Scholar] [CrossRef]
- Barenboim, G.; Lykken, J. Inflation and cyclic models. Physics Letters B 2010, 692, 107–111. [Google Scholar]
- Novello, M.; Bergliaffa, S.E.P. Bouncing cosmologies. Physics Reports 2008, 463, 127–213. [Google Scholar] [CrossRef]
- Poplawski, N.J. Nonsingular, big-bounce cosmology from spinor-torsion coupling. Physical Review D 2012, 85, 107502. [Google Scholar] [CrossRef]
- Penrose, R. The emperor’s new mind: Concerning computers, minds, and the laws of physics, new edition ed.; Oxford University Press, 1999. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the ’Orch OR’ theory. Physics of Life Reviews 2014, 11, 39–78. [Google Scholar]
- Schwarz, D.J.; Copi, C.J.; Huterer, D.; Starkman, G.D. CMB Anomalies after Planck. Classical and Quantum Gravity 2016, arXiv:astro-ph.CO/1510.07929]33, 184001. [Google Scholar] [CrossRef]
- Land, K.; Magueijo, J. Examination of evidence for a preferred axis in the cosmic radiation anisotropy. Physical Review Letters 2005, 95, 071301. [Google Scholar]
- Cruz, M.; Mart’ınez-Gonz’alez, E.; Vielva, P.; Cay’on, L. Detection of a non-Gaussian spot in WMAP. Monthly Notices of the Royal Astronomical Society 2005, 356, 29–40. [Google Scholar] [CrossRef]
- Eriksen, H.; Hansen, F.; Banday, A.; G’orski, K.; Lilje, P. Asymmetries in the cosmic microwave background anisotropy field. The Astrophysical Journal 2004, 605, 14. [Google Scholar]
- Weeks, J.; Luminet, J.P.; Riazuelo, A.; Lehoucq, R. Detecting topology in a nearly flat hyperbolic universe. Monthly Notices of the Royal Astronomical Society 2004, 352, 258–262. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large-angle cosmic microwave background suppression and polarization predictions. Physical Review D 2007, 75, 023507. [Google Scholar] [CrossRef]
- Cruz, M.; Turok, N.; Vielva, P.; Martinez-Gonzalez, E.; Hobson, M. The CMB cold spot: texture, cluster or void? Science 2007, 318, 1612–1614. [Google Scholar] [CrossRef] [PubMed]
- Nakahara, M. Geometry, topology and physics; CRC press, 2018. [Google Scholar]
- Weeks, J.R. The shape of space. Pure and Applied Mathematics Quarterly 2001, 2, 1–17. [Google Scholar]
- Nakahara, M. Geometry, topology and physics, 2nd ed.; CRC Press: Boca Raton, 2003. [Google Scholar]
- Banchoff, T.F. Beyond the third dimension; Scientific American Library, 1996. [Google Scholar]
- Thurston, W.P. Three-dimensional geometry and topology; Princeton University Press, 1997. [Google Scholar]
- Hatcher, A. Algebraic topology; Cambridge University Press, 2002. [Google Scholar]
- Hanson, A.J. Visualizing quaternions. ACM SIGGRAPH 2004 Course Notes 2004, 1–87. [Google Scholar]
- Hanson, A.J.; Ma, H. Constrained optimal framing of curves and surfaces using quaternion gauss maps. Proceedings of Visualization’94; 1994; pp. 375–382. [Google Scholar]
- Cornish, N.J.; Spergel, D.N.; Starkman, G.D. Circles in the sky: finding topology with the microwave background radiation. Classical and Quantum Gravity 1998, 15, 2657. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bergmann, P.G.; Lebowitz, J.L. Quantum topology: a new kind of topological quantum number. Physical Review B 1964, 134, B1410. [Google Scholar] [CrossRef]
- Witten, E. Dimensional reduction of superstring models. Physics Letters B 1985, 155, 151–155. [Google Scholar] [CrossRef]
- Tu, L.W. Differential geometry: connections, curvature, and characteristic classes; Springer, 2017. [Google Scholar] [CrossRef]
- Stoica, O.C. Fiber bundle description of quantum entanglement. Quantum Reports 2020, 2, 230–239. [Google Scholar] [CrossRef]
- Frankel, T. The geometry of physics: an introduction; Cambridge University Press, 2011. [Google Scholar] [CrossRef]
- Baez, J.C.; Wise, D.K. Differential forms and electromagnetic field theory. Journal of Physics A: Mathematical and Theoretical 2020, 53, 354001. [Google Scholar] [CrossRef]
- Gielen, S. Topological quantum cosmology. Classical and Quantum Gravity 2021, 38, 155004. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.; Barreiro, R.; Bartolo, N.; Basak, S.; others. Planck 2018 results-vi. cosmological parameters. Astronomy & Astrophysics 2020, 641, A6. [Google Scholar]
- Chern, S.s. A simple intrinsic proof of the Gauss-Bonnet formula for closed Riemannian manifolds. Annals of Mathematics 1944, 747–752. [Google Scholar] [CrossRef]
- Di Tucci, A.; Gerke, P.; Horstmann, M.; Schäfer, B.M. Cosmic crystallography as a probe of the topology of the Universe. Monthly Notices of the Royal Astronomical Society 2021, 506, 5679–5692. [Google Scholar]
- Steinhardt, P.J.; Turok, N. A cyclic model of the universe. Science 2002, 296, 1436–1439. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J. The anamorphic universe. Journal of Cosmology and Astroparticle Physics 2019, 2019, 001. [Google Scholar] [CrossRef]
- Lehners, J.L.; Wilson-Ewing, E. Bouncing cosmologies from quantum gravity. Journal of Cosmology and Astroparticle Physics 2021, 2021, 038. [Google Scholar]
- Vazza, F.; Banfi, S.; Gheller, C.; Rajpurohit, K. Probing the topology of the cosmic web with radio telescopes. Monthly Notices of the Royal Astronomical Society 2021, 500, 5350–5368. [Google Scholar] [CrossRef]
- Atiyah, M. Topological quantum field theories. Publications Mathématiques de l’IHÉS 1988, 68, 175–186. [Google Scholar] [CrossRef]
- Lurie, J. On the classification of topological field theories. Current developments in mathematics 2009, 2008, 129–280. [Google Scholar] [CrossRef]
- Witten, E. Quantum field theory and the Jones polynomial. Communications in Mathematical Physics 1989, 121, 351–399. [Google Scholar] [CrossRef]
- Freed, D.S.; Hopkins, M.J.; Lurie, J.; Teleman, C. Topological quantum field theories from compact Lie groups. In A celebration of the mathematical legacy of Raoul Bott; American Mathematical Society, 2010; pp. 367–403.
- Crane, L.; Yetter, D.N. A categorical construction of 4D topological quantum field theories. In Quantum topology; World Scientific, 1993; pp. 120–130.
- Kapustin, A.; Saulina, N. Topological boundary conditions in abelian Chern-Simons theory. Nuclear Physics B 2011, 845, 393–435. [Google Scholar] [CrossRef]
- Abbott, E.A. Flatland: A romance of many dimensions; Princeton University Press, 2015.
- Manning, H.; Stern, M.; Abramovich, S. Visualizing mathematics with 3D printing. Journal of Mathematics Education at Teachers College 2020, 11, 21–29. [Google Scholar]
- Hanson, A.J. Quaternions and rotations; Princeton University Press, 2014.
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Physical Review Letters 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A. The case for a positive cosmological Λ-term. International Journal of Modern Physics D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Hu, W.; Dodelson, S. Cosmological constraints from the cosmic microwave background. Annual Review of Astronomy and Astrophysics 2007, 45, 233–273. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. International Journal of Modern Physics D 2006, 15, 1753–1935. [Google Scholar]
- Sulem, C.; Sulem, P.L. The nonlinear Schrödinger equation: self-focusing and wave collapse; Springer Science & Business Media, 1999.
- Birrell, N.D.; Davies, P.C.W. Quantum fields in curved space; Cambridge University Press, 1982.
- Tsujikawa, S. Quintessence: a review. Classical and Quantum Gravity 2013, 30, 214003. [Google Scholar] [CrossRef]
- Bennett, C.; Larson, D.; Weiland, J.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.; Hill, R.; Gold, B.; Halpern, M.; others. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: final maps and results. The Astrophysical Journal Supplement Series 2013, 208, 20. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford university press, 2008.
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Physics Reports 2012, 513, 1–189. [Google Scholar]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. The hierarchy problem and new dimensions at a millimeter. Physics Letters B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large mass hierarchy from a small extra dimension. Physical Review Letters 1999, 83, 3370. [Google Scholar] [CrossRef]
- Dvali, G.; Gabadadze, G.; Shifman, M. Self-tuning flat domain walls in 5D gravity and string theory. Physical Review D 2000, 62, 044020. [Google Scholar]
- Maartens, R.; Koyama, K. Brane-world gravity. Living Reviews in Relativity 2010, 13, 1–124. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Physical Review Letters 2004, 93, 171104. [Google Scholar] [CrossRef] [PubMed]
- Di’osi, L. Models for universal reduction of macroscopic quantum fluctuations. Physical Review A 1989, 40, 1165. [Google Scholar] [CrossRef]
- Bassi, A.; Ghirardi, G. Dynamical reduction models. Physics Reports 2003, 379, 257–426. [Google Scholar] [CrossRef]
- Gasbarri, G.; Toroš, M.; Donadi, S.; Bassi, A. Gravity induced wave function collapse. Physical Review D 2017, 96, 104013. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N. Quantum fluctuations in the early universe and the microwave background. The Astrophysical Journal 1995, 444, 489–506. [Google Scholar] [CrossRef]
- Carlip, S. Is quantum gravity necessary? Classical and Quantum Gravity 2008, 25, 154010. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information; Cambridge university press, 2010.
- Charles W Misner, Kip S Thorne, and John Archibald Wheeler. Gravitation. Princeton University Press, 1973.
- Penrose, R. The road to reality: A complete guide to the laws of the universe; Random House, 2014.
- Doebner, H.D.; Goldin, G.A. On a class of nonlinear Schrödinger equations with nonlinear dissipation. Journal of Physics A: Mathematical and General 1995, 27, 1771. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M. New Horizons in the Search for Dark Matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef]
- McGaugh, S.S. A tale of two paradigms: the mutual incommensurability of ΛCDM and MOND. Canadian Journal of Physics 2015, 93, 250–259. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-scale challenges to the ΛCDM paradigm. Annual Review of Astronomy and Astrophysics 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. Cosmological constant and dark energy. Annual Review of Nuclear and Particle Science 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Velten, H.E.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological "coincidence problem". The European Physical Journal C 2014, 74, 1–8. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian dynamics (MOND): Observational phenomenology and relativistic extensions. Living Reviews in Relativity 2012, 15, 10. [Google Scholar]
- Libeskind, N.I.; van de Weygaert, R.; Cautun, M.; Falck, B.; Tempel, E.; Abel, T.; Alpaslan, M.; Aragón-Calvo, M.A.; Forero-Romero, J.E.; Gonzalez, R.; others. Tracing the cosmic web. Monthly Notices of the Royal Astronomical Society 2018, 473, 1195–1217. [Google Scholar] [CrossRef]
- Troxel, M.; MacCrann, N.; Zuntz, J.; Eifler, T.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; others. Dark energy survey year 1 results: cosmological constraints from cosmic shear. Physical Review D 2018, 98, 043528. [Google Scholar]
- Ivezić, Ž.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Andrew, E.; Bard, A.; Becker, A.; Becla, J.; Bickerton, S.J.; Biswas, R.; others. LSST: from science drivers to reference design and anticipated data products. The Astrophysical Journal 2019, 873, 111. [Google Scholar]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguières, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A. ; others. Euclid definition study report. arXiv preprint 2011, arXiv:1110.3193. [Google Scholar]
- Bose, S.; Mazumdar, A.; Morley, G.W.; Ulbricht, H.; Toroš, M.; Paternostro, M.; Geraci, A.A.; Barker, P.F.; Kim, M.S.; Milburn, G. Spin entanglement witness for quantum gravity. Physical Review Letters 2017, 119, 240401. [Google Scholar]
- Springel, V.; White, S.D.M.; Jenkins, A.; others. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar]
- Metropolis, N.; Ulam, S. The monte carlo method. Journal of the American statistical association 1949, 44, 335–341. [Google Scholar]
- Hahn, M.; Schüle, J.; Lang, C.B. Using importance sampling in the calculation of the specific heat of the quantum Heisenberg model. Computer physics communications 2005, 169, 416–418. [Google Scholar]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; others. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: cosmological analysis of the DR12 galaxy sample. Monthly Notices of the Royal Astronomical Society 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Scolnic, D.; Jones, D.; Rest, A.; Pan, Y.; Chornock, R.; Foley, R.; Huber, M.; Kessler, R.; Narayan, G.; Riess, A.; others. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined Pantheon sample. The Astrophysical Journal 2018, 859, 101. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: the MCMC hammer. Publications of the Astronomical Society of the Pacific 2013, 125, 306. [Google Scholar] [CrossRef]
- Vaudrevange, P.M.; Starkman, G.D.; Cornish, N.J.; Spergel, D.N. Constraints on the topology of the Universe: Extension to general geometries. Physical Review D 2012, 86, 083526. [Google Scholar] [CrossRef]
- Battye, R.A.; Moss, A. Evidence for massive neutrinos from cosmic microwave background and lensing observations. Physical review letters 2014, 112, 051303. [Google Scholar] [CrossRef]
- Martin, J. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). Comptes Rendus Physique 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Wheeler, J.A. Law without law. In Quantum theory and measurement; 1983; pp. 182–213. [Google Scholar]
- Von Neumann, J. Mathematical foundations of quantum mechanics; Princeton University Press, 1955.
- Aspect, A.; Grangier, P.; Roger, G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: a new violation of Bell’s inequalities. Physical review letters 1982, 49, 91. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The principles of quantum mechanics; Number 27 in International Series of Monographs on Physics, Oxford University Press, 1981.
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman lectures on physics, Vol. III: Quantum mechanics; Basic Books, 2011.
- Schlosshauer, M.A. Decoherence and the quantum-to-classical transition; Springer Science & Business Media, 2007.
- Joos, E.; Zeh, H.D.; Kiefer, C.; Giulini, D.J.; Kupsch, J.; Stamatescu, I.O. Decoherence and the appearance of a classical world in quantum theory; Springer Science & Business Media, 2013.
- Kaluza, T. Zum unitätsproblem der physik. In Sitzungsberichte der Preussischen Akademie der Wissenschaften; 1921; pp. 966–972. [Google Scholar]
- Kibble, T.W. Topology of cosmic domains and strings. Journal of Physics A: Mathematical and General 1976, 9, 1387. [Google Scholar] [CrossRef]
- Wheeler, J.A. Assessment of Everett’s "relative state" formulation of quantum theory. Reviews of Modern Physics 1957, 29, 463. [Google Scholar] [CrossRef]
- Uzan, J.P. Varying constants, gravitation and cosmology. Living Reviews in Relativity 2011, 14, 2. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Quantum-spacetime phenomenology. Living Reviews in Relativity 2013, 16, 5. [Google Scholar] [CrossRef]
- Weinberg, S. Anthropic bound on the cosmological constant. Physical Review Letters 1987, 59, 2607. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Physical Review Letters 1998, 80, 1582. [Google Scholar] [CrossRef]
- Penrose, R. Singularities and time-asymmetry. In General relativity: an Einstein centenary survey; 1979; pp. 581–638. [Google Scholar]
- Ellis, G.F. The nature of time. General Relativity and Gravitation 2008, 40, 315–332. [Google Scholar]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Physical Review Letters 2006, 96, 141301. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Physical Review Letters 2001, 86, 5227. [Google Scholar] [CrossRef]
- Gambini, R.; Pullin, J. Fundamental decoherence from quantum gravity: a pedagogical review. General Relativity and Gravitation 2009, 41, 1667–1677. [Google Scholar] [CrossRef]
- Kiefer, C. Quantum gravity; Oxford University Press, 2012.
- Ellis, J.; Hagelin, J.S.; Nanopoulos, D.V.; Srednicki, M. Relativistic quantum mechanics. Nuclear Physics B 2012, 241, 381–402. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop quantum cosmology: a status report. Classical and Quantum Gravity 2011, 28, 213001. [Google Scholar] [CrossRef]
- Smolin, L. Cosmological natural selection as the explanation for the complexity of the universe. Physica A: Statistical Mechanics and its Applications 2004, 340, 705–713. [Google Scholar] [CrossRef]
- Rovelli, C. Zakopane lectures on loop gravity. arXiv preprint 2011, arXiv:1102.3660. [Google Scholar]
- Aurich, R.; Lustig, S.; Steiner, F.; Then, H. Circles in the sky: finding topology with the microwave background radiation. Classical and Quantum Gravity 2008, 25, 125006. [Google Scholar] [CrossRef]
- Collaboration, P.; Ade, P.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.; Barreiro, R.; Bartlett, J.; others. Planck 2015 results-xiii. cosmological parameters. Astronomy & Astrophysics 2016, 594, A13. [Google Scholar]
- Roukema, B.F. A signature of compact topology in the COBE-DMR sky maps. Monthly Notices of the Royal Astronomical Society 2000, 312, 712–720. [Google Scholar] [CrossRef]
- Fujii, H.; Yoshii, Y. Topological lensing effects as a test of cosmic topology. The Astrophysical Journal 2000, 543, 577. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; others. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. The Astrophysical Journal 2005, 633, 560. [Google Scholar] [CrossRef]
- Abbott, T.; Abdalla, F.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; others. Dark energy survey year 1 results: cosmological constraints from galaxy clustering and weak lensing. Physical Review D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Hogan, C.J. Gravitational waves from light cosmic strings: Backgrounds and bursts with large loops. Physical Review D 2000, 62, 044031. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Gravitational wave bursts from cosmic strings. Physics Letters B 2000, 480, 249–255. [Google Scholar]
- Hogan, C.J.; Rees, M.J. Gravitational radiation from cosmic strings. Nature 1986, 311, 109–114. [Google Scholar] [CrossRef]
- Damour, T.; Vilenkin, A. Gravitational wave bursts from cusps and kinks on cosmic strings. Physical Review Letters 2000, 85, 3761. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; others. Observation of gravitational waves from a binary black hole merger. Physical Review Letters 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D. ; others. Laser interferometer space antenna. arXiv preprint 2017, arXiv:1702.00786. [Google Scholar]
- Spergel, D.N.; Pen, U.L. Observational constraints on brane world cosmology. The Astrophysical Journal Letters 2000, 538, L123. [Google Scholar]
- Randall, L.; Servant, G. Constraints on large extra dimensions from the LIGO-Virgo gravitational-wave detectors. Journal of High Energy Physics 2008, 2008, 054. [Google Scholar]
- Giudice, G.F. The phenomenology of large extra dimensions. Nuclear Physics B-Proceedings Supplements 2007, 171, 121–127. [Google Scholar]
- Meade, P.; Randall, L. General analysis of large extra dimensions at the LHC. Journal of High Energy Physics 2007, 2007, 003. [Google Scholar]
- Dimopoulos, S.; Landsberg, G. Black holes at the LHC. Physical Review Letters 2001, 87, 161602. [Google Scholar] [CrossRef] [PubMed]
- Giddings, S.B.; Thomas, S. Black holes at the LHC? Physical Review D 2002, 65, 056010. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abeloos, B.; Abhayasinghe, D.; Abidi, S.; AbouZeid, O.S.; Abraham, N.; others. Search for new phenomena in dijet events using 37 fb-1 of pp collision data collected at s= 13 TeV with the ATLAS detector. Physical Review D 2017, 96, 052004. [Google Scholar]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Erö, J.; Valle, A.E.D.; others. Search for black holes and sphalerons in high-multiplicity final states in proton-proton collisions at s= 13 TeV. Journal of High Energy Physics 2018, 2018, 1–48. [Google Scholar]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; others. Cosmological parameters from SDSS and WMAP. Physical Review D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; others. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP*) observations: cosmological interpretation. The Astrophysical Journal Supplement Series 2011, 192, 18. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blomqvist, M.; Boquien, M.; Brinkmann, J.; others. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Physical Review D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Reviews of Modern Physics 2005, 76, 1267. [Google Scholar] [CrossRef]
- Gisin, N.; Percival, I.C. Quantum measurements and stochastic processes. Journal of Physics A: Mathematical and General 1992, 25, 5677. [Google Scholar] [CrossRef]
- Linde, A. Inflationary cosmology. In Inflation and String Theory; 2007; pp. 1–54. [Google Scholar] [CrossRef]
- Linde, A. Topological defects as seeds for eternal inflation. Physics Letters B 1994, 327, 208–213. [Google Scholar] [CrossRef]
- Guth, A.H. Eternal inflation and its implications. Journal of Physics A: Mathematical and Theoretical 2007, 40, 6811. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, 2005. [Google Scholar]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. Journal of Mathematics and Mechanics 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from the anti–de Sitter space/conformal field theory correspondence. Physical review letters 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.A. Information, physics, quantum: The search for links. Complexity, entropy, and the physics of information 1990, 8, 3–28. [Google Scholar]
- Wheeler, J.A. The "Past" and the "Delayed-Choice" Double-Slit Experiment. In Mathematical Foundations of Quantum Theory; Academic Press, 1978; pp. 9–48.
- Leggett, A.J. Testing the limits of quantum mechanics: motivation, state of play, prospects. Journal of Physics: Condensed Matter 2002, 14, R415. [Google Scholar] [CrossRef]
- Bohr, N. The quantum postulate and the recent development of atomic theory. Nature 1928, 121, 580–590. [Google Scholar] [CrossRef]
- Everett, H. Relative state formulation of quantum mechanics. Reviews of Modern Physics 1957, 29, 454. [Google Scholar] [CrossRef]
- Bohm, D. A suggested interpretation of the quantum theory in terms of "hidden" variables. I. Physical Review 1952, 85, 166. [Google Scholar] [CrossRef]
- Smolin, L. Three roads to quantum gravity. Basic Books 2001. [Google Scholar]
- Einstein, A. Die Feldgleichungen der Gravitation. In Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin; 1915; pp. 844–847. [Google Scholar]
- Smolin, L. An invitation to loop quantum gravity. arXiv preprint hep-th/0408048 2004. [Google Scholar]
- Bojowald, M. Loop quantum cosmology. Living Reviews in Relativity 2008, 11, 1–131. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Smolin, L. Loop space representation of quantum general relativity. Nuclear Physics B 1988, 331, 80–152. [Google Scholar] [CrossRef]
- Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. General Relativity and Gravitation 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
- Kiefer, C. Consistent histories and decoherence. Physical Review D 1992, 46, 1658. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Spin networks and quantum gravity. Physical Review D 1995, 52, 5743. [Google Scholar] [CrossRef] [PubMed]
- Baez, J.C. Spin networks in gauge theory. Advances in Mathematics 1996, 117, 253–272. [Google Scholar] [CrossRef]
- Oriti, D. Group field theory as the 2nd quantization of loop quantum gravity. Classical and Quantum Gravity 2014, 31, 063001. [Google Scholar]
- Lindblad, G. On the generators of quantum dynamical semigroups. Communications in Mathematical Physics 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Thiemann, T. Quantum spin dynamics (QSD). Classical and Quantum Gravity 1998, 15, 839. [Google Scholar]
- DeWitt, B.S. Quantum theory of gravity. I. The canonical theory. Physical Review 1967, 160, 1113. [Google Scholar]
- Born, M. Zur quantenmechanik der stoßvorg"ange. Zeitschrift f"ur Physik 1926, 37, 863–867. [Google Scholar] [CrossRef]
- Connes, A. Noncommutative geometry. Publications Math’ematiques de l’IH’ES 1994, 62, 41–144. [Google Scholar] [CrossRef]
- Majid, S. Foundations of quantum group theory; Cambridge University Press, 1995.
- Garay, L.J. Quantum gravity and minimum length. International Journal of Modern Physics A 1995, 10, 145–165. [Google Scholar] [CrossRef]
- Gambini, R.; Pullin, J. Loops, knots, gauge theories and quantum gravity; Cambridge University Press, 1996.
- Kitaev, A.; Preskill, J. Topological quantum computation. Physical Review Letters 2006, 96, 110404. [Google Scholar] [CrossRef] [PubMed]
- Bekenstein, J.D. Black holes and entropy. Physical Review D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Polchinski, J. String theory. Cambridge Monographs on Mathematical Physics 1998. [Google Scholar]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Physical Review D 1986, 34, 470. [Google Scholar] [CrossRef] [PubMed]
- Connes, A.; Marcolli, M. Noncommutative geometry, quantum fields and motives; American Mathematical Society, 2008.
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Physical Review D 1976, 14, 2460. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Martin, J. Trans-Planckian issues for inflationary cosmology. Classical and Quantum Gravity 2013, 30, 113001. [Google Scholar] [CrossRef]
- Ambjørn, J.; Jurkiewicz, J.; Loll, R. Emergence of a 4D world from causal quantum gravity. Physical Review Letters 2005, 93, 131301. [Google Scholar] [CrossRef]
- Will, C.M. The confrontation between general relativity and experiment. Living reviews in relativity 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Bojowald, M. Quantum cosmology: a fundamental description of the universe; Springer Science & Business Media, 2011.
- Carlip, S. Quantum gravity: a progress report. Reports on Progress in Physics 2001, 64, 885. [Google Scholar] [CrossRef]
- Rovelli, C. Loop quantum gravity. Living Reviews in Relativity 2008, 11, 1–69. [Google Scholar] [CrossRef]
- Stapp, H.P. Mindful universe: Quantum mechanics and the participating observer; Springer Science & Business Media, 2011.
- Griffiths, R.B. Consistent quantum theory; Cambridge University Press, 2003.
- Arndt, M.; Hornberger, K. Testing the limits of quantum mechanical superpositions. Nature Physics 2014, 10, 271–277. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Reviews of Modern Physics 2014, 86, 1391. [Google Scholar] [CrossRef]
- Ellis, G.F. Physics on the edge. Nature 2014, 507, 424–425. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen der physik 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Bothwell, T.; Kedar, D.; Oelker, E.; Robinson, J.; Bromley, S.; Tew, W.; Ye, J.; Kennedy, C. JILA SrI optical lattice clock with uncertainty of 2.5×10-19. Metrologia 2019, 56, 065004. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; others. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
- Rideout, D.; Jennewein, T.; Amelino-Camelia, G.; Demarie, T.F.; Higgins, B.L.; Kempf, A.; Kent, A.; Laflamme, R.; Ma, X.; Mann, R.B.; others. Fundamental quantum optics experiments conceivable with satellites—reaching relativistic distances and velocities. Classical and Quantum Gravity 2012, 29, 224011. [Google Scholar] [CrossRef]
- Wittmann, M. Modulations of the experience of self and time. Consciousness and cognition 2016, 38, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Reviews of Modern Physics 2009, 81, 865. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Physical Review Letters 1965, 14, 57. [Google Scholar] [CrossRef]
- Petkov, V. Is there an alternative to the block universe view?; Elsevier, 2006; pp. 207–228.
- Moreva, E.; Brida, G.; Gramegna, M.; Giovannetti, V.; Maccone, L.; Genovese, M. Time from quantum entanglement: an experimental illustration. Physical Review A 2014, 89, 052122. [Google Scholar] [CrossRef]
- Lloyd, S. Ultimate physical limits to computation. Nature 2000, 406, 1047–1054. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.; Backer, D.C.; Cordes, J.M.; Lazio, T.J.W.; Stappers, B.W.; Johnston, S. Strong-field tests of gravity using pulsars and black holes. New Astronomy Reviews 2004, 48, 993–1002. [Google Scholar] [CrossRef]
- Bongs, K.; Bouyer, P.; Chormaic, S.N.; Conroy, K.; Dutta, I.; Ertmer, W.; Feast, J.; Fromhold, M.; Gleeson, P.; Hänsel, W.; others. Quantum sensors for the gravitational wave observatory eLISA. EPJ Quantum Technology 2019, 6, 1–27. [Google Scholar]
- Psaltis, D. Probing strong-field gravity through X-ray spectroscopy of relativistic Fe Kα lines. Living Reviews in Relativity 2008, 11, 9. [Google Scholar] [CrossRef] [PubMed]
- Halberg, K.A.; Kranjec, A. Time perception: The surprising effects of surprising stimuli. Journal of Cognition 2021, 4. [Google Scholar]
- George, A.; Wong, D.; Luo, B.; Cheng, S.Y. Deep learning for time series classification: a review. Data Mining and Knowledge Discovery 2018, 32, 1822–1852. [Google Scholar]
- Hooft, G. Dimensional reduction in quantum gravity. arXiv preprint gr-qc/9310026 1993. [Google Scholar]
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Physical Review D 1981, 23, 287. [Google Scholar] [CrossRef]
- Page, D.N. Information in black hole radiation. Physical review letters 1993, 71, 3743. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Annals of Physics 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Wolfram, S. A new kind of science; Wolfram media Champaign, IL, 2002.
- Preskill, J. Reliable quantum computers. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1998, 454, 385–410. [Google Scholar] [CrossRef]
- Bostrom, N. Are we living in a computer simulation? The Philosophical Quarterly 2003, 53, 243–255. [Google Scholar] [CrossRef]
- Bennett, C.H. Notes on Landauer’s principle, reversible computation, and Maxwell’s Demon. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 2003, 34, 501–510. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM journal of research and development 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Arrighi, P. Quantum cellular automata: a review. arXiv preprint 2013, arXiv:1305.5852. [Google Scholar]
- Hofstadter, D.R. G"odel, Escher, Bach: An eternal golden braid; Basic books, 1979.
- Lakoff, G.; N’u nez, R.E. Where mathematics comes from: How the embodied mind brings mathematics into being; Basic books, 2000.
- Luminet, J.P. The shape and topology of the universe. arXiv preprint 2008, arXiv:0802.2236. [Google Scholar]
- Von Neumann, J. Mathematical foundations of quantum mechanics: New edition; Princeton University Press, 2018.
- Wigner, E.P. Remarks on the mind-body question. Philosophical Reflections and Syntheses, 1995; 247–260. [Google Scholar]
- Mac Lane, S. Categories for the Working Mathematician; Springer Science & Business Media, 2013.
- Dummit, D.S.; Foote, R.M. Abstract Algebra; John Wiley & Sons, 2004.
- Hall, B.C. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction; Springer, 2015.
- Lee, J.M. Smooth Manifolds; Springer, 2013.
- Johnstone, P.T. Sketches of an Elephant: A Topos Theory Compendium; Oxford University Press, 2002.
- Bohm, D. Wholeness and the implicate order; Routledge, 1980.
- Capra, F. The web of life: A new scientific understanding of living systems; Anchor, 1996.
- Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information; Cambridge University Press, 2002.
- Li, Y.; Shen, J.; Chen, X.; Wang, S.; Taya, M. Multifunctional materials and structures. Journal of Materials Research 2016, 31, 2463–2469. [Google Scholar]
- Floreano, D.; Mattiussi, C. Bio-inspired artificial intelligence: theories, methods, and technologies. MIT press 2008. [Google Scholar]
- Nicolescu, B. Manifesto of transdisciplinarity; SUNY Press, 2002.
- Chaitin, G.J. Meta math!: the quest for omega. arXiv preprint math/0404335 2006. [Google Scholar]
- Shapiro, S. Thinking about mathematics: The philosophy of mathematics; Oxford University Press, 2000.
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 1985, 400, 97–117. [Google Scholar]
- Hersh, R. What is mathematics, really?; Oxford University Press, 1997.
- Poincar’e, H. Science and hypothesis; Science Press, 1905.
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Communications on Pure and Applied Mathematics 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Tegmark, M. The mathematical universe. Foundations of Physics 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Wolf, W.P. Mathematics for physics and physicists; Princeton University Press, 2011.
- Smolin, L. The trouble with physics: The rise of string theory, the fall of a science, and what comes next; Houghton Mifflin Harcourt, 2006.
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Review 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Harrow, A.W.; Montanaro, A. Quantum supremacy using a programmable superconducting processor. Nature 2017, 549, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Joshi, V.; Joshi, V. A review of shape memory alloys and their applications. Journal of Materials Science and Engineering 2007, 1, 1–20. [Google Scholar]
- Khoo, Z.X.; Teoh, J.E.; Liu, Y.; Chua, C.K.; Yang, S.; An, J.; Leong, K.F.; Yeong, W.Y. A review of stimuli-responsive polymers for smart textile applications. Materials & Design 2014, 78, 1–23. [Google Scholar]
- Dincer, I. Comprehensive energy systems; Elsevier, 2018.
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; others. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Baez, J.C.; Stay, M. Physics, topology, logic and computation: a Rosetta Stone. New Structures for Physics.
- Klein, J.T. Prospects for transdisciplinarity. Futures 2004, 36, 515–526. [Google Scholar] [CrossRef]
- Hu, W. Dark energy and dark matter in the universe. Astronomy 2009, 2009, 55. [Google Scholar]
- Bransford, J.D.; Brown, A.L.; Cocking, R.R.; others. How people learn: Brain, mind, experience, and school: Expanded edition; National Academies Press, 2000. [Google Scholar]
- Stephan, P. How economics shapes science; Harvard University Press, 2012.
- Weinberg, S. To explain the world: The discovery of modern science; Penguin UK, 2015.
- Vilenkin, A. Creation of universes from nothing. Physics Letters B 1982, 117, 25–28. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Physical review 1935, 47, 777. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Schroeter, D.F. Introduction to quantum mechanics; Cambridge University Press, 2018.
- Calabrese, P.; Cardy, J. Entanglement entropy and quantum field theory. Journal of Statistical Mechanics: Theory and Experiment 2004, 2004, P06002. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum discord: a measure of the quantumness of correlations. Physical review letters 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Vedral, V. Quantifying entanglement in macroscopic systems. Nature 2008, 453, 1004–1007. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, V.; Dias, O.J.; Hartnett, G.S.; Lehner, L.; Santos, J.E. Holographic thermalization, quasinormal modes and superradiance in Kerr–AdS. Journal of High Energy Physics 2014, 2014, 1–42. [Google Scholar] [CrossRef]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G. The large scale structure of space-time; Vol. 1, Cambridge University Press, 1973.
- Schwarzschild, K. "Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitzungsberichte der K"oniglich Preussischen Akademie der Wissenschaften (Berlin), 1916, Seite 189-196 1916, 1916, 189–196. [Google Scholar]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Physical Review Letters 1963, 11, 237. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Susskind, L. The cosmic landscape: String theory and the illusion of intelligent design. In The Cosmic Landscape: String Theory and the Illusion of Intelligent Design; 2005; pp. 1–473. [Google Scholar]
- Smolin, L. Temporal naturalism. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 2013, 44, 142–153. [Google Scholar]
- Hayward, S.A. Formation and evaporation of nonsingular black holes. Physical Review Letters 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Frolov, V.P.; Zelnikov, A. Black hole physics: basic concepts and new developments; Vol. 96, Springer Science & Business Media, 2012.
- Susskind, L. The world as a hologram. Journal of Mathematical Physics 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Zeh, H.D. The role of the observer in the Everett interpretation. Foundations of Physics 2007, 37, 1476–1494. [Google Scholar] [CrossRef]
- Percival, I. Quantum state diffusion; Cambridge University Press, 1998.
- Gardiner, C.W. Stochastic methods; Vol. 4, Springer Berlin, 2009.
- Bassi, A.; Lochan, K.; Satin, S.; Singh, T.P.; Ulbricht, H. Models of wave-function collapse, underlying theories, and experimental tests. Reviews of Modern Physics 2013, 85, 471. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F.; others. The theory of open quantum systems; Oxford University Presson Demand, 2002. [Google Scholar]
- Wen, X.G. Quantum field theory of many-body systems: from the origin of sound to an origin of light and electrons; Oxford University Press on Demand, 2004.
- Hu, W. Structure formation with generalized dark matter. The Astrophysical Journal 1998, 506, 485. [Google Scholar] [CrossRef]
- Dunne, M.J. Infinite regress arguments; Springer, 2009.
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine; MIT Press, 2019.
- Tegmark, M. Consciousness as a state of matter. Chaos, Solitons & Fractals 2015, 76, 238–270. [Google Scholar]
- Lovelock, J. Gaia: A new look at life on earth; Oxford University Press, 1979.
- Fuchs, C.A.; Peres, A. Quantum mechanics: an introduction; World Scientific, 2014.
- Maudlin, T. Philosophy of physics: Quantum theory; Princeton University Press, 2019.
- Zeh, H.D. Decoherence: basic concepts and their interpretation. arXiv preprint quant-ph/9506020 2003. [Google Scholar]
- Rovelli, C. Relational quantum mechanics. International Journal of Theoretical Physics 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- Barrow, J.D. The book of universes: exploring the limits of the cosmos; Random House, 2011.
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nature Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Ellis, G.F. Top-down causation and emergence: some comments on mechanisms. Interface Focus 2012, 2, 126–140. [Google Scholar] [CrossRef]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Reviews of Modern Physics 2009, 81, 1051. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Reviews of Modern Physics 2017, 89, 035002. [Google Scholar] [CrossRef]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory. Scholarpedia 2015, 10, 4164. [Google Scholar] [CrossRef]
- Kafatos, M.C.; Nadeau, R. Conscious acts of creation: The emergence of a new physics; Universal Pub, 2011.
- Wigner, E.P. Remarks on the mind-body question. In Symmetries and reflections; 1967; pp. 171–184. [Google Scholar]
- Penrose, R. Shadows of the Mind: A Search for the Missing Science of Consciousness; Oxford University Press, 1994.
- Goswami, A.; Goswami, A.; Reed, R.E.; Goswami, M. The self-aware universe: How consciousness creates the material world; Penguin, 1995.
- Stapp, H.P. Mind, matter, and quantum mechanics. Foundations of Physics 2009, 39, 1018–1018. [Google Scholar]
- Radin, D. Entangled minds: Extrasensory experiences in a quantum reality; Simon and Schuster, 2006.
- Rosenblum, B.; Kuttner, F. Quantum enigma: Physics encounters consciousness; Oxford University Press, 2011.
- Hoefer, C. Causal determinism. Stanford Encyclopedia of Philosophy 2016. [Google Scholar]
- Kane, R. The significance of free will. In Philosophical Perspectives on Free Will; Routledge, 1999; pp. 1–20.
- Laplace, P.S. A philosophical essay on probabilities; Courier Corporation, 1951.
- Searle, J.R. Rationality in action; MIT press, 2001.
- Doyle, B. Free will: The scandal in philosophy; I-Phi Press, 2011.
- Chalmers, D.J. The conscious mind: In search of a fundamental theory; Oxford University Press, 1996.
- Goff, P. Consciousness and fundamental reality; Oxford University Press, 2017.
- Nagel, T. Mind and cosmos: Why the materialist neo-Darwinian conception of nature is almost certainly false; Oxford University Press, 2012.
- Ma, X.s.; Zotter, S.; Kofler, J.; Ursin, R.; Jennewein, T.; Brukner, Č.; Zeilinger, A. Quantum entanglement with two-photon states generated in Franson-type experiments. Physical Review A 2012, 86, 010302. [Google Scholar]
- Penrose, R. On the gravitization of quantum mechanics 1: Quantum state reduction. Foundations of Physics 2014, 44, 557–575. [Google Scholar] [CrossRef]
- Everett III, H. " Relative state" formulation of quantum mechanics. Reviews of modern physics 1957, 29, 454. [Google Scholar] [CrossRef]
- Stapp, H.P. Mindful universe: Quantum mechanics and the participating observer. Springer Science & Business Media, 2007. [Google Scholar]
- Penrose, R. Fashion, faith, and fantasy in the new physics of the universe; Princeton University Press, 2016.
- Bayne, T. The unity of consciousness; Oxford University Press: Oxford, 2010. [Google Scholar]
- Nagel, T. The view from nowhere; Oxford University Press, 1986.
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: from consciousness to its physical substrate. Nature Reviews Neuroscience 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Stubenberg, L. Neutral monism. In The Stanford Encyclopedia of Philosophy, Winter 2016 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University, 2016.
- Schr"odinger, E. An undulatory theory of the mechanics of atoms and molecules. Physical review 1926, 28, 1049. [Google Scholar] [CrossRef]
- Fisher, M.P. Quantum cognition: the possibility of processing with nuclear spins in the brain. Annals of Physics 2015, 362, 593–602. [Google Scholar] [CrossRef]
- Davies, P. Cosmic Jackpot: Why Our Universe Is Just Right for Life; Houghton Mifflin Harcourt, 2007.
- Wilber, K. Integral psychology: Consciousness, spirit, psychology, therapy; Shambhala Publications, 2000.
- Becker, K.; Becker, M.; Schwarz, J.H. String theory and M-theory: A modern introduction; Cambridge University Press, 2006.
- Ambjørn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Physics Reports 2012, 519, 127–210. [Google Scholar] [CrossRef]
- Loll, R. Quantum gravity on the computer: Impressions of a workshop. Classical and Quantum Gravity 2019, 36, 033001. [Google Scholar]
- Chamseddine, A.H.; Connes, A.; Marcolli, M. Noncommutative geometry as a framework for unification of all fundamental interactions including gravity. Part I. Fortschritte der Physik 2007, 55, 761–781. [Google Scholar] [CrossRef]
- Barrett, J.W. A Lorentzian version of the non-commutative geometry of the standard model of particle physics. Journal of Mathematical Physics 2007, 48, 012303. [Google Scholar] [CrossRef]
- Carr, B. Universe or multiverse?; Cambridge University Press, 2007.
- Tegmark, M. Parallel universes. Scientific American 2003, 288, 40–51. [Google Scholar] [CrossRef] [PubMed]
- DeWitt, B.S. Quantum mechanics and reality. Physics Today 1970, 23, 30–35. [Google Scholar] [CrossRef]
- Vaidman, L. Many-worlds interpretation of quantum mechanics. The Stanford Encyclopedia of Philosophy 2008. [Google Scholar]
- Bousso, R. The holographic principle. Reviews of Modern Physics 2002, 74, 825. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Information in the holographic universe. Scientific American 2003, 289, 58–65. [Google Scholar] [CrossRef]
- Maldacena, J. The large N limit of superconformal field theories and supergravity. Advances in Theoretical and Mathematical Physics 1999, 2, 231–252. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Physics Reports 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Polchinski, J. Gauge/gravity duality. In Approaches to Quantum Gravity; 2006; pp. 169–186. [Google Scholar]
- Witten, E. Superconducting strings. Nuclear Physics B 1985, 249, 557–592. [Google Scholar] [CrossRef]
- Wilson, K.G. Confinement of quarks. Physical Review D 1974, 10, 2445. [Google Scholar] [CrossRef]
- Weinberg, S. A model of leptons. Physical review letters 1967, 19, 1264. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring theory: volume 1, introduction; Cambridge University Press, 1987.
- Witten, E. Search for a realistic Kaluza-Klein theory. Nuclear Physics B 1985, 186, 412–428. [Google Scholar] [CrossRef]
- Georgi, H.; Glashow, S.L. Unity of all elementary-particle forces. Physical Review Letters 1974, 32, 438. [Google Scholar] [CrossRef]
- Glashow, S.L. Partial-symmetries of weak interactions. Nuclear physics 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Pati, J.C.; Salam, A. Lepton number as the fourth "color". Physical Review D 1974, 10, 275. [Google Scholar] [CrossRef]
- Georgi, H.; Jarlskog, C. Hierarchy of interactions in unified gauge theories. Physics Letters B 1979, 86, 297–300. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Asymptotically free gauge theories. I. Physical Review D 1973, 8, 3633. [Google Scholar] [CrossRef]
- Nishino, H.; Clark, S.; Abe, K.; Hayato, Y.; Iida, T.; Ikeda, M.; Kameda, J.; Kobayashi, K.; Koshio, Y.; Miura, M.; others. Search for proton decay via p → e+ π0 and p →μ+ π0 in a large water Cherenkov detector. Physical Review Letters 2009, 102, 141801. [Google Scholar] [CrossRef] [PubMed]
- Minkowski, P. μ→eγ at a rate of one out of 1-billion muon decays? Physics Letters B 1977, 67, 421–428. [Google Scholar] [CrossRef]
- Hawking, S. A brief history of time: From the big bang to black holes; Bantam Books, 1988.
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; others. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physics Letters B 2012, 716, 1–29. [Google Scholar]
- Bielewicz, P.; Banday, A.J.; Górski, K.M. Cosmic topology in the search for the overall shape of the Universe. Monthly Notices of the Royal Astronomical Society 2012, 421, 1064–1072. [Google Scholar] [CrossRef]
- Baez, J.C. Quantum quandaries: a category-theoretic perspective. In The structural foundations of quantum gravity; 2006; pp. 240–265. [Google Scholar]
- Teukolsky, S.A. Spectral methods for numerical relativity. Journal of Computational Physics 2016, 312, 333–356. [Google Scholar] [CrossRef]
- Portegies Zwart, S. Astrophysics with artificial intelligence and machine learning. arXiv preprint 2020, arXiv:2009.11703. [Google Scholar]
- Punzo, D.; Van der Hulst, J.; Roerdink, J.; Oosterloo, T.; Ramatsoku, M.; Verheijen, M. The role of 3-D interactive visualization in blind surveys of HI in galaxies. Astronomy and Computing 2017, 19, 45–59. [Google Scholar] [CrossRef]
- de Oliveira-Costa, A.; Tegmark, M.; Zaldarriaga, M.; Hamilton, A. Low-order multipole maps of cosmic microwave background anisotropy derived from WMAP. Physical Review D 2004, 69, 063516. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Magueijo, J.; G’orski, K.M. Non-Gaussian cosmic microwave background fluctuations. The Astrophysical Journal Letters 1998, 503, L1. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kovetz, E.D. The Quest for B Modes from Inflationary Gravitational Waves. Annual Review of Astronomy and Astrophysics 2016, 54, 227–269. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; others. Cosmology and fundamental physics with the Euclid satellite. Living Reviews in Relativity 2018, 21, 2. [Google Scholar]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; others. A 2.4% Determination of the Local Value of the Hubble Constant. The Astrophysical Journal 2016, 826, 56. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; others. The Einstein Telescope: a third-generation gravitational wave observatory. Classical and Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves: Volume 1: Theory and Experiments; Oxford University Press: Oxford, 2008. [Google Scholar]
- Reitze, D.; others. Cosmic explorer: the US contribution to gravitational-wave astronomy beyond LIGO. Bulletin of the American Astronomical Society 2019, 51, 035. [Google Scholar]
- Collaboration, T.L.D.E.S. ; others. The LSST Dark Energy Science Collaboration (DESC) Science Requirements Document. arXiv preprint 2019, arXiv:1809.01669. [Google Scholar]
- Abe, K.; others. Indication of electron neutrino appearance from an accelerator-produced off-axis muon neutrino beam. Physical Review Letters 2011, 107, 041801. [Google Scholar] [CrossRef]
- Kocsis, B.; Frei, Z.; Haiman, Z.; Menou, K. Observable signatures of extreme mass-ratio inspiral black hole binaries embedded in thin accretion disks. The Astrophysical Journal 2006, 637, 27. [Google Scholar] [CrossRef]
- Piao, Y.S. Primordial perturbation spectra in a holographic phase of the Universe. Physical Review D 2006, 74, 047302. [Google Scholar] [CrossRef]
- Roukema, B.F.; Bajtlik, S.; Biesiada, M.; Szaniewska, A.; Jurkiewicz, H. A toroidal universe from black-hole spinors. Astronomy & Astrophysics 2004, 418, 411–415. [Google Scholar]
- Abazajian, K.; Addison, G.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Alvarez, M.; Anderson, A.; Arnold, K.; Baccigalupi, C. ; others. CMB-S4 science book, first edition. arXiv preprint 2019, arXiv:1907.04473. [Google Scholar]
- Mandelbaum, R. Weak lensing as a probe of physical properties of substructures in dark matter halos. Annual Review of Astronomy and Astrophysics 2018, 56, 393–433. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Horne, M.A.; Zeilinger, A. Experimentally verifying the quantumness of a macroscopic object. In The Physics of Quantum Information; 1999; pp. 7–22. [Google Scholar]
- Young, W.; Stebbins, R.; Thorpe, J.I.; McKenzie, K. Mission design for the Laser Interferometer Space Antenna (LISA) gravitational wave observatory. arXiv preprint 2018, arXiv:1807.09707. [Google Scholar]
- Wasserman, L. All of statistics: a concise course in statistical inference; Springer, 2010.
- Sanders, G.H. The Thirty Meter Telescope (TMT): An International Observatory. Journal of Astrophysics and Astronomy 2013, 34, 81–86. [Google Scholar] [CrossRef]
- Dravins, D. Future high-resolution studies of stars and stellar systems. Proceedings of the International Astronomical Union 2005, 1, 203–212. [Google Scholar]
- Brown, R.R.; Deletic, A.; Wong, T.H. Interdisciplinary research: Meaning, metrics and nurture. Research Policy 2015, 44, 1187–1197. [Google Scholar]
- Ries, N. The case for technology development in the environmental sciences. Environmental Science & Technology 2015, 49, 1–2. [Google Scholar]
- Carney, D.; Stamp, P.C.; Taylor, J.M. Tabletop experiments for quantum gravity: a review. Classical and Quantum Gravity 2019, 36, 034001. [Google Scholar] [CrossRef]
- Stephan, P. Research funding: trends and challenges. In The Palgrave handbook of economics and language; 2015; pp. 203–224. [Google Scholar]
- Adhikari, R.; Aguiar, O.; Altin, P.; Ballmer, S.; Barsotti, L.; Bassiri, R.; Bell, A.; Billingsley, G.; Bird, A.; Blair, C. ; others. Gravitational wave detectors: the next generation. arXiv preprint 2020, arXiv:2001.11173. [Google Scholar]
- Barish, B.C.; Weiss, R. LIGO and the detection of gravitational waves. Physics today 1999, 52, 44–50. [Google Scholar] [CrossRef]
- Collaboration, L.S.; others. Advanced LIGO. Classical and quantum gravity 2015, 32, 074001. [Google Scholar] [CrossRef]
- Battiston, R.; Berti, E.; Grimani, C.; Punturo, M.; Sesana, A.; Tamanini, N. Fundamental physics and cosmology with the Laser Interferometer Space Antenna. arXiv preprint 2021, arXiv:2108.01167. [Google Scholar]
- Ivezi’c, Ž.; Connolly, A.J.; VanderPlas, J.T.; Gray, A. Statistics, data mining, and machine learning in astronomy: a practical Python guide for the analysis of survey data; Princeton University Press, 2014.
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Eigenbrode, S.D.; O’Rourke, M.; Wulfhorst, J.D.; Althoff, D.M.; Goldberg, C.S.; Merrill, K.; Morse, W.; Nielsen-Pincus, M.; Stephens, J.; Winowiecki, L.; others. Employing philosophical dialogue in collaborative science. BioScience 2007, 57, 55–64. [Google Scholar] [CrossRef]
- Hall, K.L.; Vogel, A.L.; Huang, G.C.; Serrano, K.J.; Rice, E.L.; Tsakraklides, S.P.; Fiore, S.M. Collaboration and team science: from theory to practice. Journal of investigative medicine 2012, 60, 768–775. [Google Scholar]
- Popper, K. The logic of scientific discovery; Routledge, 2014.
- Nosek, B.A.; Alter, G.; Banks, G.C.; Borsboom, D.; Bowman, S.D.; Breckler, S.J.; Buck, S.; Chambers, C.D.; Chin, G.; Christensen, G.; others. Promoting an open research culture. Science 2015, 348, 1422–1425. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L.; O’Shea, B.W.; others. ENZO: An Adaptive Mesh Refinement Code for Astrophysics. The Astrophysical Journal Supplement Series 2014, 211, 19. [Google Scholar] [CrossRef]
- Terhal, B.M. Quantum error correction for quantum memories. Reviews of Modern Physics 2015, 87, 307. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Reviews of Modern Physics 2012, 84, 621. [Google Scholar] [CrossRef]
- Orús, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Annals of Physics 2014, 349, 117–158. [Google Scholar] [CrossRef]
- Ntampaka, M.; others. The Role of Machine Learning in the Next Decade of Cosmology. Bulletin of the American Astronomical Society 2019, 51, 14. [Google Scholar]
- Rodriguez, A.C.; Kacprzak, T.; Lucchi, A.; others. Fast Cosmic Web Simulations with Generative Adversarial Networks. Computational Astrophysics and Cosmology 2018, 5, 4. [Google Scholar] [CrossRef]
- Hezaveh, Y.D.; Levasseur, L.P.; Marshall, P.J. Fast automated analysis of strong gravitational lenses with convolutional neural networks. Nature 2017, 548, 555–557. [Google Scholar] [CrossRef] [PubMed]
- Bruschi, D.E.; Datta, A.; Ursin, R.; Ralph, T.C.; Fuentes, I. Quantum estimation of the Schwarzschild spacetime parameters of the Earth. Physical Review D 2014, 90, 124001. [Google Scholar] [CrossRef]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Physics Letters B 1993, 319, 83–86. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration. Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters 2016, 116, 061102. [Google Scholar] [CrossRef]
- Deutsch, D. The fabric of reality; Penguin UK, 1997.
- ’t Hooft, G. Quantum gravity without space-time singularities or horizons. arXiv preprint arXiv:0909.3426, arXiv:0909.3426 2009.
- Deutsch, D. Quantum mechanics near closed timelike lines. Physical Review D 1991, 44, 3197. [Google Scholar] [CrossRef]
- Penrose, R. The Emperor’s New Mind: Concerning Computers, Minds, and the Laws of Physics; Oxford University Press: Oxford, 1989. [Google Scholar]
- Searle, J.R. The mystery of consciousness; New York Review of Books, 1997.
- Bateson, G. Mind and nature: A necessary unity; Dutton, 1979.
- Kahneman, D. Thinking, fast and slow; Farrar, Straus and Giroux, 2011.
- Naess, A. The shallow and the deep, long-range ecology movement. A summary. Inquiry 1973, 16, 95–100. [Google Scholar] [CrossRef]
- Callicott, J.B. In defense of the land ethic: Essays in environmental philosophy; SUNY Press, 1989.
- Churchland, P.M. Matter and consciousness; MIT press, 2013.
- Berkeley, G. A treatise concerning the principles of human knowledge; Aaron Rhames, 1710.
- Descartes, R. Meditations on first philosophy; Paris, 1641.
- Skrbina, D. Panpsychism in the West; MIT Press, 2005.
- Whitehead, A.N. Process and reality: An essay in cosmology; Cambridge University Press, 1929.
- Conway, J.; Kochen, S. Free will, quantum mechanics, and the brain. Foundations of Physics 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Radin, D. Supernormal: Science, yoga, and the evidence for extraordinary psychic abilities; Deepak Chopra, 2013.
- Chalmers, D.J. The character of consciousness. In The Character of Consciousness; Oxford University Press, 2010; pp. 3–35.
- Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Davies, P.; Gregersen, N.H. Information and the nature of reality: From physics to metaphysics; Cambridge University Press, 2010.
- Tononi, G. An information integration theory of consciousness. BMC neuroscience 2004, 5, 1–22. [Google Scholar] [CrossRef]
- Br"untrup, G.; Jaskolla, L. Panpsychism and monism. In Panpsychism: Contemporary Perspectives; Oxford University Press, 2016; pp. 48–74.
- Nagel, T. Panpsychism. In Mortal questions; 1979; pp. 181–195. [Google Scholar]
- Seager, W. Panpsychist infusion. In Routledge Handbook of Panpsychism; 2020; pp. 229–248. [Google Scholar]
- Kane, R. The Oxford handbook of free will; Oxford University Press, 2002.
- Dennett, D.C. Freedom evolves; Viking, 2003.
- Nietzsche, F. The Gay Science: With a Prelude in Rhymes and an Appendix of Songs; Vintage Books: New York, 1974; Translated by Walter Kaufmann. [Google Scholar]
- Nahmias, E. Is free will an illusion? Confronting challenges from the modern mind sciences. In Moral psychology; MIT Press Cambridge, MA, 2014; pp. 1–25.
- Heisenberg, W. Physics and philosophy: The revolution in modern science; Harper & Row, 1958.
- Bedau, M.A.; Humphreys, P. Emergence: Contemporary readings in philosophy and science; MIT press, 2008.
- Chalmers, D.J. Strong and weak emergence. In The Re-Emergence of Emergence; Oxford University Press Oxford, 2006; pp. 244–256.
- Capra, F. The Tao of Physics: An Exploration of the Parallels Between Modern Physics and Eastern Mysticism; Shambhala Publications: Boulder, Colorado, 1975. [Google Scholar]
- Kim, J. Mind in a physical world: An essay on the mind-body problem and mental causation; MIT press, 1998.
- Searle, J.R. Minds, brains, and programs. Behavioral and brain sciences 1980, 3, 417–424. [Google Scholar] [CrossRef]
- Dennett, D.C. Consciousness explained; Little, Brown and Co, 1991.
- Chakravartty, A. Scientific ontology: Integrating naturalized metaphysics and voluntarist epistemology; Oxford University Press, 2017.
- Ladyman, J.; Ross, D.; Spurrett, D.; Collier, J. Every thing must go: Metaphysics naturalized; Oxford University Press, 2007.
- Putnam, H. What is mathematical truth? Historia Mathematica 1975, 2, 529–543. [Google Scholar] [CrossRef]
- Kauffman, S.A. The origins of order: Self-organization and selection in evolution; Oxford University Press, USA, 1993.
- Barrow, J.D.; Tipler, F.J. The anthropic cosmological principle; Oxford University Press, 1986.
- Tipler, F.J. The physics of immortality: Modern cosmology, God and the resurrection of the dead; Anchor, 1994.
- Davies, P. The Goldilocks enigma: Why is the universe just right for life?; HMH, 2008.
- Strawson, G. Realistic monism: Why physicalism entails panpsychism. Journal of Consciousness Studies 2006, 13, 3–31. [Google Scholar]
- Kane, R. The significance of free will; Oxford University Press, 1996.
- Katz, J.S.; Martin, B.R. What is research collaboration? Research Policy 1997, 26, 1–18. [Google Scholar] [CrossRef]
- Wilson, E.O. Consilience: The unity of knowledge; Vol. 31, Vintage, 1999.
- Sathyaprakash, B.; Schutz, B.F. Physics, astrophysics and cosmology with gravitational waves. Living Reviews in Relativity 2009, 12, 1–141. [Google Scholar] [CrossRef]
- Kuhn, T.S. The structure of scientific revolutions; University of Chicago press, 2012.
- Sagan, C. Cosmos; Ballantine Books, 2011.
- Ellis, G.F.R. The topology of the universe. Classical and Quantum Gravity 2014, 31, 245001. [Google Scholar]
- Linde, A. Inflationary cosmology after Planck 2013. arXiv preprint 2014, arXiv:1402.0526. [Google Scholar]
- Grigor’yan, A. Heat Kernel and Analysis on Manifolds. AMS/IP Studies in Advanced Mathematics 2009, 47. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics; Vol. 1, Academic Press: San Diego, 1980. [Google Scholar]
- Hawking, S.W. Zeta Function Regularization of Path Integrals in Curved Spacetime. Communications in Mathematical Physics 1977, 55, 133–148. [Google Scholar] [CrossRef]
- Liu, J.S. Monte Carlo Strategies in Scientific Computing; Springer: New York, 2008. [Google Scholar]
- Chib, S.; Greenberg, E. Understanding the Metropolis-Hastings Algorithm. The American Statistician 1995, 49, 327–335. [Google Scholar] [CrossRef]
- Berger, M.J.; Colella, P. Local Adaptive Mesh Refinement for Shock Hydrodynamics. Journal of Computational Physics 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, 2000. [Google Scholar]
- Bernardeau, F.; Colombi, S.; Gaztañaga, E.; Scoccimarro, R. Large-scale Structure of the Universe and Cosmological Perturbation Theory. Physics Reports 2002, 367, 1–248. [Google Scholar] [CrossRef]
- Baumann, D. TASI Lectures on Inflation. arXiv preprint arXiv:0907.5424, arXiv:0907.5424 2009.
- Hu, W.; Dodelson, S. Cosmic Microwave Background Anisotropies. Annual Review of Astronomy and Astrophysics 2002, 40, 171–216. [Google Scholar] [CrossRef]
- CMB-S4, Collaboration.; Abazajian, K.; Addison, G.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Alvarez, M.; Anderson, A.; Arnold, K. CMB-S4 Collaboration.; Abazajian, K.; Addison, G.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Alvarez, M.; Anderson, A.; Arnold, K.; others. CMB-S4 Science Case, Reference Design, and Project Plan. arXiv e-prints 2019, arXiv:[astro-ph.IM/1907.04473]. [Google Scholar]
- Skilling, J. Nested Sampling for General Bayesian Computation. Bayesian Analysis 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Trotta, R. Bayes in the sky: Bayesian inference and model selection in cosmology. Contemporary Physics 2008, 49, 71–104. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Monthly Notices of the Royal Astronomical Society: Letters 2007, 377, L74–L78. [Google Scholar] [CrossRef]
- Srednicki, M. Entropy and area. Physical Review Letters 1993, 71, 666–669. [Google Scholar] [CrossRef]
- LISA Collaboration. Laser Interferometer Space Antenna. arXiv preprint 2017, arXiv:1702.00786.
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D.J. Laboratory Tests of Chameleon Models. Physical Review D 2007, 76, 085010. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; others. Cosmology and fundamental physics with the Euclid satellite. Living Reviews in Relativity 2018, 21, 2. [Google Scholar]
- Karoubi, M. K-Theory: An Introduction; Springer-Verlag: Berlin, 1978. [Google Scholar]
- Milnor, J. Morse Theory; Princeton University Press: Princeton, 1963. [Google Scholar]
- Kress, R. Linear Integral Equations, 2 ed.; Springer: New York, 1999. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields; Vol. 1, Cambridge University Press: Cambridge, 1995. [Google Scholar]
- Bertlmann, R.A. Anomalies in Quantum Field Theory; Oxford University Press: Oxford, 1996. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos, 2 ed.; Westview Press: Boulder, 2014. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, 1982. [Google Scholar]
- Vazza, F.; Feletti, A. The Quantitative Comparison Between the Neuronal Network and the Cosmic Web. Frontiers in Physics 2019, 7, 80. [Google Scholar] [CrossRef]
- Bungartz, H.J.; Griebel, M. Sparse Grids. Acta Numerica 2004, 13, 147–269. [Google Scholar] [CrossRef]
- Ling, J.; Jewell, J.; Laszlo, I. Deep Learning for Cosmology. Journal of Cosmology and Astroparticle Physics 2016, 2016, 018. [Google Scholar]
- Jordan, S.P.; Lee, K.S.M.; Preskill, J. Quantum Algorithms for Quantum Field Theories. Science 2012, 336, 1130–1133. [Google Scholar] [CrossRef] [PubMed]
- Montanaro, A. Quantum speedup of Monte Carlo methods. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2015, 471, 20150301. [Google Scholar] [CrossRef] [PubMed]
- Mazumdar, A.; White, G. Review of cosmic phase transitions: their significance and experimental signatures. Reports on Progress in Physics 2019, 82, 076901. [Google Scholar] [CrossRef] [PubMed]
- Coleman, S. Fate of the false vacuum: Semiclassical theory. Physical Review D 1977, 15, 2929. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Physical Review D 1984, 30, 272. [Google Scholar] [CrossRef]
- Riotto, A.; Trodden, M. Recent progress in baryogenesis. Annual Review of Nuclear and Particle Science 1999, 49, 35–75. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, 2000. [Google Scholar]
- Hindmarsh, M.B.; Kibble, T.W.B. Cosmic strings. Reports on Progress in Physics 1995, 58, 477. [Google Scholar] [CrossRef]
- Vilenkin, A. Cosmic strings and domain walls. Physics Reports 1985, 121, 263–315. [Google Scholar] [CrossRef]
- Durrer, R.; Kunz, M.; Melchiorri, A. Cosmic structure formation with topological defects. Physics Reports 2002, 364, 1–81. [Google Scholar] [CrossRef]
- Wesson, P.S. Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology; World Scientific: Singapore, 2006. [Google Scholar]
- Greene, B.R. String Theory on Calabi-Yau Manifolds. arXiv preprint hep-th/9702155 1996. [Google Scholar]
- Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. Vacuum Configurations for Superstrings. Nuclear Physics B 1985, 258, 46–74. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.; Trivedi, S.P. de Sitter Vacua in String Theory. Physical Review D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Ibáñez, L.E.; Uranga, A.M. String Theory and Particle Physics: An Introduction to String Phenomenology; Cambridge University Press: Cambridge, 2012. [Google Scholar]
- Butterfield, J.; Earman, J. Philosophy of Physics; Elsevier: Amsterdam, 2007. [Google Scholar]
- Psillos, S. Scientific Realism: How Science Tracks Truth; Routledge: London, 1999. [Google Scholar]
- Ellis, G.F.R. Issues in the Philosophy of Cosmology. Handbook of the Philosophy of Science 2006, 2, 1183–1285. [Google Scholar]
- Susskind, L. The Anthropic Landscape of String Theory. arXiv preprint hep-th/0302219 2003. [Google Scholar]
- Carter, B. Large Number Coincidences and the Anthropic Principle in Cosmology. In Confrontation of Cosmological Theories with Observational Data; Longair, M.S., Ed.; Reidel: Dordrecht, 1974; pp. 291–298. [Google Scholar]
- Wen, X.G. Quantum Field Theory of Many-Body Systems; Oxford University Press: Oxford, 2017. [Google Scholar]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Reviews of Modern Physics 2010, 82, 3045. [Google Scholar] [CrossRef]
- Keimer, B.; Kivelson, S.A.; Norman, M.R.; Uchida, S.; Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 2015, 518, 179–186. [Google Scholar] [CrossRef]
- Houck, A.A.; Türeci, H.E.; Koch, J. On-chip quantum simulation with superconducting circuits. Nature Physics 2012, 8, 292–299. [Google Scholar] [CrossRef]
- Benioff, P. Space searches with a quantum robot. AMS Contemporary Mathematics Series 2002, 305, 1–12. [Google Scholar]
- Dimopoulos, S.; Graham, P.W.; Hogan, J.M.; Kasevich, M.A. Testing General Relativity with Atom Interferometry. Physical Review Letters 2007, 98, 111102. [Google Scholar] [CrossRef] [PubMed]
- Bloch, I.; Dalibard, J.; Nascimbène, S. Quantum simulations with ultracold quantum gases. Nature Physics 2012, 8, 267–276. [Google Scholar] [CrossRef]
- Ravanbakhsh, S.; Lanusse, F.; Mandelbaum, R.; Schneider, J.; Poczos, B. Enabling Dark Energy Science with Deep Generative Models of Galaxy Images. Proceedings of the AAAI Conference on Artificial Intelligence 2017, 31. [Google Scholar] [CrossRef]
- Einstein, A. Die grundlage der allgemeinen relativit"atstheorie. Annalen der Physik 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nature Physics 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Marshman, R.J.; Mazumdar, A.; Bose, S. Locality and entanglement in table-top testing of the quantum nature of linearized gravity. Physical Review A 2020, 101, 052110. [Google Scholar] [CrossRef]
- Baez, J.C. Higher-dimensional algebra and Planck-scale physics; Cambridge University Press, 2004.
- Witten, E. A new look at the path integral of quantum mechanics. arXiv preprint 2010, arXiv:1009.6032. [Google Scholar]
- Atiyah, M.F. K-theory and reality. The Quarterly Journal of Mathematics 1967, 17, 367–386. [Google Scholar] [CrossRef]
- Penrose, R. The road to reality: A complete guide to the laws of the universe; Jonathan Cape, 2004.
- Witten, E. Topological quantum field theory. Communications in Mathematical Physics 1988, 117, 353–386. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmological observations. AIP Conference Proceedings 2008, 1141, 24–35. [Google Scholar]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Communications in Mathematical Physics 1973, 31, 161–170. [Google Scholar] [CrossRef]

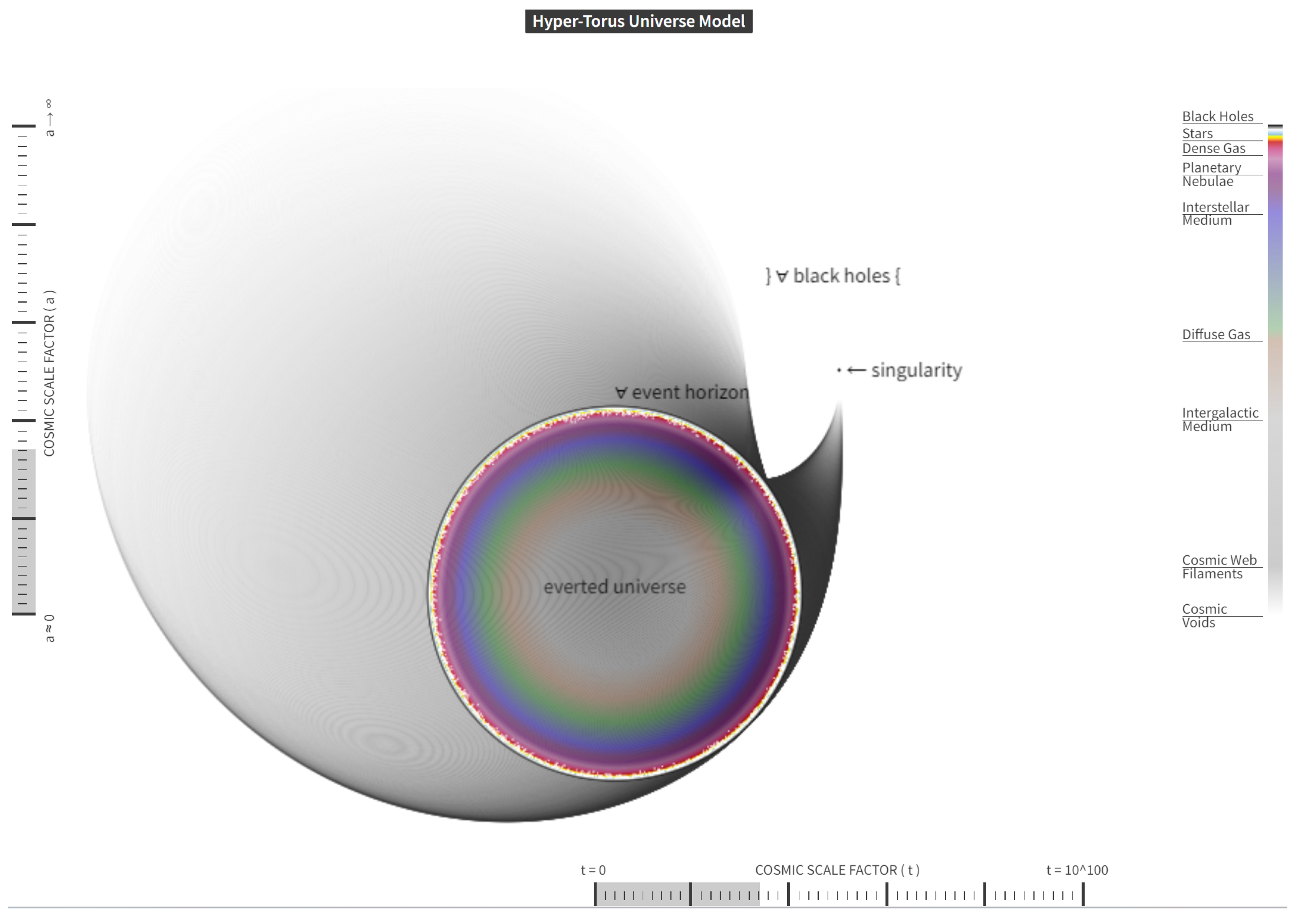
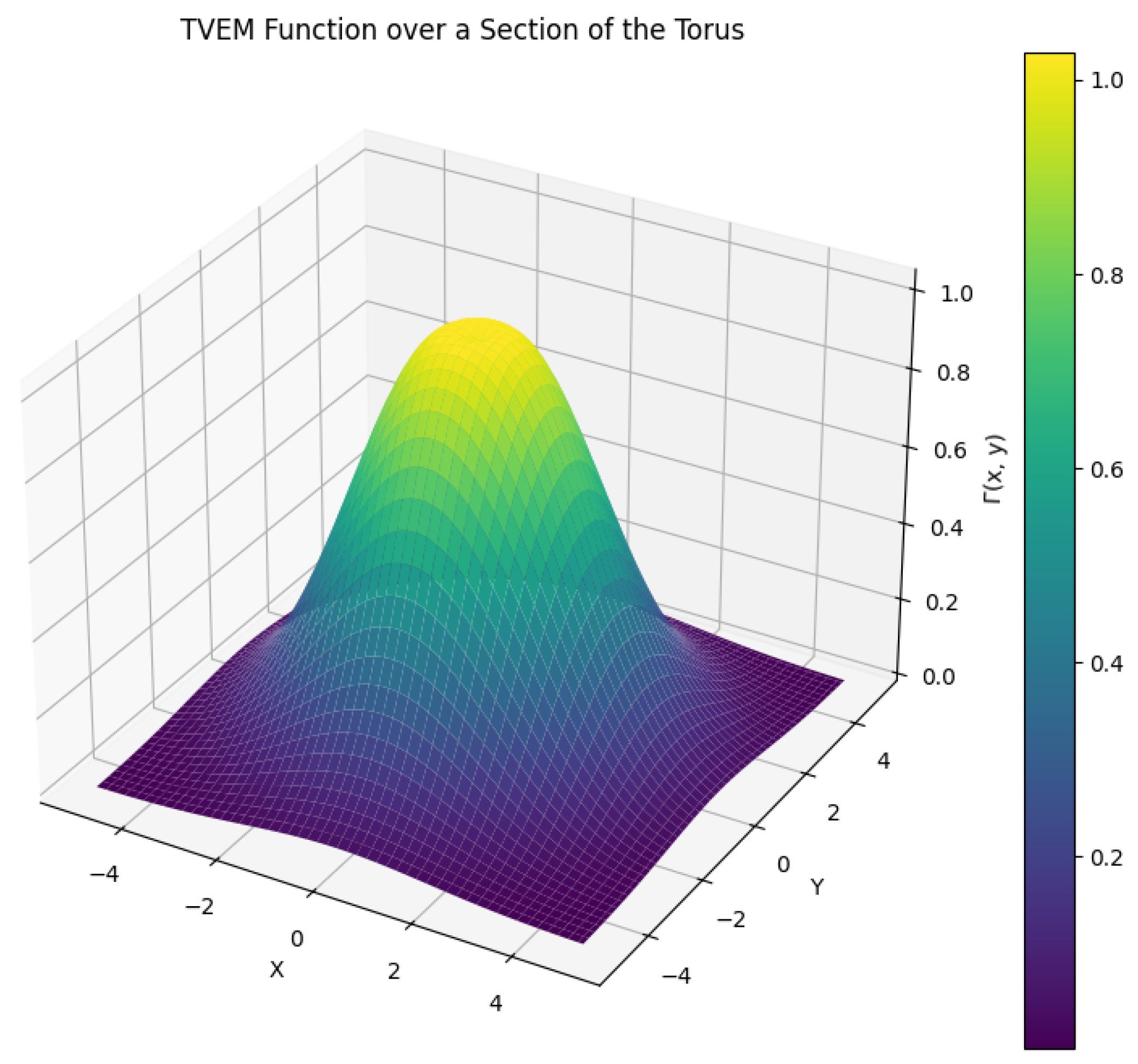
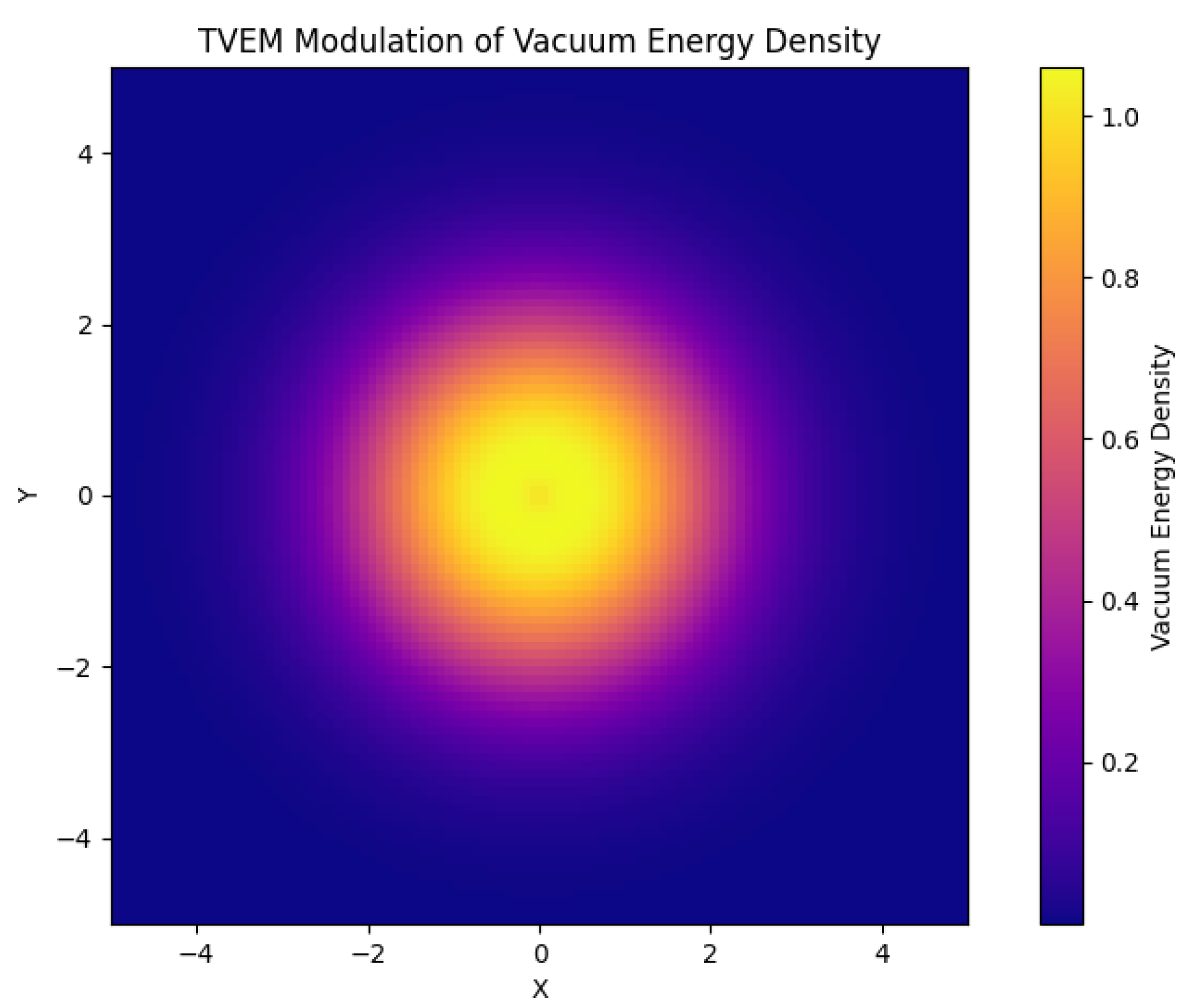
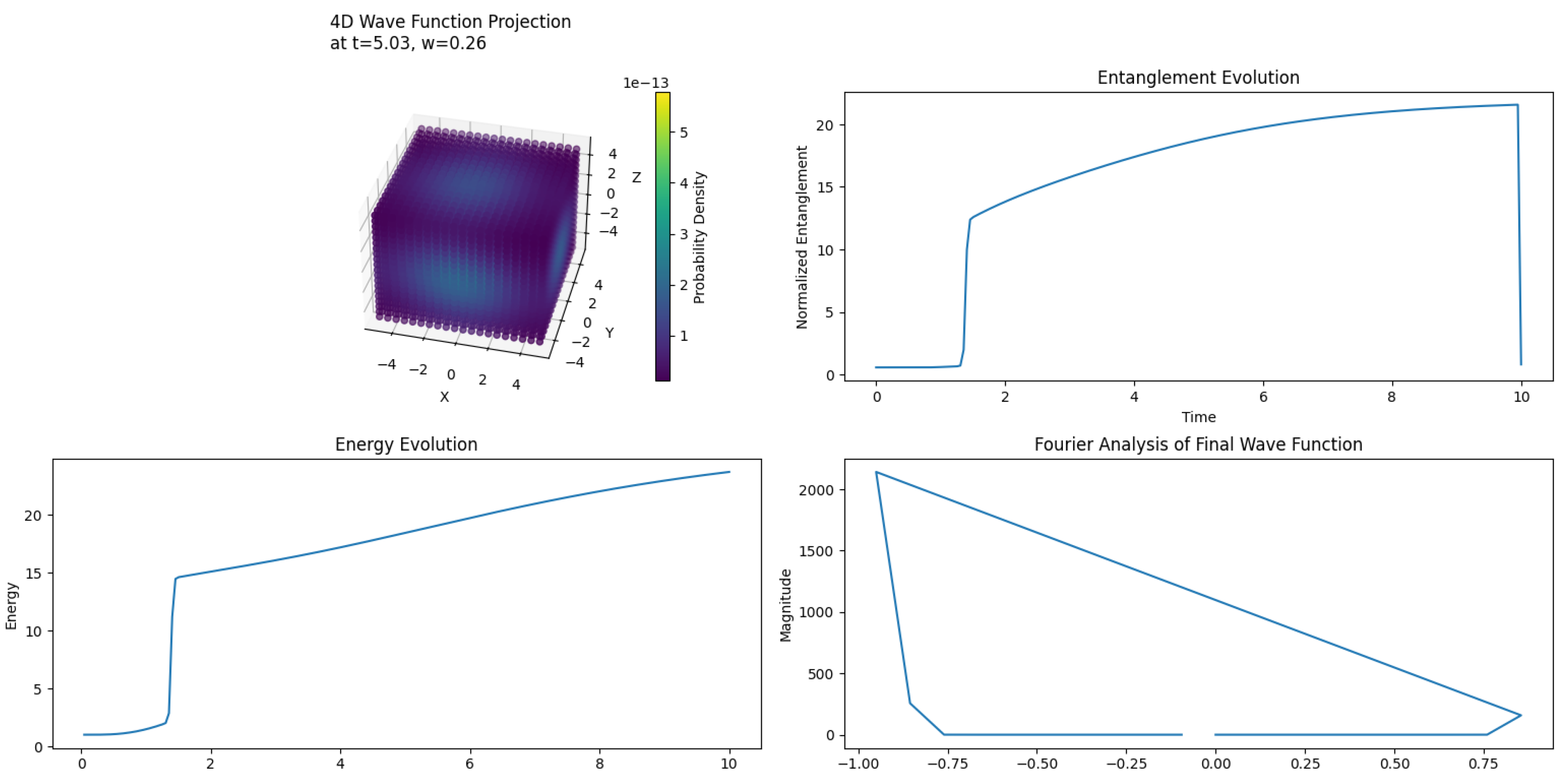
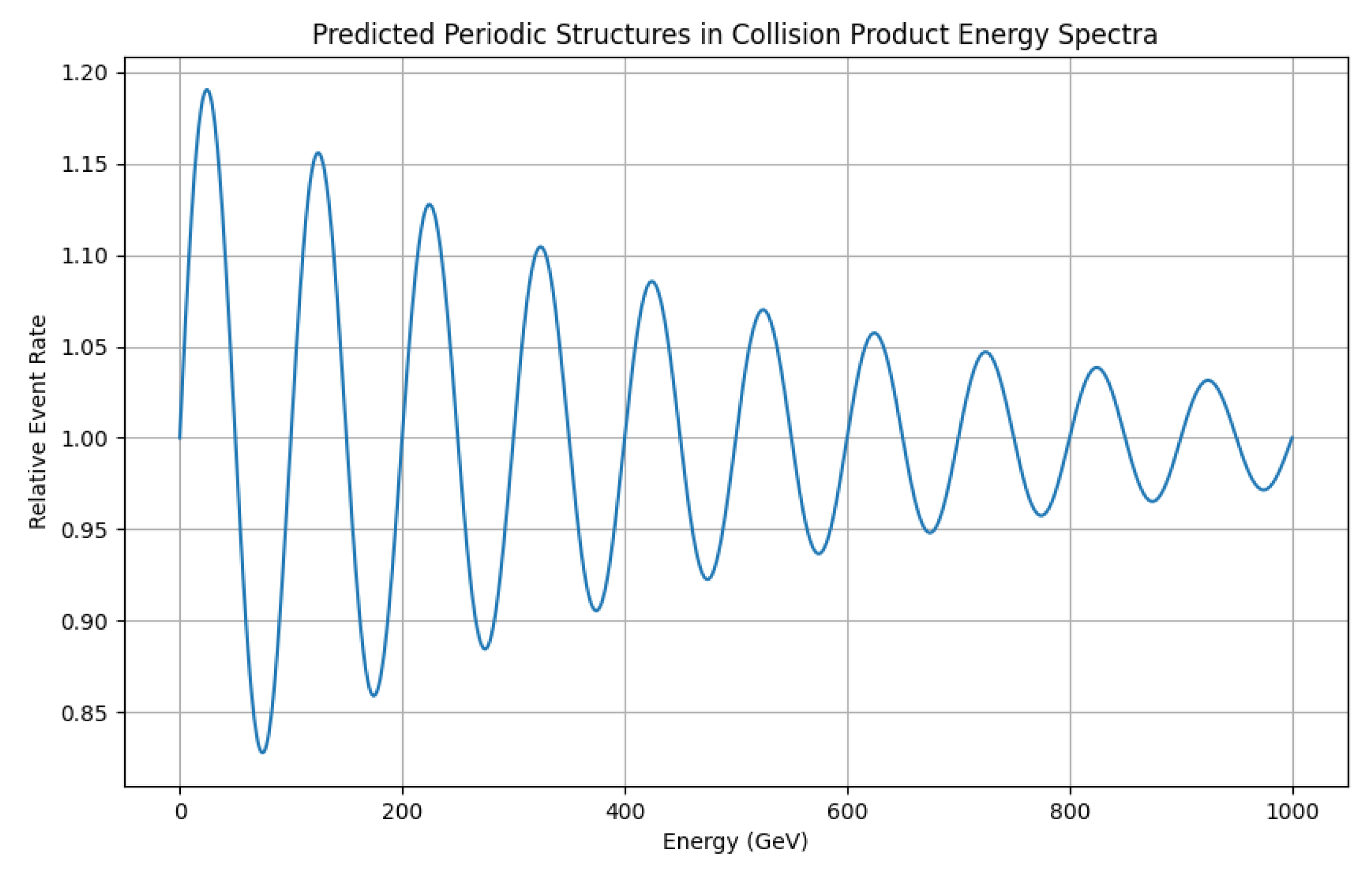
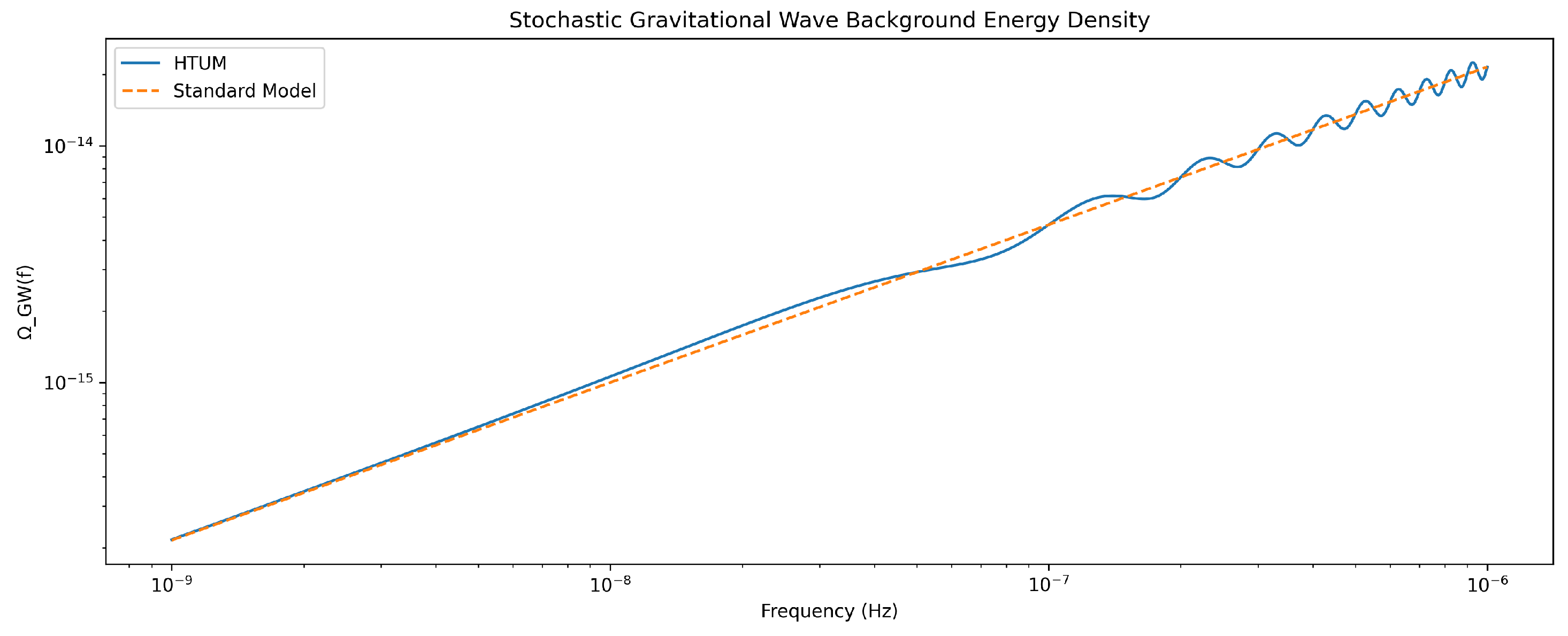
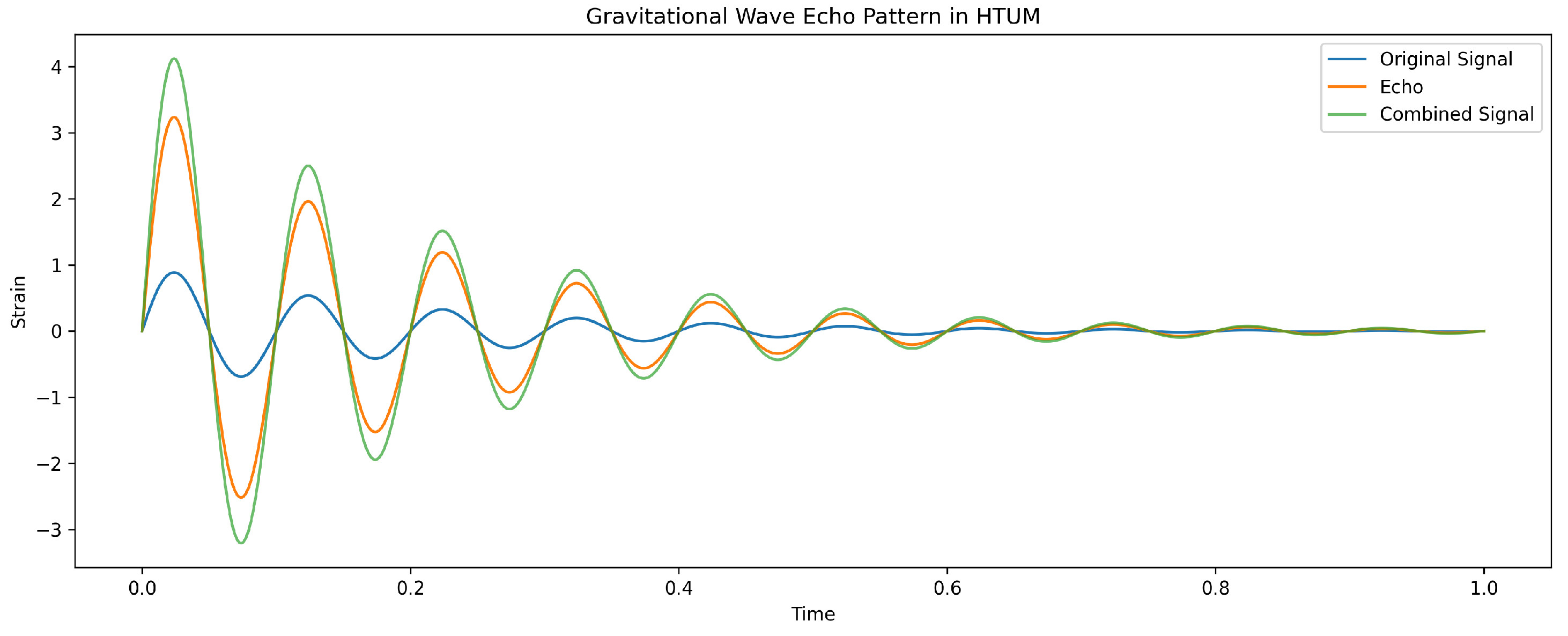
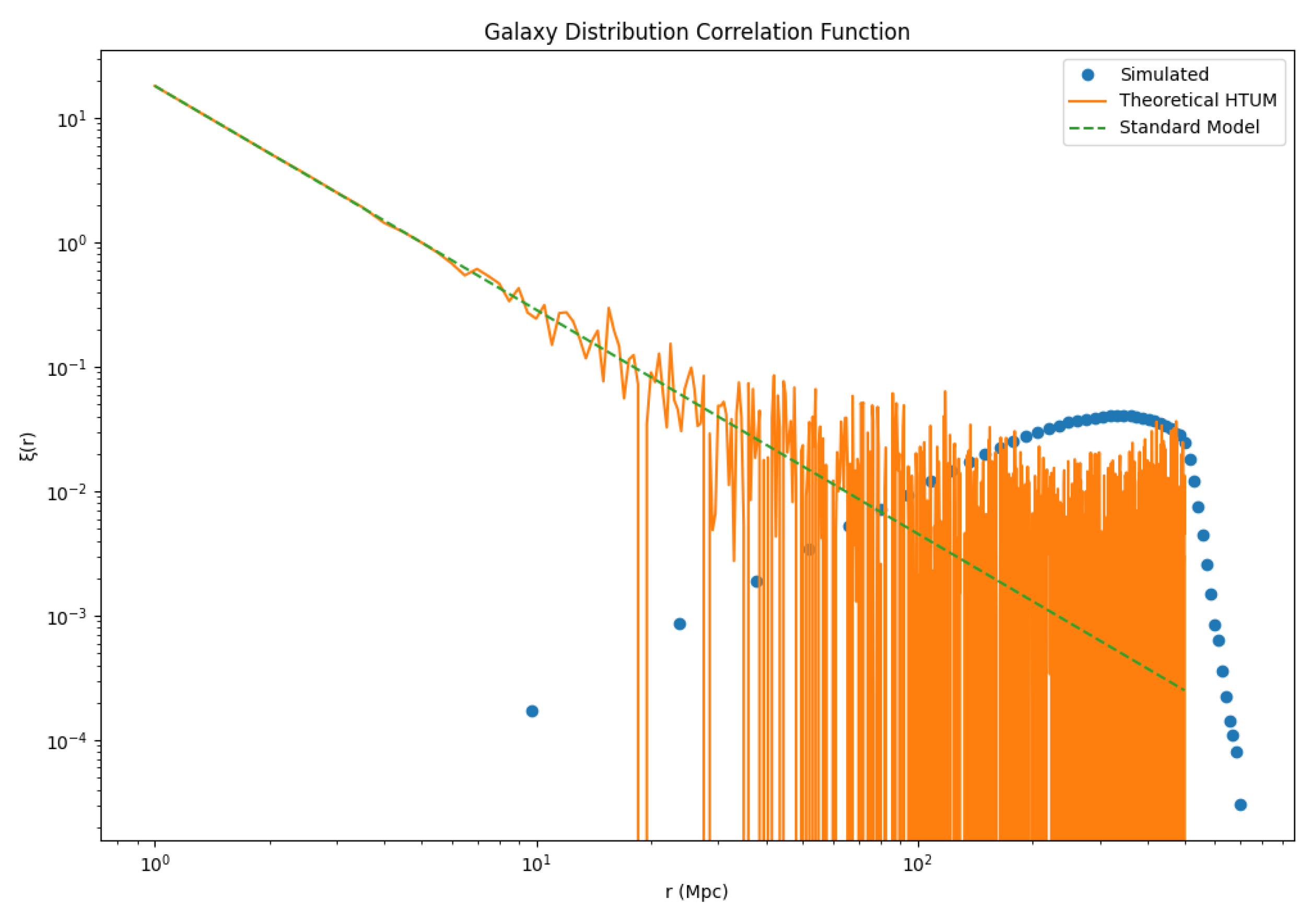
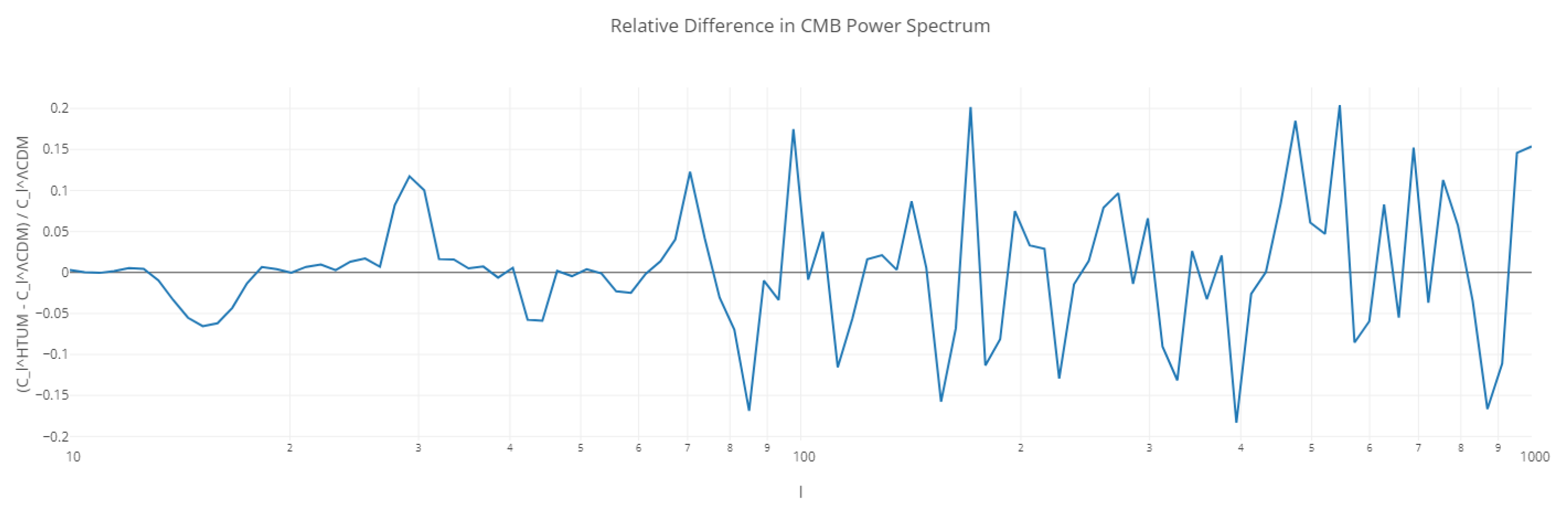
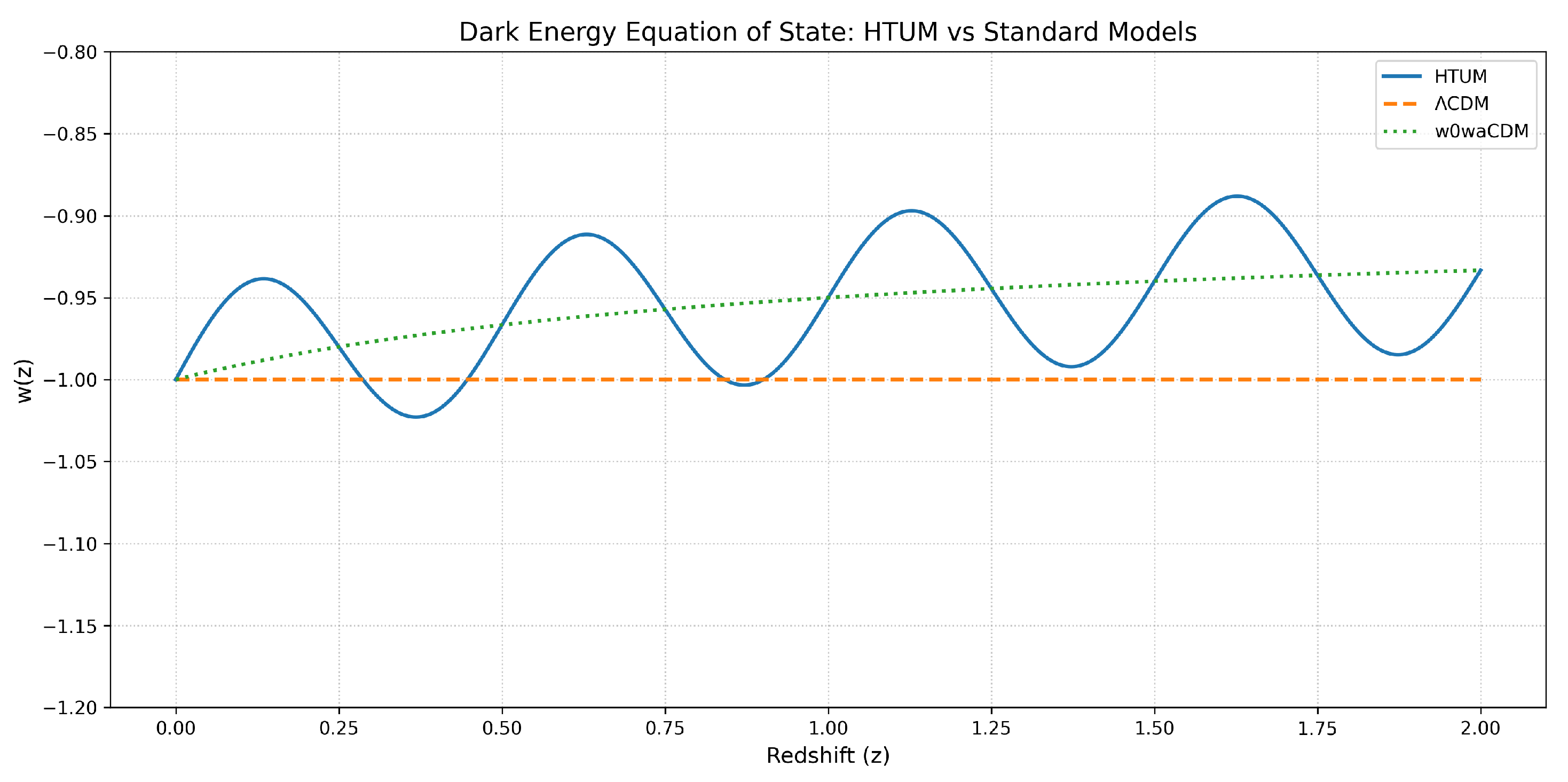

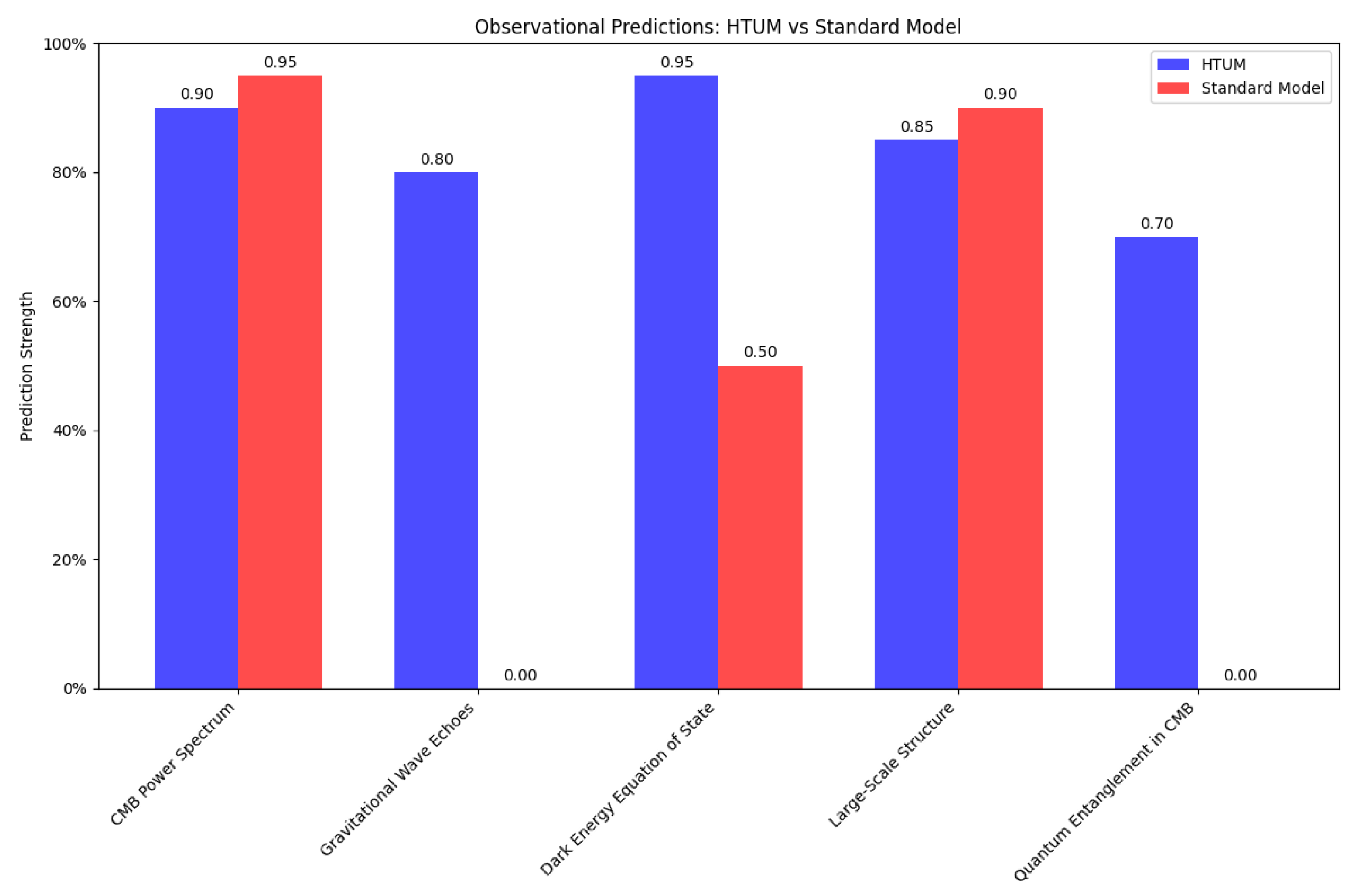
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





