1. Introduction
An important direction in modern construction is the study of lightweight concrete. The low density and high strength of such concretes distinguish them from traditional concretes. These properties make lightweight structural concrete ideal for use in a wide variety of building structures.
One of the advantages of light weight concrete for structural applications is its light weight. The use of such concrete can reduce the weight of structures and reduce the load on the foundation. This is particularly true when constructing a high-rise building or bridge structure.
The results of the experiment plan and statistical modelling indicated that it was possible to determine the optimal compositions of lightweight structural concrete using volcanic tuff. The use of statistical methods and the Design of Experiment allowed the development of a more reliable and efficient approach to determine the optimal influencing factors and properties of concrete. The study also provided insight into the variability of the optimal parameters as well as the intervals of variation of the factors. In conclusion, the results of this study can contribute to the development of more efficient and sustainable building materials.
A promising avenue of research is the use of lightweight concrete. The advantages of lightweight concretes (average density up to 1800 kg/m³) over heavyweight concretes. The primary benefits are a reduction in the weight of structures by 30-40% and an increase in the compressive strength of enclosing structures. Modern lightweight concretes can exhibit increased strength at reduced weight and belong to strength classes up to B15-20 [
1].
Volcanic tuffs represent an important local raw material base that can be utilized in the building materials industry for both masonry materials and for the preparation of masonry mortar, lightweight concrete or autoclaved aerated concrete. This paper presents the results of tests with a mathematical three-factor planning experiment conducted for lightweight structural concrete based on volcanic tuff used as aggregate.
The following study [
2] demonstrates the efficacy of polyfractional aggregate (sand and gravel up to 10 mm in size) derived from volcanic tuff in producing a rheologically stable self-compacting low-density concrete mix with a cone diameter of up to 90 cm. It is noteworthy that the utilization of polyfractional aggregate from volcanic tuff enables the creation of a rheological stable self-compacting low-density concrete mix. Moreover, the compressive strength of the hardened concrete ranged from 24-57 MPa, indicating the material’s capacity to resist compressive forces. This suggests the concrete can be utilized for structural purposes in construction. Furthermore, the average dry density of the concrete, less than 1800 kg/m³, indicates that it has a relatively low density. This can assist in reducing the overall weight of the structure, which in turn improves the material's energy efficiency. Overall, this study suggests that the use of volcanic tuff as an aggregate in the production of concrete has the potential to result in the creation of a strong, lightweight and structurally sound material.
In the aforementioned study, the proportions of the concrete mixture were defined as 1:2, 3:2, 2:2, which correspond to the quantities of cement, sand, and tuff aggregate, respectively. Consequently, the analogous proportions for conventional concrete were 1:2, 3:3.7 by mass of Portland cement, sand, and granite aggregates, respectively, in the concrete composition. The coarse aggregates of tuff and granite, occupying the same volume of approximately 63% in the unit volume of concrete, were used to determine the aforementioned mix proportions. However, it should be noted that the aggregates have different masses. Mixtures were prepared utilizing a water-cement ratio of 0.4.
The study [
4] demonstrated that tuff fillers are suitable materials for the production of low-density structural concrete with an average density of 2038 kg/m³ and compressive strength of 26.0 MPa. The compressive strength of tuff concrete exhibited a positive correlation with increasing water-cement ratio, reaching a compressive strength of 25.5 MPa at B/C ratio = 0.6. The mean density of tuff concrete is 19% lower than that of conventional concrete. Consequently, it is an appropriate material for the construction of structures with enhanced earthquake resistance.
A further study of tuff concrete examines the utilization of the waste generated during the development of volcanic tuff. This waste makes up between 30 and 50 percent by volume and can be used to produce natural porous aggregates that are currently lacking in construction. These aggregates are estimated to be missing by up to 60 million m
3 per year. Conversely, the cost of these materials will be significantly lower than that of similar concrete mortars on artificial porous aggregates. A high-quality and durable lightweight concrete is proposed for use in the manufacture of wall materials. This is to be formulated with the use of porous tuff aggregates as part of the mortar, specifically within the range of 0-5 mm and as a coarse aggregate within the range of 5-20 mm [
5].
The findings revealed that concrete comprising a 30% ratio of volcanic tuff aggregate demonstrated a 28% reduction in tensile strength compared to conventional concrete comprising limestone aggregate (R
cd = 300 kg/cm²). After 28 days of curing, these observations were recorded. In concrete production, aggregates with maximum size fractions of 10, 20 and 40 mm are utilized. It is evident that these size fractions significantly influence the strength of concrete. The relationship between the strength of concrete and the size of its aggregate fraction has been quantified. Tests demonstrated that an increase in aggregate fraction resulted in a 0.2, 5, and 14% enhancement in the strength of concrete on limestone aggregate relative to volcanic tuff [
6].
A further study [
7] also examined the possibility of using volcanic tuff as lightweight structural concrete. In order to determine the suitability of tuff for this purpose, two specimens were subjected to a series of tests. These included a determination of the tuff's specific gravity and water absorption; the measurement of its average density and porosity, which was performed in accordance with the standards set out in ASTM C29/C29M-17a; and an assessment of its readability on an abrasive machine. The analyses were conducted in the laboratories of the Department of Civil Engineering at Tafil Technical University in southern Jordan. Tuff aggregate was employed as a replacement for limestone aggregate at varying ratios, including 25%, 50%, 75%, and 100% replacement with volcanic tuff aggregate. The specimens demonstrated satisfactory porosity with a value of 0.605, corresponding to a porosity of 60.5%. The two specimens, ZT and BT, demonstrated water absorption values of 8.7% and 10.2%, respectively.
In addition, the material properties, including compressive strength and thermal conductivity, were subjected to experimental evaluation. Flow table tests were conducted in accordance with the specifications set forth in EN 12350-5 in order to produce lightweight concrete specimens with varying binders. Lightweight concrete with a density of less than 1000 kg/m
3 was produced using expanded clay lightweight aggregate and a variety of admixtures, including limestone powder, expanded clay, tuff, fly ash, and two types of sand, smooth and regular. The compressive strength of all the concretes studied by them was found to be above 18 MPa [
8].
The average void ratio of tuff samples from the studied deposits ranges from 0.12 to 0.37, with porosity values between 10 and 27 percent. The average density of the tuff samples is between 1660 and 2250 kg/m³. These values are consistent with their use as an aggregate. The high density values of the tuff samples indicate the major textural characteristics of the rock. The high void and porosity ratios in the samples indicate low density values. The compressive strength of the material was found to decrease with the increase in replacement ratio at seven days of age, with the percentage decrease observed being 11, 20, 45.8 and 53.6, respectively for replacement ratios of 5, 10, 15 and 20%. At 28 days of age, the compressive strength was observed to drop by 4.1, 9.4, 38.22 and 47.8, respectively [
9].
Upon the addition of tuff to the mixture, a slight decrease in the density of the specimens was observed, from 1700 kg/m³ (control specimen) to 1510 kg/m³. After the specimens were subjected to firing (burning) at a temperature of 900°C, the density was observed to decrease by 10.9% in comparison to the density recorded before the firing process [
10].
The specimens containing 5% zeolite tuff exhibited the highest average compressive strength over the 7-28 day period, while the specimens from the 10% group demonstrated the highest flexural strength. With regard to the specimens tested after 56 days, the highest compressive strength was observed in the 10% zeolite group, a trend that was also confirmed for the period of 90 days [
11].
The thermal conductivity of volcanic tuff is 0.55 W/m·K, as stated in the standard. This value is consistent with the results of several studies, which have shown that for higher bulk densities of about 2000-2100 kg/m³, the thermal conductivity of volcanic tuff ranges from 0.52 to 1.79 W/m·K. A comparison of the results with the standards revealed that all the tested samples exhibited a higher heat capacity than anticipated. The standards established for porous stones stipulate a specific heat capacity of 1 J/(kg·K). Consequently, the results indicate that, for instance, volcanic tuff exhibits a 30% higher heat capacity than anticipated. This is of great interest because the thermal performance of the structural system varied markedly with the specified characteristics [
12].
Nanostructured mortars with conductivity coefficients of 0.2-0.4 W/m·K were successfully produced. With the exception of the coquina mortar, the conductivity coefficients were found to be below 0.2 W/m °C, which is consistent with the category of tuff-filled insulating mortars as defined in [
13].
The hypothesis that cement concrete structures exhibit fractal characteristics was empirically substantiated. In light of the fact that the structure of concrete is susceptible to technological cracks and the potential formation of cracks between grains of aggregate, it is logical to employ the methods of mechanics of destruction in the modelling of the process of destruction. The basis of the developed model A. Griffiths is formed in concepts of Euclidean geometry. Concrete is known to have a fractal structure, which is a concept within the field of geometry. In considering the mechanisms of concrete fracture, it is important to take into account the invariant multiscale structure of the material. The hypothesis that concrete structure failure can be modelled as a discrete, quantum process has been experimentally validated [
14].
In order to ascertain the optimal characteristics of concrete and concrete mixture from their composition, and to limit the number of laboratory works, experiments are conducted utilizing mathematical methods of experimentation planning and processing of their results. The planning of an optimal experiment plan is undertaken by taking into account a number of predetermined factors. Three-factor planning models are the most prevalent models for identifying the optimal values of an output quantity, such as the compressive strength of concrete [
15]. The principles of experimental theory are of great significance in the modern world. Experimentation is a procedure for selecting the number and conditions of experiments necessary and sufficient to solve the problem with the required accuracy. In addition to the control of products, it is often necessary to control the parameters of technological processes. This task can be solved by testing statistical hypotheses. Nevertheless, the most significant impact can be achieved not by controlling quality parameters, but by organizing experiments in such a way. The objective of experimentation is to determine the minimum number of experiments and conditions required for their conduct, as well as the most appropriate methods for the mathematical processing of results and decision-making [
16].
The paper states that the organisation of experiments is of great consequence for the establishment of the minimal number of experiments, the conditions under which they are to be conducted, the selection of methods for the mathematical processing of results and decision-making. Such a goal can be achieved by subjecting statistical hypotheses to empirical testing, and controlling quality parameters.
The purpose of this article is to study the influence of volcanic tuff on the properties of lightweight structural concrete, as well as to determine the optimal compositions of such concrete, taking into account the use of tuff as a filler. The study involves developing a statistical model based on a three-factor experimental design and estimating parameters such as average density, compressive strength and thermal conductivity. Additionally, the effect of adding basalt fiber on the properties of lightweight structural concrete is investigated.
2. Materials and Methods
2.1. Materials
2.1.1. Tuff Aggregate
The research involved the use of crushed stone and sand obtained by crushing overburden volcanic rocks in jaw crushers. Subsequently, the grain mixture was subjected to sieving through a set of standard sieves, resulting in the formation of fractions. The fractions were 0.16–5 mm, 5–10 mm, and 10–20 mm. These were formed during the extraction of volcanic tuff (Chunja village, Uygur district, Almaty region) and were of lower quality, unsuitable for the manufacture of piece products. The research employed pieces of overburden volcanic rocks with a size range of 50-150 mm. In order to create aggregates, the overburden was crushed in a jaw crusher and sieved through a set of standard sieves. Consequently, aggregates were produced from tuff in fractions. The resulting fractions were 0.16-5 mm, 5-10 mm, and 10-20 mm. The first fraction corresponds to fine aggregate, which is defined as sand. The second and third fractions correspond to coarse aggregate, which is defined as crushed stone.
2.1.2. Basalt Fiber
Basalt fiber with a length of 3.2 mm was employed as a reinforcing admixture. The manufacture of basalt fiber for concrete begins with the melting of volcanic rocks at high temperatures. This process yields a high-quality natural material that is resistant to water, corrosion, fire and alkalis and chemicals.
Figure 1 shows chopped pieces of basalt fiber filament yarns for concrete.
2.1.3. Cement
The binder used in the production of lightweight structural concrete was Portland cement CEM I 32.5 H. Physical and mechanical tests demonstrated that the cement utilized corresponded to Kazakhstani quality standards, as defined by state standards GOST 310.3-76 (GOST- Government standard) [
17]. To ensure the stability and reliability of the results, the requisite quantity of cement for the entire series of experiments was determined and procured in a single transaction. The cement was stored in a dry environment to prevent the effects of moisture on its properties.
2.1.4. Superplasticizer
The MasterGlenium 51 superplasticiser additive was employed to reduce the quantity of water present in the concrete mortar, given that the incorporation of porous tuff tends to elevate the water-cement ratio (W/C). The additive was employed in all samples. The additive was employed in an amount equal to 0.8% of the weight of the cement.
2.2. Methods
2.2.1. Crushability of Volcanic Tuff Aggregate
The crushability of crushed stone is quantified through the measurement of grain destruction during a compression test, in line with the state standard GOST 8269.0-97 [
18]. The weight of the crushed stone (gravel) is poured into the cylinder from a height of 50 mm, such that after levelling the upper level of the material by approximately 15 mm, it does not reach the upper edge of the cylinder. Subsequently, the plunger is inserted into the cylinder such that the plunger plate is aligned with the top edge of the cylinder. Should the upper surface of the plunger plate fail to align with the cylinder's edge, it is necessary to either remove or add a small quantity of crushed stone (gravel) until the desired alignment is achieved. Subsequently, the cylinder is positioned on the lower platen of the press. It is recommended that the pressing force of the press be increased by 1-2 kN per second. When testing crushed stone (gravel) in a cylinder with a diameter of 75 mm, the force should be brought up to 50 kN. When testing in a cylinder with a diameter of 150 mm, the force should be increased to 200 kN. The data pertaining to the crushing process is obtained on the hydraulic press IP-1A-500, utilizing a copper cylinder with a plunger.
Calculation of tuff concrete composition was carried out according to the method given by the Departmental Construction Standards (1992) [
19].
2.2.2. Preparation of Tuff Concrete Specimens
From the compositions obtained by mathematical planning in laboratory conditions, cube samples with dimensions of 100×100×100 mm were made. The samples were manufactured in accordance with GOST 10180-2012 [
20].
2.2.3. Determination of the Average Density of Tuff Concrete Samples.
In accordance with the Government Decree, standard GOST 12730.1-78 [
21], the average density of lightweight concrete was determined. In order to calculate the density index of concrete cubes of regular shape, their volume is measured using measuring tools, such as a ruler and a caliper. In this instance, the permissible error is limited to 1 mm. In the case of irregularly shaped samples, the hydrostatic method of determining mass or the use of a volumeter is recommended. Subsequently, the volume is determined by weighing.
2.2.4. Determination of Compressive Strength of Tuff Concrete Samples
The compressive strength of the tufo concrete samples was determined in accordance with the European Standard EN 12390-3:2009 [
22]. During the compression test, the cube specimens are placed with one of the selected faces on the lower base plate of the testing machine (press), centred relative to its longitudinal axis, using the marks on the plate of the testing machine (press) or a special centering device.
Once the test specimen has been positioned on the testing machine platens or supplementary steel plates, it is necessary to align the upper platens of the testing machine with the upper support face of the test specimen, ensuring that both surfaces are in complete contact with each other. The specimen is subjected to a constant rate of load increase (0.6 ± 0.2 MPa/s) until failure.
Figure 2 presents photographic images of the tuff concrete specimen following fracture.
2.2.5. Determination of Thermal Conductivity of Tuff Concrete
The thermal conductivity of tufobeton was determined by a thermal conductivity meter, the ITP-MG4 (250), in accordance with GOST 7076-99 [
23].
The tests were conducted by measuring the temperature of both sides of the samples placed between the heater at 65 °C and laboratory conditions, in comparison to a reference material with known thermal conductivity. To ensure the accuracy of the measurements, the heat flux is determined under steady-state conditions, taking into account both heat conduction within the specimen and heat transfer through the air wall. This typically indicates that measurements were conducted approximately three to four hours after the commencement of the experiment. In this instance, six specimens with dimensions of 250×250×30 mm were prepared for the purpose of determining the thermal conductivity.
2.2.6. Determination of the Fractal Model of Concrete Strength Considering the Scale Effect
The potential for an explanation of the scale effect based on the fractal geometry of B. Mandelbrot is considered. It is demonstrated that the underlying physical essence of the scale effect can be found in the scale invariance of the structure at each scale level of the concrete structure. Consequently, the properties are found to be similar. The strength (in kilonewtons per square centimetre, megapascals) was determined on specimens in the form of cubes with dimensions of 20, 50 and 100 millimetres. Furthermore, the discrete, multilevel character of failure of concrete specimens with dimensions of 20 mm, 50 mm and 100 mm is corroborated by the deformation diagram obtained on a Wille Geotechnik testing machine (model 13-PD/104). The tests were conducted at a loading rate of 0.5 mm/min, with the measurement readings recorded at a rate of 10 readings per second.
2.2.7. Rotatable Method of Experiment Planning
In order to achieve this goal, it is necessary to determine the composition of the concrete mixture. This involves establishing the ratio between the components that form the material's structure and provide a given level of quality indicators.
The solution of such problems is carried out with the help of mathematical methods of the theory of planning the experiment. The use of these methods will allow us to obtain a mathematical model describing the dependence of quality indicators on the level of varying factors.
For the purposes of experimental study, it is recommended that a rotating central composite plan be employed in the matrix F, with n=3.
The effect of the amount of sand and demolished stone, as well as dispersed reinforcement (fiber), on the strength, average density, and thermal conductivity of tuff concrete will be investigated.
The fundamental principle underlying the three-factor planning of experiments and the optimisation of the composition of lightweight structural concrete utilising mathematical statistics is the establishment of a mathematical relationship between the given material properties and the flow rate, the properties of constituent components and the technological factors.
Table 1.
Levels of variation of influencing factors.
Table 1.
Levels of variation of influencing factors.
| No. |
Factor |
Components |
Levels of variation |
| |
|
|
-1.682 |
-1.0 |
0 |
+1.0 |
1.682 |
| 1 |
x1
|
Tuff sand (TS) |
1.318 |
2 |
3 |
4 |
4.682 |
| 2 |
x2
|
Tuff coarse aggregate (TCA) |
0.682 |
2 |
4 |
6 |
7.364 |
| 3 |
x3
|
Basalt fiber (BF) |
0.00318 |
0.01 |
0.02 |
0.03 |
0.03682 |
The efficacy of an experiment is contingent upon the meaningful formulation of the problem, the appropriate selection of research methodology, the identification of the primary factors and their variations, as well as the comprehensive interpretation of the results in a physical context. The selection of factors and parameters for the optimisation of lightweight structural concrete was based on the criteria of technological and economic feasibility.
A three-factor quadratic dependence experiment was planned, the planning conditions of which are presented in
Table 2. For all compositions, the water-cement ratio was assumed to be W/C = 0.4. In the initial stages of the study, a comprehensive factor plan was developed. Subsequently, experiments 1 to 8 were conducted. Subsequently, six parallel experiments were conducted at the centre of the plan, with experiments 15 to 20. The outcomes of these experiments provide compelling evidence that the model exhibits nonlinear characteristics. To provide a more comprehensive description, it is necessary to conduct experiments in star points (experiments 9–14).
A review of the available data suggests that the study employed an experimental design based on a full factorial plan. This involved conducting experiments at various points along the plan, as well as at the centre and at the star points. The results of the centre experiments demonstrated that the model is nonlinear, necessitating the conduct of additional experiments for a more comprehensive description. Consequently, experiments were conducted at the star points with the objective of enhancing the accuracy and completeness of the model. This iterative approach to experiment planning and data analysis is a common practice in scientific research, with the aim of ensuring the reliability and robustness of the results.
The significance of quadratic effects (nonlinearities) is confirmed by experimental data through the process of checking the conditions (Formulas 1 - 3).
Using the experimental data in
Table 2, we calculate the values of regression coefficients according to formulas 2-11. As a result, we obtain mathematical models describing the dependence of compressive strength, average density and thermal conductivity on the amount of sand, crushed stone and fiber in the form of Formulas 4-14:
The regression coefficients of the strength, average density and thermal conductivity equations are given in
Table 3.
The coded and natural values of the varied coefficients are given in
Table 4.
Statistical analysis of the obtained regression equations by F-criterion confirmed their adequacy.
The analysis of significance of regression coefficients established that the mathematical function of thermal conductivity can be simplified by taking
x3=0, and then it will have the formula 15:
The results of the experiments shown in Table 5 allow us to determine the optimal values of the coefficients
x1, x2, x3. For this purpose, we examine the obtained functions for extrema and obtain a system of equations of the formula 16:
Solving these systems sequentially, we obtain that the highest value of strength will have the composition at values (Formula 17):
The composition will have the lowest thermal conductivity if you take (Formula 18):
For this composition the compressive strength will be 8.7 MPa.
A coefficient is considered to be established if its name and area of definition are specified. In the selected area of definition, it can have several values corresponding to the number of its different states. The quantitative or qualitative states of the factor selected for the experiment are called factor levels [
24].
Compressive strength (Formula 19):
Next, we find the standard deviation (
) by expressing the Formula 20:
Which sounds as the root of the sum of squares of differences between the sample elements and the mean value divided by the number of elements in the sample.
Using Formula 20 we obtain the standard deviation for the mean values of experimental and calculated data: Std1= 8.01; Std2= 8.3.
The adequacy of the equation is checked by Fisher's criterion. The equation is adequate, because the ratio F thus compiled is less than the theoretical F (Formula 21).
Since F= 6.9>Fcr = 0.05, the model is considered adequate. Thus, all the coefficients are significant with 99% reliability.
The objective of this investigation is to examine the impact of various factors on the output parameters of lightweight structural concrete, with a particular focus on its average density and strength. The factors under investigation are the quantity of sand, crushed stone and dispersion-reinforcing admixture.
3. Results
3.1. Crushability of Volcanic Tuff Aggregate
The mass loss of the tuff following crushing was 13.5%. A special table was employed to determine the grade of the crushed rock, translating the percentage of crushability into a known grade. The grade at which it occurred is not specified. However, it may be inferred that it fell within the range of M800-M1200.
3.2. Determination of Average Density
The average density of tuff concrete, as determined by testing, is 1754.6-2112.0 kg/m³. It can be observed that the average density of formulations No. 2, 16, 18 and 20 has increased to 2114.0 kg/m
3 (
Table 5). As the ratio of components increased, the average density decreased. The lowest average density was observed in compound No. 7, with a value of 1754.6 kg/m³. There is no significant difference in the average density values of the concrete samples. The observed average density values are consistent with the values typically observed in lightweight structural concrete.
3.3. Determination of Compressive Strength
The principal findings of the experiment are presented in
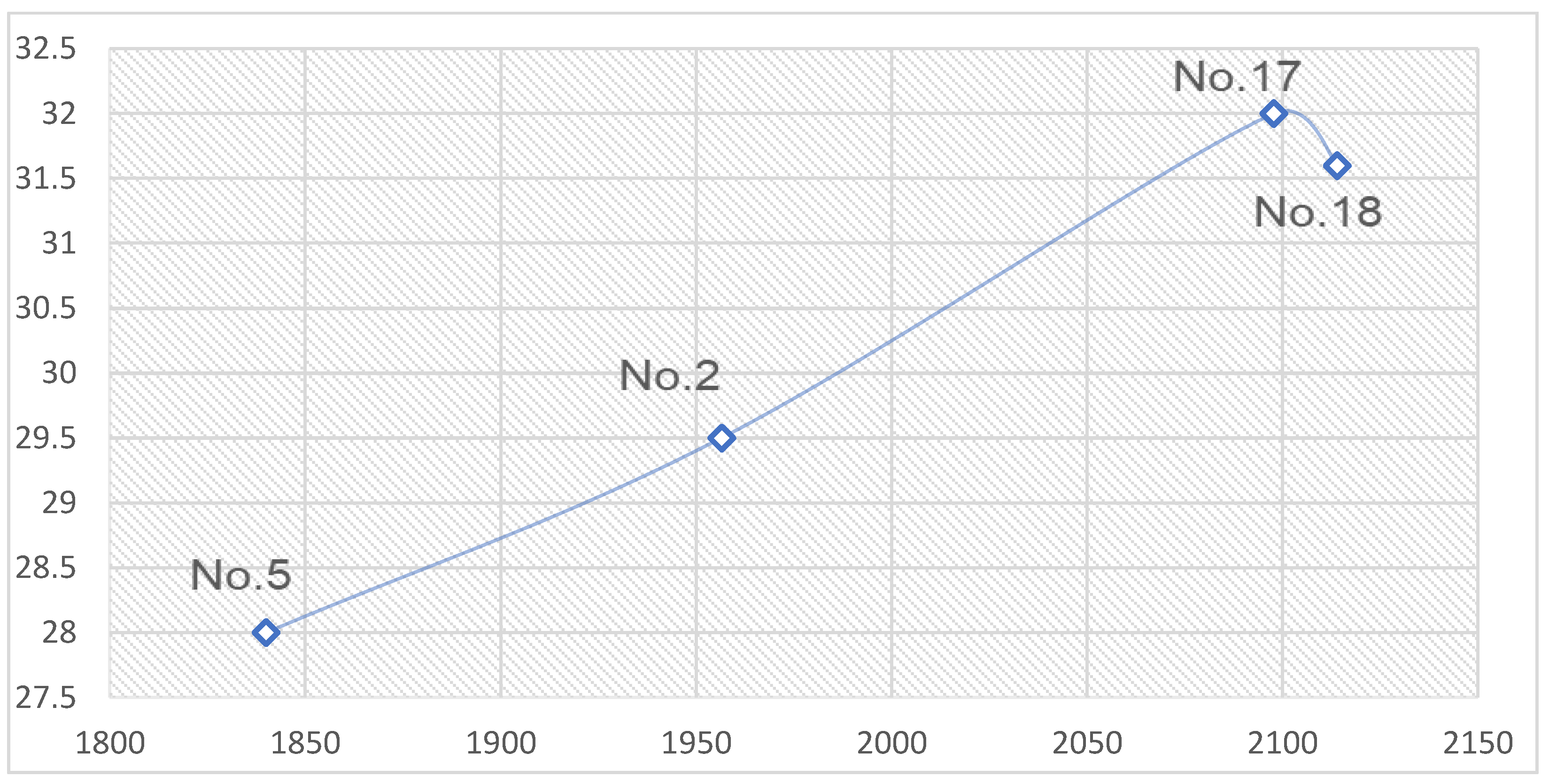
Table 5. The experiment revealed that certain compounds, namely No. 2, 5 and No. 15 to 20, exhibited higher values of compressive strength. Among the formulations, No. 17 exhibited the most pronounced increase in compressive strength, reaching 31.0 MPa after 28 days. In a comparable manner, formulations number two and number eighteen demonstrated high compressive strength values of 29.5 MPa and 31.6 MPa, respectively.
3.4. Determination of Thermal Conductivity
The thermal conductivity coefficient (λ) of lightweight structural concrete utilising volcanic tuff is found within the range of 0.661 to 0.757 W/m·K, as indicated in
Table 5. This value is notably less than that of heavy concrete with a density of 2100 to 2500 kg/m
3, which has been determined to have a thermal conductivity coefficient of 0.9 to 1.3 W/m·K.
3.5. Determination of the Fractal Model of Concrete Strength Considering the Scale Effect
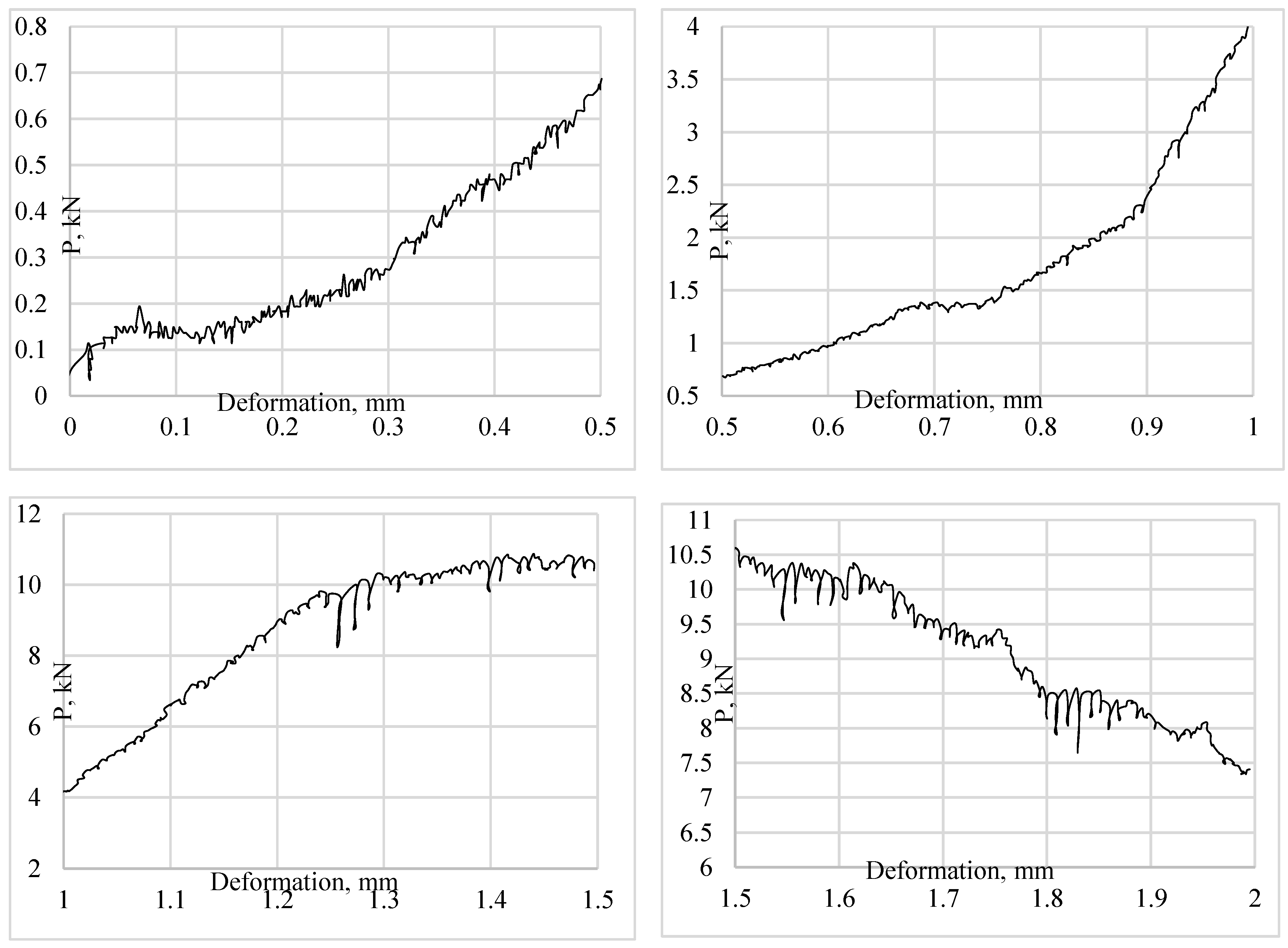
The analysis corroborates the multiscale and self-similarity of the concrete structure as an objective manifestation of the material properties, which can be quantified by the fractal dimension. The presented graphs (
Figure 2) demonstrate that the deterioration of the structure of the samples occurs gradually rather than instantaneously. The peaks denoting the moment of destruction exhibit an enlarged form, exhibiting both an increase and a decrease in amplitude. However, the graph demonstrates a fluctuating pattern as the structure is progressively dismantled.
Figure 3 presents four enlarged sections of the same graph. The figure depicts the fracture graph of samples with dimensions 50x50x50 mm.
Table 7 shows the values after testing specimens with the same composition at 7 days of age. We can see the influence of scale effect on the properties of tuff concrete specimens depending on their size.
4. Discussion
Based on the analysis of previously obtained data using mathematical planning of experiments, the optimal compositions of lightweight structural concretes using volcanic tuff were determined. In accordance with the constructed three-factor experiment plan, actual tests were conducted and the most optimal compositions of tuff concretes were identified.
Research was conducted to determine the optimum compositions of lightweight structural concretes using volcanic tuff. Mathematical planning of experiments was used in the study to identify the most optimal tuff concrete compositions based on the results of actual tests.
The study was conducted using a rotational plan with three variables that included varying factors: sand (TS), crushed stone (TCA), and basalt fiber (BF). By manipulating these factors, the study was able to identify the most optimal tuff concrete compositions.
It is likely that the results of this study can be utilized in the tuff concrete production process, helping to ensure that the final product is of high quality and meets the desired specifications. In addition, the results can be used to optimize the use of materials and resources, resulting in cost savings and increased efficiency.
A calculated crushed stone grade in the range of M800-M1200 means that tuff aggregate has favorable characteristics for construction work requiring durability and strength. This means that the aggregate can be used effectively in the production of concrete, asphalt and other building materials where high quality aggregates are required. It also indicates that tuff aggregate has the potential to meet the performance requirements of engineering projects requiring durable and stable materials.
The tests conducted showed a range of average densities for the volcanogenic tuff concrete from 1754.6 to 2112.0 kg/m3. It is particularly noteworthy that compounds No. 2, 16, 18 and 20 revealed higher average densities reaching 2114.0 kg/m3. In contrast, compound No. 7 had the lowest average density of 1754.6 kg/m3. These differences in density across formulations emphasize the effect of the component ratio on the overall density of the concrete.
Based on the information provided, it can be concluded that the optimum formulations to achieve high compressive strength values in lightweight structural concrete using volcanic tuff as filler are formulations No. 2, 5, 17 and 18. Among these compositions, No. 17 showed the highest increase in compressive strength, reaching 31.0 MPa after 28 days, followed by compositions No. 2 and No. 18 with compressive strength values of 29.5 MPa and 31.6 MPa, respectively. Hence, these compositions can be recommended for use where high compressive strength is required.
According to our analysis, compositions No. 2 and 5 showed good results due to the correct ratio of components. The correct amount of coarse aggregate, fine sand aggregate and reinforcing basalt fiber gave an optimum composition with good performance characteristics. The parallel compositions from 15 to 20 had similar proportions in the composition. These compositions have approximately the same density and thermal conductivity. Although the strength values differ by 2 to 3 megapascals. From
Figure 4, we can see that the strength values are higher depending on the increase in concrete density.
It is hypothesized that the amount of volcanic aggregate used in the compositions may have contributed to these higher compressive strength values. In particular, as the amount of fine aggregate (i.e., volcanic tuff sand) increases, the bond between fine and coarse aggregate decreases, which could result in lower compressive strengths. However, this trend does not seem to be reflected in the results obtained for formulations No. 2, 5, 17 and 18, suggesting that other factors may be influencing the compressive strength of these formulations.
Assuming that it is still a matter of compressive strength to density ratio, it is possible that the optimum values of these properties were obtained from the studies carried out on formulations No. 2, 5, 17 and 18. Based on these results, a statistical relationship between compressive strength and density of concrete in the dry state was obtained.
It is worth noting that the relationship between compressive strength and density is important because it can affect the overall performance of concrete. For example, if the density of concrete is too low, it may not be able to withstand heavy loads, which can lead to structural failure. Conversely, if the density is too high, the concrete may become brittle and more prone to cracking.
When basalt fiber reinforcement was added to lightweight structural concrete using volcanic tuff, studies were conducted that included scanning electron microscope examination of the samples. The images obtained (
Figure 5) provide valuable information on the microstructure and interaction of the components of this composite material. Raster image analysis allows us to study the dispersion of basalt fibers in the concrete matrix. The fibers have a fine but strong structure, which contributes to the strength and fracture resistance of the concrete. The images also show how the fibers interact with other components such as cement and aggregates to form strong bonds that can hold various loads and prevent cracking and failure.
Volcanic tuff helps to improve mechanical properties and reduce the weight of the structure. In general, the use of basalt fiber and volcanic tuff in lightweight structural concrete makes it possible to create a material with improved mechanical characteristics, increased strength and resistance to destruction. This opens new perspectives for the development of lightweight and strong building structures using innovative composite materials.
Apparently, the thermal conductivity values of the manufactured concrete samples using volcanic tuff decreased with increasing volume fraction of tuff, their thermal conductivity was lower than that of conventional heavy concrete by about 40-50%. The thermal conductivity of concrete is not only affected by the property of volcanic tuff, but also small permeable voids, and the use of basalt fiber can also limit the heat transfer.
As we can see from the test results, the lowest thermal conductivity has the compositions No.7 (0.687 W/m·K), No.8 (0.653 W/m·K) and No.12 (0.661 W/m·K). values among all the specimens. We can see that as the amount of aggregate in the form of volcanic tuff increases, the thermal conductivity values decrease. But we also see that these compositions have the lowest compressive strength.
Also for the optimal composition of lightweight structural concrete with volcanic tuff because of the optimal compressive strength and thermal conductivity, we take compositions No. 2, 5, 17 and 18.
According to the results of the study, the area of the most optimal values of components of lightweight structural concrete with volcanic tuff is determined. Analyzing the above data, we take the most optimal compositions No. 2, 5, 17 and 18. Compound No. 2 has a high compressive strength (29.5 MPa), low average density and the lowest thermal conductivity (0.744 W/m-K). Compound No.5 has the lowest average density (1840 kg/m3) at high strength values. Compound No.17 has the highest compressive strength (32.0 MPa) and lower average density than normal concrete.
Concrete consists of various components such as cement, aggregates and reinforcing materials. Various stresses and loads can cause the bonds between these components to break, resulting in the failure of the concrete structure. Concrete matrix is a bonding material containing reinforcing materials. Exposure to load can cause the concrete matrix to fracture and crack.
The assumption of fractal structure of cement concrete with volcanic tuff is experimentally justified. The mechanism of concrete fracture taking into account the invariant multiscale structure of the structure is considered. The discrete process of concrete structures failure has been experimentally confirmed. Depending on the size of the specimens made of tuff concrete, different strength indices for the same composition were obtained. The specimens with the smallest dimensions showed higher strength even after taking into account the correction factor. According to the test results, we observe an increase in strength for specimens with 20 mm faces in contrast to specimens with 50, 100 mm faces.
Using the constructed graphs, when determining 10 indices per second, we realize that concrete failure occurs gradually, in other words, the individual blocks of the structure fail fractally. This gives us a better understanding of the mechanical failure of the structure.
5. Conclusions
The dependency parameters and objectives of the optimized influencing factors have been determined. The intervals of variation of the factors are selected. The plan and conditions of the experiment are chosen. Processing the experimental results were carried out with the construction of mathematical models of dependence of concrete mixture and concrete properties on the selected factors. For a complete analysis of the experiment, a nomogram of optimization of the composition and technological process was constructed. The results were used to draw the following conclusions:
- -
In the experimental plan, the mean value of the data in the center of the plan is higher than the mean value of the obtained data in the core of the three-factor plan. This indicates the non-linearity of the constructed matrix. For this reason, star scores (+1.682; -1.682) were added to the experimental plan.
- -
By means of calculations and determination of Fisher's coefficient (F= 6.9 > Fcr= 0.05) and Student's coefficient, the adequacy of the constructed experiment plan was proved;
- -
The mass loss in crush tests of tuff aggregate was 13.5%, which corresponds to the strength grade M800-M1200.
- -
The average density of lightweight structural concrete using volcanic tuff was from 1754.6 to 2112.0 kg/m3.
- -
The main performance properties of lightweight structural concrete with volcanic tuff filler were studied: compressive strength R = 8.0...32.0 MPa. Optimal compositions No.17 and 18 showed the highest strength ratings of 32.0 and 31.6 MPa, respectively.
- -
The thermal conductivity λ = 0.653...0.841 W/(m·K), which corresponds to the normative values and exceeds the characteristics of traditional lightweight structural concrete due to the optimized concrete structure by using the developed and optimized composition. No. 2 and 5 with values of 0.744 W/m·K and 0.774 W/m·K were selected for the optimal composition in terms of thermal conductivity.
- -
The assumption of fractal structure of cement concrete using volcanic tuff was experimentally substantiated on the compositions and samples No. 2, 5, 17 and 18.
- -
This experimental validation of the fractal structure of cement concrete with volcanic tuff confirms the assumption of its fractal nature. The consideration of invariant multiscale structure in the failure mechanism of concrete provides insight into the discrete failure process of concrete structure, which further deepens our understanding of concrete behavior under different loading conditions.
Based on the experimental results and analysis of physical properties, it is concluded that the optimum compositions of lightweight structural concrete using volcanic tuff are No. 2, 5, 17 and 18. These compositions showed the highest values of compressive strength, with composition No.17 showing the highest value of 32.0 MPa after 28 days. At the same time, the thermal conductivity values of these compositions were within the normative values and exceeded the characteristics of traditional lightweight structural concrete due to the optimized concrete structure through the use of the developed and optimized composition. Therefore, these optimized compositions are recommended for use in structural applications where high strength and thermal insulation properties are required.
Author Contributions
Conceptualization, Y.Y.K. and M.T.Z.; methodology, Y.Y.K. and Z.O.Z.; software, Y.Y.K; validation, Y.Y.K., M.T.Z. and Z.O.Z.; formal analysis, Y.Y.K. and Z.O.Z.; investigation, Y.Y.K. and M.T.Z.; resources, Y.Y.K., E.I.K. and Z.O.Z.; data curation, R.E.N.; writing—original draft preparation Y.Y.K. and Z.O.Z.; writing—review and editing, M.T.Z., E.I.K.; visualization, Z.O.Z. and R.E.N.; supervision, E.I.K.; project administration, E.I.K. and R.E.N.; funding acquisition, E.I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. BR21882292—“Integrated development of sustainable construction industries: innovative technologies, optimization of production, effective use of resources and creation of technological park”).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bychkov, V.M.; Udodov, S. “Deformation properties of light self – compacting concrete”. Herald of Dagestan State Technical University Technical Sciences Dagestan, Russian Federation 2013, 29, 71–76. [Google Scholar] [CrossRef]
- Dipayan, J. “A New Look To An Old Pozzolan: Clinoptilolite - A Promising Pozzolan In Concrete”. In Proceedings of the twenty-ninth conference on cement microscopy, Quebec City, Canada 2007, 168-201. https://www.researchgate.net/publication/267389103_A_new_look_to_an_old_pozzolan_Clinoptilolite_-_A_promising_pozzolan_in_concrete.
- Bychkov, M.V. “Low-Density Self-Compacting Concretes Using Volcanic Tuff”. Journal Engineering Herald of the Don 2013, 128-141. http://ivdon.ru/uploads/article/pdf/Bychkov_Udodov.pdf_1774.pdf.
- Sang, G.K.; Abuodha, S.O.; Mwero, J.N. “Investigating The Potential Use of Tuff Aggregates to Produce Lightweight Concrete”. International Journal of Scientific and Research Publications 2020, 10, 458–478. [Google Scholar] [CrossRef]
- Aliev, S.; Murtazaev, S.; Salamanova, M.; Saidumov, M. “The Use Of Waste Mining Volcanic Tuff To Produce Modern Concrete Composites”. Ecology and Industry of Russia 2017, 32–35. [Google Scholar] [CrossRef]
- Jehad, A.Z.; Kamel, K.A. “Effect Of Volcanic Tuff On The Characteristics Of Cement Mortar”. Al-Huson University College, Al-Balqa' Applied University 2014, 279-284. [CrossRef]
- Reyad, A.; Al Dwairi, B.A.S.; Fathi, S.; Mohmd, S. “Characterization Of Jordanian Volcanic Tuff And Its Potential Use As Lightweight Aggregate”. Jordan Journal of Earth and Environmental Sciences 2018, 127-133. https://jjees.hu.edu.jo/files/Vol9N2/JJEES_Vol9N2_P7.pdf.
- Chung, S.Y.; Elrahman, M.A.; Stephan, D.; Kamm, P.H. “The Influence Of Different Concrete Additions On The Properties Of Lightweight Concrete Evaluated Using Experimental And Numerical Approaches”. Construction and Building Materials 2018, 189, 314–322. [Google Scholar] [CrossRef]
- Walid, F.E.; Safwat, A.; Ahmed, H.E.S.; Abd Al-Kader, A.A. “Concrete Behaviour With Volcanic Tuff Inclusion”. Civil Engineering and Architecture 2021, 9, 1434–1441. [Google Scholar] [CrossRef]
- Cobirzan, N.; Thalmaier, G.; Balog, A.A.; Constantinescu, H.; Ceclan, A.; Nasui, M. “Volcanic Tuff as Secondary Raw Material in the Production of Clay Bricks”. MDPI, Processing of End-of-Life Materials and Industrial Wastes 2021, 14, 6872. [Google Scholar] [CrossRef]
- Szulej, J.; Ogrodnik, P.; Klimek, B. “Zeolite Tuff and Recycled Ceramic Sanitary Ware Aggregate in Production of Concrete”. Sustainable Civil Engineering Materials 2019, 11, 1782. [Google Scholar] [CrossRef]
- Barbero-Barrera, M.M.; Flores-Medina, N.; Moreno-Fernández, E. “Thermal, Physical and Mechanical Characterization Of Volcanic Tuff Masonries For The Restoration Of Historic Buildings”. Mater. Construcc 2019, 69, 179. [Google Scholar] [CrossRef]
- Bogas, J.A.; Cunho, D. “Non-Structural Lightweight Concrete With Volcanic Scoria Aggregates For Lightweight Fill In Building’s Floors”. Construction and Building Materials 2017, 135, 151–163. [Google Scholar] [CrossRef]
- Selyaev, V.P.; Selyaev, P.V.; Gryaznov, S.Y.; Averkina, M.Y. “Strength and Fracture Mechanics of the Fractal Structure of Concrete”. EXPERT: THEORY AND PRACTICE 2023, 1, 35–43. [Google Scholar] [CrossRef]
- Pizhurin, A.A.; Rosenblit, M.S. “Research Of Woodworking Processes”. Forest industry 1984, 224–232. https://rusneb.ru/catalog/010003_000061_9e1f25ad65d6aa599b78a5c811cbe162/.
- Hartman, K.; Schnefer, W. “Planning The Experiment In The Study Of Technological Processes”. Publishing house MIR 1977, 553. https://lib-bkm.ru/13439.
- GOST 310.3-76 (2003) “Cements. Мethods For Determination Of Standard Consistency, Times Of Setting And Soundness (As Amended By N 1)”.
- GOST 8269.0-97 (2018) “Mauntainous Rock Road-Metal And Gravel, Industrial Waste Products For Construction Works Methods Of Physical And Mechanical Tests”. Published: SUE CPP GUP (CPP GUP 1998).
- Departmental Construction Standards (1992) “Application Of Concretes On Natural Porous Aggregates For Construction Of Transport Tunnels”. VSN, 212-91, 57.
- GOST 10180-2012 (2012) “CONCRETE. Methods for determining strength using control samples”.
- GOST 12730.1-78 (1978) “CONCRETE. Methods for density determination”.
- EN 12390-3: (2019) “Testing Hardened Concrete - Part 3: Compressive Strength Of Test Specimens”.
- GOST 7076-99 (2000) “Building Materials And Products. Method Of Determination Of Steady-State Thermal Conductivity And Thermal Resistance”.
- Spirin, N.A.; Lavrov, V.V.; Zainullin, L.A.; Bondin, A.R.; Burykin, A.A. “Methods Of Planning And Processing The Results Of Engineering Experiments: A Training Manual”. Ekaterinburg: LLC "UNITS" 2015, 290. https://elar.urfu.ru/handle/10995/39965.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).