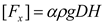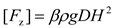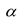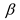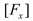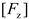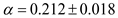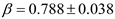1. Introduction
Oceans are the Earth’s largest receivers of solar energy and contain various renewable energy sources such as ocean wind, wave, tidal, temperature, and salt. Wave energy is particularly important for mitigating the energy crisis and environmental pollution, thus rendering its development and utilization essential. To extract and convert wave energy, various wave-energy-conversion technologies have been developed. Owing to its simple structure, few underwater moving components, and low maintenance costs, the OWC device is a promising option [
1]. The hydrodynamic performance of OWC devices has been investigated extensively over the past few decades. For instance, Bayoumi et al. [
2] developed a numerical wave energy prediction tool that was experimentally validated for an offshore Spar-Buoy OWC and discovered that the predictions aligned with the experimental results outside the resonance frequency. Evans [
3] assumed that the water surface width within an OWC chamber was significantly smaller than the wavelength; thus, they disregarded the wave-surface variation within the chamber and reduced the wave-surface motion to a rigid piston motion to ensure energy-conversion efficiency. Martins-rivas et al. [
4] investigated the effects of the shoreline angle of incident and reflective waves on power-generation efficiency under a constant water depth and a bluff coast. Nader et al. [
5] used the finite-element method to simulate single and multiple OWC devices and reported that the proximity of the devices significantly affected the power-generation efficiency. Dimakopoulos et al. [
6] developed a simple three-dimensional (3D) OWC model based on potential flow theory to investigate the effect of air compressibility on energy-conversion efficiency while considering air compressibility. Xu et al. [
7] investigated the wave-energy extraction of a 3D OWC device with a secondary power output model using physical model tests and theoretical analysis and observed that spatial non-uniformity and viscous losses significantly affected shorter waves. Hu et al. [
8]established a two-dimensional (2D) model of an offshore OWC with a rectangular chamber and used theoretical and numerical methods to examine the effects of immersion depth and chamber width on energy-conversion efficiency; their results indicated that the frequency of the peak efficiency decreased with increasing immersion depth.
However, studies regarding forces exerting on OWC wave-energy devices and related studies are few. Ashlin et al. [
9] performed physical model tests on a fixed 2D OWC to investigate wave forces in both the horizontal and vertical directions. They discovered that the peak horizontal wave forces on the OWC structure were 2.5 to 3 times higher than the peak vertical wave forces. Jakobsen et al. [
10] performed a wave-loading analysis on a hemispherical point absorber by conducting both physical model tests and numerical simulations. Elhanafi [
11] performed computational fluid dynamics (CFD) simulations to investigate wave forces on a fixed 2D rectangular OWC and observed that the horizontal wave force consistently exceeded the vertical wave force, regardless of the variation in the incident wave height and wave period. The effect of viscosity on wave force was investigated by adding an artificial viscous term to a 2D OWC through numerical simulation, which showed that the effect of viscosity on the total horizontal wave force at the front wall increased with the front wall draft [
12]. Ning et al. [
13] investigated the wave force on a 2D OWC via physical model tests and numerical simulations, where they demonstrated that the total wave force decreased with increasing wavelength and increased with increasing incident wave height. Additionally, they discovered that the wave force was affected significantly by the opening rate, with higher opening rates resulting in smaller wave forces in the low-frequency region, whereas the opposite trend was observed in the high-frequency region.
The 3D circular OWC device research has mostly concentrated on energy conversion efficiency with little attention given to force laws. Deng et al. [
14,
15] and Zhou et al. [
16] investigated the energy conversion efficiency of a 3D circular OWC using the eigenfunction-expansion method. Huang et al. [
17] as well as Xv and Huang [
18] investigated the flow-field characteristics near an OWC device. He et al. [
19,
20] experimentally verified the energy-conversion efficiency of a 3D circular OWC using a physical model. Zhou et al. [
21] investigated the energy-conversion efficiency and hydrodynamic performance of a 3D circular OWC device via numerical simulations. Zhou et al. [
22] investigated the energy-conversion efficiency and force characteristics of a 3D circular OWC device both experimentally and numerically. several researchers [
23,
24,
25] integrated a circular OWC and investigated its power-generation efficiency.
Studies pertaining to 3D circular OWC devices focus primarily on energy-conversion efficiency [
14,
15,
16,
19,
20,
22,
23,
24,
25] and flow-field characteristics [
17,
18], whereas force laws are focused less. Most previous studies regarding the force laws of OWC devices are restricted to 2D models, such as fixed 2D OWC devices [
9,
11,
12,
13]. These models cannot account for the complexity of 3D space; hence, their force characteristics cannot be utilized to analyze the forces of 3D OWC devices. In addition, experimentally verifying the overall forces of 3D OWC devices is difficult, thus rendering numerical simulations an ideal method for evaluating them.
Huang et al. [
26] investigated the forces exerting on 3D circular OWC devices under wave loading via numerical simulations. The results showed that wave loading is insensitive to changes in wavelength and period but increased with wave height. Although Huang et al. [
26] extensively investigated the force law of a 3D circular OWC device, they did not provide a quantitative law for the variation in force with wave height of the OWC device. Moreover, they did not investigate the effects of water depth on the force of the OWC device or the variation in the dynamic water pressure of the device.
Therefore, the objective of this study is to perform a more detailed examination and analysis of 3D OWC force laws. In Section I, the numerical modeling of a 3D circular OWC device is presented. In Section II, the accuracy of the model is verified. In Section III, the effects of wave period, wave height, and water depth on the forces in the OWC are analyzed, and conclusions regarding the effects of wave height on the forces in the OWC are provided; subsequently, the dynamic water pressure in the internal and external front walls of the OWC is analyzed. In Section IV, the conclusions are summarized and future endeavors are presented.
2. Materials and Methods
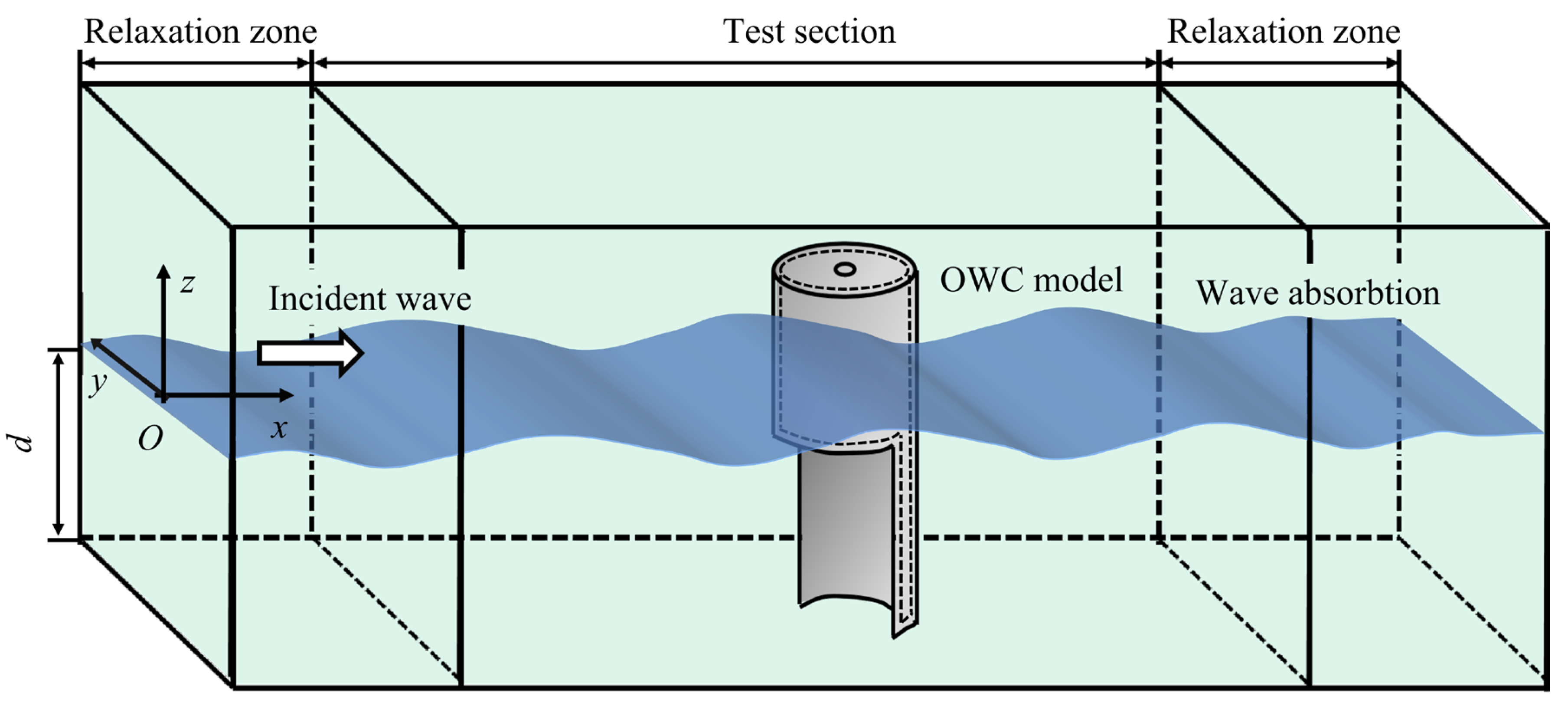
In this study, a 3D wave flume was developed using potential flow theory and the finite-volume approach for wave interactions with a 3D circular OWC-type device supported by a bottom-sitting C-shaped structure. The Cartesian coordinate system was established at the intersection of the static water surface (water depth
d = 0.3 m) and the midline of the flume side, i. e., the center point of the flume left-end rectangle, with the positive z-axis oriented vertically upward and the positive x-axis oriented horizontally to the right. A 3D diagram of the numerical wave tank is shown in
Figure 1. The device was placed at the center of the sink’s calculation area.
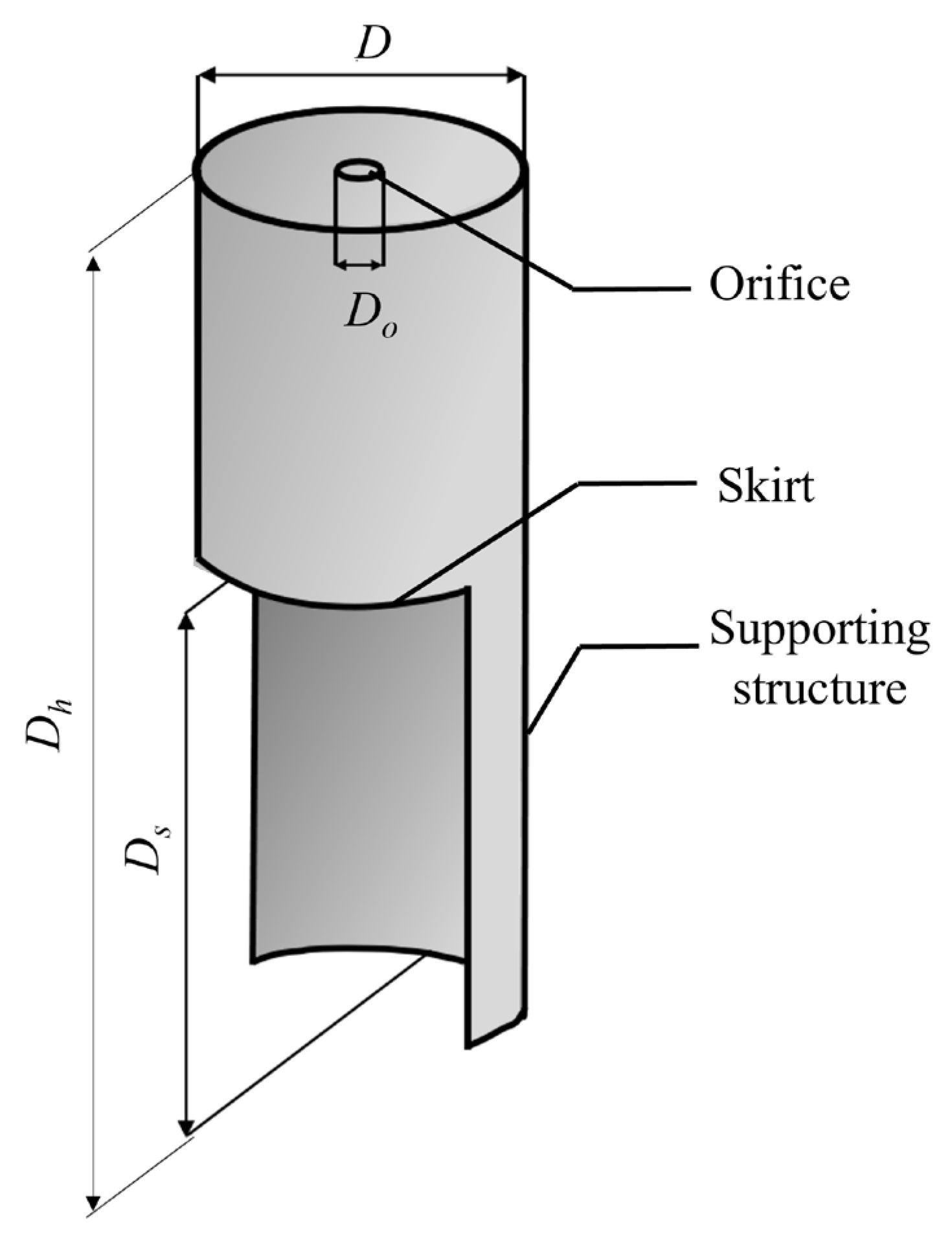
D,
DO,
Ds, and
Dh represent the outer diameter of the device, the diameter of the upper orifice, the size of the lower opening, and the column height, respectively (see
Figure 2).
The numerical model was based on OpenFOAM, with wall boundaries at the front and back of the flume, the bottom, and OWC units; and patch boundaries at the top, left, and right of the flume. The velocity inlet and pressure outlet were placed on the left and right sides of the flume, respectively, and the top of the flume was imposed with both the velocity-outlet and pressure-outlet boundary conditions (pressureInletOutletVelocity). Meanwhile, the waves2Foam relaxation zone technology was used to generate and eliminate waves [
27]. The role of the relaxation zone is to distribute weights between the calculated and theoretical values, as well as to create and eliminate waves through the transition between analytical and CFD solutions; therefore, an appropriate length of the relaxation zone for wave creation and elimination is required.
The length of the flume in this numerical model was set to 15 m, the width and height were set to 0.6 m, and the lengths of the left and right waveform relaxation zones were set as twice the wavelength
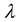
. The spatial step
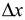
in the x-direction was set to
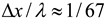
. In the z-direction,
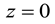
was set as the reference point. The area above and below the reference point at twice the length of the wave height 2
H was encrypted, where the spatial step
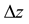
in the encrypted area was set to
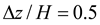
, and the spatial step in the non-encrypted area was set to
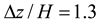
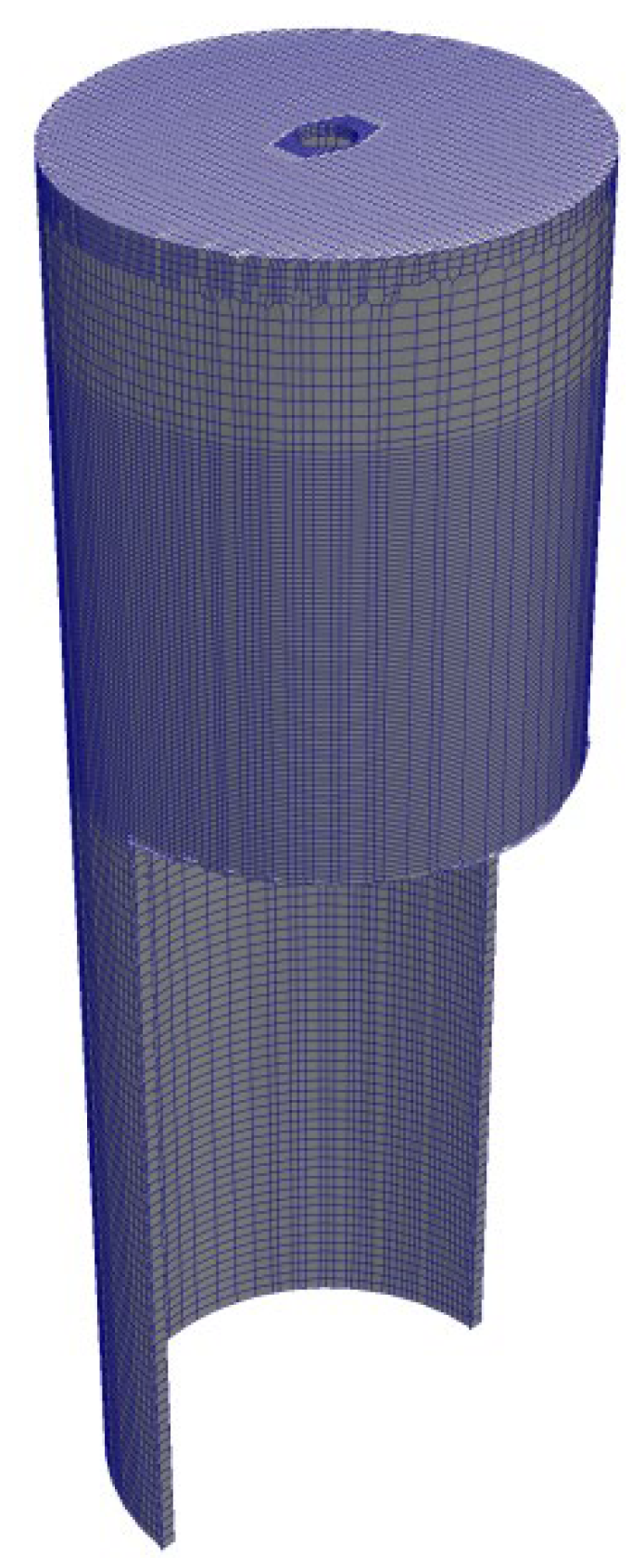
. To ensure the accuracy of the device calculations, the grid on the surface of the OWC device was encrypted, as shown in
Figure 3. The time step
Δt was calculated using the time step
Δt, which was automatically adjusted using adjustRunTime in the Controldict file.
3. Theory and validation
3.1. Governing Equations
Under a low water velocity, water is typically assumed to be an incompressible fluid, i. e., its density
ρ = 1000 kg/m
3 is constant and the fluid satisfies the continuity and momentum equations.
In Equations (1) and (2),
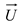
is the fluid velocity, t the time,
p the pressure,
g the acceleration owing to gravity, and
z the water surface height. The free surface of a liquid under a two-phase flow model can be modeled using the VOF method [
28] as follows:
In Equation (3),
C is the volume fraction of the fluid. The dynamic water pressure on the device is expressed as:
In Equation (4),
ϕ is the velocity potential and
p0 is the initial pressure. The wave force exerting on the device can be solved by integrating the pressure over the device surface as follows:
In Equation (5),
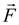
is the force applied on the structure,
p the pressure on the surface of the structure,
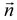
the normal vector on the surface of the device, and
τ the surface area of the structure. Because the gas pressure is extremely low relative to the wave load, the wave force is expressed as
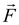
minus the hydrostatic load. The velocity potential
ϕ satisfies the boundary conditions on the free water surface and on the walls of the device.
In Equations (6) and (7), η represents the free surface.
3.2. Model Validation
The forces on the device and the dynamic water pressure on the front wall outside the gas chamber of the device were verified separately for the model with parameters D, DO, Ds, and Dh set as 0.125, 0.014, 0.244, and 0.4 m, respectively.
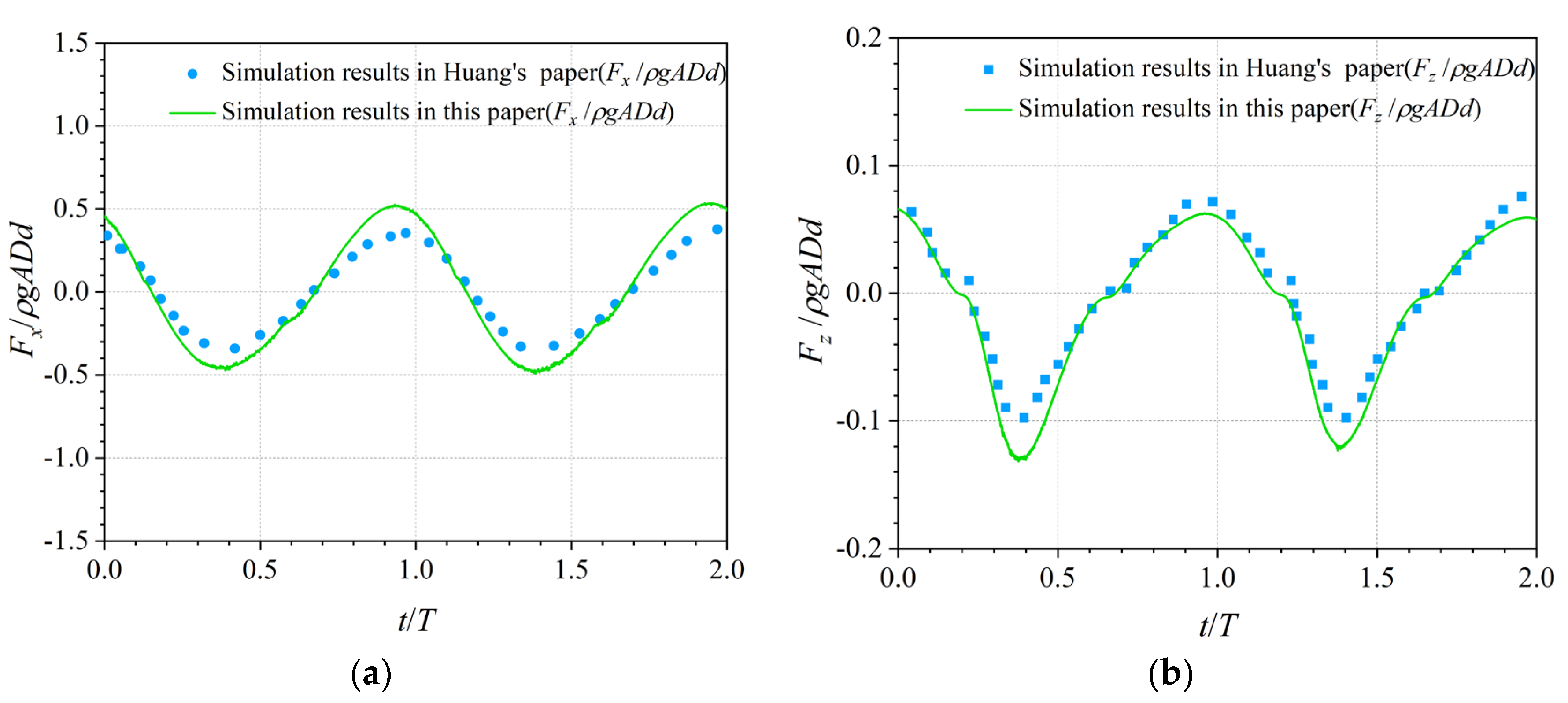
The numerical results of this study based on an incident wave period
T of 1.4 s, a water depth d of 0.3 m, and
H = 0.04 m for the horizontal wave force
Fx and vertical wave force
Fz are presented in
Figure 4a for a comparison with the numerical results of Huang et al. [
26].
Figure 4a,b show that the numerical results agreed well with each other, thus indicating that the OWC wave-energy device established in this study can accurately simulate the wave load on the device.
As shown in
Figure 5, six monitoring points, i. e., (S1 and S01), (S2 and S02), and (S3 and S03), were arranged at the hydrostatic water surface inside and outside the front wall of the device, at the midpoint of the inundation depth, and at 0.01 m from the bottom, respectively, to monitor the pressure. The dynamic water pressure is written as the sum of the first- and second-order dynamic water pressures, i. e.,
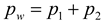
, as a theoretical value to verify the numerical results of the dynamic water pressure at three points (i. e., S1, S2, and S3) on the front wall of the gas chamber of the installation.
In Equations (8) and (9),
k denotes the wave number and
ω denotes the circular frequency; the monitoring points on the front wall of the air chamber are shown in
Figure 5.
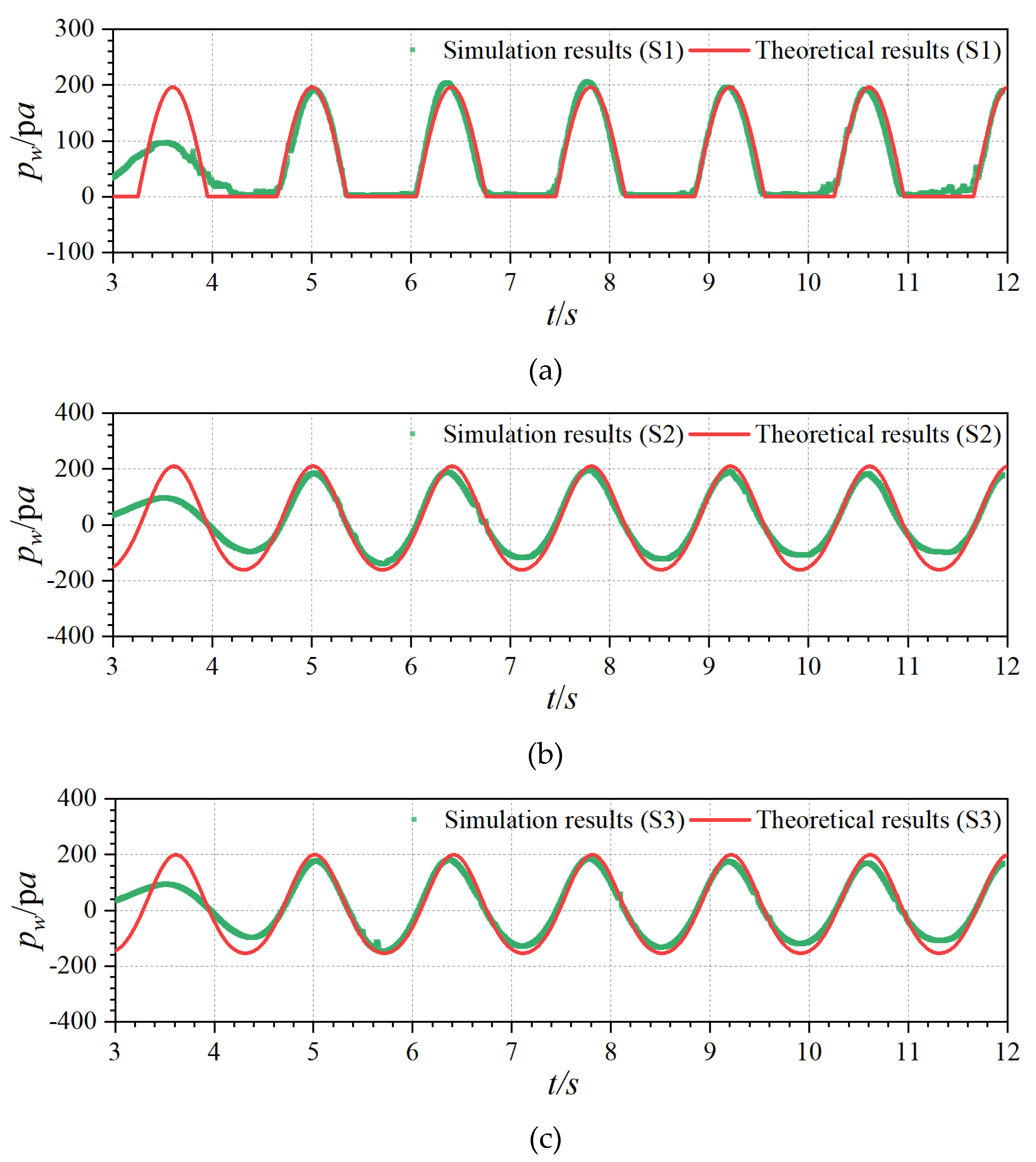
Figure 6 shows a comparison between the numerical modeling results and the theoretical results of the dynamic water pressure at three monitoring points on the outside of the front wall at
T = 1.4 s,
d = 0.3 m, and
H = 0.04 m. As shown in
Figure 6, the numerical modeling results of the dynamic water pressure at the three monitoring points agreed well with the theoretical results, thereby indicating that the OWC wave-energy device established in this study can accurately simulate the dynamic water pressure on the front wall of the installation.
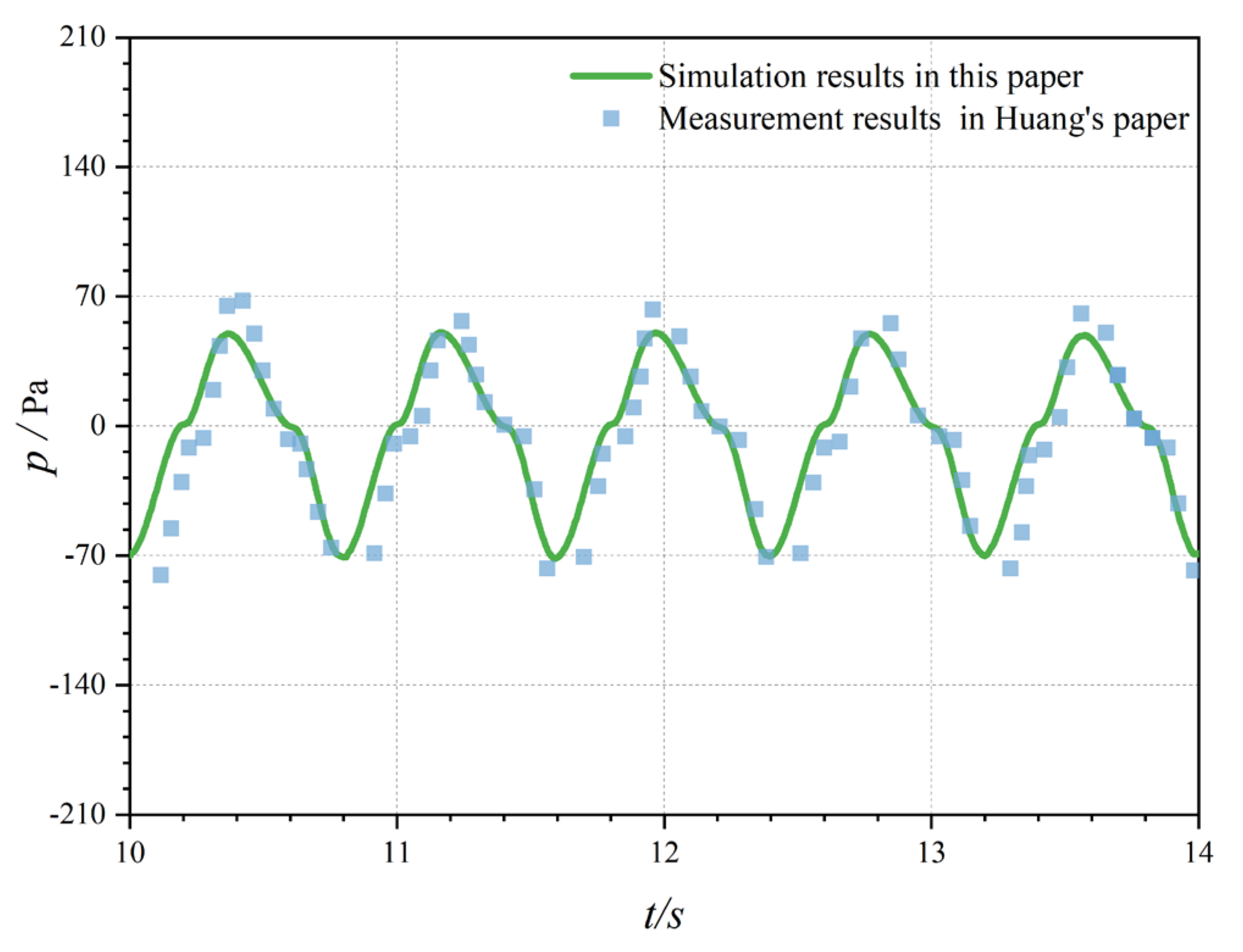
A comparison between the measured air pressure inside the chamber and the numerical model is provided in
Figure 7, which shows The measured results [
26] are consistent with the results of the numerical model, thus indicating that the numerical model established in this study can accurately simulate the relative pressure of air inside the air chamber.
4. Results
4.1. Effect of Wave Period on Forces in OWC Device
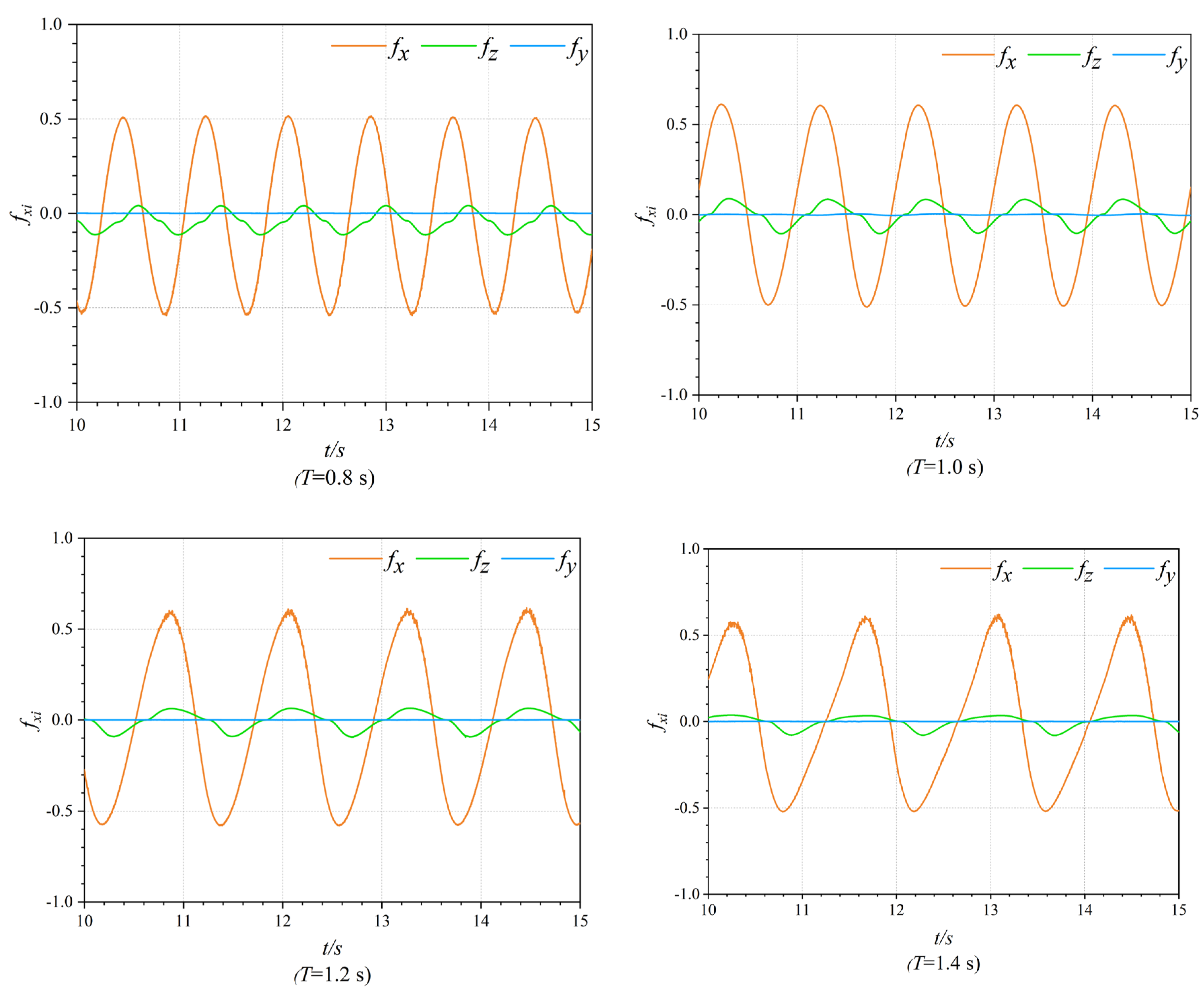
At a water depth of 0.3 m, the wave height was set to 0.04 m, whereas the wave period was varied within the range of 0.8–1.4 s. This allowed for the determination of the relationship between the wave force and wave period. To examine the wave force action law, the wave forces in the three directions were rendered dimensionless.
Here,
xi (
i = 1, 2, and 3) denotes the x-, y-, and z-directions, respectively;
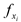
shows the dimensionless wave force in the three directions; and A is the wave amplitude.
Figure 8 shows the variation in the wave force on the OWC device in three directions (horizontal, vertical, and transverse) with time for different incident wave periods. The dimensionless wave force varied periodically in all three directions with the same period as the incident wave. The horizontal dimensionless wave force
fx reflected a regular sine curve, whereas the vertical dimensionless wave force
fz presented clear peaks and troughs but did not present the typical sine curve. The magnitude of
fx was approximately 6.6 to 7.9 times that of
fz, and the horizontal dimensionless wave force
fy was approximately zero.
According to Huang et al. [
26], the magnitude of
fy is directly related to the vorticity generated by the OWC pile, whereas vortex shedding on the device pile is related to the Keulegan–Carpenter number. Based on the model parameters of the installation, the vortex was not dislodged from the outer surface of the pile and main support structure, whereas vortex dislodgement occurred at the lower end of the pile skirt of the installation. Furthermore, because the waves were incident in the forward direction, the device was also placed on the centerline of the flume and symmetrical about the y = 0 cross-section, which explains the low
fy relative to
fx and
fz. Because
fy was extremely and thus minimally affected the device, it shall not discussed herein.
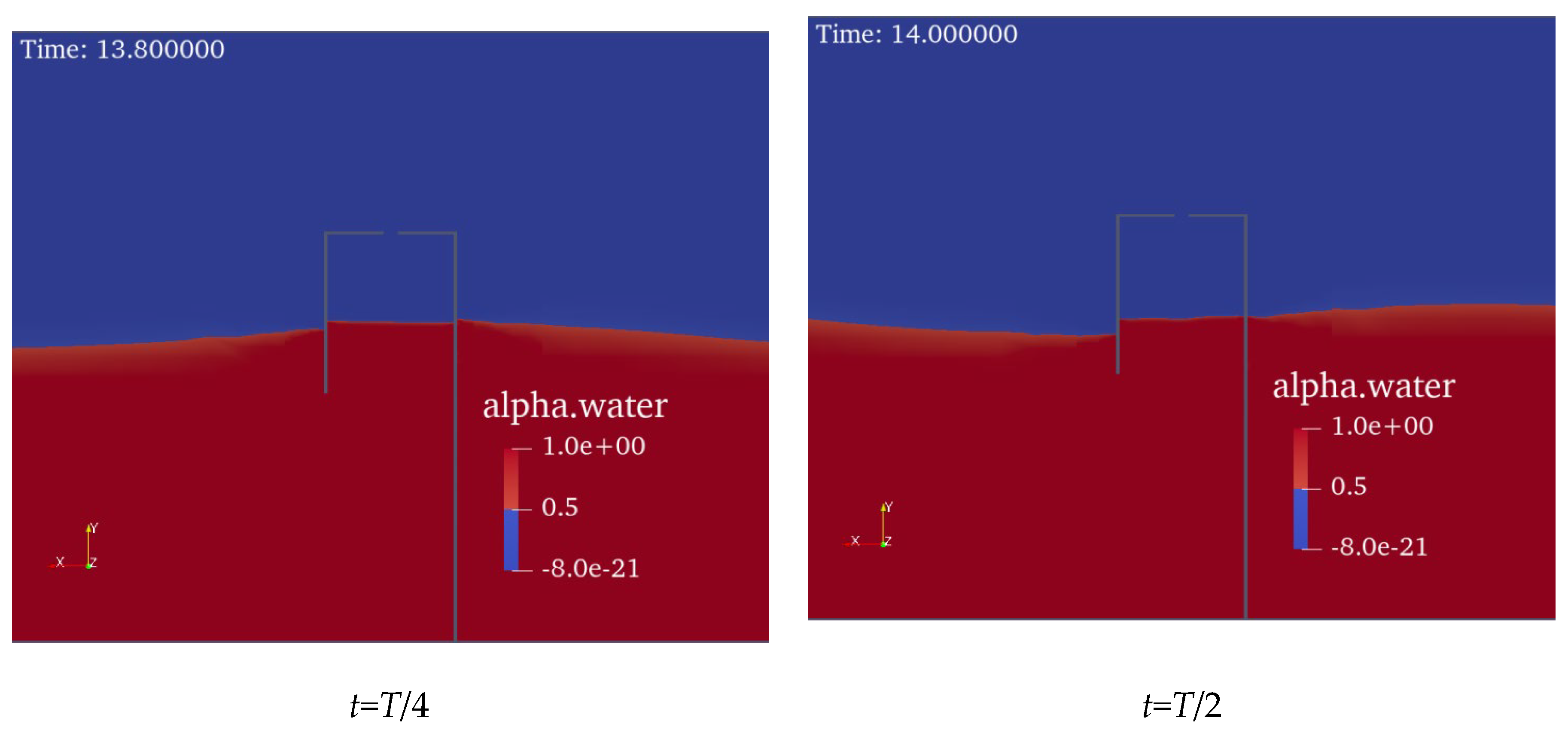
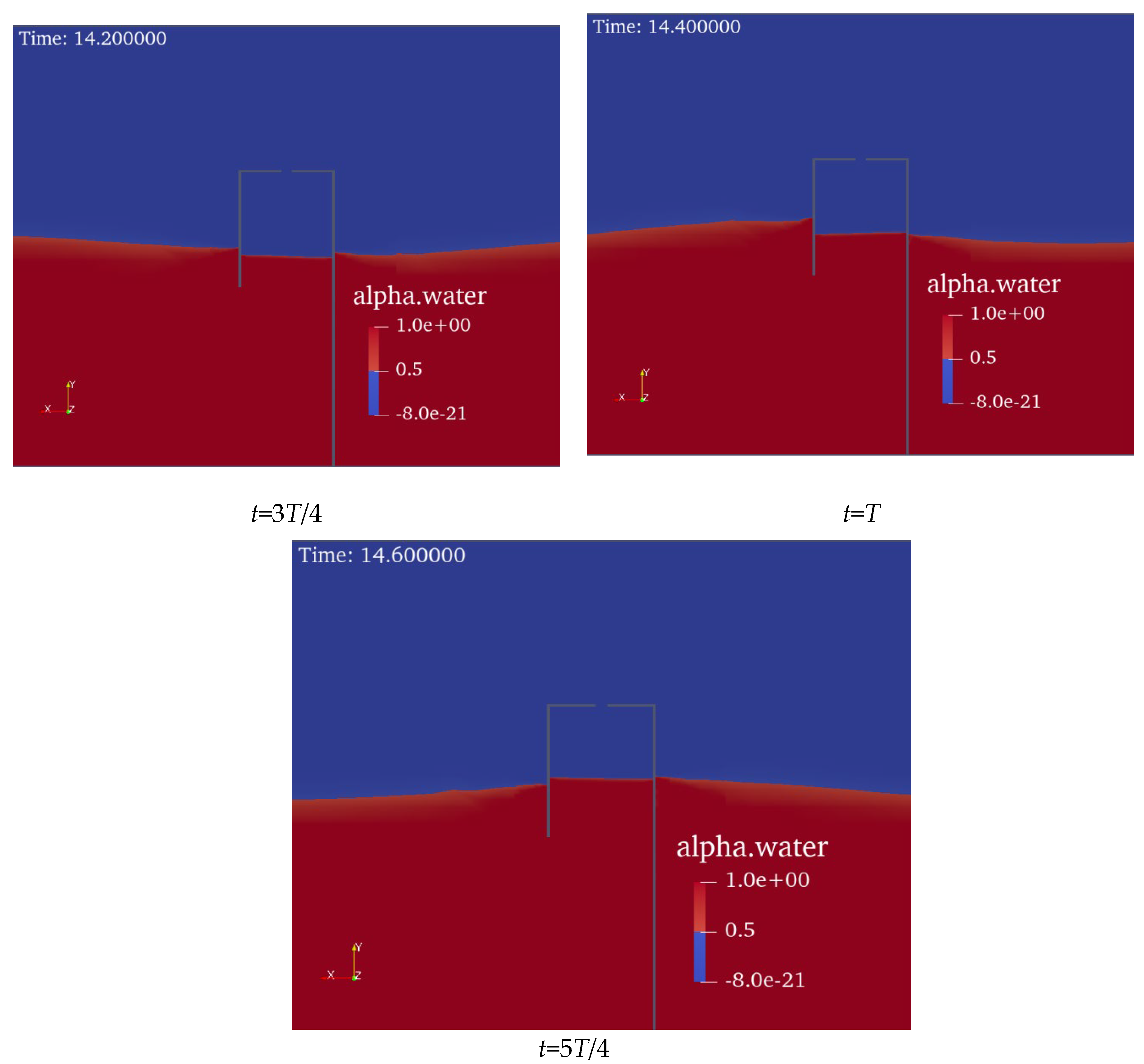
For a more intuitive observation of the water level corresponding to the force case of the device at different moments, the variation in the liquid level near the OWC device on the y = 0 cross-section during one cycle (
T = 0.8 s) is presented in
Figure 9. As shown, the liquid levels on the outside of the OWC device and inside the chamber varied periodically within one cycle, which corresponded to the force case shown in
Figure 8;
fx reached its maximum value when the water level on the outside of the front wall of the device reached its maximum, whereas the amplitude of
fz lagged slightly.
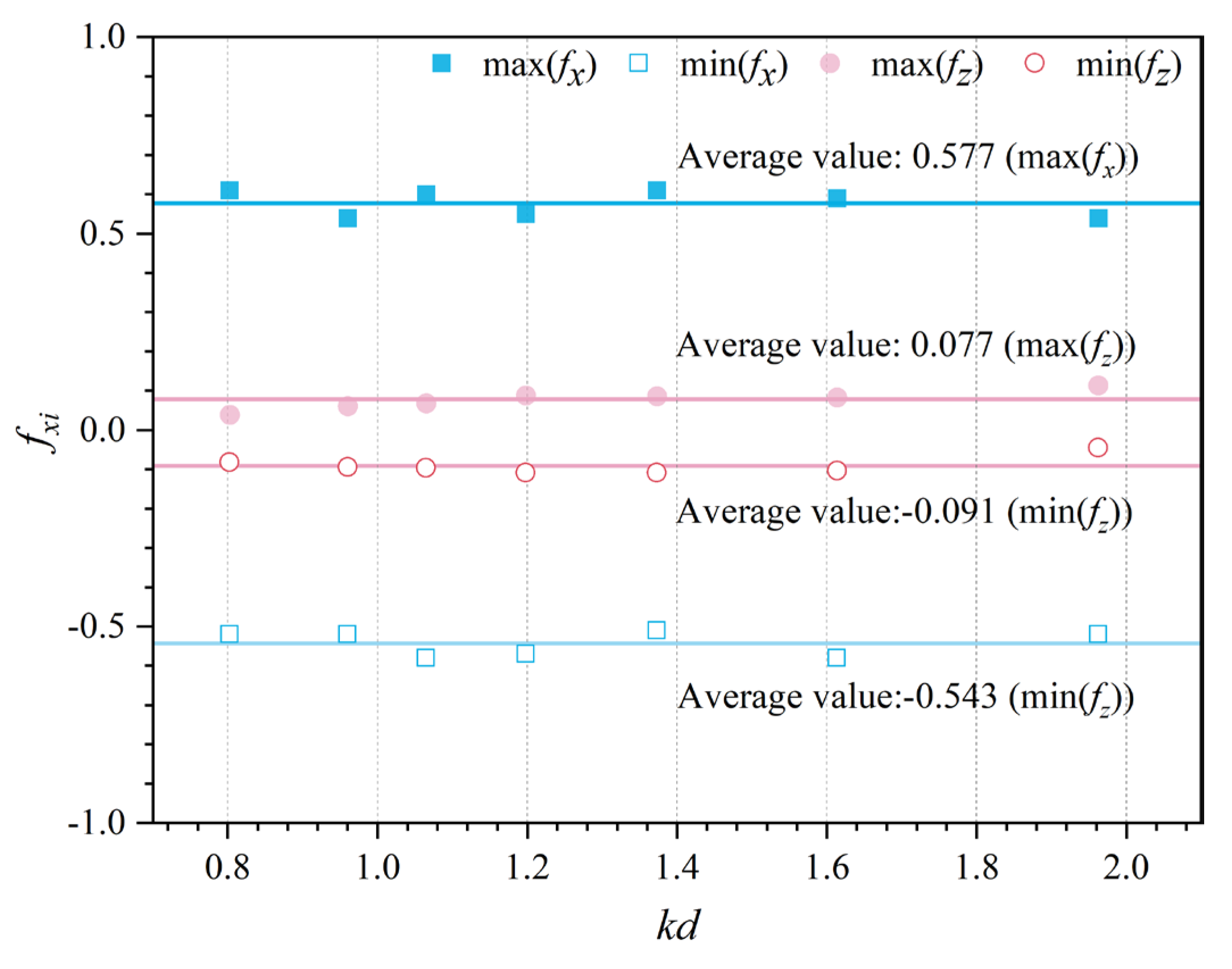
Figure 10 shows the maximum dimensionless wave force max (
fxi), the minimum dimensionless wave force min (
fx), and the corresponding mean value for wave frequencies
kd of 0.80 to 1.96 (
T = 0.8 to 1.4 s) after the wave propagation stabilized. As shown in
Figure 10, the effect of period on the horizontal and vertical dimensionless wave forces to which the device was subjected was insignificant. At
kd = 0.80–1.96, both the maximum and minimum wave forces did not vary significantly; thus, the mean values of the dimensionless wave forces at different periods can be a good estimate of the device wave force under a constant wave height and water depth.
4.2. Effect of Water Depth on Forces in OWC Device
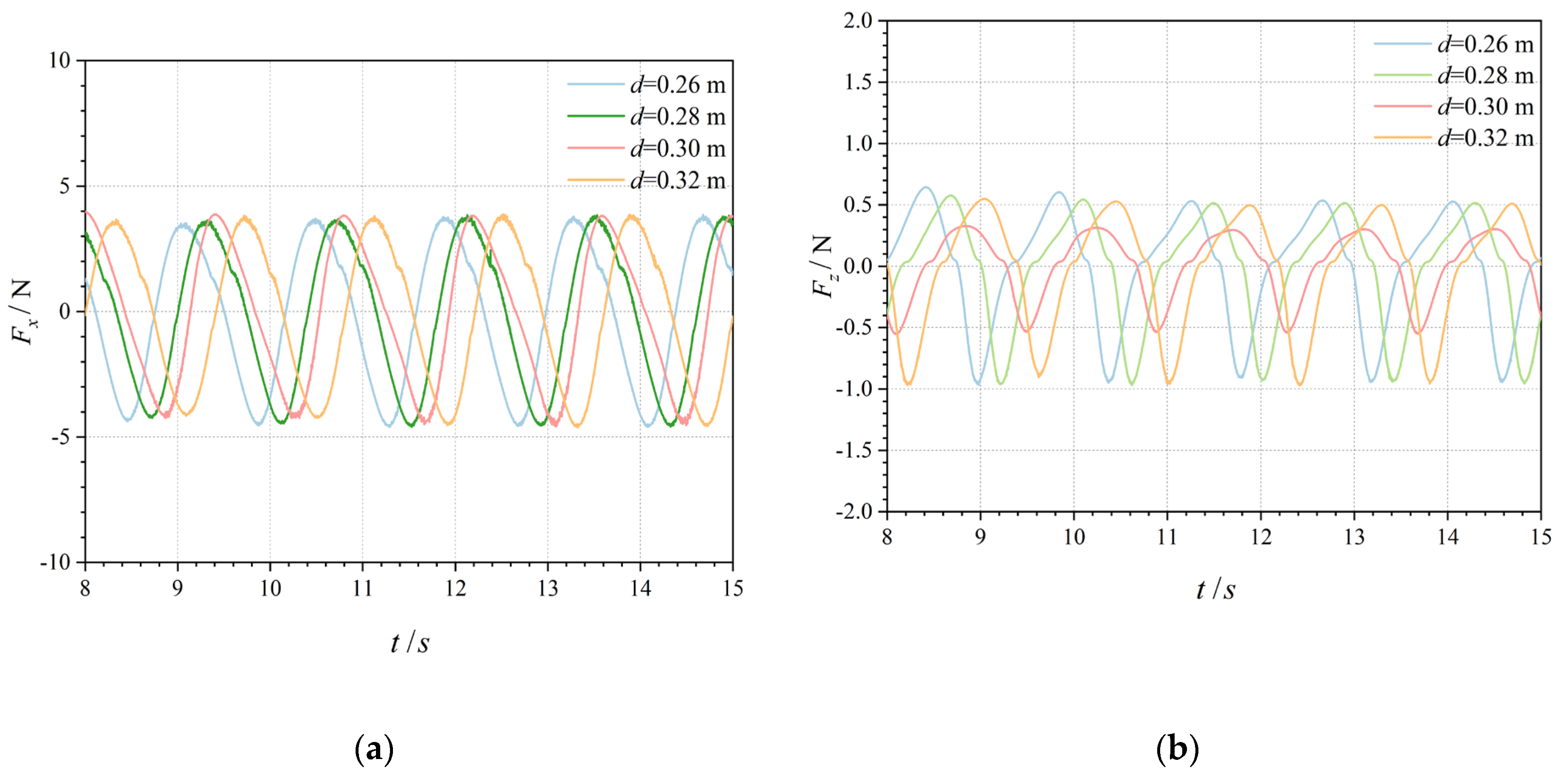
At a wave period of 1.4 s and a fixed wave height of 0.04 m, the water depth was varied within the range of 0.26–0.32 m. This allowed for the determination of the relationship between the wave force and water depth.
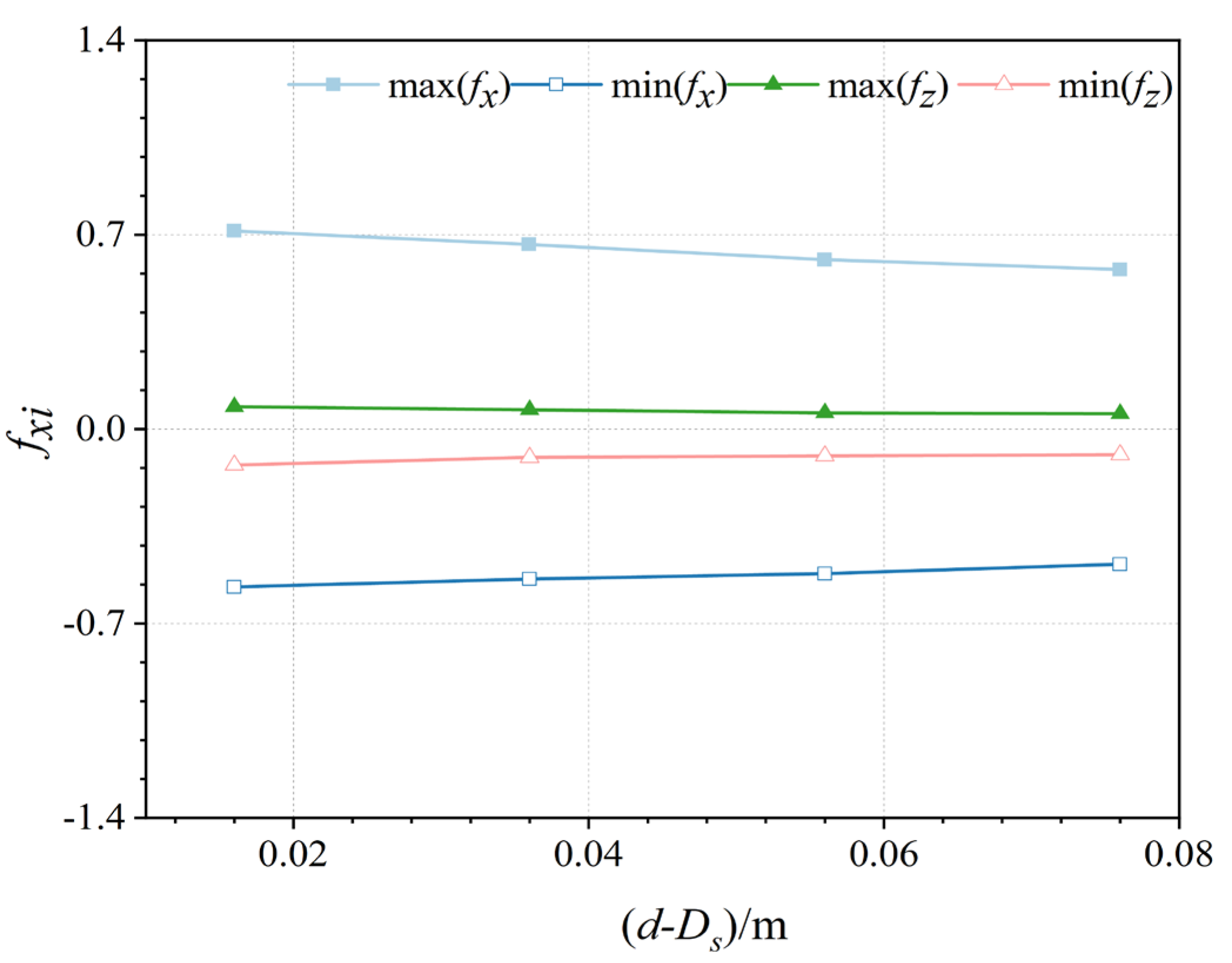
The maximum and minimum dimensionless wave loads after wave stabilization under different operating conditions are shown in
Figure 11 as a function of the relative water depth
d-
Ds. As shown in
Figure 11, the dimensionless wave force
Fxi (
i = 1 and 3) decreased as the relative water depth increased. However, the magnitudes of the horizontal and vertical wave forces exerting on the entire device were almost constant, as shown in
Figure 12a,b. The submerged section of the OWC device comprised a hollowed-out half-cylinder section and a hollowed-out cylinder section. Because the OWC device requires the water surface to be above the skirt for power generation, the area of the circular cylindrical section submerged in the water increased with the water depth. The velocity of the water quality points decreased with increasing distance from the water surface, and the movement of the water quality points contributed primarily to the wave pressure. For a specified period and wave height, the velocity of the water-quality points at the free water surface was the highest, and it increased with the water depth at the horizontal surface. By focusing only on the wave force due to the water-point velocity on the outer surface, the size of the wave loads should increase with the water depth. Therefore, the wave force on the OWC device should not only be related to the water-point velocity outside the device but also to the force on the submerged section of the structure.
4.3. Effect of Wave Height on Forces in OWC Device
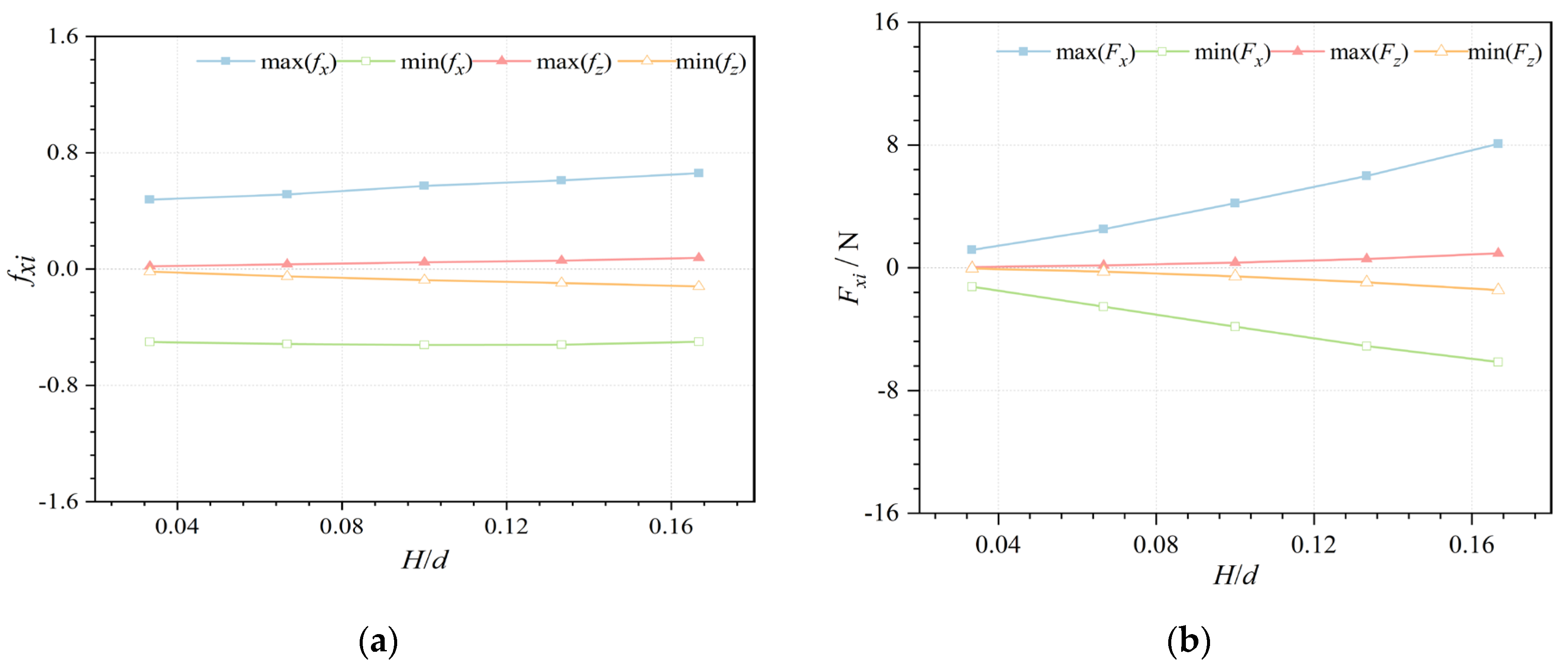
The variation in pressure with the wave height was obtained by fixing the wave period to 1.4 s and varying the wave height from 0.01 to 0.05 m at a water depth of 0.3 m.
The variations in the maximum and minimum wave forces with the relative wave height
H/
d after wave-propagation stabilization for different wave height conditions are shown in
Figure 13. As shown in
Figure 13a, the dimensionless wave force increases with the relative wave height, with the minimum dimensionless horizontal wave force min (
fx) decreasing slightly at relative water depths
H/
d of 0.1 to 0.167; however, both the maximum and minimum dimensional wave forces on the device increased significantly with the relative wave height, as shown in Figure13b.
To further investigate the relationship between the wave height and wave force, the average of the sum of the absolute values of the horizontal dimensionless wave force fx and the vertical dimensionless wave force fz crest and trough were set as the average horizontal wave force and average vertical wave force, respectively.
In Equation (11) [
fx] is the average horizontal wave force.
In Equation (12), [fz] is the average vertical wave force.
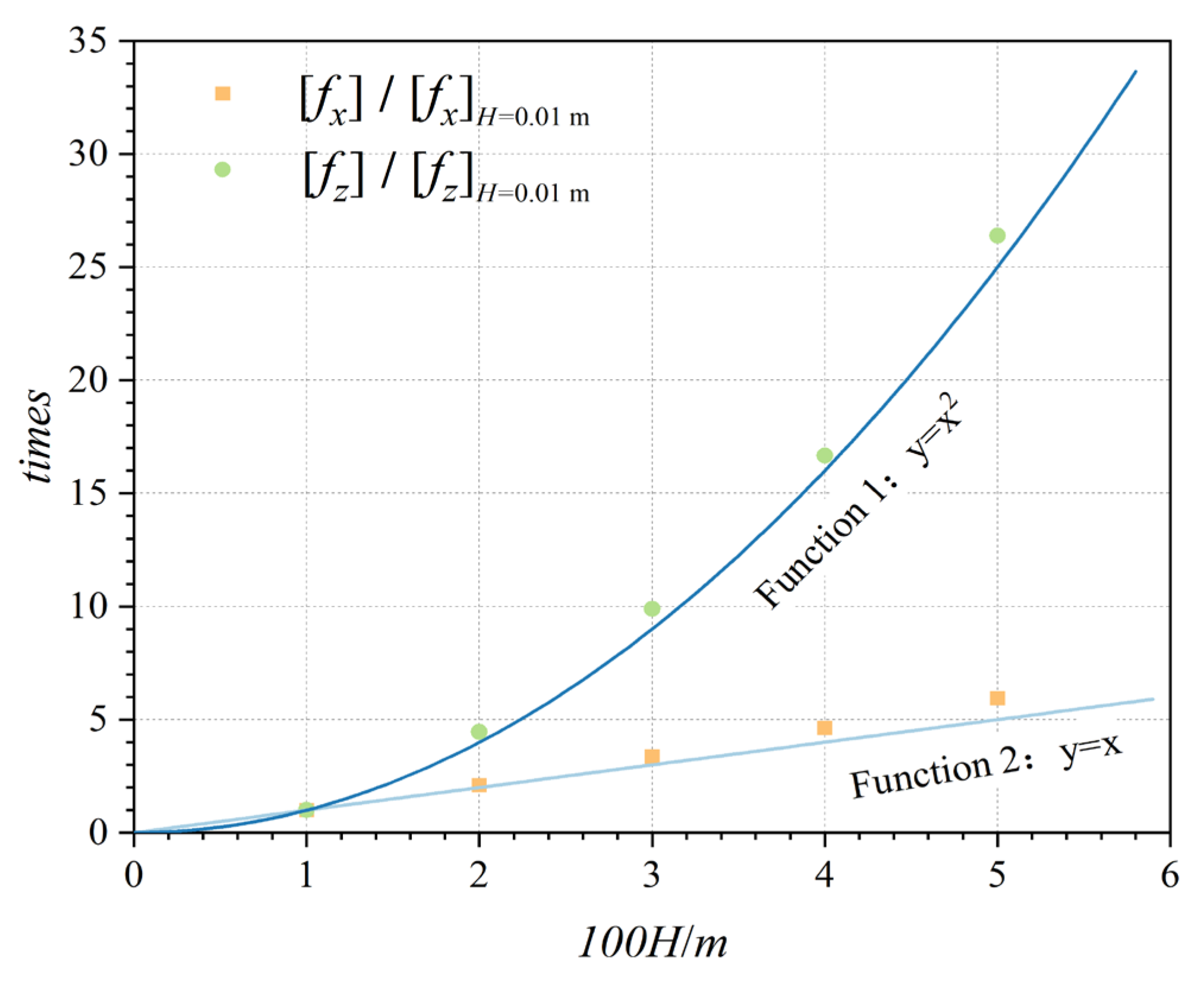
The variations of
[fx]/[
fx]
H=0. 01 m and [
fz]/[
fz]
H=0. 01 m with the wave height are shown in
Figure 14. [
fx]
H=0. 01 m and [
fz]
H=0. 01 m represent the average of the sum of the absolute values of the crests and troughs for incident wave heights of
H = 0.01 m for the horizontal and vertical dimensionless wave forces, respectively. As shown in
Figure 14, the mean horizontal wave force [
fx] increased linearly with the wave height, whereas the mean vertical wave force [
fz] increased with the square of the wave height.
To further examine the relationship between the wave height and wave force, the average value of the sum of the absolute values of the horizontal wave force
Fx and the vertical wave force
Fz peaks and troughs was set as the average horizontal wave force
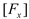
and the average vertical wave force
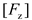
. Based on the force law of the device shown in
Figure 14 and the conclusion that the water depth is not correlated significantly with the force of the device obtained in
Section 3.2, we assumed that the magnitudes of
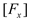
and
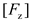
can be determined as follows, respectively:
Here,
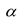
and
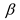
are used to estimate the
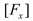
and
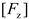
empirical formula coefficients, respectively. Based on the data presented in
Figure 13 and
Figure 14, one obtains
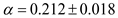
and
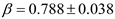
.
4. Dynamic Water Pressure at Front Wall of OWC
The dynamic water-pressure monitoring points on the front wall of the gas chamber are shown in
Figure 5.
Figure 15 shows the results of the comparison of dynamic water pressure
pw histories at each measurement point inside and outside the front wall of the gas chamber. As shown in
Figure 11b and
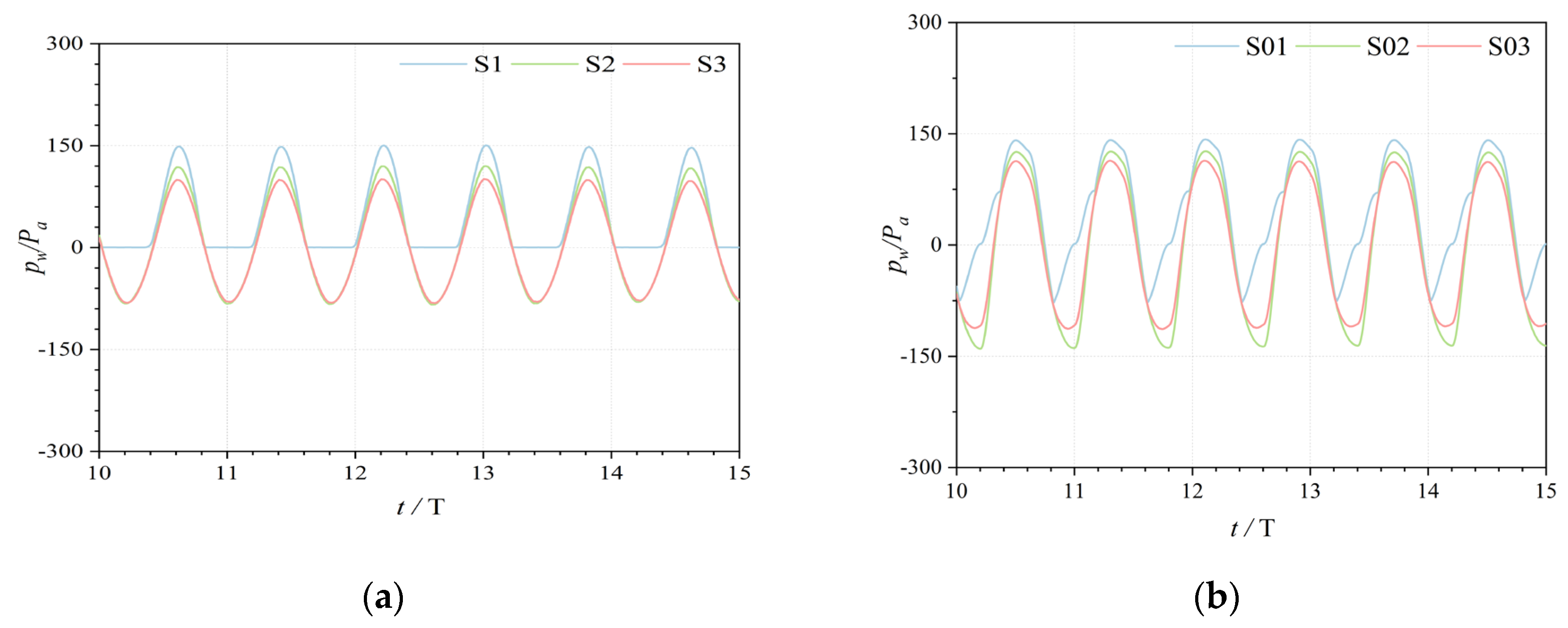
Figure 15a, the changes in the dynamic water pressure were cyclical, and the dynamic water pressure on the outside of the front wall of the gas chamber reflected a sinusoidal curve, whereas that on the inside changed relatively irregularly compared with the dynamic water pressure on the outside; this indicates that multiple wave reflections occurred inside the gas chamber of the device and were subject to the action of the air pressure inside the gas chamber. The maximum dynamic water pressure on both sides of the front wall of the gas chamber occurred at the point where it intersected the hydrostatic surface, i. e., the maximum pressures on the outside and inside occurred at points S1 and S01, respectively.
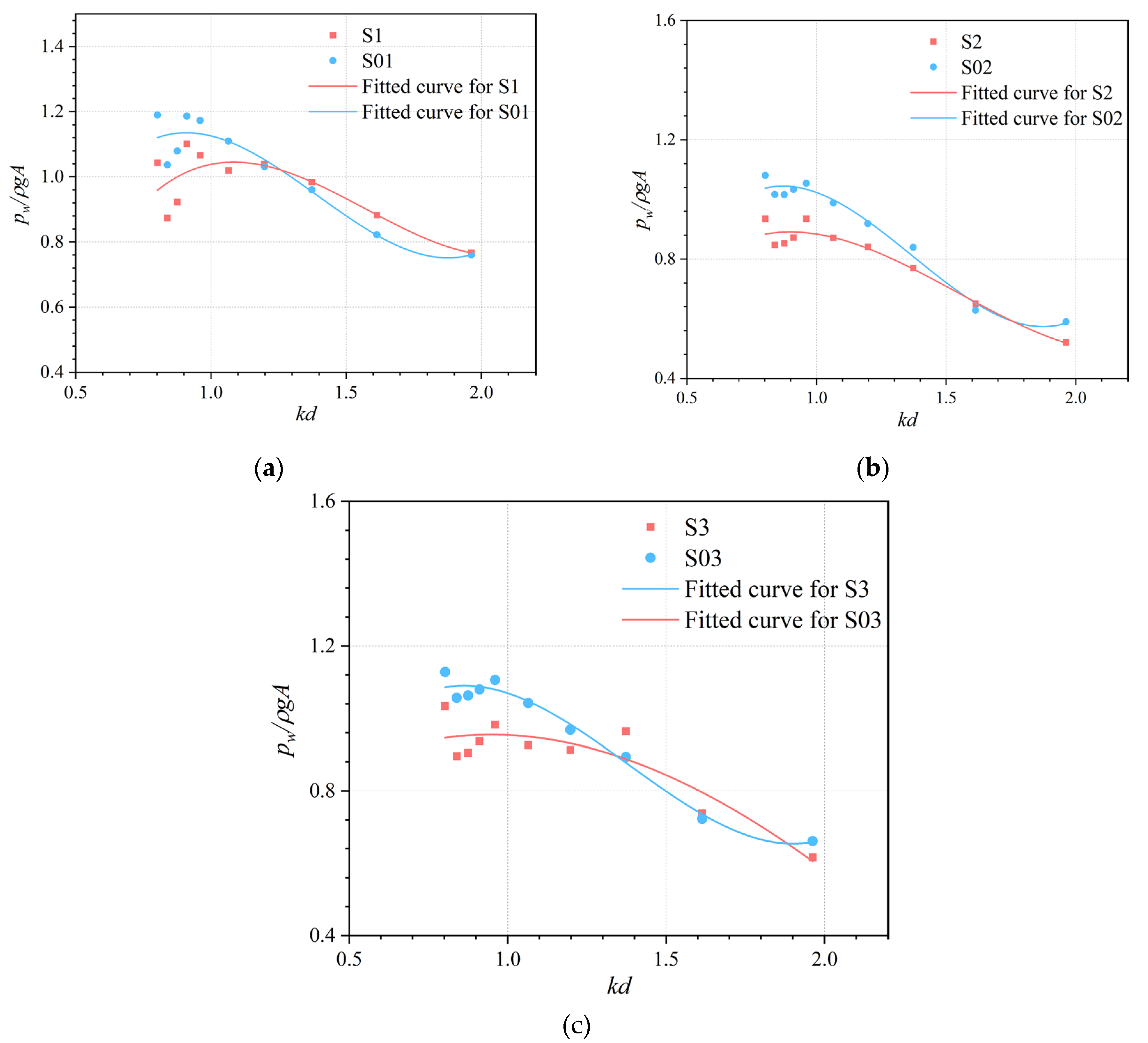
The mean value of the sum of the peaks and troughs of the dynamic water pressure at each pressure-monitoring point on the front wall is shown in
Figure 16 as a function of
kd. As shown in
Figure 16, the dynamic water pressure at each point on the inside of the front wall of the air chamber
pw increased at
kd = 0.8–1.0 and decreased at
kd = 1.0–2.0. Notably, at
kd less than 1.3 (low-frequency region), the dynamic water pressure amplitude on the inside of the front wall was greater than the outside pressure amplitude, whereas at
kd greater than 1.3 (high-frequency region), the outside amplitude is likely to exceed the inside amplitude.
5. Conclusions
In this study, simulations were conducted to analyze the wave loads on an OWC wave-energy device under forward-wave incidence conditions and dynamic water pressures on the inside and outside of the device’s front wall using OpenFOAM. The following conclusions were inferred from this study:
First, under a water depth of 0.3 m, a wave height of 0.04 m, and a wave period is 0.8–1.4 s, the horizontal wave force was approximately 6.6 to 7.9 times greater than the vertical wave force. The lateral wave force was significantly smaller than the horizontal and vertical wave forces.
Second, under a wave period of 1.4 s, wave height 0. 04 m, and water depth ranging from 0.26 to 0.32 m, the horizontal and vertical wave force on the device did not change significantly with the relative water depth. This suggests that the force on the submerged section of the device affected the force of the device.
Third, the results indicated that under a wave period of 1.4 s, a water depth of 0.3 m, and a wave height between 0.01 and 0.05 m, the horizontal wave force changed linearly as the wave height increased, whereas the vertical wave force increased with the square of the wave height.
Finally, the maximum value of the dynamic water pressure on both sides of the front wall of the device appeared at the junction between the water surface and the device. The dynamic water pressure at each point on the front wall inside the gas chamber increased with the wave frequency and then decreased. Additionally, the pressure amplitude on the front wall inside the gas chamber of the device was likely to be greater in the low-frequency region (k < 1.3) as compared with that on the external front wall.
The numerical simulation results of this study provide reference values for the design and optimization of OWC devices. Owing to the complexity of the force characteristics of OWC devices, some studies have not been conducted sufficiently. For future endeavors, the following can be considered:
(1) Consider the compressibility of air and establish a better aerodynamic model.
(2) Consider oblique incidence and investigate the hydrodynamic performance at different angles of incidence.
(3) Introduce higher-order and irregular waves to obtain a more realistic hydrodynamic performance undersea conditions.
Author Contributions
Conceptualization,J.-l.Z., P.T., H.-s.Z. and P.-b.Z.; methodology, J.-l.Z.; software,J.-l.Z.; validation, J.-l.Z., P.T. and H.-s.Z.; formal analysis, J.-l.Z.; investigation, J.-l.Z.; resources, J.-l.Z.; data curation, J.-l.Z.; writing—original draft preparation,J.-l.Z.; writing—review and editing, H.-s.Z. and P.-b.Z.; visualization, J.-l.Z.; supervision,P.T. and H.-s.Z.; project administration,P.T.; funding acquisition, P.T. and H.-s.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number Nos. 51679132, 52201321, and U22A20216.
Acknowledgments
We would like to thank Editage (
www.editage.cn) for English language editing.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ashlin, S.J.; Sundar, V.; Sannasiraj, S. Effects of bottom profile of an oscillating water column device on its hydrodynamic characteristics. Renew. Energy 2016, 96, 341–353. [Google Scholar] [CrossRef]
- Bayoumi, S.; Incecik, A.; El-Gamal, H. Dynamic modelling of Spar-Buoy oscillating water column wave energy converter. Ships Offshore Struct. 2015, 10, 601–608. [Google Scholar] [CrossRef]
- Evans, D.V. The Oscillating Water Column Wave-energy Device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Martins-Rivas, H.; Mei, C.C. Wave power extraction from an oscillating water column along a straight coast. Ocean Eng. 2009, 36, 426–433. [Google Scholar] [CrossRef]
- Nader, J.-R.; Zhu, S.-P.; Cooper, P.; Stappenbelt, B. A finite-element study of the efficiency of arrays of oscillating water column wave energy converters. Ocean Eng. 2012, 43, 72–81. [Google Scholar] [CrossRef]
- Dimakopoulos, A.S.; Cooker, M.J.; Bruce, T. The influence of scale on the air flow and pressure in the modelling of Oscillating Water Column Wave Energy Converters. Int. J. Mar. Energy 2017, 19, 272–291. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Z.; Deng, Z. Experimental and theoretical study of a cylindrical oscillating water column device with a quadratic power take-off model. Appl. Ocean Res. 2016, 57, 19–29. [Google Scholar] [CrossRef]
- Hu, H. , Deng, Z., Yao, Y., Zhao, X. Theoretical and numerical studies of off-shore oscillating water column wave energy device. J. Zhejiang Univ -Sci A (Appl. Phys. & Eng.). 2019,53(2),325-335. [CrossRef]
- Ashlin, S.J.; Sannasiraj, S.; Sundar, V. Wave Forces on an Oscillating Water Column Device. Procedia Eng. 2015, 116, 1019–1026. [Google Scholar] [CrossRef]
- Jakobsen, M.; Beatty, S.; Iglesias, G.; Kramer, M. Characterization of loads on a hemispherical point absorber wave energy converter. Int. J. Mar. Energy 2016, 13, 1–15. [Google Scholar] [CrossRef]
- Elhanafi, A. Prediction of regular wave loads on a fixed offshore oscillating water column-wave energy converter using CFD. J. Ocean Eng. Sci. 2016, 1, 268–283. [Google Scholar] [CrossRef]
- Wang, R.-Q.; Ning, D.-Z. Dynamic analysis of wave action on an OWC wave energy converter under the influence of viscosity. Renew. Energy 2020, 150, 578–588. [Google Scholar] [CrossRef]
- Ning, D.-Z.; Wang, R.-Q.; Gou, Y.; Zhao, M.; Teng, B. Numerical and experimental investigation of wave dynamics on a land-fixed OWC device. Energy 2016, 115, 326–337. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, Z.; Law, A.W. Wave power extraction by an axisymmetric oscillating-water-column converter supported by a coaxial tube-sector-shaped structure. Appl. Ocean Res. 2013, 42, 114–123. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Ning, D. Hydrodynamic Investigation of a Concentric Cylindrical OWC Wave Energy Converter. Energies 2018, 11, 985. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, S.; Xu, C. Characteristics of the flow around a circular OWC-type wave energy converter supported by a bottom-sitting C-shaped structure. Appl. Ocean Res. 2020, 101, 102228. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Z. A dual-functional wave-power plant for wave-energy extraction and shore protection: A wave-flume study. Appl. Energy 2018, 229, 963–976. [Google Scholar] [CrossRef]
- He, F.; Huang, Z. Hydrodynamic performance of pile-supported OWC-type structures as breakwaters: An experimental study. Ocean Eng. 2014, 88, 618–626. [Google Scholar] [CrossRef]
- He, F.; Li, M.; Huang, Z. An Experimental Study of Pile-Supported OWC-Type Breakwaters: Energy Extraction and Vortex-Induced Energy Loss. Energies 2016, 9, 540. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Liang, D.; Cai, S. Nonlinear hydrodynamic analysis of an offshore oscillating water column wave energy converter. Renew. Sustain. Energy Rev. 2021, 145, 111086. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Shi, W.; Johanning, L.; Liang, D. Hydrodynamic investigation on an OWC wave energy converter integrated into an offshore wind turbine monopile. Coast. Eng. 2020, 162, 103731. [Google Scholar] [CrossRef]
- Xu, C.; Huang, Z. Three-dimensional CFD simulation of a circular OWC with a nonlinear power-takeoff: Model validation and a discussion on resonant sloshing inside the pneumatic chamber. Ocean Eng. 2019, 176, 184–198. [Google Scholar] [CrossRef]
- Chen, J.; Wen, H.; Wang, Y.; Ren, B. Experimental investigation of an annular sector OWC device incorporated into a dual cylindrical caisson breakwater. Energy 2020, 211, 118681. [Google Scholar] [CrossRef]
- Wan, C.; Yang, C.; Fang, Q.; You, Z.; Geng, J.; Wang, Y. Hydrodynamic Investigation of a Dual-Cylindrical OWC Wave Energy Converter Integrated into a Fixed Caisson Breakwater. Energies 2020, 13, 896. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, Z.; Law, A.W.K. Wave power extraction from a bottom-mounted oscillating water column converter with a V-shaped channel. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2014, 470, 20140074. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, C.; Huang, S. A CFD simulation of wave loads on a pile-type oscillating-water-column device. J. Hydrodyn. 2019, 31, 41–49. [Google Scholar] [CrossRef]
- Jacobsen, N.G. , Fuhrman, D.R., Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids. 2012,70(9),1073-1088. [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
Figure 1.
Diagram of 3D numerical wave tank.
Figure 1.
Diagram of 3D numerical wave tank.
Figure 2.
Dimensions of OWC numerical model.
Figure 2.
Dimensions of OWC numerical model.
Figure 3.
OWC device grid.
Figure 3.
OWC device grid.
Figure 4.
Comparison of numerical model results for horizontal vertical wave forces on OWC (T = 1.4 s, d = 0.3 m, and H = 0.04 m). (a) horizontal direction. (b) vertical direction.
Figure 4.
Comparison of numerical model results for horizontal vertical wave forces on OWC (T = 1.4 s, d = 0.3 m, and H = 0.04 m). (a) horizontal direction. (b) vertical direction.
Figure 5.
Schematic diagram of OWC device for monitoring dynamic water pressure at section y = 0.
Figure 5.
Schematic diagram of OWC device for monitoring dynamic water pressure at section y = 0.
Figure 6.
Comparison of theoretical and numerical model results at outer monitoring point on the OWC front wall (T = 1.4 s, d = 0.3 m, and H = 0.04 m). (a) Monitoring point S1. (b) Monitoring point S2. (c) Monitoring point S3.
Figure 6.
Comparison of theoretical and numerical model results at outer monitoring point on the OWC front wall (T = 1.4 s, d = 0.3 m, and H = 0.04 m). (a) Monitoring point S1. (b) Monitoring point S2. (c) Monitoring point S3.
Figure 7.
Comparison chart of numerical model and pneumatic test (T = 0.8 s, d = 0.3 m, and H = 0.04 m).
Figure 7.
Comparison chart of numerical model and pneumatic test (T = 0.8 s, d = 0.3 m, and H = 0.04 m).
Figure 8.
Dimensionless wave forces on OWC device at different periods (T = 0.8–1.4 s, d = 0.3 m, and H = 0.04 m).
Figure 8.
Dimensionless wave forces on OWC device at different periods (T = 0.8–1.4 s, d = 0.3 m, and H = 0.04 m).
Figure 9.
Wave elevation in the vicinity of the OWC device.
Figure 9.
Wave elevation in the vicinity of the OWC device.
Figure 10.
Variation in maximum and minimum wave forces with wave frequency (T = 0.8–1.4 s, d = 0.3 m, and H = 0.04 m).
Figure 10.
Variation in maximum and minimum wave forces with wave frequency (T = 0.8–1.4 s, d = 0.3 m, and H = 0.04 m).
Figure 11.
Variation in maximum and minimum dimensionless wave forces with relative water depth (T = 1.4 s, d = 0.26–0.32 m, and H = 0.04 m).
Figure 11.
Variation in maximum and minimum dimensionless wave forces with relative water depth (T = 1.4 s, d = 0.26–0.32 m, and H = 0.04 m).
Figure 12.
Variation in horizontal and vertical wave forces with time at different water depths (T = 1.4 s, d = 0.26–0.32 m, and H = 0.04 m. (a) Horizontal wave forces. (b) Vertical wave forces.
Figure 12.
Variation in horizontal and vertical wave forces with time at different water depths (T = 1.4 s, d = 0.26–0.32 m, and H = 0.04 m. (a) Horizontal wave forces. (b) Vertical wave forces.
Figure 13.
Variation in horizontal vertical wave force with time for different wave heights (T = 1.4 s, d = 0.3 m, and H = 0.01–0.05 m). (a) Dimensionless wave force on device. (b) Gauge wave force on device.
Figure 13.
Variation in horizontal vertical wave force with time for different wave heights (T = 1.4 s, d = 0.3 m, and H = 0.01–0.05 m). (a) Dimensionless wave force on device. (b) Gauge wave force on device.
Figure 14.
Curves of [fx]/[fx]H=0.01 m and [fz]/[fz]H=0.01 m with wave height (period T = 1.4 s, water depth d = 0.3 m, and wave height H = 0.01–0.05 m).
Figure 14.
Curves of [fx]/[fx]H=0.01 m and [fz]/[fz]H=0.01 m with wave height (period T = 1.4 s, water depth d = 0.3 m, and wave height H = 0.01–0.05 m).
Figure 15.
Variation in dynamic water pressure with time at each monitoring point on both sides of front wall of OWC unit (T = 0.8 s, d = 0.3 m, and H = 0.04 m). (a) Outside of front wall (S1, S2, and S3).(b) Inside of front wall (S01, S02, and S03).
Figure 15.
Variation in dynamic water pressure with time at each monitoring point on both sides of front wall of OWC unit (T = 0.8 s, d = 0.3 m, and H = 0.04 m). (a) Outside of front wall (S1, S2, and S3).(b) Inside of front wall (S01, S02, and S03).
Figure 16.
Variation in pressure amplitude at various points on front wall with kd. (a) Monitoring point S1 and S01. (b) Monitoring point S2 and S02. (c) Monitoring point S3 and S03.
Figure 16.
Variation in pressure amplitude at various points on front wall with kd. (a) Monitoring point S1 and S01. (b) Monitoring point S2 and S02. (c) Monitoring point S3 and S03.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
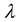 . The spatial step
. The spatial step 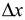 in the x-direction was set to
in the x-direction was set to 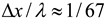 . In the z-direction,
. In the z-direction, 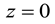 was set as the reference point. The area above and below the reference point at twice the length of the wave height 2H was encrypted, where the spatial step
was set as the reference point. The area above and below the reference point at twice the length of the wave height 2H was encrypted, where the spatial step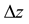 in the encrypted area was set to
in the encrypted area was set to 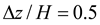 , and the spatial step in the non-encrypted area was set to
, and the spatial step in the non-encrypted area was set to 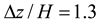 . To ensure the accuracy of the device calculations, the grid on the surface of the OWC device was encrypted, as shown in Figure 3. The time step Δt was calculated using the time step Δt, which was automatically adjusted using adjustRunTime in the Controldict file.
. To ensure the accuracy of the device calculations, the grid on the surface of the OWC device was encrypted, as shown in Figure 3. The time step Δt was calculated using the time step Δt, which was automatically adjusted using adjustRunTime in the Controldict file. 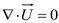
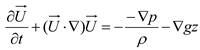
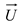 is the fluid velocity, t the time, p the pressure, g the acceleration owing to gravity, and z the water surface height. The free surface of a liquid under a two-phase flow model can be modeled using the VOF method [28] as follows:
is the fluid velocity, t the time, p the pressure, g the acceleration owing to gravity, and z the water surface height. The free surface of a liquid under a two-phase flow model can be modeled using the VOF method [28] as follows: 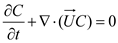
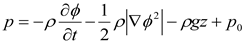
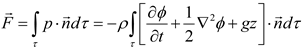
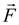 is the force applied on the structure, p the pressure on the surface of the structure,
is the force applied on the structure, p the pressure on the surface of the structure, 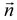 the normal vector on the surface of the device, and τ the surface area of the structure. Because the gas pressure is extremely low relative to the wave load, the wave force is expressed as
the normal vector on the surface of the device, and τ the surface area of the structure. Because the gas pressure is extremely low relative to the wave load, the wave force is expressed as 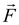 minus the hydrostatic load. The velocity potential ϕ satisfies the boundary conditions on the free water surface and on the walls of the device.
minus the hydrostatic load. The velocity potential ϕ satisfies the boundary conditions on the free water surface and on the walls of the device.
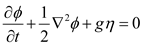
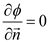
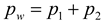 , as a theoretical value to verify the numerical results of the dynamic water pressure at three points (i. e., S1, S2, and S3) on the front wall of the gas chamber of the installation.
, as a theoretical value to verify the numerical results of the dynamic water pressure at three points (i. e., S1, S2, and S3) on the front wall of the gas chamber of the installation.
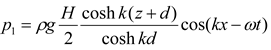
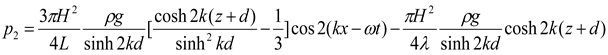
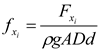
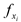 shows the dimensionless wave force in the three directions; and A is the wave amplitude.
shows the dimensionless wave force in the three directions; and A is the wave amplitude. 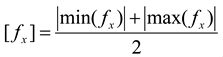
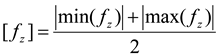
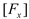 and the average vertical wave force
and the average vertical wave force 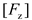 . Based on the force law of the device shown in Figure 14 and the conclusion that the water depth is not correlated significantly with the force of the device obtained in Section 3.2, we assumed that the magnitudes of
. Based on the force law of the device shown in Figure 14 and the conclusion that the water depth is not correlated significantly with the force of the device obtained in Section 3.2, we assumed that the magnitudes of 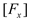 and
and 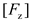 can be determined as follows, respectively:
can be determined as follows, respectively: