Prerpints.org logo
Preprint
Article

Trajectory Analysis of 6-DOF Industrial Robot Manipulators by Using Artificial Neural Networks

Altmetrics

Downloads

90

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 June 2024

Posted:

13 June 2024

You are already at the latest version

Alerts
Abstract
Robot manipulators are robotic systems that are frequently used in automation systems and able to provide increased speed, precision and efficiency in the industrial applications. Due to their nonlinear and complex nature, it is crucial to optimize the robot manipulator systems in terms of trajectory control. In this study, positioning analysis based on artificial neural networks (ANN) were performed for robot manipulator systems used in the textile industry and the optimal ANN model for the high-accuracy positioning was improved. The inverse kinematic analysis of a 6 degree of freedom (DOF) industrial denim robot manipulator were carried out via 4 different learning algorithms of Delta-Bar-Delta (DBD), Online Back Propagation (OBP), Quick Back Propagation (QBP) and Random Back Propagation (RBP) for proposed neural network predictor. From the results obtained, it was observed that QBP based 3-10-6 type ANN structure produced the optimal results in terms of estimation and modelling of trajectory control. In addition, 3-5-6 type ANN structure was also improved and its Root Mean Square Error (RMSE) and statistical R2 performances were compared to that of 3-10-6 ANN structure. Consequently, it can be concluded that the proposed neural predictors can successfully be employed in real-time industrial applications for robot manipulator trajectory analysis.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Industrial robots are capable of performing many different processes and operations accurately and do not need complex supporting elements as humans need. Robot manipulators are powerful electromechanical systems which provide effective solutions to the recent industrial applications such as picking, placing, packing, painting and welding. Especially, robot manipultors with multi-DOF are widely used at all stages of production processes such as automation systems due to their ability of performing industrial operations effectively without the need of humans. In addition, significant advantages in terms of occupational health and safety have been provided by switching from the operator-assisted production model to robot manipulator-supported structures in processes involving chemicals and carcinogens.
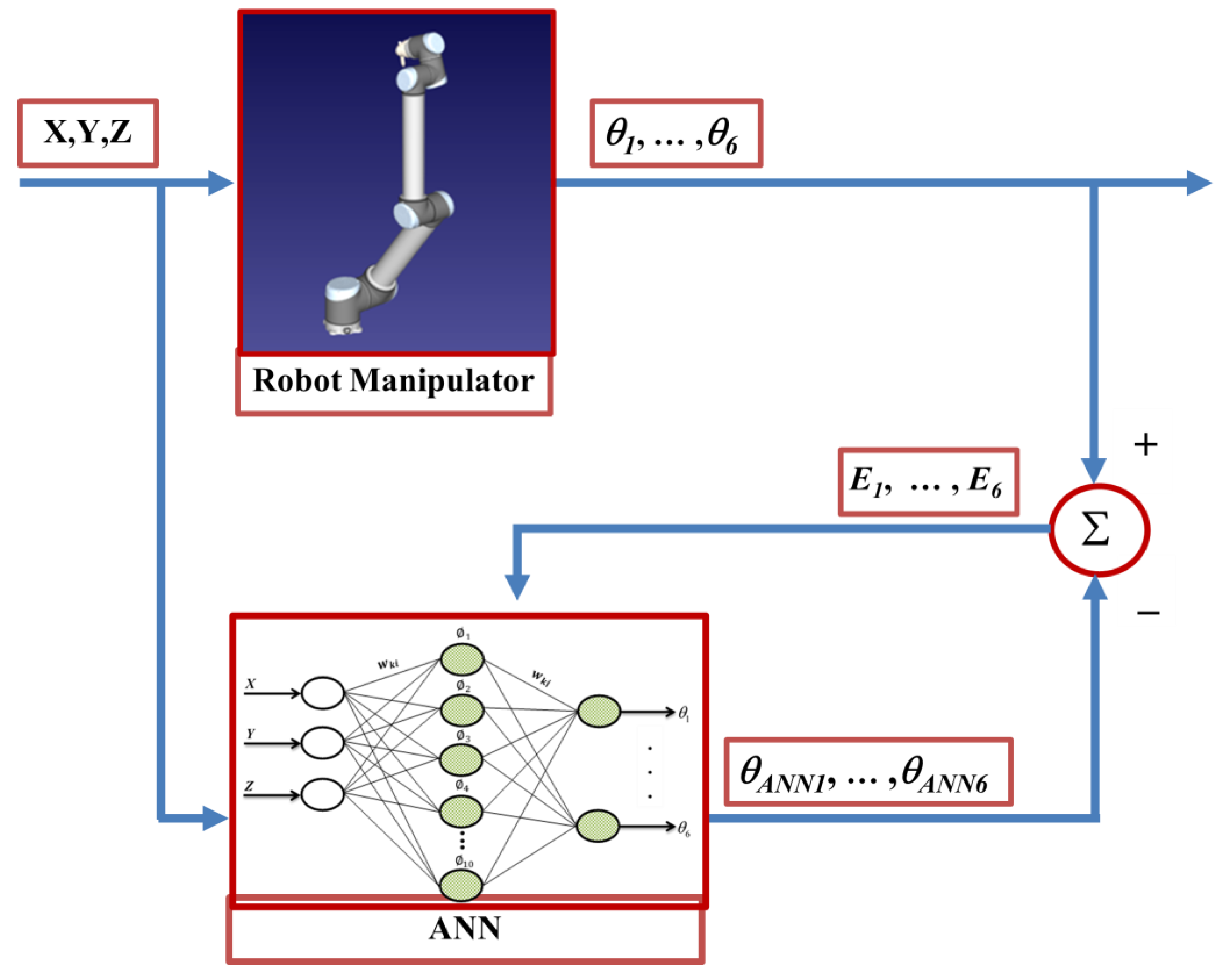
One of the most important problems encountered in robot manipulator systems is the ability to achieve high-accuracy positioning even large disturbances such as mechanical friction of the mechanical parts, ambient ventilation and mechanical strength misalignment. In this study, ANN-based detailed trajectory analyzes were carried out to enable the robot manipulator end processor to monitor the full trajectory with the highest accuracy during the denim fabric grinding process.
In the literature, there are several studies including different application areas of robot manipulator systems. Saad et al. have been developed an ANN based adaptive controller for robot manipulator applications in [1]. A geometric algorithm for fixed directional working area calculation in 6-PRRS structured robot manipulators was proposed by Boney and Ryu and its applications were analyzed [2]. In study conducted by Bonev et al. [3] on the kinematics of parallel robot manipulators with linear sensors and optimal positioning, a closed-form solution approach was developed. Detailed researches on the singularities of 3-DOF parallel robot manipulator mechanisms were carried out by Boney and his research group [4]. Tombul and Sarıtaş presented a detailed research which was conducted on inverse kinematic calculations and trajectory planning for a five-axis Edubot robot [5]. On the other hand, Khayati et al., carried out analysis on multi-stage position/force control for friction-constrained robotic systems [6]. Lessard et al. carried out analyzes on static balancing optimization by designing position and force controllers for biomedical applications, especially 3-dimensional ultrasound imaging [7]. Karahan obtained the robot inertia parameters by performing detailed dynamic model analysis for the Staubli RX-60 robot in his master thesis [8]. In another study, Janvier et al. performed detailed performance analyzes for medical robotic 3-dimensional ultrasound imaging systems [9]. A parallel medical robot design and its static balancing optimization were carried out by Lessard et al. for medical robotic applications [10]. An updated formulation and its related applications improved for a KUKA type industrial robot manipulator were presented by Bigras et al. [11]. Moreover, Yu et al. proposed a geometric approach for accuracy analysis of 3-DOF planar parallel robots [12]. Furthermore, accuracy analysis of a 3-DOF planar parallel robot structure was performed by Briot and Bonev [13]. On the other hand, parallel kinematic analyzes were carried out by Liu et al. on a two-joint robot structure and then detailed analyzes on adaptability, error optimization and size optimization were realized [14]. Bigras et al. performed detailed mathematical equation analyzes for an industrial robot and applied the results to force control [15]. Furthermore, autonomous movement capabilities of 3-DOF planar parallel robot structures were investigated in detail and then relevant analysis were carried out by Briot and Boney [16]. A novel controller structure combining the adaptive neural networks and proportional-integral-derivative (PID) control approach was presented by Perez et al. to optimize the trajectory behaivour of robot manipulators [17]. An ANN based method which is able to adapt to the characteristics of both known and unknown trajectories of 6-DOF robot manipulators was improved by Tang et al. [18]. Pham and Wang improved a robust radial basis function neural network (RBFANN) based adaptive control approach to optimize the joint position control and trajectory tracking control of robot manipulators [19]. An inverse dynamic model estimation approach based on ANNs was proposed by Moldovan et el. in study [20] to optimize the trajectory performance of a 6-DOF robot manipulator. Mahajan et al. improved an ANN based structure to optimize the trajectory tracking of a 2-DOF robotic arm by using the inverse kinematics equations [21]. Moreover, Son et al. proposed an adaptive ANN model which was strengthened by differential evolution algorithm in order to optimize the non-linear dynamics of a 5-DOF robot manipulator [22]. An ANN based control process with optimal number of hidden nodes and less computation was proposed by Liu et al. to overcome the system uncertainities and track the trajectory of robot manipulator with high accuracy [23]. Truong et al. proposed a novel adaptive tracking ANN with deadzone robust compensator for industrial robot manipulators to achieve the high precision position tracking performance [24]. On the other hand, Elsisi et al. proposed an ANN based modified adaptive tuning algorithm in order to track the trajectories of robot manipulator arms with high accuracy [25]. Finally, a multi-objective design mechanism was introduced by Kouritem to determine the optimal material type and optimal physical dimensions of the robot arm to withstand loads at vulnerable locations using stress analysis [26].

2. Materials and Methods

In this study, detailed trajectory planing and analysis of a real time 6-DOF industrial robot manipulator system were realized by using DBD, OBP, QBP and RBP based improved ANN network structures. The properties of the industrial robot manipulator system analyzed and the structure of the improved ANN networks can be explained in detail as follows.

2.1. Industrial Robot Manipulators

One of the most important stages in the production of jeans trousers is the chemical spraying process. In classical human based chemical spraying process, which was shown in Figure 1, undesirable effects such as health problems and color tone differences may occur.
In order to overcome the undesirable effects of human based spraying process, industrial robot manipulators can be preferred. In this study, firstly, kinematic analyzes of a Universal Robots UR5e model 6-DOF robot manipulator for chemical spraying were performed and then ANN based trajectory optimization was carried out. The structure and rotation axes of the 6-DOF industrial robot analyzed in this study are shown in Figure 2. As seen from the figure, the 6-DOF industrial robot structure analyzed in this study has 6 joint angels of θ 1 , θ 2 , θ 3 , θ 4 , θ 5 and θ 6 .
The technical properties and parameters of the industrial robot manipulator analyzed and designed within the scope of this study are shown in Table 2 [27]. As understood from table, the 6-DOF industrial robot structure analyzed in this study is capable of contributing significantly to production speed and precision. In addition, the fact that the robot manipulator has ( ± 360 ∘ ) rotation angle in all its joints means that the points it can reach in the working space are at the maximum level. In addition, since the operating noise level is too low, even if many robots are used in a production line, noise-related disturbances will not occur and total system performance will not negatively be affected.
Table 1. The technical properties of the Universal Robots UR5e model 6-DOF robot manipulator.
Table 1. The technical properties of the Universal Robots UR5e model 6-DOF robot manipulator.
Weight 18.4 kg
Payload Capacity 5 kg
Reachability Distance 850 mm
Max-Min rotation angles +/- 360° at all joints
Angular Velocity Joints - maximum 180° per second
Vehicle - about 1 m per second
Repeatability +/- 0.1 mm
Volume Diameter Ø 149 mm
Number of Joint 6 rotational joints
Control Box Size 475 mm x 423 mm x 268 mm (W x H x D)
I/O Ports 18 digital inputs, 18 digital outputs, 4 analog inputs, 2 analog outputs
I/O Power Supply 24V-2A in control box and 12V/24V-600 mA in vehicle
Communication TCP/IP - Modbus TCP
Programming Polyscope graphical user interface on 12 inch touch screen
Noise Low noise levels
IP Classification IP54
Power Consumption ≅ 200 W
Materials Aluminum, PP plastic
Working Temperatures 0 - 50°C
Power Source 100-240 V (AC), 50-60 Hz
The Denavit-Hartenberg (D-H) parameters representing the kinematic parameters of the robot manipulator are shown in Table 2 below. Each joint of the robot manipulator has the feature of a rotary joint and structurally there is no joint misalignment or second adjacent axis angle. Therefore, it is obvious that this structure will provide an important advantage, especially in exact positioning.
The industrial robot manipulator structure designed in this study consists of totally 6 joints, including the body, shoulder, elbow and wrist joints, as seen in Figure 3.

2.2. Artificial Neural Networks

ANNs are nonlinear mapping systems with a structure based on the principles observed in biological nervous systems. A basic ANN structure consists of input layer ( x i ), weights ( w k i , w k j ), activation level ( ϕ j ) and output layer ( y j ) as represented in Figure 4.
In this network structure, the input vector is updated via a Gaussian activation function which performs a nonlinear transformation and defined in Equation 1.
ϕ j = exp [ − ( ‖ x i − g c ‖ σ ) 2 ]
where; x i is the input vector, g c is the centre of the j th Gaussian function, σ > 0 is the spread constant parameter, finally, ‖ x i − g c ‖ defines the Euclidean distance between the two relevent vector. Afterwards, in the second level, each output of the network can be calculated via a linear transformation as defined in Equation 2.
y j = ∑ j = 1 N w k j . ϕ j
where; N is the number of hidden layers and w k j are the weight values between the hidden and output neurons.
In this study, analyzes were carried out by using an ANN network structure including two hidden layers. For rotation angle analysis of each joint of the robotic manipulator system, ANN network structures including 3 input layer cells, totally 10 hidden layer cells and 6 output layer cells were improved (3-10-6 ANN network structure). The spread constant parameter directly effects the approximating performance of the ANN network structure. In order to find the most appropriate value the simulations based on test data (30% of the experimental data) were performed for 0.1 step sizes in the range (0,1] in line with the problem structure and the optimal value of σ which produces the minimum root mean squared error (RMSE) was obtained as 0.1.
In order to determine the optimum ANN network structure, the performances of the Delta-Bar-Delta (DBD), Online Back Propagation (OBP), Quick Back Propagation (QBP) and Random Back Propagation (RBP).
DBD learning algorithm is an adaptive method in which each weight has its own learning rate. The learning rates are updated based on the change in the sign of the gradient on consecutive iterations. If the sign of the gradient does not change, the step size will be increased linearly. In contrast, if the gradient sign changes, the learning rate will be decreased exponentially. In some cases DBD seems to learn much faster than non-adaptive methods. In DBD learning algorithm, the learning rates are updated by using Equation 3,
Δ w i j ( t + 1 ) = { K ,                     i f δ ' ( t − 1 ) δ ( t ) > 0 − ϕ η ( t ) ,   i f δ ' ( t − 1 ) δ ( t ) < 0 0 ,                     e l s e
where; K and ϕ are the positive constants, η is the learning rate and finally, δ ( t ) = ∂ E ( t ) ∂ w j i ( t ) in which E ( t ) represents the instantaneous sum of the squared errors. In DBD learning algorithm, the value of the η parameter was taken as 0.1.
BP is the most widely used training algorithm for ANNs. The weights of the network are set as represented in Equation 4.
Δ w i j ( t ) = − η ∂ E ( t ) ∂ w i j ( t ) + α Δ w i j ( t − 1 )
where; η is the learning rate, E ( t ) represents the instantaneous sum of the squared errors and α determines the momentum term. In the simulations, the value of the η and α parameters were taken as 0.1 and 0, respectively. On the other hand, in OBP learning algorithm, unlike the BP algorithm, the weight values are updated after the model is presented to the ANN. OBP algorithm with randomly selected input layout order makes the learning process stochastic and is preferred in most cases.
QBP is an improved version of BP which uses the hyperbolic tangent function instead of sigmoid function. In other words, in QBP all the hidden layer neurons and all the output layer neurons use the hyperbolic tangent function while training of the network. The weights of the network are updated by using the Equation 5 at each iteration,
Δ w ( t ) = s ( t ) s ( t − 1 ) − s ( t ) Δ w ( t − 1 ) − η s ( t )
where; s ( t ) = ∂ E ( t ) ∂ w ( t ) in which E ( t ) represents the instantaneous sum of the squared errors and η represents the learning rate which was defined as 0.1.
RBP is an adaptive learning rate method where weight updates are based on the sign of the local gradients, not their magnitudes. In RBP, each weight has its own step size or update value which varies with time according to Equation 6,
Δ w i j ( t + 1 ) = { η + Δ w i j ( t − 1 ) ,                     i f ∂ E ( t − 1 ) w i j ( t − 1 ) ∂ E ( t ) w i j ( t ) > 0 η − Δ w i j ( t − 1 ) ,                     i f ∂ E ( t − 1 ) w i j ( t − 1 ) ∂ E ( t ) w i j ( t ) < 0 Δ w i j ( t − 1 ) ,                             e l s e
where; η defines the learning rate with the rule of 0 < η − < 1 < η + and E ( t ) can be defined as the instantaneous sum of the squared errors.
The structure of the ANN based analysis carried out to determine and optimize the 6 joint angels of a specifically determined trajectory for a robot manipulator is given as a block diagram in Figure 5. As seen from the figure, the learning process was optimized by using the RMSE values that are the difference between the actual angular values ​​and the angular values produced by ANN. The expression of the RMSE can be defined as given in Equation 7,
R M S E = 1 N ∑ i = 1 M I ( Y A c t u a l − Y A N N ) 2
where; MI defines the maximum number of iterations and N is the number of data which is equal to maximum number of the test data set.

3. Simulation Results

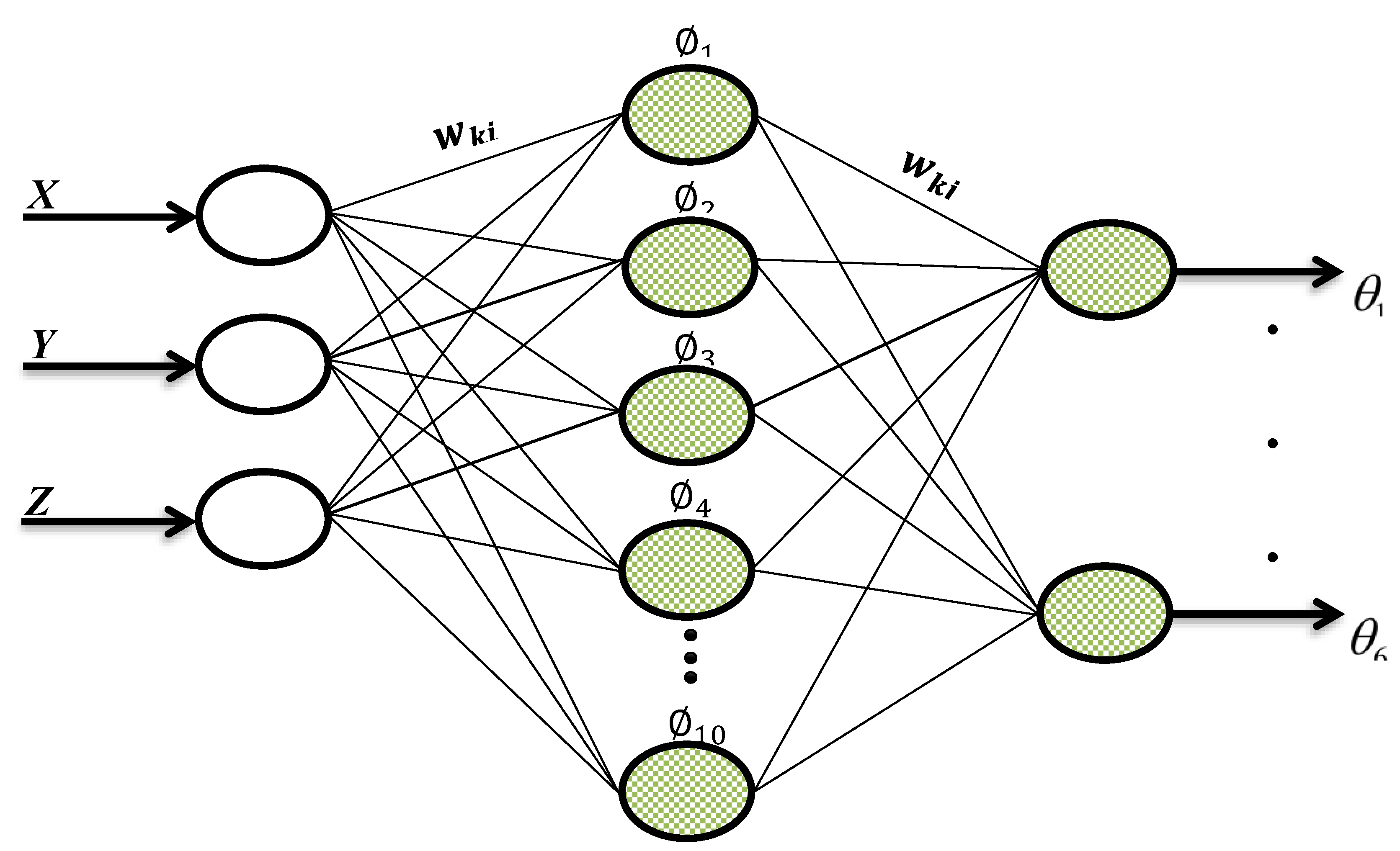
In the simulations carried out the ANN structure consists of 3 input cells (position of the end function - X, Y, Z), 10 hidden layer cells and 6 output layer cells (joint angels - θ 1 , θ 2 , θ 3 , θ 4 , θ 5 and θ 6 ) are formed. Furthermore, randomly selected %70 of the entire data set was used for the training of the ANN and the remaining %30 data were used for test phase. In all the simulations the iteration number was taken as 1000000.
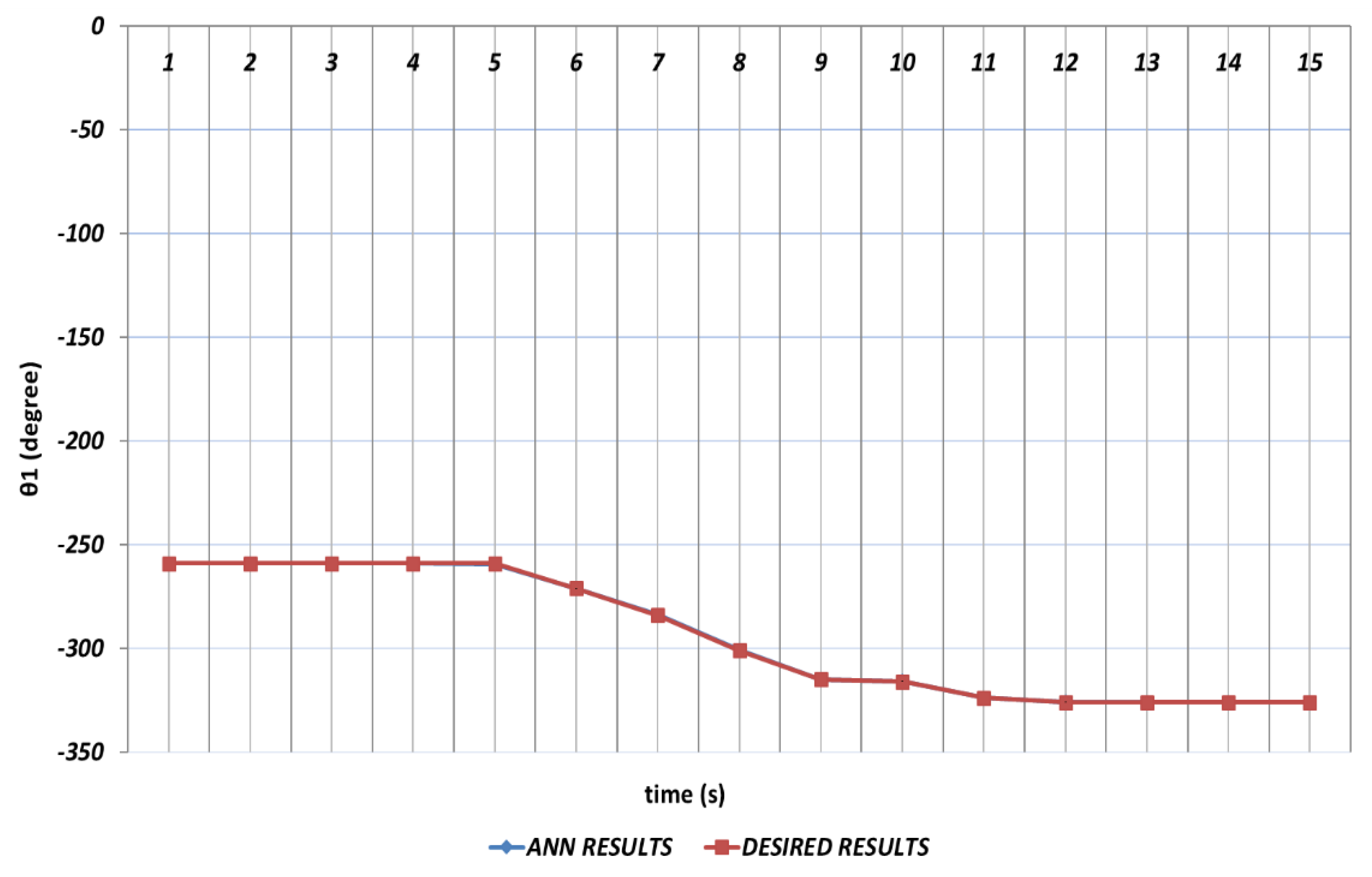
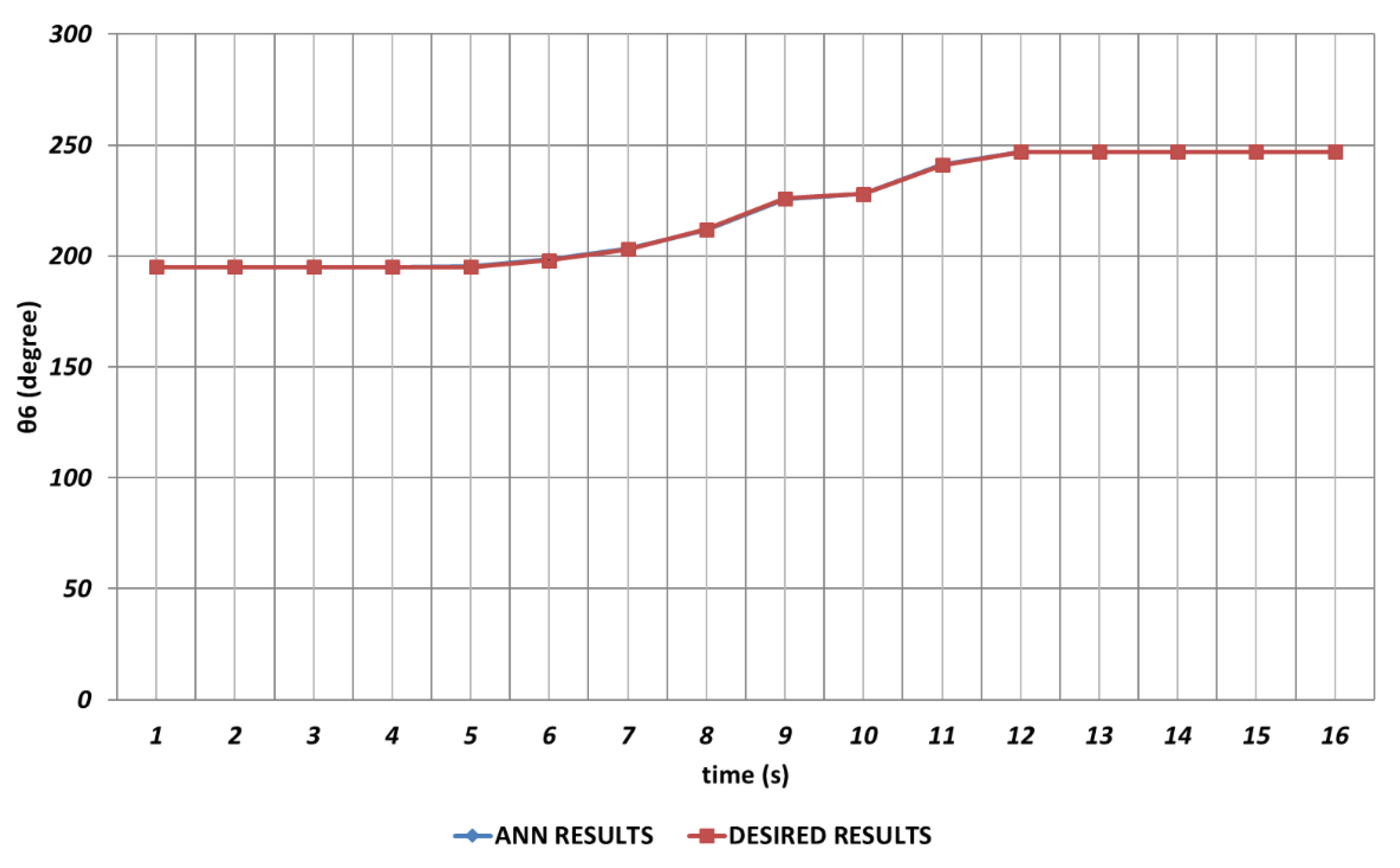
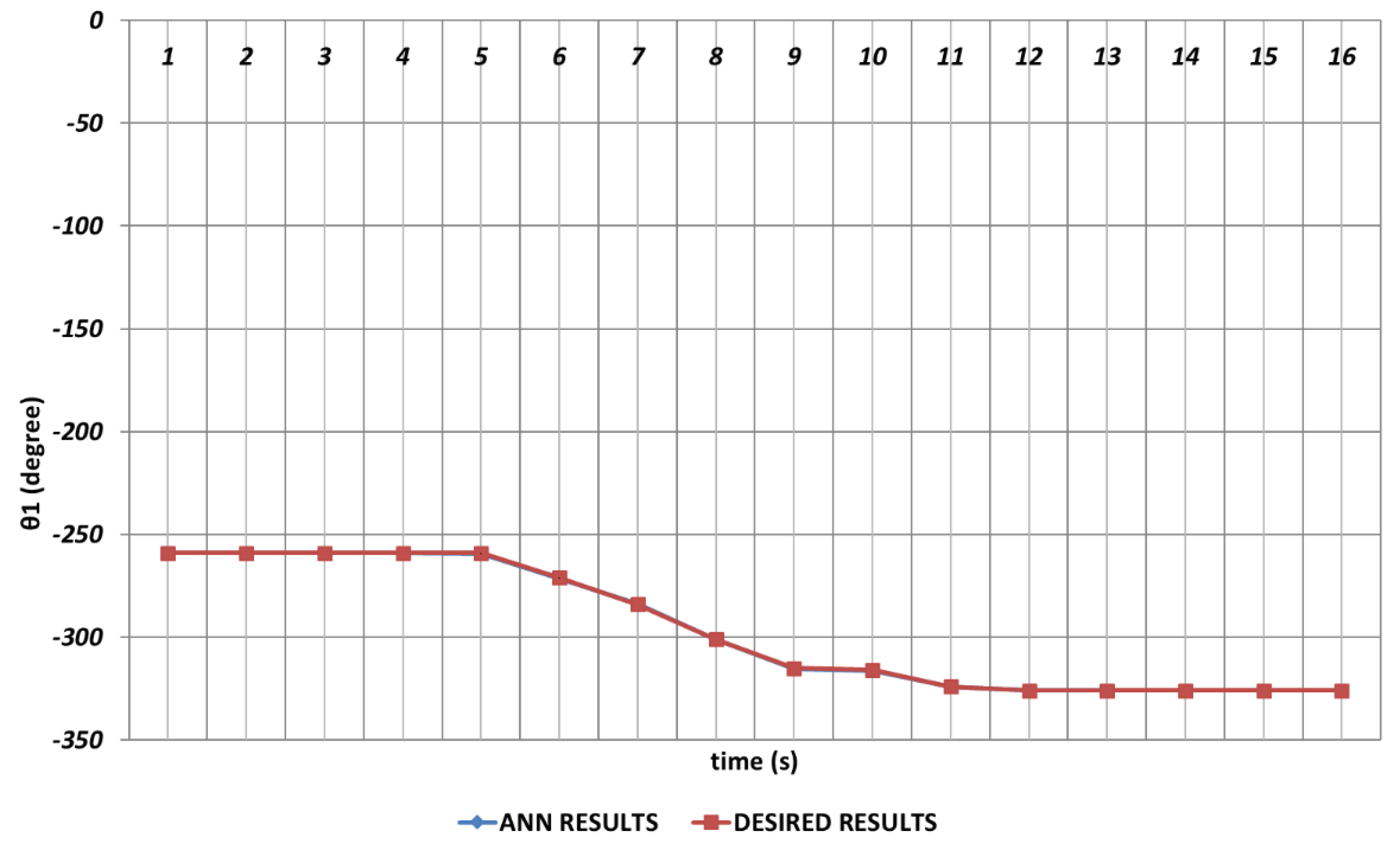
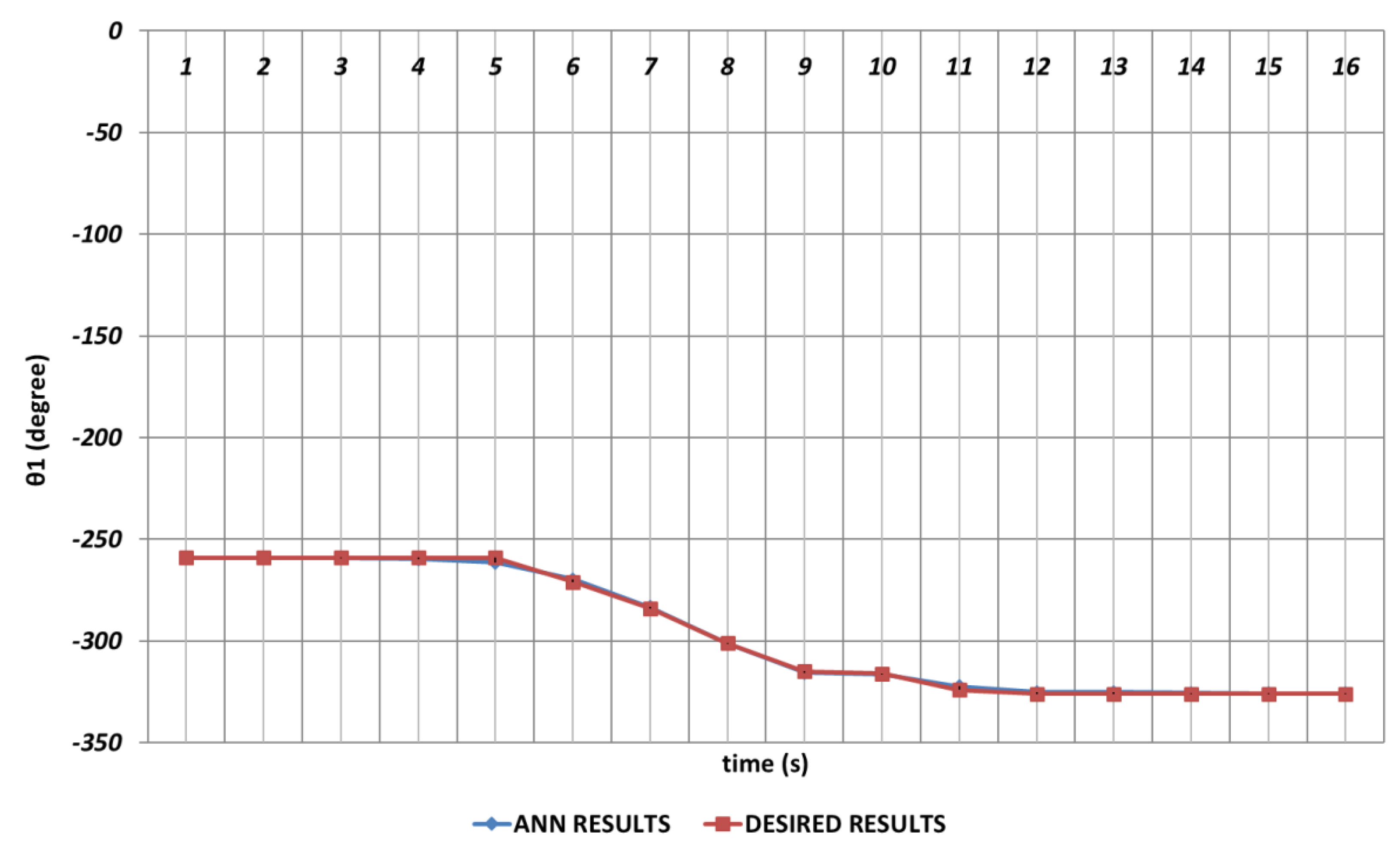
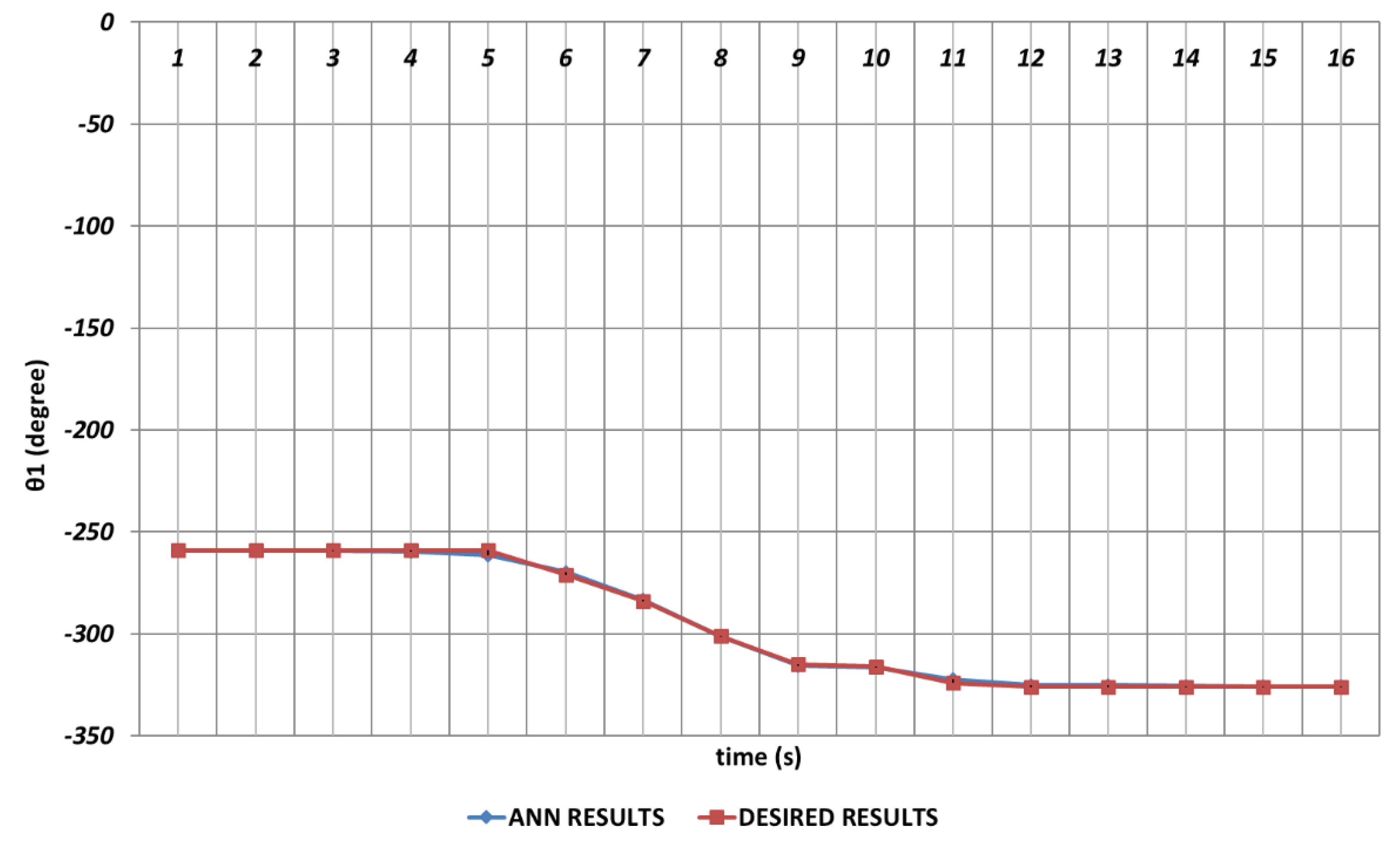
In Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, DBD learning algorithm based simulations results are presented. As seen from the Figure 6, which represents the modelling performance for θ 1 , DBD algorithm is able to predict the theoretical data with high accuracy. Although there are instantaneous angular changes at the 5th and 9th seconds, the DBD can follow these changes successfully.
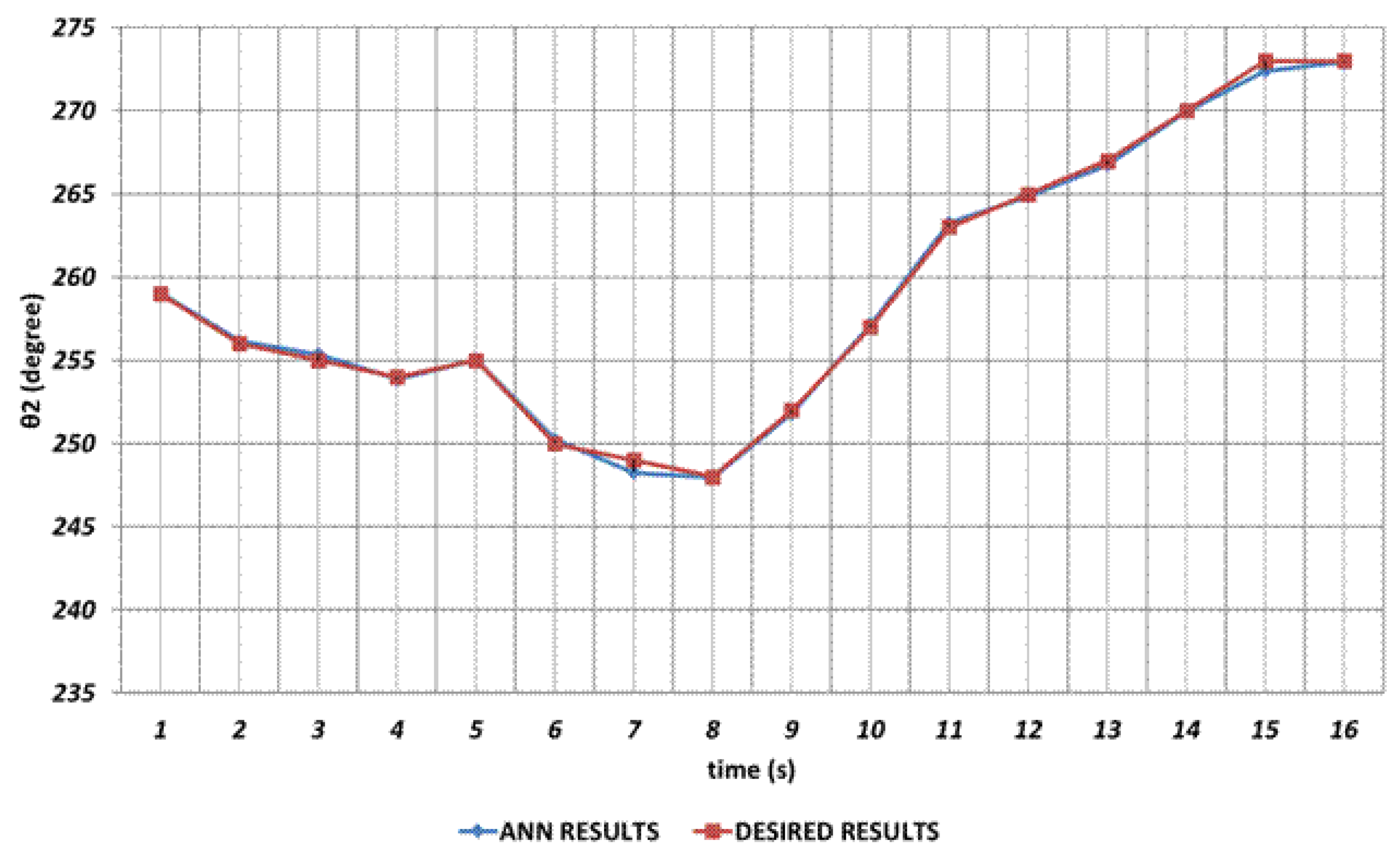
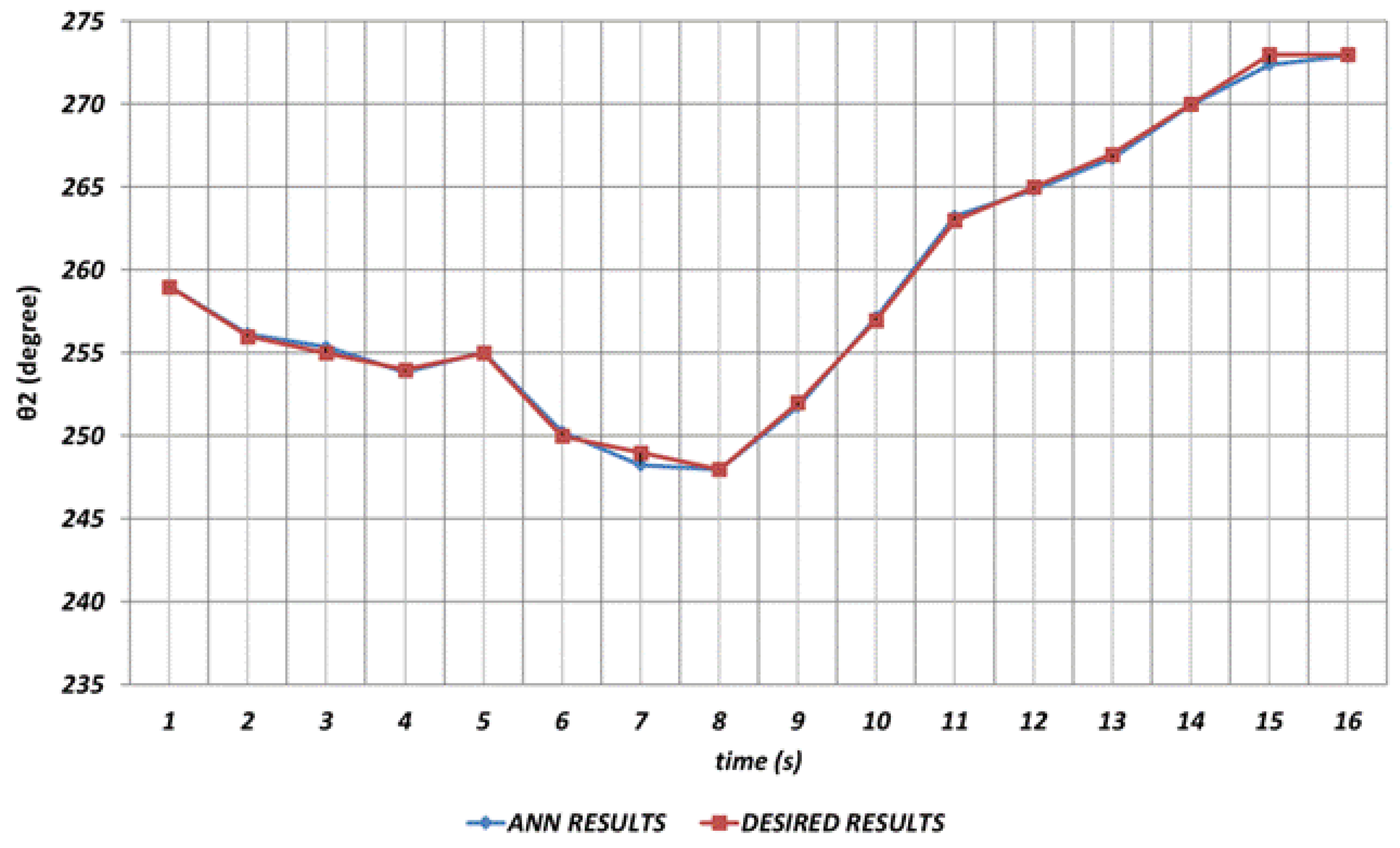
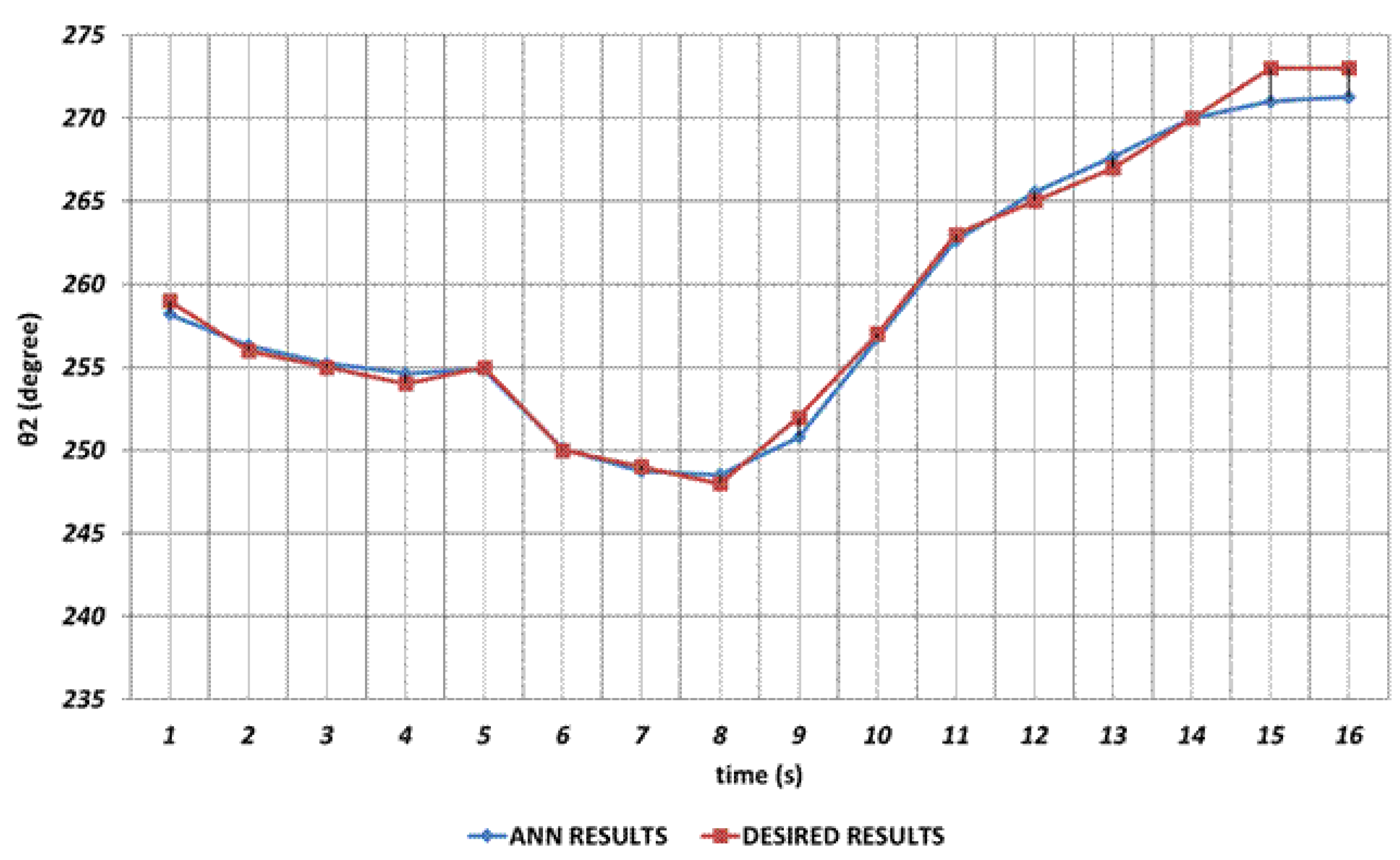
Figure 7 shows the DBD based prediction result for θ 2 . Since it is used as the shoulder angle, it is seen that there are significant prediction errors in the intervals of 2nd and 4th seconds, 6th and 8th seconds and similarly 14th and 16th seconds. Namely, DBD based estimation seems a bit insufficient in predicting instantaneous changes in the time intervals mentioned. This situation shows that an unexpected position difference will occur in serial chemical application between the fabric where the chemical will be sprayed and the ideal position.
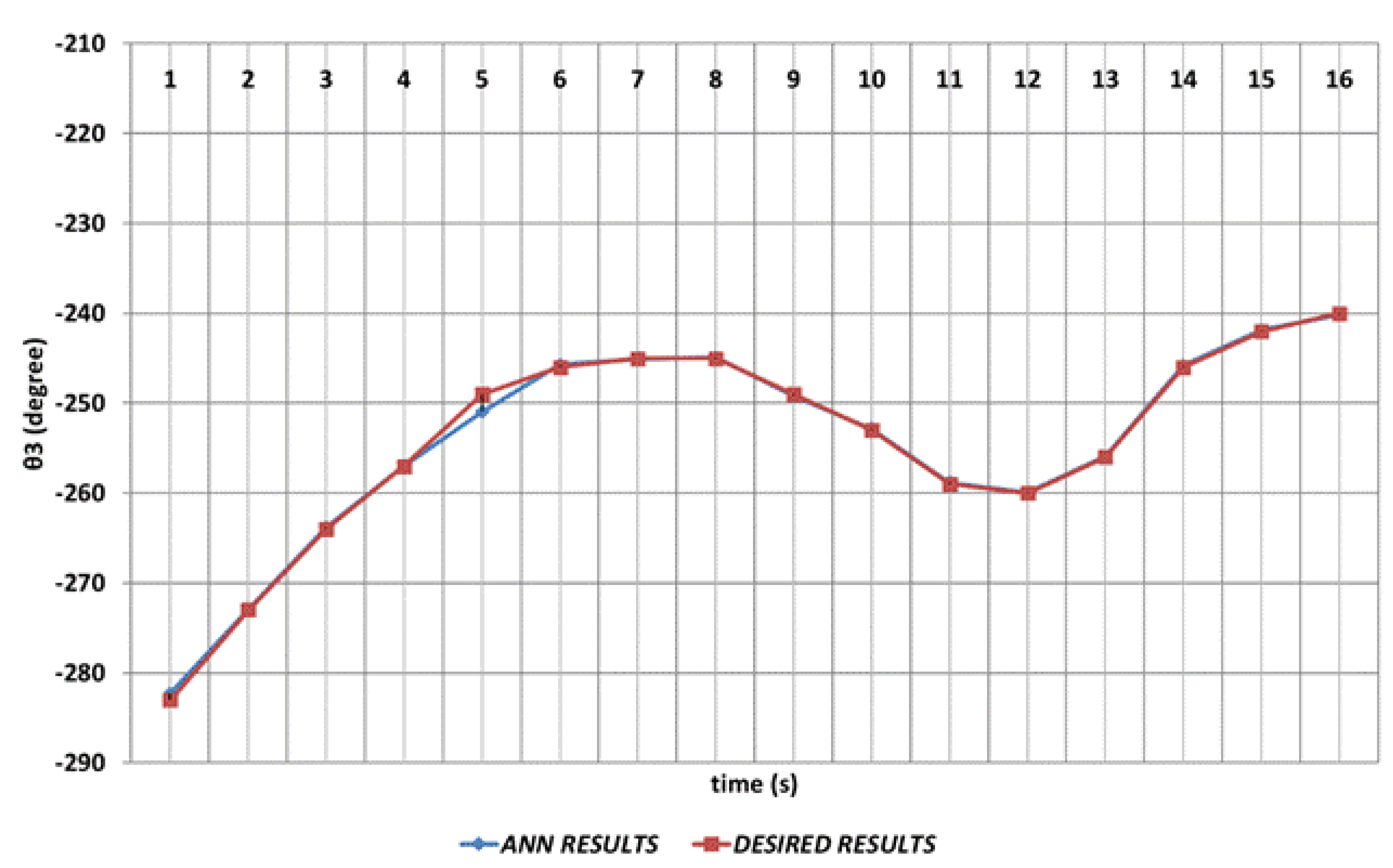
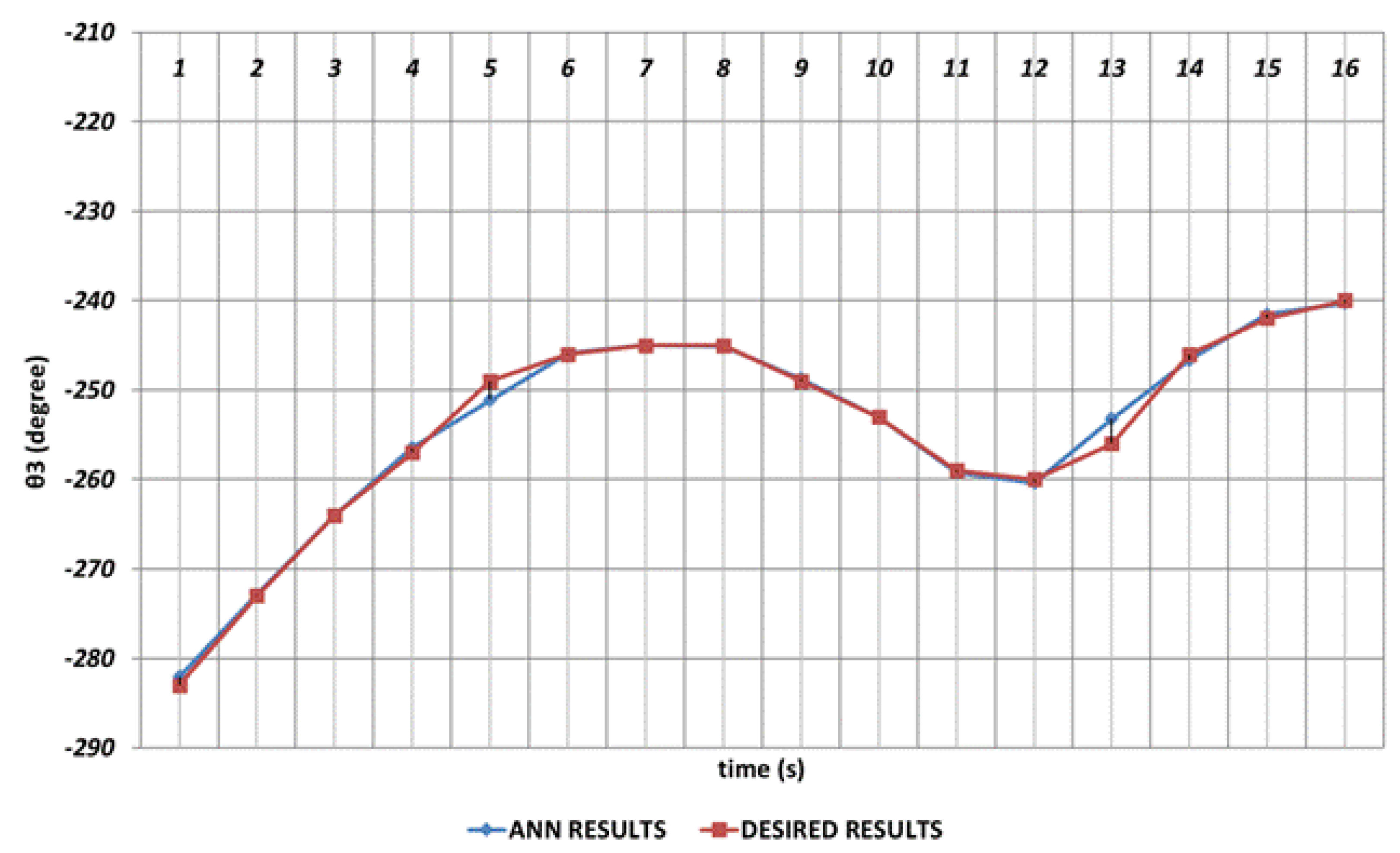
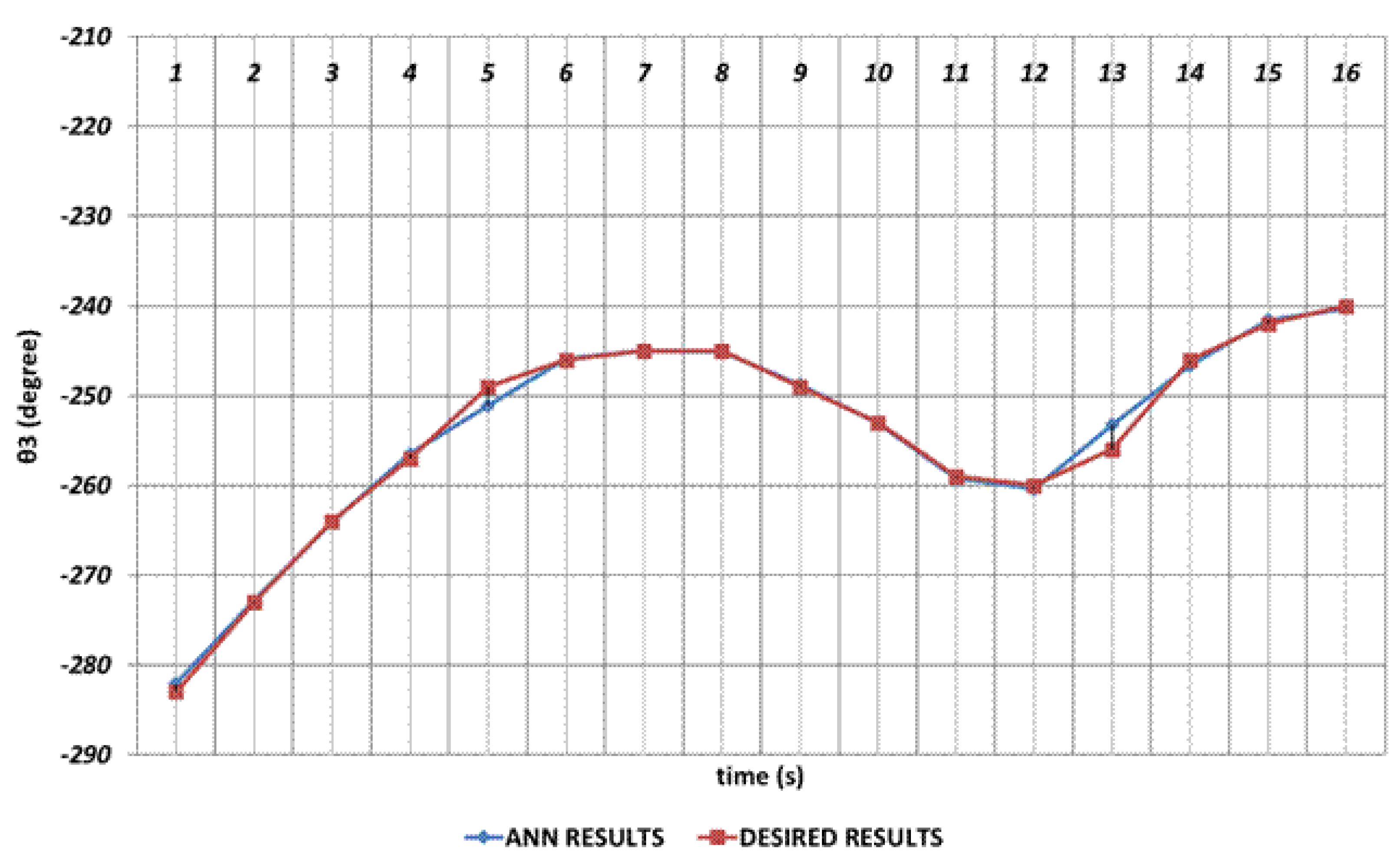
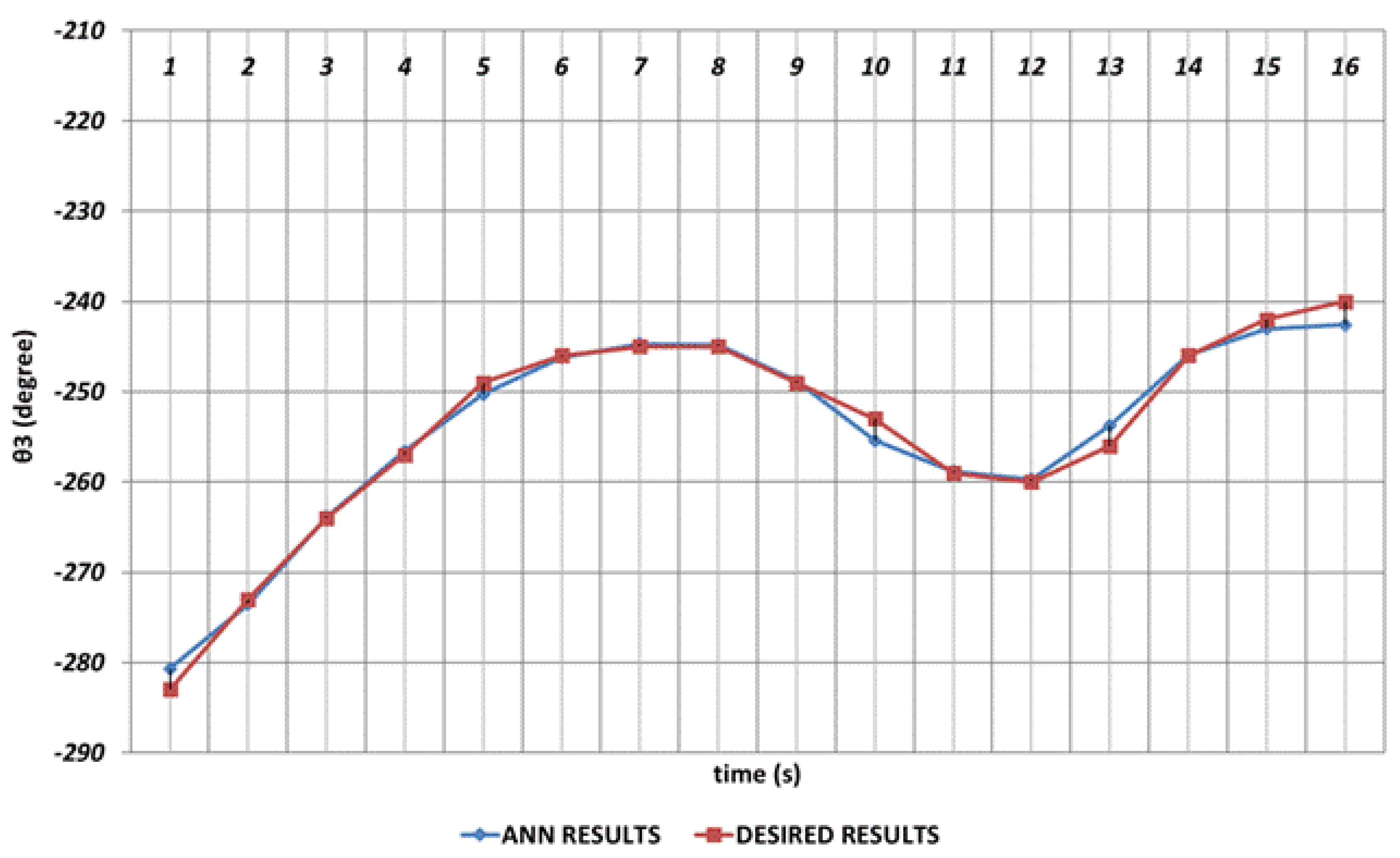
DBD based prediction results of the θ 3 , which performs the elbow function in the human structure, is demonstrated in Figure 8. Since the shoulder angle appearing after the angular change is used as the next period angle at the same time, instantaneous changes in the time intervals of 1st and 2nd seconds and also 4th and 6th seconds observed. It can be concluded that significant spray errors will occur will be observed, especially in the time interval of 4th and 6th seconds, in serial chemical applications. On the other hand, despite the errors that occur during instantaneous angular changes, the prediction performance seems successful outside of these two time intervals.
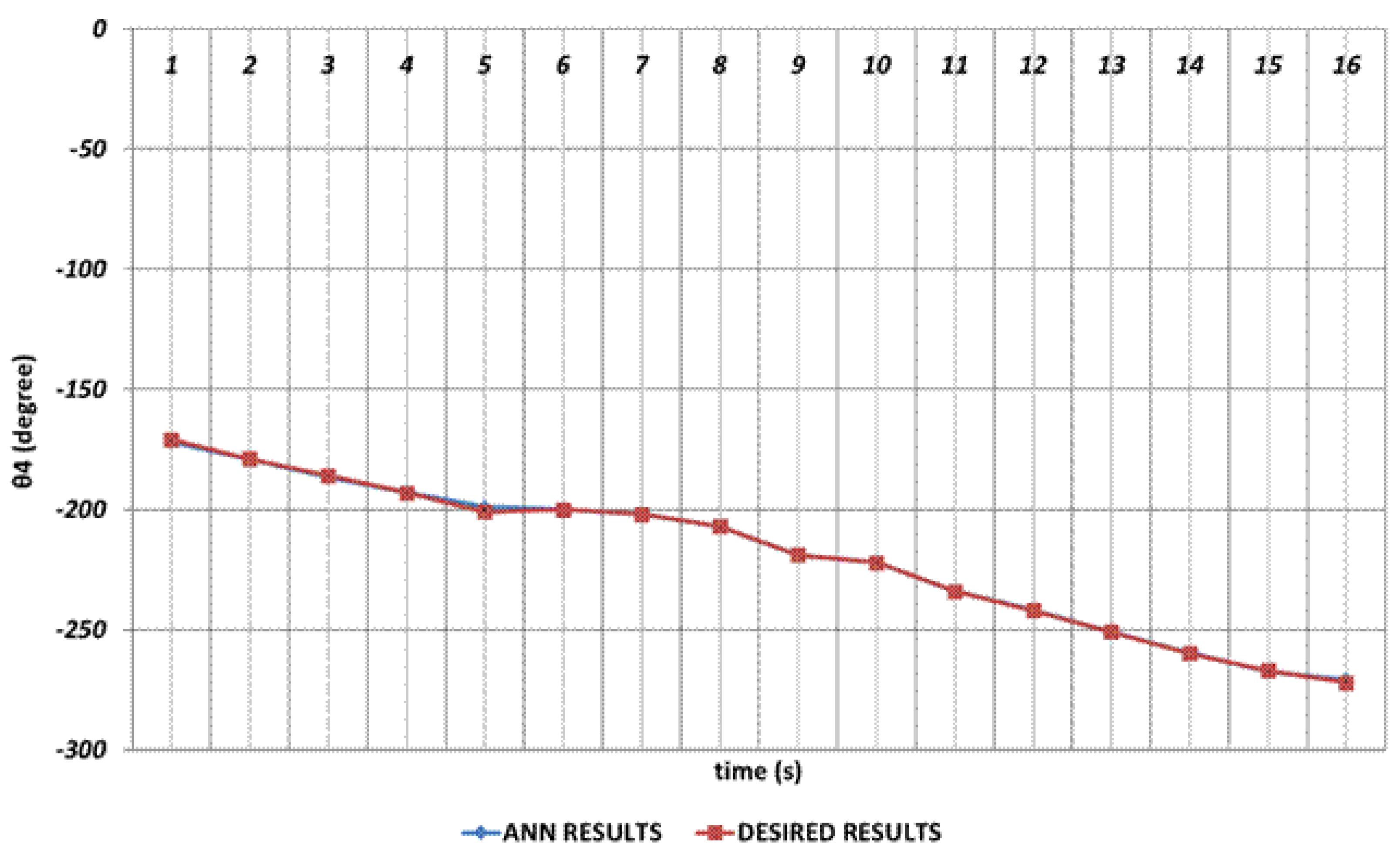
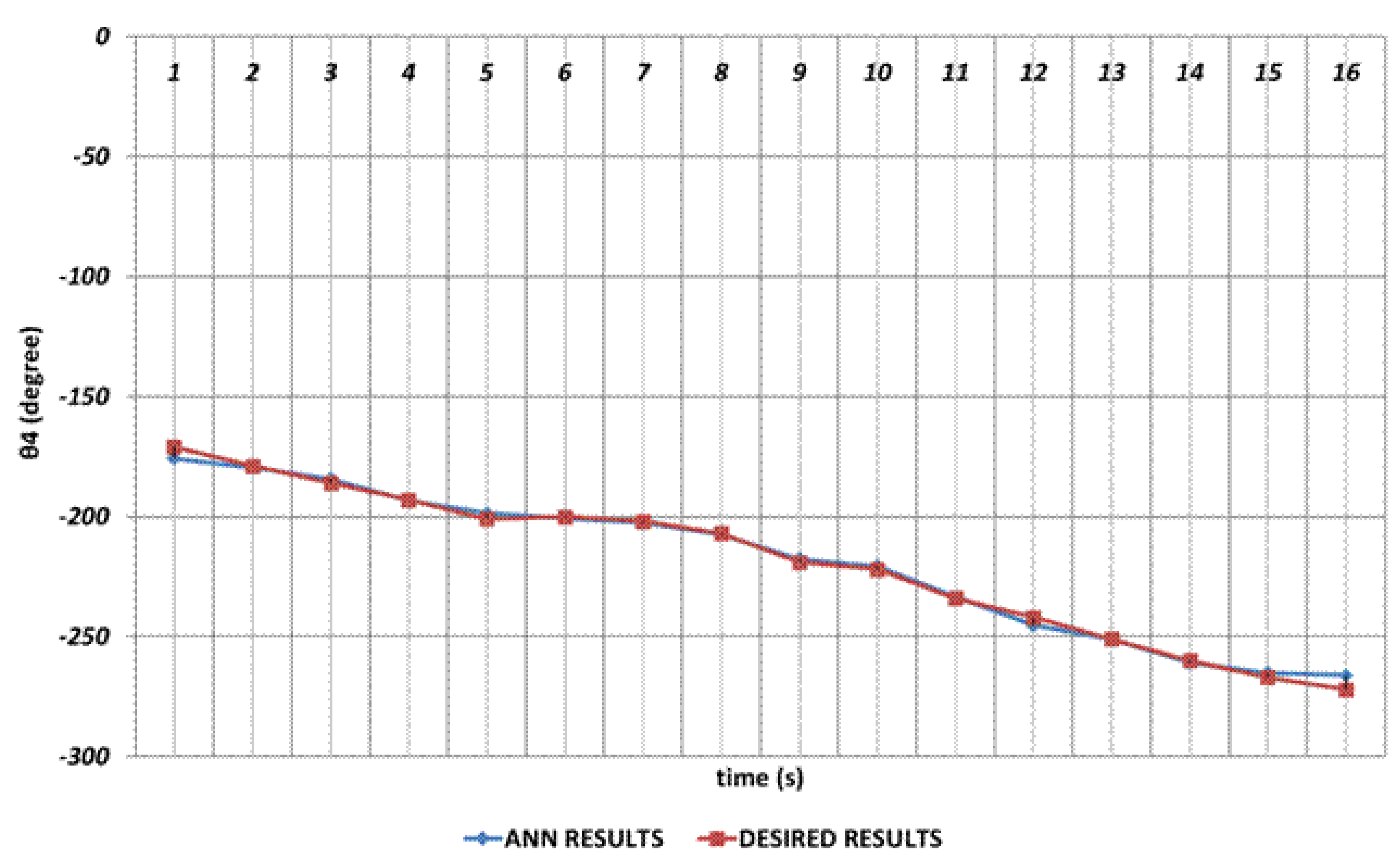
The θ 4 joint angle corresponds to the rotation angle of the robot gripper. When the DBD based prediction results anlayzed, it can be emphasized that the theoretical data can be predicted with high accuracy even in the intervals of 4th and 6th seconds and 8th and 10th seconds at which instantaneous angular changes appeared.
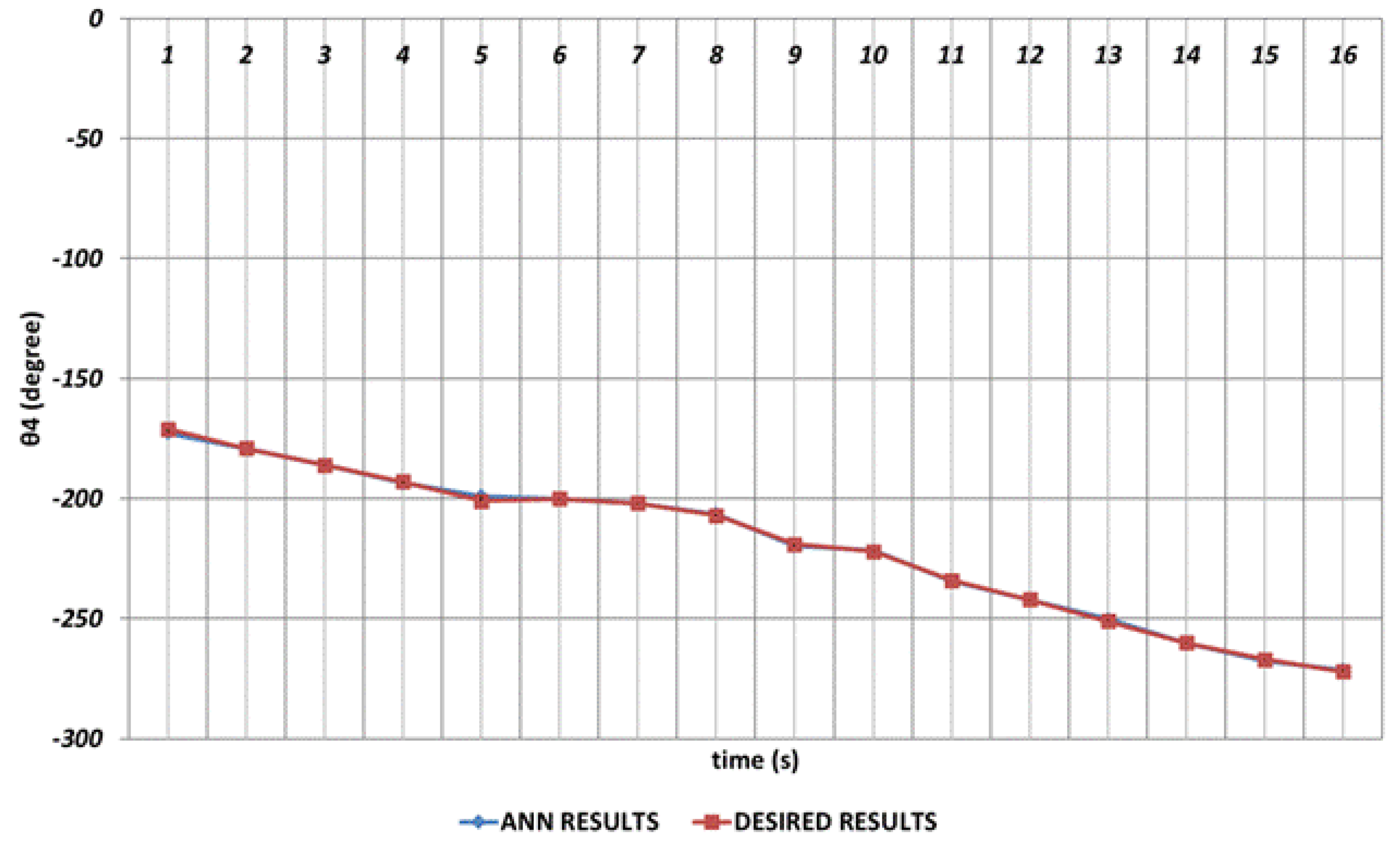
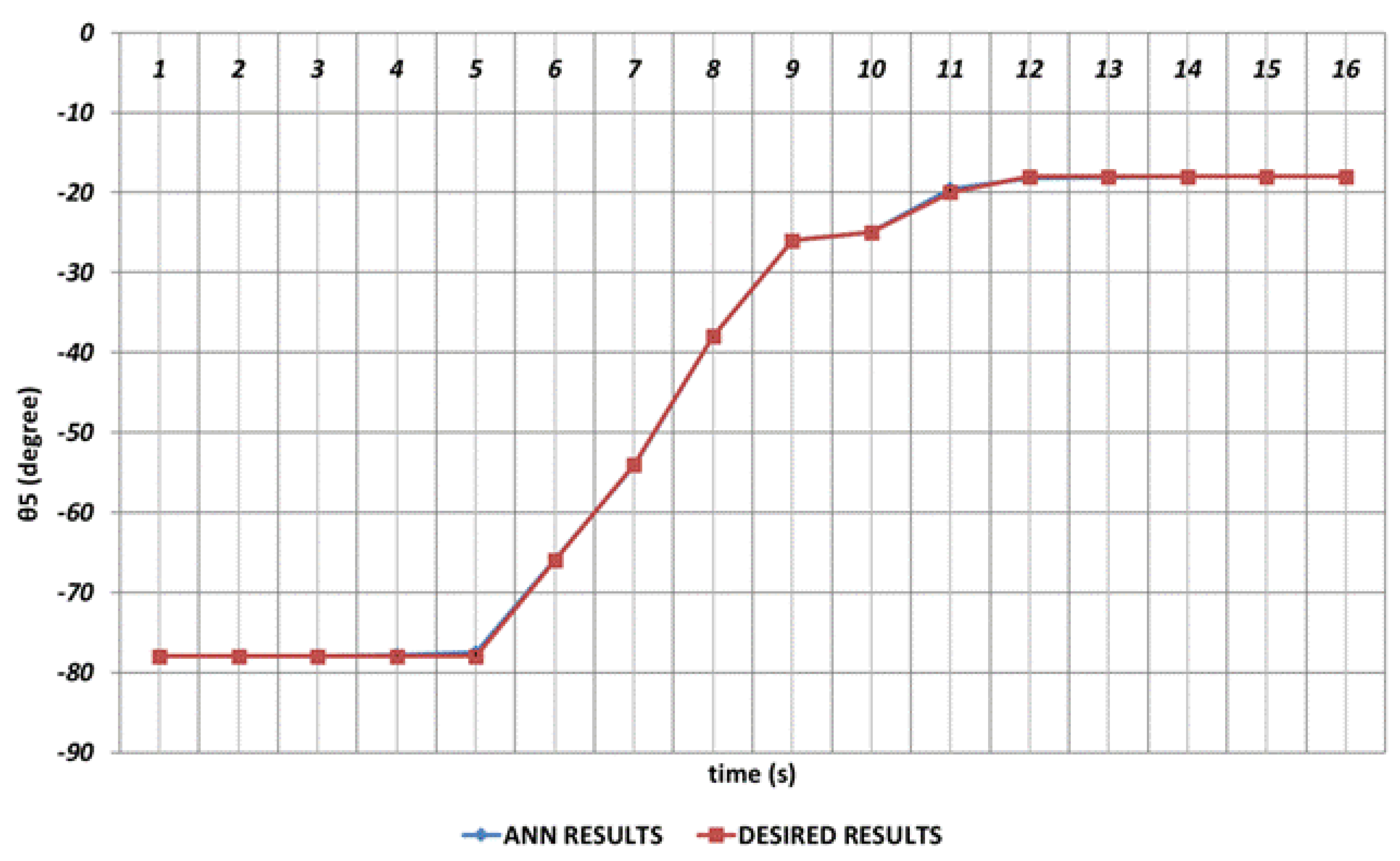
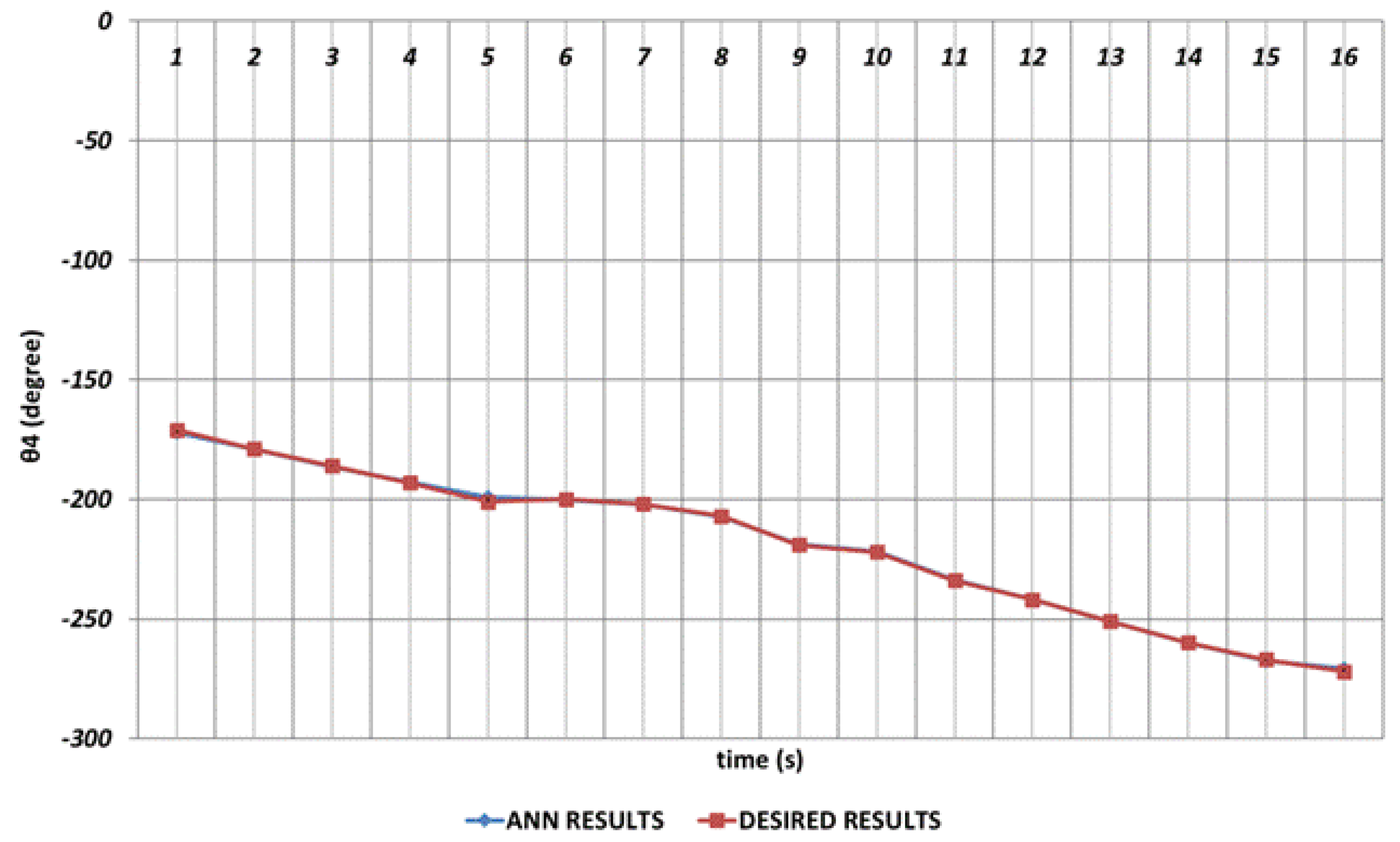
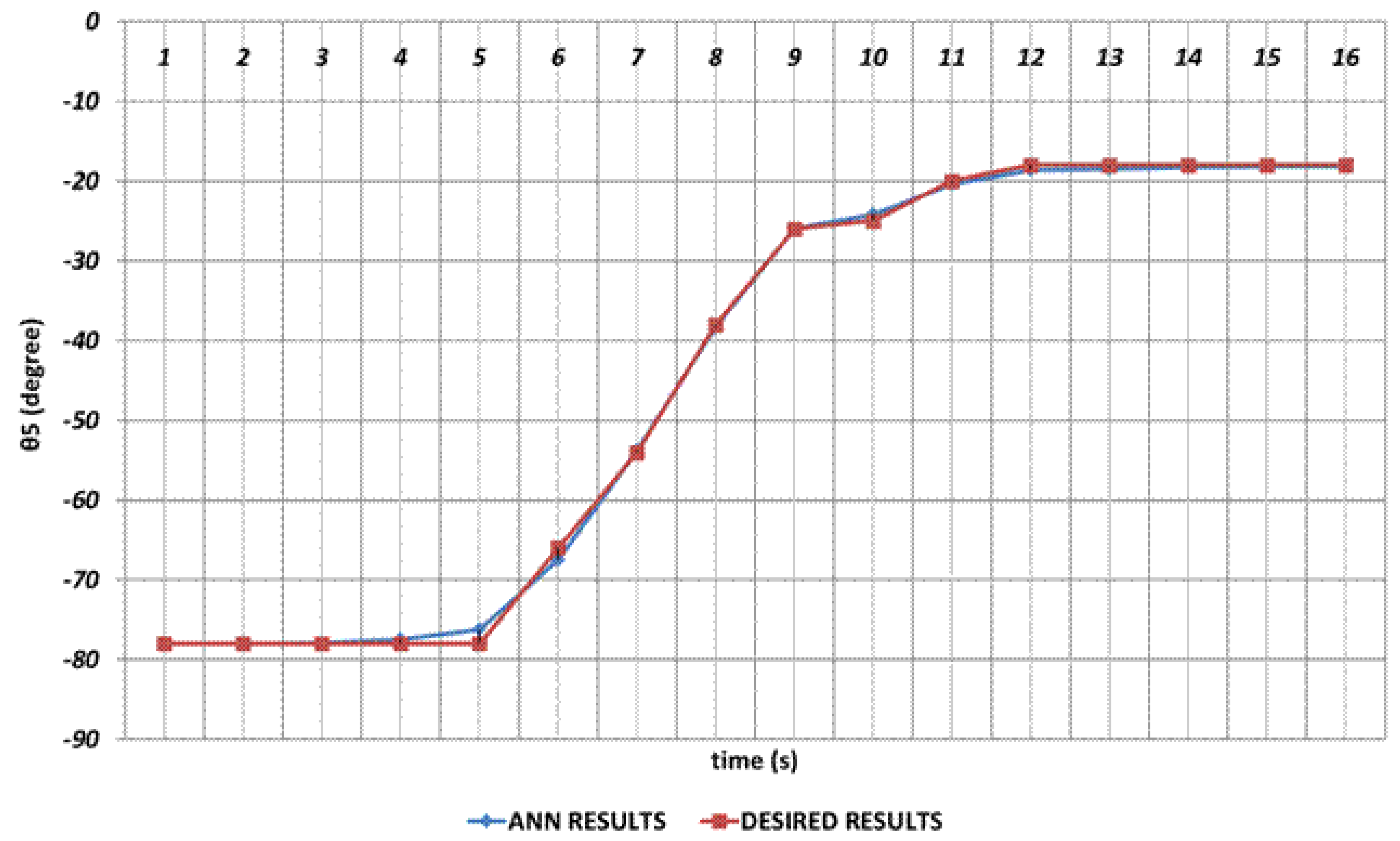
Especially the fifth joint angle has an important role in positioning structure and rotation angle and even small prediction errors for θ 5 are not acceptable. Firstly, instantaneous angular changes occur in the intervals of 4th and 5th seconds and similarly in the 10th and 12th seconds, as seen in Figure 10. As a result of these instantaneous angular changes, it is seen that deviations with too small magnitudes are occurring in the DBD based prediction results. When the prediction performance is evaluated in a general manner, it can be expressed that DBD can successfully predict the theoretical data for θ 5 .
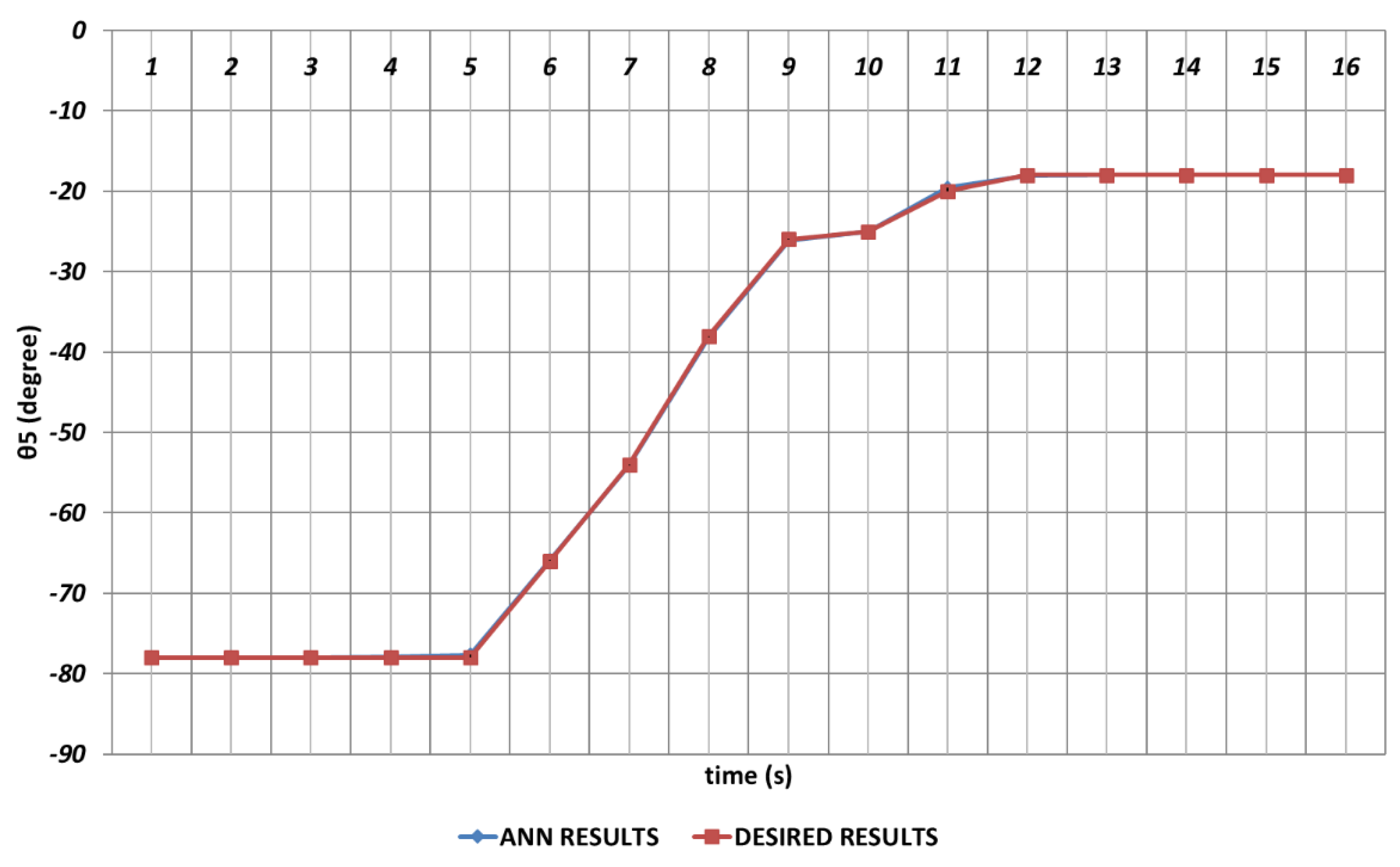
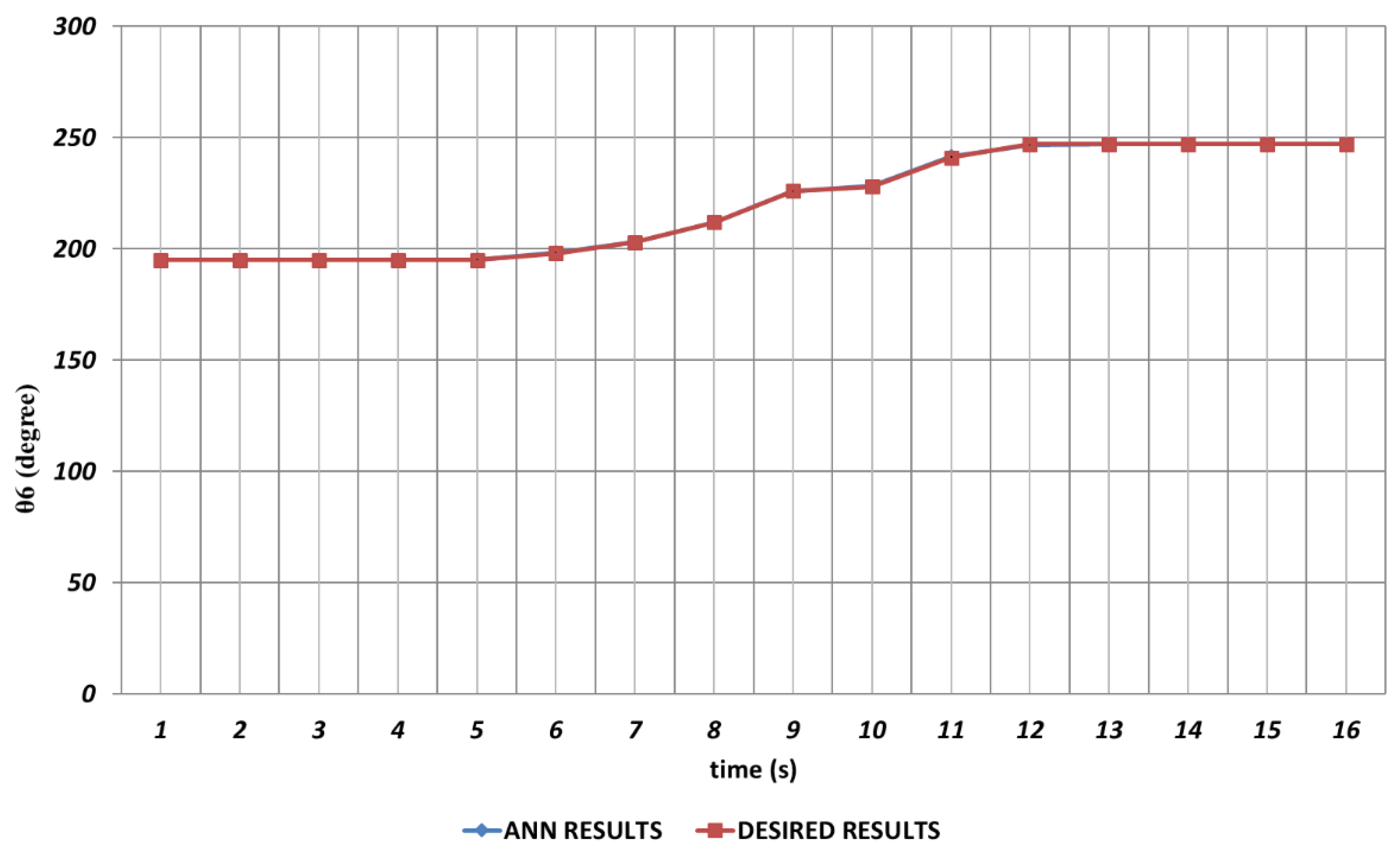
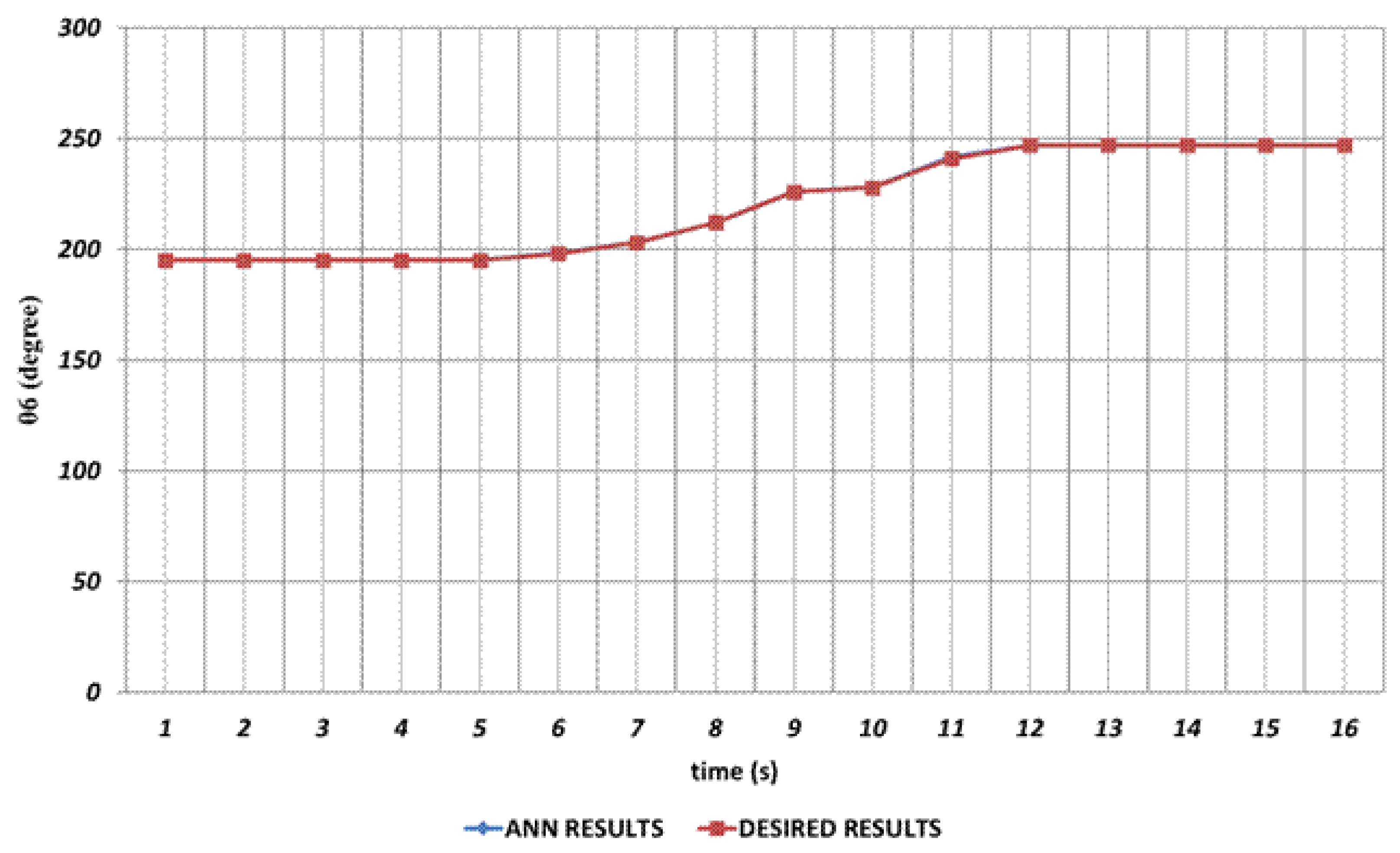
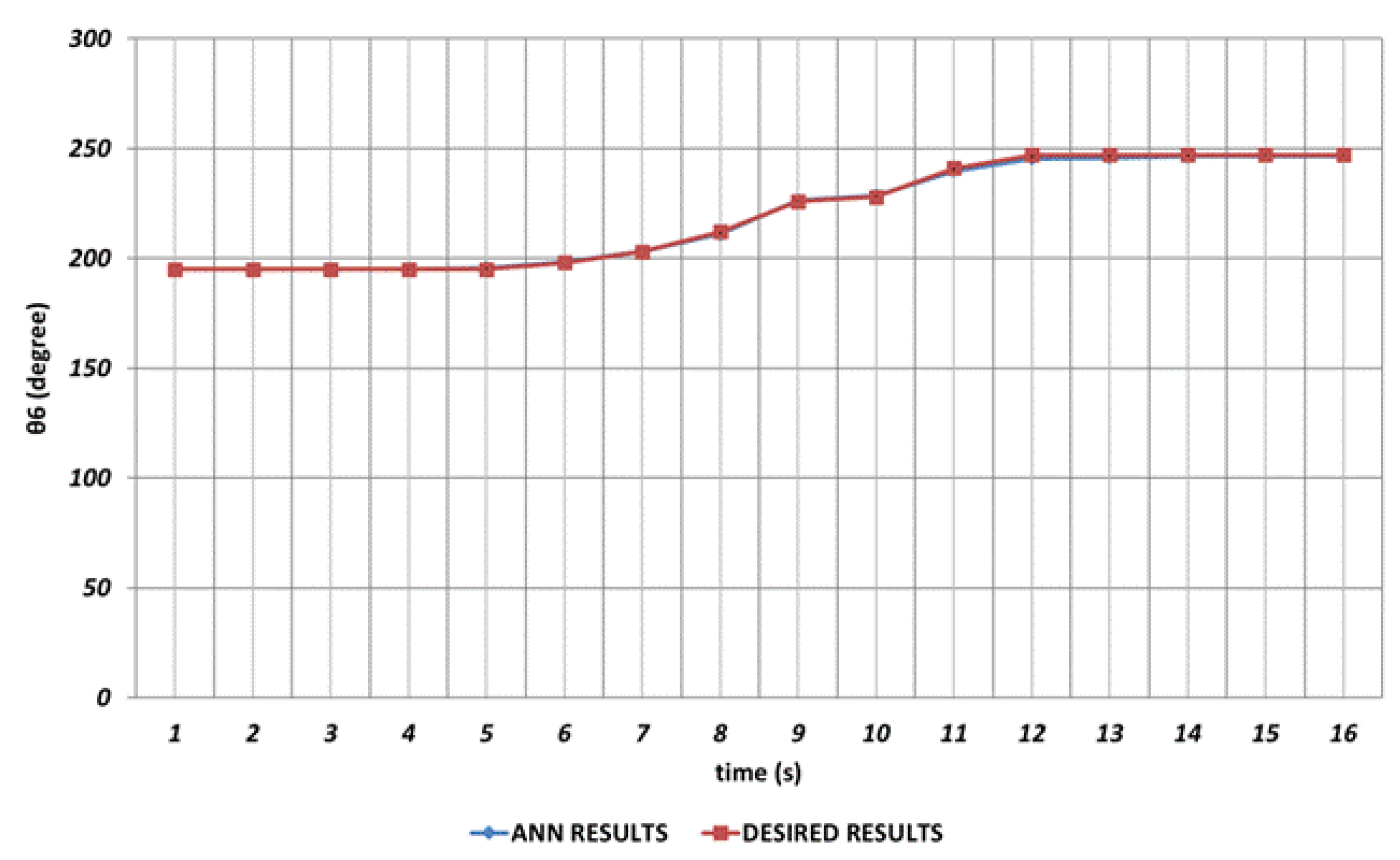
Figure 11 shows the prediction results obtained for θ 6 which is the last rotation angle of the robot manipulator. It is seen that small prediction errors are almost non-existent for the sixth joint angle. The reason of this can be expressed as no instantaneous angular changes are occurring during the entire time interval.
The analysis results obtained for the OBP learning algorithm are given in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. The prediction performance for the θ 1 joint angel is presented in Figure 12. From the figure, it is seen that OBP is able to produce superior prediction result for the first joint angle which is the body rotation angular of the robot manipulator. In other words, no instantaneous angular changes are occurring and the OBP based results converges to the theoretical results with high accuracy during the entire time interval.
In Figure 13, the prediction performance of the OBP learning algorithm is shown for the θ 2 joint angle which corresponds to the corresponds to the shoulder angle. It is seen that there are significant prediction errors in the time intervals of 2nd and 4th seconds, 6th and 8th seconds and 11th and 16th seconds due to the instantaneous angular changes. These angular differences will cause the chemical spraying process to be carried out with incorrect angle values.
Figure 14 demonstrates the OBP based prediction results obtained for θ 3 which is the third joint angle of the robot manipulator. Since the shoulder angle obtained after the angular change is used as the next period angle at the same time, it is observed that significant deviations from the theoretical data are appeared in the time intervals of 1st and 2nd seconds, 4th and 6th seconds and also 11th and 16th seconds. As a result, it can be emphasized that the prediction performance for the third joint angle seems insufficient when the OBP learning algorithm used. In contrast, OBP is able to provide better prediction performances outside of the time intervals that include instantaneous angular changes.
In Figure 15, the simulation results produced by OBP in prediction of θ 4 joint angle are presented. From the results, it can be expressed that the rotation angle of the robot gripper can successfully be predicted with high accuracy via OBP learning algorithm. However, although instantaneous angular changes have no significant effect, it is seen that prediction errors are occurring between the theoretical and ANN approach at certain rates in the time intervals of 4th and 6th seconds and 14th and 16th seconds.
θ 5 joint angle is extremely important for the positioning of the end effector used in the chemical spray system. Due to its critical role in optimizing the positioning structure of the entire system, even small prediction errors are not acceptable for this angle as mentioned before. As seen from the prediction results given in Figure 16, deviations with too small magnitudes occurring especially in the time intervals of 3rd and 6th seconds and 10th and 13th seconds
As seen from the Figure 17, which represents the OBP based prediction results obtained for θ 6 , an excellent prediction performance can be provided. The limited number of instantaneous position changes in the theoretical data ensures an effective prediction process during the entire time interval.
The prediction performance of QBP learning algorithm in terms of the joint angles are represented in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. Figure 18 proves that QBP is able to provide an excellent prediction performance for θ 1 during the entire time interval, including instantaneous angular changes.
QBP based prediction results for the robot manipulator shoulder angle θ 2 is shown in Figure 19. As can be seen from the figure, there are significant prediction errors especially in the time intervals of 2nd and 4th seconds, 6th and 8th seconds and 14th and 16th seconds due to the effect of instantaneous angular changes. In other words, the prediction results for θ 2 should not be used directly in serial chemical applications.
Figure 20 demonstrates the QBP based prediction result for the θ 3 joint angle which simulates the elbow function of humans. Due to the instantaneous angular changes in the time intervals of 1st and 2nd seconds, 4th and 6th seconds and 11th and 14th seconds, the therotical data cannot be predicted successfully. As a result, it can be emphasized that the prediction for the third joint angle is not very effective and the performance of the QBP seems insufficient at the relevant time intervals.
In Figure 21, the QBP prediction results obtained for the θ 4 joint angle are given. In general, it can be said that QBP can successfully converge to the theoretical data except the time intervals of 4th and 6th seconds and 14th and 16th seconds. On the other hand, it can also be stated that the deviations from the theoretical data are occurring with too small magnitudes in the relevant time intervals.
Due to its importance mentioned before, the prediction of the θ 5 joint angle with high accuracy is crucial. Figure 22 represents the prediction performance of the QBP learning algorithm. Due to the effect of instantaneous angular changes, it is seen that prediction errors with small magnitudes are occurring between the theoretical data and QBP approach in the time intervals of 4th and 6th seconds and 10th and 12th seconds. When the prediction performance is evaluated in a general manner, it can be expressed that QBP can successfully predict the theoretical data for θ 5 .
When the proposed QBP based approach applied to the prediction of sixth joint angel, it is seen that the θ 6 can successfully be predicted. As seen from the Figure 23, QBP is able to produce a prediction performance that almost overlapped with the theoretical data during the entire time interval. The reason for this situation may be expressed as the lack of instantaneous angular changes or their occurrence with too small magnitudes.
Figure 24, Figure 25, Figure 26, Figure 27, Figure 28 and Figure 29 represent the analysis results obtained by using RBP learning algorithm. As seen from the Figure 24, which shows the modelling performance for θ 1 , RBP is able to predict the theoretical data with high accuracy. Although there are instantaneous angular changes at the 4th and 6th seconds, the RBP can also converge to these changes successfully.
Figure 25 demonstrates the RBP based prediction result for θ 2 . As seen from the figure, the deviations with high amplitudes from the theoretical data are occurring during the entire time interval. θ 2 corresponds to the shoulder angle of the robot manipulator and it is seen that the prediction performance of the RBP in terms of θ 2 decreases significiantly as a result of the instantaneous angular changes. In other words, it will be inevitable that the lack of high prediction performance for the second joint angle will cause significant errors in chemical applications in the production process.
In Figure 26, the prediction results obtained for θ 3 by using RBP based ANN are shown. As in the prediction process of the second joint angle, the RBP produces worse prediction results during the entire time interval and also cannot converge to the theoretical data of the θ 3 joint angle enough. Namely, basic RBP learning algorithm seems insufficient in predicting the theoretical data of the third joint angle.
In predicting of θ 4 joint angle, RBP learning algorithm cannot provide a completely adequate performance as shown in Figure 27. Especially, deviations having high magnitudes from the theoretical data are occurring in the time intervals of 1st and 2nd seconds, 11th and 13th seconds and 15th and 16th seconds due to the instantaneous angular changes. In addition, deviations having small magnitudes are also observed in the time intervals of 4th and 7th seconds and 8th and 11th seconds
RBP based prediction performance for the θ 5 joint angle is given in Figure 28. Due to the effect of instantaneous angular changes, it is seen that prediction errors are occurring at unacceptable rates between the theoretical and RBP approaches in the time intervals of 3rd and 7th seconds and 9th and 16th seconds.
The the prediction results obtained for θ 6 are shown in Figure 29. From the figure, it can be seen that RBP learning algorithm is able to provide an effective prediction performance during the entire time interval except the 11th and 14th seconds. It can also be concluded that the lack of instantaneous angular changes or their occurrence with too small magnitudes results in an effective prediction performance.
In order to present a more detailed analysis, in addition to the 3-10-6 ANN network structure including 10 nonlinear cells in the hidden layer, the performance of the 3-5-6 network structure which includes 5 nonlinear cells in its hidden layer is also analyzed. The results obtained are presented in Table 3. From the results, it is seen that that the network structure including 5 nonlinear cells in its hidden layer can provide a faster learning effect. However, it is also seen that as the number of nonlinear cells in the hidden layer decreases, the error performance and therefore the prediction performance decrease. When the results are evaluated in general, it can be expressed that the QBP produces the best prediction results fot the 3-10-6 network structure while the DBD produces the best prediction results for 3-5-6 network structure.
The statistical performances of the improved ANN network structures are another important performance metric. In this study, the R2 statistical analysis approach was applied to test the reliability and stability of the results obtained. In Equation 8 given for R2,
R 2 = 1 − ∑ ( i d e a l i − i d e ^ a l i ) 2 ∑ ( i d e a l i − i d e ˜ a l i ) 2
i d e a l i can be defined as the ideal values of the joint angels, i d e ^ a l i represents the joint angel values obtained from the regression equation and finally i d e ˜ a l i is the mean value of the ideal joint angels. The value of the R2 parameter changes in the interval of [0,1], The R2 values close to 1 prove the effectiveness of the model. From the Table 4 which represents the statistical performances of each algorithm, it can be concluded that all the learning algorithms are able to provide statistically superior performance. In other words, each learning algorithm exhibits stable behavior by converging to approximately the same results at each run.

4. Conclusions

In this study, ANN based positioning analyzes were carried out to predict joint angles of a 6-DOF industrial robot manipulator system for trajectory analysis. DBD, OBP, QBP and RBP learning algorithms based ANN network structures were improved and then applied for the prediction of six joint angels with high accuracy. The applicability of ANNs in multi-DOF robot manipulator trajectory prediction was demonstrated and the superiority of ANN based apoproaches in trajectory prediction was proved.
In addition to the 3-10-6 type ANN structure, the 3-5-6 type ANN structure was also improved and applied to the prediction trajectory analysis. The simulation results obtained for the 3-10-6 type ANN structure represent that all learning algorithms can successfully predict the θ 1 , θ 4 , θ 5 and θ 6 joint angels with high accuracy. When the prediction results obtained for these joint angles are examined, it is seen that instantaneous deviations are occurring only at certain time intervals and with low magnitudes. On the other hand, the prediction performances of the algorithms for θ 2 and θ 3 seems too weak due to the instantaneous deviations with high magnitudes that occur during the entire time interval.
In order to present a detailed performance comparison between the 3-10-6 and 3-5-6 type ANN structures the RMSE and the statistical R2 values reached were also compared. The mean and maximum RMSE values reached by the algorithms represent that QBP produces the best results for the 3-10-6 ANN structure and DBD produces the best results for the 3-5-6 ANN structure. When the results are evaluated in terms of the RMSE performance, it can be expressed that RBP produces the worst results among four learning algorithms. The R2 values reached by the algorithms show that each learning algorithm is able to produce similar statistical performances but the reliability and stability of the DBD based ANN structure seems a bit better when compared to other learning algorithms.
Consequently, it can be stated that the ANN based approaches proposed in this study can be used effectively even in the optimal trajectory analysis of real-time robot manipulators operating under large disturbances.

Author Contributions

Conceptualization, M.B.Ç., K.Y. and Ş.Y.; methodology, M.B.Ç., K.Y. and Ş.Y.; software, M.B.Ç., K.Y. and Ş.Y.; validation, K.Y.; formal analysis, M.B.Ç., K.Y. and Ş.Y.; investigation, M.B.Ç., K.Y. and Ş.Y.; writing—original draft preparation, K.Y.; writing—review and editing, M.B.Ç. and Ş.Y. .

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Saad, M.; Dessaint, L.A.; Bigras, P.; Al Haddad, K. . Adaptive versus neural adaptive control: Application to robotics. International Journal of Adaptive Control and Signal Processing 1994, 8, 223–236. [Google Scholar] [CrossRef]
  2. Bonev, I.A.; Ryu, J. A geometrical method for computing the constant-orientation workspace of 6-PRRS parallel manipulators. Mechanism and Machine Theory 2001, 36, 1–13. [Google Scholar] [CrossRef]
  3. Bonev, I.A.; Ryu, J.; Kim, S.-G.; Lee, S.K. A closed-form solution to the direct kinematics of nearly general parallel manipulators with optimally located three linear extra sensors. IEEE Transactions on Robotics and Automation 2001, 17, 148–156. [Google Scholar] [CrossRef]
  4. Bonev, I.A.; Zlatanov, D.; Gosselin, C.M. Singularity analysis of 3-DOF planar parallel mechanisms via screw theory. ASME Journal of Mechanical Design 2003, 125, 573–581. [Google Scholar] [CrossRef]
  5. Tonbul, T. S.; Sarıtaş, M. Beş eksenli bir edubot robot kolunda ters kinematik hesaplamalar ve yörünge planlaması. Gazi Üniverditesi Mühendislik Mimarlık Fakültesi Dergisi, 2003; 18, 145–167. [Google Scholar]
  6. Khayati, K.; Bigras, P.; Dessaint, L.A. A multi-stage position/force control for constrained robotic systems with friction: joint-space decomposition, linearization and multi-objective observer/controller synthesis using lmi formalism. IEEE Transactions on Industrial Electronics 2006, 53, 1698–1712. [Google Scholar] [CrossRef]
  7. Lessard, S.; Bigras, P.; Bonev, I.A. ; A new medical parallel robot and its static balancing optimization. Journal of Medical Devices 2007, 1, 272–278. [Google Scholar] [CrossRef]
  8. Karahan, O. S60 Robotunun Dinamik Modelinin Çıkarılması. Master Thesis, University of Kocaeli, Turkey, 2007. [Google Scholar]
  9. Janvier, M.A.; Durant, L.G.; Roy Cardinal, M.H.; Renaud, I.; Chayer, B.; Bigras, P.; Guise, J.; Soulez, G.; Cloutier, G. Performance evaluation of a medical robotic 3D-ultrasound imaging system. Medical Image Analysis Journal 2007, 12, 275–290. [Google Scholar] [CrossRef] [PubMed]
  10. Lessard, S.; Bigras, P.; Bonev, I.A. A new medical parallel robot and its static balancing optimization. Journal of Medical Devices 2007, 1, 272–278. [Google Scholar] [CrossRef]
  11. Bigras, P.; Lambert, M.; Perron, C. New optimal formulation for an industrial robot force controller, International Journal of Robotics and Automation 2008, 23, 199-208. 23.
  12. Yu, A.; Bonev, I.A.; Zsombor-Murray, P. Geometric approach to the accuracy analysis of a class of 3-DOF planar parallel robots. Mechanism and Machine Theory 2008, 43, 364–375. [Google Scholar] [CrossRef]
  13. Briot, S.; Bonev, I.A. A new fully decoupled 3-DOF translational parallel robot for pick-and-place applications. Journal of Mechanisms and Robotics 2008, 1, 1–9. [Google Scholar]
  14. Liu, X.J.; Bonev, I.A. Orientation capability, error analysis and dimension optimization of two articulated tool heads with parallel kinematics. Journal of Manufacturing Science and Engineering 2008, 130, 1–25. [Google Scholar] [CrossRef]
  15. Bigras, P.; Lambert, M.; Perron, C. New optimal formulation for an industrial robot force controller. International Journal of Robotics and Automation 2008, 23, 199–208. [Google Scholar] [CrossRef]
  16. Briot, S.; Bonev, I.A. Accuracy analysis of 3-DOF planar parallel robots. Mechanism and Machine Theory 2008, 43, 445–458. [Google Scholar] [CrossRef]
  17. Perez, J.; Perez, J.P.; Soto, R.; Flores, A.; Rodriguez, F.; Meza, J.L. Trajectory tracking error using PID control law for two-link robot manipulator via adaptive neural networks. Procedia Technology 2012, 3, 139–146. [Google Scholar]
  18. Tang, S.H.; Ang, C.K.; Ariffin, M.K.A.; Mashohor, S.B. Predicting the motion of a robot manipulator with unknown trajectories based on an artificial neural network. International Journal of Advanced Robotic Systems 2014, 11, 1–9. [Google Scholar] [CrossRef]
  19. Pham, C.V.; Wang, Y.N. Robust adaptive trajectory tracking sliding mode control based on neural networks for cleaning and detecting robot manipulators. Journal of Intelligent & Robotic Systems 2015, 79, 101–114. [Google Scholar]
  20. Moldovan, L.; Grif, H. È.; Gligor, A. ANN based inverse dynamic model of the 6-PGK parallel robot manipulator. International Journal of Computers Communications & Control 2016, 11, 90–104. [Google Scholar]
  21. Mahajan, A.; Singh, H.P.; Sukavanam, N. An unsupervised learning based neural network approach for a robotic manipulator. International Journal of Information Technology 2017, 9, 1–6. [Google Scholar] [CrossRef]
  22. Son, N.N.; Anh, H.P.H.; Chau, T.D. Adaptive neural model optimized by modified differential evolution for identifying 5-DOF robot manipulator dynamic system. Soft Computing 2018, 22, 979–988. [Google Scholar] [CrossRef]
  23. Liu, C.; Zhao, Z.; Wen, G. Adaptive neural network control with optimal number of hidden nodes for trajectory tracking of robot manipulators. Neurocomputing 2019, 350, 136–145. [Google Scholar] [CrossRef]
  24. Truong, L.V.; Huang, S.D.; Yen, V.T.; Cuong, P.V. Adaptive trajectory neural network tracking control for industrial robot manipulators with deadzone robust compensator. International Journal of Control, Automation and Systems, 2020; 18, 2423–2434. [Google Scholar]
  25. Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An improved neural network algorithm to efficiently track various trajectories of robot manipulator arms. IEEE Access 2021, 9, 11911–11920. [Google Scholar] [CrossRef]
  26. Kouritem, S.A.; Abouheaf, M.I.; Nahas, N.; Hassan, M. A multi-objective optimization design of industrial robot arms. Alexandria Engineering Journal 2022, 61, 12847–12867. [Google Scholar] [CrossRef]
  27. Universal Robots. https://www.universal-robots.com/tr/urunler/ur5-robot/ (30.05.2024).
Preprints 109079 g001
Figure 1. Classical human based chemical spraying process on denim textile.
Figure 1. Classical human based chemical spraying process on denim textile.
Preprints 109079 g001
Preprints 109079 g002
Figure 2. Representation of the prposed 6-DOF industrial robot and its rotation axes.
Figure 2. Representation of the prposed 6-DOF industrial robot and its rotation axes.
Preprints 109079 g002
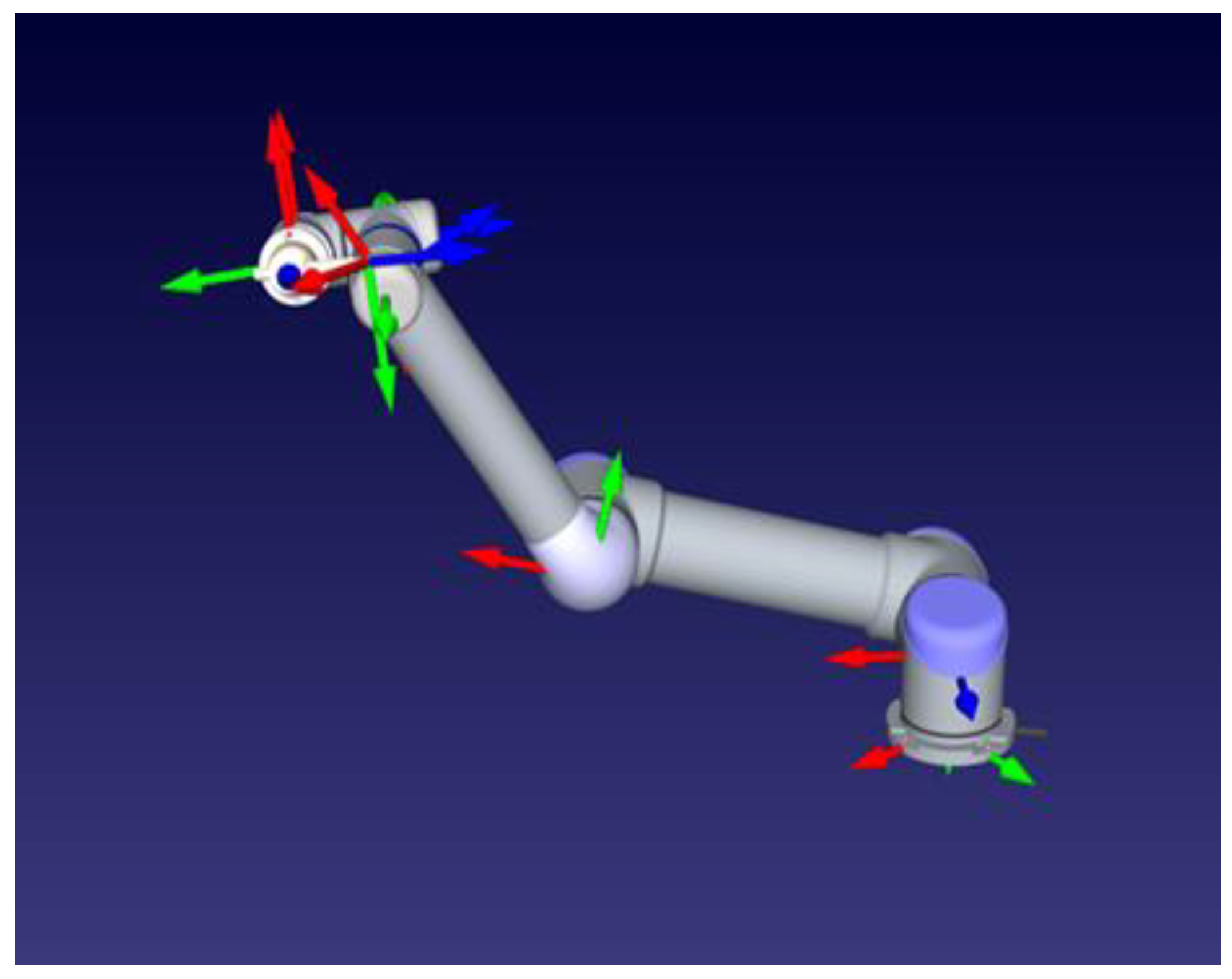
Preprints 109079 g003
Figure 3. Robot manipulator and each joint axes sets.
Figure 3. Robot manipulator and each joint axes sets.
Preprints 109079 g003
Preprints 109079 g004
Figure 4. The proposed artificial neural network representation.
Figure 4. The proposed artificial neural network representation.
Preprints 109079 g004
Preprints 109079 g005
Figure 5. ANN based modelling of a robot manipulator.
Figure 5. ANN based modelling of a robot manipulator.
Preprints 109079 g005
Preprints 109079 g006
Figure 6. DBD learning algorithm based prediction result for the first joint angle.
Figure 6. DBD learning algorithm based prediction result for the first joint angle.
Preprints 109079 g006
Preprints 109079 g007
Figure 7. DBD learning algorithm based prediction result for the second joint angle.
Figure 7. DBD learning algorithm based prediction result for the second joint angle.
Preprints 109079 g007
Preprints 109079 g008
Figure 8. DBD learning algorithm based prediction result for the third joint angle.
Figure 8. DBD learning algorithm based prediction result for the third joint angle.
Preprints 109079 g008
Preprints 109079 g009
Figure 9. DBD learning algorithm based prediction result for the fourth joint angle.
Figure 9. DBD learning algorithm based prediction result for the fourth joint angle.
Preprints 109079 g009
Preprints 109079 g010
Figure 10. DBD learning algorithm based prediction result for the fifth joint angle.
Figure 10. DBD learning algorithm based prediction result for the fifth joint angle.
Preprints 109079 g010
Preprints 109079 g011
Figure 11. DBD learning algorithm based prediction result for the sixth joint angle.
Figure 11. DBD learning algorithm based prediction result for the sixth joint angle.
Preprints 109079 g011
Preprints 109079 g012
Figure 12. OBP learning algorithm based prediction result for the first joint angle.
Figure 12. OBP learning algorithm based prediction result for the first joint angle.
Preprints 109079 g012
Preprints 109079 g013
Figure 13. OBP learning algorithm based prediction result for the second joint angle.
Figure 13. OBP learning algorithm based prediction result for the second joint angle.
Preprints 109079 g013
Preprints 109079 g014
Figure 14. OBP learning algorithm based prediction result for the third joint angle.
Figure 14. OBP learning algorithm based prediction result for the third joint angle.
Preprints 109079 g014
Preprints 109079 g015
Figure 15. OBP learning algorithm based prediction result for the fourth joint angle.
Figure 15. OBP learning algorithm based prediction result for the fourth joint angle.
Preprints 109079 g015
Preprints 109079 g016
Figure 16. OBP learning algorithm based prediction result for the fifth joint angle.
Figure 16. OBP learning algorithm based prediction result for the fifth joint angle.
Preprints 109079 g016
Preprints 109079 g017
Figure 17. OBP learning algorithm based prediction result for the sixth joint angle.
Figure 17. OBP learning algorithm based prediction result for the sixth joint angle.
Preprints 109079 g017
Preprints 109079 g018
Figure 18. QBP learning algorithm based prediction result for the first joint angle.
Figure 18. QBP learning algorithm based prediction result for the first joint angle.
Preprints 109079 g018
Preprints 109079 g019
Figure 19. QBP learning algorithm based prediction result for the second joint angle.
Figure 19. QBP learning algorithm based prediction result for the second joint angle.
Preprints 109079 g019
Preprints 109079 g020
Figure 20. QBP learning algorithm based prediction result for the third joint angle.
Figure 20. QBP learning algorithm based prediction result for the third joint angle.
Preprints 109079 g020
Preprints 109079 g021
Figure 21. QBP learning algorithm based prediction result for the fourth joint angle.
Figure 21. QBP learning algorithm based prediction result for the fourth joint angle.
Preprints 109079 g021
Preprints 109079 g022
Figure 22. QBP learning algorithm based prediction result for the fifth joint angle.
Figure 22. QBP learning algorithm based prediction result for the fifth joint angle.
Preprints 109079 g022
Preprints 109079 g023
Figure 23. QBP learning algorithm based prediction result for the sixth joint angle.
Figure 23. QBP learning algorithm based prediction result for the sixth joint angle.
Preprints 109079 g023
Preprints 109079 g024
Figure 24. RBP learning algorithm based prediction result for the first joint angle.
Figure 24. RBP learning algorithm based prediction result for the first joint angle.
Preprints 109079 g024
Preprints 109079 g025
Figure 25. RBP learning algorithm based prediction result for the second joint angle.
Figure 25. RBP learning algorithm based prediction result for the second joint angle.
Preprints 109079 g025
Preprints 109079 g026
Figure 26. RBP learning algorithm based prediction result for the third joint angle.
Figure 26. RBP learning algorithm based prediction result for the third joint angle.
Preprints 109079 g026
Preprints 109079 g027
Figure 27. RBP learning algorithm based prediction result for the fourth joint angle.
Figure 27. RBP learning algorithm based prediction result for the fourth joint angle.
Preprints 109079 g027
Preprints 109079 g028
Figure 28. RBP learning algorithm based prediction result for the fifth joint angle.
Figure 28. RBP learning algorithm based prediction result for the fifth joint angle.
Preprints 109079 g028
Preprints 109079 g029
Figure 29. RBP learning algorithm based prediction result for the sixth joint angle.
Figure 29. RBP learning algorithm based prediction result for the sixth joint angle.
Preprints 109079 g029
Table 2. D-H parameters of the Universal Robots UR5e model 6-DOF robot manipulator.
Table 2. D-H parameters of the Universal Robots UR5e model 6-DOF robot manipulator.
Number of Joint 2 Link Twist Axes Angle Link Lenght Link Offset Joint Angle Joint Variable
i αi-1 ai-1 di Θi dior Θi
1 0 L1 0 Θ1 Θ1
2 0 L2 0 Θ2 Θ2
3 0 L3 0 Θ3 Θ3
4 0 L4 0 Θ4 Θ4
5 0 L5 0 Θ5 Θ5
6 0 L6 0 Θ6 Θ6
Table 3. Performance comparison of the ANN network structures used.
Table 3. Performance comparison of the ANN network structures used.
Learning Algorithm ANN Network Structure Mean RMSE
(Training)		 Maximum RMSE
(Training)		 Mean RMSE
(Test)		 Maximum RMSE
(Test)
DBD 3-10-6 0.427328 1.20820 0.418576 1.20820
OBP 3-10-6 0.485862 1.20600 0.507729 1.20600
QBP 3-10-6 0.373176 1.19047 0.374058 1.19047
RBP 3-10-6 1.210040 2.86877 1.267080 1.27537
DBD 3-5-6 0.726305 1.60402 0.734876 1.34779
OBP 3-5-6 0.826176 1.73226 0.804328 1.73226
QBP 3-5-6 0.878670 1.98618 0.911634 1.98618
RBP 3-5-6 1.385830 2.72113 1.523790 2.72113
Table 4. R2 values obtained for each learning algorithm.
Table 4. R2 values obtained for each learning algorithm.
Learning Algorithm ANN Network Structure R 2
θ 1 θ 2 θ 3 θ 4 θ 5 θ 6
DBD 3-10-6 0.99997 0.99938 0.99773 0.99932 0.99996 0.99996
OBP 3-10-6 0.99996 0.99870 0.99310 0.99953 0.99995 0.99990
QBP 3-10-6 0.99900 0.99870 0.99310 0.99953 0.99995 0.99990
RBP 3-10-6 0.99900 0.98952 0.98709 0.99426 0.99934 0.99910
DBD 3-5-6 0.99957 0.99734 0.99349 0.99853 0.99946 0.99985
OBP 3-5-6 0.99950 0.99803 0.99355 0.99824 0.99933 0.99933
QBP 3-5-6 0.99993 0.99602 0.99449 0.99595 0.99994 0.99995
RBP 3-5-6 0.99922 0.97655 0.96693 0.99360 0.99915 0.99854
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated