The construction time of concrete structures in hydraulic tunnels is long, the construction environment is complex, and there are many influencing factors. The requirements for construction quality are high, not only to meet the strength requirements, but also to meet the design requirements of erosion resistance, crack resistance, and seepage resistance according to its specific operating environment. Therefore, evaluating the construction quality of concrete structures in hydraulic tunnels is of great significance. Considering the randomness and fuzziness of factors affecting the construction quality of concrete structures in hydraulic tunnels, this paper proposes a comprehensive evaluation model based on Combined Weighting (CWM) and Uncertainty Measurement Theory (UM). The IAHP method and CRITIC method are used to determine the subjective and objective weights of evaluation indicators, combined weighting is based on the principle of minimum entropy, and the UM method is used to evaluate the construction quality level. Finally, taking a hydraulic tunnel as an example, its construction quality grade is calculated to be III according to the evaluation model proposed in this paper, which matches with the engineering reality, and a comparative study is made with the mixture element topology theory at the same time. It is verified that the evaluation model can scientifically and reasonably evaluate the construction quality level of concrete structures in hydraulic tunnels.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

China is a vast country with abundant water resources, but they are unevenly distributed in space, with large differences between the north and the south, and the shortage of water resources restricts the development of some cities and agriculture. For this reason, China has built a series of water diversion projects such as South-to-North Water Diversion, Diversion of River to Huaihuai, Diversion of Yellow to Qingdao, etc., which basically involve the construction of a large number of hydraulic tunnels. The construction of concrete structures in hydraulic tunnels is characterized by multi-stage, multi-level and multi-factors, and the construction processes are closely connected and interact with each other, which not only have to meet the strength requirements, but also have to meet the design requirements of anti-erosion, anti-cracking, anti-seepage and anti-impact and wear-resisting according to the specific operation environment. Therefore, it is of great significance to improve the service life of hydraulic tunnels by reasonably evaluating the construction quality level of the concrete structure in hydraulic tunnels and taking scientific and effective measures to maintain it in time.

There have been a number of research results in the area of tunnel concrete structures. You Zhemin et al [1] took highway tunnels as the object of study and proposed methods to deal with the quality problems such as collapse, water gushing, large deformation of surrounding rock and cracking of support that may occur during its construction. Wu Jiming [2] made a systematic analysis for the construction quality control of hydraulic concrete structures in terms of selection and inspection of raw materials for hydraulic concrete, structural design, determination of mixing ratios, control of structural deformation, pouring and vibration construction. Lan Xiaofeng [3] combined with Jimingyi Tunnel to study the quality control of winter construction, selected the appropriate concrete ratio and raw materials, and adopted the appropriate temperature in the process of concrete mixing and transportation to ensure the quality of concrete construction and maintenance. Hu et al [4] studied the fast slope surface data acquisition and pre-processing technology based on the high slope excavation process of water conservancy project, and established the slope quality control index analysis model and real-time feedback flow, which was applied to the quality control of actual slope excavation project. Cheng Lili [5] combined the PDCA cycle method and construction project quality control for the current situation of construction quality control in Pandawling Tunnel, established a construction quality control process based on the PDCA cycle, and discussed in detail the application of the process in the preparation stage, construction stage and quality inspection stage. Qian et al [6] set up settlement and deformation observation points in the middle of the tunnel and on both sides of the elevated arch, and buried the observation elements according to the specified scheme, monitored the roadbed settlement after the construction of the railroad tunnel, and proposed the curve regression method to evaluate and predict the settlement of the tunnel foundation. Arends B J [7] proposed a method based on probabilistic risk assessment to evaluate tunnel safety based on three major aspects: economic risk, personal and social, and applied it to a real case study of a tunnel project in the Netherlands. Manchao et al [8] concluded that large deformation phenomenon occurs in tunnels during or after excavation due to poor geology, design defects, etc., for this reason, an MPM method based on finite element analysis software was introduced to simulate the deformation of materials. An evaluation technique incorporating Bayesian neural network was further proposed for the case where significant deformation occurs in tunnels. Hussain et al [9] assessed the rock quality in excavated tunnels by combining practical experience with numerical analysis and analyzed the stability of the tunnels before and after excavation.

At present, the research on tunnel condition mainly focuses on railroad and highway tunnels, while relatively few studies have been conducted on hydraulic tunnels which are in a water environment for a long time; the research mainly focuses on the construction quality control of tunnels, but ignores the evaluation of the construction quality grade; the research method cannot comprehensively take into account the actual situation of the project, and it is difficult to solve the randomness and ambiguity of the quality of tunnel construction in a better way. In conclusion, the index system and model for evaluating the construction quality grade of concrete structures in hydraulic tunnels are not perfect enough and need to be further studied.

In summary, this paper proposes a set of new methods for evaluating the construction quality level of concrete structures in hydraulic tunnels. The subjective and objective weights of the evaluation indexes are calculated by IAHP method and CRITIC method respectively, and the comprehensive weights of the evaluation indexes are calculated by using the principle of minimum entropy (MIE), and the comprehensive evaluation model based on CWM-UM theory is established. And relevant calculations are carried out with a hydraulic tunnel as the research background to verify the reasonableness and scientificity of the model in evaluating the construction quality grade of concrete structures in hydraulic tunnels.

2. The establishment of CWM-UM Evaluation Modeling

2.1. Determination of index weight

2.1.1. IAHP method to determine the subjective weight

In this paper, the IAHP method [10] is used to determine the subjective weights of construction quality evaluation indexes of hydraulic tunnels. Hierarchical analysis has a strong advantage in the process of dealing with multi-factor problems, which can split different factors, determine the corresponding level, and then construct a hierarchical relationship model between the factors to calculate their subjective weights. In this paper, the judgment matrix is established based on the theory of four scales, such as equation (1), and the scale of the scale is shown in Table 1.

A = {(a_{i j})}_{n \times n} = [\begin{matrix} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{21} & a_{22} & \dots & a_{2 n} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ a_{n 1} & a_{n 1} & \dots & a_{n n} \end{matrix}]

(1)

Where,

i = 1, 2, \cdot \cdot \cdot, n; j = 1, 2, \cdot \cdot \cdot, n

;

a_{i j}

is the result of the importance of comparing the two evaluation indicators

i

and

j

in guideline A,

a_{j i} = \frac{1}{a_{i j}}

Construct the antisymmetric matrix B of the judgment matrix A, the values of the matrix B and its element

b_{i j}

can be calculated by equation (2).

B = l g A; b_{i j} = - b_{j i}

(2)

Construct the optimal transfer matrix C of the antisymmetric matrix B. The values of the elements

c_{i j}

in the matrix C can be calculated by equation (3).

c_{i j} = \frac{1}{n} \sum_{g = 1}^{n} (b_{i g} - b_{j g})

(3)

Construct the proposed good agreement matrix

A^{'}

of the judgment matrix A. The values of the element

a_{i j}^{'}

in the matrix

A^{'}

can be calculated by equation (4).

a_{i j}^{'} = 10^{c_{i j}}

(4)

Normalize the proposed good agreement matrix

A^{'}

by columns. The values of the elements

{\bar{a}}_{i j}^{'}

in the normalized matrix can be calculated by equation (5).

{\bar{a}}_{i j}^{'} = \frac{a_{i j}^{'}}{\sum_{i}^{n} a_{i j}^{'}}

(5)

The sum vector

α_{i}^{'}

is calculated by adding rows, as shown in equation (6) :

α_{i}^{'} = \sum_{i = 1}^{n} {\bar{a}}_{i j}^{'}

(6)

The weight vector

α_{i}

can be calculated by normalizing the sum vector through equation (7).

α_{i} = \frac{α_{i}^{'}}{\sum_{i = 1}^{n} α_{i}^{'}}

(7)

AHP method [11] is used to determine the weights of evaluation indicators need to carry out consistency tests to ensure that the indicators are harmonized. This paper optimizes the hierarchical analysis method through the method of optimal matrix, which can make the calculation results reach the consistency requirement by itself.

2.1.2. CRITIC method to determine the objective weight

The CRITIC method is a method that uses standard deviation and correlation coefficient to calculate objective weights, which comprehensively takes into account the variability and conflict between indicators. It can be more reasonable and comprehensive for the assignment of weights, and the calculation process is as follows[12,13]:

Assuming that there are m evaluation objects and n construction quality evaluation indicators, the value of the evaluation object to the indicator is recorded as

x_{i k}

(

i = 1, 2, \cdot \cdot \cdot, n; k = 1, 2, \cdot \cdot \cdot, m

The evaluation data can be standardized by equation (8).

y_{i k} = \frac{x_{i k} - {m i n}_{i} (x_{i k})}{\max_{i} (x_{i k}) - {m i n}_{i} (x_{i k})}

(8)

Calculate the variability among indicators by equation (9).

V_{i} = \frac{σ_{i}}{{\bar{r}}_{i}}

(9)

Where,

V_{i}

is the coefficient of variation of the

i

th indicator;

σ_{i}

is the standard deviation of the ith indicator;

{\bar{r}}_{i}

is the mean of the ith indicator.

The conflict between indicators can be calculated through equations (10) and (11).

h_{i j} = \frac{\sum_{k = 1}^{m} (x_{i k} - {\bar{r}}_{i}) (x_{j k} - {\bar{r}}_{j})}{\sqrt{\sum_{k = 1}^{m} {(x_{i k} - {\bar{r}}_{i})}^{2} \sum_{k = 1}^{m} {(x_{j k} - {\bar{r}}_{j})}^{2}}}

(10)

R_{i} = \sum_{i = 1}^{n} (1 - h_{i j})

(11)

Where,

h_{i j}

is the correlation coefficient between indicators

i

and

j

;

R_{i}

is the value of the quantitative indicator of conflictiveness for indicator

i

The amount of information

C_{i}

for the ith indicator can be calculated through equation (12).

C_{i} = V_{i} R_{i}

(12)

The objective weight values of construction quality evaluation indicators are calculated by equation (13).

β_{i} = \frac{C_{i}}{\sum_{i = 1}^{n} C_{i}}

(13)

2.1.3. The method of calculating combination weight

(1) Rationality analysis of combination weighting

Before combining the subjective weight

α_{i}

and the objective weight

β_{i}

, their rationality should be analyzed to ensure the scientific and rational weights of the construction quality evaluation indicators of concrete structures in hydraulic tunnels. The specific process is as follows:

The subjective and objective weights of evaluation indicators are sorted, as shown in Table 2, where

α_{i}^{'}

is the sorted value of

α_{i}

and

β_{i}^{'}

is the sorted value of

β_{i}

. The sorting values range from 1 to n. The index with the largest weight value is sorted as 1, and the index with the smallest weight value is sorted as n.

The correlation between the two sets of variables can be tested by Spearman's consistency coefficient

ρ

[14] as in equation (14).

ρ = 1 - \frac{6}{n (n^{2} - 1)} \sum_{i = 1}^{n} {(α_{i}^{'} - β_{i}^{'})}^{2}

(14)

Where, the value range of

ρ

[- 1, 1]

, when

ρ \in [- 1, 0)

, it means that there is a lack of consistency between subjective and objective weights; when

ρ = 0

, it means that the correlation between subjective and objective weights is 0; when

ρ \in (0, - 1]

, it indicates that there is consistency between subjective and objective weights, which can be combined and assigned.

(2) Calculating the combination weights

The weights of evaluation indexes calculated based on IAHP method and CRITIC method are

α_{i}

and

β_{i}

, respectively. In order to make the combination weight

ω_{i}

as close as possible to

α_{i}

and

β_{i}

, the combination weights

ω_{i}

are calculated based on the MIE principle, the calculation model is as follows [15]:

\{\begin{matrix} m i n J (ω) = \sum_{i = 1}^{n} (ω_{i} \ln \frac{ω_{i}}{α_{i}} + ω_{i} \ln \frac{ω_{i}}{β_{i}}) \\ s . t . \sum_{i = 1}^{n} ω_{i} = 1, ω_{i} \geq 0, i = 1, 2, \cdot \cdot \cdot, n \end{matrix}

(15)

Solving this optimization model based on the Lagrange's algorithm, the combination weights can be obtained as:

ω_{i} = \frac{\sqrt{α_{i} β_{i}}}{\sum_{i = 1}^{n} \sqrt{α_{i} β_{i}}}

(16)

2.2. Uncertainty Measure Evaluation Model

This paper uses the uncertainty measurement theory to evaluate the construction quality of hydraulic tunnels. The uncertainty measurement theory mainly includes two parts: single-indicator and multiple-indicator uncertain measurement. The evaluation method and corresponding calculation formula are as follows [16,17]:

(1) Uncertainty measures for single indicators

Let the evaluation objects

T_{1}, T_{2}, \cdot \cdot \cdot T_{m}

form the object space of

T = \{T_{1}, T_{2}, \cdot \cdot \cdot T_{m}\}

. For each object to be evaluated

T_{j} \in T (j = 1, 2 \cdot \cdot \cdot, m)

, there exist n indicators

C_{1}, C_{2}, \cdot \cdot \cdot C_{n}

, then

C = \{C_{1}, C_{2}, \cdot \cdot \cdot C_{n}\}

is called the evaluation space.

x_{i j}

is the measured value of the

i

th indicator for the

j

th object to be evaluated

(i = 1, 2 \cdot \cdot \cdot, n)

, and the indicator is classified into

q

levels

U_{1}, U_{2}, \cdot \cdot \cdot U_{q}

, where

U_{t}

is the

t

th evaluation level

(t = 1, 2 \cdot \cdot \cdot, q)

. If the effect of class

t

is better than that of class

t + 1

, denoted as

U_{t} > U_{t + 1}

, then

U = \{U_{1}, U_{2}, \cdot \cdot \cdot U_{q}\}

is the ordered segmentation class on evaluation space C [18].

z_{i j t} = z (x_{i j} \in U_{t})

is used to indicate that the measured value

x_{i j}

belongs to the range of the

t

th evaluation grade

U_{t}

, and the following conditions must be met:

0 \leq z (x_{i j} \in U_{t}) \leq 1

(17)

z (x_{i j} \in C) = 1

(18)

z (x_{i j} \in ⋃_{t = 1}^{q} U_{t}) = \sum_{t = 1}^{q} z (x_{i j} \in U_{t})

(19)

Equation (17) is non-negative boundedness, equation (18) is normalization, and equation (19) is additivity. When z satisfies all three of these formulas at the same time, z is said to be uncertain measure.

Construct the uncertainty measurement function

z (x_{i j} \in U_{t})

of each evaluation index, substitute the measurement value

x_{i j}

, calculate the uncertainty measurement value

z_{i j t}

, which can form the single-indicator measurement evaluation matrix shown in equation (20).

{(z_{i j t})}_{n \times q} = [\begin{matrix} z_{j 11} & z_{j 12} & \dots & z_{j 1 q} \\ z_{j 21} & z_{j 22} & \dots & z_{j 2 q} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ z_{j n 1} & z_{j n 2} & \dots & z_{j n q} \end{matrix}]

(20)

(2) Uncertainty measures for multiple indicators

z_{j t} = z (T_{j} \in U_{t})

represents the degree to which the

T_{j}

th evaluation object belongs to the

t

th evaluation level

U_{t}

, then there is:

z_{j t} = \sum_{i = 1}^{n} ω_{i} z_{i j t} (j = 1, 2, \cdot \cdot \cdot, m; t = 1, 2, \cdot \cdot \cdot, q)

(21)

Where

z_{j t}

satisfies

0 \leq z_{j t} \leq 1

\sum_{t = 1}^{q} z_{j t} = 1

. Then called

z_{j} = [z_{j 1}, z_{j 2}, \cdot \cdot \cdot, z_{j q}]

is the evaluation vector of

T_{j}

's multi-index comprehensive measure [19].

(3) Confidence identification criteria

The calculation results are analyzed according to the confidence identification criteria, and the confidence is set as

λ (λ \geq 0.5)

[20]. If

λ

satisfies equation (22), it can be determined that the evaluation object

T_{j}

belongs to the

t_{0}

th evaluation level

U_{t 0}

t_{0} = m i n \{t : \sum_{j = 1}^{t} z_{j} \geq λ, t = 1, 2, \cdot \cdot \cdot, q\}

(22)

3. Construction quality evaluation process of concrete structure in hydraulic tunnel

The construction quality evaluation of concrete structure in hydraulic tunnel is to analyze the factors that affect its construction quality, take appropriate methods to organize and evaluate these factors, and determine the grade of tunnel construction quality. This paper first defines the concrete structure in hydraulic tunnel to be evaluated, and constructs the construction quality evaluation index system from six aspects: construction measurement, tunnel excavation, support construction, anti-drainage construction, secondary lining concrete construction and tunnel grouting. IAHP method and CRITIC method are used to determine the subjective and objective weights of evaluation indicators respectively, and combined weights are given based on the principle of minimum entropy. The uncertain measure function and matrix of single index are constructed, and the uncertain measure vector of multiple index is calculated. Finally, the construction quality grade of concrete structure in hydraulic tunnel is determined based on the confidence criterion. The specific evaluation process is shown in Figure 1.

4. Examples of engineering applications

In order to verify the rationality and scientificity of the method, a hydraulic tunnel is applied in this paper. According to the characteristics and general construction procedures of concrete structure in hydraulic tunnel, it can be divided into six main stages: construction survey, tunnel excavation, support construction, anti-drainage construction, secondary lining concrete construction and tunnel grouting.

4.1. Reasons affecting construction quality

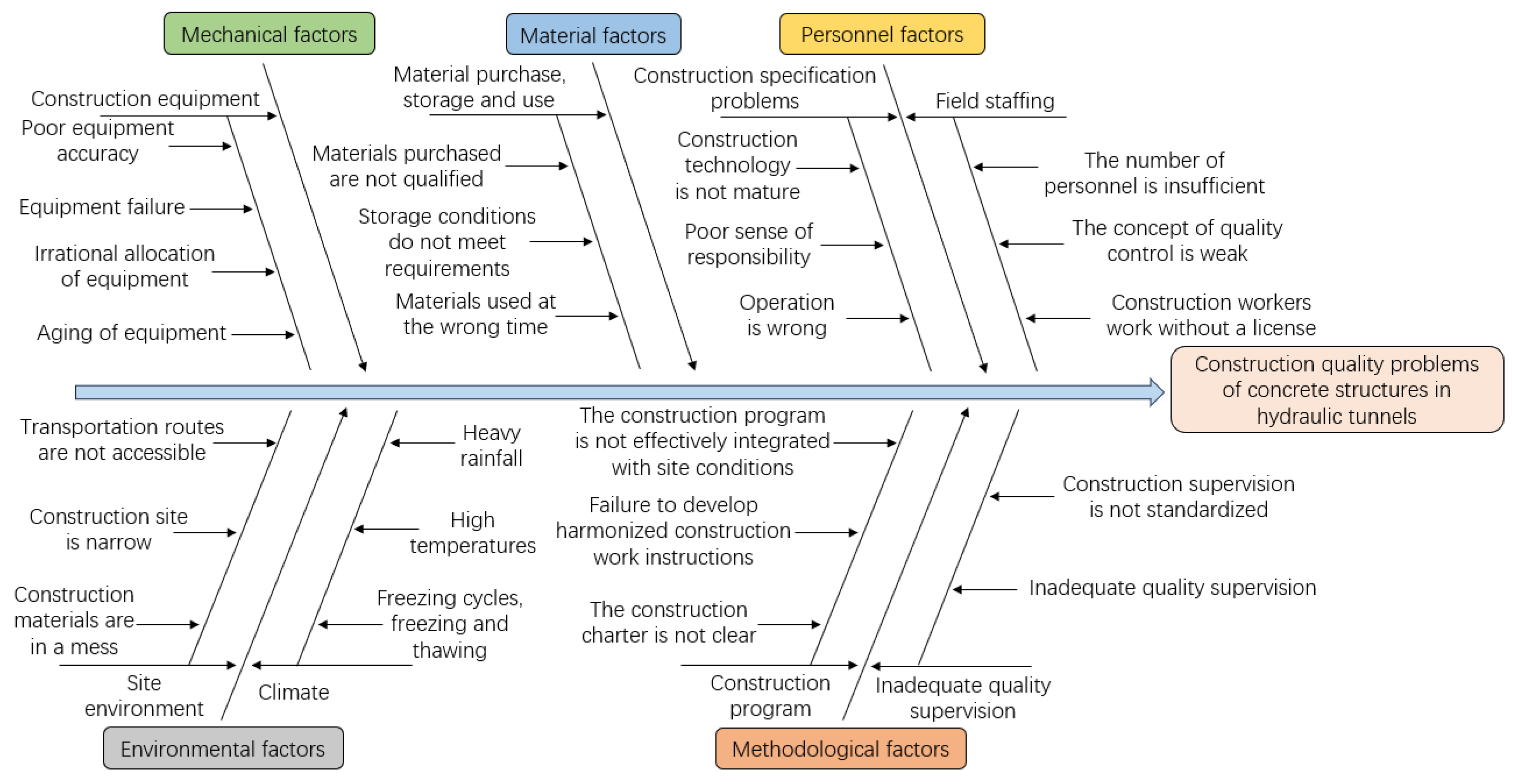
The construction process of concrete structure in hydraulic tunnels is complex, and there are more uncertainty factors affecting its construction quality, which can be basically summarized as five aspects of personnel, materials, machinery, methods and environment according to the quality management theory. Therefore, according to the actual situation of the project and the existing literature, this paper adopts the fishbone diagram method [21] to carry out a hierarchical analysis from the aspects of people, materials, machines, methods and environment to summarize the reasons affecting the construction quality.

(1) In the process of construction measurement, due to the unskilled surveyors and the unfavorable influence of the environmental factors such as heavy rain, gale, high temperature, etc., it will cause the quality problems such as horizontal penetration error, vertical penetration error and marking the wrong direction of digging.

(2) In the process of tunnel excavation, due to the unskilled tunneling operators and the low level of construction site management and monitoring, there will be quality problems such as uneven excavation surface, groundwater seepage caused by excavation, and tunnel over-excavation and under-excavation.

(3) In the process of support construction, due to the low business level of the constructor and poor inspection and management, it caused problems such as collapsed holes, deviation of the position and direction of anchor holes, low stability of steel arches, insufficient thickness of sprayed concrete, and lagging of the sprayed concrete construction surface.

(4) In the process of anti-drainage construction, the performance and laying of waterproof materials are not qualified due to non-timely testing; improper treatment of construction joint and deformation joint due to insufficient construction technology level; the drainage system is unreasonable due to lack of scientific planning.

(5) In the process of secondary lining concrete construction, the performance of concrete materials and mixing ratios do not meet the design requirements due to the lack of timely testing; insufficient maintenance of concrete, low strength of concrete demolding, and inadequate concrete pouring and vibration due to the low level of construction management and poor construction environment, and other quality problems. In addition, the quality of secondary lining concrete construction will also be affected by factors such as non-standardized concrete pouring, failure to clean the surface of the formwork in time, insufficient reinforcement of the formwork, and incomplete assembly.

(6) In the process of tunnel grouting, due to the unskilled construction personnel, it is impossible to strictly control the key parameters such as hole diameter, hole position, verticality, etc., resulting in irrational disposal of the drilled holes; due to the lack of advance hydrogeological and engineering geological exploration, it is not possible to effectively predict the ambient temperature of the construction area, which results in the grouting temperature being too large or too small; due to the irregularities in the grouting test, resulting in too high or too low a grouting pressure being selected. low.

In summary, the fishbone diagram of the quality problems of concrete structure construction of hydraulic tunnels is shown in Figure 2.

4.2. Selection of construction quality evaluation indicators.

Through the investigation of the construction site and the combing of the contents of section 4.1, 21 factors affecting the construction quality of concrete structures in hydraulic tunnels are summarized and their causal factor types are analyzed. The results are shown in Table 3.

According to Table 3, the construction process and the construction quality problems of each process are taken as primary and secondary evaluation indexes respectively. The construction quality evaluation index system is constructed to evaluate the construction quality of concrete structures in hydraulic tunnels.

4.3. Construction quality grading

According to the Technical Procedure for Detection and Evaluation of Defects in Hydraulic Concrete Buildings (DL/T5251-2010) [22] and the Code for the Design of Hydraulic Tunnels (SL279-2016) [23], the construction quality condition of the concrete structures in hydraulic tunnels is categorized into five grades. Where, Grade I indicates that the quality of tunnel construction is excellent, with few or no quality problems, and only normal inspection of the construction process is required; Grade II indicates that the quality of tunnel construction is good, with relatively small problems, and the construction process needs to be strengthened to prevent; Grade III indicates that the quality of tunnel construction is qualified, with relatively more problems, and the construction process needs to formulate the appropriate monitoring and management system; Grade IV indicates that the quality of tunnel construction is basically qualified, with more problems, but still within the permissible range, and the construction needs to be strictly prevented from the construction, and the quality problems can be corrected by appropriate means. Grade IV means that the construction quality of the tunnel is basically qualified, but there are many problems, but still within the permitted range, the construction should be strictly prevented, and appropriate means can be adopted to correct the quality problems to avoid unqualified construction quality; Grade V means that the construction quality of the tunnel is unqualified, and there are many problems, and the construction process must put forward targeted quality control and corrective measures for the quality problems, to avoid quality and safety incidents.

Due to the large number of tunnel construction processes, each quality indicator is defined in a different range, and it is impossible to carry out an accurate quantitative description, therefore, this paper suggests that the indicators and grades should be evaluated by the percentage standard, and the division of evaluation criteria is shown in Table 4.

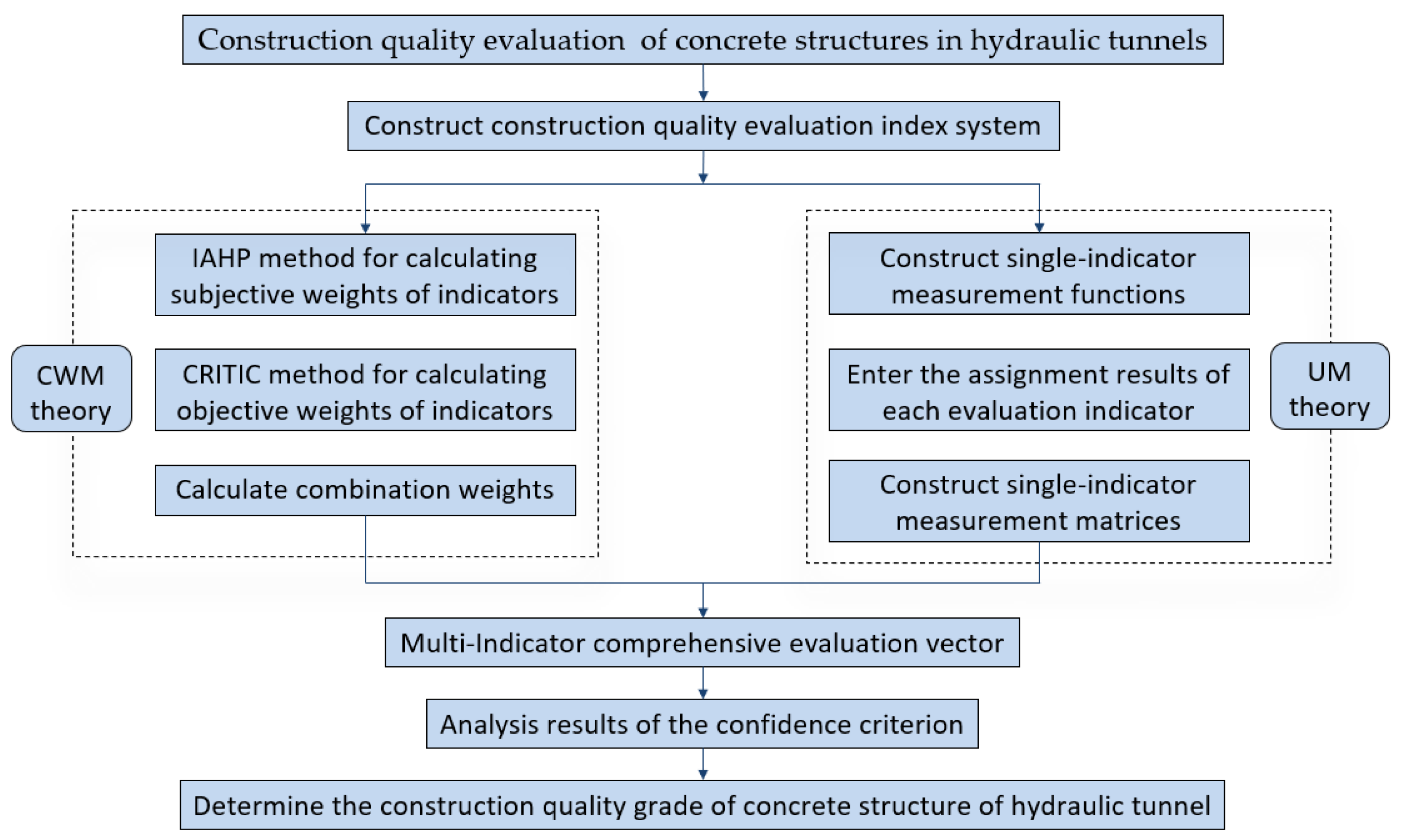
4.4. Construction quality evaluation process of concrete structures in hydraulic tunnels

This paper takes a concrete structure of a hydraulic tunnel as an example to carry out construction quality evaluation research. Indicator grading and grading standards are shown in Table 4.In order to ensure the validity and accuracy of the evaluation results, this paper assigns values to the construction quality indicators by inviting five experts in different aspects, including design units, construction units, construction units, supervisory units and scientific research institutes, with the score range of [0,100], and the better the quality control of the indicators is, the larger the score is. The results of the assigned values are shown in Table 5.

4.4.1. IAHP method to determine the subjective weight

(1) According to Table 1, the evaluation indexes of the construction quality of hydraulic tunnels are compared two by two to quantify their relative importance, and the judgment matrix of the evaluation indexes is established as shown below:

The judgment matrix of the construction quality index layer of hydraulic tunnels is as follows:

A_{1} = [\begin{matrix} 1 & 2 & 2 & 3 & 0.5 & 3 \\ 0.5 & 1 & 2 & 3 & 1 / 3 & 2 \\ 0.5 & 0.5 & 1 & 2 & 0.5 & 2 \\ 1 / 3 & 1 / 3 & 0.5 & 1 & 1 / 3 & 2 \\ 2 & 3 & 2 & 3 & 1 & 4 \\ 1 / 3 & 0.5 & 0.5 & 0.5 & 0.25 & 1 \end{matrix}]

The judgment matrix of the construction measurement indicator layer is as follows:

A_{2} = [\begin{matrix} 1 & 1 & 2 & 0.5 \\ 1 & 1 & 2 & 0.5 \\ 0.5 & 0.5 & 1 & 1 / 3 \\ 2 & 2 & 3 & 1 \end{matrix}]

The judgment matrix of the tunnel excavation index layer is as follows:

A_{3} = [\begin{matrix} 1 & 0.5 & 2 & 0.5 \\ 2 & 1 & 3 & 0.5 \\ 0.5 & 1 / 3 & 1 & 1 / 3 \\ 2 & 2 & 3 & 1 \end{matrix}]

The judgment matrix of the support construction indicator layer is as follows:

A_{4} = [\begin{matrix} 1 & 0.5 & 1 \\ 2 & 1 & 2 \\ 1 & 0.5 & 1 \end{matrix}]

The judgment matrix of the anti-drainage construction indicator layer is as follows:

A_{5} = [\begin{matrix} 1 & 0.5 & 1 / 3 \\ 2 & 1 & 0.5 \\ 3 & 2 & 1 \end{matrix}]

The judgment matrix of the secondary lining concrete construction index layer is as follows:

A_{6} = [\begin{matrix} 1 & 3 & 2 & 2 \\ 1 / 3 & 1 & 0.5 & 1 / 3 \\ 0.5 & 2 & 1 & 0.5 \\ 0.5 & 3 & 2 & 1 \end{matrix}]

The judgment matrix of the tunnel grouting index layer is as follows:

A_{7} = [\begin{matrix} 1 & 0.5 & 0.5 \\ 2 & 1 & 0.5 \\ 2 & 2 & 1 \end{matrix}]

(2) According to equations (2) to (7), the subjective weight value of each indicator is calculated, see Table 6.

4.4.2. CRITIC method to determine the objective weight

According to the assignment results of quality indicators in Table 5, it is standardized through equation (8) to obtain a standardized matrix. Then, according to equations (9) ~ (13), the variability, conflict, information content and weight values of evaluation indicators can be calculated by writing MATLAB code in turn, as shown in Table 7.

4.4.3. Calculate combination weights

(1) Rationality analysis of combined weights

According to the subjective and objective weights calculated by the above IAHP method and CRITIC method, the weights are sorted, as shown in Table 8.

The consistency coefficient can be calculated from equation (14) as

ρ = 0.5045 \in (0,1]

, the calculation shows that the weights calculated by IAHP method and CRITIC method satisfy the consistency requirements and can be combined and assigned.

(2) Calculate combination weights

Finally, the MIE principle is utilized to eliminate the subjective and objective weight bias, and by substituting the calculation results into equation (16), the final combined weight calculation results can be obtained, as shown in Table 9.

4.4.4. Construct uncertain measure function and matrix of single index

In the process of using unascertained measure theory to evaluate construction quality, it is necessary to construct uncertain measure function and matrix of single index scientifically and reasonably.

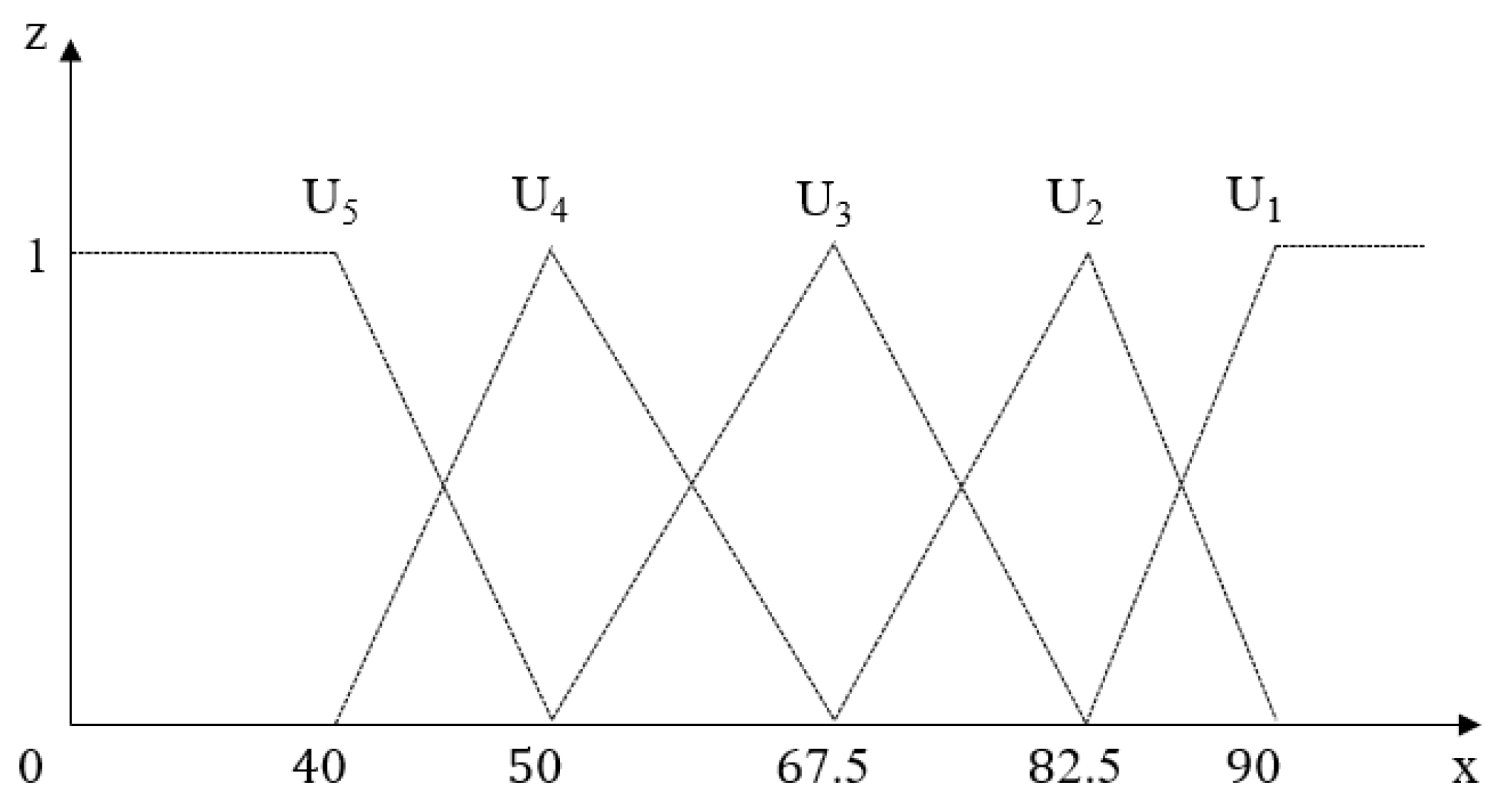
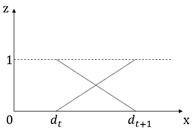
The evaluation level space must conform to a certain order, that is

U_{1} > U_{2} > \cdot \cdot \cdot > U_{q}

U_{1} < U_{2} < \cdot \cdot \cdot < U_{q}

, where

U_{t}

represents the

t

th evaluation level, and its corresponding grading standard is represented as

d_{t}

, then

d_{t}

conforms to

d_{1} > d_{2} > \cdot \cdot \cdot > d_{q}

d_{1} < d_{2} < \cdot \cdot \cdot < d_{q}

. Assuming that the measured value of the indicator at

d_{t}

belongs to level

t

, when the measured value changes from

d_{t}

d_{t + 1}

, its state value at level

t

gradually changes from 1 to 0, and its state value at level

t + 1

gradually changes from 0 to 1.

The change trend of the evaluation index value can be expressed by the uncertain measure function. The common forms of the uncertain measure function are mainly four types: straight line, parabola, exponential curve and sinusoidal curve type [24], of which the more widely used is the straight line type, and its corresponding graph and function expression are shown in Table 10.

Based on the classification standard of tunnel construction quality in Table 4 and the graph and expression of unascertained measure function in Table 10, the unascertained measure function and graph of index can be determined as follows:

z (X \in U_{1}) = \{\begin{matrix} 1, X > 90 \\ \frac{X - 82.5}{90 - 82.5}, 82.5 < X \leq 90 \\ 0, X \leq 82.5 \end{matrix} z (X \in U_{2}) = \{\begin{matrix} \frac{90 - X}{90 - 82.5}, 82.5 < X \leq 90 \\ \frac{X - 67.5}{82.5 - 67.5}, 67.5 < X \leq 82.5 \\ 0, X \leq 67.5 \end{matrix}

z (X \in U_{3}) = \{\begin{matrix} \frac{82.5 - X}{82.5 - 67.5}, 67.5 < X \leq 82.5 \\ \frac{X - 67.5}{82.5 - 67.5}, 50 < X \leq 67.5 \\ 0, X \leq 50 \end{matrix} z (X \in U_{4}) = \{\begin{matrix} \frac{67.5 - X}{67.5 - 50}, 50 < X \leq 67.5 \\ \frac{X - 40}{50 - 40}, 40 < X \leq 50 \\ 0, X \leq 40 \end{matrix}

z (X \in U_{5}) = \{\begin{matrix} \frac{50 - X}{50 - 40}, 40 < X \leq 50 \\ 0, X > 50 \\ 1, X \leq 40 \end{matrix}

Figure 3. Measure function graph.

Based on the evaluation results of quality evaluation indicators in Table 5, the expected value of five experts' scores for each indicator is taken as the measurement value, as shown in Table 11, and it is put into the unascertained measure function, and the unascertained measure matrix of single indicator can be calculated as follows:

[\begin{matrix} 0 & 0 & 0.949 & 0.051 & 0 \\ 0 & 0.087 & 0.913 & 0 & 0 \\ 0 & 0 & 0.846 & 0.154 & 0 \\ 0 & 0.567 & 0.433 & 0 & 0 \\ 0 & 0 & 0.834 & 0.166 & 0 \\ 0.173 & 0.827 & 0 & 0 & 0 \\ 0 & 0.913 & 0.087 & 0 & 0 \\ 0 & 0.607 & 0.393 & 0 & 0 \\ 0.413 & 0.587 & 0 & 0 & 0 \\ 0 & 0.247 & 0.753 & 0 & 0 \\ 0 & 0.780 & 0.220 & 0 & 0 \\ 0 & 0.113 & 0.887 & 0 & 0 \\ 0 & 0 & 0.743 & 0.257 & 0 \\ 0 & 0.780 & 0.220 & 0 & 0 \\ 0 & 0.873 & 0.127 & 0 & 0 \\ 0 & 0.940 & 0.060 & 0 & 0 \\ 0 & 0 & 0.800 & 0.200 & 0 \\ 0 & 0.460 & 0.540 & 0 & 0 \\ 0 & 0.193 & 0.807 & 0 & 0 \\ 0 & 0 & 0.800 & 0.200 & 0 \\ 0 & 0.020 & 0.980 & 0 & 0 \end{matrix}]

4.4.5. Calculate multi-index unascertained measure vector

According to the combined weights of the evaluation indicators in Table 9 and the unascertained measure matrix of the single index mentioned above, the multi-index unascertained measure vector of the construction quality of hydraulic tunnel can be calculated by equation (21):

Construction measurement:

(0, 0.1948, 0.7616, 0.0436, 0)

Tunnel excavation:

(0.0450, 0.5804, 0.3348, 0.0398, 0)

Support construction:

(0.1380, 0.5119, 0.3420, 0, 0)

Anti-drainage construction:

(0, 0.3323, 0.5874, 0.0803, 0)

Secondary lining concrete construction:

(0, 0.5648, 0.3860, 0.0491, 0)

Tunnel grouting:

(0, 0.0637, 0.8686, 0.0676, 0)

Total weight value:

(0.0290, 0.4008, 0.5252, 0.0450, 0)

4.4.6. Construction quality evaluation of concrete structures in hydraulic tunnels

According to the multi-indicator unconfirmed measurement vector of hydraulic tunnel construction quality in section 4.4.5, set the confidence level

λ = 0.5

, and the quality evaluation results of each stage and the whole in the tunnel construction process can be obtained from equation (22), which is shown in Table 12.

4.5. Comparative study

In order to illustrate the science and rationality of the method, this paper adopts the matter-element extension theory to evaluate the construction quality of hydraulic tunnels, which is used as a comparative study with the above. No further explanation about the matter-element extension theory is given, and specific reference can be made to the literature [25,26], and the focus here is on the calculation of the correlation function value of the matter-element grade of hydraulic tunnels to be evaluated.

(1) Correlation of evaluation indicators

The correlation of the construction quality level t of the hydraulic tunnel to be evaluated is shown in equation (23):

K_{t} (x_{i}) = \{\begin{matrix} \frac{ρ (x_{i}, x_{i t})}{ρ (x_{i}, x_{i p}) - ρ (x_{i}, x_{i t})} ， x_{i} \notin x_{i t} \\ \frac{- ρ (x_{i}, x_{i t})}{|x_{i t}|} ， x_{i} \in x_{i t} \end{matrix}

(23)

Where:

ρ (x_{i}, x_{i t}) = |x_{i} - \frac{a_{i t}^{+} + a_{i t}^{-}}{2}| - \frac{a_{i t}^{+} - a_{i t}^{-}}{2}

(24)

ρ (x_{i}, x_{i p}) = |x_{i} - \frac{a_{i p}^{+} + a_{i p}^{-}}{2}| - \frac{a_{i p}^{+} - a_{i p}^{-}}{2}

(25)

Where,

x_{i}

is the

i

th construction quality evaluation index;

x_{i t} = (a_{i t}^{+}, a_{i t}^{-})

is the magnitude range of the

i

th index divided by the evaluation grade

U_{t}

;

x_{i p} = (a_{i p}^{+}, a_{i p}^{-})

is the magnitude range of the

i

th index divided under each level;

|x_{i t}|

is the interval length.

(2) Determine the construction quality evaluation grade of hydraulic tunnel

By combining the weights of the indicators and the value of the correlation function, the comprehensive correlation of the evaluation object can be calculated, see equation (26), if

K_{t_{0}} (T_{0}) = m a x K_{t} (T_{0})

, the evaluation object

T_{0}

belongs to level

t_{0}

K_{t} (T_{0}) = \sum_{i = 1}^{n} ω_{i} K_{t} (x_{i})

(26)

Where,

K_{t} (T_{0})

is the comprehensive correlation degree of

T_{0}

with respect to grade

t

;

ω_{i}

take the objective weight value

β_{i}

of CRITIC method.

According to the grading standards of each evaluation index in Chapter 4.3, the classical domain and node domain of the construction quality evaluation index of hydraulic tunnel can be determined, as shown in Table 13.

Based on the expected value of each evaluation indicators in table 11, the correlation degree matrix of the evaluation indicators of hydraulic tunnel construction quality can be obtained from equations (23) to (25):

[\begin{matrix} - 0.4120 & - 0.2010 & 0.4400 & - 0.1650 & - 0.4433 \\ - 0.4046 & - 0.1658 & 0.4133 & - 0.2200 & - 0.4800 \\ - 0.4172 & - 0.2247 & 0.3200 & - 0.1200 & - 0.4133 \\ - 0.3684 & 0.0667 & - 0.0400 & - 0.4000 & - 0.6000 \\ - 0.4178 & - 0.2271 & 0.3067 & - 0.1150 & - 0.4100 \\ - 0.2768 & 0.4133 & - 0.3520 & - 0.5950 & - 0.7300 \\ - 0.3188 & 0.4133 & - 0.2480 & - 0.5300 & - 0.6867 \\ - 0.3641 & 0.1067 & - 0.0640 & - 0.4150 & - 0.6100 \\ - 0.2340 & 0.2933 & - 0.4240 & - 0.6400 & - 0.7600 \\ - 0.3950 & - 0.1166 & 0.2533 & - 0.2800 & - 0.5200 \\ - 0.3418 & 0.2800 & - 0.1680 & - 0.4800 & - 0.6533 \\ - 0.4031 & - 0.1585 & 0.3867 & - 0.2300 & - 0.4867 \\ - 0.4219 & - 0.2449 & 0.2000 & - 0.0750 & - 0.3833 \\ - 0.3418 & 0.2800 & - 0.1680 & - 0.4800 & - 0.6533 \\ - 0.3264 & 0.3733 & - 0.2240 & - 0.5150 & - 0.6767 \\ - 0.3134 & 0.4400 & - 0.2640 & - 0.5400 & - 0.6933 \\ - 0.4194 & - 0.2340 & 0.2667 & - 0.1000 & - 0.4000 \\ - 0.3786 & - 0.0229 & 0.0400 & - 0.3600 & - 0.5733 \\ - 0.3984 & - 0.1345 & 0.3067 & - 0.2600 & - 0.5067 \\ - 0.4194 & - 0.2340 & 0.2667 & - 0.1000 & - 0.4000 \\ - 0.4081 & - 0.1827 & 0.4800 & - 0.1950 & - 0.4633 \end{matrix}]

The weight value of each secondary index calculated by CRITIC method is as follows:

(0.2937, 0.2196, 0.1930,0.2937); (0.2603, 0.2405, 0.2088, 0.2904); (0.3903, 0.3303,0.2794); (0.3475,0.2852,0.3674);

(0.2383, 0.2275, 0.3172, 0.2169); (0.2850,0.3569,0.3580).

According to equation (26), the comprehensive correlation degree of the evaluation level t for the construction quality of the hydraulic tunnel can be calculated as:

Construction measurement:

(- 0.3986, - 0.1192, 0.2700, - 0.2374, - 0.4916)

Tunnel excavation:

(- 0.3476, 0.1576, - 0.0752, - 0.4042, - 0.6028)

Support construction:

(- 0.3173, 0.1542, - 0.1288, - 0.4764, - 0.6509)

Anti-drainage construction:

(- 0.3859, - 0.0220, 0.1297, - 0.2776, - 0.5184)

Secondary lining concrete construction:

(- 0.3643, 0.1099, - 0.0202, - 0.3554, - 0.5703)

Tunnel grouting:

(- 0.4093, - 0.1873, 0.3544, - 0.1796, - 0.4531)

The weight values of the primary indicators calculated by CRITIC method are: (0.1723, 0.1890, 0.1818, 0.1377, 0.2043, 0.1150). According to equation (26), the comprehensive correlation degree of the target layer for the hydraulic tunnel construction quality with respect to the evaluation level

t

can be calculated as:

Overall Construction:

(- 0.3667, 0.0352, 0.0634, - 0.3354, - 0.5569)

According to the principle of maximum affiliation, the construction quality evaluation grade of the hydraulic tunnel can be determined, as shown in Table 14.

Comparative analysis of the evaluation results of section 4.4 and section 4.5 shows that the results of both are consistent. And this paper adopts IAHP method and CRITIC method to calculate the subjective and objective weights of the evaluation indexes respectively, which avoids the one-sidedness of the weight calculation, and gives comprehensive consideration to the subjective intention of the decision maker and the objective attributes of the data itself, and the evaluation results are more scientific and reasonable. In summary, the evaluation index system and evaluation model of concrete structure construction quality of hydraulic tunnels established in this paper are scientific and reasonable.

5. Conclusions

(1) According to the analysis and summarization of the factors affecting the quality of tunnel construction, 21 factors such as excessive horizontal penetration error, over-excavation of the tunnel, low stability of the steel arch, unreasonable drainage system, and insufficient maintenance of the concrete were selected from five aspects, including construction measurement, tunnel excavation, support construction, anti-drainage construction, concrete secondary lining construction and grouting of the tunnel. Constructing a more scientific and reasonable construction quality evaluation index system of concrete structures in hydraulic tunnels.

(2) The subjective and objective weights calculated by IAHP method and CRITIC method are optimized and synthesized by using the combination assignment method, which avoids the one-sidedness of weight calculation. The subjective intention of the decision maker and the objective attributes of the data itself are considered comprehensively, which improves the reasonableness and reliability of the weights of the tunnel construction quality evaluation indexes and makes the evaluation results more in line with reality.

(3) Taking a hydraulic tunnel as an example, the CWM-UM comprehensive evaluation model constructed in this paper is used to calculate its construction quality level, and the results are as follows: the quality level of tunnel excavation, support construction and secondary lining concrete construction are all of grade II, and the quality level of construction measurement, anti-drainage construction, tunnel grouting and overall construction of the hydraulic tunnel are all of grade III. At the same time, a comparative study is made with the matter-element extension theory to verify the applicability and reasonableness of the model, thus providing a basis for the subsequent construction.

References

You, Z.M.; Chen, J.P. Research on Controlling the Quality of Highway Tunnels: Taking Shi-Man Highway Tunnel for Example. Safety and Environmental Engineering 2009, 16, 111–114. [Google Scholar]
Wu, J.M. Design of concrete structures for hydraulic buildings and their construction quality control. Technical Supervision in Water Resources 2011, 19, 26–28. [Google Scholar]
Lan, X.F. Quality control of winter construction of concrete in Jimingyi Tunnel of Dazhun Railway Additional Second Line. Railway Engineering 2013, 26, 49–50. [Google Scholar]
Hu, C.; Zhao, C.-J.; Zhou, Y.-H.; et al. Excavation surface quality real-time control for high slope in hydropower engineering. Water Resources and Power 2017, 35, 125–128. [Google Scholar]
Cheng, L.L. Study on Quality Control of Pandaoling Tunnel Project Construction. Liaoning Technical University, 2019. [Google Scholar]
Jin, Q.; Yanhui, Z. Study on quality and safety monitoring scheme of tunnel construction based on 3D laser scanning. IOP Conference Series: Earth and Environmental Science 2021, 804. [Google Scholar]
Arends, B.J.; Jonkman, S.N.; Vrijling, J.K.; et al. Evaluation of tunnel safety: towards an economic safety optimum. Reliability Engineering & System Safety 2005, 90, 217–228. [Google Scholar]
Manchao, H.; Sousa RL, E.; Mueller, A.; et al. Analysis of excessive deformations in tunnels for safety evaluation. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research 2015, 45, 190–202. [Google Scholar]
Hussain, S.; Rehman, Z.U.; Mohammad, N.; et al. Numerical modelling for engineering analysis and designing of optimum support systems for headrace tunnel. Advances in Civil Engineering 2018.
Mao, X.; Hu, A.; Zhao, R.; et al. Evaluation and Application of Surrounding Rock Stability Based on an Improved Fuzzy Comprehensive Evaluation Method. Mathematics 2023, 11. [Google Scholar] [CrossRef]
Zhi, L.; Xianqing, M.; Dunwen, L.; et al. Disaster Risk Evaluation of Superlong Highways Tunnel Based on the Cloud and AHP Model. Advances in Civil Engineering 2022. [Google Scholar]
Xingang, W.; Zhuan, Z.; Licheng, S.; et al. Research on the evaluation index system of “new energy cloud” operation mode based on CRITIC weighting method and AHP method. IOP Conference Series: Earth and Environmental Science 2021, 831. [Google Scholar]
Wu, B.; Zhou, L.; Liu, C. Evaluation of Water-rich Soft Rock Mountain Ridge Tunnel Collapse Risk Based on Game-combination Empowerment-TOPSIS Method. Science Technology and Engineering 2023, 23. [Google Scholar]
Hu, Y.; Zhu, C. Credit evaluation model of road transportation enterprises based on the combination weighting method. Mathematical Problems in Engineering 2021, 2021, 1–10. [Google Scholar]
Qiu, D.H.; Chen, Q.Q.; Xue, Y.G.; et al. A new method for risk assessment of water inrush in a subsea tunnel crossing faults. Marine Georesources Geotechnology 2022, 40, 679–689. [Google Scholar] [CrossRef]
Changfu, H.; Shuguang, T.; Qun, L.; et al. Evaluation of Rock Quality of Tunnel Wall Rock Based on Rough Set Theory and Unascertained Measurement Theory. Mathematical Problems in Engineering 2018, 20181–10. [Google Scholar]
Jia, Q.; Wu, L.; Li, B.; et al. The Comprehensive Prediction Model of Rockburst Tendency in Tunnel Based on Optimized Unascertained Measure Theory. Geotechnical and Geological Engineering 2019, 37, 3399–3411. [Google Scholar] [CrossRef]
Mu, C.L.; Huang, R.Q.; Pei, X.J.; et al. Evaluation of rock stability based on combined weighting-unascertained measurement theory. Chinese Journal of Geotechnical Engineering 2016, 38. [Google Scholar]
Li, X.; Jiangwen, Q.; Tang, J.; et al. Study on combination weighting method-TOPSIS methodbased risk assessment of water in-rush in construction of North Tianshan Mountain Tunnel. Water Resour. Hydropower Eng 2019, 50, 114–119. [Google Scholar]
Huang, R.; Zhang, F.X. Method of Comprehensively Evaluating Water Quality Based on Optimal Set Pair Analysis. Journal of Changjiang River Scientific Research Institute 2016, 33, 6–10. [Google Scholar]
Pi, S.L. Research on the PRS Integrated Fishbone Diagram and Its Application in Project Management. China Soft Science 2009, 19, 92–97. [Google Scholar]
DL/T5251-2010, Technical code for detection and evaluation of hydraulic concrete structure [S].
SL279-2016, Specification for design of hydraulic tunnel [S].
Chen, C.M. Research on Evaluation Method of Eco-city Construction Based on Unascertained Mesure Theory. Tianjin University, 2013. [Google Scholar]
Qingfu, L.; Huade, Z.; Hua, Z. Durability evaluation of highway tunnel lining structure based on matter element extension-simple correlation function method-cloud model: A case study. Mathematical biosciences and engineering: MBE 2021, 18, 4027–4054. [Google Scholar]
Sun, X.R. Safety evaluation of sluice based on matter-element extension theory. Harnessing the Huaihe River 2018, 45, 19–21. [Google Scholar]

Figure 1. Construction quality evaluation process of concrete structures in hydraulic tunnels. based on CWM-UM modeling.

Figure 2. Fishbone diagram of construction quality problems of concrete structures in hydraulic tunnels.

Table 1. Numerical values and significance relationships.

Elemental	Numerical value	Degree
$a_{i j}$	1	Indicator $i$ is as important as indicator $j$
	2	Indicator $i$ is slightly more important than indicator $j$
	3	Indicator $i$ is more important than indicator $j$
	4	Indicator $i$ is very important compared to indicator $j$

Table 2. Sorting result of indicator weights.

Weights	Indicator 1	Indicator 2	$\cdot \cdot \cdot$	Indicator n
Subjective weights	$α_{1}^{'}$	$α_{2}^{'}$	$\cdot \cdot \cdot$	$α_{n}^{'}$
Objective weights	$β_{1}^{'}$	$β_{2}^{'}$	$\cdot \cdot \cdot$	$β_{n}^{'}$

Table 3. Summary of factors affecting construction quality.

Main body of construction	Construction process	Construction quality problems	Types of causal factors
Construction of concrete structures in hydraulic tunnels	Construction measurement X₁	Horizontal penetration error is too large X_1-1	People, methods
		Vertical penetration error is too large X_1-2	People, methods
		Marking the wrong direction of digging X_1-3	People, methods
		Inclement weather X_1-4	Environment
	Tunnel excavation X₂	Over-excavation of tunnels X_2-1	People, methods
		Under-excavation of tunnels X_2-2	People, methods
		Unevenness of excavated surface X_2-3	People, machinesmethods
		Groundwater seepage due to excavation X_2-4	Machines, methods
	Support construction X₃	Deviation in anchor hole position and hole orientation X_3-1	People, methods
		Low stability of steel arch X_3-2	People, materials, methods, environment
		Insufficient sprayed concrete thickness X_3-3	People, machinesmethods
	Anti-drainage construction X₄	Unreasonable drainage system X_4-1	People, methods
		Waterproofing materials and laying don’t meet the requirements X_4-2	People, materials
		Improper treatment of deformation joints and construction joints X_4-3	People, machinesmethods
	Secondary lining concrete construction X₅	Raw materials and mixing ratios don’t meet the requirements X_5-1	People, materials, methods
		Inadequate concrete placement and vibration X_5-2	People, methods, environment
		Inadequate concrete maintenance X_5-3	People, methods, Environment
		Lower concrete demolding strength X_5-4	People, materials, methods
	Tunnel grouting X₆	Unreasonable disposal of drilled holes X_6-1	People, methods
		Grouting pressure is too high / too small X_6-2	People, methods
		Grouting temperature is too high/too low X_6-3	People, methods, Environment

Table 4. Tunnel construction quality evaluation grading.

Constructionquality grade	Grading standard	Construction quality performance status
Grade I	(90,100)	Construction quality is excellent, with few or no problems
Grade II	(75,90)	Construction quality is good, with few problems
Grade III	(60,75)	Construction quality is satisfactory, with general problems
Grade IV	(40,60)	Construction quality is generally satisfactory, with major problems
Grade V	(0,40)	Construction quality is substandard, with significant problems

Table 5. Assigned results of quality indicators.

Quality evaluation indicators	Score
Quality evaluation indicators	Expert 1	Expert 2	Expert 3	Expert 4	Expert 5
Horizontal penetration error is too large X_1-1	68	56	73	61	75
Vertical penetration error is too large X_1-2	75	65	60	74	70
Marking the wrong direction of digging X_1-3	65	66	58	70	65
Inclement weather X_1-4	75	85	70	65	85
Over-excavation of tunnels X_2-1	70	65	60	62	66
Under-excavation of tunnels X_2-2	81	75	90	85	88
Unevenness of excavated surface X_2-3	85	80	76	80	85
Groundwater seepage due to excavation X_2-4	70	85	74	75	79
Deviation in anchor hole position and hole orientation X_3-1	92	86	89	81	80
Low stability of steel arch X_3-2	60	70	83	77	66
Insufficient sprayed concrete thickness X_3-3	80	70	85	86	75
Unreasonable drainage system X_4-1	72	67	58	84	65
Waterproofing materials and laying don’t meet the requirements X_4-2	53	65	59	70	68
Improper treatment of deformation joints and construction joints X_4-3	78	84	86	69	79
Raw materials and mixing ratios don’t meet the requirements X_5-1	81	75	77	88	82
Inadequate concrete placement and vibration X_5-2	89	70	83	76	90
Inadequate concrete maintenance X_5-3	63	78	60	55	64
Lower concrete demolding strength X_5-4	74	80	69	76	73
Unreasonable disposal of drilled holes X_6-1	70	75	56	80	71
Grouting pressure is too high / too small X_6-2	58	66	55	70	71
Grouting temperature is too high/too low X_6-3	65	59	67	75	73

Table 6. Subjective weighting values of evaluation indicators.

Indicators	Single weight						Weighted value
	X₁	X₂	X₃	X₄	X₅	X₆
	0.2324	0.1611	0.1279	0.0829	0.3286	0.0671
X_1-1	0.2274						0.0528
X_1-2	0.2274						0.0528
X_1-3	0.1222						0.0284
X_1-4	0.4231						0.0983
X_2-1		0.1867					0.0301
X_2-2		0.2922					0.0471
X_2-3		0.1078					0.0174
X_2-4		0.4133					0.0666
X_3-1			0.2500				0.0320
X_3-2			0.5000				0.0639
X_3-3			0.2500				0.0320
X_4-1				0.1634			0.0135
X_4-2				0.2970			0.0246
X_4-3				0.5396			0.0447
X_5-1					0.4133		0.1358
X_5-2					0.1078		0.0354
X_5-3					0.1867		0.0614
X_5-4					0.2922		0.0960
X_6-1						0.1958	0.0131
X_6-2						0.3108	0.0209
X_6-3						0.4934	0.0331

Table 7. The calculated result of CRITIC method.

Indicators	Variability	Conflict	Information content	Weight values
X_1-1	0.7565	21.3548	16.1546	0.0506
X_1-2	0.7160	16.8724	12.0807	0.0378
X_1-3	0.6359	16.6904	10.6140	0.0332
X_1-4	0.8131	19.8678	16.1548	0.0506
X_2-1	0.8363	18.7835	15.7090	0.0492
X_2-2	0.6790	21.3728	14.5115	0.0455
X_2-3	0.7373	17.0894	12.6003	0.0395
X_2-4	0.8611	20.3544	17.5273	0.0549
X_3-1	0.9158	24.7301	22.6473	0.0709
X_3-2	0.8070	23.7479	19.1654	0.0600
X_3-3	0.7348	22.0673	16.2151	0.0508
X_4-1	0.8643	17.6678	15.2698	0.0478
X_4-2	0.6964	17.9953	12.5323	0.0393
X_4-3	0.6481	24.9121	16.1455	0.0506
X_5-1	0.8982	17.3025	15.5411	0.0487
X_5-2	0.7381	20.1038	14.8379	0.0465
X_5-3	0.9526	21.7187	20.6888	0.0648
X_5-4	0.7477	18.9209	14.1463	0.0443
X_6-1	0.6223	16.8129	10.4625	0.0328
X_6-2	0.7974	16.4305	13.1012	0.0410
X_6-3	0.7294	18.0165	13.1412	0.0412

Table 8. Ranking results of weight values for evaluation indicators.

Indicators	X_1-1	X_1-2	X_1-3	X_1-4	X_2-1	X_2-2	X_2-3	X_2-4	X_3-1	X_3-2	X_3-3
IAHP method	7	7	16	2	15	9	20	4	13	5	13
CRITIC method	6	19	20	6	9	13	17	4	1	3	5
Indicators	X_4-1	X_4-2	X_4-3	X_5-1	X_5-2	X_5-3	X_5-4	X_6-1	X_6-2	X_6-3
IAHP method	19	17	10	1	11	6	3	21	18	12
CRITIC method	11	18	6	10	12	2	14	21	16	15

Table 9. The result of calculating the combined weights of evaluation indicators.

Primary indicators	Combination weight	Secondary indicators	Subjective weight	Objective weight	Combination weight
X₁	0.1970	X_1-1	0.0528	0.0506	0.0504
		X_1-2	0.0528	0.0378	0.0472
		X_1-3	0.0284	0.0332	0.0389
		X_1-4	0.0983	0.0506	0.0605
X₂	0.1838	X_2-1	0.0301	0.0492	0.0441
		X_2-2	0.0471	0.0455	0.0477
		X_2-3	0.0174	0.0395	0.0374
		X_2-4	0.0666	0.0549	0.0546
X₃	0.1506	X_3-1	0.0320	0.0709	0.0503
		X_3-2	0.0639	0.0600	0.0552
		X_3-3	0.0320	0.0508	0.0451
X₄	0.1268	X_4-1	0.0135	0.0478	0.0388
		X_4-2	0.0246	0.0393	0.0396
		X_4-3	0.0447	0.0506	0.0484
X₅	0.2266	X_5-1	0.1358	0.0487	0.0673
		X_5-2	0.0354	0.0465	0.0449
		X_5-3	0.0614	0.0648	0.0557
		X_5-4	0.0960	0.0443	0.0587
X₆	0.1153	X_6-1	0.0131	0.0328	0.0336
		X_6-2	0.0209	0.0410	0.0390
		X_6-3	0.0331	0.0412	0.0427

Table 10. The graph and expression of the uncertain measure function.

Method	Graph	Function expression
Linear form		${\begin{matrix} z_{t} (x) = {\begin{matrix} \frac{- x}{d_{t + 1} - d_{t}} + \frac{d_{t + 1}}{d_{t + 1} - d_{t}} d_{t} < x \leq d_{t + 1} \\ 0 x > d_{t + 1} \end{matrix} \\ z_{t + 1} (x) = {\begin{matrix} 0 x \leq d_{t} \\ \frac{x}{d_{t + 1} - d_{t}} - \frac{d_{t}}{d_{t + 1} - d_{t}} d_{t} < x \leq d_{t + 1} \end{matrix} \end{matrix}$

Table 11. Expected value of evaluation indicators.

Indicators	X_1-1	X_1-2	X_1-3	X_1-4	X_2-1	X_2-2	X_2-3	X_2-4	X_3-1	X_3-2	X_3-3
Expected value	66.6	68.8	64.8	76	64.6	83.8	81.2	76.6	85.6	71.2	79.2
Indicators	X_4-1	X_4-2	X_4-3	X_5-1	X_5-2	X_5-3	X_5-4	X_6-1	X_6-2	X_6-3
Expected value	69.2	63	79.2	80.6	81.6	64	74.4	70.4	64	67.8

Table 12. Construction quality evaluation grade of concrete structures in hydraulic tunnels.

Stage	Construction measurement	Tunnel excavation	Support construction	Anti-drainage construction	Secondary lining concrete construction	Tunnel grouting	Tunnel whole
Evaluation grade	III	II	II	III	II	III	III

Table 13. Classical domain and node domain of construction quality evaluation indicators of hydraulic tunnel.

Evaluation indicators	Classical domain					Node domain
Evaluation indicators	I	II	III	IV	V	Node domain
X_1-1~ X_6-3	（90,100）	（75,90）	（60,75）	（40,60）	（0,40）	（0,100）

Table 14. Evaluation grade.

Stage	Construction measurement	Tunnel excavation	Support construction	Anti-drainage construction	Secondary lining concrete construction	Tunnel grouting	Tunnel whole
Evaluation grade	III	II	II	III	II	III	III

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Construction Quality Evaluation of Concrete Structures in Hydraulic Tunnels Based on CWM-UM Modeling

Abstract

1. Introduction

2. The establishment of CWM-UM Evaluation Modeling

2.1. Determination of index weight

2.1.1. IAHP method to determine the subjective weight

2.1.2. CRITIC method to determine the objective weight

2.1.3. The method of calculating combination weight

2.2. Uncertainty Measure Evaluation Model

3. Construction quality evaluation process of concrete structure in hydraulic tunnel

4. Examples of engineering applications

4.1. Reasons affecting construction quality

4.2. Selection of construction quality evaluation indicators.

4.3. Construction quality grading

4.4. Construction quality evaluation process of concrete structures in hydraulic tunnels

4.4.1. IAHP method to determine the subjective weight

4.4.2. CRITIC method to determine the objective weight

4.4.3. Calculate combination weights

4.4.4. Construct uncertain measure function and matrix of single index

4.4.5. Calculate multi-index unascertained measure vector

4.4.6. Construction quality evaluation of concrete structures in hydraulic tunnels

4.5. Comparative study

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe