Multidimensional Data Analysis of Deep–Language in J.R.R. Tolkien and C.S. Lewis Reveals Tight Mathematical Connections

Preprint

Article

Multidimensional Data Analysis of Deep–Language in J.R.R. Tolkien and C.S. Lewis Reveals Tight Mathematical Connections

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Emilio Matricciani^*

This version is not peer-reviewed

Submitted:

17 June 2024

Posted:

18 June 2024

You are already at the latest version

Alerts

Abstract

Scholars of the English Literature unanimously say that J.R.R. Tolkien and C.S. Lewis influenced each other writings. For the first time we have investigated this issue mathematically by using an original multi–dimensional analysis of linguistic parameters, based on surface deep–language variables and linguistic channels. To set our investigation in the framework of the English Liter-ature, we have considered some novels written by earlier authors, such as C. Dickens, G. Mac-Donald and others. The deep–language variables and the linguistic channels, discussed in the paper, are likely due to writers’ unconscious design and have revealed connections between texts far beyond writers’ awareness. In summary, the capacity of the extended short–term memory required to readers, the universal readability index of texts, the geometrical representation of texts and the fine tuning of linguistic channels within texts – all tools largely discussed in the paper – have revealed strong connections between The Lord of the Rings (Tolkien), The Chronicles of Narnia, The Space Trilogy (Lewis) and novels by MacDonald, therefore in agreement with what scholars of the English Literature say.

Keywords:

Subject: Arts and Humanities - Literature and Literary Theory

1. Introduction

Unanimously, in a large number of papers – some of which are here recalled [1,2,3,4,5,6,7,8] from the vast literature on the topic – scholars of the English Literature state that J.R.R. Tolkien and C.S. Lewis influenced each other writings. The purpose of the present paper is not to review this large literature based on the typical approach used by scholars of literature – which is not our speciality – but to investigate this issue mathematically and statistically – study never done before – by using recent methods devised by researching the impact of the surface deep–language variables [9,10,11] and linguistic channels [12] in literary texts. Since scholars mention also the influence by George MacDonald on both, we consider also some novels written by this earlier author. To set all these novels in the framework of the English Literature, we consider also some novels written by other earlier authors, such as C. Dickens and others.

After this introduction, in Section 2 we introduce the literary texts (novels) studied. In Section 3 we report the series of words, sentences and interpunctions versus chapters for some novels, and define an index useful to synthetically describe regularity due to what we think is a consciouos design by authors. In Section 4 we start exploring the four deep−language variables; to avoid misunderstaning, these variables, and the linguistic channels derived from them, refer to the “surface” structure of texts, not to the “deep” structure mentioned in cognitive theory. In Section 5 we report results concerning the extended short–term memory and a universal readability index; both topics address human short–term memory buffers. In Section 6 we represent literary texts geometrically in the Cartesian plane by defining linear combinations of deep‒language variables and calculate the probability that a text can be confused with another. In Section 7 we show the linear relationships existing between linguistic variables in the novels considered. In Section 8 we report the theory of linguistic channels and in Section 9 we apply it to the novels presently studied. Finally, in Section 10 we summarise the main findings and conclude. Several Appendices report numerical data.

2. Database of Literary Texts (Novels)

Let us first introduce the database of literary texts used in the present paper. Table 1 lists some basic statistics of the novels by Tolkien, Lewis and MacDonald. To set these texts in the framework of earlier English Literature, we consider novels by Charles Dickens (Table 2) and other authors (Table 3). Notice that these statistics refer only to the main text because titles, footnotes and other extraneous material present in the digital texts have been deleted.

Some homogeneity can be noted in novels of the same author. The stories in The Space Trilogy and The Chronicles of Narnia, by Lewis, are told with about the same number of chapters, words and sentences, as is also for couples of MacDonald’s novels, such as At the Back of the North Wind and Lilith: A Romance. The stories in David Copperfield, Bleak House and Our Mutual Friend (by Dickens) are also told in this way as The Adventures of Oliver Twist and A Tale of Two Cities. These numerical values, we think, are not due to chance but consciously managed by the authors, a topic we purse more in the next Section.

3. Conscious Design of Texts: Words, Sentences and Interpunctions Versus Chapters

First, we study the linguistic variables which we think the authors deliberately designed. In the specific, we show the series of words, sentences and interpunctions versus chapter.

Let us consider a literary work (a novel) and its subdivision in disjoint blocks of text long enough to give reliable average values. Let

n_{S}

be the number of sentences contained in a text block,

n_{W}

the number of words contained in the

n_{S}

sentences,

n_{C}

the number of characters contained in the

n_{W}

words and

n_{I}

the number of punctuation marks (interpunctions) contained in the

n_{S}

sentences.

Figure 1 shows the series

n_{W}

versus the normalized chapter number for The Lord of the Rings, The Chronicles of Narnia, The Space Trilogy.

For example, the normalized value of chapter 10 in The Chronicles of Narnia, is

10 / 110 = 0.09

in the

x -

scale of Figure 1. This normalization allows to show synoptically novels of different number of chapters.

In The Chronicles of Narnia (in the following Narnia, for brevity. We can notice a practically constant value

n_{W}

compared to The Lord of the Rings (Lord) and The Space Trilogy (Trilogy).

Let us define a synthetic index to describe the series drawn in Figure 1, namely the coefficient of dispersion

δ

, given by the standard deviation

σ_{n_{W}}

divided by the mean value

< n_{W} >

δ = \frac{σ_{n_{W}}}{< n_{W} >}

(1)

Table 4 and Table 5 report

δ

for

n_{W}

n_{S}

and

n_{I}

. Since

n_{S}

and

n_{I}

(series not shown for brevity) are very well correlated with

n_{S}

, the three coefficients of dispersion are about the same.

In Narnia

δ = 0.16

, in Lord

δ = 0.34

and in Trilogy

δ = 0.60

. Let us also notice the minimum value

δ = 0.07

in The Screwtape Letters (Screwtape).

The overal (words, sentences and interpunctions mixed together) mean value is

< δ > = 0.44

, the standard deviation

σ_{δ} = 0.18

. Therefore, Screwtape is practically more than

{2 \times σ}_{δ}

from the mean – as also is Silmarillion on the other side – Narnia is at about

1.5 \times σ_{δ}

. In contrast, Trilogy, Lord and The Hobbit (Hobbit) are whithin

1 \times σ_{δ}

From these results, it seems that Lewis designed the chapters of Narnia and Screwtape with an almost uniform distribution of words, sentences and interpunctions, very likely because of the intended audience in Narnia (i.e., kids) and the “letters” fiction tool used in Screwtape. In Trilogy the design seems very different (

δ = 0.60

, well within

1 \times σ_{δ}

) likely due to the development of the science fiction story narrated.

Tolkien acted differently from Lewis, because he seems to have designed chapters more randomly and within

1 \times σ_{δ}

, as Hobbit and Lord show. An exception is The Silmarillion, published posthumously, a text far from being a “novel”.

Finally, notice that the novels by MacDonald show more homogeneous values, very similar to Hobbit and Trilogy and to the other novels listed in Table 5.

In conclusion, the analysis of series of words, sentences and interpunctions per chapter does not indicate likely connections between Tolkien, Lewis and MacDonald. Each author distributed words, sentences and interpunctions according to some plan different from author to author and also from novel to novel of the same author.

There are, however, linguistic variables that – as we have reported for modern and ancient literary texts [13,14,15] – are not consciously designed/managed by authors, therefore, these variables are the best candidates to reveal hidden mathematical/statistical connections between texts. In the next section we start dealing with these variables, with the specific purpose of comparing Tolkien and Lewis, although this comparison is set in the more general framework of the authors mentioned in Section 2.

4. Surface Deep–Language Variables

We start exploring the four stochastic variables we called deep−language variables, following our general statistical theory on alphabetical languages [9,10,11]. To avoid possible misunderstaning, these variables, and the linguistic channels derived from them, refer to the “surface” structure of texts, not to the “deep” structure mentioned in cognitive theory.

Contrarily to the variables studied in Section 3, the deep–language variables are likely due to unconscious design. As shown in [9,10,11], they reveal connections between texts far beyond writers’ awarness, therefore, the geometrical representation of texts [10] and the fine tuning of linguistic channels [12,13,14,15], are tools better suited to reveal connections. They can likely indicate also the influence of an author on another.

Defined the number of characters per chapter

n_{C}

and the number of

I_{P}' s

per chapter

n_{I_{P}}

, the four deep−language variables are [9]:

The number of characters

C_{P}

C_{P} = \frac{n_{C}}{n_{W}}

(2)

The number of words per sentence

P_{F}

P_{F} = \frac{n_{W}}{n_{S}}

(3)

The number of interpunctions per word, referred to as the word interval,

I_{P}

I_{P} = \frac{n_{I}}{n_{W}}

(4)

The number of word intervals per sentence

M_{F}

M_{F} = \frac{n_{I_{P}}}{n_{S}}

(5)

Equation (5) can be written also as

M_{F} = P_{F} / I_{P}

Table 6, Table 7, Table 8 and Table 9 reports mean and standard deviation of these variables. Notice that these values have been calculated by weighing each chapter with its number of words to avoid that short chapters weigh as much as long ones. For example, chapter 1 of Lord has

10097

words, therefore its statistical weight is

10097 / 472173 \approx 0.021

not

1 / 62 \approx 0.016

. Notice, also, that the coefficient of dispersion used in Section 2 was calculated by weighting each chapter

1 / 62

, not

10097 / 472173,

to visually agree with the series drawn in Figure 1.

Specifically, let

M

be the number of samples (i.e., chapters), then the mean value

< P_{F} >

is given by:

< P_{F} > = \sum_{k = 1}^{M} P_{F, k} \times (n_{W, k} / \sum_{k = 1}^{M} n_{W, k})

(6)

Therefore, notice, for not being misled, that

< P_{F} > \neq \frac{1}{M} \sum_{k = 1}^{M} P_{F, k} \neq \sum_{k = 1}^{M} n_{W, k} / \sum_{k = 1}^{M} n_{S, k}

W / S

. In other words,

< P_{F} >

is not given by the total number of words

W

divided by the total number of sentences

S

, or by assigning the weight

1 / M

to every chapter. The three values coincide only if all text blocks contain the same number of words and the same number of sentences, a case never found. The same observations apply to all other variables.

From Table 6, Table 7, Table 8 and Table 9 we can notice the following characteristcs. Lord and Narnia share the same

< P_{F} >

. Silmarillion is distinctly different from Lord and Hobbit, in agreement with the different coefficient of dispersion. Screwtape is distinctly different from Narnia and Trilogy. There is a great homogeneity in Dicken’s novels and a large homogeneity in

{< C}_{P} >

in all novels.

In the next sections we use

< P_{F} >

{< I}_{P} >

and

< M_{F} >

to calculate interesting indices connected to the short–term memory of readers–

5. Extended Short–Term Memory of Writers/Readers and Universal Readability Index

In this section we deal with the linguistic variables that, very likely, are not consciously managed by writers who, of course, act also as readers of their own text. We first report findings concerning the extended short–term memory and then those concerning a universal readability index. Both topics address human short–term memory buffers.

5.1. Extended Short–Term Memory and Multiplicity Factor

In [16,17], we have conjectured that the human short–term memory is sensitive to two independent variables, which apparently engage two short–term memory buffers in series, constituents of what we have called the extended short–term memory (E–STM). The first buffer is modelled according to the number of words between two consecutive interpunctions—i.e., the variable

I_{P}

, the word interval—which follows Miller’s

7 \pm 2

law [18]; the second buffer is modelled according to the number of word intervals,

I_{P}' s

, contained in a sentence —i.e., the variable

M_{F}

– ranging approximately for 1 to 7.

In [17] we studied the patterns (which depend on the size of the two buffers) that determine the number of sentences that theoretically can be recorded in the E–STM of a given capacity. These patterns were then compared with the number of sentences actually found in novels of Italian and English literature. We have found that most authors write for readers with short memory buffers and, consequently, are forced to reuse sentence patterns to convey multiple meanings. This behavior is quantified by the multiplicity factor

α

, defined as the ratio between the number of sentences in a novel and the number of sentences theoretically allowed by the two buffers, a function of

I_{P}

and

M_{F}

We found that

α > 1

is more likely than

α < 1

and often

α ≫ 1

. In the latter case, writers reuse many times the same pattern of number of words. Few novels show

α < 1

, in this case writers do not use some or most of them. The values of

α

found in the novels presently studied are reported in Table 10 and Table 11.

5.2. Universal Readability Index

In Reference [19], we have proposed a universal readability index given by:

G_{U} = 89 - 10 k C_{P} + 300 / P_{F} - 6 (I_{P} - 6)

(7)

k = < C_{P, I T A} > / < C_{P, E n g} >

(8)

In Eq. (8)

{< C}_{p, I T A} > = 4.48

{< C}_{p, E N G} > = 4.24

. By using Eqs. (7)(8), the average value

{< k C}_{P} >

of any language is forced to be equal to that found in Italian, namely

4.48

. The rationale for this choice is that

C_{P}

is a parameter typical of a language which, if not scaled, would bias

G_{U}

without really quantifying the reading difficulty of readers, who in their language are used, on the average, to read shorter or longer words than in Italian. This scaling, therefore, avoids changing

G_{U}

for the only reason that a language has, on the average, words shorter (as English) or longer than Italian. In any case,

C_{p}

affects Eq.(7) much less than

P_{F}

I_{P}

The values of

< G_{U} >

– calculated as the other linguistic variables, i.e., by weighting chapters (samples) according to the number of words – are reported in Table 10 and Table 11. The reader may be tempted to calculate Eq.(7) by introducing the mean values reported in Table 6, Table 7, Table 8 and Table 9. This, of course, can be done but it should be noted that the values so obtained are always less or equal (hence they are lower bounds) to the means calculated from the samples (see Appendix A). For example, for Lord, instead of 64.9 we would obtain 61.9.

It is interesting to “decode” these mean values into the minimum number of school years,

Y

necessary to make a novel “easy” to read, according to the Italian school system, assumed as the reference, see Figure 1 of [19]. The results are also listed in Table 10 and Table 11.

5.3. Discussion

There are several interesting facts to be noticed from the results reported in the previous sub–sections.

Silmarillion with

α = 0.2

is quite diverse from other Tolkien’s writings. Mathematically, this is due to its large

< M_{F} > = 3.62

and

< I_{P} > = 8.58

. In practice, the number of theoretical sentences allowed by the E–STM to read this text is only

1 / α = 5

times the number of sentence patterns actully used in the text. The reader needs a powerful E–STM and reading ability, since

G_{U} = 38.7

and

Y > 13

. This does not occur for Hobbit (

α = 39.4,

G_{U} = 52.4

Y =

9.9) and Lord (

α = 368.1, G_{U} = 64.2,

Y = 7.4

) in which Tolkien reuses patterns many times, especially in Lord.

Lord and Narnia show very large values,

α = 368.1

and

α = 297.7

, and very similar

G_{U}' s

and school years:

G_{U} = 64.2

Y = 7.4

and

G_{U} = 61.1

Y = 7.9

, respectively. Sentence patterns are reused many times by Lewis in this novel, but not in Screwtape (

α = 1.4)

, which is more difficult to read (

G_{U} = 33.5

) and requires more years of schooling,

Y > 13

. Moreover, Lord and Narnia have practically the same

< P_{F} > \approx 14

In general, Narnia is closer to Lord than to Trilogy, although the number of words and sentences in Trilogy and Narnia are quite similar (Table 1). This difference between Trilogy (

G_{U} = 56.2

Y = 9

) and Narnia (

G_{U} = 61.1

Y = 7.9

) might depend on the different readers addressed, kids for Narnia, adults for Trilogy, with different reading ability, as

G_{U}

indicates.

The novels by MacDonald show values of

α

and

G_{U}

very similar to those of the other English novels.

Notice the homogeneity in Dicken’s novels, which require about

Y = 7 ~ 8

years of school and readability index

< G_{U} > = 59 ~ 65

In conclusion, Lord and Narnia are the novels that address readers with very similar E–STM buffers, re–use sentence patterns in similar way, contain the same number of words per sentence, require the same reading ability and school years compared to other Tolkien’s and Lewis’ novels. The mathematical connections between Lord and Narnia will be further pursued in the next Section, where the four deep–language parameters are used to represent texts geometrically.

6. Geometrical Representation of Texts

The mean values of Table 6, Table 7, Table 8 and Table 9 can be used to assess how texts are “close”, or mathematically similar, in the Cartesian coordinate plane, by defining linear combinations of deep‒language variables. Texts are then modelled as vectors, representation discussed in detail in [9,10] and here briefly recalled. An extension of this geometrical representation of texts allows to calculate the probability that a text may be confused with another one, an extension in two dimensions of the problem discussed in [20].

6.1. Vector Representation of Texts

Let us consider the following six vectors of the indicated components of deep‒language variables

:

\vec{R_{1}} = ({< C}_{P} >, {< P}_{F} >

\vec{R_{2}} = ({< M}_{F} >, {< P}_{F} >

\vec{R_{3}} = (< I_{P} >, < P_{F} >

\vec{R_{4}} = ({< C}_{P} >, {< M}_{F} >

\vec{R_{5}} = ({< I}_{P} >, {< M}_{F} >

\vec{R_{6}} = ({< I}_{P} >, < C_{P} >

) and their resulting vector sum:

\vec{R} = \sum_{k = 1}^{6} \vec{R_{k}} = x \vec{i} + y \vec{j}

(9)

The choice of which parameter represents the component in abscissa and ordinate axes is not important because, once the choice is made, the numerical results will depend on it, but not the relative comparisons and general conclusions.

In the 1st quadrant of the Cartesian coordinate plane two texts are likely mathematically connected ‒ they show close ending points of vector (9) ‒ if their relative Pythagorean distance is small. A small distance means that texts share a similar mathematical structure, according to the four deep–language variables.

By considering the vector components

x

and

y

of Eq. (9), we obtain the scatterplot shown in Figure 2 where

X

and

Y

are normalized coordinates calculated by setting Lord at the origin

(X = 0, Y = 0)

and Silmarillion at

(X = 1, Y = 1)

, according to the linear tranformations:

X = \frac{x - x_{L o r d}}{x_{S i l m a} - x_{L o r d}}

(10)

X = \frac{y - y_{L o r d}}{y_{S i l m a} - y_{L o r d}}

(11)

From Figure 2 we can notice that Silmarillion and Screwtape are distinctly very far from all other texts examined, marking their striking diversity, as already remarked, therefore in the following we neglect them. Moreover, Pride, Vanity, Moby and Floss are grouped together and far from Trilogy, Narnia and Lord, therefore in the following we will not consider them further.

The complete set of the Pythagorean distance

d

between couples of texts is reported in Appendix B. These data synthetically describes proximity of texts and may indicate to scholars of literature connections between texts not considered before.

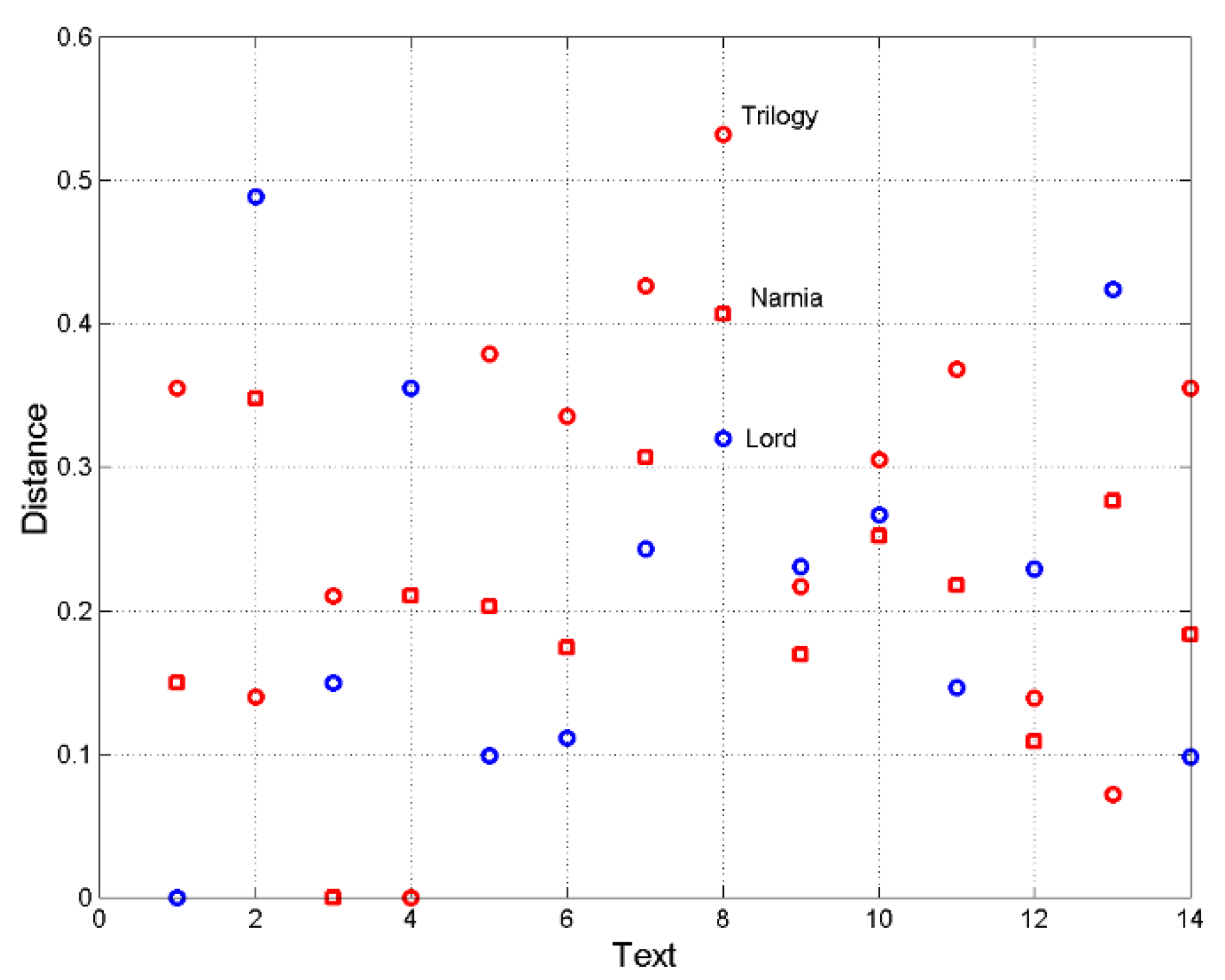
Figure 3 shows example of these distances concerning Lord (text 1), Narnia (text 3) and Trilogy (text 4). By referring to the cases in which

d < 0.2

, we can observe:

The closest texts to Lord are Narnia (3), Back (5), Lilith (6), Mutual (11) and Peter (14).

The closest texts to Narnia (1) are Lord (1), Lilith (6), Bleak (9), Martin, Peter (14)

The closest texts to Trilogy (3) are Hobbit (2), Martin (12), Peter (14).

Besides the proximity with earlier novels, Lord and Narnia show close proximity with each other and with two novels by MacDonald.

These remarks, however, refer to the “average” display of vectors whose ending point depends only on mean values. The standard deviation of the four deep–language variables, reported in Table 6, Table 7, Table 8 and Table 9, do introduce data scattering, therefore in the next sub–section we study and discuss this issue by calculating the probability (called “error” probability) that a text may be mathematically confused with another one.

6.2. Error Probability

Besides the vector

\vec{R}

of Eq. (9) – due to mean values – we can consider another vector

\vec{ρ}

, due to the standard deviation of the four deep–language variables, that adds to

\vec{R}

. In this case, the final random vector describing a text is given by:

\vec{T} = \vec{R} + \vec{ρ}

(12)

Now, to get some insight into this new description, we consider the area of a circle centered at the ending point of

\vec{R}

We fix the magnitude (radius)

ρ

as follows. First, we add the variances of the deep–language variables that determine the components

x

and

y

\vec{R}

– let them be

σ_{x}^{2}

σ_{y}^{2}

– then we calculate the average value

σ_{ρ}^{2} = 0.5 \times (σ_{x}^{2} + σ_{y}^{2})

and finally we set:

ρ = σ_{ρ}

(13)

Now, since in calculating the coordinates

x

and

y

\vec{R}

a deep–language variable can be summed twice or more, we add its standard deviation (referred to as sigma) twice or more times before squaring. For example, in the

x -

component

I_{P}

appears three times, therefore its contribution to the total variance in the

x - a x i s

is 9 times the variance calculated from the standard deviation reported in Table 6, Table 7, Table 8 and Table 9. For Lord, for example, it is

9 \times {0.51}^{2}

. After these calculations, the values of the 1–sigma circle are transformed into the normalized coordinates

X, Y

according to Eqs (10)(11).

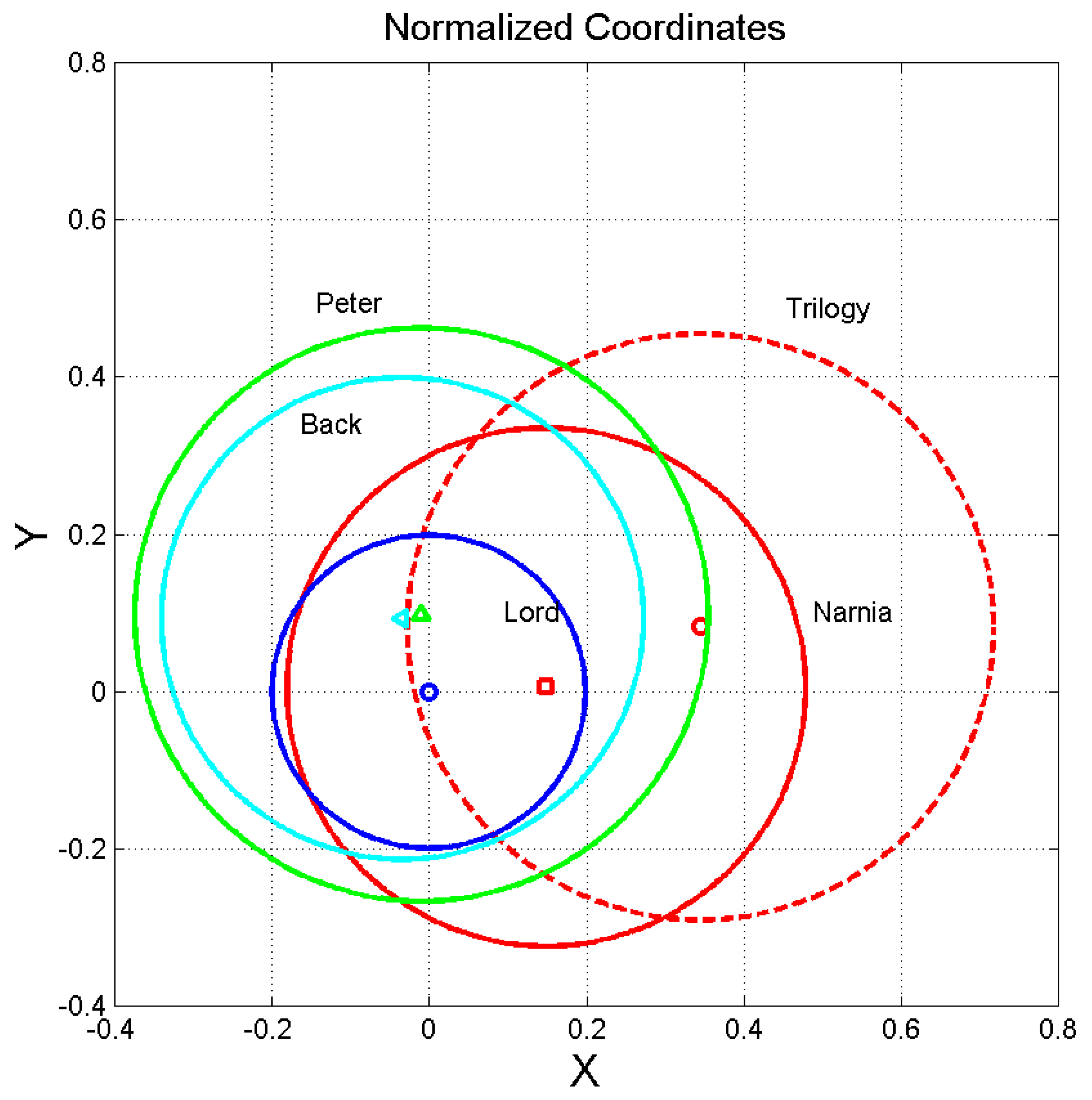
Figure 4 shows a significant example involving Lord, Narnia, Trilogy, Back and Peter. We see that Lord can be almost fully confused with Narnia, and partially with Trilogy, but not vice versa. Lord can also be confused with Peter and Back, therefore indicacting strong connections with these earlier novels.

Now, we can estimate the (conditional) probability that a text is confused with another by calculating ratios of areas. This procedure is correct if we assume that the bivariate density of the normalized coordinates

ρ_{X}, ρ_{Y}

, centred at

\vec{R}

, is uniform. By assuming this hypothesis we can calculate probabilities as ratios of areas [21,22].

The hypothesis of substantially uniformity around

\vec{R}

should be justified by noting that the coordinates

X, Y

are likely distributed according to a log–normal bivariete density because the logarithm of the four deep–language variables, which combine in Eq.(9) linearly, can be modelled as Gaussian. For the central limit theorem we should expect approximately a Gaussian model on the linear values, but with a signficantly larger standard deviation that that of the single variables. Therefore, in the area close to

\vec{R}

the bivariate density function should not be very peaked, hence the uniform density modelling.

Now we can calculate the following probabilities. Let

A

be the common area of two 1–sigma circles (i.e., the area proportional to the joint probability of two texts), let

A_{1}

be the area of 1–sigma circle of text 1 and

A_{2}

the area of 1–sigma circle of text 2. Now, since probabilities are proportional to areas, we get the following relationships:

\frac{A}{A_{1}} = \frac{P (A_{1}, A_{2})}{P (A_{1})} = \frac{P (A_{2} / A_{1}) P (A_{1})}{P (A_{1})} = P (A_{2} / A_{1})

(14)

\frac{A}{A_{2}} = \frac{P (A_{1}, A_{2})}{P (A_{2})} = \frac{P (A_{1} / A_{2}) P (A_{2})}{P (A_{2})} = P (A_{1} / A_{2})

(15)

In other words,

A / A_{1}

gives the conditional probability

P (A_{2} / A_{1})

that part of text 2 can be confused (or “contained”) in text 1;

A / A_{2}

gives the conditional probability

P (A_{1} / A_{2})

that part of text 1 can be confused with text 2. Notice that these conditional probabilities depend on the distance between two texts and on the 1–sigma radii (Appendix C)

Of course, these joint probabilities can be extended to three or more texts, e.g., in Figure 4 we could calculate the area shared by Lord, Narnia and Trilogy and the corresponding joint probability, not done in the present paper.

We think that the conditional probabilities and the visual display of 1–sigma circles give useful clues to establish possible hidden connections between texts and, maybe, even between authors, because the variables involved are not consciously managed by them.

In Table 12 the conditional probability

P (A_{2} / A_{1})

is reported in the columns, therefore

A_{1}

refers to the text indicated in the upper row;

P (A_{1} / A_{2})

is reported in the rows, therefore

A_{2}

refers to the text indicated the left column.

Notice that

P (A_{2} / A_{1}) = 1

means

A = A_{1}

, therefore text 1 can be fully confused with text 2 and

P (A_{1} / A_{2}) = 1

means

{A = A}_{2}

, therefore text 2 can be fully confused with text 1.

For example, assuming Lord as text 1 (column 1 of Table 12) and Narnia as text 2 (row 3), we find

P (A_{2} / A_{1}) = 0.974

. Viceversa, if we assume Narnia as text 1 (column 3) and Lord as text 2 (row 1), we find

P (A_{2} / A_{1}) = 0.356

. These data indicate that Lord can be confused with Narnia with probability close to 1, but not vice versa. In other words, in the data bank considered in this paper, if a machine randomly extracts a chapter from Lord, another machine, unaware of this choice, could attribute it to Lord, of course, but also, with decreasing probability, to Back, Peter, Narnia and Lilith.

On the contrary, if the text is extracted from Narnia, then it is more likely attributed to Peter or Trilogy than to Lord or other texts.

Now, we can define a synthetic parameter which highlights how much, on the average, two texts can be erroneously confused with each other. The parameter is the average conditional probability (see [20] for a similar problem):

p_{e} = P (A_{2} / A_{1}) P (A_{1}) + P (A_{1} / A_{2}) P (A_{2})

(16)

Now, since in comparing two texts we can assume

P (A_{1}) = P (A_{2}) = 0.5

, we get:

p_{e} = 0.5 \times [P (A_{2} / A_{1}) + P (A_{1} / A_{2})]

(17)

p_{e} = 0

, there is no intersection between the two 1–sigma circles, the two texts cannot be each other confused, therefore there is no mathematical connection involving the deep–language parameters (this happens for Screwtape and Silmarillion, which can be each other confused, but not with the other texts). If

p_{e} = 1

the two texts can be totally confused, the two 1–sigma circles coincide. Appendix D reports the values of

p_{e}

for all couples of novels.

Now, just to allow some rough analysis, it is reasonable to assume

p_{e} = 0.5

as a reference threshold, i.e., the probability of getting heads or tails in flipping a fair coin: if

p_{e} > 0.5

, then two texts can be confused not by chance; if

p_{e} \leq 0.5

, then two texts cannot be likely confused.

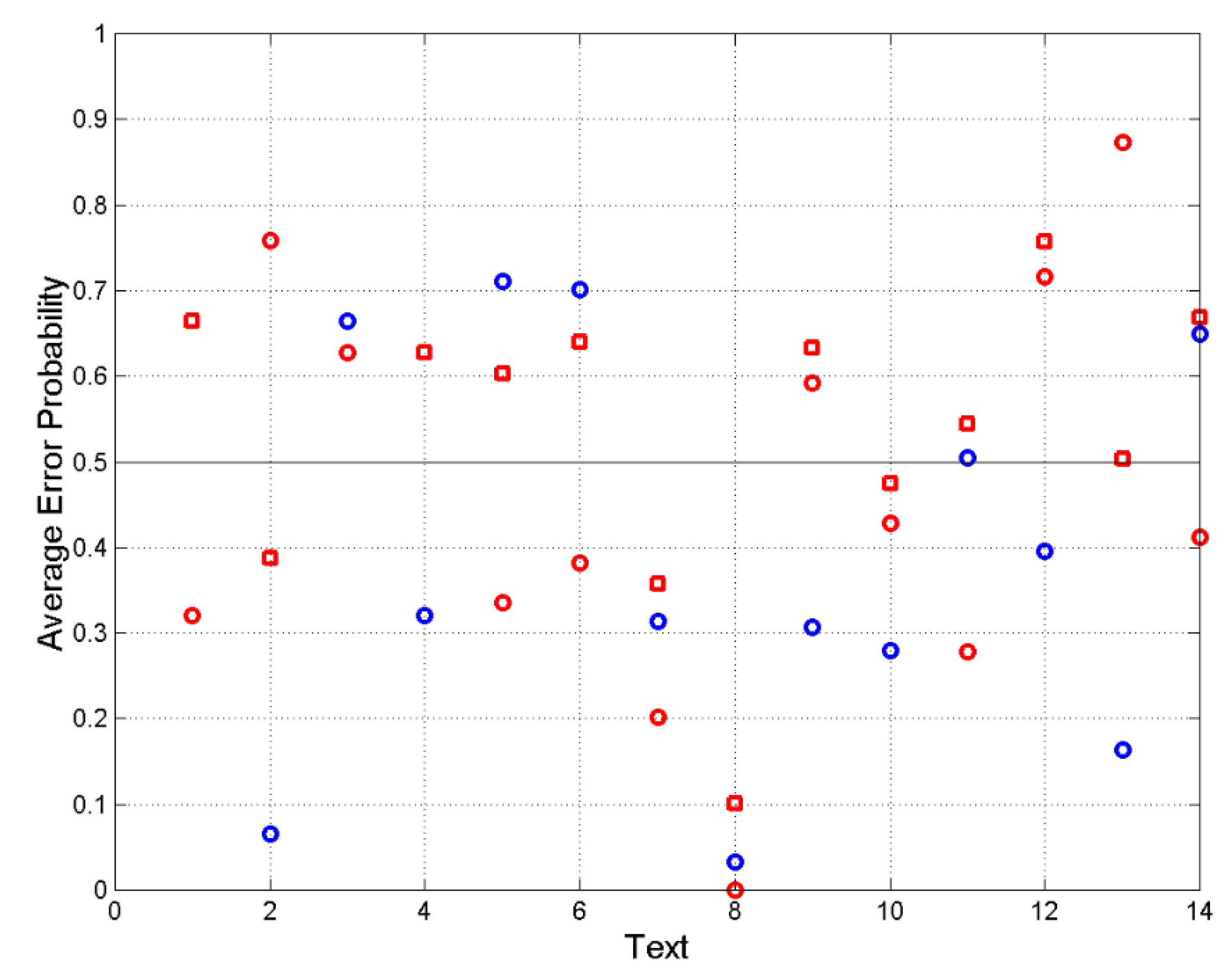
To visualize

p_{e}

, Figure 5 draws

p_{e}

when text 1 is Lord (column 1 of Table 12), Narnia (column 3) or Trilogy (column 4). We notice that

p_{e} > 0.5

in the following cases:

Lord as text 1: Narnia, Back, Lilith, Mutual, Peter.

Narnia as text 1: Lord, Trilogy, Back, Lilith, Bleak, Mutual, Martin, Peter.

Trilogy as text 1: Hobbit, Narnia, Bleak, Martin, Bask.

We can reiterate that Tolkien (Lord) appears significantly connected to Lewis (Narnia), to MacDonald (Back, Lilith) and Barrie (Peter), but not to Dicken’s novels as, on the contrary, does Lewis.

In the next Section the four deep–language variables are singled out to consider linguistic channels existing in texts. This is the analysis we have called the “fine tuning” of texts [12].

7. Linear Relationships in Literary Texts

The theory of linguistic channels, which we will recall in the next Section, is based on the regression line between linguistic variables:

y = m x

(18)

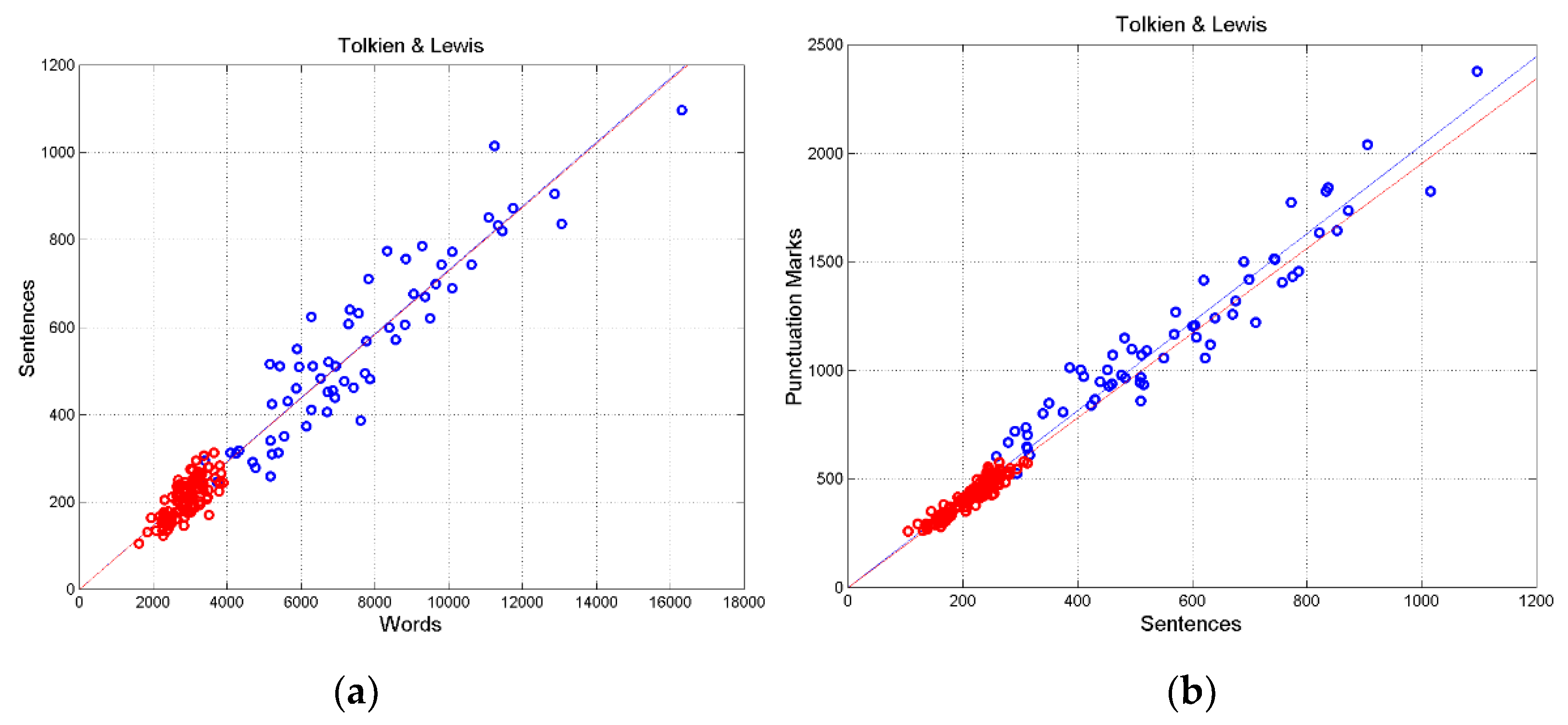
Therefore, we show examples of these linear relationships found in Lord and Narnia.

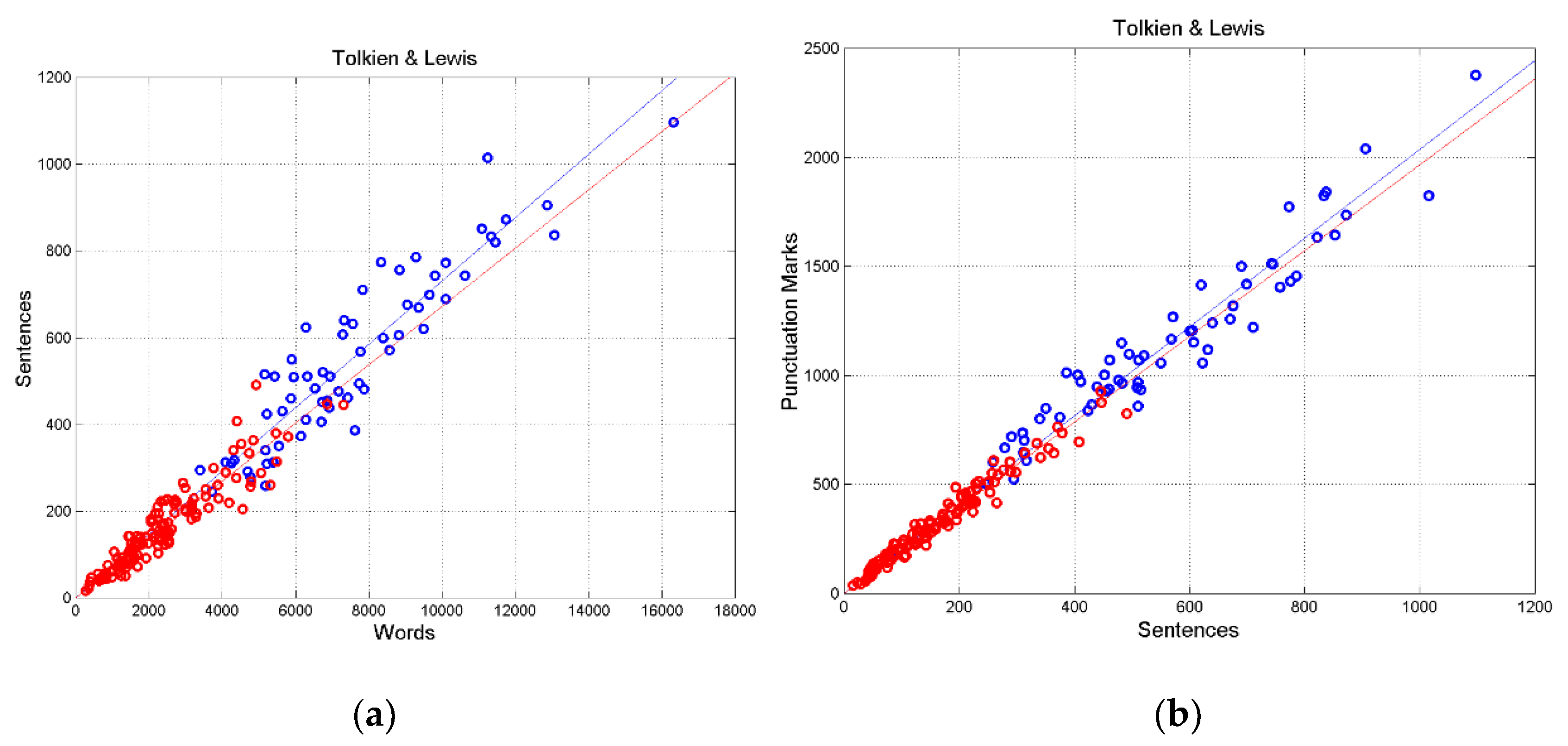
Figure 6a shows the scatterplot of

n_{S}

versus

n_{W}

of Lord and Narnia. In Narnia the slope of the regression line is

m = 0.0729

, the correlation coefficient

r = 0.7610 .

In Lord,

m = 0.0731

and

r = 0.9199

, therefore the average relationships – i.e., Eq.(18) – are practically identical – see also the values of

< P_{F} >

in Table 6 and Table 7 – while the correlation coefficients – i.e., the scattering of the data – are not and this fact will impact on the sentence channel discussed in Section 9.

Similar observations can be done for Figure 6b, which shows

n_{I}

versus

n_{S}

in Lord and Narnia. We find

m = 2.0372,

r = 0.9609

in Lord, and

m = 1.9520

and

r =

0.9384 in Narnia. Appendix E reports the complete set of these parameters.

Figure 7 shows the scatterplots of Lord and Trilogy. In Trilogy, for

n_{S}

versus

n_{W}

m = 0.0672

r = 0.9325

; for

n_{I}

versus

n_{S}

m = 1.9664, r = 0.9830

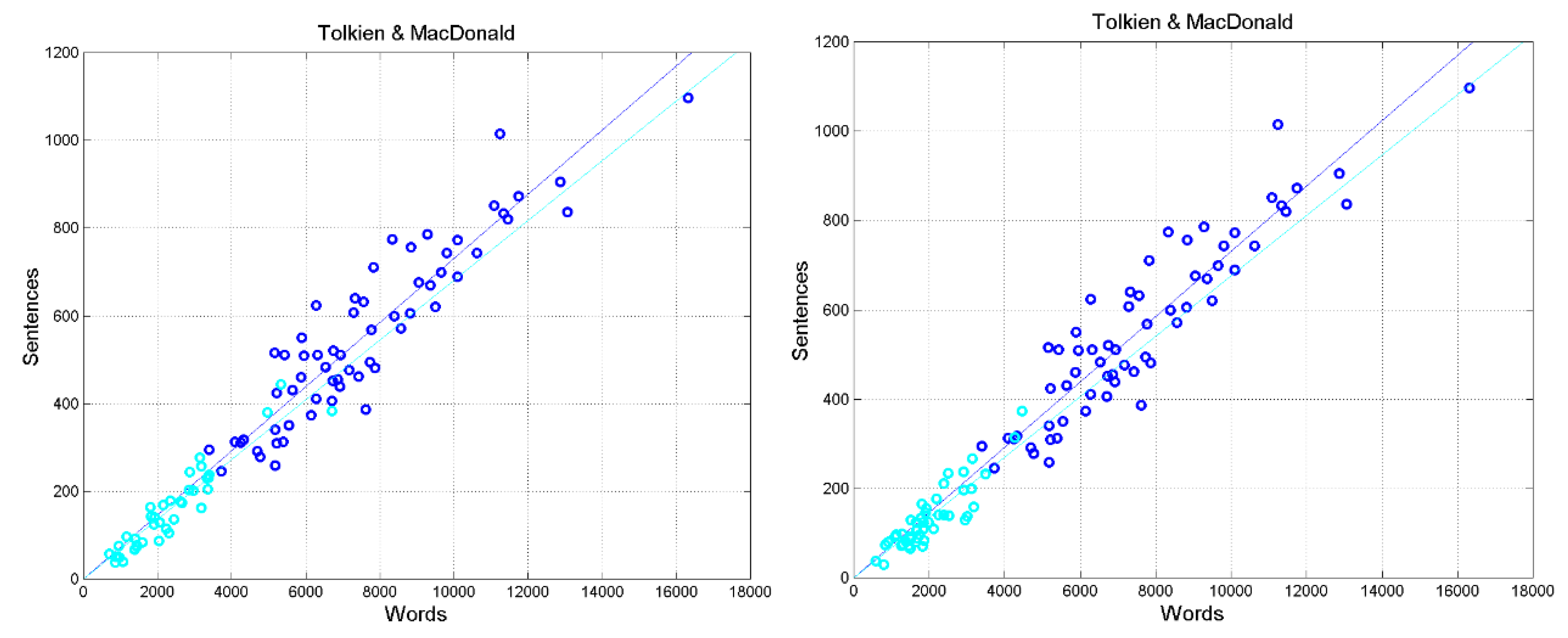
Figure 8 shows the scatterplots for Lord and Back or Lilith. We see similar regression lines and data scattering. In Back (left panel), the regression line between

n_{S}

and

n_{W}

gives

m = 0.0681

r = 0.9416

; in Lilith (right panel),

m = 0.0676

r =

0.8890. These results likely indicate the influence of MacDonald on Tolkien’s writing because they are different from most other novels.

In conclusion, the regression lines of Lord, Narnia and Trilogy are very similar, but they can differ in the scattering of the data. Regression lines, however, describe only one aspect of the relationship, namely the relationship between conditional average values Eq. (18), they do not consider the other aspect of the relationship, namely the scattering of data, which may not be the same even when two regression lines almost coincide, as shown above. The theory of linguistic channels, discussed in the next Section, on the contrary, considers both slopes and correlation coefficients and provides a “fine tuning” tool to compare two sets of data by singling out each of the four deep–language parameters.

8. Theory of Linguistic Channels

In this section we recall the general theory of linguistic channels [12]. In a literary work, an independent (reference) variable

x

(e.g.,

n_{W})

and a dependent variable

y

(e.g.,

n_{S})

can be related by the regression line given by Eq. (18).

Let us consider two different text blocks

Y_{k}

and

Y_{j}

, e.g., the chapters of work

k

and work

j

. Eq. (18) does not give the full relationship between two variables because it links only conditional average values. We can write more general linear relationships, which take care of the scattering of the data, – measured by the correlation coefficients

r_{k}

and

r_{j}

, respectively – around the average values (measured by the slopes

m_{k}

and

m_{j}

y_{k} = m_{k} x + n_{k}

(19)

y_{j} = m_{j} x + n_{j}

(20)

The linear models Eqs. (19)(20) introduce additive “noise” through the stochastic variables

n_{k}

and

n_{j}

, with zero mean value [9,12,20]. The noise is due to the correlation coefficient

|r| \neq 1

We can compare two literary works by eliminating

x

, therefore we compare the output variable

y

for the same number of the input variable

x

. For example, we can compare the number of sentences in two novels ‒ for an equal number of words ‒ by considering not only the average relationship, Eq. (18), but also the scattering of the data, measured by the correlation coefficient, Eqs. (19)(20). We refer to this communication channel as the “sentences channel”, S–channel and to this processing as “fine tuning” because it deepens the analysis of the data and can provide more insight into the relationship between two literary works, or any other texts.

By eliminating

x

, from Eqs. (19)(20) we get the linear relationship between, now, the input number of sentences in work

Y_{k}

(now the reference, input text) and the number of sentences in text

Y_{j}

(now the output text):

y_{j} = \frac{m_{j}}{m_{k}} y_{k} - \frac{m_{j}}{m_{k}} n_{k} + n_{j}

(21)

Compared to the new reference work

Y_{k}

, the slope

m_{j k}

is given by:

m_{j k} = m_{j} / m_{k}

(22)

The noise source that produces the correlation coefficient between

Y_{k}

and

Y_{j}

is given by:

n_{j k} = - \frac{m_{j}}{m_{k}} n_{k} + n_{j} = {- m}_{j k} n_{k} + n_{j}

(23)

The “regression noise−to−signal ratio”,

R_{m},

due to

|m_{j k}| \neq 1

, of the new channel is given by:

R_{m} = {(m_{j k} - 1)}^{2}

(24)

The unknown correlation coefficient

r_{j k}

between

y_{j}

and

y_{k}

is given by:

r_{j k} = c o s |a r c o s (r_{j}) - a r c o s (r_{k})|

(25)

The “correlation noise−to−signal ratio”,

R_{r}

, due to

|r_{j k}| < 1

, of the new channel from text

Y_{k}

to text

Y_{j}

is given by:

R_{r} = \frac{1 - r_{j k}^{2}}{r_{j k}^{2}} m_{j k}^{2}

(26)

Because the two noise sources are disjoint and additive, the total noise−to−signal ratio of the channel connecting text

Y_{k}

to text

Y_{j}

is given by:

R = R_{m} + R_{r}

(27)

Notice that Eq. (27) can be represented graphically [10]. Finally, the total and the partial signal−to−noise ratios are given by:

Γ_{d B} = - 10 \times {l o g}_{10} R

(28)

Γ_{m, d B} = - 10 \times {l o g}_{10} R_{m}

(29)

Γ_{r, d B} = - 10 \times {l o g}_{10} R_{r}

(30)

Of course, we expect that no channel can yield

|r_{j k}| = 1

and

|m_{j k}| = 1

, therefore

Γ_{d B} = \infty

, a case referred to as the ideal channel, unless a text is compared with itself. In practice, we always find

|r_{j k}| < 1

and

|m_{j k}| \neq 1

. The slope

m_{j k}

measures the multiplicative “bias” of the dependent variable compared to the independent variable; the correlation coefficient

r_{j k}

measures how “precise” the linear best fit is.

In conclusion, the slope

m_{j k}

is the source of the regression noise

R_{m}

, the correlation coefficient

r_{j k}

is mostly the source of the correlation noise of the channel

R_{r}

9. Linguistic Channels

In long texts (such as novels, essays etc.) we can define at least four linguistic linear channels [12], namely:

Sentence channel (S–channel)

Interpunctions channel (I–channel)

Word interval channel, WI–channel

Characters channel (C–channel).

In S‒channels, the number of sentences of two texts is compared for the same number of words. These channels describe how many sentences the author of text

j

writes, compared to the writer of text

k

(reference text), by using the same number of words. Therefore these channels are more linked to

P_{F}

than to other parameters. Very likely they reflect the style of the writer.

In I‒channels, the number of word intervals of two texts is compared for the same number of sentences. These channels describe how many short texts between two contiguous punctuation marks (of length

I_{P}

) two authors use, therefore these channels are more linked to

M_{F}

than to other parameters. Since

M_{F}

is very likely connected with the E–STM, I‒channels are more related to the second buffer of readers‘ E–STM than to the style of the writer.

In WI‒channels, the number of words contained in a word interval (i.e.,

I_{P}

) is compared for the same number of interpunctions. These channels are more linked to

I_{P}

than to other parameters. Since

I_{P}

is very likely connected with the E–STM, WI‒channels are more related to the first buffer of readers‘ E–STM than to the style of the writer.

In C‒channels, the number of characters of two texts is compared for the same number of words. They are more related to the language used, e.g., English, than to the other parameters, unless essays or scientific/academic texts are considered because these latter texts use, on the average, longer words [9].

As an example, Table 13 reports the total and the partial signal–to–noise ratios

Γ_{d B}

Γ_{m, d B}

Γ_{r, d B}

in the four channels by considering Lord as reference (input) text. In other words text

j

is compared to text

k

(reference text, i.e., Lord).

Appendix F reports

Γ_{d B}

for all novels considered in the paper.

Let us make some fundamental remarks on Table 13, applicable whichever is the reference text. The signal–to–noise ratios of C‒channels are practically the largest ones, ranging from 19.17 dB (Lilith) to 31.19 dB (Back). These results are simply saying that all authors use the same language and write texts of the same kind, novels not essays or scientific/academic papers. These channels are not apt to distinguish or assess large differences between texts or authors.

In the three other channels we can notice that Trilogy, Back and Lilith have the largest signal–to–noise ratios, about

~ 19 t o ~ 22

dB, therefore these novels are very similar to Lord. In other words, these channels seem to confirm the likely influence by MacDonald on both Lord and Trilogy, and the connection between Lord and Trilogy.

On the contrary, Narnia shows poor values in the S–Channel (10.12 dB) and WI–Channel (7.94 dB). These low values are determined by the correlation noise because

R = R_{m} + R_{r} \approx R_{r}

. If we consider only

Γ_{m, d B}

– i.e., only the regression line – then we notice a strong connection with Lord since

Γ_{m, d B} = 51.26

dB. As we have already observed regarding Figure 6, the regression lines are practically identical but the spreading of the data is not. Lewis in Narnia is less “regular” than in Trilogy or Tolkien in Lord in shaping (unconsciously) these two linguistic channels.

10. Summary and Conclusions

To set our investigation in the framework of the English Literature, we have also considered some novels written by earlier authors, such as Charles Dickens and others, including George MacDonald, because scholars mention his likely influence on Tolkien and Lewis.

In our multidensional analysis, only the series of words, sentences and interpunctions per chapter, in our opinion, were consciously planned by the authors and, specifically, they do not indicate strong connections between Tolkien, Lewis and MacDonald. Each author distributed words, sentences and interpunctions differently from author to author and, sometimes, even from novel to novel of the same author.

On the contrary, the deep–language variables and the linguistic channels, discussed in the paper, are likely due to unconscious design and can reveal connections between texts far beyond writers’ awarness.

In summary, the buffers of the extended short–term memory required to readers, the universal readability index of texts, the geometrical representation of texts and the fine tuning of linguistic channels – all tools largely discussed in the paper – have revealed strong connections between The Lord of the Rings (Tolkien), The Cronicles of Narnia and The Space Triology (Lewis) on one side, and the strong connection also with some novels by MacDonald, on the other side, therefore substantially in agreement with what scholars of the English Literature say.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author wishes to thank the many scholars who, with great care and love, maintain digital texts available to readers and scholars of different academic disciplines, such as Perseus Digital Library and Project Gutenberg.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Universal Readability Mean Index Lower Bound

The mean value of

G_{U}

is given by:

{< G}_{U} > = 89 - 10 k {< C}_{P} > + 300 < 1 / P_{F} > - 6 ({< I}_{P} > - 6)

(A1)

The value calculated by introducing the mean of the variables is given by:

G_{U, m e a n} = 89 - 10 k {< C}_{P} > + 300 / {< P}_{F} > - 6 ({< I}_{P} > - 6)

(A2)

Therefore

{< G}_{U} > - G_{U, m e a n} = 300 \times (\frac{1}{< P_{F} >} - < \frac{1}{P_{F}} >)

(A3)

Now, it can be proved with the Cauchy–Schwarz inequality that

1 / < x > \geq < 1 / x >

, therefore

{< G}_{U} > - G_{U, m e a n} \geq 0

, hence

{< G}_{U} > \geq G_{U, m e a n}

Appendix B. Pythagorean Distance $d$ between Couples of Texts

Table A1. Pythagorean distance

d

between couples of texts.

Table A1. Pythagorean distance

d

between couples of texts.

Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	0
Hobbit	0.488	0
Narnia	0.150	0.348	0
Trilogy	0.355	0.140	0.211	0
Back	0.099	0.499	0.203	0.379	0
Lililth	0.112	0.453	0.174	0.336	0.048	0
Oliver	0.244	0.518	0.307	0.426	0.146	0.141	0
David	0.320	0.620	0.407	0.532	0.222	0.234	0.106	0
Bleak	0.231	0.312	0.170	0.217	0.201	0.153	0.211	0.316	0
Tale	0.267	0.381	0.252	0.305	0.201	0.161	0.143	0.239	0.096	0
Mutual	0.146	0.479	0.218	0.369	0.055	0.044	0.099	0.190	0.170	0.151	0
Martin	0.230	0.2612	0.109	0.139	0.241	0.197	0.294	0.400	0.096	0.192	0.230	0
Bask	0.424	0.0964	0.277	0.072	0.451	0.408	0.496	0.602	0.286	0.371	0.441	0.211	0
Peter	0.098	0.4744	0.183	0.355	0.025	0.024	0.146	0.232	0.177	0.182	0.048	0.217	0.427	0

Appendix C. Common Area between Circles

We list the Matlab code to calculate the common area between text, downloaded from (last access, 15, June, 2024):

https://it.mathworks.com/matlabcentral/answers/273066–overlapping–area–between–two–circles.

Let the distance between the centers of two circles be d and their two radii be r1 and r2. Then the area, A, of the overlap region of the two circles can be calculated as follows using Matlab’s ‘atan2’ function:

t = sqrt((d+r1+r2)*(d+r1–r2)*(d–r1+r2)*(–d+r1+r2));

A = r1^2*atan2(t,d^2+r1^2–r2^2)+r2^2*atan2(t,d^2–r1^2+r2^2)–t/2;

Appendix D. Conditional Error Probability

Table A2. Error probability between the indicated texts.

	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	−−
Hobbit	0.065	−−
Narnia	0.665	0.387	−−
Trilogy	0.320	0.759	0.627	−−
Back	0.711	0.148	0.603	0.335	−−
Lililth	0.701	0.173	0.639	0.382	0.866	−−
Oliver	0.314	0.051	0.358	0.203	0.666	0.641	−−
David	0.033	0	0.101	0	0.496	0.372	0.664	−−
Bleak	0.307	0.387	0.633	0.593	0.543	0.560	0.397	0.040	−−
Tale	0.280	0.270	0.475	0.428	0.554	0.601	0.615	0.300	0.725	−−
Mutual	0.505	0.036	0.545	0.279	0.633	0.681	0.686	0.273	0.428	0.558	−−
Martin	0.395	0.499	0.757	0.716	0.478	0.528	0.273	0.003	0.732	0.517	0.367	−−
Bask	0.164	0.830	0.504	0.873	0.211	0.241	0.077	0	0.439	0.286	0.095	0.591	−−
Peter	0.649	0.231	0.669	0.412	0.853	0.761	0.687	0.568	0.642	0.644	0.594	0.587	0.294	−−

Appendix E. Slope and Correlation Coefficient of the Regression Lines

Table A3. Slope/correlation coefficient of the regresson line

y = m x

, Eq.(18), modelling the indicated variables (dependent/independent). We keep four digits because some novels differ only at the third, fourth digit.

Table A3. Slope/correlation coefficient of the regresson line

y = m x

, Eq.(18), modelling the indicated variables (dependent/independent). We keep four digits because some novels differ only at the third, fourth digit.

Novel	Sentences/Words	Interpunctions/Sentences	Words/Interpunctions	Characters/words
Lord	0.0731/0.9199	2.0372/0.9609	6.6134/0.9609	4.0367/0.9982
Hobbit	0.0608/0.9532	2.1010/0.9936	7.6902/0.9532	4.1014/0.9996
Narnia	0.0729/0.7610	1.9520/0.9384	6.9062/0.7991	4.0907/0.9919
Trilogy	0.0672/0.9325	1.9664/0.9830	7.3380/0.9696	4.2002/0.9976
Back	0.0681/0.9416	2.1640/0.9759	6.6045/0.9799	3.8496/0.9976
Lililth	0.0676/0.8890	2.2619/0.9488	6.2926/0.9800	4.1174/0.9863
Oliver	0.0566/0.9059	3.0893/0.9544	5.6302/0.9638	4.2248/0.9977
David	0.0537/0.9390	3.2949/0.9657	5.5775/0.9882	4.0474/0.9966
Bleak	0.0600/0.9258	2.5324/0.9715	6.51250.9694	4.2235/0.9923
Tale	0.0573/0.9574	2.7972/0.9785	6.1323/0.9912	4.2417/0.9983
Mutual	0.0618/0.9299	2.6814/0.9549	5.9766/0.9740	4.2197/0.9940
Martin	0.0658/0.8583	2.2243/0.9364	6.6785/0.9514	4.3171/0.9939
Bask	0.0684/0.7706	1.8517/0.9366	7.6984/0.9005	4.1320/0.9949
Peter	0.0687/0.8686	2.3080/0.9679	6.1018/0.9152	4.1117/0.9968

Appendix F. Total Signal–to–Noise Ratios $Γ_{d B}$ , in the Four Linguistic Channels

Table A4, Table A5, Table A6 and Table A7 report the signal–to–noise ratio

Γ_{d B}

in the channels between the input text

k

(reference) reported in the first row, and the output text

j

reported in the left column. For example, in Table A4, if the input text is Lord and the output text is Trilogy then

Γ_{d B} = 21.27

dB; vice versa,

Γ_{d B} = 20.44

. A slight asymmetry is typical of linguistic channels [12,15].

Table A4. Total signal–to–noise ratios

Γ_{d B}

, S–Channels.

Table A4. Total signal–to–noise ratios

Γ_{d B}

, S–Channels.

Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	∞	12.65	10.08	20.44	20.23	18.92	10.61	8.68	13.19	10.18	14.63	14.51	9.79	17.14
Hobbit	14.60	∞	8.21	19.11	19.02	14.75	15.97	17.00	21.64	24.02	23.05	12.73	8.50	13.08
Narnia	10.12	5.30	∞	8.21	7.70	11.54	6.81	4.19	6.85	4.15	7.11	13.32	23.39	13.54
Trilogy	21.27	18.00	9.58	∞	30.77	19.49	13.81	11.96	18.29	14.21	21.14	15.10	9.69	16.57
Back	21.10	17.94	8.87	30.56	∞	17.45	12.67	11.43	16.83	14.07	19.31	13.65	8.86	15.12
Lililth	19.92	13.16	12.79	19.39	17.58	∞	13.99	10.37	15.86	10.98	16.86	23.03	13.29	26.92
Oliver	12.87	17.07	10.19	15.51	14.60	15.61	∞	19.50	22.67	16.83	19.93	15.65	11.20	14.50
David	11.43	18.20	8.42	13.92	13.49	12.83	20.29	∞	19.17	21.60	17.53	12.38	9.09	11.86
Bleak	14.91	21.86	9.79	19.30	18.05	17.27	21.95	18.12	∞	19.17	30.17	15.67	10.43	15.34
Tale	12.66	24.57	7.84	15.85	15.69	13.21	16.61	20.78	19.89	∞	19.45	11.91	8.23	11.93
Mutual	16.13	22.78	9.70	21.87	20.24	18.07	18.92	16.27	29.88	18.43	∞	15.64	10.19	15.76
Martin	16.00	11.43	14.86	15.46	14.23	23.46	13.93	9.79	14.29	9.78	14.62	∞	16.34	26.65
Bask	10.92	6.53	23.97	9.38	8.78	13.09	8.49	5.56	8.33	5.38	8.51	15.69	∞	15.21
Peter	18.10	11.21	14.52	16.19	14.96	26.66	12.56	9.04	13.59	9.38	14.24	26.20	15.13	∞

Table A5. Total signal–to–noise ratios

Γ_{d B}

, I–Channels.

Table A5. Total signal–to–noise ratios

Γ_{d B}

, I–Channels.

Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	∞	15.57	21.18	19.50	21.74	19.50	9.35	8.36	14.05	11.16	12.37	19.14	17.61	18.44
Hobbit	15.04	∞	11.25	19.77	19.33	13.61	9.23	8.52	13.97	11.74	11.60	12.29	10.07	16.07
Narnia	21.83	12.48	∞	15.46	16.18	17.10	8.65	7.72	12.20	9.93	11.23	18.24	25.28	15.11
Trilogy	20.07	20.66	15.33	∞	20.28	15.03	8.61	7.83	12.86	10.53	11.05	14.25	14.16	15.95
Back	20.96	18.83	14.72	19.35	∞	19.45	10.31	9.26	16.69	12.90	13.81	17.18	12.61	23.09
Lililth	18.47	12.40	15.76	13.22	18.74	∞	11.43	10.00	17.75	13.45	16.06	27.65	12.92	23.22
Oliver	5.72	5.21	4.61	4.42	7.06	8.72	∞	22.73	12.64	16.56	16.36	8.04	3.42	9.25
David	4.18	4.22	3.04	3.25	5.57	6.66	22.01	∞	10.38	14.45	12.63	5.99	1.96	7.38
Bleak	12.10	11.84	9.57	10.56	15.30	16.42	14.53	12.69	∞	20.10	21.84	14.23	7.91	20.13
Tale	8.26	9.01	6.36	7.46	10.66	11.20	17.84	16.02	19.15	∞	19.40	9.88	5.04	13.18
Mutual	9.97	8.68	8.40	8.02	11.71	14.57	17.59	14.48	21.08	20.07	∞	13.28	6.83	15.34
Martin	18.04	11.32	17.10	12.46	16.71	27.92	10.97	9.59	15.87	12.48	15.04	∞	13.93	19.38
Bask	18.77	12.04	25.74	15.14	14.57	14.71	7.92	7.11	10.98	9.06	10.12	15.52	∞	13.36
Peter	17.31	14.69	13.28	14.34	22.40	22.88	11.85	10.47	20.95	14.94	16.77	18.77	11.10	∞

Table A6. Total signal–to–noise ratios

Γ_{d B}

, WI–Channels.

Table A6. Total signal–to–noise ratios

Γ_{d B}

, WI–Channels.

Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	∞	16.96	8.69	19.72	21.94	20.11	15.14	12.42	28.75	14.96	18.33	29.47	13.83	15.46
Hobbit	15.61	∞	7.80	22.03	13.72	11.77	8.65	7.24	14.25	9.46	10.34	16.38	16.86	10.64
Narnia	7.94	9.59	∞	7.96	6.03	5.48	5.46	3.05	6.96	3.80	5.44	8.92	13.77	10.57
Trilogy	18.74	22.69	6.92	∞	18.24	15.14	10.32	9.40	17.94	12.40	12.81	18.24	13.92	10.84
Back	21.96	15.48	6.80	19.30	∞	26.10	14.37	14.32	26.03	19.46	19.22	19.02	11.69	12.07
Lililth	20.86	13.90	7.07	16.59	26.52	∞	17.01	17.17	24.86	22.59	24.34	18.32	11.15	12.89
Oliver	16.54	11.40	8.63	12.64	15.98	18.25	∞	18.55	17.28	16.43	23.12	15.86	10.46	16.18
David	14.43	10.55	6.50	12.03	15.89	18.35	18.72	∞	15.66	20.68	20.29	13.45	9.04	11.74
Bleak	29.00	15.86	7.97	18.98	26.27	24.36	15.99	13.95	∞	17.22	20.71	23.33	12.70	14.34
Tale	16.13	12.16	5.82	14.41	20.40	23.01	15.15	19.82	18.16	∞	19.83	14.60	9.60	10.71
Mutual	19.40	12.72	7.83	14.60	20.15	24.90	22.43	19.37	21.49	20.26	∞	17.75	10.94	14.62
Martin	29.30	17.61	9.50	19.33	18.82	17.40	14.28	11.19	22.92	13.25	16.43	∞	14.97	16.69
Bask	11.77	16.84	12.10	13.11	9.38	8.32	7.06	4.92	10.38	6.29	7.77	13.14	∞	11.52
Peter	16.67	13.01	12.48	13.17	13.36	13.42	14.94	10.26	15.40	10.80	14.27	17.92	13.59	∞

Table A7. Total signal–to–noise ratios

Γ_{d B}

, C–Channels.

Table A7. Total signal–to–noise ratios

Γ_{d B}

, C–Channels.

Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
Lord	∞	29.12	23.37	27.97	26.10	19.51	26.91	32.93	22.42	26.31	23.84	21.90	26.70	31.43
Hobbit	28.87	∞	20.03	26.66	22.08	17.21	26.33	24.95	20.20	27.13	21.51	20.64	22.77	25.73
Narnia	23.14	20.07	∞	24.11	21.11	28.25	23.63	26.63	30.01	22.43	29.10	25.22	31.08	26.48
Trilogy	27.61	26.30	23.69	∞	20.81	19.94	44.44	27.92	25.21	36.70	27.87	26.30	28.81	32.34
Back	26.52	22.80	21.89	21.57	∞	19.06	21.03	25.94	19.85	20.63	20.44	18.83	22.56	23.80
Lililth	19.17	17.15	28.14	20.28	18.09	∞	20.09	21.25	26.43	19.28	24.45	23.08	23.79	21.31
Oliver	26.50	25.91	23.13	44.38	20.22	19.65	∞	26.67	24.97	39.76	27.56	26.57	27.81	30.39
David	32.88	25.17	26.81	28.28	25.48	21.54	27.08	∞	24.77	25.80	26.30	23.38	31.25	36.01
Bleak	21.76	19.71	29.73	25.11	18.84	26.05	24.98	24.22	∞	23.63	36.70	31.88	29.79	25.53
Tale	25.88	26.71	21.87	36.57	19.78	18.78	39.69	25.31	23.56	∞	25.70	25.32	25.80	28.24
Mutual	23.24	21.04	28.76	27.79	19.51	24.05	27.59	25.83	36.72	25.79	∞	32.93	32.78	27.93
Martin	21.11	19.88	24.71	25.90	17.72	22.43	26.23	22.73	31.63	25.03	32.73	∞	26.77	24.53
Bask	26.34	22.64	30.92	29.07	21.84	23.73	28.13	30.99	30.08	26.19	32.99	27.17	∞	33.27
Peter	31.19	25.68	26.39	32.56	23.22	21.33	30.67	35.87	25.93	28.59	28.28	25.08	33.36	∞

References

Carpenter, H., The Inklings: C. S. Lewis, J.R.R. Tolkien, Charles Williams, and Their Friends. Houghton Mifflin, 1979.
Glyer, D. P., The Company They Keep. C. S. Lewis and J. R. R. Tolkien as Writers in Community. Kent OH: Kent State University Press, 2007.
Duriez, C., Porter, D., The Inklings Handbook: A Comprehensive Guide to the Lives, Thought, and Writings of C.S. Lewis, J.R.R. Tolkien, Charles Williams, Owen Barfield, and Their Friends. Chalice Press, 2001.
Isley, W.L., C. S. Lewis on Friendship, Inklings Forever, 6, 2008. Colloquium Proceedings 1997–2016: Vol. 6, Article 9. Available at: https://pillars.taylor.edu/inklings_forever/vol6/iss1/9.
Sammons, M. C., War of the Fantasy Worlds: C.S. Lewis and J.R.R. Tolkien on Art and Imagination. Praeger, 2010.
Duriez, Colin. The Oxford Inklings. Lewis, Tolkien, and Their Circle. Oxford: Lion Books, 2015.
Hooper, Walter. The Inklings, in Roger White, Judith Wolfe, and Brendan N. Wolfe, eds., C. S. Lewis and His Circle. Essays and Memoirs from the Oxford C. S. Lewis Society. New York/Oxford: Oxford University Press, 2015, 197–213.
Gokulapriya T., J.R.R. Tolkien’s Literary Works: A Review, International Review of Literary Studies, 2022, 4, 31–39.
Matricciani, E. Deep Language Statistics of Italian throughout Seven Centuries of Literature and Empirical Connections with Miller’s 7 ∓ 2 Law and Short–Term Memory. Open Journal of Statistics 2019, 9, 373–406. [Google Scholar] [CrossRef]
Matricciani, E. , A Statistical Theory of Language Translation Based on Communication Theory. Open Journal of Statistics 2020, 10, 936–997. [Google Scholar] [CrossRef]
Matricciani, E. The Theory of Linguistic Channels in Alphabetical texts, 2024, Cambridge Scholars Publishing, Newcastle upon Tyne, UK.
Matricciani, E., Multiple Communication Channels in Literary Texts. Open Journal of Statistics, 2022, 12, 486–520. [CrossRef]
Matricciani, E. Linguistic Communication Channels Reveal Connections between Texts: The New Testament and Greek Literature. Information 2023, 14, 405. [Google Scholar] [CrossRef]
Matricciani, E., Short–Term Memory Capacity across Time and Language Estimated from Ancient and Modern Literary Texts. Study–Case: New Testament Translations. Open Journal of Statistics, 2023, 13, 379–403. [CrossRef]
Matricciani, E. Capacity of Linguistic Communication Channels in Literary Texts: Application to Charles Dickens’ Novels. Information 2023, 14, 68. [Google Scholar] [CrossRef]
Matricciani, E. Is Short–Term Memory Made of Two Processing Units? Clues from Italian and English Literatures down Several Centuries. Information 2024, 15, 6. [Google Scholar] [CrossRef]
Matricciani, E. A Mathematical Structure Underlying Sentences and Its Connection with Short–Term Memory. AppliedMath 2024, 4, 120–142. [Google Scholar] [CrossRef]
Miller, G.A. The Magical Number Seven, Plus or Minus Two. Some Limits on Our Capacity for Processing Information, 1955, Psychological Review, 343−352.
Matricciani, E. Readability Indices Do Not Say It All on a Text Readability. Analytics 2023, 2, 296–314. [Google Scholar] [CrossRef]
Matricciani, E. Linguistic Mathematical Relationships Saved or Lost in Translating Texts: Extension of the Statistical Theory of Translation and Its Application to the New Testament. Information 2022, 13, 20. [Google Scholar] [CrossRef]
Papoulis Papoulis, A. Probability & Statistics; Prentice Hall: Hoboken, NJ, USA, 1990. [Google Scholar]
Lindgren, B.W. Statistical Theory, 2nd ed.; MacMillan Company: New York, NY, USA, 1968. [Google Scholar]

Figure 1. Series of words versus the normalized chapter number. Blue line: The Lord of the Rings (Lord); red line: The Chronicles of Narnia (Narnia). Green line: The Space Trilogy (Trilogy).

Figure 2. Normalized coordinates

X

and

Y

of the ending point of vector (5) such that Lord, blue square, is at (0,0) and Silmarillion, blue triangle pointing left, is (1,1). Narnia: red square); Trilogy: red circle; Hobbit: blue triangle pointing right; Screwtape: red triangle pointing upward; Back: cyan triangle pointing left; Lilith: cyan triangle pointing downward; Back: cyan triangle pointing left; Phantastes: cyan triangle pointing right; Princess: cyan triangle pointing upward; Oliver: blue circle; David: green circle; Tale: cyan circle; Bleak: magenta circle; Mutual: black circle; Pride: magenta triangle pointing right; Vanity: magenta triangle pointing left; Moby: magenta triangle pointing downward; Mill: magenta triangle pointing upward; Alice: yellow triangle pointing right; Jungle: yellow triangle pointing downward; War: yellow triangle pointing right; Oz: green triangle pointing left; ; Bask: green triangle pointing right; ; Peter: green triangle pointing upward; Martin: green square; ; Finn: black triangle pointing right.

Figure 2. Normalized coordinates

X

and

Y

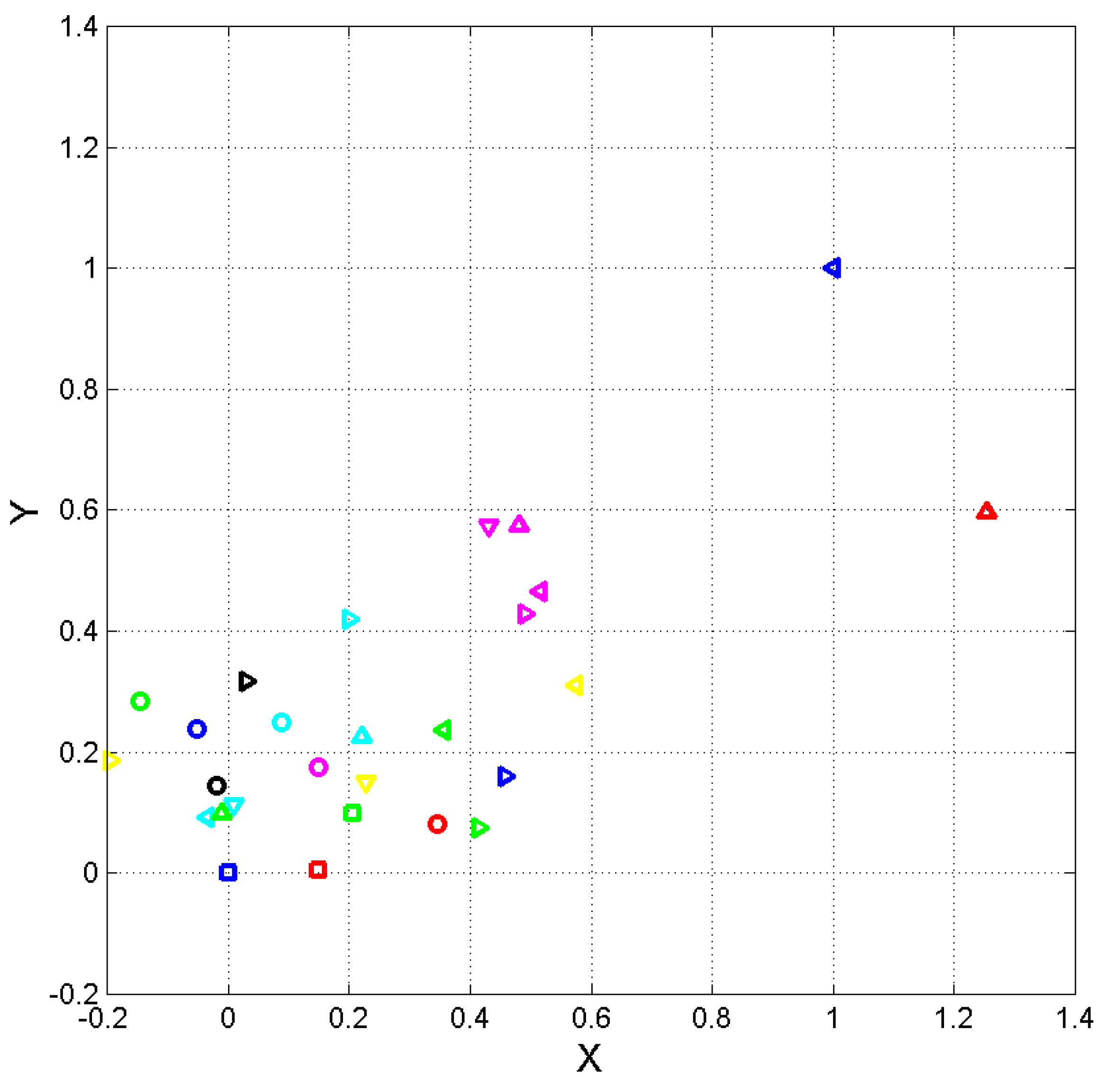
Figure 3. Pythagorean distance

d

between couples of texts considering Lord (the distances referring to this case are labelled with blue circles), Narnia (red squares) and Trilogy (red circles). Key: Lord 1, Hobbit 2, Narnia 3, Trilogy 4, Back 5, Lilith 6, Oliver 7, David 8, Bleak 9, Tale 10, Mutual 11, Martin 12, Bask 13, Peter 14.

Figure 3. Pythagorean distance

d

Figure 4. Normalized coordinates

X

and

Y

of the ending point of vector (5) and 1–sigma circles, such that Lord, blue square, is at (0,0) and Silmarillion, blue triangle pointing left, is (1,1). Lord: blue square (blue 1–sigma circle); Narnia: red square (red 1–sigma circle); Trilogy: red circle (dashed red 1–sigma circle); Back: cyan triangle pointing left (cyan 1–sigma circle); Peter: green triangle pointing upward (green 1–sigma circle).

Figure 4. Normalized coordinates

X

and

Y

Figure 5. Error probability

p_{e}

versus Text 2. Lord (the probabilities referring to this case are labelled with blue circles), Narnia (red squares) and Trilogy (red circles). Text key: Lord 1, Hobbit 2, Narnia 3, Trilogy 4, Back 5, Lilith 6, Oliver 7, David 8, Bleak 9, Tale 10, Mutual 11, Martin 12, Bask 13, Peter 14.

Figure 5. Error probability

p_{e}

Figure 6. (a) Scatterplot of

n_{S}

versus

n_{W}

in Lord (blue) and Narnia (red); (b)

n_{I}

versus

n_{S}

in Lord (blue) and Narnia (red).

Figure 6. (a) Scatterplot of

n_{S}

versus

n_{W}

in Lord (blue) and Narnia (red); (b)

n_{I}

versus

n_{S}

in Lord (blue) and Narnia (red).

Figure 7. (a) Scatterplot of

n_{S}

versus

n_{W}

in Lord (blue) and Trilogy (red); (b)

n_{I}

versus

n_{S}

in in Lord (blue) and Trilogy (red).

Figure 7. (a) Scatterplot of

n_{S}

versus

n_{W}

in Lord (blue) and Trilogy (red); (b)

n_{I}

versus

n_{S}

in in Lord (blue) and Trilogy (red).

Figure 8. Scatterplot of the number of sentences

n_{S}

versus the number of words

n_{W}

: (a) Lord (blue) and Back (cyan); (b) Lord (blue) and Lilith (cyan).

Figure 8. Scatterplot of the number of sentences

n_{S}

versus the number of words

n_{W}

: (a) Lord (blue) and Back (cyan); (b) Lord (blue) and Lilith (cyan).

Table 1. Novels written by Tolkien, Lewis and MacDonald, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentences (

S

). Titles, footnotes and other extraneous material present in the digital texts have been deleted.

Table 1. Novels written by Tolkien, Lewis and MacDonald, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentences (

S

). Titles, footnotes and other extraneous material present in the digital texts have been deleted.

John R.R. Tolkien (1892–1973)	Chapters ( $M$ )	Characters ( $C)$	Words $(W)$	Sentences ( $S$ )
The Hobbit (1937)	19	394,154	95,914	5890
The Lord of the Rings (1954–1955)	62	1,906,531	472,173	34,601
The Silmarillion (posthumous, 1977)	24	429,639	101,627	3346
Clive S. Lewis (1898–1963)
The Screwtape Letters (1942)	31	135,204	31,040	1330
The Space Trilogy (1938–1945)	123	1,243,141	295,240	20,124
The Chronicles of Narnia (1950–1956)	110	1,318,482	322,544	23,515
George MacDonald (1824–1905)
Phantastes: A Fairie Romance for Men and Women (1858)	25	283,676	67,551	3274
At the Back of the North Wind (1871)	38	349,041	90,697	5017
The Princess and the Goblin (1872)	32	208,325	51,090	3205
Lilith: A Romance (1895)	47	386,522	94,127	6271

Table 2. Novels by Charles Dickens, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentencens (

S

Table 2. Novels by Charles Dickens, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentencens (

S

Novel (year of publication)	$Chapters (M$ )	$Characters (C)$	$Words (W)$	$Sentences (S$ )
The Adventures of Oliver Twist (1837–1839)	53	679,008	160,604	9121
David Copperfield (1849–1850)	64	1,469,251	363,284	19610
Bleak House (1852–1853)	64	1,480,523	350,020	20967
A Tale of Two Cities (1859)	45	607,424	142,762	8098
Our Mutual Friend (1864–1865)	67	1,394,753	330,593	17409

Table 3. Novels by authors of the English Literature, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentencens (

S

Table 3. Novels by authors of the English Literature, with year of publication. Number of chapters (

M

, i.e., the number of samples considered in calculating the regression lines reported below), total number of characters contained in the words (

C)

, total number of words

W

and sentencens (

S

Novel (Author, Year)	$Chapters (M$ )	$Characters (C)$	$Words (W)$	$Sentences (S$ )
Pride and Prejudice (J. Austen, 1813)	61	537,005	121,934	6,013
Vanity Fair (W. Thackeray, 1847– 1848)	66	1,285,688	277,716	13,007
Moby Dick (H. Melville, 1851)	132	92,2351	203,983	9,582
The Mill On The Floss (G. Eliot, 1860)	57	888,867	207,358	9,018
Alice’s Adventures in Wonderland (L. Carroll, 1865)	12	107,452	27,170	1,629
Adventures of Huckleberry Finn (M. Twain, 1884)	42	427473	110,997	5887
The Jungle Book (R. Kipling, 1894)	9	209,935	51,090	3,214
The War of the Worlds (H.G. Wells, 1897)	27	265,499	60556	3,306
The Wonderful Wizard of Oz (L.F. Baum, 1900)	22	156,973	39,074	2,219
The Hound of The Baskervilles (A.C. Doyle, 1901–1902)	15	245,327	59,132	4,080
Peter Pan (J.M. Barrie, 1902)	17	194105	47,097	31,77
Martin Eden (J. London, 1908–1909)	45	601,672	139,281	9,173

Table 4. Coefficient of dispersion in the series of words, sentences and interpunctions in the indicated novels by Tolkien, Lewis and MacDonald.

Novel	Words	Sentences	Interpunctions	Average
The Hobbit	0.49	0.48	0.50	0.49
The Lord of the Rings	0.34	0.36	0.34	0.35
The Silmarillion	0.73	0.86	0.80	0.80
The Screwtape Letters	0.07	0.17	0.14	0.13
The Space Trilogy	0.60	0.61	0.58	0.59
The Chronicles ofNarnia	0.16	0.20	0.20	0.19
At the Back of the North Wind	0.54	0.61	0.56	0.57
Phantastes: A Fairie Romance for Men and Women	0.66	0.73	0.63	0.67
Lilith: A Romance	0.43	0.53	0.46	0.47
The Princess and the Goblin	0.53	0.75	0.62	0.64

Table 5. Coefficient of dispersion in the series of words, sentences and interpunctions in the indicated novels.

Novel	Words	Sentences	Interpunctions	Average
The Adventures of Oliver Twist	0.31	0.33	0.32	0.32
David Copperfield	0.37	0.38	0.37	0.37
Bleak House	0.28	0.31	0.30	0.30
A Tale of Two Cities	0.52	0.57	0.52	0.54
Our Mutual Friend	0.26	0.29	0.27	0.27
Martin Eden	0.29	0.33	0.29	0.31
The Hound of The Baskervilles	0.26	0.29	0.25	0.27
Peter Pan	0.29	0.41	0.33	0.34

Table 6. John R.R. Tolkien. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Table 6. John R.R. Tolkien. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Novel	$C_{p}$	$P_{F}$	$I_{P}$	$M_{F}$
The Hobbit	4.11 (0.06)	16.54 (2.03)	7.93 (0.98)	2.09 (0.12)
The Lord of the Rings	4.04 (0.08 )	13.92 (1.98)	6.68 (0.51)	2.08 (0.20)
The Silmarillion	4.23 (0.08)	31.21 (5.32)	8.58 (0.58)	3.62 (0.42)

Table 7. Clive S. Lewis. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Table 7. Clive S. Lewis. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Novel	$C_{p}$	$P_{F}$	$I_{P}$	$M_{F}$
The Screwtape Letters	4.36 (0.12)	23.95 (3.82)	9.72 (1.00)	2.47 (032)
The Space Trilogy	4.21 (0.16)	15.25 (3.05)	7.47 (0.98)	2.03 (0.22)
The Chronicles ofNarnia	4.09 (0.09)	13.97 (1.94)	7.10 (0.89)	1.97 (0.15)

Table 8. George MacDonald. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Table 8. George MacDonald. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

At the Back of the North Wind	3.85 (0.11)	15.52 (3.34)	6.76 (0.77)	2.29 (0.35)
Phantastes: A Fairie Romance for Men and Women	4.20 (0.12)	21.15 (3.58)	6.43 (0.49)	3.28 (0.45)
Lilith: A Romance	4.11 (0.25)	15.87 (3.89)	6.43 (0.57)	2.45 (0.42)
The Princess and the Goblin	4.08 (0.14)	17.81 (4.05)	7.09 (1.22)	2.46 (0.53)

Table 9. Other authors. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Table 9. Other authors. Mean value and standard deviation (in parentheses) of

{< C}_{P} >

{< P}_{F} >

{< I}_{P} >

{< M}_{F} >

in the indicated novels. Mean and standard deviation have been calculated by weighting each chapter with its number of words.

Novel	${< C}_{P} >$	$< P_{F} >$	${< I}_{P} >$	$< M_{F} >$
The Adventures of Oliver Twist	4.23 (0.09)	18.04 (3.13)	5.70 (0.52)	3.16 (0.34)
David Copperfield	4.04 (0.12)	18.83 (2.50)	5.61 (0.30)	3.35 (0.33)
Bleak House	4.23 (0.14)	16.95 (2.21)	6.59 (0.49)	2.57 (0.21)
A Tale of Two Cities	4.26 (0.12)	18.27 (4.24)	6.19 (0.46)	2.93 (0.46)
Our Mutual Friend	4.22 (0.12)	16.46 (2.01)	6.03 (0.37)	2.73 (0.27)
Pride and Prejudice	4.40 (0.14)	21.31 (5.02)	7.16 (0.46)	2.95 (0.46)
Vanity Fair	4.63 (0.08)	21.95 (3.67)	6.73 (0.63)	3.25 (0.39)
Moby Dick	4.52 (0.16)	23.82 (7.44)	6.45 (0.99)	3.64 (0.80)
The Mill On The Floss	4.29 (0.13)	23.84 (4.99)	7.09 (0.69)	3.35 (0.48)
Alice’s Adventures in Wonderland	3.96 (0.08)	17.19 (3.20)	5.79 (0.55)	2.95 (0.28)
Adventures of Huckleberry Finn	3.85 (0.10)	19.39 (3.12)	6.63 (0.67)	2.94 (0.48)
The Jungle Book	4.11 (0.09)	16.46 (3.09)	7.14 (0.53)	2.29 (0.30)
The War of the Worlds	4.38 (0.18)	19.22 (4.13)	7.67 (0.92)	2.48 (0.31)
The Wonderful Wizard of Oz	4.02 (0.10)	17.90 (2.23)	7.63 (0.64)	2.34 (0.15)
The Hound of The Baskervilles	4.15 (0.12)	15.07 (3.16)	7.83 (0.94)	1.91 (0.22)
Peter Pan	4.12 (0.09)	15.65 (3.98)	6.35 (0.92)	2.44 (0.37)
Martin Eden	4.32 (0.13)	15.61 (2.71)	6.76 (0.64)	2.30 (0.26)

Table 10. Multiplicity factor

α

, universal readability index

{< G}_{U} >

and number of school years

Y

in the indicated novels by Tolkien, Lewis, MacDonald.

Table 10. Multiplicity factor

α

, universal readability index

{< G}_{U} >

and number of school years

Y

in the indicated novels by Tolkien, Lewis, MacDonald.

Novel	$α$	${< G}_{U} >$	$Y$
The Hobbit	39.4	52.4	9.9
The Lord of the Rings	368.1	64.2	7.4
The Silmarillion	0.2	38.7	>13
The Screwtape Letters	1.4	33.5	>13
The Space Trilogy	186.3	56.2	9.0
The Chronicles ofNarnia	297.7	61.1	7.9
At the Back of the North Wind	26.3	63.9	7.5
Phantastes: A Fairie Romance for Men and Women	24.3	56.6	8.9
Lilith: A Romance	1.4	63.0	7.5
The Princess and the Goblin	8.5	58.2	8.4

Table 11. Multiplicity factor

α

, universal readability index

{< G}_{U} >

and number of school years in the indicated novels of the English Literature (see []).

Table 11. Multiplicity factor

α

, universal readability index

{< G}_{U} >

and number of school years in the indicated novels of the English Literature (see []).

Novel	$α$	$< G_{U} >$	$Y$
The Adventures of Oliver Twist	9.46	63.19	7.5
David Copperfield	12.63	64.78	7.2
Bleak House	56.98	58.74	8.3
A Tale of Two Cities	11.89	59.91	8.0
Our Mutual Friend	43.41	62.68	7.6
Pride and Prejudice	5.20	50.33	10.4
Vanity Fair	5.26	49.74	10.5
Moby Dick	1.56	52.63	9.9
The Mill On The Floss	2.17	50.22	10.5
Alice’s Adventures in Wonderland	2.90	59.27	8.1
Adventures of Huckleberry Finn	7.05	60.42	8.0
The Jungle Book	14.10	57.59	8.6
The War of the Worlds	6.72	49.05	10.8
The Wonderful Wizard of Oz	7.02	53.83	9.5
The Hound of The Baskervilles	43.87	54.87	9.2
Peter Pan	13.07	63.60	7.5
Martin Eden	46.33	58.53	8.2

Table 12. Conditional probability between the indicated novels.

P (A_{2} / A_{1})

is reported in the columns, therefore

A_{1}

refers to the text indicated in the upper row;

P (A_{1} / A_{2})

is reported in the rows, therefore

A_{2}

refers to the text indicated the left column. For example, assuming Lord as text 1 (column 1 of Table xx) and Narnia as text 2 (row 3), we find

P (A_{2} / A_{1}) = 0.974

. Viceversa, if we assume Narnia as text 1 (column 3) and Lord as text 2 (row 1), we find

P (A_{2} / A_{1}) = 0.356

Table 12. Conditional probability between the indicated novels.

P (A_{2} / A_{1})

is reported in the columns, therefore

A_{1}

refers to the text indicated in the upper row;

P (A_{1} / A_{2})

is reported in the rows, therefore

A_{2}

refers to the text indicated the left column. For example, assuming Lord as text 1 (column 1 of Table xx) and Narnia as text 2 (row 3), we find

P (A_{2} / A_{1}) = 0.974

. Viceversa, if we assume Narnia as text 1 (column 3) and Lord as text 2 (row 1), we find

P (A_{2} / A_{1}) = 0.356

	Novel	Lord	Hobbit	Narnia	Trilogy	Back	Lilith	Oliver	David	Bleak	Tale	Mutual	Martin	Bask	Peter
1	Lord	1	0.031	0.356	0.142	0.423	0.511	0.277	0.041	0.307	0.231	0.619	0.301	0.078	0.299
2	Hobbit	0.099	1	0.421	0.731	0.171	0.225	0.074	0	0.592	0.376	0.060	0.665	0.833	0.227
3	Narnia	0.974	0.354	1	0.550	0.647	0.781	0.489	0.166	0.927	0.625	0.886	0.949	0.462	0.602
4	Trilogy	0.498	0.786	0.704	1	0.400	0.510	0.297	0	0.921	0.608	0.473	0.978	0.908	0.421
5	Back	1	0.124	0.559	0.270	1	0.997	0.866	0.796	0.763	0.692	1	0.566	0.179	0.707
6	Lililth	0.891	0.121	0.498	0.254	0.735	1	0.741	0.559	0.762	0.661	1	0.546	0.169	0.521
7	Oliver	0.352	0.029	0.227	0.108	0.466	0.540	1	0.913	0.444	0.579	0.917	0.239	0.043	0.378
8	David	0.024	0	0.035	0	0.195	0.186	0.416	1	0.029	0.173	0.262	0.001	0	0.168
9	Bleak	0.307	0.182	0.339	0.264	0.323	0.437	0.350	0.051	1	0.598	0.526	0.558	0.208	0.296
10	Tale	0.330	0.165	0.327	0.248	0.417	0.541	0.650	0.427	0.852	1	0.774	0.484	0.176	0.385
11	Mutual	0.390	0.012	0.204	0.085	0.266	0.361	0.454	0.285	0.331	0.342	1	0.205	0.031	0.188
12	Martin	0.490	0.333	0.565	0.455	0.389	0.509	0.307	0.004	0.906	0.551	0.529	1	0.396	0.384
13	Bask	0.250	0.826	0.545	0.838	0.244	0.312	0.110	0	0.669	0.397	0.160	0.785	1	0.289
14	Peter	1	0.234	0.736	0.403	1	1	0.996	0.968	0.988	0.904	1	0.790	0.300	1

Table 13. Total and the partial signal–to–noise ratios

Γ_{d B}

Γ_{m, d B}

Γ_{r, d B}

in the four channels by considering Lord as reference (input) text.

Table 13. Total and the partial signal–to–noise ratios

Γ_{d B}

Γ_{m, d B}

Γ_{r, d B}

in the four channels by considering Lord as reference (input) text.

	S–Channel			I–Channel			WI–Channel			C–Channel
Novel	$Γ_{d B}$	$Γ_{m, d B}$	$Γ_{r, d B}$	$Γ_{d B}$	$Γ_{m, d B}$	$Γ_{r, d B}$	$Γ_{d B}$	$Γ_{m, d B}$	$Γ_{r, d B}$	$Γ_{d B}$	$Γ_{m, d B}$	$Γ_{r, d B}$
Hobbit	14.60	15.48	21.94	15.04	30.08	15.18	15.61	15.77	30.19	28.87	35.90	29.83
Narnia	10.12	51.26	10.12	21.83	27.57	23.18	7.94	27.08	7.99	23.14	37.47	23.30
Trilogy	21.27	21.86	30.24	20.07	29.18	20.64	18.74	19.21	28.63	27.61	27.85	40.30
Back	21.10	23.30	25.11	20.96	24.12	23.82	21.96	57.42	21.96	26.52	26.68	41.05
Lililth	19.92	22.47	23.44	18.47	19.15	26.87	20.86	26.28	22.33	19.17	33.98	19.31
Oliver	12.87	12.93	31.51	5.72	5.74	29.30	16.54	16.56	40.83	26.50	26.63	41.73
David	11.43	11.52	28.37	4.18	4.19	30.77	14.43	16.10	19.37	32.88	51.53	32.94
Bleak	14.91	14.93	38.01	12.10	12.29	25.80	29.00	36.33	29.88	21.76	26.69	23.45
Tale	12.66	13.31	21.25	8.26	8.56	19.99	16.13	22.76	17.20	25.88	25.89	55.01
Mutual	16.13	16.22	33.05	9.97	10.00	31.20	19.40	20.33	26.55	23.24	26.87	25.70
Martin	16.00	20.01	18.20	18.04	20.74	21.38	29.30	40.14	29.68	21.11	23.16	25.34
Bask	10.92	23.84	11.14	18.77	20.81	23.03	11.77	15.70	14.02	26.34	32.54	27.53
Peter	18.10	24.41	19.25	17.31	17.53	30.45	16.67	22.23	18.09	31.19	34.62	33.81

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multidimensional Data Analysis of Deep–Language in J.R.R. Tolkien and C.S. Lewis Reveals Tight Mathematical Connections

Abstract

1. Introduction

2. Database of Literary Texts (Novels)

3. Conscious Design of Texts: Words, Sentences and Interpunctions Versus Chapters

4. Surface Deep–Language Variables

5. Extended Short–Term Memory of Writers/Readers and Universal Readability Index

5.1. Extended Short–Term Memory and Multiplicity Factor

5.2. Universal Readability Index

5.3. Discussion

6. Geometrical Representation of Texts

6.1. Vector Representation of Texts

6.2. Error Probability

7. Linear Relationships in Literary Texts

8. Theory of Linguistic Channels

9. Linguistic Channels

10. Summary and Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Universal Readability Mean Index Lower Bound

Appendix B. Pythagorean Distance d between Couples of Texts

Appendix C. Common Area between Circles

Appendix D. Conditional Error Probability

Appendix E. Slope and Correlation Coefficient of the Regression Lines

Appendix F. Total Signal–to–Noise Ratios Γ d B , in the Four Linguistic Channels

References

MDPI Initiatives

Important Links

Subscribe

Appendix B. Pythagorean Distance $d$ between Couples of Texts

Appendix F. Total Signal–to–Noise Ratios $Γ_{d B}$ , in the Four Linguistic Channels