Prerpints.org logo
Preprint
Article

Cavity-Induced Optical Nonreciprocity Based on Degenerate Two-Level Atoms

Altmetrics

Downloads

129

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 June 2024

Posted:

18 June 2024

You are already at the latest version

Alerts
Abstract
We propose and experimentally realize a scheme of the optical nonreciprocity (ONR) using degenerate two-level atoms embedded in an optical ring cavity. For the degenerate transition Fg=4→Fe=3, we first study the cavity-transmission property in different coupling field, and verify that within the strong-coupling regime, the single-dark-state peak formed by electromagnetically induced transparency (EIT) shows ONR. Qualitative theoretical analysis shows that the stable ground-state Zeeman coherence is necessary for intracavity EIT. However, due to the frequency degeneracy, the large Rabi frequency of counter-propagating coupling field can reduce the number of effective atoms and weaken the strong-coupling of the atom-cavity, which determines that ONR based on intracavity EIT occurs only at weaker probe intensity. Furthermore, the ONR transmission with high contrast, linewidth-narrowed and broadband is experimentally demonstrated.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Optical nonreciprocity (ONR) has attracted widespread interest due to its important applications in optical communications and optical information processing [1,2,3]. Traditionally, ONR has been achieved through the magneto-optical effect [4], which poses challenges in miniaturization and integration. Thus, the exploration of magnet-free ONR avenues has emerged in recent years. Significant advancements have been made using methods such as nonlinear optics [5,6,7], optomechanical interactions [8,9,10], chiral quantum optics [11,12,13], tunable photonic crystals [14,15], cold atomic Bragg lattices [16,17], and hot atoms [18,19,20,21,22].
One of the important methods to realize ONR is the utilization of the thermal motion as a useful resource. For instance, considering an ensemble of Λ-type three-level hot atoms, when the probe beam and coupling beam co-propagate in the atoms, the electromagnetically-induced-transparency (EIT) effect forms (the two-photon resonance can be satisfied because of the Doppler-free) [23]. However, if the probe beam counter-propagates with the coupling beam, strong absorption of the hot atoms prohibits the transmission of the probe beam due to the Doppler shift. This chiral response of atoms dependent on unidirectional coupling field breaks the system's time-reversal symmetry and enables ONR transmission of the probe light [18]. Furthermore, when combining this ensemble with an optical cavity, the enhancement of atomic nonlinearity can boost ONR's efficiency and sensitivity [21,22], which has facilitated the development of quantum devices, such as optical isolator [24,25], optical switching and routing [26,27,28,29,30], and all-optical logic gates [31,32,33].
In this paper, we experimentally demonstrated a scheme for performing ONR with a degenerate two-level atom-cavity system. For the degenerate transition Fg↔Fe with the ground-state angular momentum Fg is larger than the excited-state angular momentum Fe, we firstly study the transmission of the probe beam in free space. It is found that the ONR based on free-space EIT is not perfect due to the frequency degeneracy. Embedding the thermal degenerate atoms in a ring cavity, however, the cavity transmission can achieve ONR at the lower probe intensity, which benefits from the strong coupling property of the atom-cavity system. Qualitatively, combing all Zeeman sublevels of the atoms and the strong-coupling characteristics of the atom-cavity, we explained the experimental results. Finally, by changing the parameters of the coupling field, the ONR with high contrast and wide frequency-tuning range were experimentally investigated.

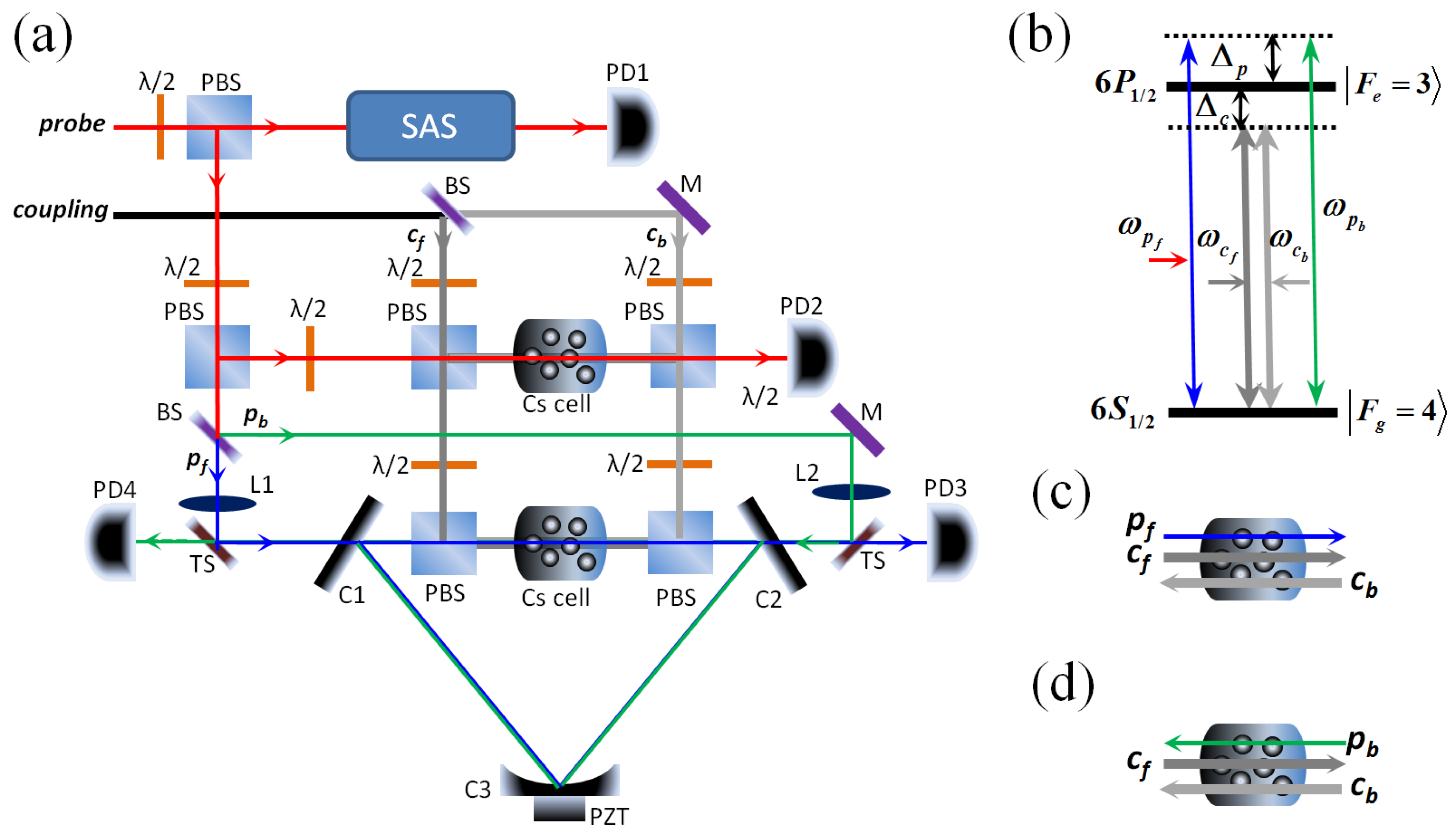
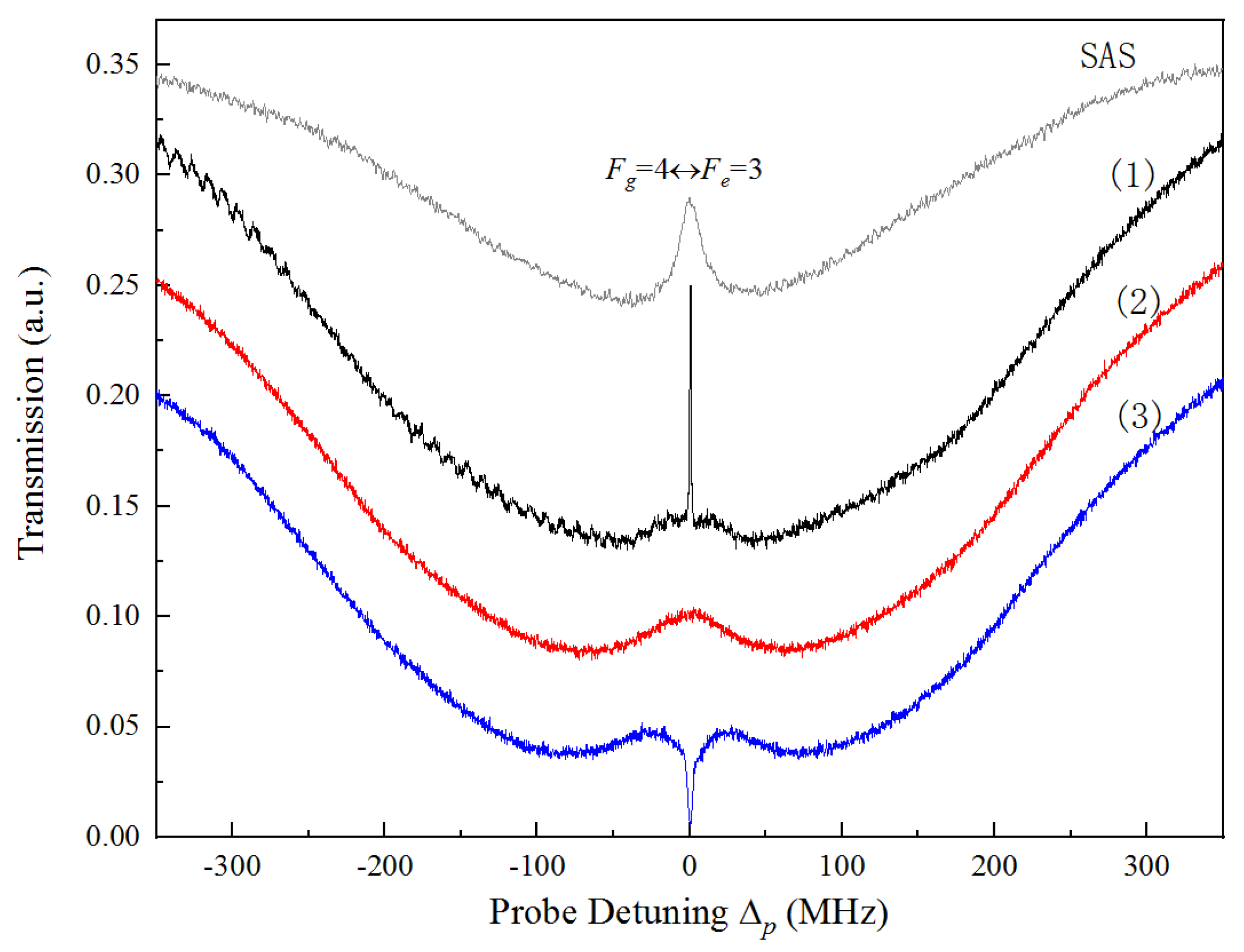
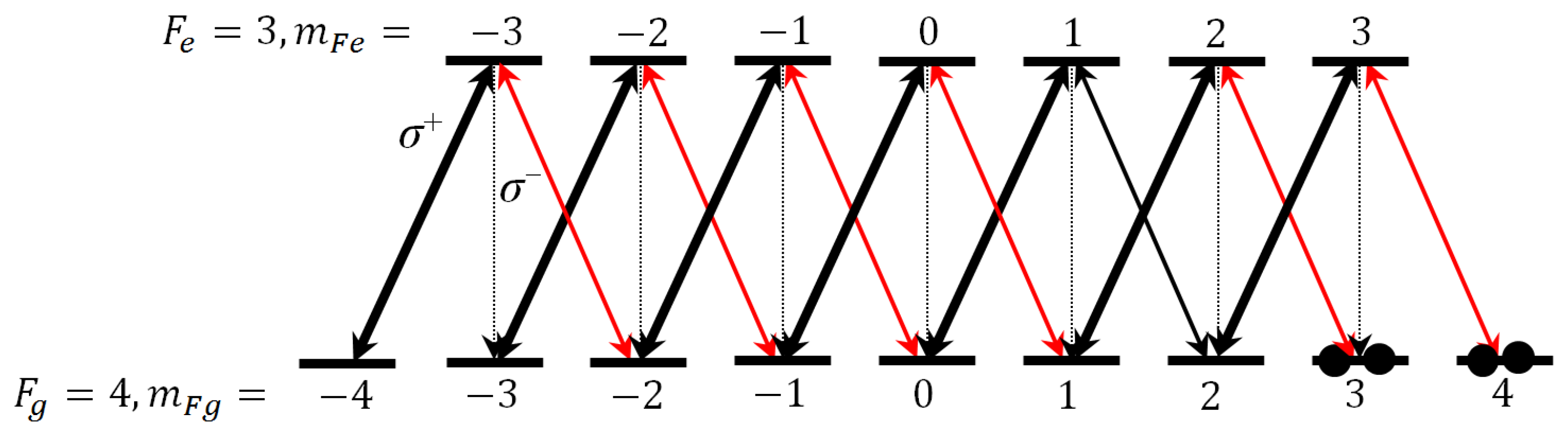
2. Experimental Arrangement and Results

The schematic diagram of our experimental setup is shown in Figure 1a. Two independent extended cavity diode lasers (ECDLs) with wavelength 894.5 nm are used as probe and coupling laser, respectively. In our experimental setup, we define the direction in which light travels from left to right as forward and the opposite direction as backward. The probe laser is divided into three parts by two combination of half-wave plate (λ/2) and polarization beam splitter (PBS): The first part is used for saturation absorption spectrum (SAS) and is detected by a photo detector (PD1); The second part is as the probe light of free-space EIT system and is detected by PD2; The third is also split into two parts (denoted by pf and pb) by a 50/50 beam-splitter (BS). A three-mirror ring cavity consists of two plane mirror C1 and C2 with the same transmissivity of 3%, and a plano-concave super mirror C3 with radius of curvature of 1000 mm and reflectivity of 99.99%, mounted on a piezoelectric transducer (PZT) for cavity frequency scanning and locking. The single cavity length L is about 530 mm. A 75-mm-long intracavity Cs cell with anti-reflection coated end windows is wrapped with µ-metal sheets for magnetic field shielding and wrapped in a heat tape for temperature-controlling. The weaker probe light pf (pb) with horizontal polarization reflected by transmissivity 90% beam-splitter (TS) is injected into C1 (C2) along the forward (backward) direction, and circulates in the atomic-cavity system as the cavity mode, then its output is detected by PD3 (PD4). The coupling laser is split into two parts (denoted by cf and cb) by a BS. The stronger coupling light cf (cb) with vertical polarization reflected by PBS passes through the Cs cell along the forward (backward) direction. Notably, the two counter-propagating coupling beams form a SW in the intracavity Cs cell and then are reflected out by two PBSs in void of circulation in the cavity. At the center of the cavity, the effective diameters of the probe and coupling lights are about 380 μm and 575 μm, respectively. The finesse of the ring cavity is degraded from 100 to 36 because of the linear loss of the inserted Cs cell and the two PBSs. The temperature of the Cs cell both in the free space and in the cavity is controlled at 40ºC.
The energy level diagrams of the atoms are shown in Figure 1b. Our experiment is performed in the D1 line of the 133Cs atoms. The probe and coupling lasers drive the same transition |62S1/2, Fg=4⟩↔|62P1/2, Fe=3⟩. The coupling laser is frequency-locked to the nearby of transition frequency ωge with detuning Δc(Δc=ωc-ωge), and the probe laser is frequency-scanned across ωge with detuning Δp(Δp=ωp-ωge). Figure 1c,d show the interaction process of atom-cavity system when only pf or only pb injects the intracavity Cs vapor, respectively. We define Δq=ωq-ωge as the detuning of the qth probe cavity mode from the atomic resonance frequency.
Figure 2 compares the transmission spectra of the probe light under the condition of different coupling field in free space, which is detected by PD2 in Figure 1a. The gray curve is the SAS of the probe laser, which is used to calibrate the transition level of the atom and judge the frequency detuning of the coupled laser. When only the co-propagating coupling field cf is injected the Cs cell, a narrow transparency peak with linewidth ～1.2 MHz is obtained because the two photon resonance can be satisfied (that is Doppler free, Δp =Δc), i.e. the so-called EIT effect [23], as shown black curve (1) in Figure 2. Predictably, when only the counter-propagating cb is injected, the EIT peak disappears due to the Doppler shift of the hot atom, as shown red curve (2) in Figure 2. However, a transparency with linewidth-broaden appears near the center of the two-photon resonance. This is because the frequency of the coupling light is the same as that of the probe light, and the stronger Rabi frequency of the coupling light occupies more the same ground state population of the atom. Thus the absorption of the atom to probe light is weakened. Notably, this is independent of the propagating direction of the coupling light. Therefore, there is still a weak probe light that can pass through the Cs cell, which leads to imperfect ONR. The standing-wave (SW) field cs forms when cf and cb are simultaneously injected, which causes the periodic modulation on the refractive index of the atom, accompanied by anomalous dispersion and strong absorption of the probe light [34]. So a strong absorption pit appears at the center of two photon resonance, as shown blue curve (3) in Figure 2. That is so-called electromagnetically induce absorption effect (EIA) [35]. Here the probe light is forbidden to pass through the Cs cell whether it propagates along the forward or backward direction.
Inspired by the generation of ONR of three-level atom-cavity systems [18,22], we place degenerate two-level atoms in a three-mirror ring cavity (see Figure 1). Figure 3 plots the cavity transmission spectra of probe light at Δq=Δc=0. In the case of forward pf [Figure 1c], when only forward cf is injected ( P c f = 20   mW ), apart from two vacuum Rabi splitting (VRS) peaks which are resulted from the strong-coupling of the atom-cavity [36], a narrowed single dark-state peak (intracavity EIT) is observed at the atomic resonance center (Δp=0), as shown black line (1) in Figure 3a. Comparing to the EIT of free space, the linewidth of the single dark-state peak is narrowed to two times (～0.6 MHz), as shown embedded in Figure 3a. When only backward cb is injected with P c b = 20   mW , a wide cavity mode without vacuum-Rabi-splitting appears at the atomic resonance center, as shown red line (2) in Figure 3a. When only the backward pb is injected [Figure 1d], the results are just the opposite, as shown lines (1) and (2) in Figure 3b. Under the action of SW coupling field ( P c s = 20   mW ), however, regardless of pf or pb, the cavity transmission spectrum is similar: the central single-dark-state peak disappears because of EIA, meanwhile, the symmetrical double-dark peaks appear on either side of the atomic resonance center, as shown blue lines (3) in Figure 3a,b. It is worth emphasizing that although for pf and pb, their double dark-state peaks exhibit optical reciprocity (OR) due to the symmetry of the system, the transmission efficiencies are much lower than that of the single dark-state peak because the frequency position of the double dark-state peaks is not resonant with the cavity mode ( Δ q = 0 ).
From Figure 3 we can see, when the probe light counter-propagates with the single coupling light, the cavity transmission show imperfect ONR (or OR) at the atom resonance center, which is different from that of the Λ-type three level atom-cavity system [18]. The reason is because in our experiment, the counter-propagating coupled light occupies part of the degenerate ground state atomic population, which reduces the absorption of intracavity atoms to the probe cavity mode and inhibits the strong-coupling efficiency of the atom-cavity system. When decreasing the input power of the probe light, the strong-coupling effect of the atom-cavity can be shown. Figure 4 shows the cavity transmission at P p f = P p b = 0.4   mW . When only co-propagating pf(b) and cf(b) are injected, a linewidth-narrowed intracavity EIT peak can be obtained at Δp=Δc=0, as shown in black line (1) in Figure4a or red line (2) in Figure 4b. When only counter-propagating pf(b) and cb(f) are injected, the cavity mode at atom resonance center disappears due to VRS effect, as shown in red line (2) in Figure 4a or black line (1) in Figure 4b. So the ONR of the probe cavity mode based on intracavity EIT is realized. Here, we define the contrast of ONR as η = ( T c o − T c o u n ) / ( T c o + T c o u n ) [14], where T c o ( c o u n t ) is the intensity of the cavity transmission of the probe light co(counter)-propagates with the coupling field at Δp=Δc=0,. Whether it is pf or pb, the contrast η reaches nearly 90% (see embedded in Figure 4). Notably, at low probe power, due to the large absorption and linear loss of the atom-cavity system, both VRS peaks are very weak to almost invisible, which improves the contrast of ONR. In addition, the double dark-state peaks generated by the SW coupling field are also lost to be completely invisible, as shown in blue lines (3) in Figure 4.

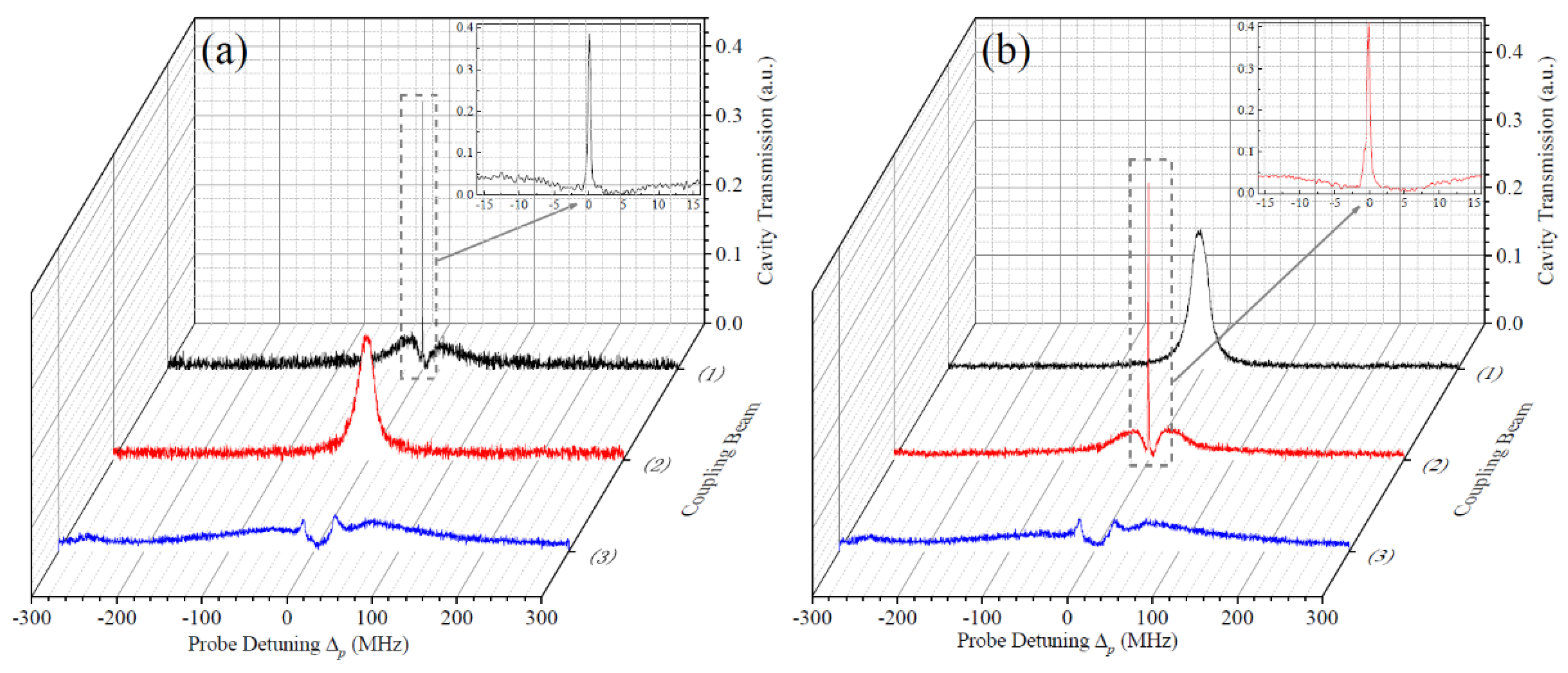
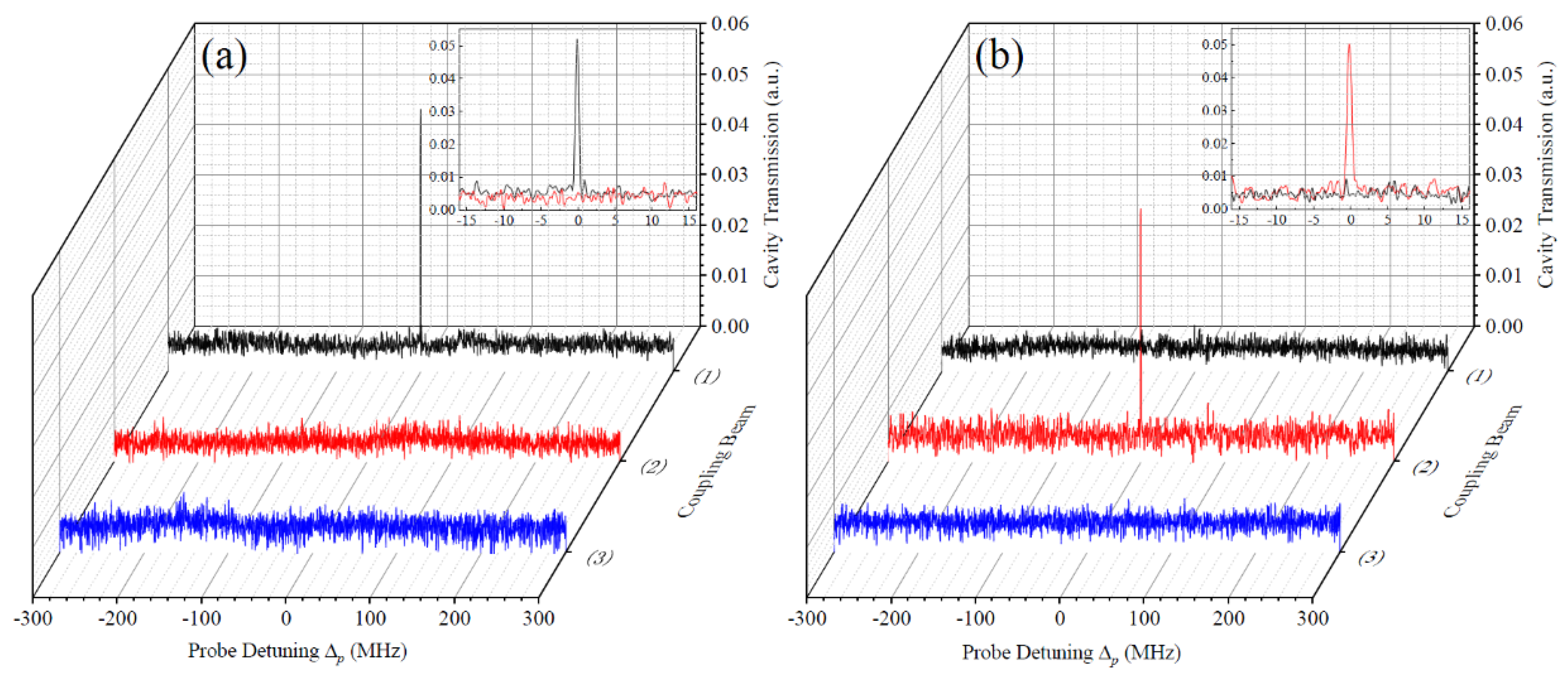
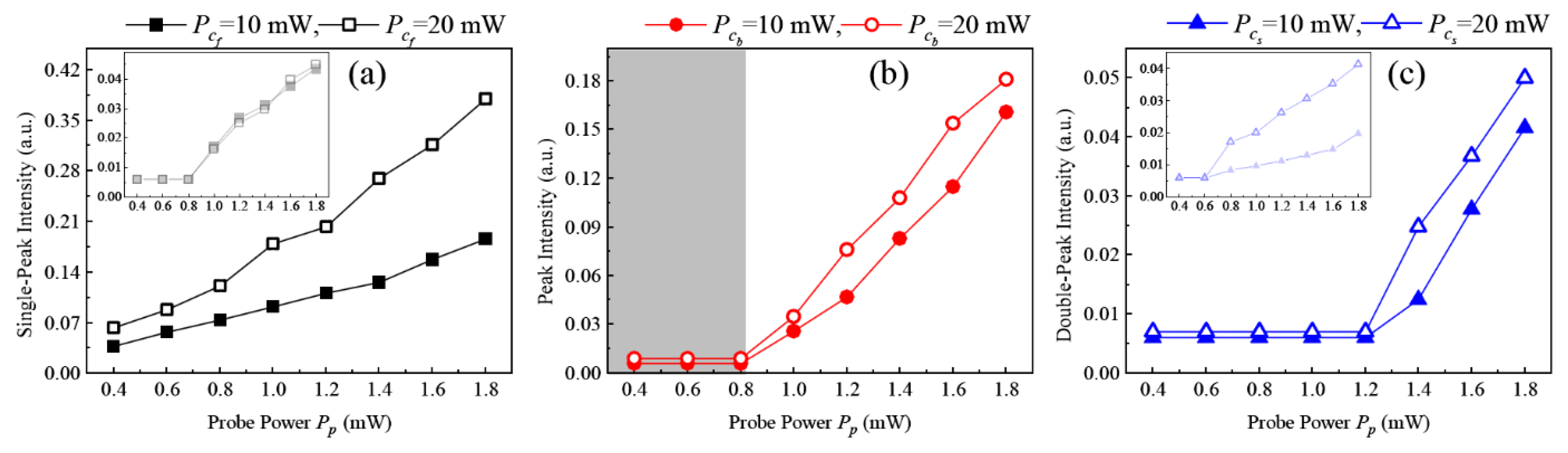
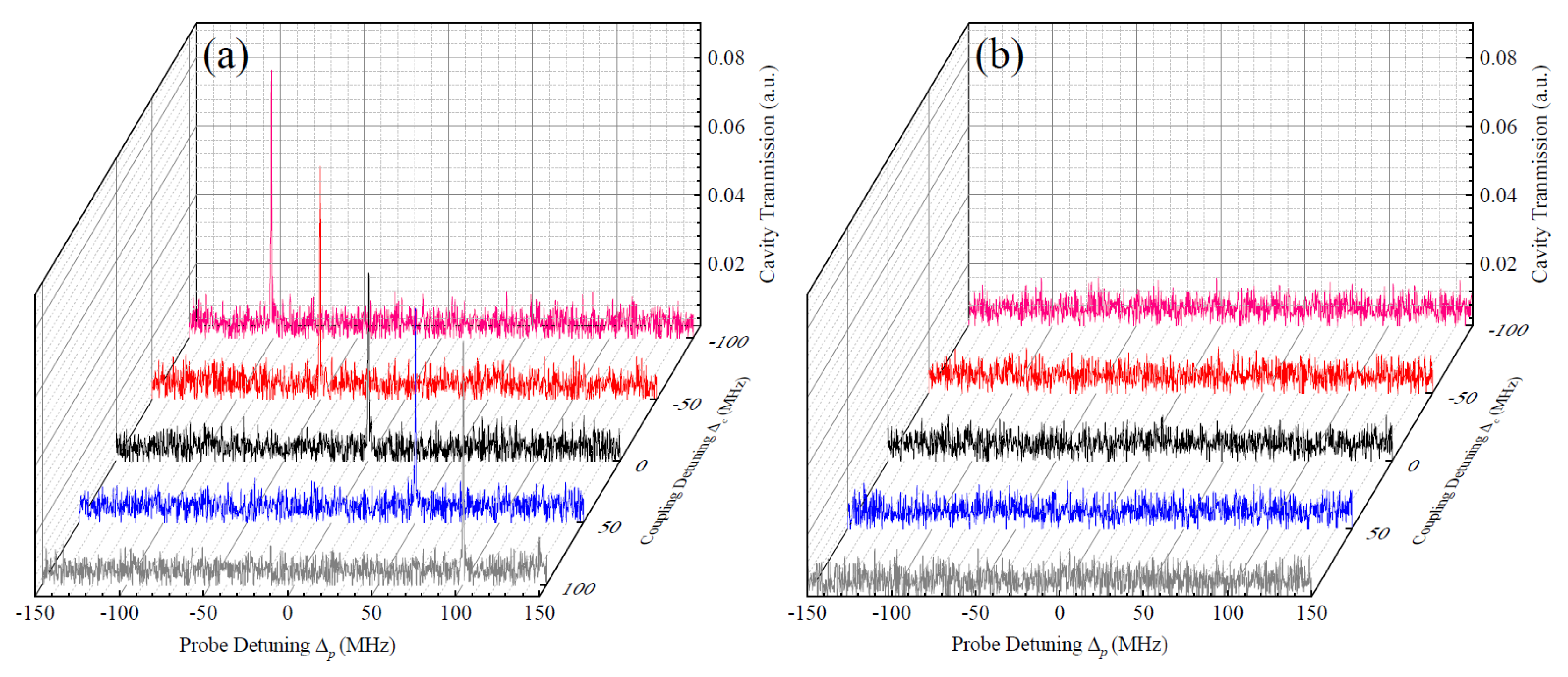
3. Theoretical Analysis and Further Experimental Investigation

Here, taking into account all Zeeman sublevels of the degenerate transition F g = 4 ↔ F e = 3 , we provide a qualitative explanation of the experimental results. As is known, a linearly polarized beam consists of left-handed (σ+) and right-handed (σ–) circularly polarized components, which couple the corresponding σ transition. In our experiment, the coupling and probe beams are both linearly polarized and perpendicular to each other. For the co-propagating coupling and probe lights, the interaction between the σ+ component of the coupling light and the σ– component of the probe light (and vice versa) establishes (Doppler free), which leads to the formation of coherent population trapping (CPT) of all the Zeeman sublevels of the ground state and two stable Λ-type EIT chains [37], as shown in Figure 5. Therefore, the transmission of probe light in free space is transparency under the two-photon resonant condition (see Figure 2), which is the superposition of two Λ-type sublevel’s action. Furthermore, with the help of the resonance filtering characteristics of the cavity, the intracavity EIT peak with linewidth-narrowed can also be obtained (see Figure 3 and Figure 4).
Based on above consideration, the degenerate two-level transition F g = 4 ↔ F e = 3 can be simplified as a three-level system. Therefore, using the susceptibility theory of dicromatic coupling field acting on three-level atoms, the physical mechanism of single-double dark-state peak formation in two-level atom-cavity system can be well explained, and the detailed see Refs. [22,34]. As for the ONR based on intracavity EIT, however, the strong coupling effect of the degenerate two atom-cavity systems is different. The provision of a rigorous theoretical calculation is highly complex due to the necessity of accounting for all Zeeman sublevels. As such, here solely presents a qualitative analysis.
For the three-level atom-cavity, the coupling strength (the frequency space of VRS) is expressed as g 2 N + 4 − 1 Ω c 2 [36,38], where g is the single photon coupling rate for the probe light, N is the number of involved intracavity atoms, and Ω c is the Rabi frequency of the control field. So at the same Temperature (N) and coupling power ( Ω c ), the strong coupling between the probe cavity mode and intracavity atoms induces a large VRS, which strongly suppresses the transmission of the probe light counter-propagating with the control field. This is more likely to induce the generation of ONR via EIT [18]. Differently, for the degenerate two-level atom-cavity, since the coupled light and probe light act on the same ground state, and Ω c ≫ Ω p , the coupled light pumps more the same ground state atoms and reduces the effective atom number N. Although the coupling light also plays a role in improving the coupling intensity, there is competition behavior here. Clearly, weakening the coupling strength played a dominant role in our experiment. Therefore, on the basis of the presence of intracavity EIT, changing the probe optical power is an effective means to achieve ONR.
Experimentally, taking forward pf for example, Figure 6 compares the variation of the cavity transmission intensity as a function of the probe power under different coupled light conditions. When only co-propagating cf is injected, the intensity of single dark-state peak increases almost linearly with the probe power. Moreover, the stronger the coupling power, the steeper the slope of intensity growth. Here, the slope is defined as the ratio of the difference in cavity transmission intensity to the difference in input probe power. Such as, the growth slope of single dark-state peak increases from 0.11 to 0.22 when the power of cf increases from 10 mW to 20 mW, as shown in solid and hollow squares in Figure 6a. For the case of only counter-propagating cb, when P p ≤ 0.8   mW , there is no probe cavity mode transmission due to the strong-coupling. That is, the ONR based on intracavity EIT is satisfied in this range, as shown the gray are in Figure 6b. Until P p > 0.8   mW , the cavity transmission without VRS which destroy the ONR occurs, and increases lineally with the probe power, as shown in the circles in Figure 6b. As for the case of SW coupling field, due to the lower transmission efficiency and larger intracavity loss, the double dark-state peaks cannot appear until the probe power P p > 1.2   mW , as shown in blue triangles in Figure 6c. The embedded in Figure 6a,c show the intensity of two VRS peaks under the condition of single co-propagating and SW coupling fields, respectively. Similar results can also be obtained for backward pb and not repeated here.
Furthermore, the impact of frequency detuning of the coupling field on ONR has also been experimentally investigated. Based on Figure 2a, Figure 7 presents the cavity transmission of pf under the different coupling detuning Δc. For the case of only co-propagating cf, the intracavity EIT peak shifts with Δc, as shown in Figure 7a. Notably the cavity mode detuning Δq hardly changes the frequency point, but it affects the intensity of intracavity EIT. The optimal transmission output occurs at Δc=Δc. For the case of only counter-propagating cb, there is no transmission (including VRS) detected, as shown in Figure 7b. Experimentally, the ONR transmission with high contrast (up to 90%) and narrowed linewidth (about 0.6 MHz) can be obtained in the range of Δc=±150 MHz. Actually, there is still intracavity EIT signal at larger coupling detuning, but the transparency efficiency is very weak due to far-off atomic resonance, which should reduce the contrast of ONR.
It is worth emphasizing that the temperature of intracavity Cs cell is also a factor affecting the cavity transmission. In our experiment, there is a good ONR transmission within the range of 35ºC～50 ºC. Certainly, the other parameters range which confirm to ONR should vary slightly.

4. Conclusions

In conclusion, using degenerate two-level atom-cavity combined system, we have experimentally implemented ONR based on intracavity EIT. For the degenerate transition Fg↔Fe (Fg>Fe), the linewidth-narrowed single dark-state peak generates when the probe cavity mode co-propagates with the coupling field (Doppler free), which results from the stable Λ-type coherence chains of all the Zeeman sublevels of the ground state. This is similar to the result for three-level atom-cavity system. But differently, when the two beams counter-propagate, the larger Rabi frequency of the coupling field can consume more of the population of the same ground state due to the frequency degeneracy, which reduces the number of effective atoms acted on the cavity mode and weakens the strong-coupling strength of the atom-cavity. Therefore, the ONR based on intracavity EIT can only be satisfied at very weak probe intensity. The study further enriches the physical extension of ONR and also can be applied in quantum information processing. Furthermore, due to the same frequency of the lights, only one laser is needed to implement our experimental scheme, which should indeed be highly useful in the design of integrated optical quantum devices, such as optical switching and routing, logical gate manipulation.

Author Contributions

Conceptualization, C.-Z.Q. and H.-T.Z.; methodology, C.-Z.Q. and D.W.; software, R.-N.L.; validation, J.-R.Z. and Y.-H.T.; formal analysis, C.-Z.Q. and L.-H.H.; investigation, C.-Z.Q. and H.-T.Z.; resources, H.-T.Z. and L.-H.H.; data curation, C.-Z.Q.; writing—original draft preparation, C.-Z.Q.; writing—review and editing, H.-T.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (Grant Nos. 61975102, and 11704235); Natural Science Foundation of Shanxi Province, China (Grant No. 20210302123437), and the Fund for Shanxi Key Subjects Construction.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Estep, N.D.; Sounas, J.; Soric, A.; Alù, A. Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nature Phys. 2014, 10, 923–927. [Google Scholar] [CrossRef]
  2. Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef] [PubMed]
  3. Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; Vanwolleghem, M.; Doerr, C.R.; Renner, H. What is — and what is not — an optical isolator. Nature Photon. 2013, 7, 579–582. [Google Scholar] [CrossRef]
  4. Aplet, L.J.; Carson, J.W. A Faraday effect optical isolator. Appl. Opt. 1964, 3, 544–545. [Google Scholar] [CrossRef]
  5. Peng, B.; Özdemir, S.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
  6. Ganainy, R.E.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
  7. Buddhiraju, S.; Song, A.; Papadakis, G.T.; Fan, S.H. Nonreciprocal metamaterial obeying time-reversal symmetry. Phys. Rev. Lett. 2020, 124, 257403. [Google Scholar] [CrossRef]
  8. Xu, W.; Iyer, A.; Jin, L.; Set, S.Y.; Renninger, W.H. Strong optomechanical interactions with long-lived fundamental acoustic waves. Optica 2023, 10, 206–213. [Google Scholar] [CrossRef]
  9. Xu, H.; Jiang, L.Y.; Clerk, A.A.; Harris, J.G.E. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature 2019, 568, 65–69. [Google Scholar] [CrossRef]
  10. Lépinay, L.M.; Ockeloen-Korppi, C.F.; Malz, D.; Sillanpää, M.A. Nonreciprocal transport based on cavity floquet modes in optomechanics. Phys. Rev. Lett. 2020, 125, 023603. [Google Scholar] [CrossRef]
  11. Scheucher, M.; Hilico, A.; Will, E.; Volz, J.; Rauschenbeutel, A. Quantum optical circulator controlled by a single chirally coupled atom. Science 2016, 354, 1577–1580. [Google Scholar] [CrossRef] [PubMed]
  12. Söllner, I.; Mahmoodian, S.; Hansen, S.L.; Midolo, L.; Javadi, A.; Kiršanské, G.; Pregnolato, T.; El-Ella, H.; Lee, E.H.; Song, J.D.; Stobbe, S.; Lodahl, P. Deterministic photon–emitter coupling in chiral photonic circuits. Nat. Nanotechnol. 2015, 10, 775–778. [Google Scholar] [CrossRef]
  13. Hua, S.; Wen, J.; Jiang, X.; Hua, Q.; Jiang, L.; Xiao, M. Demonstration of a chip-based optical isolator with parametric amplification. Nat. Commun. 2016, 7, 13657. [Google Scholar] [CrossRef] [PubMed]
  14. Wang, D.W.; Zhou, H.T.; Guo, M.J.; Zhang, J.X.; Evers, J.; Zhu, S.Y. Optical diode made from a 289 moving photonic crystal. Phys. Rev. Lett. 2013, 110, 093901. [Google Scholar] [CrossRef]
  15. Biancalana, F.; Amann, A.; Uskov, A.V.; O’Reilly, E.P. Dynamics of light propagation in spatiotemporal dielectric structures. Phys. Rev. E 2007, 75, 046607. [Google Scholar] [CrossRef] [PubMed]
  16. Horsley, S.A.R.; Wu, J.H.; Artoni, M.; La Rocca, G.C. Optical nonreciprocity of cold atom Bragg mirrors in motion. Phys. Rev. Lett. 2013, 110, 223602. [Google Scholar] [CrossRef]
  17. Yang, P.F.; Xia, X.W.; He, H.; Li, S.K.; Han, X.; Zhang, P.; Li, G.; Zhang, P.F.; Xu, J.P.; Yang, Y.P.; Zhang, T.C. Realization of nonlinear optical nonreciprocity on a few-photon level based on atoms strongly coupled to an asymmetric cavity. Phys. Rev. Lett. 2019, 123, 233604. [Google Scholar] [CrossRef]
  18. Zhang, S.; Hu, Y.; Lin, G.; Niu, Y.; Xia, K.; Gong, J.; Gong, S. Thermal-motion-induced non-reciprocal quantum optical system. Nat. Photon. 2018, 12, 744–748. [Google Scholar] [CrossRef]
  19. Lin, G.W.; Zhang, S.C.; Hu, Y.Q.; Niu, Y.P.; Gong, J.B.; Gong, S.Q. Nonreciprocal amplification with four-level hot atoms. Phys. Rev. Lett. 2019, 123, 033902. [Google Scholar] [CrossRef]
  20. Hu, H.Q.; Zhang, S.H.; Kuang, X.Y.; Qi, Y.H.; Lin, G.W.; Gong, S.Q.; Niu, Y.P. ; Reconfigurable nonreciprocity with low insertion loss using a simple two-level system. Opt. Express 2020, 28, 38710–38717. [Google Scholar] [CrossRef]
  21. Liang, C.; Liu, B.; Xu, A.N.; Wen, X.; Lu, C.C.; Xia, K.Y.; Tey, M.K.; Liu, Y.C.; You, L. Collision-induced broadband optical nonreciprocity. Phys. Rev. Lett. 2020, 125, 123901. [Google Scholar] [CrossRef] [PubMed]
  22. Zhou, H.T.; Xie, S.Y.; Li, X.; Wang, D.; Yang, B.D.; and Zhang, J.X. Manipulation of optical nonreciprocity in hot atom-cavity system. J. Phys. B: At. Mol. Opt. Phys. 2021, 54, 195001. [Google Scholar] [CrossRef]
  23. Harris, S.E.; Field, J.E.; Imamoğlu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 1990, 64, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
  24. Khanikaev, A.B.; Alù, A. Nonlinear dynamic reciprocity. Nat. Photon. 2015, 9, 359–361. [Google Scholar] [CrossRef]
  25. Chen, W.T.; Liu, L.; Zhao, J.; Zhang, C. On-chip broadband, compact TM mode Mach–Zehnder optical isolator based on InP-on-Insulator platforms. Nanomaterials 2024, 14, 709. [Google Scholar] [CrossRef] [PubMed]
  26. Dawes, A.; Illing, L.; Clark, S.M.; Gauthier, D.J. All-optical switching in rubidium vapor. Science 2005, 29, 672–674. [Google Scholar] [CrossRef] [PubMed]
  27. Wang, C.Y.; Chen, Y.F.; Lin, S.C.; Lin, W.H.; Kuan, P.C.; Yu, I.A. Low-light-level all-optical switching. Opt. Lett. 2006, 31, 2350–2352. [Google Scholar] [CrossRef] [PubMed]
  28. Sheng, J.; Khadka, U.; Xiao, M. Realization of All-Optical Multistate Switching in an Atomic Coherent Medium. Phys. Rev. Lett. 2012, 109, 223906. [Google Scholar] [CrossRef] [PubMed]
  29. Chang, D.E.; Sørensen, A.S.; Demler, E.A.; Lukin, M.D. A single-photon transistor using nanoscale surface plasmons. Nat. Phys. 2007, 3, 807–812. [Google Scholar] [CrossRef]
  30. Saha, S.; Diroll, B.T.; Ozlu, M. G.; Chowdhury, S. N.; Peana, S.; Kudyshev, Z.; Schaller, R. D.; Jacob, Z.; Shalaev, V. M.; Kildishev, A. V. Engineering the temporal dynamics of all-optical switching with fast and slow materials. Nat. Commun. 2023, 14, 5877. [Google Scholar] [CrossRef]
  31. Mondal, H.; Goswami, K.; Sen, M.; Khan, W.R. Design and analysis of all-optical logic NOR gate based on linear optics. Opt. Quant. Electron. 2022, 54, 272. [Google Scholar] [CrossRef]
  32. de Clercq, L.E.; Lo, H.Y.; Marinelli, M.; Nadlinger, D.; Oswald, R.; Negnevitsky, V.; Kienzler, D.; Keitch, B.; Home, J.P. Parallel transport quantum logic gates with trapped ions. Phys. Rev. Lett. 2016, 116, 080502. [Google Scholar] [CrossRef] [PubMed]
  33. Babazadeh, A.; Erhard, M.; Wang, F.; Malik, M.; Nouroozi, R.; Krenn, M.; Zeilinger, A. High-dimensional single-photon quantum gates: Concepts and experiments. Phys. Rev. Lett. 2017, 119, 180510. [Google Scholar] [CrossRef]
  34. Zhang, J.X.; Zhou, H.T.; Wang, D.W.; Zhu, S.Y. Enhanced reflection via phase compensation from anomalous dispersion in atomic vapor. Phys. Rev. A 2011, 83, 053841. [Google Scholar] [CrossRef]
  35. Lezama, A.; Barreiro, S.; Akulshin, A.M. Electromagnetically induced absorption. Phys. Rev. A 1999, 59, 4732–4735. [Google Scholar] [CrossRef]
  36. Wu, H.B.; Gea-Banacloche, J.; Xiao, M. Observation of intracavity electromagnetically induced transparency and polariton resonances in a Doppler-broadened medium. Phys. Rev. Lett. 2008, 100, 173602. [Google Scholar] [CrossRef]
  37. Zhou, H.T.; Guo, M.J.; Wang, D.; Gao, J.R.; Zhang, J.X.; Zhu, S.Y. Angular momentum and two-photon detuning dependence of reflection spectrum on degenerate two-level systems in Cs vapour. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 225503. [Google Scholar] [CrossRef]
  38. Mücke, M.; Figueroa, E.; Bochmann, J.; Hahn, C.; Murr, K.; Villas-Boas, C.J.; Rempe, G. Electromagnetically induced transparency with single atoms in a cavity. Nature 2010, 465, 755–758. [Google Scholar] [CrossRef]
Preprints 109591 g001
Figure 1. (a) Schematic of experimental setup. (b) Diagram of energy levels for the atoms. Two types for only pf (c) or only pb (d) is seeded into the atom-cavity system.
Figure 1. (a) Schematic of experimental setup. (b) Diagram of energy levels for the atoms. Two types for only pf (c) or only pb (d) is seeded into the atom-cavity system.
Preprints 109591 g001
Preprints 109591 g002
Figure 2. Transmission spectra of the probe light under different configurations of the coupling fields in free space: (1) only cf with power P c f = 1   mW , (2) only cb with P c b = 1   mW , and (3) SW cs with P c f = P c b = P c s = 1   mW . The other experimental parameters are: P p = 10   μ W , Δ c = 0 .
Figure 2. Transmission spectra of the probe light under different configurations of the coupling fields in free space: (1) only cf with power P c f = 1   mW , (2) only cb with P c b = 1   mW , and (3) SW cs with P c f = P c b = P c s = 1   mW . The other experimental parameters are: P p = 10   μ W , Δ c = 0 .
Preprints 109591 g002
Preprints 109591 g003
Figure 3. Cavity transmission spectra of the forward probe light pf (a) and backward pb (b) under three different coupling light conditions: (1) only cf with P c f = 20   mW , (2) only cb with P c b = 20   mW , and (3) cs with P c s = 20   mW . The other experimental parameters are P p f = P p b = 1.8   mW T = 40 ∘ C , and Δ q = Δ c = 0 .
Figure 3. Cavity transmission spectra of the forward probe light pf (a) and backward pb (b) under three different coupling light conditions: (1) only cf with P c f = 20   mW , (2) only cb with P c b = 20   mW , and (3) cs with P c s = 20   mW . The other experimental parameters are P p f = P p b = 1.8   mW T = 40 ∘ C , and Δ q = Δ c = 0 .
Preprints 109591 g003
Preprints 109591 g004
Figure 4. Cavity transmission spectra of the forward probe light pf (a) and backward pb (b) with power P p f = P p b = 0.4   mW . The other experimental parameters are the same as those in Figure 3.
Figure 4. Cavity transmission spectra of the forward probe light pf (a) and backward pb (b) with power P p f = P p b = 0.4   mW . The other experimental parameters are the same as those in Figure 3.
Preprints 109591 g004
Preprints 109591 g005
Figure 5. Zeeman sublevels for the degenerate transitions F g = 4 ↔ F e = 3 .
Figure 5. Zeeman sublevels for the degenerate transitions F g = 4 ↔ F e = 3 .
Preprints 109591 g005
Preprints 109591 g006
Figure 6. The cavity transmission intensity of pf versus the input probe power. The other experimental parameters are the same as in Figure 3.
Figure 6. The cavity transmission intensity of pf versus the input probe power. The other experimental parameters are the same as in Figure 3.
Preprints 109591 g006
Preprints 109591 g007
Figure 7. Cavity transmission spectra of pf under various coupling detuning. (a) only cf, and (b) only cb. The other experimental parameters are the same as those in Figure 3.
Figure 7. Cavity transmission spectra of pf under various coupling detuning. (a) only cf, and (b) only cb. The other experimental parameters are the same as those in Figure 3.
Preprints 109591 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated