Seasonal Variations in Hydraulic Regulation of Whole-Tree Transpiration in Mongolian Pine Plantations: Insights From Semiarid Deserts in Northern China

Seasonal precipitation variance significantly alters soil water content, potentially inducing water stress and affecting plant transpiration in semiarid deserts. This study explored the effects of environmental variables and hydraulic conductance on whole-tree transpiration (ET) in Mongolian pines (Pinus sylvestris var. mongolica) across different forest stages in the semiarid deserts of northern China. We measured ET using sap flow in mature (MMP), half-mature (HMP), and young (YMP) Mongolian pine plantations. Measurements included soil-leaf water potential difference (ΔΨ), atmospheric conditions, and soil moisture contents on sunny days, both in dry and wet periods. Seasonally variable rainfall distinctly affected soil moisture, correlating ET with photosynthetically active radiation (PAR) and vapor pressure deficit (VPD). Notable nocturnal sap flow occurred during the growing season. During the dry periods, both stomatal and hydraulic conductance influenced ET, whereas during the wet periods, stomatal conductance primarily regulated it. Discrepancies between predicted and measured ET were noticed: compared to the predicted ET, measured ET was lower during dry periods while higher during wet periods. Hydraulic conductance (KT) increased with tree height (H) and ΔΨ, although tall trees exhibited lower KT rates, suggesting that hydraulic compensation had occurred. This compensation, observed between 11:00 and 13:00, aligned with increased hydraulic resistance during dry periods. Decreasing hydraulic conductance intensified leaf water stress in dry periods, especially during the time when PAR and VPD were heightened, potentially increasing stomatal sensitivity to drought, promoting water conservation and plant survival. A linear relationship between predawn and midday leaf water potentials was noticed, indicating extreme anisohydric behavior across forest stages during both dry and wet periods. Although both stomatal and hydraulic conductance influenced ET during the dry period, MMP and YMP were more susceptible to drought conditions. Understanding these dynamics could help evaluate semiarid desert ecological functions for water conservation amidst uneven seasonal precipitation in Northern China.

Keywords:

Subject: Biology and Life Sciences - Forestry

1. Introduction

Drought significantly affects the distribution of tree species in semiarid deserts [1,2,3]. Climate projections for the next decade indicate increased dryness in this region [4,5], potentially impacting global forest ecosystems and ecosystem services [6], reducing terrestrial net productivity [7], and altering carbon dynamics [8]. China grapples with desertification in vast areas (approximately 2.61 billion ha) due to high human population density and limited natural resources [9,10]. Mu Us (107°20–111°30E, 37°30–39°20N), and Horqin (118°35–123°30E, 42°21–42°21N) deserts in Northern China face soil erosion and sand drift issues [10,11,12]. In recent decades, soil restoration and sand transformation methods, including mechanical sand barriers [13], biological soil crusts [14], and afforestation [15], have been implemented. These artificial plantations have been successfully established as a feasible method of environmental management for desertification control in the Mu Us and Horqin Deserts [16,17,18].

Scots pine, widely distributed across the globe, thrives primarily in boreal regions. It also occupies large areas in relatively dry regions within the Mediterranean basin, from the Iberian Peninsula to Turkey and north China [16,19]. Mongolian pine (Pinus sylvestris var. mongolica) is a major shelterbelt tree species in the desert that has been largely introduced to northern China (121°11–127°10E, 50°10–53°33N) [20]. The planted forest cover in the desert currently spans 7.0 × 10⁵ ha in the northern part of China [21]. This wide range offers an ideal opportunity to study the geographic variabilities in the hydraulic properties of Mongolian pine [19]. Beyond its economic and landscape importance, Mongolian pine inevitably encounters a diverse range of environmental conditions within its habitat [17]. Under drought conditions, P. mongolica adjusts its leaf-to-sapwood area ratio, hydraulic conductivity, total leaf area, etc [19]. Although the artificial plantations have adapted well, signs of slowed growth and dieback have been observed in Mongolian pine growth [22]. Projected climate change may push the semiarid area beyond the ecological niche of the species [23]. These concerns have led researchers to attribute the massive degeneration of P. mongolica to a high transpiration rate, uneven precipitation distribution, and the limitations posed by the natural rainfall patterns in the region [21,24].

Plants inevitably lose water through their stomata during carbon assimilation, which must be compensated for by water uptake from the roots to the leaves against negative hydrostatic pressure [25]. Prolonged and severe water scarcity causes the collapse of the plant hydraulic system, leading to tree mortality [26]. However, plants can partly cope with water limitations by applying physiological adaptation across the soil-plant-atmosphere continuum [27]. These physiological adaptations include adjustments in whole-tree hydraulic conductance (K_T), increased water storage, nocturnal sap flow refilling, and regulation of transpiration (e.g., decreasing the leaf-sapwood area ratio or increasing the sensitivity of stomata to vapor pressure deficit (VPD)) [19]. This concept can also be defined as isohydric/anisohydric behavior [28,29,30]. To date, only a few studies have focused on assessing the variability of these hydraulic traits, plant water regulation, or water-use strategies, especially in Mongolian pine tree species [17,31].

The uneven distribution of precipitation (P) over time significantly alters forest soil moisture between dry and wet periods and likely causes water stress during the dry period [21,32]. This difference in soil water availability creates a large difference between the predawn leaf water potential and midday minimum water potential in the dry period, resulting in increased resistance in water transfer along the soil-leaf hydraulic path [33], decreased stomatal opening of leaves, and decreased transpiration [34]. However, trees, under available light and heat resources, regulate excessive stomatal closure by adjusting hydraulic conductivity. This ensures adequate CO₂ absorption, maintaining moderate growth. This compensatory effect of hydraulic conductivity on transpiration serves as an important ecological strategy for forest tree species to adapt to soil water stress in the dry season while optimizing light and heat resources [35,36]. However, the effectiveness and safety of the water transport structures cannot be achieved for most tree species [19,37].

Although it is hypothesized that plants can adjust hydraulic conductivity to offset transpiration, few studies have explored the link between hydraulic characteristics and water transport compensation in arid environments. Most studies focus on hydraulic compensation under specific conditions like tree height (H) and leaf loss [38]. For example, research on coniferous forests in the Rocky Mountains indicates that during the late succession period, the rise in H completed offsets the increasing hydraulic constraints, whereas species in the early succession period can only partially counteract the impact of H [36]. The hurricane caused a 41% decrease in the leaf area of Taxodium distichum and only an 18% decrease in sap flow density and tree transpiration, and plants properly adjusted their hydraulic conductivity to compensate for the transpiration [39]. The leaf area of 8-year-old loblolly pine (Pinus taeda L.) trees, a shade-intolerant pioneer species common in the southeastern USA, was reduced by 55%, whereas transpiration was still fully compensated [40].

Two key questions regarding this species remain unanswered: First, how does hydraulic compensation impact Mongolian pine plantations in arid regions? Second, if the phenomenon of hydraulic compensation exists, what are the mechanisms for regulating plant water relations under seasonal changes (i.e., isohydric vs. anisohydric)? During these experiments, three different stands (mature (MMP), half-mature (HMP), and young (YMP) forest) were assessed. We measured sap fluxes (Section 2.1.) in dry and wet seasons based on regional precipitation characteristics. These stands conformed to the reasonable afforestation densities of P. sylvestris, potentially impacting sap fluxes beyond forest management [41,42]. In this study, we hypothesized that: (1) P. sylvestris should demonstrate higher transpiration rates in the wet period than in the dry period, especially in MMP and YMP, whereas HMP maintains a certain level of transpiration due to more uniformly distributed precipitation throughout the growing season. Even during the dry period, MMP, with its larger tree size, should retain substantial transpiration through nocturnal transpiration. Similarly, YMP should maintain a consistent transpiration rate due to the higher air temperature (T_a) and evaporative demand in its introduction region. (2) During the wet period, P. sylvestris faces stomatal limitation, while in the dry period, transpiration is co-regulated by hydraulic and stomatal factors. This means that P. sylvestris can adjust its hydraulic conductivity to manage water stress under certain stomatal controls. The compensatory effect of K_T on stomatal-limited transpiration is notable. Considering recent studies indicate that P. sylvestris exhibits stomatal conductance highly sensitive to VPD, the canopy and atmosphere are highly coupled, and stomata exhibit more control over transpiration, we hypothesized that (3) P. sylvestris is an anisohydric plant during the wet period, whereas isohydric behavior should be observed during the dry period.

2. Materials and Methods

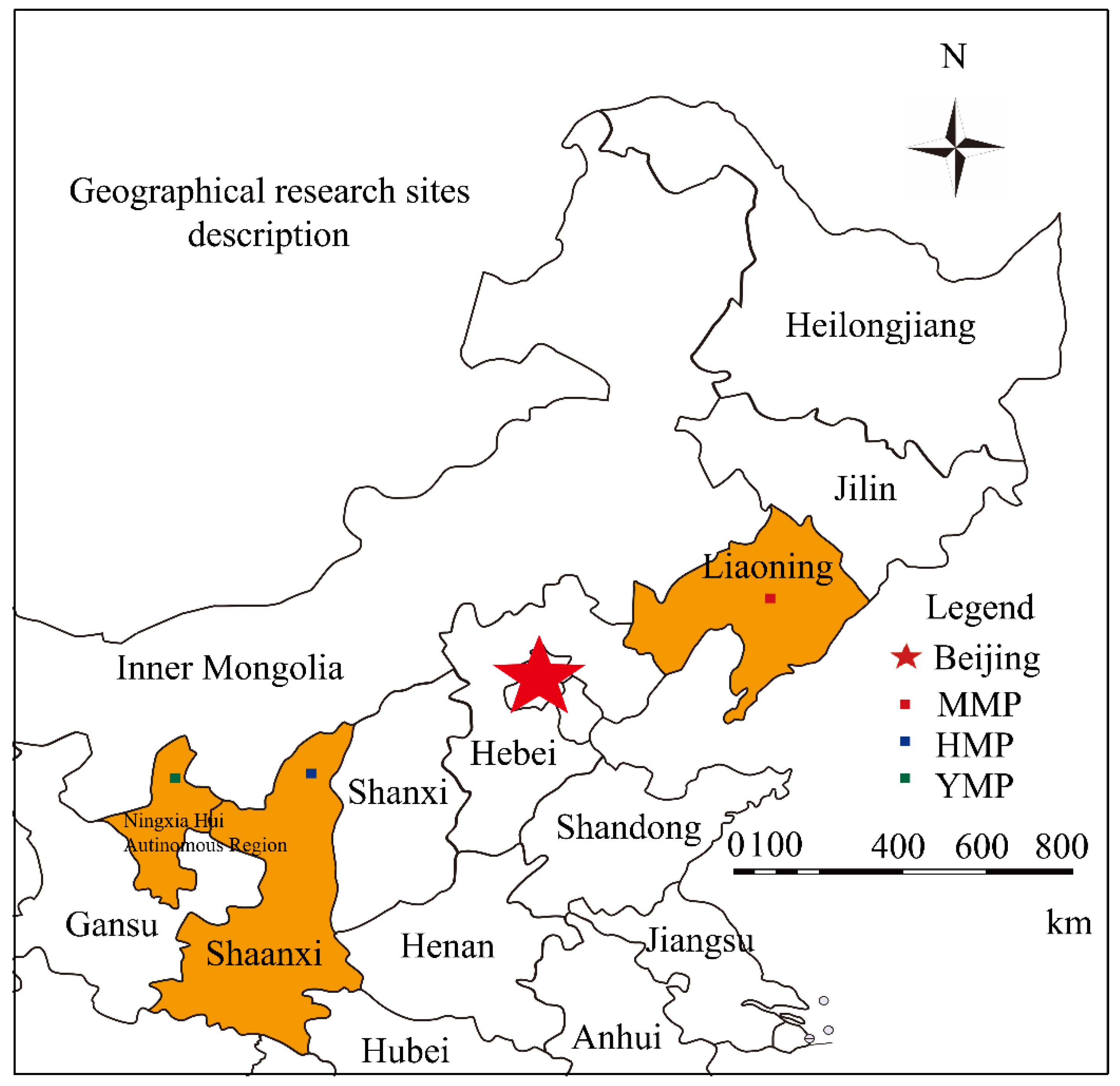
2.1. Study Sites

The Magu Forest Ecosystem Research Station (123°32′E–124°26′E, 42°33′N–43°29′N), the Rare Psammophytes Protection Botanical Base (109°42′54″E, 38°20′11″N) and the Ningxia Yanchi Research Station of State Forestry Administration (106°300′E–107°410′E, 37°04′N–38°10′N) were surveyed separately in this research (Figure 1). Three observation stations represented the three different stand ages of Mongolian pine plantations, with a mature forest (MMP; stand age, 45 y; stand density, 275 trees ha⁻¹), half-mature forest (HMP; stand age, 30 y; stand density, 1475 trees ha⁻¹), and young forest (YMP; stand age, 11 y; stand density, 850 trees ha⁻¹). The plot area of the MMP is 10,000 m², the HMP is 900 m², and the YMP is 900 m². The seed source originated from the same region of provenance for the MMP, HMP, and YMP. The area of MMP is dominated by a continental, monsoon-influenced semi-arid climate where mean P is 420 mm, mean T_a is 7.9 °C, the annual evaporation is 1078 mm, and the landscape is characterized by fixed sand dunes, which consist of areas with dark brown forest soil and eolian sandy soil; the area of HMP has a semi-arid continental climate, mean P is 400 mm, mean T_a is 8.7 °C, and the landscape is characterized by fixed desert, with eolian sandy soil; the area of YMP has a semi-arid continental monsoonal climate of the mid-temperate zone, mean P is 300 mm, annual potential evaporation averages 1273 mm, and the landscape is characterized by dark loessial, eolian sandy, and sierozem soils [17].

2.2. Sap Flow and Leaf Area/Sapwood Area

Sap flow observations were conducted from May 1 to October 20 at the study sites (MMP in 2018, HMP in 2014, and YMP in 2012). Nine, nine, and three tree samples were selected, and the minimum, maximum, and mean diameter at breast height (DBH) values of the selected sampled tree traits in the MMP, HMP, and YMP are shown in Table 1.

The sap flux densities (J_s, g cm^–2 s⁻¹) were measured using Granier-type thermal dissipation probes [43] in the MMP and HMP. Each sensor consisted of a pair of probes, 20-mm long and 2 mm in diameter, and a copper-constantan thermocouple, which were inserted into the sapwood (on the north-facing side of the sampled trees, into the tree trunk at a height of 1.3 m above the ground) [44]. The upper probe included a heater with a constant power of 0.15 W and the lower probe was unheated as the reference [45]. The temperature difference between the upper and lower probes (ΔTa, °C) was measured every 10 s, and 15 min averages were recorded on a data logger (CR1000; Campbell Scientific Inc., Logan, UT, USA) with a multiplexer (AM16/32A; Campbell Scientific). J_s was calculated as:

J_{s} = 0.0119 \times {(\frac{Δ T_{a} \max - Δ T_{a}}{Δ T_{a}})}^{1 . 231}

(1)

where ΔT_a max ( °C) is the maximum temperature difference between the sensors when J_s is close to 0 [46].

Model SGB25 gauges (Flow32 meters; Dynamax Inc., Houston, TX, USA) were applied to the stems of the YMP. Data were recorded at 10 s intervals and stored as 15 min averages using a CR1000 data logger (Campbell Scientific) [11]. J_s was calculated as:

J_{s} = \frac{Q_{f}}{c_{p} \times (Δ T)}

(2)

where Q_f is the energy of the sap flow and c_p is the specific heat of water (4.168 J g °C⁻¹) [47]. Total tree water consumption (E_T, kg d⁻¹) was estimated directly by multiplying J_s by the sapwood area (SA, cm²). The DBH was measured 1.3 m above the ground using a DBH ruler, and the tree core samples were obtained using an increment borer. The total SA for the plots in the MMP, HMP, and YMP were calculated as 99,000, 27,141, and 1338 cm², respectively. The LAI (m² m^–2) was determined to be 1.42, 1.54, and 0.96 m² m^–2 in the MMP, HMP, and YMP, respectively. Whole-tree leaf area/sapwood area ratio (A_L: A_S; m² cm^–2) was obtained from five or six trees per site, and mean A_L: A_S, were 0.14, 0.095, 0.23 m² cm^–2 in the MMP, HMP, and YMP, respectively.

2.3. Leaf and Soil Water Potentials

Leaf water potential measurements were taken under sunny days as follows: For the MMP plot on May 20 and 21, June 2 and 3, July 25, August 23, September 6 and 7, and October 12 and 13. For the HMP plot on Mau 19 and 20, June 2 and 13, August 15 and 17, September 6 and 12, and October 13 and 14. For the YMP plot on May 5 and 13, June 5 and 8, August 24 and 28, September 4 and 8, and October 11 and 12. We harvested sun-exposed branches using a pruning hook and immediately picked leaves from the branches. Leaf water potential (Ψ_L, MPa) was measured by using a PMS pressure chamber (PMS Instruments, Albany, OR, USA) immediately after leaf removal. Soil water potentials (Ψ_S, MPa) were investigated using five multi-voltmeter sensors (HR33T, Wescor, Inc., USA). The Ψ_L and Ψ_S were measured between 05:00 h to 20:00 h at time intervals of 1 h.

2.4. Hydraulic Conductance

The hydraulic conductance of the soil/root/leaf pathway was determined as:

K_{T} = \frac{E_{T}}{S A \times (Δ ψ - h \times ρ_{w} \times g)}

(3)

where ΔΨ is the difference between soil water potential and plant water potential and E_T is the amount of water lost through transpiration at the time when plant water potential was determined, g represents the acceleration of gravity (N kg⁻¹), h represents the xylem length from root to tree canopy, ρ_w represents water density (kg m³), K_T was normalized to whole-plant stem-specific hydraulic conductance (kg m⁻² s⁻¹ MPa). This equation is useful for exploring the significance of the interrelationships among stomatal conductance, soil and leaf water potentials, and plant hydraulic conductance [48,49,50,51,52].

2.5. Environmental Variables

In the MMP plot, an automatic weather station was located approximately 85 m from the studied plot. The mean T_a (°C), P (mm), RH (%), and PAR (µmol s^–2 m^–2) were measured by the automatic weather station at a height of 15 m. In the HMP plot, meteorological data were collected using a water vapor flux tower, which was 30.0 m high and located 75.0 m away from the surveyed plot. The water vapor flux tower measured PAR, T_a, RH, barometric pressure, and P (Campbell Scientific). P was collected at a height of 25 m, whereas other meteorological data were collected at a height of 14 m above the ground. At the MMP and HMP study sites, 0–100 cm soil profile samples were collected every 15 d, and additional measurements were taken after each P event. In the YMP plot, meteorological data were obtained using a meteorological monitoring station (Campbell Scientific) that measured the PAR, RH, P, and T_a. The soil volumetric content (cm³ cm^–3) was measured using a soil volumetric moisture detector (HH2 Soil Moisture Probe type ML2x and Meter type HH2; Dynamax Inc.).

VPD was calculated by combining Ta and RH, as follows:

V P D = a \times \exp [b \times T_{a} (T_{a} + c)] \times (1 - R H)

(4)

where a is 0.611 KPa, b is 17.502, and c is 240.97 °C [17,53].

2.6. Hydraulic Compensation

The theoretical basis for hydraulic compensation is presented in Equation 4: A similar derivation of Darcy’s Law for stomatal conductance (g_s, m s⁻¹) can be written in which the soil-to-leaf water potential difference (ΔΨ, MPa) is explicit [54]:

g_{s} = \frac{K_{T} \times A_{S} \times Δ Ψ}{H \times η \times A_{L} \times V P D}

(5)

where the effect of gravity at a given tree height (H, m), η (kg m⁻¹ s⁻¹) is the dynamic viscosity.

J_{s} = T_{r} = Ω E_{e q} + (1 - Ω) E_{i m p} = g_{s} \times V P D

(6)

In a previous study, researchers stated that under steady-state conditions characterized by negligible boundary-layer resistance and low hydraulic capacitance, J_s may be equated to the leaf-level transpiration rate (T_r, g cm^–2 s⁻¹), which is further linked to g_s [55]. E_eq is the transpiration rate obtained in equilibrium with an extensive, homogeneous wet surface and a good energy balance, which is dominated by the airflow on the canopy, and E_imp is the transpiration rate affected by the VPD [52]: The extent of canopy decoupling from the atmosphere can be described by a dimensionless coefficient (Ω) that expresses the relative sensitivity of canopy transpiration to marginal changes in g_s [56]. In the previous study mentioned above, P. sylvestris was coupled with atmospheric conditions [17], Ω values were too little to be neglected, and J_s is directly link to the g_s, then the formula was modified to:

\frac{J_{s}}{V P D} ~ \frac{E_{T}}{V P D} ~ g_{s} = \frac{K_{T} \times A_{S} \times Δ Ψ}{H \times η \times A_{L} \times V P D}

(7)

In this case, the denominator from Equation 7 is expressed as ΔΨ /H, the soil-to-leaf water potential gradient, and all other variables are defined as above. This derivation shows that, similar to K_T, J_s and E_T are inversely related to height if all other variables remain constant. However, if the other variables do not remain constant, compensation for H may occur. Increasing K_T may balance the effect of H on K_T; additionally, increasing ΔΨ may balance the effect of H on g_s / J_s / E_T-limited transpiration [35].

To further quantify the hydraulic compensation values, the relationships of measured E_T (M-E_T) with ΔΨ and A_L, A_S were established as functional relationship models (E_T = f(ΔΨ, A_L, A_S)) for both the dry and wet periods separately. The estimated transpiration values (P-E_T) at the corresponding time was obtained by substituting ΔΨ and A_L, A_S into the former functional relationship models. Hydraulic compensation usually occurs from early noon to late afternoon, when PAR and VPD values reach their maximum. Plants can avoid excessive stomatal closure by adjusting hydraulic conductivity, which may have a compensatory effect on transpiration. Therefore, changes in whole-tree transpiration, since the maximum PAR and VPD values were obtained (the time interval was 1.0 h), reflects the response sensitivity of whole-tree transpiration to hydraulic conductivity, and may be representative of the transpiration amount due to the hydraulic compensation effect. Specifically, if ΔE_T does not have a significant relationship with K_T, transpiration is mainly limited by g_s; in contrast, if they have a 1:1 linear relationship, transpiration is mainly controlled by K_T. Otherwise, if they have a non-linear relationship, transpiration is co-regulated by g_s and K_T, that is, K_T, has a compensatory effect on g_s-limited transpiration.

2.6. Plant Water Transport Regulation: Isohydric / Anisohydric Behaviors

Plants require effective mechanisms to regulate water transport at a variety of scales. Here, we adopted a theoretical framework describing plant responses to drying soil based on the relationship between midday (12:00 h) and pre-dawn (05:00–06:00 h) soil water potential. The intercept of the relationship (Λ) characterizes the maximum transpiration rate per unit of hydraulic transport capacity, whereas the slope (δ) measures the relative sensitivity of the transpiration rate and plant hydraulic conductance to declining water availability [27].

The relationship between the pre-dawn soil and midday water potentials, according to the theoretical model mentioned above, assumes a linear relationship. Four different behaviors are depicted, all sharing the same intercept (Λ): strict isohydric (δ = 0), partial isohydric (0 < δ < 1), strict anisohydric (δ = 1) and extreme anisohydric (δ > 1). For isohydric behaviors, Ψ_pre-dawn = Ψ_midday; while for anisohydric relationships, Ψ_midday represents the point at which plant hydraulic conductance is completely lost [27]. Importantly, Isohydric species are characterized by tighter stomatal closure, whereas anisohydric species are characterized by avoidance of complete stomatal closure [57].

Statistical analyses were conducted using SPSS software version 22.0 (SPSS Inc., Chicago, IL, USA). SciDAVis (DHI Group, Inc., NY, USA) was used to draw all figures.

3. Results

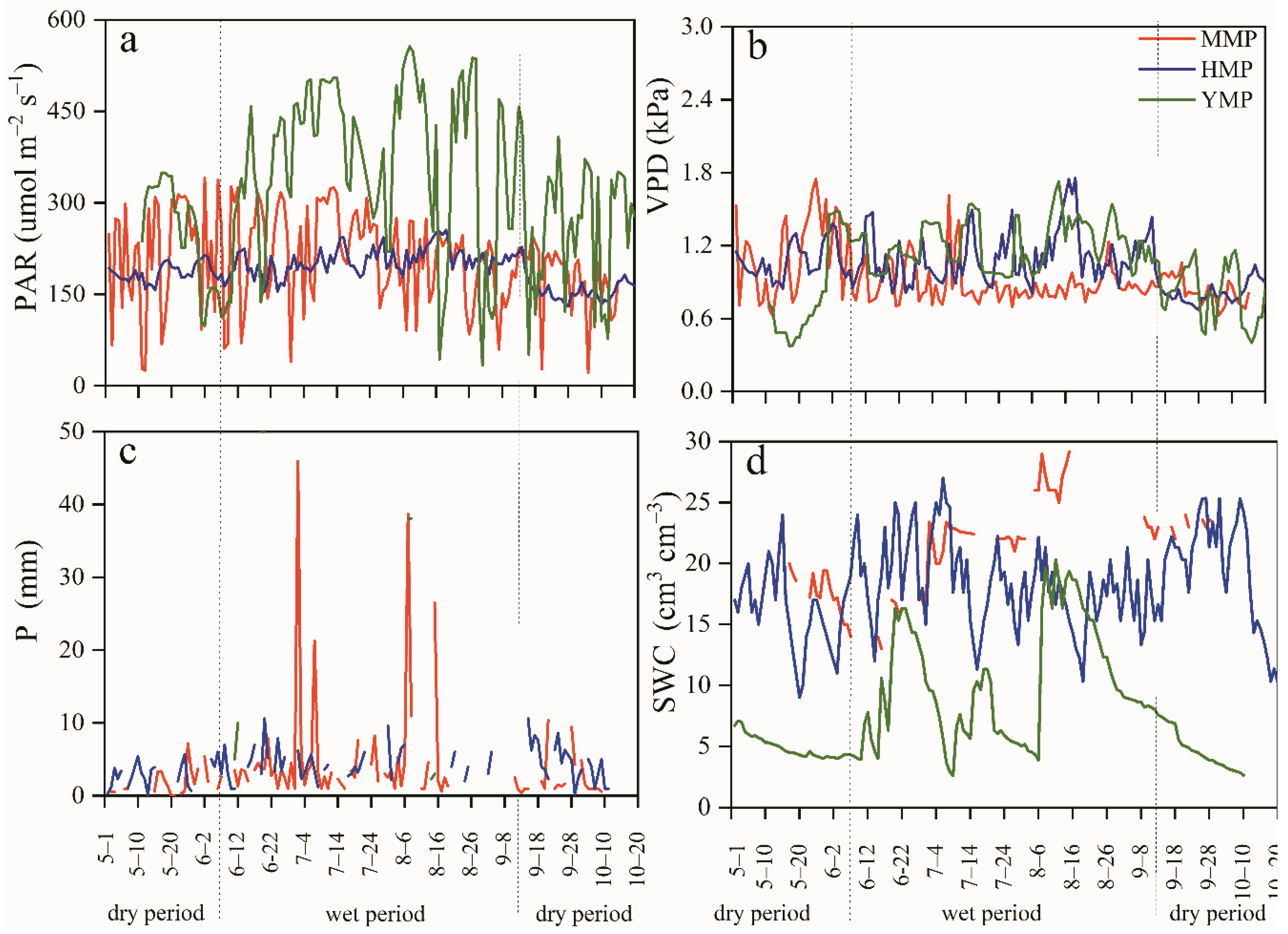
3.1. Atmospheric and Soil Moisture Changes

All environmental factors indicated distinct but similar seasonal changes in the MMP, HMP, and YMP. According to the precipitation characteristics, the growing season (from May 1 to October 20) was divided into dry (May 1 to June 10 and September 15 to October 20) and wet (June 11 to September 14) periods. Over the whole growing season, the daily PAR averaged 207.09, 190.45, and 322.17 μmol m s⁻¹ for the MMP, HMP, and YMP, respectively (Figure 2a). The daily mean VPD averaged 0.93, 1.04, and 1.05 kPa for MMP, HMP, and YMP, respectively (Figure 2b). The accumulated P over the entire study period was 274.8, 387.1, and 402.5 mm in MMP, HMP, and YMP, respectively (Figure 2c). SWC ranged from 2.60 to 20.33 cm³ cm^–3 for MMP, 9.00 to 27.00 cm³ cm⁻³ for HMP, and 12.00 to 29.20 cm³ cm^–3 for YMP (Figure 2d). In the dry period, the daily PAR ranged from 22.14 to 341.14 μmol m s⁻¹ in MMP, 130.55 to 214.35 μmol m s⁻¹ in HMP, and 51.63 to 408.20 μmol m s⁻¹ in YMP, with mean values of 195.57, 170.61, and 248.84 μmol m s⁻¹, respectively (Figure 2a). The daily mean VPD ranged from 0.62 to 1.75 KPa in MMP, 0.67 to 1.38 KPa in HMP, and 0.38 to 1.48 KPa in YMP, with mean values of 0.99, 0.95, and 0.83 KPa, respectively (Figure 2b). The accumulated P over the entire study period was 4.0, 160.5, and 50.1 mm in the MMP, HMP, and YMP treatments, respectively (Figure 2c). SWC ranged from 9.00 to 25.35 cm³ cm^–3 with a mean value of 17.00 cm³ cm^–3 for the MMP, 12.00 to 24.00 cm³ cm^–3 with the mean value of 16.01 cm³ cm^–3 for the HMP, and 2.63 to 7.23 cm³ cm^–3 with the mean value of 4.69 cm³ cm^–3 for the YMP (Figure 2d). In the wet period, the daily PAR ranged from 39.80 to 325.42 μmol m s⁻¹ in the MMP, 154.76 to 255.55 μmol m s⁻¹ in the HMP, and 33.56 to 556.29 μmol m s⁻¹ in the YMP, with mean values of 215.86, 206.68, and 373.84 μmol m s⁻¹, respectively (Figure 2a). The daily mean VPD ranged from 0.69 to 1.61 KPa in the MMP, 0.80 to 1.75 KPa in the HMP, and 0.94 to 1.73 KPa in the YMP, with mean values of 0.88, 1.12, and 1.21 KPa, respectively (Figure 2b). The accumulated P over the entire study period was 270.8, 226.6, and 270.3 mm in the MMP, HMP, and YMP, respectively (Figure 2c). SWC ranged from 13.00 to 29.20 cm³ cm^–3 with the mean value of 22.53 cm³ cm^–3 for MMP, 10.32 to 27.00 cm³ cm^–3 with the mean value of 18.30 cm³ cm^–3 for HMP, and 2.60 to 20.33 cm³ cm^–3 with the mean value of 10.56 cm³ cm^–3 for YMP (Figure 2d). During the wet period, the daily PAR ranged from 39.80 to 325.42 μmol m s⁻¹ in MMP, 154.76 to 255.55 μmol m s⁻¹ in HMP, and 33.56 to 556.29 μmol m s⁻¹ in YMP, with mean values of 215.86, 206.68, and 373.84 μmol m s⁻¹, respectively (Figure 2a). The daily mean VPD ranged from 0.69 to 1.61 kPa in MMP, 0.80 to 1.75 kPa in HMP, and 0.94 to 1.73 kPa in YMP, with mean values of 0.88, 1.12, and 1.21 kPa, respectively (Figure 2b). The cumulative precipitation over the entire study period was 270.8, 226.6, and 270.3 mm in MMP, HMP, and YMP, respectively (Figure 2c). SWC ranged from 13.00 to 29.20 cm³ cm^–3, with a mean value of 22.53 cm³ cm^–3 for MMP; 10.32 to 27.00 cm³ cm^–3, with a mean value of 18.30 cm³ cm^–3 for HMP; and 2.60 to 20.33 cm³ cm^–3, with a mean value of 10.56 cm³ cm^–3 for YMP (Figure 2d).

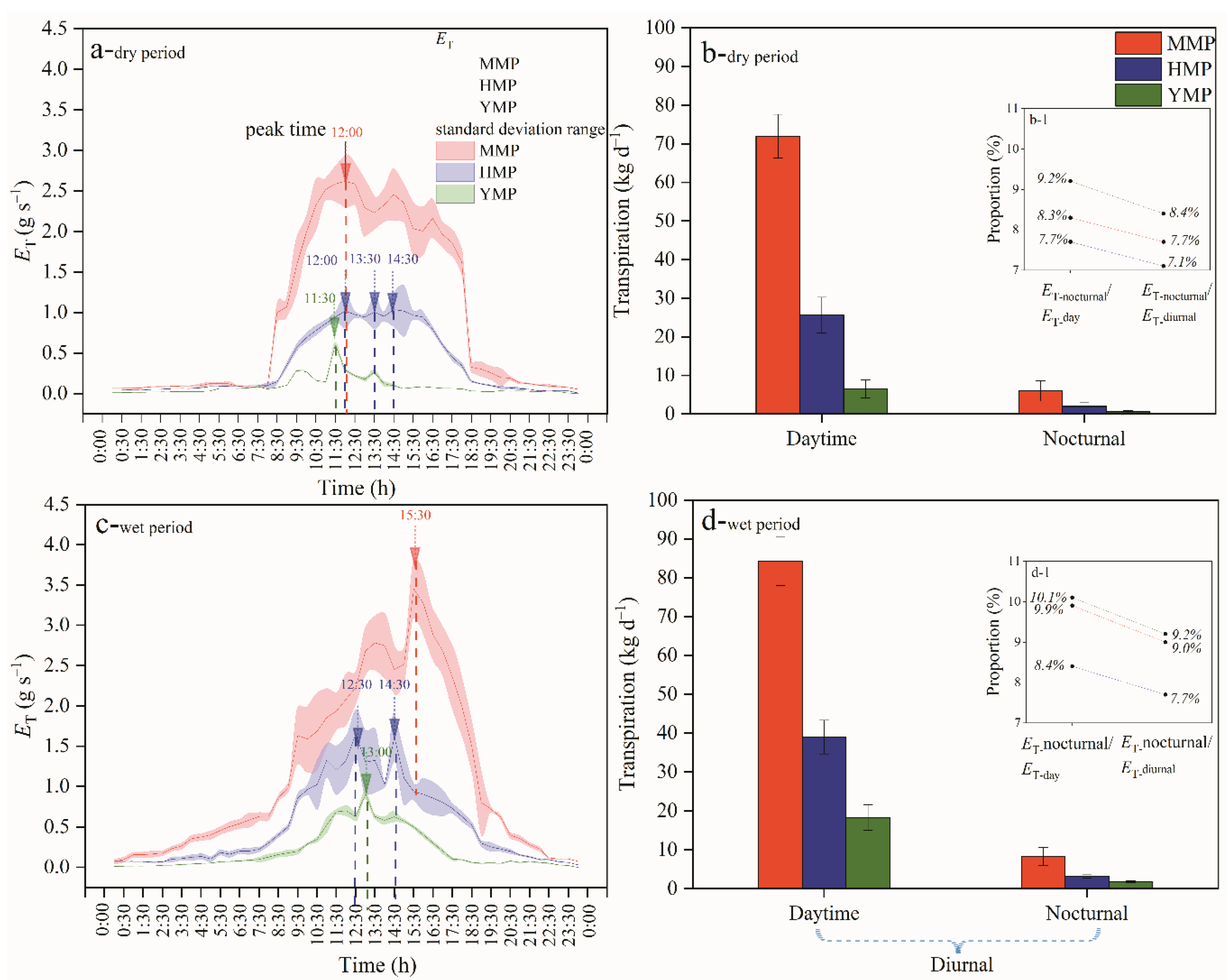
3.2. Tree Water Consumption

The diurnal courses of E_T showed similar patterns for the MMP, HMP, and YMP. Generally, J_s increased in the morning as PAR and VPD increased and reached a maximum, then decreased in the afternoon and reached a minimum late at night (Figure 3a,c). The time when the variables started to grow differed by 0.5–1.5 h but the time when they started to decreased differed by 1.0–6.0 h. During the dry period, E_T reached its peak at 12:00 with a maximum value of 2.62 g s⁻¹ in the MMP. For the HMP, E_T peaked at 12:00, 13:30, and 14:30 with values of 1.02 g s⁻¹, 1.00 g s⁻¹, and 1.04 g s⁻¹, respectively; while for the YMP, E_T peaked at 11:30 with a value of 0.600 g s⁻¹ in YMP (Figure 3a). In the wet period, E_T peaked at 15:30 with 3.45 g s⁻¹ in the MMP, it peaked at 12:30 and 14:30 with 1.65 g s⁻¹ and 1.60 g s⁻¹ in the HMP, respectively; and at 13:00 with 0.90 g s⁻¹ in the YMP (Figure 3c). During this study, J_s occurred at night. In the dry period, the total daytime ET averaged 72.00, 25.63, and 6.55 kg d⁻¹ for the MMP, HMP, and YMP. The total nocturnal E_T averaged 6.00, 1.96, and 0.60 kg d⁻¹ for the MMP, HMP, and YMP, respectively. The total nocturnal E_T was 8.3%, 7.7%, and 9.2% of the daytime E_T in the wet period and the total nocturnal ET was 7.7%, 7.1%, and 8.4% of the diurnal E_T in the dry period, respectively (Figure 3b-1). In the wet period, the total daytime E_T averaged 84.32, 39.00, and 18.33 kg d⁻¹ and the total nocturnal E_T averaged 8.32, 3.26, and 1.86 kg d⁻¹ for MMP, HMP, and YMP, respectively. Additionally, the total nocturnal E_T was 9.9%, 8.4%, and 10.1% of the daytime E_T and the total nocturnal E_T was 9.0%, 7.7%, and 9.2% of the diurnal E_T, respectively (Figure 3d-1).

The linear regression relationships between E_T and PAR, as well as VPD in the dry and wet periods for the MMP (R² = 0.847 and 0.886), HMP (R² = 0.871 and 0.963), and YMP (R² = 0.789 and 0.810) show that E_T has a good relationship with PAR, as well as VPD, especially during the wet period (Table 2).

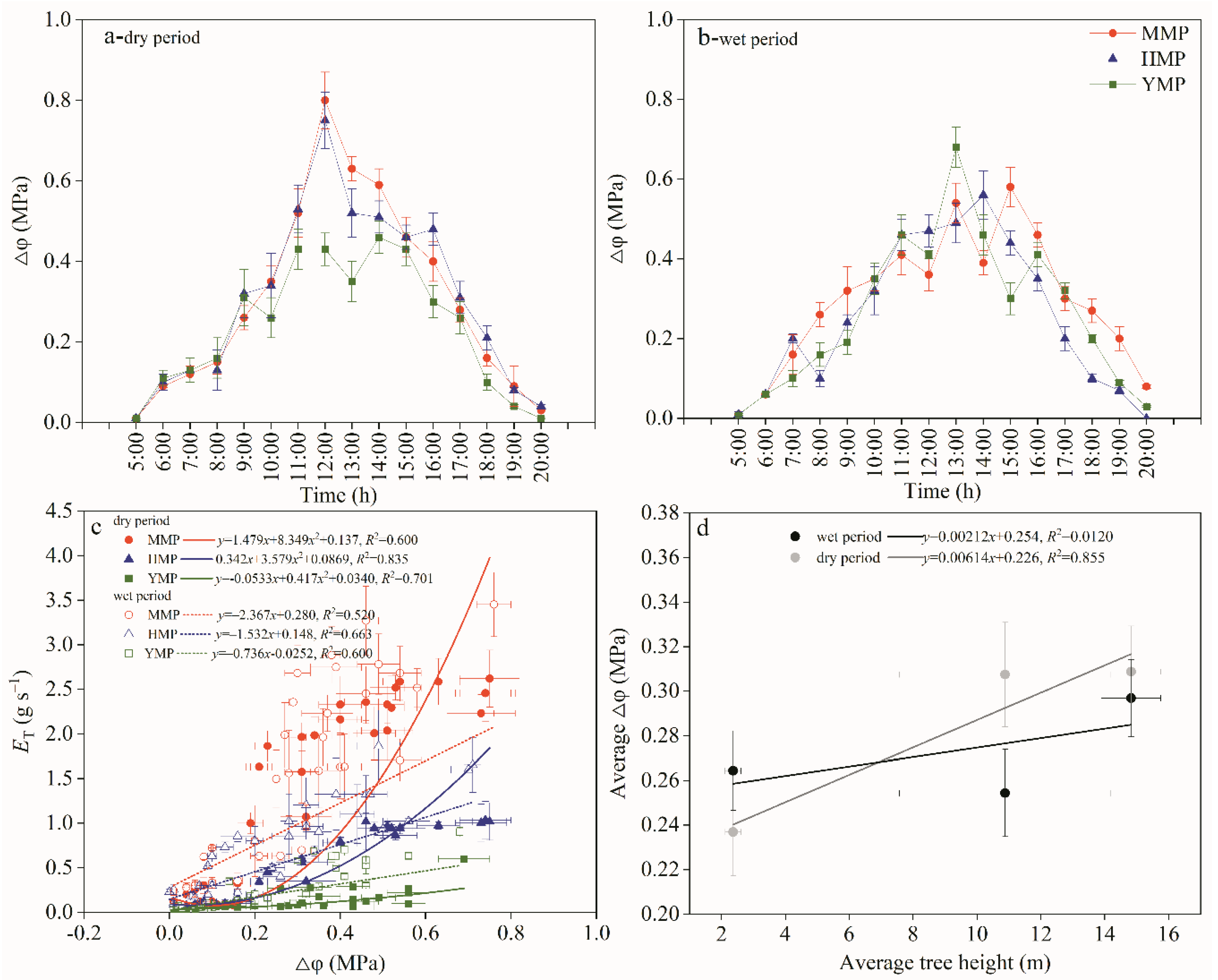
3.3. Relations Between Tree Water Consumption and Soil to Leaf Water Potential Difference

For the whole tree, the leaf has the lowest water potential, and the plant needs to overcome the pressure caused by the water potential difference in the process of absorbing water. With the opening of leaf stomata, transpiration begins to consume water in the leaves, resulting in a gradual decrease in water potential. The diurnal courses of ΔΨ had similar patterns for the three forest types. In the dry period, ΔΨ averaged 0.32, 0.33, and 0.27 MPa for the MMP, HMP, and YMP, respectively (Figure 4a). In the dry period, ΔΨ averaged 0.31, 0.26, and 0.26 MPa for the MMP, HMP, and YMP, respectively (Figure 4b). In the dry period, the functions of E_T and ΔΨ followed a non-linear relationship, where the functions of E_T and ΔΨ equated to y = 1.479x + 8.349x² + 0.173, R² = 0.600, y = 0.342x + 3.579x² + 0.0869, R² = 0.835, y = −0.0533x + 0.417x² + 0.0340, R² = 0.701 for the MMP, HMP, and YMP, respectively. In the wet period, the functions of E_T and ΔΨ demonstrated linear relationships, which equated to y = −2.367x + 0.280, R² = 0.520, y = −1.532x + 0.148, R² = 0.663, and y = −0.736x − 0.0252, R² = 0.600 for the MMP, HMP, and YMP, respectively (Figure 4c). Additionally, with H rising, ΔΨ values were elevated especially in the dry period, when y = 0.00614x + 0.226, and determination coefficient was 0.855.

3.4. Whole Tree Hydraulic Conductance Changes

Whole-tree hydraulic conductivity is an indirect expression of the effect of tree hydraulic structure on water transport efficiency. Figure 5 shows that K_T was higher in the morning and gradually decreased over time. The change in K_T in the morning was gentle but drastic in the afternoon and in the dry period than in the wet period. The K_T values in the dry period were lower than those in the wet period, indicating that the hydraulic resistance in the dry period was higher (Figure 5a,b). A comparison of K_T during the dry and wet periods is shown in Figure 5c. The K_T was higher during the dry period. The adjustment of a tree's hydraulic structure, water storage, and other biological characteristics may affect hydraulic resistance. Drought increased the hydraulic resistance between the soil and roots and decreased the hydraulic conductivity of sapwood. In addition, since transpiration increases the water column tension of the xylem conduit, water transport resistance depending on the hydraulic structure and soil water condition will restrict excessive transpiration and avoid the joint action of transpiration pull and water column gravity to cause the water column to fracture, or induce cavitation, and stomata are appropriately closed to maintain water balance. Therefore, the hydraulic resistance during the dry period can increase further. The functions of K_T and H showed a non-linear relationship, where the functions of KT and H equated to y = −0.218x + 0.0246x² + 1.136, R² = 0.899, y = −0.111x + 0.0143x² + 0.676, R² = 0.777 for the three forest types, respectively (Figure 5d). The reduction rates in K_T from wet to dry periods in MMP, HMPP, and YMP were 12%, 36%, and 22%, respectively (Figure 5d-1).

3.5. Hydraulic Compensation

Since the estimated value of transpiration is calculated by substituting the actual ΔΨ measured at each moment of the wet and dry season test day into the transpiration and water potential difference equation of the corresponding time period, the estimated value of transpiration clearly is highly correlated with the measured value. In the dry period, the functions of the measured E_T and estimated E_T were y = 0.545x + 0.0118, R² = 0.559; y = 0.961x + 0.173, R² = 0.948; and y = 0.785x − 0.0233, R² = 0.930 for MMP, HMP, and YMP, respectively (Figure 6). During the wet period, the functions of the measured E_T and estimated E_T were y = 1.172x + 0.0712, R² = 0.820, y = 0.722x + 0.00249, R² = 0.718, and y = 0.973x + 0.173, R² = 0.508 for MMP, HMP, and YMP, respectively (Figure 6). However, the dry and wet periods were clearly different, that is, a distinct discrepancy between the predicted and measured E_T was apparent: the measured E_T were 0.90, 0.72, and 0.92 times of the predicted E_T for MMP, HMP, and YMP in the dry period, respectively, while in the wet period, the measured E_T T were 1.10-, 1.36, and 1.50 times the predicted values, respectively (Figure 6). Compared with the wet period, the soil water supply was lower during the dry period (see Figure 2). When the VPD was high, the stomata were partially closed to prevent excessive water loss, while the temperature was suitable for growth. Therefore, plants balance the relationship between preventing excessive water loss and effectively utilizing light and heat resources by adjusting their hydraulic conductivity. During the wet period, the water supply is sufficient, solar radiation is also high, and suitable water and heat conditions are available to meet the vigorous growth of plants. Plant transpiration is not restricted by water and heat resources; consequently, the measured value was less than and greater than the predicted value in the dry and wet periods, respectively. The results demonstrated that tree transpiration during the dry season was not only controlled by gs but also by K_T.

The K_T in dry season had an obvious compensation effect on E_T, and the hydraulic compensation effect appeared from 12:00 to 14:00, when the PAR and VPD reached their highest values (means were 1024.54 μmol m s⁻¹ and 2.10 Kpa, respectively), and the average compensation value was 0.097 g s⁻¹ in the MMP. Further, the hydraulic compensation effect appeared from 12:00 to 13:00, mean PAR and VPD were 956.31 μmol m s⁻¹ and 2.03 KPa, the mean compensation value was 0.12 g s⁻¹ in the HMP. Additionally, the hydraulic compensation effect appeared at 11:00, mean PAR and VPD were 986.31 μmol m s⁻¹ and 2.08 Kpa, and the average compensation value was 0.022 g s⁻¹ in the YMP. Meanwhile, during the wet period, no compensating effect was found (Figure 7). The pattern of hydraulic compensation changes was the same as that of transpiration variations.

3.6. Water Transport Regulation in Plants

According to Equation 7, the theoretical model assumes a linear relationship between predawn and midday leaf water potentials. From the Figure 7, we can see in the dry period, mean σ was 1.314, 1.749, and 1.033 in the MMP, HMP, and YMP, respectively (Figure 8a, b, c). While, in the wet period, mean σ was 2.105, 1.931, and 2.046 in the MMP, HMP, and YMP, respectively (Figure 8d, e, f). These results indicated that in both the dry and wet periods, MMP, HMP, and YMP all showed the extreme anisohydric behavior (Figure 8g). Even from wet to dry periods, the reduction rates of σ in the MMP, HMPP, and YMP showed that MMP, HMP, and YMP all showed extreme anisohydric behavior (Figure 8h).

4. Discussion

4.1. Seasonal Transpiration Dynamics

The study area experienced marked seasonal variations in precipitation, PARs, VPDs, and SWCs. During the dry period, the transpiration rates of Mongolian pine plantations were higher in the morning than in the afternoon and declined during the wet period in response to increasing PARs and VPDs. Interestingly, such patterns were not evident in HMP compared to MMP and YMP. The primary reason for this transpiration rate difference in plantation stage between dry and wet periods appears to be caused by a less distinct contrast between dry and wet periods in HMP in the study area. For example, the total rainfall was evenly spread throughout the growing season, with 160.5 and 266.6 mm for dry and wet periods, respectively. SWC averaged 16.01 and 18.30 cm³ cm^–3, respectively, resulting in consistent transpiration rates in HMP across both periods. Transpiration rates surged in the morning with increasing PAR and VPD, peaked in the early afternoon, and declined toward dusk [58]. A slight midday dip indicated stomatal control, corresponding with the declining leaf water potential earlier in the morning [59]. This result is consistent with expectations in this region given the extended seasonal drought, where many species exhibited decreased leaf stomatal conductance and predawn leaf water potential [59,60]. However, the relatively high transpiration rates during the dry period suggest that soil water availability was not a limiting factor. Possibly, larger tree sizes enabled greater water storage, or nocturnal transpiration may have replenished daytime water loss during the extended dry period [11,61,62]. In addition, the increased evaporative demand over the dry period exceeded the decline in g_s resulting from the increased VPD and PAR and reduced predawn leaf water potential [60]. Elevated air and leaf temperatures resulted in increased vapor pressure within the leaves, driving transpiration rates [63]. These findings mirror patterns seen in P. sylvestris forests in other regions and in this study [63,64], corroborating our first hypothesis. This finding further highlights the challenges in extrapolating leaf scale findings to larger scales, such as whole-tree or stand responses. Factors like internal water storage, nighttime transpiration, and fluctuating PAR and VPDs contribute to diverse tree transpiration rates, resulting in species-specific variations.

4.2. Hydraulic Compensation Effect

Our study assessed the complex issue of the regulation of forest transpiration, an area of research that, despite making some progress, still lacks a clear consensus. For example, Pataki et al. [65] assessed transpiration sensitivity in different plant species and found that Populus tremuloides exhibited high sensitivity to VPD, whereas Pinus fexilis demonstrated the lowest sensitivity. Similarly, Granier et al. [66] reported a stronger correlation between J_s and VPD than that between PAR and T_a in 21-year-old Norwegian spruce (Picea abies). The sap flow of Hedysarum scoparium in large plants was more sensitive to environmental factors, exhibiting daily J_s variation that correlated with T_a, VPD, wind speed, relative humidity, soil temperature, and soil surface heat flux. Moreover, substantial nocturnal transpiration was detected, exhibiting seasonal variations similar to daytime transpiration patterns [11]. Notably, nocturnal transpiration in smaller plants was more sensitive to meteorological factors. In semiarid regions, studies on Tamarix elongata, and Juniperus scopulorum suggested that even at relatively high T_a and VPD (1.5 KPa and 2.5 KPa, respectively), nighttime sap flow remained elevated [67,68]. Studies on Carya tomentosa and Quercus alba indicated that drought does not alter transpiration but accelerates leaf aging and decay after the growing season [69]. Previous research has primarily focused on the external environmental influences on plant transpiration [70]. However, the impact of environmental factors on plant physiology should not be overlooked, especially since specific combinations of environmental factors likely influence plant respiration. For example, the semiarid regions of northern China experience prolonged water-deficit periods alongside high PAR and VPD values. These variables are correlated with each other, potentially with a compensatory effect that influences plant growth under adverse environmental conditions. It is possible that plants in this region may have acquired genetic characteristics (physiology), enabling them to dynamically respond to varying environmental factors [11]. As the predominant shelterbelt tree species, P. sylvestris has adapted to endure harsh environmental conditions by adjusting transpiration [22,24,42]. Our study findings revealed that PAR and VPD strongly controlled the transpiration rates in P. sylvestri forests during both the dry and wet periods, although the degree of control varied over time. It has been speculated that the internal regulation of trees might contribute to these varying degrees of control. Therefore, the synergistic effects of meteorological factors and internal hydraulic characteristics on P. sylvestris transpiration rates are crucial. The understanding of water transport in plants is based on the cohesive tension theory. Soil water deficits caused by an imbalance of water input (rainfall) and output (transpiration + evaporation) change the cohesion and tension of plant water, resulting in changes in hydraulic characteristics [71,72]. The cohesion tension theory is widely supported as an effective theory, consistent with the preponderance of data on water transport in plants [71]. Studies have shown that continuous tracheid/catheter cavitation caused by a long-term soil water deficit weakens the water transport capacity of the xylem, disrupts water transport from the xylem to the leaves in plants, and disrupts xylem function, leading to canopy drying, top dieback, and telome withering [71]. However, after long-term adaptive evolution, plants maintain a safe distance between their hydraulic tension and hydraulic limit threshold by continuously adjusting their hydraulic conductivity to avoid hydraulic imbalances and disasters [73]. Thus, there is not always a linear relationship between transpiration and the direct driving force (i.e., soil/leaf water potential difference, PAR, VPD), especially when soil water deficit (in dry period), PAR and VPD are high, and trees are trying to reduce water loss and prevent leaf water potential from falling below the minimum threshold, resulting in excessive hydraulic tension, and functional imbalance of xylem disaster degeneration, and gs tends to non-linearly decline with the increase of VPD, e.g. the response pattern of H. scoparium transpiration to VPD showed two distinct stages: the minimum threshold of VPD driving force was 1.5 KPa and the optimal T_a was about 20 °C, when VPD < 1.5 kPa, canopy transpiration increased linearly; When VPD is greater than this value, the change of transpiration is non-linear and decreases somewhat, indicating that stomatal conductivity is limited by hydraulic conductivity at this time [11]. Pinus pinaster, Pinus nigra, and P. sylvestris displayed higher water use efficiency, which is the result of their high sensitivity to VPD and stomatal closure [74,75].

The trade-off between hydraulic safety and efficiency is crucial for drought tolerance in tree species under water-limited conditions. Lower hydraulic conductance (K_T) limits water movement from the roots to the leaves, promoting conservative water use and thus, aiding plant survival [37,75]. However, our research findings are in contrast with previous intraspecific and interspecific studies that suggested lower K_T (more K_T reduction rates in taller trees) maintained higher xylem water potential gradients and embolism. This relationship was observed across P. sylvestris populations [19], Pinus sp. [19,75], and Abies sp. [76], where hydraulic conductance strongly correlated with gs and photosynthetic capacity in the conifers [77]. Similar to other studies, in our study, the K_T declined from the wet to dry periods, potentially due to greater investment in photosynthetic capacity, especially notable in YMP. This investment helps plant survival but might lead to xylem cavitation due to reduced short-term transpiration and water potential in the dry season [73,78,79]. However, Leyre et al. [37] found no evidence of a trade-off between hydraulic conductivity and resistance to xylem embolism in P. sylvestris populations, and it is unclear whether the loss of hydraulic conductivity in response to drought is related to tree survival under field conditions [73,78,80]. Therefore, the link between stomatal function and plant hydraulics needs to be further explored in the future [27]. In summary, based on the hydraulic compensation theory by Mcdowell et al. [35], when variables like A_L: A_S, ΔΨ, and VPDs fluctuate, an increase in KT and ΔΨ along with the H (or less K_T reduction rates in taller trees from wet to dry period) may balance the effect of H on g_s, potentially resulting in compensation for H-induced hydraulic changes. Moreover, we estimated ET based on AL: AS and ΔΨ. Interestingly, E_T was underestimated during the wet period but overestimated in the dry period. This finding indicates that during the dry period, transportation is co-controlled by gs and K_T when PAR and VPD values peaked. This adjustment ensured adequate CO₂ absorption and maintain moderate tree growth, confirming our second hypothesis.

4.3. Quantification the Mechanisms of Plant Water Transport Regulation

Plant functions require effective mechanisms to regulate water transport on a variety of scales. In this study, we adopted the equation developed by Martínez-Vilalta et al. [27] based on the relationship between midday and predawn leaf water potentials. The intercept of this relationship measures the relative sensitivity of transpiration rate and plant hydraulic conductance to declining water availability. This method helps normalize differences in rooting systems across species [81]. We noticed a σ > 1 during both dry and wet periods, suggesting extreme anisohydric behavior in Mongolian pine plantations. This behaviour implies an increased pressure drop within the plant as ΨS declines. While a reduction in σ values from the wet to dry period indicates a tendency for P. sylvestris forests to moderately close their stomata and adjust the whole tree hydraulic conductance, the σ values still remain >1 in this study. This observation suggests that stomata are insensitive to environmental changes. Although increased g_s could enhance CO₂ uptake and subsequent photosynthesis and growth [57,63], the current precipitation levels in these regions cannot meet the water needs of P. sylvestris. Canopy interception accounted for about 36.0% of P [9,21], making this phenomenon much harsher. Surprisingly, in mature and young forests, the transpiration rate remained consistent, which was contrary to the hydraulic limitation hypothesis and our third hypothesis. This finding challenges the hydraulic limitation hypothesis as an explanatory mechanism for tree size and transpiration characteristics in Mongolian pine plantations, aligning with previous research [17]. Ryan and Yoder [82] proposed that hydraulic conductance and transpiration decrease as trees grow taller, affecting carbon assimilation. However, our study, akin to the frequently observed parabolic mortality pattern with plant DBH [83,84], notes the highest dieback and decline rates in the smallest and largest trees.

5. Conclusions

In this study, we assessed the hydraulic responses governing whole-tree transpiration (E_T) in mature, half-mature, and young Mongolian pine plantations in the Mu Us and Horqin Deserts of China. Our investigation revealed a significant correlation between E_T and environmental factors like PAR and VPD in both the dry and wet periods. However, during the dry period, E_T was co-regulated by both stomatal and hydraulic conductance (K_T), whereas in the wet season, it was primarily regulated by stomatal conductance due to adequate water supply and favorable atmospheric conditions. A critical observation was the occurrence of hydraulic compensation for E_T, occurring between 11:00 and 13:00 during the dry period. The compensation values measured 0.097 g s⁻¹, 0.12 g s⁻¹, and 0.022 g s⁻¹ for mature, half-mature, and young plantations, respectively. Further, our study established a linear relationship between predawn and midday leaf water potentials, exhibiting extreme anisohydric behavior across plantation stages during the growing season. Although both stomatal and hydraulic conductance played roles in regulating E_T during the dry period, environmental conditions likely led to variations among plantation stages. These findings hold promise for informing forest management practices in semiarid regions, offering valuable insights into the complex dynamics of water transportation regulation in Mongolian pine plantations.

Author Contributions

Formal analysis, Jifeng Deng and Yanfeng Bao; Investigation, Jifeng Deng, Longyan Wan and Qingbin Jia; Methodology, Longyan Wan, Yanfeng Bao and Minghan Yu; Project administration, Yanfeng Bao; Resources, Yanfeng Bao, Minghan Yu and Qingbin Jia; Software, Jifeng Deng and Longyan Wan; Supervision, Jifeng Deng and Yanfeng Bao; Validation, Qingbin Jia; Visualization, Minghan Yu; Writing – original draft, Jifeng Deng and Longyan Wan.

Funding

The work was supported by the National Natural Science Foundation of China Special Project “Research on Intelligent Control of Seabuckthorn Fruit in Naiman Banner Based on Multi-Platform Remote Sensing and iot Perception” (grant number M2242005) and National Natural Science Foundation of China “Isohydric versus anisohydric behavior characteristics and adaptive mechanisms of Pinus sylvestris var. mongolica in typical Sandy land in northern China” (grant number 31800609). We would like to thank Editage (www.editage.cn) for English language editing.

Acknowledgments

Many thanks to Xinxing Wang, Daiqing Gele, Yihan Wang, Congcong Zhang, Xiaobo Liu, Yang Liu, Jiaqi Yao, Changyuan Liu and Miao Yu for their support in preparing the experiments, collecting data, analyzing data.

Conflicts of Interest

The authors declare no conflict of interest.

References

DeKauwe, M.G.; Medlyn, B.E.; Zaehle, S.; Walker, A.P.; Dietze, M.C.; Hickler, T.; Jain, A.K.; Luo, Y. Forest water use and water use efficiency at elevated CO₂: a model-data intercomparison at two contrasting temperate forest FACE sites. Global Change Biol. 2013, 19, 1759–1779. [Google Scholar] [CrossRef] [PubMed]
Gordo, O.; Sanz, J.J. Impact of climate change on plant phenology in Mediterranean ecosystems. Global Change Biol. 2010, 16, 1082–1106. [Google Scholar] [CrossRef]
Xu, C.; McDowell, N.G.; Sevanto, S.; Fisher, R.A. Our limited ability to predict vegetation dynamics under water stress. New Phytol. 2013, 200, 298–300. [Google Scholar] [CrossRef] [PubMed]
Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global semi-arid climate change over last 60 years. Clim. Dynam. 2015, 46, 1131–1150. [Google Scholar] [CrossRef]
Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Change. 2016, 6, 166–171. [Google Scholar] [CrossRef]
Anderegg, W.R.L.; Kane, J.M.; Anderegg, L.D.L. Consequences of wide spread tree mortality triggered by drought and temperature stress. Nat. Clim. Change. 2013, 3, 30–36. [Google Scholar] [CrossRef]
Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
Jones, C.; Lowe, J.; Liddicoat, S.; Betts, R. Committed terrestrial ecosystem changes due to climate change. Nat. Geosci. 2009, 2, 484–487. [Google Scholar] [CrossRef]
Deng, J.; Yu, Y.; Shao, J.; Lu, S.; Liu, F.; Li, Z.; Shi, X. Rainfall interception using the revised Gash analytical model for Pinus sylvestris var. mongolica in a semi-humid region of NE China. Ecol. Indic. 2022, 143, 109399. [Google Scholar] [CrossRef]
Zheng, X.; Zhu, J.J.; Yan, Q.L.; Song, L.N. Effects of land use changes on the groundwater table and the decline of Pinus sylvestris var. mongolica plantations in southern Horqin Sandy Land, Northeast China. Agr. Water Manage. 2012, 109, 94–106. [Google Scholar] [CrossRef]
Deng, J.F.; Ding, G.D.; Gao, G.L.; Wu, B.; Zhang, Y.Q.; Gao, S.; Fan, W.H. The sap flow dynamics and response of Hedysarum scoparium to environmental factors in semiarid Northwestern China. Plos One 2015, 10, e0131683. [Google Scholar] [CrossRef] [PubMed]
Wu, B.; Ci, L.J. Landscape change and desertification development in the Mu Us Sandy land, Northern China. J. Arid Environ. 2002, 50, 429–444. [Google Scholar] [CrossRef]
Bo, T.L.; Ma, P.; Zheng, X.J. Numerical study on the effect of semi-buried straw checkerboard sand barriers belt on the wind speed. Aeolian Res. 2015, 16, 101–107. [Google Scholar] [CrossRef]
Li, X.R.; Ji, R.L.; Chen, Y.W.; Huang, L.; Zhang, P. Association of ant nests with successional stages of biological soil crusts in the Tengger Desert, Northern China. Appl. Soil Ecol. 2011, 47, 59–66. [Google Scholar] [CrossRef]
Tang, Y.; Li, X. Simulating effects of precipitation and initial planting density on population size of Mongolian pine in the Horqin Sandy Land, China. Agroforest Syst. 2018, 92, 1–9. [Google Scholar] [CrossRef]
Chen, F.S.; Zeng, D.H.; Zhou, B.; Singh, A.N.; Fan, Z.P. Seasonal variation in soil nitrogen availability under Mongolian pine plantations at the Keerqin Sand Lands, China. J. Arid Environ. 2006, 67, 226–239. [Google Scholar] [CrossRef]
Deng, J.F.; Yao, J.Q.; Zheng, X.; Gao, G.L. Transpiration and canopy stomatal conductance dynamics of Mongolian pine plantations in semiarid deserts, Northern China. Agr. Water Manage. 2021, 249, 106806. [Google Scholar] [CrossRef]
Zeng, D.H.; Hu, Y.L.; Chang, S.X.; Fan, Z.P. Land cover change effects on soil chemical and biological properties after planting Mongolian pine (Pinus sylvestris var. mongolica) in sandy lands in Keerqin, northeastern China. Plant Soil. 2009, 317, 121–133. [Google Scholar] [CrossRef]
Martínez-Vilalta, J.; Cochard, H.; Mencuccini, M.; Sterck, F.; Herrero, A.; Korhonen, J.F.J.; Llorens, P.; Nikinmaa, E.; Nolc, A.; Poyatos, R.; Ripullone, F.; Sass-Klaassen, U.; Zweifel, R. Hydraulic adjustment of Scots pine across Europe. New Phytol. 2009, 184, 353–364. [Google Scholar] [CrossRef]
Song, L.N.; Zhu, J.J.; Li, M.C.; Zhang, J.X.; Zheng, X.; Wang, K. Canopy transpiration of Pinus sylvestris var. mongolica in a sparse wood grassland in the semiarid sandy region of Northeast China. Agr. Forest Meteorol. 2018, 250–251, 192–201. [Google Scholar] [CrossRef]
Deng, J. Fitting the revised Gash analytical model of rainfall interception to Mongolian Scots pines in Mu Us Sandy Land, China. Trees Forest. People 2020, 1, 100007. [Google Scholar] [CrossRef]
Song, L.; Zhu, J.; Li, M.; Zhang, J.; Lv, L. Sources of water used by Pinus sylvestris var. mongolica trees based on stable isotope measurements in a semiarid sandy region of Northeast China. Agr. Water Manage. 2016, 164, 281–290. [Google Scholar] [CrossRef]
Lenoir, J.; Gegout, J.C.; Marquet, P.A.; Ruffray, P.D.; Brisse, H. A significant upwards hift in plant species optimum elevation during the 20th century. Science 2008, 320, 1768–1771. [Google Scholar] [CrossRef] [PubMed]
Song, L.N.; Li, M.C.; Zhu, J.J.; Zhang, J.X. Comparisons of radial growth and tree ring cellulose δ¹³C for Pinus sylvestris var. mongolica in natural and plantation forests on sandy lands. J. Forest Res-Jpn. 2017, 22, 160–168. [Google Scholar] [CrossRef]
Pockman, W.T.; Sperry, J.S.; O’Leary, J.W. Sustained and significant negative water pressure in xylem. Nature 1995, 378, 715–716. [Google Scholar] [CrossRef] [PubMed]
McDowell, N.G.; Ryan, M.G.; Zeppel, M.J.B.; Tissue, D.T. Improving our knowledge of drought-induced forest mortality through experiments, observations, and modeling. New Phytol. 2013, 200, 289–293. [Google Scholar] [CrossRef] [PubMed]
Martínez-Vilalta, J.M.; Poyatos, R.; Aguadé, D.; Retana, J.; Mencuccini, M. A new look at water transport regulation in plants. New Phytol. 2014, 204, 105–115. [Google Scholar] [CrossRef] [PubMed]
Martínez-Sancho, E.; Dorado-Liñán, I.; Hacke, U.G.; Seidel, H.; Annette, M. Contrasting hydraulic architectures of Scots Pine and Sessile Oak at their southernmost distribution limits. Front. Plant Sci. 2017, 8, 598. [Google Scholar] [CrossRef]
Martínez-Vilalta, J.; Sala, A.; Piñol, J. The hydraulic architecture of Pinaceae—a review. Plant Ecol. 2004, 171, 3–13. [Google Scholar] [CrossRef]
Poyatos, R.; Martínez-Vilalta, J.; Cěrmák, J.; Ceulemans, R.; Granier, A.; Irvine, J.; Köstner, B.; Lagergren, F.; Meiresonne, L.; Nadezhdina, N.; Zimmermann, R.; Llorens, P.; Mencuccini, M. Plasticity in hydraulic architecture of Scots pine across Eurasia. Oecologia 2007, 153, 245–259. [Google Scholar] [CrossRef]
Anderegg, L.D.L.; Hillerislambers, J. Drought stress limits the geographic ranges of two tree species via different physiological mechanisms. Global Change Biol. 2016, 22, 1029–1045. [Google Scholar] [CrossRef]
Naithani, K.J.; Ewers, B.E.; Pendall, E. Sap flux-scaled transpiration and stomatal conductance response to soil and atmospheric drought in a semi-arid sagebrush ecosystem. J. Hydrol. 2012, 464–465, 176–185. [Google Scholar] [CrossRef]
Martre, P.; North, G.B.; Nobel, P.S. Hydraulic conductance and mercury-sensitive water transport for roots of Opuntia acanthocarpa in relation to soil drying and rewetting. Plant Physiol. 2001, 126, 352–362. [Google Scholar] [CrossRef]
Williams, M.; Bond, B.J.; Ryan, M.G. Evaluating different soil and plant hydraulic constraints on tree function using a model and sap flow data from ponderosa pine. Plant, Cell and Environ. 2010, 24, 679–690. [Google Scholar] [CrossRef]
McDowell, N.G.; Phillips, N.; Lunch, C.; Bond, B.J.; Ryan, M.G. An investigation of hydraulic limitation and compensation in large, old Douglas-fir trees. Tree Physiol. 2002, 22, 763–774. [Google Scholar] [CrossRef] [PubMed]
Sala, A. Hydraulic compensation in northern Rocky Mountain conifers: does successional position and life history matter? Oecologia 2006, 149, 1–11. [Google Scholar] [CrossRef] [PubMed]
Leyre, C.; Eustaquio, G.P.; Eduardo, N. Differences in hydraulic architecture between mesic and xeric Pinus pinaster populations at the seedling stage. Tree Physiol. 2012, 32, 1442–1457. [Google Scholar] [CrossRef] [PubMed]
Wullschleger, S.D.; Wilson, K.B.; Hanson, P.J. Environmental control of whole-plant transpiration, canopy conductance and estimates of the decoupling coefficient for large red maple trees. Agr. Forest Meteorol. 2000, 104, 157–168. [Google Scholar] [CrossRef]
Oren, R.; Phillips, N.; Ewers, B.E.; Pataki, D.E. Sap-flux-scaled transpiration responses to light, vapor pressure deficit, and leaf area reduction in a flooded Taxodium distichum forest. Tree Physiol. 1999, 19, 337–347. [Google Scholar] [CrossRef]
Pataki, D.E.; Oren, R.; Phillips, N. Responses of sap flux and stomatal conductance of Pinus taeda L. trees to stepwise reductions in leaf area. J. Exp. Bot. 1998, 49, 871–878. [Google Scholar] [CrossRef]
Deng, J.; Ma, C.; Yu, H. Different soil particle-size classification systems for calculating volume fractal dimension-A case study of Pinus sylvestris var. Mongolica in Mu Us Sandy Land, China. Appl. Sci-Basel. 2018, 8, 1872. [Google Scholar] [CrossRef]
Song, L.N.; Zhu, J.J.; Li, M.C.; Zhang, J.X.; Zheng, X.; Wang, K. Canopy transpiration of Pinus sylvestris var. mongolica in a sparse wood grassland in the semiarid sandy region of Northeast China. Agr. Forest Meteorol 2018, 250–251, 192–201. [Google Scholar] [CrossRef]
Granier, A. A new method of sap flow measurement in tree stems. Ann. Sci. Forest. 1985, 42, 193–200. [Google Scholar] [CrossRef]
Du, S.; Wang, Y.L.; Kume, T.; Zhang, J.G.; Otsuki, K.; Yamanaka, N.; Liu, G.B. Sapflow characteristics and climatic responses in three forest species in the semiarid Loess Plateau region of China. Agr. Forest Meteorol. 2011, 151, 1–10. [Google Scholar] [CrossRef]
James, S.A.; Clearwater, M.J.; Meinzer, F.C.; Goldstein, G. Heat dissipation sensors of variable length for the measurement of sap flow in trees with deep sapwood. Tree Physiol. 2002, 22, 277–283. [Google Scholar] [CrossRef] [PubMed]
Zhu, J.J.; Fan, Z.P.; Zeng, D.H.; Jiang, F.Q.; Matsuzaki, T. Comparison of stand structure and growth between artificial and natural forests of Pinus sylvestiris var. mongolica on sandy land. J. Forestry Res. 2003, 14, 103–111. [Google Scholar] [CrossRef]
Steinberg, S.L.; Mcfarland, M.J.; Worthington, J.W. Comparison of trunk and branch sap flow with canopy transpiration in Pecan. J. Exp. Bot. 1990, 41, 635–659. [Google Scholar] [CrossRef]
Comstock, J. Variation in hydraulic architecture and gas exchange in two desert sub-shrubs, Hymenoclea salsola (T. & G.) and Ambrosia dumosa. Oecologia 2000, 125, 1–10. [Google Scholar] [CrossRef]
Mencuccini, M.; Comstock, J. Variability in hydraulicarchitecture and gas exchange of common bean (Phaseolus vulgaris) cultivars under well–watered conditions: interactionswith leaf size. Aust. J. Plant Physiol. 1999, 26, 115–124. [Google Scholar] [CrossRef]
Qiu, R.; Kang, S.; Du, T.; Tong, L.; Hao, X.; Chen, R.; Chen, J.; Li, F. Effect of convection on the Penman–Monteith model estimates of transpiration of hot pepper grown in solar greenhouse. Sci. Hortic-Amsterdam. 2013, 160, 163–171. [Google Scholar] [CrossRef]
Shelburne, V.B.; Hedden, R.L.; Allen, R.M. The effectsof site, stand density, and sapwood permeability on the relationship between leaf area and sapwood area in loblolly pine (Pinus taeda L.). Forest Ecol. Manag. 1993, 58, 193–209. [Google Scholar] [CrossRef]
Zhang, Z.Z.; Zhao, P.; McCarthy, H.R.; Zhao, X.H.; Niu, J.F.; Zhu, L.W.; Ni, G.Y.; Ouyang, L.; Huang, Y.Q. Influence of the decoupling degree on the estimation of canopy stomatal conductance for two broadleaf tree species. Agr. Forest Meteorol. 2016, 221, 230–241. [Google Scholar] [CrossRef]
Khamzina, A.; Sommer, R.; Lamers, J.P.A.; Vlek, P.L.G. Transpiration and early growth of tree plantations established on degraded cropland over shallow saline groundwater table in northwest Uzbekistan. Agr. Forest Meteorol. 2009, 149, 1865–1874. [Google Scholar] [CrossRef]
Whitehead, D.; Hinckley, T.M. Models of water flux through forest stands: critical leaf and stand parameters. Tree Physiol. 1991, 9, 35–57. [Google Scholar] [CrossRef] [PubMed]
Köstner, B.M.M.; Schulze, E.-D.; Kelliher, F.M.; Hollinger, D.Y.; Byers, J.N.; Hunt, J.E.; McSeveny, T.M.; Meserth, R.; Weir, P.L. Transpiration and canopy conductance in a pristine broad-leaved forest of Nothofagus: an analysis of xylem sap flow and eddy correlation measurements. Oecologia 1992, 91, 350–359. [Google Scholar] [CrossRef]
Jarvis, P.G.; McNaughton, K.G. Stomatal control of transpiration: scaling up from leaf to region. Adv. Ecol. Res. 1986, 15, 1–49. [Google Scholar] [CrossRef]
Hochberg, U.; Rockwell, F.E.; Holbrook, N.M.; Cochard, H. Iso/Anisohydry: A plant-environment interaction rather than a simple hydraulic trait. Trends Plant Sci. 2018, 23, 112–120. [Google Scholar] [CrossRef]
O'Grady, A.P.; Eamus, D.; Hutley, L.B. Transpiration increases during the dry season: patterns of tree water use in eucalypt open-forests of northern Australia. Tree Physiol. 1999, 19, 591–597. [Google Scholar] [CrossRef] [PubMed]
Myers, B.A.; Duff, G.A.; Eamus, D.; Fordyce, I.R.; A, O.G.; Williams, R.J. Seasonal variation in water relations of trees of differing leaf phenology in a wet--dry tropical savanna near Darwin, northern Australia. Aust. J. Bot. 1997, 45, 225–240. [Google Scholar] [CrossRef]
Prior, L.D.; Eamus, D.; Duff, G.A. Seasonal and diurnal patterns of carbon assimilation, stomatal conductance and leaf water potential in Eucalyptus tetrodonta saplings in a wet-dry savanna in northern Australia. Aust. J. Bot. 1997, 45, 241–258. [Google Scholar] [CrossRef]
Cook, P.G.; Hatton, T.J.; Pidsley, D.; Herczeg, A.L.; Held, A.A.; O’Grady, A.; Eamus, D. Water balance of a tropical woodland ecosysytem, northern Australia: a combination of micrometeorological, soil physical and groundwater chemical approaches. J. Hydrol. 1998, 210, 161–177. [Google Scholar] [CrossRef]
Liu, X.; Zhang, B.; Zhuang, J.Y.; Han, C.; Zhai, L.; Zhao, W.Z.; Zhang, J.C. The relationship between sap flow density and environmental factors in the Yangtze River Delta region of China. Forests 2017, 8, 74. [Google Scholar] [CrossRef]
Song, L.; Zhu, J.; Zheng, X.; Wang, K.; Lü, L.; Zhang, X.; Hao, G. Transpiration and canopy conductance dynamics of Pinus sylvestris var. mongolica in its natural range and in an introduced region in the sandy plains of Northern China. Agr. Forest Meteorol. 2020, 281, 107830. [Google Scholar] [CrossRef]
Urban, J.; Rubtsov, A.V.; Urban, A.V.; Shashkin, A.V.; Benkova, V.E. Canopy transpiration of a Larix sibirica and Pinus sylvestris forest in Central Siberia. Agr. Forest Meteorol. 2019, 271, 64–72. [Google Scholar] [CrossRef]
Pataki, D.E.; Oren, R.; Smith, A.W. Sap flux of co-occurring species in a western subalpine forest during seasonal soil drought. Ecology 2000, 81, 2557–2566. [Google Scholar] [CrossRef]
Granier, A.; Huc, R.; Barigah, S.T. Transpiration of natural rainforest and its dependence on climatic factors. Agr. Forest Meteorol. 1996, 78, 19–29. [Google Scholar] [CrossRef]
Moore, G.W.; Cleverly, J.R.; Owens, M.K. Nocturnal transpiration in riparian Tamarix thickets authenticated by sap flux, eddy covariance and leaf gas exchange measurements. Tree Physiol. 2008, 28, 521–528. [Google Scholar] [CrossRef] [PubMed]
Sellin, A.; Lubenets, K. Variation of transpiration within a canopy of silver birch: effect of canopy position and daily versus nightly water loss. Ecohydrology 2010, 3, 467–477. [Google Scholar] [CrossRef]
Pataki, D.E.; Oren, R. Species differences in stomatal control of water loss at the canopy scale in amature bottom land deciduous forest. Adv. Water Resour. 2003, 26, 1267–1278. [Google Scholar] [CrossRef]
Liu, B.; Zhao, W.Z.; Jin, B.W. The response of sap flow in desert shrubs to environmental variables in an arid region of China. Ecohydrology 2011, 4, 448–457. [Google Scholar] [CrossRef]
Brown, H.R. The theory of the rise of sap in trees: some historical and conceptual remarks. Phys. Perspect. 2013, 15, 320–358. [Google Scholar] [CrossRef]
Lu, P.; Biron, P.; Granier, A.; Cochard, H. Water relations of adult Norway spruce (Picea abies (L) Karst) under soil drought in the Vosges mountains: water potential, stomatal conductance and transpiration. Ann. Forest Sci. 1996, 53, 113–121. [Google Scholar] [CrossRef]
Sperry, J.S. Hydraulic constraints on plant gas exchange. Agr. Forest Meteorol. 2000, 104, 13–23. [Google Scholar] [CrossRef]
Loustau, D.; Berbigier, P.; Roumagnac, P.; Arruda-Pacheco, C.; David, J.S.; Ferreira, M.I.; Pereira, J.S.; Tavares, R. Transpiration of a 64 year old maritime pine stand in Portugal. 1. Seasonal course of water flux through maritime pine. Oecologia 1996, 107, 33–42. [Google Scholar] [CrossRef] [PubMed]
Martínez-Vilalta, J.; Prat, E.; Oliveras, I.; Piñol, J. Hydraulic properties of roots and stems of nine woody species. Oecologia 2002, 133, 19–29. [Google Scholar] [CrossRef]
Peguero-Pina, J.J.; Sancho-Knapik, D.; Cochard, H.; Barredo, G.; Villarroya, D.; Gil-Pelegrín, E. Hydraulic traits limit the distribution range of two closely related Mediterranean firs, Abies alba Mill. and Abies pinsapo Boiss. Tree Physiol. 2011, 31, 1067–1075. [Google Scholar] [CrossRef] [PubMed]
Brodribb, T.J.; Holbrook, N.M.; Zwieniecki, M.A.; Palma, B. Leaf hydraulic capacity in ferns, conifers and angiosperms: impacts on photosynthetic maxima. New Phytol. 2005, 165, 839–846. [Google Scholar] [CrossRef]
Tsuda, M.; Tyree, M.T. Plant hydraulic conductance measured by the high pressure flow meter in crop plants. J. Exp. Bot. 2000, 51, 823–828. [Google Scholar] [CrossRef]
Tyree, M.T.; Ewers, F.W. The hydraulic architecture of trees and other woody plants. New Phytol. 1991, 119, 345–360. [Google Scholar] [CrossRef]
Vilagrosa, A.; Bellot, J.; Vallejo, R.; Gil-Pelegrín, E. Cavitation, stomatal conductance, and leaf dieback in seedlings of two co-occurring Mediterranean shrubs during an intense drought. J. Am. Coll. Surgeons. 2003, 54, 2015–2024. [Google Scholar] [CrossRef]
Martínez-Vilalta, J.; Garcia-Forner, N. Water potential regulation, stomatal behaviour and hydraulic transport under drought: deconstructing the iso/anisohydric concept. Plant Cell and Environ. 2017, 40, 962–976. [Google Scholar] [CrossRef] [PubMed]
Ryan, M.G.; Yoder, B.J. Hydraulic limits to tree height and tree growth. Bioscience 1997, 47, 235–242. [Google Scholar] [CrossRef]
Liu, H.; Williams, A.P.; Allen, C.D.; Guo, D.; Wu, X.; Anenkhonov, O.A.; Liang, E.; Sandanov, D.; Yin, Y.; Qi, Z.; Badmaeva, N.K. Rapid warming accelerates tree growth decline in semi-arid forests of Inner Asia. Global Change Biol. 2013, 19, 2500–2510. [Google Scholar] [CrossRef]
McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; Yepez, E.A. Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Geographical research sites description.

Figure 2. Variations in daily photosynthetically active radiation (PAR, a), vapor pressure deficit (VPD, b), precipitation (P, c) and soil volumetric water content (SWC, d) during the growing season (the growing season is divided into dry and wet periods according to the characteristics of precipitation, split by dot lines) for the mature (MMP), half-mature (HMP), and young (YMP) forests.

Figure 3. Diurnal course of tree water consumption (E_T, a,c), total tree water transpiration in the daytime and nocturnal during the dry and wet periods (b,d), and the proportion of nocturnal tree water consumption to the daytime consumption and diurnal tree water consumption during the dry and wet periods (b-1, d-1) for the mature (MMP), half-mature (HMP), and young (YMP) forests.

Figure 4. Diurnal course of leaf to soil water potential difference in the dry and wet seasons (a,b) and the relationship between diurnal course of tree water consumption and leaf to soil water potential difference in the dry and wet periods (c,d) for the mature (MMP), half-mature (HMP), and young (YMP) forests.

Figure 5. Daily variation of whole tree hydraulic conductance of the MMP, HMP, and YMP forests in dry and wet periods (a,b), and comparison of whole tree hydraulic conductance in dry and wet periods (c), whole tree hydraulic conductance versus tree height of the MMP, HMP, and YMP forests (d), and reduction rates in whole tree hydraulic conductance from wet to dry periods in the mature (MMP), half-mature (HMP), and young (YMP) forests (d-1).

Figure 6. Deviation between measured and predicted transpiration for the mature (MMP), half-mature (HMP), and young (YMP) forests in dry and wet periods.

Figure 7. Hydraulic compensation for transpiration during the time period of 11:00–16:00 for the mature (MMP, a), half-mature (HMP, b), and young (YMP, c) forests in dry and wet periods.

Figure 8. Relationship between predawn and midday leaf water potentials in the mature (MMP; a, d), half-mature (HMP; b, e), and young (YMP; c, f) forests in dry and wet periods. Further, to determine the isohydric and anisohydric tree water transport regulation based on the slope value σ in the MMP, HMP, and YMP forests in dry and wet periods (g), and reduction rates σ from wet to dry season in the MMP, HMP, and YMP forests (h).

Table 1. Minimum, maximum, and mean, values of selected sampling tree traits in the mature, half-mature, and young Mongolian pine plantation forests (MMP, HMP, and YMP, respectively).

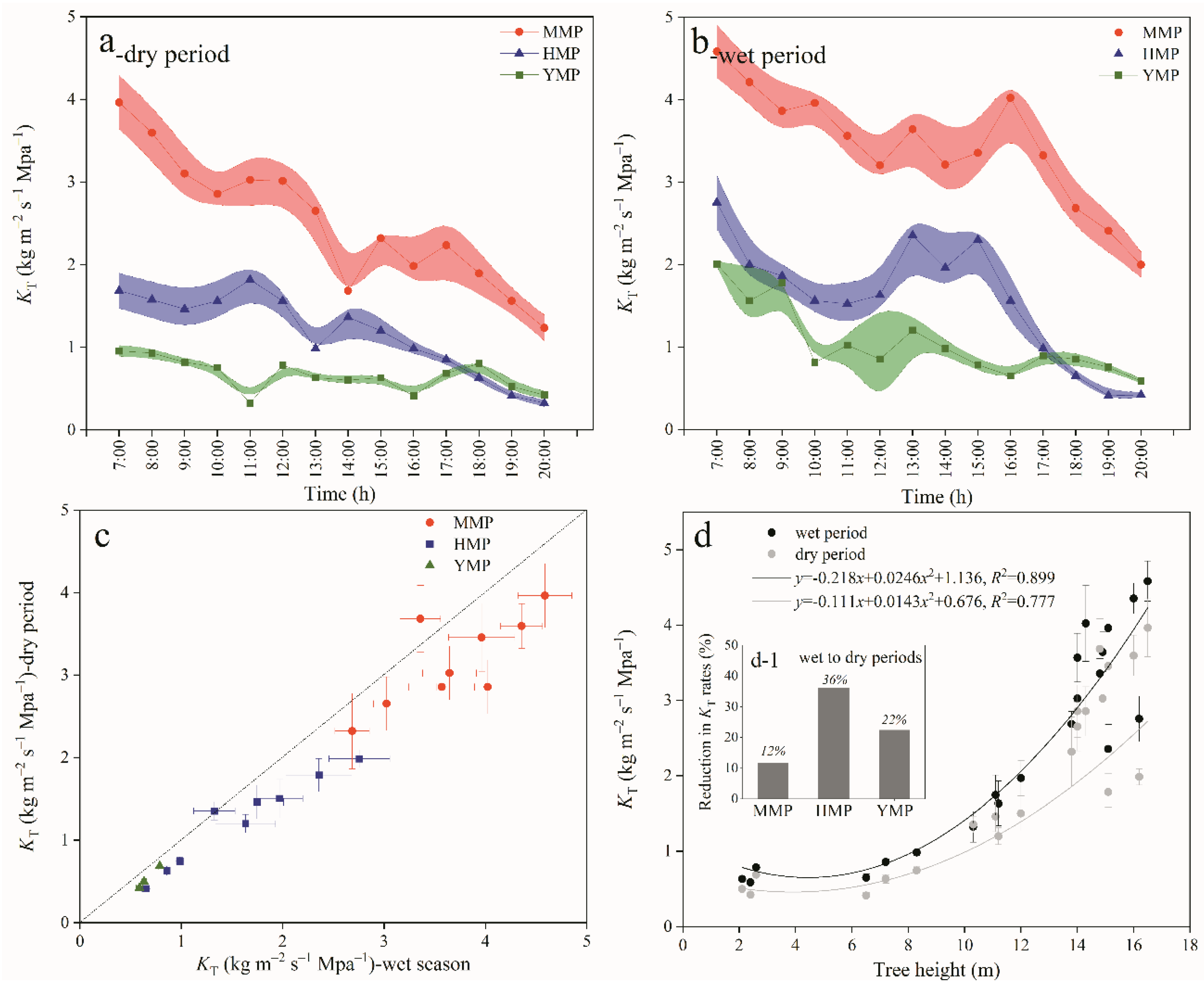
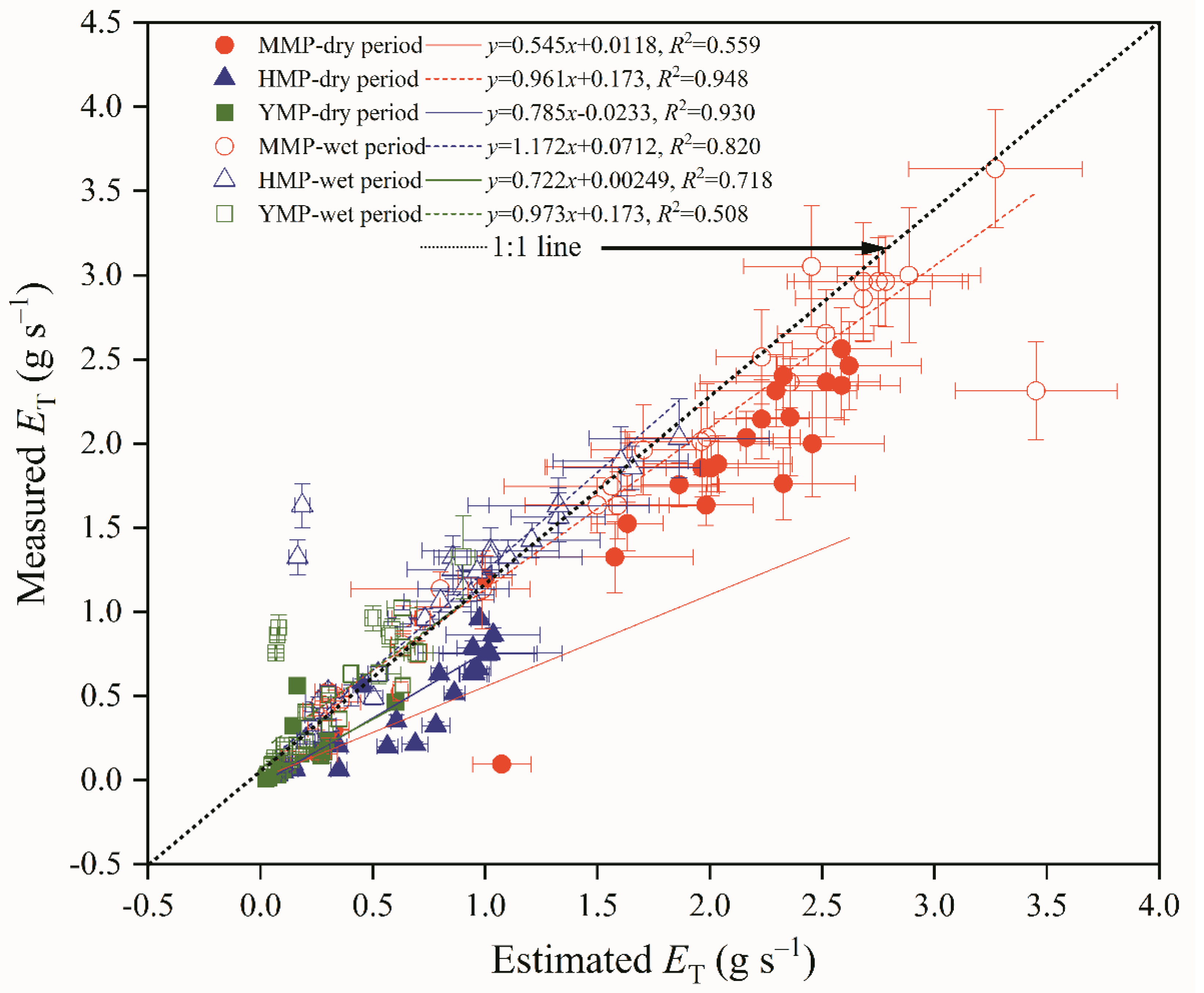
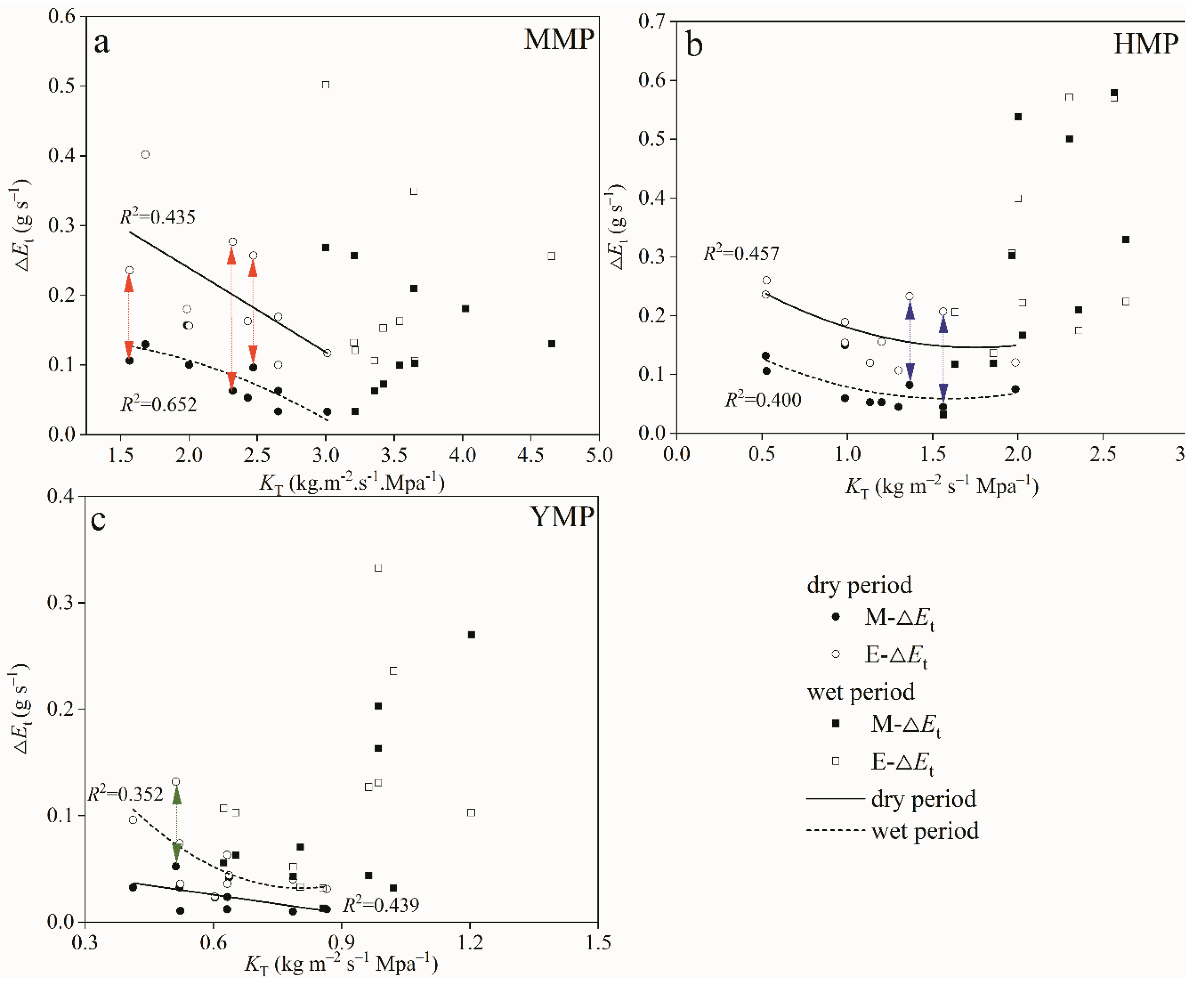
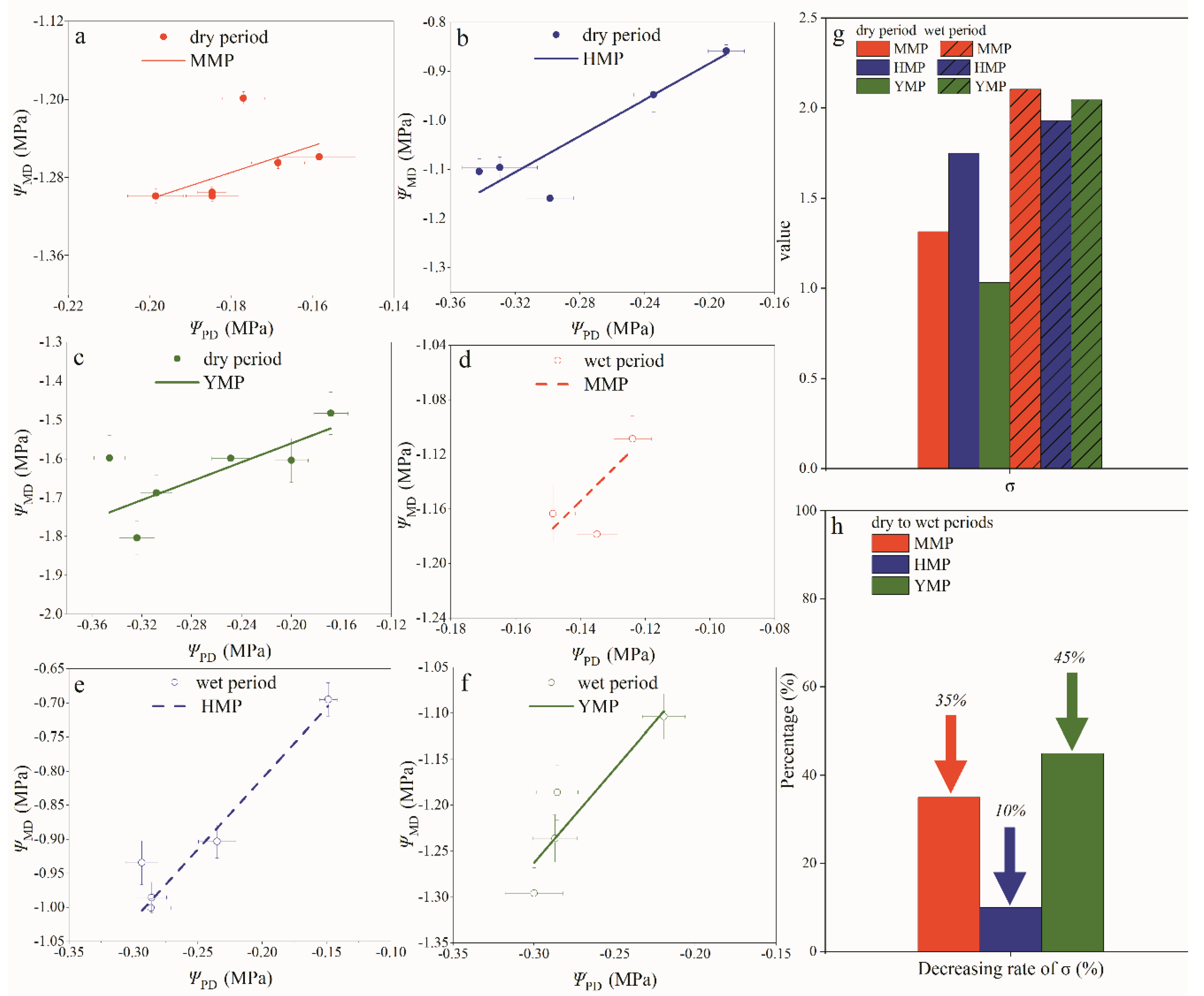
Tree number	Height (m)	DBH (cm)	Height under branch (m)	Crown diameter (m)	SA (cm²)
Max (MMP)	16.5	33.0	7.1	3.8 × 3.8	460.3
Mean (MMP)	14.8	30.9	6.4	3.2 × 3.2	410.6
Min (MMP)	13.8	26.0	5.8	2.6 × 2.7	375.3
Max (HMP)	16.2	28	1.7	2.6 × 2.8	380.6
Mean (HMP)	10.9	18.7	1.5	1.7 × 2.0	215.6
Min (HMP)	6.5	10	1.3	1.1 × 14	67.2
Max (YMP)	2.6	2.8	0.4	1.0 × 1.0	11.3
Mean (YMP)	2.4	2.8	0.3	1.0 × 1.0	10.1
Min (YMP)	2.1	2.7	0.3	0.9 × 1.0	9.5

* DBH: diameter at breast height, SA: sapwood area.

Table 2. Linear regression relationship between E_T and PAR, as well as VPD in the dry and wet periods for MMP, HMP, and YMP.

Season		Linear regression equation	R²
MMP	dry	E_T = 0.132PAR + 117.167VPD − 83.299	0.847
MMP	wet	E_T = 0.243PAR + 68.615VPD − 39.984	0.886
HMP	dry	E_T = 0.106PAR + 0.946VPD − 3.268	0.871
HMP	wet	E_T = 0.127PAR + 2.134VPD − 3.323	0.963
YMP	dry	E_T = 4.795PAR + 0.00420VPD − 2.744	0.789
YMP	wet	E_T = 0.00737PAR + 10.071VPD − 9.384	0.810

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer