Estimation of Inferior Vena Cava Size from Ultrasound Imaging in X-Plane

Preprint

Technical Note

Estimation of Inferior Vena Cava Size from Ultrasound Imaging in X-Plane

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 June 2024

Posted:

20 June 2024

You are already at the latest version

Alerts

Abstract

Ultrasound (US) scans of the inferior vena cava (IVC) provide useful information on the volume status of a patient. However, their investigation is user-dependent and prone to measurement errors. An important technical problem is the objective difficulty in studying a very compliant blood vessel like IVC, which makes large respirophasic movements and shows a complicated three dimensional geometry. Using bi-dimensional (2D) B-mode views either in long or short axis has improved the characterization of IVC dynamics compared to a measurement along a single direction (M-mode). However, specific movements of the IVC can challenge also the information provided by these 2D sections. Thus, these two orthogonal views, provided by an US system in X-plane, are here integrated by an innovative method. It is tested on simulated videos of the IVC performing complicated movements, that are compensated by the new method, overcoming the biased measurements provided by 2D scans. The method is then applied on example experimental data.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

Inferior vena cava (IVC) reflects information on the volume status of patients [1,2,3,4]. Its investigation by ultrasound (US) is low cost and non invasive. It allows to measure the diameter of IVC and its respirophasic variations, quantified in terms of the caval index (CI), defined as the relative variation of the diameter during the respiratory cycle with respect to the maximal diameter [5]. However, this method raises many concerns about standardization, operator-dependence and measurement errors [6,7,8]. Specifically, movements of the IVC [5] and non-uniform pulsatility [9,10] challenge the investigation along a single direction. Thus, different methods have been proposed to compensate movements [11] and to process two dimensional (2D) IVC sections from B-mode US scans [9,10,12,13,14]. However, it is expected that also advanced methods based on 2D processing of IVC sections in long [9,12,13] or short axis [10,14] could have problems in managing the third dimension orthogonal to the insonation plane [15].

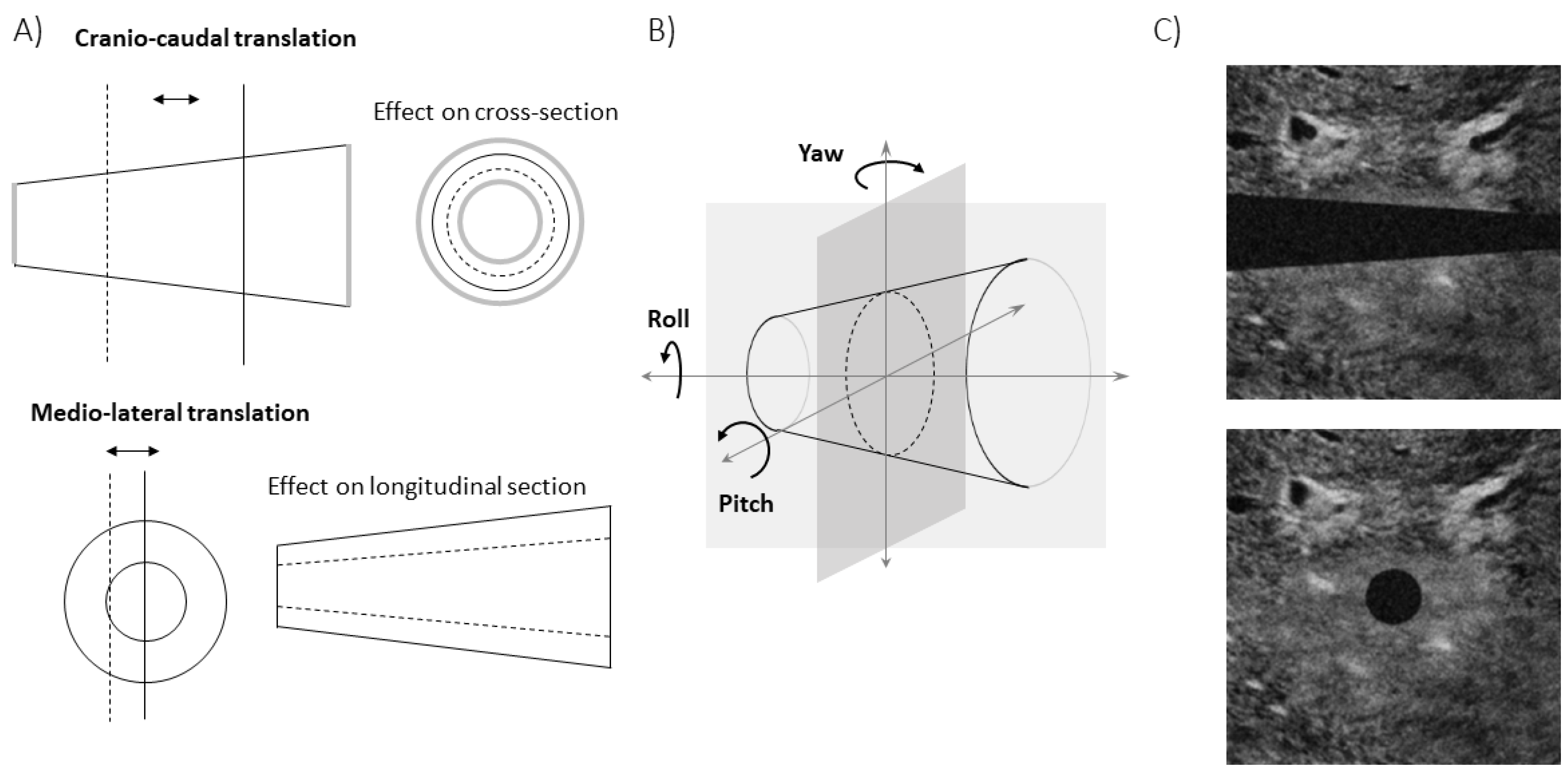
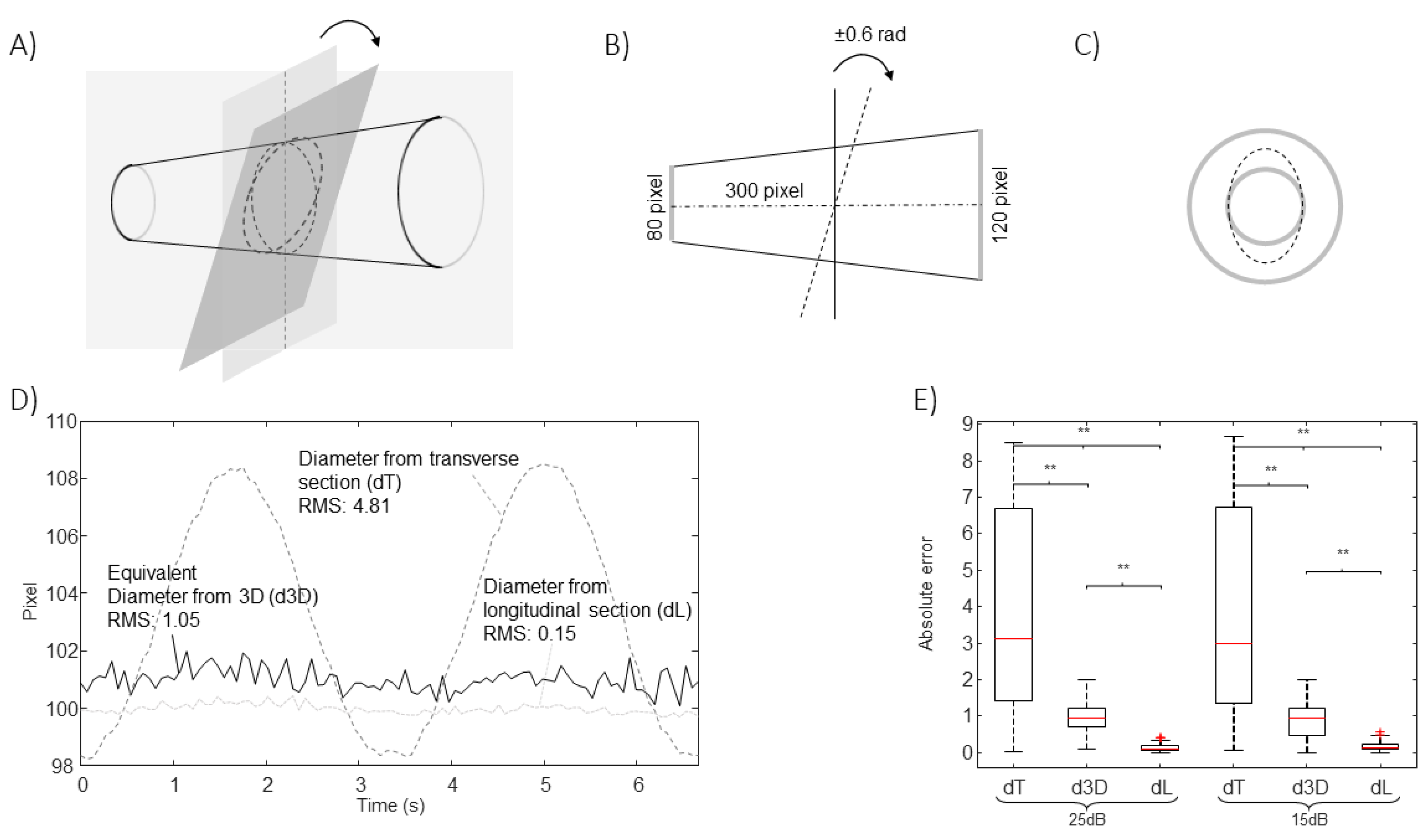
Specifically, B-mode US scans provide information on the IVC geometry in a single plane. Referring to Figure 1A, the intersection between IVC and such a plane changes when respirophasic movements induce translations in cranio-caudal and medio-lateral directions [5]. The first affects the cross-section visualized in the short axis view, whereas the latter influences the long axis section. Moreover, small rotations of the IVC with respect to the US probe are expected, as the transducer is following abdominal movements during the recording. Referring to Figure 1B, the pitch (i.e., an in-plane rotation of the IVC) can be compensated in the long axis view, if a 2D processing is used. On the other hand, the short axis view is directly affected by such a rotation: for example, if the IVC is a perfect cylinder with circular section, the cross-section is circular only if the vector orthogonal to the insonation plane is parallel to the axis of the cylinder, otherwise it is an ellipse, with area increasing with the pitch. The roll (i.e., a rotation of the IVC around its axis) does not affect the transverse view (as the entire cross-section is visualized), but it influences the long axis view, except in the case in which the cross-section is a perfect circle. The yaw (i.e., a rotation of the IVC around a vertical axis) would make the IVC out of plane, generating a variation of the visualized sections in both long and short axis views.

In this paper, we discuss the limitations of short and long axis views of IVC and introduce a method to integrate their information, conveniently acquired synchronously, by an US system with X-plane visualization. The method is here described and tested in simulations. The method is applied on experimental data in [16].

2. Methods

An algorithm (implemented in Matlab, the Mathworks) was developed to integrate the outputs of two edge tracking algorithms, processing US scans of IVC either in long [9] or in short axis view [10]. The method (described below) was then tested on simulated videos, representing translations and rotations of the IVC.

Algorithm

The long and short axis views can be measured synchronously by an US system in X-plane. They were simulated and then used to estimate the volume of a small portion of the IVC, from which an average diameter was computed as a measure of IVC size. The two views provide, for each frame, the section of the IVC in two orthogonal planes. This is a limited information on the geometry of the IVC. Thus, we made an approximate estimation of the volume of a portion of IVC, based on the following hypotheses.

H1: The portion of IVC has a cross-section with same shape along the longitudinal direction.
H2: The axis of the IVC (i.e., the geometric locus of the centroids of the cross-sections) is on a plane parallel to the long axis section.

Notice that, in a general IVC, the cross-section can change shape in time, as monitored by the short axis view. Shape variations are due both to the displacements of the IVC and to the pulsations induced by changes of transmural pressure. Exploring the longitudinal view, the translations of the IVC can be estimated, but the concomitant pressure variations are unknown, so that the information on IVC shape out of the visualized sections is not completely available. Thus, the first hypothesis H1 (even if arbitrary) is needed to fix this lack of information. It can be only approximately true, as it is expected that the shape of the cross-section of IVC can change with location, e.g., due to the presence of tissues leaning against or anchoring the vessel. However, selecting wisely a small portion of the vein, the approximation is expected to be reasonably good.

The second hypothesis H2 fixes another indeterminacy. In fact, an infinite number of vessels could have the same intersections with the two orthogonal insonation planes on which long and short axis views are taken. Indeed, different complicated geometries could be thought if we imagine a vessel with a curvilinear axis and cross-sections that adapt their dimension (and possibly also their shape, if neither the first hypothesis holds) in order that the long axis view is matched. Thus, a constraint is again needed. Our hypothesis assumes that the distance from the barycenter of each cross-section and the longitudinal plane is constant. This could be considered again valid within reasonable approximation under the hypotheses that the operator is careful to measure a section parallel to the longitudinal course of the vein and that the IVC does not bend (and therefore it has an almost straight axis). Again, this condition could be met more easily if the considered portion of IVC is small.

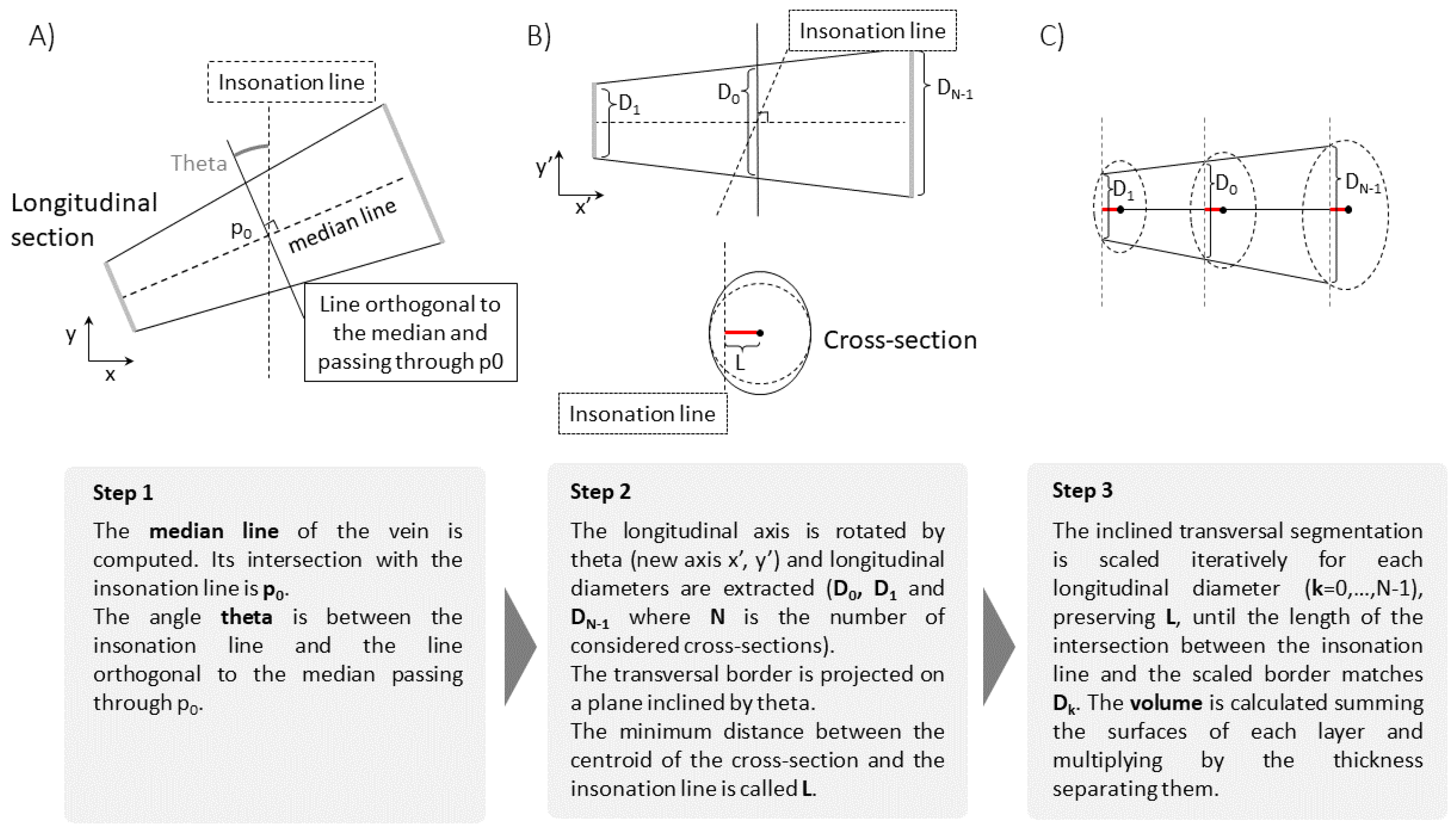
Under the above mentioned hypotheses, the volume of the portion of IVC can be computed as follows (see Figure 2).

From the longitudinal view, the IVC midline is computed as the mean of the two estimated edges.
The edges estimated in the transverse view are projected on a plane passing through the point $p_{0}$ of intersection of the short axis section with the midline and orthogonal to it.
The volume integral is computed as sum of layers, parallel to the projected cross-section computed on the previous step and all with same shape (following the first hypothesis H1). These layers are scaled in order that their intersections with the longitudinal plane match the long axis view. The optimal scaling is computed by the interior point algorithm, imposing the following requirements: matching of the diameter D found on the longitudinal section; maximal scale variation of 10% with respect to $D / D_{0}$ , where $D_{0}$ is the diameter in direction orthogonal to the midline and in the plane through $p_{0}$ ; fixed distance L from the axis (following the second hypothesis H2).

Notice that the cranio-caudal movements of the IVC are tracked in the longitudinal view, but the transverse cross-section is fixed. Thus, the longitudinal range of integration changes according to IVC movements. In order to better fit the hypotheses of our interpretation model, it is advisable that the transverse section is around the mean location of the portion of IVC that is integrated, which oscillates with the respiratory cycles, so that in the average the central cross-section of the volume portion is monitored by the short axis view.

Once the volume of the portion of IVC of interest has been calculated, a 1D size measurement, i.e., an equivalent diameter, is determined, in order to be comparable with estimates obtained using either the longitudinal or the transverse section, from which average diameters are also derived. Specifically, an equivalent diameter is computed for each estimated cross-section using the formula

D_{i} = 2 \sqrt{\frac{A_{i}}{π}}

(1)

where the subscript i indicates the

i^{t h}

cross-section and

A_{i}

is its area. Then the estimates are averaged

D = \frac{\sum_{i = 1}^{N} D_{i}}{N}

(2)

where N is the number of cross-sections considered.

Simulations

The estimations of the new algorithm have been compared to those obtained from the 2D views (longitudinal and transverse), when applied on simulated frames. A rigid IVC in the shape of a truncated cone was simulated, either translating or rotating with respect to the two orthogonal insonation planes, providing long and short axis views, respectively. Once found the intersections of the cone with the two planes, a simulated echographic frame was built, as follows. At the exterior of the cone, a portion of a real frame showing tissues around the IVC was placed. The lumen of the IVC was dark. Then, additive Gaussian and speckle noises were added, with different energies, in order to test the stability of the estimations when processing noisy data. Figure 1C shows an example of frame in long and short axis view.

3. Results

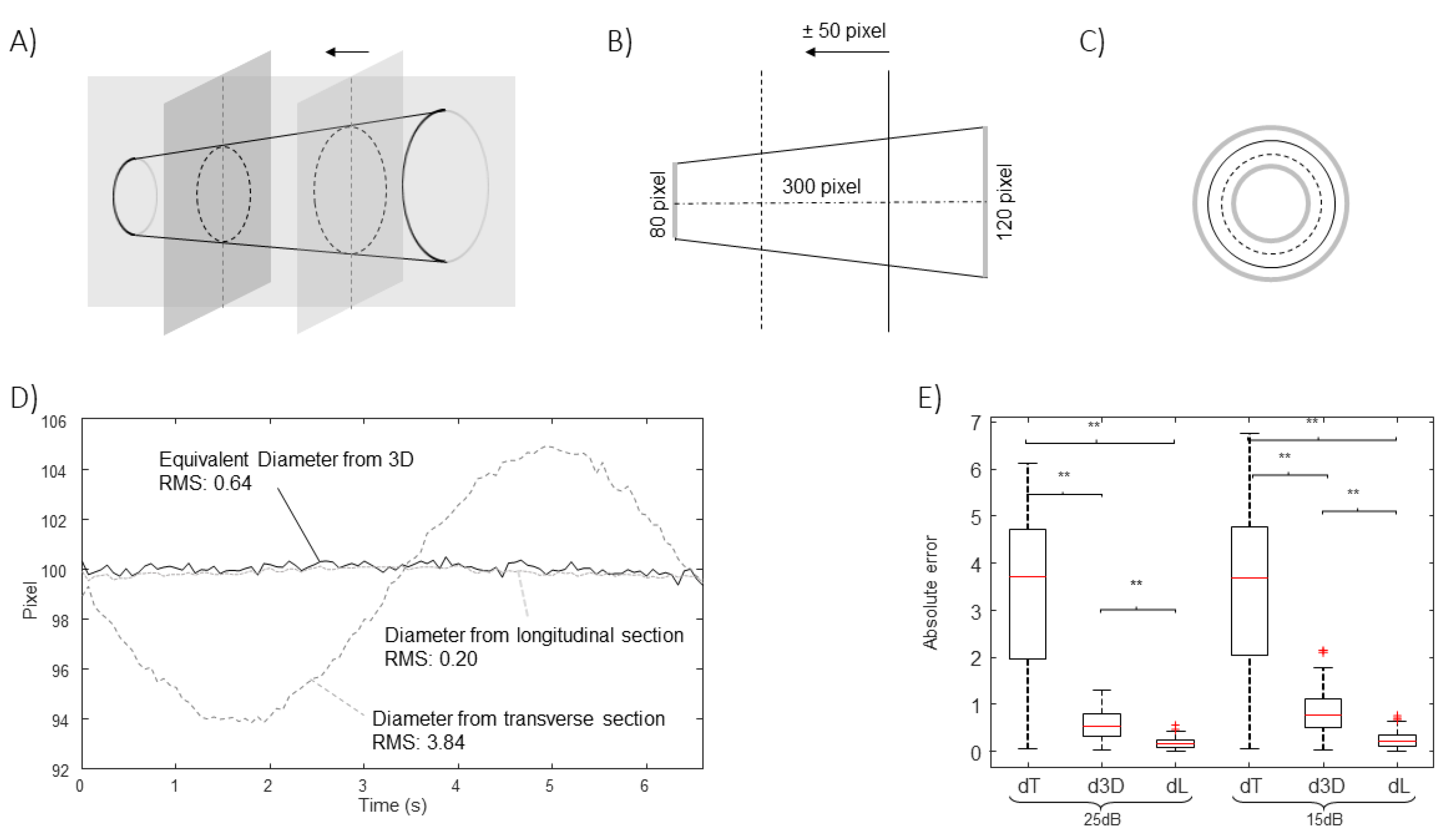
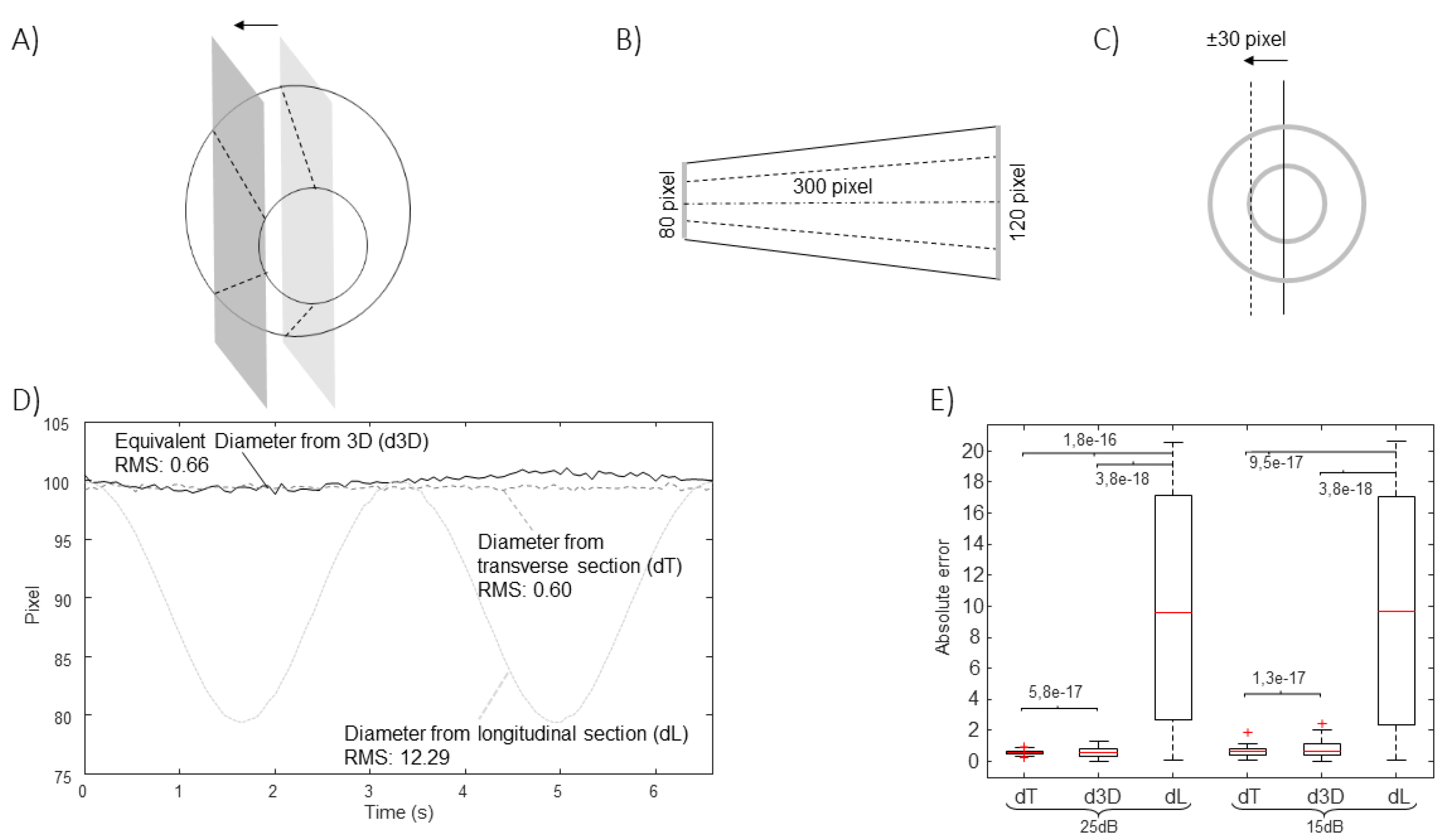
Figure 3, Figure 4, Figure 5 and Figure 6 show the estimation of the equivalent diameter obtained considering either the 2D approaches (long and short axis views) or the new one. The methods are applied to simulated frames, showing a rigid IVC with the shape of a cone making different movements. Thus, the correct diameter to be estimated is a constant value (100 pixels for Figure 3, Figure 4 and Figure 5 and 105.8 pixels for Figure 6).

Figure 3 considers translations along the longitudinal directions. The location of the IVC is making an oscillation, moving first toward left and then on the right of the initial position. The transverse section is largely affected by the displacement, which is orthogonal to the directions which are visualized, whereas the long axis view is unaffected, as the tracking compensates movements in the longitudinal plane.

Figure 4 shows the effect of translations along the medio-lateral direction. As for Figure 3, a cycle of an oscillation is considered. In this case, the diameter estimation in the long axis view is largely affected, whereas the cross-section could be correctly tracked in the transverse plane.

Figure 5 shows the effect of an oscillation of the value of the pitch (with a maximal rotation angle of 18^o). The algorithm processing the longitudinal section is able to compensate for this rotation (as it develops within the long axis plane). On the other hand, the short axis view is affected.

In all cases, the new algorithm was able to compensate the simulated movements. The estimation errors were larger when increasing the noise level, as expected. The extent of the problem depends on the extension of the movement and on the shape of the IVC.

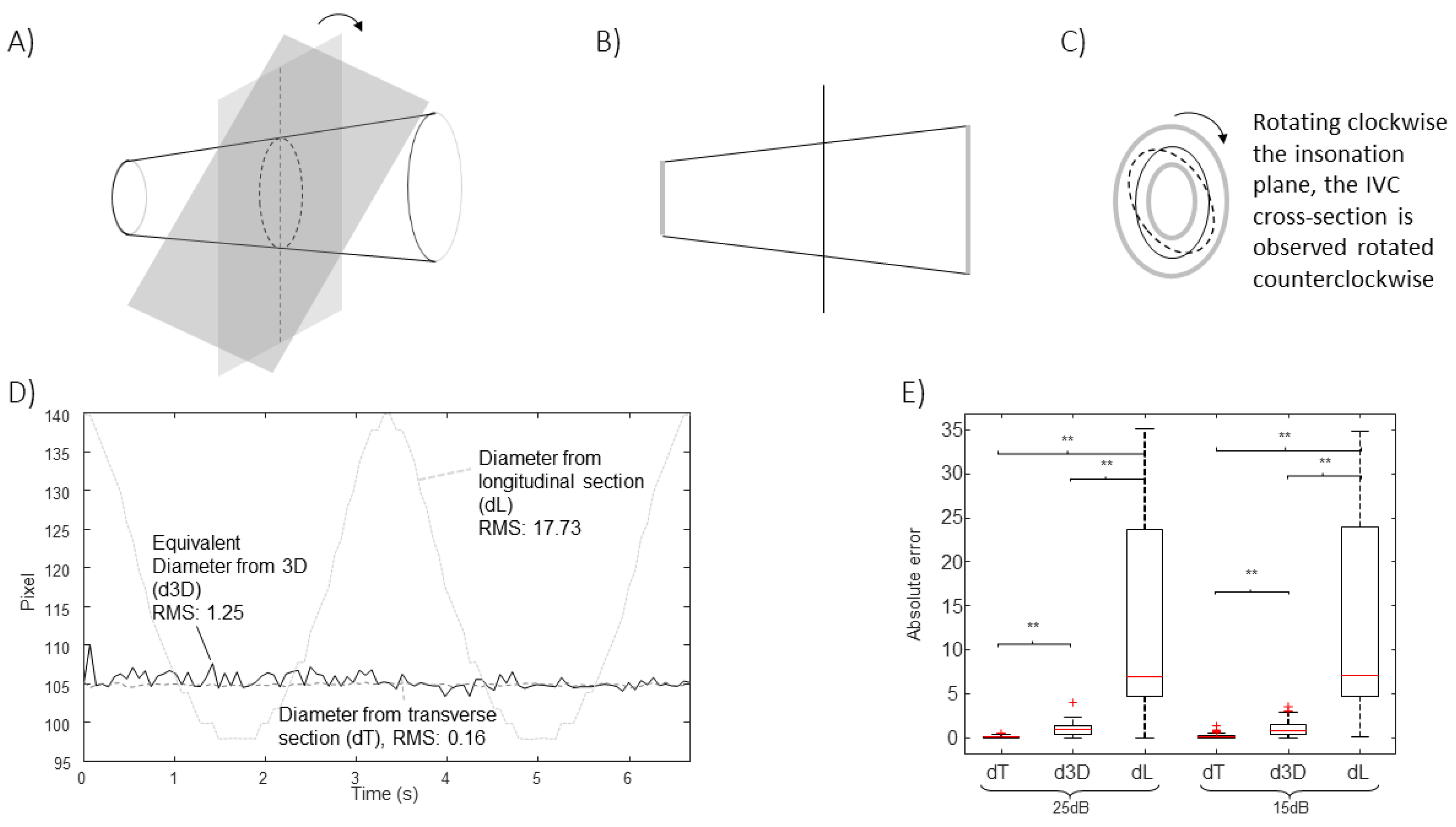
Other movements are possible. For example, the roll would not affect the estimations for the cone-shaped IVC considered in Figure 3, Figure 4 and Figure 5, as the cross-section is circular, but it would change the long axis view if the cross-section had any other arbitrary shape. As an example, Figure 6 shows the case of a simulated IVC with ellipsoidal cross-section while it is rolling.

Moreover, the yaw would affect the estimations, as the IVC would be out of plane and there’s no way to understand it from the two views.

In practice, a combination of different movements of IVC is expected in experimental recordings. They cannot be inspected in details by two sequential acquisitions in B-mode in long and short axis (which could be aligned by synchronizing them with respect to the respiration and heart cycles). Indeed, the additional information of the relative position of the two scanning planes would not be available in that case, but it is fundamental. Figure 7 provides a sketchy representation of this situation, considering a pair of frames of experimental data in B-mode. They show the IVC in long and short axis, respectively. As it is not possible to control exactly the relative locations of the scanned planes in B-mode, we assumed that the recorded frames resulted from two different sections, related by a longitudinal displacement of the cross-section (as in Figure 3) together with a medio-lateral shift of the longitudinal section (as in Figure 4) to get compatible configurations. Two very different IVC geometries are required to justify the two recorded frames in those conditions. Accordingly, different volumes and equivalent diameters would be needed to correctly characterize the vein, which are not available by neither single nor sequential B-mode acquisitions. Notice that Figure 7 shows only two examples of configurations, but the considered two frames could have been taken from IVCs with other geometries: for example, the cross-section could have been acquired with a pitch angle with respect to the IVC axis (investigated in Figure 5), providing a bias in estimating the equivalent diameter, which would be larger than that of the true cross-section of the studied portion.

These observations were recently confirmed using experimental data from 8 healthy subjects recorded by a US system in X-plane configuration, where we documented the problems induced by movements of the IVC outside the section displayed in B-mode scans (either in long or short axis) [16]. We have compared the here proposed estimation of IVC diameter with those obtained by 2D US scans. The following problems were observed: median error of 17% using long axis view of IVC affected by medio-lateral displacements (median of 4 mm); 7% and 9% of median error when measuring the IVC diameter from a short axis view in the presence of pitch angle (median of 0.12 radians) and cranio-caudal movement (median of 15 mm), respectively.

4. Discussion

This paper introduces an innovative method to estimate size changes of blood vessels from synchronous US scans acquired from two orthogonal insonation planes, providing short and long axis views. The algorithm is supposed to be applied on the inferior vena cava (IVC), which is a large and deep blood vessel that undergoes important movements and deformations.

The Need of Investigating IVC in 3D

The geometry of IVC can be very complicated and various in different patients: its section can vary a lot along a direction longitudinal to the axis [9,11]; the cross-section can be very different [10], as a function of the specific anatomy and the level of filling (that also changes during respirophasic pulsations). For these reasons, exploring the IVC edges in an entire section provides a more reliable characterization than along a single direction [9,10], as done in the clinical practice.

However, even an entire section is affected by IVC movements, that can affect measurements: for example, a displacement off-midline results in a smaller measurement of IVC size in the longitudinal view [5] and a roll makes exploring a different section (which is different if the cross-section is not a perfect circle); movements in cephalic or caudal direction affect the short axis view as it is taken at different anatomic sections [5] and a relative rotation pitch between IVC and probe increases the measured cross-section (which is minimal when the insonation plane is orthogonal to the IVC axis).

The only solution would be exploring the IVC in 3D [18]. However, taking a full 3D IVC scan could take long or provide images with low resolution, impeding the study of the dynamics of its pulsations. As an approximation, long and short axis views can be acquired synchronously by an US system in X-plane mode. In this way, the two sections are acquired at the same time and information from the two views can be integrated. Moreover, the two sections can have good spatial resolution and a sampling frequency still sufficient to follow IVC dynamics (for example, in our recent study [16], the frame rates dropped from about 60 Hz in B-mode to 30 Hz in X-plane, which is still sufficient to investigate IVC collapsibility). Here, we propose to make an approximate estimation of the volume of a portion of IVC. The vessel is tracked in order to compensate movements in the cranio-caudal and medio-lateral directions. Moreover, the cross-section is projected in the direction orthogonal to the midline. In this way, the aforementioned limits of the two views are overcome.

The method is validated using simulations as gold standard. The estimations are stable to cranio-caudal movements (Figure 3), medio-lateral movements (Figure 4), pitch rotations (Figure 5) and roll (Figure 6), whereas the method cannot compensate for a yaw rotation (i.e., the IVC is out of plane) or complicated geometries of the vein (e.g., bending or cross-sections along the longitudinal course which are much different from a linear scaling of the recorded short axis view). The comparison of the equivalent IVC diameters estimated by the proposed method and using single B-mode scans have been recently investigated with experimental data, showing relevant effects of IVC movements out of the visualized planes [16].

Limitations

The proposed method makes some assumptions on insonation planes and on the shape of IVC in order to estimate its volume. In fact, the shape of IVC out of the two insonation planes is not known and infinite geometries could perfectly fit the recorded scans. Specifically, we assumed that the IVC is straight and aligned to the long axis plane; moreover, we supposed that the cross-section has the same shape and changes only the dimension along the course of the blood vessel. We could say that we are making a first order approximation that can hold as long as the portion of investigated IVC is small. The extension of the IVC portion guaranteeing that the approximation is feasible should depend on the size of the vessel, e.g., we advise not to go beyond 2-3 times the IVC diameter. Beyond this limit, we expect that it is difficult to fit the hypotheses that the IVC is straight, the shape is constant and the long axis section is aligned to the midline.

A further limitation is the need of using an advanced echography system, with 2D probe allowing for X-plane acquisition. Using separate long and short axis views and then synchronizing them (e.g., considering short acquisitions in breath-holding and synchronizing with respect to the heartbeat) would not provide complete information, as only using X-plane the location and orientation of each insonation plane is available.

Another marginal problem is that the frame rate is twice lower when acquiring in X-plane than in B-mode. However, usually the sampling rate is still sufficient to recover information on IVC size and pulsatility, which are of main interest.

Future Perspectives

The use of US videos in X-plane allows to compensate for possible problems due to translations or rotations of IVC relative to the probe. These movements are expected to be in phase with respiration, so that their effect is superimposed to IVC respirophasic pulsatility. Thus, being able to compensate for them can improve the reliability of the assessment of IVC size and pulsatility. In prospective, this could allow to get more stable information on patient hydration and central venous pressure.

Conclusions

We introduced an algorithm to integrate the information from US videos in short and long axis views recorded by a system in X-plane configuration, to estimate the volume of a small portion of a vessel. Different translations and rotations of the US probe with respect to the blood vessel can affect the assessment of its size from a single 2D view, but they are compensated by our algorithm.

Author Contributions

Conceptualization, L.M.; methodology, L.M., P.P.; software, P.P.; validation, L.M., P.P.; data preparation, L.M.; investigation, L.M., P.P.; writing–original draft preparation, L.M., P.P.; writing–review and editing, L.M.; visualization, L.M., P.P.; supervision, L.M. The authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

An instrument implementing the 2D algorithms used in this paper was patented by Politecnico di Torino and Universitá di Torino (patent number WO 2018/134726) and was taken in license by VIPER s.r.l.

Abbreviations

The following abbreviations are used in this manuscript:

2D	two-dimensional
3D	three-dimensional
CI	caval index
IVC	Inferior Vena Cava
US	Ultrasound

References

Lichtenstein, D. Inferior vena cava. General ultrasound in the critically ill. Berlin: Springer 2005, 23, 82. [Google Scholar]
Mesin, L.; Roatta, S.; Pasquero, P.; Porta, M. Automated Volume Status Assessment Using Inferior Vena Cava Pulsatility. Electronics 2020, 9. [Google Scholar] [CrossRef]
Mesin, L.; Albani, S.; Policastro, P.; Pasquero, P.; Porta, M.; Melchiorri, C.; Leonardi, G.; Albera, C.; Scacciatella, P.; Pellicori, P.; Stolfo, D.; Grillo, A.; Fabris, B.; Bini, R.; Giannoni, A.; Pepe, A.; Ermini, L.; Seddone, S.; Sinagra, G.; Antonini-Canterin, F.; Roatta, S. Assessment of Phasic Changes of Vascular Size by Automated Edge Tracking-State of the Art and Clinical Perspectives. Front. Cardiovasc. Med. 2022, 8, 775635. [Google Scholar] [CrossRef] [PubMed]
Policastro, P.; Mesin, L. Processing Ultrasound Scans of the Inferior Vena Cava: Techniques and Applications. Bioengineering 2023, 10, 1076. [Google Scholar] [CrossRef]
Blehar, D.; Resop, D.; Chin, B.; Dayno, M.; Gaspari, R. Inferior vena cava displacement during respirophasic ultrasound imaging. Critical Ultrasound Journal 2012, 4, 1–5. [Google Scholar] [CrossRef] [PubMed]
Wallace, D.; Allison, M.; Stone, M. Inferior vena cava percentage collapse during respiration is affected by the sampling location: an ultrasound study in healthy volunteers. Acad Emerg Med 2010, 17, 96–99. [Google Scholar] [CrossRef] [PubMed]
Resnick, J.; Cydulka, R.; Platz, E.; Jones, R. Ultrasound Does Not Detect Early Blood Loss In Healthy Volunteers Donating Blood. J Emer Med. 2011, 41, 270–275. [Google Scholar] [CrossRef]
Zhang, Z.; Xu, X.; Ye, S.; Xu, L. Ultrasonographic Measurement of the Respiratory Variation in the Inferior Vena Cava Diameter Is Predictive of Fluid Responsiveness in Critically Ill Patients: Systematic Review and Meta-analysis. Ultrasound Med Biol 2014, 40, 845–853. [Google Scholar] [CrossRef]
Mesin, L.; Pasquero, P.; Roatta, S. Tracking and Monitoring Pulsatility of a Portion of Inferior Vena Cava from Ultrasound Imaging in Long Axis. Ultrasound Med Biol. 2019, 45, 1338–1343. [Google Scholar] [CrossRef] [PubMed]
Mesin, L.; Pasquero, P.; Roatta, S. Multi-directional assessment of Respiratory and Cardiac Pulsatility of the Inferior Vena Cava from Ultrasound Imaging in Short Axis. Ultrasound Med Biol. 2020, 46, 3475–3482. [Google Scholar] [CrossRef] [PubMed]
Mesin, L.; Pasquero, P.; Albani, S.; Porta, M.; Roatta, S. Semi-automated tracking and continuous monitoring of inferior vena cava diameter in simulated and experimental ultrasound imaging. Ultrasound Med Biol 2015, 41, 845–857. [Google Scholar] [CrossRef] [PubMed]
Sonoo, T.; Nakamura, K.; Ando, T.; Sen, K.; Maeda, A.; Kobayashi, E.; Sakuma, I.; Doi, K.; Nakajima, S.; Yahagi, N. Prospective analysis of cardiac collapsibility of inferior vena cava using ultrasonography. J Crit Care 2015, 30, 945–948. [Google Scholar] [CrossRef] [PubMed]
Mesin, L.; Giovinazzo, T.; D’Alessandro, S.; Roatta, S.; Raviolo, A.; Chiacchiarini, F.; Porta, M.; Pasquero, P. Improved repeatability of the estimation of pulsatility of inferior vena cava. Ultrasound Med Biol. 2019, 45, 2830–2843. [Google Scholar] [CrossRef] [PubMed]
Nakamura, K.; Tomida, M.; Ando, T.; Sen, K.; Inokuchi, R.; Kobayashi, E.; Nakajima, S.; Sakuma, I.; Yahagi, N. Cardiac variation of inferior vena cava: new concept in the evaluation of intravascular blood volume. J Med Ultrasonics 2013, 40, 205–209. [Google Scholar] [CrossRef] [PubMed]
Huguet, R.; Fard, D.; d’Humieres, T.; Brault-Meslin, O.; Faivre, L.; Nahory, L.; Dubois-Randé, J.; Ternacle, J.; Oliver, L.; Lim, P. Three-Dimensional Inferior Vena Cava for Assessing Central Venous Pressure in Patients with Cardiogenic Shock. J Am Soc Echocardiogr. 2018, 31, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
Policastro, P.; Ermini, L.; Civera, S.; Albani, S.; Musumeci, G.; Roatta, S.; Mesin, L. Effects of respirophasic displacements of inferior vena cava on size measurements from two dimensional ultrasound imaging. Ultrasound Med Biol. 2024. [Google Scholar]
Pocus 101, IVC Ultrasound STEP by STEP - Easiest Method. https://www.youtube.com/watch?v=vmmrjy1bhEc, 2015. Accessed: 2024-06-17.
Huang, Q.; Zeng, Z. A Review on Real-Time 3D Ultrasound Imaging Technology. BioMed Research International 2017, 2017. [Google Scholar] [CrossRef]

Figure 1. A) Possible translations of the inferior vena cava (IVC) with respect to the insonation plane. B) Possible rotations of IVC with respect to the insonation plane. C) Example of simulated frames in long and short axis views.

Figure 2. Illustration of the method to estimate the volume of a portion of IVC from long and short axis views.

Figure 3. Effect of translations along the longitudinal directions on the equivalent diameter estimated by 3 methods, based on 2D longitudinal and transverse views, or the 3D approach. The location of the IVC is making an oscillation, moving first toward left and then on the right of the initial position. A) Representation of the movement in 3D. B) Illustration of the long axis view. C) Cross-section. D) Estimations of IVC diameter obtained considering SNR of 25 dB (the correct diameter is 100 pixels). The root mean squared errors are indicated in the figure. E) Absolute error of diameter estimation by the transverse view (dT), the new approach (d3D) and the long axis section (dL), considering noise with different power.

Figure 4. Same format as Figure 3, but considering translations along the medio-lateral direction.

Figure 5. Same format as Figure 3, but considering oscillations of the value of pitch, varying between about ±34.4^o.

Figure 6. Same format as Figure 3, but considering oscillations of the value of roll varying between ±45^o and a vein with ellipsoidal cross-section, with semiaxes in the central section (visualized by the short view) of 40 and 70 pixels, so that the correct equivalent diameter is 105.8 pixels.

Figure 7. Representative example of two different IVC geometries compatible with the same two B-mode acquisitions in A) long and B) short axis, respectively (frames extracted from [17]). The two frames are assumed to be taken in the same conditions (i.e., ideally in the same time sample or at the same point along the respiratory and heatbeat cycles), but without knowing the direction of each scanning plane (available only in X-plane mode). Very different IVC geometries can be deduced, depending on the relative positions of the scanning planes, obtaining different estimations of equivalent diameters (D_L, D_T and D₃D are the estimated equivalent diameters from the longitudinal, transversal and X-plane views, respectively). C) If the long axis plane is displaced in the medio-lateral direction with respect to the center of the IVC, the two frames are compatible with an IVC with a large volume (notice that the green segment has the same length in the frames shown in the top panel). D) If the long axis section is on the IVC axis, the volume of the vein is much smaller than in the previous case (notice that the yellow segment has the same length in the frames shown in the top panel).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Estimation of Inferior Vena Cava Size from Ultrasound Imaging in X-Plane

Abstract

1. Introduction

2. Methods

Algorithm

Simulations

3. Results

4. Discussion

The Need of Investigating IVC in 3D

Limitations

Future Perspectives

Conclusions

Author Contributions

Funding

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe