Prerpints.org logo
Preprint
Article

Feasibility Assessment of Implementing Semi-interlocking Masonry As Infill Panels in Framed Building Construction

Altmetrics

Downloads

83

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts
Abstract
Semi-Interlocking Masonry (SIM) represents an innovative building system developed at the Centre for Infrastructure Performance and Reliability at The University of Newcastle, Australia. This system employs a unique approach to interlocking mortar-less engineered masonry panels constructed from SIM units. These units are designed to offer substantial energy dissipation capacity, primarily attributed to the friction occurring on the sliding bed joints between the units within the panel during seismic events. The primary aim of this study is to evaluate the viability of incorporating semi-interlocking masonry as infill panels in the construction of multi-storey buildings across diverse geographical locations with varying seismic conditions in Australia. To assess the feasibility of SIM panels in different conditions (according to Australian Standard AS1170) in Australia, a comprehensive analysis using Strand7 is conducted on a three-storey structure incorporating traditional masonry infill panels and SIM panels. The comparison of displacement and base shear capacities is carried out in response to seismic events across various scenarios in different locations within Australia. The insights gained from this comparative analysis contribute valuable information regarding the viability of implementing SIM as a contemporary construction material.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Masonry has been a foundational construction material globally for millennia, contributing significantly to the built environment. Evidenced in some of the most notable historical structures, masonry stands as a testament to the ingenuity and enterprise of ancient cultures throughout history. Masonry has evolved significantly over time, witnessing numerous enhancements in both the constituent materials and the functional role of masonry elements as structural components. Nevertheless, the application of infill panels constructed from traditional Unreinforced Masonry (URM) is constrained in seismic regions due to inadequate ductility. Masonry is a composite material, comprising solid or hollow blocks, mortar or mortar-less joints, grout, and reinforced bars, each exhibiting distinct material properties [1,2]. The interfaces between masonry units serve as vulnerable planes due to their limited tensile and shear bond strength in traditional masonry [3]. This susceptibility can result in failures, often yielding catastrophic consequences such as loss of life and irreparable damage to structures, as shown in Figure 1. Damage is observed in traditional masonry structures during earthquakes due to their inefficiency in dissipating the seismic energy introduced [2]. To enhance the energy dissipation capacity of masonry, certain researchers explore investigations involving mortarless constructions (dry-stacked masonry), while others introduce interlocking mechanisms between brick units (interlocking masonry). Dry-stacked masonry consists of the assembly of bricks or blocks without mortar, resulting in a distinct contact behavior between masonry units compared to traditional masonry with mortar. Noteworthy ancient dry-stack masonry structures, such as the pyramids in Egypt and the ruins in Zimbabwe, continue to exist [4]. These structures, having withstood numerous seismic events, demonstrate ongoing structural stability and integrity, affirming the resilience of dry-stacked masonry against seismic forces. Madan et al. [5] and Uzoegbo et al. [4] conducted research on both in-plane and out-of-plane seismic behavior of masonry walls, culminating in the development of an interlocking block termed Hydraform Interlocking Dry-Stack Block. Their findings suggest that the strength of dry-stack units does not significantly impact the resistance to lateral loads. Instead, the lateral load-bearing capacity of dry-stack masonry is contingent upon the effectiveness of the interlocking mechanism and inter-brick friction within the infill panels.
To enhance the energy dissipation capabilities of framed masonry structures, a novel concept in framed masonry panels, constructed with mortar-less semi-interlocking units, has been developed at the University of Newcastle, Australia [8]. It is referred to as a Semi-Interlocking Masonry (SIM) system, which introduces units in masonry infill panels (SIM panels) designed for relative sliding in-plane while interlocking to prevent relative sliding out-of-plane. As a result, the SIM panel exhibits reduced stiffness and susceptibility to damage, simultaneously amplifying its ability to dissipate seismic energy. Two distinct types of SIM units have been created: topological and mechanical, as illustrated in Figure 2 [9]. Topological SIM units leverage the natural contours of the units to facilitate in-plane movement, while mechanical SIM units employ a system of slots and sockets to allow controlled in-plane movement [10].
The initial design of the SIM system envisioned it as a dry stack, meaning the structure would be assembled solely with blocks, without mortar. However, practical concerns emerged, particularly related to water penetration and thermal properties. Forghani et al. [11] conducted an investigation into the water penetration and thermal insulation performance of SIM panels using various joint fillers, such as linseed oil-based putty and tape, between the units. Their conclusion highlighted that panels constructed with putty exhibited superior performance in terms of both thermal insulation and resistance to water penetration. Additionally, Hossain et al. [12] explored the variation of the coefficient of friction of SIM units with different bedding materials, including linseed oil-based putty and tape. Their findings indicated that surfaces treated with putty demonstrated a higher coefficient of friction compared to the other tested surfaces.
A comprehensive assessment of the structural performance of SIM panels was conducted through the testing of six full-scale panels under cyclic in-plane displacement, reaching up to 5% storey drift (100 mm displacement). The analysis focused on evaluating the load-displacement behavior and energy dissipation capacity of the SIM panels. The findings concluded that SIM panels could serve as a viable alternative to URM in-fill panels in seismic regions, given their superior energy dissipation capacity compared to traditional URM [13]. Therefore, it is imperative to evaluate the viability of the novel panel system in Australia. This study developed an analytical model to evaluate the feasibility of implementing SIM panels as infill components in Australian construction practices. The assessment considered a typical three-story, three-bay structure with 4m x 3m panels subjected to the typical load imposed by Australian Standard AS 1170.4:2007 [14]. Two distinct analytical models were created—one for the SIM panel with an open gap and another for the SIM panel with a closed gap at the top between the upper edge of the panel and the surrounding frame. The results obtained from the analytical study were then compared with the experimental findings, providing valuable insights into the potential application of SIM panels as a modern-day construction material in seismic regions of Australia.

2. Formulation of Analytical Model

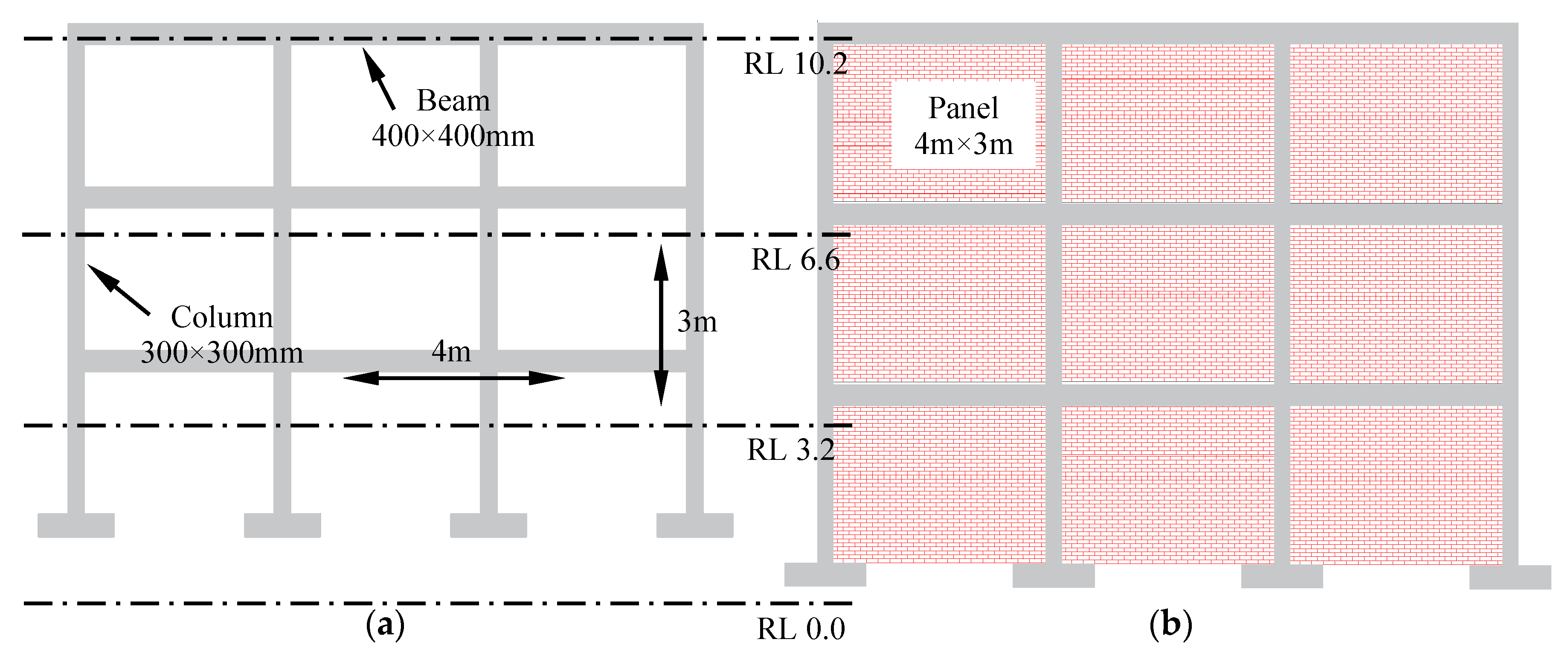
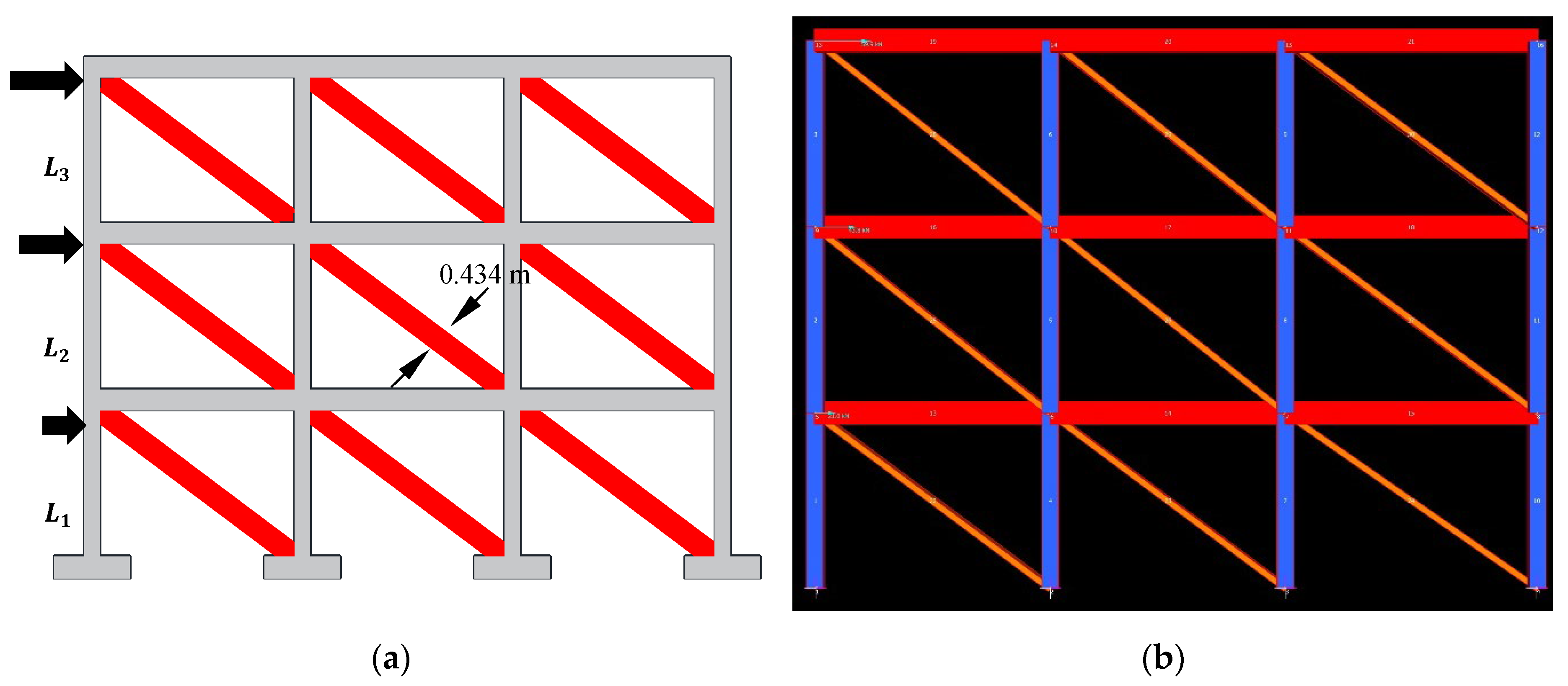
An analytical method has been developed in this study to determine the suitability of SIM panels as a replacement of URM panels. As SIM will be used as an infill panel, it is necessary to quantify the displacement and base shear capacities of the bare frame (no infill), frame with URM panels and frame with SIM panels. The elevation is depicted in Figure 3, while Table 1 provides a comprehensive overview of the specific characteristics of both the bare frame and the framed structure with infill panels used in this study to establish a simplified method.
The current study has taken into account the linear elastic behavior of the RC frame along with the nonlinear (frictional sliding) behavior in the SIM panel, as discussed in Section 2.3. As this comparative study focuses on the behavior of bare frame, traditional masonry, and SIM panels, the interaction of concrete beams and frame remains consistent across all structures. While the study does not specifically address this interaction, the comparative analysis ensures a comprehensive understanding of the infill panel's demands within the broader structural context.
It is important to highlight that the coefficients of friction for SIM panels are based on the topological and mechanical SIM bed joints, with values of 0.75 and 0.72 respectively [12]. Given the closely aligned coefficient of friction for both SIM units, the analysis in this study focuses solely on panels featuring topological SIM units, as presented in Table 1. The seismic loading configuration adhered to the standard specifications outlined in the Australian Standard AS1170.4 [14], specifically following the typical loading configuration for a residential building. Analyzing the structural behavior under seismic forces poses a complex challenge due to the dynamic nature of earthquake loading. The Australian Standard provides various methods for such analyses. In this study, a simplified approach known as the 'equivalent static method' was adopted to assess the behavior of the bare frame, traditional masonry, and SIM panels. This method conceptualizes earthquake loading as a series of static loads applied to each level of the structure. While static analysis is commonly employed in preliminary structural assessments, the equivalent static method is particularly useful for comparative research, as demonstrated in this study.
The base shear (V) of the structure for earthquake actions can be determined using the equivalent static method, as expressed in Equation (1) [14].
V = k p Z C h ( T 1 ) S p μ W t
Where k p is the probability factor which is a function of design life and importance level of the structure. For this study, assuming a typical design life of 50 years, as commonly adopted in Australia [16], the probability factor is solely dependent on the importance levels. The consequences of failure corresponding to different importance levels have been adopted from AS 1170.0:2002 [17]) and are summarized in Table 2, with the assessment focusing on importance levels 2, 3, and 4 in this study.
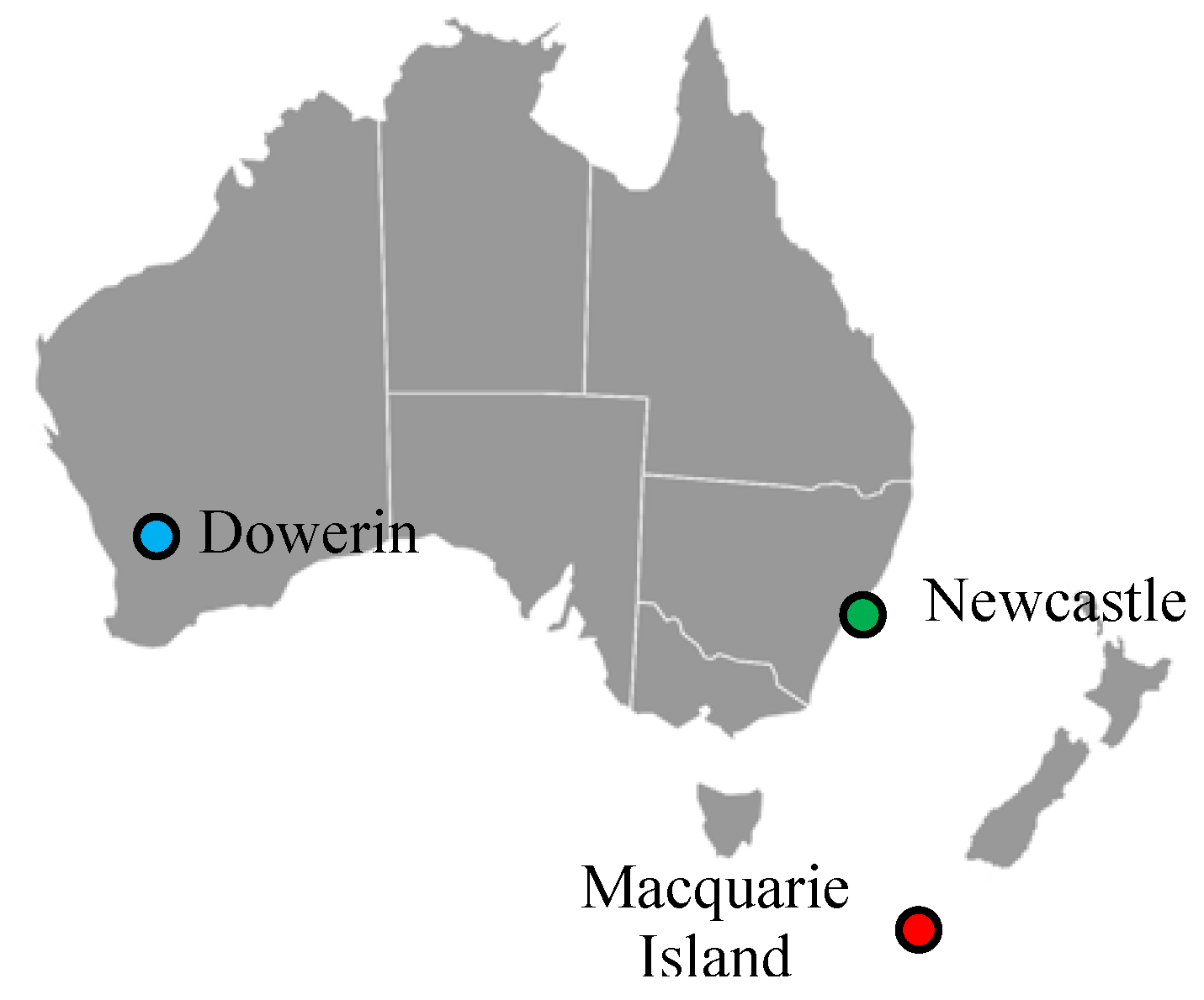
Z is the hazard factor, signifying that the geographic location of the building impacts the magnitude of static loads. Three locations, as shown in Figure 4 were chosen for this study, categorized as low-risk (Newcastle), medium-risk (Dowerin), and high-risk (Macquarie Island) seismic areas, each associated with distinct hazard design factors (Z).
Ch(T1) represents the spectral shape factor and is dependent on the fundamental period of the structure and the building’s site class. The fundamental period of the structure (T1) is determined using the formula T1 = 1.25ktkn0.75, resulting in 0.54 seconds for a braced frame with a building height of 10.2m. This study incorporates two different site sub-soil classes, namely shallow soil Ce and deep or soft soil De. The Ch(T1) value is interpolated to 0.54 according to Australian Standard AS1170.4-2007 based on the specific site sub-soil class [14].
Sp/µ represents the ratio of the structural performance factor to the structural ductility factor. This factor, as stipulated in AS 1170.4-2007 [14], is designated as 0.22. The selection of this ratio is contingent upon the material properties and load-resisting mechanisms of the frames, assumed here as a reinforced concrete moment resisting frame.
Wt denotes the seismic weight of the structure, computed as the sum of the weights across all levels. The seismic weight (Wi) at each level is determined using the following Equation (2) [14]:
W i = ∑ G i + ∑ Ψ E Q i
The calculated base shear is then distributed at each level using Equation (3) [14]. Equation (3) outlines a method for determining the lateral force acting on each level of a structure in a seismic analysis. This force is crucial for assessing the structural response to seismic forces and designing buildings to withstand such events.
F i = W i h i ∑ j = 1 j = n W i h i V
Where Fi represents the horizontal equivalent static force at the i'th level, hi is the height of the level above the base of the structure, and n is the number of levels in a structure.
In this study, the calculation of equivalent static forces on the structure involved three key criteria: location, importance level, and site class. Utilizing a comprehensive approach, three distinct locations, three importance levels, and two site sub-soil classes across Australasia were selected for the equivalent static analysis. The specific criteria employed for calculating equivalent static forces are detailed in Table 3. The combination of these criteria resulted in the development and analysis of 18 unique load cases for each structure, as outlined in Table 4.
A total of 72 load cases for the bare frame, the frame with traditional masonry, and the frame with SIM panels (Type 1 and Type 2, discussed in detail in Section 2.3) were meticulously analyzed using Strand7, a widely used finite element package for structural analysis in Australia. Strand7 integrates a comprehensive visual environment with robust solvers, providing unparalleled functionality. Users can effortlessly construct structural models (consisting of reinforced, steel, timber members) using an extensive element library, conduct analyses, and review results in real-time through an intuitive interface. Employing linear static analysis for various load cases, the study focused on determining the displacements of the structure based on the results obtained from the Strand7 analysis.

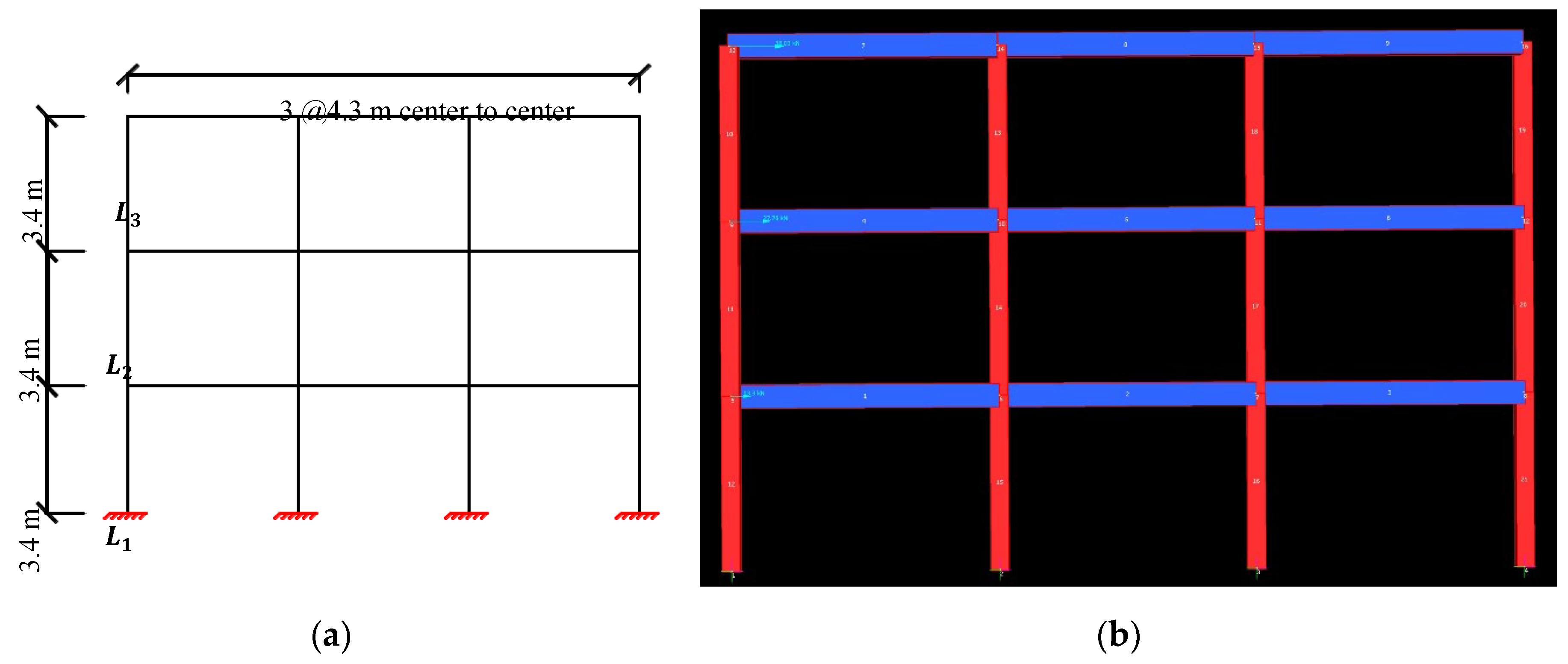
2.1. Modelling strategy of bare frame

This study involved the analysis of the bare frame for the 18 different load cases using the Strand7. The bare frame was modelled as a reinforced concrete moment-resisting frame. Figure 5 illustrates the dimensions of the bare frame and outlines the modelling strategy employed in the analysis. The horizontal equivalent static design force at each level for every load case was applied, as depicted in Figure 5b. The resulting displacement was then obtained through the detailed analysis process.

2.2. Modelling Strategy of Traditional Masonry Panel

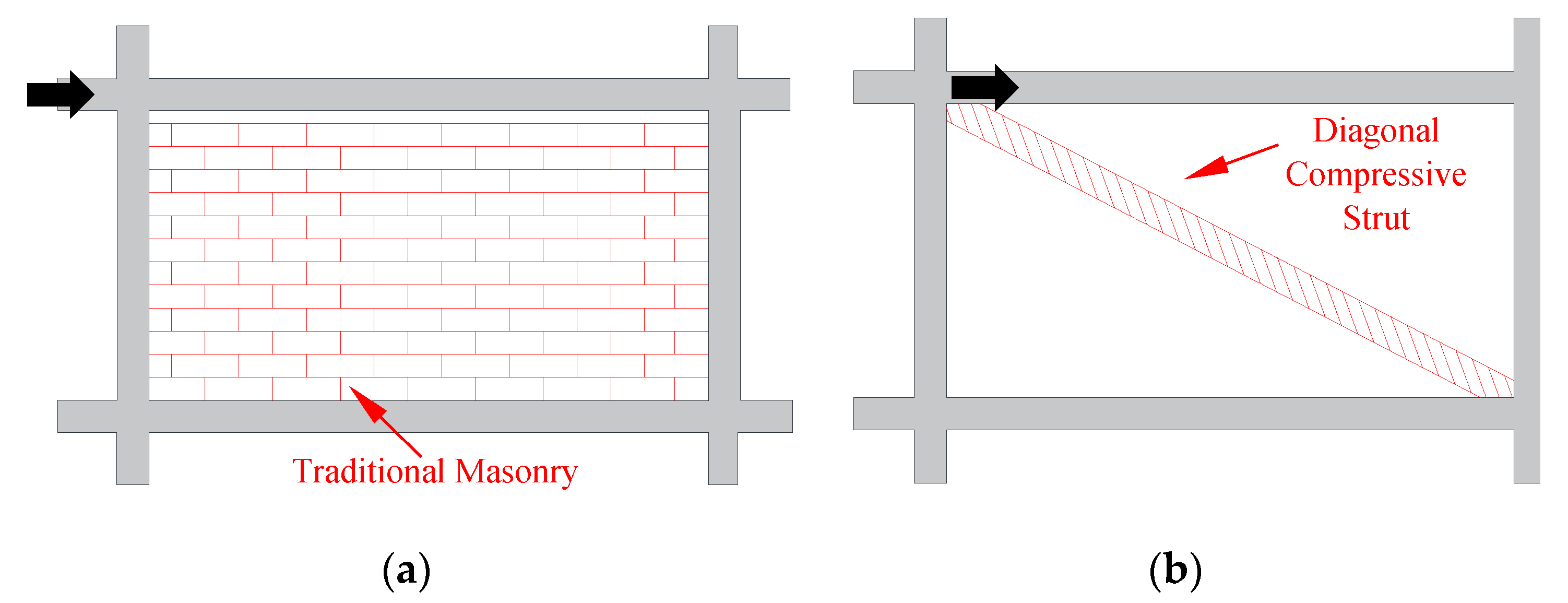
In this study, the equivalent compressive strut model was employed to evaluate the impact of a traditional infill masonry panel in comparison with the SIM panel. The initial development of the strut model can be attributed to Polyakov (1960), who formulated the concept based on elastic theory [19]. Polyakov proposed that the response of traditional infill masonry panels under lateral loads could be effectively analyzed by representing their impact through an equivalent diagonal compressive strut. Various types of strut models are available in the literature, with the most commonly used ones being the Single, Double, and Triple Strut models. Crisafulli (1997) conducted a comprehensive study comparing the impact of the three different types of strut models on the structural response of an infilled frame, utilizing finite element analysis and contrasting the findings with experimental results [20]. The findings from the study indicated that while the single strut model is the simplest rational representation for analyzing infilled frames, it falls short in describing the local effects of interaction between the frame and the infill panel. Crisafulli suggested that the use of multi-strut models (double and triple strut) can address this limitation without significantly increasing the complexity of the analysis. It was also reported that the single strut model is the most widely used and suitable for large structures.
In this study, the single strut model was chosen, as the local effects of panel and frame interaction are not the primary focus. Furthermore, within the context of this investigation, a three-bay, three-storey structure qualifies as a large structure for an equivalent compressive strut model. As previously mentioned, the reinforced concrete frame with a traditional masonry panel can be effectively modeled as an equivalent braced frame featuring an equivalent diagonal compressive strut, as illustrated in Figure 6.
Various studies in the literature offer methodologies for determining the width of the equivalent diagonal strut. To model SIM panels, trial and error analysis were used as the in-panel capacity of the SIM panels also depends on the displacement. In this study, the selection of an empirical equation to represent the equivalent width of the diagonal compressive strut for the traditional masonry panel is crucial. FEMA273 [21] recommends the use of the empirical equation proposed by Mainstone and Weeks [22] for quantifying the strength, stiffness, and deformation capacity of the traditional masonry panel (Equation (4)). For static analysis in Strand7, the equivalent width of the compressive strut was set at 0.434 m for this study. The response of the traditional masonry panel to lateral load is depicted in Figure 7a, and the corresponding Strand7 model is illustrated in Figure 7b.
W s t r u t = 0.175 λ H i n f − 0.4 d i n f
Where λ = E i n f t i n f S i n 2 θ 4 E c I c H i n f 1 4 Einf, tinf, dinf and Hinf are the modulus of elasticity, thickness, diagonal between two compressed corners and height of the infill respectively, θ is the angle between diagonal of the infill and the horizontal, Ec and Ic are the modulus of elasticity and second moment of inertia of the column respectively.

2.3. Modelling strategy of SIM panel

SIM panels can be constructed in two alternative ways, introducing distinct structural characteristics. It can be built with a gap between the top of the panel and the frame (Type 1: SIM panel with gap) or without any gap between the top of the SIM panel and frame (Type 2: SIM panel without/close gap). The presence or absence of this gap, and its width, significantly influences the structural response of the SIM panel to lateral loads, as indicated by Totoev [23,24]. In this study, the modelling strategy for the two types of SIM panels is distinct, and its responses to lateral loads are analyzed separately.

2.3.1. Type 1 SIM Panel with an Open Gap

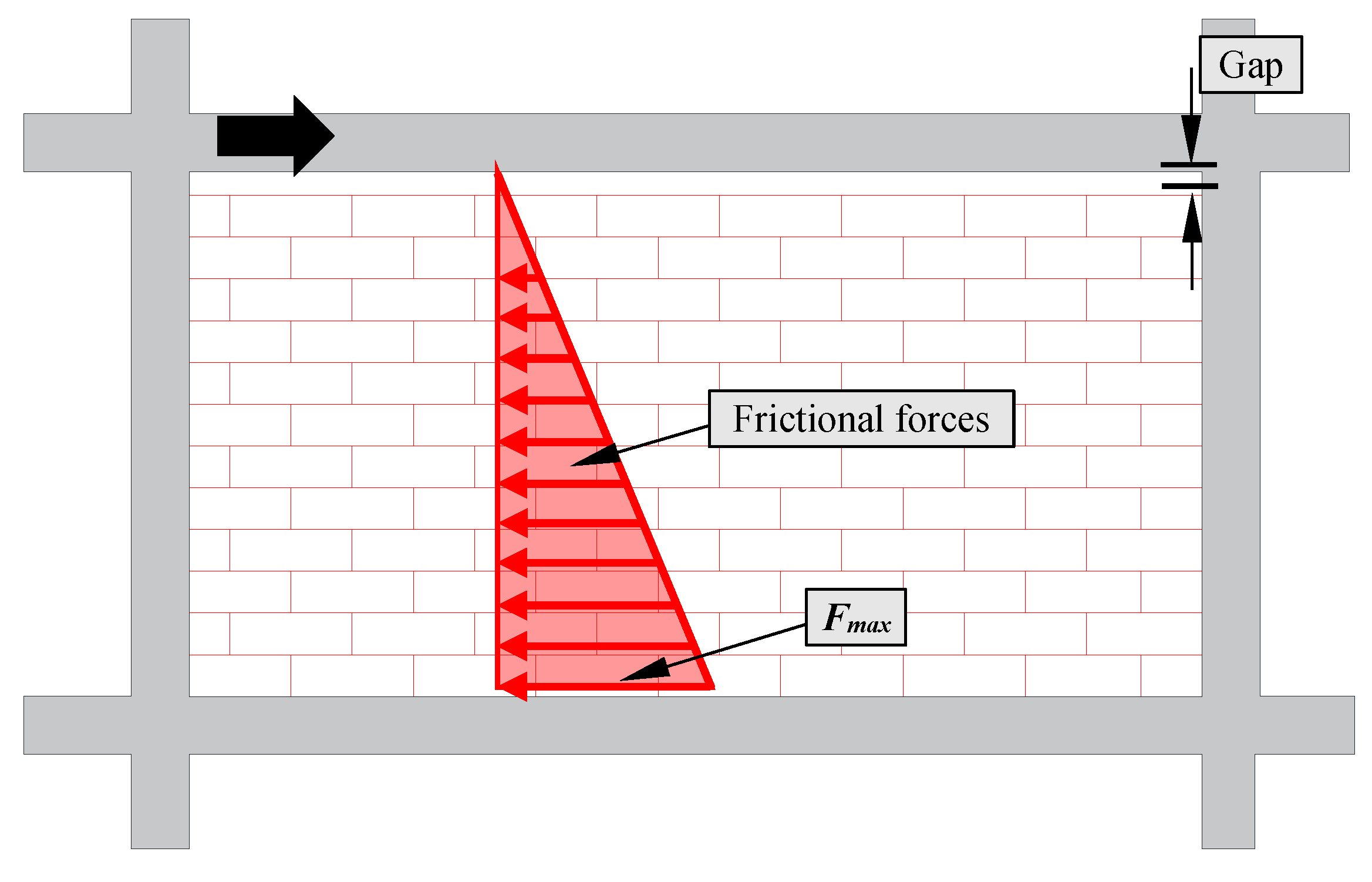
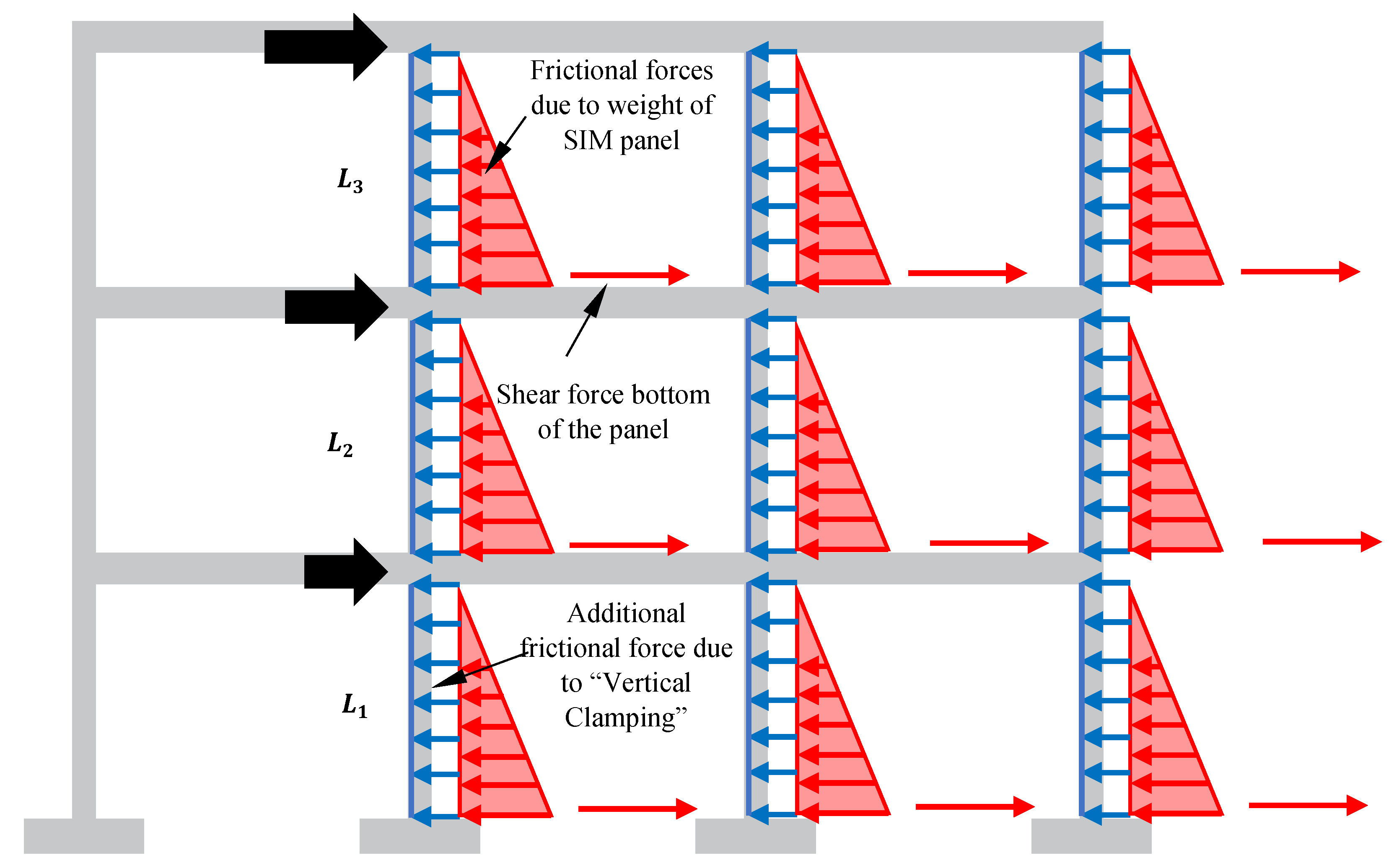
In Type 1 construction, the SIM panel is positioned tightly against the columns, featuring a gap between the top of the panel and the frame, as illustrated in Figure 8. This configuration implies that the frame interacts with the SIM panel solely through the columns. The gap remains open during a seismic event, and no compressive force on the panel originates from the top of the frame. As the frame experiences lateral loads, frictional forces emerge on the bed joints of the panel due to its self-weight. The distribution of the friction force can be conceptualized as a triangular force, as depicted in Figure 8.
The maximum theoretical frictional force at the bottom of the panel (Fmax) is determined by Equation (5) [23], with the notations for the equation already outlined in Table 1.
F m a x = H p L p t p ρ S I M g μ S I M
It is crucial to compare the theoretical Fmax value with the experimental results. For comparison, panels with an open gap (Panel TO and Panel MO) and panels with foam (Panel TF and Panel MF) are categorized as Type 1 SIM panels with a gap, experimental details can be found [9,13]. It is noteworthy that the Fmax remains constant, independent of the displacement or storey drift of the panel. 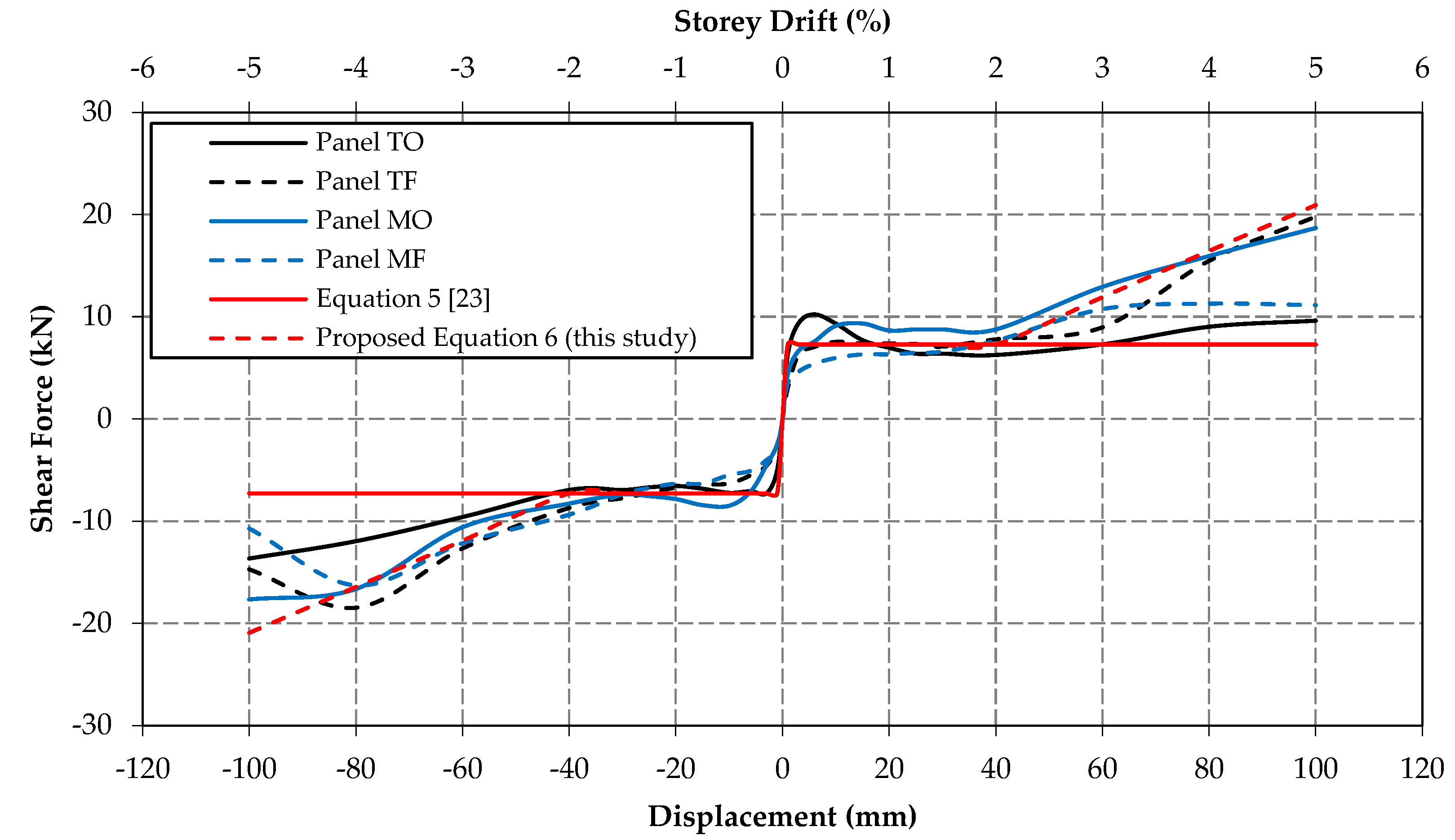For the tested panels, Fmax is a constant value of 7.28 kN, resulting in a total frictional force (represents the area of the triangle in Figure 8) of 7.28 kN for the 2m × 2m experimentally tested panel. The response of the Type 1 SIM panel (SIM panel with a gap) to lateral loads in this study is depicted in Figure 9.
It is noted that the theoretical value obtained from Equation (5) aligns well with the experimental results of up to 40mm displacement. However, beyond 40mm of in-plane displacement (2% of the storey drift), the behavior of open gap panels becomes similar to that of the Type 2 SIM panel (SIM panel without a gap). This transition occurs because, after 40mm of in-plane displacement (2% of the storey drift), panels with a gap and panels with foam experience an additional lateral load due to the development of extra frictional forces on each SIM bed joint, attributed to the 'Vertical Clamping' of the panel, as detailed in Section 2.3.2. In this study, the following equation is proposed to model the behavior of SIM panels with a gap (Type 1 SIM panel).
F m a x = H p L p t p ρ S I M g μ S I M + 4 × 10 − 5 ∆ t − 0.002 H p − 1.017 × E S I M ∆ t 2 L p t p μ S I M 4 H p 2
where ∆t and ESIM are the in-plane displacement of the panel and modulus of elasticity of SIM panel respectively.
It is essential to highlight that the proposed Equation (6) for the Type 1 SIM panel with a gap cannot account for the shear force resulting from the cracking of the units, as evidenced in Figure 9 after a displacement of -80mm. Nevertheless, the proposed equation (Equation (6)) demonstrates good correlation with the experimental results. Notably, Fmax is calculated as 21.85kN, and the total frictional force is 32.78kN for the 4m × 3m panel. The idealized response of the Type 1 SIM panel, up to 40 mm in-plane displacement, to the lateral load in this study is depicted in Figure 10.

2.3.2. Type 2 SIM panel without a gap (Close gap)

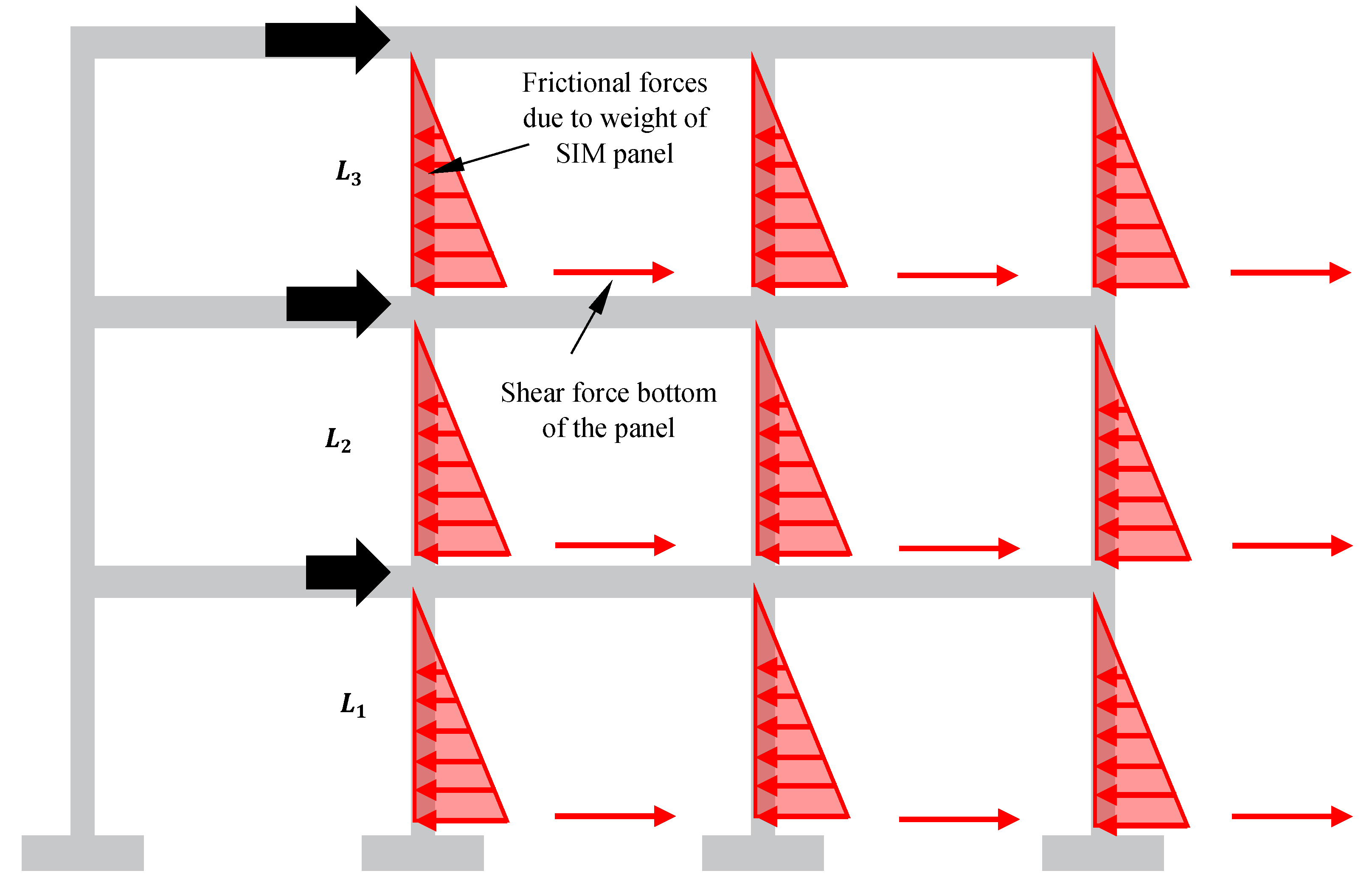
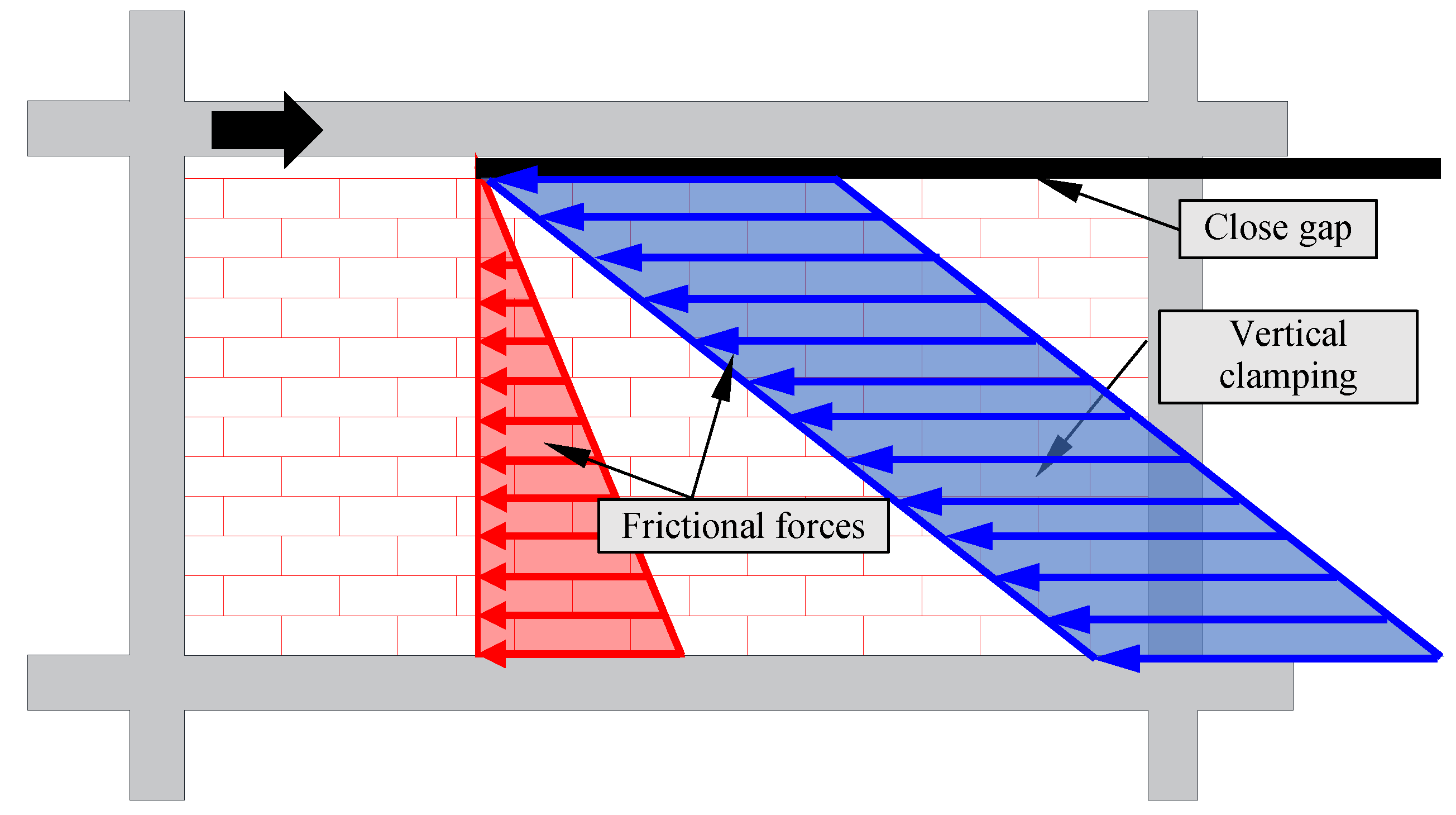
The Type 2 SIM panel is constructed firmly against all sides of the frame without any gap between the top of the panel and the frame, as illustrated in Figure 11. This design enables the SIM panel to withstand additional lateral loads generated by the development of extra frictional forces on each SIM bed joint, attributed to the 'vertical clamping' of the panel. The response to this additional frictional force is similar to the idealization of an equivalent compressive strut for traditional masonry (refer to Section 2.2). However, it is crucial to note that the interaction between the frame and panel differs for traditional masonry and SIM, and the equivalent compressive strut model is not applicable to the SIM panel [23].
The additional frictional force at each SIM bed joint of the panel, denoted as FC(∆t), due to the vertical clamping effect of the panel, is determined by Equation (7), as recommended by Totoev [23].
F C ( ∆ t ) = E S I M ∆ t 2 L p t p μ S I M 4 H p 2
The total frictional forces for the Type 2 SIM panel without a gap can be computed using the following equation, as outlined in Totoev [23].
F m a x = H p L p t p ρ S I M g μ S I M + E S I M ∆ t 2 L p t p μ S I M 4 H p 2
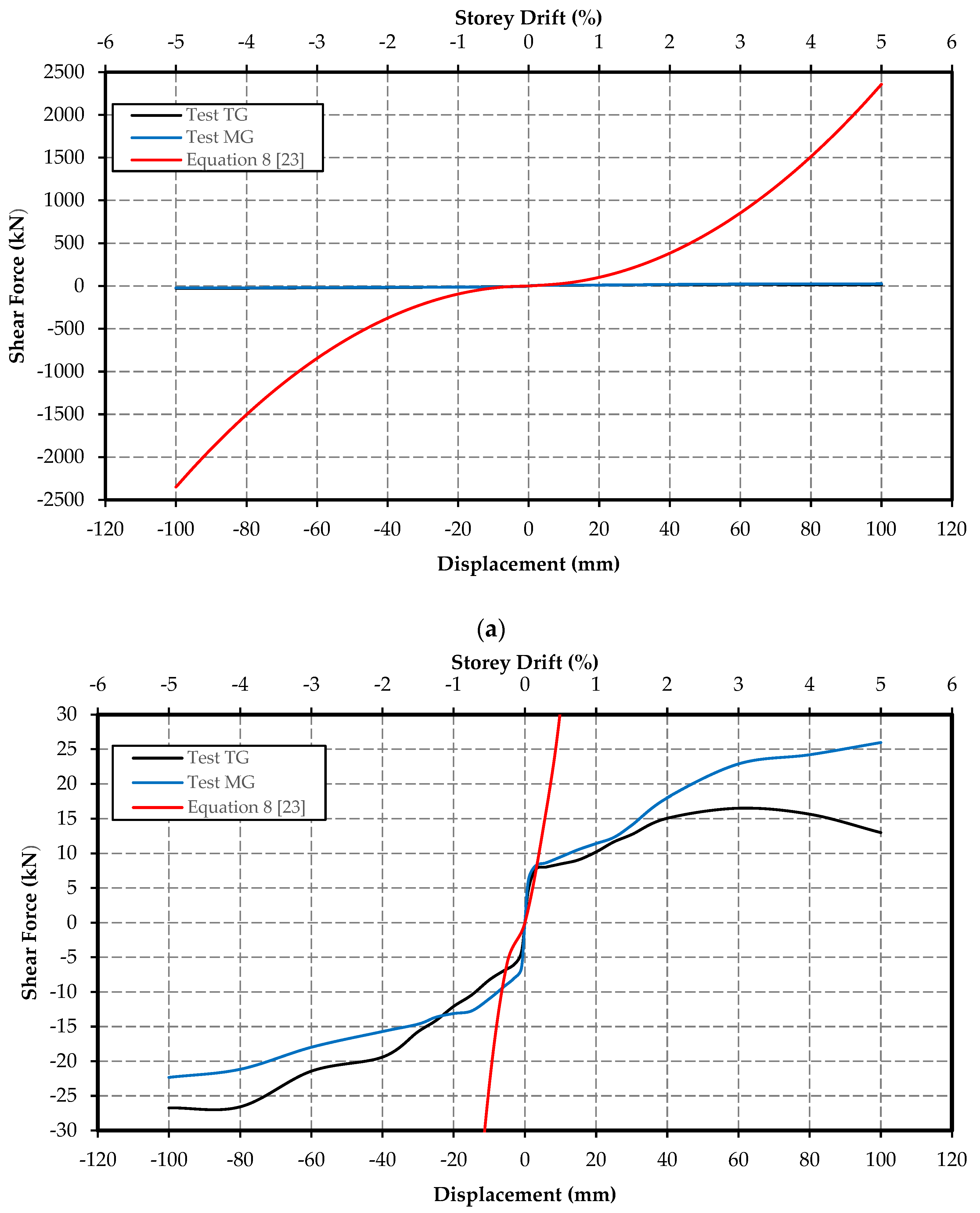
The comparison between the theoretical frictional force and the experimental results is presented in Figure 12. It is essential to note that the vertical scaling of the graphs in Figure 12 is not same. The observed discrepancy between the theoretical (based on previously developed equation by Totoev [23]) and experimental values is substantial, with the theoretical values often exceeding the experimental ones by more than 100 times. However, a closer alignment is observed for smaller displacements, typically around 1mm. This disparity is attributed to assumptions made during the derivation of Equation (8) and the impact of additional frictional forces due to vertical clamping, which significantly relies on the second-order displacement component. To address this discrepancy, a reduction factor is introduced to better align the theoretical predictions with the experimental results. The proposed equation (Equation (9)) in this study aims to predict the shear force response for the Type 2 SIM panel without a gap.
F m a x = H p L p t p ρ S I M g μ S I M + R T y p e 2 E S I M ∆ t 2 L p t p μ S I M 4 H p 2
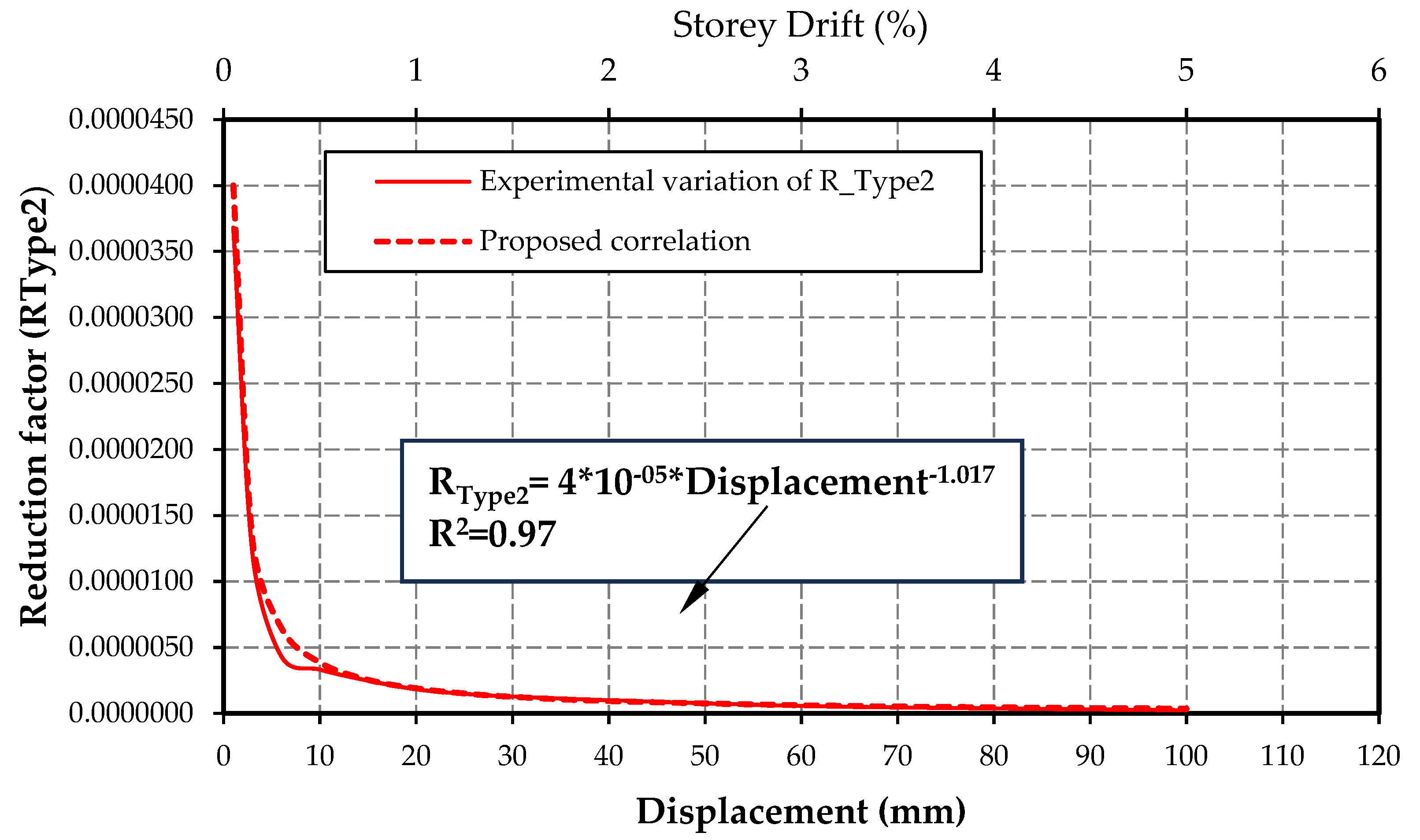
Where RType2 is the reduction factor to match the experimental results. RType2 was determined based on the collective variation observed in Panel TO, Panel TF, Panel MO, and Panel MF for both push and pull directions of shear forces. The correlation between the reduction factor and collective variation of in-plane displacement is illustrated in Figure 13.
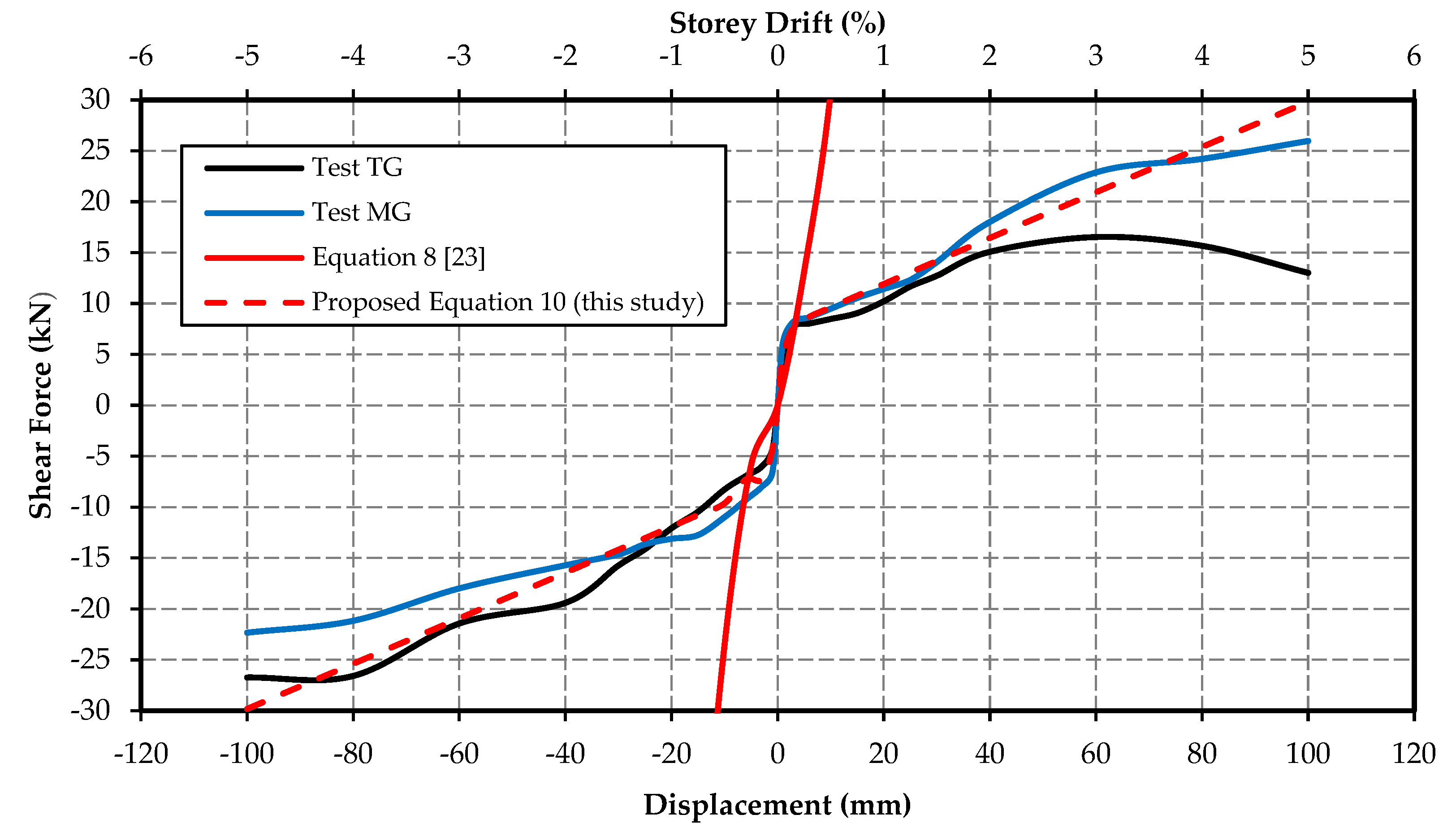
The determined value of Rtype2 is substituted into Equation (9), and the resulting equation for calculating the total frictional force for the Type 2 SIM panel is presented in Equation (10). Figure 14 depicts the variation of the proposed theoretical model with the experimental results for the Type 2 SIM panel without a gap.
F m a x = H p L p t p ρ S I M g μ S I M + 4 × 10 − 5 ∆ t − 1.017 × E S I M ∆ t 2 L p t p μ S I M 4 H p 2
Figure 14 illustrates that the proposed theoretical model cannot predict the drop of shear force due to unit cracking. Furthermore, the additional frictional force due to clamping of the panel is also a function of displacement/storey drift of the structure. To achieve the correct response of the additional frictional force due to clamping of the panel, an iterative process was adopted in static analysis. The iterative method was applied until the assumed roof displacement was within 5% of the roof displacement in the Strand7 model. In this study, the frictional force developed on the bed joint, and the additional frictional force developed due to clamping can be idealized as trapezoidal resistance, as illustrated in Figure 15. 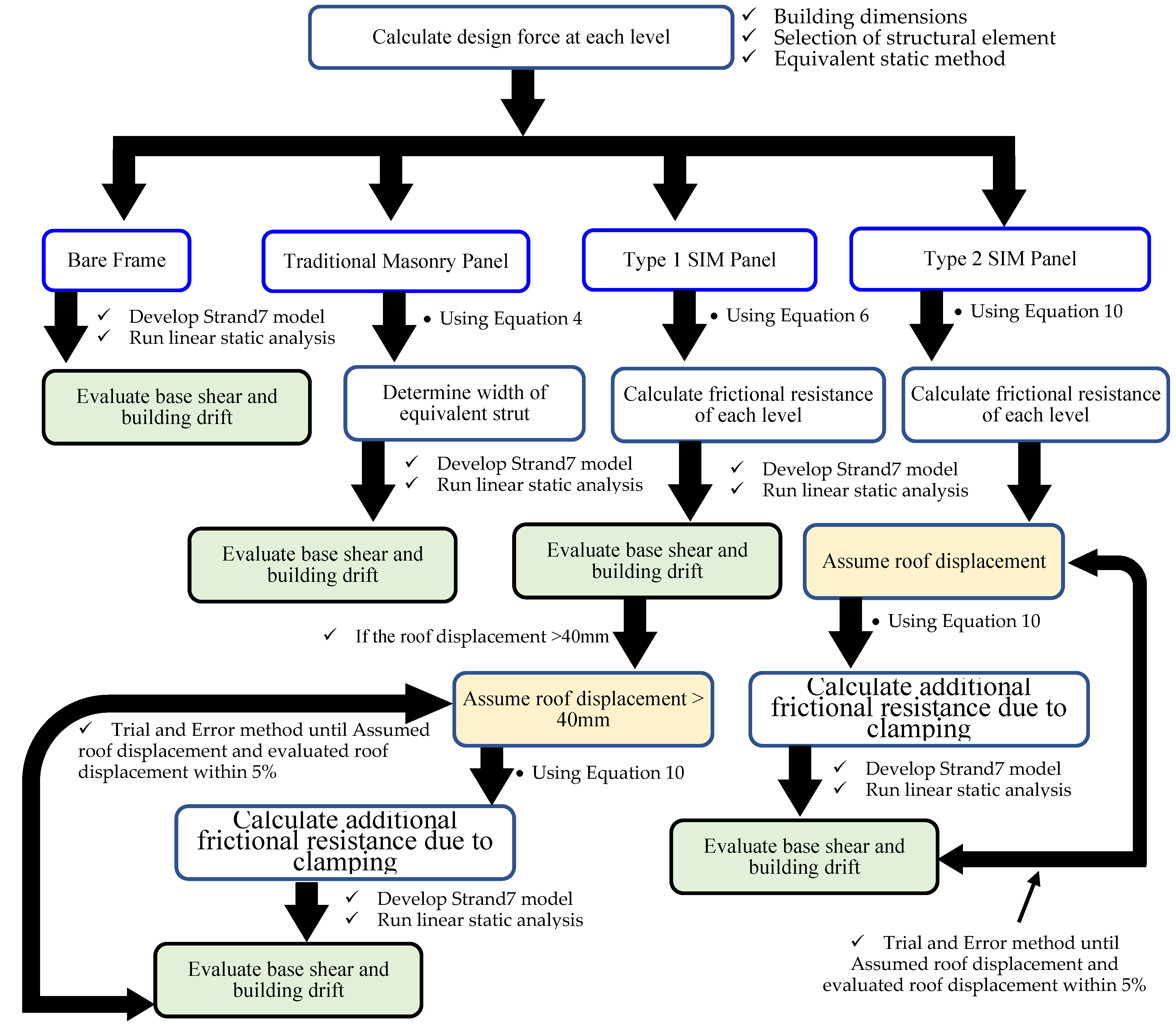The model used for Type 1 and Type 2 SIM panels in Strand7 is presented in Figure 16. The overall workflow adopted in this study is illustrated in Figure 17. The presented workflow, incorporating these calculations and analyses, provides a comprehensive understanding of the building's behavior under seismic conditions and is essential for evaluating its seismic performance.

3. Results and Discussion

The objective of this study was to investigate the response of a building featuring structural frames filled with semi-interlocking masonry (SIM) panels when exposed to lateral forces under varying seismic conditions. To achieve this, a model incorporating SIM infill panels was created in Strand7 to capture the impact of SIM panel implementation in multi-storey buildings. This section presents an evaluation of the results derived from the simplified models across three seismic risk categories: low (Newcastle), medium (Dowerin), and high (Macquarie Island) seismic locations in Australia. The analysis focuses on building base shear and displacement (drift) to ascertain the feasibility of integrating SIM infill panels in each seismic risk category.

3.1. Assessment of building base shear and displacement (drift)

The results were analyzed in this study, focusing on building base shear and displacement (drift ratio), with the aim of determining the feasibility of implementing SIM infill panels in the locations of each seismic risk category. The base shear was derived from the horizontal reaction force at the supports, while drift was determined from the horizontal displacement output obtained from the Strand7 analysis. Building drift is defined as the horizontal displacement at the top of the building relative to the horizontal displacement at the ground surface. As per AS 1170.4-2007 standards, the drift ratio of each storey should not exceed 1.5% [14]. Table 5 presents the base shear and building drift for all cases obtained from the Strand7 analyses. Figure 18 illustrates the variation of the drift ratio for all cases. Notably, as expected, traditional masonry exhibits minimal displacement (drift) compared to both types of SIM panels. This is attributed to the stiff response of traditional masonry elements to lateral loads due to their inherent rigidity. In scenarios with high base shear, panels attempt to dissipate earthquake-induced energy by forming structural cracks, which may lead to building failure. SIM panels, however, allow more displacement than traditional masonry panels, reducing the base shear force and mitigating cracks in the building. Furthermore, it is observed that, for a given location, base shear increases with higher importance levels. Additionally, base shear shows higher values for deep/soft soil compared to shallow soil. It is crucial to evaluate which SIM panel reached its maximum frictional capacity for different cases.
The percentage of SIM panel frictional capacity for each case is detailed in Table 6. The assessment of SIM panel frictional capacity is based on the ratio of the required frictional resistance for a given load case to the maximum capacity of the panel's frictional resistance, as written as “FULL” in Table 6. To assess the contribution of SIM panels to resisting the lateral load, a decision was made to allocate two-thirds of the horizontal equivalent static design force at each level of the infilled frame to be resisted by the frictional force developed on the bed joints of the panel, considering its capacity [23]. The remaining one-third of the force would be borne by the structural frame. This allocation methodology was employed to ensure a balanced and optimized distribution of forces, considering both the inherent capabilities of the SIM panels and the structural integrity of the frame. It is noted that the maximum capacity of the frictional force for each panel is 32.78 kN. As anticipated, the panels at Level 1 demonstrate a higher resistance to lateral forces compared to those at Level 2 and Level 3. This discrepancy is due to the higher horizontal static load at Level 1 than at other levels. Notably, in the Newcastle region, no panel reached its maximum capacity, while all Level 1 panels reached their full capacity in Macquarie Island. A more in-depth analysis of the results is provided based on the specific locations.

3.1.1. Newcastle - low risk seismic area

Newcastle, characterized as a low seismic risk area with minimal historical earthquake occurrences and a low hazard factor of 0.11, exhibits relatively low seismic forces, as depicted in Figure 19a and Figure 19b showcasing the shear force and building drift variations, respectively. In this low-risk region, the base shear is limited to approximately 200kN, with a building drift of around 20mm. Consequently, the feasibility of employing SIM panels for multi-storey buildings in Newcastle appears limited. However, for structures with an importance level of 4 and soft soil conditions (e.g., Case 6), the use of SIM panels may be considered. Nevertheless, the recommendation is to continue using traditional masonry panels for multi-storey infill panels in this region.

3.1.2. Dowerin - medium risk seismic area

Dowerin, categorized as a moderate seismic risk location in Australia with a hazard design factor of 0.20, demonstrates an increase in base shear force compared to traditional masonry panels, as illustrated in Figure 20.
The base shear ranges from approximately 120kN to 400kN in Dowerin. This significant base shear force raises concerns due to the limited movement allowed in traditional masonry before unit cracking occurs. Consequently, the utilization of SIM panels emerges as a feasible solution for this region, offering greater flexibility and reduced risk of structural damage.
The implementation of SIM panels, both Type 1 with a gap and Type 2 without a gap, resulted in a notable reduction in base shear, ranging from 61% to 77% and 73% to 86%, respectively. The effectiveness of Type 1 SIM panels with a gap in mitigating the risk of structural failure due to seismic events in multi-storey buildings is particularly evident in this region. However, for Case 12, characterized by high importance levels and soft soil conditions, the use of Type 2 SIM panels without a gap is recommended, as they exhibit lower drift compared to Type 1 SIM panels.

3.1.3. Macquarie Island - high risk seismic area

Macquarie Island, characterized by a high seismic risk with a hazard factor of 0.6 in this study, presents significant challenges for structural resilience. Figure 21 depicts the variation of shear force (Figure 21a) and building drift (Figure 21b) for the Macquarie Island region. The base shear force for traditional masonry in this region ranged from approximately 430kN to 1225kN, signifying a considerable magnitude. The adoption of SIM panels, both Type 1 with a gap and Type 2 without a gap, demonstrated a substantial reduction in base shear to the range of 41% to 59% and 69% to 87%, respectively, when compared with traditional masonry. However, it was observed that all SIM panels in Level 1 for this location reached their maximum frictional capacity.
The implementation of Type 1 SIM panels with a gap, designed to resist the substantial horizontal force, resulted in a maximum drift of approximately 100mm, raising concerns about potential structural damage. Consequently, the feasibility of using Type 1 SIM panels in high seismic areas like Macquarie Island is questionable. On the other hand, Type 2 SIM panels without a gap exhibited lower drift and reduced the base shear by up to 87%, making them a potentially effective solution for this region.

4. Conclusions

In this study, structural models were created in Strand7 to simulate the impact of various seismic loads on a bare reinforced concrete frame, a traditional unreinforced masonry infilled reinforced concrete frame, and a semi-interlocking masonry (SIM) infilled reinforced concrete frame. The study considered three locations, representing low, medium, and high-risk seismic areas in Australia, as well as additional factors such as building subsoil classes and importance levels. The feasibility of utilizing SIM as a construction material was assessed based on these considerations. The analysis yielded the following key observations.
  • The assessment of the feasibility of implementing Semi-Interlocking Masonry (SIM) Panels was predicated on two primary considerations: first, whether the base shears for a given location were of sufficient magnitude to accommodate the use of the system; and second, whether the implementation of the SIM system resulted in acceptable storey drift. As anticipated, traditional masonry panels demonstrated substantial base shears and minimal displacements, while SIM panels exhibited heightened displacements and reduced base shears for equivalent locations, subsoil classifications, and importance levels.
  • The outcomes derived from this analysis, which considered seismic forces anticipated in a low-risk seismic area in Australia, demonstrated a noteworthy reduction in base shears. The observations indicated that the base shears for low-risk seismic areas are comparatively low, posing no significant challenges for traditional masonry structures in these regions. Consequently, the utilization of SIM panels in low-risk seismic areas is deemed impractical.
  • The adoption of SIM panels emerges as a more practical option for regions with a medium to high seismic risk in Australia. The findings revealed the development of substantial base shears ranging from 120kN to 350kN for traditional masonry panels in a medium seismic risk area. Such elevated base shears have the potential to induce structural damage in traditional masonry due to its inherent rigidity, leading to the appearance of structural cracks while mitigating earthquake energy. In contrast, SIM panels with an open gap exhibit a less rigid response, reducing the base shear at the ground floor column by a minimum of 61% (depending on the seismic load case). Consequently, SIM panels with an open gap prove to be more efficient in dissipating earthquake energy compared to traditional masonry, while maintaining drift ratios well below the maximum limit of 1.5%.
  • In the context of forces simulating those anticipated in a high seismic risk area, the utilization of the SIM system demonstrates enhanced performance during seismic events. In the high-risk seismic area, while base shears remain considerable, drift levels become particularly concerning for Type 1 SIM panels. Conversely, Type 2 SIM panels showcase improved outcomes in terms of both base shear and building drift when compared to Type 1 SIM panels. As a result, the implementation of SIM panels with a close gap is recommended for areas characterized by very high seismic risk.

Author Contributions

Conceptualization, M.A.H., Y.Z.T. and M.J.M.; methodology, M.A.H. and Y.Z.T.; software, M.A.H.; resources, Y.Z.T. and M.J.M.; writing—original draft preparation, M.A.H.; writing—review and editing, Y.Z.T. and M.J.M.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. Friction on mortar-less joints in semi interlocking masonry. Proceedings of 16th International Brick and Block Masonry Conference, Padova, Italy; 2016. [Google Scholar]
  2. Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. In-plane cyclic behavior of Semi Interlocking Masonry panel under large drift. Proceedings of 13th Canadian Masonry Symposium, Halifax, Canada; 2017. [Google Scholar]
  3. Shing, P.B.; Mehrabi, A.B. Behaviour and analysis of masonry-infilled frames. Progress in Structural Engineering and Materials, 2002, 4, 320–331. [Google Scholar] [CrossRef]
  4. Uzoegbo, H.C.; Senthivel, R.; Ngowi, J.V. Load Capacity of Dry-Stack Masonry Wall. The Masonry Society Journal, 2007, 25, 41–52. [Google Scholar]
  5. Madan, A.; Senthivel, R.; Uzoegbo, H.; Jäger, W. Influence of Masonry Infills on the Dynamic Response of R/C Framed Structures. Proceedings of 13th International Brick and Block Masonry Conference, Amsterdam, The Netherlands; 2004. [Google Scholar]
  6. Thurston, S.J.; Beattie, G.J. Seismic performance of brick veneer houses. Phase 1. Cyclic and elemental testing of clay brick veneer construction, BRANZ Ltd: Judgeford, New Zealand, 2008.
  7. Lourenço, P.B.; Leite, J.C.; Pereira, M.F.P. Masonry infills and earthquakes. Proceedings of 11th Canadian Masonry Symposium, Toronto, Canada; 2009. [Google Scholar]
  8. Totoev, Y.Z., Mortarless Masonry. Australian Patent Application No. 2010905681, filed date December 24, 2010.
  9. Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. Application of Digital Image Correlation (DIC) Technique for Semi Interlocking Masonry (SIM) Panels under Large Cyclic In-Plane Shear Displacement. Experimental Techniques, 2021, 45, 509–530. [Google Scholar] [CrossRef]
  10. Lin, K.; Totoev, Y.Z.; Liu, H.J.; Guo, T. In-Plane Behaviour of a Reinforcement Concrete Frame with a Dry Stack Masonry Panel. Materials 2016, 9, 497–509. [Google Scholar] [CrossRef] [PubMed]
  11. Forghani, R.; Totoev, Y.Z.; Kanjanabootra, S.; Davison, A. Experimental Investigation of Water Penetration through Semi-Interlocking Masonry Walls. Journal of Architectural Engineering 2016, 04016017-1-9. [Google Scholar] [CrossRef]
  12. Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. Experimental Investigation of Frictional Behavior of Mortarless Surface in Semi-Interlocking Masonry under Cyclic Displacement. Journal of Materials in Civil Engineering, 2020, 32, 04020259. [Google Scholar] [CrossRef]
  13. Hossain, M.A.; Totoev, Y.Z.; Masia, M.J. Experimental assessment of large displacement cyclic in-plane shear behaviour of semi-interlocking masonry panels. International Journal of Masonry Research and Innovation, 2019, 4, 378–399. [Google Scholar] [CrossRef]
  14. AS 1170.4-2007. Australian standards for structural design actions, part 4: Earthquake actions in Australia.<italic> Standards Australia Limited and Standards New Zealand Limited</italic>, Australia and New Zealand, 2007.
  15. Lin, K.; Totoev, Y.Z.; Liu, H.J.; Page, A.W. Modeling of dry-stacked masonry panel confined by reinforced concrete frame. Archives of Civil and Mechanical Engineering, 2014, 14, 497–509. [Google Scholar] [CrossRef]
  16. Safe Work Australia, Safe design of structure: Code of practice.<italic> Safe work Australia</italic>, <bold>2018</bold>.
  17. AS 1170.0:2002. Australian standards for structural design actions, part 0: General principles.<italic> Standards Australia Limited and Standards New Zealand Limited</italic>, Australia and New Zealand, 2002.
  18. NCC 2022, NCC 2022 Volume One-Building Code of Australia Class 2 to 9 buildings.<italic> Australian Building Codes Board</italic>, 2021.
  19. Polyakov, S.V. On the interaction between masonry filler walls and enclosing frame when loaded in the plane of the wall.<italic> Translations in Earthquake Engineering</italic>, Earthquake engineering Research Institute, Oakland, California, 1960, pp. 36–42.
  20. Crisafulli, F.J. Seismic behaviour of reinforced concrete structures with masonry infills. PhD (Civil Engineering) thesis, University of Canterbury, Christchurch, New Zealand, 29 July 1997.
  21. FEMA273, NEHRP Commentary on the Guidelines for the Rehabilitation of Building. Washington DC: Federal Emergency Management Agency, Washington DC, USA, 1996.
  22. Mainstone, R.J.; Weeks, G.A. The influence of Bounding Frame on the Racking Stiffness and Strength of Brick Walls. In Proceedings of the 2nd International Brick Masonry Conference, Building Research Establishment, Watford, England; pp. 165–171.
  23. Totoev, Y.Z. Design Procedure for Semi Interlocking Masonry. Journal of Civil Engineering and Architecture, 2015, 9, 517–525. [Google Scholar]
  24. Totoev, Y.Z. Classification of SIM infill panels/Klassifikation von SIM-Ausfachungswänden. Ernst & Sohn Verlag für Architektur und technische Wissenschaften,. Mauerwerk 2015, 19, 74–79. [Google Scholar]
Preprints 109724 g001
Figure 1. Typical structural damage in masonry infill panels caused by seismic activities [6,7].
Figure 1. Typical structural damage in masonry infill panels caused by seismic activities [6,7].
Preprints 109724 g001
Preprints 109724 g002
Figure 2. Semi-Interlocking Masonry (SIM) unit types: (a) Topological SIM unit; (b) Mechanical SIM unit.
Figure 2. Semi-Interlocking Masonry (SIM) unit types: (a) Topological SIM unit; (b) Mechanical SIM unit.
Preprints 109724 g002
Preprints 109724 g003
Figure 3. Elevation of models: (a) Bare frame; (b) Masonry panels infill.
Figure 3. Elevation of models: (a) Bare frame; (b) Masonry panels infill.
Preprints 109724 g003
Preprints 109724 g004
Figure 4. Geographic (Australasia) locations of structure considered in this study.
Figure 4. Geographic (Australasia) locations of structure considered in this study.
Preprints 109724 g004
Preprints 109724 g005
Figure 5. Modelling of bare frame: (a) Geometry of bare frame; (b) Model of bare frame in Strand7.
Figure 5. Modelling of bare frame: (a) Geometry of bare frame; (b) Model of bare frame in Strand7.
Preprints 109724 g005
Preprints 109724 g006
Figure 6. Representation of diagonal compressive strut for traditional masonry: (a) Traditional masonry panel; (b) Replacement of traditional panel by equivalent diagonal compressive strut.
Figure 6. Representation of diagonal compressive strut for traditional masonry: (a) Traditional masonry panel; (b) Replacement of traditional panel by equivalent diagonal compressive strut.
Preprints 109724 g006
Preprints 109724 g007
Figure 7. Modelling of bare frame: (a) Geometry of bare frame; (b) Model of bare frame in Strand7.
Figure 7. Modelling of bare frame: (a) Geometry of bare frame; (b) Model of bare frame in Strand7.
Preprints 109724 g007
Preprints 109724 g008
Figure 8. Type 1 SIM panels with gap, adopted from Totoev [23].
Figure 8. Type 1 SIM panels with gap, adopted from Totoev [23].
Preprints 109724 g008
Preprints 109724 g009
Figure 9. Comparison of experimental and analytical results for Type 1 SIM panel.
Figure 9. Comparison of experimental and analytical results for Type 1 SIM panel.
Preprints 109724 g009
Preprints 109724 g010
Figure 10. Idealised lateral load response for Type 1 SIM panel up to 2% storey drift.
Figure 10. Idealised lateral load response for Type 1 SIM panel up to 2% storey drift.
Preprints 109724 g010
Preprints 109724 g011
Figure 11. Type 2 SIM panels without a gap, adopted from Totoev [23].
Figure 11. Type 2 SIM panels without a gap, adopted from Totoev [23].
Preprints 109724 g011
Preprints 109724 g012
Figure 12. Comparison of theoretical and experimental results for Type 2 SIM panel without gap: (a) Shear force presented up to 3000kN; (b) Shear force presented up to 30kN.
Figure 12. Comparison of theoretical and experimental results for Type 2 SIM panel without gap: (a) Shear force presented up to 3000kN; (b) Shear force presented up to 30kN.
Preprints 109724 g012
Preprints 109724 g013
Figure 13. Variation of reduction factor for Type 2 SIM panel.
Figure 13. Variation of reduction factor for Type 2 SIM panel.
Preprints 109724 g013
Preprints 109724 g014
Figure 14. Comparison between the experimental results and the proposed theoretical model.
Figure 14. Comparison between the experimental results and the proposed theoretical model.
Preprints 109724 g014
Preprints 109724 g015
Figure 15. Idealized lateral load response for Type 2 SIM panel without gap.
Figure 15. Idealized lateral load response for Type 2 SIM panel without gap.
Preprints 109724 g015
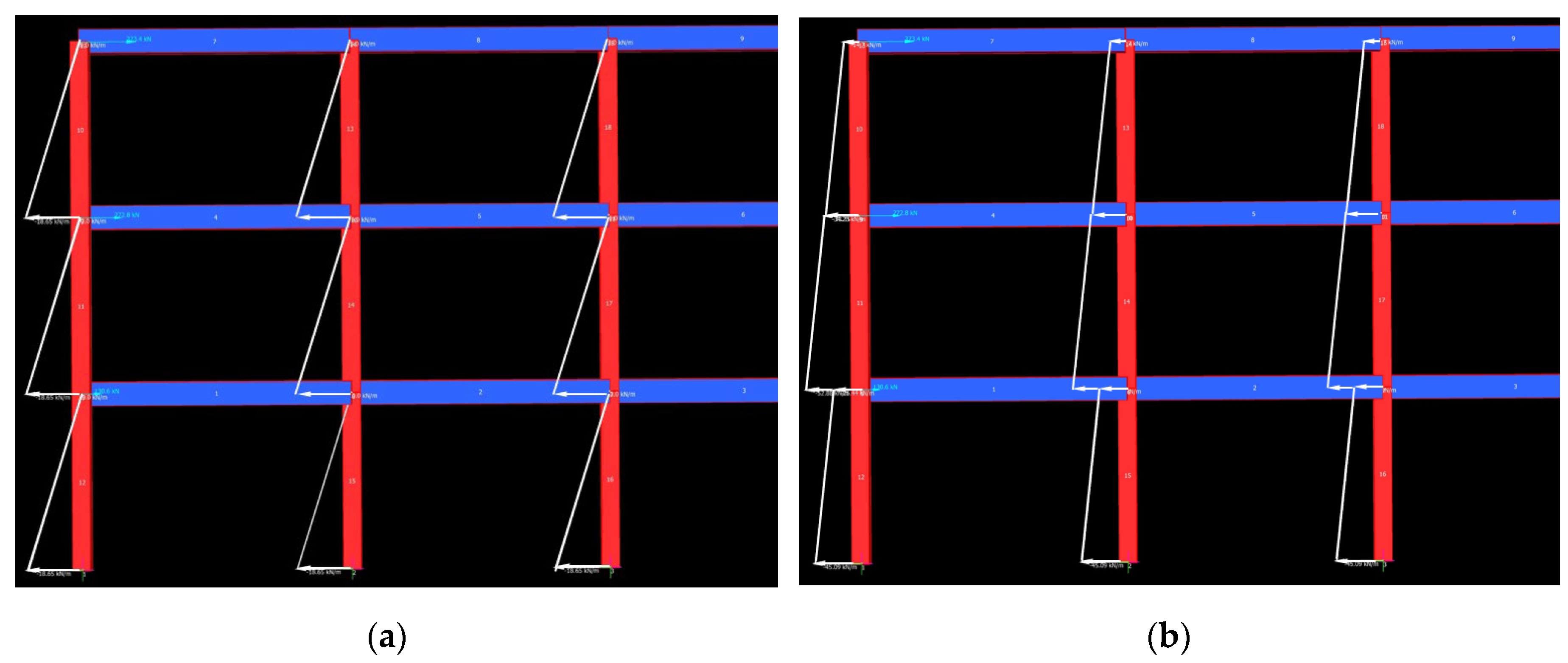
Preprints 109724 g016
Figure 16. Model of SIM panel: (a) Strand7 model of Type 1 SIM panel with gap of up to 40 mm in-plane displacement; (b) Strand7 Model of Type 1 SIM panel for after 40 mm displacement and Type 2 SIM panel without gap.
Figure 16. Model of SIM panel: (a) Strand7 model of Type 1 SIM panel with gap of up to 40 mm in-plane displacement; (b) Strand7 Model of Type 1 SIM panel for after 40 mm displacement and Type 2 SIM panel without gap.
Preprints 109724 g016
Preprints 109724 g017
Figure 17. Overall workflow for this study.
Figure 17. Overall workflow for this study.
Preprints 109724 g017
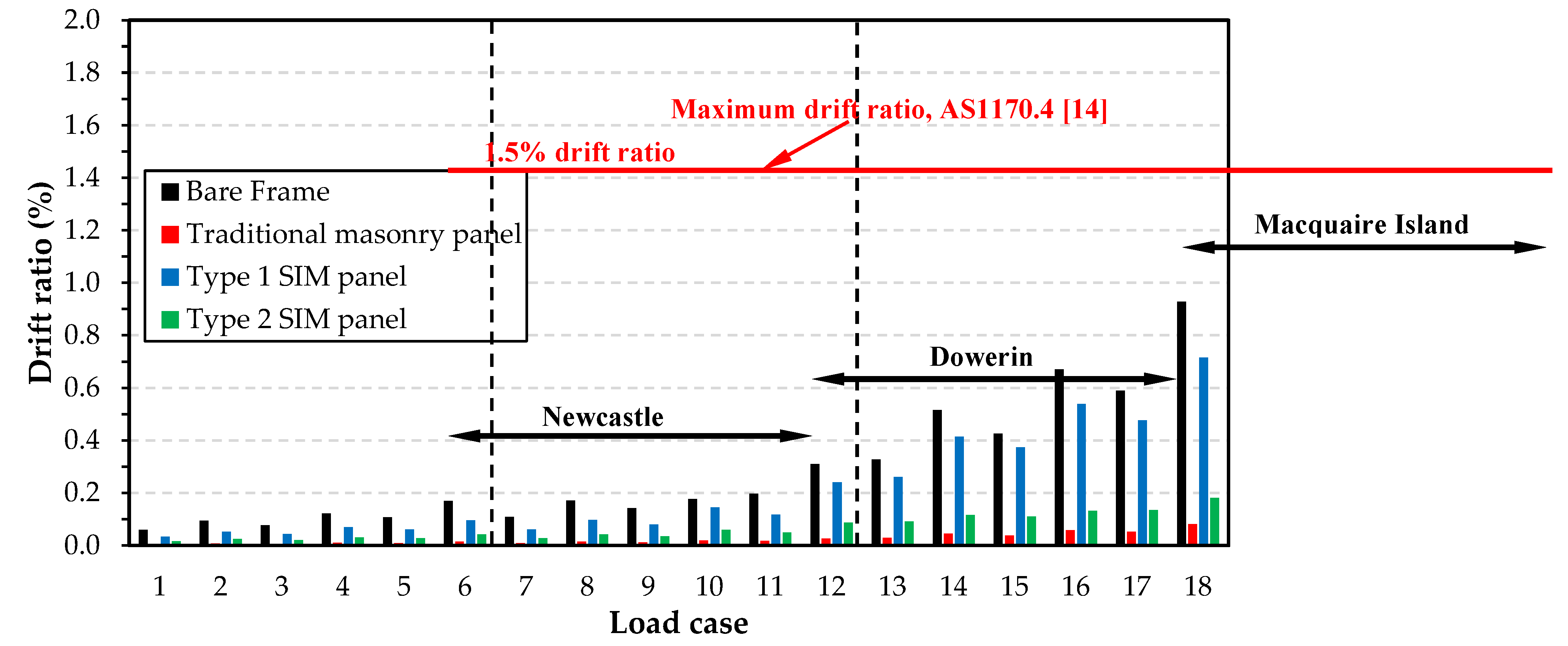
Preprints 109724 g018
Figure 18. Variation of drift ratio of different structures for all load cases.
Figure 18. Variation of drift ratio of different structures for all load cases.
Preprints 109724 g018
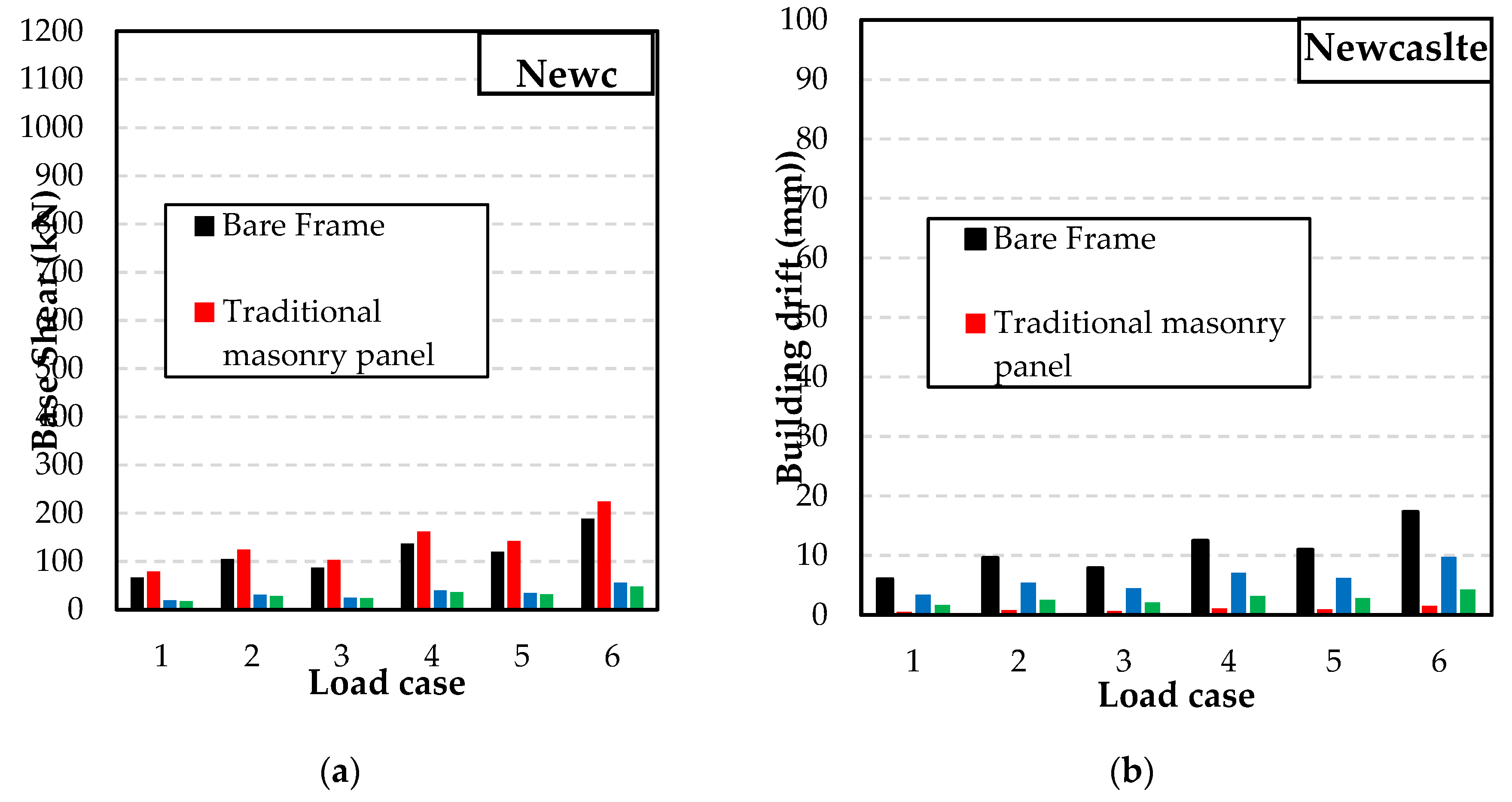
Preprints 109724 g019
Figure 19. Variation of shear force and building drift for low risk seismic region: (a) Base shear; (b) Building drift.
Figure 19. Variation of shear force and building drift for low risk seismic region: (a) Base shear; (b) Building drift.
Preprints 109724 g019
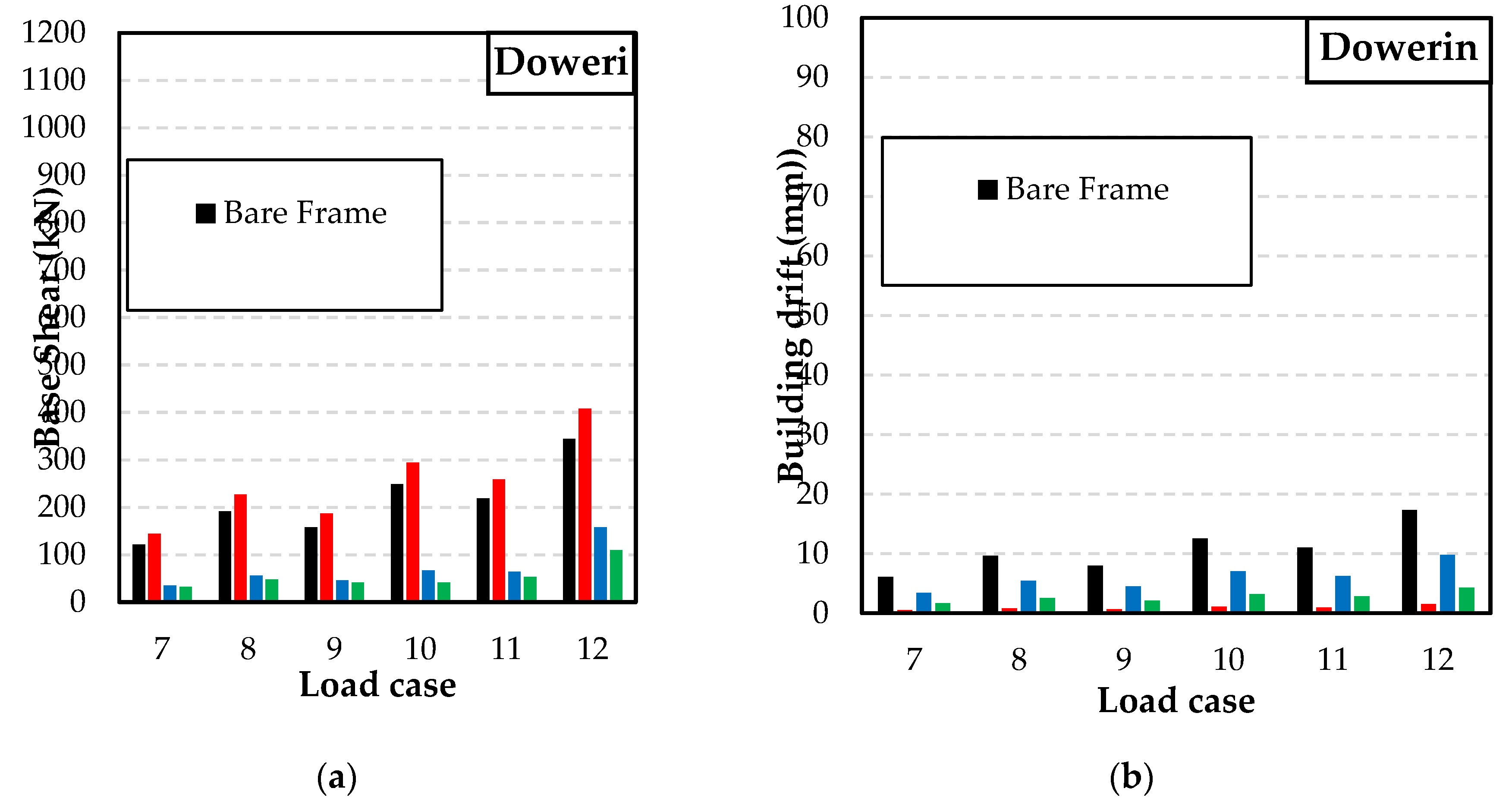
Preprints 109724 g020
Figure 20. Variation of shear force and building drift for medium risk seismic region: (a) Base shear; (b) Building drift.
Figure 20. Variation of shear force and building drift for medium risk seismic region: (a) Base shear; (b) Building drift.
Preprints 109724 g020
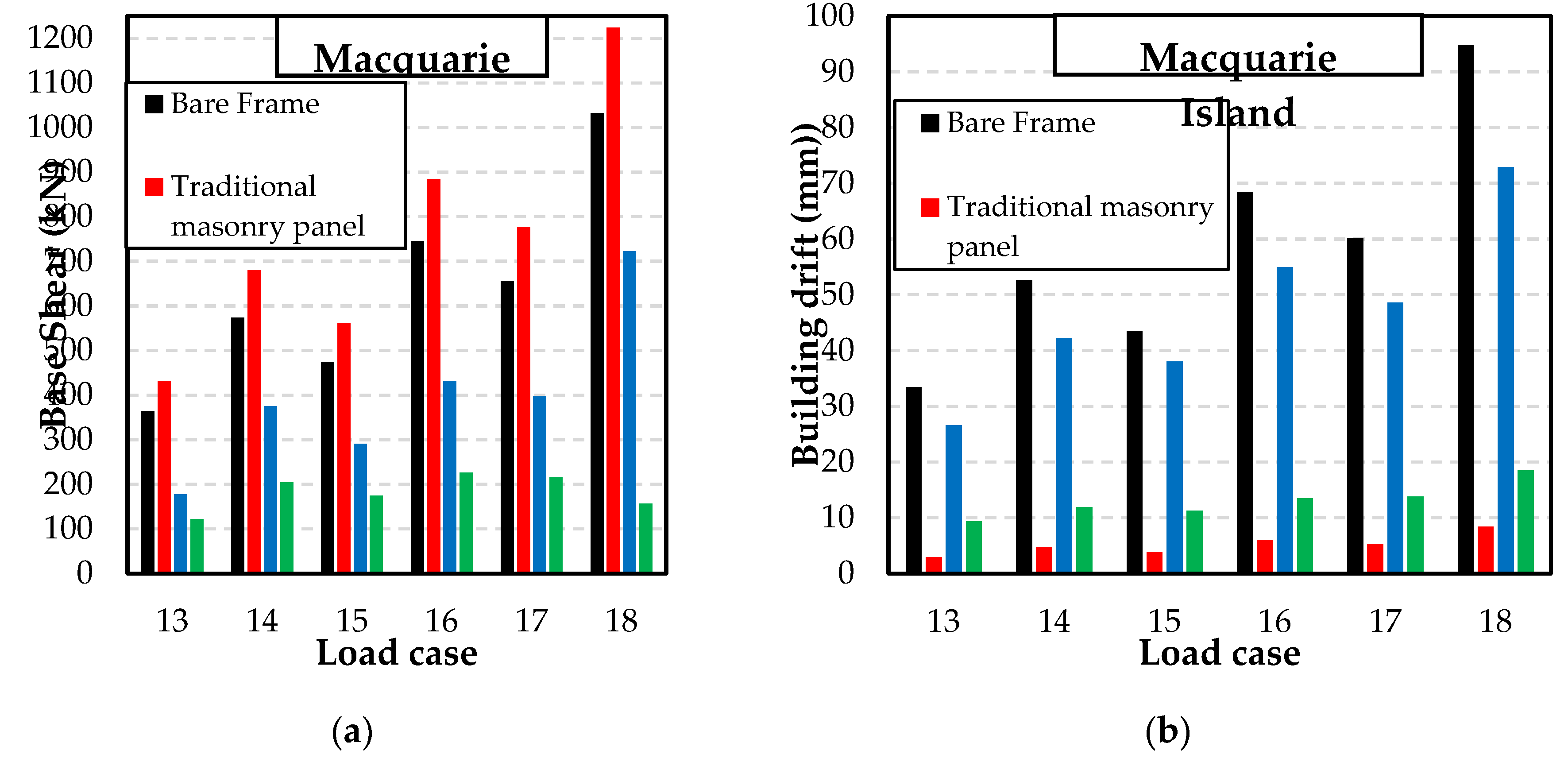
Preprints 109724 g021
Figure 21. Variation of shear force and building drift for high risk seismic region: (a) Base shear; (b) Building drift.
Figure 21. Variation of shear force and building drift for high risk seismic region: (a) Base shear; (b) Building drift.
Preprints 109724 g021
Table 1. Key properties of bare frame, masonry panels and loading conditions.
Table 1. Key properties of bare frame, masonry panels and loading conditions.
Parameter Notation Value
Panel length Lp 4 m
Panel height Hp 3 m
Panel thickness tp 0.11 m [15]
Density of SIM and masonry panel ρSIM 22.1 kg/m3 [11]
Coefficient of friction of SIM units μSIM 0.75 [12]
Column width bc 0.3 m
Column depth dc 0.3 m
Concrete column unit weight γc 24.5 kN/m3 [15]
Beam width bb 0.4 m
Beam depth db 0.4 m
Permanent load G 0.5 kPa [14]
Imposed load Q 2 kPa [14]
Width of slab w 4 m
Earthquake combination factor for live load ΨE 0.3 [14]
Design life of structure - 50 years [16]
Modulus of elasticity of column Ec, 32000 MPa [15]
Modulus of elasticity of beam Eb 33000 MPa [15]
Density of column ρc 2281 kg/m3 [15]
Density of beam ρb 2350 kg/m3 [15]
Elastic modulus of SIM unit ESIM 26365 MPa [15]
Table 2. Consequences of failure corresponding to different importance levels, as adopted from NCC 2022 [18].
Table 2. Consequences of failure corresponding to different importance levels, as adopted from NCC 2022 [18].
Importance level Building Types
1 Buildings or structures presenting a low degree of hazard to life and other property in the case of failure
2 Buildings or structures not included in Importance Level 1, 3 and 4
3 Buildings or structures that are designed to contain a large number of people
4 Buildings or structures that are essential to post-disaster recovery or associated with hazardous facilities
Table 3. Criterions employed for determination of equivalent static force.
Table 3. Criterions employed for determination of equivalent static force.
Criteria 1 Criteria 2 Criteria 3
Location Hazard design
factor, Z		 Importance
level		 Probability
factor, kp 		Site
class		 Spectral shape
factor, Ch(T1)
Newcastle 0.11 (Low risk) 2 1 Ce 2.34
Dowerin 0.2 (Medium risk) 3 1.3 De 3.68
Macquarie Island 0.6 (High risk) 4 1.8 - -
Table 4. Case details for each structure.
Table 4. Case details for each structure.
Load case Location Importance level Site class
1 Newcastle 2 Ce
2 Newcastle 2 De
3 Newcastle 3 Ce
4 Newcastle 3 De
5 Newcastle 4 Ce
6 Newcastle 4 De
7 Dowerin 2 Ce
8 Dowerin 2 De
9 Dowerin 3 Ce
10 Dowerin 3 De
11 Dowerin 4 Ce
12 Dowerin 4 De
13 Macquarie Island 2 Ce
14 Macquarie Island 2 De
15 Macquarie Island 3 Ce
16 Macquarie Island 3 De
17 Macquarie Island 4 Ce
18 Macquarie Island 4 De
Table 5. Summary of base shear and drift ratio for all 18 load cases.
Table 5. Summary of base shear and drift ratio for all 18 load cases.
Load
Case		 Bare frame Traditional masonry
panel		 Type 1 SIM panel Type 2 SIM panel
Base Shear (kN) Drift
(mm)		 Drift ratio Base Shear (kN) Drift
(mm)		 Drift ratio Base Shear (kN) Drift
(mm)		 Drift ratio Base Shear (kN) Drift
(mm)		 Drift ratio
1 66.7 6.12 0.06% 79.1 0.54 0.01% 19 3.45 0.03% 18 1.7 0.02%
2 105.1 9.65 0.09% 124.6 0.85 0.01% 31 5.44 0.05% 28 2.5 0.02%
3 86.8 7.96 0.08% 102.8 0.7 0.01% 25 4.49 0.04% 24 2.1 0.02%
4 136.7 12.54 0.12% 162 1.11 0.01% 40 7.08 0.07% 36 3.2 0.03%
5 120.1 11.02 0.11% 142.4 0.97 0.01% 35 6.23 0.06% 32 2.9 0.03%
6 189.3 17.37 0.17% 224.3 1.53 0.02% 56 9.79 0.10% 48 4.3 0.04%
7 121.4 11.14 0.11% 143.8 0.98 0.01% 35 6.29 0.06% 32 2.9 0.03%
8 191.2 17.54 0.17% 226.6 1.55 0.02% 56 9.9 0.10% 48 4.3 0.04%
9 157.8 14.48 0.14% 187 1.28 0.01% 46 8.25 0.08% 41 3.7 0.04%
10 248.5 18.02 0.18% 294.6 2.01 0.02% 67 14.78 0.14% 41 6.1 0.06%
11 218.4 20.04 0.20% 258.9 1.77 0.02% 64 11.96 0.12% 53 5.1 0.05%
12 344.1 31.57 0.31% 407.9 2.79 0.03% 158 24.47 0.24% 110 8.9 0.09%
13 364.1 33.4 0.33% 431.5 2.95 0.03% 178 26.56 0.26% 122 9.4 0.09%
14 573.5 52.62 0.52% 679.8 4.65 0.05% 375 42.23 0.41% 204 11.9 0.12%
15 473.3 43.43 0.43% 561 3.84 0.04% 291 38.05 0.37% 175 11.3 0.11%
16 745.5 68.41 0.67% 883.7 6.04 0.06% 432 54.96 0.54% 226 13.5 0.13%
17 655.3 60.12 0.59% 776.7 5.31 0.05% 394 48.62 0.48% 216 13.8 0.14%
18 1032.3 94.72 0.93% 1223.6 8.37 0.08% 723 72.89 0.71% 157 18.5 0.18%
Table 6. Contribution of SIM panels to resisting the lateral load in Strand7 analysis.
Table 6. Contribution of SIM panels to resisting the lateral load in Strand7 analysis.
Load case Location Frictional capacity of the SIM panels (Type 1 and Type 2)
Level 3 (L3) panel Level 2 (L2) panel Level 1 (L1) panel
1 Newcastle 12% 22% 27%
2 Newcastle 19% 34% 42%
3 Newcastle 15% 28% 36%
4 Newcastle 23% 44% 59%
5 Newcastle 19% 39% 56%
6 Newcastle 31% 61% 82%
7 Dowerin 18% 39% 54%
8 Dowerin 32% 62% 85%
9 Dowerin 23% 51% 65%
10 Dowerin 33% 79% FULL
11 Dowerin 37% 71% 94%
12 Dowerin 52% FULL FULL
13 Macquarie Island 58% FULL FULL
14 Macquarie Island 92% FULL FULL
15 Macquarie Island 77% FULL FULL
16 Macquarie Island FULL FULL FULL
17 Macquarie Island FULL FULL FULL
18 Macquarie Island FULL FULL FULL
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated