A New Fuzzy Backstepping Control Based on RBF Neural Network for Vibration Suppression of Flexible Manipulator

Preprint

Article

A New Fuzzy Backstepping Control Based on RBF Neural Network for Vibration Suppression of Flexible Manipulator

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhiyong Wei,

Qingchun Zheng,

Peihao Zhu^*,Wenpeng Ma,Jieyong Deng

Zhiyong Wei,

Qingchun Zheng,

Peihao Zhu^*,Wenpeng Ma,Jieyong Deng

This version is not peer-reviewed

Submitted:

19 June 2024

Posted:

20 June 2024

You are already at the latest version

Alerts

Abstract

Flexible manipulators have been widely used in industrial production. However, due to the poor rigidity of the flexible manipulator, it is easy to generate vibration. It will reduce the working accuracy and service life of the flexible manipulator. It is necessary to suppress the vibration during the operation of the flexible manipulator. Based on the energy method and Hamilton principle, the partial differential equations of the flexible manipulator are established. Secondly, an improved radial basis function (RBF) neural network is combined with the fuzzy backstepping method to identify and suppress the random vibration during the operation of the flexible manipulator, and the Lyapunov function and control law are designed. Finally, Simulink was used to build a simulation platform, three different external disturbances were set up, and the effect of vibration suppression was observed through the change curves of the final velocity error and displacement error. Compared with RBF neural network boundary control method and RBF neural network inversion method, the simulation results show that the effect of RBF neural network fuzzy inversion method is better than the previous two control methods, the system convergence is faster, and the equilibrium position error is smaller.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

With lower power consumption, lighter weight and higher flexibility, flexible manipulators have been largely used in industrial production, aerospace, search in some complex environments, expanding the use of manipulators [1,2]. However, because flexible manipulators use flexible materials, rigidity of the whole system is poor, and it is easy to produce vibration. Therefore, how to suppress the vibration of the flexible manipulators has become one of the hottest issues now.

The vibration suppression of the flexible manipulator is divided into passive sup-pression in the early stage and active suppression in the present stage. In the early passive suppression, accurate dynamic models were established, and the structure of the manipulator was optimized by finite element method [3,4]. This method has a long development cycle and cannot guarantee good vibration suppression effect.

Active suppression is to control the manipulators through the control algorithm [5,6] to achieve vibration suppression of the flexible manipulators. With the emergence of intelligent control algorithms, neural networks have also been applied to the vibration suppression of flexible manipulators. Li et al. [7] use Particle Swarm Optimization (PSO) intelligent search algorithm and Back Propagation Neural Networks (BPNN) to suppress the vibration of flexible manipulators. Jia et al. [8] proposed a neural network based adaptive integral sliding-mode observer to suppress vibration of the flexible space manipulators. Based on rigid-flexible manipulators, Liu et al. [9] proposed an adaptive neural network sliding mode control strategy is designed to estimate the un-known disturbances and uncertain parameter. Mei et al. [10] introduced Radial Basis Neural Network Functions (RBNNFs) to cope with system parameter uncertainties and input saturations.

As a common control method, the boundary control method is often used to sup-press the vibration of the manipulators. Liu et al. [11] devise a boundary control approach to suppress distributed elastic deformation and vibration. However, there are still large errors in angle tracking. Zhou et al. [12] proposed an adaptive boundary iterative learning vibration control is developed for a class of the rigid-flexible manipulator system under distributed disturbances and input constraints. However, the design of control law is complicated. Li et al. [13] proposes a novel boundary control strategy for a vibrating single-link flexible manipulator system modeled by partial differential equations. In the design of the control law, the expression is still complicated, and there are some small high-frequency vibrations in the control input of simulation results. Liu et al. [14] proposed two boundary control laws putting forward to manage vibration suppression and angular position tracking of manipulator system. However, there are some problems that the suppression effect of some parameters is not good.

To sum up, the hybrid control method combining intelligent control and traditional control method has become the main method for vibration suppression of manipulators at present. The boundary control method is also widely used in vibration suppression, but the design control law is complicated and sometimes the vibration suppression effect is not good. Based on these, the main contributions of this paper are as follows:

(1) Based on the energy method and Hamilton principle, the partial differential equation of a planar single-link flexible manipulator is established.

(2) A fuzzy backstepping control method based on RBF neural network is proposed. An RBF neural network is combined with backstepping control method, and unknown parameters are compensated by RBF neural network.

(3) A controller was designed, and nonlinear state space equations are established. Simulated platform was built by Simulink, and vibration suppression effect was analyzed by two parameters: the error of displacement and the error of velocity.

The rest of the paper is as follows: In the second part, partial differential equations of the flexible manipulator is established based on energy method and Hamilton principle. In the third part, an improved RBF neural network is designed, a new back-stepping control method is proposed, and Lyapunov function and control law are designed. In the fourth part, the simulation platform is established by Simulink. The effect of vibration sup-pression is measured by displacement error and velocity error, stable frequency, and stable point, compared with the RBF neural network boundary control method and RBF neural network backstepping control. The fifth part summarizes the work and looks forward to the future.

2. Dynamic Model

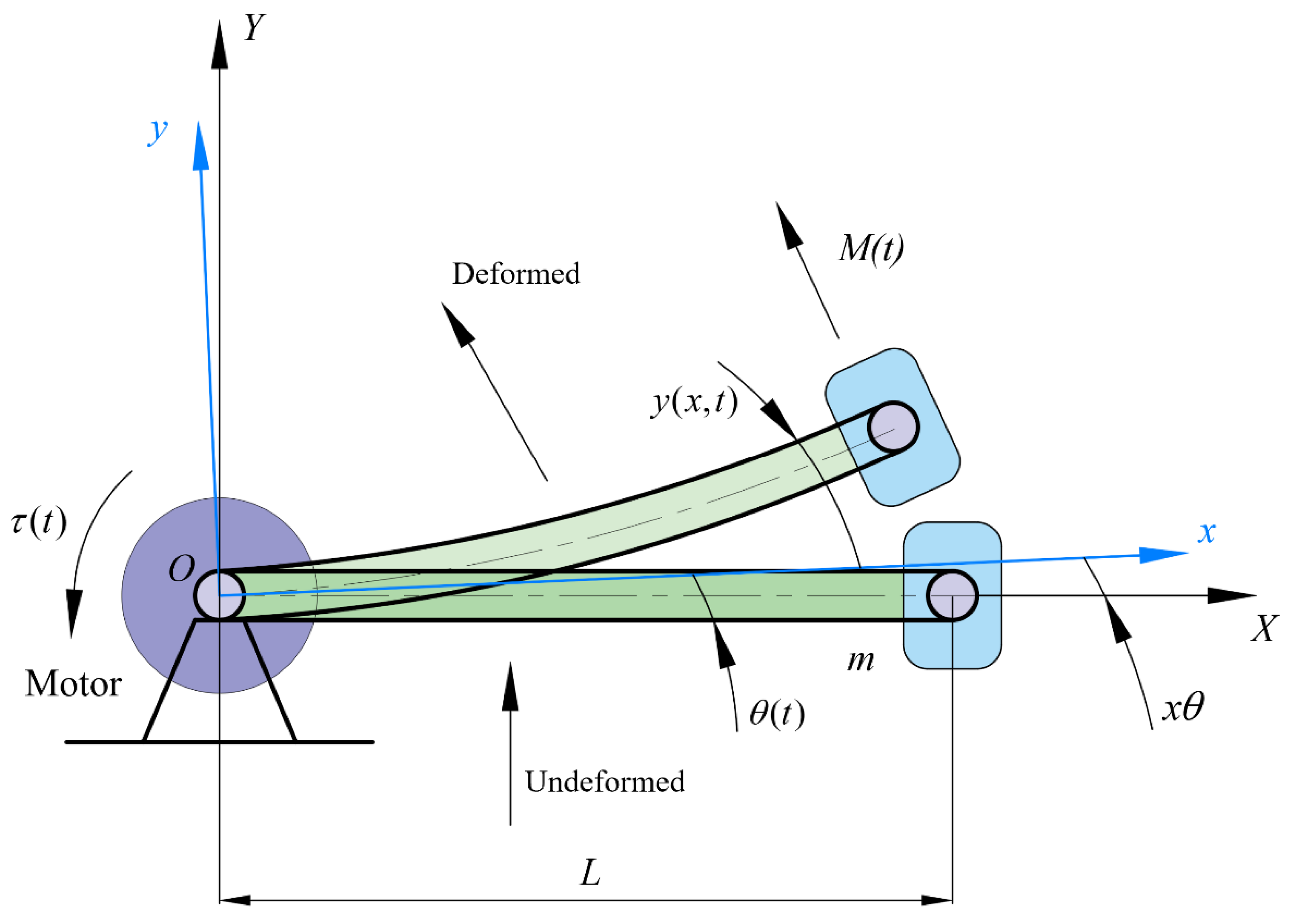
The system studied in this paper is a flexible single-link manipulator at the end of the arm in a plane. The schematic diagram of the system is shown in Figure 1. In the natural state of flexible manipulator, with the central axis of flexible manipulator as the axis and the rotation axis of motor and flexible manipulator as the origin, a world coordinate system is established. After the deformation, the direction of tangent line of central axis of flexible manipulator is y axis, and fix coordinate system is still established with the origin of world coordinate system. Some basic parameters and units of flexible manipulator defined below are shown in Table 1:

According to Hamilton's principle [15,16,17,18], the relationship between kinetic energy of system and potential energy, as well as non-conservative force, is expressed during the time interval from

t_{1}

t_{2}

\int_{t_{1}}^{t_{2}} (ε T - ε U - ε W_{n c}) d t = 0

(1)

Where

T

is the kinetic energy of the flexible manipulator.

U

is the potential energy of the flexible manipulator,

W_{n c}

is the power by non-conservative force of the flexible manipulator.

ε

(A) means the variation of (A) The kinetic energy of the system is expressed as following equation:

T = \frac{1}{2} I {\dot{θ}}^{2} (t) + \frac{1}{2} \int_{0}^{L} ρ {\dot{u}}^{2} (y, t) d y + \frac{1}{2} m {\dot{u}}^{2} (L, t)

(2)

The potential energy of the system is expressed as following equation:

U = \frac{1}{2} \int_{0}^{L} E I x''^{2} (y, t) d y

(3)

The power by non-conservative force of the flexible manipulator is expressed as following equation:

W_{n c} = τ (t) θ (t) + F (t) u (L, t)

(4)

Where

u (x, t)

is the offset of the flexible manipulator at any time

t

. In the case of initial position 0, the boundary conditions are

u (0, t) = 0

u' (0, t) = θ

. Bring Equations (2), (3) and (4) into the Equation (1). A following equation can be obtained:

\int_{t_{1}}^{t_{2}} (ε T - ε U + ε W_{n c}) d t = - \int_{t_{1}}^{t_{2}} \int_{0}^{L} A ε u (x, t) d y d t - \int_{t_{1}}^{t_{2}} B ε u' (0, t) d t - \int_{t_{1}}^{t_{2}} C ε u (L, t) d t - \int_{t_{1}}^{t_{2}} D ε u' (L, t) d t = 0

(5)

Parameters of A, B, C and D are respectively expressed as:

A = ρ \ddot{u} (x, t) + E I u^{(4)} (L, t)

B = I \ddot{u}' (0, t) - E I u'' (0, t) - τ (t)

C = m \ddot{u} (L, t) - E I u^{(3)} (L, t) - M (t)

D = E I u'' (L, t)

. As

ε u (x, t)

ε u' (0, t)

ε u (L, t)

and

ε u' (L, t)

are independent variables, so all of these equations are linearly independent, A=B=C=D=0. Thus, these partial differential equations (PDEs) [19,20] of the flexible manipulator are established as following:

ρ \ddot{u} (x, t) = - E I u^{(4)} (x, t)

(6)

τ (t) = I \ddot{u} (0, t) - E I u'' (0, t)

(7)

M (t) = m \ddot{u} (L, t) - E I u^{(3)} (L, t)

(8)

u'' (L, t) = 0

(9)

3. Control Law and Stability

Neural network [21,22,23] has good adaptability for unknown parameters, it does not need very accurate mathematical models and can be suitable for nonlinear, strongly coupled systems with many unknown parameters.

Backstepping control method is a step-by-step recursive design method, the introduction of virtual control in the design of this method is essentially a static compensation idea, the front subsystem must pass the virtual control of the back subsystem to achieve the purpose of stabilization. Therefore, this method requires that the structure of the system must design the robust controller or adaptive controller of the uncertain system (especially when the interference or uncertainty does not meet the matching conditions), which has shown its advantages. In this paper, a fuzzy backstepping control method based on RBF neural network is proposed to control flexible manipulators.

3.1. The Description of System

According to partial differential equations established above, the flexible manipulator is a nonlinear multiple-input multiple-output system. For this system, the flexible manipulator can be written as a nonlinear state space:

{\begin{cases} {\dot{x}}_{i} (t) = b_{i} x_{i + 1} (t) + f_{i} (x_{1} (t), x_{2} (t), ..., x_{i} (t)) + w_{i} (t), i \leq i \leq n - 1 \\ {\dot{x}}_{n} (t) = b_{n} u (t) + f_{n} (x_{1} (t), x_{2} (t), ..., x_{n} (t)) + w_{n} (t) \\ y (t) = x_{1} (t) \end{cases}

(10)

Where

x = {[x_{1}, x_{2}, \dots, x_{n}]}^{T} \in R^{n}

u \in R

y \in R

are the state variable of the system, control input and object output.

w_{i} (t)

is external interference,

f_{i}

is unknown nonlinear function, and

b_{i}

is unknown constant.

Hypothesis 1

There is a positive constant b_im and b_iM satisfies the inequality: 0 < b_im ≤ |b_i| ≤ b_iM, i = 1,2, …, n.

Hypothesis 2

For smooth functions

f (x)

and fuzzy systems, there is an optimal constant parameter

{\vec{θ}}^{*}

that minimizes the approximation error. Where the optimal parameter constant is defined as

{\vec{θ}}^{*} = \underset{θ \in Ω_{0}}{\arg \min} [\sup_{x \in Ω} | f (x) - {\vec{θ}}^{T} ξ (x) |]

Ω_{0}

and

Ω

are the bounded sets of

\vec{θ}

and x.

The control goal is to make the output y(t) of the system well clear of vibration errors, and all signals are bounded. For simplicity, the symbols

{\bar{x}}_{i}

and

y_{d i}

are introduced. Where

{\bar{x}}_{i} = {[x_{1}, x_{2}, ..., x_{i}]}^{T} \in R^{i}

(i = 1,2, …, n) is the input of the system,

y_{d i} = {[y_{d}, {\dot{y}}_{d}, ..., y_{d}^{(i)}]}^{T} \in R^{i}

(i = 1,2, …, n-1) is the expected trajectory value of the system.

Using single value simulator, product inference machine and barycentric average defuzzer, then for fuzzy rules: IF x₁ is

F_{1}^{j}

and … and x_n is

F_{n}^{j}

Then y is

B^{j}

( j=1,2, …, N). The fuzzy output is:

y (x) = \frac{\sum_{j = 1}^{N} θ_{j} Π_{i = 1}^{n} μ_{i}^{j} (x_{i})}{\sum_{j = 1}^{N} [Π_{i = 1}^{n} μ_{i}^{j} (x_{i})]}

(11)

Where

x = {[x_{1}, x_{2}, ..., x_{n}]}^{T} \in R^{n}

and

μ_{i}^{j} (x_{i})

are the membership function

μ_{i}^{j}

θ_{j} = \max_{y \in R} B^{j} (y)

. Defining

ξ (x) = {[ξ_{1} (x), ξ_{2} (x), ..., ξ_{N} (x)]}^{T}

\vec{θ} = {[θ_{1}, θ_{2}, ..., θ_{N}]}^{T}

, then the equation can be obtained:

y (x) = ξ^{T} (x) \vec{θ}

According to the fuzzy universal approximation theorem, if

f (x)

is a continuous function defined on a compact set

Ω

, then for any constant

ε > 0

, there exists a fuzzy system as shown above that satisfies

\sup_{y \in Ω} | f (x) - y (x) | \leq ε

3.2. The Design of Backstepping Controller

The design process of backstepping method [24,25,26,27] is completed by constructing intermediate quantity

e_{i} = x_{i} - α_{i - 1}

step by step. Where

α_{i}

is the virtual control quantity of step i. The final virtual control quantity

α_{n}

is part of the actual control quantity

u (t)

applied to the system.

The backstepping method is adopted to reconstruct the system formula (10) as follows:

Step 1. For the first subsystem

{\dot{x}}_{1} (t) = b_{1} x_{2} (t) + f_{1} (x_{1}) + w_{1} (t)

, defining

e_{1} = y - y_{d}

, where

y_{d}

is the expected tracking trajectory, and virtual control signal

α_{1}

is introduced, a equation can be obtained as follows:

{\dot{e}}_{1} = {\dot{x}}_{1} - {\dot{y}}_{d} = b_{1} e_{2} - b_{1} α_{1} + f_{1} (x_{1}) + w_{1} (t) - {\dot{y}}_{d}

(12)

Where

e_{2} = x_{2} - α_{1}

Step 2. By introducing the virtual control quantity

α_{2}

into the second subsystem, the following equation can be obtained:

{\dot{e}}_{2} = {\dot{x}}_{2} - {\dot{α}}_{1} = b_{2} e_{3} + b_{2} α_{2} - {\dot{α}}_{1} + f_{2} ({\bar{x}}_{2}) + w_{2}

(13)

Where

e_{3} = x_{3} - α_{2}

Step k. By analogy, a virtual control quantity

α_{k}

is introduced into the k subsystem, defining

e_{k + 1} = x_{k + 1} - α_{k}

, the following equation can be obtained:

{\dot{e}}_{k} = {\dot{x}}_{k} - {\dot{α}}_{k - 1} = b_{k} e_{k + 1} + b_{k} α_{k} - {\dot{α}}_{k - 1} + f_{k} ({\bar{x}}_{k}) + w_{k}

(14)

Let

e_{n} = x_{n} - α_{n - 1}

, then for the last subsystem:

{\dot{e}}_{n} = {\dot{x}}_{n} - {\dot{α}}_{n - 1} = b_{n} u + f_{n} ({\bar{x}}_{n}) + w_{n} - {\dot{α}}_{n - 1}

(15)

Therefore, the system Equations (10) can be converted to these equations:

{\begin{cases} {\dot{e}}_{k} = b_{k} e_{k + 1} + b_{k} α_{k} - {\dot{α}}_{k - 1} + f_{k} ({\bar{x}}_{k}) + w_{k}, 1 \leq k \leq n - 1 \\ {\dot{e}}_{n} = b_{n} u - {\dot{α}}_{n - 1} + f_{n} ({\bar{x}}_{n}) + w_{n} \end{cases}

(16)

Where

α_{0} = y_{d}

By determining the virtual control quantity

α_{k}

and u, the system is stable and can reach the desired tracking trajectory, and the vibration error is eliminated.

When k=1, choosing the Lyapunov function is the following equation:

V_{1} = \frac{1}{2 b_{1}} e_{1}^{2}

(17)

Taking the derivative of V₁ gives the following equation:

{\dot{V}}_{1} = e_{1} (e_{2} + α_{1} + {\hat{f}}_{1}) + \frac{1}{b_{1}} e_{1} w_{1}

(18)

Where

{\hat{f}}_{1} = \frac{f_{1} ({\bar{x}}_{1}) - {\dot{y}}_{d}}{b_{1}}

Defining

α_{1} = - λ_{1} e_{1} - φ_{1}

λ_{1} > 0

φ_{1}

is used to approximate a fuzzy system with nonlinear function

{\hat{f}}_{1}

. An equation can be obtained as follows:

{\dot{V}}_{1} = - λ_{1} e_{1}^{2} + e_{1} e_{2} + e_{1} ({\hat{f}}_{1} - φ_{1}) + \frac{1}{b_{1}} e_{1} w_{1}

(19)

When k=2, designing the Lyapunov function is the following equation:

V_{2} = V_{1} + \frac{1}{2 b_{2}} e_{2}^{2}

(20)

Defining

α_{2} = - λ_{2} e_{2} - e_{1} - φ_{2}

λ_{2} > 0

φ_{2}

is used to approximate a fuzzy system with nonlinear function

{\hat{f}}_{2}

. An equation can be obtained as follows:

{\dot{V}}_{2} = - \sum_{i = 1}^{2} λ_{i} e_{i}^{2} + \sum_{i = 1}^{2} e_{i} ({\hat{f}}_{i} - φ_{i}) + e_{2} e_{3} + \sum_{i = 1}^{2} e_{i} w_{i}

(21)

Where

{\hat{f}}_{2} = \frac{f_{2} - {\dot{α}}_{1}}{b_{2}}

Defining

α_{k - 1} = - λ_{k - 1} e_{k - 1} - e_{k - 2} - φ_{k - 1}

λ_{k - 1} > 0

φ_{k - 1}

is used to approximate a fuzzy system with nonlinear function

{\hat{f}}_{k - 1}

, then the derivative of the k-1 Lyapunov function can be recursively obtained as:

{\dot{V}}_{k - 1} = - \sum_{i = 1}^{k - 1} λ_{i} e_{i}^{2} + \sum_{i = 1}^{k - 1} e_{i} ({\hat{f}}_{i} - φ_{i}) + e_{k - 1} e_{k} + \sum_{i = 1}^{k - 1} e_{i} w_{i}

(22)

Designing the Lyapunov function at step k, an equation can be obtained as follows:

V_{k} = V_{k - 1} + \frac{1}{2 b_{k}} e_{k}^{2}

(23)

Taking the derivative of V_k gives the following equation:

{\dot{V}}_{k} = - \sum_{i = 1}^{k - 1} λ_{i} e_{i}^{2} + \sum_{i = 1}^{k - 1} e_{i} ({\hat{f}}_{i} - φ_{i}) + e_{k} (e_{k + 1} + α_{k} + e_{k - 1} + {\hat{f}}_{k}) + \sum_{i = 1}^{k} e_{i} w_{i}

(24)

For k=n, designing the Lyapunov function, an equation can be obtained as follows:

V_{n} = V_{n - 1} + \frac{1}{2 b_{n}} e_{n}^{2}

(25)

Taking the derivative of

V_{n}

, it can be obtained as follows:

{\dot{V}}_{n} = - \sum_{i = 1}^{n - 1} λ_{i} e_{i}^{2} + \sum_{i = 1}^{n - 1} e_{i} ({\hat{f}}_{i} - φ_{i}) + e_{n} (u + e_{n - 1} + \frac{1}{b_{n}} (f_{n} - {\dot{α}}_{n - 1})) + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

(26)

Where

{\hat{f}}_{n} = \frac{1}{b_{n}} (f_{n} - {\dot{α}}_{n - 1})

Defining

φ_{n}

is used to approximate a fuzzy system with nonlinear function

{\hat{f}}_{n}

, the design control law is expressed as follows:

u = - λ_{n} e_{n} - e_{n - 1} - φ_{n} (λ_{n} > 0)

(27)

Putting into

{\dot{V}}_{n}

, the equation can be obtained as follows:

{\dot{V}}_{n} = - \sum_{i = 1}^{n - 1} λ_{i} e_{i}^{2} + \sum_{i = 1}^{n - 1} e_{i} ({\hat{f}}_{i} - φ_{i}) + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

(28)

3.3. The Design of RBF Nerual Network

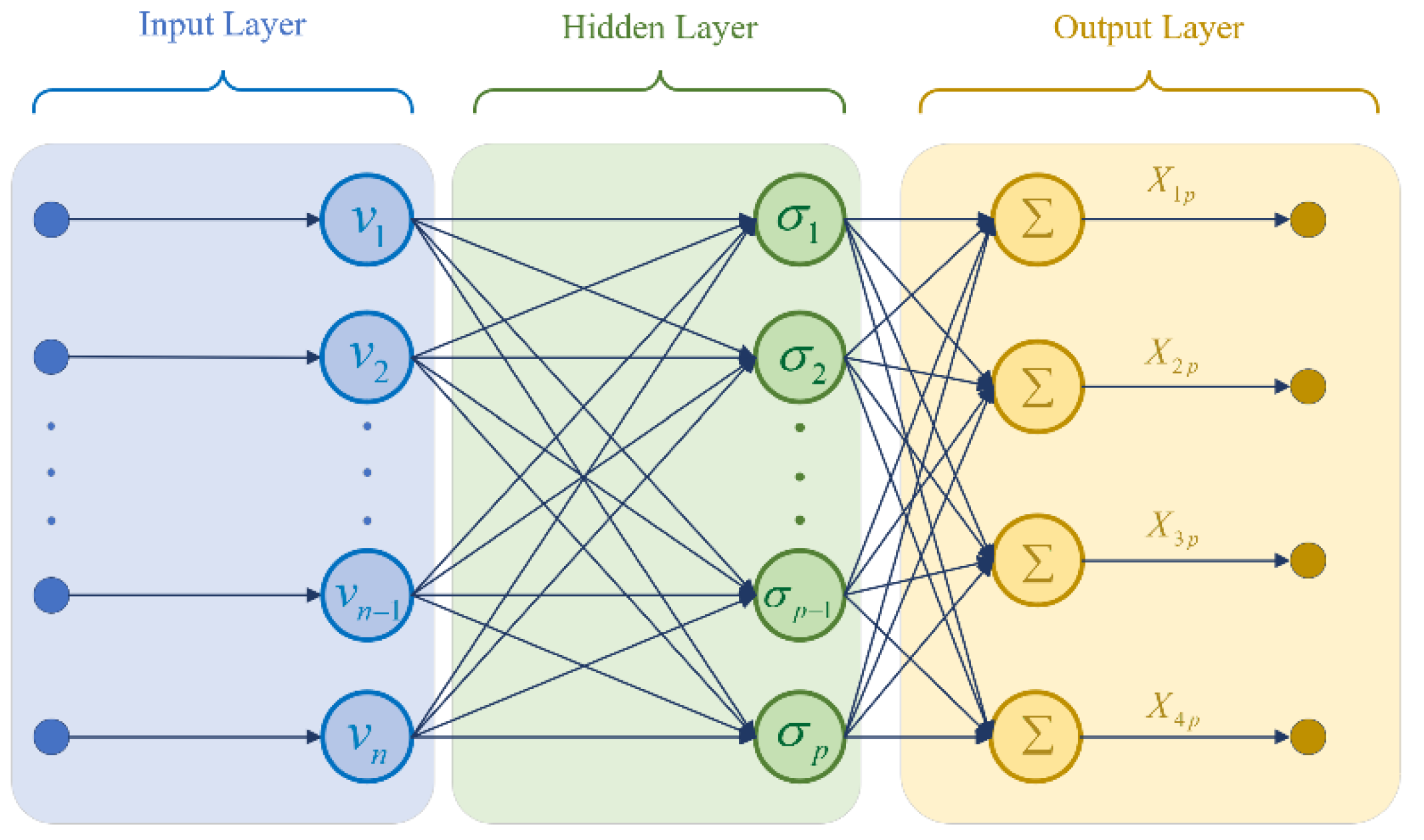
As an intelligent control, neural network can compensate unknown parameters and uncertain disturbances greatly. In this paper, unknown disturbances and random vibration of the system are estimated and compensated based on RBF neural network. The Gaussian function expression of RBF neural network is as follows:

σ_{i} = \frac{2 b_{i}^{2}}{1 + e^{- 2 V_{i} {\hat{\bar{Y}}}_{i}}}

(29)

Where

V_{i} = {[v_{1}, v_{2}, ..., v_{n}]}^{T}

is the input vector of the RBF neural network.

n

is the number of input layers of neural network.

s

is defined as the number of hidden layers of the neural network.

{\hat{\bar{Y}}}_{i}

in above equation is the input vector in the world coordinate system.

b_{i}

is width of the Gaussian Function of the i th neuron in hidden layer of neural network. Defining the ideal weight of neural network as

w = {[w_{1}, w_{2}, ..., w_{s}]}^{T}

. Then the output of the RBF neural network is

{\hat{X}}_{i s} = w^{T} σ

(i = 1, 2, 3, 4)

. The structure of this neural network is shown in Figure 2.

In the whole neural network, the weighted gain is entered into the RBF neural network for calculation. Therefore, factors affecting the input variables are complicated and difficult to control. Moreover, external interference has produced many uncertainties. Through the good adaptability of RBF neural network, unknown disturbances and the multi-order differential coupling terms in the system can be compensated.

3.4. The Design of Adaptive Fuzzy Control Based on Backstepping Method

f_{k}

is unknown function approximated by

φ_{k} = ξ^{T} (\bar{x}) \vec{θ}

. There is an optimal approximation vector

{\vec{θ}}_{k}^{*}

for a given arbitrarily small constant

ε_{k} > 0

| {\hat{f}}_{k} - {\vec{θ}}_{k}^{*} ξ ({\bar{x}}_{k}) | \leq ε_{k}

(k =1,2, …, n).

Defining

{\tilde{\vec{θ}}}_{k} = {\vec{θ}}_{k}^{*} - {\vec{θ}}_{k}

{\tilde{\vec{θ}}}_{k}

is the error of

{\vec{θ}}_{k}

. The control law designed by equation (27) above is adopted, and the adaptive control law is designed:

{\dot{\vec{θ}}}_{i} = r_{i} e_{i} ξ_{i} ({\bar{x}}_{i}) - 2 k_{i} {\vec{θ}}_{i}, (i = 1, 2, ..., n)

(30)

Where

r_{i}

is correction factor,

k_{i}

is gain factor. The signals of all closed-loop systems are bounded, and for A given attenuation coefficient

ρ > 0

, the tracking performance index satisfies the following expression:

\sum_{i = 1}^{n} \int_{0}^{T} e_{i}^{2} (s) d s \leq \frac{1}{d_{0}} V (0) + \frac{1}{d_{0}} T b_{0} + \sum_{i = 1}^{n} \frac{1}{2 d_{0}} \int_{0}^{T} ρ^{2} w_{i}^{2} d t, T \in [0, \infty]

(31)

Where

d_{0}

and

b_{0}

are constants.

Stability certificate. Designing the Lyapunov function is the following equation:

V = V_{n} + \sum_{i = 1}^{n} \frac{1}{2 r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\tilde{\vec{θ}}}_{i}, {\tilde{\vec{θ}}}_{i} = {\vec{θ}}_{i}^{*} - {\vec{θ}}_{i}

(32)

Taking the derivative of V the following equation can be obtained:

\dot{V} = {\dot{V}}_{n} + \sum_{i = 1}^{n} \frac{1}{r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\dot{\tilde{\vec{θ}}}}_{i} = - \sum_{i = 1}^{n} λ_{i} e_{i}^{2} + \sum_{i = 1}^{n} e_{i} ({\hat{f}}_{i} - {\vec{θ}}_{i}^{*}^{T} ξ_{i} ({\bar{x}}_{i})) + \sum_{i = 1}^{n} e_{i} {\tilde{θ}}_{i}^{T} ξ_{i} ({\bar{x}}_{i}) - \sum_{i = 1}^{n} \frac{1}{r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\dot{\vec{θ}}}_{i} + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

(33)

By reducing the above equation, the following inequality can be obtained:

\dot{V} \leq - \sum_{i = 1}^{n} λ_{i} e_{i}^{2} + \sum_{i = 1}^{n} {\tilde{\vec{θ}}}_{i}^{T} (e_{i} ξ_{i} ({\bar{x}}_{i}) - \frac{1}{r_{i}} {\dot{\vec{θ}}}_{i}) + \sum_{i = 1}^{n} | e_{i} ε_{i} | + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

(34)

Defining an equation is

S = - \sum_{i = 1}^{n} λ_{i} e_{i}^{2} + \sum_{i = 1}^{n} {\tilde{\vec{θ}}}_{i}^{T} (e_{i} ξ_{i} ({\bar{x}}_{i}) - \frac{1}{r_{i}} {\dot{\vec{θ}}}_{i}) + \sum_{i = 1}^{n} | e_{i} ε_{i} | + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

. At the same time, defining

a_{i} = λ_{i} - \frac{1}{2} - \frac{1}{2 ρ^{2} b_{i}^{2}}

, solving for

λ_{i}

and put it into S to get the following equation:

S = - \sum_{i = 1}^{n} a_{i} e_{i}^{2} - \frac{1}{2} \sum_{i = 1}^{n} e_{i}^{2} - \sum_{i = 1}^{n} \frac{1}{2 ρ^{2} b_{i}^{2}} e_{i}^{2} + \sum_{i = 1}^{n} {\tilde{\vec{θ}}}_{i}^{T} (e_{i} ξ_{i} ({\bar{x}}_{i}) - \frac{1}{r_{i}} {\dot{\vec{θ}}}_{i}) + \sum_{i = 1}^{n} | e_{i} ε_{i} | + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i}

(35)

Shrinking the above equation, because of inequalities

- \frac{1}{2} \sum_{i = 1}^{n} e_{i}^{2} + \sum_{i = 1}^{n} | e_{i} ε_{i} | \leq \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2}

- \sum_{i = 1}^{n} \frac{1}{2 ρ^{2} b_{i}^{2}} e_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{b_{i}} e_{i} w_{i} \leq \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2}

, considering the adaptive Equation (30), the following inequalities is obtained:

S \leq - \sum_{i = 1}^{n} a_{i} e_{i}^{2} + \sum_{i = 1}^{n} \frac{k_{i}}{r_{i}} (2 {\vec{θ}}_{i}^{*}^{T} {\vec{θ}}_{i} - 2 {\vec{θ}}_{i}^{T} {\vec{θ}}_{i}) + \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2}

(36)

According to inequality

{\vec{θ}}_{i}^{T}^{*} θ_{i}^{*} + {\vec{θ}}_{i}^{T} {\vec{θ}}_{i} \geq 2 {\vec{θ}}_{i}^{*}^{T} {\vec{θ}}_{i}

, it can be gotten an inequality

2 {\vec{θ}}_{i}^{*}^{T} {\vec{θ}}_{i} - 2 {\vec{θ}}_{i}^{T} θ_{i} \leq {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*} - {\vec{θ}}_{i}^{T} {\vec{θ}}_{i}

, if the original expression is reduced, the following expression can be obtained:

\dot{V} \leq - \sum_{i = 1}^{n} a_{i} e_{i}^{2} + \sum_{i = 1}^{n} \frac{k_{i}}{r_{i}} (- {\vec{θ}}_{i}^{T} {\vec{θ}}_{i} - {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*}) + \sum_{i = 1}^{n} \frac{2 k_{i}}{r_{i}} {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*} + \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2}

(37)

According to inequality

- \frac{1}{2} {\tilde{\vec{θ}}}_{i}^{T} {\tilde{\vec{θ}}}_{i} \geq - {\vec{θ}}_{i}^{T} {\vec{θ}}_{i} - {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*}

, shrinking the above expression again to get the following expression:

\dot{V} \leq - \sum_{i = 1}^{n} a_{i} \frac{2 b_{i m}}{2 b_{i}} e_{i}^{2} - \sum_{i = 1}^{n} \frac{k_{i}}{2 r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\tilde{\vec{θ}}}_{i} + \sum_{i = 1}^{n} \frac{2 k_{i}}{r_{i}} {\vec{θ}}_{i}^{T}^{*} θ_{i}^{*} + \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2}

(38)

Defining

λ_{i} \geq \frac{1}{2} + \frac{1}{2 ρ^{2} b_{i}^{2}}

and let

a_{i} > 0

, next defining

a_{0} = \min {2 b_{i m} a_{i}, k_{i}, i = 1, 2, ..., n}

b_{0} = \sum_{i = 1}^{n} \frac{2 k_{i}}{r_{i}} {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*} + \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2}

, the primitive can be written as the following expression:

\dot{V} \leq - a_{0} (\sum_{i = 1}^{n} \frac{1}{2 b_{i}} e_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{2 r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\tilde{\vec{θ}}}_{i}) + b_{0} + \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2} = - a_{0} V + b_{0} + c_{0}

(39)

Where

w_{i}^{2} \leq c_{i}

c_{0} = \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} c_{i}

To solve the above first order linear differential equation, the solution of equation (39) is obtained:

V (t) \leq (V (0) - \frac{b_{0} + c_{0}}{a_{0}}) e^{- a_{0} t} + \frac{b_{0} + c_{0}}{a_{0}} \leq V (0) e^{- a_{0} t} + \frac{b_{0} + c_{0}}{a_{0}} \leq V (0) + \frac{b_{0} + c_{0}}{a_{0}}, t \geq 0

(40)

Defining the compact set

Ω_{0} = {X | V (X) \leq C_{0}}

C_{0} = V (0) + \frac{b_{0} + c_{0}}{a_{0}}

, from the definition of equation (31), it can be seen that all signals of the closed-loop system are bounded:

{(e_{1}, e_{2}, ..., e_{n}, {\tilde{θ}}_{1}, {\tilde{θ}}_{2}, ..., {\tilde{θ}}_{n})}^{T} \in Ω_{0}

Let

d_{0} = \min {a_{i}; 1, 2, ..., n}

, the following equation can be obtained from Equation (38):

\dot{V} \leq - \sum_{i = 1}^{n} a_{i} e_{i}^{2} - \sum_{i = 1}^{n} \frac{k_{i}}{2 r_{i}} {\tilde{\vec{θ}}}_{i}^{T} {\tilde{\vec{θ}}}_{i} + \sum_{i = 1}^{n} \frac{2 k_{i}}{r_{i}} {\vec{θ}}_{i}^{T}^{*} {\vec{θ}}_{i}^{*} + \frac{1}{2} \sum_{i = 1}^{n} ε_{i}^{2} + \sum_{i = 1}^{n} \frac{1}{2} ρ^{2} w_{i}^{2} = - d_{0} \sum_{i = 1}^{n} e_{i}^{2} + b_{0} + \frac{1}{2} ρ^{2} w_{i}^{2}

(41)

Integrating the above equation in [0, T], because of

- \frac{1}{d_{0}} V (T) \leq 0

, then the convergence result of the system is as follows:

\sum_{i = 1}^{n} \int_{0}^{T} e_{i}^{2} (s) d s \leq \frac{1}{d_{0}} V (0) + \frac{1}{d_{0}} b_{0} T + \sum_{i = 1}^{n} \frac{1}{2 d_{0}} \int_{0}^{T} ρ^{2} w_{i}^{2} d t

(42)

According to the above equation, the system converges, and the convergence accuracy of the final error depends on the upper bounds of the perturbation and approximation error.

4. Simulation

4.1. Simulation Platform and Parameter

According to the dynamic model and control law established in the above chapter, this section simulates the nonlinear space state equation of the flexible manipulator by designing a controller. This simulation compares the dynamic surface method of backstepping space state equation with the boundary control method of linear state equation. Generally, displacement, velocity, angle, angular velocity, force, torque, and other variables are used to measure the quality of vibration suppression. In this paper, the error analysis method is used to compare the two variables of displacement and velocity. Simulink platform is used to build the controller. The designed controller structure is shown in Figure 3, where C is the fourth-order unit matrix.

In this simulation, because the external disturbance of the manipulator is random and uncertain, the type of vibration is also very complex and changeable, so it cannot be simulated one by one. Therefore, this paper sets three different vibration types to inter-fere with the vibration of the manipulator to analyze the vibration suppression effect of the proposed algorithm. The selected vibration interference is shown as follows:

{\begin{cases} w_{1} = 0.06 \sin (t) \\ w_{2} = 0.06 \sin (t) + 0.04 \sin (3 t) \\ w_{3} = 0.06 \sin (t) + 0.04 \sin (3 t) + 0.06 \sin (3 t) \end{cases}

(43)

Where is the simplest harmonic vibration wave, the amplitude is 0.06 mm, the frequency is 0.159 Hz. For easily comparison, is based on adding a low amplitude, high frequency harmonic vibration. When the frequency of simple harmonic vibration is increased and the amplitude is superimposed, the vibration suppression effect of the proposed control algorithm on the manipulator is observed. The maximum amplitude is 0.1mm and the maximum frequency is 0.4774 Hz. is based on adding a simple harmonic vibration with higher relative amplitude and higher frequency. Three different simple harmonic vibrations are superimposed on each other to simulate the external interference of the manipulator in a complex environment. has a maximum frequency of 0.4774 Hz and a maximum amplitude of 0.16 mm.

A flexible manipulator driven by a motor is used for simulation. The dynamic equation of the system is as follows:

{\begin{cases} {\dot{x}}_{1} = x_{2} \\ {\dot{x}}_{2} = - \frac{B}{M_{t}} x_{2} + \frac{N}{M_{t}} f (x_{1}, x_{2}) + \frac{K_{t}}{M_{t}} x_{3} \\ {\dot{x}}_{3} = - \frac{R}{L} x_{3} - \frac{K_{b}}{L} x_{2} + \frac{1}{L} u - w \\ y = x_{1} \end{cases}

(44)

Where parameters are

x_{1} = θ

x_{2} = \dot{θ}

x_{3} = I

M_{t} = J + \frac{1}{3} m l^{2} + \frac{1}{10} M l^{2} D

N = m g l + M g l

. Where

f

is nonlinear unknown function.

θ

is connecting rod angle. I is Electric current. u is control voltage of the motor. The physical meanings and parameter settings of the variables in the above expression are as follows:

Taking the expected trajectory is

y_{d} = \sin (t)

, nonlinear function is

f = \sin (θ)

, controller parameters are

ρ = 1

，

λ_{1} = 3

，

λ_{2} = 8.5

，

λ_{3} = 8.5

，

k_{1} = k_{2} = k_{3} = 1.5

，

r_{1} = r_{2} = r_{3} = 2

. The initial system status is

x (0) = {[0.5 π 0 0]}^{T}

. Initial value

θ_{1} (0)

and

θ_{2} (0)

is zero.

The first set of boundary control method based on linear state space equations based on RBF neural network is designed for comparison. The dynamic equations established are as follows:

{\begin{cases} {\dot{x}}_{1} = x_{2} \\ {\dot{x}}_{2} = - \frac{1}{I_{L}} [m_{L} g L_{L} x_{2} + E I (x_{1} - x_{3})] \\ {\dot{x}}_{3} = x_{4} \\ {\dot{x}}_{4} = - \frac{1}{I_{m}} [m_{m} g L_{m} - E I (x_{1} - x_{3}) - u] \end{cases}

(45)

Where x₁ and x₂ are respectively displacement error and velocity error of the flexible manipulator. x₃ and x₄ are respectively displacement error and velocity error of motor shaft. IL is the moment of inertia of the flexible manipulator. I_m is the moment of inertia of the motor. m_L is the mass of the flexible manipulator. mm is the mass of the motor shaft. g is the gravitational acceleration. The variable parameters of the linear space equation of state are shown in Table 3:

The second set of backstepping control method based on nonlinear state space equations based on RBF neural network is designed for comparison. The dynamic equations established are as follows:

{\begin{cases} {\dot{x}}_{1} = x_{2} \\ {\dot{x}}_{2} = - \frac{E I_{s}}{I_{h}} x_{1} + \frac{E I_{m}^{2} E I_{g}^{2}}{R_{m} I_{h}} x_{4} - \frac{E I_{m} E I_{g}}{R_{m} I_{h}} u - \frac{m_{m} g L_{L}}{I_{L}} \sin (x_{1} + x_{3}) \\ {\dot{x}}_{3} = x_{4} \\ {\dot{x}}_{4} = \frac{E I_{s}}{I_{h}} x_{1} - \frac{E I_{m}^{2} E I_{g}^{2}}{R_{m} I_{h}} x_{4} + \frac{E I_{m} E I_{g}}{R_{m} I_{h}} u \end{cases}

(46)

Parameters of the nonlinear state equations are shown in Table 4 :

4.2. Analysis of Simulation Results

4.2.1. Curve Analysis When the External Disturbance with w₁

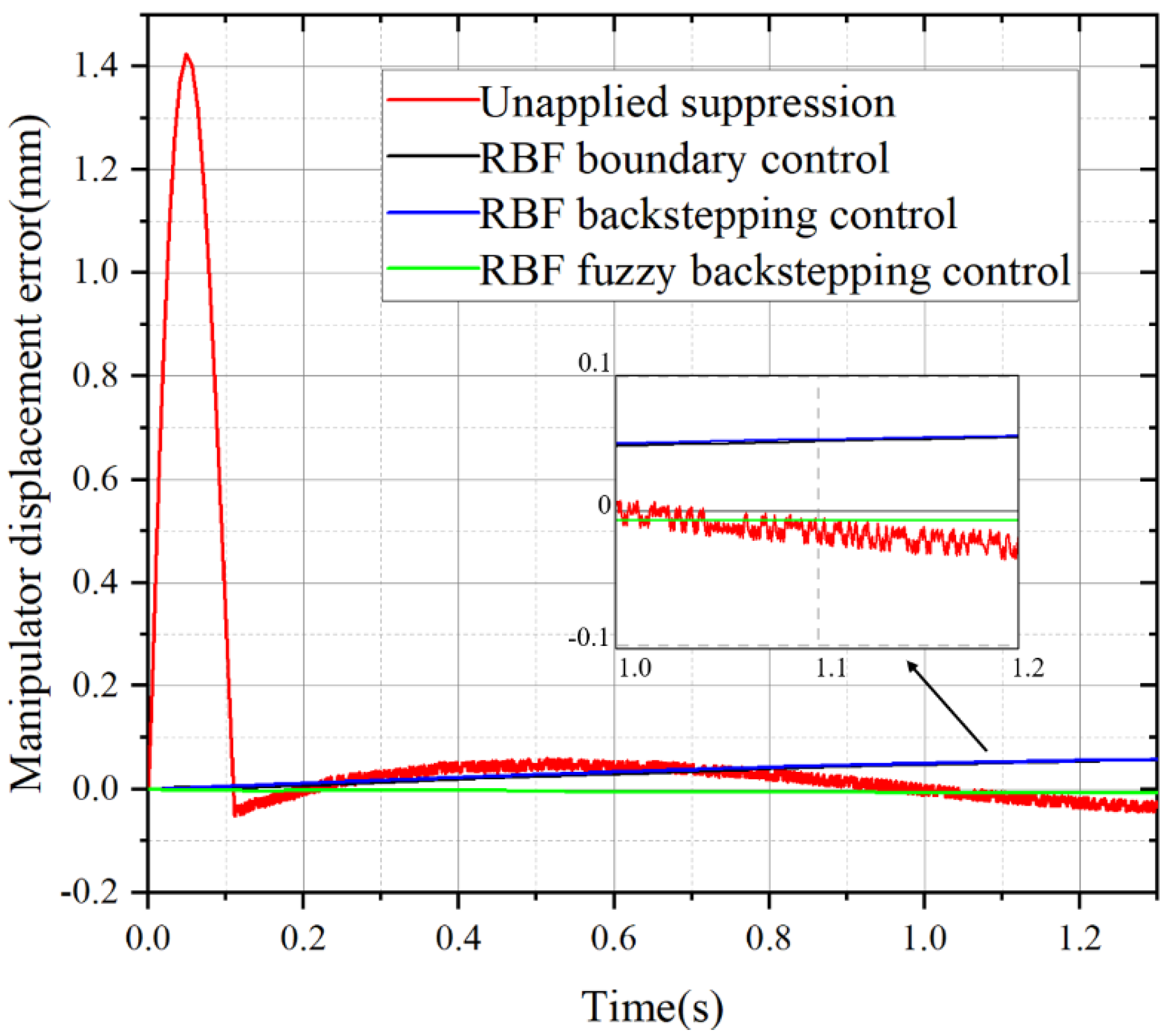
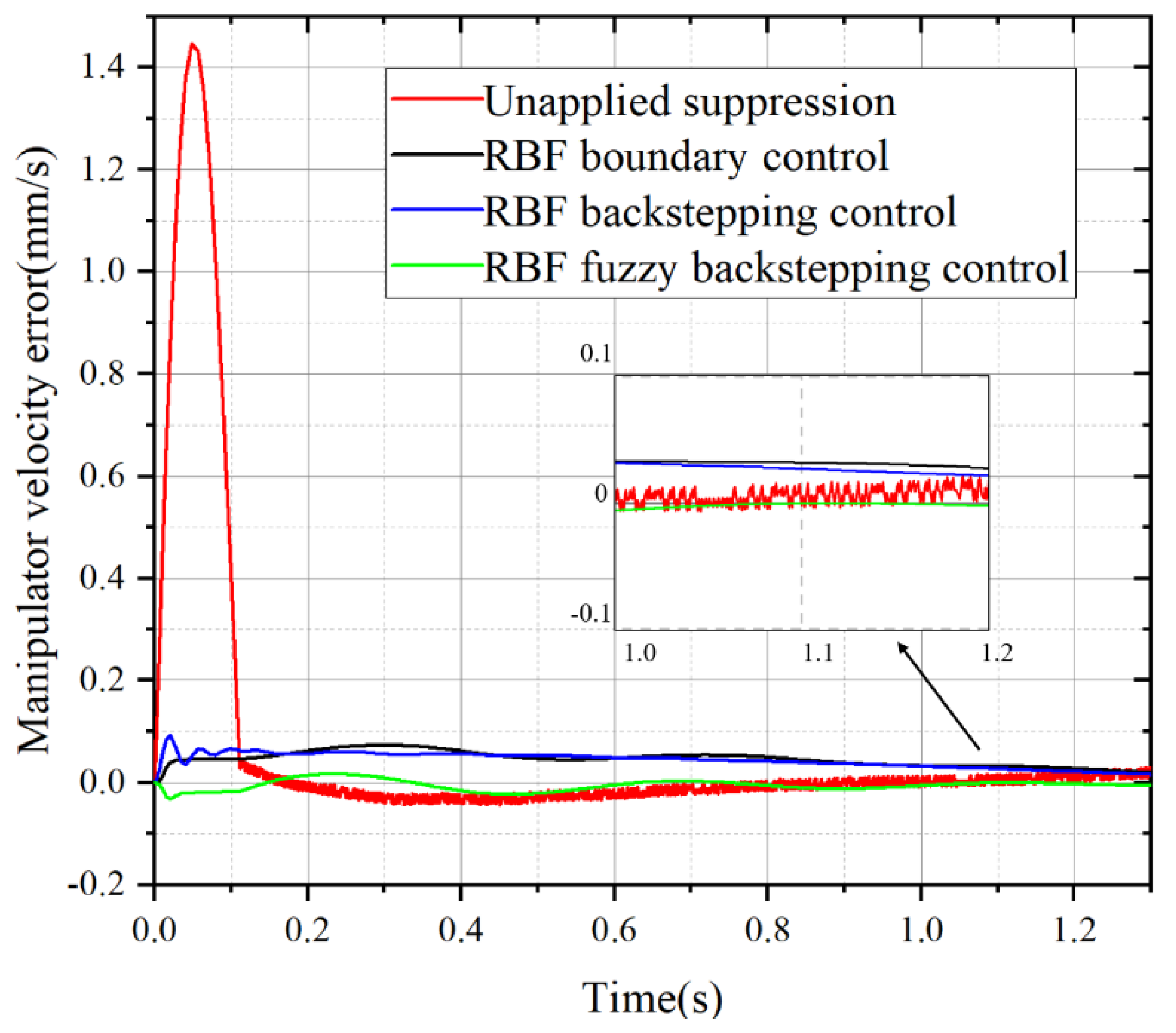
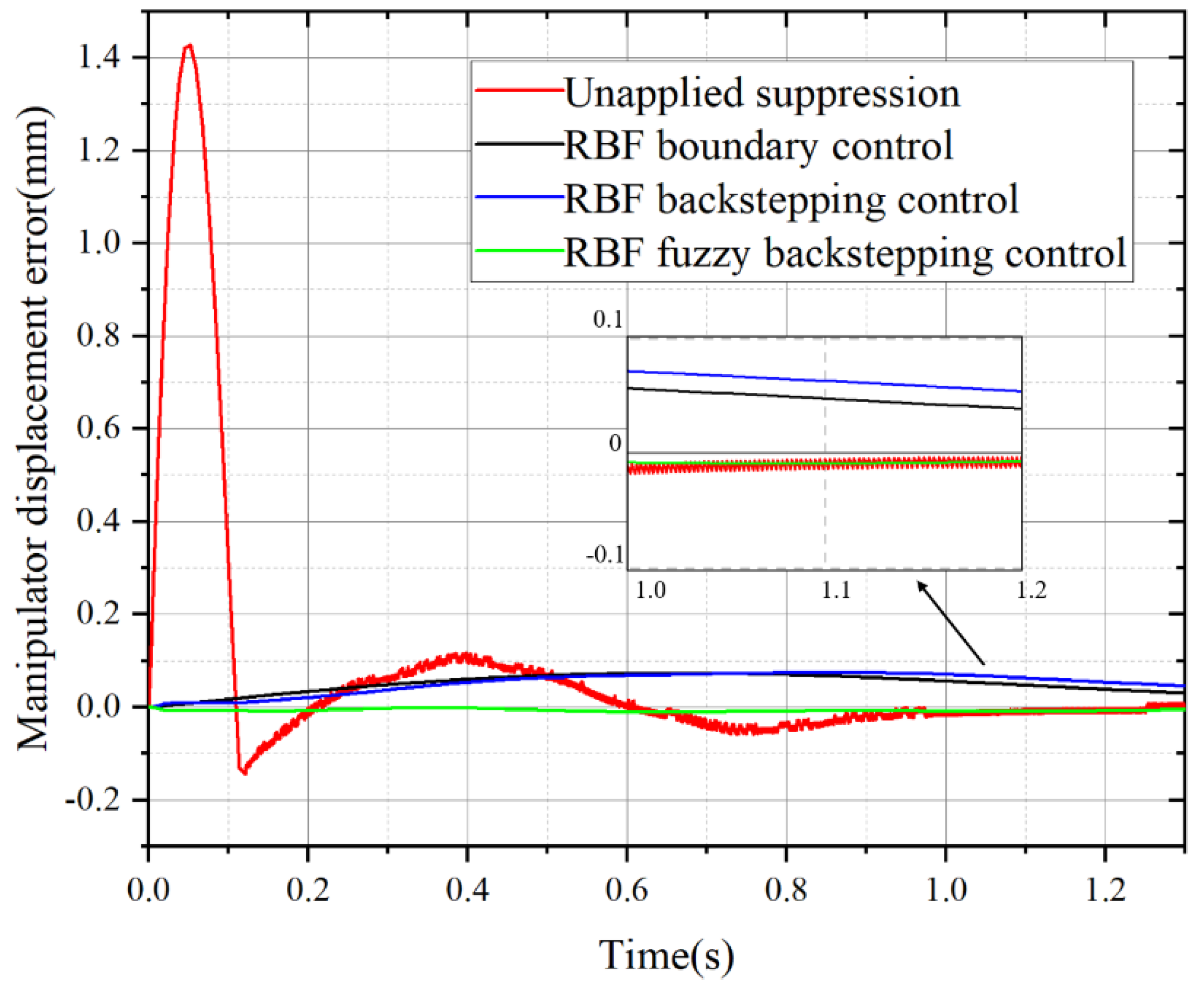
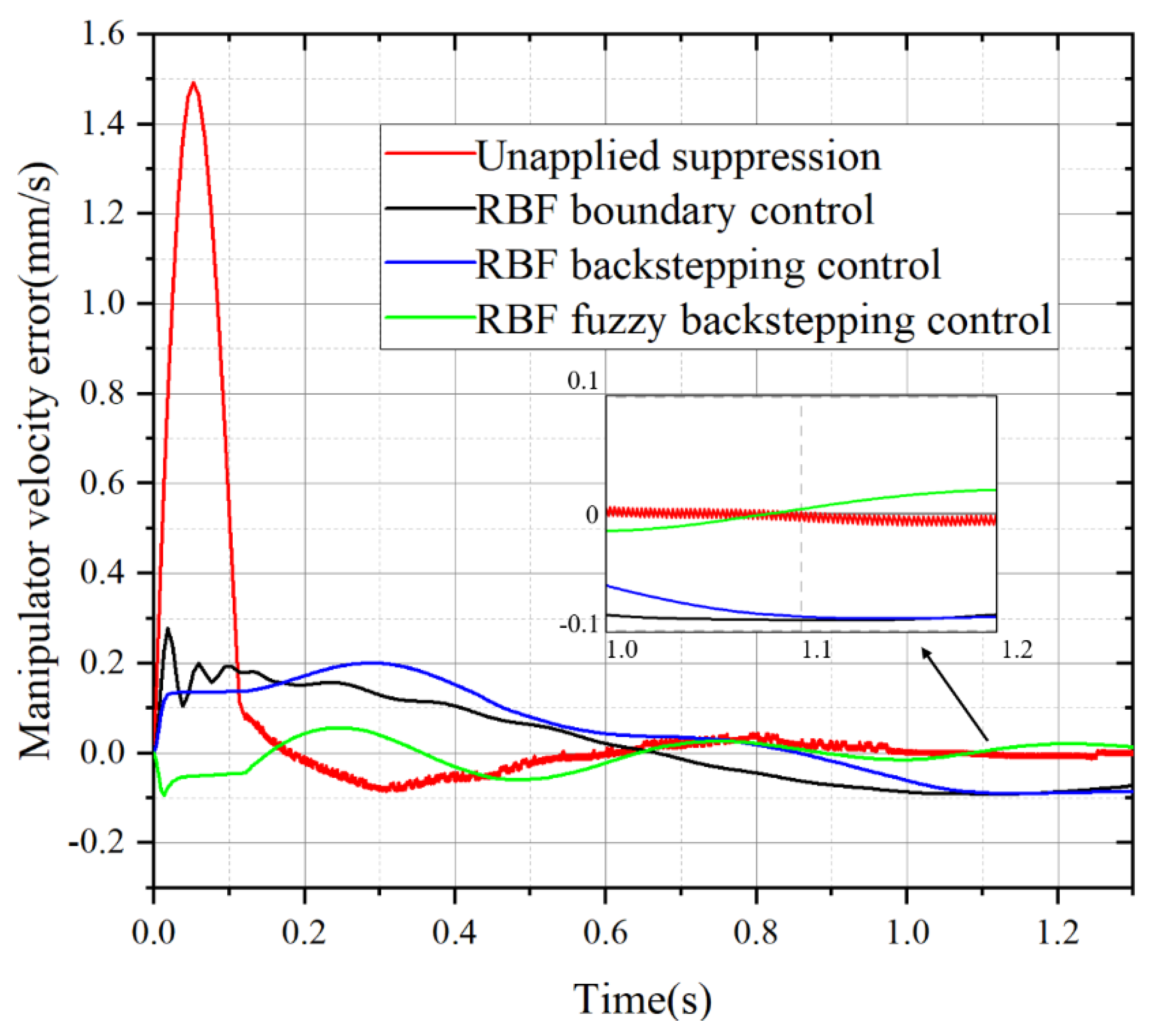
Figure 4 and figure 5 show the displacement error and velocity error curves of each system when the manipulator is subjected to external interference w₁, in which the red curve is the error curve when the vibration suppression of the system is not applied, the black curve is the error curve using RBF neural network boundary control method, and the blue curve is the error curve using RBF neural network inversion control method. The green curve is the error curve of RBF neural network fuzzy backstepping control method. It can be seen from the displacement error of the manipulator in Figure. 4, there will be an unusual displacement error of the manipulator at the start of the motor, which is mainly due to the sudden change of force and the change of motion state at the start of the motor. Then it fluctuates within a smaller range. Under the interference of simple harmonic vibration, the error fluctuation is not obvious. However, the small fluctuation frequency in the local range is very high. It is about 1000 Hz. Long-term and high-frequency vibration will affect the working accuracy and service life of the manipulator, so vibration suppression is needed. Under the vibration suppression of RBF neural network boundary control method and RBF neural network backstepping control method, the vibration frequency of the flexible arm can be well suppressed, and the vibration displacement error is suppressed to about 0.05 mm. The RBF neural network fuzzy backstepping control method not only restrains the vibration frequency well, but also restrains the displacement error of the manipulator, so that the final convergence result is close to 0. The velocity error curve is similar to the displacement error curve when the vibration is not suppressed. After the three control methods start vibration suppression, there is a certain fluctuation frequency in the initial operation, in which RBF neural network backstepping control method is the largest, RBF neural network boundary control method is the second, and RBF neural network fuzzy inversion control method is the least. In the final convergence results, RBF neural network fuzzy inversion control method is still the best, and the velocity error and vibration frequency error are almost eliminated. Table 5 gives a detailed analysis of the data.

4.2.2. Curve Analysis When the External Disturbance with w₂

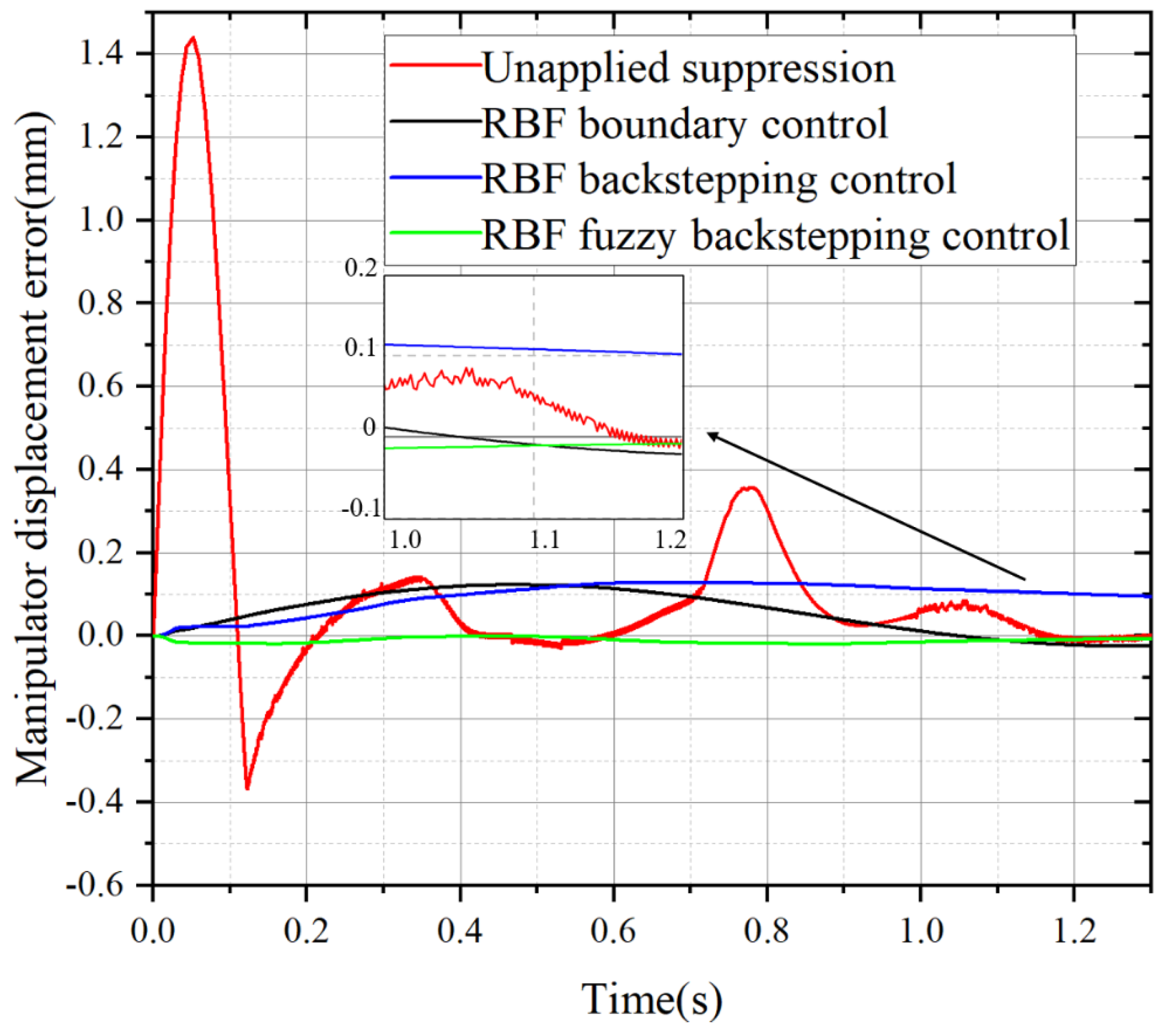
Figure 6 and Figure 7 are the variation curves of displacement error and velocity error of the flexible manipulator when it is subjected to external interference w₁ during operation. As shown in Figure 6, in the displacement error curve, due to the superposition of two simple harmonic motions, the overall displacement error fluctuates more, and so does the velocity error. However, in the wave frequency, due to the combination of two simple harmonic motions, when the two simple harmonic motions have the same di-rection, there will be a superposition of each other. When the two harmonic motion directions are opposite, the frequency and amplitude will also cancel each other. In this simulation, the two sets of simple harmonic motion cancel each other, making the maximum frequency about 400Hz. However, in terms of fluctuation error, if the

instantaneous error at startup is not considered, the maximum fluctuation error reaches 0.1448 mm, so vibration suppression is required. Both RBF neural network boundary control method and RBF neural network backstepping control method can restrain the vibration frequency well and limit the displacement error to less than 0.1 mm. RBF neural network fuzzy inversion control method can eliminate the vibration frequency and displacement error well under the external interference of w₂, and almost eliminate the vibration error and displacement error. In the velocity error curve in Figure 7, although the velocity error is not large, the fluctuation frequency is 500 Hz. Although the RBF neural network boundary control method and RBF neural network backstepping control method have a certain fluctuation frequency at the initial stage of operation, they both suppress the fluctuation frequency well in the end, and the final convergence equilibrium position is -0.1 mm/s. RBF neural network fuzzy backstepping control method also has certain fluctuation frequency and velocity errors when the system starts running, but in the final fluctuation frequency and velocity error balance point is better than the first two control methods, and the speed error is better suppressed. Table 6 gives a detailed analysis of the data.

4.2.3. Curve Analysis When the External Disturbance with w₃

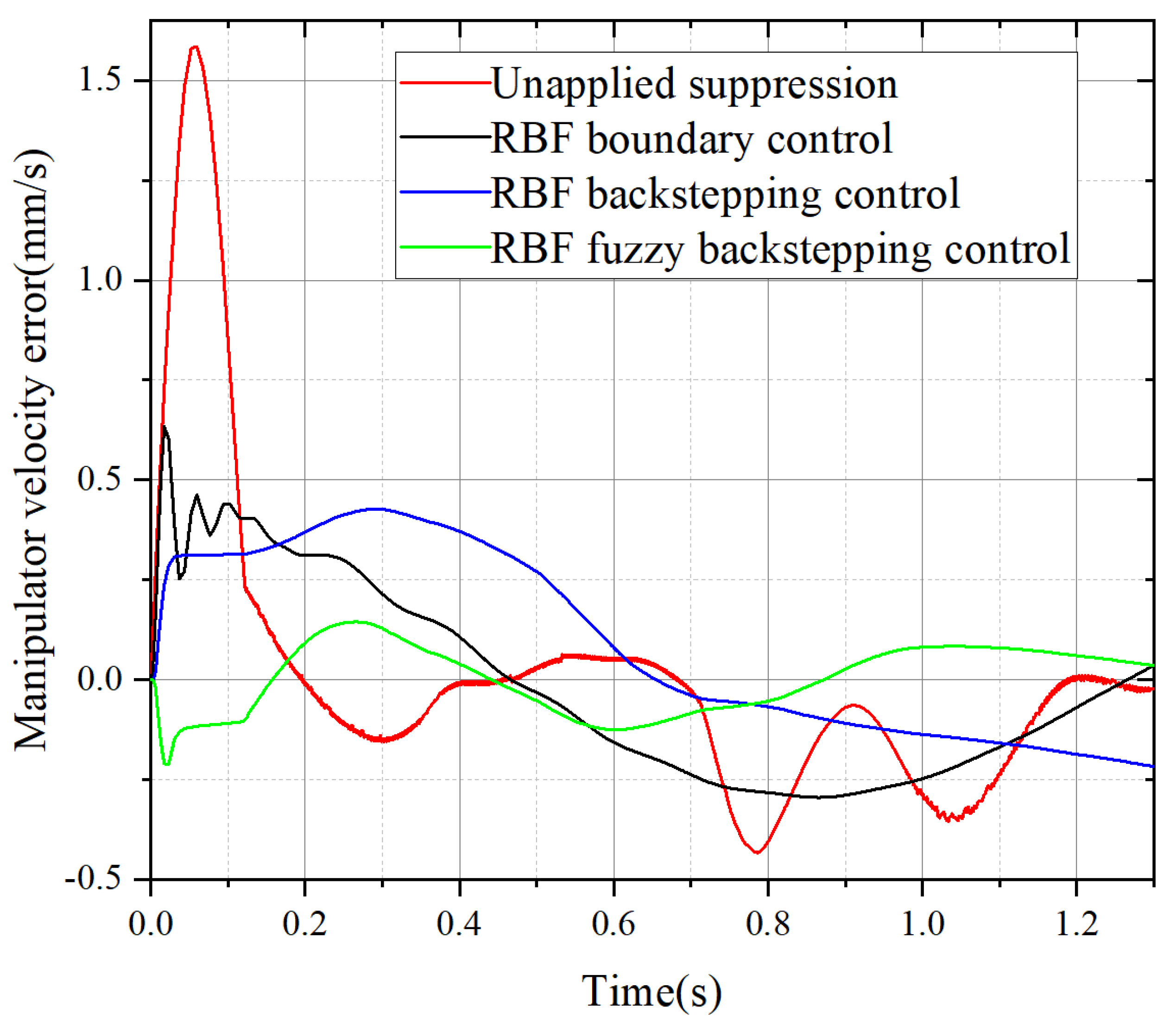
Figure 8 and Figure 9 are the variation curves of displacement error and velocity error of the flexible manipulator when it is subjected to external interference w₃ during operation. As shown in Figure 8, with the combination of three simple harmonic motions, the superposition and cancelling effects of displacement fluctuations are further enhanced. Sometimes the amplitude is very large, sometimes it is at the equilibrium point, the maximum frequency is 500 Hz, and the amplitude of the wave comes to 0.4 mm. The three control methods also suppress the fluctuation frequency well. In terms of final convergence, the RBF neural network backstepping control method finally converges at the equilibrium position where the displacement error is 0.1 mm. RBF neural network boundary control method and RBF neural network fuzzy backstepping control method have smaller error at the final convergence point, but RBF neural network fuzzy inversion control method has better inhibition effect and shorter convergence time. In the velocity error curve shown in Figure 9, the three simple harmonics are superimposed on each other, and both the fluctuation frequency and the velocity error of the unsuppressed curve are large. There is not only a small fluctuation frequency in the fluctuation frequency, but also a velocity error fluctuation frequency. The small fluctuation frequency is 300 Hz, and the maximum velocity error fluctuation frequency is 2.5 Hz. The maximum velocity error is 1.5 mm/s. The RBF neural network boundary control method and the inversion control method cannot suppress the vibration well, the RBF neural network backstepping method has a large convergence equilibrium position error, and the RBF neural network boundary control method has a high vibration frequency at the beginning of operation. According to the image, RBF neural network fuzzy backstepping control method has the best effect on vibration frequency and velocity error suppression. Table 7 gives a detailed analysis of the data.

Through the analysis of the above simulation results, RBF neural network fuzzy backstepping control method has better vibration suppression effect than RBF neural network boundary control method and RBF neural network backstepping control method, no matter from simple harmonic motion or multiple harmonic motion phase superposition. In most cases, the vibration frequency and vibration error can be quickly suppressed, and the final convergence equilibrium position error is small.

5. Conclusions

In this paper, the single-link flexible manipulator at the end of the manipulator is studied. The partial differential equations of the flexible manipulator are established firstly, and then the fuzzy backstepping control algorithm is designed, and the algorithm is combined with RBF neural network. The Lyapunov function is designed, and the stability of the system is proved. Finally, Simulink was used to build a simulation platform, and three different groups of external interference were simulated by the proposed algorithm and compared with RBF neural network boundary control method and RBF neural network inversion control method. From the two dimensions of displacement error and velocity error, the two parameters of stable convergence equilibrium position and stable frequency are quantified and compared. The effect of vibration suppression can also be roughly analyzed by the trend of the curve. The simulation results show that the RBF neural network fuzzy backstepping control method is superior to the two control algorithms, and the vibration is well suppressed and the whole system converges to an equilibrium position with less error.

In the future research, it can be considered to expand to three-dimensional to study the vibration suppression of the robot arm, and it can be considered to add practical experiments to verify the algorithm and add a variety of complex vibration types, to make the simulation and experimental environment more real.

Funding

This work was supported by the National Natural Science Foundation of China (62073239).

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflicts of interest.” Authors must identify and declare any personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results”.DD

References

Kim, W.; Tendick, F.; Ellis, S.; Stark, L. A comparison of Position and Rate Control for Telemanipulations with Consideration of Manipulator System Dynamics. IEEE Journal on Robotics and Automation 1987, 3, 426–436. [Google Scholar] [CrossRef]
Yun, A.; Moon, D.; Ha, J.; Kang, S.; Lee, W. Modman: An Advanced Reconfigurable Manipulator System with Genderless Connector and Automatic Kinematic Modeling Algorithm. IEEE Robotics and Automation Letters 2020, 5, 4225–4232. [Google Scholar] [CrossRef]
Mohamed, Z.; Tokhi, M.O. Hybrid Control Schemes for Input Tracking and Vibration Suppression of a Flexible Manipulator. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering 2003, 217, 23–34. [Google Scholar] [CrossRef]
Uyar, M. Comparison of Classical and Newly Designed Motion Profiles for Motion-Based Control of Flexible Composite Manipulator. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2022, 44, 414. [Google Scholar] [CrossRef]
Shi, M.; Cheng, Y.; Rong, B.; Zhao, W.; Yao, Z. Research on Vibration Suppression and Trajectory Tracking Control Strategy of a Flexible Link Manipulator. Applied Mathematical Modelling 2022, 110, 78–98. [Google Scholar] [CrossRef]
Alandoli, E.A.; Lee, T.S.; Lin, T.S.; Mohammed, M.Q. Dynamic Modelling and Intelligent Hybrid Optimal Controller of Hybrid Manipulator for Vibration Suppression and Tracking Control. Arabian Journal for Science and Engineering 2023, 1–17. [Google Scholar] [CrossRef]
Li, Y.; Ge, S.S.; Wei, Q.; Gan, T.; Tao, X. An Online Trajectory Planning Method of a Flexible-Link Manipulator Aiming at Vibration Suppression. IEEE Access 2020, 8, 130616–130632. [Google Scholar] [CrossRef]
Jia, S.; Shan, J. Velocity-Free Trajectory Tracking and Active Vibration Control of Flexible Space Manipulator. IEEE Transactions on Aerospace and Electronic Systems 2021, 58, 435–450. [Google Scholar] [CrossRef]
Liu, S.; Yang, H.; Liu, Z.; Langari, R. Adaptive Neural Network Independent Joint-Based Control for an ODE-PDE Rigid-Flexible Manipulator with Multiple Constraints. Journal of Vibration and Control 2024, 30, 1647–1658. [Google Scholar] [CrossRef]
Mei, Y.; Liu, Y. ILC-RBNNF-Based Vibration Control of a Rotatable Manipulator with Time-Varying Output Constraints. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2023, 53, 6416–6425. [Google Scholar] [CrossRef]
Wang, J.; Liu, J.; Ji, B.; He, Y.; Xia, S.; Zhou, Y. Vibration Suppression and Boundary Control for Nonlinear Flexible Rotating Manipulator in Three-Dimensional Space Subject to Output Restrictions. Communications in Nonlinear Science and Numerical Simulation. 2023, 120, 107151. [Google Scholar] [CrossRef]
Zhou, X.; Wang, H.; Tian, Y. Adaptive Boundary Iterative Learning Vibration Control Using Disturbance Observers for a Rigid-Flexible Manipulator System with Distributed Disturbances and Input Constraints. Journal of Vibration and Control. 2022, 28, 1324–1340. [Google Scholar] [CrossRef]
Li, L.; Liu, J. Nussbaum Function-Based Adaptive Boundary Control for Flexible Manipulator with Unknown Control Directions and Nonlinear Time-Varying Actuator Faults. International Journal of Robust and Nonlinear Control. 2023, 33, 6778–6798. [Google Scholar] [CrossRef]
Liu, Y.; Zhan, W.; Xing, M.; Wu, Y.; Xu, R.; Wu, X. Boundary Control of a Rotating and Length-Varying Flexible Robotic Manipulator System. IEEE Transactions on Systems Man Cybernetics-System. 2020, 52, 377–386. [Google Scholar] [CrossRef]
Liu, C.; Gao, W.; Gao, P. Vibration Suppression Method for a Two-Link Flexible Manipulator Based on Adaptive Iterative Learning Algorithm. Journal of Vibration Engineering & Technologies. 2024, 12, 587–599. [Google Scholar] [CrossRef]
Li, L.; Liu, J. Consensus Tracking Control and Vibration Suppression for Nonlinear Mobile Flexible Manipulator Multi-Agent Systems Based on PDE Model. Nonlinear Dynamics. 2023, 111, 3345–3359. [Google Scholar] [CrossRef]
Li, L.; Cao, F.; Liu, J. Adaptive Vibration Control for Constrained Moving Vehicle-Mounted Nonlinear 3D Rigid-Flexible Manipulator System Subject to Actuator Failures. Journal of Vibration and Control. 2023, 29, 4155–4171. [Google Scholar] [CrossRef]
Zhu, J.; Zhang, J.; Tang, X.; Pi, Y. Adaptive Boundary Control of a Flexible-Link Flexible-Joint Manipulator Under Uncertainties and Unknown Disturbances. Journal of Vibration and Control. 2023, 29, 169–184. [Google Scholar] [CrossRef]
Han, F.; Jia, Y. Bipartite Consensus and Distributed Boundary Control for Multiple Flexible Manipulators Associated with Signed Digraph. IEEE Transactions on Systems, Man, and Cybernetics: Systems. 2021, 52, 3005–3014. [Google Scholar] [CrossRef]
Wang, T.; Umemoto, K.; Endo, T.; Matsuno, F. Modeling and Control of a Quadrotor UAV Equipped with a Flexible Arm in Vertical Plane. IEEE Access. 2021, 9, 98476–98489. [Google Scholar] [CrossRef]
Tao, W.; Jiang, F.; Li, L.; Zhang, D.; Guo, X. Dynamical Analysis and Vibration Estimation of a Flexible Plate with Enhanced Active Constrained Layer Damping Treatment by Combinatorial Neural Networks of Surrogates. Aerospace Science and Technology. 2023, 133, 108136. [Google Scholar] [CrossRef]
Shang, D.; Li, X.; Yin, M.; Liu, J. Rotation tracking control strategy for space flexible structures based on neural network compensation. Advances in Space Research. 2024, 73, 2004–2023. [Google Scholar] [CrossRef]
Song, H.; Shan, X.; Zhang, L.; Wang, G.; Fan, J. Research on Identification and Active Vibration Control of Cantilever Structure Based on NARX Neural Network. Mechanical System and Signal Processing. 2022, 171, 108872. [Google Scholar] [CrossRef]
He, W.; Kang, F.; Kong, L.; Feng, Y.; Feng, Y.; Cheng, G.; Sun, C. Vibration Control of a Constrained Two-Link Flexible Robotic Manipulator with Fixed-Time Convergence. IEEE Transactions on Cybernetics. 2021, 52, 5973–5983. [Google Scholar] [CrossRef] [PubMed]
Zhao, Z.; Cai, S.; Ma, G.; Yu, F.R. Vibration Control of an Experimental Flexible Manipulator Against Input Saturation. IEEE/CAA Journal of Automatica Sinica. 2023, 10, 1340–1342. [Google Scholar] [CrossRef]
Wang, T.; Chen, Y. Event-Triggered Control of Flexible Manipulator Constraint System Modeled by PDE. Mathematical Biosciences and Engineering. 2023, 20, 10043–10062. [Google Scholar] [CrossRef]
Esmaeilzadeh, S.M.; Zeyghami, M.S. Nonlinear Finite Time Attitude Control of Flexible Spacecraft Based on a Novel Output Redefinition Method. Chinese Journal of Aeronautics. 2023, 36, 373–385. [Google Scholar] [CrossRef]

Figure 1. Structure diagram of the flexible manipulator.

Figure 2. RBF neural network structure diagram.

Figure 3. Structure diagram of the controller.

Figure 4. Displacement error of manipulator under the w₁ interference.

Figure 5. Velocity error of manipulator under the w₁ interference.

Figure 6. Displacement error of manipulator under the w₂ interference.

Figure 7. Velocity error of manipulator under the w₂ interference.

Figure 8. Displacement error of manipulator under the w₃ interference.

Figure 9. Velocity error of manipulator under the w₃ interference.

Table 1. The basic parameters and units of the flexible manipulator.

Symbol	Physical meaning	Unit
$L$	Length of the flexible manipulator in natural state	$m$
$E I$	Load mass at end of the flexible manipulator	$N \cdot m^{2}$
$m$	Load mass at end of the flexible manipulator	$k g$
$I$	Moment of inertia of the flexible manipulator	$k g \cdot m^{2}$
$τ (t)$	Input torque of the initial end motor	$N \cdot m$
$M (t)$	End load motor input control torque	$N \cdot m$
$θ (t)$	Rotation angle of joint of the flexible manipulator	$r a d$
$ρ$	Mass per unit length of the flexible manipulator	$k g / m$
$y (x, t)$	Elastic deformation of the flexible manipulator at point $x$	$m$

Table 2. The physical meaning of parameters in dynamic equations.

Symbol	Physical meaning	Unit and size
B	Bearing viscous friction coefficient	0.015
$L$	Reactance	0.0008 $Ω$
D	Load diameter	0.05 m
$R$	Resistance	0.075 $Ω$
$m$	Connecting rod mass	0.5 kg
J	Actuator torque	0.05 $N \cdot m$
l	Connecting rod length	0.6 m
K_b	Back electromotive force coefficient	0.085
$M$	Load mass	0.05 kg
K_t	Torque constant	1
g	Acceleration of gravity	9.8 m/s²

Table 3. Parameters of the linear state space equations for the flexible manipulator.

Symbol	Physical meaning	Unit and size
$m_{m}$	Mass of the motor shaft	$1.5 k g$
$L_{m}$	Length of the motor shaft	$10 m m$
$I_{m}$	Moment of inertia of the motor	$0.4 k g \cdot m$
$m_{L}$	Mass of the flexible manipulator	$500 g$
$L_{L}$	Moment of inertia of the flexible manipulator	$0.4 k g \cdot m$
$g$	Acceleration of gravity	$9.8 m / s^{2}$
$E I$	Stiffness coefficient	$0.8 N \cdot m$

Table 4. Nonlinear state space equations parameters of the flexible manipulator.

Symbol	Physical meaning	Unit and size
$E I_{s}$	Bottom stiffness of the flexible manipulator	$1.61 N \cdot m$
$I_{h}$	Moment of inertia at bottom of the flexible manipulator	$0.0021 k g \cdot m$
$E I_{m}$	Stiffness coefficient of the motor	$70 N \cdot m$
$E I_{g}$	Stiffness coefficient at top of the flexible manipulator	$0.00767 N \cdot m$
$I_{L}$	Moment of inertia at top of the flexible manipulator	$0.0059 k g \cdot m$
$R_{m}$	Damping coefficient of the motor	$2.6 N \cdot s / m$

u is the input of the controller, u = k₁x₁ + k₂x₂ +k₃x₃ +k₄x₄. In this equation, k₁=1, k₂=0.02, k₃=10 and k₄=0.01 are the gain coefficients of each item. The simulation time is set to 1.3s.

Table 5. Comparison of the data when the manipulator interferes with

w_{1}

Table 5. Comparison of the data when the manipulator interferes with

w_{1}

Control Method	Displacement error		Velocity error
Control Method	Steady displacement error(mm)	Stable frequency (Hz)	Steady velocity error(mm/s)	Stable frequency (Hz)
RBF boundary control	0.0578	Approximately equal to 0	0.0162	Approximately equal to 0
RBF backstepping control	0.0574	Approximately equal to 0	0.02	Approximately equal to 0
RBF fuzzy backstepping control	0.0071	0	0.0049	0

Table 6. Comparison of the data when the manipulator interferes with w₂.

Control Method	Displacement error		Velocity error
Control Method	Steady displacement error(mm)	Stable frequency (Hz)	Steady velocity error(mm/s)	Stable frequency (Hz)
RBF boundary control	0.04536	Approximately equal to 0	0.0867	1
RBF backstepping control	0.03059	Approximately equal to 0	0.0721	0.714
RBF fuzzy backstepping control	0.00533	0	0.0133	0.333

Table 7. Comparison of the data when the manipulator interferes with w₃.

Control Method	Displacement error		Velocity error
Control Method	Steady displacement error(mm)	Stable frequency (Hz)	Steady velocity error(mm/s)	Stable frequency (Hz)
RBF boundary control	0.02289	Approximately equal to 0	0.0232	0.56
RBF backstepping control	0.09486	Approximately equal to 0	0.2173	0.714
RBF fuzzy backstepping control	0.00646	0	0.0354	0.83

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A New Fuzzy Backstepping Control Based on RBF Neural Network for Vibration Suppression of Flexible Manipulator

Abstract

1. Introduction

2. Dynamic Model

3. Control Law and Stability

3.1. The Description of System

3.2. The Design of Backstepping Controller

3.3. The Design of RBF Nerual Network

3.4. The Design of Adaptive Fuzzy Control Based on Backstepping Method

4. Simulation

4.1. Simulation Platform and Parameter

4.2. Analysis of Simulation Results

4.2.1. Curve Analysis When the External Disturbance with w1

4.2.2. Curve Analysis When the External Disturbance with w2

4.2.3. Curve Analysis When the External Disturbance with w3

5. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.2.1. Curve Analysis When the External Disturbance with w₁

4.2.2. Curve Analysis When the External Disturbance with w₂

4.2.3. Curve Analysis When the External Disturbance with w₃