Prerpints.org logo
Preprint
Article

Compressive Sensing-Based Spectral Inversion Algorithm and Its Application in Detailed Fault Characterization

Altmetrics

Downloads

71

Views

28

Comments

0

Submitted:

19 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts
Abstract
The relentless advancement and integration of mechanization and intelligence within the coal mining industry, combined with the increasing depths of mining operations, necessitate significantly higher safety standards. This necessity arises due to the increasingly complex geological and coal seam conditions encountered as mining operations delve deeper into the earth. Traditionally, 3D seismic exploration technology has been fundamental in ensuring both operational efficiency and safety in the coal mining sector. However, despite its critical role, this technology still has limitations in detecting and characterizing small-scale geological structures which can pose substantial risks if not accurately identified and mitigated. To address these challenges, this paper introduces a sparsity-constrained adaptive hard thresholding algorithm designed to tackle the spectral inversion optimization problem with an norm constraint for the enhanced retrieval of reflection coefficients, thereby establishing a comprehensive workflow for enhancing seismic data resolution through compressed sensing spectral inversion. Real data validation has demonstrated that this method significantly enhances the resolution of seismic data while maintaining the amplitude integrity and fidelity of the original signals. This improvement allows for a more detailed and accurate characterization of small-scale geological features, which are critical in identifying and mitigating potential hazards within coal mining operations, thus offering robust support for the implementation of more effective safety protocols and disaster prevention strategies in coal mines.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology
norm constraint for the enhanced retrieval of reflection coefficients, thereby establishing a comprehensive workflow for enhancing seismic data resolution through compressed sensing spectral inversion. Real data validation has demonstrated that this method significantly enhances the resolution of seismic data while maintaining the amplitude integrity and fidelity of the original signals. This improvement allows for a more detailed and accurate characterization of small-scale geological features, which are critical in identifying and mitigating potential hazards within coal mining operations, thus offering robust support for the implementation of more effective safety protocols and disaster prevention strategies in coal mines.

1. Introduction

With the continuous advancement of mechanization and automation in coal mining, the industry has enjoyed remarkable improvements in productivity and efficiency. However, as mining operations reach greater depths, the geological and coal seam conditions become increasingly complex and challenging to manage [1,2,3,4,5]. This added complexity introduces a host of hidden geological factors that, if not properly addressed, can rapidly escalate into severe disasters [6,7,8]. Faults are among the most prevalent and impactful geological factors in coal mining, significantly affecting production efficiency and posing hidden disaster risks. Fault zones exhibit pronounced tectonic stress, extensive coal seam fractures, poor rock integrity, and low strength. These conditions severely impact the deployment of mining faces and mechanized extraction. Additionally, faults often serve as direct channels for water inrush disasters, posing substantial threats to mining safety [9]. Effective management strategies, including advanced geophysical detection and risk mitigation techniques, are essential to address these challenges and ensure safe, efficient mining operations.
Currently, 3D seismic exploration technology has established a comprehensive technical framework for studying disaster risks in coal mining. It has become the optimal method for identifying significant geological features such as major faults, collapse columns, mined-out areas, and other problematic geological structures [10,11,12,13,14]. This advanced technology provides critical insights essential for ensuring the safety and efficiency of mining operations. However, it is important to note that while 3D seismic exploration offers superior lateral resolution compared to conventional drilling methods, its vertical resolution is considerably lower. This limitation poses a challenge, as the technology's ability to accurately detect and resolve smaller faults and intricate geological structures remains insufficient. Therefore, there is an urgent need for high-resolution processing methods to improve the vertical resolution of seismic data, thereby enhancing the geological support capabilities of 3D seismic exploration for safe coal mining operations. In recent years, scholars have recognized this need and proposed various high-resolution processing techniques for seismic data. These methodologies include deconvolution [15,16,17], time-frequency analysis [18,19,20,21,22,23,24,25,26,27], inverse Q-filtering [28,29,30,31,32], spectral whitening [33,34,35], broadband constrained inversion [36,37,38,39,40,41], among others. Each of these techniques has demonstrated varying degrees of success in practical applications, offering promising prospects for the advancement of seismic exploration technology.
Yilmaz [15] introduced the class of deconvolution methods, which is designed to enhance the resolution of seismic data by compressing the seismic wavelet. Since then, a variety of practical algorithms have been developed to achieve this goal. Among these algorithms are pulse deconvolution, predictive deconvolution, homomorphic deconvolution, and surface-consistent deconvolution. Although these deconvolution methods have proven to be effective in enhancing the resolution of seismic data, they come with certain limitations and challenges. One of the primary issues is that these methods are based on several assumptions that may not always hold true in real-world scenarios. For instance, they often assume that the seismic wavelet is minimum phase or that the subsurface is horizontally layered, which may not be accurate. Moreover, the application of deconvolution can lead to a reduction in the signal-to-noise ratio (SNR).
Time-frequency analysis methods have garnered significant attention in geophysics, primarily for enhancing the resolution of seismic data. Huang [24] introduced a high-resolution processing technique for seismic data utilizing the generalized S-transform. Mao [22] proposed an adaptive continuous wavelet domain method tailored specifically for high-resolution seismic data processing. They provided detailed guidelines for selecting reference frequencies and calculating the frequency extension range, which enable effective enhancement of seismic data resolution while maintaining a high signal-to-noise ratio.
The application of inverse Q filtering techniques in seismic data processing is aimed at mitigating the attenuation effects caused by subsurface materials. By compensating for amplitude decay and frequency loss, this method effectively improves the phase characteristics and continuity of seismic records. Currently, three main types of inverse Q filtering methods are employed both internationally and domestically: series expansion-based approximate high-frequency compensation methods, wavefield extrapolation-based inverse Q filtering methods, and other inverse Q filtering techniques [32]. Accurate estimation of the subsurface quality factor Q is crucial for the successful application of inverse Q filtering methods. However, further research is needed to overcome the challenges of accurately and efficiently applying inverse Q filtering in complex underground structures.
The spectral whitening method aims to flatten the high-frequency portion of seismic data by adjusting the amplitude spectral distribution to compensate for missing components. When employing this method, the phase spectrum of seismic data remains unaltered, with only the high-frequency amplitude spectrum being elevated accordingly. This approach is known for its simplicity and robustness. However, it is worth noting that it may have the drawback of relatively poor fidelity.
Spectral inversion technology is widely recognized as an effective method for enhancing resolution in wideband constrained inversion techniques. Puryear and Castagna [36] proposed the reflection coefficient parity decomposition theory, which decomposes the reflection coefficient into odd and even components. By leveraging the distinct resolution capabilities of these components for thin layers, spectral inversion target functions yield a high-resolution reflection coefficient. This theory has significantly advanced the application of spectral inversion in enhancing the resolution of seismic data processing. However, conventional spectral inversion methods usually solve the objective function under L 2 norm constraints, resulting in limited effectiveness for resolution enhancement.
Spectral inversion relies on the crucial assumption that reflection coefficients are sparse. To address this, we introduce compressed sensing theory [42,43,44,45] into the spectral inversion. Spectral inversion is typically an underdetermined optimization problem, where the number of unknowns exceeds the number of equations. In this study, we employ the L 0 norm for sparse constraints, given its effectiveness in promoting sparsity. We propose a novel sparsity-adaptive hard thresholding pursuit algorithm to solve the sparse-constrained optimization problem, aiming to accurately estimate the reflection coefficients. It does not require the use of the Matching Pursuit algorithm to obtain initial sparse reflection coefficients [46]. Furthermore, we present a comprehensive method to enhance the resolution of stabilized seismic data. First, the sparsity-adaptive hard thresholding pursuit algorithm is used to solve the L 0 norm-constrained optimization problem, yielding the reflection coefficients. Following this, we perform wavelet extraction based on shaping regularization to ensure that the extracted wavelets are stable and consistent, followed by wavelet decomposition and high-frequency wavelet replacement, ultimately achieving the objective of improving seismic data resolution. Applying this processing workflow to actual coal mine seismic data significantly enhances data resolution. This improvement aids in the identification of small-scale fault systems, which are often difficult to detect with conventional methods. Consequently, this enhanced capability provides better geological support, greatly contributing to the safe production and operation of coal mines.

2. Methods

2.1. Spectral Inversion Objective Function

Based on the convolution model, seismic records can be represented as the convolution of reflection coefficients and a wavelet:
d ( t ) = w ( t ) ∗ r ( t ) + n ( t )
where n ( t ) is noise. By applying the Fourier transform to the above equation, we get:
D ( f ) = W ( f ) ∗ R ( f ) + N ( f ) = ∑ n = 1 N A n ⋅ W ( f ) e − i ⋅ 2 π f τ n + N ( f )
Here, A n represents the amplitude of the reflection coefficients. For a specific frequency component f m ( k = 1 , … , M ) , it can be written as:
D ( f m ) = ∑ n = 1 N A n ⋅ W ( f m ) e − i ⋅ 2 π f m τ n + N ( f )
Letting Q = e − i ⋅ 2 π f m τ n , the equation can be rewritten in matrix form as:
d = W Q x + N = Φ x + N
Where Φ = W Q , d is the observed seismic data, W is the diagonal matrix of seismic wavelets, Q is the Fourier basis matrix, and x is the sequence of reflection coefficient amplitudes. Applying the L 0 norm for sparse constraint, the optimization problem can be formulated as:
x ^ = arg min ‖ x ‖ 0 ,   s . t . Φ x = d
The L 0 norm is defined as the number of non-zero elements in a vector. By incorporating the L 0 norm sparse constraint, the spectral inversion method can obtain reflection coefficients that better approximate actual conditions.

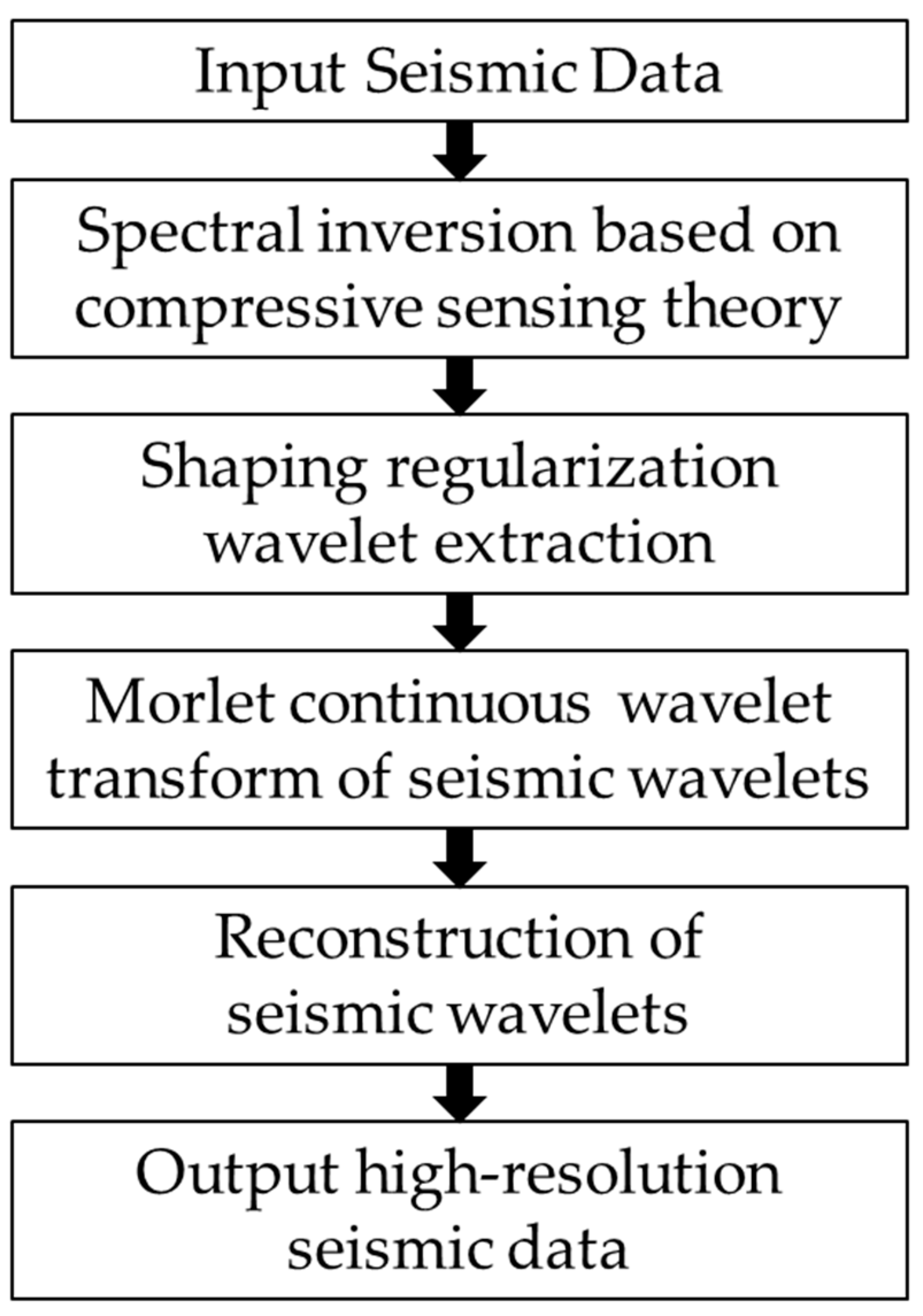
2.2. High-Resolution Seismic Data Processing Workflow

This paper introduces a robust approach for improving seismic data resolution using the spectral inversion algorithm. The proposed method consists of two crucial steps:
(1) Employ the sparsity adaptive hard thresholding pursuit algorithm to solve the norm-constrained optimization problem and obtain accurate reflection coefficients.
(2) Apply shaping regularization for wavelet extraction, followed by wavelet decomposition and high-frequency wavelet replacement, thereby effectively enhancing the overall resolution.

2.2.1. Spectral Inversion Algorithm Based on Compressed Sensing Theory

As shown in the equation (5), we solved the optimization problem to obtain the reflection coefficients.
While threshold algorithms [47,48] provide fast computational results for solving sparse constrained problems, they often yield subpar outcomes compared to matching pursuit class algorithms [49,50]. The latter has gained significant attention due to its superior practical application results. The orthogonal matching pursuit algorithm, for instance, selects only one atom in each iteration that best matches the residuals. However, this selection process becomes inefficient when dealing with high-dimensional signals. Building upon the IHT algorithm, Foucart [51] introduced the Hard Thresholding Pursuit (HTP) algorithm. In each iteration, HTP selects the atoms corresponding to the largest K elements in the sparsity coefficients of the signal. The sparsity coefficients of the signal are then obtained by solving a minimization problem. The iterative process of the algorithm can be described as follows:
s n + 1 = { indices   of   K   largest   entries   of   x n + Φ T ( d − Φ x n ) }
x n + 1 = a r g m i n { ‖ d − Φ z ‖ 2 , s u p p ( z ) ⊆ S n + 1 }
where s u p p ( z ) express the support set of z . During the second step, the minimization problem can be solved using either the least squares algorithm or the gradient descent algorithm. However, when the signal's dimensionality is large or when it contains a significant number of non-zero elements, the least squares algorithm becomes computationally challenging due to the calculation of a high-dimensional inverse matrix. To address this issue, we employ the Nesterov accelerated gradient (NAG) algorithm, known for its fast convergence and high efficiency, to solve the minimization problem in Equation (5). The process of reconstructing sparse signals using the HTP algorithm can be summarized as follows:
Input: sensing matrix Φ ∈ R M × N ( M ≤ N ) , measurement vector d ∈ R M × 1 , sparse level K ;
Initialization: sparse coefficient approximation x ∈ 0 , index set Λ 0 = ∅ , atomic matrix Φ 0 = ∅ ;
Loop:
(1) calculate ϒ n = x n + Φ T ( d − Φ x n ) (2) remain the index Λ n of the maximum K elements in ϒ n , and the atomic matrix in this index is Φ n ;
(3) solve min ‖ d − Φ x ‖ 2 2 ,   s . t . ‖ x ‖ 0 ≤ K by the Nesterov accelerate algorithm:
Input: learning rate η , attenuation rate ε Initialization: initial velocity v 0 = 0 , objective function J ( x ) = min ‖ d − Φ x ‖ 2 2 ,   s . t . ‖ x ‖ 0 ≤ K
Loop:
①   Calculate   v t = ε v t − 1 + η ∇ x J ( x − ε v t − 1 )
② Update   x t = x t − 1 − v t
If the condition is met, stop iteration; else , return step① continue iteration.
(4) if the condition is met, stop iteration; else n = n +1, return step①continue iteration.
In addition, the sparsity of reflection coefficients in the transform domain is often unknown, and the accuracy of capturing this sparsity directly impacts the reconstruction accuracy. Therefore, it is crucial to develop a reconstruction algorithm that can automatically adapt to the signal's sparsity. In this paper, we propose a sparsity-adaptive hard threshold pursuit algorithm. The algorithm consists of the following steps:
Input：sensing matrix Φ ∈ R M × N ( M ≤ N ) , measurement vector d ∈ R M × 1 , noise level ε ;
Initialization: K 1 = 0 ， K 2 = max ( 0.001 N , 1 ) ， x 1 = 0 , F ( x 1 ) = ‖ Φ x 1 − d ‖ / ‖ d ‖ = 1 , solve x 2 in the condition of ‖ x 0 ‖ ≤ K 2 , F ( x 2 ) = ‖ Φ x 2 − d ‖ / ‖ d ‖ , t = 1 ;
Loop:
(1) K t + 2 = K t + 1 + ( ε − F ( x t + 1 ) ) ( K t + 1 − K t ) / ( F ( x t + 1 ) − F ( x t ) ) (2) solve x t + 2 by the Hard Thresholding pursuit algorithm
(3) calculate F ( x t + 2 ) = ‖ Φ x t + 2 − d ‖ / ‖ d ‖
(4) if the condition is met, stop iteration; else, t = t + 1 , return step (1) continue iteration;
Output: sparse level K , sparse coefficient x .
To compare the effects of solving the objective function under different norm constraints, we replace the L 0 norm constraint in equation (5) with an L 2 norm constraint of the optimization problem. We present the inversion results under the two norm constraints using a seismic data example, as shown in Figure 1. The comparison results reveals that the L 0 norm results exhibit a higher level of sparsity and signal-to-noise ratio compared to the L 2 norm constraint. This enables a broader bandwidth seismic reflection coefficient model.

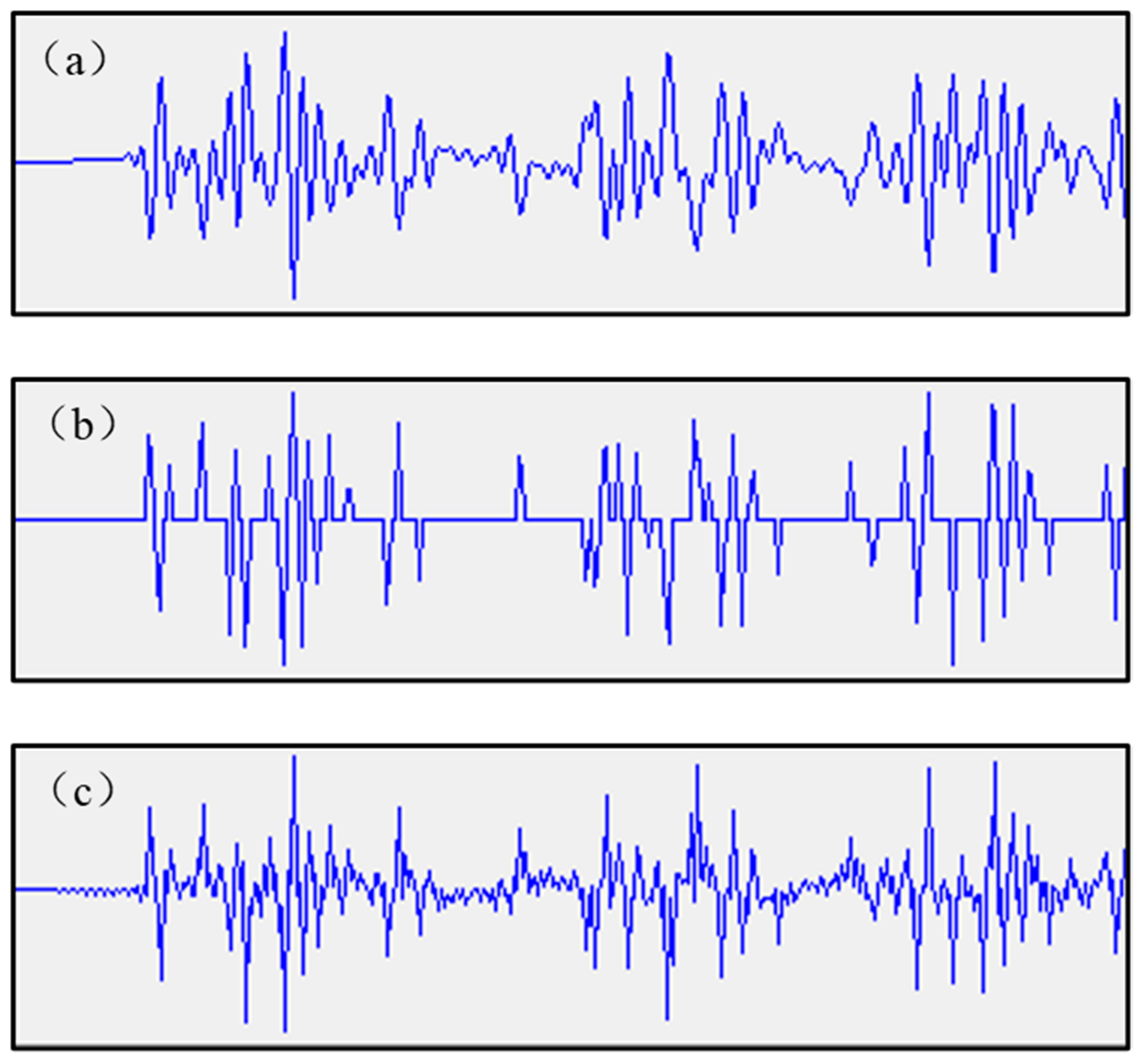
2.2.2. Continuous Wavelet Transform

The Morlet wavelet ψ ( t ) can be viewed as a complex sinusoid modulated by a Gaussian envelope (Morlet J, 1982):
ψ ( t ) = e − t 2 2 e j σ t + j φ
Here, σ represents the modulation frequency of the Morlet wavelet, which typically needs to be greater than 5.33. The Fourier transform of the Morlet wavelet is:
ψ ^ A ( ω ) = 2 π e j φ e − ( ω − σ ) 2 2
Subsequently, the optimal scale of the Morlet wavelet is obtained by optimizing the Fourier transform of the seismic trace D ( ω ) and the Fourier transform of the reflection coefficient R ( ω ) . The optimal scale a o p t can be determined by minimizing the objective function in equation (10):
arg min | | D ( ω ) | − | R ( ω ) ψ ^ A ( a ω ) | | 2
Using the wavelet ψ ( t a o p t ) with the optimal scale a o p t and the positions of the reflection coefficients, decompose the seismic data to obtain the coefficients of each reflected wavelet. Assuming the positions of the reflection coefficients are τ 1 , τ 2 , ⋯ , τ q , the coefficients α 1 , α 2 , ⋯ , α q of each reflected wavelet can be obtained by minimizing the objective function in equation (11):
‖ d − ∑ m = 1 q α m ψ ( t − τ m a o p t ) ‖ 2
Finally, replace and reconstruct ψ ( t ) using high-frequency Morlet wavelets or other high-frequency wavelets, which can naturally extending low- and high-frequency energy of seismic data.
d n e w = ∑ m = 1 q α m ψ h i g h ( t − τ m )
Applying the aforementioned steps to seismic data processing can significantly improve the resolution of the seismic profile.
Building on the outlined key steps, this paper introduces a robust resolution enhancement technique for spectral inversion by leveraging compressive sensing theory (shown in Figure 2). To ensure stability during the wavelet calculation process, a shaping regularization wavelet extraction approach is employed. This technique enhances the estimation stability of wavelets, particularly in regions exhibiting low reflection coefficients or a low signal-to-noise ratio in seismic data.

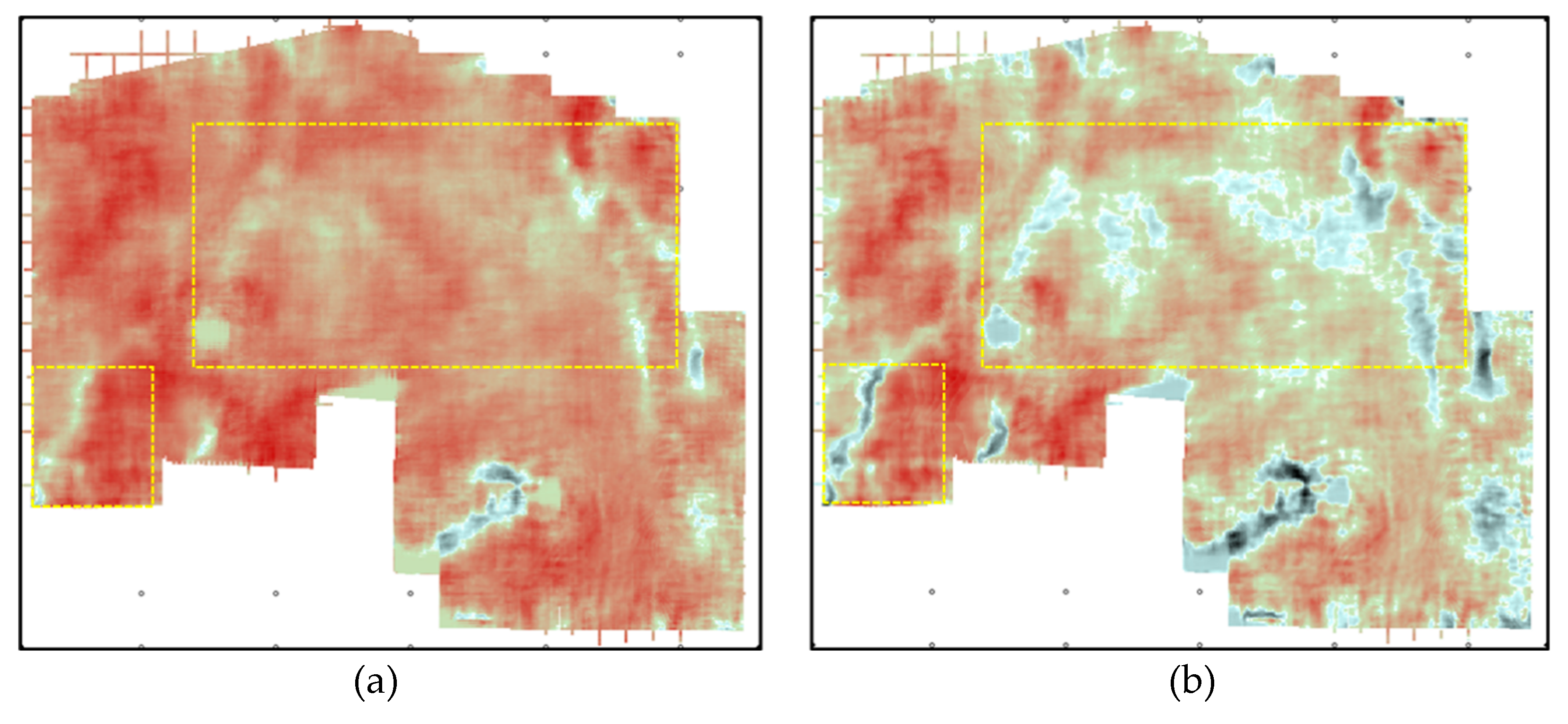
3. Results

The effectiveness of the aforementioned method was validated by applying it to the processing of three-dimensional seismic data in a coal mine. The exploration area is currently in the design stage, and in order to ensure the smooth development of the exploration area and normal production after the mining area goes into operation, maximize the advantages of mechanized mining and ensure production safety, therefore, three-dimensional seismic exploration was implemented in the exploration area to gain early insights into underground structures and geological anomalies and to take necessary precautionary measures in advance. It was confirmed through drilling and actual mining operations that the 12th coal seam developed in the area is approximately 2 meters thick. Reflection character analysis revealed that this coal seam (T12) exhibits a relatively simple phase and strong energy, allowing for continuous tracking throughout the entire region. However, the coal seam is affected by small faults, which pose risks to mining safety. Therefore, it is necessary to characterize the distribution of fault planes in the T12 coal seam in this area. High-resolution processing of the seismic data was performed, and the obtained results are shown in Figure 3. It can be observed that this technique can recover thinner layer information (circled in yellow and blue) and provide clearer fault identification(circled in red) while preserving low frequencies effectively. It also improves the signal-to-noise ratio and enhances the temporal and spatial resolution of the data. The processing yields high-fidelity, high-resolution, and high signal-to-noise ratio results.
Further validation of the reliability and effectiveness of high-resolution seismic data processing was conducted by extracting attributes along layers and comparing them with those from the original data. From the amplitude attribute map along the T12 horizon of the survey area, it can be seen that the high-resolution processing results provide a more detailed depiction of formations and faults compared to the original seismic data (annotated with yellow dashed boxes), while also revealing more geological details, as shown in Figure 4. This indicates that, after enhancing resolution, broadband seismic data can better delineate stratigraphic information and small-scale structures.
Due to the extensive development and regional distribution of small faults within the coal seam, areas where the integrity of the coal seam is compromised exhibit weakened reflected energy and reduced relative impedance. Therefore, impedance attribute maps (shown in Figure 5) along T12 (annotated with red line) have also been created. The impedance attributes along the original seismic data can reflect the main area of small fault distribution, while the impedance data processed with improved resolution can display the impedance reduction phenomenon caused by the development of small faults with greater precision. The process of enhancing seismic data resolution allows for a more precise visualization of the subtle variations in impedance caused by the presence of small faults (annotated with black dashed boxes). Furthermore, this expanded resolution enables us to capture a wider range of small fault distribution, resulting in a more comprehensive and accurate depiction of their planar layout.

4. Discussion and Conclusions

The mechanization and intelligence of coal mining are continuously improving, along with increasing mining depths. Complex geological conditions and coal seam characteristics pose higher demands for safety in coal mine production. While 3D seismic exploration has evolved into a comprehensive technical system capable of detecting geological structures, spatial positioning, and lithology interpretation, its ability to identify small-scale structures remains limited. To address this limitation, this paper proposes a technical workflow based on compressed sensing spectral inversion, aimed at enhancing the resolution of seismic data. By effectively improving the resolution while preserving amplitude and fidelity, this method allows for a more precise characterization of small-scale geological information embedded within the seismic data. In order to validate the efficacy of this approach, the method was applied to real 3D seismic data obtained from a coal mining, resulting in enhanced data resolution and a more detailed depiction of stratigraphic information and faults. This enhancement provides robust support for subsequent safe production measures.

Author Contributions

Conceptualization, G.S.; methodology, G.S.; software, G.S.; validation, L.L. and M.S.; investigation, S.M.; resources, X.M.; data curation, M.S and L.L..; writing—original draft preparation, G.S.; writing—review and editing, X.M.; supervision, X.M.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Key R&D Program of China, grant number 2023YFC3807604; the National Natural Science Foundation of China, grant number (41974161, 42174160); the National Key Research and Development Program of China (2021YFA0716901, 2022YFB3904601)

Data Availability Statement

The data presented in this study are available on request from the corresponding author due to privacy and ethical restrictions to ensure lawful use of the data.

Acknowledgments

Thanks for the great effort by editors and reviewers.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Peng, S.P.; Zhao, J.T.; Sheng, T.J.; Yang J.; Tao, J.H. Status and advance of seismic diffraction exploration in coalfield[J]. Coal Geology & Exploration,2023,51(1),1−20. [CrossRef]
  2. Peng, S.P. Current status and prospects of research on geological assurance system for coal mine safe and high efficient mining[J]. Journal of China Coal Society,2020,45(7): 2331-2345. [CrossRef]
  3. Luo, Z.Q.; Liu, P.; Tang, J.Y.; Liu, Z.L. Present situation and development direction of seismic exploration technology for hidden disaster-causing factors in coal mine[J]. ChinaCoal,2023,49 (1), 16-29.
  4. Wang, G.F.; Meng, L.Y. Development of coal mine intelligence and its technical equipment[J]. China Coal,2023,49(7):1-13.
  5. Wang, H.J.; Cao Y.; Wang H.L. Research and practice on key technologies for intelligentization of coal mine[J]. Coal Geology & Exploration,2023,51(1):44-54.
  6. Li, B.Q. Research on the technologies and application of general survey and treatment of hidden disaster causing geological factors in zhaozhuang Coal Mine[J]. China Coal,2022,48(S2):117-122.
  7. Wang J.W.; Wang H.J.; Wu H.; Wu Y.; Han K.; Cheng X.; Dong M.T. Research on transparency of hidden disaster causing factors in coal mines based on 3D geological modeling technology[J]. Journal of Mine Automation,2024,50(3):71-81,121. [CrossRef]
  8. Yuan, L.; Zhang P.S. Development status and prospect of geological guarantee technology for precise coal mining[J]. Journal of China Coal Society, 2019,44(8):2277-2284. [CrossRef]
  9. Zhang, E.W.; Zhou, J.J. Application research on three-dimensional seismic fine processing and recognition technology of small fault structure in Yuwu Mine[J]. Coal and Chemical Industry, 2023,46(9):79-82.
  10. Cheng, Y.L.; Wang, Z.F. Research and application of high-density 3D seismic exploration technology for in fault detection[J]. China Coal. 2022,48(S1):197-205.
  11. Yu, Z.M.; Han, D.F. Exploration and application of 3D seismic technology in first mining area of Hujiahe Coal Mine[J]. Coal Science & technology magazine,2023,44(4):156-161.
  12. Yang, C.M. Research and application of high precision 3D seismic prospecting technology in coal mining area[J]. China Energy and Environmental Protection,2017,39(11):238-241,245.
  13. Wang, X.D.; Liu, L. The application of shallow high accuracy 3D seismic exploration method to exploring burned area of Ningtiaota coal mine[J]. Chinese Journal of Engineering Geophysics,2019,16(2):174-183.
  14. Jin, Z.L.; Liu, X.; Gao P. Application of high-precision 3D seismic exploration technology in Buertai coal mine[J]. China Coal,2022,48(S1):180-187.
  15. Yilmaz, Öz.; Doherty, S. M. “Seismic data processing.” (1987).
  16. Gao, J.H.; Wang, L.L.; Zhao W. Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J]. Chinese Journal of Geophysics (in Chinese), 2009, 52(5): 1289-1300. [CrossRef]
  17. Jin, M.X.; Zhang, B.; Yi, S.C. Research on the application to seismic data in Bohai bay based on Gabor deconvolution[J]. Progress in Geophysics, 2017, 32(2): 856-861. [CrossRef]
  18. Mallat, S. A Wavelet Tour of Signal Processing, Third Edition: The Spare Way[M]. Academic Press, 2008.
  19. Wan, T.; Gao, J.H.; Chen, W.C.; Wang, B.J. TP wavelet and its applications to analysis of seismic data of thin interbeds[J]. COAL GEOLOGY & EXPLORATION, 2005, 33(4): 69-72.
  20. Portniaguine O.; Castagna J. Inverse spectral decomposition[J]. Seg Technical Program Expanded Abstracts, 2004, 23(1): 2586. [CrossRef]
  21. Smith, M.; Gary, P.; Jaime, S. Extending seismic bandwidth using the continuous wavelet transform [J]. First Break, 2008, 26: 97-102. [CrossRef]
  22. Mao, H.B.; Fan, X.; Yang, X.H.; Huang, J.; Chen, W.C. Application research on improving the resolution of broadband land post-stack seismic data in wavelet domain[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 541-546, 579. [CrossRef]
  23. Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: the S-transform[J]. IEEE Trans on Signal Processing,1996,44(4):998-1001. [CrossRef]
  24. Huang, H.D.; Feng, N.; Wang, Y.C. Cai Yanjie. High-resolution seismic processing based on generalized S transform. OGP, 2014, 49(1): 82-88.
  25. Yang, K.; Liu, W. The marine seismic data high resolution processing based on Hilbert-Huang transform [J]. Chinese Journal of Engineering Geophysics, 2015, 12(1): 22-26.
  26. Pham, D. H.; Meignen, S. High-Order Synchrosqueezing Transform for Multicomponent Signals Analysis With an Application to Gravitational-Wave Signal[J]. IEEE Transactions on Signal Processing, 2017, 65 (12), pp.3168-3178. [CrossRef]
  27. Dragomiretskiy, K.; Zosso, D. Variational mode decomposition[J]. IEEE Tran on Signal Processing, 2014, 62(3): 531-544. [CrossRef]
  28. Hale, D. An inverse Q-filter[A]. Stanford Exploration Project [C], 1981, 28: 289—298.
  29. Wang, J.; Yang, C.C.; Qiao, Y.L. Improve the seismic resolution with a stable and efficient inverse Q filter[J]. Progress in Geophysics, 2008, 23(2): 456-463.
  30. Chopra, S.; Alexeev, V.; Sudhakar, V. et al. High-frequency restoration of surface seismic[J]. The Leading Edge,2003,22(8):730-738. [CrossRef]
  31. Cheng, L.; Kong, Q.F.; Song, J.G. A step-by-step iteration for joint frequency expanding. OGP, 2017, 52(4): 696-703.
  32. Yu Z.; Wang, Y.C.; He, J.; Yang, R. A review of inverse Q filtering methods [J]. Progress in Exploration Geophysics,2009,32(05):309-314+325+307.
  33. Chen, C.R.; Zhou, X.X. Improving resolution of seismic data using wavelet spectrum whitening. OGP, 2000, 35(6): 703-709.
  34. Lu, W.K.; Ding, W.L.; Zhang, S.W.; Xiao, H.Q.; Zhao, M.H. A high-resolution processing technique for 3_D seismic data based on signal subspace decomposition[J]. Chinese Journal of Geophysics (in Chinese), 2005, 48(4): 896-901.
  35. Yan, Z.H.; Fang, G.; Xu, H.N.; Liu, J.; Shi, J.; Pan, J.; Wang, J.Q. The application of Hilbert spectral whitening method to high resolution processing of marine seismic data[J]. Marine Geology & Quaternary Geology, 2018, 38(4): 212-220. [CrossRef]
  36. Puryear, C.I.; Castagna, J.P. Layer-thickness determination and stratigraphic interpretation using spectral inversion: Theory and application[J]. Geophysics, 2008, 73(2): R37-R48. [CrossRef]
  37. Chopra, S.; Castagna, J.P.; Xu, Y. Thin-bed reflectivity inversion and some applications[J]. First Break, 2009, 31(1299):27-34.
  38. Chopra, S.; Castagna, J.P.; Xu, Y. Relative acoustic impedance application for thin-bed reflectivity inversion[C]. 2009 SEG Annual Meeting, Houston, 2009, 1-5.
  39. Zhang R, Castagna J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. [CrossRef]
  40. Zhang R, Sen M K, Srinivasan S. A prestack basis pursuit seismic inversion[J]. Geophysics, 2012,78(1): R1-R11. [CrossRef]
  41. Cao, J.H.; Qiu, Z.H.; Guo, D.H.; Wang, X.Y. Post-stack seismic spectral-inversion technique and its application[J]. Progress in Geophysics, 2013, 28(1): 387-393. [CrossRef]
  42. Candès, E. J. Compressive Sampling. International Congress of Mathematicians, 2006, ICM 2006 3:1433–52.
  43. Candès, E. J., Justin, K. Romberg, and Terence, T. “Stable Signal Recovery from Incomplete and Inaccurate Measurements.” Communications on Pure and Applied Mathematics,2006, 59(8):1207–23. [CrossRef]
  44. Donoho, D.L. Stable Recovery of Sparse Overcomplete Representations in the Presence of Noise. IEEE Transactions,2006, 52(10):6–18. [CrossRef]
  45. Baraniuk, Richard G. More Is Less: Signal Processing and the Data Deluge. Science,2011,331(6018):717–19. [CrossRef]
  46. Shu, M.C.; Zhang, F.; Zou, J.R.; Huo, S.D.; Luo, M.; Zhang W.D.; Li W.T.; Mu, S.Q.; Liang Y. Spectral inversion algorithm based on compressive sensing and its applications while drilling. Chinese Journal of Geophysics (in Chinese), 2023, 66(1): 34-45. [CrossRef]
  47. Blumensath, T.; Mike E. D. Iterative Thresholding for Sparse Approximations. Journal of Fourier Analysis and Applications,2008, 14(5–6):629–54. [CrossRef]
  48. Blumensath, T.; Mike E. D. Iterative Hard Thresholding for Compressed Sensing. Applied and Computational Harmonic Analysis,2009 27(3):265–74. [CrossRef]
  49. Bergeaud, F.; and Stéphane M. Matching Pursuit of Images. Pp. 285–300 in Wavelet Analysis and Its Applications, 1998,Vol. 7.
  50. Needell, D., and Tropp, J. A. CoSaMP: Iterative Signal Recovery from Incomplete and Inaccurate Samples. Applied and Computational Harmonic Analysis,2009, 26(3):301–21. [CrossRef]
  51. Foucart, S. Hard thresholding pursuit: an algorithm for compressive sensing. SIAM Journal on Numerical Analysis, 2011,49(5/6), 2543–2563. [CrossRef]
Preprints 109833 g001
Figure 1. (a) Input seismic data reflection coefficients; (b) L 0 -norm inversion; (c) L 2 -norm inversion.
Figure 1. (a) Input seismic data reflection coefficients; (b) L 0 -norm inversion; (c) L 2 -norm inversion.
Preprints 109833 g001
Preprints 109833 g002
Figure 2. High-resolution data processing workflow using spectral inversion based on compressed sensing theory.
Figure 2. High-resolution data processing workflow using spectral inversion based on compressed sensing theory.
Preprints 109833 g002
Preprints 109833 g003
Figure 3. Comparison of Data Before and After High-Resolution Processing: (a)Original Data vs. (b)High-Resolution Data.
Figure 3. Comparison of Data Before and After High-Resolution Processing: (a)Original Data vs. (b)High-Resolution Data.
Preprints 109833 g003
Preprints 109833 g004
Figure 4. Comparison of amplitude slices along the layer T12. (a)original seismic data;(b) high resolution seismic data.
Figure 4. Comparison of amplitude slices along the layer T12. (a)original seismic data;(b) high resolution seismic data.
Preprints 109833 g004
Preprints 109833 g005
Figure 5. Comparison of relative impedance slices along the layer T12. (a)original seismic data;(b) high resolution seismic data.
Figure 5. Comparison of relative impedance slices along the layer T12. (a)original seismic data;(b) high resolution seismic data.
Preprints 109833 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated