Prerpints.org logo
Preprint
Article

Sensor Systems for Measuring Force and Temperature with Fiber-Optic Bragg Gratings Embedded in Composite Materials

Altmetrics

Downloads

99

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts
Abstract
Currently, there is a high interest in smart sensors and integrated composite materials in various industries such as construction, aviation, automobile, medical, information technology, communication, and manufacturing. Here, a new conceptual design for a force and temperature sensor system is developed by integrating fiber optic Bragg grating sensors embedded within composite materials, and a mathematical model is proposed that allows one to estimate strain and temperature based on signals obtained from optical Bragg gratings. This is important for understanding the behaviors of sensors under different conditions and for creating effective monitoring systems. Describing the strain gradient distribution, especially considering different materials with different values of Young's modulus, provides insight into how different materials respond to applied forces and temperature changes. The shape of the strain gradient distribution was obtained, which is a quadratic function with a maximum value of 1500 µ, with a maximum value at the center of the lattice and a symmetrically decreasing strain value with distance from the central part of the fiber Bragg grating. With axial strain at the installation site of the Bragg grating sensor under applied force values ranging from 10 to 11 N, the change in strain was linear. As a result of theoretical research, it was found that the developed system with fiber-optic sensors based on Bragg gratings embedded in composite materials is resistant to external influences and temperature changes.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

Sensors play a crucial role in various industries such as factory automation, aerospace, automotive and construction in making the system intellectual, and have used for different applications. Fiber reinforced polymer composites have been widely used in the sensors due to their excellent properties - lightness, high strength, corrosion resistance, and structural properties [1,2,3,4,5]. Specially, composites show high potential as structural materials for spacecraft. Although the space environment in which spacecraft are operated can significantly degrade the performance of composites due to the infinitely harsh data of high vacuum, thermal cycling, atomic oxygen, ultraviolet radiation, radiation, and the presence of space debris [6,7,8]. A fiber reinforced composite exposed to the space environment suffers from changes in strength, interface delamination, surface cracking, weak fracture, molecular chain breakage and other types of damage [9,10,11,12,13,14,15,16].
Thus, the best way to predict the performance of fiberglass composites has the main property of providing them with long-term strength in service. Multiple methods have been proposed for predicting the condition of composites, such as ultrasonic detection, radiographic inspection, sound emission observation, strain gauge testing and optical fiber installation [17,18,19,20,21,22,23,24,25]. Although ultrasonic and radiographic inspection methods appear to be mature and freely used, they can only be used for offline testing. Frequent collapse of the interface between piezoelectric sensors and composites during acoustic emission testing makes noise during the propagation of elastic waves in materials. Strain gauges are free-standing, integrated into composite materials, but their electrical signals are susceptible to electromagnetic interference. In contrast, fiber Bragg grating (FBG) sensors have attracted impressive research interest in damage detection due to their embeddability, electromagnetic interference immunity capabilities, and encoded wavelength data. Previous studies have documented the adaptability of the integrated FBG sensor for dynamic stress prediction, thermal cycle reading, and thermal strain measurement [26,27,28,29,30]. However, harsh environmental circumstances may also have some impact on the monitoring method itself. When FBG sensors are adapted to the radiation sensing environment, it has been discovered that high energy ionizing radiation can cause signal deflection and transmission loss in the FBG, which can lead to errors in temperature or strain measurements [31,32,33]. Based on this, relevant studies have focused on increasing the radiation resistance of FBGs, mainly through modulation of fiber composition, grating inscription methods, and pre-treatment methods to mitigate the effects of radiation on FBGs [34,35,36]. However, it is still unknown whether FBG sensors are designed for monitoring materials in radiative environments.
The FBG sensor is an optical fiber with a uniformly distributed grating. The grating fits inside the fiber core through exposure to ultraviolet light or a femtosecond laser. The refractive index of an optical fiber is periodically modified over a certain length. It is noteworthy that FBG is a kind of unrivaled bandpass filter, which can reflect a small spectrum of incident light and simultaneously transmit another region [37]. Sensitivity coefficients to strain and temperature, respectively, which are associated with fiber and lattice parameters [38]. The wavelength shift is linearly proportional to the change in temperature and strain, which guarantees the probability of composition and temperature prediction by FBG.
For a reliable monitoring and sensing strategy in radiation environments, FBG sensors that are constant to radiation must be carefully selected. It is currently believed that FBGs deposited on purified silica or doped fibers have low radiation sensitivity, resulting in less emission loss and wavelength shift than FBGs deposited on standard Ge-doped fibers [39,40,41]. In addition, FBGs fabricated using femtosecond laser research in recent years, compared with the traditional UV laser inscription method, exhibit better stability at high temperatures and better reliability against radiation-induced wavelength shift [42,43,44,45]. The radiation reliability and commercialization of various types of FBG sensors were comprehensively provided for.
In this study, we address a new conceptual design for a force and temperature sensor system by integrating FBG sensors embedded within composite materials, and propose a mathematical model to estimate strain and temperature based on signals obtained from FBG sensors. The results give an important understanding for the sensor behaviors under different conditions and for creating effective monitoring systems.

2. Materials and Methods

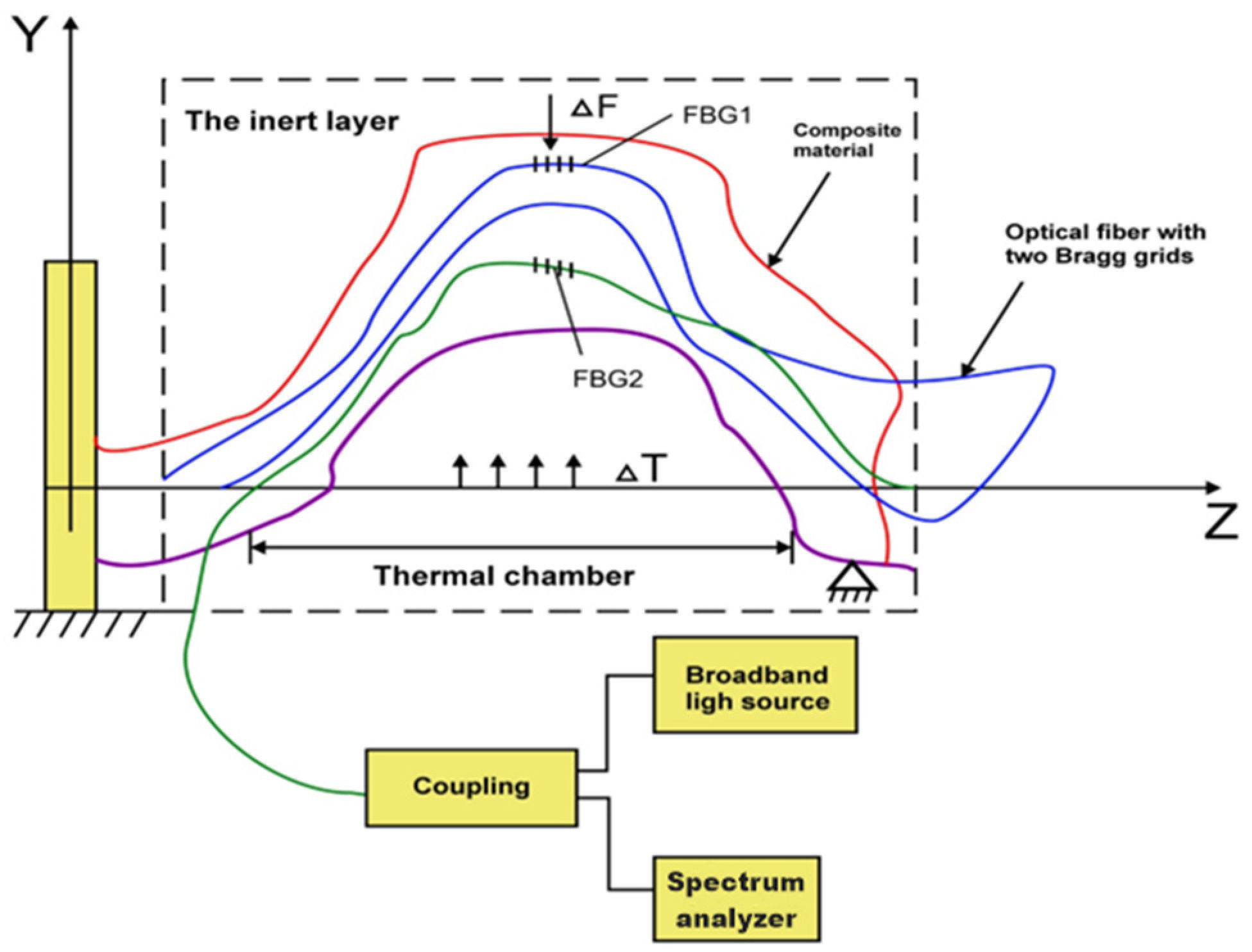
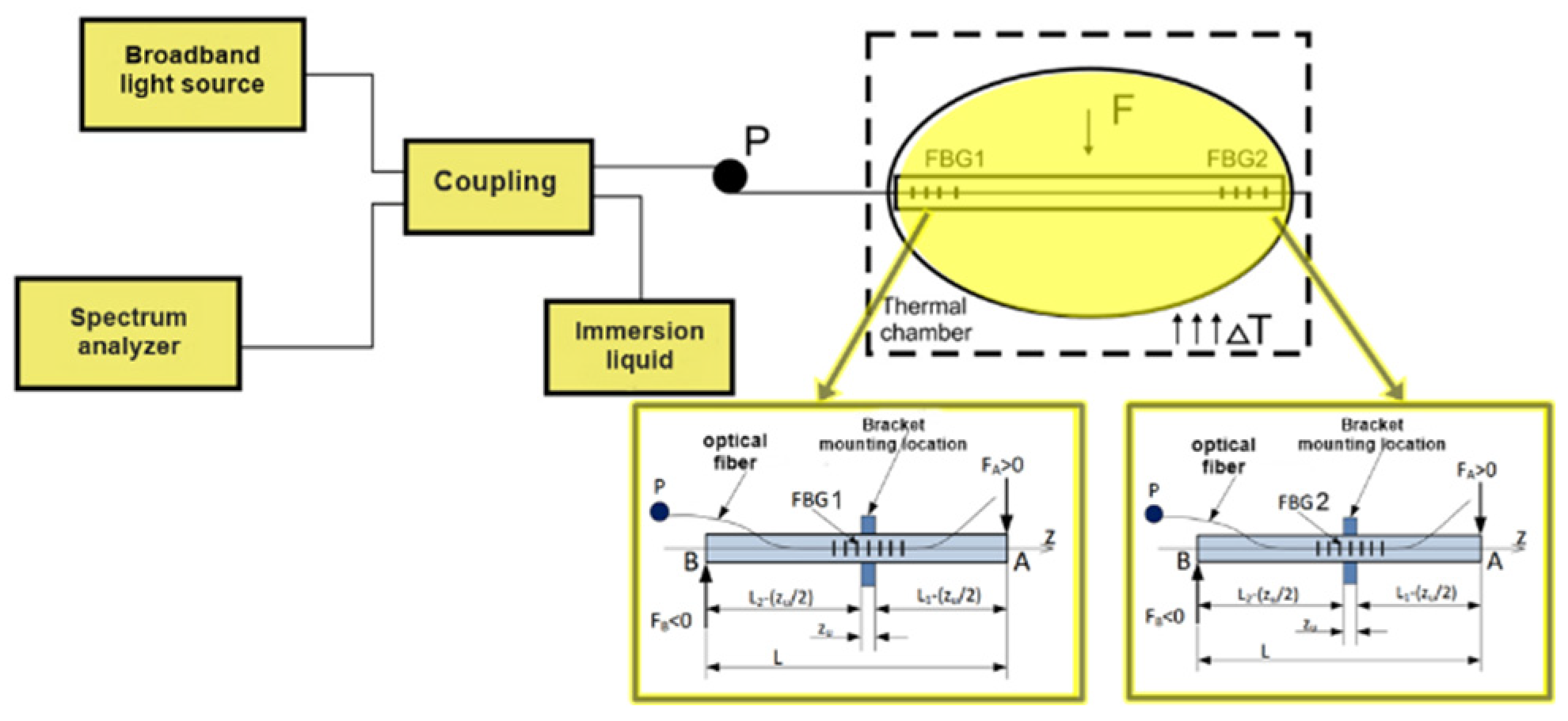
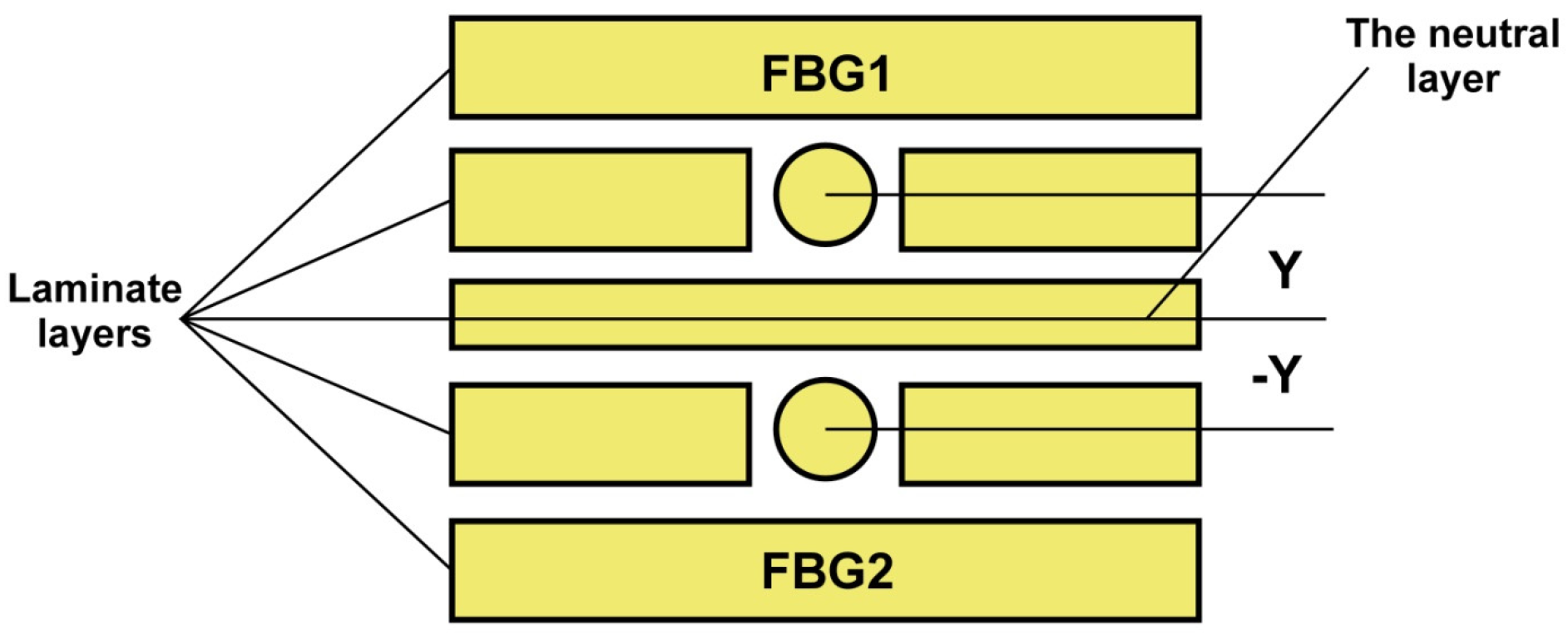
2.1. Sensor Diagram

Practical solutions for force measurement use optical Bragg gratings embedded in composite materials. a system in which Bragg gratings are mounted in a composite material in an arc shape is shown in Figure 1.
The sensor consists of two Bragg gratings built into a composite material, taking the shape of an arc. When a lateral force F is applied to the sensor, its bending will lead to strain of the lattice located below the neutral layer, as well as to shortening of the lattice located above this layer. The solution shown in Figure 1 takes advantage of the fact that the two resonant wavelengths of the gratings shift independently as the lateral force changes and simultaneously shift as the ambient temperature changes [46].
In this work we consider the simultaneous measurement of force and temperature using fiber-optic sensors with Bragg gratings. The indicated dependencies are linear. The use of all these elements makes it possible, respectively, to increase the sensitivity of the measurement of a particular physical quantity, to make the measurement insensitive to temperature, and to increase the linear resolution.
It is also possible to prove the dependence (preferably linear) of the grating spectral width on the force causing the grating strain. FBG-based force and temperature sensors are currently under investigation, in which gratings are mounted in such a way as to allow their inhomogeneous strain under a transverse force. When installing Bragg gratings in composite materials, it is assumed that the dimensions of the optical fiber are significantly smaller compared to the sensor module, so its effect on sensor strain is negligible.
Due to the specific nature of the measured quantities, the results of an analysis of mechanical conditions and groups of sensor systems currently being developed for simultaneous measurement of force and temperature are presented. Thanks to the method of determining the measured value (forces and temperatures).
This method can also be used in variable temperature conditions. The chirp caused by the transfer of the measured force to the lattice strain can then be described by an appropriate mathematical function. Figure 2 shows a schematic view of a device for measuring force and temperature using a Bragg grating mounted on a special holder that transfers the applied force to a linear, quadratic chirp, and is described by a specially designed function.
The measurement setup shown in Figure 2 uses a specially designed holder on which the FBG is mounted. In this case, the rectangular holder has length L, thickness g and width s. The two ends A and В are free, and the middle part of the holder is fixed. A Bragg grating of length L and Bragg wavelength λB is installed on the surface of the middle part of the holder. The grille is installed in such a way that the lengths of the fixed parts of the grille and the holder are the same. In this case they are designated as zu. Thus, the holder is divided into two parts of length L1 - zu / 2 and L2 - zu / 2. The parts are intentionally designated by different indices because L1 ≠ L2. From the analysis of Figure 3 it also follows that L = L1 + L2. In such sensors, two parts of the beam are subjected to opposing forces FA and FB. This design of the sensor leads to a shift in the spectrum towards longer wavelengths of the part of the grating that is being stretched - the right side of the holder in Figure 3. At the same time, there is a shift in the spectrum towards shorter wavelengths of the part of the FBG that is being compressed - located on the left side holder. In the area where the holder and grille are fixed, i.e., − zu / 2 < z < zu / 2, the strain value is theoretically zero. However, assuming that the holder is elastic and that the region zu is very small, the FBG strain distribution within z does not change dramatically. We assume that this is a quasi-homogeneous change in the gradient from the minimum value ( − zu / 2 < z < zu / 2) to the maximum (|z| = zu / 2). Thus, a uniform Bragg grating is subject to chirp caused by strain of the holder. The closer to the stationary part, the greater the FBG strain value. The holder on which the grille is fixed is symmetrical, so the FBG has a certain strip width. However, the grating spectrum does not consist of a single Bragg resonance, but of many resonance peaks.

2.2. Theory

The solution presented in Figure 1 takes advantage of the fact that the two resonant wavelengths of the gratings shift independently when the lateral force changes and simultaneously shift when the ambient temperature changes [46]. The indicated dependencies are linear. In sensors for measuring force and temperature, a Bragg grating (or several solutions, for example, two placements in different places [47] is also installed on special supports. Their shape and design transmit the lateral force applied to the strain support of the mesh attached to it [48,49].
When installing Bragg gratings in composite materials, it is assumed that the dimensions of the optical fiber are much smaller compared to the sensor module, so its effect on sensor strain is negligible. A change in the lateral force F and the associated change in strain Δε will cause changes in the Bragg wavelength, which are denoted as ∆ λ B ε .
∆ λ B ε = K ε Δ ε ,
where K ε is the sensitivity of the Bragg wavelength shift under the strain. At the same time, changing the temperature ΔT of the environment will also lead to a change in the Bragg wavelength of each of the gratings, which in turn is denoted as ∆ λ B T .
∆ λ B T = K T Δ T ,
where K T is the sensitivity of the Bragg wavelength shift at the temperature.
The total change Δ λ B in Bragg wavelength of each grating can be expressed as:
Δ λ B = K ε Δ ε + K T Δ T .
Since the described design is used for simultaneous measurement of force and temperature, the dependence of the wavelength of both gratings on the applied lateral force was established. According to Hooke’s law, the strain ε z along the z axis marked in Figure 1 can be described as
ε z = σ z E ,
where E is the Young’s modulus of the material from which the composite is made. The stresses σ z along the z axis depend on the bending moment M that occurs when a force F is applied, the distance y from the Bragg grating to the neutral layer and the moment of inertia I, according to the following relationship
σ z = M y I
and
I = s g 3 12 ,
where s is the width of the composite, g is its thickness, and the bending moment is equal to:
M = F z 2 .
To simplify calculations and due to the symmetry of the design, only the left half of the sensor can be considered, so the z variable can be limited to the range 0 ≤ z ≤ L/2. Consequently, the sensor experiences maximum strain along the z-axis in the central part, where z = L/2. Considering relations Equations (5)–(7), ε z can be described by the following equation:
ε z = y z 2 I E × F ( 0 ≤ z ≤ L 2 ) .
The strain in the central part of the sensor, at the location where the Bragg grating is attached, can be expressed by the following relationship:
ε z ( z = L 2 ) = L y 4 I E × F ,
which the outcome of Equation (6) takes the form
ε z ( z = L 2 ) = 3 L y s g 3 E × F .
The product K ε Δ ε from Equation (3) can be represented as:
K ε Δ ε = 3 L y s g 3 E × Δ F
where the sensitivity of the array to changes in force, K F , is described by the following equation:
K F = 3 L y s g 3 E
For a sensor designed to simultaneously measure force and temperature in the configuration shown in Figure 2, it can be expressed as follows:
Δ λ B 1 Δ λ B 2 = K T 1 K F 1 K T 2 K F 2 × Δ T Δ F ,
where K T 1 and K F 1 are the sensitivities of the Bragg wavelength shift Δ λ B 1 of the corresponding Bragg grating, denoted as FBG1, respectively to changes in temperature ΔT and force ΔF, and K T 2 and K F 2 are the sensitivities of the Bragg wavelength shift Δ λ B 2 of the Bragg grating, denoted as FBG2, also to a change in temperature ΔT and force ΔF, respectively. The force sensitivity of the gratings, according to Equation (12), can be easily controlled by changing the width and thickness of the composite in which the grating is installed. Equation (13) allows us to write down the changes in wavelength FBG1 and FBG2 in the following form:
Δ λ B 1 = K T 1 Δ T + K F 1 Δ F
and
Δ λ B 2 = K T 2 Δ T + K F 2 Δ F
Figure 3 shows the arrangement of two FBGs in the laminate. Based on the analyzes performed, we can conclude that the sensitivity coefficients to the applied force of both gratings in the system shown in Figure 3 satisfy the following equality:
K F 1 = − K F 2 .
The temperature sensitivity coefficients of FBG1 and FBG2 will remain as follows:
K T 1 = K T 2
in case the gratings have approximately the same Bragg wavelength and are made of the same optical fiber using the same phase mask.
Simultaneous measurement of temperature change ΔT and force change ΔF in the presented system can be performed based on Equations (16) and (17), by performing operations of addition or subtraction of the Bragg wavelengths of both lattices, by the following dependencies:
Δ λ B 1 + Δ λ B 2 = 2 K T 1 Δ T
and
Δ λ B 1 − Δ λ B 2 = 2 K F 1 Δ F .
This allows temperature and force to be measured simultaneously by detecting the wavelengths FBG1 and FBG2, since the equation holds:
Δ F = Δ λ B 1 − Δ λ B 2 2 K F 1
and at the same time the equation is executed:
Δ T = Δ λ B 1 + Δ λ B 2 2 K T 1 .
In the case when Bragg gratings, which are elements of a force and temperature sensor, are installed in composite materials, the process of curing the entire sensor containing the composite along with the gratings is very important. The type of composite material, as well as its structure and shape, play a significant role in increasing sensitivity to lateral force.
Below is a method for deriving matrix equations for force sensors operating in the system shown in Figure 2. It is assumed that for a system with a linearly chirped homogeneous lattice, the forces applied to the free ends are equal in magnitude:
F 1 = − F 2 = F .
Information about changes in temperature and strength is contained in the sum and difference of wavelengths between two parts of the grating: stretched - marked on the right in Figure 3. and compressed - marked on the left in Figure 3. Denoting the sum of changes in wavelengths of both parts of the gratings as:
Δ λ 1 + 2 = Δ λ B 1 + Δ λ B 2
and their difference, respectively, as:
Δ λ 1 − 2 = Δ λ B 1 − Δ λ B 2 .
The matrix equation of such a designed sensor for simultaneous measurement of temperature and force will take the following form:
| Δ λ 1 − 2 | Δ λ 1 + 2 = K F 1 K T 1 K F 2 K T 2 × F Δ T ,
where K F 1 and K T 1 are the sensitivity coefficients of the absolute difference in wavelengths Δ λ 1 − 2 , respectively, to force and temperature change, and K F 2 and K T 2 denote the sensitivity of the sum of the wavelengths of both parts of the grating Δ λ 1 + 2 , respectively, to force and temperature change.
Equation (23) describes the dependence of the change in wavelength on the quantities under consideration (force and temperature). This pattern can be proved using analytical relations, bearing in mind the principles of mechanics. The equation describing the dependence of the change in the Bragg wavelength of the first part of the grating on the applied force Δ λ 1 = f ( F 1 ) will take the following form:
Δ λ 1 ( F ) = 6 ( 1 − p e ) ( L 1 − z u 2 ) E s g 2 × F 1 × λ B ,
where p e is the photoelastic constant, λ B is the wavelength used for the Bragg grating (the nominal one for which the grating was designed and tuned. A similar equation Δ λ 2 = f ( F 2 ) can be written for the second part of the grating.
Δ λ 2 ( F ) = 6 ( 1 − p e ) ( L 2 − z u 2 ) E s g 2 × F 2 × λ B ,
The wavelength value for both parts of the grating also changes due to temperature changes, reflected based on the coefficient of thermal expansion of the stand on which the Bragg grating is installed, using the following equation:
Δ λ 1 ( Δ T ) = Δ λ 2 ( Δ T ) = α Λ + α n + ( 1 − p e ) ( α w ) × Δ T × λ B ,
where α w is coefficient of thermal expansion of the rack, α n is coefficient of thermal expansion of the holder, and α w is the coefficient of thermal expansion of the stand on which the Bragg grating is installed, depending on the material of the stand.
Analyzing this Equation (26), it can be noted that the difference in the change in wavelength for both parts of the array will be zero, which contributes to a better matrix condition due to the zeroing of one of the sensitivity coefficients in the sensor processing matrix. To prove this statement, the equations describing the dependence of wavelength shifts on the measured values are written as follows:
Δ λ 1 ( F , ⁡ Δ T ⁡ ) = 6 ( 1 − p e ) ( L 1 − z u 2 ) E s g 2 × F 1 + α Λ + α n + ( 1 − p e ) ( α w − α Λ ) Δ T λ B
Δ λ 2 ( F , ⁡ Δ T ⁡ ) = 6 ( 1 − p e ) ( L 1 − z u 2 ) E s g 2 × F 2 + α Λ + α n + ( 1 − p e ) ( α w − α Λ ) Δ T λ B
Thus, the processing equations will take the following form:
Δ λ 1 + 2 F , Δ T = 6 1 − p e L 1 + L 2 − z u λ B E s g 2 F + 2 λ B α Λ + α n + 1 − p e α w − α Λ Δ T
Δ λ 1 − 2 ( F , Δ T ) = 6 ( 1 − p e ) ( L 1 − L 2 − z u ) λ B E s g 2 F
Based on Equation (23), the values of the individual sensitivity coefficients can be determined because the following equations occur:
Δ λ 1 − 2 ( F , Δ T ) = K F 1 F + K T 1 Δ T
Δ λ 1 + 2 ( F , Δ T ) = K F 2 F + K T 2 Δ T
Analyzing Equations (31) and (32) and the derived processing Equations (29) and (30), it can be seen that one of the sensitivity coefficients (KT1) takes the value of zero. The matrix Equation (23) can be inverted. In view of the fulfillment of the equation KT1 = 0, it will take the form:
F Δ T = D − 1 K T 2   0 − K F 2 K F 1 × | Δ λ 1 − 2 | Δ λ 1 + 2
where in this case the determinant of the matrix is equal to:
D = K F 1 K T 2
and the following inequality holds:
K F 1 / K F 2 ≠ K T 1 / K T 2 .
It should be noted that the sensor is capable of measuring the applied force and at the same time the temperature change. In the case under consideration, the lattice parameters are the Bragg wavelength λ B and the width of the grating reflection spectrum, which is designated as ΔFWHM.
The equation describing the dependence of the Bragg wavelength of the sensor on the applied force and temperature change λB= f (F, ΔT) will take the form:
λ B F , Δ T = 32 1 − p e 2 n e f f Λ z ( 1 + z / L ) 3 E π d 3 × F + α Λ + α n + ( 1 − p e ) ( α w − α Λ ) 2 n e f f Λ × Δ T
where n e f f is the effective refractive index of the fiber on which the Bragg grating is applied, and Λ is its period.
A similar equation ΔFWHM = f (F, ΔT) can be written as follows:
Δ F W H M F , Δ T = 64 n e f f Λ 1 − p e E π d 3 × z 2 ( 1 + z 2 / L ) 3 − z 1 ( 1 + z 1 / L ) 3 × F
In this case, Equation (23) will take the form:
Δ F W H M λ B = K F 1 K T 1 K F 2 K T 2 × F Δ T .
Based on Equation (38), it is possible to calculate the values of each of the sensitivity coefficients, since the following equalities are satisfied:
Δ F W H M F , Δ T = K F 1 F + K T 1 Δ T
and
λ B ( F , Δ T ) = K F 2 F + K T 2 Δ T
Again, analyzing Equations (39) and (40) and processing Equations (36) and (37), it can be seen that one of the sensitivity coefficients (KT1) takes on a zero value. The matrix Equation (38) can be inverted. In this situation, in view of the fulfillment of the equality KT1 = 0, Equation (33) can be rewritten by
F Δ T = D − 1 K T 2   0 − K F 2 K F 1 × Δ F W H M λ B
In addition, analyzing Equation (37), one can notice that the width of the spectral characteristic depends linearly on the applied force and does not depend on temperature changes.
In theoretical studies for the steel, the temperature sensitivity of FBG1 K T 1 =9.45 pm/0C, FBG2 K T 2 =14.34 pm/0C.
Δ F W H M λ B = 2,6 × 10 − 3 9.45 1,2 × 10 − 3   14.34 × F Δ T
Also the sensitivity coefficient K F is equal to:
K F = ∆ F W H M ∆ F
From here we can find
F Δ T = 1 16,8 × 10 − 3 14.34 0 − 1,2 × 10 − 3 2,6 × 10 − 3 × Δ F W H M λ B
Table 1 shows the parameters used in this work.

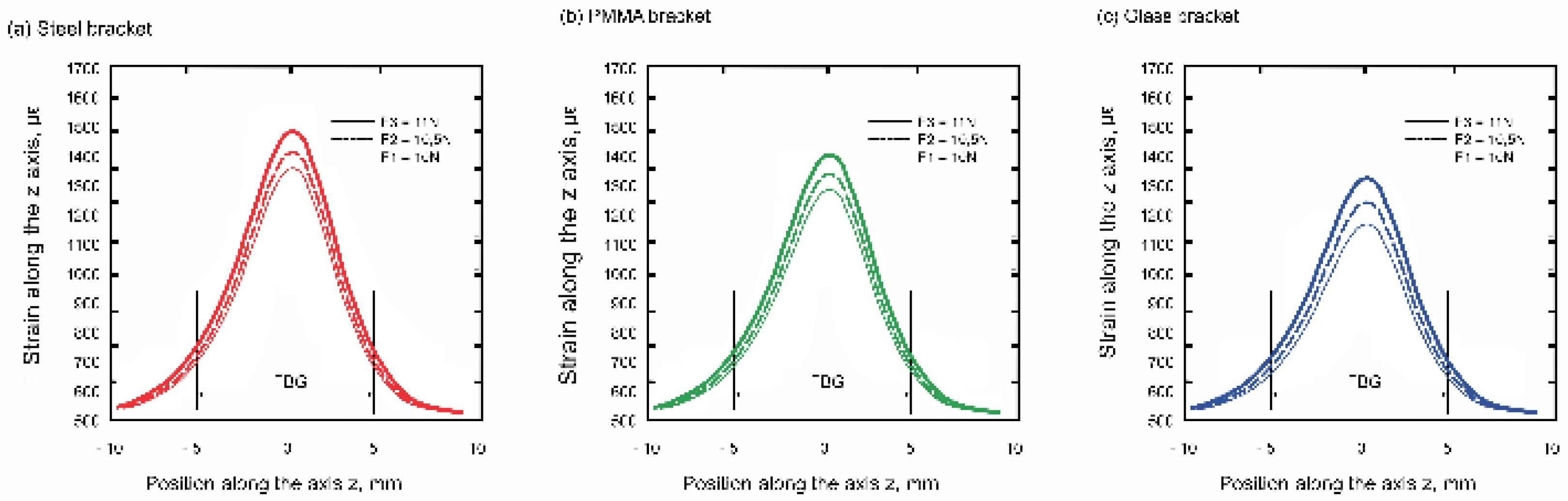
3. Results

This work is focusing on measuring temperature and strain simultaneously. The of proposed methods involves simultaneous relative methods and forces acting in two directions, uneven stresses and their distribution, including theoretical preconditions for developing specific methodological solutions.
In this study, integrated composite materials are used. Each type of bracket made of a different material (steel, PMMA, and glass) has unique mechanical, thermal conductive, and optical properties. Studying different brackets allows us to evaluate how these differences in material properties can affect the behavior of the sensor system under different operating conditions. Thus, studying three types of brackets in this study aims to provide insight into how different materials affect the performance of integrated sensors and help select the best option for specific applications.
When a vertical force is applied to the measurement section as shown in Figure 2, the grid experiences inhomogeneous deformation, resulting in inhomogeneous deformation. Figure 4 shows the axial strain shape of the grid corresponding to different values of the applied force. The graphs indicate the location where the Bragg grating is mounted. Using Equations (20)~(26) and data in Table 1, the calculations are given by applied force values F=10N, F=10.5N, F=11N.
Where the mesh is located, the shape of the strain gradient distribution is quadratic, with the maximum value in the center of the mesh and the strain value symmetrically decreasing as we move away from the central part of the FBG.
At the grating position, the shape of the gradient strain distribution is quadratic function parabola and has a maximum value in the center of the bracket and the strain value decreases symmetrically as it moves away from the center part of the FBG.
The maximum strains of the steel, PMMA, and glass brackets are 1430, 1535, and 1345 με, respectively.
Figure 5a shows plots of axial strain for different values of applied forces. Figure 5b shows plots of axial strain at the location of Bragg gratings. According to them, it can be assumed that for given values of force (10-11 N), the change in strain is linear. Also important from the point of view of the amount of strain is the material from which the bracket in Figure 6a,(a1)–(a3). The characteristics shown here were obtained for three different materials with different Young’s modulus values. The materials considered were steel (Young’s modulus around 200 GPa - red line in Figure 6(a1)–(a3), glass (Young’s modulus about 73.5 GPa - blue line in Figure 6(c1)–(c3) and PMMA - polymethyl methacrylate (Young’s modulus about 3 GPa – green line in Figure 6(b1)–(b3). Figure 6 shows the strain characteristics for different values of the cantilever length. Note that it is possible to choose a length such that the direction of strain varies. In this way, it is possible to cause an increase or decrease in the strain values along the z-axis.
Examples of processing characteristics for force and temperature measurements using an optical Bragg grating, in which linear chirp is induced by its placement on a special support, are presented in Figure 7 and Figure 8.
Figure 7 shows examples of the difference and sum characteristics of the Bragg wavelength variation of a sensor with a linear chirp at constant temperature under varying force conditions. Analogous results for wavelength and bandwidth measurements as a function of temperature for a system using a Bragg grating with a quadratic chirp function are shown in Equations (3) and (4).
Figure 7 shows examples of the difference and sum characteristics of the Bragg wavelength variation of a sensor with a linear chirp at constant temperature under varying force conditions. Analogous results for wavelength and bandwidth measurements as a function of temperature for a system using a Bragg grating with a quadratic chirp function are shown in Figure 3 and Figure 4.
As shown in Figure 8, the change in grating spectral width with temperature is negligible compared to the difference in Bragg wavelength caused by temperature changes. Based on the slope of the characteristics from Figure 5 and Figure 6, it is possible to determine the values of all sensitivity coefficients of the characteristic parameters of the gratings (for example, Bragg wavelength, grating spectral width) for force and temperature, and it is also possible to determine the discussed quantities from indirect measurements of the Bragg grating parameters. According to the theoretical results of the work, the new model has improved sensitivity compared to the existing model.
When comparing the results of this study with the results of previous studies, it can be said that, moreover, systems have been developed in which Bragg modes with chirps intentionally caused during measurement by non-uniform strain are being developed [51,52], and force and temperature sensors are also being investigated based on FBGs, in which the meshes are installed in such a way as to ensure their uneven strain as a result of the appearance of shear force [53].

4. Discussion

The discrepancy in the results for the Glass bracket, compared to other materials, is predominantly attributed to the material’s intrinsic mechanical properties, most notably its Young’s modulus. The Young’s modulus of a material is a measure of its stiffness and is a fundamental factor in determining how it will deform under stress. Glass typically has a higher Young’s modulus than many polymers, including polymethyl methacrylate (PMMA), which means it deforms less under the same applied force.
During the application of force, as outlined in Figure 2 of the provided documentation, inhomogeneous strain occurs in the Bragg grating. This strain affects the grating’s reflected wavelength due to the strain experienced by the grating’s fibers. Given that the glass bracket has a different Young’s modulus (approximately 73.5 GPa, as per the context provided), the strain gradient distribution across it would naturally differ from that of brackets made of other materials, such as steel or PMMA. In Figure 4 and Figure 5, the graphs exhibit a linear change in strain for forces ranging between 10 to 11 N, which is expected behavior under elastic strain.
Furthermore, it is crucial to consider the implications of the composite structure in which the FBG sensors are embedded. The composite matrix’s behavior, including its response to temperature changes and external influences, can also impact the measurement and performance of the sensor system. In particular, the response of the composite material to environmental factors and its subsequent impact on the embedded FBG sensors are critical to the sensors’ ability to measure force and temperature accurately. It is plausible that the distinct axial strain of the Glass bracket under the same applied forces may be the combined result of the Glass’s high modulus of elasticity and its interaction within the composite structure.
In addition to the material properties, the FBG sensor system’s design-namely, the symmetry of the holder and the Bragg grating’s mounting location-can influence the spectral width and wavelength shift, further affecting the strain measurement. As such, the resulting graphs indicate that the developed system exhibits improved sensitivity and the ability to withstand external and temperature-induced influences, as observed in the theoretical findings.
The observed difference in the strain characteristics of the Glass bracket, therefore, underpins the importance of material selection in designing FBG sensor systems for specific applications, especially when considering the composite materials’ mechanical properties and the operational environment.
In summary, the disparity in the strain behavior of the Glass bracket is a multifactorial outcome, determined by the material’s Young’s modulus, the structural design of the FBG sensor system, and the composite material’s response to force and temperature. Further research should consider these aspects to optimize the sensor system for diverse materials and applications.

5. Conclusions

In this paper, a new conceptual framework was developed for a system with fiber-optic Bragg lattice sensors for strength and temperature measurement embedded in composite materials. As a result of the study, it can be noted that the width of the spectral characteristic linearly depends on the applied force and does not depend on temperature changes, and also calculate the values of each of the sensitivity coefficients and strain characteristics for different values of the length of the holder. When calculating the strain, attention should be paid to the possibility of choosing a length that can lead to a change in the direction of strain. Thus, it is possible to create increasing or decreasing strain values along the z-axis. The characteristics of the change in the difference and sum of Bragg wavelengths for a fiber-optic sensor with a linear chirp signal at a constant temperature under conditions of varying force for different values of applied axial deforming forces along a holder in the form of a truncated cone at different lengths are constructed. The temperature change has a more significant effect on the Bragg wavelength than on the width of the lattice spectrum. This is because temperature changes lead to a change in the optical refractive index in the optical fiber, which, in turn, causes a change in the Bragg wavelength. Further research will focus on working with three, four, and five sensors, as well as creating a simulation model for monitoring the system using sensors for engineering structures.

6. Patents

Patent for utility model “Cable temperature measurement system with a fiber Bragg grating” / Kalizhanova A.U., Kunelbaev M., Kozbakova A.Kh. No. 8209, Reg. application number 2023/0373.2, dated 04/07/2023.

Author Contributions

The following statements should be used “Conceptualization, A. Kalizhanova, A. Kozbakova, M. Kunelbayev; software, Zh. Aitkulov, A. Utegenova, U. Imanbekova; validation, A. Kalizhanova, A. Kozbakova, M. Kunelbayev; investigation, X.X.; resources Zh. Aitkulov, A. Utegenova, U. Imanbekova.; data curation, A. Kalizhanova, A. Kozbakova, M. Kunelbayev; supervision, A. Kalizhanova, A. Kozbakova; project administration, A. Kalizhanova.

Funding

The work was supported by a grant and funding the Ministry of Science and Higher Education of the Republic of Kazakhstan within the framework of the Project № AP19679153, Institute Information and Computational Technologies CS MSHE RK.

Institutional Review Board Statement

The Science Committee of the Institute of Information and Computational Technologies CS MSHE RK, Kazakhstan has granted approval for this study on DATE. 03 August 2023 (Ref. No298/23-25.).

Acknowledgments

The work was supported by a grant and funding the Ministry of Science and Higher Education of the Republic of Kazakhstan within the framework of the Project № AP19679153, Institute Information and Computational Technologies CS MSHE RK.

Conflicts of Interest

No.

References

  1. Xian, G., Guo, R., Li, C. (2022). Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/ glass fiber reinforced polymer composite. Composite Structures, 281, 115060. [CrossRef]
  2. Das, T.K., Ghosh, P., Das, N.C. (2019). Preparation, development, outcomes, and application versatility of carbon fiber-based polymer composites: a review. Advanced Composites and Hybrid Materials, 2(12), 214-233. [CrossRef]
  3. Chung, D.D.L. (2017). Processing-structure-property relationships of continuous carbon fiber polymer-matrix composites. Materials Science and Engineering R Reports, 113,1-29. [CrossRef]
  4. Akman, F., Ogul, H., Ozkan, I., Kaçal, M.R., Agar, O., Polat, H., Dilsiz, K. (2022). Study on gamma radiation attenuation and non-ionizing shielding effectiveness of niobium-reinforced novel polymer composite, Nuclear Engineering and Technology, 54(1), 283-292. [CrossRef]
  5. Ramadan, W., Sakr, K., Sayed, M., Maziad, N., El-Faramawy, N. (2020). Investigation of acrylic/boric acid composite gel for neutron attenuation, Nuclear Engineering and Technology, 52, 2607-2612. [CrossRef]
  6. Jang, J., Hong, S., Kim, J., Goo, N., Yu, W. (2021). Accelerated testing method for predicting long-term properties of carbon fiber-reinforced shape memory polymer composites in a low earth orbit environment, Polymers, 13 (10) 1628. [CrossRef]
  7. Wang, L., Zhang, F., Liu, Y. (2019). Y-rays radiation resistant shape memory cyanate ester resin and its composites with high transition temperature, Smart Materials and Structures, 28(7), 075039. [CrossRef]
  8. Nishida, M., Hongo, A., Hiraiwa, Y., Higashide, M. (2019). Effects of gamma ray irradiation on penetration hole in and fragment size from carbon fiber reinforced composite plates in hypervelocity impacts, Composites Part B Engineering, 169(1–4), 229-238. [CrossRef]
  9. Pastore, R., Delfini, A., Albano, M., Vricella, A., Marchetti, M., Santoni, F., Piergentili, F. (2020). Outgassing effect in polymeric composites exposed to space environment thermal-vacuum conditionsю Acta Astronautica, 170(6). 466-471. [CrossRef]
  10. Jang, J.H., Hong, S.B., Kim, J., Goo, N.S., Lee, H., Yu, W. (2019). Long-term properties of carbon fiber-reinforced shape memory epoxy/polymer composites exposed to vacuum and ultraviolet radiation, Smart Materials and Structures, 28, 115013. [CrossRef]
  11. Zheng, L., Wang, L., Wang, Z., Wang, L. (2018) Effects of g-ray irradiation on the fatigue strength, thermal conductivities and thermal stabilities of the glass fibres/ epoxy resins composites, Acta Metallurgica Sinica (English Letters), 31, 105-112. [CrossRef]
  12. Sekulic, D., Stevanovic, M.M. (2011). Effects of gamma irradiation and post-irradiation annealing on carbon/epoxy UDC properties deduced by methods of local loading, Journal of Nuclear Materials, 412(1),190-194. [CrossRef]
  13. Wu, Z.X., Li J.W., Huang, C.J., Huang, R.J., Li, L.F. (2013). Effect of gamma irradiation on the mechanical behavior, thermal properties and structure of epoxy/glassfiber composite. Journal of Nuclear Materials, 441(s 1–3),67–72. [CrossRef]
  14. Liu, L., Feng, L., Ma, T., Xu, Z., Pei, X., Liu, Y., Shi, H., Tang, Y., Liu, L., Deng, H., Wang, C. (2022). Mechanical properties, thermal stability and microstructure evolution of carbon fiber-reinforced epoxy composites exposed to high-dose grays. Radiation Physics and Chemistry, 194(4),110056. [CrossRef]
  15. Li, R., Gu, Y., Yang, Z., Li, M., Wang, S., Zhang, Z. (2015). Effect of g irradiation on the properties of basalt fiber reinforced epoxy resin matrix composite. Journal of Nuclear Materials, 466. [CrossRef]
  16. Hoffman, E.N., Skidmore, T.E. (2009). Radiation effects on epoxy/carbon-fiber composite. Journal of Nuclear Materials, 392(2):371-378. [CrossRef]
  17. Hassani, S., Mousavi, M., Gandomi, A.H. (2022). Structural health monitoring in composite structures: a comprehensive review. Sensors, 22(1),153. [CrossRef]
  18. Goossens, S., Berghmans, F., Sharif Khodaei, Z., Lambinet, F., Karachalios, E., Saenz-Castillo, D., Geernaert, T. (2021). Practicalities of BVID detection on aerospacegrade CFRP materials with optical fibre sensors, Composite Structures, 259 113243. [CrossRef]
  19. Tuloup, C., Harizi, W., Aboura, Z., Meyer, Y., Khellil, K., Lachat, R. (2019). On the use of insitu piezoelectric sensors for the manufacturing and structural health monitoring of polymer-matrix composites: a literature review. Composite Structures, 215, 127-149. [CrossRef]
  20. Wronkowicz, A., Dragan, K., Lis, K. (2018). Assessment of uncertainty in damage evaluation by ultrasonic testing of composite structures. Composite Structures, 203, 71-84. [CrossRef]
  21. Sikdar, S., Liu, D., Kundu, A. (2022). Acoustic emission data based deep learning approach for classification and detection of damage-sources in a composite panel. Composites Part B Engineering, 228,109450. [CrossRef]
  22. Grassia, L., Iannone, M., Califano, A., D’Amore, A. (2019). Strain based method for monitoring the health state of composite structures. Composites Part B Engineering, 176, 107253. [CrossRef]
  23. Ahmed, O., Wang, X., Tran, M., Ismadi, M. (2021). Advancements in fiber-reinforced polymer composite materials damage detection methods: towards achieving energy-efficient SHM systems. Composites Part B Engineering, 223, 109136. [CrossRef]
  24. Rifaie-Graham, O., Apebende, E.A., Bast, L.K., Bruns, N. (2018). Self-reporting fiberreinforced composites that mimic the ability of biological materials to sense and report damage, Advanced Materials, 30(19):1705483. [CrossRef]
  25. Di Sante, R. (2015). Fibre optic sensors for structural health monitoring of aircraft composite structures: recent advances and applications. Sensors, 15, 18666-18713. [CrossRef]
  26. Frieden, J., Cugnoni, J., Botsis, J., Gmür, T., Coric, D. (2010). High-speed internal strain measurements in composite structures under dynamic load using embedded FBG sensors. Composite Structures, 92, 1905-1912. [CrossRef]
  27. Kim, H., Yoon, J., Kim, H., Han, J. (2010). Measurement of the thermal expansion of space structures using fiber Bragg grating sensors and displacement measuring interferometers. Measurement Science and Technology, 21(8), 085704. [CrossRef]
  28. Mulle, M., Yudhanto, A., Lubineau, G., Yaldiz, R., Schijve, W., Verghese, N. (2019). Internal strain assessment using FBGs in a thermoplastic composite subjected to quasistatic indentation and low-velocity impact. Composite Structures, 215, 305-316. [CrossRef]
  29. Szebenyi, G., Bloßl, Y., Hegedüs, G., Tabi, T. T, Czigany, T., Schledjewski, R. (2020). Fatigue monitoring of flax fibre reinforced epoxy composites using integrated fibreoptical FBG sensors, Composites Science and Technology, 199(6),108317. [CrossRef]
  30. Mohanta, S., Padarthi, Y., Chokkapu, S., Gupta, J., Neogi, S. (2023). Ultra-violet health monitoring of smart composite laminate using embedded fiber Bragg grating sensors. Journal of Composite Materials, 54(22),002199832091170. [CrossRef]
  31. Gusarov, A.I., Starodubov, D.S., Berghmans, F. (1999). Design of a radiation-hard optical fiber Bragg grating temperature sensor. Proc. SPIE Vol. 3872, Conference on Photonics for Space and Enhanced Radiation Environments, EOS/SPIE Symposium on Remote Sensing, Florence, Italy, 43-50.
  32. Faustov, A.V., Gusarov, A.I., Megret, P., Wuilpart, M., Kinet, D., Zhukov, A.V., Novikov, S.G., Svetukhin, V.V., Fotiadi, A.A. (2016). Gamma radiation-induced blue shift of resonance peaks of Bragg gratings in pure silica fibres. Quantum Electronics. 46(2),150-154. [CrossRef]
  33. Girard, S., Kuhnhenn, J., Gusarov, A., Brichard, B., Van Uffelen, M., Ouerdane, Y., Boukenter, A., Marcandella, C. (2013). Radiation effects on silica-based optical fibers: recent advances and future challenges, IEEE Transactions on Nuclear Science, 60(3), 2015-2036. [CrossRef]
  34. Gusarov, A., Hoeffgen, S.K. (2013). Radiation effects on fiber gratings. IEEE Transactions on Nuclear Science, 60(3),2037-2053. [CrossRef]
  35. Kinet, D., Broadway, C., Gusarov, A., Megret, P., Caucheteur, C., Kalli, K., O’Keeffe, S.O., Brambilla, G. (2019). Fibre Bragg gratings wavelength evolution and thermal sensitivity under gamma irradiation. Conference: Seventh European Workshop on Optical Fibre Sensors, Limassol, Cyprus. [CrossRef]
  36. Zaghloul, M.A.S, Wang, M., Huang, S., Hnatovsky, C.,., Mihailov, S., D. Carpenter, Li, M., Hu,L., Daw, J., Laffont, G., Nehr, S., Chen, K.P. (2018). Radiation resistant fiber Bragg grating in random air-line fibers for sensing applications in nuclear reactor cores. Optics Express, 26(9),11775. [CrossRef]
  37. He, J., Xu, B., Xu X., Liao, C., Wang, Y. (2021). Review of femtosecond-laser-inscribed fiber Bragg gratings: fabrication technologies and sensing applications. Photonic Sensors, 11(8). [CrossRef]
  38. Chen, J., Wang, J., Li, X., Sun, L., Li, S. (2020). Ding A., Monitoring of temperature and cure-induced strain gradient in laminated composite plate with FBG sensors. Composite Structures, 242(17), 112168. [CrossRef]
  39. Birri, A., Wilson, B.A., Blue, T.E. (2019). Deduced refractive index profile changes of type I and type II gratings when subjected to ionizing radiation. IEEE Sensors Journal, PP(99), 1-1. [CrossRef]
  40. Mihailov, S.J. (2012). Fiber Bragg grating sensors for harsh environments. Sensors, 12(2),1898-918. [CrossRef]
  41. Henschel, H., Grobnic, D., Hoeffgen, S.K., Kuhnhenn, J., Mihailov, S.J., Weinand, U. (2011). Development of highly radiation resistant fiber Bragg gratings. IEEE Transactions on Nuclear Science, 58(4),2103-2110. [CrossRef]
  42. Theodosiou, A., Leal-Junior, A., Marques, C., Frizera, A., Fernandes, A.J.S., Stancalie, A., Ioannou, A., Ighigeanu, D., Mihalcea, R., Negut, C.D., Kalli, K. (2021). Comparative study of g- and e-radiation-induced effects on FBGs using different femtosecond laser inscription methods. Sensors, 21(24),8379. [CrossRef]
  43. Morana, A., Girard,S., Marin, E., Marcandella, C., Rizzolo, S., Perisse, J., Mace, J., Taouri, A., Boukenter A., Cannas M., Ouerdane Y., Radiation vulnerability of fiber Bragg gratings in harsh environments. Journal of Lightwave Technology, 33(12), 2646-2651. [CrossRef]
  44. Remy, L., Cheymol, G., Gusarov, A. (2016). Compaction in optical fibres and fibre Bragg gratings under nuclear reactor high neutron and gamma fluence. IEEE Trans. Nucl. Sci. 63, 2317-2322. [CrossRef]
  45. Yang, X.; Lin, M.; Shoulin, J.; Zuyuan, H. (2017). Effect of kGy dose level gamma radiation on Ge-doped FBGs and femtosecond-laser-inscribed pure-silica-core FBGs. 16th International Conference on Optical Communications and Networks, Wuzhen, China. [CrossRef]
  46. Hao, J.Z., Ong, L.C., Gong, Y.D., Cai, Z.H., Ng, J.H., Varghese P. (2007). A Temperature-independent Lateral Force Sensor using a Pair of FBGs. Proceedings of Asia-Pacific Microwave Conference. [CrossRef]
  47. Pant J., Mitra A., Tiwari U., Mondal S., Singh N., Jain S., Kapur P. (2008) Temperature Compensated Transverse Load Sensor Based on Dual FBG Sensor. Proceedings of International Conference on Microwave-08, IEEE. 395-397. [CrossRef]
  48. Dong B, Zhao Q., Zhao L., Jin L., Miao Y., Liao T., Zeng X. (2008). Simultaneous measurement of temperature and force based on a special- strain-function-chirped FBG. Sensors and Actuators A Physical, 147(1), 169-172. [CrossRef]
  49. Sorensen L., Botsis J., Gmur T., Cugnoni J. (2007). Delamination detection and characterisation of bridging tractions using long FBG optical sensors. Composites Part A Applied Science and Manufacturing, 38(10), 2087-2096. [CrossRef]
  50. Shen C., Zhong C. (2011). Novel temperature-insensitive fiber Bragg grating sensor for displacement measurement. Sensors and Actuators A Physical, 170,51-54. [CrossRef]
  51. Zhang W., Dong X., Zhao Q., Kai G., Yuan S. (2001). FBG-Type Sensor for Simultaneous Measurement of Force (or Displacement) and Temperature Based on Bilateral Cantilever Beam. IEEE Photonics Technology Letters, 13, 1340-1342. [CrossRef]
  52. Dong B., Zhao Q., Liu L., Huang G., Jin L., Zhou J., Liao T. (2008). Tunable Chirped Fiber Bragg Grating Filter Based on Special Strain Function Modulation and Its Application in Fiber Sensor. Journal of Lightwave Technology, 26, 4, 2286- 2290. [CrossRef]
  53. Zhi, Zh., Thomas, W.G., Luke, H., Jin-ping, O. (2003). Techniques of Advanced FBG sensors: fabrication, demodulation, encapsulation and their application in the structural health monitoring of bridges. Pacific Science Review, 5, 116-121.
Preprints 109979 g001
Figure 1. Sensor diagram for simultaneous force and temperature measurement with designated FBG mounting location.
Figure 1. Sensor diagram for simultaneous force and temperature measurement with designated FBG mounting location.
Preprints 109979 g001
Preprints 109979 g002
Figure 2. Schematic of the sensor design for simultaneous measurement of strain and temperature based on a single FBG, mounted on a specially designed holder that ensures the transfer of shear force to the chirp.
Figure 2. Schematic of the sensor design for simultaneous measurement of strain and temperature based on a single FBG, mounted on a specially designed holder that ensures the transfer of shear force to the chirp.
Preprints 109979 g002
Preprints 109979 g003
Figure 3. View of a laminate section with a schematic.
Figure 3. View of a laminate section with a schematic.
Preprints 109979 g003
Preprints 109979 g004
Figure 4. Distributions of axial strains along the measuring arm of the sensor in Figure 2 for different brackets with different applied forces. (a) Steel, (b) PMMA, and (c) glass brackets.
Figure 4. Distributions of axial strains along the measuring arm of the sensor in Figure 2 for different brackets with different applied forces. (a) Steel, (b) PMMA, and (c) glass brackets.
Preprints 109979 g004
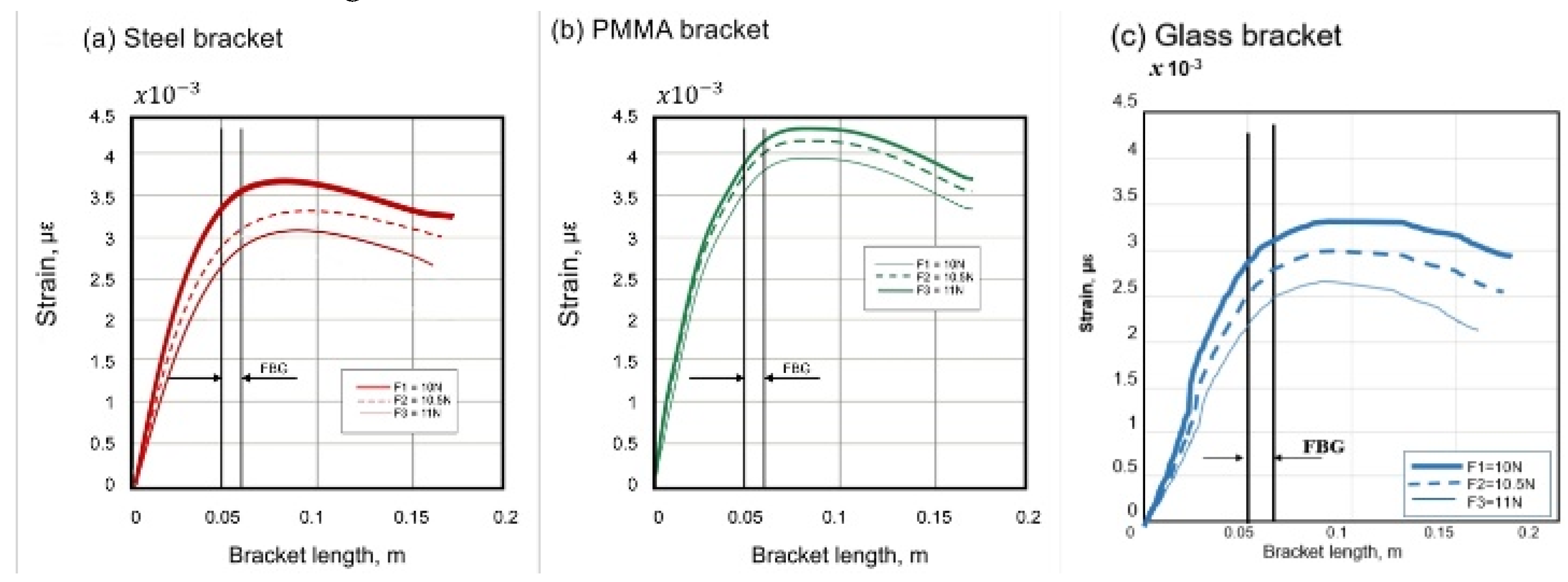
Preprints 109979 g005
Figure 5. Graph of axial strain along the support in the form of a truncated cone with the Bragg grating location marked, (a), (b) graphs plotted for different values of applied forces.
Figure 5. Graph of axial strain along the support in the form of a truncated cone with the Bragg grating location marked, (a), (b) graphs plotted for different values of applied forces.
Preprints 109979 g005
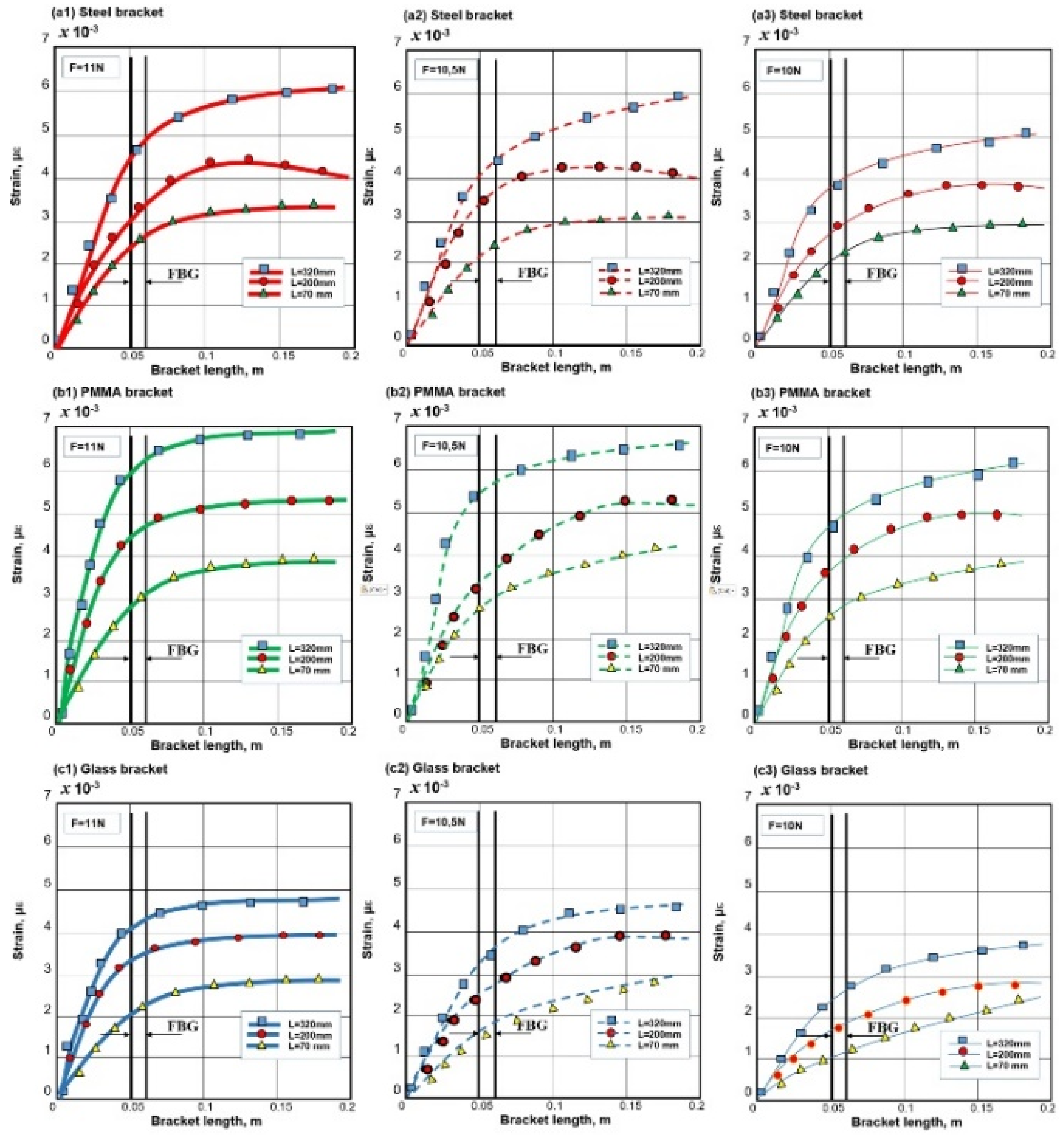
Preprints 109979 g006
Figure 6. Graph of axial strain along the support in the form of a truncated cone with the Bragg grating location marked.
Figure 6. Graph of axial strain along the support in the form of a truncated cone with the Bragg grating location marked.
Preprints 109979 g006
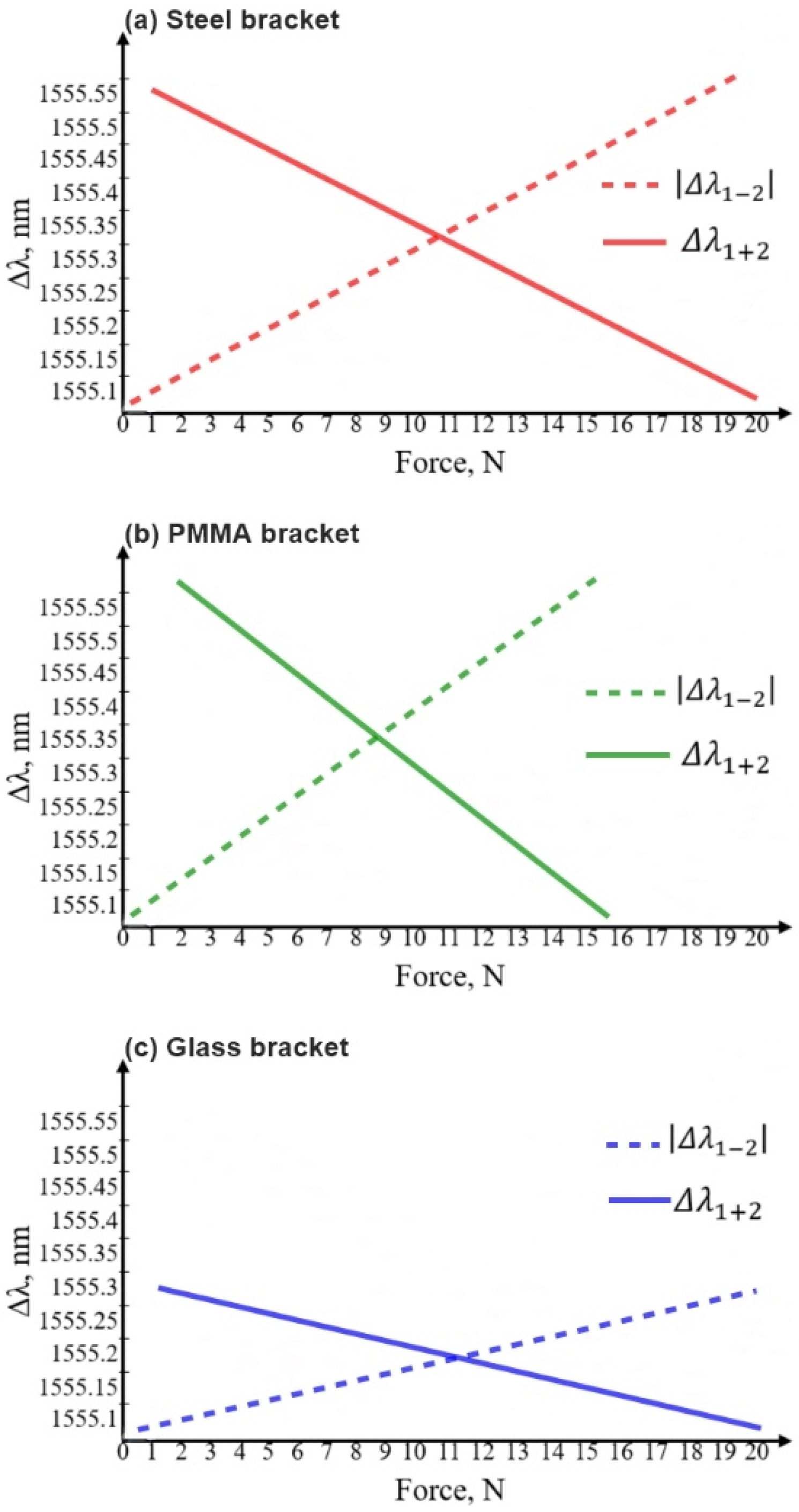
Preprints 109979 g007
Figure 7. Processing characteristics of an optical Bragg grating sensor in which a linear chirp is caused by an applied force when the force value changes and the temperature is constant.
Figure 7. Processing characteristics of an optical Bragg grating sensor in which a linear chirp is caused by an applied force when the force value changes and the temperature is constant.
Preprints 109979 g007
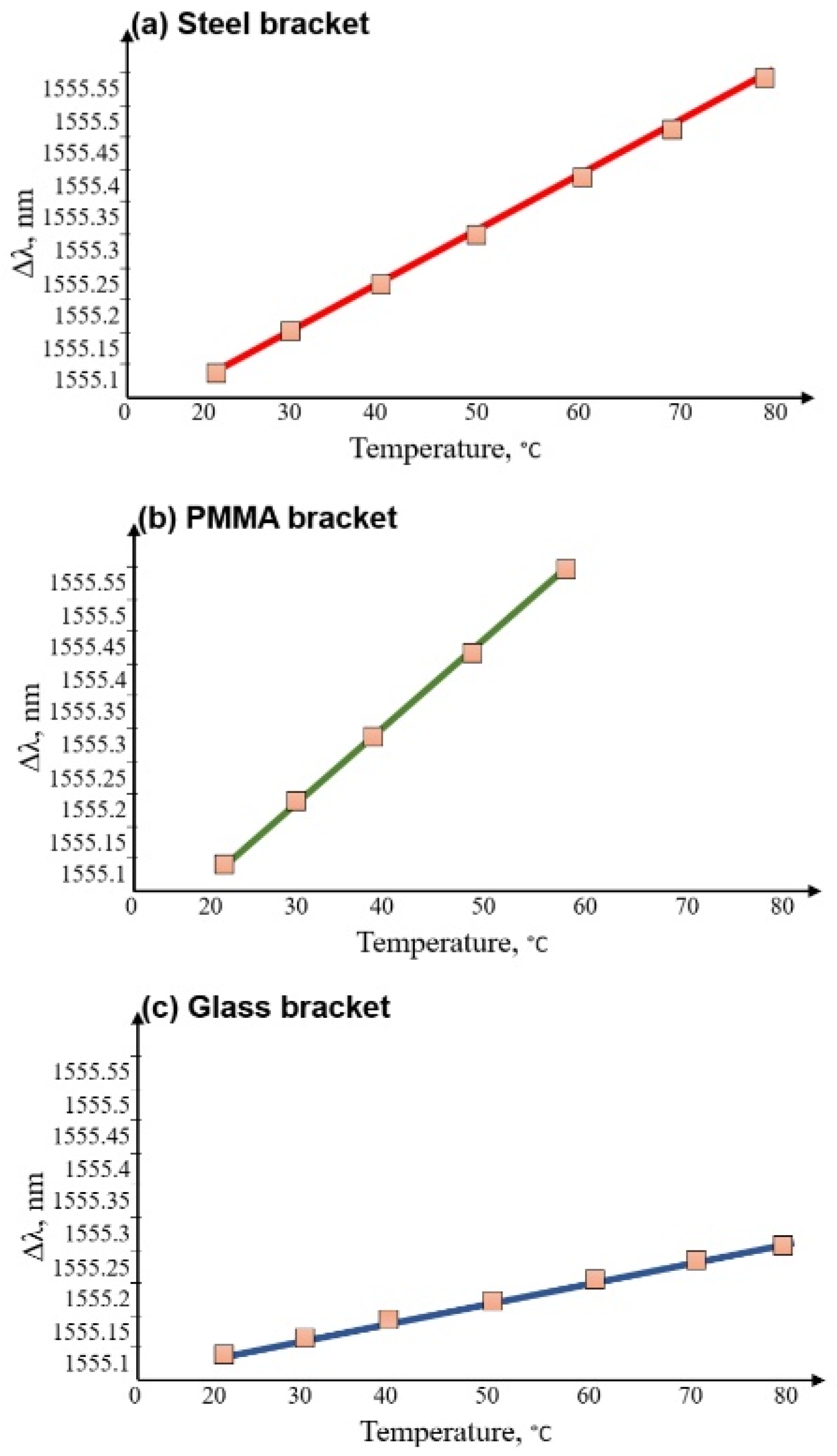
Preprints 109979 g008
Figure 8. Processing characteristics of an optical Bragg grating temperature sensor in which the linear chirp is induced by an applied force. There is a change in temperature and no load (no applied force).
Figure 8. Processing characteristics of an optical Bragg grating temperature sensor in which the linear chirp is induced by an applied force. There is a change in temperature and no load (no applied force).
Preprints 109979 g008
Table 1. Parameters used in this work.
Table 1. Parameters used in this work.
Bracket Steel (unit) PMMA (unit) Glass (unit)
Parameters
K ε 1,2nm/mε 0,554mn/mε 0,987 mn/mε
E Young’s modulus 200GPa 3GPa 73,5GPa
s the width of the composite 10mm 10mm 10mm
g is its thickness 1mm 1mm 1mm
K T 1 9,45pm/0C 7,6745pm/0C 14,3445pm/0C
K F 1 2,6*10-3nm/N 1,2*10-3nm/N 3,5*10-3nm/N
K T 2 8,35 pm/0C 5,57 pm/0C 6,24 pm/0C
K F 2 1,2*10-3km/N 2,78*10-3km/N 3,89*10-3km/N
p e photo elastic constant 210 GPa 45 GPa 71,4 GPa
λ B the wavelength used for the Bragg grating 1555nm 1555nm 1555nm
α Λ coefficient of thermal expansion of the rack 1,2*10-5 1/K 5*10-51/K 5,8*10-71/K
α n coefficient of thermal expansion of the holder 1,3*10-61/K 4,6*10-61/K 8,6*10-61/K
α w the coefficient of thermal expansion of the stand 0,55*10-61/K 3,5*10-61/K 4*10-61/K
z u the length of the Bragg grating 530 nm 530nm 530nm
n e f f the effective refractive index of the fiber 100 100 150
Λ period 100mkm 100mkm 100mkm
z 1 55nm 55nm 55nm
z 2 60nm 60nm 60nm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated