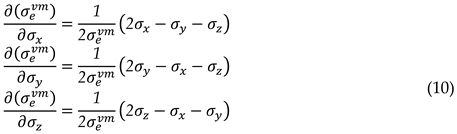Prerpints.org logo
Preprint
Article

BESO and SESO: Comparative Analysis of Spatial Structures Considering Self-Weight and Structural Reliability

Altmetrics

Downloads

90

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (11.29MB )

Submitted:

21 June 2024

Posted:

24 June 2024

You are already at the latest version

Alerts
Abstract
A comparative analysis between Bidirectional Evolutionary Structural Optimization (BESO) and Smoothing-ESO (SESO), simultaneously considering Reliability-Based Topology Optimization (RBTO) and the structure's self-weight in the case of three-dimensional elasticity, is presented in this study. Due to the important role of the existence of uncertainties in making the structural design more realistic, geometry, volumetric fraction, modulus of elasticity, compliance, and loading are considered random variables with normal probability distribution. When adopting the First Order Reliability Method (FORM), the failure probability is calculated based on the reliability index. Furthermore, considering the influence of self-weight in problems involving large structures in civil engineering, especially in the case of bridges, makes the optimal configuration more reliable for design. A series of examples are covered to validate the methods presented, showing their efficiency and robustness.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Topological Optimization (TO) is a technique used to find the ideal distribution of the material in a structure, maximizing its performance under certain constraints. In recent decades this approach has been used by several researchers in the field of structural engineering to reduce weight, improve efficiency, and increase the strength of materials. As algorithms evolve, this technique has played an important role in the production of complex and innovative structures, contributing to the advancement of civil, aerospace, mechanical and naval engineering. However, many TO designs do not consider the structure's self-weight, which can be a problem when considering large structures in civil engineering, especially in the case of bridges, viaducts, large buildings, and towers.
Several methods have been developed for OT, including the Moving Asymptote Method by Svanberg (1987), the density-based Solid Isotropic Material Penalty (SIMP) by Bendsøe (1989); Zhou and Rozvany (1991), the Bubble Method by Eschenauer et al. (1994), the Level-Set Method, by Allaire (2002), Wang et al. (2003) and Xia and Shi (2016). In this article, we highlight evolutionary methods such as Evolutionary Structural Optimization (ESO) by Xie and Steven (1993,1997), Querin et al. (1998), and Bidirectional Evolutionary Structural Optimization (BESO) by Yang et al. (1999), Querin et al. (2000) Huang and Xie (2007) and ESO Smoothing called SESO by Almeida et al. (2013) and Simonetti et al. (2014).
In this article, is propose a comparative analysis of three-dimensional elastic structures between the methods: a) BESO - Which was developed from ESO, and has a bidirectional optimization procedure, allowing the addition and removal of inefficient elements of the structure. This method is efficient and robust and has been successfully applied to a wide variety of OT problems for two-dimensional structures, including compliance minimization Shobeiri (2017,2019), frequency maximization, and displacement constraint Huang et al. (2010). BESO for compliance minimization was applied to three-dimensional structures by Zuo and Xie (2015), who presented a code in Python, Shobeiri (2017) applying it to strut-and-tie models, Bi et al. (2020) in continuous structures with self-supporting geometric constraints. Habashneh et al. (2022) extend the BESO method to the RBTO of three-dimensional structures considering an elastic-plastic topology optimization. Eom et al. (2011) use BESO for RBTO for 3-D structures in conjunction with the standard response surface method and, b) SESO – Which is also a bidirectional TO procedure and is efficient and robust in several problems with restriction of displacement, voltage, compliance, and frequency. Recently, it was extended to spatial structures in the work of Simonetti et al. (2022,2023) which uses as a restriction the minimization of compliance coupled with the reliability analysis procedure via the FORM method, considering geometry, elastic modulus, compliance, force, and von Mises stress as random variables with normal probability distribution.
For the comparative analysis, RBTO-BESO (Reliability - Based Topology Optimization BESO) and RBTO-SESO (Reliability – Based Topology Optimization SESO) were implemented, inserting the structure's self-weight, making the optimal configurations more realistic in structural design. Furthermore, the proposed algorithm can determine the tensile (blue) and compression (red) regions in the optimized structure using a modal filter and the partial derivative of the von Mises stress field.
The remainder of the article is organized as follows: In Section 2, the formulation for topological optimization considering the self-weight is described in general terms for the methods, including the formulation of the structure's self-weight. Section 3 contains the RBTO formulation in general and with the consideration of self-weight and sensitivity analysis to determine the tensile and compression regions. Then, in section 4, the examples presented are: cantilever to validate the formulation of the tensile and compressed regions, a natural optimization under the action of only the structure's self-weight with the aim of validating the procedure and the examples of bridges, in Section 5. Finally, conclusions are drawn.

2. SESO—Subject to Self-Weight Loads

The SESO method aims to optimize structural efficiency by removing or adding elements to the structure. In the search for the topology of maximum stiffness, it is common to use the minimization of the compliance or the maximum von Mises stress as an objective function, while the constraint is imposed on the structural weight, limiting the maximum volume of material allowed. Compliance represents the work done by the loads applied in the structure's equilibrium state. An alternative approach to maximum stiffness design is to use elastic strain energy as a measure of structural stiffness. Therefore, the compliance minimization problem can be reformulated as a problem of minimizing the total elastic strain energy. Thus, the formulation of the TO problem can be defined as:
M i n i m i z e : U x = 1 2 U T ( x ) K ( x ) U ( x ) S u b j e c t t o : K ( x ) U ( x ) = F ( x ) F x = f e x t ( x ) + f g r a v ( x ) V x = ∑ i = 1 N E x i V i − V ≤ 0 x = x 1   x 2     x 3   …   x n ,     x i = 1   o u     x i = 10 − 9
where U x is the nodal displacement vector, K ( x ) is the global stiffness matrix and V i is the volume of the element. K ( x ) U ( x ) = F ( x ) is the equilibrium equation, F ( x ) is the global force vector, f e x t ( x ) the external force vector and f g r a v ( x ) the force vector inertia forces of the structure, x i is the design variable of the ith element, x is the vector of design variables. The design is binary and x i = 10 − 9 is imposed in order to avoid a singular FEM problem when solving the equilibrium.
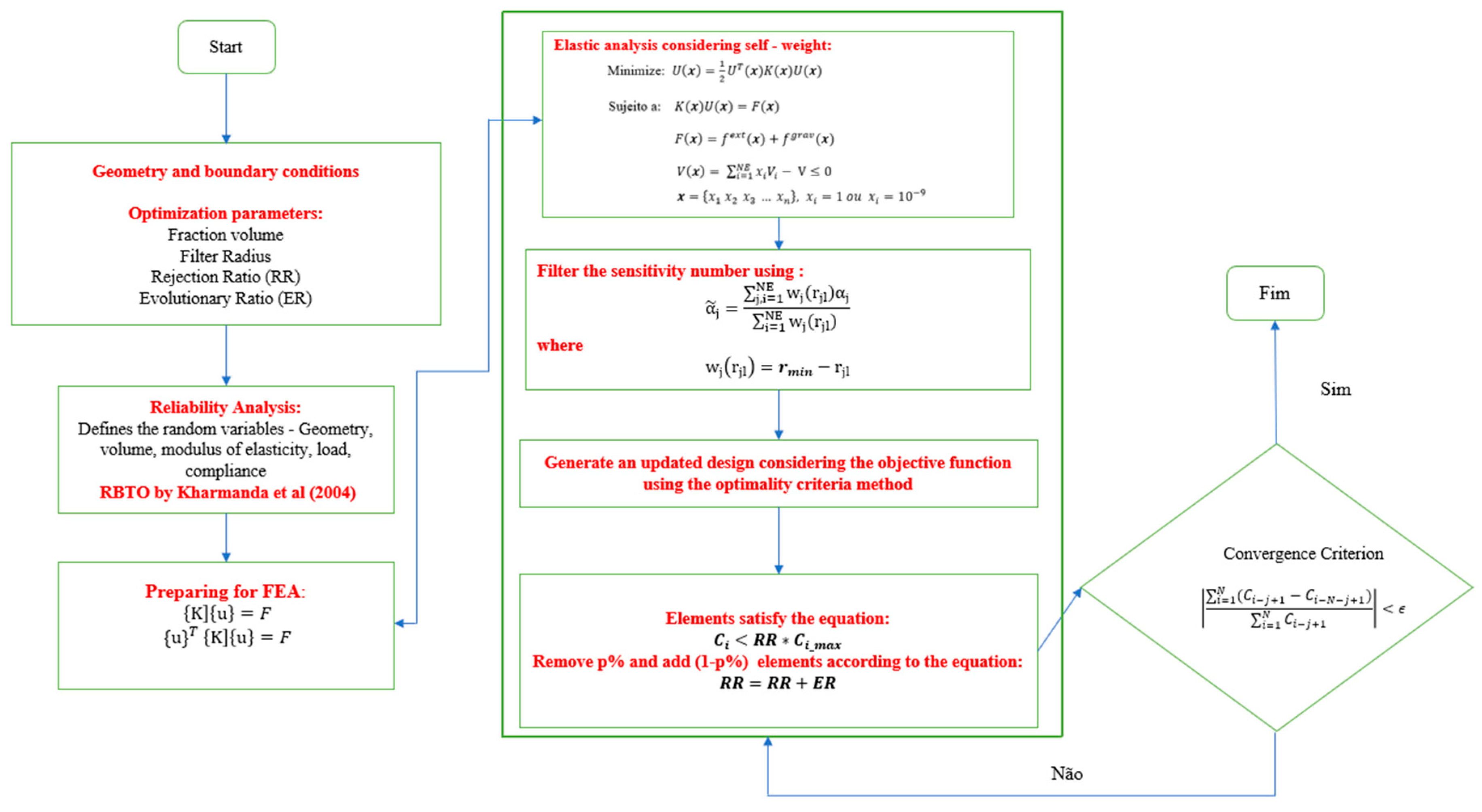
To start the SESO process it is necessary to define a problem that specifies a design domain and boundary conditions. Then, a finite element analysis is performed to determine the stiffness distribution. The heuristic of SESO is that the structure evolves into a stationary optimal solution, systematically removing inefficient elements. Through a sensitivity analysis, it is possible to calculate a sensitivity number α j for each element, which indicates the magnitude of the change in global elastic strain energy resulting from the removal of that element. Elements with a low sensitivity number can be removed without significantly affecting the overall stiffness of the structure. The steps of the SESO method can be summarized according to the flowchart, see Figure 1.

2.1. Formulation for Self-Weight Structure

Self-weight loads depend on gravitational acceleration and material properties, in particular, material density. As such, in OT problems formulated with SESO-3D approaches, the self-weight loads also depend on the set of design variables. Thus, it is possible to calculate and apply the self-weight at the nodes of the elements and the main advantage is that the load is directly proportional to the amount of material used in the structure. For the hexahedral element proposed by Liu et al. (2014) a gravitational load is obtained by assigning 1/8 of the element's weight to each node according to equation 2.
f i g r a v = ρ i * V i * g * ζ = 1 8 d x i d y i d z i ρ i g ζ
where ρ i   is the density of the i-th element, g is the acceleration of gravity ( g = 9.81   m / s ² ) and ζ is given by:
ζ = ζ 1 ζ 2         ζ 3 ζ 4 ζ 5         ζ 6 ζ 7 ζ 8 T
with ζ n is expressed by the nodal coordinates as:
ζ n = 0 − 1 0   com   n = 1 ,   2 ,   3 ,   … ,   8
Thus f g r a v defined in equation 5 can be expressed as:
f g r a v = ∑ i = 1 N f i g r a v
It should be noted that SESO is a suitable optimization method for this type of problem considering the self-weight of the structure as it is a bidirectional method that allows the addition of elements that were removed in a given iteration. It should be noted that the direction and magnitude of design-dependent loads will change as the material distribution of the design domain changes. Therefore, loading conditions in the early stages of the process can change drastically after a few iterations. In this paper, self-weight is coupled with the Method of Moving Asymptotes (MMA) in the TO program SESO-3D to make the optimization procedure more realistic. Furthermore, the Structural Reliability procedure is coupled and an analysis of the strut-and-tie models is carried out.

3. Reliability Analysis

3.1. Formulation of the RBTO

For the mathematical model of RBTO it is sufficient to transform the stress constraint in equation 6 as follows:
M i n i m i z e : V ( x i , X j , u ) = ∑ i = 1 N E x i V i ( x i , X j , u ) s u b j e c t t o :   P f = P G x i , X j ≤ 0 = ∫ … ∫ G x i ,   X ≤ 0 f X ( X ) d x K ( x i , X j , u ) U ( x i , X j , u ) = F ( X j , u ) β ( u ) = β t x i = 1       o r   x i = 10 − 9       i = 1 ,   … ,   N E     a n d     j = 1 ,   … ,   m    
with x i being the finite element, X j is the j-th random variable, V is the volume of the total structure, P S is the probability of success, P t is the target probability of success, G is the limit state function, NE is the number of variables and m the number of uncertain variables. To control the topologies obtained by the RBTO model the reliability index β ( u ) , see Kharmanda et al. (2004), is introduced with a normalized vector u .
G x i , X j = R − S = σ * − σ e v m ( x i , X j )
where R denotes the structural strength and S denotes the load variable. In this paper, we consider the possibility that random variables may cause the von Mises stress to exceed the yield strength limit of the material, thus causing the failure of the structure. Here, R indicates the allowable stress for the material ( σ * ) and S indicates the von Mises stress of the element σ e v m ( x i , X j ) . Thus, if G > 0 , the structure is reliable, if G < 0 the structure failure and if G = 0 the structure is in the limit state.

3.2. Formulation of the RBTO Problem Considering the Self-Weight

The objective of analyzing strut-and-tie models using the TO strategy is to find a reinforcement arrangement within the design domain that minimizes the maximum von Mises stress of the structure for given loading and boundary conditions. Mathematically, the problem can be stated as:
M i n i m i z e : V = ∑ e = 1 n e x e V e         s u b j e c t t o : K ( x ) U ( x ) = F ( x ) F x = f e x t x + f g r a v x σ e v m − σ * ≤ 0 V x = ∑ i = 1 N E x i V i − V ≤ 0 β ( u ) = β t x = x 1   x 2     x 3   …   x n ,     x i = 1   o u     x i = 10 − 9
Where the von Mises stress σ e v m   on each element is calculated using equation 9.
σ e v m = σ x 2 + σ y 2 + σ z 2 − σ x σ y − σ x σ z − σ y σ z + 3 τ x y 2 + 3 τ x z 2 + 3 τ y z 2 1 / 2
where V is the volume of the whole structure, V e is the volume of the e-th element, K is the stiffness matrix of the structure, U is the displacements vector , F is the force vector, ne is the total number of finite elements of the structure, σ e v m is the von Mises stress of element e, σ * is an admissible stress, x e = 0 denotes empty material and x e = 1 denotes solid material. This formulation shows that the optimization procedure aims to minimize the amount of elements and therefore minimize the volume of the structure. This structure is subject to the equilibrium equations as well as a stress constraint for each element that must be less than or equal to the permissible stress.

3.3. Sensitivity Analysis for Determining Tensile and Compression Regions

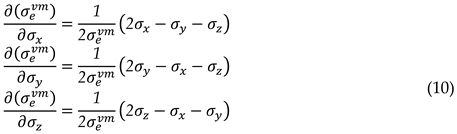
Taking the local calculation of the derivative of the von Mises stress of the element with respect to the components of the stress vector described respectively as: Preprints 110019 i002
Considering equation 10 and making ∂ ( σ e v m ( x ) ) ∂ σ x > 0 then the elements are preponderantly tensile (blue color - ties) while ∂ ( σ e v m ( x ) ) ∂ σ z < 0 are preponderantly compressed (red color - strut).

4. Numerical Examples

In this article, we present the application of the BESO and SESO methods to generate models of optimal topologies in three-dimensional elastic structural systems, aiming to provide engineers with an automated tool to determine the regions of tensile (highlighted in blue) and compression (highlighted in red), as illustrated in the figures. This approach brings something new because, in a three-dimensional regime, the traction and compression regions were defined by the partial derivatives of the von Mises stress tensor in the directions where traction and compression predominate. Thus, it is possible to provide the designer with the best choice for concrete reinforcement, ensuring greater efficiency and safety in structures. Furthermore, this article addresses a reliability analysis considering the structure's self-weight, emphasizing the influence of this factor on the optimization procedure. The following examples of structure engineering focus on TO based on minimizing compliance. The following examples of structure engineering focus on TO based on minimizing compliance. The geometry and boundary conditions for numerical applications are represented in each case. All numerical examples were processed on a Core i7-2370, 8th Gen notebook, 2.8 GHz CPU with 20.0 GB (RAM).

4.1. Cantilever Beam

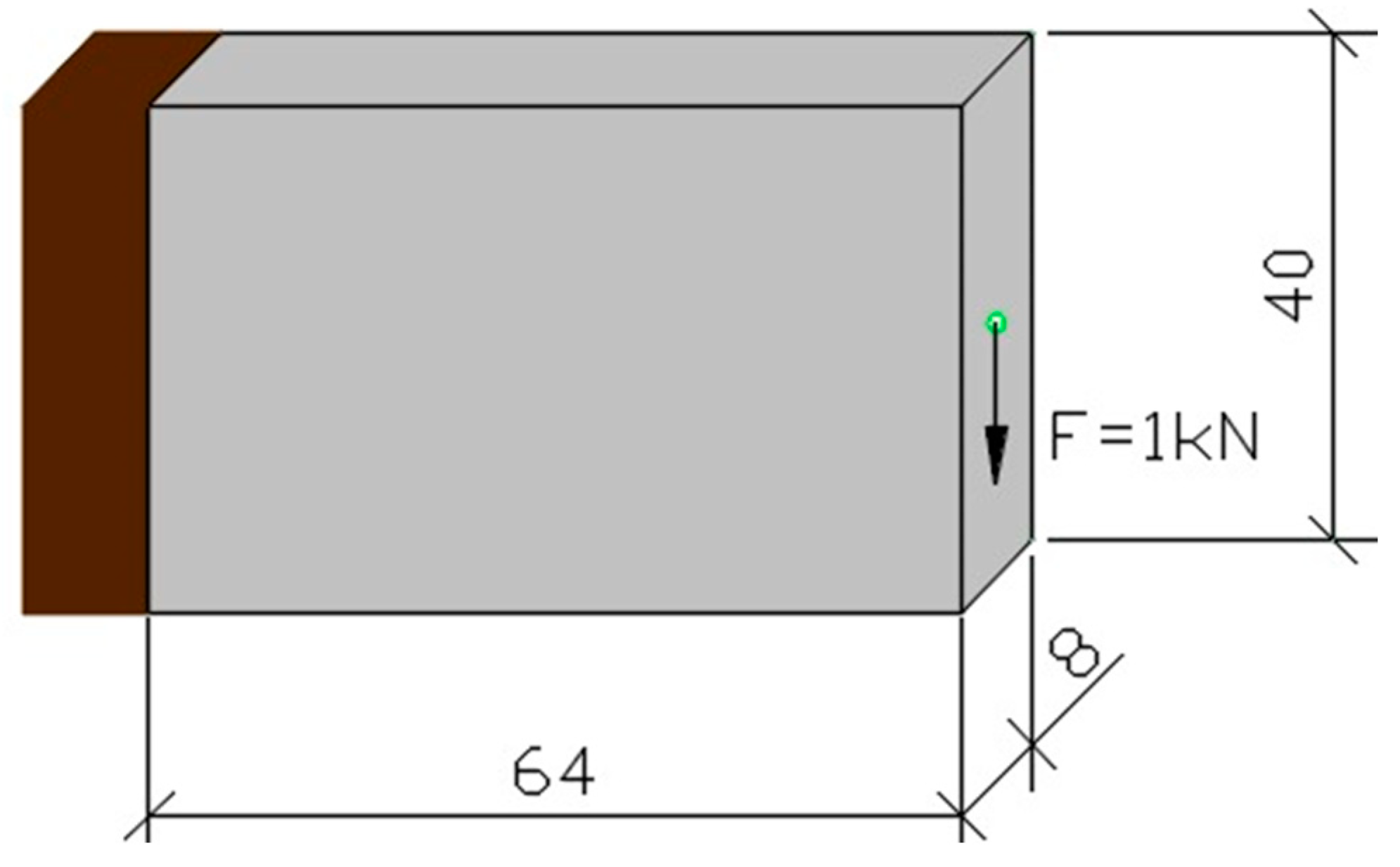
This classic example from the literature is presented with the aim of validating the formulation presented in this article. The design domain, boundary conditions and optimal topologies of a cantilever with a single, isotropic material are presented in Figure 2 and Figure 3. In Figure 3(a) we have the cantilever optimized using the BESO method and in Figure 3(b) the same cantilever was optimized using the SESO method. The cantilever is fixed at the left end and subjected to a concentrated load of F = 1 k N in the center of the free end as illustrated in Figure 2. The volume fraction is prescribed at V f = 0.20 and the radius used in the filter at r = 2 m m . A 64x8x40 mesh is defined. In this example, the self-weight of the structure was not considered.
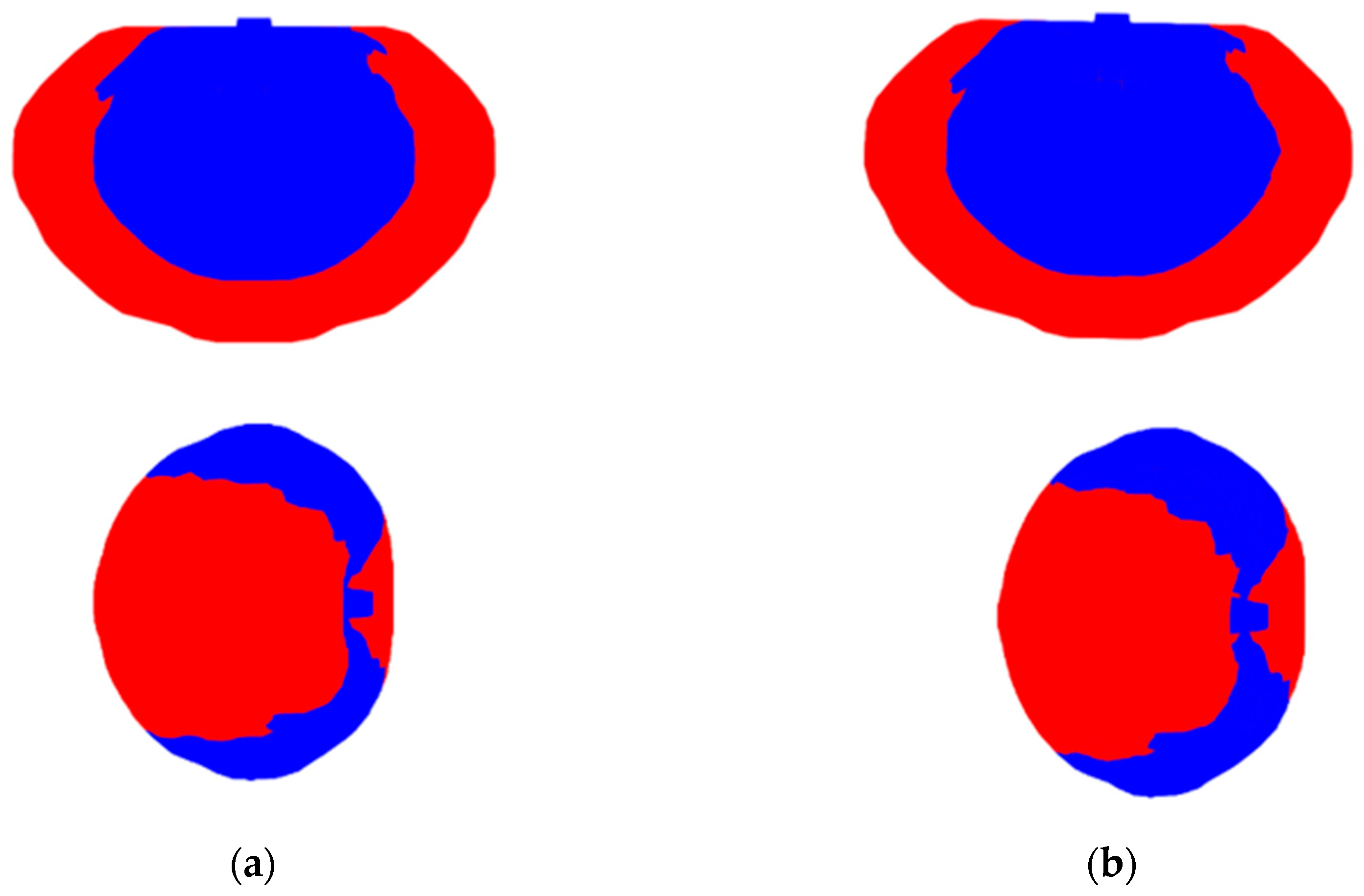
The optimization procedure with the BESO method was carried out with an evolutionary ratio E R = 0.03   with a computational cost of 47.8 minutes and compliance of 11.3334 N.mm. While in the SESO method, a rejection ratio R R = 0.01   and an E R = 0.02 were used with a computational cost of 32.5 minutes and compliance of 11.5428 N.mm. It can be seen that the upper part of the cantilever is in tensile (blue color) while the lower part is compressed.

4.2. Example 2—Application of BESO and SESO to the Design of An Apple

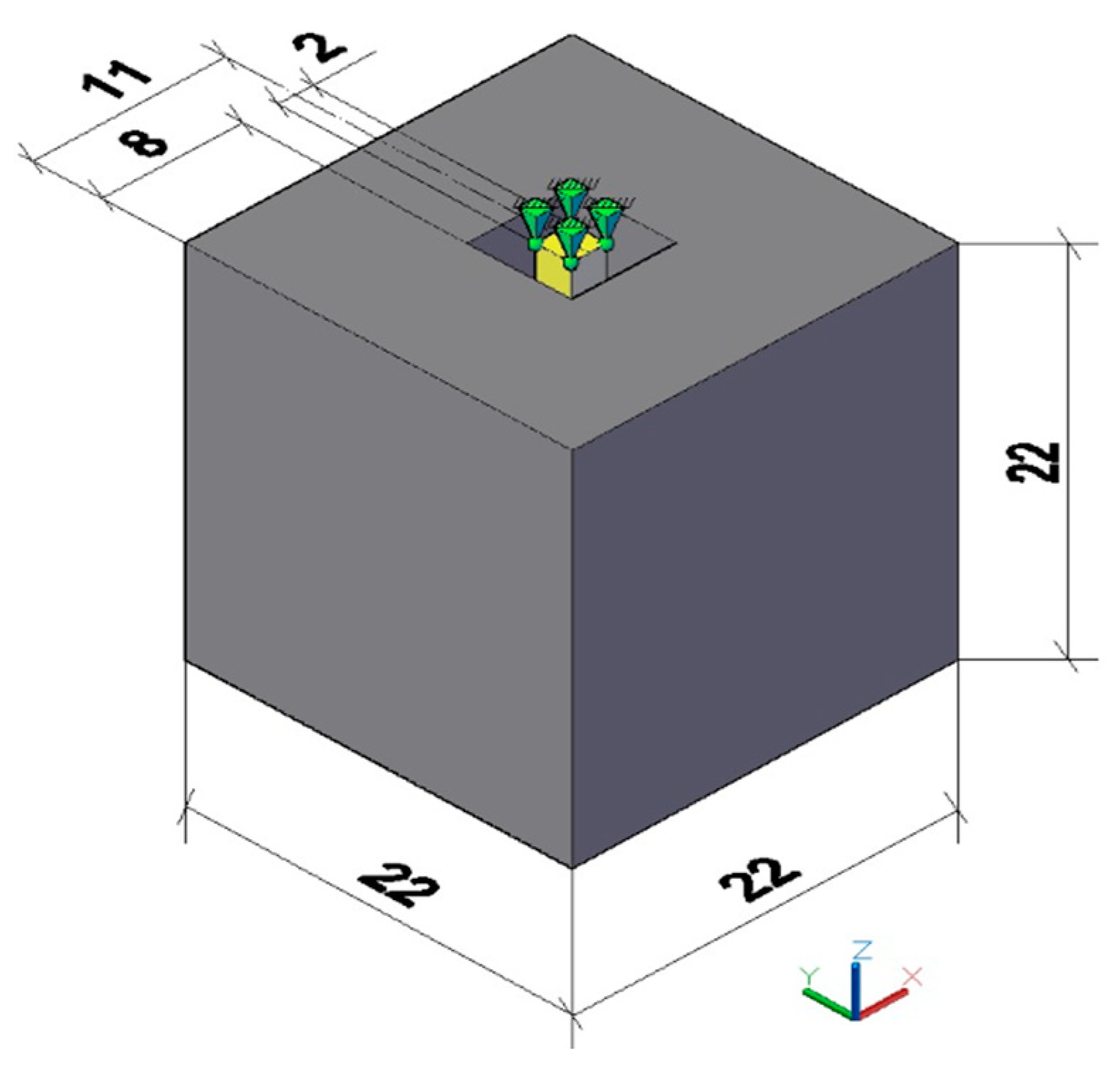
One of the most intriguing questions about the nature and structures that evolve naturally is: "What is the reason for them to have the optimal configuration they do?". To answer this question and validate the implementation of the structure's self-weight, the evolutionary optimization methods BESO and SESO, for three-dimensional structures, are applied in a natural optimization design. Figure 4 presents the design domain and boundary conditions of a structure that will only be subjected to the action of its weight. Thus, it would be possible to verify whether these methods could reproduce the same shape of an apple created by nature, in order to determine whether its appearance was influenced by a genetic or structural perspective.
The design domain was subdivided using 8-node hexahedral elements, as proposed by Liu et al. (2014), with dimensions of 1x1x1 mm. The applied load consists of a downward acceleration of 1g, equivalent to -9.8 m/s². The assumed density for all elements was 2700 kg/m³, and the modulus of elasticity of the material was assumed to be 70x10³ MPa, as proposed by Querin (1998). Figure 5 illustrates that the optimal configurations obtained by the methods presented in this article resemble the shape of a fruit, specifically that of an apple. This result is notable, as the final topology was achieved exclusively through structural constraints. This suggests that, at least for this domain, the final form was predominantly developed from a structural perspective rather than biological reasons,
In Figure 5, it is observed that both by the BESO method, Figure 5a,b and by the SESO method, Figure 5c,d the influence of self-weight results in traction in the structure. This effect causes tensile in the elements located close to the center of gravity, evidenced by the blue color. On the other hand, the elements closest to the ends of the structure are subject to compression, indicated by the color red.

4.3. Example 3—Deterministic Analysis: Bridge Topology Optimization

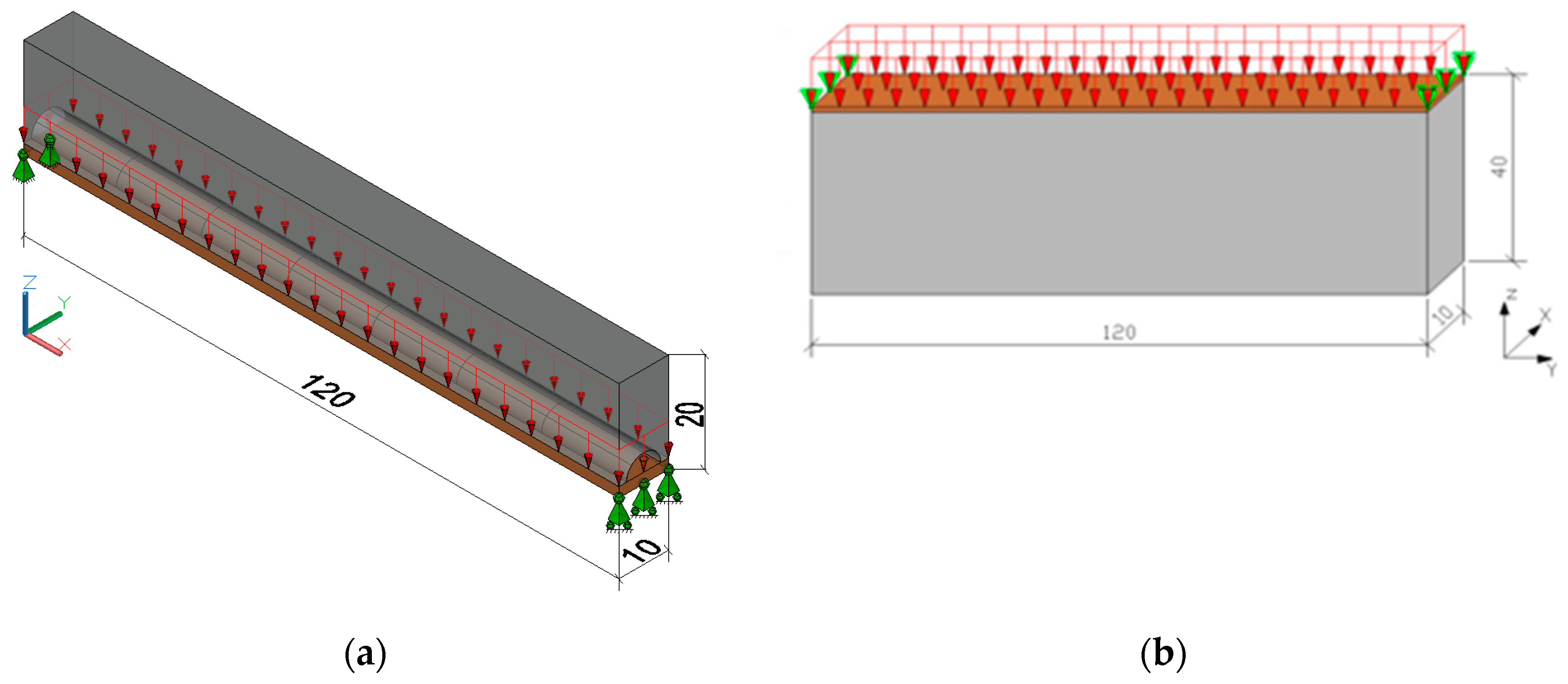
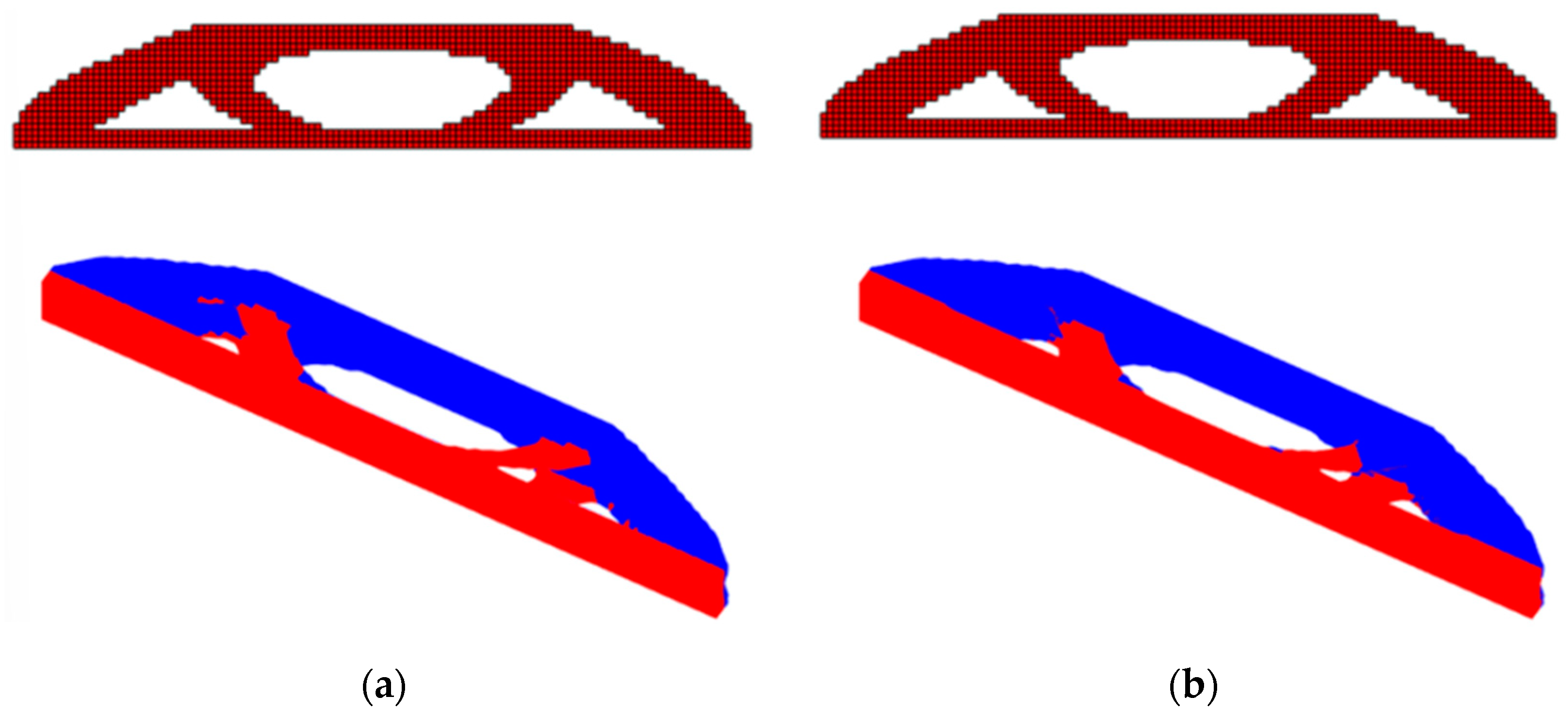
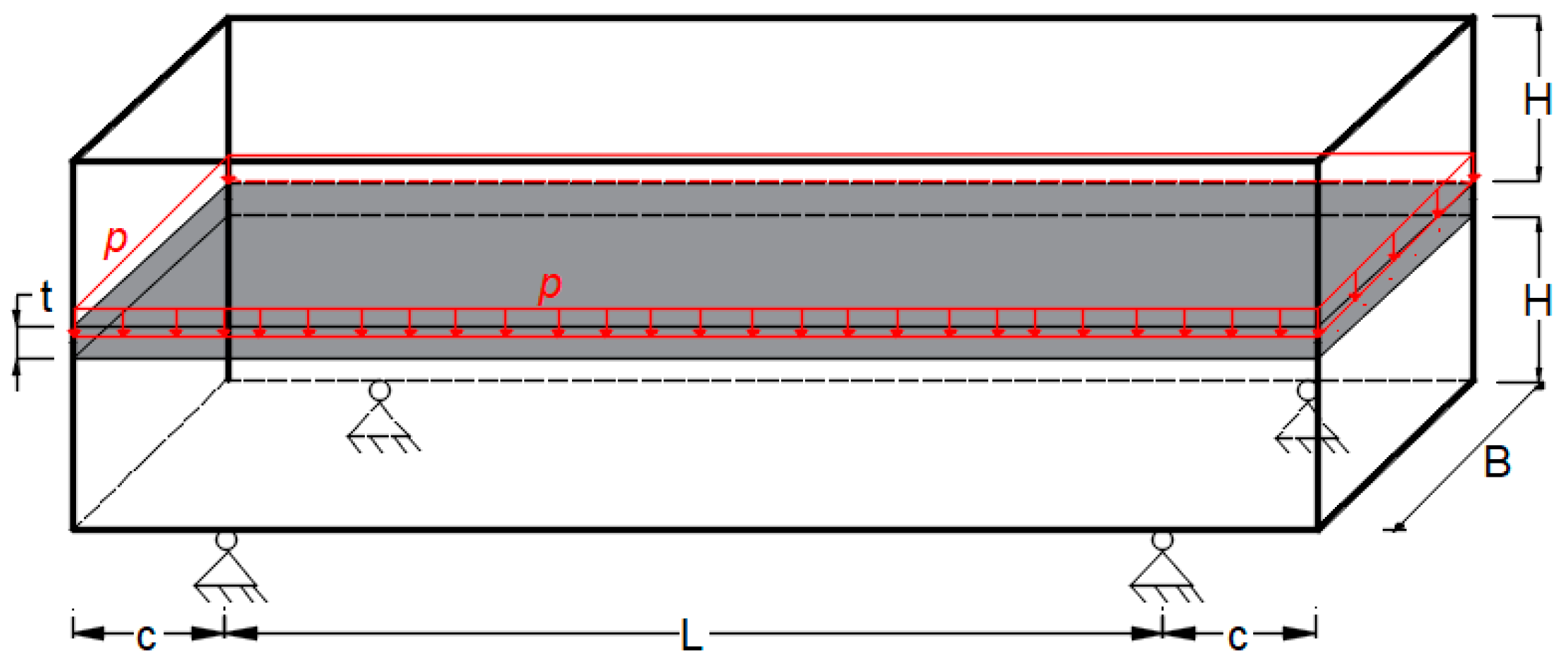
The optimization procedure via BESO and SESO methods will be carried out for the examples of bridges shown in Figure 6a,b with a span of 120m, a width of 10m, and a height of 20m. In Figure 6(a) there is a bridge with a lower deck designed with a semicircular space in the x direction intended for traffic and will be considered a non-design domain. The lower left end of the board is fixed in all directions, while the right end allows movement in the x direction. The bridge illustrated in Figure 6 (b) has an upper deck with the left end fixed in the x, y and z directions, while the right end allows movement in the x direction. The load used in both designs is uniformly distributed with F = 1 e 5   N / m ² . The prescribed final volume is V f = 0.30 and the filter radius is r = 3   m . The board is defined as a non-design domain region. In the evolutionary optimization procedure, the evolutionary ratio used in BESO was E R = 0.03 , while in SESO R R = 0.01 and E R = 0.02   were considered.
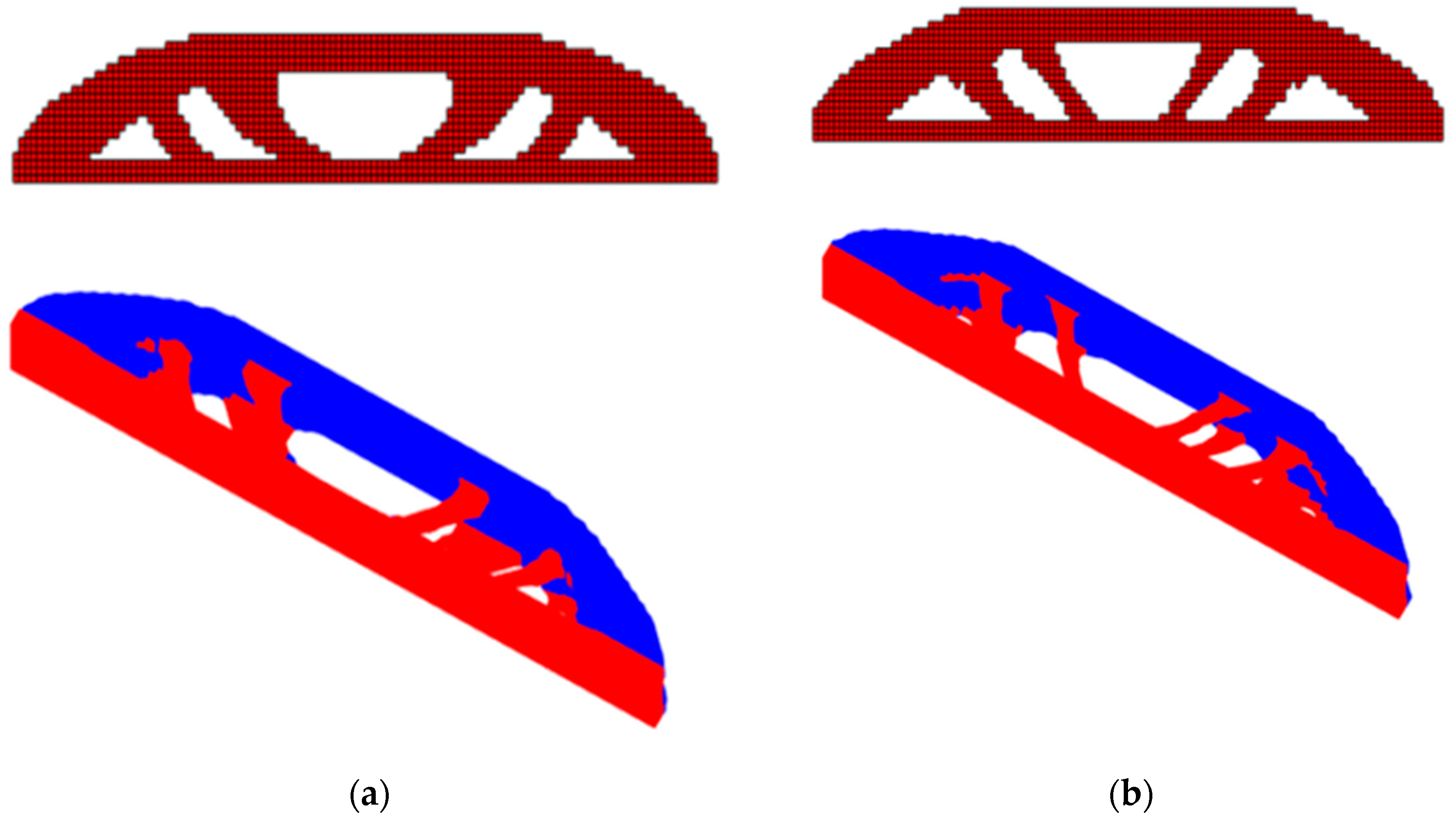
In case (a), a bridge that has a hole in the x direction, the optimized structure resembles tied arch bridges, with concrete (blue color) shaping the arch above the deck, while steel is used in the tie rods and the deck (red), see Figure 7a,b. Aesthetically, the cables take the form of catenaries due to the influence of gravity. In contrast, case (b), see Figure 8a,b, presents a substantially different configuration, with the majority of the structure located below the bridge deck. In this situation, an arch in the opposite direction to that in case (a) is formed, with the steel playing the main role by composing a brace that supports the main load of the bridge. Concrete, in turn, is used to build the deck and the small inclined columns that connect the deck to the belt. However, it is possible to observe that BESO presents a topology with the internal arc above the deck that is clearer than SESO, which presents a topology in the shape of two oblique cables.
In case (b), the deterministic optimal topologies presented in Figure 8a,b, the presence of regions that transmit efforts (blue) and regions that are compressed (red) is evident. In this article, allowable stress values for tensile and compression were incorporated, and, in the case of rods subjected to compression, it is essential to consider the possibility of failures due to buckling (slenderness) when sizing the designs.

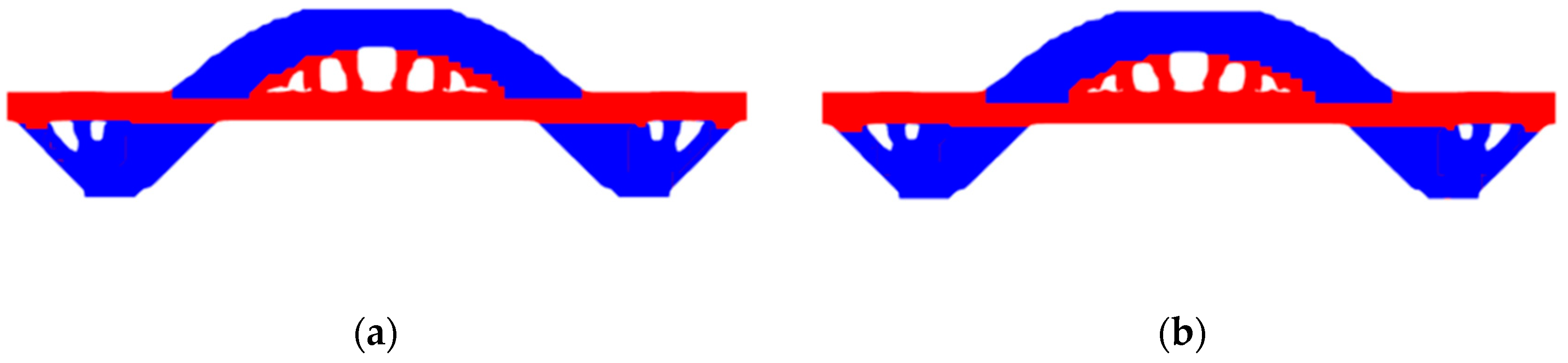
4.4. Example 4—Reliability-Based Topology Optimization without Considering Self-Weight

The optimization process in example 4.3 was developed based on the reliability analysis proposed by Kharmanda et al. (2004). In this example, geometry, volume, modulus of elasticity, and compliance obtained from the deterministic analysis were considered as random variables. Coupling structural reliability analysis into the BESO-3D and SESO-3D methods demonstrated effectiveness and robustness when optimizing the bridges illustrated in Figure 6a,b. It is worth mentioning that the optimal configurations obtained are as slender as the previous ones, without significant differences in terms of structural design. For this analysis, a target reliability index β t = 3.0 was considered, which is equivalent to a probability of structure failure equal to P f = 0.001358 .
The initial design parameters are presented in Table 1, where nelx (length), nely (height), nelz (width) represent the geometry of the structure, F, represents the distributed external load, E, represents the modulus of elasticity, V, the volume of the structure, C, compliance and are considered random variables with normal distribution, while Poisson's ratio (ν) have a constant distribution
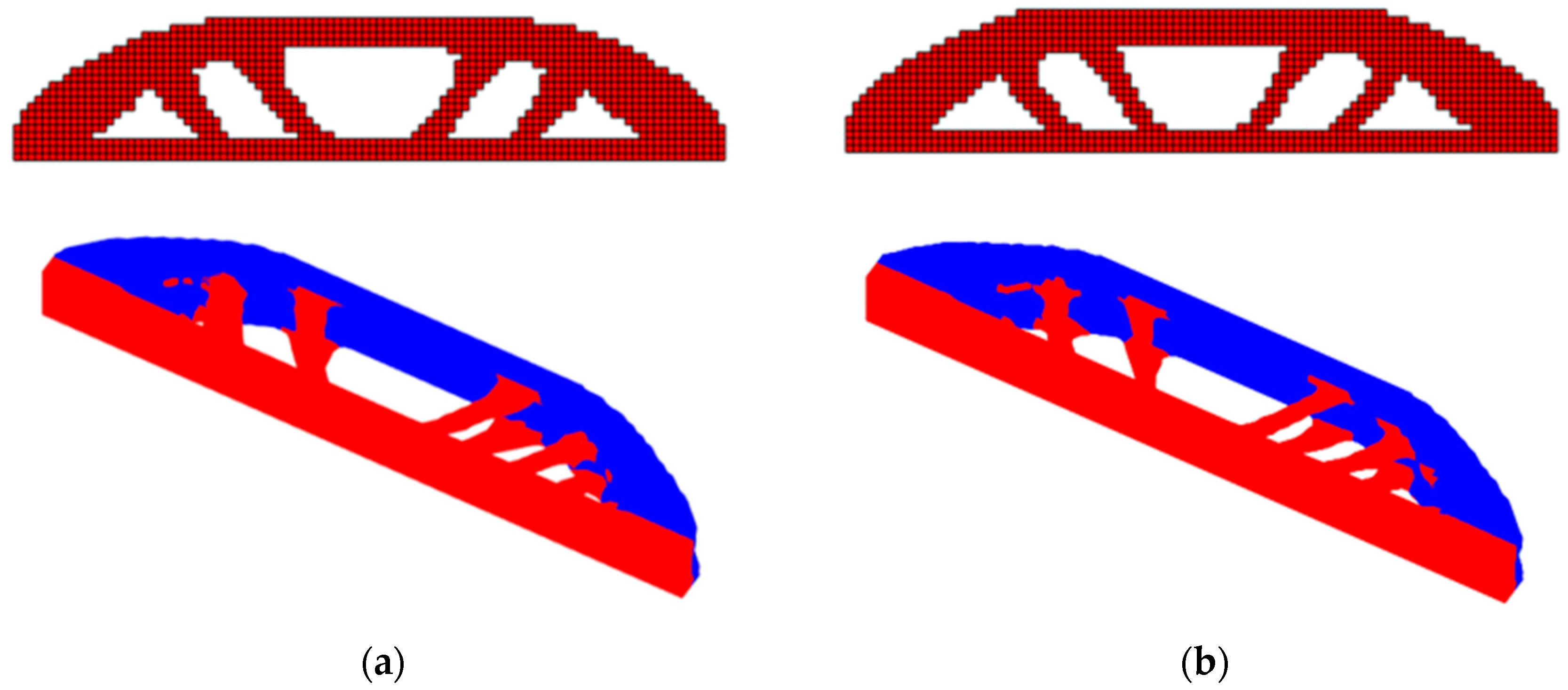
Figure 9a,b illustrate, respectively, the optimal configurations obtained by the two methods presented in this article. It is noteworthy that both BESO and SESO converged with 3 FORM iterations, 81 topology iterations with computational costs, respectively, equal to 73.02 min and 50.41 minutes. It is noteworthy that the computational performance of SESO for all examples presented in this article is superior to BESO.
It is observed that the optimal configuration for both methods are equivalent. It is noteworthy that BESO has a configuration closer to SESO when considering the reliability analysis of the structure, the arc presented in Figure 6(a) tends here for inclined cables.

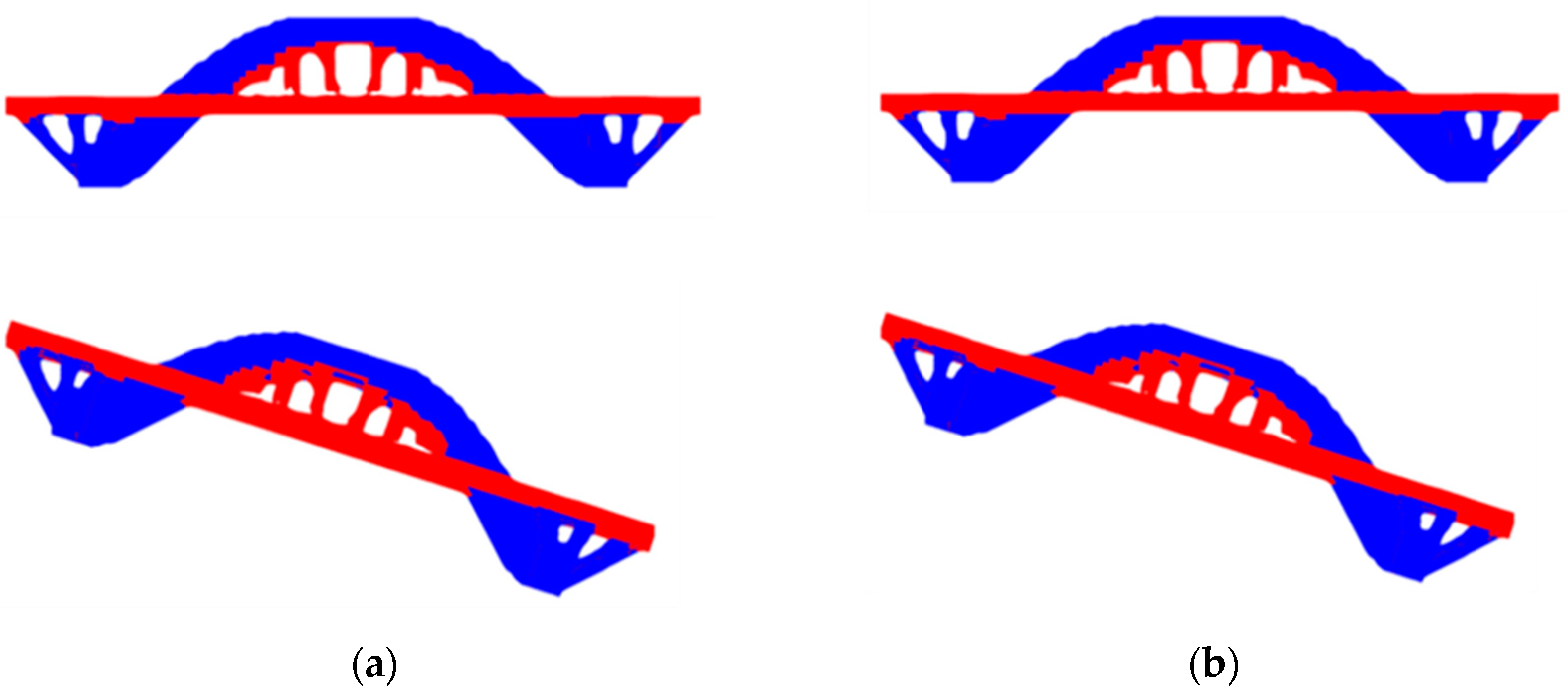
4.5. Example 5—Reliability-Based Topology Optimization Considering Self-Weight

The bridge shown in Figure 6(a) was analyzed by coupling the structure's own weight in the optimization procedure with the aim of analyzing the influence of the self-weight on the optimal configuration. It is worth mentioning that the optimal configurations obtained by the RBTO-BESO_3D and RBTO-SESO_3D methods are different in terms of structural design. However, when examining the optimal configurations, considering the self-weight, see Figure 10, we observed that the two models produced similar configurations with just a denser arc in the shape of a catenary. These changes in topology are attributable to the influence of gravitational force and have important implications for engineers. This is due to the fact that optimizing the structure taking into account its self-weight can result in more efficient and safe solutions.

4.6. Example 6—Reliability Analysis—Effects of Boundary Conditions and Self-Weight on Bridge Topology

Figure 11 displays the design domain and boundary conditions of a bridge with three different support locations. The objective is to analyse the influence of the location of the supports on the optimal configuration for different reliability indices. Furthermore, we consider geometry, volume, loading, compliance, and elastic modulus as random variables with normal distribution and standard deviation equal to 0.1. In this study, we consider the self-weight of the structure during the optimization process. The material density was defined for a steel structure ρ = 7,800 k g / m ³ . The volume fraction is set to V = 0.25   and the filter radius is set to r = 1.5   m . In each case, the mesh is defined as 120x30x10, totaling 36,000 hexahedral finite elements with eight nodes according to Liu et al. (2014). The deck with a thickness t = 1.0 m is defined as a non-design domain area shown as the darker area in Figure 11, H = 14.5   m , L = 90   m , c = 15   m and B = 10.0   m . Therefore, the region in the highlighted region will not be allowed to remove solid elements.
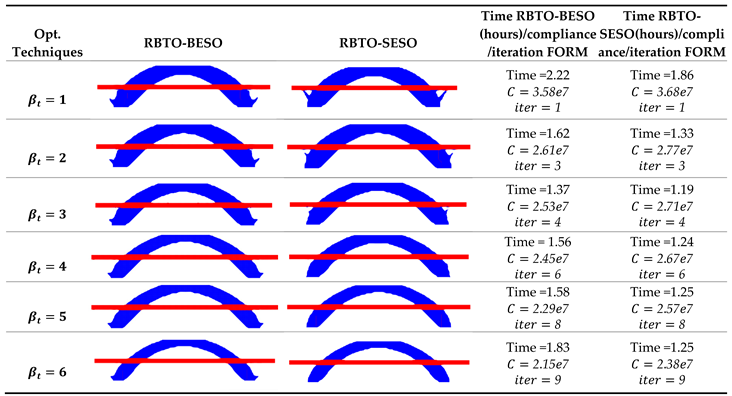
Figure 12 displays the deterministic optimal topologies obtained by the two methods covered in this article. Although the topologies are identical, the SESO method required a computational cost of 1.5 hours resulting in a compliance of C = 6.479 e 5 N . m ,, while the BESO method required t i m e = 1.6 hours of computational cost and resulted in a compliance of C = 6.495 e 5 N . m .
In the optimal configurations shown in Figure 13(a) BESO and 13(b) SESO, reliability analysis was considered with an equal reliability index β t = 3 but the structure's weight was not considered. It is noted that the topologies are similar, with a final volume 15% smaller than in deterministic topologies and computational costs 8% lower for SESO. It is worth mentioning that the compliance presented by BESO is 0.2% lower than in SESO. Additionally, SESO introduced more tensile cables on tensile arch bridges to help support the bridge load and distribute it effectively. In a tensile arch bridge, the arch supports most of the load through compression, but the tensile cables help distribute some of this load laterally to the supporting piers and ends of the bridge. These tensile cables help to stabilize the bridge structure and prevent excessive deformation under load, thus ensuring the safety and stability of the bridge.
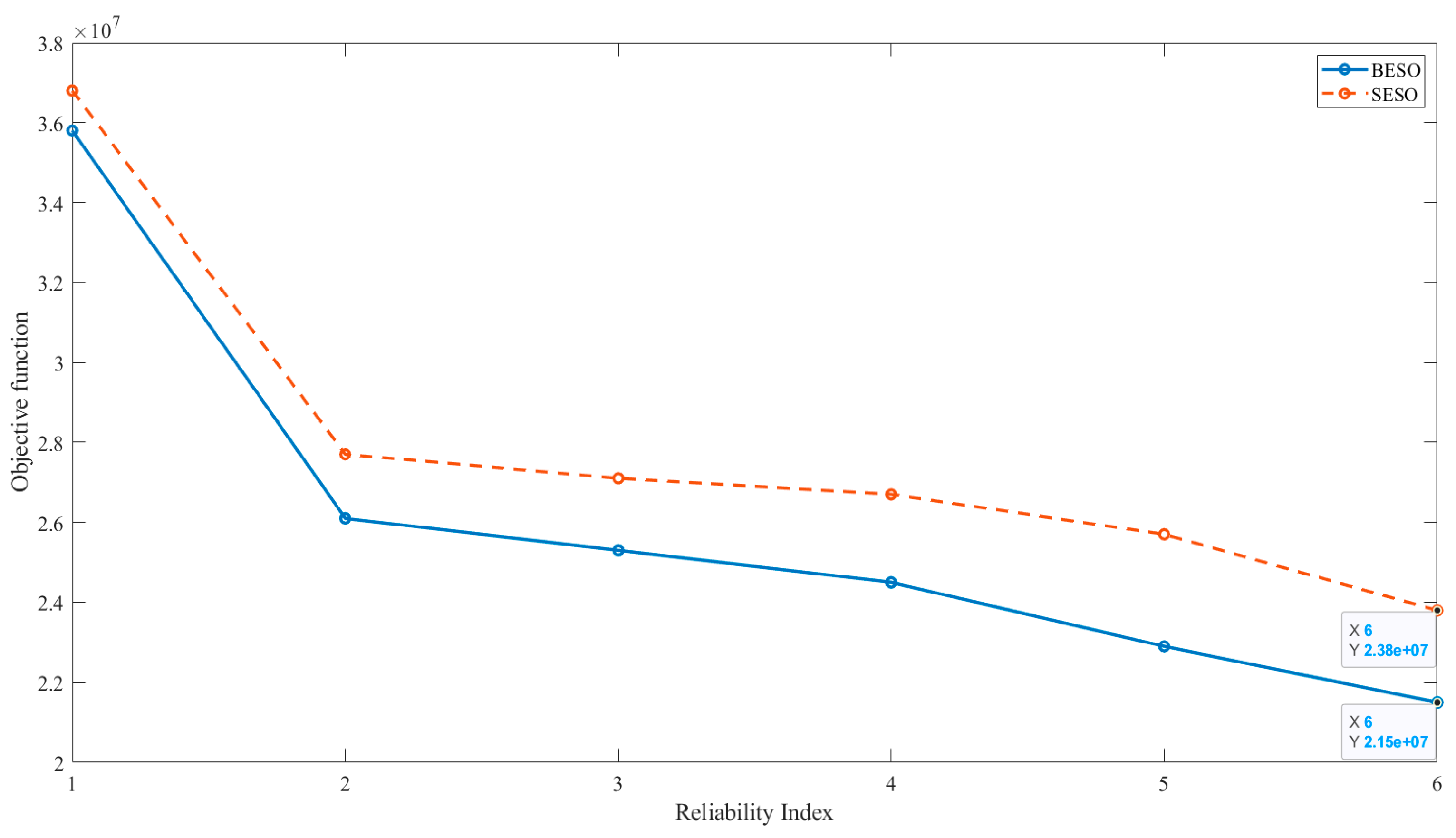
The example represented in Figure 11 was analyzed for different reliability indices, as shown in Table 2, for the two methods proposed in this article. The random variables follow the data in table 1. It is noteworthy that the RBTO models provided a volume reduction in relation to the DTO models of approximately 9%. It can be seen that the optimal topologies presented considering the structure's weight are different from the deterministic optimal topologies without considering the self-weight. This is because the tensile arch is mainly responsible for supporting compression loads, while the bridge deck, which is under compression, is responsible for transmitting these loads to the supports. In this case, cables are not needed because the loads are being transferred directly through the arch and deck without the need for an additional tensile cable structure.
When considering the structure's self-weight, a fully distributed load and the influence of gravity throughout the analyzed domain are taken into account. Therefore, it results in lighter and more efficient structures, as expected, according to Jain and Saxena (2018).
It is worth mentioning that the computational cost of SESO is much lower than that of BESO. However, BESO presents lower compliance for the reliability indices analyzed. Figure 14 displays this behavior.

5. Conclusions

This article addresses a qualitative comparison between the BESO and SESO methods, revealing that both are effective in generating optimal topologies for three-dimensional structural systems, considering compliance minimization and the influence of the structure's self-weight. The examples analyzed show that these methods produce configurations that meet safety and structural efficiency requirements, being robust even in the face of variations in boundary conditions and design parameters. Furthermore, the coupling of the structure's self-weight, in the two methods analyzed, with the reliability analysis, represents a significant contribution in the field of optimal topology for structural systems. It is worth mentioning that SESO presents a lower computational cost in all examples, while BESO results in lower compliance. These approaches offer engineers an advanced and reliable tool for the automated design of structures by distinguishing between tensile (blue) and compression (red) regions, ensuring greater safety and efficiency in practical applications.

Author Contributions

The authors have been working together for over 9 years, and the tasks in this article were developed as follows: (1) H.L.S.—Implemented BESO-3D and SESO-3D programs in MATLAB code and responsible for writing and structuring the article. (2) V.S.A.— helped with the implementation of the SESO-3D codes and responsible for reviewing the article. Participated in the data analysis of the numerical examples in the article. (3) F.d.A.d.N.—Contributions to the preparation of the article: reading, review and suggestions for examples. (4) S.Z.A.— Implemented self-weight for SESO. (5) M.M.d.S—Participated in reading and reviewing the article. All authors have read and agreed to the published version of the manuscript.

Funding

Instituto Federal de Educação Ciência e Tecnologia de Minas Gerais–IFMG, CNPq (National Council of Scientific and Technological Development) under Grant Number 306721/2023-6 and 316771/2023-6

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to the Instituto Federal de Educação Ciência e Tecnologia de Minas Gerais–IFMG, CNPq (National Council of Scientific and Technological Development) under Grant Number 306721/2023-6 and 316771/2023-6.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Svanberg, K. Method of moving asymptotes — a new method for structural optimization. Int. J. Num. Meth. Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
  2. Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
  3. Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: topological, geometrical and generalized shape optimization. Comp. Meth. Appl. Mech. Engrg. 1991, 89, 309–330. [Google Scholar] [CrossRef]
  4. Eschenauer, H.A.; Kobelev, V.V.; Schumacher, A. Bubble method for topology and shape optimization of structures. Structural optimization 1994, 8, 42–51. [Google Scholar] [CrossRef]
  5. Allaire, G.; Jouve, F.; Toader, A.-M. A level set method for shape optimization. C. R. Acad. Sci. Paris, Série I 2002, 334, 1125–1130. [Google Scholar] [CrossRef]
  6. Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Engrg. 2003, 192, 227–246. [Google Scholar] [CrossRef]
  7. Xia, Q.; Shi, T. Topology optimization of compliant mechanism and its support through a level set method. Computer Methods in Applied Mechanics and Engineering 2016, 305, 359–375. [Google Scholar] [CrossRef]
  8. Xie, Y.M.; Steven, G.P. (1997) Evolutionary Structural Optimization. Springer-Verlag, Berlin. [CrossRef]
  9. Xie, Y.M.; Steven, G.P. (1997) Evolutionary Structural Optimization. Springer-Verlag, Berlin. [CrossRef]
  10. Querin, O.M.; Steven, G.P.; Xie, Y.M. Evolutionary structural optimisation (ESO) using a bidirectional algorithm. Engineering computations 1998, 15, 1031–1048. [Google Scholar] [CrossRef]
  11. Yang, X.Y.; Xie, Y.M.; Steven, G.P.; Querin, O.M. Topology optimization for frequencies using an evolutionary method. Journal of Structural Engineering 1999, 125, 1432–1438. [Google Scholar] [CrossRef]
  12. Querin, O.M.; Young, V.; Steven, G.P.; Xie, Y.M. Computational efficiency and validation of bi-directional evolutionary structural optimisation. Computer methods in applied mechanics and engineering 2000, 189, 559–573. [Google Scholar] [CrossRef]
  13. Huang, X.; Xie, Y.M.; Burry, M.C. Advantages of bi-directional evolutionary structural optimization (BESO) over evolutionary structural optimization (ESO). Advances in Structural Engineering 2007, 10, 727–737. [Google Scholar] [CrossRef]
  14. Almeida, V.S.; Simonetti, H.L.; Neto, L.O. Comparative analysis of strut-and-tie models using Smooth Evolutionary Structural Optimization. Engineering Structures 2013, 56, 1665–1675. [Google Scholar] [CrossRef]
  15. Simonetti, H.L.; Almeida, V.S.; de Oliveira Neto, L. A smooth evolutionary structural optimization procedure applied to plane stress problem. Engineering structures 2014, 75, 248–258. [Google Scholar] [CrossRef]
  16. Shobeiri, V.; Ahmadi-Nedushan, B. Bi-directional evolutionary structural optimization for strut-and-tie modelling of three-dimensional structural concrete. Engineering Optimization 2017, 49, 2055–2078. [Google Scholar] [CrossRef]
  17. Shobeiri, V. Determination of strut-and-tie models for structural concrete under dynamic loads. Canadian Journal of Civil Engineering, 2019, 46, 1090–1102. [Google Scholar] [CrossRef]
  18. Huang, X.; Zuo, Z.H.; Xie, Y.M. Evolutionary topological optimization of vibrating continuum structures for natural frequencies. Computer Structure 2010, 88, 357–64. [Google Scholar] [CrossRef]
  19. Zuo, Z.H.; Xie, Y.M. A simple and compact Python code for complex 3D topology optimization. Advances in Engineering Software 2015, 85, 1–11. [Google Scholar] [CrossRef]
  20. Bi, M.; Tran, P.; Xie, Y.M. Topology optimization of 3D continuum structures under geometric self-supporting constraint. Additive Manufacturing 2020, 36, 101422. [Google Scholar] [CrossRef]
  21. Habashneh, M.; Movahedi Rad, M. Reliability based geometrically nonlinear bi-directional evolutionary structural optimization of elasto-plastic material. Scientific Reports 2022, 12, 5989. [Google Scholar] [CrossRef]
  22. Eom, Y.S.; Yoo, K.S.; Park, J.Y.; Han, S.Y. Reliability-based topology optimization using a standard response surface method for three-dimensional structures. Structural and Multidisciplinary Optimization 2011, 43, 287–295. [Google Scholar] [CrossRef]
  23. Simonetti, H.L.; Almeida, V.S.; de Assis das Neves, F.; Del Duca Almeida, V.; de Oliveira Neto, L. Reliability-Based Topology Optimization: An Extension of the SESO and SERA Methods for Three-Dimensional Structures. Appl. Sci. 2022, 12, 4220. [Google Scholar] [CrossRef]
  24. Simonetti, H.L.; Almeida, V.S.; Neves FdAd Almeida, V.D.D.; Cutrim, M.D.S. 3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms. Applied Sciences 2023, 13, 6215. [Google Scholar] [CrossRef]
  25. Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Structural and multidisciplinary optimization 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
  26. Kharmanda, G.; Olhoff, N.; Mohamed, A.; Lemaire, M. Reliability-based topology optimization. Structural and Multidisciplinary optimization 2004, 26, 295–307. [Google Scholar] [CrossRef]
  27. Jain, N.; Saxena, R. Effect of self-weight on topological optimization of static loading structures. Alexandria Engineering Journal 2018, 57, 527–535. [Google Scholar] [CrossRef]
Preprints 110019 g001
Figure 1. SESO Flowchart with Own Weight.
Figure 1. SESO Flowchart with Own Weight.
Preprints 110019 g001
Preprints 110019 g002
Figure 2. Design domain and boundary conditions.
Figure 2. Design domain and boundary conditions.
Preprints 110019 g002
Preprints 110019 g003
Figure 3. Optimal topologies: (a) BESO and (b) SESP.
Figure 3. Optimal topologies: (a) BESO and (b) SESP.
Preprints 110019 g003
Preprints 110019 g004
Figure 4. Design domain and boundary conditions.
Figure 4. Design domain and boundary conditions.
Preprints 110019 g004
Preprints 110019 g005
Figure 5. Optimal topologies: (a ) SESO and (b) BESO.
Figure 5. Optimal topologies: (a ) SESO and (b) BESO.
Preprints 110019 g005
Preprints 110019 g006
Figure 6. Design domain and boundary conditions: (a) Bridge with lower deck and semicircular opening in the x direction and (b) Bridge with upper deck.
Figure 6. Design domain and boundary conditions: (a) Bridge with lower deck and semicircular opening in the x direction and (b) Bridge with upper deck.
Preprints 110019 g006
Preprints 110019 g007
Figure 7. Deterministic Optimal Topologies: (a) BESO and (b) SESO.
Figure 7. Deterministic Optimal Topologies: (a) BESO and (b) SESO.
Preprints 110019 g007
Preprints 110019 g008
Figure 8. Deterministic Optimal Topologies: (a) BESO and (b) SESO.
Figure 8. Deterministic Optimal Topologies: (a) BESO and (b) SESO.
Preprints 110019 g008
Preprints 110019 g009
Figure 9. RBTO: (a) BESO and (b) SESO.
Figure 9. RBTO: (a) BESO and (b) SESO.
Preprints 110019 g009
Preprints 110019 g010
Figure 10. RBTO with own weight: (a) BESO and (b) SESO.
Figure 10. RBTO with own weight: (a) BESO and (b) SESO.
Preprints 110019 g010
Preprints 110019 g011
Figure 11. Design domain and boundary conditions.
Figure 11. Design domain and boundary conditions.
Preprints 110019 g011
Preprints 110019 g012
Figure 12. Deterministic procedure topology optimization: (a) BESO and (b) SESO.
Figure 12. Deterministic procedure topology optimization: (a) BESO and (b) SESO.
Preprints 110019 g012
Preprints 110019 g013
Figure 13. RBTO considering self-weight: (a) BESO and (b) SESO.
Figure 13. RBTO considering self-weight: (a) BESO and (b) SESO.
Preprints 110019 g013
Preprints 110019 g014
Figure 14. Graph – Objective Function by reliability index.
Figure 14. Graph – Objective Function by reliability index.
Preprints 110019 g014
Table 1. Coefficients in constitutive relations.
Table 1. Coefficients in constitutive relations.
Distribution parameter Distribution type Mean (μ) Standard deviation
(σ)
nelx (mm) Normal 120 0.1
nely (mm) Normal 20 0.1
nelz (mm) Normal 10 0.1
E (GPa) Normal 1 0.1
v Constant 0.30 0
F (1000N/m²) Normal 1 0.1
Volume (mm³) Normal 0.30 0.1
Compliance (N.mm) Normal 4.82e6 0.1
Table 2. Influence of the reliability index β t on Topology Optimization.
Table 2. Influence of the reliability index β t on Topology Optimization.
Preprints 110019 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated