1. Introduction

2. Materials and Methods

3. Results

4. Discussion

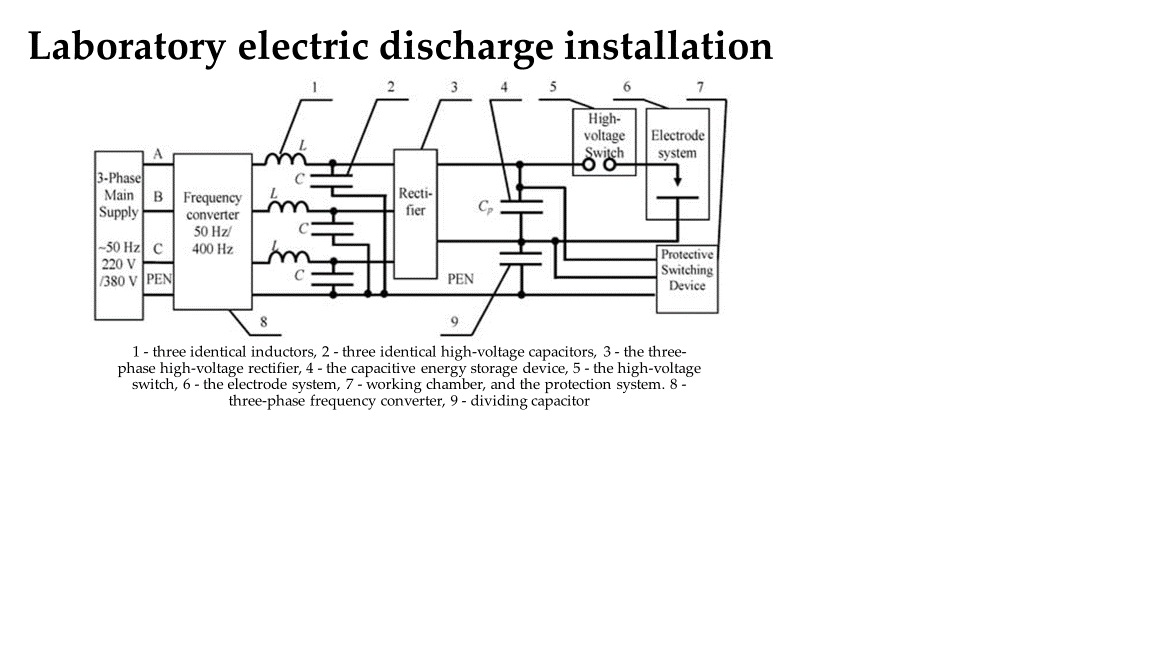
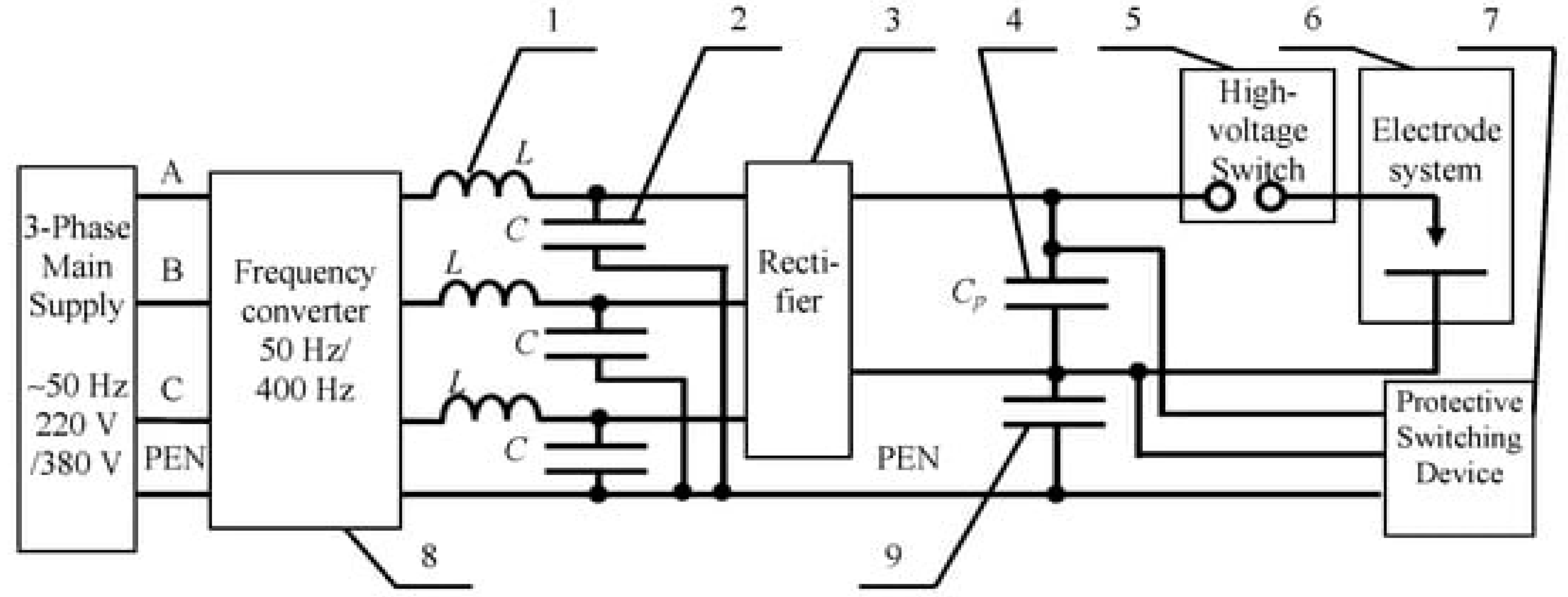
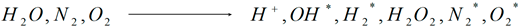4.1. Physical Phenomena Accompanying Electric Discharge Cavitation

Obvious factors that are characteristic of an underwater electrical discharge and affect biological objects are: ultraviolet and thermal radiation, primary pressure waves and secondary acoustic waves, and radical particles that arise in the working environment.

When acoustic waves of high intensity propagate in the medium, nonlinear effects occur that depend on the amplitude of the wave (second-order effects). These include, for example, acoustic streams (together with the acoustic turbulence they cause) and pulsations of gas bubbles. Pulsations induce some concomitant phenomena: flotation effect, rectified diffusion, local shock waves. In addition, second-order phenomena are ponderomotive forces, surface effects, radiation pressure, and cavitation. Cavitation is accompanied by both the flotation effect and rectified diffusion, as well as microfluid streams, microflows, and local shock waves.

Acoustic streams are stationary vortex flows of fluid that occur in an inhomogeneous acoustic field, both in free space and near obstacles of various kinds. In addition, the occurrence of acoustic streams is also possible in the vicinity of pulsating and oscillating bodies. The reason for the occurrence of various acoustic streams is the same – irreversible losses of energy and momentum of the acoustic wave in the medium. If you cross an acoustic wave with an imaginary plane, then from the side the energy density of an incident wave is greater than that of the same volume behind the plane, on the side of the passing wave. Thus, a force will act on the plane, tending to move it away from the source of acoustic vibrations. This force, which is equal to the energy density gradient and is directed towards the propagation of the wave, causes the medium to move. Energy losses in the medium, which cause acoustic streams, can occur both in the entire volume occupied by the acoustic field and in part of the volume. Acoustic streams are more intense and their speed is greater the greater the loss of acoustic energy in the medium. It does not matter whether the loss mechanism is related to the viscosity of the medium or due to the inhomogeneity of the medium (suspended particles, gas bubbles, cavitation region). The only thing that matters is the irreversibility of the loss of energy and momentum of the acoustic wave [28]. Streams arising in an acoustic field are usually divided into three groups: streams in an inhomogeneous space of limited volume; streams originating outside the acoustic boundary layer; streams that occur in a viscous boundary layer near obstacles.

Ponderomotive forces include: the Bjerkenss force, the Stokes force, associated with the change in viscosity; the force associated with the distortion of the wave form; and the force generated by the interaction of a pulsating bubble with an acoustic field. The transition from acoustic oscillations with a low amplitude to oscillations with a high amplitude, in which the continuity of the fluid is broken and cavitational bubbles appear in it, is due to a qualitative change in the oscillatory process in the liquid. These changes are due the presence of cavitational bubbles changes the properties of the medium and its characteristics become nonlinear [29]. In addition, with developed cavitation, there is a process of periodic propagation of the hydrodynamic rupture in the form of a wavefront of collapsing bubbles. Note that gas bubbles, unlike cavitational bubbles, exist in a liquid even in the absence of acoustic vibrations. The equation describing the pulsation of a cavitational bubble in an acoustic field is a second-order differential equation and cannot be solved in general by analytical methods [5], taking into account the compressibility of the fluid, this equation was obtained by Herring and is written as follows (formula 1):

$$R\left(1-\frac{2U}{c_0}\right)\frac{d^{2}R}{d{t}^2}+\frac{3}{2}\left(1-\frac{4}{3}\frac{U}{c_0}\right){\left(\frac{dR}{dt}\right)}^2-{\displaystyle \underset{P\infty 0}{\overset{P(R)}{\int }}\frac{dP}{\rho }}-\frac{R}{\rho }\frac{U}{c_0}\left(1-\frac{U}{c_0}-\frac{U^2}{c_0^2}\right)\frac{dP(R)}{dR}=0$$

(1)

(1)

where U – bubble velocity, R – bubble radius, с0 – local velocity of acoustic bubble oscillation.

Member ${\displaystyle \underset{P\infty }{\overset{P(R)}{\int }}\frac{dP}{\rho }}=h$ is an enthalpy on the surface of the vesicle, in which P∞ – pressure in the medium at infinity (in the special case, hydrostatic pressure), and P(R) – pressure on the surface of the bubble cavity. If use the Nolting–Nepayras equation and the equation of state of water [30], recorded in the form , where А, B and n – constants for water (А = 3,001∙108 Pа, В=3∙108 Pа, n=7), ρ and ρ0 – density of the fluid at the present moment and the moment of determination of the constants A and B. The enthalpy on the surface of the cavitating bubble can be expressed as follows (formula 2):

$$h=\frac{n}{n-1}\frac{A^{1/n}}{{\rho }_0}{\left[\left({\rho }_0+\frac{2\sigma }{R_0}\right){\left(\frac{R_0}{R}\right)}^{3\gamma }-\frac{2\sigma }{R}+B\right]}^{\frac{n-1}{n}}-{\left(P_0-P_{{\hspace{0.25em}}^m}\sin \omega t+B\right)}^{\frac{n-1}{n}}$$

(2)

where σ – surface tension of fluid; γ – polytropic indicator, which determines the state of the gas in the cavity; ω – cyclic frequency of acoustic vibrations.

The local velocity of the acoustic oscillation c0 in formula (1) can be represented as follows (formula 3):

$$c_0=\sqrt{c^2+(n-1)h}$$

(3)

where с – velocity of acoustic vibrations in the fluid as a whole.

From the above expression, it can be seen that the local velocity is a function of the enthalpy of the bubble’s surface. Equation (1) is solved by numerical integration methods under certain initial conditions and using equations (2) and (3). The solution of the equations for various initial conditions showed that the oscillations of the cavitating bubble are not harmonic. This is manifested in the fact that the bubble’s growth time is four to five times longer than the time it collapses, and there are modes where the collapse-time is only one-tenth of the growth time. It also follows from the calculations that the radii of bubbles of sub-resonance size increase with an increase in acoustic intensity and at the same time the time of collapse increases. From the solution of equation (1), an important conclusion was made about the possibility of controlling the bubble collapsing time by changing the external pressure. The time for collapsing is dramatically reduced if the bubble collapses in the initial pressure wave of the subsequent liquid breakdown. In the case of high external pressure, the velocity of bubble collapsing varies for two reasons. Firstly, the mass of the liquid attached to the bubble decreases and the pressure inside the cavity is remain the same, these contribute to an increase in the velocity of the bubble walls in the collapsing phase, and secondly, the collapsing phase changes relative to the period of acoustic oscillations, which in turn leads to an increase in the effective pressure acting on the cavity in the compression phase.

The movement of bubbles in the liquid as a result of interaction with each other is random. At the same time, since each bubble has a runoff at the interface, the movement of the bubbles to the interface is unidirectional. This pattern of motion can be described by the equation of diffusion kinetics with a source in the volume of the fluid and a runoff at its boundary (formula 4):

$$\frac{\partial C}{\partial t}+(\overrightarrow{U}\nabla )\cdot C=D\Delta C+Q_w$$

(4)

where С – concentration of cavitational bubbles, D – a coefficient similar to the diffusion coefficient, Qw– cavitational bubble source power.

When acoustic waves propagate, short wavelengths are formed at the “soft” interface between two media (liquid-gas, for example). These surface waves are also called “capillary waves” because their parameters depend on the surface tension of the liquid. The length of such waves can be determined from the equation: $\lambda =\sqrt[3]{8\pi \sigma /\rho f^2}$. Capillary oscillations at the interface are stable as long as their frequency is half the frequency of the acoustic vibrations that cause them. Acoustic stream that occur at the surface of pulsating bubbles are a source of acoustic turbulence. The occurrence of acoustic turbulence here is associated with the inhomogeneity of the field, where high transverse and longitudinal gradients of high pressure are formed. The stream is also turbulent at the interface between the direct and the reverse acoustic flow, as the phenomenon is observed in a limited volume.

According to the theory of isotropic turbulence, when vortices reach the “internal” scale, the properties of the medium become isotropic, that is, independent of the direction of acoustic flows. The frequency of pulsations also becomes independent of the scale of the flows, in this case it will be constant and equal to the highest value. In an acoustic field, the internal scale of turbulence is defined as follows (formula 5) [31]:

$${\lambda }_0=\frac{b^{3/4}}{{\rho }^{3/4}{\epsilon }^{1/4}}=\sqrt[4]{\frac{b^3{\lambda }_{п}}{u^3{\rho }^3}}$$

(5)

where b – a constant that takes into account, in addition to viscous energy losses, also losses inherent in an oscillating medium; λп – acoustic flow scale; u – velocity of fluid in acoustic flow; ε=u3/ λп – dissipation of energy in the medium. The constant b is often referred to as acoustic viscosity, and it can be calculated by the formula 6 [31]:

$$b=\frac{4\eta }{3}+\frac{\gamma \text{'}-1}{c_p}\chi +\eta \text{'}$$

(6)

where η − shearing viscosity; γ’ – modulus of bulk elasticity of fluid at atmospheric pressure related to its internal pressure; ср – heat capacity of liquid at constant pressure; χ – thermal conductivity coefficient; η’ – bulk viscosity of fluid.

The internal scale of water turbulence in real conditions is within the range of 5∙10-5…1∙10-4 m.

In the presence of long-lived (pulsating) bubbles in the liquid, a flotation effect is manifested in the acoustic field. Around each bubble, small particles suspended in the liquid are concentrated. To elucidate the mechanism of this phenomenon in [32] a solitary pulsating spherical bubble was considered, the expansion time of such a bubble is longer than the collapse time. In the frequency range 1∙10-4...1∙105 Hz with a bubble size of up to 1∙10-5 m, the authors consider water to be an incompressible liquid. The velocity field that pulsating bubble creates in a fluid can be represented as the equation of continuity in spherical coordinates and the symmetry of the problem:$div{U}_r=\frac{1}{r^2}\frac{d}{dr}\left({\overrightarrow{r}}^2{\overrightarrow{V}}_r\right)=0$, where r – bubble radius.

Particles in a liquid are thought to be suspended and spherical in shape. Falling into the vicinity of a pulsating bubble, such a particle finds itself in its velocity field. However, since the radius of friction and inertial forces are different, there is a boundary radius beyond which the bubble does not trap the particle. As the particle moves away from the bubble (beyond the capture radius), its velocity first increases and then drops to zero. As the particle moves toward the bubble, its velocity gradually increases. As the size of the particles decreases or their density decreases, the effective capture radius decreases, so that for particles smaller than the limit the capture radius, the gripping radius is smaller than the radius of the pulsating bubble. In this case, only the Stokes force will act on the particle, removing the particles from the bubble. In this way, very small particles are repelled by a pulsating bubble. However, it should not be thought that small particles are blocked from reaching the surface of the bubble. Forming strong aggregates that are not destroyed by alternating flows, such particles can also be trapped by the bubble.

The term “rectified diffusion” refers to the transfer of the mass of a gas from a liquid to a bubble as a result of its oscillations in an acoustic field [33]. The mechanism of this process can be represented as follows. When the bubble is compressed, the concentration of gas in it increases, and at some point begins to exceed the concentration of gas in the surrounding liquid, at which point the gas begins to diffuse from the bubble into the liquid. When the bubble expands, the reverse process occurs, a diffusion flow occurs in the opposite direction. The phenomenon of unilateral diffusion is explained by the fact that when the bubble expands, the surface through which the diffusion occurs is much larger than during compression, so the flow of gas directed into the bubble is much greater than the flow in the opposite direction.

As the frequency of oscillations increases, the density of the diffusion stream under the action of microflows decreases, while the density of the stream, which is due to the pulsations of the bubble, increases.

Cavitational bubbles are also a source of microflows in the acoustic field. If the bubble retains its spherical shape when oscillating, a so-called vortex-free motion occurs, where the velocity potential satisfies Laplace’s equation [34]. The value of this velocity is in the range of 2∙10-4... 6∙10-3 m/s.

One of the properties of cavitational bubbles is the generation of intense local shock waves. Shock waves are pressure pulses propagating in a medium at a speed greater than the speed of acoustic waves. When a cavitational bubble collapses due to a sudden stop of the entire mass of fluid involved in the motion, pressure appears at the point of collapse and a pressure pulse is generated that propagates through the fluid [34]. To calculate the pressure of the resulting shock waves, it is customary to use the equation of fluid motion in a potential approximation as a starting point: $\frac{{\partial }^2\psi }{\partial t^2}=a^2{\nabla }^2\psi -\frac{\partial {(\nabla \psi )}^2}{\partial t}$where ψ − speed potential, а – velocity of sound in perturbed fluid. Despite the rapid decrease in pressure in the shock wave as it moves away from the point of origin, it is very powerful at the distance of the initial radius of the bubble. It is also possible to estimate the pressure that develops when a cavitational bubble collapses using an empirical formula [26]: $p_{\max }=\frac{p_g^4}{81p_h^3}$, , where pg – the pressure acting in the medium at the beginning of the collapse, ph is the pressure determined by the presence of gas residues in the bubbles. The pressure increases very strongly nonlinearly when the cavitational bubble is collapses while the radius of the cavitational nucleus decreases. This can be expressed in terms of the gas content parameter: $\delta =\frac{p_0+2\sigma R_0}{p_0}{\left(\frac{R_0}{R_{\max }}\right)}^3$Some cavitation parameters obtained experimentally in [26] are shown in Table 2. It can be seen that true shock waves are generated in the course of electric discharge cavitation processes.

Table 2. Typical parameters of electric discharge cavitation.

Table 2. Typical parameters of electric discharge cavitation.

Initial bubble radius, R0, cm	Maximum bubble radius, Rmax, cm	Minimum bubble radius Rmin, cm	Gas content, δ	Pressure developed when the bubble collapses pmax, Pa	Ratio of the sound speed in the medium to the velocity of the leading edge of the microcavitation wave
1∙10-3	2.9∙10-3	5.8∙10-5	4.8∙10-2	7.4∙103	4.5
5∙10-4	2.6∙10-3	2.5∙10-5	1.0∙10-2	1.9∙104	6.2
1∙10-4	2.3∙10-3	0.9∙10-6	2.1∙10-4	2.8∙107	13.3

The time of the cavitational bubble collapse ultimately determines the duration of the leading edge of the microcavitation waves: $\tau =F{R}_{\max }\sqrt{\frac{\rho }{p_{\max }}}$ , where the F is coefficient for water is close to unity. The characteristic value of the leading edge duration of microcavitation shock waves ranges from 0.5∙10-7 to 0.5∙10-8 s.

When the microcavitational bubbles collapse, high-velocity microjets of liquid are produced. The above model of the cavitational bubble collapsing assumes that it is perfectly spherical. In real conditions, the sphericity of the bubble is broken when it is at the liquid-solid interface, if the plane of the solid surface is significantly larger than the size of the bubble (for example, the walls of an electric discharge reactor). The extremely distorted cavitational bubble (hemispherical, when it’s base is on a solid surface) slamming, if compressibility, viscosity and surface tension are neglected, can be described by the differential equation of the form presented in the paper [35]: ${\nabla }^2\cdot \Phi (r,\Theta ,t)=0$ , where Ф – scalar potential function.

The solution of this equation shows that when the current radius approaches zero, the shape changes according to a very complex law. The deformation of the bubble is so great that its walls hit a solid surface before the radius reaches zero. At the same time, the speed of microjets can reach several hundred meters per second.

All of the second-order effects described above accompany a high-voltage electrical discharge in the liquid are also characteristic for ultrasonic fluid treatment. These two ways of influencing a substance are united by cavitation, as well as macro- and microflows. All the second-order effects that accompany cavitation have a strong impact on water treatment processes, especially in terms of disinfection. In addition, chemical reactions also take place directly in the cavitational bubbles. At the same time, high-voltage electrical discharge is characterized by phenomena that affect chemical reactions: ultraviolet radiation and a strong electric field.

Given a constant gas content in the bubble and the pressure of the surrounding liquid, the minimum radius of the cavitational bubble is determined by the formula: $R_{\min }=R_{\max }{\left(\frac{p}{(\gamma -1)p_0}\right)}^{\frac{1}{3(\gamma -1)}}$ , at the same time, the pressure will be expressed by the formula: $p=p_{\max }{\left(\frac{R_{{\hspace{0.25em}}^{\max }}}{R_{\min }}\right)}^{3\gamma }$ , where pmax – gas pressure in bubble at maximum radius, p0 – hydrostatic pressure, γ – ratio of heat capacities of gas in bubble at constant pressure and volume. With the adiabatic nature of the bubble collapsing, the temperature in it is: $T_{\max }=T_0{\left(\frac{(\gamma -1)p_0}{p}\right)}^{3(\gamma -1)}$, where Т0 – initial fluid temperature. For example, when Rmin=0,1Rmax, p0=105 Pа, γ=3/4, T0=300 К the pressure of the gas in the bubble at the moment it reaches its maximum radius will be р=3,3∙103 Pа. Substituting these values into the equations above, we get that when the bubble is collapses, the pressure reaches рmax≈3∙107 Pа, and the temperature Tmax≈3000 К. Such high temperatures, which occur in a gas-filled cavity of a small volume, create conditions for the appearance of electric charges, luminescence, dissociated and ionized molecules, as well as atoms and free radicals.

4.2. Chemical Processes in Electric Discharge Cavitation

In general, the chemical reactions in aqueous solutions that are initiated in a liquid by an electric discharge in the cavitation mode are well explained by the theory of free radicals. Molecules of water and gas dissolved in it undergo the following transformations in aqueous solutions under the influence of cavitation:

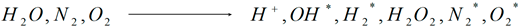
The yield of the formed products of the chemical reaction is greatly influenced by the mixing of the liquid, which is automatically provided by first-order effects when the liquid is broken down (hydraulic flows). For example, hydrogen peroxide is emitted 10 times less in the absence of hydraulic flows than in the presence of them. Authors of [36] explain this by the enrichment of the liquid with air during mixing and the reduction of concentration resistance. If solutes and micro-objects are present in the liquid, they react with excited gas molecules or formed radicals.

Second-order electric discharge effects can play an important role in providing chemical action, with volumetric cavitation playing a very important role. According to several researchers [16], when cavitation occurs in a liquid medium, chemical bonds are broken, and as a result, ions and free radicals appear near the cavitational pocket. These reactive particles can react with substances located at the gas-vapor cavity-liquid interface. According to the authors [38,39], the bubble collapses at an increasing rate. At the same time, the temperature of the gas in the bubble rises all the time and, starting from a certain moment, bubble’s collapse occurs under adiabatic conditions. Using some assumptions, the authors derived an equation that makes it possible to calculate the temperature in a cavitating bubble at any stage of its compression under adiabatic conditions: $T_0{r}_0{\hspace{0.25em}}^{3(\gamma -1)}=T{r}^{3(\gamma -1)}$, where r0 – maximum bubble radius, r – bubble’s radius at a given compression stage, Т0 – gas temperature at the beginning of bubble compression, Т – temperature at the moment of compression. According to the authors’ calculations, with a certain ratio of the maximum radius of the bubble and the value of the γ for the gas that fills the bubble, the temperature in the compressed bubble reaches 2000 K or more. Such high temperatures can contribute, according to the [40] initiation of almost all possible chemical reactions taking place in the cavitational volume. The products of gas reactions, thermally specifed in the cavitational pocket, diffuse into the surrounding solution, where, interacting with solutes, they cause some chemical processes – secondary reactions. For example, to the secondary ones in the paper [41] refers to the formation of hydrogen peroxide, which occurs in the treated water only in the presence of oxygen:

$$H_{2}O+\frac{1}{2}{O}_2\to H_2{O}_2$$

Moreover, this reaction takes place at a lower temperature than the next one: $2H_{2}O\to H_2{O}_2+H_2$ . Products of water molecules’ thermal splitting – free radicals OH* – cause intensive oxidation processes in the working environment. At the same time, the yield of the reaction depends on the ratio of the heat capacities of the gases penetrating the cavitation pocket. For example, in paper [42] it has been shown that when carbon tetrachloride is sonicated in water, more chlorine is converted into the active form in a solution saturated with noble gases (γ=1.66) than in a solution containing oxygen and nitrogen (γ=1.4).

Chemical mechanisms of cavitation work not only due to the mechanical and thermal forces that develop as the result of the resonating bubbles collapse. Chemical reactions can also occur as a result of electrochemical and photochemical processes that arise due to the appearance of high electrical voltages in cavitational pocket. According to Frenkel’s theory, the electric field strength in a cavitational pocket can be determined by the following equation: $E=\frac{4e}{r}\sqrt{N\alpha }$ , where α – distance between ruptured fluid layers, r – cavitation rupture radius, е – monovalent ion charge, N – number of dissociated molecules per volume unit. Suppose, N equally 1∙1018, α and r equal 5∙10-8 сm и 1∙10-4 сm, accordingly, then Е will be equal to 600 kV/сm, and there are conditions for the ionization of gas particles in the cavity. If, as a result of ionization, there is an electrical breakdown between the walls of the cavity, then a significant part of the channel’s radiation lies in the ultraviolet part of the spectrum. This will contribute to the photochemical nature of some of the chemical processes in the working medium.

A water molecule can split to form atomic hydrogen H*, and radical OH*, hence valence-unsaturated particles with high reactivity appear in the solution. Under the influence of the energy released during the high-voltage breakdown of the liquid, an electron is knocked out of the water molecule, it leads to the formation of an ionized water particle (Н₂О – е→H₂O+). This water particle, in turn, breaks down into the hydrogen ion H+ and the free radical OH*. An electron knocked out of a molecule travels a distance that is determined by the energy of the impact on the molecule and the properties of the medium. On its way, it can attach to a water molecule or a hydrogen ion, resulting in atomic hydrogen formation. The formation of hydrogen atoms occurs at a noticeable distance from free OH* radicals, which makes their recombination difficult. There is a high probability of interaction between free radicals and individual atoms, as a result of this process other chemical compounds and free radicals emerge. For example, the following reactions are possible:

$$O{H}^{*}+O{H}^{*}\to H_2{O}_2$$

$$H^{+}+H^{+}\to H_2$$

$$O{H}^{*}+O{H}^{*}\to H_{2}O+O^{-}$$

$$O^{-}+O^{-}\to O_2$$

$$H_2{O}_2+O{H}^{*}\to H_{2}O+H{O}_2{\hspace{0.25em}}^{*}$$

$$H{O}_2{\hspace{0.25em}}^{*}+H^{+}\to H_2{O}_2$$

$$H_2{O}_2+H{O}_2{\hspace{0.25em}}^{*}\to H_{{\hspace{0.25em}}_{{\hspace{0.25em}}^{{\hspace{0.25em}}^2}}}O+O_2+O{H}^{*}$$

For the first time, the formation of hydrogen ions (H+) during cavitation was experimentally demonstrated as early as 1955, and later free OH* radicals were experimentally detected [30].

In addition to the above-mentioned reactions leading to the formation of radicals and radical groups, the hypothesis of the formation of hydrogen peroxide H₂O₄ owing to the interaction of a hydrogen atom with molecular oxygen and the subsequent recombination of low-stable HO2* radicals is considered: $H{O}_2{\hspace{0.25em}}^{*}+H{O}_2{\hspace{0.25em}}^{*}\to H_2{O}_4$ [43].

Thus, the decomposition of water molecules under the influence of factors characterizing cavitation consists in the occurrence of two parallel reactions leading to the formation of free radicals, hydrogen peroxide molecules and atomic hydrogen. Ionization of water molecules is carried out in the gas phase – in cavitational bubbles, during their collapse chemically active objects pass into the working medium. They cause oxidation processes (e.g., iron ions) even in the absence of oxygen molecules. In the presence of molecular oxygen, the process of oxidation of iron ions is enhanced by the formation of a hydroperoxide radical in the solution, it can provide the following reactions:

$$F{e}^{2+}+H{O}_2\to H{O}_2^{*}+F{e}^{3+}$$

$$H+H{O}_2{\hspace{0.25em}}^{*}\to H_2{O}_2$$

$$H+H{O}_2{\hspace{0.25em}}^{*}\to H_2{O}_2$$

Oxidation reactions of iron ions have not been detected in aqueous solutions degassed purposefully. This is the evidence that the reactions are specified by the primary chemical reactions taking place in the cavitational pockets [44].

The analysis of the described phenomena allowed us to put forward a hypothesis about the presence of two steps in chemical reactions initiated by cavitation. Each of these stages is associated with a specific stage of the cavitational bubble development.

Stage 1. Photo- and electrochemical phenomena take place in the cavitation pocket when the pressure in the cavity is very low. At this stage, conditions are created in the cavitation region that are analogous to electric discharges in a medium of vapor and gas at low pressures. The gases in the cavity are ionized and activated. The process of formation of activated and ionized particles is completed by an electronic breakdown of the cavity.

Stage 2. Further development of the cavitational pocket is accompanied by an increase in pressure in it, and then collapse. At the same time, the formed relatively long-lived active radicals and atoms are transferred into the medium. In addition, the collapse of the cavitational bubble is accompanied by the occurrence of a local shock wave acting on the molecules of the substance, as shown above.

So, the chemical reactions initiated by cavitation can be divided into the following groups:

• reactions occurring in a gaseous medium (cavitational pocket);
• reactions occurring at the cavitational pocket-liquid interface as a result of the interaction of radicals and atoms occurring in the cavity with molecules at the interfacial area;
• reactions that are caused by active substances formed in the gas phase and penetrating into surrounding liquid (water) as a result of the collapse of cavitational bubbles;
• reactions occurring in a liquid medium under the influence of local shock waves, the source of which is collapsing cavitational pocket.

The presence of a particular gas in an aqueous solution not only causes the acceleration or deceleration of chemical processes, specific gas also causes the nature of the chemical reactions in the cavitation fields. For example, in the presence of hydrogen, the oxidation of iodine ions completely stops, but under the same conditions, iodine molecules dissociate into individual atoms, then they rebuild as a result of interaction with hydrogen atoms. The process of iodine rebuilding appears to take place in the gas phase, i.e. in cavitational bubbles. During cavitation in an aqueous solution with molecular iodine and molecular hydrogen in it, both water vapor and the above-mentioned substances diffuse into the cavitational pockets. The energy of dissociation of iodine molecules into atoms is 1.53 eV. In the case of photodissociation (ultraviolet radiation from the plasma channel of the main discharge and discharges in cavitational bubbles), the iodine molecule is split into an iodine atom and an excited radical of this element: $I_2+hv\to I+I^{*}$ . The limiting quantum capable of triggering the process of photodissociation must have an energy that is equal to or greater than the sum of the dissociation energy and the excitation energy of the radical or atom. For example, in the above case, this energy is 8.45 eV.

The hydrogen molecule can dissociate directly in the cavitational pocket: $H_2\to H^{*}+H^{*}$. Hydrogen atoms, on the other hand, can be produced by the reaction of molecular hydrogen with OH* radicals:$H_{2}O\to H^{*}+O{H}^{*}$, $H_2+O{H}^{*}\to H_{2}O+H^{*}$. This means that when one molecule of water interacts with one molecule of hydrogen, two hydrogen atoms emerge, they can rebuild two atoms of dissolved iodine. The amount of atomic iodine depends on the concentration of molecular iodine in the reaction mixture. At low concentrations of molecular iodine, only a fraction of the hydrogen atoms formed recombine to form molecular hydrogen. In the region of low concentrations, under the same physical conditions of cavitation, the amount of rebuilt iodine increases if the initial concentration of molecular hydrogen is increased. It is this phenomenon that we used in our experimental work to determine the intensity of cavitation [45]. With a further increase in iodine concentration, it may turn out that all the hydrogen atoms formed bind only a part of the halogen present. Similar patterns were obtained in paper [46] during the oxidation of iodine ions in a cavitation field. In [46], similar data were obtained during the study of the effect of carbon tetrachloride on the kinetics of iodine ions in the cavitation field oxidation. The amount of iodine released in the presence of CCl₄ in an aqueous solution increases by 10... 12 times. Starting with a certain concentration of potassium iodide (0.5 n. KI), the amount of iodine excreted in both the absence and presence of CCl₄ remains constant. This means that under the same physical conditions, the same number of active products capable to oxidize the substance under study is formed in a unit volume of an aqueous solution. The amount of CCl₄ decomposition products that enhance oxidation processes also remains constant under the same conditions. The decomposition products primarily include atomic chlorine, which segregates from carbon tetrachloride under the action of cavitation. As a result of this reaction, hexachloroethane C2Cl₆ can be obtained as the end product; that would indicate the appearance of the CCl₃ radical. Under the influence of cavitation, not only the bond of the halogen with the carbon atom is broken, but also the sulfur segregates from the carbon atom. For example, carbon disulfide (CS₂) in an aqueous solution forms a very stable colloid-sol under cavitation action [47]. The same stable sol was obtained by sonication of the aqueous solution of ethyl sulfide. Qualitative analysis showed that the resulting solutions contain colloidal sulfur micelles of various sizes.

The issue of activation of molecules of various gases in the cavitational pocket also arises when analyzing the reactions of the formation of hydrogen peroxide in sonicated water. The formation of peroxide was predominantly observed when the water contained dissolved oxygen [48]. This is explained by the fact that in the absence of oxygen, most of the products of the ionized water particles decomposition recombine: $H^{+}+O{H}^{-}\to H_{2}O$ . In the presence of oxygen, the recombination of the free hydroxyl radical and atomic hydrogen slows down as a result of the reaction: $H^{+}+O_2\to H{O}_2{\hspace{0.25em}}^{*}$ appearance of a radical НО₂* enhances oxidation processes, which are accompanied by the formation H₂O₂: $H{O}_2{\hspace{0.25em}}^{*}+H{O}_2{\hspace{0.25em}}^{*}\to H_2{O}_2+O_2$. The formation of hydrogen peroxide also occurs when a mixture of oxygen and hydrogen is forced into sonicated water. They interact with the products of the water molecules decomposition as follows:

$$,H_{2}O\to H^{+}+O{H}^{-},$$

$$H^{+}+O_2\to H{O}_2{\hspace{0.25em}}^{*},$$

$$O{H}^{*}+H_2\to H_{2}O+H^{\hspace{0.25em}},$$

$$H^{+}+O_2\to H{O}_2{\hspace{0.25em}}^{*},$$

$$2H{O}_2{\hspace{0.25em}}^{*}\to H_2{O}_2+O_2.$$

Under these conditions, for every water molecule decomposed there should also be one newly formed hydrogen peroxide molecule. However, the HO₂* radical interacts more easily with the hydroxyl radical than with the hydrogen molecules in the solution. Thus, the process represented as $O{H}^{*}+H_2\to H_{2}O+H^{+}$ , inhibited by a more easily occurring reaction: $O{H}^{*}+H{O}_2\to H_{2}O+O_2$. The largest amount of hydrogen peroxide is formed when the ratio of dissolved hydrogen and oxygen in the sonicated medium is 1:4. Oxygen molecules decompose directly in the cavitation pocket and ozone forms: $O_2\to O^{*}+O^{*}$ , $O^{*}+O_2\to O_3$.

In the cavitation region, nitrogen molecules from the air dissolved in water also dissociate. They interact with products of oxygen dissociation, form nitric oxide - a chemically highly reactive free radical that can act as both an oxidizing agent and a reducing agent. The primary elementary process that determines nitrogen oxidation reactions mainly comes down to the ionization of the nitrogen molecules N₂. The resulting particle dissociates into atomic nitrogen and a cation, then they interact with molecular oxygen:

$$N_2^{+}+O_2\to N{O}^{+}+N{O}^{+},$$

$$N_2^{+}+O_2\to N{O}_2+N^{*}$$

$$N+O_2\to NO+O^{*},$$

$$N^{*}+O_2\to N{O}^{+}+O^{*}$$

In this case, the reaction rate of the nitrogen oxidation is proportional to the efficiency of nitrogen ionization under the influence of secondary electric discharge factors, especially in cavitational bubbles.

Nucleic acids (including DNA and RNA) must be very sensitive to the effects of cavitation. A decrease in the relative viscosity of the DNA solution by ultrasonic cavitators is detected after just one minute of treatment; with increasing exposure, the relative viscosity of the DNA solution continues to decrease [49]. This decrease is persistent; the sonicated solution does not change the viscosity even after 24 ... 48 hours of sedimentation. Qualitative tests for the presence of free monosaccharides, phosphoric acid, purine and pyrimidine bases in the treated DNA solutions did not give positive results, i.e. degradation of the DNA molecule is observed. However, degradation of fragments formed in the field of ultrasonic waves does not occur if sonication of DNA solutions occurs in the presence of gases that prevent the development of oxidative reactions. In the paper [49] it is assumed that the decomposition of a giant nucleic acid molecule into separate fragments is caused by destructive mechanical effects that occur in the cavitation region. We think that such decomposition occurs not only as a result of mechanical action, but mainly due to the formation of free hydroxyl radicals in the solution under the influence of physical and chemical factors. For example, it is known [50], that depolymerization of thymonucleic acid occurs quickly in the presence of hydrogen peroxide and ferrous, their interaction is accompanied by the appearance of free hydroxyl radicals:  . As shown above, the active formation of such chemically active particles is a phenomenon accompanying cavitation in aqueous solutions. In sonificated protein solutions protein peroxide radicals appear with a lifespan of 5...10 minutes the main condition for their occurrence is the saturation of the solutions with oxygen, and not with hydrogen or an inert gas [51]. According to the authors, organic peroxides arise from the direct interaction of an oxygen molecule with an excited molecule:  . According to their data, peroxide compounds are formed during the auto-oxidation of hydrocarbons under the influence of ionizing radiation. This is preceded by the appearance of peroxyl radicals, which react with hydrocarbon radicals. According to [5], complex molecules that are in a metastable state are highly reactive and are biradicals. The lifespan of biradicals is hundredths of a second, whereas electronically excited molecules lose their energy within 1∙10-8... 1∙10-9 s. When biradicals interact with molecular oxygen, biradicals form probably, the lifetime of them is already several minutes. The long lifespan of the peroxide radical and the high reactivity significantly contribute to the conversion of the excitation energy into a chemical form.

5. Conclusions

• Powerful volumetric cavitation, indused by electrodischarges in cavitation modes, is a driving force of significant decrease in the quantity of chemical reagents, temperature and treatment time of water dezinfection. The primary factor, inherent in electrodischarge cavitation is emergence of great number of chemically active particles in working medium and following oxidation processes’ intensification. Other factors of electrical discharge are next in importance: local shock waves, acoustic flows and turbulences, flotation effects and rectified diffusion.
• The similarity of the effect of ultrasound and electric discharge in the cavitation mode on water systems has been experimentally proved, the frequencies of 70−120 kHz emerging in the spectrum of acoustic radiation of an underwater electric discharge in cavitation modes have been revealed. Intensive degradation of microorganisms is observed when the frequency of acoustic vibrations is sufficient to induce the resonant oscillation of cavitational bubbles. Discharge in the cavitation mode generates frequencies of acoustic radiation that correspond to the resonance conditions of bubbles presented in the working medium. Thus, acoustic waves of a certain frequency and intensity indirectly ensure an inactivation of microbiological objects in treated water.
• It is revealed that the intensity of the high-frequency part of the spectrum of acoustic radiation of an electric discharge in water is adjustable by the change of the discharge circuit inductance and the non-insulated end of the electrode-anode protruding into the discharge gap.
• Underwater electrical discharge as a source of cavitation does not have such intrinsic constraints as erosion resistance of the ultrasonic emitters themselves, cavitation does not have a direct effect on the plasma channel of the electrical discharge in the liquid. Besides, both the intensity and the total power of cavitational processes that are induced by underwater electrical discharges are always higher compared to ultrasonic treatment due to more wide range of generated acoustic frequencies. Hereupon, the possibilities of industrial application of water disinfection by electric discharge in cavitation mode are much wider than in the case of ultrasonic treatment. This is crucial for the practical use of underwater electrical discharges not only for acceleration of oxidation, but also for another chemical-engineering processes’ intensification.

References

1. Bezsonov, Ye.; Mitryasova, O.; Smyrnov, V.; Smyrnova, S. 2017. Influence of the South-Ukraine electric power producing complex on the ecological condition of the Southern Bug River. Eastern-European Journal of Enterprise Technologies, 4/10 (88), 20–28. [CrossRef]
2. Bernatska, N.; Dzhumelia, E.; Dyakiv, V.; Mitryasova, O., Salamon, I. 2023. Web-Based Information and Analytical Monitoring System Tools–Online Visualization and Analysis of Surface Water Quality of Mining and Chemical Enterprises, Ecological Engineering & Environmental Technology, 24(3), 99–108. [CrossRef]
3. Mitryasova, O.; Pohrebennyk, V.; Salamon, I.; Oleksiuk, A.; Mats, A. 2021. Temporal Patterns of Quality Surface Water Changes, Journal of Ecological Engineering, 22(4), 283–295. [CrossRef]
4. Mitryasova, O.; Pohrebennyk, V. 2020. Hydrochemical Indicators of Water System Analysis as Factors of the Environmental Quality State. In: Królczyk G., Wzorek M., Król A., Kochan O., Su J., Kacprzyk J. (eds) Sustainable Production: Novel Trends in Energy, Environment and Material Systems. Studies in Systems, Decision and Control, vol 198. Springer, Cham. 91−104. URL. [CrossRef]
5. Smyrnov, V.; Mitryasova, O.; Salamon, I.; Smyrnova, S.; Chvyr, V.; Mats, A. 2013. The Distribution of Heavy Metals Mobile Forms in the Industrial Urban Agglomeration Soil, Journal of Ecological Engineering, 24(11), 317–327.
6. Ponnusami, A.B.; Sinha, S.; Ashokan, H.; Paul, M.V.; Hariharan, S.P.; Arun, J.; Gopinath, K.P.; Le, Q.H.; Pugazhendhi, A. 2023. Advanced oxidation process (AOP) combined biological process for wastewater treatment: A review on advancements, feasibility and practicability of combined techniques. Environmental Research, 237 (1), URL. [CrossRef]
7. Zver, M.; Dobnik, D.; Zaplotnik, R.; Mozetič, M.; Filipić, A.; Primc, G. 2023. Non-thermal plasma inactivation of viruses in water solutions. Journal of Water Process Engineering, 53, 103839. [CrossRef]
8. Dymaczewski, Z.; Jeż-Walkowiak, J.; Michałkiewicz, M.; Sozański, M.M.; 2019. The importance of the disinfection process in ensuring the microbiological safety of water intended for human consumption, Environmental Protection, 41,1.
9. Fisher, I.; Kastl, G.; Sathasivan, A. 2017. New model of chlorine-wall reaction for simulating chlorine concentration in drinking water distribution systems. Water Research, Vol. 125, 2017, pp. 427–437. [CrossRef]
10. Gelete, G.; Gokcekus, H.; Ozsahin, D.U.; Uzun, B.; Gichamo, T. 2020. Evaluating disinfection techniques of water treatment, Desalination and Water Treatment, 177 408–415.
11. Olsińska, U; 2017, Characteristics of bromate formation prevention methods in water intended for human consumption. Environmental Protection, vol. 39, nr 2, ss. 17–26.
12. Huang, Y.; Zhang, H.; Zamyadi, A.; Andrews, S.; Hofmann, R. 2017. Predicted impact of aeration on toxicity from trihalomethanes and other disinfection byproducts. Journal – American Water Works Association, Vol. 109, No. 10, pp. 13–21. [CrossRef]
13. Selbes, M.; Brown, J.; Lauderdale, C.; Karanfil, T. 2017. Removal of selected C- and N-DBP precursors in biologically active fi lters. Journal – American Water Works Association Vol. 109, No. 3, pp. E73–E84.
14. Wang,Q.; Yang, Z.; Ma, J.; Wang, J.; Wang, L.; Guo, M. 2016. Study on the mechanism of cerium oxide catalytic ozonation for controlling the formation of bromate in drinking water. Desalination and Water Treatment, Vol. 57, No. 33, pp. 15533–15546. [CrossRef]
15. Bromine as a Drinking-water Disinfectant. WHO, Geneva 2018.
16. Foster, J.E. 2017. Plasma-based water purification: Challenges and prospects for the future, Phys Plasmas. 24, 055501. [CrossRef]
17. Malyushevskaya, A.; Koszelnik, P.; Yushchishina, A.; Mitryasova, O.; Mats, A.; Gruca-Rokosz, R. 2023. Eco-Friendly Principles on the Extraction of Humic Acids Intensification from Biosubstrates. J. Ecol. Eng. 24(2), 317−327.
18. Malyushevskaya, A.P. 2011. Properties of starch size treated by an electric discharge in the mode of nonlinear volume cavitation. Surf. Engin. Appl. Electrochem. 47, 555–557. [CrossRef]
19. Malyushevskaya, A.P.; Malyushevskii, P.P. 2008. Electrodischarge cavitation intensification in the processes of fibrous material treatment. Surf. Engin. Appl.Electrochem. 44, 253–256. [CrossRef]
20. Song, K.; Liu, Y.; Umar, A.; Ma, H.; Wang, H. 2024. Ultrasonic cavitation: Tackling organic pollutants in wastewater. Chemosphere, 350, 141024. [CrossRef]
21. Zeghioud, H.; Nguyen-Tri, P.; Khezami, L.; Amrane, A.; Assadi, A.A. 2020. Review on discharge Plasma for water treatment: mechanism, reactor geometries, active species and combined processes. Journal of Water Process Engineering, 38, 101664. [CrossRef]
22. Malyushevskaya, A.P.; Koszelnik, P.; Yushchishina, A.; Mitryasova, O.; Mats, A.; Gruca-Rokosz, R. 2023. Synergy Effect during Water Treatment by Electric Discharge and Chlorination. Environments, 10, 93. [CrossRef]
23. Akdoğan, E.; Şirin, H.T. 2021. Plasma surface modification strategies for the preparation of antibacterial biomaterials: A review of the recent literature. Materials Science and Engineering: C, 131, 112474. Materials Science and Engineering: C, 131, 112474, URL. [CrossRef]
24. Wu, U.; Nyborg, W.L. 2008. Ultrasound, cavitation bubbles and their interaction with cells. Advanced Drug Delivery Reviews, 60(10), 1103−1116. [CrossRef]
25. Lauterborn, W.; Mettin, R. 2015. 3-Acoustic cavitation: bubble dynamics in high-power ultrasonic fields, Editor(s): Juan A. Gallego-Juárez, Karl F. Graff, Power Ultrasonics, Woodhead Publishing, 37−78. [CrossRef]
26. Malyushevskaya, A.P.; Malyushevskij, P.P.; Levda, V.I. 2004. Electroexplosive nonlinear, volumetric cavitation in technological reactors. Part I (Electrodischarge generation of a gas phase − nucleus of cavitation). Electronic processing of materials, 40(1), 46–53.
27. Malyushevskaya, A.P.; Kataev, N.M.; Malyushevsky, P.P. 1999. Establishing the acoustic characteristics of underwater electrical discharges and environments. Electronic Materials Processing, 6, 33−36. (Maliushevskaia, A.P.; Kataev, N.M.; Maliushevskyi, P.P. 1999. Ustanovlenye akustycheskykh kharakterystyk podvodnykh elektrycheskykh razriadov y sredy. Elektronnaia obrabotka materyalov, 6, 33−36).
28. Islam, Md.H.; Pollet, B.G. 2022. Chapter 15 − Acoustic cavitation and sonochemistry in industry: State of the art, Editor(s): Oualid Hamdaoui, Kaouther Kerboua. Energy Aspects of Acoustic Cavitation and Sonochemistry, Elsevier, 265−279. [CrossRef]
29. Vargel, C. 2020. Chapter C.11 − Erosion and cavitation, Editor(s): Christian Vargel. Corrosion of Aluminium (Second Edition), Elsevier, 283−288. [CrossRef]
30. Graff, K.F. 1981. 1 − A History of Ultrasonics, Editor(s): WARREN P. MASON, R.N. THURSTON. Physical Acoustics, Academic Press, 15, 1−97. [CrossRef]
31. Zhou, Ye. 2021. Turbulence theories and statistical closure approaches. Physics Reports, 935, 1−117. [CrossRef]
32. Bulatovic, S.M. 2007. 6 − Summary of the Theoretical Aspects of Flotation, Editor(s): Srdjan M. Bulatovic, Handbook of Flotation Reagents, Elsevier, 87−124. [CrossRef]
33. Crum, L.A. 1984. Acoustic cavitation series: part five rectified diffusion. Ultrasonics, 22(5), 215−223. L. [CrossRef]
34. Frommelt, T.; Schneider, M.; Wixforth, A. 2008. 8 − Acoustic Methods for Manipulating Droplets, Editor(s): Jean Berthier. Micro and Nano Technologies, William Andrew Publishing, 353−388. [CrossRef]
35. Blake, W.K. 2017. Chapter 1 − Hydrodynamically Induced Cavitation and Bubble Noise, Editor(s): William K. Blake. Mechanics of Flow-Induced Sound and Vibration, 2 (Second Edition), Academic Press, 1−80. [CrossRef]
36. Hegedűs, F.; Kalmár, C.; Turányi, T.; Gy, I.; Papp, Z. 2022. Chapter 4 − Sonochemical reactions, when, where and how: Modelling approach, Editor(s): Oualid Hamdaoui, Kaouther Kerboua. Energy Aspects of Acoustic Cavitation and Sonochemistry, Elsevier, 49−77. [CrossRef]
37. Gogate, P.R. 2011. Cavitation in Biotechnology, Editor(s): Murray Moo-Young, Comprehensive Biotechnology (Second Edition), Academic Press, 2011, 957−965. [CrossRef]
38. Ming, Lü.; Zhi, N.; Chunhua, S. 2007. Numerical simulation of cavitation bubble collapse within a droplet. Computers & Fluids, 152, 157−163. [CrossRef]
39. Zularisam, A.W.; Ismailand, A.F.; Sakinah, M. 2010. Application and Challenges of Membrane in Surface Water Treatment. Journal of Applied Sciences, 10. /. [CrossRef]
40. Song, K.; Liu, Y.; Umar, A.; Ma, H.; Wang, H. 2024. Ultrasonic cavitation: Tackling organic pollutants in wastewater. Chemosphere, 350, 141024. [CrossRef]
41. Agarkoti, C.; Gogate, P.R., Pandit, A.B. 2022. Coupling of acoustic/hydrodynamic cavitation with ozone (O3), hydrogen peroxide (H2O2), magnesium oxide (MgO) and manganese dioxide (MnO2) for the effective treatment of CETP effluent. Separation and Purification Technology, 284, 120281. [CrossRef]
42. Dehane, A.; Merouani, S.; Hamdaoui, O. 2021. Effect of carbon tetrachloride (CCl4) sonochemistry on the size of active bubbles for the production of reactive oxygen and chlorine species in acoustic cavitation field. Chemical Engineering Journal, 426, 130251. [CrossRef]
43. Nowak, K.M.; Schwartz, M.R.; Breza, V.R.; Price, R.J. 2022. Sonodynamic therapy: Rapid progress and new opportunities for non-invasive tumor cell killing with sound. Cancer Letters, 532, 215592. [CrossRef]
44. Rooze, J.; Rebrov, E.V.; Schouten, J.C.; Keurentjes, J.T.F. 2013. Dissolved gas and ultrasonic cavitation – A review. Ultrasonics Sonochemistry, 20(1), 1−11. [CrossRef]
45. Yushchyshyna A.N.; Maliushevskii P.P.; Smalko A.A.; Petrichenko L.A.; Tyhonenko S.M. 2002. Iodometric determination of electric discharge volume cavitation. Electronic processing of materials, 2, 76–80.
46. Agarkoti, C.; Thanekar, P.D.; Gogate, P.R. 2021. Cavitation based treatment of industrial wastewater: A critical review focusing on mechanisms, design aspects, operating conditions and application to real effluents. Journal of Environmental Management, 300, 113786. [CrossRef]
47. Gągol, M.; Soltani, R.D.C.; Przyjazny, A.; Boczkaj, G. 2019. Effective degradation of sulfide ions and organic sulfides in cavitation-based advanced oxidation processes (AOPs). Ultrasonics Sonochemistry, 58, 104610. [CrossRef]
48. Ji, H.; Lan, Yu; Nie, S.; Qin, T.; Nie, S.; Zhou, J. 2022. Synergistic effect of hydrodynamic cavitation characteristics of self-excited oscillation cavity for degradation of dye wastewater. Journal of Cleaner Production, 380, 2, 135116. [CrossRef]
49. Kudo, K.; Ito, H.; Ihara, S.; Terato, H. 2015. Quantitative analysis of oxidative DNA damage induced by high-voltage pulsed discharge with cavitation. Journal of Electrostatics, 73, 131−139. [CrossRef]
50. Fuciarelli, A.F.; Sisk, E.C.; Thomas, R.M.; Miller, D.L. 1995. Induction of base damage in DNA solutions by ultrasonic cavitation. Free Radical Biology and Medicine, 18(2), 231−238. [CrossRef]
51. Kamal, H.; Ali, A.; Manickam, S.; Le, C.F. 2023. Impact of cavitation on the structure and functional quality of extracted protein from food sources – An overview. Food Chemistry, 407, 135071. [CrossRef]