Constraint on the Cosmic Curvature in a Model with the Schwarzschild-De Sitter Metric from Supernovae and Gamma-Ray Burst Observational Data

Preprint

Article

Constraint on the Cosmic Curvature in a Model with the Schwarzschild-De Sitter Metric from Supernovae and Gamma-Ray Burst Observational Data

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Vladimir N. Yershov^*

This version is not peer-reviewed

Submitted:

25 June 2024

Posted:

25 June 2024

You are already at the latest version

Alerts

Abstract

In developing his cosmological model of 1917, de Sitter theoretically predicted the phenomenon of cosmological redshift (the de Sitter effect), which he did long before the discovery of this phenomenon in observations. The de Sitter effect is gravitational by its nature, as it is due to differences between the coordinate systems of the observer and the distant source. However, the relationship between the redshift and distance derived from the de Sitter metric is at odds with observations, since this relationship is nonlinear (quadratic) for small redshifts, while the observed relationship between the same quantities is strictly linear. This paper discusses the possibility that cosmological redshift is gravitational by its nature, as in de Sitter’s 1917 model. At the same time, here, as in de Sitter’s model, an elliptical space is used, the main characteristic of which is the identification of its antipodal points. But, unlike de Sitter’s model, here, in order to ensure a strict linear dependence of the redshift on distance, the origin of the reference system is transferred to the observer’s antipodal point. The Schwarzschild-de Sitter metric used in this model allows you to estimate the curvature of space from observational data. To do this, a theoretical Hubble diagram is built within the framework of the model with the Schwarzschild-de Sitter metric, which is compared with observations from the Pantheon+ catalogue of type Ia supernovae and the Amati catalogue of gamma-ray bursts in the redshift range of 0<z<8. As a results of the comparison, the lower estimate of the radius of curvature of space turned out to be quite large: 2.3·1015 Mpc. This means that the observational data indicate a negligible curvature of space.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

The first exact solutions of Einstein’s field equations were spherically symmetric. The Schwarzschild metric [1] corresponds to the following interval in spherical coordinates

r, θ, ϕ

d s^{2} = g_{t t}^{Sch} c^{2} d t^{2} - \frac{d r^{2}}{g_{t t}^{Sch}} - r^{2} (d θ^{2} + {sin}^{2} θ d φ^{2}),

(1)

with its metric coefficient associated with time

g_{t t}^{Sch} = 1 - \frac{r_{g}}{r},

(2)

where

r_{g} = 2 G M / c^{2}

, is the gravitational radius, M is central mass, c is the speed of light, and G is the gravitational constant. This solution is symmetric with respect to the local centre of a spherical mass distribution. Two other exact solutions to Einstein’s field equations were found, one by Einstein [2]:

d s^{2} = c^{2} d t^{2} - d r^{2} - R^{2} {sin}^{2} \frac{r}{R} (d θ^{2} + {sin}^{2} θ d φ^{2})

(3)

and the other by de Sitter [3]:

d s^{2} = {cos}^{2} \frac{r}{R} c^{2} d t^{2} - d r^{2} - R^{2} {sin}^{2} \frac{r}{R} (d θ^{2} + {sin}^{2} θ d φ^{2}) .

(4)

These two solutions are also spherically symmetrical, but their symmetry is not local because the solutions are not related to the preferred center of curvature or the central mass distribution. The curvature

R^{- 2}

is global by definition, so the symmetry of these models is spherical with respect to any arbitrary point in space.

In the Schwarzschild solution (1), the metric coefficient

g_{t t}

implies a transformation (dilation) of time along the radial coordinate r. It follows from the coefficient (2) that this transformation leads to a complete halt in the flow of time at the Schwarzschild radius

r = r_{g}

. A similar cessation of time is inherent in the de Sitter metric (4), since the time coordinate in this metric is also subject to dilatation along the radial coordinate r due to the metric coefficient

g_{t t}^{dS} = {cos}^{2} \frac{r}{R} = {cos}^{2} χ .

(5)

Here the projective angle

χ

is such that

r = R χ .

(6)

Thus, according to the expression (5), time stops at a large distance from the observer, corresponding to

χ = \frac{π}{2}

, when

cos χ = 0

. At closer distances to the observer, time dilation leads to a decrease in the frequencies of the spectral lines of light sources. On the basis of this property, de Sitter theoretically predicted the possibility of cosmological redshift, which was called the de Sitter effect. This prediction was experimentally confirmed ten years later

As can be seen from the comparison of the metrics (1) and (4), the de Sitter effect is gravitational by its nature, since it is caused by the difference between the coordinate systems of the source and the observer in curved spacetime, similar to what happens in the Schwarzschild metric. But, unlike the gravitational redshift in the Schwarzschild metric, the de Sitter gravitational redshift is global and isotropic: its character remains the same, regardless of the choice of the observer’s point in space and the direction of observation.

In Einstein’s metric (3), the metric coefficient associated with time is identical to unity; therefore, in Einstein’s cosmological model, there is no effect of time dilation, and time is universal for all space. Einstein’s metric (3) corresponds to the Riemannian space

S^{3}

with a constant positive curvature

λ = R^{- 2}

, due to the presence of a non-zero density of matter distribution over space,

ρ > 0

. In the case of the de Sitter metric (4),

λ = 3 R^{- 2}

, and

ρ_{0} = 0

(i.e. the space is empty). The distance

d_{o s}

from the observer (o) to the source (s) is measured by the radial coordinate r:

\underset{| r = 0}{o} \overset{r = R χ \equiv d_{o s}}{\to} s \overset{}{\to} a .

(7)

The notation ‘a’ is used here for the observer’s antipodal point in space

S^{3}

. This point corresponds to the projective angle

χ = π

, which marks a very large distance from the observer. In principle, light from the source can reach the observer from this point as well, although in practice this is unlikely due to the presence of horizons, which will be discussed below. In addition, there is a coordinate ambiguity for

χ > π / 2

, as discussed by de Sitter in [3].

To avoid this ambiguity, de Sitter replaced the Riemannian sphere

S^{3}

with an elliptical (projective) space, the main property of which is the identification of its antipodal points (

o \equiv a

). The same elliptical space was used in subsequent cosmological models by Lemaître [4], Tolman [5] and Robertson [6], from where elliptical space transitioned into the standard cosmological model

Λ

CDM of cold dark matter with the cosmological term

Λ

In 1939, R.C. Tolman proposed a general method for finding exact solutions to Einstein’s field equations [7]. One of the new solutions found by Tolman combines the Schwarzschild metric with the de Sitter metric (SdS):

d s^{2} = g_{t t} c^{2} d t^{2} - \frac{d r^{2}}{g_{t t}} - R^{2} {sin}^{2} \frac{r}{R} (d θ^{2} + {sin}^{2} θ d φ^{2}) .

(8)

In this metric, the metric coefficient associated with time

g_{t t} = 1 - \frac{r_{g}}{r} - \frac{r^{2}}{R^{2}}

(9)

includes the curvature parameter

R^{- 2}

. Therefore, the SdS solution can be used to estimate the curvature of space. However, this cannot be done directly, because, as with the Schwarzschild metric, the SdS metric is local and anisotropic. The problem is solved by using the main property of elliptic space, i.e., the connectivity between its antipodal points. In this case, it is also necessary to transfer the origin of the coordinate system from the point where the observer is located to his antipodal point. We will discuss this in Section 2, and then in Section 3 we will estimate the R parameter by calculating the theoretical distance moduli for the SdS metric and comparing them to the distance moduli derived from observations of distant sources such as supernovae and gamma-ray bursts.

2. Materials and Methods

2.1. Elliptical Space

Luminosity distances calculated with the use of the metric coefficient

g_{t t}^{d S} = {cos}^{2} \frac{r}{R}

(10)

in the de Sitter metric are not consistent with observations because here the theoretical relationship between luminosity distances and redshifts is nonlinear (quadratic) near the origin. At the same time, observational data show a strictly linear relationship between luminosity distances and redshifts at low redshifts.

Notwithstanding, one can avoid nonlinearity by moving the origin of the coordinate system from the observer point (o) to the antipodal point (a):

o \overset{d_{s o}}{\leftarrow} s \overset{r = r_{s}}{\leftarrow} \underset{r = 0 |}{a} \equiv o

(11)

[compare with the diagram (7)]. In this coordinate system, distances are calculated as in the normal coordinate system associated with an observer. Here,

r_{s}

is the radial distance between the antipodal point (a) and the source location (s). In order to use the Schwarzschild-de Sitter metric in the calculations, let us bring to bear the main property of elliptic space, the connectivity between its antipodal points (see below). Our goal is to calculate the source-to-observer distance (

d_{s o}

) in the SdS metric and compare it with the redshift z of the source. Using the above notations, we obtain the distance between the observer and his antipodal point in the form

r_{o} = r_{s} + d_{s o} .

(12)

In this configuration, the center of symmetry of the SdS metric is located at the observer’s antipodal point (a). From the observer’s perspective, this point looks like a distant sphere with a large (or infinite) radius. It encompasses the entire celestial sphere (

4 π

steradian) around the observer. In this way, the SdS metric becomes spherically symmetric and isotropic for any arbitrary point in space, provided that the antipodal points are endowed with this metric.

Endowing an elliptical space with the SdS metric is possible if the mathematical identification of distant points is materialised through their physical connectivity by means of a structure with a metric that is an exact solution of Einstein’s field equations. Such an exact solution to the field equations was found in 1935 by Einstein and Rosen [8]. This solution interconnects two different spaces or two different regions of the same space. Therefore, it was called the Einstein-Rosen bridge, but more often it is called the "wormhole" [9]. In the simplest case, the exterior space around a wormhole is described by the Schwarzschild metric or by the Schwarzschild-de Sitter metric (if space has a curvature of

R^{- 2}

). In both metrics, the redshift is gravitational by its nature, so it can be calculated using the metric coefficient (9). Such a calculation within the scheme (11) makes it possible to obtain theoretical cosmological redshifts of distant sources.

As shown by Morris, Thorne, and Yurtsever [10], it is most likely that wormholes are microscopic objects with dimensions of the order of the Planck-Wheeler length,

ℓ_{P} = \sqrt{G ℏ / c^{3}} = 1.62 \cdot 10^{- 33}

cm. This determines the scale of the difference between the idealised (mathematical) elliptical space and its physical counterpart, the space whose antipodal regions are connected through microscopic Einstein-Rosen wormholes.

There is a widespread belief that wormholes are unstable and that even the slightest disturbance associated with the passage of particles of matter or radiation through their throats destroys them. However, most publications on the stability or instability of wormholes are based on the concept of their traversability [12,13,14]. Other publications discuss this topic either in terms of exotic theories of gravity [15], or within the framework of the theory of quantum gravity [16], which does not yet exist. Therefore, such publications can be disregarded.

In classical general relativity, wormholes are the smallest possible objects. As such, they are not traversable and therefore they are stable by definition. Moreover, according to the ideas of Einstein, Rosen, and Wheeler, the answer to the question of the relationship between the discrete (particles of matter) and the continuous (space) lies precisely in the possibility of the existence of microscopic structures within the framework of general relativity. Thus, the question of where matter particles and radiation can come from at all is clarified by the possibility of the existence of microscopic wormholes, proved by Einstein and Rosen.

A static wormhole is described by the Schwarzschild metric (1). But our goal here is to estimate the curvature of space

R^{- 2}

, which is encoded in the Schwarzschild-de Sitter metric (8). Therefore, we use this metric, with its free parameter of R to be evaluated using observations.

The observer is located near one of the throats of the wormhole (hereinafter referred to as the near throat), and the observed source is somewhere between the observer and the far throat of the observer’s antipodal point. According to our choice of coordinate system, any distance is now measured from the origin of that coordinate system (a) to the source (

r_{s}

) or to the observer (

r_{o}

), with the origin being the large antipodal sphere surrounding the observer. Our goal is to find the relationship between the redshift of the source (z) and the distance from the source to the observer:

d_{s o} (z) = r_{o} - r_{s} .

(13)

Any point slightly offset from the observer’s location corresponds to a slightly offset antipodal sphere, virtually indistinguishable from the observer’s antipodal sphere because of the enormous distance

χ = 2 π

. Since each antipodal sphere has a gravitational radius associated with it, the antipodal spheres of neighbouring points form a collective Schwarzschild horizon with a radius

r_{g}

, which corresponds to some (quite large from the observer’s point of view) neighbourhood around the observer.

2.2. Redshift-Distance Relationship

In our scheme (11) there are two unknown distances,

r_{o}

and

r_{s}

. The latter can be replaced by the distance from the source to the observer (13):

d = r_{o} - r_{s}

. The gravitational radius

r_{g}

and the global radius of curvature R are also unknown. Thus, in total, our model has three free parameters:

r_{o}

r_{g}

and R, which should be determined from observations.

Both the source and the observer are in the SdS metric (8) with its redshift-defining coefficient (9). Thus, the redshift of the source with respect to the observer is

z = \sqrt{\frac{g_{t t}^{o}}{g_{t t}^{s}}} - 1

(14)

or, taking into account (9),

{(z + 1)}^{2} = \frac{1 - \frac{r_{g}}{r_{o}} - \frac{r_{o}^{2}}{R^{2}}}{1 - \frac{r_{g}}{r_{s}} - \frac{r_{s}^{2}}{R^{2}}} .

(15)

At this point, we can set the parameter

r_{g}

as the distance unit, thus using it as the unit of distance for our measurements:

r_{g} = 1

. Later, this parameter can be translated into some generally accepted units of distance measurement, for example, in light years or megaparsecs. Thus,

{(1 + z)}^{2} = (1 - r_{o}^{- 1} - r_{o}^{2} R^{- 2}) {(1 - r_{s}^{- 1} - r_{s}^{2} R^{- 2})}^{- 1} .

(16)

From (13)

r_{s} = r_{o} - d_{s o},

(17)

which gives

{(r_{o} - d_{s o})}^{- 1} = 1 - (1 - r_{o}^{- 1} - r_{o}^{2} R^{- 2}) {(1 + z)}^{- 2} - {(r_{o} - d_{s o})}^{2} R^{- 2} .

(18)

Then the distance from the source to the observer is equal to

d_{s o} = r_{o} - {[1 - (1 - r_{o}^{- 1} - r_{o}^{2} R^{- 2}) {(1 + z)}^{- 2} - {(r_{o} - d_{s o})}^{2} R^{- 2}]}^{- 1},

(19)

which is a recursive expression [in units

r_{g}

] to find the distance from the source to the observer as a function of the source redshift. To get the luminosity distance to the source, the expression (19) should be multiplied by the scaling factor

{(1 + z)}^{2}

d_{L} (z) = d_{s o} {(1 + z)}^{2},

(20)

with one of the

(1 + z)

-factors accounting for the loss of luminosity due to the cosmological redshift z, as well as for the lower rate at which the photons reach the observer because of the cosmological time dilatation due to the non-unit metric coefficient

g_{t t}

. The other

(1 + z)

-factor takes into account the distortion of the photon’s trajectory (coefficient

g_{t t}^{- 1}

in the Schwarzschild-de Sitter metric. The expression (20) can be used to determine the free parameters of our model by comparing the theoretical distance moduli

μ = 5 log d_{L} + 25

(21)

(in stellar magnitudes) with the distance moduli obtained from observations. The numerical coefficients in (21) correspond to the luminosity distances

d_{L}

, expressed in Mpc.

2.3. Observational Data

The formulae (19) - (21) describe the theoretical relationship between distances to remote sources and redshifts. Distances are expressed as photometric properties of sources. Thus, the assessment of theoretical parameters should be based on observational photometric data for a wide range of cosmological redshifts. One of the most accurate sets of observational data of this kind is the photometric catalogue Pantheon+ [19,20], which contains data on 1701 Type Ia supernovae in the redshift range of

0 < z_{SN} < 2.26

Yet, this range of redshifts is not wide enough to distinguish cosmological models, since differences between the models are manifested significant only for redshifts

z > 3

. The range of redshifts can be expanded by using additional observational data from the gamma-ray burst (GRB) catalogue compiled by Amati et al. [17]. This catalogue contains 193 moduli of gamma-ray burst distances

μ_{GRB}

, calculated and calibrated using the Amati relation [18]. The range of redshifts covered by this catalogue,

0.03 < z_{GRB} < 8.1

, is significantly wider than in the case of Type Ia supernovae.

The

μ_{GRB}

data are much noisier than

μ_{SNe}

, and they are also slightly biased systematically within the redshift range

0 < z < 0.7

, where all cosmological models and data must coincide. This bias is calculated to be

- 0.258

[mag] by minimising the Pearson’s

χ^{2}

for 27 GRBs within the mentioned redshift range (the GRB data are corrected for this bias).

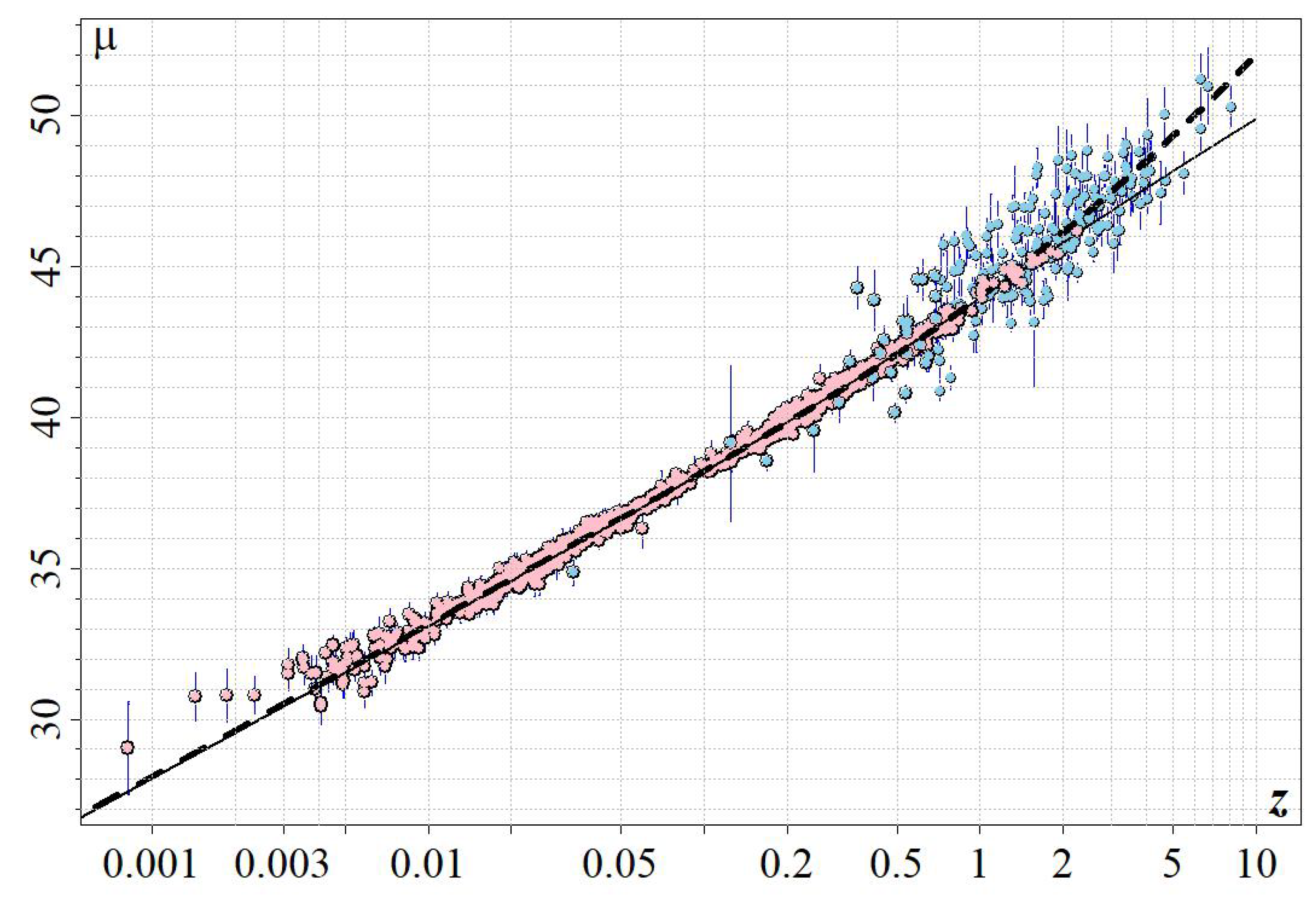
3. Results

Calculations using the formulas (19) - (21) give estimates of the parameters R,

r_{o}

and

r_{g}

within the framework of the SdS model. The parameters are estimated by minimising the

χ^{2}

Pearson criterion and comparing the theoretical and observational distance modules

μ

of the SNe and GRB datasets. This comparison is shown graphically in Figure 1, where the distance moduli of the observational data are shown as pink and blue dots depicting, respectively, the Type Ia supernovae from the Pantheon+ catalogue and the gamma-ray bursts from the Amati dataset. The calculated theoretical distance moduli for the SdS model are shown as a bold dashed curve, while the thin solid curve shows the theoretical distance moduli for the

Λ

CDM cosmological model with its parameters

H_{0} = 73.6 \pm 1.1

[km/s/Mpc],

Ω_{M} = 0.334 \pm 0.018

and

Ω_{k} = 0

, taken from the publication [20], which also used the Pantheon+ catalogue. The match of the

Λ

CDM model with these parameters to the Pantheon+ data corresponds to

χ_{Λ CDM}^{2} = 906.1

The estimated value of the SdS model parameter

R = (1 . 08_{- 0.83}^{+ \infty}) \cdot 10^{5}

, shown in the second column of the Table 1, is derived from 1701 distance moduli for Type Ia supernovae from the Pantheon+ catalogue. The quality of the model fit into the observational data is characterized by the minimum value of the Pearson criterion

χ^{2} = 887.6

(the last row of the Table 1), which indicates a slightly better binding of the theory to the observational data, compared to the

Λ

CDM model. The value

R = 1.08 \cdot 10^{5}

is the lower estimate of the radius of curvature of the universe, since any other value of R greater than

1.08 \cdot 10^{5}

keeps

χ^{2}

at almost the same level – just marginally above

χ_{\min}^{2} = 887.6

The third column of this table shows the same parameters R,

r_{o}

, and

r_{g}

, estimated for the joint data sample (SNe+GRB with 1894 data points spanning the

0 r e d s h i f t < z < 8.1

redshift interval). In this case, the lower limit on the radius of spatial curvature increases to

R = (1 . 17_{- 0.83}^{+ \infty}) \cdot 10^{5}

, which is within the statistical error. The other two parameters (

r_{o}

and

r_{g}

) in the third column of Table 1 do not change compared to their values obtained for the Type Ia supernovae only.

The data from the first row of Table 1 combined with the scale factor

r_{g}

suggest that spatial curvature of the Universe is constrained from above by the value

1 / R^{2} \approx 1.89 \cdot 10^{- 31}

Mpc⁻².

The pink circles in Figure 1 mark the observational distance moduli of Type Ia supernovae from the Pantheon+ catalogue [20], and the blue circles indicate the gamma-ray burst distance moduli, calibrated using the Amati relation [18]. The theoretical distance moduli

μ

found using the formulae (19) - (21) for the model with the SdS metric and minimising the

χ_{SdS}^{2}

criterion are shown as a bold dashed curve, and the theoretical curve for the parameters of the standard cosmological model

Λ

CDM from the [20] publication, is shown as a continuous thin curve.

4. Conclusions

Observations of 1701 Type Ia supernovae collected in the Pantheon+ catalogue, combined with observations of 193 gamma-ray bursts from the Amati catalogue, make it possible to determine the lower possible value of the radius of curvature of the Universe in a cosmological model with the Schwarzschild-de Sitter metric. It turns out to be very large:

2.3 \cdot 10^{15}

Mpc. Moreover, it was not possible to determine the upper limit for this radius using the available observational data. Accordingly, the curvature of space in this model is constrained from above by the value

1.89 \cdot 10^{- 31}

Mpc⁻², the lower bound being zero. That is, the observational data used in this work for these estimates are compatible with the possibility that space is flat.

Funding

This research received no external funding.

Institutional Review Board Statement

Institutional ethical review and approval are not applicable to this study, as it does not involve animals or humans.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used for preparing this manuscript are available at https://pantheonplussh0es.github.io and in the table from the work [17].

Acknowledgments

This research has made use of the following archives: The Pantheon+ Type Ia supernova distance moduli from [19,20] and the gamma-ray burst distance moduli prepared by Amati et al. [17]. I am also acknowledging the use of the cosmoFns software package developed by Andrew Harris and available at the following web page: github.com/cran/cosmoFns. I would like to thank Dr Paul Kuin, Dr Leslie Morrison, Dr Alice Breeveld, Prof. Victor Tostykh and Prof. Mat Page for useful discussions on the matters in this paper.

Conflicts of Interest

The author declares no conflict of interest.

Sample Availability

Samples of the compounds ... are available from the authors.

Abbreviations

The following abbreviations are used in this manuscript:

GRB	gamma-ray burst
JWST	James Webb Space Telescope
$Λ$ CDM	Lambda-Cold-Dark-Matter (cosmological model)
SN	supernova.
dS	de Sitter (metric)
SdS	Schwarzschild-de Sitter (metric)

References

Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitz. Preuss. Akad. Wiss. 1916, 3, 189–196. [Google Scholar]
Einstein, A. Kosmologische betrachtungen zur allgemeinen Relativitätstheorie, Sitz. Preuss.Akad.Wiss Phys. 1917, VL, 142–152. [Google Scholar]
de Sitter, W. On Einstein’s theory of gravitation, and its astronomical consequences. Third paper, MNRAS 1917, 78, 3–28. [Google Scholar] [CrossRef]
Lemaître, G. Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques, Ann. Soc. Sci. Bruxelles A. 1927, 47, 49–59. [Google Scholar]
Tolman, R.C. On the estimation of distances in a curved universe with a non-static line element. Proc. Nat. Acad. Sci. USA 1930, 16, 511–520. [Google Scholar] [CrossRef]
Robertson, H.P. Kinematics and world structure, ApJ 1935, 82, 284–301; ApJ 1936,83, 187–201, 257–271. [CrossRef]
Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, time machines, and the weak energy condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar] [CrossRef] [PubMed]
Fuller, R.W.; Thorne, K.S. Causality and multiply connected space-time. Phys. Rev. 1962, 128, 919–929. [Google Scholar] [CrossRef]
Bronnikov, K.; Lipatova, L.; Novikov, I.; Shatskiy, A. Example of a stable wormhole in general relativity. Grav. Cosmol. 2013, 19, 269–274. [Google Scholar] [CrossRef]
Blázquez-Salcedo, J.-L.; Knoll, C.; Radu, E. Traversable wormholes in Einstein-Dirac-Maxwell theory. Phys. Rev. Lett. 2021, 2021 126, 101102. [Google Scholar] [CrossRef]
Koiran, P. Infall time in the Eddington–Finkelstein metric, with application to Einstein–Rosen bridges. Int. J. Mod. Phys. 2021, 30, 2150106. [Google Scholar] [CrossRef]
Rosa, J.L. Double gravitational layer traversable wormholes in hybrid metric-Palatini gravity. Phys. Rev. D 2022, 104, 064002. [Google Scholar] [CrossRef]
Cox, P.H.; Harms, B.C.; Hou, S. Stability of Einstein-Maxwell-Kalb-Ramond wormholes. Phys. Rev. D 2016, 2016 93, 044014. [Google Scholar] [CrossRef]
Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the Ep-EISO correlation of gamma-ray bursts. MNRAS 2019, 486, L46–L51. [Google Scholar] [CrossRef]
Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the Cosmological Parameters with the E_p,i–E_iso Correlation of Gamma-Ray Bursts. MNRAS 2008, 391, 577–584. [Google Scholar] [CrossRef]
Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; et al. The Pantheon+ Analysis: The Full Dataset and Light-Curve Release. ApJ 2022, 938, 113. [Google Scholar] [CrossRef]
Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; et al. The Pantheon+ Analysis: Cosmological Constraints. ApJ 2022, 938, 110. [Google Scholar] [CrossRef]

Figure 1. Comparison of the theoretical distance moduli

μ

(dashed and solid curves) with the observational distance moduli of the joint data sample, including 1701 Type Ia supernovae from the Pantheon+ catalogue (pink circles) and 193 gamma-ray bursts from the Amati catalogue (blue circles). The bold dashed curve corresponds to the model based on the Schwarzschild-de Sitter metric, and the thin solid curve shows the theoretical distance moduli within the standard

Λ

CDM cosmological model. The abscissa corresponds to the redshifts z of Type Ia supernovae and gamma-ray bursts.

Figure 1. Comparison of the theoretical distance moduli

μ

Λ

CDM cosmological model. The abscissa corresponds to the redshifts z of Type Ia supernovae and gamma-ray bursts.

Table 1. Fitting of the SdS theoretical model to observational data.

Parameter	SNe	SNe+GRB	Units
R	$(1 . 08_{- 0.83}^{+ \infty}) \cdot 10^{5}$	$(1 . 17_{- 0.94}^{+ \infty}) \cdot 10^{5}$	[ $r_{g}$ ]¹
$r_{o} - 1$	$(9.91 \pm 0.15) \cdot 10^{- 8}$	$(9 . 91_{- 0.06}^{+ 0.18}) \cdot 10^{- 8}$	[ $r_{g}$ ]
$r_{g}$	$(2.13 \pm 0.03) \cdot 10^{10}$	$({2.13}_{- 0.04}^{+ 0.03}) \cdot 10^{10}$	[Mpc]
$χ_{\min}^{2}$	887.6	2033.7	–

T¹ Only the lower limit is determinable.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Constraint on the Cosmic Curvature in a Model with the Schwarzschild-De Sitter Metric from Supernovae and Gamma-Ray Burst Observational Data

Abstract

1. Introduction

2. Materials and Methods

2.1. Elliptical Space

2.2. Redshift-Distance Relationship

2.3. Observational Data

3. Results

4. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Sample Availability

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe