Prerpints.org logo
Preprint
Article

Securitising Infrastructure Sustainability: A Case Study on Implementing Resilience Bonds in a China Supply Chain

Altmetrics

Downloads

108

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

25 June 2024

Posted:

26 June 2024

You are already at the latest version

Alerts
Abstract
In response to the escalating climate-related catastrophes of recent decades and their significant impacts on global transportation systems, this study explores the concept of resilience bonds as a novel financial tool for enhancing supply chain sustainability. The research applies a case study from China to demonstrate the application of resilience bonds in funding infrastructure projects that aim to enhance the sustainability and resilience of supply chain networks. The study examines the market mechanisms and valuation models of resilience bonds, assessing their potential to mitigate risks associated with transportation failures and to reduce economic losses from unexpected disruptions. By applying empirical data, the research quantitatively evaluates the impact of resilience bonds on the sustainability and reliability of transportation systems. The findings show that resilience bonds can significantly contribute as a sustainable solution to enhance supply chain resilience and sustainability, offering insightful alternatives for financing resilient infrastructure projects. This study not only supports policymakers, investors, and business leaders in understanding innovative funding mechanisms but also makes a significant contribution to resilience financing for sustainable transportation within supply chains, especially in the context of global disruptions.
Keywords: 
Subject: Business, Economics and Management  -   Finance

1. Introduction

In today’s modern society, physical and social infrastructure networks are crucial for societal functioning. However, these systems face increasing challenges from dynamic environmental changes, especially climate-related catastrophes (Hao et al. 2015). The global insured losses from natural and man-made disasters amounted to USD 89 billion, with over 70% attributed to secondary perils such as severe convective storms and wildfires, which have been prevalent over the past decade; The growing peak-loss potential from primary perils like hurricanes, predicting possible combined annual losses up to USD 300 billion (Bevere and Weigel 2021). Supply chains play a crucial role in today’s competitive business landscape and supporting the operations of various industries. As these chains expand and become more complex, they grow increasingly vulnerable to catastrophic events (Schmitt and Singh 2009; Wagner and Neshat 2010). Notably, around 43% of businesses rely on 20 to 100 key suppliers, making even minor disruptions significant (Zurich 2016). For example, after the 9/11 terrorist attacks, Chrysler switched from air to road transport for critical components from Virginia to Mexico (Erlinghagen and Markard 2012). Such catastrophic disruptions, including operational errors, goods shortages, and natural or human-made disasters, can cause unforeseeable financial losses. They may disrupt supply chain links, necessitating immediate rerouting and imposing instant adverse effects on businesses (Ishfaq 2012). Furthermore, the risks associated with such disruptions often exceed what forecasts can predict, leading to higher costs and poorer services if logistics operations are unprepared for contingent disruptions (Barad and Sapir 2003).
As Thacker et al. (2019) highlight that infrastructure systems constitute the backbone of any nation. Enhancing the resilience of nations and communities against catastrophes is crucial and has become a main point in the sustainability development of international strategies by the United Nations. Prioritising the resilience of infrastructure systems is essential to mitigate unforeseen economic losses, as opposed to only responding to inevitable catastrophes. As per Berkeley and Wallace (2010), resilient infrastructure should not only diminish the impact of catastrophic events but also accelerate recovery. It should maintain its core functions despite internal or external risks. Thus, building a resilient supply chain, which can rapidly respond to unexpected losses and enable quick business recovery, is a key goal for suppliers and customers (Wu et al. 2007). As Rice and Caniato (2003) state that investing in infrastructure projects is an effective way to foster resilience in supply chain networks. However, infrastructure development relies heavily on government support (Gichoya 2005). Public resources contain high opportunity costs, which imposes many restrictions on the usage. As a result, turning to capital markets is increasingly seen as a dynamic and innovative financing approach. For instance, in 2016, the UK government’s infrastructure investment is £18.9 billion, of which £10.3 billion of the funds derived from market sector investment.
The potential of bonds to shift financial leverage from solely public investments to public-private partnerships is significant. According to Orr and Kennedy (2008) and Walter (2016), investments from the private sector, including both private and institutional investors are gaining recognition as crucial partners alongside governments in supplying the capital for financing infrastructure projects. Applying bonds could create a novel infrastructure financing stream to combine public and private sectors, potentially adaptable for supporting supply chains against disasters. Resilience bonds are proposed by Re:Focus (2015), which is tailored to fund eligible resilient infrastructure projects. The bond is aiming to escalating demand for investment in resilient projects, such as enhancing supply chain resilience and emphasising the importance of these investments to help ease the pressure on public resources. The case study in this paper demonstrate the implementation of resilience bonds within a China-based supply chain to enhance infrastructure resilience against catastrophic events. Using empirical data from Willis Tower Watson (Shanghai), the study analyses the application of resilience bonds to fund the enhancement of intermodal transportation ports, that are designed to withstand and recover from severe disruptions.
This paper contributes significantly to the literature on financing supply chain resilience. It introduces the innovative concept of resilience bonds and bridges the gap in existing research by providing a practical financial solution to the often underfunded area of sustainable infrastructure development. The paper’s exploration of the market mechanism and valuation model for resilience bonds is particularly noteworthy, offering new insights into how these bonds can mitigate risks associated with supply chain disruption. Moreover, the case study from China adds empirical weight to the theoretical framework, illustrating the practical application and effectiveness of resilience bonds in real-world scenarios. This research opens new avenues for further exploration in the fields of sustainable finance in supply chain networks, and offering critical guidance for decision-makers on implementing these financial tools to bolster supply chain resilience.

2. Literature Review

In recent years, global market competition between enterprises has gradually shifted to competition between supply chains, since every industry requires support from operation chains behind the business. Supply chains allow entities to share logistics activities with different partners around the world. Christopher (2016) state that supply chain networking is a business integration that will add value to raw materials and transfer them to end-users. It secures the supply and demand and helps businesses be more competitive in the market. However, supply chain management has also become increasingly vulnerable (Jayaram et al. 2000; Warren and Hutchinson 2000). Zsidisin et al. (2005) showed that, as modern supply chains have grown increasingly complex, enterprises are becoming more aware of the unforeseen disruptions. Although these disruptions are statistically rare, their occurrence can have significant impacts on supply chain operations and affect customer demand.

2.1. Vulnerability in Supply Chains: The Need for Resilience

Unforeseen events expose vulnerabilities in supply chain networks because catastrophic events often occur in clusters, showing spatial or temporal correlations, or both.(Hao et al. 2015). Some supply chain infrastructures are overexposed and underinsured against unforeseen catastrophe risks, so the question of how to prepare the supply chain against disruptions has gained much attention. As supply chain complexity and distance grow, so does the uncertainty level with regard to the intermodal transportation supply network. The rationale behind the intermodal transport, as defined by the European Conference of Ministers of Transport (ECMT), involves transferring goods using at least two different transport modes within the same loading unit for logistics (Arnold et al. 2004). Disruptions at key intermodal ports can cascade, impacting entire supply chains and delaying deliveries, thereby affecting business competitiveness. PwC’s research indicates that enhancing supply chain resilience can lead to a 7% increase in stock prices and significant market share gains (PwC 2016). Various strategies have emerged to reinforce supply chains against catastrophic disruptions, such as Global (2007) advocates that just-in-time inventory and other lean manufacturing techniques may reduce the supply chain risk significantly; Li and Wang (2015) also show that the most common way for some businesses is to continuously hold buffer stock and keep several alternative suppliers in case one is disrupted by catastrophe losses. However, strategies like continuous inventory or over-reliance on alternative suppliers can be costly and not always optimal (Christopher and Lee 2004; Tomlin 2006). In a dynamic world, maintaining an efficient and effective supply chain is challenging which often vulnerable by unforeseen disruptions (Christopher and Peck 2004). Focusing on resilience is crucial in reducing failure probabilities and recovery times since as it is more cost-effective than post-disaster rebuilding (Bruneau et al. 2003; Mottahedi et al. 2021). A resilient supply chain is defined by its readiness for disruptions and ability to maintain continuity in goods movement (Sawyerr and Harrison 2020). The ports are important to many communities, which are critical infrastructure and can be severely affected by catastrophes. Traditional logistics are inadequate for modern global supply chains, the demand of resilient infrastructure projects like intermodal transportation port upgrades is increasing (Ishfaq and Sox 2010). Thus, enhancing port resiliency is a priority for both private and public sectors, especially in the European Union (Bontekoning and Priemus 2004). With infrastructure systems often exposed to catastrophe risks, investment in resilient supply chain infrastructure is essential, though it requires significant funding often beyond what public sectors can provide, which requiring the involvement of private investment.

2.2. The Effectiveness of Implementing Resilience Bond

Although many approaches and tools have been developed for supply chain resilience, researchers need to look beyond these methods and prioritise considering the financing of resilient infrastructure projects. Bonds are widely used in fixed-income investment to allow investor loans to corporations, states or governments. The bond principal from investors is borrowed for a pre-defined period, investors receive fixed interest payments every year and get back the principal of the bond until the bond matures. Whereas the newer resilience bond is a financial tool designed to transfer risks to the capital market and provide both financial coverage and investment for resilient infrastructure projects (Vaijhala and Rhodes 2018). Resilience bond, as a recent innovation in the bond market represent a financial arrangement where investors lend money to an issuer in exchange for regular fixed interest payments. The bond is instrumental for (re)insurers in complementing traditional markets, effectively transferring risk to capital market investors. Besides, resilience bond uniquely combines insurance, rebate, and resilient project support functionalities, it differentiates by funding resilient infrastructure projects via “rebate” thereby proactively mitigating risks. The rebate mechanism directing the value from the mitigated risks back into supporting the infrastructure projects (Re:Focus 2015).
Trade globalisation brings more pressures to businesses to deliver supplies better than their competitors. A resilient supply chain is likely to raise customer confidence as well as reduce the risk of unforeseen losses. An upgrading of resilient infrastructure project therefore has more advantages, with its flexibility and efficiency in freight shipments, than a traditional logistics transport port. For example, upgrading the traditional port into a modern intermodal transportation port. BLG Logistics group in Bremen is one of the most advanced logistics parks in the world, and is ideally linked to European road, rail and waterway (Waters 2003). Freight shipments through the BLG intermodal transportation port from countries are transferred using different transport modes with several combinations. It not only provides flexibility to entities but also brings resilience to the supply chain network. Besides, by applying the intermodal service, the goods will be handled by standard containers, thus mitigating the movement time and cost. However, catastrophic disruptions have a low probability of happening, when they do occur, they significantly break the connection of the supply chain system and bring unpredictable losses for businesses. Shippers and carriers may prefer to seek financial protection from insurance companies to offset the missing market opportunities, and take on the risk of losing money. Resilience bonds could be considered as an effective financial tool to share the risks in the capital market and mitigate the risk of collapse to the supply chain by offering funds for the enhancement to port’s infrastructure in advance.
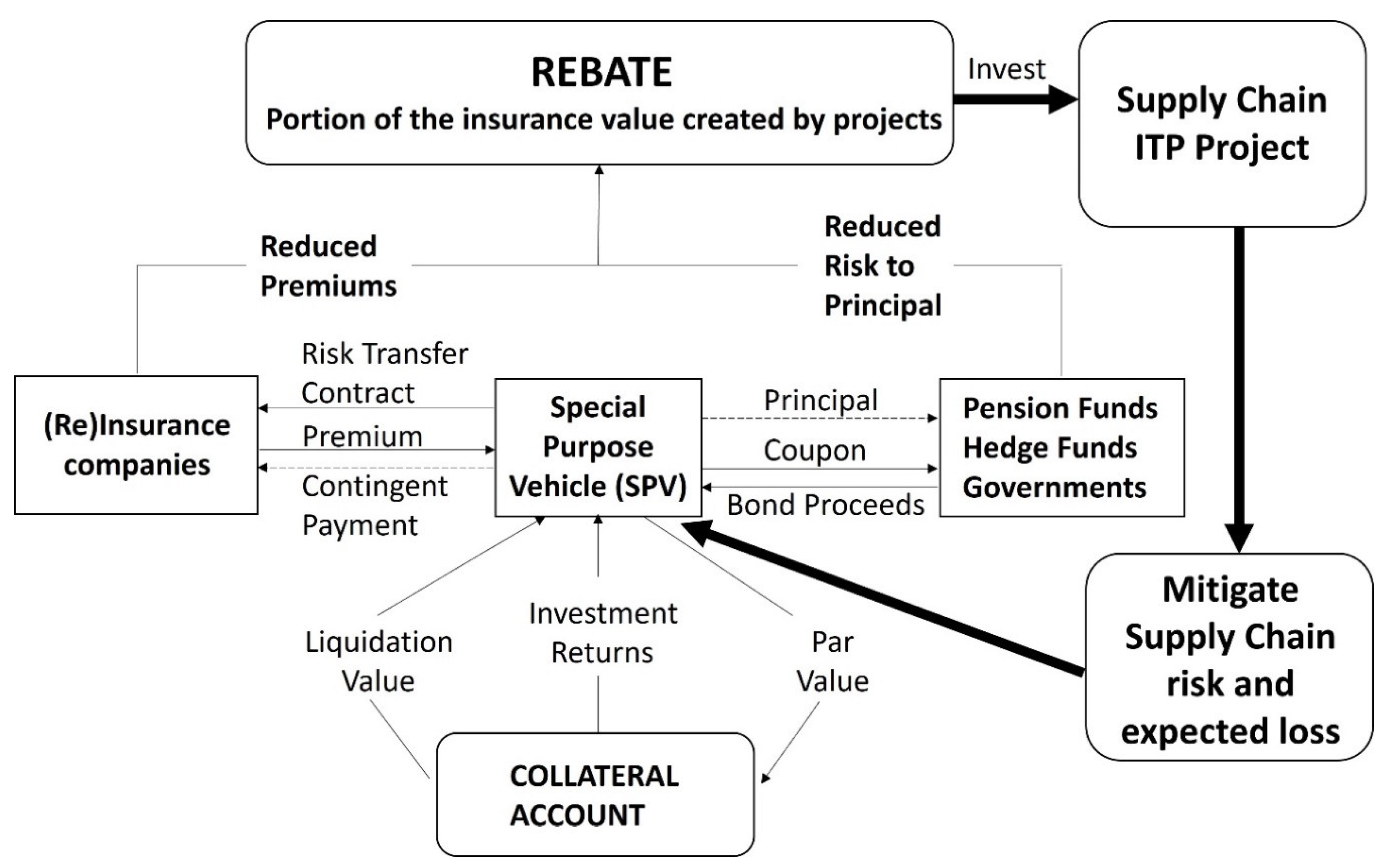
According to Re:Focus (2015), the payout mechanism of a resilience bond is based on a predefined set of resilience objectives that the issuer must meet to qualify for payment. If these objectives are not achieved, the payout may be reduced or withheld entirely. The payout can be either a fixed or variable coupon, depending on the specific terms outlined in the bond agreement. A unique feature of the resilience bond is that it generates rebates based on the overall risk reduction achieved by the resilient projects, for example, an upgrade of intermodal transportation port (IPT) project. Specifically, a designated third party predicts and quantifies the mitigated risks resulting from the ITP project. The assessed economic value of these reduced risks is then deducted from the premium and principal, transforming the deducted amount into a rebate. This rebate is reinvested into the ITP project during the initial construction stages. This mechanism ensures that the value from risk mitigation is immediately reinvested, enhancing the overall effectiveness and resilience of the system. (Vajjhala 2015).
As shown in Figure 1, the mechanism is designed to incentivise private issuers to enhance supply chain resilience while also attracting both public and private investors who are interested in collaborating on socially responsible projects. This approach aims to foster partnerships that generate positive social and environmental impacts. These projects have the potential to yield significant social and environmental benefits, making them appealing investment opportunities. (Vaijhala and Rhodes 2018). Conventional bonds typically have a maturity period of one to three years, which is also suitable for resilience bonds, aligning well with the construction timelines of resilient projects. However, some projects may require longer durations. Therefore, resilience bonds can be issued in multiple tranches to accommodate flexible construction periods. Continuous evaluation of risk mitigation efforts allows for the distribution of rebates, which can be reinvested into the project, further supporting its progression and ensuring sustained enhancement of resilience.

3. Materials and Methods

Valuing the implementation of resilience bonds for upgrading an Intermodal Transportation Port (ITP) project within a China-based supply chain involves several key steps. These steps ensure a comprehensive assessment of the project’s effectiveness and the accurate valuation of the resilience bonds. Initially, the effectiveness of the ITP project upgrade on the entire supply chain is measured. This involves simulating and calculating the economic losses from disruptions at specific nodes within the supply chain. It is assumed that upgrading the ITP project will effectively mitigate these anticipated losses. Following this, a compound Poisson process is utilised to represent the economic impact of such catastrophic disruptions. This process helps simulate and calculate the economic losses at specific nodes in the supply chain, providing a clearer picture of potential financial impacts. Then, a stochastic model is employed to analyse time-series data, assess the instantaneous interest rate, and simulate random catastrophic supply chain disruptions. This valuation model serves as a practical tool for decision-makers, assisting in determining the fair market price for resilience bonds. By offering a clearer understanding of associated risks and returns, this mechanism can enhance the bonds’ attractiveness to investors. To simplify the valuation of the supply chain resilience bond, the study considers it as a zero-coupon bond. Zero-coupon bonds, typically traded below their face value, present a viable option for funding public resilience projects against such disruptions. This simplification is particularly useful in the context of supply chain disruption events, where rapid assessment and decision-making are crucial. In summary, the main components for valuing the supply chain resilience bond include the effectiveness of the resilient infrastructure project, the dynamic processes of expected losses from catastrophic events and the dynamic interest rates.

3.1. Measurement of the Effectiveness of Resilient Infrastructure Project

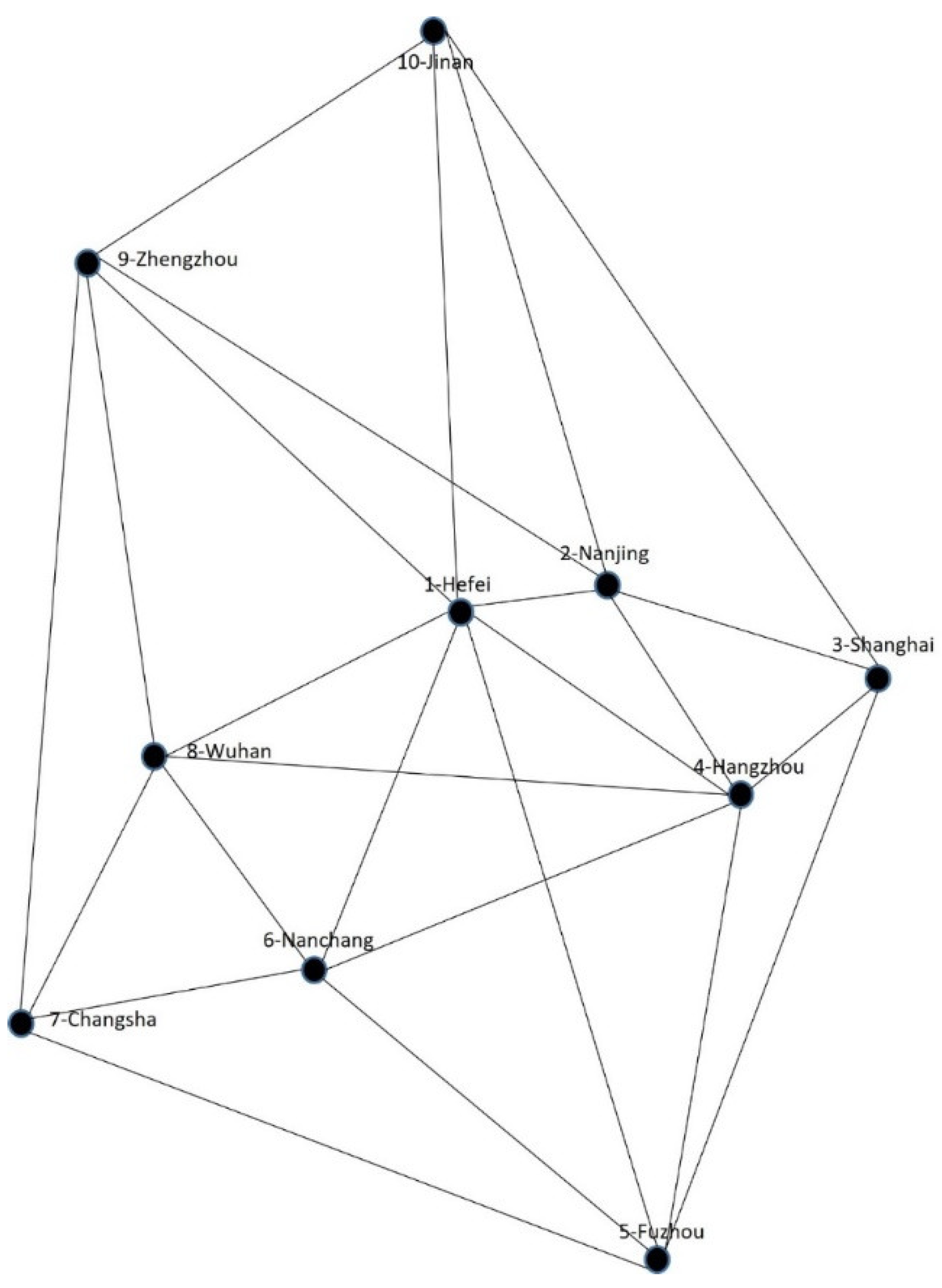
A resilience bond will only be issued for an eligible project that can be specified to offer potential risk reductions to the whole system. As per Murray-Tuite (2008), resilience can be measured as the comparison between a system with or without a strategy which brings the ratio of applying a strategy with no action taken case. The value of the resilience bond is largely in the assessment of the percentage of risk and cost mitigated by the eligible project to the whole system. According to Re:Focus (2015), the resilience bond is modelled using two scenarios to estimate the risk reduction: pre-resilient projects and post-resilient projects. Therefore, resilience in this study understood as the percentage of recovered performance due to the intermodal transportation port (ITP) project with respect to the performance without the ITP project. An impact parameter is proposed to represent the change with and without the upgrade of an ITP project. In this measurement, we simulate the cities in China as the supply chain nodes based on the historical data from Willis Tower Watson (Shanghai) and 1-tonne of general goods will be moved from Changsha (7) to Shanghai (3) within the supply chain network between several cities in China, which includes 10 node cities and 25 links.
Preprints 110291 g002
Figure 2. Simulation of supply chain network in China.
Figure 2. Simulation of supply chain network in China.
Preprints 110291 g002
Goods will be transported using standard containers, with a set transfer time of 1 hour and an assumed transfer cost of 200 yuan by Ishfaq (2012). This study considers only two transportation modes: rail and road. Any node on the route that involves both modes and requires an interchange during transit is treated as a node in an intermodal transportation port (ITP). Subsequently, we simulate and test the supply network under a catastrophic event that disconnects the ITP. Such an event can increase the cost of goods movement due to delays, damage to goods, or additional rerouting and mode-changing expenses. The effectiveness measure is based on the cost mitigated by the ITP node, comparing the total cost of moving 1 tonne of general goods from the original node to the destination with and without the target upgrade of ITP node.
All costs will be computed and compared based on real-time data in 2018 from the official website. The data include price and distance of every path in the supply chain network indicated by roadway p r d / d r d and railway p r l / d r l . To satisfy the common selection of route, we assume that logistics companies will choose the cheapest cost combination of transport modes to move goods. The cheapest cost path of moving 1-tonne of general goods using any transport modes will be calculated to fulfil the function:
C r d = f ( p r d , d r d ) C r l = f ( p r l , d r l ) C d e c i s i o n = m i n   C r d , C r l ,  
Where
C r d / C r l is the cost of using roadway / railway
p r d / d r d is the price / distance of using roadway
p r l / d r l is the price / distance of using railway
C d e c i s i o n is the choice to use roadway or railway transport based on cost comparison.
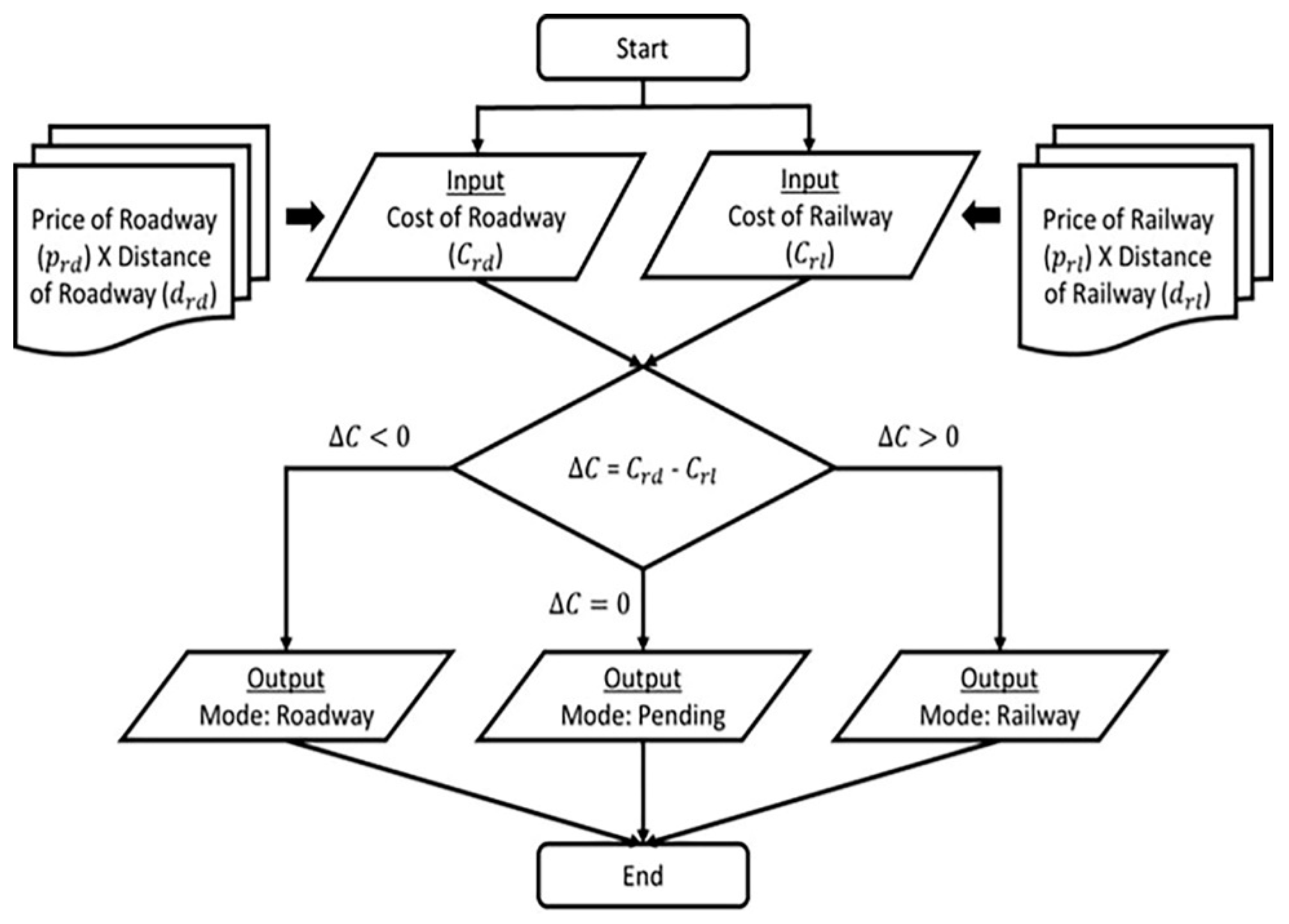
To determine the shortest path, Dijkstra’s algorithm is used to find the minimum weight from a selected node to every other node in the graph. The data structure will be evaluated and compared for each node reachable from the initial node. The costs of railway and roadway are weighted on the graph, with these weights representing the distance along the edges. The cheapest cost and transport mode for each path within the supply chain network will then be selected using the flowchart shown in Figure 3.
In the next step, the cheapest combination route to move 1-tonne of general goods from Changsha (7) to Shanghai (3) will be found based on our database. According to Zhang (2012), the shortest path problem can be applied to find a path that contains a minimum weight sum between two known nodes. The weight in the problem can be replaced as distance, flux and cost, and so forth. Therefore, we first build up a supply network, then apply the data to process the selection through the following function:
C i j = m i n C i j , C i s + C s j , i , j = 1,2 , 3 , … , 10
where
C i s a n d C s j represent transport cost for each path between i,j.
As Murray-Tuite (2008) notes that resilience has not been strictly defined or measured in the transportation field. To address this, they propose the Measures of Effectiveness (MOEs) method, which quantifies the impact by comparing scenarios with and without specific actions. To address the effectiveness of an upgrade ITP project, this study quantifies the impact by comparing scenarios with and without specific actions. Accordingly, the effectiveness parameter (ѯ), which indicates the effect of upgrading ITP project to the supply network.
E f f e c t i v e n e s s ѯ = C o s t n o − I T P − C o s t I T P C o s t n o − I T P
where
C o s t I T P is the cost of goods movement with an upgrade of ITP project;
C o s t n o − I T P is the cost of goods movement without an upgrade of ITP project.

3.2. Dynamic Modeling of Expected Losses and Interest Rate

In this section, the methodology integrates the approach for modeling expected losses, the interest rate model, and the subsequent payoff function to form a cohesive analysis. Dynamic losses in supply chains are influenced by factors such as disruptions caused by the disconnection between nodes due to catastrophic events. Modeling these dynamic losses and subtracting the mitigated losses from an upgrading ITP project are crucial components of the supply chain resilience bond. This feature sets resilience bonds apart from other financial instruments, as it uniquely quantifies and incorporates the benefits of enhanced infrastructure resilience into the bond’s valuation. To value the resilience bond, the process of losses will be assumed to follow the compound Poisson process, which considers the probability of occurrence and severity of future catastrophic disruptions based on historical data.
The dynamic process can be defined by the following
L T = ∑ t j < τ X j = ∑ j = 1 N t X j ,
where
L T is the dynamic loss, L T = 0 when N t = 0 ;
N t is the random variable number of losses event up to time t, ( t ∈ [ 0 , T ] ) ;
X j is the losses size of the jth event, which is independent to N t .
The Poisson process is applied to indicate the dynamic losses process, where N = N t , ( 0 < t < T ) . Following the Poisson law, catastrophic events X 1 , X 2 , … , X j are counting by N t with the intensity of λ . All catastrophic event losses are non-negative, independent and identically distributed values [ X j ] , with no events occurring at the same time. Let the distribution function F(x) represent the distribution of X 1 , X 2 , … , X j , where F x = P ( X j < x ) . Then, the historical economic losses data from Willis Tower Watson (Shanghai) will be fitted by heavy-tailed distributions to the calibration of the distortion operator.
Simultaneously, the dynamic interest rate is another variable needing to be defined. We assume the dynamic movement of interest rates follows the Wiener process, which describes continuous-time and independent incremental stochastic processes, also known as Brownian motion in quantitative finance. According to Brigo and Mercurio (2007), this study define the dynamic interest rate by applying the Cox-Ingersoll-Ross (CIR) model under the risk-neutral measure, Q, expressed as:
d r t = k θ − r t d t + σ r t d W t
where
r t is dynamic interest rate;
W t is a Wiener process.
k θ − r t is the drift factor, where k is the speed of reverting to the average rate θ ; σ is volatility; k , θ , σ are all positive constant and satisfy the condition 2 k θ ≥ σ 2 ;
An upgraded Intermodal Transportation Port (ITP) project is expected to enhance supply chain resilience and reduce the aggregate losses ( L T ) from catastrophic events based on the effectiveness ( ѯ ) of the project. Consequently, the pre-defined contract terms follow the below payoff function, which considers whether the aggregate losses have surpassed the predefined threshold (D).
P R B = F ρ       i f   L T − ѯ L T > D       b o n d   i s   t r i g g e r e d ,         F                   i f   L T − ѯ L T ≤ D       o t h e r w i s e ,                                
where
P R B – is the payoff amount of resilience bond at maturity;
ρ – represents the proportion of the face value repaid to investors;
F – is the face value of the resilience bond;
L T – is aggregate losses;
D – represents trigger value;
ѯ – is the impact of the resilient project, where 0 < ѯ < 1 .
In sum, the prices of the zero-coupon resilience bond at maturity T under the risk-neutralised pricing measure Q, is given by
V t = E Q e − ∫ t T r s d s P R B T = E Q e − ∫ t T r s d s • E Q P R B T
The expectation of risk-neutral pricing measure is equal to the price of a pure-discount bond
E Q e − ∫ t T r s d s = B C I R t , T
Then,
V t = E Q e − ∫ t T r s d s P R B T
= B C I R ( t , T ) • F • ( E t P C T )
= B C I R t , T • ρ • F • P L − ѯ L > D + F • P L − ѯ L ≤ D
= B C I R t , T • F • [ ρ • ( 1 − P L − ѯ L ≤ D ) + P L − ѯ L ≤ D ]
Therefore, the final resilience bond valuation model becomes
B C I R t , T • F • ρ + 1 − ρ • F l T , L − ѯ L ≤ D ,
where
ρ – is the proportion of the face value repaid to investors;
F – is face value of resilience bond;
B C I R t , T – is the dynamic interest rate by using the CIR model;
F l T , L − ѯ L ≤ D is the distribution of the losses less than or equal to threshold D.

4. Data Description

This study explores the implementation of resilience bonds as a financial tool to enhance infrastructure sustainability within a China-based supply chain. To analyse the economic impact and effectiveness of these bonds, comprehensive data were collected from the Logistics, China Federation of ‘Freight Index’ and the official website for railway pricing in China. The 2018 data on road and rail transportation costs and distances between key cities provided a robust foundation for simulating potential disruptions and evaluating the cost mitigation benefits of resilience bonds. This methodological approach ensures accurate and reliable insights into the logistics and financial mechanisms that can support resilient infrastructure development.
Table 1. Road distance/ price of 1-tonne of general goods movement between node cities (2018).
Table 1. Road distance/ price of 1-tonne of general goods movement between node cities (2018).
Km/
Yuan/Ton		 Shang Hai (3) Hang Zhou (4) Nan Jing (2) Ji Nan (10) Fu Zhou (5) He Fei (1) Nan Chang (6) Wu Han (8) Chang Sha (7) Zheng Zhou (9)
Shang Hai (3) N/A 198/84 313/113 824/226 868/283 N/A N/A N/A N/A N/A
Hang Zhou (4) 197/79 N/A 315/114 N/A 686/294 427/142 557/189 746/331 N/A N/A
Nan Jing (2) 306/107 316/109 N/A 645/174 N/A 216/79 N/A N/A N/A 673/186
Ji Nan (10) 827/252 N/A 647/244 N/A N/A 672/179 N/A N/A N/A 471/177
Fu Zhou (5) 870/232 679/109 N/A N/A N/A 911/324 596/205 N/A 891/328 N/A
He Fei (1) N/A 411/136 217/82 658/126 907/264 N/A 514/151 458/149 N/A 596/164
Nan Chang (6) N/A 558/159 N/A N/A 595/216 487/149 N/A 377/110 345/127 N/A
Wu Han (8) N/A 746/191 N/A N/A N/A 458/113 377/144 N/A 385/148 550/133
Chang Sha (7) N/A N/A N/A N/A 902/236 N/A 399/144 391/108 N/A 851/185
Zheng Zhou (9) N/A N/A 671/169 468/147 N/A 604/162 N/A 550/165 853/268 N/A
Table 2. Rail distance/price of 1-tonne of general goods movement between node cities (2018).
Table 2. Rail distance/price of 1-tonne of general goods movement between node cities (2018).
Km/
Yuan/Ton		 Shang Hai (3) Hang Zhou (4) Nan Jing (2) Ji Nan (10) Fu Zhou (5) He Fei (1) Nan Chang (6) Wu Han (8) Chang Sha (7) Zheng Zhou (9)
Shang Hai (3) N/A 202/108 301/124 968/241 584/240 N/A N/A N/A N/A N/A
Hang Zhou (4) 202/108 N/A 488/143 N/A 473/204 344/155 566/184 638/217 N/A N/A
Nan Jing (2) 301/124 429/143 N/A 667/188 N/A 156/120 N/A N/A N/A 697/197
Ji Nan (10) 968/241 N/A 667/188 N/A N/A 614/183 N/A N/A N/A 668/168
Fu Zhou (5) 612/240 455/204 N/A N/A N/A 492/265 581/169 N/A 518/232 N/A
He Fei (1) N/A 445/155 254/120 614/183 494/265 N/A 462/153 608/168 N/A 602/180
Nan Chang (6) N/A 764/185 N/A N/A 581/169 462/153 N/A 344/136 419/145 N/A
Wu Han (8) N/A 411/217 N/A N/A N/A 360/168 344/136 N/A 398/146 585/161
Chang Sha (7) N/A N/A N/A N/A 410/232 N/A 419/145 262/146 N/A 898/235
Zheng Zhou (9) N/A N/A 697/197 668/168 N/A 730/180 N/A 580/161 898/235 N/A
Unforeseen catastrophic disruptions have led to unpredictable economic losses for supply chain businesses, resulting in insured claims for (re)insurance companies. The historical dataset used in this study on these supply chain disruption claims were provided by Willis Tower Watson (Shanghai). Typically, insurance companies retain client data for three to four years, using this information to evaluate premiums. Our dataset comprises 691 insurance claims, detailing the dates, events, and amounts of losses from 2015 to 2018. By analysing this historical data and estimating the frequency and severity of events, we developed the supply chain resilience bond valuation model. The claim amounts in the dataset were adjusted to 2018 price levels using the consumer price index.
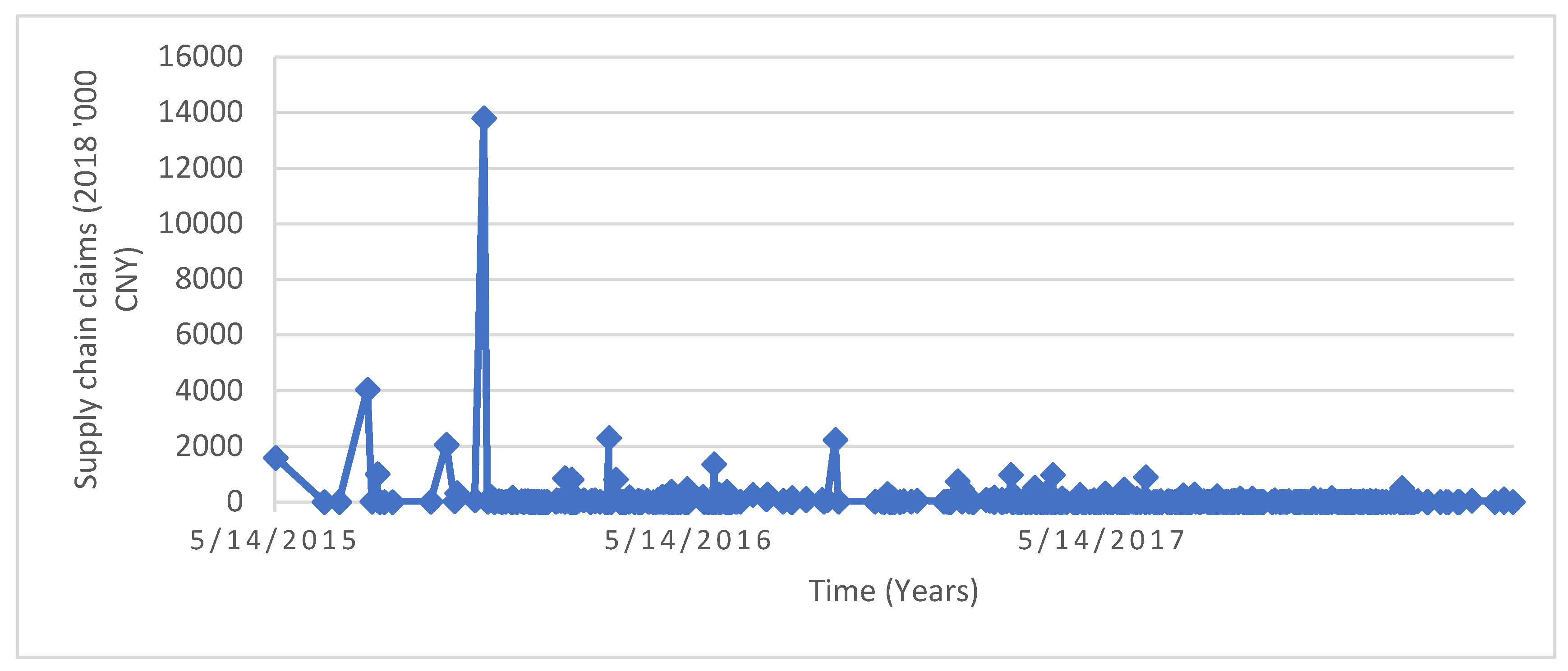
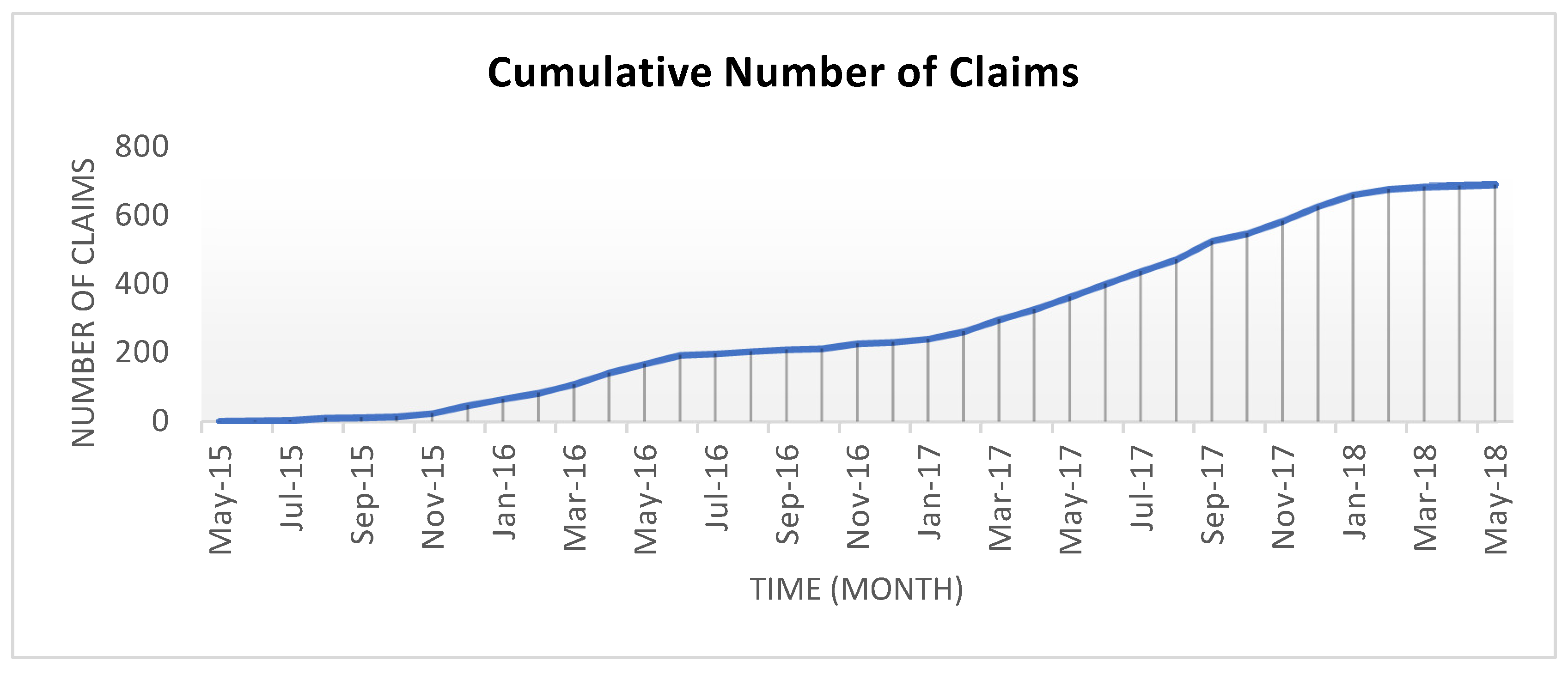
Figure 4 depicts the supply chain disruption claims between 14 May 2015 and 14 March 2018 from Willis Tower Watson (Shanghai). We later use the historical claims dataset to simulate the distribution of the consequences of the supply chain disruptions to define the aggregate claim severity X j .
The Poisson process serves as a versatile model for forecasting the expected number of future failure events, such as catastrophic disruptions. Historical monthly claims data were employed to simulate the claim arrival process, denoted as N ( t ) . Due to the irregular pattern of catastrophic disruptions observed, it was challenging to define their occurrence trend clearly. Consequently, it was assumed that the occurrence of catastrophic disruptions follows a homogeneous Poisson process with a monthly intensity of λ = 18.6486 . To define the distribution of claim severity ( X j ) , the historical data were calibrated to several distributions: Lognormal, Inverse Gaussian, Generalised Extreme Value, and Weibull. Then, the Kolmogorov-Smirnov, Anderson-Darling, and Chi-Squared tests were subsequently employed to evaluate the goodness of fit for each distribution. The Lognormal distribution emerged as the most suitable model, providing the best fit for describing the supply chain insurance claims data from Willis Tower Watson (Shanghai). The parameters derived from this distribution are σ=1.8568, μ=1.8542. Additionally, the interest rate process was modelled using the Cox–Ingersoll–Ross (CIR) framework. To calibrate the stochastic interest rate parameters, the 12-month LIBOR historical rates were utilised to calculate the price of the resilience bond. Although LIBOR ceased to be used at the beginning of 2022, it is applied in this paper to align with the claim dataset, which predates LIBOR’s discontinuation. The calibrated parameters include a reverting speed of k = 0.2124 , an average interest rate θ = 1.0847 , and the volatility σ = 42.0791 % . Using historical LIBOR rates allows the study to accurately model the financial environment during the period under investigation, ensuring that the resilience bond’s pricing and its impact on infrastructure sustainability are appropriately captured. Therefore, the initial value will be set as r 0 = 1.13 % that corresponds to the actual LIBOR rate in December 2011 and the market price of risk γ r was a constant -0.01.

5. Empirical Results and Analysis

To evaluate the effectiveness of the resilient infrastructure project, we conducted simulations to compare the economic costs with and without the upgrading of Intermodal Transportation Port (ITP) project. The first step involved calculating the most cost-effective transport mode between each pair of node cities, as detailed below:
Table 3. The cheapest transport mode between node cities Note: (Rail = rl, Road = rd).
Table 3. The cheapest transport mode between node cities Note: (Rail = rl, Road = rd).
Yuan/
Mode		 Shang Hai (3) Hang Zhou (4) Nan Jing (2) Ji Nan (10) Fu Zhou (5) He Fei (1) Nan Chang (6) Wu Han (8) Chang Sha (7) Zheng Zhou (9)
Shang Hai (3) N/A 16,632/
rd		 35,369
/rd		 186,224/
rd		 140,102/rl N/A N/A N/A N/A N/A
Hang Zhou (4) 15,563/
rd		 N/A 35,910/
rd		 N/A 96,303/
rl		 53,286/
rl		 104,370/
rl		 138,382/rl N/A N/A
Nan Jing (2) 32,742/
rd		 34,444/
rd		 N/A 112,230/
rd		 N/A 17,064/
rd		 N/A N/A N/A 125,178/
rd
Ji Nan (10) 208,404/rd N/A 125,596/
rl		 N/A N/A 112,055/rl N/A N/A N/A 83,367/
rd
Fu Zhou (5) 146,819/rl 92,638/
rl		 N/A N/A N/A 130,134/rl 98,015/
rl		 N/A 120,176/rl N/A
He Fei (1) N/A 55,896/
rd		 17,794/
rd		 82,908/
rd		 130,663/rl N/A 70,778/
rl		 68,242/
rd		 N/A 97,744/
rd
Nan Chang (6) N/A 88,722/
rd		 N/A N/A 98,015/
rl		 70,778/
rl		 N/A 41,470/
rd		 43,815/
rd		 N/A
Wu Han (8) N/A 89,146/
rl		 N/A N/A N/A 51,754/
rd		 46,853/
rl		 N/A 56,980/
rd		 73,150/
rd
Chang Sha (7) N/A N/A N/A N/A 95,120/
rl		 N/A 45,486/
rd		 38,121/
rl		 N/A 157,435/
rd
Zheng Zhou (9) N/A N/A 113,399/
rd		 68,796/
rd		 N/A 97,848/
rd		 N/A 89,650/
rd		 210,581/rl N/A
Subsequently, we ran the simulation and obtained the following results: The most cost-effective route to transport 1 tonne of general goods from Changsha (Node 7) to Shanghai (Node 3) follows the path 7-8-1-2-3. This route involves using the railway from Node 7 to Node 8, and then switching to roadway transportation from Node 8 through Nodes 1 and 2 to Node 3. The total cost for transporting goods from Node 7 to Node 3 is 140,411 yuan, with an additional interchange fee of 200 yuan incurred at Node 8.
Preprints 110291 g006
Figure 6. Cheapest cost route selection.
Figure 6. Cheapest cost route selection.
Preprints 110291 g006
In the next stage, we simulated a scenario where Node 8 is blocked due to a catastrophic disruption, resulting in a disconnection between Node 8 and other nodes. Consequently, the new most cost-effective route to transport 1 tonne of goods from Node 7 to Node 3 changes to 7-6-4-3, with a total cost of 149,771 yuan, utilising roadway transportation exclusively for each segment. To quantify the effectiveness of the Intermodal Transportation Port (ITP) at Node 8 on the entire supply chain network, we used the equation (3) and obtained the results:
E f e c t i v e n e s s ѯ = ( 149,711 − ( 140411 + 200 ) ) 149711 = 6.07 %
This result demonstrates that the ITP at Node 8 significantly reduces transportation costs within the supply chain, lowering them by 6.07%. This cost reduction translates into decreased expenses for supply chain recovery after disasters, reducing post-disaster recovery costs by the same percentage. When pricing resilience bonds, the expected loss differences with and without the project will be measured. These differences will be captured as rebates to reinvest in enhancing the infrastructure at Node 8. Therefore, by upgrading Node 8 in advance, the severity of potential losses from unforeseen catastrophic disruptions can be mitigated by 6.07%. Lastly, we conducted simulations to determine the value of a 5-year resilience bond for the supply chain. In our calculations, we assumed that the proportion of the face value ( ρ ) repaid to investors is 0.5, and the bond’s threshold is within the range of 2 to 10 million yuan. The resulting bond price for the intermodal transportation port is detailed below:
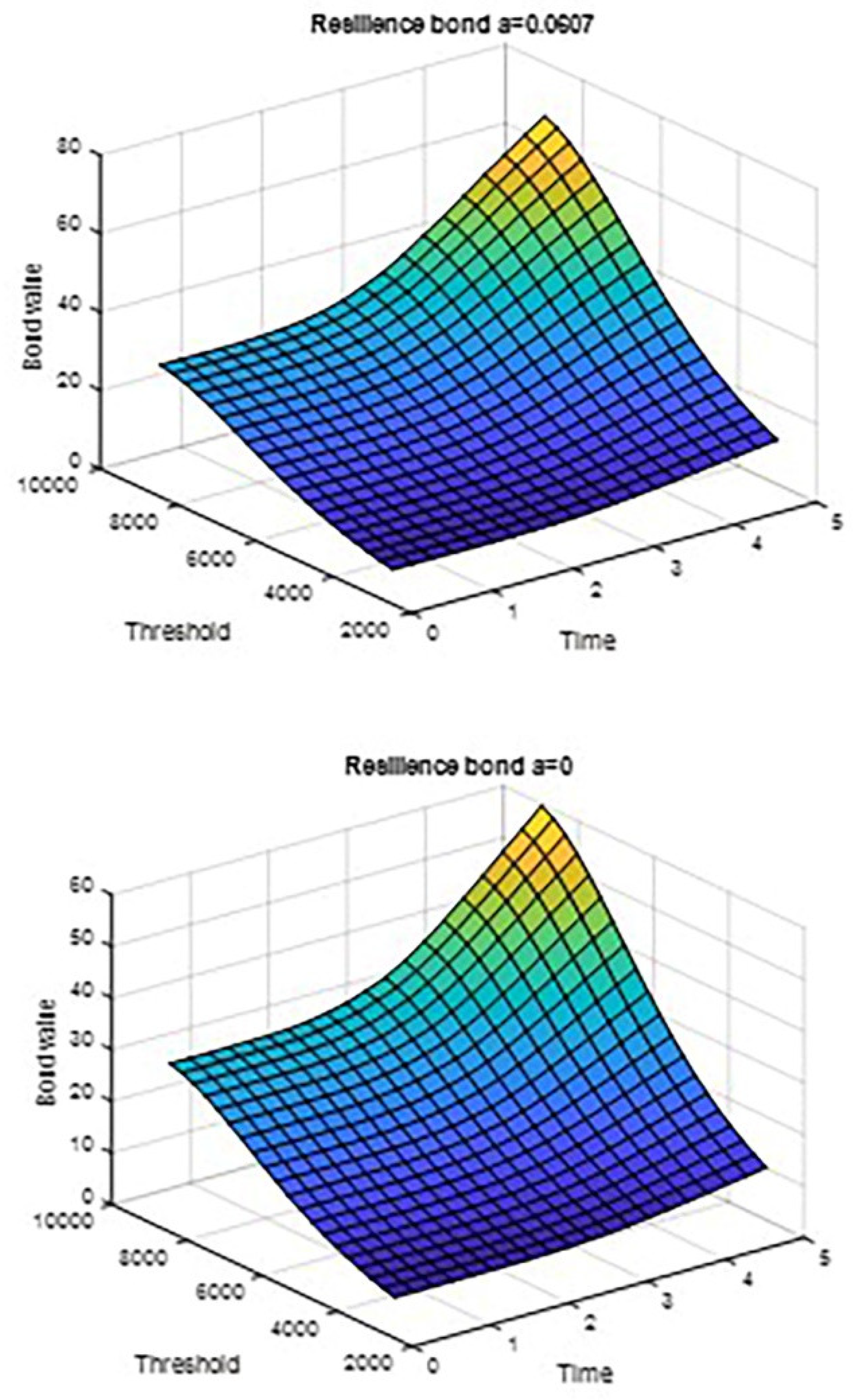
Figure 7 illustrates the pricing dynamics of the resilience bond under varying impact factors. Specifically, when an Intermodal Transportation Port (ITP) project is implemented, the price of the bond for the supply chain at the maturity of five years reaches 66.8 yuan per 100 yuan face value, assuming a threshold of approximately 10 million yuan. In contrast, without the upgrading of an ITP project, the bond price stands at 60.4 yuan, which is comparable to a resilience bond without a resilient project and similar as the catastrophe bond. The yield for a five-year maturity resilience bond is 8.41% with the upgrading ITP project, compared to 10.61% without it. This discrepancy underscores that bonds with higher yields are typically associated with higher default risk, implying that a higher quality sponsor would issue bonds with lower yields. The results indicate that the 6.07% effectiveness of the ITP project translates to a 2.2% reduction in returns when applying the resilience bond with an resilient infrastructure project. This 2.2% reduction can be redirected into upfront investments for further development of resilient infrastructure projects, thereby enhancing the overall sustainability of the infrastructure system. By calculating the value of a supply chain resilience bonds base on the case study, issuers can strategically plan the number of bonds to be issued, ensuring comprehensive preparation and investment in resilience infrastructure projects.

6. Conclusion

The financial market has immense potential to absorb the risks associated with catastrophic events. Resilience and sustainability are two critical concepts with significant applications in infrastructure and environmental management. This study introduces resilience bonds as an innovative financial instrument designed to enhance infrastructure resilience and achieve sustainability goals. Through a detailed case study of a China-based supply chain, the research demonstrates the significant potential of resilience bonds to mitigate risks associated with catastrophic events and supply chain disruptions. Resilience bonds provide a dual benefit by transferring risk to capital market investors and reinvesting insurance rebates into resilient infrastructure projects. This approach not only supports the development of sustainable and resilient supply chains but also reduces the default risk for sponsors and lowers investment risks for investors. The valuation model presented offers clear guidance on potential yields and marginal profits, making resilience bonds an attractive option for both public and private investors. The empirical data from Willis Tower Watson (Shanghai) validates the theoretical framework, showcasing the practical application and effectiveness of resilience bonds in real-world scenarios. The study highlights that the performance of eligible resilient projects significantly influences bond valuation, emphasising the importance of investing in high-quality resilient infrastructure. However, the implementation of resilience bonds involves complex dynamic modeling and relies heavily on accurate historical data. The success of these bonds in the market will depend on overcoming these complexities and gaining acceptance among investors and stakeholders. Overall, resilience bonds present a promising solution for financing resilient infrastructure projects, promoting long-term sustainability and enhancing the resilience of supply chain networks. Future research and practical applications should focus on addressing the challenges of implementation and exploring the broader applicability of resilience bonds in diverse geographical and economic contexts.

References

  1. Arnold, Pierre, Peeters, Dominique, and Thomas, Isabelle (2004), ‘Modelling a rail/road intermodal transportation system’, Transportation Research Part E: Logistics and Transportation Review, 40 (3), 255-70.
  2. Barad, M and Sapir, D Even (2003), ‘Flexibility in logistic systems—modeling and performance evaluation’, International Journal of Production Economics, 85 (2), 155-70.
  3. Berkeley, Alfred R. and Wallace, Mike (2010), ‘A Framework for Establishing Critical Infrastructure Resilience Goals’, Final Report and Recommendations by the Council.
  4. Bevere, Lucia and Weigel, Andreas (2021), ‘sigma 1/2021 - Natural catastrophes in 2020’, Swiss Re Institute.
  5. Bontekoning, Yvonne and Priemus, Hugo (2004), ‘Breakthrough innovations in intermodal freight transport’, Transportation Planning and Technology, 27 (5), 335-45. [CrossRef]
  6. Brigo, Damiano and Mercurio, Fabio (2007), Interest rate models-theory and practice: with smile, inflation and credit (Springer Science & Business Media).
  7. Bruneau, Michel, et al. (2003), ‘A framework to quantitatively assess and enhance the seismic resilience of communities’, Earthquake spectra, 19 (4), 733-52. [CrossRef]
  8. Christopher, Martin (2016), Logistics & supply chain management (Pearson Higher Ed).
  9. Christopher, Martin and Peck, Helen (2004), ‘Building the resilient supply chain’, The international journal of logistics management, 15 (2), 1-14.
  10. Christopher, Martin and Lee, Hau (2004), ‘Mitigating supply chain risk through improved confidence’, International journal of physical distribution & logistics management, 34 (5), 388-96.
  11. Erlinghagen, Sabine and Markard, Jochen (2012), ‘Smart grids and the transformation of the electricity sector: ICT firms as potential catalysts for sectoral change’, Energy Policy, 51, 895-906. [CrossRef]
  12. Gichoya, David (2005), ‘Factors affecting the successful implementation of ICT projects in government’, the Electronic Journal of e-government, 3 (4), 175-84.
  13. Hao, Yan, Armbruster, Dieter, and Hütt, Marc-Thorsten (2015), ‘Node survival in networks under correlated attacks’, PloS one, 10 (5), e0125467. [CrossRef]
  14. Ishfaq, Rafay (2012), ‘Resilience through flexibility in transportation operations’, International Journal of Logistics Research and Applications, 15 (4), 215-29. [CrossRef]
  15. Ishfaq, Rafay and Sox, Charles R (2010), ‘Intermodal logistics: The interplay of financial, operational and service issues’, Transportation Research Part E: Logistics and Transportation Review, 46 (6), 926-49.
  16. Jayaram, Jayanth, Vickery, Shawnee K, and Droge, Cornelia (2000), ‘The effects of information system infrastructure and process improvements on supply-chain time performance’, International Journal of Physical Distribution & Logistics Management, 30 (3/4), 314-30. [CrossRef]
  17. Li, Xinjun and Wang, Lijie (2015), ‘Strategy decision of business interruption insurance and emergency supply strategy based on supply disruptions’, Journal of Industrial Engineering and Management, 8 (1), 110-21. [CrossRef]
  18. Mottahedi, Adel, et al. (2021), ‘The resilience of critical infrastructure systems: A systematic literature review’, Energies, 14 (6), 1571. [CrossRef]
  19. Murray-Tuite, Pamela (2008), ‘Evaluation of strategies to increase transportation system resilience to congestion caused by incidents’, Mid-Atlantic University Transportation Center.
  20. Orr, Ryan J and Kennedy, Jeremy R (2008), ‘Highlights of recent trends in global infrastructure: new players and revised game rules’, Transnational Corporations, 17 (1), 99-133.
  21. PwC (2016), ‘Enhancing supply chain resilience.’. https://www.pwc.com/sg/en/industries/assets/enhancing-supply-chain-resilience.pdf.
  22. Re:Focus (2015), ‘LEVERAGING CATASTROPHE BONDS: As a Mechanism for Resilient Infrastructure Project Finance’, RE bound insurance report.
  23. Rice, James B and Caniato, Federico (2003), ‘Building a secure and resilient supply network’, SUPPLY CHAIN MANAGEMENT REVIEW, V. 7, NO. 5 (SEPT./OCT. 2003), P. 22-30: ILL.
  24. Sawyerr, Emmanuel and Harrison, Christian (2020), ‘Developing resilient supply chains: lessons from high-reliability organisations’, Supply Chain Management: An International Journal, 25 (1), 77-100. [CrossRef]
  25. Schmitt, Amanda J and Singh, Mahender (2009), ‘Quantifying supply chain disruption risk using Monte Carlo and discrete-event simulation’, Simulation Conference (WSC), Proceedings of the 2009 Winter (IEEE), 1237-48.
  26. Thacker, Scott, et al. (2019), ‘Infrastructure for sustainable development’, Nature Sustainability, 2 (4), 324-31.
  27. Tomlin, Brian (2006), ‘On the value of mitigation and contingency strategies for managing supply chain disruption risks’, Management Science, 52 (5), 639-57. [CrossRef]
  28. Vaijhala, Shalini and Rhodes, James (2018), ‘Resilience Bonds: a business-model for resilient infrastructure’, Field Actions Science Reports. The journal of field actions, (Special Issue 18), 58-63.
  29. Vajjhala, Shalini (2015), ‘Financing infrastructure through resilience bonds’, Available at: https://www.brookings.edu/blog/the-avenue/2015/12/16/financing-infrastructure-through-resilience-bonds/.
  30. Wagner, Stephan M and Neshat, Nikrouz (2010), ‘Assessing the vulnerability of supply chains using graph theory’, International journal of production economics, 126 (1), 121-29. [CrossRef]
  31. Walter, Ingo (2016), The infrastructure finance challenge (Open Book Publishers).
  32. Warren, Matthew and Hutchinson, William (2000), ‘Cyber attacks against supply chain management systems: a short note’, International Journal of Physical Distribution & Logistics Management, 30 (7/8), 710-16. [CrossRef]
  33. Waters, C Donald J (2003), Global logistics and distribution planning: strategies for management (Kogan Page Publishers).
  34. Wu, Teresa, Blackhurst, J, and O’grady, P (2007), ‘Methodology for supply chain disruption analysis’, International Journal of Production Research, 45 (7), 1665-82. [CrossRef]
  35. Zhang, WenJun (2012), Computational Ecology: Graphs, Networks and Agent-based Modeling (World Scientific).
  36. Zsidisin, George A, Melnyk, Steven A, and Ragatz, Gary L (2005), ‘An institutional theory perspective of business continuity planning for purchasing and supply management’, International journal of production research, 43 (16), 3401-20. [CrossRef]
  37. Zurich (2016), ‘SUPPLY CHAIN RESILIENCE REPORT’, Business Continuity Institute .
Preprints 110291 g001
Figure 1. Mechanisms of implementing resilience bond to finance supply chain resilience. Source: adapted from (Re:Focus 2015)
Figure 1. Mechanisms of implementing resilience bond to finance supply chain resilience. Source: adapted from (Re:Focus 2015)
Preprints 110291 g001
Preprints 110291 g003
Figure 3. Cheapest cost transport mode selection.
Figure 3. Cheapest cost transport mode selection.
Preprints 110291 g003
Preprints 110291 g004
Figure 4. Supply chain claim database, 2015-2018 (currency value adjusted to 2018).
Figure 4. Supply chain claim database, 2015-2018 (currency value adjusted to 2018).
Preprints 110291 g004
Preprints 110291 g005
Figure 5. Cumulative number of claims.
Figure 5. Cumulative number of claims.
Preprints 110291 g005
Preprints 110291 g007
Figure 7. Five-year supply chain resilience bond price with/without the ITP project.
Figure 7. Five-year supply chain resilience bond price with/without the ITP project.
Preprints 110291 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated