Prerpints.org logo
Preprint
Article

Accuracy Assessment of Estimated River Water Surface Elevations from Landsat 8 and 9 Imagery among Twenty Water Indices

Altmetrics

Downloads

104

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 June 2024

Posted:

26 June 2024

You are already at the latest version

Alerts
Abstract
A method for estimating river water surface elevation (WSE) from Landsat imagery using the river inundation area - water surface elevation (RIA-WSE) rating curve constructed from the U.S. Geological Survey Topobathymetric Elevation Model (TEM) data was developed and tested at six gauging stations along the upper Mississippi River. The Otsu's automatic threshold selection algorithm was employed for the image classification and estimation of inundation areas within each pre-defined polygon around each gauging station. In addition to the commonly used green-band based water indices, Landsat 8 and 9 OLI's ultra-blue, blue, and red band-based water indices were also tested in this study, which resulted in twenty different water indices: NDWIv (Normalized Difference Water Index), MNDWI1v and MNDWI2v (Modified Normalized Difference Water Index), AWEIsv (Automatic Water Extraction Index with shadow), and AWEInsv (AWEI without shadow), where v represents the visible light band used in the water index. At each station, about 60-80 Landsat 8 or 9 images during 2013-2023 were used for assessing the performances of the twenty water indices through comparing the estimated WSEs with the measured WSEs. Results showed that the ultra-blue or red band-based AWEIs yielded the most accurate estimations of WSEs among the twenty tested water indices.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

River stage is referred to water surface height above the gage datum at a stream gauging station. The sum of river stage and gage datum is the river water surface elevation (WSE) relative to the mean sea level. Either river stage or river WSE is a key variable measured at any stream gauging station, since many gauging stations first directly measure river stages or WSEs and then estimate river discharges based on the stations’ stage-discharge rating curves [1,2]. Both river stage and discharge are fundamental hydrologic variables for water cycle study [3,4], flood frequency analysis [5,6,7], flood forecast and prevention [8,9], water resources management [10,11], ecosystem services [12], reservoir management [13], river navigation [14], riverine recreation [15], and other applications.
It is well known that automatically measuring river stages at gauging stations can save time and effort, but it still requires operational costs [16] for equipment repair and maintenance, data collecting and transmission, and others. Because of lack of funding, the number of gauging stations in the United States has declined since the late 1990s [17,18,19,20]. Numerous major flood events around the world were not sufficiently measured [21] and many stream gauging networks for global major rivers shrank, not to mention medium and small rivers [20].
Two noticeable problems that the hydrology and water resources community is facing are missing data at gauging stations due to equipment failure and non-monitoring at ungauged river cross sections. To fill data gaps at gauging stations or to monitor WSEs at any ungauged river cross sections, remote sensing is one of economical, effective and efficient approaches that can play a significant role in solving these two problems. Since the 1990s, substantial progress has been made in remote sensing of river stage [22,23,24].
There are two types of remote sensing approaches for monitoring river stage or WSE [25,26,27], i.e., directly measuring river WSE using spaceborne or airborne LiDAR or altimetry radar [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46], and indirectly estimating river WSE from remote sensing imagery based on relationships between river width or river inundation area versus WSE established from the topographic information [25,26,27,39,40,47,48,49,50,51,52,53,54,55,56,57,58]. Both methods have advantages and limitations. Although the direct method is straightforward for measuring river WSE without any assistance from other remotely sensed data, satellites carrying radars or lasers usually have low sampling frequency, i.e., satellite overhead period or revisit time is long. On the other hand, even if the satellites are overhead, if the radar or laser scanning points are not falling on the river cross sections of interest, no river WSE data are available for these river cross sections. However, one major advantage associated with the direct method is that the accuracy of the measured WSEs is usually very high and can be at the centimeter level. Although the indirect method may not be able to achieve a better accuracy than the direct method, the indirect method can be used to estimate river stage or WSE at any river cross sections from remotely sensed imagery if the river basin is covered by satellite or aerial imagery.
This study aims to improve the accuracy of the estimated river WSEs using the indirect method, and specifically to address three key questions related to the accuracy of the estimated river WSEs from Landsat 8 and 9 Operational Land Imager (OLI) imagery using the constructed river inundation area (RIA) – WSE rating curves, i.e., 1) which water indices are the best for distinguishing water and non-water pixels in Landsat 8-9 OLI images? 2) which image resampling method(s) can improve the accuracy of the estimated WSEs? 3) under what flow conditions the constructed RIA-WSE rating curves fail to yield accurate estimations of river WSEs? A detailed description of these three questions and the suggested methods for solving them are presented in Section 3.
The arrangement of this paper is as follows. Section 2 describes study sites and data. Section 3 introduces methods. Section 4 contains results and discussion. Conclusions are presented in Section 5.

2. Study Sites and Data

Six stream gauging stations along the upper Mississippi river (UMR) were chosen for this study, because the topobathy elevation model (TEM) data with one-meter resolution along the UMR produced by the Upper Mississippi River System (UMRS) are available [59] for establishing the RIA-WSE rating curves. Topobathy is a seamless surface model that contains terrestrial and riverbed elevation. The UMRS utilized airborne Lidar to map the terrestrial elevation and the Acoustic Doppler Current Profile (ADCP) to survey river bathymetry [60].
Among the six selected stations, five stations are managed by the U.S. Geological Survey (USGS) and one station is operated by the U.S. Army Corps of Engineers (USACE). Table 1 lists the station name, station ID, UMRS Topobathy Pool ID, latitude, longitude, gage datum, temporal resolution of river stage data, and number of Landsat images used for each selected station. Considering some stations only have river stage data after 2013, while Landsat 5 was deactivated in June of 2013, this study only used Landsat 8 and 9 OLI images downloaded from the USGS EarthExplorer.
To understand the errors in the estimated river WSEs from Landsat 8-9 OLI imagery, high spatial resolution (1 m prior to 2018, and 0.6 m 2018-current) aerial images acquired by the National Agricultural Imagery Program (NAIP) downloaded from the USGS EarthExplorer were also used to extract river inundation areas for estimating river WSEs and assessing differences in the estimated river WSEs between Landsat 8-9 OLI and NAIP imagery.
Station USGS
Station
ID		 UMRS Pool
Topobathy		 Latitude Longitude Gage
Datum (ft)		 River Stage Data
Temporal
Resolution		 Number of Landsat 8-9 OLI Images
Grafton, IL 05587450 Pool26 38°58′5”N 90°25′44”W 403.79 30-min 70
Prescott, WI 05344500 Pool 3 44°44′45”N 92°48′0”W 649.67 Hourly (15-min after 2013/3/29) 80
Red Wing, MN 05355250 Pool 3 44°33′55”N 92°32′33”W 664.82 15-min 71
St. Louis, MO 07010000 ORN@ 38°37′44”N 90°10′47”W 379.58 Hourly (30-min after 2019/4/17) 63
Wabasha, MN USACE* Pool4 44°23′14”N 92°2′13”W elevation Daily 62
Winona, MN 05378500 Pool6 44°03′20”N 91°38′15”W 639.64 Hourly (15-min after2009/12/14) 65
* Station operated by the U.S. Army Corps of Engineers @Open River North.

3. Methods

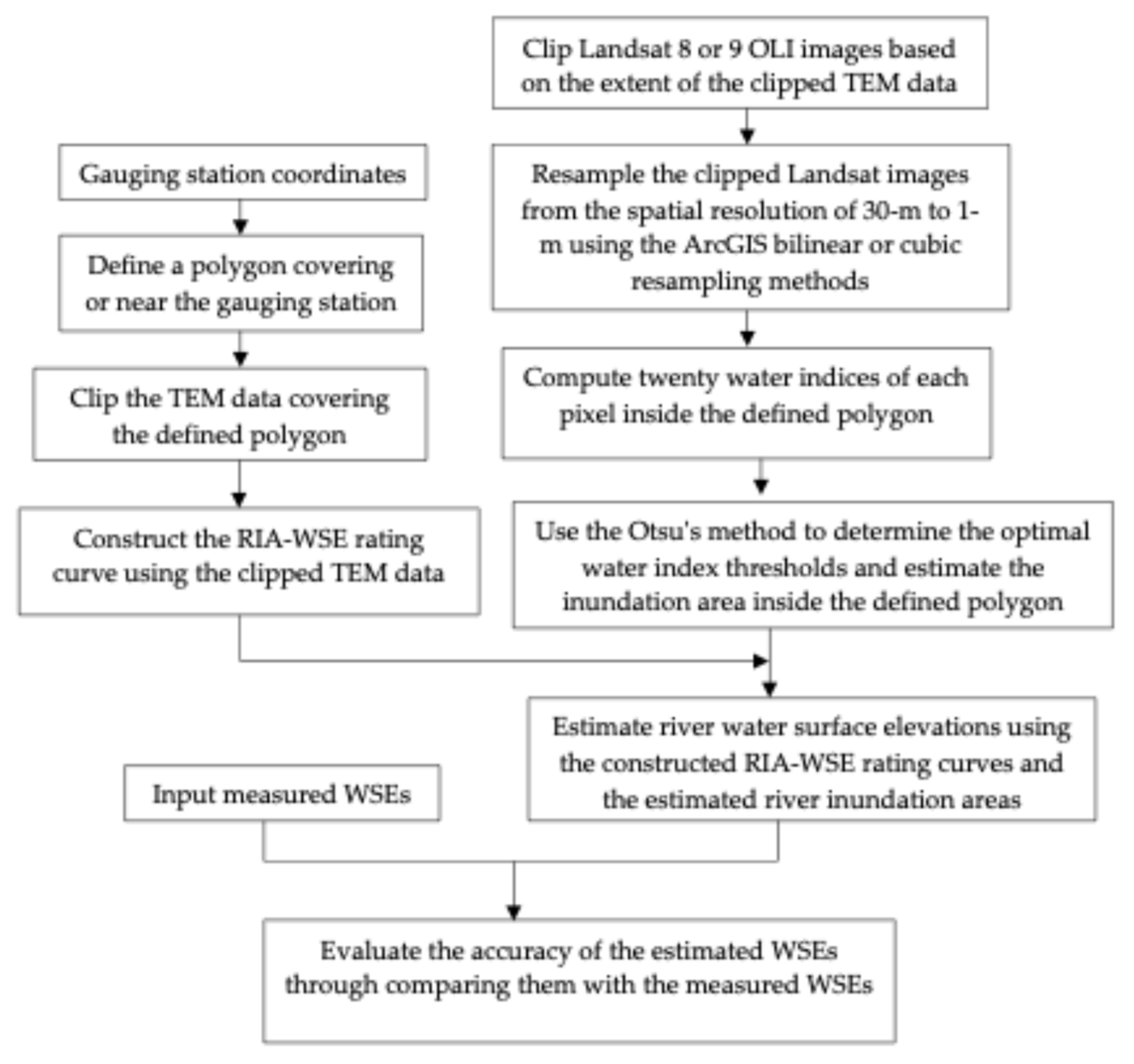
3.1. Overall Method and Flowchart

This study evaluates the accuracy of the estimated river WSEs from Landsat 8-9 OLI imagery among twenty water indices through comparing the estimated river WSEs with the measured WSEs at six gauging stations along the upper Mississippi River from Minnesota to Missouri. The overall method employed in this study is illustrated in the flowchart as shown in Figure 1.
According to the coordinates of each gauging station, a polygon is defined covering the gauging station if there is no bridge or other man-made structures, and no dense vegetation on the riverbanks within the polygon. Otherwise, a polygon is chosen near the gauging station to ensure that no bridge, or man-made structures, or densely vegetative riverbanks exist inside the polygon.
The USGS TEM data is first clipped to cover the pre-defined polygon, and then the clipped TEM data is used in constructing the RIA-WSE rating curve inside the pre-defined polygon. The principle of constructing the RIA-WSE rating curves using the TEM data is the same as constructing the RIA-WSE using the digital elevation model (DEM) data [25,26,27,56]. However, the RIA-WSE rating curves constructed from the DEM data are only valid for estimating river stages or WSEs that are above the lowest elevations in the DEM data inside the pre-defined polygon. The lowest elevations in the DEM data are the river water surface elevations as the ground, airborne or spaceborne surveys were carried out to measure terrain elevations for producing the DEM data. Unlike the DEM data, the TEM data contain the information of riverbed elevations, and thus the RIA-WSE rating curves constructed from the TEM data are valid for the entire dynamic range of river stages or WSEs at the corresponding river cross sections.

3.2. Construct the RIA-WSE Rating Curves

To explain the method of constructing the RIA-WSE rating curves from the TEM data, a hypothetical TEM dataset inside a pre-defined polygon is shown in Figure 2. The number within each cell stands for the elevation (in meters) of riverbank or riverbed, and the grid cell size is 1m x 1m. Starting from the minimum elevation (i.e., 10m) inside the polygon, let river water surface elevation rise toward the maximum elevation inside the polygon (i.e., 16m) with an incremental interval of 1m. For a TEM dataset with an elevation precision of 1 cm or 1 mm, an incremental interval of 1 cm or 1 mm should be used. Based on each water surface elevation, the river inundation area (RIA) inside the pre-defined polygon corresponding to that water surface elevation is calculated. The calculated RIAs are as follows: 2 m2 (10 m), 5 m2 (11 m), 10 m2 (12 m), 15 m2 (13 m), 23 m2 (14 m), 29 m2 (15 m), and 30 m2 (16 m), where numbers inside the parentheses are the corresponding river WSEs.
Based on the computed RIAs, a RIA-WSE rating curve is constructed and plotted in Figure 2. Actually, a RIA-WSE look-up table might be more useful than a RIA-WSE rating curve for determining river WSEs. For example, if the RIA extracted from Landsat imagery is between RIAi and RIAi+1, we can use the linear interpolation to estimate the WSE as follows:
W S E = W S E i + ( W S E i + 1 − W S E i R I A i + 1 − R I A i ) ( R I A − R I A i )
where WSEi and WSEi+1 are WSEs corresponding to RIAi and RIAi+1, respectively.

3.3. Twenty Water Indices

The commonly used water indices are green band based [61] and include the normalized difference water index (NDWI) [62], the modified normalized difference water index (MNDWI) [63], and the automatic water extraction index for non-shadow (AWEIns) and shadow (AWEIs) [64]. The formulas of these five water indices are given as follows.
N D W I = r G − r N I R r G + r N I R ; M N D W I 1 = r G − r S W I R 1 r G + r S W I R 1 ; M N D W I 2 = r G − r S W I R 2 r G + r S W I R 2
A W E I n s = 4 r G − r S W I R 1 − 0.25 r N I R + 2.75 r S W I R 2
A W E I s = r B + 2.5 r G − 1.5 r N I R + r S W I R 1 − 0.25 r S W I R 2
where rG rNIR, rSWIR1, rSWIR2, rB are spectral reflectance of green, near infrared, shortwave infrared 1, shortwave infrared 2 and blue bands, respectively. Pan et al. (2020) suggested that the ultra-blue, blue, and red bands of Landsat 8 and 9 OLI imagery could also be used in computing water index [61], as blue or ultra-blue band might work better for clear water, and red band for water containing a large amount of sediments. Therefore, if all four visible light bands of Landsat 8 and 9 OLI imagery are used to compute water index, twenty water indices can be yielded as follows:
N D W I V = r V − r N I R r V + r N I R ; M N D W I 1 V = r V − r S W I R 1 r V + r S W I R 1 ; M N D W I 2 V = r V − r S W I R 2 r V + r S W I R 2
A W E I n s V = 4 r V − r S W I R 1 − 0.25 r N I R + 2.75 r S W I R 2
A W E I s V = r B + 2.5 r V − 1.5 r N I R + r S W I R 1 − 0.25 r S W I R 2
where rV is the spectral reflectance of one of four visile light bands, i.e., ultra-blue (rUB), blue (rB), green (rG), and red (rR).

3.4. The Otsu Method

In this study, the Otsu method [65], an unsupervised image classification method was used to determine the optimal water index threshold for differentiating water and non-water pixels in Landsat 8-9 OLI imagery. The principle of the Otsu method is to determine the optimal water index threshold for maximizing an objective function given as follows:
M A X f = M A X { P w P n w ( μ w − μ n w ) 2 }
where Pw and Pnw are probabilities of water and non-water pixels, respectively; and μw and μnw are mean water index values of water and non-water pixels, respectively. The optimal water index threshold (OWI) is determined through iterating the water index threshold between -1 and 1 with an interval of 0.01 for achieving the maximum value of the objective function as shown in Eq.(8). All terms on the right-hand side of Eq.(8) are computed as follows:
P w = n w n , P n w = n n w n , μ w = ∑ i = 1 i = n w W I i n w , μ n w = ∑ i = 1 i = n n w W I i n n w
where WIi is the water index of pixel i, n, nw, nnw are number of total pixels, number of pixels with a water index greater than OWI, and number of pixels with a water index less than or equal to OWI, inside the pre-defined polygon, respectively.

3.5. Resample Landsat 8-9 OLI Imagery

The spatial resolution of Landsat 8-9 OLI imagery is 30 m, which is much coarser than the spatial resolution of the TEM data (i.e., 1 m) used in this study for constructing the RIA-WSE rating curves. To reduce errors and uncertainty in the extracted RIAs from the Landsat 8-9 OLI imagery due to the coarse resolution of the Landsat 8-9 OLI imagery, two raster resampling methods (bilinear and cubic) embedded in the ArcGIS Pro software were used to resample each Landsat 8-9 OLI imagery from the cell size of 30 m to 1 m.

3.6. Accuracy Assessment

To assess the accuracy of the estimated river WSEs, the measured river WSEs at the time close to the scene center times of Landsat 8-9 OLI images used for extracting river inundation areas were used for computing the errors (i.e., WSEest - WSEobs ). For the NAIP imagery, the measured river WSEs at 12:00pm local standard time were used to compute the errors in the estimated WSEs from the NAIP imagery, since most of the NAIP images were collected between 10:00am and 2:00pm local standard time [66]. Since at the Wabasha station operated by the U.S. Army Corps of Engineers, only daily mean WSE data are available, the observed daily mean WSEs were used for computing the errors.

3.7. The K-Nearest Neighbor (KNN) Method

Since no metadata of the NAIP aerial photos downloaded from the USGS EarthExplorer are available for converting the digital number (DN) of each pixel into all required spectral reflectance for computing all twenty water indices described in Section 3.3, the K-Nearest Neighbor (KNN) classifier [67], a supervised image classification method, was used for identifying water and non-water pixels in the NAIP aerial photos. Applying the KNN method to determine if an unknown pixel x belongs to water or non-water class, two training sample sets (i.e., water and non-water) are selected first, and then the spectral distance in the near infrared band of the NAIP imagery between pixel x and each training pixel is computed. The sum of the inverse distances between pixel x and all water training pixels (SIDw) is compared with the sum of the inverse distance between pixel x and all non-water training pixels (SIDnw). If SIDw>SIDnw, pixel x belongs to water class, otherwise x belongs to non-water class [56]. After the RIAs inside the predefined polygon were computed, they were used to estimate WSEs based on the constructed RIA-WSE rating curves.

4. Results and Discussion

4.1. Construction of the RIA-WSE Rating Curves

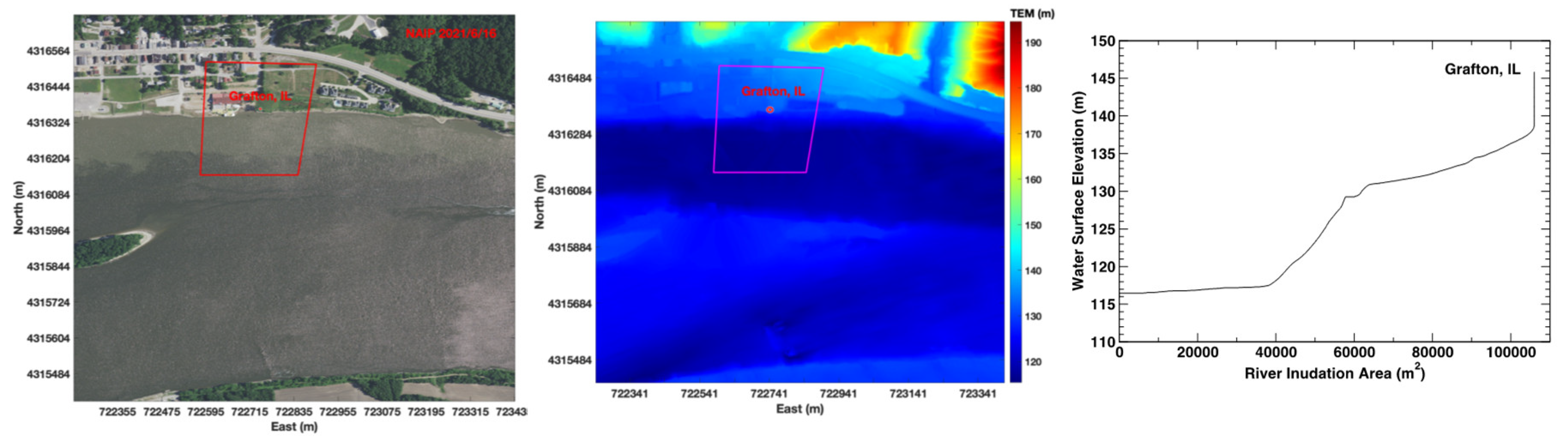
4.1.1. Grafton

The USGS gauging station 05587450 along the Mississippi River at Grafton, Illionis is located at (East 722743m, North 4316370m, UTM15) and shown as a red dot in Figs.4a (NAIP) and 4b (Topobathy). The red polygon shown in Figure 4a and 4b is the polygon for constructing the RIA-WSE rating curve. The constructed RIA-WSE rating curve is plotted in Figure 4c.

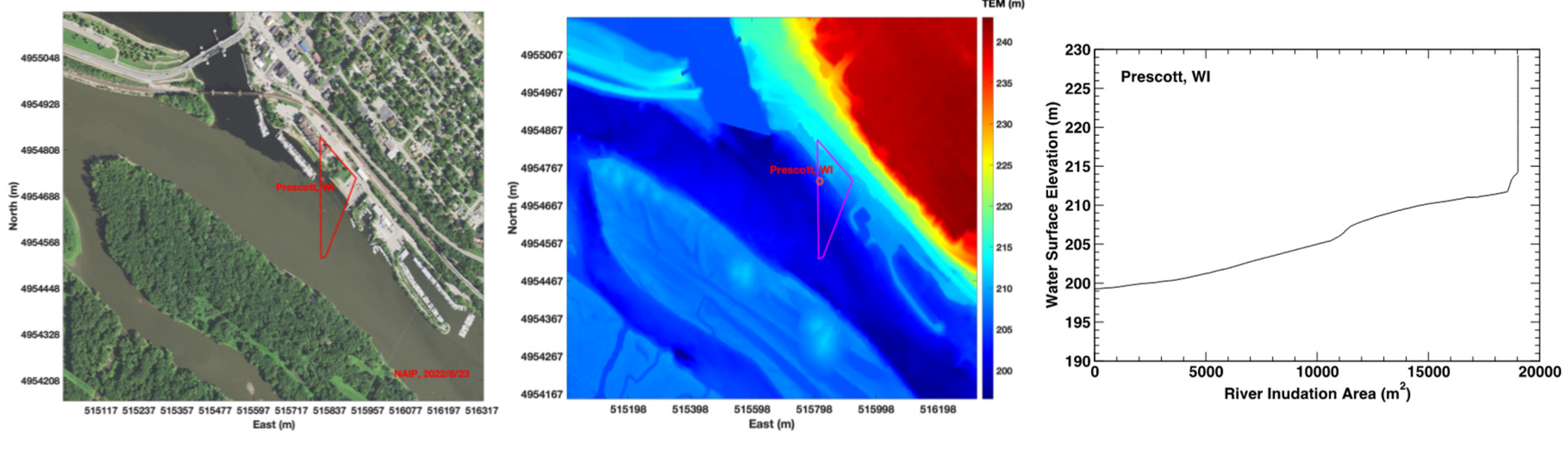
4.1.2. Prescott

The USGS gauging station 05344500 along the Mississippi River at Prescott, Wiscosin is located at (East 515817m, North 4954732m, UTM15) and shown as a red dot in Figs.5a (NAIP) and 5b (Topobathy). A polygon for constructing the RIA-WSE rating curve was chosen over the the gauging station shown as a red polygon in Figs.5a and 5b. The constructed RIA-WSE rating curve is plotted in Figure 5c.

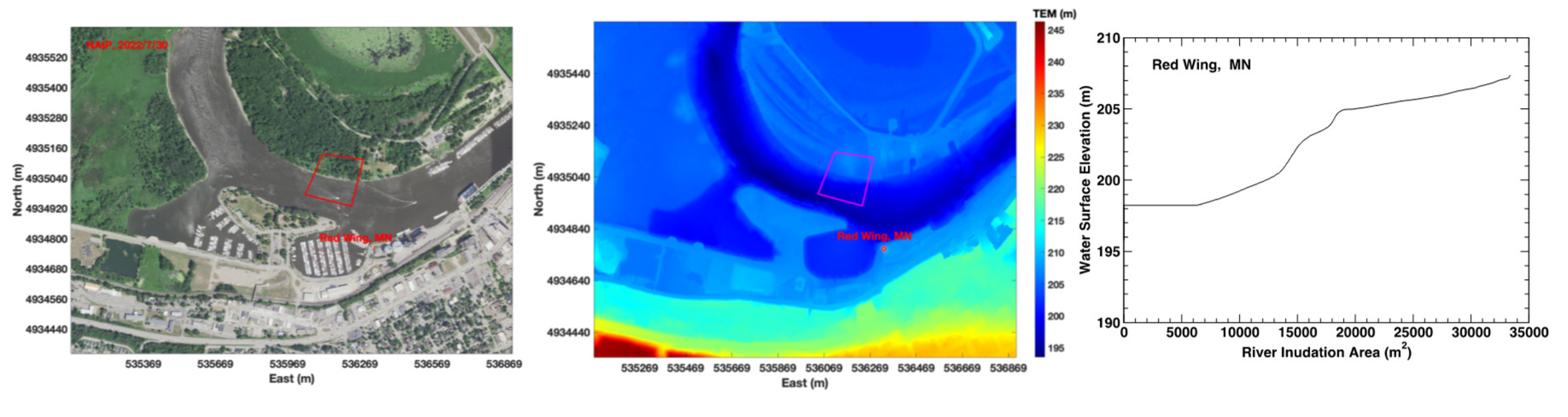
4.1.3. Red Wing

The USGS gauging station 05355250 along the Mississippi River at Red Wing, Minnesota is located at (East 536330m, North 4934762m, UTM15) and shown as a red dot in Figs.6a (NAIP) and 6b (Topobathy). This gauging station is located around an area with some man-made structures. To reduce the impact of man-made structures on the extracted RIAs inside the polygon, a polygon was chosen at the opposite riverbank shown as a red polygon in Figs.6a and 6b. The constructed RIA-WSE rating curve is plotted in Figure 6c.

4.1.4. St. Louis

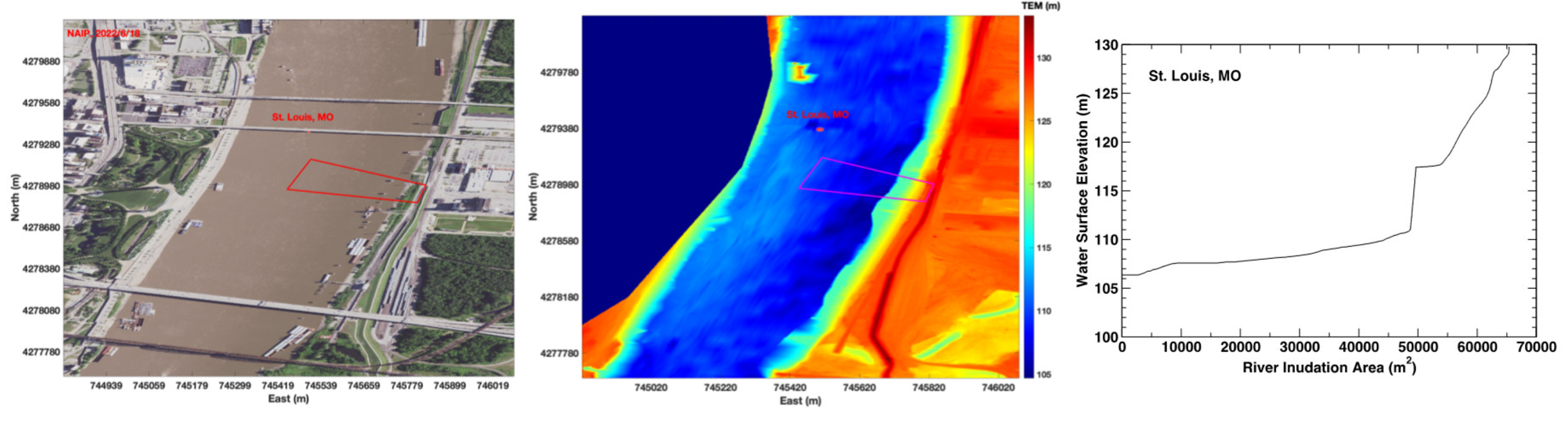
The USGS gauging station 07010000 along the Mississippi River at St. Louis, Missouri is located at (East 745505m, North 4279369m, UTM15) and shown in Figure 8a (NAIP) and 8b (Topobathy) as a red dot. This gauging station is located near a bridge. To reduce the impact of the bridge in the extracted RIAs from Landsat imagery, a polygon was chosen at the downstream of the gauging station shown as a red polygon in Figs.7a and 7b. The constructed RIA-WSE rating curve is plotted in Figure 7c.

4.1.5. Wabasha

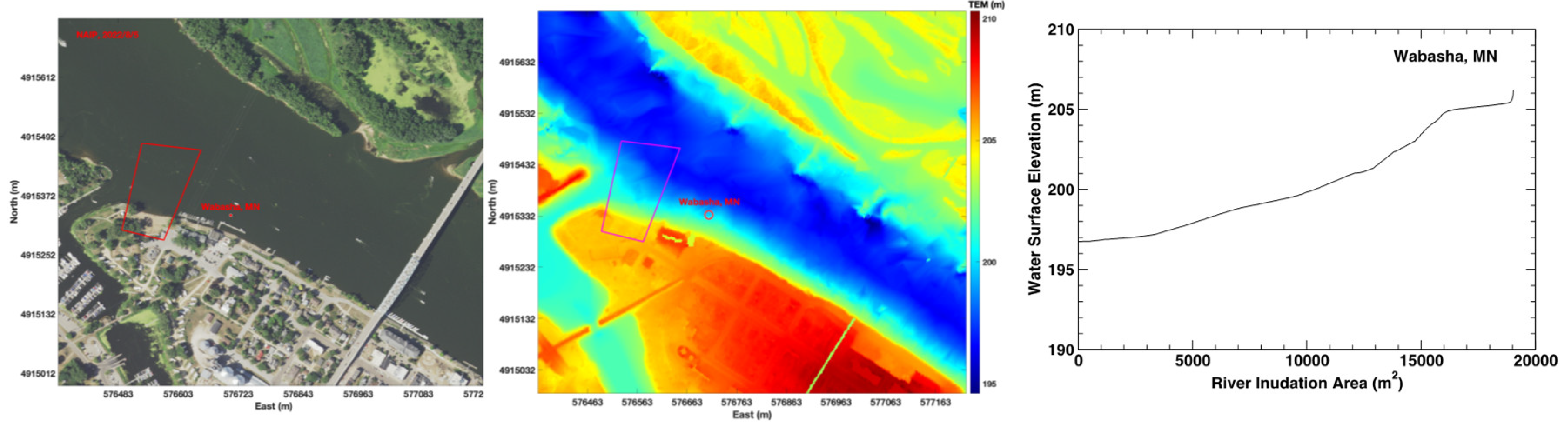
The USACE gauging station along the Mississippi River at Wabasha, Minnesota is located at (East 576708m, North 4915333m, UTM15) and shown as a red dot in Figs.8a (NAIP) and 8b (Topobathy). This gauging station is located around an area with some man-made structures. To reduce the impact of man-made structures, a polygon was chosen at the upstream of the gauging station shown as a red polygon in Figs.8a and 8b. The constructed RIA-WSE rating curve is plotted in Figure 8c.

4.1.6. Winona

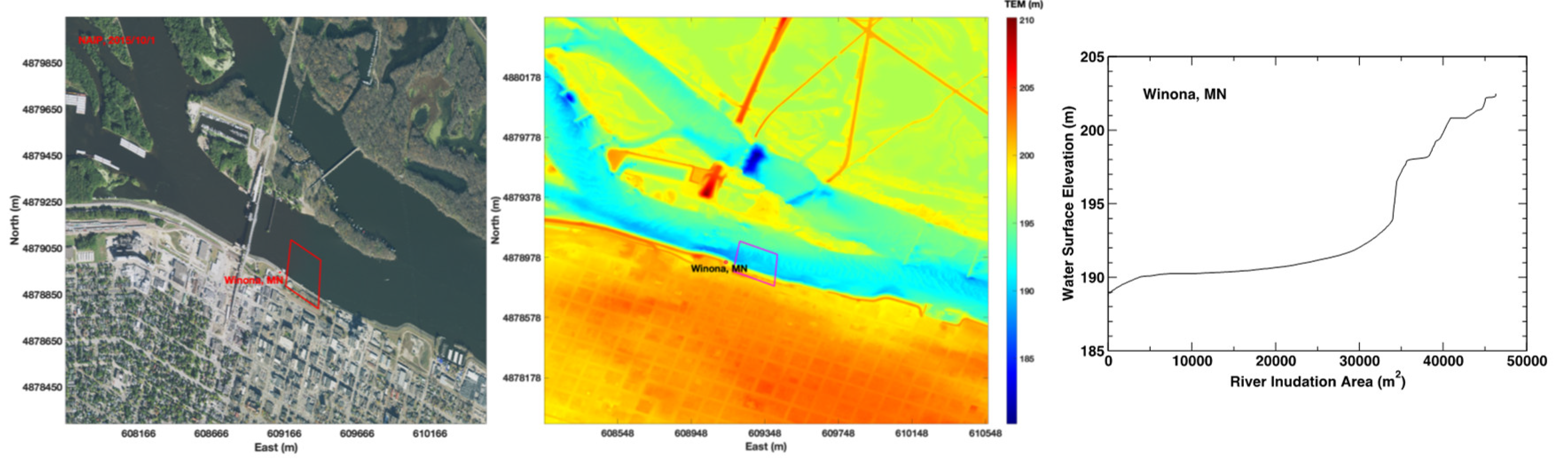
The USGS gauging station 05378500 along the Mississippi River at Winona, Minnesota is located at (East 609136m, North 4878946m, UTM15) and shown in Figs.9a (NAIP) and 9b (Topobathy) as a red dot. This gauging station is located around an area with some man-made structures. To reduce the impact of man-made structures, a polygon was chosen at the slightly downstream of the gauging station shown as a red polygon in Figs.9a and 9b. The constructed RIA-WSE rating curve is plotted in Figure 9c.

4.2. Comparison of the Bilinear and Cubic Resampling Methods

In this study, the topobathy elevation model (TEM) data used for constructing the RIA-WSE rating curves has a spatial resolution of 1 m, while the spatial resolution of Landsat 8-9 OLI imagery is 30 m. To match the finer resolution of the TEM data, all Landsat images used in this study were resampled (downscaled) from 30 m to 1 m using two resampling methods in the ArcGIS Pro, i.e., bilinear and cubic.
Table 2 shows that among the six selected stations, the percentage of the estimated WSEs from the resampled Landsat 8-9 OLI imagery using the cubic resampling method being more accurate than the estimated WSEs using the bilinear resampling method ranged from 58.3% (Red Wing) to 86.8% (St. Louis), which indicates that the cubic resampling method is better than the bilinear resampling method in terms of the accuracy of the estimated WSEs based on the extracted RIAs from the resampled Landsat 8-9 OLI imagery. The reason why the cubic resampling method is better than the bilinear resampling method for downscaling Landsat 8-9 OLI imagery from 30 m to 1m might be due to that the cubic resampling method has one more parameter than the bilinear method.

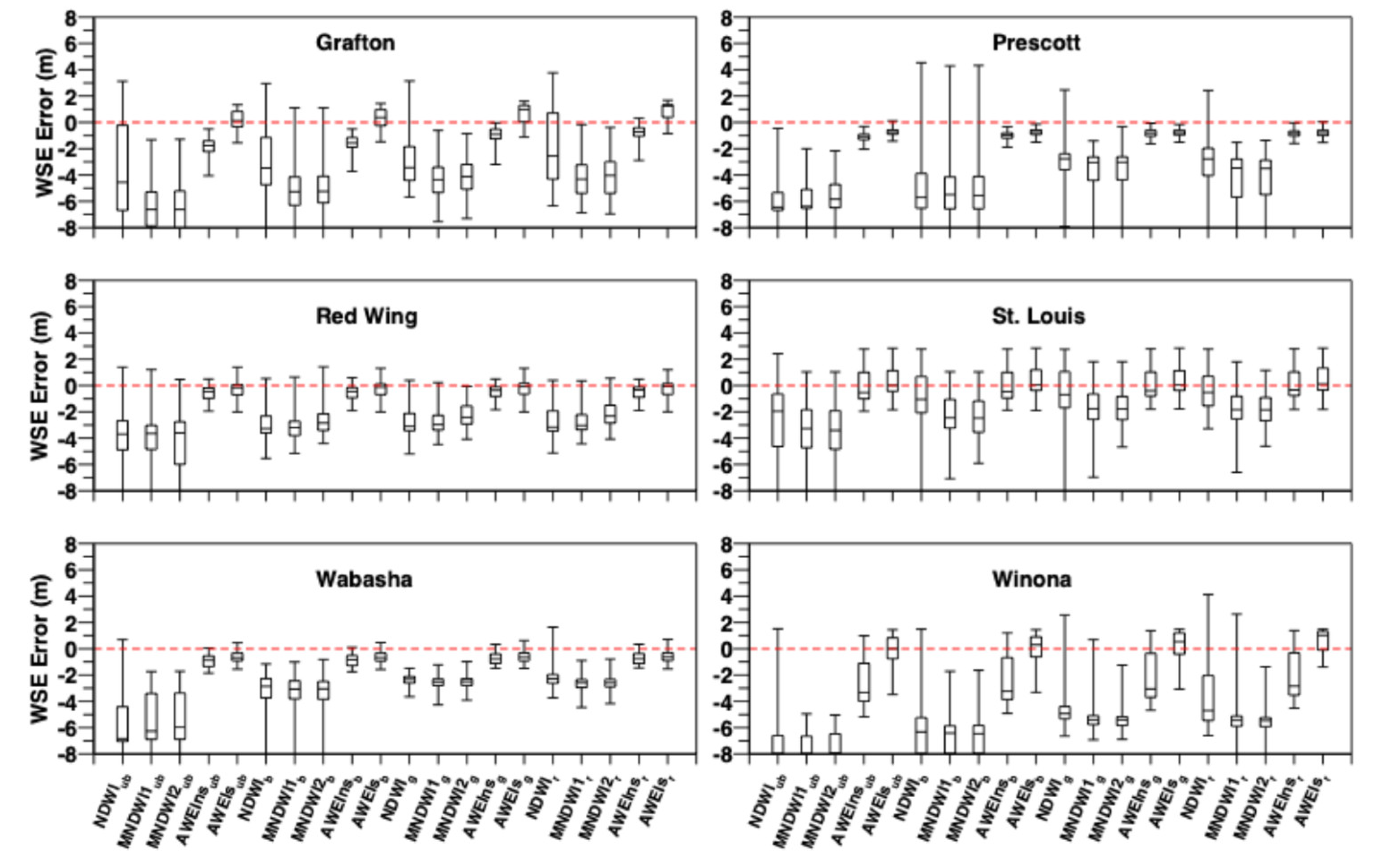
4.3. Comparison of the Estimated WSEs among Twenty Water Indices

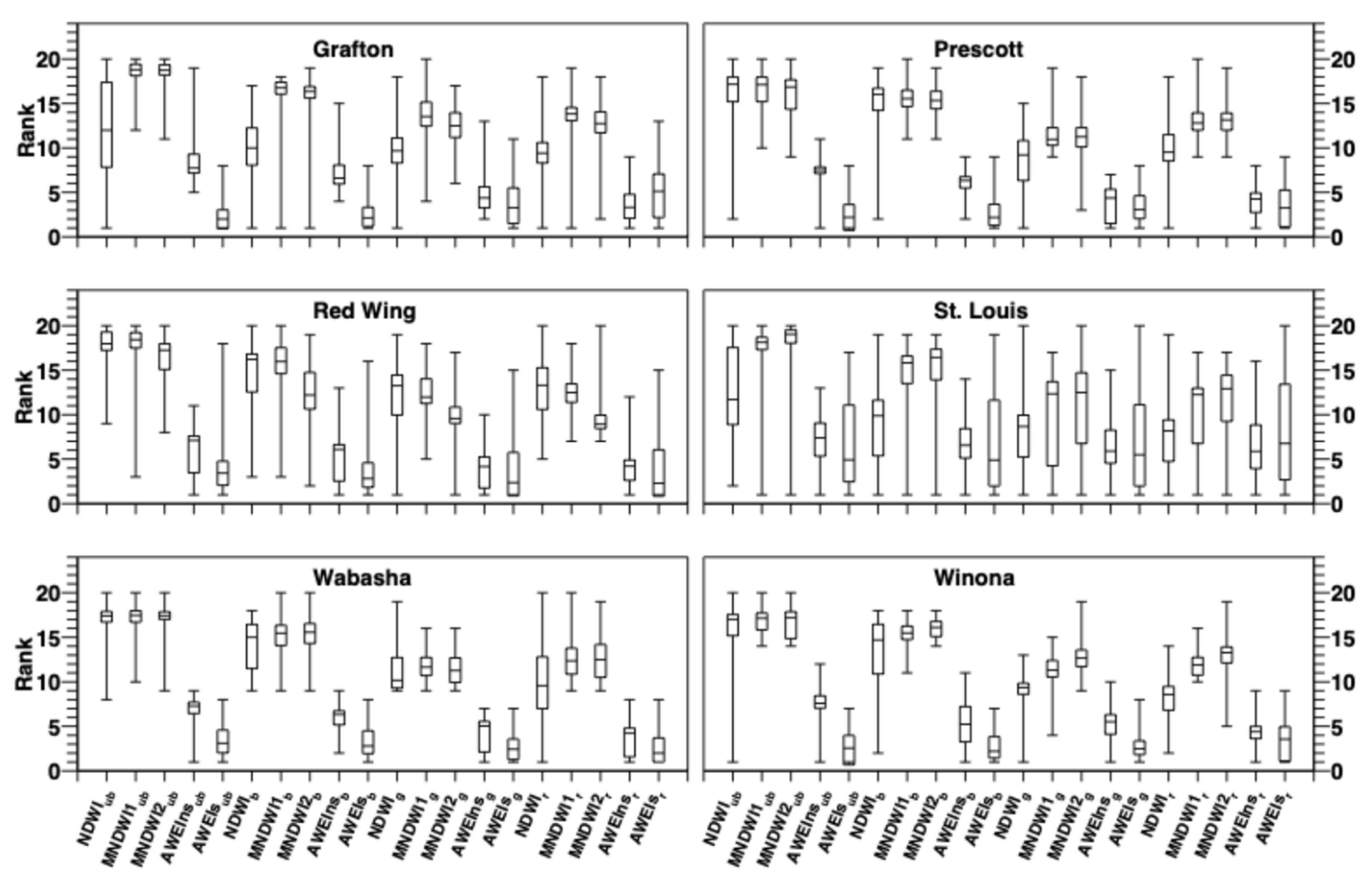
As described in Section 3.3., there are twenty water indices that can be used for differentiating water and non-water pixels in Landsat 8-9 OLI imagery. To compare these twenty water indices, two criteria were employed in this study. First, at each station, the estimated WSEs using the twenty water indices were ranked from 1 which is associated with the smallest error (compared with the observed WSEs) to 20 (the largest error) for each of the selected Landsat 8-9 OLI images. Then these ranking data were used for making the box plots as shown in Figure 11 (bilinear resampling) and Figure 12 (cubic resampling).
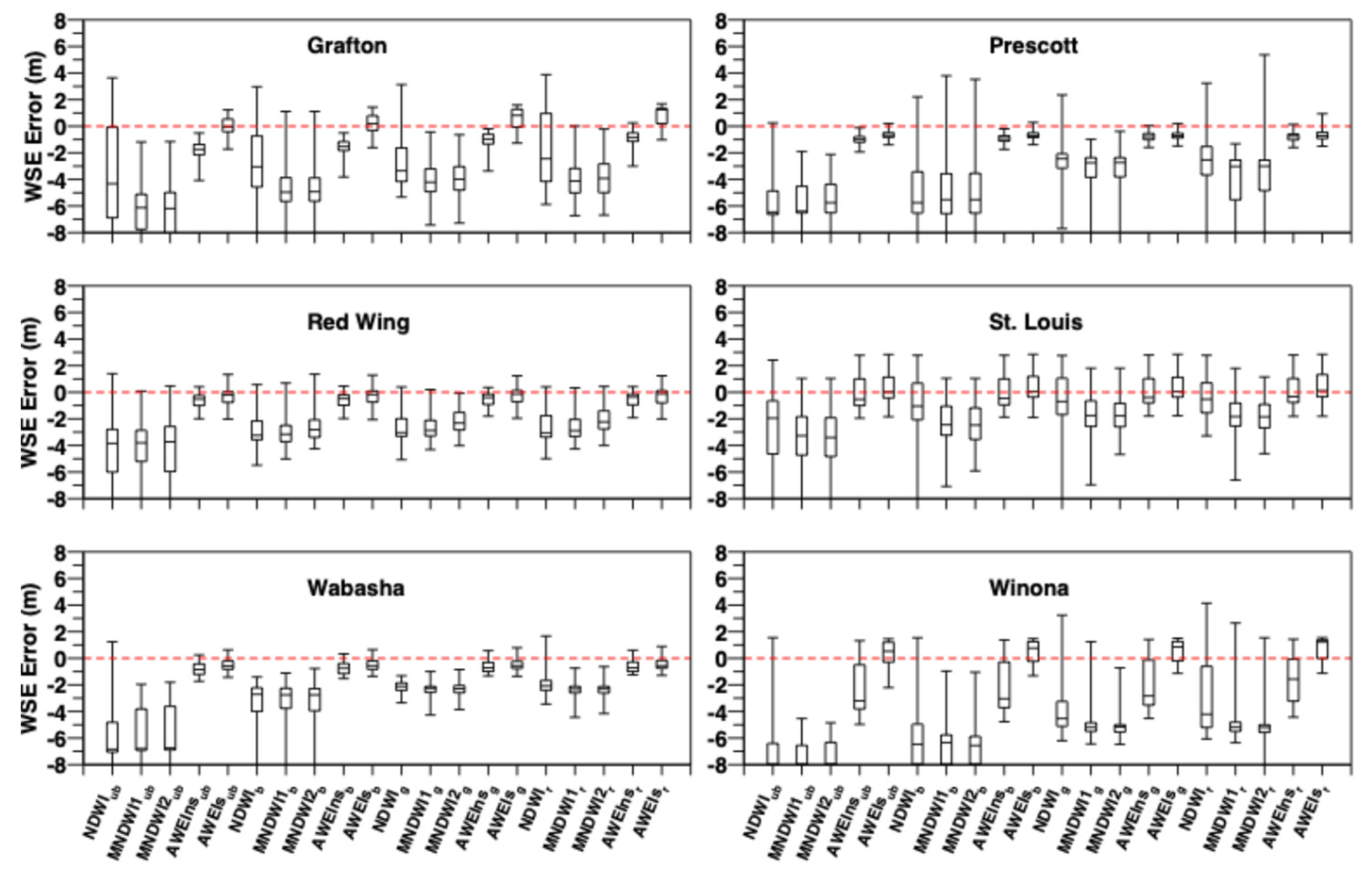
The second criterion for evaluating twenty water indices is the box plot of the errors in the estimated WSEs at each station as shown in Figure 13 (bilinear resampling) and 14 (cubic resampling).
Figure 11, Figure 12, Figure 13 and Figure 14 all demonstrate that the automatic water extraction index for non-shadow (AWEIns) and shadow (AWEIs) are better than other water indices in terms of the accuracy of the estimated WSEs at all six selected stations, no matter the bilinear resampling method or the cubic resampling method was used for downscaling Landsat 8-9 OLI imagery from 30 m to 1 m.

4.4. Comparison of the Estimated WSEs between AWEIns and AWEIs

To compare the performance of AWEIns and AWEIs, percentages of the absolute errors in the estimated WSEs using AWEIns that are equal to (i.e., |err|AWEIns=|err|AWEIs), less than (i.e., |err|AWEIns<|err|AWEIs), and greater than (i.e., |err|AWEIns>|err|AWEIs) the absolute errors in the estimated WSEs using AWEIs at each of six selected stations were computed and listed in Table 3. Among these six stations, only the station at St. Louis exhibited that more than 50% of the absolute errors in the estimated WSEs uisng AWEIns are less than that of AWEIs, and the other five stations all showed that AWEIs performed better than AWEIns.

4.5. Comparison of the Estimated WSEs among Four AWEIs

Since four visible light bands (i.e., ultra-blue, blue, green, and red) were used in this study for computing the automatic water extraction index for shadow (AWEIs), while AWEIs performed better than other water indices, it is necessary to compare the errors in the estimated WSEs among these four visible light band-based AWEIs. Table 4 lists the percentages of the absolute errors in the estimated WSEs associated with each of AWEIs that are the smallest among the four visible light band-based WAEIs at each station.
It should be noted that the sum of the percentages of the smallest absolute errors among four visible light band-based AWEIs at each station is not necessarily equal to 100%, because multiple visible light band-based AWEIs could yield the same lowest absolute errors at the same time.
According to Table 4, either ultra-blue or red band-based AWEIs performed better than blue or green band-based AWEIs in terms of the accuracy of the estimated WSEs from Landsat 8-9 OLI imagery, although the green band-based water indices are commonly used.
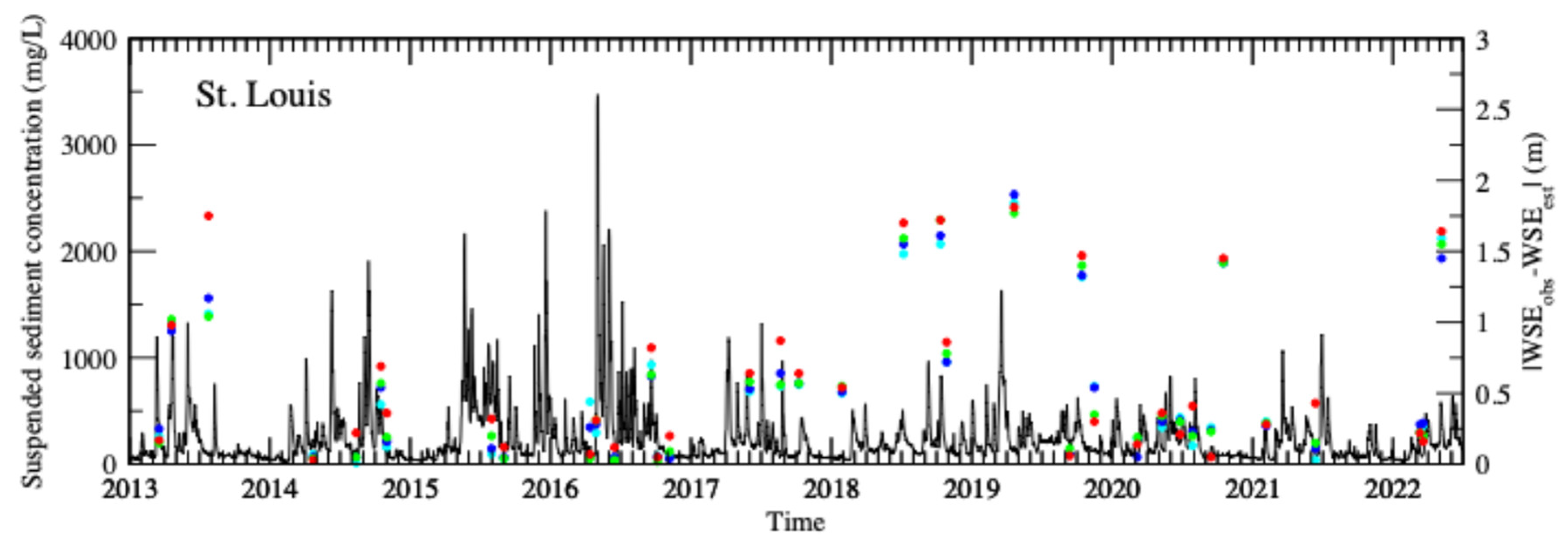
Pan et al. (2020) suggested that the ultra-blue band might work better than other visible light bands for clear water, and red band might perform well for water with a large amount of sediments. Table 4 only shows the overall performance of AWEIs among 60-80 imaging dates during the period of 2013-2024. We understand that water quality is a dynamic variable that varies with time, atmospheric conditions, weather patterns, land use and land cover change, and others. To reveal the water quality impact on the performance of four visible light band-based AWEIs, the suspended sediment concentration data collected at the St. Louis station (only this station has daily water quality data during a portion of this study period) were used to make a time series plot as shown in Figure 15. The absolute errors of the estimated WSEs by the four AWEIs versus time were also plotted in Figure 15.
Figure 15 shows that at St. Louis station, most of the estimated WSEs using the ultra-blue band-based AWEIs are more accurate that the estimated WSEs using other three visible light band-based AWEIs, which is consistent with Table 4. Figure 15 also shows that as the suspended sediment concentration decreased, the difference in the absolute errors of the estimated WSEs between red and ultra-blue band-based AWEIs increased, especially on July 25 of 2013. This result suggests that the red band-based AWEIs works better for water with high sediment loads while the ultra-blue band-based AWEIs is suitable for clear water.

4.6. The Dependence of the Errors in the Estimated WSEs by AWEIns and AWEIs on River Stages

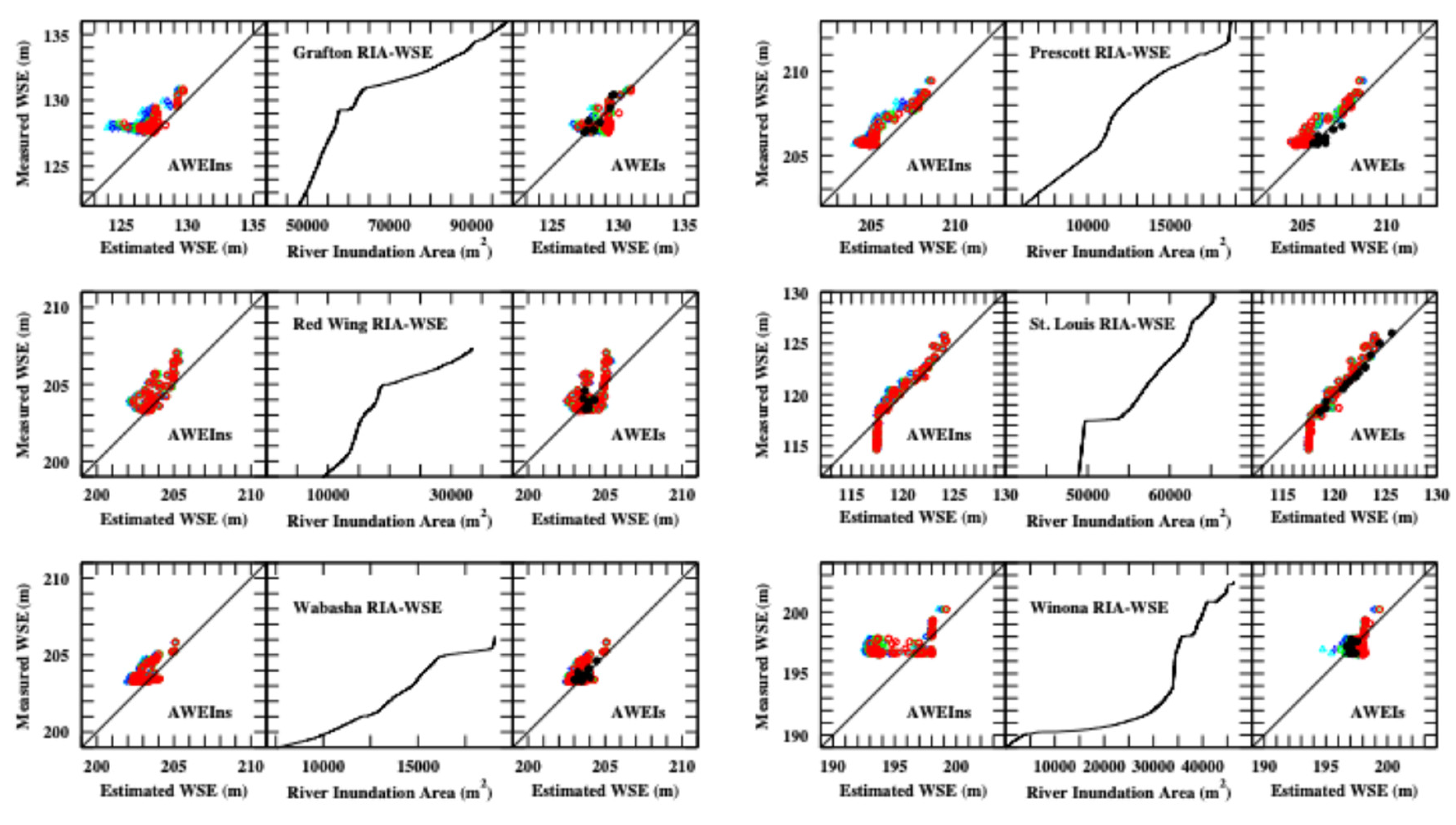
To investigate how the errors in the estimated WSEs by AWEIns and AWEIs vary with river stages, the scatter plots of measured WSEs versus estimated WSEs using AWEIns and AWEIs are illustrated in Figure 16, along with the constructed RIA-WSE rating curve at each station. Four colored-dots, i.e., cyan, blue, green, and red in Figure 16 represent estimated WSEs using ultra-blue, blue, green and red band-based AWEIns or AWEIs, respectively. Figure 16 shows that overall AWEIs performed better than AWEIns, especially at Winona station, which is consistent with Table 3. Since AWEIs is better than AWEIns, let us focus on the AWEIs results in Figure 16. To understand the error behavior of the estimated WSEs using the AWEIs, the scatter plots of the measured WSEs versus the estimated WSEs from the NAIP imagery at each station were also plotted in the same plots of the AWEIs results in Figure 16.
Figure 16 shows that at Grafton station, as WSEs above 129m, the estimated WSEs are more accurate that those below 129m. The constructed RIA-WSE rating curve at Grafton plotted in Figure 16 exhibits a sharp increase in the slope as the WSE drops below 129m, i.e., a small change in RIA is associated with a large change in WSE. This sharp increase in the slope of the RIA-WSE rating curve could induce the uncertainty in the extracted RIAs from Landsat 8-9 OLI imagery, although Landsat 8-9 OLI images used in this study were downscaled from 30m to 1m. The black dots shown in Figure 16 at Grafton do not show the same error behavior as the Landsat results, because the NAIP imagery has a spatial resolution of 1m prior to 2018 and 0.6 after 2018.
At Prescott station, the estimated WSEs were more accurate as the WSEs above 207m than those below 207m due to a slight increase in the slope of the constructed RIA-WSE rating curve. There is no NAIP imagery acquired during the time as the WSE is below 207m. The estimated WSEs based on NAIP imagery at Prescott as WSE below 207m are more accurate than the Landsat results as shown in Figure 16.
At Red Wing station, the errors in the estimated WSEs from Landsat imagery as WSE below 205 m are due to the steep slope in the constructed RIA-WSE rating curve, and the errors in the Landsat estimated WSEs as WSE above 205 m are probably caused by the dense plant canopy cover (see Figure 6a) that blocks remote sensing of water on the ground and in turn decreases the extracted RIAs from the Landsat 8-9 OLI imagery. The NAIP results shown in Fi.16 are better than the Landsat results as WSE below 205m. There is no NAIP imagery acquired at the time as WSE above 205 m.
Results at St. Louis, Wabasha and Winona all demonstrate that a sharp increase in the constructed RIA-WSE rating curves could increase the errors of the Landsat estimated WSEs, especially at St. Louis station as WSE below 108m, while such impact did not appear in the estimated WSEs from NAIP imagery (unfortunately no NAIP images are available at St. Louis as WSE below 108m), and the main reason is that the NAIP imagery has a very high spatial resolution, although the Landsat imagery was resampled from 30m to 1m in this study.

5. Conclusions

Topobathymetric elevation model (TEM) data are more useful than the DEM data in constructing the RIA-WSE rating curves because the constructed RIA-WSE rating curves from the TEM data can be used for estimating river WSEs over the whole dynamic range of the river stages especially at the low flow conditions, while the constructed RIA-WSE rating curves from the DEM data are only valid above the minimum elevations in the DEM data at river cross sections, which actually are the water surface elevations as ground survey was conducted collecting elevation data for producing DEM data.
The selection of a polygon for constructing the RIA-WSE rating curve is critical, as shown in this study, an optimal polygon should cover the riverbank and a portion of river without any man-made structures and dense vegetation cover. However, sometimes we may need to choose a polygon far away from the cross section of interest, as the distance from the cross section increases, the errors in the estimated WSEs would also increase since the water surface elevation can vary significantly along the river especially during high flow conditions. If this is the case, the direct method seems a better choice as the radar altimeter or laser scanning points can directly struck on the water surface.
As Landsat imagery has a spatial resolution of 30m, to improve the accuracy of the estimated WSEs, resampling or downscaling Landsat imagery is necessary. This study found that the cubic resampling method is better than the bilinear resampling method in terms of the accuracy of the Landsat estimated WSEs. If the slope in the RIA-WSE rating curve is not very steep, and no dense vegetation cover in the predefined polygon, the resampled Landsat imagery could yield high accurate results. However, the Landsat imagery might have trouble to achieve a centimeter-level accuracy in the estimated WSEs as the WSE is at the range where the slope in the constructed RIA-WSE rating curve is steep. Under these river stage conditions high resolution imagery is needed to accurately estimate WSEs.
The results of this study demonstrate that in addition to the green band-based water indices, other three visible light bands (i.e., ultra-blue, blue, and red) in the Landsat 8-9 OLI imagery can also be used to compute water index. Although the green band-based water indices are commonly used in the literature, this study showed that the ultra-blue or red band-based AWEIs performed better in terms of the accuracy of the estimated WSEs from Landsat 8-9 OLI imagery.

Funding

This research received no external funding.

Data Availability Statement

All data used in this study are available to everyone through email communication with the author (feifei.pan@unt.edu). After the author receives the request of data, the author will share the data with the requester through uploading data to the Google Drive and sending the Google Drive link to the requester.

Acknowledgments

The author thank the Upper Mississippi River System (UMRS) for producing the topobathy elevation model (TEM) data along the Upper Mississippi River and making the TEM data available to public.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Buchanan, T.J.; Somers, W.P. Discharge measurements at gaging stations. Techniques for water resources investigation of the United States Geological Survey. TWRI, 1969, 3, A8.
  2. Olson, S.A.; Norris, J.M. U.S. Geological Survey Stream gaging. U.S. Geological Survey Fact Sheet, 2005, 3131.
  3. Abbott, B.W.; et al. Human domination of the global water cycle absent from depictions and perceptions. Nature Geoscience, 2019, 12,533-540.
  4. Gleeson T.; et al. Illumination water cycle modifications and Earth system resilience in the Anthropocene. Water Resources Research, 2020, doi.org/10.1029/2019/WR024957.
  5. Hamed, K.; Rao, A.R. Flood Frequency Analysis, 1st Edition; CRC Press: Boca Raton, 2000; p.376.
  6. Bhat, M.S.; Alam, A.; Ahmad, B.; Katlia, B.S.; Farooq, H.; Taloor A.K.; Ahmad, S. Flood frequency analysis of river Jhelum in Kashmir basin. Quaternary International, 2019, 507, 288-294.
  7. Faulkner, D.; Warren, S.; Spencer, P.; Sharkey, P. Can we still predict the future from the past? Implementing non-stationary flood frequency analysis in the UK. Journal of Flood Risk Management, 2019, doi.org/10.1111/jfr3.12582.
  8. Bischiniotis, K.; de Moel, H.; van den Homberg, M.; Couasnon, A.; Aerts, J.; Nobre, G.G.; Zsoter, E.; van den Hurk, B. A framework for comparing permanent and forecast-based flood risk-reduction strategies. Science of The Total Environment, 2020, 720, 137572.
  9. Speight, L.J.; Cranston, M.D.; White, C.J.; Kelly, L. Operational and emerging capabilities for surface water flood forecasting. WIREs Water, 2021, doi.org/10.1002/wat2.1517.
  10. Jain, S.K.; Singh, V.P. Water Resources Systems Planning and Management, 2nd Edition, Elsevier: Amsterdam, Netherlands, 2023; p.893.
  11. Niu, W.; Feng, Z. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow times series for sustainable water resources management. Sustainable Cities and Society, 2021, 64, 102562.
  12. Grizzetti, B.; Liquete, C.; Pistocchi, A.; Vigiak, O.; Zulian, G.; Bouraoui, F.; De Roo, A.; Cardoso, A.C. Relationship between ecological condition and ecosystem services in European rivers, lakes and coastal waters. Science of The Total Environment, 2019, 671, 452-465.
  13. Suwal, N.; Huang, X.; Kuriqi, A.; Chen, Y.; Pandey, K.P.; Bhattarai, K.P. Optimisation for cascade reservoir operation considering environmental flows for different environmental management classes. Renewable Energy, 2020, 158, 453-464.
  14. Zhang, S.; Jing, Z.; Li, W.; Wang, L.; Liu, D.; Wang, T. Navigation risk assessment method based on flow conditions: A case study of the river reach between the Three Gorge Dam and the Gezhouba Dam. Ocean Engineering, 2019, 175, 71-79.
  15. Kwon, S.; Seo, I.; Kim, B.; Jung, S.; Kim Y. Assessment of river recreation safety using spatial river recreational index by integration of hydrodynamic model and fuzzy logic. Research Square, 2023, do.org/10.21203/rs.3.rs-2827493/v1.
  16. Fekete, B.M.; Vörösmarty, C.J. The current status of global river discharge monitoring and potential new technologies complementing traditional discharge measurements. In Proceedings of the PUB Kick-off meeting held in Brasilia, 20-22 November 2002, IAHS Publication, 2007, pp.309.
  17. Vörösmarty, C.J.; Willmott, C.J.; Choudhyry, B.J.; Scholss, A.L.; Stearns, T.K.; Robeson, S.M.; Dorman T.J. Analyzing the discharge regime of a large tropical river through remote sensing, ground-based climatic data and modeling. Water Resources Research, 1996, 32, 3137-3150.
  18. IAHS Ad Hoc Committee. Global Water Data: A newly endangered species. EOS Transactions, American Geophysical Union, 2001, 54-58.
  19. Bjerklie, D.M.; Dingman, S.L.; Vörösmarty, C.J.; Holster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. Journal of Hydrology, 2003, 278, 17-38.
  20. Hannah, D.M.; Demuth, S.; van Lanen, H.A.J.; Looser, U.; Prudhomme, C.; Rees, G.; Stahl, K.; Tallaken, L.M. Large-scale river flow archives: importance, current status and future needs. Hydrological Processes, 2011, 25, 1191-1200.
  21. Cloke, H.L.; Pappernberger, F. Ensemble flood forecasting: a review. Journal of Hydrology, 2009, 375(3-4), 613-626.
  22. Smith, L.C. Satellite remote sensing of river inundation area, stage, and discharge: a review. Hydrological Processes, 1997, 11, 1427-1439.
  23. Alsdorf, D.E.; Rodriguez, E.; Letternmaier, D.P. Measuring surface water from space. Reviews of Geophysics, 2007, 45, RG2002. http://dx.doi.org/10.1029/2006RG000197.
  24. Schumann, G.; Bates, P.D.; Horritt, M.S.; Matgen, P.; Pappernberger, F. Progress in integration of remote sensing-derived flood extend and stage data and hydraulic models. Reviews of Geophysics, 2009, 47, RG4001.
  25. Pan, F. Remote sensing of river stage and discharge. SPIE Newsroom, 2013, doi:10.1117/2.120121204611.
  26. Pan, F.; Nichols, J. Remote sensing of river stage using the cross sectional inundation area - river stage relationship (IARSR) constructed from digital elevation model data. Hydrological Process, 2012, doi:10.1002/hyp.9469.
  27. Pan, F.; Liao J.; Li, X.; Guo, H. Application of the inundation area-lake level rating curves constructed from the SRTM DEM to retrieving lake levels from satellite measured inundation areas. Computers & Geosciences, 2013, 52, 168-176.
  28. Koblinsky, C.J.; Clarke, R.T., Brenner, A.C.; Frey, H. Measurement of river level variations with satellite altimetry. Water Resources Research, 1993, 29(6), 1839-1848.
  29. Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: application of satellite radar altimetry. Journal of Geophysical Research-Atmospheres, 2002, 107(D20), Art.No.8059.
  30. Coe, M.T.; Birkett, C.M. Calculation of river discharge and prediction of lake height from satellite radar altimetry: example for the Lake Chad basin. Water Resources Research, 2004, 40, W10205, doi:10.1029/2003WR002543.
  31. Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, C. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992-2002). Remote Sensing of Environment, 2004, 93, 238-245.
  32. Calmant, S.; Seyler, F. Continental surface waters from satellite altimetry. Comptes Rendus Geoscience, 2006, 338, 113-1122.
  33. Leon, J.G.; Calmant, S.; Seyler, F.; Bonnet, M.P.; Cauhopé M.; Frappart, F.; Filizola, N.; Fraizy, P. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. Journal of Hydrology, 2006, 328, 481-496.
  34. Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrological Processes, 2010, 24(26), 3811-3825.
  35. Bhang, K.J.; Schwartz, F.W.; Park, S. Estimating historic lake stages from one-time snapshot, the Shuttle Radar Topography Mission of 2020. Hydrological Processes, 2010, 34, 1834-1843.
  36. Altenau, E.H.; Pavelsky, T.M.; Moller, D.; Pitcher, L.H.; Batest, P.D.; Durand M.T.; Smith, L.C. Temporal variations in river water surface elevation and slope captured by AirSWOT. Remote Sensing of Environment, 2019, 224, 304-316.
  37. Chipman, J.W. A multisensory approach to satellite monitoring of trends in lake area, water level and volume. Remote Sensing, 2019, 11(2), 158.
  38. Jiang, L.; Andersen, O.B.; Nielsen, K.; Zhang, G.; Bauer-Gottwein, P. Influence of local geoid variation on water surface elevation estimates derived from multi-mission altimetry for Lake Namco. Remote Sensing of Environment, 2019, 221, 65-79.
  39. Li, X.; Long, D.; Huang, Q.; Han, P.; Zhao, F.; Wada, Y. High-temporal-resolution water level and storage change data sets for lakes on the Tibetan Plateau during 2000-2017 using multiple altimetric missions and Landsat-derived lake shoreline positions. Earth System Science Data, 2019, 11, 1603-1627.
  40. Ma, Y.; Xu, N.; Sun, J.; Wang, X.; Yang, F.; Li, S. Estimating water levels and volumes of lakes dated back to the 1980s using Landsat imagery and photon-counting lidar datasets. Remote Sensing of Environment, 2019, 212, 111287.
  41. Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s lake level and volume changes from NASA’s ICESat/ICESat-2 and Landsat Missions. Geophysical Research Letters, 2019, 15, doi: 10.1029/2019GL085032.
  42. Bandini, F.; Sunding, T.P.; Linde, J.; Smith, O.; Jensen, I.K.; Koppl, C.J.; Butts, M.; Bauer-Gottwein, P. Unmanned aerial system (UAS) observations of water surface elevation in a small stream: comparison of radar altimetry, Lidar and photogrammetry techniques. Remote Sensing of Environment, 2020, 237, 111487.
  43. Tortini, R.; Noujdina, N.; Yeo, S.; Ricko, M.; Birkett, C.; Khandelwal, A.; Kumar, V.; Marlier, M.A.E.; Lettenmaier, D.P. Satellite-based remote sensing data set of global surface water storage change from 1992 to 2018. Earth System Science Data, 2020, 12(2), 1141-1151.
  44. Yuan, C.; Gong, P.; Bai, Y. Performance assessment of ICESat-2 laser altimeter data for water level measurement over lakes and reservoirs in China. Remote Sensing, 2020, 12(5), 770.
  45. Frappart, F.; Blarel, F.; Fayad, I.; Berge-Nguyen, M.; Crétaus, J.F.; Shu, S.; Schregenberger, J. Badhdadi, N. Evaluation of the performances of radar and lidar altimetry mission for water level retrievals in mountainous environment: The case of the Swiss lakes. Remote Sensing, 2021,13(11), 2196.
  46. Wu, G.; Liu, Y.; Liu R. Assessing the performance of the Tianggong-2 wide-swath imaging altimeter observations for water level monitoring over complex and shallow lake. Journal of Hydrology, 2022, 612, 128164.
  47. Hamilton, S.K.; Sipple, S.J.; Melack, J.M. Inundation patterns in the Pantanal wetland of South America determined from passive microwave remote sensing. Archives of Hydrobiology, 1996, 137, 115-141.
  48. Brakenridge, G.R.; Tracy, B.T.; Knox, J.C. Orbital SAR remote sensing of a river flood wave. International Journal of Remote Sensing, 1998, 19, 1439-1445.
  49. Pietroniro, A.; Prowse, T.; Peters, D.L. Hydrologic assessment of an inland freshwater data using multi-temporal satellite remote sensing. Hydrological Processes, 1999, 13, 2483-2498.
  50. Al-Khudhairy, D.H.A.; Leemhuis, C.; Hoffmann, V.; Shepherd, I.M.; Calaon, R.; Thompson, J.R.; Gavin , H.; Casca-Tucker, D.L.; Zalidis, G.; Bilas, G.; Papadimos, D. Monitoring wetland ditch water levels using Landsat TM and ground-based measurements. Photogrammetric Engineering and Remote Sensing, 2002, 68, 809-818.
  51. Temimi, M.; Leconte, R.; Brissette, F.; Chaouch, N. Flood monitoring over the Mackenzie River Basin using passive microwave data. Remote Sensing of Environment, 2005, 98, 344-355.
  52. Matgen, P.; Schumann, G.; Henry, J.P.; Hoffmann, L.; Pfister, L. Integration of SAR-derived river inundation areas, high-precision topographic data and a river flow model toward near real-time flood management. International Journal of Applied Earth Observation and Geoinformation, 2007, 9(3), 247-263.
  53. Schumann, G.; Pappernberger, F.; Matgen, P. Pappenberger, F. Estimating uncertainty associated with water stages from a single SAR image. Advances in Water Resources, 2008, 31(8), 1038-1047.
  54. Schumann, G.; Pappernberger, F.; Matgen, P. Conditioning water stages from satellite imagery on uncertain data points. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4), 810-813.
  55. Smith, L.C.; Pavelsky, T.M. Remote sensing of volumetric storage changes in lakes. Earth Surface Processes and Landforms, 2009, 34, 1353-1358.
  56. Pan, F.; Wang, C.; Xi, X. Constructing river stage-discharge rating curves using remotely sensed river cross-sectional inundation areas and river bathymetry. Journal of Hydrology, 2016, 540, 670-687.
  57. Dong, Y.; Fan, L.; Zhao J.; Huang S.; Geiß, C.; Wang, L.; Taubenböck, H. Mapping of small water bodies with integrated spatial information for time series images of optical remote sensing. Journal of Hydrology, 2022, 614, 128580.
  58. Kebede, M.G.; Wang, L.; Li, X.; Hu, Z. Remote sensing-based river discharge estimation for a small river flowing over the high mountain regions of the Tibetan Plateau. International Journal of Remote Sensing, 2019, 41(9), 3322-3345.
  59. Stone, J.M.; Hanson, J.L.; Sattler, S.R. The Upper Mississippi River System-Topobathy: U.S. Geological Survey Fact Sheet, 2017, 2016-3097, https://doi.org/10.3133/fs20163097, 4p.
  60. Rogala, J.T. Methodologies Employed for Bathymetric Mapping and Sediment Characterization as Part of the Upper Mississippi River System Navigation Feasibility Study. ENV Report 13, Interim Report for the Upper Mississippi River – Illinois Waterway System Navigation Study; prepared for U.S. Army Engineers District, Rock Island, U.S. Army Engineers District, St. Louis, and U.S. Army Engineers District, St. Paul, 1999.
  61. Pan, F.; Xi, X.; Wang, C. A comparative study of water indices and image classification algorithms for mapping inland surface water bodies using Landsat imagery. Remote Sensing, 2020, 12(10), 1611, https://doi.org/10.3390/rs12101611.
  62. McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432.
  63. Xu, H. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033.
  64. Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35.
  65. Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Mancybernetics, 1979, 9, 62–69.
  66. Bunis, L.; Mootz, J. Aerial Photography Field Office—National Agriculture Imagery Program (NAIP) Suggested Best Practices–Final Report. 2007, Performed for USDA under contract: CDRL A006 Submitted Under GSA Contract Number GS-23F-0284M, SIN 871_2.
  67. Richards, J.A. Remote Sensing Digital Image Analysis: An Introduction, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 494.
Preprints 110306 g001
Figure 1. Flowchart.
Figure 1. Flowchart.
Preprints 110306 g001
Preprints 110306 g002
Figure 2. Constructing the RIA-WSE from a hypothetical TEM data.
Figure 2. Constructing the RIA-WSE from a hypothetical TEM data.
Preprints 110306 g002
Preprints 110306 g003
Figure 4. a. NAIP image (left), Figure 4b. Topobathy image (center), Figure 4c. Constructed RIA-WSE rating curve (right) at Grafton.
Figure 4. a. NAIP image (left), Figure 4b. Topobathy image (center), Figure 4c. Constructed RIA-WSE rating curve (right) at Grafton.
Preprints 110306 g003
Preprints 110306 g004
Figure 5. a. NAIP image (left), Figure 5b. Topobathy image (center), Figure 5c. Constructed RIA-WSE rating curve (right) at Prescott.
Figure 5. a. NAIP image (left), Figure 5b. Topobathy image (center), Figure 5c. Constructed RIA-WSE rating curve (right) at Prescott.
Preprints 110306 g004
Preprints 110306 g005
Figure 6. a. NAIP image (left), Figure 6b. Topobathy image (center), Figure 6c. Constructed RIA-WSE rating curve (right) at Red Wing.
Figure 6. a. NAIP image (left), Figure 6b. Topobathy image (center), Figure 6c. Constructed RIA-WSE rating curve (right) at Red Wing.
Preprints 110306 g005
Preprints 110306 g006
Figure 7. a. NAIP image (left), Figure 7b. Topobathy image (center), Figure 7c. Constructed RIA-WSE rating curve (right) at St. Louis.
Figure 7. a. NAIP image (left), Figure 7b. Topobathy image (center), Figure 7c. Constructed RIA-WSE rating curve (right) at St. Louis.
Preprints 110306 g006
Preprints 110306 g007
Figure 8. a. NAIP image (left), Figure 8b. Topobathy image (center), Figure 8c. Constructed RIA-WSE rating curve (right) at Wabasha.
Figure 8. a. NAIP image (left), Figure 8b. Topobathy image (center), Figure 8c. Constructed RIA-WSE rating curve (right) at Wabasha.
Preprints 110306 g007
Preprints 110306 g008
Figure 9. a. NAIP image (left), Figure 9b. Topobathy image (center), Figure 9c. Constructed RIA-WSE rating curve (right) at Winonna.
Figure 9. a. NAIP image (left), Figure 9b. Topobathy image (center), Figure 9c. Constructed RIA-WSE rating curve (right) at Winonna.
Preprints 110306 g008
Preprints 110306 g009
Figure 11. Box plots of the error ranks (among twenty water indices) of the estimated WSEs from the resampled Landsat 8-9 OLI imagery using the bilinear resampling method.
Figure 11. Box plots of the error ranks (among twenty water indices) of the estimated WSEs from the resampled Landsat 8-9 OLI imagery using the bilinear resampling method.
Preprints 110306 g009
Preprints 110306 g010
Figure 12. Box plots of the error ranks (among twenty water indices) of the estimated WSEs from the resampled Landsat 8-9 OLI imagery using the cubic resampling method.
Figure 12. Box plots of the error ranks (among twenty water indices) of the estimated WSEs from the resampled Landsat 8-9 OLI imagery using the cubic resampling method.
Preprints 110306 g010
Preprints 110306 g011
Figure 13. Box plots of the errors in the estimated WSEs from the resampled Landsat 8-9 OILI imagery using the bilinear resampling method.
Figure 13. Box plots of the errors in the estimated WSEs from the resampled Landsat 8-9 OILI imagery using the bilinear resampling method.
Preprints 110306 g011
Preprints 110306 g012
Figure 14. Box plots of the errors in the estimated WSEs from the resampled Landsat 8-9 OILI imagery using the cubic resampling method.
Figure 14. Box plots of the errors in the estimated WSEs from the resampled Landsat 8-9 OILI imagery using the cubic resampling method.
Preprints 110306 g012
Preprints 110306 g013
Figure 15. Time series plots of daily suspended sediment concentration and the absolute errors in the estimated WSEs using ultra-blue (cyan dots), blue (blue dots), green (green dots), and red (red dots) band-based AWEIs at St. Louis.
Figure 15. Time series plots of daily suspended sediment concentration and the absolute errors in the estimated WSEs using ultra-blue (cyan dots), blue (blue dots), green (green dots), and red (red dots) band-based AWEIs at St. Louis.
Preprints 110306 g013
Preprints 110306 g014
Figure 16. Scatter plots of measured vs estimated WSEs using AWEIns (left box) and AWEIs (right box), and the constructed RIA-WSE rating curve (center box) at each of six selected stations.
Figure 16. Scatter plots of measured vs estimated WSEs using AWEIns (left box) and AWEIs (right box), and the constructed RIA-WSE rating curve (center box) at each of six selected stations.
Preprints 110306 g014
Table 2. Comparison of the errors in the estimated WSEs between bilinear and cubic resampling methods.
Table 2. Comparison of the errors in the estimated WSEs between bilinear and cubic resampling methods.
Error Comparison Grafton Prescott Red Wing St. Louis Wabasha Winona
|err|bilinear=|err|cubic 10.5% 15.1% 7.3% 1% 9.9% 15.1%
|err|bilinear<|err|cubic 27.7% 8.6% 34.4% 12.2% 8.6% 21.1%
|err|bilinear>|err|cubic 61.8% 76.3% 58.3% 86.8% 81.5% 63.9%
Table 3. Comparison of the errors in the estimated WSEs between AWEIns and AWEIs.
Table 3. Comparison of the errors in the estimated WSEs between AWEIns and AWEIs.
Error Comparison Grafton Prescott Red Wing St. Louis Wabasha Winona
|err|AWEIns=|err|AWEIs 0% 1.9% 2.8% 0% 1.6% 0%
|err|AWEIns<|err|AWEIs 28.2% 25% 34.2% 56.3% 24.6% 23.5%
|err|AWEIns>|err|AWEIs 71.8% 73.1% 63% 43.7% 73.8% 76.5%
Table 4. Percentages of the smallest absolute errors of the estimated WSEs among four visible light band (VLB) -based AWEIs.
Table 4. Percentages of the smallest absolute errors of the estimated WSEs among four visible light band (VLB) -based AWEIs.
VLB Grafton Prescott Red Wing St. Louis Wabasha Winona
Ultra-blue 55.7% 40% 33.8% 55.6% 16.1% 56.9%
Blue 31.4% 28.8% 21.1% 34.9% 16.1% 13.8%
Green 20% 15% 38% 30.2% 33.9% 12.3%
Red 21.4% 31.2% 40.8% 19% 41.9% 27.7%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated