Prerpints.org logo
Preprint
Article

Research on Optimizing Low-Saturation Intersection Signals with Consideration for Both Efficiency and Fairness

Altmetrics

Downloads

72

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 June 2024

Posted:

27 June 2024

You are already at the latest version

Alerts
Abstract
In response to the fairness issue arising from the unequal delay of vehicles in different phases at intersections, considering the actual situation of small and variable delays for vehicles in low-saturation intersection phases, this paper proposes the concept of "sacrificing efficiency for fairness." Firstly, the universality of unfair delay phenomena at intersection phases is explained, especially at low-saturation intersections where the fluctuation in phase delays is 1.87 times higher than at other intersections. Then, a fairness evaluation index is constructed using information entropy, and the feasibility of the proposed approach is demonstrated. Subsequently, a signal optimization model that balances efficiency and fairness is proposed. Finally, the proposed model is validated through case studies, showing that it not only simultaneously considers efficiency and fairness but also has minimal impact on efficiency. Moreover, the changes to timing schemes in the efficiency model are much smaller compared to the model that only considers fairness. Sensitivity analysis reveals that the model performs better under low-saturation intersection conditions.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

In recent years, China’s comprehensive strength has significantly increased, and socialist development has become more democratized, leading to a higher happiness index among the people. However, there are still areas that require improvement. At the 19th National Congress of the Communist Party of China, General Secretary Xi Jinping pointed out, “Socialism with Chinese characteristics has entered a new era, and the principal contradiction in our society has evolved into the contradiction between unmet growing needs for a better life and unbalanced and inadequate development.”[1] With the stable development and improvement of China’s social productivity, imbalances in social development have emerged as a major constraint to people’s pursuit of a better life. Throughout history, social fairness has always been a common aspiration of humanity, and achieving social fairness is one of the greatest demands for social development. To meet the people’s aspirations for a better life, the central leadership of the Party attaches great importance to the issue of social fairness, repeatedly emphasizing its importance, and stressing the need to focus more on social fairness and prioritize people’s well-being in the construction process across various domains. Transportation is an integral component of socioeconomic development, and to some extent, reflects social fairness.[2] Improving transportation fairness can contribute to enhancing social fairness. Currently, in various aspects of our daily lives, we have adopted strategies to improve transportation fairness. For instance, there is a strong emphasis on developing priority for public transportation. Measures such as creating dedicated bus lanes and HOV lanes aim to enhance the efficiency and environment of bus travel, thus reducing the commuting disparity among different income groups. Putting people first, facilities such as tactile paving on pedestrian walkways and barrier-free elevators at subway transfer stations are installed to meet the travel needs of special populations. These are all effective strategies for enhancing both transportation fairness and social fairness.
Urban road intersections serve as crucial nodes in urban road networks, with signal control playing a pivotal role. However, they also represent bottlenecks causing traffic delays. According to the “2020 Second Quarter Analysis Report on Traffic in Major Cities in China” released by Gaode Map, the average delay at intersections during peak hours in major Chinese cities exceeds 30 seconds per vehicle, with Shenzhen recording the highest delay at 39.22 seconds per vehicle. In urban signalized intersections, the most direct manifestation of fairness is the consistency of average delay across different phases. However, currently, most signal timing plans are designed with the objective of minimizing overall delay for vehicles, without considering the unfairness caused by differences in average delay among phases before establishing the optimization model. Equal average delay among phases is only achieved when the saturation levels of each phase are equal. The distribution of urban traffic volume over time is uneven, with significantly lower traffic during off-peak hours compared to rush hours. For example, during off-peak hours, the hourly traffic volume in cities like Shenzhen and Guangzhou is only one-third of that during rush hours. Therefore, sacrificing intersection delay during off-peak hours to achieve fairness is feasible.
Considering the sustained attention to transportation fairness in society and the actual situation of low saturation at intersections during off-peak periods, this paper proposes a signal timing optimization approach for low-saturation intersections, sacrificing some delay to achieve fairness. Through in-depth analysis of intersection efficiency and fairness, the paper first illustrates the universality of fairness issues in intersection phase delay. Next, the feasibility of the proposed approach is verified. Furthermore, a signal timing optimization model considering both efficiency and fairness is constructed. Finally, the effectiveness of the model is validated using case studies, and sensitivity analysis is conducted on intersection saturation. The first section of the paper summarizes the current research status in related fields domestically and outlines the main research content. The second section delves into the fairness of each phase of the Webster model from both theoretical and simulation perspectives. The third section introduces a fairness evaluation function based on information entropy, upon which a signal optimization model for low-saturation intersections considering delay and fairness is built. In the fourth section, the effectiveness of the model is analyzed using case studies, and sensitivity analysis is conducted on intersection saturation.

2. Literature Review

In the past, research on signal timing optimization at intersections has primarily focused on minimizing delay, with the most classic being the Webster timing optimization scheme.[3] In recent years, on one hand, scholars have innovated signal timing optimization schemes based on considering delay. On the other hand, foreign scholars have also been continuously exploring the consideration of fairness in the signal optimization process

2.1. Traffic Signal Timing Optimization

Signal timing control schemes directly impact the operational effectiveness of intersections. In foreign research, many scholars[4,5,6,7] often construct mathematical function models targeting one or more parameters in the evaluation criteria for signal timing optimization. They utilize methods like genetic algorithms to solve the established models, followed by simulation. Results indicate that the proposed schemes can reduce intersection delay. Weal et al.[8] formulated an optimization model targeting the minimization of average delay at signalized intersections. Murat[9] and Schmoecker[10] proposed a multi-objective control model for single intersections based on fuzzy logic methods, selecting multiple performance indicators as optimization objectives. Chen[11] introduced a multi-objective optimization and decision-making method to optimize signal timing at individual intersections. Additionally, Deng et al.[12] applied data fusion technology to propose a new multi-objective signal control parameter optimization model for urban intersections.
Currently, there has been a significant amount of research in China as well. Scholars[13,14,15,16] are constructing signal timing models for intersections, aiming to optimize multiple objectives by targeting one or more parameters in the intersection evaluation criteria and assigning different weights to these criteria based on varying traffic flow conditions. Li Xun et al.[17] investigated signal control issues at urban arterial road intersections, focusing on multiple intersections and establishing signal control function models. The results of model solutions effectively reduced average delay per vehicle and improved intersection capacity. Li Juan et al.[18] proposed a signal timing optimization model aimed at minimizing average delay per person at intersections based on total delay for motor vehicles, non-motor vehicles, and pedestrians, while considering the differences in two crossing modes for non-motor vehicles. Chen Song et al.[19] introduced conditions suitable for left-turning on opposing lanes and established an optimization model for intersection signal control methods, which was solved using genetic algorithms. Jiang Tao et al.[20] designed a method that matches signal control schemes with lane functions based on varying traffic demands on inbound lanes at intersections.

2.2 Transportation Fairness

The current recognized concept of transportation fairness originates from the project report of the International Joint Highway Research in 1994: “Transportation fairness refers to the allocation of costs and benefits generated by a policy, typically considering various demographic groups.”[21,22] Litman[23] provided a comprehensive overview of this concept, suggesting that transportation fairness should include horizontal fairness, vertical fairness considering different classes and incomes, and vertical fairness considering differences in transportation abilities and needs.
Scholars have not only researched the influencing factors of transportation fairness, but also explored the fairness issues between different modes of transportation. For instance, Kawabata[16] compared the accessibility of employment and travel time for employment trips among residents of different generations, analyzing the differences between car travel and public transportation, thereby discussing the fairness issues between different modes of travel. Furthermore, Lu Dandan[24] et al. analyzed factors such as residents’ travel efficiency, road infrastructure quality, travel costs, and the impact of transportation facilities on the environment, summarizing the impact of these factors on transportation fairness. Scholars have also studied various approaches to measuring transportation fairness. For example, Delbose and Currie[20] utilized mathematical models such as Lorenz curves and the Gini coefficient to investigate transportation fairness issues in the Melbourne area.
As the principle of people-oriented development gains increasing recognition, scholars have also studied the application of fairness in signal timing optimization research. ZhiChun[25] developed a heuristic solving algorithm that combines penalty functions and simulated annealing methods, incorporating both environmental and fairness objectives into traffic signal timing problems by maximizing traffic capacity and minimizing traffic emissions. Ozgur Baskan[26] proposed a heuristic solving algorithm based on harmony search and penalty function methods, optimizing traffic signal timing schemes in urban road networks by considering traffic capacity and fairness constraints. Liang Zheng[27] proposed a dual-objective signal timing simulation optimization model based on uncertainty by balancing the Atkinson index (evaluating transportation fairness) and average travel time (evaluating transportation efficiency). With the widespread application of information entropy in engineering, technology, and socioeconomics, explorations in the field of transportation have also been conducted. Shi Jing[28] and others proposed a transportation fairness evaluation method considering regional fairness and fairness of benefit attribution to different groups based on the Wilson entropy model. Lv Bin[29] and others designed a phase difference optimization algorithm for the line control system using information entropy theory and multi-attribute decision-making methods, with travel time, vehicle delay, and queue length as evaluation indicators.

2.3 Summary

(1) Existing signal timing methods often optimize for one or several objectives and construct optimization functions, primarily focusing on delay as the target, with relatively few studies considering both delay and fairness.
(2) Information entropy is widely used in various fields, but there are relatively few studies applying it to signal timing optimization.
(3) Currently, research on fairness in the transportation field is relatively broad, with increasing attention being paid to fairness in signal control. However, there are relatively few studies on fairness regarding delay fairness for each phase.
In order to comprehensively consider the various objectives in signal timing optimization for low-saturation intersections and to reflect fairness, this paper proposes incorporating the differences in phase delay fairness into the optimization objectives. It utilizes information entropy and the Webster delay model as the basis to construct a fairness evaluation function, further establishing a signal timing optimization model considering both delay and fairness. The results validate the feasibility of sacrificing delay for fairness in this paper’s approach. Finally, a multi-objective model incorporating delay, fairness, and emissions is constructed, and the model is verified through case studies, with sensitivity analysis conducted on intersection saturation.

Intersection Delay Fairness Analysis

Based on the actual conditions of the research object, this section first identifies Webster as the delay model. Subsequently, it analyzes the fairness of the Webster model from both theoretical and empirical perspectives. Finally, it utilizes information entropy to design a fairness evaluation function for intersection delay.

3.1 Delay Model Determination

Currently, the models used to calculate delay at signalized intersections mainly include the Webster delay model[30], the ARRB model[31], the HCM1985 model[32], and the HCM2000 model[33]. In estimating delay at low-saturation signalized intersections, these models are generally consistent because the latter three are derived from the Webster delay model and are more widely applicable. However, as saturation increases, the trend of consistency gradually weakens. When saturation is below 0.8, the relative error percentage of the average delay per vehicle obtained from the Webster model compared to simulation models falls within the range of 0 to 30% for over 95% of cases, significantly better than the other three delay models[31]. Since this study focuses on low-saturation conditions during off-peak periods, the Webster model is chosen as the delay calculation model. The phase-average delay in the Webster model consists of three parts: uniform delay, random delay, and delay correction, as follows:
d i = C ( 1 − λ i ) 2 2 ( 1 − λ i x i ) + x i 2 2 q i ( 1 − x i ) − 0.65 ( C q i 2 ) 1 3 x i ( 2 + 5 λ i )
In the equation, d i represents the phase i average delay; λ i represents the phase i green time ratio, in the equation of λ i = x i x , x i represents the phase i saturation, x represents the total intersection saturation; C represents the signal cycle length; qi represents the flow of the phase i .
Since the last two terms in Equation (1) are much smaller compared to the first term, they can usually be ignored in analysis. Therefore, Equation (1) can be simplified to:
d i = C ( 1 − λ i ) 2 2 ( 1 − λ i x i )
Then substituting λ i = x i x into the above equation gives：
d i = C ( 1 − x i x ) 2 2 ( 1 − x i 2 x )

3.2 Delay Model Fairness Analysis

3.2.1 Theory Analysis

(1) Prevalence of unfairness
Equation (3) is derived for x i to give the following equation:
Since the study is on low saturation intersections, so 0 < x i < x < 1 , therefore Equation(4) < 0 is constant. From this, we can get that the phase vehicle average delay is monotonically decreasing, so there is only one case that each phase saturation is equal, i.e., x 1 = x 2 = ⋯ = x i = ⋯ = x m = x m . The conclusion can be illustrated that signalized intersections designed based on the Webster model can only appear in specific cases that the phase vehicle average delays are equal, i.e., the phenomenon of absolute fairness, whereas the phenomenon of inequality is universal.
d d x i ( d i ) = C 1 − x i ( x i x − 1 ) 2 x ( 1 − x i 2 x ) 2
(2) The less saturated, the less fair
It is not difficult to find that the numerator part of equation (4) monotonically decreasing with x, the denominator part can be simplified to the following equation 5, due to 0 < x i < x < 1 can be known as its monotonically increasing with x, so the formula (4) monotonically decreasing with x, i.e., the smaller the degree of saturation, the greater the change in the phase car average, the more unfair.
x + x i 4 x − 2 x i 2

3.2.2 Example Generation

(1) Basic situation of the intersection
The research object of this paper is a typical intersection with four lanes in both directions, east-west and north-south, with separate left-turn lanes in each direction and assuming no right-turn vehicles.
(2) Traffic flow setting
Referring to the “Urban Road Capacity Table of Various Levels” in China, and according to the actual experience value, the saturation capacity of each lane is set at 1200 pcu/h/lane according to the urban trunk road lanes.
The traffic volume of each lane is randomly generated within [0, 1200] pcu/h.
(3) Phase setting
Considering the crossover practical situation, this paper chooses the classical opponent four-phase, and the following figure gives the schematic diagram.
Preprints 110420 g001
Figure 1. Classic opposite four-phase indication.
Figure 1. Classic opposite four-phase indication.
Preprints 110420 g001
(4) Arithmetic example generation
This paper utilizes Python to randomly generate 2500 sets of traffic flow data for each lane, and since the research object of this paper is low-saturation intersections, 362 sets of data in which the intersection saturation is located in [0.0, 0.8] are selected as the arithmetic examples.
(5) Example description
Since the data is randomly generated, the data distribution is relatively uniform, the average value of intersection traffic volume is 8448pcu/h, the highest is 14976pcu/h, and the lowest is 960pcu/h; the corresponding average value of intersection saturation is 0.45, the highest is 0.78, and the lowest is 0.07.

3.2.3 Example Analysis

To further analyze, this study takes a four-phase single-point intersection as an example and randomly generates 362 sets of effective basic data for different intersections. Using the Webster model, the cycle length, green time ratio, and phase-average delay of each intersection in each group are calculated. Considering that the coefficient of variation can eliminate the influence of measurement scales and dimensions, it is chosen as a parameter to measure the degree of difference in data such as phase-average delay.
(1) Prevalence of unfairness
The results indicate that unfairness is indeed widespread. The coefficient of variation for phase delay among the 362 intersection groups is greater than zero, with a mean of 0.37. Moreover, there is a roughly proportional relationship between the coefficient of variation for phase saturation and the coefficient of variation for phase-average delay. In other words, the greater the difference in phase saturation, the worse the fairness of phase-average delay. The scatter plot below illustrates the relationship between the coefficient of variation for phase saturation and the coefficient of variation for delay.
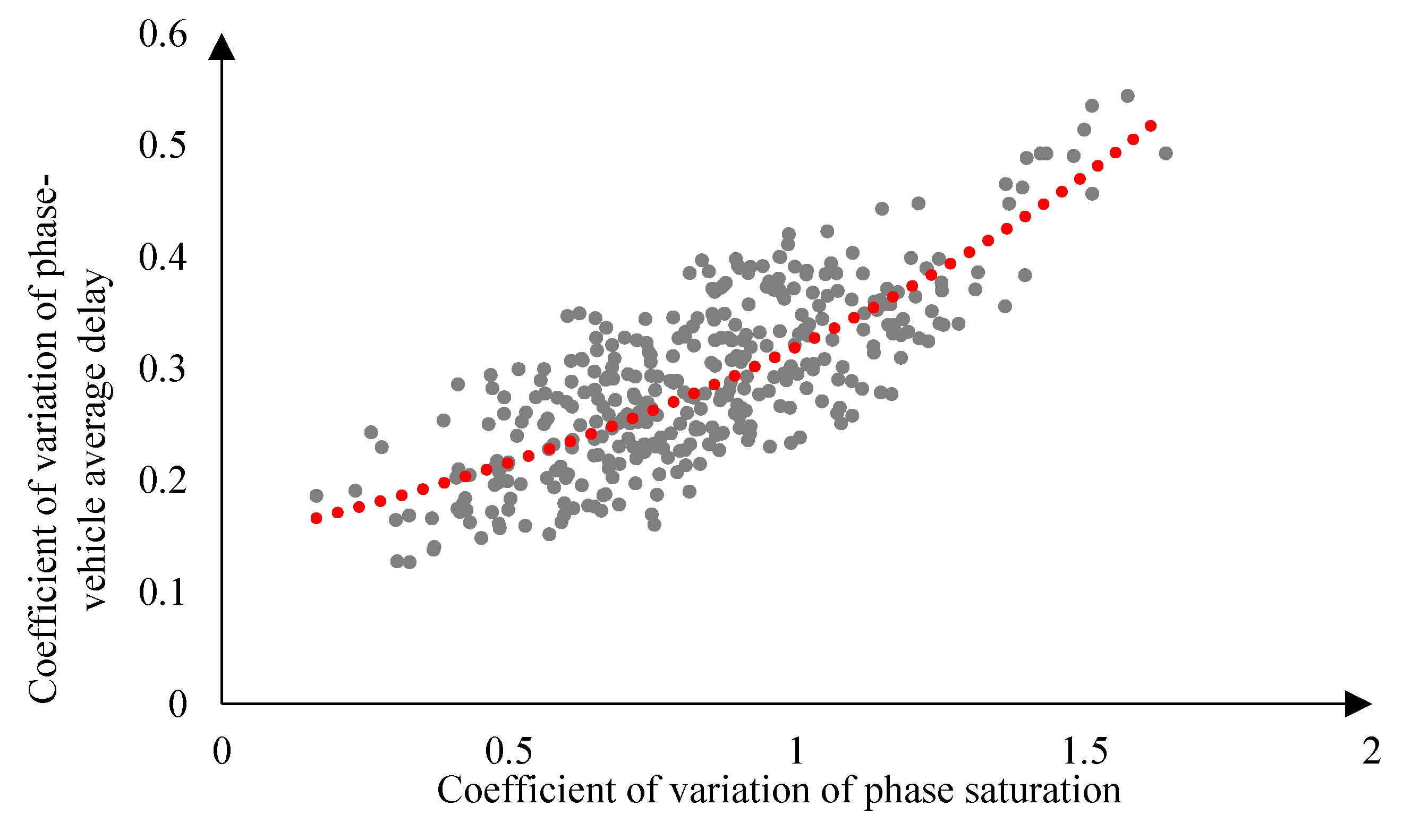
Preprints 110420 g002
Figure 2. Phase Delay Coefficient of Variation Scatter.
Figure 2. Phase Delay Coefficient of Variation Scatter.
Preprints 110420 g002
(2) The less saturated, the less fair
By dividing the 362 sets of data into three saturation intervals, it is observed that the lower the intersection saturation, the greater the coefficient of variation of phase-average delay. The average coefficient of variation for saturation in the [0.0-0.2] range is 0.56, which is 1.87 times that of the other three saturation groups. This indicates a more severe unfairness phenomenon. The figure below presents the curves of different saturation coefficient of variation.In the figure below, the orange curve represents a saturation level of 0.0-0.2, the blue curve represents a saturation level of 0.2-0.4, the green curve represents a saturation level of 0.4-0.6, and the yellow curve represents a saturation level of 0.6-0.8.
Combining the above analysis, it can be inferred that under low saturation conditions, with lower traffic volume and poorer fairness, there is a larger space for adjusting traffic efficiency and a greater necessity for improving the fairness of phase-average delay.
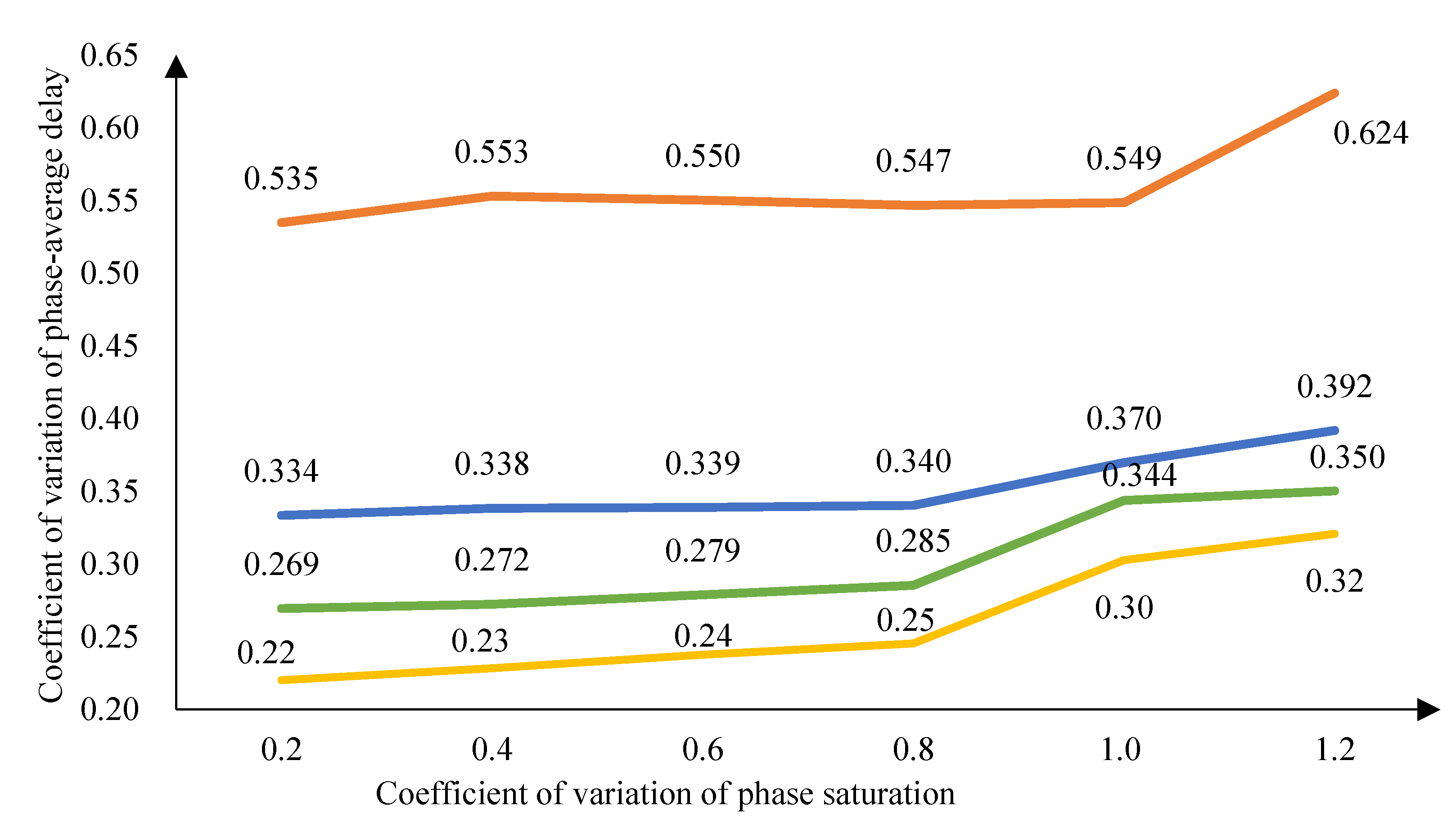
Preprints 110420 g003
Figure 3. Four-saturation coefficient of variation curve.
Figure 3. Four-saturation coefficient of variation curve.
Preprints 110420 g003

3.3 Delay Model Fairness Evaluation

Cross-intersection delay fairness mainly manifests in the consistency of average delay across phases. Descriptive parameters typically include variance, standard deviation, and, to eliminate the influence of scales and dimensions, the coefficient of variation. However, the ranges of these parameters are uncertain, posing difficulties in effectively integrating multiple objectives. Information entropy can also describe data consistency, and for specific problems, its range of values is fixed. Therefore, this study selects information entropy as the descriptive parameter for cross-intersection delay fairness.

3.3.1 Information Entropy

In 1948, Shannon introduced the concept of “information entropy,” addressing the quantification issue of information. For an uncertain system Y, if its source symbols have n possible values with corresponding probabilities P 1 , … , P i , … , P n , and each occurrence of values is independent of others, then the average uncertainty of the source should be the statistical mean ( E ) of the individual symbol uncertainties ( − log ⁡ P i ) , known as information entropy, denoted as:
H X = E − log ⁡ P i = − ∑ i = 1 n P i log ⁡ P i
In equation (6), the base of the logarithm is not specified, typically chosen as 2, e , or 10. Different bases represent information units differently. In this paper, the base e is selected.
Information entropy can be used to evaluate the equilibrium of a system. The closer the individuals are to each other, the less significant the differences, and the larger the information entropy, indicating a more balanced system. Conversely, smaller entropy values imply greater system uncertainty and higher information content. When ∃ P i = 1 , entropy is minimal; when and only when P i = 1 n , entropy is maximal. For a four-phase delay problem, this is calculated as approximately − ∑ i = 1 4 1 4 ln ⁡ 1 4 ≈ 1.386 .

3.3.2 Fairness Evaluation Index

To calculate the information entropy of a system, we need the number of information sources and the probabilities associated with each source. In the context of delay systems for various phases, the number of information sources equals the number of phases, and the probability associated with each phase delay is the proportion of the delay of each phase to the total delay of all phases. Therefore, the evaluation index for the fairness of intersection delay based on information entropy is:
H ( k ) = − ∑ i = 1 m k i l n k i
In Equation (7) k i represents the ratio of the average delay of each phase to the sum of the average delays of all phases, k i = d i ∑ i = 1 m d i ; m represents the number of phases. When and only when k 1 = k 2 = ⋯ = k m , the evaluation index the maximum of − ∑ i = 1 m 1 m ln ⁡ 1 m .

4. Efficiency and Fairness Signal Optimization Model

4.1 Feasibility Analysis

Considering equity will have an impact on delays and will require sacrificing delays for fairness, but is the sacrifice worth it? This section discusses this issue by analyzing the delay-to-fairness conversion rate.

4.1.1 The Delay-to-Fairness Conversion Rate

In the context discussed in this paper, it can be considered that sacrificing delay for equivalent or greater benefits is worthwhile or feasible; otherwise, it is not feasible. The paper proposes to use the delay-to-fairness conversion rate to measure the feasibility of sacrificing delay for fairness. The delay-to-fairness conversion rate represents the ratio between the benefits of fairness and the sacrifice of delay. If this ratio is greater than 1, it indicates feasibility; if less than 1, it indicates infeasibility. The fairness improvement ratio is used to represent the benefits of fairness, while the delay increase ratio represents the sacrifice of delay. The baseline fairness and delay are respectively referenced to the fairness evaluation index and total delay obtained from the signal timing scheme calculated based on the Webster model.

4.1.2 Feasibility Discussion

In order to realize the feasibility discussion, this section first gives the conversion rate calculation method and provides an in-depth discussion of the results, confirming the feasibility of livestock delays in exchange for fairness.
(1) Calculation Method
The first step involves calculating the average delay per vehicle D ′ and the corresponding fairness evaluation index H ′ based on the intersection data using the Webster model.
In the second step, building upon the classical signal timing optimization model, the objective function is replaced with the fairness evaluation index H. Additionally, to further explore delay sacrifice, a constraint on delay sacrifice is added to the model, as shown in Equation (8):
D′≤D≤w_2 D′
The third step involves using the results from the second step to calculate fairness indexes and total delay for each set of intersection data, with total delay sacrifice levels ranging from [0%, 5%], [5%, 10%], [10%, 15%], [15%, 20%], [20%, 25%], to [25%, 30%]. Based on the results obtained in the first step, the conversion rates are then calculated accordingly.
(2) Results
After conducting the calculations six times for the 362 sets of data, the results indicate that the overall conversion rate is not favorable, with a mean value of only 0.69. As the sacrifice level increases, the average conversion rate decreases at an average rate of 29%. However, at a delay sacrifice level of [0%, 5%], the average conversion rate is 1.78, exceeding 100%. For other sacrifice levels, the average conversion rate is only 0.48, with [25%, 30%] being as low as 0.28. This suggests that sacrificing delay for fairness is feasible when the delay sacrifice is small, indicating that this approach has minimal impact on delay, with an average impact of only 2.5%.
Regarding saturation, as saturation increases, the average conversion rate gradually decreases. The saturation range of [0, 0.2] has the highest average conversion rate of 1.25, which remains the highest across all sacrifice levels. At a sacrifice level of [0%, 5%], it even reaches 3.08. In contrast, the saturation range of [0.6, 0.8] has an average conversion rate of only 0.46. This indicates that sacrificing delay for fairness is more effective in low-saturation scenarios. The figure below illustrates the conversion rate curves for different saturation levels and sacrifice levels.In the figure below, the orange curve represents a saturation level of 0.0-0.2, the blue curve represents a saturation level of 0.2-0.4, the green curve represents a saturation level of 0.4-0.6, and the yellow curve represents a saturation level of 0.6-0.8.The black dashed line represents y=x, indicating a conversion efficiency of 100%.
In conclusion, sacrificing delay for fairness is feasible and has minimal impact on delay, making it more suitable for low-saturation intersections.
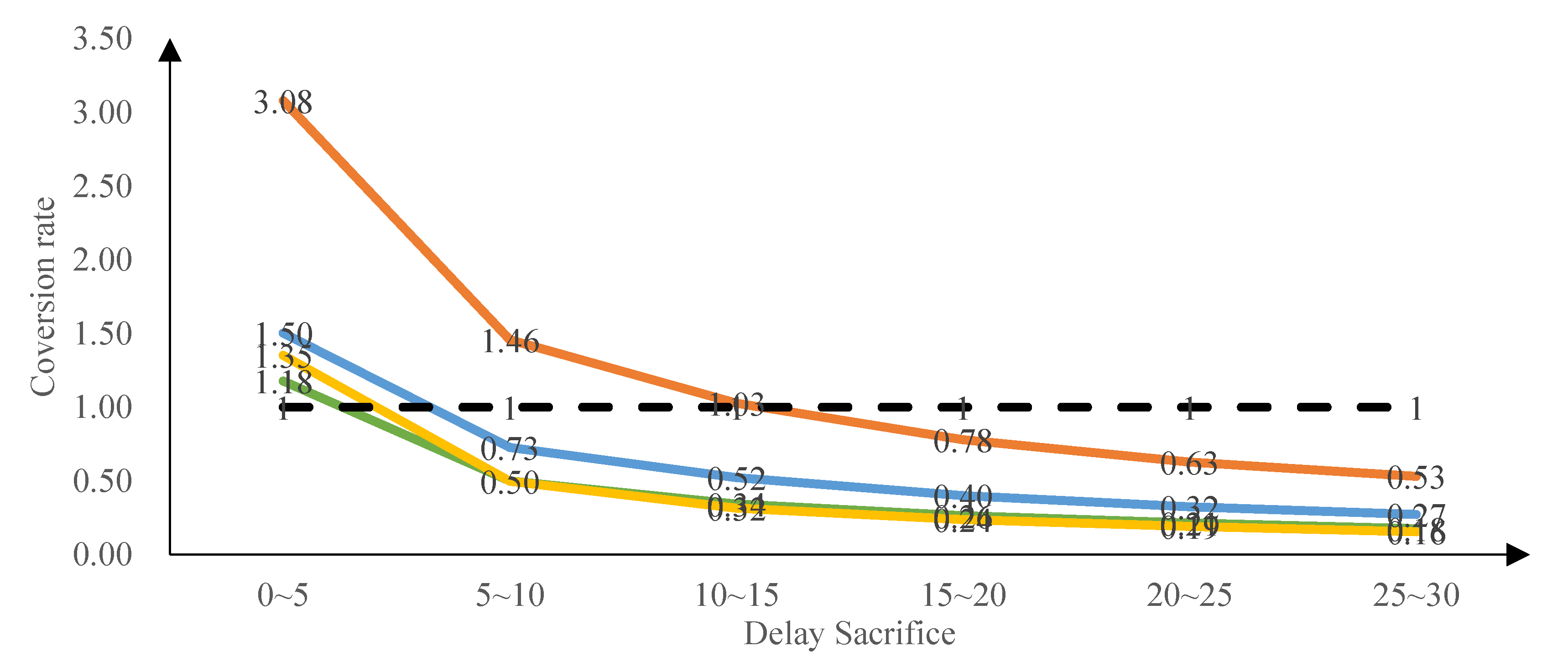
Preprints 110420 g004
Figure 4. Four-saturation conversion rate curve.
Figure 4. Four-saturation conversion rate curve.
Preprints 110420 g004

4.2 Optimization Model Construction

Considering the idea of feasibility analysis in 4.1, in order to realize the organic combination of fairness and efficiency, this paper proposes to take the conversion rate as the objective function, and at the same time take the degree of delay sacrifice as the constraint.

4.2.1 Objection Function Construction

The delay-to-fairness conversion rate represents the ratio between the fair gain and the sacrifice of delay, where the fair gain is described by the proportion of fairness enhancement and the sacrifice of delay is described by the proportion of delay increase. This is specified in equation (9) below:
( H − H ′ ) / H ′ ( D − D ′ ) / D ′
In Equation (9), D ′ and H ′ denote the average intersection vehicle delays calculated using the Webster model, and the corresponding fairness evaluation indexes; D and H denote the average intersection vehicle delays and fairness indexes, respectively.
4.2.2 Optimization Model Construction
In this paper, based on the classical signal timing optimization model, the objective function is replaced with ( H − H ′ ) / H ′ ( D − D ′ ) / D ′ proposed in the previous section, and the constraints on the conversion rate and the degree of delay sacrifice are added. Thus, the signal optimization model considering fairness is obtained, with the following equation (10) as the objective function and equation (11) as the constraints, where the 1st and 2nd in equation (11) are the phase green time length constraints; the 3rd is the cycle length constraint; the 4th is the conversion rate constraint, which is required to be greater than or equal to 1; and the 5th is the delay sacrifice degree constraint.
max   ( H − H ′ ) / H ′ ( D − D ′ ) / D ′
s t   5 < g i < ( C − L )   g i > C − L q i / s i           15 m ≤ C ≤ 220 ( H − H ′ ) / H ′ ( D − D ′ ) / D ′ ≥ 1 D ≤ w D ′ i = 1,2 ⋯ m
In Equation(10), D = ∑ i = 1 m q i ∙ d i ∑ i = 1 m q i , H = − ∑ i = 1 m k i l n k i , k i = d i ∑ i = 1 m d i . In Equation (11), g i represents the phase i green time, g i = ( C − L ) ∙ λ i , s i represents the phase i saturation flow, L represents lost time; w represents delay sacrifice and its value is greater than 1.

5. Model Examples Validation

To validate the model, this section first adopts the traditional Webster model as the efficiency model and constructs the fairness model with the fairness evaluation index as the target number. Then, using the case study employed in the feasibility analysis in Section 2.2, this section conducts a comprehensive comparative analysis of the proposed efficiency-fairness trade-off model, fairness model, and efficiency model from two aspects: the effectiveness of the model and the sensitivity of parameters. Metrics such as delay, fairness evaluation index, cycle change rate, and green ratio change rate are utilized for the comparison and analysis.

5.1 Fairness Model

To further validate the model, a signal optimization model focusing solely on fairness was constructed based on the model from the previous section. Specifically, the objective function was replaced with the fairness evaluation index H, and the fourth conversion rate constraint was removed. Equation (12) represents the objective function, while Equation (13) represents the constraint.
m a x   H
s t   5 < g i < ( C − L )   g i > C − L q i / s i           15 m ≤ C ≤ 220 D ≤ w D ′ i = 1,2 ⋯ m

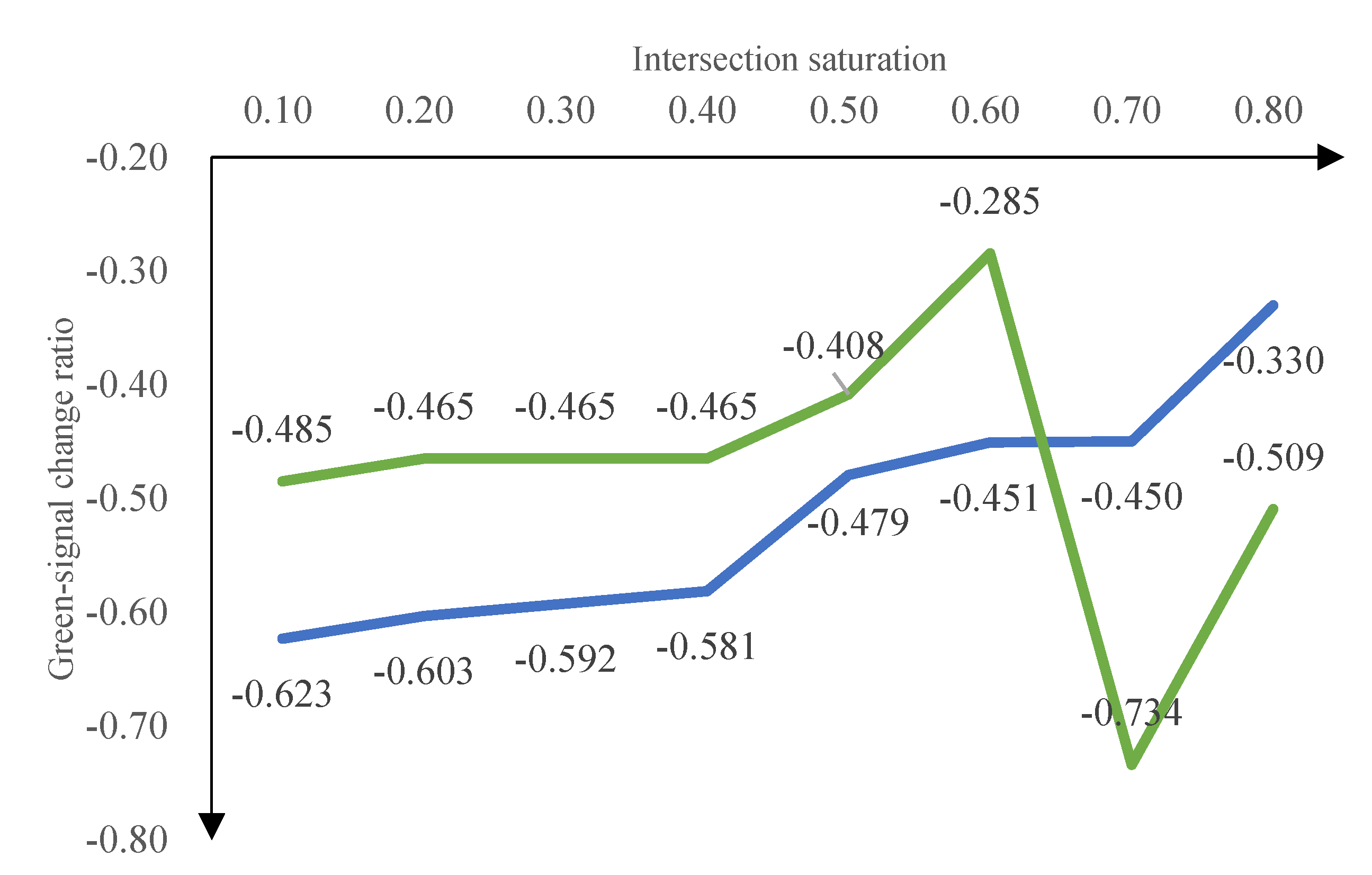
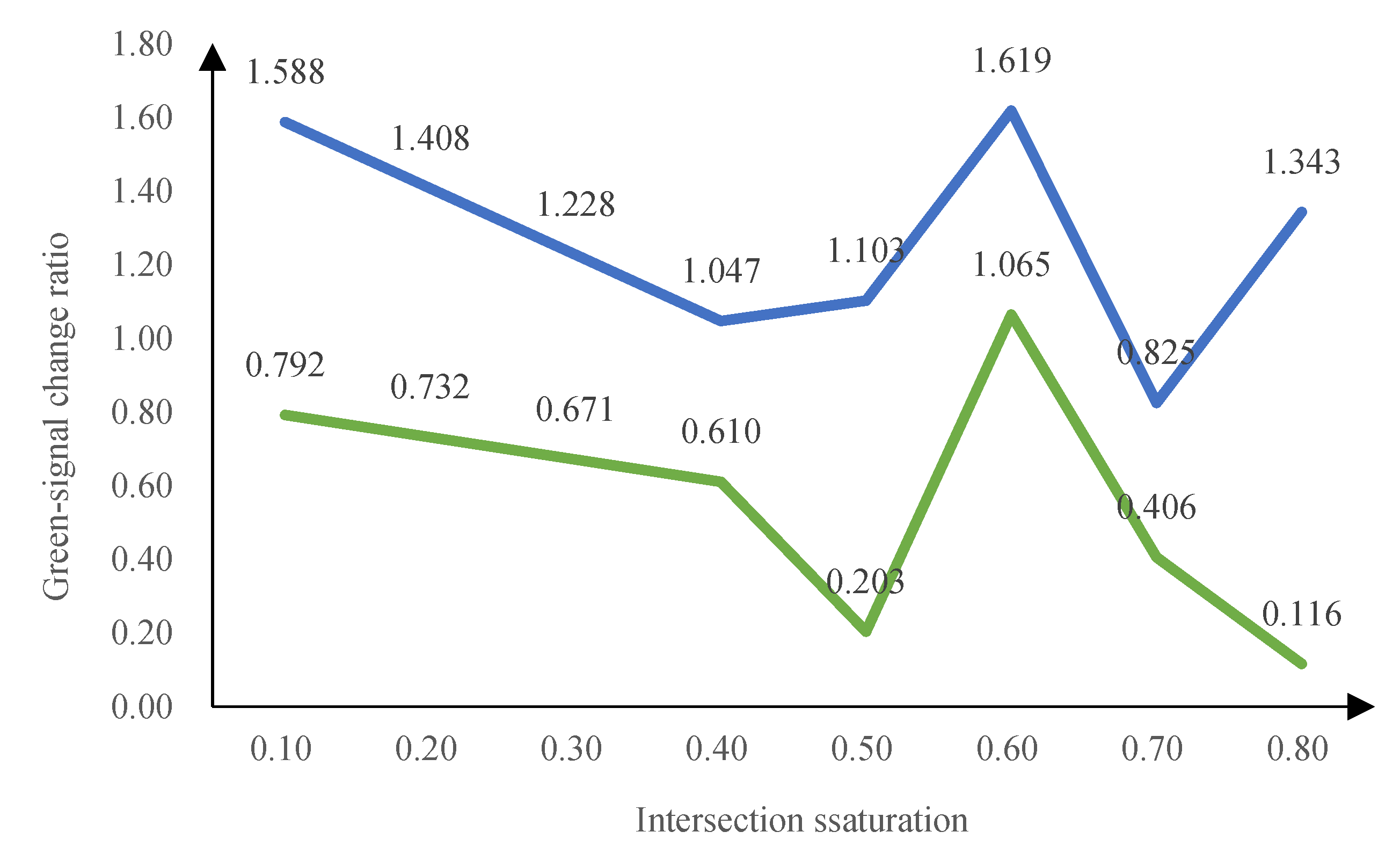
5.2 Validity and Sensitivity Analysis

This section will analyze the validity of the model in terms of both model effectiveness and impact on the efficiency model, as well as perform a sensitivity analysis for intersection saturation.

5.2.1 Comparative Analyses of Validity

(1) Fairness
In terms of the model performance, overall, the fairness model performed the best, followed by the efficiency-fairness model, and the efficiency model performed the worst. Furthermore, the difference between the efficiency-fairness model and the fairness model was significantly smaller than that between the efficiency-fairness model and the efficiency model, with mean fairness evaluation index values of 1.37, 1.32, and 1.21, respectively.
Regarding saturation, under low saturation conditions, the efficiency-fairness model showed better performance. The mean improvement in the fairness evaluation index for saturation levels between 0.1 and 0.4 was 0.16, while for saturation levels between 0.5 and 0.8, it was only 0.075. In terms of trend, higher saturation levels correlated with higher fairness evaluation index values. At saturation levels of 0.1 and 0.8, the mean fairness evaluation index values were 1.27 and 1.33, respectively. Furthermore, the higher the saturation level, the smaller the differences between the models. At saturation levels of 0.1 and 0.8, the mean differences between the models were 0.115 and 0.03, respectively, especially notable between the efficiency-fairness model and the efficiency model, with differences of 0.16 and 0.09 at saturation levels of 0.1 and 0.8, respectively. The following figure illustrates the fairness evaluation index curves for each model. In the figure, the orange curve represents the Webster model, the blue curve represents the fairness model, and the green curve represents the efficiency and fairness model.
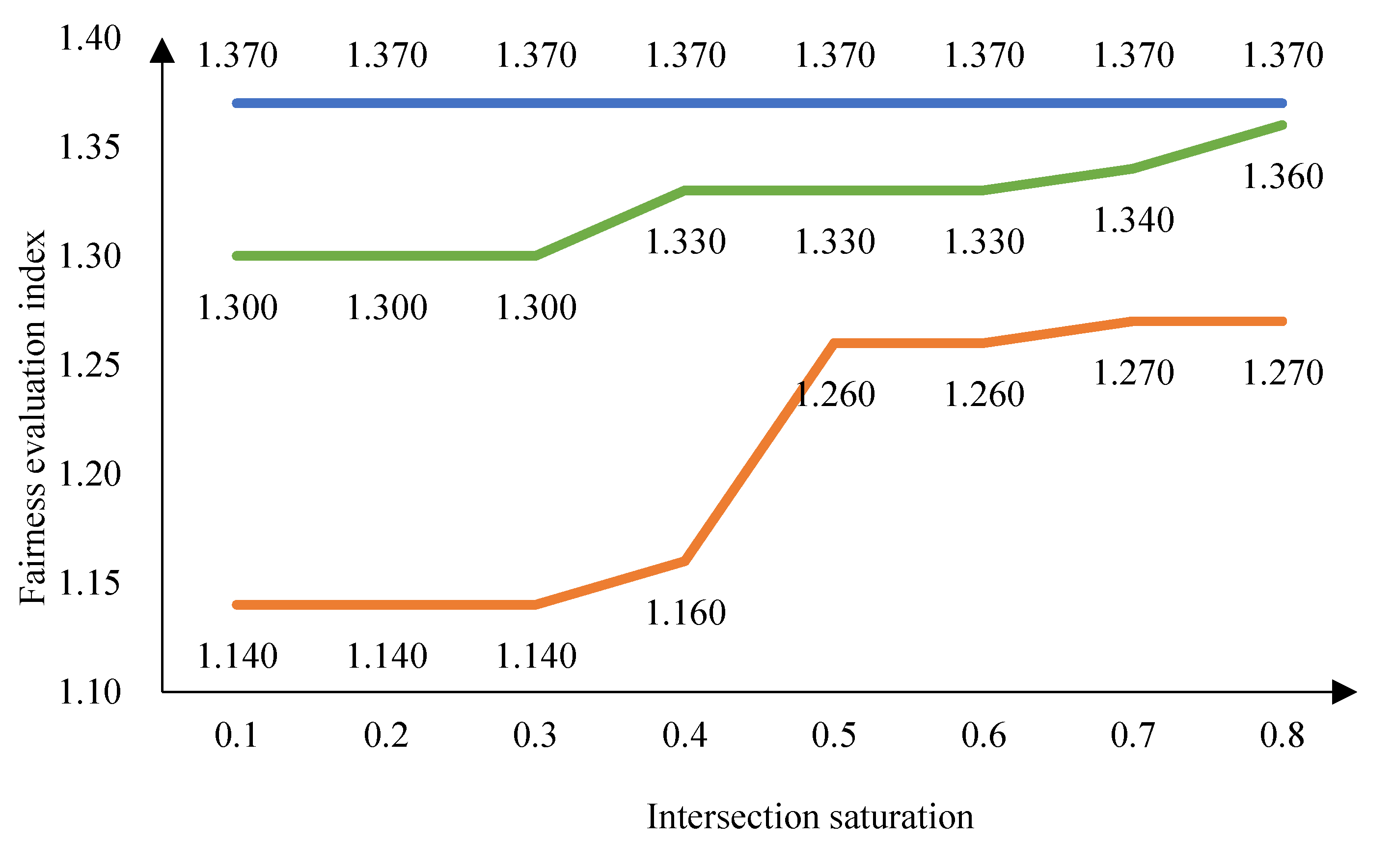
Preprints 110420 g005
Figure 5. Three-model fairness evaluation index curve.
Figure 5. Three-model fairness evaluation index curve.
Preprints 110420 g005
(2) Efficiency
In terms of the models, overall, the efficiency model performed the best, followed by the efficiency-fairness model, and the fairness model performed the worst. Furthermore, the difference between the efficiency-fairness model and the efficiency model was significantly smaller than the difference between the efficiency-fairness model and the fairness model. The mean vehicle delay values were 13.72, 14.08, and 35.12, respectively.
Regarding saturation, the saturation level had little impact on the efficiency-fairness model. As for the trend, higher saturation levels correlated with greater vehicle delays. At saturation levels of 0.1 and 0.8, the mean vehicle delays were 18.4 and 24.98, respectively. Additionally, as saturation levels increased, the differences between the models did not change significantly, with a mean difference of 10.7. At saturation levels of 0.1 and 0.8, the differences were 10.16 and 11.12, respectively. The following figure illustrates the delay curves for each model.In the figure, the orange curve represents the Webster model, the blue curve represents the fairness model, and the green curve represents the efficiency and fairness model.
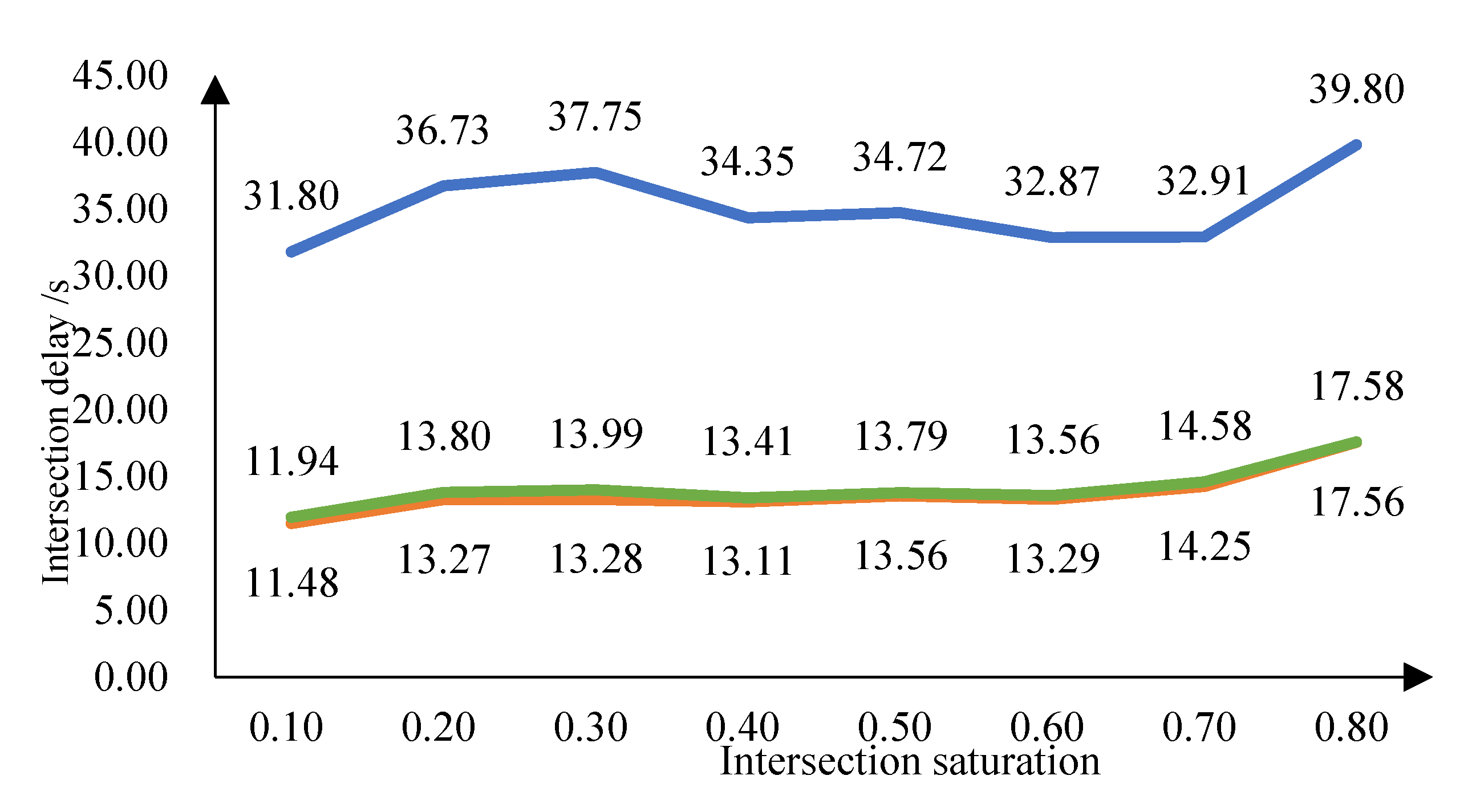
Preprints 110420 g006
Figure 6. Three-model delay curve.
Figure 6. Three-model delay curve.
Preprints 110420 g006
Conversion rate
In terms of the models, overall, the efficiency-fairness model significantly outperformed the fairness model, with mean conversion rates of 0.09 and 9.6, respectively, a difference exceeding 100 times. Furthermore, the efficiency-fairness model ranged from a minimum of 2.37 to a maximum of 0.14 for the fairness model, representing a difference of over 16 times.
Regarding saturation, under low saturation conditions, the efficiency-fairness model exhibited better performance. Excluding the outlier at saturation level 0.8, the mean conversion rates for saturation levels 0.1 to 0.4 were 4.0, greater than the rates for saturation levels 0.5 to 0.7, which were 2.76. With changes in saturation levels, the two models showed different trends. While the fairness model exhibited a decreasing conversion rate with increasing saturation levels, the efficiency-fairness model showed fluctuations in its conversion rate with changes in saturation levels, without a clear trend. The figure below illustrates the conversion rate curves for both models.In the figure, the blue curve represents the fairness model, and the green curve represents the efficiency and fairness model.
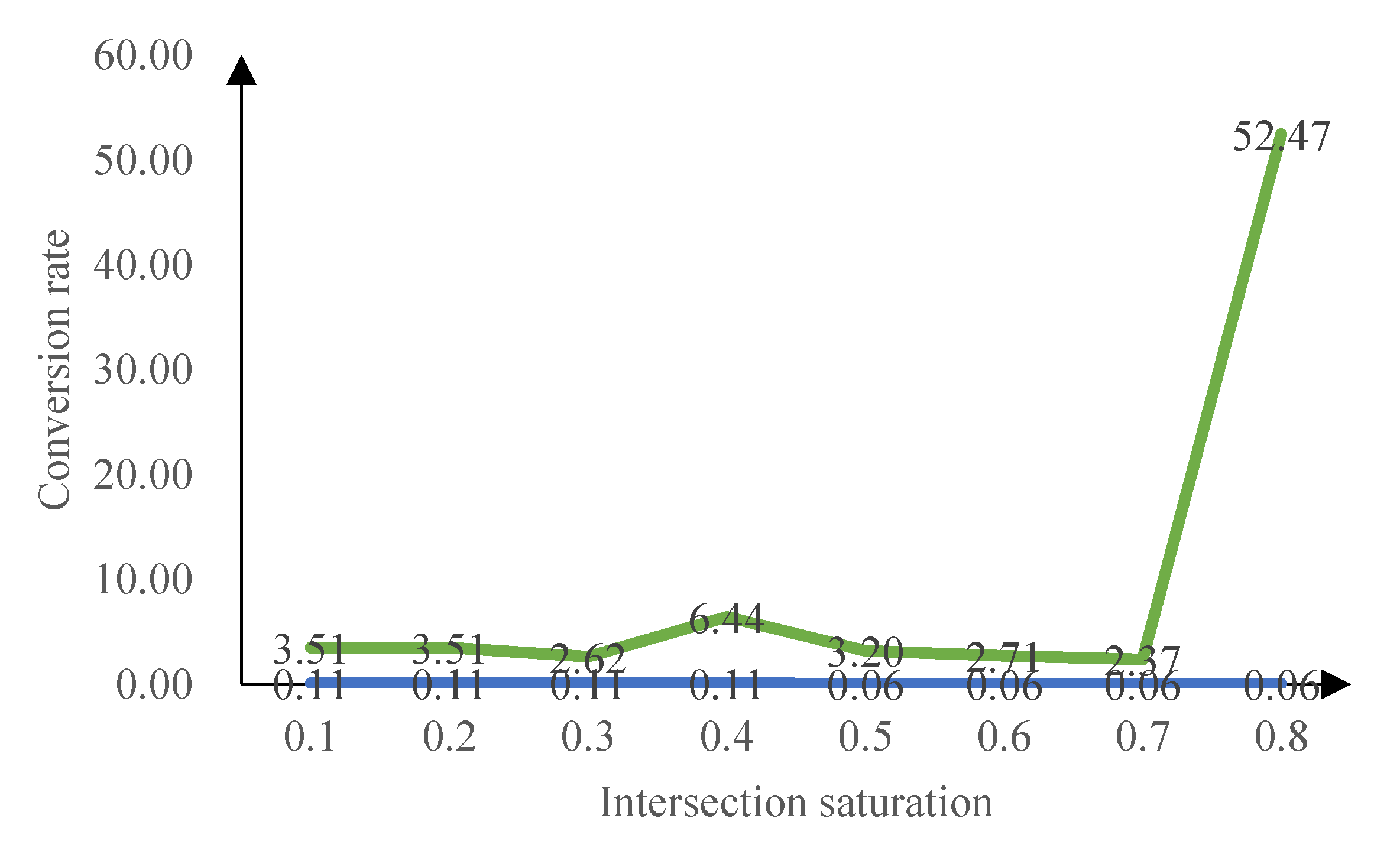
Preprints 110420 g007
Figure 7. Two-model conversion rate curve.
Figure 7. Two-model conversion rate curve.
Preprints 110420 g007

5.2.2 Comparative Analyses of Fluctuations

This section analyzes the fluctuations of the two models relative to the efficiency model based on changes in cycle length and green time ratio.
Cycle Length
Overall, the cycle lengths mostly increased. Concerning the models, the efficiency-fairness model significantly outperformed the fairness model, with mean change ratios of 0.013 and 0.88, respectively, representing a difference exceeding 67 times. Furthermore, the efficiency-fairness model ranged from a maximum of 0.04 to a minimum of 0.62 for the fairness model, a difference exceeding 15 times.
Regarding saturation levels, under low saturation conditions, the efficiency-fairness model exhibited better performance. The mean change ratio for saturation levels 0.1 to 0.4 was 0.0035, whereas for saturation levels 0.5 to 0.8, it was as high as 0.026. In terms of trends, with changes in saturation levels, the two models showed different trends. While the fairness model exhibited an initially increasing and then decreasing trend in change ratio with increasing saturation levels, with significant fluctuations, the efficiency-fairness model showed fluctuations without a clear trend with changes in saturation levels. The figure below illustrates the change ratio curves for cycle lengths for both models.In the figure, the blue curve represents the fairness model, and the green curve represents the efficiency and fairness model.
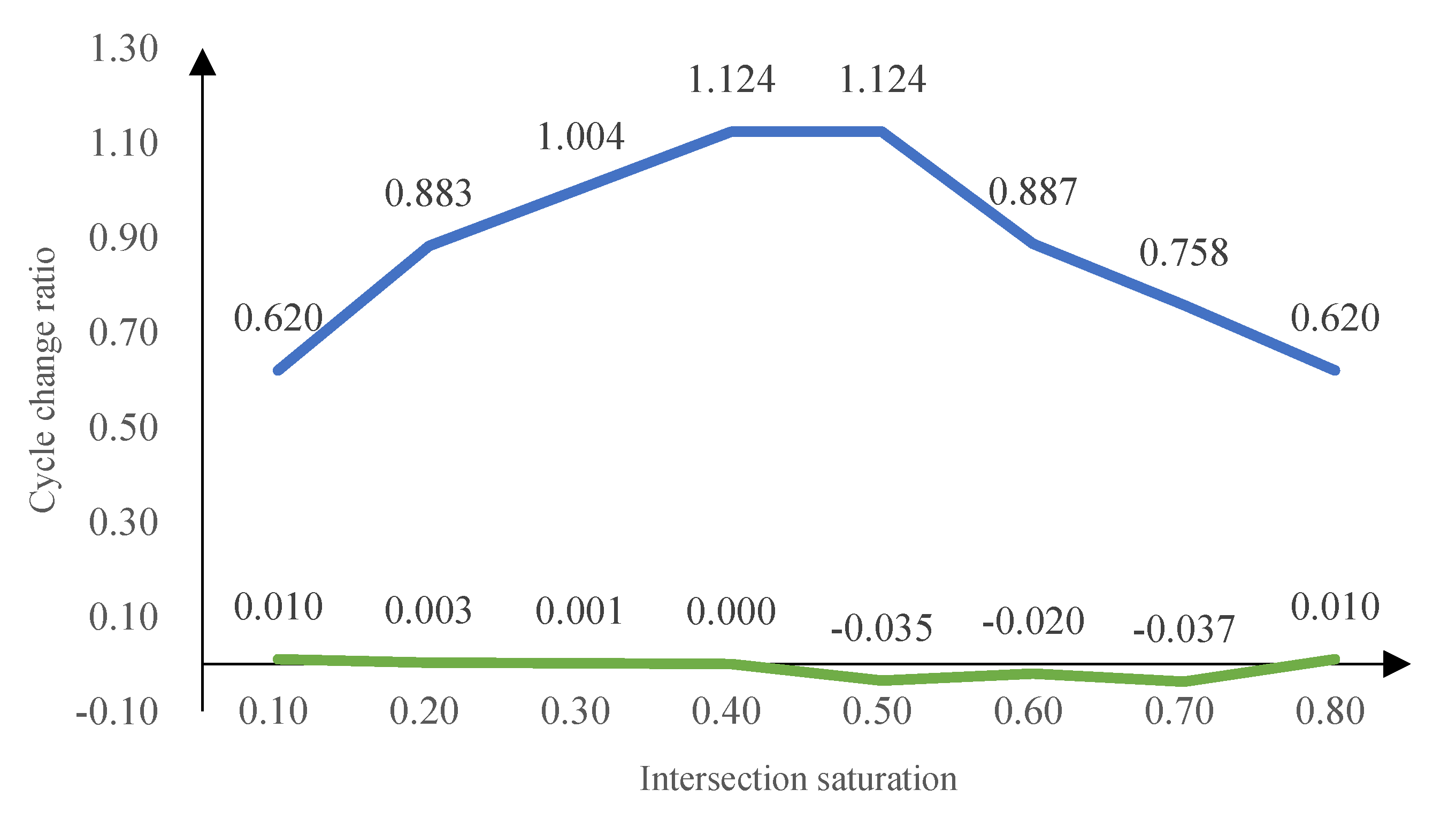
Preprints 110420 g008
Figure 8. Two-model period change proportional curve.
Figure 8. Two-model period change proportional curve.
Preprints 110420 g008
Green time ratio
Additionally, to visually represent the changes in phase green time ratio for these two models relative to the efficiency model, this section selected the two phases with the lowest and highest average delay in the efficiency model for comparison.
Overall, for phases with low green time ratios, the ratios further decreased, while for phases with high green time ratios, the ratios increased. Concerning the models, the efficiency-fairness model generally outperformed the fairness model. The mean change ratios for phases with low green time ratios were -0.48 and -0.51 for the efficiency-fairness and fairness models, respectively, while for phases with high green time ratios, the mean change ratios were 0.57 and 1.27, respectively. Only for phases with low green time ratios and saturation levels of 0.7 and 0.8 did the efficiency-fairness model slightly outperform the fairness model.
Regarding saturation levels, although the efficiency-fairness model exhibited slightly higher change ratios under low saturation conditions, its fluctuation was significantly smaller than under high saturation conditions. For saturation levels of 0.1 to 0.4, the mean change ratios for both low and high green time ratios were 0.47 and 0.7, respectively, with standard deviations of 0.01 and 0.08. For saturation levels of 0.5 to 0.8, the mean change ratios were 0.484 and 0.446, respectively, with standard deviations of 0.19 and 0.43. In terms of trends, the change rate for phases with low saturation levels increased with saturation levels, while for phases with high saturation levels, the change rate decreased with saturation levels. The figures below illustrates the change ratio curves for green time ratios for both models.In the figures, the blue curve represents the fairness model, and the green curve represents the efficiency and fairness model.
Preprints 110420 g009
Figure 9. Proportional curve of green-signal ratio change of the lowest phase of average vehicle delay.
Figure 9. Proportional curve of green-signal ratio change of the lowest phase of average vehicle delay.
Preprints 110420 g009
Preprints 110420 g010
Figure 10. Curve of green-signal ratio change with the highest average delay.
Figure 10. Curve of green-signal ratio change with the highest average delay.
Preprints 110420 g010
In summary, the efficiency and fairness model proposed in this paper not only balances efficiency and fairness simultaneously but also has minimal impact on efficiency. Furthermore, the changes to the timing schemes in the efficiency model are much smaller compared to the fairness model. Therefore, it can be concluded that the proposed model in this paper is valid and effective. Sensitivity analysis indicates that the efficiency and fairness model is more effective in low saturation conditions.

6. Conclusion

To further advance fairness-related research in the transportation field, this paper addresses the issue of fairness in the average delay per vehicle at low-saturation intersection phases. It proposes a strategy of sacrificing efficiency for fairness. Initially, it constructs a fairness evaluation metric for intersection phase delay using information entropy. Then, it validates the feasibility of this approach based on simulated data. Subsequently, it introduces the concept and calculation formula of efficiency-fairness conversion rate, and uses it to develop a signal optimization model that balances efficiency and fairness. Finally, the proposed model is validated using simulated data, showing that it not only achieves a balance between efficiency and fairness but also has minimal impact on efficiency compared to fairness-oriented models. Sensitivity analysis reveals that the model performs better in low-saturation intersection scenarios.

Author Contributions

Conceptualization, L.Z. (Liang Zou) and L.Y.; methodology, L.Y.; software, L.Y. and L.Z. (Lingxiang Zhu); validation, L.Y.; formal analysis, L.Z. (Lingxiang Zhu); writing—original draft preparation, L.Y.; writing—review and editing, L.Z. (Liang Zou). All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by Shenzhen Science and Technology Plan Project (No.KJZD20230923115223047) & Shenzhen Higher Education Stable Support Plan Project(No.20231123103157001).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

  1. Xi Jinping. Secure a Decisive Victory in Building a Moderately Prosperous Society in All Respects and Strive for the Great Success of Socialism with Chinese Characteristics for a New Era: Report to the 19th National Congress of the Communist Party of China [M]. Beijing: People’s Publishing House, 2017: 11-12.
  2. Zhang Zehua. Research on Equity Measurement of Transportation Development in China from the Perspective of Equalization of Public Services [D]. Beijing Jiaotong University, 2019.
  3. Australia S. Guide to traffic engineering practice: part 7: traffic signals[J]. 2003.
  4. Wang P, Yang Q. Genetic Algorithms Based Traffic Signal Optimization at a Congested Intersection[J]. Applied Mechanics & Materials, 2012,209-211:814-817.
  5. Kesur K B. Multiobjective Optimization of Delay and Stops in Traffic Signal Networks[J]. 2013.
  6. A, Ceder, I, et al. An algorithm to minimize queues at signalized intersections[J]. Journal of the Operational Research Society, 2001.
  7. Liu H, Balke K N, Lin W H. A reverse causal-effect modeling approach for signal control of an oversaturated intersection[J]. Transportation Research Part C Emerging Technologies, 2008,16(6):742-754. [CrossRef]
  8. Alhajyaseen W, Najjar M, Ratrout N T, et al. The effectiveness of applying dynamic lane assignment at all approaches of signalized intersection[J]. Case Studies on Transport Policy, 2017:65-72. [CrossRef]
  9. Murat Y S, Gedizlioglu E. A fuzzy logic multi-phased signal control model for isolated junctions[J]. Transportation Research Part C, 2005,13(1):19-36. [CrossRef]
  10. Schmoecker J D, Ahuja S, Bell M. Multi-objective signal control of urban junctions – Framework and a London case study[J]. Transportation Research Part C Emerging Technologies, 2008,16(4):454-470. [CrossRef]
  11. Chen J, Jia M. Robust Multi-objective Optimization and Decision for Signal Timing at Single Intersection: 2016 International Conference on Automatic Control and Information Engineering, 2016[C].
  12. Deng W, Jia L M, Dong H H. Multi-Objective Optimization Model for Urban Traffic Intersection Control Based on Data Fusion[J]. Advanced Materials Research, 2011,156-157:505-510.
  13. Gao Yunfeng, Xu Lihong, Hu Hua, et al. Multi-objective optimization method for fixed-cycle signal control at intersections[J]. China Journal of Highway and Transport, 2011, 24(05):82-88.
  14. Liu Quanfu, Lu Baichuan, Ma Qinglu, et al. Research on multi-objective optimization of signal control at signalized intersections[J]. Journal of Traffic Science and Engineering, 2014, 16(01):47-50.
  15. Wang Yuquan, Jiang Xinyue, Guo Weiwei. Research on optimization method of signalized intersection cycle length considering travel cost[J]. Journal of Chang’an University (Natural Science Edition), 2015, 35(S1):104-107.
  16. Liu Quanfu, Lu Baichuan, Ma Qinglu, et al. Research on multi-objective optimization of signal control at signalized intersections[J]. Journal of Traffic Science and Engineering, 2014, 16(01):47-50.
  17. Li Xun, Liu Yao, Zhou Jian, et al. Traffic signal timing optimization model based on improved genetic algorithm[J]. Industrial Instrumentation & Automation, 2017(04):125-130.
  18. Li Juan, Jia Tingyong. Signal timing optimization at signalized intersections based on per capita delay[J]. Journal of Highway Traffic Science and Technology, 2021, 38(11):134-141.
  19. Chen Song, Li Xiansheng, Wang Yunhao, et al. Optimization of traffic control scheme for left-turning intersections with opposing exit lanes[J]. Journal of Harbin Institute of Technology, 2018, 50(03):74-82.
  20. Jiang Tao, Ma Qiannan. Setting and signal optimization method for variable guidance lanes in multiple time periods[J]. Journal of Traffic Science and Engineering, 2019, 35(01):86-93.
  21. Cai Shiyao. Traffic network design model and application based on traffic fairness[D]. Huazhong University of Science and Technology, 2016.
  22. Zhu Zhaoming. Research on multi-mode traffic congestion charging methods considering fairness[D]. Southeast University, 2016.
  23. Litman T. EVALUATING TRANSPORTATION EQUITY - METHODS FOR INCORPORATING DISTRIBUTIONAL IMPACTS INTO TRANSPORT PLANNING[J]. Costs, 2005,8.
  24. Lu Dandan, Zhang Shengrui, Guo Meng. Analysis and Countermeasures of Urban Traffic Fairness[J]. Journal of Transportation Science and Engineering, 2008(02):103-105.
  25. Zhi C L, Xiao Y G. Traffic signal timing problems with environmental and equity considerations[J]. Journal of Advanced Transportation, 2014,48(8).
  26. Baskan O, Ozan C. Reserve Capacity Model for Optimizing Traffic Signal Timings with an Equity Constraint[M]. Highway Engineering, 2017.
  27. Liang Z, Xinfeng X, Chengcheng X, et al. A stochastic simulation-based optimization method for equitable and efficient network-wide signal timing under uncertainties[J]. Transportation Research Part B, 2019,122.
  28. Shi Jing, Yang Lang, Ying Xiwen, et al. Quantitative Evaluation Model of Traffic Fairness Based on Wilson Entropy Distribution Assumption[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2008(01):1-4.
  29. Lv Bin, Niu Huimin. Optimization Method of Phase Difference in Urban Traffic Line Control System[J]. Journal of Transportation Engineering, 2011, 11(04):103-107.
  30. Webster F V. Traffic signal settings[J]. Road Research Technical Paper, 1958,39.
  31. Akcelik R. TRAFFIC SIGNALS: CAPACITY AND TIMING ANALYSIS[J]. publication of australian road research board, 1981.
  32. Council W D N R. Transportation Research Board (TRB). Highway capacity manual 1985[R].1985.
  33. Council W D N R. Transportation Research Board (TRB). Highway capacity manual 1985[R].2000.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated