Prerpints.org logo
Preprint
Article

Impact of Residual Strains on the Carrier Mobility and Sability of Perovskite Films

Altmetrics

Downloads

117

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 June 2024

Posted:

28 June 2024

You are already at the latest version

Alerts
Abstract
Solution-based inorganic-organic halide perovskites are of great interest to researchers because of their unique optoelectronic properties and easy processing. However, polycrystalline perovskite films often show inhomogeneity due to residual strain induced during the film’s post-processing phase. In turn, these strains can impact both their stability and performances. An exhaustive study of residual strains can provide a better understanding and control of how they affect the performance and stability of perovskite films. In this work, we explore this complex interrelationship between residual strains and electrical properties for methylammonium \chemform{CH_3NH_3PbI_{3-x}Cl_x} films using grazing incident X-ray diffraction (GIXRD). We correlate with their resistiviy and carrier mobility using Hall effect. The sin^2($\psi$) technique is used to optimize the annealing parameters for the perovskite films. We also establish that temperature-induced relaxation can yield significant enhancement of the charge carrier transports in perovskite films. Finally, we also use Raman micro-spectroscopy to assess the degradation of perovskite films as a function of their residual strains.
Keywords: 
Subject: Chemistry and Materials Science  -   Nanotechnology

1. Introduction

Perovskite is a promising material with unique optical and electrical properties [1]. However can be very sensitive to environmental factors including humidity, oxygen and heat [2,3]. They can make the perovskites unstable and limit their integration into commercial devices. Recently, reports have suggested that stability enhancement could be achieved by the release of residual strains [4]. Although residual strains are well known, , the first studies on strains in perovskites were reported less than a decade ago [5]. The problems associated with residual strains and their impact on material and device stability remains an active research field [6]. In time, this deeper understanding could translate into significant improvement of perovskite devices. In this work, we use thermally-induced strain release to explore the origin of residual strains in perovskite films and their impact on the electrical and optical properties, as well as their stability.

1.1. Stress Origin in Perovskite Films

Generally, stresses in perovskite films mainly have three origins: intrinsic, mechanical, and thermal [7]. Because of the polycrystalline and heterogeneous nature of perovskite films, residual strains can stem from macroscopic, mesoscopic or microscopic deformations [8,9]. Residual strains in thin films are usually the consequence of thermal stresses or other external conditions occurring during grain coalescence or growth [4,10]. Indeed, it is largely due to the coefficient of thermal expansion (CTE) and lattice offset between the film and substrate [5,11]. These stresses can modify the structure of the crystal lattice and consequently impact the mobility of charge carriers, band gap and the stability of the film [12,13].

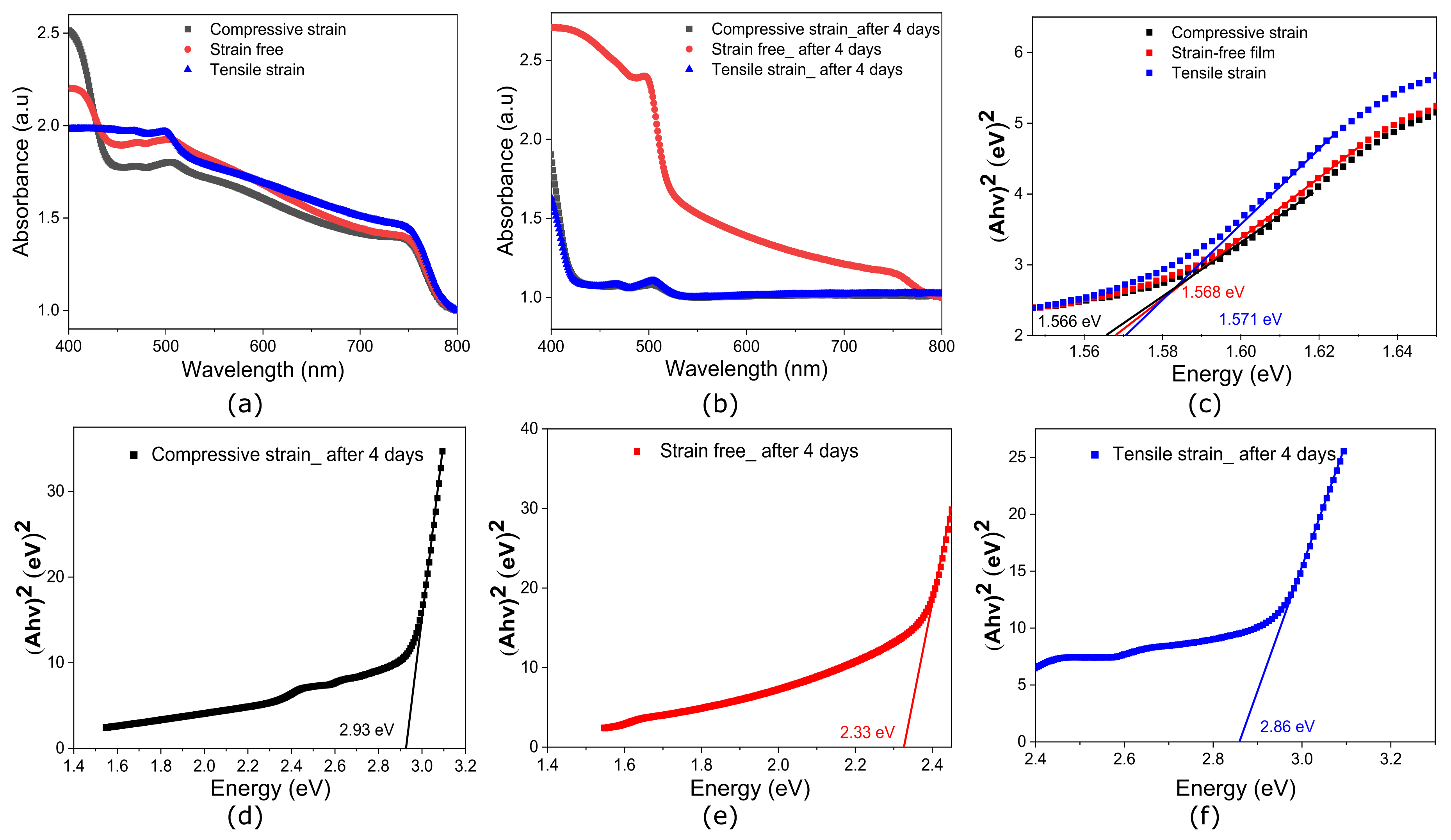
1.2. Impact on Electrical, Optical Properties and Stability

Perovskite-based solar cells (PSCs) have achieved efficiencies up-to 24.2 % in just a few years [14], However, their instability remains the main factor limiting their large-scale commercialization [15]. Efforts were made to reduce the moisture sensitivity of perovskite materials and improve the chemical stability of the electron and hole transport layers [16,17]. Strains can cause distortion of the crystal structure of perovskite [4,18]. Band structure calculations suggest that the band gap increases as the strain changes from compressive to tensile [19]. Small lattice strains in perovskite thin films can have major consequences on carrier recombination, electronic band structure, crystallinity, and crystal phase stability [20,21,22]. The bandgap variations due to strains can result in a change of the absorption spectrum of the perovskite film [5]. The presence of surface defects and grain boundaries in perovskite films can also create trap states impacting their stability [23]. It is also well known that strains can weaken the bonds and increase the defect density and degradation in perovskite films [12,24,25].

1.3. Regulation of Strain in Perovskite Films

Residual strains in perovskite films can affect their physical, optical, and electrical properties and impact their stability [26]. In turn, releasing residual strains in perovskite films could potentially be used to controllably improve their properties or stability. Several techniques can be used to release strains, including (1) regulation of local strains through the synthesis, (2) stress release by thermal expansion, or (3) adjusting the lattice offset between film and substrate [5]. It has been established that the intrinsic instability of perovskite films can result from annealing-induced residual strain accelerating their degradation [12,27]. This work will focus exclusively on the temperature-induced strain relaxation of methylammonium lead-halide provskite films in order to improve their optical and electrical properties and increase their stability. We measure the residual strains in perovskite films after annealing using the Williamson-Hall technique and GIXRD. We correlate these results with Hall effect measurements to improve the optoelectronic properties of our perovskite films. We also use Raman micro-spectroscopy measurements to probe the impact of thermally-induced strain release on the stability of perovskite films. Our findings indicate that achieving temperature-induced relaxation requires annealing within the temperature range 75 to 85 ​ ∘ C to achieve high carrier mobility, low activation energy, high average speed, and improved stability. We also find that this optimized annealing process reduces defect density.

2. Experimental Section

Perovskite layers are prepared on glass substrates by cleaning them sequentially with acetone, isopropanol, and DI solution for 15 minutes each. A layer of commercial C H 3 N H 3 P b I 3 − x C l x ink from Ossila (used as received) is deposited on the substrates by spin-coating at 2000 rpm for 30 s . The resulting films are annealed on a hot plate for 2 hours at different temperatures, ranging from 50 ​ ∘ C to 110 ​ ∘ C . The residual strains are characterized by using XRD. Hall effect measurements are used for carrier mobility. Finally, UV-Vis absorption and Raman micro-spectroscopy are used to assess perovskite film degradation.

3. Results and Discussion

In Figure 1, characterization of the films by X-ray diffraction (XRD) confirms the crystallization of the sample in a perovskite structure, with the presence of the standard peaks associated with the (110), (220), and (330) reflection planes, respectively. The peak intensity at 14° suggests that the main orientation of the perovskite film is (110) [28]. XRD can also characterize the residual strains through the lattice parameters. Indeed, the tensile or compressive strains can be respectively associated with the shift of the peaks to lower or higher diffraction angles. Residual strains are often non-uniform and complex to analyze from the peak position alone. Another indicator of strains is the broadening of the XRD peaks compared to the fully-relaxed state [19,29].

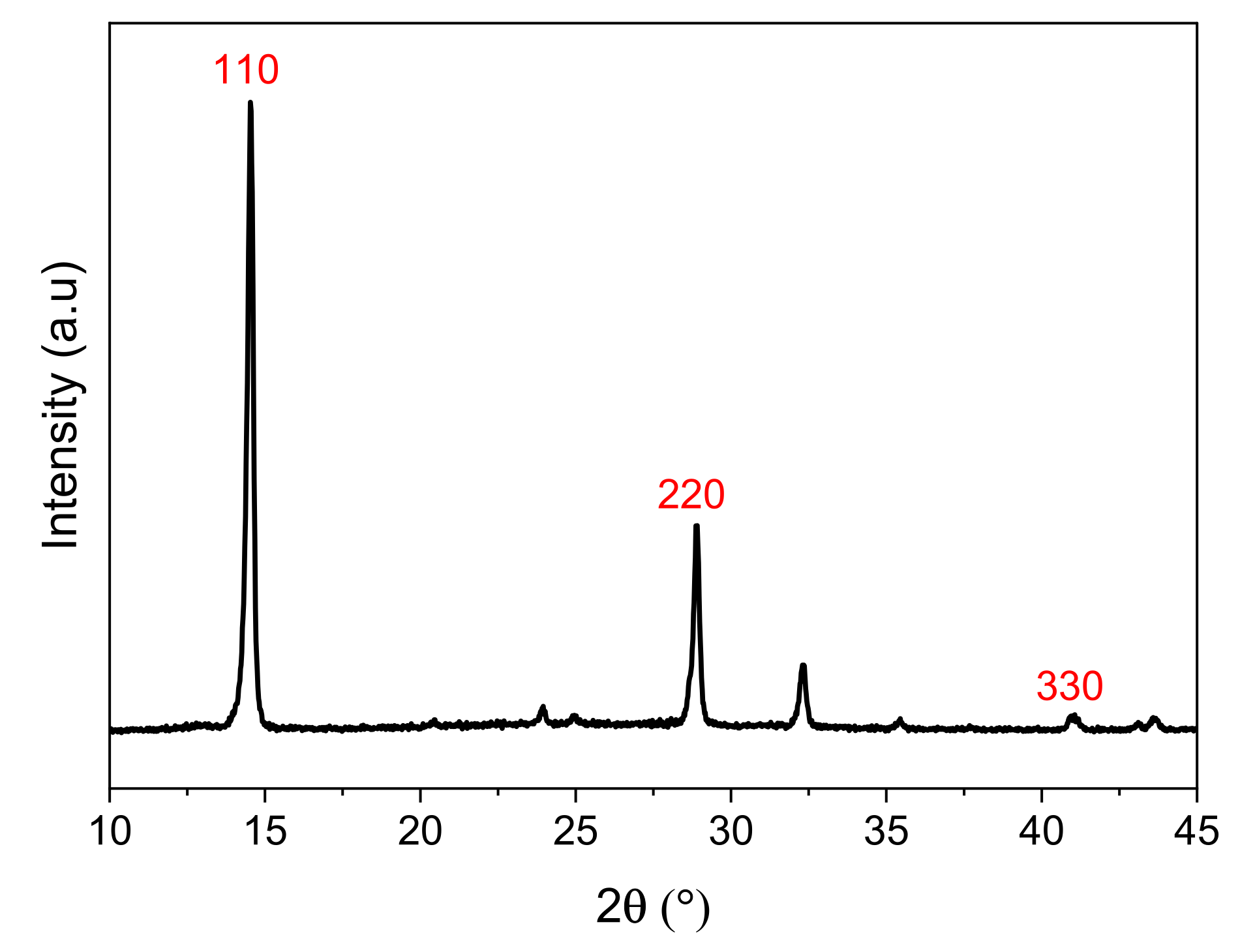
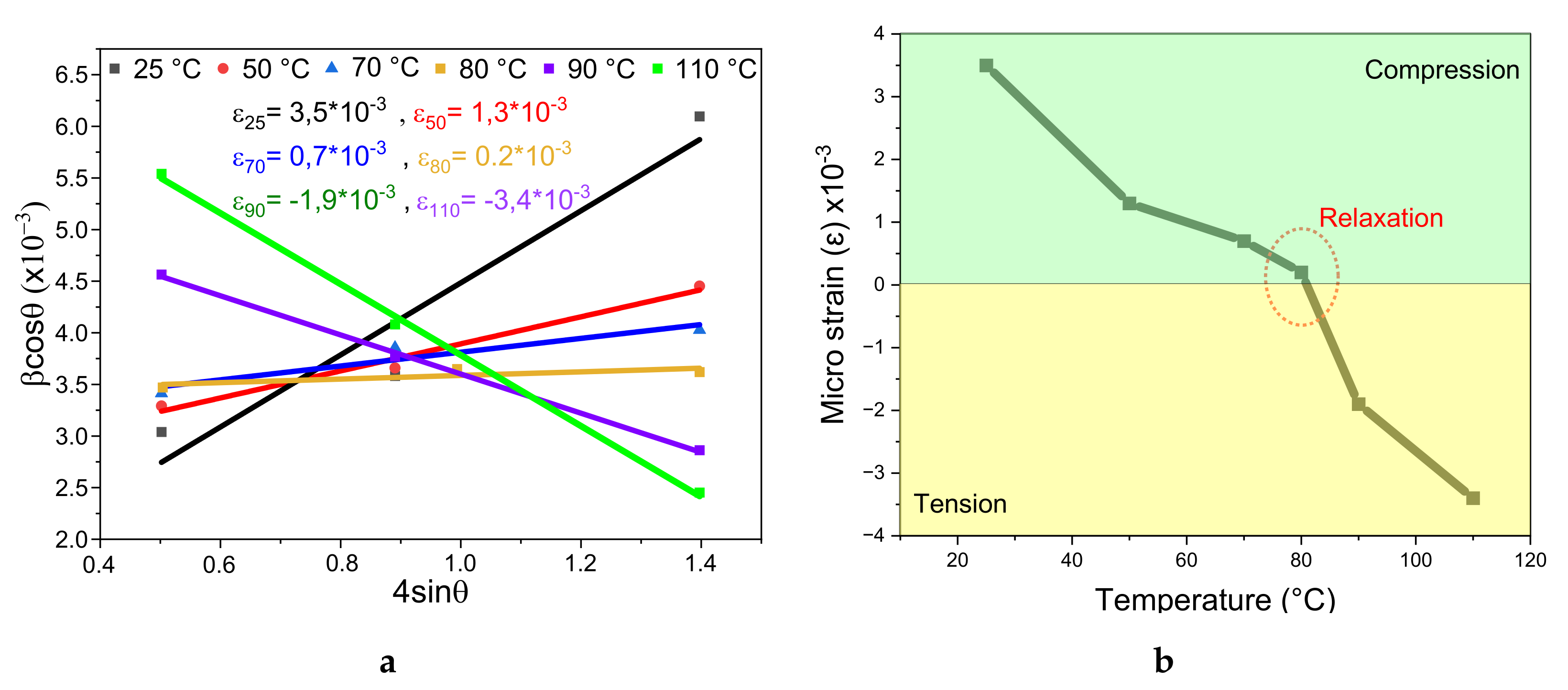
3.1. Williamson Hall Characterization

The Williamson Hall (W-H) equation 1 can be used to quantify the strain-induced broadening resulting from crystal imperfections [30,31,32], and structural imperfections such as dislocations, vacancies, stacking defects [33,34]:
β h k l . c o s Θ h k l = k λ D + 4 ε . s i n Θ
where β h k l is the fullwidth halfmaximum (FWHM) of the peak, k is the Scherrer constant equal to 0.94, λ is the X-ray source wavelength and D is the crystallite size, θ h k l is the peak position ( ​ ∘ ) and ϵ is the strain. The fundamental difference between WH’s method and Scherrer’s method is that WH considers both the crystallite size and microstrains which are often interrelated.
Williamson-Hall curves in Figure 2 show the cos θ h k l vs 4. sin θ h k l evolution measured from C H 3 N H 3 P b I 3 − x C l x films annealed at 25, 50, 70, 90 and 110 ​ ∘ C . The residual strain can be calculated directly from the slope for each curve fitting. In Figure 2, the strain values calculated reveal an interesting trend. It starts with relatively high compressive strain at low annealing temperatures (below 40 ​ ∘ C ). The residual strains decrease as the annealing temperature increases to 70 ​ ∘ C . Over 90 ​ ∘ C , the residual strains become increasingly tensile. We can conclude from this first test that the annealing temperature can generates three areas of strains: compressive, tensile, and a relaxed zone at a temperature around 80 ​ ∘ C . Based on our observations, we can expect an improved performance of the perovskite films.

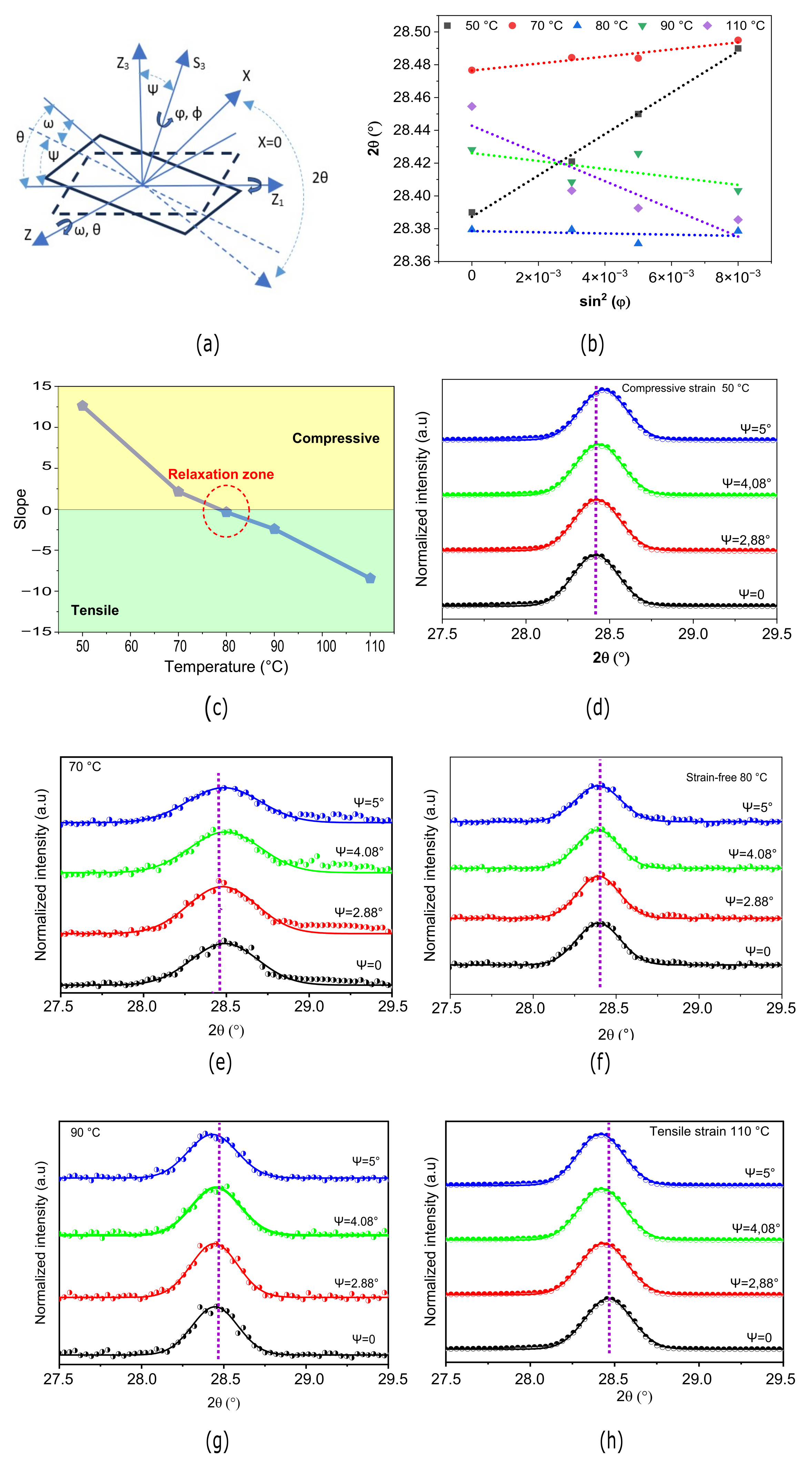
3.2. GIXRD Characterization

Grazing incidence XRD is a very useful technique to characterize the structure of thin films. It can also directly probe the strain distribution in perovskite films [5]. As such, we can use GIXRD to analyze the variations in the in-plane residual strains for the perovskite films annealed at different temperatures. The measurements shown in Figure 3a are performed in the ω -mode [5,35], by fixing the angle θ h k l and varying the instrument tilt angle ψ .
In Figure 3b,c, we analyze the strains in perovskite films annealed at 50, 70, 90, and 110 ​ ∘ C using GIXRD. Figure 3b illustrates the plot of 2 θ vs s i n 2 ( ϕ ), where the slope of the fitted curves yields the strain coefficients. A negative slope suggests tensile strains, while a positive slope suggest compressive strains. Figure 3d–h clearly indicate the distribution of compressive and tensile strain gradients for annealing temperatures from 50 to 110° C, respectively. While thermal energy can cause significant strain levels in the crystal lattice, it should be noted that the perovskite crystal structure still remains thermally stable between 50 ​ ∘ C and 110 ​ ∘ C [36]. These GIXRD strain measurements are consistent and strongly support the W-H measurements from Figure 2. In Figure 3, residual strains appear compressive at temperatures below 70 ​ ∘ C and tensile at temperatures above 90 ​ ∘ C . We can infer that strain relaxation can be achieved between 75-85 ​ ∘ C . Based on the XRD (W-H) and GIXRD analysis, we concur that C H 3 N H 3 P b I 3 − x C l x has a relaxed cubic structure at 80 ± 5 ​ ∘ C (from 80 ​ ∘ C the mixed crystals of perovskite transform from tetragonal to cubic phase) this relaxed symmetrical structure is favorable to improved electrical properties [36,37].

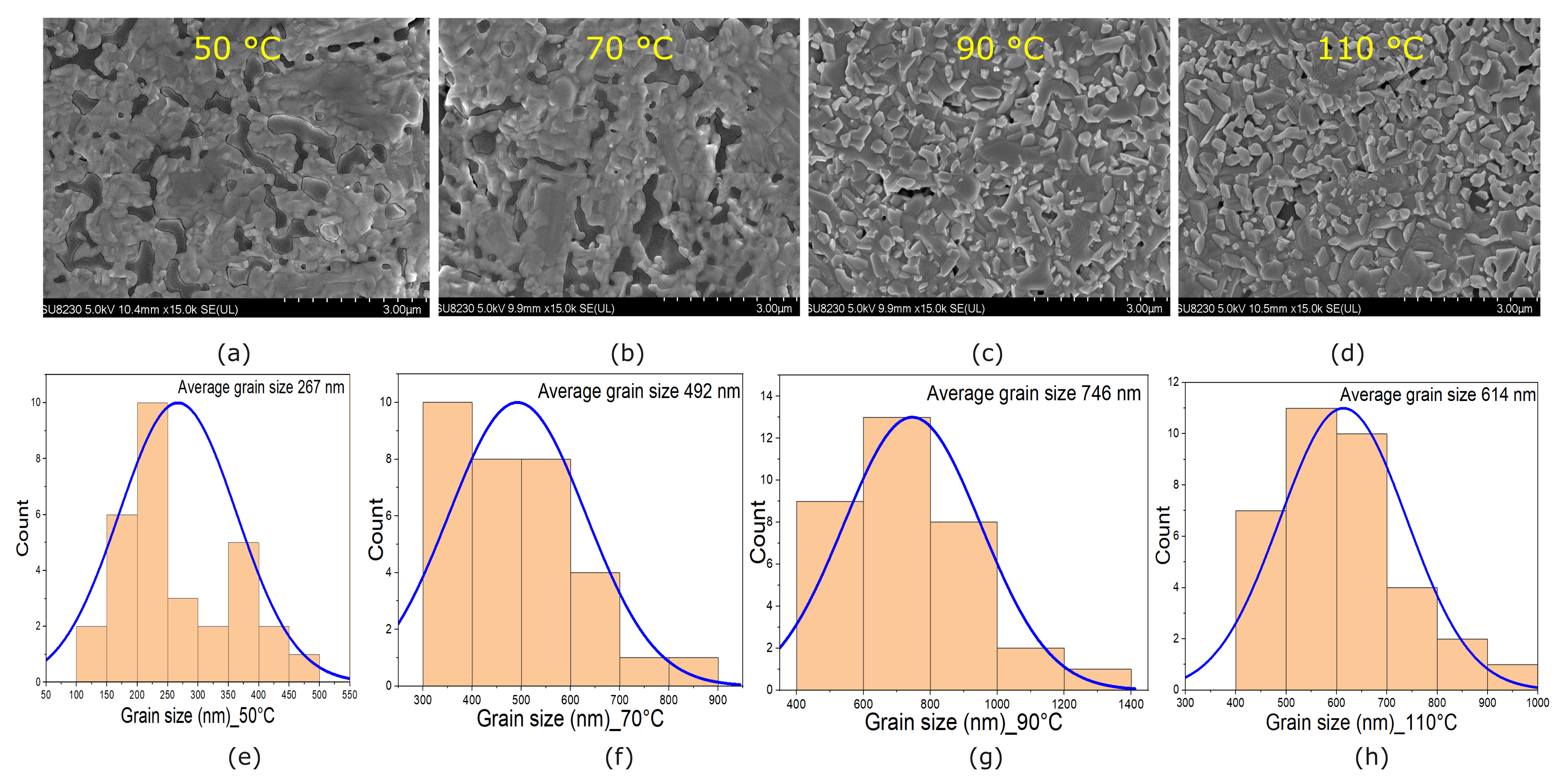
3.3. SEM Characterization

SEM analysis can be used to examine the change in granularity and microstructure caused by the residual strains. Distortions and internal strains can arise from the growth of superstructures and nanostructures, as well as from the substitutions with elements with different sizes [6]. Figure 4a–d show SEM micrographs for the perovskite films after annealing at 50, 70, 90, and 110 ​ ∘ C . The grain size evolution indicates that grains appear at 50 ​ ∘ C (Figure 4a). The presence of solvents in the precursor leads to high pinhole densities due to minimal evaporation. Increasing the annealing temperature reduces pinhole density and increases the average grain size [38]. The maximum average size of 746 n m is achieved with 90 ​ ∘ C annealing (Figure 4g). At 110 ​ ∘ C and above, microstructural changes (grain size and surface filing) start to appear (Figure 4d,h). These strain-induced alterations in the perovskite film’s granularity and microstructure potentially compromise its stability and accelerate its degradation.

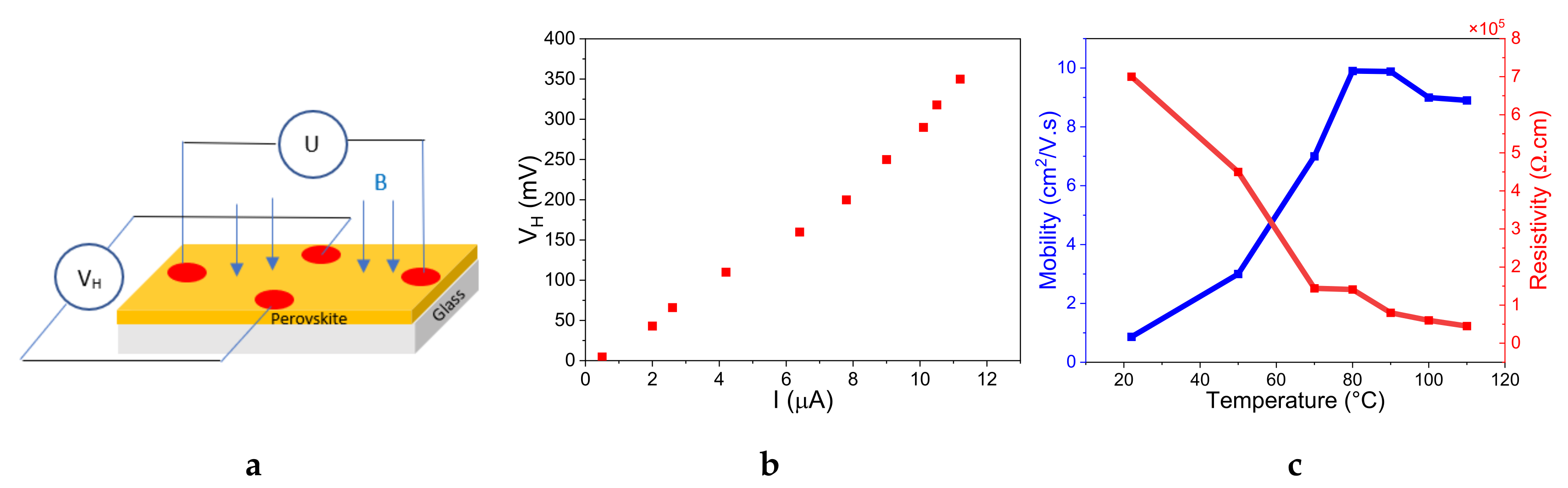
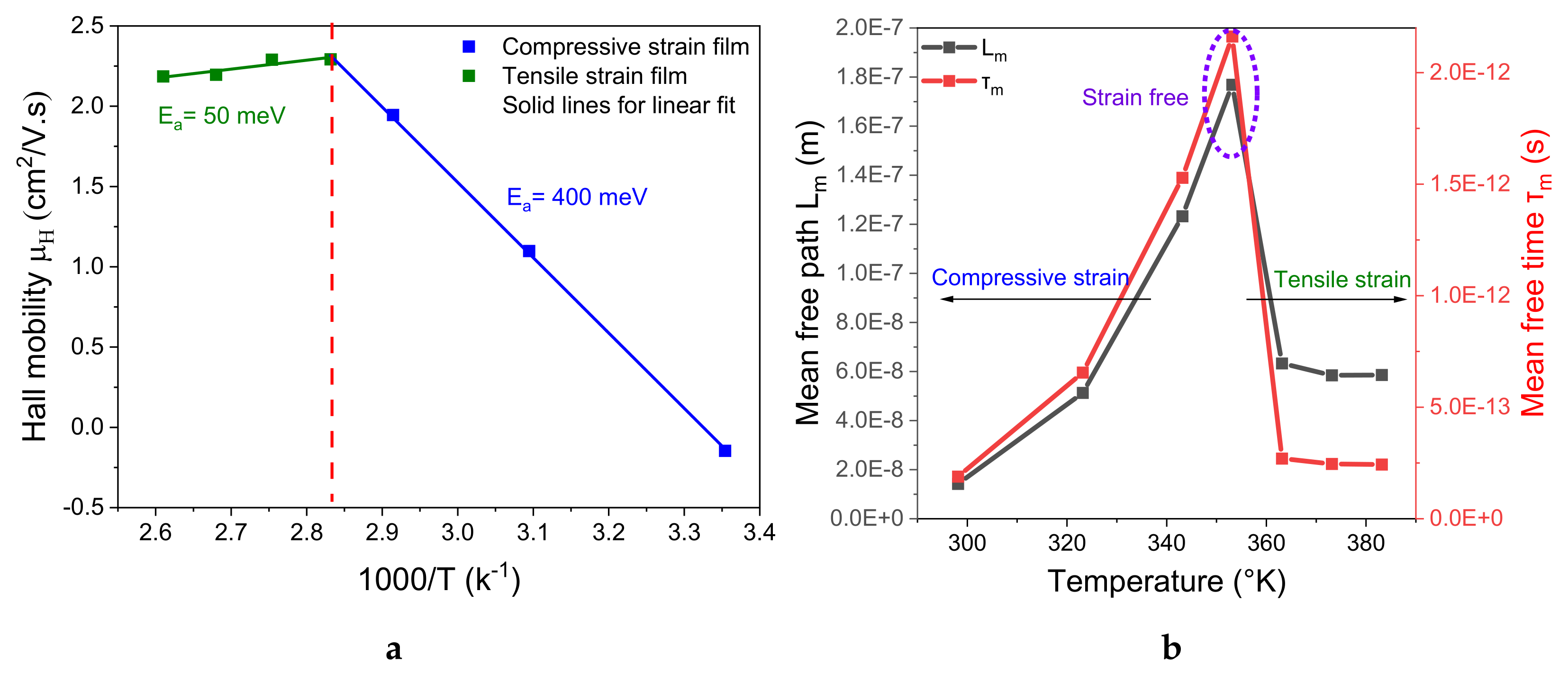
3.4. Hall Effect Characterization

Carrier mobility can be directly measured using the Hall-effect technique represented in Figure 5. Here, a transverse magnetic field of 0.7 T is applied to all samples. In Figure 5, all samples display a p-type behavior indicated by the positive Hall voltage. This expected result can be explained by the large amounts of Pb, C H 3 N H 3 I , Cl vacancies and I present in the film [39,40]. Due to lower formation energies, Pb and C H 3 N H 3 vacancies are known to play a significant role in the p-type behavior of C H 3 N H 3 P b I 3 − x C l x thin films [41,42]. Due to lower formation energies, Pb and C H 3 N H 3 vacancies are known to play a significant role in the p-type behavior of C H 3 N H 3 P b I 3 − x C l x thin films [42,43,44]. Figure 5 shows the Hall effect measurements used to identify the corresponding change in carrier mobilities and resistivities with increasing annealing temperatures. The carrier mobility reaches its highest value of 10 c m / V / s at 80 ​ ∘ C , which is consistent with previous reports [45,46]. We already established that C H 3 N H 3 P b I 3 − x C l x films annealed at this temperature are strain-relaxed. Above 75 ​ ∘ C (relaxation zone), the structure adopts cubic symmetry and can achieve high stability since the entropy reduction in the inorganic cage compensates for the high dynamic disorder of the organic cations methylammonium [37,47]. This cubic phase is also known to offer better electronic properties than the orthorhombic and tetragonal phases for symmetry reasons [48,49,50].
The thermal behavior for the Hall mobility can be described by the expression [51]:
μ T ( T ) = μ 0 ( T ) . e x p E a k B . T
where, μ 0 is the exponential prefactor, k B is the Boltzmann constant and Ea is the activation energy. Figure 6 shows ln( μ H ) as a function of 1000/T measured between 298 and 385 ° K . The activation energy Ea corresponds to the potential energy barrier height [51], and it can be directly extracted from the slope of the linear fit. From Figure 6, the activation energy for perovskite films with compressive strains is found to be 400 m , while tensile strain reduces the activation energy to 50 m . These results are also consistent with previous reports [52]. This change in activation energy originates from the slope at approximately 80 ​ ∘ C , suggesting significantly-reduced activation energy due to film relaxation. It has been previously reported that C H 3 N H 3 + and I − vacancies can easily migrate to a neighboring site due to their low activation energy [53]. This variation of the activation energy with temperature can be directly associated with the film’s residual strains [54].
Using the Hall mobility measurements from Figure 6, it becomes possible to access the mean carrier path length Lm and the mean free time ( τ m ) (Figure 6) in the C H 3 N H 3 P b I 3 − x C l x thin films using the conventional Drude-Sommerfeld model [42]:
μ T ( T ) = μ 0 ( T ) . e x p E a k B . T
L m = μ H ( 3 m h * . k B . T ) 2 e
Where m h * is the effective mass of the hole given by the expression:
E a = e 4 . m h * 2 ( 2 ε 0 . ε r . h ) 2
Where ϵ 0 is the permittivity of free space, and ϵ r is the relative dielectric constant used between 5.6 (high frequency) and 25.7 (low frequency) [42]. For the calculation of m h * we assumed ϵ r = 9 based on the hydrogen model [55]. The values of m h * are estimated at 0.3 m and 2.4 m for the tensile and compressive films respectively [42,56,57], where m e represents the rest mass of the electron. Results from Figure 6 suggest that films subjected to compressive and tensile strains respectively have lower Lm and τ m , respectively. Both parameters peak at 80 ​ ∘ C , which corresponds to the relaxation region (strain-free) regime. At this temperature, mixed halide perovskites make the transition from the tetragonal to the cubic phase due to the tilt of the inorganic P b I 6 octahedron and the rotational shift of the organic C H 3 N H 3 + , resulting in their increased average mobilities [50]. Consequently, these results confirm reports that phase shift can change the physical properties of mixed halide perovskites films and positively influence their electrical properties [42].
Figure 7a,b displays the absorption spectrum for samples annealed at 60 ​ ∘ C , 80 ​ ∘ C , and 110 ​ ∘ C exhibiting compressive, relaxed, and tensile residual strains, respectively. The spectra in Figure 7a show stronger UV absorption for the tensile-strained and relaxed samples. When the residual strains transition from compressive to tensile, the bandgap of the film in Figure 7c show a slight increase from 1.56 to 1.57 . After four days of storage in an ambient environment, the absorption spectra from Figure 7b appearsis significantly reduced for both tensile- and compressively-strained samples, compared to the sample annealed at 80 ​ ∘ C . Moreover, this degradation as the strained samples become transparent also translates in a significant bandgap increase from 1.59 to 2.34 seen in Figure 7d–f. The low absorption of these samples can be attributed to incomplete crystallization during annealing at 60 ​ ∘ C . Poor-quality perovskite films often result from incomplete solvent DMF evaporation. Conversely, high-temperature annealing at 100 ​ ∘ C promotes rapid solvent evaporation, preventing uniform surface filling and poor film quality as shown in Figure 4d.

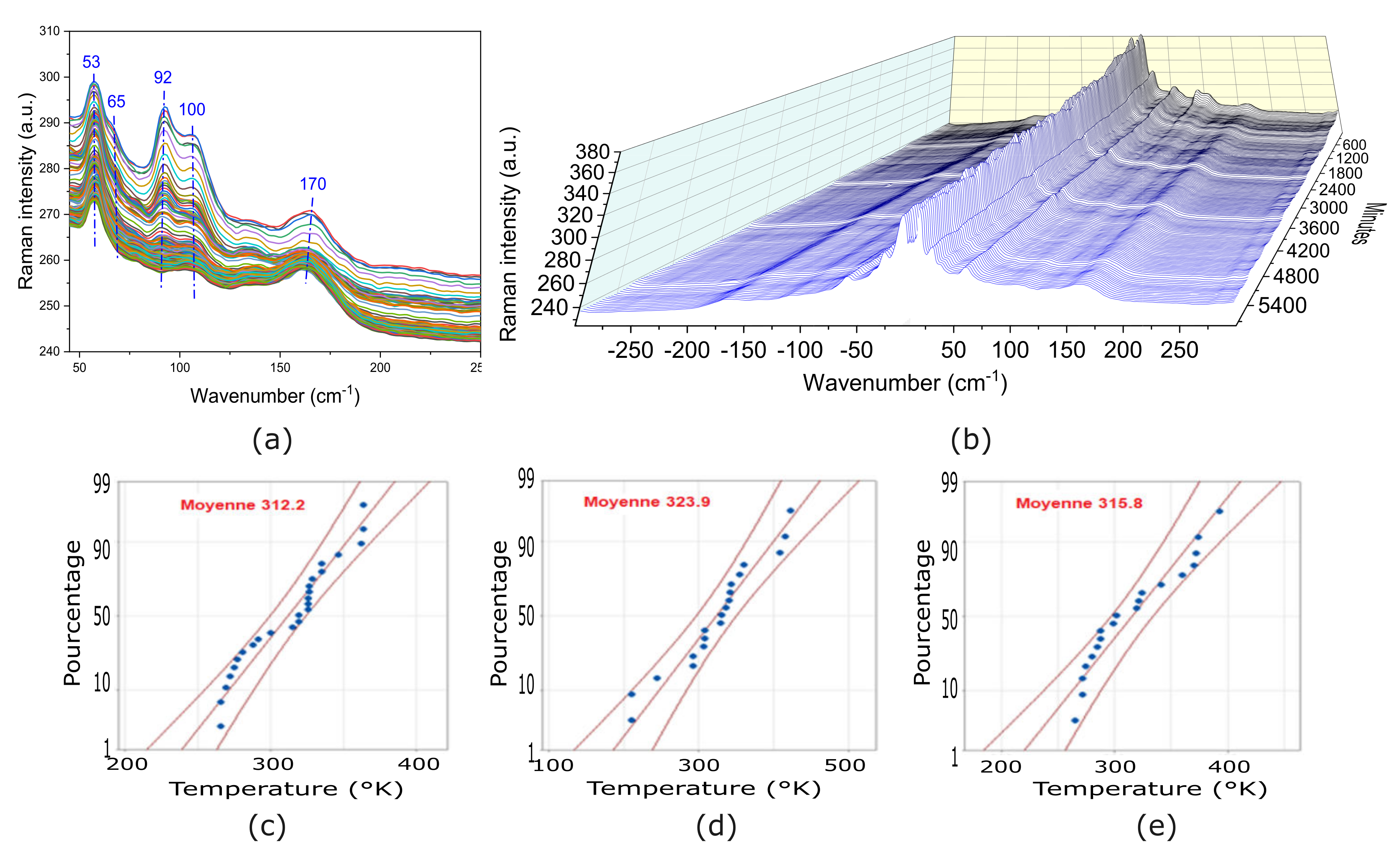
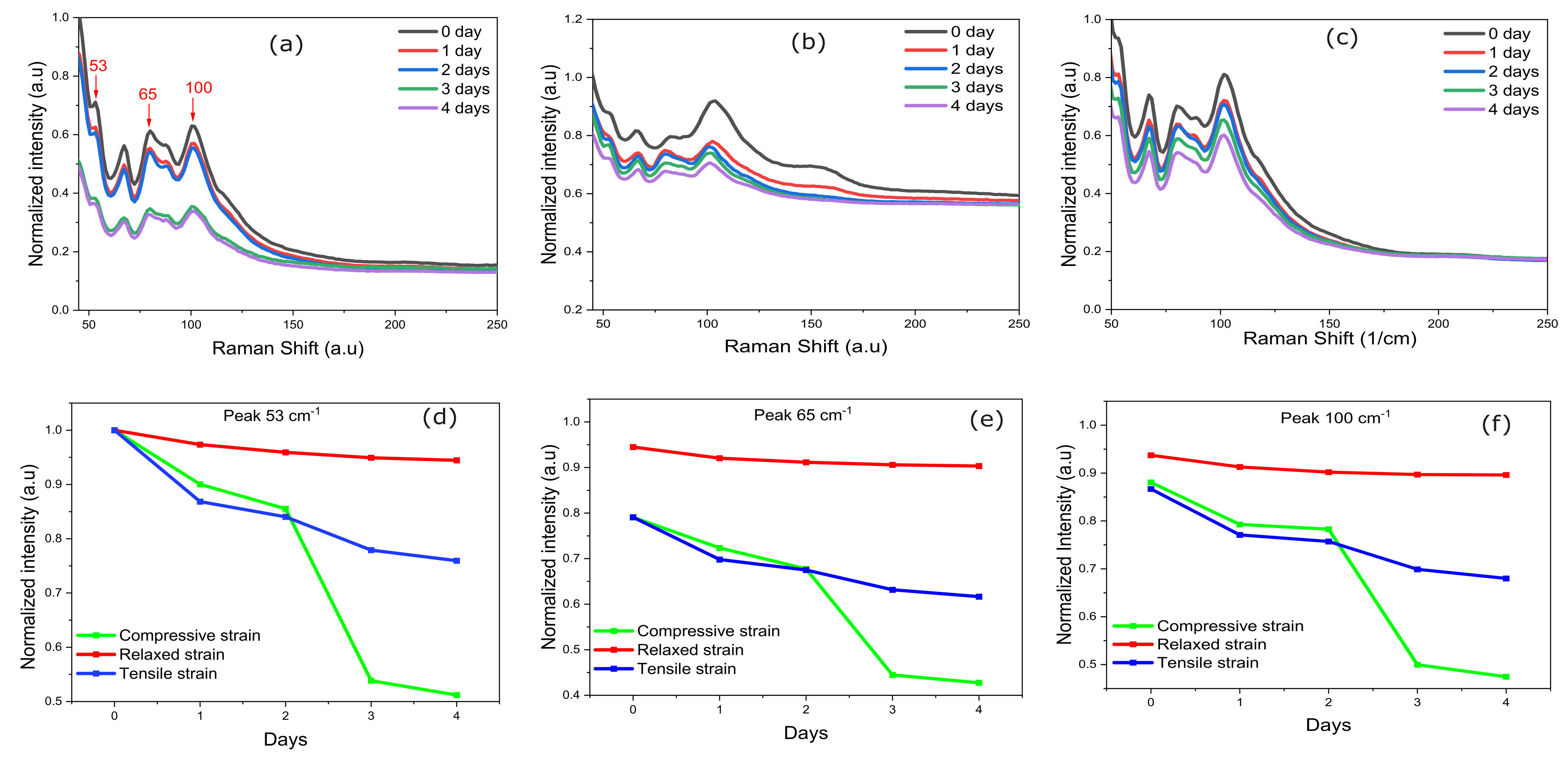
3.5. Raman Characterization

Raman micro-spectroscopy measurements from Figure 8a,b are performed with a very low laser power of 0.5 m W at 532 n m wavelength to avoid any laser-induced damage. For the same reason, the laser beam as focused with a 10x objective. All measurements are done under ambient conditions. To perform the Raman measurements, we slowly increase the laser power until the main perovskite peaks are visible. Then the laser is shifted to a new position to record the Raman spectrum for a pristine perovskite. To avoid the laser intensity from impacting the perovskite film’s crystallization, we utilized Equation 6 to estimate the sample’s temperature based on the intensity ratio between Stokes/Anti-Stokes peaks [58,59] as shown in Figure 8b:
I s I a s = ϑ 0 + ϑ v ϑ 0 − ϑ v 4 e x p E p k B . T
Where k B is the Boltzmann constant, ν 0 is the frequency of the excitation source, and T is the sample’s temperature.
The inorganic-organic sublattices of the perovskite have different vibrational frequencies covering the range from 50 to 150 / c m with phonon energies of 6-11 m (50- 90 / c m ) and 11-20 m (90- 150 / c m ) [60]. Figure 8c–e display the statistical temperature graphics calculated using Equation 6, for samples with residual tensile strains, no strains, and compressive strains for a phonon energy of 12 m at peak 100 / c m [60]. The maximum temperature reached by the samples due to laser-induced heating is 324 °K. This value remains lower than the lowest annealing temperatures, ensuring that the 532 n m laser-induced heating does not impact the crystalline structure of the different perovskite samples.
Finally, we can also evaluate the impact of different strain levels on the film degradation using Raman micro-spectroscopy. To do so, measurements are performed every 30 minutes for 4 days at a sufficiently low excitation power to prevent laser-induced heating. The Raman spectrum in Figure 8a clearly indicates the presence of vibrational peaks at 53, 65, 92, and 100 / c m with a broader Raman band at 170 / c m , which can be attributed to the Pb-I and Pb-Cl perovskite layers [61]. The sharp peaks between 53 / c m and 92 / c m are attributed to the bending and stretching of Pb-I bonds, which are modes of inorganic cages [62]. Meanwhile, the bands at 100 / c m can be attributed to the vibrations of the organic C H 3 N H 3 + cations [63]. After 24 hours, the peak intensity decreases, and no new vibrational bands are observed, implying the structure remained unaltered. It is known that incorporation of H 2 O into the crystal lattice is measured by solvating of M A + and the dissolving of the cations [64,65]. The absence of M A + can increase defect density and cause a slight displacement of atoms in the crystalline structure, leading to fluctuations in vibrational bands [65,66]. Figure 8a shows a redshift for all bands, suggesting an increased length of the chemical bond. Previous research confirms that the redshift in these bands results from stress exerted by the H 2 O molecule on the atomic bond related to this vibrational mode and the shift induced by the M A + vacancies [65]. However, the observed shift is not consistent, as the penetration of moisture in the film is not uniform due to the heterogeneity of the microstructural morphology, defects, and internal stresses.
In Figure 9a–c we compare the degradation of the strained films. As expected, results from Figure 9d–f clearly suggest that thermally-relaxed films show lower degradation compared with tensile- or compressively-strained films. Indeed, the average peak intensity decrease for the thermally-relaxed film never exceeds 10 %. In constrast, films with residual tensile and compressive strains respectively show a decrease in peak intensity of more than 20 % and 45 %. This is consistent with previous observations that strained films degrade more rapidly due to their crystal structure enabling easier incorporation of H 2 O molecules. Surface defects and strain-induced distortions in the crystal lattice weaken the structure, rendering it less resilient to external factors and thus accelerating its degradation [67,68].

4. Conclusions

This study shows a clear interrelationship between temperature-induced strains, charge carrier mobility, and the stability in solution-based perovskite films. Our findings show that these factors are interrelated and must be carefully considered in order to optimize the performance of perovskite materials. Our findings indicate that achieving temperature-induced relaxation requires annealing within the temperature range of 75 to 85 ​ ∘ C for this specific precursor formulation. As a result, the C H 3 N H 3 P b I 3 − x C l x films annealed at 80 ​ ∘ C demonstrate optimal performance due to their higher carrier mobilities, lower activation energies, high average speed, and improved stability. We find that these annealing temperatures reduce defect density and promote strain relaxation. These results could potentially minimize the impact of residual strain on optoelectronic properties and offer an alternative approach to optimize the performance of perovskite solar cells and other perovskite-based optoelectronic devices.

Author Contributions

Writing - original draft, Methodology, Resources, Conceptualization, Characterization, Formal analysis, Data curation M.A.S; Raman test Review and editing L.F.G; Supervision, visualization, validation, Review and editing, RI and S.G.C. All authors have read and agreed to the publication of the manuscript.

Funding

The authors would like to acknowledge the financial support received from NSERC with the following Discovery grants (RGPIN-2023-05211, RGPIN 2022-03083) as well as the Canada Research Chairs (CRC-2021-00490)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GIXRD grazing incident X-ray diffraction
CTE coefficient of thermal expansion
PSC perovskite solar cell
XRD X-ray diffraction
FWHM full-width half-maximum

References

  1. Rong, Y.; Hu, Y.; Mei, A.; Tan, H.; Saidaminov, M.I.; Seok, S.I.; McGehee, M.D.; Sargent, E.H.; Han, H. Challenges for commercializing perovskite solar cells. Science 2018, 361, eaat8235. [Google Scholar] [CrossRef]
  2. Kim, H.; Seo, J.; Park, N. Material and device stability in perovskite solar cells. ChemSusChem 2016, 9, 2528–2540. [Google Scholar] [CrossRef] [PubMed]
  3. Liu, S.C.; Yang, Y.; Li, Z.; Xue, D.J.; Hu, J.S. GeSe thin-film solar cells. Materials Chemistry Frontiers 2020, 4, 775–787. [Google Scholar] [CrossRef]
  4. Wang, H.; Zhu, C.; Liu, L.; Ma, S.; Liu, P.; Wu, J.; Shi, C.; Du, Q.; Hao, Y.; Xiang, S. Interfacial residual stress relaxation in perovskite solar cells with improved stability. Advanced Materials 2019, 31, 1904408. [Google Scholar] [CrossRef] [PubMed]
  5. Wu, J.; Liu, S.C.; Li, Z.; Wang, S.; Xue, D.J.; Lin, Y.; Hu, J.S. Strain in perovskite solar cells: origins, impacts and regulation. National science review 2021, 8, nwab047. [Google Scholar] [CrossRef] [PubMed]
  6. Grote, C.; Berger, R.F. Strain tuning of tin–halide and lead–halide perovskites: a first-principles atomic and electronic structure study. The Journal of Physical Chemistry C 2015, 119, 22832–22837. [Google Scholar] [CrossRef]
  7. Hutchinson, J.W. Stresses and failure modes in thin films and multilayers. Notes for a Dcamm Course. Technical University of Denmark, Lyngby 1996, 1, 14. Type: Journal Article.
  8. Peng, J. Determination of residual stresses in coating by pseudo-grazing incidence X-Ray diffraction method. Thesis, 2006.
  9. Tennyson, E.M.; Doherty, T.A.; Stranks, S.D. Heterogeneity at multiple length scales in halide perovskite semiconductors. Nature Reviews Materials 2019, 4, 573–587. [Google Scholar] [CrossRef]
  10. Abadias, G.; Chason, E.; Keckes, J.; Sebastiani, M.; Thompson, G.B.; Barthel, E.; Doll, G.L.; Murray, C.E.; Stoessel, C.H.; Martinu, L. Stress in thin films and coatings: Current status, challenges, and prospects. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films 2018, 36, 020801. [Google Scholar]
  11. Namvar, A.; Dehghany, M.; Sohrabpour, S.; Naghdabadi, R. Thermal residual stresses in silicon thin film solar cells under operational cyclic thermal loading: A finite element analysis. Solar Energy 2016, 135, 366–373. [Google Scholar] [CrossRef]
  12. Rolston, N.; Bush, K.A.; Printz, A.D.; Gold-Parker, A.; Ding, Y.; Toney, M.F.; McGehee, M.D.; Dauskardt, R.H. Engineering stress in perovskite solar cells to improve stability. Advanced Energy Materials 2018, 8, 1802139. [Google Scholar] [CrossRef]
  13. Lee, J.H.; Deng, Z.; Bristowe, N.C.; Bristowe, P.D.; Cheetham, A.K. The competition between mechanical stability and charge carrier mobility in MA-based hybrid perovskites: insight from DFT. Journal of Materials Chemistry C 2018, 6, 12252–12259. [Google Scholar] [CrossRef]
  14. Qiu, L.; He, S.; Ono, L.K.; Liu, S.; Qi, Y. Scalable fabrication of metal halide perovskite solar cells and modules. ACS Energy Letters 2019, 4, 2147–2167. [Google Scholar] [CrossRef]
  15. Mohammad, A.; Mahjabeen, F. Promises and Challenges of Perovskite Solar Cells: A Comprehensive Review. BULLET: Jurnal Multidisiplin Ilmu 2023, 2, 1147–1157. [Google Scholar]
  16. Hu, Q.; Chen, W.; Yang, W.; Li, Y.; Zhou, Y.; Larson, B.W.; Johnson, J.C.; Lu, Y.H.; Zhong, W.; Xu, J. Improving efficiency and stability of perovskite solar cells enabled by a near-infrared-absorbing moisture barrier. Joule 2020, 4, 1575–1593. [Google Scholar] [CrossRef]
  17. Rong, Y.; Hou, X.; Hu, Y.; Mei, A.; Liu, L.; Wang, P.; Han, H. Synergy of ammonium chloride and moisture on perovskite crystallization for efficient printable mesoscopic solar cells. Nature communications 2017, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
  18. Lei, Y.; Liu, W.; Li, C.; Da, S.; Zheng, Y.; Wu, Y.; Ran, F. Microstress for metal halide perovskite solar cells: from source to influence and management. Nanoscale.
  19. Zhu, C.; Niu, X.; Fu, Y.; Li, N.; Hu, C.; Chen, Y.; He, X.; Na, G.; Liu, P.; Zai, H.; et al. Strain engineering in perovskite solar cells and its impacts on carrier dynamics. Nature Communications 2019, 10, 815. [Google Scholar] [CrossRef] [PubMed]
  20. Jones, T.W.; Osherov, A.; Alsari, M.; Sponseller, M.; Duck, B.C.; Jung, Y.K.; Settens, C.; Niroui, F.; Brenes, R.; Stan, C.V. Lattice strain causes non-radiative losses in halide perovskites. Energy & Environmental Science 2019, 12, 596–606. [Google Scholar]
  21. Qiao, L.; Fang, W.H.; Long, R.; Prezhdo, O.V. Elimination of Charge Recombination Centers in Metal Halide Perovskites by Strain. Journal of the American Chemical Society 2021, 143, 9982–9990. [Google Scholar] [CrossRef] [PubMed]
  22. Wang, S.; Hu, J.; Wang, A.; Cui, Y.; Chen, B.; Niu, X.; Hao, F. Facile lattice tensile strain compensation in mixed-cation halide perovskite solar cells. Journal of Energy Chemistry 2022, 66, 422–428. [Google Scholar] [CrossRef]
  23. Zheng, X.; Chen, B.; Dai, J.; Fang, Y.; Bai, Y.; Lin, Y.; Wei, H.; Zeng, X.C.; Huang, J. Defect passivation in hybrid perovskite solar cells using quaternary ammonium halide anions and cations. Nature Energy 2017, 2, 1–9. [Google Scholar] [CrossRef]
  24. Ghosh, D.; Aziz, A.; Dawson, J.A.; Walker, A.B.; Islam, M.S. Putting the squeeze on lead iodide perovskites: pressure-induced effects to tune their structural and optoelectronic behavior. Chemistry of Materials 2019, 31, 4063–4071. [Google Scholar] [CrossRef] [PubMed]
  25. Steele, J.A.; Jin, H.; Dovgaliuk, I.; Berger, R.F.; Braeckevelt, T.; Yuan, H.; Martin, C.; Solano, E.; Lejaeghere, K.; Rogge, S.M. Thermal unequilibrium of strained black CsPbI3 thin films. Science 2019, 365, 679–684. [Google Scholar] [CrossRef] [PubMed]
  26. Jin, B.; Cao, J.; Yuan, R.; Cai, B.; Wu, C.; Zheng, X. Strain relaxation for perovskite lattice reconfiguration. Advanced Energy and Sustainability Research 2023, 4, 2200143. [Google Scholar] [CrossRef]
  27. Zhao, J.; Deng, Y.; Wei, H.; Zheng, X.; Yu, Z.; Shao, Y.; Shield, J.E.; Huang, J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Science advances 2017, 3, eaao5616. [Google Scholar] [CrossRef] [PubMed]
  28. Głowienka, D.; Miruszewski, T.; Szmytkowski, J. The domination of ionic conductivity in tetragonal phase of the organometal halide perovskite CH3NH3PbI3-xClx. Solid State Sciences 2018, 82, 19–23. [Google Scholar] [CrossRef]
  29. Zak, A.K.; Majid, W.A.; Abrishami, M.E.; Yousefi, R. X-ray analysis of ZnO nanoparticles by Williamson–Hall and size–strain plot methods. Solid State Sciences 2011, 13, 251–256. [Google Scholar]
  30. Hall, W. X-ray line broadening in metals. Proceedings of the Physical Society. Section A 1949, 62, 741. [Google Scholar] [CrossRef]
  31. Mote, V.; Purushotham, Y.; Dole, B. Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles. Journal of theoretical and applied physics 2012, 6, 1–8. [Google Scholar] [CrossRef]
  32. Nishimura, K.; Hirotani, D.; Kamarudin, M.A.; Shen, Q.; Toyoda, T.; Iikubo, S.; Minemoto, T.; Yoshino, K.; Hayase, S. Relationship between lattice strain and efficiency for Sn-perovskite solar cells. ACS applied materials & interfaces 2019, 11, 31105–31110. [Google Scholar]
  33. Pramanick, A.; Wang, X.; Hoffmann, C.; Diallo, S.; Jørgensen, M.; Wang, X.L. Microdomain dynamics in single-crystal BaTi O 3 during paraelectric-ferroelectric phase transition measured with time-of-flight neutron scattering. Physical Review B 2015, 92, 174103. [Google Scholar] [CrossRef]
  34. Robinson, I.; Harder, R. Coherent X-ray diffraction imaging of strain at the nanoscale. Nature materials 2009, 8, 291–298. [Google Scholar] [CrossRef] [PubMed]
  35. Song, H. Analyse expérimentale et numérique de la distribution des contraintes résiduelles induites par choc-laser dans les alliages d’aluminium. Thesis, 2010.
  36. Murali, B.; Yengel, E.; Peng, W.; Chen, Z.; Alias, M.S.; Alarousu, E.; Ooi, B.S.; Burlakov, V.; Goriely, A.; Eddaoudi, M. Temperature-induced lattice relaxation of perovskite crystal enhances optoelectronic properties and solar cell performance. The journal of physical chemistry letters 2017, 8, 137–143. [Google Scholar] [CrossRef] [PubMed]
  37. Francisco-López, A.; Charles, B.; Alonso, M.I.; Garriga, M.; Campoy-Quiles, M.; Weller, M.T.; Goñi, A.R. Phase diagram of methylammonium/formamidinium lead iodide perovskite solid solutions from temperature-dependent photoluminescence and Raman spectroscopies. The Journal of Physical Chemistry C 2020, 124, 3448–3458. [Google Scholar] [CrossRef]
  38. Ren, X.; Yang, Z.; Yang, D.; Zhang, X.; Cui, D.; Liu, Y.; Wei, Q.; Fan, H.; Liu, S.F. Modulating crystal grain size and optoelectronic properties of perovskite films for solar cells by reaction temperature. Nanoscale 2016, 8, 3816–3822. [Google Scholar] [CrossRef] [PubMed]
  39. Xiong, S.; Hou, Z.; Zou, S.; Lu, X.; Yang, J.; Hao, T.; Zhou, Z.; Xu, J.; Zeng, Y.; Xiao, W. Direct observation on p-to n-type transformation of perovskite surface region during defect passivation driving high photovoltaic efficiency. Joule 2021, 5, 467–480. [Google Scholar] [CrossRef]
  40. Xie, Z.; Feng, K.; Xiong, Y.; Chen, X.; Liang, Y.; Abid, K.; Xu, L. A High Seebeck Voltage Thermoelectric Module with P-type and N-type MAPbI3 Perovskite Single Crystals. Advanced Electronic Materials 2021, 7, 2001003. [Google Scholar] [CrossRef]
  41. Yin, W.J.; Shi, T.; Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Applied Physics Letters 2014, 104, 063903. [Google Scholar] [CrossRef]
  42. Karim, A.; Khan, M.; Hossain, M. Temperature dependency of excitonic effective mass and charge carrier conduction mechanism in CH3NH3PbI3- xClx thin films. Scientific reports 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
  43. Wang, Q.; Shao, Y.; Xie, H.; Lyu, L.; Liu, X.; Gao, Y.; Huang, J. Qualifying composition dependent p and n self-doping in CH3NH3PbI3. Applied Physics Letters 2014, 105, 163508. [Google Scholar] [CrossRef]
  44. Frolova, L.A.; Dremova, N.N.; Troshin, P.A. The chemical origin of the p-type and n-type doping effects in the hybrid methylammonium–lead iodide (MAPbI 3) perovskite solar cells. Chemical Communications 2015, 51, 14917–14920. [Google Scholar] [CrossRef]
  45. Wehrenfennig, C.; Eperon, G.E.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. High charge carrier mobilities and lifetimes in organolead trihalide perovskites. Advanced materials 2014, 26, 1584–1589. [Google Scholar] [CrossRef] [PubMed]
  46. Luo, D.; Yu, L.; Wang, H.; Zou, T.; Luo, L.; Liu, Z.; Lu, Z. Cubic structure of the mixed halide perovskite CH 3 NH 3 PbI 3- x Cl x via thermal annealing. RSC Advances 2015, 5, 85480–85485. [Google Scholar] [CrossRef]
  47. Saffari, M.; Mohebpour, M.A.; Soleimani, H.R.; Tagani, M.B. DFT analysis and FDTD simulation of CH3NH3PbI3- xClx mixed halide perovskite solar cells: role of halide mixing and light trapping technique. Journal of Physics D: Applied Physics 2017, 50, 415501. [Google Scholar] [CrossRef]
  48. Leguy, A.M.; Azarhoosh, P.; Alonso, M.I.; Campoy-Quiles, M.; Weber, O.J.; Yao, J.; Bryant, D.; Weller, M.T.; Nelson, J.; Walsh, A. Experimental and theoretical optical properties of methylammonium lead halide perovskites. Nanoscale 2016, 8, 6317–6327. [Google Scholar] [CrossRef]
  49. Berdiyorov, G.R.; Kachmar, A.; El-Mellouhi, F.; Carignano, M.A.; El-Amine Madjet, M. Role of cations on the electronic transport and optical properties of lead-iodide perovskites. The Journal of Physical Chemistry C 2016, 120, 16259–16270. [Google Scholar] [CrossRef]
  50. Berdiyorov, G.; Madjet, M.; El-Mellouhi, F.; Peeters, F. Effect of crystal structure on the electronic transport properties of the organometallic perovskite CH3NH3PbI3. Solar Energy Materials and Solar Cells 2016, 148, 60–66. [Google Scholar] [CrossRef]
  51. Shan, D.; Tong, G.; Cao, Y.; Tang, M.; Xu, J.; Yu, L.; Chen, K. The effect of decomposed PbI2 on microscopic mechanisms of scattering in CH3NH3PbI3 films. Nanoscale Research Letters 2019, 14, 1–6. [Google Scholar] [CrossRef] [PubMed]
  52. Brenner, T.M.; Egger, D.A.; Kronik, L.; Hodes, G.; Cahen, D. Hybrid organic—inorganic perovskites: low-cost semiconductors with intriguing charge-transport properties. Nature Reviews Materials 2016, 1, 1–16. [Google Scholar] [CrossRef]
  53. Eames, C.; Frost, J.M.; Barnes, P.R.; O’regan, B.C.; Walsh, A.; Islam, M.S. Ionic transport in hybrid lead iodide perovskite solar cells. Nature communications 2015, 6, 1–8. [Google Scholar] [CrossRef]
  54. Bhargava, R.; Sharma, P.K.; Kumar, S.; Pandey, A.C.; Kumar, N. Consequence of doping mediated strain and the activation energy on the structural and optical properties of ZnO: Cr nanoparticles. Journal of Solid State Chemistry 2010, 183, 1400–1408. [Google Scholar] [CrossRef]
  55. Miyata, A.; Mitioglu, A.; Plochocka, P.; Portugall, O.; Wang, J.T.W.; Stranks, S.D.; Snaith, H.J.; Nicholas, R.J. Direct measurement of the exciton binding energy and effective masses for charge carriers in organic–inorganic tri-halide perovskites. Nature Physics 2015, 11, 582–587. [Google Scholar] [CrossRef]
  56. Yang, J.; Meissner, M.; Yamaguchi, T.; Zhang, X.; Ueba, T.; Cheng, L.; Ideta, S.; Tanaka, K.; Zeng, X.; Ueno, N. Band dispersion and hole effective mass of methylammonium lead iodide perovskite. Solar RRL 2018, 2, 1800132. [Google Scholar] [CrossRef]
  57. Davies, C.L.; Filip, M.R.; Patel, J.B.; Crothers, T.W.; Verdi, C.; Wright, A.D.; Milot, R.L.; Giustino, F.; Johnston, M.B.; Herz, L.M. Bimolecular recombination in methylammonium lead triiodide perovskite is an inverse absorption process. Nature communications 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
  58. Kauffmann, T.H.; Kokanyan, N.; Fontana, M.D. Use of Stokes and anti-Stokes Raman scattering for new applications. Journal of Raman Spectroscopy 2019, 50, 418–424. [Google Scholar] [CrossRef]
  59. Barbillat, J.; Bougeard, D.; Buntinx, G.; Delhaye, M.; Dhamelincourt, P.; Fillaux, F. Spectrométrie raman. Techniques de l’ingénieur. Analyse et caractérisation 1999, 4, P2865.1–P2865.31. [Google Scholar] [CrossRef]
  60. Chang, A.Y.; Cho, Y.; Chen, K.; Chen, C.; Kinaci, A.; Diroll, B.T.; Wagner, M.J.; Chan, M.K.; Lin, H.; Schaller, R.D. Slow organic-to-inorganic sub-lattice thermalization in methylammonium lead halide perovskites observed by ultrafast photoluminescence. Advanced Energy Materials 2016, 6, 1600422. [Google Scholar] [CrossRef]
  61. Singh, R.K.; Jain, N.; Singh, J.; Kumar, R. Stability behavior of chemically synthesized organic electrolyte salts and methylammonium lead halide perovskite light harvester. Adv Mater Lett 2017, 8, 707–711. [Google Scholar] [CrossRef]
  62. Ardimas.; Pakornchote, T.; Sukmas, W.; Chatraphorn, S.; Clark, S.J.; Bovornratanaraks, T. Phase transformations and vibrational properties of hybrid organic–inorganic perovskite MAPbI3 bulk at high pressure. Scientific Reports 2023, 13, 16854. [CrossRef] [PubMed]
  63. Liang, Z.; Zhang, S.; Xu, X.; Wang, N.; Wang, J.; Wang, X.; Bi, Z.; Xu, G.; Yuan, N.; Ding, J. A large grain size perovskite thin film with a dense structure for planar heterojunction solar cells via spray deposition under ambient conditions. RSC advances 2015, 5, 60562–60569. [Google Scholar] [CrossRef]
  64. Leguy, A.M.; Hu, Y.; Campoy-Quiles, M.; Alonso, M.I.; Weber, O.J.; Azarhoosh, P.; Van Schilfgaarde, M.; Weller, M.T.; Bein, T.; Nelson, J. Reversible hydration of CH3NH3PbI3 in films, single crystals, and solar cells. Chemistry of Materials 2015, 27, 3397–3407. [Google Scholar] [CrossRef]
  65. Segovia, R.; Qu, G.; Peng, M.; Sun, X.; Shi, H.; Gao, B. Evolution of Photoluminescence, Raman, and Structure of CH 3 NH 3 PbI 3 Perovskite Microwires Under Humidity Exposure. Nanoscale research letters 2018, 13, 1–8. [Google Scholar] [CrossRef] [PubMed]
  66. Byranvand, M.M.; Saliba, M. Defect passivation of perovskite films for highly efficient and stable solar cells. Solar Rrl 2021, 5, 2100295. [Google Scholar] [CrossRef]
  67. Chen, B.; Rudd, P.N.; Yang, S.; Yuan, Y.; Huang, J. Imperfections and their passivation in halide perovskite solar cells. Chemical Society Reviews 2019, 48, 3842–3867. [Google Scholar] [CrossRef] [PubMed]
  68. Aydin, E.; De Bastiani, M.; De Wolf, S. Defect and contact passivation for perovskite solar cells. Advanced Materials 2019, 31, 1900428. [Google Scholar] [CrossRef] [PubMed]
Preprints 110460 g001
Figure 1. XRD spectra of perovskite film annealed at 80 °C.
Figure 1. XRD spectra of perovskite film annealed at 80 °C.
Preprints 110460 g001
Preprints 110460 g002
Figure 2. a) Williamson-Hall analysis of perovskite films annealed at 50, 70, 80, 90 and 110 °C, b) Residual strain extracted from the slope using Equation 1.
Figure 2. a) Williamson-Hall analysis of perovskite films annealed at 50, 70, 80, 90 and 110 °C, b) Residual strain extracted from the slope using Equation 1.
Preprints 110460 g002
Preprints 110460 g003
Figure 3. (a) Schematic representation of the GIXRD angle geometry in mode- ω . (b) GIXRD analysis of the perovskite films annealed at 50, 70, 90 and 110 ​ ∘ C , (c) Strain coefficients extracted from the GIXRD slope. (d, e) Compressively-strained films annealed below 80 ​ ∘ C . (f) strain-free film (g, h) Tensile-strained films annealed above 80 ​ ∘ C .
Figure 3. (a) Schematic representation of the GIXRD angle geometry in mode- ω . (b) GIXRD analysis of the perovskite films annealed at 50, 70, 90 and 110 ​ ∘ C , (c) Strain coefficients extracted from the GIXRD slope. (d, e) Compressively-strained films annealed below 80 ​ ∘ C . (f) strain-free film (g, h) Tensile-strained films annealed above 80 ​ ∘ C .
Preprints 110460 g003
Preprints 110460 g004
Figure 4. SEM micrographs for the perovskite films annealed (a) 50 ​ ∘ C , (b) 70 ​ ∘ C , (c) 90 ​ ∘ C and (d) 110 ​ ∘ C . The scale bars are 3 μ m . (e-h) Grain size distributions extracted from these images using ImageJ.
Figure 4. SEM micrographs for the perovskite films annealed (a) 50 ​ ∘ C , (b) 70 ​ ∘ C , (c) 90 ​ ∘ C and (d) 110 ​ ∘ C . The scale bars are 3 μ m . (e-h) Grain size distributions extracted from these images using ImageJ.
Preprints 110460 g004
Preprints 110460 g005
Figure 5. (a) Hall effect measurement setup, (b) Hall-voltage measured as a function of the current flowing through the device. (c) Resistivity and mobility values extracted from the Hall measurements for different annealing temperatures.
Figure 5. (a) Hall effect measurement setup, (b) Hall-voltage measured as a function of the current flowing through the device. (c) Resistivity and mobility values extracted from the Hall measurements for different annealing temperatures.
Preprints 110460 g005
Preprints 110460 g006
Figure 6. (a) Activation energy ( E a ) and (b) Mean free path (Lm) and mean free time ( τ m ) for the C H 3 N H 3 P b I 3 − x C l x films as a function of their annealing temperature.
Figure 6. (a) Activation energy ( E a ) and (b) Mean free path (Lm) and mean free time ( τ m ) for the C H 3 N H 3 P b I 3 − x C l x films as a function of their annealing temperature.
Preprints 110460 g006
Preprints 110460 g007
Figure 7. Absorption spectra for perovskite films annealed at 60, 80 and 110 °C. (a) Pristine films following fabrication (b) After 4 days of degradation in ambient conditions. (c) Tauc plot showing the bandgap evolution under temperature induced strain variation.(d,e,f) Tauc plots measured after 4 days in ambient environment.
Figure 7. Absorption spectra for perovskite films annealed at 60, 80 and 110 °C. (a) Pristine films following fabrication (b) After 4 days of degradation in ambient conditions. (c) Tauc plot showing the bandgap evolution under temperature induced strain variation.(d,e,f) Tauc plots measured after 4 days in ambient environment.
Preprints 110460 g007
Preprints 110460 g008
Figure 8. (a) Raman peaks shifting of the thermally-relaxed sample during 4 days of analysis, b) Stokes/ani-Stokes for samples without strain. Evaluation of the samples based on Stokes/anti-Stokes intensity ratios. Calculated temperature of the (c) compressively-strained sample annealed at 60 ​ ∘ C , (d) thermally-relaxed sample annealed at 80 ​ ∘ C and (e) tensile-strained sample annealed at 110 ​ ∘ C .
Figure 8. (a) Raman peaks shifting of the thermally-relaxed sample during 4 days of analysis, b) Stokes/ani-Stokes for samples without strain. Evaluation of the samples based on Stokes/anti-Stokes intensity ratios. Calculated temperature of the (c) compressively-strained sample annealed at 60 ​ ∘ C , (d) thermally-relaxed sample annealed at 80 ​ ∘ C and (e) tensile-strained sample annealed at 110 ​ ∘ C .
Preprints 110460 g008
Preprints 110460 g009
Figure 9. Raman spectra of film degradation of a different time from 0 day to 4 days. (a) With residual compressive strains, (b) Thermally-relaxed, (c) tensile-strained film. (d,e,f) Degradation measured from Raman peaks evolutions at 53, 65 and 100 / c m
Figure 9. Raman spectra of film degradation of a different time from 0 day to 4 days. (a) With residual compressive strains, (b) Thermally-relaxed, (c) tensile-strained film. (d,e,f) Degradation measured from Raman peaks evolutions at 53, 65 and 100 / c m
Preprints 110460 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated