On Lyapunov Stability of Caputo Fractional Dynamic Equations on Time Scale using a New Generalized Derivative

Preprint

Article

On Lyapunov Stability of Caputo Fractional Dynamic Equations on Time Scale using a New Generalized Derivative

Altmetrics

Downloads

140

Views

Comments

A peer-reviewed article of this preprint also exists.

Michael Precious Ineh^*

,Edet Peter Akpan,

Hossam Nabwey^*

Michael Precious Ineh^*

,Edet Peter Akpan,

Hossam Nabwey^*

This version is not peer-reviewed

Submitted:

28 June 2024

Posted:

28 June 2024

You are already at the latest version

Alerts

Abstract

In this work, we introduce a new and generalized concept (herein referred to as Caputo fractional delta derivative and Caputo fractional delta dini derivative of order $\alpha\in(0,1)$) for Caputo fractional derivatives on an arbitrary time domain $\mathbb{T}$ which is a closed subset of $\mathbb{R}$. Combining the continuous and discrete time domains, we create a unified framework for stability analysis on time scales. Comparison results and stability criteria for the considered Caputo fractional dynamic equations are presented based on a new definition for Caputo fractional delta derivative of a Lyapunov function, contributing to the broader understanding of fractional calculus on time scales. The work also incorporates an illustrative example to demonstrate the relevance, effectiveness and applicability of the established stability results over that of the integer order.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 34A08; 34A34; 34D20; 34N05

1. Introduction

In recent years, the study of fractional calculus has gained significant attention due to its ability to capture complex dynamics and model real-world problems more accurately and efficiently. In-fact, it is a generalization of the integer-order derivatives and integrals, it is also referred to as differentiation and integration to an arbitrary order [28]. Numerous studies have utilized Lyapunov second method, also known as the Lyapunov direct method, with remarkable outcomes in comprehending the qualitative and quantitative characteristics of dynamical systems. One benefit of using the Lyapunov direct method is that it does not require knowledge of the solution to the differential equation under study([30]).In [1,2,3,6,8], several types of fractional derivatives of Lyapunov functions used in stability investigations of differential equations, including Caputo fractional derivative, Dini fractional derivative, and Caputo fractional Dini derivative were applied. However, the most preferred as pointed out by the authors is the Caputo Fractional derivative

_{t_{0}}^{C} D_{t}^{α} V (t, x (t)) = \frac{1}{Γ (1 - α)} \int_{t_{0}}^{t} {(t - s)}^{- α} \frac{d}{d s} (v (s, x (s))) d s, t \in [t_{0}, T)

this is due to the fact that it is easier to handle and has a more realistic application. Still, the authors noted that the function

V (t, x (t))

need be continuously differentiable which posses another challenge. This disadvantage does not affect the other Lyapunov function derivatives, so the authors obtained sufficient conditions for these derivatives using a continuous Lyapunov function that needs not be continuously differentiable. In [2] it was noted that the Dini fractional derivative

^{C} D_{+}^{α} V (t, x (t)) = \underset{h \to 0 +}{lim sup} \frac{1}{h^{α}} {V (t, x (t)) - \sum_{r = 1}^{[\frac{t - t_{0}}{h}]} {(- 1)}^{r}^{α} C_{r} V (t - r h, x (t) - h^{α} f (t, x (t)))}

maintains the idea of fractional derivatives since it depends not only on the present state but also on the initial state. Yet, it doesnt depend on the initial state

V (t_{0}, x_{0})

. So a better definition

\begin{matrix} _{t_{0}}^{C} D_{+}^{α} V (t, x (t)) \\ = \underset{h \to 0 +}{lim sup} \frac{1}{h^{α}} \{V (t, x (t)) - V (t_{0}, x (t_{0})) - \sum_{r = 1}^{[\frac{t - t_{0}}{h}]} {(- 1)}^{r + 1}^{α} C_{r} [V (t - r h, x (t) - h^{α} f (t, x (t))) - V (t_{0}, x (t_{0}))]\} \end{matrix}

(1)

was considered as more suitable. (see[1])

The Caputo fractional Dini derivative (1) has been utilized to examine various types of stability in Caputo fractional differential equations with continuous domain as seen in [1,4]. As explained in [23] and [11], a more holistic and practicable examination of stability can be achieved if it can be done across different time domains. The existing research considers a time domain of real numbers which ignores discrete details while in [12,20,24,25], the domain considered are discrete domains ignoring the continuous time domains. However, in practicability, some systems undergo smooth and abrupt changes almost simultaneously while others could have more than one time scale or frequency. Modeling such phenomenon is more realistically represented as a dynamic system that includes continuous and discrete times, that is, time as an arbitrary closed subset of real numbers known as the time scale or measure chain and denoted by

T

. Dynamic equations on time scale are defined on discrete, continuous (connected) or combination of both. It is a bedrock for a broader analysis of difference and differential systems [17].This work focuses on the Lyapunov stability analysis of Caputo fractional dynamic equations on time scale using a new definition for the delta derivative of a Lyapunov function known herein as the Caputo fractional delta derivative on a time scale, aiming to provide a unified and comprehensive understanding as well as extending the stability properties from the classical sense to the fractional-order sense. The inclusion of time scales in fractional calculus will bridge the gap between continuous and discrete mathematical frameworks, offering a versatile platform for modeling and analyzing dynamic systems.

The study of dynamic systems on time scales has seen significant development since the foundational work by Hilger (see [15]). This pioneering work laid the ground work for subsequent research including [7,11,18,19] which provided comprehensive introductions and analyzed several qualitative properties of solutions of dynamic equations on time scales, such as existence and uniqueness, stability, and instability. More recently, in [17], the boundaries were pushed even further by analyzing the existence and uniqueness of solutions to dynamic equations on time scales via generalized ordinary differential equations. These results were then extended from integer order to a more generalized form (fractional order) in [8,9,13,29,31].

Building on the existence and uniqueness results for Caputo-type fractional dynamic equations on time scales established in [8], we extend the stability results in [18] to fractional order and the Lyapunov stability results for Caputo fractional differential equations in [1] to a more generalized (unified) domain (time scale). This unification of continuous and discrete calculus gives rise to fractional difference equations in discrete time, fractional differential equations in continuous time, and fractional calculus on time scale in combined continuous and discrete time.

The investigation unfolds by delving into the basic definitions of some important terminologies, remarks, and a basic theorem which sets the stage for our contributions. New definitions and vital remarks were given which are important in establishing crucial comparison results and stability criteria for Caputo fractional dynamic equations. These results contribute not only to the theoretical advancements in fractional calculus but also extends the results on integer order dynamic equations on time scales to fractional order. To emphasize the relevance and effectiveness of the derived stability criteria, we present a detailed example, illustrating the importance and applicability of our results.

2. Preliminaries, Definitions and Notations

The foundational principles of dynamic equations, encompassing derivatives and integrals, can be extended to noninteger orders through the application of fractional calculus. This generalization to noninteger orders becomes particularly relevant when exploring dynamic equations on a time scale, allowing for a versatile and comprehensive analysis of system behavior across both continuous and discrete time domains. See [9,13,22,27],and [29]. In this section we shall set the foundation, introduce notations and give definitions that will be used in the main results.

Definition 1.

For

t \in T

, the forward jump operator

σ : T \to T

is defined as

σ (t) = inf {s \in T : s > t}

while the backward jump operator

ρ : T \to T

is defined as

ρ (t) = s u p {s \in T : s < t} .

(i): if $σ (t) > t$ , t is right scattered,
(ii): if $ρ (t) < t$ , t is left scattered,
(iii): if $t < m a x T$ and $σ (t) = t$ , then t is called right dense,
(iv): if $t > m i n T$ and $ρ (t) = t$ , then t is called left dense.

Definition 2.

The graininess function

μ : T \to T

for

t \in T

is defined as

μ (t) = σ (t) - t

The derivative makes use of the set

T^{k}

, which is derived from the time scale

T

as follows.

T

has a left scattered maximum M, then

T^{k} = T ∖ {M}

. Otherwise

T^{k} = T

Definition 3

(Delta Derivative). Let

h : T \to R

and

t \in T^{k}

. We define the delta derivative

h^{Δ}

also known as the Hilger derivative as

h^{Δ} (t) = lim_{s \to t} \frac{h (σ (t)) - h (s)}{σ (t) - s}, s \neq σ (t) .

provided the limit exists.

The function

h^{Δ} : T \to R

is called the (Delta) derivative of h on

T^{k}

If t is right dense, the delta derivative of

h : T \to R

, becomes

h^{Δ} (t) = lim_{s \to t} \frac{h (t) - h (s)}{t - s}

and if t is right scattered, the Delta derivative becomes

h^{Δ} (t) = \frac{h^{σ} (t) - h (t)}{μ (t)}

For a function

h : T \to R

h^{σ}

denotes

h (σ (t))

Definition 4.

A function

h : T \to R

is right dense continuous if it is continuous at all right dense points of

T

and its left sided limits exists and is finite at left dense points of

T

. The set of all right dense continuous function is denoted by

C_{r d} = C_{r d} (T)

Definition 5.

Assume

[a, b]

is a closed and bounded interval in

T

. Then a function

H : [a, b] \to R

is called a delta antiderivative of

h : [a, b] \to R

provided F is continuous on

[a, b]

, delta differentiable on

[a, b)

, and

H^{Δ} (t) = h (t)

for all

t \in [a, b)

. Then, we define the Delta integral by

\int_{a}^{b} h (t) = H (b) - H (a) \forall a, b \in T

Remark 1.

All right dense continuous functions are delta integrable.

Definition 6.

A function

ϕ : [0, r] \to [0, \infty)

is of class

K

if it is continuous, and strictly increasing on

[0, r]

with

ϕ (0) = 0

Definition 7.

A continuous function

V : R^{n} \to R

with

V (0) = 0

is called positive definite(negative definite) on the domain D if there exists a function

ϕ \in K

such that

ϕ (| x |) \leq V (x) (ϕ (| x |) \leq - V (x))

for

x \in D

Definition 8.

A continuous function

V : R^{n} \to R

with

V (0) = 0

is called positive semidefinite (negative semi-definite) on D if

V (x) \geq 0 (V (x) \leq 0)

for all

x \in D

and it can also vanish for some

x \neq 0

Definition 9.

Assume

V \in C_{r d} [T \times R^{n}, R_{+}]

and

μ (t)

is the graininess function then we define the dini derivative of

V (t, x)

as:

D_{-} V^{Δ} (t, x) = \underset{μ (t) \to 0}{lim inf} \frac{V (t, x) - V (t - μ (t), x - μ (t) h (t, x))}{μ (t)}

(2)

D^{+} V^{Δ} (t, x) = \underset{μ (t) \to 0}{lim sup} \frac{V (t + μ (t), x + μ (t) h (t, x)) - V (t, x)}{μ (t)}

(3)

If V is differentiable, then

D_{-} V^{Δ} (t, x) = D^{+} V^{Δ} (t, x) = V^{Δ} (t, x)

Definition 10.

(Fractional Integral on Time Scales).. Let

α \in (0, 1)

[a, b]

be an interval on

T

and h an integrable function on

[a, b]

. Then the fractional integral of order α of h is defined by

_{a}^{T} I_{t}^{α} h^{Δ} (t) = \int_{a}^{t} \frac{{(t - s)}^{α - 1}}{Γ (α)} h (s) Δ s

Definition 11.

(Riemann-Liouville Derivative on Tme Scale).Let

T

be a time scale,

t \in T, 0 < α < 1

, and

h : T \to R

. The Riemann-Liouville fractional derivative of order α of h is defined by

_{a}^{T} D_{t}^{α} h^{Δ} (t) = \frac{1}{Γ (1 - α)} {(\int_{a}^{t} {(t - s)}^{- α} h (s) Δ s)}^{Δ}

Definition 12.

(Caputo Derivative on Time Scale).Let

T

be a time scale,

t \in T, 0 < α < 1

, and

h : T \to R

. The Caputo fractional derivative of order α of h is defined by

_{a}^{T} D_{t}^{α} h^{Δ} (t) = \frac{1}{Γ (1 - α)} \int_{a}^{t} {(t - s)}^{- α} h^{Δ} (s) Δ s

Theorem 1.

[19] Let

T

be a time scale with minimal element

t_{0} \geq 0

. Assume that for any

t \in T

, there is a statement

A (t)

such that the following conditions are verified:

(i): $S (t_{0})$ is true;
(ii): If t is right scattered and $A (t)$ is true, then $S (σ (t))$ is also true;
(iii): For each right-dense t, there exists a neighbourhood $U$ such that whenever $S (t)$ is true, $S (t^{*})$ is also true for all $t^{*} \in U$ , $t^{*} \geq t$

Then the statement

S (t)

is true for all

t \in T

Remark 2.

When

T = N

, then Theorem 1 reduces to the well known principle of mathematical induction. That is

1.: $S (t_{0})$ is true is equivalent to the statement is true for $n = 1$
2.: $S (t)$ is true then $S (σ (t))$ is true is equivalent to if the statement is true for $n = k$ , then the statement is true for $n = k + 1$

Definitions 1 to 12 are contained in [7,10,11,14,16,17,21,23,31]. We give the following definitions and remarks.

Definition 13.

Let

T

be a time scale. A point

t_{0} \in T

is said to be a minimal element of

T

if for any

t \in T

t > t_{0}

whenever

t \neq t_{0}

Remark 3.

The concept of minimal element is important in the study of dynamic equations because it establishes a starting point, a reference time from which the dynamics of the system evolve. In the study of difference equations (a discrete-time setting),

t_{0}

represents the initial time step. Similarly, in differential equations (a continuous-time setting),

t_{0}

represents the initial time instant.

Definition 14.

The Grunwald-Letnikov fractional delta derivative is given by

^{G L T} D_{0}^{α} h^{Δ} (t) = lim_{μ \to 0 +} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ)] t \geq t_{0}

(4)

and the Grunwald-Letnikov fractional delta dini derivative is given by

^{G L T} D_{0^{+}}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ)] t \geq t_{0}

(5)

where

0 < α < 1

^{α} C_{r}

are the binomial coefficients and

[\frac{(t - t_{0})}{μ}]

denotes the integer part of the fraction

\frac{(t - t_{0})}{μ}

observe that if the domain is

R

, then (5) becomes

^{G L T} D_{0^{+}}^{α} h^{Δ} (t) = \underset{d \to 0 +}{lim sup} \frac{1}{d^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{d}]} {(- 1)}^{r}^{α} C_{r} [h (t - r d)] t \geq t_{0}

Remark 4.

It is necessary to note that the relationship between the Caputo fractional delta derivative and the Grunwald-Letnikov fractional delta derivative is given by

^{C T} D_{0}^{α} h^{Δ} (t) =^{G L T} D_{0}^{α} [h (t) - h (t_{0})]^{Δ}

(6)

substituting (4) into (6) we have that the Caputo fractional delta derivative becomes

\begin{matrix} ^{C T} D_{0}^{α} h^{Δ} (t) = lim_{μ \to 0 +} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})] t \geq t_{0} \\ ^{C T} D_{0}^{α} h^{Δ} (t) = lim_{μ \to 0 +} \frac{1}{μ^{α}} \{h (σ (t)) - h (t_{0}) + \sum_{r = 1}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})]\} \end{matrix}

(7)

and the Caputo fractional delta dini derivative becomes

^{C T} D_{0^{+}}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})] t \geq t_{0}

(8)

Which is equivalent to

^{C T} D_{0^{+}}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \{h (σ (t)) - h (t_{0}) + \sum_{r = 1}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})]\} t \geq t_{0}

(9)

for notation simplicity, we shall represent the Caputo fractional delta derivative of order

α

^{C T} D^{α}

and the Caputo fractional delta dini derivative of order

α

^{C T} D_{+}^{α}

3. Statement Of Problem

Let

T

be a time scale with

t_{0} \geq 0

as a minimal element.

Consider the Caputo fractional dynamic system of order

α

with

0 < α < 1

\begin{matrix} ^{C T} D^{α} x^{Δ} = f (t, x), t \in T, \\ x (t_{0}) = x_{0}, t_{0} \geq 0 \end{matrix}

(10)

where

f \in C_{r d} [T \times R^{n}, R^{n}]

f (t, 0) \equiv 0

and

^{C T} D^{α} x^{Δ}

is the Caputo fractional delta derivative of

x \in R^{n}

of order

α

with respect to

t \in T

. Let

x (t) = x (t, t_{0}, x_{0}) \in C_{r d}^{α} [T, R^{n}]

be a solution of (10) and assume the solution exists and is unique (results on existence and uniqueness of (10) are contained in [8,13,22]), the aim of this work is to study the stability of the system (10).

To do this, we shall use the Caputo fractional dynamic system of the form

^{C T} D^{α} u^{Δ} = g (t, u), u (t_{0}) = u_{0} \geq 0

(11)

where

u \in R_{+}

g : T \times R_{+} \to R_{+}

and

g (t, 0) \equiv 0

. (11) is called the comparison system. for the purpose of this work we will assume that the function

g \in [T \times R_{+}, R_{+}]

is such that for any initial data

(t_{0}, u_{0}) \in T \times R_{+}

, the system (11) with

u (t_{0}) = u_{0}

has a unique solution

u (t) = u (t; t_{0}, u_{0}) \in C_{r d}^{α} (T, R_{+})

see [8].

Definition 15.

The trivial solution

x = 0

of (10) is called stable if given

ϵ > 0

and

t_{0} \in T

there exists a

δ = δ (ϵ, t_{0}) > 0

such that for any

x_{0} \in R^{n}

the inequality

∥ x_{0} ∥ < δ

implies

∥ x (t; t_{0}, x_{0}) ∥ < ϵ

, for

t \geq t_{0}

Now, we introduce the derivative of the Lyapunov function using the Caputo fractional delta dini derivative of

h (t)

given in (8).

Definition 16.

We define the Caputo fractional delta dini derivative of the Lyapunov function

V (t, x) \in C_{r d} [T \times R^{n}, R_{+}]

(which is locally Lipschitzian with respect to its second argument and

V (t, 0) \equiv 0

) along the trajectories of solutions of the system (10) as:

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t, x) = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} [\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [V (σ (t) - r μ, x (σ (t)) - μ^{α} f (t, x (t)) - V (t_{0}, x_{0})]] \end{matrix}

and can be expanded as

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t, x) = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (σ (t), x (σ (t)) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [V (σ (t) - r μ, x (σ (t)) - μ^{α} f (t, x (t)) - V (t_{0}, x_{0})]} \end{matrix}

(12)

where

t \in T, x, x_{0} \in R^{n}

μ = σ (t) - t

and

x (σ (t)) - μ^{α} f (t, x) \in R^{n}

T

is discrete and

V (t, x (t))

is continuous at t, we have that

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t, x) = \frac{1}{μ^{α}} [\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) (V (σ (t), x (σ (t))) - V (t_{0}, x_{0}))] \end{matrix}

(13)

and if

T

is Continuous that is

T = R

, and

V (t, x (t))

is continuous at t, we have that

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t, x) = \underset{d \to 0^{+}}{lim sup} \frac{1}{d^{α}} {V (t, x (t)) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t - t_{0}}{d}]} {(- 1)}^{r + 1} (^{α} C_{r}) [V (t - r d, x (t)) - d^{α} f (t, x (t)) - V (t_{0}, x_{0})]} \end{matrix}

(14)

Notice that (14) is the same in [1] where

d > 0

Given that

lim_{N \to \infty} \sum_{r = 0}^{N} {(- 1)}^{r}^{α} C_{r} = 0

where

α \in (0, 1)

, and

lim_{μ \to 0^{+}} [\frac{(t - t_{0})}{μ}] = \infty

then it is easy to see that

lim_{μ \to 0^{+}} \sum_{r = 1}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} = - 1

(15)

Also from (8) and since the Caputo and Riemann-Liouville formulations coincide when

h (t_{0}) = 0

, ([1]) then we have that

^{C T} D_{+}^{α} h^{Δ} (t) =^{R L T} D_{+}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ)], t \geq t_{0}

(16)

setting

h (σ (t) - r μ = 1

we obtain

^{C T} D_{+}^{α} h^{Δ} (t) = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} =^{R L T} D^{α} (1) = \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)}, t \geq t_{0}

(17)

4. Inequalities on Fractional Dynamic Equations on Time scale and Comparison results

Lemma 1.

Assume

h, m \in C_{r d} (T, R)

, suppose there exists

t_{1} > t_{0}, t_{1} \in T

such that

h (t_{1}) = m (t_{1})

and

h (t) < m (t)

for

t_{0} \leq t < t_{1}

. Then if the Caputo fractional delta dini derivatives of h and m exist at

t_{1}

, then the inequality

^{C T} D_{+}^{α} h^{Δ} (t_{1}) >^{C T} D_{+}^{α} m^{Δ} (t_{1})

holds.

Proof.

Applying (8), we have

^{C T} D_{+}^{α} {(h (t) - m (t))}^{Δ} = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \{\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} α C_{r} [h (σ (t) - r μ) - m (σ (t) - r μ)] - [h (t_{0}) - m (t_{0})]\}

^{C T} D_{+}^{α} h^{Δ} (t) -^{C T} D_{+}^{α} m^{Δ} (t) = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \{\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} q C_{r} [h (σ (t) - r μ) - m (σ (t) - r μ)] - [h (t_{0}) - m (t_{0})]\}

t_{1}

, we have that

^{C T} D_{+}^{α} h^{Δ} (t_{1}) = - \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \{\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} α C_{r} [h (t_{0}) - m (t_{0})]\} +^{C T} D_{+}^{α} m^{Δ} (t_{1})

(18)

Applying (17) to (18), we have

\begin{matrix} ^{C T} D_{+}^{α} h^{Δ} (t_{1}) & = & - \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} [h (t_{0}) - m (t_{0})] +^{C T} D_{+}^{α} m^{Δ} (t_{1}) \end{matrix}

but from the statement of the lemma, we have that

\begin{matrix} h (t) < m (t) f o r t_{0} \leq t < t_{1} \\ \Rightarrow h (t) - m (t) < 0, f o r t_{0} \leq t < t_{1} \end{matrix}

And so it follows that

\begin{matrix} - \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} [h (t_{0}) - m (t_{0})] > 0 \end{matrix}

implying that

\begin{matrix} ^{C T} D_{+}^{α} h^{Δ} (t_{1}) >^{C T} D_{+}^{α} m^{Δ} (t_{1}) \end{matrix}

□

Theorem 2.

Assume that

(i): $g \in C_{r d} [T \times R_{+}, R_{+}]$ and $g (t, u) μ$ is non-decreasing in u.
(ii): $V \in C_{r d} [T \times R^{N}, R_{+}]$ be locally Lipschitzian in the second variable such that

$^{C T} D_{+}^{α} V^{Δ} (t, x) \leq g (t, V (t, x)), (t, x) \in T \times R^{N}$

(19)
(iii): $z (t) = z (t; t_{0}, u_{0})$ is the maximal solution of (11) existing on $T$ .

Then

$V (t, x (t)) \leq z (t), t \geq t_{0}$

(20)

provided that

$V (t_{0}, x_{0}) \leq u_{0}$

(21)

where $x (t) = x (t; t_{0}, x_{0})$ is any solution of (10), $t \in T$ , $t \geq t_{0}$

Proof.

Apply the principle of induction as stated in Theorem 1 to the statement

S (t) : V (t, x (t)) \leq z (t), t \in T, t \geq t_{0}

(i): $S (t_{0})$ is true since $V (t_{0}, x_{0}) \leq u_{0}$
(ii): Let t be right-scattered and $S (t)$ be true. We need to show that $S (σ (t))$ is true; that is

$V (σ (t), x (σ (t))) \leq z (σ (t))$

(22)

set $h (t) = V (t, x (t))$ then $h (σ (t)) = V (σ (t), x (σ (t)))$ but from (8), we have that

$^{C T} D_{+}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})] t \geq t_{0}$

also

$^{C T} D_{+}^{α} z^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [z (σ (t) - r μ) - z (t_{0})] t \geq t_{0}$

so that

$\begin{matrix} ^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t) \\ = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [z (σ (t) - r μ) - z (t_{0})] - \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [h (σ (t) - r μ) - h (t_{0})] \end{matrix}$

$^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t) = \underset{μ \to 0 +}{lim sup} \frac{1}{μ^{α}} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [[z (σ (t) - r μ) - z (t_{0})] - [h (σ (t) - r μ) - h (t_{0})]]$

$(^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t)) μ^{α} = \underset{μ \to 0 +}{lim sup} \sum_{r = 0}^{[\frac{(t - t_{0})}{μ}]} {(- 1)}^{r}^{α} C_{r} [[z (σ (t) - r μ) - z (t_{0})] - [h (σ (t) - r μ) - h (t_{0})]]$

$(^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t)) μ^{α} \leq [z (σ (t)) - z (t_{0})] - [h (σ (t)) - h (t_{0})]$

$(^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t)) μ^{α} \leq [z (σ (t)) - h (σ (t))] - [z (t_{0}) - h (t_{0})]$

$[z (σ (t)) - h (σ (t))] \geq (^{C T} D_{+}^{α} z^{Δ} (t) -^{C T} D_{+}^{α} h^{Δ} (t)) μ^{α} + [z (t_{0}) - h (t_{0})]$

$[h (σ (t)) - z (σ (t))] \leq (^{C T} D_{+}^{α} h^{Δ} (t) -^{C T} D_{+}^{α} z^{Δ} (t)) μ^{α} + [h (t_{0}) - z (t_{0})] \leq (g (t, h (t)) - g (t, z (t))) μ^{α} + [h (t_{0}) - z (t_{0})]$

Since $g (t, u) μ$ is non decreasing in u and $S (t)$ is true, then $h (σ (t)) - z (σ (t)) \leq 0$ so (22) holds.
(iii): Let t be right dense and $N$ be a right neighborhood of $t \in T$ . We need to show that $S (t^{*})$ is true for $t^{*} \in N$ . This follows from the comparison theorem for Caputo fractional differential equations since at every right dense point $t^{*} \in N$ , $σ (t^{*}) = t^{*}$ . See [1].

Let $ω$ be a small enough arbitrary positive number such that $ω \leq B_{T}$ (where $B_{T}$ is a small enough number on the time scale $T$ ) and consider the initial value problem

$^{C T} D^{α} u^{Δ} = g (t^{*}, u) + ω, u (t_{0}) = u_{0} + ω$

(23)

for $t^{*} \in N$ .

The function $u_{ω} (t^{*}) = u (t^{*}) + ω$ is a solution of (23) if and only if it satisfies the delta Integral equation

$u_{ω} (t^{*}) = u_{0} + ω + \frac{1}{Γ (α)} \int_{t_{0}}^{t^{*}} {(t^{*} - s)}^{α - 1} (g (s, u_{ω} (s)) + ω) Δ s, t^{*}, s \in N$

(24)

Let $h (t^{*}) \in C_{r d} (T, R_{+})$ be such that $h (t^{*}) = V (t^{*}, x^{*} (t^{*}))$ , where $x^{*} (t^{*})$ is any other solution of (10). We show that

$h (t^{*}) < u_{ω} (t^{*}), f o r t^{*} \in N$

(25)

the inequality (25) holds for $t^{*} = t_{0}$ since

$h (t_{0}) = V (t_{0}, x_{0}) \leq u_{0} < u_{α} (t_{0})$

Assume that the inequality (25) is not true, then there exist a point $t_{1}^{*} > t_{0}$ such that

$h (t_{1}^{*}) = u_{ω} (t_{1}^{*}) a n d h (t^{*}) < u_{ω} (t^{*}) f o r t_{0} \leq t^{*} < t_{1}^{*}, t^{*}, t_{1}^{*} \in N$

From lemma (1) it follows that

$^{C T} D_{+}^{α} h^{Δ} (t_{1}^{*}) >^{C T} D_{+}^{α} u_{ω}^{Δ} (t_{1}^{*})$

So that

$^{C T} D_{+}^{α} V^{Δ} (t_{1}^{*}, x^{*} (t_{1}^{*})) >^{C T} D_{+}^{α} u_{ω}^{Δ} (t_{1}^{*})$

and using (23) we arrive at

$^{C T} D_{+}^{α} V^{Δ} (t_{1}^{*}, x^{*} (t_{1}^{*})) > g (t_{1}^{*}, u_{ω} (t_{1}^{*})) + ω) > g (t_{1}^{*}, h (t_{1}^{*}))$

Therefore,

$^{C T} D_{+}^{α} h^{Δ} (t_{1}^{*}) > g (t_{1}^{*}, h (t_{1}^{*}))$

(26)

Now,

$\begin{matrix} ^{C T} D_{+}^{α} h^{Δ} (t^{*}) \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \{h (t^{*}) - h (t_{0}) - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [h (t^{*} - r μ) - h (t_{0})]\}, f o r t^{*} \in N \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (t^{*}, x^{*} (t^{*})) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [V (t^{*} - r μ, x^{*} (t^{*} - r μ) - V (t_{0}, x_{0})]} \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (t^{*}, x^{*} (t)) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [[V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) - V (t_{0}, x_{0})] \\ - [V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) - V (t_{0}, x_{0})] \\ + [V (t^{*} - r μ, x^{*} (t^{*} - r μ)) - V (t_{0}, x_{0})]]} \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (t^{*}, x^{*} (t^{*})) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [[V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) - V (t_{0}, x_{0})] \\ - V [(t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*})))] + V (t^{*} - r μ, x^{*} (t^{*} - r μ))]} \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (t^{*}, x^{*} (t^{*})) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [[V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) - V (t_{0}, x_{0})] \\ + [V (t^{*} - r μ, x^{*} (t^{*} - r μ)) - [V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*})))]]} \end{matrix}$

$\begin{matrix} = & \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (t^{*}, x^{*} (t^{*})) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r} [V (t^{*} - r μ, x^{*} (t^{*} - μ^{α} f (t^{*}, x^{*} (t^{*})) - V (t_{0}, x_{0})]} \\ - \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {\sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [V (t^{*} - r μ, x^{*} (t^{*} - r μ)) \\ - V (t^{*} - r μ, x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*})))]} \end{matrix}$

Since $V (t^{*}, x)$ is locally Lipschtzian in the second variable, we have

$\begin{matrix} ^{C T} D_{+}^{α} h^{Δ} (t^{*}) & \leq & ^{C T} D_{+}^{α} V^{Δ} (t^{*}, x^{*} (t^{*})) + L \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \sum_{r = 1}^{[\frac{t^{*} - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) \\ ∥ x^{*} (t^{*} - r μ) - (x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) ∥ \end{matrix}$

Where $L > 0$ is a Lipschitz constant.

As $μ \to 0, ∥ x^{*} (t^{*} - r μ) - (x^{*} (t^{*}) - μ^{α} f (t^{*}, x^{*} (t^{*}))) ∥ \to 0$ , so that from (19) we have

$\begin{matrix} ^{C T} D_{+}^{α} h^{Δ} (t^{*}) =^{C T} D_{+}^{α} V^{Δ} (t^{*}, x^{*} (t^{*})) \leq g (t^{*}, V (t^{*}, x^{*} (t^{*}))) = g (t^{*}, h (t^{*})) \end{matrix}$

(27)

Now (27) with $t^{*} = t_{1}^{*}$ contradicts (26), hence (25) is true. For $t^{*} \in N$ , we now show that whenever $ω_{1} < ω_{2}$ , then

$u_{ω_{1}} (t^{*}) < u_{ω_{2}} (t^{*})$

(28)

Notice that (28) holds for $t^{*} = t_{0}$ since $u (t_{0}) + ω_{1} < u (t_{0}) + ω_{2}$ $\Rightarrow ω_{1} < ω_{2}$ . Assume the inequality (28) is not true. Then there exist a point $t_{1}^{*}$ such that $u_{ω_{1}} (t_{1}^{*}) = u_{ω_{2}} (t_{1}^{*})$ and $u_{ω_{1}} (t^{*}) < u_{ω_{2}} (t^{*})$ for $t_{0} \leq t^{*} < t_{1}^{*} t^{*} \in N$ .

By Lemma (1), we have that

$^{C T} D_{+}^{α} u_{ω_{1}}^{Δ} (t_{1}^{*}) >^{C T} D_{+}^{α} u_{ω_{2}}^{Δ} (t_{1}^{*})$

However,

$\begin{matrix} ^{C T} D_{+}^{α} u_{ω_{1}}^{Δ} (t_{1}^{*}) -^{C T} D_{+}^{α} u_{ω_{2}}^{Δ} (t_{1}^{*}) & = & g (t_{1}^{*}, u_{ω_{1}} (t_{1}^{*})) + ω_{1} - [g (t_{1}^{*}, u_{ω_{2}} (t_{1}^{*})) + ω_{2}] \\ = & ω_{1} - ω_{2} < 0 \end{matrix}$

which is a contradiction and so (28) is true. Now from (28) and since $ω \leq B_{T}$ , we deduce that

$\begin{matrix} u_{ω_{1}} (t^{*}) < u_{ω_{2}} (t^{*}) < . . . < u (t^{*}) + ω_{i} \leq | u (t^{*}) + B_{T} | \leq M \end{matrix}$

and therefore we can say that the family of solutions ${u_{ω_{i}} (t^{*})}$ is uniformly bounded with bound $M > 0$ on $T$ . This means that $| u_{ω_{i}} (t^{*}) | \leq M$ for $t^{*} \in N$ and $ω \in (0, B_{T}]$

We now show that the family ${u_{ω_{i}} (t^{*})}$ is equicontinuous on $T$ . Assume $S = sup {| g (t^{*}, x^{*}) | : (t^{*}, x^{*}) \in N \times [- M, M]}$ . Now let us take ${ω_{i}}_{i = 1}^{\infty} (t^{*})$ , as a decreasing sequence, such that $lim_{i \to \infty} ω_{i} = 0$ and consider a sequence of functions $u_{ω_{i}} (t^{*})$ and take $t_{1}^{*}, t_{2}^{*} \in N$ with $t_{1}^{*} < t_{2}^{*}$ , then we have the following estimate

$\begin{matrix} | u_{ω_{i}} (t_{2}^{*}) - u_{ω_{i}} (t_{1}^{*}) | & = & | u_{0} + ω_{i} + \frac{1}{Γ (α)} \int_{t_{0}}^{t_{2}^{*}} {(t_{2}^{*} - s)}^{α - 1} (g (s, u_{ω_{i}} (s)) + α_{i}) Δ s \\ - (u_{0} + ω_{i} + \frac{1}{Γ (α)} \int_{t_{0}}^{t_{1}^{*}} {(t_{1}^{*} - s)}^{α - 1} (g (s, u_{ω_{i}} (s)) + ω_{i})) Δ s | \end{matrix}$

$\begin{matrix} = & \frac{1}{Γ (α)} | \int_{t_{0}}^{t_{2}^{*}} {(t_{2}^{*} - s)}^{α - 1} (g (s, u_{ω_{i}} (s))) Δ s \\ - \int_{t_{0}}^{t_{1}^{*}} {(t_{1}^{*} - s)}^{α - 1} (g (s, u_{ω_{i}} (s))) Δ s | \end{matrix}$

$\begin{matrix} \leq & \frac{1}{Γ (α)} [|\int_{t_{0}}^{t_{2}^{*}} {(t_{2}^{*} - s)}^{α - 1}| Δ s | (g (s, u_{ω_{i}} (s))) | \\ + |\int_{t_{0}}^{t_{1}^{*}} {(t_{1}^{*} - s)}^{α - 1} Δ s| | (g (s, u_{ω_{i}} (s))) |] \end{matrix}$

$\begin{matrix} \leq & \frac{S}{Γ (α)} [|\int_{t_{0}}^{t_{2}^{*}} {(t_{2}^{*} - s)}^{α - 1} Δ s | + | \int_{t_{0}}^{t_{1}^{*}} {(t_{1}^{*} - s)}^{α - 1} Δ s|] \end{matrix}$

$\begin{matrix} = & \frac{S}{Γ (α)} [|\int_{t_{0}}^{t_{1}^{*}} {(t_{2}^{*} - s)}^{α - 1} Δ s + \int_{t_{1}^{*}}^{t_{2}^{*}} {(t_{2}^{*} - s)}^{α - 1} Δ s | + | \int_{t_{0}}^{t_{1}^{*}} {(t_{1}^{*} - s)}^{α - 1} Δ s|] \end{matrix}$

$\begin{matrix} = & \frac{S}{Γ (α)} [|- [\frac{{(t_{2}^{*} - t_{1}^{*})}^{α}}{α} - \frac{{(t_{2}^{*} - t_{0})}^{α}}{α}] + \frac{{(t_{2}^{*} - t_{1}^{*})}^{q}}{α}| + |\frac{{(t_{1}^{*} - t_{0})}^{α}}{α}|] \end{matrix}$

$\begin{matrix} = & \frac{S}{Γ (α)} [|- \frac{{(t_{2}^{*} - t_{1}^{*})}^{α}}{α} + \frac{{(t_{2}^{*} - t_{0})}^{α}}{α} + \frac{{(t_{2}^{*} - t_{1}^{*})}^{α}}{α}| + |\frac{{(t_{1}^{*} - t_{0})}^{α}}{α}|] \end{matrix}$

$\begin{matrix} = & \frac{S}{Γ (α)} [|\frac{{(t_{2}^{*} - t_{0})}^{α}}{α}| + |\frac{{(t_{1}^{*} - t_{0})}^{α}}{α}|] \end{matrix}$

$\begin{matrix} = & \frac{S}{Γ (α + 1)} [{(t_{2}^{*} - t_{0})}^{α} + {(t_{1}^{*} - t_{0})}^{α}] \end{matrix}$

$\begin{matrix} \leq & \frac{2 S}{Γ (α + 1)} [{(t_{2}^{*} - t_{0})}^{α}] \end{matrix}$

A family of solutions ${u_{ω_{i}} (t^{*})}$ is said to be equicontinuous if given $ϵ > 0$ , we can find $δ > 0$ such that $| u_{ω_{i}} (t_{2}^{*}) - u_{ω_{i}} (t_{1}^{*}) | < ϵ$ whenever $| t_{2}^{*} - t_{1}^{*} | < δ$ .

implying that $| u_{ω_{i}} (t_{2}^{*}) - u_{ω_{i}} (t_{1}^{*}) | \leq \frac{2 S}{Γ (α + 1)} [{(t_{2}^{*} - t_{0})}^{α}] < ϵ$ provided $| t_{2}^{*} - t_{1}^{*} | < δ$

Now, we choose $δ = {(\frac{ϵ Γ (α + 1)}{2 S})}^{\frac{1}{α}}$ , ${(\frac{ϵ Γ (α + 1)}{2 S})}^{\frac{1}{α}} > {(\frac{2 S {(t_{2}^{*} - t_{0})}^{α}}{Γ (α + 1)} \times \frac{Γ (α + 1)}{2 S})}^{\frac{1}{α}} = (t_{2}^{*} - t_{0})$ but $(t_{2}^{*} - t_{0}) > | t_{2}^{*} - t_{1}^{*} |$ so since $(t_{2}^{*} - t_{0}) < δ$ , then $| t_{2}^{*} - t_{1}^{*} | < δ$ . Proving that the family of solutions ${u_{ω} (t^{*})}$ is equi-continuous. By the Arzela-Ascoli theorem, ${u_{ω_{i}} (t^{*})}$ has a sub-sequence ${u_{ω_{i_{j}}} (t^{*})}$ which converges uniformly to a function $z (t^{*})$ on $T$ . We then show that $z (t^{*})$ is a solution of (11). Equation (24) becomes

$u_{ω_{i_{j}}} (t^{*}) = u_{0} + ω_{i_{j}} + \frac{1}{Γ (α)} \int_{t_{0}}^{t^{*}} {(t^{*} - s)}^{α - 1} (g (s, u_{ω_{i_{j}}} (s)) + ω_{i_{j}}) Δ s$

(29)

Taking the limit as $i_{j} \to \infty$ , then $u_{ω_{i_{j}}} (t^{*}) \to z (t^{*})$ on $T$ . Now (29) yields

$z (t^{*}) = u_{0} + \frac{1}{Γ (α)} \int_{t_{0}}^{t^{*}} {(t^{*} - s)}^{α - 1} (g (s, z (t^{*}))) Δ s$

(30)

Thus, $z (t^{*})$ is a solution of (11) on $T$ . Since $lim_{j \to \infty} u_{ω_{i_{j}}} (t^{*}) = z (t)$ exists, then for any $u_{ω_{i}}$ that satisfies the dynamic equation (11), $u_{ω} (t^{*}) \leq z (t^{*})$ . So from (25), we have that $h (t^{*}) < u_{ω} (t^{*}) \leq z (t^{*})$ on $T$ .

Therefore by induction principle, the statement $S (t)$ is true, and this completes the proof

□

Theorem 3.

Assume the following conditions are satisfied:

1.: the function $V (t, x (t)) \in C_{r d} [T \times R^{N}, R_{+}]$ , $V (t, x (t))$ is locally Lipschitzian with respect to x, $V (t, 0) \equiv 0$ and the inequality

$ϕ (∥ x ∥) \leq V (t, x (t))$

(31)

holds for all $(t, x) \in T \times R$ and $ϕ \in K$
2.: $g \in C_{r d} [T \times R_{+}, R_{+}]$ is nondecreasing with respect to u at all $t \in T$ , $g (t, 0) \equiv 0$ , and

$^{C T} D_{+}^{α} V^{Δ} (t, x (t)) \leq g (t, V (t, x (t)))$
3.: the zero solution of the comparison equation (11) is stable.

Then the zero solution of the system (10) is stable.

Proof.

By condition (3) of Theorem 3, we have that the zero solution of (11) is stable, so let

ϵ > 0

be given, and for

ϕ (ϵ)

and

t_{0} \in T

, let there exists

λ = λ (t_{0}, ϵ) > 0

such that

z (t) < ϕ (ϵ) a t a l l t \geq t_{0}

(32)

whenever

u_{0} < λ

, where

z (t) = z (t, t_{0}, u_{0})

is the maximal solution of the comparison system (11).

Now,

V (t, 0) = 0

and

V \in C_{r d}

this implies that V is continuous at the origin, then given

λ > 0

, we can find a

δ = δ (t_{0}, λ) > 0

such that for

x_{0} \in R^{n}

, we have that,

∥ x_{0} ∥ < δ

implies

V (t_{0}, x_{0}) < λ

Claim that

∥ x_{0} ∥ < δ

implies

∥ x (t) ∥ < ϵ

at all

t \in T

where

x (t) = x (t, t_{0}, x_{0})

is any solution of the system (10). If this is not true, then there would exists a time

t_{1} \in T

t_{1} > t_{0}

such that the solution

x (t)

of the dynamic system (10) at the instant time

t_{1}

leaves the

ϵ - n e i g h b o r h o o d

of the zero solution. That is

∥ x (t) ∥ < ϵ

t_{0} \leq t < t_{1}

and

∥ x (t_{1}) ∥ \geq ϵ

(33)

but from Theorem 2, we have that

V (t, x (t)) \leq z (t), t_{0} \leq t \leq t_{1}

(34)

provided

V (t_{0}, x_{0}) \leq u_{0}

, where

z (t)

is maximal solution of the comparison system (11).

Combining (31),(32), (34), and (33) for

t = t_{1}

we obtain

ϕ (∥ x (t_{1}) ∥) \leq V (t_{1}, x (t_{1})) \leq z (t_{1}) < ϕ (ϵ) \leq ϕ (∥ x (t_{1})) ∥

\Rightarrow ϕ (∥ x (t_{1}) ∥) < ϕ (∥ x (t_{1})) ∥

(35)

The contradiction (35) shows that

t_{1} \notin T

and therefore

∥ x (t) ∥ < ϵ

at all

t \in T

whenever

∥ x_{0} ∥ < δ

and such the zero solution (10) is stable. □

5. Application

Consider the system of dynamic equations

\begin{matrix} \begin{matrix} x_{1}^{Δ} (t) & = & x_{1} {sec}^{2} t - {tan}^{2} t (x_{2} + x_{1}) + x_{2} {cot}^{2} t \\ x_{2}^{Δ} (t) & = & 2 (x_{1} - x_{2}) + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t \end{matrix} \end{matrix}

(36)

for

t \geq t_{0}

, with initial conditions

x_{1} (t_{0}) = x_{10} a n d x_{2} (t_{0}) = x_{20}

where

x_{1}, x_{2} \in R^{2}

f = (f_{1}, f_{2})

Consider

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

, for

t \in T

and

x_{1}, x_{2} \in R^{2}

, where

x \in S (ρ)

ρ > 0

. Then we compute the dini derivative for

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

as follows from (3) we have that

\begin{matrix} D^{+} V^{Δ} (t, x) = \underset{μ (t) \to 0}{lim sup} \frac{V (t + μ (t), x + μ (t) f (t, x)) - V (t, x)}{μ (t)} \end{matrix}

\begin{matrix} = \underset{μ (t) \to 0}{lim sup} \frac{| x_{1} + μ (t) f_{1} (t, x) | + | x_{2} + μ (t) f_{2} (t, x) | - [| x_{1} | + | x_{2} |]}{μ (t)} \end{matrix}

\begin{matrix} \leq \underset{μ (t) \to 0}{lim sup} \frac{| x_{1} | + | μ (t) f_{1} (t, x) | + | x_{2} | + | μ (t) f_{2} (t, x) | - | x_{1} | - | x_{2} |}{μ (t)} \end{matrix}

\begin{matrix} = \underset{μ (t) \to 0}{lim sup} \frac{| μ (t) f_{1} (t, x) | + | μ (t) f_{2} (t, x) |}{μ (t)} \end{matrix}

\begin{matrix} = \underset{μ (t) \to 0}{lim sup} \frac{μ (t) [| f_{1} (t, x) | + | f_{2} (t, x) |]}{μ (t)} \end{matrix}

\begin{matrix} \leq | f_{1} (t, x) | + | f_{2} (t, x) | \end{matrix}

\begin{matrix} = | x_{1} {sec}^{2} t - {tan}^{2} t (x_{2} + x_{1}) + x_{2} {cot}^{2} t | + | 2 (x_{1} - x_{2}) + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t | \end{matrix}

\begin{matrix} = | x_{1} {sec}^{2} t - x_{2} {tan}^{2} t - x_{1} {tan}^{2} t + x_{2} {cot}^{2} t | + | 2 x_{1} - 2 x_{2} + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t | \end{matrix}

\begin{matrix} = | x_{1} ({sec}^{2} t - {tan}^{2} t) - x_{2} ({tan}^{2} t - {cot}^{2} t) | + | 2 x_{1} (1 - {cos}^{2} t) - x_{2} (2 - {cosh}^{2} t) | \end{matrix}

\begin{matrix} = |x_{1} (\frac{1}{{cos}^{2} t} - \frac{{sin}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{2} t}{{cos}^{2} t} - \frac{{cos}^{2} t}{{sin}^{2} t})| + |2 x_{1} ({sin}^{2} t) - x_{2} (2 - \frac{1}{{cos}^{2} t})| \end{matrix}

\begin{matrix} \leq |x_{1} (\frac{1 - {sin}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{4} t - {cos}^{4} t}{{cos}^{2} t {sin}^{2} t})| + | 2 x_{1} | | {sin}^{2} t | + | x_{2} | (| 2 | + |\frac{1}{{cos}^{2} t}|) \end{matrix}

\begin{matrix} \leq |x_{1} (\frac{{cos}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{2} t - {cos}^{2} t) ({sin}^{2} t + {cos}^{2} t)}{{cos}^{2} t {sin}^{2} t})| + 2 | x_{1} | + 3 | x_{2} | \end{matrix}

\begin{matrix} \leq | x_{1} | + | x_{2} | | (\frac{{sin}^{2} t - {cos}^{2} t}{{cos}^{2} t {sin}^{2} t}) | + 2 | x_{1} | + 3 | x_{2} | \end{matrix}

\begin{matrix} = | x_{1} | + | x_{2} | | (\frac{1}{{cos}^{2} t} - \frac{1}{{sin}^{2} t}) | + 2 | x_{1} | + 3 | x_{2} | \end{matrix}

\begin{matrix} \leq 3 | x_{1} | + | x_{2} | (| \frac{1}{{cos}^{2} t} | + | \frac{1}{{sin}^{2} t} |) + 3 | x_{2} | \end{matrix}

\begin{matrix} \leq 3 | x_{1} | + 5 | x_{2} | \leq 5 [| x_{1} | + | x_{2} |] \end{matrix}

D^{+} V^{Δ} (t, x) \leq 5 V (t, x_{1}, x_{2}) = g (t, V)

Now consider the consider the comparison equation

D^{+} u^{Δ} = 5 u > 0, u (0) = u_{0}

(37)

with solution

u (t) = u_{0} e^{5 t}

(38)

Even though conditions (i)-(iii) of [18] are satisfied that is

V \in C_{r d} [T \times R^{n}, R_{+}]

D^{+} V^{Δ} (t, x_{1}, x_{2}) \leq g (t, V (t, x))

and

\sqrt{x_{1}^{2} + x_{2}^{2}} \leq | x_{1} | + | x_{2} | \leq 2 (x_{1}^{2} + x_{2}^{2})

, for

b (∥ x ∥) = r

and

a (∥ x ∥) = 2 r^{2}

, it is obvious to see that the solution (38)of the comparison system (37) is not stable, so we can not deduce the stability properties of the system (36) by applying the basic definition of the Dini-derivative of a Lyapunov function of dynamic equation on time scale to the Lyapunov function

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

Now, we will apply our new definition on the same system but as a Caputo fractional dynamic system

\begin{matrix} \begin{matrix} ^{C T} D^{α} x_{1}^{Δ} (t) & = & x_{1} {sec}^{2} t - {tan}^{2} t (x_{2} + x_{1}) + x_{2} {cot}^{2} t \\ ^{C T} D^{α} x_{2}^{Δ} (t) & = & 2 (x_{1} - x_{2}) + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t \end{matrix} \end{matrix}

(39)

for

t \geq t_{0}

, with initial conditions

x_{1} (t_{0}) = x_{10} a n d x_{2} (t_{0}) = x_{20}

where

x_{1}, x_{2} \in R^{2}

f = (f_{1}, f_{2})

Consider

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

, for

t \in T

and

x_{1}, x_{2} \in R^{2}

, where

x \in S (ρ)

ρ > 0

. Then condition 1 of Theorem (3) is satisfied, for

ϕ = \frac{1}{2} r

, where

ϕ \in K

with

x = (x_{1}, x_{2}) \in R^{2}

, so that the associated norm

∥ x ∥ = \sqrt{x_{1}^{2} + x_{2}^{2}}

Since

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

then

ϕ (∥ x ∥) \leq V (t, x_{1}, x_{2})

. From (12), we compute the Caputo fractional Dini derivative for

V (t, x_{1}, x_{2}) = | x_{1} | + | x_{2} |

as follows

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t, x) \\ = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {V (σ (t), x (σ (t)) - V (t_{0}, x_{0}) \\ - \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r + 1} (^{α} C_{r}) [V (σ (t) - r μ, x (σ (t)) - μ^{α} f (t, x (t))) - V (t_{0}, x_{0})]} \end{matrix}

\begin{matrix} = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {(| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) - (| x_{10} | + | x_{20} |) + \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) \\ [| x_{1} (σ (t)) - μ^{α} f_{1} (t, x_{1}) | + | x_{2} (σ (t)) - μ^{α} f_{2} (t, x_{2}) | - (| x_{10} | + | x_{10} |)]} \end{matrix}

\begin{matrix} \leq \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {(| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) - (| x_{10} | + | x_{20} |) + \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) \\ [| x_{1} (σ (t)) | + | μ^{α} f_{1} (t; x_{1}) | + | x_{2} (σ (t)) | + | μ^{α} f_{2} (t; x_{2}) | - (| x_{10} | + | x_{10} |)]} \end{matrix}

\begin{matrix} \leq \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {(| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) - (| x_{10} | + | x_{20} |) \\ + \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{1} (σ (t)) | + | x_{2} (σ (t)) |] \\ + \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) | [| μ^{α} f_{1} (t; x_{1}) | + | μ^{α} f_{2} (t; x_{2}) |] \\ - \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{10} | + | x_{10} |]} \end{matrix}

\begin{matrix} = \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} {(| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) + \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{1} (σ (t)) | + | x_{2} (σ (t)) |] \\ - (| x_{10} | + | x_{20} |) - \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{10} | + | x_{10} |] \\ + μ^{α} \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) | [| f_{1} (t; x_{1}) | + | f_{2} (t; x_{2}) |]} \end{matrix}

\begin{matrix} \leq \underset{μ \to 0^{+}}{lim sup} \frac{1}{μ^{α}} \{\sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{1} (σ (t)) | + | x_{2} (σ (t)) |] - \sum_{r = 0}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) [| x_{10} | + | x_{10} |]\} \\ + \underset{μ \to 0^{+}}{lim sup} \sum_{r = 1}^{[\frac{t - t_{0}}{μ}]} {(- 1)}^{r} (^{α} C_{r}) | [| f_{1} (t; x_{1}) | + | f_{2} (t; x_{2}) |] \end{matrix}

Applying (15) and (17) we have

\begin{matrix} = \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} (| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) - \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} (| x_{10} | + | x_{10} |) - [| f_{1} (t; x_{1}) | + | f_{2} (t; x_{2}) |] \end{matrix}

\begin{matrix} \leq \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} (| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) - [| f_{1} (t; x_{1}) | + | f_{2} (t; x_{2}) |] \end{matrix}

t \to \infty, \frac{{(t - t_{0})}^{- α}}{Γ (1 - α)} (| x_{1} (σ (t)) | + | x_{2} (σ (t)) |) \to 0

, then

\begin{matrix} ^{C T} D_{+}^{α} V^{Δ} (t; x_{1}, x_{2}) \leq - [| f_{1} (t; x_{1}) | + | f_{2} (t; x_{2}) |] \end{matrix}

\begin{matrix} = - [| x_{1} {sec}^{2} t - {tan}^{2} t (x_{2} + x_{1}) + x_{2} {cot}^{2} t | + | 2 (x_{1} - x_{2}) + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t |] \end{matrix}

\begin{matrix} = - [| x_{1} {sec}^{2} t - x_{2} {tan}^{2} t - x_{1} {tan}^{2} t + x_{2} {cot}^{2} t | + | 2 x_{1} - 2 x_{2} + x_{2} {cosh}^{2} t - 2 x_{1} {cos}^{2} t |] \end{matrix}

\begin{matrix} = - [| x_{1} ({sec}^{2} t - {tan}^{2} t) - x_{2} ({tan}^{2} t - {cot}^{2} t) | + | 2 x_{1} (1 - {cos}^{2} t) - x_{2} (2 - {cosh}^{2} t) |] \end{matrix}

\begin{matrix} = - [|x_{1} (\frac{1}{{cos}^{2} t} - \frac{{sin}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{2} t}{{cos}^{2} t} - \frac{{cos}^{2} t}{{sin}^{2} t})| + |2 x_{1} ({sin}^{2} t) - x_{2} (2 - \frac{1}{{cos}^{2} t})|] \end{matrix}

\begin{matrix} \leq - [|x_{1} (\frac{1 - {sin}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{4} t - {cos}^{4} t}{{cos}^{2} t {sin}^{2} t})| + | 2 x_{1} | | {sin}^{2} t | + | x_{2} | (| 2 | + |\frac{1}{{cos}^{2} t}|)] \end{matrix}

\begin{matrix} \leq - [|x_{1} (\frac{{cos}^{2} t}{{cos}^{2} t}) - x_{2} (\frac{{sin}^{2} t - {cos}^{2} t) ({sin}^{2} t + {cos}^{2} t)}{{cos}^{2} t {sin}^{2} t})| + 2 | x_{1} | + 3 | x_{2} |] \end{matrix}

\begin{matrix} \leq - [| x_{1} | + | x_{2} | | (\frac{{sin}^{2} t - {cos}^{2} t}{{cos}^{2} t {sin}^{2} t}) | + 2 | x_{1} | + 3 | x_{2} |] \end{matrix}

\begin{matrix} = - [| x_{1} | + | x_{2} | | (\frac{1}{{cos}^{2} t} - \frac{1}{{sin}^{2} t}) | + 2 | x_{1} | + 3 | x_{2} |] \end{matrix}

\begin{matrix} \leq - [3 | x_{1} | + | x_{2} | (| \frac{1}{{cos}^{2} t} | + | \frac{1}{{sin}^{2} t} |) + 3 | x_{2} |] \end{matrix}

\begin{matrix} \leq - 3 | x_{1} | - 5 | x_{2} | \leq - 3 [| x_{1} | + | x_{2} |] \end{matrix}

Therefore

^{C T} D_{+}^{α} V^{Δ} (t; x_{1}, x_{2}) \leq - 3 V (t, x_{1}, x_{2})

(40)

Consider the comparison system

^{C T} D_{+}^{α} u^{Δ} = g (t, u) \leq - 3 u

(41)

using the Laplace transform method

^{C T} D_{+}^{α} 3 u^{Δ} + u = 0

\begin{matrix} L {^{C T} D_{+}^{α} u^{Δ}} + 3 L {u} = 0 \\ \Rightarrow & S^{α} U (s) - S^{α - 1} u_{0} + 3 U (s) = 0 \\ U (s) (s^{α} + 3) = u_{0} S^{α - 1} U (s) = \frac{u_{0} S^{α - 1}}{S^{α} + 3} \end{matrix}

taking the inverse Laplace transform we have

u (t) = u_{0} L^{- 1} \{\frac{S^{α - 1}}{S^{α} + 3}\}

(42)

Recall that

L^{- 1} \{\frac{S^{α - β}}{S^{α} - λ}\} = t^{β - 1} E_{α, β} (λ t^{α})

(43)

Comparing (43) and (42), we have

q - β

\Rightarrow β = 1

S^{α} - λ = S^{α} + 3

\Rightarrow λ = - 3

so we have,

\begin{matrix} u (t) = u_{0} E_{α, 1} (- 3 t^{α}), f o r α \in (0, 1), \end{matrix}

(44)

where

E_{α} (z)

is the Mittag-Leffler functions of one-varriable which can be approximated as:

E_{α, 1} (- t^{α}) = \sum_{n = 0}^{\infty} {(- 1)}^{n} \frac{t^{n α}}{Γ (α k + 1)} = 1 - \frac{t^{α}}{Γ (1 + α)} + . . . \approx exp [- \frac{t^{α}}{Γ (1 + α)}]

Now, let

| u_{0} | < δ

, then from (44), we have

| u (t) | = | 3 u_{0} E_{α, 1} (- t^{α}) | = |3 u_{0} exp [- \frac{t^{α}}{Γ (1 + α)}]| < 3 |exp [- \frac{t^{α}}{Γ (1 + α)}]| δ < ϵ

whenever

| u_{0} < δ = \frac{ϵ}{3 |exp [- \frac{t^{α}}{Γ (1 + α)}]|}

Therefore given

ϵ > 0

, we can find a

δ > 0

such that

| u (t) | < ϵ

whenever

| u_{0} | < δ

Since all the conditions of Theorem 3 are satisfied, and trivial solution of the comparison system (41) is stable, then we conclude that the trivial solution of system (39) is stable.

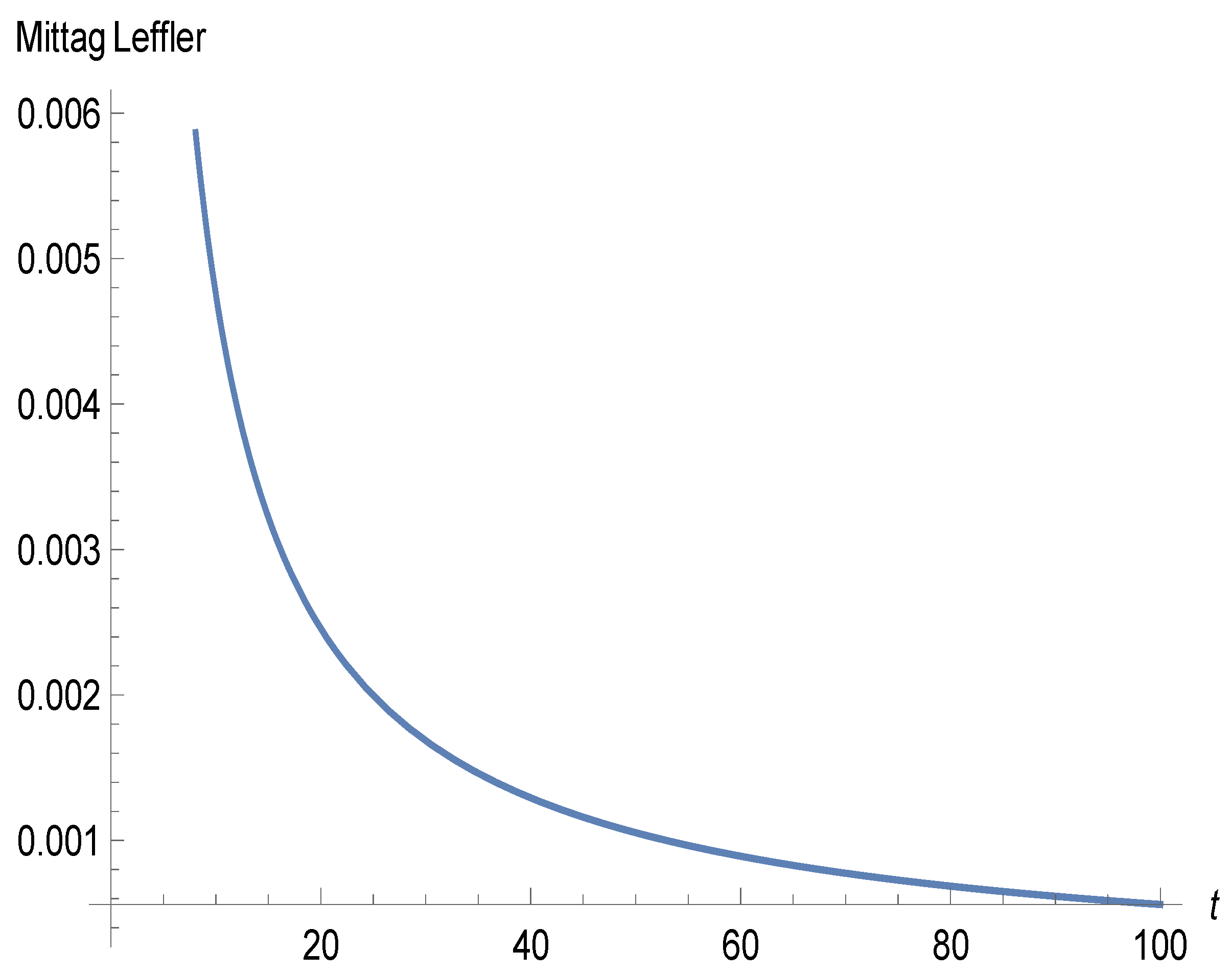
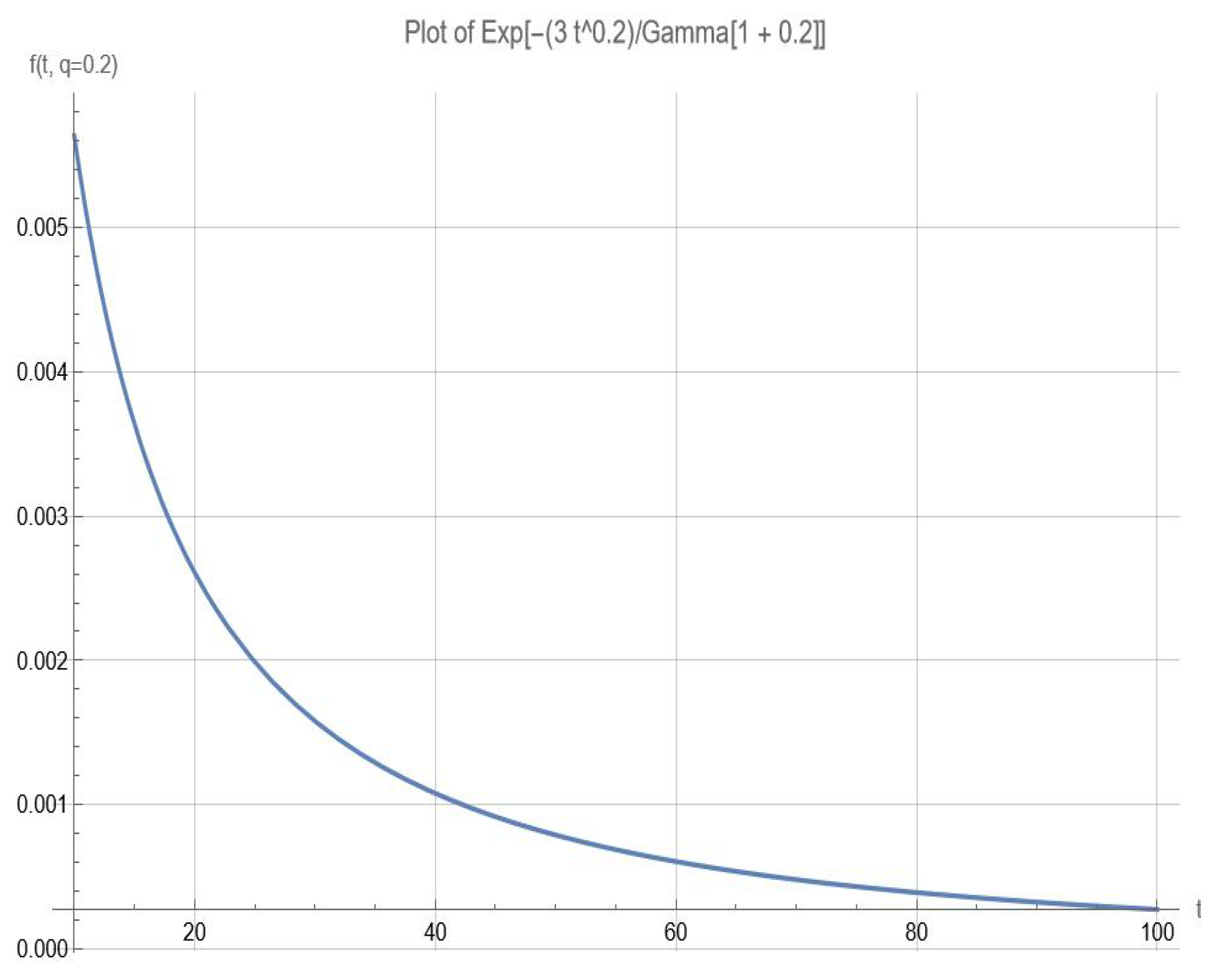
Figure 1 below is the graphical representation of

E_{α, 1} (- 3 t^{α})

which was then approximated in Figure 2 as

exp [- \frac{t^{α}}{Γ (1 + α)}]

and the behaviour of the curve shows stability over time.

6. Conclusion

In conclusion, our study significantly advances the understanding of Lyapunov stability for Caputo fractional dynamic equations on time scale. The new concept developed in this work successfully contributes to the advancement of the Fractional Calculus in general and stability theory in particular from a continuous domain to a unified continuous and discrete domain which is a breakthrough for modeling and other practical application. Through the establishment of a comparison results and stability criteria, we have provided a solid theoretical foundation for analyzing the stability properties of these equations across different time scales. The inclusion of an application further showcases the applicability and effectiveness of our results over existing results in integer order and continuous domain.

Author Contributions

M.P.I. made conceptualization, methodology and writing draft preparation. E.P.A. performed supervision and editing. H.A.N. made investigation, review and validation. All authors read and approved the final version.

Funding

This work does not receive any external funding.

Institutional Review Board Statement

This article does not contain any studies with human participants or animals performed by any of the authors.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

Agarwal, Ravi, Donal O’Regan, and Snezhana Hristova, Stability of Caputo fractional differential equations by Lyapunov functions, Applications of Mathematics, 60, (2015): 653–676.
Agarwal, Ravi, Snezhana Hristova, and Donal O’Regan. Applications of Lyapunov functions to Caputo fractional differential equations, Mathematics 6, no. 11 (2018): 229.
Agarwal, Ravi P., Snezhana Hristova, and Donal O’Regan. Lyapunov Functions and Stability Properties of Fractional Cohen–Grossberg Neural Networks Models with Delays, Fractal and Fractional 7, no. 10 (2023): 732.
Agarwal, Ravi, Donal O’Regan, S. Hristova, and Muhammed Cicek. Practical stability with respect to initial time difference for Caputo fractional differential equations,Communications in Nonlinear Science and Numerical Simulation, 42 (2017): 106-120.
Agarwal, Ravi, Snezhana Hristova, and Donal O’Regan. Lyapunov functions and strict stability of Caputo fractional differential equations, Advances in Difference Equations 2015, (2015): 1-20.
Agarwal, Ravi P., Donal O’Regan, and Snezhana Hristova. Stability with initial time difference of Caputo fractional differential equations by Lyapunov functions, Zeitschrift für Analysis und ihre Anwendungen 36, no. 1 (2017): 49-77.
Agarwal, Ravi, Martin Bohner, Donal o’Regan, and Allan Peterson. Dynamic equations on time scales: a survey, Journal of Computational and Applied Mathematics, 141, No. 1-2 (2002): 1–26.
Ahmadkhanlu, A., & Jahanshahi, M., On the existence and uniqueness of solution of initial value problem for fractional order differential equations on time scales, Bulletin of the Iranian Mathematical Society, 38 No 1 (2012), 241–252.
Bastos, Nuno RO, Fractional calculus on time scales. arXiv preprint arXiv:1202.2960 2012 (2012).
Bhatia, Nam P., and George P. Szegö, Dynamical systems: stability theory and applications, Vol. 35. Springer, 2006, (2006).
Bohner, Martin, and Allan Peterson, Dynamic equations on time scales: An introduction with applications, Springer Science & Business Media, 2001, (2001).
Čermák, Jan, Tomáš Kisela, and Luděk Nechvátal, Stability and asymptotic properties of a linear fractional difference equation, Advances in Difference Equations, 2012, (2012): 1-14.
Georgiev, S. G. Fractional dynamic calculus and fractional dynamic equations on time scales Vol. 196. Berlin: Springer. 2018, (2018).
Gusein Sh. Guseinov, Integration on time scales, Journal of Mathematical Analysis and Applications, 285, No 1, 2003, 107-127,.
Hilger, S. Analysis on Measure Chains — A Unified Approach to Continuous and Discrete Calculus, Results, Math. 18, 18–56 (1990). [CrossRef]
Hoffacker, Joan, and Christopher C. Tisdell. Stability and instability for dynamic equations on time scales, Computers & Mathematics with Applications 49, No. 9-10 (2005): 1327–1334.
Igobi, D.K and Ineh, M.P. Results On Existence and Uniqueness Of Solutions of Dynamic Equations on Time Scale via Generalized Ordinary Differential, International Journal of Applied Mathematics 37, No. 1 (2024): 1-20.
Kaymakçalan, Billur. Lyapunov stability theory for dynamic systems on time scales, International Journal of Stochastic Analysis No. 5, (1992): 275-281.
Kaymakcalan, B. I. L. L. U. R. Existence and comparison results for dynamic systems on a time scale, Journal of mathematical analysis and applications, 172, No. 1 (1993): 243-255.
Koksal, Mehmet Emir. Stability analysis of fractional differential equations with unknown parameters, arXiv preprint arXiv:1709.05402, (2017).
Kuehn, Christian, Multiple time scale dynamics, Vol. 191. Switzerland: Springer International Publishing, 2015 (2015).
Kumar, V. & Malik, M. Existence, stability and controllability results of fractional dynamic system on time scales with application to population dynamics, International Journal of Nonlinear Sciences and Numerical Simulation, 22, No 6 (2021), 741–766.
Lakshmikantham, Vangipuram, Seenith Sivasundaram, and Billur Kaymakçalan, Dynamic systems on measure chains, Vol.370. Springer Science & Business Media, 2013 (2013).
Laledj, Nadjet, Abdelkrim Salim, Jamal Eddine Lazreg, Saïd Abbas, Bashir Ahmad, and Mouffak Benchohra. On implicit fractional q-difference equations: Analysis and stability, Mathematical Methods in the Applied Sciences, 45, no. 17 (2022): 10775-10797.
Liu, Xiang, Baoguo Jia, Lynn Erbe, and Allan Peterson. Stability analysis for a class of nabla (q,h)-fractional difference equations, Turkish Journal of Mathematics, 43, no. 2 (2019): 664-687.
Martynyuk, Anatoly A. Stability theory for dynamic equations on time scales, Basel, Switzerland: Springer International Publishing, 2016.
Mekhalfi, Kheira, and Delfim FM Torres, Generalized fractional operators on time scales with application to dynamic equations, The European Physical Journal Special Topics, 226, no. 16 (2017): 3489–3499.
Miller, Kenneth S., and Bertram Ross. An introduction to the fractional calculus and fractional differential equations. John Wiley& Sons INC, 1993, (1993).
Rashid, S., Aslam Noor, M., Nisar, K. S., Baleanu, D., & Rahman, G., A new dynamic scheme via fractional operators on time scale, Frontiers in Physics, No 8, (2020), 165.
Sadati, S. J., R. Ghaderi, and N. Ranjbar. "Some fractional comparison results and stability theorem for fractional time delay systems." Romanian Reports in Physics 65, no. 1 (2013): 94-102.
Segi Rahmat, Mohamad Rafi, and Mohd Salmi Md Noorani, Caputo type fractional difference operator and its application on discrete time scales, Advances in Difference Equations 2015 (2015): 1–15.

Figure 1. Graph of

E_{α, 1} (- 3 t^{α})

against t

Figure 1. Graph of

E_{α, 1} (- 3 t^{α})

against t

Figure 2. Graph of

exp [- \frac{3 t^{α}}{Γ (1 + α)}]

against t

Figure 2. Graph of

exp [- \frac{3 t^{α}}{Γ (1 + α)}]

against t

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Lyapunov Stability of Caputo Fractional Dynamic Equations on Time Scale using a New Generalized Derivative

Abstract

1. Introduction

2. Preliminaries, Definitions and Notations

3. Statement Of Problem

4. Inequalities on Fractional Dynamic Equations on Time scale and Comparison results

5. Application

6. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe