1. Introduction
The domain of online retailing has witnessed consistent expansion in recent years, with a pronounced upsurge in e-commerce activity during the COVID-19 pandemic. In the United States, online sales experienced a median growth of 14.2% in the half-decade preceding the pandemic, only to see a substantial leap to a 50.5% increase in 2021 from 2019 levels [
1]. Globally, e-commerce sales soared by 25.7% in 2020, amassing a record total of 4.213 trillion dollars, off the back of a 20.5% growth rate in 2019 [
2].
Within this burgeoning landscape, two principal selling channels have emerged: agency selling and reselling. The agency model positions the online platform as a marketplace, facilitating direct sales from upstream firms to consumers in exchange for commissions. In contrast, the reselling model sees the platform act as a traditional intermediary, purchasing products from upstream firms and then reselling to end consumers. Notable examples of platforms adopting dual-channel strategies include Amazon.com, which began as a book reseller, and JD.com, which started as an online retailer. Meanwhile, platforms like Taobao.com and Tmall.com remain purely marketplaces, focusing solely on agency sales. Conversely, Zappos.com and VIP.com have established themselves as pure resellers in their respective markets.
Despite these advances, the proliferation of counterfeit products poses a significant threat to brand reputation and consumer confidence. Even with concerted efforts to combat these issues, the presence of counterfeits on online platforms remains a considerable challenge [
3][
4].
Blockchain technology offers a beacon of hope in this context, with its potential to revolutionize supply chain management and enhance transaction transparency. As a distributed ledger technology, blockchain records transactions across a network of nodes, ensuring stability and real-time transparency through its tamper-resistant consensus algorithms [
5]. The technology’s strengths—transparency, traceability, irreversibility, cost-efficiency, speed, and reduced risk—are particularly advantageous in verifying the authenticity of products and preventing counterfeiting [
6].
JD.com’s blockchain traceability solution, Zhiyi, exemplifies this potential, having amassed 1.3 billion data entries and managing over 60,000 products across more than 700 brands [
7]. Similarly, luxury and fresh produce sectors have increasingly turned to blockchain to assure consumers of product authenticity [
8]. Projections indicate that blockchain adoption will become widespread, with an estimated 25% of the top 2,000 global enterprises, and 20% in China, expected to integrate the technology into their operations, according to IDC China [
8].
By integrating such innovative technologies, online retail platforms are not only enhancing their operational efficiency but also contributing to sustainable e-commerce practices. This shift towards transparency and authenticity aligns with the broader goals of sustainable development, ensuring that e-commerce growth is not only rapid but also responsible and trustworthy.
Inspired by empirical observations and anecdotal evidence, this study seeks to shed light on the interplay between blockchain technology and online retail platform channel structures. To be specific, the research questions are examined as follows:
When should the manufacturer participate in the blockchain, and how does the channel structure affect the participation decision?
What are the implications of blockchain technology on channel structures (i.e., the agency channel, the reselling channel, and the dual-channel) choice of the platforms?
How do the blockchain technology participation decision and channel structure choice depend on factors (i.e., the consumer’s belief in the reselling channel, the commission fee in the agency channel, and the substitutability between channels)?
To address these questions, we have constructed a game theory model that encompasses a manufacturer (he), an online retail platform (she), and a representative consumer (it). The manufacturer sells products through the platform, which may operate an agency channel, a reselling channel, or both. We acknowledge that products in the reselling channel typically face brand dilution due to counterfeits, an issue that blockchain can mitigate. Accordingly, we postulate that products in the agency channel are perceived more favorably than those in the reselling channel when the manufacturer remains outside the blockchain framework. This valuation advantage dissipates once the manufacturer adopts blockchain.
Our analysis yields several compelling findings. Notably, in an agency channel setup, manufacturers are disinclined to adopt blockchain. However, in reselling and dual-channel scenarios, low blockchain costs can incentivize participation. The decision to engage with blockchain is a balance between the technology’s quality assurance benefits and its associated costs. The reselling channel, in particular, prompts greater blockchain participation due to the heightened consumer trust it fosters, despite increased channel competition.
Secondly, the manufacturer’s blockchain adoption and the platform’s channel strategy are shown to be mutually reinforcing. This relationship indicates that when a manufacturer participates in blockchain within the reselling channel, it expands the strategic options available to the reselling channel structure. The rationale is straightforward: blockchain participation in the reselling channel boosts sales volume, prompting the platform to increase the wholesale price, thus capturing additional profits.
In a dual-channel context, while the manufacturer’s blockchain engagement may escalate competition and diminish profits from the agency channel, the benefits accruing from the reselling channel outweigh these losses.
Thirdly, a manufacturer is more likely to embrace blockchain when consumer confidence in the reselling channel is low. Under such circumstances, blockchain’s quality assurance attributes are more pronounced, and the reduced substitutability between channels alleviates market competition, benefiting the manufacturer. Additionally, blockchain participation results in a lower commission-sharing rate for the agency channel, allowing the manufacturer to optimize profit distribution across channels.
Conversely, the platform is inclined toward the reselling channel when consumer trust in it is lacking, as the quality assurance from blockchain cannot be replicated. Increased channel substitutability, in this case, diminishes the appeal of the dual-channel approach due to heightened competitive pressures. Moreover, a reduced agency income-sharing rate detracts from the attractiveness of the agency channel model.
The rest of this study is organized as follows. In section 2, we briefly summarize the related literature and highlight the contribution to the existing literature. In section 3, we describe our game theory model in detail. In section 4, we derive and analyze the equilibrium wholesale and retail price decisions (short-term decisions). In section 5, we derive and analyze the optimal channel structure and blockchain participation decisions (long-term decisions). In section 6, we summarize the insights drawn from the analysis and suggest areas for future research. We present the proofs and technical details of all the main results in the appendix.
2. Related Literature
This study investigates the effect of blockchain technology on channel structure. Accordingly, there are two related streams of literature: blockchain technology in supply chain management and channel structure (i.e., agency channel and reselling channel) in online retail platforms.
The existing literature on blockchain technology has primarily studied why, when, and how to apply this emerging technology in operations management. Babich and Hilary [
9] and Olsen and Tomlin [
10] comprehensively describe the operations management implications of blockchain technology. Hastig and Sodhi [
11] guide operations management on when and how to implement blockchain-based supply chain traceability systems. To address the counterfeiting problem specifically, Pun et al. [
12] examine the effectiveness of blockchain as a solution. They demonstrate that blockchain should be employed when the quality of the counterfeit is intermediate. However, Shen et al. [
13] suggest that brand name companies may reduce product quality when using blockchain, despite the technology’s potential to reveal product authenticity and mitigate counterfeiting issues. Tan [
14] proposes that implementing a blockchain-based marketplace for pre-owned virtual goods allows developers to adjust prices more strategically, benefiting both developers and consumers. Wang et al. [
15] tackle the issue of distrust in shared data between supply chain partners by designing a blockchain-based data sharing marketplace, aiming to overcome barriers in data sharing. Cong and He [
16] analyze the correlation between decentralized blockchain technology and consensus quality, and its impact on supply chain competition, finding that blockchain-based smart contracts can mitigate asymmetric information while potentially encouraging collusion. Wei et al. [
17] and Chen and Chen [
18] introduce new perspectives on blockchain’s role in supply chain management. Wei et al. [
17] construct an evolutionary game model based on prospect theory to study the tripartite relationship between government, manufacturers, and retailers within the context of blockchain-based data governance for manufacturing supply chains. They highlight the importance of government incentives in fostering data governance and sustainable development. Chen and Chen [
18] apply Stackelberg game theory to compare optimal operational strategies across different supply chain finance scenarios, emphasizing the impact of blockchain on reducing interest rate thresholds and its preference over traditional financing methods. Abbas and Myeong [
19] contribute to the literature by conducting a systematic literature review on the role of blockchain in promoting sustainability and circularity across large-scale industries. Their study provides an in-depth discussion of blockchain demand, implementation gaps, and the contribution of various blockchain platforms to sustainability, offering a comprehensive overview of the practical implications of blockchain in large-scale industries.
The literature on channel structure in online retail platforms has significantly expanded with recent studies addressing the complexities of agency versus reselling formats. Mantin et al. [
20] suggest that introducing the agency channel alongside the reselling channel increases the retailer’s bargaining power in negotiations with the manufacturer. Hagiu and Wright [
21] investigate the preferences of both suppliers and retailers for agency and reselling channels, illustrating that these preferences depend on the information advantage of the supplier and retailer. Abhishek et al. [
22] extend the literature by considering retailer competition, finding that the retailer’s channel structure decision depends on the effect of sales in the electronic channel on the conventional channel. This preference can be mediated by retailer competition. Kwark et al. [
23] consider the role of third-party information (e.g., product reviews) in upstream pricing schemes. They confirm that the retailer prefers the reselling format for increased upstream competition, as product quality information homogenizes consumers’ perceived utility differences. Conversely, the retailer prefers the agency format for decreased upstream competition, aligning with the heterogeneous consumer’s estimated fit for the products. Geng et al. [
24] explore the interaction between the supplier’s add-on strategy and the retailer’s distribution contract choice. Their results reveal that the supplier prefers bundling the core product with the add-on product under the wholesale contract, while preferring to separate the add-on product from the core product under the agency contract. Tian et al. [
25] consider the upstream competition between suppliers and the order-fulfillment cost in the retailer’s channel structure decision, suggesting that the trade-off between the reselling mode and the agency mode is between the responsibility for order fulfillment and pricing rights. Jerath and Zhang [
26] demonstrate that the key benefit of the agency channel is channel coordination, where the retailer gives autonomy to the supplier in its retail space. Ha et al. [
27] study the effect of the platform’s demand enhancement service on channel structure choice, indicating that the flexibility of sales shifts between agency and reselling channels can increase the platform’s incentive for promotion. Hu et al. [
28] extend the literature by considering retail pass-through behavior, confirming that the trade-off between the agency and reselling channels is between channel efficiency and the intensity of supplier competition. Li et al. [
29] explore optimal strategies for platform channel configuration and slotting fee contracts, considering competition and quality investment. They indicate that a dual-channel structure contributes to sustainable operations by increasing selling prices, sales volumes, and consumer willingness, especially when channel introduction costs are low. Fu et al. [
30] examine the channel preferences of a platform and a green manufacturer in an online market, concluding that the manufacturer’s channel choice is influenced by the interaction of green investment, commission rate, and competition intensity. Meanwhile, the online platform prefers a hybrid channel under moderate commission rates and green investment inefficiencies. Zhang et al. [
31] utilize a game theory model to assess the impact of adding an offline channel to online recovery platforms, revealing that a dual-channel structure can always yield more profit for the platform and allow for lower recovery prices, despite potentially lower recovery quantities due to high shipping costs.
The most relevant paper, which requires special mention, is by Jiang and Chen [
32]. They also study the use of blockchain technology to eradicate product counterfeiting in e-commerce platforms. However, they compare the profits of all agents in traditional and blockchain-supported supply chains to measure the actual benefits of blockchain technology, while our paper emphasizes the strategic role of online retail platforms in designing channel structures (agency, reselling, or dual-channel) to encourage or discourage blockchain participation by manufacturers. A key contribution of our study is the insight that the platform can use the channel structure to strategically influence blockchain adoption and that there is a complementarity between blockchain participation and channel structure.
3. Model Setup
The research questions of interest include: (1) Given the platform’s channel structure, when should the manufacturer participate in the blockchain? (2) What is the optimal channel structure for the platform? Is it beneficial for the platform to induce the manufacturer to encroach on the market (choose the dual-channel structure)? The answers to these questions depend on consumer trust in the reselling channel, the substitutability between channels, and the commission fee in the agency channel. Thus, we first describe the model in this section and answer the questions in
Section 5.
We study a stylized supply chain comprising of a manufacturer (he, denoted as
M), who sells through an online retail platform (she, denoted as
P). The platform operates an agency channel and/or a reselling channel. Thus, there are three possible channel structures, including the agency channel (denoted as
A), the reselling channel (denoted as
R), and the dual channel (denoted as
D). To be specific, under the agency channel structure, the manufacturer directly sells his product to end consumers. He charges an agency price
for the product and pays the platform a unit commission fee
. We assume that the commission fee is proportional to the sales revenue of the agency channel. To capture the practice of platforms like JD.com and Amazon, which often charge an identical commission fee for all products within a certain category, we assume the commission fee is exogenous. The official websites of these platforms provide public access to the commission fees. For instance, the commission fees range from
to
on JD.com, determined by the product category, whereas the fees range from
to
on Amazon. Moreover, due to the wide variety of products offered within each category, platforms cannot consider the effect of each individual product when determining commission fees for each category. We consider a representative consumer who has a utility of
, where
denotes the consumer’s highest willingness to pay for the product sold through channel
i (
or
),
and
represent the sales quantity and the retail price in channel
i, respectively. This utility function has been extensively adopted in existing research [
33,
34,
35,
36,
37,
38,
39]. The demand function can be determined by maximizing the consumer’s utility, which is written as follows:
Subsequently, we consider the reselling channel structure. In this structure, the platform first procures products from the manufacturer and then resells them to the end consumer. Since the products sold via the reselling channel are subject to counterfeiting, consumers perceive the product as low quality. To capture this dilution of brand value, we assume , where the parameter and , which has a mean of zero and variance , represent the deterministic and random parts of the consumer’s belief, respectively. Without loss of generality, we normalize to a. To eliminate consumers’ concerns about counterfeits, the manufacturer can participate in the blockchain. This makes an online certificate for the product available to consumers. The certificate is encrypted and signed by the brand and all other parties involved in its supply chain (i.e., design, raw materials, production, and distribution). As a result, consumers then perceive the reselling channel products as high quality (i.e., ). However, participating in blockchain incurs a fixed cost F for the manufacturer. As mentioned in the introduction, this cost largely comprises purchasing and deploying the machines used to establish blockchain certification.
In the dual channel, the manufacturer serves as both the platform’s upstream partner and downstream competitor. To model the downstream competition, the utility of the representative consumer becomes
, where the parameter
indicates the degree of substitutability between the products sold in the two channels. When
, the consumer recognizes the products from the two channels as independent; when
, the consumer considers the products from the two channels as perfect substitutes or homogeneous. The demand function can be determined by maximizing the utility of the consumer, which is written as:
Note that the total potential market size in the dual channel is larger than that in the agency channel and the reselling channel if the products from the two channels are not completely substitutable.
To focus on how the channel structure is influenced by blockchain technology, we abstract the unit production cost of the manufacturer and the unit operating cost of the platform to zero. Positive production and operating costs do not change our main insights. Additionally, to capture the manufacturer’s less efficient handling of consumer service, logistics, and other operations compared to the platform’s reselling channel, we consider that the manufacturer incurs a unit channel operating cost c. Since our main insights remain unchanged with a non-negative cost c, we also assume this cost to be zero.
The sequence of decisions is as follows:
When the platform chooses the agency channel structure, the subsequent decision sequence is:
When the platform selects the reselling channel structure, the subsequent decision sequence is:
When the platform chooses the dual-channel structure, the subsequent decision sequence is:
The manufacturer sets the wholesale price w.
The manufacturer sets the agency price , and the platform sets the reselling price simultaneously.
In general, the channel structure decision, which requires substantial and continuous financial and managerial support, is a long-term strategic decision for a firm. Relatively, the blockchain participation decision is a medium-term decision. Thus, we assume that the manufacturer’s decision on blockchain participation is made after the platform’s decision on the channel structure. After making long-term and medium-term decisions, the manufacturer and the platform negotiate short-term pricing contracts based on the channel structure and blockchain participation. We solve the game backward, starting with the determination of the retail price, to ensure sub-game perfection.
We use superscripts and to denote the platform’s decision on channel structure and the manufacturer’s blockchain participation decision, respectively. Here, , R, or D, where A stands for the agency channel, R stands for the reselling channel, and D stands for the dual channel. or B, where N denotes the manufacturer does not participate in the blockchain and B denotes blockchain participation. Variables denotes the equilibrium wholesale price, agency price, reselling price, platform’s profit, and manufacturer’s profit, respectively. For instance, denotes the equilibrium agency price when the platform selects the agency channel and the manufacturer participates in the blockchain.
Assumption A1. , where is the smaller real root of equation .
This assumption ensures that the substitutability between the products sold in the two channels is neither so low nor so high that the wholesale price, retail prices, and sales quantities are non-positive.
4. Price Decisions
4.1. Scenario AN: Agency Channel without Blockchain
In this scenario, the manufacturer maximizes his profit by deciding the agency price:
The equilibrium agency price is given by
We substitute the equilibrium agency price back to the sales quantity and profit functions to yield the equilibrium:
4.2. Scenario AB: Agency Channel with Blockchain
Likewise, in this scenario, the manufacturer maximizes his profit by deciding the agency price:
The equilibrium agency price is given by
We substitute the equilibrium agency price back to the sales quantity and profit functions to get the equilibrium:
4.3. Scenario RN: Reselling Channel without Blockchain
In this scenario, we first solve the platform’s problem as given any wholesale price
w:
We yield the best-response reselling price:
By anticipating the best response to reselling price, the manufacturer maximizes this expected profit:
Solving the maximization problem gets the equilibrium wholesale price and substituting it back to the platform’s response function, we obtain the following equilibrium:
Next, we substitute the equilibrium back to the sales quantity and profit functions and yield the equilibrium:
4.4. Scenario RB: Reselling Channel with Blockchain
With the same pattern, in this scenario, we first solve the platform’s problem as given any wholesale price
w:
We yield the best-response reselling price:
By anticipating the platform’s best response to the reselling price, the manufacturer charges a wholesale price to maximize his profit:
Solving the maximization problem gets the equilibrium wholesale price and substituting it back to the platform’s response function, we yield:
Subsequently, we substitute the equilibrium back to the sales quantity and profit functions and yield the following equilibrium:
4.5. Scenario DN: dual-channel without Blockchain
In this scenario, given any wholesale price
w, the platform maximizes her expected profit
by charging the reselling price
to
The manufacturer maximizes his expected profit
by charging the agency price
to
Simultaneously solving the two best-response functions, we yield:
By considering the platform’s and the manufacturer’s best responses, the manufacturer solves the following problem:
Subsequently, We yield the equilibrium:
We substitute the equilibrium back to the sales quantities and profit functions to yield
4.6. Scenario DB: dual-channel with Blockchain
In the same manner, given any wholesale price
w, the platform maximizes her profit
by charging reselling price
to
The manufacturer maximizes his profit
by charging agency price
to
Simultaneously solving the above two best-response functions, we yield
By taking the platform’s and the manufacturer’s best responses into account, the manufacturer solves the following problem:
Solving the equilibrium wholesale price
and substituting it to the platform’s and the manufacturer’s best-response functions, we yield the equilibrium as follows:
We substitute the equilibrium back to the sales quantities and profit functions to yield
5. Channel Structure and Blockchain Participation Decisions
5.1. Blockchain Participation Decision in Agency Channel
Based on the comparison of the equilibrium in scenarios AB (agency channel with blockchain participation) and AN (agency channel without blockchain participation), we derive the blockchain participation decision in the agency channel.
Theorem 1. Suppose the platform chooses the agency channel.
, .
In equilibrium, there is no blockchain participation in the agency channel.
Theorem 1 shows that blockchain participation by the manufacturer harms the manufacturer’s profit while having no impact on the platform’s profit when the platform operates only an agency channel. The intuition behind this result is that, in the agency channel, the manufacturer directly interacts with the consumer. Thus, the consumer does not need to question the authenticity of the product. For the manufacturer, participating in the blockchain does not enhance consumer trust, yet it incurs a fixed cost F. Consequently, the manufacturer chooses not to participate in the blockchain if the platform selects the agency channel.
5.2. Blockchain Participation Decision in Reselling Channel
We examine the manufacturer’s decision on whether to participate in blockchain in the reselling channel by comparing the equilibrium in scenarios RN (reselling channel without blockchain participation) and RB (reselling channel with blockchain participation). Based on the results, the following Lemma and Theorem are derived.
Lemma 1. Suppose the platform chooses the reselling channel.
The equilibrium wholesale price in RN is lower than that in RB, i.e., .
The equilibrium reselling price in RN is lower than that in RB, i.e., .
The equilibrium sales quantity in RN is lower than that in RB, i.e., .
Theorem 2. Suppose the platform chooses the reselling channel.
when , where . .
In equilibrium, the manufacturer participates in the blockchain in the reselling channel if the blockchain cost is low.
Theorem 2 shows that blockchain participation by the manufacturer may benefit the manufacturer but always benefits the platform. The intuition is as follows: to gain consumer trust in the quality of the product sold through the reselling channel, the manufacturer bears the blockchain cost. If this cost is relatively lower than the benefit derived from the improved quality image, the manufacturer should participate in the blockchain. Although the platform raises the wholesale price to encourage the manufacturer to participate in the blockchain, it benefits from a higher reselling price and a larger sales quantity. These benefits outweigh the loss due to the increase in procurement cost (i.e., the wholesale price). Thus, participation in the blockchain by the manufacturer is always beneficial for the platform.
Theorem 3. The cost threshold of blockchain participation is
decreasing in the consumer’s willingness to pay in the reselling channel, i.e., ;
increasing in the consumer’s willingness to pay in the agency channel, i.e., ;
and thus increasing in the difference between the above two willingness to pay, i.e., .
Theorem 3 illustrates that the larger the difference between the consumer’s willingness to pay in the agency and reselling channels, the greater the opportunity for blockchain participation by the manufacturer. The insight is that the difference in willingness to pay reflects the consumer’s perceived improvement in product quality, which is the source of the benefits.
5.3. Blockchain Participation Decision in dual-channel
We analyze the manufacturer’s decision on whether to participate in blockchain in the dual channel by comparing the equilibrium in scenarios DN (dual channel without blockchain participation) and DB (dual channel with blockchain participation). Based on the results, the following Lemma and Theorem are derived.
Lemma 2. Suppose the platform chooses the dual channel.
The equilibrium wholesale price in DN is lower than that in DB, i.e., .
The equilibrium agency and reselling price in DN is lower than that in DB, i.e., and .
The equilibrium sales quantity of the agency channel in DB is lower than that in DN, whereas the equilibrium sales quantity of reselling channel in DN is lower than that in DB, i.e., and .
Theorem 4. Suppose the platform chooses the dual channel.
-
when , where . when , where and
.
In equilibrium, the manufacturer participates in the blockchain in the dual channel at a low blockchain cost.
The intuition behind Lemma 2 is as follows. Due to the quality assurance effect of the blockchain, the willingness to pay for the product in the reselling channel increases, directly boosting the sales quantity in this channel. The manufacturer, anticipating this increased sales quantity, is encouraged to raise the wholesale price and the reselling price charged by the platform. Moreover, the increased wholesale price forces the platform to further raise the reselling price. Additionally, the increased wholesale price can lead to a higher agency price. However, the heightened competition between the reselling and agency channels, due to increased willingness to pay, indirectly pushes down the agency price. The positive effect of the increased wholesale price always dominates the negative effect from intensified market competition, resulting in a higher agency price. Furthermore, the increased reselling price causes a reduction in the sales quantity in the agency channel, which cannot be compensated by the increased agency price, leading to a smaller market share in the agency channel.
Theorem 4 reveals that blockchain participation by the manufacturer can be beneficial. The manufacturer’s expected profit comprises two parts: the wholesale income from selling to the platform in the reselling channel and the agency income from direct sales to consumers in the agency channel. First, blockchain participation leads to a higher wholesale price and a larger market share in the reselling channel, thereby increasing wholesale income. Second, although the agency price is higher, the reduced market share in the agency channel results in lower agency income. When the increased wholesale income compensates for the decreased agency income, the manufacturer benefits from blockchain participation if the blockchain cost is lower than the remaining wholesale income, i.e., . The platform’s expected profit also includes reselling income from the reselling channel and commission income from the agency channel. Theorem 4 also illustrates that the platform may suffer from the manufacturer’s blockchain participation when the substitutability between the agency and reselling channels is at a moderate level, i.e., . On one hand, high substitutability implies that products from both channels are nearly perfect substitutes, making the difference in sales quantities between channels negligible. Due to double marginalization, channel efficiency is lower in the reselling channel compared to the agency channel, making the blockchain’s quality assurance effect more significant for the reselling income. In such cases, the reselling income increase outweighs the commission income decrease. On the other hand, extremely low substitutability suggests significant differentiation between channels, with consumers treating products from each channel as independent. Here, the blockchain’s quality assurance effect primarily benefits reselling income, which is higher with blockchain participation. Thus, the platform prefers the manufacturer not to participate in the blockchain when the substitutability is moderate.
Theorem 5. The cost threshold of blockchain participation is expressed as follows:
decreasing in the consumer’s willingness to pay in the reselling channel, i.e., ,
decreasing in the substitutability between channels, i.e., ,
and decreasing in the commission fee in the agency channel, i.e., .
Theorem 5 reveals that the manufacturer is more likely to benefit from blockchain participation under conditions of low consumer willingness to pay in the reselling channel, high differentiation between the agency and reselling channels, and low agency income shared with the platform. The smaller the consumer’s willingness to pay in the reselling channel, the greater the perceived quality improvement from blockchain participation. When channel differentiation is high and agency income shared with the platform is low, competition between the two channels is softened, allowing the manufacturer to better balance profits across both channels. Thus, the manufacturer reaps greater benefits from blockchain participation.
Corollary 1. The cost threshold of blockchain participation in the dual channel is lower than that in the agency channel, i.e., .
Corollary 1 reveals that the dual-channel structure can deter the manufacturer from participating in the blockchain. Thus, the platform can maintain its competitive advantage by strategically choosing the channel structure.
5.4. Channel Structure Decision
By anticipating the manufacturer’s decision on blockchain participation, the platform makes the channel structure decision, summarized in Theorem 6 and Corollary 2.
Theorem 6.
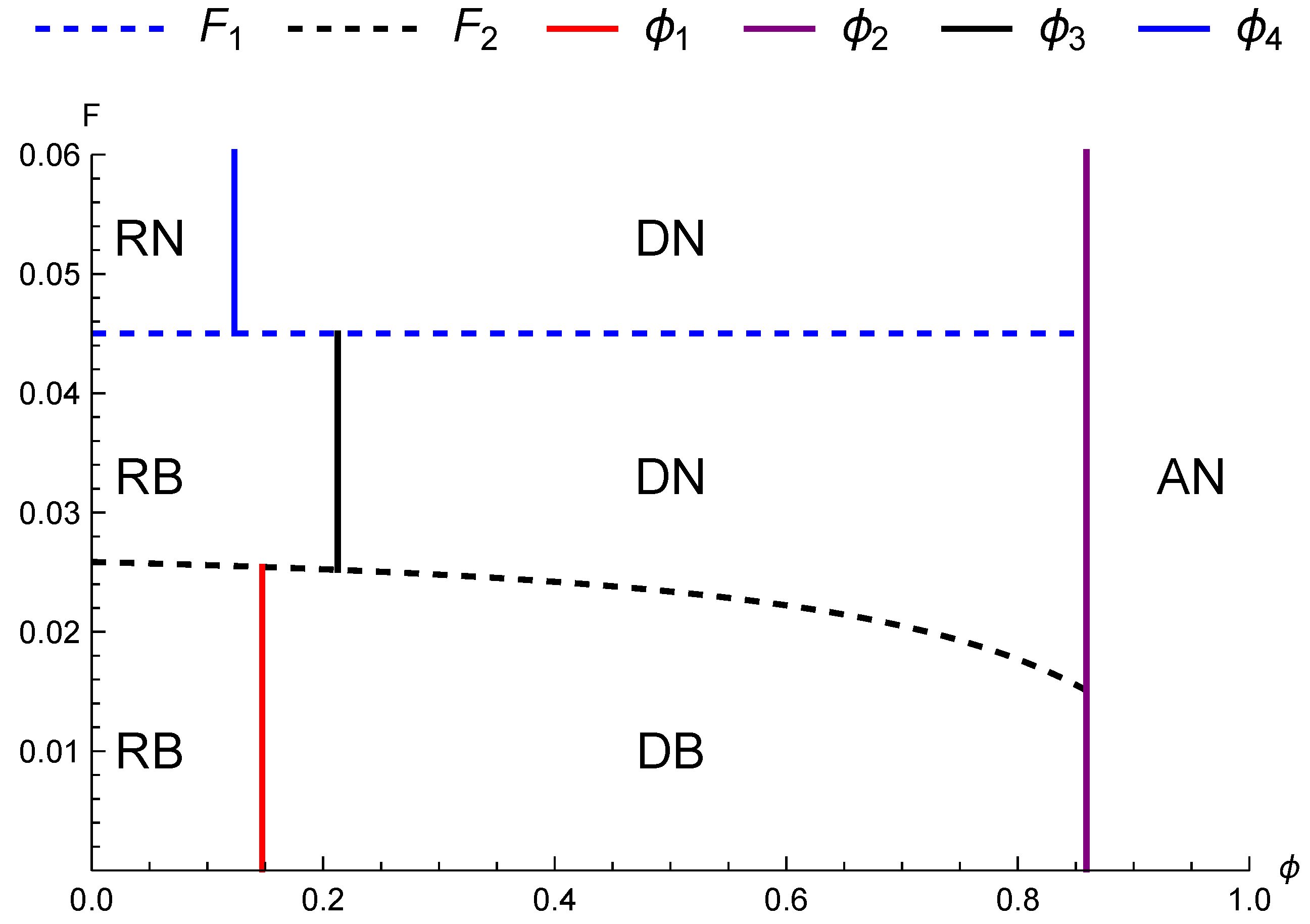
When , the platform chooses the reselling channel if ; chooses the dual-channel if ; and chooses the agency channel if .
When , the platform chooses the reselling channel if ; chooses the dual-channel if ; and chooses the agency channel if .
When , the platform chooses the reselling channel if ; chooses the dual-channel if ; and chooses the agency channel if .
Note is the real root of the equation between 0 and , is the real root of the equation between and 1, is the real root of the equation between 0 and , and is the real root of the equation between 0 and .
Corollary 2. The relationship among the thresholds of channel structure choice is .
Theorem 6 reveals that regardless of the manufacturer’s blockchain participation decision, the platform selects:
the agency channel if the commission fee is high;
the reselling channel if the commission rate is low;
the dual-channel when the commission rate is mid-range.
The intuition behind this is straightforward. In the agency channel, the platform transfers the pricing right to the manufacturer in exchange for commission income proportional to the manufacturer’s agency income. This eliminates the well-known double marginalization effect in the reselling channel, resulting in total profit in the agency channel that is identical to profit in a centralized supply chain and higher than in the reselling channel. Thus, the higher the commission rate, the greater the advantage of the agency channel. Since the dual-channel is a combination of the agency and reselling channels, its commission fee threshold lies between those of the agency and reselling channels.
Corollary 2 demonstrates the complementarity between the manufacturer’s blockchain participation decision and the platform’s channel structure decision. Specifically, participating in the blockchain in the dual-channel (or the reselling channel) expands the dual-channel structure’s choice space (or the reselling channel structure’s choice space), i.e., ().
We present
Figure 1 to provide a visual illustration of Theorem 6.
Theorem 7.
The threshold of channel structure choice is independent of the consumer’s willingness to pay in the reselling channel, i.e., and increasing in substitutability between channels, i.e., .
The threshold of channel structure choice is independent of the consumer’s willingness to pay in the reselling channel, i.e., and first decreasing and then increasing in the substitutability between channels, i.e., when and when , where .
The threshold of channel structure choice is decreasing in the consumer’s willingness to pay in the reselling channel, i.e., and increasing in substitutability between channels, i.e., .
The threshold of channel structure choice is increasing in the consumer’s willingness to pay in the reselling channel, i.e., and increasing in substitutability between channels, i.e., .
Theorem 7 illustrates how the consumer’s willingness to pay and the substitutability between channels affect the choice of channel structures. As the substitutability between channels increases, implying intensified competition, it becomes more beneficial for the platform to choose the reselling channel structure at a low commission rate. However, at a high commission rate, the platform should first choose the agency channel structure and then the dual-channel as substitutability increases. As the consumer’s willingness to pay in the reselling channel decreases, indicating a greater potential benefit from blockchain participation, it becomes more beneficial for the platform to induce the manufacturer to embrace blockchain, with greater benefits in the reselling channel.
6. Conclusion
With the rise of online retailing, many platforms have redesigned their channel structures to enhance sustainability and combat counterfeiting. Examples include Amazon.com and JD.com, which operate both agency and reselling channels, Taobao.com and Tmall.com, which use pure agency channels, and Zappos.com and VIP.com, which use pure reselling channels. Counterfeiting remains a significant issue for these platforms, often resulting in a tarnished reputation for quality. To address this, many large platforms have adopted blockchain technology within their supply chain systems to ensure product authenticity and enhance consumer trust.
We develop a game theory model to explore how blockchain technology affects channel structure and vice versa in the context of sustainable e-commerce. Our study first derives the equilibrium decisions regarding blockchain participation by the manufacturer and the platform’s channel structure. Our findings indicate that blockchain participation does not occur in the agency channel. However, in both reselling channel and dual channels, manufacturers are likely to participate in the blockchain when the blockchain cost is low. The platform’s choice of channel structure is influenced by the commission rate: it opts for the reselling channel at a low commission rate, the dual channel at a mid-range commission rate, and the agency channel at a high commission rate. Furthermore, our results show that the reselling channel structure more effectively encourages manufacturers to adopt blockchain technology compared to the dual channel, highlighting a complementarity between blockchain participation and channel structure. We also examine the effects of consumers’ beliefs in the reselling channel, the substitutability between channels, and the commission fee in the agency channel on equilibrium outcomes. Our results demonstrate that the opportunity for blockchain participation by manufacturers increases with the difference in consumers’ willingness to pay between the agency and reselling channels and the consumer’s sensitivity to products sold through these channels. It decreases with the profit differential between the agency and reselling channels. Platforms benefit from inducing manufacturers to embrace blockchain technology due to this complementarity. At a low commission rate, greater substitutability between channels makes the reselling channel more appealing to the platform. Conversely, at a high commission rate, increased substitutability prompts the platform to first select the agency channel structure, followed by the dual channel.
A limitation of this study is its focus on the interactions between blockchain technology and channel structure, omitting many factors that could also significantly impact blockchain participation decisions and channel structure choices. These factors include competition among upstream and downstream firms, information asymmetry between these firms, and other considerations. Future research can investigate the effects of blockchain technology on channel structure under more complex and realistic settings, contributing to a more comprehensive understanding of sustainable e-commerce practices.
Author Contributions
Conceptualization, Wu, X., Jiang, W., and Meng, L.; methodology, Wu, X.; software, Wu, X.; validation, Wu, X.; formal analysis, Wu, X.; investigation, Wu, X.; writing—original draft preparation, Wu, X., Jiang, W., and Meng, L.; writing—review and editing, Wu, X., Jiang, W., and Meng, L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Project of NSFC Youth Fund Project: “Research on Robust Group Decision Making of SME Credit Scoring in Supply Chain Finance Based on Multi Agent” (No.72101098), Project of National key R&D plan of the Ministry of Science and Technology: "Research on collaborative optimization and trusted control technology of the value chain of large-scale manufacturing industry" (No.2021YFB3301702).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Acknowledgments
The authors would like to thank the anonymous review team for helpful comments on earlier drafts of this paper. This research was financially supported by Project of NSFC Youth Fund Project: “Research on Robust Group Decision Making of SME Credit Scoring in Supply Chain Finance Based on Multi Agent” (No.72101098), Project of National key R&D plan of the Ministry of Science and Technology: "Research on collaborative optimization and trusted control technology of the value chain of large-scale manufacturing industry" (No.2021YFB3301702). The authors would like to thank the anonymous review team for helpful comments on earlier drafts of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof
Proof of Theorem 1. Theorem 1 can be derived by comparing the equilibrium outcomes in scenario AB and scenario AN. By comparing with , we have . Similarly, we have . □
Proof of Lemma 1.
According to , , and , we obtain Lemma 1. □
Proof of Theorem 2.
According to and , we obtain Theorem 2. □
Proof of Theorem 3.
Theorem 3 can be derived by calculating the first-order derivatives of . Taking the first order derivative of , we have , , and . □
Proof of Lemma 2.
According to , , , , and , we obtain Lemma 2. □
Proof o
f Theorem 4.
According to , we obtain Theorem 2(i). Solving the inequality , we get that , where
and . □
Proof of Theorem 5.
Theorem 5 can be derived by calculating the first-order derivatives of . Taking the first order derivative of , we have ,
,
and . □
Proof of Corollary 1.
According to , we obtain Corollary 1 □
Proof of Theorem 6.
Comparing the platform’s profit with , we have when . Comparing the platform’s profit with , we have when . Comparing the platform’s profit with , we have when . Comparing the platform’s profit with , we have when . Comparing the platform’s profit with , we have when . Now, we complete the proof of Theorem 6. □
Proof of Corollary 2.
Corollary 2 can be derived by directly comparing , , , and . □
Proof of Theorem 7.
Theorem 7 can be derived by directly calculating the first order derivatives of , , , and . □
References
- Conley, P. US ecommerce in 2022 tops $1 trillion for first time, 2023. https://www.digitalcommerce360.com/article/us-ecommerce-sales/, Last accessed on 2023-3-5.
- von Abrams, K. Global Ecommerce Forecast 2021, Digital Leads the Way, Building on 2020’s Growth, 2021. https://www.emarketer.com/content/global-ecommerce-forecast-2021, Last accessed on 2023-3-5.
- Levy, A. Amazon counterfeiters wreak havoc on artists and small businesses, 2016. https://www.cnbc.com/2016/05/25/amazon-counterfeiters-wreak-havoc-on-artists-and-small-businesses.html, Last accessed on 2023-3-5.
- Wang, Y. Alibaba’s Struggle For E-Commerce Legitimacy Is Undermined By Fake Gucci And Refugee Boats, 2017. https://www.forbes.com/sites/ywang/2017/08/14/alibabas-struggle-for-e-commerce-legitimacy-is-undermined-by-fake-gucci-and-refugee-boats/?sh=79a12b1152d0, Last accessed on 2023-3-5.
- Katalyst. How Blockchain Can Improve Manufacturing In 2020, 2020. https://katalysttech.com/blog/blockchain-for-manufacturing/, Last accessed on 2023-3-5.
- Columbus, L. How Blockchain Can Improve Manufacturing In 2019, 2018. https://www.forbes.com/sites/louiscolumbus/2018/10/28/how-blockchain-can-improve-manufacturing-in-2019/?sh=467196df5db6, Last accessed on 2023-3-5.
- Wood, M. Chi-X voices competition concerns over ASX blockchain project, 2019. https://www.ledgerinsights.com/chi-x-competition-concerns-asx-blockchain/, Last accessed on 2023-3-5.
- Song, J. JD uses blockchain to increase traceability of its supply chain, 2017. https://global.chinadaily.com.cn/a/201711/14/WS5a0d2841a31061a7384095e0.html, Last accessed on 2023-3-5.
- Babich, V.; Hilary, G. OM Forum—Distributed Ledgers and Operations: What Operations Management Researchers Should Know About Blockchain Technology. Manufacturing & Service Operations Management 2020, 22, 223–240. [Google Scholar]
- Olsen, T.L.; Tomlin, B. Industry 4.0: Opportunities and Challenges for Operations Management. Manufacturing & Service Operations Management 2020, 22, 113–122. [Google Scholar]
- Hastig, G.M.; Sodhi, M.S. Blockchain for Supply Chain Traceability: Business Requirements and Critical Success Factors. Production and Operations Management 2020, 29, 935–954. [Google Scholar] [CrossRef]
- Pun, H.; Swaminathan, J.M.; Hou, P. Blockchain Adoption for Combating Deceptive Counterfeits. Production and Operations Management 2021, 30, 864–882. [Google Scholar] [CrossRef]
- Shen, B.; Dong, C.; Minner, S. Combating Copycats in the Supply Chain with Permissioned Blockchain Technology. Production and Operations Management 2022, 31, 138–154. [Google Scholar] [CrossRef]
- Tan, Y.R. Implications of blockchain-powered marketplace of preowned virtual goods. Production and Operations Management 2022. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Z.E.; Jiang, W.; Tang, S. Blockchain-Enabled Data Sharing in Supply Chains: Model, Operationalization, and Tutorial. Production and Operations Management 2021, 30, 1965–1985. [Google Scholar] [CrossRef]
- Cong, L.W.; He, Z. Blockchain Disruption and Smart Contracts. The Review of Financial Studies 2019, 32, 1754–1797. [Google Scholar] [CrossRef]
- Wei, J.; Yi, X.; Yang, X.; Liu, Y. Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance. Sustainability 2023, 15. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, X. Blockchain-Enabled Supply Chain Internal and External Finance Model. Sustainability 2023, 15. [Google Scholar] [CrossRef]
- Abbas, Z.; Myeong, S. A Comprehensive Study of Blockchain Technology and Its Role in Promoting Sustainability and Circularity across Large-Scale Industry. Sustainability 2024, 16. [Google Scholar] [CrossRef]
- Mantin, B.; Krishnan, H.; Dhar, T. The Strategic Role of Third-Party Marketplaces in Retailing. Production and Operations Management 2014, 23, 1937–1949. [Google Scholar] [CrossRef]
- Hagiu, A.; Wright, J. Marketplace or Reseller? Management Science 2015, 61, 184–203. [Google Scholar] [CrossRef]
- Abhishek, V.; Jerath, K.; Zhang, Z.J. Agency Selling or Reselling? Channel Structures in Electronic Retailing. Management Science 2016, 62, 2259–2280. [Google Scholar] [CrossRef]
- Kwark, Y.; Chen, J.; Raghunathan, S. Platform or Wholesale? A Strategic Tool for Online Retailers to Benefit from Third-Party Information. Management Information Systems Quarterly 2017, 41, 763–785. [Google Scholar] [CrossRef]
- Geng, X.; Tan, Y.R.; Wei, L. How Add-on Pricing Interacts with Distribution Contracts. Production and Operations Management 2018, 27, 605–623. [Google Scholar] [CrossRef]
- Tian, L.; Vakharia, A.J.; Tan, Y.R.; Xu, Y. Marketplace, Reseller, or Hybrid: Strategic Analysis of an Emerging E-Commerce Model. Production and Operations Management 2018, 27, 1595–1610. [Google Scholar] [CrossRef]
- Jerath, K.; Zhang, Z.J. Platform retailing: from offline “stores within a store” to online “marketplaces”. In Handbook of Research on Distribution Channels; Edward Elgar Publishing: Cheltenham, UK, 2019; pp. 52–74. [Google Scholar]
- Ha, A.Y.; Tong, S.; Wang, Y. Channel Structures of Online Retail Platforms. Manufacturing & Service Operations Management 2021.
- Hu, H.; Zheng, Q.; Pan, X.A. Agency or Wholesale? The Role of Retail Pass-Through. Management Science 2022. [Google Scholar] [CrossRef]
- Li, C.; Xing, P.; Li, Y. Sustainable Strategy Analysis: Platform Channel Configuration and Slotting Fee Design under Differentiated Quality Investment. Sustainability 2022, 14. [Google Scholar] [CrossRef]
- Fu, Y.; Wu, J.; Ma, C.; Fu, X. Agency, Reselling, or Hybrid: Strategic Channel Selection in a Green Supply Chain. Sustainability 2023, 15. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, X.; Wang, F. A Dual-Channel Strategy for Online Recovery Platforms to Increase Recovery Quantity and Profits. Sustainability 2023, 15. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, J. Managing the Product-Counterfeiting Problem with a Blockchain-Supported E-Commerce Platform. Sustainability 2021, 13. [Google Scholar] [CrossRef]
- Singh, N.; Vives, X. Price and Quantity Competition in a Differentiated Duopoly. The RAND Journal of Economics 1984, 15, 546–554. [Google Scholar] [CrossRef]
- Thisse, J.F.; Vives, X. On The Strategic Choice of Spatial Price Policy. The American Economic Review 1988, 78, 122–137. [Google Scholar]
- Choi, S.C. Price Competition in a Channel Structure with a Common Retailer. Marketing Science 1991, 10, 271–296. [Google Scholar] [CrossRef]
- Amir, R.; Jin, J.Y. Cournot and Bertrand equilibria compared: substitutability, complementarity and concavity. International Journal of Industrial Organization 2001, 19, 303–317. [Google Scholar] [CrossRef]
- Cachon, G.P.; Kök, A.G. Competing Manufacturers in a Retail Supply Chain: On Contractual Form and Coordination. Management Science 2010, 56, 571–589. [Google Scholar] [CrossRef]
- Farahat, A.; Perakis, G. TECHNICAL NOTE—A Comparison of Bertrand and Cournot Profits in Oligopolies with Differentiated Products. Operations Research 2011, 59, 507–513. [Google Scholar] [CrossRef]
- Zheng, Q.; Pan, X.A.; Vakharia, A.J. Common Retailer Channel Revisited: The Role of Supply Network Size. Production and Operations Management 2020, 29, 2175–2181. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).