Prerpints.org logo
Preprint
Article

Open-ended Ridged Waveguide Elements for LEO Direct Radiating Arrays in Ka-band

Altmetrics

Downloads

123

Views

78

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 July 2024

Posted:

02 July 2024

You are already at the latest version

Alerts
Abstract
This paper presents an extensive performance analysis of open-ended waveguide elements for direct radiating arrays with high scan angle (± 50º/60º). The evaluated designs are based on square and hexagonal apertures loaded with ridges. Both square and triangular lattices are considered in the framework of Ka-band downlink design requirements for future LEO mega-constellations. The parameter space defined by the monomodal condition has been explored to find an optimum value for each structure. The analyses are validated with both infinite and finite full-wave models in terms of active reflection coefficient, scan loss and cross-polar discrimination.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

The new generation 6G paradigm is expected to offer uninterrupted connectivity and coverage everywhere through non-terrestrial networks (NTN). The key aspect is the usage of satellite communications (SatCom) to complement the terrestrial networks in both fixed and mobile scenarios (SatCom on the move). To this end, low Earth orbit (LEO) satellites are the most promising solution in terms of lower attenuation and smaller latency [1] compared to medium Earth orbit or geostationary orbit.
Nowadays, SatCom user link generally operates at Ku- and Ka-bands. Multibeam antennas are required to send the information to different spots on the Earth, maximizing spatial diversity and covering wide areas [1,2]. At LEO orbits, direct radiating array (DRA) antennas are a suitable candidate for flexible multibeam operation. However, a significant scan range of ±50   ∘ /60   ∘ is required [3,4] which is a challenging aspect in the antenna design in terms of impedance matching and polarization purity. Other important figures-of-merit are radiation efficiency, cost and weight.
In this framework, few radiating elements have been presented in the literature such as waveguide apertures (open-ended waveguides) [5,6,7], Vivaldi [8,9], microstrip patch [10,11] and substrated integrated waveguide (SIW) antennas [12]. Among the different solutions, all-metal ones are promising thanks to their good power handling capabilities and higher radiation efficiency. An all-metal evanescent quadridge antenna (EQA, square waveguide loaded with four ridges [13,14]), operating in the Ku-band has been proposed in [5]. The antenna works in a 4.5% bandwidth with good performance up to ±50   ∘ scanning angle. Unfortunately, such design does not cover the full downlink Ka-band (17.7 - 20.2 GHz) where the bandwidth is instead 13.2%. A waveguide-based aperture and all-metal Vivaldi radiating element covering the full Ka-band are presented in [15,16]. The first one provides low performance at the E-plane, where a ±60   ∘ scan blindness appears at 20 GHz. Concerning the all-metal Vivaldi radiating element, both E- and H-planes provides good performance when it scans up to ±40   ∘ with an active reflection coefficient (ARC) lower than -10 dB. Circular polarization is instead difficult to achieve with such Vivaldi arrays.
In this paper, we provide an extensive study of open-ended ridged waveguides to assess their performance as array elements. We present results for square and hexagonal waveguides in square [14] and triangular lattices [17,18], respectively (such geometries are sketched in Figure 1). Differently from [5], we only consider the element at aperture level i.e. without the matching section in order to find intrinsic peculiarities and limitations of each configuration. In this way, this study offers a starting point to design more complex elements integrating the aperture itself and cascaded discontinuities for matching improvement and polarization conversion.
The novelty aspect of this paper is the study of such square and hexagonal ridged waveguide apertures in array environment to cover a bandwidth of 13.2% i.e. the downlink Ka-band in terms of ARC, scan loss and cross-polar discrimination (XPD). For all configurations, we provide cut-off, parametric and the complete performance analyses for the optimum parameter sets in both linear and circular polarization. Even if the system operates in circular polarization, the linear one provides additional physical insight.
To the best of the author’s knowledge, this is the first paper analyzing the quadridge element design in the 13.2% bandwidth. This is also the first paper providing results on the hexagonal ridged waveguide in triangular lattice.
The paper is organized as follows: Section 2 describes the main parameters for a LEO array design such as periodicity and configuration. Section 3 presents the cut-off analyses for both quadridge and hexagonal waveguides. Section 4 discusses and compares the performance of the proposed radiating elements in terms of S-Parameters, scan loss and XPD. Section 5 validates the results using both infinite and finite array approaches. Conclusion is reported in Section 6.

2. Array Design for LEO

As far as antennas for LEO satellites are concerned, typical requirements for array gain are in the order of 35 dBi. Considering an element gain of 6 dBi with a scan loss of 3 dB at maximum scan angle, the resulting number of elements is in the order of 48x48 elements.
The inter-element spacing providing grating-lobe-free condition is defined in Equation (1) [19,20].
p λ ≤ 1 s i n θ L 1 − 1 N 1 + s i n θ S
where θ L defines the lattice angle (i.e, see Figure 2, 90   ∘ for square lattice and 60   ∘ for triangular lattice), θ S is the maximum scan angle and N is the number of elements in a row/column.
According to Equation (1) and considering both the highest frequency of the band (20.2 GHz) and a scan limit of 60   ∘ , the period is equal to 7.8 mm (0.52 λ ) and 9 mm (0.61 λ ) for square (Figure 2(a)) and triangular lattice (Figure 2(b)), respectively. Both arrangements are studied in this paper.
The inter-element spacings reported above have been computed considering a finite array approach, which is suitable for a future prototype. Nevertheless, the large number of elements, i.e. 48x48, justifies an infinite array approach for the element design.

3. Cut-Off analysis

The inter-element spacing was computed in the previous section to satisfy the grating-lobe-free condition. With reference to Figure 1, waveguide apertures should be smaller than the inter-element spacing to provide a minimum metal thickness of 1 mm for manufacturability [21]. Therefore, the maximum waveguide sizes are 6.8 mm and 8 mm for square and triangular lattices, respectively. Such sizes does not allow fundamental degenerate modes propagation in the operative band if square or circular/hexagonal waveguides are considered. Dielectric filling has been proposed in [7] to lower the cut-off frequencies of such waveguides. Similarly to [5], in this work we instead propose the use of ridges to achieve fundamental mode propagation in the frequency band together with low losses (all-metal solutions) and easier manufacturing. All-metal antennas are also generally preferred for space applications.
The design of the ridged waveguides in terms of cut-off frequencies are reported in the next subsections.

3.1. Quadridge Waveguide

The geometry of the quadridge waveguide [13,14] and its parameters can be seen in Figure 3. As written above, the waveguide side a is 6.8 mm. The iso-level curves of the cut-off frequencies for the two fundamental degenerate modes f c 1 , 2 and the higher-order one f c 3 are shown in Figure 4(a) and Figure 4(b), respectively, as a function on the width w R and the height h R of the ridges. Even if the waveguide supports two degenerate modes (one for each polarization) the interval f c 1 , 2 and f c 3 can be referred to as monomodal bandwidth.
The dashed line corresponds to the lower limit of the operative bandwidth ( F m i n = 17.7 GHz). Therefore, the useful ridge parameter combinations lay on the right-hand side of Figure 4(a) ( f c 1 , 2 < F m i n ). On the other hand, the dash-dotted line in Figure 4(b) shows the upper limit of the operative bandwidth ( F m a x = 20.2 GHz). The dashed curve is reported again in Figure 4(b) to obtain the parameter region where only the two fundamental degenerate modes are propagating within the frequency band (17.7 - 20.2 GHz). It can be seen that low values of w R provide a larger available range of ridge height, h R . However, such region should be further reduced considering a manufacturing constraint of 1 mm for the minimum ridge width. An optimal value (OV) has been chosen to be almost equally spaced from both cut-off frequency limits. The resulting dimensions are h R equal to 1.5 mm and w R equal to 1 mm, providing cut-off frequencies of 17.6 GHz (see Figure 4(a)) for the fundamental degenerate modes f c 1 , 2 and 20.5 GHz (see Figure 4(b)) for the third mode f c 3 . The performance of this waveguide as a radiating element will be shown in Section 4.1.
From the previous analysis, it is apparent that the quadridge configuration does not provide large margins between the operative band and the corresponding cut-off frequencies. This is consistent to the significant bandwidth limitations for this type of element shown in Section 4.1. For this reason, the hexagonal waveguide with three and six ridges is studied in the next subsection.

3.2. Hexagonal Ridged Waveguides

Hexagonal designs are presented to overcome the limitation found in the quadridge structure. Although in triangular lattice the inter-element spacing and the dimensions of the waveguide are larger than in the previous case, it is still necessary to load with ridges. Two configurations have been considered with three [22] and six ridges [18] (Figure 1). The former (three-ridges) leads to a simple manufacturing whereas better polarization performance is expected from the latter (six-ridges) due to the two-fold symmetry.
As reported in Section 2, the waveguide size a is 8 mm. The iso-level curves of the cut-off frequencies for the two fundamental degenerate modes f c 1 , 2 and the higher-order one f c 3 are shown in Figure 6, as a function on the width w R and the height h R of the ridges.
As far as three-ridged waveguide is concerned (Figure 6(a,c), it can be seen that with a parameter combination of w R = 2.5 mm and h R = 3 mm (close to upper right corner) the maximum bandwidth approaches 3:1. Therefore, in principle this waveguide can cover both Ka-band downlink (17.7 - 20.2 GHz) and Ku-band downlink (10.7 - 12.75 GHz).
The dashed line corresponds to the lower limit of the operative bandwidth ( F m i n = 17.7 GHz). Therefore, the useful ridge parameter combinations lay on the right-hand side of Figure 6 ( f c 1 , 2 < F m i n ).The dash-dotted line showing the upper limit ( F m a x = 20.2 GHz) is only visible in Figure 6(d) for the six ridges configuration. As mentioned above, the three ridges does not provide limitations related to the higher order mode ( f c 3 > F m a x for all the considered parameters values). The benefits of the triangular symmetry ( 60 ∘ rotational symmetry) in terms of very high cut-off frequency/resonance of the higher-order mode have been also used in [23,24].
It is apparent that both solutions in Figure 1 allow a larger range of parameters w R and h R with respect to the quadridge (see Figure 4). In this case, the optimal value (OV) has been determined using full-wave simulations presented in Section 4.2.

4. Parametric Analyses and Performance Evaluation

The results shown in this section have been obtained with unit cell boundary conditions using CST software [25], considering a waveguide excitation with the two fundamental degenerate modes and Floquet port with 18 modes at 4.40 mm from the aperture (0.25 λ 0 at 17 GHz). Scan angles of 0   ∘ , 30   ∘ and 60   ∘ are presented to investigate the limits of the structure. For brevity, 50   ∘ is only reported in the final comparison table in Section 4.3.

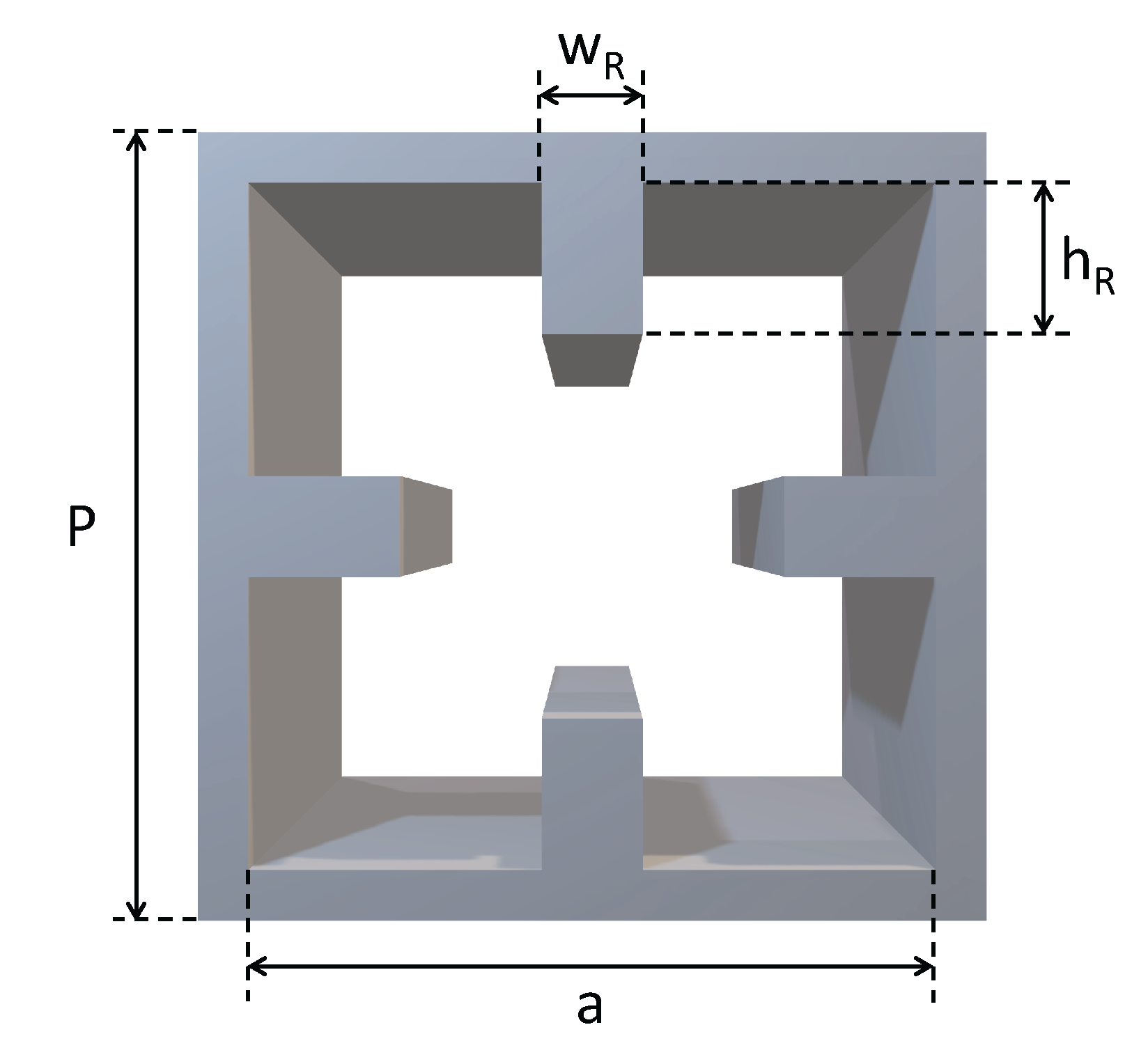
4.1. Quadridge Radiating Elements

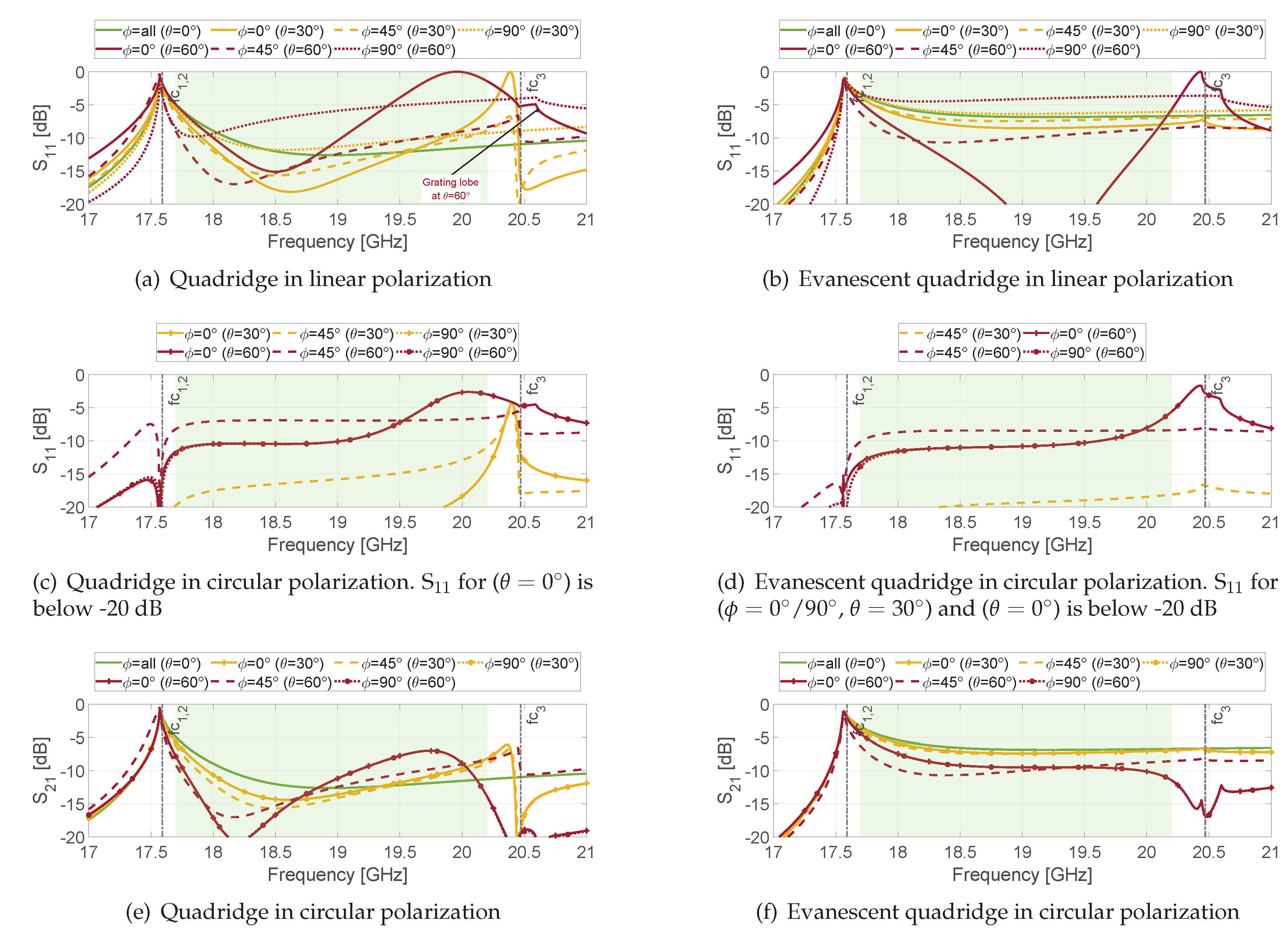
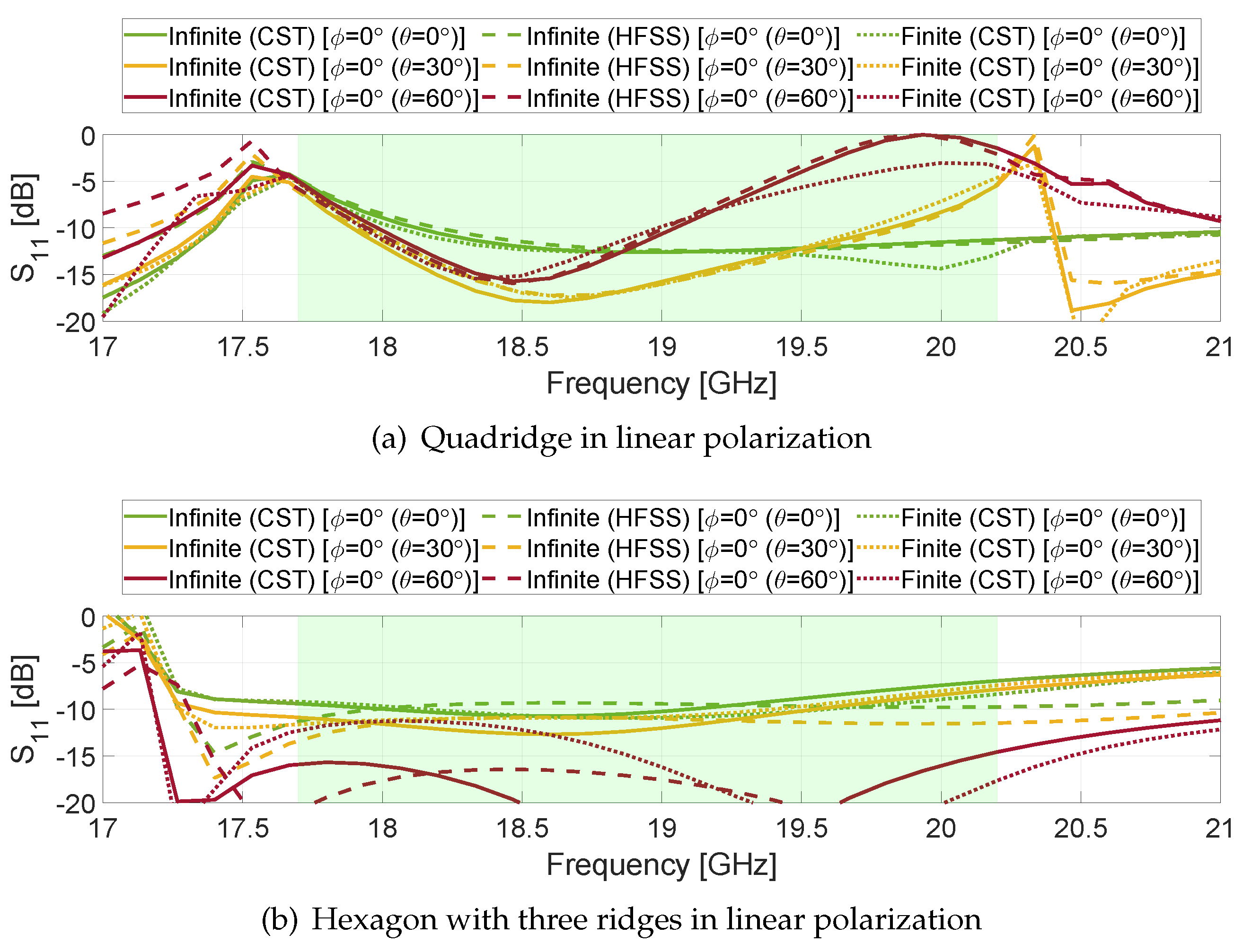
The ARC of the open-ended quadridge waveguide reported in Section 3.1, whose parameters are summarized in Table 1, is reported in Figure 7(a) for linear polarization. The solid, dashed and dotted lines refer to the E- ( ϕ = 0 ∘ ), D- ( ϕ = 45 ∘ ) and the H-plane ( ϕ = 90 ∘ ), respectively. The line colours identify the scanning angles. The vertical black dash-dotted lines indicate the cut-off frequencies of the waveguide, and the green box highlights the operative bandwidth. The ARC for only one of the two fundamental degenerate modes is shown due to the 90   ∘ rotational symmetry along the propagation axis.
It can be seen that the open-ended quadridge waveguide does not provide satisfactory matching level even at broadside (green solid line). This is related to the proximity of the lower cut-off frequency (vertical black dash-dotted line). In addition, when scanning up to 60   ∘ in the E-plane (red solid line), a scan blindness is observed at 20 GHz i.e. the signal is completed reflected at this frequency, reducing the bandwidth even further. The other principal plane (dotted red line) instead shows reflection level of about -5 dB in the overall band.
Two sharp features on the S   11 curves are visible above the upper limit of the frequency band. The first one, located at 20.47 GHz (vertical black dash-dotted line), is due to the higher-order mode of the waveguide. It is related to the waveguide geometry, therefore it is independent of the scan angle. However, it does not appear at ϕ = 90 ∘ (dotted line) because of the symmetry of the structure i.e the fundamental mode is not coupled to the third one along such a plane (H-plane). The second sharp feature is at 20.61 GHz (black arrow), this is instead due to the appearance of the grating lobes at this frequency (see Equation (1)).
Concerning the coupling in linear polarization, it is only significant in the D-plane where it reaches -6.5 dB when the scan angle goes up to 60   ∘ . These curves are not shown for brevity. However, their effect is included in the circular polarization behaviour discussed hereafter.
As far as the ARC in circular polarization is concerned, this scan blindness decreases by almost 3 dB (red solid line in Figure 7(c)) because, as stated above, only one of the two linear components is completely reflected. The results shown in circular polarization have been calculated taking into account an ideal polarizer (the parameters simulated in linear polarization have been combined according to Equations (2) and (3)).
S 11 C i r c = 1 2 S 11 − S 22 − j S 12 + S 21
S 21 C i r c = 1 2 S 21 − S 12 − j S 11 + S 22
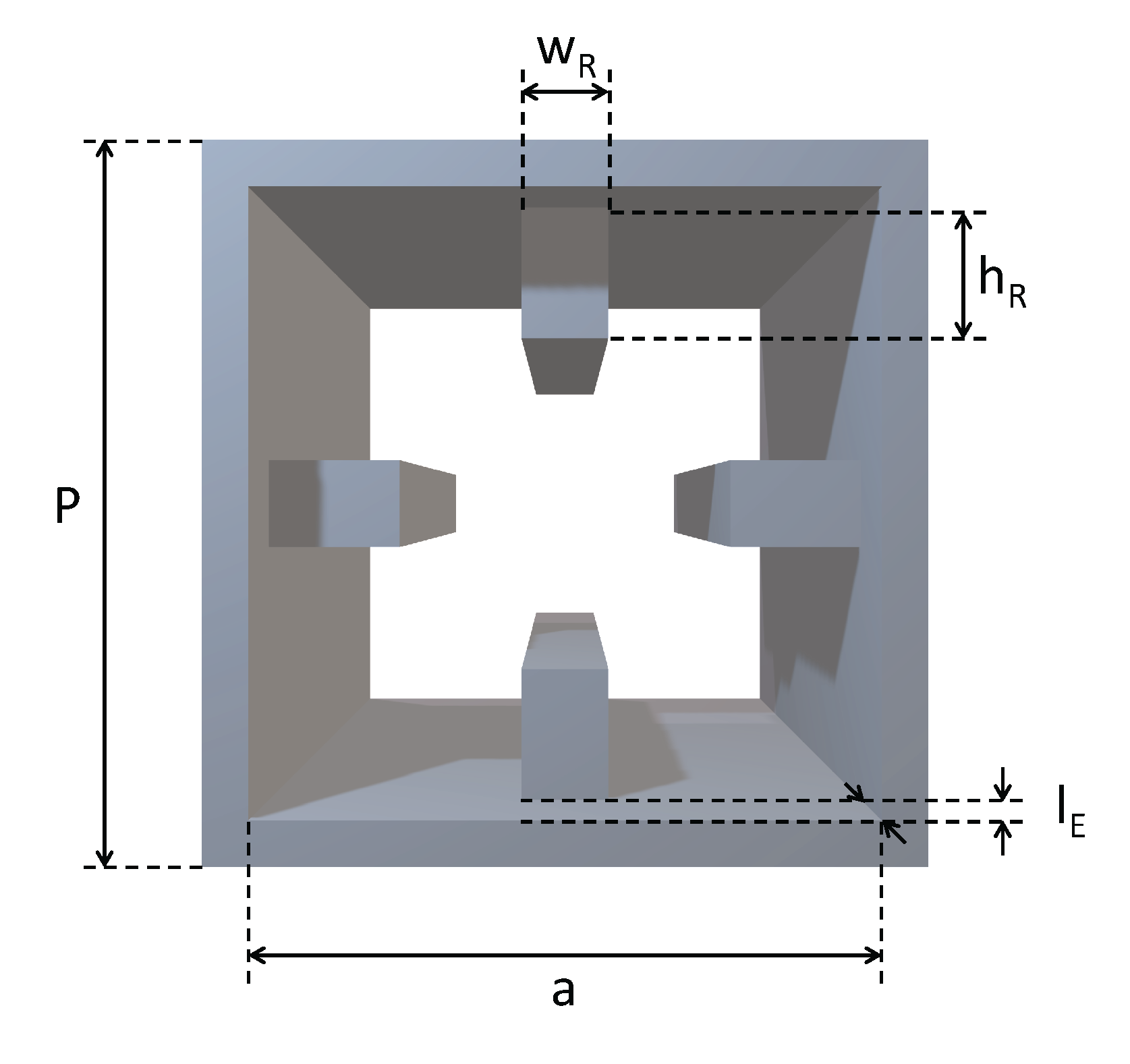
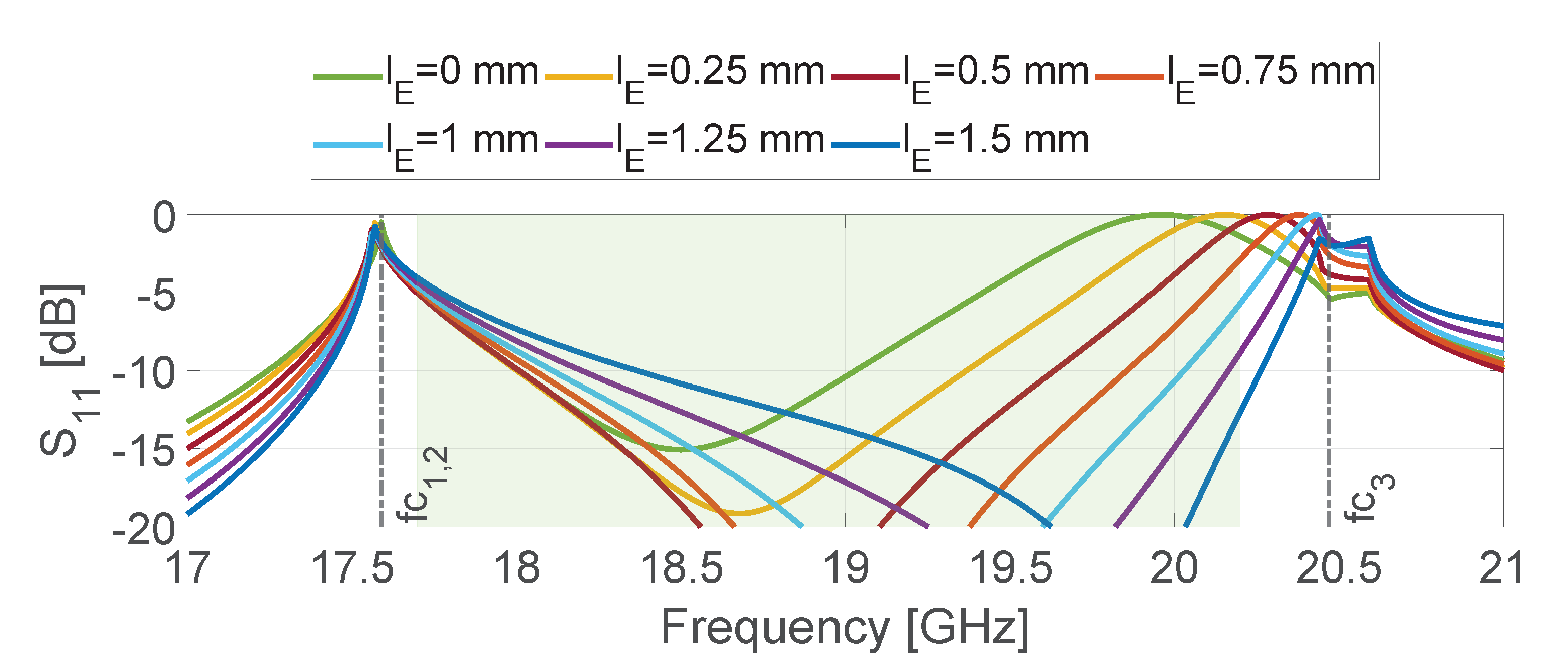
To overcome this scan blindness, a square waveguide section can be placed between the end of the ridges and the aperture (see Figure 8). Its effect on the E-plane response is shown in Figure 9 as a function of the length l E . The same phenomenon, also called spurious resonance, has been studied in [5] considering circular polarization. Here, the impact is even more apparent in linear polarization (Figure 9), where the scan blindness is shifted to higher frequencies and then out of the band increasing the length l E . An optimal value of l E , 1 mm, has been chosen to achieve the same reflection coefficient value at the two ends of the band (around -5 dB).
The whole phenomenon of the scan blindness reduction is complex because it involves multimodal interaction between the end of the ridges and the aperture. In the quadridge-to-free space discontinuity (Figure 3), the higher-order mode of the quadridge is strongly excited on the aperture because its cut-off frequency f c 3 = 20.4 GHz is close to the upper limit of the frequency band. On the contrary, when the square waveguide section is added (Figure 8), both fundamental degenerate (TE   10 , TE   01 ) and higher-order modes (TE   11 , TM   11 ) are excited at the end of the ridges. However, the TE   11 and TM   11 are significantly attenuated (4.3 dB/mm at 20.2 GHz) because their cut-off frequency (31.1 GHz) is far from the operative bandwidth. In this way, the contribution of such higher-order modes to radiation is reduced with respect to the abrupt quadridge-free space interface. It should be mentioned that the TE   10 is also below cut-off (about 22 GHz). Nevertheless, as shown in Figure 7(b), such slightly evanescent mode (1.6 dB/mm) does not prevent radiation. However, the overall ARC is higher (at broadside and 30   ∘ ) with respect to the quadridge element (see Figure 7(a)). The S   11 levels are quite acceptable in circular polarization (see Figure 7(d)) because (due to the polarizer) such reflection coefficient basically depends on the difference between ARCs for the two linear polarizations which is related to the difference response in the two orthogonal planes (see Equation (2)).
A further increment in l E will result in a lower and flatter S   11 in circular polarization, but the S   21 will increase in proximity of the lower end of the bandwidth. For this reason, l E = 1 mm can be considered as an optimum value also for circular polarization.
As far as circular polarization is concerned, the evanescent quadridge provides an improvement of about 2-3 dB and overall bandwidth enlargement (Figure 7(d)) with respect to the nominal one (Figure 7(c)). The coupling S   21 shows values equals to -5 dB at the lower end of the band due to the proximity of the cut-off frequency in both designs (Figure 7(e,f)). The impact of the increased ARC of the evanescent quadridge at low scanning angles is visible on S   21 (about -6 dB) through all the band.
In conclusion, the quadridge with evanescent section, which does not show the blindness at the expense of a higher reflection coefficient in linear polarization (and higher S   21 in circular), can be suitable for single-pol DRAs, where the port of the unexcited polarization is closed on a matched load (with reduction of the overall efficiency).
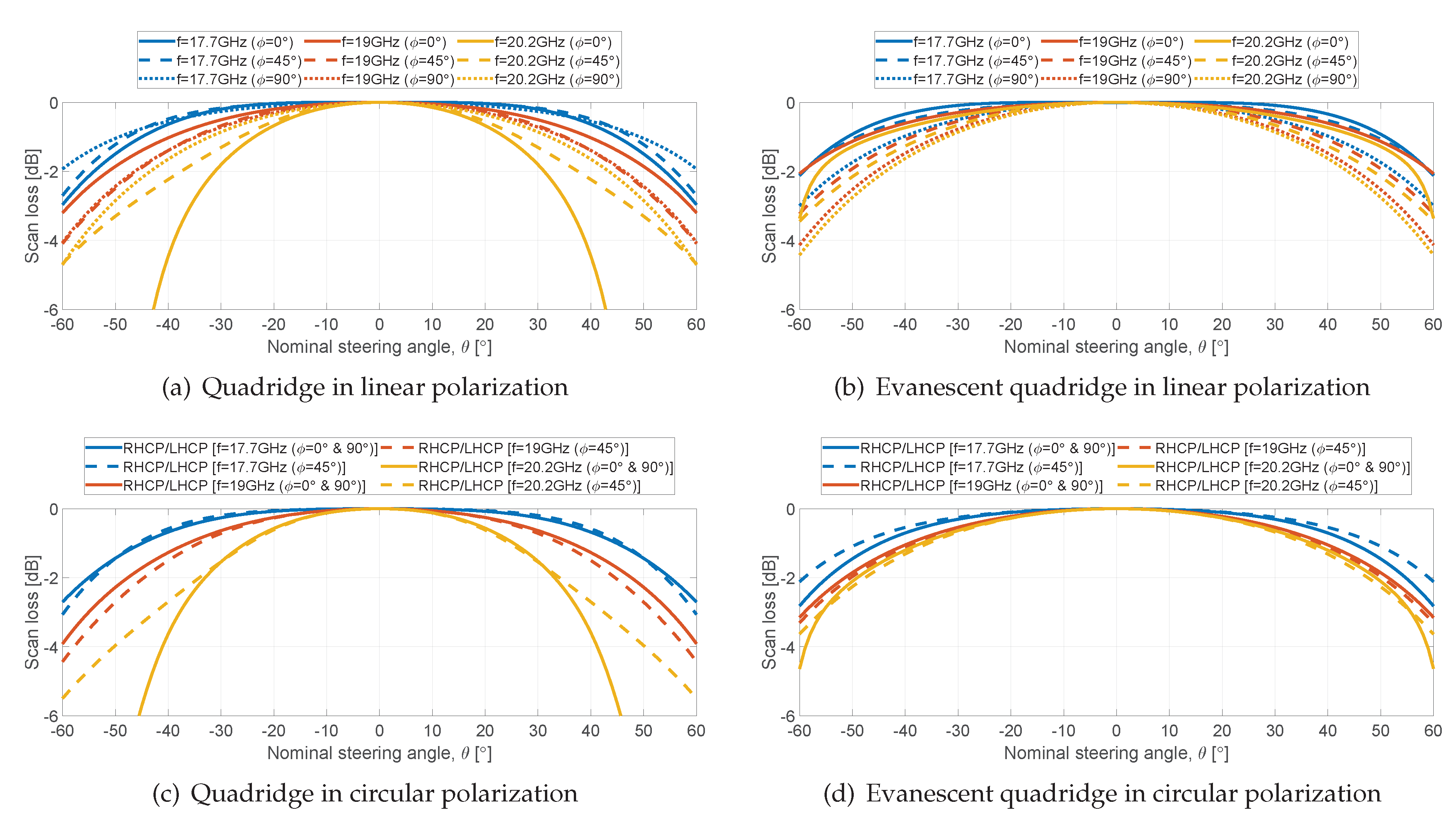
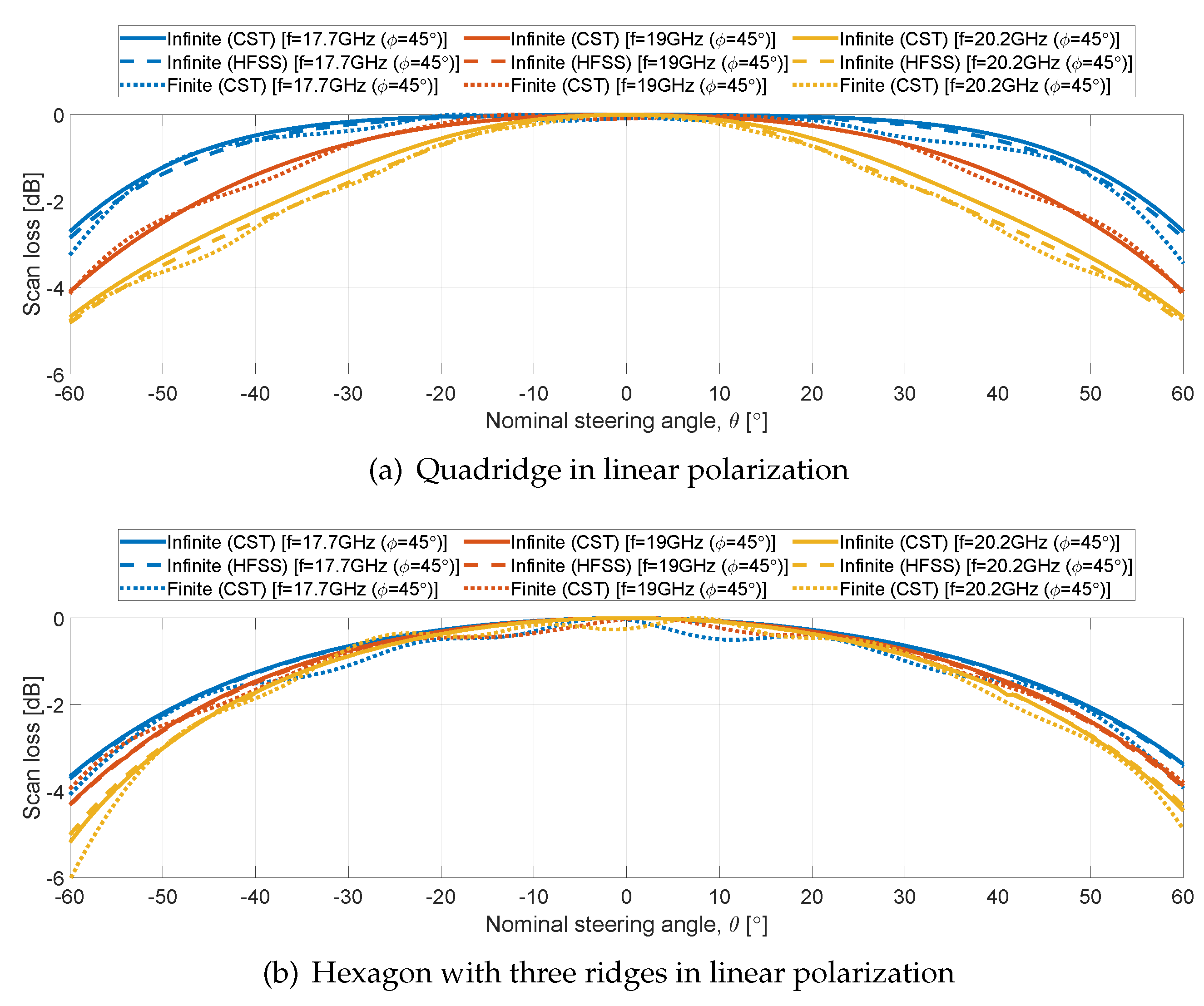
Figure 10 shows the scan loss at the band limits and center frequency when scanning from − 60 ∘ to 60 ∘ for both quadridge designs in both linear and circular polarization. The circular polarization data have been computed according to Equations (4) and (6) as a function of the radiated field in linear polarization.
E c o , L H = 1 2 E θ , 1 + j E θ , 2 − j E ϕ , 1 + j E ϕ , 2
E c r o s s , L H = 1 2 E θ , 1 + j E θ , 2 + j E ϕ , 1 + j E ϕ , 2
E c o , R H = 1 2 E θ , 1 − j E θ , 2 + j E ϕ , 1 − j E ϕ , 2
E c r o s s , R H = 1 2 E θ , 1 − j E θ , 2 − j E ϕ , 1 − j E ϕ , 2
From Figure 10(a), a maximum difference of 2 dB is observed between planes at 17.7 GHz (blue lines) and 19 GHz (red lines). At 20.2 GHz (yellow lines) the scan loss drops more than 6 dB due to the scan blindness discussed above. The same consideration applies for circular polarization (Figure 10(c)). When the evanescent section is added (Figure 10(b)), the drop due to scan blindness at the upper frequency of the band disappears, obtaining values between -2 and -4 dB for all the planes and frequencies. Similar values are visible in circular polarization.
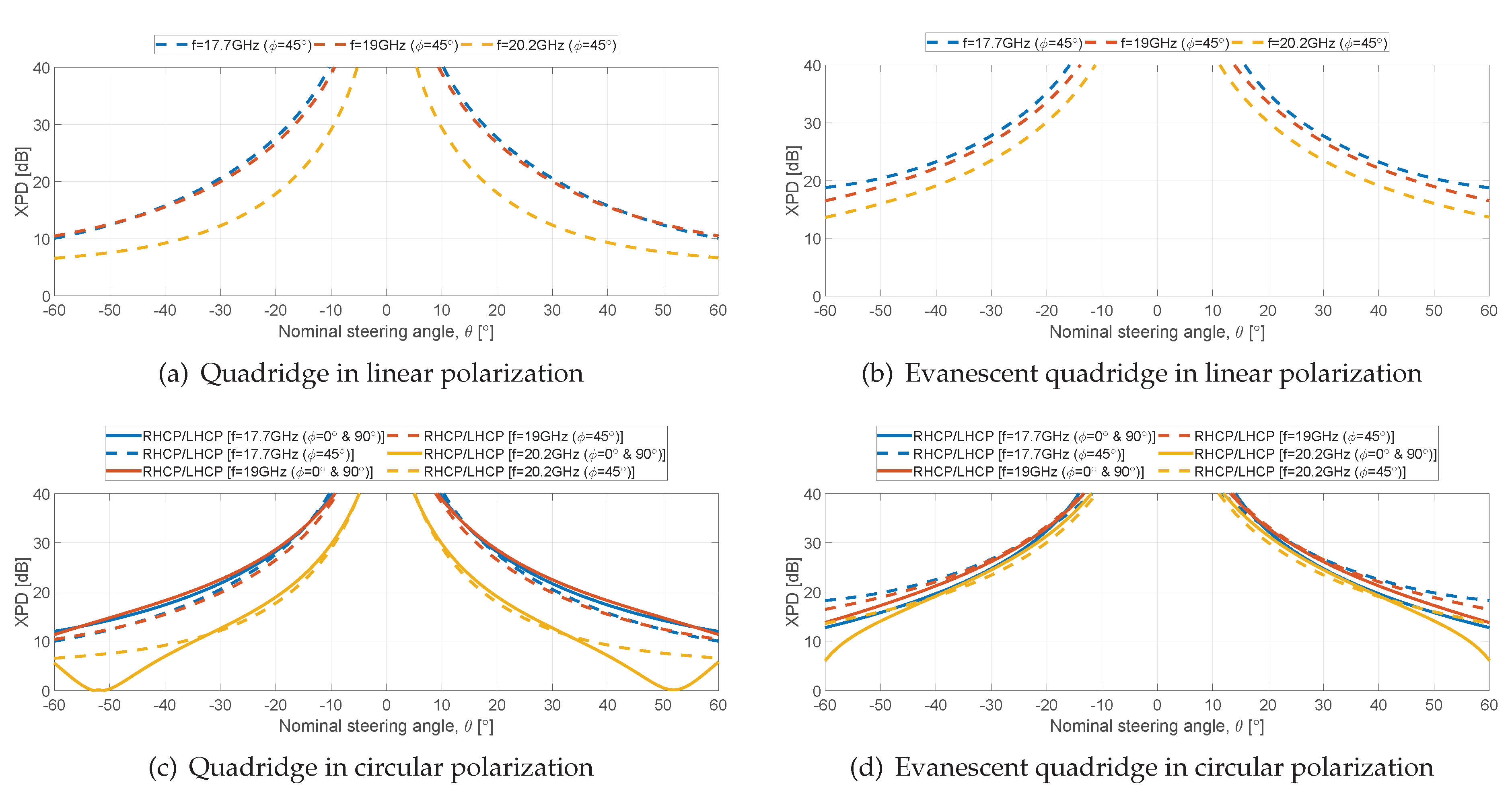
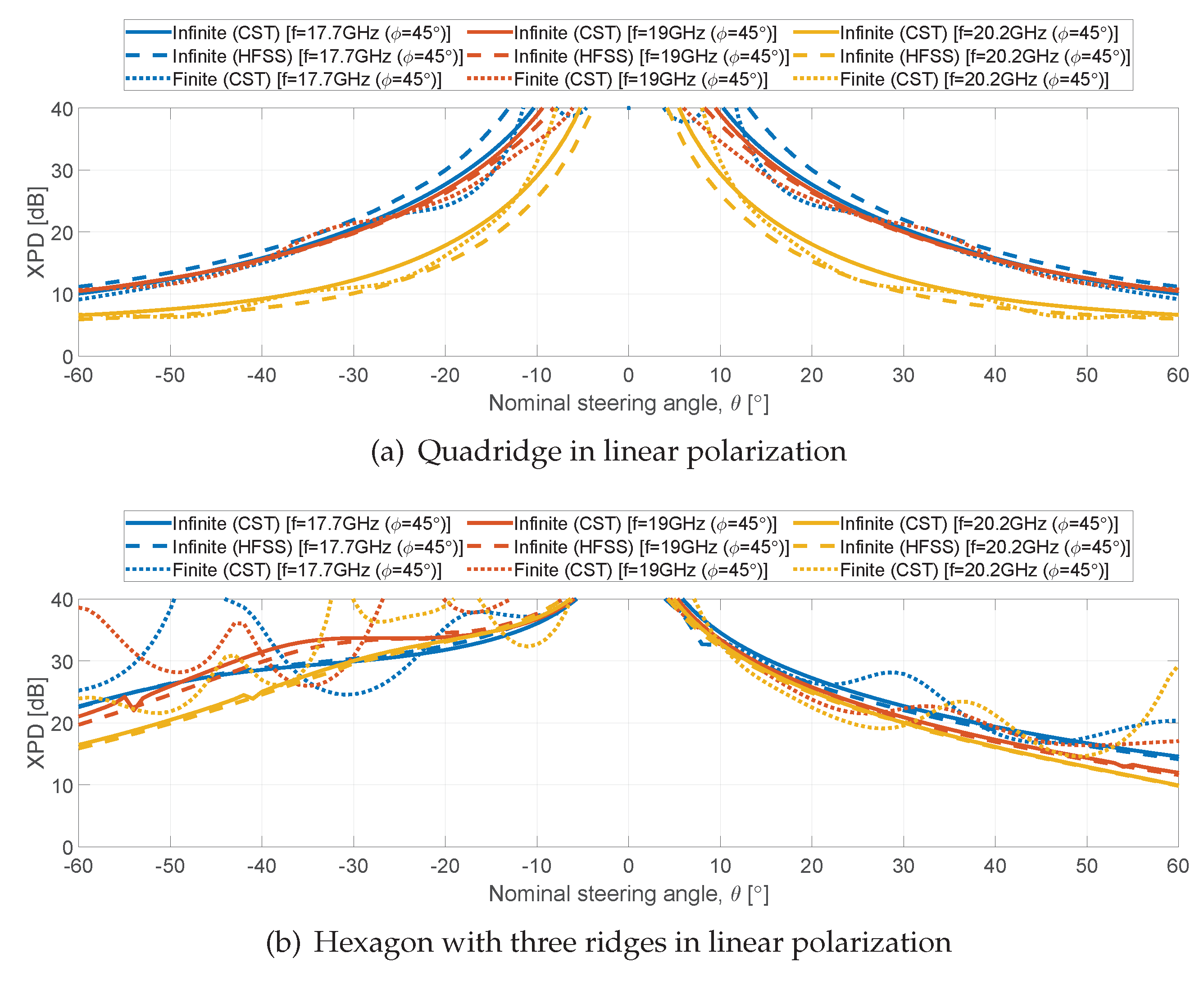
The XPD performance in D-plane (Ludwig 3) is shown in Figure 11. The E- and H-planes are not reported due to the two-fold symmetry (the simulated values are above 40 dB). Circular polarization data have been computed as the ratio between the Equations (4) and (5), and Equations (6) and (7). The quadridge in linear polarization (Figure 11(a)) provides values around 10 dB at 17.7 and 19 GHz, and a value of about 7 dB at the upper frequency. The presence of the blindness is clearly visible in circular polarization (Figure 11(c)), where XPD approaches 0 dB. This happens because one of the two linear components is completely reflected and hence the radiated field is linearly polarized. The values at the scan limits improve for the evanescent quadridge, being higher than 14 dB for the three frequencies in linear polarization (Figure 11(b)). In terms of circular polarization (Figure 11(d)), there is a decrease at 20.2 GHz in the planes ϕ = 0 ∘ / 90 ∘ . This is due to the different radiation patterns for the two principal polarizations at high scan angles, as it can be seen comparing solid and dotted lines in Figure 10(b) (see Equations (4)–(7)).

4.2. Hexagonal Ridged Radiating Elements

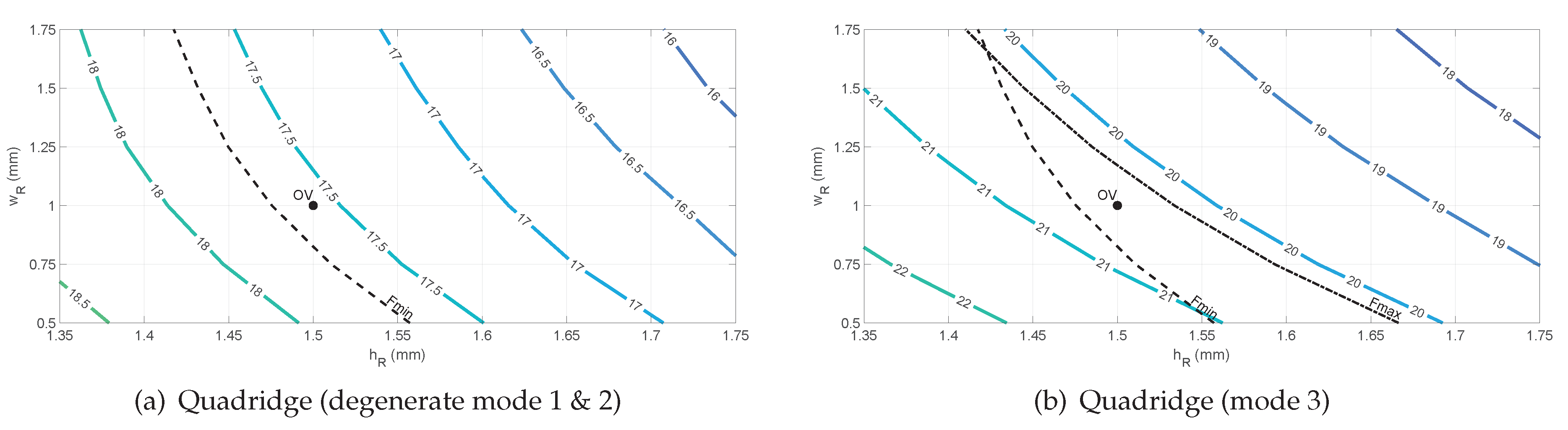
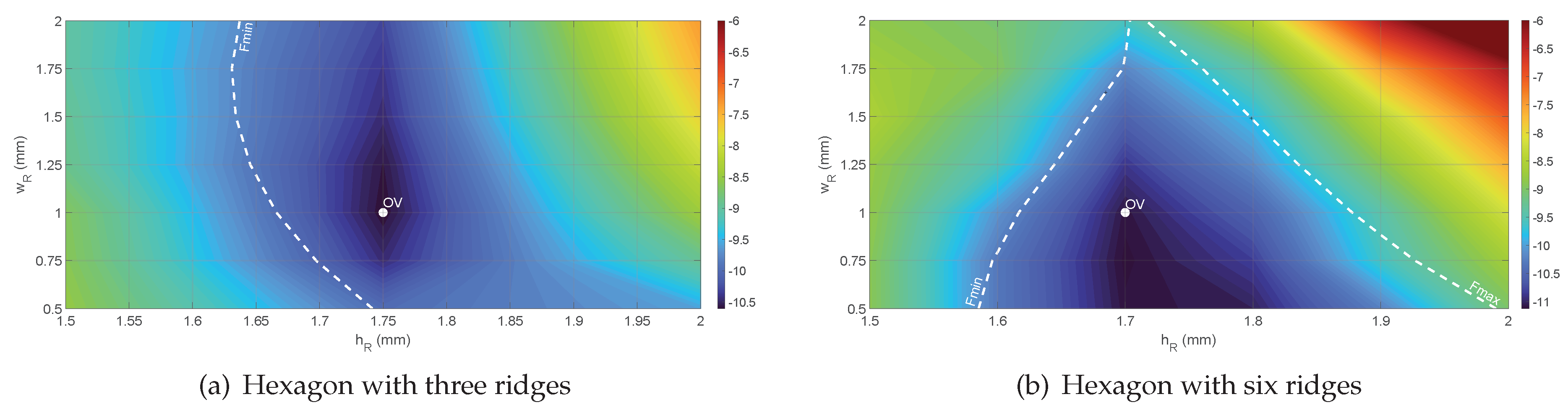
Differently from the quadridge, where the optimum value (OV) of the ridge dimensions was selected on the basis on the cut-off analysis only, the hexagonal structures allow a larger range of parameters (see Section 3.2). For this reason, full-wave analyses have been carried out to determine the OVs for the three and six ridges configurations. Figure 12 shows the contour plots of ARC averaged on scan range as a function of the ridge parameters. For both configurations, where the optimal region is apparent, the selected OVs are shown in Table 2. The manufacturing constraint of 1 mm for the ridge width has been also considered. The optimum values for the hexagon with three ridges (Figure 12(a)) are 1 mm and 1.75 mm for width and height, respectively. The resultant cut-off frequencies are 17.4 GHz and 30.7 GHz for the fundamental and higher-order modes. In the case of six ridges (Figure 12(b)), optimum values are 1 mm and 1.7 mm for width and height, respectively. In this case, cut-off frequencies are 17.4 GHz and 21.7 GHz for the fundamental and higher-order modes.
The S-Parameters of both hexagonal designs in the E-, D- and H-planes at different scan angles are reported in Figure 13(a,b). No scan blindness is visible due to the high cut-off frequency of the third mode. The worst value is around -4 dB in the H-plane when scanning to the 60   ∘ limit (dotted red line). For smaller scan angles (green and yellow lines), the six-ridges solution provides an improvement of about 2 dB in E- and D-planes above 18.5 GHz. Scattering parameters for the other fundamental mode (S   22 , i.e. other polarization) are similar to S   11 , therefore they are not reported for brevity. S   21 in linear polarization (not shown) is in the order of -10 dB and its effect is accounted in the circular polarization data.
As far as the circular polarization is concerned, both hexagonal designs (Figure 13(c,d)) have similar behaviour. The three-ridges solution has a flatter behaviour due to the higher cut-off frequency of the third mode. The overall levels are similar to the evanescent quadridge one Figure 7(d). The coupling in circular polarization for the hexagon with three ridges is shown in Figure 13(e). The values are below of -10 dB for scanning angles up to 30   ∘ for each principal plane. A value of about -5 dB is obtained at the scanning angle limit for ϕ = 90 ∘ (dotted red line). Comparing Figure 13(c,d), it can be observed that the six-ridges solution exhibits worse performance at the upper frequency limit of the band (i.e. some bandwidth reduction). Again, this is due to lower cut-off frequency of the higher-order mode (21.7 GHz) with respect to the three-ridges counterpart (30.7 GHz). Similar values are obtained for the coupling in circular polarization of the six ridges configuration (Figure 13(f)). In this case, there is less variations between planes. The worst value is obtained at 60   ∘ for ϕ = 90 ∘ (dotted red line), being -5 dB at higher frequencies.
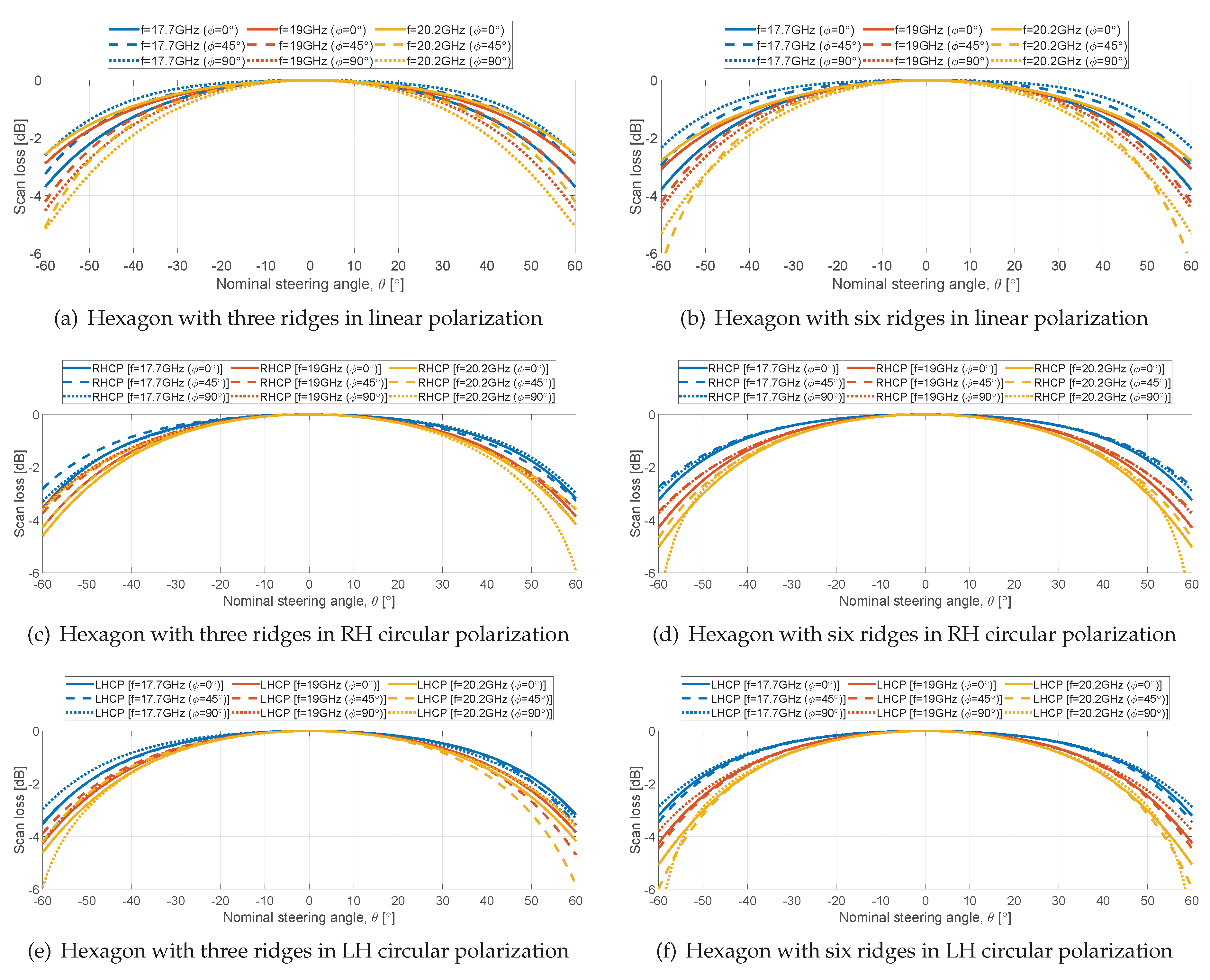
Concerning the scan loss, Figure 14 shows the results of both hexagonal designs within the scan range of -60   ∘ to 60   ∘ in both linear and circular polarization. In terms of linear polarization, both hexagonal apertures (Figure 14(a,b)) show a decay between 2.5 and 3.5 dB at ± 60 ∘ in the E-plane for the three considered frequencies (solid lines). These values increase up to 5 dB for the hexagonal aperture with three ridges and up to 6 dB for the hexagonal aperture with six ridges, in both D- and H-planes (dashed and dotted lines).
Differently from the quadridge structure, the hexagonal waveguide apertures do not have 90   ∘ rotational symmetry. Therefore, a full set of scan loss and XPD data is provided for both left hand (LH) and right hand (RH) circular polarization. For both solutions, the scan loss ranges from 3 to 6 dB (Figure 14(c,e)). Minor differences are visible between the two circular polarizations.
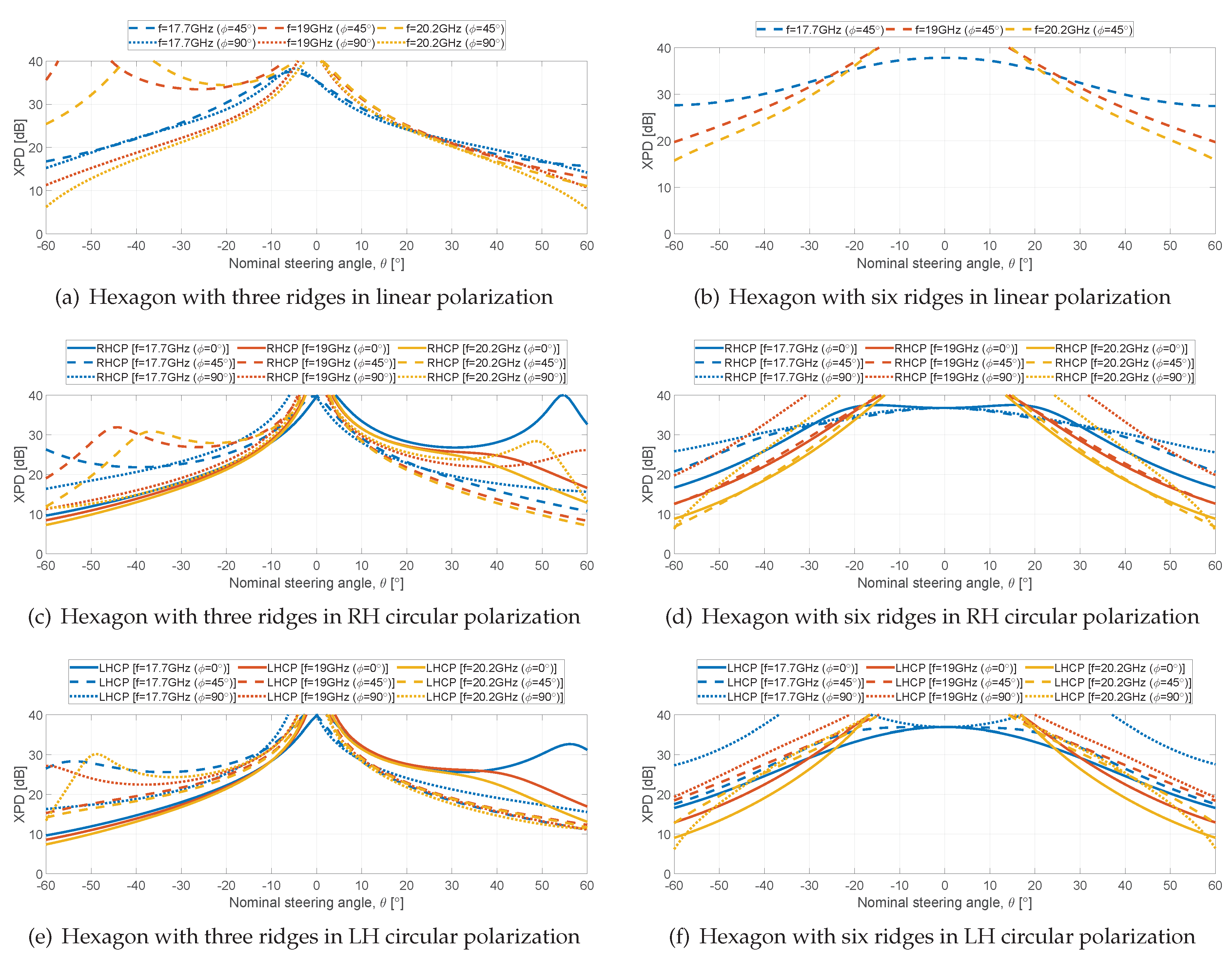
The XPD is reported in Figure 15. The curves for the three-ridged aperture are not symmetrical along the scan range (fig:XPD-lineal-hexagon-threeridges,fig:XPD-circular-hexagon-threeridges1,fig:XPD-circular-hexagon-threeridges2) due to the one-fold symmetry of the geometry. Symmetrical curves are instead observed for the six ridges solution thanks its two-fold symmetry. XPD values ranging from 8 to 10 dB are observed at the scan limits. As already discussed for the quadridge, these values are related to the different behaviour of the structure for the two principal polarizations along the scan planes. It should be noted that the complete scan loss and polarization analyses reported in fig:scanloss-hexagon,fig:XPD-hexagon are required to appreciate the performance variation along the various planes for both polarizations and asses the worst cases.

4.3. Performance Comparison

The performance of the proposed designs is listed in Table 3. The scan angle of 50   ∘ is also reported to provide direct comparison to the literature data. All the data refer to circular polarization.
Reference [5] reports an EQA with a matching section providing acceptable reflection and coupling up to ± 50 ∘ within a bandwidth of 4.5%. The worst case XPD level is only 8 dB.
For the radiated elements presented in this work, no matching section is included. In this way, the reported data show the intrinsic performance of such radiating apertures (open-ended waveguides) i.e. the performance that can be achieved with minimum complexity. The reported data can be used as a reference for the future design of more complex elements including matching discontinuities.
The quadridge without evanescent section has been reported for completeness. However, it is apparent that the scan blindness impairs the overall performance in terms of both reflection (-4 dB) and XPD (0 dB) for high scan angles.
The evanescent quadridge instead provides good performance in terms of matching (-11 dB), scan loss (2 dB) and XPD (14 dB) within 13.2% bandwidth up to 50   ∘ scan angle. The coupling S   21 is -3 dB at the lower limit of the band. Such level is actually -8 dB above 18.5 GHz (see Figure 7(f)).
The hexagon with three ridges reports an improvement on the coupling S   21 (-6 dB) with respect to the evanescent quadridge up to 50   ∘ scan angle. Moreover, acceptable values have been obtained for scan loss (3 dB) and XPD (11 dB).
The hexagon with six ridges shows the best performance in terms of coupling S   21 (-8 dB). The XPD (12 dB), scan loss (3 dB) and matching S   11 (-10 dB) are comparable to the three ridges. The quadridge provides better performance in terms of XPD.
The performance for scan angles of 60   ∘ is not satisfactory for all the elements. The coupling is above -10 dB even at 50   ∘ scan angles. From these considerations, we can conclude that such elements can be suitable for single polarized DRAs (which, to the best of the author’s knowledge are the currently adopted configuration nowadays in LEO satellites) operating up to 50   ∘ scan angles, when the unexcited port is closed on a matched load. This will reduce the element radiation efficiency. However, it will provide a smooth frequency response (without spurious resonances/spikes).

5. Validation

This section provides a validation of the results presented in the paper. Two relevant configurations have been selected i.e. quadridge in square lattice and the hexagon with three ridges in triangular lattice. The quadridge is significant because of its scan blindness. The hexagon with three ridges is interesting because of its one-fold symmetry and the triangular lattice arrangement. The validation has been carried out comparing three sets of results: infinite approach (unit cell) in both CST and HFSS software, and finite array simulation in CST.
For the hexagonal structure, a simple transition with two steps from a smaller waveguide to the aperture has been introduced to avoid overlapping of waveguide ports in the finite array configuration. The same transition has also been included in the infinite simulation for consistency. Therefore, the presented results are slightly different from the ones presented in Section 4.2.
In the infinite approach, a Floquet port has been used instead of the perfect matched layer (PML) due to its better absorption for higher scan angles [26]. Up to 18 Floquet modes have been considered in both lattices for CST. The number of modes in HFSS has been instead increased to 30 and 42 for the square and triangular lattice, respectively, to achieve an attenuation of 50 dB for the last considered mode [27]. In both infinite models, the distance between the Floquet port and the aperture has been set to 0.25 λ 0 at 17 GHz. Both the S-Parameters for ARC and the active element pattern (AEP) for the scan loss and XPD were computed with both simulators.
The unit cell has been replicated in both directions to obtain a finite array model. PML boundary conditions have been applied at a certain distance from the model in all directions including the back. Both the number of elements and the PML distance will be discussed in the convergence analysis reported hereafter. Regarding the S-Parameters, the calculation of the ARC has been performed summing the self contribution of the central element and the coupling from all the other ones with the required weight for beam scanning [28]. The excitation of the central element has been considered to compute the embedded element pattern (EEP). This approach has been preferred over the scan of the whole finite array due to the limited number of elements in a row/column.
Figure 16(a,b) show the convergence analysis of the finite array model and its comparison to the infinite CST one. The most critical condition is θ = 60 ∘ where the scan blindness is present at about 20 GHz for the quadridge in square lattice. This phenomenon is difficult to model with a small finite array simulation where the contribution of the farther elements is missing. Nevertheless, both the red and cyan dashed curves (11x11 and 13x13, respectively) approach the purple curve (infinite) quite well. The convergence analysis stopped at 13x13 elements due to peak memory (150 GB) and time consumptions (9 hours in a Intel Xeon with two processors at 3 GHz). It can be observed that it is not only necessary to increase the number of elements, but also the PML distance (see yellow and red dashed curves where the PML distance is 0.25 λ and 1.5 λ , respectively, at 17 GHz) to achieve convergence between finite and infinite simulations. Such distance is required to attenuate the evanescent wave interaction occurring at high scan angles.
Figure 17 shows the ARC for the E-plane ( ϕ = 0 ∘ ) for both considered designs using the three simulation methods described above. For the quadridge (Figure 17(a)), the infinite models are in very good agreement at all scan angles. The finite array simulation (11x11) follows the same trend but with the expected discrepancy at 20 GHz. As for the hexagonal waveguide (Figure 17(b)), the larger differences occurs when the reflection level of the infinite array is below -15 dB. An overall agreement is achieved between curves confirming good consistency of the results. This analysis is also useful to asses the minimum number of elements that should be considered for array prototyping. This number is smaller than 48x48 discussed in Section 2.
Figure 18 shows the scan loss across D-plane at three frequencies ranging from 17.7 GHz to 20.2 GHz within ± 60 ∘ scan angle. The three different methods are presented with solid, dashed and dotted curves (see legend). A remarkable agreement is visible for both designs.
A similar comparison is provided for the XPD in Figure 19. Good agreement between the three methods has been achieved for the quadridge. As far as the hexagonal structure is concerned, the infinite methods are in perfect agreement. The finite one shows a consistent trend. However, a significant ripple is visible on such EEP. Additional simulation effort should be carried out to achieve a higher degree of convergence.

6. Conclusions

This work studied open-ended ridged waveguide solutions as array radiating elements for Ka-band downlink (relative bandwidth 13.2%). Both cut-off and full-wave parametrical analyses have been carried out to find optimal design parameters for each structure. ARC, coupling, scan loss and XPD have been determined for both linear and circular polarizations. The impact of cut-off frequencies on the achievable element bandwidth, the presence of blindness and the effect of the structure symmetry on the radiation pattern have been discussed. The validity of the results has been verified by comparing finite and infinite approaches in both CST and HFSS.
Good performance has been achieved in both square and triangular lattices with the evanescent quadridge and three/six-ridges hexagonal waveguide, respectively. All elements show limitations in terms of coupling at high scan angles. Therefore, they will be more suitable for single-polarized DRAs operating up to 50   ∘ scan angles, with a consequent slight reduction of the radiation efficiency due to the power dissipated on the matched load at the unexcited port. In this configuration, they will still provide a smooth frequency response (without spurious resonances/spikes).
Future research on this topic includes the design of suitable transitions/discontinuities for a better matching across the full scan angle. Moreover, modifications of the radiating aperture to improve both XPD and coupling should be investigated to achieve high-performance dual-polarized DRAs.

Author Contributions

Conceptualization, G.V.; data curation, C.V-S. and R.M-R.; formal analysis, C.V-S. and R.M-R.; funding acquisition, G.V.; investigation, G.A., O.P. and G.V.; methodology, G.A., O.P. and G.V.; project administration, G.V.; resources, O.P.; software, G.A.; supervision, G.A. and G.V; validation, G.A., O.P. and G.V.; visualization, C.V-S. and R.M-R.; writing—original draft preparation, C.V-S. and R.M-R.; writing—review and editing, G.A., O.P. and G.V. All authors have read and agreed to the published version of the manuscript.

Funding

Funded by the European Union, under ANTERRA 101072363 HORIZON-MSCA-2021-DN-01. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
LEO Low Earth Orbit
LoS Line of Sight
SatCom Satellite Communications
DRA Direct Radiating Array
EQA Evanescent Quadridge Antenna
ARC Active Reflection Coefficient
XPD Cross-Polar Discrimination
TE Transverse Electric
TM Transverse Magnetic
RH Right Hand
LH Left Hand
PML Perfect Matched Layer
AEP Active Element Pattern
EEP Embedded Element Pattern

References

  1. M. Giordani and M. Zorzi. Non-Terrestrial Networks in the 6G Era: Challenges and Opportunities. IEEE Network 2021, 35, 244–251.
  2. S. K. Rao. Advanced Antenna Technologies for Satellite Communications Payloads. IEEE Transactions on Antennas and Propagation 2015, 63, 1205–1217.
  3. J. C. Lafond et al. Thales Alenia Space multiple beam antennas for telecommunication satellites. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP), The Hague, Netherlands, September 2014. 20 September.
  4. G. Araniti, A. Iera, S. Pizzi and F. Rinaldi. Toward 6G Non-Terrestrial Networks. IEEE Network 2022, 36, 113–120.
  5. L. Polo-López, E. Menargues, S. Capdevila, G. Toso and M. García-Vigueras. Solving Sub-Wavelength Lattice Reduction in Full-Metal Front-Ends for Dual-Polarized Active Antennas. IEEE Transactions on Antennas and Propagation 2022, 70, 7413–7426.
  6. J. A. Vásquez-Peralvo et al. Flexible Beamforming for Direct Radiating Arrays in Satellite Communications. IEEE Access 2023, 11, 79684–79696.
  7. X. Liang, Z. Zhang, J. Zeng, F. Guan, X. Liu and J. Zi. Scan Blindness Free Design of Wideband Wide-Scanning Open-Ended Waveguide Phased Array. IEEE Access 2021, 9, 68127–68138.
  8. H. H. Kähkönen, J. Ala-Laurinaho and V. Viikari. A Modular Dual-Polarized Ka-Band Vivaldi Antenna Array. IEEE Access 2022, 10, 36362–36372.
  9. R. W. Kindt and J. T. Logan. Benchmarking Ultrawideband Phased Antenna Arrays: Striving for Clearer and More Informative Reporting Practices. IEEE Antennas and Propagation Magazine 2018, 60, 34–37.
  10. A. Barka, A. De Oliveira Cabral and A. Dorlé. Manufacture and Measurement of Circularly Polarized Ka-Band Radiating Elements for SatCom Wide-Angle Phased Arrays Tiles. In Proceedings of the 2023 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Venice, Italy, October 2023.
  11. P. Gorski, M. C. Vigano and D. Llorens del Rio. Developments on phased array for low-cost, high frequency applications. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, March 2017.
  12. T. Jaschke, H. K. Mitto and A. F. Jacob. An SIW fed dual-band and dual-polarized lens antenna at K/Ka-band. In Proceedings of the 2017 47th European Microwave Conference (EuMC), Nuremberg, Germany, October 2017.
  13. J. Montgomery. Ridged waveguide phased array elements. IEEE Transactions on Antennas and Propagation 1976, 24, 46–53. [CrossRef]
  14. SWISSTO12 SA, E. Menargues Gomez. Radiofrequency module (Patent No. WO2019229515A1). European Patent Office. 2019.
  15. R. Montoya-Roca, C. Vazquez-Sogorb, G. Virone and G. Addamo. Array Elements for LEO SatCom Payloads. In Proceedings of the 2023 IEEE Conference on Antenna Measurements and Applications (CAMA), Genoa, Italy, November 2023.
  16. C. Vazquez-Sogorb, R. Montoya-Roca, G. Addamo, O. Peverini and G. Virone. Multi-Beam Arrays for Future LEO SatCom Payloads. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, United Kingdom, March 2024.
  17. E. Menargues, M. García-Vigueras, S. Capdevila, P. Angeletti and G. Toso. Meandered Waveguides for Active Antennas. In Proceedings of the 15th European Conference on Antennas and Propagation (EuCAP), Dusseldorf, Germany, 2021.
  18. THALES SA, T. Girard, M. Etcharren & A. Cot. Antenna source for an array antenna with direct radiation, radiating panel and antenna comprising a plurality of antenna sources (Patent No. EP4012834A1). European Patent Office. 2022.
  19. F. A. Dicandia and S. Genovesi. Exploitation of Triangular Lattice Arrays for Improved Spectral Efficiency in Massive MIMO 5G Systems. IEEE Access 2021, 9, 17530–17543.
  20. R. L. Haupt. Array Factor Analysis. In Antenna Arrays: A Computational Approach. Wiley-IEEE Press, Hoboken, NJ, USA.2010.
  21. G. Addamo et al. 3-D Printing of High-Performance Feed Horns From Ku- to V-Bands. IEEE Antennas and Wireless Propagation Letters 2018, 17, 2036–2040.
  22. SWISSTO12 SA, E. Menargues Gomez, T. Debogovic, S. Capdevila Cascante & E. De Rijk. Radiofrequency component having a plurality of waveguide devices provided with ridges (Patent No. WO2020194270A1). European Patent Office. 2020.
  23. O. A. Peverini et al. On-board calibration system for millimeter-wave radiometers based on reference-polarized signal injection. IEEE Transactions on Microwave Theory and Techniques 2006, 54, 412–420. [CrossRef]
  24. R. Orta, I. P. Savi and R. Tascone. Numerical Green’s function technique for the analysis of screens perforated by multiply connected apertures. IEEE Transactions on Antennas and Propagation 1996, 44, 765–776.
  25. CST Studio Suite. High Frequency Simulation. Version 2020.0 - 8/16/2019.
  26. A. Bhattacharyya. Introduction to Floquet Modes in Infinite Arrays. In Phased Array Antennas: Floquet Analysis, Synthesis, BFNs, and Active Array Systems Wiley-Interscience, Hoboken, N.J.; y John Wiley & Sons, Inc. USA, 2006; pp. 61–83.
  27. ANSYS, Inc. Getting Started with HFSS: Floquet Ports. Release 2020 R2 - July 2020.
  28. A. Bhattacharyya. Finite Array Analysis Using Infinite Array Results: Mutual Coupling Formulation. In Phased Array Antennas: Floquet Analysis, Synthesis, BFNs, and Active Array Systems Wiley-Interscience, Hoboken, N.J.; y John Wiley & Sons, Inc. USA, 2006; pp. 129–156.
Preprints 111028 g001
Figure 1. Open-ended ridged waveguide elements in square and triangular lattices.
Figure 1. Open-ended ridged waveguide elements in square and triangular lattices.
Preprints 111028 g001
Preprints 111028 g002
Figure 2. Lattice geometry.
Figure 2. Lattice geometry.
Preprints 111028 g002
Preprints 111028 g003
Figure 3. Proposed quadridge waveguide aperture for square lattice array.
Figure 3. Proposed quadridge waveguide aperture for square lattice array.
Preprints 111028 g003
Preprints 111028 g004
Figure 4. Cut-off frequency map for the quadridge waveguide. OV indicates the optimum value.
Figure 4. Cut-off frequency map for the quadridge waveguide. OV indicates the optimum value.
Preprints 111028 g004
Preprints 111028 g005
Figure 5. Proposed hexagonal ridged waveguide elements for triangular lattice array.
Figure 5. Proposed hexagonal ridged waveguide elements for triangular lattice array.
Preprints 111028 g005
Preprints 111028 g006
Figure 6. Cut-off frequency map for the hexagonal waveguide. OV indicates the optimum value.
Figure 6. Cut-off frequency map for the hexagonal waveguide. OV indicates the optimum value.
Preprints 111028 g006
Preprints 111028 g007
Figure 7. S-Parameters for both quadridge designs. The dashed lines indicate the cut-off frequencies and the green box the operative frequency band.
Figure 7. S-Parameters for both quadridge designs. The dashed lines indicate the cut-off frequencies and the green box the operative frequency band.
Preprints 111028 g007
Preprints 111028 g008
Figure 8. Evanescent quadridge waveguide geometry.
Figure 8. Evanescent quadridge waveguide geometry.
Preprints 111028 g008
Preprints 111028 g009
Figure 9. Scan blindness effect on the ARC depending on the evanescent length at ϕ = 0 ∘ and θ = 60 ∘ .
Figure 9. Scan blindness effect on the ARC depending on the evanescent length at ϕ = 0 ∘ and θ = 60 ∘ .
Preprints 111028 g009
Preprints 111028 g010
Figure 10. Scan loss for both quadridge designs.
Figure 10. Scan loss for both quadridge designs.
Preprints 111028 g010
Preprints 111028 g011
Figure 11. XPD for both quadridge designs.
Figure 11. XPD for both quadridge designs.
Preprints 111028 g011
Preprints 111028 g012
Figure 12. ARC averaged on scan range as a function of the ridge parameters. OV indicates the optimum value.
Figure 12. ARC averaged on scan range as a function of the ridge parameters. OV indicates the optimum value.
Preprints 111028 g012
Preprints 111028 g013
Figure 13. S-Parameters for both hexagonal designs. The dashed lines indicate the cut-off frequencies and the green box the operative frequency band.
Figure 13. S-Parameters for both hexagonal designs. The dashed lines indicate the cut-off frequencies and the green box the operative frequency band.
Preprints 111028 g013
Preprints 111028 g014
Figure 14. Scan loss for both hexagonal designs.
Figure 14. Scan loss for both hexagonal designs.
Preprints 111028 g014
Preprints 111028 g015
Figure 15. XPD for both hexagonal designs.
Figure 15. XPD for both hexagonal designs.
Preprints 111028 g015
Preprints 111028 g016
Figure 16. Effect of the number of radiating elements and PML distance for the converge of finite array against infinite approach.
Figure 16. Effect of the number of radiating elements and PML distance for the converge of finite array against infinite approach.
Preprints 111028 g016
Preprints 111028 g017
Figure 17. ARC convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST. The green box indicates the operative frequency band.
Figure 17. ARC convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST. The green box indicates the operative frequency band.
Preprints 111028 g017
Preprints 111028 g018
Figure 18. Scan loss convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST.
Figure 18. Scan loss convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST.
Preprints 111028 g018
Preprints 111028 g019
Figure 19. XPD convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST.
Figure 19. XPD convergence analysis between infinite approaches in CST and HFSS, and finite array simulation in CST.
Preprints 111028 g019
Table 1. Quadridge element dimensions.
Table 1. Quadridge element dimensions.
Parameter Description Value (mm)
P Period 7.8
a Aperture side 6.8
h R Ridge height 1.5
w R Ridge width 1
l E Evanescent section length 1
Table 2. Hexagon element dimensions.
Table 2. Hexagon element dimensions.
Parameter Description Value (mm)
P Period 9
a Aperture side 8
h R 1 Ridge height (three ridges) 1.75
w R 1 Ridge width (three ridges) 1
h R 2 Ridge height (six ridges) 1.7
w R 2 Ridge width (six ridges) 1
Table 3. Performance comparison between proposed designs. All the data refer to circular polarization.
Table 3. Performance comparison between proposed designs. All the data refer to circular polarization.
Radiating element Lattice BW (%) Scan
angle, θ
(   ∘ )		 S   11
(dB)		 S   21
(dB)		 Scan
loss
(dB)		 XPD
(dB)
Evanescent quadridge [5] Square 4.5 0 -32 -12 - 32
30 -15 -13 1 15
50 -10 -6 2 8
60 NA NA NA NA
Preprints 111028 i001 Square 13.2 0 -53 -4 - 40
30 -11 -6 2 12
50 -4 -6 9 0
60 -3 -7 7 6
Preprints 111028 i002 Square 13.2 0 -41 -3 - 40
30 -18 -4 1 23
50 -11 -4 2 14
60 -6 -4 5 6
Preprints 111028 i003 Triangular 13.2 0 -35 -8 - 40
30 -21 -9 1 18
50 -11 -6 3 11
60 -8 -4 6 8
Preprints 111028 i004 Triangular 13.2 0 -31 -8 - 40
30 -21 -9 1 25
50 -10 -8 3 12
60 -6 -6 6 6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated