Prerpints.org logo
Preprint
Article

Quantum Transport Through a Quantum Dot Coupled to Majorana Nanowire and Two Ferromagnets With Noncollinear Magnetizations

Altmetrics

Downloads

115

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts
Abstract
We study the electron tunneling (ET) and local Andreev reflection (AR) processes in a quantum dot (QD) coupled to the left and right ferromagnetic leads with noncollinear ferromagnetisms. In particular, we consider that the QD is also side-coupled to a nanowire hosting Majorana bound states (MBSs) at its ends. Our results show that when one mode of the MBSs is coupled simultaneously to both spin-up and spin-down electrons on the QD, the height of the central peak is quite different from that if the MBS is coupled to only one spin component electrons. The ET and AR conductances which are mediated by the dot-MBS hybridization strongly depend on the angle between the left and right magnetic moments in the leads, which result in sign change of the angle-dependent tunnel magnetic resistance. This result is very different from case when the QD is coupled to regular fermonic mode, and can be used for detecting the existence of MBSs, a current challenge in condensed matter physics under extensive investigations.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

With the rapid development of information technology, there is a growing demand for information storage setups possessing faster response speed, lower energy consumption, and higher integration density. This is then continuously challenging the control methods and hosting materials of electrons’ spin degree of freedom in addition to their charge counterpart. In this context, much recent work has been devoted to the research subject of non-collinear magnetoelectronics, [1,2,3] regarding to the manipulation of electron transport by the configuration changes of the magnetic moments in ferromagnetic [4,5,6,7,8], antiferromagnetic [9,10], or ferrimagnetic [11,12] multilayers and tunnel junctions. In metallic ferromagnets, the differences between electronic bands and tunneling rates of electrons for majority and minority spins at the Fermi energy induce spin-dependent mobilities, and the directions of the magnetic moments in different ferromagnets are either parallel or antiparallel to each other. In the presence of applied electric fields and weak spin-flip scattering processes, a two-channel resistor model can be applied to explain the transport processes and spin-up and spin-down currents flow in parallel. When the magnetic moments of two ferromagnets are in noncollinear configuration (i.e., neither parallel nor antiparallel), the injected spin currents are also noncollinear and may induce spin states in the ferromagnets or the spacer between them pointing in arbitrary directions [1,2,3,7,8], which is tunable by the device materials and noncollinearity angles. Correspondingly, the spin states prepared in the device and the spin currents transport through the system can be effectively modulated via the relative angles between the magnetic moments, and thus the instruments is called evocatively as spin valves.
Noncollinear ferromagnetic materials bring about unique physical phenomena that are absent in collinear ones, such as the interesting magnetoelectric coupling between the noncollinear spin states and spin spiral order, which may lead to the simultaneous broken of both spatial inversion symmetry and the time-reversal symmetry [1,2,8,9,11,13,14]. It was shown that in system composed of a quantum dot (QD) sandwiched between the left and right ferromagnetic leads with noncollinear magnetizations (FM-QD-FM), the spin valve effect can serve as an effective modulation means of the subtle Kondo resonance, resonant tunneling and Coulomb blockade phenomena because the spin-polarized current carried by transport processes is variable by changing both the spin polarization and magnetizations of the ferromagnets [4,5,15,16,17,18]. The spin polarization and noncollinearity of the spin valve strongly affects the photon-assisted tunneling and thermoelectric processes when the FM-QD-FM is driven by a high-frequency ac voltage bias [19].
In recent investigations, although as two conventionally antagonistic phenomena, the combination of ferromagnetism and superconductivity has attracted much attention since several intriguing novel effects emerge in the superconductor/ferromagnet heterostructures. It was found that a ferromagnetic nanowire can be driven to a nontrivial chiral topological superconducting state when it is deposited on a spin-orbit coupled superconducting substrate, and then a pair of Majorana bound states (MBSs) may be prepared at the ends of the nanowire [20]. The massless and neutral MBSs are of their own antiparticles, and topologically protected. These exotic characters enable them promising in fault-tolerant quantum computation [21,22,23]. Since the MBSs are realizable in superconductor/ferromagnet heterostructures in the absence of magnetic fields generally required in most of other schemes [21], many similar platforms were put forward in recent years, such as unconventional superconductor/ferromagnet heterostructures [24], ferromagnetic wires in proximixed to conventional superconductors [25] and ferromagnetic chains with magnetic impurities deposited on top of conventional superconductors [26]. Ferromagnetic metallic nanowire sandwiched between two conventional superconductors in proximity to ferromagnetic insulators were also proposed in theory to prepare the MBSs, a platform free from spin-orbit interaction and relies on the interplay of the supercurrents and exchange fields arising from the ferromagnetic insulators [27,28]. Very recently, it was found that topological superconductors with Majorana flat edge mode can be realized when noncollinear magnetic textures are in contact with the s-wave superconductor [29].
In view of the successful applications of superconductor/ferromagnets heterostructures in preparation and manipulation of MBSs, here we study quantum transport through a QD simultaneously coupled to a nanowire hosting MBSs and two ferromagents individually acting as source and drain leads (FM-MQD-FM in Figure 1). One of the motivations of the present paper is to exploit the possibility of detecting the existence of MBSs, an unsolved research issue yet [21,30,31,32,33], by means of transport quantities related to materials’ magnetization, such as the tunnel magnetoresistance (TMR) [11,15,17,18,34,35,36]. To distinguish the unique properties induced by the presence of MBSs, we compare the results obtained in this FM-MQD-FM with those when the QD is coupled to regular fermonic zero mode, such as another QD, a system denoted by FM-TDQDs-FM. Our numerical results find that the Andreev reflection (AR) processes induced by the MBSs exert strong impacts on the linear conductance and TMR, while leave the electron tunneling (ET) processes almost unchanged. The resonant peak value mediated by the MBSs in the presence of ferromagnetic leads are quite different from that when the QD is coupled to normal metallic leads. Especially, both the linear conductance and TMR are sensitive to the relative angles between the leads’ magnetizations. The TMR can even change its sign by the dot-MBS coupling, which is beyond the reach of coupling between QD and regular fermionic mode under similar parameters. This phenomenon thus may serve as detection method for the existence of MBSs. The present system is realizable within current nanofabrication technologies and may find use in superconductor/ferromagnets devices.

2. Model and Method

The structure studied here is described by the Hamiltonian of H = H Q D + H l e a d s + H M N W s + H T [4,5,36,37,38], in which
H Q D = ε d ∑ σ d σ † d σ ,
H l e a d s = ∑ α = L , R ; k , σ ε α k σ c α k σ † c α k σ ,
H M N W s = i δ M γ 1 γ 2 + ∑ σ λ σ ( d σ − d σ † ) γ 1 ,
H T = ∑ k , σ [ V k L σ c k L σ † d σ + V k R σ ( cos θ 2 c k R σ † + σ sin θ 2 c k R σ ¯ † ) d σ + H . c . ] ,
where the creation (annihilation) operator d σ † ( d σ ) is for electrons in the QD with spin-independent energy level ε d , which is tunable via gate voltage. The energy of conduction electrons with spin direction σ = ↑ , ↓ and wave vector k in lead α is denoted by ε α k σ = ε α k + σ M α , where M α is the amplitude of the magnetic moment in lead α [4,5]. In the present paper, we assume that the direction of the magnetic moment M → L of the left lead is aligned with the z axis, while that of the right lead M → R has a tilted angle θ with respective to M → L , forming a noncollinear magnetic configuration [4,5,18,19]. The quantity δ M in the Hamiltonian H M N W s is for direct hybridization strength between the MBSs with self-conjugate operators γ 1 , 2 , i.e., γ i = γ i † ( i = 1 , 2 ) , and { γ i , γ j } = 2 δ i , j [37,39,40,41,42]. Here we consider that only one mode of the MBSs γ 1 is coupled to the QD with spin-dependent coupling strength λ σ [38,41,42]. The Hamiltonian H T in Eq. (1) describes tunneling between the QD and the leads with amplitude of V k α σ . To proceed, we make make an unitary transformation to change the Majorana fermion representation to a conventional fermion one [37,41,42], f = ( γ 1 + i γ 2 ) / 2 and f † = ( γ 1 − i γ 2 ) / 2 . Then the total Hamiltonian is rewritten in a matrix form to calculate the Green’s functions needed for the electrical current through the QD. In the basis of Ψ † = ( d ↑ † , d ↓ , d ↓ † , d ↑ , f † , f ) , the retarded Green’s function is calculated from the Dyson equation method as [37,41,42,43]:
G r = g r + g r Σ r G r ,
in which g r is the retarded Green’s function of the isolated QD and MBSs and Σ r represents the self-energy due to QD-leads and QD-MBS couplings. The diagonal g r is given by,
g r = diag ( ε − ε d , ε + ε d , ε − ε d , ε + ε d , ε − δ M , ε − δ M ) − 1 ,
while Σ r is
Σ r = Σ L r + Σ R r Λ Λ T 0 .
The self-energy Σ L / R r is contributed from coupling between the QD and the left/right ferromagnetic lead, with [4,19,43]
Σ L r = − i 2 diag ( Γ L ↑ , Γ L ↓ , Γ L ↓ , Γ L ↑ ) ,
where Γ L σ is the spin-dependent coupling strength defined by Γ L σ = 2 π ρ L σ | V k L σ | 2 with ρ L σ the density of states of spin σ band in the left ferromagnetic lead. The matrix elements of Σ R r are individually given by [4,19,43] Σ R ; 11 r = Σ R ; 44 r = cos 2 θ 2 Γ R ↑ + sin 2 θ 2 Γ R ↓ , Σ R ; 22 r = Σ R ; 33 r = cos 2 θ 2 Γ R ↓ + sin 2 θ 2 Γ R ↑ , Σ R ; 13 r = Σ R ; 31 r = Σ R ; 24 r = Σ R ; 42 r = sin θ 2 ( Γ R ↑ − Γ R ↓ ) . The coupling strength between the QD and the right lead Γ R σ is defined similarly to that of Γ L σ , i.e., Γ R σ = 2 π ρ R σ | V k R σ | 2 . The self-energy due to the dot-MBS coupling is as follows [37,38,40,41,42]
Λ = 1 2 − λ ↑ − λ ↑ λ ↓ λ ↓ − λ ↓ − λ ↓ λ ↑ λ ↑ ,
and Λ T is the transposed matrix of Λ (here we have assumed that λ σ is real).
To calculate the current flowing through the system, one need also the lesser Green’s function for the electrons on the QD. We then extract the matrix elements in lines and columns from one to four from the Green’s functions in Eq. (2) to form the retarded Green’s function for the QD, i.e., G r = G r ( 1 : 4 ; 1 : 4 ) . The 4 × 4 QD lesser Green’s function is then defined as G < = G r Σ < G a , where G a = ( G r ) † is the advanced Green’s function and Σ < = Σ L < + Σ R < the lesser self-energy contributed from the two leads. By applying the fluctuation-dissipation theorem, one obtains that Σ α < = F α ( Σ α a − Σ α r ) with the advanced self-energy Σ α a = ( Σ α r ) † and [43,44,45]
F α = diag ( f α , f ˜ α , f α , f ˜ α ) ,
where f α = 1 / { exp [ ( ε − μ α ) / k B T ] + 1 } and f ˜ α = 1 / { exp [ ( ε + μ α ) / k B T ] + 1 } are individually the electron and hole Fermi distribution functions in lead α . In the above expression, μ α , T and k B denote chemical potential, system temperature and Boltzmann constant, respectively.
The electronic current J L flowing from the left lead to the QD is obtained in terms of the Green’s functions of G r and G < as [43,44,45,46]
J L = J L ↑ + J L ↓ = e h ∫ d ε [ ( G Σ L ) < + H . c . ] 11 + 33 ,
in which ( G Σ L ) < = G r Σ L < + G < Σ L a , and [ ] 11 + 33 = [ ] 11 + [ ] 33 . In the present paper, we consider that an opposite bias V is applied between the two leads, μ L = − μ R = e V / 2 . In such a case, we have J L = − J R , f L = f ˜ R and only ET and local AR processes are allowed to occur [43,47]. Taking the explicit expressions of the above Green’s functions and self-energies into consideration, the current J L is finally written as
J L = e h ∫ d ε [ T E T ( ε ) + T A R ( ε ) ] ( f L − f R ) ,
in which the transmission of ET transport process is [43,44,45,46]
T E T ( ε ) = ( cos 2 θ 2 Γ R ↑ + sin 2 θ 2 Γ R ↓ ) ( Γ L ↑ | G 11 r | 2 + Γ L ↓ | G 31 r | 2 ) + ( cos 2 θ 2 Γ R ↓ + sin 2 θ 2 Γ R ↑ ) ( Γ L ↑ | G 13 r | 2 + Γ L ↓ | G 33 r | 2 ) + sin θ ( Γ R ↑ − Γ R ↓ ) Re ( Γ L ↑ G 11 r G 13 r * + Γ L ↓ G 33 r G 31 r * ) ,
and
T A R ( ε ) = Γ L ↑ ( Γ L ↑ | G 14 r | 2 + Γ L ↓ | G 34 r | 2 ) + Γ L ↓ ( Γ L ↑ | G 12 r | 2 + Γ L ↓ | G 32 r | 2 ) .

3. Numerical Results

In numerical calculations, the ferromagnetism on the leads is described by the spin-polarization parameter defined as [4,5,18,19] P α = ( Γ α ↑ − Γ α ↓ ) / ( Γ α ↑ + Γ α ↓ ) . We then obtain Γ α σ = Γ α ( 1 + σ P α ) with Γ α = ( Γ α ↑ + Γ α ↓ ) . In the present paper, we consider the case of the two leads are made of the same material having the same spin polarization, i.e., P L = P R = P , and set Γ L = Γ R = Γ to be the energy unit. The spin-up and spin-down dot-MBS coupling strengths are also given with the help of a spin-polarization parameter P M as λ ↑ = λ 0 ( 1 − P M ) and λ ↓ = λ 0 P M [38,41]. Moreover, we consider the zero temperature case which is favorable for the preparation of MBSs. Therefore, the linear conductances are G E T = ( 2 e 2 / h ) [ T E T ( μ ) ] and G A R = ( 2 e 2 / h ) [ T A R ( μ ) ] [47]. In previous work on a spinless QD coupled to normal metal leads, the conductance peak at zero temperature is suppressed to be half of its quantum value e 2 / ( 2 h ) by QD-MBS coupling when the QD is on resonance and symmetrically coupled to the leads [37]. Whereas if the dot is coupled to a regular fermionic zero mode (such as another QD), the conductance is suppressed to be 0 [48,49]. This a strong evidence of the existence of MBSs. One of the main tasks of the present paper is to examine how the conductance is changed when the QD is coupled to ferromagnetic leads, in particular when their magnetic moments are arranged in noncollinear configuration.
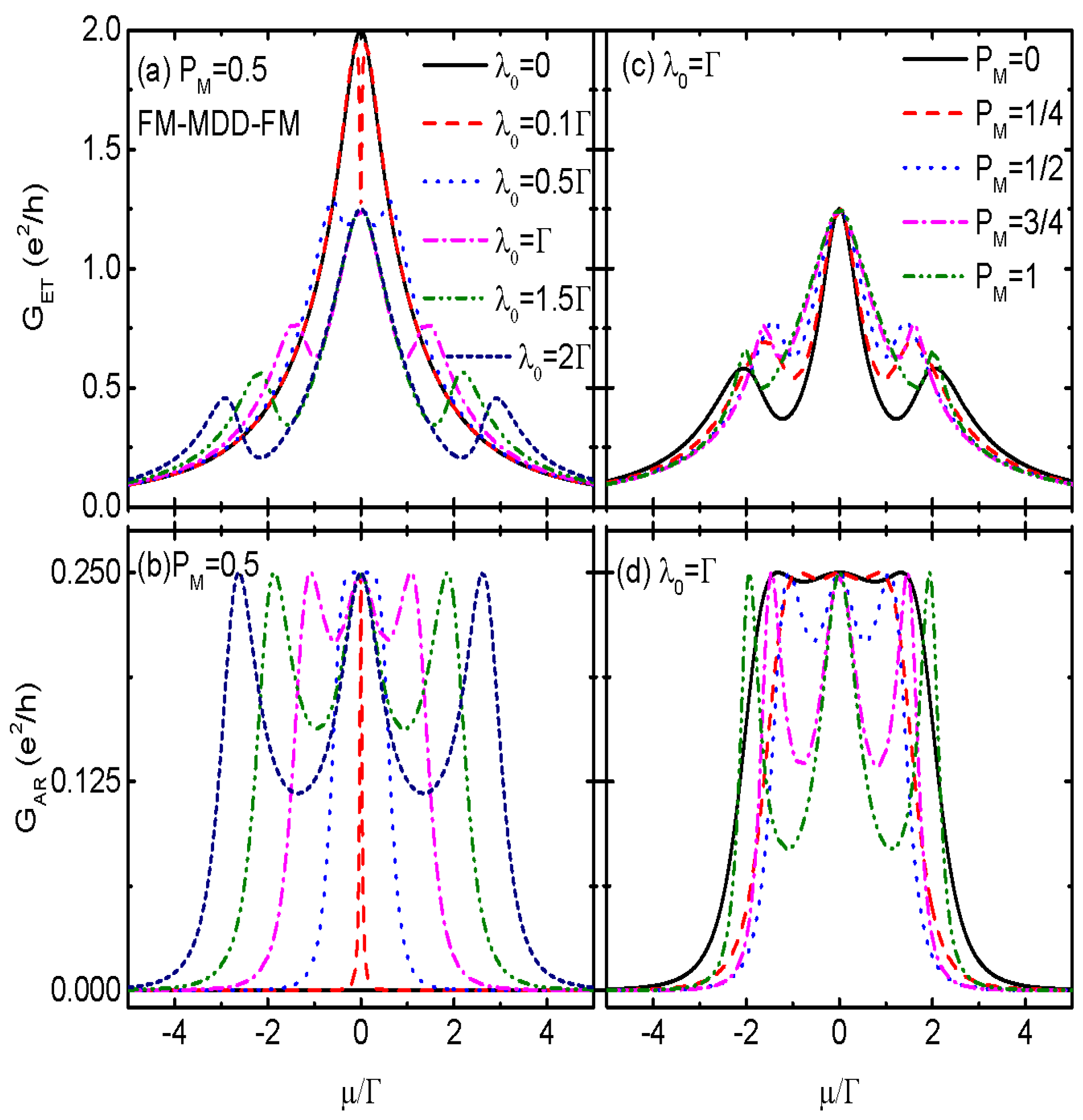
Figure 2 shows G E T and G A R varying with respective to the chemical potential μ under the conditions of θ = 0 , P = 0 . 5 and ε d = 0 . The spin-polarization of dot-MBS coupling is fixed to be P M = 0 . 5 which means that spin-up and spin-down electrons are coupled to the MBS with equal strength, λ ↑ = λ ↓ = λ 0 / 2 . When the QD is decoupled from the MBSs ( λ 0 = 0 ), the system becomes to be FM-QD-FM and the ET conductance is characterized by a single-peak configuration. The central peak value of G E T ( μ = 0 ) reaches its quantum value 2 e 2 / h as indicated by the black solid line in Figure 2a. Now the AR process is absence and G A R = 0 which is shown by the black solid line in Figure 2b [37,47]. Turing on the QD-MBS coupling λ 0 ≠ 0 and the system becomes to be FM-MQD-FM, the conductance peak of G E T in Figure 2a is split and lowered to a fixed value of 1 . 25 e 2 / h . With increasing λ 0 , the peak height of G E T ( μ = 0 ) remains unchanged, with the two satellite peaks locate individually at ε d = ± 2 λ ↑ 2 + λ ↓ 2 . In the presence of dot-MBS coupling, AR process occurs and G A R develops three peaks with equal height of 0 . 25 e 2 / h . Moreover, the peaks’ positions of G A R and G E T are the same. The height of the central peak in total conductance G ( μ = 0 ) = G E T ( μ = 0 ) + G A R ( μ = 0 ) = 1 . 5 e 2 / h . Since now electrons of the two spin directions couple to the MBS with equal strength λ ↑ = λ ↓ , we have G ↑ ( μ = 0 ) = G ↓ ( μ d = 0 ) = 0 . 75 e 2 / h [38], which is quite different from the case when the MBS is coupled to spinless QD in which G ( μ = 0 ) = e 2 / ( 2 h ) [37,47].
In fact, under this simple case, the analytical expression of the spin-dependent total conductance can be obtained as,
G σ = e 2 h Γ σ Γ σ Γ σ ¯ λ σ ¯ 2 + [ ( μ − ε d ) 2 + Γ σ ¯ 2 ] λ σ 2 / 2 [ ( μ − ε d ) 2 + Γ σ 2 ] Γ σ ¯ λ σ ¯ 2 + [ ( μ − ε d ) 2 ) + Γ σ ¯ 2 ] Γ σ λ σ 2 ,
in which Γ σ = ( Γ L σ + Γ R σ ) / 2 . Results presented in Figure 2 are in consistent with the analytical expression of G σ . Note that similar result was also found in system of the QD coupled to nonmagnetic leads and Majorana nanowire [38]. In Figure 2c,d we present G E T and G A R as function of the chemical potential for fixed λ 0 and different values of spin polarization P M . Both of the two conductances remain the triple-peak configurations, and the the peaks’ values at μ = 0 are also fixed as P M is varied. As a result of it, the central peak value of the total conductance G keeps at 1 . 5 e 2 / h regardless of the value of coupling strengths between the dot and the two spin components electrons. Under the conditions of strong asymmetric coupling with P M = 0 and P M = 1 , the values of ( λ ↑ , λ ↓ ) are individually ( λ 0 , 0 ) and ( 0 , λ 0 ) and the MBS couples only to one spin level of the dot. Assuming that spin- σ electrons of the QD is coupled to the MBS, one finds the spin-dependent total conductance G σ ( μ = 0 ) = e 2 / ( 2 h ) which is independent of the dot level and dot-lead coupling strength, and G σ ¯ ( μ = 0 ) = e 2 Γ σ ¯ 2 / [ h ( ε d 2 + Γ σ ¯ 2 ) ] being in consistent with the result in FM-QD-FM [5,19].
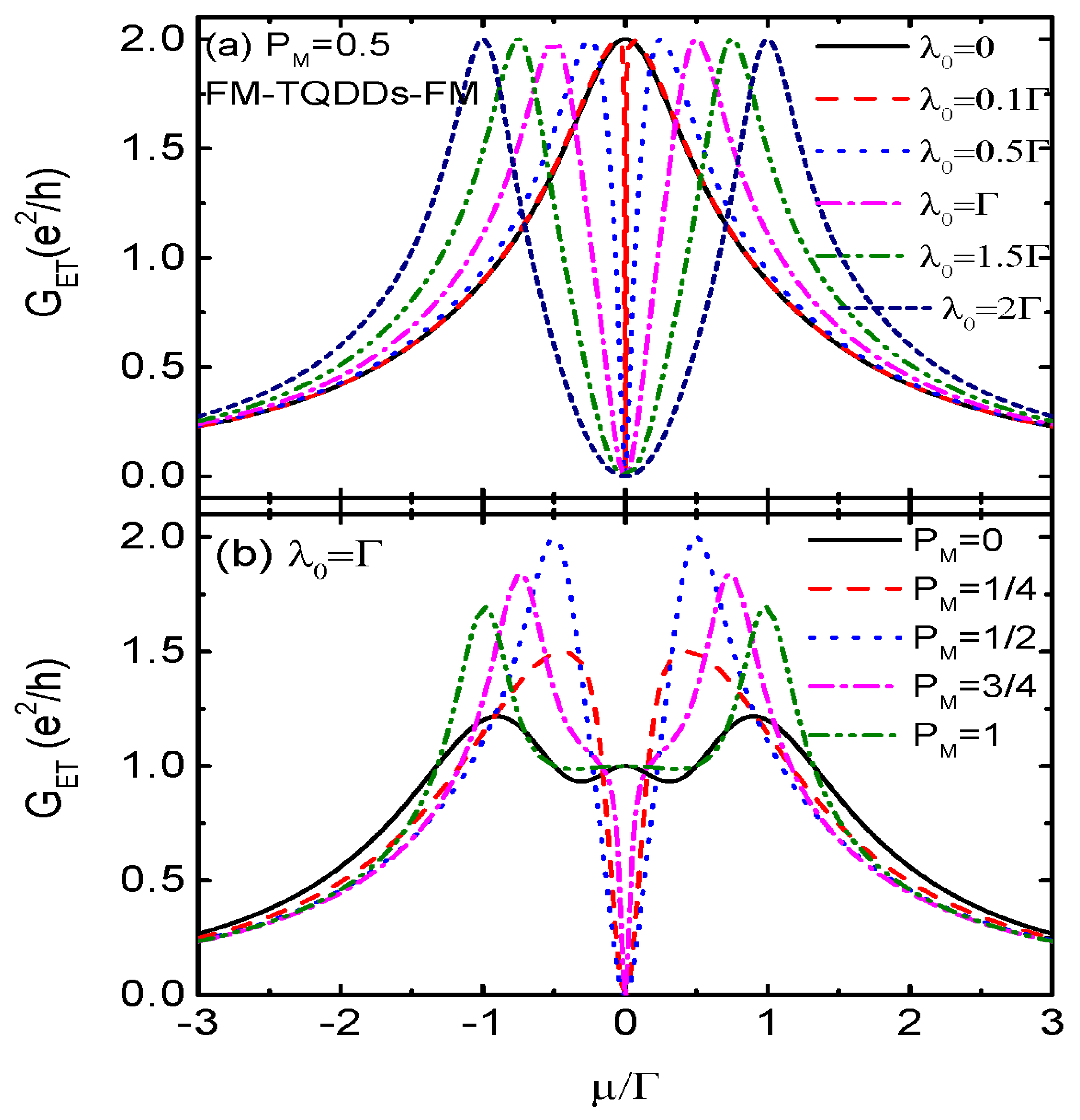
To recognize the exotic characterize in the transport properties brought about by the MBSs, we present in Figure 3 the conductance when the QD is coupled to another one behaving as a regular fermionic zero mode, and forms a T-shaped double QDs (TDQDs) configuration [48,49]. We denote the creation (annihilation) operator, energy level and coupling strength between the dots by the same symbols as those of the MBSs for the sake of consistency, and the Hamiltonian of the TDQDs is written as,
H T D Q D s = ε d ∑ σ d σ † d σ + δ M γ 1 † γ 1 + ∑ σ λ σ ( γ 1 † d σ + d σ † γ 1 ) ,
and the spin-dependent conductance is obtained as
G σ = 2 e 2 h Γ σ 2 ( μ − δ M ) 2 [ ( μ − ε d ) ( μ − δ M ) − λ σ 2 ] 2 + Γ σ 2 ( μ − δ M ) 2 ,
which indicates that G σ ( μ = 0 ) = 2 e 2 / h in the cases of λ 0 = δ M = 0 as is shown by the black solid line in Figure 3a. When the central QD is coupled to another dot ( λ 0 ≠ 0 ), the single peak in G σ is split into two positioned at μ = ( ε d + δ M ) / 2 ± ( ε d − δ M ) 2 / 4 + λ σ 2 , and the dip at μ = 0 is suppressed to be zero. With increasing λ 0 , the heights of the two peaks in G remain unchanged and are shifted toward negative and positive energy regimes, respectively. Note that in this TDQDs, G A R ≡ 0 since the AR process is forbidden. These results are totally different from those of FM-MQD-FM presented in Figure 2a [37,47].
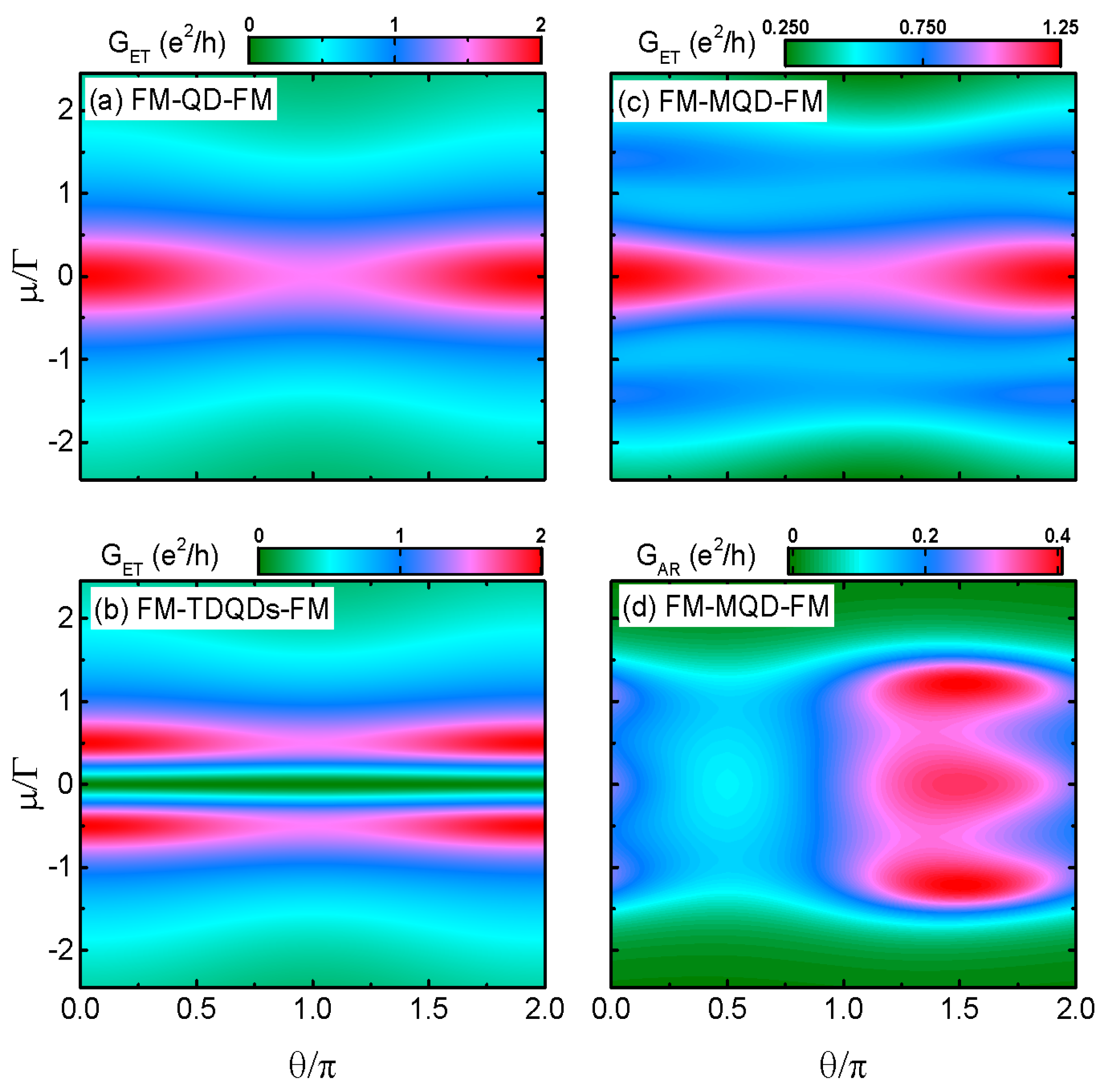
We now study in Figure 4 the angle θ between the magnetizations of the left and right leads on the transport properties. When the QD is decoupled from the Majorana nanowire (configuration of FM-QD-FM), the line-shape of G E T varying with respective to chemical potential μ at θ = 0 in Figure 4a is the same as the black solid line in Figure 2a which is characterized by single-peak configuration. With increasing θ from 0 (parallel configuation) to π (antiparallel configuration), G E T is monotonously suppressed which is the so-called spin valve effect [4,5,18,19]. This is induced by the difference between Γ L σ (ingoing tunneling rate) and Γ R σ (outgoing tunneling rate). When the magnetizations on the two leads are in parallel configuration ( θ = 0 ), Γ L σ = Γ R σ and electrons of both the two spin components will tunnel resonantly from the left lead to the right one through the QD if μ = ε d , and the total conductance reaches its quantum value 2 e 2 / h . For the case of noncollinearity angles θ = π and the two leads are in antiparallel configuration, the ingoing and outgoing tunneling rates of the two spin directions are Γ L ↑ = ( 1 + 0 . 5 ) Γ , Γ R ↑ = ( 1 − 0 . 5 ) Γ , and Γ L ↓ = ( 1 − 0 . 5 ) Γ , Γ R ↓ = ( 1 + 0 . 5 ) Γ . This imbalance between the tunneling rates induces spin accumulation on the QD and suppresses the conductance amplitude. When the angle changes from π to 2 π , the imbalance between the ingoing and outgoing tunneling rates of each spin component is reduced and the conductance is enhanced accordingly. Therefore, in this FM-QD-FM system the conductance obeys the relationship of G E T ( θ ) = G E T ( 2 π − θ ) . As for the FM-TDQDs-FM system, the line-shape of the conductance G E T in Figure 4b also resemble that in Figure 3. There are two Breit-Wigner resonances in G E T and the dip at μ = 0 is suppressed to be zero. Such a behavior of G E T remains unchanged regardless of the value of θ , and also fulfills the the relation of G E T ( θ ) = G E T ( 2 π − θ ) as in system of FM-QD-FM.
It is shown in Figure 4c that the resonant peak of ET conductance in FM-MQD-FM resembles those in FM-QD-FM and FM-TDQDs-FM, except that the peak’s height becomes to be 1 . 25 e 2 / h as in Figure 2. The behaviors of the satellite peaks are also unchanged by the value of θ . As for the AR conductance in Figure 4c, its line-shape is quite different from that of G E T , and the tripe-peak configuration at θ = 0 is changed. Firstly, a dip in G E T ≈ 0 . 1 e 2 / h emerges around θ = π / 2 . Secondly, the triple-peak configuration reappears around θ = 3 π / 2 . Thirdly, the peak value around θ = 3 π / 2 is enhanced about to 0 . 4 e 2 / h other than the value of 0 . 25 e 2 / h for θ = 0 and obeys the relationship of G E T ( θ ) = G E T ( 2 π + θ ) . As a result of it, the dependence of the total conductance in FM-MQD-FM on the noncollinearity angle θ is totally different from those in both FM-QD-FM and FM-TDQDs-FM, and can be used for distinguishing the MBSs from the regular fermionic zero mode.
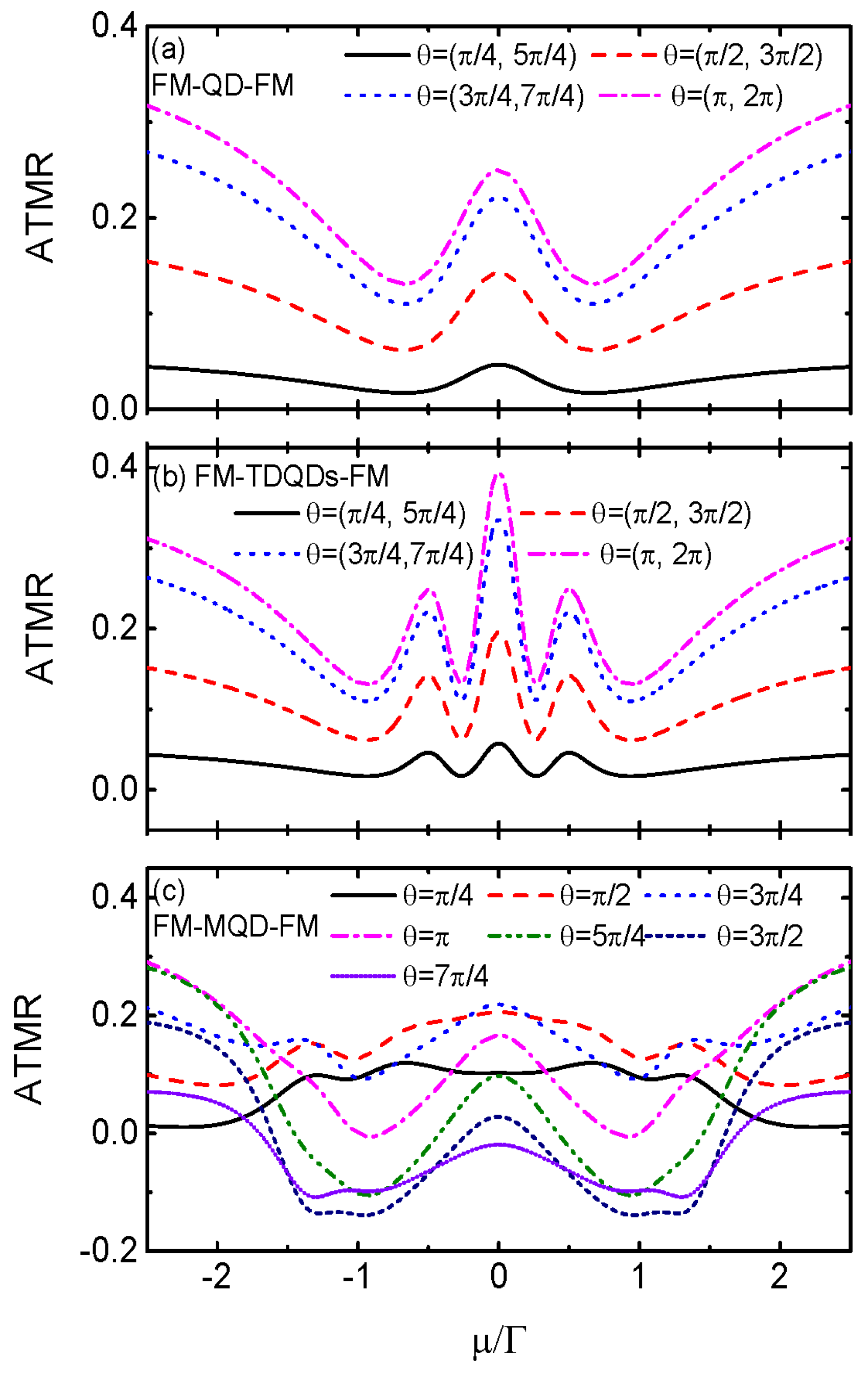
The impacts of the MBSs on the transport processes can also be shown via the angle-dependent TMR (ATMR) besides the conductances [15,17]. Figure 5a presents the ATMR for the case of FM-QD-FM ( λ 0 = 0 ) varying as a function of chemical potential and different values of the noncollinearity angles. The ATMR is positive regardless of the values of the chemical potential and angle θ , and is characterized by a resonant peak centered at μ = 0 . It is monotonously enhanced when the angle is changed from 0 to π , and obeys the relationship of ATMR ( θ ) = ATMR ( 2 π − θ ) [15,17,18]. This is because that the magnitude of the conductance is monotonously suppressed during this process as is compared to the case of θ = 0 . In the system of FM-TDQDs-FM, the behavior of the ATMR in Figure 5b essentially resembles that of FM-QD-FM, but now the central peak is split into three due to the quantum interference effect. When the QD is coupled to MBS as shown in Figure 5c, the ATMR depends on the angle θ nonlinearly and even can change its signs. During the chemical regimes of μ < | λ 0 | , the magnitude of the ATMR essentially first increases and then decreases with increasing θ . For θ > π , the ATMR value may change from positive to negative, which serves as a detection mean for the existence of MBSs. Moreover, the relationship between ATMR and the angle is ATMR ( θ ) = ATMR ( 2 π + θ ) , which is quite different from that in the cases of FM-QD-FM and FM-TDQDs-FM.
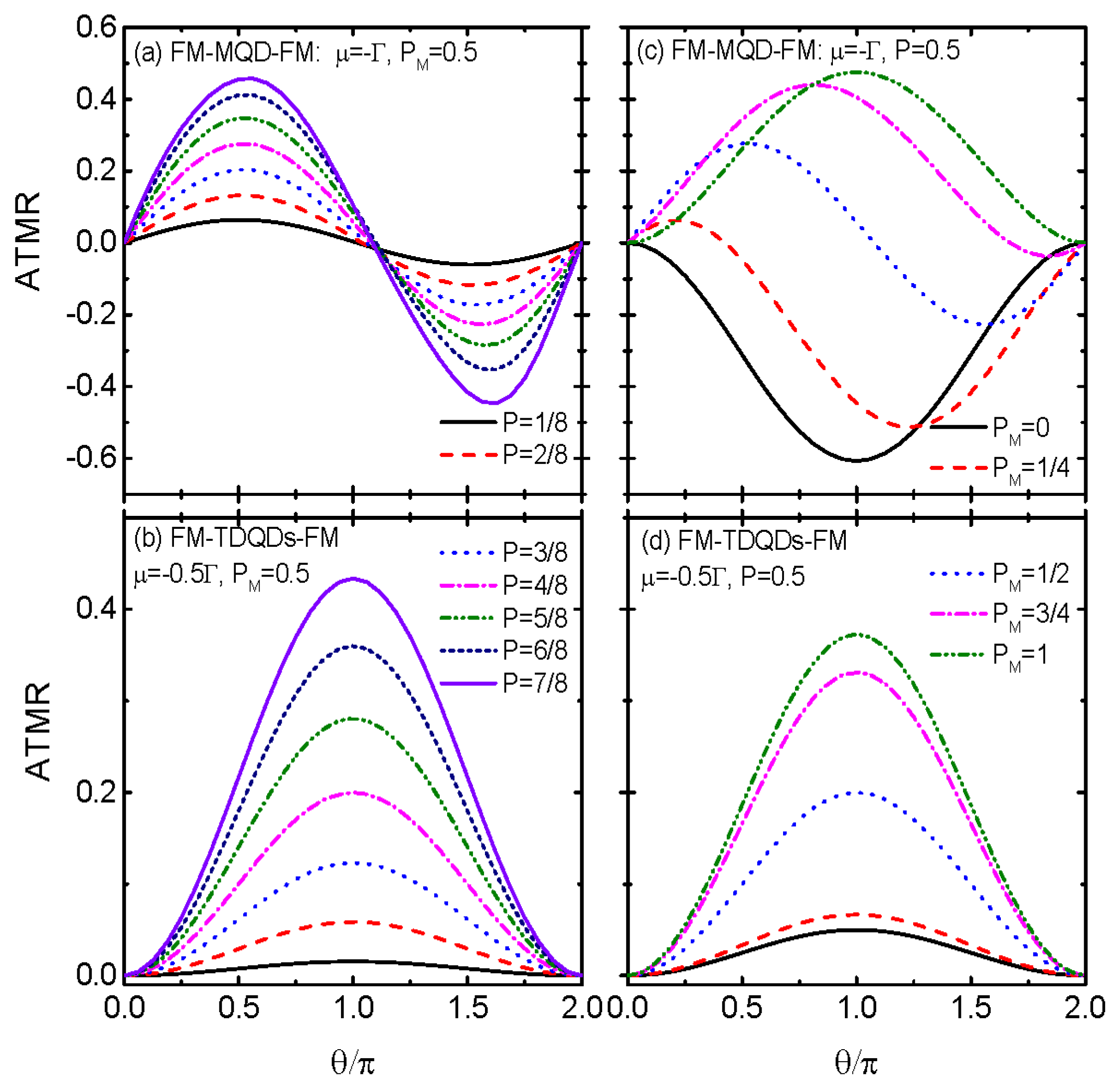
In Figure 6 we fix μ = − λ 0 , around which obvious negative ATMR emerges, and examine the variation of ATMR with respective to the angle θ . When the QD is coupled to MBS as shown in Figure 6a, the ATMR oscillates with respective to θ in the form of a sinusoidal function. With increasing spin-polarization P of the leads, the magnitude of ATMR is enhanced obviously with the sinusoidal line-shape remains unchanged. In contrast, the ATMR of FM-TDQDs-FM in Figure 6b shows a broad Breit-Wigner resonance centered at θ = π , and increases monotonously with increasing P. The enhancement of the ATMR arises from the increased imbalance of the ingoing and outgoing tunnelling rates due to increased spin-polarization of the leads. Figure 6c indicates that the ATMR is negative characterized by a broad Breit-Wigner resonance at θ = π for P M = 0 and λ ↑ = 0 , λ ↓ = λ 0 , i.e., the MBS couples only to spin-down electrons. With increasing P M and the MBS couples to both of the two spin states on the QD, the absolute value of ATMR is suppressed and the resonance position is changed. Interesting, the ATMR in the case of P M = 1 and the MBS couples only to spin-up state on the QD is totally opposite to that of P M = 0 , i.e., ATMR | P M = 1 =-ATMR | P M = 0 . The ATMR for the case of FM-TDQDs-FM in Figure 6d, however, is positive regardless of the value of P M and remains as the single broad peak configuration.

4. Summary

In summary, we studied electronic transport through a QD sandwiched between two ferromagnetic leads with noncollinear magnetizations. We find that when the QD is additionally side-coupled to a semiconductor nanowire hosting MBSs at its ends, the linear conductance and ATMR are significantly changed. When the MBS couples simultaneously to both of the spin states on the QD, the spin-up and spin-down resonant conductance peak value is 0 . 75 e 2 / h but not 0 . 5 e 2 / h previously found in the case of the MBS is coupled to only one spin state. If the QD is coupled to regular fermonic zero mode and when the Fermi level is aligned to the dot level, however, the conductance is suppressed to be zero. We find that the conductance and ATMR in the presence of dot-MBS coupling depends on the noncollinearity angle in a way quite different from the case of the QD interacting with regular fermonic zero mode. It is also found that both the magnitude and sign of the ATMR can be adjusted by the dot-MBS coupling strength and its spin polarization. Such a sign change of the ATMR can hardly emerge in system of the QD coupled to regular fermonic zero mode, where the ATMR remains to be positive and is characterized by a broad Breit-Wigner regime.

Author Contributions

Writing—original draft preparation, Y.M. Gao, F. Chi; writing review and editing, Y. H. Shen, Z.C. Yi, L.M. Liu and F. Chi. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Education Science Planning Project of the Department of Education in Guang-dong Province (no. 2023GXJK542), the Educational Quality Project of the Department of Education in Guang-dong Province of China (no. SJD202302), the Innovation Team of Colleges and Universities in Guangdong Province (Grant No. 2021KCXTD040), Guangdong Province Education Department (Grant No. 2023KTSCX174), the Key Laboratory of Guangdong Higher Education Institutes (Grant No. 2023KSYS011), and Science and Technology Bureau of Zhongshan (Grant No. 2023B2035).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data included in this study are available upon request by contact with the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Brataas, A.; Bauer, G.E.W.; Kelly, P.J. Non-collinear magnetoelectronics. Phys. Rep. 2006, 427, 157. [CrossRef]
  2. Qin, P.X.; Yan, H.; Wang, X.N. et al. Noncollinear spintronics and electric-field control: a review. Rare Met. 2020, 39, 95. [CrossRef]
  3. Xie, H.; Luo, X.; Ye, Z. et al. Evidence of non-collinear spin texture in magnetic moir— superlattices. Nat. Phys. 2023, 19, 1150. [CrossRef]
  4. Sergueev, N.; Sun, Q.F.; Guo, H.; Wang, B.G.; Wang J. Spin-polarized transport through a quantum dot: Anderson model with on-site Coulomb repulsion. Phys. Rev. B 2002, 65, 165303. [CrossRef]
  5. Braun, M, Kong, J, Martinek, J. Theory of transport through quantum-dot spin valves in the weak-coupling regime. Phys. Rev. B 2004, 70, 195345. [CrossRef]
  6. Yuan, Z.; Hals, K.M.D.; Liu, Y. et al. Gilbert Damping in Noncollinear Ferromagnets. Phys. Rev. Lett. 2014, 113, 266603. [CrossRef]
  7. Jimenez-Bustamante, J.; Lindner, A.; Koyun, H.N.; et al. Static and dynamic properties of noncollinear magnetized ferromagnetic films. Phys. Rev. B 2024, 109, 094403. [CrossRef]
  8. Lertzman-Lepofsky, G.; Terko, F.; Koraltan, F. et al. Energy landscape of noncollinear exchange coupled magnetic multilayers. Phys. Rev. B 2024, 109, 224421. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.109.224421.
  9. Huang, J.; Liu, C.; Cui, Y. et al. Non-collinear magnetic configuration mediated exchange coupling at the interface of antiferromagnet and rare-earth nanolayers. Sci. Rep. 2022, 12, 21836. [CrossRef]
  10. Deng, S.; Gomonay, O.; Chen, J. et al. Phase transitions associated with magnetic-field induced topological orbital momenta in a non-collinear antiferromagnet. Nat. Commun. 2024, 15, 822. [CrossRef]
  11. Chen, D.D; Xu, Y.H.; Tong, S.C.; et al. Noncollinear spin state and unusual magnetoresistance in ferrimagnet Co-Gd. Phys. Rev. Materials 2022, 6, 014402. [CrossRef]
  12. Zemen. J. Collinear and noncollinear ferrimagnetic phases in Mn4N investigated by magneto-optical Kerr spectroscopy. J. Appl. Phys. 2023, 134, 203902. [CrossRef]
  13. Yu, S.Q.; Xu, Y.S.;, Dai, Y. et al. Electrical control of noncollinear magnetism in VAl2S4 van der Waals structures. Appl. Phys. Lett. 2024, 124, 212903. [CrossRef]
  14. Wang W.H.; Pan, C.Y.; Liu, C.M. et al. Chirality-Induced Noncollinear Magnetization and Asymmetric Domain-Wall Propagation in Hydrogenated CoPd Thin Films. ACS Appl. Mater. Interfaces 2022, 14, 20151. [CrossRef]
  15. Swirkowicz, R.; Wilczynski, M.; Wawrzyniak, M.; Barnas, J. Kondo effect in quantum dots coupled to ferromagnetic leads with noncollinear magnetizations. Phys. Rev. B 2006, 73, 193312. [CrossRef]
  16. Simon, P.; Cornaglia, P.S.; Feinberg, D.; Balseiro, C.A. Kondo effect with noncollinear polarized leads: A numerical renormalization group analysis. Phys. Rev. B 2007, 75, 045310. [CrossRef]
  17. Hornberger, R.; Koller, S.; Begemann, G.et al. Transport through a double-quantum-dot system with noncollinearly polarized leads. Phys. Rev. B 2008, 77, 245313. [CrossRef]
  18. Chi, F.; Bai, X.F.; Huang, L.; Zhao, J. Spin-dependent transport in a Rashba ring connected to noncollinear ferromagnetic leads. J. Appl. Phys. 2010, 108, 073702. [CrossRef]
  19. Chen, X.B.; Liu, D.P.; Duan, W.H.; Guo, H. Photon-assisted thermoelectric properties of noncollinear spin valves. Phys. Rev. B 2013, 87, 085427. [CrossRef]
  20. Dumitrescu, E.; Roberts, B.; Tewari, S. et al. Majorana fermions in chiral topological ferromagnetic nanowires. Phys. Rev. B 2015, 91, 094505. [CrossRef]
  21. Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [CrossRef]
  22. Alicea, J.; Oreg, Y.; Refael, G. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 2011, 7, 412. [CrossRef]
  23. Lian, B.; Sun, X.Q.; Vaezi, A.; Zhang, S.C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl. Acad. Sci. 2018, 115, 10938. [CrossRef]
  24. Takei, S.; Fregoso, B.M.; Galitski, V.; Sarma, S.D. Topological superconductivity and Majorana fermions in hybrid structures involving cuprate high-Tc superconductors. Phys. Rev. B 2013, 87, 014504. [CrossRef]
  25. Sau, J.D.; Brydon, P.M.R. Bound States of a Ferromagnetic Wire in a Superconductor. Phys. Rev. Lett. 2015, 115, 127003. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.115.127003.
  26. Schneider, L.; Beck, P.; Posske, T.; et al. Topological Shiba bands in artificial spin chains on superconductors. Nat. Phys. 2021, 17, 943–C948. [CrossRef]
  27. Livanas, G.; Vanas, N.; Varelogiannis, G. Majorana Zero Modes in Ferromagnetic Wires without Spin-Orbit Coupling. Condens. Matter 2021, 6, 44. [CrossRef]
  28. Livanas, G., Vanas, N., Sigrist, M. et al. Platform for controllable Majorana zero modes using superconductor/ferromagnet heterostructures. Eur. Phys. J. B 95, 47 (2022). [CrossRef]
  29. Chatterjee, P.; Banik, S.; Bera, S. et al. Topological superconductivity by engineering noncollinear magnetism in magnet/superconductor heterostructures: A realistic prescription for the two-dimensional Kitaev model. Phys. Rev. B 2024, 109, L121301. [CrossRef]
  30. Lee, E.J.H.; Jiang, X.C.; Aguado, R. et al. Zero-Bias anomaly in a nanowire quantum dot coupled to superconductors. Phys. Rev. Lett. 2012, 109, 186802. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.109.186802.
  31. Lopez, R.; Lee, M.; Serra, L.; Lim, J. Thermoelectrical detection of majorana states. Phys. Rev. B 2014, 89, 205418. [CrossRef]
  32. Prada, E.; Aguado, R.; San-Jose, P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys. Rev. B 2017, 96, 085418. [CrossRef]
  33. Jack, B.; Xie, Y.; Yazdani, A. Detecting and distinguishing Majorana zero modes with the scanning tunnelling microscope. Nat. Rev. Phys. 2021, 3, 541. [CrossRef]
  34. Stefanski, P. Tunneling magnetoresistance anomalies in a Coulomb blockaded quantum dot. Phys. Rev. B 2009, 79, 085312. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.79.085312.
  35. Chi, F.; Zeng, H.; Yuan, X.Q. Flux-dependent tunnel magnetoresistance in parallel-coupled double quantum dots. Superlattice. Microst. 2009, 46, 523. [CrossRef]
  36. Tang, L.W.; Mao, W.G. Detection of Majorana Bound States by Sign Change of the Tunnel Magnetoresistance in a Quantum Dot Coupled to Ferromagnetic Electrodes. Front. Phys. 2020, 8, 00147. https://www.frontiersin.org/journals/physics/articles/10.3389/fphy.2020.00147/full.
  37. Liu, D.E.; Baranger, H.U. Detecting a majorana-fermion zero mode using a quantum dot. Phys. Rev. B 2011, 84, 201308R. [CrossRef]
  38. Gorski, G.; Kucab, K. The Spin-Dependent Coupling in the Hybrid Quantum Dot-Majorana Wire System. Phys. Status Solidi B 2019, 256, 1800492. [CrossRef]
  39. Gao, Y.; Zhang, X. Tunable Josephson Current through a Semiconductor Quantum Dot Hybridized to Majorana Trijunction. Coatings 2023, 13, 1627. [CrossRef]
  40. Gao, Y.; Zhang, X.; Yi, Z. et al. Thermophase Seebeck Coefficient in Hybridized Superconductor-Quantum-Dot-Superconductor Josephson Junction Side-Coupled to Majorana Nanowire. Nanomaterials 2023, 13, 2489. [CrossRef]
  41. Chi, F.; Jia, Q.S.; Liu, J.; Gao, Q.G.; Yi, Z.C.; Liu, L.M. Enhancement of the Josephson Current in a Quantum Dot Connected to Majorana Nanowires. Nanomaterials 2023, 13, 1482. [CrossRef]
  42. Xu, L.T.; Li, X.Q.; Sun, Q.F. Majorana dc Josephson current mediated by a quantum dot.J. Phys.: Condens. Matter 2017, 29, 195301. DOI 10.1088/1361-648X/aa6661.
  43. Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev reflection through a quantum dot coupled with two ferromagnets and a superconductor. Phys. Rev. B 2001, 65, 024516. [CrossRef]
  44. Sun, Q.F.; Wang, J.; Lin, T.H. Photon-assisted Andreev tunneling through a mesoscopic hybrid system. Phys. Rev. B 1999, 59, 13126. [CrossRef]
  45. Sun, Q.F.; Wang, J.; Lin, T.H. Control of the supercurrent in a mesoscopic four-terminal Josephson junction. Phys. Rev. B 2000, 62, 648. [CrossRef]
  46. Zhu, Y.; Sun, Q.F.; Lin, T.H. Andreev bound states and the π-junction transition in a superconductor/quantum-dot/superconductor system. J. Phys. Condens. Matter 2001, 13, 8783. [CrossRef]
  47. Mathe, L.; Sticlet, D.; Zarbo, L.P. Quantum transport through a quantum dot side-coupled to a Majorana bound state pair in the presence of electron-phonon interaction. Phys. Rev. B 2022, 105, 155409. [CrossRef]
  48. Cheng, S.G.; Sun, Q.F. Josephson current transport through T-shaped double quantum dots. J. Phys. Condens. Matter 2008, 20, 505202. [CrossRef]
  49. Zhang, H.R.; Sun, L.L.; Liu, J. Josephson dc Current through T-Shaped Double-Quantum-Dots Hybridized to Majorana Nanowires. Coatings 2023, 13, 523. [CrossRef]
Preprints 111109 g001
Figure 1. Schematic setup of a quantum dot inserted between two ferromagentic leads whose magnetic moments form an angle θ . The dot is also side-coupled to a Majorana nanowire (purple band) hosting MBSs (yellow circles), which are denoted individually by γ 1 and γ 2 . The MBSs are coupled to the QD with strength of λ σ , and to each other by δ M .
Figure 1. Schematic setup of a quantum dot inserted between two ferromagentic leads whose magnetic moments form an angle θ . The dot is also side-coupled to a Majorana nanowire (purple band) hosting MBSs (yellow circles), which are denoted individually by γ 1 and γ 2 . The MBSs are coupled to the QD with strength of λ σ , and to each other by δ M .
Preprints 111109 g001
Preprints 111109 g002
Figure 2. (Color online)Electron tunneling conductance G E T in (a) and (c), Andreev reflection conductance G A R in (b) and (d) for the case of FM-MQD-FM as functions of chemical potential μ for different values of dot-MBSs coupling strength λ 0 in (a) and (b), and different spin-polarization of the dot-MBSs coupling strength P M in (c) and (d). Other parameters except those listed in the figures are, spin-polarization of the ferromagnetic leads P L = P R = P = 0 . 5 , angle between the left and right magnetizations θ = 0 , MBS-MBS overlap amplitude δ M = 0 , and dot level ε d = 0 .
Figure 2. (Color online)Electron tunneling conductance G E T in (a) and (c), Andreev reflection conductance G A R in (b) and (d) for the case of FM-MQD-FM as functions of chemical potential μ for different values of dot-MBSs coupling strength λ 0 in (a) and (b), and different spin-polarization of the dot-MBSs coupling strength P M in (c) and (d). Other parameters except those listed in the figures are, spin-polarization of the ferromagnetic leads P L = P R = P = 0 . 5 , angle between the left and right magnetizations θ = 0 , MBS-MBS overlap amplitude δ M = 0 , and dot level ε d = 0 .
Preprints 111109 g002
Preprints 111109 g003
Figure 3. Electron tunneling conductance G E T for the case of FM-TDQDs-FM as a function of chemical potential μ for different values of coupling strength between the dots λ 0 in (a), and different spin-polarization of dot-dot coupling strength P M in (b). Other parameters are as in Figure 2. Note that when the central QD is coupled to another QD behaving as a regular fermion, the AR conductance G A R ≡ 0 .
Figure 3. Electron tunneling conductance G E T for the case of FM-TDQDs-FM as a function of chemical potential μ for different values of coupling strength between the dots λ 0 in (a), and different spin-polarization of dot-dot coupling strength P M in (b). Other parameters are as in Figure 2. Note that when the central QD is coupled to another QD behaving as a regular fermion, the AR conductance G A R ≡ 0 .
Preprints 111109 g003
Preprints 111109 g004
Figure 4. Counter plots of electron tunneling conductance as a function of μ and θ for the cases of FM-SQD-FM in (a) and FM-TDQDs-FM in (b), in which the AR conductance is zero. Figs. (c) and (d) are counter plots of the electron tunneling and AR conductances as functions of ε d and θ in structure of FM-MQD-FM. In the above figures, we set λ 0 = Γ 0 , P = P M = 0 . 5 , and other parameters are as in Figure 2.
Figure 4. Counter plots of electron tunneling conductance as a function of μ and θ for the cases of FM-SQD-FM in (a) and FM-TDQDs-FM in (b), in which the AR conductance is zero. Figs. (c) and (d) are counter plots of the electron tunneling and AR conductances as functions of ε d and θ in structure of FM-MQD-FM. In the above figures, we set λ 0 = Γ 0 , P = P M = 0 . 5 , and other parameters are as in Figure 2.
Preprints 111109 g004
Preprints 111109 g005
Figure 5. ATMR as a function of the chemical potential μ and different values of θ for the cases of FM-SQD-FM ( λ 0 = 0 ) in (a), FM-TDQDs-FM in (b), and FM-MQD-FM in (c), respectively. Other parameters are as in Figure 4.
Figure 5. ATMR as a function of the chemical potential μ and different values of θ for the cases of FM-SQD-FM ( λ 0 = 0 ) in (a), FM-TDQDs-FM in (b), and FM-MQD-FM in (c), respectively. Other parameters are as in Figure 4.
Preprints 111109 g005
Preprints 111109 g006
Figure 6. ATMR as a function of the angle θ and different spin-polarization of the leads P in (a) and (b), and varying P M in (c) and (d). (a) and (c) are for the case of FM-MQD-FM, and (b) and (d) are for FM-TDQDs-FM, respectively. Other parameters are as in Figure 2 unless listed in the figures.
Figure 6. ATMR as a function of the angle θ and different spin-polarization of the leads P in (a) and (b), and varying P M in (c) and (d). (a) and (c) are for the case of FM-MQD-FM, and (b) and (d) are for FM-TDQDs-FM, respectively. Other parameters are as in Figure 2 unless listed in the figures.
Preprints 111109 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated