Prerpints.org logo
Preprint
Article

A Novel Geothermal Wellbore Model Based on the Drift-Flux Approach

Altmetrics

Downloads

137

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts
Abstract
Geothermal energy, being a clean energy source, has immense potential, and accurate wellbore modeling is crucial for optimizing the drilling process and ensuring safety. This paper presents a novel geothermal wellbore model based on the drift-flux approach, tested under three different temperature and pressure well conditions. The proposed model integrates the conservation equations of mass, momentum, and energy, incorporating the gas-liquid two-phase flow drift-flux model and heat transfer model. Key features include handling heat transfer between the for-mation and the wellbore, addressing the slip relationship between gas and liquid phases, and accounting for wellbore friction. The nonlinear equations are discretized using the finite differ-ence method, and the highly nonlinear system is solved using the Newton-Raphson method. Numerical simulation, validation, and comparison with existing models demonstrate the en-hanced accuracy of this model. In our tests, the model achieved high accuracy in calculating bottom hole pressure and temperature, with Mean Relative Errors (MRE) significantly lower than those of other models. These results offer valuable insights for optimizing drilling parameters and ensuring drilling safety. Comparisons indicate that this approach significantly outperforms others in capturing the complex dynamics of geothermal wellbores, making it a superior tool for geo-thermal energy development.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Geothermal energy, characterized by its low carbon footprint and abundant reserves, has emerged as a highly promising renewable energy source, garnering ever-growing interest. However, as drilling depths escalate, the operational environment within geothermal wells deteriorates significantly, posing challenges for accurate parameter measurements. Consequently, Therefore, employing numerical simulation for modeling geothermal wells is an excellent choice. It allows for an in-depth study of the complex subsurface environment, enabling the prediction of parameters such as bottom hole pressure and temperature. This predictive capability is instrumental in optimizing drilling parameters to ensure safe drilling practices.
In recent years, many researchers have conducted modeling of geothermal wells. Bjornsson et al. have developed HOLA, a steady-state simulator for geothermal wells [1]. Tian et al. have developed a geothermal wellbore model based on the two-phase flow conservation equations. This model is used to simulate multiphase flow inside the wellbore and the heat transfer process between the well and the formation. It is capable of handling complex drilling scenarios and achieves this functionality through input data [2]. Because steady-state geothermal wellbore models cannot accurately reflect the actual flow conditions inside the wellbore, many scholars have begun to use transient models to model geothermal wellbores. Khasani et al. used numerical simulation to establish a wellbore model to investigate the presence of CO2 gas in geothermal water and the effect of scale deposition formed in the wellbore on the flow characteristics of fluids in geothermal wells [3]. Gao et al. developed a coupled THM(Thermo-Hydro-Mechanical) semi-numerical model for fractured reservoirs with three types of flow modes based on porous media theory, including non-local thermal equilibrium and non-Darcy law. The study analyzed the impact of CO2 thermal properties on heat transfer and flow inside the wellbore [4]. The drift-flux model is commonly used to describe multiphase flow, particularly in cases of gas-liquid two-phase flow, making it especially significant for modeling flow in geothermal wells. The drift-flux model was first proposed by Zuber and Findlay [5] in 1965. Hasan et al. used the drift-flux method to establish a robust model for two-phase flow in geothermal wells [6]. Akbar et al. developed a model that utilizes the finite element method to solve heat and fluid flow in high enthalpy deep geothermal wellbores. Additionally, they employed the drift-flux model to simulate the transient heat flow of a compressible, two-phase fluid traveling along the wellbore [7]. Tonkin et al. conducted a review of mathematical models for simulating geothermal wellbores, detailing parameter definitions and differences between models. In 2023, they developed a transient geothermal wellbore simulator based on a mathematical model comprising three conservation equations (mass, momentum, and energy), and incorporating the drift-flux model established by Shi et al [8,9,10]. Lei et al. used the drift-flux model to establish a geothermal wellbore model for controlling two-phase flow containing CO2 in the wellbore. They proposed a robust computational method and applied this model to three production wells in the Yangba geothermal field [11]. Xu et al. developed a transient non-isothermal two-phase flow model for dynamic simulation of multiphase flow in gas kick wellbores, with the ability to predict the temperature and pressure distribution inside the wellbore [12]. Hajidavalloo et al. developed conservation equations for the steady-state annulus and drill string, solved using the finite difference method. They analyzed the impact of temperature changes on predicting bottom hole pressure [13].
From the above literature, it is evident that many researchers have modeled wellbores. However, steady-state wellbore models often have low accuracy and cannot adequately reflect the true conditions inside the wellbore. Some geothermal drilling models include the energy conservation equation, which is essential. Although some models can simulate complex multiphase flows, their descriptions of heat transfer behavior within the wellbore are insufficient, leading to less accurate predictions. Due to inaccuracies in temperature predictions, and since temperature can significantly affect the properties of the fluid in the well, pressure predictions also have inaccuracies.
This paper establishes a comprehensive geothermal wellbore model using the conservation equations of mass, momentum, and energy, combined with Shi et al.'s drift-flux model [10] and Hasan et al.'s heat transfer model [14]. The highly nonlinear equations are discretized using the finite difference method and solved using the Newton-Raphson iteration method. The model is analyzed and validated through numerical simulation software, demonstrating promising application prospects. Furthermore, comparisons with models mentioned in the literature highlight the accuracy and superiority of this model.

2. Model formulation

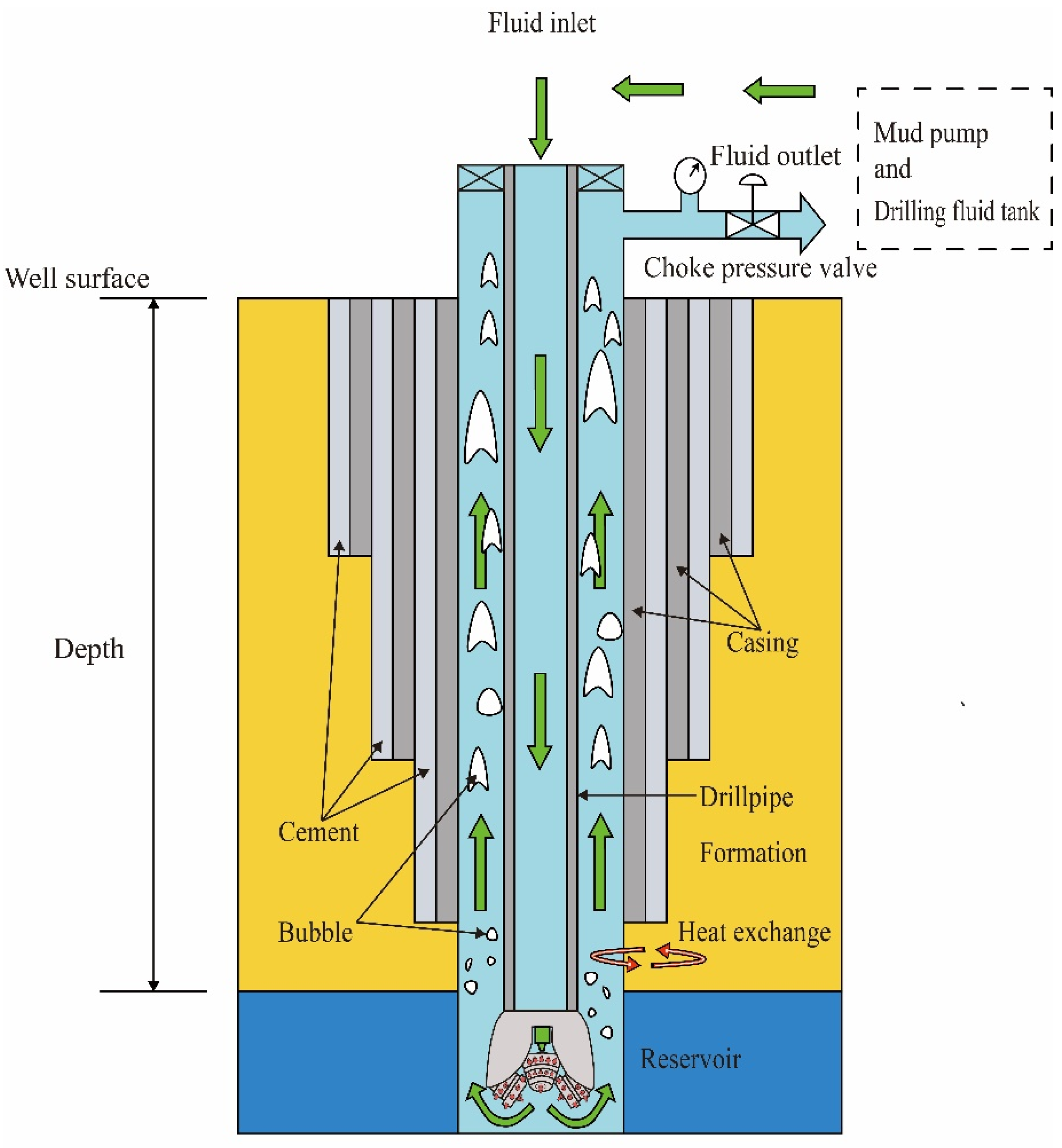
As shown in Figure 1, the drilling fluid exits through the drill bit nozzles and enters the wellbore annulus, carrying bottom-hole cuttings and gas-liquid mixtures back to the surface while exchanging heat with the formation in the annulus. To establish the geothermal wellbore model, the following assumptions are made:
  • The gas-liquid mixture flows one-dimensionally along the wellbore;
  • Disregard axial heat conduction within the wellbore;
  • Disregard the impact of drill cuttings;
  • Consider the impact of the casing and cement sheath on heat transfer;
  • Consider the slip relationship between the gas and liquid phases.

2.1. Conservation equations for gas-liquid two-phase flow

In geothermal drilling, gas-liquid two-phase flow must satisfy the conservation laws of mass, momentum, and energy. The equations are as follows:
Mass conservation equation
∂ ∂ t ρ g α g + ρ l α l + ∂ ∂ x ρ g α g v g + ρ l α l v l = 0
ρg andρl are the densities of the gas phase and liquid phase, respectively. vg and vl are the velocities of the gas phase and liquid phase, respectively. αg and αl are the cross-sectional gas content and cross-sectional liquid content.
Momentum conservation equation
∂ ∂ t ρ g α g v g + ρ l α l v l + ∂ ∂ x P + ρ g α g v g 2 + ρ l α l v l 2 = − ρ m v m g sin ⁡ θ − F f
P is the wellbore pressure, ρm and vm are the density and velocity of the gas-liquid mixture, respectively, f is the wellbore friction coefficient, and D is the wellbore diameter.
Energy conservation equation
∂ ∂ t ρ g α g e g + 1 2 v g 2 + ρ l α l e l + 1 2 v l 2 + ∂ ∂ x ρ g α g v g h T g + ρ l α l v l h T l + Q π r i 2 = 0
eg and el are the specific internal energies of the gas and liquid phases, respectively. hTg and hTl are the total specific enthalpies, defined as the sum of specific enthalpy, kinetic energy, and potential energy. Q represents the energy change due to heat exchange between the formation and the wellbore. ri is the wellbore radius.
e g = h g − P ρ g
e l = h l − P ρ l
h T g = h g + v g 2 2 − g x
h T l = h l + v l 2 2 − g x
Where hg and hl represent the specific enthalpies of the gas phase and liquid phase, respectively.

2.2. Constitutive equations

Due to the large number of unknowns in these conservation equations, it is necessary to supplement them with constitutive equations. In geothermal wellbore modeling, considerations include the slip between gas and liquid phases, friction with the wellbore wall, and heat transfer between the wellbore and the surrounding formation.

2.2.1. Mixture equation

The relationship between the cross-sectional gas content and the mass liquid content is as follows:
α l + α g = 1
The mixture density is described as:
ρ m = α g ρ g + α l ρ l

2.2.2. Wellbore friction

In geothermal drilling, the gas-liquid mixture flowing upward along the wellbore causes a significant frictional pressure drop. The expression for Ff is as follows:
F f = f ρ m v m | v m | 2 D
The f in Equation (7) represents the wellbore friction coefficient, which can be expressed as:
  f = 16 R e R e ≤ 2400 1 16 l o g ξ 3.7 r i − 5.02 R e l o g ξ 3.7 r i + 13 R e − 2 R e > 2400
Where Re is the Reynolds number, ξ is the wellbore roughness. In this paper, the roughness is assumed to be 0.00175 millimeters. The Reynolds number is calculated as follows:
R e = ρ m | v m | 2 r i μ m
In Equation (9), μm represents the viscosity of the gas-liquid mixture, and its expression is as follows:
μ m = α g μ g + α l μ l

2.2.3. Formation-Wellbore Heat Exchange

In geothermal drilling, there is heat transfer between the formation and the wellbore. Heat is transferred from the formation through the cement and casing into the wellbore, and the fluid inside the wellbore is transferred back to the formation through the same path. Here, we use a heat transfer equation developed by Hasan [14], applicable to any wellbore, which is expressed as follows:
Q = 2 π r t i U t k f T e i − T f k f + r t i U t T D
kf is the formation thermal conductivity, Tei is the formation temperature unaffected by wellbore heat transfer, and Tf is the fluid temperature inside the drill string. Radial heat exchange occurs between the formation and the wellbore fluid. When heat is transferred from the formation to the wellbore, it first passes through the cement, then the casing, and finally through the outer wall of the drill string into the fluid inside the drill string. Each of these parts has its own thermal resistance, so the overall heat transfer coefficient Ut can be considered as the series combination of these individual resistances, as represented by Equation (16), TD is a temperature function related to the dimensionless time td.
1 U t = 1 h t i + r t i l n r t o r t i k t + r t i r t o h c + h r + r t i l n r c o r c i k c + r t i l n r w b r c o k c e m
T D = l n e − 0.2 t d + 1.5 − 0.3719 e − t d t d 1 2

2.2.4. Slip Model

In the wellbore, the gas moves faster than the liquid, often resulting in slip. Since Zuber and Findlay introduced the drift-flux model, many researchers have studied various drift-flux models [15,16,17,18,19]. Investigations have shown that among these models, the one developed by Shi et al [10] has better applicability. Therefore, this paper adopts the drift-flux model established by Shi et al [10]. The two-phase velocity formula is described as：
v g = C 0 v m + v d
Where vm is the mixture velocity, and vd is the drift velocity.
v m = v s g + v s l = α g v g + α l v l
v d = m θ 1 − C 0 α g K α g v c C 0 α g ρ g ρ l + 1 − C 0 α g
In this slip model, m(θ) is a function of the wellbore inclination angle, C0​ is the profile coefficient, K is a function of the cross-sectional gas content, and vc is the characteristic velocity.
In a gas-water dominated system, the expression for m(θ) is:
m θ = 1.85 c o s θ 0.21 1 + s i n θ 0.95
Here, the improved K by Pan et al. [17]. based on Shi's model [10] is used.
K α g =                 1.53                                                                                                                                                                     α g ≤ α 1   1.53 + 0.5 C 0 K u − 1.53 1 − c o s π α g − α 1 α 2 − α 1       α 1 < α g <   α 2                     C 0 K u                                                                                                                                                                 α g ≥ α 2
where Ku is the "critical Kutateladze number" related to the pipe diameter.
K D ^ = g ρ l − ρ g σ g l 1 2 D
The expression for the characteristic velocity vc is:
v c = σ g l ρ l − ρ g ρ l 2 1 4
The formula for the profile parameter C0 is:
C 0 = A 1 + A − 1 γ 2
This equation ensures that C0 has a constant value during bubble flow or slug flow, and equals 1 during annular mist flow. The expression for the parameter γ is:
γ = β − B 1 − B
β = m a x α g , F v α g v m v s g f
Fv is a constant used to adjust the sensitivity of C0 to velocity. vsgf is the critical velocity value that prevents the liquid film from falling back with the gas flow.
v s g f = K u ρ l ρ g 1 2 v c
After experiments conducted by Shi et al., [10] it was found that in the gas-water system, the optimal parameter A is equal to 0, α1 = 0.06, and α2 = 0.21. Therefore, the calculated value of C0 is equal to 1.

3. Numerical methods

Finite Difference Method (FDM) is a common numerical analysis technique used to solve differential equations. It discretizes the differential equations in a specified region, transforming continuous problems into discrete ones. It has been widely applied in wellbore modeling [20,21]. Due to the highly nonlinear and strongly coupled nature of the geothermal wellbore model, analytical solutions are not feasible. Therefore, numerical methods are needed to approximate the desired solutions. The flowchart below illustrates the solution process in this paper.
  • Initialize Pressure and Temperature: First, set the initial pressure and temperature values, then divide the wellbore into grids.
  • Calculate Velocity and Phase Fractions: Use the mass conservation equation and momentum conservation equation to determine the fluid velocities and phase fractions. This step involves calculating the movement properties of the fluids within the wellbore.
  • Calculate Temperature: Apply the energy conservation equation to compute the temperature, considering the heat conduction within the wellbore fluids.
  • Newton-Raphson Iteration: Since the discretized equations form a nonlinear system, use the Newton-Raphson iteration method. Based on the current values of velocity, phase fractions, temperature, and pressure, compute the Jacobian matrix and iterate to solve the nonlinear equations.
  • Error and Convergence Check: Compare the calculated residuals with the convergence criteria. If the error is less than the threshold of 10-6, the solution is considered converged, and the loop can end.
  • Update Solution and Continue Loop: If the solution has not converged, update the velocity, phase fractions, temperature, and pressure values based on the Newton-Raphson iteration results and error assessment. Then, return to step 1 to continue the iteration process.
  • Advance to Next Time Step: Once the simulation converges, proceed to the next time step and continue simulating the wellbore conditions at the next moment.

3.1. Discretization of Equations

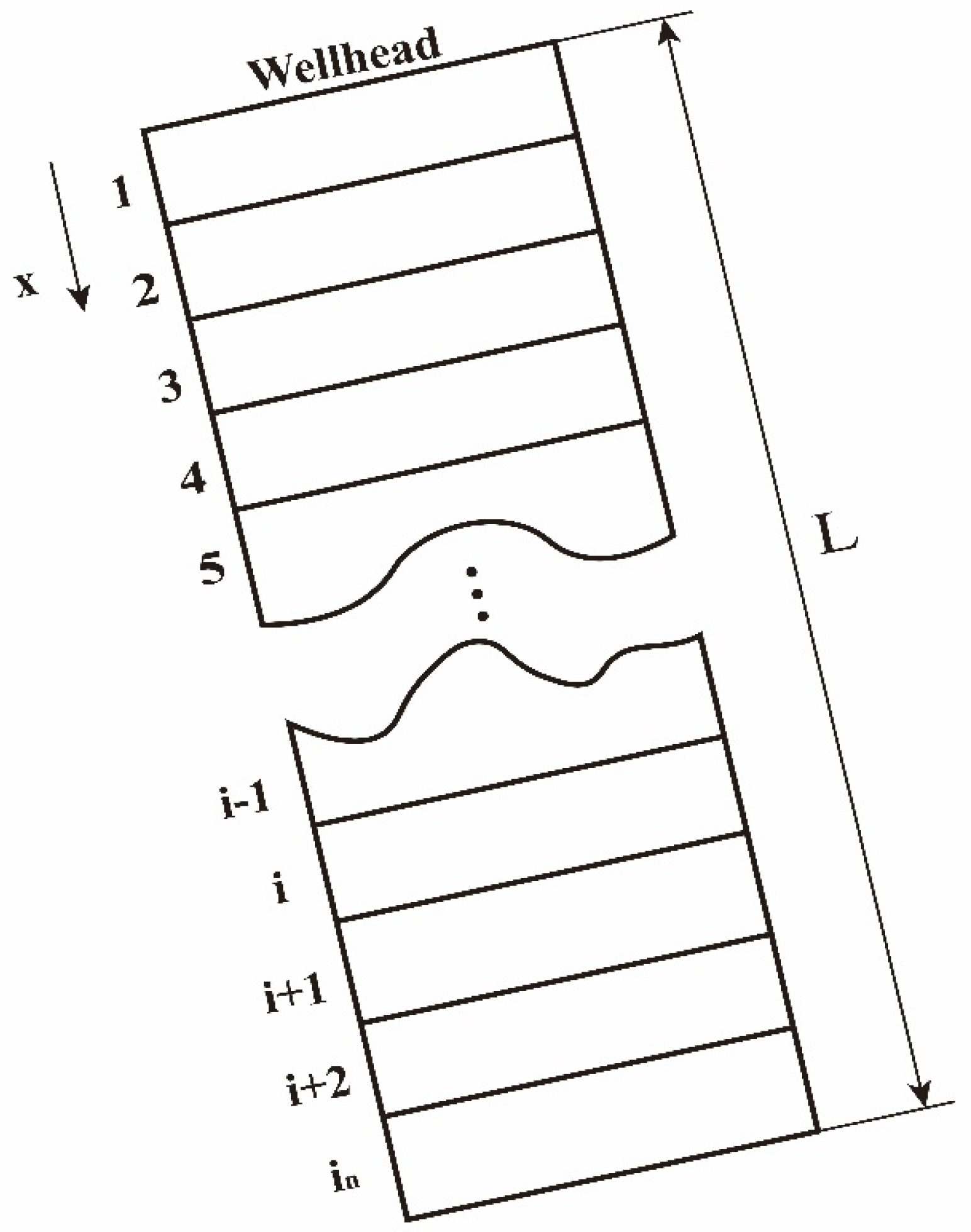
3.1.1. Grid Division

To accurately simulate the geothermal wellbore model, the wellbore is divided into in discrete grid cells along its length, with a total length of L and an increment of Δx for each segment (see Figure 2). Detailed calculations of pressure, temperature, velocity, and phase fractions are performed from the initial grid point at the wellhead, iterating down to the bottom of the well.

3.1.2. Mass conservation equation

The mass conservation equation is discretized in time and space using a forward difference scheme, given as follows:
ρ g α g + ρ l α l i n + 1 − ρ g α g + ρ l α l i n ∆ t + ρ g α g v g + ρ l α l v l i + 1 n − ρ g α g v g + ρ l α l v l i n ∆ x = 0

3.1.3. Momentum conservation equation

The momentum conservation equation is discretized as follows:
ρ g α g v g + ρ l α l v l i n + 1 − ρ g α g v g + ρ l α l v l i n ∆ t + P + ρ g α g v g 2 + ρ l α l v l 2 i + 1 n − P + ρ g α g v g 2 + ρ l α l v l 2 i n ∆ x = − ρ m v m i + 1 n − ρ m v m i n ∆ x g sin ⁡ θ − f 2 D ρ m v m | v m | i + 1 n − ρ m v m | v m | i n ∆ x

3.1.4. Energy conservation equation

The Energy conservation equation is discretized as follows:
ρ g α g e g + 1 2 v g 2 + ρ l α l e l + 1 2 v l 2 i n + 1 − ρ g α g e g + 1 2 v g 2 + ρ l α l e l + 1 2 v l 2 i n ∆ t + ρ g α g v g h T g + ρ l α l v l h T l i + 1 n − ρ g α g v g h T g + ρ l α l v l h T l i n ∆ x + Q π r i 2 = 0

3.2. Boundary conditions

Boundary conditions in the geothermal wellbore model are crucial for the model's accuracy and need to be precisely defined.

3.2.1. At the wellhead

The temperature at the wellhead is determined by the temperature of the drilling fluid at the wellhead, and is thus expressed as:
T h 0 , t = T m
The pressure at the wellhead is the sum of the dynamic pressure and the backpressure, thus the expression for the pressure at the wellhead is:
P 0 , t = P C + 1 2 ρ m t , x v m t , x 2

3.2.1. At the bottom-hole

Due to the significant influence of the formation temperature at the bottom of the wellbore, the temperature inside the wellbore is expressed as Equation (34), where ΔT represents the temperature loss, determined according to Fourier's law of heat conduction, and ΔZ represents the distance between the wellbore and the formation.
T L , t = T e i − ∆ T
∆ T = Q ∆ Z k f
Assume the bottom-hole pressure is equal to the formation pressure.
P L , t = P f

3.3. Newton-Raphson Iteration

After discretization, the conservation equations remain nonlinear. Therefore, the Newton-Raphson method is used for iterative solution. The Newton-Raphson method has many advantages, such as efficiency and fast convergence, and it has shown good application effects in wellbore modeling [22,23,24].
Assuming the solution vector is:
u = u ρ g , α g , v g , P , T T
The residual vector F is calculated from the conservation equations. The mass conservation equation, momentum conservation equation, and energy conservation equation are represented as F1, F2, and F3 respectively. Additionally, the equations from the drift-flux model and the heat transfer model are used as auxiliary residual equations F4 and F5.
F u = F 1 ρ g , α g , v g , P , T F 2 ρ g , α g , v g , P , T F 3 ρ g , α g , v g , P , T F 4 ρ g , α g , v g , P , T F 5 ρ g , α g , v g , P , T
The increment Δu is obtained by multiplying the inverse of the Jacobian matrix by the residual vector.
∆ u = ∂ F 1 ∂ ρ g ∂ F 1 ∂ α g ∂ F 1 ∂ v g ∂ F 1 ∂ P ∂ F 1 ∂ T ∂ F 2 ∂ ρ g ∂ F 2 ∂ α g ∂ F 2 ∂ v g ∂ F 2 ∂ P ∂ F 2 ∂ T ∂ F 3 ∂ ρ g ∂ F 3 ∂ α g ∂ F 3 ∂ v g ∂ F 3 ∂ P ∂ F 3 ∂ T ∂ F 4 ∂ ρ g ∂ F 4 ∂ α g ∂ F 4 ∂ v g ∂ F 4 ∂ P ∂ F 4 ∂ T ∂ F 5 ∂ ρ g ∂ F 5 ∂ α g ∂ F 5 ∂ v g ∂ F 5 ∂ P ∂ F 5 ∂ T − 1 F 1 ρ g , α g , v g , P , T F 2 ρ g , α g , v g , P , T F 3 ρ g , α g , v g , P , T F 4 ρ g , α g , v g , P , T F 5 ρ g , α g , v g , P , T
The iterative formula for solving the solution vector in conjunction with the auxiliary equations mentioned earlier is given by Equation (40).
u i + 1 = u i + ∆ u

4. Model verification and analysis

To validate the effectiveness of the model, three sets of comparative experiments were conducted using geothermal wells from different locations. The first set involved a geothermal well in the Rongxi area of Xiongan, China. The parameters of this well are listed in Table 1. The second set of experiments used the SNLG87-29 well data from Garg et al. [25]. Finally, the third set utilized data from the No. 6 well at point D in northwest Iran, as mentioned in the article by Zolfagarroshan et al. [26]. First, the parameters of the well in the Rongxi area of Xiongan are listed in Table 1.
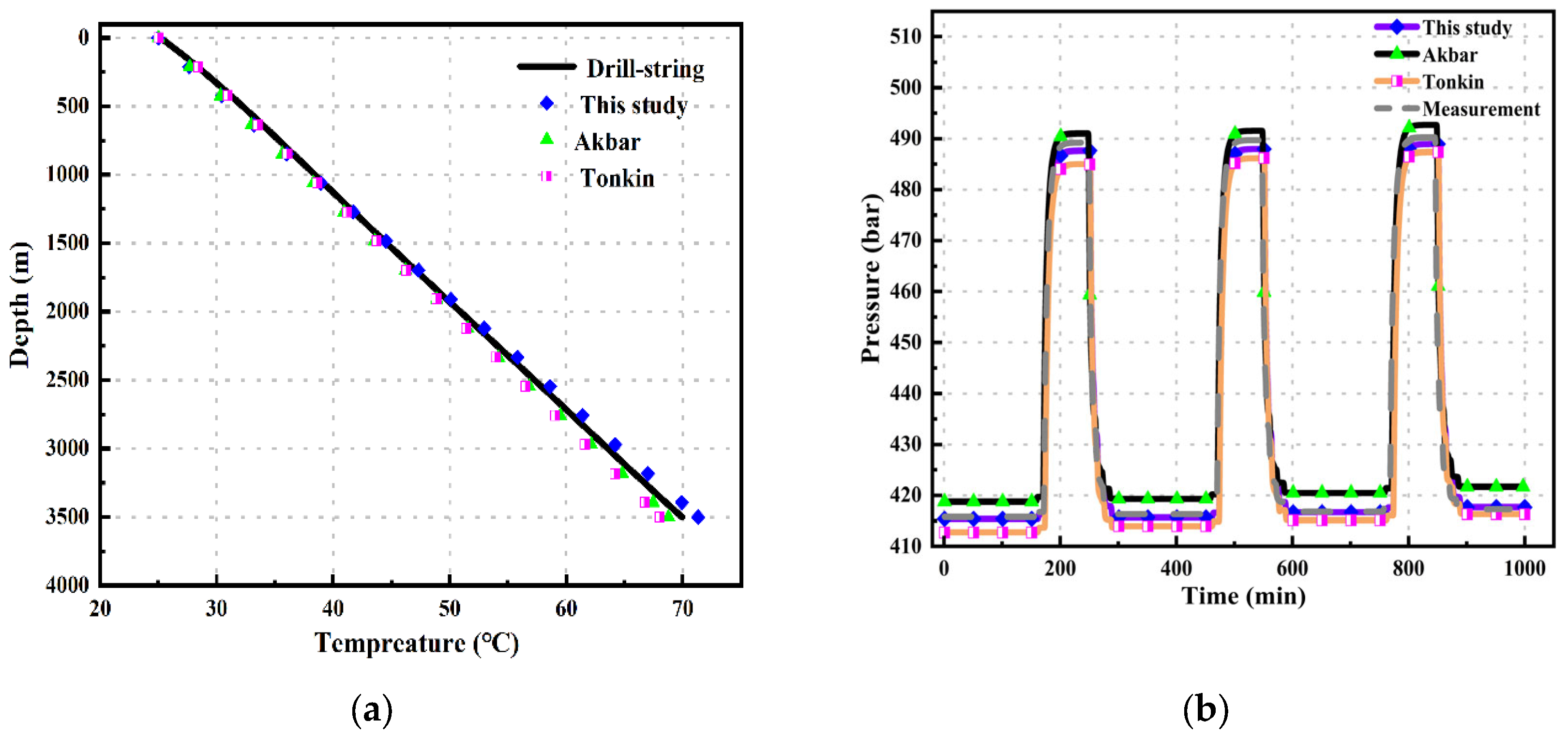
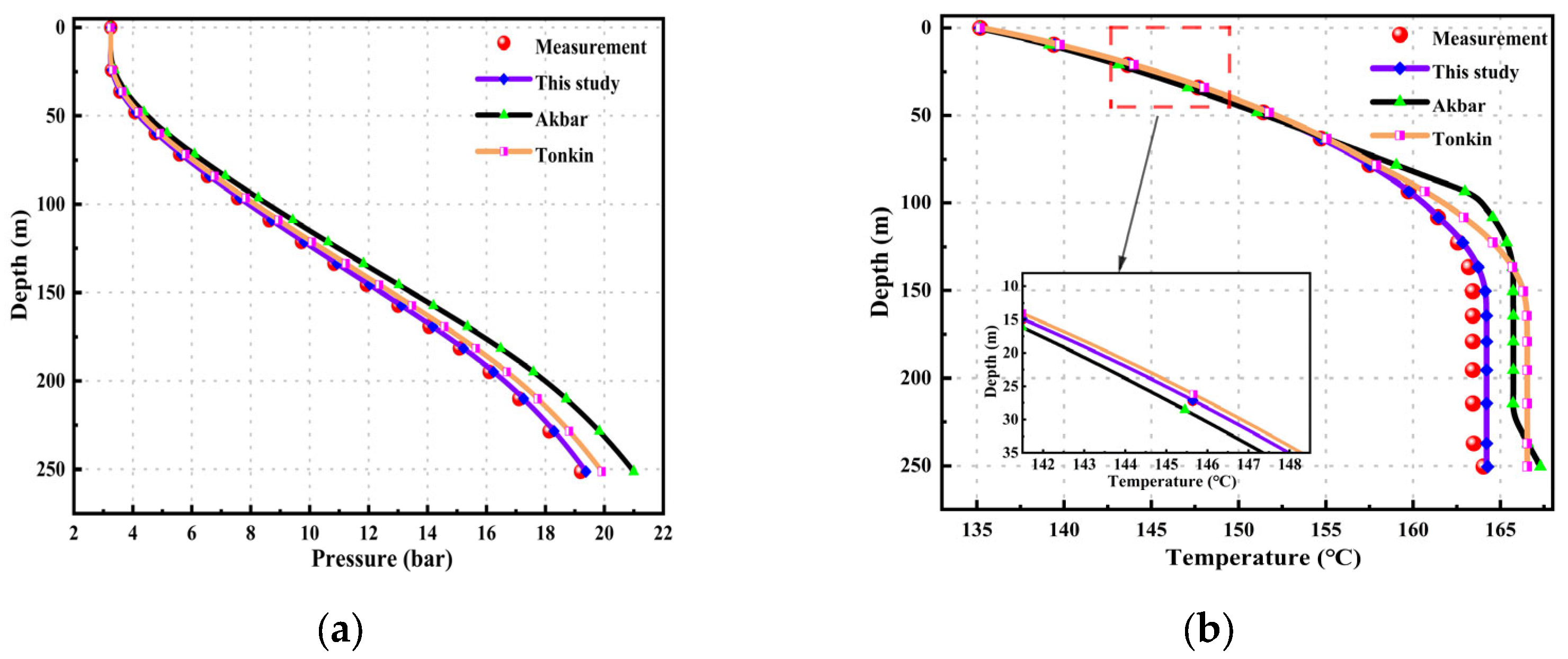
Based on the data in the table, calculations using the model produced results as shown in Figure 3. Figure 3-a presents the measured temperature data inside the drill pipe. After comparing and validating with the models by Akbar et al. and Tonkin et al., the results are as follows: all three wellbore models provide accurate temperature calculations. The mean relative error (MRE) for this model is 1.323%. For Akbar's model, the MRE is 1.999%, and for Tonkin et al.'s model, the errors are 1.78%. This indicates that the temperature calculation model in this study is relatively accurate.
Figure 3-b shows the trend of bottom hole pressure over time. As the drilling depth increases over time, the bottom hole pressure increases. However, due to various uncertainties in the formation, the bottom hole pressure may suddenly change, necessitating adjustments to the surface backpressure to control the bottom hole pressure. The figure shows that the model in this study provides a good fit during the stable drilling phase, outperforming the other two models. When the bottom hole pressure suddenly changes, the MRE in the calculated results is 1.491%, which is smaller than the MRE calculated by the other two models.
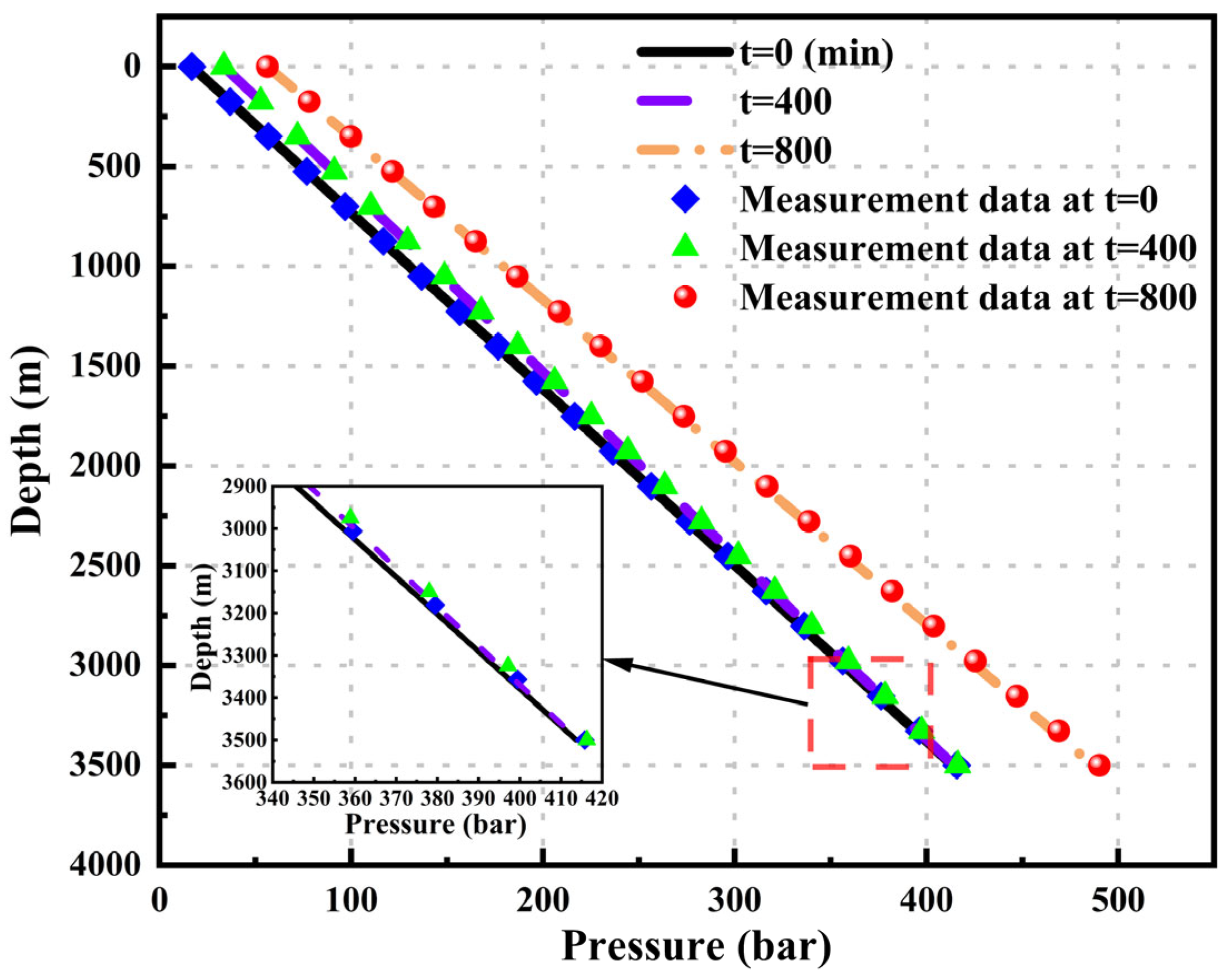
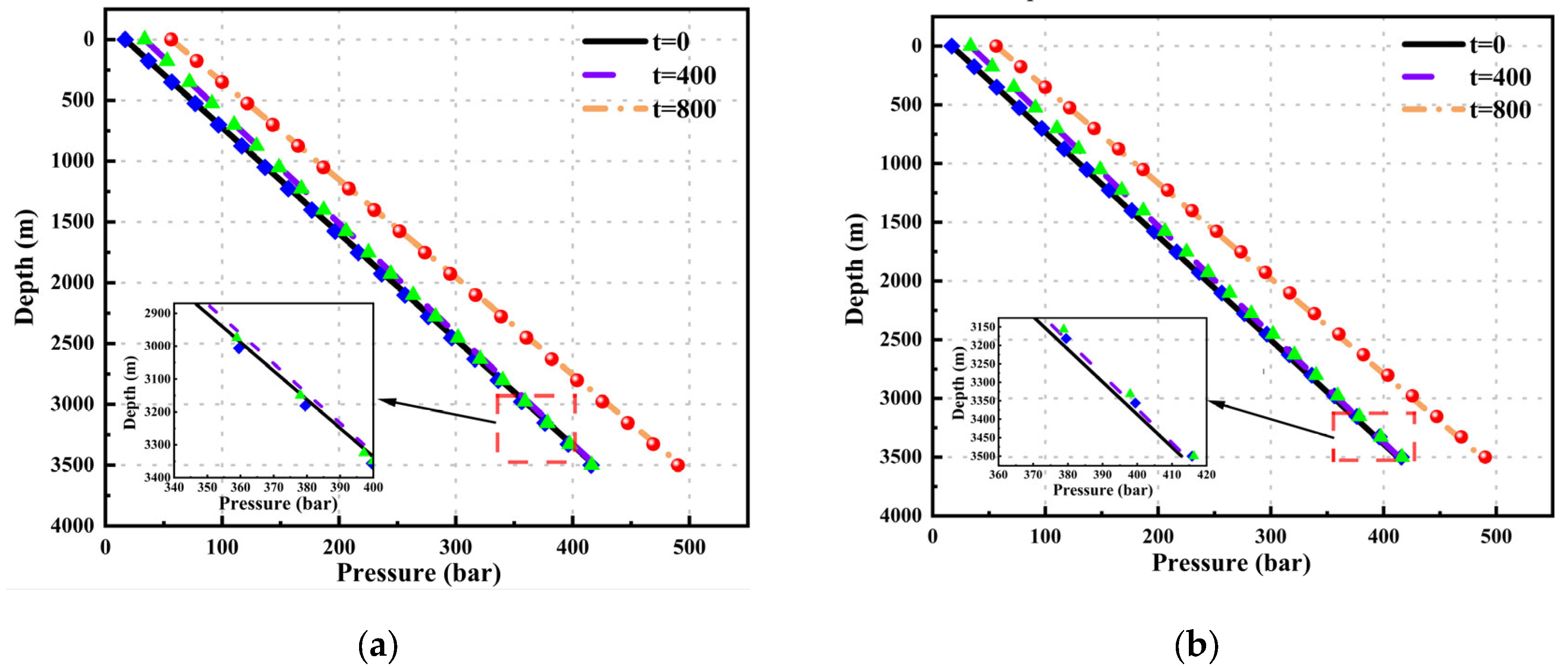
To clearly and intuitively demonstrate the pressure calculation results of various geothermal wellbore models, pressure-depth curves were plotted at different time points: t=0, 400, and 800.
Figure 5 shows that both the wellhead pressure and the bottom hole pressure increase with time. The pressure-depth curves calculated by this model at different time points match well with the actual measured data. The Mean Relative Errors (MRE) at the three different time points are 1.254%, 1.254%, and 1.339, respectively.
Figure 6 shows the pressure results calculated by Akbar's model and Tonkin's model. The Mean Relative Errors (MRE) calculated by Akbar's model at different time points are 2.036%, 2.035%, and 2.025%, while the MREs calculated by Tonkin's model at different time points are 2.037%, 2.029%, and 2.029%.
The SNLG87-29 well was designed to match the temperature and pressure data recorded in 1993. The parameters are listed in Table 2.
Based on the existing parameters and some initial parameter assumptions, calculations were performed for this geothermal well. The results are shown in Figure 6.
Figure 6-a illustrates the pressure variation with depth. It can be clearly observed that the measured data align well with the model presented in this study, with an MRE of: 1.824%. Given the shallow depth and low pressure of the well, all three models show good fitting results. The MRE for Akbar's model is 4.624%, and for Tonkin's model, it is: 3.213%.
Figure 6-b depicts the temperature variation with depth. In the initial 75 meters, all three models fit the measured data well. However, as the temperature gradient changes, the temperature variation with depth decreases. Akbar's model retains the trend of the original data curve but has a higher MRE, which is: 2.203%. The model presented in this study shows a similar trend to Tonkin's model, but with an MRE of: 1.209%, which is lower than Tonkin's.
This indicates that the model presented in this study performs well even in high-temperature, low-pressure wells.
Zolfagharroshan et al. [26] mentioned detailed parameters of Well No. 6, listed in Table 3.
Based on the parameters of Well No. 6 listed in Table 3, a comparison of the results calculated by the three models with the measured data is shown below:
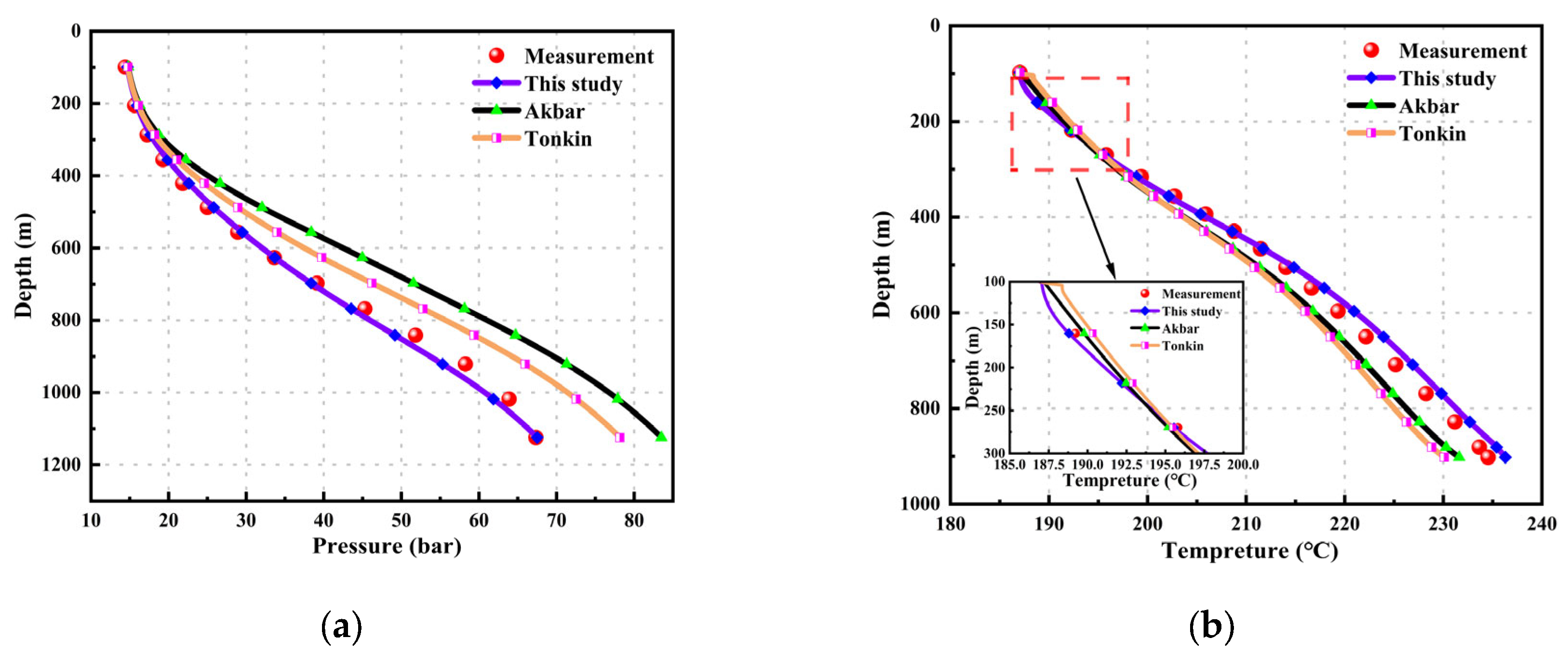
Figure 7(a) shows that the pressure-depth curve of this well has two inflection points, where the rate of pressure change with depth significantly varies. The model proposed in this paper closely matches the measured data, with a calculated Mean Relative Error (MRE) of 2.937%. The Akbar model and the Tonkin model also exhibit good pressure curves but show larger errors compared to the measured data and lag in the pressure increasing trend. The calculated MREs are 6.55% and 3.185%, respectively.
Figure 7 illustrates that the temperature calculation results of the three models have relatively small errors. However, this model has an MRE of 0.912%, which is lower than the other two models. Meanwhile, the temperature calculation results of the Akbar model are superior to those of the Tonkin model, with MREs of 1.553% and 1.814%, respectively.

5. Conclusions

This paper presents a geothermal wellbore model that demonstrates strong adaptability under three different temperature and pressure well conditions. The model integrates conservation equations with the drift-flux model and heat transfer model. After discretizing the equations, the Newton-Raphson iteration method is used to calculate pressure and temperature. Validation results show that the model performs well in three different wellbore environments, achieving high accuracy by taking into account multiple factors affecting heat transfer. Experimental comparison results indicate that the model has a low Mean Relative Error (MRE), demonstrating its high precision and reliability in calculating bottom hole pressure and temperature. Overall, this model provides reliable and accurate results, making it a valuable tool for optimizing drilling parameters and ensuring drilling safety in the geothermal energy field.

Author Contributions

Conceptualization, Y.Y. and J.Z.; methodology, Y.Y.; software, Y.Y.; validation, Y.Y., X.X. and J.L.; formal analysis, L.B.; investigation, J.Z.; resources, J.L.; data curation, J.L.; writing—original draft preparation, Y.Y.; writing—review and editing, Y.Y.; visualization, J.Z.; supervision, W.L.; project administration, W.L.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Special Project of Xiongan New Area of the Ministry of Science and Technology of the People's Republic of China (2022XAGG0500).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bjornsson, G., Bodvarsson, G.S., A Multi-Feedzone Wellbore Simulator. Geotherm. Resour. Counc. Trans. 1987, 11, 503–507.
  2. Tian, S., Finger, J.T., Advanced Geothermal Wellbore Hydraulics Model. J. Energy Resour. Technol. 2000, 122, 142–146. [CrossRef]
  3. Khasani, Deendarlianto, K., and Itoi, R. Numerical study of the effects of CO2 gas in geothermal water on the fluid-flow characteristics in production wells. Eng. Appl. Comput. Fluid Mech. 2021, 15, 111-129.
  4. Gao, X.; Wang, Z.-Y.; Qiao, Y.-W.; Li, T.-L.; Zhang, Y. Effects of seepage flow patterns with different wellbore layout on the heat transfer and power generation performance of enhanced geothermal system. Renew. Energy. 2024, 223, 120065. [Google Scholar] [CrossRef]
  5. Zuber, N., and Findlay, J. Average volumetric concentration in two-phase flow systems. J Heat Transf. 1965, 87, 453–468.
  6. Hasan, A.R., Kabir, C.S., Modeling two-phase fluid and heat flows in geothermal wells. J. Pet. Sci. Eng. 2010, 71, 77–86. [CrossRef]
  7. Akbar, S., Fathianpour, N., Al-Khoury, R., A finite element model for high enthalpy two-phase flow in geothermal wellbores. Renew. Energy 2016, 94, 223–236. [CrossRef]
  8. Tonkin, R.A., O’Sullivan, M.J., O’Sullivan, J.P., A review of mathematical models for geothermal wellbore simulation. Geothermics. 2021, 97, 102255. [CrossRef]
  9. Tonkin, R.A., O’Sullivan, J.P., Gravatt, M, O’Sullivan, M.J., A transient geothermal wellbore simulator. Geothermics. 2023, 110, 102653.
  10. Shi, H., Holmes, J.A., Durlofsky, L.J., Aziz, K., Diaz, L.R., Alkaya, B., Oddie, G. Drift-flux modeling of two-phase flow in wellbores. SPE J. 2005, 10, 24–33. [CrossRef]
  11. Lei, H.-W.; Xie, Y.-C.; Li, J.; Hou, X.-W. Modeling of two-phase flow of high temperature geothermal production wells in the Yangbajing geothermal field,Tibet. Front. Earth Sci. 2023, 11, 1019328. [Google Scholar] [CrossRef]
  12. Xu, Z.-M.; Song, X.-Z.; Li, G.-S.; Wu, K.; Pang, Z.-Y.; Zhu, Z.-P. Development of a transient non-isothermal two-phase flow model for gas kick simulation in HTHP deep well drilling. Appl. Therm. Eng. 2018, 141, 1055–1069. [Google Scholar] [CrossRef]
  13. Hajidavalloo, E., Daneh-Dezfuli, A., Falavand Jozaei, A. Effect of temperature variation on the accurate prediction of bottom-hole pressure in well drilling. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1-21.
  14. Hasan, A.R., Kabir, C.S., Wellbore heat-transfer modeling and applications. J. Pet. Technol. 2012, 86-87, 127-136.
  15. Orkiszewski, J., Predicting Two-Phase Pressure Drops in Vertical Pipe. J. Pet. Technol. 1967, 19, 829–838. [CrossRef]
  16. Rouhani, S.Z., Axelsson, E., Calculation of void volume fraction in the subcooled and quality boiling regions. Int. J. Heat Mass Transf. 1970, 13, 383–393. [CrossRef]
  17. Pan, L., Oldenburg, C.M., Wu, Y-S., Pruess, K., T2Well/ECO2N Version 1.0: Multiphase and Non-Isothermal Model for Coupled Wellbore-Reservoir Flow of Carbon Dioxide and Variable Salinity Water. Report LBNL-4291E, Earth Sciences Division. Lawrence Berkeley Laboratory, University of California, Berkeley, California, 2011.
  18. Hibiki, T, Tsukamoto, N, Drift-flux model for upward dispersed two-phase flows in vertical medium-to-large round tubes. Prog. Nucl. Energy. 2023, 158, 104611. [CrossRef]
  19. Barati, H, Hibiki, T, Schlegel, J.P., Tsukamoto, N, Two-group drift-flux model for dispersed gas-liquid flow in large-diameter pipes. Int. J. Heat Mass Transfer. 2024, 218, 124766.
  20. Chen, X.; Wang, S.-W.; He, M.; Xu, M.-B. A comprehensive prediction model of drilling wellbore temperature variation mechanism under deepwater high temperature and high pressure. Ocean Eng. 2024, 296, 117063. [Google Scholar] [CrossRef]
  21. Meng, L.-D.; Zhang, X.-L.; Jin, Y.-J.; Yan, K.; Li, S. Numerical simulation of fracture temperature field distribution during oil and gas reservoir hydraulic fracturing based on unsteady wellbore temperature field model. Geophysics. 2024, 89, 1–15. [Google Scholar] [CrossRef]
  22. Liu, W.-Z.; Zeng, Q.-D.; Yao, J. Poroelastoplastic Modeling of Complex Hydraulic-Fracture Development in Deep Shale Formations. SPE J. 2021, 26, 2626–2650. [Google Scholar] [CrossRef]
  23. He, Y.-T.; Yang, Z.-Z.; Jiang, Y.-F.; Li, X.-G.; Zhang, Y.-Q.; Song, R. A full three-dimensional fracture propagation model for supercritical carbon dioxide fracturing. Energy Sci. Eng. 2020, 8, 2894–2906. [Google Scholar] [CrossRef]
  24. Yue, P.; Yang, H.-G.; He, C.-J.; Yu, G.-M.; Sheng, J.-J.; Guo, Z.-L.; Guo, C.-Q.; Chen, X.-F. Theoretical Approach for the Calculation of the Pressure Drop in a Multibranch Horizontal Well with Variable Mass Transfer. ACS Omega. 2020, 45, 29209–29221. [Google Scholar] [CrossRef] [PubMed]
  25. Garg, S.K.; Pritchett, J.W.; Alexander, J.H. Development of New Geothermal Wellbore Holdup Correlations Using Flowing Well. 2004. Available online: https://doi.org/10.2172/910629. [CrossRef]
  26. Zolfagharroshan, M. , Khamehchi, E. A rigorous approach to scale formation and deposition modelling in geothermal wellbores. Geothermics. 2020, 87, 101841. [Google Scholar] [CrossRef]
Preprints 111130 g001
Figure 1. Schematic of Drilling circulation.
Figure 1. Schematic of Drilling circulation.
Preprints 111130 g001
Preprints 111130 g002
Figure 2. Wellbore Grid Division.
Figure 2. Wellbore Grid Division.
Preprints 111130 g002
Preprints 111130 g003
Figure 3. This is Xiongan Rongxi District Well: (a) Temperature Results Performance of Different Models; (b) Pressure Results over Time for Different Models.
Figure 3. This is Xiongan Rongxi District Well: (a) Temperature Results Performance of Different Models; (b) Pressure Results over Time for Different Models.
Preprints 111130 g003
Preprints 111130 g004
Figure 4. Comparison of the pressure-depth curves calculated by this model with the measured results.
Figure 4. Comparison of the pressure-depth curves calculated by this model with the measured results.
Preprints 111130 g004
Preprints 111130 g005
Figure 5. The pressure results calculated at different time points as a function of depth: (a) Akbar's model; (b) Tonkin's model.
Figure 5. The pressure results calculated at different time points as a function of depth: (a) Akbar's model; (b) Tonkin's model.
Preprints 111130 g005
Preprints 111130 g006
Figure 6. This is SNLG87-29 well. (a) Pressure vs. Depth Curve; (b) Temperature vs. Depth Curve.
Figure 6. This is SNLG87-29 well. (a) Pressure vs. Depth Curve; (b) Temperature vs. Depth Curve.
Preprints 111130 g006
Preprints 111130 g007
Figure 7. This is well number 6. (a) Pressure vs. Depth Curve; (b) Temperature vs. Depth Curve.
Figure 7. This is well number 6. (a) Pressure vs. Depth Curve; (b) Temperature vs. Depth Curve.
Preprints 111130 g007
Table 1. Parameters of a Geothermal Well in the Rongxi Area.
Table 1. Parameters of a Geothermal Well in the Rongxi Area.
Parameter Value
Depth (m) 3500
Wellbore diameter (mm) 222
Drillpipe ID (mm) 119
Drillpipe OD (mm) 159
Gas injection rate (m3/s) 0.263
Surface temperature (℃) 25
Bottomhole temperature (℃) 71.1
Casing ID (mm) 306
Casing OD (mm) 350
Mud density (kg/m3) 1066.45
Table 2. Parameters of SNLG87-29 well.
Table 2. Parameters of SNLG87-29 well.
Parameter Value
Depth (m) 248.4
Vertical Depth (m) 248.4
Angle with Vertical (Degrees) 0
0-159.7m Internal Diameter (mm) 102
159.7-248.4m Internal Diameter (mm) 99
Depth (m) 248.4
Surface temperature (℃) 22
Bottomhole temperature (℃) 163.5
Table 3. Parameters of No. 6 well.
Table 3. Parameters of No. 6 well.
Parameter Value
Depth (m) 2377
Production casing depth (m) 1250
Wellbore diameter (mm) 244.5
Slotted liner depth (m) 2371
Slotted liner size (mm) 177.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated