Prerpints.org logo
Preprint
Article

Comparative Study of Rapid Assessment Methods of Earthquake-Triggered Landslides Based on Newmark Model - A Case Study of The 2022 Luding Ms6.8 Earthquake

Altmetrics

Downloads

89

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 July 2024

Posted:

09 July 2024

You are already at the latest version

Alerts
Abstract
Earthquake-triggered landslides represent a significant seismic-related disaster, posing threats to both the lives and properties of individuals in affected areas. Furthermore, they can result in road and river blockages, as well as other secondary disasters, significantly impacting post-earthquake rescue efforts. Efficient and accurate rapid assessment of high-risk landslide zones carries important implications for decision-making in disaster response and for mitigating potential secondary disasters. This study uses the high-intensity Zone VII to IX of the 5 September 2022 Luding Ms6.8 earthquake as a case study. The "difference method" and the "cumulative displacement method," based on the simple Newmark model, are employed to assess earthquake-triggered landslides. The evaluation results from both methods demonstrate that the areas posing an ex-tremely high risk of earthquake-triggered landslides are predominantly situated on the western side of the Xianshuihe Fault. Actual landslide data verification shows that both models have high predictive accuracy, with the difference method model slightly outper-forming the cumulative displacement method model. Moreover, the study recommends determining threshold values for each landslide hazard interval with significant physical meaning using past strong earthquake data as soon as possible when utilizing the difference method to assess the risk of earthquake-triggered landslides.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Earthquake-triggered landslides occur when slope materials slide due to the strong seismic motion. These landslides directly jeopardize the lives and property of individuals in earthquake-prone areas. For instance, the 2008 Wenchuan earthquake led to a landslide in the western region of Beichuan County, resulting in the burial of approximately 1600 people and the destruction of hundreds of houses [1]. Additionally, earthquake-triggered landslides can disrupt traffic, damage critical infrastructure, and create blockages in rivers, leading to the formation of barrier lakes in affected areas, all of which have detrimental effects on rapid rescue efforts [1,2,3]. Therefore, the efficient and accurate rapid assessment of high-risk areas for earthquake-triggered landslides holds great significance in reducing losses caused by secondary disasters during the rapid response stage following earthquakes.
Currently, there are numerous rapid assessment methods for regional earthquake-triggered landslides, which can be broadly categorized into two groups.The first category consists of the indicator system methods, which involve developing evaluation techniques based on various parameters related to earthquake-triggered landslides and faults, such as magnitude, distance to the epicenter, and the distribution of rivers and roads. These methods include models such as logistic regression [4,5], support vector machines [6,7], and neural networks [8,9]. The second category is the Newmark method, which is based on the principle of mechanical equilibrium and has been widely applied in earthquake landslide risk assessment worldwide [10,11,12,13,14,15,16,17,18,19,20]. Unlike the indicator system method, the Newmark method is not constrained by geological background differences and provides evaluation results with relatively clear physical significance. This method has been used in various earthquake cases globally [21].
Within the Newmark method, there are two main approaches for determining earthquake landslide risk: the “difference method” and the “cumulative displacement method”. The difference method assesses risk based on the magnitude of the difference between Peak Ground Acceleration (PGA) and the critical acceleration of rock-soil mass, with a larger difference indicating a higher risk of earthquake-triggered landslides [16,17,19,22,23]. On the other hand, the cumulative displacement method uses the relationship between PGA and permanent cumulative displacement to calculate the displacement of rock-soil mass and determine landslide risk based on the magnitude of the displacement value[20,24,25,26,27]. While both methods have shown effectiveness in previous earthquake case studies, further comparative research is required to fully understand their respective advantages, disadvantages, and applicability.
On September 5, 2022, Luding County in Sichuan Province was struck by a magnitude 6.8 earthquake, with its epicenter located at (29.25°N, 102.08°E) and a focal depth of 16km. The earthquake reached an intensity of Ⅸ according to the China Earthquake Networks Center (www.cenc.ac.cn), causing widespread damage to infrastructure, including transportation networks, power systems, and buildings. Additionally, the seismic event triggered a substantial number of landslides, exacerbating the devastation [27,28,29,30]. By the end of the emergency response phase on September 11th, the earthquake had claimed 118 lives, with 86% attributed to secondary geological disasters such as landslides and collapses.
Following the earthquake, researchers conducted extensive field investigations and utilized remote sensing data to compile distribution data on the earthquake-triggered landslides, providing valuable insights for studying rapid assessment methods in such scenarios. This study focuses on high-intensity areas, notably Moxi Town and Detuo Town, during the Luding earthquake (rated VII~IX), employing the “difference method” and “cumulative displacement method” to assess the risk of earthquake-induced landslides in the region. The validation of these methods relies on actual landslide data, allowing for a comprehensive analysis of their strengths, weaknesses, and applicability in similar contexts.

2. Method and Data

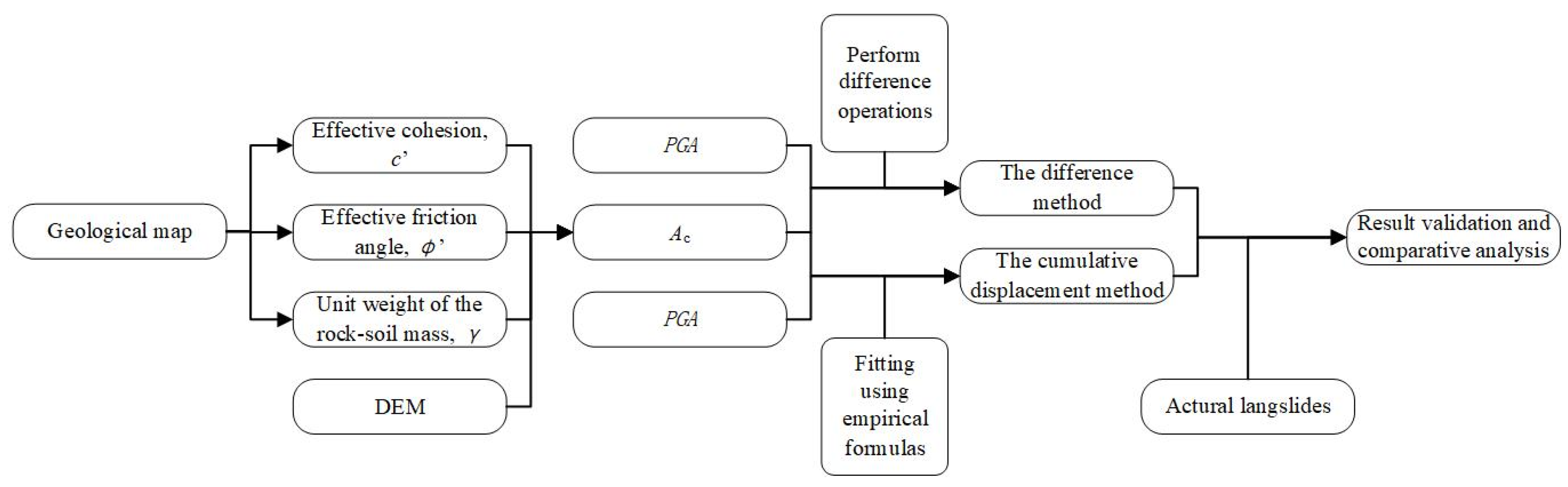
2.1. Two Assessment Methods Based on Newmark Method

The Newark model, introduced by Newmark in 1965, was originally developed to assess the stability of dams in response to seismic activity. According to this method, when ground motion produces peak acceleration surpassing the critical acceleration (Ac) associated with the most precarious surface, the slider is initiated to slide along this surface, leading to cumulative displacement. Essentially, the model posits that a rock-soil mass with a higher Ac necessitates a greater peak ground acceleration (PGA) to induce cumulative displacement, indicating that a larger Ac generally corresponds to enhanced stability during seismic events. Furthermore, in the absence of external forces, the static safety coefficient can be computed using the principle of limit equilibrium [31].
F s = c ' γ t sin α + tan φ ' tan α - m γ w tan φ ' γ tan α
In formula (1), Fs represents the static factor of safety, while c’, φ’, and γ denote the physical and mechanical parameters of the rock-soil mass, specifically the effective cohesion (kPa), effective friction angle (°), and unit weight (kN/m³) respectively. The variable t represents the thickness of the failure slab, which, in the context of this earthquake, where landslides are predominantly small to medium-sized, is considered as 3m. The slope angle (°), denoted by α, is determined using Digital Elevation Models (DEMs) within the study area, while m signifies the proportion of the slab thickness that is saturated. Given the absence of rainfall during this seismic event, the value of m is assumed to be 0. Ac, representing the critical acceleration of the rock-soil mass in the study area, can be computed from Fs using formula (2):
A c = ( F s − 1 ) g sin α
By employing the difference method and cumulative displacement method, the seismic-triggered landslide risk of the rock-soil mass in the study area can be evaluated based on the critical acceleration (Ac) and peak ground acceleration (PGA). The difference method involves treating PGA and Ac as distinct entities and utilizing their difference as the primary metric for assessing the risk of earthquake-induced landslides. A larger difference indicates a heightened risk of such landslides, while a smaller difference suggests a lower risk.
On the other hand, the cumulative displacement method involves fitting Ac with PGA to directly determine the permanent cumulative displacement of the rock-soil mass (DN) under the influence of ground motion. DN serves as the basis for assessing the risk of earthquake-induced landslides. It is important to note that the empirical formula used to calculate DN exhibits regional characteristics, and the same formula may yield significantly different fitting results in various regions. Therefore, it is advisable to employ fitting formulas that are most suitable for the specific study area. Figure 1 illustrates the processes of these two assessment methods.

2.2. Data source

This study utilized 1:200,000 scale geological map data obtained from the National Geological Data Center (www.ngac.cn). Slope data was derived from pre-earthquake SRTM 30m resolution Digital Elevation Models (DEMs), sourced from the official website of the United States Geological Survey (www.usgs.gov).
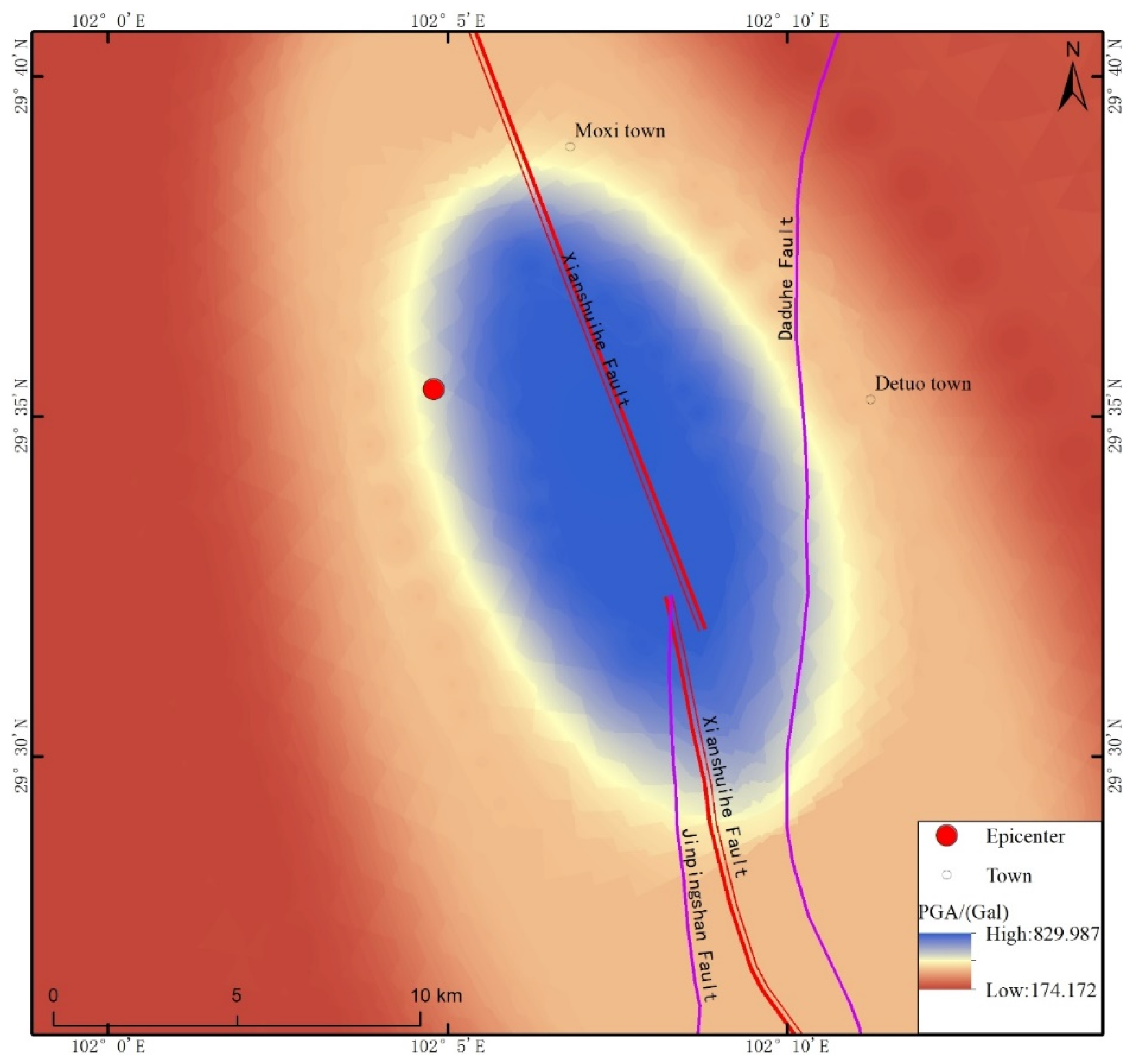
Given the limited number of seismic stations within the earthquake zone, only one station is situated in the study area, located at the perimeter. Consequently, PGA data for this study were acquired through transformation and interpolation analysis, leveraging the earthquake intensity map released by the Ministry of Emergency Management of the People’s Republic of China (www.mem.gov.cn) and the Chinese seismic intensity scale (refer to Figure 2) [32].The interpolated PGA data ranged from 174 to 830 gal, exhibiting consistency with both the seismic station recordings within the earthquake zone and the seismic intensity map released by the Ministry of Emergency Management of the People’s Republic of China.
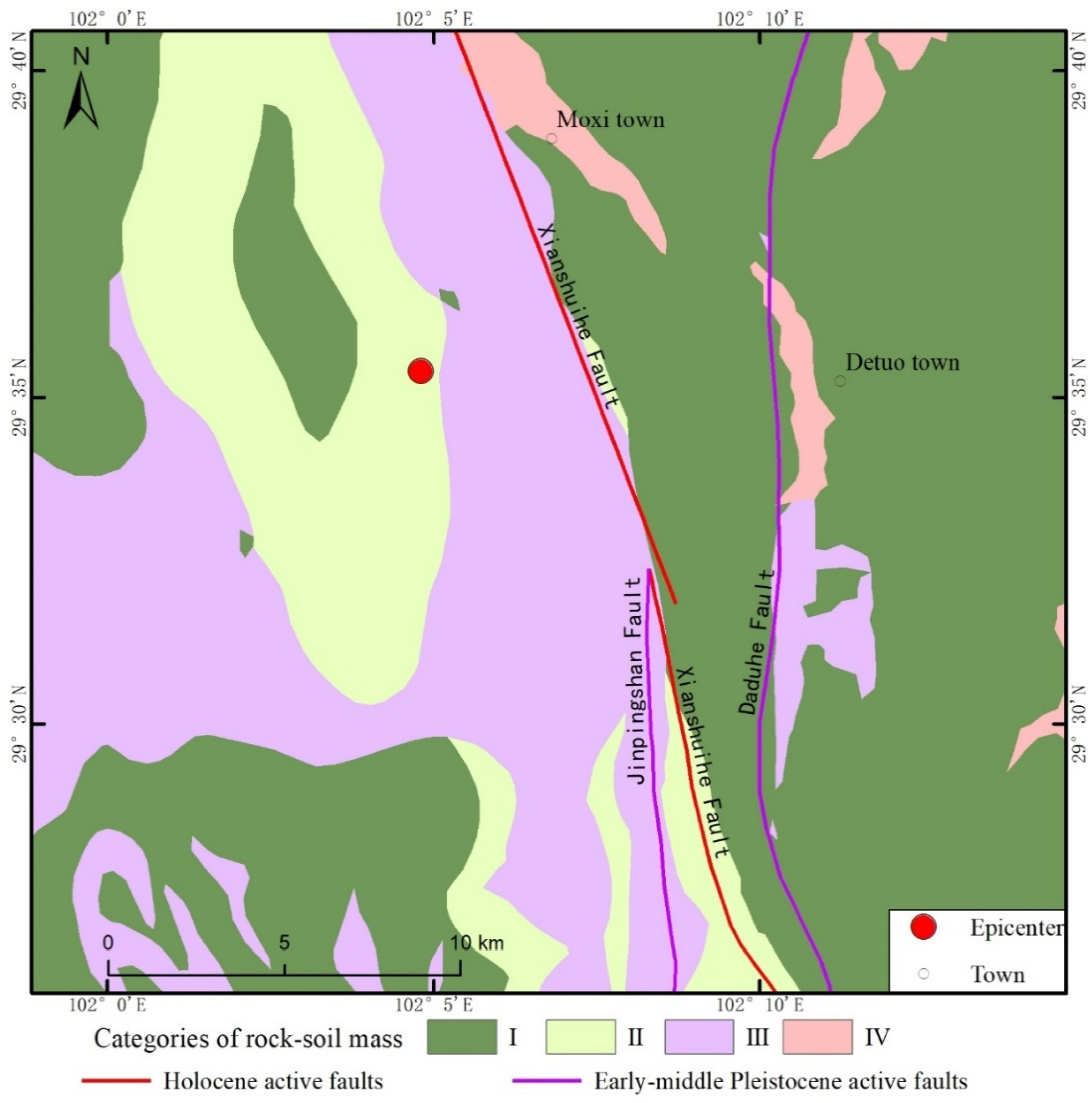
The physical and mechanical parameters of the rock-soil mass utilized in this study were derived from regional 1:200,000 large-scale geological maps. In accordance with the engineering classification standard for rock mass [33], the rock-soil mass within the research area was categorized into four groups (refer to Figure 3): very hard (I), harder (II), softer (III), and extremely soft (IV).
In detail, the very hard category predominantly encompasses intermediate acidic intrusive rocks such as granite and diorite, while the harder types include limestone, dolomite, calcareous dolomite, and dolomitic limestone. The softer types comprise sedimentary rocks like conglomerate, mudstone, and slate, while the extremely soft type refers to loose deposits of the Holocene series. Drawing upon the aforementioned standards and relevant studies in neighboring regions [11,16,17,18], we assigned specific values to the physical and mechanical parameters of various rock-soil masses (see Table 1).

3. Results

3.1. The Susceptibility of Earthquakes-Triggered Landslides in the Research Area

Leveraging the physical and mechanical parameters, as well as the slope data of the rock-soil mass within the study area, we computed the critical acceleration (Ac) of the rock-soil mass using formulas (1) and (2) (refer to Figure 4). The results of the calculations reveal that the critical acceleration of the rock-soil mass within the area is constrained by the Xianshuihe Fault. Notably, there exists a distinct numerical pattern characterized by lower values in the west and higher values in the east. This suggests a higher propensity for earthquake-triggered landslides on the western side of the Xianshuihe Fault under ground motion.

3.2. Assessment Results of Difference Method

Conducting a differential analysis between PGA and Ac, we then utilize the natural breaks method—an approach characterized by small intra-class differences and significant inter-class differences—to classify the earthquake landslide risk into five distinct categories: extremely low risk area, low risk area, medium risk area, high risk area, and extremely high risk area.
Observing Figure 5, the earthquake-triggered landslide hazard evaluation conducted using the difference method exhibits a distinctive pattern of high risk in the west and low risk in the east, delineated by the Xianshuihe Fault. Particularly noteworthy is the concentration of the extremely high hazard zone predominantly on the western side of the fault line. Additionally, the seismic landslide hazard classification demonstrates a gradual decrease towards the surrounding regions, mirroring the distribution trend of PGA. Statistical analysis reveals that the distribution of earthquake-triggered landslide hazard classification, ranging from extremely high to extremely low in the study area, stands at 8.27%, 22.77%, 27.21%, 21.50%, and 20.25%, respectively.

3.3. Assessment Results of Cumulative Displacement Method

In this study, we employed empirical formulas to compute the permanent cumulative displacement of the rock-soil mass within the study area under ground motion. Subsequently, we assessed the earthquake-triggered landslide hazard by evaluating the magnitude of the cumulative displacement value. To ensure regional applicability, we utilized an empirical formula derived from previous research, specifically based on cumulative displacement records from the Wenchuan strong earthquake, to calculate the cumulative displacement of the rock-soil mass in the current earthquake event (refer to Formula 3) [26].
lg D N = 0.194 + lg [ ( 1 − A c P G A ) 2.262 * ( A c P G A ) − 1.754 ]
The formula utilizes DN to represent the permanent cumulative displacement (in cm), while Ac and PGA denote the critical acceleration (in g) and peak ground acceleration (in g), respectively. Notably, the empirical formula boasts an impressive judgment coefficient R2 of 91.4%. Integrating the results derived from this formula with the critical displacement values determined in prior studies [13,27,34,35], the earthquake-triggered landslide risk within the study area is classified into extremely low risk, low risk, medium risk, high risk, and extremely high risk zones, with boundary values set at 0.5, 1, 2, and 5 cm.
Derived from Figure 6, the earthquake-triggered landslide risk classification obtained through this method spans from extremely high to extremely low, encompassing 19.8%, 3.67%, 3.10%, 3.15%, and 70.26% of the study area, respectively.

4. Analysis and Discussion

4.1. Analysis of Assessment Results

On the whole, the evaluation results from both methods demonstrate that the areas posing an extremely high risk of earthquake-triggered landslides are predominantly situated on the western side of the Xianshuihe Fault, exhibiting a similar distribution pattern to that of the critical acceleration of the rock-soil mass. Concurrently, the difference method identifies elevated earthquake-triggered landslide risks on both sides of the Daduhe Fault, aligning with the observed real-world scenario. Conversely, the cumulative displacement method indicates a relatively heightened risk of earthquake-triggered landslides on the eastern side of the Daduhe Fault, accompanied by isolated high-risk zones on the western side. Notably, the actual distribution of seismic landslides deviates somewhat from the assessment results.
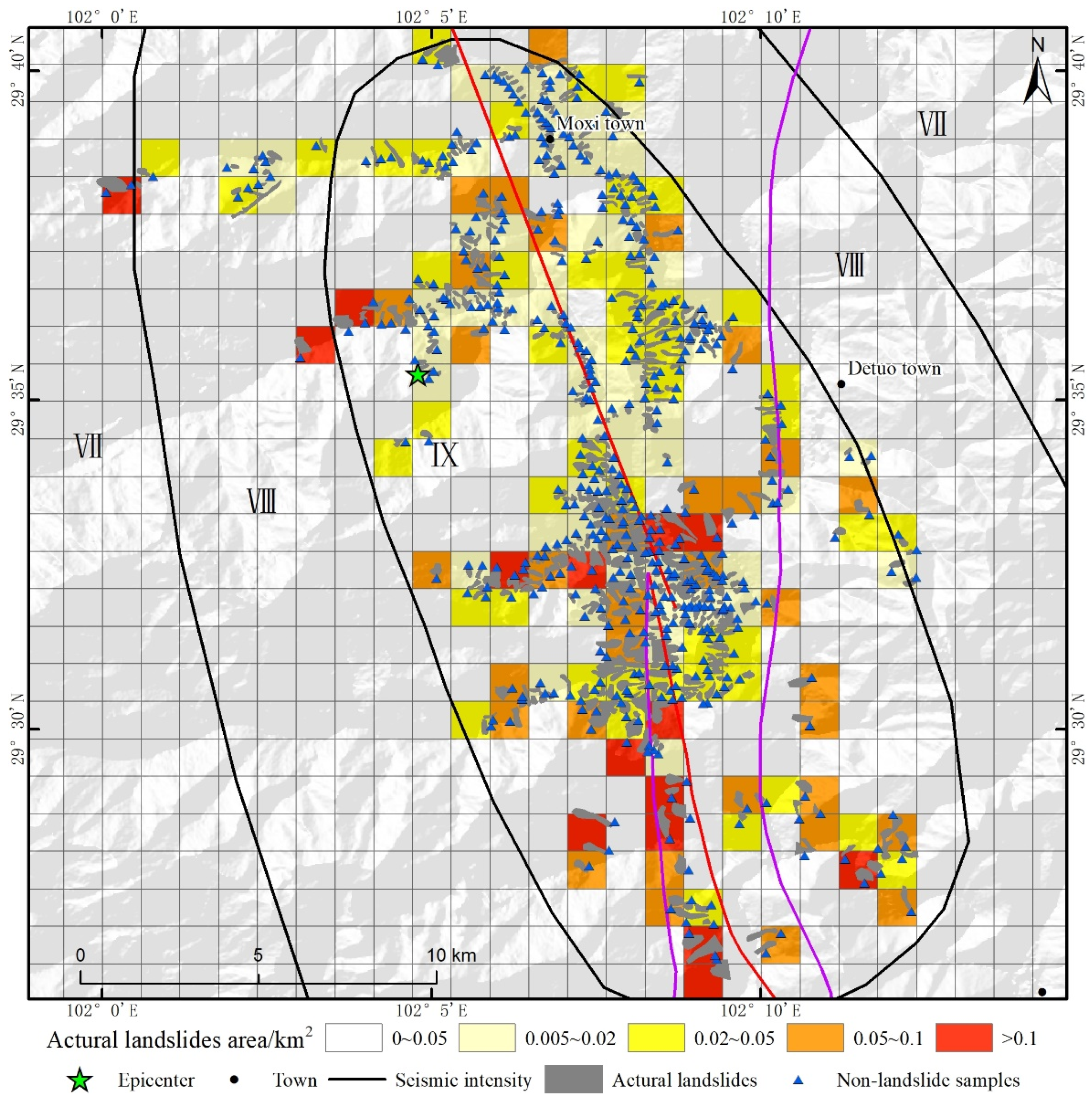
In the study area, a comprehensive collection of 476 earthquake-triggered landslides was amassed [29], covering an approximate total area of 17.81 km2. This data was employed in this study as validation data to facilitate a comparative analysis of the assessment results derived from the two methods.
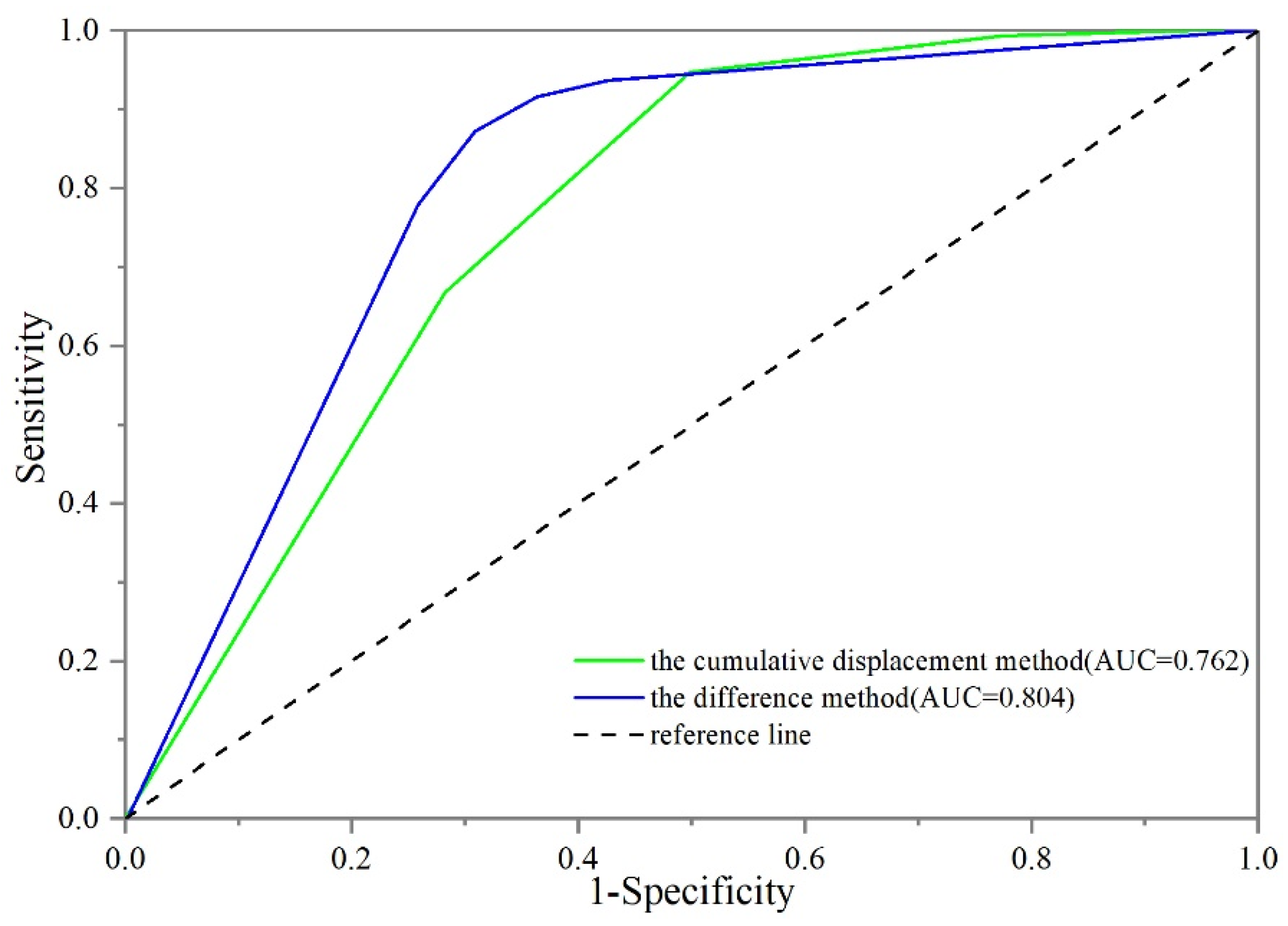
We evaluated the accuracy of two models using ROC curves, which are Receiver Operating Characteristic curves, a comprehensive indicator reflecting sensitivity and specificity of continuous variables [36]. The evaluation criteria are as follows: when AUC < 0.5, the prediction results are opposite; when AUC = 0.5, it indicates a random model; AUC between 0.5 and 0.7 suggests low accuracy; AUC between 0.7 and 0.9 indicates high accuracy; and when AUC > 0.9, the model accuracy is very high [37].
We used 476 actual landslides triggered by the earthquake as landslide samples. Additionally, we randomly selected 476 non-landslide samples outside a 100-meter buffer zone from the actual landslide samples, totaling 952 sample points (Figure 7). Based on this, we calculated the predictive accuracy of different models. The results show that both models have high predictive accuracy (both exceeding 0.7), with the difference method model slightly outperforming the cumulative displacement method model (Figure 8).

4.2. Discussion

This article employs the Luding 6.8 earthquake as a case study, utilizing both the difference method and the cumulative displacement method based on the Newmark model to evaluate the risk of earthquake-triggered landslides and conduct a comparative analysis.
The validation results show that both evaluation methods have high reliability, with the difference method slightly outperforming the cumulative displacement method. Unlike the complex cumulative displacement fitting formula, the difference method directly performs the difference operation between PGA and Ac. As a result, the assessment results obtained by this method not only reflect the characteristics of seismic landslide susceptibility of rock-soil mass but also capture the distribution and attenuation of PGA. The difference method has demonstrated effective performance in the study of earthquake landslides across numerous earthquake cases [17,19,22,23,38].
Nevertheless, it is important to note that the natural breaks method, which forms the basis of the difference method for classifying the risk level of earthquake-triggered landslides, lacks clear physical significance in its natural break values [19,38]. Consequently, different sample data may result in varying break points, potentially leading to the classification of the same risk level by different thresholds in distinct earthquake case studies, thus potentially impacting the assessment results.
The cumulative displacement method employs empirical formulas to calculate the permanent cumulative displacement values of rock-soil mass for assessing earthquake-triggered landslide risk. This method not only facilitates a rapid evaluation of such risks but also enables predictions regarding potential loosening points within the rock-soil mass induced by earthquakes. It is crucial to bear in mind that the regional applicability of the empirical formula utilized for calculating permanent cumulative displacement must be considered when employing this method [25,26,39]. Selecting an appropriate empirical formula tailored to the specific study area is imperative to avoid potential deviations in the assessment results.
In conclusion, the regional earthquake-triggered landslide risk assessment technology based on the Newmark method has significantly advanced from its initial stage; however, there are still numerous shortcomings that require urgent improvement. Regarding the difference method, it is imperative to determine threshold values for each landslide risk interval with clear physical significance through the study of previous significant earthquake data. This approach will ensure that the assessment results not only receive verification-level support but also possess a solid theoretical foundation. As for the cumulative displacement method, establishing a fitting formula with a high regression coefficient between ground motion and cumulative displacement in each earthquake-prone area is crucial. Furthermore, improving the Newmark method itself entails establishing a more refined database of physical and mechanical parameters for rock-soil mass, along with regular updates of high-precision terrain data [13,18,40,41]. These measures will contribute to enhancing the accuracy and reliability of the method’s assessment results.

5. Conclusion

(1) The evaluation results from both methods demonstrate that the areas posing an extremely high risk of earthquake-triggered landslides are predominantly situated on the western side of the Xianshuihe Fault, exhibiting a similar distribution pattern to that of the critical acceleration of the rock-soil mass.
(2) Actual landslide data verification shows that both models have high predictive accuracy (both AUC exceeding 0.7), with the difference method model slightly outperforming the cumulative displacement method model.
(3) When employing the difference method to analyze the risk of earthquake-triggered landslides, it is imperative to determine threshold values for each landslide risk interval with clear physical significance through the study of previous significant earthquake data.

Author Contributions

Data curation, Jing-fei Yin; Formal analysis, Min Li; Funding acquisition, Huan-yu Li and Dong-ping Li; Investigation, Hai-qing Sun; Methodology, Huan-yu Li; Resources, Jing-fei Yin and Chen-bing Dai; Writing—original draft, Huan-yu Li; Writing—review & editing, Dong-ping Li.All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by “Key Tasks for Youth in Earthquake Emergency Response of China Earthquake Administration”, grant number “CEAEDEM20240206”, “Natural Science Foundation of Zhejiang Province”, grant number “LTGG24D040002”, “Research on Major Policy Theory and Practice Issues of China Earthquake Administration”, grant number “CEAZY2024JZ01” and The APC was funded by “Natural Science Foundation of Zhejiang Province”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in publicly accessible website.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Yin Y. P. Researches on The Geo-Hazards Triggered by Wenchuan Earthquake, Sichuan. Journal of Engineering Geology, 2008, 16(04), 433-444 (in Chinese).
  2. Kong J. M., A F. Y., Deng H. Y., et al. Classification and Typical Case Analysis of Wenchuan Earthquake-induced Dammed Lakes Based on Landslide Formation Mechanism. Journal of Sichuan University (Engineering Science Edition), 2010, 42(5), 44-51 (in Chinese).
  3. Li H. Y., Chen T., Yang F. P., et al. Rapid Estimation of Road Landslides Based on Newmark Method for The 6.1 Magnitude Earthquake in Lushan, Sichuan. North China Earthquake Sciences, 2023, 41(02), 16-21 (in Chinese).
  4. Xu C., Xu X. W., Zhou B. G., et al. Probability of Coseismic Landslides: A New Generation of Earthquake-Triggered Landslide Hazard Model. Journal of Engineering Geology, 2019, 27(05), 1122-1130 (in Chinese).
  5. Ma S. Y., Xu C., Tian Y. Y., et al. Application of Logistic Regression Model for Hazard Assessment of Earthquake-Intriggered landslides: A Case Study of 2017 Jiuzhaigou(China) Ms7.0 Event. Seismology and Geology, 2019, 41(01): 162-177 (in Chinese).
  6. Xu C., Dai F. C., Xu X. W., et al. Gis-Based Support Vector Machine Modeling of Earthquake-Triggered Landslide Susceptibility in the Jianjiang River Watershed, China. Geomorphology, 2012, 145-146(2012), 70-80. [CrossRef]
  7. Lin Q. G., Liu Y. Y.,Liu L. Y., et al. Earthquake-triggered landslide susceptibility assessment based on support vector machine combined with Newmark displacement model. Journal of Geo-information Science, 2017, 19(12), 1623-1633 (in Chinese).
  8. Chen X. Li., Zhao J.,Ye H. Application of RBPNN in The Research of Earthquake-Induced Landslide. Seismology and Geology, 2006, 28(3), 430-440 (in Chinese).
  9. Pradhan B., Lee S. Landslide Susceptibility Assessment and Factor Effect Analysis: Backpropagation Artificial Neural Networks and their Comparison with Frequency Ratio and Bivariate Logistic Regression Modelling. Environmental Modelling & Software, 2010, 25(6), 747-759. [CrossRef]
  10. Newmark, N. M. Effects of Earthquakes on Dams and Embankments. Géotechnique, 1965, 15 (2), 139–160.
  11. Chen Q. G., Ge H., Zhou H. F. Mapping of Seismic Triggered Landslide through Newmark Method-An Example from Study Area Yingxiu. Coal Geology of China, 2011, 23(11), 44-48 (in Chinese).
  12. Chen X. L., Yuan R. M., Yu L. Applying The Newmark’s Model to The Assessment of Earthquake-Triggered Landslides During The Lushan Earthquake. Seismology and Geology, 2013, 35(03), 661-670 (in Chinese).
  13. Wang T., Wu S. R., Shi J. S., et al. Case Study on Rapid Assessment of Regional Seismic Landslide Hazard Based On Simplified Newmark Displacement Model: Wenchuan Ms 8.0 Earthquake. Journal of Engineering Geology, 2013, 21(01), 16-24 (in Chinese).
  14. Yang Z. H., Zhang Y. S., Guo C. B., et al. Landslides Hazard Rapid Assessment in The Nepal Ms8.1 Earthquake-Impacted Area, Based on Newmark Model. Journal of Geomechanics, 23(01), 2017, 115-124 (in Chinese).
  15. Liu J. M., Wang T., Shi J. S., et al. Emergency Rapid Assessment of Landslides induceds by The Jiuzhaigou Ms 7.0 Earthquake, Sichuan, China.Journal of Geomechanics, 2017, 23(05): 639-645 (in Chinese).
  16. Chen X. L., Shan X. J.,Zhang L., et al.. Quick Assessment of Earth-triggered Landslide Hazards: A Case Study of The 2017 Ms7.0 Jiuzhaigou Earthquake. Earth Science Frontiers, 2019, 26(02), 312-320 (in Chinese).
  17. Chen X. L., Liu C. G., “Assessment of Landslides Triggered by Earthquakes Based On the Combination of Peak Ground Motion and Critical Acceleration Analysis”. in IAEG/AEG Annual Meeting Proceedings, San Francisco, California Cham: Springer, 2019, 123–129. [CrossRef]
  18. Ma S. Y., Xu C., Wang T., et al. Application of Two Simplified Newmark Models to The Assessment of Landslides Triggered by the 2008 Wenchuan Earthquake. Seismology and Geology, 2019, 41(03), 774-788 (in Chinese).
  19. Wei Y. K., Chen X. L. Applicability of Different Seismic Landslide Risk Assessment Methods: A Case Study of Maduo Ms 7.4 Earthquake. Seismology and Geology, 2022, 44(03), 590-603 (in Chinese).
  20. Jia Z. L., Zheng C., Wu Y. M., et al. Risk Assessment of The Hazard-bearing Bodies by Earthquake-induced Landslides Based on The Newmark Mode: A case study of 2014 Ludian, Yunnan Ms 6.5 Earthquake. Journal of Seismological Research. 2023, 46(03), 366-375 (in Chinese).
  21. Wang T., Liu J. M., Li. Z. T., et al. Seismic Landslide Hazard Assessment of China and Its Impact on National Territory Spatial Planning. Geology in China, 2021, 48(1), 21-39 (in Chinese).
  22. Chen X. L., Liu, C. G., Yu, L., et al. Critical Acceleration as a Criterion in Seismic Landslide Susceptibility Assessment. Geomorphology, 2014, 217,15–22. [CrossRef]
  23. Maharjan S., Gnyawali K. R., Tannant D. D., et al. Rapid Terrain Assessment for Earthquake-Triggered Landslide Susceptibility with High-Resolution Dem and Critical Acceleration. Frontiers in Earth Science, 2021, 9,689303. [CrossRef]
  24. Ambraseys N. N., Menu J. M. Earthquake-Induced Ground Displacements. Earthquake Engineering & Structural Dynamics , 1988, 16 (985-1006). [CrossRef]
  25. Jibson R. W. Regression Models for Estimating Coseismic Landslide Displacement. Engineering Geology, 2007, 91 (2-4), 209–218. [CrossRef]
  26. Xu G. X., Yao L. K., Li Chao Hong, et al. Predictive Models for Permanent Displacement of Slopes Based on Recorded Strong-motion Data of Wenchuan Earthquake. Chinese Journal of Geotechnical Engineering, 2012, 34(6), 1131-1136 (in Chinese).
  27. Liu J. M., Wang T., Du J. J., et al. Emergency Rapid Assessment of Landslides Induced by The Luding Ms 6.8 Earthquake in Sichuan of China. Hydrogeology & Engineering Geology, 2023, 50(02), 84-94 (in Chinese).
  28. Tie Y. B., Zhang X. Z., Lu J. Y., et al. Characteristics of Geological Hazards and It’s Mitigations of The Ms6.8 Earthquake in Luding County, Sichuan Province. Hydrogeology & Engineering Geology, 2022, 49(06), 1-12 (in Chinese).
  29. Zhang J. J., Chen L., Li Y. L., et al. Development Characteristics and Controlling Factors of Coseismic Geohazards Triggered by The Luding Ms 6.8 Earthquake Occurred on September 5. 2022. Acta Seismologica Sinica, 2023, 45(02), 167-178 (in Chinese).
  30. Wang W. Q., Li Y. L., Zhang Z. G., et al. Rapid Estimation of Disaster Losses for The M6.8 Luding Earthquake on September 5. 2022, Science China Earth Sciences, 2023 53(06): 1342-1352 (in Chinese).
  31. Jibson R. W., Harp E. L., Michael J. A. A method for producing digital probabilistic seismic landslide hazard maps. Engineering Geology, 2000, 58 (3～4), 271-289. [CrossRef]
  32. State Administration For Market Regulation. The Chinese Seismic intensity Scale(GB /T 17742-2020). Beijing, Standards Press of China, 2020 (in Chinese).
  33. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. (). Standard For Engineering classification of Rock Mass(GB /T 50218-2014). Beijing, China Planning Press, 2015.
  34. Wieczorek G. F, Wilson R C, Harp E L. Map Showing Slope Stability During Earthquakes in San Mateo County, California. U.S. Geological Survey Miscellaneous Investigations Series Map, I,1257E, 1985．.
  35. Wang X. Y.,Nie G. Z.,Wang S. Ground motion acceleration criterion for judging landslide induced by the 2008 Wenchuan earthquake. Acta Seismologica Sinica, 2011, 33(1), 82-90 (in Chinese).
  36. Swets J.A., Measuring the accuracy of diagnostic systems. Science, 1988. 240(4857): 1285-1293. [CrossRef]
  37. Brenning. A., Spatial prediction models for landslide hazards; review, comparison and evaluation. Natural hazards and earth system sciences, 2005. 5(6): 853-862. [CrossRef]
  38. Chen X. L., Shan, X. J., Wang, M.-M., et al. Distribution Pattern of Coseismic Landslides Triggered by the 2017 Jiuzhaigou Ms 7.0 Earthquake of China: Control of Seismic Landslide Susceptibility. ISPRS International Journal of Geo-Information, 2020, 9 (4), 198. [CrossRef]
  39. Roberto R., Seismically induced landslide displacements: a predictive model. Engineering Geology, 2000. 58(3): 337-351. [CrossRef]
  40. Bojadjieva J., Sheshov V., Christophe B., Hazard and risk assessment of earthquake-induced landslides—case study. Landslides, 2018. 15(1): 161-171. [CrossRef]
  41. Dreyfus D. K., Rathje E.M., Jibson R. W., The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake. Engineering Geology, 2013. 163: 41-54. [CrossRef]
Preprints 111490 g001
Figure 1. Research flowchart
Figure 1. Research flowchart
Preprints 111490 g001
Preprints 111490 g002
Figure 2. Distribution of PGA
Figure 2. Distribution of PGA
Preprints 111490 g002
Preprints 111490 g003
Figure 3. Categories of rock-soil mass
Figure 3. Categories of rock-soil mass
Preprints 111490 g003
Preprints 111490 g004
Figure 4. Critical acceleration of rock-soil mass
Figure 4. Critical acceleration of rock-soil mass
Preprints 111490 g004
Preprints 111490 g005
Figure 5. Risk assessment results of earthquake-triggered landslides (by the difference method)
Figure 5. Risk assessment results of earthquake-triggered landslides (by the difference method)
Preprints 111490 g005
Preprints 111490 g006
Figure 6. Risk assessment results of earthquake-triggered landslides (by the cumulative displacement method)
Figure 6. Risk assessment results of earthquake-triggered landslides (by the cumulative displacement method)
Preprints 111490 g006
Preprints 111490 g007
Figure 7. Actual landslides and non-landslide samples
Figure 7. Actual landslides and non-landslide samples
Preprints 111490 g007
Preprints 111490 g008
Figure 8. Actual landslides and non-landslide samples
Figure 8. Actual landslides and non-landslide samples
Preprints 111490 g008
Table 1. Physical and mechanical parameters of the rock-soi masss in the study area
Table 1. Physical and mechanical parameters of the rock-soi masss in the study area
Rock-soil mass c’（kPa） φ’（°） γ（kN/m3）
Ⅰ 35 38 26
Ⅱ 28 33 23
Ⅲ 22 24 22
Ⅳ 15 10 16
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated