Submitted:
04 July 2024
Posted:
09 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
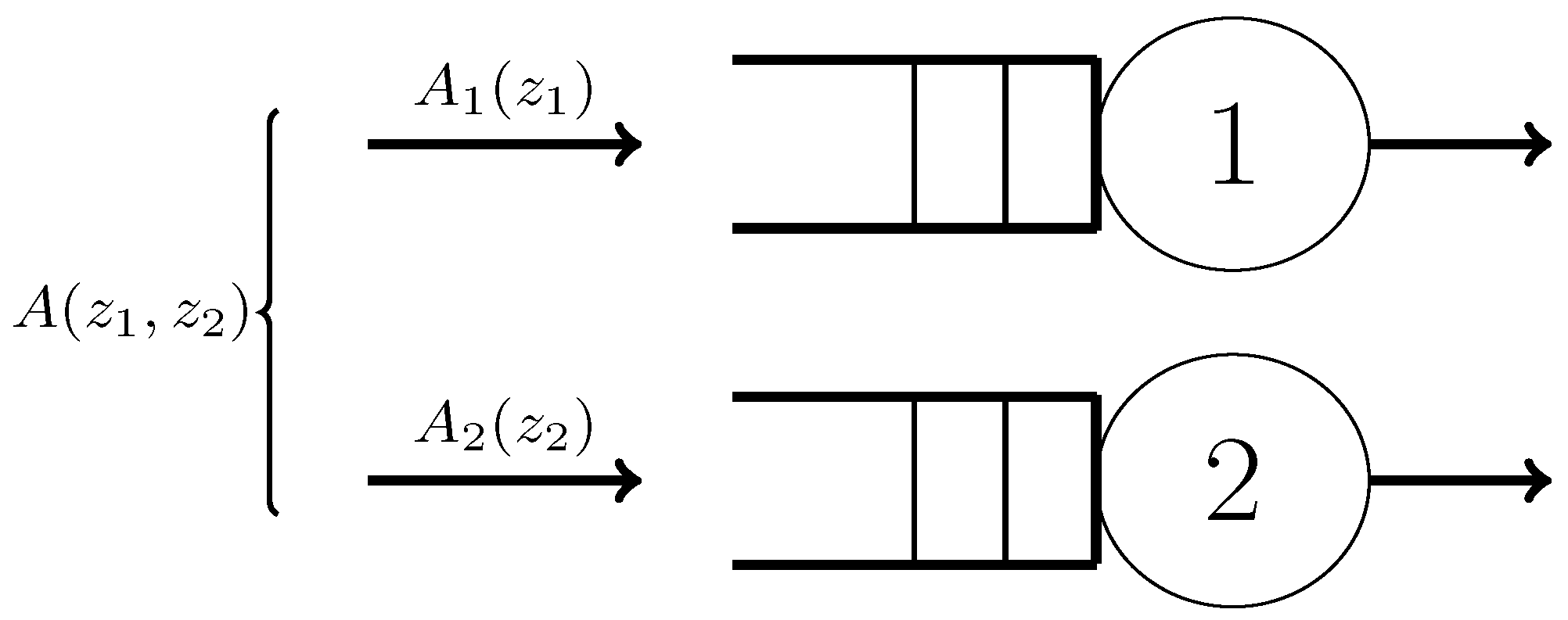
2. Mathematical Model and Queueing Analysis
3. Defining a Class of Arrival pgfs
4. The Main Result
4.1. Some Remarks on the Terms of Theorem 1
4.2. Proving Theorem 1
5. Subclasses A, B and C
5.1. Subclass A:
5.2. Subclass B:
5.3. Subclass C: No Linear Terms in and
6. Special Cases within Subclasses A, B and C
6.1. Special Cases within Subclass A
6.1.1. At Most One Arrival per Slot in Queue 1
6.1.2. The Case
6.1.3. Geometric f-Distributions
6.1.4. Binomial f-Distributions
6.1.5. Batch-2-Geometric f-Distributions
6.2. Special Cases within Subclass B
6.2.1. The Case
6.2.2. The Case
6.3. Special Cases within Subclass C
6.3.1. Bernoulli c-Distributions
6.3.2. Geometric c-Distributions
6.3.3. Negative Binomial c-Distributions
7. Inverting the Joint pgf
7.1. Some Comments
7.2. Specific Examples
7.2.1. An Example within Subclass A
7.2.2. An Example within Subclass B
7.2.3. An Example within Subclass C
8. Concluding REMARKS
References
- Jaffe, S. The equilibrium distribution for a clocked buffered switch. Probability in the Engineering and Informational Sciences 1992, 6, 425–438. [Google Scholar] [CrossRef]
- Boxma, O.; van Houtum, G. The compensation approach applied to a 2x2 switch. Probability in the Engineering and Informational Sciences 1993, 7, 471–493. [Google Scholar] [CrossRef]
- Cohen, J. On the determination of the stationary distribution of a symmetric clocked buffered switch. In Proc. ITC-15, Teletraffic Contributions for the Information Age; Ramaswami, V.; Wirth, P., Eds.; Elsevier, 1997; Vol. 2a, pp. 297–307.
- Adan, I.; Boxma, O.; Resing, J. Queueing models with multiple waiting lines. Queueing Systems 2001, 37, 65–98. [Google Scholar] [CrossRef]
- Bruneel, H. Some thoughts on the analysis of coupled queues. Queueing Systems 2022, 100, 185–187. [Google Scholar] [CrossRef]
- Bruneel, H.; Devos, A. Asymptotic behavior of a system of two coupled queues when the content of one queue is very high. Queueing Systems 2023, 105, 189–232. [Google Scholar] [CrossRef]
- Cohen, J. Analysis of the asymmetrical shortest two-server queueing model. Journal of Applied Mathematics and Stochastic Analysis 1998, 11, 115–162. [Google Scholar] [CrossRef]
- Dimitriou, I. Analysis of the symmetric join the shortest orbit queue. Operations Research Letters 2021, 49, 23–29. [Google Scholar] [CrossRef]
- Adan, I.; Boxma, O.; Kapodistria, S.; Kulkarni, V. The shorter queue polling model. Annals of Operations Research 2016, 241, 167–200. [Google Scholar] [CrossRef]
- Wright, P.E. Two parallel processors with coupled inputs. Advances in Applied Probability 1992, 24, 986–1007. [Google Scholar] [CrossRef]
- Bruneel, H.; Devos, A. Coupled queues whose stationary joint content distribution is a finite sum of bivariate geometric terms. submitted 2024. [Google Scholar]
- Takagi, H. Queuing analysis of polling models. ACM Computing Surveys (CSUR) 1988, 20, 5–28. [Google Scholar] [CrossRef]
- Levy, H.; Sidi, M. Polling systems: applications, modeling, and optimization. IEEE Transactions on Communications 1990, 38, 1750–1760. [Google Scholar] [CrossRef]
- Vishnevskii, V.; Semenova, O. Mathematical methods to study the polling systems. Automation and Remote Control 2006, 67, 173–220. [Google Scholar] [CrossRef]
- de Haan, R.; Boucherie, R.; van Ommeren, J. A polling model with an autonomous server. Queueing Systems 2009, 62, 279–308. [Google Scholar] [CrossRef]
- Al Hanbali, A.; de Haan, R.; Boucherie, R.; van Ommeren, J. Time-limited polling systems with batch arrivals and phase-type service times. Annals of Operations Research 2012, 198, 57–82. [Google Scholar] [CrossRef]
- Saxena, M.; Boxma, O.; Kapodistria, S.; Nunez Queija, R. Two queues with random time-limited polling. Probability and Mathematical Statistics 2017, 37, 257–289. [Google Scholar]
- Borst, S.; Boxma, O. Polling: past, present, and perspective. Top 2018, 26, 335–369. [Google Scholar] [CrossRef]
- Vishnevsky, V.; Semenova, O. Polling systems and their application to telecommunication networks. Mathematics 2021, 9, 117. [Google Scholar] [CrossRef]
- Eisenberg, M. Two queues with alternating service. SIAM Journal on Applied Mathematics 1979, 36, 287–303. [Google Scholar] [CrossRef]
- Coffman, E.; Fayolle, G.; Mitrani, I. Two queues with alternating service periods. Proceedings of the 12th IFIP WG 7.3 International Symposium on Computer Performance Modelling, Measurement and Evaluation, 1987, pp. 227–239.
- Feng, W.; Kowada, M.; Adachi, K. A two-queue model with Bernoulli service schedule and switching times. Queueing Systems 1998, 30, 405–434. [Google Scholar] [CrossRef]
- Devos, A.; Fiems, D.; Walraevens, J.; Bruneel, H. An approximate analysis of a Bernoulli alternating service model. International Conference on Queueing Theory and Network Applications. Springer, 2019, pp. 314–329.
- Devos, A.; Walraevens, J.; Fiems, D.; Bruneel, H. Approximations for the performance evaluation of a discrete-time two-class queue with an alternating service discipline. Annals of Operations Research 2020, 1–27. [Google Scholar] [CrossRef]
- Devos, A.; Walraevens, J.; Fiems, D.; Bruneel, H. Heavy-Traffic Comparison of a Discrete-Time Generalized Processor Sharing Queue and a Pure Randomly Alternating Service Queue. Mathematics 2021, 9, 2723. [Google Scholar] [CrossRef]
- Devos, A. Analysis of a two-class queueing model with randomly alternating service. PhD thesis, Ghent University, 2022.
- Devos, A.; Walraevens, J.; Fiems, D.; Bruneel, H. Analysis of a discrete-time two-class randomly alternating service model with Bernoulli arrivals. Queueing Systems 2020, 96, 133–152. [Google Scholar] [CrossRef]
- Devos, A.; De Muynck, M.; Bruneel, H.; Walraevens, J. A product-form solution for a two-class Geo/Geo/D/1 queue with random routing and randomly alternating service. EAI International Conference on Perfor- mance Evaluation Methodologies and Tools. Springer, 2022, pp. 81–95.
- Walraevens, J.; Steyaert, B.; Bruneel, H. Delay characteristics in discrete-time GI-G-1 queues with non- preemptive priority queueing discipline. Performance Evaluation 2002, 50, 53–75. [Google Scholar] [CrossRef]
- Walraevens, J.; Steyaert, B.; Bruneel, H. Performance analysis of a single-server ATM queue with a priority scheduling. Computers & Operations Research 2003, 30, 1807–1829. [Google Scholar]
- Walraevens, J.; Steyaert, B.; Bruneel, H. Performance analysis of a GI-Geo-1 buffer with a preemptive resume priority scheduling discipline. European Journal of Operational Research 2004, 157, 130–151. [Google Scholar] [CrossRef]
- Walraevens, J.; Steyaert, B.; Bruneel, H. A packet switch with a priority scheduling discipline: Performance analysis. Telecommunication Systems 2005, 28, 53–77. [Google Scholar] [CrossRef]
- Walraevens, J.; Steyaert, B.; Moeneclaey, M.; Bruneel, H. Delay analysis of a HOL priority queue. Telecom- munication Systems 2005, 30, 81–98. [Google Scholar] [CrossRef]
- Walraevens, J.; Fiems, D.; Bruneel, H. The discrete-time preemptive repeat identical priority queue. Queueing Systems 2006, 53, 231–243. [Google Scholar] [CrossRef]
- Maertens, T.; Walraevens, J.; Bruneel, H. On priority queues with priority jumps. Performance Evaluation 2006, 63, 1235–1252. [Google Scholar] [CrossRef]
- Walraevens, J.; Steyaert, B.; Bruneel, H. A preemptive repeat priority queue with resampling: Performance analysis. Annals of Operations Research 2006, 146, 189–202. [Google Scholar] [CrossRef]
- Maertens, T.; Walraevens, J.; Bruneel, H. A modified HOL priority scheduling discipline: performance analysis. European Journal of Operational Research 2007, 180, 1168–1185. [Google Scholar] [CrossRef]
- Walraevens, J.; Wittevrongel, S.; Bruneel, H. A discrete-time priority queue with train arrivals. Stochastic models 2007, 23, 489–512. [Google Scholar] [CrossRef]
- Maertens, T.; Walraevens, J.; Bruneel, H. Priority queueing systems: from probability generating functions to tail probabilities. Queueing Systems 2007, 55, 27–39. [Google Scholar] [CrossRef]
- Maertens, T.; Walraevens, J.; Bruneel, H. Performance comparison of several priority schemes with priority jumps. Annals of Operations Research 2008, 162, 109–125. [Google Scholar] [CrossRef]
- Walraevens, J.; Steyaert, B.; Bruneel, H. Analysis of a discrete-time preemptive resume priority buffer. European Journal of Operational Research 2008, 186, 182–201. [Google Scholar] [CrossRef]
- Walraevens, J.; Fiems, D.; Bruneel, H. Time-dependent performance analysis of a discrete-time priority queue. Performance Evaluation 2008, 65, 641–652. [Google Scholar] [CrossRef]
- Walraevens, J.; Maertens, T.; Bruneel, H. A semi-preemptive priority scheduling discipline: performance analysis. European Journal of Operational Research 2013, 224, 324–332. [Google Scholar] [CrossRef]
- Walraevens, J.; Bruneel, H.; Fiems, D.; Wittevrongel, S. Delay analysis of multiclass queues with correlated train arrivals and a hybrid priority/FIFO scheduling discipline. Applied Mathematical Modelling 2017, 45, 823–839. [Google Scholar] [CrossRef]
- De Clercq, S.; Walraevens, J. Delay analysis of a two-class priority queue with external arrivals and correlated arrivals from another node. Annals of Operations Research 2020, 293, 57–72. [Google Scholar] [CrossRef]
- Walraevens, J.; Van Giel, T.; De Vuyst, S.; Wittevrongel, S. Asymptotics of waiting time distributions in the accumulating priority queue. Queueing Systems 2022, 101, 221–244. [Google Scholar] [CrossRef]
- Konheim, A.; Meilijson, I.; Melkman, A. Processor-sharing of 2 parallel lines. Journal of Applied Probability 1981, 18, 952–956. [Google Scholar] [CrossRef]
- Parekh, A.; Gallager, R. A generalized processor sharing approach to flow control in integrated services networks: the single-node case. IEEE/ACM transactions on networking 1993, 1, 344–357. [Google Scholar] [CrossRef]
- Núnez-Queija, R. Sojourn times in a processor sharing queue with service interruptions. Queueing systems 2000, 34, 351–386. [Google Scholar] [CrossRef]
- Walraevens, J.; van Leeuwaarden, J.; Boxma, O. Power series approximations for generalized processor sharing systems. Queueing Systems 2010, 66, 107–130. [Google Scholar] [CrossRef]
- Vanlerberghe, J.; Walraevens, J.; Maertens, T.; Bruneel, H. A procedure to approximate the mean queue content in a discrete-time generalized processor sharing queue with Bernoulli arrivals. Performance Evaluation 2019, 134, 102001. [Google Scholar] [CrossRef]
- Gail, H.; Grover, G.; Guérin, R.; Hantler, S.; Rosberg, Z.; Sidi, M. Buffer size requirements under longest queue first. Performance Evaluation 1993, 18, 133–140. [Google Scholar] [CrossRef]
- Pedarsani, R.; Walrand, J. Stability of multiclass queueing networks under longest-queue and longest- dominating-queue scheduling. Journal of Applied Probability 2016, 53, 421–433. [Google Scholar] [CrossRef]
- Perel, E.; Perel, N.; Yechiali, U. A polling system with ‘Join the shortest-serve the longest’policy. Computers & Operations Research 2020, 114, 104809. [Google Scholar]
- Perel, E.; Perel, N.; Yechiali, U. A 3-queue polling system with join the shortest-serve the longest policy. Indagationes Mathematicae 2023, 34, 1101–1120. [Google Scholar] [CrossRef]
- Van Leeuwaarden, J.; Resing, J. A tandem queue with coupled processors: computational issues. Queueing Systems 2005, 51, 29–52. [Google Scholar] [CrossRef]
- Resing, J.; Ormeci, L. A tandem queueing model with coupled processors. Operations Research Letters 2003, 31, 383–389. [Google Scholar] [CrossRef]
- Malyshev, V. An analytical method in the theory of two-dimensional positive random walks. Siberian Mathematical Journal 1972, 13, 917–929. [Google Scholar] [CrossRef]
- Cohen, J. Analysis of a two-dimensional algebraic nearest-neighbour random walk (queue with paired services). Technical report, CWI, Amsterdam, 1994.
- Cohen, J. On a class of two-dimensional nearest-neighbour random walks. Journal of Applied Probability 1994, 31, 207–237. [Google Scholar] [CrossRef]
- Fayolle, G.; Malyshev, V.; Iasnogorodski, R. Random walks in the quarter-plane; Vol. 40, Springer, 1999.
- Adan, I.; van Leeuwaarden, J.; Raschel, K. The compensation approach for walks with small steps in the quarter plane. Combinatorics Probability & Computing 2013, 22, 161–183. [Google Scholar] [CrossRef]
- Cohen, J. On the asymmetric clocked buffered switch. Queueing Systems 1998, 30, 385–404. [Google Scholar] [CrossRef]
- Bruneel, H.; Kim, B. Discrete-time models for communication systems including ATM; Kluwer Academic Publisher: Boston, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




