Prerpints.org logo
Preprint
Article

Estimating Evapotranspiration of Rainfed Winegrapes Combining Remote Sensing and the SIMDualKc Soil Water Balance Model

Altmetrics

Downloads

144

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (127.15KB )

Submitted:

08 July 2024

Posted:

10 July 2024

You are already at the latest version

Alerts
Abstract
Soil water balance (SWB) in woody crops is sometimes difficult to estimate with one-dimensional models because these crops do not completely cover the soil and usually have a deep root system, particularly when cropped under rainfed conditions in a Mediterranean climate. In this study, the actual crop evapotranspiration (ETc act) is estimated with the soil water balance model SIMDualKc which uses the dual-Kc approach (relating the fraction of soil cover with the crop coefficients) to improve the estimation of the water requirements of a rainfed vineyard, using data from a deep soil profile. The actual basal crop coefficient (Kcb act) obtained using the SIMDualKc model was compared with the Kcb act estimated using the A&P approach, which is a simplified approach based on measurements of the fraction of ground cover and crop height. Spectral vegetation indices derived from Landsat-5 satellite data were used to determine the fraction of ground cover (fc VI) and thus, the density coefficient (Kd). The SIMDualKc model was calibrated using soil water content (SWC) measurements down to a depth of 1.85 meters, which significantly improved the conditions for using a SWB estimation model. The test of the model was performed using a different SWC dataset. A good agreement between simulated and field measured SWC was observed for both data sets along the crop season, with RMSE<12.0 mm, NRMSE <13%. The calibrated Kcb values were 0.15, 0.60 and 0.52 for the initial, mid-season, and end season, respectively. The ratio between actual (ETc act) and crop evapotranspiration (ETc) was quite low between veraison and maturity (mid-season), corresponding to 36%, indicating that the rainfall was not sufficient to satisfy the vineyards water requirements. Spectral vegetation indices used to compute fc VI were unable to fully track the plants’ conditions when water stress. However, ingestion of data from remote sensing showed promising results that could be used to support decisions making in irrigation scheduling. Further studies on the use of the A&P approach using remote sensing data are required.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

Estimating the evapotranspiration of orchards and vineyards using the soil water balance approach is often difficult due to the soil extent explored by the root system, especially under rainfed conditions [1,2,3]. Under such conditions, the root system varies between 0.5 and 6 m, although it is suggested that a small fraction of roots can grow to greater depths [4,5,6,7], at which soil water content measurements are not normally surveyed. Additionally, the root system of these crops tends to explore the soil further into the inter-row spacing. Grapevine root systems were studied across a wide range of climates and soil textures and showed that most active roots (about 80%) are located in the first 1.0 m of soil [7,8]. Vineyards have long been rainfed [6,9,10] as the species is inherently adapted to tolerate dry periods, typical of many wine-growing regions [6]. However, nowadays irrigation is commonly adopted because it allows improving the wine quantity and quality [11,12,13,14,15,16,17]. Vineyards have mechanisms to control transpiration, the most relevant of which is the pronounced stomatal control [5,6,11,18,19]. These plants also have a strategy to further explore the water reservoir in the soil by using a deep root system [5,6,13,20,21,22]. Both mechanisms allow for efficient use of available water [5,6,11,19,20,21,22], particularly in drier periods. Under rainfed conditions, the root system can be expected to develop further than in a comparable irrigated vineyard. There are few studies reporting a maximum rooting depths of vines greater than 6 m [23], however, it has been suggested that a small fraction of roots can grow to a depth of 20 m in the absence of impermeable barriers [4,5,6,7]. The root system of the vine depends on the characteristics of the soils, the planting density, and the crop management used. Soil characteristics that have the greatest impact on root distribution include the soil bulk density, resistance to soil penetration, and texture [19].
Soil water content is difficult to quantify due to the heterogeneity of the water distribution in the soil [3]. However, it is possible to assess the vineyard water status by analyzing the relationship between the actual crop evapotranspiration and its partitioning and the predawn leaf water potential (ψb) of grapevines. For instance, [24] reported a threshold of -0.3 MPa as limit for irrigating vineyards cv. Moscatel Galego-Branco. For water stress conditions, [25] also reported ψb ranging from -0.1 MPa to -0.36 MPa as indicative of weak to moderate water stress for rainfed vineyards. In addition, [18] quantified ψb varying of -0.3 MPa to -0.47 MPa for cv. Semillon and from -0.30 MPa to -1.07 MPa for cv. Muscat, both vineyards in rainfed conditions. [26] defined the water stress limits as follows: no water deficit (0 MPa ≥ ψb ≥ -0.2 MPa), mild to moderate water deficit (-0.2 MPa ≥ ψb ≥ -0.4 MPa), moderate to severe water deficit (-0.4 MPa ≥ ψb ≥ -0.6 MPa), severe to high water deficit (-0.6 MPa ≥ ψb ≥ -0.8 MPa), and high-water deficit (< -0.8 MPa).
A common approach to estimate crop water requirements is the FAO two-step approach which combines the climate conditions (reference crop evapotranspiration, ETo) with the crop characteristics (crop coefficient, Kc) also named Kc-ETo approach. This approach was proposed in FAO56 [27] and has been widely adopted [28]. The FAO56 Kc-ETo approach can be applied with a single or a dual crop coefficient. In the first case, soil evaporation and crop transpiration are combined into a single Kc value for each crop stage; for the latter, daily plant transpiration is based on the basal crop coefficient (Kcb), while daily soil evaporation is estimated using an evaporation coefficient (Ke). Thus, ETc is divided into crop transpiration (Tc = Kcb ETo) and soil evaporation (Es = Ke ETo).
The standard tabulated values of Kc and Kcb allow the assessment of ETc under potential and well-watered conditions [27]. The standard tabulated Kc and Kcb values for trees and vines were recently reviewed and updated by [29]. However, under natural field conditions, the crop is often subject to biotic and abiotic stress due to water deficits caused by inadequate irrigation, improper management practices, soil quality and salinity, unsuitable crop varieties or rainfed conditions. Therefore, a water stress coefficient, Ks, in the range between 0 and 1.0 is introduced as a multiplicative factor to estimate actual values of Kc or Kcb, i.e., Kc act or Kcb act [27,28,30,31]. The actual crop evapotranspiration (ETc act) is generally smaller than the potential value (ETc) and can be defined as:
ETc act = (Ks Kcb + Ke) ETo = Kc act ETo
The actual crop transpiration may be measured using the eddy covariance technique e.g. [32,33,34], the Bowen ratio energy balance method, soil water balance or a lysimeter as reviewed by [35]. The partitioning of evapotranspiration may be performed combining soil evaporation measured in micro-lysimeters or mini-lysimeters [36] with actual crop transpiration estimations with sap flow methods [37,38,39]. In addition, models properly calibrated allows assessing crop water requirements, to auxiliar adequately in the management of irrigation, and analysing the impact of crops and management, including under water deficit conditions. These models employ different functions and frequently do not use the FAO Kc-ETo approach, e.g., the transient model Hydrus-2D [40]. Other examples have recently been reviewed [35]. Models applying the dual-Kc approach, include the SIMDualKc [41,42], which has been shown to be suitable for olive orchards [31,34,38,43] and other woody perennial crops, such as vineyards [44,45], peach trees [46] and almond, citrus, and pomegranate [43,47].
Alternatively to the models’ usage, [48] suggested an approach to obtain the basal crop and crop coefficients (Kcb, Kc) using a density coefficient (Kd), which calculated is estimated with information of fraction of the ground covered by the plants’ canopy (fc) and crop height (h) [31,48]. In this approach, the estimation of Kcb considers two other parameters, the multiplier on fc, which describes the influence of canopy density (ML) and the resistance correction factor (Fr). ML characterizes the transparency of the canopy to solar radiation while Fr is an empirical downward adjustment when vegetation exhibits tight stomatal control to transpiration. In the case of fc, the value may be measured using ground or remote sensing data [35,49,50]. Application examples are provided by [38,50] and [35]. A full review of the parameter values for ML and Fr is provided by [28].
In the last decades, remote sensing (RS) data have been used to estimate crop evapotranspiration considering two main approaches: (i) satellite-based surface energy balance models (SEB) [32,51,52,53,54] and (ii), spectral vegetation indices for estimation of basal crop coefficient (Kcb) based on FAO56 method, Kcb-VI [49,50,55,56,57]. The Kcb-VI approach requires information for a smaller number of variables than the SEB models, being based on elementary principles. Nevertheless, in contrast to the SEB models, the Kcb-VI approach ignores the effect of stomata closure related to the occurrence of water stress and assumes that this effect does not significantly affect the reduction in evapotranspiration compared to the effect of crop size [57].
The estimation of Kcb based on spectral vegetation indices has already been performed with different approximations. An overview on this topic is given by [49]. Two of the world’s most widely used spectral indices for this approximation are the Normalized Difference Vegetation Index, NDVI [58] and the Soil Adjusted Vegetation Index, SAVI [59]. The formulation of NDVI and SAVI combines red and near infrared (NIR) reflectance to provide an indirect measure of red-light absorption by chlorophyll (a and b) and reflectance of NIR by the mesophyll structure in leaves [49,60,61]. Compared to NDVI, SAVI is less sensitive to the soil backscatter effect, which is an advantage in crops with discontinuous ground cover, such as vineyards [59,62]. These spectral vegetation indices have also been used to determine the fraction of soil covered by the crop, fc.
Significant gaps exist in the determination of the soil water available for the evapotranspiration process due to the uncertainty in the volume of soil explored by the root system of vines. Consequently, this uncertainty also occurs when modelling the soil water balance (SWB), particularly in the case of one-dimensional models. To improve the soil water balance and actual crop ET estimates in a rainfed managed vineyard, the current study uses a combined approach of ground and remote sensing data ingested in the SWB model SIMDualKc. To support the everyday decision making, the A&P approach was also tested using the estimates of SIMDualKc model. Thus, a comparison of the Kcb SIMDualKc with the Kcb derived from the observed values of fc and h (Kcb A&P) [48] was included. The A&P approach is considered a useful approach to improve irrigation management and parameterize water balance models. The novelty of the current study lies in the precise determination of the soil water balance in a deep soil profile that can be explored by the roots, combined with a set of ground-truth data including predawn water potential measurements. The soil water content data allowed to perform an adequate parameterization, and calibration of a modelling tool. To the authors knowledge, this is the first time that the A&P approach has been used to estimate rainfed vineyard evapotranspiration.

2. Materials and Methods

In the present study, the ground data set was collected in a vineyard experimental site located in the Ribatejo region (Center Portugal). The remote sensing (RS) data characterizing the vineyard development was acquired by the Landsat 5 satellite (downloaded from the Earth Explorer portal; https://earthexplorer.usgs.gov/). The following subsections provide a detailed description of all data sets and modeling tool.

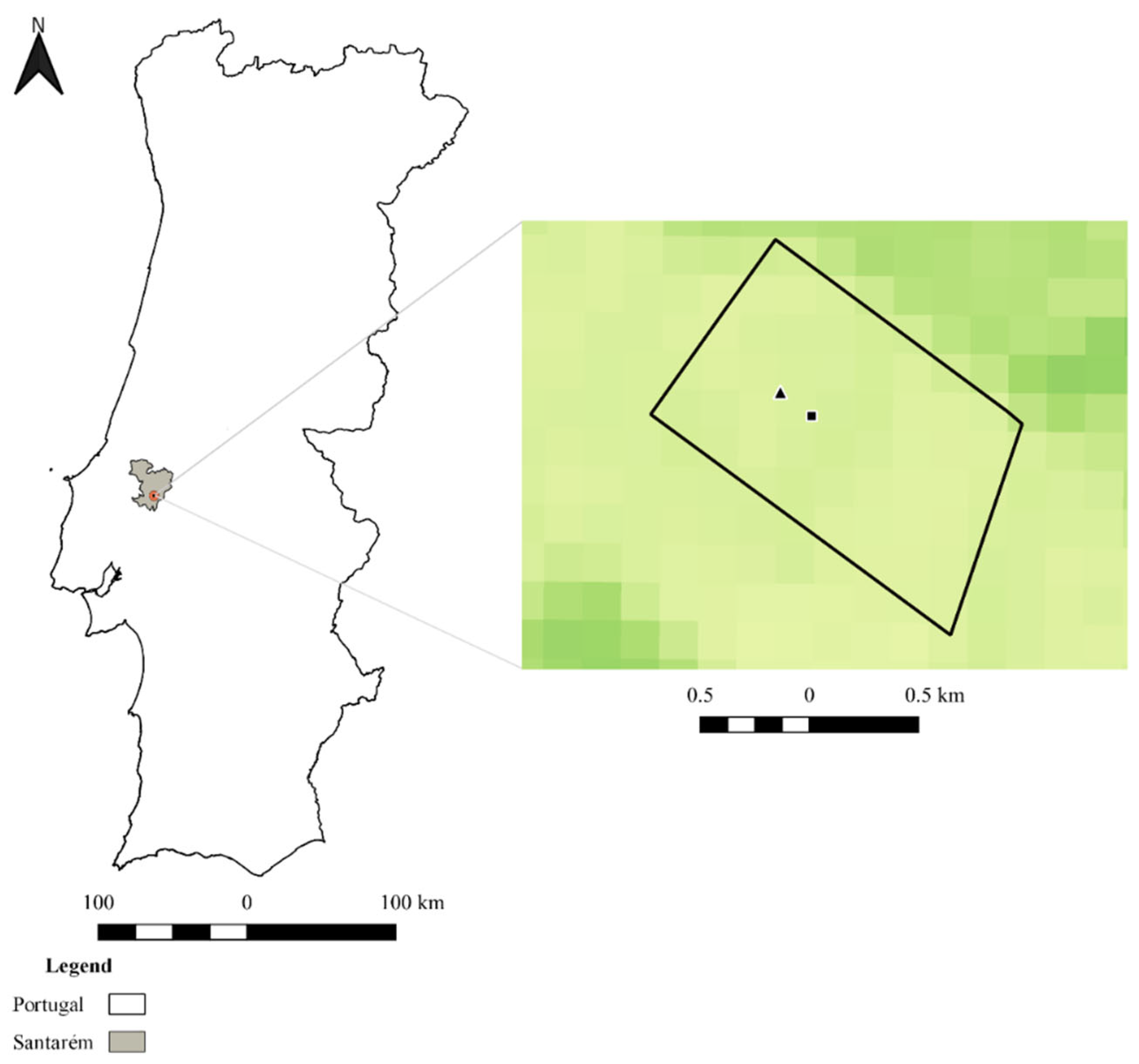
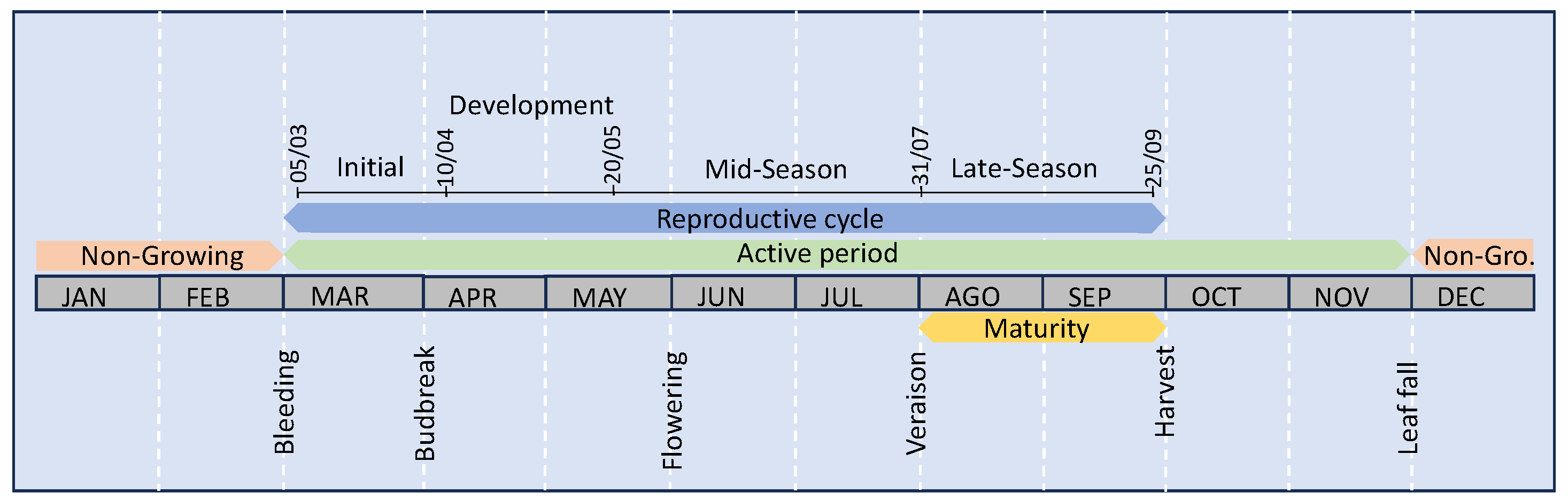
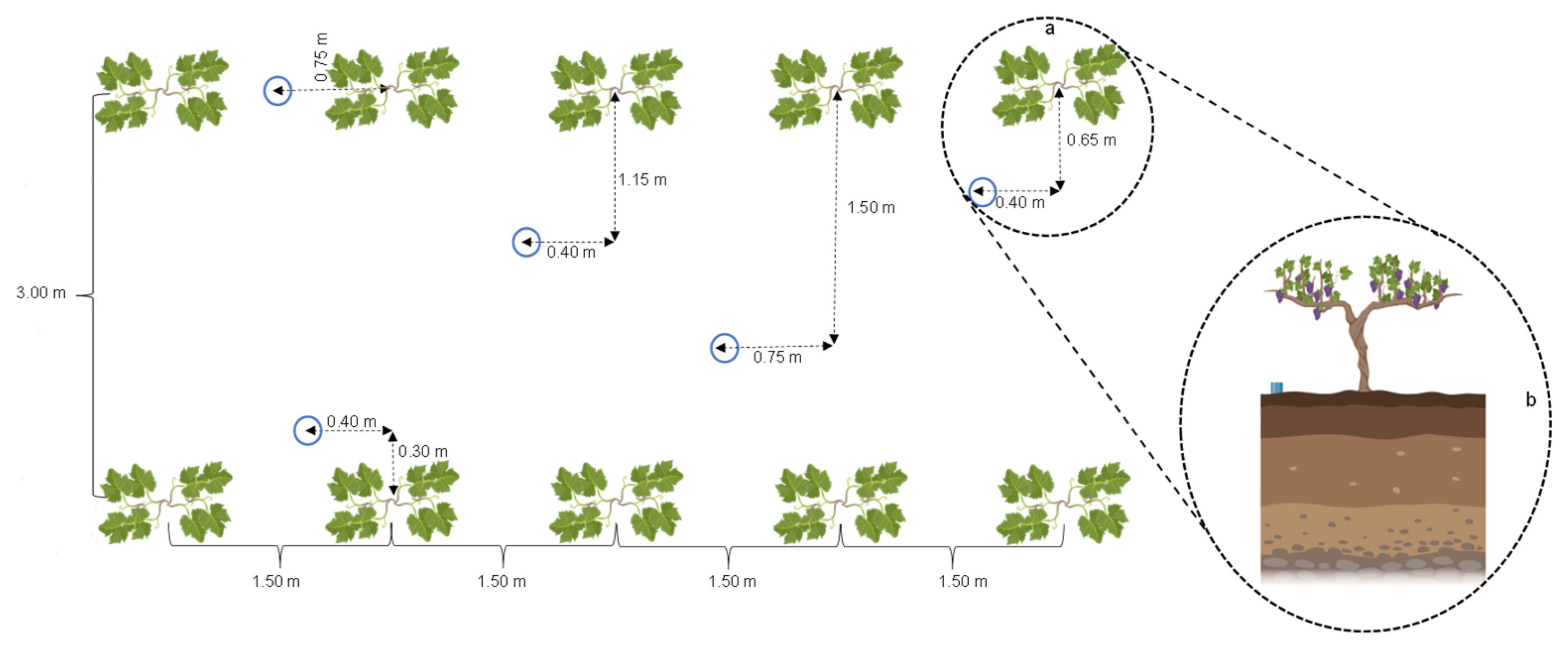
2.1. Study area and crop characterization

The experiments were developed in a 2.13 ha vineyard plot of Escola Superior Agrária (School of Agriculture), located in Santarém, Ribatejo region (39º 15' 38.15'' N, 8º 42' 37.7'' W) (Figure 1).
Data were collected in 1987, on a 20-year-old vineyard, cv. black Trincadeira, grafted on rootstock R110, planted at 3.0 m x 1.5 m, trained in a vertical shoot positioned trellis, pruned to the bead of 2 to 3 buds and a total load ranging between 6 to 10 buds, and with a high plant vigor. The vineyard was aligned, trellised, and oriented in the SSW-NNE direction. The timing of the phenological stages was recorded according to the Bagiolini scale as follows [19]: (i) cotton bud (bud swelling) in the first week of March, (ii) green tip (bud opening) occurred ten days later, (iii) onset flowering occurred between April 10 and 15, (iv) end of flowering between May 20 and 25, (v) pea-berry stage normally occurred in the first week of July and, (vi) complete ripening took place in the last week of September. These stages were then converted to those proposed by [27] as follows: initial stage from 05/03–09/04, development from 10/04–19/05, mid-season stage from 20/05–30/07, and late-season from 31/07–25/09 (Figure 2). Weed control in the inter-row was carried out with herbicides in April.
The vineyard predawn leaf water potential (ψb) and available soil water content relationship was analyzed as an indicator of the vineyard water stress level, and to better understand the soil-plant water relationships. Predawn leaf water potential measurements were carried out using a pressure chamber [63] on a total of nine dates, from June to September, on 7 to 10 leaves of different plants in each date. These measurements were considered to be representative of the vineyard. To minimize measurement errors, all ψb measurements were carried out close to the vines, with a time interval of around one minute between cutting the leaf and reaching the balance between the pressure in the chamber and the pressure in the xylem [19].

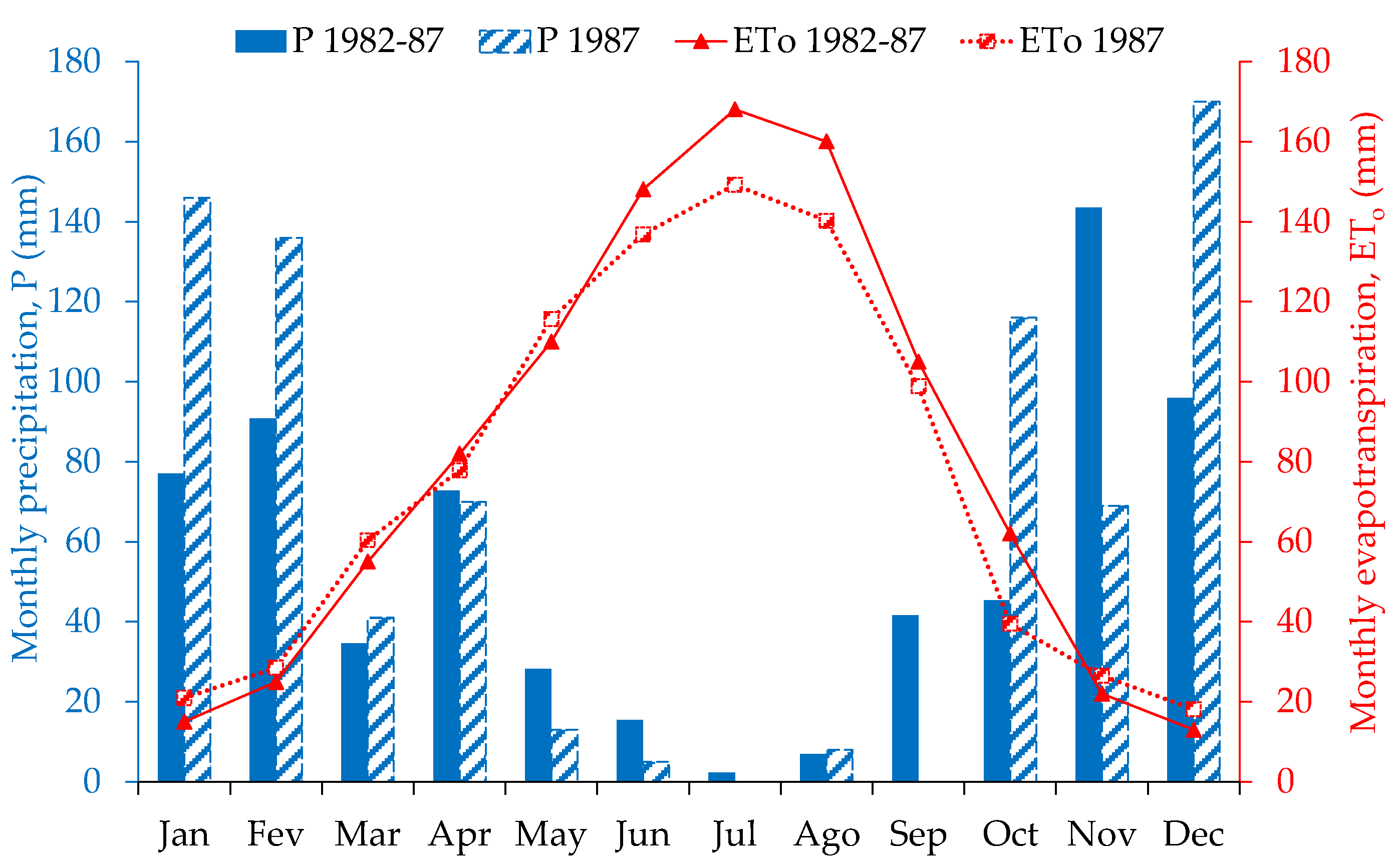
2.2. Climate Characterization

According to the Köppen-Geiger climate classification [64], the study area has a warm temperate climate (Csa), with dry and hot summers (Tair>22 ºC) and mild rainy winters, thus a typical Mediterranean climate. Average annual evapotranspiration ranges from 712 mm to 815 mm while average annual precipitation ranges from 674 mm to 844 mm, mostly concentrated in the winter months considering the years 1982-1987 [19].
Weather data were obtained from the Santarém weather station of (39º15'N, 8º42'W, 73 m a. s. l.), located 1 km away from the experimental site.
Daily data collected included maximum and minimum temperature (Tmax and Tmin, ºC), solar radiation (Rs, W m-2), and average relative humidity (RH, %). The station is under reference site conditions [27], which allows the estimation of the reference evapotranspiration (PM-ETo). Daily precipitation (mm) was also collected in the station. Based on [65], weather data were assessed in terms of quality and integrity. A brief characterization of the prevailing weather conditions in the study year is shown in Figure 3. Although the annual precipitation was 784 mm, it is clear that most of the precipitation was concentrated in the months of November to February, when the vineyards were dormant.

2.3. Soil characterization and soil water content monitoring

Soil properties were assessed by collecting disturbed soil samples at different depths. The vineyard soil in the studied area is an Anthrosol [66] with a sandy loam texture, down to a depth of 1.90 m, most of the sand being fine. Collection of undisturbed soil samples for determination of volumetric water content at field capacity was not possible due to the unstable soil surface layer and significant structural discontinuities. In addition, some soil layers exhibited very low saturated hydraulic conductivity (Ks<0.5 cm d−1), which also made it difficult to determine soil moisture at field capacity. Thus, the volumetric soil water content at field capacity and at permanent wilting point were obtained using the pedotransfer functions determined for the Portuguese conditions [67] using the particle size and the soil bulk density.
A neutron probe (Humiterra, Laboratório Nacional de Engenharia e Tecnologia Industrial, Portugal) was used to monitor soil water content at each 0.10 m, up to 1.85 m, in two locations. Before use, the probe was calibrated following the procedures of [68] and [69]. As suggested by [68], special calibration of the probe was performed for the surface layers up to 0.15 m. Several transparent access tubes were placed surrounding the plants as shown in Figure 4. The measurements were carried out on seven dates every 16 days from 23 April to 8 September 1987.

2.4. Modelling approach

It was assessed the accuracy of a SWB model fed with ground truth data after proper calibration and a simplified approach that combines ground truth data with remote sensing data.

2.4.1. SIMDualKc modelling tool

The SIMDualKc modelling tool was developed with the aim of simplifying the implementation and computation of water use and irrigation requirements using the dual crop coefficient approach. The tool can be applied to a wide variety of situations including crops that do not fully cover the soil (e.g., orchards), intercropping systems, mulching impacts (plastic and organic), active ground cover, and soil and water salinity.
SIMDualKc is a one-dimension soil water balance modeling tool, that daily estimates the crop water requirements as follows [27,41], as:
D r , i = D r , i − 1 − P − R O i − I i − C R i + E T c a c t , i + D P i
where Dr represents depletion in the root zone (mm), P represents the rainfall amount (mm), RO refers to the surface runoff (mm), I represents the net irrigation (mm), CR describes the capillary rise (mm) obtained of the groundwater table (mm), ETc act is the actual crop evapotranspiration (mm), and DP is the is the root zone deep percolation (mm), all referring to days i or i-1.
The actual ETc is partitioned into actual crop transpiration (Tc act) and soil evaporation (Es) as:
T c a c t = K s K c b E T o = K c b a c t E T o
E s = K e E T o
The stress coefficient (Ks) is calculated daily as a linear function of the root zone depletion Dr (mm):
K s = T A W − D r T A W − R A W = T A W − D r 1 − p T A W   for   D r > R A W
K s = 1   for   D r ≤ R A W
wherever TAW represents the total available soil water (mm) and RAW is the readily available soil water (mm), with RAW= p TAW, and p is the soil water depletion fraction for conditions of no-stress [27,48]. When the root zone depletion is higher than RAW, i.e., in situations of the water depleted fraction is larger than p, the stress coefficient is lower than one (Ks < 1.0).
The evaporation coefficient (Ke) will be the maximum immediately after rainfall or irrigation events occur and the wetted soil surface is being partially covered by plants canopy. This higher Ke value is dependent of Kc value be maximum (i.e., Kc max), which signifies the upper threshold of evaporation and transpiration from any cropped surface and reflects the natural restrictions imposed by the available energy on the transpiration coefficient Kcb on the same day, and thus on Kc max – Kcb [48,70]. Nevertheless, it changes day-to-day as a function of the total water available for evaporation in the soil surface layer; thus, the estimative of Ke is made by a dimensionless reduction factor, Kr, as:
K e = K r   K c m a x − K c b ≤ f e w K c m a x
being few the wetted soil fraction exposed to direct solar radiation, which is calculate as few= min (1 – fc, fw) according to the fractions of ground covered by plants’ canopy (fc) and wetted by irrigation (fw).
The value of Kr depends on the cumulative depth of water depleted from the topsoil and is daily calculated through the soil water balance considering the soil evaporation layer’s thickness (Ze, m). Calculations are based on the assumption that the drying cycle happens in two stages, with the water in the topsoil and the energy available at the soil's surface limiting the first stage [36,48], thus with Kr reducing once the evaporated depleted water exceeds the readily evaporable water (REW). Thus, Kr is computed as:
K r   =   1   for   D e , i − 1 ≤ R A W
K r = T E W − D e , i − 1 T E W − R E W   for   D e , i − 1 > R E W
where De,i-1 is the amount of water evaporated from the evaporable soil layer at the end of day i-1.
The adjusted Kcb calculation already includes a water stress coefficient (Ks), that represents situations where water is a limiting factor. The soil evaporation coefficient (Ke) in turn is calculated by separating this coefficient into two parts: the Kei relative to the fraction of soil wetted by irrigation and precipitation (fewi); and the Kep, which is based on the fraction of soil wetted only by precipitation (fewp).
Mandatory SIMDualKc input data include: i) weather data required for calculation of the PM-ETo or computed elsewhere, precipitation and, in case of adjustment of Kc/Kcb to weather conditions, u2 and RHmin; ii) crop characteristics data, which include the dates of the diverse crop growth stages, the crop height, rooting depth, the depletion fraction for no stress, the basal crop coefficients and the fraction of ground cover or the LAI for each defined stage; iii) soil characteristics, such as the soil water holding characteristics (soil water at field capacity and wilting point), or the TAW, or, as in the case of the current study, the use of pedotransfer functions (PTF) used to derive the TAW for diverse soil layers; iv) the surface layer characteristics: depth (m), total evaporable water (TEW, mm) and readily evaporable water (REW, mm); v) irrigation schedules that include different options, such as rainfed.
Other model functions were used to improve the SWB estimates. Therefore, other input data used with SIMDualKc in the current study included: i) the deep percolation or drainage fluxes (mm d−1) is calculated with a decay function over time describing the soil water storage (W) close to saturation in the period following events of intense rainfall or irrigation. The SIMDualKc model uses a decay function [71] for the estimation of the deep percolation as follows:
W = a D t b D
where parameter aD is the soil water storage value comprised between the field capacity and the saturation, and bD < -0.0173 for soils draining quickly and b > -0.0173 for soils with slow drainage.
(ii) capillary rise computed using the parametric equations developed by Liu et al. (2006) which parameters (a1, b1, a2, b2, a3, b3, a4 and b4) depend on the soil’s physical and hydraulic characteristics, were subjected to the model’s calibration process [41,71] (Table 1); and (iii) surface runoff which is estimated with the curve number (CN, dimensionless) method [72]. CN ranges from 0 to 100, meaning there is no runoff, and all rainfall becomes runoff, respectively. Runoff (RO) was estimated using the curve number (CN) approach [51,72], in which CN value changes depending on the soil and vegetation type, and the antecedent moisture in soil. SIMDualKc model adjusts CN daily to represent the influences of adding or subtracting soil water content on soil infiltration properties, by linking the CN value to soil water depletion in the surface layer.
A complete description of the calibration and testing of the SIMDualKc model is provided by [41,42,73,74].

2.5. Estimating Kcb values using the A&P approach and remote sensing data

In the A&P approach [48], Kcb A&P is computed with the equation below [41,48] where impacts of plant density and/or leaf area are taken into consideration as a function of a density coefficient (Kd):
K c b A & P = K c m i n + K d K c b f u l l − K c m i n
To consider the influence of crop height and density on Kcb, [48] proposed a density coefficient (Kd) (equation 9) that allows adjusting the Kcb of vegetation and ground cover conditions [48,51]. This Kd is calculated through the factors: fc eff that corresponds to the fraction of ground effectively covered or shaded by plants at midday, ML, which is a multiplicative factor of fc eff, representative of the fraction of ET per unit area of horizontal vegetation to the ETo on the same area, and h that is the vegetation height.
K d = m i n   1 ,  ;  M L f c   e f f ,   f c e f f 1 1 + h
Kd has also been used in other studies to adjust Kcb to actual density conditions for full cover crops [35] and in partial cover crops using both ground [75] or remote sensing data [49,50,76].
The Kcb full represents a ceiling limit on Kcb mid for vegetation under no-water stress and with a full ground cover and LAI value higher than 3. Following [27], the Kcb full is estimated as a function of mean plant height (h) and corrected for climate conditions as:
K c b f u l l = F r m i n 1.0 + k h , 1.20 + 0.04 u 2 − 2 − 0.004 R H m i n − 45 h 3 0.3
wherever u2 is the daily mean wind speed (m s-1) considered of 2 m above ground level through the growth period, RHmin (%) is the daily mean of minimum relative humidity over the growth cycle, and h is the average plant height (m) for the mid-season stage. Previously to the climatic correction, a value of 1.20 is considered as a superior threshold for Kcb full. The crop height influence is considered in the sum 1 + kh h, with kh = 0.1 for tree and vine crops, as recommended by [28,35].
Taller crops and situations where the local climate is windier or drier than typical (standard) climatic conditions (RHmin = 45% and u2 = 2 m s-1) are expected to have higher total Kcb full values. When vegetation shows greater stomatal adjustment transpiration, as is common in most annual crops, the Fr parameter applies an empirical correction (Fr ≤ 1.0). When crops show strong vegetative vigor and decline consequently by training and pruning, as well as when water availability is restricted, Fr is high for trees and vines. As proposed by [27], Fr, can be estimated as:
F r = ∆   +   γ   1   +   0.34   u 2 ∆   +   γ   1   +   0.34   u 2   r l r t y p
where rl and rtyp are, respectively, the average of leaf resistance and the typical leaf resistance (s m-1) for the considered plant, Δ is the slope of the saturation vapor pressure vs. air temperature curve, kPa, and γ is the psychrometric constant, kPa °C-1, both for the same period when Kcb full is calculated. The earliest established version of that equation considered a fixed rtyp = 100 s m-1, a normal value for yearly crops, however default Fr values for trees and vines and several annual crops were recently revised and updated by [28].
[35] provided examples of the Kcb A&P approach's application to a variety of annual and perennial crops, as well as active soil cover in the interrow for wine vineyards. The Kcb A&P technique does not require any calibration/test process when using the tabulated parameters [28,31].
Alternatively, in the A&P approach, the Kd can be estimated under actual conditions using remote sensing data of the fraction of soil covered by vegetation (fc VI). In the present study, we have assumed that fc eff is approximately equal to the fc VI derived from spectral vegetation indices computed with RS data. This data was derived from spectral vegetation indices obtained through satellite data, namely Landsat 5 images for the period under analysis. Five Landsat-5 images covering the study area, relative to the path/row 204-033, were available and downloaded from Earth Explorer portal (https://earthexplorer.usgs.gov/), for the study period (dates 26/04/1987, 28/05/1987, 29/06/1987, 31/07/1987, and 17/09/1987). From each of these images, 12 pixels covering the vineyard under study were selected.
The Soil Adjusted Vegetation Index (SAVI) was considered to calculate the fc VI, as it presents less sensitive to soil background reflectance variability than other VI [49,50].
S A V I = ρ N I R − ρ r e d 1 + L ρ N I R − ρ r e d + L
where the ρred and ρNIR are the reflectance at red and NIR spectral domains, and L is the soil conditioning factor varying between 0 and 1. A value of L equal to 0.5 is considered for the most common environmental conditions and was found to minimize the effects of soil brightness variation and eliminate the need for calibration under different soil conditions [49,50,77].
The fc VI was computed as:
f c V I = S A V I − S A V I m i n S A V I m a x − S A V I m i n
where fc is the fraction of ground cover by vegetation, SAVI, SAVImax and SAVImin correspond to the vegetation index for a specific date and pixel, vegetation index at maximum vegetation cover, and vegetation index at minimum vegetation cover (bare soil), respectively. The SAVImax and SAVImin values were obtained from the literature considering woody crops [78] and [49,50]. In the present study, the SAVImax and SAVImin values considered were 0.75 and 0.09, respectively.
When calculating Kd, it was assumed that the fraction of soil effectively covered at solar noon (fc eff) was equal to the fraction of soil covered by vegetation (fc). The ML factor, used to calculate Kd was not changed and remained equal to 1.5 [48].

2.4.3. Parameterization and calibration procedures of SIMDualKc model

The first step in the calibration procedure was to define the upper and lower boundary conditions. A value of 1.20 is assumed as an upper limit for Kcb full, before climate adjustment. As above mentioned, for different conditions from those standards, i.e., considering taller crops and local climate windier/drier or windier than RHmin = 45% and u2 = 2 m s-1, higher Kcb full values can be obtained. The lower boundary conditions are Kcb ini equal to 0.15, which corresponds to bare soil conditions.
The observed parameters of weather data, dates of the crop growth stage, crop height (h), root depth (Zr), and soil characteristics were input into the modelling tool. The weather data used were the daily maximum and minimum temperatures (°C), Tmax and Tmin, respectively, the daily average wind speed, measured by an anemometer at a height of 6 meters (km h-1), the daily average relative humidity (%), RHmed, the daily number of sunshine hours (h) and the daily precipitation (mm), corresponding to the year of 1987.
The initial values for the non-observed parameters (Kcb, depletion factor p, aD, bD) were set using diverse sources of information. Based on the vineyard density, the training system and the fc, the Kcb value was taken from [28]; for the depletion factor, the soil evaporative layer (Total Evaporable Water - TEW, Readily Evaporable Water - REW, evaporable layer - Ze), and aD, the values were calculated according to the soil textural characteristics (sandy loam soil); and for bD, values were retrieved from [71].
The calibration procedure followed that described by [73]. Thus, the initial Kcb values used in the simulation were those tabulated by [28] for vineyards. The p factor was considered as a constant value throughout the cycle, considering that the study was performed in a 20-year rainfed vineyard and that, during these stages, the activation of deeper roots is to be expected, increasing the plant's ability to cope with water scarcity, as discussed by [79].
Regarding the evaporable soil layer (Ze), the initial values for TEW and REW were derived from the characteristics of the soil, i.e., field capacity and the permanent wilting point values, and the textural characteristics, for the selected thickness of the evaporative layer.
In the following procedures, the DP, CN and CR parameter values were adjusted. The initial values for the deep percolation parameters, aD and bD were respectively 275 and -0.0173. CN value was assumed equal to 68 [72], according to soil characteristics. The water table depth (WTD) varied from 4.2 m to 4.61 m during the crop season. The measured values of WTD were taken from a piezometric station nearby the experimental plot which belongs to Portugal's National Water Resources Information System (https://snirh.apambiente.pt/). The values of the parameters a1, a2, b1, b2, a3, b3, a4 and b4 that vary according to soil texture were based on those proposed by [71] for loamy sandy soils. The maximum root depth was based upon measurements taken in open soil profiles in the studied vineyard, thus Zr max = 1.85 m.
Since the weeds in the vineyard under study were controlled by tillage and herbicide, respectively in the inter-row and row, neither mulching, nor active ground cover were considered in the simulations.
The model was run until no further improvements were obtained and the best values of the variables were retained.
As already mentioned, two sets of measured SWC were used for the calibration and test of the SIMDualKc model. The data set called 1D (Figure 1) on SWC was used for calibration as it provided 10 observations, while the data set called 2A was chosen for testing (n=7). Due to restrictions in observed data sets it was therefore not possible to validate the model, but the calibrated parameters were tested using measured SWC from a different location within the same field.

2.4.4. Modeling tool accuracy assessment

The accuracy of the calibration and test was assessed using a set of goodness-of-fit indicators described below. These indicators have been used in other modeling performance evaluations, e.g. [45,44], and [47] for vineyard, [31] to evaluate olive grove, or by [30,80].
The calibration/test procedure was considered acceptable once the test results indicators’ accuracy was judged comparable to those obtained for the calibration dataset. The selected goodness-of-fit indicators are detailed in [73], including the targeted values, and include:
i) the regression coefficient (b0, dimensionless) of the linear regression pushed to the origin between the measured and simulated variables; the goal value is b0 = 1.0, which implies that the projected values are statistically equivalent to the observed ones;
ii) the coefficient of determination (R2, dimensionless) of the ordinary least-squares regression between the simulated and observed values should be close to 1.0, indicating that the model explains the majority of the variance in the observed values;
iii) root mean square error (RMSE, mm), the desired value of which is zero, demonstrating a perfect match between simulated and observed variables, the value of which must be much smaller than the mean of the observed values;
iv) the normalized root mean square error (NRMSE, %), whose target value is zero, signifying a perfect match between simulated and observed variables, must be much smaller than the mean of the observed values;
v) the average absolute error (AAE, mm day-1), represents the average error related to the estimations and ought to be significantly less than the average of the observed values;
vi) the target value of average relative error (ARE), which represents the magnitude of the error in relative terms, is zero, signifying a perfect match between the values of the simulated and observed variables;
vii) the ratio of the mean square error (MSE) to the variance of the observed variable is the Nash and Sutcliffe efficiency of modelling (EF, dimensionless) [81,82], whose target value of 1.0 denotes that MSE is negligible for observed variables.

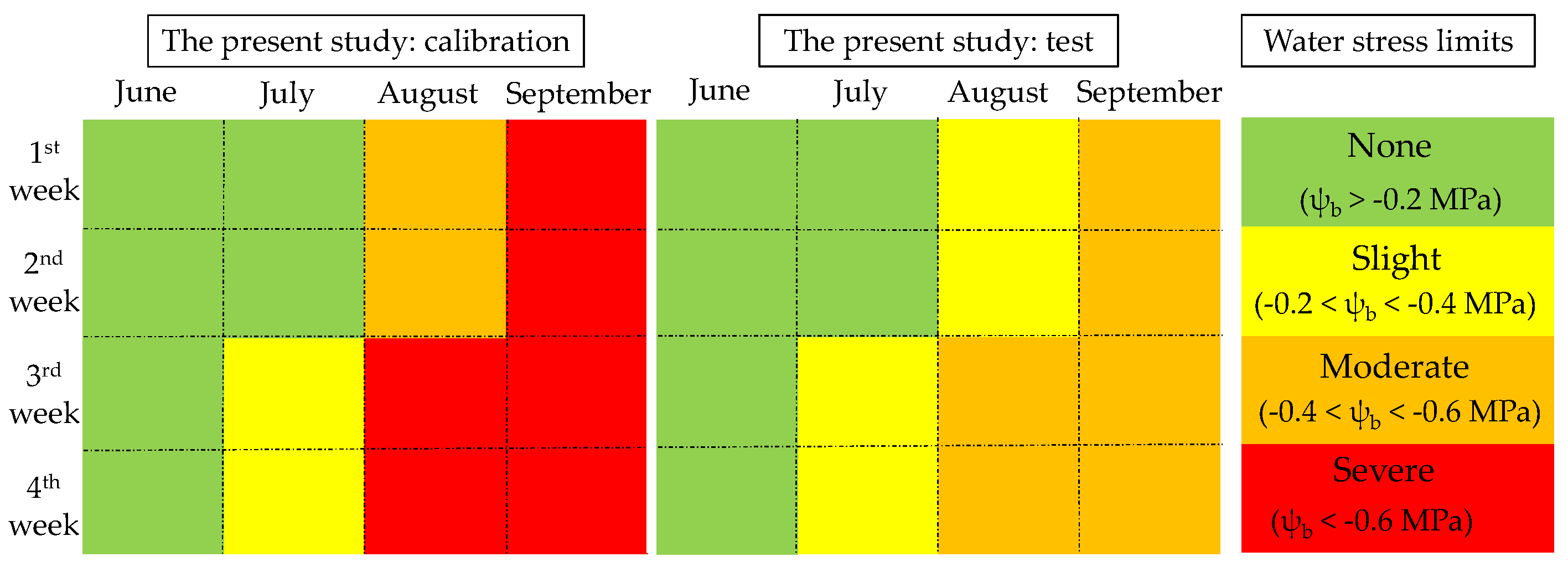
3. Results and Discussion

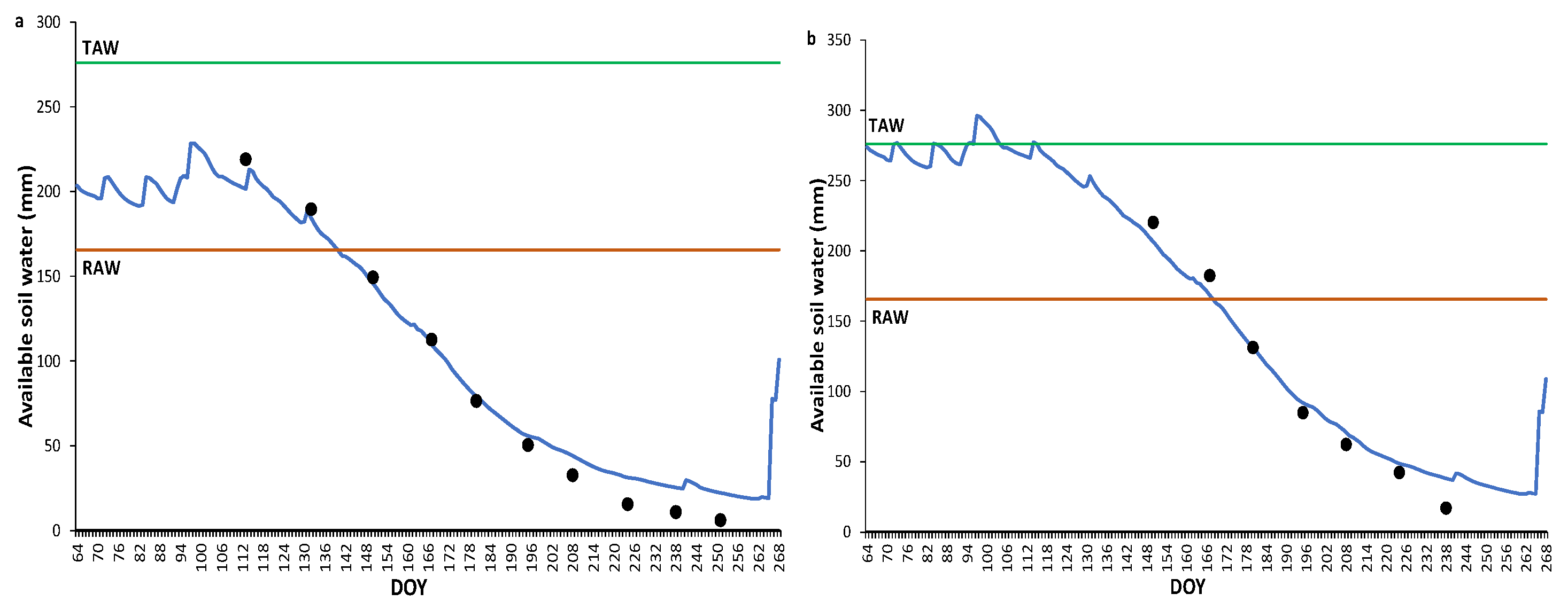
3.1. Performance of the SIMDualKc Model in Calculating Soil Water Content

The crop characterization in the SIMDualKc model was done by entering the dates of its vegetative cycle with an indication of root depth, plant height (h), and soil water depletion fraction (p). The characterization of the crop relative to the Kcb values for the different phases of the cycle (initial, intermediate, and final), and soil characteristics (soil evaporation layer, runoff and deep percolation, capillary rise) are shown on Table 2. These initial values of Kcb, h and p were from [28]. The initial p value, proposed by FAO [27] was adjusted during calibration since this is a rainfed vineyard adapted to water stress.
Results in Table 2 show that, for most cases, the values of the parameters used for initializing the model are relatively close to those obtained after proper model calibration (the variation was 12.2% on average, with Kcb end and p factors responding for the higher variation, respectively increasing 23% and 25%). The depletion fraction p's calibrated values (Table 2) are greater than those suggested by [27,28] which relates to the fact that the vineyard was rainfed and, therefore, well adapted to low water availability conditions. The calibrated p value is in the range of those reported for rainfed vineyard [44,45]. A slightly lower p value was reported by [83] for irrigated cv. Loureiro vineyards. Differently, [55] reported a p value of 0.65 for a drip irrigated vineyard.
The textural characteristics of the soil and the water-retention capacity of the soil evaporation layer were used to estimate the initial values for Ze, REW, and TEW calculations, as proposed in [27]. In this way, the values of these calibrated soil evaporation parameters are the same as those indicated by [27] for sandy loam textured soils. Similarly, the calibrated runoff parameter CN was kept unchanged from the initial value proposed by [51] and [72], considering the soil texture. One of the parameters associated with deep percolation, aD, was estimated from the water available in the soil, at saturation and field capacity, and it was slightly changed from the initial values, decreasing 3.5%. The bD parameter, estimated from the drainage characteristics of the soil [71], was left unchanged.
Figure 5 shows the simulated and observed available soil water (ASW) dynamics throughout the season. Results in Figure 5 show, that the model is able to adequately simulate the dynamics of the ASW observations. The differences between observations and simulations in the calibration set (Figure 5a), were lower in the intermediate and higher in the final stage of the crop. In other words, the ASW dynamics simulated with SIMDualKc agree well with the ASW observations. In addition, the results agree with the predawn leaf water potential (ψb) observations. The model simulates water stress from DOY 136 onwards while the ψb observations range from -0.2 to -0.4 MPa, thus presenting a slight water stress (Figure 6). The decreasing in the ψb, increase in the plant water stress, well matches the simulations of ASW from then onwards. The ψb reached values close to -1.0 MPa in the second week of September, and the daily minimum leaf water potential varied between -1.4 MPa and -1.6 MPa [19], which agrees well with the intense soil water stress simulated with SIMDualKc.
Rainfed vineyards show similar ψb dynamics during the June-August period in south Portugal (typical mediterranean climatic conditions) i.e., the occurrence of slight to moderate water stress, reaching severe water stress (-1.56 MPa and -1.96 MPa) by September as reported by [84]. Differently, in a rainfed vineyard in Douro Wine Region, located in the North of Portugal, where climatic demand is lower during July-September, [24] reported ψb ranging from -0.3 to -0.5 MPa, indicating slight to moderate water stress.
In a study developed in rainfed vineyards cv. Chardonnay in Catalonia, Spain [85,86] low ψb values up to -1.36 MPa. Similar finds were reported by [87], and [88], for mediterranean climatic conditions.
Figure 5 shows a slight mismatch for the extremes of the period considered, suggesting a more abrupt progression over time of the measured values. However, the statistical indicators showed a good performance of the model (Table 3). Both, the calibration and the test comparing available soil water simulated by the SIMDualKc model and available soil water measured using a neutron probe have a good correlation, with a regression coefficient (b0) of 0.97 (Table 3). The coefficient of determination (R2) is equal to 1 in both cases, which indicates that the model can explain the variance of the data. Regarding the modelling efficiency (EF) the values also show a good result with values equal to or higher than 0.97, which indicates that the residual variance due to modelling is comparable to the variance of the measured data, as depicted in [81]. The values of root mean square error were quite similar in both the calibration and test, with RMSE of 11.1 and 11.9 mm respectively, while the mean absolute error (AAE, mm) was 9.5 to 10.2, respectively. Additionally, the NRMSE presents a good result with values below 13%. Similar to the other indicators, ARE showed a good agreement between simulated and observed SWC values, with an error of less than 0.60.
For vineyards, there are only a few results in the literature regarding the calibration of the SIMDualKc model using soil water content data. The RMSE and NRMSE (11.5 mm and 12%, respectively) obtained in the present study are higher than those verified by [83] for a rainfed vineyard cv. Loureiro in Ponte de Lima, northwest Portugal, by [44], working in a vineyard cv. Godello and cv. Mencía in Galicia, Spain and also higher than those estimated by [45], for a vineyard cv. Albariño in Pontevedra, Spain. Likewise in the present study, a small error (RMSE) was reported by [89] simulating water flow within the Hydrus (2D/3D) model towards a two-year set of soil water content measurements from a rainfed vineyard cv. Aglianico. Similarly, [90] found small values of RMSE comparing soil water content measured with TDR probes and estimated using the SWAP model for irrigated crops (passion fruit and pastures). On the contrary, [91] found RMSE values higher than those reported in the present study assessing soil moisture profiles with HYDRUS-1D model for several Mediterranean rainfed vineyards. Although the values of RMSE and NRMSE reported in the present study indicate errors of estimation, they represent less than 4.17% and 4.35% of the TAW for RMSE and NRMSE, respectively. [47] also obtained RMSE and NRMSE lower than the values verified in the present study for a rainfed vineyard in Monferrato, northern Italy. In the reported studies [44,45,47,83], the soil depth was 1.20 m, 1.0 m, 0.60 m, and 0.80 m, respectively, therefore lower than that considered in the present study (1.85 m). Nonetheless, given the very different edaphoclimatic characteristics, in places where annual rainfall is higher, the root system is expected to explore more superficial layers and the lower limit of the control volume in the modelling process can be located at a depth closer to the surface than in the current situation, unlike in places with lower rainfall and deeper soils. Moreover, in situations where the plants are under greater water stress, either due to more demanding environmental conditions or to the absence of irrigation (as in the present study), there will be a tendency for the root system to grow deeper, easily surpassing the common threshold (approx. 1.0 m) as depicted by several authors [4,5,6,7,23], sometimes deeper than 2 m (for an irrigated vineyard under extremely arid conditions) [92], or even higher than 6 m, as reported by [7].

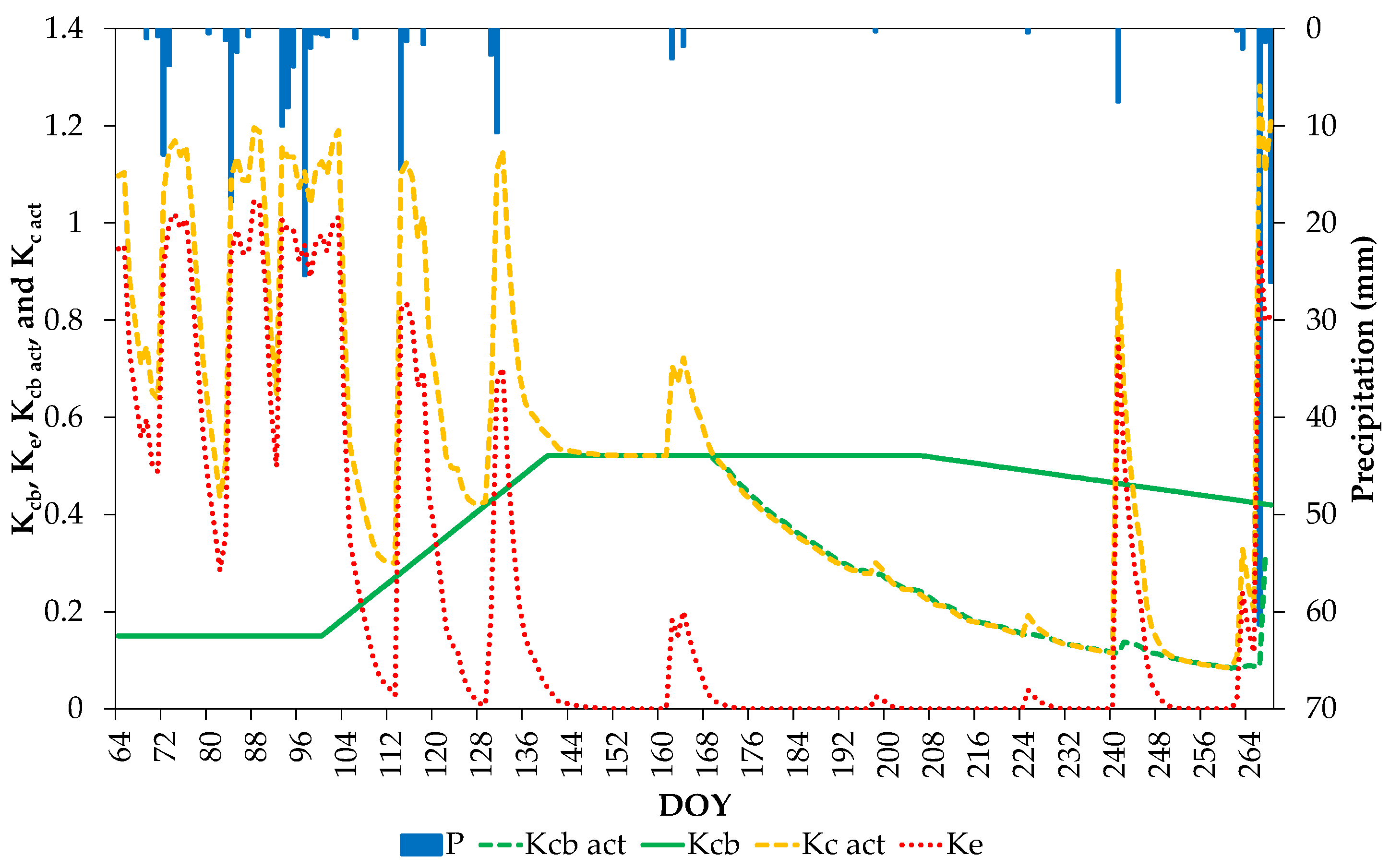
3.2. Crop Coefficients Dynamics over the Season

The daily values of precipitation, the potential basal crop coefficient (Kcb), the actual basal crop coefficient (Kcb act), the soil evaporation coefficient (Ke), and the actual crop coefficient (Kc act = Kcb act + Ke) calculated by SIMDualKc model are shown in Figure 7. For both, calibration and test, the Kcb act and the Kcb values are coincident during most of the crop cycle, except for part of the mid-season (DOY 196), till harvesting, when rainfall events are not sufficient to avoid water stress (as seen in Figure 6), i.e., few rainfall events occurred during spring, winter, and autumn. The value of Kcb ini calibrated is equal to the standard value proposed in [28] for vineyards (0.15). However, during mid-season and late-season, the calibrated values of Kcb are quite different from standard values (Kcb mid = 0.65 and Kcb end = 0.40), being Kcb mid = 0.60 and Kcb end = 0.52 (as shown in Table 2). These differences are related to the rainfed conditions of the studied vineyard, which reflect its tolerance to water stress. The calibrated Kcb values (Kcb ini, Kcb mid, and Kcb end, respectively) in the present study are lower than those reported by [44] for vineyard cv. Godello (0.30, 0.80, and 0.60) and cv. Mencía (0.20, 0.75, and 0.60) in Galicia, Spain, probably related to the higher annual rainfall amount in that location. In the same way, the Kcb calibrated here are lower than those obtained by [45] for a vineyard cv. Albariño, under irrigation conditions, which can explain the differences in comparison to the values verified in the present study. The results of Kcb obtained in [45] for the Kcb mid (mean 0.57) with moderate stress, are quite similar to the Kcb mid values calibrated in the present study. [83] also reported calibrated Kcb values ranging from 0.09-0.13, 0.21-0.25, and 0.27-0.22 (for development, mid-season and late-season) for a vineyard cv. Loureiro under rainfed treatment, which are lower than those calibrated in the present study. The difference can be related to higher amounts of precipitation in the location reported in [83].
As verified for Kcb and Kcb act, the Kc act and Ke have a similar pattern, especially in the initial and final stages. The Kc act peaks occur mainly when the soil is wetted, after rainfall events, and the evapotranspiration process is dominated by soil evaporation, i.e., the transpiration amount is small in this period. Furthermore, in Figure 7, it is possible to find times (especially in the early growth phases) when the Ke values are very similar to the Kc act values, close to 1.2, in the end season with Kc act close to 1.0, and close to harvest, when the Kc act values are close to and higher than 1.2. This pattern is mainly related to the rainfall during these periods (Figure 7), as well as the absence of ground cover vegetation. Similar trends in Ke and Kc act values were observed by [44], for the cultivars cv. Godello and Mencía in Galicia, NW Spain and [83] to cv. Loureiro in Ponte de Lima, Portugal.
Numerous Ke peaks on the soil evaporation curves (Figure 7) show how the vineyard responded to rainfall events at its distinctive growth stages. These Ke peaks occur mostly at the initial, start of rapid growth and at the beginning of mid-season periods. Ke peaks respond to the total soil wetting that occurs from rain events (fw = 1). During almost all mid-season, maturity and harvesting stages, Ke peaks are small and not very frequent due to the dry soil conditions with the absence of rain. This pattern Ke response to rainfall was also reported by [44,45] and [83] for vineyards cv. Godello and cv Mencía, cv. Albariño, and cv. Loureiro, respectively, under a rainfed treatment in Spain and Portugal.

3.3. Estimation of the Fraction of Ground Cover from Vegetation Indices

The fc retrieved from SAVI (fc VI; Equation (14)) was estimated for five dates, those with cloud-free images for the period under study (Table 4). The lowest fc VI value was estimated for the beginning of the growing season (DOY 116, fc 0.174) and the highest fc VI was verified for the mid-season (DOY 148, fc 0.286). The temporal evolution of SAVI is similar to the fc VI, with the lowest SAVI value estimated for the beginning of the growing season (start rapid growth) and the highest value observed in the mid-season. This tendency was observed for table grapes using NDVI [93], and for other crops and VIs, like maize, barley, and olive, using SAVI and NDVI [50].
The fc VI obtained in the present study (ranging from 0.17 to 0.28, Table 4) are lower than those reported by [93] for a fc VI relationship of table grapes vineyards cv. Perlette and Superior in the semi-arid region of Northwest Mexico. However, [93] used NDVI for the computation of fc VI instead of NDVI. Additionally, the fc values of the present study are closer to the limit values presented in [27] for vines and other perennial crops. The authors reported fc values ranging from 0.25 to 0.45, with Kcb mid values between 0.46 and 0.80 and Kcb end values varying from 0.20 to 0.60. On the other hand, [10] reported fc values ranging from 0.04 to 0.28 and from 0.06 to 0.33, for 2017 and 2018 seasons, respectively, in a rainfed vineyard cv. Monastrell, in Albacete, Spain, with maximum values similar to those observed in the present study. [47] reported fc values ranging from 0.15 to 0.28 for an Italian rainfed vineyard, which is similar compared to the fc values verified in the present study. It important to take into account the spatial resolution of the Landsat-5 images available at the time of the study, 30 m x 30 m, which means that no more than 12 pixels per image can be used to estimate the fc for the vineyard studied.

3.4. Comparison between Kcb obtained with SIMDualKc model and predicted with the A&P approach

The Kcb A&P values obtained through fc, derived from remote sensing (fc VI), and applying equation 9 [48], were compared with the Kcb obtained through the SIMDualKc model, to verify the accuracy of using the A&P approach combined with RS data. The five Kcb values obtained by SIMDualKc, for each day where Kcb A&P was estimated using the fc VI, were compared.
Table 5 shows that the Kcb A&P values are close to the values obtained by the calibrated SIMDualKc (Kcb SIMDualKc_1D), especially for 26/05 and 29/06/1987. For these dates, the plants were not under water stress (shown in Figure 6) and both, SIMDualKc model and A&P approach, were able to precisely estimate the Kcb values. On the contrary, the Kcb A&P values for the final stages (after July 31) are greater than those for Kcb SIMDualKc. It is noteworthy that vegetation indices (VI) detect crop stress when a reduction in chlorophyll green cover or changes in canopy geometry occur, and thus do not immediately detect the slight water stress conditions in plants, when the effect is only noticeable in the transpiration rates and predawn water potential (Figure 6). During the two first weeks of August, the water stress increase was moderate and after the third week onwards it was severe (Figure 6), which can explain the higher deviation between Kcb SIMDualKc and Kcb A&P values occurred on September 17 (Table 5). For these stress conditions, it is necessary to add ancillary modelling approaches based on soil water balance, as also reported by [94] and [50], or based on a thermal signal, as demonstrated by [95], or even using a combined Kcb-VI approach, with soil water balance for assessing actual Kc, as demonstrated in [49,50].
Regarding the test process, the Kcb A&P and Kcb SIMDualKc values are very similar and the deviation between them is low, except for the value corresponding to the late-season stage, following the same pattern observed in the calibration (Table 5). As shown in Table 5, the deviation between Kcb A&P and Kcb SIMDualKc values starts when plants suffer slight water stress (confirmed by Figure 6), and the highest difference between Kcb A&P and Kcb SIMDualKc_2A occurs for the last crop stage, when the plant water stress is moderate, as also observed for calibration (Kcb SIMDualKc_1D).
The modelling efficiency was low for test (poor results with values between 0.03 and 0.38) and it presented a lower coefficient of determination (R2) than model calibration. However, the low number of Landsat-5 images available for the study period somehow affects the results of the quality of fit indicators. Nevertheless, the difference between the Kcb A&P and the Kcb SIMDualKc is small for most of dates, mainly when the plants are not under water stress. Differently, when moderate (or severe) water stress starts, (after 31/07/1987), the difference between the Kcb A&P and the Kcb SIMDualKc values is greater (specially for 31/07/1987 and 17/09/1987).
It is also worth mentioning that, while the results obtained with SIMDualKc refer to specific positions in the plot, namely the measurement position considered for the model calibration (1D) and the position considered for the test (2A), the results for the A&P approach, use the fc VI values from SAVI derived from satellite images. The Landsat-5 satellite images, available in the study period, have a pixel size of 30 m x 30 m, thus representing an area on the ground where the variability of soil conditions is higher than the variability of the soil water content measurement positions.
The SIMDualKc model and the A&P approach were not able to explain the entire variance of the data, due to the small number of observations of the fc VI data. This small number of available satellite images was pointed as a limitation in a study by [55]. Moreover, reduced efficacy in the A&P approach as a result of insufficient fc and h field observations was also reported by [31]. The current availability of a large number of satellite missions with improved spatial and temporal resolutions (e.g., Landsat 8, Landsat 9, Sentinel-2) can help overcome this data availability limitation.

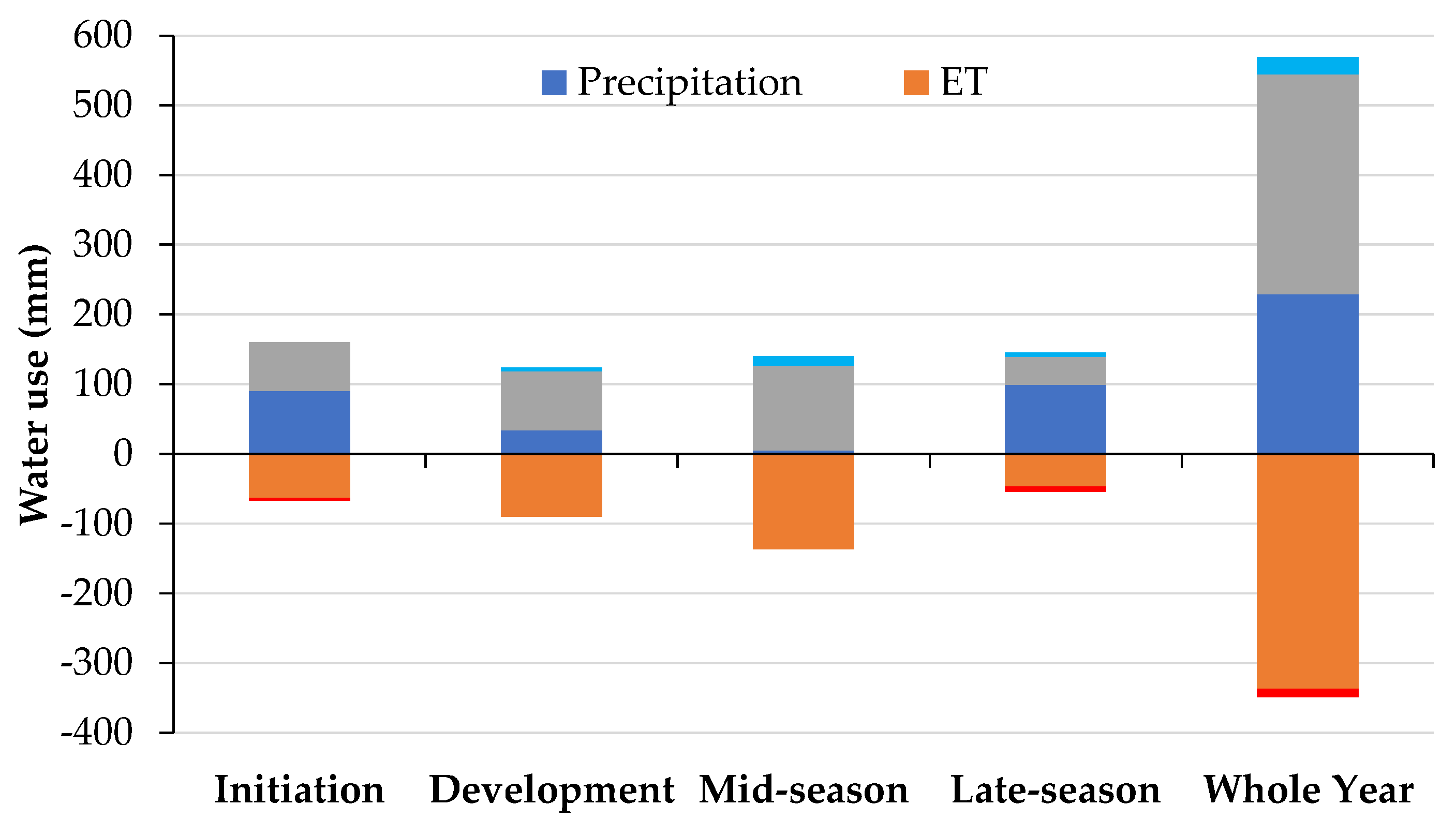
3.5. Water Balance and Respective Components

Figure 8 summarizes the various soil water balance components for the studied year that were estimated using SIMDualKc model. For calibration (1D), regarding the runoff process (RO), it occurred only for two periods, in the initial crop stage (3.60 mm), and at the late season (with 7.70 mm). The capillary rise (CR) contribution to soil water balance, for the calibration process was estimated as a total of 25.16 mm from development till late-season stage, with 52% of the total CR occurring on mid-season. For test (2A), the CR contribution was 15.80 mm, from the mid-season up to the late-season stage. The difference in CR between the two positions (1D and 2A) can be explained by the variability of the soil in the vineyard area, which is composed, as described by [19], of calcareous and non-calcareous materials in the form of complexes, such as fine sandstones, clays, and argillites with a texture variation from loamy to clayey. Besides that, in this area, there is a variation in the slope of the terrain (approximately 2.5%), and position 1D (used for to calibrate the model) is located in a higher landscape position than position 2A (used for testing the model). Naturally, it is expected that greater accumulation of water in the soil will occur in lower topographical positions, associated with the soil's water retention capacity, as demonstrated in Figures 5 (available soil water) and 6 (predawn leaf water potential). Furthermore, [19] mentioned that this is an area intensely marked by crops and with frequent annual plowing up to 0.20-0.30 m, sometimes reaching 0.65-0.80 m. Thus, the natural soil horizons are mixed to a greater or lesser extent. Therefore, taking this into account and as the soil is an Anthrosol, it is understandable to have this variation in CR, as verified in the present study. Even so, it is worth mentioning that there was no significant difference in vine yield in the year under study between the two positions evaluated, with 5.22 kg plant-1 in 1D and 3.80 kg plant-1 in 2A, as described in [19].
Variability in precipitation and its distribution across the different stages of crop growth were verified for the study year (1987), which had less precipitation and was drier than the previous five years' average (1982–1987) (as depicted in Figure 3). The runoff (RO, mm) represents 5% of precipitation, and capillary rise (CR, mm) represents 7.02% (position 1D) and 11.18% (position 2A), respectively. These percentages show that rainfall was primarily utilized for crop evapotranspiration. The highest quantities of RO and CR were verified at the maturity and end-season crop phases, when crop evapotranspiration was lowest (Table 6).
The soil water balance values (average values for calibration and test) estimated with the SIMDualKc model are summarized in Table 6. The actual evapotranspiration (ETc act) ranges from 68 mm to 55 mm, in the initiation stage to late-season, respectively. The higher value is observed in the mid-season (143 mm), which represents 40.4% of the total in the crop cycle. Most of the ETc act (84.7%) occurs between the beginning and mid-season stages, with higher precipitation in March and April having a significant effect on this. A similar pattern occurs for the actual transpiration (Tc act), with 82% occurring from initiation to mid-season stages. Since the vineyard was not irrigated, the contribution from precipitation and the capacity of the soil to store water (Δ SWC, Figure 8), and to contribute to ETc act (including capillary rise), are higher during mid-season, indicating that the water stored in the soil (especially in the deeper layers) played an important role in the actual crop evapotranspiration for the studied area. The daily actual transpiration (Tc act) and soil evaporation (Es) for the year of study estimated with SIMDualKc model are presented on supplementary Figure S1 (Annex I).
By analyzing the consumptive use of water (Table 6), it can be observed that in the ETc act partitioning, the soil evaporation (Es) was the main component of the evapotranspiration process, particularly during the initial and development crop phases. Es values were 83.8% and 51.6% of the total ETc act on the aforementioned stages. This variation is related to higher precipitation on these periods, which kept the soil wet. On the other hand, Es contribution to ETc act was smaller than Tc act at mid-season and late-season stages, with values ranging from 3.5% to 23.6% of ETc act. During these stages, the transpiration becomes more important and is the main consumptive water use, representing 97.2% and 74.54% of ETc act. Once again, these values are explained by the influence of precipitation, soil water storage and capillary rise, therefore the rainfed condition of the vineyard. In general, it was found that Es and Tc act values represents 36% and 64% of ETc act during the entire crop season. Similar results for evapotranspiration partition occurring during the mid-season and, however less important, during the late season, were observed by [10] and by [47] for rainfed vineyards. [10] studied vineyards under two watering regimes that are frequently applied in the Mediterranean region for this crop (rainfed and deficit irrigation) and [47] evaluated a rainfed Italian vineyard, also in a Mediterranean condition. The differences between these studies and the present study can be explained by different amounts of rain and soil water storage capacity of the respective locations.
Results regarding the ETc act/ETc ratio (Table 6) show that ETc act was smaller by 17% relative to the potential ETc in the studied year. During the mid-season, that ratio ETc act/ETc was small, when ETc act was smaller by 13% comparatively to the potential ETc. These reductions are probably low in non-irrigated scenarios with low rainfall, as analyzed above, which did not affect yields (as reported by [19]), comparing calibration and test positions.

4. Conclusions

In the present study, soil water balance modelling using SIMDualKc was evaluated in a rainfed vineyard, in Santarém, Portugal, using as reference soil water content field data. These data were collected at a depth (1.85 m) greater than that commonly used for modelling and therefore, allowing to better represent the soil volume explored by the roots. Additionally, the actual crop coefficient (Kcb act) obtained in SIMDualKc model (Kcb SIMDualKc) was compared with Kcb estimated using the A&P approach [48] (Kcb A&P), where fc was estimated from spectral vegetation indices derived from Landsat 5 images to further estimate Kd.
For the specific characteristics of this study area, namely, the soil, the climate, and the studied vineyard cultural practices (spacing, crop height, inter-row management), the calibration and test of the SIMDualKc model were successfully performed, proving that it is possible to calibrate the model considering a soil profile depth greater than those that are normally used for vineyard ET modelling with soil water content.
Previous studies that adopted a similar calibration procedure of SIMDualKc with soil water content values were carried out in areas with higher annual rainfall and milder temperatures than those recorded in the region of Santarém. Although these studies provided good results for the application of SIMDualKc model, this was performed for less deeper soil profiles (up to 1.0 m).
For the study year (1987), a good fit was achieved between the soil water content values measured in the field with the neutron probe and the values simulated with the SIMDualKc model, both for the calibration and the test performed.
Furthermore, the comparison between Kcb SIMDualKc and the Kcb A&P showed a small difference for most values throughout the different crop stages. However, the reduced number of satellite images to estimate fc VI and derive Kd in the A&P approach was a limitation in obtaining a good fit between the Kcb act simulated by the SIMDualKc model and the Kcb act estimated by the A&P approach. Nevertheless, nowadays increasingly available satellite missions can potentially contribute to better approximating the soil water balance modeling to the real conditions of vegetation development.
We can reckon that the present study allowed improving the knowledge about the application of the SIMDualKc model in vineyards, exploring the application of the model for conditions of increased root depth, as expected in rainfed conditions under Mediterranean influence, and thus potentially contributing to better water management.
Moreover, model fitting results (namely, modelling efficiency and variance explained by the model) were very good, indicating an enhanced accuracy of the model when using increased depth for calibration field data of vineyards.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Actual evapotranspiration (ETc act), plant transpiration (Tc act), soil evaporation (Es), and precipitation (P), computed by SIMDualKc model in a rainfed vineyard, in Santarém, Portugal.

Author Contributions

Conceptualization, T.A.P., I.P., and P.P.; methodology, I.P., P.P., J.B., W.S.A., and T.A.P.; software, W.S.A., I.P., P.P., and T.A.P.; validation, W.S.A., J.B., I.P., P.P., and T.A.P.; formal analysis, W.S.A., P.P., and T.A.P.; investigation, W.S.A., and J.B.; resources, C.A.P., T.A.P, I.P., and P.P.; data curation, W.S.A.; writing—original draft preparation, W.S.A., P.P., and T.A.P.; writing—review and editing, P.P., I.P., J.B., C.A.P., W.S.A., and T.A.P.; visualization, W.S.A., P.P. and T.A.P.; supervision, T.A.P., I.P., and P.P..; project administration, T.A.P.; funding acquisition, C.A.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Centro de Pedologia da Universidade Técnica de Lisboa (INIC) and Instituto Superior de Agronomia/Universidade de Lisboa.

Data Availability Statement

The data presented in this study are available in the article.

Acknowledgments

The authors acknowledge the Centro de Pedologia of Technical University of Lisbon (INIC) and the School of Agriculture; the School of Agriculture of Santarém; and the "Institut National Agronomique Paris-Grignon (Chaire d'Agronomie)".

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Fernandes-Silva A, Oliveira M, A. Paço T, Ferreira I (2019) Deficit Irrigation in Mediterranean Fruit Trees and Grapevines: Water Stress Indicators and Crop Responses. In: Ondrašek G (ed) Irrigation in Agroecosystems. IntechOpen. [CrossRef]
  2. Ferreira MI, Silvestre J, Conceição N, Malheiro AC (2012) Crop and stress coefficients in rainfed and deficit irrigation vineyards using sap flow techniques. Irrig Sci 30:433–447. [CrossRef]
  3. Groenveld T, Obiero C, Yu Y, et al (2023) Predawn leaf water potential of grapevines is not necessarily a good proxy for soil moisture. BMC Plant Biology 23:369. [CrossRef]
  4. Edwards E j., Clingeleffer P r. (2013) Interseasonal effects of regulated deficit irrigation on growth, yield, water use, berry composition and wine attributes of Cabernet Sauvignon grapevines. Australian Journal of Grape and Wine Research 19:261–276. [CrossRef]
  5. Keller M (2010) The Science of Grapevines - 1st Edition. https://shop.elsevier.com/books/the-science-of-grapevines/keller/978-0-12-374881-2. Accessed 19 Jun 2023.
  6. Savi T, Petruzzellis F, Moretti E, et al (2019) Grapevine water relations and rooting depth in karstic soils. Science of The Total Environment 692:669–675. [CrossRef]
  7. Smart DR, Schwass E, Lakso A, Morano L (2006) Grapevine Rooting Patterns: A Comprehensive Analysis and a Review. Am J Enol Vitic 57:89–104. [CrossRef]
  8. Celette F, Wery J, Chantelot E, et al (2005) Belowground Interactions in a Vine (Vitis vinifera L.)-tall Fescue (Festuca arundinacea Shreb.) Intercropping System: Water Relations and Growth. Plant Soil 276:205–217. [CrossRef]
  9. Iland P, Dry P, Proffitt T, Tyerman S (2011) The Grapevine: from the science to the practice of growing vines for wine - Patrick Iland Wine Books. https://www.piwpwinebooks.com.au/wine-books/the-grapevine-from-the-science-to-the-practice-of-growing-vines-for-wine. Accessed 19 Jun 2023.
  10. Valentín F, Sánchez JM, Martínez-Moreno A, et al (2023) Using on-the-ground surface energy balance to monitor vine water status and evapotranspiration under deficit irrigation and rainfed conditions. Agricultural Water Management 281:108240. [CrossRef]
  11. Chaves MM, Zarrouk O, Francisco R, et al (2010) Grapevine under deficit irrigation: hints from physiological and molecular data. Annals of Botany 105:661–676. [CrossRef]
  12. Chaves MM, Santos TP, Souza CR, et al (2007) Deficit irrigation in grapevine improves water-use efficiency while controlling vigour and production quality. Ann Applied Biology 150:237–252. [CrossRef]
  13. Costa JM, Oliveira M, Egipto RJ, et al (2020) Water and wastewater management for sustainable viticulture and oenology in South Portugal – a review. Ciência Téc Vitiv 35:1–15. [CrossRef]
  14. De Souza CR, Maroco JP, Dos Santos TP, et al (2005) Control of stomatal aperture and carbon uptake by deficit irrigation in two grapevine cultivars. Agriculture, Ecosystems & Environment 106:261–274. [CrossRef]
  15. De Souza CR, Maroco JP, Dos Santos TP, et al (2005) Impact of deficit irrigation on water use efficiency and carbon isotope composition (δ13C) of field-grown grapevines under Mediterranean climate. Journal of Experimental Botany 56:2163–2172. [CrossRef]
  16. Ferreira MI, Conceição N, Malheiro AC, et al (2017) Water stress indicators and stress functions to calculate soil water depletion in deficit irrigated grapevine and kiwi. Acta Hortic 119–126. [CrossRef]
  17. MacMillan P, Teixeira G, Lopes CM, Monteiro A (2021) The role of grapevine leaf morphoanatomical traits in determining capacity for coping with abiotic stresses: a review. Ciência Téc Vitiv 36:75–88. [CrossRef]
  18. Dinis L-T, Correia CM, Ferreira HF, et al (2014) Physiological and biochemical responses of Semillon and Muscat Blanc à Petits Grains winegrapes grown under Mediterranean climate. Scientia Horticulturae 175:128–138. [CrossRef]
  19. Pacheco CMA (1989) Influência de técnicas de não mobilização e de mobilização sobre aspectos estruturais e hídricos de solos com vinha, bem como sobre o respectivo sistema radical. Consequencias das relações hídricas solo - vinha na produção. Tese de doutoramento, Insituto Superior de Agronomia – Universidade Técnica de Lisboa.
  20. Costa JM, Vaz M, Escalona J, et al (2016) Modern viticulture in southern Europe: Vulnerabilities and strategies for adaptation to water scarcity. Agricultural Water Management 164:5–18. [CrossRef]
  21. Dal Santo S, Palliotti A, Zenoni S, et al (2016) Distinct transcriptome responses to water limitation in isohydric and anisohydric grapevine cultivars. BMC Genomics 17:815. [CrossRef]
  22. Flexas J, Carriquí M, Nadal M (2018) Gas exchange and hydraulics during drought in crops: who drives whom? Journal of Experimental Botany 69:3791–3795. [CrossRef]
  23. Savi T, Petruzzellis F, Martellos S, et al (2018) Vineyard water relations in a karstic area: deep roots and irrigation management. Agriculture, Ecosystems & Environment 263:53–59. [CrossRef]
  24. Malheiro AC, Gonçalves IN, Fernandes-Silva AA, et al (2011) Relationships between relative transpiration of grapevines and plant and soil water status in Portugal’s Douro wine region. Acta Hortic 261–267. [CrossRef]
  25. Pellegrino A, Lebon E, Voltz M, Wery J (2004) Relationships between plant and soil water status in vine (Vitis vinifera L.). Plant Soil 266:129–142. [CrossRef]
  26. Carbonneau A (1998) Irrigation, vignoble et produits de la vigne. In: Traité d’irrigation, Tiercelin, J.R. (ed.). Lavoisier Tec & Doc, Paris, pp 257–276.
  27. Allen RG, Pereira LS, Raes D, Smith, M (1998) FAO Irrigation and Drainage Paper. 326.
  28. Pereira LS, Paredes P, Hunsaker DJ, et al (2021) Standard single and basal crop coefficients for field crops. Updates and advances to the FAO56 crop water requirements method. Agricultural Water Management 243:106466. [CrossRef]
  29. Rallo G, Paço TA, Paredes P, et al (2021) Updated single and dual crop coefficients for tree and vine fruit crops. Agricultural Water Management 250:106645. [CrossRef]
  30. Liu M, Shi H, Paredes P, et al (2022) Estimating and partitioning maize evapotranspiration as affected by salinity using weighing lysimeters and the SIMDualKc model. Agricultural Water Management 261:107362. [CrossRef]
  31. Puig-Sirera À, Rallo G, Paredes P, et al (2021) Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach. Water 13:2466. [CrossRef]
  32. Cammalleri C, Anderson MC, Ciraolo G, et al (2012) Applications of a remote sensing-based two-source energy balance algorithm for mapping surface fluxes without in situ air temperature observations. Remote Sensing of Environment 124:502–515. [CrossRef]
  33. Conceição N, Häusler M, Lourenço S, et al (2017) Evapotranspiration measured in a traditional rainfed and an irrigated intensive olive orchard during a year of hydrological drought. Acta Hortic 281–288. [CrossRef]
  34. Paço TA, Pôças I, Cunha M, et al (2014) Evapotranspiration and crop coefficients for a super intensive olive orchard. An application of SIMDualKc and METRIC models using ground and satellite observations. Journal of Hydrology 519:2067–2080. [CrossRef]
  35. Pereira LS, Paredes P, Melton F, et al (2020) Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agricultural Water Management 241:106197. [CrossRef]
  36. Allen RG, Pereira LS, Smith M, et al (2005) FAO-56 Dual Crop Coefficient Method for Estimating Evaporation from Soil and Application Extensions. J Irrig Drain Eng 131:2–13. [CrossRef]
  37. Er-Raki S, Chehbouni A, Boulet G, Williams DG (2010) Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agricultural Water Management 97:1769–1778. [CrossRef]
  38. Paço T, Paredes P, Pereira L, et al (2019) Crop Coefficients and Transpiration of a Super Intensive Arbequina Olive Orchard using the Dual Kc Approach and the Kcb Computation with the Fraction of Ground Cover and Height. Water 11:383. [CrossRef]
  39. Rallo G, Baiamonte G, Juárez JM, Provenzano G (2014) Improvement of FAO-56 Model to Estimate Transpiration Fluxes of Drought Tolerant Crops under Soil Water Deficit: Application for Olive Groves. J Irrig Drain Eng 140:A4014001. [CrossRef]
  40. Autovino D, Rallo G, Provenzano G (2018) Predicting soil and plant water status dynamic in olive orchards under different irrigation systems with Hydrus-2D: Model performance and scenario analysis. Agricultural Water Management 203:225–235. [CrossRef]
  41. Rosa RD, Paredes P, Rodrigues GC, et al (2012) Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agricultural Water Management 103:8–24. [CrossRef]
  42. Rosa RD, Paredes P, Rodrigues GC, et al (2012) Implementing the dual crop coefficient approach in interactive software: 2. Model testing. Agricultural Water Management 103:62–77. [CrossRef]
  43. Ramos TB, Darouich H, Oliveira AR, et al (2023) Water use and soil water balance of Mediterranean tree crops assessed with the SIMDualKc model in orchards of southern Portugal. Agricultural Water Management 279:108209. [CrossRef]
  44. Cancela JJ, Fandiño M, Rey BJ, Martínez EM (2015) Automatic irrigation system based on dual crop coefficient, soil and plant water status for Vitis vinifera (cv Godello and cv Mencía). Agricultural Water Management 151:52–63. [CrossRef]
  45. Fandiño M, Cancela JJ, Rey BJ, et al (2012) Using the dual-Kc approach to model evapotranspiration of Albariño vineyards (Vitis vinifera L. cv. Albariño) with consideration of active ground cover. Agricultural Water Management 112:75–87. [CrossRef]
  46. Paço TA, Ferreira MI, Rosa RD, et al (2012) The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model versus eddy covariance measurements. Irrig Sci 30:115–126. [CrossRef]
  47. Darouich H, Ramos TB, Pereira LS, et al (2022) Water Use and Soil Water Balance of Mediterranean Vineyards under Rainfed and Drip Irrigation Management: Evapotranspiration Partition and Soil Management Modelling for Resource Conservation. Water 14:554. [CrossRef]
  48. Allen RG, Pereira LS (2009) Estimating crop coefficients from fraction of ground cover and height. Irrig Sci 28:17–34. [CrossRef]
  49. Pôças I, Calera A, Campos I, Cunha M (2020) Remote sensing for estimating and mapping single and basal crop coefficientes: A review on spectral vegetation indices approaches. Agricultural Water Management 233:106081. [CrossRef]
  50. Pôças I, Paço T, Paredes P, et al (2015) Estimation of Actual Crop Coefficients Using Remotely Sensed Vegetation Indices and Soil Water Balance Modelled Data. Remote Sensing 7:2373–2400. [CrossRef]
  51. Allen RG, Wright JL, Pruitt WO, et al (2007) Water requirements. In: Design and Operation of Farm Irrigation Systems, 2nd Edition, 1st ed. American Society of Agricultural and Biological Engineers, St. Joseph, MI, pp 208–288.
  52. Anderson MC, Kustas WP, Alfieri JG, et al (2012) Mapping daily evapotranspiration at Landsat spatial scales during the BEAREX’08 field campaign. Advances in Water Resources 50:162–177. [CrossRef]
  53. Bastiaanssen WGM, Menenti M, Feddes RA, Holtslag AAM (1998) A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. Journal of Hydrology 212–213:198–212. [CrossRef]
  54. French AN, Hunsaker DJ, Thorp KR (2015) Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sensing of Environment 158:281–294. [CrossRef]
  55. Campos I, Neale CMU, Calera A, et al (2010) Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agricultural Water Management 98:45–54. [CrossRef]
  56. Jayanthi H, Neale CMU, Wright JL (2007) Development and validation of canopy reflectance-based crop coefficient for potato. Agricultural Water Management 88:235–246. [CrossRef]
  57. Mateos L, González-Dugo MP, Testi L, Villalobos FJ (2013) Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agricultural Water Management 125:81–91. [CrossRef]
  58. Rouse W, Haas R, Scheel J, Deering W (1973) Monitoring Vegetation Systems in Great Plains with ERST, Proceedings of the Third ERTS Symposium, NASA SP-351. US Government printing office, Washington, DC, pp. 309–317.
  59. Huete AR (1988) A soil-adjusted vegetation index (SAVI). Remote Sensing of Environment 25:295–309. [CrossRef]
  60. Glenn EP, Neale CMU, Hunsaker DJ, Nagler PL (2011) Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems: VEGETATION INDEX-BASED CROP COEFFICIENTS. Hydrol Process 25:4050–4062. [CrossRef]
  61. Jensen JR (2000) Remote Sensing of Environment. An Earth Resource Perspective. Prentice Hall, Inc., New Jersey.
  62. Qi J, Chehbouni A, Huete AR, et al (1994) A modified soil adjusted vegetation index. Remote Sensing of Environment 48:119–126. [CrossRef]
  63. Scholander PF, Bradstreet ED, Hemmingsen EA, Hammel HT (1965) Sap Pressure in Vascular Plants. Science 148:339–346. [CrossRef]
  64. Kottek M, Grieser J, Beck C, et al (2006) World Map of the Köppen-Geiger climate classification updated. metz 15:259–263. [CrossRef]
  65. Allen RG (1996) Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J Irrig Drain Eng 122:97–106. [CrossRef]
  66. FAO-UNESCO (1974) Soil map of the world. 1: Legend: [Erläuterungen]. Unesco, Paris.
  67. Paz AM, Cipriano D, Sequeira B, et al (2009) Funções de pedo-transferência para a curva de retenção da água no solo. [CrossRef]
  68. Bell JP (1976) Neutron probe practice. Institute of Hydrology, Wallingford, In: Report No. 19, second ed.
  69. Hodnett MG (1986) The Neutron Probe for Soil Moisture Measurement. In: Gensler WG (ed) Advanced Agricultural Instrumentation: Design and Use. Springer Netherlands, Dordrecht, pp 148–192. [CrossRef]
  70. Allen RG, Pereira LS, Howell TA, Jensen ME (2011) Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agricultural Water Management 98:899–920. [CrossRef]
  71. Liu Y, Pereira LS, Fernando RM (2006) Fluxes through the bottom boundary of the root zone in silty soils: Parametric approaches to estimate groundwater contribution and percolation. Agricultural Water Management 84:27–40. [CrossRef]
  72. USDA-SCS (2004) Chapter 10 - Estimation of Direct Runoff from Storm Rainfall. USDA-SCS. National Engineering Handbook. Curve Number (Part 630 Hydrology). In: National Engineering Handbook. p 79.
  73. Pereira LS, Paredes P, Rodrigues GC, Neves M (2015) Modeling malt barley water use and evapotranspiration partitioning in two contrasting rainfall years. Assessing AquaCrop and SIMDualKc models. Agricultural Water Management 159:239–254. [CrossRef]
  74. Rosa RD, Ramos TB, Pereira LS (2016) The dual Kc approach to assess maize and sweet sorghum transpiration and soil evaporation under saline conditions: Application of the SIMDualKc model. Agricultural Water Management 177:77–94. [CrossRef]
  75. González-Altozano P, Pavel EW, Oncins JA, et al (2008) Comparative assessment of five methods of determining sap flow in peach trees. Agricultural Water Management 95:503–515. [CrossRef]
  76. Siqueira JM, Paço TA, Silvestre JC, et al (2014) Generating fuzzy rules by learning from olive tree transpiration measurement – An algorithm to automatize Granier sap flow data analysis. Computers and Electronics in Agriculture 101:1–10. [CrossRef]
  77. Huete AR, Liu HQ (1994) An error and sensitivity analysis of the atmospheric- and soil-correcting variants of the NDVI for the MODIS-EOS. IEEE Transactions on Geoscience and Remote Sensing 32:897–905. [CrossRef]
  78. González-Dugo MP, Mateos L (2008) Spectral vegetation indices for benchmarking water productivity of irrigated cotton and sugarbeet crops. Agricultural Water Management 95:48–58. [CrossRef]
  79. Comas L h., Bauerle T l., Eissenstat D m. (2010) Biological and environmental factors controlling root dynamics and function: effects of root ageing and soil moisture. Australian Journal of Grape and Wine Research 16:131–137. [CrossRef]
  80. Liu M, Paredes P, Shi H, et al (2022) Impacts of a shallow saline water table on maize evapotranspiration and groundwater contribution using static water table lysimeters and the dual Kc water balance model SIMDualKc. Agricultural Water Management 273:107887. [CrossRef]
  81. Moriasi DN, J. G. Arnold, M. W. Van Liew, et al (2007) Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Transactions of the ASABE 50:885–900. [CrossRef]
  82. Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models part I — A discussion of principles. Journal of Hydrology 10:282–290. [CrossRef]
  83. Silva SP, Valín MI, Mendes S, et al (2021) Dual Crop Coefficient Approach in Vitis vinifera L. cv. Loureiro. Agronomy 11:2062. [CrossRef]
  84. Silvestre JMC (2003) Evapotranspiração e funcionamento hídrico em Vitis vinifera L. Dissertação de Doutoramento, Instituto Superior de Agronomia, Universidade Técnica de Lisboa 222.
  85. Serrano L, González-Flor C, Gorchs G (2010) Assessing vineyard water status using the reflectance-based Water Index. Agriculture, Ecosystems & Environment 139:490–499. [CrossRef]
  86. Serrano L, González-Flor C, Gorchs G (2012) Assessment of grape yield and composition using the reflectance-based Water Index in Mediterranean rainfed vineyards. Remote Sensing of Environment 118:249–258. [CrossRef]
  87. Ramírez-Cuesta JM, Intrigliolo DS, Lorite IJ, et al (2023) Determining grapevine water use under different sustainable agronomic practices using METRIC-UAV surface energy balance model. Agricultural Water Management 281:108247. [CrossRef]
  88. Ballesteros R, Intrigliolo DS, Ortega JF, et al (2020) Vineyard yield estimation by combining remote sensing, computer vision and artificial neural network techniques. Precision Agric 21:1242–1262. [CrossRef]
  89. Basile A, Albrizio R, Autovino D, et al (2020) A modelling approach to discriminate contributions of soil hydrological properties and slope gradient to water stress in Mediterranean vineyards. Agricultural Water Management 241:106338. [CrossRef]
  90. da Silva AJP, Pinheiro EAR, de Jong van Lier Q (2020) Determination of soil hydraulic properties and its implications for mechanistic simulations and irrigation management. Irrig Sci 38:223–234. [CrossRef]
  91. Galleguillos M, Jacob F, Prévot L, et al (2017) Estimation of actual evapotranspiration over a rainfed vineyard using a 1-D water transfer model: A case study within a Mediterranean watershed. Agricultural Water Management 184:67–76. [CrossRef]
  92. Wang S, Zhu G, Xia D, et al (2019) The characteristics of evapotranspiration and crop coefficients of an irrigated vineyard in arid Northwest China. Agricultural Water Management 212:388–398. [CrossRef]
  93. Er-Raki S, Rodriguez JC, Garatuza-Payan J, et al (2013) Determination of crop evapotranspiration of table grapes in a semi-arid region of Northwest Mexico using multi-spectral vegetation index. Agricultural Water Management 122:12–19. [CrossRef]
  94. Campos I, Villodre J, Carrara A, Calera A (2013) Remote sensing-based soil water balance to estimate Mediterranean holm oak savanna (dehesa) evapotranspiration under water stress conditions. Journal of Hydrology 494:1–9. [CrossRef]
  95. Alfieri JG, Kustas WP, Prueger JH, et al (2019) A multi-year intercomparison of micrometeorological observations at adjacent vineyards in California’s Central Valley during GRAPEX. Irrig Sci 37:345–357. [CrossRef]
Preprints 111563 g001
Figure 1. Study area location in Santarém, Portugal. (Vineyard approximate boundaries in black). 1D (▲) and 2A (▄) locations of soil water content measurements, used respectively for calibrating and testing the modelling tool.
Figure 1. Study area location in Santarém, Portugal. (Vineyard approximate boundaries in black). 1D (▲) and 2A (▄) locations of soil water content measurements, used respectively for calibrating and testing the modelling tool.
Preprints 111563 g001
Preprints 111563 g002
Figure 2. The annual cycle of the vine and the crop growth stages. The crop growth stages are delimited according to the FAO segmented curve [27].
Figure 2. The annual cycle of the vine and the crop growth stages. The crop growth stages are delimited according to the FAO segmented curve [27].
Preprints 111563 g002
Preprints 111563 g003
Figure 3. Average monthly reference evapotranspiration (ETo) and precipitation (P) data in the years 1982-1987 and for the study year (1987) at Santarém, Portugal.
Figure 3. Average monthly reference evapotranspiration (ETo) and precipitation (P) data in the years 1982-1987 and for the study year (1987) at Santarém, Portugal.
Preprints 111563 g003
Preprints 111563 g004
Figure 4. Schematic partial top view of the experimental layout and the access tubes (AT, blue circles) location at the experimental field, Santarém, Portugal.
Figure 4. Schematic partial top view of the experimental layout and the access tubes (AT, blue circles) location at the experimental field, Santarém, Portugal.
Preprints 111563 g004
Preprints 111563 g005
Figure 5. Available soil water dynamics for the calibration (a) and test (b) of the SIMDualKc model. Dots represent observations while the curve represents simulations of the available soil water (ASW). TAW represents the total available water, and RAW denotes the rapidly available water.
Figure 5. Available soil water dynamics for the calibration (a) and test (b) of the SIMDualKc model. Dots represent observations while the curve represents simulations of the available soil water (ASW). TAW represents the total available water, and RAW denotes the rapidly available water.
Preprints 111563 g005
Preprints 111563 g006
Figure 6. Vine water stress severity according to the limit values of leaf water potential (ψb) proposed by [26].
Figure 6. Vine water stress severity according to the limit values of leaf water potential (ψb) proposed by [26].
Preprints 111563 g006
Preprints 111563 g007
Figure 7. Standard and actual basal crop coefficients (Kcb, Kcb act), soil evaporation coefficient (Ke), and actual crop coefficient (Kc act = Kcb act + Ke), and precipitation (P), computed by the SIMDualKc model in a rainfed vineyard, in Santarém, Portugal.
Figure 7. Standard and actual basal crop coefficients (Kcb, Kcb act), soil evaporation coefficient (Ke), and actual crop coefficient (Kc act = Kcb act + Ke), and precipitation (P), computed by the SIMDualKc model in a rainfed vineyard, in Santarém, Portugal.
Preprints 111563 g007
Preprints 111563 g008
Figure 8. Simulated soil water balance components: precipitation, evapotranspiration (ET), soil water content variation (Δ SWC), runoff (RO), and capillary rise (CR) (all variables in mm) after accurate SIMDualKc model calibration.
Figure 8. Simulated soil water balance components: precipitation, evapotranspiration (ET), soil water content variation (Δ SWC), runoff (RO), and capillary rise (CR) (all variables in mm) after accurate SIMDualKc model calibration.
Preprints 111563 g008
Table 1. Summary of the equations used to compute capillary rise (from [41,71]).
Table 1. Summary of the equations used to compute capillary rise (from [41,71]).
Equations Conditions Parameters
Capillary rise
W c = a 1   .   D w b 1 (mm) a1 = WFC, soil water storage to maximum root depth (Zr) at field capacity (mm); a1 = θFC Zr ·1000
W s = a 2   .   D w b 2 (mm) D w   ≤   3   m b1 = −0.17
W s = 240   mm D w   >   3   m a2 = 1.1 [(θFC + θWP)/2] Zr ·1000, i.e., storage above the average between those at field capacity and the wilting point (mm)
b2 =−0.27
D w c = a 3   .   E T m + b 3 (m) E T m ≤ 4 mm d-1 a3 = −1.3
D w c = 1.4 (m) E T m > 4 mm d-1 b3 = 6.7 for clay and silty clay loam soils, decreasing to 6.2 for loamy sands
C R m a x = k .   E T m (mm d-1) D w   ≤   D w c a4 = 4.6 for silty loam and silty clay loam soils, decreasing to 3 for loamy sands
C R m a x = a 4   .   D w b 4 (mm d-1) D w > D w c b4 = −0.65 for silty loam soils and decreasing to −2.5 for loamy sand soils
k = 1 − e − 0.6   .   L A I E T m ≤ 4 mm d-1
k = 3.8 / E T m E T m > 4 mm d-1
C R = C R m a x   D w ,   E T m (mm d-1) W a < W s D w
C R = C R m a x   D w ,   E T m   W c D w − W a W c D w − W s D w (mm d-1) W s D w ≤ W a ≤ W c D w
C R = 0 W a < W c D w
Wa represents the actual root zone soil water storage (mm); Wc represents the critical soil water storage (mm); Ws is the steady soil water storage (mm); θFC is soil water content at field capacity (non-dimensional); θWP is the soil water content at the wilting point (non-dimensional); Dw is the depth of groundwater (m); Dwc is the critical depth of groundwater (m); ETm is the potential crop evapotranspiration rate (mm d−1), usually ETm = ETc (mm d−1); CRmax is the potential capillary flux (mm d−1); CR is the actual capillary flux (mm d−1); k is the factor associating the evapotranspiration with transpiration (non-dimensional); LAI is leaf area index (non-dimensional); and t is the time after occurrence of irrigation or rainfall events that produced water storage over field capacity (days).
Table 2. Initial and calibrated SIMDualKc model parameters.
Table 2. Initial and calibrated SIMDualKc model parameters.
Parameters Initial values* Calibrated values
Crop characteristics Kcb ini 0.15 0.15
Kcb mid 0.65 0.60
Kcb end 0.40 0.52
p ini 0.45 0.60
p dev 0.45 0.60
p mid 0.45 0.60
p end 0.45 0.60
Soil evaporation TEW 20 20
REW 10 10
Ze (m) 0.10 0.10
Runoff and deep percolation CN 68 68
aD 285 275
bD -0.0173 -0.0173
Capillary rise a1 260 253
b1 -0.17 -0.17
a2 200 196
b2 -0.27 -0.27
a3 -1.3 -1.3
b3 6.2 6.2
a4 3.0 3.0
b4 -2.5 -2.5
*Values taken from [27,28,48,71,72].
Table 3. Statistical indicators obtained for the comparison between soil water content simulated by the SIMDualKc model and soil water content measured using a neutron probe, for the calibration and the test positions.
Table 3. Statistical indicators obtained for the comparison between soil water content simulated by the SIMDualKc model and soil water content measured using a neutron probe, for the calibration and the test positions.
Number of observations b0 R2 RMSE (mm) NRMSE (%) AAE (mm) ARE (%) EF
Calibration 10 0.97 1.00 11.1 12.8 9.5 0.56 0.98
Test 7 0.97 1.00 11.9 11.2 10.2 0.25 0.97
b0 and R2 are the coefficients regression and determination; RMSE is the root mean square error; NRMSE is the normalized RMSE; AAE is the average absolute error; ARE is the average relative error; EF is the model efficiency.
Table 4. Soil Adjusted Vegetation Index (SAVI) and the fraction of ground cover derived from SAVI (fc VI) for a rainfed vineyard in Santarém, Portugal.
Table 4. Soil Adjusted Vegetation Index (SAVI) and the fraction of ground cover derived from SAVI (fc VI) for a rainfed vineyard in Santarém, Portugal.
DOY Date SAVI ± SD fc VI
116 26/04/1987 0.205 ± 0.012 0.174
148 28/05/1987 0.279 ± 0.066 0.286
180 29/06/1987 0.271 ± 0.065 0.275
212 31/07/1987 0.272 ± 0.081 0.276
260 17/09/1987 0.228 ± 0.058 0.209
DOY is the day of the year; SAVI values are the average of SAVI in 12 pixels for each satellite image; and SD is the standard deviation.
Table 5. Kcb estimated by SIMDualKc model for calibration (Kcb SIMDualKc_1D) and for test (Kcb SIMDualKc_2A), Kcb from A&P approach (Kcb A&P), and the deviation between Kcb SIMDualKc and Kcb A&P for a rainfed vineyard in Santarém, Portugal.
Table 5. Kcb estimated by SIMDualKc model for calibration (Kcb SIMDualKc_1D) and for test (Kcb SIMDualKc_2A), Kcb from A&P approach (Kcb A&P), and the deviation between Kcb SIMDualKc and Kcb A&P for a rainfed vineyard in Santarém, Portugal.
Date Kcb SIMDualKc_1D Kcb A&P Deviation Kcb SIMDualKc_2A Kcb A&P Deviation
26/04/1987 0.29 0.29 -0.01 0.27 0.29 0.01
28/05/1987 0.51 0.45 -0.10 0.47 0.45 -0.05
29/06/1987 0.39 0.40 0.01 0.47 0.40 -0.06
31/07/1987 0.20 0.43 0.21 0.32 0.43 0.09
17/09/1987 0.08 0.35 0.24 0.14 0.35 0.18
Table 6. Average values ± standard deviation of actual evapotranspiration (ETc act, mm), and its partition into soil evaporation (Es, mm) and actual transpiration (Tc act, mm), soil evaporation to actual evapotranspiration ratio (Es/ETc act, %), crop transpiration to actual evapotranspiration ratio (Tc act/ETc act, %) and actual evapotranspiration to maximum (potential) evapotranspiration ratio (ETc act/ETc, %), for the crop growing periods of the rainfed vineyard under study.
Table 6. Average values ± standard deviation of actual evapotranspiration (ETc act, mm), and its partition into soil evaporation (Es, mm) and actual transpiration (Tc act, mm), soil evaporation to actual evapotranspiration ratio (Es/ETc act, %), crop transpiration to actual evapotranspiration ratio (Tc act/ETc act, %) and actual evapotranspiration to maximum (potential) evapotranspiration ratio (ETc act/ETc, %), for the crop growing periods of the rainfed vineyard under study.
Initial Development Mid-season Late-season Full Year
ETc act (mm) 68 ± 1.51 89 ± 1.16 143 ± 7.80 55 ± 8.80 354 ± 16.95
Es (mm) 57 ± 1.51 46 ± 0.53 5 ± 0.15 13 ± 0.15 121 ± 2.04
Tc act (mm) 10 ± 0.00 43 ± 1.69 139 ± 7.17 41 ± 9.15 234 ± 14.63
Es/ETc act (%) 83 ± 0.57 43 ± 0.84 3 ± 0.11 16 ± 1.15 36 ± 0.09
Tc act/ETc act (%) 17 ± 0.57 57 ± 0.85 98 ± 0.50 85 ± 1.22 64 ± 0.17
ETc act/ETc (%) 100 ± 0.00 100 ± 0.00 87 ± 8.45 46 ± 8.55 83 ± 4.25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated