Reducing the Rebound Effect in Microscale Laser Dynamic Forming Through Multi-pulse Laser Shock Loading

Microscale laser dynamic forming, as a novel high-speed microforming technique, can overcome the shortcomings of traditional microforming methods. However, in practical applications, laser dynamic microforming technology is often affected by the rebound behavior of the workpiece surface, limiting the further improvement of processing quality and efficiency. This paper aims to reduce the rebound effect in laser dynamic microforming by using multi-pulse laser shock loading. The forming results of workpieces under different laser energies and laser impact numbers were studied using experimental and numerical simulation methods. Numerical simulations of the forming results after multiple laser shocks were conducted using ANSYS/LS-DYNA software. These numerical simulation results were then experimentally validated and compared. Surface morphology and microstructure of the workpieces were characterized using a confocal microscope and scanning electron microscope, and energy dispersive spectroscopy (EDS) was used to analyze the chemical element content changes in the collision regions at the bottoms of the workpieces after multi-pulse loading, revealing the collision behavior patterns during the forming process. Finally, the forming laws of workpieces under multiple laser shocks were summarized.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Laser dynamic microforming [1] technology is a novel high-precision, high-speed microforming process that does not require molds and can rapidly form complex micro-components. It has broad application prospects in industrial components [2], medical devices [3], power electronics [4], aerospace [5] and military fields [6]. However, in practical applications, the LDMF process is often affected by the rebound behavior of workpieces [7], which severely limits further improvements in processing quality and efficiency. Rebound behavior can lead to decreased forming accuracy, cause workpiece failure, and result in significant deviations between the final shape of the formed part and the design target, thereby affecting the precision and performance of the final product. Traditional single-pulse laser shock forming methods tend to induce rebound effects due to the high forming speed, concentrated energy, and high instantaneous stress.

Zheng et al. [8] utilized finite element methods to study deformation non-uniformity during the laser shock forming process and found that rebound effects occur when the laser spot diameter is too small. Gu et al. [9] analyzed and discussed the size effects in laser shock hydraulic microforming technology in terms of maximum protrusion height, surface morphology, micro-thickness, and elastic recovery. Wang et al. [10] employed the three-dimensional multi-particle finite element method (MPFEM) to investigate the dynamic response, stress-strain evolution mechanism, and rebound behavior of stamping blanks under laser loading characteristics, and studied the densification process of laser shock dynamic compaction of Al₂O₃/Al composite powder. They explored the effects of Em, hard particle Al₂O₃ content, and friction coefficient on the rebound and relative density of compacted blanks. The results showed that with the increase of laser energy and Al₂O₃ particle content, the rebound phenomenon of the compacted blanks became more pronounced; the smaller the friction coefficient and the higher the laser energy, the more evident the rebound phenomenon. To address the issue of rebound effects in LDMF, various solutions have been proposed by researchers. Among them, the multi-pulse laser loading method, as an effective technical means, has attracted wide attention. By applying multiple laser pulses, multi-pulse laser loading can reduce the forming speed, effectively reducing the severe deformation caused by single high-speed laser shocks, and thus suppressing the rebound effect of the workpieces. However, current research on the suppression of rebound effects using multi-pulse laser loading is still relatively limited, particularly in terms of systematic numerical simulation and experimental verification.

This study proposes an effective method to suppress the rebound effect in LDMF, providing a theoretical basis and technical support for improving the precision and stability of microforming technology. This method not only helps improve the quality of LDMF but also provides a reference for the optimization of other high-strain-rate forming processes [11].

2. Experimental Principles and Research Methods

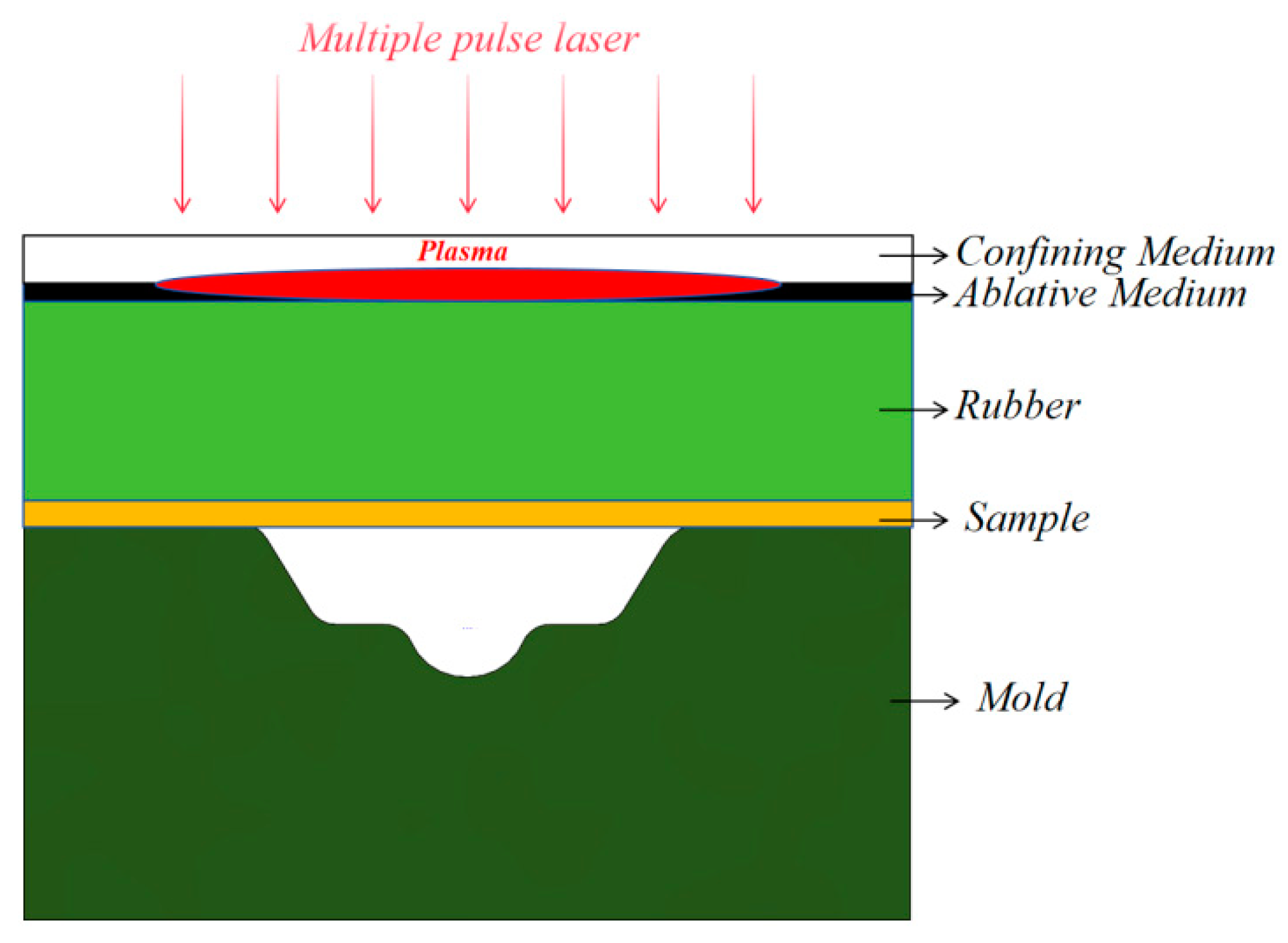
2.1. Mechanism of Multi-Pulse Laser Dynamic Microforming

Laser dynamic microforming can be categorized into single-pulse laser dynamic microforming and multi-pulse laser dynamic microforming. In single-pulse laser dynamic microforming, successful material-to-die conformity can be achieved by adjusting the energy of the pulse laser. Lower laser energy may result in poor forming quality, while higher laser energy might introduce various defects. Therefore, finding an appropriate critical point [12] for the energy is crucial for experimental research.

In this study, the experimental setup for laser dynamic microforming consists of a blank holder ring, a K9 glass constraint layer, black paint (as the ablation layer medium), a soft film, a workpiece (copper foil), and a micro-die, arranged from top to bottom. The blank holder ring is responsible for securing the entire experimental system platform, preventing displacement and ensuring tight contact between components during the forming process. K9 glass, known for its excellent optical properties and high resistance to laser-induced damage, is used as the constraint layer with a thickness of 3mm to ensure experimental accuracy and to prevent plasma dispersion and loss after the laser impacts the ablation layer medium. The ablation layer is made of black paint, which generates a significant amount of plasma when irradiated by the laser. This plasma, constrained by the glass layer, acts downward on the soft film to form the workpiece. The soft film is made of 100μm thick polyurethane material.

Multi-pulse laser dynamic forming is an advanced technology derived from single-pulse laser dynamic forming. Compared to traditional single-pulse laser dynamic forming, MPLDF increases the number of pulses, typically using multiple pulses to complete the forming process [13]. By dispersing energy, multi-pulse laser loading can effectively prevent the problem of excessive forming speed. This approach also avoids material damage defects and thermal deformation [14] caused by temperature influences, thereby ensuring the stability and quality of the forming process. The forming mechanism is illustrated in Figure 1.

As shown in Figure 1, it can be seen that multi-pulse laser dynamic forming is very similar in principle to single-pulse laser dynamic forming, with the only difference being the number of laser pulses. Compared to the energy of a single pulse, each pulse in MPLDF has much lower energy. Since multiple laser pulses act on the same position, the impact effect is more uniform and stable, resulting in better material forming outcomes, which helps enhance the strength and durability of the material surface. Additionally, the method of multi-pulse laser loading allows for more precise control of the surface forming of complex materials. Multiple low-energy laser pulses can effectively suppress the rebound effect induced by high-energy single-pulse laser forming, improving the accuracy and complexity of material forming. Overall, MPLDF leverages the cumulative effect of multiple pulses to achieve more uniform and stable processing of the workpiece material surface, thereby enhancing forming precision and efficiency.

2.2. Micro-Die

During laser shock experiments, the laser emitted by the laser device has properties such as high heat and high impact. The laser spot diameter is larger than the grooves and model features of the micro-mold, resulting in a portion of the laser spot directly impacting the surface of the micro-mold. Hence, the micro-mold design needs to possess good impact resistance. In this study, ductile iron is selected as the material for the micro-mold. The micro-die used in the experiment features two-level characteristics: trapezoidal and spherical. The more complex the shape of the micro-die, the more uneven the velocity of the workpiece when it collides with the micro-die. This allows for more convenient study of the rebound behavior and collision behavior patterns during the workpiece forming process. The two-dimensional morphology and three-dimensional contour observed under a depth-of-field microscope are shown in Figure 2, where [A-B] represents the depth after forming the spherical groove and [C-D] represents the width of the bottom surface of the trapezoidal groove. The degree of fit and smoothness between the clamping ring, constraint layer, soft film, workpiece, and micro-mold significantly influence the forming quality of the samples. The pressure applied by the 3mm thick K9 glass constraint layer alone cannot ensure the fitting accuracy of all components. Therefore, in the experiment, a clamping ring [15] is designed to be placed above the constraint layer to ensure the forming precision of the workpiece, eliminating gaps between components and improving the forming result. The mechanical performance and material properties of the designed clamping ring are not demanding, as long as it can firmly press the lower constraint layer and the components below it. Ultimately, gray cast iron is used as the material for the clamping ring.

2.3. The Scheme Design of the Comparison Experiment

In the study of numerical simulation and experimental comparison on the suppression of rebound effects in multi-pulse laser dynamic micro-forming, we designed a comparative scheme. Using T2 copper with different pulse numbers (1, 2, and 3 pulses), we conducted numerical simulations utilizing ANSYS APDL/LS-DYNA software and recorded the dynamic responses of the workpieces through actual experiments. And EDS was used to measure the chemical element changes. The effectiveness of multi-pulse loading in suppressing the rebound behavior and improving the forming quality of the workpieces was assessed. This ensured the consistency and reliability of the numerical simulations and experimental results, providing a scientific basis for enhancing the application of laser dynamic micro-forming technology.

2.4. Constitutive Model of Materials

1) Constitutive model of workpiece

In the numerical simulation of laser dynamic micro-forming, the workpiece undergoes dynamic responses to high strain and experiences plastic deformation. The Johnson-Cook model is an empirical constitutive model used to describe the plastic behavior of materials, particularly suitable for metallic materials under high strain rates and high temperature conditions. This model is widely applied in simulating and studying the behavior of metals under conditions such as impact, explosion, and high-speed deformation. In this study, the numerical simulation process of laser dynamic micro-forming adopts this model as the constitutive model for the copper foil specimen, expressed as follows [16]:

σ = (A + B ε^{n}) (1 + C l n \frac{\dot{ε}}{\dot{ε_{0}}}) [1 - {(\frac{T - T_{r}}{T_{m} - T_{r}})}^{m}]

(1)

In the equation, A, B, n,

ε_{0}

and m are material constants and are the five major material characteristic constants of this model,

σ

represents the equivalent yield strength in MPa.

T 、 T_{m} 、 T_{r}

respectively denotes the material's temperature, room temperature, and the material's melting point temperature, with C being the strain rate constant. The constitutive model parameters for T2 copper used in this study are shown in Table 1 [17,18]:

2) Constitutive model of soft membrane

In the process of laser dynamic forming, polyurethane rubber with high elasticity is selected as the material for the soft film. Polyurethane rubber is a nonlinear material. In this paper, Mooney-Rivlin constitutive model is used to characterize its behavior. The stress component expression of the model is shown in Equation (2) [19]:

σ_{i j} = \frac{\partial W}{\partial ε_{i j}}

(2)

The stress components of this model are obtained by differentiating the strain energy function with respect to the strain components, where W represents the strain energy function and

ε_{i j}

represents the strain components. For the strain energy function W, its expression is given by Equation (3):

W = \sum_{k + m = 1}^{n} C_{k m} {(I_{1} - 3)}^{k} {+ (I_{2} - 3)}^{m} + \frac{k}{2} {(I_{3} - 3)}^{2}

(3)

Where I₁, I₂, and I₃ are the invariants of the deformation tensor. Since polyurethane rubber is an incompressible material, I₃ is set to 1. k is the bulk modulus of elasticity, and Ckm are constants determining the material's dynamic response. Typically, C₀₁ and C₁₀ are used to describe the deformation behavior in the Mooney-Rivlin model. Table 2 provides the constitutive model parameters for polyurethane rubber material [20].

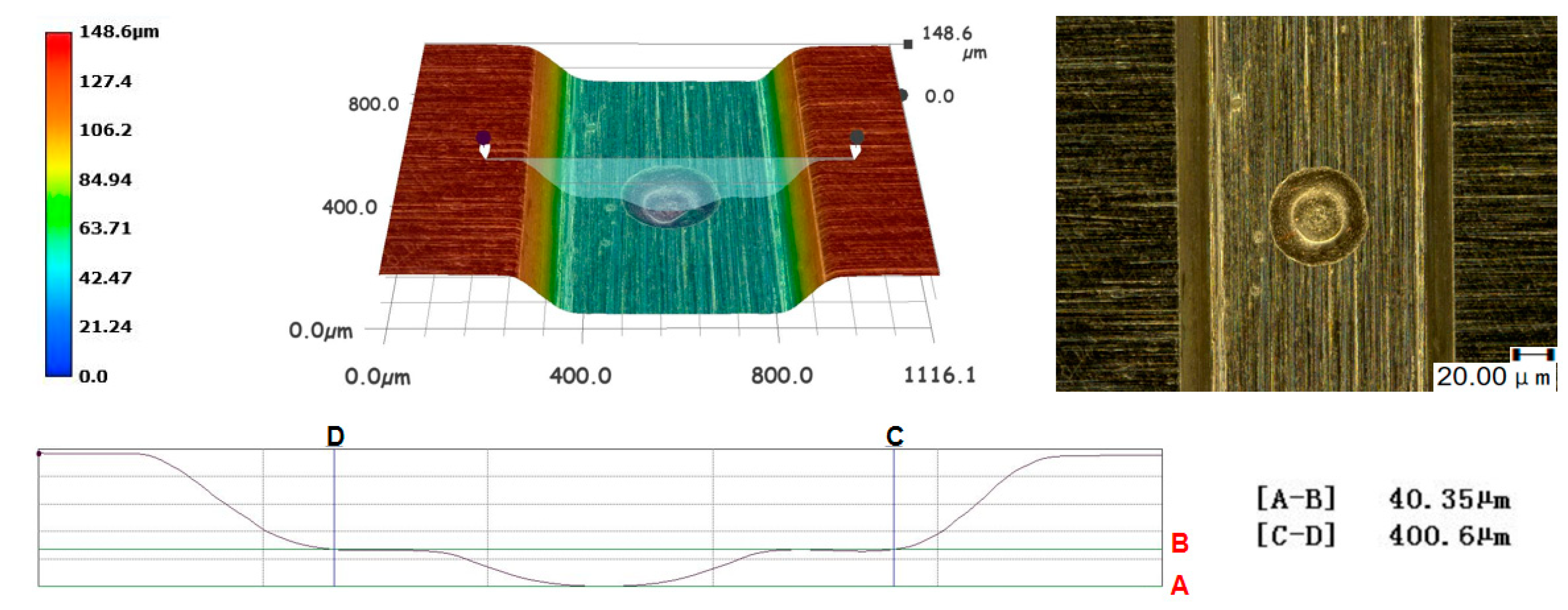
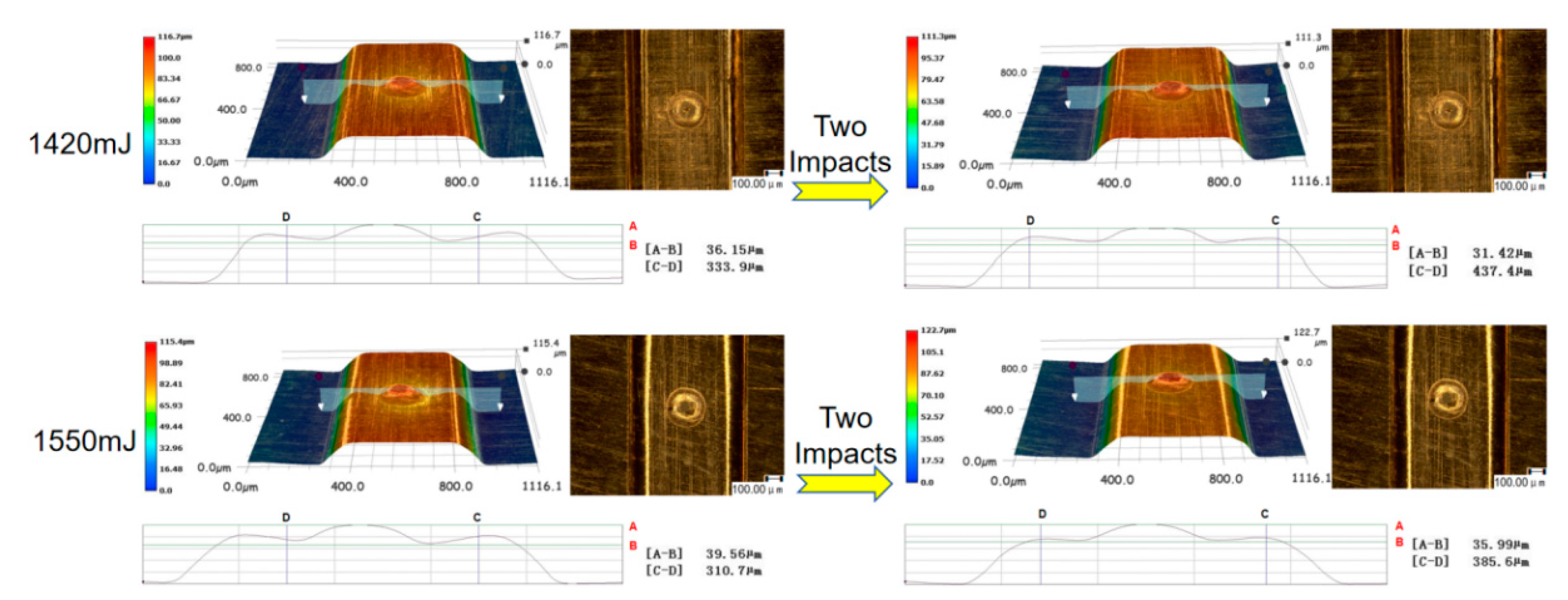
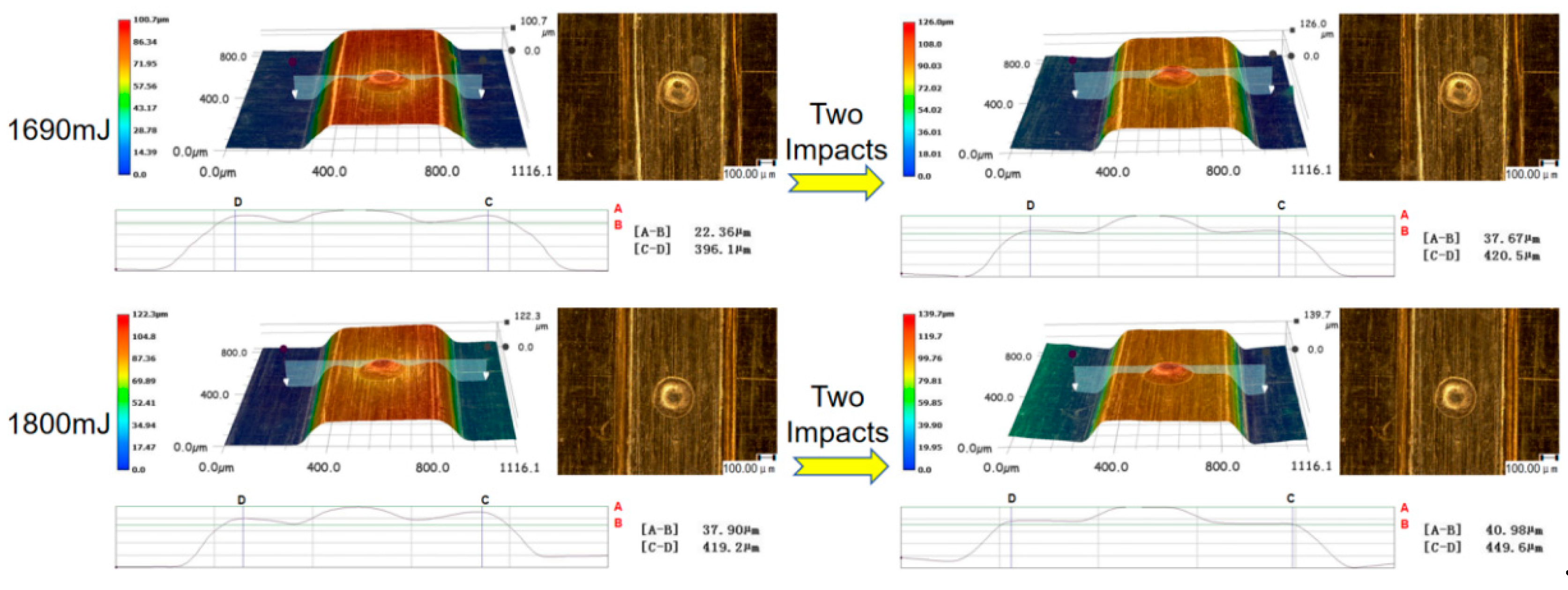
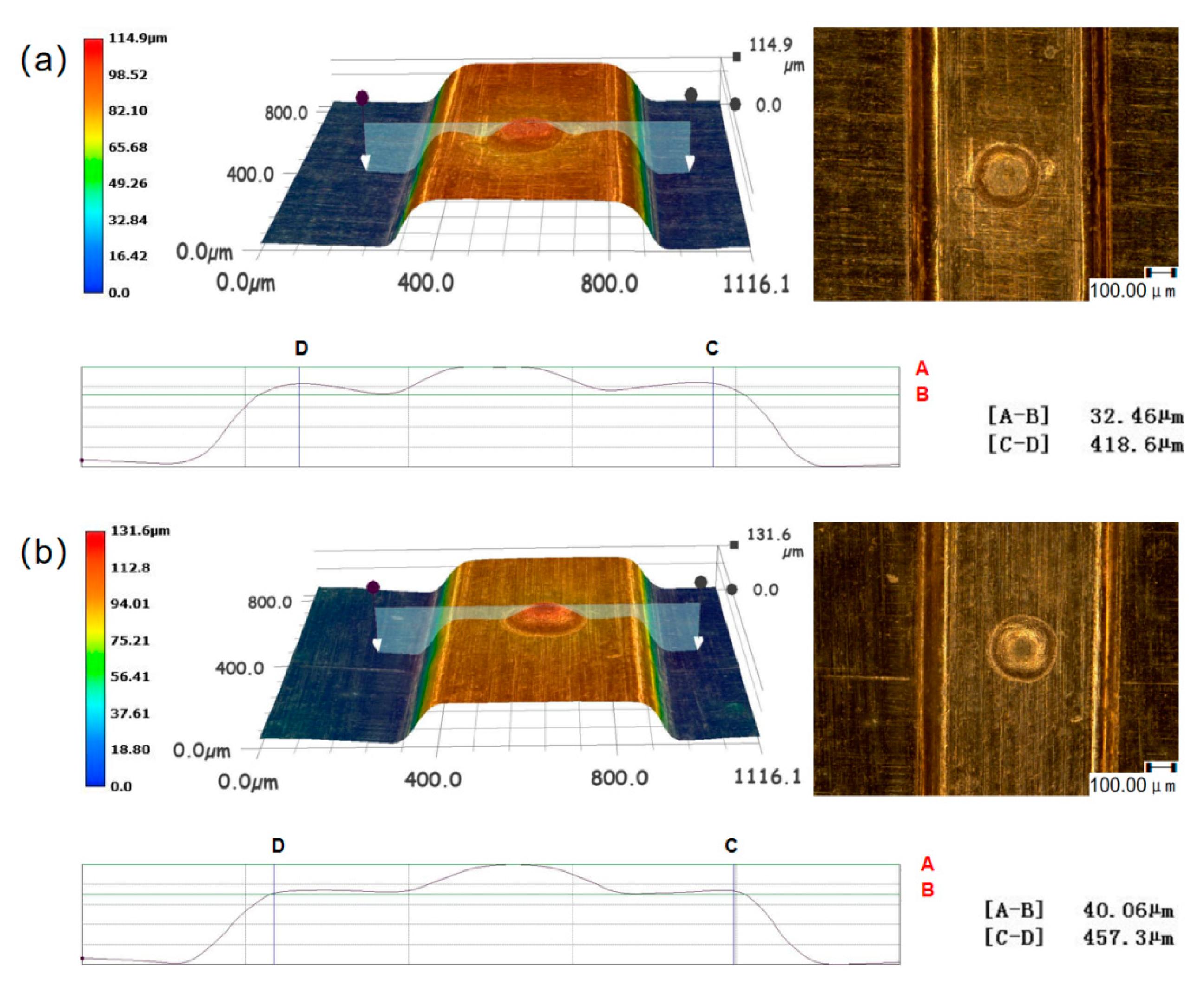
2.5. Result Characterization

After the experimental phase in this study, different experimental detection devices were utilized to examine the results. The KEYENCE VHX-1000C ultra-depth 3D microscope was employed to observe the surface morphology and three-dimensional profiles of the deformed workpieces. Additionally, the scanning electron microscope (SEM), model S-3400N manufactured by Hitachi, Japan, was used for more detailed observations of the microstructure and morphology of the workpieces. Furthermore, X-ray energy dispersive spectroscopy (EDS) was employed to detect and analyze the changes in chemical element content on the surface of the workpieces.

3. Result and Analysis

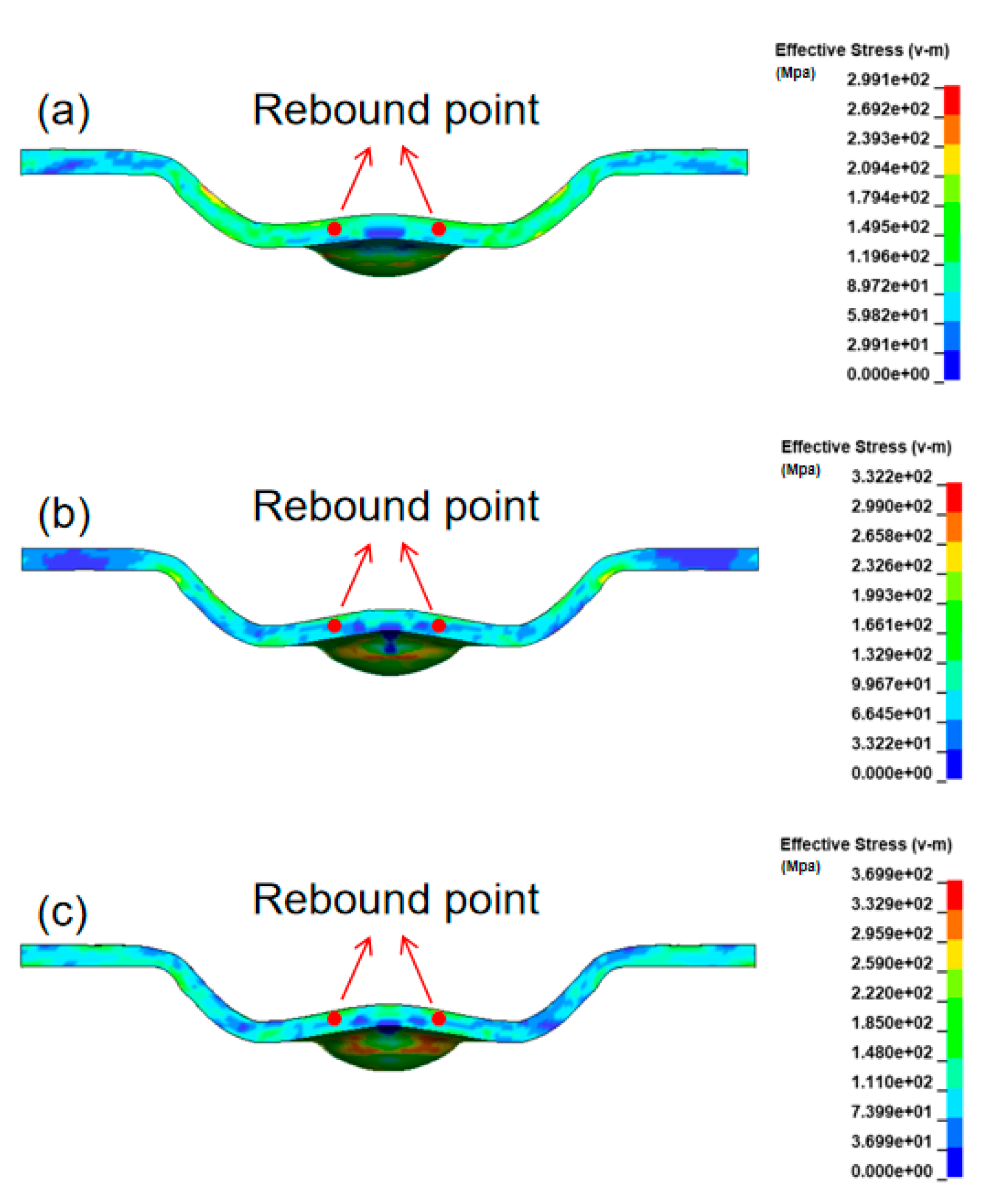
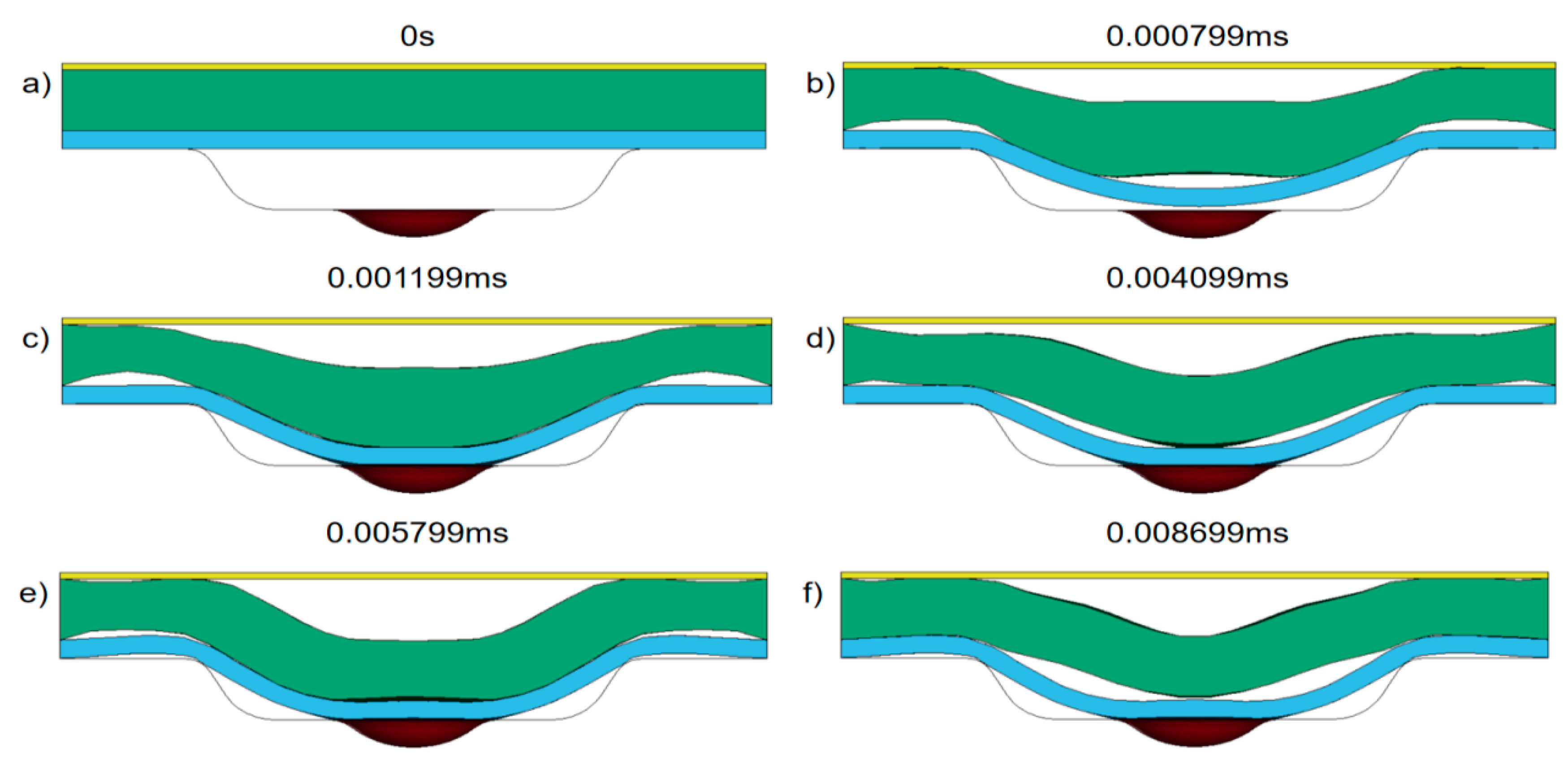
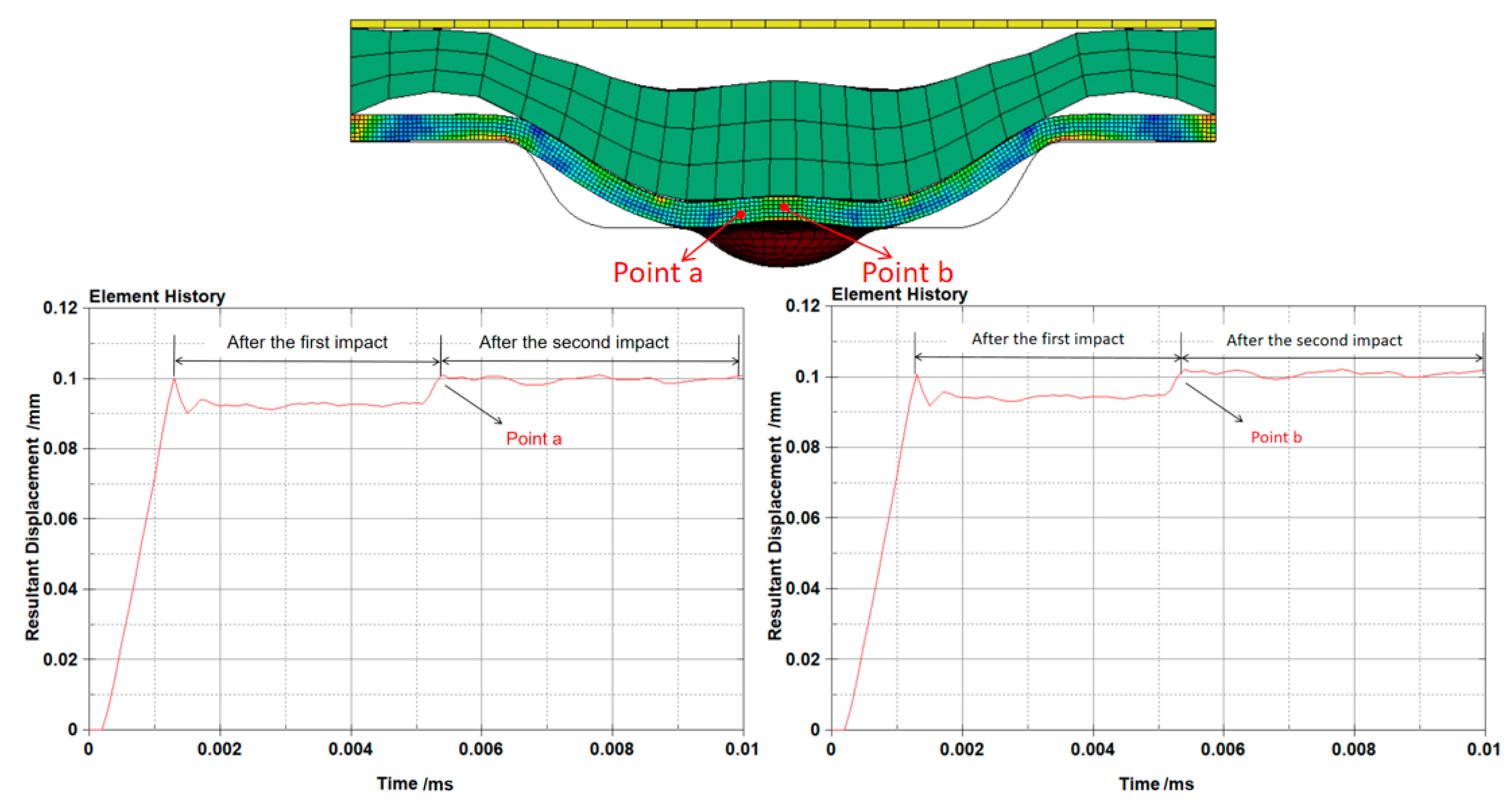
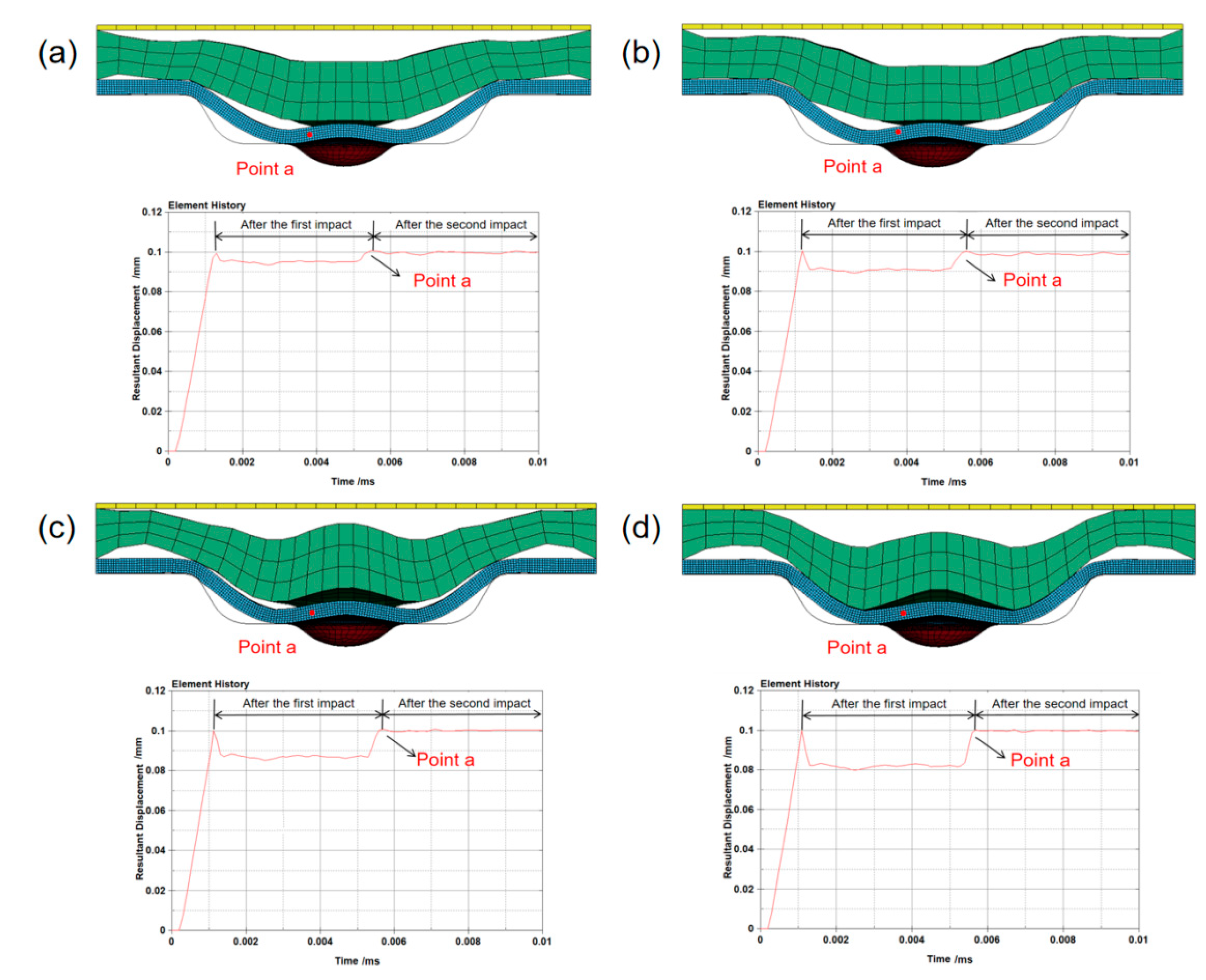
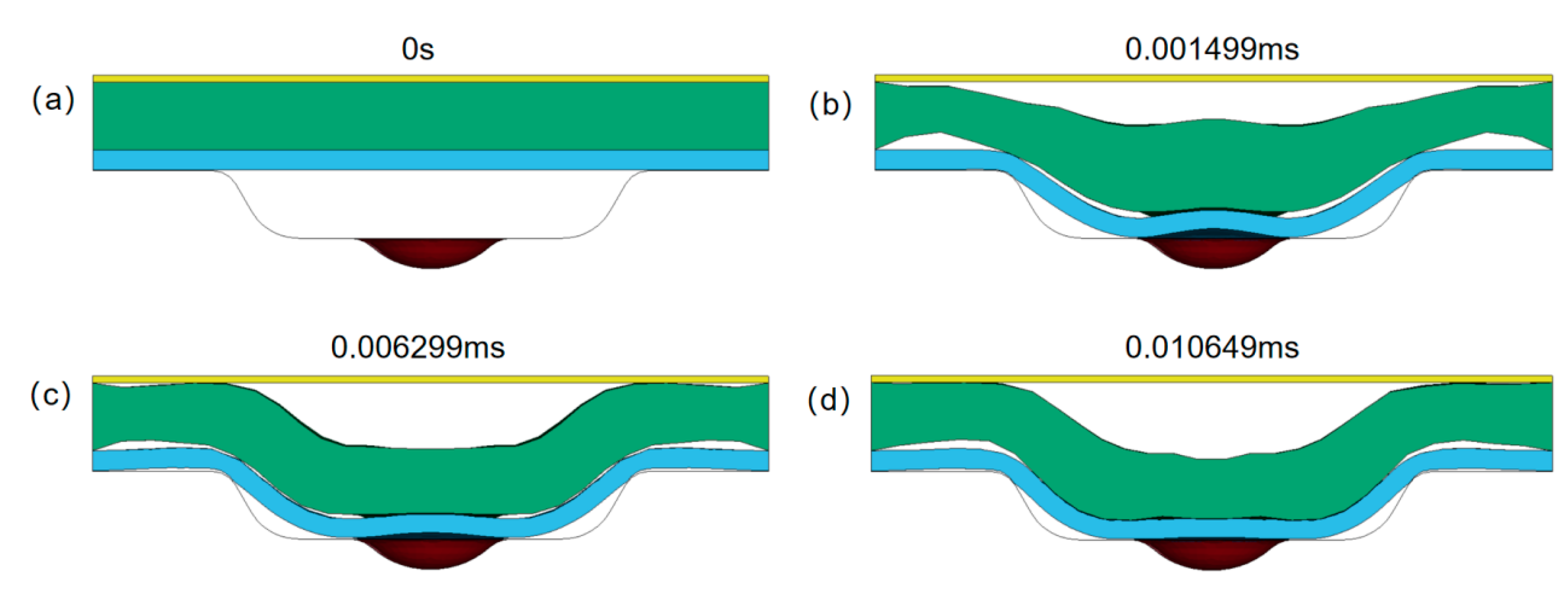
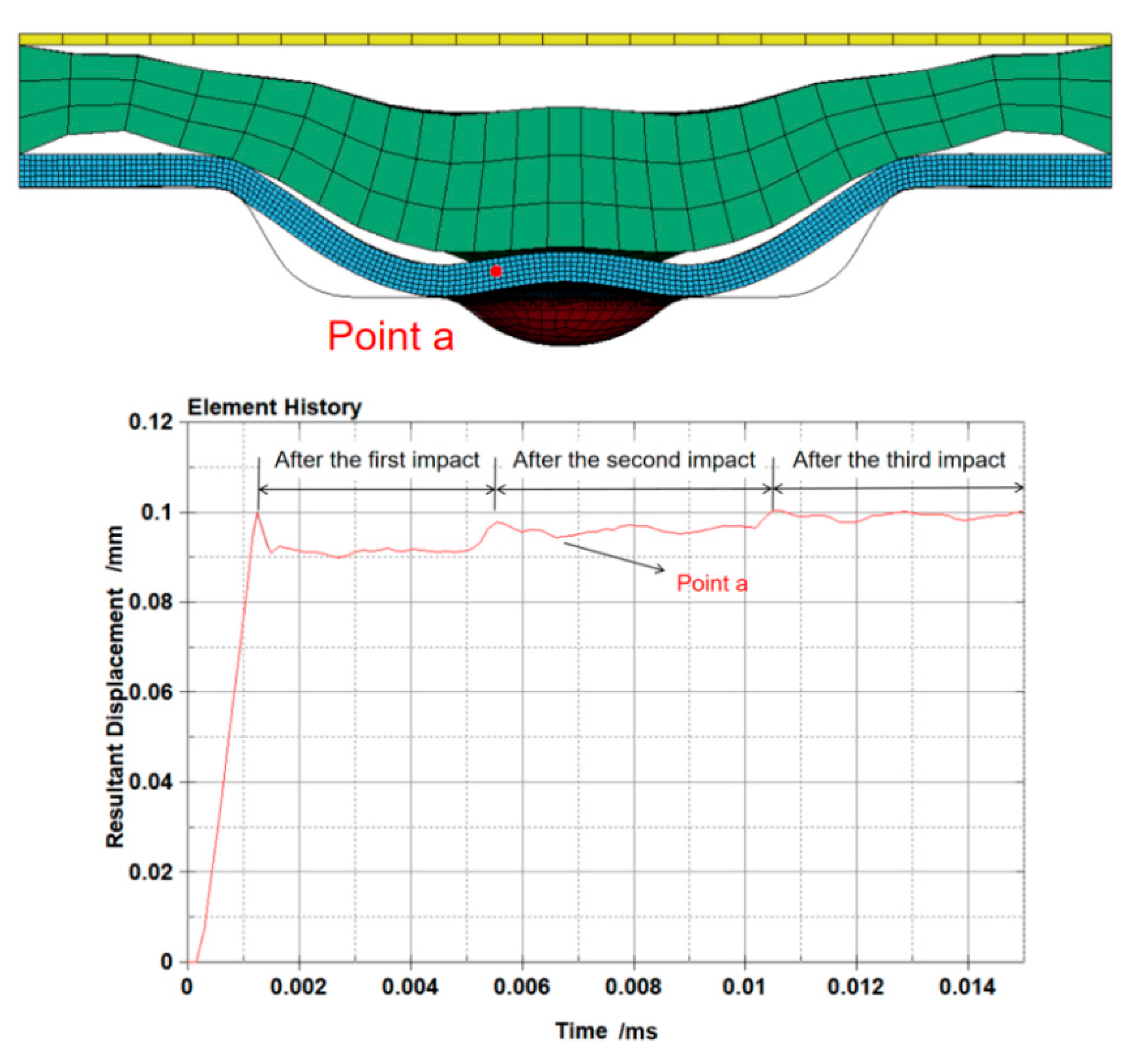
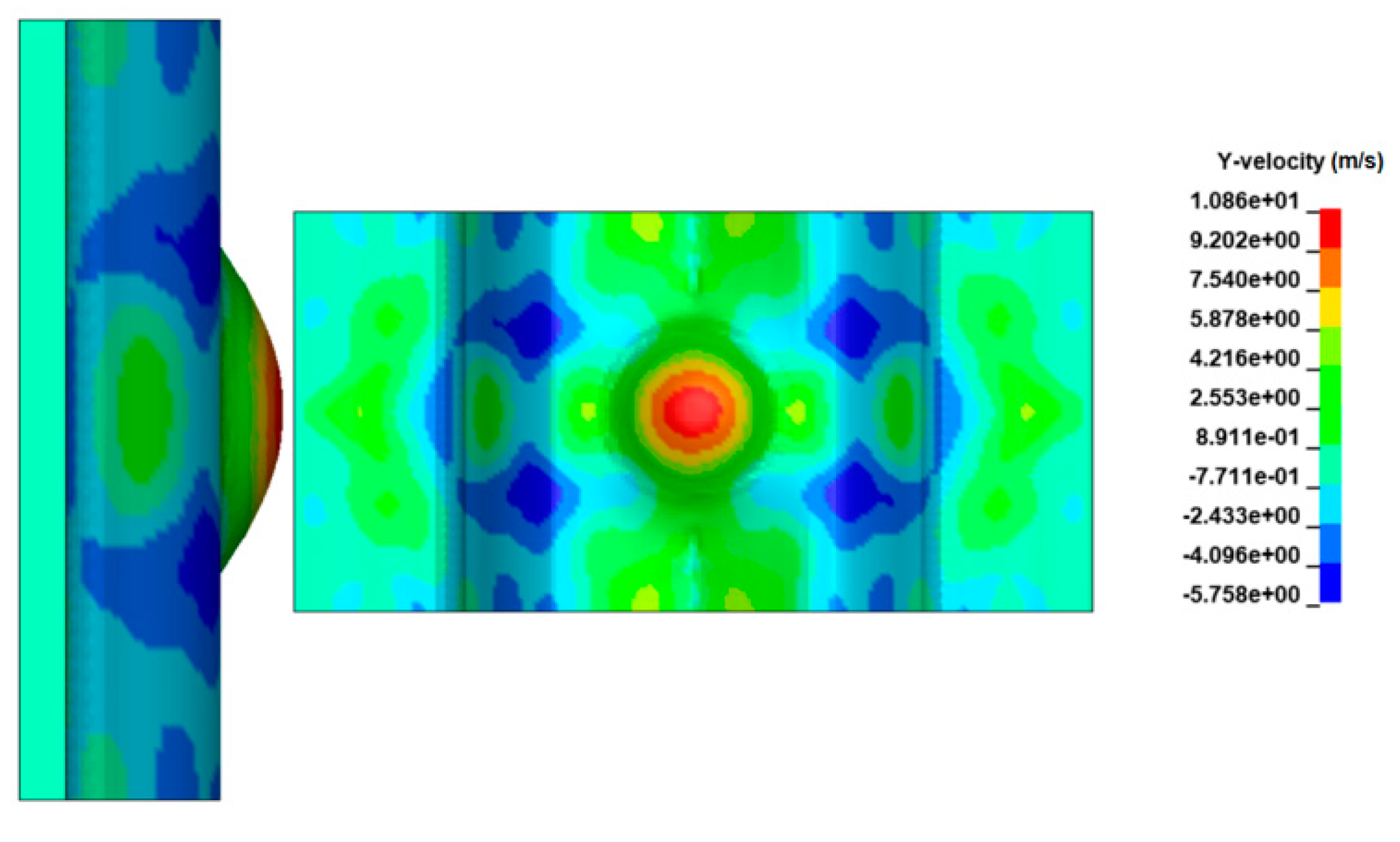
3.1. Rebound Phenomenon in Laser Dynamic Microforming

During the laser dynamic microforming process, materials undergo plastic deformation due to laser heating. However, after the heating ceases, materials may partially recover elastic deformation, leading to workpiece rebound. High material strength or hardness exacerbates the likelihood of rebound, constituting a significant factor in workpiece rebound. Additionally, inappropriate selection of laser spot size and laser impact angle can result in uneven stress distribution during workpiece forming, further increasing the likelihood of rebound. Improper support or constraint during the impact process may destabilize workpiece deformation, significantly increasing rebound potential. Figure 3. illustrates the forming results of a 30 μm workpiece after laser impact at different energy levels in numerical simulations, while Figure 4 shows the forming results of a 30μm workpiece after laser impact at different energy levels in experiments, with rebound points marked in both Figure 4. Upon comparing experimental and numerical simulation results, it was observed that areas with more severe rebound were primarily located at the junction of the bottom trapezoidal and spherical grooves of the workpiece. Subsequent detailed research on rebound suppression will be conducted through a combination of experimental and numerical simulation methods.

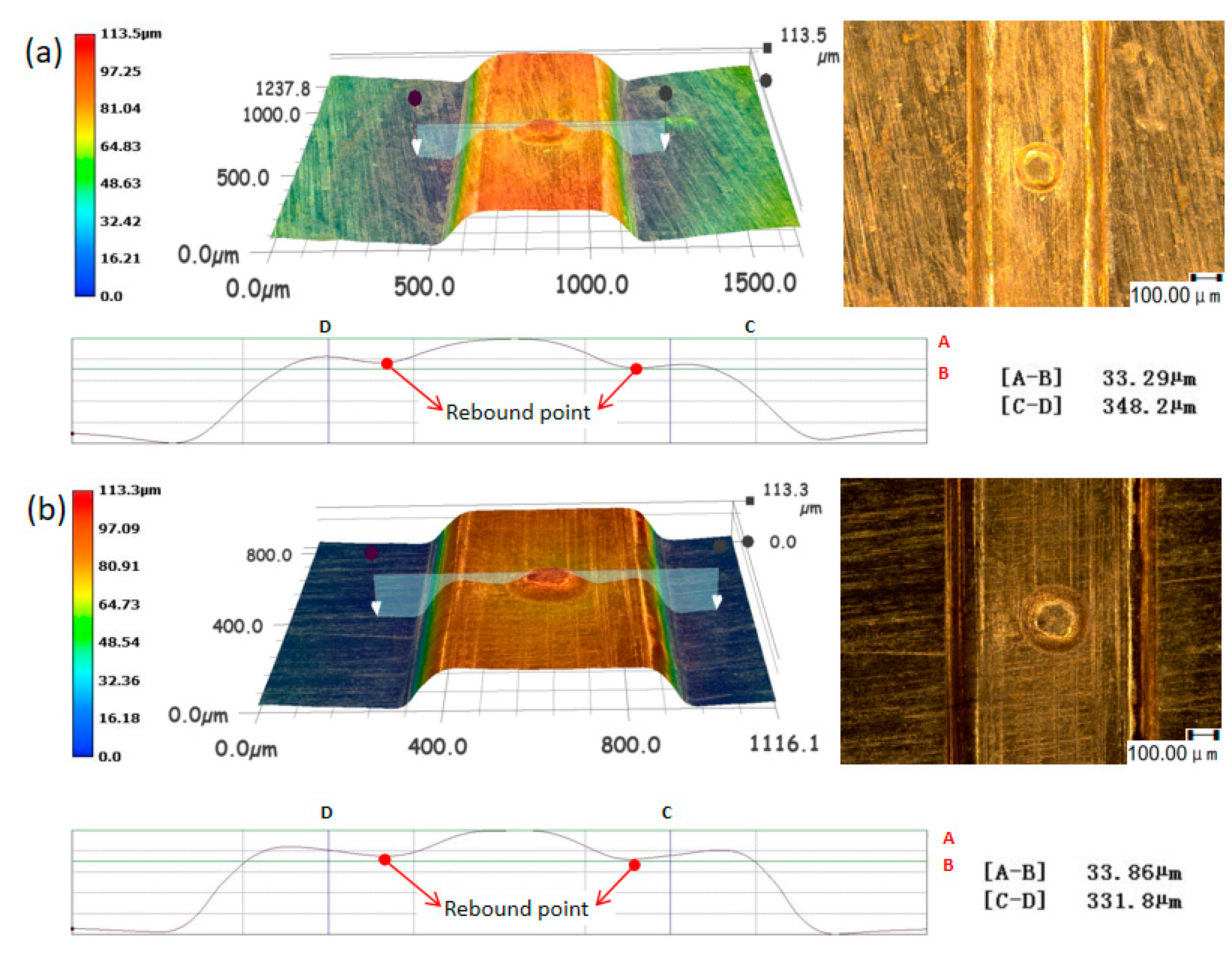
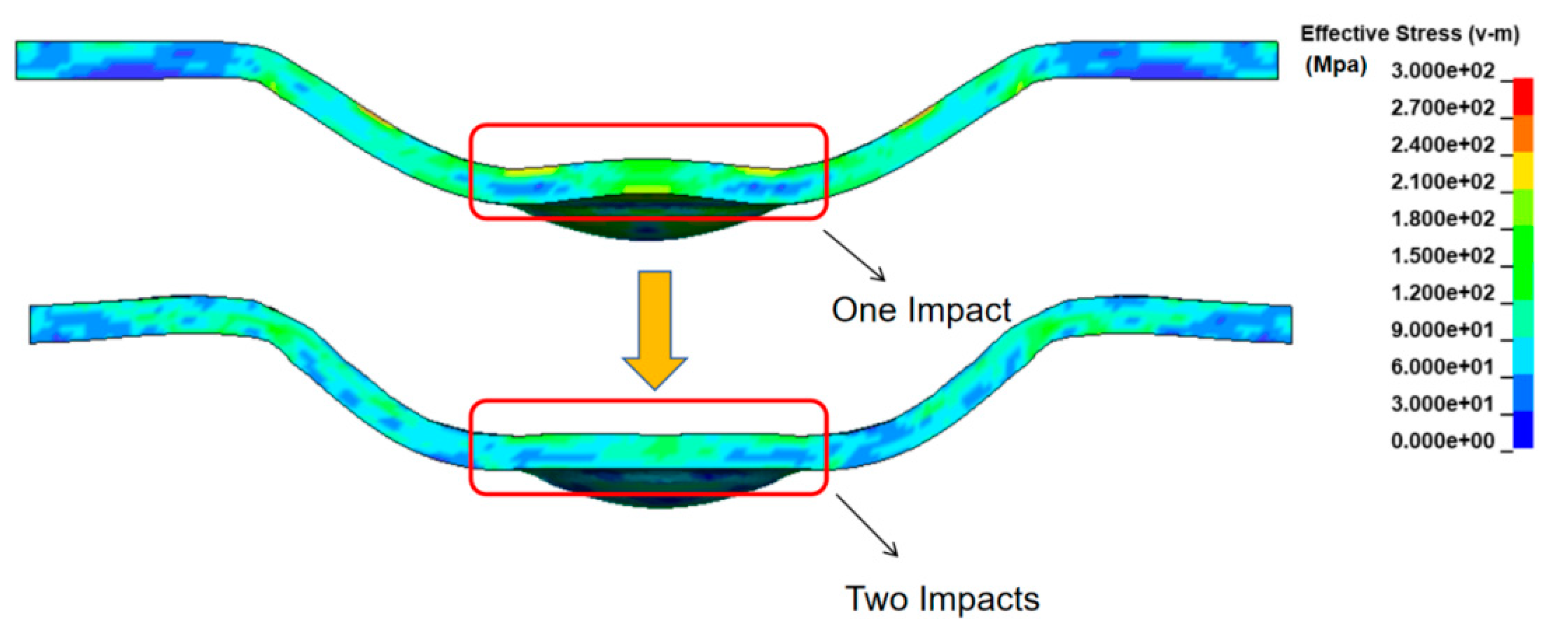
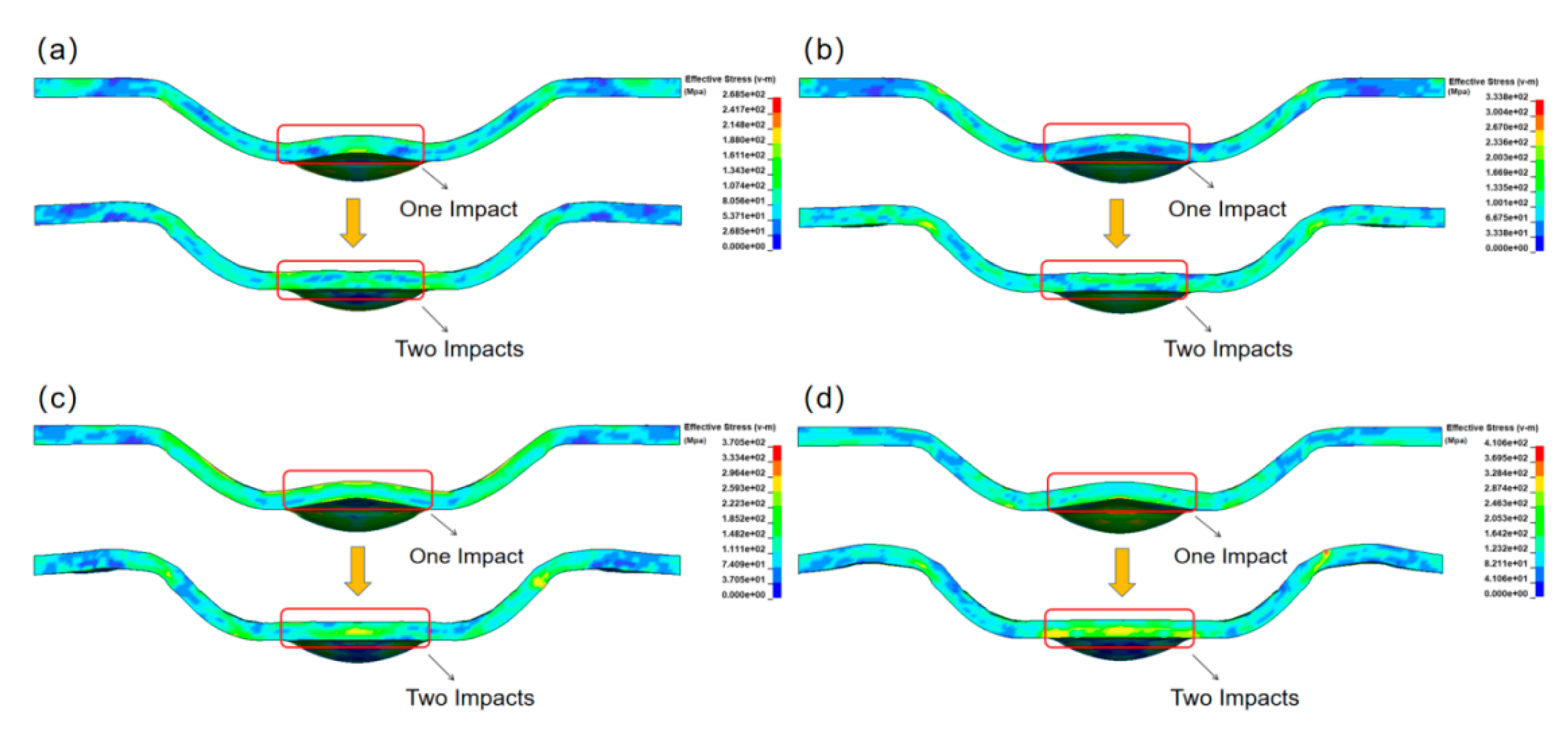
3.2. Influence of Laser Shock Frequency on Workpiece Forming Result

The forming process of multi-pulse laser dynamic microforming differs from that of single-pulse due to the involvement of multiple loading cycles, making the forming process more complex. Figure 5 illustrates the forming process when the laser impact occurs twice. The first stage represents the initial phase. The second stage depicts the loading phase of the first laser impact, where the workpiece begins to deform. The third stage represents the contact stage between the workpiece and the micro-mold, where collision occurs between the bottom of the workpiece and the micro-mold, completing the forming of the spherical and trapezoidal grooves. The fourth stage represents the rebound phase of the soft membrane, marking the end of the first laser loading. The fifth stage is the second laser loading phase, where the two-level features at the bottom of the workpiece become more aligned with the micro-mold, optimizing the forming result and suppressing the rebound effect caused by the high laser energy during the first laser loading. The sixth stage is the second rebound phase of the soft membrane, marking the end of the numerical simulation process for forming the workpiece with two laser impact loadings. When increasing the laser impact cycles, the process remains similar to the two-load scenario, with only a change in the number of laser loadings, thus repeating stages five and six. Next, a systematic numerical simulation study will be conducted on the forming results of the workpiece under different laser impact cycles.

The workpiece with a thickness of 30 μm was selected as the research object. Figure 6 compares the effects of 1 and 2 laser impacts at 1380 mJ laser energy. After a single laser impact at 1380 mJ energy, the workpiece exhibits significant rebound, particularly noticeable at the lower surface of the trapezoidal groove. However, with continued laser impact cycles, the rebound phenomenon disappears, and after 2 impacts, the bottom of the trapezoidal groove becomes smooth, indicating effective suppression of the rebound effect. Two points (points a and b) in the rebound area of the lower surface of the workpiece were selected to study their displacement histories. The displacement histories of these two points are shown in Figure 7. It can be observed from the graph that after the first laser loading, point a exhibits an initial peak displacement, followed by a sharp decrease, indicating the occurrence of rebound after the collision between the workpiece and the micro-mold. Subsequently, the displacement of point a stabilizes at a reduced value, with a rebound displacement of approximately 0.01 mm, until the second laser loading, where the displacement returns to the peak height observed after the first laser loading. This indicates the suppression of the rebound phenomenon that occurred after the first laser loading, and the displacement finally stabilizes without further changes. The displacement history of point b is similar to that of point a, but the rebound displacement after the first laser loading is around 0.005 mm, indicating a less severe rebound effect compared to point a. This observation aligns with the experimental findings, where the rebound area of the workpiece is concentrated at the junction of the trapezoidal and spherical grooves. Therefore, point a is selected as the basic point for analyzing and suppressing the rebound effect in the subsequent research.

Continuing to increase the laser energy, the forming results of the workpiece were studied at laser energy levels of 1420 mJ, 1550 mJ, 1690 mJ, and 1800 mJ. Figure 8 shows the comparison of numerical simulation results for the workpiece with a thickness of 30 μm under these four laser energy levels after 1 and 2 laser impacts. It can be observed that when the workpiece thickness is constant, increasing the laser energy leads to higher von Mises stresses within the workpiece, resulting in more severe rebound effects. However, after increasing the number of laser impacts to 2, the rebound phenomena induced by these four energy levels are all suppressed, and the rebound effect at the lower surface of the trapezoidal groove is significantly mitigated. Figure 9 depicts the displacement histories of four selected regions exhibiting rebound after laser impacts at energy levels of 1420 mJ, 1550 mJ, 1690 mJ, and 1800 mJ on a 30 μm thick workpiece. From the graphs, it is evident that after the first laser impact, point a experiences an initial peak displacement, followed by an instantaneous decrease, stabilizing at a lower level for a period. This phenomenon occurs due to the rebound of the workpiece after the first laser impact, and as the laser energy increases, the magnitude of the decrease after reaching the peak also increases, indicating a more severe rebound effect. However, after the second laser impact, point a experiences an upward displacement and eventually stabilizes near the peak height observed after the first impact. This is because the rebound effect of the workpiece is successfully suppressed after the second laser impact. Therefore, increasing the number of laser impacts can effectively mitigate the rebound effect of the workpiece.

Figure 10 presents a comparison of the three-dimensional profiles and surface morphologies of the 30 μm thick workpiece after different numbers of laser impacts at high laser energies. It can be observed from the Figure that as the laser energy gradually increases from 1420 mJ to 1800 mJ, the rebound effect of the workpiece is effectively suppressed after 2 laser impacts. As mentioned in the previous numerical simulations, under laser energies ranging from 1420 mJ to 1800 mJ, the rebound effect after 2 laser impacts is mitigated. Therefore, the experimental results are consistent with the numerical simulation results, indicating that the rebound effect of the 30 μm thick workpiece is effectively suppressed after increasing the appropriate number of laser impacts.

The numerical simulation study process of the 30 μm thick workpiece subjected to three laser impacts at different laser energies is presented above. The research indicates that after two impacts, the rebound effect of the workpiece is essentially suppressed. Next, we explore whether the rebound effect of the workpiece can be effectively suppressed after three impacts at low laser energies. Figure 11 shows the numerical simulation process of the 30 μm thick workpiece subjected to three laser impacts at 1020 mJ laser energy. It can be observed that at low laser energies, the rebound effect of the workpiece is not completely suppressed after two impacts, and it is only fully suppressed after the third impact. Additionally, the displacement history of the rebound area of the workpiece after three laser impacts is characterized, as shown in Figure 12 It can be seen that initially, the displacement history is similar to that after two impacts mentioned earlier, with an instantaneous drop after reaching the peak value, followed by recovery to near peak height after the second impact. The difference lies in the fact that at low laser energies, the displacement of the workpiece after two impacts does not reach the peak value, indicating a slight rebound effect still present after the second impact. However, after the third impact, the displacement history returns to the vicinity of the peak height and stabilizes, indicating a better suppression effect on the rebound effect of the workpiece.

Figure 13a illustrates the surface morphology and three-dimensional profile of the workpiece after two laser impacts with a laser impact energy of 1020 mJ, while Figure 13b depicts the surface morphology and three-dimensional profile of the workpiece after three laser impacts. It can be observed that in Figure 13a, the rebound phenomenon is significantly suppressed, and the forming depth of the workpiece is increased, indicating a better forming result. The process can be clearly observed to be essentially identical to the numerical simulation results. After two impacts, the rebound phenomenon on the lower surface of the trapezoidal groove has not completely disappeared; however, after the third impact, the rebound phenomenon is essentially eliminated. Therefore, the experiment serves as a good comparative verification of the numerical simulation results.

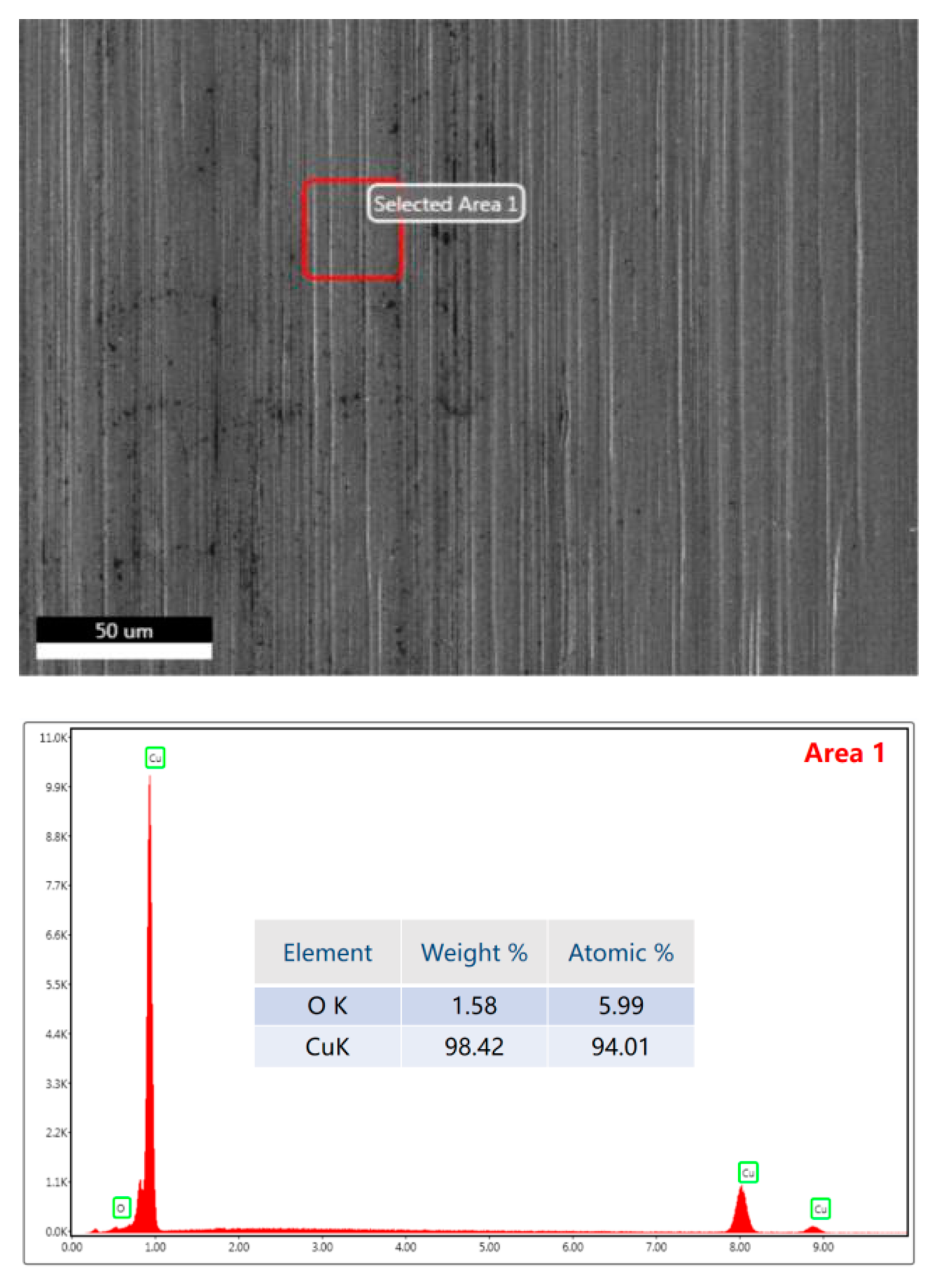
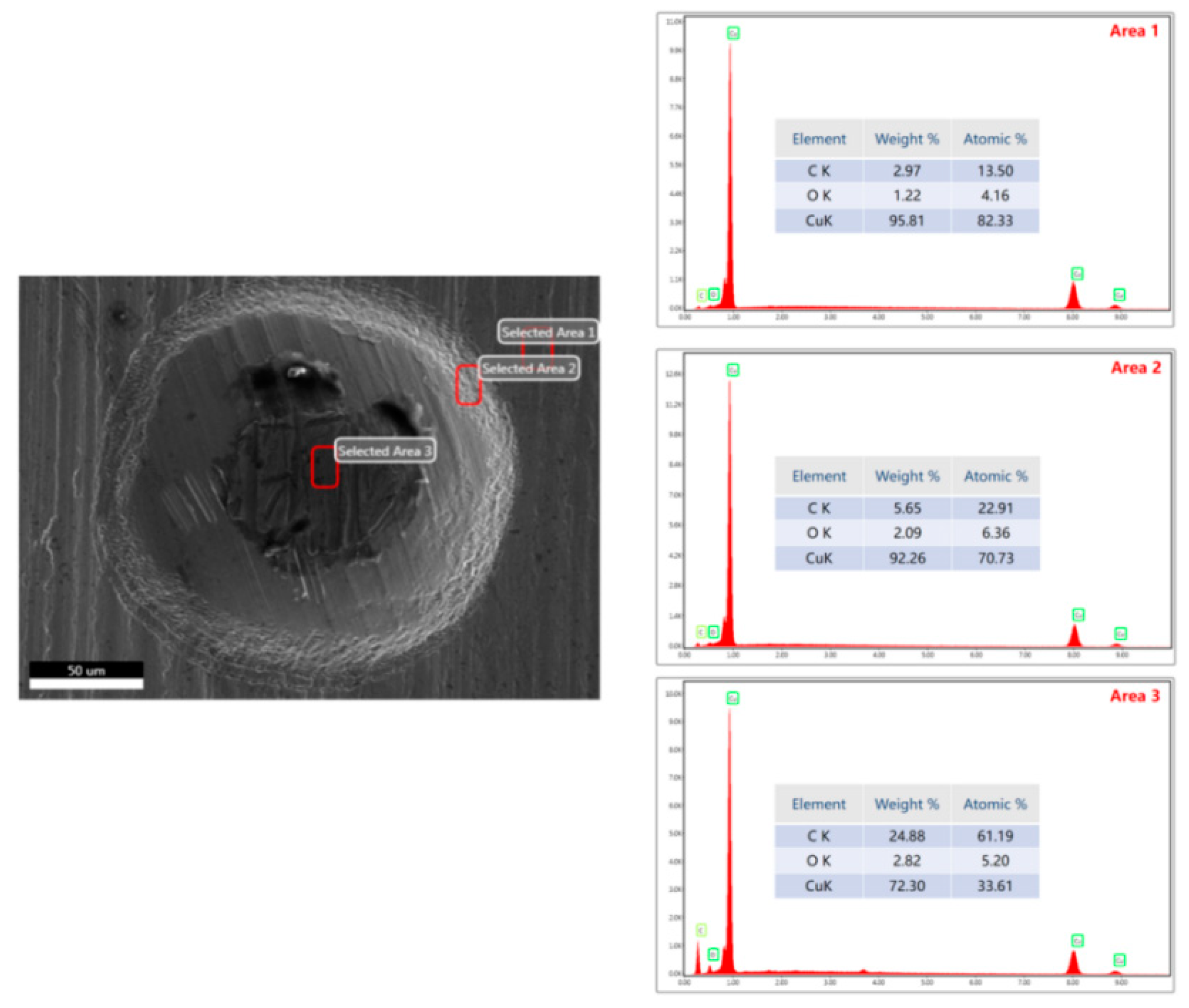
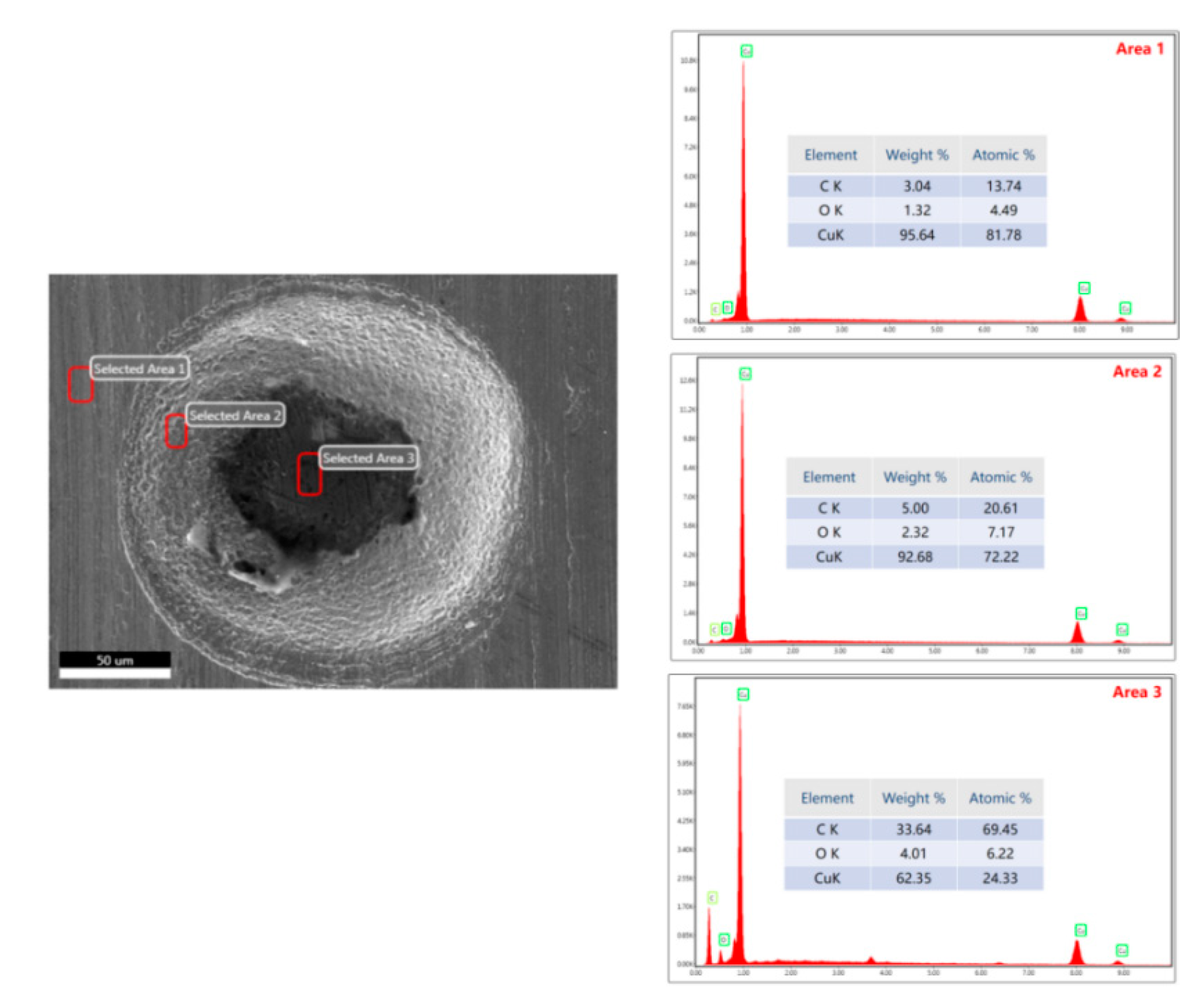
3.3. Variation Trend of Chemical Element Content on Workpiece Surface after Multi-Pulse Laser Loading

Next, we investigate the changes in surface chemical elements before and after the collision of the workpiece. The experimental instruments to be used for this purpose are the S-3400N scanning electron microscope and its associated energy dispersive X-ray spectroscopy (EDS) system. To conduct a comparative analysis of the changes in chemical elements on the surface of the workpiece before and after collision, it is necessary to first measure the chemical element content on the surface of the raw material. Figure 14 illustrates the chemical element content on the surface of the raw material before collision. All experimental raw materials used in this study are T2 copper foil, as indicated in Figure 14, with a copper (Cu) element proportion of 98.42%. Due to inevitable contact with air, the surface undergoes slight oxidation, resulting in an oxygen (O) element proportion of 1.58%.

Figure 15 illustrates the proportion of surface chemical elements in three areas after three impacts with 835mJ laser energy. The data reflect that the elements beneath the trapezoidal groove surface undergo relatively minor changes compared to before the collision. The proportion of carbon (C) elements on the wall of the spherical groove increases by approximately double compared to beneath the trapezoidal groove surface. However, upon measuring the proportion of carbon elements at the bottom of the spherical groove, the results show a proportion of 24.88%, indicating the most intense collision behavior at the bottom of the spherical groove and suggesting a significant increase in carbon atom content before and after the collision, indicating carbonization on the surface of the workpiece. Similarly, after three impacts with 1200 mJ laser energy, chemical element measurements in three different areas reveal similar patterns. The proportion of carbon elements in Area 1 exhibits minor changes compared to before the collision, while the proportion of carbon elements in Area 2 increases by approximately two-thirds. However, in the central Area 3, the proportion of carbon elements reaches 33.64%, higher than the proportion after three impacts with 835 mJ laser energy, indicating more intense collision behavior with increased laser energy and carbonization at the bottom. This trend is illustrated in Figure 16.

Figure 17 shows the velocity distribution at the bottom of the spherical groove of the workpiece in the numerical simulation. According to the Figure 17, it can be observed that the velocity at the bottom of the spherical groove is relatively high during forming. The temperature rise due to plastic deformation at high strain rates can be calculated using Equation (4), where

ρ

is the material density(

ρ

=8.9x10³kg/m³)，C_v is the specific heat capacity(C_v=394J/kg

∙

℃)，t is time, T is temperature,

μ

is the thermal conversion coefficient (usually taken as 0.9),

\dot{ε}

is the strain rate, and

δ

is the strain. During high strain rate deformation, the surface temperature of the workpiece increases rapidly, while the cooling rate is relatively slow, making it difficult for the heat to dissipate. Additionally, the increased contact with oxygen on the surface further exacerbates this effect. As a result, even with a short laser exposure time and high velocity, the surface temperature of the workpiece can become excessively high, intensifying the carbonization phenomenon. This is the fundamental reason why a significant increase in carbon atoms is observed at the bottom of the spherical groove during experimental measurements, as shown in Figure 18.

ρ C_{v} \frac{d T}{d t} = μ δ \dot{ε}

(4)

4. Conclusions

This paper conducts numerical simulations and experimental studies on multi-pulse laser dynamic micro-forming. By comparing the results of numerical simulations and experimental research, the study investigates the forming result and the suppression of rebound effects of 30 μm thick workpieces after being impacted by different numbers of pulses at various laser energies. The main conclusions are as follows:

(1): The forming result of 30 μm thick workpieces after being impacted once, twice, and three times at different laser energies was investigated. In the ANSYS post-processing software, displacement history curves of the rebound regions were characterized. The results indicate that the workpiece exhibited a rebound effect after a single impact. However, by increasing the number of laser impacts, the rebound effect can be successfully suppressed. At high laser energy densities, impacting twice is sufficient to suppress the rebound effect, while at low laser energy densities, three impacts are required to effectively eliminate the rebound effect.
(2): The numerical simulation results were verified through specific experiments, exploring the forming results of workpieces subjected to multi-pulse laser impacts in actual experiments. The surface morphology and three-dimensional contours of the formed workpieces were characterized, and the experimental results were consistent with the numerical simulations. The comparative analysis of both results indicated that appropriately increasing the number of laser impacts according to the laser energy density can effectively suppress the rebound effect during workpiece forming. Through the combined methods of numerical simulation and experimental validation, it was found that the rapid temperature rise on the material surface due to high strain rate deformation during the forming process, along with the difficulty in dissipating heat, exacerbated the occurrence of "carbonization." This phenomenon is the fundamental reason for the significant increase in C atom content measured after the experiments.

Author Contributions

Formal analysis, F.W., B.L., Y.S. and Z.S.; investigation, F.W. and B.L.; data curation, F.W., Y.S. and B.L..; writing—original draft preparation, F.W. and Z.S.; Conceptualization, F.W. and B.L.; methodology, F.W. ang Z.S.; supervision, Z.S.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by China Postdoctoral Science Foundation. (Grant No. 2019 M651724).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Zhang H, Wang X, Ma Y, et al. Formability and mechanism of pulsed current pretreatment–assisted laser impact microforming[J]. The International Journal of Advanced Manufacturing Technology, 2021, 114(3): 1-19. [CrossRef]
Tao Z, Xiao W, Di Z, et al. Laser shock micro-sheet bulk metal forming: numerical simulation and experimental validation[J]. International Journal of Material Forming, 2022, 16(1). [CrossRef]
H. M, L. K. Inhibition of neoatherosclrotic restenosis after laser angioplasty, using paclitaxel administration accompanied by 5-aminolevulinic acid-mediated B-mode ultrasound-guided extracorporeal focused low-level confocal dual pulse electrohydraulic shock wave sonodynamic therapy[J]. Atherosclerosis, 2021, 331: e285-e285.
Sato S, Hidai H, Matsusaka S, et al. Drilling, bonding, and forming conductive path in the hole by laser percussion drilling[J]. Precision Engineering, 2020, 61: 147-151. [CrossRef]
K.V. Rama Sateesh; Dinesh Kumar Harursampath. Impact damage of hemispherical shells formed by direct metal laser sintering[J]. Materials Today: Proceedings, 2020, 22(Pt 4): 2983-2989. [CrossRef]
Yuan L, Mengen D, Xixiang P, et al. Surface mechanical properties and micro-structure evolution of 7075 aluminum alloy sheet for 2-dimension ellipse ultrasonic vibration incremental forming: A pretreatment for laser shock peening[J]. Coatings, 2022, 12(12): 1914-1914. [CrossRef]
Shen Z, Zhang J, Liu H, et al. Reducing the rebound effect in micro-scale laser dynamic flexible forming through using plasticine as pressure-carrying medium[J]. International Journal of Machine Tools and Manufacture, 2019, 141: 1-18. [CrossRef]
Zheng C, Tian Z, Zhao X, et al. Effect of pulsed laser parameters on deformation inhomogeneity in laser shock incremental forming of pure copper foil[J]. Optics and Laser Technology, 2020, 127: 106205-106205. [CrossRef]
Xin G, Xiao W, Jiankun C, et al. Laser shock composite microforming of Fe-based amorphous alloys[J]. Mater Res Express, 2021, 8(3): 036511-. [CrossRef]
Tao W, Maomao C, Huixia L, et al. Effect of laser shock on the compacting characteristics and rebound behavior of composite powders (Al2O3/Al) with different alumina contents[J]. Optics and Laser Technology, 2024, 168. [CrossRef]
Feifei Z, Kai H, Zheng L, et al. Strain-rate effect on anisotropic deformation characterization and material modeling of high-strength aluminum alloy sheet[J]. Metals, 2022, 12(9): 1430-1430. [CrossRef]
Yang H, Wang X, Ni P, et al. Construction of high strain rate loading constitutive model and failure model and prediction of forming limit for la103z magnesium alloy[J]. Metals and Materials International, 2021, 28(8): 1-10. [CrossRef]
Li J, Cheng G J, Asme. Effect of multiple pulses on the deformation behavior of ultrathin metal foils in 3d micro-scale laser dynamic forming[C]//ASME International Manufacturing Science and Engineering Conference. NEW YORK. Amer Soc Mechanical Engineers, 2011: 299-306.
Wang X, Yang X, Huang W, et al. Effect of hot deformation on the dynamic precipitation and mechanical properties of AA2099 Al–Li alloy[J]. Journal of Alloys and Compounds, 2024, 985: 173928-. [CrossRef]
Shahaboddin S, Mahdi B M, Hossein T-G. Numerical-experimental investigation of using rubber blank holder on wrinkling of metallic bipolar plates formed by stamping process[J]. International Journal of Hydrogen Energy, 2023, 48(62): 23967-23991. [CrossRef]
Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[J]. Engineering Fracture Mechanics, 1983, 21: 541-548.
Christophe, Poizat, Laurence, et al. Modeling and simulation of thin sheet blanking using damage and rupture criteria[J]. International Journal of Forming Processes, 2005. [CrossRef]
Bae G, Xiong Y, Kumar S, et al. General aspects of interface bonding in kinetic sprayed coatings[J]. Acta Mater, 2008, 56(17): 4858-4868. [CrossRef]
Wang X, Du D Z, Zhang H, et al. Investigation of microscale laser dynamic flexible forming process-simulation and experiments[J]. Int J Mach Tools Manuf, 2013, 67: 8-17. [CrossRef]
Dirikolu A H, Akdemir E. Computer aided modelling of flexible forming process[J]. J Mater Process Technol, 2004, 148(3): 376-381. [CrossRef]

Figure 1. Multi-pulse laser dynamic microforming diagram.

Figure 2. 3D profile and surface topography of the mold.

Figure 3. Forming result of 30 μm thickness workpiece under different laser energies (Numerical simulation) (a) 835 mJ; (b) 1380 mJ;(c) 1550 mJ.

Figure 4. Forming result of 30μm thickness workpiece under different laser energies (Experiment). (a) 835 mJ; (b) 1380 mJ; (c) 1550 mJ.

Figure 5. The forming process of the workpiece under two laser shocks.

Figure 6. A comparison of the first and second shocks of a 30 μm thick workpiece at 1380 mJ laser energy.

Figure 7. The displacement history curve of point a and point b on the lower surface of the trapezoidal groove at the bottom of the workpiece.

Figure 8. Comparison diagram of a workpiece with a thickness of 30 μm under different laser energies (a) 1420 mJ; (b) 1550 mJ; (c) 1690 mJ; (d) 1800 mJ.

Figure 9. The displacement curve of point a on the lower surface of the trapezoidal groove at the bottom of the workpiece after two times of different laser energy impact (30μm). (a) 1420 mJ; (b) 1550 mJ; (c) 1690 mJ; (d) 1800 mJ.

Figure 10. Comparison of 3D profile and surface topography of 30 μm thick workpiece after different times of impact under different laser energies.

Figure 11. The forming process of the workpiece with a thickness of 30 μm is struck 3 times at 1020 mJ laser energy.

Figure 12. The displacement history curve of point a after the 30 μm thickness workpiece is impacted 3 times under 1020 mJ laser energy.

Figure 13. 3D profile and surface topography of 30 μm thick workpiece after different times of impact under 1020 mJ laser energy (a) 2 times; (b) 3 times.

Figure 14. Chemical element composition of the raw material.

Figure 15. The chemical element composition of the surface of 30 μm workpiece after 3 shocks at 835 mJ laser energy.

Figure 16. The chemical element composition of the surface of 30 μm workpiece after 3 shocks at 1200 mJ laser energy.

Figure 17. Velocity distribution of a 30 μm workpiece at the bottom of a spherical groove under 1200 mJ laser energy impact.

Figure 18. SEM images of macro, magnification and local detail of 30 μm workpiece after three shocks of different laser energies (a) 835 mJ; (b) 1200 mJ.

Table 1. T2 constitutive model parameters of copper.

Materials	A	B	C	n	m	$T_{r}$	$T_{m}$	$ε_{0}$
T2 copper	89.63	291.64	0.025	0.31	1.09	27	12	1.0

Table 2. Constitutive model parameters of polyurethane rubber.

Materials	A(Shore hardness)	C₀₁	C₁₀	poisson ratio
Urethanes	70	0.184	0.736	0.49997

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer