Prerpints.org logo
Preprint
Article

Coupling Analysis on Safety Influencing Factors in Subway Station Operation Under High-Pressure Gas Pipeline

Altmetrics

Downloads

80

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 July 2024

Posted:

11 July 2024

You are already at the latest version

Alerts
Abstract
The subway station operation is susceptible to safety accidents when high-pressure gas pipeline overlaying, and analyzing the correlations between the safety influencing factors (SIFs) under this operation situation can provide paths to reduce safety accidents. Thus, this paper investigated the coupling correlations between the SIFs. We firstly identified the SIFs during subway station operation under high-pressure pipeline (SSOUHP) based on the literature review and experts’ discussion. Then, the analytic hierarchy process (AHP) and coupling degree analysis (CDA) were combined to assess the coupling correlations between the SIFs. And Y subway station was selected to test the proposed hybrid coupling analysis approach. Research results show that (a) 23 second-level SIFs were identified and these SIFs can be summed up into 5 first-level SIFs, namely, human-related SIFs, pipeline-related SIFs, station-related SIFs, environment-related SIFs, and management-related SIFs; (b) the proposed hybrid approach can be used to evaluate the coupling correlations between SIFs; (c) of the coupling situations during Y subway station operation, the internal coupling correlations among environment-related SIFs, the coupling correlations between pipe-related SIFs and environment-related SIFs, and the coupling correlations among human-related SIFs, pipe-related SIFs and environment-related SIFs are with higher safety risk; (d) the overall coupling correlation among all SIFs during Y subway station operation is with lower safety risk. The research can enrich the knowledge in the safety evaluation area, and provide reference for onsite safety management.
Keywords: 
Subject: Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

The national “14th Five-Year Plan” pointed out that it is necessary to build a multi-level rail transit network in urban agglomerations and metropolitan areas, promote the rail construction of key urban agglomerations, accelerate the construction of a multi-network integration system, and make overall use of existing lines and new lines[1]. By the end of 2022, there were 308 urban rail transit lines in 55 cities in Chinese, with a total length of 10,287.45 kilometers. Among them, the subway operating lines are 8008.17 kilometers, accounting for 77.84%, and the length of the new open lines is 1080.63 kilometers[2]. With the development of network, gas pipelines and subway stations are closely related to the operation, and their spatial proximity, parallel or intersection will inevitably form a new urban safety regional coupling risk[3,4]. Leakage or damage of gas pipeline may affect the normal operation of subway line, more seriously, can cause explosion or fire and threatens the personnel’s safety in subway station or its surrounding area[5]. Furthermore, the settlement[6], high frequency vibration[7] and stray current[8] of subway station during operation also can exert an impact on the gas pipeline, and lead to the rupture or damage of the gas pipeline, and thus, an accident caused by gas leakage occurs. In 2008, a gas leak occurs in Guangzhou Subway Line 6 due to improper construction of a gas pipeline, causing an explosion and killing 7 peoples. In 2021, a gas pipeline was damaged by a construction unit, resulting in a gas pipeline leakage of about 10,000 m3 of natural gas overlaying the subway station of Hangzhou Line 9. These accidents not only bring about a large number of delays and casualties, but also spawned huge losses to the social economy.
At present, scholars have studied the safe operation of subway stations from two main aspects: identification of SIFs and coupling analysis of SIFs. In terms of identification of safety factors, most scholars attribute the safety factors to four aspects: personnel, facilities and equipment, environment and management[9,10,11]. IIn the analysis of the coupling of SIFs, scholars usually use the interpretive structure model[12], N-K model[13], coupling degree model[14], system dynamics model[15], SHEL model[16] and so on. For example, Yu et al.[13] used the N-K model to construct a coupled subway operation safety risk model, measured the risk coupling value under different coupling methods, and obtained the single-factor, two-factor, and multi-factor risk coupling probability and the risk coupling value for different coupling methods. Wang et al.[16] based on the SHEL model and AHP method, an identification and evaluation method for human error SIFs in human, machine and environment system is proposed to research the human error SIFs in subway station system. However, few people have delved into the operation safety when SSOUHP. Therefore, it is necessary to distinguish the factors affecting the safety of the SSOUHP, to find out the most unfavorable risk coupling situation of subway station and gas pipeline, to avoid the potential safety risks of subway station and gas pipeline in the space proximity, parallel or intersection complex environment, and to provide scientific basis for the safe operation of subway station.
Therefore, this paper uses the literature analysis and the expert discussion to distinguish the SIFs of SSOUHP. And the internal coupling relationship of the operational safety of subway stations was also quantitatively described using AHP and CDA. Finally, an engineering case is chosen to validate the proposed model. The coupled analysis of the SIFs carried out for this paper not only provides some enlightenment and reference for the research in related fields, but also helps the relevant departments to formulate the management regulations for the safe operation of subway stations to provide a basis.

2. Literature Review

2.1. SIFs and Coupling Analysis of Subway Station Operation

According to the 4M1E theory, most scholars attribute the safety factors to four aspects: personnel, facilities and equipment, environment and management[9,10,11]. On this basis, Liu et al.[17] introduced the concept of emergency management, and identified 18 secondary subway operation SIFs from five aspects. Starting from the five basic dimensions of the physical constituents of subway stations, Du et al. [18]established a system of indicators of SIFs with structure, equipment, management, personnel and environment as the main body. Some scholars have further analyzed the 4M1E theory, dividing “personnel” into “passengers” and “employees”, dividing “environment” into “internal environment” and “external environment”, and dividing “management” into “rules and regulations” and “prevention system” [19]. In addition, some scholars have summarized the safety influences on the operation of subway stations from other aspects. For example, Bai et al.[20] established the index system of SIFs of subway operation safety from four aspects: “safety management”, “organization management”, “equipment management”, and “environment”. Xiao et al.[21] extracted the main factors influencing the operational safety of metro stations from the aspects of “passengers”, “equipment and facilities” and “emergency response capability”. Li et al.[22] identified the SIFs of metro stations from four aspects: “operation management”, “equipment and facilities”, “employees” and “external environment”.
In a coupled study of factors affecting the safety of subway stations, scholars consider the problems from four aspects: “personnel”, “management”, “equipment” and “environment”. In order to calculate the likelihood of subway operation safety accidents and the coupling value under different coupling modes, the N-K model is used to study the degree of influence of each factor and its coupling mode on urban subway operation[23,24]. Huang et al.[25] introduced the influencing factor of “materials transported on the subway”, analyzed the formation mechanism of the coupling risk based on the N-K model and the trigger concept, and quantitatively described the internal coupling relationship of subway safety. Shi et al.[26] based on the traditional node-place theoretical model, the evaluation model is optimized by adding the “connection” evaluation dimension. And the safety of subway stations was also evaluated using the coupled coordination degree model. In addition, in order to compensate for the limitations of qualitative analysis methods and make research more objective, scientific, and operational. Drawing on the coupling degree theory, some scholars have established a coupling degree calculation model and quantitatively analyzed the coupling degree between the factors[14].

2.2. Study on the SIFs of High-Pressure Gas Pipeline

For the research on the safety factors of high-pressure gas pipelines, scholars mainly summarized from the perspectives of human factors[27], vibration[28], corrosion[29,30], equipment and operation[31], design[32,33] and so on. For example, Wang[32], Yang et al.[33] mainly consider the safety of high-pressure gas pipelines from four aspects: “third-party damage”, “corrosion”, “misoperation” and “design”. Bai et al.[34] summarized the main SIFs of high-pressure gas pipeline safety from four aspects: “third-party interference”, “environment”, “misoperation” and “material defects”. Zeng et al.[31] constructed an index system of SIFs of urban gas pipeline safety including 105 bottom factors from four aspects: “third party damage”, “corrosion”, “equipment and operation” and “intrinsic safety quality of pipeline”. Some scholars have supplemented the identification of the factors affecting the safety of high-pressure gas pipelines. For example, a risk assessment method based on cloud reasoning was suggested by Guo et al.[35] and includes a number of factors, including aging, third-party damage, biological erosion, factor misuse, corrosion damage, and design faults. Depending on the pipeline properties, Zhang et al.[36] adjusted the SIFs such as corrosion factors, manufacturing and construction defects, soil movement, misoperation, leakage influence coefficient, etc. which improved the applicability of each influencing factor to the pipeline.
In terms of coupling study on SIFs of high-pressure gas pipelines. Yang et al.[37] established a calculation model of coupling degree depended on the coupling degree theory, and used AHP and entropy weight method to quantitatively analyze the coupling degree between different levels of factors. In order to determine the probability and coupling value of various coupling modes, Fu et al.[38] analyzed the influence of multi-factor coupling on the possibility of urban gas pipeline failure from four aspects: man, machine, environment and pipe, constructed the N-K model based on complex network, and calculated the probability of occurrence of different coupling modes and the value of coupling. Based on the risk factors of human, pipeline, operation and maintenance, and environment, a comprehensive index system of SIFs was established by Wang[39]. The coupling mechanism of risk factors of gas pipeline network was analyzed, and the safety assessment of urban gas pipeline network under the coupling of complex disaster-causing factors was studied.
Comprehensive current research status, scholars’ research direction mainly focuses on the unilateral safety evaluation and coupling analysis of SIFs of subway stations and gas pipelines. Research on the coupling of SIFs under the unique operating circumstances of the SSOUHP is lacking. The coupling study of such interrelationships is important for the comprehensive evaluation of the safety of subway stations, but the research in this area is still limited. Moreover, there is also a lack of specific research processes and methods on how to accurately identify the key SIFs of the SSOUHP. Therefore, this paper will try to analyze the SIFs of the SSOUHP, and conduct a coupling analysis of its key SIFs to improve the safety management level of the subway and gas industry.

3. Identification of Operation SIFs of SSOUHP

3.1. Preliminary Identification of Operation SIFs

Identifying reasonable SIFs can help us comprehensively understand the SIFs of the SSOUHP, and thus develop scientific and reasonable management strategies and response plans. This paper combines the research results of Yao[10], Xu et al.[23], Zeng et al.[31], Fu et al.[38], and introduces the influence factor of “pipeline” according to the suggestion of the expert group, and divides the safety influence factors of the SSOUHP into five aspects: human, pipeline, station, environment, and management.
In order to make the identified SIFs more systematic, scientific and comprehensive, the “subway station” and “gas pipeline” and “SIFs”, “subway station” and “gas pipeline” and “safety evaluation” are combined and searched in databases such as CNKI and Web of Science. The publication time of the literature is set to 2000-2024. By analyzing the titles, abstracts, and keywords of the literature, 51 academic journals and 17 dissertations were finally identified for the screening of security SIFs, and 22 high-frequency SIFs were initially obtained, as shown in Appendix A.

3.2. Optimization of Operation SIFs

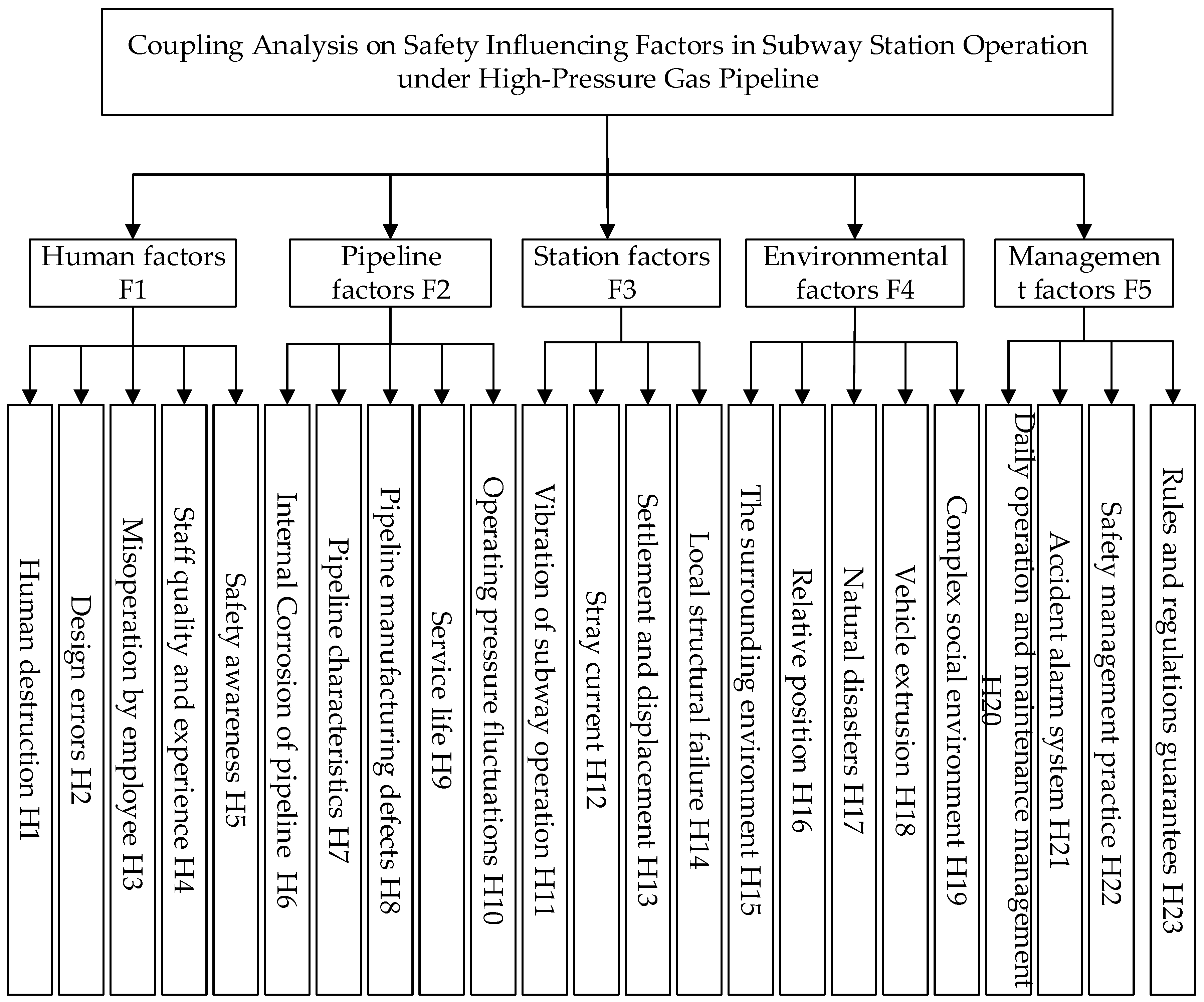
Through the method of expert discussion, 15 experts from design, owner, and research organizations were invited on-site to evaluate the acquired initial factors. According to the results of the experts’ discussion, among the 22 high-frequency SIFs initially obtained through the literature screening, the factors “pipeline characteristics” and “pipeline equipment condition” have a cross-cutting relationship, and it is recommended that the factor “pipeline equipment condition” be deleted. In response to the “station factor”, the experts suggested adding the factor of “localized structural failure”. And experts point out that the “surrounding environment” factor includes the “geological condition” factor, so experts suggest deleting the “geological condition” factor. In view of the imperfection of “environmental factors”, experts suggest adding the two factors of “complex social environment” and “vehicle squeeze”. In addition, since experts have proposed that the impact of “policy and legal protection” on the safety of SSOUHP is not applicable in this article, this factor is replaced with “regulatory protection”. Finally, the five major factors of “human”, “pipeline”, “station”, “environment”, and “management” were determined as the first-level SIFs and 23 second-level SIFs, as shown in Table 1.

4. Coupling Model of SIFs of SSOUHP

4.1. Coupling and Coupling Degree Theory

The idea of coupling first appeared in physics, and it is thought to be a phenomenon in which systems or forms of motion (two or more) interact influence or unite with each other[40]. Richard[41] first proposed the theoretical model of coupling coordination degree in 1990. Since Chinese scholar Jinchuan Huang introduced the concept of system coupling into the study of the relationship between urbanization and ecological environment in 2003, the research in this field has shown multidimensional characteristics. Coupling has been used in more disciplines, including ecology [42], agriculture [43], economy [44] and logistics [45]. Cong[46] explained and corrected the problems such as generalized expression errors, confusion of different coupling degree models, error of coupling degree value range and error of coupling stage division from the physical meaning of coupling degree and relevant literature in recent years.
The degree of coupling is an indicator for evaluating the degree of interdependence between different parts of the system[47]. The level or degree reflects the correlation and comprehensive effects among different security SIFs. The higher coupling degree indicates that the benign resonance coupling between the SIFs is achieved, and the system will gradually reach a new state of order. On the contrary, when the coupling degree is low, the system or the internal elements of the system are in an unrelated state, and the system will develop disorderly. Furthermore, each of these factors needs to be managed and controlled appropriately to ensure that the SIFs reach a benign and orderly state.
According to the coupling classification and the selection of the SIFs of the SSOUHP, the coupling of the SIFs of the SSOUHP can be divided into single-factor coupling, two-factors coupling and multi-factors coupling, as shown in Table 2.

4.2. The Efficiency Value of the Order Degree of SIFs

Firstly, 15 experts from design, owner and scientific research units are invited. The judgment matrix is determined by experts’ pairwise comparison and evaluation of the relative importance between two factors, and the importance of each influencing factor is calculated. The higher of the score, the more important of the influencing factor, and the higher of the weight. And the obtained weight is used to calculate the comprehensive index. Finally, the efficacy value of the ordering degree of the SIFs on the system is obtained through a composite index. The specific steps are as follows:
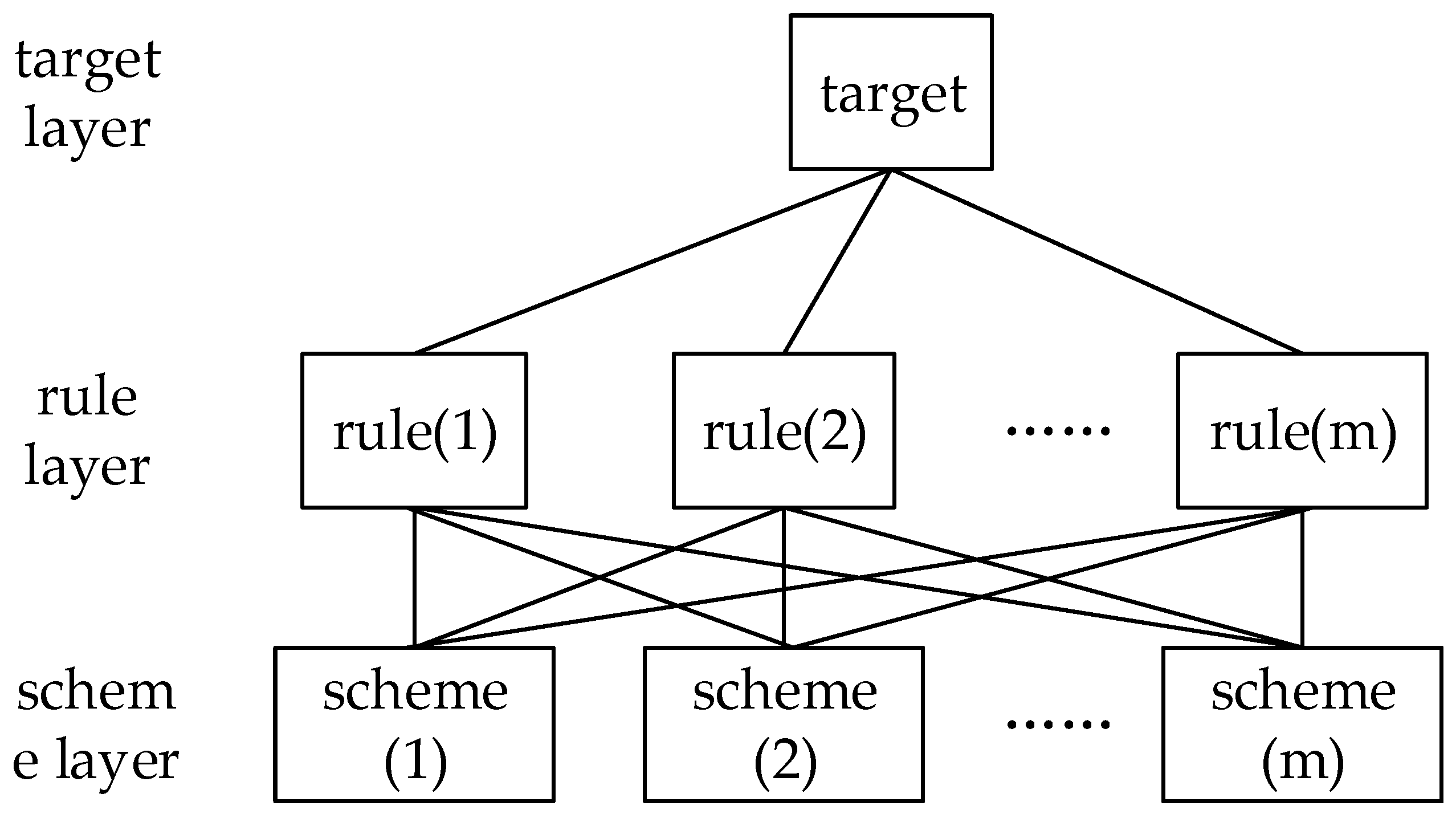
Step 1: Build the hierarchical model
Depending on the situation, the SIFs can be categorized from top to bottom as follows: target, rule and scheme levels, as shown in Figure 1.
Step 2: Build the pairwise comparison matrix
The first-level influencing factor is taken as the evaluation benchmark, and the pair comparison of the second-level influencing factor is carried out. The Satty1-9 scale method [48] (as shown in Table 3) was used to assign values to each element.
The pairwise comparison matrix is as follows:
A i = 1 a 12 … a 1 j ⋯ a 1 m 1 a 12 1 … a 2 j … a 2 m ⋮ ⋮ 1 ⋮ ⋮ ⋮ 1 a 1 j 1 a 2 j … 1 … a i m ⋮ ⋮ ⋮ ⋮ 1 ⋮ 1 a 1 m 1 a 2 m … 1 a i j … 1
A i a j i = 1 a i j  
Where Ai is the pairwise comparison matrix of first-level SIFs;
aij is the scale value of the i and j second-level SIFs.
Step 3: Consistency check
In the AHP, the subjective judgments and comparisons made by experts may involve certain subjective errors and biases. By using the consistency check, the credibility of the AHP can be enhanced. This ensures that the weight results are more reliable and accurate, thus improving the reliability of the decision-making process. When CI and CR are less than or equal to 0.1, the consistency check is passed.
C I = λ m a x − n n − 1
Where CI is the consistency index;
n is the order of pairwise comparison matrix.
C R = C I R I
Where CR is the ratio of consistency to consistency;
RI is the random consistency index, and its value can refer to the research results of Zhang et al.[49], as shown in Table 4.
Step 4: Calculate the criterion weight vector
Because the weight is the evaluation given by the subjective judgment of the experts when comparing in pairs, there is a gap with the real value to some extent. Therefore, when A is a consistent matrix, the maximum eigenvalue λmax in the A matrix is used instead. The criterion weight vector can be calculated by the following formula:
A i − λ m a x w i j = 0
Where λmax is the maximum eigenvalue of the paired comparison matrix;
wij is the criterion weight vector of the j-th second-level SIFs under the i-th firs-level SIFs.
Step 5: Calculation of the comprehensive index of SIFs
The evaluation results of the firs-level are transformed into the evaluation matrix A, and the comprehensive index of the influencing factor is calculated by the weight coefficient of the influencing factor of the middle level, which can be calculated by the following formula:
x i j = ∑ j = 1 m w i j a i j
Where m is the number of second-level SIFs (the order of matrix);
xij is the comprehensive index of the j-th second-level SIFs under the i-th first-level SIFs.
Step 6: The construction of power function
The formula for calculating the ordered positive efficacy vector of the second-level SIFs to the first-level SIFs can be adopted:
u i j = x i j − β i j α i j − β i j
The calculation formula of negative efficacy vector can be adopted:
u i j = α i j − x i j α i j − β i j
Where αij, βij are the upper and lower limits of the comprehensive index of SIFs when the system is stable;
uij is the satisfaction degree of each SIFs to achieve the goal. The larger the value, the higher the satisfaction. The uij is [0,1].
The contribution of the order parameters of each second- level SIFs to the order degree of the first- level SIFs can be calculated by using the line weighting sum method:
u i = ∑ j = 1 m w i u i j
Where m is the number of second-level SIFs (order parameter);
ui is the efficacy value of the i-th second- SIFs on the order degree of the first-SIFs.

4.3. Coupling Degree Function

The coupling function model is used to describe the interaction relationships between various parts of the system. The basic idea is to treat the various parts of the system as interrelated variables, and to describe their interactions by establishing mathematical relationships between them. Drawing on the concept of capacity coupling and the model of capacity coupling coefficients in physics, we generalize to obtain the multiple system (or element) interaction coupling degree model[50]. For example:
C = m ∗ ∏ i = 1 m u i ∑ i = 1 m u i m m
Where C is the coupling degree of the system;
m is the number of SIFs.

4.4. Coupling Coordination Degree

The coupling coordination model is a quantitative method used to evaluate the degree of coupling and coordination between different systems or factors. There are obvious differences and connections between coupling coordination degree and coupling degree[14]. The degree of coupling is difficult to reflect the “efficacy” and “synergy” of the SIFs, especially in the case of comparative studies of multiple factors. It may be misleading to use only coupling degree discrimination. The coupling coordination degree can make up for the disadvantages of coupling degree. For this reason, coupled coordination needs to be introduced to account for the degree of synergy between the systems of SIFs.
The degree of coupled coordination evaluates the extent to which elements within a system or between systems interact with each other in the development process. It can show a tendency for the system’s constituent components to move from disorder to order. Additionally, it is a quantitative index that measures the degree of coupling coordination. The level of coordination between the SIFs inside the system is worse when the coupling coordination degree is closer to 0. The level of coordination between the SIFs inside the system is better when the coupling coordination degree is closer to 1. Additionally, when the degree of coupling coordination is strong, it can effectively encourage the coordinated development of the subway station’s safe operation. The criteria for classifying the coupling coordination degree refer to the existing research results[51,52], as shown in Table 5.
The present study will utilize the research findings of Ji et al.[53] and Wang et al.[54] as references to establish a coupling coordination degree model and appraise the extent of interactive coupling coordination. The formula is as follows:
T = ∑ i = 1 m b i u i
D = C T
Where T is the index comprehensive harmonic index;
bi is the undetermined coefficient of the second-level SIFs, which is obtained by referring to the research results of Hou et al.[55], b1=b2=…bm, and ∑ i = 1 m b i = 1 ;
D is the coupling coordination degree.

5. Case Study

5.1. Case Background

The Y Station project of Line X in Zhengzhou, is an underground three-layer, double-column, three-span, island-type station. The platform width is 14 meters, and the station main body is 188.0 meters long. The standard segment width is 23.15 meters, and the expanded segment width is 23.65 to 29.65 meters. The center mileage of the station is K11+900557. It is equipped with 3 sets of wind pavilions, 1 safety entrance, 1 transfer hall, 1 transfer passage, and 1 connecting passage. The project is located on the north side of the intersection of two main roads. The east-west and north-south roads are both eight lanes in two-way. The planned road width is 60 meters. The road traffic is busy and the traffic flow is large. Due to the existence of water supply pipe, heat pipe, sewage pipe, power, communication and other facilities near the roof of the station, the surrounding environment of the subway station is too complex to bypass the high-pressure gas pipeline. Therefore, after the completion of the project, it is necessary to permanently relocate the high-pressure gas pipeline to the station cover above the laying. In addition, the elevation of the bottom of the high-pressure gas pipeline is -1.962 meters, while the elevation of the station roof is -3.254 meters, which leads to the close distance between the high-pressure gas pipeline and the station roof, and there are certain safety hazards. Therefore, it is necessary to analyze the coupling factors influencing the safety of HPGPOSS.

5.2. The Construction of Hierarchy Model of SIFs in Case Study

The SIFs of the project have been identified through Section 3.1. Therefore, for the coupling analysis of the SIFs of this case, the optimized influencing factor in Section 3.2 can be directly applied to construct the hierarchical structure model figure shown in Figure 2.

5.3. Determination of the Efficacy Value of SIFs for System Orderliness

Firstly, 15 experts in the field were invited to score the second-level evaluation SIFs (1-9 points). Then take the average value as the initial value vector of each second-level SIFs. Finally, the relative importance of the second-level SIFs (see Section 3.1 and Section 3.2 for details) is compared to form a pairwise comparison matrix.
A 1 = 1 1 4 2 1 2 1 1 4 2 1 2 1 4 1 4 1 1 2 1 5 1 2 1 2 2 1 1 3 2 2 5 3 1 A 2 = 1 1 2 1 2 1 4 2 2 1 1 1 2 4 2 1 1 1 2 4 4 2 2 1 5 1 2 1 4 1 4 1 5 1 A 3 = 1 3 1 2 1 4 1 3 1 1 4 1 5 2 4 1 1 3 4 5 3 1
A 4 = 1 1 4 1 3 2 1 2 4 1 2 5 3 3 1 2 1 3 2 1 2 1 5 1 3 1 1 3 2 1 3 1 2 3 1 A 5 = 1 1 2 1 4 1 4 2 1 1 3 1 3 4 3 1 1 4 3 1 1
The maximum eigenvalues of each pair of comparison matrix calculated by Matlab2018b software are as follows:
λmax1=5.0257，λmax2=5.0267，λmax3=4.0277，λmax4=5.0860，λmax5=4.0206。
The CI and CR values of each matrix calculated by equations (3) and (4) are shown in Table 6.
Both CI and CR are less than 0.1, and the consistency check meets the requirements.
Calculated by Formula (5) and corrected by Matlab2018b software, the weight values of each l SIFs are obtained, as shown in Table 7.
According to Formula (6), the comprehensive index vectors of the SIFs are calculated as follows:
x1j=(1.108, 1.108, 0.306, 0.586, 1.917)T x2j=(0.545, 1.090, 1.090, 1.999, 0.302)T
x3j=(0.615, 0.288, 1.001, 2.214)T x4j=(0.502, 2.139, 1.283, 0.338, 0.825)T
x5j=(0.351, 0.574, 1.548, 1.548)T
The efficacy vectors of the SIFs are calculated by Formulas (7) and (8) as follows:
u1j=(0.498, 0.498, 0.000, 0.174, 1.000)T u2j=(0.143, 0.464, 0.464, 1.000, 0.000)T
u3j=(0.170, 0.000, 0.370, 1.000)T u4j=(0.091, 1.000, 0.524, 0.000, 0.271)T
u5j=(0.000, 0.186, 1.000, 1.000)T
The efficacy values of various SIFs on the system order degree are calculated using Formula (9) as shown in Table 8.

5.4. Determination of Coupling Degree and Coupling Coordination Degree

According to the coupling degree model, the coupling degree and coupling coordination degree among the SIFs are calculated by Formulas (10)–(12), and the results are shown in Table 9.
The following conclusions are drawn from the analysis of the coupling degree and coupling coordination degree of each influencing factor.
(1) The analysis of the single-factor coupling results shows that the coupling degree of the internal SIFs is 1.000, indicating that the single-factor system is in a state of benign resonance coupling and orderly development. The order of coupling coordination degree of internal SIFs from large to small is management, station, human, pipeline, environment, and the coupling coordination degree of internal SIFs of management and station is greater than 0.8. It shows that the coordination level between the internal factors of management and station is good, and they promote each other and develop coordinately.
(2) The analysis of the two-factor coupling results shows that the coupling degree between human and pipeline, human and station, human and environment, pipeline and station, pipeline and environment is 1.000, and the coupling degree between the other SIFs is greater than 0.9. It shows that the two-factor system is in a state of benign resonance coupling and orderly development. The order of coupling coordination degree of SIFs from large to small is station and management, human and management, pipeline and management, environment and management, human and station, pipeline and station, station and environment, human and pipeline, human and environment, pipeline and environment. Among them, the four types of two-factor coupling between station and management, human and management, pipeline and management, environment and management are good coordination levels, and the remaining six types of two-factor coupling are moderate coordination levels.
(3) The analysis of multi-factor coupling results shows that the coupling degree of multi-factor coupling is greater than 0.9, indicating that the system is in a state of benign resonance coupling and orderly development under the action of multi-factor coupling. Under the coupling effect of the three-factor, the three-factor of human pipeline station, human station environment, pipeline station environment and human pipeline environment are coupled with each other to a moderate coordination level, and the remaining six types of three-factor are coupled with each other to a good coordination level. Under the coupling of four-factor, the four-factor of human pipeline station environment are coupled to each other at a moderate coordination level, and the remaining four-factor are coupled to each other at a good coordination level. Under the coupling of five-factor, the coupling coordination degree is greater than 0.8, which indicates that the system of the SSOUHP is at a good coordination level.
(4) Compared with the results of single factor, two-factor and multi-factor coupling, it can be found that with the coupling of environment, pipeline and human, the coupling coordination degree between the SIFs will decrease. It is noteworthy that the environmental factors have the strongest influence, followed by management factors, and finally human factors. As the station and management factors participate in the coupling, the coupling coordination degree between the SIFs will increase, and the management factors have the strongest influence. In addition, with the increase of the SIFs involved in coupling coordination, the coupling degree decreases. When the coupling degree is too high, it will affect the level of coupling coordination, and the frequency of coupling dispatch higher than 0.8 is increasing. When all the SIFs of the system participate in coupling, the coupling degree and coupling coordination degree are at a high level. Therefore, when analyzing the factors affecting the safety of SSOUHP, the more comprehensive the factors considered, the easier it is for the system to achieve benign resonance coupling, high-quality coordination, and orderly development.

6. Discussion and Management Implication

This paper identifies 23 SIFs in five dimensions: human, pipeline, station, environment, and management through literature research and expert discussion. In the existing research on the factors affecting the safety of subway stations, scholars have mainly considered the influence of “human”, “mechanical equipment”, “environment”, “management” and other aspects[17,56,57]. Few people consider the impact of gas pipelines on the operation safety of subway stations. For example, Du et al.[18] considered the safety impacts of urban subway systems from the perspectives of resilient cities in terms of five aspects: “structure”, “equipment”, “management”, “personnel” and “environment”. This paper focuses on the safe operation of subway stations under the special perspective of the HPGPOSS. In combination with the actual situation of the project, the main SIFs of the three dimensions of human, environment and management are identified through literature research. For the safety influencing factor of “environment”, we categorize it into natural and social environments. This categorization was also used by some scholars in earlier studies to consider issues and make specific statements[58]. Based on the actual situation of the project and the conjunction of the expert discussion, we have replaced the influence factor of “mechanical equipment and facilities” with “station” factor, and, together with the factor of “pipeline”, we have adopted it as the first-level influence factor. In response to this categorization, some scholars have summarized the first-level influences in terms of the physical components of the HPGPOSS[59].This approach makes our categorization more rational, comprehensive and scientific.
In this paper, AHP is combined with coupled coordination model to analyze the factors affecting the safety of the HPGPOSS. Based on the literature research, it is found that the commonly used coupling models are explanatory structure model, N-K model, coupling degree model, SD model, SHEL model and so on. Where interpretive structural models are suitable for analyzing systems with relatively complex relationships[60]. The N-K model is computationally demanding and labor intensive in terms of the data used[61]. The SD model can only analyze and evaluate the coupling of two nonlinear systems, and the model requires a high sample size of data[15]. The elements in the SHEL model must be matched around people[62]. The coupling degree model is suitable for describing the coupling strength between systems or elements with coupling relationship, and it can realize quantitative evaluation of the coupling strength between elements with coupling relationship[14]. Therefore, based on a comparison of commonly used coupling models in the literature, the coupling analysis model used in this paper makes it easier to analyze the magnitude of the coupling effects between the SIFs and the degree of mutual coordination.
In the case study section, this paper analyzes and studies the role of single-factor coupling, two-factor coupling and multi-factor coupling, respectively. The results of the study show that environmental, pipeline, and human factors are the main influences on the safety of the HPGPOSS, and with the participation of environment, pipeline, and human factors in the coupling, the degree of coordination of the coupling between the SIFs will decrease. However, in existing research on the role of subway station coupling, scholars regard personnel, equipment, and environmental factors as important factors in the safe operation of subway stations. For example, Yu et al.[13] concluded that personnel factors and equipment factors are important factors affecting the safety of subway operations. Xu et al.[23] identified four factors, namely human, equipment, nature and management, as the main factors contributing to risk events in metro operations. Zhao et al.[24] concluded that equipment and personnel are the main SIFs in single-factor risk coupling, while personnel, equipment, and management are the main SIFs in multi-factor coupling. In addition, for the increase in the number of SIFs involved in the coupling coordination, the degree of coupling has decreased, and the level of coupling coordination tends to stabilize the state of good coordination level. Some scholars have explained this, for example, Xue et al.[63] believe that the coupling degree and coordination degree of each influencing factor of the subsystem varies greatly numerically. But all with the increase in the number of SIFs, the overall coupling is a decreasing trend, and the level of coupling and coordination tends to a stable state. It is also reflected that the level of coupled coordination between the SIFs has a positive impact on the resilience of the sub-systems in the subway station[64].
Through the coupling analysis of the SIFs of the SSOUHP, it is suggested that the relevant managers should control the interaction among the three key factors of environment, pipeline and human factors, so as to avoid the coupling of unsafe influencing factors from the source of safety accidents. For example, (a) with regard to environmental factors, it is necessary to take into account not only the impact of the natural environment, but also the complex social environment, and to strengthen public safety education, the dissemination of safety knowledge, and public morality among members of social groups; (b) strengthening the management of human factors, reinforcing staff safety awareness, improving staff quality and experience; (c) focusing on the management of coupled risks, combining the influencing factors with the characteristics of the pipeline itself, so as to avoid safety accidents caused by pipeline failures. In addition, when managing the safe operation of subway stations, not only human factors, pipelines and environmental factors are considered, but also some other factors. For example, (a) focus on the impact of subway operation vibration, stray current, settlement and displacement, and local structural failure on the safe operation of subway stations; (b) strengthening the daily operation and maintenance management of subway stations, regularly checking the accident alarm system, and improving safety and protection emergency measures and regulatory safeguards.

7. Conclusions

(1) Aiming at the working conditions of SSOUHP, this paper summarizes 23 SIFs from five aspects, namely, human-related SIFs, pipeline-related SIFs, station-related SIFs, environment-related SIFs, and management-related SIFs. And constructs the hierarchical structure model of SIFs of SSOUHP.
(2) The AHP and CDA were combined to assess the coupling correlations between the SIFs. And Y subway station was selected to test the proposed hybrid approach can be used to evaluate the coupling correlations between SIFs.
(3) In the coupling situations during Y subway station operation, the internal coupling correlations among environment-related SIFs, the coupling correlations between pipe-related SIFs and environment-related SIFs, and the coupling correlations among human-related SIFs, pipeline-related SIFs and environment-related SIFs are with higher safety risk. The overall coupling correlation among all SIFs during Y subway station operation is with lower safety risk.
(4) In the future, we will improve the safety factors of SSOUHP. And we will conduct specific analysis on the relationship between coupling degree and coupling coordination among the influencing factors, as well as the causes and consequences of accidents.

Author Contributions

Conceptualization and formal analysis, W.Y.; investigation and writing—original draft, Y.W.; methodology and writing—review & editing, J.C.; resources and supervision, H.L.; project administration, J.G.; validation, L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grand number U1810203, 52178388), the Zhengzhou Metro Group Co. Ltd. (grand number H22-541); the Fundamental Research Funds for the Universities of Henan Province (grand number NSFRF230426), and the Doctoral fund of Henan Polytechnic University (grand number B2022-23).

Data Availability Statement

The data is available by querying the authors.

Acknowledgments

The research would like to thank Henan Polytechnic University for providing research facilities.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Initial Table of SIFs.
First-level SIFs Second-level SIFs Source
Human factors Human destruction [35,65,66,67]
Design errors [35,65]
Misoperation by employees [33,35,65,66,68]
Staff quality and experience [10,58,65]
Safety awareness [10,58,69]
Pipeline factors Internal corrosion of pipeline [34,35,65,58]
Pipeline characteristics [35,65,70]
Pipeline manufacturing defects [35,58,65,67]
Service life [65]
Operating pressure fluctuation [35,65,70]
Pipeline equipment condition [58,65,71]
Station factors Vibration of subway operation [71,72]
Stray current [71,73,74]
Settlement and displacement [73]
Environmental factors The surrounding environment [58,75,76]
Relative position [70,73]
Geological conditions [72,75]
Natural disasters [33,66,67]
Management factors Daily operation and maintenance management [58,77,78]
Accident alarm system [65,75,79]
Safety management practice [10,58,75,79]
Policy and legal protection [10,58,65,75]

References

  1. “The 14th Five-Year Plan: Accelerating the Construction of Urban (Suburban) Railroads and Promoting the Development of Urban Rail Transit in an Orderly Manner. China Metros 2021, (03), 6 (In Chinese).
  2. Urban Rail Transit 2022 Annual Statistics and Analysis Report. China Metros 2023, (04), 13-15 (In Chinese).
  3. Wu, B.; Gao, B.; Suo, X.M.; Liu, W.N.; Shi, Y.X., Study on Influence of Metro Tunnel Excavation on Buried Pipelines. Rock and Soil Mechanics 2004, (04), 657-662 (In Chinese).
  4. Shi, J.H., Revised Calculation and Numerical Analysis on Peck Formula for Safety of Metro Passage with Underneath Crossing Gas Pipeline. Journal of Safety Science and Technology 2018, 14, (06), 182-186 (In Chinese).
  5. Yan, Q.S.; Zhang, Y.N.; Sun, Q.W., Characteristic Study on Gas Blast Loadings in an Urban Utility Tunnel. Journal of Performance of Constructed Facilities 2020, 34, (4). [CrossRef]
  6. Zheng, S.F.; Wen, J., Analysis and Prediction of Subway Settlement Deformation Based on Grey Model. IOP Conference Series: Earth and Environmental Science 2021, 638, (1).
  7. Li, J.W., Review of Testing and Analysis on Metro-Induced Vibration. Applied Mechanics and Materials 2014, 3307, (580-583). [CrossRef]
  8. Wang, C.T.; Li, W.; Wang, Y.Q., Remaining Lifetime Assessment of Gas Pipelines Subjected to Stray Current Interference Using an Integrated Electric-electrochemical Method. Engineering Failure Analysis 2021, 127. [CrossRef]
  9. Luan, X., Safety Risk Assessment of Metro Operation Period Based on AHP and Entropy Weight Method: Taking Nanjing Metro as an Example. Intelligent City 2023, 9, (06), 44-47 (In Chinese).
  10. Yao, S.Y. Research on Safety Risk Assessment of Metro Station in Integrated Transportation Hub Based on Fuzzy Bayesian Network. South China University of Technology, 2022 (In Chinese).
  11. Xiao, X.M.; Wang, Y.H.; Jia, L.M., Safety Assessment Model for Urban Rail Transit Network Operations Based on Complex Network and Entropy Theory. China Safety Science Journal 2011, 21, (11), 41-48 (In Chinese).
  12. Liu, P.; Li, Q.M.; Bian, J.; Song, L.L.; Hou, X.X., Using Interpretative Structural Modeling to Identify Critical Success Factors for Safety Management in Subway Construction: A China Study. International Journal of Environmental Research and Public Health 2018, 15, (7), 1359. [CrossRef]
  13. Yu, M.Y.; Zhu, L.; Liu, Z.G., Coupling Analysis of Subway Operation Safety Risk Factors Based on N-K Model. Logistics Sci-tech 2022, 45, (17), 1-4, 9 (In Chinese).
  14. Pan, H.Z.; Gou, J.; Wan, Z.H.; Ren, C.X.; Chen, M.J.; Gou, T.Q.; Luo, Z.H., Research on Coupling Degree Model of Safety Risk System for Tunnel Construction in Subway Shield Zone. Mathematical Problems in Engineering 2019, 2019. [CrossRef]
  15. Wang, F.; Ding, L.Y.; E D Love, P.; J Edwards, D., Modeling Tunnel Construction Risk Dynamics: Addressing the Production Versus Protection Problem. Safety Science 2016, 87. [CrossRef]
  16. Wang, J.; Fang, W.N.; Zhang, Y., Identification and Evaluation of Human Error Influential Factors in Subway Scheduling System. China Safety Science Journal 2011, 21, (08), 74-79 (In Chinese).
  17. Liu, J.; Wan, L.T.; Wang, W.Q.; Yang, G.D.; Ma, Q.; Zhou, H.W.; Zhao, H.Y.; Lu, F., Integrated Fuzzy DEMATEL-ISM-NK for Metro Operation Safety Risk Factor Analysis and Multi-Factor Risk Coupling Study. Sustainability 2023, 15, (7), 5898. [CrossRef]
  18. Du, X.L.; Zhang, Y.; Miao, H.Q.; Li, Y.; Zhong, Z.L.; Jiang, L.Z.; Hou, B.W., Indicator System for the Evaluation of Metro System Safe Operation from the Perspective of Resilient Cities. Journal of Natural Disasters 2023, 32, (3), 1-13 (In Chinese).
  19. Ren, G.; Chen, J.J.; Gao, J.Y.; Wang, Y.; Yuan, C.Q.; Jiang, Q.Y., Safety Assessment of Metro Station Operation Based on Improved Extension and Matter Element Method. Urban Mass Transit 2020, 23, (3), 136-139 (In Chinese).
  20. Bai, S.M.; Sun, H.S.; Zhao, Y.C., Study of the Safety Evaluation of Urban Subway Operation Based on Extenics. Advanced Materials Research 2014, 3149, (919-921). [CrossRef]
  21. Xiao, X.M.; Wang, Y.H.; Jia, L.M., Safety Assessment of Subway Station Operation Based on Grey Clustering Method. Advanced Materials Research 2013, 2493, (748-748). [CrossRef]
  22. Li, J.; Song, R.; Jiang, J.L., Safety evaluation of rail transit based on comprehensive fuzzy evaluation model. Journal of Transport Science and Engineering 2011, 27, (2), 91-95 (In Chinese).
  23. Xu, H.; Yue, J.C.; Du, M.K.; Jiao, L.D., Analysis of Urban Rail Transit Coupling Operation Risks Based on N-K Model. Urban Mass Transit 2020, 23, (10), 105-108 (In Chinese).
  24. Zhao, J.X.; Liu, L.Y.; Wang, F.; Mao, N., The Subway Operation Safety Risk Based on N-K Model Coupling Research. Journal of Civil Engineering and Management 2023, 40, (2), 31-36 (In Chinese).
  25. Huang, W.C.; Shuai, B.; Sun, Y., Study on Coupling Risk Formation Mechanism of Railway Dangerous Goods Transportation System Based on N-K Model. Journal of the China Railway Society 2019, 41, (05), 1-9 (In Chinese).
  26. Shi, J.R.; Lv, Q.W.; Jin, S.M., Coupling Coordination Analysis of Urban Metro Station Catchment Area Development Based on Urban Multi-Source Data. School of Tourism and Urban-Rural Planning, Zhejiang Gongshang University (China) 2022.
  27. Balali, A.; Valipour, A.; Edwards, R.; Moehler, R., Ranking Effective Risks on Human Resources Threats in Natural Gas Supply Projects Using ANP-COPRAS Method: Case study of Shiraz. Reliability Engineering & System Safety 2021, 208, 107442.
  28. Jiang, N.; Gao, T.; Zhou, C.; Luo, X., Safety Assessment of Upper Buried Gas Pipeline Under Blasting Vibration of Subway Tunnel: a Case Study in Beijing Subway Line. Journal of Vibroengineering 2019, 21, (4), 888-900. [CrossRef]
  29. Li, Y.Q.; Liao, Q.; Hao, Z.F.; Yin, X.F.; Liu, B., Influence Factors and Mathematical Modeling of the Security of Underground Gas Conduit Network. Journal of South China University of Technology(Natural Science Edition) 2004, (02), 89-93 (In Chinese).
  30. Ba, Z.N.; Han, Y.X.; Liang, J.W., Risk Assessment of the Gas Pipeline Corrosion Based on the Improved AHP and Fuzzy Comprehensive Evaluation Method. Journal of Safety and Environment 2018, 18, (06), 2103-2109 (In Chinese).
  31. Zeng, X.K.; Feng, Y.; Lai, W.Q.; Tang, B.K.; Wu, T.; Fu, X.B.; Huang, X.B.; Zhong, S.C.; Zhong, J.F., Risk Assessment of Urban Gas Pipeline Based on AHP and Entropy Weight Method. Journal of Safety Science and Technology 2021, 17, (05), 130-135 (In Chinese).
  32. Wang, C. Research on Risk Assessment of Urban Gas Pipelines and Management. Xi’an University of Architecture and Technology, 2013 (In Chinese).
  33. Yang, Z.H.; Can, W.; Hu, S.J., Study on Fuzzy Comprehensive Evaluation System of City Gas Pipeline Based on AHP. Journal of Safety and Environment 2013, 13, (02), 257-260 (In Chinese).
  34. Bai, Y.P.; Wu, J.S.; Ren, Q.R.; Jiang, Y.; Cai, J.T., A BN-Based Risk Assessment Model of Natural Gas Pipelines Integrating Knowledge Graph and DEMATEL. Process Safety and Environmental Protection 2023, 171. [CrossRef]
  35. Guo, Y.B.; Meng, X.L.; Meng, T.; Wang, D.G.; Liu, S.H., A Novel Method of Risk Assessment Based on Cloud Inference for Natural Gas Pipelines. Journal of Natural Gas Science and Engineering 2016, 30. [CrossRef]
  36. Zhang, H.B.; Cheng, W.Y.; Zhou, L.J.; Feng, Q.S.; Zheng, H.L.; Dai, L.S.; Xiang, X.Q.; Cao, T.; Liu, Y., Pipeline Risk Assessment Practice of PetroChina Pipeline Company. Oil & Gas Storage and Transportation 2012, 31, (02), 96-98 (In Chinese).
  37. Yang, Y.; Cai, Z.; Jiang, N.; Zhou, C.; Li, H., Safety Evaluation of Underground Gas Pipe under Blasting of Subway Connected Aisle: A Case Study. KSCE Journal of Civil Engineering 2022, 26, (2), 921-932. [CrossRef]
  38. Fu, B.W.; Jiang, H.Y.; Xu, T.L.; Lin, Y.A., Coupling Analysis on Failure Possibility Factors of Urban Gas Pipeline Based on N-K Model. Journal of Safety Science and Technology 2018, 14, (02), 145-149 (In Chinese).
  39. Wang, M.S. Operation Safety Risk Assessment of Municipal Gas Pipeline Network Under Multi Factor Coupling Effect. Tianjin University, 2020 (In Chinese).
  40. Huang, J.C.; Fang, C.L., Analysis of Coupling Mechanism and Rules Between Urbanization and Eco-Environment. Geographical Research 2003, (02), 211-220 (In Chinese).
  41. Norgaard, R.B., Economic Indicators of Resource Scarcity: A Critical Essay. Journal of Environmental Economics and Management 1990, 19, (1). [CrossRef]
  42. Tao, J.; Xie, Y.; Zhou, H.; Xu, Y.; Zhao, G., Cross-County Characteristics of Water–Ecology–Economy Coupling Coordination in the Wuding River Watershed, China. Land 2022, 11, (12). [CrossRef]
  43. Wang, R.X.; Chen, J.C.; Li, M.H., Coupling and Coordinating Relationship between Agricultural Eco-Efficiency and Food Security System in China. International Journal of Environmental Research and Public Health 2023, 20, (1). [CrossRef]
  44. Yan, B.R.; Dong, Q.L.; Qian, L.; Fei, H.M.; Wu, J.N., A Study on the Coupling and Coordination between Logistics Industry and Economy in the Background of High-Quality Development. Sustainability 2021, 13, (18). [CrossRef]
  45. Gong, Y.; Yang, X.Q.; Ran, C.Y.; Shi, V.; Zhou, Y.F., Evaluation of the Sustainable Coupling Coordination of the Logistics Industry and the Manufacturing Industry in the Yangtze River Economic Belt. Sustainability 2021, 13, (9). [CrossRef]
  46. Cong, X.N., Expression and Mathematical Property of Coupling Model, and Its Misuse in Geographical Science. Economic Geography 2019, 39, (04), 18-25 (In Chinese).
  47. Xue, Y.; Liu, Y.L.; Zhang, T.T., Research on Formation Mechanism of Coupled Disaster Risk. Journal of Natural Disasters 2013, 22, (02), 44-50 (In Chinese).
  48. L., V.V.; A., W.L., Application of New Fuzzy-Weighted Average (NFWA) Method to Engineering Design Evaluation. International Journal of Production Research 2001, 39, (6).
  49. Zhang, K.; Zheng, W.B.; Xu, C.; Cheng, S.E., An Improved Extension System for Assessing Risk of Water Inrush in Tunnels in Carbonate Karst Terrain. KSCE Journal of Civil Engineering 2019, 23, (5). [CrossRef]
  50. Illingworth, V., The Penguin dictionary of physics. 2nd ed. ed.; Penguin Books: London, England, 1991; p 544.
  51. Wang, Y.F.; Geng, Q.J.; Si, X.H.; Kan, L.P., Coupling and Coordination Analysis of Urbanization, Economy and Environment of Shandong Province, China. Environment, Development and Sustainability 2020, 23, (7). [CrossRef]
  52. Dong, G.L.; Ge, Y.B.; Liu, J.J.; Kong, X.K.; Zhai, R.X., Evaluation of Coupling Relationship between Urbanization and Air Quality Based on Improved Coupling Coordination Degree Model in Shandong Province, China. Ecological Indicators 2023, 154. [CrossRef]
  53. Ji, Y.; Sheng, Q.Q.; Zhu, Z.L., Assessment of Ecological Benefits of Urban Green Spaces in Nanjing City, China, Based on the Entropy Method and the Coupling Harmonious Degree Model. Sustainability 2023, 15, (13). [CrossRef]
  54. Wang, M.; Chen, F.R.; Zhang, D.Q.; Rao, Q.Y.; Li, J.J.; Tan, S.K., Supply–Demand Evaluation of Green Stormwater Infrastructure (GSI) Based on the Model of Coupling Coordination. International Journal of Environmental Research and Public Health 2022, 19, (22). [CrossRef]
  55. Hou, X.F.; Zhang, D.F.; Fu, L.Y.; Zeng, F.; Wang, Q., Spatio-Temporal Evolution and Influencing Factors of Coupling Coordination Degree between Urban–Rural Integration and Digital Economy. Sustainability 2023, 15, (12). [CrossRef]
  56. Suo, Q.; Wang, L.Y.; Yao, T.Z.; Wang, Z.H., Promoting Metro Operation Safety by Exploring Metro Operation Accident Network. Journal of Systems Science and Information 2021, 9, (04), 455-468. [CrossRef]
  57. Zhang, M., Risk Assessment of Metro Operation Based on G1-EW Combination Weighting Cloud Model. China Safety Science Journal 2022, 32, (06), 163-170 (In Chinese).
  58. Fang, F. Coupling Analysis and Simulation of Human and Environment Factors in Gas Pipeline Safety Risk. Anhui Jianzhu University, 2021 (In Chinese).
  59. Li, D.N.; Zhao, B.K.; Xu, S.M., Research on Safety Evaluation System of Underground Pipelines Adjacent to Metro Construction Based on Pipelines Properties and Pipe-tunnel Position Relationship. Journal of Municipal Technology 2023, 41, (04), 206-215 (In Chinese).
  60. Sreenivasan, A.; Ma, S.; Nedungadi, P.; Sreedharan, V.R.; Raman, R.R., Interpretive Structural Modeling: Research Trends, Linkages to Sustainable Development Goals, and Impact of COVID-19. Sustainability 2023, 15, (5). [CrossRef]
  61. Yan, H.Y.; Zheng, Z.W.; Huang, H.J.; Zhou, X.Y.; Tang, Y.Z.; Hu, P., Risk Coupling Evaluation of Social Stability of Major Engineering Based on N-K Model. Buildings 2022, 12, (6). [CrossRef]
  62. Molloy, G.J.; O’Boyle, C.A., The SHEL Model: a Useful Tool for Analyzing and Teaching the Contribution of Human Factors to Medical Error. Academic medicine : journal of the Association of American Medical Colleges 2005, 80, (2). [CrossRef] [PubMed]
  63. Xue, F.; He, C.L.; Huang, Q.; Luo, J., Coordination Degree of Multimodal Rail Transit Network. Journal of Jilin University(Engineering and Technology Edition) 2021, 51, (06), 2040-2050 (In Chinese).
  64. Yao, X.H. Analysis on the Current Situation, Internal Coupling and Influencing Factors of the Urban Resilience of China’s Provincial Capital Cities. Zhejiang University, Zhejiang, 2022 (In Chinese).
  65. Wang, Q.S.; Tan, Y.F.; Qi, H.Y., Mutual Coupling Analysis of Safety Impact Factors of Gas Network. Gas & Heat 2010, 30, (11), 22-26 (In Chinese).
  66. Zhang, Y.; Lv, S.R.; Wang, W.Q., Risk Analysis of High Pressure Gas Pipeline Leakage Based on Bow-tie Model and IAHP. IOP Conference Series: Earth and Environmental Science 2020, 461, (1). [CrossRef]
  67. Sheng, K.; Lai, X.L.; Chen, Y.; Jiang, J.C.; Zhou, L., Risk Assessment of Urban Gas Pipeline Based on Different Unknown Measure Functions. Tehnički vjesnik 2021, 28, (5).
  68. Li, J.; Zhang, H.; Han, Y.S.; Wang, B.D., Study on Failure of Third-Party Damage for Urban Gas Pipeline Based on Fuzzy Comprehensive Evaluation. PLoS ONE 2017, 11, (11). [CrossRef] [PubMed]
  69. Han, W.; Qian, Z.X.; Wang, J.W., A Safety Risk Evaluation Index System of Subway Projects Based on the Analytic Hierarchy Process. Journal of Physics: Conference Series 2020, 1676, (1).
  70. Gao, B.L.; Xi, R.J., Safety Risk Assessment for Adjacent Underground Pipelines in Metro Construction. Modern Tunnelling Technology 2016, 53, (03), 118-123 (In Chinese).
  71. Wu, B.B.; Qiu, P.Y.; Shi, J.H.; Liu, J.J., Analysis on the Interaction Between Subway and Gas Pipeline. Journal of Safety Science and Technology 2021, 17, (S2), 64-67 (In Chinese).
  72. Zou, B.P.; Sun, D.; Mu, J.D.; Xu, Z.P., Comprehensive Risk Evaluation in the Long-Term Operation of Urban Subway Based on Multiple Indices. Mathematical Problems in Engineering 2021, 2021. [CrossRef]
  73. Yao, X.J.; Zhang, W.; Wu, Z.Z.; Lu, Q.C.; Xia, D.L., Safety Protection Standards for Oil and Gas Pipelines Adjacent to A Subway. Oil & Gas Storage and Transportation 2018, 37, (12), 1380-1384 (In Chinese).
  74. Saeed, R.A.; Michael, I.; Mohammad, D.; Masoud, S.; Hojjat, S.; Ashkan, R., Investigation on corrosion rate and a novel corrosion criterion for gas pipelines affected by dynamic stray current. Journal of Natural Gas Science and Engineering 2015, 26.
  75. Wu, Q.T. Resilience Evaluation and Promotion of Urban Metro Network. China University of Mining and Technology, 2022 (In Chinese).
  76. Hu, Y.W. Research on Reliability of Safety Management System for Subway Shield Construction. China Three Gorges University, 2020 (In Chinese).
  77. Long, Y.T. Study on the Risk Evaluation of Operation and Maintenance of X Integrated Pipeline Corridor Project in F City Based on Cloud Model. Jiangxi University of Science and Technology, 2022 (In Chinese).
  78. Pan, K.; Wang, H.D.; Shi, J.Y., Application of Multi-level Extensible Method to Urban Subway Operation Safety Evaluation. Journal of the China Railway Society 2011, 33, (05), 14-19 (In Chinese).
  79. Jiang, T.T.; Yao, C.Q.; Tong, Z.J., Safety Evaluation of Deep Foundation Pit Construction in Subway Stations Based on Game Theory-Extenics Theory. Journal of North China Institute of Science and Technology 2023, 20, (01), 103-110 (In Chinese).
Preprints 111794 g001
Figure 1. Hierarchy model diagram.
Figure 1. Hierarchy model diagram.
Preprints 111794 g001
Preprints 111794 g002
Figure 2. Hierarchy model of SIFs.
Figure 2. Hierarchy model of SIFs.
Preprints 111794 g002
Table 1. SIFs.
Table 1. SIFs.
First-level SIFs Second-level SIFs Interpretation
Human factors Human destruction Damage caused by third-party construction, terrorist attacks, etc.
Design errors The design rationality, material selection, safety factor design and other potential errors caused by the experience and qualification of the designers of the special design scheme.
Misoperation by employees Daily operational errors in pipeline or station caused by employees’ lack of concentration, misunderstanding, work pressure, etc.
Staff quality and experience Including staff mental health, basic quality, responsibility, similar project experience and regular training sessions.
Safety awareness Daily operation and maintenance staff education, training, safety awareness, safety attitude, safety knowledge popularization and so on.
Pipeline factors Internal corrosion of pipeline The interaction between the inner wall of the pipeline and the impurities contained in the transported gas causes the explosion accident caused by the gas leakage after pipeline corrosion.
Pipeline characteristics Mainly for the thickness of the pipeline, material, the ability of gas leakage after destruction, etc.
Pipeline manufacturing defects The explosion accident caused by gas leakage caused by pipeline damage, small crack, wrinkle bending, welding defect or insufficient strength.
Service life Mainly due to disrepair and long time of use appear fatigue damage.
Operating pressure fluctuation When the pipeline pressure is large, the explosion caused by gas leakage will aggravate the accident.
Station factors Operation vibration Fatigue damage to gas pipelines caused by the continuous cyclic action of vibration generated in subway operation.
Stray current Subway operation has some current leakage to form stray currents, which can cause galvanic corrosion on pipeline.
Settlement and displacement The effect of settlement and displacement generated by the main structure of the subway station during the operational phase on the overall system.
Local structural failure Impact on the overall system after failure of the main structure such as beams, slabs and columns in the subway station due to abnormal factors.
Environmental factors The surrounding environment When the surrounding buildings form a relatively enclosed area, the explosion caused by gas leakage will exacerbate the impact of the accident.
Relative position The clear distance between the bottom of the high-pressure gas pipeline and the roof of the subway station.
Natural disasters It is mainly the impact of natural disasters such as earthquake, high temperature, rainstorm, flood, and soil settlement on high-pressure gas pipeline and subway station.
Vehicle squeeze The gas pipeline is laid under the road, and the long-term extrusion of the vehicle will aggravate the wear of the pipeline. When the pipeline reaches the limit, the pipeline damage will cause a gas leakage accident.
Complex social environment It mainly refers to the public safety awareness of the social group, the popularization of safety knowledge, the ability to prevent security, and the ability to report problems in time.
Management factors Daily operation and maintenance management Configuration, installation and maintenance of software and hardware for the entire system of the gas pipeline and subway station.
Accident alarm system Monitor the status of the gas pipeline and subway station, and find out whether the problem can be timely alarm and information transmission and sharing.
Safety management practice Including the preparation of emergency plans, emergency equipment configuration, accident management, etc.
Rules and regulations guarantee Whether the safety regulations and responsibility system are sound, whether the safety responsibility system is clear, and the implementation and supervision of responsibilities.
Table 2. Coupling of SIFs.
Table 2. Coupling of SIFs.
Single-factor coupling Two-factor coupling Multi-factor coupling
Three-factor coupling Four-factor coupling Five-factor coupling
Human - Human Human - Pipeline Human - Pipeline - Station Human - Pipeline - Station - Environment Human - Pipeline - Station - Environment - Management
Human - Pipeline Human - Pipeline - Environment
Pipeline - Pipeline Human - Environment Human - Pipeline - Management Human - Pipeline - Station - Management
Human - Management Human - Station - Environment
Station - Station Pipeline - Station Human - Station - Management Human - Pipeline - Environment - Management
Pipeline - Environment Human - Environment - Management
Environment - Environment Pipeline - Management Pipeline - Station - Environment Human - Station - Environment - Management
Station - Environment Pipeline-Station-Management
Management - Management Station - Management Pipeline - Environment - Management Pipeline - Station - Environment - Management
Environment - Management Station - Environment - Management
Table 3. The meaning of scale method assignment.
Table 3. The meaning of scale method assignment.
Scale Meaning
1 Both factors are equally important.
3 Factor i is slightly more important than factor j.
5 Factor i is more important than factor j.
7 Factor i is significantly more important than factor j.
9 Factor i is extremely important compared to factor j.
2、4、6、8 Scale between two neighboring levels of importance.
Count backwards The importance of factor i relative to j is aij, and the importance of j relative to i is aji=1/aij.
Table 4. RI Value.
Table 4. RI Value.
Order 3 4 5 6 7 8
RI value 0.52 0.89 1.12 1.26 1.36 1.41
Table 5. Standard for classification of coupling coordination degree.
Table 5. Standard for classification of coupling coordination degree.
Coupling coordination degree interval Degree of coordination Coordinated contrast type
[0.0～0.1] Dysfunctional recession Extreme disorder
(0.1～0.2] Severe disorder
(0.2～0.3] Moderate disorder
(0.3～0.4] Mild disorder
(0.4～0.5] Transitional coordination Critical coordination
(0.5～0.6] Barely coordination
(0.6～0.7] Junior coordination
(0.7～0.8] Coordination development Moderate coordination
(0.8～0.9] Good coordination
(0.9～1.0] High-quality coordination
Table 6. CI and CR values.
Table 6. CI and CR values.
A1 A2 A3 A4 A5
CI 0.00642 0.00667 0.00923 0.02150 0.00687
CR 0.00574 0.00596 0.01037 0.01920 0.00772
Table 7. Weight value of each SIFs.
Table 7. Weight value of each SIFs.
First-level SIFs Second-level SIFs Weight value
Human factors Human destruction 0.221
Design errors 0.221
Misoperation by employees 0.061
Staff quality and experience 0.117
Safety awareness 0.382
Pipeline factors Internal corrosion of pipeline 0.108
Pipeline characteristics 0.217
Pipeline manufacturing defects 0.217
Service life 0.398
Operating pressure fluctuation 0.060
Station factors Operation vibration 0.149
Stray current 0.070
Settlement and displacement 0.243
Local structural failure 0.538
Environmental factors The surrounding environment 0.099
Relative position 0.421
Natural disasters 0.252
Vehicle squeeze 0.067
Complex social environment 0.162
Management factors Daily operation and maintenance management 0.087
Accident alarm system 0.143
Safety management practice 0.385
Rules and regulations guarantee 0.385
Table 8. Efficacy values of various SIFs on system order degree.
Table 8. Efficacy values of various SIFs on system order degree.
U1 U2 U3 U4 U5
Value 0.621 0.615 0.653 0.606 0.796
Table 9. Coupling degree and coupling coordination degree.
Table 9. Coupling degree and coupling coordination degree.
Factors set Coupling degree C Coupling coordination degree U Coupling coordination type
Single-factor F1F1 1.000 0.788 moderate coordination
F2F2 1.000 0.784 moderate coordination
F3F3 1.000 0.808 good coordination
F4F4 1.000 0.778 moderate coordination
F5F5 1.000 0.892 good coordination
Two-factor F1F2 1.000 0.786 moderate coordination
F1F3 1.000 0.798 moderate coordination
F1F4 1.000 0.783 moderate coordination
F1F5 0.992 0.839 good coordination
F2F3 1.000 0.796 moderate coordination
F2F4 1.000 0.781 good coordination
F2F5 0.992 0.836 moderate coordination
F3F4 0.999 0.793 good coordination
F3F5 0.995 0.849 moderate coordination
F4F5 0.991 0.833 good coordination
Multi-factor Three-factor F1F2F3 1.000 0.793 moderate coordination
F1F2F4 1.000 0.783 moderate coordination
F1F2F5 0.993 0.820 good coordination
F1F3F4 1.000 0.791 moderate coordination
F1F3F5 0.994 0.828 good coordination
F1F4F5 0.992 0.818 good coordination
F2F3F4 0.999 0.790 moderate coordination
F2F3F5 0.994 0.826 good coordination
F2F4F5 0.992 0.816 good coordination
F3F4F5 0.993 0.824 good coordination
Four-factor F1F2F3F4 1.000 0.790 moderate coordination
F1F2F3F5 0.994 0.817 good coordination
F1F2F4F5 0.993 0.809 good coordination
F1F3F4F5 0.994 0.816 good coordination
F2F3F4F5 0.994 0.814 good coordination
Five-factor F1F2F3F4F5 0.995 0.809 good coordination
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated