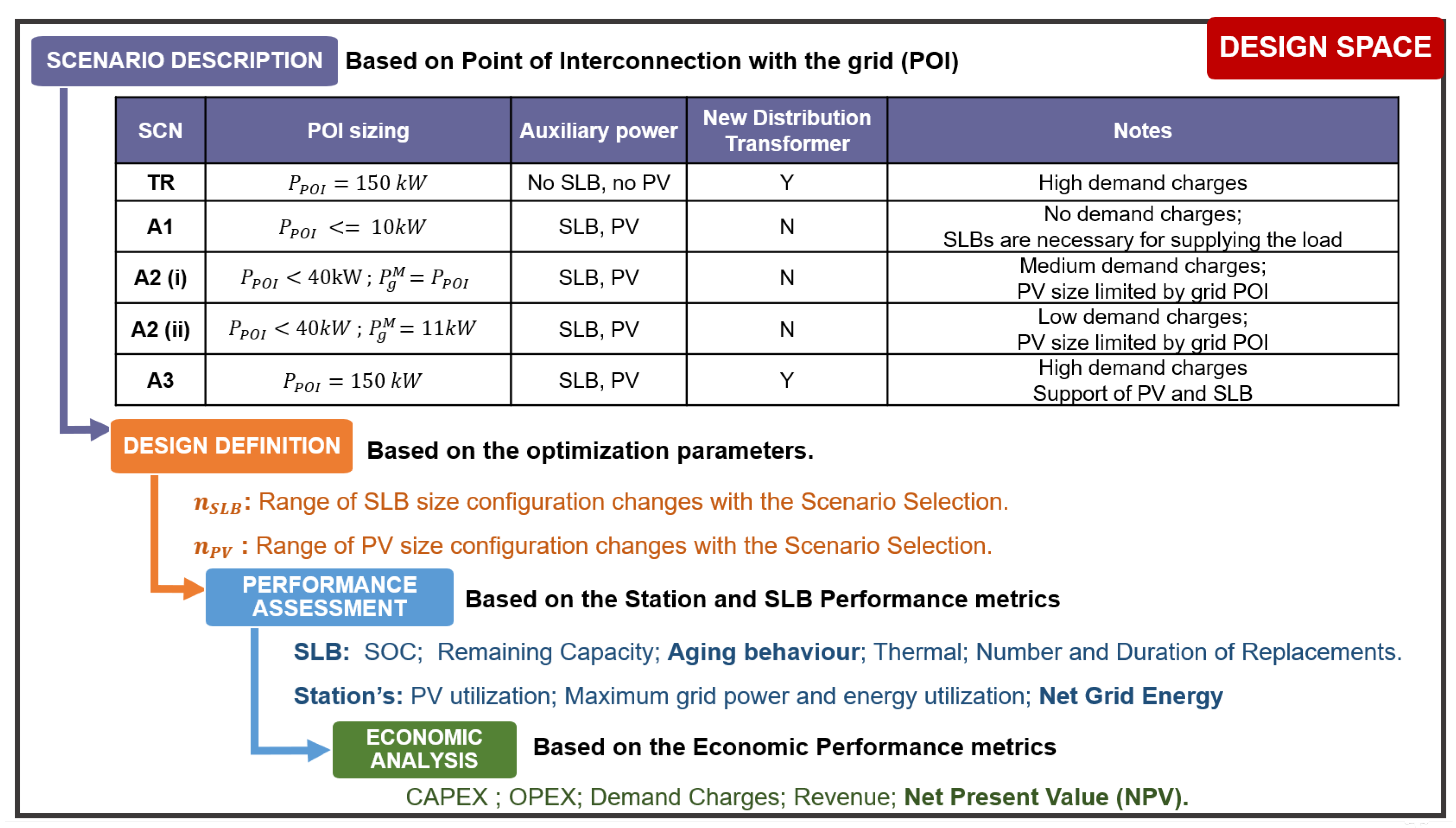
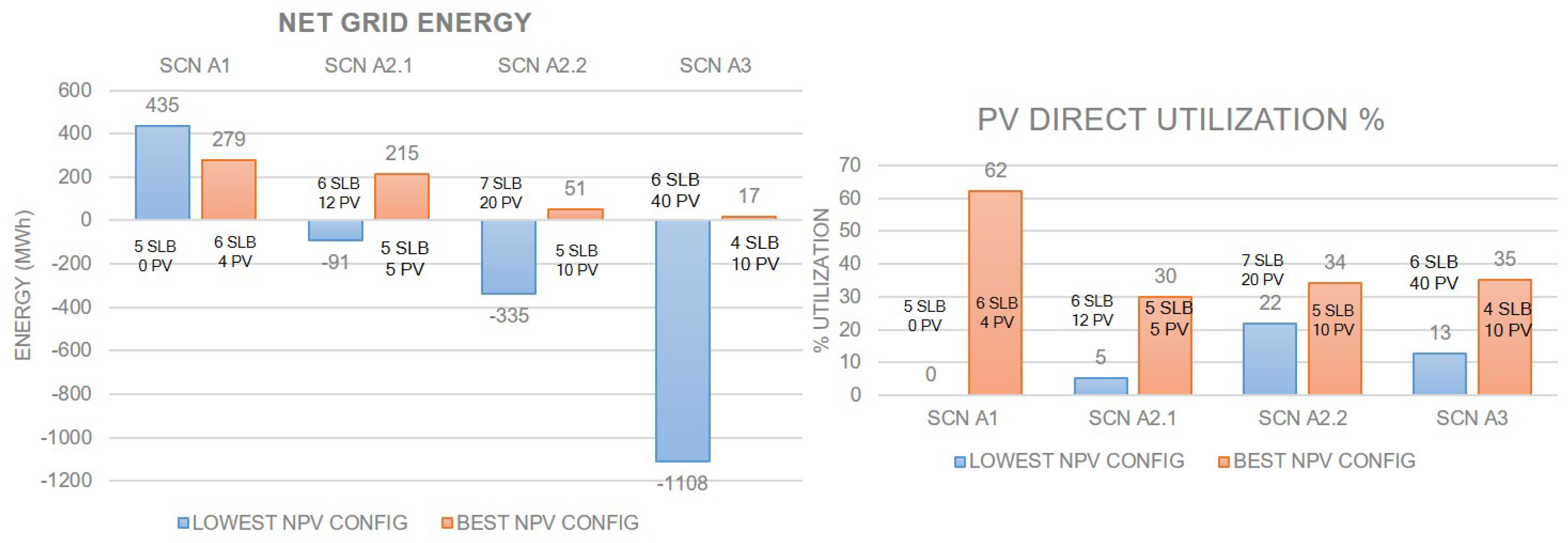
The DCFC station considered in this work includes SLBs and PV systems connected with a low-power bi-directional connection to the grid (Point of Interconnection or POI). Further, a 150-kW charging station is considered as an example, however, this architecture design can be extended to various power levels of DCFC stations. The proposed architecture is an evolution of the concept proposed in [
28,
42].
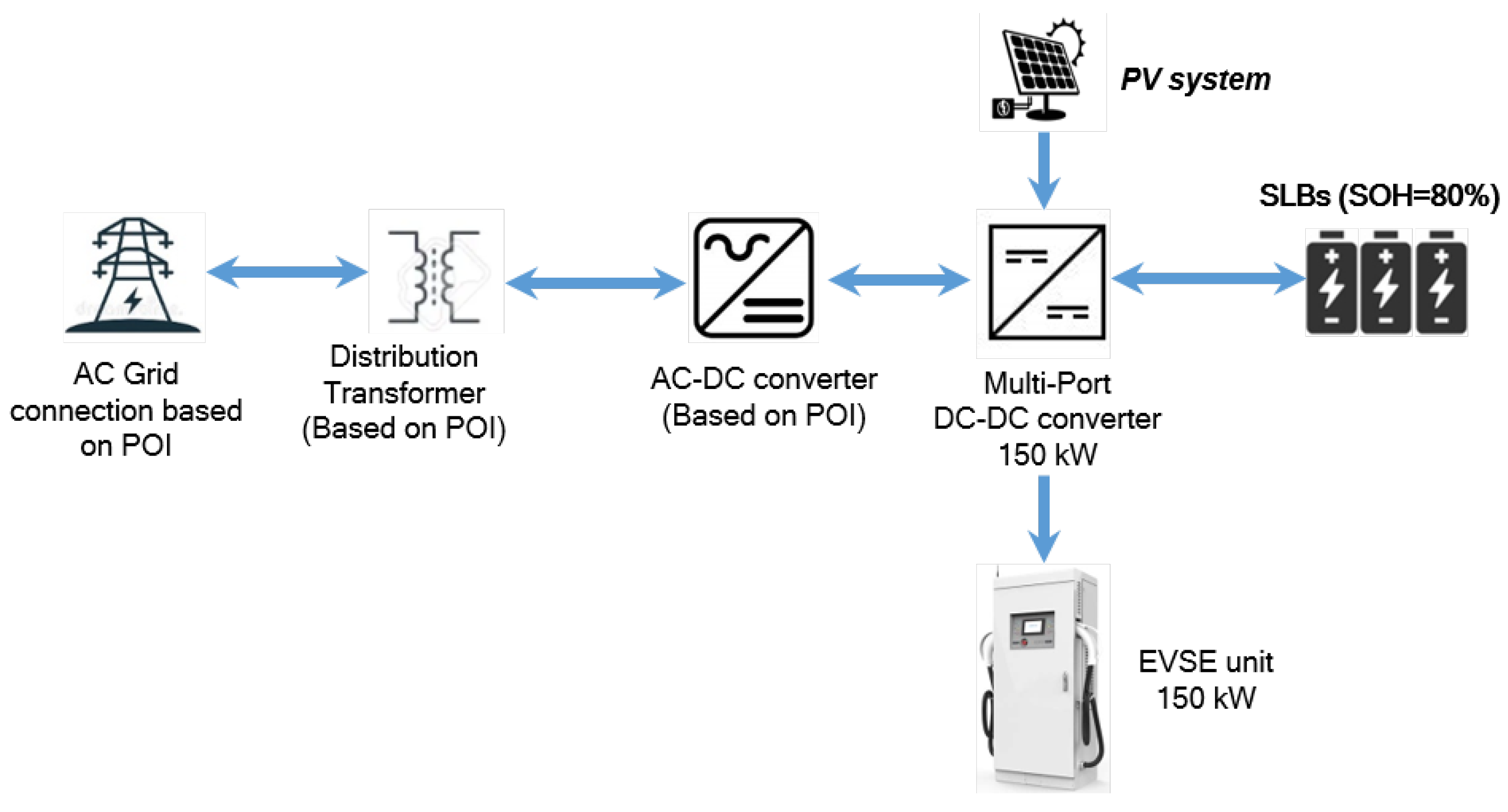
Figure 1 shows the architecture of the proposed DCFC station with connection to its sub-components. The SLBs are connected to the grid using a secondary distribution level transformer and a bidirectional AC-DC converter with a maximum power connection from the grid rating
. The distribution transformer is not considered to be part of the DCFC station when power of the POI is lower than 120 kW, as defined by [
43]. A bidirectional DC-DC converter, rated up to the maximum power of EVs charging, is located on the other side of the SLBs and connects the batteries to the EVs and PV system. The PV is capable of providing power through the DC-DC converters. However, SLB and grid can have bi-directional power flow. The bidirectional flow with the grid enables additional PV power, more than the station’s self-consumption to be sent back to the grid (according to the Net Metering rules [
43]). On the EV side, the connection is made using an Electric Vehicle Supply Unit (EVSE) and unidirectional power flow. The Vehicle-to-Grid (V2G) capability is not considered for this study.
An Energy Management Controller (EMC) has been developed to prioritize the charging power availability for EV users and maintain the battery’s SOC within safe operating ranges. The energy required by the EVs can be delivered by the stored energy in the SLBs. Additionally, the remaining energy requirement of the EVs can be supplied by two sources - PV and the grid. Using SLBs as the direct supply of power reduces the power dependence of the EVs on the grid. Further, the SLBs can be charged using sources PV and the grid. The proportion of the power provided by either of the sources is dependent on the availability of solar energy.
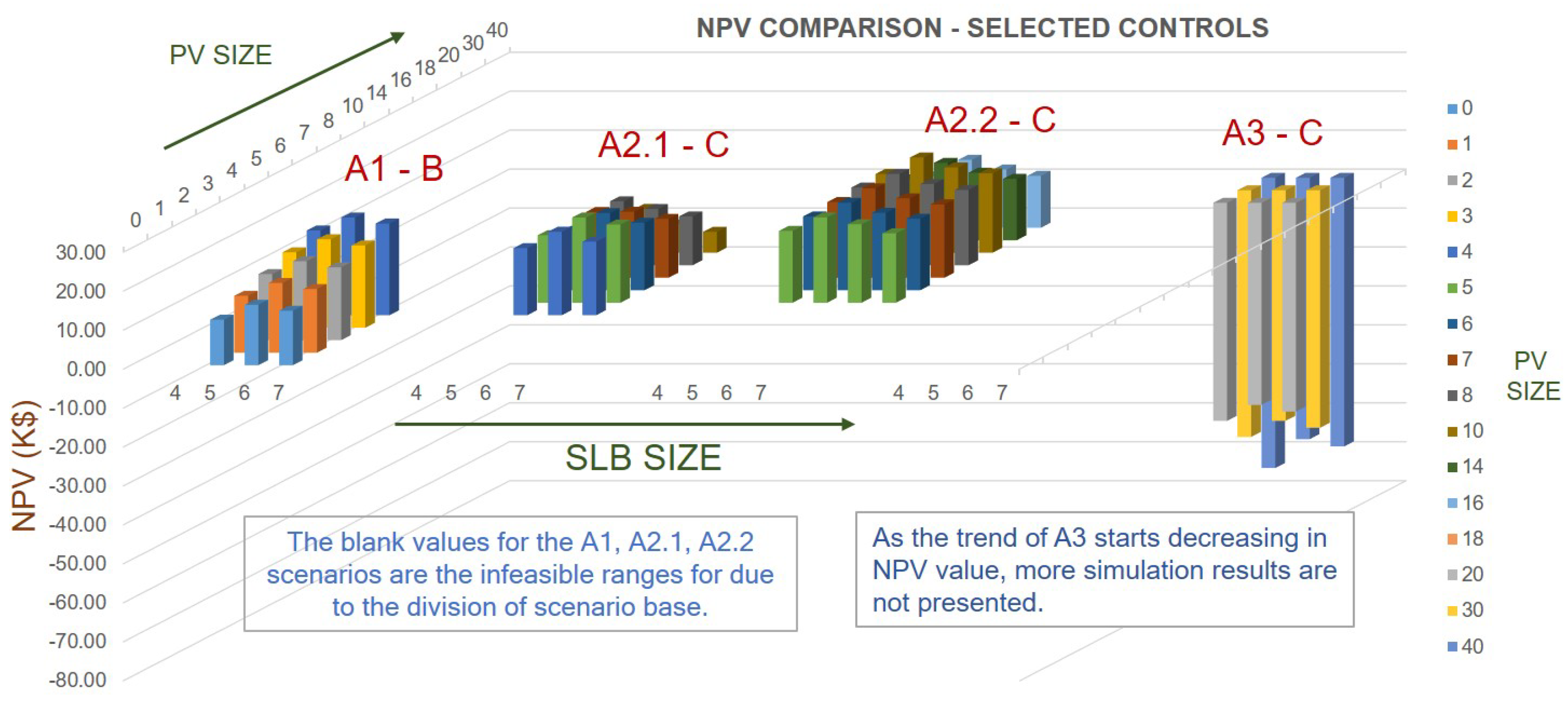
To maximize the station’s performance and economic benefits, interaction of the DERs (SLBs and PVs) and the grid needs to be optimally configured. A sub-optimal configuration could lead to over-sizing or under-sizing of the sources or DERs causing economic and energy loss. Design parameters for this work are chosen as the sizes of SLBs () and PVs (), and the grid interconnection power ().
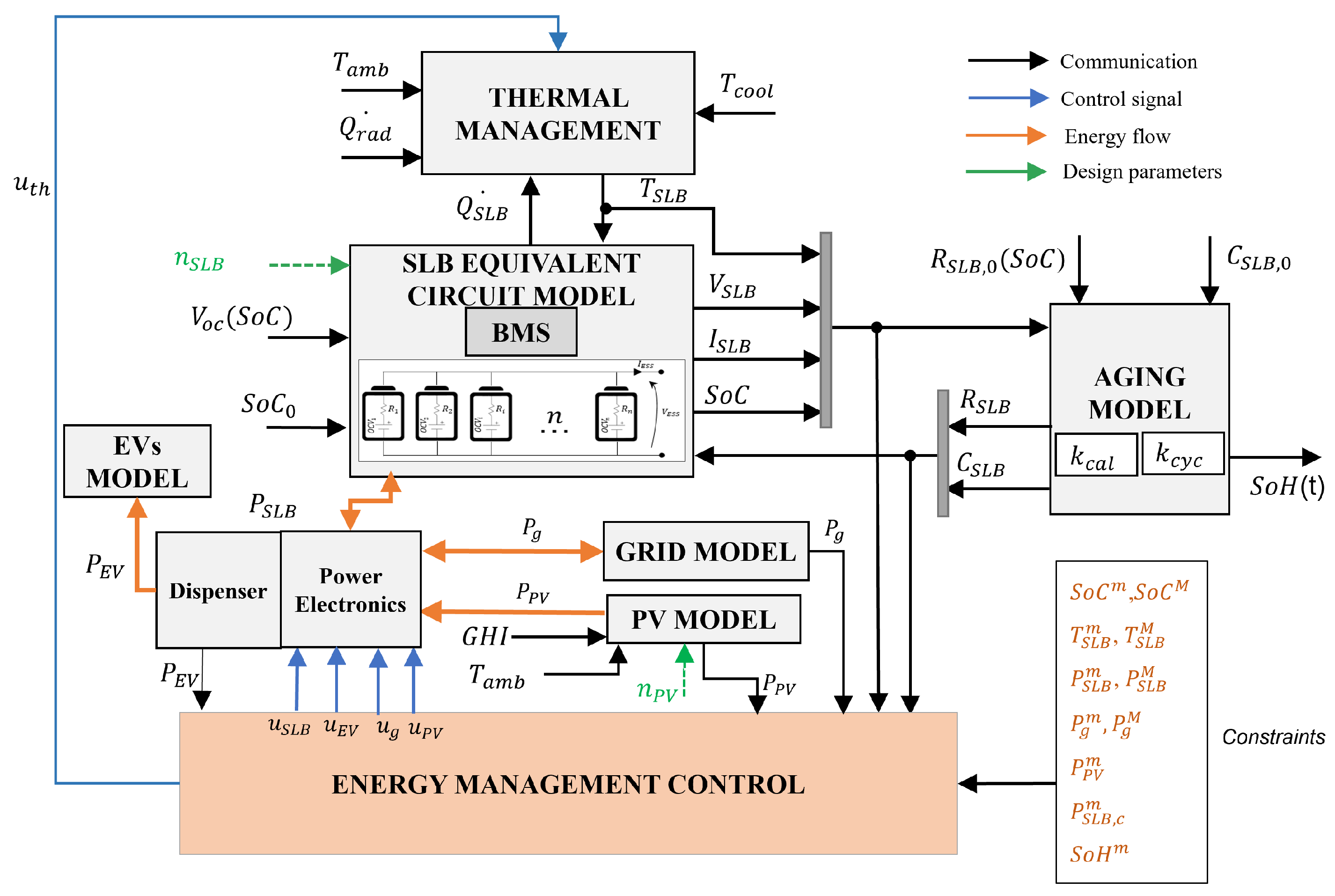
This section describe the thermo-electric model of the station and the financial model of the investment. The station model receives design inputs along with environmental factors and daily EV demands. Each sub-system outputs the daily energy requirements of the station and its components along with the estimate of the SLB’s State Of Heath (SOH). The power, energy requirements, and SLB replacement factor are given to the economic model that provides daily, monthly, and yearly cash flow which is discussed in the later subsection. Multiple pieces of literature and data from national labs are used to calibrate all of the sub-system model and economic model parameters.
2.1. System Modeling
The architecture of the DCFC station model has been referred from [
28,
41,
42,
44,
45,
46], and updated for this work. The details of the components with their respective models are given in the
Table 1. An overview of the system model architecture is shown in
Figure 2. The model design is augmented considering a multi-source DCFC station including a grid connection, PV model, and SLB packs.
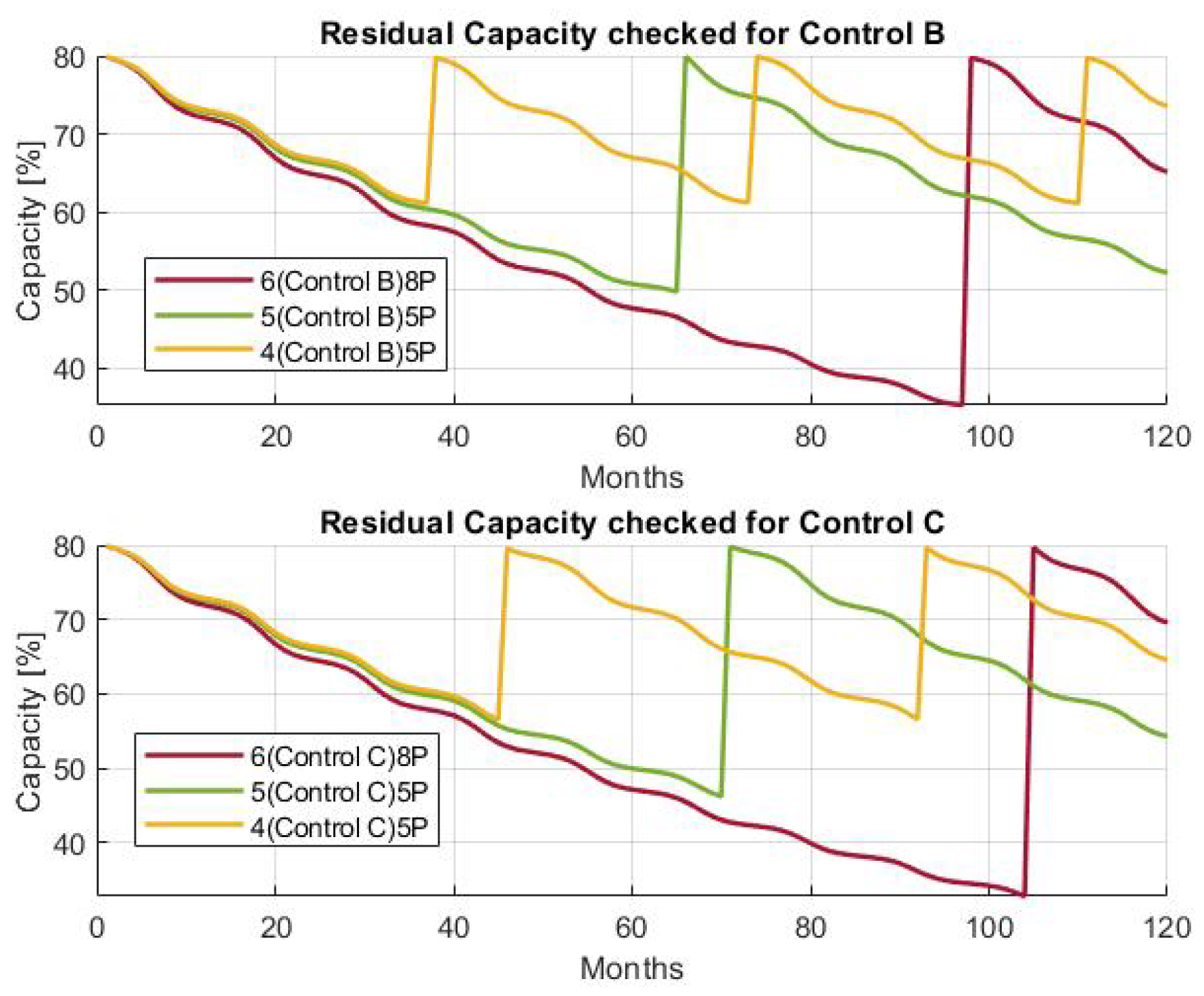
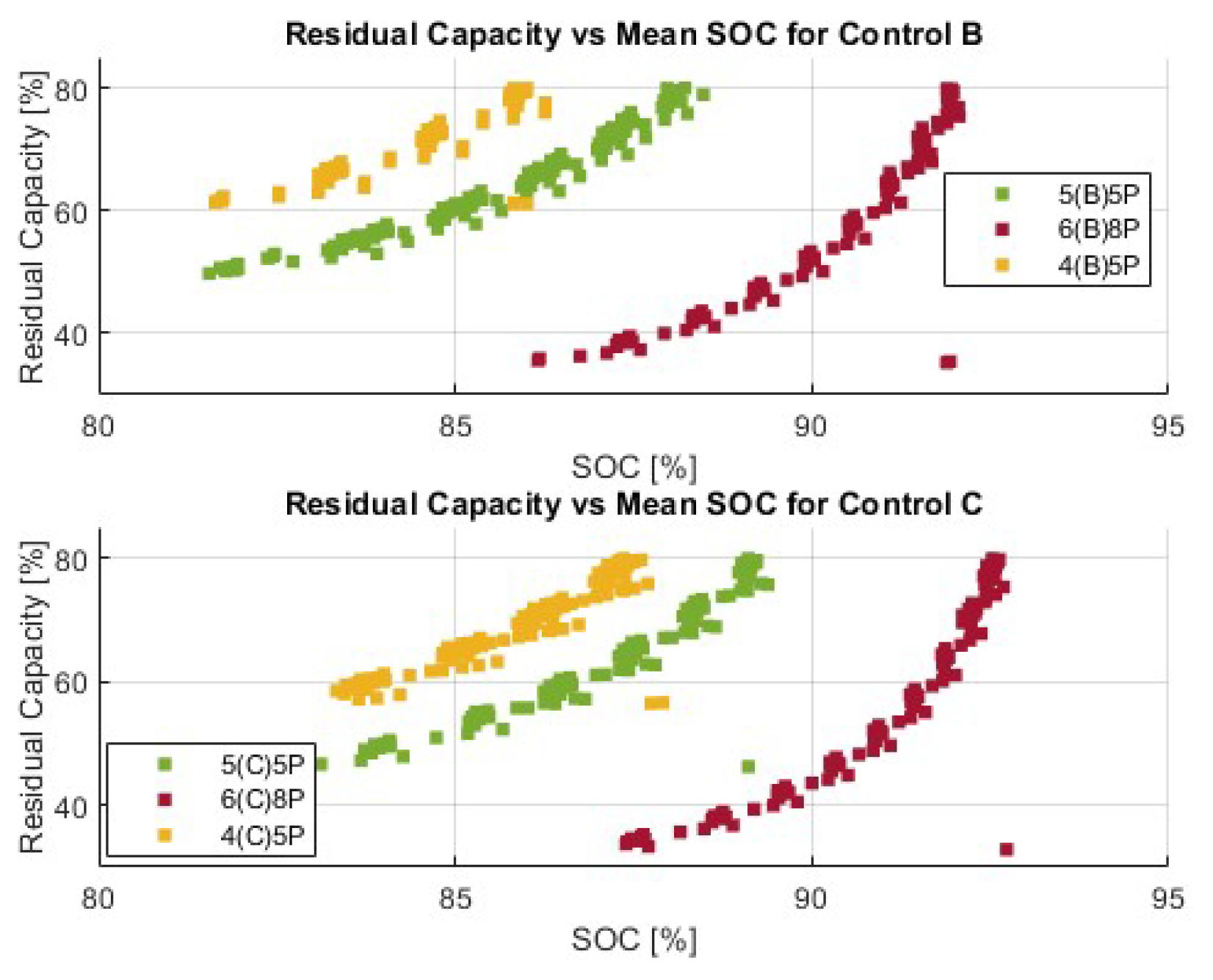
The battery pack model includes electrical, thermal and degradation performance. The aging method estimates the capacity and internal resistance of the batteries based on the cycle and calendar life using the realistic operating conditions of the battery estimated by the battery electro-thermal model. A thermal management model is emulating a liquid cooling system and related control. The battery model has been incorporated with a Battery Management System (BMS) model to keep the battery’s parameters in the safe operating region (voltage, current, temperature, state of charge limits) [
46]. The battery capacity and internal resistance are degraded overtime on the basis of the current, state of charge and temperature of operation. The model used in this work includes both calendar and cycling aging and is inspired to the empirical aging model reported in [
45] The PV model is based on the real solar irradiation and weather data from Columbus, Ohio, year 2020 [
47] and the PV panel used is BP 3 SERIES 235 Watt [
48]. The EV model acts as a load when EVs are present, power converters model provides efficiency based on system power and voltage. The EV load is modeled as a series of pulses distributed in time, as developed in [
41]. The grid model outputs the power based on the request from the Energy Management Controller (EMC). The grid’s initial boundary conditions are set up to maintain the system parameters within defined ranges of several predetermined scenarios.
Table 1.
Details of the models used in DCFC station model architecture.
Table 1.
Details of the models used in DCFC station model architecture.
| Components |
Model used |
References |
| SLB |
Zero-order Equivalent Circuit Model |
[28,42] |
| SLB Thermal |
Lumped Parameter Thermal Model |
[28,42] |
| SLB BMS |
State flow |
[46] |
| SLB Aging |
Daikin’s battery aging model |
[28,42,45] |
| PV |
5 parameter model |
[49] |
| AC-DC and DC-DC |
Efficiency based model |
[41] |
| EV Load |
Event based profile |
[41] |
An EMC is included to enable a proper operation of the station over the lifetime and ensuring power readily available for EVs under realistic system constraints. To select the power source, EMC collects the battery information in terms of
, temperature
and voltage
from the SLB model, PV available power
and the load request
from EVs at time
t to define the power reference for SLB, PV and grid (
,
,
, respectively). The other tasks are to fully utilize the PV energy and maintaining the battery SOC within a certain operating range. The EMC operates in such a way to maintain SLB charging while maximizing PV utilization when EVs are not present at the station. If there is surplus PV energy available, net metering [
43] will be used. The SLB charge is allowed only if EVs are not present. The control strategy allows SLB to be charged through PV whenever solar irradiation is available. If the PV power is more than the minimum charging power threshold of SLB
, all the available PV power is given to the SLB charging and no power is used from the grid. However, if the PV power is less than the charging power threshold
, the grid supplements the SLB charging up to the minimum charging power of SLB. Note that
varies with the selection of scenarios, discussed in the
Section 3 and is considered as the maximum power used from the grid
. When the PV is available and SLB is fully charged (SOC > 95%), the PV residual power is fed into the grid and will be operated in net metering mode. The details of SLB and EV charging controls are given in
Table 2 and
Table 3, respectively.
For EV and SLB charging mode, the power balance equation is given in (
1).
During EV charging, three types of control strategies for EV charging are considered. These strategies change the dependence on the grid and PV for EV charging and the ways they are used to support SLBs during EV charging.
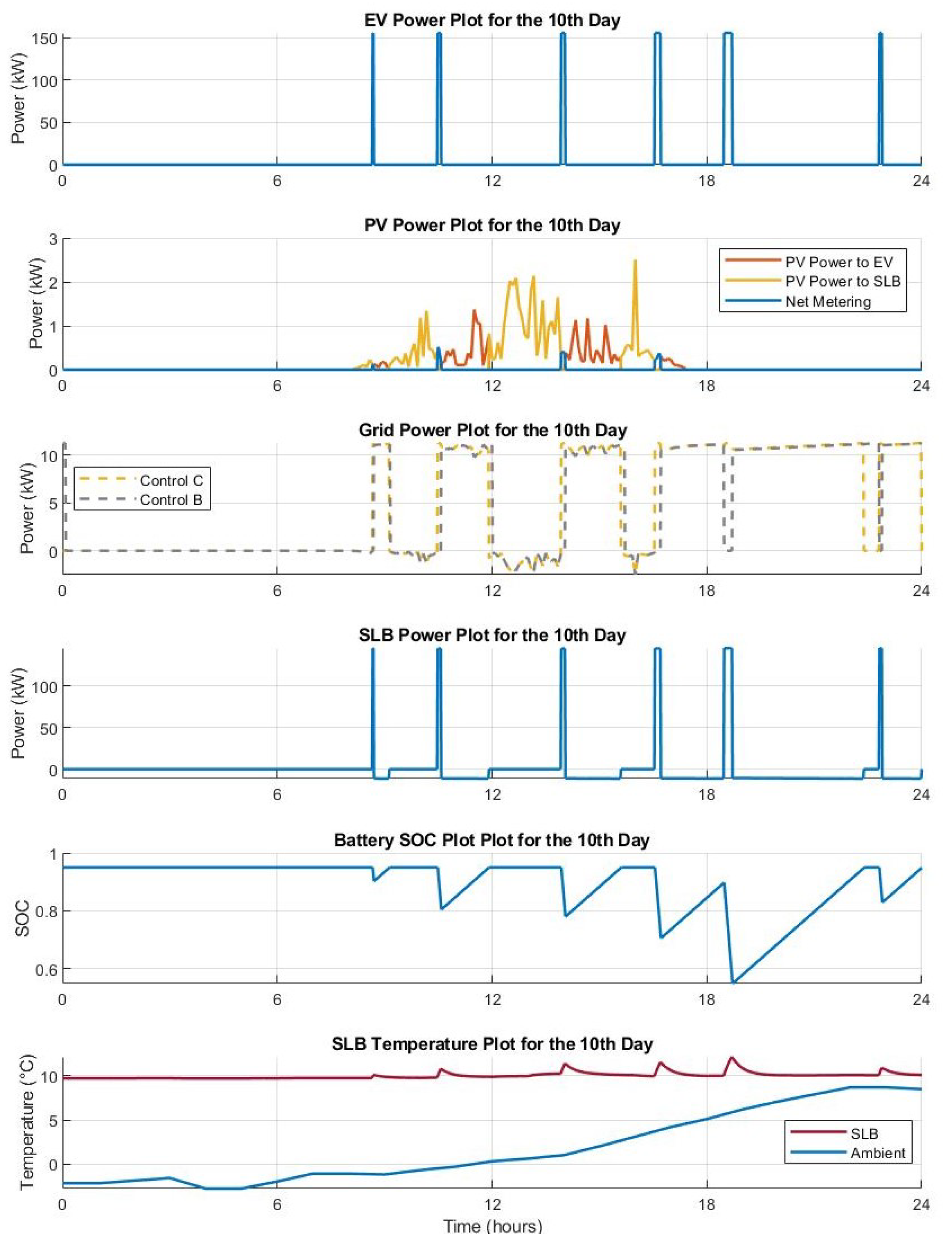
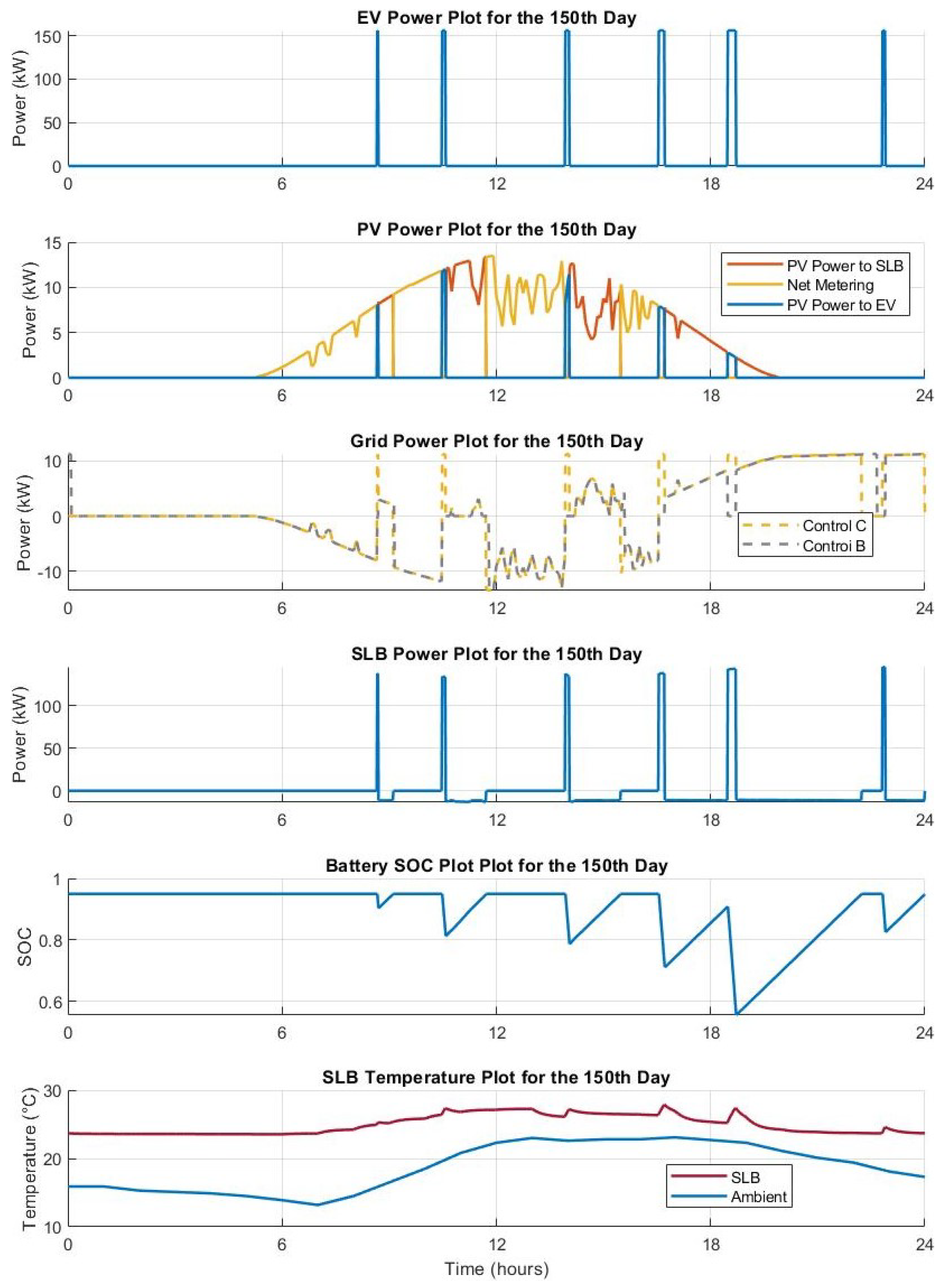
CONTROL A: Charge EV only from SLB. In this control strategy, the EVs are directly charged from the SLBs and no other source is used.
CONTROL B: Charge EV from SLB and PV. In this control strategy the PV power, if available, has the priority when an EV request to be charged with the aim of maximizing the energy from renewable resources. The PV power is equal to the Maximum Power Point
[
50]. Then, the remaining power required by the EVs is supplied by the SLB. There is no use of grid energy to charge EVs in this control.
CONTROL C: Charge EV from SLB, grid and PV. In this control strategy the PV power, if available, has the priority when an EV request to be charged with the aim of maximizing the energy from renewable resources. The PV power is equal to the Maximum Power Point . Then, the remaining power required by the EVs is supplied by the SLB and the grid. The grid power supplies the maximum interconnection power .
2.2. Economic Modeling
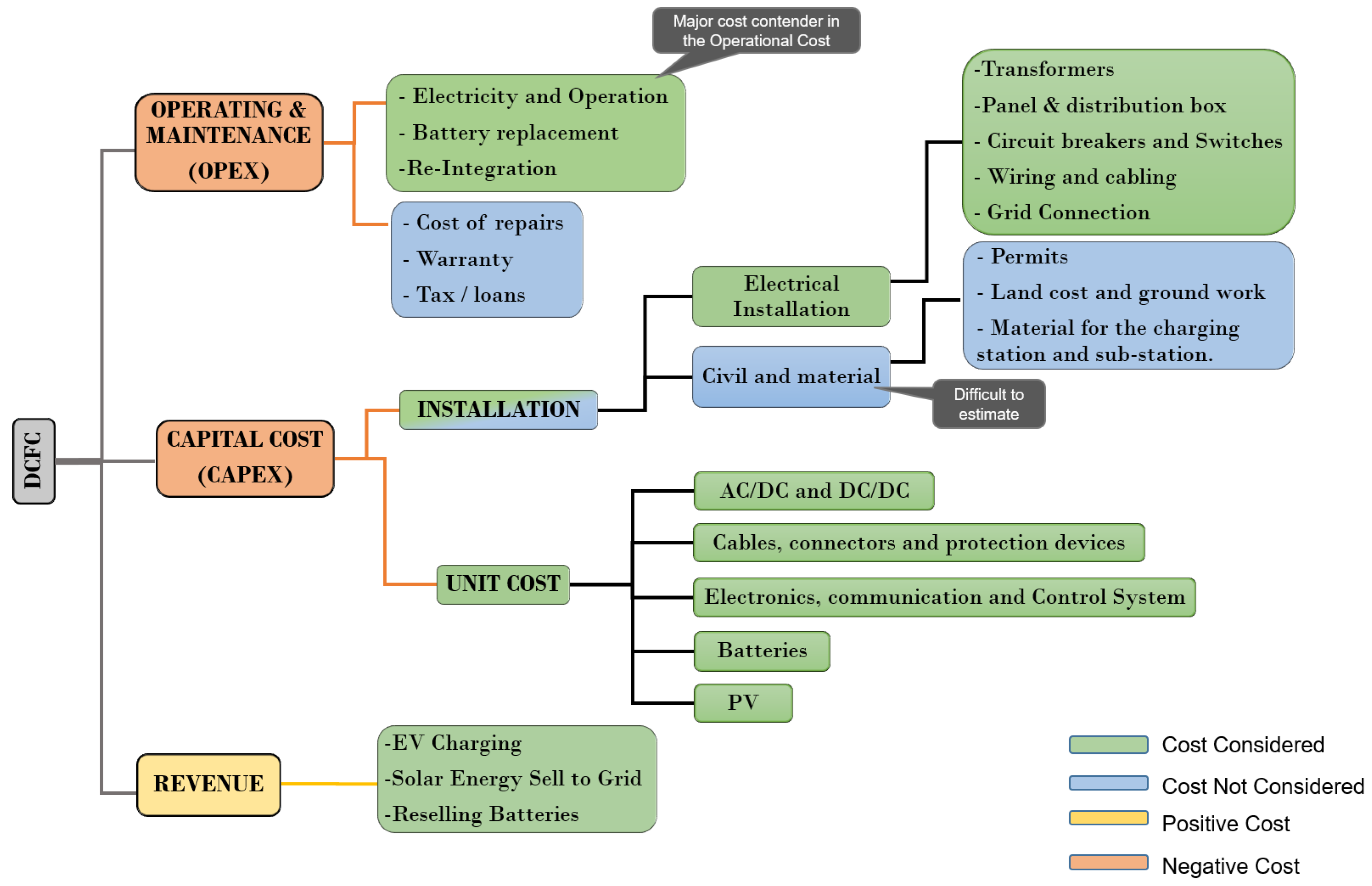
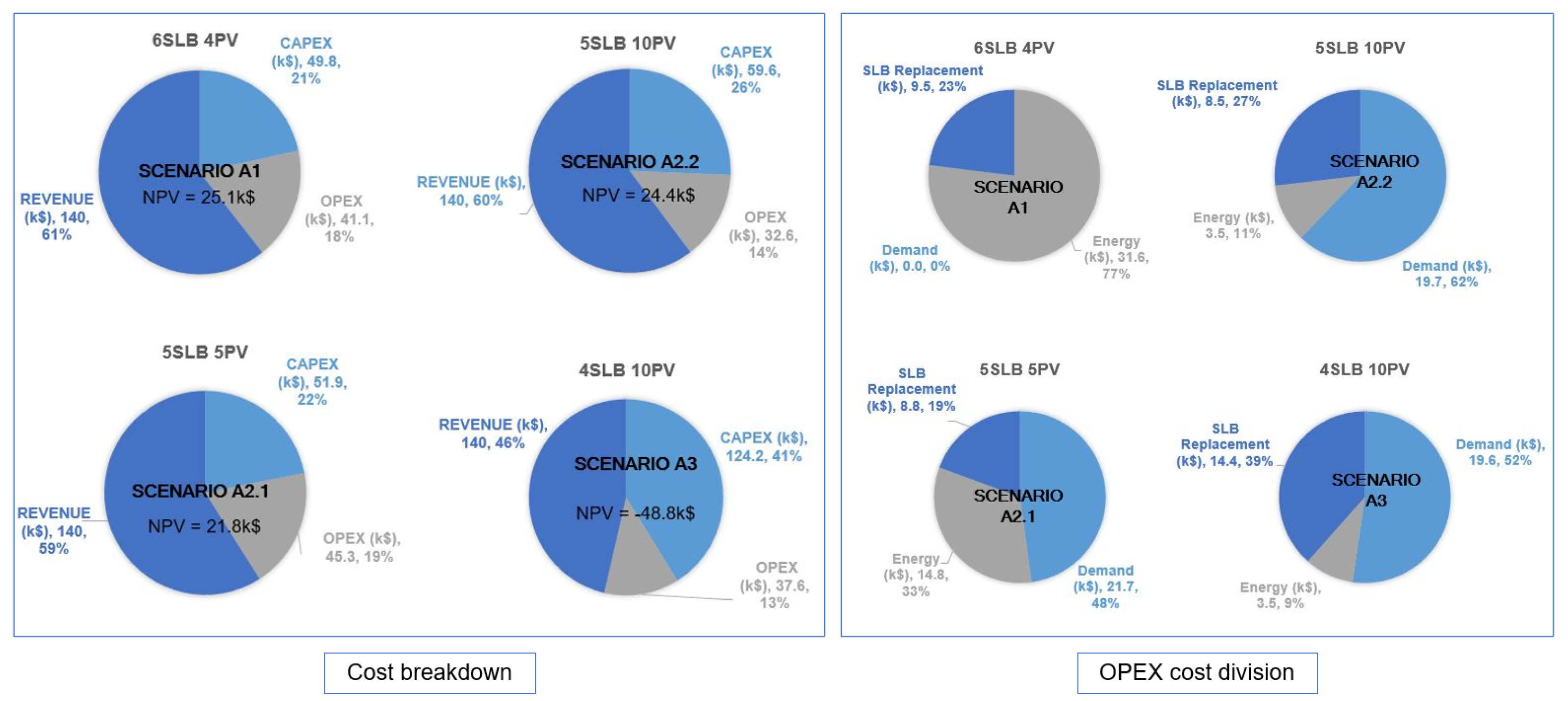
In this sub-section, the cost of ownersip of the EV DCFC station is evaluated and the economic value of the station is assessed through Net Present Value (NPV) method. The breakdown of cost structure by owning, maintaining, and operating a DCFC station is considered for both the traditional and proposed station models which is later compared in the results section. The cost can be categorized as capital cost (CAPEX), operating cost (OPEX), and revenue. The description of components for the DCFC cost is shown in
Figure 3 which includes all major cost components of the proposed DCFC station.
The capital investment cost, or CAPEX, is based on the price of the materials and the cost of their installation related to DCFC’s components. Because it is challenging to predict the site and land needs, permitting and civil costs are outside the scope of this work. The operational cost, also known as OPEX, is the variable cost that fluctuates with time and consumption depending on how the sources are used, such as the cost of the electricity in terms of energy and power. The cost of charging station maintenance, which primarily consists of SLB replacement needs, is also included. The replacement of PV modules and station maintenance is not taken into account as the components’ and PV life exceeds the project’s total life. Taxes are paid for electricity use and EV charging, warranties and location-based taxes are not taken into account. The station’s expenses are its CAPEX and OPEX costs, while revenue represents cash inflow from the EV charging events, and various revenue sources such as solar credits and battery resale earnings.
The cost parameters with their descriptions and references are listed in the
Table 4,
Table 5 and
Table 6. A detailed survey of recent literature and data has been performed to accurately evaluate the values of each cost component and for each of the cost categories. The data have been collected from a multitude of publications from industry, national laboratories, academia, and energy reports.
The Balance of System (BOS) is part of the CAPEX that includes components of a BESS excluding the battery pack’s cost. The segregation is done from the BESS to cost per unit basis in terms of energy for BESS and in terms of power for BOS . BOS includes BMS, Thermal Management System (TMS), wiring and cabling, connectors isolation system and protection circuits, and Fire Management System (FMS). Re-purposing or re-integrating the SLBs also added cost to the CAPEX value.
The parameters for the demand charges and the electricity charges have been referenced from the Ohio Electricity Tariff rules [
51]. The values of the bill have been normalized to obtain
$/kWh value for the energy or electricity consumption in terms of kWh used and in
$/kW for the demand charges to account for the power in kW used.
The revenues have three contributors, the earnings from EV charging, the earnings from selling the batteries after the end of the project with the energy capacity remaining, and finally the earnings from Solar Renewable Credits (SREC) for the extra energy produced from PV and sold to the grid (in compliance with net metering rules of Ohio [
43]). The SREC values are based on Locational Marginal Price (LMP) in real cases and change dynamically like a stock market. Hence for simplicity, an average value has been considered from Ohio’s history of SREC prices over a year [
52,
53].
From the values of CAPEX, OPEX, and Revenues, the following equations are used.
is the number of PV panel arrays in parallel (number of panels in series is decided as per the battery pack max voltage) and
is the number of battery packs in parallel. Sizing details are explained in
Section 3.
The operational cost is divided into two parts which includes the cost of paying the electricity bills which constitute demand charges and energy charges as given in (
6).
The other part of the operational cost is due to the SLBs when they need the replacement. Equation (
7) breaks down the replacement cost of batteries.
gives the cost of replacing the SLBs after their End of Life (EOL) and
gives the operational cost of integrating the replaced SLB packs.
The revenues is represented as
given in Equation (
8) has 3 contributors as the earnings from EV charging
, the earnings from selling the batteries after the end of the project with the energy capacity remaining
, and finally the earnings from Solar Renewable Credits for the extra energy produced from PV and sold to the grid
.
Table 4.
CAPEX cost parameters with their description, unit, variables and values.
Table 4.
CAPEX cost parameters with their description, unit, variables and values.
| Description |
Symbol |
Unit |
Value |
References |
| Unit Cost of SLB |
|
$/kWh
|
63.2 |
[27,28,54,55,56,57,58] |
| Unit Cost of PV |
|
$/kW
|
410 |
[27,29,30,54,55,56,57,58] |
| Unit Cost of AC-DC |
|
$/kW
|
108.5 |
[27,29,54,55,56,57,58] |
| Unit Cost of DC-DC |
|
$/kW
|
100 |
[27,29,54,55,56,57,58] |
| Unit Cost of SLB integration |
|
$/kWh
|
55 |
[59,60,61,62,63] |
| Unit Cost of SLB modification |
|
$/kW
|
50 |
[59,60,61,62,63] |
| Unit Cost of BOS |
|
$/kW
|
40 |
[54,55,56,57,58] |
| Unit Cost of AC connection |
|
$/kW
|
100 |
[54,55,56,57,58] |
| Unit Cost of Distribution transformer |
|
$/kW
|
250 |
[64,65,66] |
| Unit Cost of EVSE |
|
$/kW
|
100 |
[54,55,56,57,58] |
Table 5.
OPEX cost parameters with their description, unit, variables and values.
Table 5.
OPEX cost parameters with their description, unit, variables and values.
| Description |
Symbol |
Unit |
Value |
|
| Unit Cost of SLB replacement |
|
$/kWh
|
63.2 |
[27,28,54,55,56,57,58] |
| Unit Cost of replaced SLB integration |
|
%/kWh
|
55 |
[59,60,61,62,63] |
Table 6.
Revenue cost parameters with their description, unit, variables and values.
Table 6.
Revenue cost parameters with their description, unit, variables and values.
| Description |
Symbol |
Unit |
Value |
References |
| Unit Cost of EV charging |
|
$/kWh |
0.32 |
[67,68,69] |
| Unit Cost of selling battery with remaining capacity |
|
%/kWh |
63.2 |
[27,28,54,55,56,57,58] |
| Unit Cost of Solar Renewable Energy Credits (SREC) |
|
$/kWh |
0.03 |
[52,53] |
Table 7.
Unit costs in various scenarios.
Table 7.
Unit costs in various scenarios.
The relations of unit cost and the total cost values are shown below in
Table 8. The variables with ‘
E’ denote the energy and ‘
P’ is the power. The superscript ‘
M’ is the maximum value. The variable
is the energy capacity of each pack which is 23 kWh, and
is the maximum energy capacity of all SLB packs together (based on the number of SLB packs
) on which the total cost of SLB
is based on. Similarly,
is the maximum power for a single PV module, and the total cost of PV
depends on the total number of modules used
. The
is the replacement index of the SLBs defining the number of replacements.
Table 8.
Relation of Cost Parameters.
Table 8.
Relation of Cost Parameters.
| Description |
Symbol |
Equation |
| Cost of SLB |
|
|
| Cost of PV |
|
|
| Cost of AC-DC |
|
|
| Cost of DC-DC |
|
|
| Cost of SLB integration |
|
|
| Cost of SLB modification |
|
|
| Cost of BOS |
|
|
| Cost of AC connection |
|
|
| Cost of Distribution transformer |
|
|
| Cost of EVSE |
|
|
| Cost of SLB replacement |
|
|
| Cost of integrating replaced SLB |
|
|
| Revenue from EV Charging |
|
|
| Revenue from selling battery with remaining capacity |
|
|
| Revenue from SREC |
|
|
Revenue from SREC is earned when Net Metered energy is negative (supplied back to the grid).
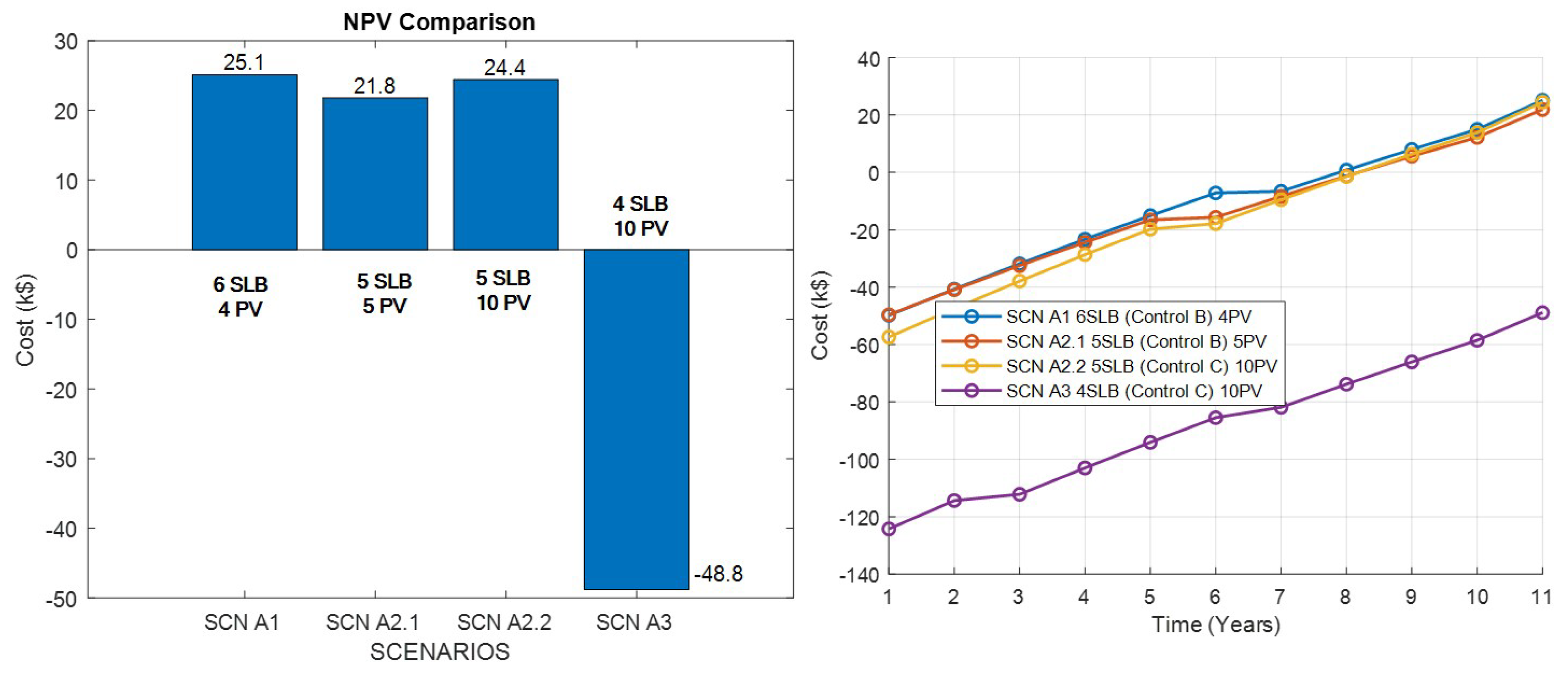
Net Present Value (NPV) is the present value of the cash flows at the required rate of return of a project compared to the initial investment. It is calculated by estimating future cash flows related to a project. Then, these cash flows are discounted to present value using a discount rate representing the project’s capital costs, operating costs, and desired rate of return. NPV gives the overall value of the project from the investment and earnings point of view [
70]. The NPV is calculated as:
where
is net cash inflow-outflows during a single period
t.
t is the number of time periods, and years in our case and the
d is the discount factor. To account for the NPV cash flow, it is important to consider the following parameters:
Discount Factor: Accounts for the change in the power of money over the years.
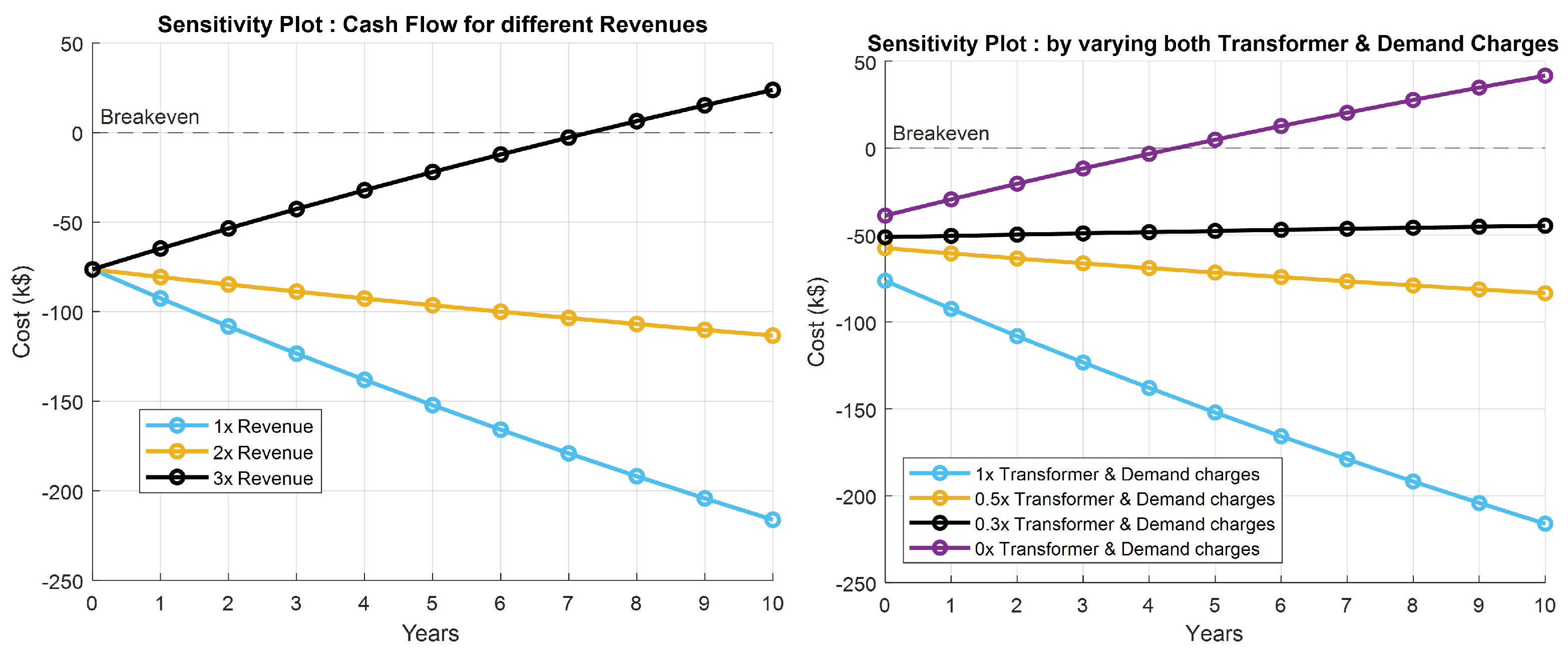
Electricity Charges Inflation: Due to the change in means of resources and overall inflation, electricity charges inflate over the years. From the historical trend of electricity rates in the US and in Ohio, the inflation percentage has been taken as constantly growing per year. To account for both demand and energy charges inflation, the rate of inflation has been considered the same.
Revenue Inflation: Same consideration and the percentage growth of inflation has been taken as the electricity charges inflation due to dependence of revenue earned in $/kWh by charging EVs has electricity charges as a major contributor apart from the other earnings to recover the cost of the station.
Battery Prices: Battery prices are forecasted to decrease over the years due to more supply and demand matching and technology getting better. This is depreciation or negative inflation and its value has been chosen as a rate from forecast reports and historical data studies.
The inflation parameters are given in
Table 9, that are the early percentage inflation rates multiplied with their cost parameters after the zeroth year (the year of investment). The investment has a 0th-year cash value that is negative. The discounted normalization is added to the OPEX and Revenue to determine the real cost incurred and earned. The deferred difference between OPEX and Revenue for each year is used to determine the present value of money. The cash flow
is derived as the product of the project’s cash in the prior year and its present value for the current year. The cash flow fluctuates each year according to the present value, which depends on earnings and expenditures.