Submitted:
15 July 2024
Posted:
17 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Site Description
1.2. Reservoir Geology and Fluid
1.3. Production History
2. Materials and Methods

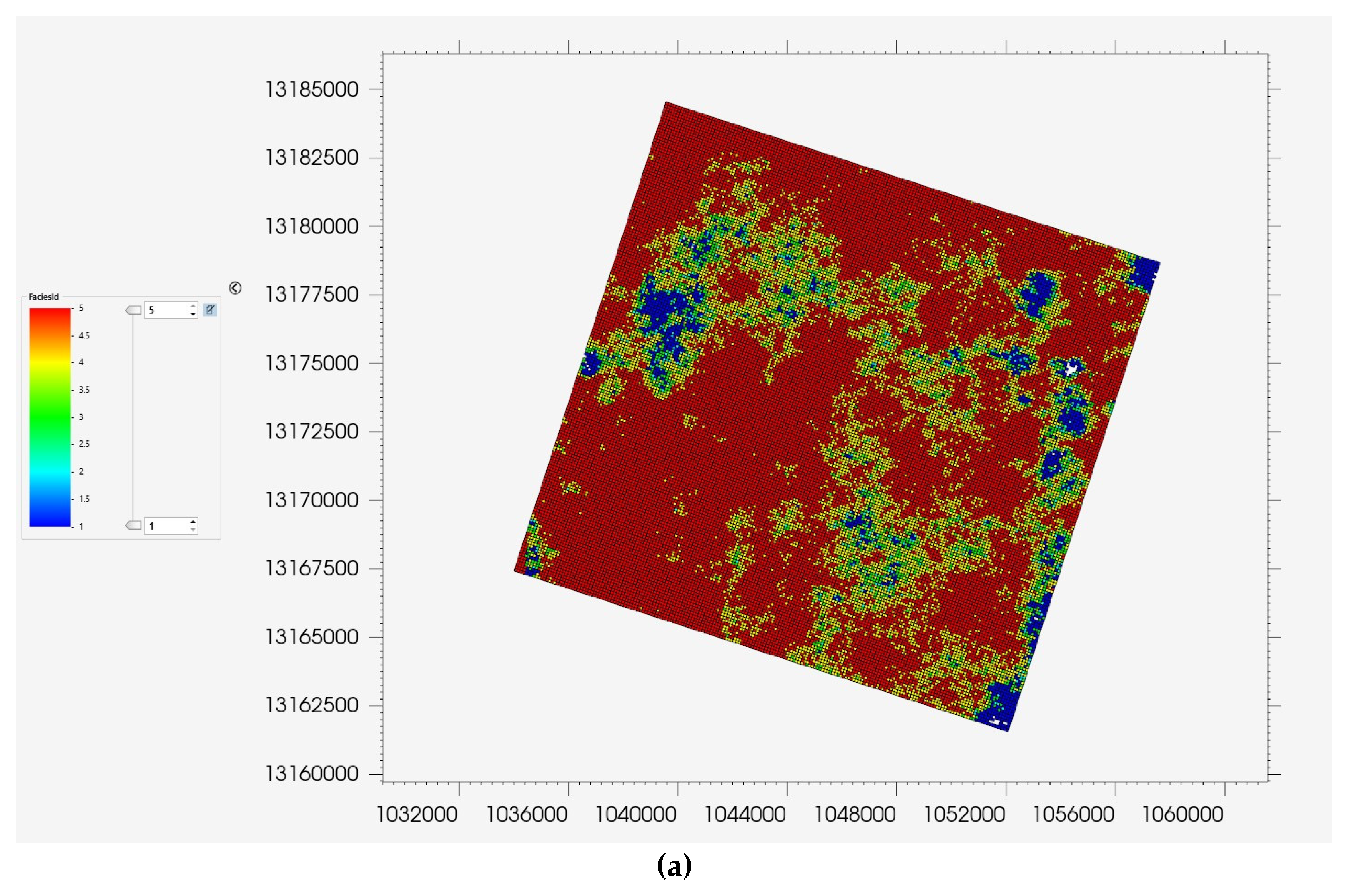
2.1. Construction of Reservoir Model
2.2. Dynamic Reservoir Model
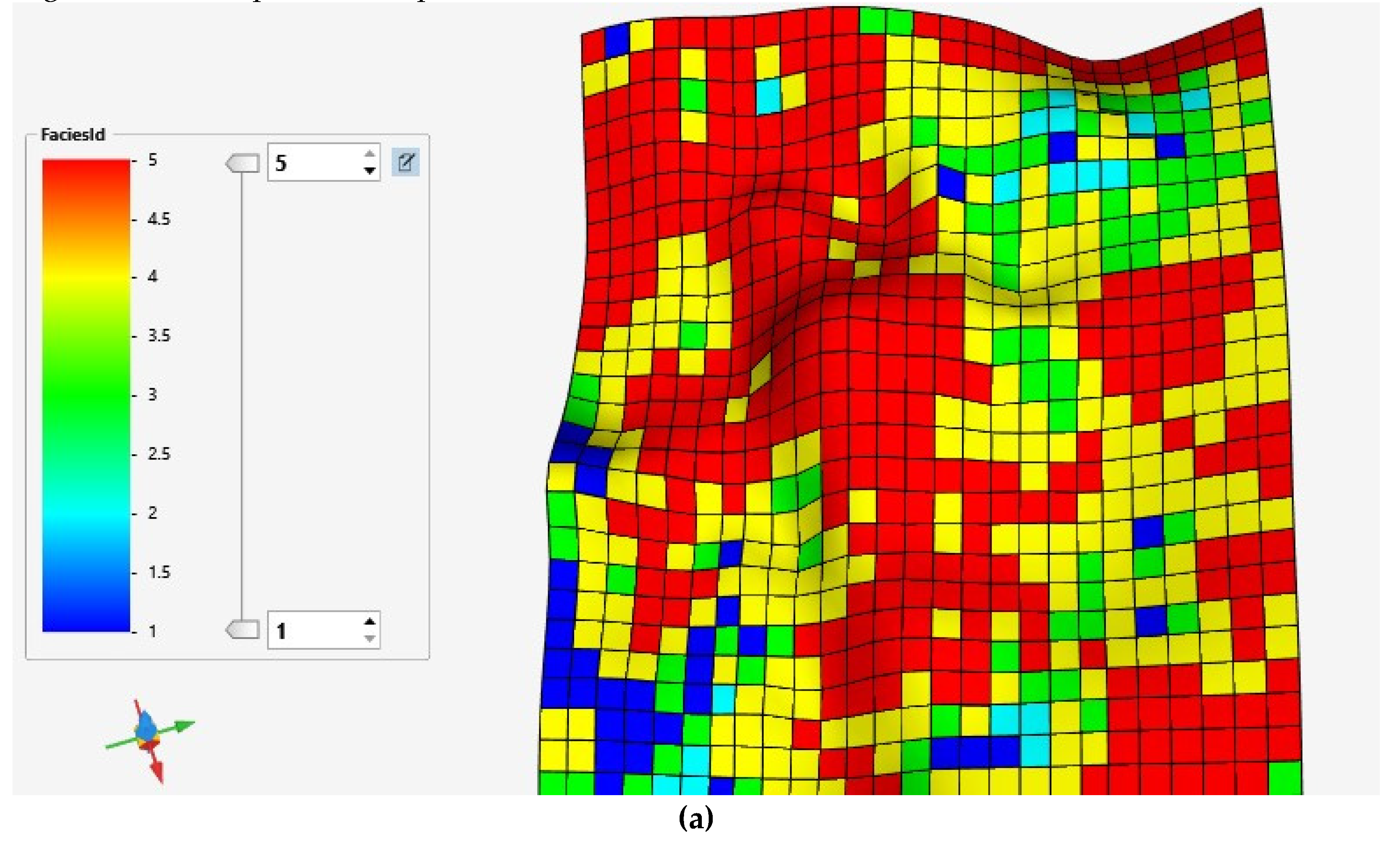
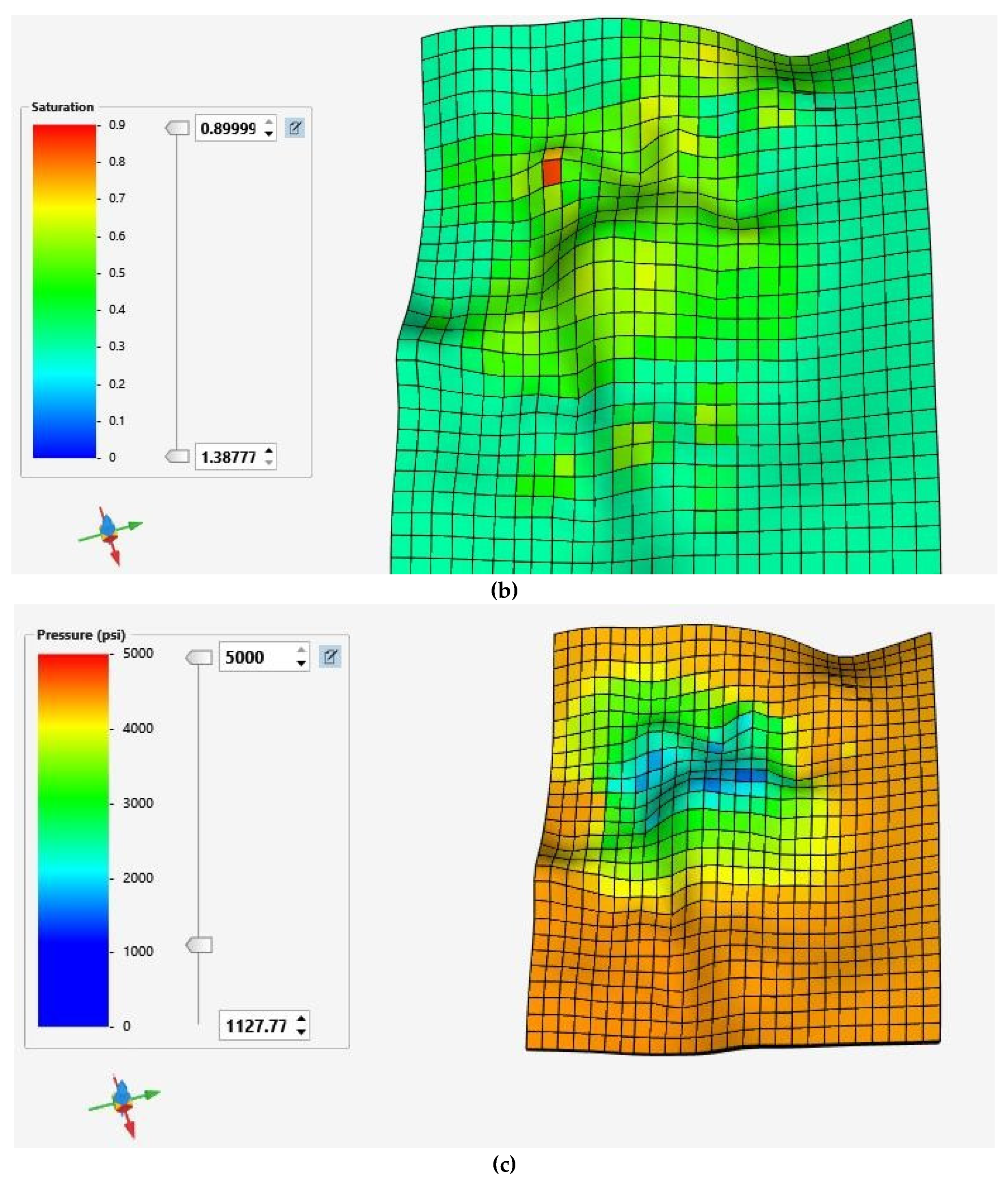
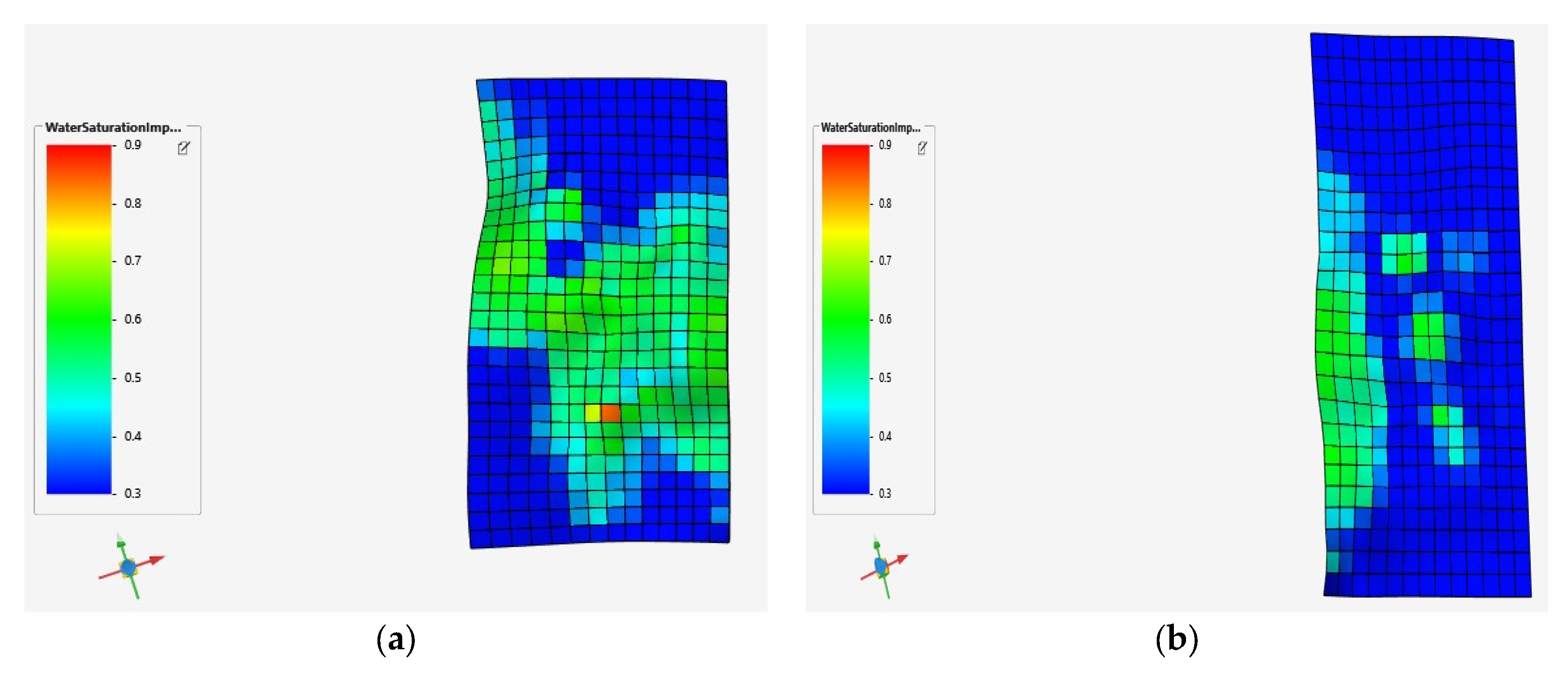
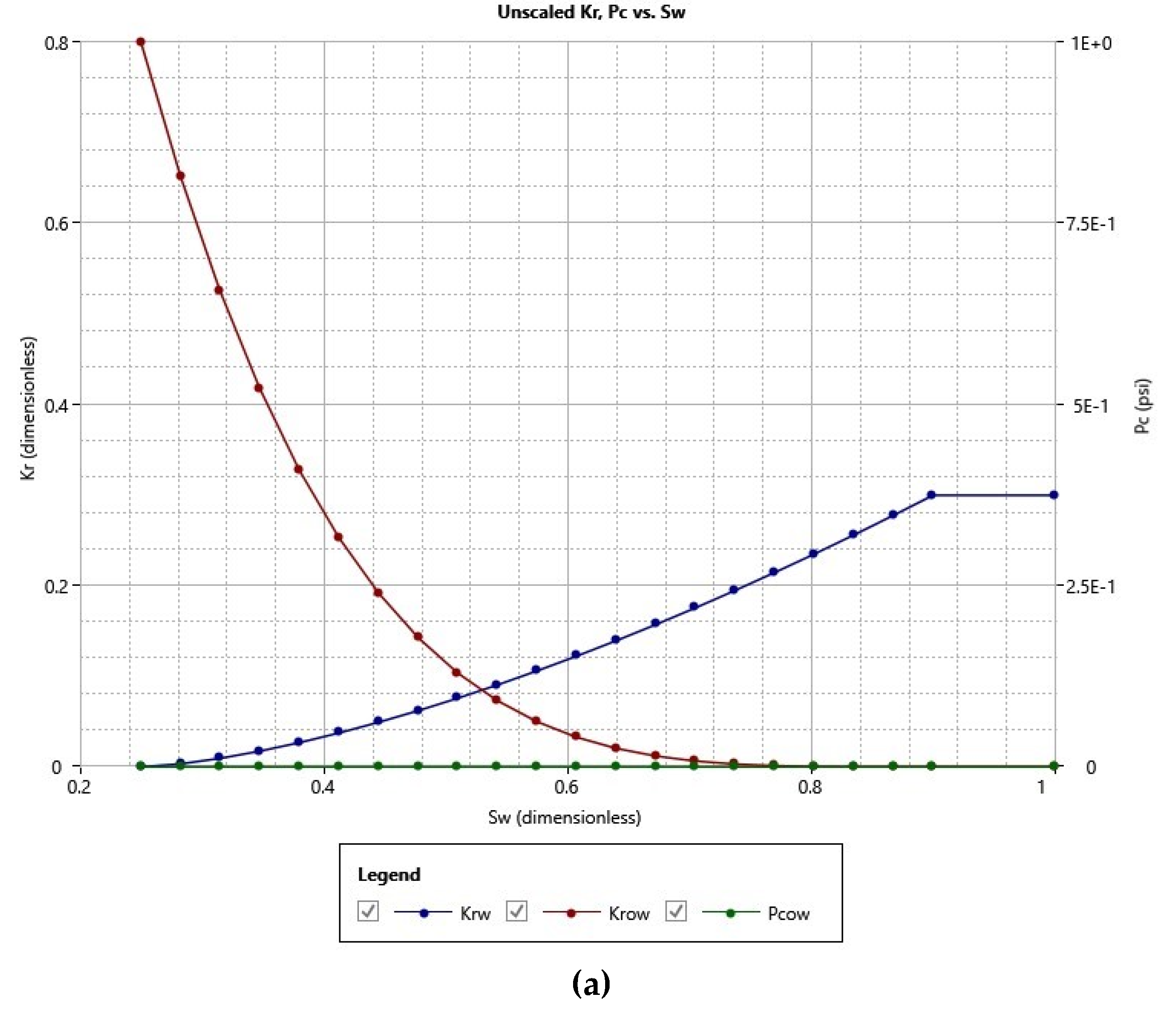

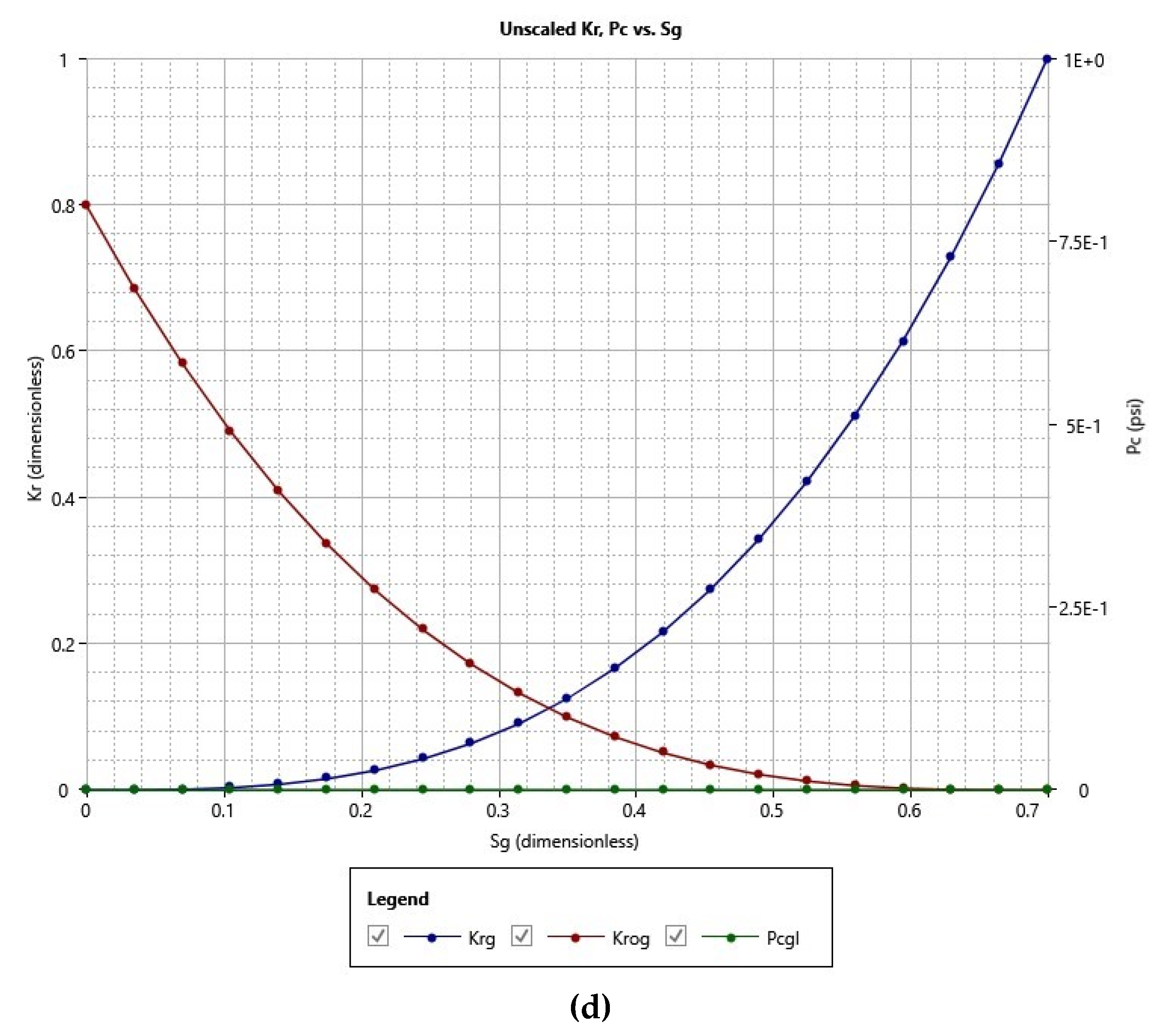
2.3. Wells
2.4. Surface Facility
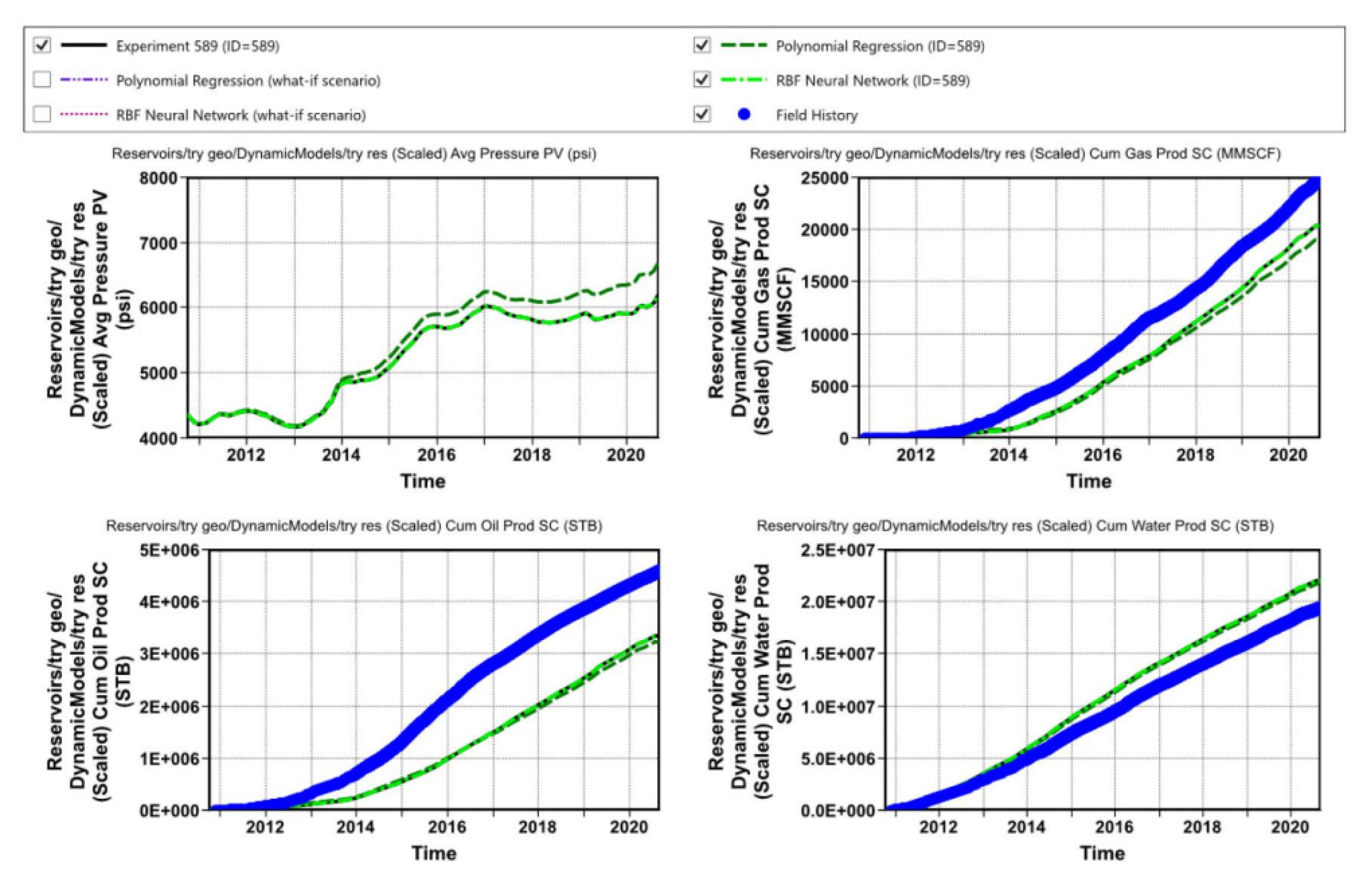
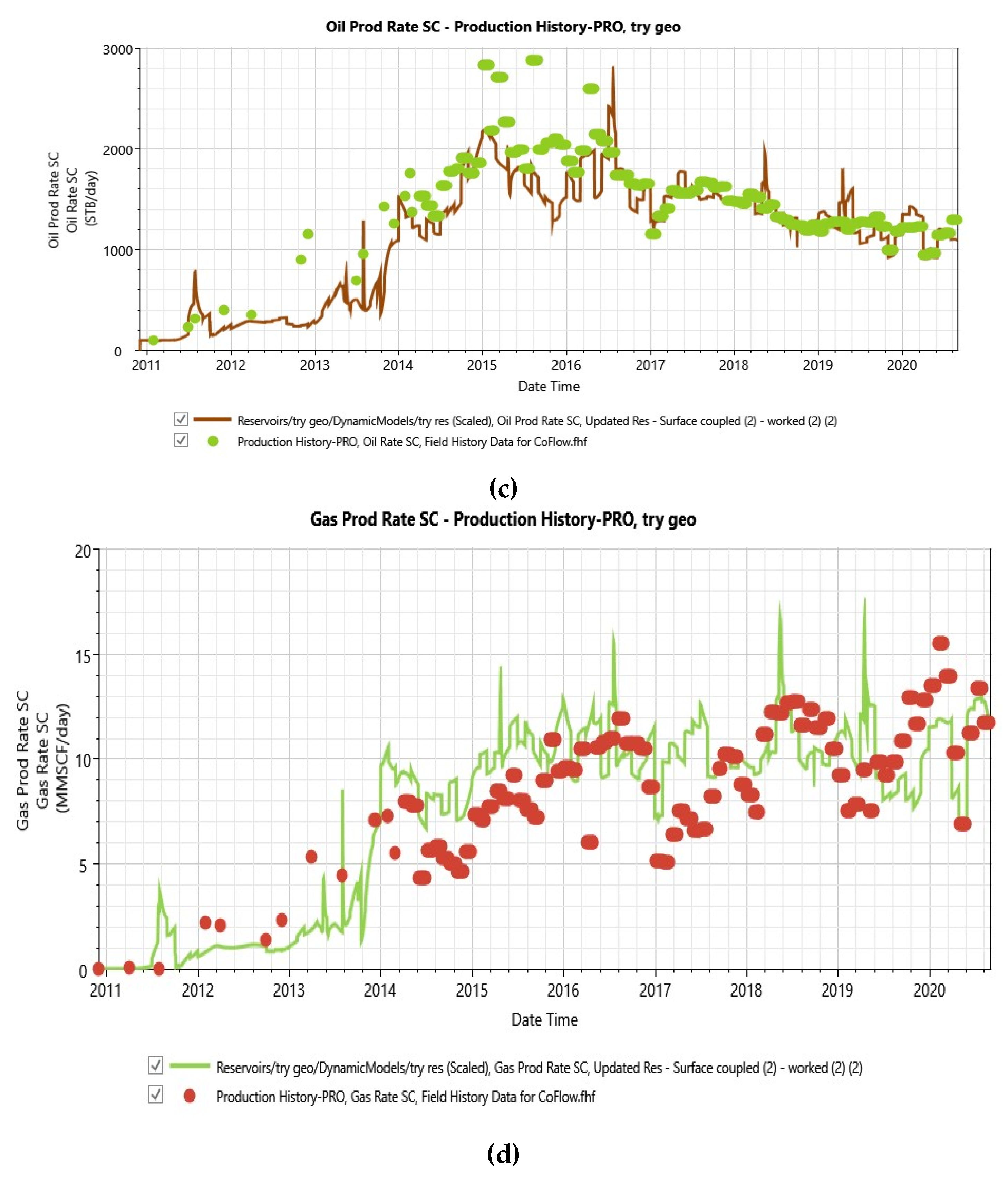
2.5. History Matching
- (a)
- Parameterization
- (b)
- Sensitivity Analysis and Proxy Modeling
- (c)
- Optimization
2.6. Simulation and Forecast
2.8. Optimization of Development Strategy
| Parameters | Default |
|---|---|
| Pressure on Production Manifold, psi | 90 |
| Injection Group 1 (gas/water), months | 2/2 |
| Injection Group 2 (gas/water), months | 3/1 |
| Injection Group 3 (gas/water), months | 9/1 |
| Injection Group 4 (gas/water), months | 3/3 |
| Compressor Rate, MMSCF/Day | 34 |
| High Separator Pressure, psi | 62 |
| Parameters | Default | Minimum | Maximum |
|---|---|---|---|
| Pressure on Production Manifold, psi | 90 | 60 | 120 |
| Injection Group 1 (gas/water), months | 2/2 | (1:1) | (12:3) |
| Injection Group 2 (gas/water), months | 3/1 | (1:1) | (12:3) |
| Injection Group 3 (gas/water), months | 9/1 | (1:1) | (12:3) |
| Injection Group 4 (gas/water), months | 3/3 | (1:1) | (12:3) |
| Compressor Rate, MMSCF/Day | 34 | 17 | 34 |
| High Separator Pressure, psi | 62 | 30 | 70 |
| Parameters | Cost |
|---|---|
| Price of CO2 transport and storage, $/t | 11.2 |
| Recycle Compression, $/MCF | 0.4 |
| Surface Facility Maintenance and Well Workover, $/bbl | 20.92 |
| Water Management Cost, $/bbl | 2.64 |
| Price of oil, $/bbl | 60 |
| Tax Benefit for CO2 stored, $/t | 24 |
3. Results and Discussion
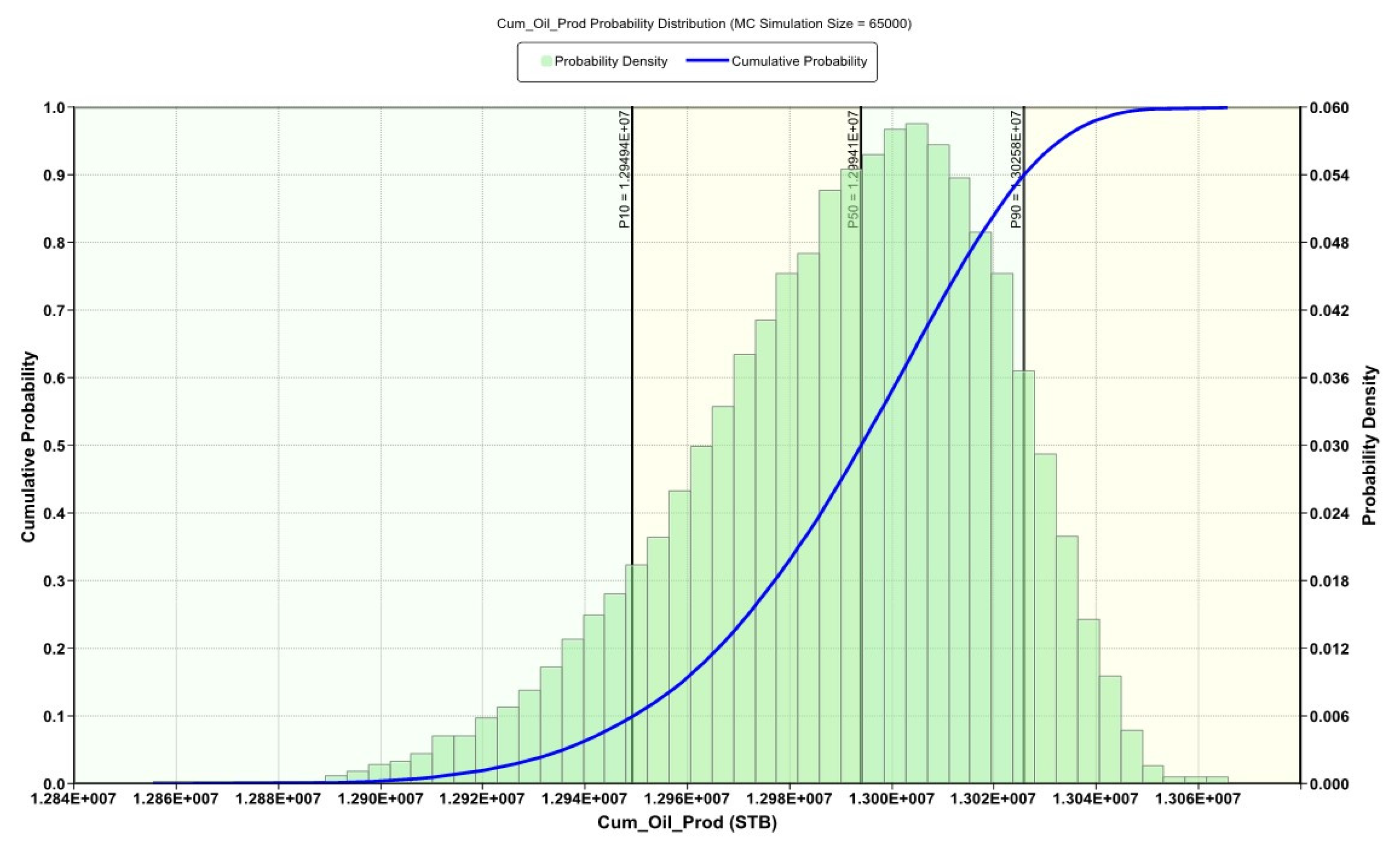
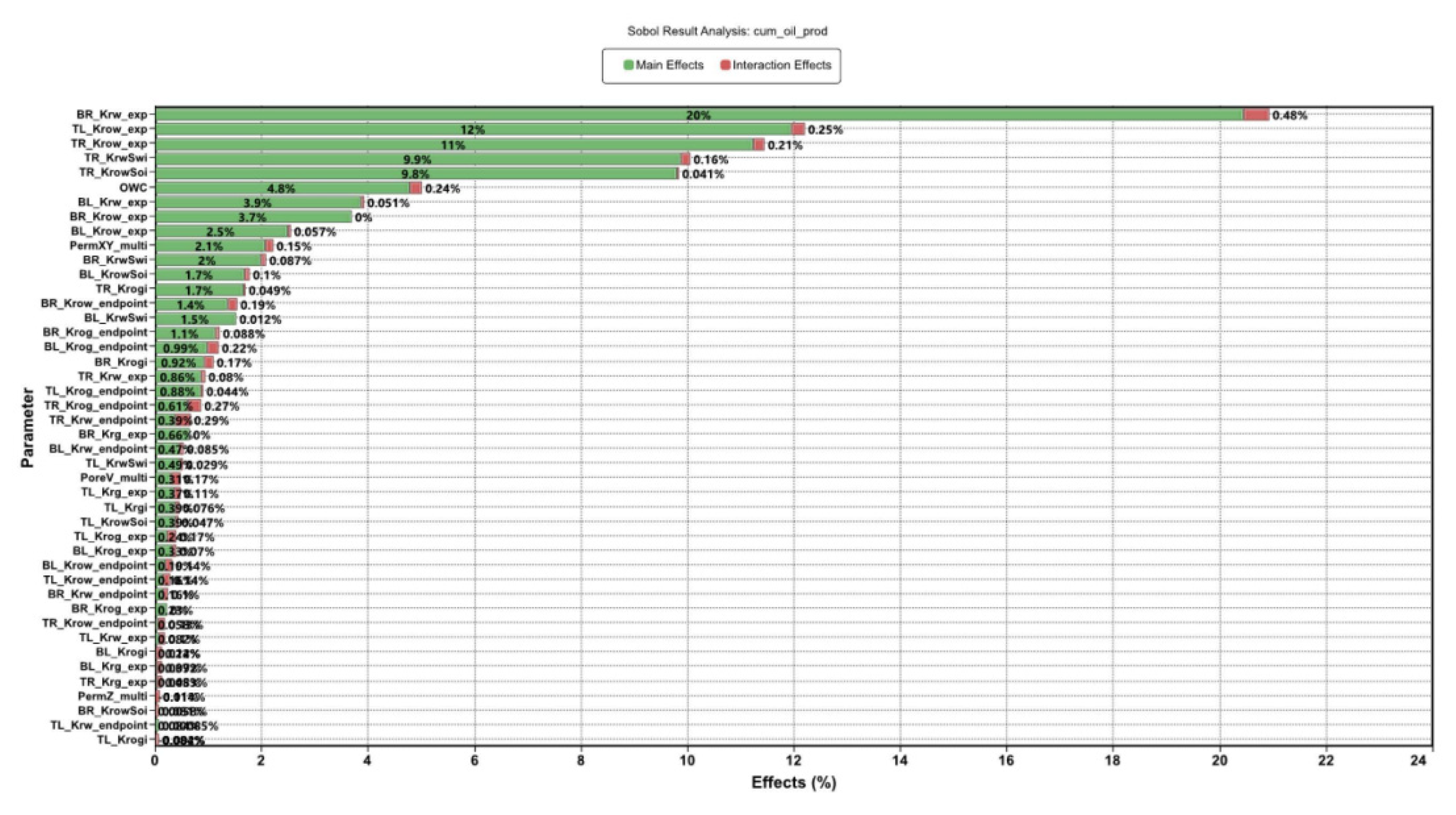
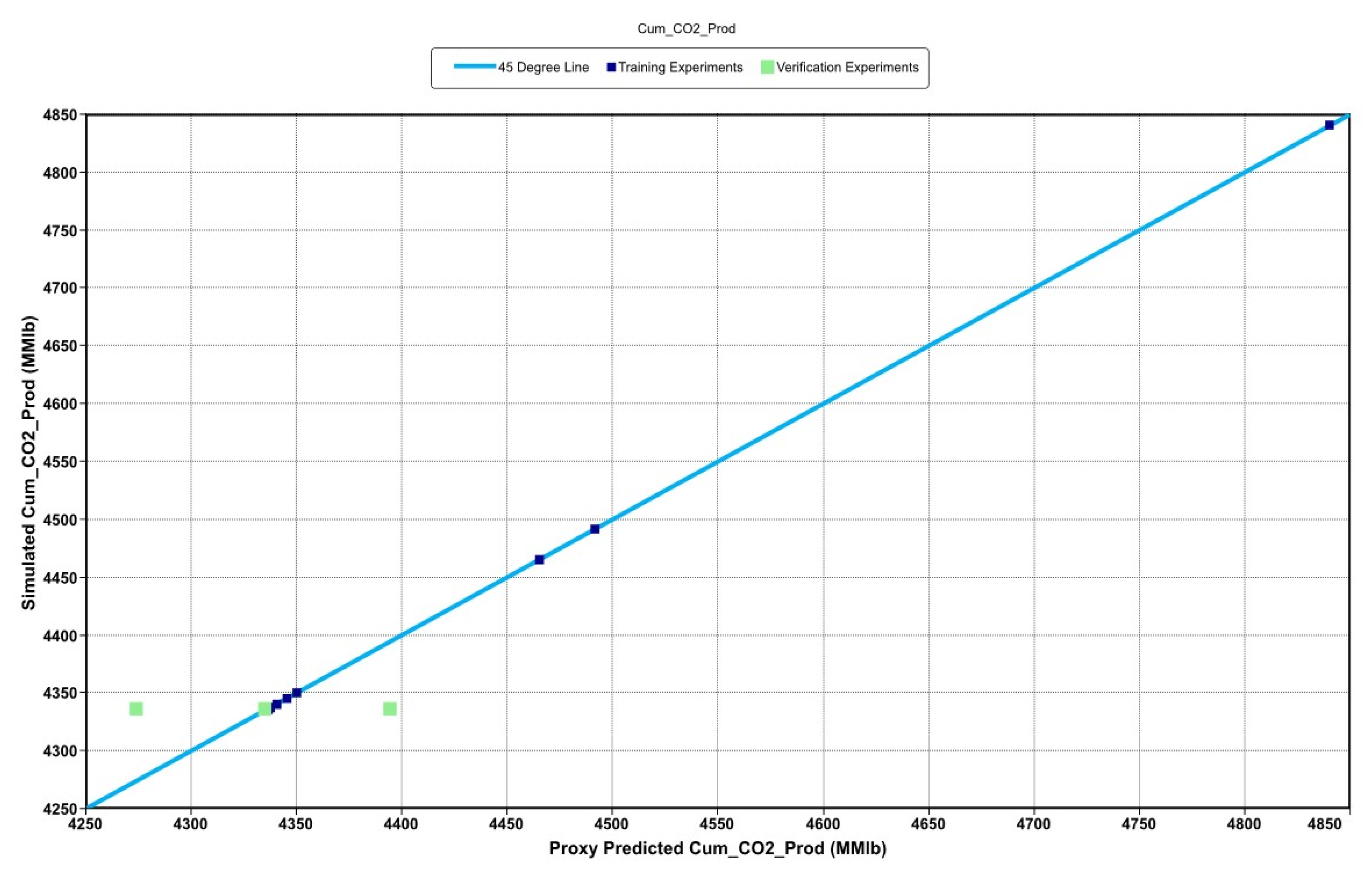
3.1. Proxy Modeling and Sensitvity Analysis
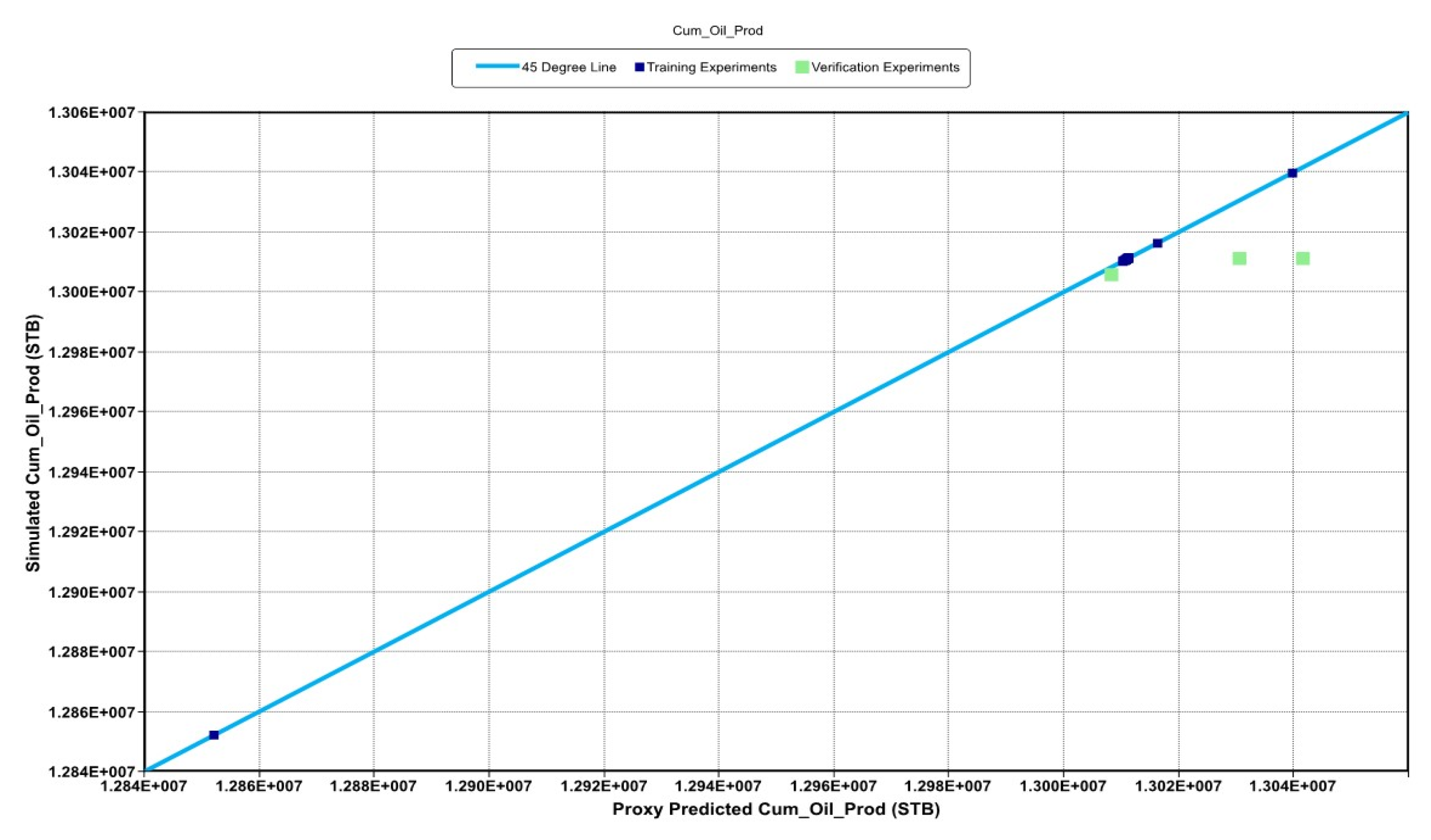
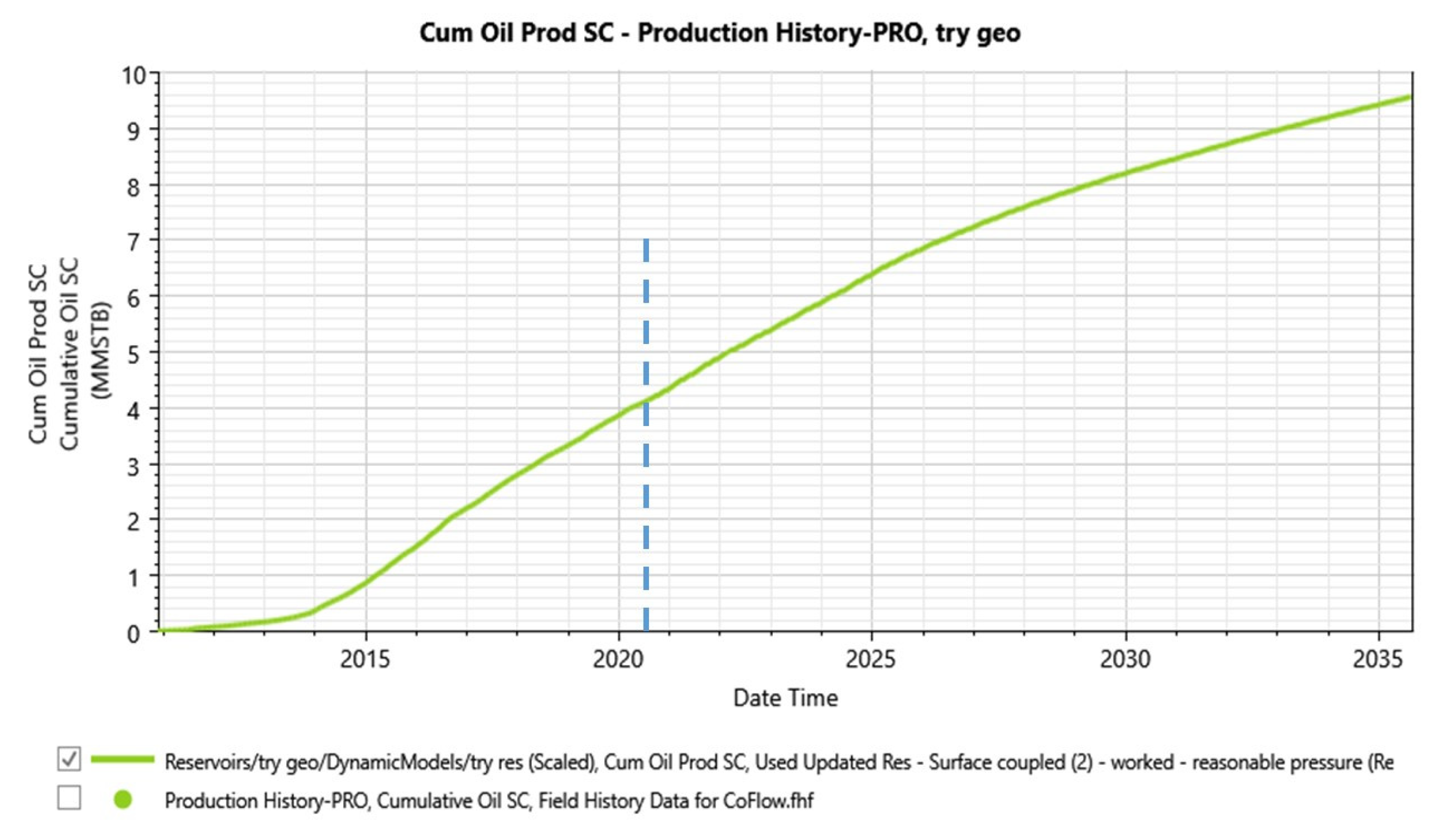
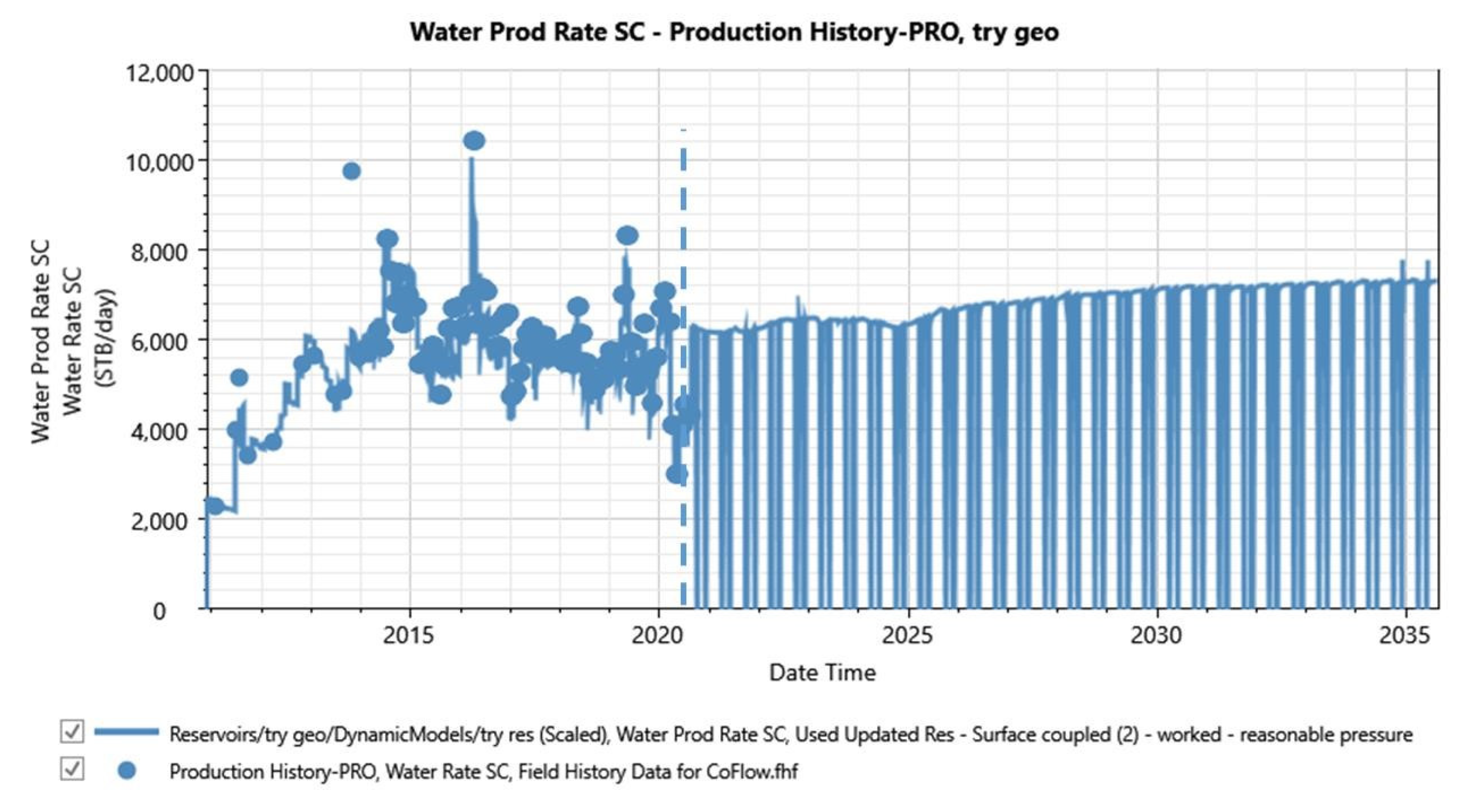
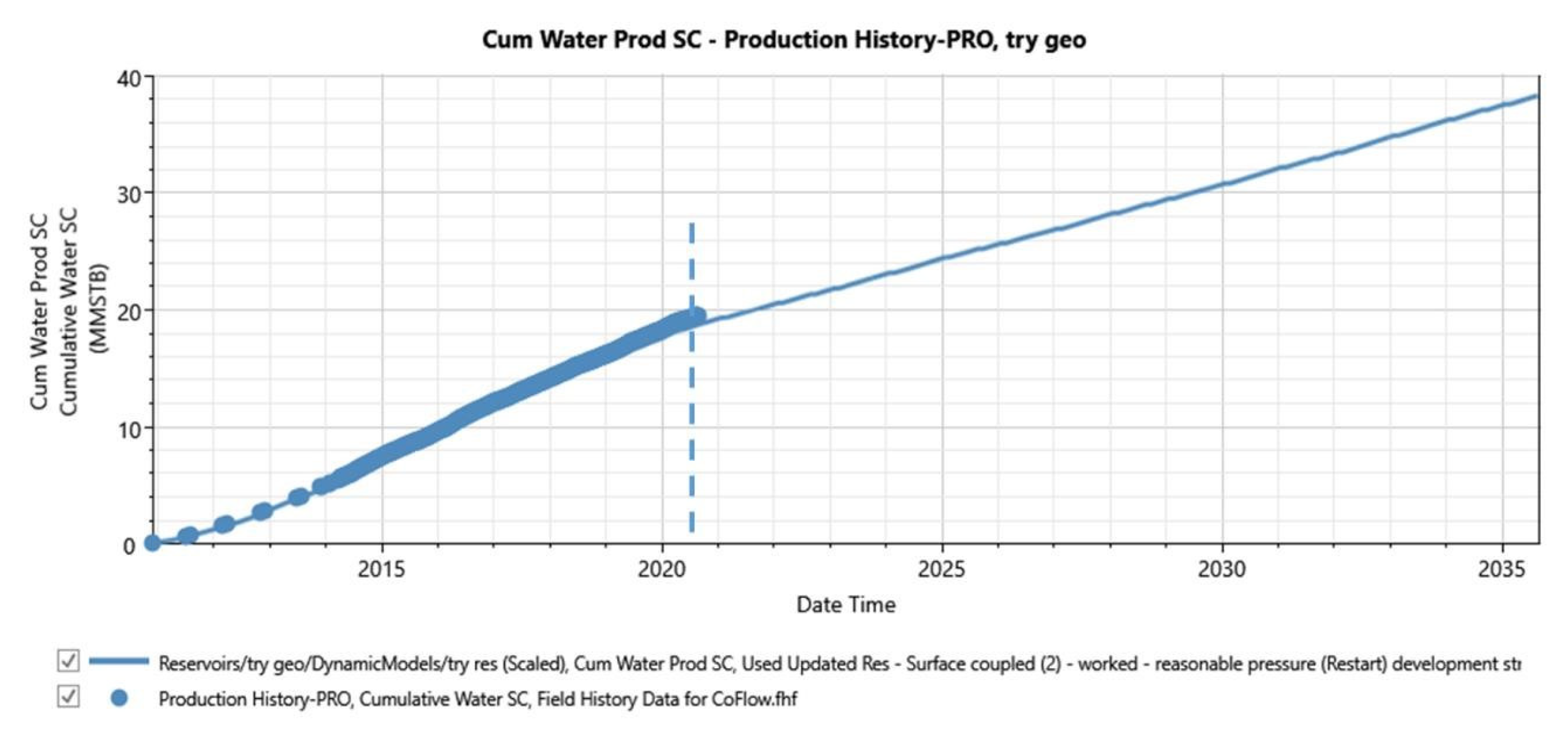
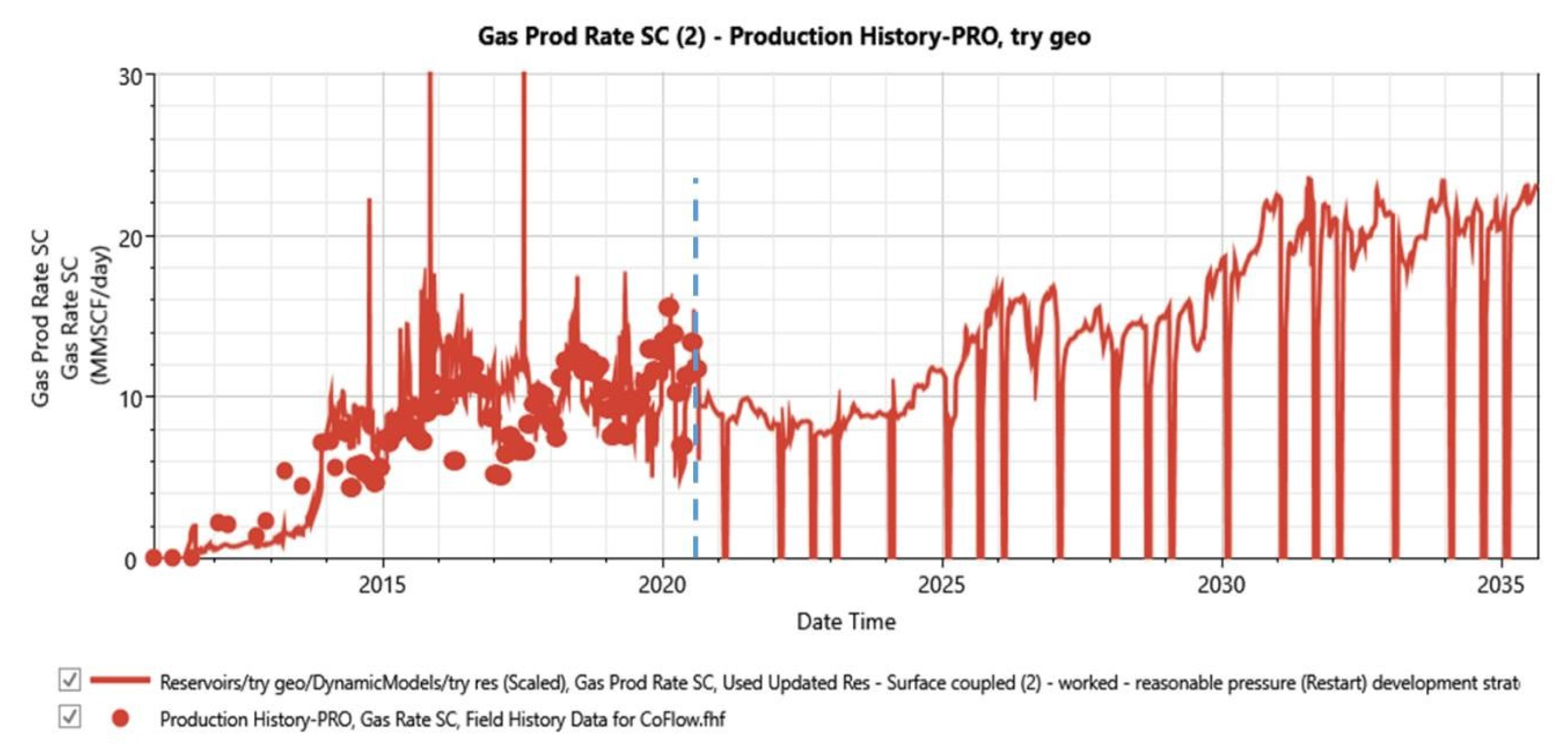
3.2. History Matching
3.3. Simulation and Forecast
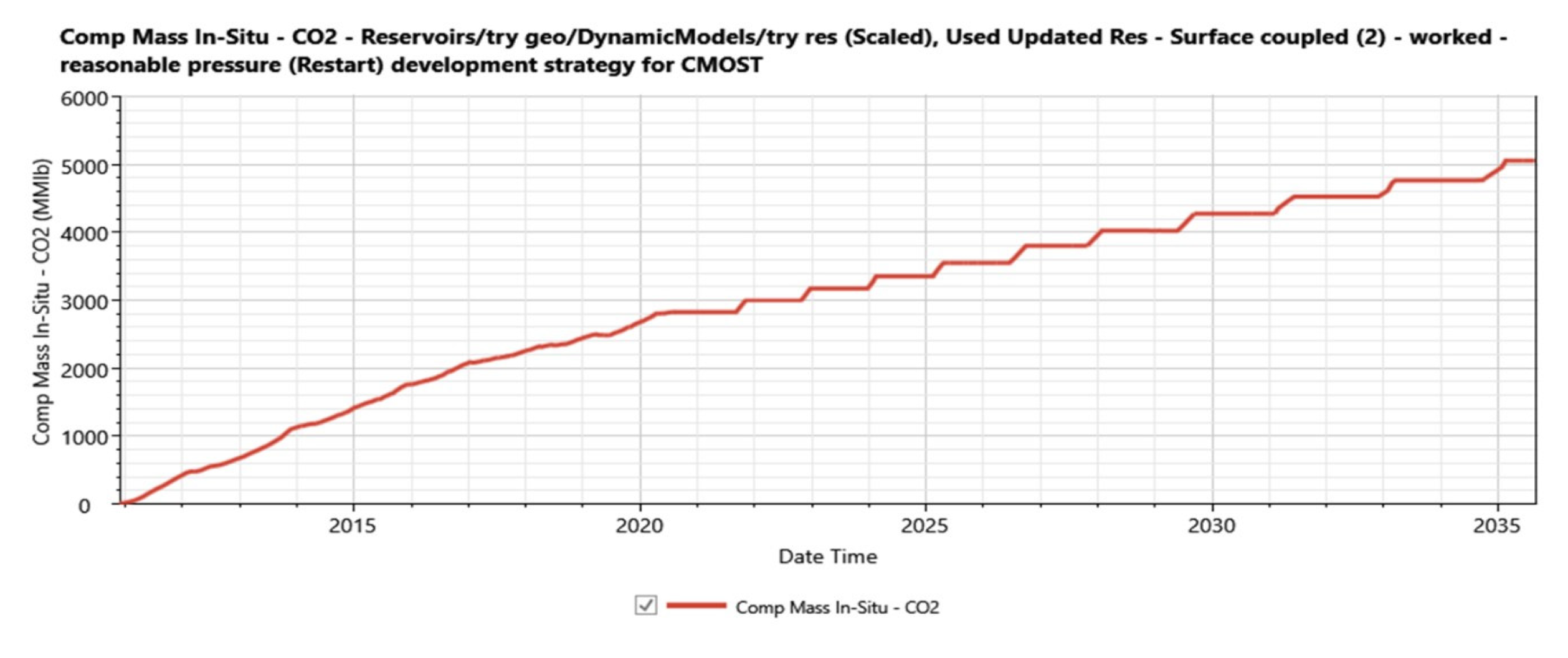
3.3.1. Do-Nothing Forecast
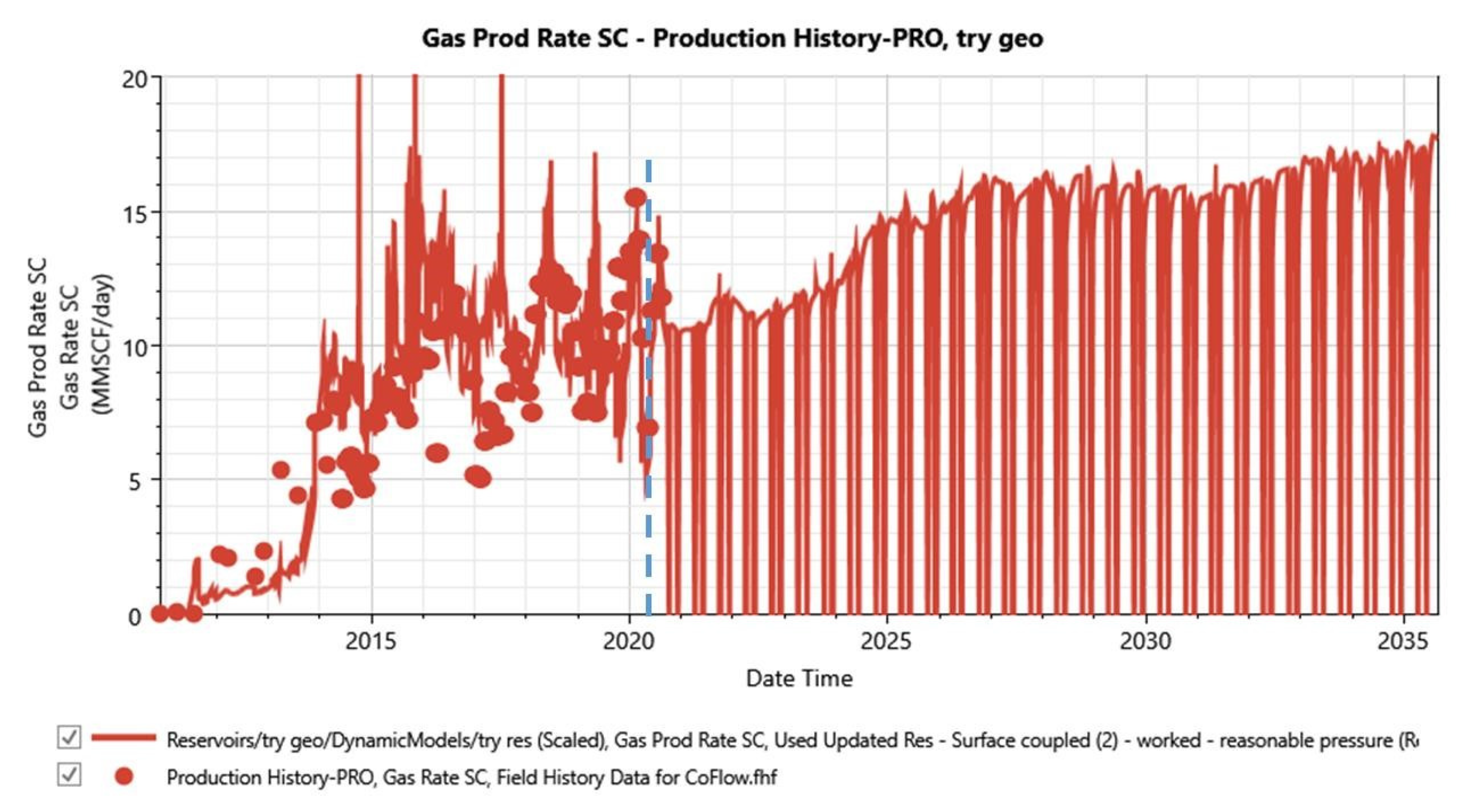
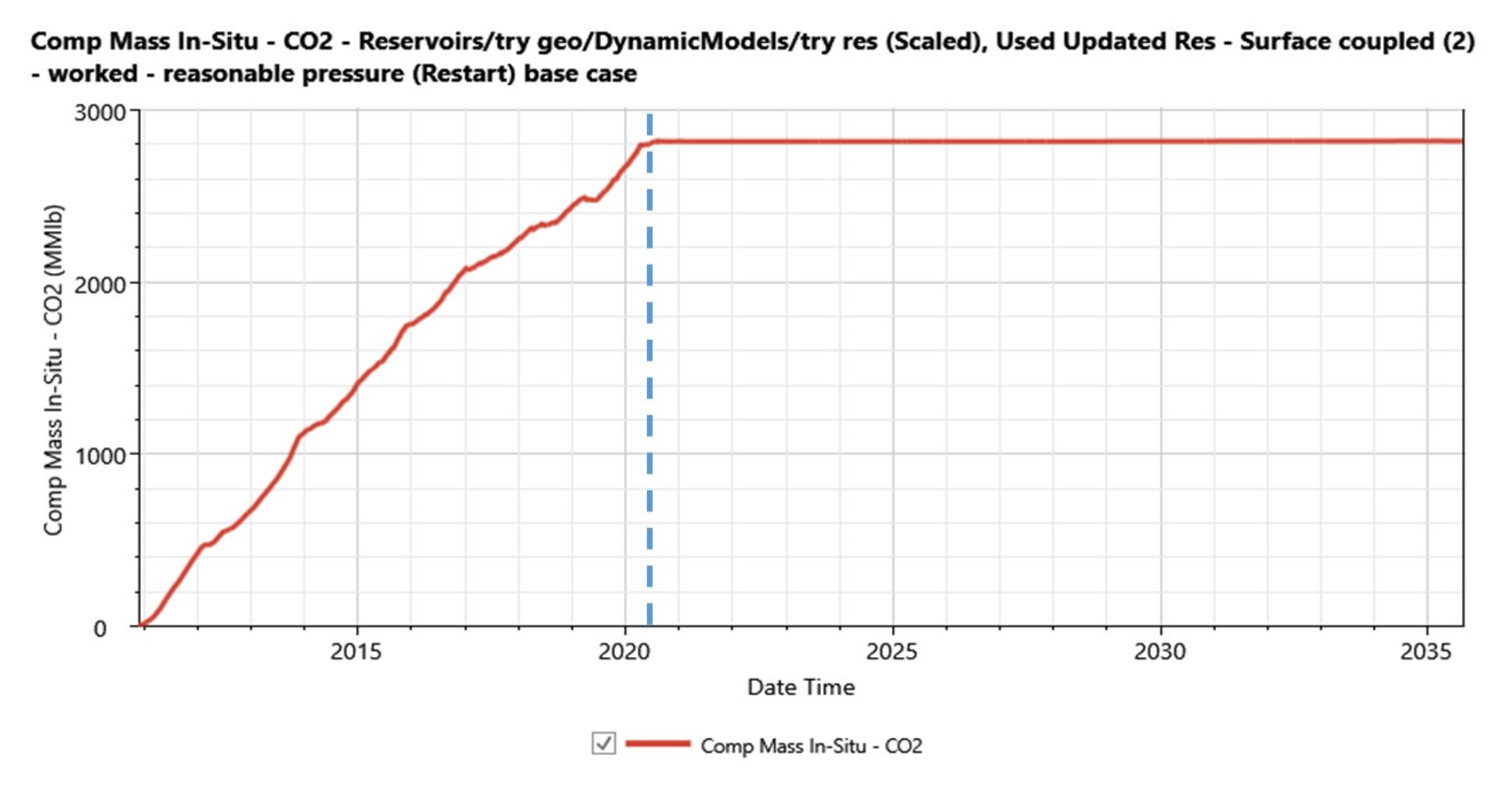
| Parameters | Cumulative Value |
|---|---|
| Oil Production, MMSTB | 9.57 |
| Water Production, MMSTB | 50.44 |
| Gas Production, MMSCF | 94,669.58 |
| CO2 Stored, MMIbs | 2,822.70 |
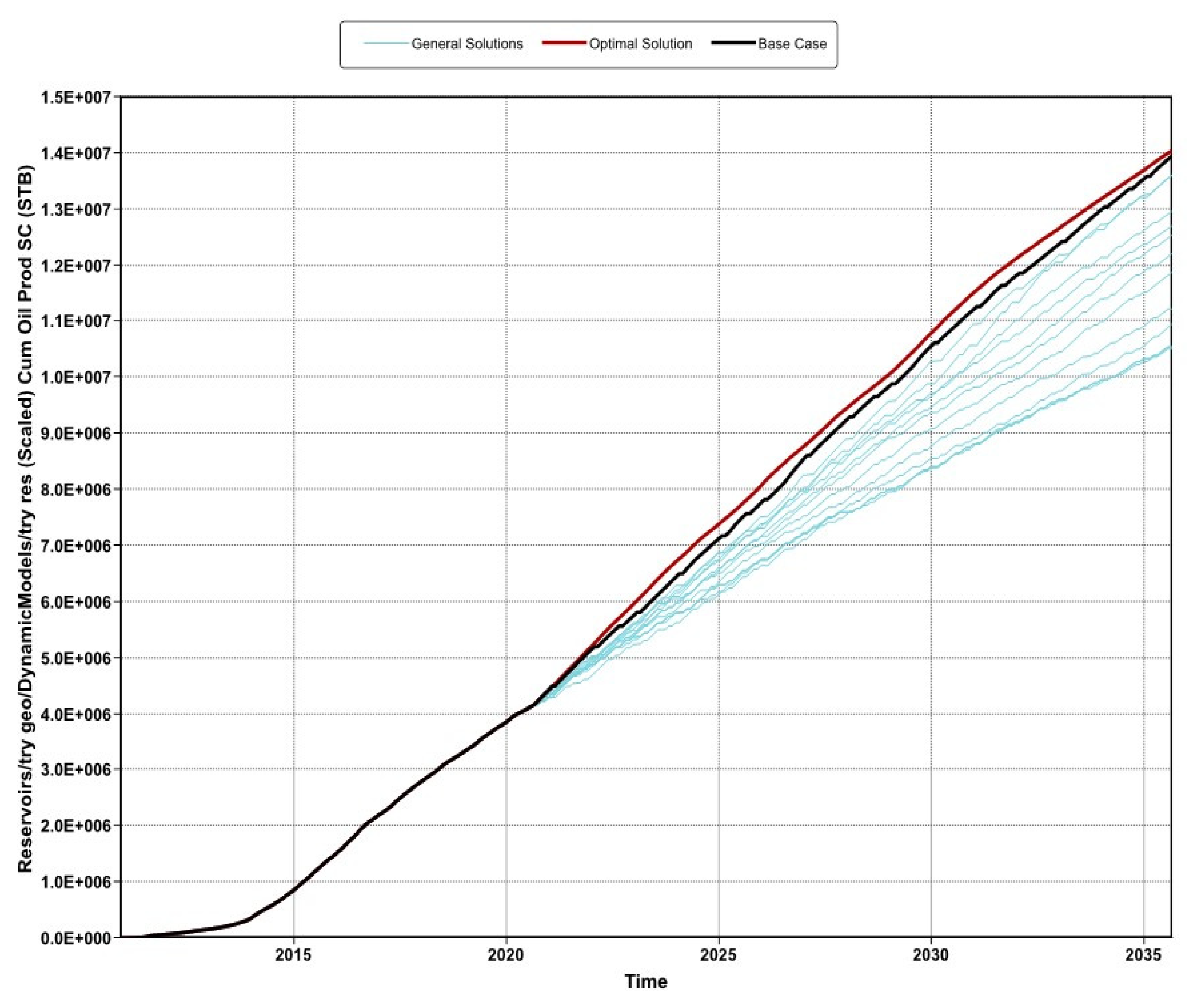
3.3.2. Development Scenario Forecast

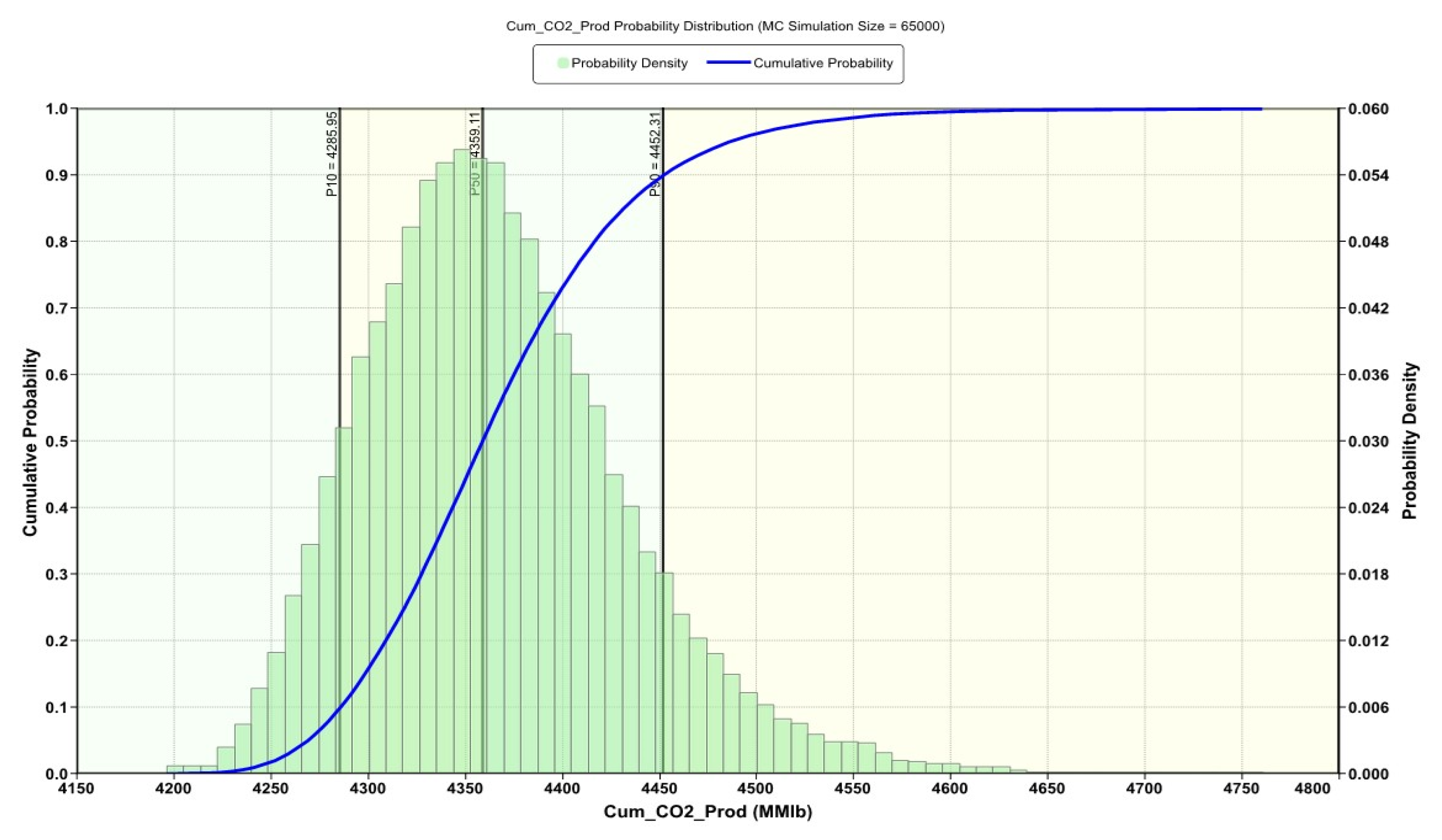
3.4. Optimization
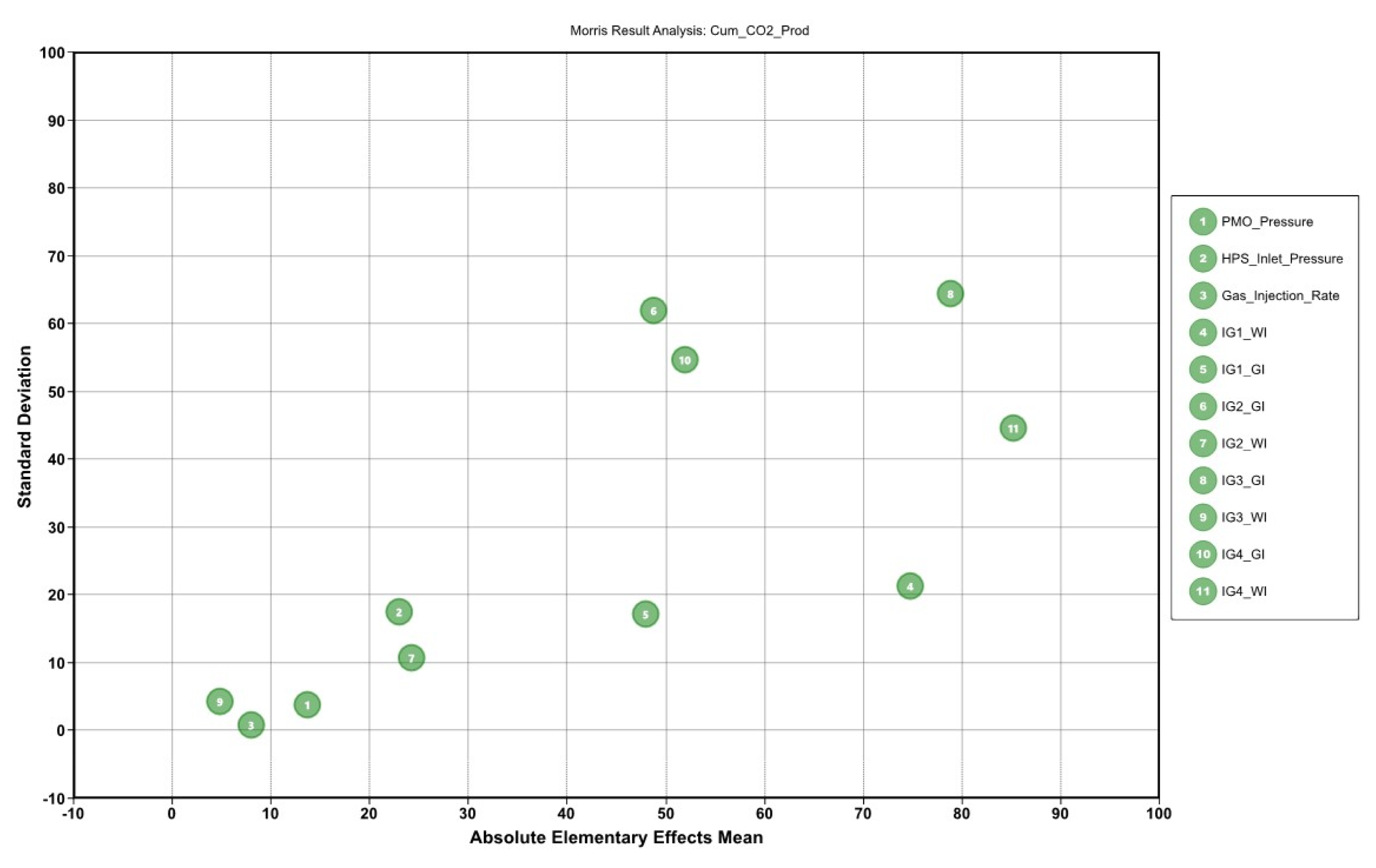
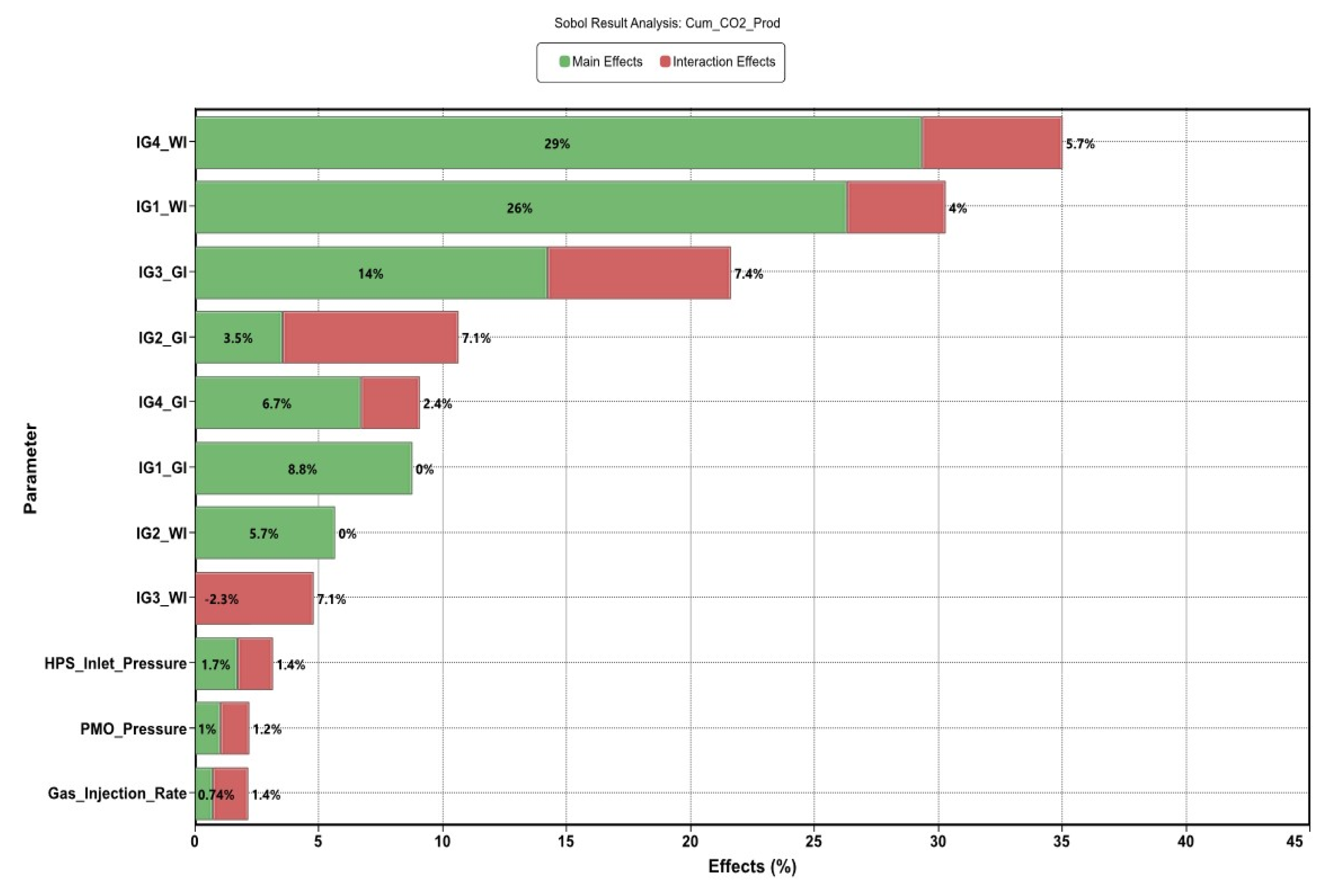
3.4.1. Parameterization and Sensitivity Analysis
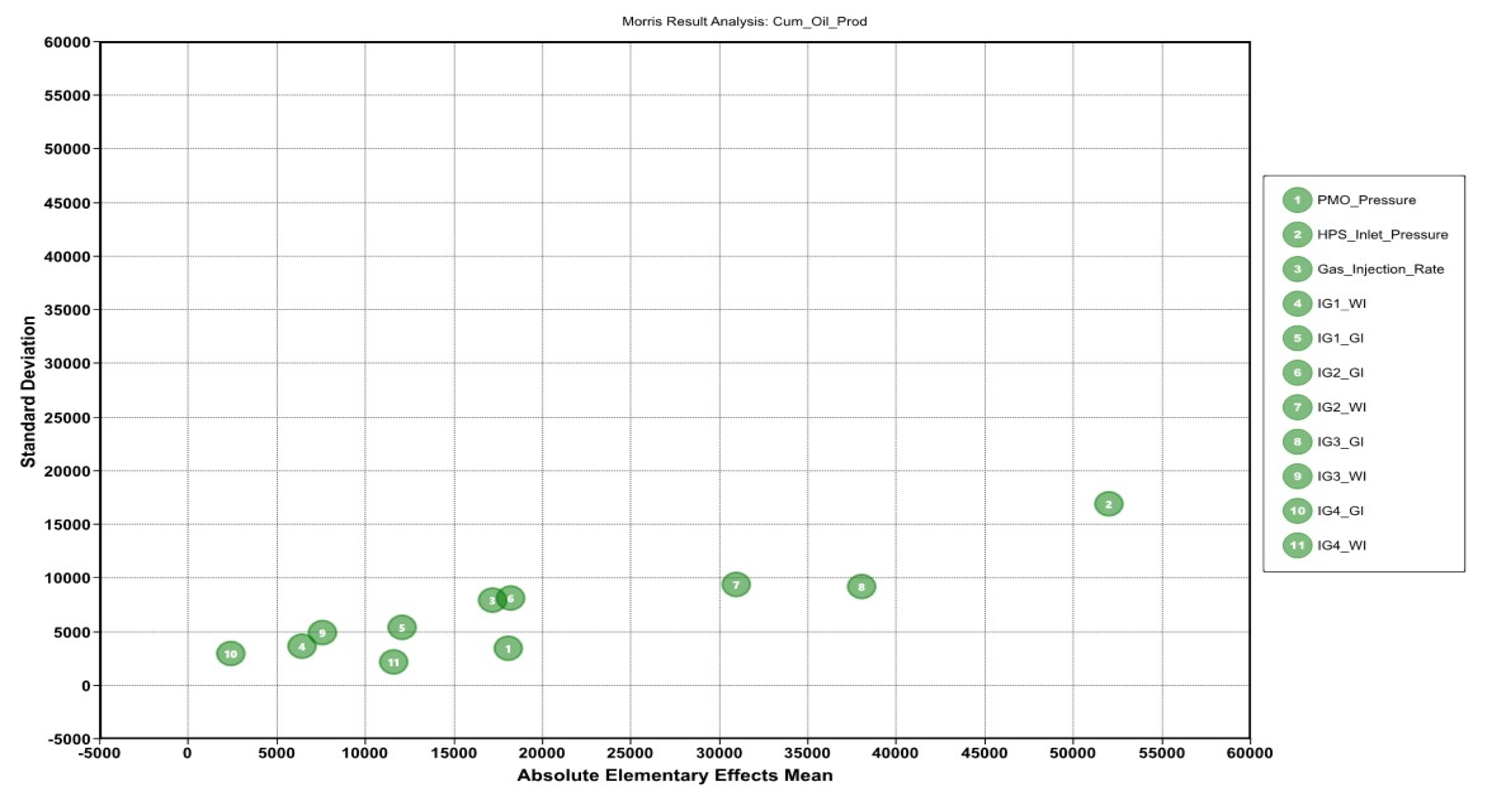
- PMO_Pressure = Pressure on Production Manifold
- HPS_Inlet Pressure = High Separator Pressure
- Gas_Injection_Rate = Compressor Rate
- IG1_GI = Injection Group 1—Gas Injection Cycle Duration
- IG1_WI = Injection Group 1—Water Injection Cycle Duration
- IG2_GI = Injection Group 2—Gas Injection Cycle Duration
- IG2_WI = Injection Group 2—Water Injection Cycle Duration
- IG3_GI = Injection Group 3—Gas Injection Cycle Duration
- IG3_WI = Injection Group 3—Water Injection Cycle Duration
- IG4_GI = Injection Group 4—Gas Injection Cycle Duration
- IG4_WI = Injection Group 4—Water Injection Cycle Duration
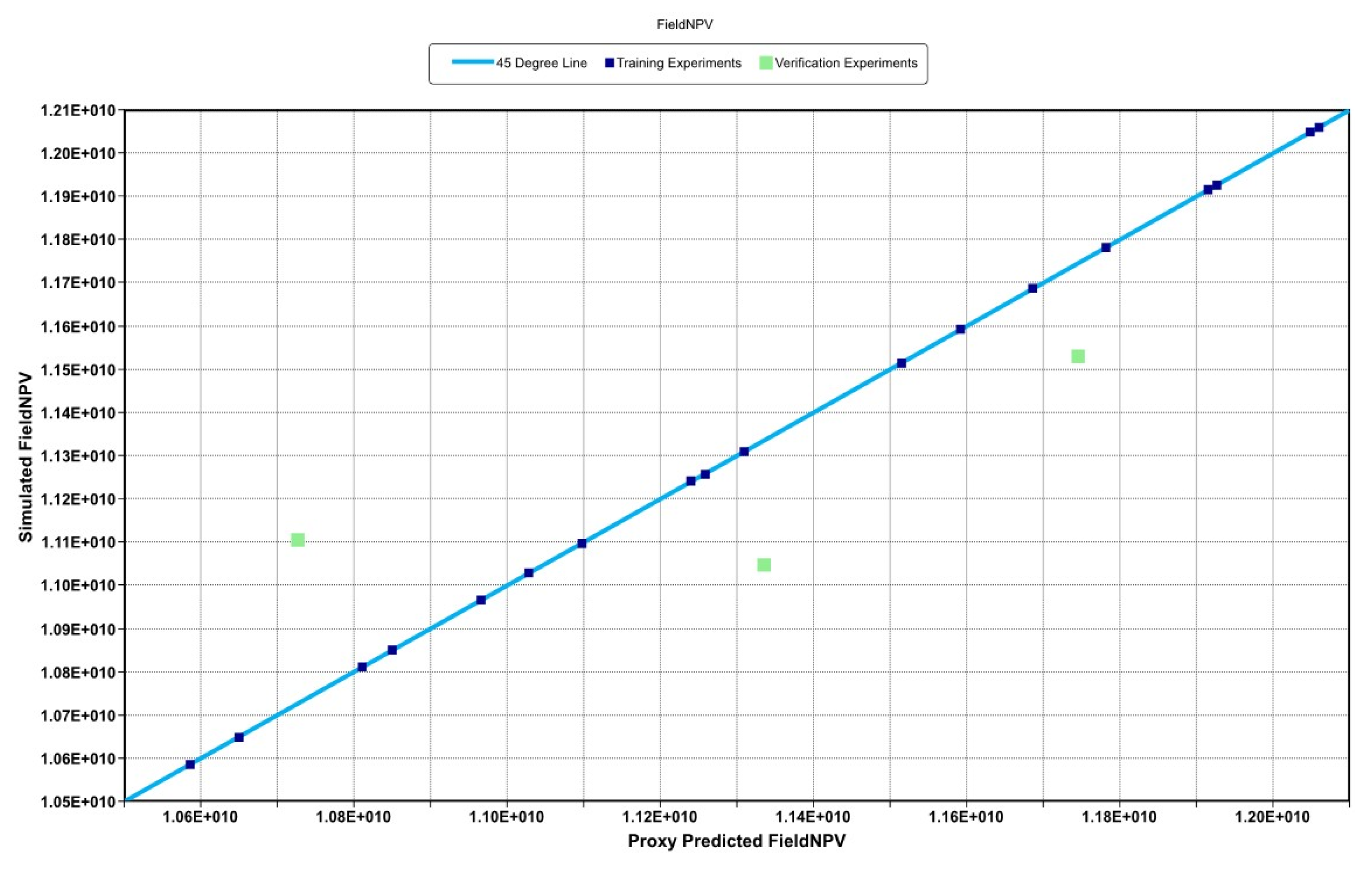
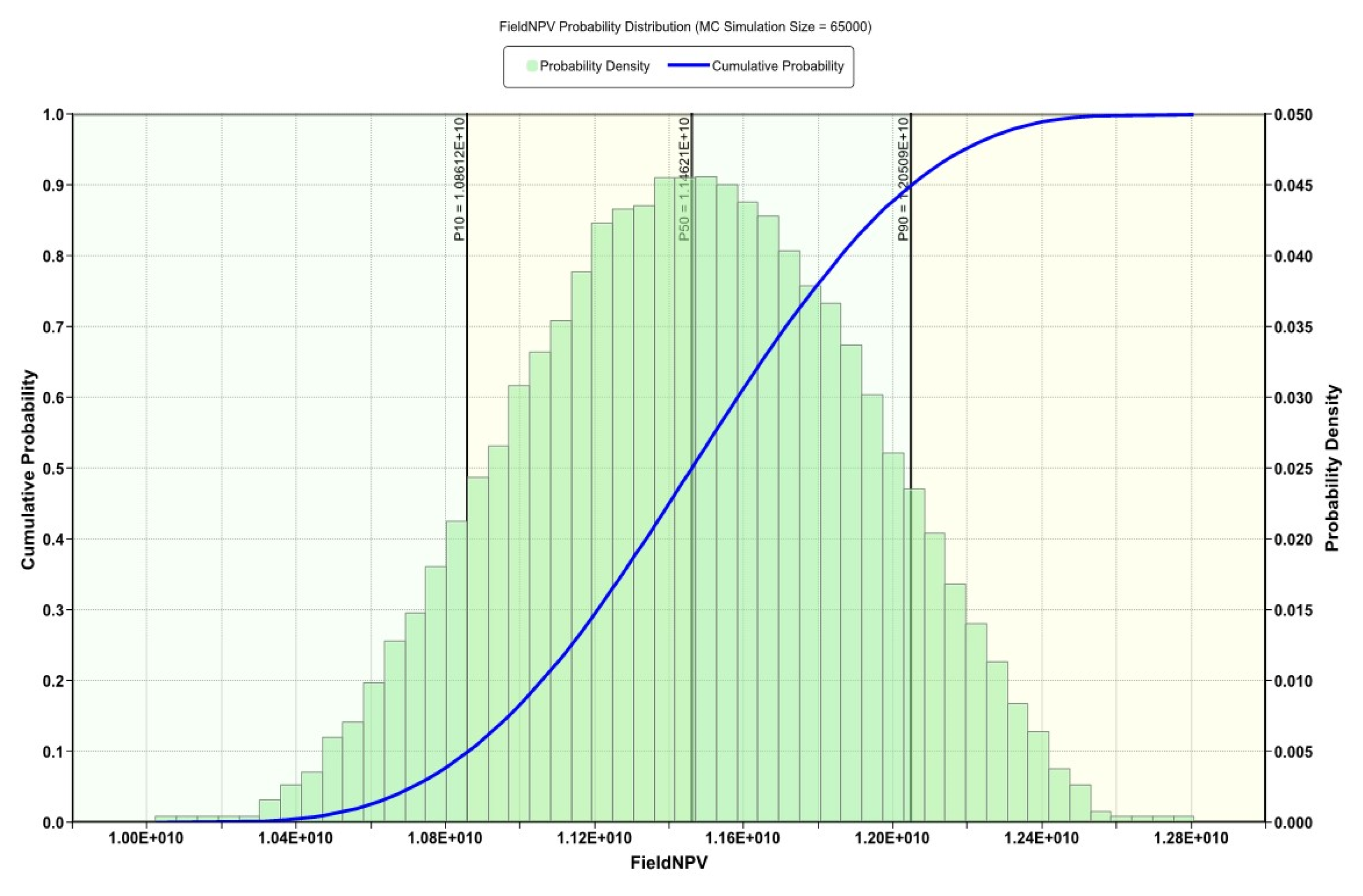
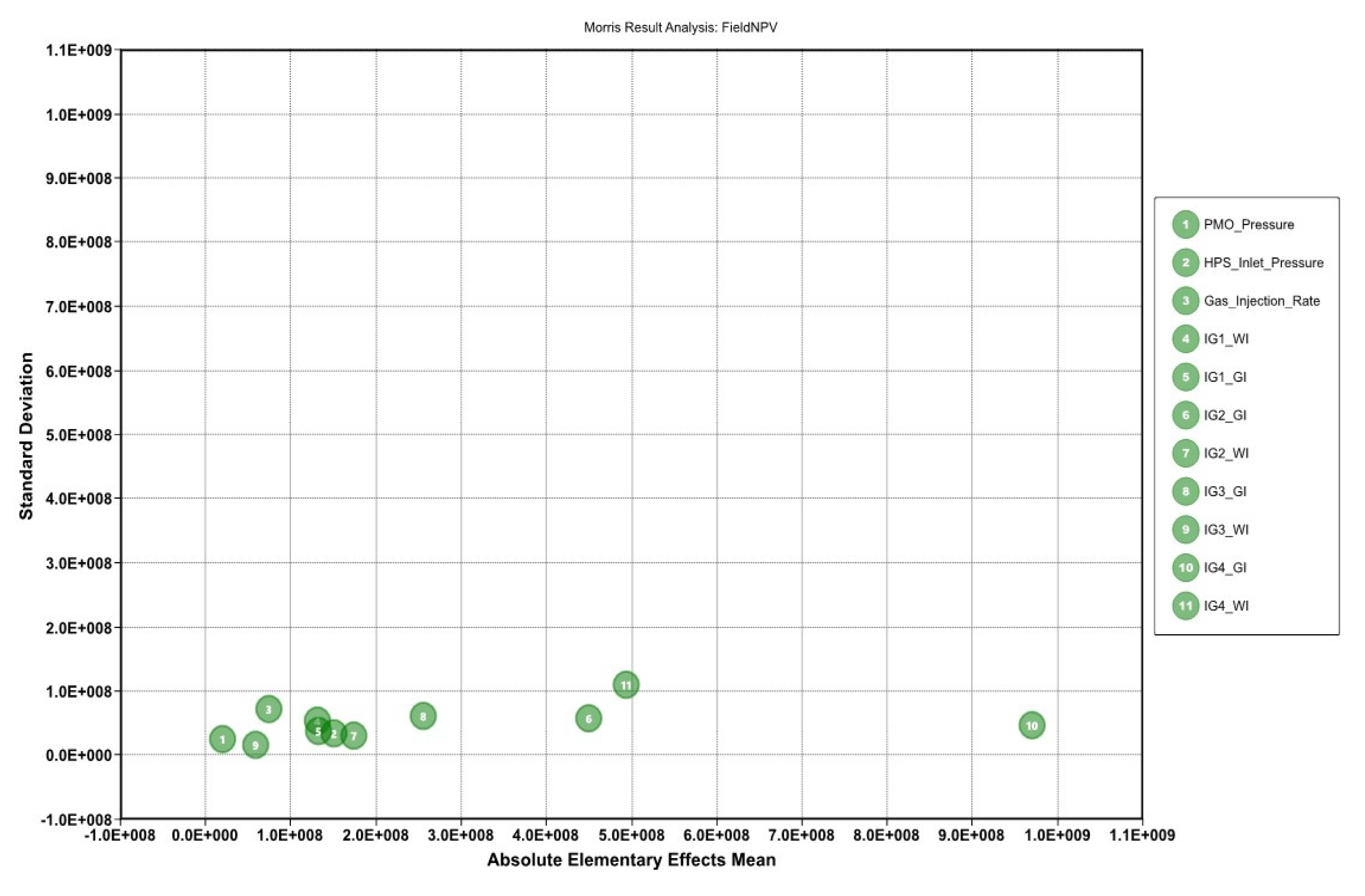
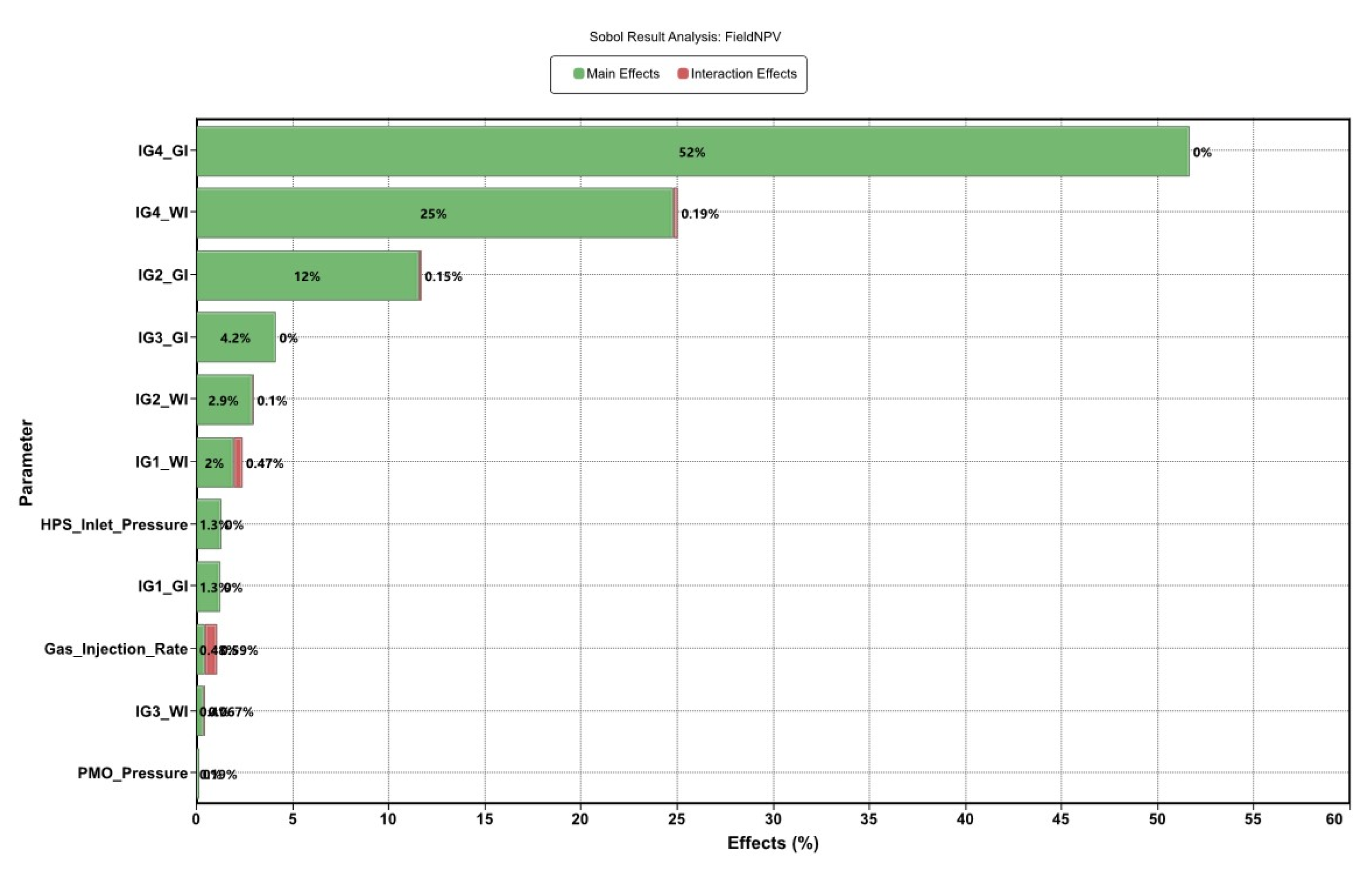
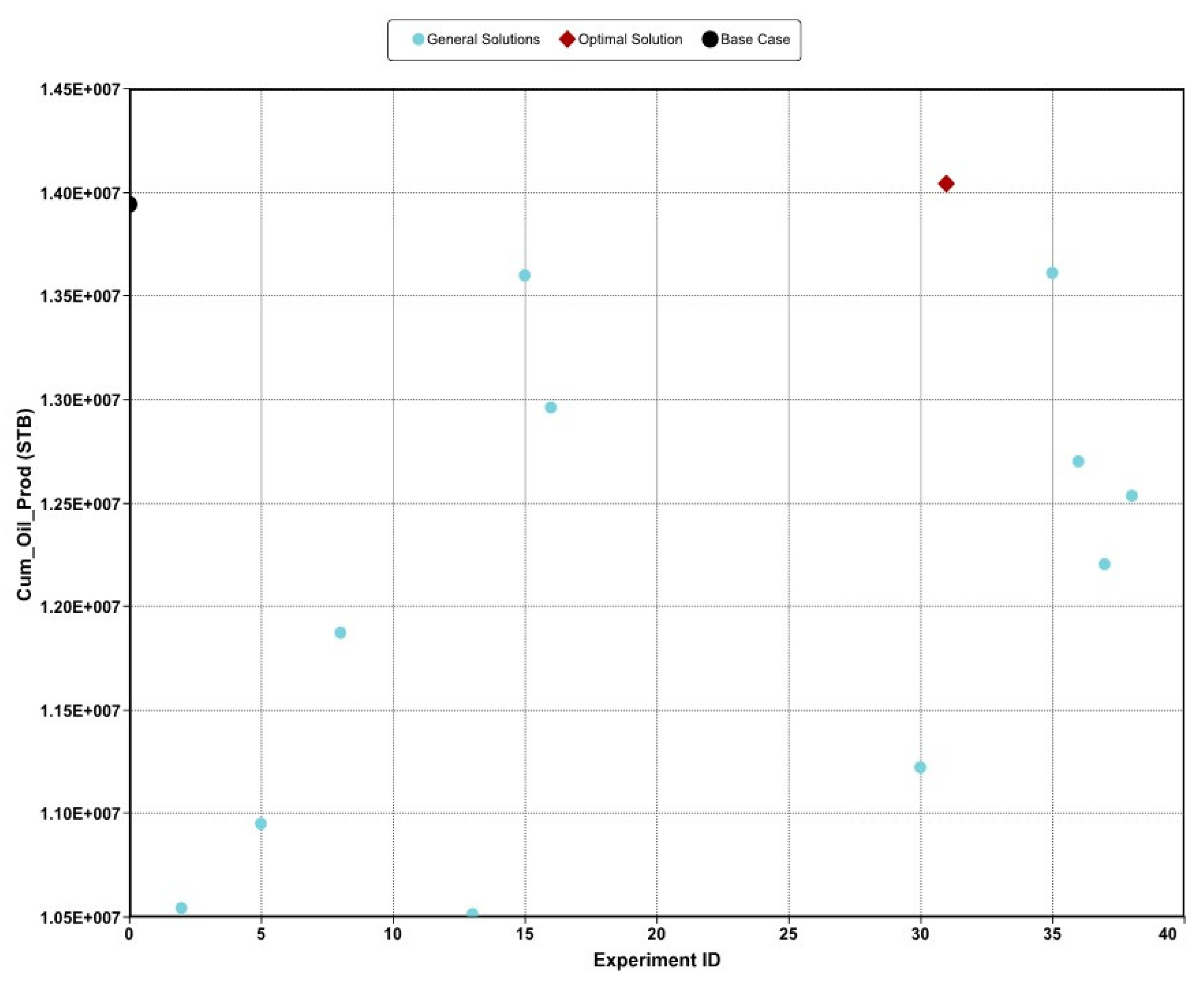
3.4.2. Optimized Operating Conditions
| Experiment ID | Cumulative Oil Produced (STB) |
Incremental Oil Recovered (STB) |
Percentage Increment |
|---|---|---|---|
| Development Case | 13,946,568 | ||
| Optimal Strategy | 14,043,372 | 96,804 | 0.694 |
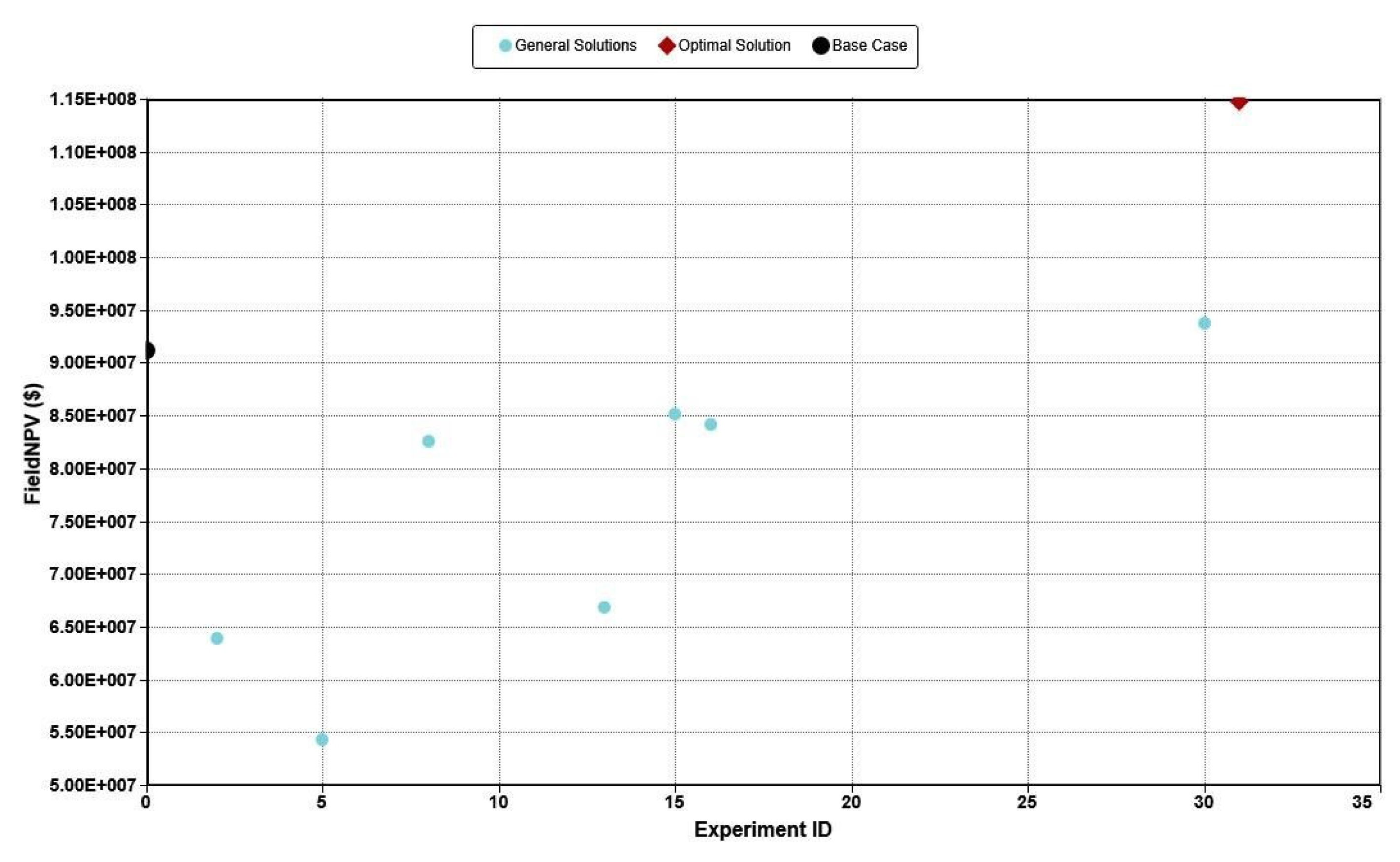
| Experiment ID | Field NPV ($) | Incremental Field NPV ($) | Percentage of Incremental Field NPV |
|---|---|---|---|
| Development Case | 91,281,921 | ||
| Optimal Strategy | 114,871,730 | 23,589,809 | 25.84 |
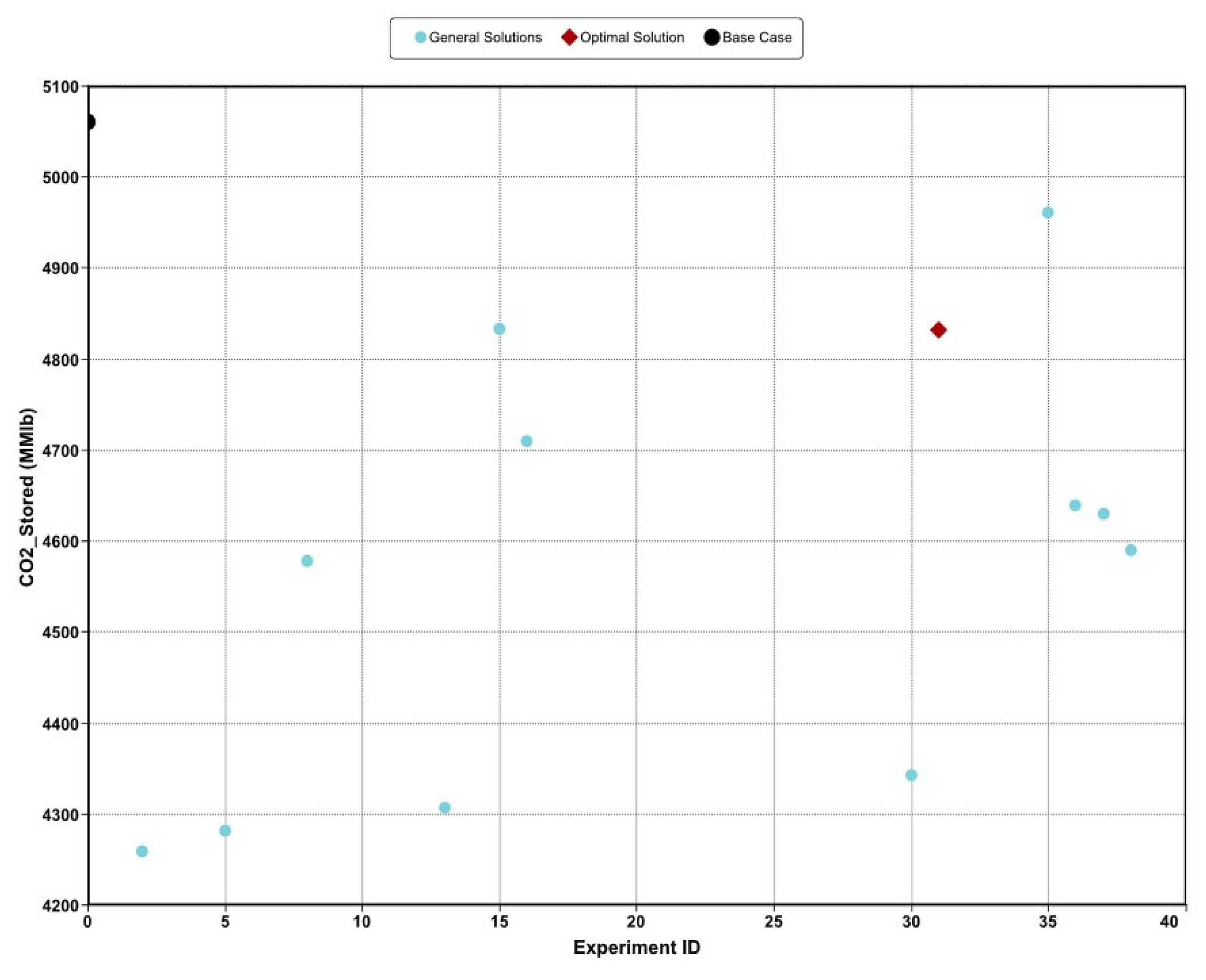
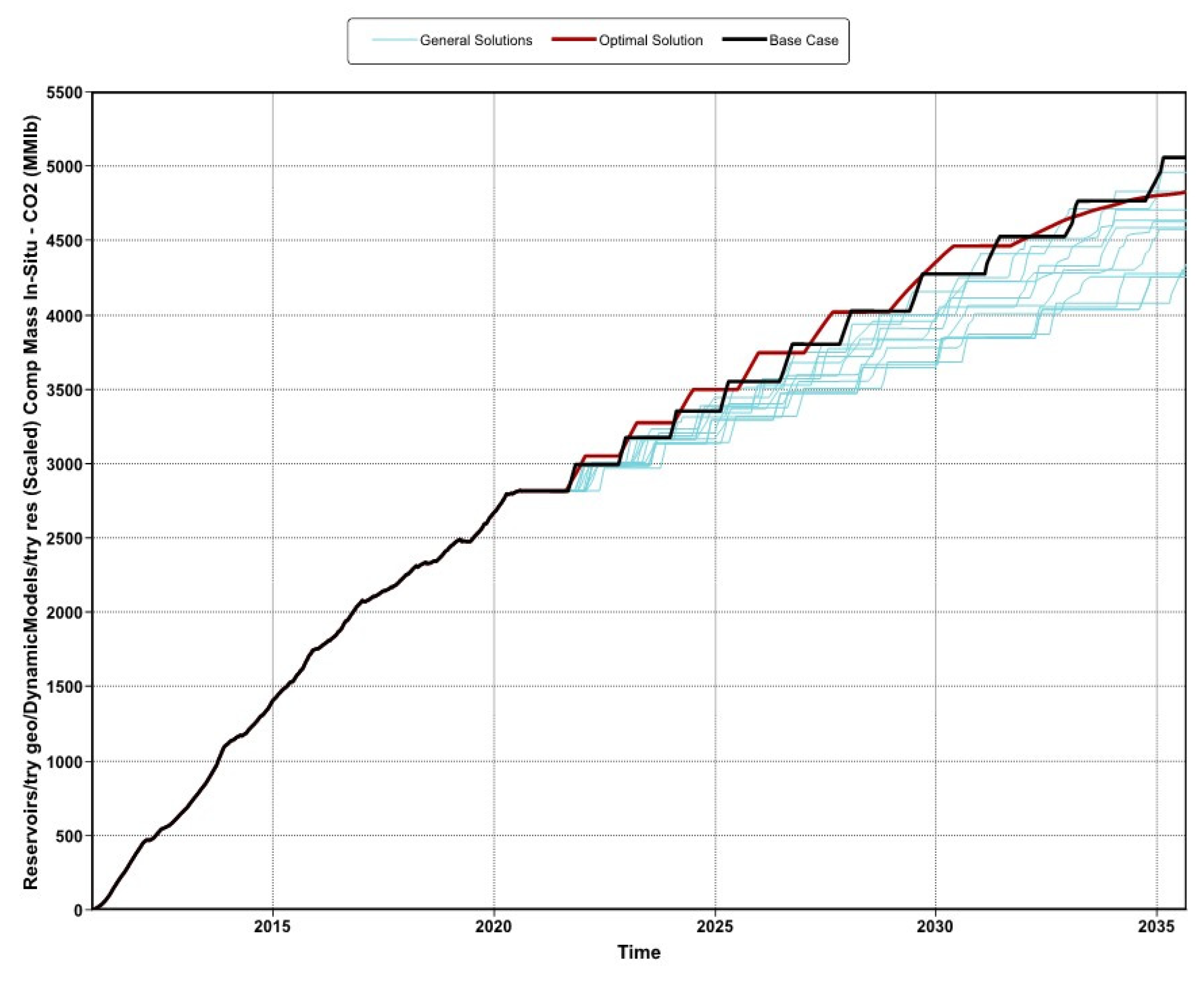
| Experiment ID | Cumulative CO2 stored (MMIbs) | Incremental Storage (MMIbs) | Percentage Decrement |
|---|---|---|---|
| Development Case | 5,061.68 | ||
| Optimal Strategy | 4,832.18 | -229.5 | 4.53 |
4. Recommendation and Conclusion
4.1. Conclusion
4.2. Recommendations
- Replace Surface Network Connections with Actual Pipe Models: Employing pipe models that consider length, diameter, and appropriate flow correlations will provide more precise simulations of surface network dynamics. This improvement can lead to more accurate predictions of fluid behavior and pressure losses, enhancing the overall reliability of the integrated model.
- Incorporate Historical Fluid Composition in History Matching: Including the historical fluid composition sampled at the surface in the history-matching process can help reduce the non-uniqueness of the solution. This addition will provide a more detailed understanding of the reservoir’s fluid characteristics and improve the accuracy of the model’s predictions.
- Develop a Comprehensive Life-Cycle Assessment (LCA): Conducting a full LCA for the integrated asset model will provide a holistic view of the environmental impacts associated with CO2-EOR and CO2 storage processes. This assessment can identify areas for reducing carbon footprints and improving sustainability, thereby aligning the model with environmental regulations and sustainability goals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on C8limate Change; Pachauri, R., Meyer, L., Eds.; IPCC: Geneva, Switzerland, 2014; pp. 40–54. [Google Scholar]
- Houghton, J. Global Warming: The Complete Briefing; Cambridge University Press: Cambridge, UK, 2009; pp. 3–11. [Google Scholar]
- NASA. The Effects of Climate Change. Available online: https://climate.nasa.gov/effects/ (accessed on 10 March 2024).
- Koottungal, L. 2012 Worldwide EOR Survey. Oil Gas J. 2012, 110, 57–69. [Google Scholar]
- Al-Mutairi, S.M.; Kokal, S.L. EOR Potential in the Middle East: Current and Future Trends. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, Vienna, Austria, 23-26 May 2011. [Google Scholar]
- Kuuskraa, V.; Wallace, M. CO2-EOR Set for Growth as New CO2 Supplies Emerge. Oil Gas J. 2014, 112, 92–105. [Google Scholar]
- Allan, D. Integrated Asset Modeling. Oilfield Review 2016.
- Temizel, C.; Jia, B.; Ranjith, R.; Suhag, A.; Balaji, K.; Putra, D.; Saracoglu, O. Integrated Asset Modeling through Optimization of Multiple Reservoirs Using Next-Generation Reservoir Simulators. In Proceedings of the SPE Europec Featured at 79th EAGE Conference and Exhibition, Paris, France, 12-15 June 2017. [Google Scholar] [CrossRef]
- Primera, A.; Sifuentes, W.; Rodríguez, N. CO2 Injection and Storage: A New Approach Using Integrated Asset Modeling. In Proceedings of the EUROPEC/EAGE Conference and Exhibition, Amsterdam, The Netherlands, 8-11 June 2009. [Google Scholar] [CrossRef]
- Roadifer, R.D.; Sauvé, R.; Torrens, R.; Mead, H.W.; Pysz, N.P.; Uldrich, D.O.; Eiben, T. Integrated Asset Modeling for Reservoir Management of a Miscible WAG Development on Alaska’s Western North Slope. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8-10 October 2012. [Google Scholar] [CrossRef]
- Araya, A.; Cullick, S.; Smyth, J. Holistic Approach for CO2 Underground Geological Storage. Energy Procedia 2011, 4, 2645–2653. [Google Scholar] [CrossRef]
- Carpenter, C. Integrated Asset Modeling: An Approach to Long-Term Production Planning. J. Pet. Technol. 2016, 68, 43–44. [Google Scholar] [CrossRef]
- Balch, R.; McPherson, B. Integrating Enhanced Oil Recovery and Carbon Capture and Storage: Farnsworth Field. J. Pet Technol. 2017, 69, 80–82. [Google Scholar] [CrossRef]
- Al-Mutairi, S.; Hayder, E.; Munoz, A.; Al-Shammari, A.; Al-Jama, N. A Study of Coupling Surface Network to Reservoir Simulation Model in a Large Middle East Field. In Proceedings of the North Africa Technical Conference and Exhibition, Cairo, Egypt, 14-17 February 2010. [Google Scholar] [CrossRef]
- Beliakova, N.; van Berkel, J.T.; Kulawski, G.J.; Schulte, A.M.; Weisenborn, A.J. Hydrocarbon Field Planning Tool for Medium to Long Term Production Forecasting from Oil and Gas Fields Using Integrated Subsurface—Surface Models. In Proceedings of the SPE European Petroleum Conference, Paris, France, 24-25 October 2000. [Google Scholar] [CrossRef]
- Wilson, A. A Fully Coupled Network Model: Comparison with Other Integrated Models on Field Cases. J. Pet. Technol. 2015, 67, 90–91. [Google Scholar] [CrossRef]
- Coats, B.K.; Fleming, G.C.; Watts, J.W.; Ramé, M.; Shiralkar, G.S. A Generalized Wellbore and Surface Facility Model, Fully Coupled to a Reservoir Simulator. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, USA, 3-5 February 2003. [Google Scholar] [CrossRef]
- Ghorayeb, K.; Holmes, J.; Torrens, R. Field Planning Using Integrated Surface/Subsurface Modeling. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Kingdom of Bahrain, 12-15 March 2005. [Google Scholar] [CrossRef]
- Pathak, V.; Mirzabozorg, A.; Zuloaga, P.; Dorival Vargas, J.M.; Klix, B. Solving the Challenges of a Complex Integrated Production System in Camisea Field Using Novel Modeling Techniques. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Virtual, 27-31 July 2020. [Google Scholar] [CrossRef]
- Rotondi, M.; Cominelli, A.; Di Giorgio, C.; Rossi, R.; Vignati, E.; Carati, B. The Benefits of Integrated Asset Modeling: Lesson Learned from Field Cases. In Proceedings of the EUROPEC/EAGE Conference and Exhibition, Rome, Italy, 9-12 June 2008. [Google Scholar] [CrossRef]
- Shammari, B.A.; Putra, S.A.; Nooruddin, H.A.; Bellaci, I.J.; Shammari, A.T. European Association of Geoscientists & Engineers, IPTC 2014: International Petroleum Technology Conference, Doha, Qatar, January 2014. [CrossRef]
- Bowen, D.W.; Weimer, P. Reservoir Geology of the Morrow Formation, Eastern Colorado and Western Kansas: Implications for CO2 Sequestration and EOR. NETL Proceeding, 2005. Available online: http://www.netl.doe.gov/publications/proceedings/05/carbon-seq/Poster (accessed on 12 March 2024).
- Ampomah, W.; Balch, R.; Cather, M.; Rose-Coss, D.; Dai, Z.; Heath, J.; Dewers, T.; Mozley, P. Reservoir Modeling of CO2 Storage and Enhanced Oil Recovery at the Morrow Formation, Farnsworth Unit, Texas. Energy Fuels 2016, 30, 8545–8555. [Google Scholar] [CrossRef]
- Kolodzie, S. Analysis of Pore Throat Size and Use of the Waxman-Smits Equation to Determine OOIP in Spindle Field, Colorado. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, USA, 21-24 September 1980. [Google Scholar] [CrossRef]
- Balch, R.; McPherson, B.; Will, R.; Ampomah, W. Recent Developments in Modeling: Farnsworth Texas, CO2 EOR Carbon Sequestration Project. In Proceedings of the 15th Greenhouse Gas Control Technologies Conference, Virtual, 15-18 March 2021. [Google Scholar] [CrossRef]
- Rasmussen, L.; Fan, T.; Rinehart, A.; Luhmann, A.; Ampomah, W.; Dewers, T.; Heath, J.; Cather, M.; Grigg, R. Carbon Storage and Enhanced Oil Recovery in Pennsylvanian Morrow Formation Clastic Reservoirs: Controls on Oil–Brine and Oil–CO2 Relative Permeability from Diagenetic Heterogeneity and Evolving Wettability. Energies 2019, 12, 3663. [Google Scholar] [CrossRef]
- Ross-Coss, D.; Ampomah, W.; Cather, M.; Balch, R.S.; Mozley, P.; Rasmussen, L. An Improved Approach for Sandstone Reservoir Characterization. In Proceedings of the SPE Western Regional Meeting, Anchorage, USA, 23-26 May 2016. [Google Scholar] [CrossRef]
- Sun, Q.; Ampomah, W.; Kutsienyo, E.J.; Appold, M.; Adu-Gyamfi, B.; Dai, Z.; Soltanian, M.R. Assessment of CO2 Trapping Mechanisms in Partially Depleted Oil-Bearing Sands. Fuel 2020, 278, 118356. [Google Scholar] [CrossRef]
- Moch, J.M.; Xue, W.; Holdren, J.P. Carbon Capture, Utilization, and Storage: Technologies and Costs in the U.S. Context. Harvard Kennedy School Belfer Center Policy Brief 2022. 2022.
- Smith, E.; Morris, J.; Kheshgi, H.; Teletzke, G.; Herzog, H.; Paltsev, S. The cost of CO2 transport and storage in global integrated assessment modeling. Int. J. Greenh. Gas Control 2021, 109, 103367. [Google Scholar] [CrossRef]




| Parameter (Reference Name) | Default | Minimum | Maximum |
|---|---|---|---|
| X, Y Permeability Multiplier (PermXY multi) | 1.0 | 0.6 | 0.6 |
| Z Permeability Multiplier (PermZ multi) | 1.0 | 1.0 | 1.0 |
| Porosity Multiplier (PoreV multi) | 1.0 | 0.80 | 1.50 |
| Oil-Water Contact (OWC) | -6500 | -6500 | -4600 |
| Residual Water Saturation (KrwSwi) | 0.15 | 0.10 | 0.36 |
| Water Curve Endpoint (Krw endpoint) | 0.50 | 0.15 | 0.60 |
| Water Saturation Exponent (Krw exp) | 3.0 | 1.0 | 7.0 |
| Residual Oil Saturation (KrowSoi) | 0.1 | 0 | 0.3 |
| Oil Curve Endpoint (Krow endpoint) | 0.8 | 0.7 | 1.0 |
| Oil Saturation Exponent (Krow exp) | 4.0 | 1.0 | 8.0 |
| Residual Gas Saturation (Krgi) | 0 | 0 | 0.15 |
| Gas Curve Endpoint (Krg endpoint) | 1.0 | 0.8 | 1.0 |
| Gas Saturation Exponent (Krg exp) | 1.0 | 1.0 | 3.0 |
| Residual Liquid Saturation (Krogi) | 0.1 | 0.1 | 0.5 |
| Liquid Curve Endpoint (Krog endpoint) | 1.0 | 0.7 | 1.0 |
| Liquid Saturation Exponent (Krog exp) | 4.0 | 1.0 | 5.0 |
| Parameters | Cumulative Value |
|---|---|
| Oil Production, MMSTB | 13.95 |
| Water Production, MMSTB | 38.39 |
| Gas Production, MMSCF | 100,353.7 |
| CO2 Stored, MMIbs | 5,061.68 |
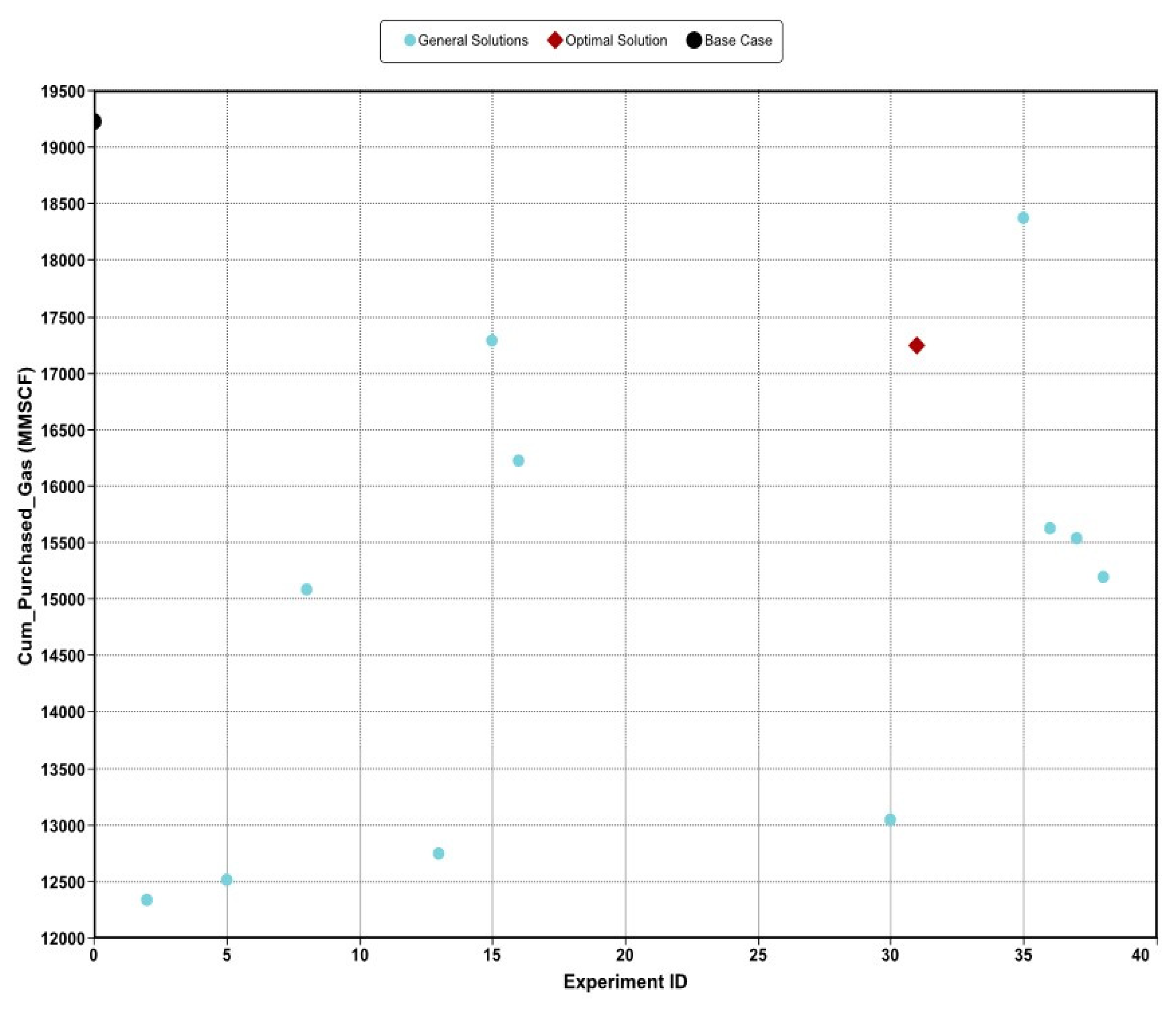
| Experiment ID | Cumulative Gas Produced (MMSCF) |
Amount of CO2 Not Purchased (STB) |
Percentage of Purchased CO2 Less |
|---|---|---|---|
| Development Case | 19,236.79 | ||
| Optimal Strategy | 17,252.12 | 1,984.668 | 10.317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




