In the past few decades, functional data analysis has been widely developed and applied in various fields, such as medicine, biology, economics, environmetrics, chemistry (see [1,2,3,4,5]). An important model in functional data analysis is partial functional linear model, which includes the parametric linear part and the functional linear part. To make the relationships between variables more flexible, the parametric linear part is usually replaced by the non-parametric part. This model is known as functional partially model, which has been studied in [6,7,8]. The functional partially linear regression model is defined as follows: where Y is response variable, $X(·)$ is functional predictor with mean ${\mu }_0(·)$ and covariance operator $\mathcal{C}$. The slope function $\alpha (·)$ is an unknown function. $g(·)$ is a general continuous function defined on a compact support $\Omega$. $\epsilon$ is a random error with mean zero and finite variance ${\sigma }^2$, and is independent of the predictor $X(·)$. When the $g(·)$ is constant, the model (1) becomes a functional linear model. See [9,10,11]. When $g(·)$ is parametric linear part, the model (1) becomes a partially functional linear model, which has been studied in [12,13,14].

Hypothesis testing plays a critical role in statistical inference. For testing the linear relationship between the response and the functional predictor in functional linear model, functional principal component analysis (FPCA) of the functional predictor $X(·)$ in the literature is a major idea to construct test statistic. See [9,10,15]. Taking into account the flexibility of non-parametric functions, [6] introduced the functional partially linear regression model. [7] and [8] constructed the estimators of the slope functions based on spline and FPCA respectively, and the estimate of non-parametric components in their papers adopted B-spline. When the predictors are measured with additive error, [16] studied the estimators of slope function and non-parametric function by FPCA and kernel smoothing techniques. [17] established the estimators of slope function, non-parametric component and mean of response variable when existing missing responses at random.

However, testing the relationship between the response variable and the functional predictor in functional partially linear regression model has been rarely considered so far. In this paper, the following hypothesis testing for model (1) will be considered: where ${\alpha }_0\left(t\right)$ is an assigned function. Without loss of generality, let ${\alpha }_0\left(t\right)=0$. For testing (2), [18] constructed a chi-square test using FPCA when the functional data can be approximated with a few principal components. In particular, when the functional data cannot be approximated with a few principal components, only several researches have considerated this situation in functional data analysis. [19] constructed a FLUTE test based on order-four U-statistic for the testing in functional linear model, which can be computationally very costly. In order to save calculation time, [20] developed a faster test using a order-two U-statistic. Motivated by this, we propose a non-parametric U-statistic that combines the functional data analysis with the classical kernel method for testing (2).

The paper is organized as follows. In Section 2, we construct a new test procedure for testing in functional partially linear regression model. The theoretical properties of the proposed test statistic under some regularity conditions will be considered in Section 3. Simulation study is conducted in Section 4 to assess the finite sample performance of our proposed test procedure. Section 5 reports the testing result for spectrometric data. All the proofs of main theoretical results are presented in Appendix.

Suppose that Y and U are real-valued random variables. $\left\{X\right(·\left)\right\}$ is a stochastic process with sample paths in $L^2[0,1]$, which is the set of all square integrable functions defined on $[0,1]$. Let $\langle ·,·\rangle$, $\Vert ·\Vert$ represent the inner product and norm in $L^2[0,1]$, respectively. {$(Y_i,X_i(·),U_i),i=1,2,\dots ,n$} is a random sample from model (1), For any given $\alpha \left(t\right)\in L^2[0,1]$, we move $\alpha \left(t\right)$ to the left, Then model (4) becomes classical non-parametric model. A pseudo kernel estimate of the non-parametric function using Nadaraya-Watson regression method can be constructed as follows: where $K_h(·)=K(·/h)/h$ with $K(·)$ being a preselected kernel function and h being the bandwidth whose optimal value can be determined by some data-driven methods such as the cross-validation methods. Here we estimate non-parametric $g\left(U_i\right)$ without ith sample.

Let where $W_{ij}=K_h(U_j-U_i)/{\sum }_{k\ne i}{K}_h(U_k-U_i)$. So the pseudo estimate (5) of non-parametric function can be rewritten in matrix as If we replace $g\left(U_i\right)$ by $\check{g}\left(U_i\right)$ in the model (3), we have where ${\check{X}}_i\left(t\right)=X_i\left(t\right)-{\mathbf{W}}_{-i}^T{\mathbf{X}}_{-i}\left(t\right)$, ${\check{Y}}_i=Y_i-{\mathbf{W}}_{-i}^T{\mathbf{Y}}_{-i}$. If we denote ${\mu }_{it}\triangleq \mu (U_i,t)=E\left[X_1\left(t\right)\right|U_i]$, where “≜” stand for “defined as”. Then ${\widehat{\mu }}_{it}={\mathbf{W}}_{-i}^T{\mathbf{X}}_{-i}\left(t\right)$ can be estimator of the conditional expectation ${\mu }_{it}$ for any $t\in [0,1]$.

For an arbitrary orthonormal basis ${\left\{{\varphi }_j\right\}}_{j=1}^{\infty }$ in $L^2[0,1]$, the predictor $X(·)$ and the slope function $\alpha (·)$ have following expansions. Denote the number of truncated basis function by p, where ${\xi }_{ij}=\langle X_i,{\varphi }_j\rangle$, ${\beta }_j=\langle \alpha ,{\varphi }_j\rangle$. Let ${\check{\xi }}_{ij}=\langle {\check{X}}_i,{\varphi }_j\rangle$, the model (7) can be rewritten as follows: Denote ${\xi }_i={({\xi }_{i1},{\xi }_{i2},\dots ,{\xi }_{ip})}^T$, which has mean $\mu$ and covariance matrix $\Sigma$. Let

For model (3), we define the approximation error as

To analyze the effect of the approximation error, we impose following condition on functional predictors and regression function.

(C1) Functional predictors $\{X_i,i=1,\dots ,n\}$ and regression function $\alpha \left(t\right)$ satisfy:

(i) Functional predictors $\{X_i,i=1,\dots ,n\}$ belongs to a Sobolev ellipsoid of order-two, then there exists a universal constant C, such that ${\sum }_{j=1}^{\infty }{\xi }_{ij}^2{j}^4\le C^2,\mathrm{for}i=1,\dots ,n.$

(ii) Regression function satisfies $\int {\alpha }^2\left(t\right)dt\le K,$ where K is a constant.

Using Cauchy-Schwarz inequality, we have Then the approximation error can be ignored as $p\to \infty$. Model (7) becomes: which is a high-dimensional partial linear model. Since can be used as an effective measure of the distance between $\alpha (·)$ and 0 when testing (2). Motivated by [21], we construct following test statistic by estimating (11). where where $\overline{\check{X}}\left(t\right)$ and $\overline{\check{Y}}$ are sample means of ${\check{X}}_i\left(t\right)$ and ${\check{Y}}_i$. By some calculations, we can get $E\left[{\Delta }_{ij}\left(\check{X}\right)\right]=0$, $E\left[{\Delta }_{ij}\left(\check{Y}\right)\right]=0$. The test statistic $T_{np}$ can served as a measurement of distance between $\alpha (·)$ and 0 under null hypothesis. Large values of test statistic $T_{np}$ are in favor of alternative hypothesis and leads to rejection of null hypothesis.

To achieve the asymptotic properties of the proposed test, we first suppose following conditions based on [19] and [21]. Denote A condition on the dimension of matrix ${\Sigma }_{*}$ is:

(C2) As $n\to \infty$, $p\to \infty$; ${\Sigma }_{*}>0$, $\mathrm{tr}\left({\Sigma }_{*}^4\right)=o\left({\mathrm{tr}}^2\left({\Sigma }_{*}^2\right)\right)$.

(C3) There exists a m-dimensional random vector $Z_i={(Z_{i1},\dots ,Z_{im})}^T$ for a constant $m\ge p$ so that ${\xi }_i=E\left[{\xi }_i\right|U_i]+\mathbf{\Gamma }\left(U_i\right)Z_i.$ Here $Z_i$ satisfies $E\left(Z_i\right)=0$, $\mathrm{var}\left(Z_i\right)=I_m$, and for any $U_i$, $\mathbf{\Gamma }\left(U_i\right)$ is a $p\times m$ matrix such that $\mathbf{\Gamma }\left(U_i\right){\mathbf{\Gamma }}^T\left(U_i\right)={\Sigma }_{*}\left(U_i\right)$. Each random vector $\{Z_i,i=1,\dots n\}$ is assumed to have finite 4th moments and $E\left(Z_{ij}^4\right)=3+\Delta$ for some constant $\Delta$. Furthermore, we assume for ${\sum }_{k=1}^d{l}_k\le 4$ and $j_1\ne j_2\ne \cdots \ne j_d$, where d is a positive integer.

(C4) ${\mathsf{\beta }}^T{\Sigma }_{*}\mathsf{\beta }=o\left(h^2\right)$, and ${\mathsf{\beta }}^T{\Sigma }_{*}^3\mathsf{\beta }=o(\mathrm{tr}\left({\Sigma }_{*}^2\right)/n)$.

(C5) The error term satisfies $E\left[{\epsilon }^4\right]<+\infty$.

(C6) The random variable U has a compact support $\Omega$, and its density function $f(·)$ has continuous second order derivative and bounded away from 0 on its support. The kernel function $K(·)$ is a symmetric probability density function with a compact support. Also, it is Lipschitz continuous.

(C7) $E\left({\xi }_1\right|U_1)$ and $g(·)$ are Lipschitz continuous, and have continuous second order derivatives.

(C8) The sample size n and the smoothing parameter h are assumed to satisfy $\underset{n\to \infty }{lim}h=0,\underset{n\to \infty }{lim}nh=\infty ,\underset{n\to \infty }{lim}n{h}^4=0$.

(C9) The truncated number p and the sample size n are assumed to satisfy $p=o\left(n^2{h}^2\right)$.

Condition (C2) has been adopted in many studies about high-dimensional data (see [21,22,23]). Condition (C3) resembles a factor model. To analyze the local power, we also impose the condition (C4) on the coefficient vector $\mathsf{\beta }$. In fact, (C4) can be served as the local alternatives as its distance measurement between $\mathsf{\beta }$ and 0. This local alternative can be also found in [21]. (C5) is the typical assumptions for the error term $\epsilon$. Conditions (C6-C8) are very common in non-parametric smoothing. (C9) is a technical condition which is needed to derive the theorems.

We will show the asymptotic theory of our proposed test statistic under the null hypothesis and the local alternative (C4) in the following two theorems.

Theorem 2 indicates that under the local alternative hypothesis (C4), the proposed test statistic has the following asymptotic local power for the nominal level $\alpha$, where $\Phi (·)$ is the cumulative distribution function of the standard normal distribution, and $z_{\alpha }$ denotes its upper $\alpha$ quantile. Let $\eta \left(\alpha \right)={\mathcal{C}}^{*}\left(\alpha \right)/{\sigma }^2\sqrt{2\mathrm{tr}\left({\Sigma }_{*}^2\right)}$, and this quantity can be viewed as a signal-to-noise ratio. When the term $\eta \left(\alpha \right)=o(1/n)$, the power converges to $\alpha$, then the power converge to 1 if it has a high order of $1/n$. This implies that the proposed test is consistent. Our proposed test statistic also process the identical asymptotic local power. The performance of the power will be shown by simulation in Section 4.

By Theorem 2, the proposed test statistic rejects $H_0$ at a signification level $\alpha$ if where ${\widehat{\sigma }}^2$ and $\widehat{\mathrm{tr}\left({\Sigma }_{*}^2\right)}{z}_{\alpha }$ are consistent estimators of ${\sigma }^2$ and $\mathrm{tr}\left({\Sigma }_{*}^2\right)$, respectively. We use the similar method as in [24] to estimate the trace. That is, where $Y_{1n}={\displaystyle \frac{1}{A_n^2}}\sum _{i\ne j}{\langle {\check{X}}_i^T,{\check{X}}_j\rangle }^2$, $Y_{2n}={\displaystyle \frac{1}{A_n^3}}\sum _{i\ne j\ne k}\langle {\check{X}}_i^T,{\check{X}}_j\rangle \langle {\check{X}}_j^T,{\check{X}}_k\rangle$, $Y_{2n}={\displaystyle \frac{1}{A_n^4}}\sum _{i\ne j\ne k\ne l}\langle {\check{X}}_i^T,{\check{X}}_j\rangle \langle {\check{X}}_k,{\check{X}}_l\rangle$ with $A_n^m=n!/(n-m)!$. And the simple estimator ${\widehat{\sigma }}^2={(n-1)}^{-1}{\sum }_{i=1}^n{({\check{Y}}_i-\overline{\check{Y}})}^2$ is used, which is consistent under the null hypothesis testing.

In this section, to evaluate the finite sample performance of the proposed test, some simulation studies are conducted. We generate 1,000 Monte Carlo samples in each simulation. For basis expansion and FPCA, we use the implementation in the R package fda.

Here we compare the proposed test $T_{np}$ with the chi-square test $T_n$ constructed by [18]. The cumulative percentage of total variance (CPV) method is used to estimate the number of principal components in $T_n$. Define CPV explained by the first m empirical functional principal components as where ${\left\{{\widehat{\lambda }}_i\right\}}_{i=1}^p$ is the estimate of the eigenvalue of covariance operator. The minimal m for which CPV(m) exceeds a desired level, 95% is chosen in this section. We denote p as the number of basis functions used to fit curves. The simulated data is generated from the following model: where $g\left(U_i\right)=2U_i$ or $g\left(U_i\right)=2+sin\left(2\pi U_i\right)$, and $\{U_i,i=1,2,\dots ,n\}$ is independently generated from the uniform distribution $\mathrm{U}(0,1)$. To analyze the impact of different error distributions, the following four distributions will be selected: (1) ${\epsilon }_i\sim N(0,1)$, (2) ${\epsilon }_i\sim t\left(3\right)/\sqrt{3}$, (3) ${\epsilon }_i\sim \mathbf{\Gamma }(1,1)-1$, (4) ${\epsilon }_i\sim (\mathrm{lnorm}(0,1)-\sqrt{e})/\sqrt{e(e-1)}$. All results about $g\left(U_i\right)=2U_i$ are presented in supplementary materials.

We next report the simulation results for two data structures of the predictor $X\left(t\right)$. Because fitting curves with several basis functions are not reasonable for functional data that cannot be approximated by a few principal components, the performance of $T_n$ and $T_{np}$ will be compared based on the change in the number of basis functions used in the fitting curves, and the performance of the proposed test $T_{np}$ when the number of basis functions used to fit curves is large enough (at this point, the value of $T_n$ cannot be calculated) will be presented.

1. The predictor $X\left(t\right)={\sum }_{j=1}^{50}{\xi }_j{\varphi }_j\left(t\right)$, where ${\xi }_j$ follows a normal distribution with mean zero and variance ${\lambda }_j=10{\left((j-0.5)\pi \right)}^{-2}$, ${\varphi }_j\left(t\right)=\sqrt{2}(j-0.5)\pi t$ for $j=1,2,\dots ,50$. The slope function $\alpha \left(t\right)=c(\sqrt{2}\sin (\pi t/2)+3\sqrt{2}\sin (3\pi t/2))$ with c varying from 0 to 0.2. $c=0$ corresponds to the null hypothesis. The number of basis functions used to fit curves and the sample size are taken as: $p=11,49$, $n=50,100$. Under different error distributions, Table 1 and Table 2 evaluate the empirical size and power of both tests for different non-parametric functions when the nominal level $\alpha$ is $0.05$.

From Table 1 and Table 2, it can be seen that, (i) For different error distributions and different non-parametric functions, the performance of both tests is stable; (ii) Due to the asymptotic distribution of $T_{np}$ is for functional data that cannot be approximated by a few principal components, the power of proposed test is slightly lower than that of $T_n$. (iii) As the sample size n increases, the power increases, while the power does not increase or decrease significantly as the value of p increases. In fact, for this data structure of the predictor, no matter how many basis functions are selected to fit the function curves, the number of principal components we finally select is very small.

2. The functional predictor is generated based on the expansion (8), where ${\varphi }_k$’s are Fourier basis functions on [0,1] defined as ${\varphi }_1\left(t\right)=1$, ${\varphi }_2\left(t\right)=\sqrt{2}\sin \left(2\pi t\right)$, ${\varphi }_3\left(t\right)=\sqrt{2}\cos \left(2\pi t\right)$, ${\varphi }_4\left(t\right)=\sqrt{2}\sin \left(4\pi t\right)$, ${\varphi }_4\left(t\right)=\sqrt{2}\cos \left(4\pi t\right),\dots$. The first p of these basis functions will be used to generate the prediction function and slope function. Let $X_i\left(t\right)={\sum }_{j=1}^p{\xi }_{ij}{\varphi }_j\left(t\right)$, $\alpha \left(t\right)={\sum }_{j=1}^p{\beta }_j{\varphi }_j\left(t\right)$, where $p=11,49,201,365$, $n=50,100,200$, the coefficient of slope function $\{{\beta }_i=|\beta |/\sqrt{p},i=1,\dots ,p\}$ with ${\left|\beta \right|}^2=c\ast {10}^{-2}$ and c varying from 0 to 1. $c=0$ corresponds to the case in which $H_0$ is true. The coefficients of predictor ${\xi }_{ij}$ follow the moving average model: where the constant T controls the range of dependence between the components of predictor $X\left(t\right)$. $\{Z_{ij},Z_{i(j+1)},\dots ,Z_{i(p+T-1)}\}$ are independently generated from the normal distribution $N(0,I_{p+T-1})$ with $T=10$. The element at $(j,k)$ position of the covariance matrix $\Sigma$ for coefficient vector ${\xi }_i$ is ${\sum }_{l=1}^{T-|j-k|}{\rho }_l{\rho }_{l+|j-k|}I\left\{\right|j-k|<T\},$ where $\{{\rho }_k,k=1,\dots ,T\}$ is independently generated from the uniform distribution on [0,1].

The Epanechnikov kernel is adopted in estimating non-parametric part $g(·)$. we select the bandwidth with cross validation (CV). When the significant level $\alpha$ is 0.05, Table 3 and Table 4 show the empirical size and power of both tests for different non-parametric functions with different error distributions.

From Table 3 and Table 4, the number of basis functions used for fitting functions has a very important impact on the test. Specifically, (i) Under different error distributions, with the increase of p, the empirical size of test $T_n$ is much greater than the nominal level, while our proposed test $T_{np}$ has a stable performance; (ii) As the sample size n increases, the power increases, while the power decreases as the value of p increase. In fact, for this data structure of the predictor, the number of selected principal components is too large to make the test statistics based on FPCA perform well. Instead, the proposed test has great advantages(see bold numbers in Table 3 and Table 4).

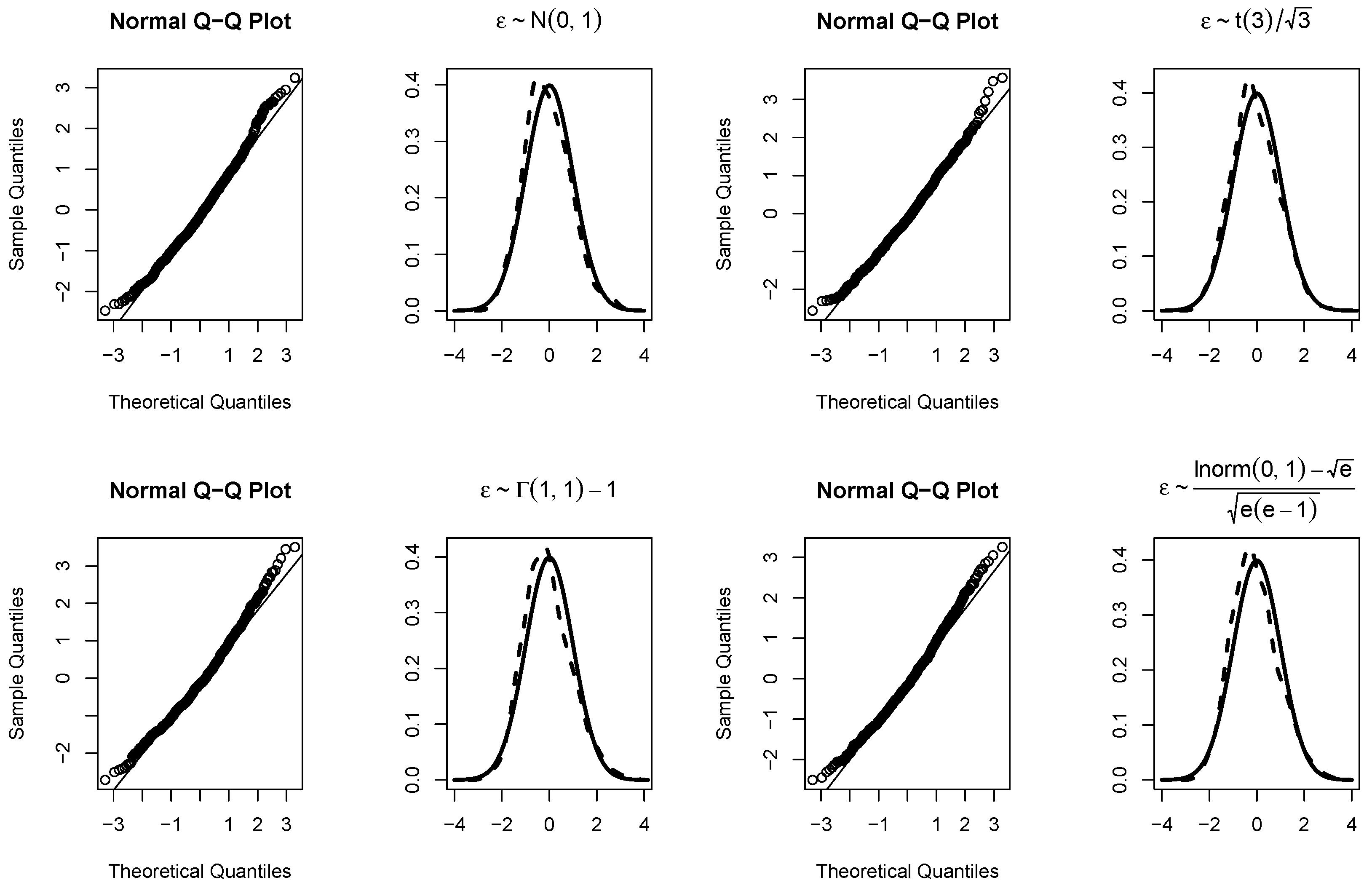
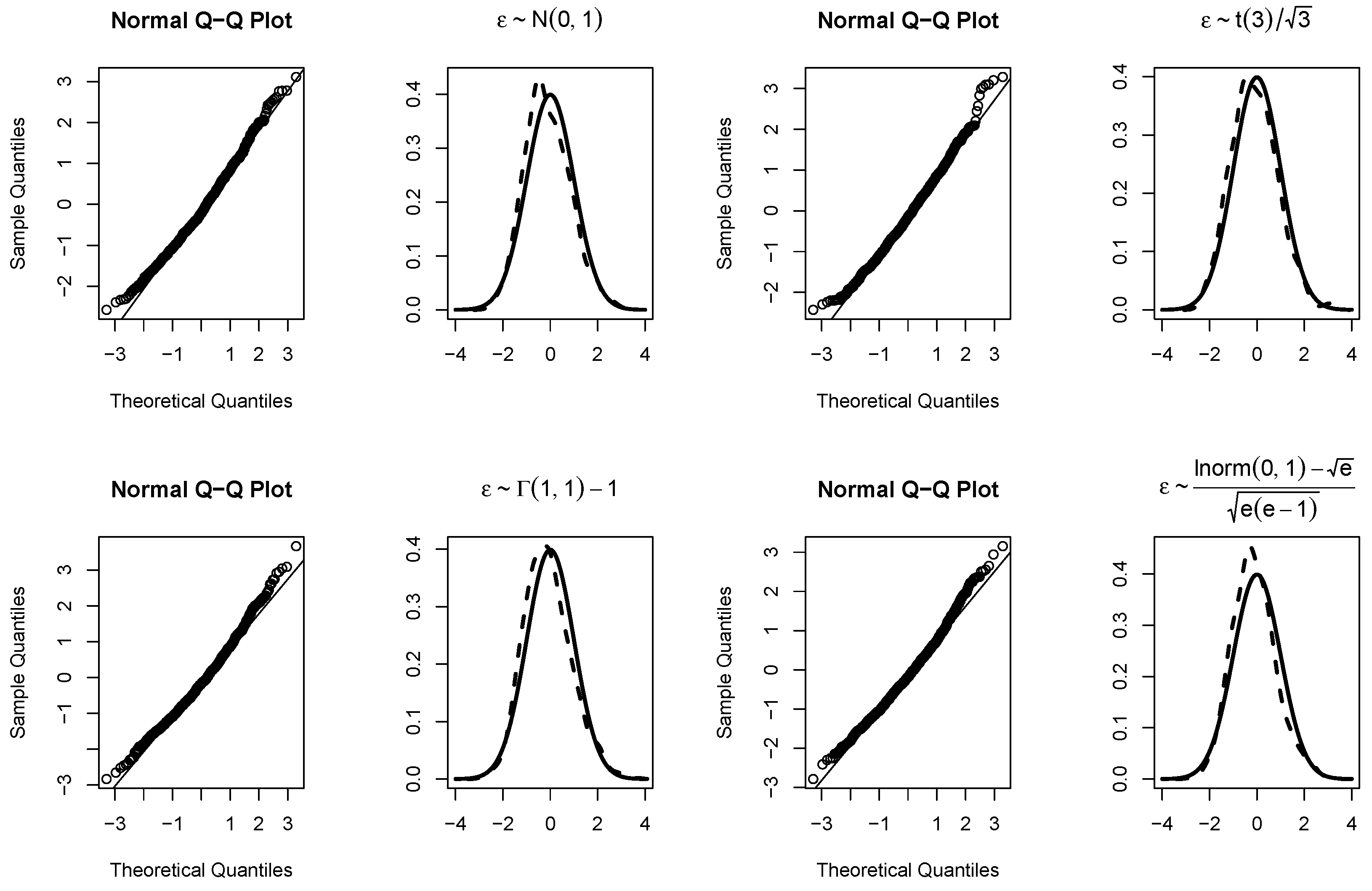
Furthermore, to verify the asymptotic theory of our proposed test, when $(n,p)=(200,365)$, Figure 1 and Figure 2 draw the null distributions and the q-q plots of $T_{np}$ for $g\left(u\right)=2u$ and $g\left(u\right)=2+sin\left(2\pi u\right)$, respectively. The null distributions are represented by the dashed lines, while the solid lines are density function curves of standard normal distributions. 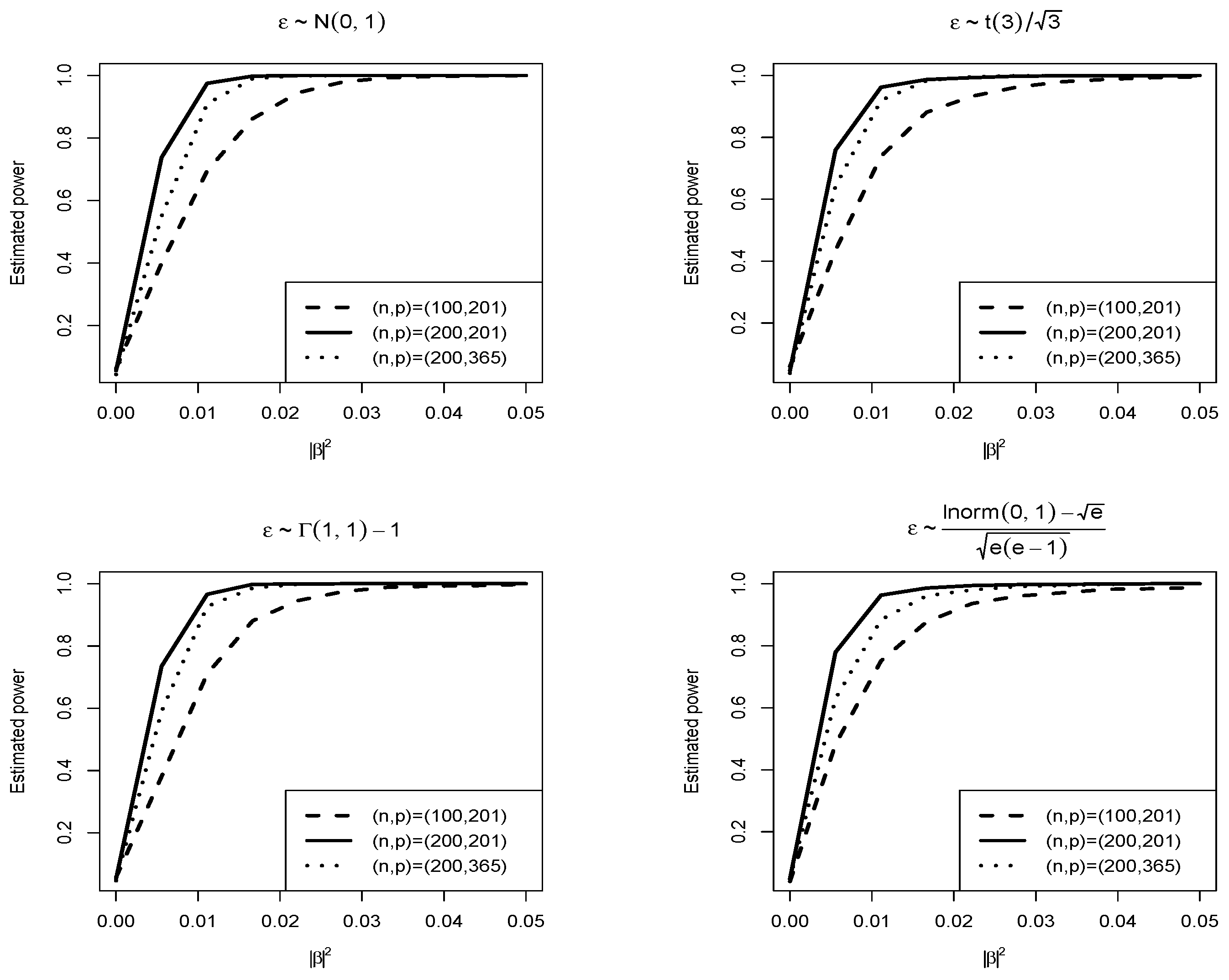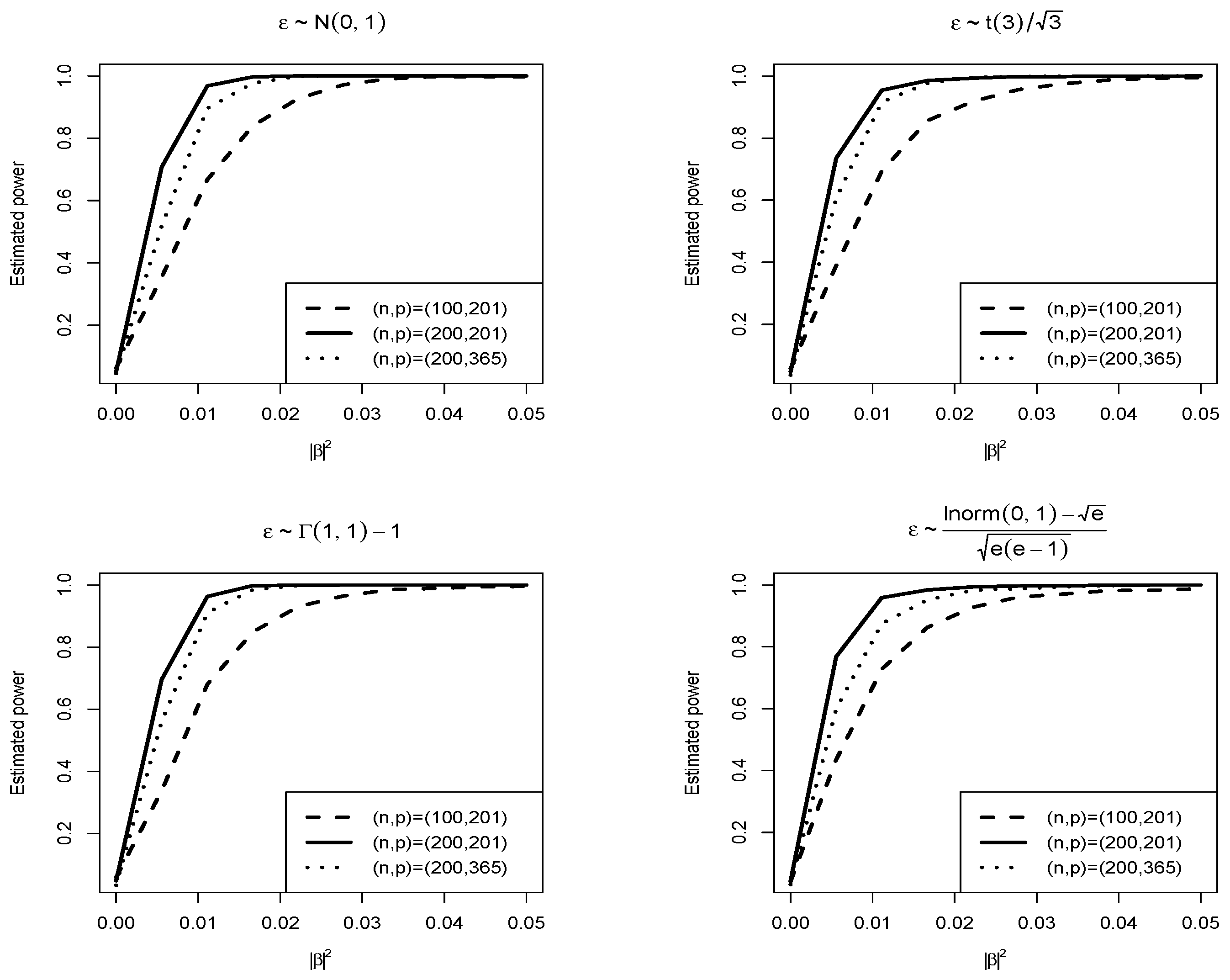For different $n,p$, Figure 3 and Figure 4 respectively show the empirical power functions of the proposed test statistics under four different error distribution functions when the non-parametric function is a linear function and a trigonometric function. When $(n,p)=(200,201),(100,201),(200,365)$, the empirical power functions of the proposed test are represented by solid lines, dashed lines and dotted lines respectively. It can be seen that from Figure 3 and Figure 4, the power increases rapidly as long as c increases slightly. As the sample size n increases, the power increases, while the power decreases as p increases. The proposed test is stable under different error distributions. These are consistent with the conclusions in Table 3 and Table 4 (i.e.$p<n$).

This section applies the proposed test to the spectral data, which has been described and analyzed in the literature (see [25,26]). This dataset can be obtained on the following platforms: http://lib.stat.cmu.edu/datasets/tecator. There are 215 meat samples. Each sample contains chopped pure meat, which contains different absorption spectra and fat, protein and water contents. The observations of the spectral measurement are some curves, denoted by $X_i(·)$, which corresponds to the absorbance measured on the grid with 100 wavelengths ranging from 850nm to 1050nm in step. Fat, protein and water content (in percentage) are measured by chemical analysis method. Denote the fat contents as response variable $Y_i$, the protein contents as $Z_i$, and the moisture content as $U_i$. Similar to [27], the following two models will be used to assume the relationship between them:

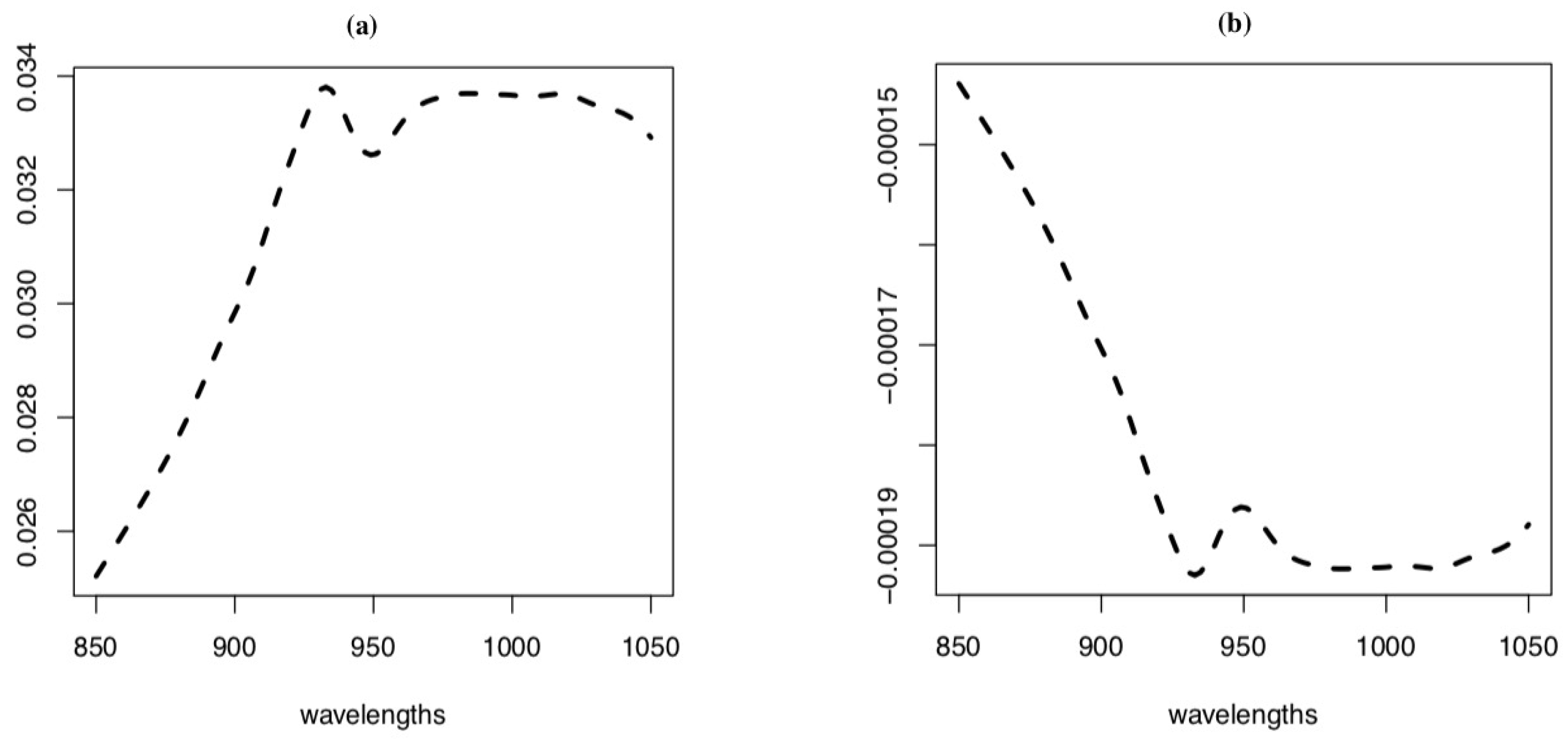
Here we mainly study the test in models (14) and (15): $\alpha \left(t\right)=0$. The number of basis functions used for fitting function curves p is selected as 129. Figure 5 shows the estimation of slope function $\alpha \left(t\right)$ in models (14) and (15).

The calculation results are as follows: (i) For model (14), the value of statistic is $T_{np}=31.186$; p-value is 0. (ii) For model (15), the value of statistic is $T_{np}=-0.867$; p-values are 0.386.

From this we can seen that the conclusions. The test on model (14) is significant, while the test on model (15) is not significant. This result can also be reflected from Figure 5. It is obvious that the estimated value of $\alpha \left(t\right)$ on the right side of Figure 5 is much smaller than that on the left side.

In this paper, we constructed a U-statistic of order-two for testing linearity between the functional predictor and the response variable in functional partially linear regression model. The proposed test procedure didn’t depend on the estimate of covariance operator of predictor function. The asymptotic distribution of proposed test statistic is normal under a null hypothesis and a local alternative assumption. Furthermore, numerical simulations show that our proposed test performs well when functional data cannot be approximated by a few principal components. Finally, the real data has applied to our proposed test to verify its feasibility.