Prerpints.org logo
Preprint
Review

Recent Advances in Numerical Simulation of Ejector Pumps for Vacuum Generation: A Review

Altmetrics

Downloads

161

Views

62

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 July 2024

Posted:

22 July 2024

You are already at the latest version

Alerts
Abstract
This review paper provides an overview of recent advances in computational fluid dynamics (CFD) simulations of ejector pumps for vacuum generation. It examines various turbulence models, multiphase flow approaches, and numerical techniques employed to capture complex flow phenomena like shock waves, mixing, phase transitions, and heat/mass transfer. Emphasis is placed on comprehensive assessment of flow characteristics within ejectors, including condensation effects such as nucleation, droplet growth, and non-equilibrium conditions. The review highlights efforts in optimizing ejector geometries and operating parameters to enhance the entrainment ratio, a crucial performance metric for ejectors. The studies reviewed encompass diverse working fluids, flow regimes, and geometric configurations, underscoring the significance of ejector technology across various industries. While substantial progress has been made in developing advanced simulation techniques, several challenges persist, including accurate modeling of real gas behavior, phase change kinetics, and coupled heat/mass transfer phenomena. Future research efforts should focus on developing robust multiphase models, implementing advanced turbulence modeling techniques, integrating machine learning based optimization methods, and exploring novel ejector configurations for emerging applications.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Ejectors stand as versatile and vital components in the realm of fluid dynamics, finding application across a spectrum of industries ranging from refrigeration and air conditioning to aerospace propulsion. These devices harness the kinetic energy of a high-pressure primary flow to induce and accelerate a secondary fluid stream based on the principle of entrainment. A typical ejector comprises main component such as primary nozzle, mixing chamber, throat, and diffuser. Figure 1 shows the schematic of a typical ejector main components. Notable benefits of ejectors include their simple design, no moving parts, no electricity required, no contamination, and scalability to accommodate various flow rates and pressure requirements. The drawbacks of ejectors are low efficiency, limited suction capability, dependence on motive fluid properties, complexity in design and operation, as well as noise and vibration.
Chen and colleagues [2] pointed out the critical role of ejectors with respect to energy recovery systems and their integration with other technologies, highlighting the necessity for more dependable ejector and system modeling under both steady-state and transient conditions. Elbel et al. [3] presented an overview of advancements in utilizing ejectors for recovering expansion work in vapor-compression systems. They suggested further research and development efforts in this field to enhance the adaptability of ejectors for broader applications. Besagni et al. [4] conducted a comprehensive review on ejector refrigeration systems, exploring their diverse applications alongside various other technologies. They presented an analysis of the relationship between the working fluids and ejector performance, emphasizing historical, current, and future trends. Little and Garimella [5] offered a review while highlighting particular aspects of ejector traits and their application within chiller systems. Aidoun et al.[6,7] contributed to two review papers. The first paper [6], focusing on single-phase ejectors, outlined recent research on heat-driven ejectors and ejector-based machines using low boiling point fluids. They discussed ejector physics principles, recent technological developments, and achievements in thermally activated ejectors for compressible fluids. The emphasis was on design, operation, theoretical and experimental approaches, complex phenomena analysis, and performance evaluation. The subsequent paper by Aidoun et al. [7], which concentrated on two-phase ejectors, provided substantial insights into the design, functioning, and effectiveness of these components. They extensively discussed the impact of geometry, operating conditions, and recent advancements in theoretical and experimental approaches, evaluation methods, and applications. Tashtoush et al. [1] focused on various geometrical factors influencing ejector performance, such as entrainment ratio, pressure ratio, primary nozzle position, area ratio, and mixing suction length. They also covered mathematical models for studying ejector behavior, experimental flow visualization techniques, primary ejector refrigeration systems, and the effects of different working fluids on system performance. Koirala et al. [8] aimed to evaluate primary water jet ejectors for active vapor transport and condensation in compact domestic water desalination systems, with the goal of replacing vacuum pumps and condensers. Besagni [9] analyzed ejector technology, refrigerant properties, and their impact on performance, categorizing the technologies into past, present, and future trends.
For a significant duration, design of ejector systems has largely leaned towards empirical or semi-empirical methods due to the intricate flow physics involved. Leveraging numerical techniques and mathematical models, CFD simulation provide a virtual window into the inner workings of ejectors, enabling detailed analysis of pertinent parameters. By synthesizing the collective knowledge and expertise from diverse disciplines including fluid mechanics and numerical analysis, this review seeks to offer a holistic understanding of the intricacies involved in the CFD-based investigation of ejectors.

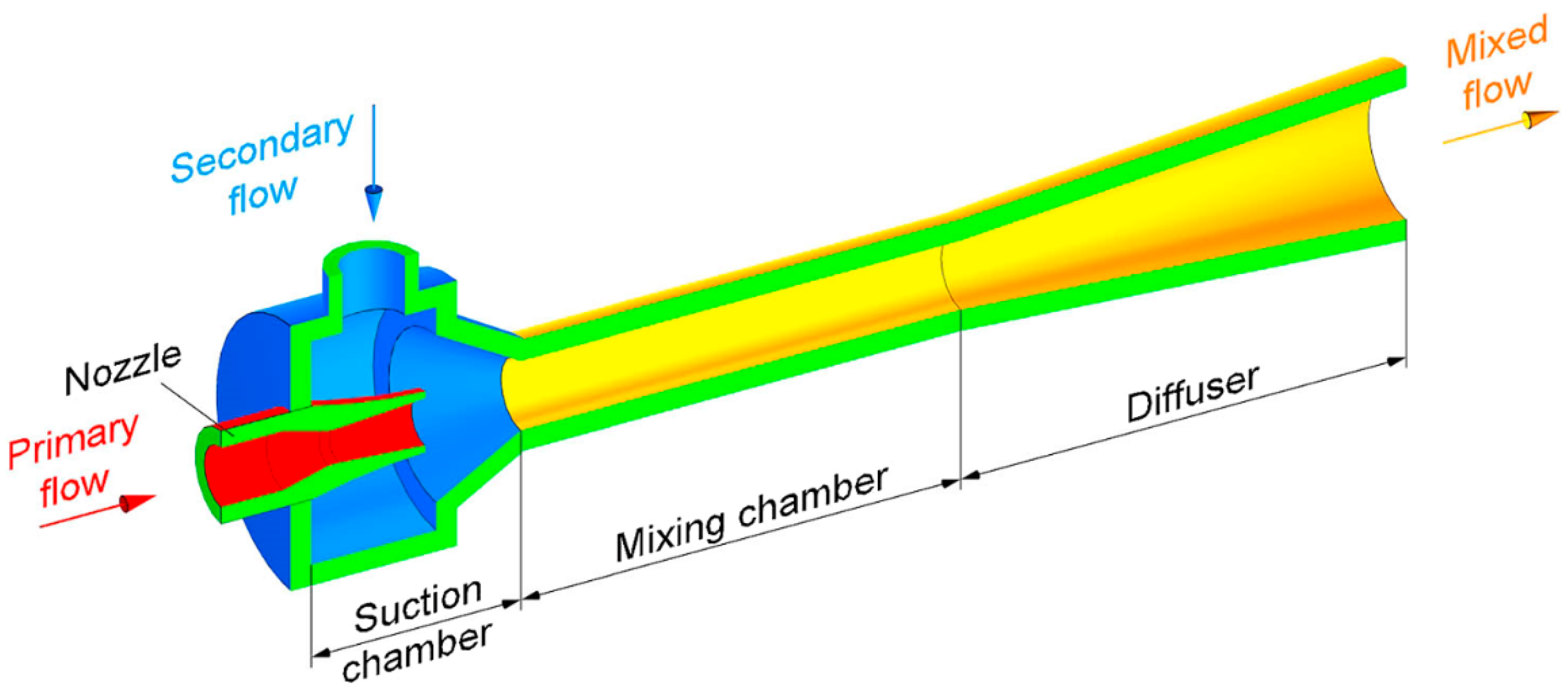
2. Fundamental of Ejectors

Ejectors function to convey energy from either a liquid or gas primary fluid to a secondary fluid. The following processes occur in the components of an ejector:
  • The primary fluid’s pressure energy is converted into kinetic energy within the nozzle
  • The low-velocity secondary fluid is entrained and mixed with the high-velocity primary fluid in the mixing throat, driven by viscous friction and the suction created by the pressure drop at the nozzle exit
  • The combined fluid’s kinetic energy is transformed back into pressure energy within the diffuser.
Within the mixing region, turbulent shear stress generates a velocity distribution that steeply increases towards the ejector axis. If the primary flow is supersonic, a series of shock waves will appear along the mixing zone, undergoing multiple reflections. Additionally, Phase-change phenomena inside ejectors may happen in different ways depending on the application. Condensation effect is one of the most sophisticated phenomena which may occur due to expansion of either primary or secondary fluid within the two-phase boundary. Due to the high velocity, compressibility, and turbulence involved, the study of this effect becomes more intricate[10,11,12,13].

2.1. Entrainment Ratio

The entrainment ratio M refers to the ratio of entrained fluid flow rate m ˙ s to the primary fluid flow rate m ˙ p , indicating the effectiveness of fluid entrainment and mixing within the ejector system, which is defined as follows[14]:
M = m ˙ s m ˙ p

2.2. Pressure Ratio

The pressure ratio N represents the ratio of pressure increase in the secondary flow to the pressure drop in the primary flow by the ejector system, which can be defined as follows [14]:
N = P d − P s P p − P d
where P d , P s , and P p denote diffuser outlet pressure, secondary fluid pressure, and primary fluid pressure, respectively.

2.3. Efficiency of Ejector

Efficiency of ejector η , in essence, refers to the relationship between the power generated by the ejector (output power E ˙ o u t ) and the power consumed by the ejector (input power E ˙ i n ). Based on the one-dimensional theory assuming that mixing is completed in the constant area mixing throat and also, spacing between the nozzle exit and the mixing throat entrance is zero, the efficiency of ejector can be defined as follows[15,16]:
η = E ˙ o u t E ˙ i n = M N
where M, N are entrainment ratio and pressure ratio.

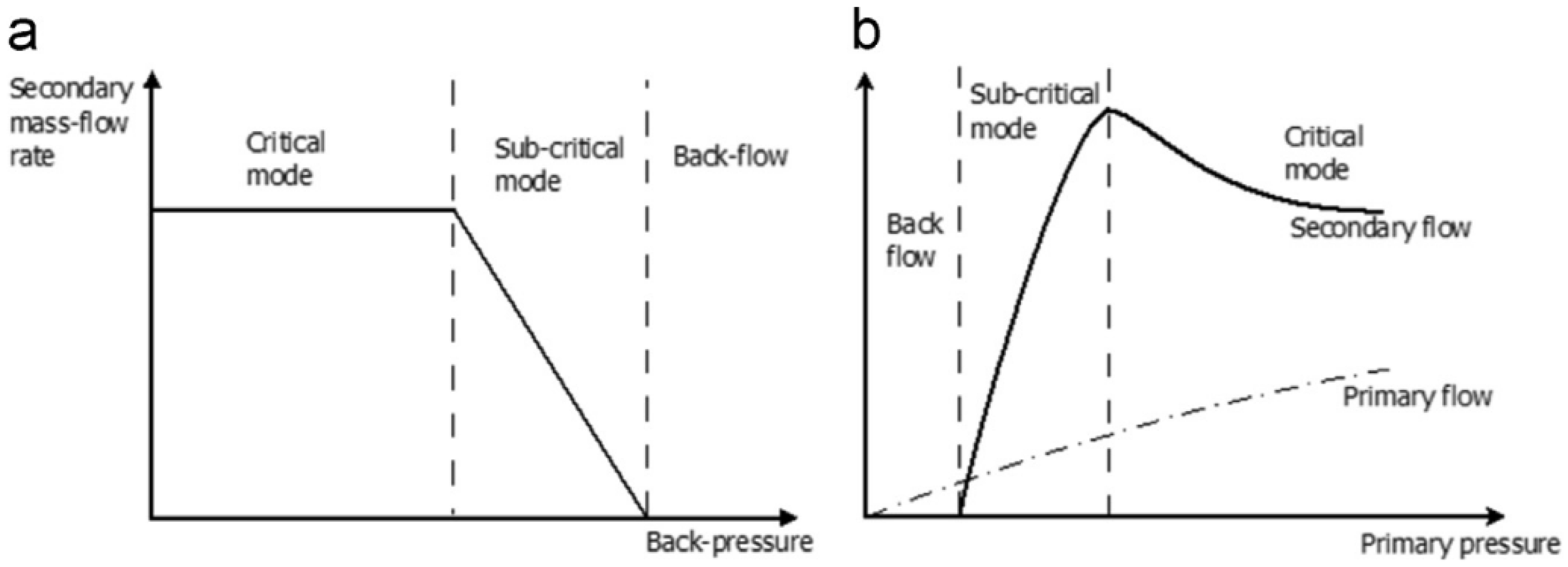
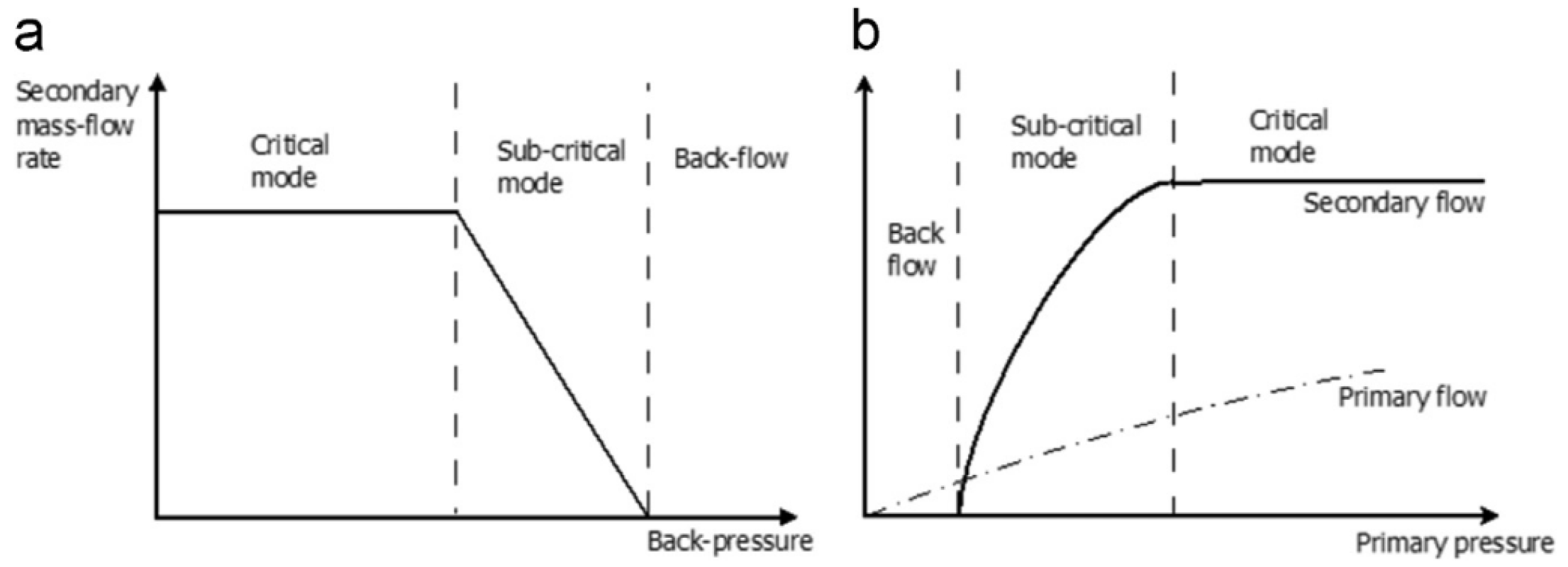
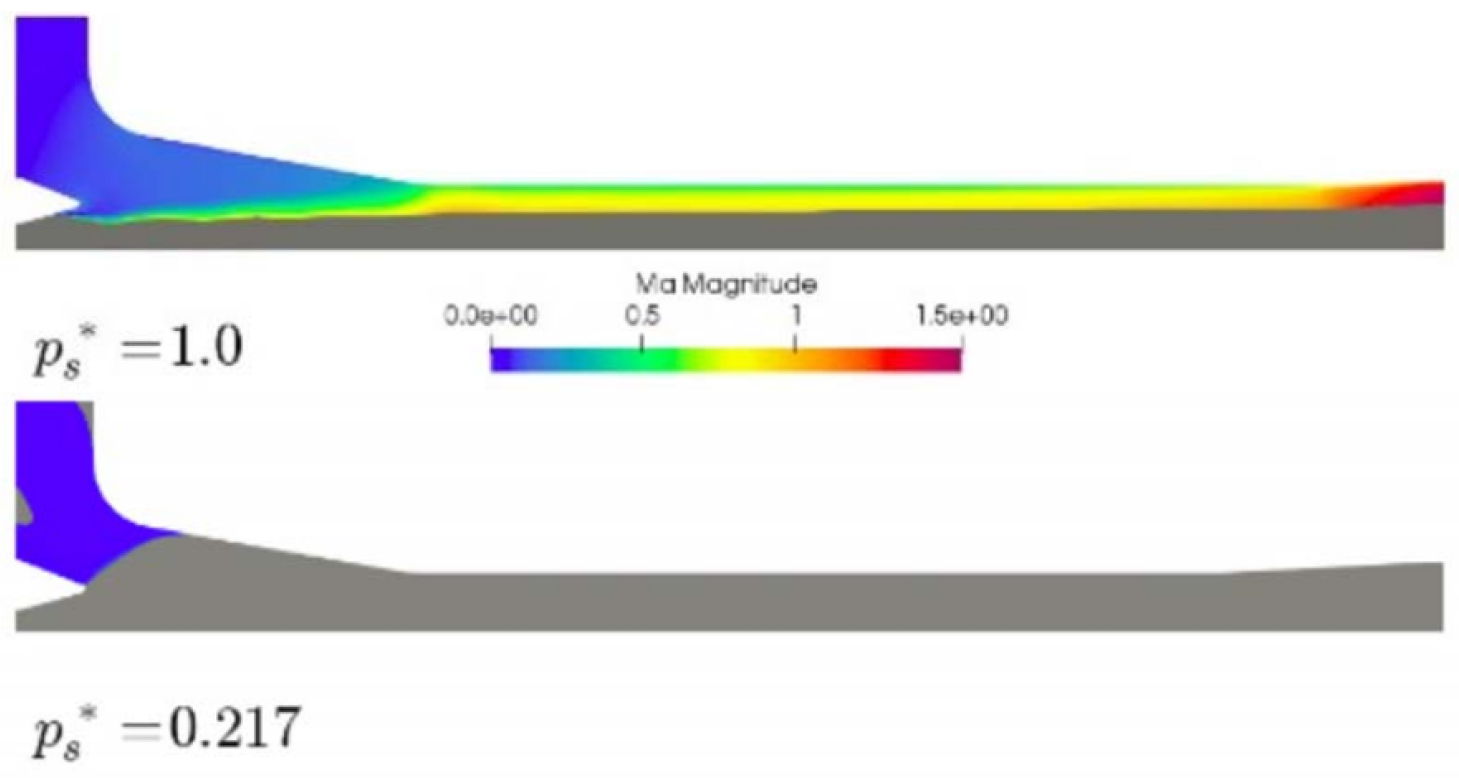
2.4. Subsonic Ejectors

Subsonic ejectors can operate in three modes namely stable, critical, and unstable, as shown in Figure 2. At the stable mode, the entrainment ratio stays constant until it reaches its critical value of compression ratio. At the critical compression ratio, the suction reaches its peak, in other words, it is called the maximum discharge point (MDP). At the unstable mode, fluctuations and declines in the entrainment ratio are noted, along with reversed flows. The reversed flow condition occurs when the entrainment ratio reaches its minimum threshold, causing the motive flow to reverse within the system.

2.5. Supersonic Ejectors

The supersonic ejector operates in three distinct modes, illustrated in Figure 3. In the critical mode, also known as double-choking, the entrainment ratio remains constant due to the choking of both primary and secondary flows. In the subcritical mode, or single-choking, the primary flow is choked, leading to a linear change in entrainment ratio with backpressure. In the malfunction mode, referred to as back-flow, the reversal of the secondary flow causes the ejector to malfunction.

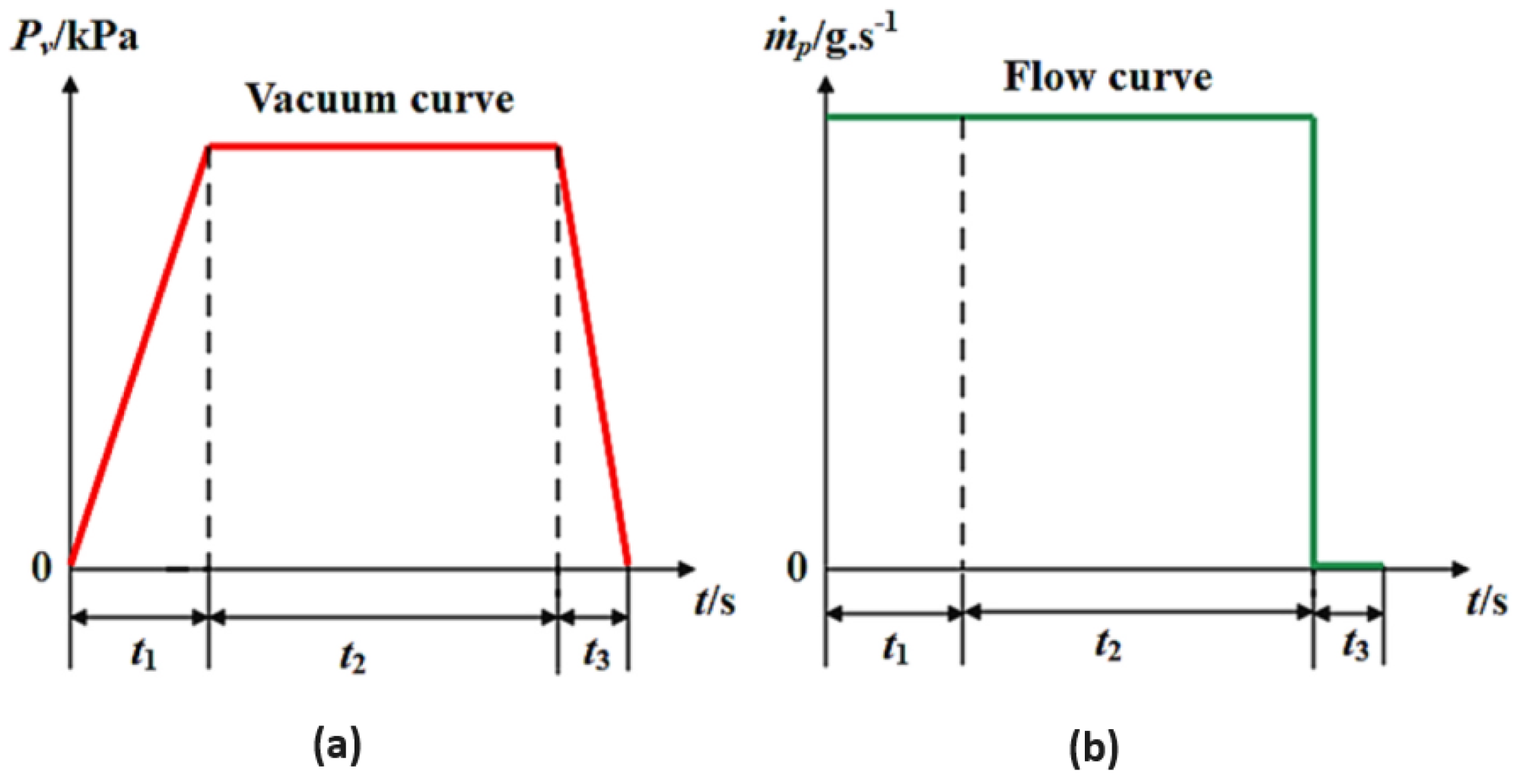
2.6. Vacuum Ejectors

One of the most common applications of ejectors is their use in creating vacuum environments without any need for electricity while producing no contaminants. Working cycle including vacuum curve as well as flow curve accounts for vacuum ejectors which involve three stages: vacuum generation or response time t 1 , vacuum holding t 2 , and vacuum release t 3 , as shown in Figure 4. In vacuum ejectors:
  • The response time t 1 of the vacuum system is important - if it is too long, it can reduce work efficiency and increase air consumption.
  • The vacuum maintenance time or workpiece suction time t 2 is a significant portion of the overall work cycle, 50-80%. During this time, high-pressure air is continuously supplied to maintain the vacuum level.
  • In practice, the priority should be minimizing the response time, even if it means using a lower supply pressure to reduce energy consumption.
  • Improving the entrainment capacity of the vacuum ejector or reducing air consumption during the vacuum holding stage could lead to more energy-efficient and effective vacuum system applications.
The main focus is on optimizing the response time, vacuum maintenance time, and energy consumption of the vacuum system to improve overall efficiency and performance.

2.7. Applications

Depending on the specific use case, the primary fluid might be either liquid or gas, while the secondary fluid can be liquid, gas, or solid particles[6,18,19,20,21].

2.7.1. Single-Phase and Two-Phase Ejectors

Single-phase ejectors work with a single phase, typically either gas or liquid. They find applications in various industries where fluid transportation or mixing is required. Two-phase ejectors refer generally to the condensing ejector (vapor stream condenses in the ejector), or to the conventional two-phase ejector (two-phase, liquid–vapor flow throughout the ejector). Finding an increased use as expansion devices, they reduce throttling losses and recover expansion work (replacement of expansion valves) in heat pumps, air-conditioning and refrigeration systems.
In summary, ejectors involve a wide range of technologies and applications such as:
  • vacuum pumping and degassing; power cycle [22]
  • desalination
  • air-conditioning, heating, and refrigeration [23,24]
  • aeronautics and space applications
  • enhancing gas turbine performance[25]
  • fluid mixing and separation[26]
  • fuel cell applications [27]
  • natural gas recompression

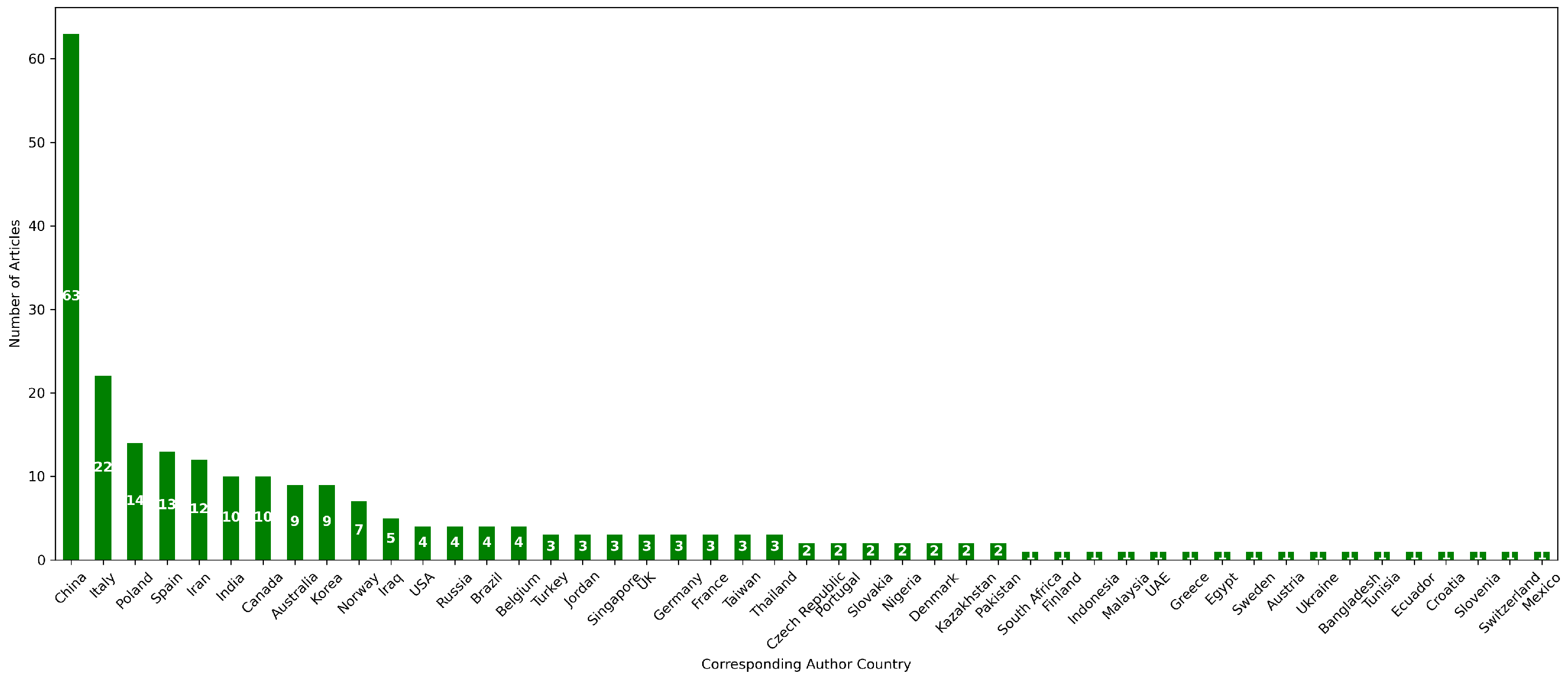
2.7.2. Geography of Ejectors Research

Geographically, conducting research through applications of ejectors are dispersed globally, with prominent centers in regions like North America, Europe, Africa and Asia-Pacific. This distribution often aligns with the necessities and concentration of industries requiring technologies such as vacuum technology, distillation, desalination, refrigeration, etc. For instance, there are some researches in the literature reporting methods in purifying Persian Gulf seawater using desalination systems based on vacuum ejectors [28,29]. Also, other noteworthy practical researches available in the literature refers to the use of vacuum ejectors in advanced MED solar desalination plants in Almeria, Spain [30,31]. The bar chart in Figure 5 provides a visual representation of the contribution of 47 counties in the world in publishing articles associated with numerical simulation of ejectors from 2014 to 2024.

3. Computational Fluid Dynamics Modeling of Ejectors

Computational fluid dynamics as a powerful tool helps in creating detailed model to capture the complex fluid interactions and turbulence within ejectors[32]. It also allows for the optimization of ejector design by providing insights into pressure distribution, velocity fields, and mixing behaviors. Among the published works correspond to ejectors in this review, some adopted the flow inside ejectors as single phase and the others undertook two-phase simulation.

3.1. Single-Phase Ejector CFD Simulation

As indicated in Table 1, from the perspective of primary and secondary flows subjected to single-phase ejectors in recent CFD studies, Gas-gas both as ideal gas [33] , Air-air both as ideal gas[34,35] steam-steam both as ideal saturated steam[36], steam-steam both as ideal gas[37] were taken into account as primary and secondary flows subjected to single-phase ejectors.

3.2. Two-Phase Ejectors CFD Simulation

Likewise, according to data available in Table 1, saturated steam-water [38], Subcooled water- vapor[39], vapor-liquid [40] , and wet steam[41,42] were employed as primary and secondary flows, functioning in two-phase ejectors. Modeling two-phase flows, including phenomena like flashing liquid or vapor condensation, remains challenging. Many aspects at the local scale, such as nucleation characteristics and the growth of bubbles and droplets, are still not fully understood. Developing accurate models for the complex gas-liquid interface and transfer mechanisms requires more sophisticated approaches, often relying on empirical correlations or assumptions that have yet to be rigorously tested.

3.3. Numerical Methods

Various numerical techniques including finite volume method, finite difference method and the finite element method can be used for computational fluid dynamics simulations of ejectors. The finite volume method is more conventional for solving the Navier-Stokes equations and other governing equations associated with flow inside ejectors. Some key aspects of the finite volume method include second-order upwind discretization scheme [33,34,37,41,43,44,45,46,47,48] and coupled algorithm for pressure-velocity coupling [33,34,37,41,43,44,45,47], which have been widely used among the papers in this review. Although Koirala et al. [39] employed several numerical schemes in their study. They utilized the phase coupled SIMPLE scheme (also used by [45])for phase coupling. The least-squares cell-based model was used for the spatial discretization of gradients. The pressure was discretized using the PRESTO model. For the remaining terms, they applied the first-order upwind scheme. With regard to multiphase flow modeling, eulerian-eulerian model is a popular method for simulating multiphase flows inside ejectors which have been commonly employed. Other multiphase models used in ejector simulations include:
  • Volume of Fluid (VOF): Suitable for simulating fluids with a sharp interface, such as liquid-gas flows.
  • Mixture model: often used for simulating homogeneous multiphase flows or when the interface is not of primary interest.

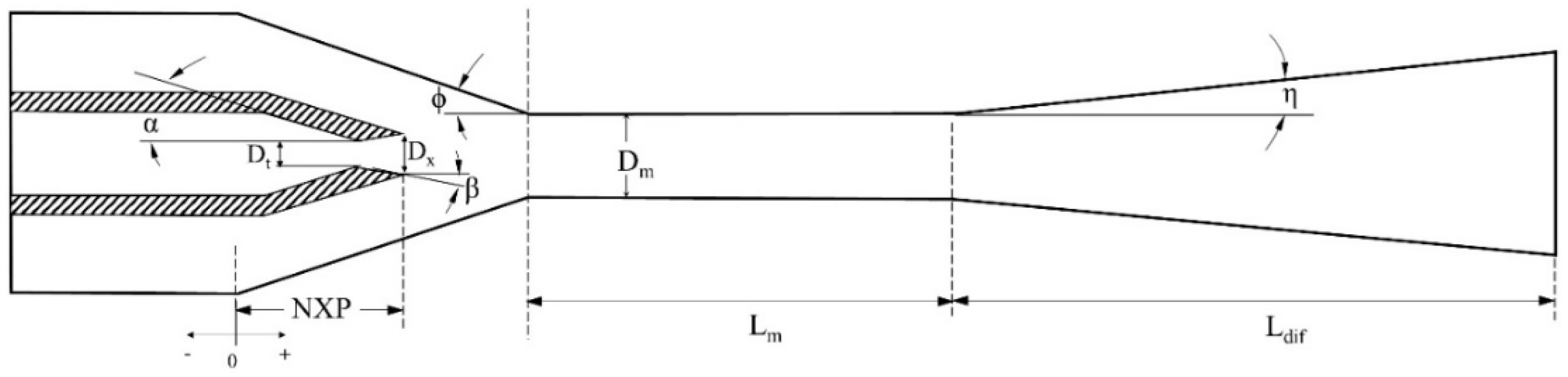
3.4. Geometry and Mesh

Here, the geometry and computational mesh used in CFD studies of ejectors are reviewed. Various types of geometries used are presented in Table 1. Chai et al. [38] , Hou[36], Koirola et al. [39] Banu and Mani [37] utilized 3-dimensional models, while, Talebiyan et al.[33], Singer et al. [44], Feng et al. [49], Kus and Madjeski [45], Tavakoli et al. [34], dadpour et al. [46], Wen et al. [40], Macia et al. [35], Han et al. [47] Giacomelli et al. [41], and Ariafar et al. [48] used 2D axis-symmetric model of ejector in their simulations. According to Besagni et al. [9], there are no substantial differences in the results obtained from 2D and 3D models. This claim is further supported by Feng et al. [50], who validated the assertions made by previous researchers [51] regarding the accuracy of two-dimensional models in predicting flow behavior. Thus, more investigations need to be undertaken about the comparison between 2D and 3D ejector models. with regard to types of mesh, both structured, consist of hexahedral (3D) or quadrilateral (2D) elements and Unstructured Mesh consist of tetrahedral (3D) or triangular (2D) elements have been used. Also, Table 1 demonstrates the number of elements number in the studies.

3.5. Boundary Conditions

Properly defining boundary conditions is crucial for accurate simulation of ejectors, i.e. specifying inlet conditions, outlet conditions, and wall boundary conditions. Table 2 depicts all types of boundary conditions used in detail. While pressure boundary conditions were mostly used for both inlet and outlet of ejector by authors, Chai et al. [38], Singer et al. [44], and Tavakoli et al. [34] used mass flow rate as inlet boundary conditions of primary flow. Hence, Kus and Madjeski [45] utilized the velocity condition alongside pressure for primary inlet boundary condition. Besides, generally, the inside wall of the ejector is assumed to be adiabatic and Non-slip condition for wall is considered.

3.6. Solvers and Software

Prior researchers indicated that selection of appropriate solvers and turbulence models [52] significantly influences the accuracy of ejector simulations in CFD studies. As depicted in Table 2, various solver algorithms, such as pressure-based [33,36,38,39]or density-based solvers [35,37], were employed based on the flow regime and physics of the ejector system. With regard to commercial packages, different versions of Ansys Fluent was widely used by the authors. However, Lucas et al. [53], Novais and Scalon [54], Macia et al. [35] Fang et al. [49], and Klyuyev et al. [55] used Open FOAM in recent years.

3.7. Turbulence Modeling

In terms of turbulence modeling, Direct Numerical Simulation (DNS), the two-equation eddy viscosity models based on Reynolds-Averaged Navier-Stokes (RANS) or Large Eddy Simulation (LES) have been utilized to model turbulent flow behavior within ejectors. Although RANS-based turbulence models have been predominantly used by the authors in recent years, using LES simulation by Zaheer et al. [56]and Croquer et al. [57] are noteworthy. Among the RANS-based turbulence models, the k- ω SST [33,34,35,40,43] has been favored as a strong turbulence model in capturing flow features inside ejectors compared to other turbulence models. However, others used standard k- ϵ [34,38] and realizable k- ϵ [36,42] in their simulation. Recently, Singer et al. [44] employed three methods—Direct Numerical Simulation (DNS), Large Eddy Simulation (LES), and Reynolds-averaged Navier-Stokes equations (RANS)—to characterize turbulent flow within an ejector in PEM fuel cell applications. They found that the RSM GEKO turbulence model, with adjusted parameters, effectively achieved an average deviation of 6.1% across the entire operating range, outperforming traditional eddy viscosity turbulence models in predicting flow features particularly shock propagation inside the hydrogen ejectors. Table 2 provides detailed information about turbulence modeling and wall function used by authors. Additionally, as outlined in Table 3, the k- ω SST as being the best turbulence model in simulation of the flow inside ejectors was emphasized by Talebyian et al.[33] and Chen et al. [40]. However, Tavakoli et al.[34] reported that there were no differences between the results yielded by k- ω SST and standard k- ϵ in their work.

3.8. Validation and Verification

Validation and verification of CFD models against experimental data, analytical solutions, or numerical results are essential steps to ensure the reliability and accuracy of simulated ejector performance [58]. Experimentally, There haven’t been too many references for validation of two-phase ejectors flow features. However, Moore [59], Moses and Stein [60], and Bakhtar[61] were the first researchers who provided test rigs regarding two-phase steam condensation which are still widely used as case for validation. Subsequently, Kwidzinsky [62,63] published experimental study on two-phase steam ejectors. Also, other experimental data related to gaseous ejectors by Karthick et al.[64,65] and Al-Rbaihat et al. [66] are available in the literature review. An important point among the published experimental works is the lack of experimental data based on subcooled water as the primary fluid and steam as the secondary fluid, corresponding to the condensation or evaporation process in the ejector systems. Therefore, the necessity of conducting such an experiment is inevitable. Table 2 demonstrates the validation or verification cases used by selected papers in this review.

3.9. Parametric Study

Conducting parametric study involves systematically varying input parameters, such as nozzle exit position, throat area ratio, or operating conditions, to analyze their effects on ejector performance and optimize design parameters.

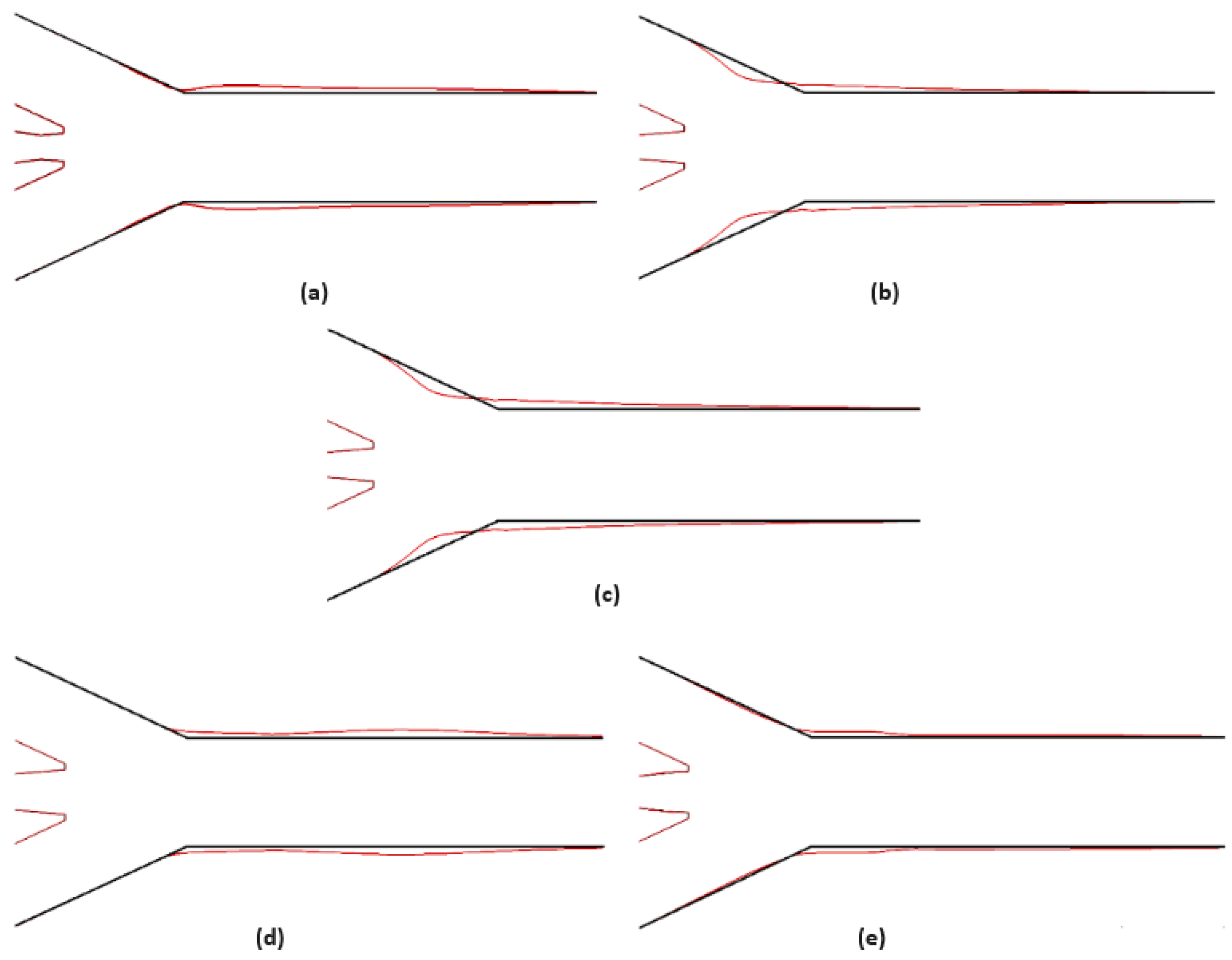
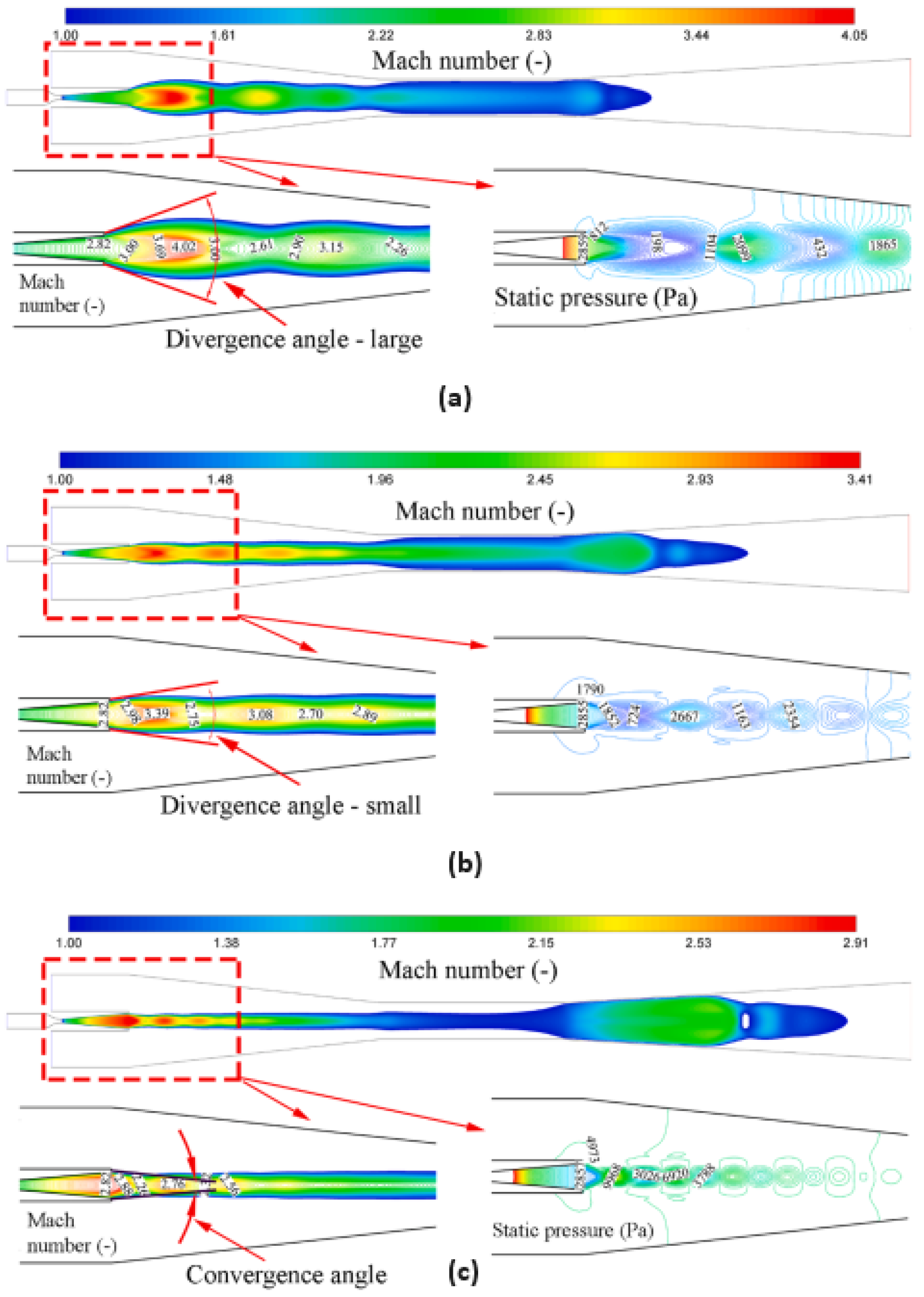
3.9.1. Nozzle exit position

The nozzle exit position NXP parameter is defined as the distance between the exit plane of the primary nozzle and the entry plane of the converging entrance zone of the mixing chamber, as shown in Figure 6.
Han [47] identified an optimal NXP value of 10 mm for a steam ejector refrigeration system. Exceeding this optimum value led to decline in enrainment ratio and performance of ejector. Tavakoli et al. [34] investigated the influence of NXP and mixing chamber height to reach the highest entrainment ratio. They found that the optimal ratios of the NXP to the primary nozzle throat height, and the mixing chamber height to the primary nozzle throat height were 3.63 and 5, respectively.

3.9.2. Nozzle Area Ratio

The geometry of primary nozzle in ejectors can also be described by the nozzle exit area ratio D x / D t , shown in Figure 4, which is known to impact ejector performance. Variation of nozzle area ratio was the subject of the parametric study in Ariafar’s et al. work[48]. They simulated nozzles with overall area ratios of 11, 18, and 25. They reported identical curves when they plotted the results of each nozzle performance versus area ratio.

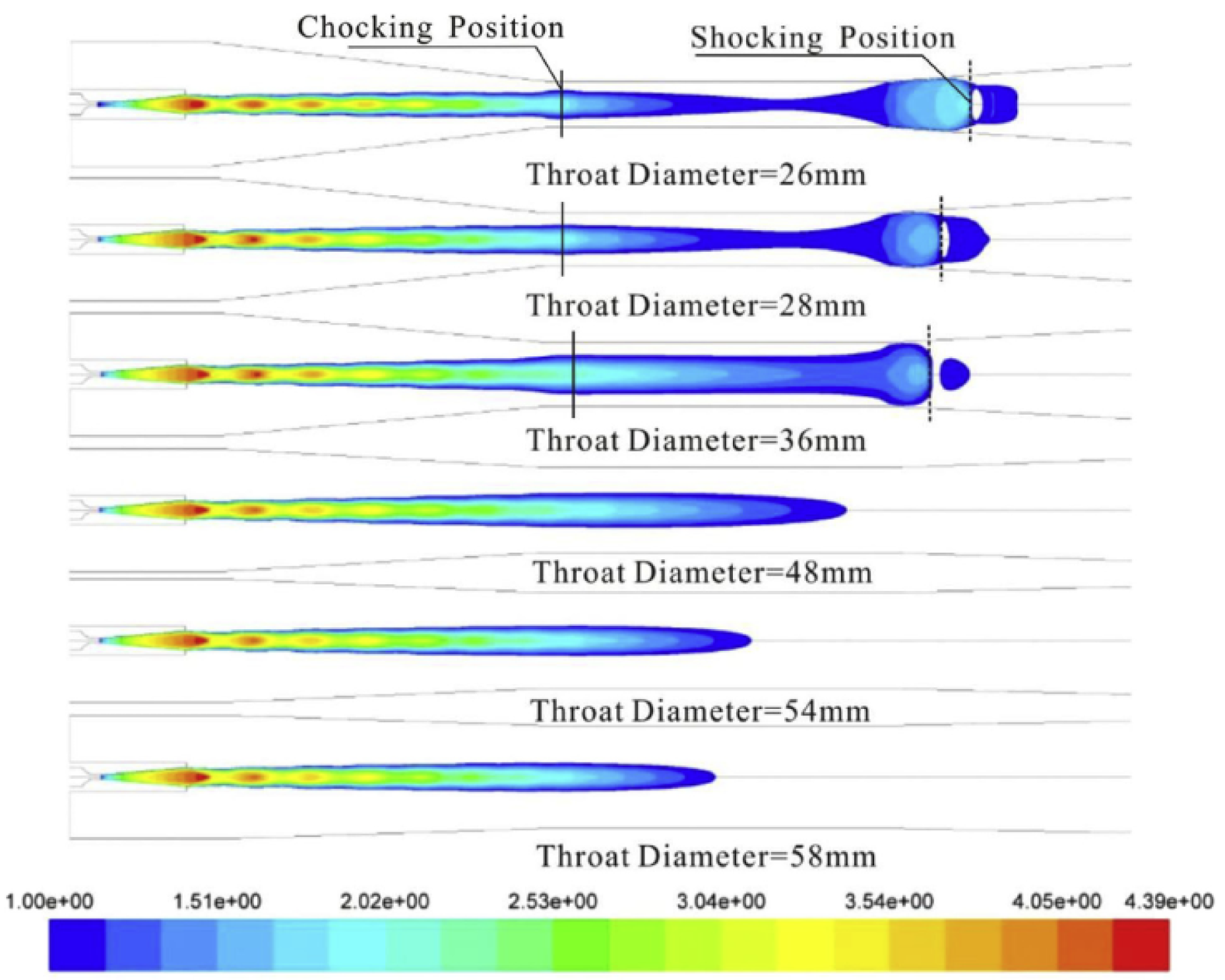
3.9.3. Mixing Throat Diameter

Constant-area mixing section diameter D m is another important geometric parameters in ejector. Han et al. [47] investigated the formation of the boundary layer by varying the mixing throat diameter. They concluded that boundary layer separation occurs when the throat diameter is either too large or too small, emphasizing its negative impact on ejector performance. They also assessed the variation of throat diameter on the entrainment ratio and observed that as the throat diameter increases, both the entrainment ratio and the mass flow rate of the secondary fluid continue to rise, but they begin to decline after reaching a peak at 48 mm.

3.9.4. Other Geometric Aspects

Banu and Mani [37] investigated two types of swirl generators: solid type and cavity type, as shown in Figure 7. They found that the solid vane type provided minimal performance with about 2% improvement, while the cavity type, due to its sweep and camber angles, improved performance by up to 5%. For the cavity type with a 10° camber angle, sweep angles of 10°, 20°, and 30° the entrainment ratio increased by 5-8%, 10-12%, and 15%, respectively. The study concluded that the combined sweep and camber angles in cavity types significantly enhance ejector performance by increasing swirl intensity, unlike the solid vane type.
Hou et al. [36] explored the impact of nozzle displacement and inclination angle on the entrainment ratio. They found that a large displacement of the primary nozzle significantly reduces the critical back pressure and entrainment ratio under certain conditions. However, the inclination of the primary nozzle has minimal effect on the entrainment ratio when the ejector operates in critical mode. Additionally, small displacements and inclinations of the primary nozzle do not affect the entrainment ratio in critical mode, which remains consistent with the ratio when there is no deviation in the primary nozzle. Claiming that the number of nozzles affects the performance of ejector, Li et al. [43] compared the characteristics of single-nozzle and four-nozzle ejectors through experiment and numerical simulation. The findings indicated that the four-nozzle setup was more efficient when the compression ratio surpassed 8 or the entrainment ratio dropped below 0.068. Nevertheless, choosing the correct length for the mixing chamber was essential to improve the ejector’s performance.

3.9.5. Operating Conditions

Koirola et al. [39] investigated the performance of a two-phase ejector, focusing on the effects of back pressure, primary flow temperature, and condensation. They found that increasing back pressure initially has little impact on the entrainment ratio, but as it approaches to the critical pressure, the entrainment ratio drops sharply and eventually causes backflow. Higher primary fluid temperatures result in lower entrainment ratios due to the reduced condensation. Additionally, using non-condensing air demonstrated a lower entrainment ratio, indicating that thermal interaction enhances entrainment in two-phase flow mode.
In addition, Dadpour et al. [46] investigated the effect of droplet injection in the secondary fluid of a wet steam ejector and concluded that the injection leads to a decrease in the entrainment ratio by approximately 22.93%. Feng et al. [50] studied the impact of droplets in the primary flow on the performance and condensation behavior of ejectors. They found that an increase in droplet mass fraction led to a 9.15% decrease in the ejector’s entrainment ratio. Conversely, a reduction in droplet radius caused the entrainment ratio to fluctuate within 1.5%. Overall, smaller droplet mass fractions and radii were found to enhance the performance of both the ejector and the system.

3.10. Optimization

Optimization techniques, including artificial neural networks (ANN), genetic algorithms, adjoint optimization, or gradient-based optimization methods can be applied for CFD models of ejectors to improve performance and achieve desired objectives, such as maximizing entrainment ratio or minimizing pressure losses etc. [67,68,69]. Talebiyan et al. [33] employed parametric study and adjoint optimization to explore the performance of a supersonic ejector. They focused on varying the height of the mixing chamber by adjusting outlet-to-throat height ratios of the primary nozzle. The adjoint optimization method notably improved entrainment ratio by around 20.8%, 15.3%, and 16.5% for different operating modes. Interestingly, combining parametric and adjoint methods yielded similar maximum entrainment ratios across all modes. Hence, the optimized ejectors showed broader performance ranges, particularly in under-expanded mode, indicating better performance against increased back pressure. As can be seen in Figure 8, they suggested a wavy-like configuration for ejector walls resulted from adjoint optimization.

3.11. Entropy Loss

Most of the irreversibilities within ejectors are primarily situated in the mixing chamber and diffuser. Generally, irreversibilities inside the ejector can be categorized as following processes [70,71,72,73]:
  • Entropy generation through viscous dissipation caused by average velocity gradients.
  • Entropy Generation through heat conduction resulting from average temperature gradients.
  • Entropy generation through viscous dissipation caused by fluctuating velocity gradients (turbulent dissipation).
  • Entropy generation through heat conduction due to fluctuating temperature gradients (turbulent heat transfer).
Wen et al. [40] clarified that the transition of flow structures from under-expanded to over-expanded flow significantly augments entropy loss in the steam ejector. They employed entropy loss coefficients to evaluate energy loss in a MED-TVC desalination system and found that the entropy loss coefficient increases as the suction chamber pressure in the steam ejector rises.

3.12. Entrainment Ratio Behavior

Entrainment ratio is recognized as the most crucial parameter in evaluating the performance of an ejector. All the efforts are implemented to increase the entrainment ratio although critical back pressure limits them. Different methods for improving entrainment ratio in numerical simulation of ejector can be listed as follows:
  • implementing advanced turbulence models
  • optimizing geometry; involving nozzle design, mixing chamber shape, diffuser design
  • adjusting operating conditions
  • utilizing adjoint optimization.
    Additional factors can also be added to this list such as:
  • incorporation of real gas effects
  • boundary layer control involving wall treatments.
Hence, in case of multi-phase flow considerations, accurately modeling phase changes as well as optimizing the size and distribution of droplets in applications involving condensation or evaporation can effectively improve the entrainment ratio.
Table 3 provides various approaches performed by authors to assess the variation of entrainment ratio in ejectors include: pressure ratio, outlet back pressure, inlet pressure of suction chamber, primary flow temperature, entrainment pressure, time, and condensation effect.
Table 1. List of main reviewed papers with primary and secondary working fluids, fluid flow type, geometry and mesh sizes.
Table 1. List of main reviewed papers with primary and secondary working fluids, fluid flow type, geometry and mesh sizes.
Paper Primary-secondary flow Fluid flow Geometry Elements no.
Chai et al. 2024 [38] Saturated steam-water two-phase supersonic 3D 294480
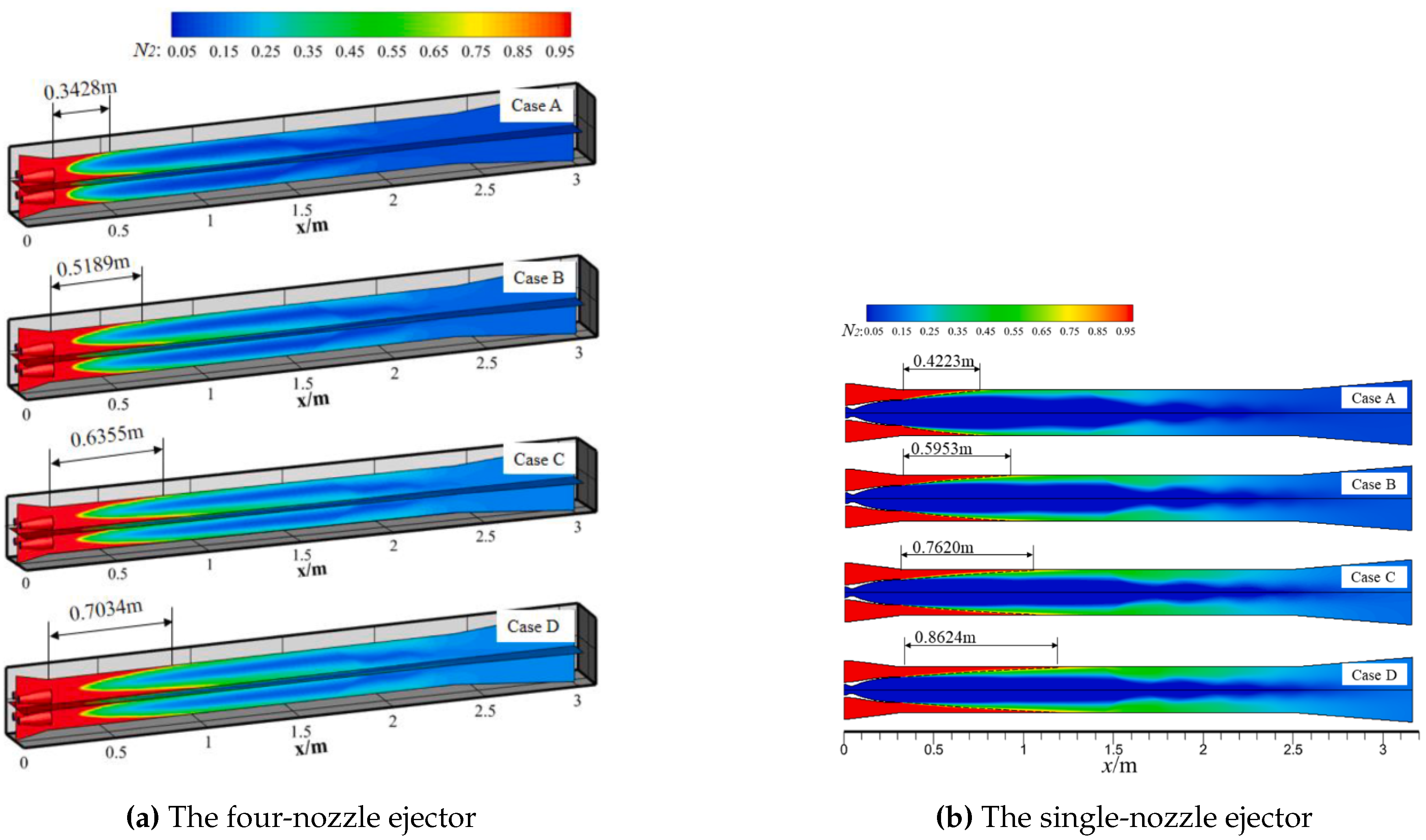
Li et al. 2024 [43] Nitrogen-air single phase Supersonic 2D for single nozzle and 3D for 4-nozzles 374000 for single nozzle 16 million for 4-nozzles
Talebiyan et al. 2024 [33] Gas-gas (both ideal gas) single phase supersonic 2D with rectangular cross-section 430000
Singer et al. 2024 [44] Pure hydrogen-mixed H 2 / N 2 single phase supersonic 2D axis-symmetric 330000
Feng et al. 2024 [50] Steam-water two-phase supersonic 2D axis-symetric 140,000
Kus and Madejski [45]2024 water- C o 2 two-phase subsonic 2D axis-symetric 28299
Tavakoli et al. 2023 [34] Air-air (both ideal gas) single phase subsonic 2D without and with fluidic oscillator 50000
Hou et al. 2022[36] Steam-steam (both ideal saturated steam) single phase supersonic 3D 982,362
Dadpour et al. 2022 [46] Wet steam- wet steam two phase supersonic 2D 40000
Koirala et al. 2022 [39] Sub-cooled water- vapor two-phase subsonic 3D 1.8 million
Wen et al. 2020 [40] Vapour-liquid two phase supersonic 2D 73000
Macia et al. 2019 [35] Air-air(both ideal gas) single phase supersonic 2D axisymmetric 20300
Han et al. 2019 [47] Steam-steam(both ideal gas) single phase supersonic 2D axisymmetric 46352
Banu and Mani 2019 [37] Steam-steam (both ideal gas) single phase - 3D 700000
Giacomelli et al. 2016 [41] wet steam-wet steam two phase supersonic 2D axis-symmetric 45000
Ariafar et al. 2014 [48] wet steam nozzle (of an ejector) two phase supersonic 2D axis-symmetric with rectangular cross section 6510
Table 2. List of main reviewed papers with boundary conditions, solver and software, turbulence modeling and wall function, validation and verification methods .
Table 2. List of main reviewed papers with boundary conditions, solver and software, turbulence modeling and wall function, validation and verification methods .
Paper Boundary conditions Solver and Software Turbulence modeling and wall function Validation and verification
Chai et al. 2024 [38] Inlet: mass flow rate for primary and secondary, P p = 0.6 − 2.9 M P a , Outlet: P o u t = 500 k P a Pressure based Ansys Fluent k- ϵ ,Scalable wall function -
Li et al. 2024 [43] m ˙ p = 6.84 k g / s , T p = 316.2 K , m ˙ s = 0.61 k g / s , T s = 315.9 K , P o u t = 101 k P a , T o u t = 303.2 K coupled implicit density-based, FLUENT 19 k- ω SST Experimental
Talebiyan et al. 2024 [33] Inlet: P p = 600 k P a , T p = 300 K , P s = 100 k P a , T s = 300 K , Outlet: P o u t = 200 k P a , T o u t = 300 K Pressure based Ansys Fluent 2022 R2 k- ω SST Karthick et al. 2016(exp), Samsam-Khayani et al. 2022(Num)
Singer et al. 2024 [44] Inlet: m ˙ p = 0.645 − 0.323 , P s = 1.38 − 1.18 k P a Outlet: P o u t = 1.60 − 1.38 k P a with variation of pure hydrogen and mixed H 2 / N 2 volume percentage pressure-based using pressure-velocity coupling, Ansys Fluent 2023 R1 Spallart allmaras, Standard k- ϵ wall function:Enhanced Wall Treatment, RNG k- ϵ , Realizable k- ϵ , k- ω , SST k- ω , Generalized k- ω (GEKO), RSM stress-BSL Experimental
Feng et al. 2024 [50] Inlet: P p = 550 P a , T p = 435 K , P s = 8.87 k P a , T s = 375 K Outlet: P o u t = 53.3 k P a , T o u t = 385 K density-based implicit, FLUENT 19.2 k- ω SST Experimental and CFD by Sriveerakul [74]
Kus and Madejski [45]2024 Inlet: V p = 0.67 m / s , P p = 12 b a r , T p = 17 C , m ˙ s = 10 g / s , P s = 0.9 − 0.84 b a r , T s = 150 C Outlet: P o u t = 1.13 b a r Segregated flow model, Siemens StarCCM+ 2022.1.1 Realizable k- ϵ -
Tavakoli et al. 2023 [34] Inlet: m ˙ p = 1.5 k g / s , P s = 99961.75 P a , Outlet: P o u t = 102161 P a URANS equations (unsteady) Ansys Fluent 2022 R2 k- ϵ and k- ω SST -
Hou et al. 2022[36] Inlet: P p = 27100 P a , T p = 130 ∘ C , P s = 1250 , T s = 10 ∘ C Outlet: P o u t : an independent variable, T o u t : saturated steam temperature corresponding to the P o u t l e t Pressure-based (steady state) Fluent Realizable k- ϵ ,standard wall function Numerical
Dadpour et al. 2022 [46] B-Moore nozzle: P i n = 25 k P a , T i n = 357.6 K , P o u t = 6.3 , T o u t = 310.4 K , Ejector: P p = 270 k P a , T p = 403 K , P s = 1.2 k P a , T s = 283 K Outlet: P o u t = 4 , T o u t = 302.1 K using Gauss-Seidel method coupled with implicit scheme, Open FOAM k- ω model B-Moore nozzle
Koirala et al. 2022 [39] Inlet: P p = 1 M P a , T p = 25 ∘ C , P s = 0.045 , 0.06 , 0.08 , 0.105 M P a , Outlet: P o u t l e t = 0.1 M P a Pressure based (steady and unsteady) Ansys Fluent 2019 R2 k- ω model Zhang et al. 2012
Wen et al. 2020 [40] total pressure and total temperature for the entrances and exit URANS equations (unsteady) Ansys Fluent 19 k- ω SST Sharifi and Boroomand 2013(exp) Laval nozzle Moses and Stein 1978 (exp) Starzman et al. 2018
Macia et al. 2019 [35] Inlet: P p = 6 b a r , Neumann condition for velocity, P s = 0 b a r , Outlet: P o u t = 0 Density-based explicit (rhoCentralFoam) implicit (HiSA) solvers OpenFOAM k- ω SST Experimental
Han et al. 2019 [47] Inlet: P p = 310 − 390 k P a , P s = 2330 − 3170 P a , Outlet: P o u t = 3500 − 7000 P a ANSYS Fluent 17 Standard k- ϵ , RNG k- ϵ , realizable k- ϵ , with Standard Wall Function and Enhanced Wall Function, and k- ω SST Experimental
Banu and Mani 2019 [37] Inlet: P p = 1 − 5 b a r , P s = 0.8 b a r Density-based (steady) Ansys Fluent k- ω SST Experimental Banu et al. 2014 PIV study
Giacomelli et al. 2016 [41] Inlet: T S A T , p = 80 ∘ C , T S A T , s = 7 ∘ C ;primary and secondary pressures are the saturation pressures corresponding to T S A T Ansys Fluent - WS model in Fluent
Ariafar et al. 2014 [48] I n l e t : P i n l e t = 270 k P a , T i n l e t = 403 K , Outlet: P o u t = 1.6 k P a Coupled implicit solver Ansys Fluent 14.5 Realizable k- ϵ two experimental cases by Moor et al 1980 and Bakhtar et al. 1981
Table 3. List of main reviewed papers with two-phase model, best turbulence model reported, entrainment ratio remarks, Heat and mass transfer model and parameters.
Table 3. List of main reviewed papers with two-phase model, best turbulence model reported, entrainment ratio remarks, Heat and mass transfer model and parameters.
Paper Two-phase model Best turbulence model reported Entrainment ratio remarks Heat and mass transfer model and parameters
Chai et al. 2024 [38] inhomogeneous multiphase model - - Non-equilibrium condensation model
Li et al. 2024 [43] - - Reported versus compression ratio, non-mixing length -
Talebiyan et al. 2024 [33] - k- ω SST The adjoint optimization method notably improved entrainment ratio by around 20.8%, 15.3%, and 16.5% for different operating modes -
Singer et al. 2024 [44] - RSM with adjusted GEKO parameters Reported versus the percentage of the fuel cell stack’s maximum load point/Generalized k- ω turbulence model decreases overprediction of entrainment ratio by 25% -
Feng et al. 2024 [50] Eulerian-eulerian - Reported versus liquid mass fraction, droplet number/increase of droplet mass fraction led to a 9.15% decrease in M classical homogeneous nucleation theory
Tavakoli et al. 2023 [34] - k- ω SST k- ϵ reported versus pressure ratio/Ejector with oscillator improved entrainment ratio by 38.3%
Kus and Madejski [45]2024 * - - Direct contact condensation and Mixture multiphase mode(MMP)
Hou et al. 2022 [36] - - Reported versus oultlet back pressure -
Dadpour et al. 2022 [46] Eulerian-eulerian - Reported versus back pressure/injection leads to a decrease in M by approximately 22.93% -
Koirala et al. 2022 [39] Eulerian multiphase model - Back pressure ratio on entrainment ratio Primary flow temperature on entrainment ratio Entrainment pressure on entrainment ratio Time on entrainment ratio Condensation on entrainment ratio/ Direct contact condensation resistance models for heat transfer interaction Ranz-marshall to zero-resistance
Wen et al. 2020 [40] * k- ω SST Reported versus inlet pressure of suction chamber on entrainment ratio/ M grows as the pressure in the suction chamber increases Non-equilibrium condensation model
Macia et al. 2019 - - - -
Han et al. 2019 [47] - realizable k- ϵ Reported versus primary fluid temperature, Back pressure, Throat diameter, NXP/
Banu and Mani 2019 [37] - - Reported versus pressure drive ratio and for different sweep angles of cavity type swirl generator/ -
Giacomelli et al. 2016 [41] Eulerian multiphase model - Reported versus outlet pressure/HEM predicts a lower value of M Non-equilibrium condensation model Homogeneous Non-equilibrium model
Ariafar et al. 2014 [42] Eulerian-Eulerian approach - described without curves *

3.13. Internal Flow Visualization

Macia et al. [35] illustrated the internal flow behavior once occurring shock and then in the mode of zero secondary flow due to operating pressure, which can be seen in the Figure 9.
Wen et al. [40] found that steam’s expansion levels vary due to the surrounding pressure in the mixing section. Figure 10(a) shows that the pressure at the nozzle exit is much higher than in the mixing section, leading to over-expanded flow with a wide expansion wave and higher supersonic flow. When the suction chamber pressure reaches 1800 Pa, as depicted in Figure 10(b), the surrounding pressure in the mixing section increases, reducing the steam’s expansion downstream of the primary nozzle. As the suction chamber pressure rises further, it surpasses the nozzle outlet pressure, significantly altering the flow structure downstream of the primary nozzle, as shown in Figure 10(c). This results in under-expanded flow within the mixing section, characterized by a convergence angle, which differs markedly from the flow structures in Figure 10(a) and 10(b).
In Tavakoli et al.’s [34] work, it can be observed that the velocity has sensibly increased after adding fluidic oscillator at the entrance of the ejector nozzle, as shown in Figure 11.

3.13.1. Mixing Characteristics

Rao et al. [75] presented the concept of the non-mixing length, which can indirectly reflect the development of mixing rate. Li et al. [43] described the non-mixing length of the ejector as the distance from the nozzle exit to the farthest point where the mixing boundary reaches the ejector wall. They compared the non-mixing length of a single-nozzle ejector with that of four-nozzle ejector based on four experimental cases and concluded that the non-mixing length increased as the entrainment ratio increased. Also, as can be seen in Figure 12, their finding proposed that the non-mixing length of the four-nozzle ejector is shorter than that of the single-nozzle ejector, implying that it achieves a quicker and more efficient mixing process over a shorter distance.

3.13.2. Shock Structure

Evaulating the flow visualization, Hou et al. [36] reported that the position of secondary shock wave has undergone a change by moving toward the diffuser inlet area when the inclination angle increased from 0 to 0.6161 degree, as depicted in Figure 13.
Han et al. [47], as shown in Figure 14, found that increasing the throat diameter compresses the mixed fluid channel, leading to significant boundary layer separation. For throat diameters of 36 mm or less, shock waves prevent downstream pressure disturbances, maintaining constant flow patterns and effective areas, which allows the ejector to operate in critical mode. However, when the throat diameter reaches 48 mm or more, the mixed fluid weakens, the influence of back pressure increases, and the ejector fails, entering back-flow mode due to an inability to overcome external pressure.

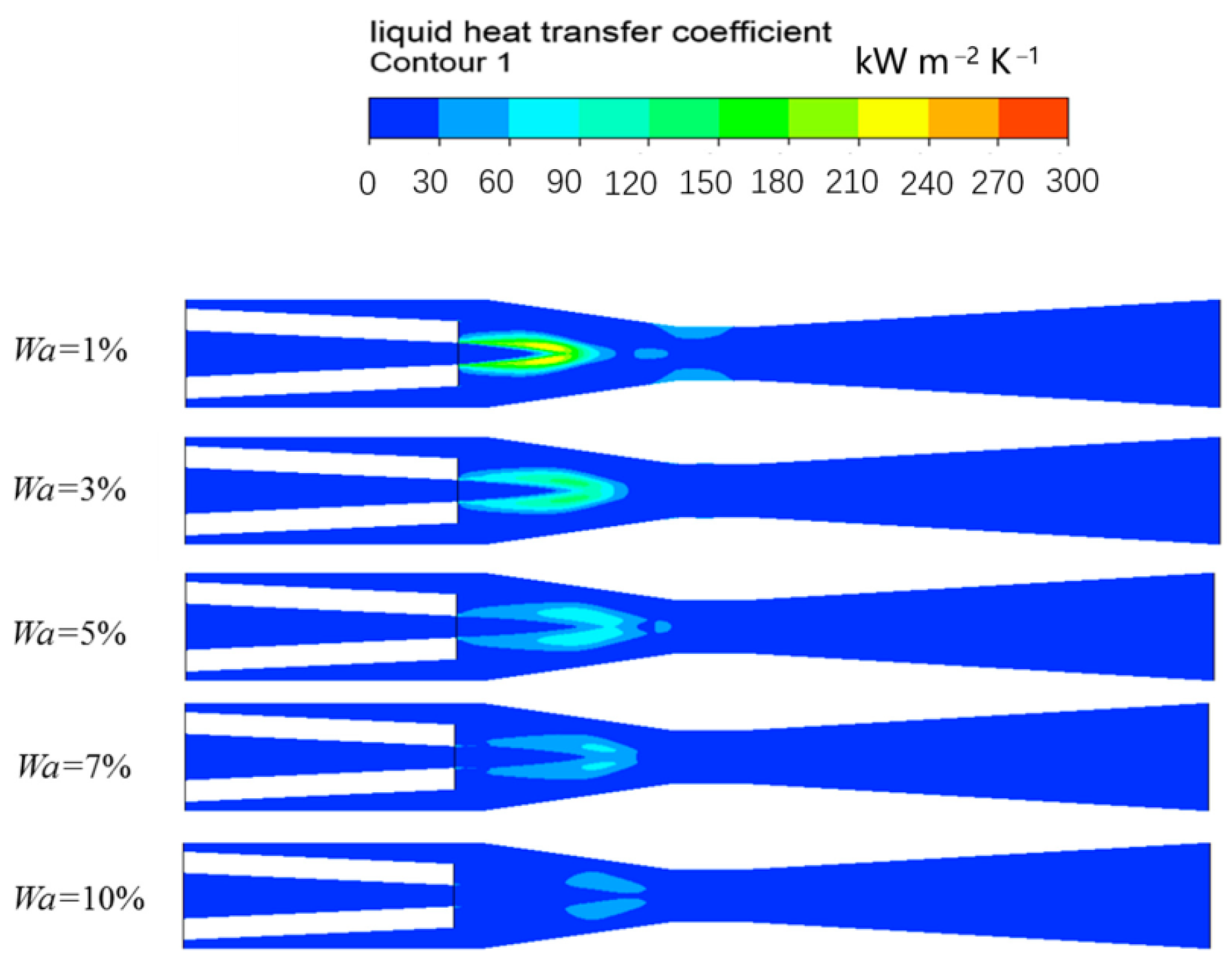
3.14. Investigation into the Properties of Heat and Mass Transfer

In this section, the influence of heat and mass transfer on the performance of ejectors among the published works is reviewed. Various models are commonly used to account for the heat and mass transfer behavior inside the ejector, including ideal gas model [76,77], mixture model [45] non-equilibrium model [78], homogeneous equilibrium model HEM [79,80], and wet steam WS models [46,81,82,83]. Table 3 presents details on two-phase models in addition to the heat and mass transfer models utilized by the authors. Giacomelli [41] compared wet steam model in the commercial code of ANSYS Fluent with a HEM model defined by User-Defined functions. They suggested that the WS model predicts less condensation, leading to a lower temperature during expansion than the HEM model. The temperatures of both phases drop below the Triple Point temperature, indicating a potential for ice formation in the ejector. Finally, they concluded that HEM overestimates the variations of main quantities during the shocks and expansion process in the ejector. Kus and Madejski [45] investigated the steam condensation phenomenon inside the ejector condenser using a mixture model for a two-phase ejector. They applied the direct contact condensation model to account for boiling and condensation processes. They determined that, in all examined scenarios, the variation in condensation rate is linked to the mass flow rate of the ingested exhaust gas. At the highest exhaust gas mass flow rate of 25 g/s, corresponding to an inlet pressure of 0.9 bar, the steam is completely condensed within the diffuser.

3.14.1. Condensation Effect

Phase-transition phenomena may take place in various manners depending on the application. The condensation of a supersaturated vapor requires the formation of droplets. When investigating condensation within a supersonic nozzle, it’s essential to differentiate between two specific phases of the process: the initial stage characterized by droplet formation, also referred to as nucleation, and the subsequent phase involving droplet growth [84,85]. Chai et al. [38] researched the exist of non-condensable gas in a two-phase (saturated steam-water) ejector using an inhomogeneous multiphase model. They found that the presence of non-condensable gas inhibited direct contact condensation between the steam and water, which means with the increases of non-condensable gas mass fraction the rate of heat transfer decreases, as depicted in Figure 15. Also, the heat transfer coefficient and plume penetration length increased with higher steam inlet pressure.

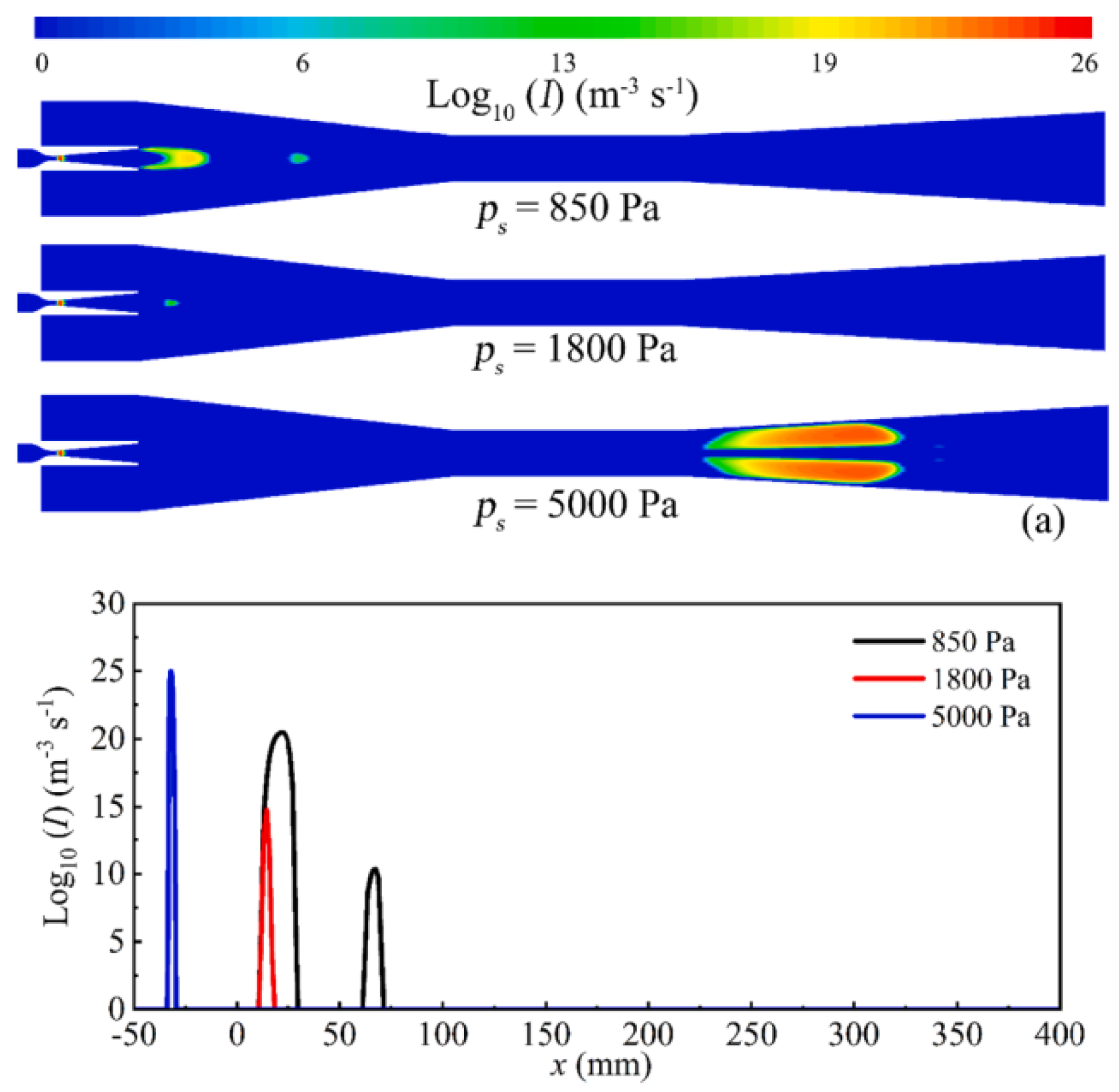
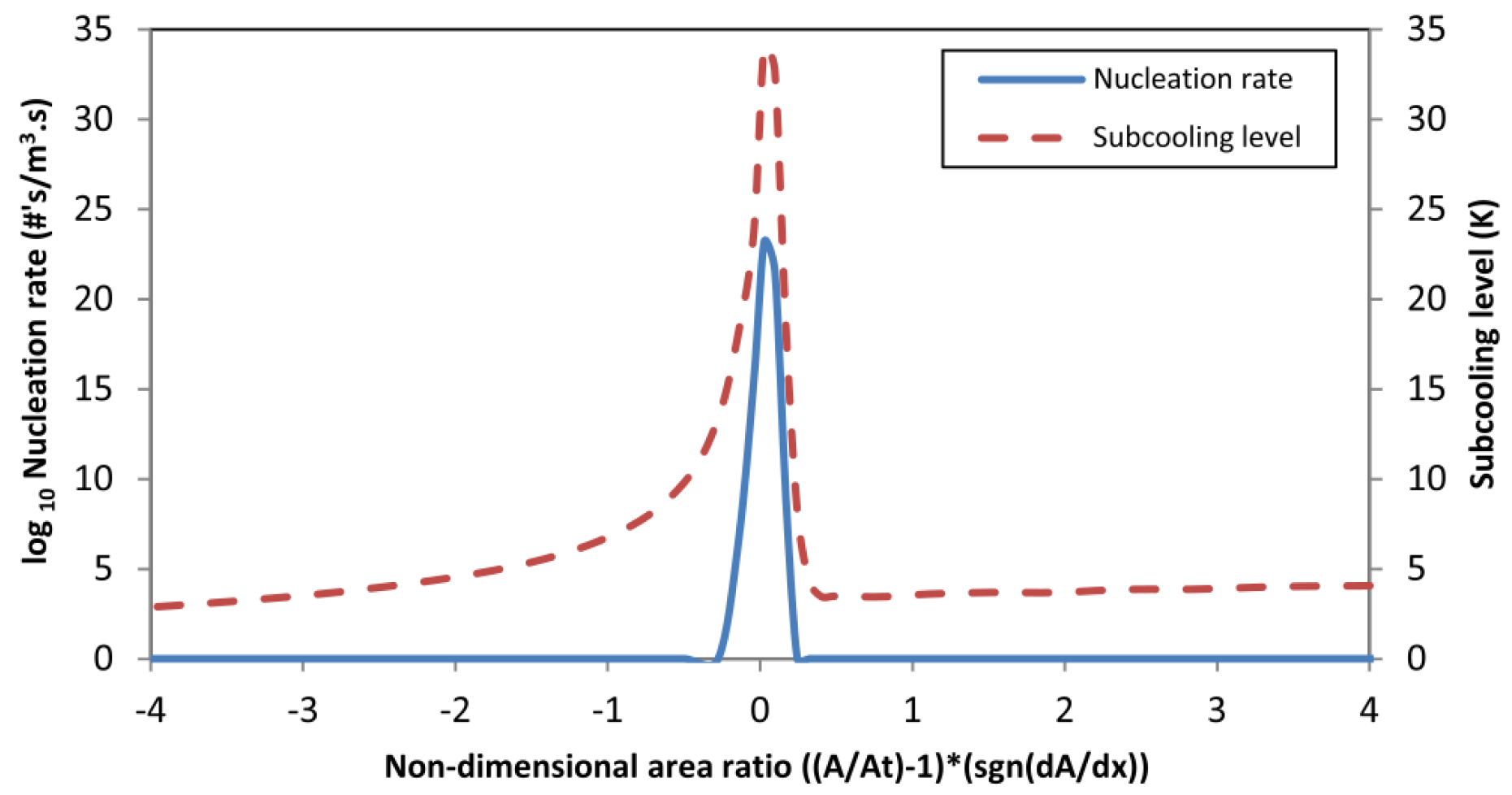
3.14.2. Nucleation

There are two primary mechanisms for the formation of critical clusters. The first mechanism occurs due to the presence of foreign particles within the vapor or surface defects on the solid walls that contain the flow. These impurities and surface imperfections act as initial sites where molecules gather to form an embryo, a process known as heterogeneous nucleation, which is typical in phase transitions within standard condensers [86,87,88,89]. The second mechanism, known as homogeneous nucleation, arises from random density fluctuations caused by the thermal motion of vapor molecules. This type of nucleation, which is a random phenomenon that requires statistical and probabilistic methods for analysis, can occur in any system but is the main way droplets form inside high-speed nozzles [88,90,91,92].

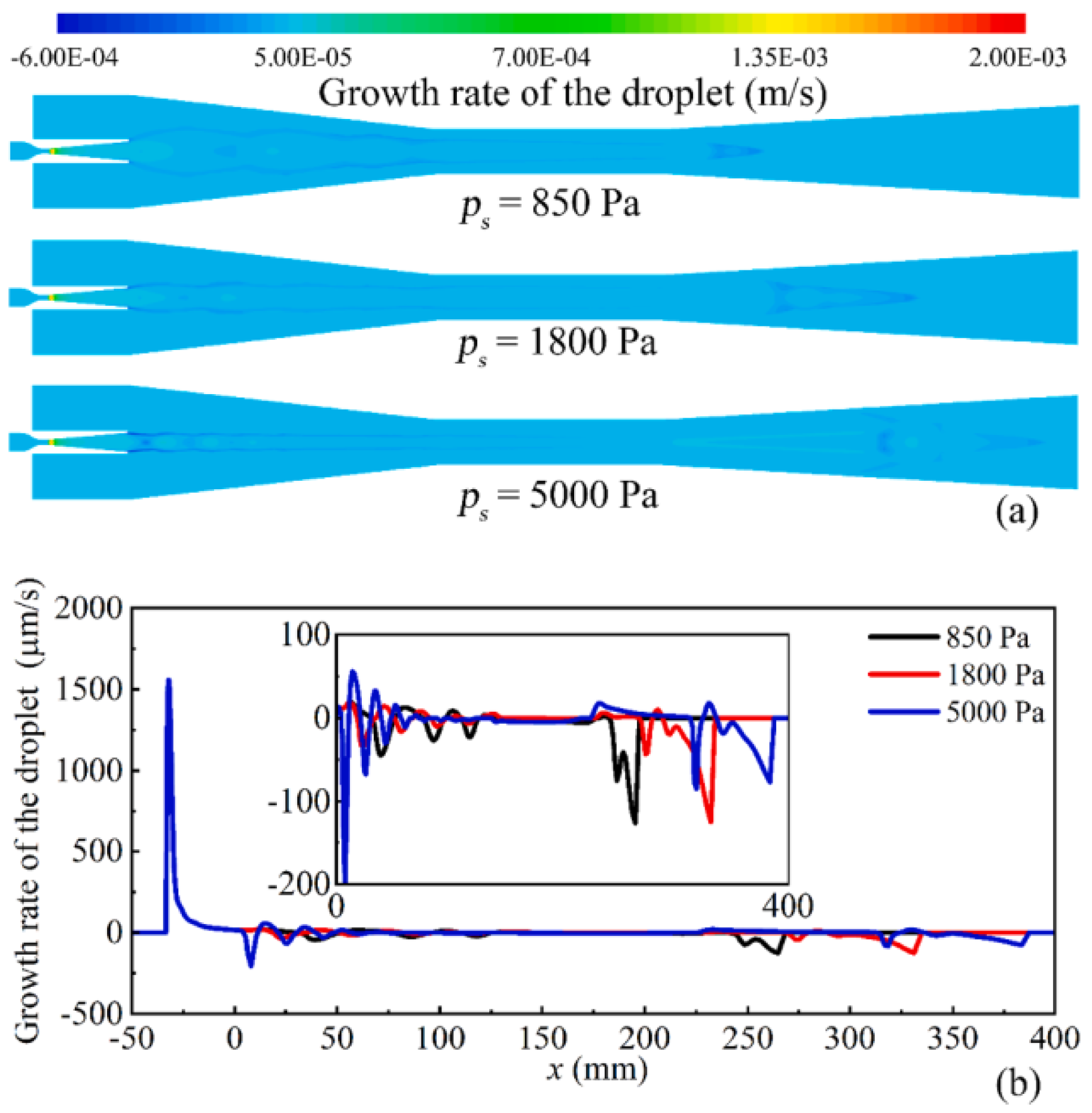
3.14.3. Droplet Growth

In high-speed condensations, the mass of the nucleus at the critical size is much smaller than the mass of the liquid that subsequently condenses on it [88,93,94]. It is the growth of these droplets that causes significant changes in the nozzle and ejector dynamics [46,47]. Therefore, accurately calculating this final stage of the condensation process is crucial to understanding the behavior of the mixture flow variables, such as Mach number, temperature, pressure, and entropy.
Wen et al. [40] analyzed the non-equilibrium condensation phenomenon and described the condensing parameters such as nucleation rate, droplet growth, dgree of subcooling, and liquid fraction. They demonstrated that steam reaches a peak subcooling of around 40 K within the divergent sections of the primary nozzle, generating initial condensations with a maximum nucleation rate of approximately 9.87 × 10 24 m − 3 s − 1 . This significant non-equilibrium state of the steam results in a rapid droplet growth rate, with the liquid fraction reaching approximately to 0.14 at the exit of the primary nozzle. Figure 16 and 17 show the impacts of the suction chamber pressure on non-equilibrium condensations inside the steam ejector. Furthermore, They concluded that the non-equilibrium condensations within the primary nozzles are unaffected by the inlet pressures of the suction chamber because of the substantial pressure difference between the motive and secondary flows.
The impact of droplets in the primary flow on the condensation phenomenon was studied by Feng et al. [50]. It was found that increasing the droplet mass fraction from 0 to 0.12 delays nucleation by 13 mm and increases condensation intensity at the primary nozzle outlet by 201.2%. Hence, increasing the number of droplets slightly reduces the condensation intensity. Furthermore, the relationship between the droplet radius and critical radius determines the sequence and strength of the two forms of liquid mass generation: droplet growth and nucleation.

3.14.4. Condensing Nozzle

Condensing nozzle refers to supersonic expansions in the Laval nozzles [95,96,97]. Ariafar [48] carried out simulation of wet steam flow through three distinct nozzles, each with a different overall area ratio (AR) of 11, 18, and 25. As shown in Figure 18, they demonstrated that nucleation of liquid droplets begins at an axial position upstream of the nozzle throat, peaking at an axial location of 0.067. At this point, significant droplet generation occurs, approximately 10241024 droplets per second per unit volume. The vapor phase starts to condense after experiencing substantial subcooling of around 13 K.

4. Conclusions

This review provided a comprehensive overview of the state-of-the-art in numerical simulation of ejector pumps for vacuum generation. The studies reviewed encompass a diverse range of working fluids, flow regimes, geometric configurations, and modeling approaches.
The literature demonstrates the potential of CFD simulations to accurately capture the complex flow phenomena within ejectors, including shock wave patterns, mixing processes, and phase transitions. However, the accuracy of numerical predictions heavily relies on the appropriate selection of turbulence models, multiphase flow modeling strategies, and the consideration of non-equilibrium effects, especially for condensing flows.
Significant progress has been made in developing advanced numerical techniques and models to accurately simulate condensation phenomena, such as nucleation, droplet growth, and non-equilibrium effects. These advancements have led to improved understanding and optimization of ejector performance parameters, including entrainment ratio, efficiency, and vacuum generation capability.
Despite the progress, several challenges remain, including the accurate modeling of real gas effects, phase change kinetics, and the coupling of heat and mass transfer processes. Additionally, there is a need for further validation and verification of numerical models against experimental data, particularly for complex multiphase flow scenarios.
Future research efforts should focus on developing more robust and computationally efficient multiphase flow models, incorporating advanced turbulence modeling techniques, and integrating AI-based optimization methods for ejector design. Additionally, the exploration of novel ejector configurations and the investigation of applications in emerging technologies, such as energy storage and waste heat recovery systems, present exciting opportunities for further research.
Overall, this review highlights the significant progress made in numerical simulation of ejector pumps for vacuum generation and provides a solid foundation for future advancements in this field, paving the way for more efficient and optimized ejector designs across various industrial sectors.

References

  1. Tashtoush, B.M.; Al-Nimr, M.A.; Khasawneh, M.A. A comprehensive review of ejector design, performance, and applications, 2019. [CrossRef]
  2. Chen, J.; Jarall, S.; Havtun, H.; Palm, B. A review on versatile ejector applications in refrigeration systems. Renewable and Sustainable Energy Reviews 2015, 49, 67–90. [Google Scholar] [CrossRef]
  3. Elbel, S.; Lawrence, N. Review of recent developments in advanced ejector technology, 2016. [CrossRef]
  4. Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review, 2016. [CrossRef]
  5. Little, A.; Garimella, S. A critical review linking ejector flow phenomena with component- and system-level performance. International Journal of Refrigeration 2016, 70. [Google Scholar] [CrossRef]
  6. Aidoun, Z.; Ameur, K.; Falsafioon, M.; Badache, M. Current advances in ejector modeling, experimentation and applications for refrigeration and heat pumps. Part 2: Two-phase ejectors. Inventions 2019, 4. [Google Scholar] [CrossRef]
  7. Aidoun, Z.; Ameur, K.; Falsafioon, M.; Badache, M. Current advances in ejector modeling, experimentation and applications for refrigeration and heat pumps. Part 2: Two-phase ejectors. Inventions 2019, 4. [Google Scholar] [CrossRef]
  8. Koirala, R.; Ve, Q.L.; Zhu, B.; Inthavong, K.; Date, A. A review on process and practices in operation and design modification of ejectors, 2021. [CrossRef]
  9. Besagni, G.; Cristiani, N.; Croci, L.; Guédon, G.R.; Inzoli, F. Computational fluid-dynamics modelling of supersonic ejectors: Screening of modelling approaches, comprehensive validation and assessment of ejector component efficiencies. Applied Thermal Engineering 2021, 186. [Google Scholar] [CrossRef]
  10. G.Cunningham, R., JetPumpTheory-1.pdf.
  11. Kwidziński, R. Control-volume-based model of the steam-water injector flow. Archives of Thermodynamics 2010, 31, 45–59. [Google Scholar] [CrossRef]
  12. Grazzini, G.; Milazzo, A.; Piazzini, S. Prediction of condensation in steam ejector for a refrigeration system. International Journal of Refrigeration 2011, 34, 1641–1648. [Google Scholar] [CrossRef]
  13. Mazzelli, F.; Giacomelli, F.; Milazzo, A. CFD modeling of condensing steam ejectors: Comparison with an experimental test-case. International Journal of Thermal Sciences 2018, 127, 7–18. [Google Scholar] [CrossRef]
  14. Elmore, E.; Al-Mutairi, K.; Hussain, B.; El-Gizawy, A.S. DEVELOPMENT OF ANALYTICAL MODEL FOR PREDICTING DUAL-PHASE EJECTOR PERFORMANCE, 2016.
  15. Winoto, S.H.; Li, H.; Shah, D.A. EFFICIENCY OF JET PUMPS, 2000.
  16. Karassik, I.J. Pump handbook; McGraw-Hill, 2001.
  17. Niu, L.; Zhang, X. Comparison of the performance enhancement of vacuum ejector by means of structure optimization and bypass methods. Energy 2024, 297. [Google Scholar] [CrossRef]
  18. Couper, J.R. Chemical process equipment: selection and design; Gulf professional publishing, 2005.
  19. Megdouli, K.; Tashtoush, B.M.; Nahdi, E.; Elakhdar, M.; Mhimid, A.; Kairouani, L. Analyse de performance d’un cycle à compression de vapeur combiné et d’un cycle à éjecteur pour la cogénération de froid. International Journal of Refrigeration 2017, 74, 515–525. [Google Scholar] [CrossRef]
  20. Zou, L.; Yu, J. 4E assessment of ejector-enhanced R290 heat pump cycle with a sub-cooler for cold region applications. Energy 2024, 131369. [Google Scholar] [CrossRef]
  21. Bruno, F.; Belusko, M.; Halawa, E. CO2 refrigeration and heat pump systems—a comprehensive review. Energies 2019, 12, 2959. [Google Scholar] [CrossRef]
  22. Mohammadi, A.; Aghaie, H.R.; Saghafian, M. Design and analysis of a suction mechanism for the vacuum degassing process. Ironmaking & Steelmaking 2021, 48, 457–465. [Google Scholar]
  23. Peris Pérez, B.; Ávila Gutiérrez, M.; Expósito Carrillo, J.A.; Salmerón Lissén, J.M. Performance of Solar-driven Ejector Refrigeration System (SERS) as pre-cooling system for air handling units in warm climates. Energy 2022, 238, 121647. [Google Scholar] [CrossRef]
  24. Braimakis, K. Solar ejector cooling systems: A review. Renewable Energy 2021, 164, 566–602. [Google Scholar] [CrossRef]
  25. Cao, Y.; Dhahad, H.A.; Hussen, H.M.; Parikhani, T. Proposal and evaluation of two innovative combined gas turbine and ejector refrigeration cycles fueled by biogas: Thermodynamic and optimization analysis. Renewable Energy 2022, 181, 749–764. [Google Scholar] [CrossRef]
  26. Gullo, P.; Hafner, A.; Banasiak, K.; Minetto, S.; Kriezi, E.E. Multi-Ejector Concept: A Comprehensive Review on its Latest Technological Developments. Energies 2019, 12. [Google Scholar] [CrossRef]
  27. Liu, Y.; Tu, Z.; Chan, S.H. Applications of ejectors in proton exchange membrane fuel cells: A review, 2021. [CrossRef]
  28. Moghimi, M.; Emadi, M.; Akbarpoor, A.M.; Mollaei, M. Energy and exergy investigation of a combined cooling, heating, power generation, and seawater desalination system. Applied Thermal Engineering 2018, 140, 814–827. [Google Scholar] [CrossRef]
  29. Hassani, M.; Kouhikamali, R. Investigation of two phase liquid jet ejector with simultaneous air and water suction in fresh water distillation system. Energy 2024, 301. [Google Scholar] [CrossRef]
  30. Milow, B.; Zarza, E. Advanced MED solar desalination plants. Configurations, costs, future — seven years of experience at the Plataforma Solar de Almeria (Spain). Desalination 1997, 108, 51–58. [Google Scholar] [CrossRef]
  31. Andrés-Mañas, J.; Requena, I.; Ruiz-Aguirre, A.; Zaragoza, G. Performance modelling and optimization of three vacuum-enhanced membrane distillation modules for upscaled solar seawater desalination. Separation and Purification Technology 2022, 287, 120396. [Google Scholar] [CrossRef]
  32. Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics.
  33. Talebiyan, M.A.; Nili-Ahmadabadi, M.; Ha, M.Y. Adjoint optimization of a supersonic ejector for under-expanded, isentropic, and over-expanded primary flow modes. Chemical Engineering Science 2024, 292, 119979. [Google Scholar] [CrossRef]
  34. Tavakoli, M.; Nili-Ahmadabadi, M.; Joulaei, A.; Ha, M.Y. Enhancing subsonic ejector performance by incorporating a fluidic oscillator as the primary nozzle: a numerical investigation. International Journal of Thermofluids 2023, 20. [Google Scholar] [CrossRef]
  35. Macia, L.; Castilla, R.; Gámez, P.J. Simulation of ejector for vacuum generation. Institute of Physics Publishing, 2019, Vol. 659. [CrossRef]
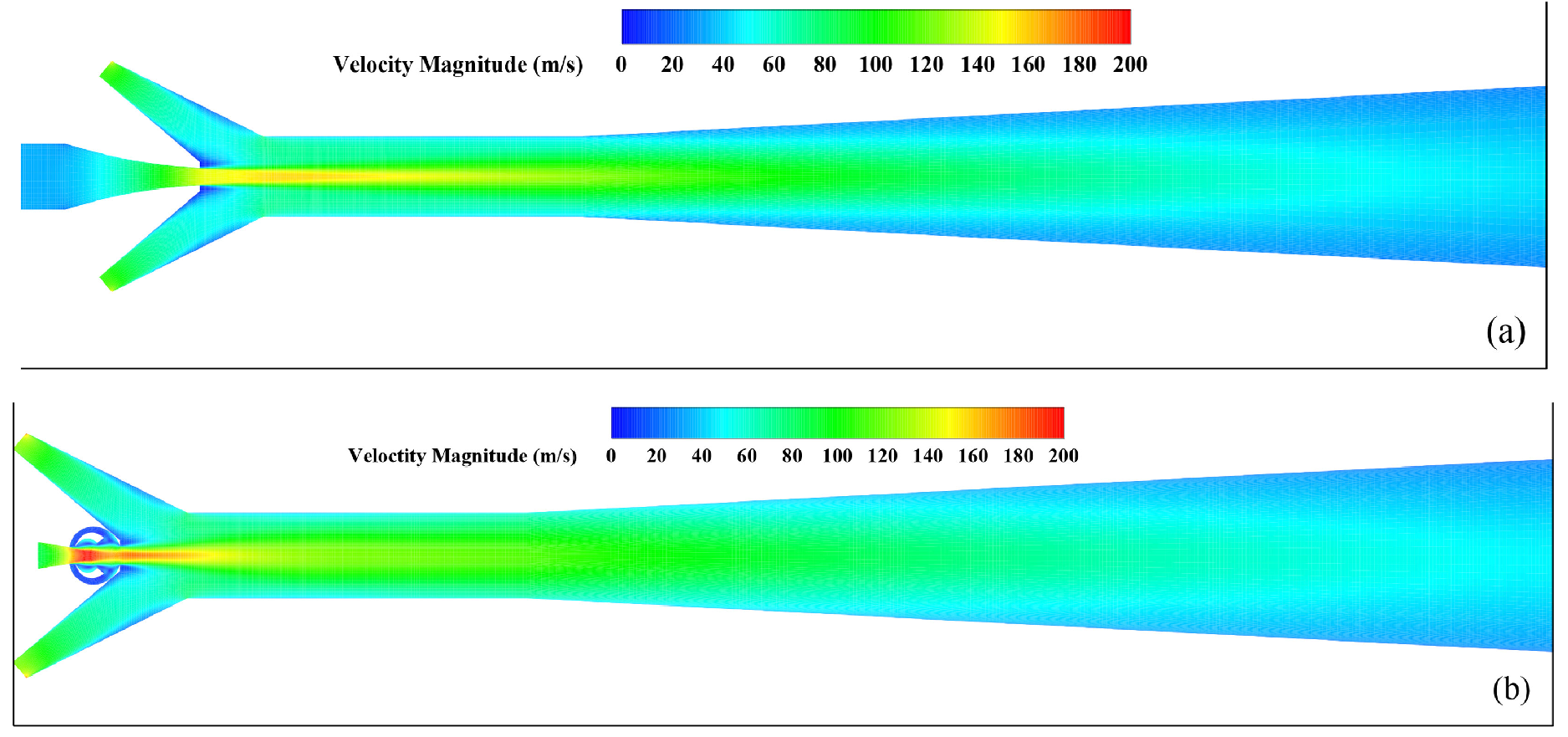
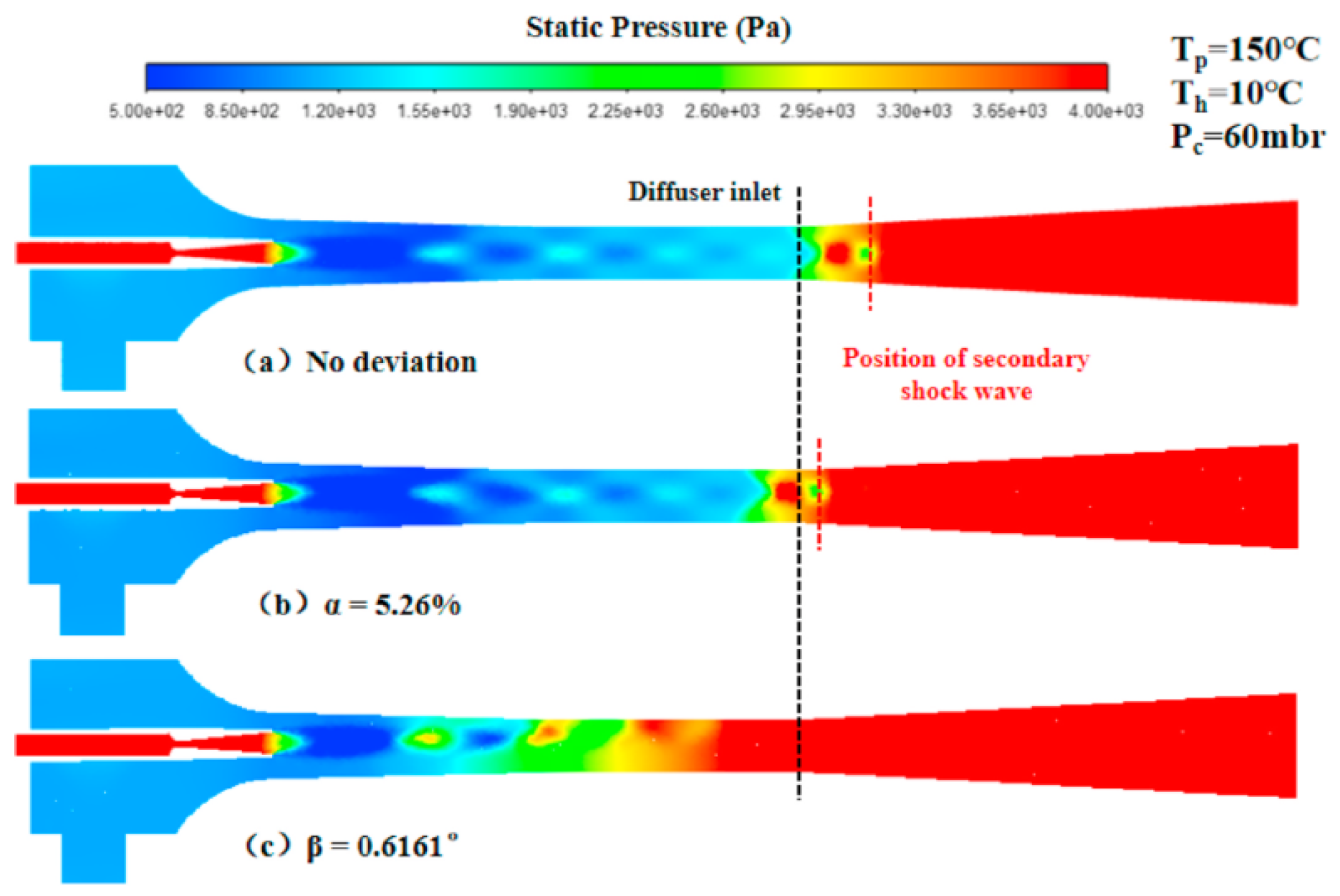
  36. Hou, Y.; Chen, F.; Zhang, S.; Chen, W.; Zheng, J.; Chong, D.; Yan, J. Numerical simulation study on the influence of primary nozzle deviation on the steam ejector performance. International Journal of Thermal Sciences 2022, 179, 107633. [Google Scholar] [CrossRef]
  37. Banu, J.P.; Mani, A. Numerical studies on ejector with swirl generator. International Journal of Thermal Sciences 2019, 137, 589–600. [Google Scholar] [CrossRef]
  38. Chai, Y.; Lin, Y.; Xiao, Q.; Huang, C.; Ke, H.; Li, B. Numerical Simulation on Two-Phase Ejector with Non-Condensable Gas. Energies 2024, 17, 1341. [Google Scholar] [CrossRef]
  39. Koirala, R.; Inthavong, K.; Date, A. Numerical study of flow and direct contact condensation of entrained vapor in water jet eductor. Experimental and Computational Multiphase Flow 2022, 4, 291–303. [Google Scholar] [CrossRef]
  40. Wen, C.; Gong, L.; Ding, H.; Yang, Y. Steam ejector performance considering phase transition for multi-effect distillation with thermal vapour compression (MED-TVC) desalination system. Applied Energy 2020, 279, 115831. [Google Scholar] [CrossRef]
  41. Giacomelli, F.; Biferi, G.; Mazzelli, F.; Milazzo, A. CFD Modeling of the Supersonic Condensation Inside a Steam Ejector. Elsevier Ltd, 2016, Vol. 101, pp. 1224–1231. [CrossRef]
  42. Ariafar, K.; Buttsworth, D.; Al-Doori, G.; Malpress, R. Effect of mixing on the performance of wet steam ejectors. Energy 2015, 93, 2030–2041. [Google Scholar] [CrossRef]
  43. Li, Z.; Xu, W.; Liang, T.; Ye, W.; Zhang, Z. Experimental and numerical studies on the performance of supersonic multi-nozzle ejector. Applied Thermal Engineering 2024, 242. [Google Scholar] [CrossRef]
  44. Singer, G.; Pinsker, R.; Stelzer, M.; Aggarwal, M.; Pertl, P.; Trattner, A. Ejector validation in proton exchange membrane fuel cells: A comparison of turbulence models in computational fluid dynamics (CFD) with experiment. International Journal of Hydrogen Energy 2024, 61, 1405–1416. [Google Scholar] [CrossRef]
  45. Kuś, T.; Madejski, P. Numerical Investigation of a Two-Phase Ejector Operation Taking into Account Steam Condensation with the Presence of CO2. Energies 2024, 17. [Google Scholar] [CrossRef]
  46. Dadpour, D.; Lakzian, E.; Gholizadeh, M.; Ding, H.; Han, X. Numerical modeling of droplets injection in the secondary flow of the wet steam ejector in the refrigeration cycle. International Journal of Refrigeration 2022, 136, 103–113. [Google Scholar] [CrossRef]
  47. Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
  48. Ariafar, K.; Buttsworth, D.; Sharifi, N.; Malpress, R. Ejector primary nozzle steam condensation: Area ratio effects and mixing layer development. Applied Thermal Engineering 2014, 71, 519–527. [Google Scholar] [CrossRef]
  49. Fang, Y.; Sen, S.; Poncet, S.; Bartosiewicz, Y.; Nesreddine, H.; Monney, D. Advanced modelling of a transcritical CO2 ejector. 2020, Vol. 2020-December. [CrossRef]
  50. Feng, H.; Yao, A.; Han, Q.; Zhang, H.; Jia, L.; Sun, W. Effect of droplets in the primary flow on ejector performance of MED-TVC systems. Energy 2024, 293. [Google Scholar] [CrossRef]
  51. Pianthong, K.; Seehanam, W.; Behnia, M.; Sriveerakul, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Conversion and Management 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
  52. Launder, B.; Spalding, D. The numerical computation of turbulent flows. Computer Methods in Applied Mechanics and Engineering 1974, 3, 269–289. [Google Scholar] [CrossRef]
  53. Lucas, C.; Rusche, H.; Schroeder, A.; Koehler, J. Numerical investigation of a two-phase CO2 ejector. International Journal of Refrigeration 2014, 43, 154–166. [Google Scholar] [CrossRef]
  54. Novais, W.R.I.; Scalon, V.L. Numerical Simulation of an Ejector Using the OpenFOAM® Solvers. Associacao Brasileira de Engenharia e Ciencias Mecanicas - ABCM, 2018. [CrossRef]
  55. Klyuyev, A.S.; Chernyshev, Y.I.; Ivanov, E.A.; Borshchev, I.O. Comparison of jet pump numerical calculation results in ansys and openfoam cfd packages. EDP Sciences, 2021, Vol. 320. [CrossRef]
  56. Zaheer, Q.; Masud, J. Visualization of flow field of a liquid ejector pump using embedded LES methodology. Journal of Visualization 2017, 20, 777–788. [Google Scholar] [CrossRef]
  57. Croquer, S.; Lamberts, O.; Poncet, S.; Moreau, S.; Bartosiewicz, Y. Large Eddy Simulation of a supersonic air ejector. Applied Thermal Engineering 2022, 209. [Google Scholar] [CrossRef]
  58. Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa Publishers, 1998.
  59. Moore, M. Predicting the fog-drop size in wet-steam turbines. Wet steam 1973. [Google Scholar]
  60. Moses, C.A.; Stein, G.D. On the Growth of Steam Droplets Formed in a Laval Nozzle Using Both Static Pressure and Light Scattering Measurements. Journal of Fluids Engineering 1978, 100, 311–322. [Google Scholar] [CrossRef]
  61. Bakhtar, F.; Mohammadi Tochai, M. An investigation of two-dimensional flows of nucleating and wet steam by the time-marching method. International Journal of Heat and Fluid Flow 1980, 2, 5–18. [Google Scholar] [CrossRef]
  62. Kwidzinski, R. Experimental and theoretical investigations of two-phase flow in low pressure steam–water injector. International Journal of Heat and Mass Transfer 2019, 144. [Google Scholar] [CrossRef]
  63. Kwidzinski, R. Condensation heat and mass transfer in steam–water injectors. International Journal of Heat and Mass Transfer 2021, 164, 120582. [Google Scholar] [CrossRef]
  64. Karthick, S.; Rao, S.M.; Jagadeesh, G.; Reddy, K. Experiments in Supersonic Gaseous Ejector Using 2D-PIV Technique. 31st International Symposium on Shock Waves 2: Applications 31. Springer, 2019, pp. 785–793.
  65. Karthick, S.; Rao, S.; Jagadeesh, G.; Reddy, K. Parametric experimental studies on mixing characteristics within a low area ratio rectangular supersonic gaseous ejector. Physics of Fluids 2016, 28. [Google Scholar] [CrossRef]
  66. Al-Rbaihat, R.; Saleh, K.; Malpress, R.; Buttsworth, D. Experimental investigation of a novel variable geometry radial ejector. Applied Thermal Engineering 2023, 233. [Google Scholar] [CrossRef]
  67. Ahmed, F.; Chen, W. Investigation of steam ejector parameters under three optimization algorithm using ANN. Applied Thermal Engineering 2023, 225. [Google Scholar] [CrossRef]
  68. Liu, G.; Pu, L.; Zhao, H.; Chen, Z.; Li, G. Multi-objective optimization of CO2 ejector by combined significant variables recognition, ANN surrogate model and multi-objective genetic algorithm. Energy 2024, 295. [Google Scholar] [CrossRef]
  69. Wang, K.; Wang, L.; Jia, L.; Cai, W.; Gao, R. Optimization design of steam ejector primary nozzle for MED-TVC desalination system. Desalination 2019, 471. [Google Scholar] [CrossRef]
  70. Arbel, A.; Shklyar, A.; Hershgal, D.; Barak, M.; Sokolov, M. Ejector irreversibility characteristics. J. Fluids Eng. 2003, 125, 121–129. [Google Scholar] [CrossRef]
  71. Sierra-Pallares, J.; García del Valle, J.; García Carrascal, P.; Castro Ruiz, F. A computational study about the types of entropy generation in three different R134a ejector mixing chambers. International Journal of Refrigeration 2016, 63, 199–213. [Google Scholar] [CrossRef]
  72. Omidvar, A.; Ghazikhani, M.; Razavi, S.M.R.M. Entropy analysis of a solar-driven variable geometry ejector using computational fluid dynamics. Energy conversion and management 2016, 119, 435–443. [Google Scholar] [CrossRef]
  73. Galanis, N.; Sorin, M. Ejector design and performance prediction. International Journal of Thermal Sciences 2016, 104, 315–329. [Google Scholar] [CrossRef]
  74. Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. International Journal of Thermal Sciences 2007, 46, 812–822. [Google Scholar] [CrossRef]
  75. Rao, S.M.V.; Jagadeesh, G. Observations on the non-mixed length and unsteady shock motion in a two dimensional supersonic ejector. Physics of Fluids 2014, 26, 036103. [Google Scholar] [CrossRef]
  76. He, S.; Li, Y.; Wang, R. Progress of mathematical modeling on ejectors. Renewable and Sustainable Energy Reviews 2009, 13, 1760–1780. [Google Scholar] [CrossRef]
  77. Śmierciew, K.; Gagan, J.; Butrymowicz, D. Application of numerical modelling for design and improvement of performance of gas ejector. Applied Thermal Engineering 2019, 149, 85–93. [Google Scholar] [CrossRef]
  78. Bodys, J.; Smolka, J.; Palacz, M.; Haida, M.; Banasiak, K. Non-equilibrium approach for the simulation of CO2 expansion in two-phase ejector driven by subcritical motive pressure. International Journal of Refrigeration 2020, 114, 32–46. [Google Scholar] [CrossRef]
  79. Smolka, J.; Bulinski, Z.; Fic, A.; Nowak, A.J.; Banasiak, K.; Hafner, A. A computational model of a transcritical R744 ejector based on a homogeneous real fluid approach. Applied Mathematical Modelling 2013, 37, 1208–1224. [Google Scholar] [CrossRef]
  80. Palacz, M.; Smolka, J.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Banasiak, K.; Hafner, A. Application range of the HEM approach for CO2 expansion inside two-phase ejectors for supermarket refrigeration systems. International Journal of Refrigeration 2015, 59, 251–258. [Google Scholar] [CrossRef]
  81. Akbarnejad, S.; Ziabasharhagh, M. A study of the application of wet steam modeling for thermocompressor simulation in TVC desalination. Desalination and Water Treatment 2024, 317. [Google Scholar] [CrossRef]
  82. Al-Manea, A.; Saleh, K. Supersonic Steam Ejectors: Comparison of Dry and Wet, 2022.
  83. Foroozesh, F.; Khoshnevis, A.B.; Lakzian, E. Improvement of the wet steam ejector performance in a refrigeration cycle via changing the ejector geometry by a novel EEC (Entropy generation, Entrainment ratio, and Coefficient of performance) method. International Journal of Refrigeration 2020, 110, 248–261. [Google Scholar] [CrossRef]
  84. Marynowski, T.; Desevaux, P.; Mercadier, Y. Experimental and numerical visualizations of condensation process in a supersonic ejector. Journal of visualization 2009, 12, 251–258. [Google Scholar] [CrossRef]
  85. Khalil, A.; Fatouh, M.; Elgendy, E. Ejector design and theoretical study of R134a ejector refrigeration cycle. International Journal of refrigeration 2011, 34, 1684–1698. [Google Scholar] [CrossRef]
  86. Carey, V.P.; Oyumi, S.M.; Ahmed, S. Post-nucleation growth of water microdroplets in supersaturated gas mixtures: a molecular simulation study, 1997.
  87. Banasiak, K.; Hafner, A. 1D Computational model of a two-phase R744 ejector for expansion work recovery. International Journal of Thermal Sciences 2011, 50, 2235–2247. [Google Scholar] [CrossRef]
  88. Grazzini, G.; Milazzo, A.; Mazzelli, F.; Grazzini, G.; Milazzo, A.; Mazzelli, F. Physics of the Ejectors. Ejectors for Efficient Refrigeration: Design, Applications and Computational Fluid Dynamics 2018, 21–69. [Google Scholar]
  89. Yadav, S.K.; Pandey, K.M.; Gupta, R. Recent advances on principles of working of ejectors: A review. Materials Today: Proceedings 2021, 45, 6298–6305. [Google Scholar] [CrossRef]
  90. Wegener, P.; Mack, L. Condensation in Supersonic and Hypersonic Wind Tunnels; Elsevier, 1958; Vol. 5, Advances in Applied Mechanics, pp. 307–447. [CrossRef]
  91. Wang, C.; Wang, L.; Zhao, H.; Du, Z.; Ding, Z. Effects of superheated steam on non-equilibrium condensation in ejector primary nozzle. International Journal of Refrigeration 2016, 67, 214–226. [Google Scholar] [CrossRef]
  92. Starzmann, J.; Hughes, F.R.; Schuster, S.; White, A.J.; Halama, J.; Hric, V.; Kolovratník, M.; Lee, H.; Sova, L.; Št’astný, M.; Grübel, M.; Schatz, M.; Vogt, D.M.; Patel, Y.; Patel, G.; Turunen-Saaresti, T.; Gribin, V.; Tishchenko, V.; Gavrilov, I.; Kim, C.; Baek, J.; Wu, X.; Yang, J.; Dykas, S.; Wróblewski, W.; Yamamoto, S.; Feng, Z.; Li, L. Results of the International Wet Steam Modeling Project. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy 2018, 232, 550–570. [Google Scholar] [CrossRef]
  93. Hill, P.G. Condensation of water vapour during supersonic expansion in nozzles. Journal of Fluid Mechanics 1966, 25, 593–620. [Google Scholar] [CrossRef]
  94. Zhou, H.; Gué, A. Simulation model and droplet ejection performance of a thermal-bubble microejector. Sensors and Actuators B: Chemical 2010, 145, 311–319. [Google Scholar] [CrossRef]
  95. Yang, Y.; Walther, J.H.; Yan, Y.; Wen, C. CFD modeling of condensation process of water vapor in supersonic flows. Applied Thermal Engineering 2017, 115, 1357–1362. [Google Scholar] [CrossRef]
  96. High Pressure Subsonic Nucleation in 1D Nozzles — An Experimental Study, Vol. Volume 1B: Marine; Microturbines, Turbochargers and Small Turbomachines; Steam Turbines, Turbo Expo: Power for Land, Sea, and Air, 2014, [https://asmedigitalcollection.asme.org/GT/proceedings-pdf/GT2014/45585/V01BT27A051/2422848/ v01bt27a051-gt2014-27241.pdf]. [CrossRef]
  97. Starzmann, J.; Hughes, F.R.; Schuster, S.; White, A.J.; Halama, J.; Hric, V.; Kolovratník, M.; Lee, H.; Sova, L.; Št’astný, M.; Grübel, M.; Schatz, M.; Vogt, D.M.; Patel, Y.; Patel, G.; Turunen-Saaresti, T.; Gribin, V.; Tishchenko, V.; Gavrilov, I.; Kim, C.; Baek, J.; Wu, X.; Yang, J.; Dykas, S.; Wróblewski, W.; Yamamoto, S.; Feng, Z.; Li, L. Results of the International Wet Steam Modeling Project. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy 2018, 232, 550–570. [Google Scholar] [CrossRef]
Preprints 112475 g001
Figure 1. Schematic of a typical ejector indicating its main components, reproduced from [1]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 1. Schematic of a typical ejector indicating its main components, reproduced from [1]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g001
Preprints 112475 g002
Figure 2. Schematic of subsonic ejector. performance curve (a) fixed primary pressure (b) fixed back pressure, reproduced from [4]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 2. Schematic of subsonic ejector. performance curve (a) fixed primary pressure (b) fixed back pressure, reproduced from [4]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g002
Preprints 112475 g003
Figure 3. Schematic of supersonic ejector performance curve. (a) fixed primary pressure (b) fixed back pressure, reproduced from [4]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 3. Schematic of supersonic ejector performance curve. (a) fixed primary pressure (b) fixed back pressure, reproduced from [4]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g003
Preprints 112475 g004
Figure 4. Vacuum ejector working cycle: (a) vacuum curve (b) flow curve, reproduced from [17]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 4. Vacuum ejector working cycle: (a) vacuum curve (b) flow curve, reproduced from [17]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g004
Preprints 112475 g005
Figure 5. Number of articles versus corresponding authors countries.
Figure 5. Number of articles versus corresponding authors countries.
Preprints 112475 g005
Preprints 112475 g006
Figure 6. Schematic of a typical ejector geometric parameters [7].
Figure 6. Schematic of a typical ejector geometric parameters [7].
Preprints 112475 g006
Preprints 112475 g007
Figure 7. Types of swirl generator used in Banu and Mani’s work [37]: (a) Solid type (b) cavity type (c) different sweep and chamber angels in cavity type, reproduced from Banu and Mani[37]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 7. Types of swirl generator used in Banu and Mani’s work [37]: (a) Solid type (b) cavity type (c) different sweep and chamber angels in cavity type, reproduced from Banu and Mani[37]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g007
Preprints 112475 g008
Figure 8. Comparison of parameterically optimized (gray lines) and adjoint- optimized (red lines) ejectors, reproduced from Talebiyan et al. [33]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 8. Comparison of parameterically optimized (gray lines) and adjoint- optimized (red lines) ejectors, reproduced from Talebiyan et al. [33]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g008
Preprints 112475 g009
Figure 9. Internal flow showing occurrence of shock and zero secondary flow [35].
Figure 9. Internal flow showing occurrence of shock and zero secondary flow [35].
Preprints 112475 g009
Preprints 112475 g010
Figure 10. Contours of Mach number and static pressure in three flow modes: a) over-expanded b)slight over-expanded c) under-expanded, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 10. Contours of Mach number and static pressure in three flow modes: a) over-expanded b)slight over-expanded c) under-expanded, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g010
Preprints 112475 g011
Figure 11. Contour of velocity with and without fluidic oscillator, reproduced from [34]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 11. Contour of velocity with and without fluidic oscillator, reproduced from [34]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g011
Preprints 112475 g012
Figure 12. The mass fraction contour of N2 and the non-mixing length for two ejectors, reproduced from [43]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 12. The mass fraction contour of N2 and the non-mixing length for two ejectors, reproduced from [43]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g012
Preprints 112475 g013
Figure 13. Contour of static pressure indicating shock position, reproduced from [36]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 13. Contour of static pressure indicating shock position, reproduced from [36]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g013
Preprints 112475 g014
Figure 14. Mach cloud diagram representing chock and shock positions in different throat diameter of the ejector, reproduced from [47]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 14. Mach cloud diagram representing chock and shock positions in different throat diameter of the ejector, reproduced from [47]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g014
Preprints 112475 g015
Figure 15. Heat transfer coefficient distributions at different non-condensable gas mas fractions [38].
Figure 15. Heat transfer coefficient distributions at different non-condensable gas mas fractions [38].
Preprints 112475 g015
Preprints 112475 g016
Figure 16. Variation of droplet growth rate versus the suction chamber pressure inside the steam ejector, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 16. Variation of droplet growth rate versus the suction chamber pressure inside the steam ejector, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g016
Preprints 112475 g017
Figure 17. Variation of nucleation rate versus the suction chamber pressure inside the steam ejector, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 17. Variation of nucleation rate versus the suction chamber pressure inside the steam ejector, reproduced from [40]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g017
Preprints 112475 g018
Figure 18. Variations of nucleation rate and subcooling level, reproduced from [48]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Figure 18. Variations of nucleation rate and subcooling level, reproduced from [48]. Copyright © 2024 Elsevier Masson SAS. All rights reserved.
Preprints 112475 g018
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated