Optimization of Spatial Windshield Wiper Linkages by Using the Differential Evolution Method

Preprint

Article

Optimization of Spatial Windshield Wiper Linkages by Using the Differential Evolution Method

Altmetrics

Downloads

Views

Comments

Tsai-Jung Chen^*,Tien-Shun Chung

This version is not peer-reviewed

Submitted:

22 July 2024

Posted:

24 July 2024

You are already at the latest version

Alerts

Abstract

This study developed a three-dimensional kinematic and dynamic model of a center-driven linkage system (CDLS). Force analysis was conducted to determine the required driving torque to ensure that the input link of the CDLS rotates at a constant speed with a certain angular velocity, even in the presence of frictional resistance torque. The primary objective was to optimize the maximum angular acceleration of the output links to reduce wiper noise. This optimization can enhance the stability of the linkage system while maintaining its operational functionality. In the adopted methodology, the frames of the fixed links are assumed to remain unchanged, and the input link is considered to operate at a constant angular speed and have a constant length. To meet standard vehicle windshield wiper requirements, 10 constraints were imposed on the optimization problem, which was solved using the differential evolution method. The lengths of both output links were reduced by over 10% after optimization.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Spatial four-bar linkages are employed to achieve mechanical input–output relationships between spatially oriented axes of movement. A revolute–spherical–spherical–revolute (RSSR) spatial four-bar mechanism features two revolute joints of arbitrary orientation that are attached to a fixed link and two spherical joints that connect cranks to a coupler link. The analysis and development of these linkages are interesting and challenging problems. Numerous researchers have made significant contributions to the study of rigid-link RSSR mechanisms [1,2,3,4,5,6,7,8,9,10,11,12]. A center-driven linkage system (CDLS) comprises two RSSR linkage systems driven by a single central input link. In the present study, we developed a three-dimensional kinematic and dynamic model of a CDLS for windshield wipers. Chen et al. [13,14] proposed that appropriately reducing the magnitude of a wiper's acceleration (or deceleration) helps decrease vibrations, which can reduce unpleasant rubber wiper noises on vehicle windshields. We adopted the objective function and constraints presented in their study to optimize the link lengths in a wiper linkage system by employing a differential evolution (DE) search method.

DE was introduced by Storn and Price in 1995 [15,16,17] and rapidly gained widespread adoption because of its simplicity and experimental efficiency. Numerous variants of DE have been developed to enhance its optimization capabilities, including DE with trigonometric mutation [18], opposition-based learning (OBL) DE [19,20,21], DEGL (DE with global and local neighborhoods) incorporating neighborhood-based mutation [22], and self-adaptive DE [23,24,25]. These innovations have considerably bolstered DE’s robustness and adaptability, making it a versatile tool for diverse optimization problems. The equilibrium optimizer, introduced by Faramarzi et al. [26], is inspired by the principles of dynamic and equilibrium states in physics. This algorithm has been demonstrated to outperform DE and other optimization techniques because it effectively balances the exploration and exploitation phases. In addition, Mallipeddi et al. [27] investigated various mutation strategies and parameter settings within DE and substantially improved its robustness and adaptability across various optimization scenarios. Wang et al. [28] conducted a scalability analysis of DE enhanced with generalized OBL and achieved significant performance gains for large-scale optimization tasks. Similarly, Choi et al. [29] introduced a stochastic variant of OBL for DE, which substantially enhanced the convergence speed and solution quality for numerical optimization problems.

Wang et al. integrated the gray wolf optimizer with DE to improve feature selection and demonstrated that their method was more effective than conventional DE and other methods were. Heidari et al. [30] explored integrating the Harris Hawks Optimization algorithm with DE and highlighted the superior efficiency of this integrated method for solving intricate engineering optimization challenges.

Collectively, the aforementioned studies underscore the versatility and effectiveness of DE for solving sophisticated optimization challenges in various domains. Ongoing enhancements to DE and the introduction of novel DE variants ensure the enduring relevance and applicability of DE in solving increasingly complex optimization problems. The objective function for optimization in this study is defined as follows:

f (r_{3}, r_{4}, r_{5}, r_{6}) = \max_{{0 \leq θ}_{2} \leq 2 π} |α_{4} (r_{2}, r_{3}, r_{4}, θ_{2})| + \max_{{0 \leq θ}_{2} \leq 2 π} |α_{6} (r_{2}, r_{5}, r_{6}, θ_{2})|

(1)

where

α_{4}

and

α_{6}

represent the angular accelerations of the output links on the driver and passenger sides of the CDLS, respectively.

This optimization problem is subject to 10 constraints derived from typical requirements for vehicle windshield wipers. The aforementioned objective function is a function of the parameters of the connecting and output links on the driver and passenger sides of the CDLS. Additional details on this objective function are provided in Section 2. The input link of the CDLS is assumed to rotate at a constant speed with an angular velocity of 1 rad/s. Our optimization calculations for this linkage system indicate that the maximum angular acceleration of the output link on the driver side of the CDLS can be reduced by 13.64%. Additionally, the calculations show that the maximum angular acceleration of the output link on the passenger side can be reduced by 14.38%. In addition, we developed a dynamic model of the CDLS. Through force analysis, we determined the required motor torque to ensure that the input link of the CDLS rotates at a constant speed with a given angular velocity, even in the presence of frictional resistance torque.

2. Materials and Methods

A flowchart of our method is shown in Figure 1. This section discusses a kinematic model of the CDLS. Mathematical formulas based on this model were established for the angles, angular velocities, angular accelerations, and transmission angles of various parts of the CDLS. Numerical simulations of CDLS motion were then performed in MATLAB by using these mathematical formulas.

Mathematical formulas for

α_{4}

and for

α_{6}

are provided in Section 2.1. Section 2.2 presents the mathematical formulas for the magnitudes of the joint forces acting on each link and the driving torque of the motor. Finally, Section 2.3 describes the use of DE to minimize the objective function of the present study under the 10 considered constraints. Finally, this section discusses a dynamic model of the CDLS. This model and Euler’s laws of motion can be used to determine the magnitudes of the joint forces acting on each link and the driving torque of the motor. The torque exerted by an external load on the output links is considered in the analysis to ensure that the crank rotates at a constant speed.

2.1. Wiper Linkage Motion Model

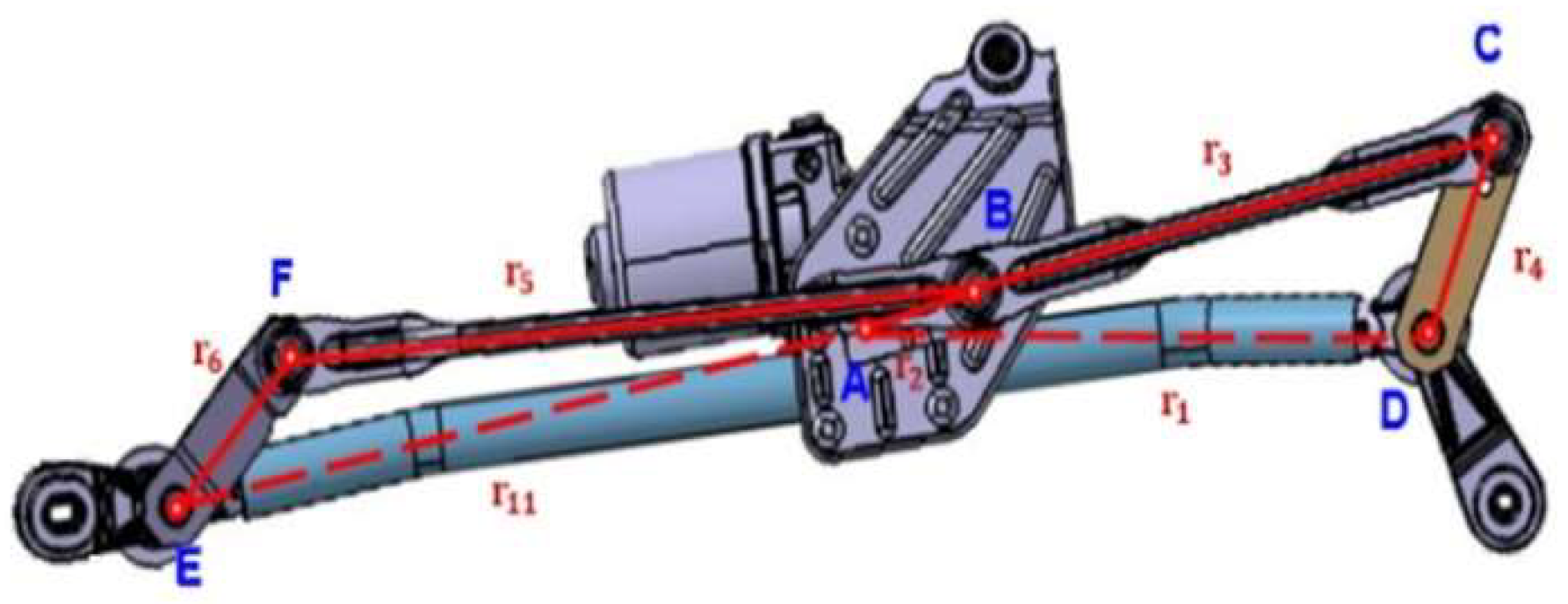
Figure 2 displays the structure of a CDLS. The vectors of the crankshaft’s axis are not mutually parallel with the vectors of the output links of the wipers on both sides; therefore, the linkages cannot be simplified into a planar model. 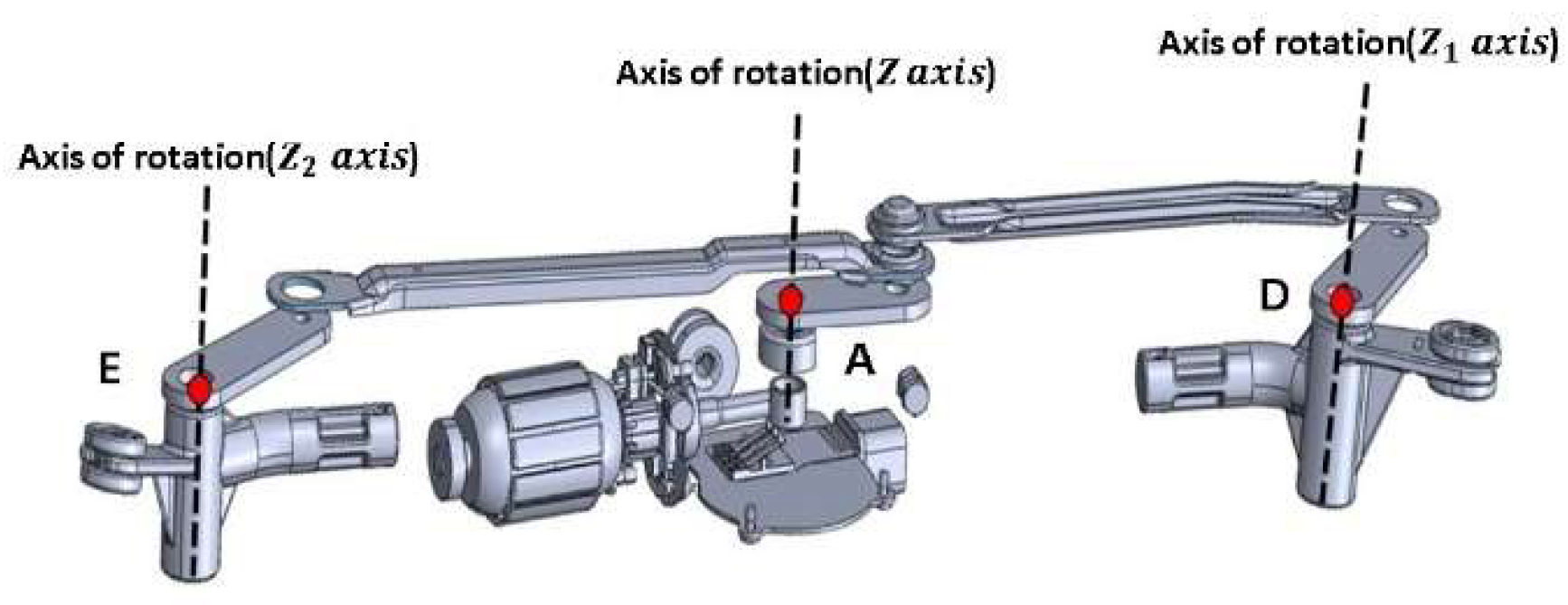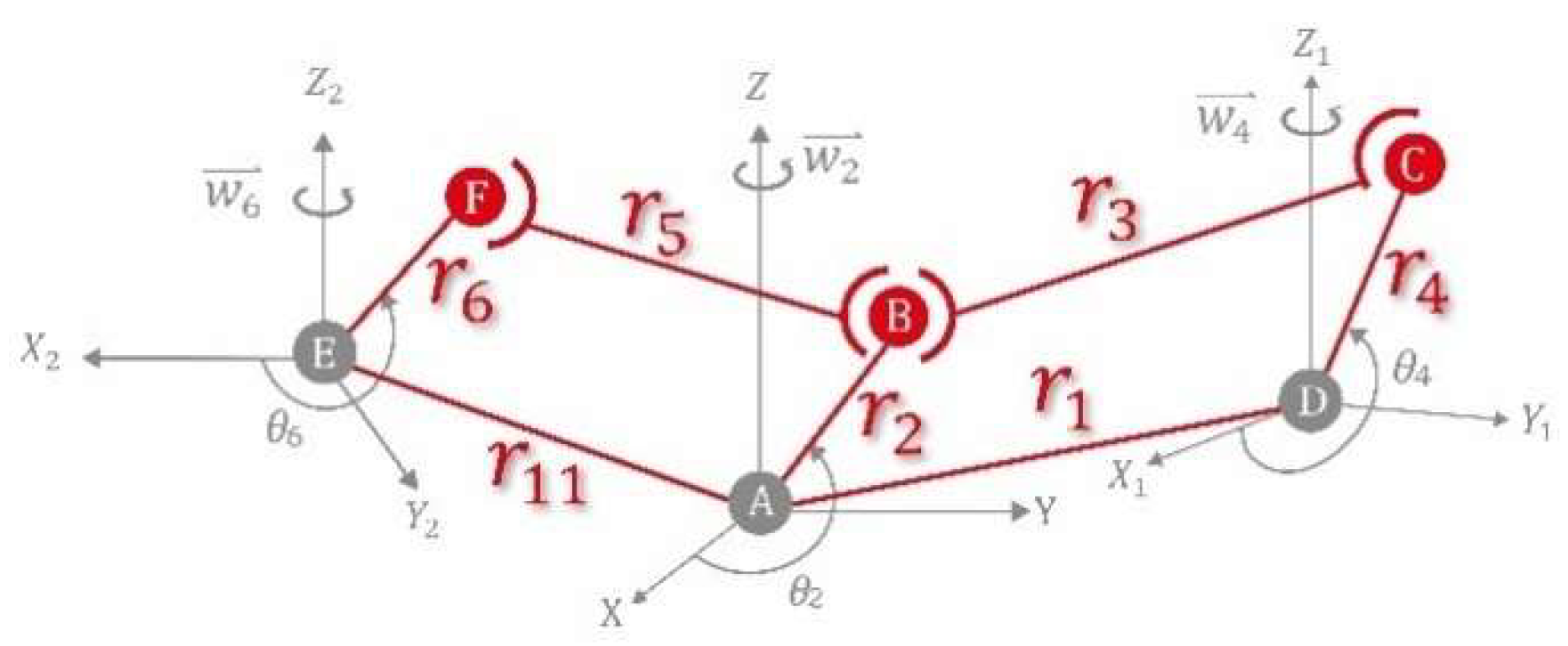To precisely optimize the rod lengths and meet the requirements of practical applications, we established a simplified three-dimensional kinematic model of a CDLS (Figure 4). For this model, three Cartesian coordinate systems were established:

X Y Z

X_{1} Y_{1} Z_{1}

, and

X_{2} Y_{2} Z_{2}

. Point A is the origin of coordinate system

X Y Z

, and the motor shaft vector is aligned along the

Z

-axis. Link AB rotates in the

X Y

plane around the

Z

-axis. Point D is the origin of coordinate system

X_{1} Y_{1} Z_{1}

, and Link CD rotates about the

Z_{1}

-axis within the

X_{1} Y_{1}

plane. Finally, point E is the origin of coordinate system

X_{2} Y_{2} Z_{2}

, and Link EF rotates about the

Z_{2}

-axis within the

X_{2} Y_{2}

plane.

Figure 2. Structure of a CDLS.

Figure 3. Rotating shafts, coordinate origins, and axes of rotation.

Figure 4. Simplified three-dimensional kinematic model of a CDLS.

The link components of the CDLS were measured in millimeters, and angles were measured in radians .

The linkage system, which includes Links AB, BC, CD, and AD, drives the wiper on the driver side of the CDLS. Link AD is fixed, and Link AB, commonly referred to as the crankshaft, is the input link that receives power to drive Links BC and CD. Link BC is a connecting link, and Link CD is the output link on the driver side of the CDLS. Link AB is the shortest link and can rotate 360°. The lengths of these four driver-side links must satisfy Grashof's law [14]. ABCD is a spatial four-bar linkage mechanism; points A, B, C, and D have a rotational joint R, spherical joint S, spherical joint S, and rotational joint R, respectively. This mechanism is commonly known as an RSSR mechanism. The angle

μ_{4}

between Links BC and CD is commonly referred to as the transmission angle on the driver side of the CDLS [31], and

μ_{4}

varies as the input link (Link AB) rotates. The mechanism achieves optimal efficiency (maximized effective torque) when the transmission angle is π/2 radians. Typically, the transmission angle must be able to vary from 40° to 140° [31].

The linkage responsible for driving the wiper on the passenger side of the CDLS comprises Links AB, BF, AE, and EF. Link AE is a fixed link, and Link AB is the input link (crankshaft) that powers Links BF and EF. Link BF and Link EF are the connecting and output links, respectively, on the passenger side of the CDLS, and the angle

μ_{6}

between Links BF and FE is the transmission angle on the passenger side of the CDLS. For the driver side, the efficiency is optimized when the transmission angle is π/2 radians.

The lengths of Links AB, BC, CD, and AD are denoted as

r_{2}

r_{3}

r_{4}

and

r_{1}

, respectively. In addition, the angles between Link AB and the X-axis, Link DC and the X₁-axis, and Link EF and the X₂-axis are denoted as

θ_{2}

θ_{4}

, and

θ_{6}

, respectively (refer to Figure 4). Similarly, the lengths of Links BF, FE, and AE are denoted as

r_{5}, r_{6}

, and

r_{11}

respectively. The lengths of Links AB, BC, CD, and AD (passenger-side links) must also satisfy Grashof's law. ABFE is also a spatial four- bar linkage mechanism with a rotational joint R, spherical joint S, spherical joint S, and rotational joint R at points A, B, F, and E, respectively (Figure 4).

The following paragraphs discuss the mathematical formulas for the established model.

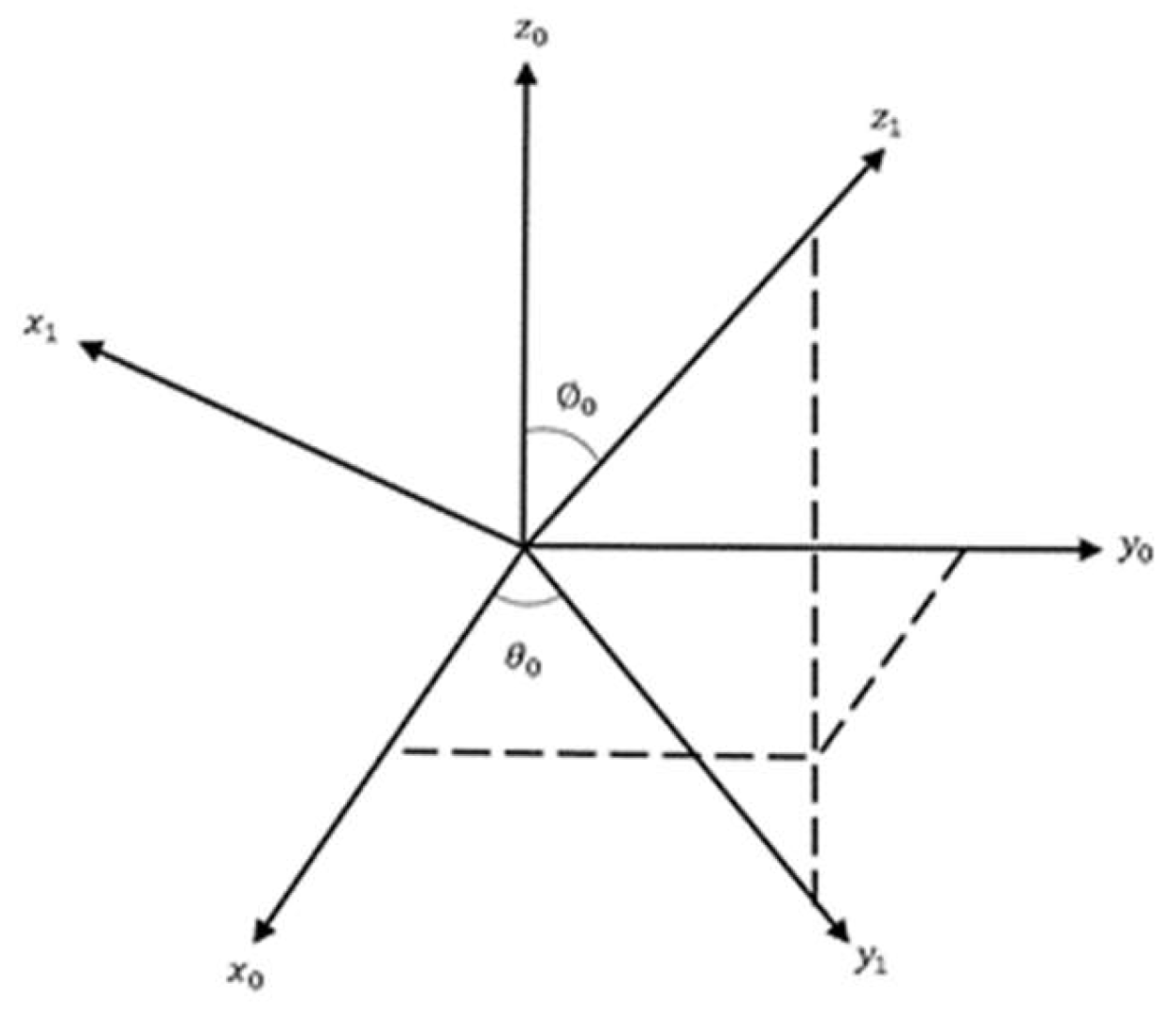
2.1.1. Matrices for Three-Dimensional Rotations

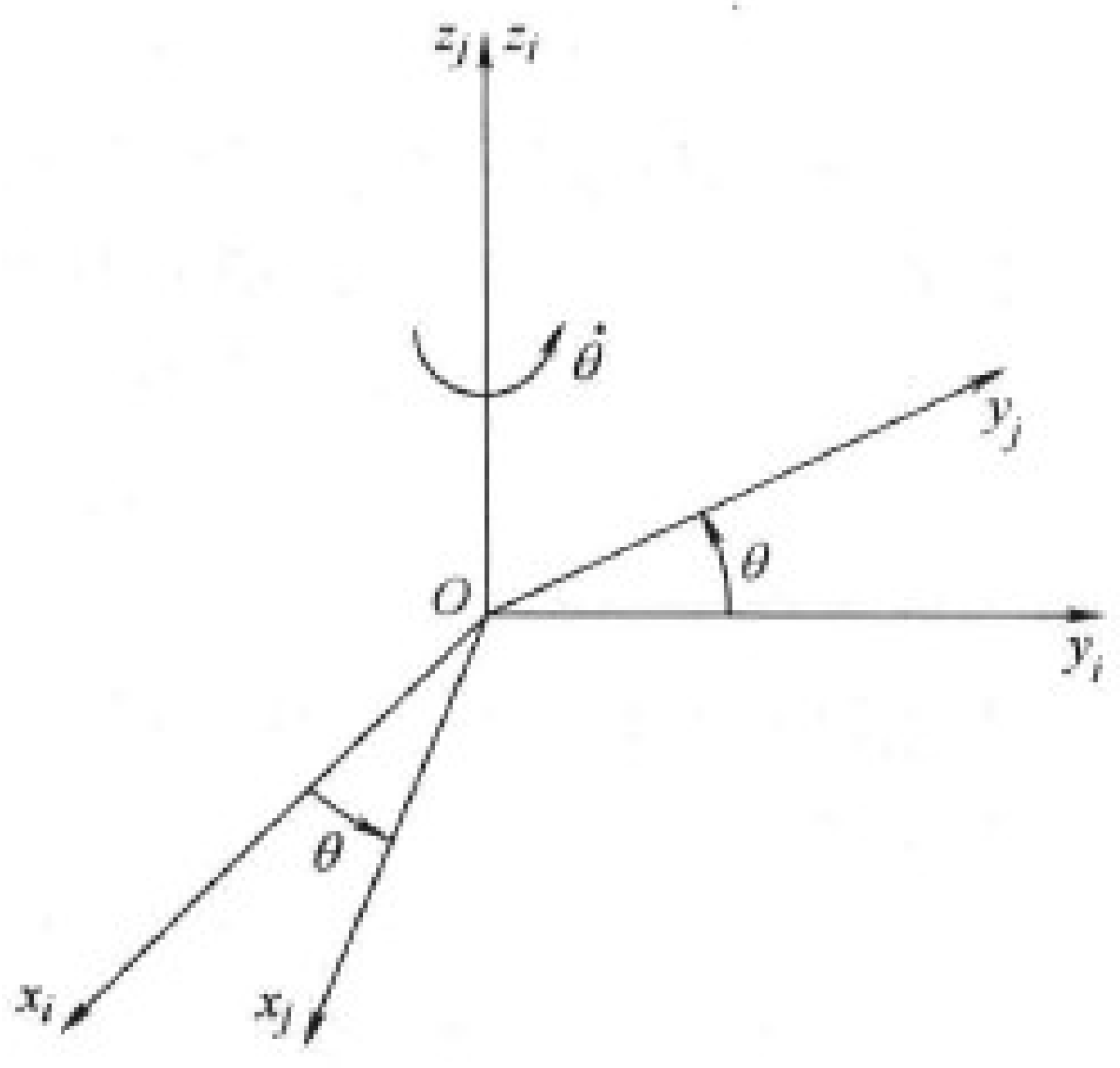
The

y_{i}

-axis is defined as running horizontally left and right on the paper, and the

z_{i}

-axis is defined as running vertically up and down on the paper. The diagonal line represents the

x_{i}

-axis, which is perpendicular to the other two axes; its positive direction is out of the paper, and its negative direction is into the paper. The positive axes of the standard

x_{i} y_{i} z_{i}

coordinate frame point in the out, right, and up directions (Figure 5). The standard definitions of the rotations about the three principle axes are first explained. Consider two right-handed rectangular coordinate systems with a common origin, as depicted in Figure 5. The coordinate system

x_{j} y_{j} z_{j}

can be obtained from the coordinate system

x_{i} y_{i} z_{i}

by performing a counterclockwise rotation about the

z_{i}

-axis by an angle

θ

. The sign of

θ

follows the right-hand rule: When the thumb points in the positive direction of the

z_{i}

-axis, a counterclockwise rotation from the

x_{i}

-axis to the

x_{j}

-axis indicates a positive

θ

value, whereas a clockwise rotation indicates a negative

θ

value. The coordinate transfer matrix is expressed as follows:

[{C_{i j}}^{(θ)}] = [\begin{matrix} \cos (θ) & \sin (θ) & 0 \\ - \sin (θ) & \cos (θ) & 0 \\ 0 & 0 & 1 \end{matrix}]

where (

θ

) in the upper right corner of the square matrix indicates that the coordinate system

x_{j} y_{j} z_{j}

is obtained by rotating the coordinate system

x_{i} y_{i} z_{i}

about the

z_{i}

-axis by the angle

θ

. Two vectors in the

O_{x_{i} y_{i} z_{i}}

and the

O_{x_{j} y_{j} z_{j}}

systems, namely (

x, y, z

) and (

x', y', z'

), respectively, have the following relationship:

[\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix}] = [{C_{i j}}^{(θ)}] [\begin{matrix} x \\ y \\ z \end{matrix}]

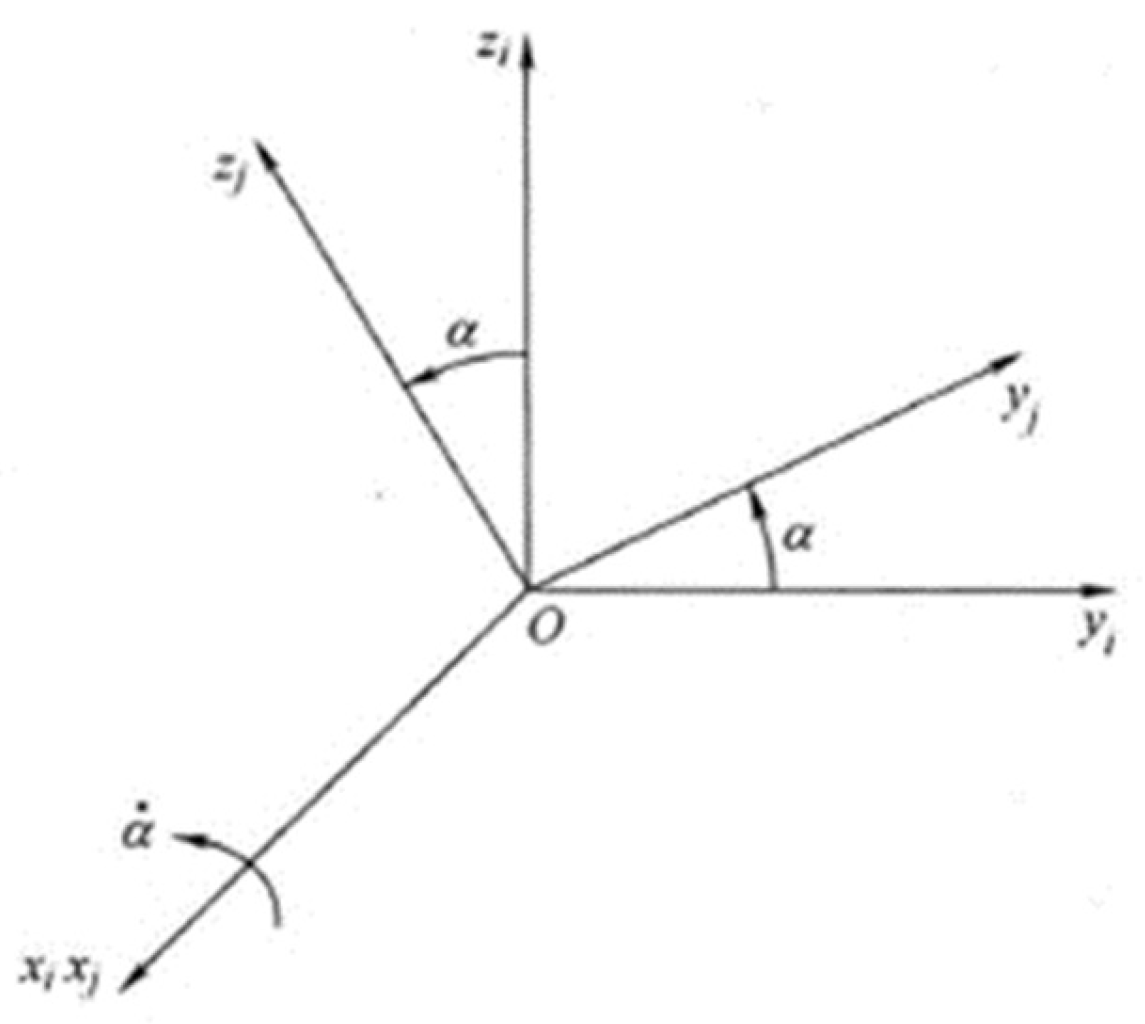
As shown in Figure 6, the coordinate system

x_{j} y_{j} z_{j}

can be obtained from the coordinate system

x_{i} y_{i} z_{i}

by performing a counterclockwise rotation about the

x_{i}

-axis by an angle

α

. The relevant coordinate transfer matrix is expressed as follows:

[{C_{i j}}^{(α)}] = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (α) & \sin (α) \\ 0 & - \sin (α) & \cos (α) \end{matrix}]

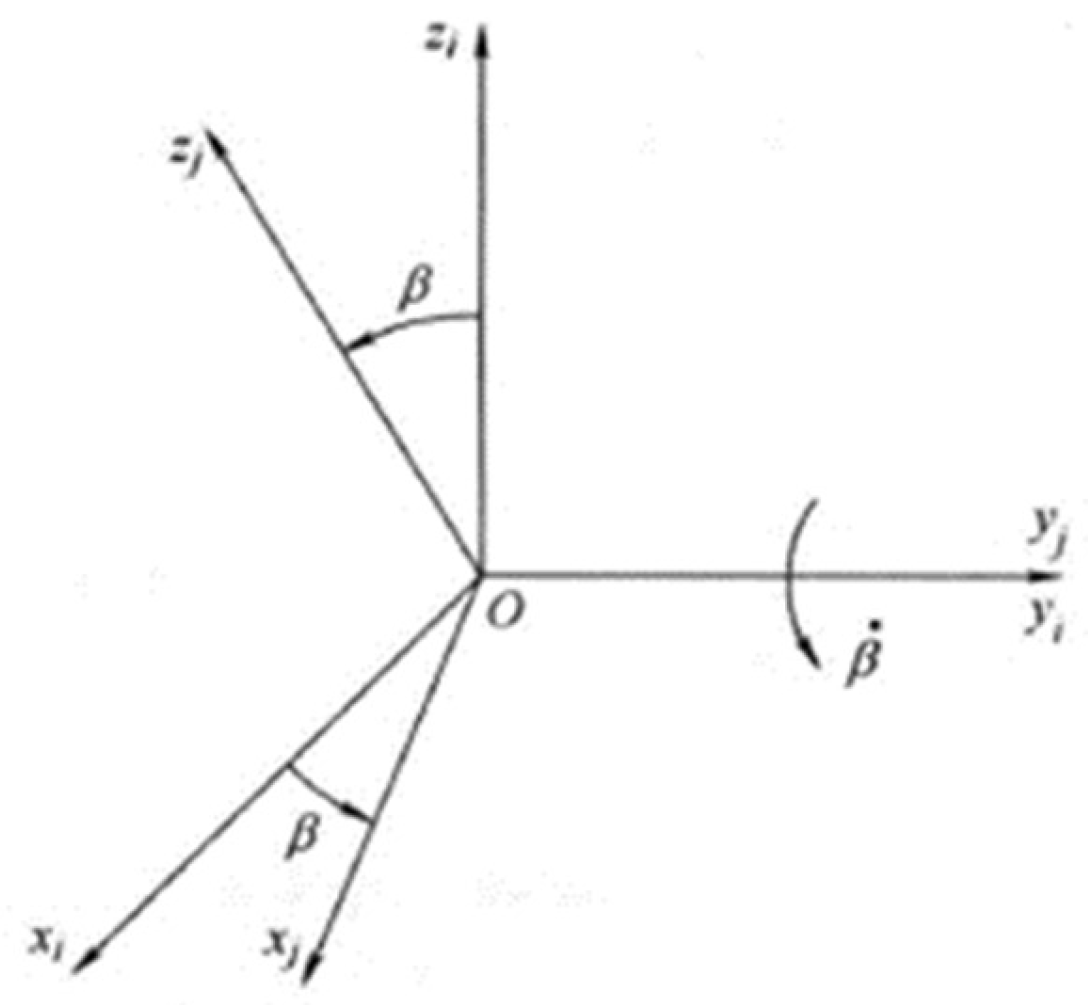
Similarly, coordinate system

x_{j} y_{j} z_{j}

is obtained from coordinate system

x_{i} y_{i} z_{i}

by performing a counterclockwise rotation about the

y_{i}

-axis by an angle

β

(Figure 7). The relevant coordinate transfer matrix is expressed as follows:

[{C_{i j}}^{(β)}] = [\begin{matrix} \cos (β) & 0 & - \sin (β) \\ 0 & 1 & 0 \\ \sin (β) & 0 & \cos (β) \end{matrix}]

2.1.2. Multiple Rotations

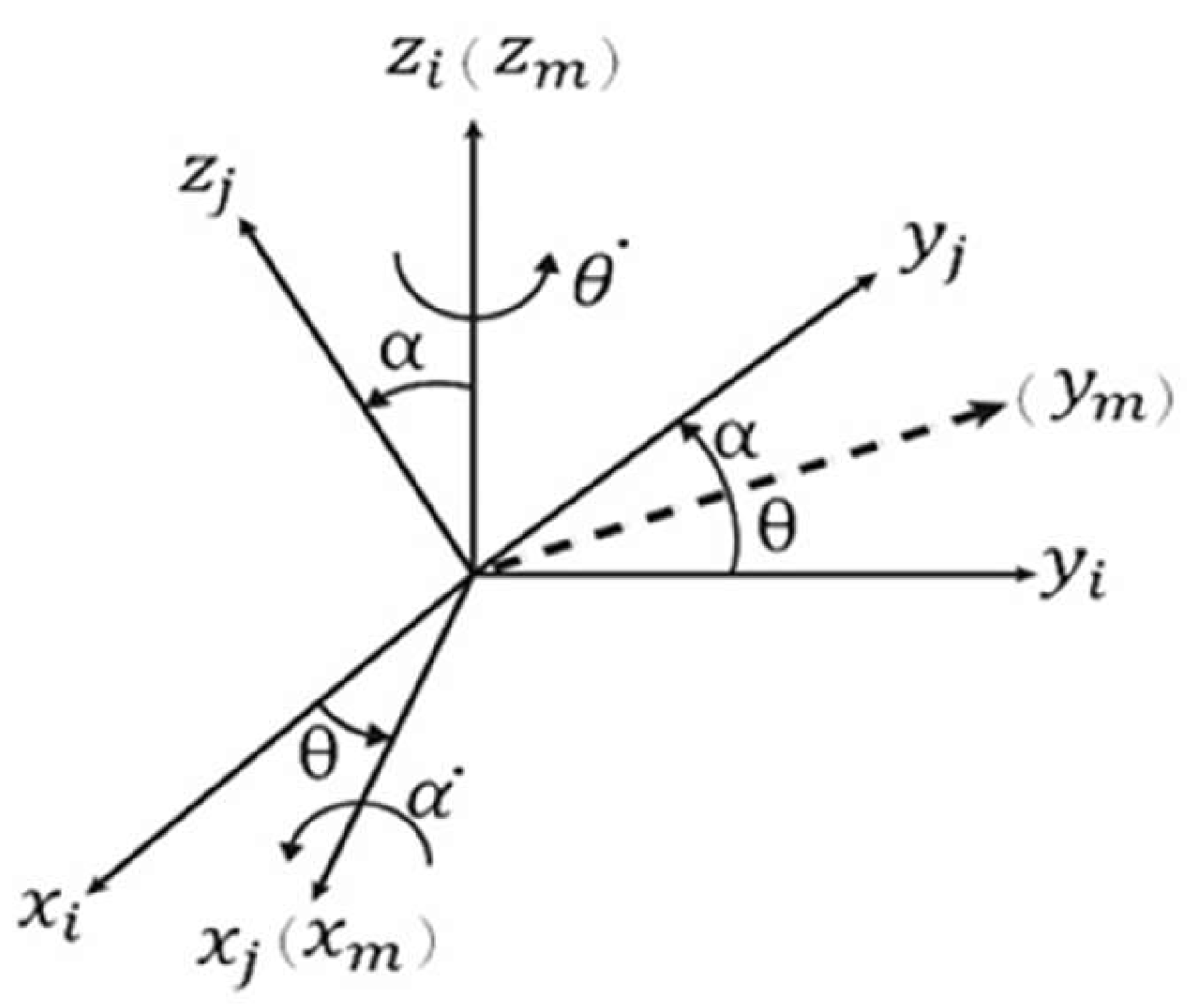
As displayed in Figure 8, the orientation of the

x_{j} y_{j} z_{j}

coordinate system relative to the

x_{i} y_{i} z_{i}

coordinate system can be regarded as a transformation involving two steps. First, the

x_{i} y_{i} z_{i}

coordinate system is rotated around the

z_{i}

-axis by θ, resulting in the

x_{m} y_{m} z_{m}

coordinate system. The matrix relationship for this transformation is given as follows:

{\overset{⃑}{r}}_{x_{m} y_{m} z_{m}} = [{C_{i m}}^{(θ)}] {\overset{⃑}{r}}_{x_{i} y_{i} z_{i}} = [\begin{matrix} \cos (θ) & \sin (θ) & 0 \\ - \sin (θ) & \cos (θ) & 0 \\ 0 & 0 & 1 \end{matrix}] {\overset{⃑}{r}}_{x_{i} y_{i} z_{i}},

(2)

where

{\overset{⃑}{r}}_{x_{i} y_{i} z_{i}}

is a vector in the

x_{i} y_{i} z_{i}

coordinate system. This vector can be expressed in the

x_{m} y_{m} z_{m}

coordinate system as

{\overset{⃑}{r}}_{x_{m} y_{m} z_{m}}

by using Equation (2).

Second, the

x_{m} y_{m} z_{m}

coordinate system is rotated around the

x_{m}

-axis by an angle

α

to become the

x_{j} y_{j} z_{j}

coordinate system; the corresponding coordinate transformation matrix relationship can be expressed as follows:

{\overset{⃑}{r}}_{x_{j} y_{j} z_{j}} = [{C_{m j}}^{(α)}] {\overset{⃑}{r}}_{x_{m} y_{m} z_{m}} = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos (α) & \sin (α) \\ 0 & - \sin (α) & \cos (α) \end{matrix}] {\overset{⃑}{r}}_{x_{m} y_{m} z_{m}},

(3)

where

{\overset{⃑}{r}}_{x_{m} y_{m} z_{m}}

is a vector in the

x_{m} y_{m} z_{m}

coordinate system. This vector can be expressed in the

x_{i} y_{i} z_{i}

system as follows:

{\overset{⃑}{r}}_{x_{j} y_{j} z_{j}} = [{C_{m j}}^{(α)}] {\overset{⃑}{r}}_{x_{m} y_{m} z_{m}} = [{C_{m j}}^{(α)}] [{C_{i m}}^{(θ)}] {\overset{⃑}{r}}_{x_{i} y_{i} z_{i}},

(4)

Equation (4) can be used to achieve continuous transformations between coordinate systems.

If an axis of a reference frame is specified, its coordinate system can be conveniently selected, as shown in Figure 9. If

z_{1}

is the specified axis of the system

x_{0} y_{0} z_{0}

, the polar and azimuthal angles are

ϕ_{0}

and

θ_{0}

, respectively. First, the coordinate system

x_{0} y_{0} z_{0}

is rotated around the

z_{0}

-axis clockwise by an angle

\frac{π}{2} - θ_{0}

, resulting in the

x_{m} y_{m} z_{m}

coordinate system. Next, the

x_{m} y_{m} z_{m}

coordinate system is rotated around the

x_{m}

-axis clockwise by an angle

ϕ_{0}

, transforming it into the

x_{1} y_{1} z_{1}

coordinate system. Here

, {\overset{⃑}{r}}_{x_{0} y_{0} z_{0}}

is a vector in the

x_{0} y_{0} z_{0}

coordinate system. This vector can be expressed in the

x_{1} y_{1} z_{1}

coordinate system as follows:

{\overset{⃑}{r}}_{x_{1} y_{1} z_{1}} = [{C_{m 1}}^{(- ϕ_{0})}] [{C_{0 m}}^{(- (\frac{π}{2} - θ_{0}))}] {\overset{⃑}{r}}_{x_{0} y_{0} z_{0}},

(5)

2.1.3. Motion of the Driver-Side Linkage of the CDLS

The

Z

-axis of the

X Y Z

coordinate system is aligned with the crankshaft axis, and the crank itself is positioned in the

X Y

plane of this coordinate system. Assume that the unit vector of the main output shaft's axis

Z_{1}

is (

c o s (θ_{0}) s i n (ϕ_{0}), s i n (θ_{0}) s i n (ϕ_{0}), c o s (ϕ_{0})

). A reference coordinate system

X_{1} Y_{1} Z_{1}

is defined for the main output shaft. Here,

{\overset{⃑}{r}}_{X Y Z}

is a vector in the

X Y Z

coordinate system. This vector can be expressed in the

X_{1} Y_{1} Z_{1}

coordinate system as follows by using Equation (5):

{\overset{⃑}{r}}_{X_{1} Y_{1} Z_{1}} = [\begin{matrix} s i n θ_{0} & - c o s θ_{0} & 0 \\ c o s θ_{0} c o s ϕ_{0} & s i n θ_{0} c o s ϕ_{0} & - s i n ϕ_{0} \\ s i n ϕ_{0} c o s θ_{0} & s i n ϕ_{0} s i n θ_{0} & c o s ϕ_{0} \end{matrix}] {\overset{⃑}{r}}_{X Y Z},

(6)

Let R = [\begin{matrix} s i n θ_{0} & - c o s θ_{0} & 0 \\ c o s θ_{0} c o s ϕ_{0} & s i n θ_{0} c o s ϕ_{0} & - s i n ϕ_{0} \\ s i n ϕ_{0} c o s θ_{0} & s i n ϕ_{0} s i n θ_{0} & c o s ϕ_{0} \end{matrix}],

(7)

Assume that vectors

\overset{⃑}{A B}

and

\overset{⃑}{A D}

are defined as follows in the

X Y Z

coordinate system:

\overset{⃑}{A B} = [\begin{matrix} r_{2} \cos (θ_{2}) \\ r_{2} \sin (θ_{2}) \\ 0 \end{matrix}], \overset{⃑}{A D} = [\begin{matrix} r_{1} \sin (ϕ_{1}) \cos (θ_{1}) \\ r_{1} \sin (ϕ_{1}) \sin (θ_{2}) \\ r_{1} \cos (ϕ_{1}) \end{matrix}]

Vector

\overset{⃑}{A B} - \overset{⃑}{A D}

can then be expressed in the

X_{1} Y_{1} Z_{1}

coordinate system as follows:

[\begin{matrix} r_{2 x} \\ r_{2 y} \\ r_{2 z} \end{matrix}] = R [\begin{matrix} r_{2} \cos θ_{2} \\ r_{2} \sin θ_{2} \\ 0 \end{matrix}] - R [\begin{matrix} r_{1} \sin ϕ_{1} \cos θ_{1} \\ r_{1} \sin ϕ_{1} \sin θ_{1} \\ r_{1} \cos ϕ_{1} \end{matrix}],

(8)

Similarly, assume that vectors

\overset{⃑}{D C}

and

\overset{⃑}{B C}

are defined as follows in the

X_{1} Y_{1} Z_{1}

coordinate system:

\overset{⃑}{D C} = [\begin{matrix} r_{4} \cos (θ_{4}) \\ r_{4} \sin (θ_{4}) \\ 0 \end{matrix}], \overset{⃑}{B C} = [\begin{matrix} r_{3} \sin (ϕ_{3}) \cos (θ_{3}) \\ r_{3} \sin (ϕ_{3}) \sin (θ_{3}) \\ r_{3} \cos (ϕ_{3}) \end{matrix}]

The following equality can be derived by considering Figure 3 and using the vector loop method:

\overset{⃑}{A B} + \overset{⃑}{B C} + \overset{⃑}{C D} + \overset{⃑}{D A} = \overset{⃑}{0},

(9)

Expressing this vector equality in terms of the

X_{1} Y_{1} Z_{1}

coordinate system results in the following relations:

r_{2 x} + r_{3} s i n ϕ_{3} c o s θ_{3} - r_{4} c o s θ_{4} = 0,

(10)

{r_{2 y} + r}_{3} s i n ϕ_{3} s i n θ_{3} - r_{4} s i n θ_{4} = 0,

(11)

r_{2 z} + r_{3} c o s ϕ_{3} = 0,

(12)

The solution of Equation (12) is given as follows:

ϕ_{3} = {c o s}^{- 1} (r_{2 z}),

(13)

Squaring Equations (10) and (11) and adding them results in the following relation without

θ_{3}

A \cos θ_{4} + B \sin θ_{4} + C = 0,

(14)

where

A = 2 r_{4} r_{2 x}, B = 2 r_{4} r_{2 y},

and

C = {r_{3}}^{2} {s i n ϕ_{3}}^{2} - {r_{2 x}}^{2} - {r_{4}}^{2} - {r_{2 y}}^{2}

Let

\tan \frac{θ_{4}}{2} = β

The half-angle formula for tangent can be used to express Equation (14) in the following form:

(C - A) β^{2} + 2 B β + (C + A) = 0,

(15)

The following expression is obtained by solving Equation (15) for

β

β = \frac{- B \pm \sqrt{B^{2} - (C^{2} - A^{2})}}{(C - A)}

Thus, the following equation is obtained:

θ_{4} = 2 \cdot \arctan (\frac{- B \pm \sqrt{B^{2} - (C^{2} - A^{2})}}{(C - A)}),

(16)

In Equation (16),

θ_{4}

has two solutions representing the motion of the linkage above or below the

x_{1}

-axis. The following solution is obtained for

θ_{4}

when the positive square root is considered:

θ_{4} = 2 \cdot \arctan (\frac{- B + \sqrt{B^{2} - (C^{2} - A^{2})}}{(C - A)}),

(17)

The following expression is obtained by substituting Equation (17) into Equations (10) and (11):

θ_{3} = \arctan (\frac{- r_{2 y} + r_{4} s i n θ_{4}}{- r_{2 x} + r_{4} c o s θ_{4}}),

(18)

The angular velocity

ω_{2}

(the derivative of

θ_{2}

with respect to time) of Link AB is fixed at 1 rad/s. The time derivatives of

ϕ_{3}

(

ϕ_{3}

'),

θ_{3}

(

ω_{3}

), and

θ_{4}

(

ω_{4}

), which is the angular velocity of Link DC) for Link DC are obtained by differentiating Equations (10)–(12) with respect to time (t).

ϕ_{3}' = \frac{r_{2 z}^{'}}{r_{3} \sin (ϕ_{3})},

(19)

w_{3} = \frac{{(r}_{2 x}^{'} \cos (θ_{4}) + r_{2 y}^{'} \sin (θ_{4})}{r_{3} \sin (ϕ_{3}) \sin (θ_{4} - θ_{3})} + \frac{r_{3} c o s (ϕ_{3}) c o s (θ_{3} - θ_{4}) ϕ_{3}')}{r_{3} s i n (ϕ_{3}) s i n (θ_{4} - θ_{3})},

(20)

w_{4} = \frac{- r_{2 x}^{'} \cos (θ_{3}) - r_{2 y}^{'} \sin (θ_{3}) - r_{3} \cos (ϕ_{3}) ϕ_{3}^{'}}{r_{4} s i n (θ_{4} - θ_{3})},

(21)

The angular velocity of Link AB is fixed at 1 rad/s; therefore, the angular acceleration

α_{2}

of this link is 0. Equations (10)–(12) are differentiated twice with respect to time (t) to obtain

{ϕ_{3}}^{″}

from

{ϕ_{3}}^{'}

α_{3}

from

ω_{3}

, and

α_{4}

from

ω_{4}

for Link DC;

ω_{4}

is the angular acceleration of Link DC.

ϕ_{3}^{″} = \frac{{r_{2 z}}^{″} - r_{3} \cos ϕ_{3} {ϕ_{3}}^{2}}{r_{3} \sin (ϕ_{3})},

(22)

α_{3} = \frac{r_{2 x}^{″} \cos (θ_{4}) + r_{2 y}^{″} \sin (θ_{4})}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})} - \frac{r_{3} \sin (ϕ_{3}) {ϕ_{3}'}^{2} \cos (θ_{4} - θ_{3})}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})} + \frac{r_{3} \cos (ϕ_{3}) ϕ_{3}^{″} \cos (θ_{4} - θ_{3})}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})} - \frac{r_{3} \sin (ϕ_{3}) \cos (θ_{4} - θ_{3}) {w_{3}}^{2}}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})} - \frac{2 r_{3} \cos (ϕ_{3}) ϕ_{3}^{'} w_{3} \sin (θ_{3} - θ_{4})}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})} + \frac{r_{4} {w_{4}}^{2}}{r_{3} \sin (ϕ_{3}) \sin (θ_{3} - θ_{4})},

(23)

and

α_{4} = \frac{r_{2 x}^{″} \cos (θ_{3}) + r_{2 y}^{″} \sin (θ_{3})}{r_{4} \sin (θ_{3} - θ_{4})} + \frac{r_{3} \cos (ϕ_{3}) ϕ_{3}^{″}}{r_{4} \sin (θ_{3} - θ_{4})} - \frac{(r_{3} \sin (ϕ_{3}) {ϕ_{3}'}^{2} + r_{3} \sin (ϕ_{3}) {w_{3}}^{2})}{r_{4} \sin (θ_{3} - θ_{4})} + \frac{r_{4} {w_{4}}^{2} \cos (θ_{4} - θ_{3})}{r_{4} s i n (θ_{3} - θ_{4})},

(24)

The transmission angle

μ_{4}

for the driver side of the CDLS can be expressed as follows by using the dot product of vectors CD and CB:

μ_{4} = \arccos (\frac{\overset{\cdot}{C D} \cdot \overset{⃑}{C B}}{r_{3} r_{4}}),

(25)

2.1.4. Motion of the Passenger-Side Linkage of the CDLS

Assume that the unit vector of the main output shaft's axis

Z_{2}

is (

c o s (θ_{01}) s i n (ϕ_{01}), s i n (θ_{01}) s i n (ϕ_{01}), c o s (ϕ_{01})

). An

X_{2} Y_{2} Z_{2}

coordinate system is established on the auxiliary output shaft, where the

Z_{2}

- axis is aligned with the auxiliary output shaft’s axis of rotation. The matrix relationship between the

X Y Z

and

X_{2} Y_{2} Z_{2}

coordinate systems is as follows:

{\overset{⃑}{r}}_{X_{2} Y_{2} Z_{2}} = [\begin{matrix} s i n θ_{01} & - c o s θ_{01} & 0 \\ c o s θ_{01} c o s ϕ_{01} & s i n θ_{01} c o s ϕ_{01} & - s i n ϕ_{01} \\ s i n ϕ_{01} c o s θ_{01} & s i n ϕ_{01} s i n θ_{01} & c o s ϕ_{01} \end{matrix}] {\overset{⃑}{r}}_{X Y Z},

(26)

Let R_{1} = [\begin{matrix} s i n θ_{01} & - c o s θ_{01} & 0 \\ c o s θ_{01} c o s ϕ_{01} & s i n θ_{01} c o s ϕ_{01} & - s i n ϕ_{01} \\ s i n ϕ_{01} c o s θ_{01} & s i n ϕ_{01} s i n θ_{01} & c o s ϕ_{01} \end{matrix}],

(27)

Assume that vectors

\overset{⃑}{A B}

and

\overset{⃑}{A E}

are defined as follows in the

X Y Z

coordinate system:

\overset{⃑}{A B} = [\begin{matrix} r_{2} \cos (θ_{2}) \\ r_{2} \sin (θ_{2}) \\ 0 \end{matrix}], \overset{⃑}{A E} = [\begin{matrix} r_{11} \sin (ϕ_{11}) \cos (θ_{11}) \\ r_{11} \sin (ϕ_{11}) \sin (θ_{11}) \\ r_{11} \cos (ϕ_{11}) \end{matrix}]

The vector

\overset{⃑}{A B} - \overset{⃑}{A E}

can be expressed in

X_{2} Y_{2} Z_{2}

[\begin{matrix} r_{21 x} \\ r_{21 y} \\ r_{21 z} \end{matrix}] = R_{1} [\begin{matrix} r_{2} \cos θ_{2} \\ r_{2} \sin θ_{2} \\ 0 \end{matrix}] - R_{1} [\begin{matrix} r_{11} \sin ϕ_{11} \cos θ_{11} \\ r_{11} \sin ϕ_{11} \sin θ_{11} \\ r_{11} \cos ϕ_{11} \end{matrix}],

(28)

Similarly, assume that vectors

\overset{⃑}{E F}

and

\overset{⃑}{B F}

are defined as follows in the

X_{2} Y_{2} Z_{2}

coordinate system:

\overset{⃑}{E F} = [\begin{matrix} r_{6} \cos (θ_{6}) \\ r_{6} \sin (θ_{6}) \\ 0 \end{matrix}], \overset{⃑}{B F} = [\begin{matrix} r_{5} \sin (ϕ_{5}) \cos (θ_{5}) \\ r_{5} \sin (ϕ_{5}) \sin (θ_{5}) \\ r_{5} \cos (ϕ_{5}) \end{matrix}]

Similar mathematical formulas are valid for the motion of the passenger-side linkage of the CDLS. In this case,

θ_{2}

is the input variable of the input link AB, and

θ_{6}

is the unknown output of the output link EF. The following expressions are obtained by using the vector loop method and the half-angle formula for tangent:

ϕ_{5} = a r c c o s (r_{21 z}),

(29)

θ_{6} = 2 \cdot \arctan (\frac{- E \pm \sqrt{E^{2} - (F^{2} - D^{2})}}{(F - D)}),

(30)

θ_{5} = \tan^{- 1} (\frac{- r_{21 y} + r_{6} s i n θ_{6}}{- r_{21 x} + r_{6} c o s θ_{6}}),

(31)

with

D = 2 r_{6} r_{21 x}, E = 2 r_{6} r_{21 y},

and

F = {r_{5}}^{2} {s i n ϕ_{5}}^{2} - {r_{21 x}}^{2} - {r_{6}}^{2} - {r_{21 y}}^{2}

The solution adopted for

θ_{6}

is expressed as follows:

θ_{6} = 2 \cdot \arctan (\frac{- E + \sqrt{E^{2} - (F^{2} - D^{2})}}{(F - D)}),

(32)

The time derivatives of

ϕ_{5}

(

{ϕ_{5}}^{'}

θ_{5}

(

ω_{5}

)_, and

θ_{6}

(

ω_{6}

), which is the angular velocity of Link EF) for Link EF are obtained as follows by using the method introduced in Section 2.1.3:

{ϕ_{5}}^{'} = \frac{r_{21 z}^{'}}{r_{5} \sin (ϕ_{5})},

(33)

ω_{5} = \frac{r_{21 x}^{'} \cos (θ_{6}) + r_{21 y}^{'} \sin (θ_{6})}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} + \frac{r_{5} \cos (ϕ_{5}) \cos (θ_{5} - θ_{6}) ϕ_{5}'}{(r_{5} s i n (ϕ_{5}) s i n (θ_{5} - θ_{6}))},

(34)

and

ω_{6} = \frac{- r_{21 x}^{'} \cos (θ_{5}) - r_{21 y}^{'} \sin (θ_{5}) - r_{5} \cos (ϕ_{5}) ϕ_{5}^{'}}{(r_{6} s i n (θ_{6} - θ_{5}))},

(35)

Similarly, the time derivatives of

{ϕ_{5}}^{'}

(

{ϕ_{5}}^{'}'

ω_{5}

(

α_{5}

), and

ω_{6}

(

α_{6}

), which is the angular acceleration of Link EF) for Link EF are expressed as follows:

ϕ_{5}^{″} = \frac{{r_{21 z}}^{″} - r_{5} \cos ϕ_{5} {ϕ_{5}}^{2}}{r_{5} \sin (ϕ_{5})},

(36)

α_{5} = \frac{- r_{21 x}^{″} \cos (θ_{6}) - r_{21 y}^{″} \sin (θ_{6})}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} + \frac{r_{5} \sin (ϕ_{5}) {ϕ_{5}'}^{2} \cos (θ_{5} - θ_{6})}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} - \frac{2 r_{5} \cos (ϕ_{5}) ϕ_{5}^{'} w_{5} \sin (θ_{6} - θ_{5})}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} - \frac{r_{5} \cos (ϕ_{5}) ϕ_{5}^{″} \cos (θ_{5} - θ_{6})}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} + \frac{r_{5} \sin (ϕ_{5}) \cos (θ_{5} - θ_{6}) {w_{5}}^{2}}{(r_{5} \sin (ϕ_{5}) \sin (θ_{5} - θ_{6}))} - \frac{r_{6} {w_{6}}^{2}}{(r_{5} s i n (ϕ_{5}) s i n (θ_{5} - θ_{6}))},

(37)

α_{6} = \frac{r_{21 x}^{″} \cos (θ_{5}) + r_{21 y}^{″} \sin (θ_{5})}{r_{6} \sin (θ_{5} - θ_{6})} - \frac{r_{5} \sin (ϕ_{5}) {ϕ_{5}'}^{2}}{r_{6} \sin (θ_{5} - θ_{6})} + \frac{r_{5} \cos (ϕ_{5}) ϕ_{5}^{″} - r_{5} \sin (ϕ_{5}) {w_{5}}^{2}}{r_{6} \sin (θ_{5} - θ_{6})} + \frac{r_{6} {w_{6}}^{2} \cos (θ_{5} - θ_{6})}{r_{6} \sin (θ_{5} - θ_{6})},

(38)

The transmission angle

μ_{6}

on the passenger side of the CDLS can then be expressed as follows:

μ_{6} = \cos^{- 1} (\frac{\overset{⃑}{F E} \cdot \overset{⃑}{F B}}{r_{5} {\times r}_{6}}),

(39)

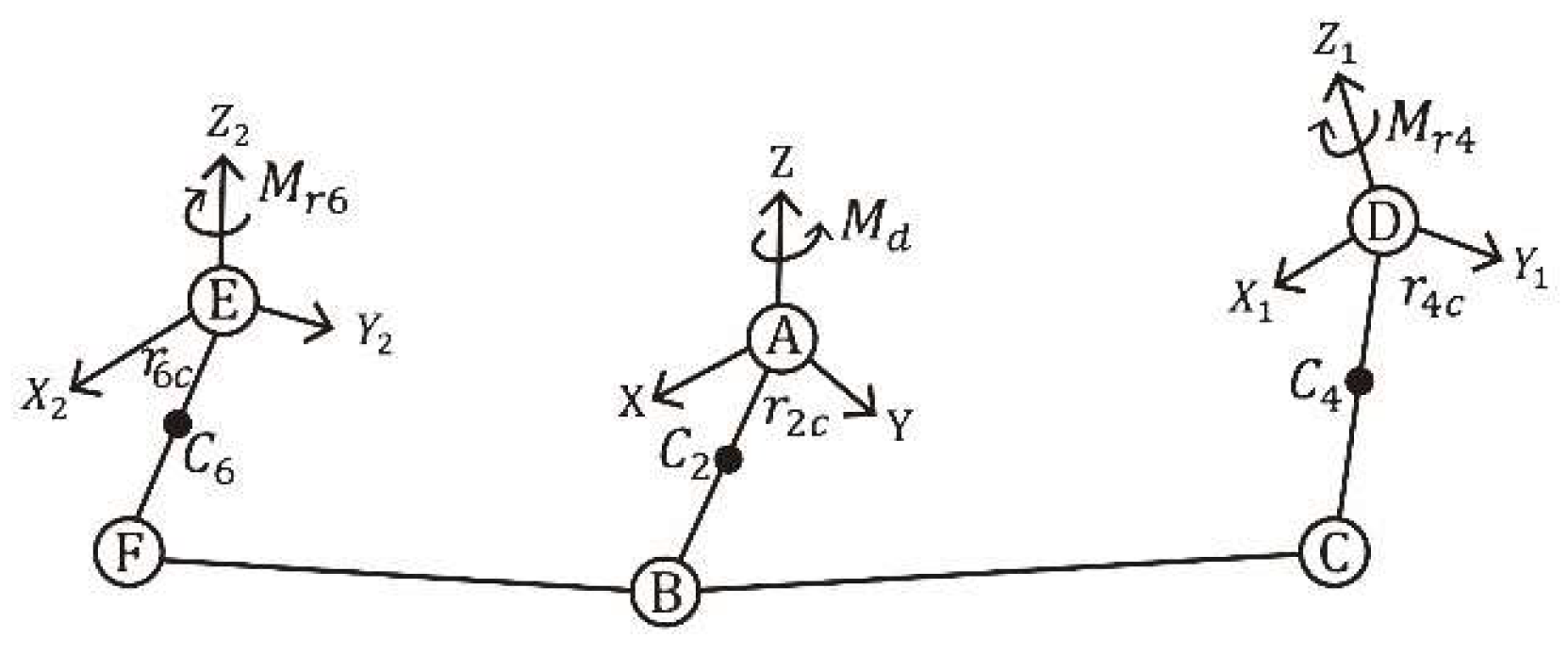
2.2. Dynamic Analysis of the Linkage System

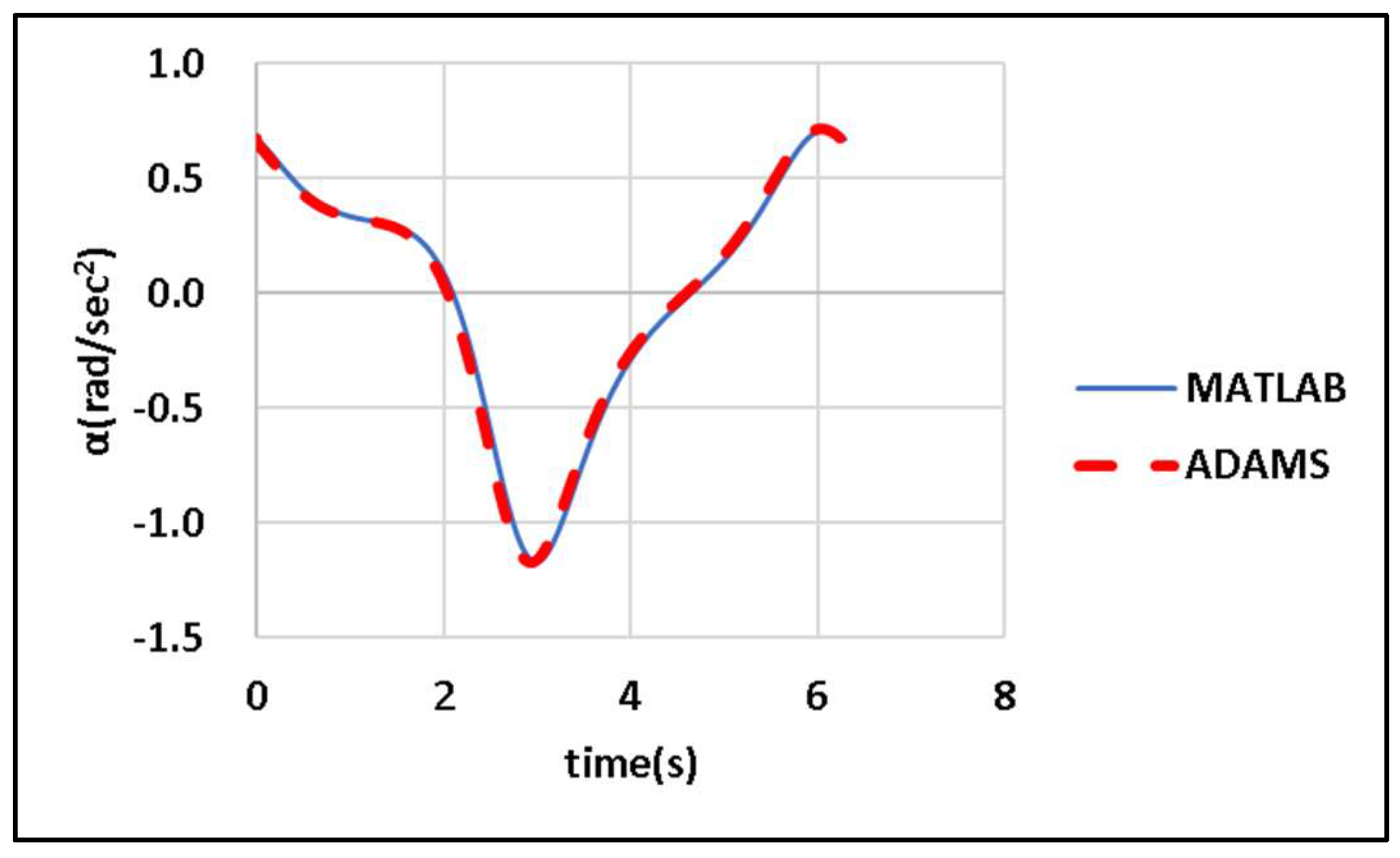
In Figure 10,

M_{d}

represents the driving torque in the

Z

direction at point A. The terms

M_{r 4}

and

M_{r 6}

represent external torques at point D in the

Z_{1}

direction and at point E in the

Z_{2}

direction respectively; both have known magnitudes. The driving torque required for Link AB to maintain a constant angular velocity is calculated. The joint forces, bearing forces, and driving torque in the CDLS are derived using Newton–Euler equations of motion. To simplify the dynamic analysis model, the following three assumptions are made:

Friction at the joints can be neglected.
All links are rigid bodies.
The effects of gravity are negligible.
All links in the mechanism are homogeneous.

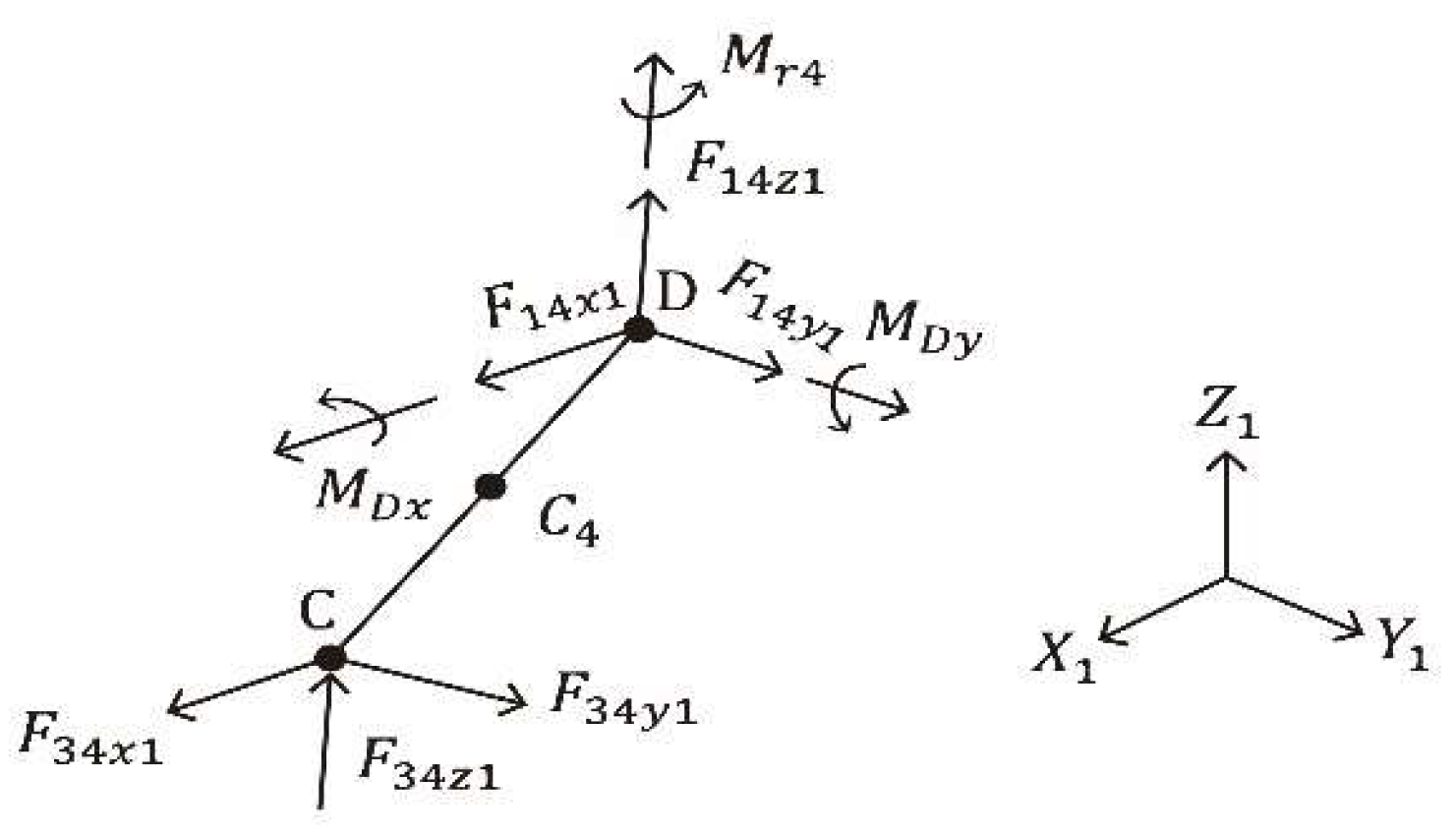
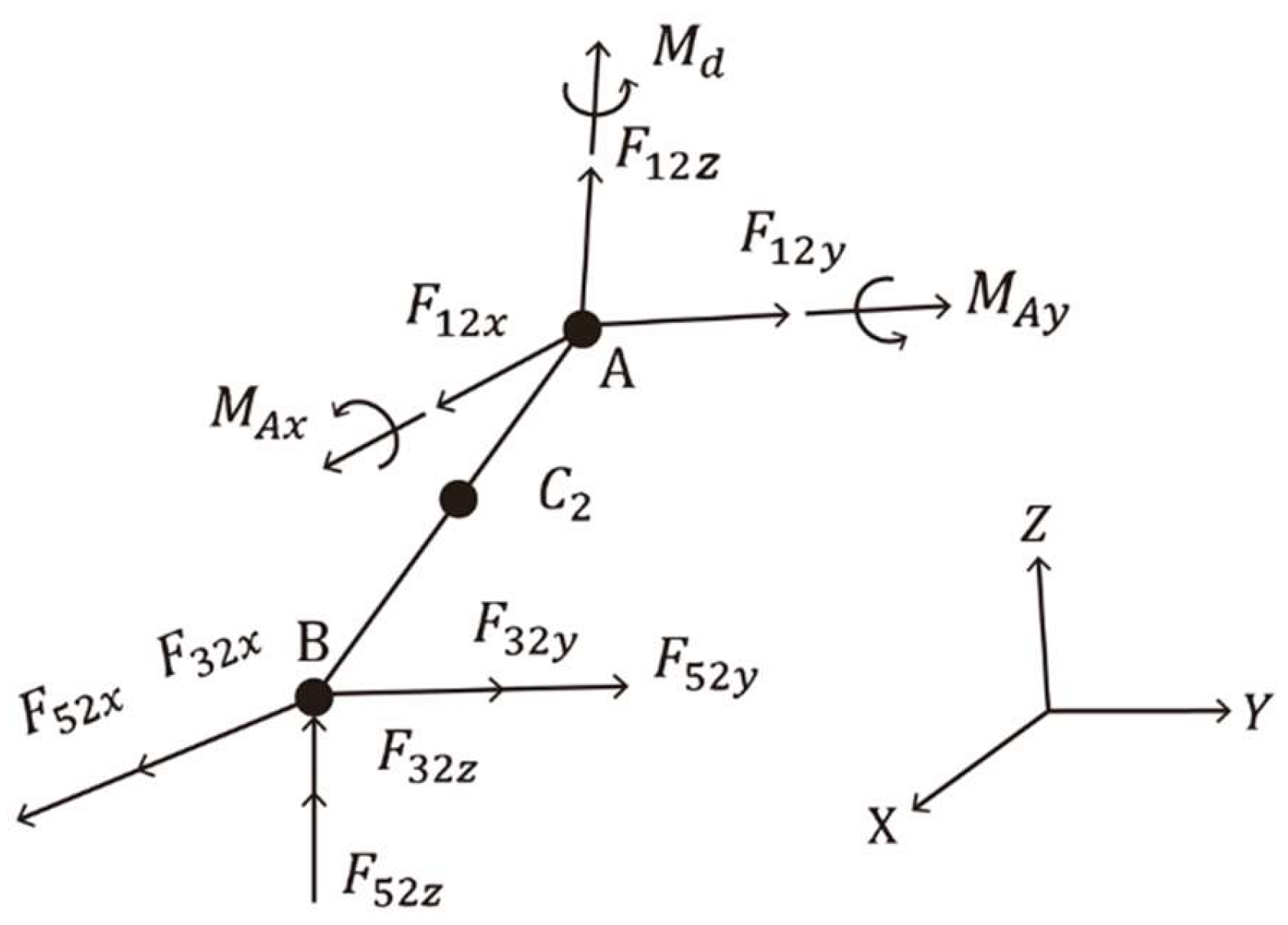
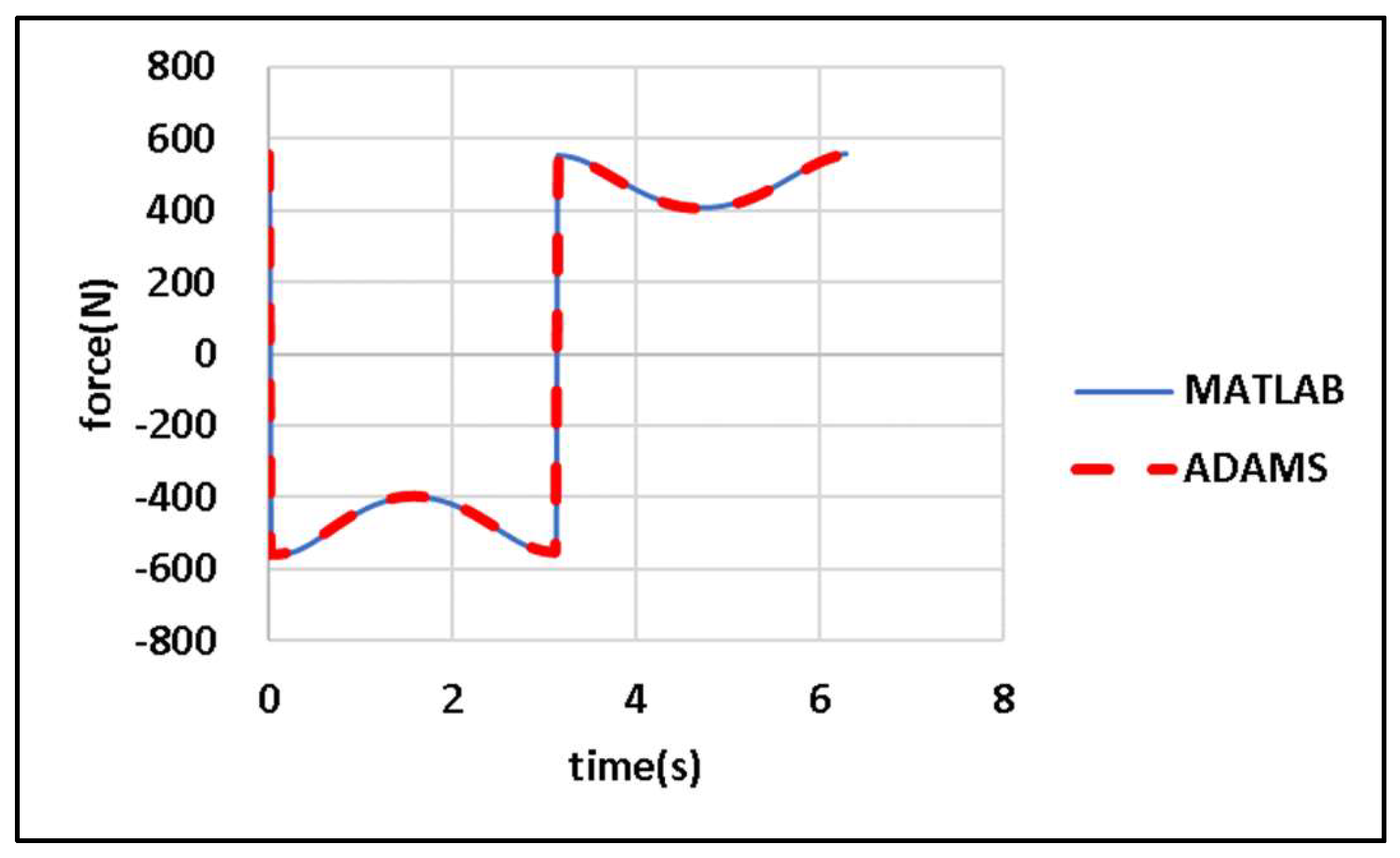
In Figure 11,

F_{14 x 1}

F_{14 y 1}

, and

F_{14 z 1}

represent the reaction forces in the

X_{1}

Y_{1}

, and

Z_{1}

directions, respectively, at bearing D. The terms

F_{34 x 1}

F_{34 y 1}

, and

F_{34 z 1}

represent the components of the joint force exerted by Link BC on Link AB in the

X_{1}

Y_{1}

, and

Z_{1}

directions. The masses of Links AB, BC, and CD are denoted by

m_{2}

m_{3}

, and

m_{4}

, respectively, and

a_{4 c x}

a_{4 c y}

, and

a_{4 c z}

are the acceleration components of the center of mass

C_{4}

of Link CD in each direction. The term

I_{4}

represents the mass moment of inertia of Link CD relative to its center of mass, and

M_{D x}

and

M_{D y}

are the reaction moments in the

X_{1}

and

Y_{1}

directions, respectively, at bearing D. The position vector of the center of mass

C_{4}

of Link CD is denoted by

\overset{⃑}{D C_{4}}

and expressed as follows:

\overset{⃑}{D C_{4}} = (r_{4 c} \cos θ_{4}, r_{4 c} \sin θ_{4}, 0),

(40)

where

\overset{⃑}{a_{4}}

is the acceleration of the center of mass

C_{4}

of Link CD in the

X_{1} Y_{1} Z_{1}

coordinate system.

\overset{⃑}{a_{4 c}} = (a_{4 c x}, a_{4 c y}, a_{4 c z}),

(41)

Differentiating each component of vector

\overset{⃑}{D C_{4}}

with respect to t twice yields the following expressions:

a_{4 c x} = - r_{4 c} {ω_{4}}^{2} \cos θ_{4} - r_{4 c} α_{4} \sin θ_{4} a_{4 c y} = - r_{4 c} {ω_{4}}^{2} \sin θ_{4} + r_{4 c} α_{4} \cos θ_{4} a_{4 c z} = 0

Suppose that the force vector

\overset{⃑}{F_{34}}

is scaled by a factor of

K

in the direction of the unit vector of BC; that is,

(F_{34 x 1}, F_{34 y 1}, F_{34 z 1}) = K_{1} (s i n ϕ_{3} c o s θ_{3}, s i n ϕ_{3} \sin θ_{3}, c o s ϕ_{3})

The force balance equations and torque equations are as follows :

F_{14 x 1} + F_{34 x 1} = m_{4} a_{4 c x},

(42)

F_{14 y 1} + F_{34 y 1} = m_{4} a_{4 c y},

(43)

F_{14 z 1} + F_{34 z 1} = m_{4} a_{4 c z},

(44)

- F_{14 z 1} r_{4 c} \sin (θ_{4}) + F_{34 z 1} (r_{4} - r_{4 c}) \sin (θ_{4}) + M_{D x} = 0,

(45)

F_{14 z 1} r_{4 c} \cos (θ_{4}) - F_{34 z 1} (r_{4} - r_{4 c}) \cos (θ_{4}) + M_{D y} = 0,

(46)

F_{14 x 1} r_{4 c} \sin (θ_{4}) - F_{14 y 1} r_{4 c} \cos (θ_{4}) - F_{34 x 1} (r_{4} - r_{4 c}) \sin (θ_{4}) + F_{34 y 1} (r_{4} - r_{4 c}) \cos (θ_{4}) = I_{4} α_{4} - M_{r 4},

(47)

Using the Equation (41), (42), (43), (44 ), (45) and (46) we may obtain

K_{1}, F_{14 x 1}

F_{14 y 1}

F_{14 z 1}

, F_{34 x 1}, F_{34 y 1}, F_{34 z 1}, M_{D x},

and

M_{D y}

as follow:

[\begin{matrix} K_{1} \\ F_{14 x 1} \\ F_{14 y 1} \\ F_{14 z 1} \\ \begin{matrix} F_{34 x 1} \\ \begin{matrix} F_{34 y 1} \\ \begin{matrix} F_{34 z 1} \\ \begin{matrix} M_{D x} \\ M_{D y} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix}] = {[\begin{matrix} G_{1} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ G_{2} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ G_{3} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & G_{4} & 0 & 0 & G_{5} & 1 & 0 \\ 0 & 0 & 0 & G_{6} & 0 & 0 & G_{7} & 0 & 1 \\ 0 & G_{8} & G_{9} & 0 & G_{10} & G_{11} & 0 & 0 & 0 \end{matrix}]}^{- 1} [\begin{matrix} 0 \\ 0 \\ 0 \\ m_{4} a_{4 c x} \\ \begin{matrix} m_{4} a_{4 c y} \\ m_{4} a_{4 c z} \\ \begin{matrix} 0 \\ 0 \\ I_{4} α_{4} - M_{r_{4}} \end{matrix} \end{matrix} \end{matrix}],

(48)

in which

G_{1} = - s i n ϕ_{3} c o s θ_{3}, G_{2} = - s i n ϕ_{3} s i n θ_{3}, G_{3} = - c o s ϕ_{3}, G_{4} = - r_{4 c} s i n θ_{4},

G_{5} = (r_{4} - r_{4 c}) s i n θ_{4}, G_{6} = r_{4 c} c o s θ_{4}, G_{7} = - (r_{4} - r_{4 c}) c o s θ_{4}

and

G_{8} = r_{4 c} s i n θ_{4}

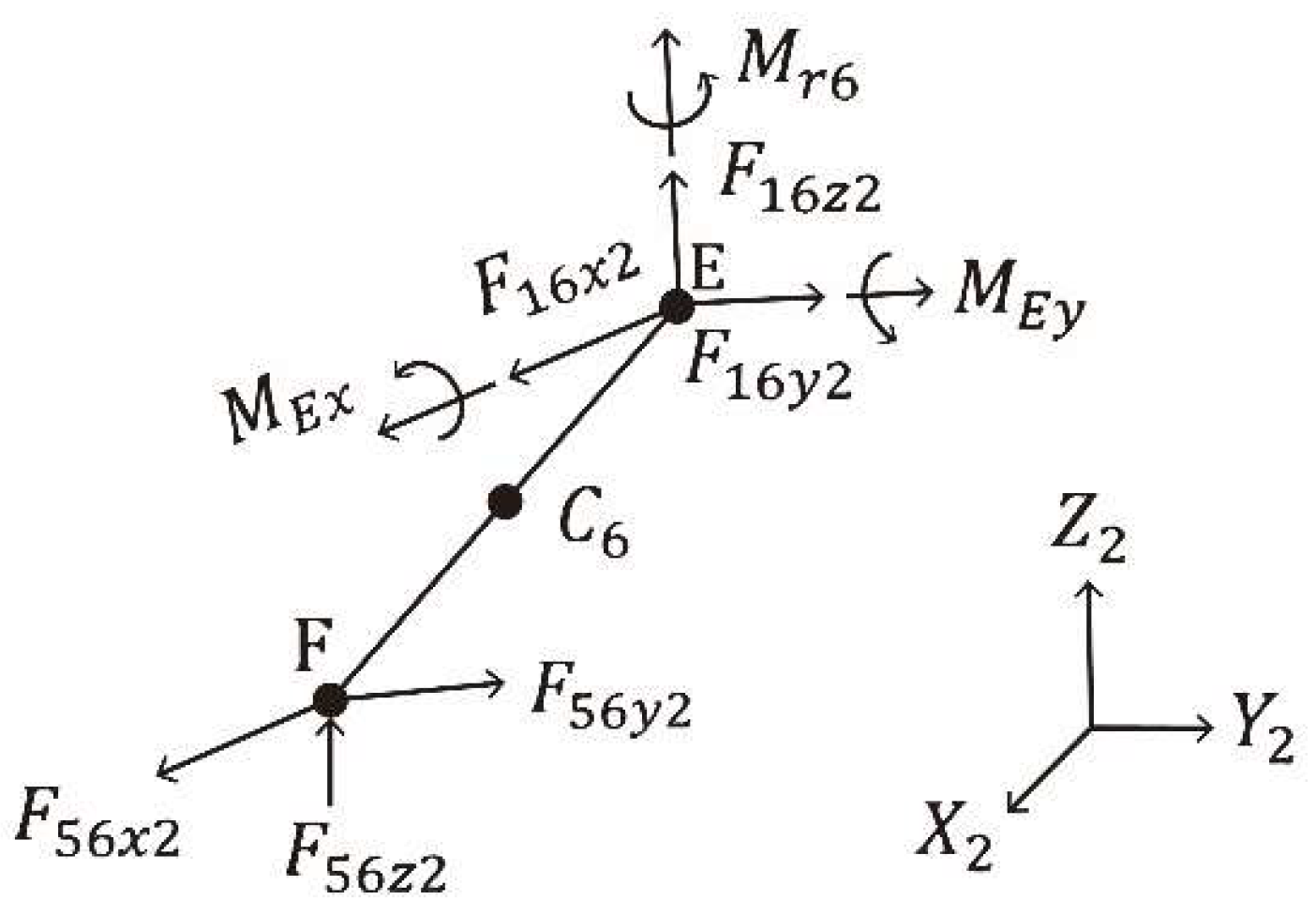
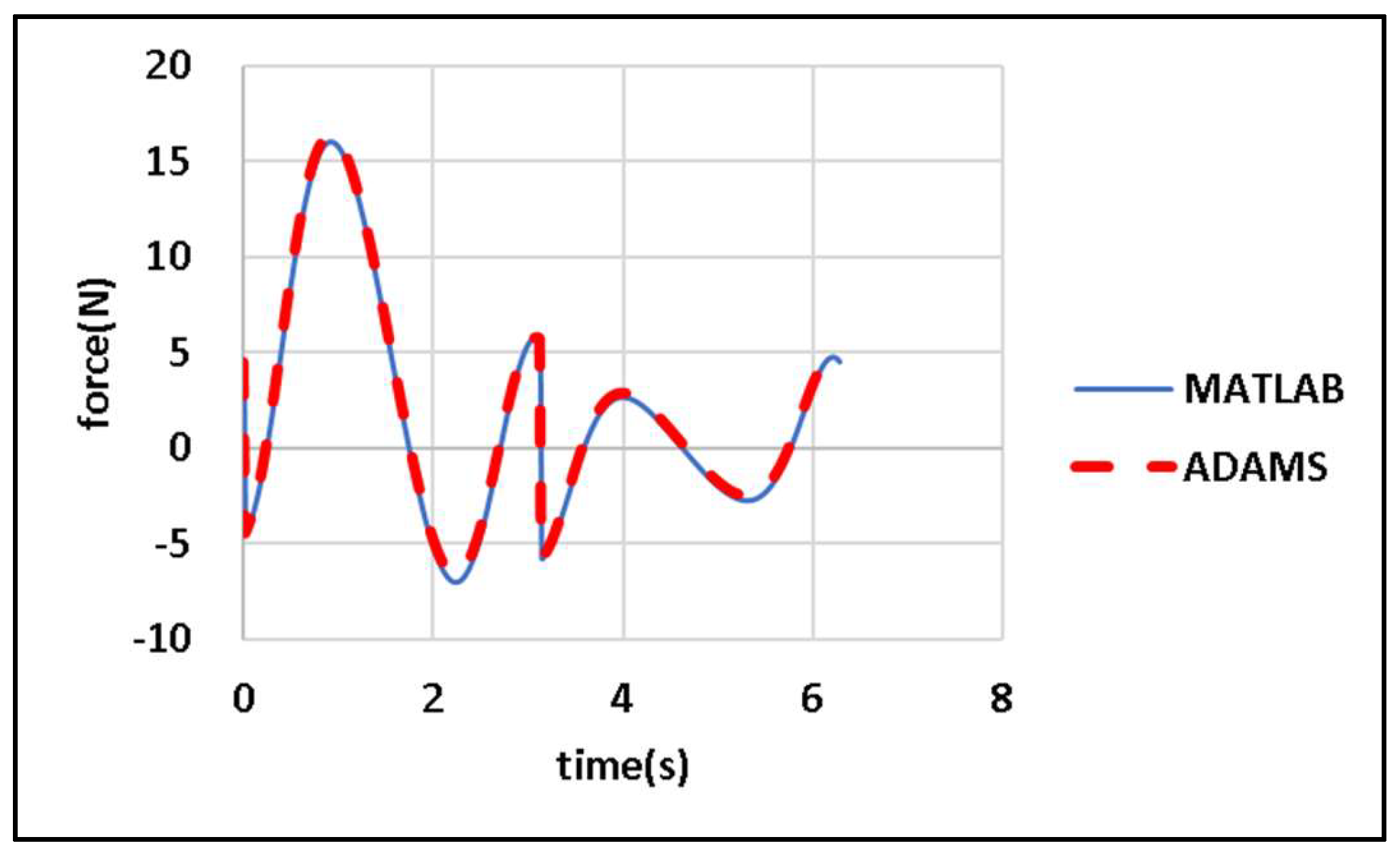
In Figure 12,

F_{16 x 2}

F_{16 y 2}

, and

F_{16 z 2}

represent the reaction forces in the

X_{2}

Y_{2}

, and

Z_{2}

directions, respectively, at bearing E. Moreover,

F_{56 x 2}

F_{56 y 2}

, and

F_{56 z 2}

are the components of the joint force exerted by Link BF on Link EF in the

X_{2}

Y_{2}

, and

Z_{2}

directions, respectively. The terms

a_{6 c x}

, a_6cy, and a_6cz represent the acceleration components of the center of mass

C_{6}

of Link EF in the

X_{2}

Y_{2}

, and

Z_{2}

directions, respectively. The term I₆ denotes the mass moment of inertia of Link EF relative to its center of mass;

M_{E x}

and

M_{E y}

are the reaction moments in the

X_{2}

and

Y_{2}

directions, respectively, at bearing E; and m₅ and m₆ represent the masses of Links BF and EF, respectively.

The following matrix can be obtained in the

X_{2} Y_{2} Z_{2}

coordinate system by using the same method as that used for Figure 11:

[\begin{matrix} K_{2} \\ F_{16 x 2} \\ F_{16 y 2} \\ F_{16 z 2} \\ \begin{matrix} F_{56 x 2} \\ \begin{matrix} F_{56 y 2} \\ \begin{matrix} F_{56 z 2} \\ \begin{matrix} M_{E x} \\ M_{E y} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix}] = {[\begin{matrix} H_{1} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ H_{2} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ H_{3} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & H_{4} & 0 & 0 & H_{5} & 1 & 0 \\ 0 & 0 & 0 & H_{6} & 0 & 0 & H_{7} & 0 & 1 \\ 0 & H_{8} & H_{9} & 0 & H_{10} & H_{11} & 0 & 0 & 0 \end{matrix}]}^{- 1} [\begin{matrix} 0 \\ 0 \\ 0 \\ m_{6} a_{6 c x} \\ \begin{matrix} m_{6} a_{6 c y} \\ m_{6} a_{6 c z} \\ \begin{matrix} 0 \\ 0 \\ I_{6} α_{6} - M_{r_{6}} \end{matrix} \end{matrix} \end{matrix}],

(49)

in which

H_{1} = - s i n ϕ_{5} c o s θ_{5}, H_{2} = - s i n ϕ_{5} s i n θ_{5}, H_{3} = - c o s ϕ_{5}, H_{4} = - r_{6 c} s i n θ_{6},

H_{5} = (r_{6} - r_{6 c}) s i n θ_{6}, H_{6} = r_{6 c} c o s θ_{6}, H_{7} = - (r_{6} - r_{6 c}) c o s θ_{6}, H_{8} = r_{6 c} s i n θ_{6}, H_{9} = - r_{6 c} c o s θ_{6}

Let [\begin{matrix} F_{32 x} \\ F_{32 y} \\ F_{32 z} \end{matrix}] = R^{- 1} [\begin{matrix} F_{32 x 1} \\ F_{32 y 1} \\ F_{32 z 1} \end{matrix}] and [\begin{matrix} F_{52 x} \\ F_{52 y} \\ F_{52 z} \end{matrix}] = {R_{1}}^{- 1} [\begin{matrix} F_{52 x 2} \\ F_{52 y 2} \\ F_{52 z 2} \end{matrix}]

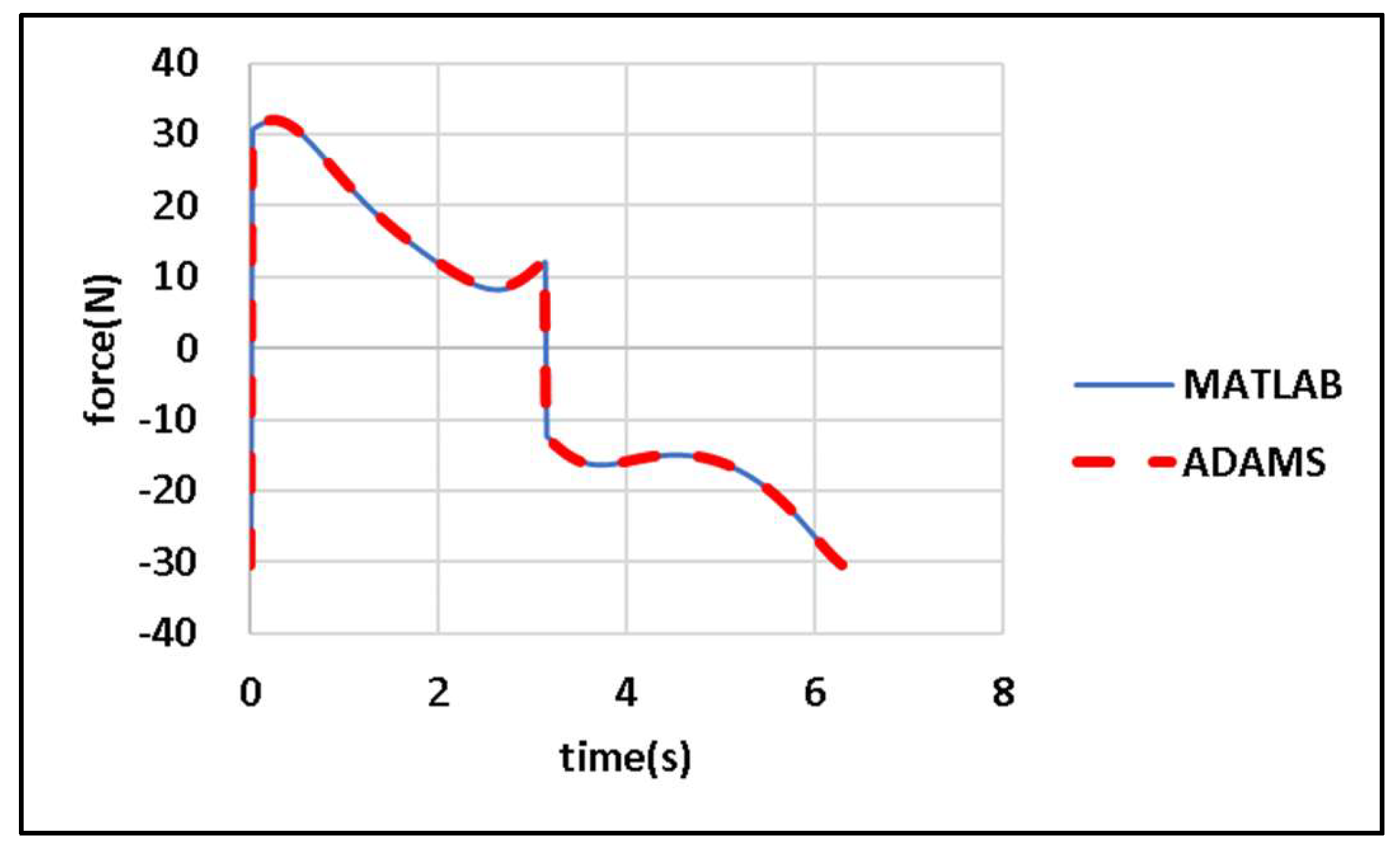
In Figure 13,

F_{12 x}

F_{12 y}

, and

F_{12 z}

represent the reaction forces in the

X

Y

, and

Z

directions, respectively, at bearing A. The acceleration components of the center of mass

C_{2}

of Link AB in the

X

Y

, and

Z

directions are

a_{2 c x}

a_{2 c y}

, and

a_{2 c z}

, respectively. The term

I_{2}

represents the mass moment of inertia of Link AB relative to its center of mass. Moreover,

M_{A x}

and

M_{A y}

are the reaction moments in the

X

and

Y

directions, respectively, at bearing A. The following matrix is obtained in the

X Y Z

coordinate system by using the same method as that used for Figure 11:

[\begin{matrix} F_{12 x} \\ F_{12 y} \\ F_{12 z} \\ M_{A x} \\ M_{A y} \\ M_{d} \end{matrix}] = {[\begin{matrix} 0 & 0 & J_{1} & 1 & 0 & 0 \\ 0 & 0 & J_{2} & 0 & 1 & 0 \\ J_{3} & J_{4} & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}]}^{- 1} [\begin{matrix} - (F_{32 z} + F_{52 z}) (r_{2} - r_{2 c}) s i n θ_{2} \\ (F_{32 z} + F_{52 z}) (r_{2} - r_{2 c}) c o s θ_{2} \\ I_{2} α_{2} + (F_{32 x} + F_{52 x}) (r_{2} - r_{2 c}) s i n θ_{2} - (F_{34 y} + F_{52 y}) (r_{2} - r_{2 c}) c o s θ_{2} \\ m_{2} a_{2 c x} - (F_{32 x} + F_{52 x}) \\ m_{2} a_{2 c y} - (F_{32 y} + F_{52 y}) \\ m_{2} a_{2 c z} - (F_{32 z} + F_{52 z}) \end{matrix}]

(50)

in which

J_{1} = - r_{2 c} s i n θ_{2}, J_{2} = r_{2 c} c o s θ_{2}, J_{3} = r_{2 c} s i n θ_{2},

and

J_{4} = - r_{2 c} c o s θ_{2} .

2.3. Optimization of the Angular Acceleration of the Output Links of the CDLS

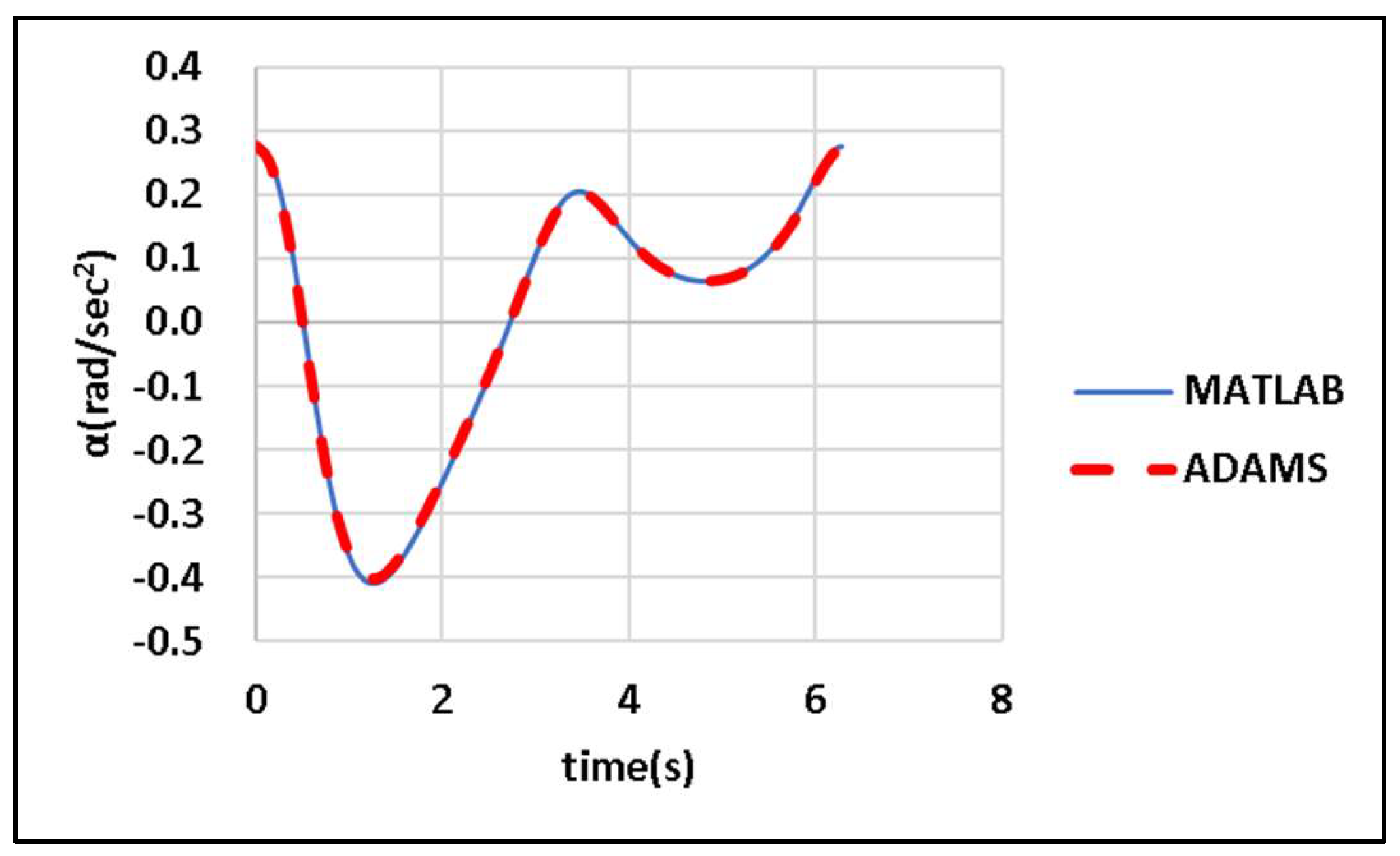
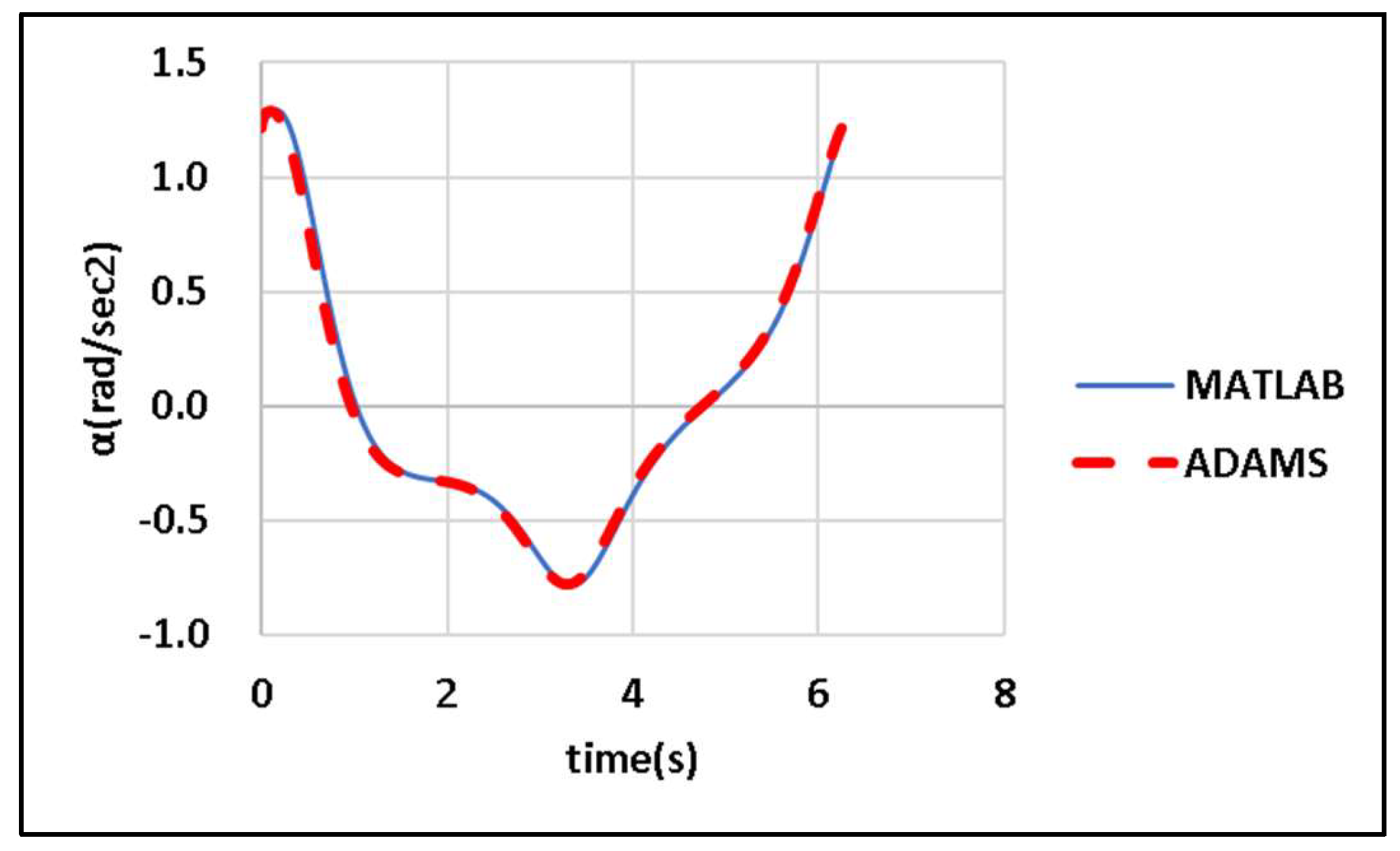
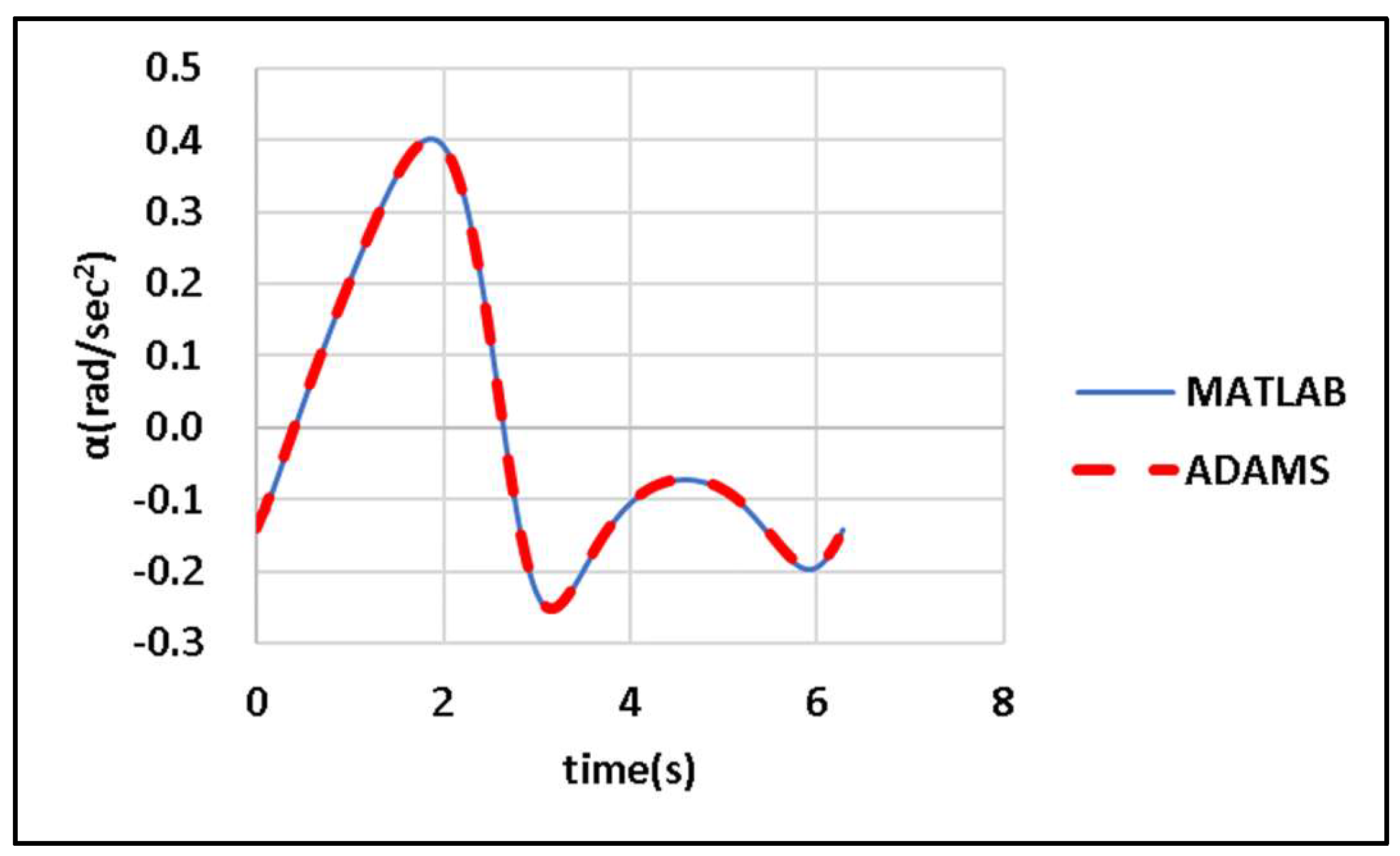
DE is applied to maximize the angular acceleration of the output links of the designed CDLS for windshield wipers. The objective function f is as shown in equation (1).

A detailed explanation of the model is presented in Section 2.1. The input link AB of the designed CDLS is assumed to rotate at a constant angular velocity

ω_{2}

= 1 rad/s, as illustrated in Figure 4. Relevant items are recorded or calculated at an interval of

π / 180

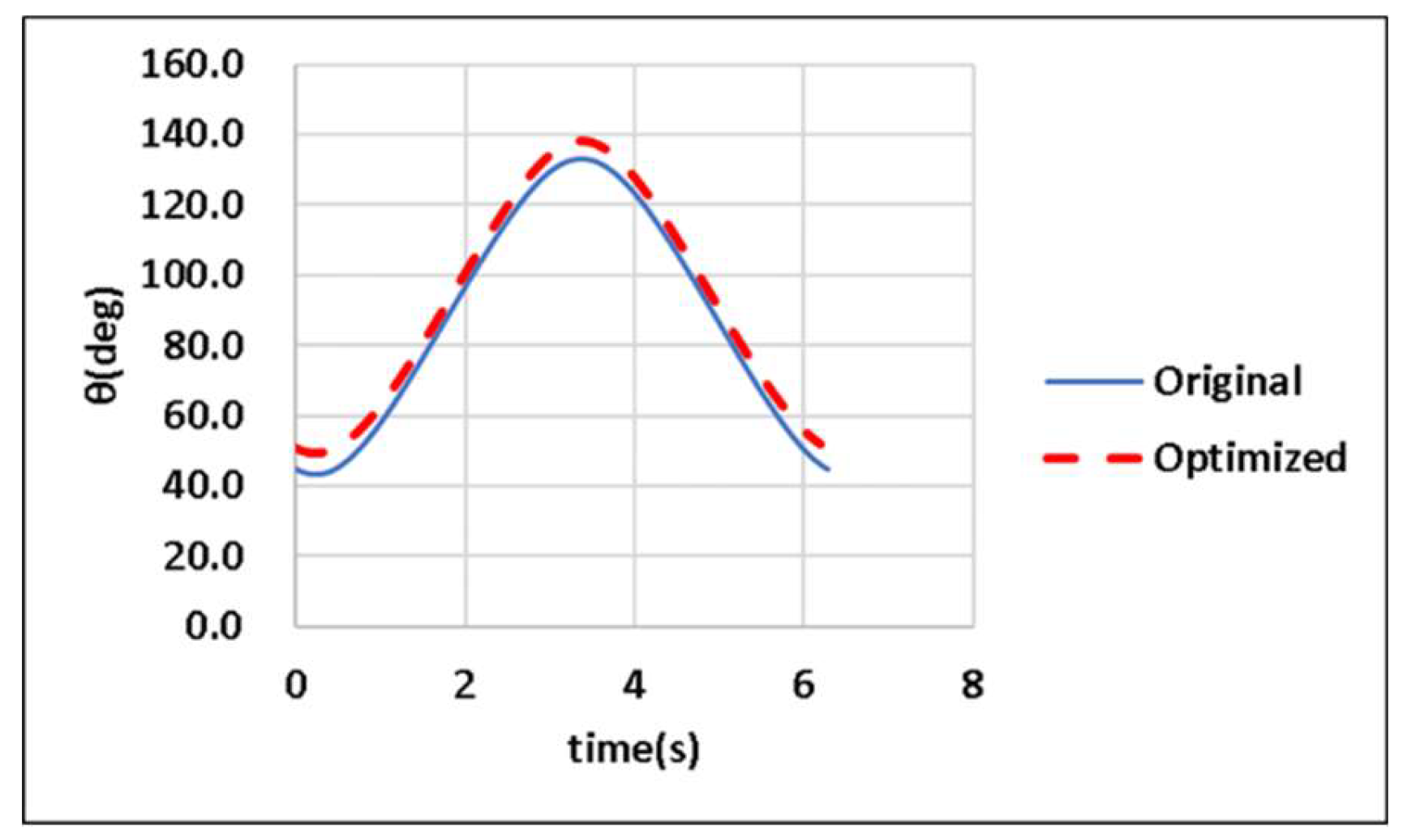
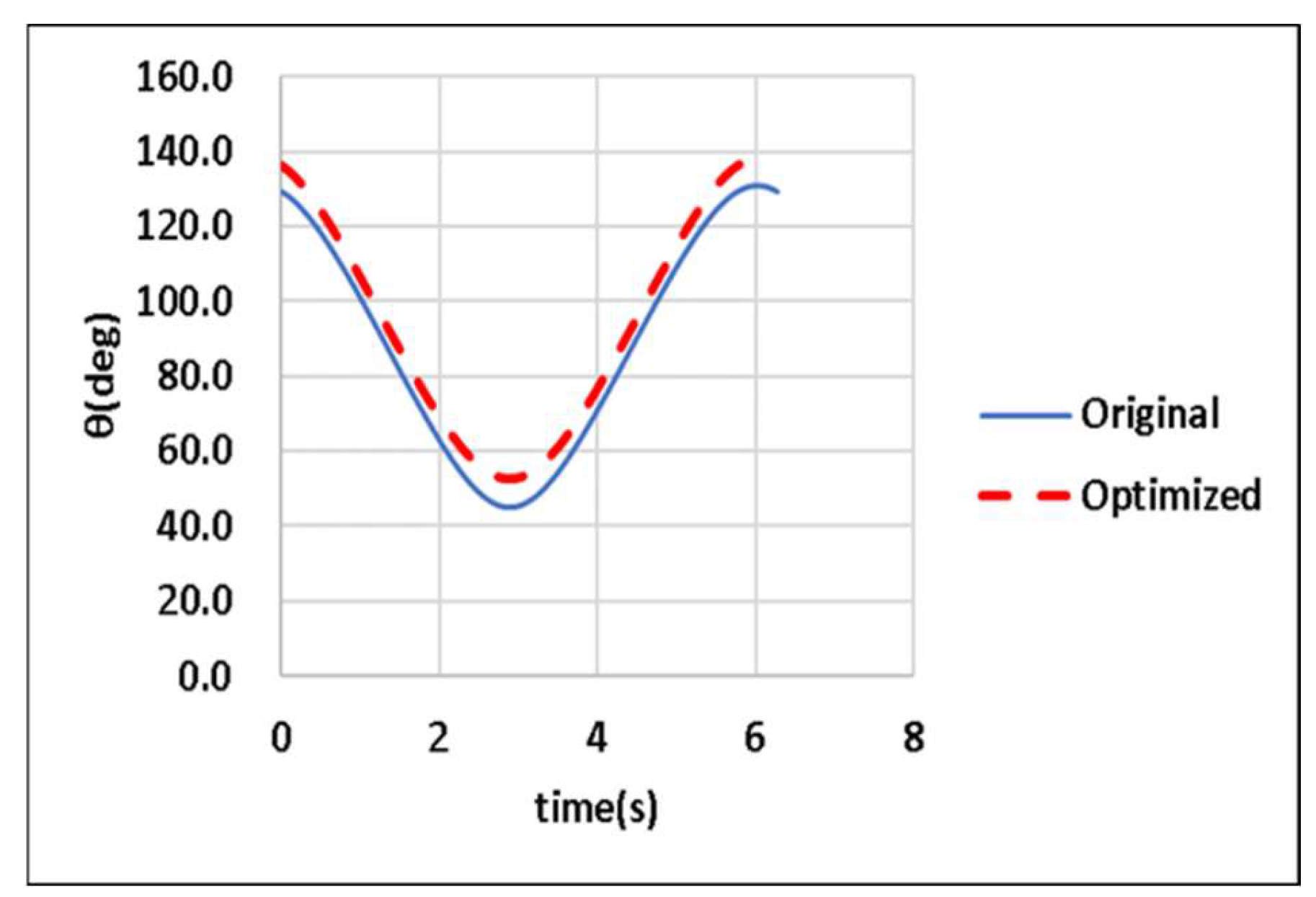
seconds. The widths of the wiping regions on the driver and passenger sides of the CDLS are

85 π / 180

and

80 π / 180

rad, respectively, with the permitted error margin being

1 π / 1800

rad. The patterns of the wiping region are regulated in accordance with the guidelines provided in [14].

DE is employed to minimize f subject to 10 constraints. For the CDLS, the fixed constants are

r_{1}

= 233.9 mm,

r_{11}

= 232.4 mm,

ω_{2}

= 1 rad/sec,

α_{2}

= 0 rad/s², and

r_{2}

= 50 mm. Table 1 presents detailed information on the angle-related parameters used in the simulations. The constraints for the objective function

f

are listed as follows:

(1)

190 \leq r_{3} \leq 400

(mm)

(2)

50 \leq r_{4} \leq 80

(mm)

(3)

190 \leq r_{5} \leq 400

(mm)

(4)

50 \leq r_{6} \leq 80

(mm)

(5)

|\max_{0 \leq θ_{2} \leq 2 π} θ_{4} - \min_{0 \leq θ_{2} \leq 2 π} θ_{4} - \frac{85 π}{180}| \leq \frac{0.1 π}{180}

(rad)

(6)

\frac{40 π}{180} \leq μ_{4} \leq \frac{140 π}{180}

(rad)

(7)

|ω_{4}| \leq 0.3 π

(rad/s)

(8)

|\max_{0 \leq θ_{2} \leq 2 π} θ_{6} - \min_{0 \leq θ_{2} \leq 2 π} θ_{6} - \frac{80 π}{180}| \leq \frac{0.1 π}{180}

(rad)

(9)

\frac{40 π}{180} \leq μ_{6} \leq \frac{140 π}{180} (r a d)

(10)

|ω_{6}| \leq 0.3 π

(rad/s)

The parameter values for DE in this study are as follows:

(1): Crossover ratio CR = 0.6.
(2): Scale factor F = 0.6.
(3): Population size M = 150.
(4): Maximum number of iterations G_max = 100.

3. Results

Section 3.1 discusses the validation of our modeling approach. The results obtained from calculations using the mathematical formulas derived in Section 2.1 and those from the commercial software ADAMS were compared to validate the proposed model. Section 3.2 presents the optimized results obtained after using the DE method.

3.1. Comparison with ADAMS Results

We used MATLAB to calculate

α_{3}

α_{4}

α_{5}

, and

α_{6}

in accordance with the formulas derived in Section 2.1. The calculated parameter values are listed in Table 1 and Table 2. The time interval and sampling time for the MATLAB computations were

[0, 2 π]

and

π / 180

, respectively. The initial value of

θ_{2}

was

0 °

To validate the proposed model, the simulation parameters used in MATLAB were also input into the commercial software ADAMS. Figure 14, Figure 15, Figure 16 and Figure 17 present a comparison between the results obtained from MATLAB and ADAMS for

α_{3}

α_{4}

α_{5}

, and

α_{6}

_, respectively.

We calculated

F_{12 x}

F_{12 y}

F_{12 z}

and

M_{d}

MATLAB by using the formulas derived in Section 2.2. The parameter values used in the calculations are listed in Table 1, Table 2 and Table 3. To validate the proposed model, we input the same parameters into the commercial software ADAMS. Figure 18, Figure 19, Figure 20 and Figure 21 depict the MATLAB and ADAMS results obtained for

F_{12 x}

F_{12 y}

F_{12 z}

and

M_{d}

respectively.

A comparison of the results calculated with MATLAB and those obtained from ADAMS suggest that our modeling method is accurate and reliable.

3.2. DE Results for Linkage Length Optimization

Table 4 presents the optimized linkage lengths obtained after DE for minimizing the absolute angular accelerations |

α_{4}

| and |

α_{6}

| of the CDLS.

Figure 22 and Figure 23 reveal that DE optimization decreased the maximal absolute values of

α_{4}

and

α_{6}

of the output links on the driver and passenger sides of the CDLS.

Figure 24, Figure 25 and Figure 26 reveal that the transmission angles were closer to

90 °

after optimization, which slightly reduced the maximum motor driving torque.

Table 5 and Table 6 presents the values of various parameters before and after DE optimization. Optimization reduced the maximum angular accelerations of the driver- and passenger-side output links of the CDLS (max|

α_{4}

| and max|

α_{6}

| respectively) by 13.64% and 14.38%, respectively.

4. Discussion

In this study, we successfully established the kinematics of a three-dimensional CDLS for windshield wipers. We designed a method for enhancing the stability of the system while maintaining its functionality. This improvement was achieved by minimizing the maximal absolute angular acceleration of the system's output links through DE optimization. The designed method was applied to a commercially available CDLS for vehicle wipers. We also developed a dynamic model of the center-driven linkage to determine the driving torque required from the motor to maintain constant crank rotation under a fixed frictional resistance torque.

In future research, we plan to use the Ansys/Fluent software program to perform numerical simulations of the wiper blade's interaction with the windshield to obtain lift and drag coefficients. Moreover, we intend to incorporate a wiper arm into the current CDLS model to simulate the forces during wiper operation on a glass surface with a given friction coefficient. This approach will provide a more accurate description of the wiper linkage system's dynamic behavior.

Author Contributions

Methodology, T.-J.C.; Software ,Tien-Shun Chung .

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

Freudenstein, F.; Kiss, I.S. Type Determination of Skew Four-bar Mechanisms. ASME J. Eng. Ind. 1969, 91, 220–223. [Google Scholar] [CrossRef]
Sticher, F.C.O. Mobility Limit Analysis of RSSR Mechanisms by “Ellipse diagram”. Journal of Mechanisms 1970, 5(3), 393–415. [Google Scholar] [CrossRef]
Bottema, O. The Motion of the Skew Four-bar. Journal of Mechanisms 1971, 6(1), 69–79. [Google Scholar] [CrossRef]
Hamid, S.; Soni, A.H. Design of an RSSR Crank-rocker Mechanism for Optimum Force Transmission. In Proceedings of the 2nd OSU Applied Mechanisms Conference; 1971; 17, pp. 171–176. [Google Scholar]
Freudenstein, F.; Primrose, E. On the Criteria for the Rotatability of the Cranks of Skew Four-bar Linkage. Trans. ASME, J. Eng. Ind. 1976, 98, 1285–1288. [Google Scholar] [CrossRef]
Alizade, R.A.; Freudenstein, F.; Pamidie, P.R. Optimum Path Generation by Means of the Sew Four-bar linkage. Mechanism and Machine Theory 1976, 11(4), 295–302. [Google Scholar] [CrossRef]
Balaji, R.L.V.; Lakshminarayana, K. Optimal Designs of the RSSR Crank-rocker Mechanism-1. General time ratio. Mechanism and Machine Theory 1984, 19, 431–441. [Google Scholar] [CrossRef]
Zhang, W.; Zhang, D. Conditions of Crank Existence for a Particular Case of the RSSR Linkage. Mechanism and Machine Theory 1993, 28(6), 845–850. [Google Scholar] [CrossRef]
Söylemez, E. Transmission Optimization of Right-angled Four-bar Mechanisms. Mechanism and Machine Theory 1993, 28(4), 539–552. [Google Scholar] [CrossRef]
Saka, Z. The RSSR Mechanisms with Partially Constant Transmission Angle. Mechanism and Machine Theory 1996, 31(6), 763–769. [Google Scholar] [CrossRef]
Chung, W.Y. Mobility Analysis of RSSR Linkage and Type Maps of Special Cases. Mechanism and Machine Theory 2004, 39(4), 379–393. [Google Scholar] [CrossRef]
Mirja, Rotzolla.; Margaret H., Reganb.; Manfred L., Hustyc.; M. John D., Hayesa. Kinematic Geometry of Spatial RSSR Mechanisms. Mechanism and Machine Theory 2023, 185, p105335. [Google Scholar]
Chen, T.-J.; Hong, Y.-J. Geometric Analysis of the Vibration of Rubber Wiper Blade. Taiwanese Journal of Mathematics 2021, 25, 491–516. [Google Scholar] [CrossRef]
Chen, T.-J.; Hong, Y.-J.; Lin, C.-H.; Wang, J.-Y. Optimization on Linkage System for Vehicle Wipers by the Method of Differential Evolution. Applied Sciences 2023, 13(1), 1–19. [Google Scholar] [CrossRef]
Storn, R.; Price, K.V. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report, TR-95-012; International Computer Science Institute (ICSI) of University of California: Berkeley, CA, USA, 1995. [Google Scholar]
Storn, R.; Price, K.V. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
Storn, R.; Price, K.V.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
Fan, Y.-F.; Lampinen, J. A Trigonometric Mutation Operation to Differential Evolution. Journal of Global Optimization 2003, 27(1), 105–129. [Google Scholar] [CrossRef]
Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation, Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
Tizhoosh, H.R. Reinforcement Learning Based on Actions and Opposite Actions. In Proceedings of the ICGST International Conference on Artificial Intelligence and Machine Learning (AIML-05), Cairo, Egypt, 19-21 December 2005. [Google Scholar]
Tizhoosh, H.R. Opposition-based Reinforcement Learning. Journal of Advanced Computational Intelligence and Intelligent Informatics 2006, 10(4), 578–585. [Google Scholar] [CrossRef]
Das, S.; Abraham, A.; Chakraborty, U.K.; Konar, A. Differential Evolution using a Neighborhood Based Mutation Operator. IEEE Transactions on Evolutionary Computation 2009, 13(3), 526–553. [Google Scholar] [CrossRef]
Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Transactions on Evolutionary Computation 2009, 13(2), 398–417. [Google Scholar] [CrossRef]
Brest, J.; Sepesy Maučec, M. Self-Adaptive Differential Evolution Algorithm Using Population Size Reduction and Three Strategies. Soft Computing 2011, 15(11), 2157–2174. [Google Scholar] [CrossRef]
Lou, Y.; Yuen, S.Y.; Chen, G. Non-Revisiting Stochastic Search Revisited: Results, Perspectives, and Future Directions. Swarm and Evolutionary Computation 2021, 61, 100828. [Google Scholar] [CrossRef]
Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential Evolution Algorithm with Ensemble of Parameters and Mutation Strategies. Appl. Soft Comput. 2010, 11, 1679–1696. [Google Scholar] [CrossRef]
Wang, H.; Wu, Z.J.; Rahnamayan, S.; Kang, L.S. A Scalability Test for Accelerated DE Using Generalized Opposition-based Learning. In Proceedings of the International Conference on Intelligent System Design and Applications, Location, Country; 2009; pp. 1090–1095. [Google Scholar]
Choi, T.J.; Togelius, J.; Cheong, Y.G. A Fast and Efficient Stochastic Opposition-Based Learning for Differential Evolution in Numerical Optimization. Swarm Evol. Comput. 2021, 60, 100768. [Google Scholar] [CrossRef]
Heidari, A.A.; Abbaspour, R.A.; Mirjalili, S. Harris hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
Balli, S.S.; Chand, S. Transmission Angle in Mechanisms. Mech. Mach. Theory 2002, 37, 175–195. [Google Scholar] [CrossRef]

Figure 1. Flowchart of our research method.

Figure 5. Rotation about the

z_{i}

-axis.

Figure 5. Rotation about the

z_{i}

-axis.

Figure 6. Rotation about the

x_{i}

-axis.

Figure 6. Rotation about the

x_{i}

-axis.

Figure 7. Rotation about the

y_{i}

-axis.

Figure 7. Rotation about the

y_{i}

-axis.

Figure 8. Coordinate transformation through rotation around two axes.

Figure 9. Relationship between the

x_{0} y_{0} z_{0}

and

x_{m} y_{m} z_{m}

coordinate systems.

Figure 9. Relationship between the

x_{0} y_{0} z_{0}

and

x_{m} y_{m} z_{m}

coordinate systems.

Figure 10. Simplified three-dimensional model of a CDLS.

Figure 11. Free-body diagram of Link CD in the

X_{1} Y_{1} Z_{1}

coordinate system.

Figure 11. Free-body diagram of Link CD in the

X_{1} Y_{1} Z_{1}

coordinate system.

Figure 12. Free-body diagram of Link EF in the

X_{2} Y_{2} Z_{2}

coordinate system.

Figure 12. Free-body diagram of Link EF in the

X_{2} Y_{2} Z_{2}

coordinate system.

Figure 13. Free-body diagram of Link AB in the

X Y Z

coordinate system.

Figure 13. Free-body diagram of Link AB in the

X Y Z

coordinate system.

Figure 14. Comparison of the MATLAB and ADAMS results for

α_{3}

Figure 14. Comparison of the MATLAB and ADAMS results for

α_{3}

Figure 15. Comparison of the MATLAB and ADAMS results for

α_{4}

Figure 15. Comparison of the MATLAB and ADAMS results for

α_{4}

Figure 16. Comparison of the MATLAB and ADAMS results for

α_{5}

Figure 16. Comparison of the MATLAB and ADAMS results for

α_{5}

Figure 17. Comparison of the MATLAB and ADAMS results for

α_{6}

Figure 17. Comparison of the MATLAB and ADAMS results for

α_{6}

Figure 18. Comparison of the MATLAB and ADAMS results for

F_{12 x}

Figure 18. Comparison of the MATLAB and ADAMS results for

F_{12 x}

Figure 19. Comparison of of the MATLAB and ADAMS results for

F_{12 y}

Figure 19. Comparison of of the MATLAB and ADAMS results for

F_{12 y}

Figure 20. Comparison of the MATLAB and ADAMS results for

F_{12 z}

Figure 20. Comparison of the MATLAB and ADAMS results for

F_{12 z}

Figure 21. Comparison of the MATLAB and ADAMS results for

M_{d}

Figure 21. Comparison of the MATLAB and ADAMS results for

M_{d}

Figure 22. Optimized and unoptimized angular acceleration

α_{4}

of the driver-side output link of the CDLS.

Figure 22. Optimized and unoptimized angular acceleration

α_{4}

of the driver-side output link of the CDLS.

Figure 23. Optimized and unoptimized angular acceleration

α_{6}

of the passenger-side output link of the CDLS.

Figure 23. Optimized and unoptimized angular acceleration

α_{6}

of the passenger-side output link of the CDLS.

Figure 24. Motor driving torque

M_{d}

before and after DE optimization.

Figure 24. Motor driving torque

M_{d}

before and after DE optimization.

Figure 25. Ttransmission angle

μ_{4}

for the driver-side output link of the CDLS before and after DE optimization.

Figure 25. Ttransmission angle

μ_{4}

for the driver-side output link of the CDLS before and after DE optimization.

Figure 26. Transmission angle

μ_{6}

for the passenger-side output link of the CDLS before and after DE optimization.

Figure 26. Transmission angle

μ_{6}

for the passenger-side output link of the CDLS before and after DE optimization.

Table 1. Angle-related parameters used in simulations.

$θ_{1}$ (rad)	$ϕ_{1}$ (rad)	$θ_{11}$ (rad)	$ϕ_{11}$ (rad)	$θ_{0}$ (rad)	$ϕ_{0}$ (rad)	$θ_{01}$ (rad)	$ϕ_{01}$ (rad)
0.2279	1.6961	2.8886	1.6236	0	0	0.1368	0.1301

Table 2. Length, angular velocity, and angular acceleration parameters used in simulations.

$r_{1}$ (mm)	$r_{11}$ (mm)	$r_{3}$ (mm)	$r_{4}$ (mm)	$r_{5}$ (mm)	$r_{6}$ (mm)	$α_{2}$ $(rad / {s e c}^{2}$ )	$w_{2}$ (rad/sec)
233.9	232.4	229.9	71.4	227.5	75.1	0	1

Table 3. Parameter values used in simulations.

$m_{2}$ (kg)	$m_{4}$ (kg)	$m_{6}$ (kg)	$I_{2}$ $(kg - {m m}^{2}$ )	$I_{4}$ $(kg - {m m}^{2}$ )	$I_{6}$ $(kg - {m m}^{2}$ )	$M_{r 4}$ (N-m)	$M_{r 6}$ (N-m)
0.204	0.271	0.283	13.194	17.650	18.415	15	15

Table 4. Linkage lengths before and after DE optimization.

	$r_{3}$ (mm)	$r_{4}$ (mm)	$r_{5}$ (mm)	$r_{6}$ (mm)
Linkage length before DE	229.9	71.4	227.5	75.1
Linkage length after DE	228.9	74.1	224.1	76.4

Table 5. Values of

α_{4}

and

ω_{4}

for the driver-side output link of the CDLS before and after DE optimization.

Table 5. Values of

α_{4}

and

ω_{4}

for the driver-side output link of the CDLS before and after DE optimization.

	$\max_{0 \leq θ_{2} \leq 2 π} α_{4}$	$\min_{0 \leq θ_{2} \leq 2 π} α_{4}$	$\max_{0 \leq θ_{2} \leq 2 π} ω_{4}$	$\min_{0 \leq θ_{2} \leq 2 π} ω_{4}$
Before DE	1.290	-0.783	0.787	-0.701
After DE	1.114	-0.825	0.728	-0.683
Change	-13.64%	5.36%	-7.50%	-2.57%

Table 6. Values of

α_{6}

and

ω_{6}

for the passenger-side output link of the CDLS before and after DE optimization.

Table 6. Values of

α_{6}

and

ω_{6}

for the passenger-side output link of the CDLS before and after DE optimization.

	$\max_{0 \leq θ_{2} \leq 2 π} α_{6}$	$\min_{0 \leq θ_{2} \leq 2 π} α_{6}$	$\max_{0 \leq θ_{2} \leq 2 π} ω_{6}$	$\min_{0 \leq θ_{2} \leq 2 π} ω_{6}$
Before DE	0.716	-1.168	0.742	-0.667
After DE	0.782	-1.000	0.681	-0.651
Change	9.21%	-14.38%	-8.22%	-2.40%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimization of Spatial Windshield Wiper Linkages by Using the Differential Evolution Method

Abstract

1. Introduction

2. Materials and Methods

2.1. Wiper Linkage Motion Model

2.1.1. Matrices for Three-Dimensional Rotations

2.1.2. Multiple Rotations

2.1.3. Motion of the Driver-Side Linkage of the CDLS

2.1.4. Motion of the Passenger-Side Linkage of the CDLS

2.2. Dynamic Analysis of the Linkage System

2.3. Optimization of the Angular Acceleration of the Output Links of the CDLS

3. Results

3.1. Comparison with ADAMS Results

3.2. DE Results for Linkage Length Optimization

4. Discussion

Author Contributions

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe