Prerpints.org logo
Preprint
Concept Paper

This version is not peer-reviewed.

Open Problems in Synthetic Multicellularity

Submitted:

22 July 2024

Posted:

24 July 2024

You are already at the latest version

Abstract
Multicellularity is one of the major evolutionary transitions, and its rise provided the ingredients for the emergence of a biosphere inhabited by complex organisms. Over the last decades, the potential for bioengineering multicellular systems has been instrumental in interrogating nature and exploring novel paths to regeneration and disease, as well as cognition and behaviour. Here, we provide a list of open problems that encapsulate many of the ongoing and future challenges in the field, and we suggest conceptual approaches that may facilitate progress.
Keywords: 
Synthetic Biology
;  
multicellularity
;  
collective computation
;  
regeneration
;  
self-organization
;  
biobots
Subject: 
Biology and Life Sciences  -   Cell and Developmental Biology

I. Introduction

Life forms in our biosphere fall into two categories: unicellular (UC) and multicellular (MC). UC organisms act independently, dealing with their environments autonomously, while MC organisms consist of various cell types with division of labor and cooperation [1,2]. UC complexity is energetically favorable, involving simple replication and minimal life cycles. MC systems exhibit complex traits like developmental programs, self-maintenance, and spatial patterns [3].
The study of MC has traditionally been helped by experimental and comparative methods, theoretical models and the revolutionary tools provided by molecular phylogenetics [9,10,11]. These studies have revealed unexpected insights concerning the tempo and mode of MC change and the role played by dynamical patterning modules [12,13]. However, thinking at the organism level beyond structural patterns, MC also includes other phenomena, such as movement or cognition, both relevant to our understanding of MC evolution. This paper considers the potential insights provided by synthetic alternatives based on diverse approaches to build cellular assemblies, from microbial consortia on a Petri Dish or cell clusters to organoids and living bots. Some examples are displayed in Figure 1, with three examples from biology (first column) and several synthetic MC case studies with different levels of complexity. The first two rows are related to hierarchical and emergent mechanisms of pattern generation [14]. These correspond to top-down (predictable) versus bottom-up (emergent) mechanisms, respectively, and both are relevant for our understanding (and engineering) of MC systems. Programmable MC synthetic systems shown in Figure 1(b–d) include gradient-forming microbial consortia, multistable cell fates. On the other hand, many crucial developmental processes shaping embryos (Figure 1e) include emergent phenomena captured by some synthetic MC systems, including organoids, branching bacterial populations and Anthrobots (Figure 1f-h). Finally, the third row showcases the use of evolutionary strategies in the design of MC assemblies. The challenge here is to generate simple synthetic organisms, such as Placozoans (Figure 1i). Successful evolution in vitro of simple multicellular systems [7,15] has been achieved (Figure 1 j, k) while in silico evolutionary algorithms have been used to design reconfigurable organisms [16,17].
Multicellular complexity is a tale of multiple scales, and understanding its origins, universal properties and contingencies inevitably call for an interdisciplinary picture where theory has played a crucial role. As pointed out by the late Brian Goodwin [18] the traditional, reductionist approach to the problem led to an inadequate view of the nature of organisms. Additionally, the presence of feedback loops connecting different levels (such as genes, gene networks and cell-cell interactions) are deeply constrained by the laws governing pattern formation [19,20]. This includes symmetry breaking [21], the structure of attractor landscapes [22,23] or collective properties [24,25]. Synthetic alternatives [26] provide a unique opportunity of dissecting MC complexity [27,28]. Importantly, they allow the study of emergent form and function without an explicit evolutionary history [17]. Unlike traditional biological model systems, sculpted by aeons of selection, synthetic organisms allow us to observe the plasticity of life’s agential materials as they solve new problems [29,30]. Adaptive structure and behaviour arise in real-time in novel configurations not previously tested by evolution.
The early days of synthetic biology were largely dominated by modifying microorganisms, which have become the perfect chassis to build complex cellular circuits capable of sensing and reacting to their environments in complex ways. On the other hand, stem cell technology and new cell culture methods have made it possible to reach new complexity levels associated with tissue or even organs [31,32]. Because of their relevance in bioengineering and potential biomedical impact, organoids have emerged as a unique opportunity for the study of diseases and as a complement to animal models. Finally, engineering behaviour, motion and even self-repair in embodied, motile living systems have provided unexpected insights [33,34].
In most case studies, the complexity of synthetic living agents is achieved through a combination of design and self-organization. Far from standard engineering, synthetic MC exploits intrinsic properties of living matter and offers opportunities for predictable design based on computational modelling and evolution in silico. Sometimes, the design principles depart from both natural and human-designed solutions. The current landscape of synthetic MC systems can be roughly decomposed into three (partially overlapping) classes:
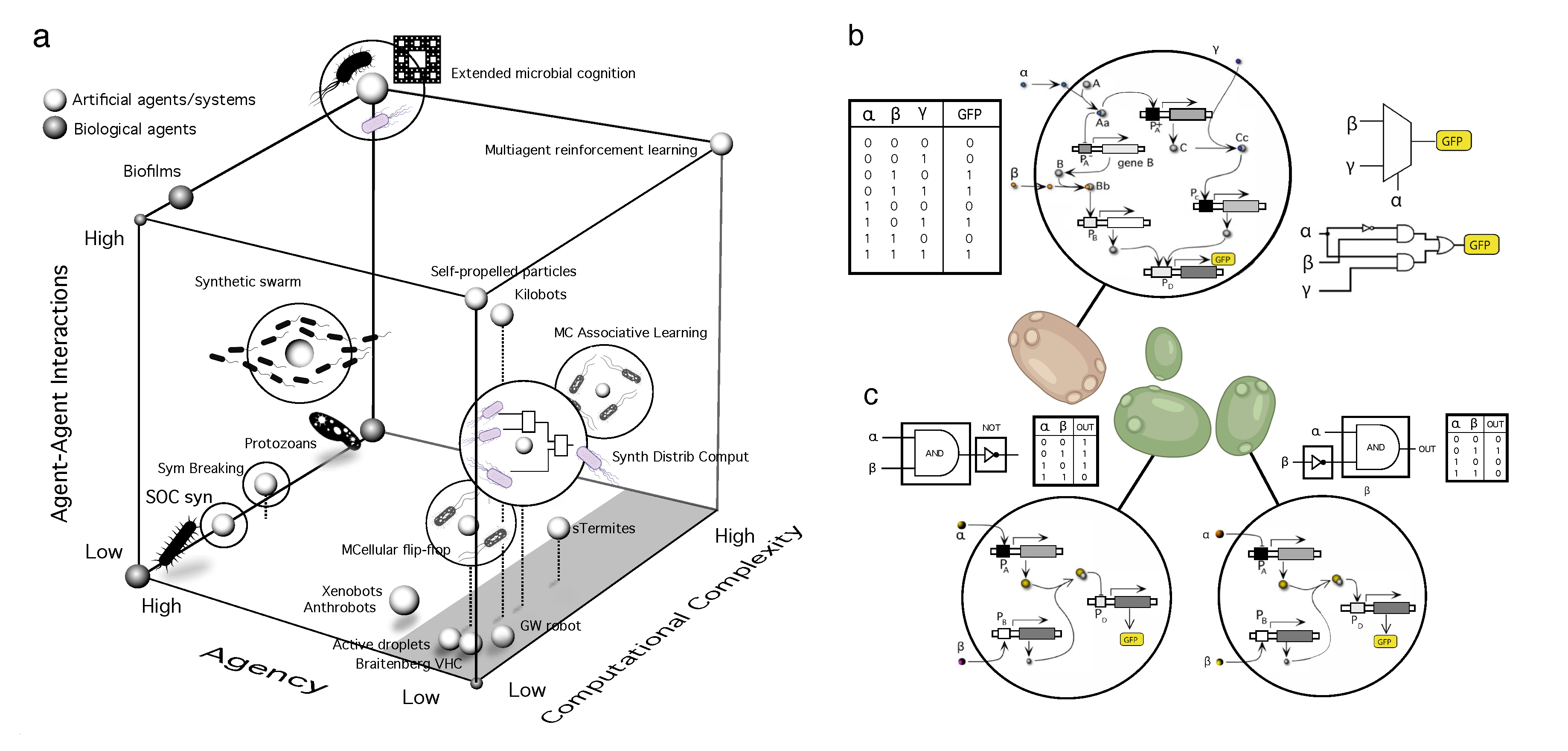
  • Synthetic multicellular circuits. This class involves cellular circuits that have been modified or introduced through genetic engineering within living cells, typically used as a chassis [35,36,37,38,39]. Many designs within this domain rely on a modular approach to circuit complexity based on standard combinatorial circuit design [40,41,42]. Cellular consortia have been used as MC implementations of all kinds of simple responses, from combining Boolean gates [43,44,45,46] to pattern formation [4,47]. These designs involve strains interacting through chemical signals propagating in a liquid medium or diffusing over short distances on an agar plate.
  • Programmable synthetic assemblies. The next step towards engineering MC systems exploits the predictable properties displayed by adhesion-driven spatial morphodynamics. Again, this bottom-up engineering allows predicting (i. e. programming) the outcome of the final spatial structure. It was early understood that cell sorting due to different adhesion energies could easily explain the self-organized aggregation of a set of randomly mixed cells [48,49]. Despite the self-organized nature of the process, it is possible to make some predictions concerning the spatial arrangements at steady state.
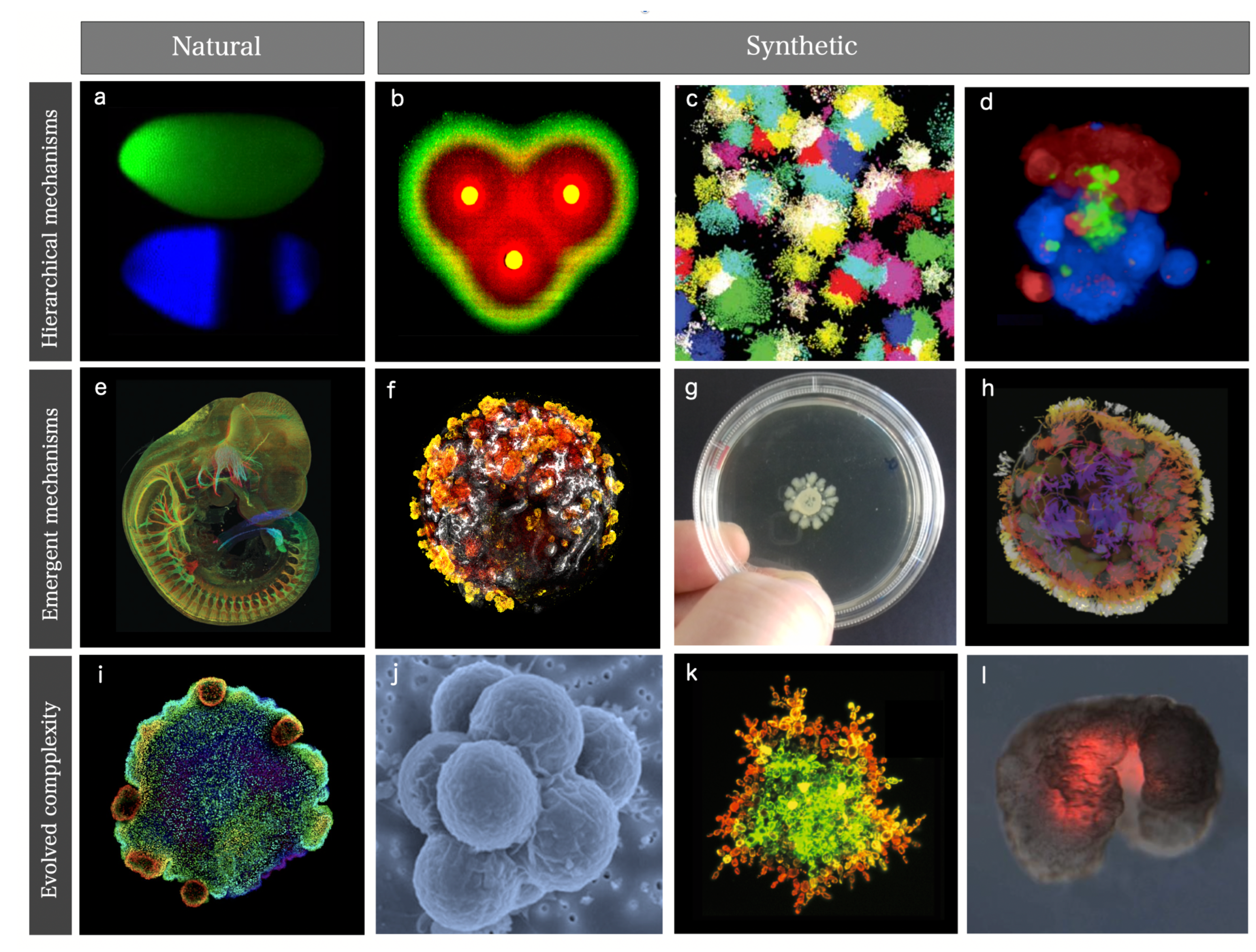
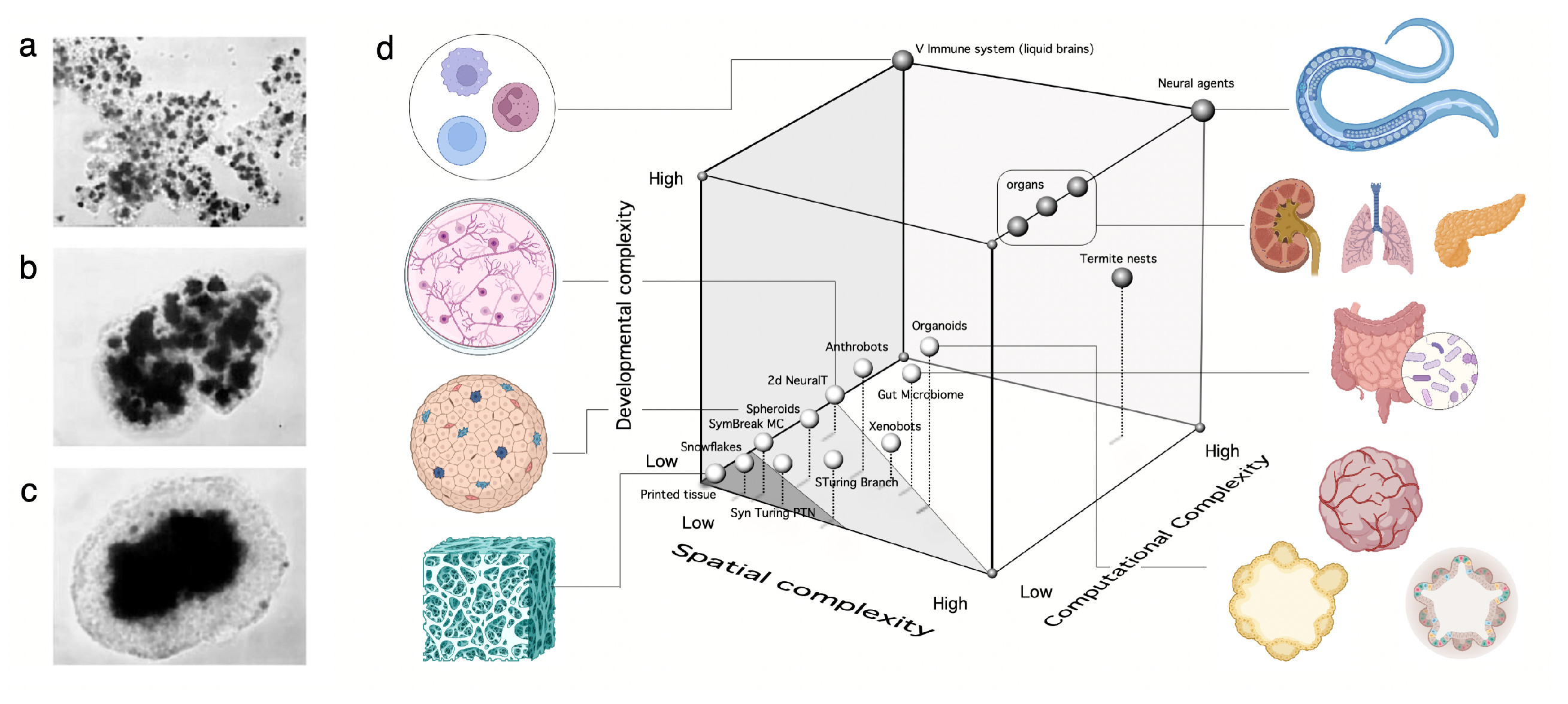
  • Synthetic morphology and agential materials. One way of moving beyond cell-level engineering involves considering cell collectives as agential materials. These systems exhibit emergent properties at the system level that cannot be understood in terms of the properties of the constituents (genes and cells). This approach takes advantage of higher-order properties of embodied living matter (such as memory, context-sensitive navigation of problem spaces and homeostasis) to perform computations and design morphologies beyond the bottom-up principles of synthetic biology [29,50]. This class includes organoids and biobots and other MC assemblies capable of collective responses in space and time and novel forms of behaviour.

II. Synthetic Multicellular Classes

The three domains listed above have contributed to a new wave of exploring biological complexity and interrogating the principles of living systems. They have also provided a great source for novel biomedical research and applications. While some constraints need to be addressed (such as the limits to organoid size), some engineered constructs have revealed unique properties that question some old assumptions concerning the nature of computation or agency. The next section summarises each class’s key features before defining our challenges and open questions.

A. Synthetic Multicellular Circuits 

While standard engineering design has exploited inert matter, bioengineering constructs are made of molecular and cellular substrates tied to living structures (or their components). What is different? If we compare with physical systems, physicist John Hopfield argued that what makes biology different is its potential to perform computations [54]. More precisely, biological agents that navigate their environments searching for resources (and thus involving purpose) “compute” incoming information (internal and external) and respond to it in adaptive ways. The first (but incomplete) layer to approach this problem from synthetic biology involves building logic circuits, including a whole array of logic gates, oscillators, band-pass filters, sensing-reacting networks and even sophisticated circuits capable of making decisions, such as targeting and killing cancer cells [55,56,57,58,59]. Complex dynamical states (such as critical states) have also been engineered [60]. Some of these examples, associated with UC implementations, are depicted on the left lower wall in Figure 2a., where a space of synthetic biology designs has been depicted. One axis introduces the main target of most designs: computational complexity, which describes the diversity of computational tasks performed by each circuit design. A second axis weights the relative role played by interactions between different engineered strains. Moving up, MC designs are represented by swarms [61], learning consortia [52], or MC computation [62]. Some examples, such as synthetic swarms, still need to be implemented. In all these examples, cell populations live in a well-mixed medium.
As the field advanced, a limitation in engineered design predictability became evident. Circuit design complexity in cells often causes cross-talk: a transcription factor linking genes disrupts other processes. This “wiring problem” arises from the evolved nature of cellular circuits, differing from standard designs due to natural selection and reuse of parts [63]. This is particularly relevant when comparing computers and living systems regarding hardware and software separation. In living systems, modularity and integration are intertwined. Experiments in evolutionary computation highlight this difference [64]: in silico evolved circuits perform better and are more reliable than human-made ones, though harder to understand.
To address this, a standard approach isolates circuit modules within cellular circuitry, and modularisation has become a design principle [65]. However, a different MC design allows a combinatorial approach, differing from traditional engineering [44,53]. We will use this approach to illustrate the potential for non-standard solutions within bioengineered agents. This uses distributed computation logic, creating a cell library with minimal engineering and no connections, producing an OR logic output [53]. Figure 2b–c illustrates this with a three-input, one-output multiplexer. While the UC design (b) requires several wires to connect the different genes, an MC alternative (c) shows that very simple, reusable constructs can be engineered within two cells, both including a GFP reporter gene and not connected to each other. If one of the reporters is expressed, we take the system’s response as one (“ON”), whereas if none does, the output is zero (“OFF”).
We have skipped the third axis of our space in Figure 2a. It is labelled as “agency” and reconnects us with Hopfield’s conjecture about the nature of living systems. Within the context of cells, agency refers to their ability to sense, respond to, and adapt to their environment through autonomous processes [66,67]. They expend effort to attain specific preferred states, using different degrees of problem-solving competency, learning, and active inference to resist perturbations and autonomously project their actions into new problem spaces. Living systems display agency, and we situate synthetic UC designs on the left wall since the individual agency is not modified by adding an extra genetic construct. Instead, complex circuits generated by means of cellular consortia (grey area) lack this property due to their disconnected nature and their special implementation, which requires all cellular components to perform the computation but not the interaction as a system with their environments. To incorporate this feature within synthetic MC systems, we must expand the reach of standard biocomputation designs. In this context, a pluralist stance, known as polycomputation [34], suggests that living organisms harness various forms of information processing across different scales and contexts to control their development, behaviour, and adaptation. As discussed in the next sections, the embodied nature of MC complexity facilitates such multiscale processing, sometimes in unexpected directions.

B. Programmable Synthetic Assemblies 

Developing complex multicellular agents requires two important features: (1) a mechanism to generate cellular diversity and (2) a predictable spatial organization that allows coherent system-level responses. Increasing cell types displays an evolutionary trend: with the rise of animals, the number of different cellular phenotypes has increased [68,69]. The current understanding of generating different cell states is grounded on the concept of attractors [70,71]. By using simple models of gene-gene interactions, it is possible to show that different stable expression states are accessible from different initial conditions. Small two-gene cross-inhibitory networks have achieved this [72], and synthetic implementations exist [73]. But only recently has it been possible to design a circuit capable of displaying many different states ([5] see Box 1).
Preprints 112964 i001
How can we build MC systems with a spatial organization that can be predicted from the basic units (genes, molecules and cells) and their interactions? Getting closer to organs, organisms, and embryos implies introducing several extra layers of complexity, and the mapping between these components and the system-level properties is known to be highly nonlinear (Box 2). In other words, the nonlinear dynamics connecting gene network states with the unfolding of cell-cell interactions is far from trivial. This is particularly true with growing systems, where even the boundary conditions change through development. However, there is a domain of predictability given by engineering strategies that exploit some hierarchical cell-cell interactions. The best candidate, which has a long tradition within embryology and theoretical biology, is based on combining adhesion molecules.
Adhesion dynamic and the associated cell displacements occur via energy minimisation [48,76]. A model can be easily defined by a cell population on a discrete lattice. Cell states (cell types or engineered strains) are indicated as σ n ∈ { 0 , 1 , 2 , . . . } and cells can move to neighbouring sites. To illustrate how the model works, consider a three-state example: two cell types plus empty space, to be indicated as σ 1 , σ 2 and σ 0 , respectively.
Different cells have different adhesion strengths. These are defined by means of an adhesion matrix W :
W = ω ( σ 0 , σ 0 ) ω ( σ 0 , σ 1 ) ω ( σ 0 , σ 2 ) ω ( σ 1 , σ 0 ) ω ( σ 1 , σ 1 ) ω ( σ 1 , σ 2 ) ω ( σ 2 , σ 0 ) ω ( σ 2 , σ 1 ) ω ( σ 2 , σ 2 ) .
As defined, we have: ω ( a , b ) = ω ( b , a ) , and ω ( σ 0 , σ 0 ) = 0 . An energy function H that is defined for each lattice site μ i. e. :
H μ = ∑ σ η ∈ Γ μ ω ( σ μ , σ η )
where Γ μ is the set defined by the nearest neighbours of a cell in position μ each of which occupies a position η , and has a defined state σ η . If we try to swap one cell to one of its nearest locations, we first determine the new energy H ′ using the same expression. The energy difference between the original and the chosen location is Δ H = H ′ − H * . The probability associated to this is given by the so-called Boltzmann rule:
P ( σ μ → σ η ) = 1 1 + e Δ H / T
where the parameter T is a noise factor tuning the degree of randomness associated to our model. The Boltzmann factor e Δ H / T acts in such a way that if Δ H = 0 , the probability of swapping is 1 / 2 . For small T, the probability of swapping rapidly increases when Δ H > 0 , whereas is very small when Δ H < 0 . The relative weights of the matrix elements induce a hierarchy that allows to predict the kinds of patterns that can result from a given engineering design associated to adhesion properties (see [77] for details).
This simple microscopic set of rules provides the causal framework that explains re-aggregation experiments, as shown in the sequence of Figure 3a-c) displaying a set of dissociated cells (two types of retinal cells) evolves to a segregated structure [78]. Following these basic principles, orthogonal cell adhesion toolboxes have been designed to exploit the weight hierarchy, leading to synthetic programmable morphologies [79,80]. Furthermore, using a stochastic recombinase genetic switch allows programmable symmetry breaking and commitment to downstream cell fates [6]. This synthetic induction of SB could be an important step towards inducing differentiation in organoids.
The predictable nature of these designs faces challenges when dealing with the reality of more complex cellular aggregates and developmental processes. Along with symmetry breaking, population growth and the role played by physical forces beyond differential adhesion need to be considered, as well as intrinsic properties of cells and tissues as agential materials [29].
Preprints 112964 i002

C. Synthetic Morphology and Agential Materials 

The predictable nature of the previous examples becomes less reliable as we move towards complex MC systems, from organs to full organisms. The lack of predictability is due to the nonlinear nature of the genotype-phenotype mapping (see Box 2). In a formal fashion, it is a mapping Ω between the space of genotypes G and the space of (possible) phenotypes Φ :
Ω : G ⟶ Φ
In a nutshell, while the nature of adhesion rules allows programmable designs, living agents are the result of developmental programs that require growth and self-organisation, as well as regeneration, reproduction and behaviour. The information at the level of genes and gene-gene interactions will typically be incomplete in explaining the next complexity layers because the phenotype is not only the result of open-loop emergent complexity, but of directed navigation of anatomical morphospace guided by perception-action loops and setpoints encoded in bioelectrical, biochemical, and biomechanical properties. One crucial but traditionally ignored aspect is the presence of agency, i.e., the capacity for goal-directed changes to one’s self and the environment [94]. Agency itself is not only a general feature of life but also a multiscale property, because living organisms are composed of numerous layers of overlapping cooperating and competing agents which distort the option landscape for their parts and provide abstraction layers of competent subroutines for the systems they in turn comprise [30]. Two synthetic counterparts to these MC agents are discussed here: organoids and living robots.
One successful implementation of embodied MC systems is provided by organoids, representing the last part of a timeline starting from re-aggregation experiments [95,96]. In a nutshell, organoids are in vitro tissue-engineered cell models that can behave as miniature versions of the full-fledged organs they represent. Along with the self-organised component of their development [97], we need to use adult stem cells or pluripotent stem cells. The latter, in particular, have been exploited to generate different organoids, bringing the right conditions for a given set of cell types to emerge and get together. Afterwards, cell-cell interactions, both in signalling and mechanic forces, take control of morphodynamics.
Stem cell engineering has been used to study gene circuits and physical cues in morphogenesis. One particularly groundbreaking work was the self-organized emergence of optic cup organoids, later followed by brain organoids with regional identities using soluble compounds [97]. In all these cases, one major challenge is reproducibility and making organoids scalable and closer to their organs of reference, as well as the generation of vascular or neural networks for realistic contexts. It is worth noting that improvements in the field have benefited from the emulation of native tissue properties like stiffness and geometry. Similar results in whole embryo models, known as gastruloids, reveal symmetry-breaking mechanisms and axis formation in models of early embryogenesis [98,99].
The previous case studies lack two important components of MC complexity. One is the order for free resulting from intrinsic system properties, which allow the material to exploit its nested multiscale competency. Secondly, two innovations were required for the rise of cognitive complexity in metazoans: movement and sight [100]. Movement is likely to be a precondition for the rise of cognitive agents [101,102]. Along with sensors, it allows the existence of behavioural patterns. Can these nontrivial features be implemented in engineered MC agents? Are the synthetic designs necessarily grounded in engineered gene networks or signalling circuits?
Biology features problem-solving at each level of organisation—a kind of agential material with agendas, homeostatic loops, and the ability to maximize or minimize specific goal states with various degrees of robustness despite novel circumstances. This is well-known in neuroscience, where the CNS provides a learning interface that allows simple stimuli, such as reward and punishment, to drive complex internal rearrangements that the trainer could not achieve via micromanaging the molecular details. Numerous examples of learning [103], problem-solving, and optimization in biological systems such as molecular networks, cells, and tissues represent highly tractable targets for engineering top-down. The previously discussed examples cannot incorporate many aspects of agency that we can find in the living world. The gap in the space of Figure 2a is a reminder that designed computational circuits and programmable spheroids impose some restrictions to the behavioural repertoire of these constructs. There is a twilight zone that requires extra features capable of exploiting the intrinsic agential properties of cells and tissues.
A novel approach to the previous questions that provides one way to explore the voids in these spaces is provided by Xenobots [16] and Anthrobots [104], which show that endogenous functional capacities can be reached with no genetic editing or synthetic circuits. Xenobots are constructed from the skin and heart cells of the African clawed frog (Xenopus laevis). These choices allow them to move in predictable ways, pushing objects and working in collective ways (although their learning capacity and ability to achieve specific ends is only beginning to be investigated). Moreover, because of the chosen cells, they have self-repair properties. Importantly, they were designed using an evolutionary optimization algorithm that explored the space of soft physical shapes that could crawl in (a virtual) space. The optimal shapes were then sculpted in living tissue using microsurgery [16,17]. Anthrobots, on the other hand, are self-constructed spheroidal living bots obtained out of human lung cells that allow cilia-driven propulsion. By contrast to Xenobots, they require no evolutionary algorithms, manual sculpting, or embryonic tissues. In both cases, instead of implementing desired functionality explicitly with transcriptional circuits, these living robots featured no genetic editing or synthetic circuits. Their capabilities, such as kinematic self-replication, repair of neural wounds, etc., are endogenous and novel functions that can be controlled by behaviour-shaping, not bottom-up engineering.
Regenerating and developing systems offer numerous examples of biological systems navigating the anatomical morphospace to solve novel problems. This capacity is a highly tractable set of built-in software modules accessible to the bioengineer, in addition to the specific pathways and molecules that are usually targeted. More recently, it has been claimed that living tissue can be understood (and efficiently controlled) as an agential material—a substrate with its own competencies and agendas in transcriptional, anatomical and physiological problem spaces that can be manipulated using the tools of behavior science, not only biochemistry [105]. Indeed, work to understand the policies by which the homeodynamic set points scale, from the humble metabolic goals of single cells to the dynamic maintenance of grandiose construction projects such as regenerating limbs, has led to new approaches to combat the failure of this scaling, in the form of cancer [106,107].
The three classes of synthetic MC systems reveal a very wide space of possibilities for further exploration. On one hand, the combinatorial nature of genetic circuits and programmable adhesion hierarchies provides a potential source of logic functionalities that can be combined with other features, particularly embodied architectures. On the other hand, the realization that key aspects of agency can be available for free, both in living tissues and in engineered biobots, reveals some unexpected properties of living matter that could be exploited to understand evolutionary constraints to the evolution of MC forms [18,19,108] while pushing the boundaries of the possible. In the next section, we propose several open problems regarding this potential for synthetic multicellularity.

III. Open Problems

Synthetic developmental programs: the possible and the actual. The suggestion that there is a universal toolkit defining a finite set of dynamical patterning modules [13] could be studied within the synthetic MC framework. The programmable design of MC aggregates using adhesion molecules and symmetry-breaking mechanisms [6] would be one example within this validation of the theory. The advantages provided by scalable generation of cell types [5] and that can recapitulate the Waddington landscape concept [109], combined with using other developmental modules (introducing polarity or dynamic oscillations), could lead to a taxonomy of possible embodied designs.
Embodied memory and learning. Current synthetic designs dealing with memory circuits rely on the standard approach of electronic switches. Synthetic flip-flops have been implemented using MC consortia [51], and theoretical models have shown how learning could be implemented using MC consortia [52]. Can we move beyond these standard metaphors? It has been shown that learning in living systems can occur without a neural substrate [103] and that GRNs and pathways can learn with no genetic changes needed [110,111]. Moreover, memory can also be mediated by electrical, rather than biochemical, signals, as shown recently in bacterial biofilms [112]. Learning can also be implemented at the global regulatory network level to interpret the nonlinear high-dimensional projection of time-dependent external signals by intracellular recurrent networks of genes and proteins [113,114]. New MC constructs using organoids or biobots could benefit from memory enhancements grounded in these novel views.
Synthetic collective intelligence. One dominant form of intelligent behaviour that rules the biosphere outside standard brains is based on collective intelligence (CI). In general terms, it refers to the enhanced capacity that emerges from the collective interactions among agents in a group, resulting in solutions that cannot be explained in terms of single individual actions. The standard example is provided by insect societies [115,116,117,118]. It has been conjectured that the conceptual basis for CI can be translated into synthetic CI counterparts [61]. Moreover, electrical transmission of information in biofilms has shown the unexpected potential [119,120] that reminds us of some general principles of neuronal tissue dynamics [121]. In recent years, collective intelligence has been recognized as a general principle in agential MC systems beyond animal societies [25]. Moreover, it has been pointed out that multicellular organisms and social insect colonies share fundamental common organizing principles [122]. Could we use synthetic MC designs to explore this connection? Can we exploit general principles of information sharing and processing in MC agents to build novel forms of embodied CI?
Synthetic neural cognition. Recent advances in microfabrication are allowing the development of precision neuroengineering methods through which neurons in in vitro cultures can be connected to one another in pre-designed ways [123]. These advances are revealing, for instance, the importance of modularity in the emerging activity of neural networks [124], and pave the way for the design of prescribed collective activity in neuronal assemblies. Can they inspire the development of augmented embodied agents to expand the cognitive potential of spheroids, organoids or Xenobots? One obvious possibility is to follow the path of standard synthetic circuit design on a new scale: instead of using single cells as a chassis for engineered circuits, use whole cell assemblies as the chassis for engineered cell types carrying computational circuits.
Synthetic proto-organisms and life cycles. One challenge for synthetic MC designs is the design and development of complex assemblies that can be considered simple forms of organisms, developing from single cells in predictable ways and able to self-replicate themselves. A minimal synthetic design should include the growth of a whole assembly from a single cell and the potential for some cells in the assembly to leave it by detaching from other cells, which should then be able to repeat the growth process. Anthrobots already possess some key components for such a goal: they develop in a predictable way from single stem cells, complete their developmental path into a multicellular spheroid (with variable size), display phenotypic traits (also associated with a variable shape), and display simple behavioural patterns including the ability to heal neural wounds. Xenobots, on the other hand, can display a remarkable (and once again, unexpected) property of organismality: self-reproduction [125]. However, this is a completely novel path based on kinematic self-replication: the Xenobot autonomously constructs copies of itself using available materials in its environment. Is this an indication that there are multiple paths to build autonomous organisms and their life cycles?
Building new organs. The organ level of organization is a missing component of current theories of organismality. Although they are identified as discrete modules within animal bodies1, we do not have a systems-level theory that provides predictable insights concerning their expected agency, number, nature and embedding within systems [77,126]. One possible path towards a better understanding of these mesoscale structures would be the synthesis of novel organs. A proof of concept would require building a stable, self-maintaining structure within a model organism and being able to perform a given functionality. Some inspiration in this context can come from the developmental processes leading to nest construction in social insects [127,128,129], where selforganization, broken symmetries and specialised parts emerge (and are maintained and regenerated) out of swarm intelligence.
Multiscale synthetic holobionts. Current and future synthetic biology applications in the biomedical context often involve single UC agents as potential carriers. One major field of research involves the study of synthetic microbes used to repair dysbiotic microbiomes [130,131] or even terraforming extant ecosystems [132,133]. In all these cases, we deal with the holobiont: an organism that contains other organisms, defining an ecological unit [134]. However, ongoing research reveals that we might need to expand this towards how MC agents can also interact with a context defined by tissues, organs or another organism. This includes the repair behaviour displayed by Anthrobots [104] and the swimming microrobots made out of algae and coated with nanoparticles, used to deliver drugs directly to metastatic lung tumours [135]. Could MC agents persistently coexist (maintaining their individuality) with tissues and organs within organisms, defining a new class of synthetic holobionts?
Synthetic behaviour. Work in minimal animals such as C. elegans has shown that sophisticated experience-dependent behaviour, such as salt attraction or repulsion depending on previous cultivation conditions [136,137], is encoded by small protein circuits in a single synapse [138]. This multiscale simplicity level encourages designing similarly complex behaviours in synthetic minimal animals. Moreover, the study of basal cognition opens new avenues to define behaviour [139]. Robots have been extensively used to study the evolution of adaptive behaviour [140,141] An interesting avenue could be to use Xenobots to study fossil behaviour [142] as represented by the tracks or burrows of ancient animals, which has been studied using robot models [143]. Could living robots with different levels of behavioural complexity recapitulate the taxonomy of fossil traces and help understand their origins?
Predictable designs? A generic problem, namely, to what extent the predictability of the MC designs is feasible, remains to be addressed [144,145]. Most synthetic systems, from UC to MC, are built to live under in vitro conditions, and those used to target tissues or organs are used as a chassis for an isolated design that is largely disconnected from the rest of the cellular circuitry. The dream of understanding biological complexity under a top-down view, in ways close to standard engineering [146] might be limited by the non-standard, tangled nature of cellular circuits and the presence of emergent phenomena. Although emergence is on our side in many ways [27], shaping organoids and allowing behaviour out of form, we lack a general picture of the limits of what can be predicted. The voids within the spaces shown in Figure 2 and Figure 3 are a reminder of the difficulties associated with building MC complexity from scratch without the natural developmental context. Perhaps we must accept that we cannot engineer the way we did so far with passive materials, micromanaging everything from the bottom up. We need to collaborate with the materials and take advantage of their basal cognition.

IV. Discussion

What determines the intrinsic complexity of organisms and developmental paths? Morphological complexity results from a highly non-linear mapping between genotype and phenotype [147]. In this context, self-organization processes beyond the gene level must be considered when dealing with tissue, organ and organismal complexity. A universal outcome of SO is the presence of emergent properties, i.e., qualitative properties exhibited by a system that results from interactions between units but that cannot be reduced to the properties of those units. Recent theoretical and experimental studies have shown that inspiration from the physics of phase transitions might help to deal with these emergent properties and their universal patterns [148,149,150]. The growing ambitions of bioengineering towards creating artificial macroscopic systems face dealing with emergent patterns, emergent (primitive) cognition and their scalability. All in all, we have a real world where our goal of designing increasingly complex cell assemblies is challenged by the underlying nonlinearities that connect genotypes and phenotypes. In Figure 4, we summarise these difficulties using a metaphor: Waddington’s Demon2. Using all the available molecular information at the cellular and subcellular scales, the Demon tries to predict the final outcome of all the microscopic interactions, failing to succeed due to the emergent nature of multicellular systems.
Is the emergent nature of MC complexity a sharp obstacle to our understanding of how cells self-organize into tissues, organs or even organisms? Perhaps not. Synthetic biology, stem cell-derived organoids, and the synthesis of living robots allow us to interrogate nature in novel ways, considering emergent properties in explicit ways that allow experimental validation of hypotheses and formulating models that deal with self-organization and agency. These tools can collectively bridge the gap between cellular- and tissue/organ-level biological models, resulting in a more realistic, functionally meaningful representation of the in vivo tissue spatial organization and the interactions between the cellular and extracellular environments. Organoid designs offer a unique opportunity to analyse the nature of emergence and the limits imposed by context and self-organization on the generative potential of bioengineering, while Xenobots and Anthrobots are the front layers that will help us understand complex biology at the organismal level, from development to behaviour. All the lessons obtained by answering the open problems discussed above will be instrumental to understanding the evolution of complexity, but they also allow the development of new ways to deal with health and disease beyond the molecular and cellular scales. Agential interventions (using patient-specific Anthrobots injected into the body) could be used to learn about the state of tissues or to execute repairs.

Acknowledgments

R.S., N.C. and J.P.M. thank the members of the Complex Systems Lab for useful discussions and Aurora Picornell for her inspiring ideas. This work has been supported by an AGAUR 2021 SGR 0075 grant and the Santa Fe Institute. J.P.M. was supported by funding from the Spanish government “PRE2020-091968” (MCIN/AEI) grant. J.G.O. was supported by the Spanish Ministry of Science and Innovation, the Spanish State Research Agency and FEDER (project PID2021-127311NB-I00), by the Maria de Maeztu Programme for Units of Excellence in R&D (project CEX2018-000792-M), and by the ICREA Academia programme. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program ERCCoG-2020 101002478 ENGINORG to N.M. M.L. gratefully acknowledges the support of Grant 62212 from the John Templeton Foundation and Grant Number W911NF-23-1-0100 from the Army Research Office. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government.

References

  1. Knoll, A.H. The multiple origins of complex multicellularity. Annual Review of Earth and Planetary Sciences 2011, 39, 217–239. [Google Scholar] [CrossRef]
  2. Grosberg, R.K.; Strathmann, R.R. The evolution of multicellularity: a minor major transition? Annu. Rev. Ecol. Evol. Syst. 2007, 38, 621–654. [Google Scholar] [CrossRef]
  3. Levin, M. The Computational Boundary of a “Self”: Developmental Bioelectricity Drives Multicellularity and Scale-Free Cognition. Frontiers in Psychology 2019, 10. [Google Scholar] [CrossRef] [PubMed]
  4. Basu, S.; Gerchman, Y.; Collins, C.H.; Arnold, F.H.; Weiss, R. A synthetic multicellular system for programmed pattern formation. Nature 2005, 434, 1130–1134. [Google Scholar] [CrossRef]
  5. Zhu, R.; del Rio-Salgado, J.M.; Garcia-Ojalvo, J.; Elowitz, M.B. Synthetic multistability in mammalian cells. Science 2022, 375. [Google Scholar] [CrossRef]
  6. Wauford, N.; Patel, A.; Tordoff, J.; Enghuus, C.; Jin, A.; Toppen, J.; Kemp, M.L.; Weiss, R. Synthetic symmetry breaking and programmable multicellular structure formation. Cell Systems 2023, 14, 806–818. [Google Scholar] [CrossRef] [PubMed]
  7. Herron, M.D.; Borin, J.M.; Boswell, J.C.; Walker, J.; Chen, I.C.K.; Knox, C.A.; Boyd, M.; Rosenzweig, F.; Ratcliff, W.C. De novo origins of multicellularity in response to predation. Scientific reports 2019, 9, 2328. [Google Scholar] [CrossRef] [PubMed]
  8. Bozdag, G.O.; Libby, E.; Pineau, R.; Reinhard, C.T.; Ratcliff, W.C. Oxygen suppression of macroscopic multicellularity. Nature communications 2021, 12, 2838. [Google Scholar] [CrossRef] [PubMed]
  9. Ruiz-Trillo, I.; Burger, G.; Holland, P.W.; King, N.; Lang, B.F.; Roger, A.J.; Gray, M.W. The origins of multicellularity: a multi-taxon genome initiative. TRENDS in Genetics 2007, 23, 113–118. [Google Scholar] [CrossRef]
  10. Ruiz-Trillo, I.; Nedelcu, A.M. Evolutionary transitions to multicellular life: principles and mechanisms; Vol. 2, Springer, 2015; pp. 53–0763. [CrossRef]
  11. Sebé-Pedrós, A.; Degnan, B.M.; Ruiz-Trillo, I. The origin of Metazoa: a unicellular perspective. Nature Reviews Genetics 2017, 18, 498–512. [Google Scholar] [CrossRef]
  12. Newman, S.A.; Bhat, R. Dynamical patterning modules: a “pattern language” for development and evolution of multicellular form. International Journal of Developmental Biology 2009, 53, 693. [Google Scholar] [CrossRef] [PubMed]
  13. Newman, S.A. Physico-genetic determinants in the evolution of development. Science 2012, 338, 217–219. [Google Scholar] [CrossRef] [PubMed]
  14. Salazar-Ciudad, I.; Newman, S.; Solé, R. Phenotypic and dynamical transitions in model genetic networks I. Emergence of patterns and genotype-phenotype relationships. Evolution & development 2001, 3, 84–94. [Google Scholar] [CrossRef]
  15. Ratcliff, W.C.; Denison, R.F.; Borrello, M.; Travisano, M. Experimental evolution of multicellularity. Proceedings of the National Academy of Sciences 2012, 109, 1595–1600. [Google Scholar] [CrossRef] [PubMed]
  16. Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. A scalable pipeline for designing reconfigurable organisms. Proceedings of the National Academy of Sciences 2020, 117, 1853–1859. [Google Scholar] [CrossRef]
  17. Blackiston, D.; Kriegman, S.; Bongard, J.; Levin, M. Biological Robots: Perspectives on an Emerging Interdisciplinary Field. Soft Robotics 2023, 10, 674–686. [Google Scholar] [CrossRef] [PubMed]
  18. Goodwin, B. How the leopard changed its spots: The evolution of complexity; Vol. 24, Princeton University Press, 2001.
  19. Alberch, P. The logic of monsters: Evidence for internal constraint in development and evolution. Geobios 1989, 22, 21–57. [Google Scholar] [CrossRef]
  20. Alberch, P. From genes to phenotype: dynamical systems and evolvability. Genetica 1991, 84, 5–11. [Google Scholar] [CrossRef] [PubMed]
  21. Turing, A.M. The chemical basis of morphogenesis. Bulletin of mathematical biology 1990, 52, 153–197. [Google Scholar] [CrossRef]
  22. Huang, S. The molecular and mathematical basis of Waddington’s epigenetic landscape: A framework for post-Darwinian biology? Bioessays 2012, 34, 149–157. [Google Scholar] [CrossRef]
  23. Furusawa, C.; Kaneko, K. Origin of complexity in multicellular organisms. Physical review letters 2000, 84, 6130. [Google Scholar] [CrossRef] [PubMed]
  24. Nadell, C.D.; Bucci, V.; Drescher, K.; Levin, S.A.; Bassler, B.L.; Xavier, J.B. Cutting through the complexity of cell collectives. Proceedings of the Royal Society B: biological sciences 2013, 280, 20122770. [Google Scholar] [CrossRef] [PubMed]
  25. McMillen, P.; Levin, M. Collective intelligence: A unifying concept for integrating biology across scales and substrates. Communications Biology 2024, 7, 378. [Google Scholar] [CrossRef] [PubMed]
  26. Solé, R. Synthetic transitions: towards a new synthesis. Philosophical Transactions of the Royal Society B: Biological Sciences 2016, 371, 20150438. [Google Scholar] [CrossRef] [PubMed]
  27. Ebrahimkhani, M.R.; Ebisuya, M. Synthetic developmental biology: build and control multicellular systems. Current opinion in chemical biology 2019, 52, 9–15. [Google Scholar] [CrossRef] [PubMed]
  28. Martínez-Ara, G.; Stapornwongkul, K.S.; Ebisuya, M. Scaling up complexity in synthetic developmental biology. Science 2022, 378, 864–868. [Google Scholar] [CrossRef] [PubMed]
  29. Davies, J.; Levin, M. Synthetic morphology with agential materials. Nature Reviews Bioengineering 2023, 1, 46–59. [Google Scholar] [CrossRef]
  30. Levin, M. Darwin’s agential materials: evolutionary implications of multiscale competency in developmental biology. Cellular and Molecular Life Sciences 2023, 80. [Google Scholar] [CrossRef] [PubMed]
  31. Kamm, R.D.; Bashir, R. Creating Living Cellular Machines. Annals of Biomedical Engineering 2013, 42, 445–459. [Google Scholar] [CrossRef]
  32. Kamm, R.D.; Bashir, R.; Arora, N.; Dar, R.D.; Gillette, M.U.; others. Perspective: The promise of multi-cellular engineered living systems. APL Bioengineering 2018, 2. [Google Scholar] [CrossRef]
  33. Bongard, J.; Levin, M. Living Things Are Not (20th Century) Machines: Updating Mechanism Metaphors in Light of the Modern Science of Machine Behavior. Frontiers in Ecology and Evolution 2021, 9. [Google Scholar] [CrossRef]
  34. Bongard, J.; Levin, M. There’s Plenty of Room Right Here: Biological Systems as Evolved, Overloaded, Multi-Scale Machines. Biomimetics 2023, 8, 110. [Google Scholar] [CrossRef] [PubMed]
  35. Bashor, C.J.; Horwitz, A.A.; Peisajovich, S.G.; Lim, W.A. Rewiring cells: synthetic biology as a tool to interrogate the organizational principles of living systems. Annual review of biophysics 2010, 39, 515–537. [Google Scholar] [CrossRef] [PubMed]
  36. Nielsen, A.A.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic circuit design automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed]
  37. Cameron, D.E.; Bashor, C.J.; Collins, J.J. A brief history of synthetic biology. Nature Reviews Microbiology 2014, 12, 381–390. [Google Scholar] [CrossRef] [PubMed]
  38. Ma, Y.; Budde, M.W.; Mayalu, M.N.; Zhu, J.; Lu, A.C.; Murray, R.M.; Elowitz, M.B. Synthetic mammalian signaling circuits for robust cell population control. Cell 2022, 185, 967–979. [Google Scholar] [CrossRef] [PubMed]
  39. Youk, H.; Lim, W.A. Secreting and Sensing the Same Molecule Allows Cells to Achieve Versatile Social Behaviors. Science 2014, 343. [Google Scholar] [CrossRef] [PubMed]
  40. Amos, M. Cellular computing; Systems Biology, 2004. [CrossRef]
  41. Grozinger, L.; Amos, M.; Gorochowski, T.E.; Carbonell, P.; Oyarzún, D.A.; Stoof, R.; Fellermann, H.; Zuliani, P.; Tas, H.; Goñi-Moreno, A. Pathways to cellular supremacy in biocomputing. Nature communications 2019, 10, 5250. [Google Scholar] [CrossRef] [PubMed]
  42. Goñi-Moreno, Á. Biocomputation: Moving Beyond Turing with Living Cellular Computers. Communications of the ACM 2024, 67, 70–77. [Google Scholar] [CrossRef]
  43. Tamsir, A.; Tabor, J.J.; Voigt, C.A. Robust multicellular computing using genetically encoded NOR gates and chemical `wires’. Nature 2011, 469, 212–215. [Google Scholar] [CrossRef]
  44. Regot, S.; Macia, J.; Conde, N.; Furukawa, K.; Kjellén, J.; Peeters, T.; Hohmann, S.; de Nadal, E.; Posas, F.; Solé, R. Distributed biological computation with multicellular engineered networks. Nature 2011, 469, 207–211. [Google Scholar] [CrossRef]
  45. Moon, T.S.; Lou, C.; Tamsir, A.; Stanton, B.C.; Voigt, C.A. Genetic programs constructed from layered logic gates in single cells. Nature 2012, 491, 249–253. [Google Scholar] [CrossRef]
  46. Macia, J.; Manzoni, R.; Conde, N.; Urrios, A.; de Nadal, E.; Solé, R.; Posas, F. Implementation of Complex Biological Logic Circuits Using Spatially Distributed Multicellular Consortia. PLOS Computational Biology 2016, 12, e1004685. [Google Scholar] [CrossRef]
  47. Song, H.; Ding, M.Z.; Jia, X.Q.; Ma, Q.; Yuan, Y.J. Synthetic microbial consortia: from systematic analysis to construction and applications. Chemical Society Reviews 2014, 43, 6954–6981. [Google Scholar] [CrossRef] [PubMed]
  48. Steinberg, M.S. Differential adhesion in morphogenesis: a modern view. Current opinion in genetics & development 2007, 17, 281–286. [Google Scholar] [CrossRef]
  49. Krens, S.G.; Heisenberg, C.P. Cell sorting in development. Current topics in developmental biology 2011, 95, 189–213. [Google Scholar] [CrossRef] [PubMed]
  50. Davies, J.A. Synthetic morphology: prospects for engineered, self-constructing anatomies. Journal of anatomy 2008, 212, 707–719. [Google Scholar] [CrossRef]
  51. Urrios, A.; Macia, J.; Manzoni, R.; Conde, N.; Bonforti, A.; de Nadal, E.; Posas, F.; Solé, R. A Synthetic Multicellular Memory Device. ACS Synthetic Biology 2016, 5, 862–873. [Google Scholar] [CrossRef] [PubMed]
  52. Macia, J.; Vidiella, B.; Solé, R.V. Synthetic associative learning in engineered multicellular consortia. Journal of The Royal Society Interface 2017, 14, 20170158. [Google Scholar] [CrossRef]
  53. Macia, J.; Sole, R. How to Make a Synthetic Multicellular Computer. PLoS ONE 2014, 9, e81248. [Google Scholar] [CrossRef]
  54. Hopfield, J. Physics, computation, and why biology looks so different. Journal of Theoretical Biology 1994, 171, 53–60. [Google Scholar] [CrossRef]
  55. Voigt, C.A. Genetic parts to program bacteria. Current opinion in biotechnology 2006, 17, 548–557. [Google Scholar] [CrossRef] [PubMed]
  56. Ruder, W.C.; Lu, T.; Collins, J.J. Synthetic biology moving into the clinic. Science 2011, 333, 1248–1252. [Google Scholar] [CrossRef]
  57. Benenson, Y. Biomolecular computing systems: principles, progress and potential. Nature Reviews Genetics 2012, 13, 455–468. [Google Scholar] [CrossRef] [PubMed]
  58. Brophy, J.A.; Voigt, C.A. Principles of genetic circuit design. Nature methods 2014, 11, 508–520. [Google Scholar] [CrossRef] [PubMed]
  59. Dannenfelser, R.; Allen, G.M.; VanderSluis, B.; Koegel, A.K.; Levinson, S.; Stark, S.R.; Yao, V.; Tadych, A.; Troyanskaya, O.G.; Lim, W.A. Discriminatory Power of Combinatorial Antigen Recognition in Cancer T Cell Therapies. Cell Systems 2020, 11, 215–228. [Google Scholar] [CrossRef]
  60. Vidiella, B.; Guillamon, A.; Sardanyés, J.; Maull, V.; Pla, J.; Conde, N.; Solé, R. Engineering self-organized criticality in living cells. Nature communications 2021, 12, 4415. [Google Scholar] [CrossRef]
  61. Solé, R.; Amor, D.R.; Duran-Nebreda, S.; Conde-Pueyo, N.; Carbonell-Ballestero, M.; Montañez, R. Synthetic collective intelligence. Biosystems 2016, 148, 47–61. [Google Scholar] [CrossRef]
  62. Solé, R.V.; Macia, J. Expanding the landscape of biological computation with synthetic multicellular consortia. Natural Computing 2013, 12, 485–497. [Google Scholar] [CrossRef]
  63. Solé, R.; Valverde, S. Evolving complexity: how tinkering shapes cells, software and ecological networks. Philosophical Transactions of the Royal Society B: Biological Sciences 2020, 375, 20190325. [Google Scholar] [CrossRef]
  64. Koza, J.R.; Keane, M.A.; Streeter, M.J. Evolving inventions. Scientific American 2003, 288, 52–59. [Google Scholar] [CrossRef] [PubMed]
  65. Wang, B.; Kitney, R.I.; Joly, N.; Buck, M. Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology. Nature communications 2011, 2, 508. [Google Scholar] [CrossRef] [PubMed]
  66. Moreno, A.; Etxeberria, A. Agency in natural and artificial systems. Artificial Life 2005, 11, 161–175. [Google Scholar] [CrossRef] [PubMed]
  67. Moreno, A. On minimal autonomous agency: natural and artificial. Complex Systems 2018, 27, 289–313. [Google Scholar] [CrossRef]
  68. Bonner, J.T. The evolution of complexity by means of natural selection; Princeton University Press, 1988. [CrossRef]
  69. Valentine, J.W.; Collins, A.G.; Meyer, C.P. Morphological complexity increase in metazoans. Paleobiology 1994, 20, 131–142. [Google Scholar] [CrossRef]
  70. Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of theoretical biology 1969, 22, 437–467. [Google Scholar] [CrossRef] [PubMed]
  71. Huang, S. Multistability and multicellularity: cell fates as high-dimensional attractors of gene regulatory networks. In Computational Systems Biology; Elsevier, 2006; pp. 293–326. [CrossRef]
  72. Koseska, A.; Zaikin, A.; Kurths, J.; García-Ojalvo, J. Timing Cellular Decision Making Under Noise via Cell–Cell Communication. PLoS ONE 2009, 4, e4872. [Google Scholar] [CrossRef] [PubMed]
  73. Gardner, T.S.; Cantor, C.R.; Collins, J.J. Construction of a genetic toggle switch in Escherichia coli. Nature 2000, 403, 339–342. [Google Scholar] [CrossRef]
  74. Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
  75. Zhou, J.X.; Huang, S. Understanding gene circuits at cell-fate branch points for rational cell reprogramming. Trends in Genetics 2011, 27, 55–62. [Google Scholar] [CrossRef]
  76. Deutsch, A.; Dormann, S. Mathematical modeling of biological pattern formation; Springer, 2005; pp. 49–61. [CrossRef]
  77. Ollé-Vila, A.; Duran-Nebreda, S.; Conde-Pueyo, N.; Montañez, R.; Solé, R. A morphospace for synthetic organs and organoids: the possible and the actual. Integrative Biology 2016, 8, 485–503. [Google Scholar] [CrossRef]
  78. Mombach, J.C.; Glazier, J.A.; Raphael, R.C.; Zajac, M. Quantitative comparison between differential adhesion models and cell sorting in the presence and absence of fluctuations. Physical Review Letters 1995, 75, 2244. [Google Scholar] [CrossRef]
  79. Glass, D.S.; Riedel-Kruse, I.H. A synthetic bacterial cell-cell adhesion toolbox for programming multicellular morphologies and patterns. Cell 2018, 174, 649–658. [Google Scholar] [CrossRef] [PubMed]
  80. Stevens, A.J.; Harris, A.R.; Gerdts, J.; Kim, K.H.; Trentesaux, C.; Ramirez, J.T.; McKeithan, W.L.; Fattahi, F.; Klein, O.D.; Fletcher, D.A.; others. Programming multicellular assembly with synthetic cell adhesion molecules. Nature 2023, 614, 144–152. [Google Scholar] [CrossRef]
  81. Mjolsness, E.; Sharp, D.H.; Reinitz, J. A connectionist model of development. Journal of theoretical Biology 1991, 152, 429–453. [Google Scholar] [CrossRef] [PubMed]
  82. Salazar-Ciudad, I.; Garcia-Fernández, J.; Solé, R.V. Gene networks capable of pattern formation: from induction to reaction–diffusion. Journal of theoretical biology 2000, 205, 587–603. [Google Scholar] [CrossRef]
  83. Solé, R.V.; Salazar-Ciudad, I.; Garcia-Fernández, J. Common pattern formation, modularity and phase transitions in a gene network model of morphogenesis. Physica A: Statistical Mechanics and its Applications 2002, 305, 640–654. [Google Scholar] [CrossRef]
  84. Koch, A.J.; Meinhardt, H. Biological pattern formation: from basic mechanisms to complex structures. Reviews of modern physics 1994, 66, 1481. [Google Scholar] [CrossRef]
  85. Murray, J.D. Mathematical biology II, 3 ed.; Interdisciplinary applied mathematics, Springer: New York, NY, 2002. [Google Scholar]
  86. Sagués, F.; Sancho, J.M.; García-Ojalvo, J. Spatiotemporal order out of noise. Reviews of Modern Physics 2007, 79, 829–882. [Google Scholar] [CrossRef]
  87. Munteanu, A.; Sole, R.V. Neutrality and robustness in evo-devo: emergence of lateral inhibition. PLoS computational biology 2008, 4, e1000226. [Google Scholar] [CrossRef]
  88. Cotterell, J.; Sharpe, J. An atlas of gene regulatory networks reveals multiple three-gene mechanisms for interpreting morphogen gradients. Molecular systems biology 2010, 6, 425. [Google Scholar] [CrossRef] [PubMed]
  89. Solé, R.V.; Fernández, P.; Kauffman, S.A. Adaptive walks in a gene network model of morphogenesis: insights into the Cambrian explosion. arXiv preprint q-bio/0311013, -8. [CrossRef]
  90. Stern, M.; Murugan, A. Learning without neurons in physical systems. Annual Review of Condensed Matter Physics 2023, 14, 417–441. [Google Scholar] [CrossRef]
  91. Stern, M.; Liu, A.J.; Balasubramanian, V. Physical effects of learning. Physical Review E 2024, 109, 024311. [Google Scholar] [CrossRef] [PubMed]
  92. Pfeifer, R.; Scheier, C. Understanding intelligence; MIT press, 2001. [CrossRef]
  93. De Domenico, M.; Solé-Ribalta, A.; Cozzo, E.; Kivelä, M.; Moreno, Y.; Porter, M.A.; Gómez, S.; Arenas, A. Mathematical formulation of multilayer networks. Physical Review X 2013, 3, 041022. [Google Scholar] [CrossRef]
  94. Ball, P. Organisms as agents of evolution. John Templeton Foundation: West Conshohocken, PA, USA.
  95. Corrò, C.; Novellasdemunt, L.; Li, V.S. A brief history of organoids. American Journal of Physiology-Cell Physiology 2020, 319, C151–C165. [Google Scholar] [CrossRef] [PubMed]
  96. Lancaster, M.A.; Knoblich, J.A. Organogenesis in a dish: modeling development and disease using organoid technologies. Science 2014, 345, 1247125. [Google Scholar] [CrossRef] [PubMed]
  97. Sasai, Y. Cytosystems dynamics in self-organization of tissue architecture. Nature 2013, 493, 318–326. [Google Scholar] [CrossRef]
  98. Moris, N.; Anlas, K.; van den Brink, S.C.; Alemany, A.; Schröder, J.; Ghimire, S.; Balayo, T.; van Oudenaarden, A.; Martinez Arias, A. An in vitro model of early anteroposterior organization during human development. Nature 2020, 582, 410–415. [Google Scholar] [CrossRef] [PubMed]
  99. Beccari, L.; Moris, N.; Girgin, M.; Turner, D.A.; Baillie-Johnson, P.; Cossy, A.C.; Lutolf, M.P.; Duboule, D.; Arias, A.M. Multi-axial self-organization properties of mouse embryonic stem cells into gastruloids. Nature 2018, 562, 272–276. [Google Scholar] [CrossRef]
  100. Lane, N. Life ascending: the ten great inventions of evolution; WW Norton: New York, NY, 2010. [Google Scholar]
  101. Llinás, R.R. I of the vortex: From neurons to self; A Bradford Book, Bradford Books: Cambridge, MA, 2002. [Google Scholar]
  102. Jablonka, E.; Lamb, M.J. The evolution of information in the major transitions. Journal of theoretical biology 2006, 239, 236–246. [Google Scholar] [CrossRef]
  103. Gunawardena, J. Learning Outside the Brain: Integrating Cognitive Science and Systems Biology. Proceedings of the IEEE 2022, 110, 590–612. [Google Scholar] [CrossRef]
  104. Gumuskaya, G.; Srivastava, P.; Cooper, B.G.; Lesser, H.; Semegran, B.; Garnier, S.; Levin, M. Motile Living Biobots Self-Construct from Adult Human Somatic Progenitor Seed Cells. Advanced Science 2024, 11, 2303575. [Google Scholar] [CrossRef] [PubMed]
  105. Fields, C.; Levin, M. Competency in Navigating Arbitrary Spaces as an Invariant for Analyzing Cognition in Diverse Embodiments. Entropy 2022, 24, 819. [Google Scholar] [CrossRef] [PubMed]
  106. Chernet, B.T.; Levin, M. Transmembrane voltage potential is an essential cellular parameter for the detection and control of tumor development in aXenopusmodel. Disease Models & Mechanisms 2013, 6, 595–607. [Google Scholar] [CrossRef]
  107. Levin, M. Bioelectrical approaches to cancer as a problem of the scaling of the cellular self. Progress in Biophysics and Molecular Biology 2021, 165, 102–113. [Google Scholar] [CrossRef]
  108. Smith, J.M.; Burian, R.; Kauffman, S.; Alberch, P.; Campbell, J.; Goodwin, B.; Lande, R.; Raup, D.; Wolpert, L. Developmental constraints and evolution: a perspective from the Mountain Lake conference on development and evolution. The Quarterly Review of Biology 1985, 60, 265–287. [Google Scholar] [CrossRef]
  109. Ferrell, J.E. Bistability, Bifurcations, and Waddington’s Epigenetic Landscape. Current Biology 2012, 22, R458–R466. [Google Scholar] [CrossRef] [PubMed]
  110. Biswas, S.; Manicka, S.; Hoel, E.; Levin, M. Gene regulatory networks exhibit several kinds of memory: Quantification of memory in biological and random transcriptional networks. iScience 2021, 24, 102131. [Google Scholar] [CrossRef] [PubMed]
  111. Biswas, S.; Clawson, W.; Levin, M. Learning in Transcriptional Network Models: Computational Discovery of Pathway-Level Memory and Effective Interventions. International Journal of Molecular Sciences 2022, 24, 285. [Google Scholar] [CrossRef]
  112. Yang, C.Y.; Bialecka-Fornal, M.; Weatherwax, C.; Larkin, J.W.; Prindle, A.; Liu, J.; Garcia-Ojalvo, J.; Süel, G.M. Encoding Membrane-Potential-Based Memory within a Microbial Community. Cell Systems 2020, 10, 417–423. [Google Scholar] [CrossRef]
  113. Gabalda-Sagarra, M.; Carey, L.B.; Garcia-Ojalvo, J. Recurrence-based information processing in gene regulatory networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 2018, 28, 106313. [Google Scholar] [CrossRef] [PubMed]
  114. Vidal-Saez, M.S.; Vilarroya, O.; Garcia-Ojalvo, J. Biological computation through recurrence. Biochemical and Biophysical Research Communications 2024, 728, 150301. [Google Scholar] [CrossRef]
  115. Wilson, E.O. The insect societies; Harvard University Press: London, England, 1971. [Google Scholar]
  116. Bonabeau, E.; Theraulaz, G.; Deneubourg, J.L.; Aron, S.; Camazine, S. Self-organization in social insects. Trends in ecology & evolution 1997, 12, 188–193. [Google Scholar] [CrossRef]
  117. Gordon, D.M. Ants at work: how an insect society is organized; Simon and Schuster, 1999.
  118. Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm intelligence: from natural to artificial systems; Oxford university press, 1999; pp. I–XII, 1–307. [CrossRef]
  119. Prindle, A.; Liu, J.; Asally, M.; Ly, S.; Garcia-Ojalvo, J.; Süel, G.M. Ion channels enable electrical communication in bacterial communities. Nature 2015, 527, 59–63. [Google Scholar] [CrossRef] [PubMed]
  120. Larkin, J.W.; Zhai, X.; Kikuchi, K.; Redford, S.E.; Prindle, A.; Liu, J.; Greenfield, S.; Walczak, A.M.; Garcia-Ojalvo, J.; Mugler, A.; Süel, G.M. Signal Percolation within a Bacterial Community. Cell Systems 2018, 7, 137–145. [Google Scholar] [CrossRef] [PubMed]
  121. Martinez-Corral, R.; Liu, J.; Prindle, A.; Süel, G.M.; Garcia-Ojalvo, J. Metabolic basis of brain-like electrical signalling in bacterial communities. Philosophical Transactions of the Royal Society B 2019, 374, 20180382. [Google Scholar] [CrossRef]
  122. Libby, E.; Rainey, P.B. A conceptual framework for the evolutionary origins of multicellularity. Physical biology 2013, 10, 035001. [Google Scholar] [CrossRef] [PubMed]
  123. Yamamoto, H.; Moriya, S.; Ide, K.; Hayakawa, T.; Akima, H.; Sato, S.; Kubota, S.; Tanii, T.; Niwano, M.; Teller, S.; Soriano, J.; Hirano-Iwata, A. Impact of modular organization on dynamical richness in cortical networks. Science Advances 2018, 4. [Google Scholar] [CrossRef] [PubMed]
  124. Yamamoto, H.; Spitzner, F.P.; Takemuro, T.; Buendía, V.; Murota, H.; Morante, C.; Konno, T.; Sato, S.; Hirano-Iwata, A.; Levina, A.; Priesemann, V.; Muñoz, M.A.; Zierenberg, J.; Soriano, J. Modular architecture facilitates noise-driven control of synchrony in neuronal networks. Science Advances 2023, 9. [Google Scholar] [CrossRef]
  125. Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. Kinematic self-replication in reconfigurable organisms. Proceedings of the National Academy of Sciences 2021, 118, e2112672118. [Google Scholar] [CrossRef]
  126. Gregory, T.R. The evolution of complex organs. Evolution: Education and Outreach 2008, 1, 358–389. [Google Scholar] [CrossRef]
  127. Theraulaz, G.; Bonabeau, E.; Deneubourg, J.L. The origin of nest complexity in social insects. Complexity 1998, 3, 15–25. [Google Scholar] [CrossRef]
  128. Bonabeau, E.; Theraulaz, G.; Deneubourg, J.L.; Franks, N.R.; Rafelsberger, O.; Joly, J.L.; Blanco, S. A model for the emergence of pillars, walls and royal chambers in termite nests. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 1998, 353, 1561–1576. [Google Scholar] [CrossRef]
  129. Turner, J.S. Termites as models of swarm cognition. Swarm intelligence 2011, 5, 19–43. [Google Scholar] [CrossRef]
  130. Foo, J.L.; Ling, H.; Lee, Y.S.; Chang, M.W. Microbiome engineering: Current applications and its future. Biotechnology journal 2017, 12, 1600099. [Google Scholar] [CrossRef] [PubMed]
  131. Dou, J.; Bennett, M.R. Synthetic biology and the gut microbiome. Biotechnology journal 2018, 13, 1700159. [Google Scholar] [CrossRef]
  132. Solé, R.V.; Montañez, R.; Duran-Nebreda, S. Synthetic circuit designs for earth terraformation. Biology Direct 2015, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
  133. Conde-Pueyo, N.; Vidiella, B.; Sardanyés, J.; Berdugo, M.; Maestre, F.T.; De Lorenzo, V.; Solé, R. Synthetic biology for terraformation lessons from mars, earth, and the microbiome. life 2020, 10, 14. [Google Scholar] [CrossRef] [PubMed]
  134. Foster, K.R.; Schluter, J.; Coyte, K.Z.; Rakoff-Nahoum, S. The evolution of the host microbiome as an ecosystem on a leash. Nature 2017, 548, 43–51. [Google Scholar] [CrossRef]
  135. Zhang, F.; Guo, Z.; Li, Z.; Luan, H.; Yu, Y.; Zhu, A.T.; Ding, S.; Gao, W.; Fang, R.H.; Zhang, L.; others. Biohybrid microrobots locally and actively deliver drug-loaded nanoparticles to inhibit the progression of lung metastasis. Science Advances 2024, 10, eadn6157. [Google Scholar] [CrossRef]
  136. Kunitomo, H.; Sato, H.; Iwata, R.; Satoh, Y.; Ohno, H.; Yamada, K.; Iino, Y. Concentration memory-dependent synaptic plasticity of a taste circuit regulates salt concentration chemotaxis in Caenorhabditis elegans. Nature Communications 2013, 4. [Google Scholar] [CrossRef] [PubMed]
  137. Hiroki, S.; Yoshitane, H.; Mitsui, H.; Sato, H.; Umatani, C.; Kanda, S.; Fukada, Y.; Iino, Y. Molecular encoding and synaptic decoding of context during salt chemotaxis in C. elegans. Nature Communications 2022, 13. [Google Scholar] [CrossRef] [PubMed]
  138. Vidal-Saez, M.S.; Vilarroya, O.; Garcia-Ojalvo, J. A multiscale sensorimotor model of experience-dependent behavior in a minimal organism. Biophysical Journal 2024, 123, 1654–1667. [Google Scholar] [CrossRef] [PubMed]
  139. Lyon, P.; Keijzer, F.; Arendt, D.; Levin, M. Reframing cognition: getting down to biological basics. Philosophical Transactions of the Royal Society B: Biological Sciences 2021, 376, 20190750. [Google Scholar] [CrossRef] [PubMed]
  140. Bongard, J.C. Evolutionary robotics: Taking a biologically inspired approach to the design of autonomous, adaptive machines. Communications of the ACM 2013, 56, 74–83. [Google Scholar] [CrossRef]
  141. Nolfi, S.; Bongard, J.; Husbands, P.; Floreano, D. , Evolutionary Robotics. In Springer Handbooks; Springer International Publishing, 2016; p. 2035–2068. [CrossRef]
  142. Seilacher, A. Fossil behavior. Scientific American 1967, 217, 72–83. [Google Scholar] [CrossRef]
  143. Plotnick, R.E. Behavioral biology of trace fossils. Paleobiology 2012, 38, 459–473. [Google Scholar] [CrossRef]
  144. Andrianantoandro, E.; Basu, S.; Karig, D.K.; Weiss, R. Synthetic biology: new engineering rules for an emerging discipline. Molecular systems biology 2006, 2, 2006–0028. [Google Scholar] [CrossRef] [PubMed]
  145. Lopatkin, A.J.; Collins, J.J. Predictive biology: modelling, understanding and harnessing microbial complexity. Nature Reviews Microbiology 2020, 18, 507–520. [Google Scholar] [CrossRef]
  146. Lazebnik, Y. Can a biologist fix a radio?—Or, what I learned while studying apoptosis. Cancer cell 2002, 2, 179–182. [Google Scholar] [CrossRef]
  147. Lobo, D.; Solano, M.; Bubenik, G.A.; Levin, M. A linear-encoding model explains the variability of the target morphology in regeneration. Journal of The Royal Society Interface 2014, 11, 20130918. [Google Scholar] [CrossRef] [PubMed]
  148. Corominas-Murtra, B.; Petridou, N. Viscoelastic Networks: Forming Cells and Tissues. Frontiers in Physics 2021, 9. [Google Scholar] [CrossRef]
  149. Petridou, N.I.; Corominas-Murtra, B.; Heisenberg, C.P.; Hannezo, E. Rigidity percolation uncovers a structural basis for embryonic tissue phase transitions. Cell 2021, 184, 1914–1928. [Google Scholar] [CrossRef] [PubMed]
  150. Lenne, P.F.; Trivedi, V. Sculpting tissues by phase transitions. Nature Communications 2022, 13, 664. [Google Scholar] [CrossRef] [PubMed]
1
Plants follow a very different organization plant and developmental trajectories, with no fixed numbers of organs, such as leaves, that are highly redundant parts.
2
This hypothetical creature is inspired by Laplace’s Demon, proposed by Pierre-Simon Laplace, capable of knowing the precise location and momentum of every atom in the universe. With this information, it could predict the past and future of every particle, demonstrating a deterministic universe where the future is entirely predictable given complete knowledge of the present.
Preprints 112964 g001
Figure 1. Natural and synthetic multicellularity. These case studies include three natural examples (left column) of patterns and processes associated with hierarchical and emergent mechanisms and evolutionary dynamics. A classic example of a top-down mechanism in morphogenesis is the formation of gradients and stripes in Drosophila (a). These processes can be approached by (b) a synthetic band-pass filter using engineered E coli (after [4]), (b) the generation of multiple coexisting cell fates [5] and (d) programmable symmetry breaking-induced structure formation (from [6]). Morphogenetic processes are spatially organized through multiscale feedback loops shaping embryos (e; image courtesy of James Sharpe). Synthetic counterparts of the underlying emergent phenomena include (f) kidney organoid development, (g) Turing-like branching morphogenesis of bacteria (g) and (h) the development of Anthrobots. The simplest, aneural metazoans are exemplified by Placozoans (image by Sebastian R. Najle, CRG) (i), while evolved cell assemblies emerge under synthetic selection mechanisms, including cell-cell adhesion to escape from predators (j; adapted from [7]), yeast MC aggregates (k; adapted from [8]) and Xenobots (l). The latter were obtained through a combination of in silico evolutionary algorithms and bioengineering.
Figure 1. Natural and synthetic multicellularity. These case studies include three natural examples (left column) of patterns and processes associated with hierarchical and emergent mechanisms and evolutionary dynamics. A classic example of a top-down mechanism in morphogenesis is the formation of gradients and stripes in Drosophila (a). These processes can be approached by (b) a synthetic band-pass filter using engineered E coli (after [4]), (b) the generation of multiple coexisting cell fates [5] and (d) programmable symmetry breaking-induced structure formation (from [6]). Morphogenetic processes are spatially organized through multiscale feedback loops shaping embryos (e; image courtesy of James Sharpe). Synthetic counterparts of the underlying emergent phenomena include (f) kidney organoid development, (g) Turing-like branching morphogenesis of bacteria (g) and (h) the development of Anthrobots. The simplest, aneural metazoans are exemplified by Placozoans (image by Sebastian R. Najle, CRG) (i), while evolved cell assemblies emerge under synthetic selection mechanisms, including cell-cell adhesion to escape from predators (j; adapted from [7]), yeast MC aggregates (k; adapted from [8]) and Xenobots (l). The latter were obtained through a combination of in silico evolutionary algorithms and bioengineering.
Preprints 112964 g001
Preprints 112964 g002
Figure 2. Synthetic cellular computation. Engineering cells at the gene level have provided a broad range of simple computational circuits, including both unicellular (UC) and multicellular (MC) designs. In (a), a biocomputation space involving implementations based on consortia is shown. Here, the locations are relative to each other. We use three axes in this space: agency, computational complexity and the diversity of network interactions among cells. The bottom left of this cube includes several implementations that use a unicellular chassis, whereas MC consortia are found close to the right wall (grey area). Some designs, such as flip-flop memory devices [51] or learning systems [52], are obtained using a microbial consortium. However, computational designs can depart from nature and engineering, as shown by synthetic Distributed Computation models [44,46,53]. An illustration is provided in (b-c). In (b), a single-cell implementation of a multiplexer circuit (MUX), along with the truth table (left) and the corresponding combinatorial circuit (right). A simpler two-cell MUX is shown in (c) and involves much simpler circuits and reusable parts; notice that the two cells are not connected.
Figure 2. Synthetic cellular computation. Engineering cells at the gene level have provided a broad range of simple computational circuits, including both unicellular (UC) and multicellular (MC) designs. In (a), a biocomputation space involving implementations based on consortia is shown. Here, the locations are relative to each other. We use three axes in this space: agency, computational complexity and the diversity of network interactions among cells. The bottom left of this cube includes several implementations that use a unicellular chassis, whereas MC consortia are found close to the right wall (grey area). Some designs, such as flip-flop memory devices [51] or learning systems [52], are obtained using a microbial consortium. However, computational designs can depart from nature and engineering, as shown by synthetic Distributed Computation models [44,46,53]. An illustration is provided in (b-c). In (b), a single-cell implementation of a multiplexer circuit (MUX), along with the truth table (left) and the corresponding combinatorial circuit (right). A simpler two-cell MUX is shown in (c) and involves much simpler circuits and reusable parts; notice that the two cells are not connected.
Preprints 112964 g002
Preprints 112964 g003
Figure 3. A space for synthetic embodied MC.. Spatial self-organization rules associated with cell-cell nonlinear interactions are responsible for SO phenomena such as re-aggregation of tissues (a-c) due to differential adhesion (image adapted from [78]). This SO rule is part of the processes shaping MC embodied complexity, captured in (d) using a 3D space for natural (dark spheres) and engineered or artificially evolved multicellular systems (light spheres). Each system is located in terms of its relative positions, not in quantitative terms. Here, the three axes include (a) spatial complexity (how different cells are distributed over space), (b) developmental complexity (the relative relevance of self-organization and hierarchy participates in the building of the agent) and (c) computational complexity axis. The latter aims to capture the complexity of the computational decision-making actions displayed by each system. The current synthetic MC designs occupy the left corner, where synthetic circuits (dark grey) and embodied systems (light grey) are highlighted. A large void on the right reminds us of the large gap between current achievements and the natural counterparts of MC complexity.
Figure 3. A space for synthetic embodied MC.. Spatial self-organization rules associated with cell-cell nonlinear interactions are responsible for SO phenomena such as re-aggregation of tissues (a-c) due to differential adhesion (image adapted from [78]). This SO rule is part of the processes shaping MC embodied complexity, captured in (d) using a 3D space for natural (dark spheres) and engineered or artificially evolved multicellular systems (light spheres). Each system is located in terms of its relative positions, not in quantitative terms. Here, the three axes include (a) spatial complexity (how different cells are distributed over space), (b) developmental complexity (the relative relevance of self-organization and hierarchy participates in the building of the agent) and (c) computational complexity axis. The latter aims to capture the complexity of the computational decision-making actions displayed by each system. The current synthetic MC designs occupy the left corner, where synthetic circuits (dark grey) and embodied systems (light grey) are highlighted. A large void on the right reminds us of the large gap between current achievements and the natural counterparts of MC complexity.
Preprints 112964 g003
Preprints 112964 g004
Figure 4. Prediction and emergence in multicellularity. One major challenge for synthetic multicellular designs is associated with the lack of predictability that would be in place if the genotype-phenotype map were simple and different scales reducible to lower-level entities. Here we depict the “Waddington demon”: an idealized entity trying to predict higher-scale structures (organs, embryos or organisms) from the observable microscopic dynamics (genes, gene interactions and early developmental states). This cartoon summarizes the difficulties in predicting multicellular complexity, both within developmental biology and in bioengineering. Because of the presence of emergent phenomena, such a prediction might be difficult to achieve unless we use the right scale, ignoring the details on the lower levels (drawing by R. Solé).
Figure 4. Prediction and emergence in multicellularity. One major challenge for synthetic multicellular designs is associated with the lack of predictability that would be in place if the genotype-phenotype map were simple and different scales reducible to lower-level entities. Here we depict the “Waddington demon”: an idealized entity trying to predict higher-scale structures (organs, embryos or organisms) from the observable microscopic dynamics (genes, gene interactions and early developmental states). This cartoon summarizes the difficulties in predicting multicellular complexity, both within developmental biology and in bioengineering. Because of the presence of emergent phenomena, such a prediction might be difficult to achieve unless we use the right scale, ignoring the details on the lower levels (drawing by R. Solé).
Preprints 112964 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated