Meta-Analysis of Genuine and Fake p-Values

Preprint

Article

Meta-Analysis of Genuine and Fake p-Values

This version is not peer-reviewed.

This version is not peer-reviewed.

Altmetrics

Downloads

115

Views

Comments

Submitted:

23 July 2024

Posted:

24 July 2024

You are already at the latest version

Abstract

For Sir Ronald Fisher, it is important to consistently obtain significant p-values to support an experimental hypothesis. So, replicating experiments to obtain independent p-values is a legitimate and desirable research practice. Several simple statistics have been proposed to meta-analyze p-values, all assuming that they are genuine, i.e. observations from independent standard Uniform random variables. But, as publication bias favors the studies that report "significant" p-values, when a p>0.05 is obtained for the outcome of an experiment, some researchers will "fall into temptation" and decide to replicate the experiment in the hope of getting a smaller second p-value, ideally a significant one. Consequently, if the smallest of two p-values is reported, this is a Beta(1,2) distributed "fake" p-value, not a uniformly distributed genuine p-value. This is an unacceptable scientific research practice, and moreover the detection of fake p-values is unpractical. Even when it is possible, the analytic results to accommodate their existence in combined tests are cumbersome. For an informed decision, inclusive when the presence of fake p-values in a sample of p-values to be meta-analyzed is probable, tables with simulated critical values for the usual combined testing are supplied. This will also allow comparisons to be made between several combined tests.

Keywords:

Subject:

Computer Science and Mathematics - Probability and Statistics

Supplementary Material

supplementary.pdf (3.92MB )

1. Introduction

The use of p-values, defined as the probability of obtaining a result equal to or more extreme than what was actually observed, under a null hypothesis of no effect or no difference, is generally credited to Pearson [1], although Kennedy-Shaffer [2] extensively lists its previous use, tracing it back to Arbuthnott [3].

Fisher [4,5] popularized the concept, which plays a central role in his theory of significance testing. According to Fisher [6], a p-value should function as an informal index to evaluate the discrepancy between the data and the hypothesis under investigation. This closely matches the meaning of significance of Edgeworth [7], who considered a difference to be "significant and not accidental" if it was unlikely to have resulted from chance alone. On the other hand, a p-value smaller than 0.05, considered by Fisher [4,5] to be a threshold for a significant value, only hints that the experiment should be repeated. If subsequent studies also generate significant p-values, then it is fair to conclude that the observed effects are unlikely to result from chance alone. In this regard, Fisher [8] states that “A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this[P=0.05]level of significance”. Therefore, a significant p-value just indicates that further experiments should be carried out.

Obtaining significant p-values raises the issue of reproducibility (cf. Utts [9], Greenwald et al. [10], or Colquhoun [11]), which in turn requires that the p-values obtained from the repeated experiments must be summarized into a combined p-value. Being well-aware of this, Fisher [6] was one of the first to meta-analyze p-values. Note, however, that a combined p-value is not, in general, a p-value in the strict sense of the definition (Vovk and Wang [12]).

Taking a different approach, Neyman and Pearson [13,14] developed a theory for hypothesis testing. Significance testing and hypothesis testing were in Fisher’s [15] and E. Pearson’s [16] points of view incompatible, but they have become so intertwined that they are regarded by most users as part of a single and coherent approach to statistical inference (Lehman [17]). The work of Cox et al. [18] is an excellent critical overview of significance testing, with stimulating discussions and reply.

Despite the original Neyman-Pearson standpoint that hypothesis testing limits the number of mistaken conclusions in the long run, the discomforting price of abandoning the ability to measure evidence and assess the truth from a single experiment was soon forgotten in favor of the methodology of using p-values. In other words, taking for granted that each study originates conclusions with certain error rates instead of adding evidence to that provided by other sources and other studies. This clearly generated plenty of bad science, raising doubts on many scientific papers, with p-values adding nothing to true scientific knowledge (Ioannidis [19,20]).

The editorials in The American Statistician vol. 70 (Wasserstein and Lazar [21]) and vol. 73 (Wasserstein et al. [22]), introducing issues discussing the dangers of abuse when using p-values and significance testing, summarize, to a certain extent, the fierce debate on the matter and have originated a warning on p-values in Nature (Baker [23]). To cite some highlights of the debate, while Goodman [24,25] and Kühberger et al. [26] warn on the fallacies and misconceptions of p-values, Benjamini [27] claims that the abuse is not the fault of the p-values, and Greenland [28] states that valid p-values behave exactly as they should. Critics of the p-values question why is it so hard to get rid of significance testing and p-values (Goodman [29]; Halsey [30]), or to put forward the need to complement p-values with effect size, sample size, or Bayes factors (Colquhoun [31]; Goodman et al. [32]; Rougier [33]), or even to recommend lowering the significance threshold to 0.005, cf. Di Leo and Sardanelli [34]. Murdoch et al. [35] emphasize that p-values are random variables and the innovating paper of Fraser [36] argues that the p-value function should be used instead of p-values.

The heart of the matter is that a single p-value should not be used as a sound basis for decision. As already mentioned, a low p-value is just an indication that the experiment should be repeated, and that only consistently obtaining low p-values uphold the conviction that the null hypothesis should be rejected, as both Fisher and Neyman and Pearson originally defended, although on opposite sides when it comes to statistical inference understanding. Therefore, replicating to obtain independent p-values in such contexts is legitimate, even desirable, and the resulting combined p-values are relevant for decision making under uncertainty.

The classical test statistics

T (P_{1}, \dots, P_{n})

for combining p-values assume that the p-values are all genuine (or bona fide), i.e. that under a null hypothesis the

P_{k}

’s are independent and identically distributed standard Uniform random variables. The combination of genuine p-values either relies on algebraic properties of Uniform random variables (order statistics, sums, products), or on transformations of standard Uniform random variables. In Section 2, a preliminary discussion of combining genuine p-values is undertaken.

However, the assumption that all

p_{k}

’s are genuine can be false, namely since the bias that results from some publication policies is the source of selective reporting of scientific findings. The greater opportunity researchers have to publish significant results than non-significant ones originates a so-called file drawer problem, thus exacerbating the publication bias phenomenon, which is discussed in Section 3. In addition to censoring p-values above traditional thresholds, publication bias can increase the temptation to replicate experiments in the hope of obtaining significant results.

Such scientific malpractice originates the report of fake p-values, as described in Section 4, where Mendel random variables, inspired by the Mendel-Fisher controversy, discussed in Fisher [37], Franklin et al. [38], and Pires and Branco [39], are introduced. While it is acceptable to think that the replication of p-values may strengthen the confidence in the idea that observed effects are unlikely to result from chance alone, the replication of p-values with the sole purpose of keeping only the most favorable ones is methodologically wrong, even possibly fraud, as Fisher [37] hinted in his discussion of Mendel’s results. The new trend of retaining only the p-values less than some specified cut-off value (Zaykin [40]; Neuhäuser and Bretz [41]; Zhang et al. [42]), or to use the product of the most significant p-values (Dudbridge and Koeleman [43]), have a similar effect of favoring the rejection of an overall null hypothesis, which in our opinion biases the conclusions. An extension of Deng and George’s [44] contraction, considered in SubSection 4.1, leads to ways of testing independence versus correlated P-values, in SubSection 4.2. In SubSection 4.3, the combination of genuine and fake p-values is investigated. This is a simple issue using Tippett’s [45] minimum method, but the analytical results for other ways of combining p-values, exemplified in SubSection 4.3, are complex to work with, even in the simplest case of just one fake p-value being present, making them useless from a practical point of view.

In these complex settings, simulation is a good tool for obtaining estimates of critical values for combined tests. Tables are supplied as Supplementary Materials, and in Section 5 their usefulness for an overall informed decision is illustrated. Section 6 summarizes the main findings with a comparison of different scenarios.

2. Combining Genuine $p$ -Values

Let us assume that the p-values

p_{k}

1 \leq k \leq n

, are known for testing

H_{0 k}

versus

H_{A k}

k = 1, \dots, n

, in n independent studies on some common topic, and that the objective is to achieve a decision on the overall problem

H_{0}^{*}

: all of the

H_{0 k}

are true versus

H_{A}^{*}

: some of the

H_{A k}

are true.

As there are many different ways in which

H_{0}^{*}

can be false, selecting an appropriate test is in general unfeasible. On the other hand, combining the available

p_{k}

’s so that

T (p_{1}, \dots, p_{n})

is the observed value of a random variable whose sampling distribution under

H_{0}^{*}

is known is a simple issue, since under

H_{0}^{*}

p = (p_{1}, \dots, p_{n})

is the observed value of a random vector

P = (P_{1}, \dots, P_{n})

with independent

Uniform (0, 1)

univariate margins, i.e. genuine p-values.

The classical statistics

T (P_{1}, \dots, P_{n})

for combining independent genuine p-values use:

—: transformations of the $P_{k} \sim Uniform (0, 1)$ random variables, namely $- 2 ln P_{k} \sim χ_{2}^{2}$ , $Φ^{- 1} (P_{k}) \sim Gaussian (0, 1)$ , where $Φ$ is the standard Gaussian cumulative distribution function, or $ln (\frac{P_{k}}{1 - P_{k}}) \sim Logistic (0, 1)$ (SubSection 2.1), or
—: sums, products and order statistics of $P_{1}, \dots, P_{n}$ , namely the Pythagorean harmonic, geometric and arithmetic means (SubSection 2.2).

Note, however, that there are good reasons to believe that not all

p_{k}

’s are genuine, either because some of the

H_{A k}

are true, or because there is truncation (Zaykin et al. [40]; Neuhäuser and Bretz [41]; Zhang et al. [42]) or censoring due to publication bias (two issues that will be addressed in Section 3), or even because of poor scientific methodology (possibly fraud) leading to the generation of fake p-values, as described in Section 4 in the context of the Mendel-Fisher controversy (Fisher [37]; Franklin et al. [38]; Pires and Branco [39]) and Mendel random variables.

2.1. Combining Transformed Genuine p-Values

In 1932, Fisher [6] (Section 21.1), from the fact that

- 2 ln P_{k} \sim χ_{2}^{2}

when

P_{k} \sim Uniform (0, 1)

, used the statistic

T_{F} (P_{1}, \dots, P_{n}) = - 2 \sum_{k = 1}^{n} ln P_{k} | H_{0}^{*} \sim χ_{2 n}^{2} .

Thus, the overall hypothesis

H_{0}^{*}

is rejected at a significance level

α

- 2 \sum_{k = 1}^{n} ln p_{k} > χ_{2 n, 1 - α}^{2}

, where

χ_{m, q}^{2}

denotes the q-th quantile of the chi-square distribution with m degrees of freedom.

In what concerns the use of Gaussian transformed p-values, Stouffer et al. [46] used as a test statistic

T_{S} (P_{1}, \dots, P_{n}) = \sum_{k = 1}^{n} \frac{Φ^{- 1} (P_{k})}{\sqrt{n}} .

\sum_{k = 1}^{n} \frac{Φ^{- 1} (P_{k})}{\sqrt{n}} | H_{0}^{*} \sim Gaussian (0, 1),

H_{0}^{*}

is rejected at a significance level

α

|\sum_{k = 1}^{n} \frac{Φ^{- 1} (p_{k})}{\sqrt{n}}| > z_{1 - α}

, with

z_{q}

denoting the q-th quantile of the standard Gaussian distribution.

Since

{[Φ^{- 1} (P_{k})]}^{2} | H_{0}^{*} \sim χ_{1}^{2}

, an alternative to Fisher’s method is to use the statistic

T_{C} (P_{1}, \dots, P_{n}) = \sum_{k = 1}^{n} {[Φ^{- 1} (P_{k})]}^{2} | H_{0}^{*} \sim χ_{n}^{2},

as observed in Chen [47]. Note that Liu et al. [48] and Cinar and Viechtbauer [49] prefer an inverse chi-square method, more precisely,

T_{L} (P_{1}, \dots, P_{n}) = \sum_{k = 1}^{n} F_{χ_{1}^{2}}^{- 1} (1 - P_{k}),

where

F_{χ_{1}^{2}}^{- 1}

is the inverse cumulative distribution function of the chi-square distribution with one degree of freedom.

Mudholkar and George [50] propose the use of the statistic

T_{M G} (P_{1}, \dots, P_{n}) = - \sum_{k = 1}^{n} ln (\frac{P_{k}}{1 - P_{k}}),

based on the logit transformation

ln (\frac{P_{k}}{1 - P_{k}}) | H_{0}^{*} \sim Logistic (0, 1)

, and which combines together

1 - P_{k}

and

P_{k}

Due to the approximation

T_{M G}^{*} = - \frac{\sum_{k = 1}^{n} ln (\frac{P_{k}}{1 - P_{k}})}{\sqrt{\frac{n π^{2} (5 n + 2)}{3 (5 n + 4)}}} \approx t_{5 n + 4},

H_{0}^{*}

is rejected at significance level

α

t_{M G}^{*} = \frac{|\sum_{k = 1}^{n} ln (\frac{p_{k}}{1 - p_{k}})|}{\sqrt{\frac{n π^{2} (5 n + 2)}{3 (5 n + 4)}}} > t_{5 n + 4, 1 - α},

where

t_{m, q}

represents the q-th quantile of Student’s t-distribution with m degrees of freedom. Or alternatively, as

ln (\frac{P_{k}}{1 - P_{k}}) | H_{0}^{*} \approx G a u s s i a n (0, \frac{π^{2}}{3}),

H_{0}^{*}

is rejected if

- \sum_{k = 1}^{n} ln (\frac{p_{k}}{1 - p_{k}}) / π \sqrt{\frac{n}{3}} > z_{1 - α}

2.2. Should You Mean It?

An interesting way of combining p-values is to consider an average-like function

M_{Ψ, n} (P_{1}, \dots, P_{n}) = Ψ^{- 1} (\frac{\sum_{k = 1}^{n} Ψ (P_{k})}{n}),

(1)

where

Ψ : [0, 1] \to [- \infty, \infty]

is a continuous strictly monotonic function (Kolmogorov [51]).

If in (1),

Ψ (p) = p^{r}

r \in [- \infty, \infty]

, this is the so-called mean of order r

T_{r} (P_{1}, \dots, P_{n}) = M_{r, n} (P_{1}, \dots, P_{n}) = {(\frac{\sum_{k = 1}^{n} P_{k}^{r}}{n})}^{1 / r},

(2)

with the understanding that the case

r = 0

is the limit as

r \to 0

, i.e.

T_{0} (P_{1}, \dots, P_{n}) = M_{0, n} (P_{1}, \dots, P_{n}) = exp (\frac{\sum_{k = 1}^{n} ln P_{k}}{n}) = {(\prod_{k = 1}^{n} P_{k})}^{1 / n} .

r_{1} \leq r_{2}

, then

T_{r_{1}} (p_{1}, \dots, p_{n}) \leq T_{r_{2}} (p_{1}, \dots, p_{n})

(Theorem 16 in Hardy et al. [52]). The means of order r for combining p-values are invariant for any permutation of

p_{1}, \dots, p_{n}

, which is a useful property for the simulations carried out to obtain the results in Section 5.

The most used means of order r, defined in (2), are the Pythagorean means, namely

—: Harmonic mean:

$T_{- 1} (P_{1}, \dots, P_{n}) = \frac{n}{\sum_{k = 1}^{n} 1 / P_{k}} = T_{H_{n}} (P_{1}, \dots, P_{n}) (Ψ (P) = 1 / P);$
—: Geometric mean:

$T_{0} (P_{1}, \dots, P_{n}) = {(\prod_{k = 1}^{n} P_{k})}^{1 / n} = T_{G_{n}} (P_{1}, \dots, P_{n}) (Ψ (P) = ln P);$
—: Arithmetic mean:

$T_{1} (P_{1}, \dots, P_{n}) = \frac{\sum_{k = 1}^{n} P_{k}}{n} = {\bar{P}}_{n} (Ψ (P) = P) .$

Other special cases are

T_{- \infty} (P_{1}, \dots, P_{n}) = min \{P_{1}, \dots, P_{n}\} = P_{1 : n}

and

T_{+ \infty} (P_{1}, \dots, P_{n}) = max \{P_{1}, \dots, P_{n}\} = P_{n : n} .

From now on, we shall use the notations

T_{- \infty} = T_{T}

T_{1} = T_{E}

and

T_{\infty} = T_{W}

, due to their use in the combined tests of Tippett [45], Edgington [53] and Wilkinson [54], respectively.

Tippett [45] was the first one to meta-analyze p-values using the statistic

T_{T} (P_{1}, \dots, P_{n}) = P_{1 : n} .

P_{1 : n} | H_{0}^{*} \sim Beta (1, n)

, the decision is to reject

H_{0}^{*}

at a significance level

α

if the minimum observed p-value

p_{1 : n} < 1 - {(1 - α)}^{1 / n}

Tippett’s minimum method is a special case of Wilkinson’s method (Wilkinson [54]), which recommends the rejection of

H_{0}^{*}

if some order statistic

p_{k : n} < c

. As

T_{W_{k}} (P_{1}, \dots, P_{n}) = P_{k : n} | H_{0}^{*} \sim Beta (k, n + 1 - k),

the cut-of-point c to reject

H_{0}^{*}

at a significance level

α

is the solution of

\int_{0}^{c} u^{k - 1} {(1 - u)}^{n - k} d u = α B (k, n + 1 - k) .

Note that Tippett’s and Wilkinson’s methods use drastically restricted information, contrasting with the efficient way in which Fisher’s and Stouffer’s methods use all available information.

In 1933, Pearson [55] expressed the distribution of

T_{P} (P_{1}, \dots, P_{n}) = \prod_{k = 1}^{n} P_{k}

as a function of the upper incomplete Beta function,

B_{z} (p, q) = \int_{z}^{1} x^{p - 1} {(1 - x)}^{q - 1} d x, p, q > 0, z \in (0, 1) .

In fact, the product of n independent random variables

P_{k} \sim Uniform (0, 1)

verifies

\prod_{k = 1}^{n} P_{k} \overset{d}{=} Y_{1, 1, 1, n} \sim BetaBoop (1, 1, 1, n),

where

Y_{p, q, P, Q} \sim BetaBoop (p, q, P, Q)

is a random variable with probability density function

f_{Y_{p, q, P, Q}} (x) = \frac{x^{p - 1} {(1 - x)}^{q - 1} {[- ln (1 - x)]}^{P - 1} {(- ln x)}^{Q - 1}}{\int_{0}^{1} t^{p - 1} {(1 - t)}^{q - 1} {[- ln (1 - t)]}^{P - 1} {(- ln t)}^{Q - 1} d t} I_{(0, 1)} (x),

with

p, q, P, Q > 0

such that

\int_{0}^{1} t^{p - 1} {(1 - t)}^{q - 1} {[- ln (1 - t)]}^{P - 1} {(- ln t)}^{Q - 1} d t < \infty

, cf. Brilhante et al. [56] and Brilhante and Pestana [57].

Y_{p, 1, 1, Q}^{1 / α} \overset{d}{=} Y_{α p, 1, 1, Q}

p, Q, α > 0

, we conclude that the geometric mean

G_{n} = T_{0} (P_{1}, \dots, P_{n}) = {(\prod_{k = 1}^{n} P_{k})}^{1 / n}

of n independent

P_{k} \sim Uniform (0, 1)

is a

BetaBoop (n, 1, 1, n)

random variable with probability density function

f_{G_{n}} (x) = \frac{n^{n}}{Γ (n)} x^{n - 1} {(- ln x)}^{n - 1} I_{(0, 1)} (x),

where

Γ (α) = \int_{0}^{\infty} x^{α - 1} e^{- x} d x, α > 0,

is the Euler’s Gamma function, being

I_{A}

the indicator function of A.

Therefore, the cumulative distribution function of

G_{n}

F_{G_{n}} (x) = \frac{Γ (n, - n ln x)}{Γ (n)} I_{(0, 1)} (x) + I_{[1, \infty)} (x),

where

Γ (α, z) = \int_{z}^{\infty} x^{α - 1} e^{- x} d x

α, z > 0

, is the upper incomplete Gamma function. Critical quantiles

g_{n, 1 - α}

for

G_{n}

can easily be computed from the critical quantiles

g_{n, 1 - α}^{*}

G_{n}^{n} = \prod_{k = 1}^{n} P_{k}

, where

\int_{0}^{g_{n, 1 - α}^{*}} \frac{{(- ln x)}^{n - 1}}{(n - 1)!} d x = 1 - α

, since

g_{n, 1 - α} = {(g_{n, 1 - α}^{*})}^{1 / n}

Observe, however, that using products of standard uniform random variables, or adding their exponential logarithms, provides essentially the same information. Pearson [55] acknowledged that combining p-values using

T_{P} (P_{1}, \dots, P_{n}) = {[G_{n} (P_{1}, \dots, P_{n})]}^{n} = \prod_{k = 1}^{n} P_{k}

is equivalent to Fisher’s [6] earlier combination method based on

T_{F} (P_{1}, \dots, P_{n}) = - 2 \sum_{k = 1}^{n} ln P_{k},

as described in SubSection 2.1.

In 1934, Pearson [58] observed that in bilateral contexts it would be more adequate to combine

\prod_{k = 1}^{n} P_{k}

and

\prod_{k = 1}^{n} (1 - P_{k})

, namely using

T_{P^{*}} (P_{1}, \dots, P_{n}) = min \{\prod_{k = 1}^{n} P_{k}, \prod_{k = 1}^{n} (1 - P_{k})\} .

(3)

As already observed,

T_{P}

is equivalent to

T_{F}

. Similarly, using Fisher’s transformation,

T_{P^{*}}

defined in (3) is equivalent to

\begin{matrix} T_{PF} & = max \{- 2 ln (\prod_{k = 1}^{n} P_{k}), - 2 ln (\prod_{k = 1}^{n} (1 - P_{k}))\} \\ = max \{- 2 \sum_{k = 1}^{n} ln P_{k}, - 2 \sum_{k = 1}^{n} ln (1 - P_{k})\}, \end{matrix}

(4)

which clearly is not

χ_{2 n}^{2}

-distributed. Owen [59] used the Bonferroni’s correction

α - \frac{α^{2}}{4} \leq P (T_{PF} \geq χ_{2 n, 1 - α / 2}^{2}) \leq α

to establish lower and upper bounds.

Instead of (3), we suggest the use of the minimum of the geometric means,

T_{min {G_{n}, G_{n}^{*}}} = min \{{(\prod_{k = 1}^{n} P_{k})}^{1 / n}, {(\prod_{k = 1}^{n} (1 - P_{k}))}^{1 / n}\} .

Combining p-values through their sum (Edgington [53]), or arithmetic mean,

T_{E} (P_{1}, \dots, P_{n}) = {\bar{P}}_{n},

is also feasible, but much less appealing than Fisher’s chi-square transformation method, since

{\bar{P}}_{n}

has a very cumbersome probability density function,

f_{{\bar{P}}_{n}} (x) = \frac{n}{Γ (n)} [\sum_{j = 0}^{⌊ n x ⌋} {(- 1)}^{j} (\binom{n}{j}) {(max {0, n x - j})}^{n - 1}] I_{(0, 1)} (x),

where

⌊ x ⌋

is the largest integer not greater than x. However, for moderately large values of n, an approximation based on the central limit theorem can be used to perform an overall test on

H_{0}^{*}

versus

H_{A}^{*}

. But this procedure is not consistent, in the sense that it can fail to reject the overall test’s null hypothesis, even though the results of some of the individual p-values are extremely significant.

Wilson [60] recommends the use of the harmonic mean

T_{H_{n}} (P_{1}, \dots, P_{n})

for combining mutually exclusive tests, not necessarily independent, assuming that the p-values being combined are valid. It was shown that

T_{H_{n}} (P_{1}, \dots, P_{n})

effectively controls the strong-sense familywise error rate, i.e. the probability of falsely rejecting a null hypothesis in favor of an alternative hypothesis in one or more of all tests performed. The harmonic mean of p-values, whose distribution is in the domain of attraction of the heavy-tailed Landau skewed additive (1,1)-stable law [61], is robust to positive dependency between p-values and also to the distribution of weights w used in its computation, being as well insensitive to the number of tests, aside from being mainly influenced by the smallest p-values. Based on recent developments in robust risk aggregation techniques, Vovk and Wang [12], without making any assumptions on the dependence structure of the p-values to be combined, extended those results to generalized means and showed that np-values can be combined by scaling up the harmonic mean

T_{H_{n}} (P_{1}, \dots, P_{n})

by a factor

ln n

2.3. Which Combining Rule Should Be Used?

To illustrate the application of different combined methods, Examples 1 and 2 are considered using data taken from Hartung et al. [62]. The tables in the Supplementary Materials, containing critical values for each combined method, are used (case

n_{f} = 0

, i.e. no fake p-values, compared with

n_{f} = 1, \dots, ⌊ n / 3 ⌋

fake p-values) to decide whether the hypothesis

H_{0}^{*}

should be rejected or not.

Example 1

(Table 3.1, [62], p. 31). For the meta-analysis of

n = 19

case-control studies on the risk of lung cancer in women in relation to exposure to environmental tobacco smoke the p-values are

\begin{matrix} 0.0669 & 0.2740 & 0.6844 & 0.8460 & 0.0623 & 0.1805 & 0.0990 & 0.0143 \\ 0.0580 & 0.0690 & 0.6572 & 0.0571 & 0.0027 & 0.0127 & 0.4747 & 0.1760 \\ 0.2855 & 0.0056 & 0.2411, \end{matrix}

The observed values for the above combined tests statistics are:

\begin{matrix} T_{F} (0.0669, \dots, 0.2411) = 90.0426 \\ T_{S} (0.0669, \dots, 0.2411) = - 4.7198 \\ T_{M G} (0.0669, \dots, 0.2411) = 38.4946 (t_{M G}^{*} = 4.9189) \\ T_{C} (0.0669, \dots, 0.2411) = 41.7048 \\ T_{T} (0.0669, \dots, 0.2411) = 0.0027 \\ T_{H_{19}} (0.0669, \dots, 0.2411) = 0.0233 \\ T_{G_{19}} (0.0669, \dots, 0.2411) = 0.0935 \\ T_{min {G_{19}, G_{19}^{*}}} (0.0669, \dots, 0.2411) = 0.0935 \\ T_{E} (0.0669, \dots, 0.2411) = 0.2246 \\ T_{W} (0.0669, \dots, 0.2411) = 0.8460 . \end{matrix}

In this case,

H_{0}^{*}

is rejected at the usual significance level

0.05

using all combined tests, with the exception of Tippett’s method, as expected, since only 4 of the 19 p-values are smaller than

0.05

. As can be noted, Tippett’s rule drastically discards most of the information and therefore should not be considered a reliable test to make an overall decision.

Example 2

(Table 13.1, [62], p. 172). For the meta-analysis of

n = 20

validity studies examining the correlation between ratings of the instructor and student achievement the p-values are:

\begin{matrix} 0.0153 & 0.0051 & 0.2248 & 0.0007 & 0.0041 & 0.5491 & 0.0529 & 0.0247 \\ 0.0046 & 0.2878 & 0.7385 & 0.0096 & 0.0720 & 0.00004 & 0.0010 & 0.0312 \\ 0.0053 & 0.0988 & 0.0674 & 0.2502 \end{matrix}

The observed values for the combined tests statistics are:

\begin{matrix} T_{F} (0.0153, \dots, 0.2502) = 154.5968 \\ T_{S} (0.0153, \dots, 0.2502) = - 8.0553 \\ T_{M G} (0.0153, \dots, 0.2502) = 73.8730 (t_{M G}^{*} = 9.1960) \\ T_{C} (0.0153, \dots, 0.2502) = 90.1191 \\ T_{T} (0.0153, \dots, 0.2502) < 0.0000 \\ T_{H_{20}} (0.0153, \dots, 0.2502) = 0.0007 \\ T_{G_{20}} (0.0153, \dots, 0.2502) = 0.0210 \\ T_{min {G_{20}, G_{20}^{*}}} (0.0153, \dots, 0.2502) = 0.0210 \\ T_{E} (0.0153, \dots, 0.2502) = 0.1222 \\ T_{W} (0.0153, \dots, 0.2502) = 0.7385 . \end{matrix}

The overall rejection of

H_{0}^{*}

seems more consistent in this example. However, a closer look at the data shows that 9 out of 20 p-values are greater than the usual significance level

0.05

, which is an exceptional case, since p-values greater than

0.05

often lead to the non-publication of the studies, thus creating a phenomenon known as publication bias. Four of the p-values are much greater than

0.05

, which causes the rejection of

H_{0}^{*}

when using the combined tests based on the transformations of p-values

T_{F}

T_{S}

T_{M G}

and

T_{C}

, whereas the rejection using the mean of order r tests

T_{T}

T_{H_{20}}

T_{G_{20}}

T_{min {G_{20}, G_{20}^{*}}}

T_{E}

and

T_{W}

is due to the existence of some very small p-values.

Both previous examples raise some concern on the validity and efficiency of combined tests and on the question of which one should actually be used. A common understanding on this matter is that any rational combining procedure

T (p_{1}, \dots, p_{n})

should be monotone, in the sense that if one set of p-values

(p_{1}, \dots, p_{n})

leads to the rejection of the overall null hypothesis

H_{0}^{*}

, any set of componentwise smaller p-values

(p_{1}^{'}, \dots, p_{n}^{'})

p_{k}^{'} \leq p_{k}, k = 1, \dots, n

, must also lead to its rejection.

Birnbaum [63] has shown that every monotone combined test procedure is admissible, i.e. provides a most powerful test against some alternative hypothesis for combining some collection of tests, and therefore is optimal for some combined testing situation whose goal is to harmonize eventually conflicting evidence, or to pool inconclusive evidence. In the context of social sciences, Mosteller and Bush [64] recommend Stouffer et al.’s [46] method, which is also preferred by Whitlock [65], while Littell and Folks [66,67] have shown that, under mild conditions, Fisher’s method is optimal for combining independent tests. Owen [59], showing that Birnbaum’s statement on the inadmissibility of Pearson’s two-sided combined test was wrong, recommends Pearson’s two-sided combination rule, given in (4). Marden [68], using the concepts of sensitivity and sturdiness, orders from best to worst

T_{F} ≻ T_{T} ≻ T_{S} ≻ T_{E} ≻ T_{W}

, warning that all statistics perform worse as n increases.

The thorough comparison performed by Loughin [69] concludes that the normal combining function has a good performance in problems where evidence against the combined null hypothesis is spread among more than a small fraction of the individual tests. Moreover, when the total evidence is weak, Fisher’s method is the best choice if the evidence is at least moderately strong and is concentrated in a relatively small fraction of the individual tests. The Mudholkar and George’s [50] logistic combination method provides a compromise between the two. When the total evidence against the combined null hypothesis is concentrated in one or in a very few of the tests to be combined, Tippett’s minimum function can be useful as well. See also Won et al. [70] on how to choose an optimal method to combine p-values.

Since there is no unanimity among researchers as to which procedure should be used, a reasonable approach is to compare the results for a variety of tests. For this purpose, tables with critical values for the combined test statistics discussed earlier are presented as Supplementary Materials.

For more details on the early developments of combining one-sided tests, see the first chapter of Oosterhoff [71]. In what regards recent advances on combining tests, namely in a dependence framework, or using e-values, defined by expectations, instead of p-values, defined by probabilities, see recent developments in Vovk and Wang [72], Vovk et al. [73], and Vuursteen et al. [74].

3. Publication Bias

Published results have in general significant p-values, typically less than 0.05, and this publication bias is one of the ill-resolved problems in the meta-analysis of p-values. In fact, many published studies deal with significant p-values, see for instance the insistence on

p \leq 0.05

in Zintaras et al. [75].

The influential International Committee of Medical Journal Editors (ICMJE) [76] in its Uniform Requirements for Manuscripts states that

“Editors should seriously consider for publication any carefully done study of an important question, relevant to their readers, whether the results for the primary or any additional outcome are statistically significant. Failure to submit or publish findings because of lack of statistical significance is an important cause of publication bias’’.

The Journal of Articles in Support of the Null Hypothesis [77] offers “an outlet for experiments that do not reach the traditional significance levels (p < .05)[...]reducing the file drawer problem, and reducing the bias”, considering that “without such a resource researchers could be wasting their time examining empirical questions that have already been examined”.

As with many other techniques used in meta-analysis, publication bias can easily lead to erroneous conclusions in combined testing (Pestana et al. [78]). Indeed, if the set of available p-values comes mainly from studies considered worthy of publication because the observed p-values are small, thus pointing out to significant results, then the rejection of

H_{0}^{*}

can be due to publication bias. Often, the assumption that the

p_{k}

’s are observations of independent Uniform(0,1) random variables is questionable, since they are frequently a set of low order statistics, given that p-values greater than 0.05 are less published.

Example 3

(Table B1, p. 726 in van Aert et al. [79] assessment of meta-analysis) For the set of the

n = 25

p-values

\begin{matrix} 0.0489 & 0.0690 & 0.0133 & 0.0372 & 0.0188 & 0.0457 & 0.0307 & 0.0428 \\ 0.0335 & 0.0274 & 0.0030 & 0.0531 & 0.0335 & 0.0254 & 0.0240 & 0.0023 \\ 0.0254 & 0.0263 & 0.0429 & 0.0172 & 0.0365 & 0.0287 & 0.0200 & 0.0498 \\ 0.0134 \end{matrix}

the observed values for the combined test statistics are:

\begin{matrix} T_{F} (0.0489, \dots, 0.0134) = 184.4354 \\ T_{S} (0.0489, \dots, 0.0134) = - 9.7083 \\ T_{M G} (0.0489, \dots, 0.0134) = 91.4336 (t_{M G}^{*} = 10.1611) \\ T_{C} (0.0489, \dots, 0.0134) = 96.6378 \\ T_{T} (0.0489, \dots, 0.0134) = 0.0023 \\ T_{H_{25}} (0.0489, \dots, 0.0134) = 0.0156 \\ T_{G_{25}} (0.0489, \dots, 0.0134) = 0.0250 \\ T_{min {G_{25}, G_{25}^{*}}} (0.0489, \dots, 0.0134) = 0.0250 \\ T_{E} (0.0489, \dots, 0.0134) = 0.0308 \\ T_{W} (0.0489, \dots, 0.0134) = 0.0690 . \end{matrix}

H_{0}^{*}

is rejected, as expected, whatever combined test is used. In fact, the meta-analysis of these p-values is a pointless exercise, since it is obvious that they cannot be a random sample from the standard Uniform distribution.

As a matter of fact, it seems reasonable to assume for the set of p-values in Example 3 that the distribution of the underlying

P_{k}

’s is a

Uniform (0, 0.0718)

, where the right endpoint is the unbiased estimate

p_{25 : 25} \times 26 / 25

. Consequently, dividing the values by 0.0718 we obtain a genuine standard Uniform sample, i.e. 0.6814, 0.9615, 0.1853, 0.5184, 0.2620, 0.6368, 0.4278, 0.5964, 0.4668, 0.3818, 0.0418, 0.7400, 0.4668, 0.3540, 0.3344, 0.0321, 0.3540, 0.3665, 0.5978, 0.2397, 0.5086, 0.3999, 0.2787, 0.6940, 0.1867, and the observed values of the combined tests statistics for these new values are:

\begin{matrix} T_{F} (0.6814, \dots, 0.1867) = 52.7130 \\ T_{S} (0.6814, \dots, 0.1867) = - 1.0837 \\ T_{M G} (0.6814, \dots, 0.1867) = 9.2157 (t_{M G}^{*} = 1.0241) \\ T_{C} (0.6814, \dots, 0.1867) = 14.3117 \\ T_{T} (0.6814, \dots, 0.1867) = 0.0321 \\ T_{H_{25}} (0.6814, \dots, 0.1867) = 0.2181 \\ T_{G_{25}} (0.6814, \dots, 0.1867) = 0.3485 \\ T_{min {G_{25}, G_{25}^{*}}} (0.6814, \dots, 0.1867) = 0.3484 \\ T_{E} (0.6814, \dots, 0.1867) = 0.4285 \\ T_{W} (0.6814, \dots, 0.1867) = 0.9615 . \end{matrix}

So there is no reason to reject the hypothesis that the sample of expanded values is from the standard Uniform distribution.

It is worth noting that under

H_{0}^{*}

the moment of order k of the geometric mean is

E (G_{n}^{k}) = {(1 / (1 + \frac{k}{n}))}^{n} \underset{n \to \infty}{\to} e^{- k} .

Hence,

E (G_{n}) = {(\frac{n}{n + 1})}^{n} \underset{n \to \infty}{↓} \frac{1}{e} \approx 0.3679,

the standard deviation decreases to zero, the skewness steadily decreases after a maximum 0.2645 for

n = 5

, and the kurtosis increases from

- 0.8541

(for

n = 2

) towards 0. Observe that for

n \geq 14

, the expected value of

G_{n}

is greater than 0.36 and the standard deviation is smaller than 0.1. Therefore, whenever

p_{n : n}

is smaller than a threshold

c ≪ 1 / e

, the test based on

T_{G_{n}}

will lead to the rejection of

H_{0}^{*}

, as it happens with the data from van Aert et al. [79], but a

p_{n : n}

smaller than a low threshold can just be a consequence of publication bias.

The assessment of publication bias is often performed computing the number of non-significant p-values that would be needed to reverse the decision to reject

H_{0}^{*}

based on the available p-values, which is illustrated with Examples 4 and 5.

Example 4.

For the seven p-values in Fogacci et al. [80]from studies on the effect of vitamin D supplements administered to pregnant women with risk of preeclampsia incidents:

\begin{matrix} 0.039 & 0.324 & 0.057 & 0.001 & 0.324 & 0.105 & 0.003 \end{matrix}

it follows that

T_{F} (p_{1}, \dots, p_{7}) = - 2 \sum_{k = 1}^{7} ln p_{k} = 46.667

. As

P (T_{F} > 46.667 | H_{0}^{*}) = 0.0000218

H_{0}^{*}

is rejected. In this example,

p_{2}

p_{3}

p_{5}

and

p_{6}

are greater than

0.05

, and the rejection of

H_{0}^{*}

is caused by the very small

p_{4}

and

p_{7}

values, thus raising some doubts as to whether the p-values are truly genuine. According to Hartung et al. [62], p. 177, to reverse the decision to reject

H_{0}^{*}

at the significance level

0.05

, it is necessary to compute the number

n_{0}

of non-significant additional p-values such that

- 2 \sum_{k = 1}^{7} ln p_{k} - 2 n_{0} ln \tilde{p} \leq χ_{2 (7 + n_{0}), 0.95}^{2},

where for simplicity it is assumed that

p_{8} = \dots = p_{7 + n_{0}} = \tilde{p}

. The solution of

46.667 - 2 n_{0} ln \tilde{p} \leq χ_{2 (7 + n_{0}), 0.95}^{2}

depends on the value of

\tilde{p}

. For instance, if

\tilde{p} = 0.4

, then

n_{0} = 46

, if

\tilde{p} = 0.5

, then

n_{0} = 23

, and if

\tilde{p} = 0.6

, then

n_{0} = 17

Example 5.

The p-values in Table 2 of Zintaras et al.’s [75] investigation of heterogeneity-based genome search for preeclampsia are:

\begin{matrix} 0.010 & 0.015 & 0.025 & 0.029 & 0.032 & 0.034 & 0.044 & 0.047 & 0.049 \\ 0.053 & 0.055 & 0.060 & 0.162 \end{matrix}

Since

T_{F} (0.010, \dots, 0.162) = 85.0524

H_{0}^{*}

is also rejected (

P [T_{F} > 85.0524] = 0.0000000342

). In this case, to observe

- 2 \sum_{k = 1}^{13} ln p_{k} - 2 n_{0} ln \tilde{p} \leq χ_{2 (13 + n_{0}), 0.95}^{2}

, it will be needed

n_{0} = 120

\tilde{p} = 0.4

n_{0} = 52

\tilde{p} = 0.5

, and

n_{0} = 36

\tilde{p} = 0.6

. Even if

\tilde{p} = 0.9

, it will require

n_{0} = 22

In Zintaras et al.’s [75] example, the high number of non-significant studies needed to reverse the rejection of

H_{0}^{*}

seems to indicate that the decision is the consequence of having consistently low p-values, or possibly moderate censoring of non-significant p-values (note that

p_{13 : 13} = 0.162 > 0.05

). In Fogacci et al.’s [80] example, the rejection of

H_{0}^{*}

was due to

p_{1 : 7}

, although 4 out of 7 p-values are greater than 0.05, and the fact that

p_{2 : 7}

is quite small, can be considered suspicious.

Begg and Mazumdar [81] and Egger et al. [82] devised tests to detect publication bias. Jin et al. [83] and Lin and Chu [84] present interesting overviews, and Givens et al. [85] provide a deep insight on publication bias in meta-analysis, namely using data-augmentation techniques.

It is also worth mentioning that Zaykin et al. [40], Neuhäuser and Bretz [41] and Zhang [42] advocate the use of a truncated product combination statistic of only those p-values smaller than some specified cut-off value, which in practice dismisses publication bias. Dudbridge and Koeleman [43] go even further, proposing the combination of the most significant p-values. This recommendation clearly favors the rejection of

H_{0}^{*}

, therefore increasing the probability of false positive results, and contributing to the misconception that significance implies importance.

4. Mendel Random Variables — Combined Tests with Genuine and Fake $p$ -Values

The assumption

P_{k} | H_{0} \sim Uniform (0, 1)

k = 1, \dots, n

, is rather naive. In fact, the alternative hypothesis

H_{A}^{*}

states that some of the

H_{A k}

are true, and so a meta-decision on

H_{0}^{*}

implicitly assumes that some of the

P_{k}

’s may have non-uniform distribution, cf. Hartung et al. [62], pp. 81–84; Kulinskaya et al. [86], pp. 117–119. Thus, the uniformity of the

P_{k}

’s is solely the consequence of assuming that the null hypothesis is true, and this far-fetched assumption led Tsui and Weerahandi [87] to introduce the concept of generalized p-values. See also Weerahandi [88], Hung et al. [89] and Brilhante [90], and references therein, on the promising concepts of generalized and of random p-values. Moreover, a consequence of publication bias is that most of the published studies point out to the rejection of

H_{0}

. Hence, instead of combining p-values, it would be more reasonable to combine either generalized p-values or random p-values. Assuming that the p-values being combined can come from a combination of null and alternative hypotheses, Dai and Charnigo [91] investigated a Beta mixture adjustment. For large exploratory studies, an extreme-value distribution adjustment for fixed numbers of combined evidence and a Beta distribution adjustment for the most significant evidence are accurate and efficient (Dudbridge and Koeleman [92]).

Moreover, when the result of an experiment leads to a p-value which is not highly significant or significant, there is the possibility of the researcher carrying out a new experiment, in the hope of obtaining a "better" p-value that favors the publication of his study.

Such malpractice of trying to obtain results more attuned with the researcher’s expectations (or wishes) is scientifically wrong, eventually fraud, leading to results “too good to be true”, as Fisher [37] observed in his appraisal of Mendel’s data: “the data of most, if not all, of the experiments have been falsified so as to agree closely with Mendel’s expectations”. For more details on the (in)famous Mendel-Fisher controversy, see Franklin et al. [38], and Pires and Branco [39].

If a reported

p_{k}

is the "best" of ℓ observed p-values in ℓ independent repetitions of an experiment, such "fake p-value" comes from the minimum of ℓ independent Uniform(0,1) random variables, so that

P_{k} \sim Beta (1, ℓ)

with probability density function

f_{P_{k}} (x) = ℓ {(1 - x)}^{ℓ - 1} I_{(0, 1)} (x) .

On the other hand, fake p-values demand substantial changes in the computation of combined p-values. For instance, with regard to Fisher’s method, for fake p-values

P_{k} \sim Beta (1, ℓ_{k})

, it implies that

- 2 ℓ_{k} ln (1 - P_{k}) \sim χ_{2}^{2}

. Therefore, for

ℓ_{k} = 1

, i.e. for genuine p-values

P_{k} \sim Uniform (0, 1)

, it follows that

- 2 ln P_{k} \overset{d}{=} - 2 ln (1 - P_{k}) \sim χ_{2}^{2}

. Hence, the existence of fake p-values requires the following adjustment to Fisher’s combined test:

T_{F}^{f} (P_{1}, \dots, P_{n}) = - 2 \sum_{k = 1}^{n} ℓ_{k} ln P_{k} | H_{0}^{*} \sim χ_{2 n}^{2},

but the problem is that the values

ℓ_{k}

are actually unknown.

Using the integral transform theorem,

1 - {(1 - P_{k})}^{ℓ_{k}} \sim Uniform (0, 1)

, and as far as Stouffer et al.’s method is concerned,

\frac{\sum_{k = 1}^{n} Φ^{- 1} (1 - {(1 - P_{k})}^{ℓ_{k}})}{\sqrt{n}} \sim Gaussian (0, 1),

while for Chen’s

T_{C}

statistic,

\sum_{k = 1}^{n} {[Φ^{- 1} (1 - {(1 - P_{k})}^{ℓ_{k}})]}^{2} \sim χ_{n}^{2} .

In what concerns Mudholkar and George’s

T_{M G}

statistic, if

P_{k} \sim Beta (1, ℓ_{k})

, then the cumulative distribution function and probability density function of

Y = ln (\frac{P_{k}}{1 - P_{k}})

are, respectively,

F_{Y} (y) = [1 - \frac{1}{{(1 + e^{y})}^{ℓ_{k}}}] I_{R} (y) and f_{Y} (y) = F ’_{Y} (y) = \frac{ℓ_{k} e^{y}}{{(1 + e^{y})}^{ℓ_{k} + 1}} I_{R} (y) .

The central limit theorem can be used to obtain an approximation of

\sum_{k = 1}^{n} ln (\frac{P_{k}}{1 - P_{k}})

, as long as we know which of the p-values are the fake ones and their corresponding

ℓ_{k}

values.

In fact, the main problem here is that there is no information on whether some of the reported p-values are in fact fake p-values, and if so, how many and which ones are. In the classical framework, the number n of p-values

(p_{1}, \dots, p_{n})

to be combined is generally small, and if the overall null hypothesis is true, it seems reasonable to expect that the number

n_{f}

of fake p-values with

Beta (1, ℓ)

distribution,

ℓ = 2, 3, \dots

, to be much smaller than the number

n - n_{f}

of genuine standard Uniform distributed p-values. For what follows, it is assumed that the proportion of fake p-values among the observed p-values being combined is

\frac{n_{f}}{n} = \frac{m}{2}

m \in [0, 2]

With regard to fake p-values, it is likely that in most cases

ℓ = 2

, especially when the second experiment provides a smaller p-value that supports the researcher’s expectations. Actually, if the second p-value is again non-significant, there is a good chance that this would continue to happen with other similar experiments, which have a cost attached (at least they are time-consuming). In this situation, the researcher will most likely decide to give up carrying out further experiments and no p-value will be reported.

For what follows, it is also assumed that the model for the p-values to be combined is

P_{k} \sim Beta (1, ℓ)

, with

ℓ \in {1, 2}

, i.e.

P_{k}

is a genuine p-value if

ℓ = 1

, or a fake one if

ℓ = 2

. As it is unknown whether

P_{k}

is genuine or fake, the distribution of

P_{k}

is a mixture of the minimum of two independent Uniform(0,1) random variables and of a Uniform(0,1) random variable, with weights

\frac{m}{2}

and

1 - \frac{m}{2}

, respectively.

Therefore,

P_{k}

has probability density function

f_{P_{k}} (x) = \frac{m}{2} f_{U_{1 : 2}} (x) + (1 - \frac{m}{2}) f_{U} (x) = (\frac{m}{2} 2 (1 - x) + 1 - \frac{m}{2}) I_{(0, 1)} (x),

where

U_{1 : 2}

denotes the minimum of two standard uniform random variables

U_{1}, U_{2}

, and

U \sim Uniform (0, 1)

. In other words,

f_{P_{k}} (x) = (m (1 - x) + 1 - \frac{m}{2}) I_{(0, 1)} (x) .

More generally, tilting the probability density function of

U \sim Uniform (0, 1)

with pole

(\frac{1}{2}, 1)

, for

m \in [- 2, 2]

, we obtain the probability density function of a random variable

X_{m}

given by

f_{X_{m}} (x) = (m x + 1 - \frac{m}{2}) I_{(0, 1)} (x),

and thus we shall say that

X_{m} \sim Mendel (m)

when

m \in [- 2, 2]

Note that

X_{0} \sim Uniform (0, 1)

X_{- 2} \sim Beta (1, 2)

is the minimum of two independent standard uniform random variables, and

X_{2} \sim Beta (2, 1)

is the maximum of two independent standard uniform random variables. For intermediate values of

m \in (- 2, 0)

X_{m}

is a mixture of a standard uniform random variable, with weight

1 - \frac{| m |}{2}

, and a Beta(1,2) random variable, and for

m \in (0, 2)

, it is a mixture of a standard uniform random variable and a Beta(2,1) random variable, i.e. with cumulative distribution function

F_{X_{m}} (x) = (1 - \frac{| m |}{2}) F_{U} (x) + \frac{| m |}{2} F_{U_{i : 2}} (x),

where

i = 1

m \in [- 2, 0]

and

i = 2

m \in (0, 2]

, and

U_{1 : 2}

and

U_{2 : 2}

denote, respectively, the minimum and maximum of two independent standard uniform random variables.

4.1. Deng and George’s Contractions with Mendel Random Variables

Let X and Y be independent random variables with support

S_{X} = S_{Y} = [0, 1]

. The support extension resulting from

\frac{X}{Y}

\frac{1 - X}{1 - Y}

[respectively

X + Y

] followed by the contraction

V = min \{\frac{X}{Y}, \frac{1 - X}{1 - Y}\}

[respectively

W = X + Y - ⌊X + Y⌋

], so that

S_{V} = S_{W} = [0, 1]

, restores the unit

[0, 1]

support. These contractions have been used by Deng and George [44], with

X \sim Uniform (0, 1)

— i.e.

X \sim Mendel (0)

— to obtain a useful characterization of the standard Uniform distribution. Theorem 1 extends their results to

Mendel (m), m \in [- 2, 2]

, random variables.

Theorem 1.

X_{m} \sim M e n d e l (m)

and Y, with support

[0, 1]

, are independent random variables, then

V = min \{\frac{X_{m}}{Y}, \frac{1 - X_{m}}{1 - Y}\} \sim Mendel ((2 E [Y] - 1) m) .

In particular, if

X_{m_{1}} \sim M e n d e l (m_{1})

and

X_{m_{2}} \sim M e n d e l (m_{2})

are independent, then

V_{m_{1}, m_{2}} = min \{\frac{X_{m_{1}}}{X_{m_{2}}}, \frac{1 - X_{m_{1}}}{1 - X_{m_{2}}}\} \sim Mendel (\frac{m_{1} m_{2}}{6}),

(5)

and the cumulative distribution function of

W_{m_{1}, m_{2}} = X_{m_{1}} + X_{m_{2}} - ⌊X_{m_{1}} + X_{m_{2}}⌋

F_{W_{m_{1}, m_{2}}} (x) = (1 - \frac{m_{1} m_{2}}{12}) F_{U} (x) + \frac{m_{1} m_{2}}{12} F_{X_{2, 2}} (x),

where

U \sim Uniform (0, 1)

and

X_{2, 2} \sim Beta (2, 2)

Proof.

The probability density function of

X \sim Mendel (m)

f_{X} (x) = m x + 1 - \frac{m}{2}

, so for

x \in [0, 1]

F_{X} (x) = \frac{m}{2} x^{2} + (1 - \frac{m}{2}) x

. If

\tilde{X} = 1 - X

and

\tilde{Y} = 1 - Y

, then

F_{\tilde{X}} (x) = 1 - F_{X} (1 - x)

E (\tilde{Y}) = 1 - E (Y)

and

E ({\tilde{Y}}^{2}) = 1 - 2 E (Y) + E (Y^{2})

. Therefore, for

v \in [0, 1]

\begin{matrix} F_{V} (v) & = P [X \leq v Y] + P [\tilde{X} \leq v \tilde{Y}] \\ = E [F_{X} (v Y)] + E [F_{\tilde{X}} (v \tilde{Y})] \\ = E [F_{X} (v Y)] + E [1 - F_{X} (1 - v \tilde{Y})] \\ = \frac{m}{2} [2 E (Y) - 1] v^{2} + [1 + \frac{m}{2} - m E (Y)] v, \end{matrix}

and consequently,

f_{V} (v) = [(2 E (Y) - 1) m v + 1 - \frac{m (2 E (Y) - 1)}{2}] I_{[0, 1]} (v) .

In what regards the random variable

V_{m_{1}, m_{2}}

defined in (5),

E [X_{m_{2}}] = \int_{0}^{1} x (m_{2} x + 1 - \frac{m_{2}}{2}) d x = \frac{1}{2} + \frac{m_{2}}{12},

and hence

[2 (\frac{1}{2} + \frac{m_{2}}{12}) - 1] m_{1} = \frac{m_{1} m_{2}}{6}

, i.e.

V_{m_{1}, m_{2}} \sim Mendel (\frac{m_{1} m_{2}}{6})

On the other hand, for

w \in [0, 1]

\begin{matrix} F_{W_{m_{1}, m_{2}}} (w) & = P [X_{m_{1}} + X_{m_{2}} \leq w] + P [1 < X_{m_{1}} + X_{m_{2}} \leq 1 + w] \\ = \int_{- \infty}^{\infty} F_{X_{m_{1}}} (w - y) f_{X_{m_{2}}} (y) d y + \int_{- \infty}^{\infty} [F_{X_{m_{1}}} (1 + w - y) - F_{X_{m_{1}}} (1 - y)] f_{X_{m_{2}}} (y) d y \\ = \int_{0}^{w} F_{X_{m_{1}}} (w - y) f_{X_{m_{2}}} (y) d y + \int_{w}^{1} F_{X_{m_{1}}} (1 + w - y) f_{X_{m_{2}}} (y) d y - E [F_{X_{m_{2}}} (1 - Y)] \\ = (1 - \frac{m_{1} m_{2}}{12}) w + \frac{m_{1} m_{2}}{12} (3 w^{2} - 2 w^{3}), \end{matrix}

and therefore

\begin{matrix} f_{W_{m_{1}, m_{2}}} (w) & = (1 - \frac{m_{1} m_{2}}{12} + \frac{m_{1} m_{2}}{12} 6 w (1 - w)) I_{[0, 1]} (w) \\ = (1 - \frac{m_{1} m_{2}}{12}) f_{U} (x) + \frac{m_{1} m_{2}}{12} f_{X_{2, 2}} (x), \end{matrix}

with

X_{2, 2} \sim Beta (2, 2)

. □

4.2. Testing Independence

The extension of classical methods of combining independent p-values to a more general framework of combining correlated p-values is nowadays an active area of research, with far-reaching consequences in dealing with taxa and investigation in Genomics and, more generally, with Big Data. Therefore, testing the independence of a sequence of standard uniform random variables versus autoregressive Mendel processes is relevant in the context of meta-analyzing p-values.

Let

\{X_{m, i}\}

i \in N

, be a sequence of replicas of independent Mendel random variables

X_{m}, m \in [- 2, 2]

. For

1 \leq i \leq n

and

ρ \in [0, 1)

, define

Y_{m, 0} = X_{m, 0}, Y_{m, i} = ρ Y_{m, i - 1} + (1 - ρ) X_{m, i} .

ρ = 0

, then the sequence

\{Y_{m, i}\}

i \geq 0

, is the initial one, but if

ρ > 0

, then there is serial correlation.

The inverse transformation

X_{m, i} = \frac{Y_{m, i} - ρ Y_{m, i - 1}}{1 - ρ}

, with

i = 1 \dots, n

and

J = {(\frac{1}{1 - ρ})}^{n}

, leads to

f_{Y_{m}} (y) = \prod_{i = 1}^{n} (m \frac{y_{i} - ρ y_{i - 1}}{1 - ρ} + \frac{2 - m}{2}) \frac{1}{1 - ρ} I_{S} (y),

where

Y_{m} = (Y_{m, 1}, \dots, Y_{m, n})

y = (y_{1}, \dots, y_{n})

0 \leq y_{i} \leq 1

, and

S = ⋂_{i = 1}^{n} \{(y_{1}, \dots, y_{n}) : 0 < \frac{y_{i} - ρ y_{i - 1}}{1 - ρ} < 1\} .

Since

0 < \frac{y_{i} - ρ y_{i - 1}}{1 - ρ} < 1 ⟺ \{\begin{matrix} ρ < \frac{y_{i}}{y_{i - 1}} \\ ρ < \frac{1 - y_{i}}{1 - y_{i - 1}} \end{matrix} ⟺ ρ < min \{\frac{y_{i}}{y_{i - 1}}, \frac{- 1 y_{i}}{1 - y_{i - 1}}\},

for all

i \in {1, \dots, n}

, this is equivalent to

ρ < min_{1 \leq i \leq n} min \{\frac{y_{i}}{y_{i - 1}}, \frac{1 - y_{i}}{1 - y_{i - 1}}\} = A (y) .

The following cases are considered.

—: $ρ = 0$ :

If $ρ = 0$ $(y = x)$ , the sequence $\{Y_{m, i}\}$ , $i \geq 0$ , is the initial one, and so the joint probability density function of $Y_{1}, \dots, Y_{n}$ is

$f_{Y_{1}, \dots, Y_{n}} (y) = f_{X_{1}, \dots, X_{n}} (x) = {(\frac{1}{1 - ρ})}^{n} I_{\{x \in {[0, 1]}^{n} : ρ < A (x)\}} (x),$

which requires solving the equation

$min_{1 \leq i \leq n} min \{\frac{X_{0, i}}{X_{0, i - 1}}, \frac{1 - X_{0, i}}{1 - X_{0, i - 1}}\} = min_{1 \leq i \leq n} \{U_{1}, \dots, U_{n}\},$

where $\{U_{1}, \dots, U_{n}\}$ is a sequence of independent standard uniform random variables, and therefore $min_{1 \leq i \leq n} \{U_{1}, \dots, U_{n}\} \sim Beta (1, n) .$
—: $ρ \in (0, 1)$ , $m = 0$ :

If $ρ \in (0, 1)$ and $m = 0$ , then $X_{0, i} \overset{d}{=} U_{i}$ , and

$\begin{matrix} min \{\frac{Y_{0, i}}{Y_{0, i - 1}}, \frac{1 - Y_{0, i}}{1 - Y_{0, i - 1}}\} & = min \{ρ + (1 - ρ) \frac{U_{i}}{Y_{0, i - 1}}, ρ + (1 - ρ) \frac{1 - U_{i}}{1 - Y_{0, i - 1}}\} \\ = ρ + (1 - ρ) min \{\frac{U_{i}}{Y_{0, i - 1}}, \frac{1 - U_{i}}{1 - Y_{0, i - 1}}\} \\ = ρ + (1 - ρ) U_{i}^{*}, \end{matrix}$

with $U_{i}^{*} \sim Uniform (0, 1)$ , and so $min \{\frac{Y_{0, i}}{Y_{0, i - 1}}, \frac{1 - Y_{0, i}}{1 - Y_{0, i - 1}}\} = V_{i, ρ} \sim Uniform (ρ, 1)$ . On the other hand, $V = min_{1 \leq i \leq n} V_{i, ρ}$ is the maximum likelihood estimator of $ρ$ , which is also sufficient for $ρ$ . The likelihood function is $L (ρ) = {(\frac{1}{1 - ρ})}^{n} I_{{ρ \leq V}} (ρ)$ . Therefore, the hypothesis of independence should be rejected if $V > 1 - α^{1 / n}$ , with the power of the test being equal to $\frac{α}{{(1 - ρ)}^{n}}$ if $ρ \leq 1 - α^{1 / n}$ , or 1 otherwise.
—: $ρ \in (0, 1)$ , $m \in [- 2, 2]$ :

For a general $m \in [- 2, 2]$ , it follows from $\frac{Y_{m, i}}{Y_{m, i - 1}} = ρ + (1 - ρ) \frac{X_{m, i}}{Y_{m, i - 1}}$ and $\frac{1 - Y_{m, i}}{1 - Y_{m, i - 1}} = ρ + (1 - ρ) \frac{1 - X_{m, i}}{1 - Y_{m, i - 1}}$ that

$min \{\frac{Y_{m, i}}{Y_{m, i - 1}}, \frac{1 - Y_{m, i}}{1 - Y_{m, i - 1}}\} = ρ + (1 - ρ) min \{\frac{X_{m, i}}{Y_{m, i - 1}}, \frac{1 - X_{m, i}}{1 - Y_{m, i - 1}}\},$

and with the independence of the $X_{m, i}$ ’s implying that

$min \{\frac{Y_{m, i}}{Y_{m, i - 1}}, \frac{1 - Y_{m, i}}{1 - Y_{m, i - 1}}\} \overset{d}{=} ρ + (1 - ρ) X_{\frac{m^{2}}{6}, i} .$

As $F_{X_{\frac{m^{2}}{6}, i}} (x) = ((1 - \frac{m^{2}}{12}) x + \frac{m^{2}}{12} x^{2}) I_{(0, 1)} (x) + I_{[1, \infty)} (x)$ , the cumulative distribution function of

$W = min_{1 \leq i \leq n} \{ρ + (1 - ρ) X_{\frac{m^{2}}{6}, i}\} = ρ + (1 - ρ) min_{1 \leq i \leq n} X_{\frac{m^{2}}{6}, i}$

is

$F_{W} (x) = \{\begin{matrix} 0, & x < ρ \\ 1 - {[1 - (1 - \frac{m^{2}}{12}) \frac{x - ρ}{1 - ρ} - \frac{m^{2}}{12} {(\frac{x - ρ}{1 - ρ})}^{2}]}^{n}, & ρ \leq x < 1 \\ 1, & x \geq 1 \end{matrix} .$

4.3. Combined Tests with Genuine and Fake p-values — Some Analytic Results

4.3.1. Tippett’s $T_{T} (P_{1}, \dots, P_{n})$

Provided the number

n_{f}

of fake p-values is known, it is straightforward to obtain the exact distribution of Tippett’s combined test statistic: If there are

n_{f}

fake Beta(1,2) p-values among the n available

p_{k}

’s to be combined,

T_{T} (P_{1}, \dots, P_{n}) = P_{1 : n + n_{f}}

. Therefore, the decision rule is to reject

H_{0}^{*}

at a significance level

α

if the minimum observed p-value

p_{1 : n + n_{f}} < 1 - {(1 - α)}^{1 / (n + n_{f})}

Tippett’s case is quite unique, since the analytical results for the test statistics of the other combination methods are cumbersome.

4.3.2. Pearson’s $T_{P} (P_{1}, \dots, P_{n})$

The computation of the probability density function of Pearson’s statistic

T_{P} (P_{1}, \dots, P_{n})

= \prod_{k = 1}^{n} P_{k}

when all

P_{k}

’s are independent genuine p-values is a straightforward exercise of multiplicative algebra of random variables, since

f_{T_{P}} (x) = \frac{{(- ln x)}^{n - 1}}{Γ (n)} I_{(0, 1)} (x) .

To accommodate fake p-values in the analysis, the first step is to obtain the cumulative distribution function of

\prod_{k = 1}^{n} P_{k}

when there exists just one fake p-value in the sample, and the remaining

n - 1

p-values are genuine ones (note that it is irrelevant to know which

P_{k}

is actually the fake one).

—: Probability density function of $Z_{n, 1} = Y \prod_{k = 1}^{n - 1} P_{k}$ , with independent $P_{k} \sim Uniform (0, 1)$ and $Y \sim Beta (1, 2)$

Let

Z_{n, 1} = Y P_{1} \dots P_{n - 1}

, where

P_{k} \sim Uniform (0, 1)

k = 1, \dots, n - 1

, and

Y \sim Beta (1, 2)

are independent random variables, and define

S = - ln Z_{n}

. Therefore,

S = - ln Y + \sum_{k = 1}^{n - 1} (- ln P_{k}) \overset{d}{=} W + X,

where

W = - ln Y

and

X = \sum_{k = 1}^{n - 1} (- ln P_{k}) \sim Gamma (n - 1, 1)

are independent random variables. Since the joint probability density function of the random pair

(W, X)

\begin{matrix} f_{(W, X)} (w, x) = \frac{2}{(n - 2)!} x^{n - 2} (1 - e^{- w}) e^{- (x + w)} I_{(0, \infty) \times (0, \infty)} (w, x), \end{matrix}

for

s > 0

\begin{matrix} f_{S} (s) & = \int_{0}^{s} f_{(W, X)} (s - x, x) d x = \frac{2}{(n - 2)!} e^{- s} \int_{0}^{s} x^{n - 2} (1 - e^{- s + x}) d x \\ = \frac{2}{(n - 2)!} e^{- s} [\int_{0}^{s} x^{n - 2} d x - \int_{0}^{s} x^{n - 2} e^{- s + x} d x] \\ = \frac{2}{(n - 2)!} e^{- s} \{\frac{s^{n - 1}}{n - 1} - e^{- s} {(- 1)}^{n} [Γ (n - 1, - s) - Γ (n - 1)]\} \\ = \frac{2}{(n - 2)!} \{\frac{s^{n - 1} e^{- s}}{n - 1} + {(- 1)}^{n} e^{- 2 s} [(n - 2)! - Γ (n - 1, - s)]\} . \end{matrix}

Consequently, for

z \in (0, 1)

\begin{matrix} f_{Z_{n, 1}} (z) & = \frac{2}{(n - 2)!} [\frac{{(- ln z)}^{n - 1} z}{n - 1} + {(- 1)}^{n} z^{2} [(n - 2)! - Γ (n - 1, ln z)]] \frac{1}{z} \\ = \frac{2}{(n - 2)!} [\frac{{(- ln z)}^{n - 1}}{n - 1} + {(- 1)}^{n} z [(n - 2)! - Γ (n - 1, ln z)]] . \end{matrix}

(6)

Noting that

Γ (α, z) = Γ (α) (1 - P (α, z))

, where

P (α, z) = \frac{1}{Γ (α)} \int_{0}^{z} t^{α - 1} e^{- t} d t

α, z > 0

, and in particular,

P (n, z) = 1 - e^{- z} \sum_{k = 0}^{n - 1} \frac{z^{k}}{k!}

n \in N

(cf. Abramowitz and Stegun [93], 6.5.1–6.5.3 and 6.5.13), we get

Γ (n - 1, ln z) = \frac{Γ (n - 1)}{z} \sum_{k = 0}^{n - 2} \frac{{(ln z)}^{k}}{k!} = \frac{(n - 2)!}{z} \sum_{k = 0}^{n - 2} \frac{{(ln z)}^{k}}{k!} .

Therefore, substituting the above expression in (6), it follows that

\begin{matrix} f_{Z_{n, 1}} (z) & = \frac{2 {(- ln z)}^{n - 1}}{(n - 1)!} + 2 {(- 1)}^{n} z [1 - \frac{1}{z} \sum_{k = 0}^{n - 2} \frac{{(ln z)}^{k}}{k!}] \\ = 2 {(- 1)}^{n - 1} [\frac{{(ln z)}^{n - 1}}{(n - 1)!} - z + \sum_{k = 0}^{n - 2} \frac{{(ln z)}^{k}}{k!}] \\ = 2 {(- 1)}^{n - 1} [1 - z + \sum_{k = 1}^{n - 1} \frac{{(ln z)}^{k}}{k!}] . \end{matrix}

Note that due to the contraction resulting from multiplying random variables with support

[0, 1]

\sum_{k = 1}^{n - 1} \frac{{(ln z)}^{k}}{k!} \underset{n \to \infty}{\to} e^{ln z} - 1 = z - 1,

and therefore for all

z > 0

f_{Z_{n, 1}} (z) \underset{n \to \infty}{\to} 0

. In other words,

f_{Z_{n, 1}} (z) \underset{n \to \infty}{\to} δ_{0}

, the Dirac degenerate at 0 "density", and

F_{Z_{n, 1}} (z) \underset{n \to \infty}{\to} H_{0} (z) = \{\begin{matrix} 0, & x < 0 \\ 1, & x \geq 0 \end{matrix}

, i.e. the Heaviside function.

—: Probability density function of $Z_{n, 2} = Y_{1} Y_{2} \prod_{k = 1}^{n - 2} P_{k}$ , with independent $Y_{1}, Y_{2} \sim Beta (1, 2)$ and $P_{k} \sim Uniform (0, 1)$

Let

Y_{1} \overset{d}{=} Y_{2} \sim B e t a (1, 2)

be independent random variables. The probability density function of

Z_{2, 2} = Y_{1} Y_{2}

f_{Z_{2, 2}} (z) = - 4 [2 (1 - z) + (1 + z) ln z] I_{(0, 1)} (z),

and from which we easily obtain the probability density function of

Z_{3, 2} = Y_{1} Y_{2} P_{1}

f_{Z_{3, 2}} (z) = 4 [3 - 3 z + (z + 2) ln z + \frac{{(ln z)}^{2}}{2}] I_{(0, 1)} (z) .

Applying recursive methods, the probability density function of

Z_{n, 2}

f_{Z_{n, 2}} (z) = 4 {(- 1)}^{n - 1} [n (1 - z) + z ln z + \sum_{k = 1}^{n - 1} \frac{(n - k) {(ln z)}^{k}}{k!}] I_{(0, 1)} (z) .

4.3.3. Fisher’s Statistic Sampling Distribution for Combining p-Values from a Mendel(m) Population

X_{1}, \dots, X_{n}

are independent and identically distributed random variables with probability density function f, the probability density function of the sum

X_{1} + \dots + X_{n}

is the n-fold convolution of f, denoted by

f^{n *}

, and defined as

f^{n *} = f^{(n - 1) *} * f = f * f^{(n - 1) *},

with

f^{1 *} = f

and

f^{0 *} * f = f

. As for the n-fold convolution of a finite mixture of probability density functions

f_{1}, \dots, f_{k}

, i.e. with probability density function

f (t) = \sum_{j = 1}^{k} π_{j} f_{j} (t),

where

π_{j} \geq 0

and

\sum_{j = 1}^{k} π_{j} = 1

, it is

f^{n *} (t) = \sum_{n_{1} + \dots + n_{k} = n} \frac{n!}{n_{1}! \dots n_{k}!} π_{1}^{n_{1}} \dots π_{k}^{n_{k}} f_{1}^{n_{1} *} * \dots * f_{k}^{n_{k} *} (t),

(7)

(Sarabia et al. [94]), which is also a mixture.

Let

(X_{1}, \dots, X_{n})

be a random sample with

X_{k} \overset{d}{=} X \sim Mendel (m)

m \in (- 2, 2)

k = 1, \dots, n

, i.e. with probability density function

f_{X} (x) = (m x + 1 - \frac{m}{2}) I_{(0, 1)} (x),

and define

T_{n; m} = - 2 \sum_{k = 1}^{n} ln X_{k}

m = 0

, then

T_{n; 0} = T_{F} \sim χ_{2 n}^{2}

since

X_{k} \sim Uniform (0, 1)

k = 1, \dots, n

. If

m \in (- 2, 0) \cup (0, 2)

, define

Y_{k} = - 2 ln X_{k}

k = 1, \dots, n

. Therefore, for

t > 0

, the probability density function of

Y_{k}

can be expressed as

f_{Y_{k}} (t) = \frac{m}{2} e^{- t} + (1 - \frac{m}{2}) \frac{1}{2} e^{- t / 2} = (1 + \frac{m}{2}) \frac{1}{2} e^{- t / 2} - \frac{m}{2} (e^{- t / 2} - e^{- t}) .

Consequently, if

m \in (0, 2)

, the distribution of

Y_{k}

is a convex mixture of two exponential distributions, more precisely,

f_{Y_{k}} (t) = \frac{m}{2} f_{E_{1}} (t) + (1 - \frac{m}{2}) f_{E_{2}} (t),

(8)

where

E_{j}

denotes an exponential random variable with scale parameter

j > 0

. On the other hand, if

m \in (- 2, 0)

, then the distribution of

Y_{k}

is also a convex mixture since its probability density function can be expressed as

f_{Y_{k}} (t) = (1 + \frac{m}{2}) f_{E_{2}} (t) + (- \frac{m}{2}) f_{W} (t),

(9)

where W has probability density function

f_{W} (t) = (e^{- t / 2} - e^{- t}) I_{(0, \infty)} (t)

Note that if

m \in (- 2, 0)

(respectively,

m \in (0, 2)

), probability density function (8) (respectively, probability density function (9)) can be considered a general mixture. Hence, the probability density function of

T_{n; m}

is the n-fold convolution of a finite mixture when

m \in (- 2, 0) \cup (0, 2)

Although Theorem 1 in Sarabia et al. [94] only deals with convex mixtures, it is extended in Theorem 2 to general finite mixtures, i.e. mixtures where some mixing weights are allowed to be negative.

Theorem 2.

Let

f_{j}

j = 1, \dots, k

, be probability density functions and X a random variable with probability density function defined by

f (x) = \sum_{j = 1}^{k} a_{j} f_{j} (x),

where

a_{1}, \dots, a_{k}

are real constants subject to

\sum_{j = 1}^{k} a_{j} = 1

. The probability density function of the n-fold convolution of f is

f^{n *} (x) = \sum_{n_{1} + \dots + n_{k} = n} \frac{n!}{n_{1}! \dots n_{k}!} a_{1}^{n_{1}} \dots a_{n}^{n_{k}} f_{1}^{n_{1} *} * \dots * f_{k}^{n_{k} *} (x) .

Proof.

Denoting by

ψ_{j}

the characteristic function of the probability density function

f_{j}

j = 1, \dots, k

, the characteristic function of

f^{n *}

, the probability density function of the n-fold convolution of f, is

\begin{matrix} ψ (t) & = {[E (e^{i t X})]}^{n} = {[\sum_{j = 1}^{k} a_{j} ψ_{j} (t)]}^{n} \\ = \sum_{n_{1} + \dots + n_{k} = n} \frac{n!}{n_{1}! \dots n_{k}!} a_{1}^{n_{1}} \dots a_{k}^{n_{k}} ψ_{1}^{n_{1}} (t) \dots ψ_{k}^{n_{k}} (t) . \end{matrix}

ψ_{1}^{n_{1}} \dots ψ_{k}^{n_{k}}

is the characteristic function of the convolution

f_{1}^{n_{1} *} * \dots * f_{k}^{n_{k} *}

, the probability density function of the n-fold convolution of f is

f^{n *} (x) = \sum_{n_{1} + \dots + n_{k} = n} \frac{n!}{n_{1}! \dots n_{k}!} a_{1}^{n_{1}} \dots a_{k}^{n_{k}} f_{1}^{n_{1} *} * \dots * f_{k}^{n_{k} *} (x),

which is an immediate consequence of the inversion formula for characteristic functions. □

Therefore, from Theorem 2 it follows that

T_{n; m}

is a finite mixture when

m \in (- 2, 0) \cup (0, 2)

Since probability density functions (8) and (9) are formally equivalent, for what follows, it suffices to work with probability density function (8). Thus applying (7), we get for

t > 0

f_{T_{n; m}} (t) = \sum_{k = 0}^{n} (\binom{n}{k}) {(\frac{m}{2})}^{k} {(1 - \frac{m}{2})}^{n - k} f_{E_{1}}^{k *} * f_{E_{2}}^{(n - k) *} (t),

where

f_{E_{1}} (t) = e^{- t} I_{(0, \infty)} (t)

and

f_{E_{2}} (t) = \frac{1}{2} e^{- t / 2} I_{(0, \infty)} (t)

Noticing that

f_{j}^{m *}

is the m-convolution of an exponential probability density function with scale parameter j, in other words,

f_{j}^{m *}

is the probability density function of the sum of m independent and identically distributed exponential random variables with scale parameter j,

j = 1, 2

, it follows that

f_{j}^{m *}

is the probability density function of the Gamma distribution with shape parameter m and scale parameter j, and therefore

f_{1}^{k *} (t) = \frac{t^{k - 1} e^{- t}}{Γ (k)} I_{(0, \infty)} (t) and f_{2}^{(n - k) *} (t) = \frac{t^{n - k - 1} e^{- t / 2}}{2^{n - k} Γ (n - k)} I_{(0, \infty)} (t) .

Hence,

\begin{matrix} f_{1}^{k *} * f_{2}^{(n - k) *} (t) & = \int_{- \infty}^{\infty} f_{1}^{k *} (x) f_{2}^{(n - k) *} (t - x) d x \\ = \int_{0}^{t} \frac{x^{k - 1} e^{- x} {(t - x)}^{n - k - 1} e^{- (t - x) / 2}}{2^{n - k} Γ (k) Γ (n - k)} d x \\ = \frac{e^{- t / 2}}{2^{n - k} Γ (k) Γ (n - k)} \int_{0}^{t} x^{k - 1} {(t - x)}^{n - k - 1} e^{- x / 2} d x . \end{matrix}

Using the formula

\int_{0}^{u} x^{ν - 1} {(u - x)}^{μ - 1} e^{β x} d x = B (μ, ν) {u^{μ + ν - 1}}_{1} F_{1} (ν; μ + ν; β u), μ > 0, ν > 0,

(cf. Gradshteyn and Ryzhik [95], 3.383.1), where

B (p, q) = \int_{0}^{1} x^{p - 1} {(1 - x)}^{q - 1} d x

p, q > 0

, is the Beta function and ₁

F_{1} (a; b; z) = \sum_{k = 0}^{\infty} \frac{{(a)}_{k}}{{(b)}_{k}} \frac{z^{k}}{k!}

the Kummer’s confluent hypergeometric function, we obtain

\begin{matrix} f_{1}^{k *} * f_{2}^{(n - k) *} (t) & = \frac{e^{- t / 2}}{2^{n - k} Γ (k) Γ (n - k)} B (n - k, k) {t^{n - 1}}_{1} F_{1} (k; n; - \frac{t}{2}) \\ = {\frac{t^{n - 1} e^{- t / 2}}{2^{n - k} Γ (n)}}_{1} F_{1} (k; n; - \frac{t}{2}) . \end{matrix}

Therefore, for

t > 0

\begin{matrix} f_{T_{n; m}} (t) & = \sum_{k = 0}^{n} (\binom{n}{k}) {(\frac{m}{2})}^{k} {(1 - \frac{m}{2})}^{n - k} {\frac{t^{n - 1} e^{- t / 2}}{2^{n - k} Γ (n)}}_{1} F_{1} (k; n; - \frac{t}{2}) \\ = \frac{t^{n - 1} e^{- t / 2}}{2^{n} Γ (n)} \sum_{k = 0}^{n} (\binom{n}{k}) m^{k} {(1 - \frac{m}{2})}^{n - k}_{1} F_{1} (k; n; - \frac{t}{2}) . \end{matrix}

For example, if

n = 2

and

m = 1

\begin{matrix} f_{T_{2; 1}} (t) & = \frac{t e^{- t / 2}}{4} \sum_{k = 0}^{2} (\binom{2}{k}) {(\frac{1}{2})}^{2 - k}_{1} F_{1} (k; 2; - \frac{t}{2}) \\ = \frac{1}{16} [(t + 8) e^{- t / 2} + 4 (t - 2) e^{- t}] \\ = \frac{1}{4} \frac{t e^{- t / 2}}{4} + \frac{1}{4} t e^{- t} + \frac{1}{2} (e^{- t / 2} - e^{- t}), \end{matrix}

which is a convex mixture, and if

n = 2

and

m = - 1

\begin{matrix} f_{T_{2; - 1}} (t) & = \frac{t e^{- t / 2}}{4} \sum_{k = 0}^{2} (\binom{2}{k}) {(- 1)}^{k} {(\frac{3}{2})}^{2 - k}_{1} F_{1} (k; 2; - \frac{t}{2}) \\ = \frac{1}{16} [3 (3 t - 8) e^{- t / 2} + 4 (t + 6) e^{- t}] \\ = \frac{9}{4} \frac{t e^{- t / 2}}{4} + \frac{1}{4} t e^{- t} - \frac{3}{2} (e^{- t / 2} - e^{- t}), \end{matrix}

which is a general mixture.

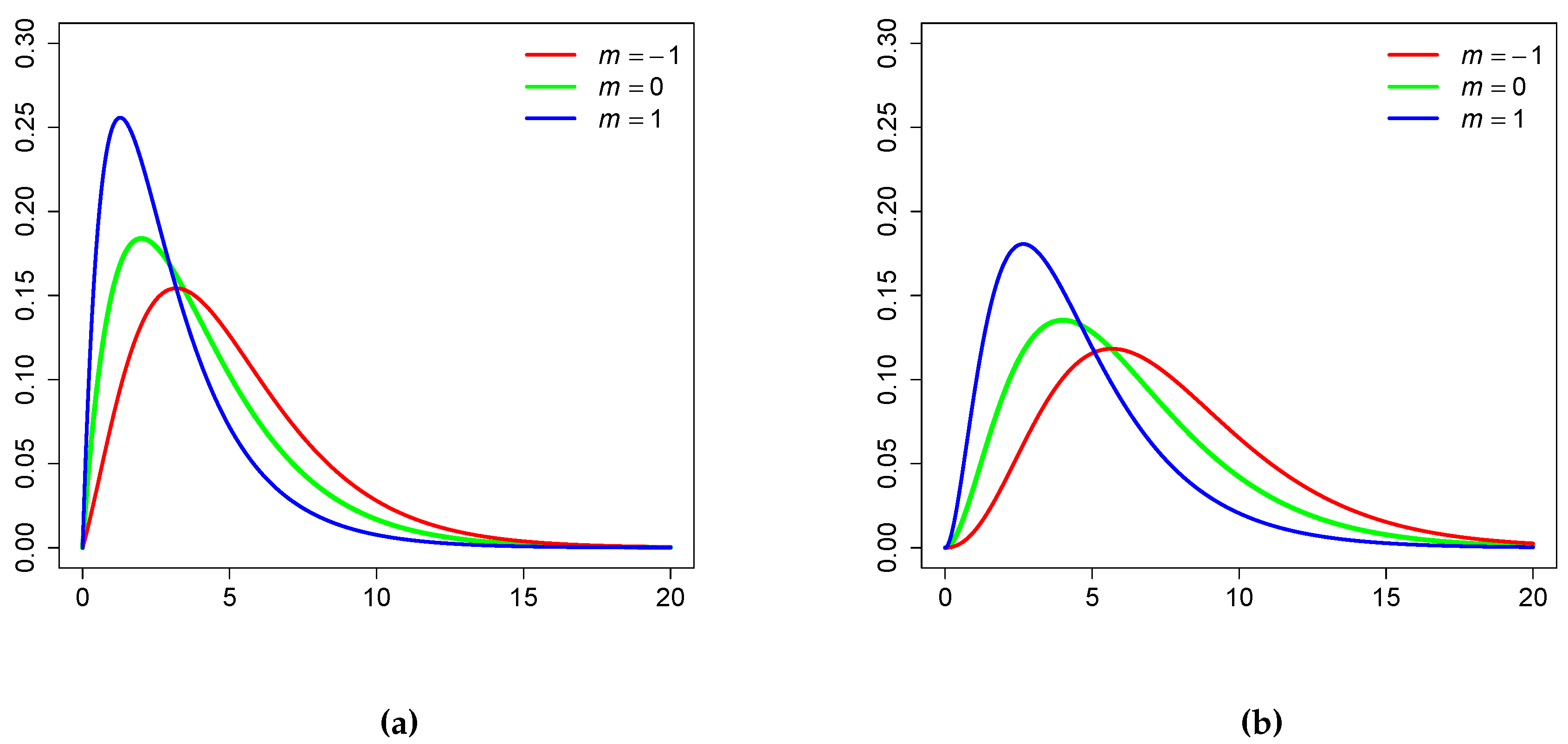
In Figure 1 we plot the probability density function of

T_{n; m}

for

n = 2, 3

and

m = - 1, 0, 1

5. Discussion

With the exception of Tippett’s

T_{T} (P_{1}, \dots, P_{n}) = P_{1 : n}

, the other combined test statistics mentioned in Section 2 have a distribution that does not allow a closed-form expression for the cumulative distribution function when there are

n_{f} \geq 1

fake p-values in the sample.

As already mentioned, it is in general impossible to know whether there exist or not fake p-values among the set of p-values to be combined. Therefore, a realistic approach is to examine possible scenarios and assess how the existence of fake p-values can affect the decision on the overall hypothesis

H_{0}^{*}

For this purpose, a simple simulation was carried out with the software R (version 4.3.1), a language and environment for statistical computing (R Core Team 2023, [96]), to obtain quantile estimates of order q (q = 0.005,0.01,0.025,0.05,0.1,0.9,0.95,0.975,0.99,0.995) for the combined test statistics indicated in Section 2, and when some of the p-values in the sample are fake ones. The guidelines in Davison and Hinkley [97] on how to estimate quantiles (pp. 18-19) were followed here. The tables with the estimated quantiles (in a few cases some are exact) are supplied in the Supplementary Materials for sample sizes

n = 3, \dots, 28

, and when there exists at most

n_{f} \leq ⌊ n / 3 ⌋

fake p-values. These tables are a useful tool to build up an overall picture, as is illustrated with Example 6.

Example 6.

For the set of

n = 18

fictional p-values:

\begin{matrix} 0.4574 & 0.0223 & 0.0371 & 0.6954 & 0.0549 & 0.2793 & 0.7928 & 0.6917 & 0.3483, \\ 0.0554 & 0.8238 & 0.8583 & 0.3824 & 0.7138 & 0.0423 & 0.0116 & 0.7543 & 0.1438 \end{matrix}

the observed values for the combined test statistics are:

\begin{matrix} T_{F} (0.4574, \dots, 0.1438) = 56.9104 \\ T_{S} (0.4574, \dots, 0.1438) = - 1.9665 \\ T_{C} (0.4574, \dots, 0.1438) = 26.1606 \\ T_{M G} (0.4574, \dots, 0.1438) = 15.9379 (t_{M G}^{*} = 2.0935) \\ T_{G_{18}} (0.4574, \dots, 0.1438) = 0.2058 \\ T_{min G_{18}, G_{18}^{*}} (0.4574, \dots, 0.1438) = 0.2058 \\ T_{H_{18}} (0.4574, \dots, 0.1438) = 0.0734 \\ T_{E} (0.4574, \dots, 0.1438) = 0.3981 \\ T_{T} (0.4574, \dots, 0.1438) = 0.0116 \\ T_{W} (0.4574, \dots, 0.1438) = 0.8583 . \end{matrix}

We reproduce below only the part for

n = 18

from the tables in the Supplementary Materials (without the standard errors), highlighting the critical quantiles that lead to the rejection of

H_{0}^{*}

with an asterisk, as well as indicating the smallest significance level

α \in {0.005, 0.01, 0.025, 0.05, 0.10}

for which this happens.

• Fisher’s Statistic

T_{F} = 56.9104

$n$	$n_{f}$	0.900	0.950	0.975	0.990	0.995	$α$
18	0	$47.2122 *$	$50.9985 *$	$54.4373 *$	$58.6192$	$61.5812$	0.025
18	1	$48.3379 *$	$52.1229 *$	$55.5203 *$	$59.7620$	$62.7232$	0.025
18	2	$49.4103 *$	$53.1857 *$	$56.6785 *$	$60.8012$	$63.7274$	0.025
18	3	$50.4540 *$	$54.3029 *$	$57.7948$	$62.0427$	$65.0779$	0.05
18	4	$51.5281 *$	$55.3389 *$	$58.8498$	$63.1156$	$66.1164$	0.05
18	5	$52.5732 *$	$56.4025 *$	$59.8978$	$64.0685$	$67.2668$	0.05
18	6	$53.6360 *$	$57.4945$	$60.9949$	$65.3194$	$68.3048$	0.10

• Stouffer’s Statistic

T_{S} = - 1.9665

$n$	$n_{f}$	0.900	0.950	0.975	0.990	0.995	$α$
18	0	$1.2815 *$	$1.6448 *$	$1.9600 *$	$2.3264$	$2.5758$	0.025
18	1	$1.1321 *$	$1.4888 *$	$1.8005 *$	$2.1669$	$2.4111$	0.025
18	2	$0.9884 *$	$1.3418 *$	$1.6537 *$	$2.0091$	$2.2655$	0.025
18	3	$0.8432 *$	$1.1942 *$	$1.5043 *$	$1.8587 *$	$2.1084$	0.01
18	4	$0.6997 *$	$1.0505 *$	$1.3625 *$	$1.7079 *$	$1.9505 *$	—
18	5	$0.5578 *$	$0.9073 *$	$1.2070 *$	$1.5548 *$	$1.8026 *$	—
18	6	$0.4117 *$	$0.7573 *$	$1.0546 *$	$1.3945 *$	$1.6334 *$	—

• Chen’s Statistic

T_{C} = 26.1606

$n$	$n_{f}$	0.900	0.950	0.975	0.990	0.995	$α$
18	0	$25.9894 *$	$28.8693$	$31.5264$	$34.8053$	$37.1564$	0.10
18	1	$26.0050 *$	$28.8614$	$31.5476$	$34.7641$	$37.2442$	0.10
18	2	$26.0007 *$	$28.8603$	$31.5185$	$34.7654$	$37.1842$	0.10
18	3	$25.9715 *$	$28.8615$	$31.5584$	$34.7827$	$37.2972$	0.10
18	4	$25.9611 *$	$28.8558$	$31.5221$	$34.8170$	$37.2941$	0.10
18	5	$25.9520 *$	$28.8359$	$31.4967$	$34.8157$	$37.2759$	0.10
18	6	$25.9417 *$	$28.8679$	$31.5524$	$34.7698$	$37.2629$	0.10

• Mudholkar and George’s Statistic

T_{M G} = 15.9379

$n$	$n_{f}$	0.900	0.950	0.975	0.990	0.995	$α$
18	0	$9.8535 *$	$12.6987 *$	$15.1577 *$	$18.0717$	$20.0749$	0.025
18	1	$10.7808 *$	$13.6068 *$	$16.0024$	$18.9023$	$20.8850$	0.05
18	2	$11.6996 *$	$14.4896 *$	$16.9051$	$19.6710$	$21.6251$	0.05
18	3	$12.6072 *$	$15.3900 *$	$17.8073$	$20.6821$	$22.6112$	0.05
18	4	$13.5400 *$	$16.2821$	$18.6795$	$21.5146$	$23.4955$	0.10
18	5	$14.4620 *$	$17.1581$	$19.5568$	$22.3635$	$24.2301$	0.10
18	6	$15.3463 *$	$18.0434$	$20.4629$	$23.1753$	$25.2362$	0.10

• Geometric Mean

T_{G_{18}} = 0.2058

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.18076$	$0.19626$	$0.22044 *$	$0.24253 *$	$0.26943 *$	0.025
18	1	$0.17517$	$0.19015$	$0.21392 *$	$0.23508 *$	$0.26114 *$	0.025
18	2	$0.17034$	$0.18474$	$0.20715 *$	$0.22824 *$	$0.25348 *$	0.025
18	3	$0.16407$	$0.17849$	$0.20082$	$0.22127 *$	$0.24623 *$	0.05
18	4	$0.15941$	$0.17324$	$0.19502$	$0.21499 *$	$0.23899 *$	0.05
18	5	$0.15439$	$0.16871$	$0.18942$	$0.20873 *$	$0.23215 *$	0.05
18	6	$0.15002$	$0.16295$	$0.18373$	$0.20250$	$0.22540 *$	0.10

• Minimum of Geometric Means

T_{min \{G_{18}, G_{18}^{*}\}} = 0.2058

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.16748$	$0.18109$	$0.20234$	$0.22089 *$	$0.24268 *$	0.05
18	1	$0.16771$	$0.18106$	$0.20210$	$0.22066 *$	$0.24246 *$	0.05
18	2	$0.16614$	$0.17955$	$0.20004$	$0.21905 *$	$0.24126 *$	0.05
18	3	$0.16209$	$0.17584$	$0.19665$	$0.21584 *$	$0.23835 *$	0.05
18	4	$0.15833$	$0.17185$	$0.19303$	$0.21195 *$	$0.23429 *$	0.05
18	5	$0.15416$	$0.16818$	$0.18850$	$0.20724 *$	$0.22955 *$	0.05
18	6	$0.14992$	$0.16267$	$0.18340$	$0.20183$	$0.22413 *$	0.10

• Harmonic Mean

T_{H_{18}} = 0.0734

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.00484$	$0.00933$	$0.02154$	$0.03932$	$0.06833$	—
18	1	$0.00470$	$0.00892$	$0.02061$	$0.03724$	$0.06481$	—
18	2	$0.00448$	$0.00850$	$0.01953$	$0.03528$	$0.06166$	—
18	3	$0.00433$	$0.00808$	$0.01860$	$0.03350$	$0.05882$	—
18	4	$0.00408$	$0.00772$	$0.01773$	$0.03213$	$0.05639$	—
18	5	$0.00395$	$0.00735$	$0.01702$	$0.03087$	$0.05413$	—
18	6	$0.00374$	$0.00707$	$0.01635$	$0.02967$	$0.05194$	—

• Arithmetic Mean

T_{E} = 0.3981

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.32566$	$0.34207$	$0.36647$	$0.38733$	$0.41222 *$	0.10
18	1	$0.31913$	$0.33507$	$0.35886$	$0.37940$	$0.40362 *$	0.10
18	2	$0.31213$	$0.32820$	$0.35130$	$0.37126$	$0.39516$	—
18	3	$0.30455$	$0.31983$	$0.34308$	$0.36304$	$0.38675$	—
18	4	$0.29747$	$0.31320$	$0.33505$	$0.35499$	$0.37860$	—
18	5	$0.28958$	$0.30480$	$0.32736$	$0.34705$	$0.37017$	—
18	6	$0.28308$	$0.29723$	$0.31931$	$0.33906$	$0.36191$	—

• Minimum

T_{T} = 0.0116

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.00028$	$0.00056$	$0.00141$	$0.00285$	$0.00584$	—
18	1	$0.00026$	$0.00053$	$0.00133$	$0.00270$	$0.00553$	—
18	2	$0.00025$	$0.00050$	$0.00127$	$0.00256$	$0.00525$	—
18	3	$0.00024$	$0.00048$	$0.00120$	$0.00244$	$0.00500$	—
18	4	$0.00023$	$0.00046$	$0.00115$	$0.00233$	$0.00478$	—
18	5	$0.00022$	$0.00044$	$0.00110$	$0.00223$	$0.00457$	—
18	6	$0.00021$	$0.00042$	$0.00105$	$0.00213$	$0.00438$	—

• Maximum

T_{W} = 0.8583

$n$	$n_{f}$	0.005	0.010	0.025	0.050	0.100	$α$
18	0	$0.74501$	$0.77426$	$0.81470$	$0.84668$	$0.87992 *$	0.10
18	1	$0.73587$	$0.76506$	$0.80672$	$0.83921$	$0.87388 *$	0.10
18	2	$0.72414$	$0.75493$	$0.79795$	$0.83189$	$0.86768 *$	0.10
18	3	$0.71307$	$0.74442$	$0.78830$	$0.82406$	$0.86091 *$	0.10
18	4	$0.70160$	$0.73412$	$0.77899$	$0.81504$	$0.85338$	—
18	5	$0.68996$	$0.72267$	$0.76825$	$0.80548$	$0.84499$	—
18	6	$0.67754$	$0.71057$	$0.75737$	$0.79515$	$0.83610$	—

Note that the conclusions with

T_{F}

and

T_{G_{n}}

are the same, but it is obviously useful to supply both tables. The example has been constructed to have p-values in the range

[0, 1]

, some of them small and some large. This is a situation where

T_{M G}

and

T_{min {G_{n}, G^{*}}}

, which use both

P_{k}

’s and

1 - P_{k}

’s, may be useful for an informed decision.

In fact, in this example,

T_{M G}

and

T_{min {G_{n}, {G_{n}}^{*}}}

perform almost as well as

T_{F}

(or

T_{G_{n}}

) and better than

T_{S}

. Moreover, the statistic

T_{C}

seems to be less reliable than

T_{S}

and

T_{M G}

, and except for the geometric (

r = 0

) mean

T_{G_{n}}

, the means of order

r \in {- \infty, - 1, 1, \infty}

, i.e.

T_{T}

T_{H_{n}}

T_{E}

and

T_{W}

, do not contribute effectively for a clearcut decision.

This example shows that the existence of fake p-values can influence the overall decision on

H_{0}^{*}

, as expected, and the most recommended Fisher’s and Stouffer et al.’s methods are clearly affected by their existence. Aside from the number of fake p-values in the sample, their magnitude has also a bearing on the smallest level

α

that leads to the rejection of

H_{0}^{*}

6. Conclusions

Although significance testing and p-values have these days plenty of bad press and detractors, reporting low p-values still has a mythic standing and influences publication acceptance. Therefore, it is possible that research teams will try to obtain smaller p-values if the first ones obtained are not significant. In these unwanted situations, which were first pointed out by Fisher [37] when denouncing the possibility of fraud in Mendel’s theories (cf. also Franklin [38], and Pires and Branco [39]), the most realistic scenarios are:

In the first experiment the p-value obtained was greater than 0.05 and the p-value obtained in the second experiment is smaller than 0.05. The first one is "hidden" and the second one is reported. However, the reported p-value is not genuine, it is the fake result of two P, and therefore it is Beta(1,2)-distributed.
The p-values obtained in the first and second experiments were both greater than 0.05. This seems to indicate that there are no grounds to reject the null hypothesis and the most plausible consequence is the abandonment of the line of research, thus leading to no p-value being published. In fact, replicating experiments has costs, at least it is time consuming, and therefore discarding further experimentation seems to be a reasonable decision.

So, when meta-analyzing p-values via combining them, one must be aware that in the Brave New World of scientific achievements, where the underlying motto is "publish or perish", eventually some — but almost certainly very few — of the the

P_{k}

’s,

k = 1, \dots, n

, to be used in statistics

T (P_{1}, \dots, P_{n})

are fake

Beta (1, 2)

p-values, although in an honest world all p-values should be genuine

Beta (1, 1) = Uniform (0, 1)

values.

It is therefore reasonable to use tools such as the extensive tables supplied in the Supplementary Materials to compare the results of several combined tests, assuming that between the

P_{k}

’s there are

n_{f} = 0, 1, \dots, j ≪ n

fake p-values.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, M.F.B., M.I.G., S.M., D.P. and R.S.; Funding acquisition, M.I.G.; Investigation, M.F.B., M.I.G., S.M., D.P. and R.S.; Methodology, M.F.B., M.I.G., S.M., D.P. and R.S.; Project administration, M.F.B., D.P. and R.S.; Resources, M.F.B., M.I.G., and R.S.; Software, M.F.B. and R.S.; Supervision, M.F.B. and D.P.; Writing – original draft, M.F.B., M.I.G., S.M., D.P. and R.S.; Writing – review & editing, M.F.B., M.I.G., S.M., D.P. and R.S.. All authors have read and agreed to the published version of the manuscript.

Funding

Research partially supported by National Funds through FCT—Fundação para a Ciência e Tecnologia, project UIDB/00006/2020 (CEAUL). (https://doi.org/10.54499/UIDB/00006/2020)

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine Series 5 1900, 50, 157–175. [Google Scholar] [CrossRef]
Kennedy-Shaffer, L. Before p<0.05 to beyond p<0.05: Using History to contextualize p-values and significance testing. Amer. Stat. 2019, 73, 82–90. [Google Scholar] [CrossRef]
Arbuthnott, J. An argument for divine providence, taken from the constant regularity observ’d in the births of both sexes. Philosophical Transactions of the Royal Society of London 1710, 27, 186–190. [Google Scholar] [CrossRef]
Fisher, R.A. On the interpretation of χ² from contingency tables, and the calculation of P. J. R. Stat. Soc. 1922, 85, 87–94. [Google Scholar] [CrossRef]
Fisher, R.A. Statistical Methods for Research Workers; Oliver and Boyd: Edinburgh, UK, 1925. [Google Scholar]
Fisher, R.A. Statistical Methods for Research Workers, 4th ed.; Oliver and Boyd: London, UK, 1932. [Google Scholar]
Edgeworth, F.Y. The calculus of probabilities applied to psychical research, Part I. In Proceedings of the Society for Psychical Research; Society for Psychical Research, 1885; Vol. 3, pp. 190–199. [Google Scholar]
Fisher, R.A. The arrangement of field experiments. Journal of the Ministry of Agriculture 1926, 33, 503–515. [Google Scholar]
Utts, J. Replication and meta-analysis in parapsychology. Statist. Sci. 1991, 6, 363–378. [Google Scholar] [CrossRef]
Greenwald, A.G.; Gonzalez, R.; Harris, R.J.; Guthrie, D. Effect sizes and p values: what should be reported and what should be replicated? Psychophysiology 1996, 33, 175–183. [Google Scholar] [CrossRef] [PubMed]
Colquhoun, D. The reproducibility of research and the misinterpretation of p-values. R. Soc. Open Sci. 2017, 4, 171085. [Google Scholar] [CrossRef] [PubMed]
Vovk, V.; Wang, R. Combining p-values via averaging. Biometrika 2020, 107, 791–808. [Google Scholar] [CrossRef]
Neyman, J.; Pearson, E. On the use and interpretation of certain test criteria for purposes of statistical inference: Part I. Biometrika 1928, 20A, 175–240. [Google Scholar] [CrossRef]
Neyman, J.; Pearson, E.S. On the problem of the most efficient tests of statistical hypotheses. Phil. Trans. R. Soc. Lond. Series A 1933, 231, 289–337. [Google Scholar] [CrossRef]
Fisher, R. Statistical methods and scientific induction. J. R. Stat. Soc. Series B Stat. Methodol. 1955, 17, 69–78. [Google Scholar] [CrossRef]
Pearson, E.S. Statistical concepts in the relation to reality. J. R. Stat. Soc. Series B 1955, 17, 204–207. [Google Scholar] [CrossRef]
Lehmann, E.L. The Fisher, Neyman-Pearson theories of testing hypotheses: one theory or two? J. Amer. Stat. Assoc. 1993, 88, 1242–1249. [Google Scholar] [CrossRef]
Cox, D.R.; Spjøtvoll, E.; Johansen, S.; van Zwet, W.R.; Bithell, J.F.; Barndorff-Nielsen, O.; Keuls, M. The role of significance tests [with discussion and reply]. Scandinavian Journal of Statistics 1977, 4, 49–70. [Google Scholar]
Ioannidis, J.P.A. Why most published research findings are false. Chance 2005, 18, 40–47. [Google Scholar] [CrossRef]
Ioannidis, J.P.A. What have we (not) learnt from millions of scientific papers with p values? Amer. Stat. 2019, 73, 20–25. [Google Scholar] [CrossRef]
Wasserstein, R.L.; Lazar, N.A. The ASA statement on p-values: context process, and purpose. Amer. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a world beyond "p<0.05". Amer. Stat. 2019, 73, 1–19. [Google Scholar] [CrossRef]
Baker, M. Statisticians issue warning on P values. Nature 2016, 531, 151–151. [Google Scholar] [CrossRef]
Goodman, S.N. Toward evidence-based medical statistics. 1: The P value fallacy. Ann. Intern. Med. 1999, 130, 995–1004. [Google Scholar] [CrossRef] [PubMed]
Goodman, S. A dirty dozen: twelve p-value misconceptions. Seminars in Hematology 2008, 45, 135–140. [Google Scholar] [CrossRef] [PubMed]
Kühberger, A.; Fritz, A.; Lermer, E.; Scherndl, T. The significance fallacy in inferential statistics. BMC Research Notes 2015, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
Benjamini, Y. It’s not the p-values’ fault. J. Amer. Stat. Assoc. 2016. Online Supplement to ASA Statement on P-values. [Google Scholar]
Greenland, S. Valid p-values behave exactly as they should: Some misleading criticisms of p-values and their resolution with s-values. Amer. Stat. 2019, 73, 106–114. [Google Scholar] [CrossRef]
Goodman, S.N. Why is getting rid of p-values so hard? Musings on science and statistics. Amer. Stat. 2019, 73, 26–30. [Google Scholar] [CrossRef]
Halsey, L.G. The reign of the p-value is over: what alternative analyses could we employ to fill the power vacuum? Biol. Lett. 2019, 15, 20190174. [Google Scholar] [CrossRef] [PubMed]
Colquhoun, D. The false positive risk a proposal concerning what to do about p-values. Amer. Stat. 2019, 73, 192–201. [Google Scholar] [CrossRef]
Goodman, W.M.; Spruill, S.E.; Komaroff, E. A proposed hybrid effect size plus p-value criterion: empirical evidence supporting its use. Amer. Stat. 2019, 73, 168–185. [Google Scholar] [CrossRef]
Rougier, J. p-Values, Bayes factors, and sufficiency. Amer. Stat. 2019, 73, 148–151. [Google Scholar] [CrossRef]
Di Leo, G.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics—reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 1–8. [Google Scholar] [CrossRef]
Murdoch, D.S.; Tsai, Y.L.; Adcock, J. P-values are random variables. Amer. Stat. 2008, 62, 242–245. [Google Scholar] [CrossRef]
Fraser, D.A.S. The p-value function and statistical inference. Amer. Stat. 2019, 73, 135–147. [Google Scholar] [CrossRef]
Fisher, R.A. Has Mendel’s work been rediscovered? Ann. Sci. 1936, 1, 115–137. [Google Scholar] [CrossRef]
Franklin, A.; Edwards, A.W.; Fairbanks, D.J.; Hartl, D.L. Ending the Mendel-Fisher Controversy; University of Pittsburgh Press: Pittsburgh, USA, 2008. [Google Scholar] [CrossRef]
Pires, A.M.; Branco, J.A. A statistical model to explain the Mendel-Fisher controversy. Stat. Sci. 2010, 25, 545–565. [Google Scholar] [CrossRef]
Zaykin, D.V.; Zhivotovsky, L.A.; Westfall, P.H.; Weir, B.S. Truncated product method for combining P-values. Genetic Epidemiology 2002, 22, 170–185. [Google Scholar] [CrossRef]
Neuhäuser, M.; Bretz, F. Adaptive designs based on the truncated product method. BMC Medical Research Methodology 2005, 5, 1–7. [Google Scholar] [CrossRef]
Zhang, H.; Tong, T.; Landers, J.; Wu, Z. TFisher: A powerful truncation and weighting procedure for combining p-values. Ann. Appl. Stat. 2020, 14, 178–201. [Google Scholar] [CrossRef]
Dudbridge, F.; Koeleman, B. Rank truncated product of P-values, with application to genomewide association scans. Genet. Epidemiol. 25, 360–366. [CrossRef]
Deng, L.Y.; George, E.O. Some characterizations of the uniform distribution with applications to random number generation. Ann. Inst. Statist. Math. 1992, 44, 379–385. [Google Scholar] [CrossRef]
Tippett, L.H.C. The Methods of Statistics; Williams & Norgate Ltd.: London, UK, 1931. [Google Scholar] [CrossRef]
Stouffer, S.A.; Schuman, E.A.; DeVinney, L.C.; Star, S.; Williams, R.M. The American Soldier: Adjustment During Army Life; Vol. I, Princeton University Press: New Jersey, USA, 1949. [Google Scholar] [CrossRef]
Chen, Z. Optimal tests for combining p-values. Appl. Sci. 2022, 12, 322–322. [Google Scholar] [CrossRef]
Liu, J.Z.; Mcrae, A.F.; Nyholt, D.R.; Medland, S.E.; Wray, N.R.; Brown, K.M.; AMFS Investigators; Hayward, N.K.; Montgomery, G.W.; Vissher, P.M.; et al. A versatile gene-based test for genome-wide association studies. The American Journal of Human Genetics 2010, 87, 139–145. [Google Scholar] [CrossRef]
Cinar, O.; Viechtbauer, W. The poolr package for combining independent and dependent p values. J. Stat. Softw. 2022, 101, 1–42. [Google Scholar] [CrossRef]
Mudholkar, G.S.; George, E.O. The logit method for combining probabilities. In Symposium on Optimizing Methods in Statistics; Rustagi, J., Ed.; Academic Press: New York, USA, 1979; pp. 345–366. [Google Scholar]
Kolmogorov, A.N. Sur la notion de la moyenne. Atti della Reale Accademia Nazionale dei Lincei. Classe di scienze fisiche, matematiche, e naturali. Rendiconti Serie VI 1930, 12, 388–391. [Google Scholar]
Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
Edgington, E.S. An additive method for combining probability values from independent experiments. J. Psychol. 1972, 80, 351–363. [Google Scholar] [CrossRef]
Wilkinson, B. A statistical consideration in psychological research. Psychol. Bull. 1951, 48, 156–158. [Google Scholar] [CrossRef]
Pearson, K. On a method of determining whether a sample of size n supposed to have been drawn from a parent population having a known probability integral has probably been drawn at random. Biometrika 1933, 25, 379–410. [Google Scholar] [CrossRef]
Brilhante, M.F.; Gomes, M.I.; Mendonça, S.; Pestana, D.; Pestana, P. Generalized Beta models and population growth, so many routes to chaos. Fractal Fract 2023, 7. [Google Scholar] [CrossRef]
Brilhante, M.F.; Pestana, D. BetaBoop function, BetaBoop random variables and extremal population growth. In International Encyclopedia of Statistical Science, 2nd ed.; Lovric, M., Ed.; Springer: Berlin, Germany, 2024. [Google Scholar]
Pearson, K. On a new method of determining "goodness of fit". Biometrika 1934, 26, 425–442. [Google Scholar] [CrossRef]
Owen, A.B. Karl Pearson’s meta-analysis revisited. Ann. Stat. 2009, 37, 3867–3892. [Google Scholar] [CrossRef] [PubMed]
Wilson, D.J. The harmonic mean p-value for combining dependent tests. In Proceedings of the of the National Academy of Sciences, Vol. 116, USA; 2019; pp. 1195–1200. [Google Scholar] [CrossRef]
Landau, L. On the energy loss of fast particles ionization. J. Phys. (USSR) 1944, 8, 201–205. [Google Scholar] [CrossRef]
Hartung, J.; Knapp, G.; Sinha, B.K. Statistical Meta-Analysis with Applications; Wiley: New Jersey, USA, 2008. [Google Scholar] [CrossRef]
Birnbaum, A. Combining independent tests of significance. J. Amer. Statist. Assoc. 1954, 49, 559–574. [Google Scholar] [CrossRef]
Mosteller, F.; Bush, R. Selected quantitative techniques. In Handbook of Social Psychology: Theory and Methods; Lidsey, G., Ed.; Addison-Wesley: Cambridge MA, USA, 1954. [Google Scholar]
Whitlock, M.C. Combining probability from independent tests: the weighted Z-method is superior to Fisher’s approach. J. Evol. Biol. 2005, 18, 1368–1373. [Google Scholar] [CrossRef]
Littell, R.C.; Folks, L.J. Asymptotic optimality of Fisher’s method of combining independent tests, I. J. Amer. Statist. Assoc. 1971, 66, 802–806. [Google Scholar] [CrossRef]
Littell, R.C.; Folks, L.J. Asymptotic optimality of Fisher’s method of combining independent tests, II. J. Amer. Statist. Assoc. 1973, 68, 193–194. [Google Scholar] [CrossRef]
Marden, J.I. Sensitive and sturdy p-values. Ann. Stat. 1991, 19, 918–934. [Google Scholar] [CrossRef]
Loughin, T.M. A systematic comparison of methods for combining p-values from independent tests. Comput. Stat. Data Anal. 2004, 47, 467–485. [Google Scholar] [CrossRef]
Won, S.; Morris, N.; Lu, Q.; Elston, R.C. Choosing an optimal method to combine P-values. Stat. Med. 2009, 28, 1537–1553. [Google Scholar] [CrossRef]
Oosterhoff, J. Combination of One-Sided Statistical Tests; Vol. 28, Mathematical Centre Tracts, Mathematical Centre Amsterdam: Amsterdam, Netherland, 1969. [Google Scholar]
Vovk, V.; Wang, R. E-values: calibration, combination and applications. Ann. Statist. 2021, 49, 1736–1754. [Google Scholar] [CrossRef]
Vovk, V.; Wang, B.; Wang, R. Admissible ways of merging p-values under arbitrary dependence. Ann. Stat. 2022, 50, 351–375. [Google Scholar] [CrossRef]
Vuursteen, L.; Szabó, B.; van der Vaart, A.; van Zanten, H. Optimal testing using combined test statistics across independent studies. Advances in Neural Information Processing Systems 2023, 36. [Google Scholar] [CrossRef]
Zintzaras, E.; Kitsios, G.; Harrison, G.A.; Laivuori, H.; Kivinen, K.; Kere, J.; Messinis, I.; Stefanidis, I.; Ioannidis, J.P.A. Heterogeneity-based genome search meta-analysis for preeclampsia. Hum Genet 2006, 120, 360–370. [Google Scholar] [CrossRef]
ICMJE. Uniform Requirements for Manuscripts Submitted to Biomedical Journals. https://web.archive.org/web/20120716211637/http://www.icmje.org/publishing_1negative.html, 2024.
JASNH. Welcome to the Journal of Articles in Support of the Null Hypothesis. https://www.jasnh.com/about.html.
Pestana, D.; Rocha, M.L.; Vasconcelos, R.; Velosa, S. Publication Bias and Meta-Analytic Syntheses. In Advances in Regression, Survival Analysis, Extreme Values, Markov Processes and other Statistical Applications; Lita da Silva, J., Caeiro, F., Natário, I., Braumann, C., Eds.; Springer: Berlin, Germany, 2013; pp. 347–354. [Google Scholar] [CrossRef]
van Aert, R.C.; Wicherts, J.M.; van Assen, M.A. Conducting Meta-Analyses Based on p Values: Reservations and Recommendations for Applying p-Uniform and p-Curve. Perspect. Psychol. Sci. 2016, 11, 713–729. [Google Scholar] [CrossRef]
Fogacci, S.; Fogacci, F.; Banach, M.; Michos, E.D.; Hernandez, A.V.; Lip, G.Y.H.; Blaha, M.J.; Toth, P.P.; Borghi, C.; Cicero, A.F.G.; et al. Vitamin D supplementation and incident preeclampsia: A systematic review and meta-analysis of randomized clinical trials. Clin. Nutr. 2020, 39, 1742–1752. [Google Scholar] [CrossRef]
Begg, C.B.; Mazumdar, M. Operating characteristics of a rank correlation test for publication bias. Biometrics 1994, 50, 1088–1101. [Google Scholar] [CrossRef]
Egger, M.; Davey, S.G.; Schneider, M.; Minder, C. Bias in meta-analysis detected by a simple, graphical test. BMJ 1997, 315, 629–634. [Google Scholar] [CrossRef]
Jin, Z.C.; Zhou, X.H.; He, J. Statistical methods for dealing with publication bias in meta-analysis. Stat. Med. 2015, 34, 343–360. [Google Scholar] [CrossRef]
Lin, L.; Chu, H. Quantifying publication bias in meta-analysis. Biometrics 2018, 74, 785–794. [Google Scholar] [CrossRef]
Givens, G.H.; Smith, D.D.; Tweedie, R.L. Publication bias in meta-analysis: a Bayesian data-augmentation approach to account for issues exemplified in the passive smoking debate. Stat. Sci. 1997, 12, 221–250. [Google Scholar] [CrossRef]
Kulinskaya, E.; Morgenthaler, S.; Staudte, R.G. Meta Analysis. A Guide to Calibrating and Combining Statistical Evidence; Wiley: Chichester, UK, 2008. [Google Scholar] [CrossRef]
Tsui, K.; Weerahandi, S. Generalized p-values in significance testing of hypothesis in the presence of nuisance parameters. J. Amer. Stat. Assoc. 1989, 84, 602–607. [Google Scholar] [CrossRef]
Weerahandi, S. Exact Statistical Methods for Data Analysis; Springer: New York, USA, 1995. [Google Scholar] [CrossRef]
Hung, H.; O’Neill, R.; Bauer, P.; Kohn, K. The behavior of the p-value when the alternative is true. Biometrics 1997, 53, 11–22. [Google Scholar] [CrossRef]
Brilhante, M.F. Generalized p-values and random p-values when the alternative to uniformity is a mixture of a Beta(1,2) and uniform. In Recent Developments in Modeling and Applications in Statistics; Oliveira, P., Temido, M., Henriques, C., Vichi, M., Eds.; Springer: Heildelberg, Germany, 2013; pp. 159–167. [Google Scholar] [CrossRef]
Dai, H.; Charnigo, R. Omnibus testing and gene filtration in microarray data analysis. J. Appl. Stat. 2008, 35, 31–47. [Google Scholar] [CrossRef]
Dudbridge, F.; Koeleman, B.P.C. Efficient computation of significance levels for multiple associations in large studies of correlated data, including genomewide association studies. Am. J. Hum. Genet. 2004, 75, 424–435. [Google Scholar] [CrossRef]
Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables, 8th ed.; Dover: New York, USA, 1972. [Google Scholar]
Sarabia, J.M.; Prieto, F.; Trueba, C. The n-fold convolution of a finite mixture of densities. Appl. Math. Comput. 2012, 218, 9992–9996. [Google Scholar] [CrossRef]
Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 5th ed.; Academic Press: San Diego, USA, 1980. [Google Scholar]
R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
Davison, A.C.; Hinkley, D.V. Bootstrap Methods and their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]

Figure 1. Probability density function of

T_{n; m}

for

m = - 1, 0, 1

: (a)

n = 2

. (b)

n = 3

Figure 1. Probability density function of

T_{n; m}

for

m = - 1, 0, 1

: (a)

n = 2

. (b)

n = 3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Meta-Analysis of Genuine and Fake p-Values

Abstract

Keywords:

Subject:

1. Introduction

2. Combining Genuine p -Values

2.1. Combining Transformed Genuine p-Values

2.2. Should You Mean It?

2.3. Which Combining Rule Should Be Used?

3. Publication Bias

4. Mendel Random Variables — Combined Tests with Genuine and Fake p -Values

4.1. Deng and George’s Contractions with Mendel Random Variables

4.2. Testing Independence

4.3. Combined Tests with Genuine and Fake p-values — Some Analytic Results

4.3.1. Tippett’s T T ( P 1 , … , P n )

4.3.2. Pearson’s T P ( P 1 , … , P n )

4.3.3. Fisher’s Statistic Sampling Distribution for Combining p-Values from a Mendel(m) Population

5. Discussion

6. Conclusions

Supplementary Materials

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2. Combining Genuine $p$ -Values

4. Mendel Random Variables — Combined Tests with Genuine and Fake $p$ -Values

4.3.1. Tippett’s $T_{T} (P_{1}, \dots, P_{n})$

4.3.2. Pearson’s $T_{P} (P_{1}, \dots, P_{n})$