Rigid Polynomial Differential Systems with Homogeneous Nonlinearities

Preprint

Article

Rigid Polynomial Differential Systems with Homogeneous Nonlinearities

This version is not peer-reviewed.

Jaume Llibre^*

This version is not peer-reviewed.

Altmetrics

Downloads

125

Views

Comments

Submitted:

23 July 2024

Posted:

24 July 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

Planar differential systems whose angular velocity is constant are called rigid differential systems. We characterize the existence and non-existence of limit cycles, and the finite and infinite singularities of the rigid polynomial differential systems with homogeneous nonlinearities of arbitrary degree in the Poincaré disc. Moreover, we classify the phase portraits in the Poincaré disc of the rigid polynomial differential systems of degree two, and of one class of rigid polynomial differential systems with cubic homogeneous nonlinearitie that can exhibit one limit cycle.

Keywords:

Subject:

Computer Science and Mathematics - Analysis

MSC: 34C05

1. Introduction and Statement of the Main Result

The rigid differential systems in the plane

R^{2}

having a focus or a center at the origin of coordinates can be written in the form

\dot{x} = \frac{d x}{d t} = - y + x F (x, y), \dot{y} = \frac{d y}{d t} = x + y F (x, y),

(1)

where

F (x, y)

is a smooth real function. Such differential systems have been studied by several authors, see for instance [1–3,5–7,9,12]. In the paper of Gasull, Prohens and Torregrosa [10] in 2005 they classify the phase portraits of the rigid cubic polynomial differential systems in the Poincaré disc.

Our objective here is to study the dynamics of the rigid polynomial differential systems with homogeneous nonlinearities of arbitrary degree in the Poincaré disc. From equation (1) a rigid polynomial differential system with homogeneous nonlinearities of degree

n > 1

in the plane

R^{2}

can be written in the form

\dot{x} = - y + x (λ + P (x, y)), \dot{y} = x + y (λ + P (x, y)),

(2)

where

P (x, y)

is a homogeneous polynomial of degree

n - 1

Roughly speaking the Poincaré disc

D^{2}

is the closed unit disc in the plane

R^{2}

, where its interior has been identified with the whole plane

R^{2}

and its boundary, the circle

S^{1}

, has been identified with the infinity of

R^{2}

. Note that in the plane

R^{2}

we can go or come from the infinity in as many directions as points has the circle

S^{1}

. A polynomial differential system defined in

R^{2}

can be extended analytically to the Poincaré disc

D^{2}

. In this way we can study the dynamics of the polynomial differential systems in a neighborhood of the infinity. In the Appendix we summarize how to work in the Poincaré disc.

Our main result is the next theorem and the two propositions.

Theorem 1.

The following statements hold for the differential systems (2).

(a): If $λ = 0$ then systems (2) have no limit cycles.
(b): If $λ \neq 0$ , then systems (2) have at most one limit cycle.
(c): Define $B = \int_{0}^{2 π} P (cos θ, sin θ) d θ = 0$ . If $λ B < 0$ and λ is sufficiently small, then n is odd and systems (2) have one limit cycle, stable if $λ > 0$ and unstable if $λ < 0$ .
(d): If $λ^{2} + B^{2} \neq 0$ and $a B \geq 0$ , then systems (2) have no periodic orbits.

Statements (c) and (d) were proved by Gasull and Torregrosa in Theorem 1.1 of [9]. Here we prove at the end of Section 2 statements (a) and (b), and we present a new proof of statment (c).

Proposition 1.

System (2) has a unique equilibrium point

p = (0, 0)

at the origin of coordinates.

(a): If $λ \neq 0$ then p is focus, stable if $λ < 0$ , unstable if $λ > 0$ .
(b): If $λ = 0$ and $B = \int_{0}^{2 π} P (cos θ, sin θ) d θ = 0$ , then p is a center.
(c): If $λ = 0$ and $B \neq 0$ , then p is a weak focus, unstable if $B < 0$ , and stable if $B > 0$ .

Statement (b) is also due to Gasull and Torregrosa, see again Theorem 1.1 of [9]. We present another proof of statement (b).

Proposition 2.

All points of the infinity of the differential system (2) are equilibrium points.

(a): The infinite equilibrium point $(u, 0)$ of the local chart $U_{1}$ in the Poincaré compactification of the differential system (2) is the α-limit (resp. ω-limit) of one orbit of system (2) if $P (1, u) > 0$ (resp. $P (1, u) < 0$ ). If $P (1, u) = 0$ then, either the infinite equilibrium point $(u, 0)$ is simultaneously the α-limit and ω-limit of two orbits of system (2), or no orbit has the infinite equilibrium point $(u, 0)$ as α-limit and ω-limit set.
(b): The infinite equilibrium point $(0, 0)$ of the local chart $U_{2}$ in the Poincaré compactification of the differential system (2) is the α-limit (resp. ω-limit) of one orbit of system (2) if $P (0, 1) > 0$ (resp. $P (0, 1) < 0$ ). If $P (0, 1) = 0$ then, either the infinite equilibrium point $(0, 0)$ is simultaneously the α-limit and ω-limit of two orbits of system (2), or no orbit has the infinite equilibrium point $(0, 0)$ as α-limit and ω-limit set.

Propositions 1 and 2 are proved in Section 2.

In the next propostion we provide the phase portraits of the rigid quadratic polynomial differential systems.

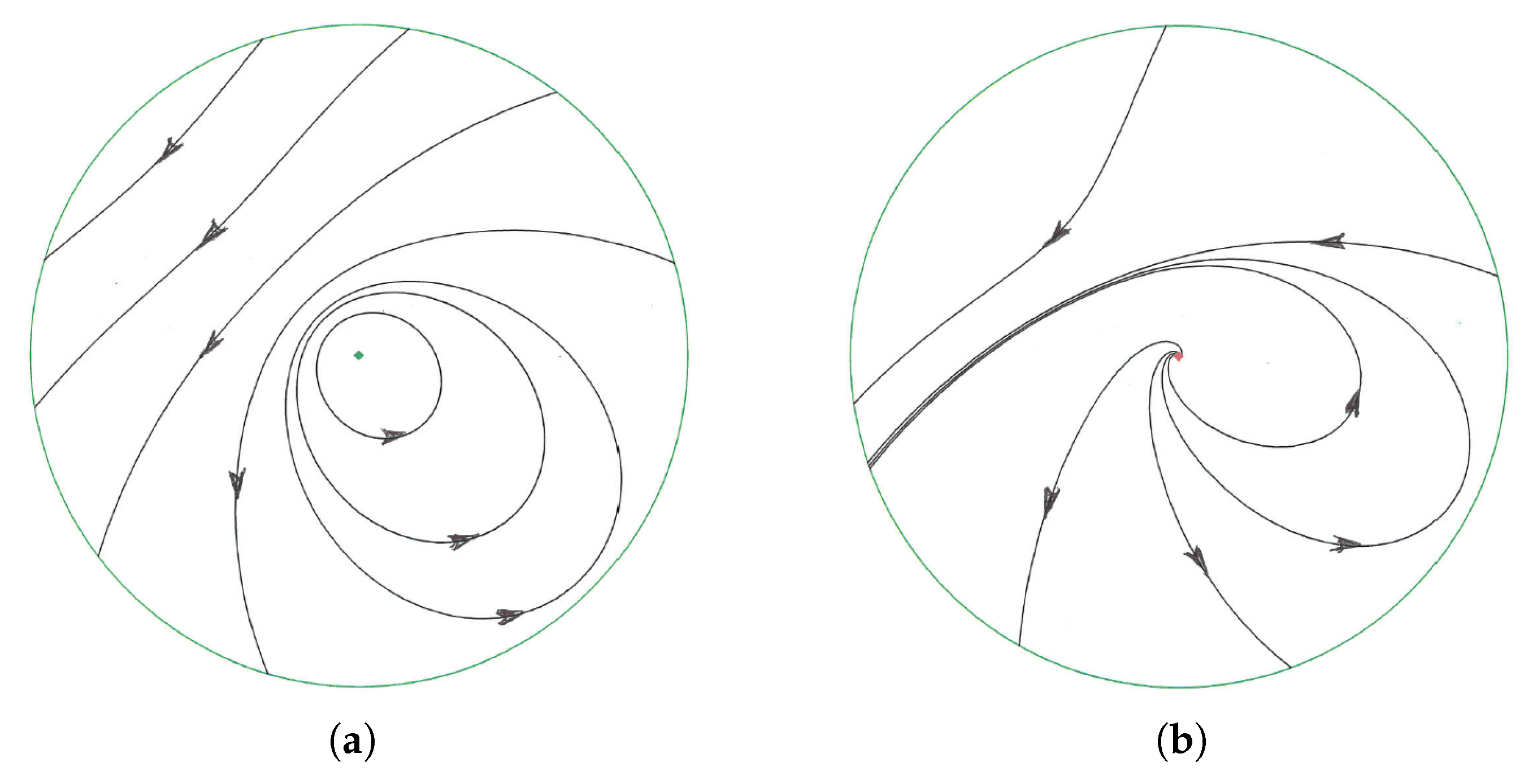
Proposition 3.

The phase portraits of the rigid quadratic polynomial differential systems in the Poincaré disc are topologically equivalent to one of the two phase portraits of Figure 1, perhaps reversing the sense of all its orbits.

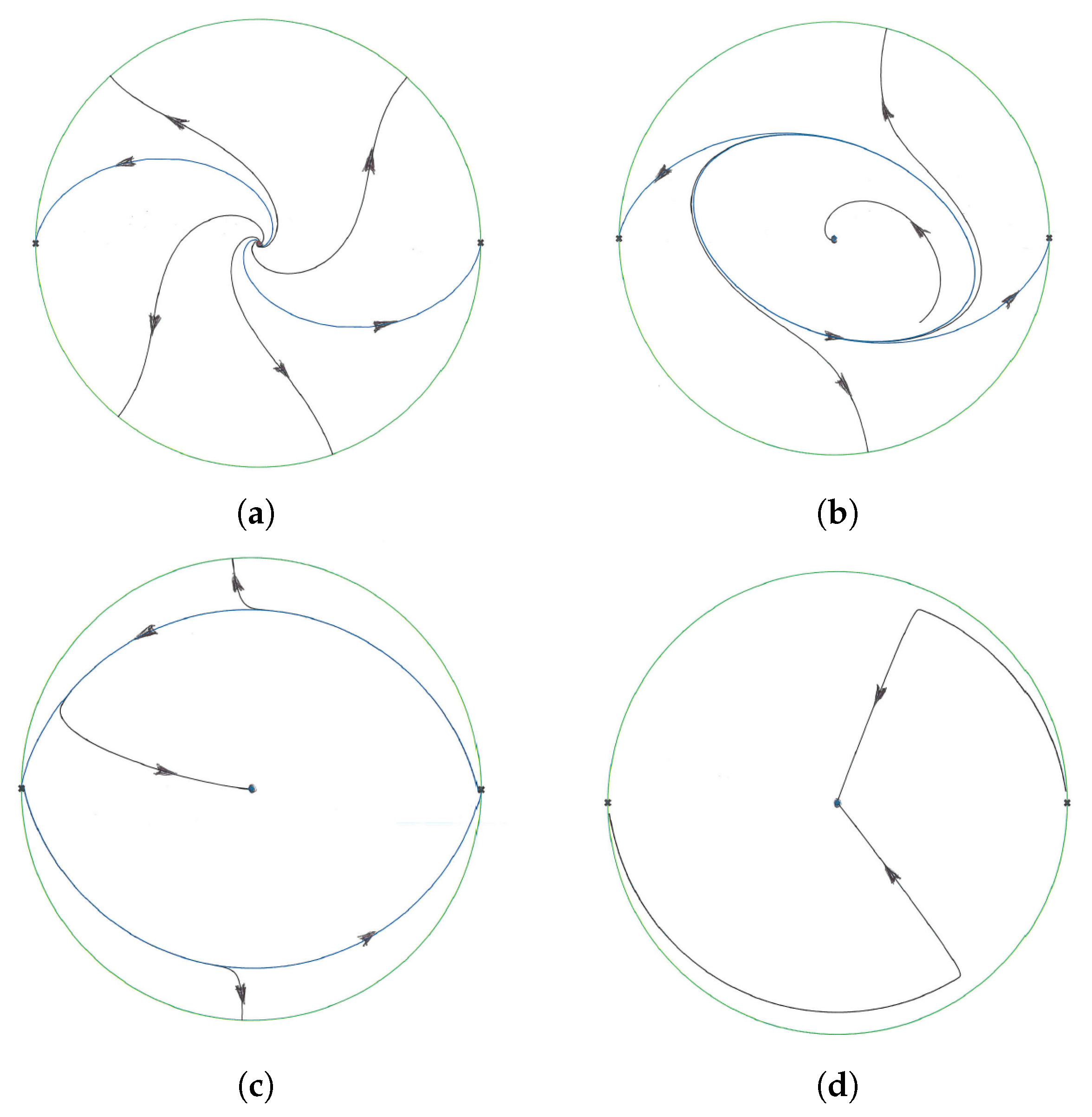
Proposition 4.

The following statements hold for the rigid cubic polynomial systems with homogeneous nonlinearities (2) with

P (x, y) = y^{2}

(a): If $λ \geq 0$ the origin is a global attractor, see Figure 2(a),
(b): An unstable limit cycle bifurcates from the origin when $λ = 0$ , see this limit cycle for the value $λ = - 1$ in Figure $2 (b)$ ,
(c): The λ-family of unstable limit cycles ends in a graphic having two equilibria at infinity, see Figure $2 (c)$ , and
(d): See the phase portrait of the system after the missing of the graphic in Figure $2 (d)$ .

Propostions 3 and 4 are proved at Section 4.

2. Proofs

For the basic notions of focus, center,

α

-limit,

ω

-limit and limit cycle that appear in this paper see for instance the book [8].

We write the differential system (2) in polar coordinates

(r, θ)

where

x = r cos θ

and

y = r sin θ

, and we obtain the system

\dot{r} = r λ + r^{n} P (cos θ, sin θ), \dot{θ} = 1 .

(3)

Taking

θ

as the new time the differential system (3) becomes the differential equation

r^{'} = \frac{d r}{d θ} = r λ + r^{n} P (cos θ, sin θ) .

(4)

Proposition 5.

Consider the differential equation (4).

(a): If $λ = 0$ equation (4) has the first integral

$H (r, θ) = r^{1 - n} + (n - 1) \int_{0}^{θ} P (cos s, sin s) d s .$
(b): If $r (θ, r_{0})$ denotes the solution of equation (4) such that $r (0, r_{0}) = r_{0} > 0$ , then

$r (θ, r_{0}) = {(e^{- (n - 1) λ θ} (r_{0}^{1 - n} - (n - 1) \int_{0}^{θ} e^{(n - 1) λ s} P (cos s, sin s) d s))}^{\frac{1}{1 - n}} .$

(5)

Proof.

Let

r (θ)

be an arbitrary solution of the differential equation (4). Since

\frac{d H (r (θ), θ)}{d θ} = \frac{\partial H (r, θ)}{\partial r} \frac{d r (θ)}{d θ} + \frac{\partial H (r, θ)}{\partial θ} = 0,

the function

H (r, θ)

is a first integral of equation (4). Statement (a) is proved.

We verify that

r (θ, r_{0})

is a solution of the differential equation (4) by direct substitution of the expression of

r (θ, r_{0})

, given in (5), into the differential equation (4). So statement (b) is proved. □

In the next proposition we study the finite equilibrium points of the differential systems (2).

Proof of Proposition 1.

Since

x \dot{y} - y \dot{x} = x^{2} + y^{2}

, it follows that p is the unique equilbrium point of system (2).

The eigenvalues of the Jacobian matrix of the system at p are

λ \pm i

. If

λ \neq 0

, by the Hartman-Grobman Theorem (see for instance [4], or Theorem 2.15 of [8]) p is a focus, stable if

λ < 0

, unstable if

λ > 0

. So statement (a) is proved.

λ = 0

from statement (b) of Proposition 5 the solution

r (θ, r_{0})

of equation (4) becomes

r (θ, r_{0}) = {(r_{0}^{1 - n} - (n - 1) \int_{0}^{θ} P (cos s, sin s) d s)}^{\frac{1}{1 - n}} .

(6)

Then

r (2 π, r_{0}) = {(r_{0}^{1 - n} - (n - 1) \int_{0}^{2 π} P (cos s, sin s) d s)}^{\frac{1}{1 - n}} .

(7)

From (6) and (7) it follows that

r (0, r_{0}) = r_{0} = r (2 π, r_{0})

if and only if

B = 0

. So statement (b) follows. If

B \neq 0

, then from (6) and (7) if follows that we have a weak focus, unstable if

B < 0

, and stable if

B > 0

, □

Now we study the infinite equilbrium points of the differential systems (2). For studying these equilibrium points we shall use the notation and results of the subsection 4.1 of the Appendix. Thus, we recall that for analyzing the local phase portraits at the infinite equilibrium points we only need to study the infinite equilibrium points of the local chart

U_{1}

and the origin of the local chart

U_{2}

Proof of Proposition 2.

From the subsection 4.1 of the Appendix we have that the differential system (2) in the local chart

U_{1}

writes

\dot{u} = (1 + u^{2}) v^{n - 1}, \dot{v} = v ((1 - λ) u v^{n - 1} - P (1, u)) .

Therefore, all the points

(u, 0)

of the infinity contained in the chart

U_{1}

are equilibrium points. Rescaling the time we eliminate the common factor v between

\dot{u}

and

\dot{v}

, and we get the differential system

\dot{u} = (1 + u^{2}) v^{n - 2}, \dot{v} = (1 - λ) u v^{n - 1} - P (1, u) .

So,

\dot{v} |_{v = 0} = - P (1, u)

. From here it follows statement (a).

In the local chart

U_{2}

system (2) writes

\dot{u} = - (1 + u^{2}) v^{n - 1}, \dot{v} = - v ((1 + λ) u v^{n - 1} + P (u, 1)) .

Therefore, the origin

(0, 0)

of the chart

U_{1}

is equilibrium point. Consequently, all the points of the infinity are equilibrium points. Again rescaling the time we eliminate the common factor v between

\dot{u}

and

\dot{v}

, and we obtain the differential system

\dot{u} = - (1 + u^{2}) v^{n - 2}, \dot{v} = - (1 + λ) u v^{n - 1} - P (u, 1) .

So,

\dot{v} |_{u = v = 0} = - P (0, 1)

. This proves statement (b). □

After determining the local phase portraits at the finite and infinite equilibrium points of the differential system (2), in order to obtain the global phase portraits in the Poincaré disc of this differential system we need to control their possible limit cycles. Of course, if

λ = 0

from it is clear that the differential systems (2) have no limit cycles. Now we shall prove that when

λ \neq 0

the differential systems (2) have no periodic orbits, and consequently no limit cycles. First we recall the following well known result.

Proof of Theorem 1.

When

λ = 0

since the first integral

H (r, θ)

given in statement (a) of Proposition 5 is defined in the whole plane

R^{2}

except at the origin of coordinates, the differential system (2) cannot have limit cycles, otherwise by continuity the first integral will be constant in a neighborhood of the limit cycle, and this is not the case for the function

H (r, θ)

. This proves statement (a).

From statement (b) of Proposition 5 for every

r_{0} > 0

the solution

r (θ, r_{0})

of the differential equation (4) such that

r (0, r_{0}) = r_{0}

verifies that

r (2 π, r_{0}) = {(e^{- (n - 1) λ 2 π} (r_{0}^{1 - n} - (n - 1) \int_{0}^{2 π} e^{(n - 1) λ s} P (cos s, sin s) d s))}^{\frac{1}{1 - n}} .

If the solution

r (θ, r_{0})

is periodic, then

r (2 π, r_{0}) = r_{0}

. From this equation we obtain the unique solution that

r_{0} = {(\frac{e^{2 π λ} - e^{2 n π λ}}{(n - 1) e^{- 2 π λ} \int_{0}^{2 π} e^{(n - 1) λ s} P (cos s, sin s) d s})}^{\frac{1}{n - 1}} .

So, if there exists a periodic solution this is unique, consequently it is a limit cycle. Statement (b) is proved.

Now assume

λ B < 0

. We have that

\int_{0}^{2 π} {cos}^{p} θ {sin}^{q} θ d θ = 0,

if p or q is odd (see formulas 2.5111 and 2.5114 of [11]), and

\int_{0}^{2 π} {cos}^{p} θ {sin}^{q} θ d θ = \frac{(q - 1)!! (p - 1)!!}{2^{p / 2} (p / 2) | (q + p) (q - 2 + p) \dots (2 + p)} \neq 0,

if p and q are even (see formulas 2.5121 and 2.5122 of [11]). As usual

(q - 1)!! = (q - 1) (q - 3) \dots 1

when q is even. Therefore, since

B = \int_{0}^{2 π} P (cos θ, sin θ) d θ \neq 0

and

P (x, y)

is a homogeneous polynomial of degree

n - 1 > 0

, it follows that n is odd.

For completing the proof of statement (c) we shall use the averaging theory of first order, see subsection 4.2 of the Appendix.

Assume that

λ > 0

. Then in the differential equation (4) we change the variable r by

r = R λ^{\frac{1}{n - 1}}

, then we obtain the differential equation

R^{'} = λ (R + R^{n} P [cos θ, sin θ]) = : λ F (θ, R) .

(8)

λ

is sufficiently small we can apply the averaging theory of first order with

λ = ε

x = R

t = θ

and

T = 2 π

. Then

f (R) = \frac{1}{2 π} \int_{0}^{2 π} F (θ, R) d θ = R + \frac{R^{n}}{2 π} \int_{0}^{2 π} P (cos θ, sin θ) d θ = : R + \frac{R^{n}}{2 π} B .

The unique positive zero of the averaged function

f (R)

R^{*} = {(- B / (2 π))}^{1 / (1 - n)}

, and since

f^{'} (R^{*}) = 1 - n < 0

, from subsection 4.2 it follows that the differential equation (8) with

λ > 0

sufficiently small has a stable limit cycle

R (θ, λ)

such that

R (0, λ) R^{*}

when

λ 0

Now assume

λ < 0

. Then doing the change of variables

r = R {(- λ)}^{\frac{1}{n - 1}}

in the differential equation (4), and working as in the case

λ > 0

we obtain that the differential equation (8) with

λ < 0

sufficiently small has an unstable limit cycle

R (θ, λ)

such that

R (0, λ) {(B / (2 π))}^{1 / (1 - n)}

when

λ \to 0

. This completes the proof of the proposition. □

3. Phase Portraits

Now we shall prove Propositions 3 and 4.

Proof of Proposition 3.

From Proposition 1 the differential system (2) for

λ = 0

and

B = 0

has a center at the origin of coordinates. Moreover, this differential system by Theorem 1 has no limit cycles, and by Proposition 2 we know its dynamics at infinity. Therefore its phase portrait in the Poincarè disc is given in Figure 2(a). That is the origin is a global repeller.

Now assume that either

λ \neq 0

, or

λ = 0

and

B \neq 0

. Now from Proposition 1 the differential system (2) has a focus at the origin of coordinates, stable if

λ < 0

and unstable if

λ > 0

. By statement (a) of Theorem 1 when

λ = 0

the system has no limit cycles, and when

λ \neq 0

, by statement (c) of Theorem 1, since the degree of the system is

n = 2

if also has no limit cycles. Again by Proposition 2 we know its dynamics at infinity. Hence its phase portrait in the Poincarè disc is given in Figure 2(b). □

Proof of Proposition 4.

Applying the arguments of the proof of Proposition 2 to the rigid systems (2) with

P (x, y) = y^{2}

and

λ \geq 0

, it follows that each infinite singular point is

ω

-limit of a unique orbit, so the infinity is an attractor. For these rigid systems we have that

B = \int_{0}^{2 π} P (cos θ, sin θ) d θ = \int_{0}^{2 π} {cos}^{2} θ d θ = π .

Then, by statement (d) of Theorem 1 when

λ \geq 0

these systems have no periodic orbits. Since the origin of coordinates is the unique equilibrium point of these systems and it is an unstable hyperbolic focus for

λ > 0

and a weak unstable focus for

λ = 0

, we obtain that their phase portraits in the Poincaré disc are given in Figure 2(a). So statement (a) is proved.

For

λ < 0

we have that

λ B < 0

, and if

λ

is sufficiently small by statement (c) of Theorem 1 an unstable limit cycle bifurcates from the equilibrium localized at the origin of coordinates. This proves statement (b).

The limit cycle bifurcating from the origin increasis with

λ

, because

λ

is a rotating parameter as it was already observed in [9], for more details on rotating families of differential systems see, for instance, Chapter 8 of [8]. Since the unique finite equilibrium is at the origin, this

λ

-family of limit cycles only can end in a graphic with equilibrium points at infinity. Due to the fact that systems (2) with

P (x, y) = y^{2}

are invariant under the symmetry

(x, y) \to (- x, - y)

, the infinite equilibrium points of that graphic are diametrally opposite in the Poincaré disc. Studying the infinite equilibrium points as we did in the proof of Proposition 2, there are only two infinite equilibrium points that are simultaneously the

α

-limit and

ω

-limit of two orbits, so the mentioned graphic has only these two infinite equilbrium points. Hence statement (c) follows.

Since the parameter

λ

is a rotating parameter after the missing of the graphic no more limit cycles can exist. Studying the infinite equilibrium points as in the proof of Proposition 2 we obtain that each infinite equilibrium is

α

-limit of a unique orbit, so the infinity is a repeller. Taking into account that the unique finite equilibrium point is a stable focus, we obtain the phase portrait of the Figure 2(d). That is, the origin is a global attractor. □

Appendix

4.1. Poincaré Compactification of Polynomial Differential Systems in $R^{2}$

In order to study the dynamics of a polynomial differential system in the plane

R^{2}

near infinity we need its Poincaré compactification. This tool was created by Poincaré in [13], for more details see Chapter 5 of [8].

Consider the polynomial differential system

\dot{x} = P (x, y), \dot{y} = Q (x, y),

(9)

where P and Q are polynomial being d the maximum of the degrees of the polynomials P and Q.

We consider the plane

{(x_{1}, x_{2}, 1); x_{1}, x_{2} \in R}

R^{3}

identified with the plane

R^{2}

, where we have the differential system (9). This plane is tangent at the nord pole

(0, 0, 1)

of the 2-dimensional sphere

S^{2} = {(x_{1}, x_{2}, x_{3}) \in R^{3}; x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 1}

. We define the northern hemisphere

H_{+} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} > 0}

, the southern hemisphere

H_{-} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} < 0}

and the equator

S^{1} \equiv {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{3} = 0}

of the sphere

S^{2}

In order to study a vector field over

S^{2}

we consider six local charts that cover the whole sphere

S^{2}

. So, for

i = 1, 2, 3

, let

U_{i} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{i} > 0} a n d V_{i} = {(x_{1}, x_{2}, x_{3}) \in S^{2}; x_{i} < 0} .

Consider the diffeomorphisms

φ_{i} : U_{i} ⟶ R^{2}

and

ψ_{i} : V_{i} ⟶ R^{2}

given by

φ_{i} (x_{1}, x_{2}, x_{3}) = ψ_{i} (x_{1}, x_{2}, x_{3}) = (\frac{x_{j}}{x_{i}}, \frac{x_{k}}{x_{i}})

with

j, k \neq i

and

j < k

. The sets

(U_{i}, φ_{i})

and

(V_{i}, ψ_{i})

are the local charts over

S^{2}

Let

f^{\pm} : R^{2} ⟶ H_{\pm}

be the central projections from the tangent plane

R^{2}

at the point

(0, 0, 1)

of the sphere

S^{2}

S^{2}

given by

f^{\pm} (x_{1}, x_{2}) = \pm (\frac{x_{1}}{Δ (x_{1}, x_{2})}, \frac{x_{2}}{Δ (x_{1}, x_{2})}, \frac{1}{Δ (x_{1}, x_{2})})

where

Δ (x_{1}, x_{2}) = \sqrt{x_{1}^{2} + x_{2}^{2} + 1}

. In other words

f^{\pm} (x_{1}, x_{2})

is the intersection of the straight line through the points

(0, 0, 0)

and

(x_{1}, x_{2}, 1)

with

H_{\pm}

. Moreover, the maps

f^{\pm}

induces over

H_{\pm}

vector fields analytically conjugate with the vector field of the differential system (9). Indeed,

f^{+}

induces on

H_{+} = U_{3}

the vector field

X_{1} (y) = D f^{+} (φ_{3} (y)) X (φ_{3} (y))

, and

f^{-}

induces on

H_{-} = V_{3}

the vector field

X_{2} (y) = D f^{-} (ψ_{3} (y)) X (ψ_{3} (y))

. Note that

f^{+} = φ_{3}^{- 1}

and

f^{-} = ψ_{3}^{- 1}

. Thus we obtain a vector field on

S^{2} ∖ S^{1}

that admits an analytic extension

p (X)

S^{2}

. The vector field

p (X)

S^{2}

is called the Poincaré compactification of the vector field

X = (P, Q)

Denote

(u, v) = φ_{i} (x_{1}, x_{2}, x_{3}) = ψ_{i} (x_{1}, x_{2}, x_{3})

. Then the expression of the differential system associated to the vector field

p (X)

in the chart

U_{1}

u^{'} = v^{d} [Q (\frac{1}{v}, \frac{u}{v}) - u P (\frac{1}{v}, \frac{u}{v})], v^{'} = - v^{d + 1} P (\frac{1}{v}, \frac{u}{v}) .

The expression of

p (X)

U_{2}

u^{'} = v^{d} [P (\frac{u}{v}, \frac{1}{v}) - u Q (\frac{u}{v}, \frac{1}{v})], v^{'} = - v^{d + 1} Q (\frac{u}{v}, \frac{1}{v}) .

The expression of

p (X)

U_{3}

u^{'} = P (u, v), v^{'} = Q (u, v) .

For

i = 1, 2, 3

the expression of

p (X)

in the chart

V_{i}

differs of the expression in

U_{i}

only by the multiplicative constant

{(- 1)}^{d - 1}

Note that we can identify the infinity of

R^{2}

with the equator

S^{1}

. Two points for each direction in

R^{2}

provide two antipodal points of

S^{1}

. An equilibrium point of

p (X)

S^{1}

is called infinite equilibrium point and an equilibrium point on

S^{2} ∖ S^{1}

is called a finite equilibrium point. Observe that the coordinates of the infinite equilibrium points are of the form

(u, 0)

on the charts

U_{1}, V_{1}, U_{2}

and

V_{2}

. Thus, if

(x_{1}, x_{2}, 0) \in S^{1}

is an infinite equilibrium point, then its antipode

(- x_{1}, - x_{2}, 0)

is also a infinite equilibrium point.

The image of the closed northern hemisphere of

S^{2}

under the projection

(x_{1}, x_{2}, x_{3}) \to (x_{1}, x_{2}, 0)

is the Poincaré disc, denoted by

D^{2}

4.2. The Averaging Theory of First Order

This theory deals with the problem of finding T-periodic solutions for a T-periodic differential system depending on a small parameter

ε

. For more details about the averaging theory of first order for finding periodic orbits see Theorems 11.5 and 11.6 of [14].

We consider the differential system

\dot{x} (t) = ε F (t, x) + ε^{2} G (t, x, ε),

(10)

where

x \in D \subset R^{n}

, D is an open set,

t \geq 0

, the functions F, G,

\partial F / \partial x

\partial^{2} F / \partial x^{2}

and

\partial G / \partial x

are defined, continous and bounded by a constant M (independent of

ε

) in

[0, \infty) \times D

0 \leq ε \leq ε_{0}

; and F and G are T-periodic in t (T independent of

ε

). If p is a zero of the averaged function

f (x) = \frac{1}{T} \int_{0}^{T} F (t, x) d t,

such that

{|\frac{\partial f (x)}{\partial x}|}_{x = p} \neq 0,

Then for

| ε |

sufficiently small, there exists a T-periodic limit cycle

x (t, ε)

of system (10) such that

x (0, ε) \to p

ε \to 0

. Moreover, If all eigenvalues of the Jacobian matrix

{\frac{\partial f (x)}{\partial x}|}_{x = p}

have negative real parts, the corresponding periodic solution

x (t, ε)

is asymptotically stable for

ε

sufficiently small. If one of these eigenvalues has positive real part,

x (t, ε)

is unstable.

That is, the simple zeros of the averaged function

f (x)

provide the initial conditions for T-periodic limit cycles of the differential system (10).

Funding

The author has been partially supported by the Agencia Estatal de Investigación of Spain grant PID2022-136613NB-100, AGAUR (Generalitat de Catalunya) grant 2021SGR00113, and by the Reial Acadèmia de Ciències i Arts de Barcelona.

Data Availability Statement

This paper has no data.

Acknowledgments

In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The author declares no conflicts of interest.

References

Algaba, A.; Reyes, M. Centers with degenerate infinity and their commutators, J. Math. Anal. Appl. 278 (2003), limno. 1, 109–124.
Algaba, A.; Reyes, M. Computing center conditions for vector fields with constant angular speed, J. Comput. Appl. Math. 154 (2003), no. 1, 143–159. [CrossRef]
Alwash, M. A. M. On the center conditions of certain cubic systems, Proc. Amer. Math. Soc. 126 (1998), no. 11, 3335–3336.
Chicone, C. Ordinary Differential Equations with Applications, Texts in Applied Mathematics. Vol. 34 (2nd ed.), Springer, 2006.
Collins, C. B. Algebraic conditions for a centre or a focus in some simple systems of arbitrary degree, J. Math. Anal. Appl. 195 (1995), no. 3, 719–735. [CrossRef]
Conti, R. Uniformly isochronous centers of polynomial systems in R2, Differential equations, dynamical systems, and control science, Lecture Notes in Pure and Appl. Math., vol. 152, Dekker, New York, 1994, 21–31.
Dias, F. S.; Mello, L. F. The center-focus problem and small amplitude limit cycles in rigid systems, Discrete Contin. Dyn. Syst. 32 (2012), no. 5, 1627–1637.
Dumortier, F.; Llibre, J.; Artés, J. C. Qualitative theory of planar differential systems, UniversiText, Springer-Verlag, New York, 2006.
Gasull, A.; Torregrosa, J. Exact number of limit cycles for a family of rigid systems, Proc. Amer. Math. Soc. 133 (2004), no. 3, 751–758.
Gasull, A.; Prohens, R.; Torregrosa, J. Limit cycles for cubic rigid systems, J. Math. Anal. Appl. 303 (2005) 391–404.
Gradshteyn, I. M.: Ryzhik, I. M. Table of integrals, series, and products, (7th ed.), Academic Press, Amsterdam, 2007.
Mazzi, J.; Sabatini, M. Commutators and linearizations of isochronous centers, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 11 (2000), no. 2, 81–98.
Poincaré, H. Mémoire sur les courbes définies par les équations différentielles, Journal de Mathématiques 37 (1881), 375–422; Oeuvres de Henri Poincaré, vol. I, Gauthier-Villars, Paris, 1951, pp 3–84.
Verhulst, F. Nonlinear differential equations and dynamical systems, (2nd ed.), Springer, Berlin, 1996.

Figure 1. Phase portraits of the differential system (2) with

n = 2

in the Poincaré disc: (a) when

λ = 0

and (b) when

λ > 0

. If

λ < 0

then we have the phase portrait (b) but its orbits are travelled in the converse sense. The infinity of the phase portraits (a) and (b) are filled with equilibrium points.

Figure 1. Phase portraits of the differential system (2) with

n = 2

in the Poincaré disc: (a) when

λ = 0

and (b) when

λ > 0

. If

λ < 0

then we have the phase portrait (b) but its orbits are travelled in the converse sense. The infinity of the phase portraits (a) and (b) are filled with equilibrium points.


(a)	(b)

Figure 2. Phase portraits of the differential system (2) with

P (x, y) = y^{2}

in the Poincaré disc: (a) when

λ \geq 0

, (b) when

λ = - 1

, (c) for the value

λ = λ^{*}

where the family of the limit cycles that exist for

0 < λ < λ^{*}

ends in a graphic, (d) for a value of

λ > λ^{*}

. The infinity of these phase portraits are filled with equilibrium points.

Figure 2. Phase portraits of the differential system (2) with

P (x, y) = y^{2}

in the Poincaré disc: (a) when

λ \geq 0

, (b) when

λ = - 1

, (c) for the value

λ = λ^{*}

where the family of the limit cycles that exist for

0 < λ < λ^{*}

ends in a graphic, (d) for a value of

λ > λ^{*}

. The infinity of these phase portraits are filled with equilibrium points.


(a)	(b)

(c)	(d)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rigid Polynomial Differential Systems with Homogeneous Nonlinearities

Abstract

Keywords:

Subject:

1. Introduction and Statement of the Main Result

2. Proofs

3. Phase Portraits

Appendix

4.1. Poincaré Compactification of Polynomial Differential Systems in R 2

4.2. The Averaging Theory of First Order

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.1. Poincaré Compactification of Polynomial Differential Systems in $R^{2}$