Enhancing Significant Wave Height Retrieval With FY-3E GNSS-R Data: A Comparative Analysis of Deep Learning Models

Significant Wave Height(SWH) is a crucial parameter in oceanographic research, essential for understanding various marine and atmospheric processes. Traditional methods for obtaining SWH, such as ship-based and buoy measurements, face limitations like limited spatial coverage and high operational costs. With the advancement of Global Navigation Satellite Systems reflectometry(GNSS-R) technology, a new method for retrieving SWH has emerged, demonstrating promising results. This study utilizes Radio occultation sounder(GNOS) data from the FY-3E satellite and incorporates the latest Vision Transformer(ViT) technology to investigate GNSS-R-based SWH retrieval. We designed and evaluated various deep learning models, including ANN-Wave, CNN-Wave, Hybrid-Wave, Trans-Wave, and ViT-Wave. Through comparative training using ERA5 data, the ViT-Wave model was identified as the optimal retrieval model. The ViT-Wave model achieved an Root Mean Square Error(RMSE) accuracy of 0.4052 meters and Mean Absolute Error(MAE) accuracy of 0.2700 meters, significantly outperforming both traditional methods and newer deep learning approaches utilizing Cyclone Global Navigation Satellite Systems(CYGNSS) data. These results underscore the potential of integrating GNSS-R technology with advanced deep learning models to enhance SWH retrieval accuracy and reliability in oceanographic research.

Keywords:

Subject: Environmental and Earth Sciences - Oceanography

1. Introduction

The retrieval of Significant Wave Height(SWH) is crucial in meteorology and oceanography as it serves as a fundamental parameter for assessing ocean wave conditions. Accurate SWH measurements are Vital for understanding sea state, which directly influences marine navigation, offshore operations, and coastal management. Utilizing remote sensing techniques to retrieval SWH allows for high-resolution, wide-coverage wave data collection, essential for improving weather forecasts, monitoring marine environments, and studying climate change impacts. Moreover, SWH data plays a significant role in validating and calibrating wave models, which are integral to predicting extreme weather events and managing coastal risks [1,2,3,4,5]. Traditional methods for retrieving SWH, such as using altimeter satellites, buoys, and ship-based observations, face several challenges, including computational complexity, data acquisition difficulties, and platform-specific limitations. Altimeter satellites like TOPEX/Poseidon, Jason-1, Jason-2, and Sentinel-3 measure the time for radar pulses to travel to the ocean surface and back, requiring sophisticated algorithms to correct for atmospheric and instrumental effects, making data processing complex and resource-intensive [6,7]. Despite offering global coverage, these satellites have temporal and spatial gaps due to specific orbital paths, and adverse weather or technical issues can disrupt data collection [8,9]. Buoys, although highly accurate and capable of providing real-time data, are limited by geographic distribution and are susceptible to damage from severe weather, necessitating regular maintenance, which is costly and logistically challenging [10,11]. Ship-based observations, while valuable for direct measurements, are infrequent, geographically constrained, and costly, often restricted to specific routes or missions, and prone to human error [12,13]. Furthermore, the calibration and validation of SWH data require continuous efforts and integration of various datasets, adding to the overall complexity and resource requirements [10,11].

GNSS-Reflectometry (GNSS-R) is an innovative remote sensing technique that leverages reflected signals from Global Navigation Satellite Systems (GNSS) to extract various environmental parameters, including surface wind speeds, ice extent, soil moisture, and SWH [25,26,27,28,33,43,50]. By processing Delay-Doppler Maps (DDMs) to correlate surface roughness with wave height, GNSS-R offers a compelling alternative to traditional SWH retrieval methods. Compared to traditional methods, GNSS-R has several advantages in SWH retrieval. Unlike altimeter satellites, which have temporal and spatial gaps due to specific orbital paths, GNSS-R provides more frequent and comprehensive coverage. It also overcomes the limitations of buoys, which are restricted by geographic distribution and susceptibility to severe weather damage, and ship-based observations, which are infrequent and geographically constrained. Additionally, GNSS-R data collection is less affected by adverse weather conditions and does not require complex and resource-intensive data processing algorithms [25]. The spaceborne GNSS-R research commenced with the TechDemoSat-1 (TDS-1) mission, launched by the UK Space Agency (UKSA), which carried the SGR-ReSI payload to demonstrate GNSS-R’s feasibility for environmental monitoring [23]. This pioneering mission paved the way for subsequent advancements, notably the Cyclone Global Navigation Satellite System (CYGNSS), launched by NASA in December 2016. Comprising eight microsatellites, CYGNSS provides frequent and comprehensive measurements. Initially scheduled to terminate on September 30, 2023, the mission has been extended due to its excellent operational performance and high-quality data products. The extension of CYGNSS’s mission underscores the significant potential and broad applicability of GNSS-R technology. This technique not only enhances our ability to monitor and understand oceanic and atmospheric conditions but also promises a robust future for environmental remote sensing. By integrating GNSS-R capabilities with advanced machine learning models, researchers can achieve unprecedented accuracy in SWH retrieval, contributing significantly to marine navigation, weather forecasting, and climate research. The continued operation of CYGNSS beyond its planned termination date highlights its importance and efficacy in environmental monitoring, affirming the broad and meaningful impact of GNSS-R technology.

Studies by Ruf et al. [48] have demonstrated strong correlations between CYGNSS-derived roughness measurements and buoy data, validating the approach for SWH retrieval. Additionally, Clarizia et al. [29] have significantly improved noise reduction in DDMs, enhancing the precision of SWH measurements. In addition to these data analysis methods, machine learning techniques have also been widely applied to SWH retrieval. These techniques have notably enhanced the capabilities of CYGNSS in retrieving various environmental parameters. For instance, neural networks have been applied to retrieve sea surface wind speeds with high accuracy. Methods developed by Stopa and Cheung [23] and Jensen et al. [24] utilize large datasets of co-located buoy and satellite data to train models that accurately retrieve wind speeds based on GNSS-R signal characteristics. Neural networks trained on extensive datasets of co-located buoy and satellite data have modeled the relationship between reflected signal characteristics and SWH with high precision. For example, Morris et al. [31] and Gleason et al. [30] used neural networks to retrieve SWH from CYGNSS data, demonstrating significant improvements in accuracy. Furthermore, deep learning approaches, such as those explored by Li et al. [32], have shown promise in extracting SWH from GNSS-R data, leveraging the ability of deep neural networks to handle complex and non-linear relationships. Recent studies, such as those by Patanè et al., have proposed the use of LSTM-based estimation models [36], while Bu et al. combined ERA5 data with CNN networks for SWH retrieval research [37].

Despite these advancements, there are still limitations in using machine learning for SWH retrieval compared to wind speed retrieval. The models used for SWH are often less sophisticated, and the amount of training data is relatively sparse. Research on SWH retrieval lags behind that of wind speed, where more advanced models like transformers have been applied. For instance, the use of hybrid transformer networks and ConvLSTM models in wind speed forecasting has shown significant improvements in accuracy and prediction horizons [34,35]. In contrast, SWH models tend to rely on older, simpler architectures, which may not capture the complex dynamics as effectively. Overall, the integration of advanced machine learning techniques with GNSS-R data from CYGNSS not only improves the accuracy and precision of SWH retrievals but also broadens the scope of applications, making it a crucial tool for contemporary remote sensing. However, the field still faces challenges, particularly in the sophistication of models used for SWH retrieval compared to wind speed retrieval.

In China, the current approach to SWH retrieval predominantly utilizes data from the Cyclone-1 (CFOSAT) satellite. Launched in 2018, CFOSAT employs GNSS-R to monitor ocean surface wind speeds and SWH. However, its single-satellite design limits both data coverage and temporal resolution. With the launch of the FY-3E series satellites in 2021, equipped with GNOS(GNSS Occultation Sounder) payloads capable of GNSS-R data collection, China’s spaceborne GNSS-R technology has seen rapid development. Comparatively, CYGNSS, composed of eight microsatellites, offers high-frequency data that is particularly useful for monitoring extreme weather conditions. CYGNSS processes DDMs from reflected GPS signals to maintain data quality under adverse weather, while FY-3E’s GNOS leverages multi-frequency DDMs to improve measurement accuracy and reduce noise [14,15,16]. The GNOS sensor on FY-3E also demonstrates superior capabilities in monitoring polar ice changes and high-latitude ocean environments, complementing the strengths of CYGNSS [17,18,19,20,21,40]. Despite significant progress in sea surface wind speed retrieval[38,44], comprehensive research on SWH retrieval using FY-3E data has yet to be conducted. Developing this capability would significantly enhance the utility and accuracy of FY-3E products. By focusing on SWH retrieval, FY-3E can provide more reliable data, crucial for applications such as marine navigation, weather forecasting, and climate research[39,41,42]. This research would not only improve the precision of FY-3E’s measurements but also extend its applicability, thereby solidifying its role in global oceanographic monitoring [21,22].

Given the challenges in machine learning-based GNSS-R retrieval methods, this study focuses on using FY-3E GNOS payload data with ERA5 as the reference data for SWH retrieval. The contributions of this paper are as follows:

First Use of FY-3E GNOS Data for SWH Retrieval: This study is the first to utilize FY-3E GNOS payload data for SWH retrieval, achieving promising accuracy.
Proposal of the ViT-Wave Model: Combining the latest transformer models with Vision Transformer (ViT) models tailored for the task, we propose a specialized model, ViT-Wave, for SWH retrieval.
Global Ocean Analysis: The global ocean analysis demonstrates that the model significantly improves the retrieval accuracy of high wave heights and enhances the overall precision distribution across different sea states.

The structure of this paper is as follows: Section 2 introduces the data encountered in the experiment. Section 3 describes the experimental methods and models. Section 4 details the experimental process. Section 5 provides a summary and discussion of the experimental results. Section 6 concludes the paper with final remarks. By advancing the application of neural network models and integrating state-of-the-art transformer techniques, this research aims to significantly improve the accuracy and reliability of SWH retrieval using FY-3E GNOS data, contributing to the broader field of oceanographic monitoring and analysis.

2. Date Description

2.1. FY-3E Data

The FY-3E satellite, is equipped with the GNOS payload, which enables the reception of GNSS-R signals, thereby facilitating research in SWH retrieval. Unlike CYGNSS, which can only receive GPS signals, FY-3E can simultaneously receive reflected signals from GPS, BeiDou, and Galileo satellites. This capability provides FY-3E with a broader observational range. Specifically, FY-3E’s observation coverage extends from 67°N to 67°S, compared to CYGNSS’s coverage from 34°N to 34°S. This wider observational range allows FY-3E to monitor a more extensive area, including high-latitude regions. Moreover, the effective scattering area for DDM data also differs between the two systems. FY-3E features an effective scattering area of 9x20 bins, while CYGNSS has an area of 17x11 bins. These distinctions enhance the observational capabilities of FY-3E, providing more detailed and accurate measurements. For this study, data from one month (August 2023 to September 2023) were selected, and their distribution is shown in Figure 1.

In the experiment, a total of 32 key data parameters were utilized. The variables sp_lat and sp_lon represent the coordinates of the specular reflection points. The following 29 variables describe various aspects of the DDM:

Ddm_brcs_factor, Ddm_effective_area, Ddm_doppler_refer, Ddm_kurtosis, Ddm_noise_m,
Ddm_noise_raw, Ddm_noise_source, Ddm_peak_column, Ddm_peak_delay,
Ddm_peak_doppler, Ddm_peak_power_ratio, Ddm_peak_raw, Ddm_peak_row,
Ddm_peak_snr, Ddm_power_factor, Ddm_quality_flag, Ddm_range_refer, Ddm_skewness, Ddm_sp_column,
Ddm_sp_delay, Ddm_sp_dles, Ddm_sp_doppler, Ddm_sp_les, Ddm_sp_nbrcs, Ddm_sp_normalized_snr,
Ddm_sp_raw, Ddm_sp_reflectivity, Ddm_sp_row, Ddm_sp_snr.

Among these, Ddm_effective_area is a 9x20 two-dimensional data, and

Sp_delay_doppler_flag serves as a quality assessment metric. The specific meaning of each variable is shown in Appendix A.

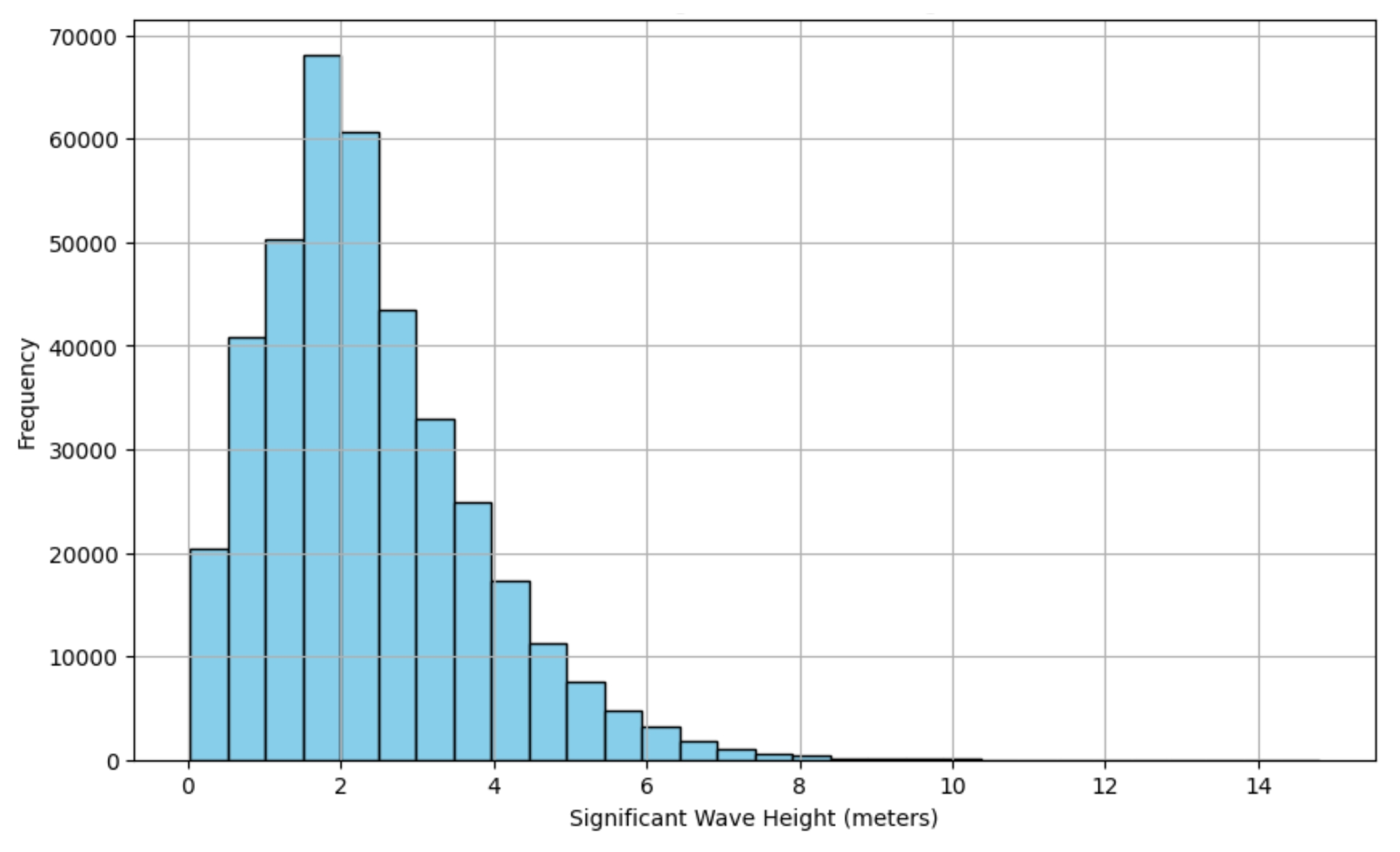
2.2. ERA5 SWH

ERA5 is a fifth-generation reanalysis dataset produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). It provides comprehensive and high-resolution climate and weather data, including SWH, on a global scale. ERA5 offers detailed temporal and spatial resolution, with hourly data on a 0.25° x 0.25° grid. This fine resolution allows for precise monitoring and analysis of wave conditions across different regions and time periods. The dataset spans several decades, enabling long-term studies and trend analysis in wave dynamics and climate change.

In numerous research studies, ERA5 SWH data has been utilized as training labels for machine learning models due to its high accuracy and consistency, which make it an ideal reference dataset[45,47]. Compared to other datasets, the integration of satellite observations, buoy measurements, and numerical weather prediction models in ERA5 provides a robust and reliable source of SWH data[46]. In this experiment, ERA5 SWH data corresponding to the same time period as the FY-3E observations was used for reference and validation.

3. Methology

This study introduces five distinct neural network models tailored for SWH retrieval: the ANN-Wave model, based on ANN; the CNN-Wave model, utilizing CNN; the hybrid-Wave model, integrating both ANN and CNN architectures; the trans-Wave model, built on the transformer framework; and the ViT-Wave model, leveraging the ViT architecture. Each model comprises different network layers and weights, as indicated in Table 1. The models are structured into several parts: the first part consists of convolutional layers that employ CNN methods to extract features from the DDM; the second part includes transformer layers that analyze DDM features using transformer techniques; the third part consists of linear layers that process the features derived from various methods in a unified manner; and the final part, also composed of linear layers, outputs the model’s final SWH retrieval results.

In the following sections, each model will be introduced and discussed in detail, highlighting their unique structures and the methodologies employed for SWH retrieval.

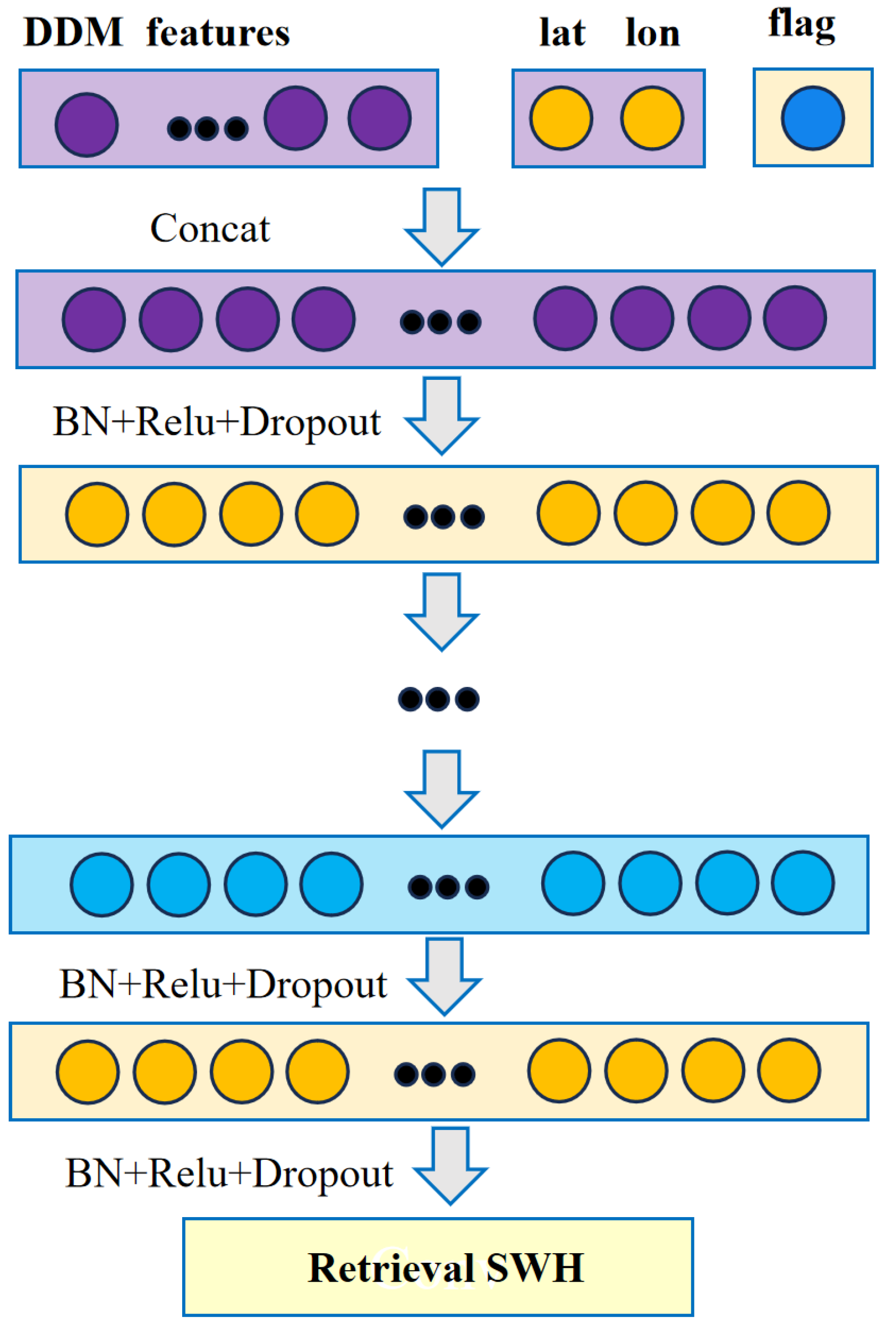
3.1. ANN-Wave

The ANN-Wave model is predominantly based on an Artificial Neural Network (ANN) architecture. The primary inputs to this model consist of spatial-temporal auxiliary information, including the latitude and longitude of the specular point (SP), one-dimensional feature data from DDMs, and quality control labels. In total, the model utilizes 31 one-dimensional features, as detailed in Appendix A, variables numbered 2-32. The network architecture is illustrated in Figure 2. The input features are concatenated and fed into the linear network structure. Initially, Batch Normalization (BatchNorm) is applied to normalize the inputs, which helps in accelerating the training process and improving the stability of the network. Following this, a Rectified Linear Unit (ReLU) activation function is employed to introduce non-linearity into the model, enabling it to learn complex patterns in the data. Subsequently, Dropout is utilized to prevent overfitting by randomly setting a fraction of the input units to zero during training, thereby promoting model generalization. The linear network consists of a total of eight layers, each incorporating BatchNorm, ReLU, and Dropout. The final layer is a fully connected layer that outputs the retrieved SWH.

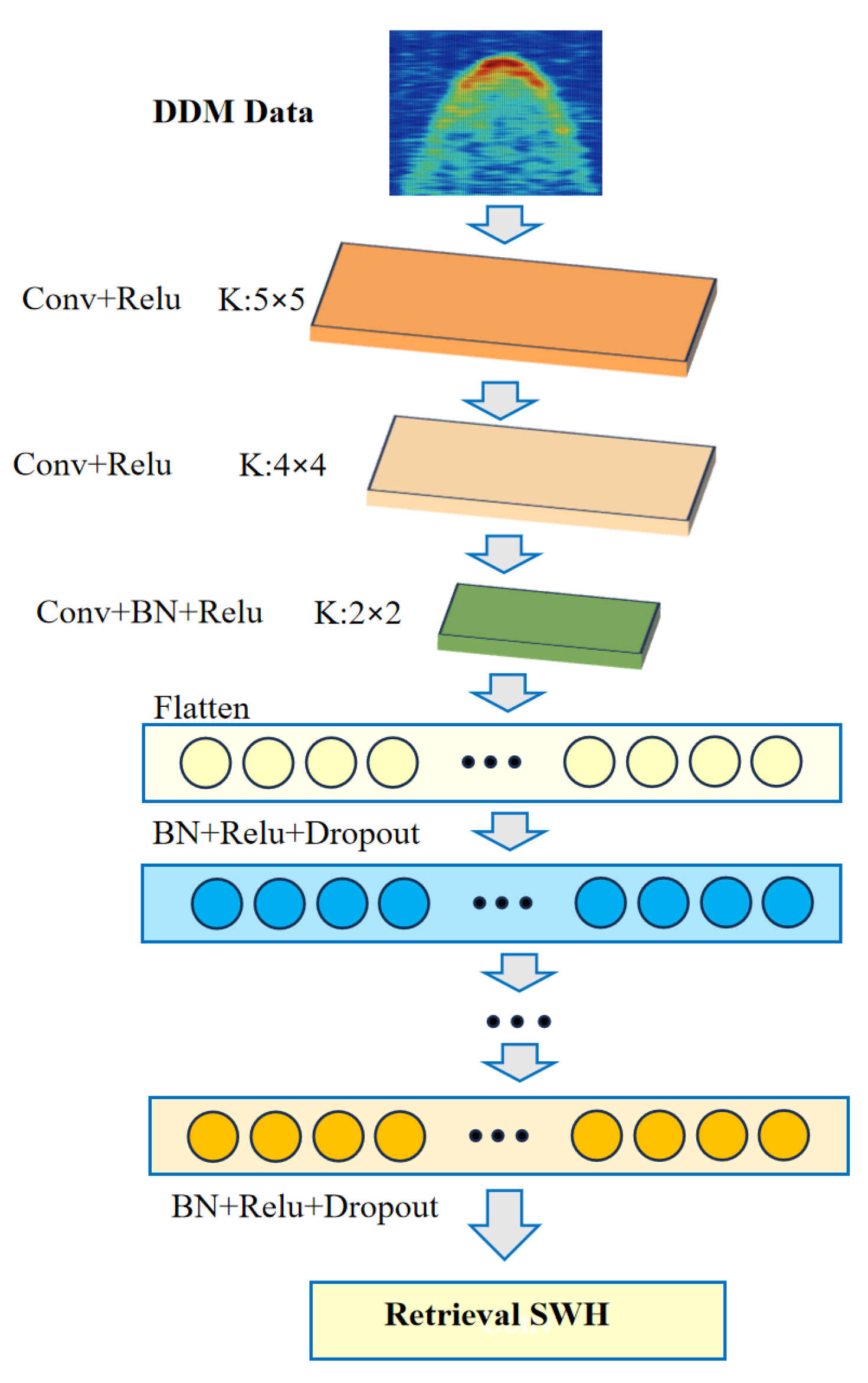
3.2. CNN-Wave

The CNN-Wave model is primarily based on a Convolutional Neural Network (CNN) architecture, designed to process two-dimensional feature data from DDMs. The primary input feature for this model corresponds to the variable listed as number 1 in Appendix A. The network architecture is illustrated in Figure 3. Initially, the model employs convolutional layers with kernel sizes of 5, 4, and 2, respectively. These varying kernel sizes enable the extraction of features at different scales, capturing both broad and fine-grained information from the input DDM data. Each convolutional layer is followed by a ReLU activation function, which introduces non-linearity and aids in learning complex patterns within the data. After the convolutional layers, the extracted features are flattened and fed into a series of linear network layers. This transformation converts the two-dimensional feature maps into a one-dimensional vector, suitable for further processing by the fully connected layers. The final layer of the CNN-Wave model is a fully connected layer that outputs the retrieved SWH. This architecture ensures that the CNN-Wave model effectively leverages the spatial structure of the DDM data to accurately predict SWH.

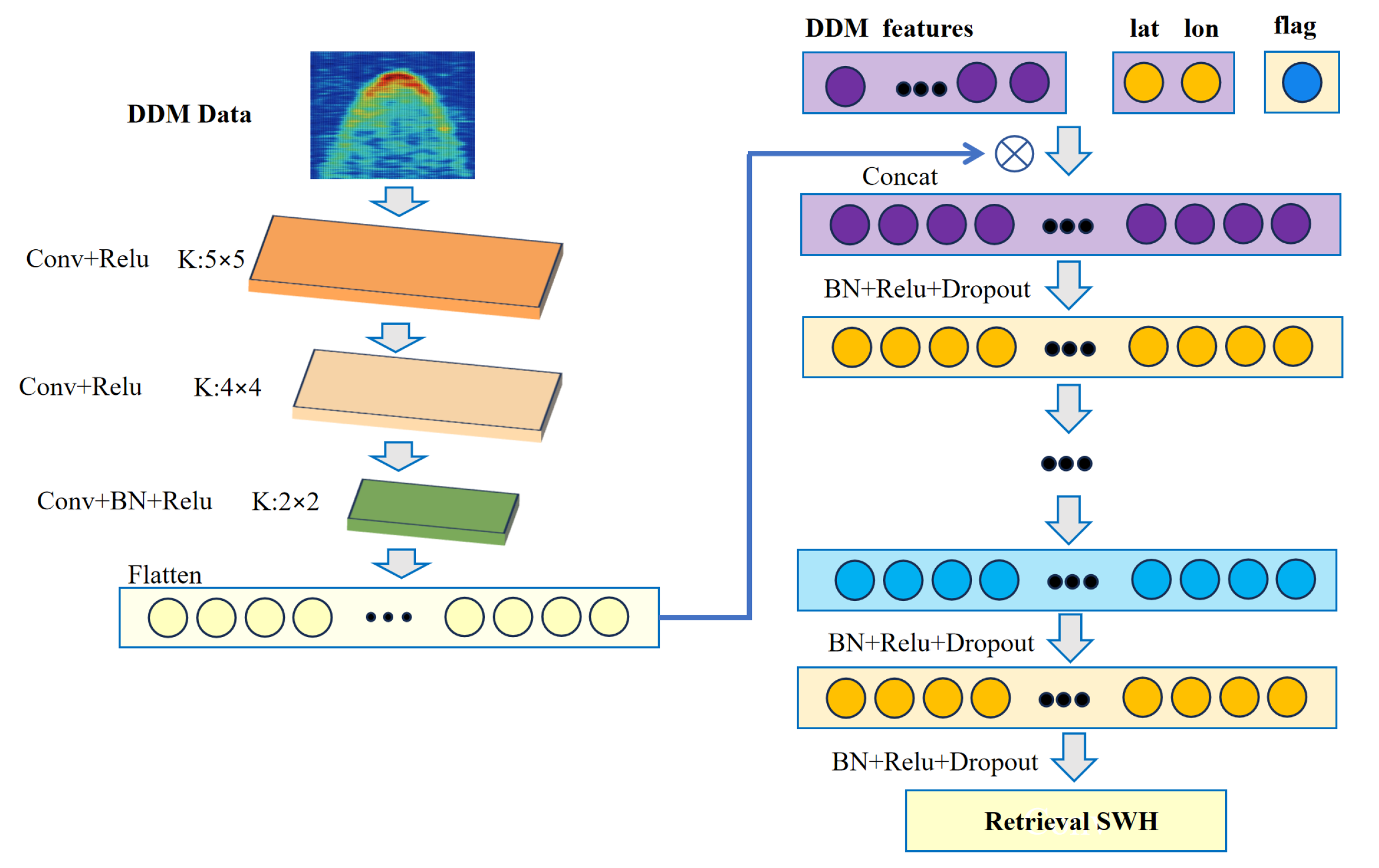
3.3. Hybrid-Wave

The Hybrid-Wave model integrates both ANN and CNN, utilizing all 32 variables listed in Appendix A as inputs. The network architecture is illustrated in Figure 4. In this model, the two-dimensional DDM data is initially fed into a Conv network, which extracts relevant features through a series of convolutional layers. These features are then flattened to form a one-dimensional vector. Simultaneously, the one-dimensional linear features are processed. The extracted features from the Conv network are concatenated with the one-dimensional linear features. This combined feature vector is then fed into a series of linear network layers. The final layer of the Hybrid-Wave model is a fully connected layer that outputs the retrieved SWH. This architecture leverages the strengths of both ANN and CNN, effectively capturing and processing the diverse input features to enhance the prediction accuracy of SWH.

3.4. Trans-Wave

The trans-Wave model, as depicted in Figure 5, is predicated on the transformer architecture, uniquely tailored for analyzing the Delay-Doppler Map (DDM) features for Significant Wave Height (SWH) retrieval. This model simplistically preprocesses the DDM data before directly inputting them into the Transformer alongside auxiliary one-dimensional features, thus forming a comprehensive set of inputs. The transformer layers, consisting of an embedding layer and a TransformerEncoder layer, transform the raw input into a dense 64-dimensional representation suitable for processing by the transformer encoder. Configured with 64-dimensional inputs, 8 attention heads, 3 encoder layers, and a feedforward dimension of 256, the encoder adeptly captures complex dependencies among features. Post-processing, the outputs are concatenated with additional auxiliary features and routed through a linear layer, concluding with a series of SWH retrieval layers. These layers comprise multiple linear layers enhanced with BatchNorm, ReLU, and Dropout, leading to the final SWH prediction. This architecture allows the trans-Wave model to effectively utilize both the spatial-temporal structure of the input data and the sequential characteristics of the DDM features.

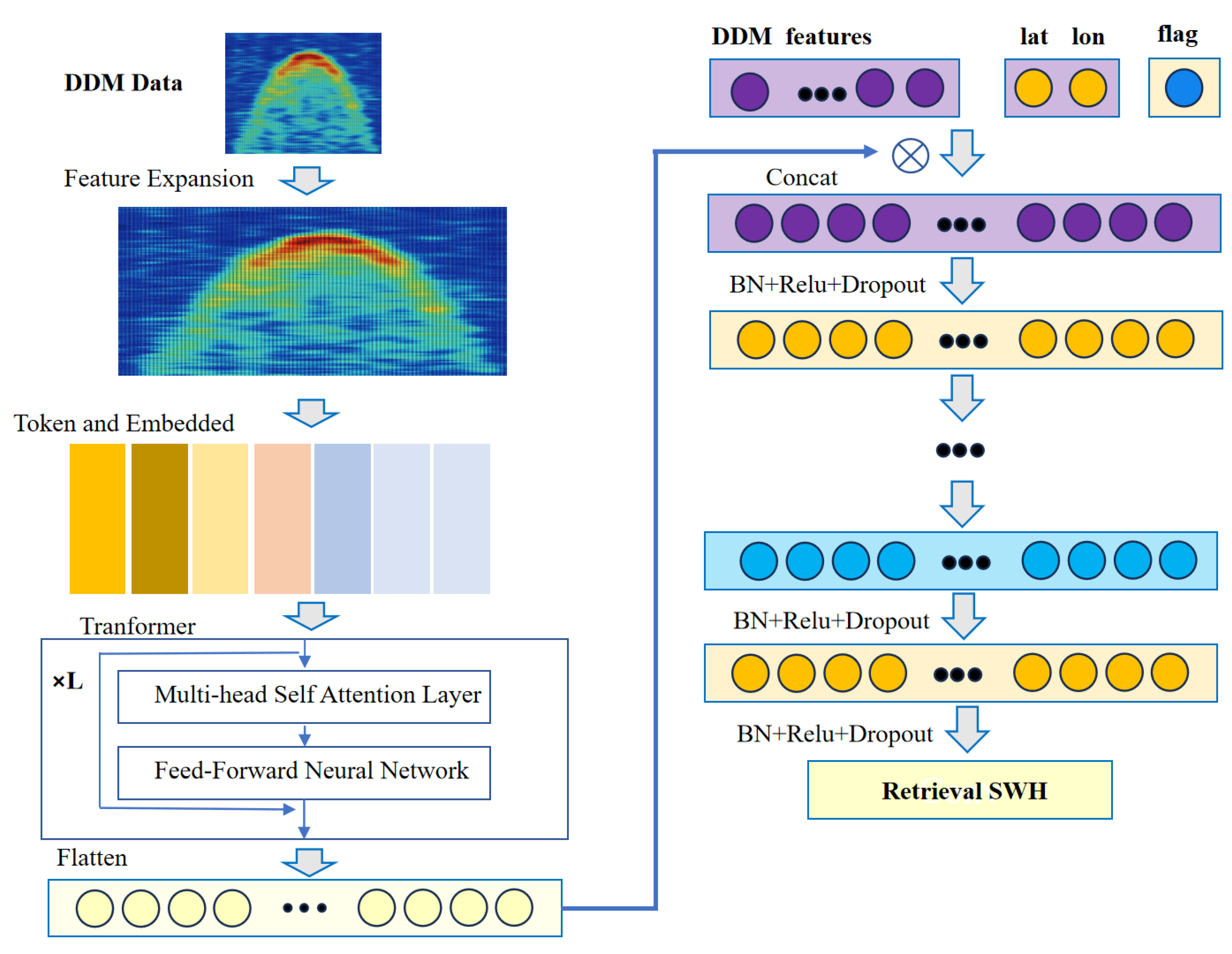
3.5. ViT-Wave

The ViT-Wave model, illustrated in Figure 6, utilizes the Vision Transformer (ViT) architecture to handle image-like input data from DDMs. Differing from the trans-Wave model, it begins by segmenting the DDM into several small patches to enhance feature learning. The primary inputs include these DDM patches and auxiliary one-dimensional features. The ViT-Wave model’s embedding layer maps each patch into a 64-dimensional space, preparing it for the VisionTransformerEncoder. This encoder, with identical configuration settings as the trans-Wave model, processes the embedded patches, meticulously capturing the relationships across the input field. Its self-attention mechanism focuses on relevant features while ignoring irrelevant ones, enhancing the model’s precision in predicting SWH. Following this, the outputs are concatenated with auxiliary features and passed through a linear layer. The final SWH retrieval layers, similar to those in the trans-Wave model, consist of multiple linear stages equipped with BatchNorm, ReLU, and Dropout, ultimately delivering the SWH prediction. This model’s structure effectively leverages the spatial structure of the DDM data and the power of self-attention to achieve high accuracy in SWH retrieval.

4. Experiment

4.1. Data Preprocessing

The data preprocessing phase involved several critical steps to ensure the integrity and reliability of the dataset used in the study. Initially, data cleaning was performed to remove outliers and NaN values, which could potentially skew the results and degrade model performance. Following this, temporal and spatial matching of the data was conducted to ensure alignment between different datasets. Specifically, the observed variables from FY-3E were interpolated onto a 0.25° x 0.25° grid. Temporally, the data was interpolated to the nearest hour using the nearest-neighbor method, ensuring consistency with the spatial and temporal resolution of the ERA5 data.

After the cleaning and matching processes, the resulting dataset comprised 390,261 entries. A significant portion of this data, 87.92%, corresponded to SWH ranging from 0 to 4 meters. Entries with SWH between 4 and 8 meters accounted for 47,148 records, representing 11.87% of the total dataset. Only 824 entries, or 0.21%, had SWH values exceeding 8 meters. Thus, the vast majority of SWH measurements were below 8 meters, making up 99.79% of the data. The maximum observed SWH was 14.80 meters, while the minimum was 0.03 meters. This distribution shown in Figure 7, highlights that extreme SWH values are relatively rare within the dataset.

4.2. Computational Platform and Resources

In this experiment, the services provided by the OpenI computing platform were utilized. OpenI is a comprehensive computational platform that offers a range of advanced computing services tailored for various scientific and engineering applications. For this study, the experiment was conducted on the Zhisuan Network Cluster (Beta), a cutting-edge computing infrastructure designed to provide high-performance computational resources. The computational resources employed in this experiment included the Tianzu Zhixin GPGPU V100, which is equipped with 30 GB of CPU memory, 32 GB of GPU memory, and 64 GB of RAM. These resources were essential in handling the computational demands of the neural network models developed in this study.

The runtime for the different neural network models varied. The ANN-Wave, CNN-Wave, and Hybrid-Wave models each took approximately one hour to run. In contrast, the more complex trans-Wave and ViT-Wave models required about two hours of computational time. This disparity in runtime reflects the varying computational complexities of the different neural network architectures

4.3. Experimental Procedure

The experimental process commenced with the random shuffling of data, followed by its division into training, validation, and test sets in a 7:2:1 ratio. The training set was utilized to train the model, the validation set to verify the results of each training iteration, and the test set to evaluate the final performance of the model. To ensure reproducibility and robustness, five different random seeds were selected, and each of the five models was trained and evaluated five times under the same experimental configuration.

In the model training phase, the loss function used was Mean Squared Error Loss (MSELoss). To prevent overfitting, a regularization parameter was introduced. The total loss during training included both the prediction loss and an L2 regularization term:

total ⎽ loss = loss + λ \sum L 2 ⎽ reg

(1)

where

λ

is the regularization parameter, and

L 2 ⎽ reg

is the sum of the L2 norms of the model parameters. This regularization helps in mitigating overfitting by penalizing large weights in the model. Additional key parameters set during the experiment included the optimizer and learning rate. The Adam optimizer was chosen with a learning rate of 0.0005 to balance the speed and stability of convergence. The number of epochs was set to 500, providing ample iterations for the model to learn from the data. Data loaders were configured with a batch size of 512, ensuring efficient data handling and processing.

The training process involved several steps. To begin with, the dataset was randomly shuffled and divided into training, validation, and test sets. Throughout each epoch of model training, the model’s parameters were updated using the training set, and the loss was calculated for each batch. This loss, combined with the L2 regularization term, was used to adjust the model parameters via backpropagation. Subsequently, the model’s performance was evaluated using the validation set, and the validation loss was recorded after each epoch. This step ensured that the model’s learning was appropriately generalized and not overfitted to the training data. Finally, after the last epoch, the model’s performance was assessed using the test set, and the test loss was recorded to evaluate the model’s prediction accuracy on unseen data. As is shown in the Table 2, after five rounds of training, the ViT-Wave model demonstrates the most superior performance across all metrics. Specifically, the ViT-Wave model achieved the lowest average training loss and validation loss, with the smallest standard deviations. This indicates that the ViT-Wave model not only converges quickly during training but also maintains high stability and consistency, highlighting its comprehensive superiority. In contrast, the CNN-Wave model with single input exhibits the poorest performance, characterized by the highest training and validation losses, along with significant error variability. Moreover, Hybrid-Wave and Trans-Wave models achieve moderate training and validation losses with relatively small standard deviations, indicating stable performance. Overall, the experimental results clearly delineate the performance differences among the models. The ViT-Wave model stands out as the best-performing model with significant advantages.

4.4. Evaluation Metrics

To comprehensively evaluate the performance of each neural network model in retrieving SWH, several key metrics were selected as evaluation standards. These metrics offer unique insights into different aspects of model accuracy and reliability. The selected evaluation metrics include Root Mean Square Error (RMSE), Bias, Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and the Coefficient of Determination (R²). The specific formulas and meanings of each metric are detailed below:

RMSE = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}

RMSE measures the average magnitude of the errors between predicted SWH values (

\hat{y}

) and observed SWH values (y). It provides a sense of how well the model’s predictions align with the actual ERA5 SWH data. Lower RMSE values indicate better model performance.

MAE = \frac{1}{n} \sum_{i = 1}^{n} | y_{i} - {\hat{y}}_{i} |

MAE quantifies the average absolute differences between the predicted and observed SWH values. It provides an intuitive measure of the model’s prediction accuracy, with lower MAE values indicating more precise predictions.

Bias = \frac{1}{n} \sum_{i = 1}^{n} (y_{i} - {\hat{y}}_{i})

Bias represents the average difference between predicted SWH values and actual ERA5 SWH values. It indicates whether the model’s predictions are systematically higher or lower than the actual values. A Bias close to zero suggests that the model is unbiased.

MAPE = \frac{100 %}{n} \sum_{i = 1}^{n} |\frac{y_{i} - {\hat{y}}_{i}}{y_{i}}|

MAPE measures the average magnitude of errors as a percentage of the actual SWH values. It provides an understanding of the model’s prediction accuracy in relative terms. Lower MAPE values indicate better model accuracy.

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

The Coefficient of Determination indicates the proportion of the variance in the observed SWH data that is predictable from the model. Values range from 0 to 1, with higher values indicating better model performance. An R² value of 1 implies perfect prediction accuracy.

Parameters -

y_{i}

: Observed SWH value (ERA5 data) -

{\hat{y}}_{i}

: Predicted SWH value (model output) - n: Number of observations -

\bar{y}

: Mean of observed SWH values -

\bar{\hat{y}}

: Mean of predicted SWH values These metrics collectively provide a robust framework for evaluating the performance of the neural network models, ensuring that various aspects of prediction accuracy and reliability are comprehensively assessed in the context of SWH retrieval using ERA5 data as the reference.

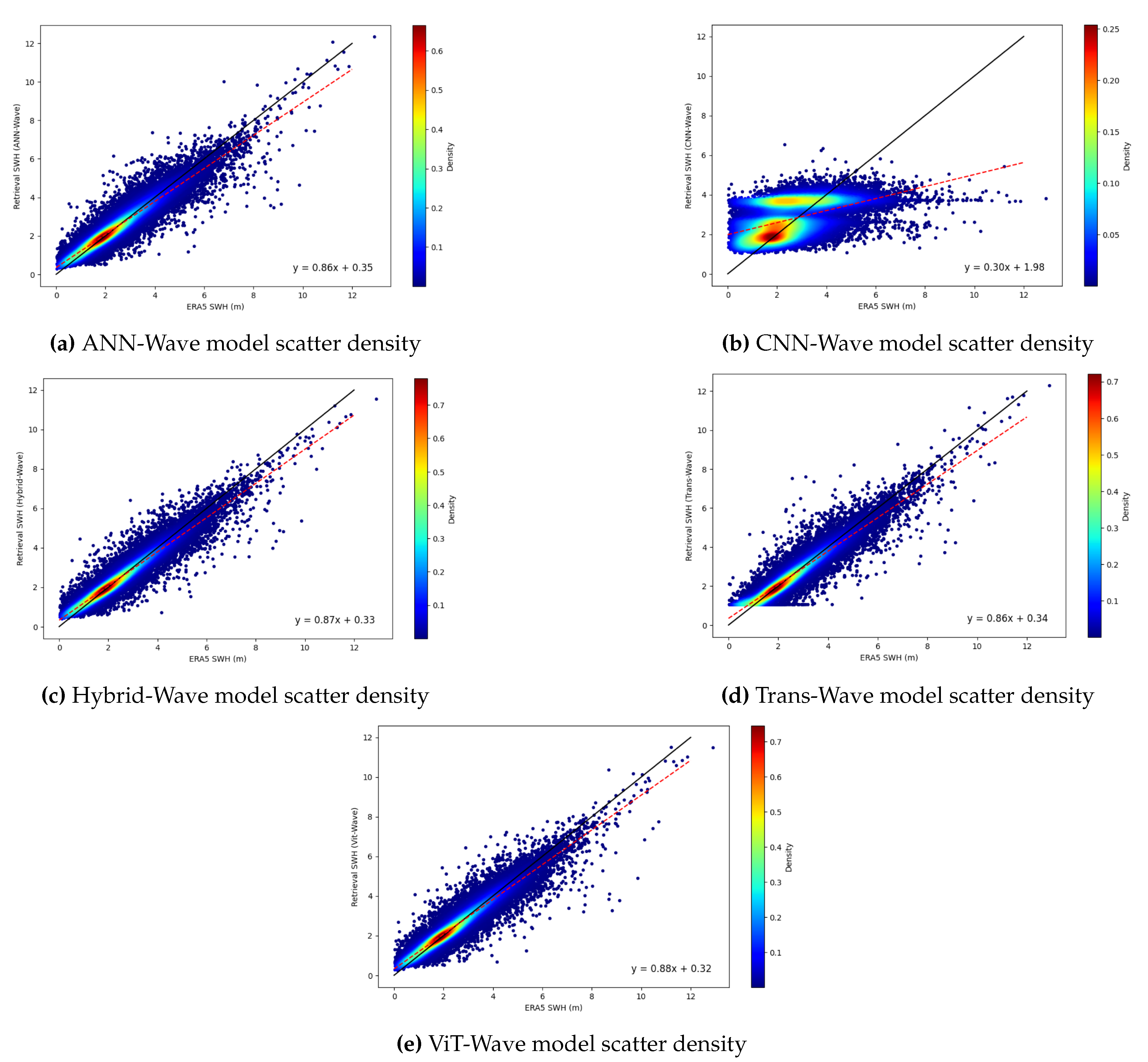
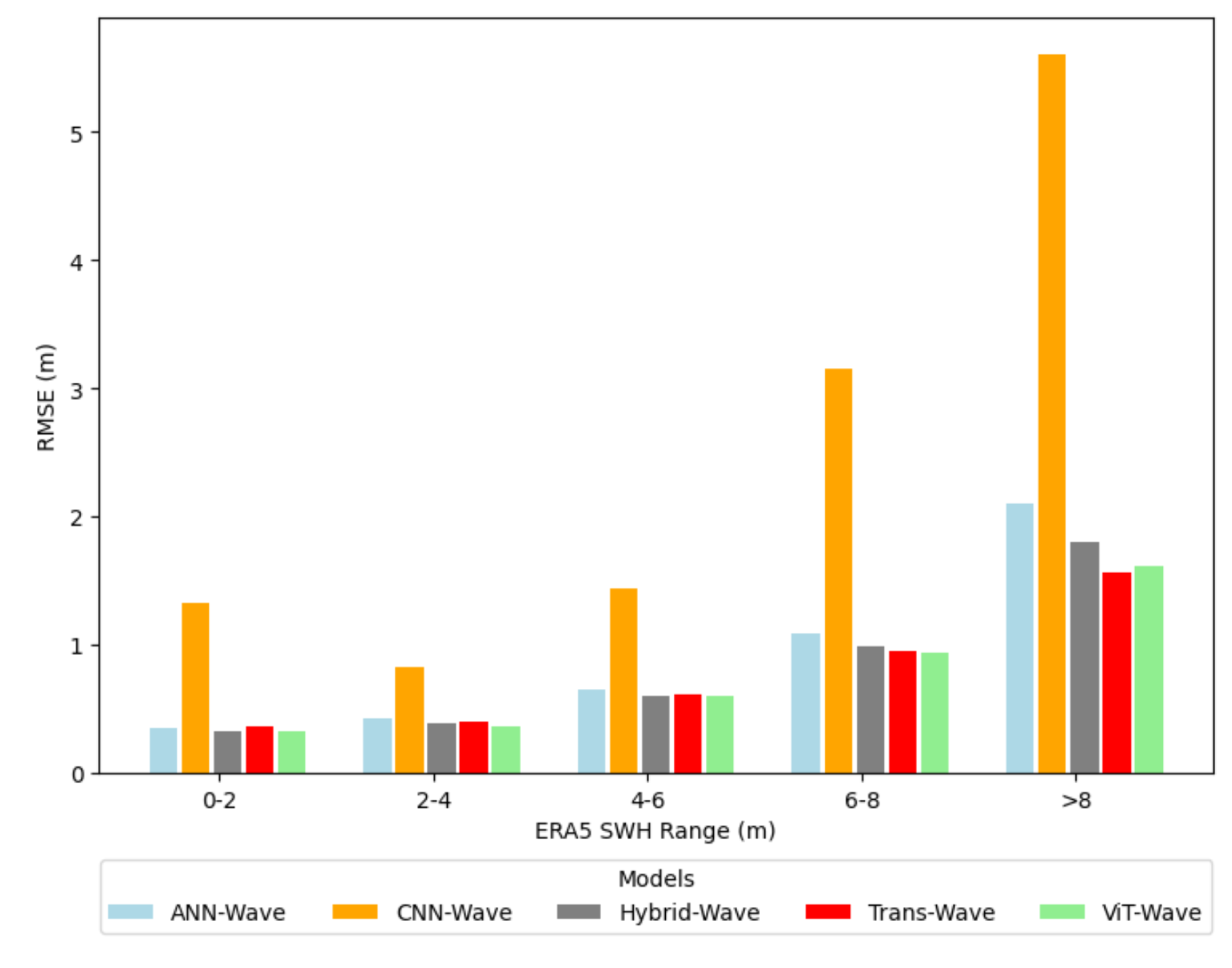
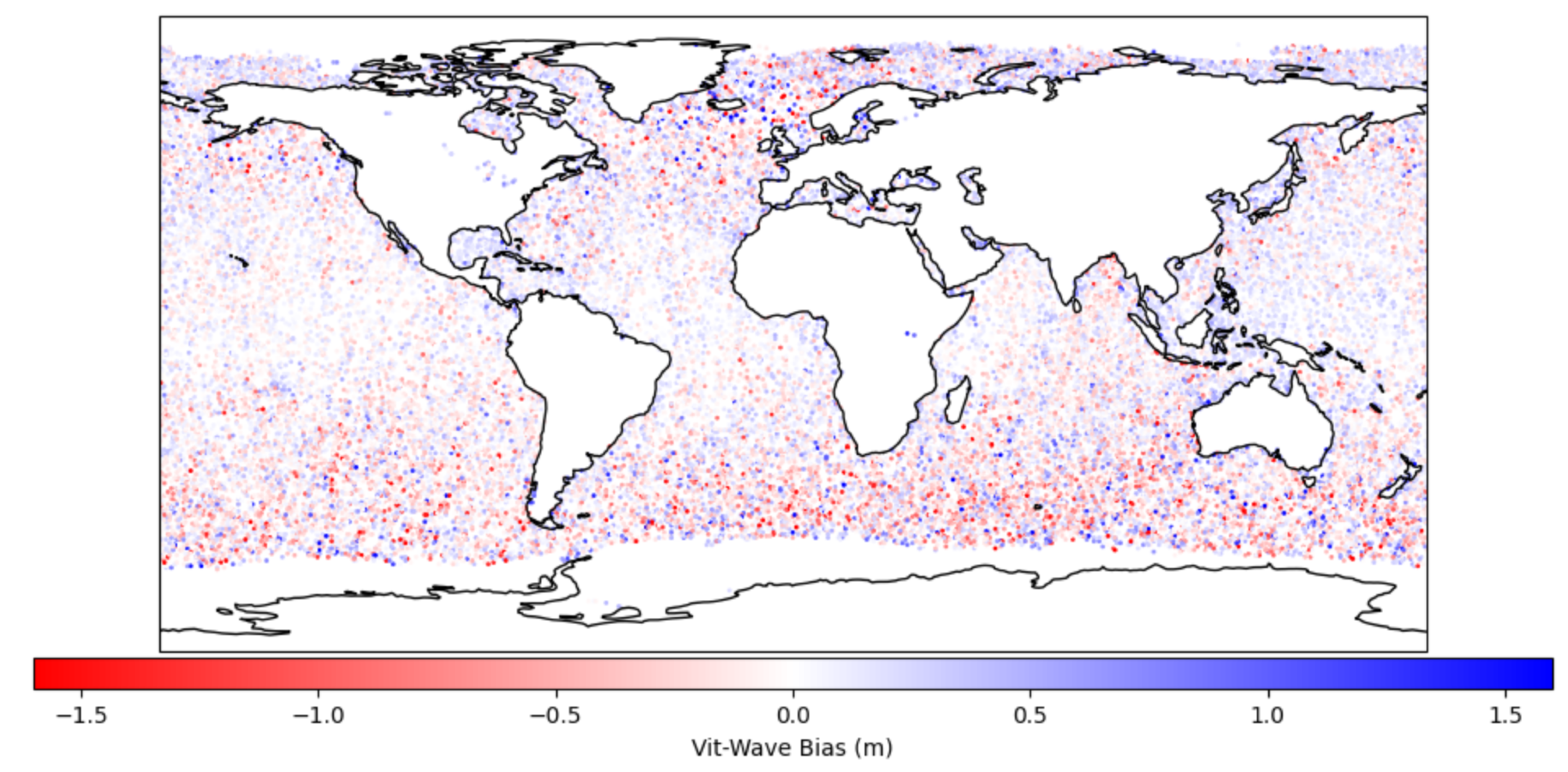
5. Result and Discussion

Upon completing the experimental tests, we evaluated the finalized models using the test dataset. The performance of these models was assessed based on several predetermined evaluation metrics: RMSE, MAE, BIAS, MAPE, and R². The test results are summarized in Table 3. Among the evaluated models, the ViT-Wave model demonstrated superior performance across all five metrics. Specifically, the ViT-Wave model achieved an RMSE of 0.4052 meters, indicating that it had the lowest overall error distribution. This suggests that the ViT-Wave model is highly effective in capturing the variability in the data and minimizing retrieval errors. The MAE for the ViT-Wave model was 0.27 meters, reflecting its capability to maintain low absolute errors, which highlights the model’s robustness in providing accurate retrievals with minimal deviations from the observed values. In terms of BIAS, the ViT-Wave model achieved a value of -0.0015 meters. This near-zero bias indicates that the model’s retrievals are almost unbiased, with negligible systematic errors, thereby enhancing its reliability for practical applications. The MAPE for the ViT-Wave model was 18.02%, highlighting its efficiency in minimizing percentage errors relative to the observed values. This metric is crucial for assessing the model’s performance in contexts where relative error measurements are critical. However, the Hybrid-Wave model achieved a slightly lower MAPE of 17.71%, indicating its superior performance in scenarios where minimizing relative errors is particularly important. This suggests that the Hybrid-Wave model may be more effective in applications requiring precise percentage error reduction, possibly because it is less influenced by extreme values. Finally, the R² value of 0.9117 for the ViT-Wave model signifies a high level of correlation between the retrieved and observed values. This strong correlation indicates that the model explains a substantial proportion of the variance in the observed data, further validating its effectiveness.

In addition to these evaluations, we conducted comparative studies with other models that utilize CYGNSS data for SWH retrieval. When compared with traditional data statistical analysis methods such as SNR[49] and NCDW LES[49], the ViT-Wave model exhibited improved performance in terms of RMSE and MAE. These improvements highlight the advantages of leveraging advanced neural network architectures over conventional statistical methods. Furthermore, the ViT-Wave model outperformed several other machine learning models, including ANN[32], BT [32], and DCNN[37]. The enhancements in retrieval accuracy with the ViT-Wave model underscore its potential for more accurate and reliable SWH retrievals compared to these existing methods.

To better illustrate the performance improvements of the ViT-Wave model, Table 4 presents the percentage enhancements of key parameters when compared to other models.

Scatter density plots were generated for each model to comprehensively evaluate their performance as shown in Figure 8. In these plots, the black solid line represents the ideal

y = x

line, indicating perfect agreement between the observed and retrieved values. Additionally, a red dashed line depicts the linear fit of the data, with the corresponding regression equation displayed in the bottom right corner of each plot. The scatter density plots reveal that the ViT-Wave model demonstrates the most favorable distribution of data points around the ideal

y = x

line, indicating a high degree of accuracy in its retrievals. The linear regression equation for the ViT-Wave model,

y = 0.88 x + 0.32

, underscores the model’s superior fitting performance. This close alignment with the ideal line suggests that the ViT-Wave model effectively captures the underlying relationship between the observed and retrieved SWH values, resulting in minimal deviations and high fidelity in its predictions.

In comparison, other models show varying degrees of dispersion around the y=x line, reflecting differences in retrieval accuracy and consistency. The scatter density plots reveal that models such as the CNN-Wave and Trans-Wave have more scattered points, indicating higher retrieval errors and less reliable performance. The fitting equations for these models also exhibit greater deviations from the ideal line, further highlighting their comparative inferiority. Overall, the scatter density analysis reinforces the earlier findings from the quantitative metrics, solidifying the ViT-Wave model’s status as the most robust and accurate model for SWH retrieval among those evaluated. Its superior performance across both quantitative metrics and visual scatter plots underscores its potential for practical applications in wave height prediction and oceanographic research.

We also conducted a segmented error analysis based on the range of SWH values. The SWH data were divided into five segments: 0-2 m, 2-4 m, 4-6 m, 6-8 m, and >8 m. The blue column represents the ANN-Wave model; the orange column represents the CNN-Wave model; the blue column represents the ANN-Wave model; the gray column represents the Hybrid-Wave model; the red column represents the Tans-Wave model; the green column represents the ViT-Wave model. The errors for each model within these segments were calculated and presented in the form of bar charts (see Figure 9 Figure 10 Figure 11). From these bar charts, it is evident that the ViT-Wave model consistently demonstrates the lowest errors across the SWH range of 0-8 meters, indicating its superior performance in this range. Notably, the error range of 0-4 meters is where all models perform best across all metrics, which may be related to the data distribution, as shown in Figure 7. This suggests that the ViT-Wave model is highly effective in accurately retrieving SWH values, particularly within the common range encountered in oceanographic observations. Interestingly, for SWH values greater than 8 meters, the Trans-Wave model shows the smallest errors, outperforming other models in this higher SWH segment. This indicates that while the ViT-Wave model excels in general SWH conditions, the Trans-Wave model has a notable advantage in extreme wave conditions, where its architecture might better capture the complex features associated with higher wave heights. This also aligns with the test results in Table 3 and Table 4, showing the ViT-Wave model’s limitations under extreme conditions. The segmented error analysis highlights the strengths of both the ViT-Wave and Trans-Wave models, each excelling in different SWH ranges and collectively offering robust solutions for a wide spectrum of wave height retrieval scenarios.

To better understand the global distribution of SWH across the ocean surface, we utilized reference points based on ERA5 SWH data along with their corresponding latitudes and longitudes. Upon evaluating the test dataset, it was observed that 95% of the SWH values were concentrated in the 0-5 meter range. To enhance the visibility of the overall SWH distribution, a customized color bar was employed, as shown in Figure 12, where darker colors indicate lower SWH values and lighter colors indicate higher SWH values. From Figure 12 and Figure 13, it can be seen that most of the colors are consistent, indicating that the ViT-Wave model’s retrieval results are close to the ERA5 SWH. However, in the central part of the Southern Hemisphere, the color in Figure 13 is lighter than in Figure 12, indicating that the ViT-Wave model underestimates the SWH compared to the ERA5 data. This suggests that the ViT-Wave model requires further optimization in high-value ranges.

From in Figure 12, which represents the ERA5 data, it is evident that SWH values tend to be higher in high latitude regions, particularly in the Southern Hemisphere. This observation cannot be made using CYGNSS data due to its limited coverage between 33°N and 33°S latitude, highlighting the advantage of FY-3E data. Overall, the ViT-Wave model shows a distribution that closely resembles the ERA5 reference, indicating its superior performance in capturing the global SWH distribution.

To evaluate the error distribution of the ViT-Wave model across the global ocean surface, we generated bias distribution maps (see Figure 14). These maps visually represent the differences between the ViT-Wave model predictions and the ERA5 reference data. In these maps, negative biases (indicating model underestimation) are shown in red, with darker shades representing larger discrepancies. Conversely, positive biases (indicating overestimation) are shown in blue, with darker shades indicating greater deviations. Regions where the model predictions match the ERA5 data are displayed in white. From Figure 14, it is evident that the ViT-Wave model tends to underestimate SWH values overall. The biases are more pronounced in high-latitude regions compared to areas near the equator, suggesting that the model’s performance is less accurate in these regions. This indicates a need for further refinement and optimization of the ViT-Wave model to improve its accuracy, particularly in high-latitude areas. Future research should focus on addressing these discrepancies to enhance the model’s reliability and performance in various oceanographic conditions.

6. Conclusions

With the rapid advancement of technology, new methodologies have emerged that enable the swift and accurate retrieval of SWH, a critical oceanographic parameter. The use of GNSS-R technology for SWH retrieval offers substantial advantages over traditional observational methods, including enhanced spatial and temporal resolution and broader coverage. This study, leveraging data from the newly launched FY-3E satellite, represents the first attempt to apply its GNSS-R data for SWH retrieval. Through the design of multiple deep learning networks, this research not only demonstrates the feasibility and efficacy of using Vision Transformers for SWH retrieval but also achieves promising results. The ViT-Wave model, in particular, shows superior performance compared to traditional methods and models based on CYGNSS data, underscoring the potential of Vision Transformers in this domain. The highest RMSE achieved was 0.4m, which surpasses the precision obtained using CYGNSS data. However, there remains room for improvement in the model’s performance concerning high wave conditions. Additionally, the global analysis revealed a significant trend of high waves in high-latitude regions, indicating the necessity for further optimization.

Moreover, this study provides a novel approach for GNSS-R based SWH retrieval and underscores the reliability and utility of FY-3E satellite data. The positive outcomes of this research pave the way for further exploration and application of FY-3E data in various oceanographic and environmental monitoring scenarios. Future work could delve deeper into expanding the use cases and enhancing the models for even better performance. This research establishes a solid foundation for the continued development and refinement of GNSS-R techniques, contributing to the broader field of oceanographic monitoring and environmental assessment. The successful implementation of the ViT-Wave model highlights the transformative potential of integrating advanced machine learning models with innovative satellite data to achieve unprecedented accuracy and coverage in SWH retrieval.

Author Contributions

Conceptualization, Z.Z and D.B.; methodology, R.K. and D.B.; software, Z.Z.; validation, Z.Z. and N.W.; investigation, C.R.; resources, D.B.; data curation, Z.Z. and R.K.; writing—original draft preparation, Z.Z.; writing—review and editing, D.B. and N.W.; visualization, C.R.; supervision, R.K.; project administration, R.K.; All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The GNSS-R data of FY-3E can be obtained from the Fengyun Data Service Network, the URL is https://satellite.nsmc.org.cn/portalsite/default.aspx; The SWH data of ERA5 can be obtained from the Climate Data Store, the URL is https://cds.climate.copernicus.eu/cdsapp!/dataset/reanalysis-era5-single-levels?tab=form

Acknowledgments

This article would like to thank the National Satellite Meteorological Center for data support and researcher Fangli Dou for her help.

Abbreviations

The following abbreviations are used in this manuscript:

SWH	Significant Wave Height
ERA5	European Centre for Medium-Range Weather Forecasts Reanalysis v5
MAE	Mean Absolute Error
RMSE	Root Mean Square Error
ViT	Vision Transformer
GNOS	GNSS Occultation Sounder
CYGNSS	Cyclone Global Navigation Satellite System
CNN	Convolutional Neural Network
ANN	Artificial Neural Network
GNSS	Global Navigation Satellite System
DDM	Delay-Doppler Map
NASA	National Aeronautics and Space Administration

Appendix A

Table A1. Explanation of Variables

#	Abbreviation	Full Name	Explanation
1	Ddm_effective_area	Effective Scattering Area	The effective scattering area of the 9x20 region of the DDM used to calculate DDM_NBRCS
2	sp_lat	Specular Point Latitude	Latitude of the specular reflection point
3	sp_lon	Specular Point Longitude	Longitude of the specular reflection point
4	Ddm_brcs_factor	BRCS Factor	Factor used to compute DDM BRCS (power/BRCS)
5	Ddm_doppler_refer	Doppler Reference	The central doppler (at column 10) of the DDM
6	Ddm_kurtosis	Kurtosis	Kurtosis of raw counts in the whole DDM
7	Ddm_noise_m	Noise M-value	The ratio of the square of the mean of the noise floor and the variance of the noise floor
8	Ddm_noise_raw	Noise Raw	The mean noise floor of the raw DDM
9	Ddm_noise_source	Noise Source	DDM noise floor source to calculate the mean noise
10	Ddm_peak_column	Peak Bin Column	The zero-based Doppler column of the peak value in the DDM
11	Ddm_peak_delay	Peak Bin Delay	Delay of the DDM peak bin, in corresponding GNSS system chip
12	Ddm_peak_doppler	Peak Bin Doppler	Doppler of the DDM peak bin
13	Ddm_peak_power_ratio	Peak Power Ratio	Sum of centered 5x3 DDM power bin values around the specular point divided by the sum of the all DDM power bin values
14	Ddm_peak_raw	Peak Raw	Peak value in DDM raw counts
15	Ddm_peak_row	Peak Bin Row	The zero-based delay row of the peak value in the DDM
16	Ddm_peak_snr	Peak SNR	10lg(S_max/N_avg-1), where S_max is the maximum value (in raw counts) in a single DDM bin and N_avg is the average per-bin raw noise counts
17	Ddm_power_factor	Power Factor	Factor used to compute DDM power (dBW) from DDM counts (counts/power)
18	Ddm_quality_flag	Quality Flag	The L1 DDM quality flag of processing, indicating various quality checks and conditions
19	Ddm_range_refer	Range Reference	The central range (at column 10) of the DDM
20	Ddm_raw_data	Raw Data	122x20 array of DDM bin raw counts
21	Ddm_skewness	Skewness	Skewness of raw counts in the whole DDM
22	Ddm_sp_column	Specular Point Column	The zero-based Doppler column of the specular point doppler in the DDM
23	Ddm_sp_delay	Specular Point Delay	Specular point delay in the DDM
24	Ddm_sp_dles	Specular Point DLES	The slope of the second derivative of the DDM’s leading edge slope
25	Ddm_sp_doppler	Specular Point Doppler	Specular point Doppler in the DDM
26	Ddm_sp_les	Specular Point LES	Leading edge slope of a 3 delay x 5 Doppler bin box centered at the specular point bin
27	Ddm_sp_nbrcs	Specular Point NBRCS	Normalized BRCS of a 3 delay x 5 Doppler bin box centered at the specular point bin
28	Ddm_sp_normalized_snr	Normalized SNR at Specular Point	SNR at specular point normalized by bistatic radar equation
29	Ddm_sp_raw	Specular Point Raw	Value of the specular point in the DDM raw counts
30	Ddm_sp_reflectivity	Specular Point Reflectivity	Signal reflectivity at the specular point assuming coherent scattering
31	Ddm_sp_row	Specular Point Row	The zero-based delay row of the specular point delay in the DDM
32	Sp_delay_doppler_flag	Delay-Doppler Flag	The method and quality flag to find specular position in DDM

References

Young, I. R. Wind Generated Ocean Waves. Elsevier, 1999.
Janssen, P. A. E. M. The Interaction of Ocean Waves and Wind. Cambridge University Press, 2004.
Queffeulou, P. Long-term validation of wave height measurements from altimeters. Marine Geodesy 2004, 27(3-4), 495-510. [CrossRef]
Ardhuin, F.; Chapron, B.; Collard, F. Observation of swell dissipation across oceans. Geophysical Research Letters 2009, 36(6). [CrossRef]
Komar, P. D. Beach processes and erosion—an introduction. In Handbook of coastal processes and erosion; CRC Press, 2018; pp. 1-20.
Chelton, D. B.; Wentz, F. J. Further development of an improved altimeter wind speed algorithm. Journal of Geophysical Research: Oceans 1986, 91(C12), 14250-14256. [CrossRef]
Stopa, J. E.; Cheung, K. F. Intercomparison of Wind and Wave Data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Modelling 2014, 75, 65-83. [CrossRef]
Fu, L.-L.; Chelton, D. B.; Traon, P.-Y. L.; Morrow, R. Eddy Dynamics from Satellite Altimetry. Oceanography 2010, 23(4), 14-25. [CrossRef]
Lambright, W. H. Adopting TOPEX/Poseidon. In NASA and the Politics of Climate Research: Satellites and Rising Seas; Springer Nature Switzerland, Cham, 2023; pp. 21-37.
Gommenginger, C. P.; Srokosz, M. A.; Challenor, P. G.; et al. Measuring ocean wave period with satellite altimeters: A simple empirical model. Geophysical Research Letters 2003, 30(22). [CrossRef]
Durrant, T. H.; Greenslade, D. J.; Simmonds, I. Validation of Jason-1 and Envisat Remotely Sensed Wave Heights. Journal of Atmospheric and Oceanic Technology 2009, 26(5), 123-134. [CrossRef]
Gemmrich, J.; Thomas, B.; Bouchard, R. Observational Changes and Trends in Northeast Pacific Wave Records. Geophysical Research Letters 2011, 38(22). [CrossRef]
Ribal, A.; Young, I. R. 33 Years of Globally Calibrated Wave Height and Wind Speed Data Based on Altimeter Observations. Scientific Data 2019, 6(1), 77.
Ruf, C. S.; et al. CYGNSS: Enabling the Future of Hurricane Forecasting. IEEE Geoscience and Remote Sensing Magazine 2019, 7(2), 52-67.
Clarizia, M. P.; et al. Analysis of GNSS-R Delay-Doppler Maps from the UK-DMC Satellite Over the Ocean. Geophysical Research Letters 2014, 41(15), 5276–5283. [Google Scholar] [CrossRef]
Li, Z.; Guo, F.; Chen, F.; et al. Wind speed retrieval using GNSS-R technique with geographic partitioning. Satellite Navigation 2023, 4(1), 4. [Google Scholar] [CrossRef]
Li, W.; Cardellach, E.; Fabra, F.; et al. Assessment of spaceborne GNSS-R ocean altimetry performance using CYGNSS mission raw data. IEEE Transactions on Geoscience and Remote Sensing 2019, 58(1), 238–250. [Google Scholar] [CrossRef]
Eroglu, O.; Kurum, M.; Boyd, D.; et al. High spatio-temporal resolution CYGNSS soil moisture estimates using artificial neural networks. Remote Sensing 2019, 11(19), 2272. [Google Scholar] [CrossRef]
Gleason, S.; Ruf, C. S.; O’Brien, A. J.; et al. The CYGNSS level 1 calibration algorithm and error analysis based on on-orbit measurements. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 12(1), 37–49. [Google Scholar] [CrossRef]
Zhao, R.; Wang, K.; Xu, X. Global precipitation from FY-3 polar orbit satellites. Science Bulletin 2024. [Google Scholar] [CrossRef] [PubMed]
Shao, W.; Sheng, Y.; Sun, J. Preliminary assessment of wind and wave retrieval from Chinese Gaofen-3 SAR imagery. Sensors 2017, 17(8), 1705. [Google Scholar] [CrossRef] [PubMed]
Sun, Y.; Wang, X.; Du, Q.; et al. The status and progress of Fengyun-3E GNOS II mission for GNSS remote sensing. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: New York, NY, USA, 2019; pp. 5181–5184. [Google Scholar]
Stopa, J. E.; Cheung, K. F. Intercomparison of Wind and Wave Data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Modelling 2014, 75, 65–83. [Google Scholar] [CrossRef]
Guo, W.; Du, H.; Guo, C.; et al. Information fusion for GNSS-R wind speed retrieval using statistically modified convolutional neural network. Remote Sensing of Environment 2022, 272, 112934. [Google Scholar] [CrossRef]
Yan, Q.; Jin, S.; Huang, W.; et al. Global soil moisture estimation using CYGNSS data. IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2020, 6182-6185.
Li, W.; Cardellach, E.; Fabra, F.; et al. Assessment of spaceborne GNSS-R ocean altimetry performance using CYGNSS mission raw data. IEEE Transactions on Geoscience and Remote Sensing 2019, 58(1), 238–250. [Google Scholar] [CrossRef]
Zribi, M.; Motte, E.; Baghdadi, N.; et al. Potential applications of GNSS-R observations over agricultural areas: Results from the GLORI airborne campaign. Remote Sensing 2018, 10(8), 1245. [Google Scholar] [CrossRef]
Strandberg, J.; Hobiger, T.; Haas, R. Real-time sea-level monitoring using Kalman filtering of GNSS-R data. GPS Solutions 2019, 23(3), 61. [Google Scholar] [CrossRef]
Clarizia, M. P.; et al. Analysis of GNSS-R Delay-Doppler Maps from the UK-DMC Satellite Over the Ocean. Geophysical Research Letters 2014, 41(15), 5276–5283. [Google Scholar] [CrossRef]
Yu, K.; Han, S.; Bu, J.; et al. Spaceborne GNSS reflectometry. Remote Sensing 2022, 14(7), 1605. [Google Scholar] [CrossRef]
Li, Z.; Guo, F.; Zhang, X.; et al. Analysis of factors influencing significant wave height retrieval and performance improvement in spaceborne GNSS-R. GPS Solutions 2024, 28(2), 64. [Google Scholar] [CrossRef]
Wang, F.; Yang, D.; Yang, L. Retrieval and assessment of significant wave height from CYGNSS mission using neural network. Remote Sensing 2022, 14(15), 3666. [Google Scholar] [CrossRef]
Cardellach, E.; Fabra, F.; Nogués-Correig, O.; et al. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Science 2011, 46(06), 1–16. [Google Scholar] [CrossRef]
Zhao D, Heidler K, Asgarimehr M, et al. DDM-Former: Transformer networks for GNSS reflectometry global ocean wind speed estimation[J]. Remote Sensing of Environment, 2023, 294: 113629. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 15, 1234-1246. [CrossRef]
Madhiarasan D M, Roy P, Pratim P. Hybrid Transformer Network for Different Horizons-based Enriched Wind Speed Forecasting[J]. arXiv preprint arXiv:2204.09019, 2022. Remote Sensing 13(5), 1257.
Patanè, L.; Iuppa, C.; Faraci, C.; et al. A deep hybrid network for significant wave height estimation. Ocean Modelling 2024, 189, 102363. [Google Scholar] [CrossRef]
Bu, J.; Yu, K.; Ni, J.; et al. Combining ERA5 data and CYGNSS observations for the joint retrieval of global significant wave height of ocean swell and wind wave: a deep convolutional neural network approach. Journal of Geodesy 2023, 97(8), 81. [Google Scholar] [CrossRef]
Huang, F.; Xia, J.; Yin, C.; et al. Assessment of FY-3E GNOS-II GNSS-R Global Wind Product. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 7899–7912. [Google Scholar] [CrossRef]
Yang, G.; Du, X.; Huang, L.; et al. An Illustration of FY-3E GNOS-R for Global Soil Moisture Monitoring. Sensors 2023, 23(13), 5825. [Google Scholar] [CrossRef] [PubMed]
Li, Z.; Verhoef, A.; Stoffelen, A.; et al. First Results from the WindRAD Scatterometer on Board FY-3E: Data Analysis, Calibration and Wind Retrieval Evaluation. Remote Sensing 2023, 15(8), 2087. [Google Scholar] [CrossRef]
Yang, G.; Bai, W.; Wang, J.; et al. FY-3E GNOS II GNSS Reflectometry: Mission Review and First Results. Remote Sensing 2022, 14(4), 988. [Google Scholar] [CrossRef]
Huang, F.; Xia, J.; Yin, C.; et al. Spaceborne GNSS Reflectometry with Galileo Signals on FY-3E/GNOS-II: Measurements, Calibration, and Wind Speed Retrieval. IEEE Geoscience and Remote Sensing Letters 2023, 20, 1–5. [Google Scholar] [CrossRef]
Wang, W.; Ren, K.; Duan, B.; Zhu, J.; Li, X.; Ni, W.; Lu, J.; Yuan, T. A four-dimensional variational constrained neural network-based data assimilation method. Journal of Advances in Modeling Earth Systems 2024, 16(1), e2023MS003687. [Google Scholar] [CrossRef]
Zhou, Z.; Duan, B.; Ren, K. Improving GNSS-R Sea Surface Wind Speed Retrieval from FY-3E Satellite Using Multi-task Learning and Physical Information. In Proceedings of the International Conference on Neural Information Processing; Springer Nature Singapore; 2023; pp. 357–369. [Google Scholar]
Wolf, J.; Woolf, D. K. Waves and climate change in the north-east Atlantic. Geophysical Research Letters 2006, 33(6). [Google Scholar] [CrossRef]
Zhang, W.; Sun, Y.; Wu, Y.; et al. A deep-learning real-time bias correction method for significant wave height forecasts in the Western North Pacific. Ocean Modelling 2023, 102289. [Google Scholar] [CrossRef]
Martinez, P.; Lopez, M.; Wang, S. Comparative Study of Significant Wave Height Datasets for Coastal Management. Marine Data Science 2023, 10(1), 45–58. [Google Scholar]
Ruf, C.; Unwin, M.; Dickinson, J.; et al. CYGNSS: Enabling the future of hurricane prediction [remote sensing satellites]. IEEE Geoscience and Remote Sensing Magazine 2013, 1(2), 52–67. [Google Scholar] [CrossRef]
Bu, J.; Yu, K. Significant wave height retrieval method based on spaceborne GNSS reflectometry. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [Google Scholar] [CrossRef]
Yuan, T.; Zhu, J.; Ren, K.; et al. Neural network driven by space-time partial differential equation for predicting sea surface temperature. In Proceedings of the 2022 IEEE International Conference on Data Mining (ICDM), 2022; IEEE: 656-665.

Figure 1. Temporal and Spatial Distribution of Observation

Figure 2. ANN-Wave model structure

Figure 3. CNN-Wave model structure

Figure 4. Hybrid-Wave model structure

Figure 5. Trans-Wave model structure

Figure 6. ViT-Wave model structure

Figure 7. Distribution of Significant Wave Height (SWH)

Figure 8. Scatter density plot of all models

Figure 9. RMSE error distribution histogram of each model

Figure 10. MAE error distribution histogram of each model

Figure 11. Bias error distribution histogram of each model

Figure 12. SWH data ocean surface distribution of ERA5 test set

Figure 13. SWH data ocean surface distribution retrieval by VIT-WAVE model

Figure 14. Bias error distribution of ViT-Wave model

Table 1. Weights for Each Layer in the models

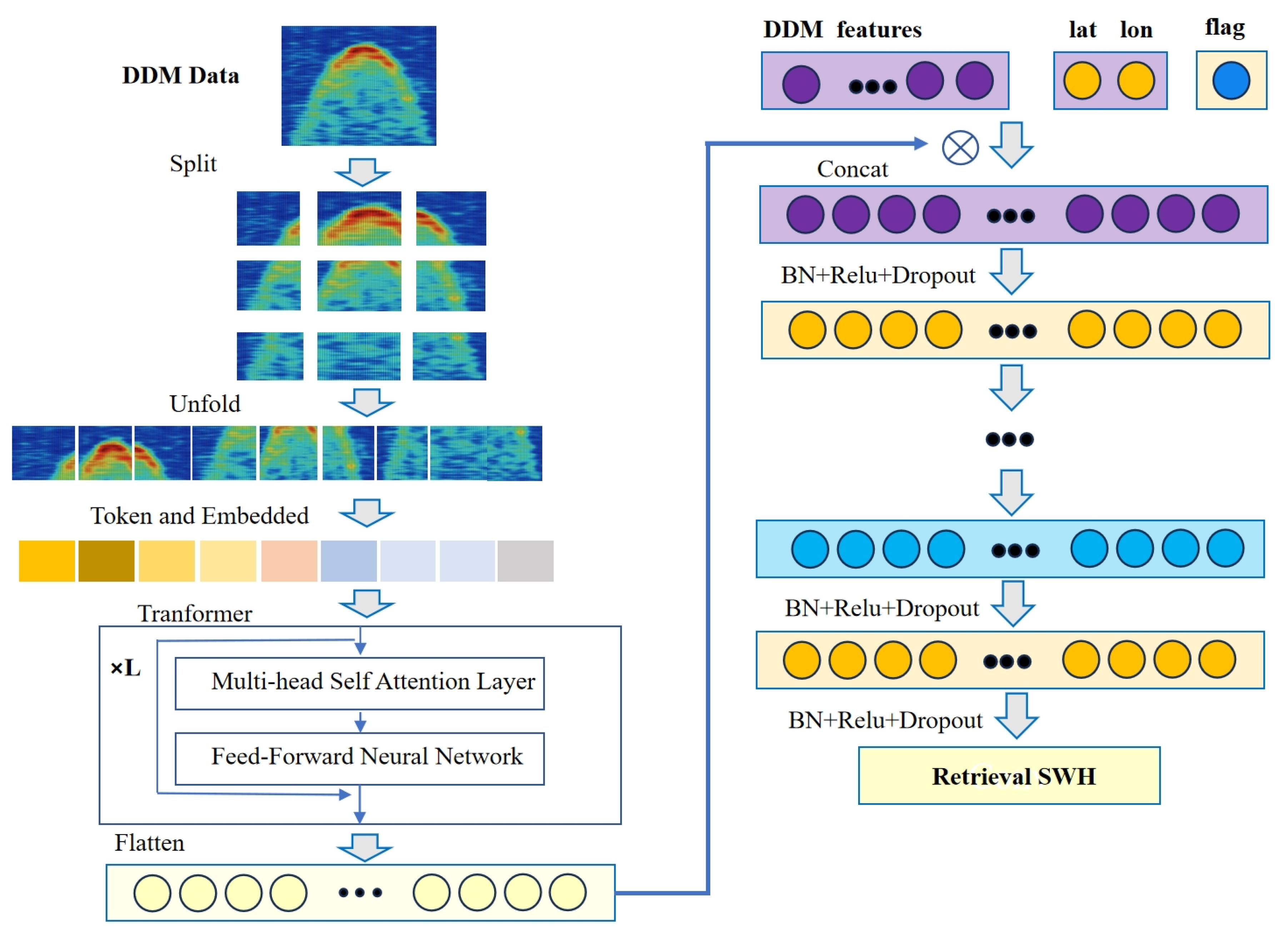
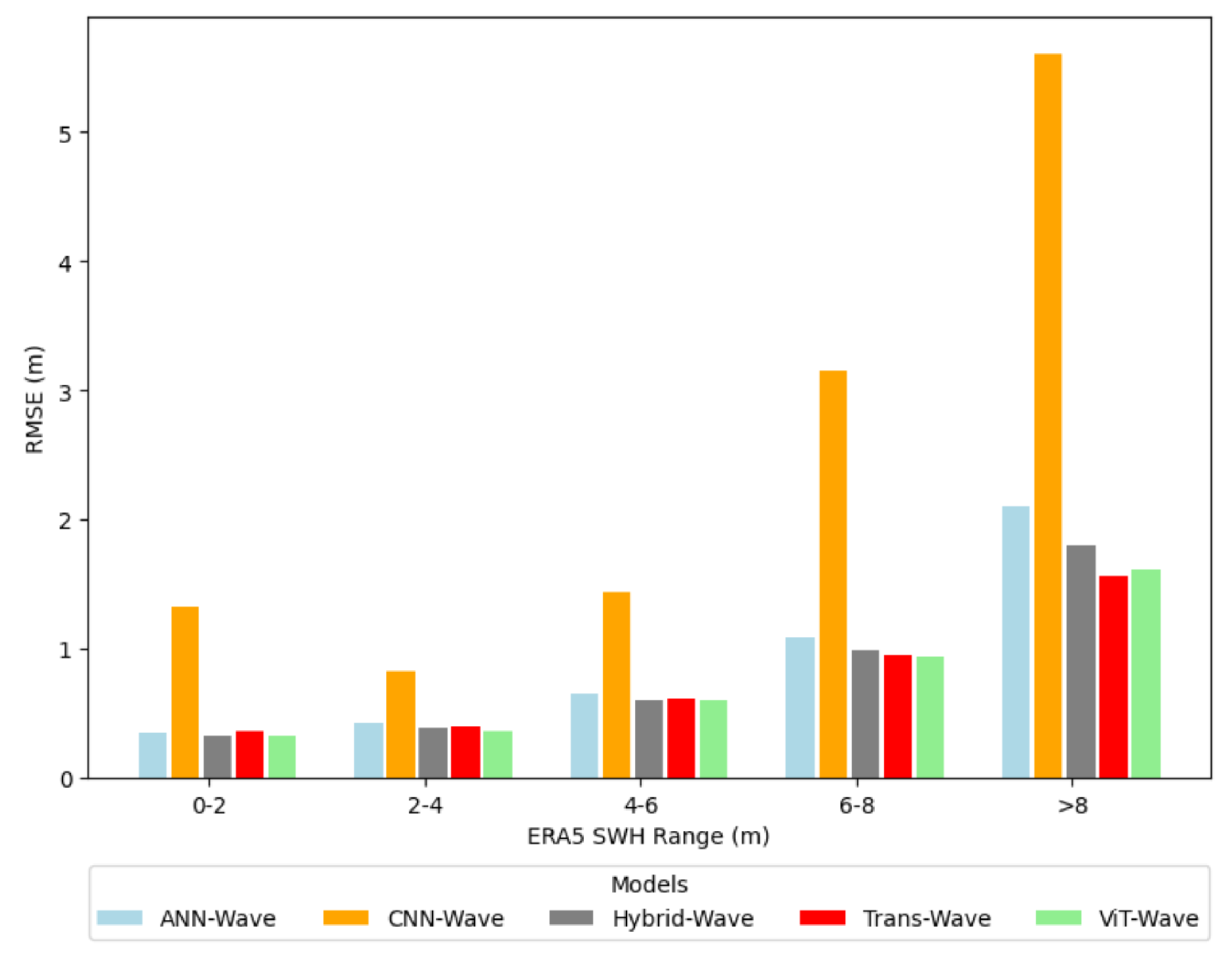
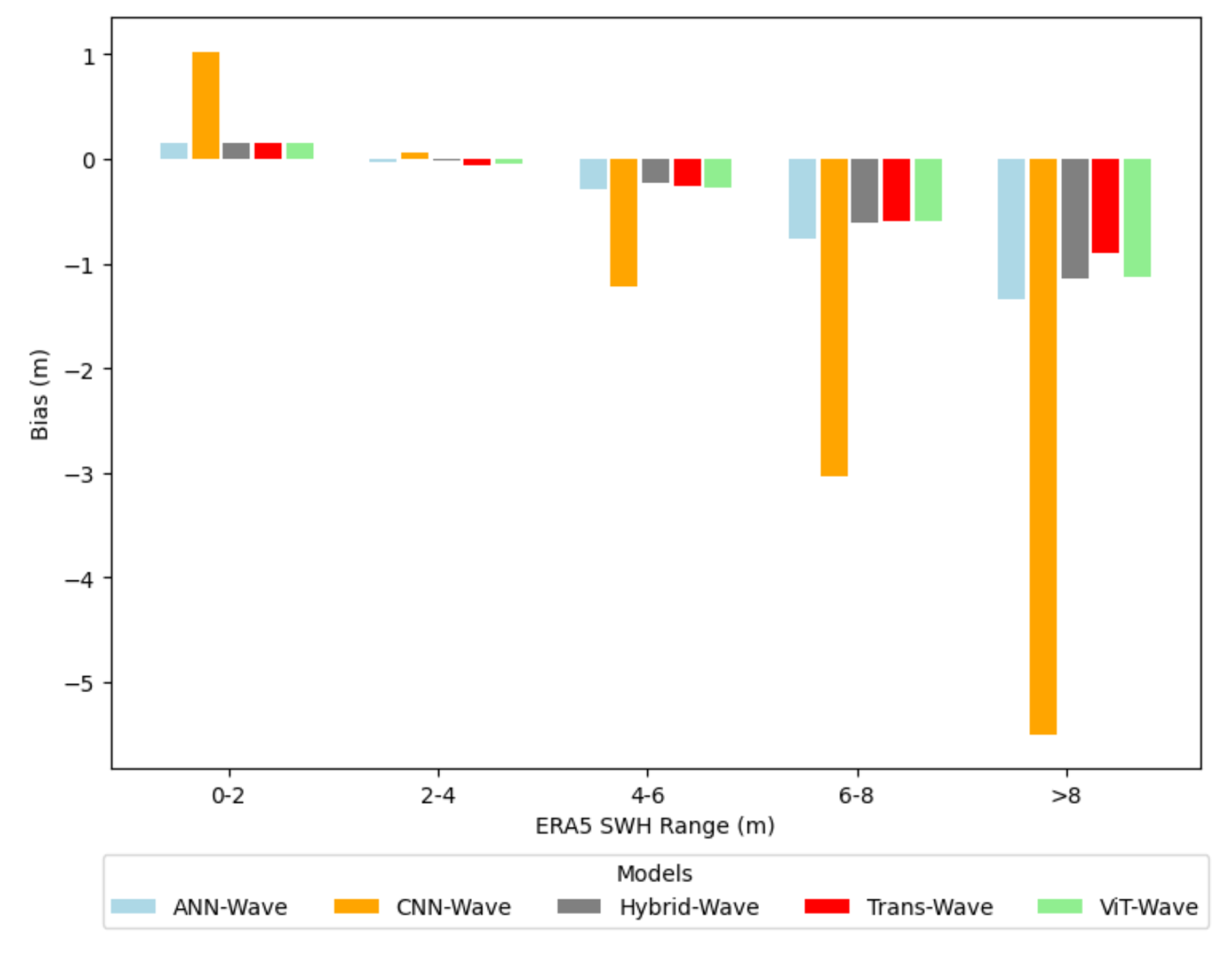
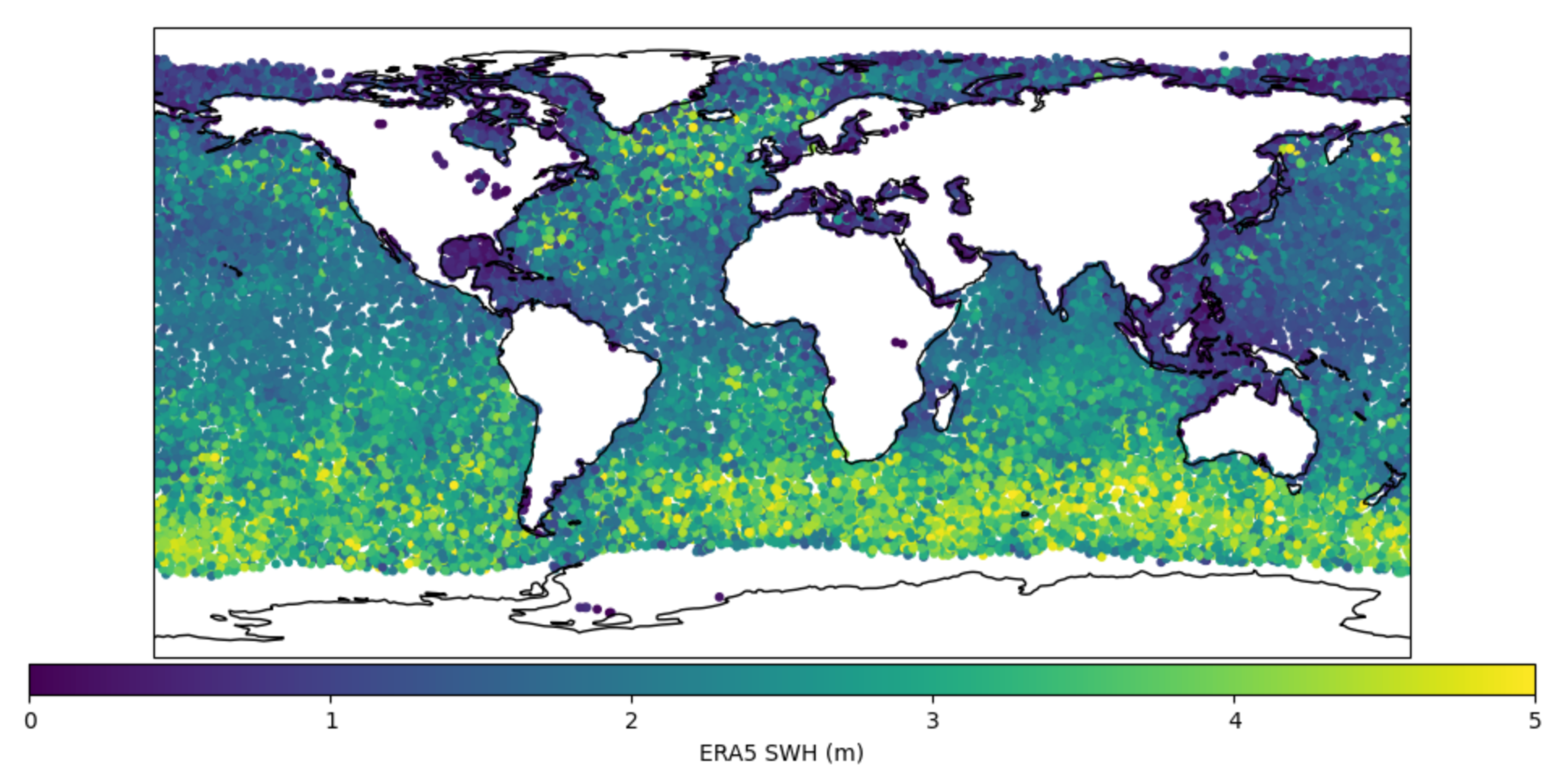
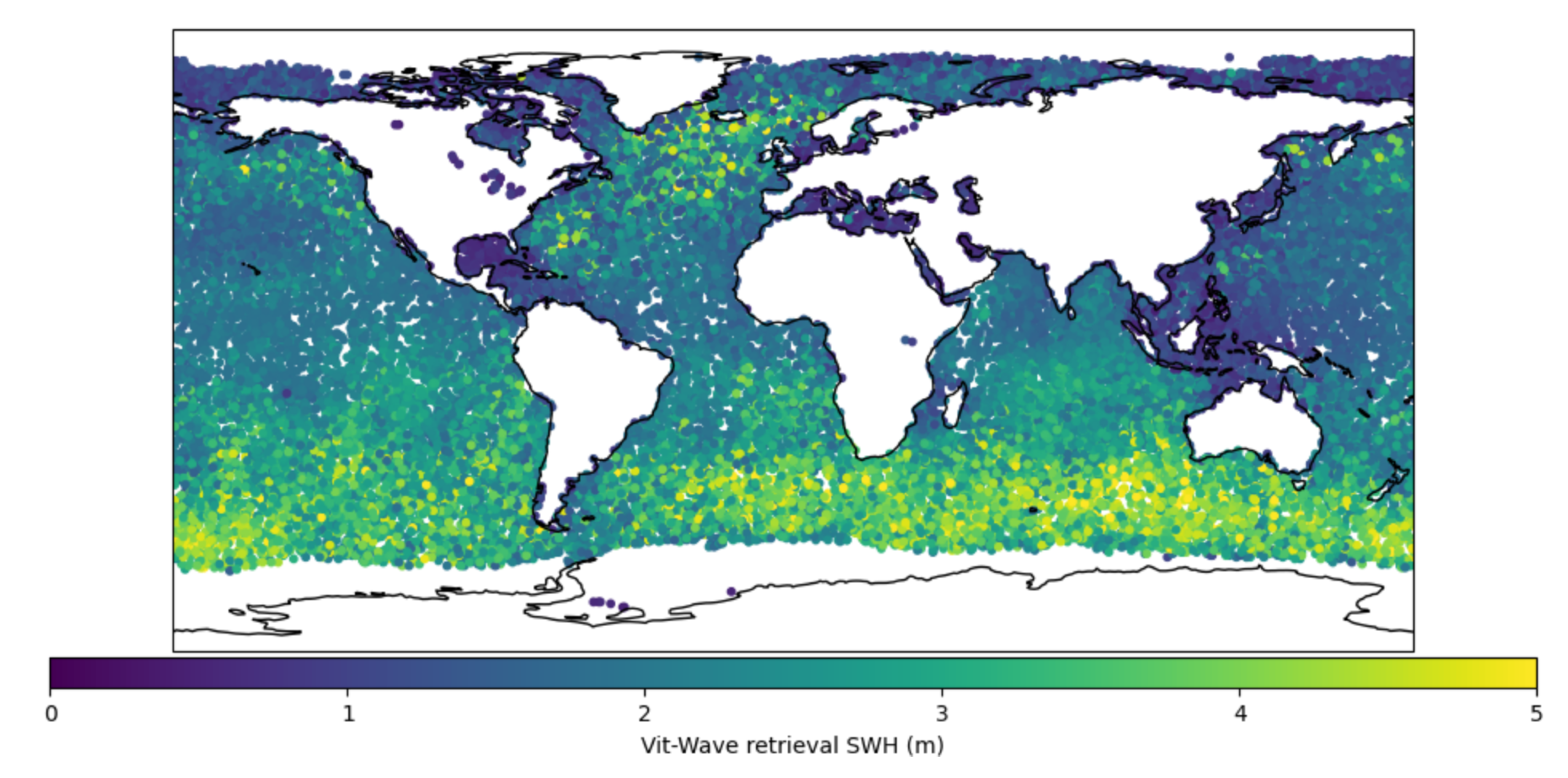
Layer	ANN-Wave	CNN-Wave	Hybrid-Wave	trans-Wave	ViT-Wave
Convolutional Layers
Conv2d	-	[128, 1, 5, 5]	[128, 1, 5, 5]	-	-
Conv2d	-	[32, 128, 4, 4]	[32, 128, 4, 4]	-	-
Conv2d	-	[1, 32, 2, 2]	[1, 32, 2, 2]	-	-
Transformer Layers
Embedding	-	-	-	[20, 64]	[4 * 4, 64]
Transformer Encoder	-	-	-	[64, 8, 3, 256]	[64, 8, 3, 256]
Linear Layer
Linear	[31, 1000]	[12, 1000]	[43, 1000]	[(9 * 64) + 31, 1000]	[(45 * 64) + 31, 1000]
SWH Retrieval Layers	Weight Dimensions
Linear	[1000, 2000]
Linear	[2000, 1500]
Linear	[1500, 500]
Linear	[500, 200]
Linear	[200, 100]
Linear	[100, 10]
Linear	[10, 1]

Table 2. Average Train and Validation Loss with Standard Deviations

Model	Train Loss ± Std	Validation Loss ± Std
ANN-Wave	0.2135 ± 0.0146	0.2177 ± 0.0044
CNN-Wave	1.1400 ± 0.0191	1.9116 ± 0.6267
Hybrid-Wave	0.2065 ± 0.0165	0.1938 ± 0.0109
Trans-Wave	0.2034 ± 0.0148	0.1955 ± 0.0086
ViT-Wave	0.1816 ± 0.0040	0.1735 ± 0.0042

Table 3. Evaluation accuracy of all models

	RMSE	MAE	Bias	MAPE	R²
ANN-Wave	0.4546	0.3048	0.0040	18.6814	0.8889
CNN-Wave	1.2337	0.9447	0.2715	74.6440	0.1819
Hybrid-Wave	0.4225	0.2799	0.0144	17.7126	0.9040
Trans-Wave	0.4344	0.2931	-0.0012	23.2238	0.8986
SNR[49]	0.534	0.421	-	21.52	-
NCDW LES[49]	0.503	0.390	-	20.02	-
ANN[32]	0.59	-	-	-	-
BT[32]	0.48	-	-	-	-
DCNN[37]	0.422	-	-	-	0.89
ViT-Wave	0.4052	0.2700	-0.0015	18.0200	0.9117

Table 4. Percentage Improvement of ViT-Wave Model Over Other Models

	RMSE	MAE	Bias	MAPE	R²
ANN-Wave	10.85%	11.45%	137.50%	3.54%	2.57%
CNN-Wave	67.15%	71.42%	100.55%	75.86%	401.10%
Hybrid-Wave	4.10%	3.53%	110.42%	-1.74%	0.83%
Trans-Wave	6.72%	7.88%	25.00%	28.28%	1.46%
SNR[49]	24.07%	35.87%	-	16.26%	-
NCDW LES[49]	19.43%	30.77%	-	10.00%	-
ANN[32]	31.36%	-	-	-	-
BT[32]	15.62%	-	-	-	-
DCNN[37]	4.00%	-	-	-	2.44%
ViT-Wave	-	-	-	-	-

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer