Ansys HFSS Evaluation of Periodic ZnO Nanorod Metamaterial Unit Cell for Terahertz Broadband Antireflection Coatings

Preprint

Article

Ansys HFSS Evaluation of Periodic ZnO Nanorod Metamaterial Unit Cell for Terahertz Broadband Antireflection Coatings

Altmetrics

Downloads

131

Views

Comments

Rishikesh Madhuvairy^*

This version is not peer-reviewed

This preprints belongs to the Topic

Advances in Computational Materials Sciences

Submitted:

24 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts

Abstract

This paper proposes a theoretical silicon dioxide (SiO2) solar cell based dielectric metamaterial unit surface consisting of zinc oxide (ZnO) periodic nanorods of bandgap energy of 2.2-2.4eV. It evaluates the absorptive efficiency of the film using S-parameter and Z-parameter testing of magnitude, return/insertion loss, and impedance matching with respect to a frequency band of 0.0014-10.5THz. Terahertz applications of the result are considered due to potential scope for infrared (IR) and microwave (MW) spectral selectivity with ZnO. Calculations of input n-impedance and loss tangents are also presented with emphasis on the exhibition of antireflection to gauge the performance of the thin-film meta-surface in tandem solar cells. The data for the reflectance parameters of this structure, primarily the S11 loss and impedance matching (dB/dB10) are compared to those of prior investigations with different metamaterial coatings on SiO2 solar photovoltaic cells, as well as ZnO nanorods used in photovoltaic applications, to ascertain the cylindrical meta-surface structure with the preset thicknesses of the study being an effective anti-reflector. Application can be extended to other broadband domains requiring plasmonic graded refractive surfaces, in further work.

Keywords:

Subject: Chemistry and Materials Science - Surfaces, Coatings and Films

1. Introduction

Metamaterial antireflection coatings have emerged to become significant in facilitating the tuneability and absorptivity of multilayered thin-films and coatings for a variety of electrical applications due to their unique bulk exhibition of negative dielectric constants – a projection of their response to external optical excitation [1]. Negative electrical permittivity is viewed in natural circumstances, particularly in some substrates resonating below the plasma frequency [2]. A negative dielectric constant, defined by a negative permittivity for individual unit cells has been achieved in the context of metamaterial multilayers. On the contrary, their ability to disrupt an incident electromagnetic field is not observed in natural materials by virtue of their properties following the right-hand rule of electromagnetic absorption, indicating positive refractive indices [2].

Metamaterial structures therefore provide insight into the potential re-tuning of solar photovoltaic cells to maximize their efficiency in terms of controlling/modulating electrical permittivity to influence amplitude and phase [1] in sunlight-deficient regions, or low frequency applications pertaining to a broadband Terahertz (THz) spectrum, which is a region of convergence between microwave (MW) and infrared (IR) radiation defined as 150GHz-10THz. Radio-frequency (RF) circuits with metamaterial antireflection coatings also serving as a layer to the transmission line of a photovoltaic have seldom been tested due to the conflict of purpose between their respective frequency bands (and magnetic permeability has a massive negative effect on the output power of the circuit at high voltages) [3]. For high-frequency applications, pushing the boundaries of metamaterial unit cells into the visible region of light has been achieved by optimizing the surface topology, proving to be more efficacious in constructing films with surfaces smaller than the wavelength of the incident light, [2,4,5,6,7,8,9], but common S11 and S21 results for the reflectance of such surfaces have proven that the transmittivity and impedance matching for such frequency bands is significantly of higher quality than THz bands – a cause for some concern at face value. This investigation deals with THz frequency bands to check the ramifications and validity of such results for planar silicon solar cells, with specific focus on the reflectance of the film for certain plasmonic preconditions.

Past investigations, however, have proved the absolute success of different meta-surfaces in such frequency bands. Some common metamaterial structures that have been proven to minimize the dielectric loss of the coating through a graded negative refractive index for MW applications are split ring resonators or square/cross patches [9, 10]. A study by Guozhang Wu et. al. [9] involving vanadium dioxide periodic structures used the former method, which demonstrated an absorption bandwidth of more than 90% in a low-THz frequency band. A study by Yue Jhun-Zheng et. al. [10] used a coplanar loading philosophy to minimize radar cross section of a wideband MW antennae using thin-films arranged according to different polarization angles, in a chessboard-like meta-surface. The study demonstrated a phase shift where destructive interference was achieved in two locations by orienting the radiation patches by a 45° difference.

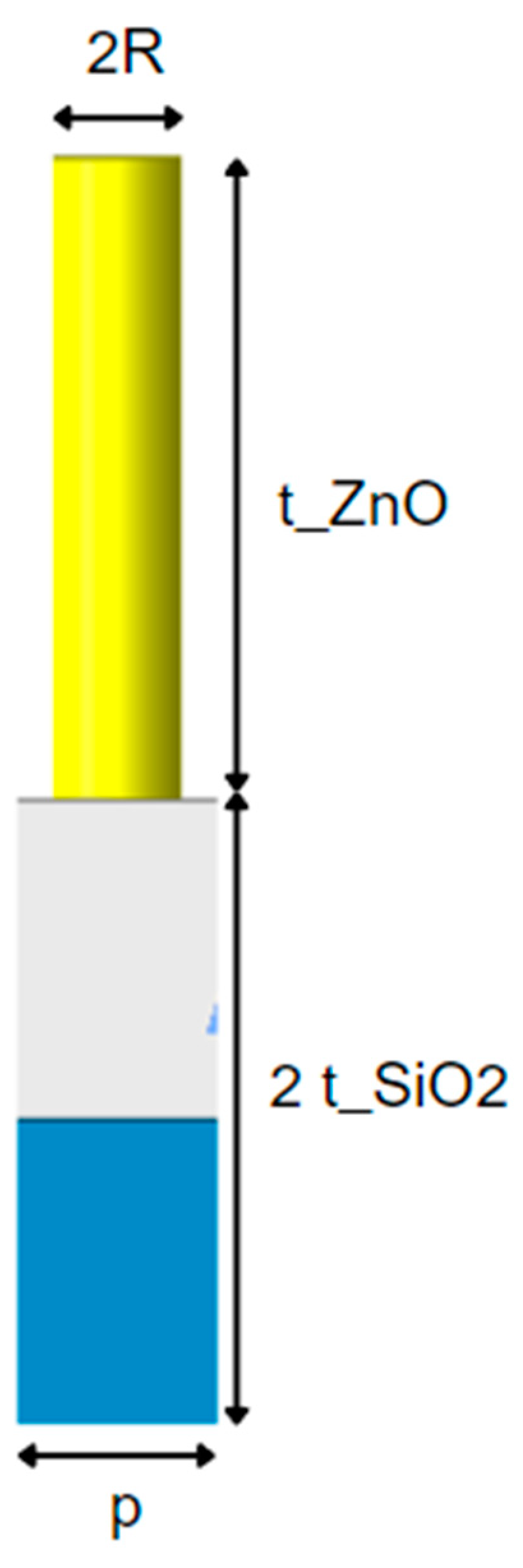
This gives tremendous hope for applications of metamaterials in any telecommunication frequency range, opening up a new domain of its usability to photovoltaic efficiency enhancement. The focus of this study, being a zinc-oxide nanorod mounted to a dual-layer SiO₂-Aluminium-ground is modelled off of the artificial periodic structure fabricated by low temperature hydrothermal methods by Abhishek Kumar et. al. [4] previously indicating a performance enhancement for high-frequency bands up to a 50% increase in absorption in the near-UV spectrum. Aside from this, ZnO nanorods have become popular periodic structures for instrumentation techniques for the evaluation of physical/chemical processes [11]. Hence, this study carries the properties of ZnO into a unique intersection between RF and silicon photonics with emphasis on the Terahertz region, to gauge the rod’s multifunctional properties at the nanoscale.

2. Materials and Methods

The purpose of antireflection coatings in high-efficiency solar cells is that it dictates the enhanced cell’s performance via high power transmission through the minimization of reflectance at the film’s surface [7]. The reflection coefficient, Ґ, is a useful parameter to gauge the appropriateness of the proposed structure as it is a function of the characteristic impedances and the magnitude of return loss of the heterostructures [Reflection Coefficient, Ґ]. Understanding the relationship between the regions of the experimental frequency band and the combinations of these parameters that can be used to find the film’s permittivity and dielectric loss tangent, new conclusions are to be drawn about the efficiency of zinc oxide (ZnO) in fulfilling the purpose of antireflection.

2.1. ZnO: Conductive/Reflective Performance, Meta-Surface Properties

The conductive and reflective properties of ZnO have been thoroughly discussed in a variety of investigations of field response and optical/photo-excited carrier frequency modulation for different parameters (high-doping, laser/thermal annealing, ion implantation for balanced plasma wavelength and minimized attenuation [12,13,14,15,16]). Some methods’ analytical components have factored in Drude damping [1] due to the Lorentzian transformation of the real permittivity of ZnO, which is the dominant contributor to the metamaterial refractive index. Specific pump fluences (correlated to intensity of impinging light with energy within or above the bandgap respectively) are attributed to changes in the photo-excited carrier frequency, resulting in changes to the saturation of the multilayer’s free carrier density.

If we were to isolate the performance of ZnO, the goal becomes to achieve desired levels of frequency modulation at the entering wave-port [1,12,15], which in the context of this study, is S-{Floquetport 1:1}, and achieve low return loss relative to the carrier modes as the pump frequency tends to the plasma frequency. From a results standpoint, this positively divulges from previous remarks on trying to achieve only perfect absorption with ZnO in similar bandgaps. Regardless, past outcomes of these analytical techniques have shown undoped, unannealed ZnO films transferred to glasses/substrates by whichever method are highly robust and tuneable [1,14]. In dynamic nanophotonic applications, the next step becomes decreasing power requirements and dissipation to enhance reflectance modulation of ZnO meta-surfaces to higher extents [1,7]. In the case of the work by S. Saha et. al. [1], a split-disk resonator geometry was used to achieve tailored resonance at telecommunication wavelengths. While a major independent variable in this paper’s extension of the work on ZnO is the cylindrical geometry of the nanorod [4,6], the aforementioned results remarkably convey ZnO’s highly adjustable antireflective properties at specific pump fluencies. ZnO is also an excellent photocatalytic semiconductor, making it useful for circuit applications of this metamaterial film [13,15,16] upon the theoretical addition of poly(3-hexylthiophene):(phenyl-C61-butyric acid methyl ester) (P3HT:PCBM) and poly(3,4-ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS) heterojunctions to the bulk material [4].

One interesting case to consider when accounting for ZnO’s reflective performance in past investigations is the study performed by Koch et. al. [12] wherein reflectance spectra remarkably suggested an increase in reflectance modulation towards the near-infrared (IR) wavelength range, except the complex permittivity of the substrate in this circumstance was measured for a case where ZnO had been implanted with Gallium ions in a hyper-dopant situation. This a unique result that deviates from the previous insights about ZnO’s individual antireflective properties but still validates the ability to achieve metamaterial spectral selectivity in the Terahertz (THz) broadband with this oxide. The wavelength threshold for which the structure’s extinction coefficient exceeds the real permittivity is not very large, which means the dopant versions of these studies can exhibit plasmonic behaviour in the THz range [12]. For the sake of simplicity (since this study is entirely simulation based), my investigation will deal with non-dopant ZnO as a comparative measure with a predefined plasma frequency.

The original study which was performed with organic growth of ZnO nanowires through coating nanoimprinted indium tin oxide (ITO) fibres with hydrochloric acid and the fabrication of the substrate’s active material with the organic dissolution of PCBM found excellent modulation patterns for a 30° angle of incidence with an absolute minimum n-reflectance at the film’s experimental bandgap energy of 2.2 eV [4]. However, it was also observed that because of the organically grown wires, their resonating modes were not synchronous due to a lack of absolute geometrical symmetry when interacting with incident rays of ultraviolet (UV) light, which widened the energy bandgap. This investigation, although theoretical, guarantees uniformity of cross-section, thickness and orientation by an explicitly parametrized cylindrical interface as demonstrated below, while still observing the effects of the plasmonic threshold of ZnO on THz reflectance through the |S21| magnitude.

For this uniformity in interaction/excitation, a theoretical method of electron-beam nanoimprinting is also suggested [8], where the fabrication of metal-oxide heterojunctions is made fast and efficient. To conceptualize the fabrication method in the context of this study in brief, ZnO mould on Aluminium foil would be compacted in exposition to an ultrasonic laser which demoulds the substrate at high temperatures and leaves behind symmetrical ZnO nanostructures with interspatial nanogaps [8]. One such period of that structure is evaluated for the remainder of the investigation.

2.2. Unit Cell Preconditions and Protocol

Figure 1. shows the geometrical setup for the calculation and post-processing of simulation data for return/insertion loss in dB, dB10 and n-dB10 (depending on conventional |S11| and |Z11| characteristics for low-frequency tailored resonance). After these setups are established, the simulation tool is run on the Ansys High Frequency Structure Simulator (HFSS) Analysis Solution Setup, where the following data is used:

Table 1. Project variables used for Ansys HFSS Simulation of Zinc Nanorod Metamaterial Periodic Oscillator [4,6]. Note that the input values are scalable and arbitrary, and can be optimized according to individual project specifications. poly(3,4-ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS) and poly(3-hexylthiophene):(phenyl-C61-butyric acid methyl ester) (P3HT:PCBM) layers [4,6] have been eliminated due to unavailability of P-type/N-type orientation. Further simulation using the steps provided here is encouraged.

Parameter	Value/Unit	Description
gm	5.75e+13s ^-1	Collision frequency of zinc oxide (ZnO) Drude Model [9]
t_SiO₂	250/nm	Thickness of silicon dioxide/indium tin oxide (SiO ₂/ITO) pillar [4]
ϕ	0/rad	Polarization angle
R	50/nm	Radius of ZnO nanorod
sg	2.22e+5/m ^-1	Conductivity of ZnO [14]
sg₀	3e+5/m^-1	Conductivity of ZnO Drude Model [14]
ϴ	80/deg	Incident angle of light (arbitrary tilt)
wp	2.53e+17	Plasma frequency of ZnO [1]
wp₀	2.94e+17	Plasma frequency of ZnO Drude Model [1]
t_ZnO	450/nm	Thickness of ZnO nanorod [4]
p	166.67/nm	Artificial period of ZnO nanorod

Table 2. Solution Setup for S/Z Parameter Interpolation of Rectangular Waveguide Analysis of ZnO Nanorod Meta-surface.

Input	Data
Frequency Range Function	1.4GHz-10.5THz
Number of passes	25
Adaptive Frequency	Single: 7THz
Maximum ΔS	0.02
Maximum refinement per pass	30% (standard)
Sweep interpolation counts	400 (standard)

An important consideration is the disallowance of radiation boundaries on the ports themselves. The waveguides (Appendix A) are defined as rectangular with gradation pertaining only to 2 primary and secondary modes. The allowance of radiation boundaries on the wave-port would allow for a continuity of transmission to be established across the line into free space, thereby nullifying any reflective effects from the analysis. Hence, it is imperative that since a reflected signal is being measured from the excited electromagnetic wave incident upon the cylindrical surface for S-parameter calculations, a lumped/floquet waveguide is used with the radiation boundary being defined as the region of excitation only. Without this, the |S11| and |S21| parameter plots obtained would not accurately display reflectance parameters at specific pump frequencies.

3. Results and Discussion

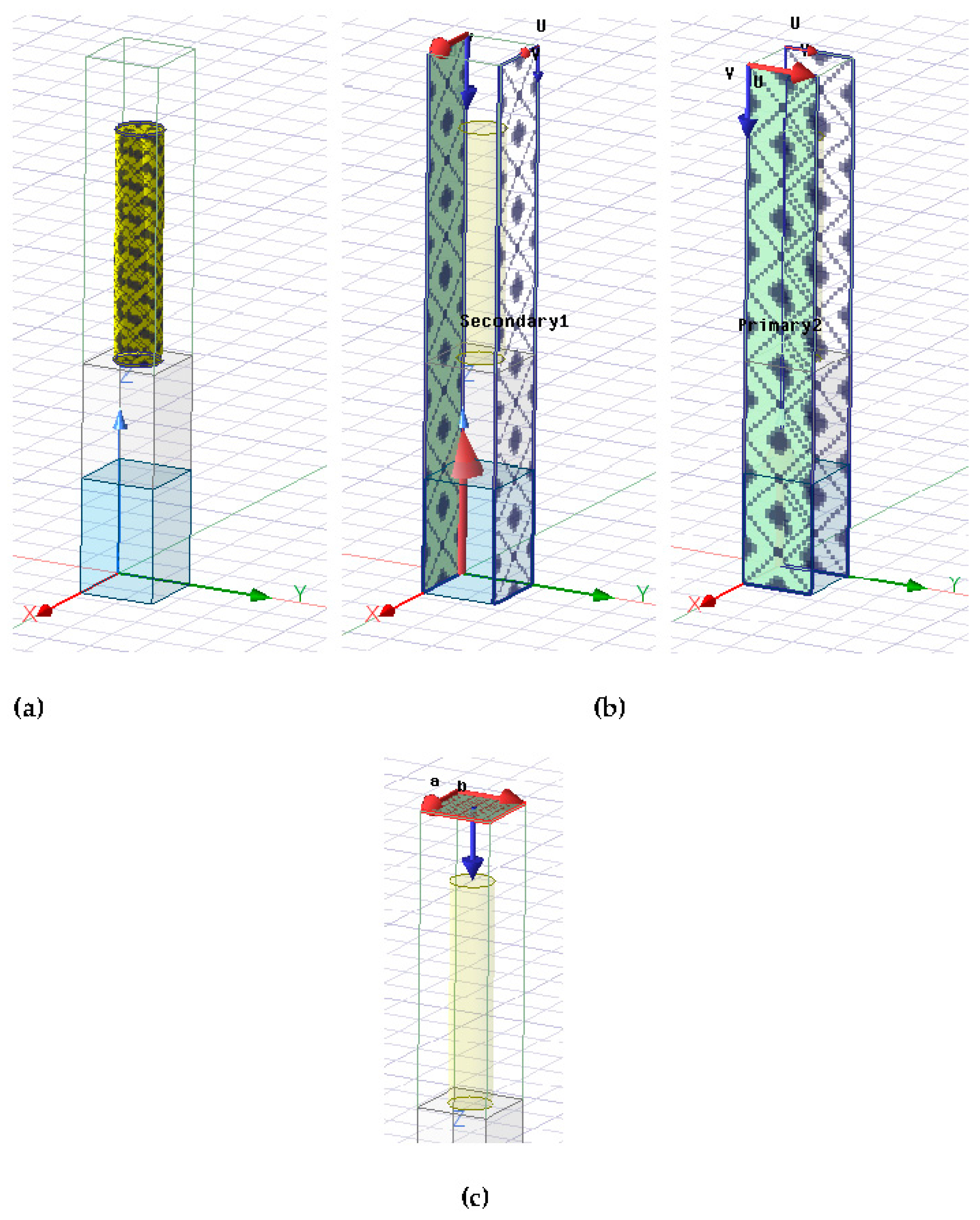
Angularly resolved return loss and normalized impedance values were generated with a three-dimensional geometry of the unit cell, such that the nanorods were parallel (Transverse Magnetic (TM) mode) to the polarized incident light [02.2. Unit Cell Preconditions and Protocol] during interaction with a varying alternating current (AC) signal. The simulation was performed with a parameter sweep, where frequency interpolation happened at a preset limit of 1 convergent pass. The solution data is far from plasmonic behavior and can be judged accurately. 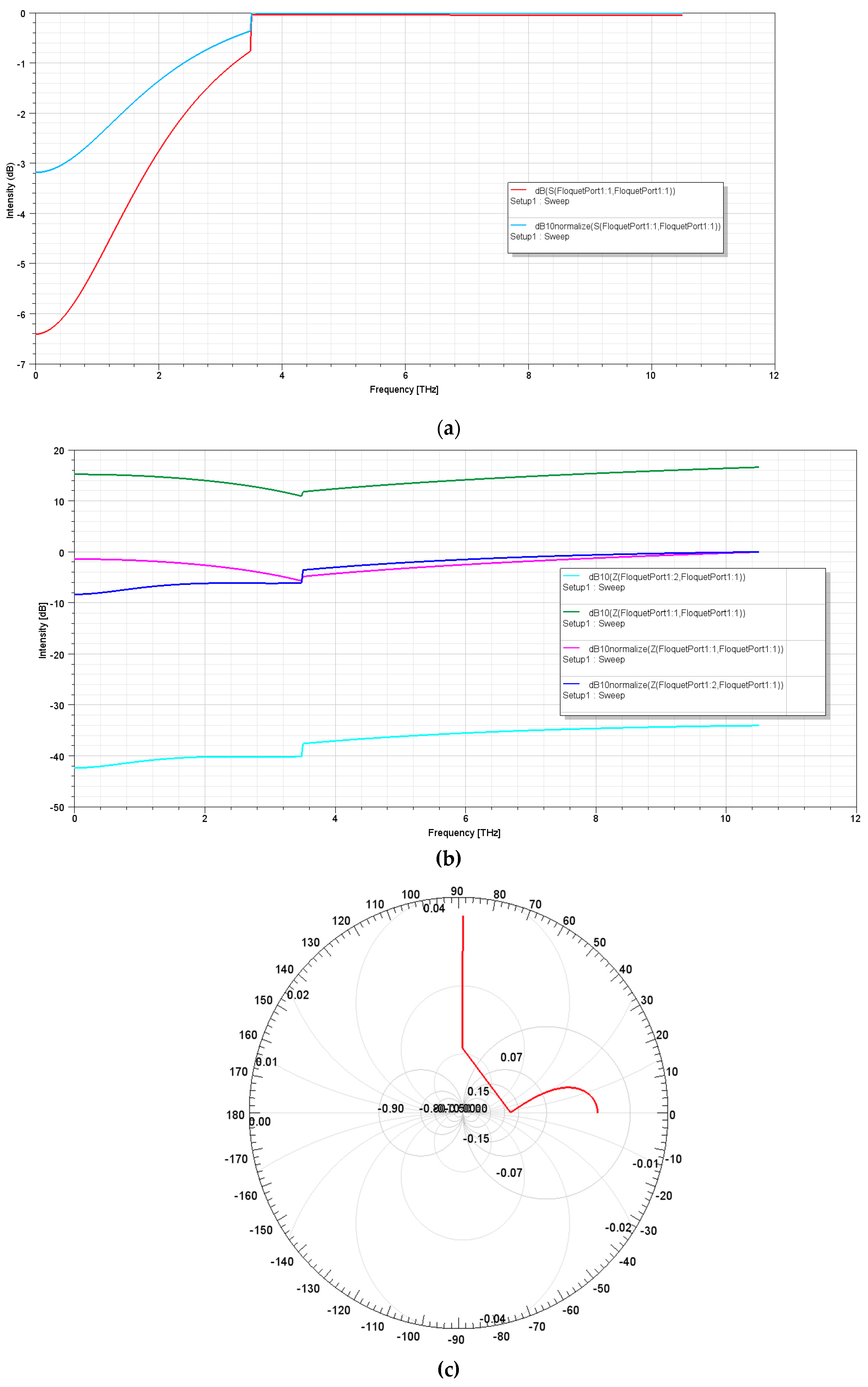Figure 2.(a) has been calibrated to display how much of incident energy has not been reflected back to the source [Reflection Coefficient, Ґ].Figure 2.(a) demonstrates a significant phase shift at approximately 3.55THz for both dB and dB10 normalized scales, minimizing the Return Loss of the unit cell to less than -0.1dB up until near-infrared wavelengths of incident light, implying almost perfect matching of the surface in the middle-to-high THz frequency broadband.

We can see that by Impedance Matching Theory, the same balance between the source and the load is maintained in Z-parameter results; Figure 2.(b) indicates a similar shift in the magnitude-phase factor at 3.55THz. An exact magnitude-phase diagram has not been produced since the interest is in the reflectivity and transmittivity coefficients, but an S-parameter plot between THz frequency and the phase angle of the input and transfer wave-ports can be generated to further analyze the specific locations of the destructive interference. This would help understand the components of complex impedance shown in Figure 2.(c) although not entirely necessary to make informed conclusions about matching in Ґ. At 3.55THz in Figure 2.(b), the Ohmic scaling difference between the input and transfer impedances corresponding to |Z11| and |Z21| (i.e., Z-{Floquetport 1:1} and Z-{Floquetport 1:2}), is shown to be approximately -14.23Ω, corresponding to a magnitude difference of approximately 26.5dB. This shows relatively good impedance matching, and extremely good impedance matching for a normalization of 10Ω, therefore aligning with the principal antireflection observed in Figure 2.(a). The significant difference between |Z11| and |Z21| also shows that for the characteristic impedance demonstrated by the convergence between the pink and blue traces (evidently and correctly normalized at 0dB), significant power transmission from the source to the load is occurring, therefore resulting in high signal integrity and minimized reflection at the source S-{Floquetport 1:1}. Power transfer ideally tends to a maximum (difference < 20Ω). While the achievement of antireflection for a unit cylindrical ZnO surface is a tremendous step further in the evaluations of the reflective and transmissive properties of similar meta-surfaces dealing with THz propagation, significant power dissipation in the near-MW region is observed as shown by the complex (capacitive) impedance value (red trace on the imaginary axis, 90° on Smith Chart) as shown in Figure 2. (c). The location of the central complex maximum corresponds to roughly 40°, indicating an imaginary value of 6.59 Ω in polar form [

\tan δ

]. This is the magnitude of the reactance component that corresponds to the upper threshold for perfect impedance matching, the far left of which is purely imaginary (frequency band of approximately 1.4GHz-500GHz), indicating an extremely high loss tangent at significantly longer incident wavelengths. This can in part be due to the conductive properties exhibited by the nanorod in a low-frequency carrier mode, if not for only dielectric loss, but power transmission is still highly inefficient.

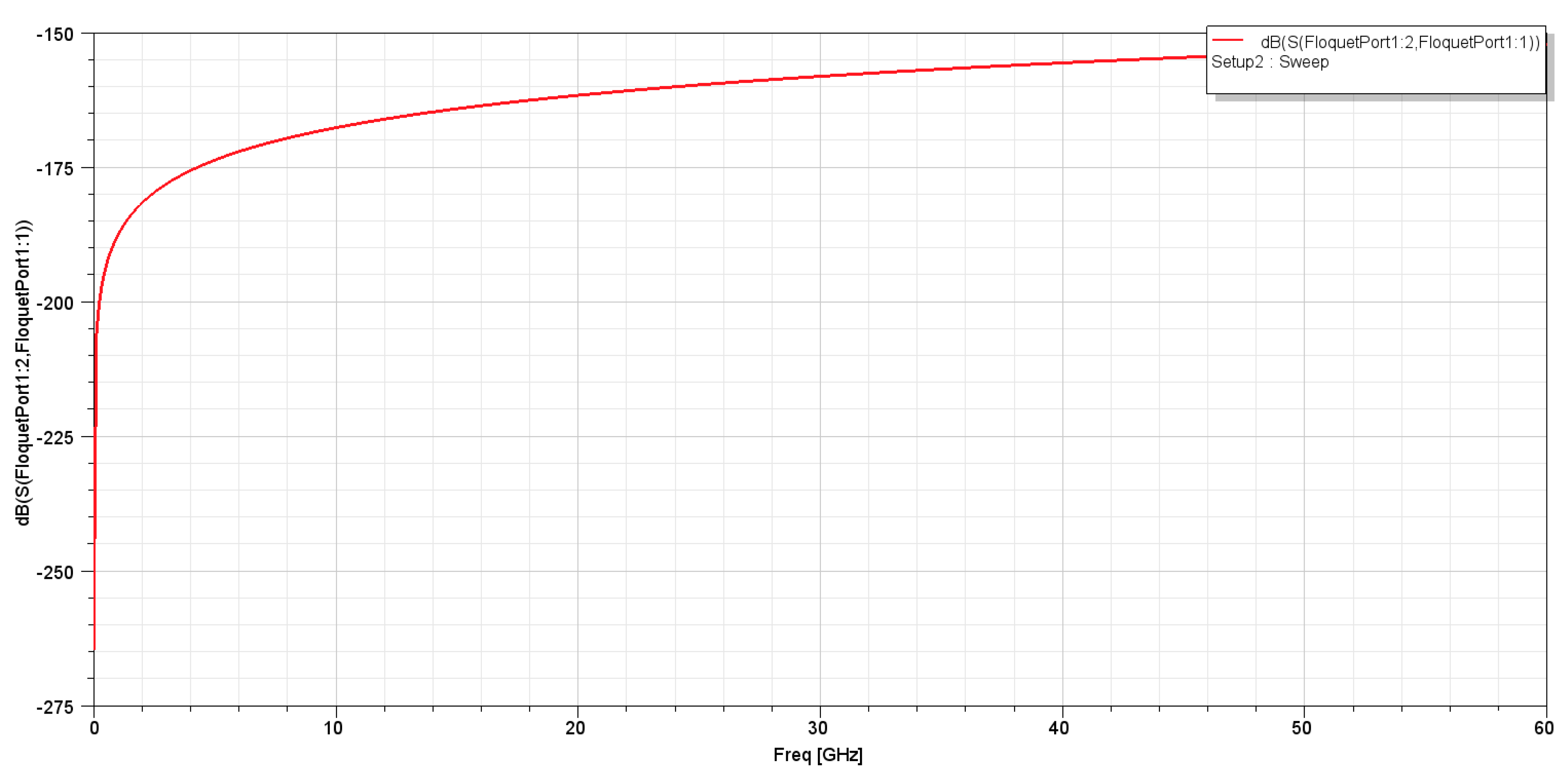
The inferences made about power dissipation suggesting the loss of the cylindrical structure occur after absorption through the excitation of the waveguide, and are further supplemented by Figure 3., which shows an infinitesimal broadband transmission between ports. Across the broader Terahertz region, till 60THz, a second sweep was setup with 50 passes a sweep interpolation count of 501. The effective transmission coefficient of the film is now estimated to be extremely marginal. A transformation to slighter linearity is observed at the phase shift. While this shows all results are coherent, the Insertion Loss value of -175 dB (corresponding to an |S21| transmission coefficient value of 1.63e-9 [Transmission Coefficient, S21]) reflects a highly negative imaginary component of permittivity contributing to the surface’s dissipation factor. The metamaterial’s negative dielectric constant has been successfully achieved simultaneously with high dielectric loss and low real permittivity ε’. 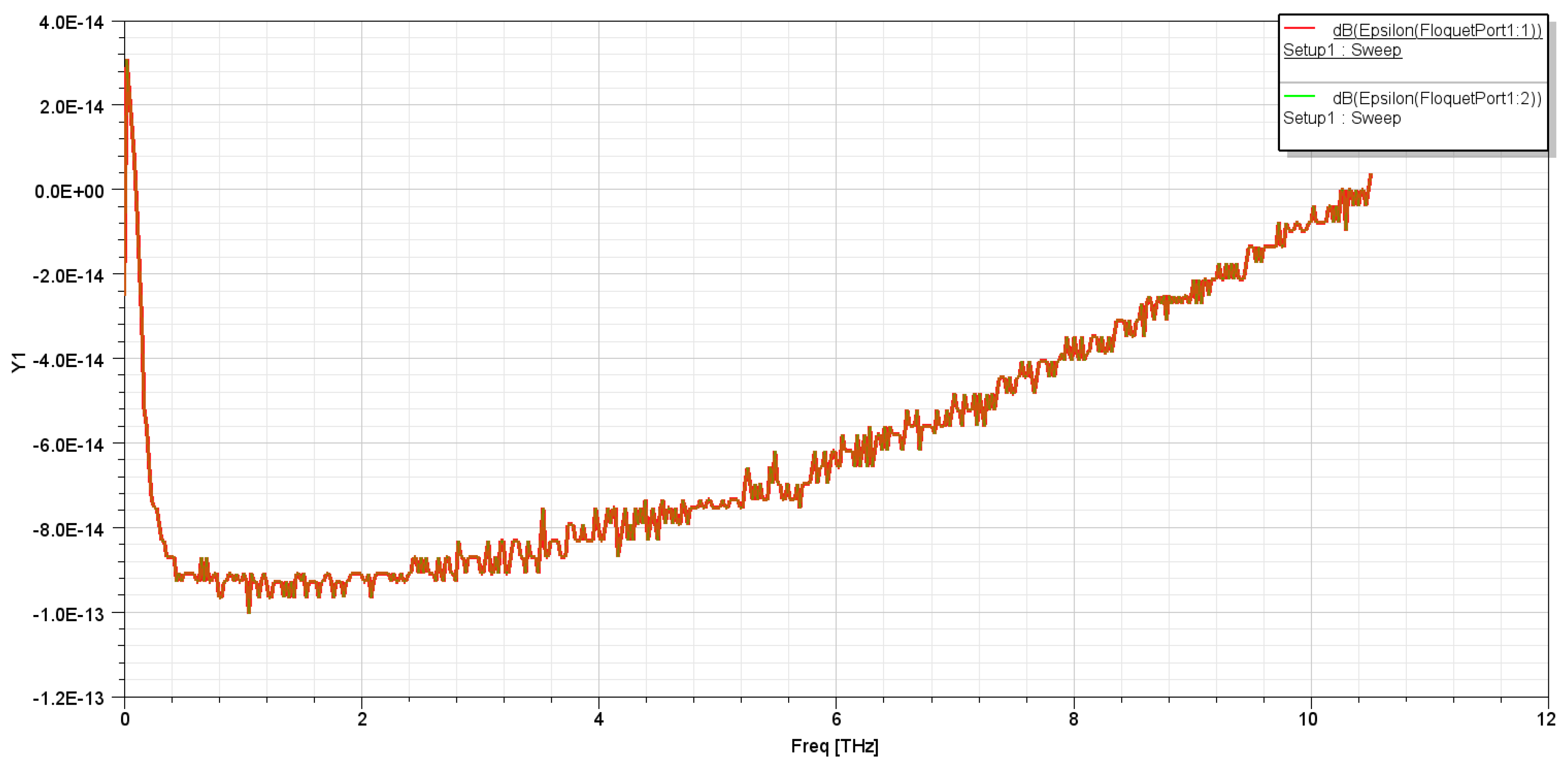Figure 4. shows almost no transmission to the load, with magnitude of -272 F/m at 3.55THz. The Epsilon Chart also demonstrates there is no location, both in terms of frequency and location on the transmission line from Port 1 to 2, where the nanorod is purely non-dissipative, suggesting that the majority of dissipation observed could be due to heat. The axis values in Figure 4. along with the correlation of |ε| to speed suggest the refractive index of the unit cell is very high in magnitude.

Connecting this back to Figure 2.(a), calculating Ґ for a range of frequencies [Reflection Coefficient, Ґ] demonstrates over 50% of reflectance at 400-600GHz, well within the far Terahertz frequency but still distant to the adjusted magnitude of the phase shift in antireflection. Such drastic changes in spite of good real n-impedance of the input port in the MW band might be due to internal reflections rather than a single interface reflection. This could also explain the observation of high reactance, and subsequently, high inefficiency in Figure 2.(c), where impedance matching is achieved at the source, but overall reflectance appears only to be minimized when the impedance matching network is adjusted specifically at 3.55THz. Internal reflectance would imply a unique case with ZnO acting as a conductor, since very high conductance observed in Figure 2. in its entirety is surely a contributory factor, but is most likely due to the geometry of the rod when treating the unit cell as a metamaterial film. That is, high dissipation could stem from the assignment of the “PerfE1” excitation boundary to the ZnO medium (Appendix A) for graded irradiation through the structure’s primary waveguide being a curved surface, but heat loss from the meta-surface instead of storage in the transmission line, thereby explaining the nonlinearity of Figure 3. when tending towards high-frequency limits. Assuming that P-type/N-type heterojunctions had constituted the multilayer as shown in [4], i.e., the external influences of a photovoltaic circumstances were applied to the network, the capacitance shown for the low-THz region in Figure 2.(c) would be partially transmitted through the RF circuit’s capacitive element (which would agree with past literature deliberating ZnO’s electrical properties in RF applications [12,13,15]), which would change the left regions of all figures substantially, but that would revert to conventional semiconduction. It is highly recommended that this computerized simulation is also replicated in a physical setting using aforementioned methods with artificial ZnO nanorods attached to SiO₂ fibres on a photovoltaic cell so see whether the results of Figure 2, Figure 3 and Figure 4 are purely immutable for the THz broadband as well as broader MW and RF applications of the antireflection philosophy.

3.1. Calculation of Relevant Coefficients

Reflection Coefficient, Ґ

Ґ = \frac{S_{11} - S_{21}}{S_{11} + S_{21}} \approx 1 - 10^{\frac{R L}{20}}

(1)

where Return Loss:

R L = - 20 {l o g}_{10} | S_{11} |

(2)

2.: Transmission Coefficient, S21

S_{21} = \frac{2 Z_{21}}{Z_{11} + Z_{22} + Z_{0} - Z_{12} - Z_{21}} = \frac{{V_{t r a n s}}^{+}}{{V_{i n p}}^{+}} \approx 10^{\frac{I L}{20}}

(3)

where Insertion Loss:

I L = - 20 {l o g}_{10} | S_{21} |

(4)

3.: Electrical Permittivity and Dielectric Loss Tangent, ε’ and $\tan δ$

| ε | = \sqrt{{ε'}^{2} + {ε''}^{2}} = - 20 {l o g}_{10} | Y 1 |

(5)

where

ε' = | ε | \cos δ and ε'' = | ε | \sin δ

(6)

δ

is calculated using a phase-angle/THz plot (Appendix B).

Table 3. Sample approximate derivations (equal intervals) of relevant parameter calculations through [Reflection Coefficient, Ґ][Transmission Coefficient, S21][

\tan δ

] for tracing of functions representing return loss, insertion loss source and load impedance, and real/complex permittivity in Figure 2, Figure 3 and Figure 4, with mathematical method taken from in-built simulation system tools in Ansys HFSS1.

Table 3. Sample approximate derivations (equal intervals) of relevant parameter calculations through [Reflection Coefficient, Ґ][Transmission Coefficient, S21][

\tan δ

Frequency/THz	$Ґ$	$\| S_{21} \|$	$ε''$	$\tan δ$
0.5	0.527	3.162e-10	14.543	0.056
1.0	0.438	5.623e-10	24.010	0.092
1.5	0.332	7.498e-10	25.180	0.096
2.0	0.259	9.441e-10	19.992	0.077
2.5	0.206	1.011e-9	14.115	0.054
3.0	0.149	1.334e-9	6.378	0.024
3.5	0.087	1.585e-9	9.116	0.035
3.55	0.014	1.631e-9	21.397	0.082
4.0	~0	1.778e-9	23.735	0.091
4.5	~0	1.799e-9	26.482	0.101

4. Conclusions

In conclusion, a computerized simulation analysis was performed using Ansys HFSS on the antireflective and transmissive properties of a cylindrical ZnO-SiO₂/ITO-Al metamaterial multilayered unit cell with Terahertz broadband specifications, as a prospective extension of the work done with ZnO nanorods for organic solar photovoltaic UV applications [4,6]. The measured S and Z parameters along with insights into dielectric loss and energy storage through an Epsilon chart modelling the dB20-logarithmic real permittivity suggest strong power transmission and extremely accurate impedance matching of the transmission line, but a high power dissipation factor contributing to an |S11| to |S21| dielectric loss. The normalized characteristic impedance in accordance with the sample calculations of

Ґ

and

\tan δ

support the deductions made about a phase shift at 3.55THz, within the defined region of incoming Terahertz radiation, as well as the minimization of return loss shown by Input S-parameter calculations. The capacitance of ZnO was also applied to impedance matching calculations in brief, and evaluated in detail based on signals of high reactance in the MW band, shown by non-resistivity between the specified GHz range. A speculation was made about the origin of internal power discharge being attributed to the artificial geometry of the metamaterial causing internal reflections independent of the transmission of power through the input wave-port, and its preconditions for photoexcitation. A high negative refractive index was demonstrated throughout the frequency band, with supporting sample values for

ε''

Low negative dB in |Z11| suggested low impedance, prospectively useful in matching specific pump load conditions when layered onto a semiconductive substrate, although composed of high reactance attributing to the high conductance of the film. Simultaneously, an evaluation of |S21| showed highly negative dB values for insertion loss indicating poor transmission efficiency.

\tan δ

data suggests phase angle being a significant contributor to parameter fluctuations, once again possibly due to the surface orientation given that it is not organic and therefore its oscillations are uniform about a non-uniform excitation boundary. The nanorod’s cylindrical structure seems to prove better results for return loss and can be considered for future low-frequency and high-power applications. Although unlikely, degradation beyond the plasmonic mode can warrant some form of high-temperature annealing to test for geometrical defects. However, some specific modifications are necessary for exploration since heat transmission has been demonstrated to significantly disaffect the efficiency of the film, which in the past has been mitigated by 2-dimensional radiation patches perpendicular to polarized light. These risks can be further investigated with the protocols provided.

Since the magnitudes and dielectric loss tangent values are calculated from metamaterial excitation boundaries alone (due to the elimination of P3HT:PCBM and PEDOT:PSS layers), results from this study can be extended in direct Radio-frequency (RF) applications to further understand ZnO’s conductive capacities as its own field, as moderate energy losses require some form of conductive use and the results are fairly acceptable for lower frequency bands such as the experimental broadband of 0.0014-10.5THz. The results overall show that for high-frequency applications like photovoltaics, such a structure is far from optimal and would likely contribute to intolerable energy efficiency or lack thereof, although further simulation in comparison to the past study on organic solar cells is encouraged.

Funding

This research paper received no external funding at the time of writing.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Acknowledgments

I acknowledge the guidance in interpretation of Ansys HFSS simulation results and sourcing of literature from Mr. Kaushal Tiwary, Indian Institute of Science (IISc), Department of Materials Engineering and the preliminary support and mentorship in the initial stages of project-work by Mr. Damian Matheson, Program Director, The Knowledge Society (TKS). Acknowledgments to the Schmidt Trust and Rhodes Future for allowing me to present earlier stages of my research work at the RISE Global Challenge Finalist Round.

Conflicts of Interest

The author declares no conflicts of interest.

Appendix A. Setup of Excitation Boundaries and Wave Ports

Figure 5. Setup of excitation boundaries for predefined network analyzer region; (a) PerfE1 activation boundary for cylindrical ZnO nanorod; (b) Primary and secondary vectors for excitation boundary of prism region, defined by areal dimensions of SiO2/ITO-Al substrate and ground; (c) Rectangular wave-port {Floquet1:1} defined by vectors parallel to polarization in TM mode, with a de-embed value of 166.67nm such that Δd=p. .

Appendix B. Setup of S-Parameter Results (Phase Angle in Degrees)

Figure 6. Function boxes with specification of entries for generation of a phase angle plot for implicit correlations between magnitude and phase. Project variables being parametrized to be specified in “Output Variables”, and Range Function to be altered according to the discretion or specific requirements of the program. Calculations in-built. .

References

Saha, S. , Dutta, A., Devault, C., Diroll, B. T., Schaller, R. D., Kudyshev, Z., Xu, X., Kildishev, A., Shalaev, V. M., & Boltasseva, A. (n.d.). Extraordinarily Large Permittivity Modulation in Zinc Oxide for Dynamic Nanophotonics.
Student, M. (2010). Absorption in Metamaterials: Turning Loss into Gain.
Fathabadi, H. (2018). Impact of high-voltage power transmission lines on photovoltaic power production. Solar Energy, 163, 78–83. [CrossRef]
Hiralal, P., Chien, C., Lal, N. N., Abeygunasekara, W., Kumar, A., Butt, H., Zhou, H., Unalan, H. E., Baumberg, J. J., & Amaratunga, G. A. J. (2014a). Nanowire-based multifunctional antireflection coatings for solar cells. Nanoscale, 6(23), 14555–14562. [CrossRef]
Abdulazhanov, S., Le, Q. H., Huynh, D. K., Wang, D., Lederer, M., Olivo, R., Mertens, K., Emara, J., Kämpfe, T., & Gerlach, G. (2021). RF-characterization of HZO thin film varactors. Crystals, 11(8). [CrossRef]
Hiralal, P., Chien, C., Lal, N. N., Abeygunasekara, W., Kumar, A., Butt, H., Zhou, H., Unalan, H. E., Baumberg, J. J., & Amaratunga, G. A. J. (2014b). Nanowire-based Multifunctional Antireflection coatings for Solar cells, Supplementary Material.
Li, M. , Shen, H., Zhuang, L., Chen, D., & Liang, X. (2014). SiO2antireflection coatings fabricated by electron-beam evaporation for black monocrystalline silicon solar cells. International Journal of Photoenergy, 2014. [CrossRef]
Ge, J. , Ding, B., Hou, S., Luo, M., Nam, D., Duan, H., Gao, H., Lam, Y. C., & Li, H. (2021). Rapid fabrication of complex nanostructures using room-temperature ultrasonic nanoimprinting. Nature Communications, 12. [CrossRef]
Wu, G. , Jiao, X., Wang, Y., Zhao, Z., Wang, Y., & Liu, J. (2021). Ultra-wideband tunable metamaterial perfect absorber based on vanadium dioxide. Optics Express, 29, 2703. [CrossRef]
Zheng, Y. J. , Gao, J., Zhou, Y. L., Cao, X. Y., Xu, L. M., Li, S. J., & Yang, H. H. (2017). Metamaterial-based patch antenna with wideband RCS reduction and gain enhancement using improved loading method. IET Microwaves, Antennas and Propagation, 11, 1183–1189. [CrossRef]
Plikusiene, I. , Maciulis, V., Graniel, O., Bechelany, M., Balevicius, S., Vertelis, V., Balevicius, Z., Popov, A., Ramanavicius, A., & Ramanaviciene, A. (2021). Total internal reflection ellipsometry for kinetics-based assessment of bovine serum albumin immobilization on ZnO nanowires. Journal of Materials Chemistry C, 9, 1345–1352. [CrossRef]
Koch, A. , Mei, H., Rensberg, J., Hafermann, M., Salman, J., Wan, C., Wambold, R., Blaschke, D., Schmidt, H., Salfeld, J., Geburt, S., Kats, M. A., & Ronning, C. (2023). Heavily Doped Zinc Oxide with Plasma Frequencies in the Telecommunication Wavelength Range. Advanced Photonics Research, 4. [CrossRef]
Prepelita, P. , Medianu, R., Garoi, F., Stefan, N., & Iacomi, F. (2010). On the structural and electrical characteristics of zinc oxide thin films. Thin Solid Films 518, 4615–4618. [CrossRef]
Ondo-Ndong, R. , Essone-Obame, H., & Koumba, N. (2017). Electrical performance of zinc oxide thin films transistors. Journal of Nano- and Electronic Physics, 9. [CrossRef]
Ondo-Ndong, R. , Essone-Obame, H., Moussambi, Z. H., & Koumba, N. (2018). Capacitive properties of zinc oxide thin films by radiofrequency magnetron sputtering. Journal of Theoretical and Applied Physics 12(4), 309–317. [CrossRef]
Smith, L. (n.d.). STARS STARS Electronic Theses and Dissertations 2007 Surface Characterization Of Thin Film Zno Capacitors By Surface Characterization Of Thin Film Zno Capacitors By Capacitance-voltage Measurements Capacitance-voltage Measurements. http://library.ucf.edu.

For a more precise interval than this sample, Ansys HFSS Solution Data under Results Modification for Rectangular Plots (S/Z-Parameter) – Report All Frequencies. This is a protocol by which primary data has been generated for the study, and no repositories other than those cited have been used for the above sample calculations.

Figure 1. (left). Simplified schematic representation of cylindrical periodic meta-surface [4,6] in unit cell boundary configurations consisting of a zinc nanorod whose dimensions are approximated to that of a cylindrical wire, layered over SiO₂/ITO dielectric nanopillar and Al substrate.

Figure 2. Frequency (THz) against Magnitude (dB) plots demonstrating characteristic parameters of ZnO-SiO2/ITO-Al nanorod meta-surface over a THz broadband of 1.4GHz-10.5THz; (a) Modelling the return loss and return loss normalized to 10Ω of the |S11| port to indicate the trendline for reflectance in a linear electrical network; (b) Modelling input |Z11| and transfer |Z21| impedance of the to indicate locations of impedance matching and/or gross impedance buildup; (c) Modelling real (resistance) and imaginary (inductance/capacitance) components of impedance when characteristics of the output port are terminated on a Smith Chart.

Figure 3. THz frequency against magnitude in dB modeling insertion loss S-Parameter |S21| showing behavior of the unit cell transmission line over Infrared-Terahertz broadband region.

Figure 4. Application of radiation boundaries on {Floquetport 1:1} modeling freely photoexcitation response of the unit cell in terms of electrical permittivity ε’ in the experimental THz broadband using an Epsilon Chart of THz Frequency against ε’ (logarithmic Y1).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ansys HFSS Evaluation of Periodic ZnO Nanorod Metamaterial Unit Cell for Terahertz Broadband Antireflection Coatings

Abstract

1. Introduction

2. Materials and Methods

2.1. ZnO: Conductive/Reflective Performance, Meta-Surface Properties

2.2. Unit Cell Preconditions and Protocol

3. Results and Discussion

3.1. Calculation of Relevant Coefficients

4. Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Setup of Excitation Boundaries and Wave Ports

Appendix B. Setup of S-Parameter Results (Phase Angle in Degrees)

References

MDPI Initiatives

Important Links

Subscribe