Prerpints.org logo
Preprint
Article

Quantification of Methane Hydration Energy Through Free Energy Perturbation Method

Altmetrics

Downloads

124

Views

79

Comments

0

This version is not peer-reviewed

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
This study presents a comprehensive approach to calculating the free energy of hydration of methane using Molecular Dynamics simulations. We employed the Free Energy Perturbation (FEP) method to determine the Gibbs free energy associated with transferring a methane molecule into water. Simulations were conducted in a cubic simulation box containing one methane molecule and 1000 TIP4P water molecules. The forward and backward routes were both analyzed, providing consistent free energy differences, which validates the robustness of our methodology. The Gibbs free energy profiles demonstrated characteristic energy barriers and stabilization points, indicative of the interaction dynamics in the solvation process. The results demonstrate the robustness of the FEP method implemented in LAMMPS, yielding free energy in close agreement with experimental data and previous computational studies. The calculated free energy differences for methane hydration exhibited deviations of 13% and 8% for the forward and backward routes, respectively, compared to experimental values. These findings underscore the accuracy and efficiency of using LAMMPS for free energy calculations, contributing to the broader understanding of solvation thermodynamics. Additionally, radial distribution functions were analyzed to provide insights into the structural arrangement of water molecules around methane, revealing strong interaction between methane's carbon atom and water molecules.
Keywords: 
Subject: Chemistry and Materials Science  -   Analytical Chemistry

1. Introduction

Computational modeling and simulation serve as valuable complements to experimental studies of energetic materials [1,2,3,4,5,6]. Atomistic simulations can accurately determine many key material properties, helping guide or supplement laboratory work. This approach can significantly reduce the scope of investigations, lowering financial costs and minimizing physical risks. To ensure thermodynamic rigor and relevance to experimental conditions, it is crucial that an atomistic model is fully characterized within its intended application range [3,7,8,9,10,11,12].
In the context of free energy, calculations of hydration play a significant role in understanding various chemical and biochemical processes, such as solubility, solvent effects on equilibrium and reaction rates, and partition coefficients. The transfer of a solute from the gas phase to a solvent, characterized by the free energy of hydration, is a fundamental thermodynamic quantity. This calculation involves determining the difference in Gibbs free energy between the solute in the gas phase and in the solution phase at a given temperature and pressure [13,14,15,16].
Statistical perturbation theory and thermodynamic integration are the predominant computational methods used for these calculations [17,18]. Statistical perturbation theory, in particular, has shown high precision for computing the hydration free energies of small organic molecules. This method involves gradually changing the interaction parameters of a solute in a solvent and calculating the corresponding free energy changes. Despite the method's precision, it has traditionally been used for relative free energy calculations rather than absolute free energies, except in a few cases such as noble gases and small molecules like methane [19,20].
Molecular dynamics (MD) simulations provide a powerful tool for studying the microscopic details of solvation processes. Among various MD simulation packages, LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) is widely used due to its flexibility and efficiency in simulating large systems. However, LAMMPS does not have built-in functions for performing free energy calculations directly. This limitation can be addressed using the Free Energy Perturbation (FEP) method, which involves the calculating the free energy difference associated with this process [21,22].
In the context of methane hydration, FEP can be utilized to compute the free energy difference when a methane molecule is transferred from the gas phase into water. This process involves simulating the methane molecule and calculating the interactions with the surrounding water molecules. William et al. calculated the free energies of hydration of methane using FEP via Monte Carlo simulations with the BOSS program, achieving results that were in good agreement with experimental data [23]. Subsequently, Shirts et al. employed the Bennett acceptance ratio method using GROMACS, which provided an improved free energy of hydration for methane, yielding results that closely matched experimental values [24]. In this study, we aim to calculate this free energy using FEP through LAMMPS to compare its effectiveness with the previous studies.
By implementing a procedure to perform these calculations in LAMMPS, we seek to provide accurate and efficient results comparable to those obtained with other MD simulation packages. This work not only demonstrates the application of FEP in LAMMPS but also contributes to the broader understanding of solvation thermodynamics in molecular simulations. The second section offers a detailed exposition of the initial force field models, molecular dynamic setup, and the FEP method. Section 3 explores our findings, highlighting the results have been presented for the absolute free energies of hydration for methane, using the TIP4P model of water. This approach has allowed for a detailed analysis of both methodological issues and the accuracy of the intermolecular potential functions used, and finally, Section 4 summarizes our finding.

2. Materials and Methods

Here's a well-organized methods section for calculating the free energy of methane in water using the Free Energy Perturbation method in LAMMPS. This section incorporates insights from the provided articles and the LAMMPS documentation [21,25].
A key aspect of free energy calculations involves the perturbation of interaction parameters and the recalculation of the pair potential energy without changing the atomic coordinates from unperturbed system. This approach can be used to calculate free energy differences. The potential energy of the system includes three terms: the background term Ubkg (interaction sites whose parameters remain constant), the reference term Uref (initial interactions of the atoms that will undergoes perturbation), and the term Upert corresponding to the final interactions of these atoms. A coupling parameter λ varying between 0 and 1 connects the reference and perturbed systems is shown as below:
U λ = U b k g + U r e f λ + U p e r t λ
In order to perform a free energy calculation, we need to define the end states. For solvation free energy calculations, one end state is the isolated molecule in the gas phase along with the solution phase in the background. The other end state is the solvated molecule in the solution phase. In the first state, the atoms of the isolated molecule interact only with each other and are decoupled from the surrounding environment. In the final state, the atoms of the molecule interact with all the atoms present in the system, including the solvent and other dissolved solutes, making it the coupled state. Two common paths are that “Forward” route (involves deleting methane from water) and the “Backward” route (involves introducing methane into water), in which interactions of sites that are being created or deleted are treated using Lennard-Jones and Coulomb potentials with soft cores [26].
To compute the total free energy difference, we sum the free energy differences between successive states along the chosen route. The free energy difference along each path is determined by computing the free energy change of turning on the Lennard-Jones (LJ) and Coulomb potentials interactions between the solute and the solution. The numerical estimation of the free energy difference between two states i and f, characterized, can be obtained using the Zwanzig formula as below:
∆ G i → f   = − k B T   ∑ j = 0 j = n − 1 ln ⁡ < exp ⁡ ( − U λ j + 1 − U λ j k B T ) >
where T is the ambient temperature, kB is the Boltzmann constant and < denotes an ensemble average by the microstates of the starting state i [17,27,28,29,30,31]. The total free energy difference is obtained by summing the individual free energy differences, which directly correlates with experimentally measurable values. To avoid singularities during free energy calculations, a soft repulsive core is used. When the parameter λ tends to 0, the pair interaction vanishes while maintaining this soft repulsive core. As λ approaches 1, the pair interaction transitions to the normal, non-softened potential [26]. Lennard-Jones and Coulomb potentials modified by a soft core as below:
U L J r , λ = λ 4 ε   1 ( 0.5 [ Å 2 ] ) 1 − λ 2 + r σ 6 2 − 1 0.5 1 − λ 2 + r σ 6    
U c o u l r , λ = λ κ q i q j ( 10 [ Å 2 ] ) ( 1 − λ ) 2 + r 2 1 / 2
where, r is the distance between two atoms, κ = N A / 4 π ε , and q is the charge of particle.
We perform hydration free energy calculations using the procedure laid out in the previous sections. A cubic simulation box with periodic boundary conditions was created by fftool, containing one methane molecule was solvated in 1000 TIP4P water molecules [32,33,34]. Lennard-Jones parameters and partial charges for methane and water were assigned according to standard OPLS-AA and TIP4P values. Interactions of sites that are being created or deleted are handled using Lennard-Jones and Coulomb potentials with soft cores to avoid singularities. The initial configuration was energy minimized to remove any bad contacts using the conjugate gradient algorithm. We used a time step of 1.0 fs. Bonds involving hydrogen atoms were constrained using the SHAKE algorithm. Nonbonded interactions were cut off at 1 nm, with long-range electrostatics managed by Particle-Particle-Particle-Mesh (PPPM) summation method. The NPT ensemble was simulated using the Nose–Hoover thermostat and barostat at a temperature of 298.15 K and a pressure of 1.0 atm. - Equilibration ensured the system reached a stable density and temperature, which are prerequisites for accurate free energy calculations. All systems were equilibrated for 4 ns followed by 10 ns data collection period. Furthermore, ∆λ choose 0.1, and the fix adapt/fep command is used to dynamically adjust simulation parameters (such as pair coefficients and atomic charges) over the course of the simulation according to the value of λ. This allows for a smooth transition between states (e.g., from non-interacting to fully interacting states). The simulations were run on a high-performance cluster (HPC) with LAMMPS as parallel tasks on 128 CPUs.

3. Results and Discussion

In this section, we present the results of the free energy calculations for the hydration of methane using the FEP method with LAMMPS. The simulations were carried out as described in the previous section, and the following results were obtained.
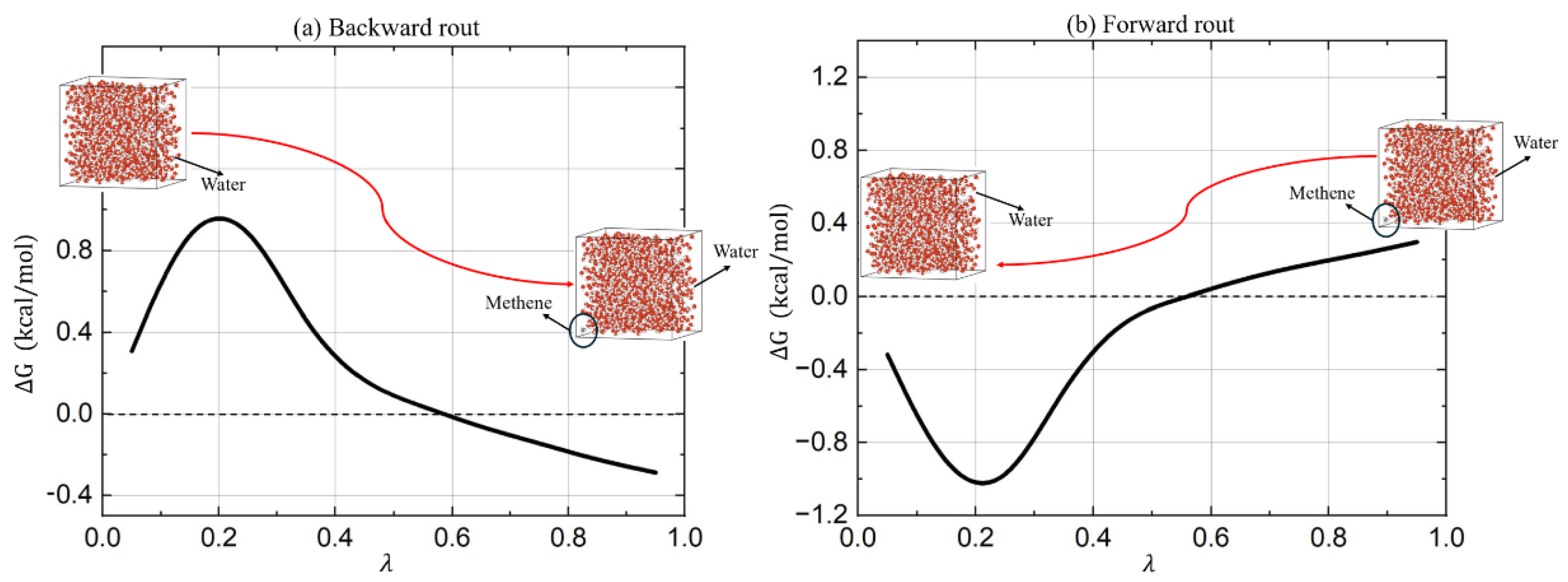
Both the forward and backward routes were tested, and the results were compared. The free energy differences obtained from both pathways were consistent, demonstrating that the methodology is robust and independent of the chosen path. The free energy difference associated with the hydration of methane was calculated by gradually varying the coupling parameter λ from 0 to 1 (backward) or from 1 to 0 (forward). Figure 1 shows the Gibbs free energy (Zwanzig equation) difference with respect to the coupling parameter λ for both processes. For the x-axis, we chose the midpoint between λi and λi+1. The smooth transition between states indicates that the FEP method was successfully implemented due to the use of soft-core potentials. In Figure 1 (a), the red arrow shows the simulation direction from λ = 0 to 1, while in Figure 1(b), it shows the direction from λ = 1 to 0.
In the backward route simulation (Figure 1 (a)), the Gibbs free energy starts from a small value, approximately 0.2, when λ change from 0 to 0.1. As λ increases, ∆ G initially rises, reaching a peak at λ ≅ 0.2. This indicates a significant energy barrier in the initial stages of coupling the methane molecule to the solvent environment. Following the peak, ∆G gradually decreases, stabilizing around λ of 0.6. This suggests that once the initial interactions are established, the system stabilizes, and the energy required for further coupling decreases. From λ of 0.6 to 1.0, the ∆G varies relatively slow, indicating that the system has reached a near-equilibrium state where additional interactions contribute minimally to the overall free energy change.
In the forward route simulation (Figure 1 (b)), the process starts at λ = 1, where the methane molecule is fully coupled with the solvent. As λ decreases, ∆G further drops, reaching a minimum at λ ≅ 0.22. This suggests that the energy cost for decoupling the methane molecule is highest at this stage of the process. Beyond λ of 0.2, ∆G begins to rise, indicating that the system starts to regain some of the energy as the interactions between the methane molecule and the solvent decrease, by λ = 0, the free energy returns close to zero, indicating the decoupled state.
Both forward and backward processes display characteristic energy profiles that reflect the stability and interaction dynamics of the methane solvation process. The backward route shows an initial energy barrier, followed by stabilization, while the forward route shows an initial stabilization followed by a decrease in energy as the solvation interactions are removed.
The total free energy was compared with experimental data and previous computational studies to validate the accuracy of our simulations. Table 1 compares the total Gibbs free energy (ΔG) for the hydration of methane obtained from various methods. This study, using FEP in LAMMPS, reports ΔGForward of -2.218 kcal/mol with a 13% deviation and ΔGBackward of 2.132 kcal/mol with an 8% deviation from experimental values. Previous studies using BAR in GROMACS [24] and FEP-MC [23] (Monte Carlo simulations were carried out with the BOSS program) reported ΔGBackward of 2.27 kcal/mol with a 15% deviation and 2.90 kcal/mol with a 48% deviation, respectively, while FEP-MC also reported ΔGForward of -2.08 kcal/mol with a 6% deviation. However, in principle, the forward and backward free energy values should be equal in magnitude but have opposite signs. The experimental values for ΔG reported a value of ± 2.005 [35] and ± 1.912 [36] kcal/mol. For comparison with computational values, we have used the average value of ± 1.9585 kcal/mol. This study's results agree to the experimental values and also the previous computational studies, especially in the backward route, indicating higher accuracy and reliability of the FEP calculations performed in LAMMPS. The observed ∆G for both routes demonstrates the hysteresis effect commonly seen in such free energy perturbation calculations, indicating that the paths are not perfectly reversible, likely due to system equilibration differences. However, compared to the previous study using the FEP-MC method, which reported a significant difference of approximately 0.82 kcal/mol between the forward and backward routes, our results demonstrate a notable improvement, with a much smaller difference of only about 0.086 kcal/mol.
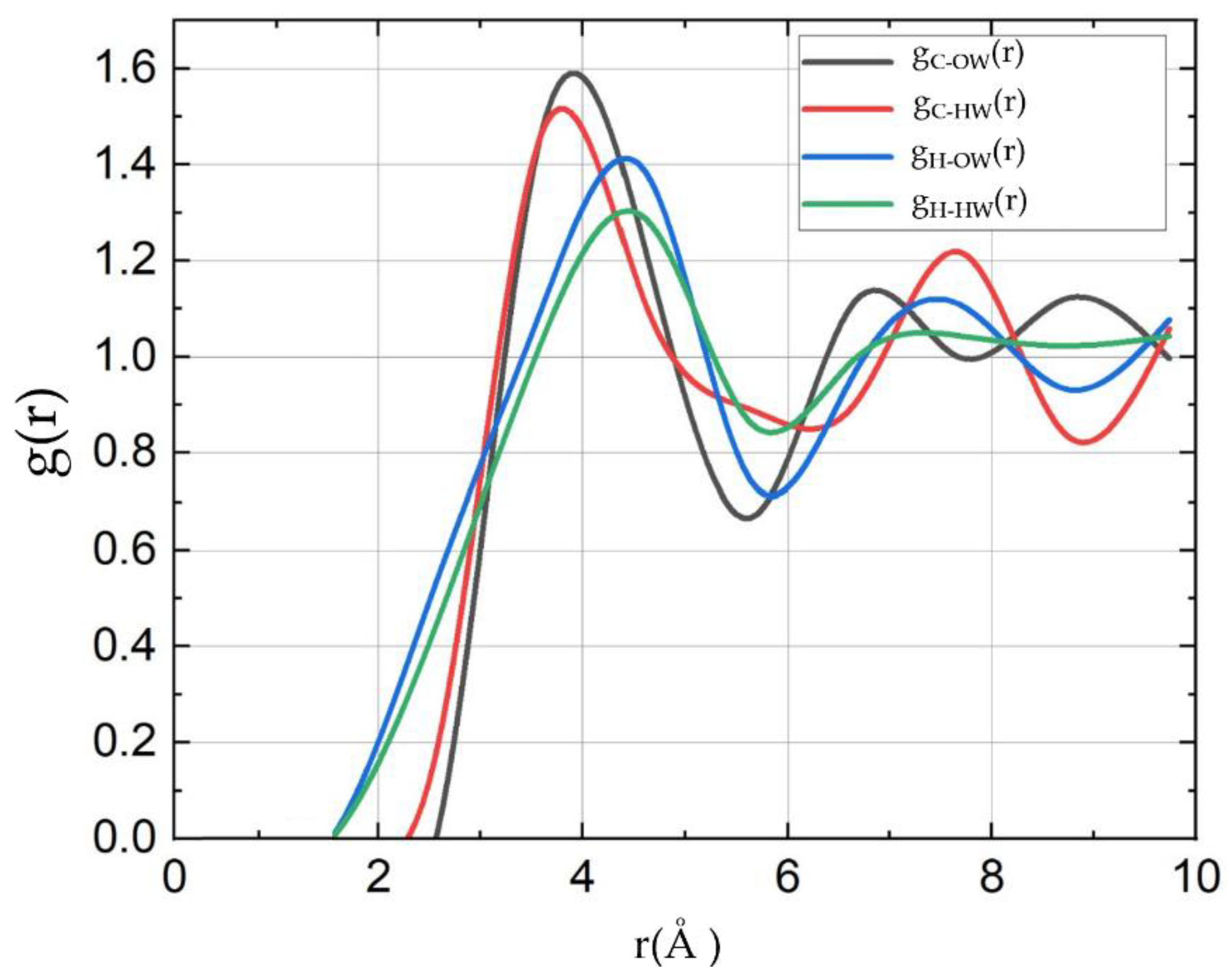
Radial distribution functions (RDFs) provide insights into the structural arrangement of molecules around a central molecule. The Figure 2 represents the RDFs for Carbon-Oxygen of water (C-Ow), Carbon-Hydrogen of water (C-HW), Hydrogen of methane-Oxygen of water (H-OW), and Hydrogen of methane-Hydrogen of water (H-HW) interactions in a methane-water system. The gC-OW(r) and gC-HW(r) RDFs both exhibit a prominent first peak at around 3.5 Å, indicating strong interactions between the carbon atom of methane and the oxygen atoms of water, as well as the hydrogen atoms of water. These peaks suggest the formation of a well-defined first hydration shell around the carbon atom, with the peak heights indicating almost equal interaction strengths for these pairs. In contrast, the gH-OW(r) and gH-HW(r) show their first peaks at around 4.7 Å. This shift to a larger distance for the first peak suggests weaker interactions between the hydrogen atoms of methane and the surrounding water molecules, both with the oxygen and the hydrogen atoms of water. The relative heights of these peaks indicate that while these interactions are significant, they are less pronounced compared to those involving the carbon atom of methane. The differences in peak positions and heights across the RDFs highlight the varying interaction strengths and spatial arrangements within the methane-water system. The closer peaks for C-Ow and C-HW reflect stronger and more immediate interactions, forming a tighter hydration shell around the carbon atom, whereas the more distant peaks for H-OW and H-HW indicate a more diffuse and less structured interaction landscape for the hydrogen atoms of methane. This structured arrangement around methane is crucial for understanding the solvation dynamics and the energetics of methane in aqueous environments. These results in agreement with previous study [37].

4. Conclusions and Future Works

We have calculated the free energy of hydration for methane using the Free Energy Perturbation method within the LAMMPS molecular dynamics simulation framework. We were able to quantify the free energy changes associated with the solvation process, providing valuable insights into the thermodynamic behavior of methane in aqueous environments. Our simulations were meticulously designed, using the TIP4P water model and Lennard-Jones and Coulomb potentials with soft cores, to ensure accurate and stable results. The consistency observed between the forward and backward free energy calculations highlights the robustness and reliability of our methodological approach. The results demonstrated good agreement with experimental data and previous computational studies, particularly in the backward route, which highlights the accuracy of the FEP calculations performed. The total Gibbs free energy difference for methane hydration of -2.218 kcal/mol (forward) and 2.132 kcal/mol (backward), with deviations of 13% and 8% from experimental values, respectively. These results were consistent with experimental values and previous computational studies. Our study highlighted the robustness and accuracy of the FEP method, particularly in the backward route, where our results showed only an 8% deviation from experimental values. Radial distribution functions revealed distinct structural arrangements in the methane-water system. Strong interactions were observed between the carbon atom of methane and both oxygen and hydrogen atoms of water, with prominent peaks at 3.5 Å, indicating a well-defined hydration shell. In contrast, interactions involving the hydrogen atoms of methane displayed peaks at around 4.7 Å, reflecting weaker interactions and a more diffuse hydration structure. These findings highlight the varying interaction strengths and spatial arrangements, consistent with previous studies, providing key insights into the solvation dynamics of methane in water.
Our findings emphasize the importance of detailed methodological setups and parameter optimization in molecular simulations, which are critical for obtaining reliable and reproducible results. This work not only validates the use of FEP in LAMMPS for free energy calculations but also enhances our understanding of solvation thermodynamics. Future studies could extend this approach to other solute-solvent systems, further exploring the capabilities and limitations of FEP and other free energy calculation methods in molecular dynamics simulations.

Author Contributions

Conceptualization, methodology, data preparation and cleaning, statistical analysis, writing, and original draft preparation, F.H.; Statistical analysis, review and editing, visualization, and project administration, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The code and data generated during the current study are accessible upon reasonable request from the corresponding request. Requests should be directed to mmoradi2@meei.harvard.edu.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Moradi, M.; Chen, Y. Monte Carlo simulation of diffuse optical spectroscopy for 3D modeling of dental tissues. Sensors 2023, 23, 5118. [Google Scholar] [CrossRef] [PubMed]
  2. Moradi, M.; Vasudevan, S.; Bhusal, A.; Weininger, S.; Chen, Y.; Pfefer, J. Modeling light-tissue interactions in pulse oximetry: effect of device design and skin pigmentation. In Proceedings of the Design and Quality for Biomedical Technologies XVII, St. Bellingham, WA, USA; 2024; p. 1283302. [Google Scholar]
  3. Hatami, F.; Moradi, M. Comparative Analysis of Machine Learning Models for Predicting Viscosity in Tri-n-Butyl Phosphate Mixtures Using Experimental Data. Computation 2024, 12, 133. [Google Scholar] [CrossRef]
  4. Hatami, F.; Moradi, M. Comparison of Different Machine Learning Approaches to Predict Viscosity of Tri-n-Butyl Phosphate Mixtures Using Experimental Data. arXiv 2023, arXiv:2311.02522. [Google Scholar]
  5. Moradi, M.; Eslami, M.; Hashemabad, S.K.; Friedman, D.S.; Boland, M.V.; Wang, M.; Elze, T.; Zebardast, N. PyGlaucoMetrics: An Open-Source Multi-Criteria Glaucoma Defect Evaluation. Investigative Ophthalmology & Visual Science 2024, 65, OD38–OD38. [Google Scholar]
  6. Hatami, F. Energy Spectrum of Primary Knock-on Atoms and Atomic Displacement Calculations in Metallic Alloys Under Neutron Irradiation. arXiv 2024, arXiv:2406.08438. [Google Scholar]
  7. Chipot, C.; Pearlman, D.A. Free energy calculations. The long and winding gilded road. Molecular Simulation 2002, 28, 1–12. [Google Scholar] [CrossRef]
  8. Cieplak, P.; Kollman, P.A. Calculation of the free energy of association of nucleic acid bases in vacuo and water solution. Journal of the American Chemical Society 1988, 110, 3734–3739. [Google Scholar] [CrossRef]
  9. Jorgensen, W.L. The many roles of computation in drug discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef] [PubMed]
  10. Wilhelm, E.; Battino, R.; Wilcock, R.J. Low-pressure solubility of gases in liquid water. Chemical reviews 1977, 77, 219–262. [Google Scholar] [CrossRef]
  11. Hine, J.; PK, M. The intrinsic hydrophilic character of organic compounds. Correlations in terms of structural contributions. 1975. [Google Scholar]
  12. Abraham, M.H. Thermodynamics of solution of homologous series of solutes in water. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases 1984, 80, 153–181. [Google Scholar] [CrossRef]
  13. Pearson, R.G. Ionization potentials and electron affinities in aqueous solution. Journal of the American Chemical Society 1986, 108, 6109–6114. [Google Scholar] [CrossRef]
  14. Garrido, N.M.; Economou, I.G.; Queimada, A.J.; Jorge, M.; Macedo, E.A. Prediction of the n-hexane/water and 1-octanol/water partition coefficients for environmentally relevant compounds using molecular simulation. AIChE journal 2012, 58, 1929–1938. [Google Scholar] [CrossRef]
  15. Yang, L.; Ahmed, A.; Sandler, S.I. Comparison of two simulation methods to compute solvation free energies and partition coefficients. Journal of Computational Chemistry 2013, 34, 284–293. [Google Scholar] [CrossRef]
  16. Bapat, D.U.; Dalvi, V.H. Molecular insights into water clusters formed in tributylphosphate–di-(2-ethylhexyl) phosphoric acid extractant systems from experiments and molecular dynamics simulations. The Journal of Physical Chemistry B 2019, 123, 1618–1635. [Google Scholar] [CrossRef]
  17. Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. The Journal of Chemical Physics 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
  18. Kirkwood, J.G. Statistical mechanics of fluid mixtures. The Journal of chemical physics 1935, 3, 300–313. [Google Scholar] [CrossRef]
  19. Straatsma, T.; Berendsen, H.; Postma, J. Free energy of hydrophobic hydration: A molecular dynamics study of noble gases in water. The Journal of chemical physics 1986, 85, 6720–6727. [Google Scholar] [CrossRef]
  20. Bash, P.A.; Singh, U.; Langridge, R.; Kollman, P.A. Free energy calculations by computer simulation. Science 1987, 236, 564–568. [Google Scholar] [CrossRef]
  21. Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. Journal of computational physics 1995, 117, 1–19. [Google Scholar] [CrossRef]
  22. Paluch, A.S.; Shah, J.K.; Maginn, E.J. Efficient solvation free energy calculations of amino acid analogs by expanded ensemble molecular simulation. Journal of Chemical Theory and Computation 2011, 7, 1394–1403. [Google Scholar] [CrossRef] [PubMed]
  23. Jorgensen, W.L.; Blake, J.F.; Buckner, J.K. Free energy of TIP4P water and the free energies of hydration of CH4 and Cl-from statistical perturbation theory. Chemical physics 1989, 129, 193–200. [Google Scholar] [CrossRef]
  24. Shirts, M.R.; Pande, V.S. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. The Journal of chemical physics 2005, 122. [Google Scholar] [CrossRef] [PubMed]
  25. Pearlman, D.A. A comparison of alternative approaches to free energy calculations. The Journal of Physical Chemistry 1994, 98, 1487–1493. [Google Scholar] [CrossRef]
  26. Beutler, T.C.; Mark, A.E.; van Schaik, R.C.; Gerber, P.R.; Van Gunsteren, W.F. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chemical physics letters 1994, 222, 529–539. [Google Scholar] [CrossRef]
  27. Jorgensen, W.L.; Thomas, L.L. Perspective on free-energy perturbation calculations for chemical equilibria. Journal of chemical theory and computation 2008, 4, 869–876. [Google Scholar] [CrossRef]
  28. Cross, A.J. Influence of hamiltonian parameterization on convergence of kirkwood free energy calculations. Chemical physics letters 1986, 128, 198–202. [Google Scholar] [CrossRef]
  29. Mezei, M.; Beveridge, D. Free energy simulations. Annals of the New York Academy of Sciences 1986, 482, 1–23. [Google Scholar] [CrossRef]
  30. Boresch, S.; Bruckner, S. Avoiding the van der Waals endpoint problem using serial atomic insertion. Journal of computational chemistry 2011, 32, 2449–2458. [Google Scholar] [CrossRef]
  31. Giese, T.J.; York, D.M. A GPU-accelerated parameter interpolation thermodynamic integration free energy method. Journal of chemical theory and computation 2018, 14, 1564–1582. [Google Scholar] [CrossRef]
  32. Gissinger, J.R.; Nikiforov, I.; Afshar, Y.; Waters, B.; Choi, M.-k.; Karls, D.S.; Stukowski, A.; Im, W.; Heinz, H.; Kohlmeyer, A. Type Label Framework for Bonded Force Fields in LAMMPS. The Journal of Physical Chemistry B 2024, 128, 3282–3297. [Google Scholar] [CrossRef] [PubMed]
  33. Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. Journal of computational chemistry 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
  34. Kumar, R.A.; Sruthi, S.; Kiruthika, A.; Karthik, V. Atomistic modelling of carbon nanotube networks and analysis of inter filler distance. Materials Today: Proceedings 2021, 39, 1791–1795. [Google Scholar]
  35. Ben-Naim, A.; Marcus, Y. Solvation thermodynamics of nonionic solutes. The Journal of chemical physics 1984, 81, 2016–2027. [Google Scholar] [CrossRef]
  36. Graziano, G. Contrasting the hydration thermodynamics of methane and methanol. Physical Chemistry Chemical Physics 2019, 21, 21418–21430. [Google Scholar] [CrossRef]
  37. Luis, D.P.; García-González, A.; Saint-Martin, H. A theoretical study of the hydration of methane, from the aqueous solution to the sI hydrate-liquid water-gas coexistence. International Journal of Molecular Sciences 2016, 17, 378. [Google Scholar] [CrossRef]
Preprints 113299 g001
Figure 1. Gibbs free energy difference (ΔG) of methane hydration as a function of the coupling parameter (λ) for (a) backward (introducing methane to water) and (b) forward (deleting methane from water) route. Red arrows show the direction of the simulation.
Figure 1. Gibbs free energy difference (ΔG) of methane hydration as a function of the coupling parameter (λ) for (a) backward (introducing methane to water) and (b) forward (deleting methane from water) route. Red arrows show the direction of the simulation.
Preprints 113299 g001
Preprints 113299 g002
Figure 2. Radial distribution functions between the methane and water atoms.
Figure 2. Radial distribution functions between the methane and water atoms.
Preprints 113299 g002
Table 1. Calculated and literature values for the free energy of hydration of methane.
Table 1. Calculated and literature values for the free energy of hydration of methane.
Method ΔGForward (kcal/mol) ΔGBackward (kcal/mol)
This study
(FEP, LAMMPS)		 -2.218(13%) 2.132 (8%)
Shirts’s work [24]
(BAR, GROMACS)		 *N/A 2.27 (15%)
Jorgensen’s work [23]
(FEP-MC)		 -2.08 (6%) 2.90 (48%)
Experimental [35,36] -2.005, -1.912 2.005, 1.912
*N/A= Not applicable.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated