Multi-objective Design and Optimization of Hardware Friendly Grid-Based Sparse MIMO Arrays

Preprint

Article

Multi-objective Design and Optimization of Hardware Friendly Grid-Based Sparse MIMO Arrays

Altmetrics

Downloads

113

Views

Comments

A peer-reviewed article of this preprint also exists.

S. Gokhun Tanyer

,Paul Dent,Murtaza Ali,Curtis Davis,SenthinelKumar Rajagopal,

Peter F. Driessen^*

S. Gokhun Tanyer

,Paul Dent,Murtaza Ali,Curtis Davis,SenthinelKumar Rajagopal,

Peter F. Driessen^*

This version is not peer-reviewed

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts

Abstract

A comprehensive design framework is proposed for optimizing sparse MIMO (multiple-input, multiple-output) arrays to enhance multi-target detection. The framework emphasizes efficient utilization of antenna resources, including strategies for minimizing inter-element mutual coupling and exploring alternative grid-based sparse array (GSA) configurations by efficiently separating interacting elements. Alternative strategies are explored to enhance angular beamforming metrics, including beamwidth (BW), peak-to-sidelobe ratio (PSLR), and grating lobe limited field of view. Additionally, a set of performance metrics is introduced to evaluate virtual aperture effectiveness and beamwidth loss factors. The study employs the desirability function and explores optimization strategies for the partial sharing of antenna elements in multi-mode radar applications. A novel machine learning initialization approach is introduced for rapid convergence. Observations include the potential for peak-to-sidelobe ratio (PSLR) reduction in dense arrays and insights into GSA feasibility and performance compared to uniform arrays. The study validates the efficacy of the proposed framework through simulated and measured results. The study underscores the importance of effective sparse array processing in multi-target scenarios and highlights the advantages of the proposed design framework, offering clarity on sparse array efficiency and applicability in processing hardware providing clarity on its advantages over uniform and nonuniform arrays.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Sensor arrays are integral components in spatio-temporal signal processing across diverse fields, including electromagnetic, acoustics, ultrasonic, and seismic processing systems. Their utility spans fundamental technologies such as radar, sonar, navigation, wireless communications, electronic surveillance, and radio astronomy [1,2,3,4].

MIMO radar leverages multiple antennas to transmit a diverse waveform, allowing for the maximization of power in specific areas of interest. The investigation of antenna pattern design for MIMO radar has garnered significant attention in recent years [5,6,7,8,9]. Prevalent in various signal processing and communication applications are sparse signal samples in time, frequency, or space domains [10,11,12]. While conventional FFT-based techniques exist, recent years have seen the emergence of novel methods that surpass them in terms of both complexity and optimality [13,14,15].

Sparse antenna arrays offer improved angular resolution through their thinned configurations, benefiting both phased array radar and MIMO radar. In contrast to the well-known repetitive sidelobe patterns inherent in Uniform Linear Arrays (ULAs) and Uniform Rectangular Arrays (URAs), sparse arrays intentionally distribute spacing unevenly to effectively mitigate grating lobes. However, the thinning of the array introduces an increase in the overall side lobe level [1,5]. In each respective field, similar tools, algorithms, and reconstruction methods have been developed for sparse signal processing. These include random sampling of bandlimited signals, compressed sensing (CS) [16], channel estimation in Orthogonal Frequency Division Multiplexing (OFDM) [15,17], and calibration for the mutual coupling between antenna elements [18,19,20,21,22,23].

In this work, without loss of generality, our focus is on automotive radars, which have undergone a significant transformation in recent years, evolving from a niche sensor to becoming standard even in middle-class cars. Radar is frequently recognized as the most suitable sensor for automated braking and pedestrian safety functionality, as required by Euro-NCAP ratings. The industry is benefiting from the adoption of new radar-on-chip technology, integrating both analog and digital circuitry on the same substrate, resulting in cost-effective products [24,25,26,27].

The remainder of this paper is organized as follows: In Section 2, we formulate the MIMO radar system model, with its radiation and receiving mechanism generalized in the Appendix A for sparse arrays—a fundamental step often overlooked in the literature.

In Section 3, we derive a classical Fourier transform-based beamforming formulation for sparse arrays. This formulation includes the calibration of imperfect elements and inter-element mutual coupling. We formulate steering vectors for targets and the beamforming matrix, incorporating physical steering vectors for transmitter and receiver elements.

Section 4 introduces a multi-objective design and optimization approach for a sparse MIMO array. Performance parameters are defined to illustrate the trade-offs in designing an effective radar system. Efficient initialization for fast convergent optimization and minimization of mutual coupling effects are proposed. This section also explores joint optimization of a multi-mode sparse array, complementary transmitter, and receiver apertures — examined together for the first time in the literature. We apply a machine learning approach to utilize adaptive desirability functions for dynamically setting hyperparameters in the optimization process.

Finally, Section 5 presents results, and Section 6 draws conclusions. The effectiveness of grid-based sparse arrays is illustrated using four grid-based sparse arrays. Simulated and measured results confirm the efficacy of grid-based sparse arrays. Additionally, potential directions for future are outlined. Detailed formulations are provided in Section 9 Appendix A.

Antenna arrays can be classified based on their inter-element spacing values and design characteristics, as illustrated in Figure 1. An antenna array is considered uniformly spaced when the inter-element spacings are constant in each orthogonal direction. Conversely, if the inter-element spacing values appear random or are non-uniform, the array is categorized as non-uniform.

Uniformly spaced arrays can be defined in 1D for the uniform linear array (ULA) and in 2D for the uniform rectangular arrays (URA). Slanted URAs can be defined for two non-orthogonal (slanted) axes, proving beneficial when the physical width and height of antenna elements differ significantly, and slanting allows for physically closer elements.

Thinned arrays are non-uniformly spaced arrays where the inter-element spacings are quantized values relative to a minimum inter-element spacing that defines the reference grid points. Thinned arrays can be grouped into two classes based on their average inter-element spacings: dense and sparse arrays. In dense arrays, the average inter-element spacings are smaller than one wavelength, while in sparse arrays, the average inter-element spacings are larger than one wavelength, as suggested in [10]. The spacing between antenna elements can be either random or calculated using an algorithm for low discrepancy (LD). In this context, ‘discrepancy’ refers to the deviation between the uniform element grid and the randomized positions, as outlined in [11]. This concept extends to non-uniformly spaced arrays, but our focus here is on inducing discrepancy from uniformly spaced arrays by under populating the grid. This specific approach is discussed in Section 2. C to facilitate the practical implementation of angle beamforming for sparse arrays.

Table 1. Common notations used throughout the paper.

$α_{a p}, α_{b w, ϕ}, α_{b w, θ}$	Aperture Loss and Beamwidth Spreading Factors
$b, B$ and $b_{s}, B_{s}$	Beamforming vector and matrices
$β (t)$	Reference phase at the origin
$C, C_{s}$	Calibration matrices; standard and for the sparse array formulation
$d, d_{λ}, Δ d$	Inter-element spacing, its value normalized to one wavelength and incremental spacing value
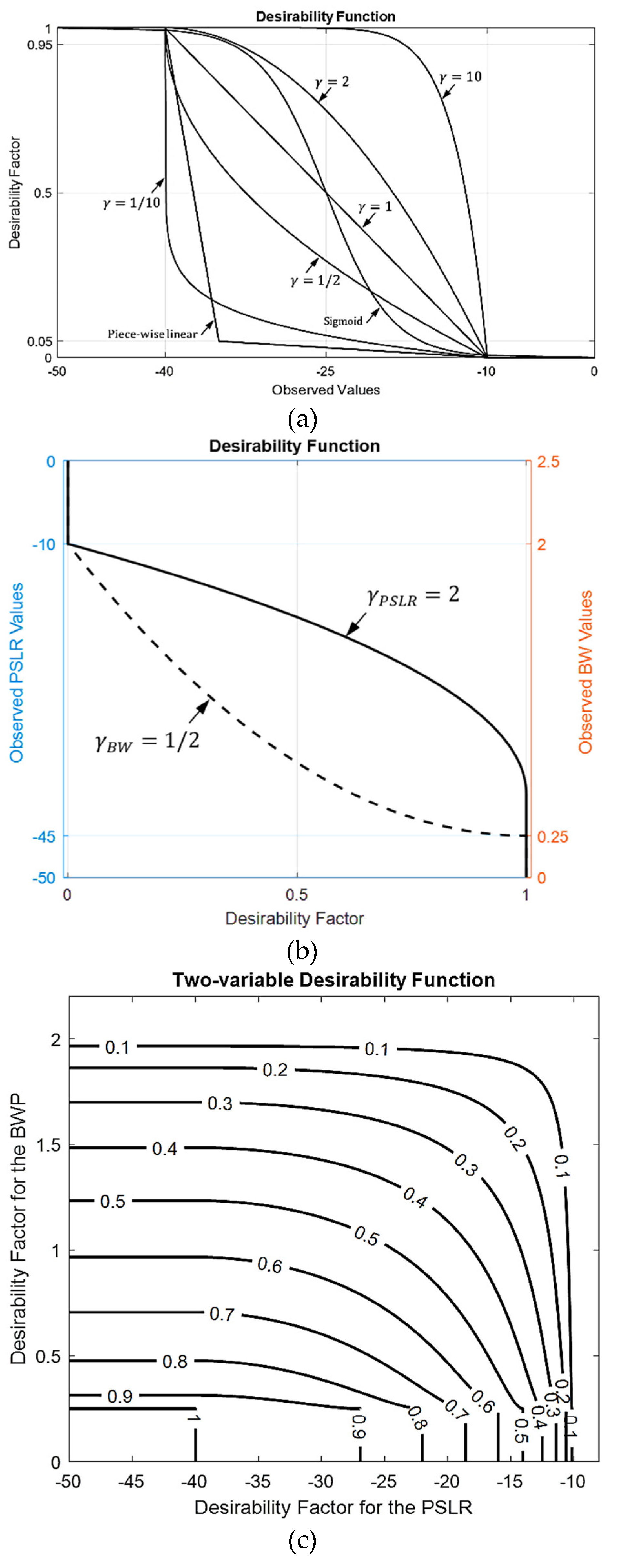
$d_{v}^{+}$ , $d_{v}^{-}$	The desirability functions for the LTB and STB cases
$f_{t x}, f_{r x}$	Antenna element gain factors
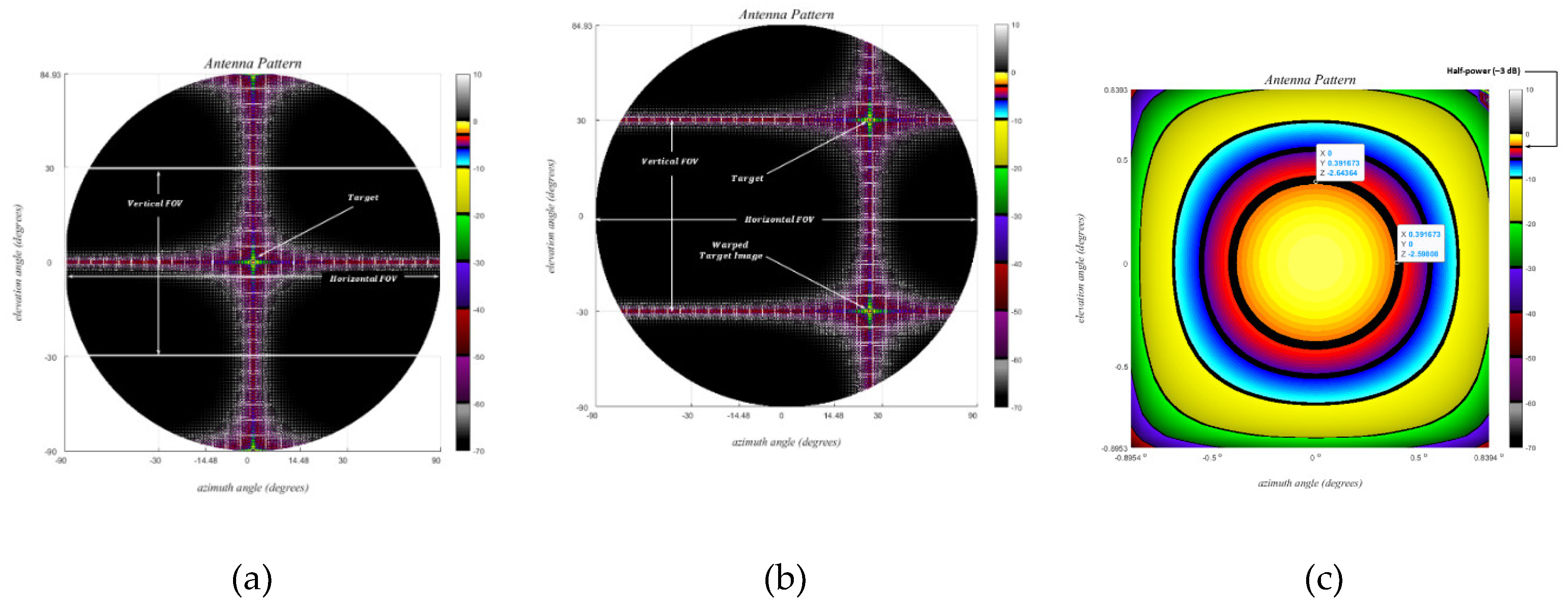
FOV, uFOV	Operational field of view (FOV) and the usable FOV
$(ϕ_{t}, θ_{t})$	Direction of the t’th target in spherical coordinates
$G, G_{s}$	Beamforming output
$\bar{k}$	Wavevector
$N_{t x}, N_{r x}, N_{v r x}$	Number of transmitter, receiver and virtual receiver elements
$p, P$	Sparse array element order number and the total number of virtual elements
$q_{ϕ}, q_{θ}$	Oversampling ratios for the field domain $(u, v)$
$s_{s}$	Far-field received pattern
$r, r_{s}$	Steering vectors
$\bar{R}, {\bar{R}}_{t x}, {\bar{R}}_{r x}$	Displacement vectors for the field point, TX and RX
$σ_{c, t}$	Radar cross-section for the t’th target
$t$	Thinning/sparsity ratio
T	Number of targets
$(u, v)$	Directional cosine terms, $(\sin (ϕ) \sin (θ), \cos (θ))$ for the field domain
$(v_{m i n}, v_{d e s i r e d})$	Expected observation range for the variable $v$
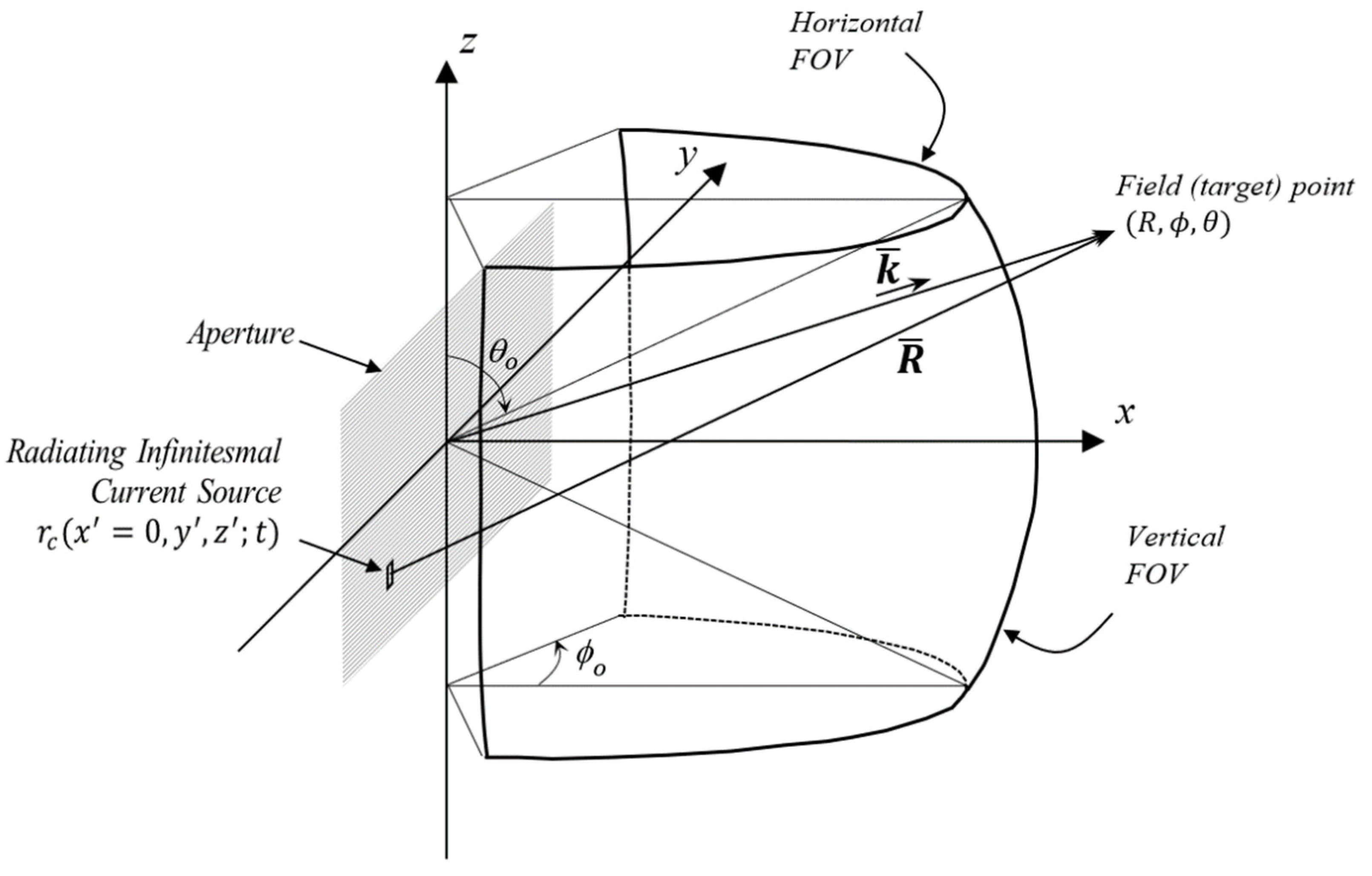
$(x, y, z)$	Field point based on the ISO/SAE coordinate system.
$(x^{'}, y^{'}, z^{'})$	Source coordinates where the aperture is located on the $x ’ = 0$ surface.
$(y_{t x}, z_{t x}), (y_{r x}, z_{r x})$	Transmitter and receiver coordinates on the aperture
$(Y_{m a x}, Z_{m a x})$	Antenna aperture dimensions along y- and z-axis.

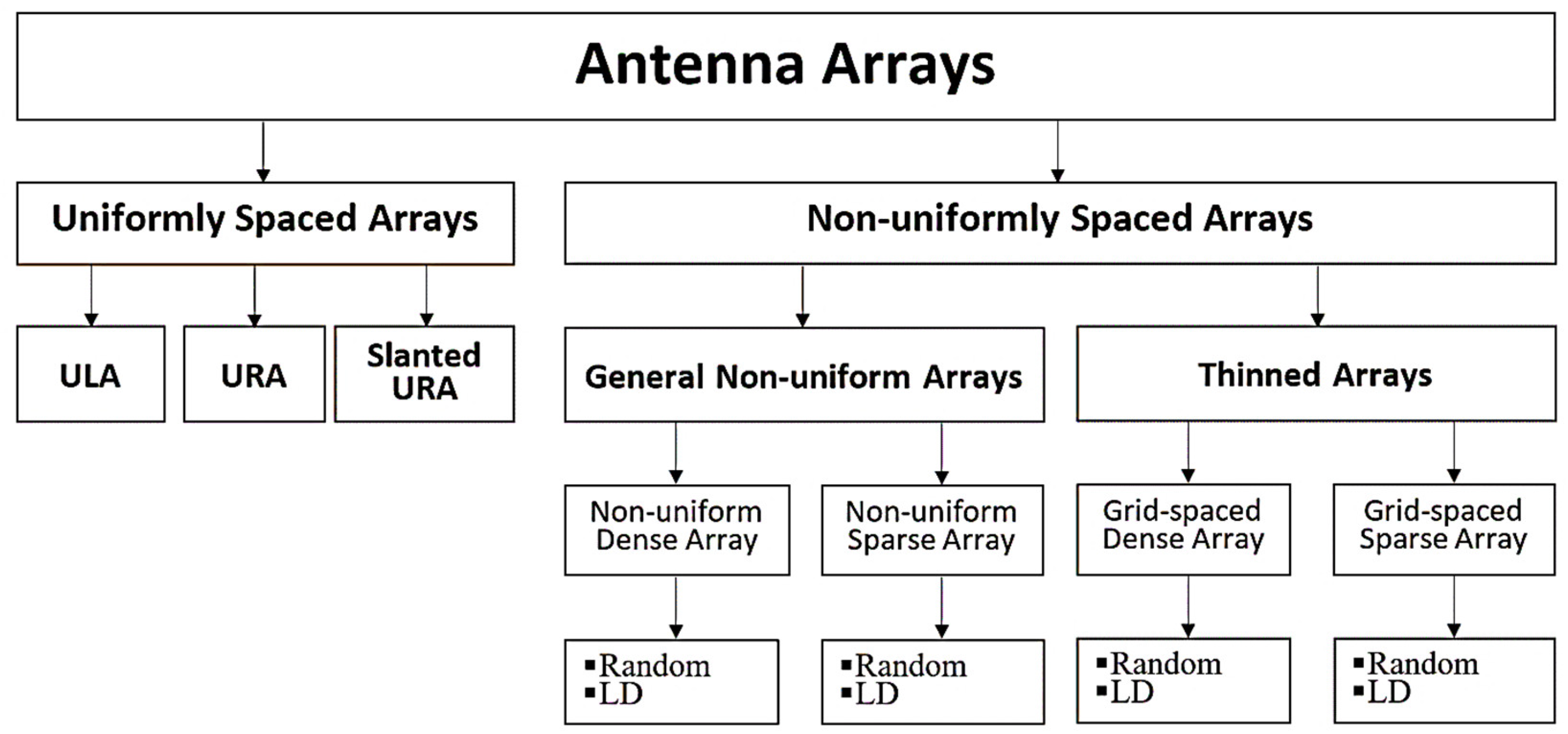
2. Sparse MIMO Radar Systems

In a multiple-input multiple-output (MIMO) radar system, each transmitter (TX) signal is distinguished from every other TX signal by utilizing appropriate modulation differences, such as different digital code sequences. Each receiver (RX) correlates with each TX signal, generating a number of correlated outputs equal to the product of the number of RXs and the number of TXs. These correlated outputs can be interpreted as having been generated by several virtual receivers (VRXs) [4,6,7,9,28].

MIMO processing enables the physical length to double in both directions, resulting in a four-fold increase in aperture area. The construction of virtual sparse arrays with different aperture sizes is demonstrated to be highly beneficial in achieving high-precision broadband direction finding [29]. Sparse arrays offer techniques for extremely large-scale (XL) arrays, providing potential solutions for overcoming severe path loss in millimeter-wave (mm Wave) and Terahertz (THz) bands [30].

Antenna aperture and the desired field of view defined in the spherical coordinate system are illustrated in Figure 2. This standard coordinate system is defined in [31,32,33,34].

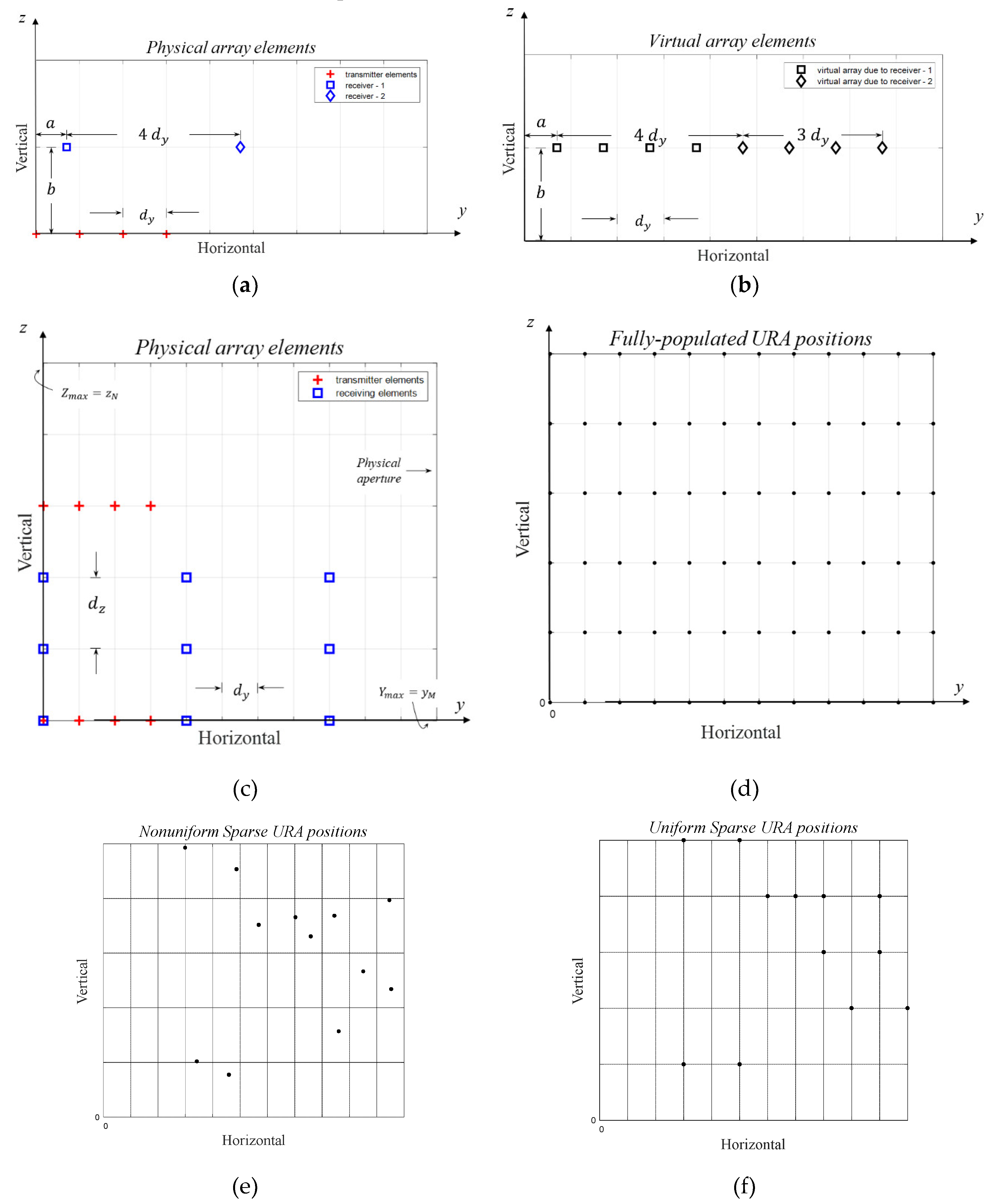
2.1. Creation of Virtual Arrays

The MIMO processing performed at the range correlator enables the received signals due to differently encoded transmitters to be separated, leading to the creation of virtual receivers for each transmitter-receiver pair. The positions for these virtual arrays can be calculated analogously to the convolution operation, taking into consideration the relative positions of transmitter (TX) and receiver (RX) elements. Specifically, virtual arrays are generated by replicating transmitter arrays through each receiver, accounting for their relative positions. A visual comparison in Figure 3 (a) and (b) illustrates that each receiver generates a replica of the transmitter array, perfectly aligned to form a virtual uniform linear array. In general, the number of virtual receivers equals the product of the number of transmitters and receivers. However, this count may decrease in instances where some of the virtual receivers (VRXs) overlap.

The relative positions between the TX and the RX elements illustrated by (a, b) and shown in Figure 3 (a) is observed to create a physical shift for the virtual array shown in Figure 3 (b). This shift introduces a common complex phase factor in radiation equations which is often ignored.

2.2. Transmitting Grid-Based Sparse Antennas

The antenna aperture is commonly shared by transmitting and receiving elements, and the physical positions for uniform linear and rectangular arrays are well-established. In contrast, sparse array elements, in general, can be positioned anywhere inside a given physical aperture. However, the elements of grid-based sparse arrays (GSAs), as proposed in this context, are constrained to specific points defined by a reference grid space, as illustrated in Figure 3.

The radiation equation for a grid-based sparse array can be formulated by selectively disabling some of the transmitting elements in (A.8) and introducing the uniform antenna element radiation pattern

s_{s} (u, v) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} r_{t x, s} (m, n) f_{t x} (u, v) e^{- j 2 π (m d_{λ, y} u + n d_{λ, z} v)},

(1)

where

(u, v) = (s i n ϕ \sin θ, c o s θ)

(ϕ, θ)

represents the direction of the field point in the spherical coordinates,

r_{t x, s} (m, n)

is the amplitude of the excitation current at the transmitter element,

d_{λ, y} = d_{y} / λ

, and

d_{λ, z} = d_{z} / λ

are the inter-element spacing values,

f_{t x} (u, v)

is the radiation pattern for the transmitting elements, and where

r_{t x, s}

is nonzero only for a selection of

(m, n)

couples for active sparse elements (transmitters) located on the reference grid space.

Without loss of generality, (1) can be simplified by assuming isotropic antenna patterns and setting half-wavelength spacings

d_{λ, y} = d_{λ, z} = 1 / 2,

s_{s} (u, v) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} r_{t x, s} (m, n) e^{- j π (m u + n v)} .

(2)

2.3. Receiving Grid-Based Sparse MIMO Antenna Arrays

Similar to (2) (A.11) can also be simplified to obtain the received signal at the virtual receiver elements

r_{r x, s} (p) = \sum_{t = 1}^{T} σ_{c, t} e^{j π (m u_{t} + n v_{t})}

(3)

for

p = 1, 2, \dots P_{s} < M N

are the active VRXs created by available TX and RXs located on the grid points

(m, n)

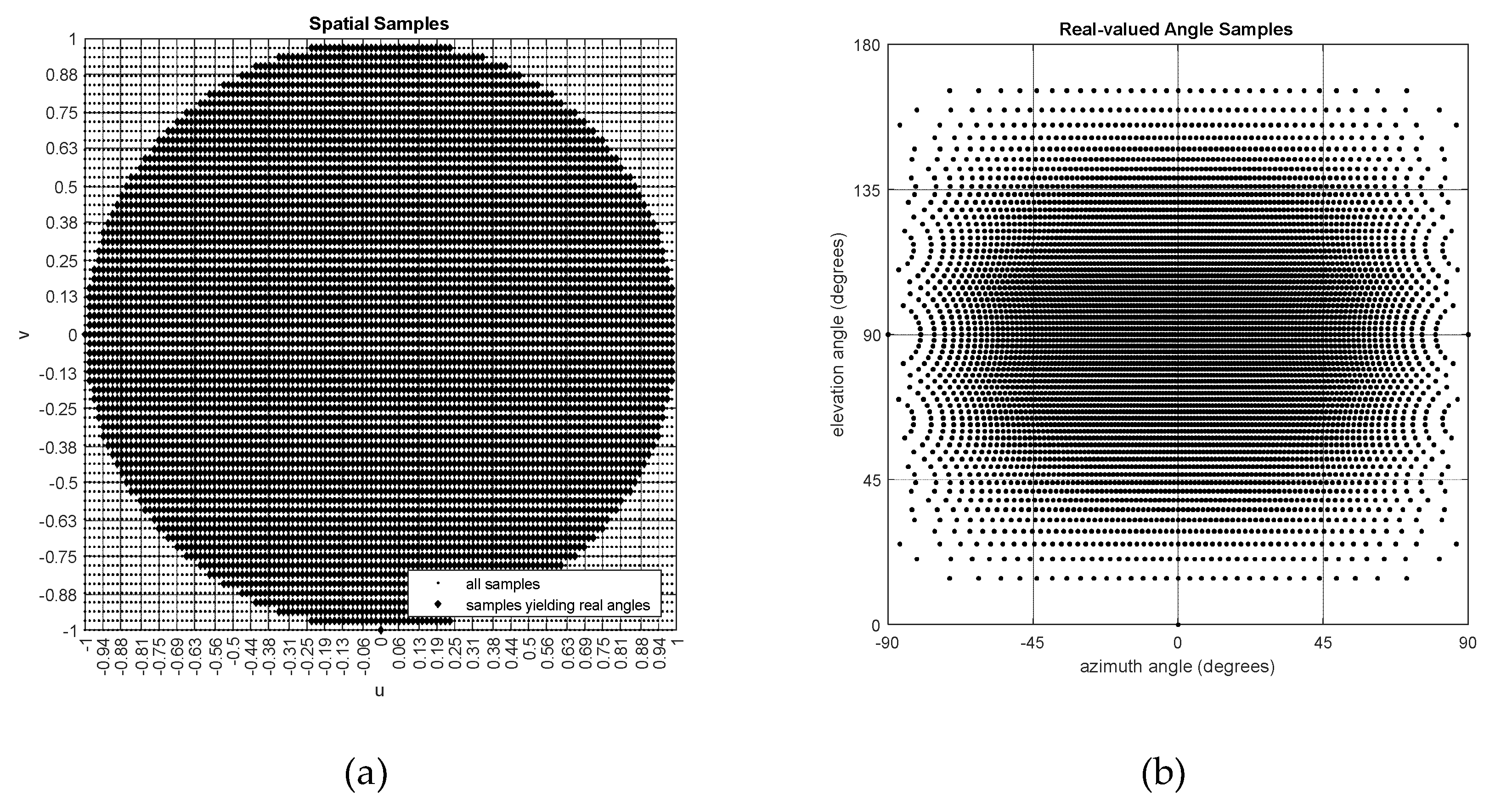
3. Angle Beamforming

Recalling the properties of Fourier transform and its inverse discussed in Section 2.1 (A.11) and using (2), and (3) the received signal pattern for a fully populated uniform array at the direction

(u, v)

can be calculated by

g (u, v) = b r

(4)

where the received signal at all available VRXs form the received signal (column) vector r of length

P

, and

b

is the steering (column) vector evaluated at

(u, v)

. One can oversample

(u, v)

uniformly for the received signal pattern

u_{m} = \frac{2 m^{'}}{M q_{ϕ}} - 1, f o r 0 \leq m^{'} < M q_{ϕ},

(5)

v_{n} = \frac{2 n^{'}}{N q_{θ}} - 1, f o r 0 \leq n^{'} < N q_{θ} .

(6)

The corresponding non uniform samples in the angular domain can be calculated using the inverse-projection equations given below (see Figure 4)

ϕ_{m^{'}, n^{'}} = asin (\frac{u}{\sin (θ_{m^{'}})}) = asin [\frac{\frac{2 m^{'}}{M q_{ϕ}} - 1}{\sqrt{1 - {(\frac{2 n^{'}}{N q_{θ}} - 1)}^{2}}}],

(7)

θ_{n^{'}} = acos v = acos (\frac{2 n^{'}}{N q_{θ}} - 1)

(8)

where the above equation is valid only for real angles satisfying

u^{2} + v^{2} \leq 1 .

Here,

q_{ϕ}

and

q_{θ}

are positive integer oversampling factors for the

ϕ

- and

θ

-axes, respectively (Figure 4).

Now let us sort those angular samples into a single (row) vector, and evaluate the steering vector at each row, yielding the angle beamforming matrix B. The received signal pattern can be calculated as

g = B r

(9)

where

g

is the column vector for the received signal pattern,

g

is calculated in (4),

r

is defined in (3), and where B is the angle beamforming matrix with a size

[(M - 1) (N - 1) q_{ϕ} q_{θ})]

P

. For the hardware implementation of a multi-resolution B, both oversampling ratios,

q_{ϕ}

and

q_{θ}

, can be set to be multiples of 2 and the largest of those can be used to calculate a vector look-up table for the list of orthogonal set of Fourier coefficients.

To obtain a 2D pattern with 512 azimuth and 256 elevation angle samples,

g

should have

512 \times 256 = 131,072

row elements. For a virtual array of 192 elements B is expected to have

192 \times 131,072 = 25,165,824

complex coefficients to be calculated or stored in the radar hardware for a general sparse array. This is especially true for non-uniform (gridless) sparse arrays [35]. However, for a grid-based sparse array (GSA) those exponential coefficients become regular, and the number goes down to only 512 values. This brings a great advantage to GSAs for their hardware implementations.

4. Multi-Objective Design and Optimization of Grid-Based Sparse Arrays

For a grid-based sparse array both the physical and virtual array elements are thinned, and

r (p)

is nonzero only for its

P_{s}

elements where

P_{s} < P

[14,36]. Deleting the zero equations (9) simplifies to

g_{s} = B_{s} r_{s}

(10)

where both columns of

B_{s}

, and rows of

r_{s}

are reduced to

P_{s}

, and the thinning/sparsity ratio is defined as

t = P_{s} / P \leq 1

, and where a fully populated array this thinning ratio is 1.

4.1. Optimizing Parameters

In practice radar design engineers often face the challenge of satisfying multiple conflicting objectives for the same desired antenna array. The main optimization constraints include;

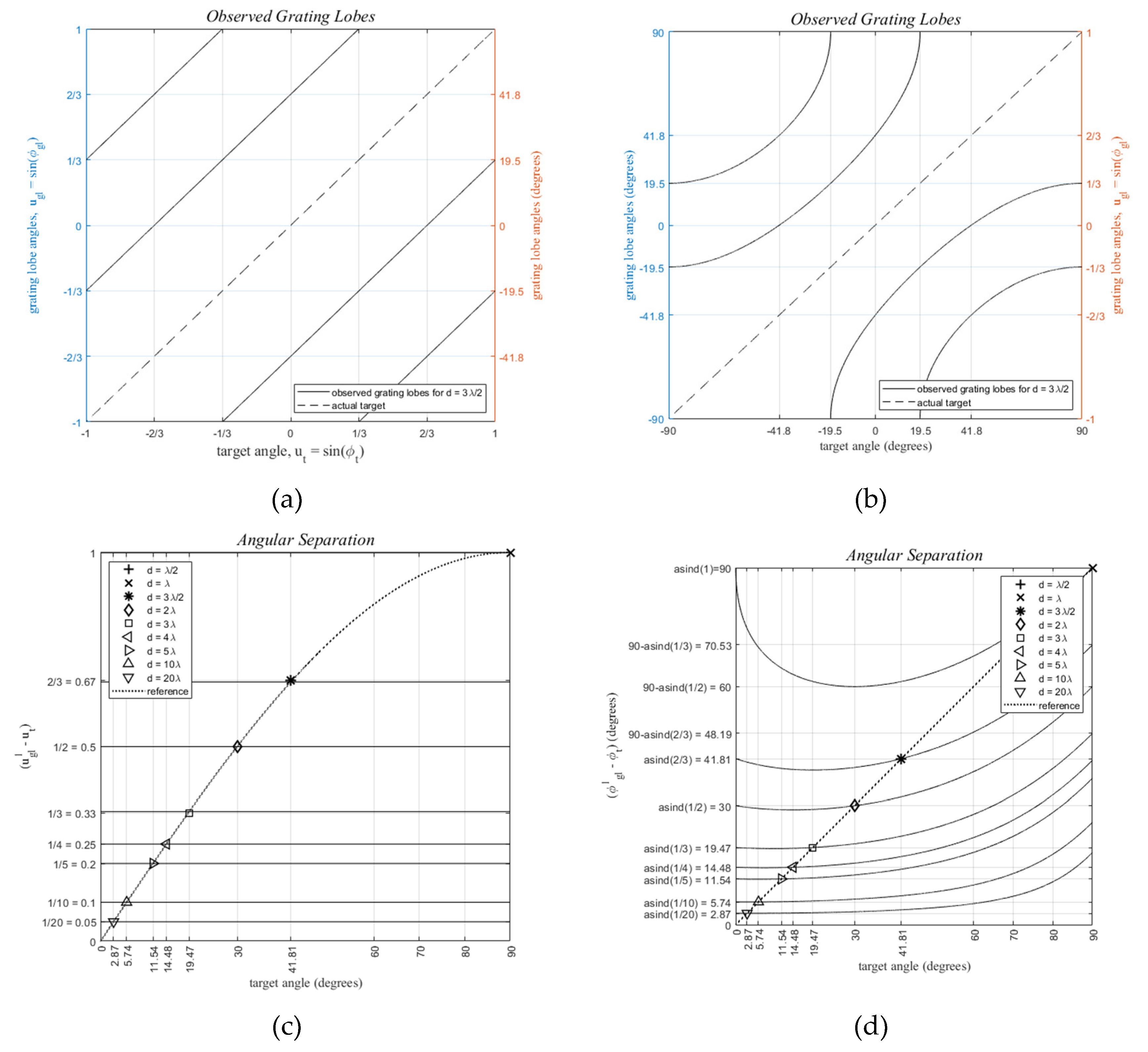
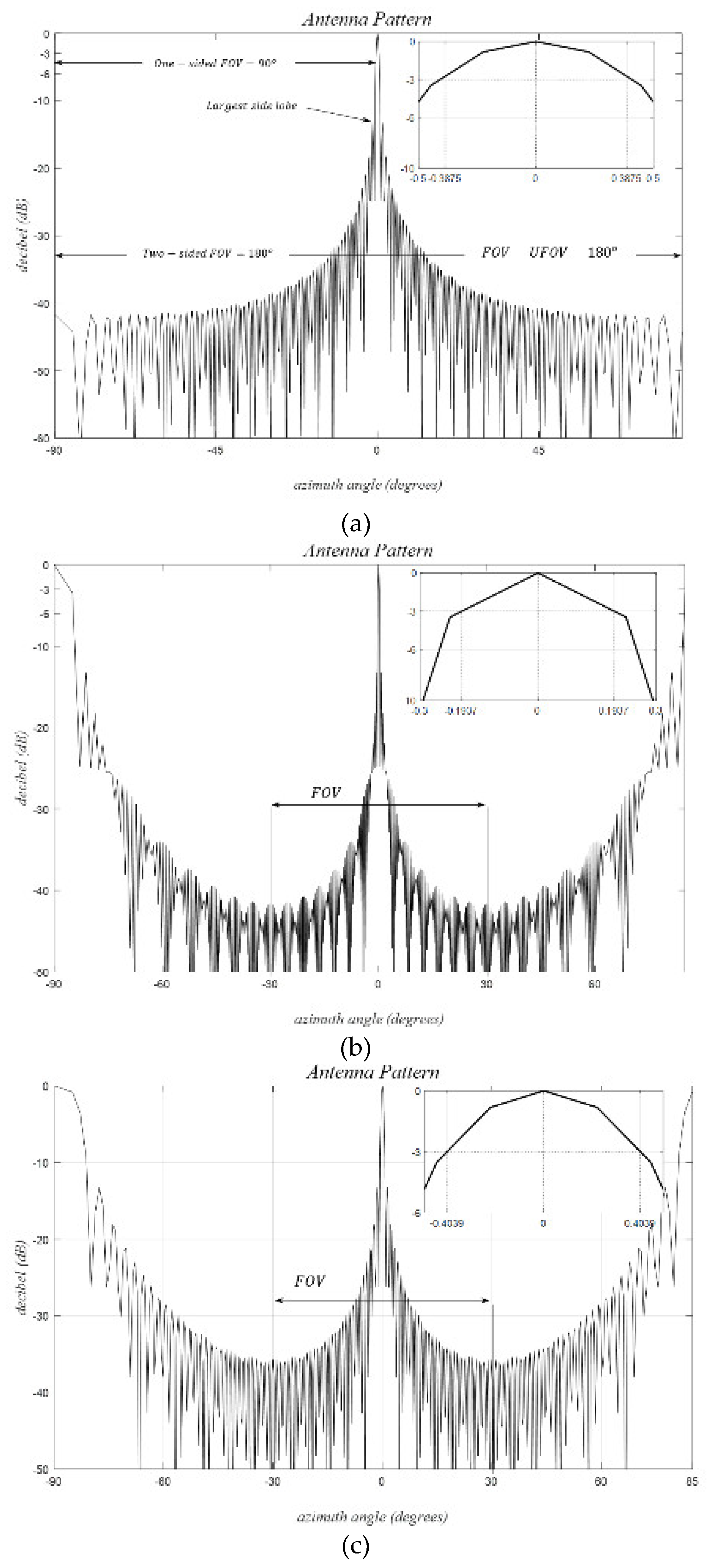
usable field of view (uFOV): The maximum grating lobe-free angular extent around broadside, beyond which lies a flipped replica of the interior pattern that carries no additional information about the target.
Beamwidth (BW): The desired angular width of the main lobe of the antenna pattern.
Total number of physical elements (NTX and NRX): The count of both transmitting (TX) and receiving (RX) elements in the antenna array.
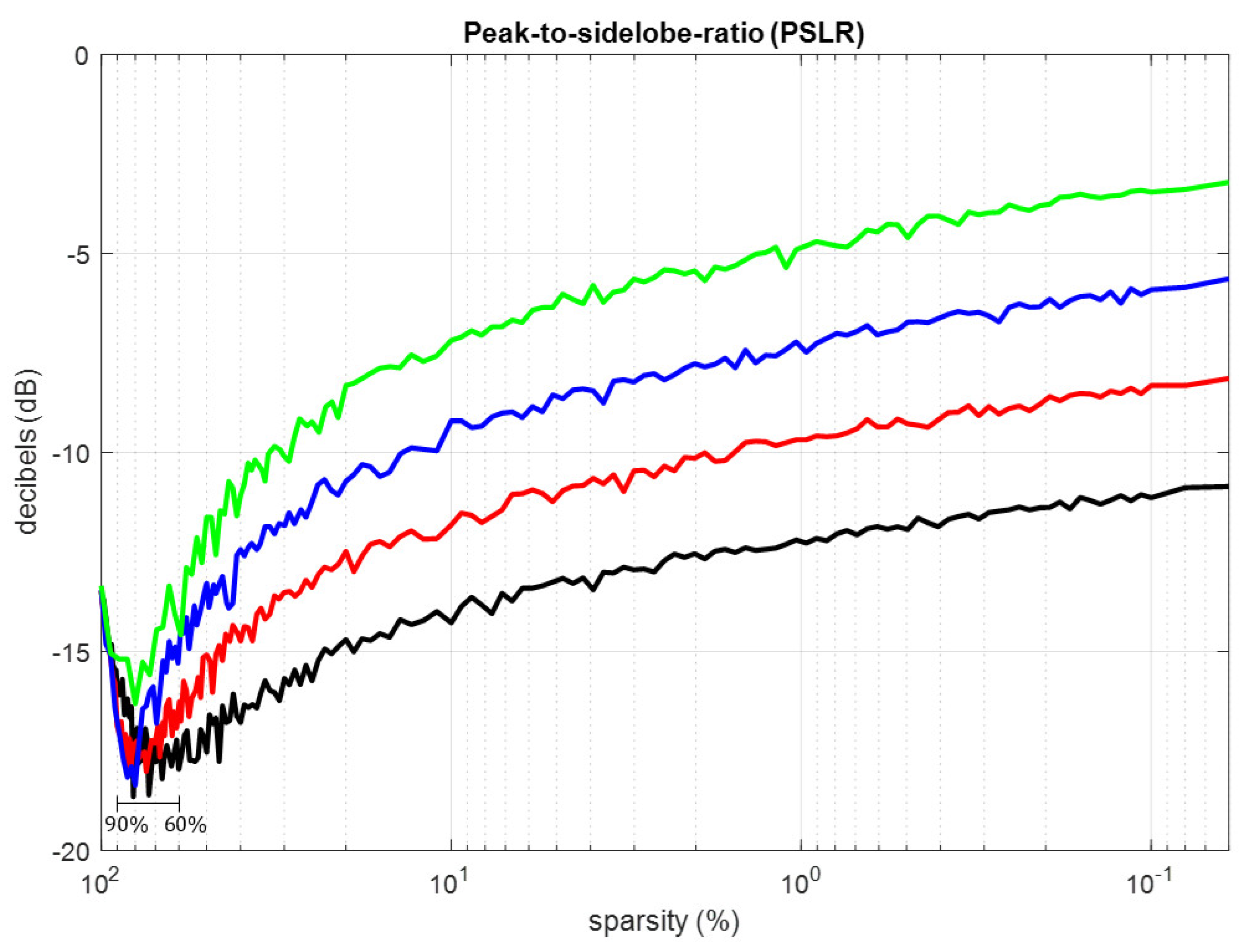
Peak-to sidelobe ratio (PSLR): A measure of the maximum amplitude of the main lobe relative to the sidelobes.

In addition to those here are practical considerations.

Physical size limitations: The TX and the RX antenna elements in practice have finite physical dimensions, namely their width and height, which impose constraints on the minimum inter-element spacing values. These spacing values limit the horizontal and vertical uFOV values, respectively. Densely packed ULA and URAs are directly affected by this limitation, especially when any size dimension is larger than $λ / 2$ .
Mutual coupling: TX and the RX groups should often be physically separated to decrease inter-group mutual coupling [1]. Mutual coupling among the same type of elements is assumed to be calibrated digitally.
Antenna element sharing of different arrays: In multi-functional radars, some of the TX and the RX elements are often shared between different scan modes. The antenna array design and optimization for all scans need to be done simultaneously. A practical approach involves forcing the physical elements for a simpler scan mode to be used in some other complicated antenna configuration, effectively utilizing the array aperture.
Hardware implementation constraints: Antenna elements are fed by transmission lines or waveguide structures, usually implemented on a separate neighboring hardware board. The layouts of transmitted and received signals should also be fed from another layer. As a design choice, a central region can be preferred to keep all the transmission lines approximately equal in length. This central region needs to be defined as a forbidden zone for the array elements.

In this work, thinning of fully populated uniform MIMO antenna arrays is examined to form effective sparse arrays, with the focus on improving the usable field of view (uFOV), beamwidth (BW), and peak-to-side lobe-ratio (PSLR) using fewer physical antenna elements simultaneously. The detailed definitions for these parameters provided in the following sub-sections.

i.: Peak-to-Side Lobe Ratio (PSLR):

Considering a given target range and velocity, the peak-to-side lobe-ratio (PSLR) is an important metric. The maximum skin return for a target is given by

g_{p e a k} = |g_{s} (ϕ_{t}, θ_{t})| = \max_{ϕ, θ in FOV} |g_{s} (ϕ, θ)|

(11)

where

(ϕ_{t}, θ_{t})

is the direction of the brightest signal observation in the FOV. The maximum side lobe level is given by

g_{m s l l} = |g_{s} (ϕ_{s}, θ_{s})| = \max_{ϕ, θ in FOV} |{\tilde{g}}_{s} (ϕ, θ)|

(12)

where

(ϕ_{s}, θ_{s})

is the direction of the largest side lobe in the uFOV, and where

{\tilde{g}}_{s}

is obtained by setting

g_{s}

to zero inside its main lobe region. This side lobe has the potential to create false targets, even when it is outside of the operational FOV, as long as oFOV

\leq

uFOV.

The peak-to-side lobe ratio (PSLR) can be calculated by

P S L R (ϕ_{t}, θ_{t}; ϕ_{s}, θ_{s}) = 20 l o g_{10} (\frac{g_{p e a k}}{g_{m s l l}}) .

(13)

Note that for uniform and isotropic elements, assuming mutual coupling to be shift-invariant, and ignoring interference between the skin returns of neighboring targets in the presence of multi-targets, the PSLR becomes independent of the target direction.

P S L R = 20 l o g_{10} (\frac{g_{p e a k}}{g_{m s l l}}) .

(14)

ii.: Beamwidth for Uniform Arrays:

The first-null-, and the half-power-beamwidth can be calculated as follows [37]

B W_{f n} = asin (\frac{1}{L_{λ}}),

(15)

B W_{h p} = 0.886 (\frac{1}{L_{λ}})

(16)

where

N

is the number of uniform linear array (ULA) elements,

B W_{h p}

and

B W_{f n}

are the half-power beamwidth (HPBW), and the first null beamwidth calculated in radians, and where

d_{λ}

and

L_{λ} = (N - 1) d_{λ}

are inter-element spacing and aperture length in terms of wavelength, respectively. Eqns (15) and (16) are valid for uniform arrays for their horizontal and the elevation cross sections, separately.

iii.: Side lobes, Grating Lobes and Usable FOV for Sparse Arrays:

ULA and URAs, by definition, have constant inter-element spacings, and at any target angle, the inter-element phase differences are also constant, ideally zero at the target angle, and all elements contribute constructively. However, for field angles retreating from the main lobe moving along one of the axes, these phase differences with respect to the array center begin to rotate for the furthest elements the fastest. First null occurs when the two elements furthest to the array center are out of phase with respect to this center by approximately

\pm π

, yielding the first minimum. Those far elements are

d (N - 1) / 2

meters away from the array center with a phase difference of

\pm π d_λ (N - 1)

. The first null is observed approximately at

\pm s i n^{- 1} (1 / d_{λ} (N - 1))

radians, respectively. This approximation is accurate within 0.6, 0.4, 0.2, and 0.1 degrees for N= 15, 18, 25, and 35, respectively. Retreating further from the broadside angle while furthest elements’ phase rotations turning back to in-phase, we observe the second to the last elements to be approximately out of phase creating the second minimum. In this narrow angular region bounded by those two minima, all except the last two elements are mostly in-phase, causing the largest side lobe. Side lobes gradually decrease due to increasing incoherence between the elements until we reach the halfway to the first grating lobe. For an odd numbered ULA, all radiations cancel each other completely leaving the only one in the center to yield the minimum side lobe level of 1/N. This phenomena /occurs independent of the number of elements or their spacings, and this first side lobe sets the PSLR approximately to –13.8 dB at

ϕ \approx {10.8}^{o}

for

s i n c (u)

where

u = 2 / 2 N

Sparse arrays find applications in diverse fields, including astronomy [38,39], and autonomous vehicle radars. A notable sparse array in New Mexico prompts a discussion on its description and implications for Discrete Fourier Transform (DFT) requirements [40]. Unlike uniform arrays, sparse arrays, including the one in New Mexico, lack positions that are accurately rounded to integer values. Consequently, hardware implementations demand precise calculations of complex numbers for each angle beam, emphasizing the need to reduce the required number of complex coefficients. This reduction is effectively achieved by employing a uniform grid space.

In nonuniform array designs, the challenge arises from working in an infinite space, making solutions elusive with certain types of random searches. However, the use of grid-based sparse arrays proves advantageous, enabling a reduction in the search space/domain to a manageable size. Unlike nonuniform arrays, which typically require discrete Fourier transform (DFT), grid-based sparse arrays (GSAs) utilize Fast Fourier Transform (FFT) with a practical list of beamforming coefficients. GSAs offer a more efficient approach, especially when considering the number of coefficients needed for a specific field of view.

Simple heuristics aid in understanding the interactions between Uniform Linear Array (ULA) and uniform rectangular array (URA) elements. These heuristics also elucidate why sparse arrays exhibit much lower skin-return near (and even inside) the expected main lobe. The irregularity of sparse element positions leads to more than just two elements being out of phase away from the main lobe, as illustrated in Figure 5. In-phase interactions between elements rapidly become incoherent, resulting in a much smaller beamwidth. Despite this, due to the conservation of radiated power, the side lobes cannot be entirely suppressed but spread across the half-hemisphere. Alternatively, they can be optimized to be pushed outside of a given field of view (FOV). This optimization is particularly crucial when dealing with a narrow FOV.

Grating lobes manifest at angles when all array elements are perfectly in-phase, constructively contributing to the received signal pattern equivalent to the main lobe. Large side lobes, distinct from grating lobes, necessitate only a comparatively large complex sum of all contributions, allowing for some inter-element phase mismatching and even some destructive interferences between elements.

For a fully populated ULA, a target located at some

ϕ_{t}

(

θ_{t} = 0

) creates grating lobes at angles given by

ϕ_{g l} = asin γ_{n}, f o r - 1 < γ_{n} \leq 1, a n d f o r n = 0, \pm 1, \pm 2 \dots

(17)

where

γ_{n} = (n / d_{λ} + \sin ϕ_{t})

and

ϕ_{g l} \neq ϕ_{t}

which yields the usable FOV (uFOV)

ϕ_{u F O V} = \pm asin (\frac{1}{2 d_{λ}}), f o r - 1 < \frac{1}{2 d_{λ}} \leq 1, a n d f o r n = \pm 1, \pm 2 \dots

(18)

For

d_{λ} = λ / 2

, and

ϕ_{t} = π / 2

, the first grating lobe occurs for

n = - 2

ϕ_{g l} = - π / 2

allowing the usable angular extend with

ϕ_{u f o v} = {- π / 2, π / 2}

(Figure 2). Similarly, for

d_{λ} = λ

ϕ_{t} = π / 6,

the closest grating lobe occurs for

n = - 2

ϕ_{g l} = - π / 6

, and the usable angular region becomes

ϕ_{u f o v} = {- π / 6, π / 6}

as suggested by (17), and (18). It is crucial to note that, in practice, the physical size of elements limits the minimum possible inter-element spacing values both horizontally and vertically. With an element width of two wavelengths, azimuthal uFOV is approximately restricted to

\pm

14.48^o, as shown in Table 2.

For field angles along the azimuth,

- π < ϕ \leq π

, as illustrated in Figure 2 and for

d_{λ} \leq λ / 2

, the condition

- π < k d u = 2 π d_{λ} u \leq π

holds where u and v are defined in (1). In this scenario, each of the observed sample,

- 1 < u \leq 1

, carries independent information, and no grating lobes are observed. Equivalently, this discussion is valid for

θ \leq π

and

- π < k d v = 2 π d_{λ} v \leq π

where each measurement at the field point

(ϕ, θ)

is unique. However, for larger inter-element spacings,

d_{y} = μ / 2

for

μ > 1

, the condition

| k d u | \leq π

is no longer satisfied. This confines the uFOV to

- 1 / μ < u < 1 / μ

and phase-wrapped target images could be created outside of this region. Conversely, real targets outside the uFOV also create their corresponding ‘target images’ inside the uFOV, making it challenging to distinguish real targets based on radar detections. This becomes a significant issue if the overall antenna patterns for the virtual receivers are not sufficiently directive to protect the uFOV.

‘Target images’, or equivalently, the grating lobes for a specific real target, emerge at angles relative to its source target angle, as shown in Figure 6. For instance, with a single broadside target,

d_{λ} = 3 / 2

, and

μ = 3

the replicas of the target-return patterns are created in regions

- 1 < u < - 1 / 3

, and

1 / 3 < u < 1

outside of the uFOV, as depicted in Figure 6 (a), with corresponding azimuth angles shown Figure 6 (b). Notably, at least three target patterns exist in the half sphere regardless of the real target angle Figure 6 (c) and (d).

Target separations remain constant in the

(u, v)

domain for varying target angles. The dotted reference line indicates the locus of target angles,

ϕ = ϕ_{t 0}

, where the first phase-wrapped target image appears on the opposite side of the uFOV edge at

ϕ = - ϕ_{t 0}

. Thus, uFOV

= 2 ϕ_{t 0}

defines the range

- ϕ_{t 0} < ϕ < ϕ_{t 0}

. In general, (

N_{t} - 1)

target images are created, separated by

π / μ

radians, where

N_{t}

is the largest integer satisfying

N_{t} \leq μ

. Target image separations decrease for larger

μ

, increasing the total number of images, as illustrated in Figure 6 (c) and (d).

Table 2 presents a concise list of calculated spacing values and their corresponding uFOV angles, providing valuable insights for design engineers. For forward-looking- (FLR) and long-range-radar (LRR) applications with narrow operational FOVs (< 30⁰), large inter-element spacings can accommodate the use of large antennas with widths,

w_{λ} \leq 2

. In mid-range-radar (MRR) scenarios with a

u F O V = 140^{o}

, smaller antenna elements with

w_{λ} \leq 0.5321

are preferable. Short-range-radar (SRR) applications requiring a wider uFOV face challenges when using large antenna elements, particularly when mitigating inter-element mutual coupling is a concern.

4.2. Design and Optimization of a Grid-Based Sparse Arrays

The preceding discussion illustrates that ULA and URAs can often become unpractical when confronted with constraints such as uFOV and element size limitations. Additional degrees of freedom become necessary to address these challenges. Sparse arrays, though known for generating undesired grating lobes [41], are purposefully designed in this work to offer optimal solutions by leveraging their irregular element positions. Furthermore, sparse arrays provide the advantage of achieving very high angular resolution by allowing much smaller inter-element spacing values. In this section, a practical design procedure for grating lobe-free sparse array with high angular resolution is proposed.

Examining Section (4.1), it becomes evident that for uniform linear (ULA) and rectangular arrays (URA), the improvement of the beamwidth (BW) for a desired uFOV BW can only be achieved only by increasing the antenna length

(L_{λ})

, aperture size

(A_{λ})

, or the number of elements

(N)

. Therefore, with a fixed FOV and

N

, BW improvement is not possible with ULA and URAs. This limitation arises since required FOV and BW values determine the size of the fully populated aperture, which may exceed practical limits. Furthermore, additional constraints, such as the physical size of elements and the mutual coupling, add complexity to the design process. There is currently a need for an efficient approach to design TX/RX arrays utilizing thinning, allowing larger apertures with fewer elements, without compromising the initial constraints significantly.

Without loss of generality, let’s assume that the maximum number of elements and the available physical antenna aperture are the only initial constraints, while all other parameters are subject to optimization. The type of radar scan, whether one-dimensional horizontal or a supporting two-dimensional elevation scan, determines the array dimension. Hardware limitations dictate the available number of array elements. Operational requirements may necessitate a minimum BW value for angular resolution. The operating frequency, preferred implementations, technology, and cost determine the element size requirements. Initial simulations for mutual couplings provide insights into the required minimum horizontal and vertical separation distances,

L_{m c, y}

, and

L_{m c, z}

to minimize these effects which are discussed in Section 4.2.ii. Physical and virtual element sharing from a previously designed array (or for a multi-mode radar) could enforce some positions as initial values for the optimization (See Table 3.)

In this initial step, the desired BW and uFOV values determine the minimum aperture length/size and the minimum inter-element spacing, respectively. Notably, at this step, there is no constraint for the element sizes to be smaller than the spacing values. This results in the largest possible grid spacing for the reference fully populated virtual array using (16), and (18) [42,43]. Reader can refer to the literature on various approaches in constructing of such virtual arrays [6,7]. The available number of TX and RX elements determines the targeted thinning ratio as discussed in (10). Initial element positions are enforced at the same grid space.

As an iterative process, a random or preferred search algorithm is performed to determine successful arrays based on PSLRs and BWs, ensuring that each candidate satisfies all constraints. The iteration terminates upon achieving the desired PSLR or reaching the maximum number of iterations. Additionally, the desired and constructing hyper-parameters can be optimized using an outer loop. While there are various approaches for improved convergence, including evolutionary algorithms and gradient descent-type analytical approaches [14], these will be explored in detail in future studies. Here, we propose a heuristic approach to illustrate rapid convergence to a satisfactory ‘local optimum’ array.

i.: Low Discrepancy (LD) Inter-Element Spacings:

A highly effective heuristic initialization approach ensures an even distribution of inter-element spacing values across the entire range, distinguishing itself from Uniform Linear Arrays (ULAs) and Uniform Rectangular Arrays (URAs). Unlike the repetitive patterns in ULAs and URAs that lead to distinct constructive and destructive interactions among radiations, sparse arrays intentionally disperse spacing distributions to effectively suppress grating lobes. The use of an initial value with a uniform distribution promotes fast convergence, especially beneficial for smaller sparsity values where the search domain size grows exponentially. This heuristic initialization approach results in a ‘good’ local array, directing the search path toward better candidates. In many instances, the optimum result is found in the vicinity of this initialization after just a few iterations.

To achieve a low PSLR, grating lobes must be spread outside the operational FOV. This sets the grid sizes according to (19) and Table 1 [44]. Subsequently, element positions are optimized for a reduced PSLR and the maximum allowable BW value(s). When the frequency of a specific inter-element spacing value is significantly larger than others, it can lead to a large side lobe with high in-phase contributions. To mitigate this, irregular spacing values (Table 3) can be employed to distribute large side lobes and grating lobes across the half-hemisphere. However, this may cause the overall rise in sidelobe levels due to the conservation of total radiated power. Grating lobe mitigation can be achieved by enforcing the Empirical Cumulative Distribution Function (ECDF),

F_{D} (d_{n})

, representing a smooth density, ideally a uniform density where the ECDF is a staircase function with a uniformly increasing steps,

F_{D} (d) = n / N

for

d_{n} \leq d < d_{n + 1}

, and

1 < n < N - 1, F_{D} (d) = 0

for

d < d_{1}

and

F_{D} (d) = 1

for

d_{N} \leq d

One method of initializing spacing values for low discrepancy is to force their ECDF to be linear, as proposed below.

A linear GSA with N elements has

(N - 1)

inter-element spacing values,

d_{n}

, which can be set to be empirically uniform.

d_{n} = d_{m i n} + (n - 1) Δ d f o r n = 1 \dots (N - 1)

(19)

where

d_{m i n}

is the minimum inter-element spacing, for

N \geq 3

Δ d = \frac{X_{m a x} - X_{m i n} - (N - 1) d_{m i n}}{\sum_{k = 1}^{N - 2} k}

(20)

and where N elements are located between

X_{m a x}

and

X_{m i n}

Let us begin by setting the reference grid space to

λ / 2

for a grating lobe-free pattern, disregarding the element size constraint at this stage. For

L_{λ} = 11

, and

N = 5

, we calculate

Δ d = 3 λ / 2

, and spacings are linearly increasing as given by

2 d_{n} / λ = {1, 4, 7, 10

}, yielding element positions

2 x_{n} / λ = {0, 1, 5, 12, 22}

for

X_{m i n} = 0

. This results a linear ECDF,

F_{D} (d_{n}) = (1 + d_{n} / λ) / 6

, ensuring that all positions fall within the reference grid space.

Next, using the same reference grid space, for an element size of

2 λ

to avoid any overlapp, we need

d_{m i n} = 2 λ

. Then, we calculate

Δ d = λ / 2

, and spacings linearly increase as

2 d_{n} / λ = {4, 5, 6, 7

}, yielding positions

2 x_{n} / λ = {0, 4, 9, 15, 22}

. This also results a linear ECDF,

F_{D} (d_{n}) = (- 3 + 2 d_{n} / λ) / 4

. No grating lobes are expected since the ECDF is smooth, and the positions are located on a uniform grid size of

λ / 2

. It is worth noting that a random shuffling of the spacing ordering will change the element positions but not the ECDF. Each alternative configuration will yield to a different signal-return pattern, requiring search iterations for the optimum spacing ordering for the best PSLR. Perturbing the spacing values during search iterations is another strategy.

Similar to the second example, let us now set

L_{λ} = 10

. Recalculating

Δ d = λ / 3

, spacings are given by

3 d_{n} / λ = {6, 7, 8, 9

} with element positions,

3 x_{n} / λ = {0, 6, 13, 21, 30}

, which do not coincide with the reference grid points. For a general sparse array there is no constraint on the element positions as proposed in Table 2. However, a ‘uniform’ sparse array (GSA), as defined in this paper, requires all its element positions to be in some uniform grid space. In this third example, we can change the reference grid size to

λ / 3

or move the elements to some neighboring grid points without causing any overlapping. Both approaches will provide the first group of initial array candidates for the optimization search. Element positions can be further perturbed to move around the neighboring grids, finding a better ‘local optimum’ PSLR value as described in Table 2. The ECDF for the optimum spacings is expected to be a smooth function with minimal repetitive spacing values to spread the grating lobes into side lobes. The ECDF is further examined in Section 5.3.

ii.: Sparse Arrays with Minimized Mutual Coupling:

The sparse array design procedure described above allows for flexible positioning of both TX and RX elements within a shared aperture, which is particularly advantageous for designing smaller BW. However, it is crucial to address potential challenges related to high mutual coupling between TX and RX groups. In cases where mutual coupling can significantly impact the system’s beamforming performance, it might be necessary to physically separate the two groups, allocating different sections of the aperture to each. This separation helps mitigate the negative effects of mutual coupling, ensuring optimal performance.

To study this scenario the beamforming equation (4) is modified to account for mutual coupling contributions

g (u, v) = \int_{S} C (x_{λ}, y_{λ}; u, v) r (x_{λ}, y_{λ}) \exp [j 2 π (x_{λ} u + y_{λ} v)] d x_{λ} d y_{λ},

(21)

and physical aperture sparsing can be done as in (10)

g_{s} = B_{s} C_{s} r_{s}

(22)

where

C_{s}

is the square mutual coupling matrix of size

P_{s}

. The optimization of sparse arrays can be further constrained by introducing a ‘forbidden zone’ that mandates a physical separation between TX and RX elements. This additional constraint simplifies (22) by assuming that the mutual couplings become negligible when distances between TX and RX elements exceed specific thresholds, denoted as

y_{m c}

, and

z_{m c}

for the horizontal and vertical dimensions, respectively. The ‘forbidden zone’ enforces a spatial segragation, mitigating mutual coupling effects and contributing to the overall optimization of the sparse array.

iii.: Efficient Design of Virtual Arrays:

The compensation for imperfections arising from mismatched antenna elements can be achieved through separate digital calibration for the TX and RX antenna groups, as discussed in [18]. However, mitigating the effects of transmitter-to-receiver coupling is a more intricate process, dependent not only on target variables but also on the field angle. In addressing this complex mutual coupling, a strategy involves physically separating the transmitter (TX) and receiver (RX) groups and implementing forbidden zones on the physical aperture. This approach minimizes mutual coupling issues but demands careful consideration during the sparse array design process. Further attention is required to avoid poor placement of transmitter and receiver elements, which could lead to aperture loss and potentially result in degradation of both PSLR and BW. Thus, a thorough understanding, and management of these factors are crucial for successful sparse array optimization.

Alternative approaches to defining forbidden zones for minimizing mutual coupling between the TX and RX elements are shown in Figure 7. In this illustration, a physical aperture of

40 λ \times 30 λ

and a uniform grid spacing of

λ / 2

are considered. Minimum inter-element distances between element groups are assumed to be

15 λ

, and

10 λ

along the azimuth and elevation, respectively. In the case of uniform arrays, the virtual aperture is created by doubling both the horizontal and vertical physical lengths, leading to a virtual aperture size four times that of the corresponding physical dimensions. All the array structures depicted in Figure 7 adopt a

40 λ 30 λ

configuration, and virtual apertures are anticipated to fall within an

80 λ 60 λ

maximum possible area. The effect of the forbidden zones is observed to create lost virtual apertures, as expected. Accounting for the physical element sizes to prevent overlapping renders certain positions unusable, leading to further aperture loss and beamwidth spreading, necessitating careful consideration.

Let us define the performance metrics for virtual aperture and BW efficiency.

Virtual Aperture Efficiency (

α_{a p}

α_{a p} = {(β_{v} A}_{p h y}) / A_{v r x}

(23)

where

A_{p h y}

and

A_{v r x}

represent the physical and virtual aperture sizes, respectively. The virtual aperture gain,

β_{v}

, takes values 2 and 4 for the 1D and 2D cases, respectively. The aperture loss factor,

α_{a p} \leq 1

assesses the efficiency of the aperture.

Beamwidth Spreading Factor (

α_{b w}

α_{b w} = {B W}_{o b s e r v e d, h p} / {B W}_{t h e o r y, h p}

(24)

where

{B W}_{o b s e r v e d, h p}

and

{B W}_{t h e o r y, h p}

denote the observed and theoretical half-power beamwidths, respectively. The beamwidth spreading factor (

α_{b w} \leq 1

) is calculated for both azimuth and elevation in Table 4 for each configuration in Figure 7. These metrics provide a quantitative evaluation of the performance of the sparse array, considering aperture loss and beamwidth spreading considerations.

The fully populated reference array is most efficient in creating the largest possible virtual aperture, providing a unity aperture loss factor. In theoretical considerations, standard ULA and URAs utilize TX and RX elements that can be co-located on a shared aperture, and their physical sizes are often ignored, as shown in Table 4 (a, b). However, in practice, this is not possible due to the physical sizes of the antenna elements.

Aperture loss factor as defined in (23), represents the ratio of the utilized virtual area to the maximum possible virtual area and gives unity for the reference URA. The available physical apertures is often divided into TX and RX sub-apertures to minimize their mutual couplings and to avoid overlapping. Different design rules for defining sub-apertures are illustrated in Table 4 (c – n ), providing a pool of positions for the algorithm given in Table 3. The efficiency of the improved four-corners case is further enhanced in Table 4 (m, n) compared to the four corners in Table 4 (g, h). Note that α_ap ≤ 1 decreases as the separation distance between the TX and the RX groups increases.

The half-power beamwidth (HPBW), as defined in (15) and (16), is a measure of the angular resolution that improves with larger aperture. Once again, the reference URA array provides the smallest value. The HPBW spreading factors,

α_{ϕ} \geq 1

, and

α_{θ} \geq 1

, are defined as the ratio between the observed HPBW and the minimum possible value given by the reference URA. The improved four-corners approach yields the best overall results for the aperture loss and the beamwidth loss factors compared to the given alternative approaches listed in Table 4. As part of future work, other alternative design approaches for achieving better performance metrics will be studied.

Thinning of arrays is widely recognized for its capacity to achieve superior angular resolution, even though it is acknowledged to lead to higher peak-to-sidelobe ratio (PSLR) values [41]. This characteristic is also evident in sparse arrays, as discussed in Section (4.1.iii), particularly when the sparsity ratio is small. Nonetheless, it is important that PSLR experiences a 5 dB reduction when the sparsity ratio falls within the range of 60 to 90 percent. This observation suggests that PSLR reduction is possible for dense arrays, as indicated by the dip in PSLR in the lower left secton of Figure 8.

4.3. Multi-Objective Optimization of Sparse Arrays Using the Desirability Function

The Desirability Function (DF) is a valuable technique in optimization, especially when dealing with multiple conflicting objectives. It enables the combination of various objectives into a single composite desirability value, allowing for the identification of solutions that are optimal for all objectives simultaneously.

The DF evaluates and assigns a score to each response based on how well it aligns with the desired target. The simplest form of the desirability function is linear, providing a score to each response based on its distance from the target value. However, more complex forms of the desirability function can capture nonlinear relationships between the objectives, offering a more nuanced evaluation of the optimization process [14].

While the algorithm proposed in Section 4.1 focuses on improving a single parameter, as illustrated for the PSLR in Table 3, real-world antenna design often involves multiple conflicting requirements. Enhancing one parameter may adversely affect others, for example, achieving a low PSLR with an excessively wide beamwidth. To address this, the Desirability Function proves beneficial by enabling the simultaneous optimization of multiple constraints [14]. Below, the one-sided DF is illustrated for three parameters: PSLR, and beamwidths along both the azimuth and elevation.

D_{O} = {(\prod_{i = 1}^{N} d_{i})}^{1 / γ_{0}},

(25)

d_{v}^{+} = \{\begin{matrix} 0 & v \leq v_{m i n} \\ {[\frac{v - v_{m i n}}{v_{d e s i r e d} - v_{m i n}}]}^{γ_{v}} & v_{m i n} \leq v \leq v_{d e s i r e d} \\ 1 & v_{d e s i r e d} \leq v \end{matrix},

(26)

d_{v}^{-} = 1 - d_{v}^{+} D_{O} = {(\prod_{i = 1}^{N} d_{i})}^{1 / γ_{0}},

(27)

where

D_{O}

is the overall desirability function for N observing parameters,

γ_{v}

, and

γ_{0} = \sum γ_{i}

are individual and overall geometrical weight coefficients for the desirability functions,

d_{v}

, and

D_{0}

, respectively for the parameter

v

where

d_{v}^{+}

, and

d_{v}^{-}

, promotes larger and smaller values respectively and where

v

v_{m i n}

, and

v_{d e s i r e d}

are the observed, minimum acceptable value and the desired value for some variable v.

For the case studied here, smaller PSLR and BW values are preferred. Consequently,

d_{P S L R}^{-}

d_{B W, ϕ}^{-}

, and

d_{B W, θ}^{-}

are the selected smaller-the-better (STB) desirability functions for the PSLR, azimuth BW, and elevation BW, respectively. Thus, the overall desirability function becomes

D_{O} = {(d_{P S L R}^{-} d_{B W, ϕ}^{-} d_{B W, θ}^{-})}^{1 / (γ_{P S L R} + γ_{B W, ϕ} + γ_{B W, θ})} .

(28)

It is evident that

0 \leq D_{O} \leq 1

holds since the inequalities

0 \leq d_{i} \leq 1

hold for each

d_{i}, (i = 1, 2, \dots N)

. One may assign equal weights to all three variables by setting

γ_{P S L R} = γ_{B W, ϕ} = γ_{B W, θ} = 1

. Alternatively, for a different emphasis, one can prioritize PSLR over beamwidth along the azimuth and the elevation, with

γ_{P S L R} = 2

γ_{B W, ϕ} = 1

, and

γ_{B W, θ} = 0.5

. Similar to (25 – 28), the LTB-DF can be constructed using the sigmoid function as illustrated in Figure 9 (a) where

d_{v}^{+} = S (x)

S (x) = 1 / (1 + e^{- x})

x = 10 \frac{v - v_{m}}{v_{e}}

v_{e} = v_{m a x} - v_{m i n}

and

v_{m} = {(v}_{m a x} + v_{m i n}) / 2

Equation (25) provides a valuable variable, the desirability function (DF), for multi-objective optimization, serving as a metric to be monitored throughout the optimization process to identify the ‘best’ antenna array. The procedure proposed in Table 3 can be adapted for any number of objectives simply by substituting

D_{b e s t}

in place of

P S L R_{b e s t}

4.4. Machine Learning for Dynamic Setting of Hyperparameters

In optimization, defining an accurate desirability function (DF) requires prior knowledge of trade-off parameter ranges and preference parameters, such as hyperparameters

v_{m i n}

, and

v_{d e s i r e d}

for each variable. The accuracy of this information significantly impacts optimization performance, and convergence may be hindered if the target bounds are incorrectly defined. Initialization of the DF plays a crucial role in the convergence rate, and designing an effective DF can be a time-consuming process.

A practical approach proposed in [14] for determining an adaptive desirability function (ADF) can be applied here. In this context, a machine learning approach is proposed, utilizing the adaptive desirability function (ADF) given below to ensure consistent progress during optimization without requiring prior knowledge. The one-sided larger-the-better (LTB) DF, DF,

d_{v}^{+} (k + 1)

, for the

(k + 1)

’th iteration is given by

d_{v}^{+} (k + 1) = S (10 \frac{v (k + 1) - v_{m} (k)}{v_{e} (k)}),

(29)

where

v_{e}

v_{m}

and S are defined earlier, and the desired parameter range is continuously updated using the most recent observations,

v_{m i n} (k) = \min \{v_{m i n} (j)\}, f o r k - 10 \leq j \leq k - 1,

(30)

v_{d e s i r e d} (k) = \max \{v_{d e s i r e d} (j)\}, f o r k - 10 \leq j \leq k - 1 .

(31)

4.5. Disadvantages of Sparse Arrays

The optimum sparse array design of Section 4.2, as illustrated in Figure 5, suggests uniformly distributed inter-element spacings, effectively attenuating and spreading the grating lobes into side lobes. Consequently, sparse arrays can provide solutions with no grating lobes. However, this comes at the cost of spreading the grating lobe power across the uFOV, leading to increased side lobe levels and reduced PSLR. This effect becomes more pronounced, especially for wider uFOV and smaller thinning ratios, as depicted in Figure 9. In general, sparse arrays often require effective specialized processing techniques to mitigate the reduction in PSLR, particularly in the multi-target scenarios. Various practical approaches addressing this challenge are readily available [24,45,46].

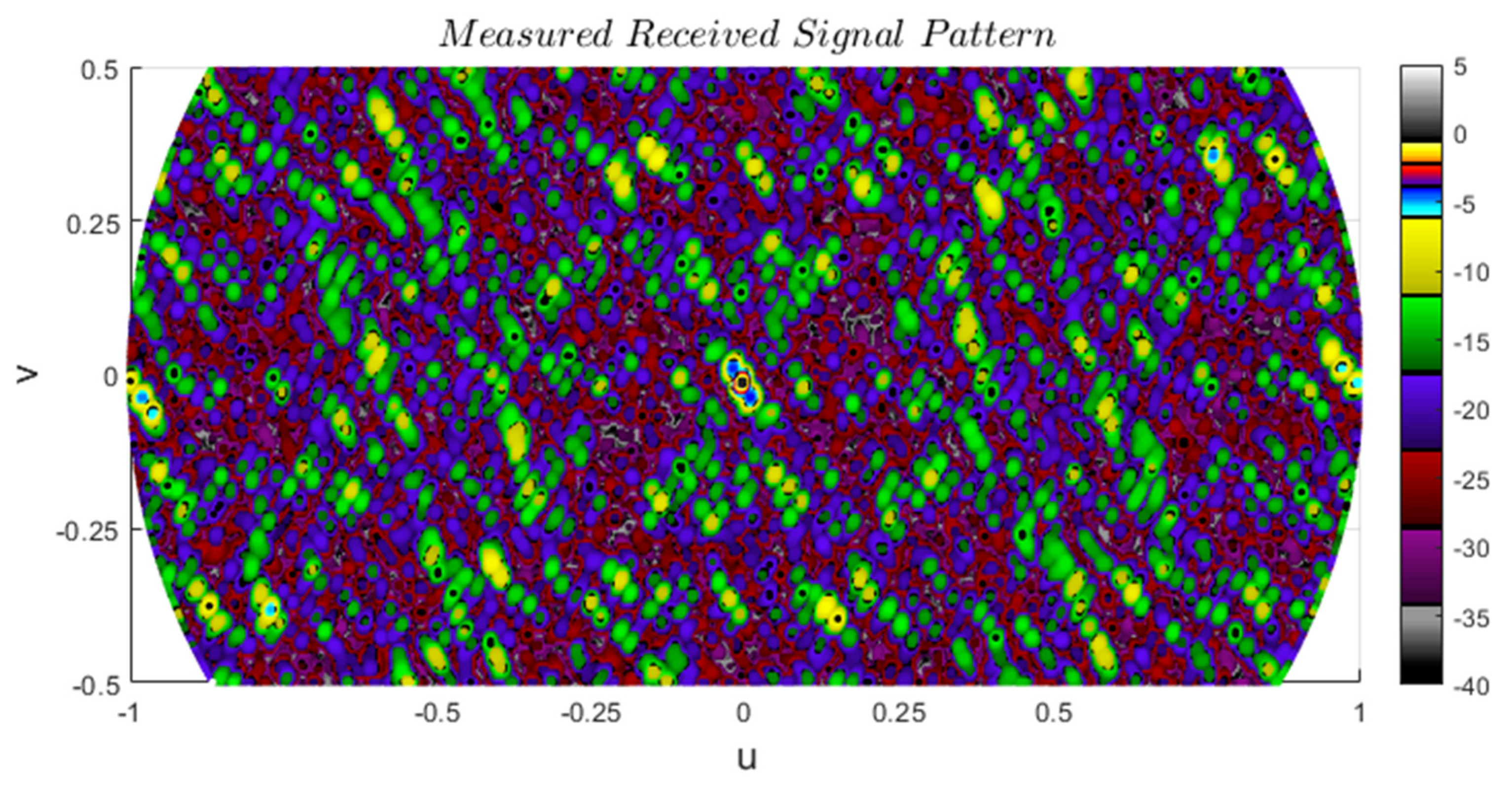
5. Results

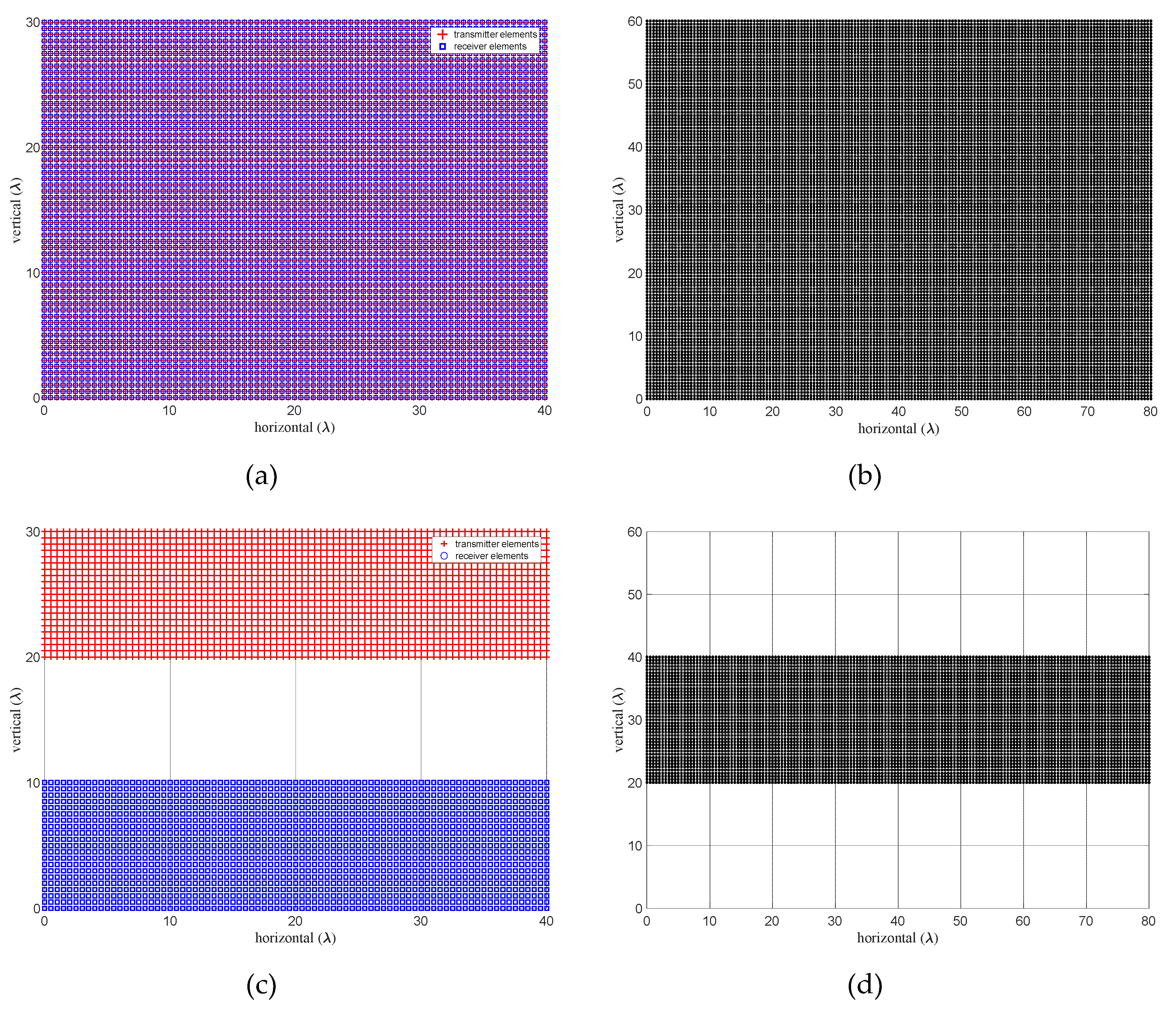
5.1. Fully Populated Uniform Arrays:

Grating lobes, uFOV and BW are examined in Figure 10. The received signal patterns illustrate the number of VRXs, inter-element spacings, aperture lengths, uFOV, and BW for the cases (a) 121, λ/2, 60λ, 180^o, 0.3875, (b) 121, λ, 120λ, 90^o, 0.1937, and (c) 61, λ, 60λ, 90^o, 0.4039, respectively. The inverse proportionality between BW and

L_{λ}

, as suggested by (15) and (16), holds true. Additionally, for

d_{λ} \geq 1 / 2

, grating lobe angles, and uFOV angles demonstrate an inverse proportionality, as indicated by (17) and (18). It is noteworthy that PSLR remains approximately constant for these cases. To simultaneously improve uFOV and BW, an increase in the number of elements is necessary, with only one degree of freedom.

The target signal return pattern is observed to shift without any distortion in the

(u, v)

plane, as shown in Figure 11 (a) and (b), where the signal is hard-limited from below to –70 dB for enhanced visual clarity. This underscores the primary reason for the preference of the

(u, v)

plane over the

(ϕ, θ)

, particularly when evaluating side lobes arising from distinct targets in a multi-target scenario.

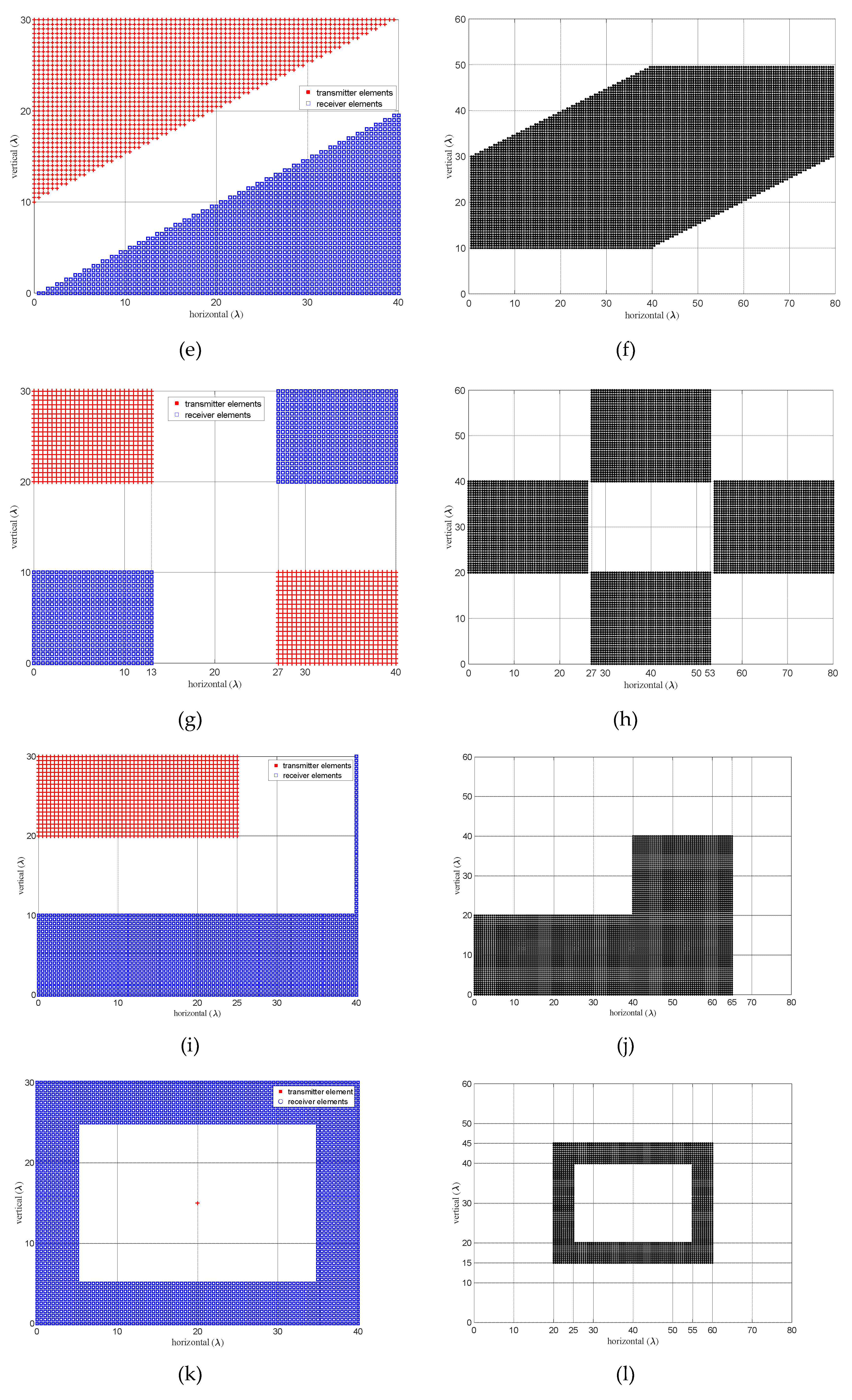
5.2. Grid-Based Sparse Arrays (GSA) with Large Antenna Elements

Here are some numerical results illustrating GSAs with no grating lobes, optimized with or without mutual coupling forbidden zones. For the optimization, A version’s 12 RXs and B version’s 8 RX positions are enforced as the initial condition. The physical aperture size is limited to

35 λ \times 35 λ

, and element sizes are

5 λ \times 2 λ

for the so-called Ankara–1 array and their versions A and B introduced in the next subsection.

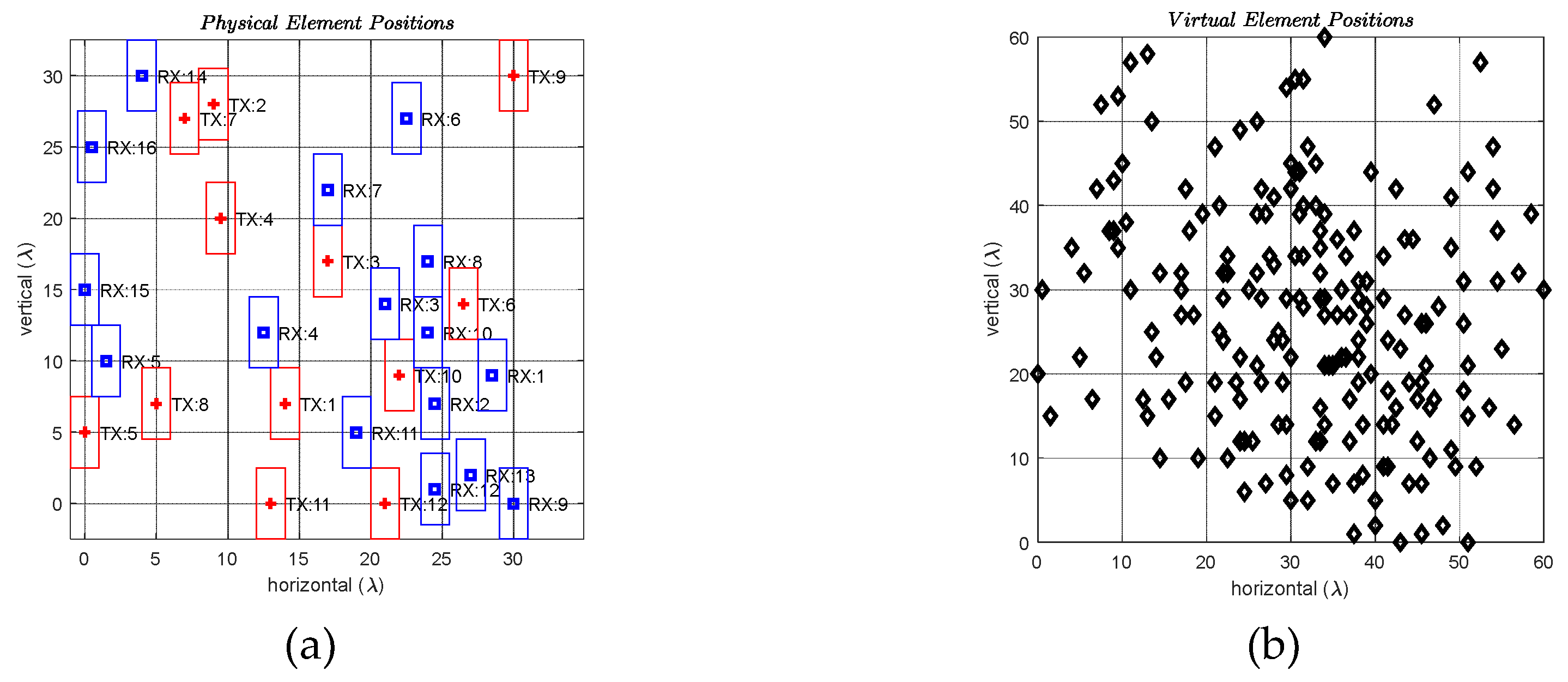
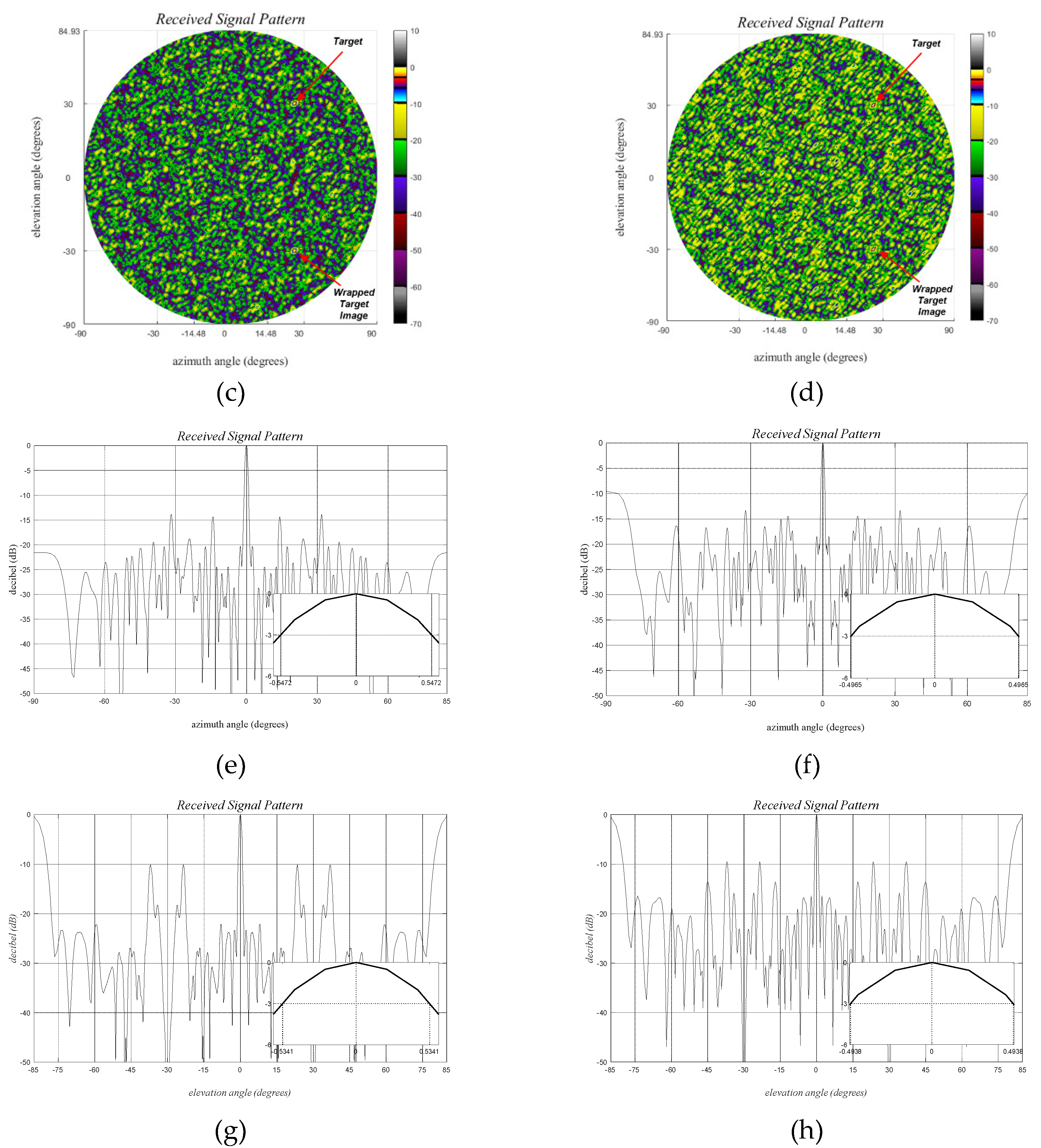
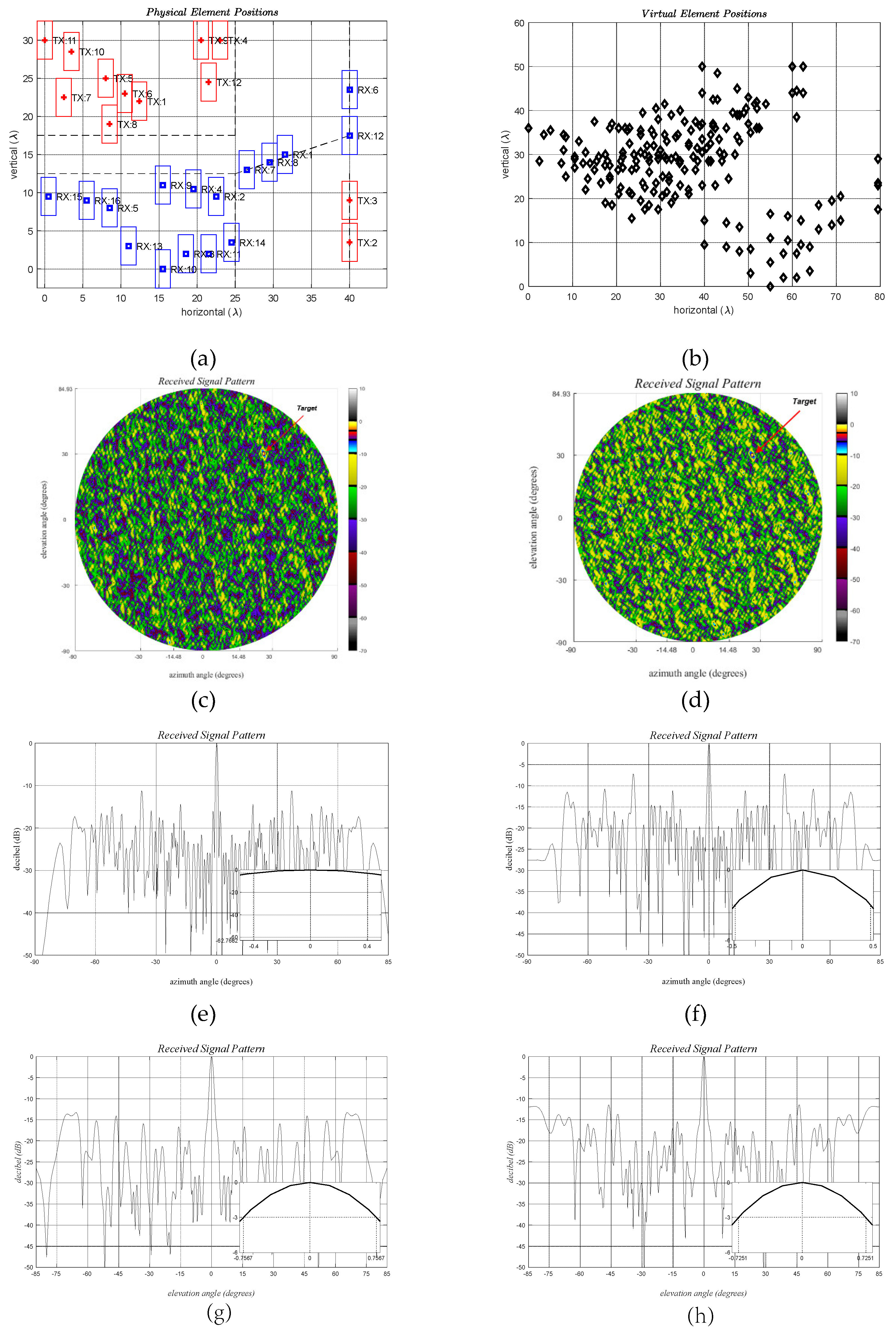
i.: GSA with no Forbidden Zones: Ankara–1 A & B Arrays

Ankara–1 A and B arrays represent the first two examples of GSA with no forbidden zones. Versions A and B have 16 and 8 RXs, respectively. Version A is enforced to use B’s 8 RXs and 12 TXs, and its remaining 8 RXs (the first 8) are optimized separately.

Sparse Ankara A and B GSAs are configured on a reference grid with dimensions

λ / 2 \times λ

, employing physical element sizes of

2 λ \times 5 λ

, ensuring freedom from grating lobes exclusively along the horizontal do not have forbidden zones as illustrated in Figure 12 (a, b). A total of 12 TX and 16 RX elements share a common usable aperture of

30 λ 30 λ

, with non-overlapping elements of size

5 λ 2 λ

, where the usable aperture refers to the available region for the element centers. The optimization outlined in Table 3 is performed in two stages. Initially, it is applied to Version B for 12 TX and 8 RX positions. Subsequently, a second run is conducted to calculate the remaining 8 RXs for Version A, using same TX positions.

The received signal pattern for a single target in the direction

(ϕ_{t}, θ_{t}) = ({30^{0}, 30}^{0})

is depicted in Figure 12 (c, d), while the broadside for the azimuth and elevation cross-sections presented in Figure 12 (e – h). Notably, no observed horizontal grating lobe is present, given that

d_{x} = λ / 2

. However, a target at an elevation angle

30^{0}

, situated located at the elevation uFOV edge, generates its image at

{- 30}^{0}

, consistent with the expectations outlined in Table 2. PSLR is noted to be below – 10 dB and – 8 dB within the uFOV for Version A and B, respectively, in accordance with the optimization hyperparameter.

The maximum PSLR values for arrays A and B are 11.23 dB, 8.64 dB, respectively. The azimuth and elevation HPBW values are [1.1⁰, 1.1⁰], [1.0⁰, 1.0⁰], respectively.

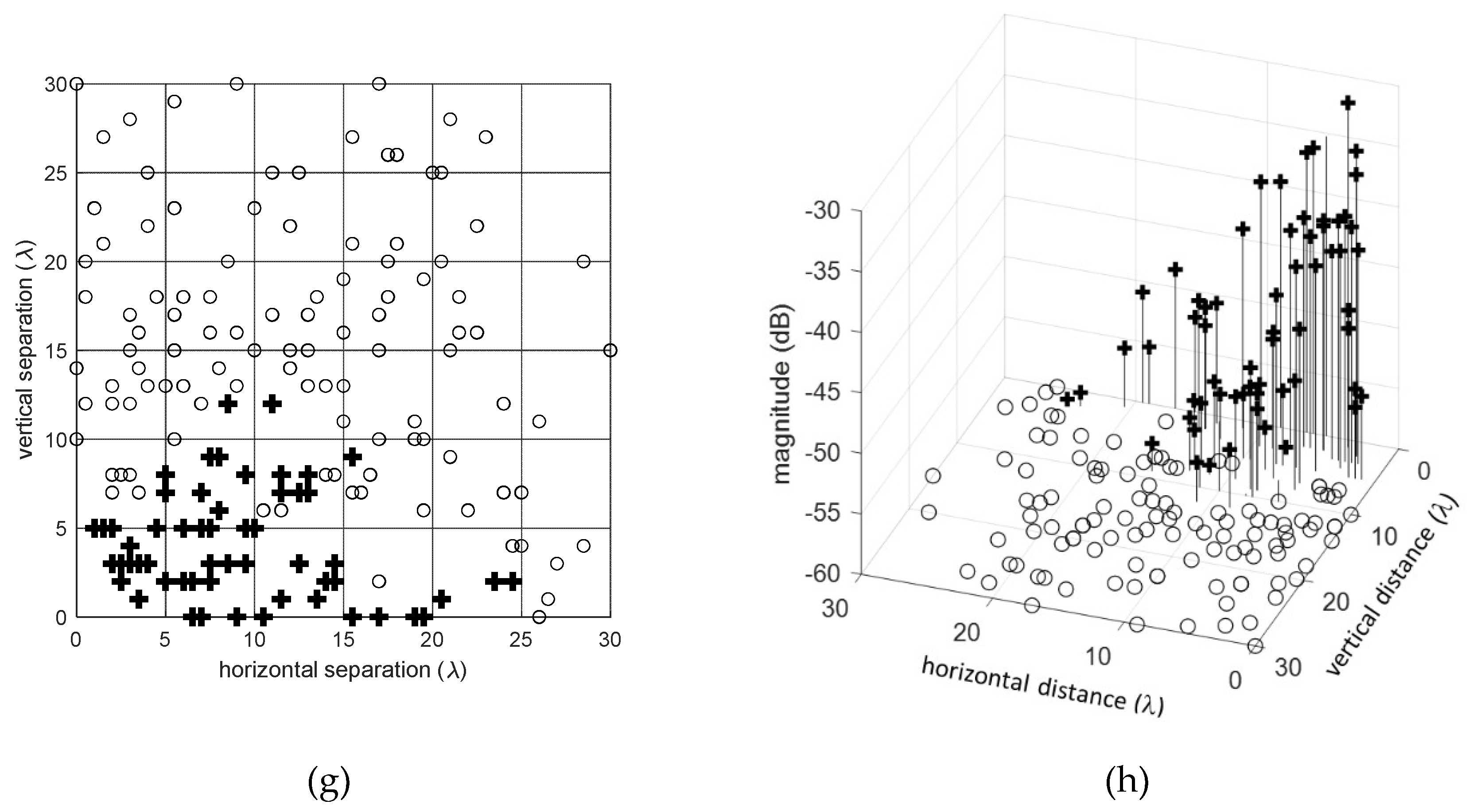
ii.: Inter-Element Mutual Coupling for Sparse Ankara-1 Array:

Inter-element mutual coupling within an antenna array is significantly influenced by the specific positions of both transmitters (TXs) and receivers (RXs). For elements of the same type, compensations are primarily achievable through laboratory measurements and signal calibration. However, coupling among those two groups strongly depends on the environment and the target angles. The simulated results for Ankara array shown in Table 5. The coupling values, denoted by K, range from–116.2 dB to –36.3 dB. The physical positions of the array elements are shown in Figure 12 (a), while coupling values are illustrated in Figure 13. Values smaller than –60 dB are ignored here due to the presence of background spurious imperfections at that level. The maximum and minimum coupling values, –36.3 dB and –116.2 dB, correspond to the coupling between the couples TX-7

(22 λ, 9 λ) :

RX-11

(28.5 λ, 9 λ)

and TX-1

(30 λ, 30 λ)

: RX-15

(24.5 λ, λ)

with separation distances

6.5 λ

and

29.5 λ

, respectively. Notably, the minimum horizontal and vertical distances of

15 λ

and

10 λ

between the element centers emerge as preferable separation distances for minimizing mutual coupling. This constraint will be rigorously applied in the subsequent section.

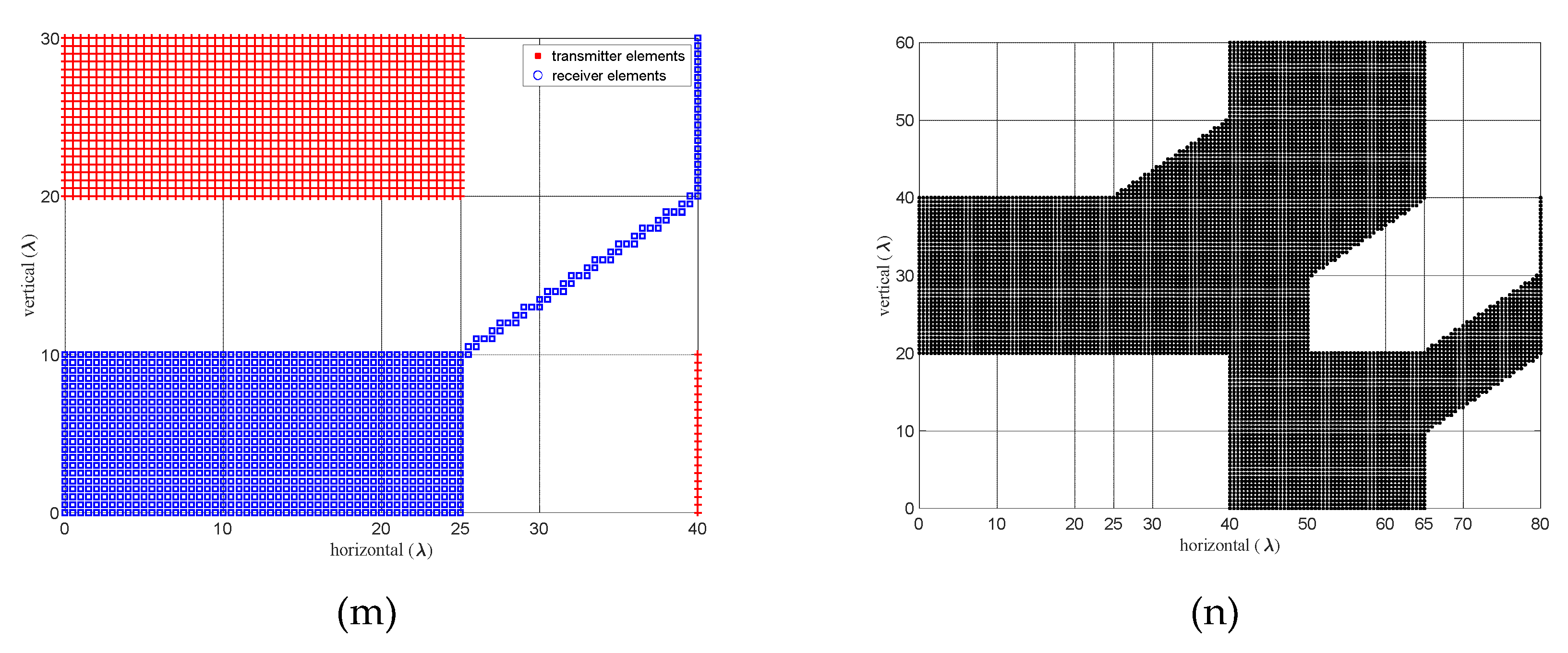
ii.: GSA with Forbidden Zones: Ankara–2 A & B Arrays

This section demonstrates the application of the improved four-corners approach proposed in Figure 7 (m and n) to the design of Ankara–2 arrays. To minimize coupling effects, forbidden distances of

y_{m c} = 10 λ

, and

z_{m c} = 15 λ

are enforced. Elements and physical sizes in versions A and B remain identical to Ankara–1 GSAs, offering improved array aperture and BW spreading efficiency as defined in equations (23) and (24).

The Ankara–2 GSAs are designed on a reference grid with dimensions

λ / 2 \times λ / 2

, utilizing physical element sizes of

2 λ \times 5 λ

. The design ensures grating lobe-free operation both horizontally and vertically, as illustrated in Figure 14 (c – h). The minimum PSLR values are observed to be 11.10 dB, and 9.14 dB. The azimuth and elevation HPBW values are

[{0.8}^{o}, {1.5}^{o}]

[{1.0}^{o}, {1.45}^{o}]

for A and B arrays, respectively.

The measured maximum PSLR outside of the main beam aligns the simulated results, revealing reduced sidelobes attributed to the directivity of radar elements contributing to MIMO directivity. The measured BW is around 0.32 degrees, and a secondary wider main lobe within (–10 dB, –6 dB) range extends to approximately 0.72 degrees. This two-tiered main lobe structure is clearly formed by the two separate grouping of the virtual array structure, as illustrated in Figure 14 (b).

The captured radar data for the received signal at the Doppler filter output for Ankara–2A is used to calculate the angle beamformer output presented in Figure 15 as a function of

[u, v]

. The angle values

(ϕ, θ)

corresponding to the

[u, v]

values can be calculated using

(u, v) = (\sin ϕ \sin θ, \cos θ)

, where the values

[0, 0.25, 0.5, 1.0]

correspond to the angles

({0, 14.48}^{o}, 60^{o}, 90^{o})

Table 6. Performance Parameter Values for Example GSAs.

	Ankara–1		Ankara–2
	A	B	A	B
PSLR (dB)	11.23	8.64	11.10	9.14
BW-azimuth (deg)	0.55	0.53	0.4	0.5
BW-elevation (deg)	0.49	0.5	0.76	0.73
# of elements (TX, RX)	12, 16	12, 8	12, 16	12, 8
# of VRX’s (generated, unique)	192, 192	96, 96	192, 190	96, 96
Thinning ratio (%)	2.6	1.3	1.09	0.68
uFOV (deg)	180	60	180	180
Reference URA size	121 $\times$ 61		156 $\times$ 112	130 $\times$ 109
# reference URA elements	7,381		17,472	14,170
Reference grid size $(λ)$	0.5, 1.0		0.5, 0.5
Physical aperture size $(λ)$	32 $\times$ 35		41.5 $\times$ 34

The novel GSA design approach outlined in Section 4 offers effective array solutions with improved FOV and BW, especially for low number of elements. Ankara arrays enable the utilization of large element sizes, ensuring that the received signal patterns are grating lobe-free along any desired axis. The results demonstrate that achieving PSLR values greater than 11 dB and BW less than 0.5 degrees is possible with only

N_{t x} = 12

N_{r x} = 16

, and

N_{v r x} = 192

. Additional measured performance values are provided in Table 4.

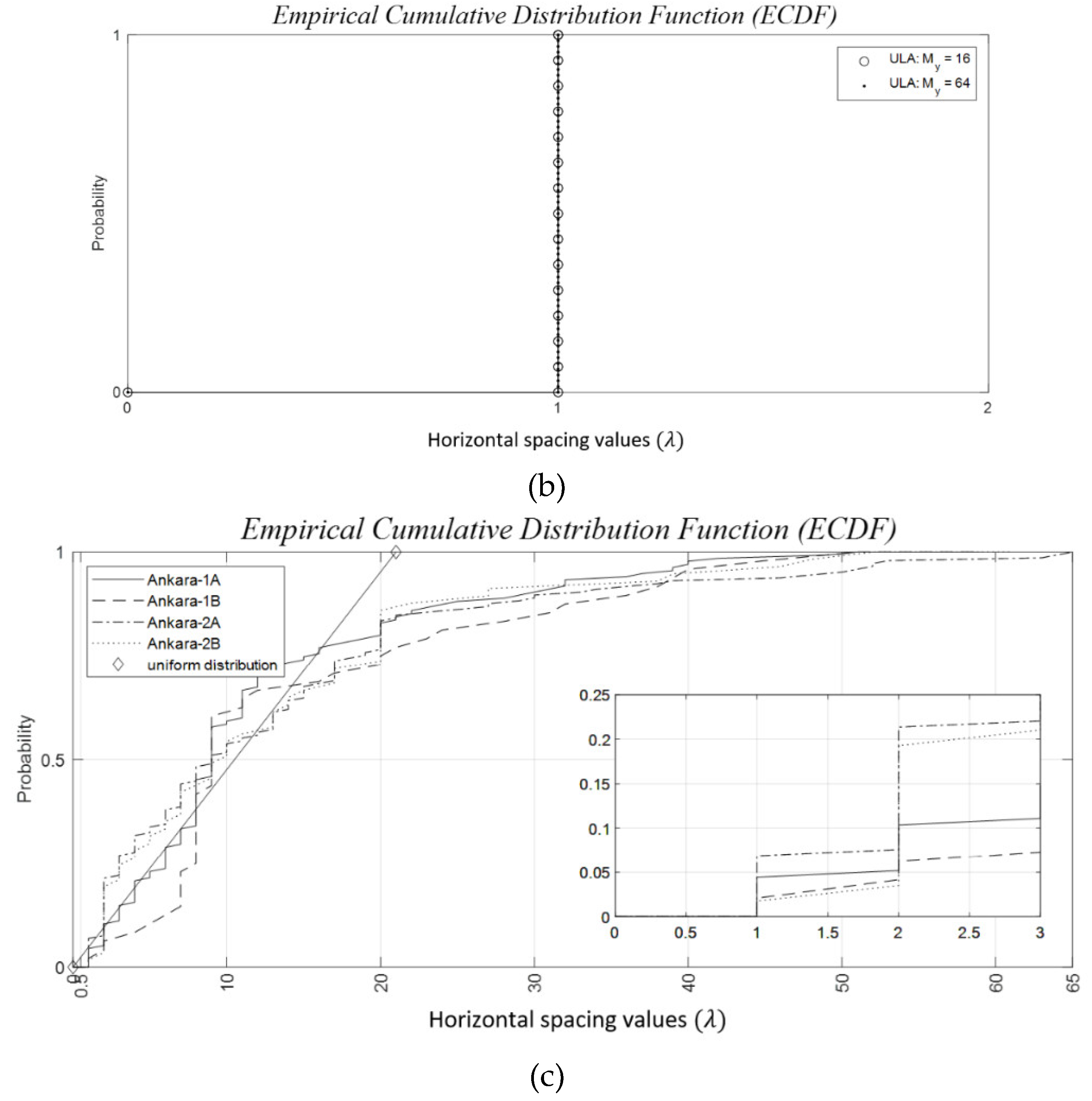
5.3. The Empirical Cumulative Distribution Functions (ECDF) for the Inter-Element Spacings

The inter-element spacings for ULAs are constant as depicted in Figure 16 (a) for both N = 16 and 64. The staircase function ECDF, as defined in Section 4.2.i, simplifies to a single step function due to constant spacing value of

d_{λ} = 1

creating grating lobes. In the case of the grid-based sparse Ankara arrays with versions A and B, illustrated in Figure 16 (b), the minimum spacing for each vertical is also

d_{λ} = 1

. This is because the closest possible distance between two elements is constrained by the width of

λ

. It is worth noting that antenna elements are freely positioned within the

λ / 2

grid space avoiding the grating lobes.

To ensure grating lobe-free operation, these spacings need to be

λ / 2

or smaller. However, when the physical size of elements and so the spacings exceed this value, the received signal pattern for ULAs becomes the sum of all image replicas for each real-valued grating lobe angle at

asin (n / 2 w

shifted along the azimuth. Similarly, for URAs, additional replica images will be added for each real-valued grating lobe at

asin (n / 2 h)

shifted along the elevation, as discussed in (17). Additionally, avoiding large side lobes is only possible if the sparse array has irregular spacing values. Irregular spacing occurs when the Empirical Cumulative Distribution Function (ECDF) lacks substantial increments in large values, and the step-increment values are relatively uniform, as shown in Figure 16 (b).

6. Conclusions

This study introduces a comprehensive design and optimization approach for sparse arrays, particularly emphasizing grid-based antenna element configurations. The proposed methodology addresses multi-objective optimization, considering higher PSLR, smaller BW, the challenge of utilization of larger antenna elements causing grating lobes, and the critical issue of minimizing mutual couplings.

By defining grid-based sparse arrays, the study presents a systematic design framework that considers the trade-offs associated with peak sidelobe ratio (PSLR), beamwidth (BW), and mutual coupling. The proposed approach offers flexibility in positioning transmitter (TX) and receiver (RX) elements within a shared aperture, enabling the creation of virtual apertures with enhanced beamforming performance.

Multi-objective optimization is a key focus, allowing for the simultaneous consideration of conflicting objectives. The Desirability Function (DF) is introduced as an effective tool to balance multiple constraints, providing valuable insights for researchers and engineers working on sparse array applications. Furthermore, the study acknowledges challenges related to antenna elements exceeding sizes and creating grating lobes. The optimization process takes these challenges into account, ensuring that the resulting sparse arrays meet specific design requirements, particularly for smaller bandwidths.

A significant aspect of the proposed methodology is its capability to minimize mutual couplings between TX and RX groups. By introducing forbidden zones based on separation distances, the study encourages the physical separation of these groups, mitigating potential negative effects on beamforming performance.

In conclusion, this study offers a holistic approach to sparse array design and optimization, addressing various challenges associated with PSLR, BW, grating lobes, and mutual couplings. The presented framework provides a valuable foundation for advancing sparse array applications in diverse domains.

Patents

Related patents resulting from this work reported in [42,43,44,45].

Author Contributions

Conceptualization, methodology, software, G.T.; validation, G.T., S.R.; formal analysis, investigation, G.T.; resources, P.F.D.; data curation, writing—original draft preparation, G.T.; writing—review and editing, P.F.D., P.D.; visualization, G.T., S.R., P.F.D.; supervision, C.D., M.A., P.F.D.; project administration, funding acquisition, P.F.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Multicoreware Inc., San Jose, in the form of a grant to the University of Victoria grant number 50566-52200, and is conducted at the Department of Electrical and Computer Engineering, University of Victoria, and INNOVTECH, Victoria, BC.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Please see the link for the digital copies of figures, data and related code scripts, Figure 1 through 16. Folder: Data-Sensors

https://drive.google.com/drive/u/0/folders/1xSsMqpVWtbVMm7yAhre5kvWA2xMJ3bz2

Acknowledgments

The authors would like to express their appreciation to Lun Chen for his contribution in capturing radar data used in Figure 14. The authors also express their appreciation to Curtis Davis for his unwavering dedication to advancing next-generation algorithms for improved angular resolution. Curtis Davis was instrumental in envisioning the symmetric four-corner approach summarized in Section 4.2.ii. Unfortunately, he passed away before the publication of his work, and his contributions are remembered with deep respect.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

In this appendix we present the formulation of the MIMO radar system model, incorporating its radiation and receiving mechanisms generalized for sparse arrays—a fundamental step often overlooked in the literature.

A.1. A Radiating Antenna Aperture

Let us examine a radiating planar aperture where the radiated signal strength is proportional to the surface integral across the aperture of the current at each point weighted by a phase factor (with reference to the origin) that is a function of the position in the aperture and the field point for which the response is to be calculated. If the current distribution is

r (y, z)

then the relative gain in the field point

(x, y, z)

is given by [47] (Figure 2)

s (R, ϕ, θ; t) = \int_{S} A r_{c} (y^{'}, z^{'}; t) e^{j β_{r} (y^{'}, z^{'}; t)} e^{- j \bar{k} \bar{R}} d y^{'} d z^{'}

(A.1)

where S represents the planar antenna aperture, A is the scaling constant,

r_{c}

is the excitation current,

r_{c} (y^{'}, z^{'}; t) = |r (y^{'}, z^{'}; t)| e^{j β_{r} (y^{'}, z^{'}; t)}

with a phase

β_{r}

with respect to the origin,

(x^{'} = 0, y^{'}, z^{'})

are the primed Cartesian (source) coordinates. The unprimed spherical (field) coordinates are

(R, ϕ, θ)

\bar{k}

is the wave vector where

k = | \bar{k} | = | k {\hat{a}}_{R} | = 2 π / λ_{0} = (2 π f_{0}) / c

λ_{o}

and

f_{0}

are the wavelength and the center frequency for the narrow band transmission respectively,

{\hat{a}}_{R}

is the radial unit vector in the direction of

(ϕ, θ)

, (

•)

is the scalar (dot) product operator,

\bar{R}

is the one way source to the field point displacement vector [48].

For field points in the far field the vectors

\bar{k}

and

\bar{R}

are approximately parallel (Figure 2)

\bar{k} • \bar{R} ≅ R + y^{'} \sin ϕ \sin θ + z^{'} \cos θ,

(A.2)

and the radiated signal with respect to the reference phase

β (t)

at the origin (1) simplifies to

s (ϕ, θ) = \int_{S} r_{c} (x^{'}, y^{'}) e^{- j k (y^{'} \sin ϕ \sin θ + z^{'} \cos θ)} d y^{'} d z^{'}

(A.3)

where the scaling factor is ignored. The above integral becomes

s (u, v) = \int_{S} r_{c} (x, z) e^{- j k (y^{'} u + z^{'} v)} d y^{'} d z^{'}

(A.4)

where

(u, v) = (\sin ϕ \sin θ, \cos θ)

. Note that

s

is the inverse Fourier transform of the aperture distribution

r

, and r is the Fourier transform of the broadside pattern

s

where this pattern is defined only for the real angles for which

u^{2} + v^{2} < 1 .

For a single infinitesimal current element at an arbitrary location

(x_{s}, y_{s})

on the aperture

r_{c} (y^{'}, z^{'}) = r_{0} δ (y^{'} - y_{s}, z^{'} - z_{s}),

(A.5)

the radiated field simplifies to

s (u, v) = r_{o} e^{- j k (y_{s} u + z_{s} v)}

(A.6)

where the current source amplitude directly contributes to the field with its propagation delay.

Let us assume a rectangular aperture defined by

0 < y < Y_{m a x},

and

0 < z < Z_{m a x}

, and uniform spatial samples are at the source points

(m d_{y}, n d_{z})

for

m = 0, 1, 2, \dots (M - 1)

, and

n = 0, 1, 2 \dots (N - 1)

, and

Y_{m a x} = (M - 1) d_{y}

and

Z_{m a x} = (N - 1) d_{z}

, and

d_{y}

and

d_{z}

are the horizontal and vertical sampling intervals (Figure 3). The infinitesimal currents are located on the rectangular

[M \times N]

grid points

r_{c} (y^{'}, z^{'}) = r_{c} (m, n) δ (y^{'} - m d_{y}, z^{'} - n d_{z}), f o r 0 < m < M - 1, 0 < n < N - 1 .

(A.7)

The superposition of individual contributions is accurate if mutual coupling between the source elements is ignored the radiated field can be calculated as follows,

s (u, v) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} r_{c} (m, n) e^{- j 2 π (m d_{λ, y} u + n d_{λ, z} v)}

(A.8)

where

d_{λ, y} = d_{y} / λ

, and

d_{λ, z} = d_{z} / λ

, and,

r_{c} (m, n)

, are the identical isotropic current elements on the radiating aperture.

A.2. A Receiving Sparse MIMO Antenna Array

For a single-input single-output (SISO) radar the induced current at the receiver, r, due to multiple targets can be assumed to be in the form (A.1)

s (u, v) = r_{o} e^{- j k (y_{s} u + z_{s} v)}

(A.9)

where A is the two-way spread factor,

σ_{c, t} {= σ}_{t} e^{{j γ}_{t}}

is the complex-valued skin return with real-valued radar cross section

σ_{t}

and the phase return

γ_{t}

for the t’th target at the field coordinates

(ϕ_{t}, θ_{t})

f_{t x}

and

f_{r x}

are the newly introduced antenna patterns for the transmitting and receiving elements,

{\bar{R}}_{t x}

and

{\bar{R}}_{r x}

are the exact transmitter to target and target to receiver displacement vectors forming the two-way propagation path, respectively and other parameters are defined in (A.1).

Ignoring common scaling terms, the received signal in the far field with respect to the reference phase

β (t)

at the origin (A.9) can be simplified similar to (A.8)

\begin{array}{l} r_{r x} (p) & = r_{p} (y_{v r x}^{p}, z_{v r x}^{p}) for p = 1, 2, \dots P, \\ = r (y_{t x}^{i}, z_{t x}^{i}; y_{r x}^{j}, z_{r x}^{j}) \\ = \sum_{t = 1}^{T} σ_{c, t} f_{t x} (ϕ_{t}, θ_{t}) f_{r x} (ϕ_{t}, θ_{t}) e^{j k (y_{v r x}^{p} \sin ϕ_{t} \sin θ_{t} + z_{v r x}^{p} \cos θ_{t})} \end{array}

(A.10)

where

r_{r x}

is the received signal at the j’th RX due to the i’th transmitted signal for the p’th of P VRXs where

y_{v r x}^{p} = y_{t x}^{i} + y_{r x}^{j}

z_{v r x}^{p} = z_{t x}^{i} + z_{r x}^{j}

are the coordinates of the p’th sum VRX created by the i’th RX and j’th TX couple located at the points

(y_{t x}^{i}, z_{t x}^{i})

and

(y_{r x}^{j}, z_{r x}^{j})

for

1 \leq i \leq M

and

1 \leq j \leq N

as illustrated in Figure 3. In this fully populated uniform rectangular array (URA) all possible TX-RX couples create

M N

virtual elements located over a virtual aperture of

{2 Y}_{m a x} \times {2 Z}_{m a x}

where a sorted list for those couples

(m, n)

can be created using an order number

p

where

1 \leq p \leq P = M N

, and each

p

corresponds to a single

(m, n)

pair where some overlapping might occur.

Assuming antenna elements located at the reference grid points as defined in (A.7) (A.10) can be simplified to yield the received signal at the p’th VRX on the virtual aperture

r_{r x} (p) = \sum_{t = 1}^{T} σ_{c, t} f_{t x} (u_{t}, v_{t}) f_{r x} (u_{t}, v_{t}) e^{j 2 π (m d_{λ, y} u_{t} + n d_{λ, z} v_{t})}

(A.11)

for

p = 1, 2, \dots P = M N,

for

m = 0, 1, 2, \dots M - 1,

and for

n = 0, 1, 2, \dots N - 1,

and where

(u_{t}, v_{t}) = (\sin ϕ_{t} \sin θ_{t}, {\cos θ}_{t})

. Note that for

d_{λ, y} = d_{λ, z} = 1 / 2

(A.8) and (A.11) carry the exponential coefficients for the Fourier and the inverse Fourier transforms.

The appendix is an optional section that can contain details and data supplemental to the main text—for example, explanations of experimental details that would disrupt the flow of the main text but nonetheless remain crucial to understanding and reproducing the research shown; figures of replicates for experiments of which representative data is shown in the main text can be added here if brief, or as Supplementary data. Mathematical proofs of results not central to the paper can be added as an appendix.

References

Z. Zheng, W. Wang, Y. Kong, and Y. D. Zhang, ‘MISC array: A new sparse array design achieving increased degrees of freedom and reduced mutual coupling effect,’ IEEE Transactions on Signal Process., Vol. 67, No. 7, 2019. [CrossRef]
H. Krim and M. Viberg, ‘Two decades of array signal processing research: The parametric approach,’ IEEE Signal Process. Mag., Vol. 13, No. 4, pp. 67–94, July 1996. [CrossRef]
B. Liao, A. Madanayake, and P. Agathoklis, ‘Array signal processing and systems,’ Multidim. Syst. Sign. Process., Vol. 29, 2018, pp. 467–473. [CrossRef]
S. Catreux, P. F. Driessen, and L. J. Greenstein, ‘Data throughputs using multiple-input multiple-output (mimo) techniques in a noise-limited cellular environment,’ IEEE Trans. on Wireless Comm., Vol. 1, No. 2, 2002, pp. 226 – 235. [CrossRef]
Z. Chen, F. Yan, X. Qiao, and Y. Zhao, ‘Sparse Antenna Array Design for MIMO Radar Using Multiobjective Differential Evolution,’, International Journal of Antennas and Propagat., Hindawi Publishing, Vol. 2016, 2016. [CrossRef]
M. Yang, L. Sun, X. Yuan, and B. Chen, ‘A New Nested MIMO Array With Increased Degrees of Freedom and Hole-Free Difference Coarray,’ IEEE Signal Process. Lett., Vol. 25, No. 1, 2018, pp. 40–44. [CrossRef]
J. Dong, F. Liu, Y. Jiang, B. Hu, and R. Shi, ‘Minimum redundancy MIMO array design using cyclic permutation of perfect distance (CPPD),’ 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), 2014.
X. Wang, and X. Wang, ‘Hole Identification and Filling in k-times Extended Co-prime Arrays for Highly-Efficient DOA Estimation,’ IEEE Transactions on Signal Process., Vol. 67, No. 10, 2019, pp. 1–14. [CrossRef]
R. Rajamaki, and V. Koivunen, ‘Sparse Linear Nested Array for Active Sensing,’ 2017 25th European Signal Processing Conference (EUSIPCO), 2017.
R.L. Haupt, ‘Thinned arrays using genetic algorithms,’ IEEE Trans. on Antennas and Propagat., Vol. 42, No. 7, 1994, pp. 993–999. [CrossRef]
T. Torres, N. Alselmi, P. Nayeri, P. Rocca, R. Haupt, ‘Low discrepancy sparse phased array antennas,’ Sensors, Vol. 21, No. 7816, 2021, pp. 1–20. [CrossRef]
N. Bruce , J. Stacey , and P. F. Driessen, ‘Visibility domain direction-of-arrival optimization for arbitrary 2-D arrays,’ IEEE Access, Vol. 10, 2022, pp. 21646 – 21654. [CrossRef]
R. Eghbali, A. Rashidinejad, F. Marvasti, ‘Iterative methods with adaptive thresholding for sparse signal reconstruction,’ Int. Workshop on Sampling Theo. and Appl. (SampTA), May 2011.
S. G. Tanyer, A. E. Yilmaz, F. Yaman, ‘Adaptive desirability function for multiobjective design of thinned array antennas,’ Journal of Electromagnetic Waves and App., Vol. 26, No. 17-18, 2012, pp. 2410-2417. [CrossRef]
F. Marvasti, A. Amini, F. Haddadi, M. Soltanolkotabi, B. H. Khalaj, A. Aldroubi, S. Holm, S. Sanei, and J. Chambers, ‘A Unified Approach to Sparse Signal Processing’, EURASIP Journal on Advances in Signal Process., Vol. 44, 2012. [CrossRef]
M. Ibrahim, V. Ramireddy, A. Lavrenko, J. König, F. Römer, M. Landmann, M. Grossmann, G. D. Galdo, R. S. Thomä, ‘Design and analysis of compressive antenna arrays for direction of arrival estimation,’ Signal Process., Vol. 138, 2017, pp. 35–47. [CrossRef]
T. Yardibi, J. Li, P. Stoica, M. Xue, A. B. Baggeroer, ‘Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares,’ IEEE Transactions on Aerospace and Electron. Sys., Vol. 46, No. 1, Jan. 2010, pp.425–443. [CrossRef]
M. Z. Ikram, M. Ali, and D. Wang, ‘Joint Antenna-Array Calibration and Direction ofArrival Estimation for Automotive Radars,’ 2016 IEEE Radar Conference, 2016.
H. T. Hui, K. Y. Chan, and E. K. N. Yung,. Wang, ‘Compensating for the Mutual Coupling Effect in a Normal-Mode Helical Antenna Array for Adaptive Nulling,’ IEEE Trans. On Vehicular Technology, Vol. 52, No. 4, July 2003.
X. H. Wu, A. A. Kishk, and A. W. Glisson, ‘Antenna Effects on a Monostatic MIMO Radar for Direction Estimation, a Cramèr-Rao Lower Bound Analysis,’ IEEE Trans. On Antennas and Propagat., Vol.59, No. 6, June 2011.
D. Qi, M. Tang, S. Chen, Z. Liu, ‘DOA estimation and self-calibration under unknown mutual coupling,’ Sensors, Vol. 19, No. 978, 2019, pp. 1 – 13. [CrossRef]
X. Chen, S. Zhang, and Q. Li, ‘A Review of Mutual Coupling in MIMO Systems,’ IEEE Access, May 24, 2018. [CrossRef]
H. Singh, H. L. Sneha, and R. M. Jha, ‘Mutual Coupling in Phased Arrays: A Review,’ International Journal of Antennas and Propagat., Hindawi Publishing, Vol. 2013.
V. Giannini, M. Goldenberg, A. Eshraghi, J. Maligeorgos, L. Lim, R. Lobo, D. Welland, C. Chow, A. Dornbusch, T. Dupuis, S. Vaz, F. Rush, P. Bassett, H. Kim, M. Maher, O. Schmid, C. Davis, and M. Hegde, ‘A 192-Virtual-receiver 77/79 GHz GMSK code-domain MIMO radar system-on-chip,’ ISSCC, 2019.
J. Hasch, R. Bosch, ‘Driving Towards 2020: Automotive Radar Technology Trends’, 2015 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility, 2015.
M. R. Zofka, R. K. Kohlhaas, C. Rist, T. Schamm, and J. M. Zollner , ‘Data-driven simulation and parameterization of traffic scenarios for the development of advanced driver assistance systems,’ 18th Int. Conf. on Information Fusion, July, 6, 2015.
W. Wiesbeck, L. Sit, M. Younis, T. Rommel, G. Krieger, and A. Moreira, ‘Radar 2020: The future of radar systems,’ IGARSS, 2015, pp. 188 – 191.
P. F. Driessen, ‘Ray tracing interpretation of multiple-input multiple-output wireless systems,’ IFAC Proceedings Volumes, Vol. 36, No. 16, Elsevier, 2003, pp. 109 – 114. [CrossRef]
M. Zhang, C. Tu, W. Zhu, C. Wu, Q. Li, C. Wang, and H. Wang, ‘BD-CVSA: A broadband direction finding method based on constructing virtual sparse arrays,’ Signal Process, Vol. 212, No. 109160, 2023, pp. 1 – 13. [CrossRef]
S. Yang, W. Lyu, Z. Zhang, and C. Yuen, ‘Enhancing near-field sensing and communications with sparse arrays: potentials, challenges, and emerging trends,’ 2309.08681, arxiv.org, 2023, pp. 1 – 8.
Road vehicles – Vehicle dynamics and road-holding ability – Vocabulary, International Standard, ISO 8855, Second Ed., 2011.
Surface Vehicle Recommended Practice, SAE, Recommendation J670, January, 2008.
T. D. Gillespie, Fundamentals of vehicle dynamics,’ Society of Automotive Engineers Inc. Warrendale, 1992.
B. C. Hamblin, R. D. Martini, J. T. Cameron, and S. N. Brennan, ‘Low-order modeling of vehicle roll dynamics,’ Proceedings of the American Control Conference, 2006.
Q. Gong, S. Zhong, S.Ren, Z. Peng, and G. Wang, ‘A gridless method for direction finding with sparse arrays in nonuniform noise,’ Digital Signal Process., Vol. 134, No. 103898, 2023, pp. 1 – 9. [CrossRef]
L. Perez-Eijo, M. Arias, B. Gonzalez-Valdes, Y. Rodriguez-Vaqueiro, O. Rubiños, A. Pino, I. Sardinero-Meirás, and J. Grajal, ‘Designing advanced multistatic imaging systems with optimal 2D sparse arrays,’ Appl. Sci, Vol. 13, No. 12138, 2023 pp. 1 – 15. [CrossRef]
W. L. Stutzman, and G. A. Thiele, Antenna Theory and Design, Third Ed., John Wiley & Sons. Inc., 2013.
R. Sharif, S. G. Tanyer, S. Harrison, W. Junor, P. Driessen, and R. Herring, ‘Locating Earth Disturbances Using the SDR Earth Imager,’ Vol. 14, No. 6393, Remote Sens., 2022, pp. 1 – 18. [CrossRef]
R. Sharif, S. G. Tanyer, S. Harrison, P. Driessen, and R. Herring, ‘Monitoring Earth using SDR Earth Imager,’ Jour. of Atmospheric and Solar-Terrestrial Physics, Vol. 235, No.105907, 2022, pp. 1 – 8.
LWA: Long Wavelength Array, accessed on Feb. 25, 2025. https://leo.phys.unm.edu/~lwa/index.html.
H. Wang, and Y. Zeng, ‘Can sparse arrays outperform collocated arrays for future wireless communications?,’ No. 2307.07925, arxiv.org, 2023, pp. 1 – 6.
S. G. Tanyer, P. Dent, M. Ali, and C. Davis, ‘Sparse antenna arrays for automotive radar,’ United States Patent, Publ. no. 20220326347, Filed: Jan. 24, 2022, Publ. Oct. 13, 2022.
P. W. Dent, S. G. Tanyer, M. Ali, F. Rush, M. Maher, A. Eshraghi, J. P. Bordes, M. Goldenberg, V. Caldeira, S. W. Alland, and C. Davis, ‘Automotive radar device,’ United States Patent, Publ. no. 20220308160, Filed on Jan. 24, 2022, Publ. Sept. 29, 2022.
S. G. Tanyer, ‘Random number generation with the method of uniform sampling: very high goodness of fit and randomness’, Engineering Letters, Vol. 26, No. 1, 2018.
A. Graff, L. Chen, M. Ali, J. Tang, S. G. Tanyer, and P. W. Dent, ‘Radar system with enhanced processing for increased contrast ratio, improved angular separability and accuracy, and elimination of ghost targets in a single-snapshot,’ United States Patent, Publ. No. 20230176179, Filed: Nov. 30, 2022, Publ. June 8, 2023.
P. Sarangi, M. C. Hucumenoglu, R. Rajamaki, and P. Pal, ‘Super-resolution with sparse arrays: a non-asymptotic analysis of spatio-temporal trade-offs,’ No. 2301.01734, arxiv.org, 2023, pp. 1 – 14.
J. Foutz, A. Spanias, and M. K. Banavar, ‘Narrowband Direction of Arrival Estimation for Antenna Arrays,’, Synthesis Lectures on Antennas #8, Morgan & Claypool Publishers, 2008.
D. K. Cheng, ‘Field and wave electromagnetics,’ Addison-Wesley Publ., Sydney, 1983.

Figure 1. Classification of antenna arrays in terms of inter-element spacing values.

Figure 2. Problem geometry for a planar antenna aperture.

Figure 3. Examples for physical and virtual arrays. (a) The physical elements for 4 TX, 2 RX ULA antenna arrays, (b) 8 element virtual ULA created by the elements given in (a). (c) The physical elements for 8 TX, 9 RX URA antenna arrays, and (d) corresponding fully populated 2D URA virtual array of 72 elements located on the reference grid space. Two other examples for virtual arrays, (e) a non-uniform, and (f) grid-based virtual sparse arrays, respectively (physical locations are ignored.).

Figure 4. (a) Uniformly sampled spatial variables, and (b) the corresponding real angles for which

(u^{2} + v^{2}) \leq 1

is satisfied.

Figure 4. (a) Uniformly sampled spatial variables, and (b) the corresponding real angles for which

(u^{2} + v^{2}) \leq 1

is satisfied.

Figure 5. Uniform linear arrays (ULA),

d_{λ} = 0.5

, (dashed)

N = 8

, (dashed dot)

N = 16

, and some examples to (dotted) a sparse array (SA) with

d_{λ} = 0.5

, and

N = 8

with nonuniform positions

d_{λ} = 0, 1.07, 2.52, 3.79, 4.48, 4.98, 5.86, 7.5

, and (solid) a grid-based sparse array (GSA) with

d_{λ} = 0.5

, and

N = 8

using the positions of as reference for which are thinned to 0, 3, 5, 7, 8, 10, 14, and 15. This figure shows how the main lobe is spread when the array is thinned.

Figure 5. Uniform linear arrays (ULA),

d_{λ} = 0.5

, (dashed)

N = 8

, (dashed dot)

N = 16

, and some examples to (dotted) a sparse array (SA) with

d_{λ} = 0.5

, and

N = 8

with nonuniform positions

d_{λ} = 0, 1.07, 2.52, 3.79, 4.48, 4.98, 5.86, 7.5

, and (solid) a grid-based sparse array (GSA) with

d_{λ} = 0.5

, and

N = 8

using the positions of as reference for which are thinned to 0, 3, 5, 7, 8, 10, 14, and 15. This figure shows how the main lobe is spread when the array is thinned.

Figure 6. Grating lobe angles with respect to the target angle. (a, and b) grating lobes with respect to the target angle for a ULA with

d_{λ} = 3 λ / 2

, (c, and d), angular separation between the first grating lobe angle,

u_{g l}^{1}

, and the target angle,

u_{t}

, for various inter-element spacings where the dotted reference line shows the locus of target angles,

ϕ = ϕ_{t 0}

, for which the first phase-wrapped target image appears on the opposite side of the uFOV at

ϕ = - ϕ_{t 0}

. All values given in the vertical axes carry the angles (left) represented in the

(u, v)

plane, and (right) given in degrees, respectively. Note that for (c) and (d) there is no grating lobe for

d = λ / 2

Figure 6. Grating lobe angles with respect to the target angle. (a, and b) grating lobes with respect to the target angle for a ULA with

d_{λ} = 3 λ / 2

, (c, and d), angular separation between the first grating lobe angle,

u_{g l}^{1}

, and the target angle,

u_{t}

, for various inter-element spacings where the dotted reference line shows the locus of target angles,

ϕ = ϕ_{t 0}

, for which the first phase-wrapped target image appears on the opposite side of the uFOV at

ϕ = - ϕ_{t 0}

. All values given in the vertical axes carry the angles (left) represented in the

(u, v)

plane, and (right) given in degrees, respectively. Note that for (c) and (d) there is no grating lobe for

d = λ / 2

Figure 7. Example array structures with mutual coupling forbidden zones, (left) physical apertures for (red) TX and (blue) for RX where the opposite also yields the same VRXs, and (right) their virtual apertures, (a, b) fully-populated URA with no forbidden zones and co-located TX and RXs, (c, d) two-vertical, (e, f) two-diagonal, (g, h) four-corners and (i, j) thick-L shaped, (k, l) wrap-around, and (m, n) improved four corner structures, respectively. Forbidden distances,

y_{m c}

and

z_{m c}

are selected to be

15 λ

and

10 λ

, respectively.

y_{m c}

and

z_{m c}

are selected to be

15 λ

and

10 λ

, respectively.

Figure 8. PSLR as a function of sparsity for ULAs with aperture lengths of 16

λ

, 32

λ

64 λ

, and

128 λ

Figure 8. PSLR as a function of sparsity for ULAs with aperture lengths of 16

λ

, 32

λ

64 λ

, and

128 λ

Figure 9. Single and two-variable LTB desirability functions, (a) linear, nonlinear (sigmoid function) and piece-wise linear functions with different weights, (b)

D_{P S L R}^{-}

and

D_{B W}^{-}

for

γ_{P S L R} = 2

, and

γ_{B W} = 0.5,

and (c)

D_{0} = D_{P S L R}^{-} D_{B W}^{-}

. Desired regions are assumed to be

(- 40 d B < P S L R < - 10 d B)

, and

({0.25}^{o} < B W < 2^{o})

Figure 9. Single and two-variable LTB desirability functions, (a) linear, nonlinear (sigmoid function) and piece-wise linear functions with different weights, (b)

D_{P S L R}^{-}

and

D_{B W}^{-}

for

γ_{P S L R} = 2

, and

γ_{B W} = 0.5,

and (c)

D_{0} = D_{P S L R}^{-} D_{B W}^{-}

. Desired regions are assumed to be

(- 40 d B < P S L R < - 10 d B)

, and

({0.25}^{o} < B W < 2^{o})

Figure 10. Received signal patterns for uniform linear MIMO arrays with different parameters; (a)

N_{v r x} = 121

d = λ / 2

, (b)

N_{v r x} = 61

d = λ / 2

, (c)

N_{v r x} = 61

d = λ

Figure 10. Received signal patterns for uniform linear MIMO arrays with different parameters; (a)

N_{v r x} = 121

d = λ / 2

, (b)

N_{v r x} = 61

d = λ / 2

, (c)

N_{v r x} = 61

d = λ

Figure 11. Received normalized signal patterns in decibels for a uniform rectangular MIMO array;

(M_{v r x}, N_{v r x}) = (121, 61)

d = λ / 2

, (a)

(ϕ_{t}, θ_{t}) = (0, 0)

, (b)

(ϕ_{t}, θ_{t}) = ({0, 30}^{0})

, (c) close up view of the beam width region.

Figure 11. Received normalized signal patterns in decibels for a uniform rectangular MIMO array;

(M_{v r x}, N_{v r x}) = (121, 61)

d = λ / 2

, (a)

(ϕ_{t}, θ_{t}) = (0, 0)

, (b)

(ϕ_{t}, θ_{t}) = ({0, 30}^{0})

, (c) close up view of the beam width region.

Figure 12. Grid-based sparse arrays,

d_{y} = λ / 2

d_{z} = λ

w_{t x} = w_{r x} = 2 λ

h_{t x} = h_{r x} = 5 λ

, no forbidden zones are defined. (left) Ankara–1A, (right) Ankara–1B, (a, and b) Physical element positions where Ankara–1A is utilizing all elements whereas for Ankara–1B the first 8 RXs are disabled, (c – h) 2D and 1D received signal patterns in the

(u, v)

planes with tick values converted to degrees. Single target angles,

(ϕ_{t}, θ_{t})

, are

({30^{0}, 30}^{0})

, and

({0^{0}, 0}^{0})

for 2D and 1D plots, respectively.

Figure 12. Grid-based sparse arrays,

d_{y} = λ / 2

d_{z} = λ

w_{t x} = w_{r x} = 2 λ

h_{t x} = h_{r x} = 5 λ

(u, v)

planes with tick values converted to degrees. Single target angles,

(ϕ_{t}, θ_{t})

, are

({30^{0}, 30}^{0})

, and

({0^{0}, 0}^{0})

for 2D and 1D plots, respectively.

Figure 13. Inter-element mutual coupling between the transmitter and receiver groups for the sparse array Ankara-1. (a, b) calculated mutual coupling values, (+)

K > - 60 d B

Figure 13. Inter-element mutual coupling between the transmitter and receiver groups for the sparse array Ankara-1. (a, b) calculated mutual coupling values, (+)

K > - 60 d B

Figure 14. Mutual coupling constrained grid-based sparse arrays,

d_{y} = d_{z} = d = λ / 2

w_{t x} = w_{r x} = 2 λ

h_{t x} = h_{r x} = 5 λ

, the forbidden distances,

y_{m c} = 10 λ

, and

z_{m c} = 15 λ

. (left) Ankara–2A, (right) Ankara–2B, (a, and b) Physical element positions where Ankara–2A is utilizing all elements whereas for Ankara–2B the first 8 RXs are disabled, (c – h) optimized 2D and 1D received signal patterns in the

(u, v)

planes with tick values converted to degrees. Single target angles,

(ϕ_{t}, θ_{t})

, are

({30^{0}, 30}^{0})

, and

({0^{0}, 0}^{0})

for 2D and 1D plots, respectively.

Figure 14. Mutual coupling constrained grid-based sparse arrays,

d_{y} = d_{z} = d = λ / 2

w_{t x} = w_{r x} = 2 λ

h_{t x} = h_{r x} = 5 λ

, the forbidden distances,

y_{m c} = 10 λ

, and

z_{m c} = 15 λ

(u, v)

planes with tick values converted to degrees. Single target angles,

(ϕ_{t}, θ_{t})

, are

({30^{0}, 30}^{0})

, and

({0^{0}, 0}^{0})

for 2D and 1D plots, respectively.

Figure 15. Measured received signal pattern for Ankara–2A with a single target at broadside.

Figure 16. The empirical cumulative distribution functions (ECDF) for the horizontal inter-element spacings of virtual arrays with physical antenna elements of width λ. (a) Horizontal ULA with number of elements of 16 and 64, , and (b) the grid-based sparse Ankara arrays with versions A and B.

Table 2. Inter-element spacings and the usable FOV values.

Spacings (λ)	0.5	0.5077	0.5321	0.5774	0.6527	0.7778	1	2	3	4	5	10	20
uFOV (deg)	180	160	140	120	100	80	60	28.96	19.19	14.36	11.48	5.73	2.87

Table 3.

Algorithm: Sparse array optimization
desired parameters:

array dimension (1D/2D/3D) and let us assume 1D as an example.
available number of TX and RX elements, $N_{t x}$ , $N_{r x}$ , respectively,
uFOV, and BW both for azimuth and elevation,

constraints:

physical dimensions of antenna elements, $w_{t x}$ , $h_{t x}$ , $w_{r x}$ , $h_{r x}$
forbidden zones for mutual coupling, $y_{m c}$ , $z_{m c}$
enforced element positions

initialize k = 0:

calculate required virtual aperture length, ${2 Y}_{λ, m a x}$ using (27) and (28)
calculate required minimum inter-element spacings, $∆ d_{λ, m i n}$ using (29) and (30)
determine reference grid space, $y_{n}$
set positions to the enforced list of positions
(optional HIA): calculate uniformly distributed set of $∆ d_{λ}$ $∆ d_{λ}^{n}$

iterate k until

({k < K}_{m a x})

(P S L R_{b e s t} > P S L R_{d e s i r e d})

random shuffling and random perturbations of $∆ d_{λ, y}^{n}$
add non-overlapping TX and RX positions satisfying constraints until all positions are calculated
calculate the received signal pattern , and calculate the PSLR,
update array positions and $P S L R_{b e s t}$ if $P S L R_{n e w} < P S L R_{b e s t}$

end
repeat: outer loop is used if desired and hyperparameters are also to optimized for a given range of values.

Table 4. Aperture loss and beamwidth spreading factors.

	$\frac{y_{m p}, z_{m p}}{λ}$	$(a, b)$ Shared fully populated aperture	$(c, d)$ Vertical	$(e, f)$ Diagonal	$(g, h)$ Four corners	$(i, j)$ L shaped receivers	(k,l) Wrap-around	(m,n) Improved four corners
$α_{a p}$	$(0, 0)$	1	0.504	0.735	0.735	0.629	0.254	1
	$(5, 5)$	1	0.438	0.613	0.681	0.535	0.235	0.670
	$(15, 10)$	1	0.3398	0.4897	0.446	0.380	0.136	0.490
	$(20, 15)$	1	0.1746	0.244	0.142	0.199	–	0.238
$α_{b w, ϕ}$	$(0, 0)$	1	1	1.013	1	1	2	1
	$(5, 5)$	1	1	1.013	1	1.067	2	1
	$(15, 10)$	1	1	1.013	1	1.231	2	1
	$(20, 15)$	1	1	1.013	1	1.455	–	1
$α_{b w, θ}$	$(0, 0)$	1	2	1.008	1	1.333	2	1
	$(5, 5)$	1	2.308	1.212	1	1.395	2	1
	$(15, 10)$	1	3	1.519	1	1.500	2	1
	$(20, 15)$	1	6	3.078	1	1.714	–	1

Table 5. Inter-element Mutual Coupling Between TX and RX elements for The Sparse Array Ankara.

	RX-1	RX-2	RX-3	RX-4	RX-5	RX-6	RX-7	RX-8	RX-9	RX-10	RX-11	RX-12	RX-13	RX-14	RX-15	RX-16
TX-1	-86.0	-77.5	-59.7	-55.6	-81.1	-80.6	-85.7	-72.5	-94.7	-91.4	-99.7	-101.4	-101.5	-109.3	-116.2	-110.9
TX-2	-41.5	-51.0	-50.1	-56.5	-67.7	-71.1	-60.7	-91.4	-63.8	-92.1	-70.8	-71.5	-97.7	-81.4	-91.4	-81.0
TX-3	-39.7	-41.1	-52.2	-79.1	-89.1	-75.5	-60.6	-77.9	-64.8	-91.6	-72.0	-69.0	-81.7	-77.0	-84.5	-78.8
TX-4	-58.3	-68.0	-57.2	-42.3	-57.2	-54.0	-84.9	-66.9	-104.2	-59.9	-85.2	-61.8	-67.0	-69.0	-72.4	-71.9
TX-5	-60.4	-78.3	-63.2	-67.3	-36.9	-63.3	-42.8	-43.0	-53.8	-66.3	-59.3	-52.5	-84.8	-65.6	-93.3	-64.7
TX-6	-78.9	-90.7	-77.2	-53.2	-40.5	-70.3	-35.3	-50.0	-34.8	-66.9	-46.2	-70.5	-53.3	-73.0	-80.9	-81.7
TX-7	-70.2	-81.2	-87.2	-82.8	-63.3	-78.0	-53.1	-54.9	-42.3	-55.2	-36.4	-36.7	-42.0	-47.3	-68.4	-50.0
TX-8	-88.7	-77.1	-85.3	-86.1	-54.3	-74.7	-47.9	-52.6	-54.7	-56.3	-49.5	-40.0	-41.0	-66.8	-70.7	-71.7
TX-9	-94.8	-97.0	-73.7	-66.4	-64.2	-51.0	-67.3	-46.0	-66.7	-40.2	-58.9	-50.9	-49.9	-76.8	-76.4	-91.2
TX-10	-101.1	-101.6	-80.0	-72.7	-70.3	-71.8	-71.8	-54.9	-76.0	-54.1	-66.1	-59.6	-55.3	-80.0	-81.2	-88.1
TX-11	-101.9	-99.9	-101.9	-92.4	-71.0	-62.0	-71.6	-84.7	-56.8	-57.6	-57.7	-52.9	-43.4	-51.5	-43.5	-48.5
TX-12	-94.0	-85.3	-105.7	-80.0	-80.8	-75.1	-72.1	-55.2	-85.8	-83.9	-52.0	-60.0	-47.7	-42.5	-31.5	-39.7

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Multi-objective Design and Optimization of Hardware Friendly Grid-Based Sparse MIMO Arrays

Abstract

1. Introduction

2. Sparse MIMO Radar Systems

2.1. Creation of Virtual Arrays

2.2. Transmitting Grid-Based Sparse Antennas

2.3. Receiving Grid-Based Sparse MIMO Antenna Arrays

3. Angle Beamforming

4. Multi-Objective Design and Optimization of Grid-Based Sparse Arrays

4.1. Optimizing Parameters

4.2. Design and Optimization of a Grid-Based Sparse Arrays

4.3. Multi-Objective Optimization of Sparse Arrays Using the Desirability Function

4.4. Machine Learning for Dynamic Setting of Hyperparameters

4.5. Disadvantages of Sparse Arrays

5. Results

5.1. Fully Populated Uniform Arrays:

5.2. Grid-Based Sparse Arrays (GSA) with Large Antenna Elements

5.3. The Empirical Cumulative Distribution Functions (ECDF) for the Inter-Element Spacings

6. Conclusions

Patents

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

A.1. A Radiating Antenna Aperture

A.2. A Receiving Sparse MIMO Antenna Array

References

MDPI Initiatives

Important Links

Subscribe