Submitted:
26 July 2024
Posted:
26 July 2024
You are already at the latest version
Abstract
Keywords:
MSC: 35A01; 35F21; 47H10; 70H20
1. Introduction
- (A1)
- , , , is an arbitrary time scale with forward jump operator and delta differentiation operator and , respectively.
2. Fuzzy Dynamic Calculus Essentials
3. The Adomian Decomposition Method on Time Scales
4. The Adomian Decomposition Method for the Problem (1), (2)
5. A Numerical Example
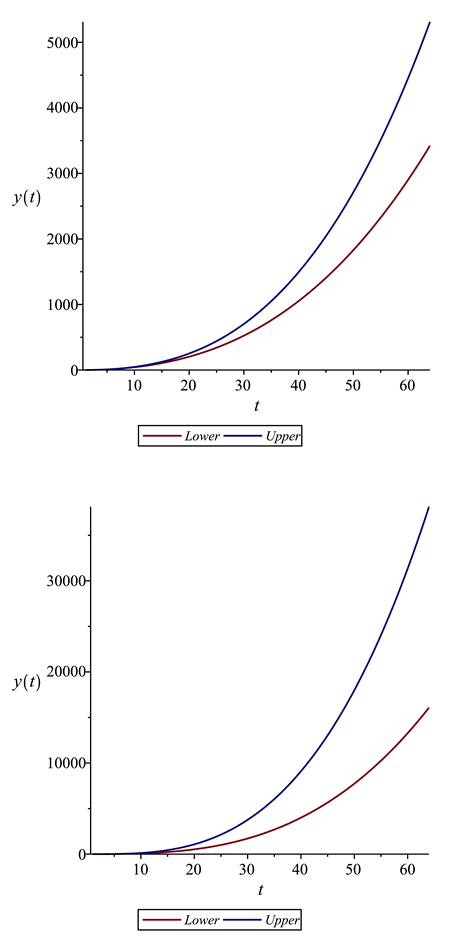
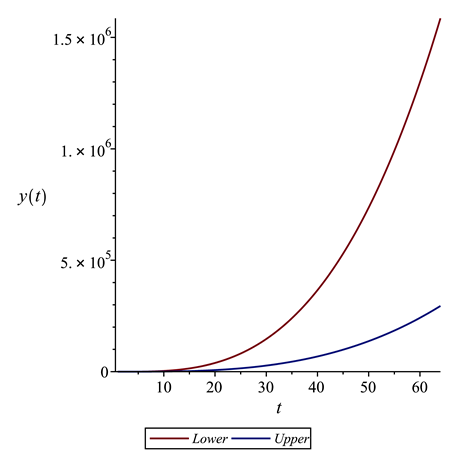
References
- R. P. Agarwal, M. Meehan and D. O’Regan, Fixed Point Theory and Applications, Cambridge University Press 12, (2001).
- S. Georgiev. Fuzzy dynamic equations, dynamic inclusions and optimal control problems on time scales, Springer, 2021.
- S. Georgiev and I. Erhan. Numerical Methods on Time Scales, De Gryuter, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



