Prerpints.org logo
Preprint
Article

Comparing Var and Artificial Neural Network Model in Forecasting Real Estate Prices during Good and Bad Times

Altmetrics

Downloads

102

Views

20

Comments

0

This version is not peer-reviewed

Submitted:

26 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts
Abstract
The financial crisis augmented the need to predict real estate prices. The current study examines the application of Artificial Neural Network (ANN) model and Vector Autoregressive (VAR) model in forecasting real estate prices. The study uses daily observations, which accounted for a total of 2955 observations collected. We found that ANN outperformed significantly the VAR model providing evidence that these models can be used for valuation purposes in the area of real estate and financial markets. These findings are novel and important as they provide evidence of the usefulness of more sophisticated methodologies for market participants and regulators in real estate and financial markets.
Keywords: 
Subject: Business, Economics and Management  -   Finance

1. Introduction

The high cost of global financial crisis and the following Covid-19 pandemic, made economic problems worse and increased the pressure to regulators and politicians, towards more accurate prediction models in markets to achieve efficient allocation of scarce resources. Neural Networks (NN) gained popularity in the past few decades [1] and the term ‘neural network and prediction’, appeared in searching engines approximately 10,850 at its peak in 2017, and resulted in 892 new publications (based on the Scopus database). This indicates that NN is an active area of research, many of which focus on solving prognostic problems. The Artificial Neural Networks (ANN) can be described as a mathematical in-put-output model inspired by a biological nervous system. The main basic element that ANN is made up of are called “artificial neurons,” which have a similar function as a real neuron. The biological neuron is constituted of dendrites, somatic cells, and axons, where the equivalent in an artificial neuron is weighted input, activation function, and output respectively.
Four main characteristics of the neural network distinguished [2] are: non-linearity the input-output function is a result not only of a complex neuron structure but also interlinks between other neurons, non-limited number of neurons, non-qualitative due to its iterative nature, non-convex the system has more than one stable equilibrium point. Most importantly neural networks have the ability to self-adaptation/learning and self-organizing.
The Artificial Neural Network is classified as a machine learning algorithm, due to its ability to recognize the patterns and memorize them. It is achieved by the complex net-work of neurons that comprises input layer, hidden layers, and output layer.
The proposed research is a comparative study between the Vector Auto Regression (VAR) model and Machine Learning (ML) based model for forecasting FTSE350 UK Real Estate Index. The study will be conducted on empirical data utilizing historical data. Based on the recent studies the novel ANN performs significantly better over VAR considering performance, better adaptability, and less limitation by the required model assumptions [3]. However, most of the research has been done using US data set and very specific applications, hence it cannot be stated that the ANN will perform better in the considered UK FTSE 350 Real Estate Index forecasting.
The real estate industry is a significant sector for each economy which is highly correlated with most sectors of the economy, currency prices, commodities, and other macroeco-nomic indicators [4]. Therefore, accurate real estate forecasting is a complex task and highly desired by many parties. One of the widely used gauges for measuring the performance of the real estate industry in the United Kingdom is the FTSE350 Real Estate Index that consists of the biggest companies in the sector listed in the FTSE350 index. Predicting the movement in the FTSE350 Real Estate Index can prove to be useful for researchers, industry, policymakers, or investors. Forecasting indexes whether, it is a single company share price, stock market index price, or other it has been a subject of research for many years. For a few decades, there have been well-known approaches for time forecasting in a classical econometrical method i.e., GARCH, ARCH, VAR [6], however over the past two decades computational intelligence methods such as Artificial Neural Networks (ANN) have been increasingly adopted [3]. Therefore, the proposed comparative study between VAR and ANN in forecasting UK Re-al Estate Index will contribute to the current knowledge.
The objective of this study is to examine differences/similarities in the characteristics, the process of model creation, and the performance of the forecast FTSE350 Real Estate Index for two models: Artificial Neural Network Model and Vector Autoregressive Model. The work focuses on the novel ANN model that will be put in perspective of the classical econometrical tool – VAR.

2. Literature Review and Hypothesis

Although the first mathematical model of the neuron has been proposed in the 1940s the empirical data suggest that the ANN started to be adopted more frequently to solve practical complex input-output problems only since around 1980 [2]. In comparison, the time-series sta-tistical analysis and forecasting have been known for a long time, for example [5] described the statistical tools available way before 1927. Over the years these statis-tical methods have been developed and gained popularity especially in the field of econ-omy and econometrics
However, along with the developments in information technology and computing the other more advanced methods such as ANN can be implemented much easier and faster than ever before, hence are a frequent subject of research [7]. In 2004, the VAR and ANN models were compared by [8] to forecast Oil prices in the US. In this research, it has been established that the lagged price is the most significant factor in predicting future prices. The work revealed significant advantages of ANN over VAR indicating that ANN is less limited by the assumptions required for VAR. Moreover, the study proved that in this application for the studied time series the NN outperformed the VAR model. Note that this study is outdated and does not prove that NN would always outperform the VAR hence, it cannot be determined which method will perform better in the proposed research. In more recent work [3] surveyed different computational intelligence and soft computing methods in an econometric domain comparing intelligent computing methods such as Artificial Neural Networks, Fuzzy Logic, Genetic Algorithms, and hybrid models and showing the results of the forecast performance for the S&P500 index, however, does not detail the process of modelling. Nevertheless, the survey demonstrated the feasibility of the use of Neural Networks models in the complex task of time series forecasting based on the S&P500 example. The feasibility of a neural network for time-series forecasting has been demonstrated in [9] where it was demonstrated that the ANN has the capability of processing and storing knowledge from the historical data through training process. Another comparative study between VAR and ANN models [10] predicted price movements for gold prices, USD/TRY ex-change rate, and BIST 100 index. It was concluded that ANN has better adaptability to the dynamic changes and was more likely to predict TRY currency crashes. In this case, the ANN also outperformed VAR giving more accurate predictions. The author supports this result providing reference to the previous research demonstrating ANN superiority. Simi-lar results were concluded by [11] who did a generic study of time series forecasting methods for land market values in the US. In this work, the ANN has significantly outperformed the VAR model in all considered criteria: MAD, MAPE, MSE, RMSE, and Theil’s. All of the above research has contributed by providing analysis of the selected time series and variables used for the forecasting model, different model comparisons, and measurement of the model performance. Although the studies provide the NN model and VAR models there is a lack of details and justification for the proposed model. It has not been proved that the proposed models are optimal. It has been observed that most of the research focuses on the datasets for the US, hence there is a lack of evidence using a dataset for other countries. This research work will fill this gap by focusing on the dataset for the UK. 
Based on the literature review, it is reasonable to state that the Neural Network based models perform better than the statistical methods. In many studies, it was discovered that the fitness of the neural network model is multiple times better than the other models. Moreover, Neural Networks models have shown a greater ability to adapt to data anomalies.
H0: Neural Network model variables do not surpass the VAR method in predicting the UK FTSE350 Real Estate index considering all common criteria for forecast performance measurement MSE and RMSE.
H1: Neural Network model with exogenous variables surpasses the VAR method in predicting UK FTSE350 Real Estate index considering all common criteria for forecast performance measurement MSE and RMSE.

3. Methodology

The previously examined literature review indicates that the performance of the Real Estate sector is correlated with other sectors and financial indicators. Therefore, based on that the following data will be required for the forecasting of the FTSE350 Real Estate Index:FTSE 350 Real Estate, 10 Years UK Treasury Yield, 1 Year UK Treasury Yield, US 1 Year Treasury Yield, FTSE350 Banking Sector Index, FTSE350 Travel and Leisure Sector and FTSE350 Brokerage & Investment Sector.
Those financial datasets are publicly available and were obtained by using Bloomberg database.
Considerations regarding sample were given to avoid bias, to capture seasonal patterns, to achieve good precision, and to capture the dynamic of the forecasted time series (Monteiro et al., 2021). Therefore, to capture the dynamics and patterns in the time series, the sample size has a daily interval for the period of 11 years - 01.02.2010 to 26.03.2021 - a total of 2955 observations. We divide the sample into 2 main groups - 2200 observations will be used for the ANN models design and VAR estimation. The remaining 755 samples will be used for forecasting and comparative analysis. This will ensure that the data used for analysis and verification were not used for the models creation hence are “new” and “unknown” and unbiased by the model design.
Furthermore, the NN model design requires additional data split to train and verify the network. For this purpose, the modelling sample for NN will be divided into 70% of the sample for training, 15% of the sample for test, and 15% of the sample for validation.
The sample division will be done to both dependent and independent variables. The example has been presented in Figure 1 where the orange vertical line indicates the point of data split. The data on the left-hand side of the orange line will be used for modelling, where the data on the right-hand side of the line will be used for forecasting and comparative analysis.
The sample division (Figure 1) will be done to both dependent and independent variables. As dataset for the time series might feature some non-regularity such as missing observation [6] such as the close price of the index which is recorded at the close of the session on the public market has only observations available for the weekdays and lacks the observation for weekends and any public holidays, we will use daily close price, and to avoid irregular missing observations it will be normalised using a linear extrapolation as per the equation below. For example, the Saturday and Sunday close prices will be linearly extrapolated using the Friday close price and Monday close price. The dependant variable is FTSE 350 Real Estate – 350 biggest companies by market cap listed in the UK publicly listed real estate sector companies. The independent variables consist of the same sample period and interval for: 10 Years UK Treasury Yield, 1 Year UK Treasury Yield, US 10 Tears Yield, US 1 Tear Yield, FTSE350 Banking Sector Index, FTSE350 Travel and Leisure Sector, and FTSE350 Brokerage & Investment Sector. We use the logarithm of the pricea and logarithmic day
The graphs for both series have been presented in Figure.
e_n=log (FTSE350_Real_Estate_Price_n)
r_n=log (FTSE350_Real_Estate_Price_n) -log(FTSE350Real_Estate_Price_(n-1))
Preprints 113376 g002
Figure 2. Logarithm of index e n (left) and logarithm of daily return r n (right) for selected sample.
Figure 2. Logarithm of index e n (left) and logarithm of daily return r n (right) for selected sample.
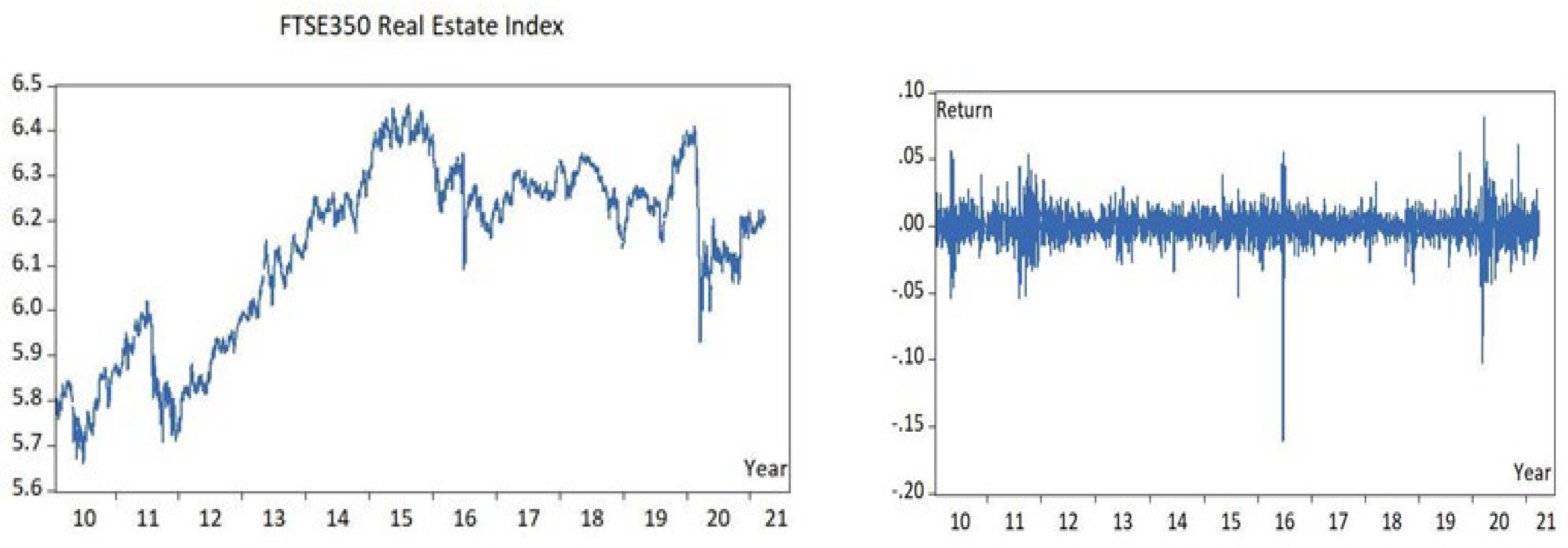
Preprints 113376 g002
Figure left-hand side graph is evidence that the index value is not normally distributed. The mean value is not constant. The Real Estate Index graph seems to have a positive slope with the intercept. Figure the right-hand side graph representing daily return seems to have a constant mean value. The variance cannot be visually confirmed to be constant across the time period. Periods with increased volatility can be observed in 2011, 2016 and 2020-21. The statistical details have been presented below.
Both data series are not normally distributed - the skewness of prices (rn) and log returns (en) are -0.379075 and -1.156150 respectively. The kurtosis of rn and en are equal to 2. and 20.31888 respectively. Comparing to the skewness of a theoretical normally distributed population (skewness 0 and kurtosis 3) it is evident that neither rn nor en are normally distributed. From the histogram presented in Figure 7 it can be observed how the theoretical distribution line compares to the rn where symmetric pattern (non-ideal) exists for real estate daily return data distribution. The standard deviation of the daily return for the Real Estate Index time series is 0.012241. To put it in perspective the standard deviation of the top 100 companies across all the sectors listed at the FTSE100 index for the same sample is 0.010211, hence the examined real estate index return is more volatile.  Based on the correlations presented in the Table 1, the strongest positive correlation can be observed between the dependent variable and FTSE350 Index, FTSE350 Travel and Leisure Index, UK 10 Year Government and US 1 Year Bond Yield. The strongest negative correlation exists between a dependent variable and UK 10 Year Government Bond Yield. The other independent variables correlations are relatively low – FTSE350 Banking Sector, UK 1 Year Government Bond Yield and US 10 Year Government bond Yield.
The autocorrelation for the dependent variable and log daily return of the dependent variable for 40 legs was examined and ACF and PACF exist and is statistically significant which indicates a correlation of residuals. For log daily return it can be observed that relatively high autocorrelation exists for 18, 23, 29. The ACF and PACF follow the same pattern which might indicate non-stationarity.. The unit root test provides evidence that the FTSE350 Real Estate Index series is stationary at 1st difference.

4. VAR Model

Vector autoregressive models (VARs) is the type of autoregressive model where there are multiple dependant variables [12] The most basic example of the VAR model is a bivariate VAR with two variables, y1 and y2. The y1 and y2 values depend on different combinations of the previous lags k of y1 and y2 values, and error terms, which can be described by a system of equations below [12].
Similarly for this research, a VAR model will give a system of equations describing dependencies between dependant variable and independent variables previous lags. First, we determine which variables are useful for the model and how many past observations affect present value (length of lag). In the next step, the model coefficients will be fitted using the modelling samples of 2200 observations, finally, the model will be evaluated.
As it was discovered during data collection/analysis the correlation between variables exists, moreover it was examined if the correlation between lagged values exists for the considered data series. Correlation analysis, presented in Table 1., indicates that FTSE350 Brokerage Index and FTSE350 Travel index are strongly correlated to the FTSE350 Real Estate Index with the correlation value of 0.90 and 0.91 respectively. On the contrary, UK 10 Years Treasury Yield is inversely correlated to the FTSE350 Real estate index, having correlation value -0.53. The number of variables and lags used in the VAR is important as it determines the degree-of-freedoms. If the variable doesn’t contribute to the predictive power of the model, then degrees of freedom are “wasted”. For these reasons VAR is feasible to be used with FTSE350 Travel index, FTSE350 Brokerage Index and UK 10 Years Treasury Yield.
Too small lag length will result in the model not capturing all available correlations, and too large amount of the lags puts constraints in terms of degrees of freedom. We therefore use the Akaike information criteria (AIC) to obtain optimum lag value, following [13] The optimal length based on the AIC criterion (AIC value 24.14983) is 4 lags, as indicated in Table 3.Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
Table 2. Lag length criteria.
Table 2. Lag length criteria.
Lag LR FPE AIC SC HQ
0 N/A 1.56E+14 44.0309 44.0413 44.0347
1 41420.7 940752.7 25.1059 25.1579 25.1249
2 2078.71 368355.8 24.1683 24.26180 24.20248
3 57.464 364044.6 24.1565 24.2916 24.2059
4 46.3418 361611.0 24.14983* 24.3264 24.2144
5 26.2725 362515.5 24.1523 24.3705 24.2321
6 28.8696 362979 24.1536 24.4133 24.2485
7 23.8937 364271.4 24.1572 24.4584 24.2673
8 25.5252 365285 24.1599 24.5027 24.2852
Granger Causality/Block Exogeneity Wald Tests for created VAR(4) model has been done. The three following null hypotheses have been tested:
H0-1: UK 10 Treasury Yield does not Granger Cause FTSE350 Real Estate index
H0-2: FTSE350 Brokerage index does not Granger Cause FTSE350 Real Estate index
H0-3: FTSE350 Travel and Leisure index does not Granger Cause FTSE350 Real Estate index
If p < 0.05 then 5% significance level that causality exists, otherwise the null hypothesis cannot be rejected. The H0-1 and H0-2 can be rejected hence with 5% significance we conclude that UK 10 Treasury Yield and FTSE350 Brokage Index Granger Cause FTSE350 Real Estate Index. It is worth to notice that none of the variables proposed for this VAR(4) model Granger Cause UK 10 Treasury Yield which makes it valuable independent variable.
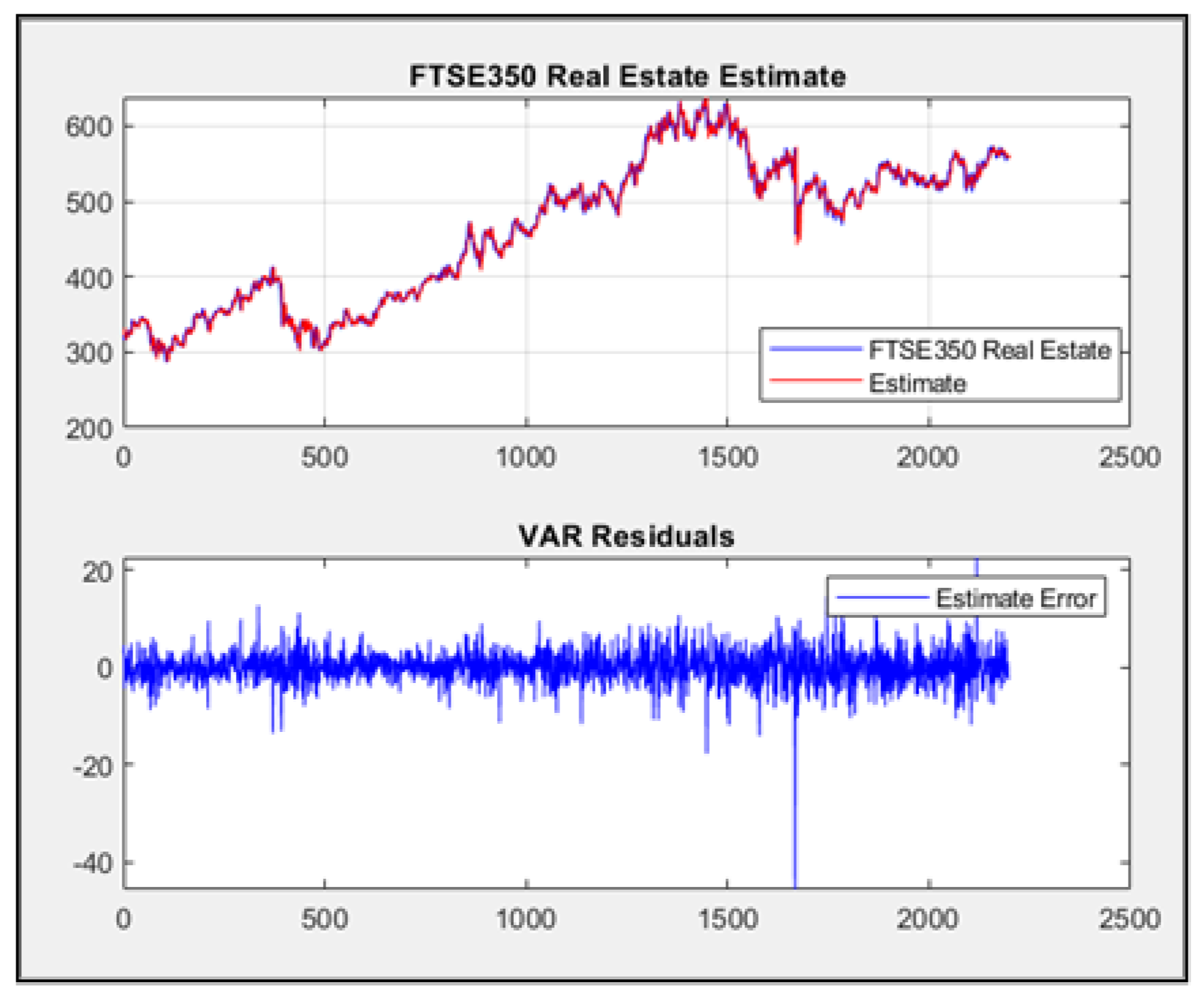
The VAR(4) estimate Mean Square error is equal to 96.5631. The VAR(4) estimate static response and residuals for the full modeling sample of 2200 observations have been presented in Figure and the zoom-in of the last 200 samples (from 2000 to 2200) has been presented in the following Figure.
Preprints 113376 g003
Figure 3. VAR(4) estimate response vs real output and error residuals for modelling sample.
Figure 3. VAR(4) estimate response vs real output and error residuals for modelling sample.
Preprints 113376 g003

5. Neural Network Model

Over the last few decades multiple types of ANN have been used across many engineering, science, and other disciplines, for example, Multi-layer Feedforward Neural Network, Elman Partial Recurrent Neural Network, Time Delay Neural Network, Auto-Regressive Neural Networks [14]. These could be applied for solving the econometric problem considered in this research.
The Artificial Neural Network (ANN) will be developed using Matlab NN toolbox application. In the first step, the most suitable neural network model type for the time series forecasting is selected based on the research. In the next steps, the model is created with the initial network size: number of hidden layers, number of neurons, and lags. Following that step, the model will be trained with the sample dedicated for ANN modelling. The process is repeated iteratively until the validation (using Mean Square Error) will show no model improvement. Additional iterations with the random parameters will be conducted to confirm no improvement in performance observed from the model over the one found in the process above.
One specific branch of the ANN type that is commonly used for time series forecasting is the autoregressive neural network. The main task of the autoregressive NN could be described as dynamic filtering, where lagged values of one time series vector are used to estimate future values [15] The autoregressive NN proved to be useful to model the behaviour of nonlinear and complex dynamic systems [16]. The two types of the autoregressive NN that will be considered for model creation are:
  • Non-linear autoregressive neural network (NAR)
  • Non-linear Autoregressive with External (exogenous) input (NARX)
Previously it was established that correlation for the selected variables exists. Therefore, Non-linear Autoregressive Neural Network with External (exogenous) input will be used.
Selection of the activation function has a significant impact on the performance and training ability of the ANN [17]. In [18] examined seven activation functions for deep learning ANN (ReLU, sigmoid, Tanh, linear, Swish, Sine and Cosine) in the application of time series prediction for 6 different currency rates. In his research, the ReLU was proved to be the best performing activation function. However as characterized [19] ReLU activation function is more suitable for deep learning neural networks and as pointed by [20] the ReLU might suffer a problem of dying cells. Therefore, since the ReLU function is similar to the slope of 0–1 as per the sigmoid function [20], the sigmoid function will be used in this research. The activation operation of the sigmoid function
Another method is available for estimating an optimal number of hidden layers was presented in [21]. Applying the number of layers [21] would equal 88 (for 7 dependent variables, 6 lags, and 1 independent variable). However, this method was only used for reference as there is no evidence provided in mentioned research that the proposed formula results in the optimal number of hidden layers.
Instead of the mentioned above methods, for the purpose of this research, an automated iterative script will be developed to search for the satisfactory solution close to the optimal solution by examining many combinations of the NN performance. The network size will be increased at each iteration and the improvement in performance will be checked. Once no significant improvement is observed the NN with the lowest MSE will be selected for forecast comparative analysis with VAR. The optimal architecture for the final model will be selected based on the lowest value of the MSE from tested Neural Networks. The results of the experiment are presented in Table 4. Note that the proposed by [21] method (88 hidden layers) did not give the optimal result.5. Conclusions
This section is not mandatory but can be added to the manuscript if the discussion is unusually long or complex.
The lags are feedback to the network input, therefore the selection of “Number of Delays” will determine the size of the NN input layer. The difference in the input layer will affect the structure of the entire network and will affect interlinks.
Based on the FTSE350 autocorrelation the NN structure for 2, 4, 6, 8, and 10 lags will be created and verified with the combination of examined hidden layer numbers searching for minimum Mean Square Error value of the network fitness (see Table 3).
Similarly, the artificial neural network requires training by repeated adjustment of the neurons using certain input data and respective reference target output. Due to the approach taken where many iterations of training will be required Lavenberg-Marquardt is the most beneficial training algorithm for the purpose of this study. Lavenberg-Marquardt is known as an error back propagation method which uses two technics: the gradient descent method and the Gauss-Newton method [22].
Open model was used for validation and the open model response to the training data, test data and validation data (modelling dataset of 2200 samples) has been presented in Figure 4
The regression graphs representing the correlation between outputs of the neural network vs targets data (actual values) for training data, validation data, test indicate good fitness of estimates for all datasets - a value of 1 means a close relationship, 0 a random relationship [15].

6. Comparative Analysis between VAR and NN Models Forecasts

Both VAR and NN models were used for forecasting FTSE350 Real Estate Index using the Forecasting sample. The sample of 755 observation has been dedicated for comparative analysis and was not used in the process of model creation hence will be new for both models. The experiments result for VAR vs. ANN have been presented below.In experiment 1 we use Forecast 710 Samples – static VAR and open-loop ANN forecast., in experiment 2 – Forecast 710 Sample – dynamic VAR with exogenous variables and closed loop ANN forecast in Experiment 3 – 30 samples – static/open loop forecast and in Experiment 4 – One month (30 samples) – dynamic/closed loop forecast.
The VAR and ANN forecasts error measures result (MSE and RMSE) for the respective experiments above have been presented in Table 4.
The summary of all experiments has been presented in Table 4 indicates on average 4.4 times worse than ANN in MSE criteria (all experiments). The highest discrepancy was observed in our experiment 2 for long-term closed loop/dynamic forecast with exogenous variables where VAR MSE was 529 and ANN resulted in MSE equal to 70. The smallest discrepancy between VAR and ANN was observed in experiment 3 for short-term open-loop/static forecast where VAR MSE was 15 and ANN MSE was 10. In experiment 2 the VAR model with exogenous variables did not follow the dynamics of the FTSE350 Real Estate Index trend as ANN, hence the MSE and RMSE were multiple times higher for VAR than ANN. Therefore, our experiment 2 provides evidence that the ANN can map a non-linear pattern better than VAR. This result is in line with [23] that compared VAR with ANN featuring one hidden layer, using Levenberg–Marquardt and the sigmoid function in the oil sector, finding, in these commodity prices, that ANN (using MSE criterion) performed multiple times better than VAR. Moreover, [23] arrived at the same conclusion - ANN performed better in periods of high volatility by being able to recognise nonlinear relations between inputs and outputs. Further alignment with achieved results can be found in [10] where it was determined that the ANN had better adaptability to the dynamic changes and was more likely to predict TRY currency crashes due to the non-linear nature of ANN. It is worth mentioning that [23] only used 1 hidden layer, and a small sample of 35 observations, hence did not demonstrate long term learning ability of the neural network. The results presented in Section 7 compared results for a larger sample - 2955 observations, allowing to utilise ANN learning capability. Another unique contribution in our study is that both models were tested in the sample that included increased volatility caused by COVID-19. In the selected sample the volatility is not constant in time due to this major event. This might explain the observed increased error value for VAR post-COVID-19 index price crash is increased. The ANN resulted in a smaller error value in the period of high volatility. It can be concluded that ANN adapts better to change in volatility than VAR. This example is evidence of the limitation of VAR. The VAR is scrutinised by the assumption that heteroscedasticity is a feature of forecasted time series. The VAR model is a statistical model, hence requires heteroscedasticity of the entire population. Therefore, with the change of statistical measures in the forecasted time series, we observe an expected downgrade in the forecast performance. In the process of the VAR modelling, it was observed that the VAR model loses its degrees of freedom with increasing lags length and independent variables. This limits the model in comparison to the ANN model where the number of used lags and variables is less significant. The ANN model’s difficulty of implementation does not change with the increased number of inputs/lags as it is still “black box” like model. The effort to create model with 5 inputs vs 10 inputs will be similar. The same is not true for the VAR model, where each additional variable increases complexity and causes limitations. Hence it can be concluded that ANN is more flexible and allow to use of a larger number of inputs to the model.

7. Conclusions

The main objective of this work was to establish which model performs better in terms of MSE and RMSE in the area of real estate prices. The results confirmed the that ANN has fewer limitations and performs better in time series forecasting than the VAR model. These results were in line with [10,23,24]. Our findings reject the hypothesis that Neural Network model variables do not surpass the VAR method in predicting the UK FTSE350 Real Estate prices. This finding bridges the gap and contributes to the field by providing further evidence of the feasibility of a novel ANN model in forecasting tasks, demonstrating its application for the FTSE350 UK Real Estate Index forecast versus a VAR model. Moreover, the research contributed by proposing the new original pragmatic approach of ANN architecture size optimisation by using an iterative process measuring the gradient of Mean Square Error of network performance for different input/hidden layer sizes. Moreover, due to the use of new data, the selected sample included increased volatility caused by COVID-19. This allowed to examine both VAR and ANN in the condition of increased volatility. The result shown that the ANN performed better forecast post COVID-19 period then VAR that indicates that there is potential for further use of ANN or hybrid algorithms that will enable to achieve better results. Future comparative study could consider long term forecasting, where the exogenous variables will be estimated in a closed loop. Nevertheless, ANN, a so-called shallow network, which is relatively simple and more complex deep learning or hybrid networks could be considered with non-time series predictors giving even further advantage against classical statistical methods.

Author Contributions

M.I and KV. Contributed equally to all parts of the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The data that support the fndings of the study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Waheeb, W. , & Ghazali, R. A novel error-output recurrent neural network model for time series forecasting. Neural Computing and Applications, 32(13), 2020, 9621–9647. [CrossRef]
  2. Wu, Y. chen, & Feng, J. wen. Development and Application of Artificial Neural Network. Wireless Personal Communications, 2018,102(2), 1645–1656. [CrossRef]
  3. Kumar, G. , Jain, S., & Singh, U. P. Stock Market Forecasting Using Computational Intelligence: A Survey. Archives of Computational Methods in Engineering, 2020, 28(3), 1069–1101. [CrossRef]
  4. Tiwari, P. , & White, M. Real estate finance in the new economy. John Wiley & Sons, 2014.
  5. Newbold, E. M. Practical applications of the statistics of repeated events’ particularly to industrial accidents. Journal of the Royal Statistical Society, 1927, 90(3), 487–547.
  6. Chatfield, C. Time-series forecasting. CRC press.2000.
  7. Tsay, R. S. Time series and forecasting: Brief history and future research. Journal of the American Statistical Association, 2000, 95(450), 638–643.
  8. Mirmirani, S. , & Cheng Li, H. A COMPARISON OF VAR AND NEURAL NETWORKS WITH GENETIC ALGORITHM IN FORECASTING PRICE OF OIL. In J. M. Binner, G. Kendall, & S.-H. Chen (Eds.), Applications of Artificial Intelligence in Finance and Economics, 2004, (Vol. 19, pp. 203–223). Emerald Group Publishing Limited. [CrossRef]
  9. Ülke, V. , Sahin, A., & Subasi, A. A comparison of time series and machine learning models for inflation forecasting: empirical evidence from the USA. Neural Computing and Applications, 2018, 30(5), 1519–1527. [CrossRef]
  10. Aydin, A. D. , & Cavdar, S. C. Comparison of Prediction Performances of Artificial Neural Network (ANN) and Vector Autoregressive (VAR) Models by Using the Macroeconomic Variables of Gold Prices, Borsa Istanbul (BIST) 100 Index and US Dollar-Turkish Lira (USD/TRY) Exchange Rates. Procedia Economics and Finance, 2015, 30(15), 3–14. [CrossRef]
  11. Md.Siraj-Ud-Doulah. Time Series Forecasting : A Comparative Study of VAR ANN and SVM Models. Journal of Statistical and Econometric Methods,2019, 8(3), 21–34.
  12. Brooks, C. , RATS Handbook to Accompany Introductory Econometrics for Finance. Cambridge University Press.2008. https://ebookcentral.proquest.com.
  13. Odel, M, F b o var m. 2010, 59–69.
  14. Luk, K. C. , Ball, J. E., & Sharma, A., A study of optimal model lag and spatial inputs to artificial neural network for rainfall forecasting. Journal of Hydrology, 2000, 227(1–4), 56–65. [CrossRef]
  15. Howard, D. , & Mark, B.,Neural Network Toolbox Documentation. Neural Network Tool, 2004, 846.
  16. Aras, S. , Nguyen, A., White, A., He, S., & Bilgisi, Y., Comparing and Combining MLP and NEAT for Time Series Forecasting. İstanbul Üniversitesi İşletme Fakültesi Dergisi, 46(2), 147–160.
  17. Ramachandran, P., Zoph, B., & Le, Q. v, Searching for Activation Functions. 2017. https://arxiv.org/abs/1710.05941.
  18. Munkhdalai, L., Munkhdalai, T., Park, K. H., Lee, H. G., Li, M., & Ryu, K. H. , Mixture of Activation Functions with Extended Min-Max Normalization for Forex Market Prediction. IEEE Access, 2019, 7, 183680–183691. [CrossRef]
  19. Mercioni, M. A. , & Holban, S., Developing Novel Activation Functions in Time Series Anomaly Detection with LSTM Autoencoder. 2021, 000073–000078. [CrossRef]
  20. Vijayaprabakaran, K. , & Sathiyamurthy, K.,Towards activation function search for long short-term model network: A differential evolution based approach. Journal of King Saud University - Computer and Information Sciences, 2020. [CrossRef]
  21. Amelot, L. M. M. , Subadar Agathee, U., & Sunecher, Y, Time series modelling, NARX neural network and hybrid KPCA–SVR approach to forecast the foreign exchange market in Mauritius. African Journal of Economic and Management Studies, 2021, 12(1), 18–54. [CrossRef]
  22. Gavin, H. P. , The Levenberg-Marquardt Algorithm For Nonlinear Least Squares Curve-Fitting Problems. Duke University,2019, 1–19. http://people.duke.edu/~hpgavin/ce281/lm.pdf.
  23. Ramyar, S. , & Kianfar, F, Forecasting Crude Oil Prices: A Comparison Between Artificial Neural Networks and Vector Autoregressive Models. Computational Economics, 2019, 53(2), 743–761. [CrossRef]
  24. Ince, H. , Cebeci, A. F., & Imamoglu, S. Z, An Artificial Neural Network-Based Approach to the Monetary Model of Exchange Rate. Computational Economics, 2019, 53(2), 817–831. [CrossRef]
Preprints 113376 g001
Figure 1. Data sampling in the time series (FTSE350 Real Estate).
Figure 1. Data sampling in the time series (FTSE350 Real Estate).
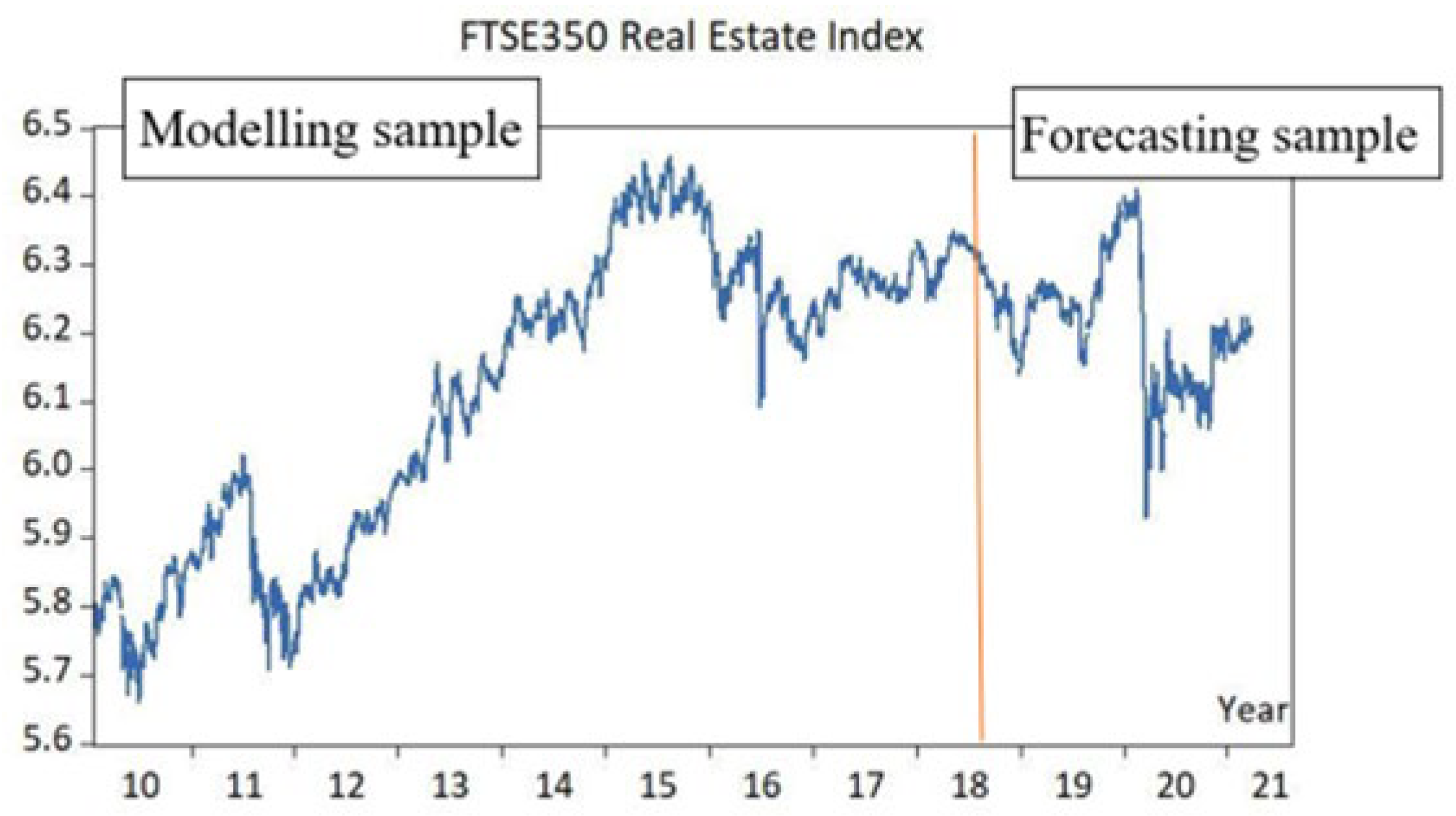
Preprints 113376 g001
Preprints 113376 g004
Figure 4. Response. Left-hand side full period (2200 samples), right-hand side zoom in last 200 samples – Open-loop mode.
Figure 4. Response. Left-hand side full period (2200 samples), right-hand side zoom in last 200 samples – Open-loop mode.
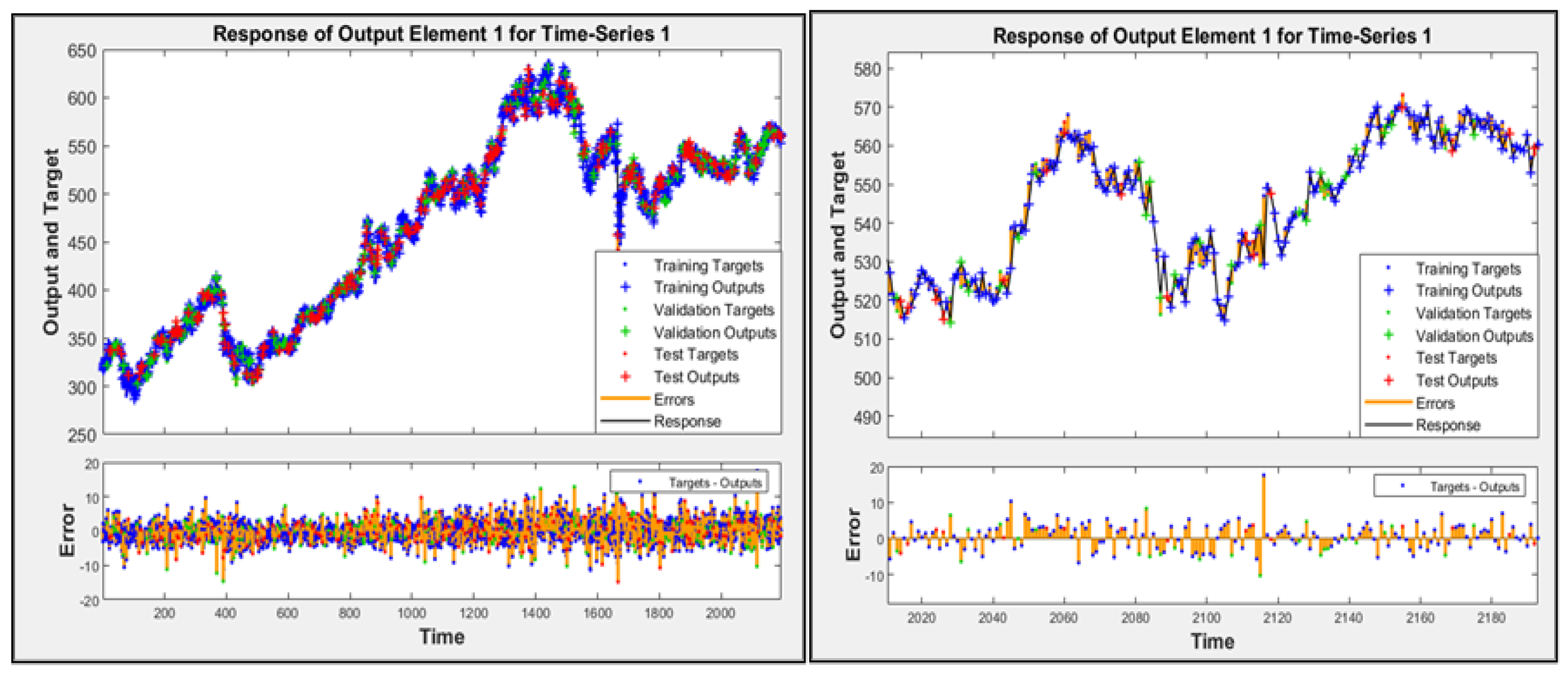
Preprints 113376 g004
Table 1. FTSE350 Daily return series statistical information- en and rn.
Table 1. FTSE350 Daily return series statistical information- en and rn.
Parameter price index log return
Mean 6.137 8.86e-05
Median 6.206 0.000362
Maximum 6.458 0.0813
Minimum 5.659 -0.1608
Standard Deviation 0.1963 0.0122
Skewness -0.624 -1.156
Kurtosis 2.197 20.31
FTSE350 Estate FTSE350 Brokage FTSE350 Banking FTSE350 Leisure and Travel UK 10 Year Bond UK 1 Year Bond US 10 Year Bond US 1 Year Bond
FTSE350 Estate 1 0.9002 0.0027 0.9183 -0.5304 -0.1835 -0.0839 0.4383
FTSE350 Brokage 0.9002 1 0.0798 0.9853 -0.5931 -0.1722 0.06112 0.7248
FTSE350 Banking
0.0027 0.0798 1 0.0168 0.47928 0.27374 0.63361 -0.0138
FTSE350 Travel 0.9184 0.9854 0.0169 1 -0.6586 -0.2557 -0.0402 0.6980
UK 10 Year Bond -0.5304 -0.5931 0.4793 -0.658 1 0.6479 0.67772 -0.5393
UK 1 Year Bond -0.1835 -0.1722 0.2737 -0.255 0.6479 1 0.64063 0.0394
US 10 Year Bond -0.0839 0.0611 0.6336 -0.04 0.67772 0.64063 1 0.16998
US 1 Year Bond 0.43827 0.7247 -0.0138 0.6980 -0.5393 0.0394 0.16998 1
Table 3. NNs Performances for various lags and hidden layers.
Table 3. NNs Performances for various lags and hidden layers.
Iteration Layers Lags MSE
1 10 2 10.62521456
2 10 4 10.43579192
3 10 6 10.40362438
4 10 8 11.10665214
5 10 10 10.27700301
6 15 2 11.18394697
7 15 4 11.58470414
8 15 6 12.04079142
9 15 8 10.43845425
10 15 10 13.22750617
11 20 2 11.18394697
12 20 4 11.58470414
13 20 6 12.04079142
14 20 8 10.43845425
15 20 10 13.22750617
16 30 2 10.3368559
17 30 4 9.500408453
18* 30* 6* 8.452163345*
19 30 8 12.68224404
20 30 10 12.95759596
21 50 2 10.32805827
22 50 4 10.25260303
23 50 6 11.23423115
24 50 8 13.50034617
25 50 10 13.44264925
26 88 6 20.12304212
Table 4. Experiments – Forecast performance measures.
Table 4. Experiments – Forecast performance measures.
Error Measure VAR Result ANN Result
Experiment 1 Mean Square Error 106.8880 50.0312
Root Mean Square Error 10.3387 7.0733
Experiment 2 Mean Square Error 529.9981 70.2729
Root Mean Square Error 23.0217 8.3829
Experiment 3 Mean Square Error 15.0500 10.3868
Root Mean Square Error 3.8794 3.2229
Experiment 4 Mean Square Error 96.7512 39.9825
Root Mean Square Error 9.8362 6.3232
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated