A Framework for Iterative Phase Retrieval Technique Integration into Atmospheric Adaptive Optics. Part I: Wavefront Sensing in Strong Scintillations

Preprint

Article

A Framework for Iterative Phase Retrieval Technique Integration into Atmospheric Adaptive Optics. Part I: Wavefront Sensing in Strong Scintillations

Altmetrics

Downloads

132

Views

100

Comments

A peer-reviewed article of this preprint also exists.

Mikhail A Vorontsov^*

,Ernst Polnau

Mikhail A Vorontsov^*

,Ernst Polnau

This version is not peer-reviewed

Submitted:

25 July 2024

Posted:

26 July 2024

You are already at the latest version

Alerts

Abstract

The objective of this study, which is divided into two parts, is twofold: to address long standing challenges in the sensing of atmospheric turbulence-induced wavefront aberrations in strong scintillation conditions via comparative analysis of several basic scintillation resistant wavefront sensing (SR-WFS) architectures and iterative phase retrieval (IPR) techniques (Part I, this paper), and to develop a framework for the potential integration of SR-WFS techniques into practical closed-loop non-astronomical atmospheric adaptive optics (AO) systems (Part II). In this paper we consider basic SR-WFS mathematical models and phase retrieval algorithms, tradeoffs in sensor design and phase retrieval technique implementation, and methodologies for WFS parameter optimization and performance assessment. The analysis is based on wave-optics numerical simulations imitating realistic turbulence-induced phase aberrations and intensity scintillations, and optical field propagation inside SR-WFSs. Several potential issues important for practical implementation of SR-WFS and IPR techniques such as requirements for phase retrieval computational grid resolution, tolerance with respect to optical element misalignments, and the impact of camera noise and input light non-monochromaticity are also considered. Results demonstrate that major wavefront sensing requirements desirable for AO operation in strong intensity scintillations can potentially be achieved by transitioning to novel SR-WFS architectures based on iterative phase retrieval techniques.

Keywords:

Subject: Physical Sciences - Optics and Photonics

1. Introduction

Operational principles of wavefront sensors (WFS) used in astronomical adaptive optics (AO) applications including Shack–Hartmann (SH) [1,2], curvature sensor [3,4], lateral shearing interferometer [5,6], pyramid WFS [7,8], etc., are based on the assumption of relatively weak intensity inhomogeneities (scintillations) in the entering WFS optical field. For this reason, it is not a surprise that these sensors are not efficient in AO applications associated with laser beam propagation over near-horizontal or slant atmospheric paths, which are commonly characterized by moderate-to-strong intensity scintillations [9]. This drawback precludes efficient utilization of AO techniques in such rapidly growing atmospheric optics areas as directed energy (DE) [10,11], remote laser power beaming [12], laser communications [13], and active (laser illumination based) imaging [14].

Several efforts were undertaken in recent years to develop wavefront sensors that are less affected by scintillations (scintillation-resistant WFS) and, hence, can be used for turbulence-induced aberration sensing in various non-astronomical atmospheric AO systems [15,16]. Despite some progress in tackling the scintillation problem, the scintillation resistant wavefront sensing (SR-WFS) approaches have not (as to our knowledge) been implemented in practical closed-loop non-astronomical atmospheric AO systems.

One of the reason for this outcome is that in addition to scintillation resistance, such sensors should meet several additional criteria: (a) high closed-loop operational bandwidth (typically close to or above 1.0 kHz); (b) sufficiently high spatial resolution in phase aberration sensing (e.g., ranging from about 10² to 10³ resolvable phase values); (c) cost efficiency; (d) robustness in operation under a wide range of turbulence and environmental conditions; (e) easy alignment and maintenance; (f) operation at a low signal to noise ratio (SNR) and with a non-monochromatic light source; and (g) high accuracy in aberration sensing with errors not exceeding a small fraction of the operational wavelength.

This list of desired WFS characteristics may require modification and/or extension for certain, specific atmospheric AO applications. However, it is quite a challenge to meet even a portion of the previously mentioned criteria with a single WFS instrument. Furthermore, some requirements may be at odds with each other. For example, increasing the WFS operational bandwidth most likely will only be achieved at the expense of wavefront sensing resolution and accuracy, and vice versa. On the other hand, the classical SH sensor represents an excellent example of wavefront sensing system that meets nearly all of the criteria outlined above with the exception of resistance to scintillations, and inadequate spatial resolution for some AO applications. In this study the SH sensor is considered as the model to be followed in the development of scintillation-resistant wavefront sensing techniques for atmospheric AO applications.

In this paper we demonstrate that most of the wavefront sensing characteristics desired for atmospheric AO can potentially be achieved by transitioning to WFS architectures based on iterative phase retrieval (IPR) techniques.

In Section 2 we provide a synopsis of basic WFS configurations and IPR algorithms that may be considered as candidates for turbulence-induced phase aberration sensing and AO mitigation in strong scintillations. These sensors can be described in terms of a generic SR-WFS model introduced here. This model is further applied to derive iterative phase and complex field (phase and magnitude) retrieval algorithms based on gradient descent optimization of a fidelity (error) metric – analogues of the classical Gerchberg-Saxton (GS) and Fienup error reduction and hybrid-input-output (HIO) phase retrieval algorithms [17,18,19,20]. We also outline the similarity of the iterative phase retrieval techniques and algorithms used for synthesis of programmable diffractive optics elements (DOE) in laser beam shaping applications [21,22]. This section also provides a description of IPR computational steps and metrics that can be utilized for phase and complex field retrieval accuracy assessment.

In Section 3 we analyze the general properties of optical field transformation in basic SR-WFS configurations which are “favorable” for achieving high performance in closed-loop operation under a wide range of turbulence conditions. This analysis is further applied to the SR-WFS optical configuration introduced here and referred to as the scintillation-resistant advanced phase contrast (SAPCO) sensor that, similarly the SH WFS, is composed of a single optical element – a specially designed phase mask. In this section we also outline and discuss several tradeoffs that should be considered in designing SR-WFS instruments for atmospheric AO applications, including tradeoffs between phase retrieval accuracy and required computational time.

Section 3 is concluded by a description of the numerical simulation setting used for analysis and parameter optimization of SR-WFSs and IPR-based wave front sensing techniques. Numerical simulations were conducted using a conventional wave-optics (split-step operator based [23]) numerical simulation approach. To imitate realistic turbulence-induced wavefront aberrations and intensity scintillations the modeling and simulation (M&S) setting included laser beacon beam propagation over 5 km to the SR-WFS input plane through atmospheric turbulence uniformly distributed along the path.

Section 4 provides examples of parameter selection and optimization for basic SR-WFS types with special emphasis on the SAPCO sensor. Optimization of WFS parameters was based on the computation of phase retrieval error in the course of HIO algorithm iterations. The corresponding dependencies (phase retrieval error evolution curves) were obtained in a set of numerical simulation trials conducted for statistically independent atmospheric turbulence realizations, WFS parameter values, and under different turbulence conditions. Trial results were averaged over turbulence realizations and the corresponding atmospheric-averaged phase retrieval error evolution curves were used for parameter optimization and comparative performance assessment of basic SR-WFS types. This methodology was applied to address issues important for practical (hardware) implementation of SR-WFS architectures based on the IPR technique such as tolerance with respect to SR-WFS parameter deviations unaccounted for in the mathematical model used for phase retrieval, and the impact of WFS photo-array (camera) noise and laser source non-monochromaticity.

In the concluding remarks (Section 5) we deliberate the path forward for SR-WFS technique integration into closed-loop AO systems. A framework for this integration with specific examples of SR-WFS-based AO architectures and performance analysis are presented in a following paper (Part II).

2. Scintillation Resistant Wavefront Sensing for Atmospheric AO

2.1. Intensity Scintillation Impact on Zonal and Modal WFSs

Due to point-to-point (or zonal) mapping of input and output field characteristics in conventional WFSs, spatial modulation of the input field intensity

I_{i n} (r)

is practically “imprinted” into the sensor output intensity

I_{o u t} (r)

used for input field phase

φ (r)

computation (retrieval), where

r = {x, y}

is a coordinate vector in the WFS input and output planes. Correspondingly, under strong scintillations the output intensity distribution in these sensors may contain low-intensity (“dark”) regions with an SNR unacceptably low for accurate phase retrieval.

At the same time, intensity inhomogeneities (e.g., resulting from turbulence-induced scintillations) are not a major concern for modal-type WFSs where input intensity “dark” regions are dispersed across the sensor output plane.1 Transformation of the optical field in these WFSs can be considered non-localized.

A simple lens with a photo-array (camera) located at its focal plane represents a canonic example of a modal-type optical system that provides non-localized mapping of input and output fields. Referred to here as the lens-based WFS, this optical system is illustrated in Figure 1. In lens-based and other modal-type WFSs the output intensity

I_{o u t} (r)

is predominantly defined by the input field phase

φ (r)

and is only weakly influenced by input field intensity inhomogeneities – the major reason why modal-type wavefront sensing systems are more resilient to intensity scintillations. This low sensitivity (resilience) with respect to intensity scintillations comes at the price of significantly more complicated and time-consuming (in comparison with conventional WFSs) signal processing requirements for phase function

φ (r)

retrieval from output intensity measurements.

Potential utilization of SR-WFSs for atmospheric AO is contingent on how efficient (fast and accurate) phase retrieval can be performed. This, in turn, largely depends on both the SR-WFS type (WFS optical configuration) defining the input-to-output field transformation, and the phase retrieval algorithm utilized. Both the WFS optical configuration (optical design) and phase retrieval algorithm should be jointly optimized while accounting for input field phase and intensity characteristics specific for A-AO applications. The following sections include discussions of both of these key matters.

Figure 1. Examples of single-camera-based modal type WFS configurations and the corresponding generic SR-WFS model (bottom right).

2.2. Basic SR-WFS Architectures

Examples of WFS types weakly affected by scintillations considered in this paper are represented in Figure 1 by notional schematics of: (a) the lens-based WFS; (b) classical Zernike filter (Zernike WFS) [25,26,27]; (c) multi-aperture phase reconstruction (MAPR) sensor [15]; (d) multi-aperture phase contrast (MAPCO) WFS [16]; and (e) a WFS based on a phase-only spatial light modulator (SLM) used for imposing a high-resolution random phase modulation pattern onto the optical field entering the sensor [28,29,30].

The optical schematics of the Zernike and MAPCO WFSs in Figure 1 include phase-shifting elements (phase masks). The Zernike sensor phase mask represents a diffraction-limited circular region (Zernike phase dot) at the lens focus that introduces a π/2 radian phase shift into the optical wave passing through the phase dot [25]. The corresponding phase mask of the MAPCO WFS is composed of a large number of differently configured Zernike phase dots that impose π radian phase shift [16].

In the SR-WFSs in Figure 1 phase masks, and phase-only SLM that can also be considered as a phase mask, provide non-localized input-to-output optical field transformation enabling mitigation of the input field intensity scintillations (dark regions) impact on sensor output intensity. Note that in the case of lens-based and MAPR WFSs non-localized optical field transformation is achieved via positioning of the photo-array in the focal plane of the correspondingly lens and lenslet array.

Characteristic output intensity patterns for the modal type basic SR-WFS configurations in Figure 1 are illustrated in Figure 2 for relatively weak (top row), moderate-to-strong (middle row), and strong (bottom row) turbulence conditions. These intensity patterns were computed using the input field intensity

I_{i n} (r)

and phase

φ (r)

distributions shown in Figure 3, which are identical for all WFSs. Note that the phase patterns in this figure (bottom row) have characteristic topological singularities (branch points [31]) and 2π phase cuts, which grow in number when turbulence strength is increased.

The impact of turbulence is characterized in Figure 2 and elsewhere in this paper by the following commonly used parameters: the ratio

D / r_{0}

of the WFS aperture size D to the Fried parameter

r_{0}

(the measure of the input field phase aberration correlation length), and the Rytov variance

σ_{R}^{2}

describing input field intensity scintillation strength [32,33,34].

For the numerical analysis in this paper the following expressions for

r_{0}

and

σ_{R}^{2}

were utilized:

r_{0} = {(0.16 C_{n}^{2} k^{2} L)}^{- 3 / 5}

and

σ_{R}^{2} = 1.23 C_{n}^{2} k^{7 / 6} L^{- 11 / 6}

[33]. Here

C_{n}^{2}

is the defining turbulence strength refractive index structure parameter,

k = 2 π / λ

is wavenumber for a monochromatic optical wave of wavelength

λ

, and L is the atmospheric propagation path length.

Comparing the input and output intensity distributions in Figure 2 and Figure 3 reveals the lack of correlation between the corresponding intensity patterns, which is typical for modal type wavefront sensors. Note that some similarity between

I_{i n} (r)

and

I_{o u t} (r)

can still be observed in Figure 2 for the Zernike WFS but only under relatively weak turbulence

(D / r_{0} = 3)

It is worthwhile to point out a distinguishing characteristic of the output intensity distributions in Figure 2 that is (as further discussed) important for selecting the SR-WFS type for atmospheric AO applications. As seen from Figure 2, when turbulence strength is increased the output intensity patterns for the lens-based WFS, MAPR, and Zernike WFS undergo quite a significant transformation. Conversely, the corresponding intensity distributions for phase contrast type sensors such as MAPCO and phase-SLM based sensors preserve a similar spatial structure (randomly scattered spots) when turbulence strength is increased. For these sensors we would expect (as further discussed in Section 3.1 and 4.3) that phase retrieval efficiency would be less affected by turbulence strength – an important advantage for closed-loop wavefront sensing and AO control under diverse turbulence conditions.

2.3. Generic Scintillation Resistance WFS: Mathematical Model

Consider a generic SR-WFS model as illustrated in Figure 1 (bottom right panel). This model provides a general framework for analysis of different WFS architectures. Transformation of a coherent monochromatic (quasi-monochromatic) input optical field with complex amplitude

A_{i n} (r)

is described in this model by accounting for the following effects: (a) input field diffraction at the WFS aperture diaphragm [pupil-plane mask

M_{i n} (r)

]; (b) propagation through SR-WFS phase-only optical element(s) located between the input (z=0) and output (

z = L_{W F S}

) planes; and (c) propagation along optical path segments between these elements. Additionally, we assume that optical power loses inside the SR-WFS are negligibly small and can be neglected.

The impact of phase-only optical elements (e.g., lenses, lenslets, phase masks, etc.) on the optical field complex amplitude

A (r, z)

, where

0 \leq z \leq L_{W F S}

, is described in the SR-WFS model by the refractive index

n_{W F S} (r, z)

dependence on the transversal and longitudinal (along the sensor optical axis) coordinates, correspondingly

r = {x, y}

and z.

For example, a thin phase-only optical element (e.g., a phase mask, lens, or lenslet array) located at the plane

z = z_{e l m}

, where

0 \leq z_{e l m} \leq L_{W F S}

, is described by the function

n_{W F S} (r, z) = n_{e l m} (r) δ (z - z_{e l m})

, where

δ (z - z_{e l m})

is a delta function and

n_{e l m} (r)

is the phase modulation introduced by the phase-only optical element. It is easy to see that the generic SR-WFS model can be applied for analysis of optical field transformation performed in all sensing systems shown in Figure 1.

In general terms, transformation of the optical field complex amplitude

A (r, z)

inside the generic SR-WFS can be described in the framework of the Fresnel approximation of diffraction theory using the following parabolic (quasi-optics propagation) equation [34]:

2 i k \frac{\partial A (r, z)}{\partial z} = \nabla_{⊥}^{2} A (r, z) + k^{2} (\frac{n_{W F S}^{2} (r, z)}{n_{0}^{2}} - 1) A (r, z), 0 \leq z \leq L_{W F S}

(1)

where

\nabla_{⊥}^{2} = \partial^{2} / \partial x^{2} + \partial^{2} / \partial y^{2}

is the Laplacian operator

n_{0}

is the undisturbed refractive index and

k = 2 π n_{0} / λ

. The boundary condition for Equation (1) is defined by the input field complex amplitude

A (r, z = 0) \equiv A_{i n} (r) = A_{0} (r) \exp [i φ (r)]

, where

A_{0} (r) = M_{i n} (r) I_{i n}^{1 / 2} (r)

is the input field magnitude within the aperture diaphragm

M_{i n} (r)

In the generic SR-WFS model considered here, it is assumed that retrieval of the input field phase

φ (r) = \arg [A (r, 0)]

inside the WFS aperture is solely based on processing of the output intensity distribution

I_{o u t} (r) = M_{P A} (r) | A (r, z = L_{W F S}) |^{2}

inside the photo-array region as described by the aperture function

M_{P A} (r)

. For simplicity we assume that

M_{i n} (r)

and

M_{P A} (r)

are window functions equal to one inside and zero outside of the corresponding squares of size

D_{W F S}

and

D_{P A}

. It is also convenient to assume that

D_{P A}

exceeds the characteristic output field footprint size and that the camera pixel size can be considered as infinitely small. This implies that

I_{o u t} (r) = | A (r, L_{W F S}) |^{2}

The SR-WFS model introduced here can be applied to describe input-to-output optical field transformation for a wide range of wavefront sensing architectures (including WFSs that are not necessarily resilient to intensity scintillations). In the following sections this SR-WFS model is utilized in derivation of IPR algorithms used in the efficiency analysis of wavefront sensing of atmospheric turbulence-induced aberrations.

2.4. Phase Retrieval via Optimization of a SR-WFS Output Field Fidelity Metric

The phase retrieval problem can be formulated as a minimization problem for the following fidelity metric (also referred to as an error metric and cost function) [20,35]:

J = {\int [{\tilde{I}}_{o u t}^{1 / 2} (r) - I_{o u t}^{1 / 2} (r)]}^{2} d^{2} r

(2)

Here

{\tilde{I}}_{o u t} (r) = | \tilde{A} (r, L_{W F S}) |^{2}

and

\tilde{A} (r, L_{W F S})

are, correspondingly, the SR-WFS output field intensity and complex amplitude computed using the input field estimation

{\tilde{A}}_{i n} (r) = {\tilde{A}}_{0} (r) \exp [i \tilde{φ} (r)]

for the “true” input field complex amplitude

A_{i n} (r) = A_{0} (r) \exp [i φ (r)]

inside WFS aperture diaphragm. Here

{\tilde{A}}_{0} (r) \geq 0

and

\tilde{φ} (r)

are corresponding estimations of the true magnitude and phase.2

The complex amplitude estimation

{\tilde{A}}_{i n} (r)

defines the boundary condition

A (r, 0) = {\tilde{A}}_{i n} (r) = {\tilde{A}}_{0} (r) \exp [i \tilde{φ} (r)]

(3)

for propagation Equation (1) that is used for computation of the output field intensity estimation

{\tilde{I}}_{o u t} (r)

and the corresponding value of the fidelity metric [Equation (2)].

Fidelity metric minimization is considered here by iterative modification (“shaping”) of the phase

\tilde{φ} (r)

and magnitude

{\tilde{A}}_{0} (r)

estimations aimed at retrieval of the true phase function

φ (r)

. Note that minimization of a fidelity metric analogous to Equation (2) is commonly used for synthesis of phase-only diffractive optics elements (DOE-based beam shapers) that perform transformation of a laser beam with a known input intensity distribution

I_{i n} (r)

into a beam with output intensity

{\tilde{I}}_{o u t} (r)

that is maximally “close” [optimal in terms of the metric (2)] to the desired intensity

I_{o u t} (r)

at a pre-defined distance

L_{D O E}

from the beam shaper [21,22].

Similar to the beam shaping problem statement mentioned above, both the input

I_{i n} (r)

and output

I_{o u t} (r)

intensity distributions are assumed to be known in the classical GS error reduction iterative phase retrieval algorithm originally developed for reconstruction of astronomical images [17,18,36]. Note that the original GS technique requires utilization of two cameras enabling synchronous measurements of both the input and output intensity distributions.

The core GS algorithm concept was further exploited to include complex field (both phase and magnitude) retrieval based on processing of a single and multiple intensity distributions (e.g., error-reduction iterative Fourier transform [18,20], phase diversity [36], incremental binary random sampling [37], beam-propagation-based random phase modulation [38], coded diffraction pattern [39], etc.).

In the single-camera based wavefront sensing configurations considered here, the input field intensity

I_{i n} (r)

is assumed to be unknown. Although knowledge of this intensity distribution is not required for AO operation, the function

I_{i n} (r)

still needs to be retrieved since the error metric (2) absolute minimum value can only be achieved when both the input field intensity and phase distributions are correctly determined. Thus, in the case of single-camera-based SR-WFS we “unavoidably” deal with the complex field retrieval problem. By keeping this in mind, we interchangeably refer in this paper to either “phase” or “complex field” retrieval.

2.5. Complex Field Retrieval for the Generic SR-WFS Model

To further proceed with phase (complex field) retrieval algorithms for the SR-WFS model, it is convenient to represent the error metric (2) in the following equivalent form:

J = \int {\tilde{I}}_{o u t} (r) d^{2} r + \int I_{o u t} (r) d^{2} r - 2 \int \tilde{A} (r, L_{W F S}) ψ (r, L_{W F S}) d^{2} r,

(4)

where

ψ (r, L_{W F S}) = I_{o u t}^{1 / 2} (r) \exp [- i \arg \tilde{A} (r, L_{W F S})]

(5)

is the complex function corresponding to formal replacement of the magnitude

| \tilde{A} (r, L_{W F S}) |

\tilde{A} (r, L_{W F S})

by the true output field magnitude

I_{o u t}^{1 / 2} (r)

Assume that the selected input field intensity

{\tilde{I}}_{i n} (r)

estimation is defined within the aperture diaphragm

M_{i n} (r)

and the function

{\tilde{A}}_{i n} (r) = {\tilde{I}}_{i n}^{1 / 2} (r) \exp [i \tilde{φ} (r)]

obeys the following condition describing preservation of the optical power

W_{0}

inside the SR-WFS:

\int {\tilde{I}}_{i n} (r) d^{2} r = \int {\tilde{I}}_{o u t} (r) d^{2} r = \int I_{o u t} (r) d^{2} r = W_{0} = c o n s t .

(6)

Under this condition, minimization of the fidelity metric (4) is equivalent to maximization of the following expression (referred to as the overlapping integral [40] or the interference metric [41]):

J_{i n t} = Re \int \tilde{A} (r, L_{W F S}) ψ (r, L_{W F S}) d^{2} r .

(7)

Assume now that the function

ψ (r, L_{W F S})

in Equation (5) defines the boundary condition for the complex amplitude

ψ (r, z)

of an auxiliary “optical wave” propagating along the SR-WFS optical axis in the reverse direction (from the output

z = L_{W F S}

to the input

z = 0

plane). Correspondingly, propagation (back-propagation) of this auxiliary wave can be described by the following quasi-optics equation similar to expression (1):

- 2 i k \frac{\partial ψ (r, z)}{\partial z} = \nabla_{⊥}^{2} ψ (r, z) + k^{2} (\frac{n_{W F S}^{2} (r, z)}{n_{0}^{2}} - 1) ψ (r, z) .

(8)

Note that the term “propagating” or “back-propagating” wave is applied to the solution (numerical solution) of either Equations (1) or (8), rather than to the propagation of real optical waves.

Using Equations (1) and (8) for the counter-propagating waves with complex amplitudes

\tilde{A} (r, z)

and

ψ (r, z)

, one can derive the following relationship coupling integral characteristics of these complex amplitudes at the SR-WFS input and output planes [41,42]:

J_{i n t} = Re \int \tilde{A} (r, L_{W F S}) ψ (r, L_{W F S}) d^{2} r = Re \int \tilde{A} (r, z) ψ (r, z) d^{2} r = Re \int \tilde{A} (r, 0) ψ (r, 0) d^{2} r,

(9)

where

\tilde{A} (r, z)

denotes the complex amplitude corresponding to the solution of Equation (1) with boundary condition (3). Note that expression (9) is valid for arbitrary boundary conditions for both Equations (1) and (8). Using expressions (3) and (5), relationship (9) can be represented in the form:

J_{i n t} = \int {\tilde{I}}_{o u t}^{1 / 2} (r) I_{o u t}^{1 / 2} (r) d^{2} r = Re \int {\tilde{A}}_{0} (r) | ψ (r, 0) | \exp [i \tilde{φ} (r) + i φ_{ψ} (r)] d^{2} r,

(10)

where

φ_{ψ} (r) = \arg [ψ (r, 0)]

Consider now an iterative procedure of metric

J_{i n t}

[Equation (10)] maximization with respect to estimations of the input field phase

\tilde{φ} (r)

and magnitude

{\tilde{A}}_{0} (r)

. Define these estimations at the n-th iteration (n=0,…,) as

{\tilde{φ}}^{(n)} (r)

and

{\tilde{A}}_{0}^{(n)} (r)

, correspondingly. In the introduced notations the right-hand side of Equation (10) is given by:

J_{i n t} = Re \int {\tilde{A}}_{0} (r) | ψ^{(n)} (r, 0) | \exp [i \tilde{φ} (r) + i φ_{ψ}^{(n)} (r)] d^{2} r,

(11)

where

ψ^{(n)} (r, 0)

and

φ_{ψ}^{(n)} (r) = \arg [ψ^{(n)} (r, 0)]

are, correspondingly, the complex amplitude and phase of the back-propagating wave at the SR-WFS input plane computed based on the estimations

{\tilde{φ}}^{(n)} (r)

and

{\tilde{A}}_{0}^{(n)} (r)

The functions

\tilde{φ} (r)

and

{\tilde{A}}_{0} (r)

in expression (11) denote the input field phase and magnitude estimations that should be selected at the next (n+1-st) iteration. It is easy to see that metric

J_{i n t}

in Equation (11) can be increased by choosing the n+1-st input field phase estimation

\tilde{φ} (r)

as the following:

{\tilde{φ}}^{(n + 1)} (r) = - \arg [ψ^{(n)} (r, 0)] .

(12)

Derived iterative procedure [Equation (12)] formally coincides with the original GS phase retrieval algorithm, assuming that both the input and output intensity distributions are known. In the single-camera-based SR-WFS model considering here, the input intensity

I_{i n} (r)

or, equivalently, the magnitude

A_{0} (r) = I_{i n}^{1 / 2} (r)

is the unknown function that should be retrieved jointly with the input field phase

φ (r)

To derive the corresponding algorithm for input field magnitude retrieval, substitute

{\tilde{φ}}^{(n + 1)} (r)

from Equation (12) into expression (11), which now reads

J_{i n t} = \int {\tilde{A}}_{0} (r) | ψ^{(n)} (r, 0) | d^{2} r .

(13)

It can be shown that the metric

J_{i n t}

in Equation (13) can be increased by selecting at the next (n+1-st) iteration the input field magnitude estimation in the form:

{\tilde{A}}_{0}^{(n + 1)} (r) = M_{i n} (r) | ψ^{(n)} (r, 0) | .

(14)

Here we used optical power conservation condition (6) and the assumption that the input field estimation

{\tilde{A}}_{0} (r)

is defined inside the aperture diaphragm

M_{i n} (r)

The update rules for input phase [Equation (12)] and magnitude [Equation (14)] estimations can be represented in the form of a single iterative equation:

{\tilde{A}}_{i n}^{(n + 1)} (r) = M_{i n} (r) | ψ^{(n)} (r, 0) | \exp [- i φ_{ψ}^{(n)} (r)] \equiv M_{i n} (r) ψ^{* (n)} (r, 0),

(15)

where the notation

ψ^{* (n)} (r, 0)

defines a complex function conjugated with respect to

ψ^{(n)} (r, 0)

Expression (15) describes an iterative procedure of back-propagating wave complex amplitude conjugation inside the aperture diaphragm

M_{i n} (r)

. It can be shown that the complex field retrieval iterative algorithm (15) is directly related to error metric (2) minimization via the conditional gradient search technique [35,43].3

Iterative equation (15) represents a formal analogous to the known in AO complex field conjugation (CFC) control algorithm in which the function

ψ^{(n)} (r, 0)

is associated with the complex amplitude of an optical wave scattered off a remotely located target and propagated back to the laser beam projection transceiver aperture (target-return wave) [44]. This resemblance between phase (complex field) retrieval and AO CFC control algorithms is further discussed in Part II. Referring to this formal analogy between the AO CFC control and the iterative algorithm for complex field retrieval via the auxiliary function conjugation (AFC) as described by iterative equation (15), the latter expression is referred to here as the AFC algorithm.

The iterative procedures described by Equations (12) and (15) belong to a wide framework of Fienup phase and complex field retrieval algorithms originally developed (see Ref. [20,45]) for astronomical imaging. One of the major issues with practical application of these algorithms for wavefront sensing in atmospheric AO systems is their relatively slow convergence resulting in potentially unacceptably low closed-loop operational bandwidth. As shown in Section 4.3, complex field retrieval convergence can be significantly improved using the AFC algorithm clone referred to as the hybrid input-output (HIO) iterative scheme introduced by Fienup (Ref [18]).

The iterative procedure for complex amplitude estimation update in the HIO algorithm is given by:

{\tilde{A}}_{i n}^{(n + 1)} (r) = M_{i n} (r) ψ^{* (n)} (r, 0) + W (r) [{\tilde{A}}_{i n}^{(n)} (r) - β ψ^{* (n)} (r, 0)],

(16)

where

β

is a tuning parameter (

β ≃ 0.95

) and

W (r) = 1 - M_{i n} (r)

is a window function that is zero inside the aperture diaphragm, and one otherwise. When compared with Equation (15), the HIO algorithm contains an additional term on the right hand side of expression (16), which affects complex amplitude estimations outside the aperture diaphragm

M_{i n} (r)

[within the window-function

W (r)

]. While the origin of this term, referred to here as Fienup’s complex field retrieval acceleration term, still lacks rigorous justification (as pointed out in Ref. [46]), its presence commonly results in noticeable acceleration of complex field retrieval process convergence [16,18,28].

2.6. Complex Field Retrieval Computational Steps

Consider now the computational steps associated with utilization of the AFC [Equation (15)], and HIO [Equation (16)] complex field retrieval algorithms.

In both cases iterations start from the selection of an initial (defined by the superscript n=0) estimation for the input field complex amplitude

{\tilde{A}}_{i n}^{(n = 0)} (r) = {\tilde{A}}_{0}^{(n = 0)} (r) \exp [i {\tilde{φ}}^{(n = 0)} (r)]

. In the M&S described in Section 4 and Section 5, the magnitude

{\tilde{A}}_{0}^{(n = 0)} (r)

was always set equal to a constant inside the SR-WFS aperture diaphragm

M_{i n} (r)

and zero otherwise. At the same time, the initial phase estimation

{\tilde{φ}}^{(n = 0)} (r)

was represented by a random realization of a delta-correlated field with zero mean and uniform probability distribution inside the interval [-π, π].

In analysis of the closed-loop wavefront sensing and AO control described in the paper that follows this study (Part II) the initial estimation

{\tilde{A}}_{i n}^{(n = 0)} (r)

was changed at each step of AO control variable update (at each AO control cycle). In this case to accelerate convergence the initial complex field estimation

{\tilde{A}}_{i n}^{(n = 0)} (r)

was set equal to the retrieved complex amplitude obtained during the preceding AO control cycle.

In both cases the initial estimation

{\tilde{A}}_{i n}^{(n = 0)} (r)

was utilized as the boundary condition

A (r, 0) = {\tilde{A}}_{i n}^{(n = 0)} (r)

for propagation Equation (1), which describes evolution of the complex amplitude

A (r, z)

along the SR-WFS optical axis from

z = 0

z = L_{W F S}

The computational steps associated with subsequent (ranging from n=1 to N_it) iterations are identical for both the AFC [Equation (15)] and HIO [Equation (16)] algorithms and include:

(1) Numerical integration of Equation (1) with the boundary condition

A (r, 0) = {\tilde{A}}_{i n}^{(n)} (r)

enabling computation of the complex amplitude

{\tilde{A}}^{(n)} (r, L_{W F S}) \equiv A (r, L_{W F S})

at the sensor output plane.

(2) Setting the boundary condition

ψ^{(n)} (r, L_{W F S}) = I_{o u t}^{1 / 2} (r) \exp [- i \arg {\tilde{A}}^{(n)} (r, L_{W F S})]

[Equation (5)] for the auxiliary complex amplitude

ψ (r, z)

(3) Numerical integration of Equation (8) from

z = L_{W F S}

z = 0

to obtain the complex amplitude

ψ^{(n)} (r, 0) \equiv ψ (r, 0)

at the SR-WFS input plane.

(4) Computation of the input field complex amplitude estimation

{\tilde{A}}_{i n}^{(n + 1)} (r)

at the n +1-st iteration using either the AFC [Equation (15)] or HIO [Equation (16)] update rule.

Steps (1) through (4) are repeated utilizing the complex field estimation

{\tilde{A}}_{i n}^{(n + 1)} (r)

as the boundary condition for Equation (1).

The complex amplitude retrieval trial ends with computation of the complex field estimation

{\tilde{A}}_{i n}^{(N_{i t} + 1)} (r)

after completing the set of N_it iterations. The number of required iterations N_it depends on the metric selected for evaluation of phase and/or complex field retrieval quality. Note that in the case of closed-loop WFS operation, the number of iterations N_it may be constrained by the duration

τ_{A O}

of the AO control cycle and the computational time

τ_{i t}

needed to perform a single phase retrieval iteration.

2.7. Complex Field and Phase Retrieval Quality Metrics

For phase retrieval quality assessment, it is necessary to account for the 2π phase ambiguity [31,47]. This implies that the phase estimation functions

\tilde{φ} (r)

which are distinguished from the true phase function

φ (r)

by points or regions having a modulo 2π difference, should be considered as equivalent. For this reason, performance evaluation of phase retrieval algorithms should be based on metrics that are insensitive to modulo 2π phase value jumps. This requirement is satisfied for the following metrics that can be used for phase retrieval accuracy evaluation at each nth iteration:

S t_{δ} (n) = S_{M}^{- 1} {| \int M_{i n} (r) \exp [i δ^{(n)} (r)] d^{2} r |}^{2}, and ε_{δ} (n) = 1 - S t_{δ} (n)

(17)

where

S_{M}

and

δ^{(n)} (r) = φ (r) - {\tilde{φ}}^{(n)} (r)

are, correspondingly, the WFS input aperture area and the residual phase computed at the nth phase retrieval iteration. Note that ideal retrieval of the true phase

φ (r)

corresponds to

S t_{δ} (n) = 1

and

ε_{δ} (n) = 0

. Metric (17a) can be associated with the Strehl ratio well-known in AO that is applied here for an optical wave with uniform intensity [

I_{i n} (r) = c o n s t

] and phase aberration

δ^{(n)} (r)

. The metric

ε_{δ} (n)

in Equation (17b) is referred to here as the phase retrieval error. This metric is convenient for estimation of the number of iterations

N_{i t} (ε_{0})

required to reach a pre-selected phase retrieval error threshold

ε_{δ} (n = N_{i t}) = ε_{0}

[16].

For quality assessment of complex field retrieval, the following metrics characterizing “matching” of the true

A_{i n} (r)

and retrieved

{\tilde{A}}_{i n}^{(n)} (r)

complex amplitudes can be used:

J_{f l d} (n) = | \int M_{i n} (r) A_{i n}^{*} (r) {\tilde{A}}_{i n}^{(n)} (r) d^{2} r | / \int I_{i n} (r) d^{2} r, ε_{f l d} (n) = 1 - J_{f l d} (n) .

(18)

Ideal input field complex amplitude retrieval (both phase and magnitude) corresponds to

J_{f l d} (n) = 1

and

ε_{f l d} (n) = 0

The spatial distribution of retrieved phase error within the WFS aperture may play an important role in AO beam projection applications in which a larger error is more “acceptable” (causes a smaller impact on AO system performance) within laser beam footprint areas with lower intensity, e.g., within the tail section of a truncated Gaussian-shaped beam formed by an off-axis type transmitter telescope (beam director). For this reason, the projected beam intensity distribution

I_{b e a m} (r)

(beam “shape”) should somehow be accounted for in the phase retrieval quality metric. This can be achieved by adding a weighting function

W_{b e a m} (r) = I_{b e a m} (r) / \max [I_{b e a m} (r)]

proportional to

I_{b e a m} (r)

into expression (17a). The corresponding phase retrieval quality metrics accounting for the transmitted beam shape are given by:

S t_{W} (n) = S_{M}^{- 1} {| \int M_{i n} (r) W_{b e a m} (r) \exp [i δ^{(n)} (r)] d^{2} r |}^{2} and ε_{W} (n) = 1 - S t_{W} (n)

(19)

Note that a similar beam shape weighting factor can also be applied into the corresponding expressions (18) for complex field retrieval quality metrics.

These introduced metrics may not be adequate for analysis of phase retrieval error impact on overall performance of closed-loop atmospheric AO systems. In addition to evaluation of phase retrieval errors, such a performance analysis may require consideration of a number of mutually dependent factors such as beam director configuration, propagation geometry, atmospheric turbulence strength, feedback control algorithm, beam control performance measures, etc. An example of such an analysis is presented in Part II of this paper.

3. Tradeoffs in SR-WFS Design and Phase Retrieval Technique Implementation

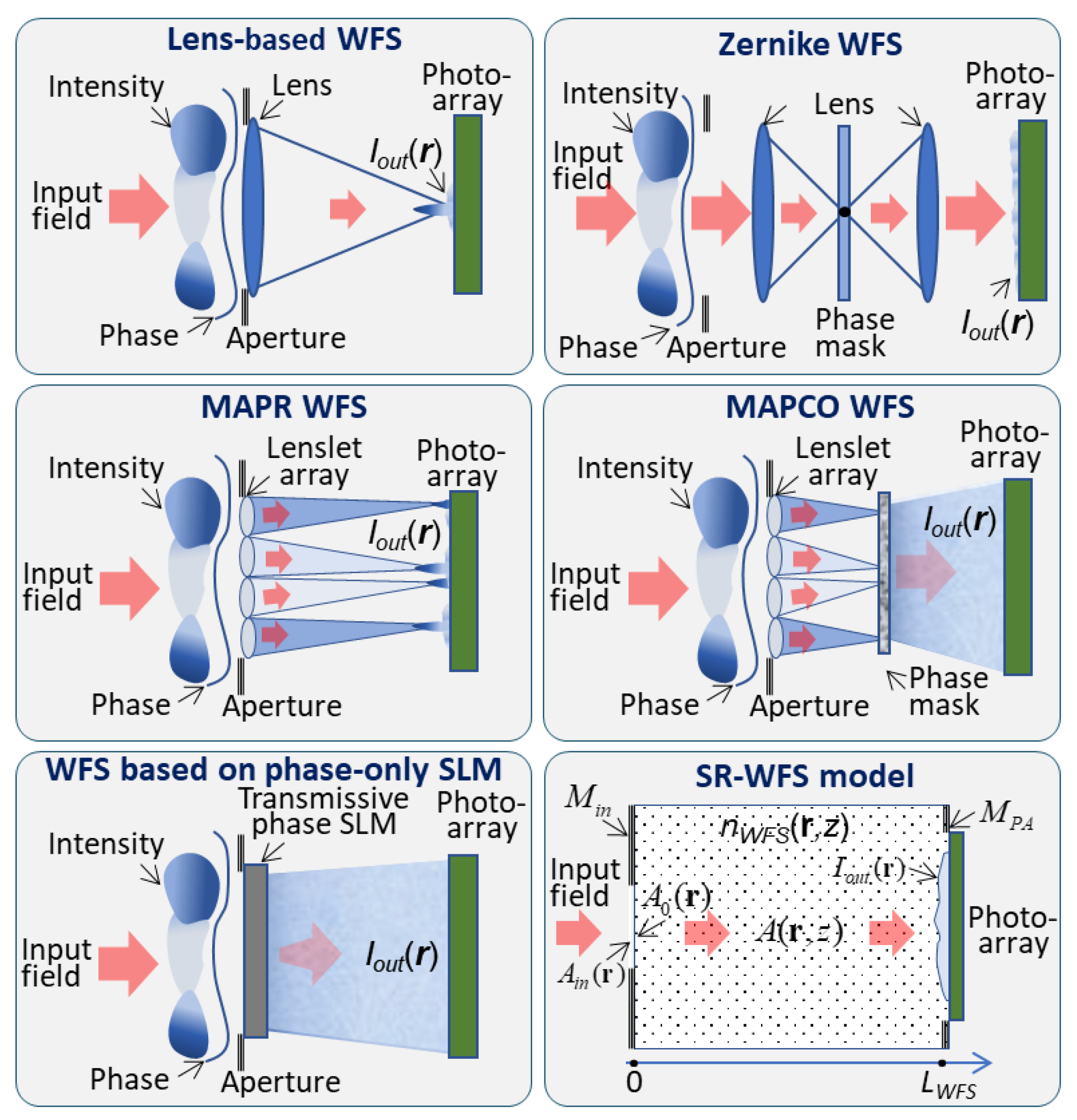
3.1. Basic Considerations for SR-WFS Design: SAPCO WFS

The phase retrieval convergence rate defined here as

R_{c o n v} = 1 / N_{i t} (ε_{0})

, represents one of the most important characteristics for assessment of IPR-based wavefront sensing technique relevance for atmospheric AO. The convergence rate depends not only on the phase retrieval algorithm, pre-selected phase error threshold

ε_{0}

, and initial complex field estimation, but to large degree on the optical configuration specific for each SR-WFS (WFS optical design/schematic) defining the input-to-output optical field transformation inside the WFS, atmospheric turbulence strength, and the propagation geometry on which the spatio-temporal characteristics of the input field phase and intensity distributions depend.

As shown in the M&S described in Section 4 a higher phase retrieval convergence rate is expected with WFS optical designs that provide highly non-localized mapping of input and output fields resulting in near homogeneous output intensity spread across the entire photo-array area with the absence of dominating intensity spikes. Such highly non-localized input-to-output mapping leads to increase SNR and mitigation of phase retrieval process stagnation.

For the atmospheric AO applications considered here, it is also important to achieve uniform phase retrieval convergence rate for a wide range of turbulence conditions - from weak turbulence characterized by the presence of smooth (low-order) phase aberrations and relatively weak intensity scintillations, to strong turbulence for which the input field phase has a complicated topological structure with a number of branch points and the intensity is highly scintillated. This suggests that more uniform convergence rates are anticipated for SR-WFS optical configurations where the variation in turbulence strength and, hence, input field characteristics do not significantly affect the general structure of the WFS output intensity patterns.

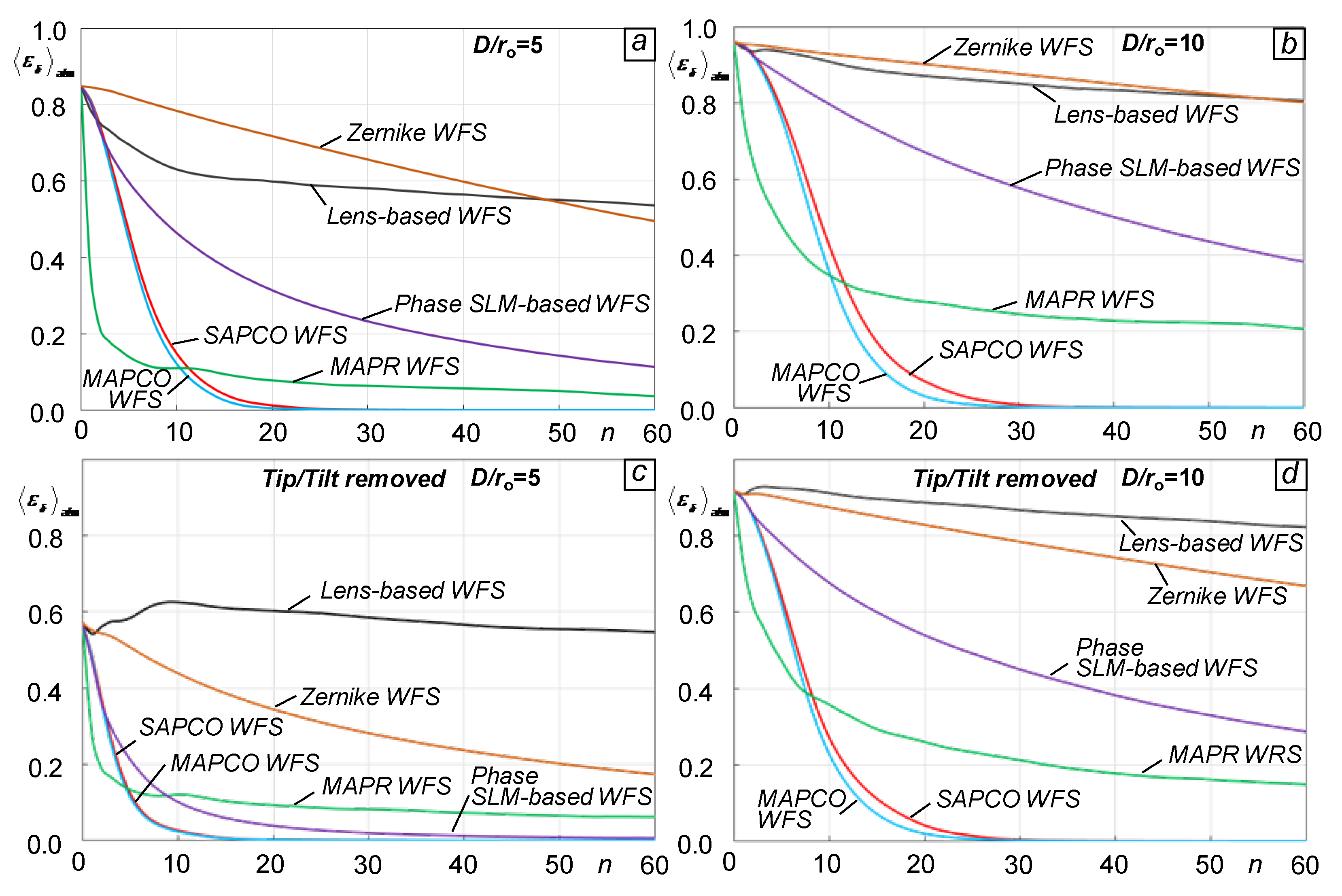
In terms of the outlined (“favorable” for achieving a high phase retrieval convergence rate) criteria, compare the basic SR-WFS architectures shown in Figure 1. The following physics-based analysis provides general guidance for development and optimization of the most promising SR-WFS architectures for atmospheric AO applications, such as the scintillation-resistant advanced phase contrast (SAPCO) WFS introduced here.

1. Lens-based WFS (top left panel in Figure 1). The output intensity distributions in this sensor (left column in Figure 2), are highly non-uniform and characterized by the presence of dominant (bright) intensity spots surrounded by relatively weak side-lobes in weak and moderate-to-strong turbulence. Turbulence strength increases result in side-lobe area widening and an associated diminishing of the bright spot, which practically vanishes under strong turbulence conditions. Note that input field phase aberrations predominantly affect the intensity distribution pattern within the side-lobe region. Correspondingly, in order to ensure an SNR sufficiently high for accurate phase retrieval under weak turbulence, lens-based WFS would require a photo-array (camera) with a large dynamical range. In addition, to scale the output intensity footprint into the camera chip area the lens, or a combination of lenses used for optical field scaling, should have a relatively long focal length F thus leading to WFS hardware implementations that are potentially bulky and sensitive to vibrations.

2. MAPR WFS (middle left panel in Figure 1). The drawbacks of the lens-based sensor are partially alleviated in the MAPR WFS design by utilization of a 2D lenslet array composed of

n_{l} \times n_{l}

densely packaged lenslets of size

d_{s u b} = D_{W F S} / n_{l}

. The lenslet array performs input field partitioning into

n_{l}

-fold smaller zones (subregions) resulting in both a general decrease in sensor output intensity spatial nonuniformity and a decrease in the impact of turbulence strength on the output intensity spatial structure inside subregions, as illustrated in Fig 2 (second column) for

n_{l} = 4

. Additionally,

n_{l}

-fold smaller size lenslets enables a proportional decrease in the focal length

f_{l} = F / n_{l}

, potentially providing for a more compact WFS hardware implementation. Another advantage of the MAPR WFS is the possibility for significant improvement in both the phase retrieval convergence rate and required computational time with processing of output intensity within subregions in parallel [15]. On the other hand, input field partitioning may lead to crosstalk between neighboring subregions (especially in strong turbulence conditions) resulting in a decline in phase retrieval accuracy (see Section 4.3).

3. Zernike WFS (top right panel in Figure 1). This sensor provides for more spatially uniform output intensity spreading across the photo-array area than both the lens-based and MAPR sensors (compare corresponding images in Figure 2). One of the major potential drawbacks of this sensor is its high sensitivity to turbulence-induced wavefront tilts leading to focal spot lateral displacements with respect to the phase shifting dot. These displacements, typical for weak turbulence conditions, result in strong variations in output intensity pattern contrast that negatively affect phase retrieval convergence. Intensity pattern contrast variations and its general decline also occur due to fluctuations of optical power within the phase shifting dot area when turbulence strength increases. Furthermore, Zernike WFS is even bulkier than are the lens-based and MAPR sensors.

4. MAPCO WFS (top middle panel in Figure 1). The shortcomings of the SR-WFS discussed above are addressed in the MAPCO WFS consisting of a densely packed array of phase contrast (Zernike-type) sensors [16]. Here the same approach as in the MAPR WFS is applied - input field partitioning with a lenslet array. Mitigation of the negative impact of local (inside lenslet subregions) wavefront tilts is achieved using a phase mask composed of a large (~ 10³) number of identical phase shifting dots arranged either randomly (random-dot phase mask) or in the form of a 2D grid (grid-dot phase mask) [16]. The optical wave entering the MAPCO sensor is focused by the lenslet array onto the phase mask and, after receiving the corresponding phase modulation, undergoes free-space propagation (diffraction) over the relatively short distance

L_{d i f}

to the photo-array. The output intensity patterns of the MAPCO sensor are comprised of a large number of spots that are nearly evenly spread across the output plane as illustrated in Figure 2 (fourth column). Note that increases in turbulence strength have little impact on the general structure and spatial extent of the output intensity patterns – a desired WFS characteristic for obtaining comparably even phase retrieval convergence rate under a wide range of turbulence conditions.

The characteristic size and configuration of spots in the MAPCO WFS output intensity depend on a set of design parameters including the propagation length

L_{d i f}

, dimension

n_{l}

and focal length

f_{l e n s l e t}

of the lenslet array, and phase dot pattern characteristics such as the phase dot size

d_{d o t}

, introduced phase modulation amplitude

Δ_{d o t}

, and the geometry and density

η_{d o t}

of dots within the phase mask. The density

η_{d o t}

is defined here as the percentage of mask area occupied by phase dots. This parameter primarily impacts the output intensity pattern contrast that reaches its maximum value when the phase dots occupy approximately 50% of the entire phase mask area, as discussed in Section 4.2.

5. WFS based on phase-only SLM (bottom left panel in Figure 1). The characteristic output intensity distributions in this WFS consist of random structures composed of bright spots (speckles) as shown in Figure 2 (right column). The characteristic size and spatial extent (spread) of these spots depend on the overall sensor length

L_{W F S}

and parameters of the random phase modulation pattern induced by the SLM, namely the phase modulation variance

σ_{S L M}^{2}

and correlation length

r_{S L M}

4 Note that increases in turbulence strength cause a noticeable increase in the characteristic speckle size and the output intensity spatial extent.

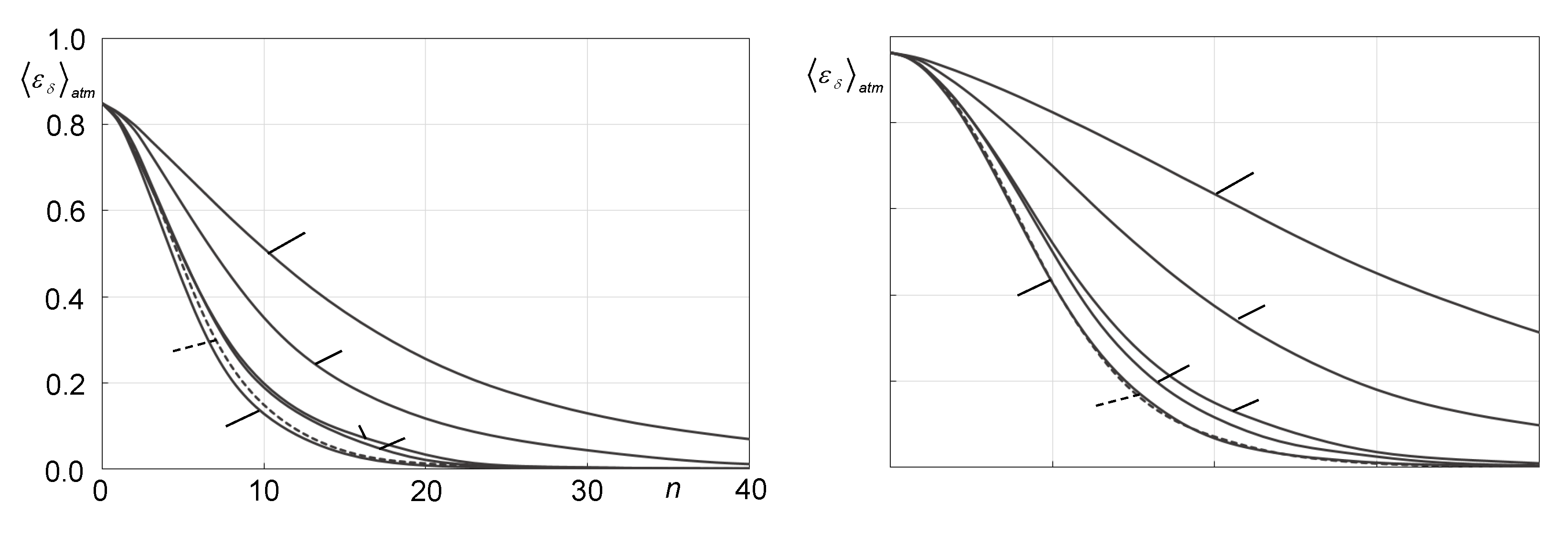
As numerical simulations shown (see Section 4), phase retrieval convergence rate for sensors considered here depends on characteristic spatial structure of output intensity distributions which can be (at some degree) engineered by turning (optimizing) WFS optical design and / or sensor parameters. From this view point the MAPCO WFS has the largest parameter space to be used for the phase retrieval convergence rate optimization.

Another important issue to be considered in selection of SR-WFS optical configuration and parameter optimization is the strong phase retrieval error dependence on the accuracy of mathematical and computational models describing the actual (implemented in hardware) sensor. Discrepancy between optical field transformation occurring in a specific WFS type and its “imitation” in phase retrieval computations may cause uncompensated phase errors that are “invisible” for AO controller.

This disparity between hardware-implemented WFS and its mathematical/computational model may emerge from a number of unaccounted for factors that can influence sensor output intensity such as misalignments, unidentified phase aberrations in the optical elements, and non-monochromaticity of the input light and/or changes in environmental conditions occurring during WFS operation.

From this viewpoint, a SR-WFS optical configuration comprised of the minimal possible numbers of optical components packaged into a compact rigid instrument has an obvious advantage, certainly, if such a SR-WFS can also provide a high convergence rate and accuracy in input field phase retrieval.

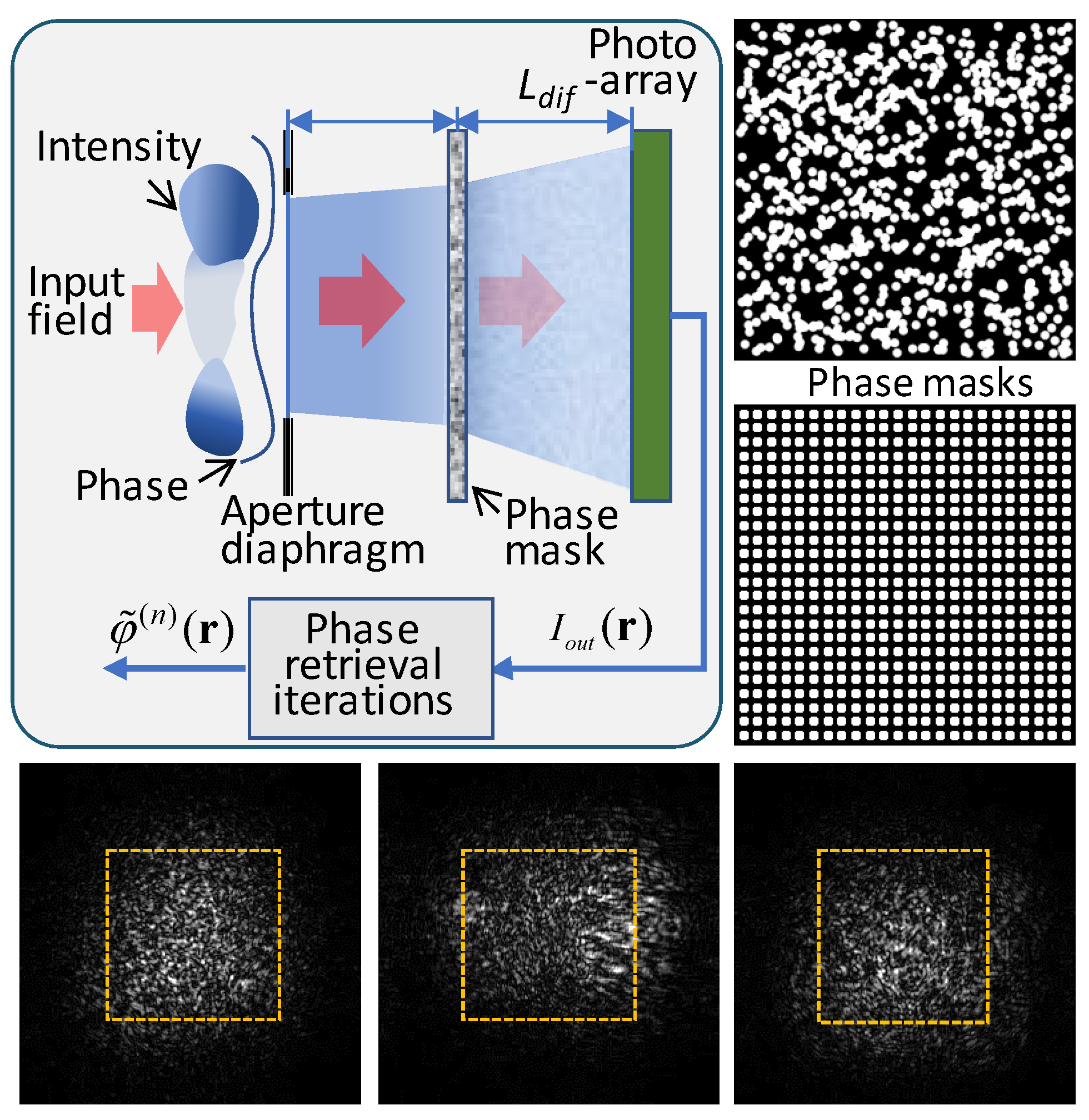
The SR-WFS design criteria discussed above were considered in the SAPCO sensor proposed here. The optical schematic of this sensor shown in Figure 4 is similar to the MAPCO WFS (middle right panel in Figure 1) with the exception that the SAPCO WFS does not have a lenslet array. Both sensors include phase masks composed of large numbers of phase dots with parameters identical or similar to the MAPCO sensor discussed above. In addition to phase mask characteristics the SAPCO sensor output intensity structure also depends on the propagation distances

L_{m a s k}

and, correspondingly, between the input aperture diaphragm and phase mask, and between the phase mask and the photo-array as shown in Figure 4. The spatial structure of output intensity patterns for both sensors are alike (compare the corresponding output intensity distributions in Figure 2 and Figure 4). As M&S shows (see Section 4.3) the absence of the lenslet array in the SAPCO sensor practically does not impact phase retrieval convergence speed while it simplifies both the WFS optical design (lesser number of optical elements) and the corresponding mathematical model used in phase retrieval computations.

3.2. Phase Retrieval Computational Time

In addition to optical design simplification and a potentially more rigorous mathematical model describing optical field transformation in the actual WFS, the lesser number of optical components is also desired to reduce the computational time

τ_{i t}

needed to perform single phase retrieval iteration (iteration time). Correspondingly, decreases in

τ_{i t}

lead to shortening the overall phase retrieval computation time

τ_{φ} = N_{i t} τ_{i t}

. Here N_it is the number of iterations associated with either the selected phase retrieval error threshold

ε_{δ} (n = N_{i t}) = ε_{0}

, as defined by Equation (17), or the limitation imposed by the AO control cycle duration.

In a simplified generic SR-WFS model comprised of

M_{e l m}

thin phase-only optical elements, the iteration time

τ_{i t}

is primarily defined by the time required for numerical integration of Equations (1) and (8) describing propagation of the outgoing and back-propagating (auxiliary) waves in an optically homogeneous media

[n_{W F S} (r, z) = n_{0}]

along

M_{e l m} + 1

consecutive non-zero-length optical path segments defined by the optical element locations inside the SR-WFS. Note that the parameter

M_{e l m}

does not account for the optical elements located at the input and output planes, e.g., the optical elements at the input plane in the SR-WFS schematics shown Figure 1 (left column) for which

M_{e l m} = 0

In the standard wave-optics based M&S technique (Ref [23]) numerical integration of the propagation equations Equations (1) and (8) includes a direct 2D fast Fourier transform (FFT), followed by multiplication of the result by a 2D array (phase term) and, further, an inverse FFT of the multiplication product [48,49]. The associated computational times required for a single FFT and multiplication by the phase term (complex 2D array) are defined, correspondingly, as

τ_{F F T}

and

τ_{m p l}

Similarly, the impact of a thin phase-only element (or phase mask) is accounted for by multiplication of the ingoing complex amplitude [complex 2D array] by a complex 2D array describing the phase-only element induced wavefront phase modulation. This operation adds an additional computational time

τ_{m p l}

Thus, the computational time required for single phase retrieval iteration for the generic SR-WFS composed of a single phase-only element at the pupil plane (lens, lenslet array or phase mask) and

M_{e l m}

phase-only elements inside the sensor can be estimated as:

τ_{i t} ≃ 4 (M_{e l m} + 1) (τ_{F F T} + τ_{m p l}) + τ_{ψ} + τ_{u p d a t e} .

(20)

Here

τ_{ψ}

and

τ_{u p d a t e}

are, correspondingly, the times required to compute the boundary condition for the back-propagating wave complex amplitude at the sensor’s output plane [Equation (5)], and to perform complex amplitude estimation update based on either AFC [Equation (15)] or HIO [Equation (16)] algorithms. Note that computational times in Equation (20) depend on the numerical grid size (resolution) and specific computational hardware and software used. In most cases the computational times

τ_{m p l}

τ_{u p d a t e}

and

τ_{ψ}

are significantly shorter than

τ_{F F T}

and can be neglected, which simplifies expression (20):

τ_{i t} ≃ 4 (M_{e l m} + 1) τ_{F F T} .

(21)

It follows from Equation (21) that the expected phase retrieval iteration time

τ_{i t}

for SR-WFS optical configurations, comprised of

M_{e l m}

optical elements located between the sensor input and output planes, is a factor

M_{e l m} + 1

longer than for the optical schematics shown in the left column in Figure 1 for which

M_{e l m} = 0

. Note that

M_{e l m} = 1

for both MAPCO and SAPCO WFSs as both sensors have a single phase-only optical element (phase mask) inside the WFS propagation path (the lenslet array of the MAPCO WFS is not accounted for as being located directly at the input plane).

Results of iteration time

τ_{i t}

benchmarking for the SR-WFS optical configuration with

M_{e l m} = 1

(MAPCO and SAPCO WFS shown in Figure 2 and Figure 4) are presented in Table 1 for a numerical grid of different resolution N_PR (numerical grid with N_PR x N_PR pixels). The simulations were performed using different NVIDIA Geforce GPU models. Iterative phase retrieval computations were performed for the HIO algorithm. The benchmarking was conducted using the CUDA-based, GPU-optimized C# WaveJet software package [50]. Note that the presented estimates for

τ_{i t}

can vary based on such factors as the specific CPU and GPU models, FFT implementation, computer code, etc.

Further phase retrieval iteration time decreases are expected with ongoing advancements in GPU technology and software optimization. More drastic phase retrieval computation acceleration by several folds is anticipated with transitioning to a specialized FPGA-based signal processing hardware. This suggests (and is further elaborated in the following Part II) potential achievements exceeding one kHz closed-loop AO control system bandwidth with utilization of IPR techniques and the SR-WFS architectures described.

Table 1. Results of phase retrieval iteration time benchmarking for MAPCO and SAPCO sensors.

Computational time $τ_{i t}$ required for single phase retrieval operation in milliseconds (ms)
GPU model	Iterative phase retrieval (PR) computational grid N_PR x N_PR pixels
GPU model	2048 x 2048	1024 x 1024	512 x 512	256 x 256
NVIDIA Geforce RTX 2080 Ti	5.15 ms	1.24 ms	0.234 ms	0.140 ms
NVIDIA Geforce RTX 3090	3.36 ms	0.84 ms	0.194 ms	0.139 ms
NVIDIA Geforce RTX 4090	1.30 ms	0.362 ms	0.157 ms	0.133 ms

3.3. Phase Retrieval Computational Grid

As indicated in Table 1, the reduction in the iteration time

τ_{i t}

desired for AO control bandwidth increase could potentially be achieved by minimizing the phase retrieval computational grid resolution (grid size N_PR). The question to ask is, how small could N_PR be without sacrificing phase retrieval convergence rate and accuracy?

From a general AO requirements viewpoint, spatial resolution in phase aberration sensing on the order of 10³ (e.g., 32x32) resolvable phase values would be sufficient for the majority of atmospheric AO applications. This may incite the idea that a numerical grid with N_WFS =32 (N_WFS x N_WFS pixels inside the SR-WFS aperture diaphragm) could be an acceptable option. However, the AO wavefront sensing resolution requirement does not imply that accurate phase retrieval computations can be performed using such a low-resolution numerical grid. There are some constraints that should be accounted for in selection of an acceptable phase retrieval numerical grid resolution (parameter N_PR) and the associated actual (physical) size D_PR for the phase retrieval computational area.

First, the SR-WFS output intensity distribution

I_{o u t} (r)

may quite significantly extend beyond the sensor aperture area of size D_WFS, as shown in Figure 2 and Figure 4. Correspondingly, both the photo-array size D_PA and physical size D_PR of the phase retrieval computational area should exceed D_WFS. It is important that the parameters D_PA and D_PR should provide accurate representation (approximation) of the measured intensity on the chosen numerical grid. As seen from Figure 2, the output intensity patterns do not extend beyond approximately twice the size of D_WFS for all SR-WFS configurations considered. Therefore, we may set D_PA =D_PR =2D_WFS, also additionally assuming that that in the course of phase retrieval computations the complex amplitudes

{\tilde{A}}^{(n)} (r, z)

and

ψ^{(n)} (r, z)

do not extend beyond the selected computational area of size D_PR. Note that for optimal SR-WFS performance, the phase retrieval computational grid (resolution and pixel pitch) should match the corresponding photo-array parameters.

Second, the computational grid resolution should provide a sufficiently accurate numerical representation of: (a) the SR-WFS optical elements; (b) characteristic spatial features of the measured output intensity pattern; and (c) the complex amplitudes

{\tilde{A}}^{(n)} (r, z)

and

ψ^{(n)} (r, z)

within the entire phase retrieval computational volume D_PR x D_PR x L_WFS. For the basic SR-WFS optical configurations considered (shown in Figure 1 and Figure 4), the smallest spatial scale is associated with phase-shifting elements: phase dots of the Zernike, MAPCO, and SAPCO WFSs, and the characteristic phase modulation correlation length

r_{S L M}

of the SLM-based WFS. Note that in the course of the phase retrieval computations the complex amplitudes

{\tilde{A}}^{(n)} (r, z)

and

ψ^{(n)} (r, z)

can be truncated by the phase mask boundary. In order to prevent such truncation, the phase mask size D_mask should exceed D_WFS_. To be on the safe side, the following SR-WFS design parameters defining the phase retrieval computational grid size N_PR were used in M&S: D_mask = D_PA =D_PR = 2D_WFS.

For estimation of the smallest acceptable grid size N_PR, consider as an example the phase mask shown in Figure 4 composed of an array of 24x24 square-shape phase dots inside the D_WFS x D_WFS area (48x48 phase dots within the entire mask of size D_mask = 2D_WFS). By assuming that each phase-shifting dot can be satisfactorily represented at the numerical grid by a 4x4 pixel square, for the smallest possible computational grid dimension we obtain N_PR =256. This implies that the phase retrieval computations at this grid will provide input field phase aberration estimation at N_WFS x N_WFS grid points, where N_WFS = N_PR / 2 =128, that is with significantly higher (4-fold) resolution than is required for the majority of atmospheric AO applications. As M&S shows, phase mask numerical representation using a smaller number of pixels (3x3 or 2x2) per phase dot aiming to potentially decrease N_PR resulted in slow convergence and unacceptably high phase retrieval errors. The origin of such errors is insufficiently accurate (for such a small number of pixels per phase dot) numerical integration of parabolic Equations (1) and (8) in the course of the phase retrieval iterations.

As mentioned above, the computational grid should also provide accurate approximation of the characteristic spatial structures for the output intensity distribution

I_{o u t} (r)

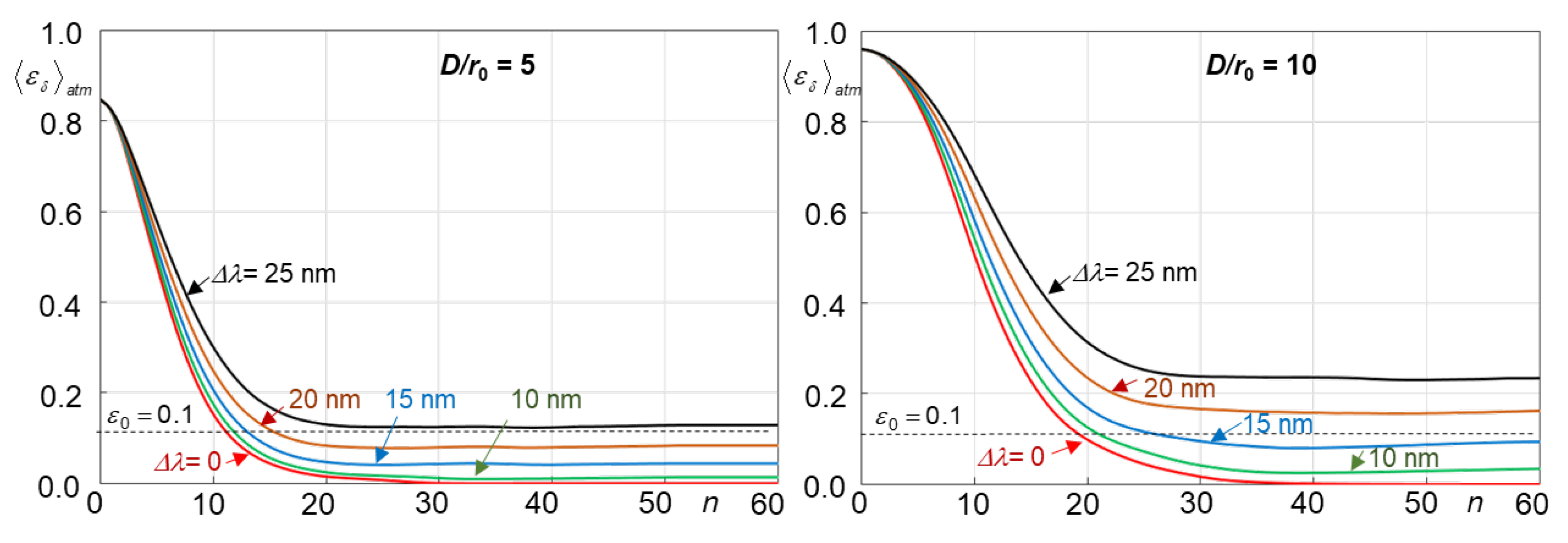
. In the case of phase contrast type sensors (Zernike, MAPCO, SAPCO, and phase SLM-based WFSs) for which the intensity patterns contain small bright spots (speckles) as shown in Figure 2 and Figure 3, the numerical grid pixel size should be several fold smaller than the characteristic speckle size l_sp. Note that for MAPCO and SAPCO sensors the speckle size l_sp can be adjusted (scaled) by changing the distance

L_{d i f}

between the phase mask and photo-array. In the numerical simulations described here, this distance was set to

L_{d i f} = 14.0

cm in order to obtain approximately 4x4 or 5x5 pixels per intensity bright spot at the numerical grid with N_PR =256. This computational grid resolution was used in M&S for all SR-WFS types considered.

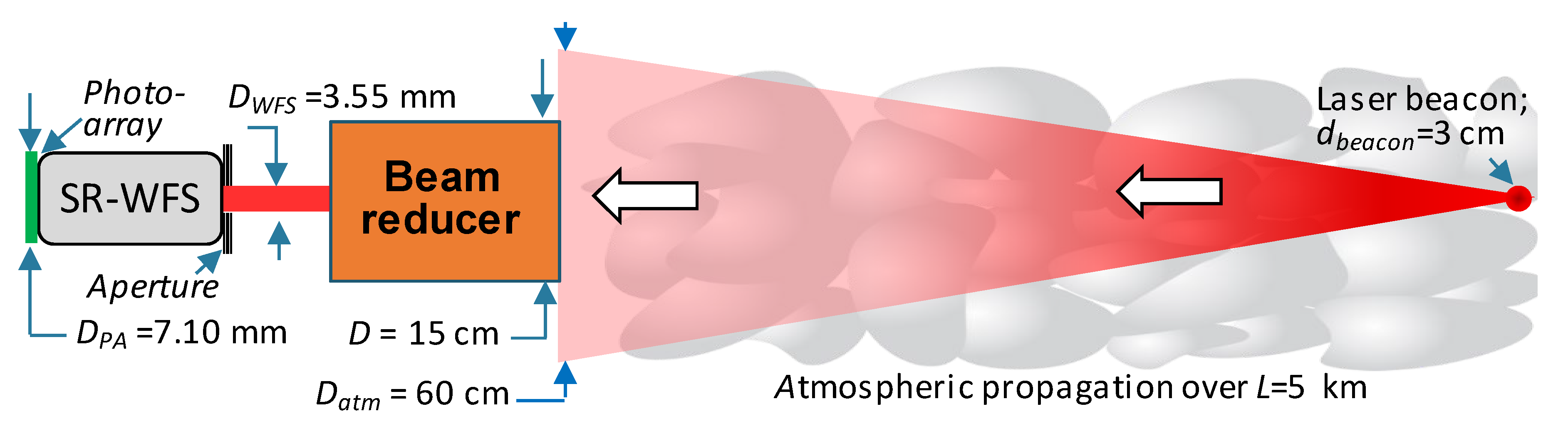
An important factor that defines the overall SR-WFS design parameter space (including the required computational grid resolution) is the photo-array size D_PA. In the numerical simulations we used D_PA = D_PR =7.10 mm (256x256 pixels) to match the smallest dimension of a commercially available CCD camera. Correspondingly, the square WFS aperture mask was set twice smaller: D_WFS = D_PA /2 = 3.55 mm (128x128 pixels).

We also assumed a receiver telescope (beam reducer) providing reimaging of the pupil square area of size D =15 cm into the WFS aperture diaphragm with the demagnification factor M=D/D_WFS =42.2 as shown in Figure 5. These parameters were identical for all SR-WFS types considered here. In M&S of phase contrast-type sensors the physical size of the phase-shifting dots was set to d_dot =100 μm. In the case of WFS based on phase-only SLM, the introduced phase modulation was modeled using random field realizations delta-correlated on the numerical grid. Other parameters of the basic SR-WFS models in Figure 1 (e.g., focal distances of lenses and lenslet arrays) were selected based on numerical analysis of phase retrieval efficiency under a wide range of atmospheric turbulence conditions.

3.4. Numerical Modeling and Simulations Setting

For numerical modeling of optical field realizations entering the SR-WFS typical of atmospheric AO applications, the M&S setting included a monochromatic (λ= 1064 nm) laser beacon located a distance L= 5 km from the beam reducer telescope as shown in Figure 5. We assumed that the collimated Gaussian beam of width d_beacon generated by a beacon laser source propagates through homogeneously distributed isotropic atmospheric turbulence prior to entering the beam reducer telescope. A lens (not shown in Figure 5) with focal distance f = L/M at the beam reducer exit plane was included into the numerical model for mitigation of static defocus type aberrations of the optical field at the SR-WFS input plane (plane of the aperture diaphragm).

Numerical simulations of beacon beam propagation in the turbulent atmosphere were based on the conventional wave-optics (split-step operator [23,48,49]) technique using a computational grid with a resolution of 1024x1024 pixels. The physical size of the simulation area corresponded to a 0.6-m square with about 0.58-mm pixel size. The beacon beam complex amplitude

A_{i n} (r)

at the beam reducer input plane was rescaled to the 512x512 pixel grid and the central 256x256 pixel section (30x30 cm²) was assigned as the phase retrieval computational grid with resolution N_PR =256 and ~1.17-mm pixel size (prior to demagnification by the beam reducer). Beacon optical wave reimaging by the beam reducer telescope with demagnification factor M=D/D_WFS =42.2 was modeled by simple reassignment (M-fold reduction) of the grid pixel size from ~1.17-mm to Δ_WFS ~27.7μm.

Turbulence-induced refractive index inhomogeneities along the beacon beam propagation path were represented by a set of N_φ =20 equally spaced 2D random thin phase screens corresponding to the Kolmogorov turbulence power spectrum [51]. A single set of the generated N_φ phase screens is referred to here as a “turbulence realization” [52]. Each turbulence realization was comprised of N_φ statistically uncorrelated phase screens.

Turbulence and intensity scintillation strength were correspondingly characterized by the

D / r_{0}

ratio and Rytov variance

σ_{R}^{2}

defined in Section 2.2. The parameter D/r₀ was altered (from zero to

D / r_{0}

=20) via equivalent changes of the phase screen modulation amplitudes in each turbulence realization. This enables simulation of SR-WFS input field realizations

{A_{i n} (r)}

with Rytov variances ranging from zero to

σ_{R}^{2} ≃ 28

. Characteristic examples of computed input field phase and intensity distributions are shown in Figure 3.

The spatial inhomogeneity of the generated input field intensity realizations

{I_{i n} (r)}

within the receiver beam reducer telescope square aperture of area S_Rx = DxD was characterized by the scintillation index

σ_{I}^{2}

[16]:

σ_{I}^{2} = S_{R x}^{- 1} \int_{} M_{R x} (r) {〈 {[I_{i n} (r) - {\bar{I}}_{i n}]}^{2} 〉}_{a t m} d^{2} r / {〈 {\bar{I}}_{i n}^{2} 〉}_{a t m},

(22)

where

{\bar{I}}_{i n}

is the mean value of the input field intensity within the receiver aperture described by the window

M_{R x} (r)

. In Equation (22) and elsewhere below < >_atm denotes averaging (also referred to as atmospheric averaging) corresponding to an ensemble of N_atm statistically independent turbulence realizations. The parameter N_atm equal to 100 was used in all M&S described below.

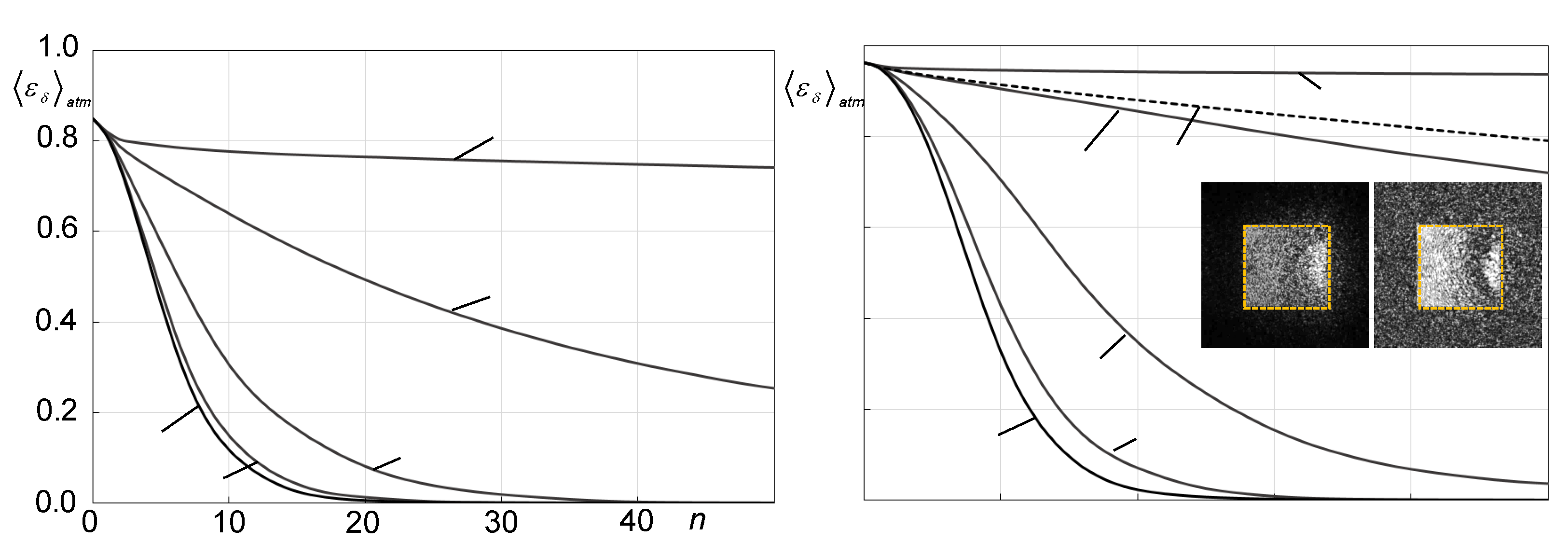
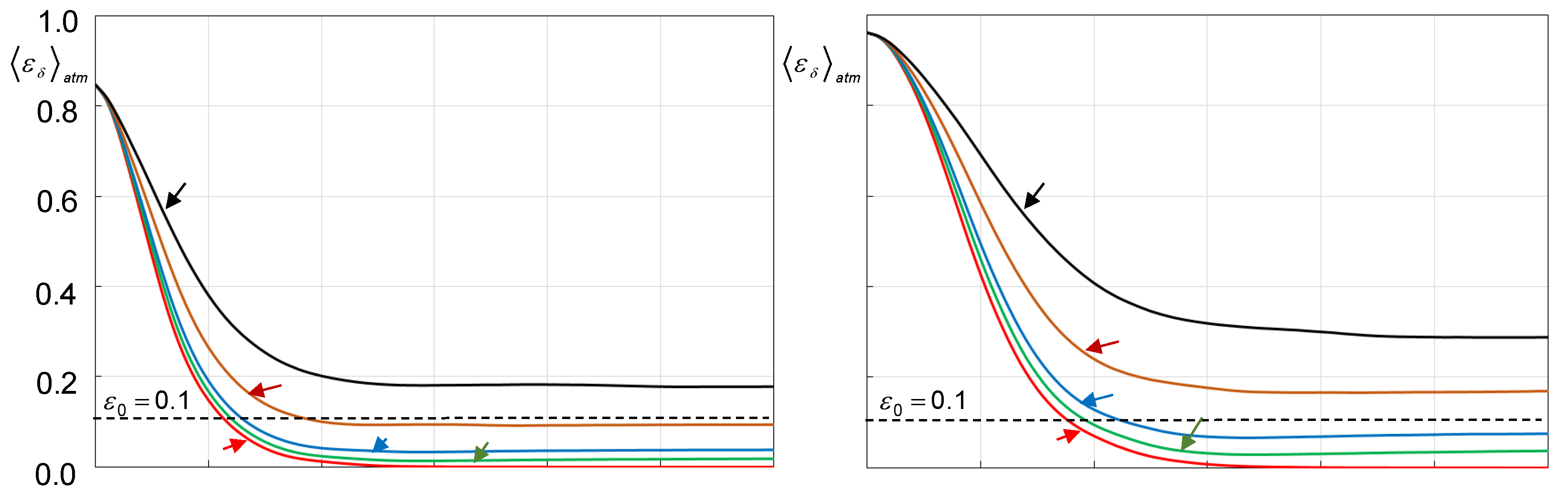
For each SR-WFS type and pre-selected

D / r_{0}

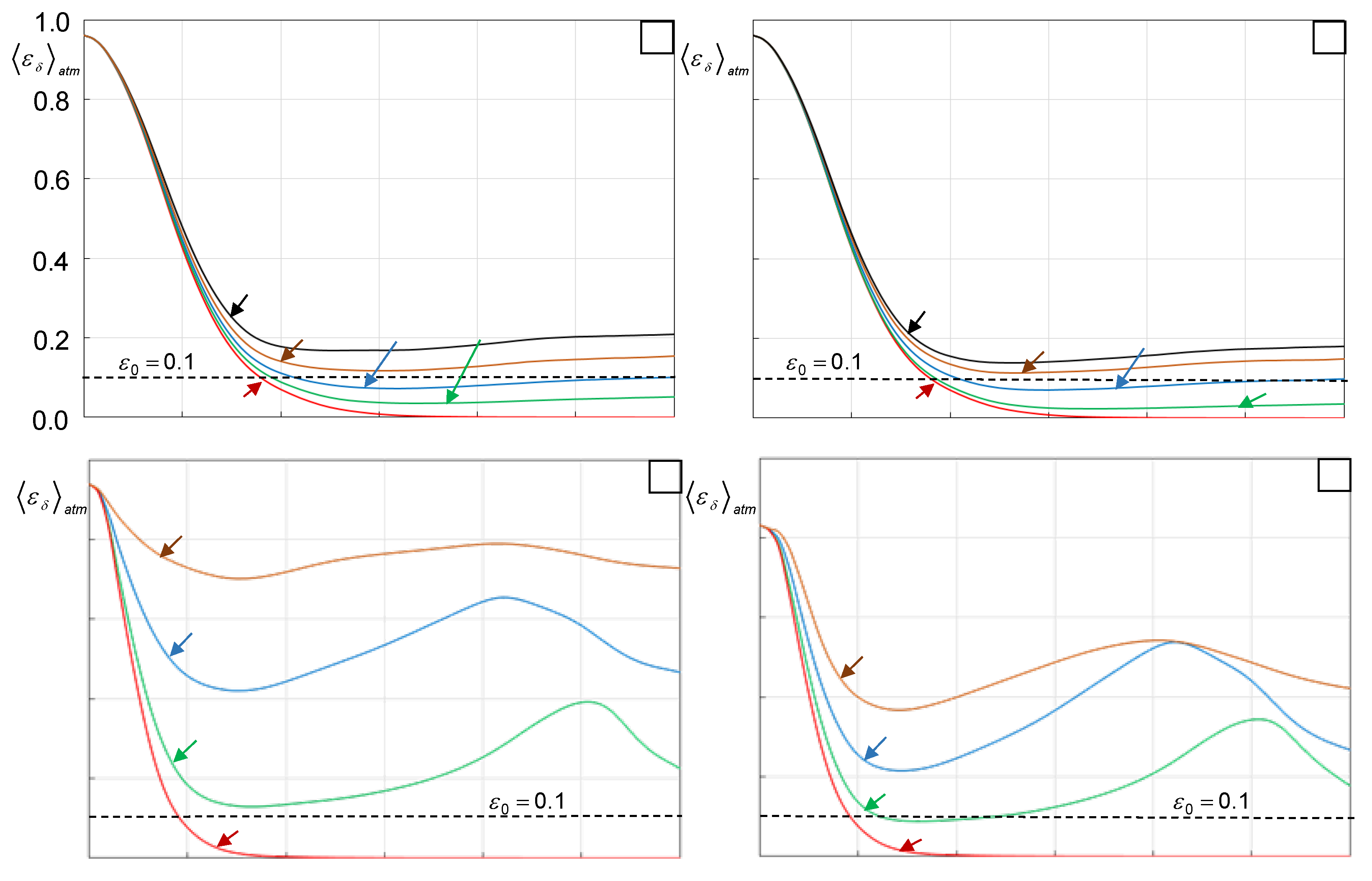
value phase retrieval performance was evaluated in a set of N_atm phase retrieval trials resulting in computation of the corresponding dependencies

{ε_{δ}^{(j)} (n, D / r_{0})}

, (j=1,…, N_atm) of the phase retrieval error [Equation (17b)] on the iteration number n, which were averaged over atmospheric trials. The obtained dependencies

{〈 ε_{δ} (n, D / r_{0}) 〉}_{a t m}

computed for different

D / r_{0}

values (referred to here as atmospheric-averaged phase retrieval error evolution curves) were used for parameter optimization and performance assessment of the basic SR-WFS types shown in Figure 1.

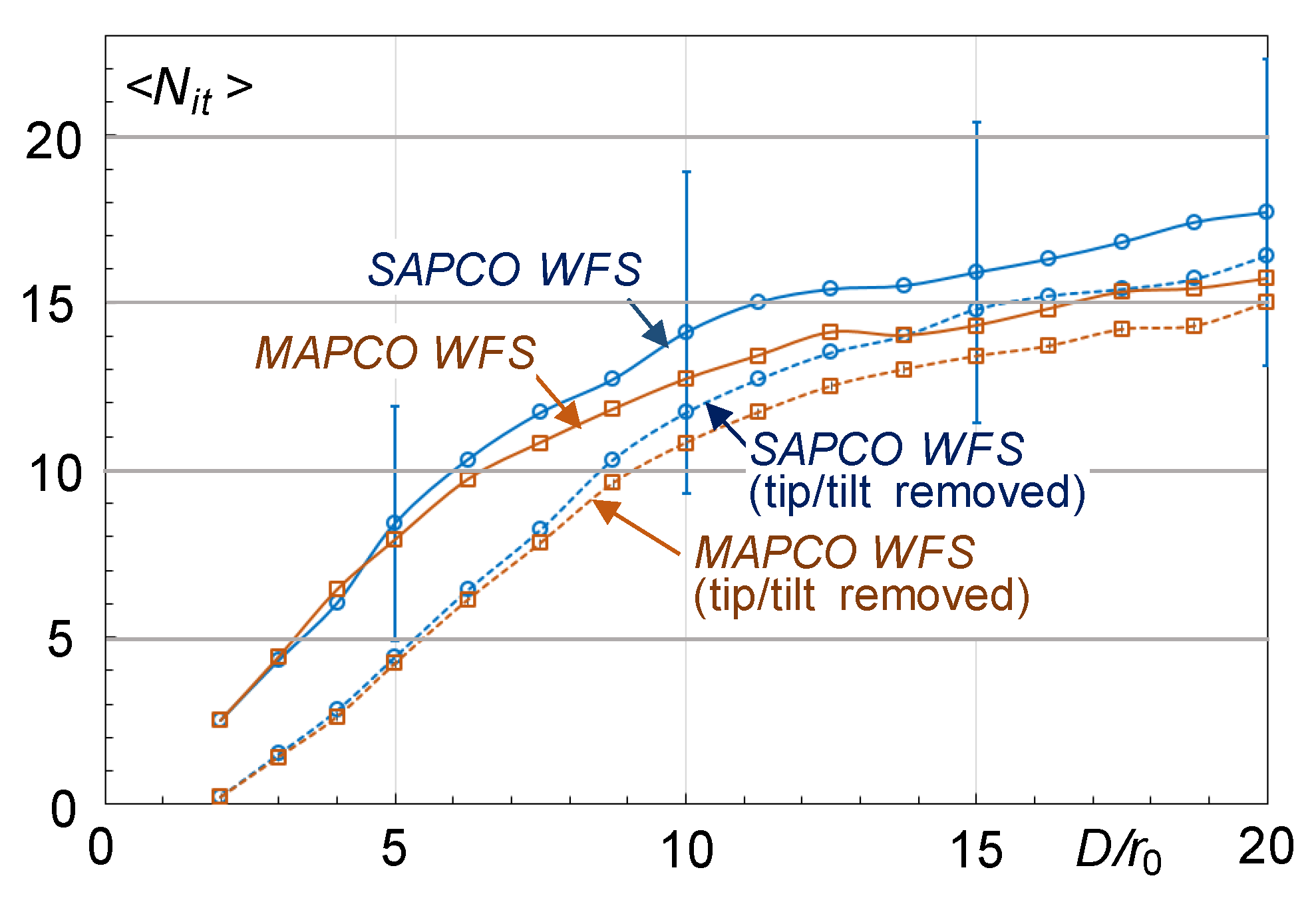
For comparative analysis of the SR-WFSs and phase retrieval algorithms we also utilized the atmospheric-averaged number of iterations

{〈 N_{i t} (D / r_{0}) 〉}_{a t m}

required for each fixed

D / r_{0}

ratio to reach a pre-selected threshold level

ε_{0}

=0.1 (a 10% phase retrieval error). The

{〈 N_{i t} (D / r_{0}) 〉}_{a t m}

values were computed by averaging the corresponding iteration numbers

{N_{i t}^{(j)} (D / r_{0})}

obtained for each phase retrieval trial, where j=1,…, N_atm.

4. SR-WFS Parameter Optimization and Performance Assessment

4.1. SR-WFS Optimization Parameter Space

As previously mentioned, phase retrieval process convergence depends on a number of parameters specific for each SR-WFS type. Correspondingly, for unbiased performance comparison of different sensors, these parameters should be independently optimized for each SR-WFS configuration. The overall parameter space for the SR-WFSs considered here is quite extensive, which makes such a comparative analysis a challenging task.

To simplify the problem, we assumed several (pre-selected) parameters common for all SR-WFS types, including phase retrieval computational grid resolution (N_PR =256) and the physical sizes of the WFS input aperture D_WFS, photo-array D_PR = 2 D_WFS, phase retrieval computational area D_PA =D_PR = 2D_WFS, photo-array D_PA = D_PR = 2 D_WFS, and the aperture size for the beam reducer D = MD_WFS.

We also used fixed and already optimized for the MAPCO WFS (see Ref [16]) the diameter and phase modulation amplitude of the phase shifting dots (correspondingly

d_{d o t} = 100

μm and

Δ_{d o t} = π

rad), and the propagation (diffraction) distance

L_{d i f}

between the phase mask and photo-array (

L_{d i f} = 14

cm). These parameters were pre-set for both the MAPCO and SAPCO sensors. Lenslet arrays composed of 4x4 densely packed lenses was used in M&S of both MAPR and MAPCO WFS, while optimal focal distance value

f_{l}

was determined separately for each sensor:

f_{l}

=28 cm for MARP and

f_{l}

=20 cm for MAPCO WFS.

As a result, the optimization parameter space was significantly reduced. It included the lens focal distance F for the lens-based and Zernike WFSs, propagation distances

L_{W F S}

and

L_{m a s k}

between the WFS aperture diaphragm and, correspondingly, the photo-array for the phase-only SLM-based WFS, and a phase mask for the SAPCO WFS. In both the SAPCO and MAPCO WFSs we also considered random-dot and grid-dot type phase masks of size D_PA and optimized the number of phase dots (N_dot) within the phase mask.

Selection and optimization of the SR-WFS parameters were based on a comparison of atmospheric-averaged phase retrieval errors

{〈 ε_{δ} (n, D / r_{0}) 〉}_{a t m}

(phase retrieval error evolution curves), which were computed using the HIO algorithm. To verify that the selected SR-WFS parameter values are satisfactory under a wide range of turbulence conditions, numerical simulations were performed for weak-to-moderate turbulence (

D / r_{0} = 5

σ_{R}^{2} = 2.76

σ_{I}^{2} = 1.2

), moderate-to-strong turbulence (

D / r_{0} = 10

σ_{R}^{2} = 8.77

σ_{I}^{2} = 3.4

) and strong turbulence (

D / r_{0} = 20

σ_{R}^{2} = 27.8

σ_{I}^{2} = 4.3

4.2. Parameter Optimization Methodology Examples

As an example of SR-WFS parameter optimization, consider the SAPCO sensor optical setting in Figure 4. The design parameters to be optimized included the distance

L_{m a s k}

between the WFS aperture diaphragm and phase mask, and the geometry and density of the phase shifting dots

η_{d o t}

of the sensor phase mask. Corresponding numerical simulation results are presented in Figure 6 and Figure 7 by sets of atmospheric-averaged phase retrieval error evolution curves

{〈 ε_{δ} (n) 〉}_{a t m}

computed using the HIO algorithm for

D / r_{0} = 5

and

D / r_{0} = 10

As can be seen from the

{〈 ε_{δ} (n) 〉}_{a t m}

curves in Figure 6, phase retrieval iterative process convergence speed strongly depends on the phase mask position (parameter

L_{m a s k}

). It is especially slow for the SAPCO WFS with phase mask located at the sensor pupil plane

(L_{m a s k} = 0)

. Note that this WFS configuration coincides with the phase-only SLM-based WFS in Figure 1 (bottom left), except that the parameters of the random phase modulation pattern for this sensor (phase modulation variance

σ_{S L M}^{2}

and correlation length

r_{S L M}

) are quite different from the phase mask parameters of the SAPCO WFS and could be separately optimized to improve convergence.

Gradually increasing the distance

L_{m a s k}

from zero to approximately 20 cm resulted in a significant acceleration of the phase retrieval convergence rate for both weak-to-moderate (

D / r_{0}

=5) and moderate-to-strong (

D / r_{0}

=10) turbulence conditions. With further parameter

L_{m a s k}

increase the iterative process convergence speed only marginally improved. This suggests that, from a practical viewpoint (WFS compactness and rigidity), the distance

L_{m a s k}

= 20 cm could be considered as a reasonable option (optimal) and was used in all numerical simulations further described.

To understand why the increase in the distance

L_{m a s k}

between the sensor aperture diaphragm and phase mask may play so a critical role in phase retrieval convergence speed, consider the grey-scale images in Figure 6 (right) for the back-propagating wave (auxiliary function) magnitude

| ψ^{(n = 0)} (r, 0) |

at the SAPCO sensor input plane for the following two cases: phase mask located either at the WFS pupil plane (

L_{m a s k}

=0), or a distance

L_{m a s k}

=20 cm from the WFS aperture diaphragm. For

L_{m a s k}

=0 (image on the left) nearly the entire back-propagated wave footprint [magnitude

| ψ^{(n = 0)} (r, 0) |

] is confined within the WFS aperture diaphragm indicated by the yellow square in Figure 6. Correspondingly, in this case the Fienup complex field retrieval process acceleration term

W (r) [{\tilde{A}}_{i n}^{(n = 0)} (r) - β ψ^{* (n = 0)} (r, 0)]

in the HIO update rule [Equation (16)], which accounts for the corresponding complex amplitudes outside the aperture diaphragm

W (r) = 1 - M_{i n} (r)

, is negligibly small. Indeed, the product

W (r) {\tilde{A}}_{i n}^{(n = 0)} (r)

in this term is zero as the initial complex field estimate is defined solely within the window function

M_{i n} (r)

. On the other hand, the complex amplitude

ψ^{* (n = 0)} (r, 0)

in this expression is primarily confined within

M_{i n} (r)

due to boundary condition (5) for the back-propagating wave describing outgoing field phase conjugation at the WFS output plane. With the negligibly small acceleration term, the HIO algorithm nearly coincides with the slow-converging AFC algorithm [Equation (15)].

In the second case (

L_{m a s k}

=20 cm) the back-propagated wave receives strong phase modulation after passing through the phase mask resulting in escalated divergence and corresponding expansion to outside the input aperture diaphragm after propagation over the distance

L_{m a s k}

as shown in Figure 6 (image at right). This back-propagated wave footprint broadening “activates” the convergence acceleration term of the HIO algorithm (16) resulting in faster complex field retrieval process convergence. Further distance

L_{m a s k}

increase eventually results in a disbalance between the convergence acceleration and AFC [

M_{i n} (r) ψ^{* (n)} (r, 0)

] terms in Equation (16) for the HIO algorithm, leading to marginal convergence speed acceleration and even slowing when the complex amplitude

ψ^{* (n)} (r, 0)

expands beyond the physical size D_PR of the phase retrieval computational area.

To emphasize the importance of the back-propagating wave footprint expansion to outside the aperture diaphragm in the SAPCO WFS, we computed the phase retrieval error evolution curve (shown by dashed line in Figure 6, right) for

L_{m a s k} = 20 cm

using the AFC algorithm [Equation (15)], which does not include the HIO algorithm acceleration term. This resulted in a significant drop in the phase retrieval convergence rate – compare the corresponding solid and dashed curves computed for

L_{m a s k} = 20 cm

using the HIO and ACF algorithms in Figure 6 (right).

The second example of SAPCO WFS design parameter optimization is illustrated in Figure 7 where the atmospheric-averaged phase retrieval error evolution curves

{〈 ε_{δ} (n) 〉}_{a t m}

were computed for the grid-dot and random-dot type phase masks (such as shown in Figure 4 right inserts) composed of different numbers N_dot of identical phase shifting dots within the mask area of size D_mask = D_PR. The grid-dot type phase masks were represented by n_dot x n_dot arrays of phase shifting dots occupying the entire mask. The dimension of the phase shifting dot grid pattern (parameter n_dot) was varied with the goal to optimize the phase retrieval convergence rate. Simulations were performed for weak-to-moderate (

D / r_{0} = 5

) and moderate-to-strong (

D / r_{0} = 10

) turbulence conditions with a fixed (previously optimized) distance

L_{m a s k} = 20 cm

between the WFS aperture diaphragm and the phase mask.

As shown in Figure 7, increases in the parameter n_dot and, consequently, density of the phase dots inside the phase mask (parameter

η_{d o t}

) from n_dot = 24 (N_dot =576,

η_{d o t} =

10%) to n_dot = 40 (N_dot =1600,

η_{d o t} =

27%) resulted in rapid phase retrieval process convergence improvement for both turbulence conditions examined. The fastest convergence was observed for the grid-dot mask with n_dot =48 (N_dot =2304,

η_{d o t} =

40%). Note that utilization of a random-dot type phase mask (dashed RND line in Figure 7) with N_dot =3600 provided a nearly optimal phase retrieval convergence rate while use of the grid-dot type mask with an equal number of phase dots (n_dot =60) resulted in noticeably slower convergence. This difference can be explained by the fact that the density parameter (percentage of mask area occupied by phase dots) for the random-dot mask was nearly 50% (

η_{d o t} =

52%) vs 61% for the corresponding grid-dot mask with an equal number of phase dots. Since the sensor output intensity distribution is formed by the interference of light components passing through and missing the phase shifting dots, the highest interference pattern visibility and, hence, the highest output intensity pattern contrast can be achieved with the phase dot density factor

η_{d o t} =

50%. Apparently, as confirmed in M&S, a higher output intensity contrast leads to faster HIO phase retrieval algorithm convergence.

In the example considered here, the random arrangement of N_dot =3600 phase dots resulted in their occasional overlapping and a corresponding decrease in the density factor from

η_{d o t} =

61% for the 60x60 grid (n_dot =60) to

η_{d o t} =

52%, which is closer to the optimal (50%) density factor value. Based on this analysis, in the following M&S of SAPCO and MAPCO WFSs we solely used a random-dot type mask with N_dot =3600 phase shifting dots.

4.3. Comparative Performance Analysis of Basic SR-WFS Configurations

The methodology of WFS parameter optimization described in section 4.2 for the SAPCO sensor was applied to the basic SR-WFS configurations shown in Figure 1. For a fair comparison of phase retrieval performance for these sensors, several parameters were set identical for all SR-WFS configurations (pre-selected parameters discussed earlier in section 4.1).

Additionally, notice that the phase retrieval convergence rate can be strongly affected by wavefront tip and tilt (tip/tilt) aberrations in the optical field entering the WFS. In practical atmospheric AO systems, this type of aberration is commonly mitigated using a separate AO control sub-system utilizing a fast-steering mirror, which typically operates with a significantly higher closed-loop frequency bandwidth enabling mitigation (or complete removal) of tip/tilt aberrations from the entering WFS optical field. In analysis of such AO system architectures, tip/tilt aberrations can be considered as absent (actively removed). In the M&S presented here we also included a SR-WFS performance analysis for the case of preliminarily removed tip/tilt aberrations. Corresponding results [atmospheric-averaged phase retrieval error evolution curves

{〈 ε_{δ} (n) 〉}_{a t m}

] computed using N_atm = 100 statistically independent turbulence realizations are presented in Figure 8.

Compare first the phase retrieval iterative process convergence in the absence of tip/tilt removal (top panels). Under both the weak-to-moderate and moderate-to-strong turbulence conditions examined, both the MAPCO and SAPCO sensors significantly overperform other sensor types providing significantly faster phase retrieval convergence and accuracy. Separately, also notice the relatively poor performance of both the Zernike- and lens-based WFSs.

Although the initial stage of phase retrieval computations for the MAPR sensor resulted in the most rapid (among all sensors) decrease in the error

{〈 ε_{δ} (n) 〉}_{a t m}

, which is due to processing of output intensity within subregions in parallel (as mentioned in section 3.1 and Ref [15]), the iterative process quickly slowed down and nearly stagnated at approximately

{〈 ε_{δ} 〉}_{a t m} ≃ 0.1

for

D / r_{0}

=5 and

{〈 ε_{δ} 〉}_{a t m} ≃ 0.3

for

D / r_{0}

=10, as can be seen in Figure 8a,b.

Removal of wavefront tip and tilt aberrations [Figure 8c,d] clearly resulted in phase retrieval process convergence acceleration for all sensors, although this does not change the overall conclusion regarding the MAPCO and SAPCO WFS dominant performance superiority. Among the most noticeable convergence speed improvements with tip/tilt aberration removal are observed for Zernike and phase SLM based sensors in the case of weak-to-medium turbulence (

D / r_{0}

=5). This result is quite expected for the Zernike WFS when considering the high sensitivity of this sensor to input field tip/tilt aberrations, as already mentioned in section 3.1. Note that in strong turbulence conditions [Figure 8d] the impact of tip/tilt aberration removal on the performance of both Zernike and SLM based WFSs is less pronounced.

Based on the apparent advantage (clearly seen in Figure 8) of the MAPCO and SAPCO WFS architectures for potential practical use in atmospheric AO systems, subsequent analysis was narrowed down to further study only these SR-WFS configurations.

To compare performance of MAPCO and SAPCO WFSs in more detail, consider the dependencies shown in Figure 9 describing the atmospheric-averaged number of iterations

< N_{i t} (D / r_{0}) >_{a t m}

required to reach a 10% residual phase retrieval error threshold

[< ε_{δ} (n = N_{i t}, D / r_{0}) > \leq ε_{0} = 0.1]

as a function of

D / r_{0}

with and without tip/tilt aberration removal. As can be seen from the presented curves, for

D / r_{0} \leq 5

(under weak-to-moderate turbulence conditions) the number of iterations

< N_{i t} >_{a t m}

is nearly equal for both WFS types. With turbulence strength increase (up to

D / r_{0} = 20

in Figure 9)

< N_{i t} >_{a t m}

is smaller for the MAPCO WFS, but the difference with the SAPCO WFS is within the standard deviation range (shown in Figure 9 by vertical error bars).

Removal of tip/tilt aberrations resulted in significant acceleration of phase retrieval convergence leading to a nearly two-fold decrease in

< N_{i t} >_{a t m}

for

D / r_{0}

values ranging from

D / r_{0} ≃ 2

D / r_{0} ≃ 7

. Under strong turbulence (

D / r_{0} \geq 10

) tip/tilt aberration removal is noticeably less beneficial for both WFSs with the difference in

< N_{i t} >_{a t m}

with and without tip/tilt aberration removal being smaller than the standard deviation of the mean.

In general, the results presented in Figure 9 demonstrate a relatively small difference in phase retrieval performance between the SAPCO and MAPCO sensors. Since from a practical viewpoint the SAPCO WFS configuration is simpler and hence, easier to align and ruggedize, this sensor may have the better (among the SR-WFS types considered here) potential for atmospheric AO applications. These factors were behind the selection of the SAPCO WFS for further analysis.

4.4. SR-WFS Tolerance Analysis Examples

In this section we consider examples of SR-WFS “tolerance” analysis in assessing the impact of the potential discrepancy between optical field transformation in a hardware-implemented SR-WFS vs one described in mathematical and/or numerical sensor models used for phase retrieval computations.

The questions to address are, how sensitive are phase retrieval computations to relatively small, unaccounted for deviations in the WFS parameters in the SR-WFS model, and how to minimize errors resulting from these deviations by tuning the WFS mathematical/numerical model and/or improving the accuracy of sensor component alignment. Since the overall WFS parameter space is quite extensive, the tolerance analysis presented here is limited to only the SAPCO WFS (Figure 4) and a specified set of parameters.

Consider first the impact of an unrevealed in the SAPCO WFS mathematical model possible longitudinal (along the sensor optical axis) deviation Δ_CCD in the photo-array (CCD camera) position with respect to its prescribed in the model (nominal) location a distance L_dif from the phase mask. Such deviation may occur due to insufficiently accurate WFS alignment, and/or environmental factors (temperature variations, mechanical jitter, etc.).

With photo-array longitudinal shift Δ_CCD, the measured sensor output intensity

I_{o u t} (r, Δ_{C C D})

corresponds to the distance L_CCD = L_dif + Δ_CCD. At the same time, phase retrieval computations are performed based on the sensor mathematical model that does not account for the photo-array position deviation (misalignment), that is, assuming Δ_CCD =0. In the course of phase retrieval iterations, this misalignment, unaccounted for in the mathematical model, results in residual phase retrieval error

δ^{(n)} (r, Δ_{C C D}) = φ (r) - {\tilde{φ}}^{(n)} (r, Δ_{C C D})

, (n=0, 1,…) that is dependent on the photo-array displacement Δ_CCD. Here

φ (r)

is the true input field phase, and

{\tilde{φ}}^{(n)} (r, Δ_{C C D})

is the phase function computed at the nth phase retrieval iteration performed based on the measured intensity

I_{o u t} (r, Δ_{C C D})

Impact of SAPCO WFS photo-array misalignment was evaluated in numerical simulations using the defined by Equation (17 b) phase retrieval error metric

ε_{δ} (n, Δ_{C C D})

. Note that, with perfect WFS alignment,

ε_{δ} (n, Δ_{C C D})

coincides with the phase error metric

ε_{δ} (n, Δ_{C C D} = 0) = ε_{δ} (n)

previously discussed.

An analogous approach was applied to evaluate tolerance requirements with respect to the longitudinal displacement Δ_aper of the sensor aperture diaphragm, and lateral shift Δ_mask of the phase mask, by computing the corresponding phase errors

ε_{δ} (n, Δ_{a p e r})

and

ε_{δ} (n, Δ_{m a s k})

. The corresponding results are presented in Figure 10 by sets of atmospheric-averaged phase retrieval error evolution curves [dependencies

< ε_{δ} (n, Δ_{C C D}) >_{a t m}

< ε_{δ} (n, Δ_{a p e r}) >_{a t m}

, and

< ε_{δ} (n, Δ_{m a s k}) >_{a t m}

], which were computed for different misalignment parameter values Δ_CCD , Δ_aper, and Δ_mask . The pre-selected phase retrieval residual error threshold

ε_{0} = 0.1

(shown in Figure 10 by horizontals dashed lines) was considered as the maximum permissible misalignment level.

By comparing the phase error evolution curves in Figure 10a-c, one can see that phase mask lateral positioning requires significantly higher accuracy than does longitudinal positioning of the photo-array and aperture diaphragm. Also, note that in the case of phase mask lateral displacement [Figure 10c,d], the smallest phase retrieval error is achieved after approximately the first n=15 iterations and only increases with successive iterations. For the phase dot size d_dot = 100 μm used in simulations, a phase retrieval error below 10%

(< ε_{δ} >_{a t m} \leq 0.1)

can be obtained with a phase mask lateral displacement Δ_mask not exceeding approximately 5 μm. Corresponding tolerances in positioning of the photo-array (Δ_CCD

\leq

0.3 mm) and aperture diaphragm (Δ_aper

\leq

2.0 mm) are significantly more relaxed.5 Note that the required alignment accuracy (including phase mask lateral positioning) can be fulfilled using commercial opto-mechanical positioners.

Compare the phase retrieval error evolution curves in Figure 10c,d corresponding to phase mask lateral misalignment, computed without and with tip/tilt aberration removal using an external fast steering mirror-based control system. The results clearly indicate that tip/tilt aberration mitigation results in a noticeably lower alignment accuracy requirement. This difference is quite easy to understand from a physics viewpoint as tip/tilt aberrations at the sensor aperture diaphragm lead to overall optical field footprint shifts in the phase mask plane, and hence cause an effect analogous to phase mask lateral shift.

Notice that the phase retrieval convergence rate for the perfectly aligned WFS in Figure 10c,d is nearly two-fold higher than the corresponding convergence rate in Figure 10a,b, while they are expected to be identical. The reason for this difference is that in analysis of phase mask lateral misalignment, the numerical grid size N_PR was doubled (from N_PR =256, which was used in all previously described simulations, to N_PR =512) to increase the number of pixels per phase dot and, hence, the accuracy in M&S of phase mask lateral misalignment. This increase in phase retrieval computation grid resolution also resulted in more accurate numerical integration of the propagation Equations (1) and (8) for the outgoing and back-propagating (auxiliary) waves in the HIO iterative algorithm [Equation (16)], thus decreasing digital noise and accelerating phase retrieval process convergence. This phase retrieval convergence improvement comes not without a price – there is a noticeable increase in the iteration time

τ_{i t}

(see Table #1) and a potential AO control bandwidth decline. The optimal choice from an AO control perspective between phase retrieval convergence acceleration via increase of the phase retrieval computational grid resolution at the expense of iteration time

τ_{i t}

increase, vs

τ_{i t}

decrease when transitioning to a lower numerical grid resolution, is an important subject to be further investigated.

Phase retrieval computations may offer useful tools for SR-WFS alignment and calibration while utilizing for this purpose a plane (reference) input optical wave

[A_{i n} (r) = c o n s t]

. For example, as numerical simulations show, in the presence of the WFS misalignment Δ_CCD or Δ_aper, phase retrieval computations result in a clearly seen random uncorrelated phase component (phase noise) vs spatially uniform phase function for the perfectly aligned sensor. The phase noise component amplitude gradually increases with either parameter Δ_CCD or Δ_aper increase. Correspondingly, the variance of random fluctuations in the retrieved phase patterns can be used as a metric to be minimized in the course of WFS alignment.

Similarly, retrieved phase patterns can also be used for phase mask lateral alignment. As M&S shows, retrieved phase patterns have characteristic (dependent on lateral shift amplitude Δ_mask) stripe-shaped spatial structures, which can provide guidance for phase mask lateral alignment during WFS calibration.

4.5. Impact of Camera Noise and Laser Beacon Linewidth

“Photon-hungry” (low input field photon flux level) operational conditions characterized by relatively low SNR are common for atmospheric optics applications. Correspondingly, phase retrieval “resilience” with respect to photo-array (camera) noise is an important matter to be considered. Camera noise impact is analyzed here for the SAPCO WFS configuration that possesses perhaps the lowest optical power loses, and, hence, potentially the highest SNR among the basic SR-WFS architectures considered above and shown in Figure 1.6

Camera noise inside the photo-array area of size D_PA =2D_WFS was represented in M&S by statistically independent delta-correlated 2D random fields

{ξ_{n} (r)}

(n=1,…, N_atm) with uniform probability distribution inside the [0,1] interval. After scaling by the factor  each noise realization

ξ_{n} (r)

was superimposed with a corresponding realization of the WFS output intensity distribution

I_{o u t}^{(n)} (r)

prior to phase retrieval computations. SNR was defined as the ratio of atmospheric-averaged (averaged over N_atm =100 turbulence and noise realizations) optical

{〈 P_{o u t} 〉}_{a t m}

and camera noise

{〈 P_{n o i s e} 〉}_{a t m}

powers inside the WFS photo-array area:

S N R = {〈 P_{o u t} 〉}_{a t m} / [ν {〈 P_{n o i s e} 〉}_{a t m}]

Phase retrieval computations with “noisy” WFS output intensity distributions

{I_{o u t}^{(n)} (r) + ν ξ_{n} (r)}

were repeated for a set of pre-selected SNR values. The computed dependencies of the atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

on iteration number n for

D / r_{0}

=5 and

D / r_{0}

=10 are presented in Figure 11 for several SNR values.

As might be expected, photo-array noise results in phase retrieval convergence rate and accuracy decrease, which are more pronounced for stronger turbulence (

D / r_{0}

=10 in Figure 11, right). For the chosen acceptable phase retrieval error

< ε_{δ} >_{a t m} \leq 0.1

the SNR should be approximately above ten for weak-to-moderate (

D / r_{0}

=5) and nearly twice higher for moderate-to-strong (

D / r_{0}

=10) turbulence conditions.

So far in our previous analysis the light source (laser beacon light) was considered monochromatic. This assumption may not be applicable for a number of atmospheric AO applications including directed energy and remote laser power beaming based on spectral beam combining (see [53]), and utilizing short pulse or wide linewidth laser systems for laser beacon generation and active imaging [54].

The question to ask is, how non-monochromaticity (non-zero spectral linewidth) of the input optical field entering the SR-WFS might potentially impact phase retrieval process accuracy and convergence speed. To address this question, consider as an example phase retrieval efficiency for the SAPCO WFS operating with a non-monochromatic laser beacon light.

In numerical simulations a non-monochromatic laser beacon was represented by a set of N_λ =11 monochromatic collimated Gaussian beams (laser beacon spectral components) having identical width d_beacon and different wavelengths {λ_n } ,(n =1,…, N_λ). It is assumed that the wavelengths {λ_n } are equidistantly distributed within a spectral band (laser beacon linewidth) centered at the wavelength λ_c = 1060 nm corresponding to the largest peak intensity value among N_λ laser beacon monochromatic components.

In the laser beacon model considered here, wavelengths (spectral lines) are symmetrical with respect to the central wavelength λ_c , and peak intensity values of the corresponding laser beacon spectral components are described by the Gaussian function of width Δλ (laser beacon linewidth) dependent on the wavelength. The linewidth is commonly defined as the full-width at half-maximum (FWHM) of the spectral band, where the peak intensity value drops to half its maximum value. In example considered here of a Gaussian spectral intensity distribution the wavelength difference between two adjacent laser beacon spectral components was equal to Δλ / 6.

The output intensity

I_{o u t} (r)

at the SAPCO sensor photo-array was obtained via averaging of N_λ output intensity distributions {

I_{o u t}^{(n)} (r)

}, which were computed by considering atmospheric propagation of individual monochromatic laser beacon components to the WFS input plane and subsequent propagation from the sensor aperture diaphragm to the photo-array plane. The output intensity distribution

I_{o u t} (r)

was further utilized for phase retrieval computations based on the WFS mathematical model corresponding to a monochromatic input light with central wavelength λ_c =1060 nm, and the HIO algorithm [Equation (16)].

In M&S of individual laser beacon component propagation, wavelength difference was accounted for via corresponding change in phase screen modulation amplitudes for each turbulence realization. A similar phase modulation amplitude scaling was applied to the SAPCO sensor phase mask (scaling of the phase dot introduced phase shift). Note that M&S parameters for both the SAPCO sensor and atmospheric turbulence were computed for the central laser beacon wavelength λ_c.

The impact of the laser beacon linewidth Δλ on phase retrieval accuracy and convergence rate is illustrated in Figure 12 by the dependence of the atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

on iteration number for

D / r_{0}

=5 and

D / r_{0}

=10.

Analogous to the impact of photo-array noise (see Figure 11), laser source linewidth broadening resulted in a decline in the phase retrieval convergence rate and accuracy, which is more evident under stronger turbulence conditions (

D / r_{0}

=10 in Figure 12). In order to quantify the potential decline in WFS performance, consider (as before) the 10% phase retrieval error as an acceptable criterion (

< ε_{δ} >_{a t m} \leq 0.1

), shown in Figure 12 by horizontal dashed lines. This criterion is met for laser sources with linewidth Δλ of approximately 22 nm for weak-to-moderate (

D / r_{0}

=5) and 15 nm for moderate-to-strong (

D / r_{0}

=10) turbulence conditions.

The results obtained indicate the potential applicability of the SAPCO WFS and iterative phase retrieval technique discussed here for atmospheric AO systems operating with broadband (several hundred GHz) continuous wave and pico-second-class pulse laser sources.

5. Concluding Remarks

Recent advances in the development of GPU and FPGA-based signal processing hardware have opened the real prospect for practical application of computationally expensive iterative phase retrieval (IPR) techniques in closed-loop atmospheric AO applications. On the other hand, these possibilities cannot be fully realized without parallel development of novel wavefront sensing architectures that are no longer constrained by the phase retrieval computational time, and are uniquely suitable for addressing one of the most challenging atmospheric AO problems related to closed-loop wavefront sensing control in the strong scintillation conditions typical for near-ground propagation scenarios.

In this paper we provide a general framework for the analysis of such scintillation-resistant wavefront sensing (SR-WFS) architectures based on IPR algorithms, which can be considered as candidates for turbulence-induced phase aberration sensing and AO control in strong scintillations. It was shown that these sensors can be described in terms of a generic SR-WFS model that was further applied for derivation of iterative phase and complex field retrieval algorithms - analogues of the classical Gerchberg-Saxton and Fienup hybrid-input-output (HIO) iterative algorithms. This general phase retrieval framework was utilized for optimization and comparative performance analysis of basic SR-WFS architectures. This analysis led to introduction of the scintillation-resistant advanced phase-contrast (SAPCO) WFS. The major advantages of the SAPCO sensor are simplicity from a practical implementation viewpoint and efficiency in phase retrieval under a wide range of turbulence conditions. The numerical simulation results provided for SAPCO WFS tolerance with respect to optical component misalignment, and ability to operate with both non-monochromatic light and under relatively low SNR, open attractive opportunities for potential utilization of this IPR technique based sensor for closed-loop AO control under strong input field intensity scintillations, as described in Part II.

Author Contributions

Problem statement, derivations and paper writing: M.V; computer code development and numerical simulations: E.P; analysis and discussions of obtained results: M.V. and E.P.; preparation of the manuscript for submission: M.V. and E.P. Both authors have read and agreed to the published version of the manuscript.

Funding

This research was funded in part by Optonica LLC projects.

Data Availability Statement

Where no new data were created.

Acknowledgments

We thank Jennifer C. Ricklin for her careful review and helpful comments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Hardy, J.W. Adaptive Optics for Astronomical Telescopes; Oxford series in optical and imaging sciences; Oxford University Press: New York, 1998; ISBN 978-0-19-509019-2.
Platt, B.C.; Shack, R. History and Principles of Shack-Hartmann Wavefront Sensing. J. Refract. Surg. 2001, 17, p. 573. [CrossRef]
Roddier, F. Curvature Sensing and Compensation: A New Concept in Adaptive Optics. Appl. Opt. 1988, 27, p. 1223. [CrossRef]
Rousset, G. Wave-Front Sensors. In Adaptive Optics in Astronomy; Roddier, F., Ed.; Cambridge University Press, 1999; p. 91, ISBN 978-0-521-55375-9.
Hardy, J.W.; Lefebvre, J.E.; Koliopoulos, C.L. Real-Time Atmospheric Compensation. J. Opt. Soc. Am. 1977, 67, p. 360. [CrossRef]
Sandler, D.G.; Cuellar, L.; Lefebvre, M.; Barrett, T.; Arnold, R.; Johnson, P.; Rego, A.; Smith, G.; Taylor, G.; Spivey, B. Shearing Interferometry for Laser-Guide-Star Atmospheric Correction a Large D/r₀. J. Opt. Soc. Am. A 1994, 11, p. 858. [CrossRef]
Ragazzoni, R. Pupil Plane Wavefront Sensing with an Oscillating Prism. Journal of Modern Optics 1996, 43, p. 289. [CrossRef]
Esposito, S.; Riccardi, A. Pyramid Wavefront Sensor Behavior in Partial Correction Adaptive Optic Systems. Astron. Astrophys. 2001, 369, p. L9. [CrossRef]
Barchers, J.D.; Fried, D.L.; Link, D.J.; Tyler, G.A.; Moretti, W.; Brennan, T.J.; Fugate, R.Q. Performance of Wavefront Sensors in Strong Scintillation. In Proc. SPIE 4839; Wizinowich, P.L., Bonaccini, D., Eds.; Waikoloa, Hawai’i, United States, February 1 2003; p. 217. [CrossRef]
Perram, G.P.; Cusumano, S.J.; Hengehold, R.L.; Fiorino, S.T. An Introduction to Laser Weapon Systems; 1st ed.; Directed Energy Professional Society: Albuquerque, NM, 2010; ISBN 978-0-9793687-4-5.
Varshney, A.K.; Mainuddin; Singhal, G.; Nayak, J. High Power Lasers for Directed Energy Applications: Developments and Challenges. Infrared Physics & Technology 2024, 136, p. 105064. [CrossRef]
Soref, R.; De Leonardis, F.; Daligou, G.; Moutanabbir, O. Directed High-Energy Infrared Laser Beams for Photovoltaic Generation of Electric Power at Remote Locations. APL Energy 2024, 2, p. 026101. [CrossRef]
Majumdar, A.K.; Ricklin, J.C. Free-Space Laser Communications: Principles and Advances; Springer: New York, NY, 2008; ISBN 978-0-387-28652-5.
Göhler, B.; Lutzmann, P.; Anstett, G. 3D Imaging with Range Gated Laser Systems Using Speckle Reduction Techniques to Improve the Depth Accuracy. In Proc. SPIE 7113; Huckridge, D.A., Ebert, R.R., Eds.; Cardiff, Wales, United Kingdom, 2008; p. 711307. [CrossRef]
Aubailly, M.; Vorontsov, M.A. Scintillation Resistant Wavefront Sensing Based on Multi-Aperture Phase Reconstruction Technique. J. Opt. Soc. Am. A 2012, 29, p. 1707. [CrossRef]
Bordbar, B.; Vorontsov, M.A. Complex Field Sensing in Strong Scintillations with Multi-Aperture Phase Contrast Techniques. J. Opt. 2020, 22, p. 10LT01. [CrossRef]
Gerchberg, R.W.; Saxton, W.O. A Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik 1972, 35, p. 237.
Fienup, J.R. Phase Retrieval Algorithms: A Comparison. Appl. Opt. 1982, 21, p. 2758. [CrossRef]
Fienup, J.R. Phase-Retrieval Algorithms for a Complicated Optical System. Appl. Opt. 1993, 32, p. 1737. [CrossRef]
Fienup, J.R. Phase Retrieval Algorithms: A Personal Tour [Invited]. Appl. Opt. 2013, 52, p. 45. [CrossRef]
Soifer, V.A.; Kotlar, V.; Doskolovich, L. Iterative Methods for Diffractive Optical Elements Computation; CRC Press, 1997; ISBN 978-1-4822-7291-8.
Vorontsov, M.A.; Matveev, A.N.; Sivokon’, V.P. Optimal Guiding of the Wave Front in the Focusing of Radiation into an Arbitrary Region. Soviet Physics Doklady 1986, 31, p. 829.
Fleck, J.A.; Morris, J.R.; Feit, M.D. Time-Dependent Propagation of High Energy Laser Beams through the Atmosphere. Appl. Phys. 1976, 10, p. 129. [CrossRef]
Ghebremichael, F.; Andersen, G.P.; Gurley, K.S. Holography-Based Wavefront Sensing. Appl. Opt. 2008, 47, p. A62. [CrossRef]
Zernike, F. How I Discovered Phase Contrast. Science 1955, 121, p. 345. [CrossRef]
Vorontsov, M.A.; Justh, E.W.; Beresnev, L.A. Adaptive Optics with Advanced Phase-Contrast Techniques: Part I. High-Resolution Wave-Front Sensing. J. Opt. Soc. Am. A 2001, 18, p. 1289. [CrossRef]
Bloemhof, E.E.; Wallace, J.K. Phase Contrast Techniques for Wavefront Sensing and Calibration in Adaptive Optics. In Proc. SPIE 5169; Tyson, R.K., Lloyd-Hart, M., Eds.; San Diego, California, USA, December 31 2003; p. 309.
Wu, Y.; Sharma, M.K.; Veeraraghavan, A. WISH: Wavefront Imaging Sensor with High Resolution. Light Sci Appl 2019, 8, p. 44. [CrossRef]
Wang, C.; Dun, X.; Fu, Q.; Heidrich, W. Ultra-High Resolution Coded Wavefront Sensor. Opt. Express 2017, 25, p. 13736. [CrossRef]
Li, X.; Liu, K.; Liu, Z.; Guo, J. High-Precision Phase Retrieval Method for Speckle Suppression Based on Optimized Modulation Masks. Opt. Express 2023, 31, p. 18824. [CrossRef]
Fried, D.L. Branch Point Problem in Adaptive Optics. J. Opt. Soc. Am. A 1998, 15, p. 2759. [CrossRef]
Fried, D.L. Optical Resolution Through a Randomly Inhomogeneous Medium for Very Long and Very Short Exposures. J. Opt. Soc. Am. 1966, 56, p. 1372. [CrossRef]
Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; 2nd ed.; SPIE Publications: Bellingham, 2005; ISBN 978-1-5106-4370-3.
Ahmanov, S.A.; Nikitin, S.Y. Physical Optics; Oxford University Press: Oxford, 1997; ISBN 978-0-19-851795-5.
Vorontsov, M.A.; Shmalgauzen, V.I. The Principles of Adaptive Optics; Izdatel’stvo Nauka: Moscow, 1985;
Paxman, R.G.; Schulz, T.J.; Fienup, J.R. Joint Estimation of Object and Aberrations by Using Phase Diversity. J. Opt. Soc. Am. A 1992, 9, p. 1072. [CrossRef]
Wang, B.-Y.; Han, L.; Yang, Y.; Yue, Q.-Y.; Guo, C.-S. Wavefront Sensing Based on a Spatial Light Modulator and Incremental Binary Random Sampling. Opt. Lett. 2017, 42, p. 603. [CrossRef]
Almoro, P.F.; Pedrini, G.; Gundu, P.N.; Osten, W.; Hanson, S.G. Enhanced Wavefront Reconstruction by Random Phase Modulation with a Phase Diffuser. Optics and Lasers in Engineering 2011, 49, p. 252. [CrossRef]
Candès, E.J.; Li, X.; Soltanolkotabi, M. Phase Retrieval from Coded Diffraction Patterns. Applied and Computational Harmonic Analysis 2015, 39, p. 277. [CrossRef]
Zel’dovich, B.Ya.; Pilipetsky, N.F.; Shkunov, V.V. Principles of Phase Conjugation; Springer Series in Optical Sciences; Springer: Berlin, Heidelberg, 1985; Vol. 42; ISBN 978-3-662-13573-0.
Vorontsov, M.A.; Shmal’gauzen, V.I. Interference Criteria for the Focusing of Light. Sov. J. Quantum Electron. 1980, 10, p. 285. [CrossRef]
Minet, J.; Vorontsov, M.A.; Polnau, E.; Dolfi, D. Enhanced Correlation of Received Power-Signal Fluctuations in Bidirectional Optical Links. J. Opt. 2013, 15, p. 022401. [CrossRef]
Levitin, E.S.; Polyak, B.T. Constrained Minimization Methods. USSR Computational Mathematics and Mathematical Physics 1966, 6, p. 1. [CrossRef]
Vorontsov, M.A.; Kolosov, V.V.; Kohnle, A. Adaptive Laser Beam Projection on an Extended Target: Phase- and Field-Conjugate Precompensation. J. Opt. Soc. Am. A 2007, 24, p. 1975. [CrossRef]
Fienup, J.R.; Marron, J.C.; Schulz, T.J.; Seldin, J.H. Hubble Space Telescope Characterized by Using Phase-Retrieval Algorithms. Appl. Opt. 1993, 32, p. 1747. [CrossRef]
Bauschke, H.H.; Combettes, P.L.; Luke, D.R. Phase Retrieval, Error Reduction Algorithm, and Fienup Variants: A View from Convex Optimization. J. Opt. Soc. Am. A 2002, 19, p. 1334. [CrossRef]
Gass, J.; Dakoff, A.; Kim, M.K. Phase Imaging without 2π Ambiguity by Multi-wavelength Digital Holography. Opt. Lett. 2003, 28, p. 1141. [CrossRef]
Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE: Bellingham, 2010; ISBN 978-0-8194-8326-3.
Roggemann, M.C.; Welsh, B.M. Imaging Through Turbulence; 1st ed.; CRC Press, 2018; ISBN 978-0-203-75128-2.
Lachinova, S.; Maynard, M.; Vorontsov, M.A.; Filimonov, G.; Spencer, M. WaveJET Software Modeling and Simulation Platform for HEL DE Applications: Overview. 21st Annual Directed Energy S&T Symposium Proceedings; Destin, Florida, 2019.
Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akademiia Nauk SSSR Doklady 1941, 30, p. 301.
Vorontsov, M.; Filimonov, G.; Ovchinnikov, V.; Polnau, E.; Lachinova, S.; Weyrauch, T.; Mangano, J. Comparative Efficiency Analysis of Fiber-Array and Conventional Beam Director Systems in Volume Turbulence. Appl. Opt. 2016, 55, 4170. [CrossRef]
Walbaum, T.; Plötner, M.; Strecker, M.; Heinzig, M.; Liem, A.; Ehrhardt, S.; Möller, F.; Damm, C.; Trautmann, S.; Rothhardt, C.; et al. Spectral Beam Combining for Security as Well as Terrestrial, Satellite, and Deep Space Communication. In Proceedings of the Fiber Lasers XXI: Technology and Systems; Jollivet, C., Ed.; SPIE: San Francisco, 2024; p. 25. [CrossRef]
DiComo, G.; Helle, M.; Kaganovich, D.; Schmitt-Sody, A.; Elle, J.; Peñano, J. Nonlinear Self-Channeling of High-Power Lasers through Controlled Atmospheric Turbulence. J. Opt. Soc. Am. B 2020, 37, p. 797. [CrossRef]

1	The term “modal WFS” is used here in spite of the fact that this most commonly refers to holographic-type WFSs performing input field transformation (mapping) into a set of highly localized spots associated with phase aberration components, which can be directly (without phase reconstruction) utilized for closed loop AO control [24].
2	A diacritic tilde symbol is used to distinguish optical field characteristics associated with input field estimation.
3	Corresponding derivations are analogous to those presented in Ref. [44].
4	The phase-only SLM in this SR-WFS type can be replaced by a specially designed phase mask providing a random phase modulation pattern with analogues parameters $σ_{S L M}^{2}$ and $r_{S L M}$ .
5	The alignment tolerance results presented are specific to the SAPCO sensor parameters selected in M&S (see section 3.4) and turbulence strength, and may vary when these parameters change.
6	In the analysis we neglect potential optical power losses in the SAPCO sensor related to imperfections in the phase mask glass plate antireflection coating.

Figure 2. Examples of output intensity patterns corresponding to the basic SR-WFS configurations in Figure 1. The input field complex amplitudes entering the sensors were obtained through numerical simulations of monochromatic (λ = 1064 nm) plane wave propagation over L = 5 km in homogeneously distributed (volume) turbulence under relatively weak (top row,

D / r_{0} = 3

σ_{R}^{2} = 1.18

), moderate-to-strong (middle row,

D / r_{0} = 10

σ_{R}^{2} = 8.77

), and strong (bottom row,

D / r_{0} = 15

σ_{R}^{2} = 17.25

) conditions. The squares indicate the sensor aperture of size D_WFS =D/M =3.55 mm, where D is the input field aperture size (D =15 cm) and M = 42.2 is the demagnification factor of the optical receiver telescope in front of the WFS. The optical wave propagation length inside the WFSs (between the input and output planes) was L_WFS = 100 cm for the lens-based WFS and L_WFS = 28 cm for all other WFS configurations. A densely packed array of 4x4 square lenses (lenslet array) was used in M&S of both the MAPR and MAPCO WFSs. The phase mask of the MAPCO sensor with size D_mask =2D_WFS was composed of randomly distributed N_dot = 3600 identical phase dots of d_dot =100 μm diameter. Grey-scale images in this and all subsequent figures correspond to the 2D_WFS x 2D_WFS square at the WFS input and output planes, and correspondingly the 2D x 2D square at the receiver telescope pupil plane.

D / r_{0} = 3

σ_{R}^{2} = 1.18

), moderate-to-strong (middle row,

D / r_{0} = 10

σ_{R}^{2} = 8.77

), and strong (bottom row,

D / r_{0} = 15

σ_{R}^{2} = 17.25

Figure 3. Input field intensity (top row) and phase (bottom row) patterns used in computation of the SR-WFS output intensity distributions shown in Figure 2:

D / r_{0} = 3

(left column),

D / r_{0} = 10

(middle column) and

D / r_{0} = 15

(right column). Phase functions are shown module 2π.

Figure 3. Input field intensity (top row) and phase (bottom row) patterns used in computation of the SR-WFS output intensity distributions shown in Figure 2:

D / r_{0} = 3

(left column),

D / r_{0} = 10

(middle column) and

D / r_{0} = 15

(right column). Phase functions are shown module 2π.

Figure 4. Optical schematic of the SAPCO WFS. The sensor is composed of an aperture diaphragm (aperture), phase mask containing large numbers of circular phase dots of diameter

d_{d o t}

that are either distributed randomly or in the form of a 2D grid (shown in right inserts), and a photo-array. The SAPCO WFS output intensity patterns (shown by grey-scale images) are computed for the numerical simulation setting and input field phase and intensity distributions (shown in Figure 3) identical to those described in Figure 2. The parameters used in M&S are: D_WFS =3.55 mm, D_mask =2D_WFS, L_mask = L_dif = 14 cm, d_dot =100 μm, and Δ_dot = π rad. Simulations were conducted for a random-dot mask (top right) composed of N_dot= 3600 dots inside the D_WFS x D_WFS area with approximately 50% density (

η_{d o t} ≃ 0.5

Figure 4. Optical schematic of the SAPCO WFS. The sensor is composed of an aperture diaphragm (aperture), phase mask containing large numbers of circular phase dots of diameter

d_{d o t}

η_{d o t} ≃ 0.5

Figure 5. Schematic diagram of the numerical simulation setting for SR-WFS performance analysis.

Figure 6. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS configuration (Figure 4) with a phase mask composed of randomly distributed phase shifting dots with density

η_{d o t} = 52 %

(N_dot=3600 dots within a square of size D_mask = 2D_WFS). Results were obtained for different parameter

L_{m a s k}

values and turbulence conditions corresponding to

D / r_{0}

= 5 (left) and

D / r_{0}

= 10 (right). Phase retrieval simulations were performed using the HIO (solid lines) and AFC (dashed line) algorithms [Equations (15) and (16)]. Averaging was performed using N_atm = 100 statistically independent turbulence realizations. Grey-scale images illustrate the auxiliary function magnitude

| ψ^{(n = 0)} (r, 0) |

within the phase retrieval grid area D_PR x D_PR at the sensor input plane prior to the first (n=1) complex field estimation update.

Figure 6. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS configuration (Figure 4) with a phase mask composed of randomly distributed phase shifting dots with density

η_{d o t} = 52 %

(N_dot=3600 dots within a square of size D_mask = 2D_WFS). Results were obtained for different parameter

L_{m a s k}

values and turbulence conditions corresponding to

D / r_{0}

= 5 (left) and

D / r_{0}

| ψ^{(n = 0)} (r, 0) |

within the phase retrieval grid area D_PR x D_PR at the sensor input plane prior to the first (n=1) complex field estimation update.

Figure 7. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for a SAPCO WFS with grid-dot type phase masks having different grid pattern dimension parameter n_dot values (solid lines), and with a random-dot type mask composed of N_dot =3600 dots randomly located across the mask area (RND dashed line) for turbulence conditions corresponding to

D / r_{0}

= 5 (left) and

D / r_{0}

= 10 (right).

Figure 7. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

D / r_{0}

= 5 (left) and

D / r_{0}

= 10 (right).

Figure 8. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the basic SR-WFS types (Figure 1) computed for turbulence conditions corresponding to

D / r_{0}

=5 (left panels) and

D / r_{0}

=10 (right panels) without (top panels) and with (bottom panels) wavefront tip and tilt aberration removal from the input optical fields.

Figure 8. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the basic SR-WFS types (Figure 1) computed for turbulence conditions corresponding to

D / r_{0}

=5 (left panels) and

D / r_{0}

=10 (right panels) without (top panels) and with (bottom panels) wavefront tip and tilt aberration removal from the input optical fields.

Figure 9. Average number of iterations <N_it > required to reach a phase retrieval residual error threshold of

ε_{0} = 0.1

(10% error) vs

D / r_{0}

ratio for MAPCO and SAPCO WFS configurations with (dotted lines) and without (solid lines) removal of tip/tilt phase aberration components from the entering WFS input field. Vertical bars indicate standard deviation characterizing fluctuations in iteration numbers

{N_{i t}^{(j)}}

computed for N_atm =100 phase retrieval trials for the SAPCO WFS with no tip/tilt aberration removal. Error bars are virtually identical for all other curves and thus are omitted here.

Figure 9. Average number of iterations <N_it > required to reach a phase retrieval residual error threshold of

ε_{0} = 0.1

(10% error) vs

D / r_{0}

{N_{i t}^{(j)}}

computed for N_atm =100 phase retrieval trials for the SAPCO WFS with no tip/tilt aberration removal. Error bars are virtually identical for all other curves and thus are omitted here.

Figure 10. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS (Figure 4) computed for turbulence conditions corresponding to

D / r_{0}

=10 in the presence of longitudinal deviations Δ_CCD and Δ_aper in the WFS photo-array (a) and aperture diaphragm (b) with respect to the nominal distances L_dif = 14 cm [for (a)] and L_mask = 20 cm [for (b)], and the phase mask lateral shift over the distance Δ_mask without (c) and with (d) removal of tip/tilt aberrations from the input wave entering the WFS.

Figure 10. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS (Figure 4) computed for turbulence conditions corresponding to

D / r_{0}

Figure 11. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS computed for turbulence conditions corresponding to

D / r_{0}

=5 (left) and

D / r_{0}

=10 (right) in the presence of photo-array noise for different SNR values. Numerical simulation parameters are presented in Fig 5 and described in Section 3.4, 4.1 and 4.2.

Figure 11. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS computed for turbulence conditions corresponding to

D / r_{0}

=5 (left) and

D / r_{0}

=10 (right) in the presence of photo-array noise for different SNR values. Numerical simulation parameters are presented in Fig 5 and described in Section 3.4, 4.1 and 4.2.

Figure 12. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS operating with a non-monochromatic laser beacon of linewidth Δλ, computed for atmospheric turbulence conditions corresponding to

D / r_{0}

=5 (left) and

D / r_{0}

=10 (right). M&S parameters are presented in Fig 5 and described in Section 3.4, 4.1 and 4.2.

Figure 12. Atmospheric-averaged phase retrieval error

{〈 ε_{δ} (n) 〉}_{a t m}

evolution curves for the SAPCO WFS operating with a non-monochromatic laser beacon of linewidth Δλ, computed for atmospheric turbulence conditions corresponding to

D / r_{0}

=5 (left) and

D / r_{0}

=10 (right). M&S parameters are presented in Fig 5 and described in Section 3.4, 4.1 and 4.2.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Framework for Iterative Phase Retrieval Technique Integration into Atmospheric Adaptive Optics. Part I: Wavefront Sensing in Strong Scintillations

Abstract

1. Introduction

2. Scintillation Resistant Wavefront Sensing for Atmospheric AO

2.1. Intensity Scintillation Impact on Zonal and Modal WFSs

2.2. Basic SR-WFS Architectures

2.3. Generic Scintillation Resistance WFS: Mathematical Model

2.4. Phase Retrieval via Optimization of a SR-WFS Output Field Fidelity Metric

2.5. Complex Field Retrieval for the Generic SR-WFS Model

2.6. Complex Field Retrieval Computational Steps

2.7. Complex Field and Phase Retrieval Quality Metrics

3. Tradeoffs in SR-WFS Design and Phase Retrieval Technique Implementation

3.1. Basic Considerations for SR-WFS Design: SAPCO WFS

3.2. Phase Retrieval Computational Time

3.3. Phase Retrieval Computational Grid

3.4. Numerical Modeling and Simulations Setting

4. SR-WFS Parameter Optimization and Performance Assessment

4.1. SR-WFS Optimization Parameter Space

4.2. Parameter Optimization Methodology Examples

4.3. Comparative Performance Analysis of Basic SR-WFS Configurations

4.4. SR-WFS Tolerance Analysis Examples

4.5. Impact of Camera Noise and Laser Beacon Linewidth

5. Concluding Remarks

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe