Submitted:
26 July 2024
Posted:
26 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Definition of MOEMS Displacement Sensing
3. Performance Indexes
4. Classifications
4.1. Guided-Wave based Techniques
4.1.1. Evanescent Coupling Scheme
4.1.2. Interference Scheme
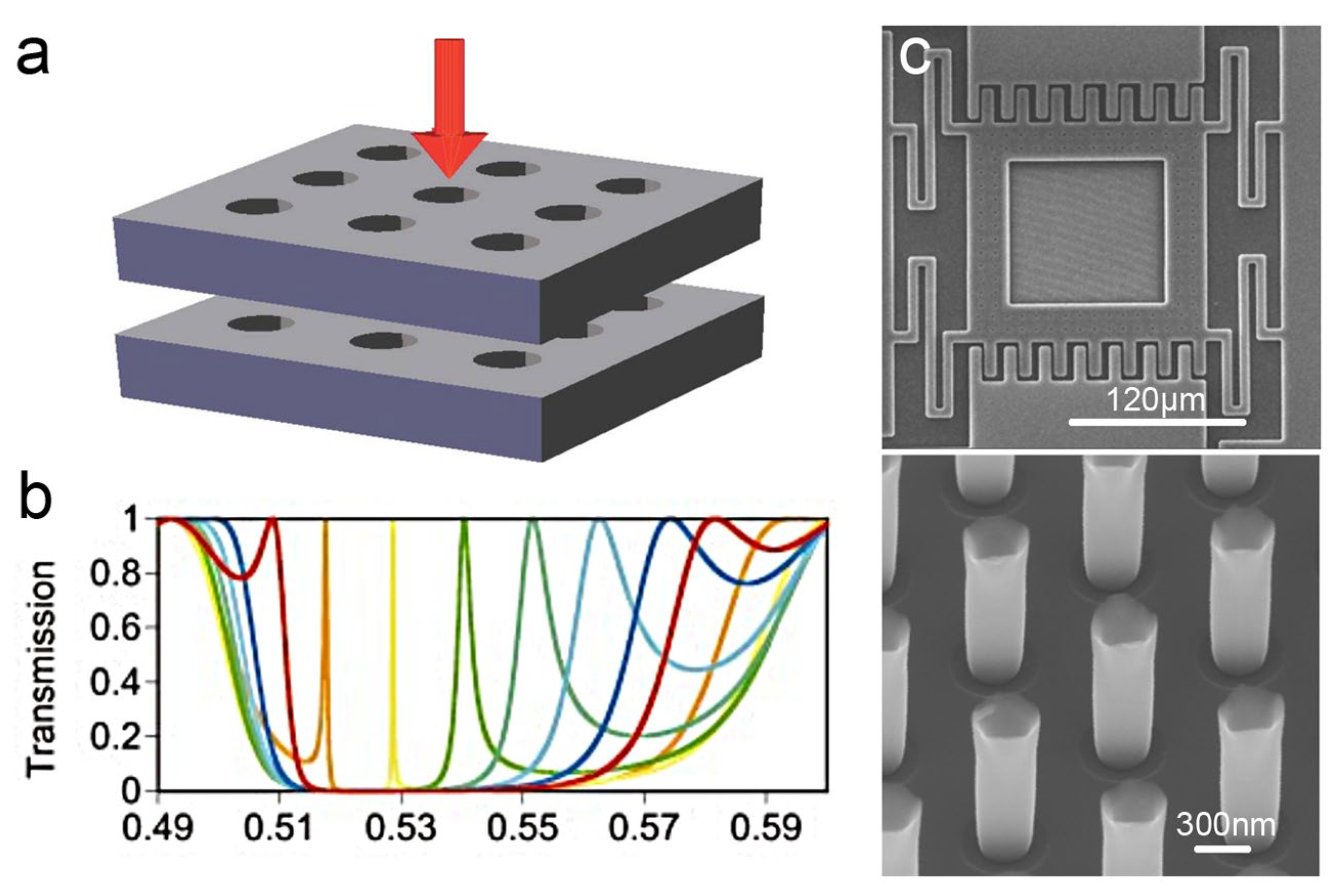
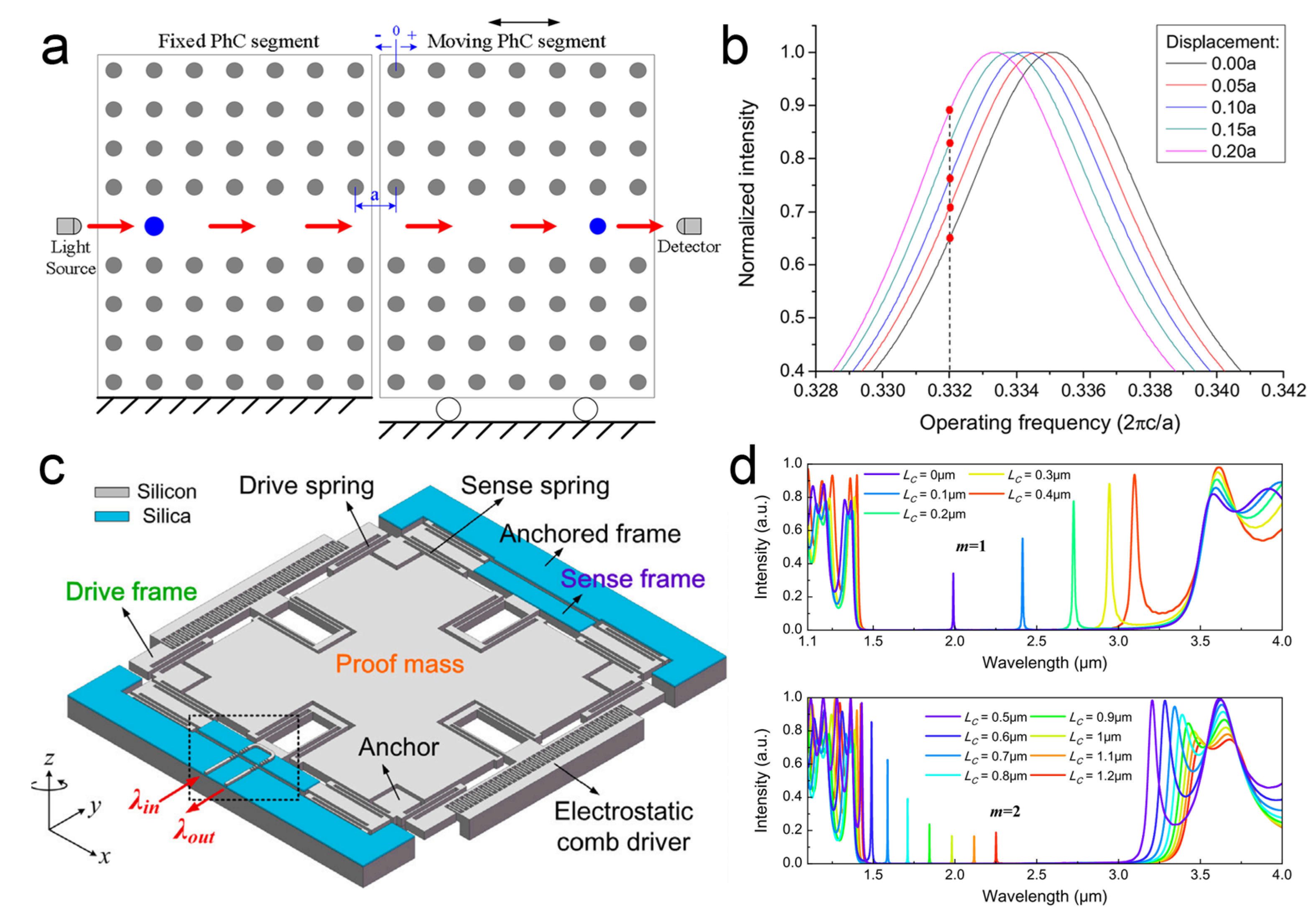
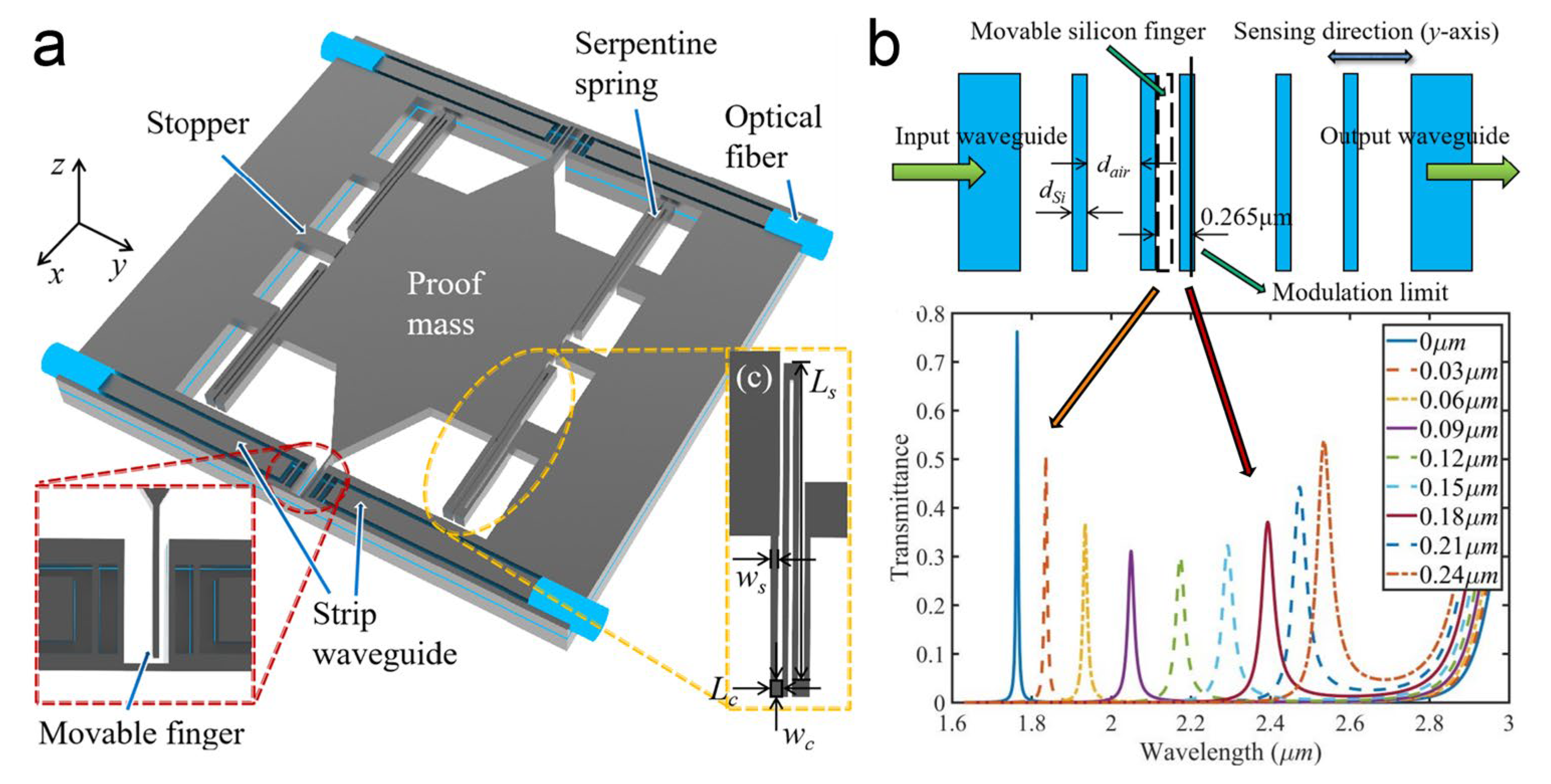
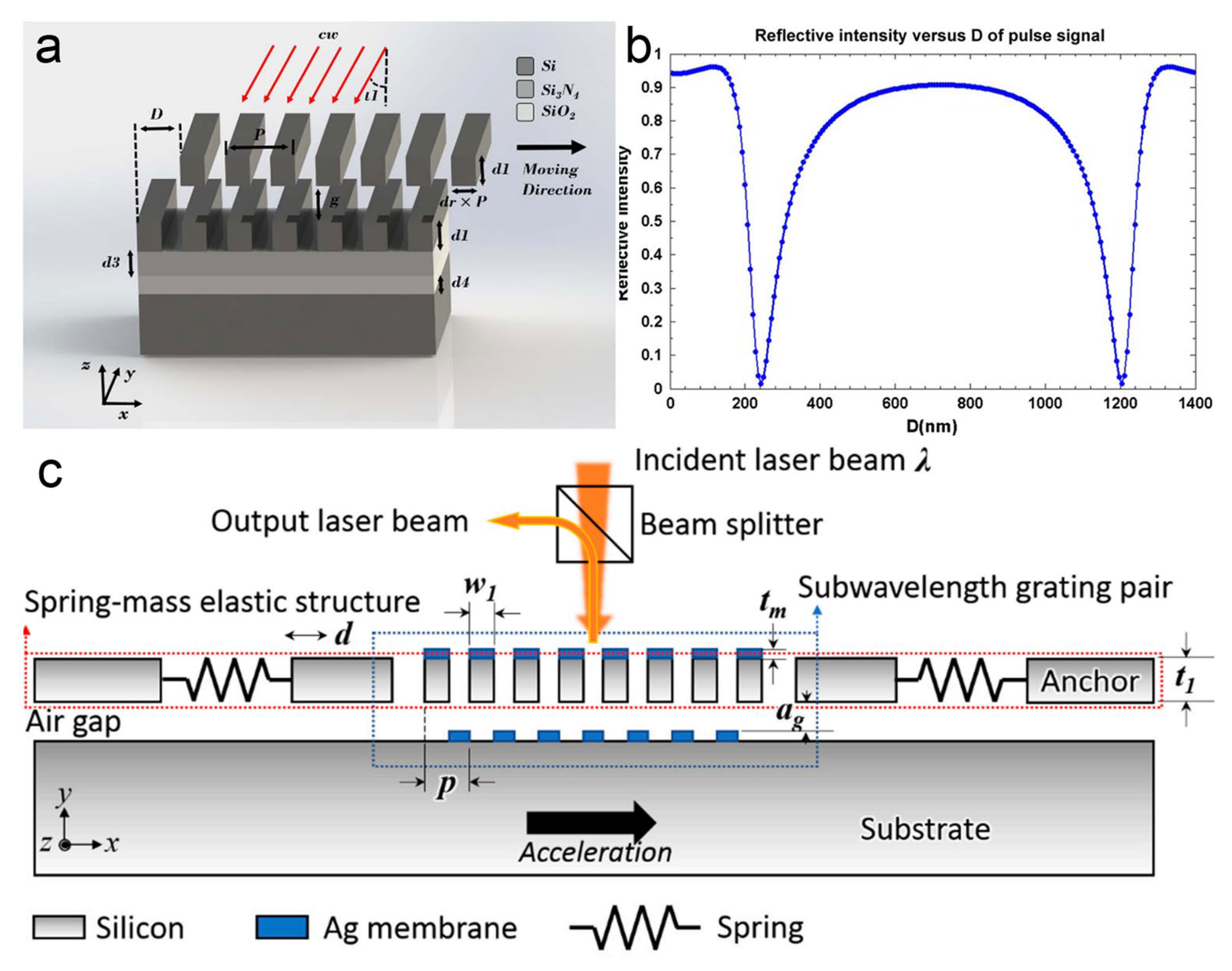
4.1.3. Bandgap Modulation Scheme
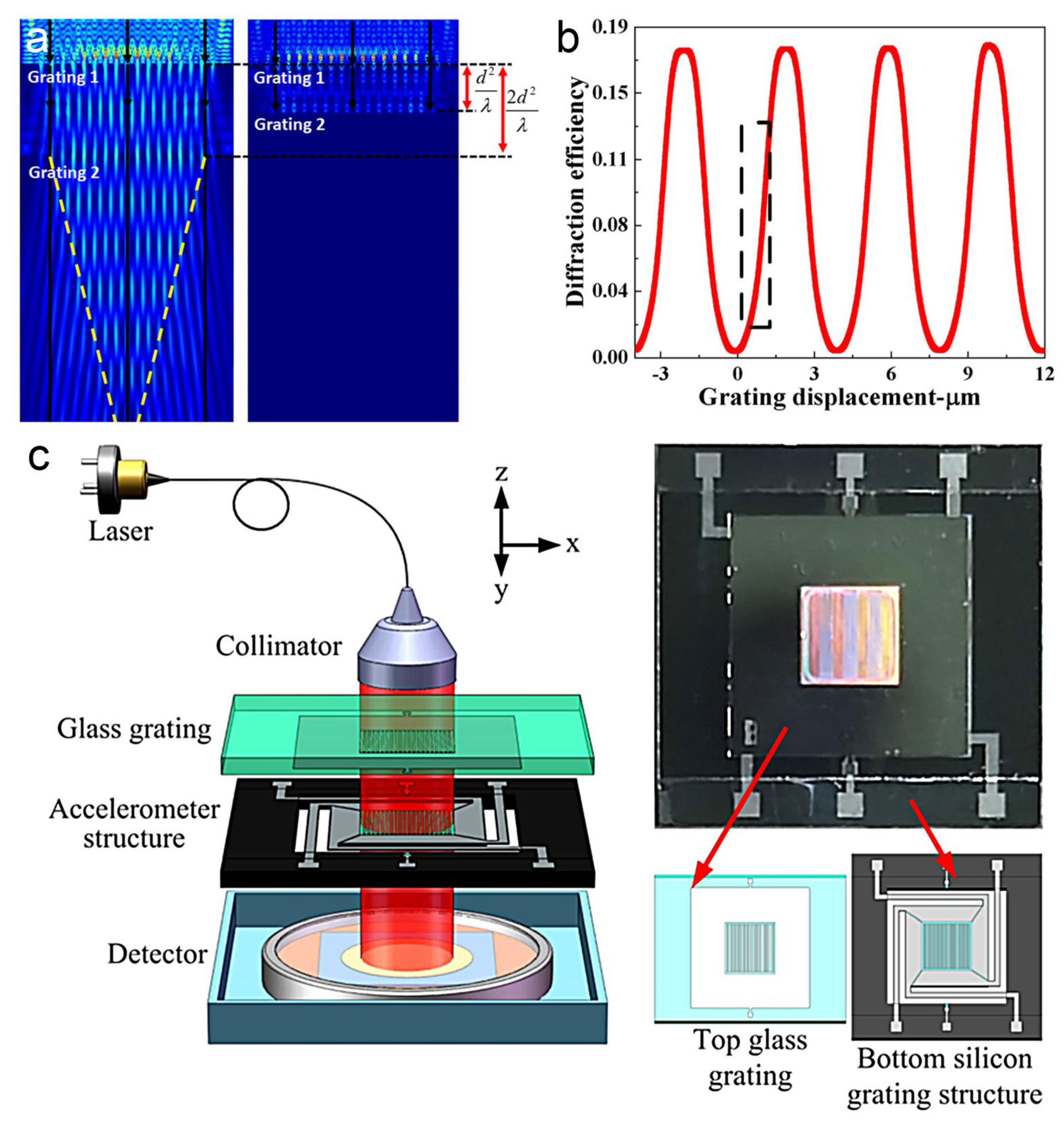
4.2. Figures, Tables and Schemes
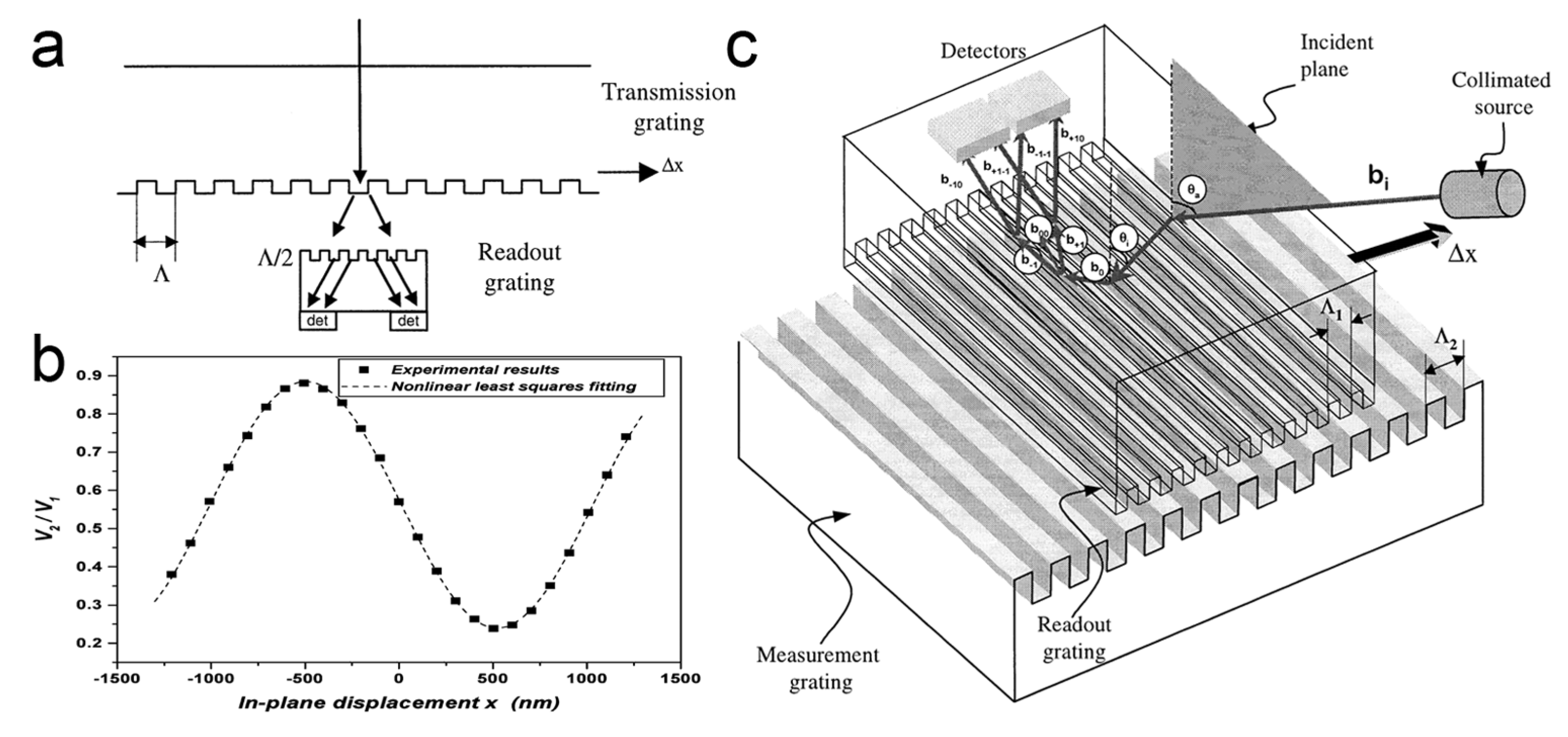
4.2.1. Transmission Scheme
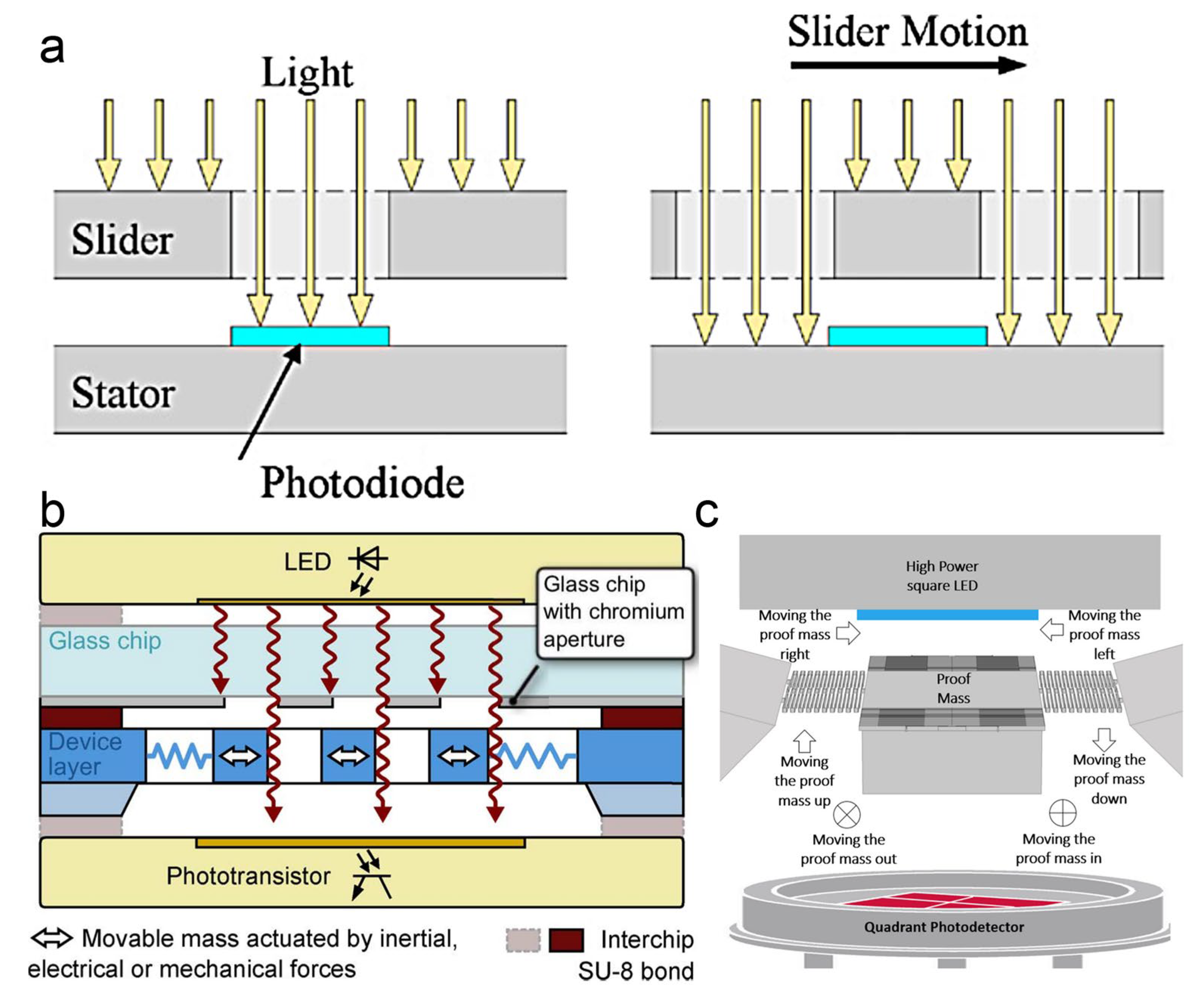
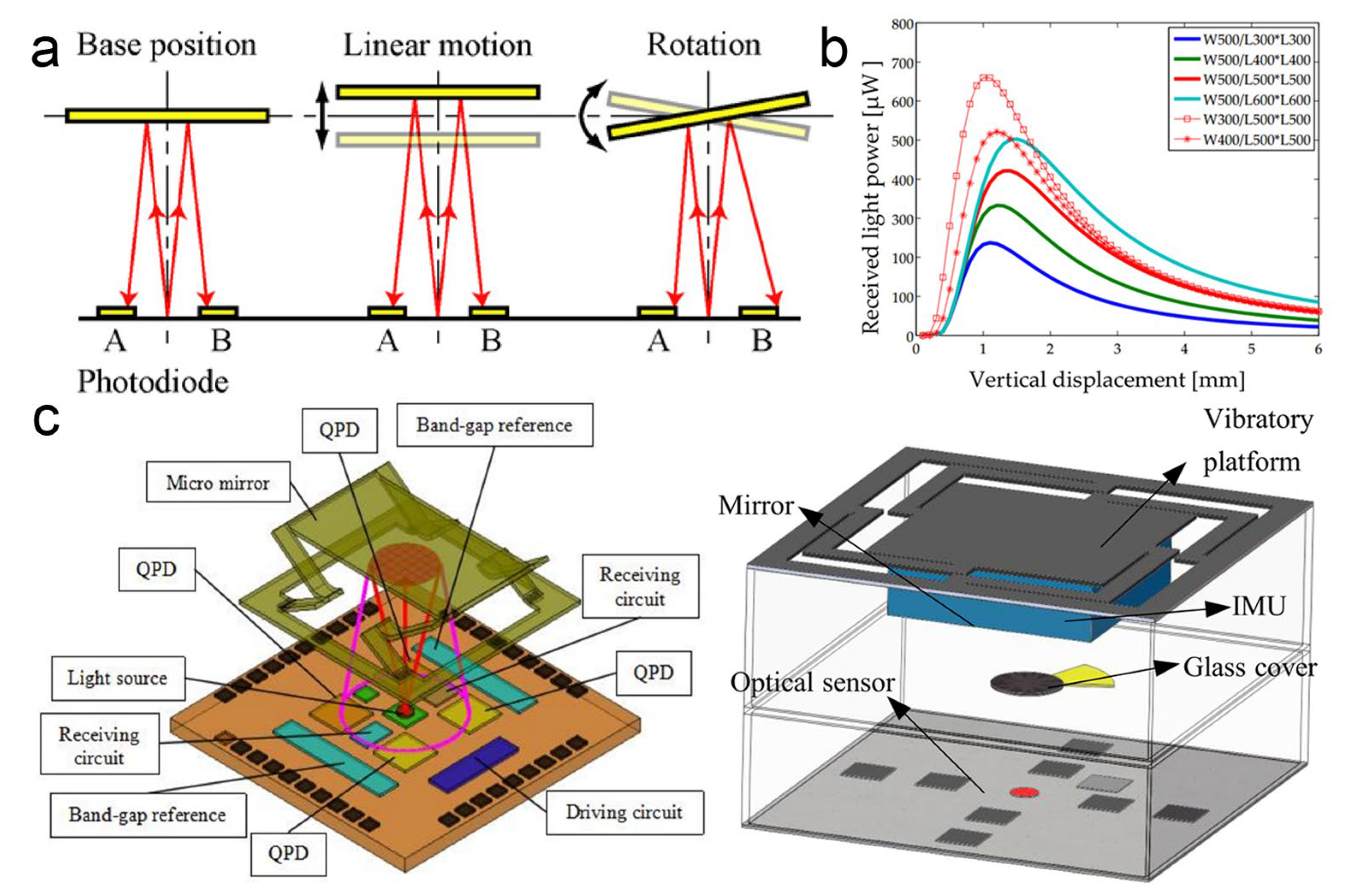
4.2.2. Reflection Scheme
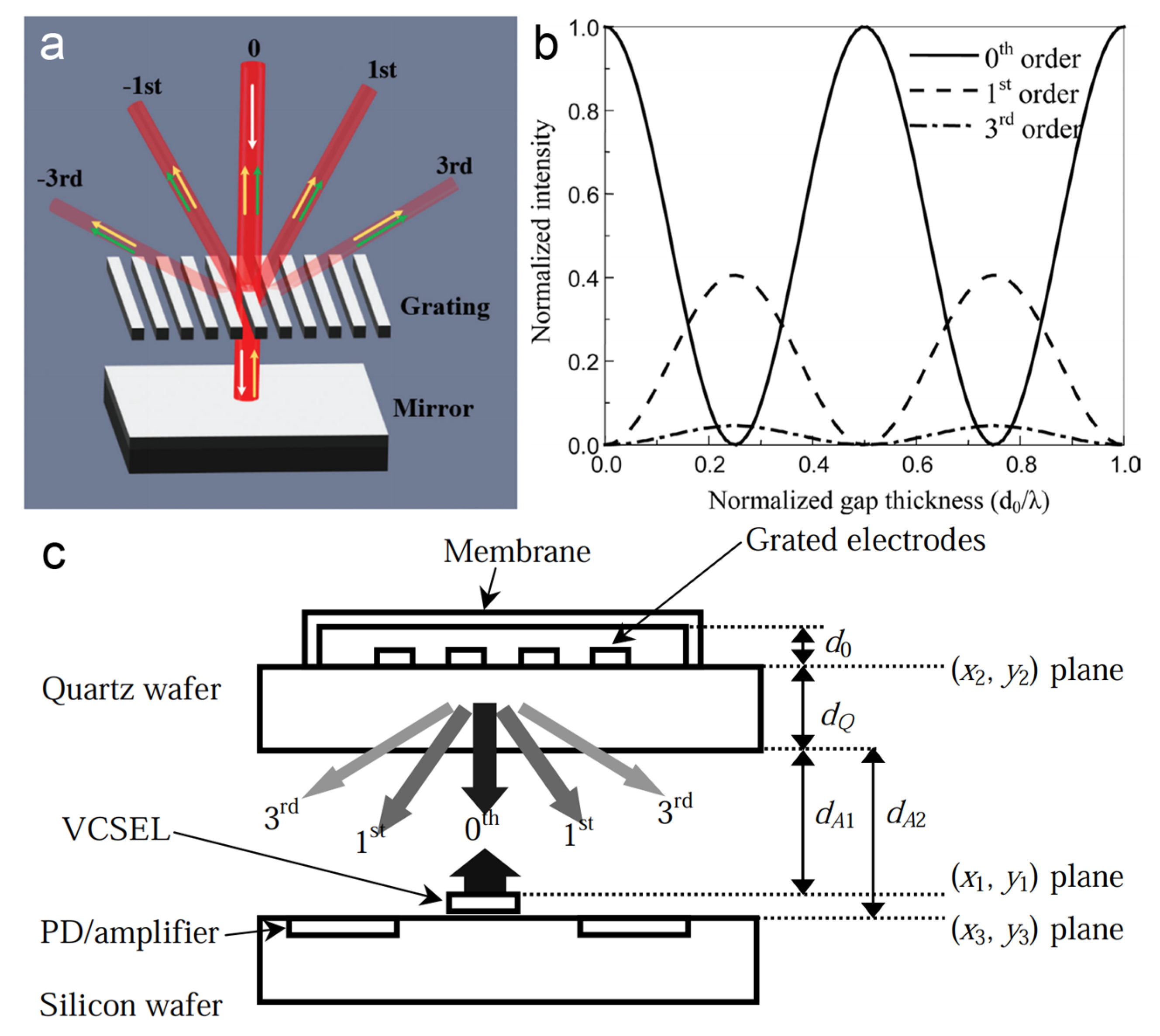
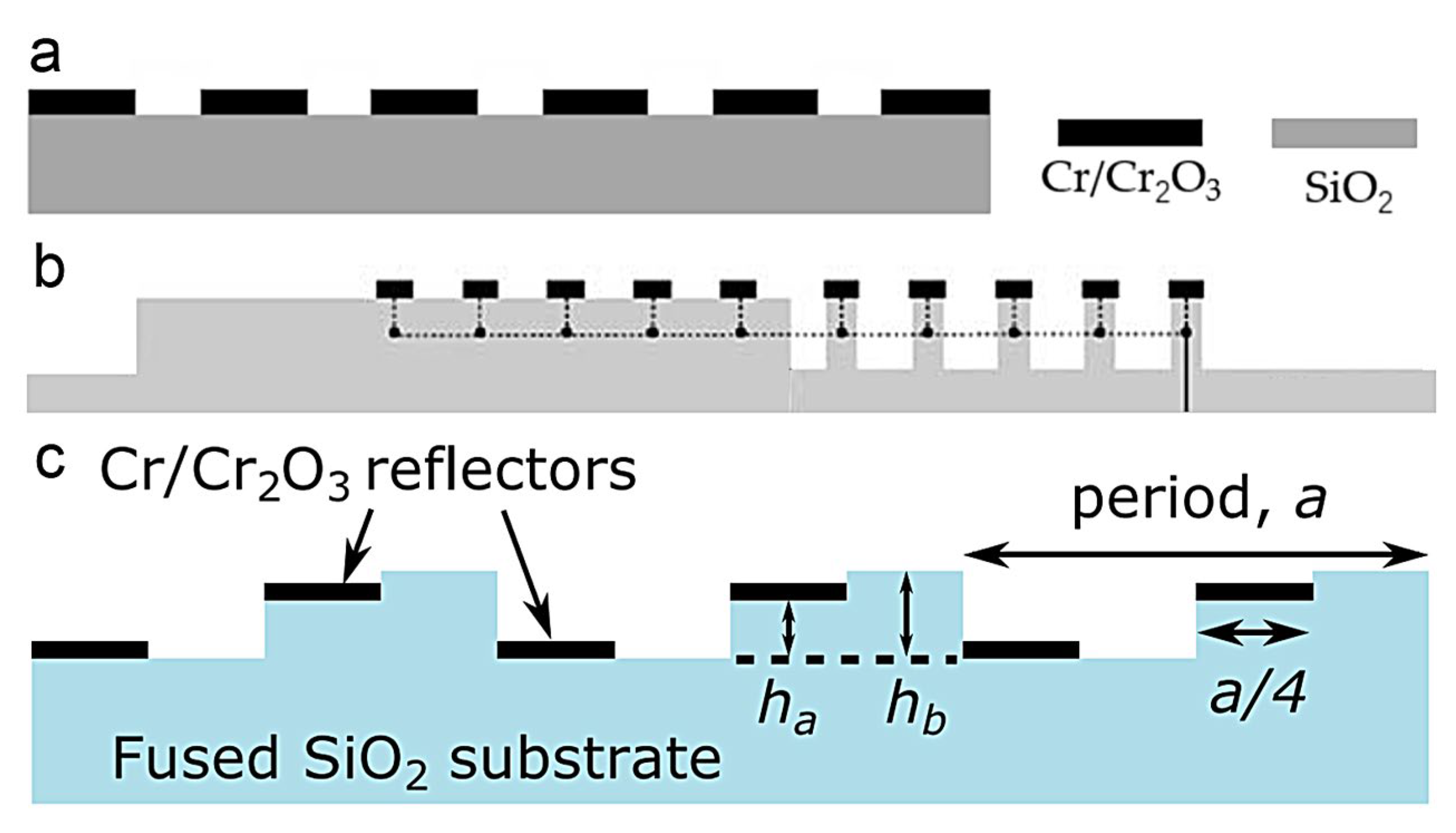
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rakich, P.T.; Popovic, M.A.; Soljacic, M.; Ippen, E.P. Trapping, corralling and spectral bonding of optical resonances through optically induced potentials. Nature Photonics 2007, 1, 658–665. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chena, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. Cirp Annals-Manufacturing Technology 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. Cirp Annals-Manufacturing Technology 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Lei, Y.-J.; Li, R.-J.; Zhang, L.-S.; Hu, P.-H.; Huang, Q.-X. Optical Accelerometers for Detecting Low-Frequency Micro-Vibrations. Applied Sciences 2022, 12. [Google Scholar] [CrossRef]
- Berkovic, G.; Shafir, E. Optical methods for distance and displacement measurements. Advances in Optics and Photonics 2012, 4, 441–471. [Google Scholar] [CrossRef]
- Tseng, V.F.G.; Xie, H. Simultaneous piston position and tilt angle sensing for large vertical displacement micromirrors by frequency detection inductive sensing. Applied Physics Letters 2015, 107. [Google Scholar] [CrossRef]
- Tseng, V.F.-G.; Xie, H. Resonant Inductive Coupling-Based Piston Position Sensing Mechanism for Large Vertical Displacement Micromirrors. Journal of Microelectromechanical Systems 2016, 25, 207–216. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, C.; He, C.; Wang, X.; Huang, J.; Deng, J. A Review on Applications of Capacitive Displacement Sensing for Capacitive Proximity Sensor. IEEE Access 2020, 8, 45325–45342. [Google Scholar] [CrossRef]
- Hu, P.-c.; Chang, D.; Tan, J.-b.; Yang, R.-t.; Yang, H.-x.; Fu, H.-j. Displacement measuring grating interferometer: a review. Frontiers of Information Technology & Electronic Engineering 2019, 20, 631–654. [Google Scholar] [CrossRef]
- Motamedi, E.; Kubby, J.; Oden, P.; Piyawattanametha, W. Emerging MOEMS Technology and Applications. Journal of Micro-Nanolithography Mems and Moems 2014, 13. [Google Scholar] [CrossRef]
- Lu, Q.; Wang, Y.; Wang, X.; Yao, Y.; Wang, X.; Huang, W. Review of micromachined optical accelerometers: from m<i>g</i> to sub-μ<i>g</i>. Opto-Electronic Advances 2021, 4. [Google Scholar] [CrossRef]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Ba Hashwan, S.S.; Junaid, M.M. A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices. Nanoscale Research Letters 2021, 16. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zeng, X.; Rao, Y.-J.; Gong, Y.; Hou, C.-L.; Yang, G.-G. MOEMS Accelerometer Based on Microfiber Knot Resonator. IEEE Photonics Technology Letters 2009, 21, 1547–1549. [Google Scholar] [CrossRef]
- Pang, C.; Bae, H.; Gupta, A.; Bryden, K.; Yu, M. MEMS Fabry-Perot sensor interrogated by optical system-on-a-chip for simultaneous pressure and temperature sensing. Optics Express 2013, 21, 21829–21839. [Google Scholar] [CrossRef] [PubMed]
- Jindal, S.K.; Raghuwanshi, S.K.; Kumar, A. Realization of MOEMS pressure sensor using mach zehnder interferometer. Journal of Mechanical Science and Technology 2015, 29, 3831–3839. [Google Scholar] [CrossRef]
- Huang, J.; Wen, Q.; Nie, Q.; Chang, F.; Zhou, Y.; Wen, Z. Miniaturized NIR Spectrometer Based on Novel MOEMS Scanning Tilted Grating. Micromachines 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- el Ahdab, R.; Sharma, S.; Nabki, F.; Menard, M. Wide-band silicon photonic MOEMS spectrometer requiring a single photodetector. Optics Express 2020, 28, 31345–31359. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, C.; Shi, X.; Wu, Z.; Fan, S.; Wan, Z.; Han, S. High-Sensitivity Graphene MOEMS Resonant Pressure Sensor. ACS Applied Materials & Interfaces 2023, 15, 30479–30485. [Google Scholar] [CrossRef]
- Mireles, J., Jr.; Sauceda, A.; Jimenez, A.; Ramos, M.; Gonzalez-Landaeta, R. Design and Development of a MOEMS Accelerometer Using SOI Technology. Micromachines 2023, 14. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Xia, D.; Fu, B.; Li, J.; Zhao, J.; Chu, Q. High-Sensitivity MOEMS Gyroscope Based on Photonic Crystal Wavelength Modulation. IEEE Sensors Journal 2024, 24, 9489–9497. [Google Scholar] [CrossRef]
- Van Gorp, B.; Onaran, A.G.; Degertekin, F.L. Integrated dual grating method for extended range interferometric displacement detection in probe microscopy. Applied Physics Letters 2007, 91. [Google Scholar] [CrossRef]
- Hadzialic, S.; Kim, S.; Sarioglu, A.F.; Sudbo, A.S.; Solgaard, O. Displacement Sensing With a Mechanically Tunable Photonic Crystal. IEEE Photonics Technology Letters 2010, 22, 1196–1198. [Google Scholar] [CrossRef]
- Miao, H.; Srinivasan, K.; Aksyuk, V. A microelectromechanically controlled cavity optomechanical sensing system. New Journal of Physics 2012, 14. [Google Scholar] [CrossRef]
- Williams, R.P.; Hord, S.K.; Hall, N.A. Optically read displacement detection using phase-modulated diffraction gratings with reduced zeroth-order reflections. Applied Physics Letters 2017, 110. [Google Scholar] [CrossRef]
- Sun, P.; She, X.; Yao, J.; Chen, K.; Bi, R.; Wang, L.; Shu, X. Monolithic Integrated Micro-Opto-Electromechanical Accelerometer Based On Michelson Interferometer Structure. Journal of Lightwave Technology 2022, 40, 4364–4372. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, X.; Shi, Q.; He, T.; Sun, Z.; Guo, X.; Liu, W.; Bin Sulaiman, O.; Dong, B.; Lee, C. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2020, 11. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Yan, X.; Zhang, S.; Li, Z.; Hassan, J.N.A.; Chen, D.; Wen, G.; Chen, K.; Deng, G.; Huang, Y. MEMS and MOEMS Gyroscopes: A Review. Photonic Sensors 2023, 13. [Google Scholar] [CrossRef]
- Qu, H. CMOS MEMS Fabrication Technologies and Devices. Micromachines 2016, 7. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Pernice, W.H.P.; Xiong, C.; Baehr-Jones, T.; Hochberg, M.; Tang, H.X. Harnessing optical forces in integrated photonic circuits. Nature 2008, 456, 480–U428. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Pagliano, F.; van Veldhoven, R.; Pogoretskiy, V.; Jiao, Y.; Fiore, A. Integrated nano-optomechanical displacement sensor with ultrawide optical bandwidth. Nature Communications 2020, 11. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Pernice, W.H.P.; Tang, H.X. Broadband all-photonic transduction of nanocantilevers. Nature Nanotechnology 2009, 4, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, A.L.; Picelli, L.; Veldhoven, R.P.J.v.; Verhagen, E.; Fiore, A. Nano-optomechanical fiber-tip sensing. Nanophotonics 2024, 1, 10. [Google Scholar] [CrossRef]
- Anetsberger, G.; Arcizet, O.; Unterreithmeier, Q.P.; Riviere, R.; Schliesser, A.; Weig, E.M.; Kotthaus, J.P.; Kippenberg, T.J. Near-field cavity optomechanics with nanomechanical oscillators. Nature Physics 2009, 5, 909–914. [Google Scholar] [CrossRef]
- Schilling, R.; Schutz, H.; Ghadimi, A.H.; Sudhir, V.; Wilson, D.J.; Kippenberg, T.J. Near-Field Integration of a SiN Nanobeam and a SiO<sub>2</sub> Microcavity for Heisenberg-Limited Displacement Sensing. Physical Review Applied 2016, 5. [Google Scholar] [CrossRef]
- Hall, N.A.; Lee, W.; Degertekin, F.L. Capacitive micromachined ultrasonic transducers with diffraction-based integrated optical displacement detection. IEEE transactions on ultrasonics, ferroelectrics, and frequency control 2003, 50, 1570–1580. [Google Scholar] [CrossRef] [PubMed]
- Cagri A., Savran; Andrew, W. Sparks; Joachim Sihler; Jian Li; Wan-Chen Wu; Dean E. Berlin; Burg, T.P. Fabrication and Characterization of a Micromechanical Sensor for Differential Detection of Nanoscale Motions. Journal of Microelectromechanical Systems 2002, 11, 703–708. [Google Scholar]
- Pruessner, M.W.; Park, D.; Stievater, T.H.; Kozak, D.A.; Rabinovich, W.S. An Optomechanical Transducer Platform for Evanescent Field Displacement Sensing. IEEE Sensors Journal 2014, 14, 3473–3481. [Google Scholar] [CrossRef]
- Orlowska, K.; Swiatkowski, M.; Kunicki, P.; Kopiec, D.; Gotszalk, T. High-resolution and wide-bandwidth light intensity fiber optic displacement sensor for MEMS metrology. Applied Optics 2016, 55, 5960–5966. [Google Scholar] [CrossRef]
- Hortschitz, W.; Steiner, H.; Sachse, M.; Stifter, M.; Kohl, F.; Schalko, J.; Jachimowicz, A.; Keplinger, F.; Sauter, T. An Optical In-Plane MEMS Vibration Sensor. IEEE Sensors Journal 2011, 11, 2805–2812. [Google Scholar] [CrossRef]
- Steiner, H.; Hortschitz, W.; Kainz, A.; Stifter, M.; Jachimowicz, A.; Schalko, J.; Keplinger, F.; Kohl, F. MOEMS transducer with a non-linear transfer characteristic for static displacement measurement applications on the example of an inclination sensor. Sensors and Actuators A: Physical 2017, 263, 727–732. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Liu, C.; Cai, G.; Wang, W. A survey on the grating based optical position encoder. Optics and Laser Technology 2021, 143. [Google Scholar] [CrossRef]
- Mohd-Yasin, F.; Nagel, D.J.; Korman, C.E. Noise in MEMS. Measurement Science and Technology 2010, 21. [Google Scholar] [CrossRef]
- Pooser, R.C.; Lawrie, B. Ultrasensitive measurement of microcantilever displacement below the shot-noise limit. Optica 2015, 2, 393–399. [Google Scholar] [CrossRef]
- Tong, L.; Lou, J.; Mazur, E. Single-mode guiding properties of subwavelength-diameter silica and silicon wire waveguides. Optics express 2004, 12, 1025–1035. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.B.; Fang, H.B.; Wang, P.; Zhang, L.; Guo, X.; Tong, L. Optical microfiber or nanofiber: a miniature fiber-optic platform for nanophotonics. Photonics Research 2024, 3, R02. [Google Scholar] [CrossRef]
- Huang, K.; Yang, S.; Tong, L. Modeling of evanescent coupling between two parallel optical nanowires. Applied Optics 2007, 46, 1429–1434. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Barker, R.F. Characterization and Testing of a Micro-g Whispering Gallery Mode Optomechanical Accelerometer. Journal of Lightwave Technology 2018, 36, 3919–3926. [Google Scholar] [CrossRef]
- Kilic, O.; Ra, H.; Akkaya, O.C.; Digonnet, M.J.F.; Solgaard, O. Haltere-Like Optoelectromechanical Gyroscope. IEEE Sensors Journal 2016, 16, 4274–4280. [Google Scholar] [CrossRef]
- Wu, X.; Tong, L. Optical microfibers and nanofibers. Nanophotonics 2013, 2, 407–428. [Google Scholar] [CrossRef]
- Povinelli, M.L.; Loncar, M.; Ibanescu, M.; Smythe, E.J.; Johnson, S.G.; Capasso, F.; Joannopoulos, J.D. Evanescent-wave bonding between optical waveguides. Optics Letters 2005, 30, 3042–3044. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wu, H.; Xin, C.; Dai, D.; Tong, L. Flexible integration of free-standing nanowires into silicon photonics. Nature Communications 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Xin, C.; Zhang, Z.; Wang, X.; Fan, C.; Li, M. Ultracompact single-layer optical MEMS accelerometer based on evanescent coupling through silicon nanowaveguides. Scientific Reports 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Cao, L.; Su, P.; He, Q.; Jin, G.; Gu, G. Micro-displacement sensor with large dynamic range based on photonic crystal co-directional coupler. IEEE Journal of Quantum Electronics 2007, 43, 182–187. [Google Scholar] [CrossRef]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nature Photonics 2012, 6, 768–772. [Google Scholar] [CrossRef]
- Soltanian, E.; Jafari, K.; Abedi, K. A Novel Differential Optical MEMS Accelerometer Based on Intensity Modulation, Using an Optical Power Splitter. IEEE Sensors Journal 2019, 19, 12024–12030. [Google Scholar] [CrossRef]
- Devrez M. Karabacak; Kamil L. Ekinci; Choon How Gan; Gregory J. Gbur; M. Selim Ünlü; Stephen B. Ippolito; Bennett B. Goldberg; Carney, P.S. Diffraction of evanescent waves and nanomechanical displacement detection. Optics Express 2007, 32, 1881-1883.
- Ab Razak, M.Z.; Reduan, S.A.; Sharbirin, A.S.; Jamaludin, N.; Zulkifli, M.Z.; Ahmad, H. Noncontact Optical Displacement Sensor Using an Adiabatic U-Shaped Tapered Fiber. IEEE Sensors Journal 2015, 15, 5388–5392. [Google Scholar] [CrossRef]
- Schliesser, A.; Anetsberger, G.; Riviere, R.; Arcizet, O.; Kippenberg, T.J. High-sensitivity monitoring of micromechanical vibration using optical whispering gallery mode resonators. New Journal of Physics 2008, 10. [Google Scholar] [CrossRef]
- Wilson, D.J.; Sudhir, V.; Piro, N.; Schilling, R.; Ghadimi, A.; Kippenberg, T.J. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature 2015, 524, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Kolli, V.R.; Dudla, P.; Talabattula, S. Integrated optical MEMS serially coupled double racetrack resonator based accelerometer. Optik 2021, 236. [Google Scholar] [CrossRef]
- Gholamzadeh, R.; Salarieh, H.; Parsanasab, G.M.; Akbari, J. A high sensitive, low foot print, SU-8 material-based, light intensity modulated MOMS accelerometer. Optical Engineering 2022, 61. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, W.; Zou, X. Design and Simulation Study of an Optical Mode-Localized MEMS Accelerometer. Micromachines 2023, 14. [Google Scholar] [CrossRef] [PubMed]
- Basumallick, N.; Biswas, P.; Dasgupta, K.; Bandyopadhyay, S. Design optimization of fiber Bragg grating accelerometer for maximum sensitivity. Sensors and Actuators A: Physical 2013, 194, 31–39. [Google Scholar] [CrossRef]
- Tosi, D.; Perrone, G.; Vallan, A. Performance Analysis of a Noncontact Plastic Fiber Optical Fiber Displacement Sensor with Compensation of Target Reflectivity. Journal of Sensors 2013, 2013. [Google Scholar] [CrossRef]
- Orlowska, K.; Slupski, P.; Swiatkowski, M.; Kunicki, P.; Sankowska, A.; Gotszalk, T. Light Intensity Fibre Optic Sensor for MEMS displacement and vibration metrology. Optics and Laser Technology 2015, 65, 159–163. [Google Scholar] [CrossRef]
- Favero, I.; Stapfner, S.; Hunger, D.; Paulitschke, P.; Reichel, J.; Lorenz, H.; Weig, E.M.; Karrai, K. Fluctuating nanomechanical system in a high finesse optical microcavity. Optics Express 2009, 17, 12813–12820. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-S.; Dagalakis, N.G.; Choi, Y.-M. Optical fiber Fabry-Perot micro-displacement sensor for MEMS in-plane motion stage. Microelectronic Engineering 2018, 187, 6–13. [Google Scholar] [CrossRef]
- Malayappan, B.; Lakshmi, U.P.; Rao, B.V.V.S.N.P.; Ramaswamy, K.; Pattnaik, P.K. Sensing Techniques and Interrogation Methods in Optical MEMS Accelerometers: A Review. IEEE Sensors Journal 2022, 22, 6232–6246. [Google Scholar] [CrossRef]
- Qu, Z.; Ouyang, H.; Xiong, W.; Xu, Q.; Wang, Y.; Liu, H. A Nano-g MOEMS Accelerometer Featuring Electromagnetic Force Balance With 157-dB Dynamic Range. IEEE Transactions on Industrial Electronics 2024, 71, 6418–6426. [Google Scholar] [CrossRef]
- Taghavi, M.; Latifi, H.; Parsanasab, G.M.; Abedi, A.; Nikbakht, H.; Poorghadiri, M.H. A Dual-Axis MOEMS Accelerometer. IEEE Sensors Journal 2021, 21, 13156–13164. [Google Scholar] [CrossRef]
- Rahimi, M.; Malekmohammad, M.; Taghavi, M.; Noori, M.; Parsanasab, G.-M.M. Design and Fabrication of a Differential MOEMS Accelerometer Based on Fabry-Perot Micro-Cavities. IEEE Sensors Journal 2022, 22, 14779–14785. [Google Scholar] [CrossRef]
- Zandi, K.; Belanger, J.A.; Peter, Y.-A. Design and Demonstration of an In-Plane Silicon-on-Insulator Optical MEMS Fabry-Perot-Based Accelerometer Integrated With Channel Waveguides. Journal of Microelectromechanical Systems 2012, 21, 1464–1470. [Google Scholar] [CrossRef]
- Trigona, C.; Ando, B.; Baglio, S. Fabrication and Characterization of an MOEMS Gyroscope Based on Photonic Bandgap Materials. IEEE Transactions on Instrumentation and Measurement 2016, 65, 2840–2852. [Google Scholar] [CrossRef]
- Di Falco, A.; O'Faolain, L.; Krauss, T.F. Photonic crystal slotted slab waveguides. Photonics and Nanostructures-Fundamentals and Applications 2008, 6, 38–41. [Google Scholar] [CrossRef]
- Wu, C.J.; Wang, Z.H. PROPERTIES OF DEFECT MODES IN ONE-DIMENSIONAL PHOTONIC CRYSTALS. Progress In Electromagnetics Research-PIER 2010, 103, 169–184. [Google Scholar] [CrossRef]
- Hosseinzadeh Sani, M.; Saghaei, H.; Mehranpour, M.A.; Asgariyan Tabrizi, A. A Novel All-Optical Sensor Design Based on a Tunable Resonant Nanocavity in Photonic Crystal Microstructure Applicable in MEMS Accelerometers. Photonic Sensors 2021, 11, 457–471. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Jafari, K.; Abedi, K. Design and Analysis of a Novel MOEMS Gyroscope Using an Electrostatic Comb-Drive Actuator and an Optical Sensing System. IEEE Sensors Journal 2019, 19, 144–150. [Google Scholar] [CrossRef]
- Suh, W.; Solgaard, O.; Fan, S. Displacement sensing using evanescent tunneling between guided resonances in photonic crystal slabs. Journal of Applied Physics 2005, 98, 033102. [Google Scholar] [CrossRef]
- Xu, Z.F.; Cao, L.C.; Gu, C.; He, Q.S.; Jin, G.F. Micro displacement sensor based on line-defect resonant cavity in photonic crystal. Optics Express 2006, 14, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Suh, W.; Yanik, M.F.; Solgaard, O.; Fan, S. Displacement-sensitive photonic crystal structures based on guided resonance in photonic crystal slabs. Applied Physics Letters 2003, 82, 1999. [Google Scholar] [CrossRef]
- Levy, O.; Steinberg, B.Z.; Nathan, M.; Boag, A. Ultrasensitive displacement sensing using photonic crystal waveguides. Applied Physics Letters 2005, 86, 104102. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Fan, C.; Jin, L.; Li, M.; Xin, C. Design and simulation of a waveguiding MOEMS gyroscope with ultrawide optical bandwidth based on tunable cascaded Fabry-Perot cavities. Optics Communications 2024, 556. [Google Scholar] [CrossRef]
- Huang, K.; Yu, M.; Cheng, L.; Liu, J.; Cao, L. A Proposal for an Optical MEMS Accelerometer With High Sensitivity Based on Wavelength Modulation System. Journal of Lightwave Technology 2019, 37, 5474–5478. [Google Scholar] [CrossRef]
- Huang, K.; Cao, L.; Zhai, P.; Liu, P.; Cheng, L.; Liu, J. High sensitivity sensing system theoretical research base on waveguide-nano DBRs one dimensional photonic crystal microstructure. Optics Communications 2020, 470. [Google Scholar] [CrossRef]
- Nie, Y.; Huang, K.; Yang, J.; Cao, L.; Cheng, L.; Wang, Q.; Tian, H.; Peihua, W.; Heng, L. A Proposal to Enhance High-Frequency Optical MEMS Accelerometer Sensitivity Based on a One-Dimensional Photonic Crystal Wavelength Modulation System. IEEE Sensors Journal 2020, 20, 14639–14645. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Abedi, K.; Jafari, K. A Proposal for an Optical MEMS Accelerometer Relied on Wavelength Modulation With One Dimensional Photonic Crystal. Journal of Lightwave Technology 2016, 34, 5244–5249. [Google Scholar] [CrossRef]
- Lee, C.K.; Radhakrishnan, R.; Chen, C.C.; Li, J.; Thillaigovindan, J.; Balasubramanian, N. Design and Modeling of a Nanomechanical Sensor Using Silicon Photonic Crystals. Journal of Lightwave Technology 2008, 26, 839–846. [Google Scholar] [CrossRef]
- Ahrnadian, M.; Jafari, K.; Sharifi, M.J. Novel graphene-based optical MEMS accelerometer dependent on intensity modulation. ETRI Journal 2018, 40, 794–801. [Google Scholar] [CrossRef]
- Afunadian, M.; Jafari, K. A Graphene-Based Wide-Band MEMS Accelerometer Sensor Dependent on Wavelength Modulation. IEEE Sensors Journal 2019, 19, 6226–6232. [Google Scholar] [CrossRef]
- Huang, K.; Nie, Y.; Liu, Y.; Liu, P.; Cao, L.; Wang, Q.; Cheng, L.; Cui, J.; Gao, X.; Li, J. A Proposal for a High-Sensitivity Optical MEMS Accelerometer With a Double-Mode Modulation System. Journal of Lightwave Technology 2021, 39, 303–309. [Google Scholar] [CrossRef]
- Sheikhaleh, A.; Abedi, K.; Jafari, K. An Optical MEMS Accelerometer Based on a Two-Dimensional Photonic Crystal Add-Drop Filter. Journal of Lightwave Technology 2017, 35, 3029–3034. [Google Scholar] [CrossRef]
- Beyaz, M.I.; McCarthy, M.; Ghalichechian, N.; Ghodssi, R. Closed-loop control of a long-range micropositioner using integrated photodiode sensors. Sensors and Actuators A: Physical 2009, 151, 187–194. [Google Scholar] [CrossRef]
- Abozyd, S.; Toraya, A.; Gaber, N. Design and Modeling of Fiber-Free Optical MEMS Accelerometer Enabling 3D Measurements. Micromachines 2022, 13. [Google Scholar] [CrossRef]
- Jin, L.; Wang, C.; Jin, L.; Chen, W.; Xu, H.; Cui, M.; Li, M. Micro-opto-electro-mechanical systems accelerometer based on the Talbot effect of double-layer diffraction gratings. Applied Optics 2022, 61, 5386–5391. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Jin, L.; Wang, Z.; Peng, H.; Li, M. Design and Demonstration of an In-Plane Micro-Optical-Electro-Mechanical-System Accelerometer Based on Talbot Effect of Dual-Layer Gratings. Micromachines 2023, 14. [Google Scholar] [CrossRef] [PubMed]
- Xin, C.; Yang, Z.; Qi, J.; Niu, Q.; Ma, X.; Fan, C.; Li, M. Ultra-compact displacement and vibration sensor with a sub-nanometric resolution based on Talbot effect of optical microgratings. Optics Express 2022, 30, 40009–40017. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.-S.; Scharf, T.; Menzel, C.; Rockstuhl, C.; Herzig, H.P. Talbot images of wavelength-scale amplitude gratings. Optics Express 2012, 20, 4903–4920. [Google Scholar] [CrossRef] [PubMed]
- Cao, B.; Zhang, R.; Niu, Q.; Ma, X.; Yang, Z.; Li, M.; Xin, C. Out-of-plane displacement sensor based on the Talbot effect in angular-modulated double-layer optical gratings. Applied Optics 2022, 61, 9873–9878. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Yang, H.; Niu, Q.; Zhang, X.; Yang, J.; Lai, J.; Fan, C.; Li, M.; Xin, C. Combined Displacement and Angle Sensor with Ultra-High Compactness Based on Self-Imaging Effect of Optical Microgratings. Sensors 2024, 24. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Ma, X.; Yu, D.; Cao, B.; Niu, Q.; Li, M.; Xin, C. An Ultracompact Angular Displacement Sensor Based on the Talbot Effect of Optical Microgratings. Sensors 2023, 23. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Geng, H.; Wu, Q.; Zhang, R.; Han, Y.; Wang, G. Application of double metal/dielectric gratings in optical displacement detection. Applied Optics 2018, 57, 3438–3443. [Google Scholar] [CrossRef] [PubMed]
- Jin, L.; Xie, K.; Du, Y.; Li, M. Linearization signal conditioning circuit for tri-axial micro-grating MOEMS accelerometer. Optics Express 2024, 32, 10241–10251. [Google Scholar] [CrossRef] [PubMed]
- Jourlin, Y.; Jay, J.; Parriaux, O. Compact diffractive interferometric displacement sensor in reflection. Precision Engineering 2002, 26, 1–6. [Google Scholar] [CrossRef]
- Fourmen, S.; Arguel, P.; Noullet, J.L.; Lozes, F.; Bonnefont, S.G.S.; Jourlin, Y.; Parriaux, O. A silicon integrated opto-electro-mechanical displacement sensor. Sensors and Actuators A: Physical 2004, 110, 294–300. [Google Scholar] [CrossRef]
- Li, M.; Liang, Z.; Zhang, R.; Wu, Q.; Xin, C.; Jin, L.; Xie, K.; Zhao, H. Large-scale range diffraction grating displacement sensor based on polarization phase-shifting. Applied Optics 2020, 59, 469–473. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Pan, D.; Wang, J.; Dong, T.; Guo, J.; Wang, C.; Geng, A.; Fang, W.; Lu, Q. Design and Modification of a High-Resolution Optical Interferometer Accelerometer. Sensors 2021, 21. [Google Scholar] [CrossRef]
- Lee, W.; Hall, N.A.; Degertekin, F.L. A grating-assisted resonant-cavity-enhanced optical displacement detection method for micromachined sensors. Applied Physics Letters 2004, 85, 3032–3034. [Google Scholar] [CrossRef] [PubMed]
- Bicen, B.; Jolly, S.; Jeelani, K.; Garcia, C.T.; Hall, N.A.; Degertekin, F.L.; Su, Q.; Cui, W.; Miles, R.N. Integrated Optical Displacement Detection and Electrostatic Actuation for Directional Optical Microphones With Micromachined Biomimetic Diaphragms. IEEE Sensors Journal 2009, 9, 1933–1941. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, J.; Hou, C.; Bai, J.; Yang, G. Optical accelerometer based on grating interferometer with phase modulation technique. Applied Optics 2012, 51, 7005–7010. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Wang, C.; Bai, J.; Wang, K.; Lou, S.; Jiao, X.; Han, D.; Yang, G.; Liu, D.; Yang, Y. Minimizing cross-axis sensitivity in grating-based optomechanical accelerometers. Optics Express 2016, 24, 9094–9111. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Bai, J.; Wang, K.; He, S. Design, Optimization, and Realization of a High-Performance MOEMS Accelerometer From a Double-Device-Layer SOI Wafer. Journal of Microelectromechanical Systems 2017, 26, 859–869. [Google Scholar] [CrossRef]
- Li, C.; Yang, B.; Zheng, X.; Sun, Z.; Zhou, L.; Huang, X.; Guo, X. An Optical Interferometry Based MEMS Accelerometer Applicable to Seismic-Grade Measurement. IEEE Transactions on Instrumentation and Measurement 2022, 71. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, Z.; Zhang, Y.; Deng, K.; Feng, L. High-resolution micro-grating accelerometer based on a gram-scale proof mass. Optics Express 2019, 27, 34299–34312. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Cai, C.; Zhang, Y.; Deng, X.; Lin, L.; Xiao, W. High Sensitivity Optical MEMS Accelerometer Based on a Metal Fabry-Prot Microcavities Wavelength Modulation System. IEEE Sensors Journal 2024, 24, 4304–4314. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Chau, F.S. Grating-Assisted Optical Microprobing of In-Plane and Out-of-Plane Displacements of Microelectromechanical Devices. Journal of Microelectromechanical Systems 2006, 15, 388–395. [Google Scholar] [CrossRef]
- Wang, C.; Lu, Q.; Bai, J.; Yang, G.; Wang, K.; Liu, D.; Yang, Y. Highly sensitive lateral deformable optical MEMS displacement sensor: anomalous diffraction studied by rigorous coupled-wave analysis. Applied Optics 2015, 54, 8935–8943. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Bai, J.; Wang, K.; Chen, P.; Fang, W.; Wang, C. Single Chip-Based Nano-Optomechanical Accelerometer Based on Subwavelength Grating Pair and Rotated Serpentine Springs. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Wood, R. Anomalous Diffraction Gratings. Physical Review 1935, 48, 928–936. [Google Scholar] [CrossRef]
- Hessel, A.; Oliner, A.A. A New Theory of Wood's Anomalies on Optical Gratings. Applied Optics 1965, 4, 1275–1297. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Geng, H.; Wu, Q.; Zhang, R.; Cui, Z.; Wang, X.; Wang, G. Structural design and simulation of a micro-gyroscope based on nano-grating detection. Microsystem Technologies 2019, 25, 1627–1637. [Google Scholar] [CrossRef]
- Ishikawa, I.; Sawada, R.; Higurashi, E.; Sanada, S.; Chino, D. Integrated micro-displacement sensor that measures tilting angle and linear movement of an external mirror. Sensors and Actuators A: Physical 2007, 138, 269–275. [Google Scholar] [CrossRef]
- Cheng, X.; Sun, X.; Liu, Y.; Zhu, L.; Zhang, X.; Zhou, L.; Xie, H. Integrated Optoelectronic Position Sensor for Scanning Micromirrors. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Zhan, H.; Zhou, W.; Ran, L.; Yu, H.; Peng, B.; Hao, R. A High-Resolution Optical Displacement Detection Method for Piezoelectric Microvibratory Stage. IEEE Transactions on Industrial Electronics 2020, 67, 10897–10904. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, Y.; Sun, X.; Zhu, L.; Cheng, X.; Chen, Q.; Liu, Y.; Xie, H. Integrated tilt angle sensing for large displacement scanning MEMS mirrors. Optics Express 2018, 26, 25736–25749. [Google Scholar] [CrossRef] [PubMed]
- Takeshita, T.; Iwasaki, T.; Harisaki, K.; Ando, H.; Higurashi, E.; Sawada, R. Development of a Piezo-driven Mechanical Stage Integrated Microdisplacement Sensor for Calibration of Displacements. Sensors and Materials 2014, 26, 547–557. [Google Scholar]
- Iwasaki, T.; Takeshita, T.; Arinaga, Y.; Uemura, K.; Ando, H.; Takeuchi, S.; Furue, M.; Higurashi, E.; Sawada, R. Shearing force measurement device with a built-in integrated micro displacement sensor. Sensors and Actuators A: Physical 2015, 221, 1–8. [Google Scholar] [CrossRef]
- Du, Y.-J.; Yang, T.-T.; Gong, D.-D.; Wang, Y.-C.; Sun, X.-Y.; Qin, F.; Dai, G. High Dynamic Micro Vibrator with Integrated Optical Displacement Detector for In-Situ Self-Calibration of MEMS Inertial Sensors. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
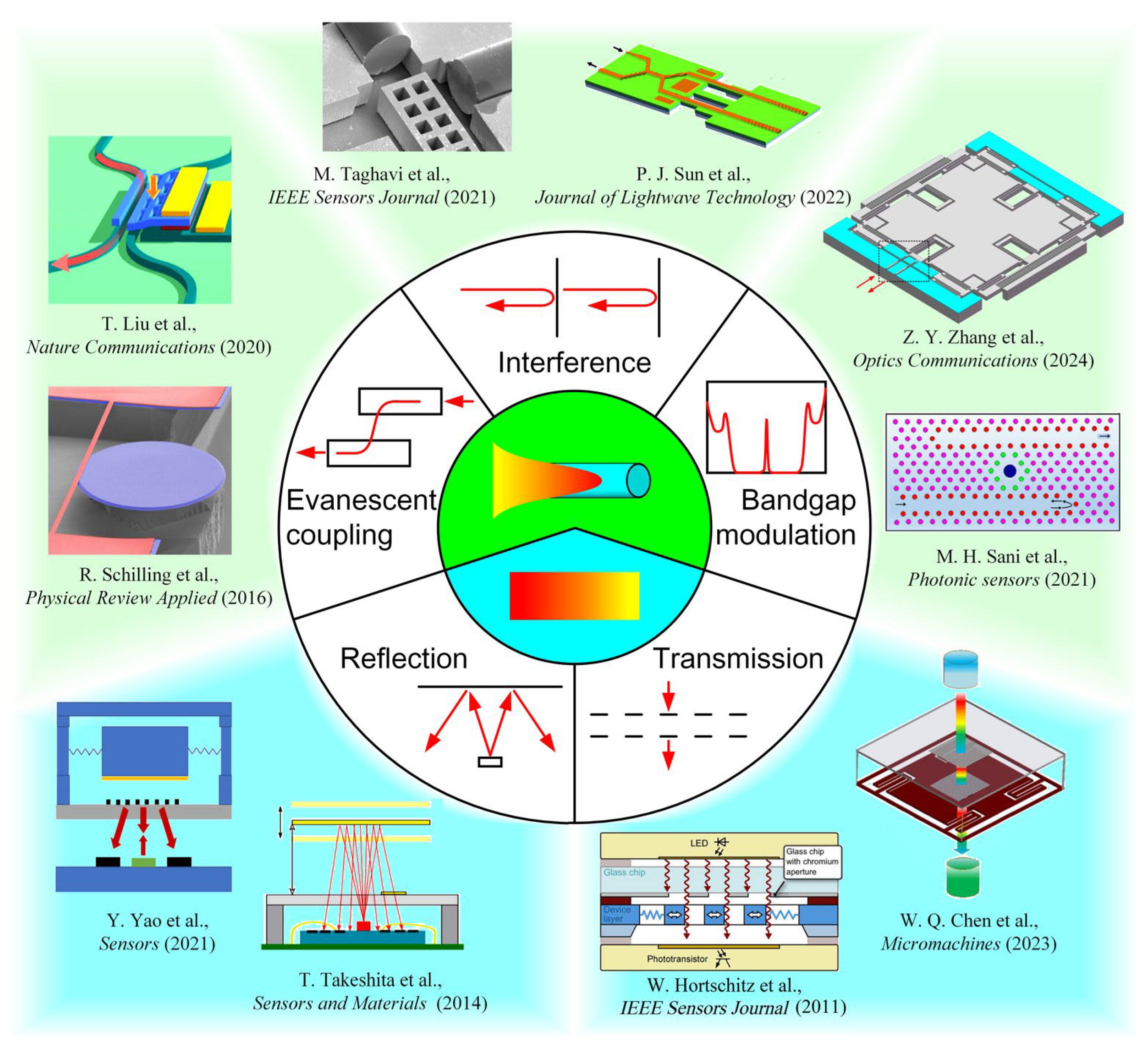
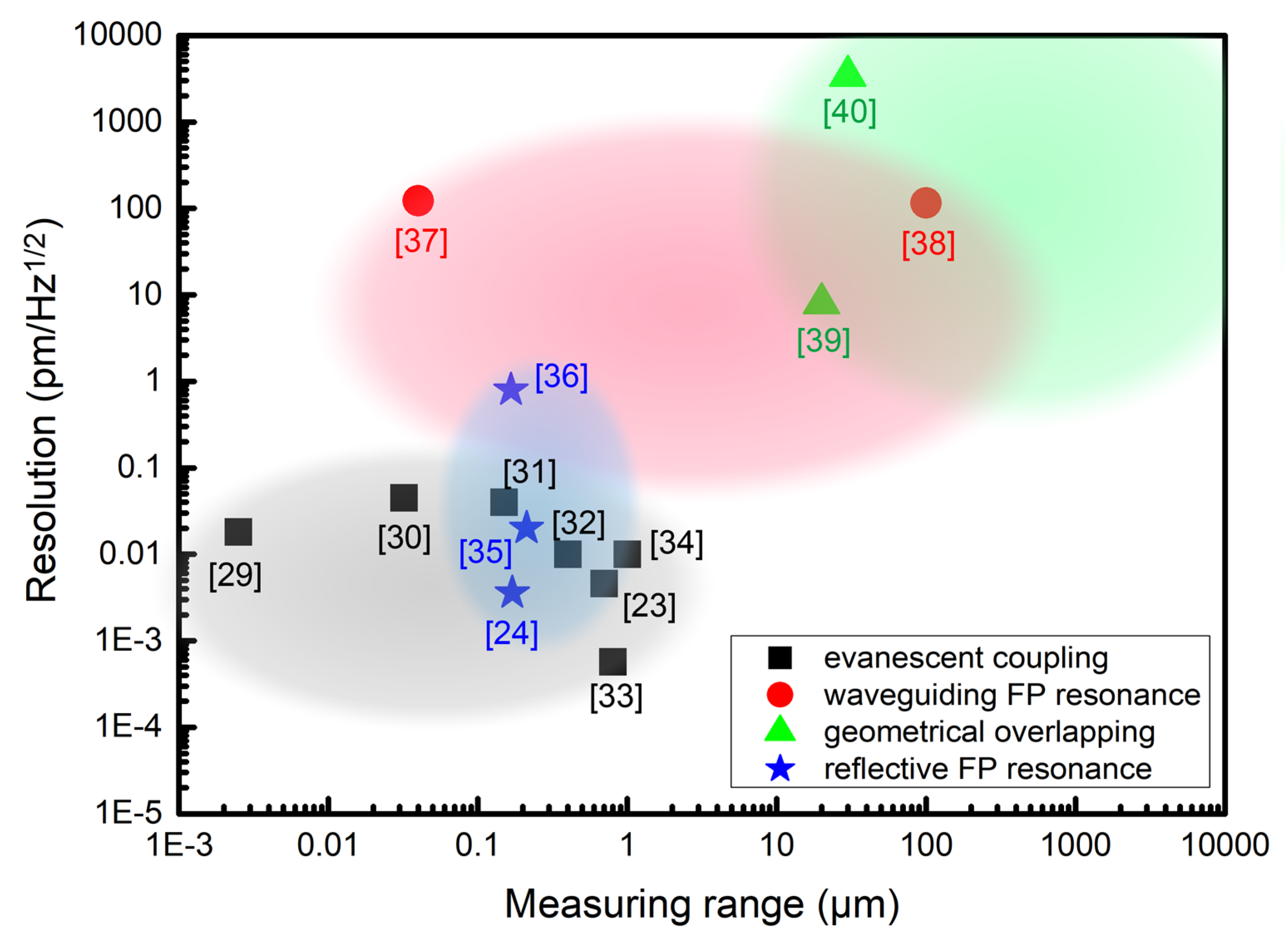
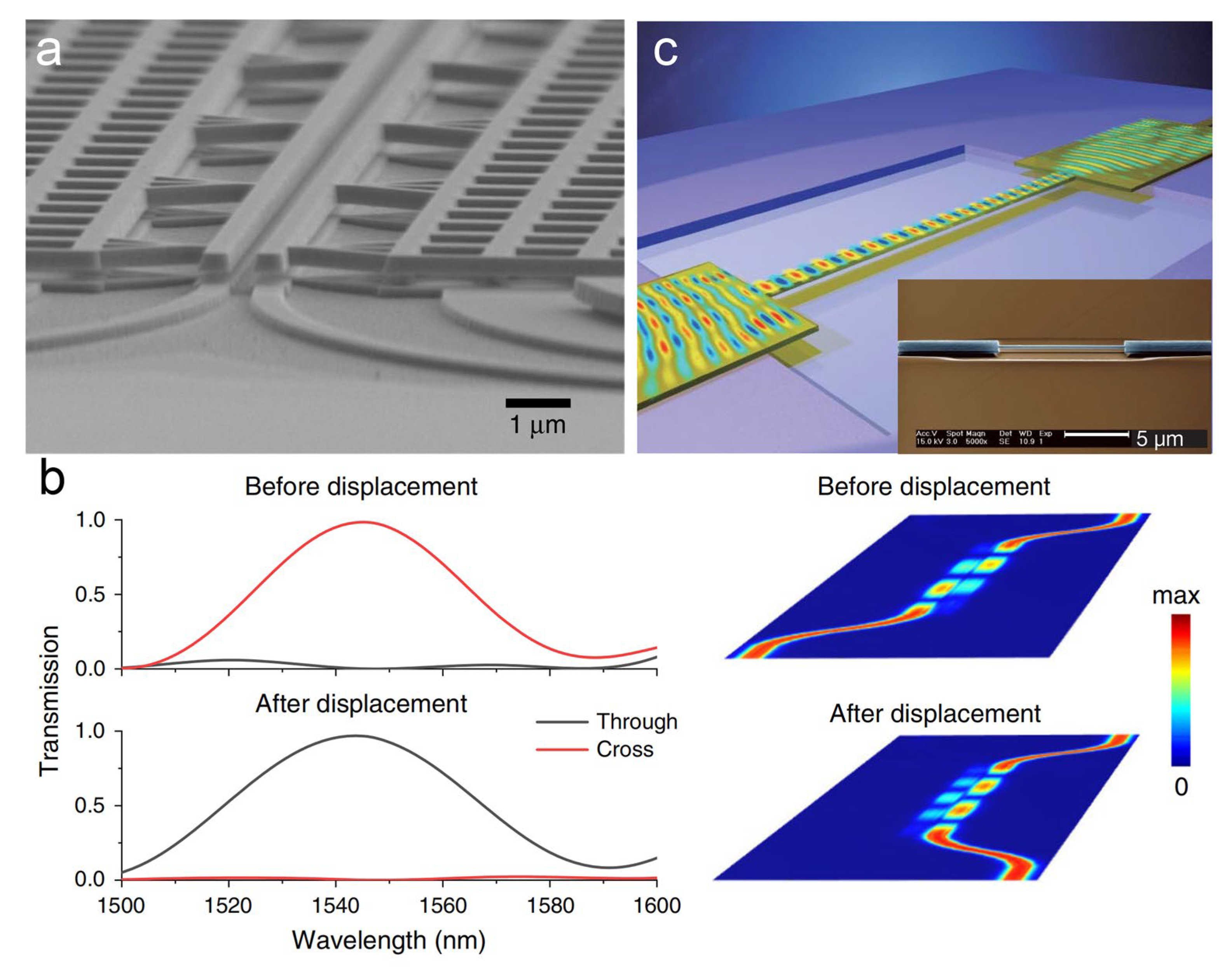
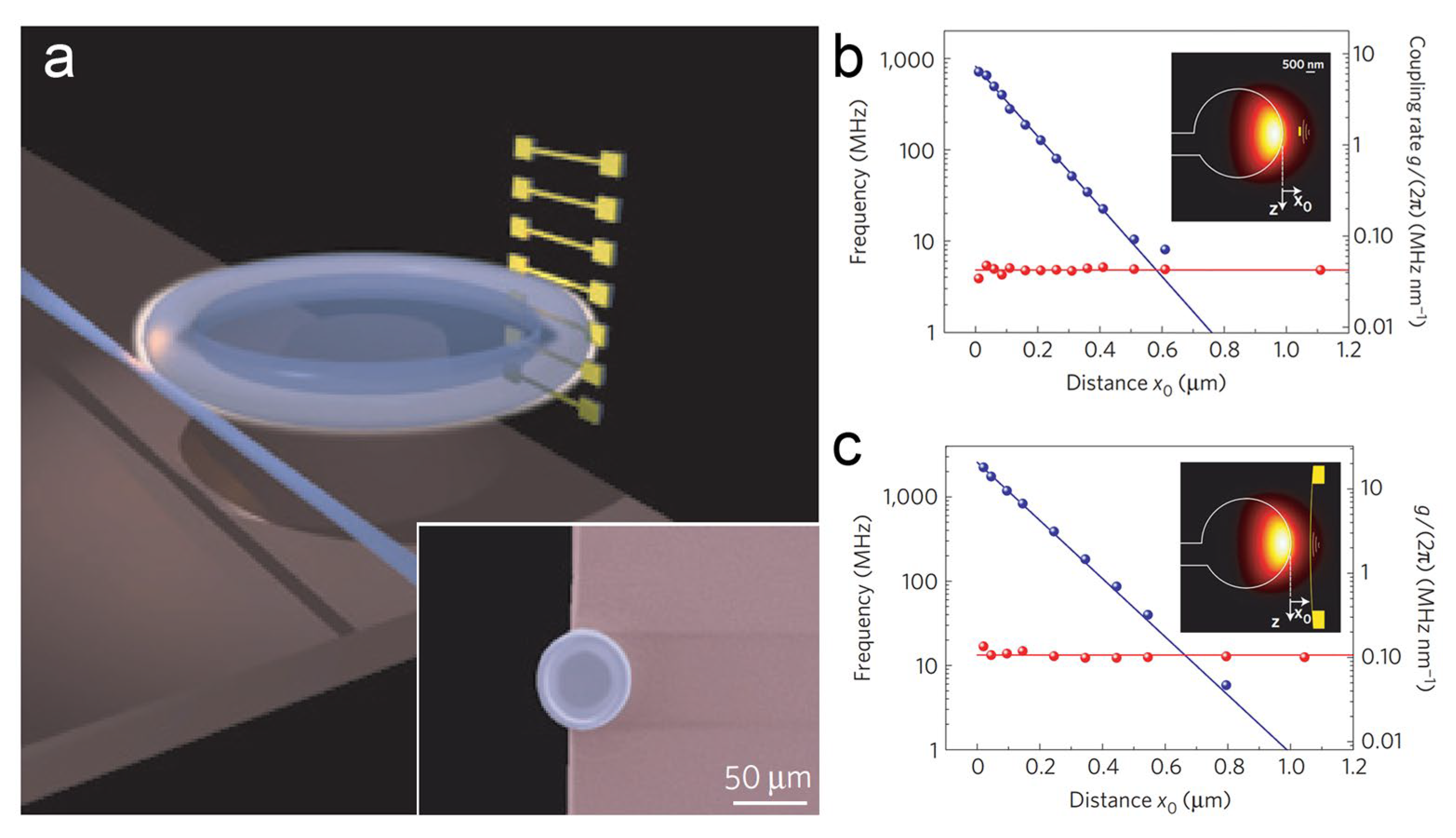
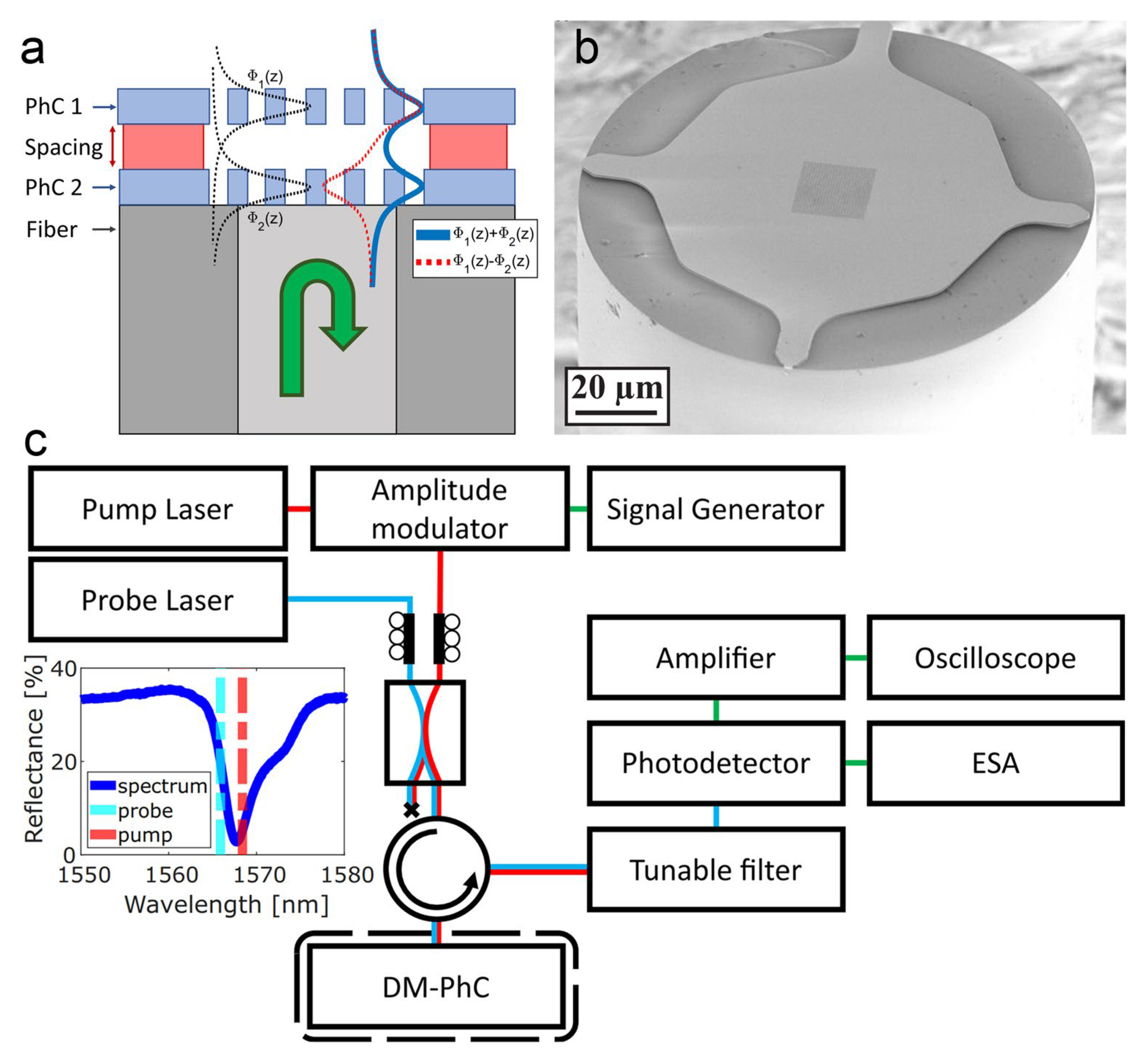
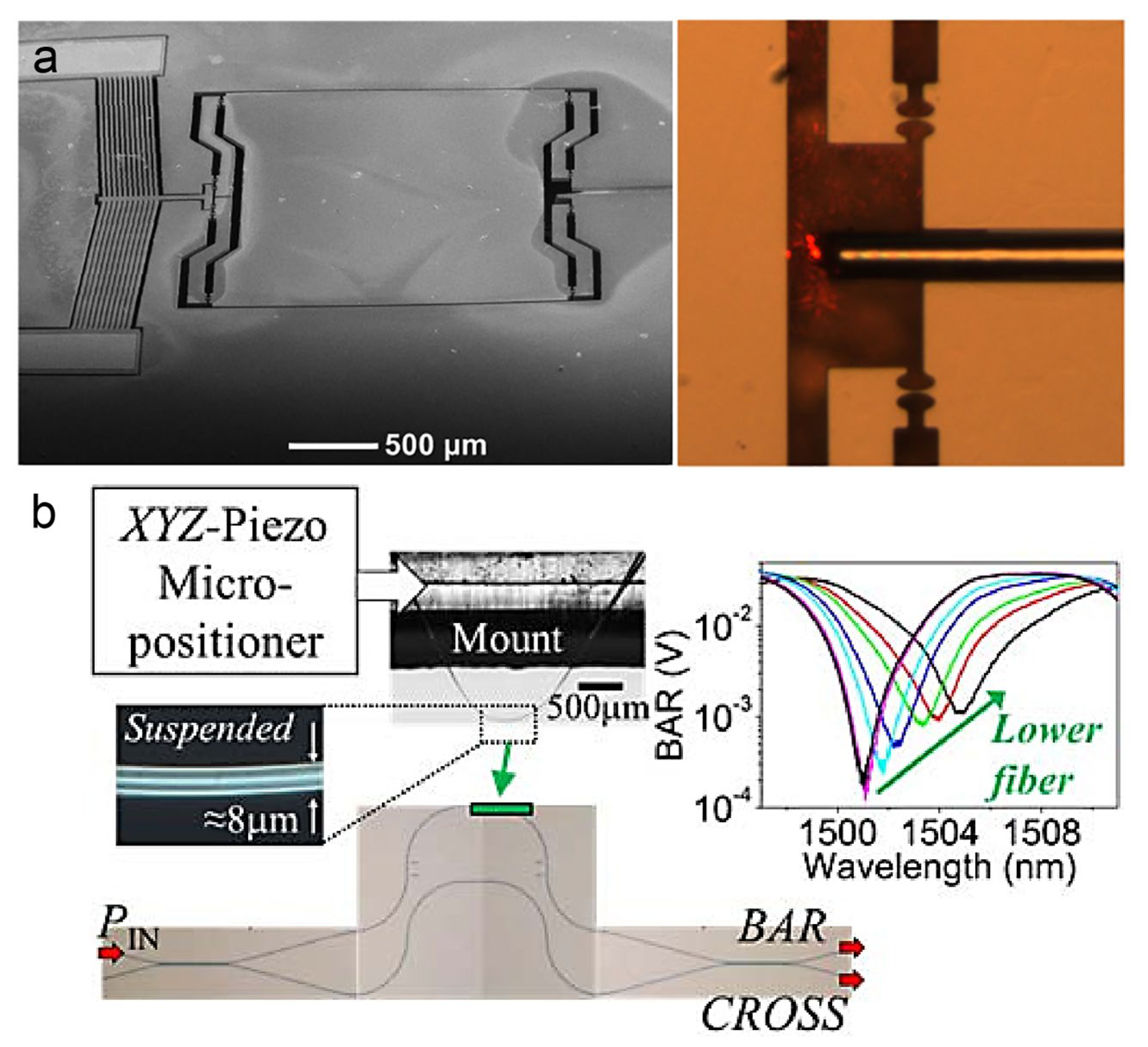
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).