1. Introduction
Holography is an advanced imaging technology where image information can be reconstructed without a lens. It is an important tool for controlling wave fields and producing highly complex and customized field distributions. Since its invention, holography has been widely used to record and reconstruct all the information of an object, and has found applications in medical observation, virtual reality displays, sensing, data storage, security, secure printing [
1,
2], and secret sharing [
3]. Recently, multiplexing techniques have been widely adopted to realize multiple holographic images or functionalities to increase the information capacity and make the optimum use of the space-bandwidth product. Particularly, with the advancement of computer-generated holograms, hologram generation can be done in an easier way through programming.
Metasurfaces offer flexible capabilities in manipulating the phase, amplitude, wavelength, and polarization of the incident wave. In addition, metasurfaces are capable of manipulating electromagnetic fields at the subwavelength scale, and enable holographic displays with higher resolution, wider field of view, and smaller geometry size [
4]. Since a plasmonic metasurface for holography generation in 2013, metasurface-based holography has emerged as a vibrant research field [
5]. Holographic multiplexing metasurfaces can record multiple images within the same spatial area, which increase information capacity while maintaining an ultrasmall footprint, subwavelength resolution, and larger field of view. So holographic multiplexing metasurfaces have received widely attention. Numerous studies have been conducted in the light frequency band: a single-layer LP metasurface for independently projecting different hologram images in transmission and reflection modes at the same frequency [
6], a single-layer transmission metasurface generating multi-channel gray images by separately and independently controlling the amplitude and phase [
7], a tri-channel single-layer transmission metasurface simultaneously recording a continuous grayscale nanoprinting image in the near field and projecting two independent holographic images in the far-field [
8], an all-dielectric transmission single-layer metasurface generating polarization-multiplexed holographic images [
9]. Significant advancements have also been achieved in the microwave frequency band: a single-layer reflective metasurface generating four-channel holographic images by simultaneous frequency and polarization multiplexing at 7.5 GHz and 13 GHz [
10], a frequency-multiplexed single layered transmission metasurface for four-channel holography images at 7.2 GHz, 9.1 GHz, 10.9 GHz, and 15.2 GHz [
11], a full-space single-layer encoding metasurface independently manipulating the images ‘F’ and ‘H’ in transmission or reflection mode based on polarization multiplexing at 10GHz [
12], reconfigurable holographic images achieved by switching the transmission metasurface shape from planar (for the letter ‘Z’ image, 14.8-15.0 GHz) to zigzag (for the letter ‘L’ image, 14.8-15.2 GHz) [
13].
Terahertz (0.1-10 THz) wireless communication is a cornerstone of the next 6G wireless. THz frequencies have the potential to dramatically increase wireless capacity performance and enable high-resolution environment sensing. THz waves can penetrate substances that are opaque to visible and infrared light and possess higher spatial resolution, penetration depth, and non-ionization safety. However, the research on THz metasurface holography images is still in its nascent stages. Reference [
14] reported single-pixel THz near-field imaging, achieving
λ0/45 resolution at 0.75 THz and
λ0/133 resolution at 0.5 THz. In reference [
15], single-pixel computational ghost imaging with reflective multilayer metasurface holography was introduced in an optical encryption scheme. A reconfigurable and multifunctional 3-bit coding reflection single layer metasurface at 0.95 THz is proposed by integrating photosensitive Ge material into the metasurface unit, and switching between vortex beams and holographic imaging was achieved under the RCP incidence by optically controlling [
16]. A multilayer metasurface achieved reconfigurable multichannel holographic imaging in the THz band by integrating vanadium dioxide (VO
2) into the metasurface unit [
17]. Holographic letters ‘R’ and ‘L’ were achieved when temperature is above 68 °C, and holographic numbers ‘2’ and ‘6’ were generated in other two channels when temperature is below 68 °C.
Graphene has garnered extensive research attention due to its mechanical robustness, outstanding thermal stability, and chemical and biological stability. Reconfigurable multi-channel reflected light beams were obtained by integrating graphene into the metasurface unit cell [
18]. A multifocal graphene orbital angular momentum (OAM) metalen was designed by using spatially multiplexed single-focus with different focal lengths and topological charges [
19].
As mentioned above, multi-channel holographic multiplexing images have been realized using transmission, reflection, or transmission-reflection mode metasurface. Full-space meta-holograms offer the advantages of miniaturization and high integration. However, to the knowledge of the authors, the above full space metasurface is realized by controlling orthogonal linearly polarized waves, and there is no dynamic modulation of dual modes (transmission and reflection) based on phase change material. In THz frequency band, there is no reflection-transmission dual mode metasurface for holographic imaging, and there is no dynamic modulation holographic imaging based on graphene. Here, reflection-transmission dynamic modulation THz single-layer propagation-geometric phase dielectric metasurface is proposed based on graphene. The reflection and transmission modes can be switched by controlling the Fermi energy level of graphene integrated into the metasurface unit. In the meantime, the metasurface is also reconfigurable in reflection or transmission mode by switching the feed polarization among RCP, LCP and LP. As example, a reflection and transmission propagation-geometric phase metasurface is designed, and reconfigurability between reflection and transmission modes is achieved by switching the graphene Fermi energy level between 0.1 eV and 0.9 eV. The operation bandwidth for reflection mode is from 1.15 THz to 1.35 THz (16%), and from 1.32 THz to 1.6 THz (19%) for transmission mode. High holographic efficiencies (42.5% to 49%), and six-channel holographic imaging are obtained.
2. Materials and Methods
Figure 1 shows the schematic diagram for the dual mode reconfigurable multifunctional metasurface, which consists of three layers: indium telluride pillar unit layer (top), F4B substrate (middle), and graphene layer (bottom).
Figure 1 shows the reconfigurable holographic imaging obtained by switching the incidence polarization in reflection and transmission modes, respectively.
Figure 1c is the phase switching sketch map: metal when
Ef = 0.9eV, insulator when
Ef = 0.1eV. The proposed metasurface works in reflection and transmission modes when
Ef =0.9eV and 0.1eV, respectively. The reconfiguration among the Chinese characters ‘

’, ‘

’ and ‘

’are achieved by switching LCP, RCP and LP incidence, respectively. The operation frequency range is 1.15THz – 1.35THz (16%) for reflection mode, and 1.32 THz - 1.6 THz (19%) for transmission mode. The holographic imaging is co- and cross- polarization for reflection and transmission modes, respectively.
2.1. Phase Change Principle of Graphene
The electric conductivity of graphene is the sum of inter-band and intra-band conductivity according to the Kubo equation. The inter-band conductivity can be neglected at room temperature in the lower THz frequency band, and the surface electric conductivity
σg(
ω) of graphene is described as follows [
20].
where
ω, e, KB, T, ℏ, τ and
Ef are the angular frequency, electron charge, Boltzmann constant, environmental temperature, Planck's constant, the relaxation time and the Fermi energy level, respectively. The conductivity of graphene can be continuously tuned by manipulating its Fermi energy via extra voltage. Graphene functions as the dielectric when
Ef = 0.1 eV, and is in metallic state when
Ef = 0.9 eV [
21]. Here, set
τ = 1
ps and T = 300
K. The conductivity of graphene is a function of
ω and
Ef according to Equation (1). In this paper, the proposed reconfigurable metasurface works in transmission mode at frequency
f1 when
Ef = 0.1 eV, and in reflection mode at frequency
f2 when
Ef = 0.9 eV. The metallic 2D graphene layer acts as ground plane in reflection mode.
2.2. The Phases (ϕx, ϕy, β) Calculation Principle for Geometry-Propagation Phase Unit
After the phase distribution map for the metasurface is calculated according to GS algorithm, a unit with phase (ϕx, ϕy, β) are designed to implement the calculated phase distribution map. The physical model of the unit phase (ϕx, ϕy, β) vs the outgoing wave phase is as follows.
When a unit with x-axis or y-axis symmetry is rotated an angle β in the xoy plane, and a propagation-geometric phase metasurface unit is formed.
For transmission metasurface, assume the transmission amplitude
tx(y) for
x- or
y- polarization approaches 1. When the transmission metasurface is excited by the normal CP incidence plane wave, the co-polarized (
Jco) and cross-polarized (
Jcross) components are given by [
19]:
where
and
are defined as polarization operators and the subscripts L and R represent LCP and RCP, respectively.
ϕx and
ϕy are the propagation phases for x and y polarization, respectively.
β is the rotated angle in the
xoy plane. From Equation (2), the amplitude (
t) and phase (
ϕ) for
Jco and
Jcross are as follows:
From Equation (4), the phase for the cross-dual CP can be independently controlled as follows:
for RCP,
for LCP. If
, the co-polarized component is suppressed according to Equation (2), and the metasurface convert RCP (LCP) incident wave to outgoing LCP (RCP) wave. Then the propagation phase and rotation angle of the unit can be derived as by Equation (4):
For reflection metasurface. Assume the reflection amplitudes for
x- or
y- polarization keeps as unity (
rx =
ry =1), and (
ϕx −
ϕy = π). When the reflection metasurface is excited by a normal CP incidence plane wave, the Jones matrix of the outgoing wave is as follows: [
23,
24]:
where
ELi,
ELLr,
ELLr and
ERRr are represent the incident LCP wave, incident RCP wave, LCP outgoing wave, and RCP outgoing wave, respectively.
,
,
and
. The cross-polarized component is suppressed, and the outgoing wave is co-polarized. The co-polarization phases for LCP and RCP waves are as follows:
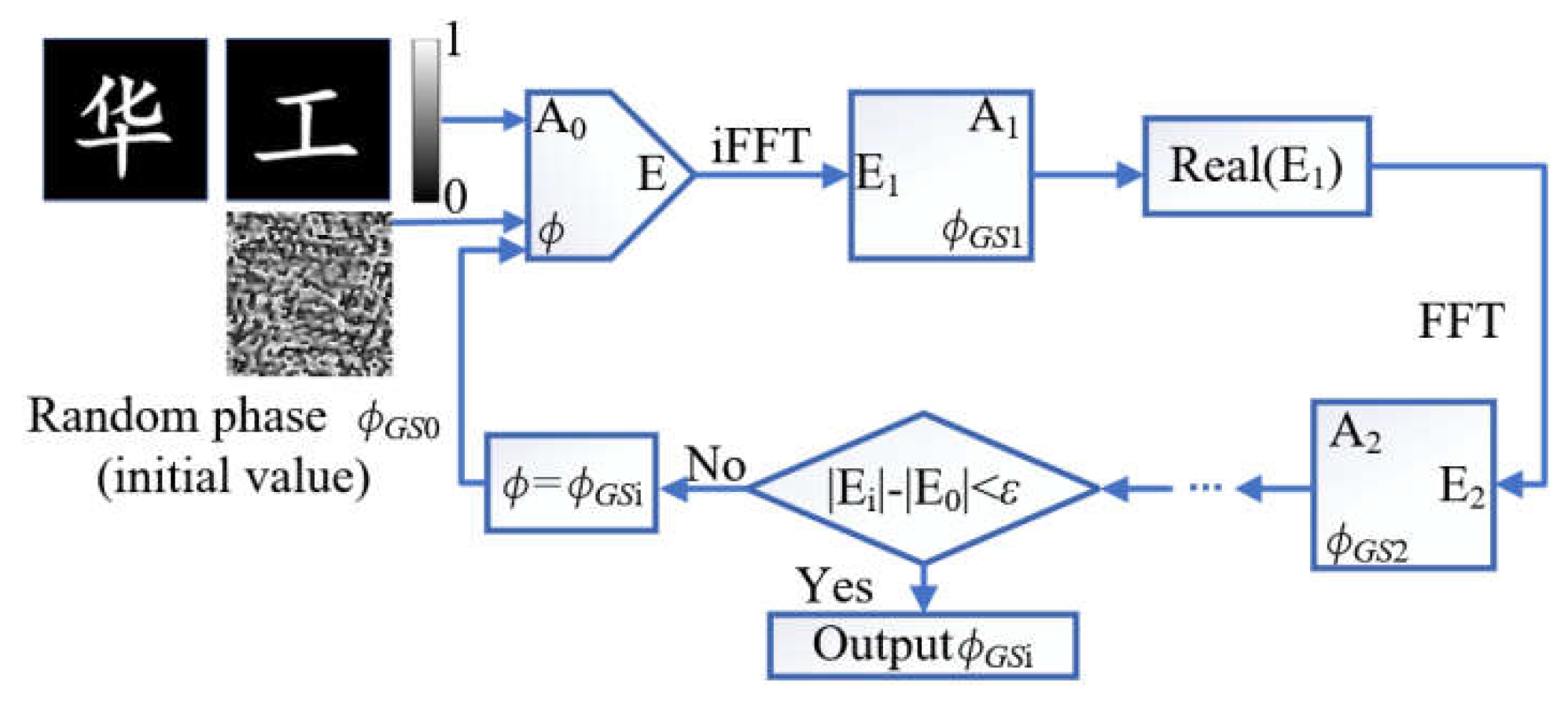
2.3. Gerchberg-Saxton (GS) Algorithm
The Gerchberg-Saxton (GS) algorithm, which was originally proposed by D. Gerchberg and W. Saxton in 1972 [
22], is an iterative algorithm commonly used in phase retrieval for holographic imaging based on Fourier transform and inverse Fourier transform. The iteration starts from the measured amplitude information of the input image, and ends until the error threshold
is met. Here GS algorithm is used to obtain the phase distribution map of the phase gradient metasurface, and the basic steps and method are shown in
Figure 2.
The required images ‘

’, ‘

’ in z axis direction are established by Computer holography technology based on MATLAB. First, painting software is used to draw the required images (including the black background and the white images). Second, the amplitude matrix A
0 (m×n) in the image area is obtained by MATLAB function ‘imread’ and ‘binary’. In A
0 (m×n), the intensities are “1” and “0” for points (
x,
y, 0) in white and black, respectively. Third, the MATLAB function ‘random’ generates a random phase matrix
ΦGS0 (m×n). Apply Fourier transform to the matrices A
0 and
ΦGS0, and obtain amplitude and phase matrices in frequency domain A
1 and
ΦGS1. Then, update all the amplitude matrix values in A
1 (m×n) into 1, that is, A
′1(
x,
y) = 1. Perform inverse Fourier transform to A
′1 and
ΦGS1, and obtain amplitude and phase matrices in time domain A
2 and
ΦGS2. Repeat iterative operations of step 2 and step 3, and update the
i-th iteration amplitude A
i (
x,
y) to A
′I (
x,
y) = 1 until the error threshold
, where
. Then the phase distribution map for the Metasurface is obtained.
2.4. The Total Compensated Phase Calculation Based on Transmission Mode
The metasurface is designed in transmission mode at
f1 when
Ef = 0.1 eV. Under LCP incidence, a holographic imaging RCP ‘

’ is generated in direction (
θ1, 0°). Under RCP incidence, a holographic imaging LCP ‘

’ is generated in direction (
θ2, 0°). The phase compensation for the metasurface obtained by GS algorithm is
ΦGS, which is for the images in normal direction. An additional compensated phase is added for the desired imaging direction (
θ, 0°), and the compensated phase for RCP ‘

’ or LCP ‘

’ for the metasurface unit located at (
x,
y, 0) is as follows:
Then the compensated phase parameters (
ϕx,
ϕy,
β) of the metasurface unit for reconfigurable multifunctional holographic imaging for ‘

’, ‘

’ and ‘

’ is calculated by Equation (5) and Equation (8).
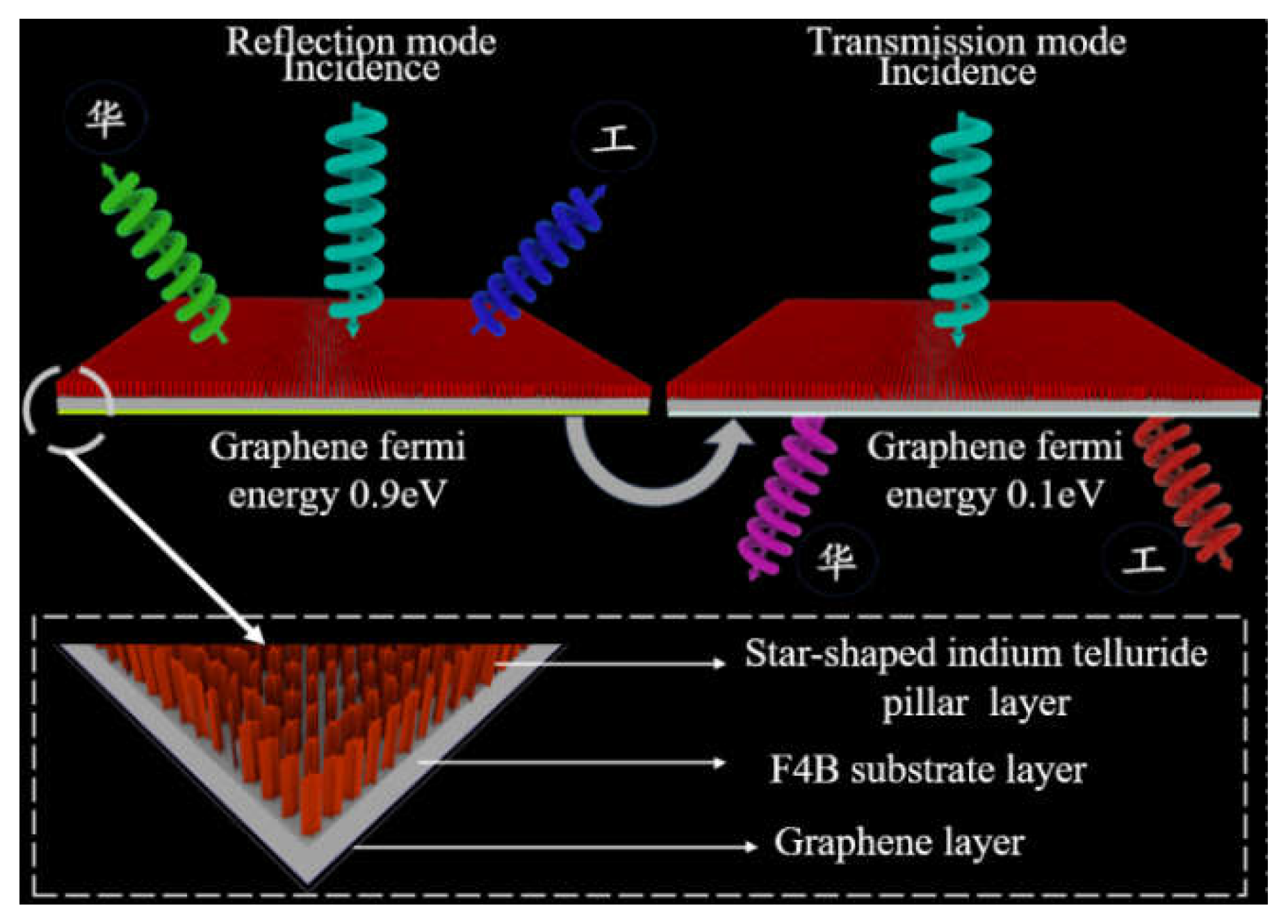
2.5. The Imaging Direction Deduction for Reflection Mode
By switching the bottom graphene layer from insulator to metal states, the metasurface designed in transmission mode can be made to work in reflection mode with the bottom graphene layer acting as a ground plane. According to Equation (6), the holographic imaging of (RCP, ‘

’,
θ1, 0°) and (LCP, ‘

’,
θ2, 0°) designed in transmission mode has changed into co-polarized imaging of (LCP, ‘

’,
θ3, 0°) and (RCP, ‘

’,
θ4, 0°) in reflection mode as shown in
Figure 3. Though the phase distribution map of the metasurface is calculated based on transmission mode, (LCP, ‘

’,
θ3, 0°) and (RCP, ‘

’,
θ4, 0°) are generated under LCP and RCP incidences in reflection mode, respectively. Because the graphene permittivity is a function of its state, the operation frequency
f2 and direction
θ3(4) for reflection mode are different from f
1 and
θ1(2) in transmission mode. The direction
θ3(4) is calculated as follows:
From Equations (8) and (9),
θ3 and
θ4 are deduced as follows.
In summary, based on the above analysis, the proposed metasurface can be switched between transmission and reflection modes, and the holographic imaging can be reconfigured by switching the incident polarization when operating in transmission or reflection mode. Six holographic imaging channels are achieved, as shown in
Table 1.
2.6. Unit Cell Design
The proposed dual-mode metasurface is excited by normal plane wave as in
Figure 1 and
Figure 3. Open boundaries were set as boundary conditions. As example, dual-mode reconfigurable multifunctional holographic imaging are designed in order to validate the above design method: (1) Reconfigurable Chinese characters with cross-polarized in transmission mode are achieved when
Ef = 0.1 eV: (a) (RCP, ‘

’, -14°, 0°), (b) (LCP, ‘

’, 17.5°, 0°), and (c) both (RCP, ‘

’, -14°, 0°) and (LCP, ‘

’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional holographic imaging (Chinese characters) with co-polarized are achieved in reflection mode when
Ef = 0.9 eV: (a) (RCP, ‘

’, -16°, 0°), (b) (LCP, ‘

’, 20°, 0°), (c) both (RCP, ‘

’, -16°, 0°) and (LCP, ‘

’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively. All the curves and field patterns are simulated by CST Microwave Studio software.
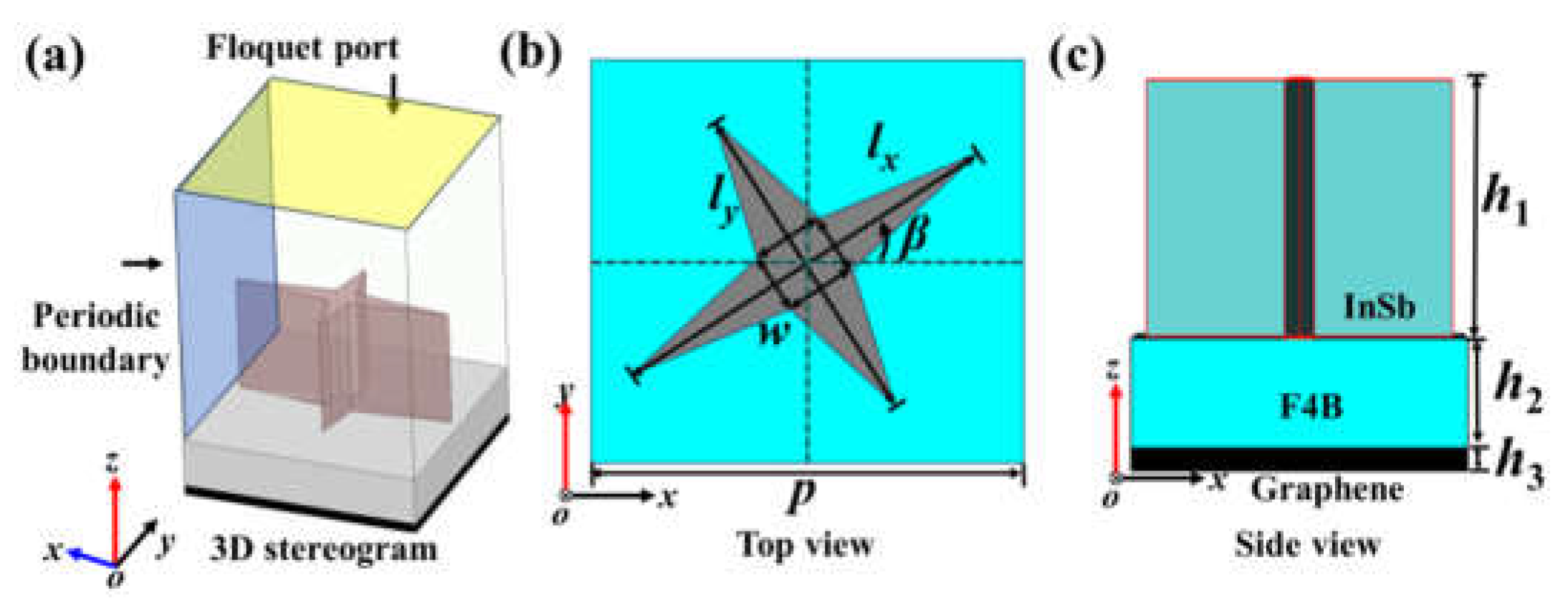
To realize the designed dual-mode reconfigurable multifunctional holographic imaging, a unit cell is proposed to implement the phase (
ϕx,
ϕy,
β) at (
x,
y, 0) calculated by Equation (5), which is shown in
Figure 4.
Figure 4a–c show the simulation Floquet model, top and side views for the unit, respectively, which consists of a star-shaped indium telluride pillar (
εr =19, tan
δ = 0.001) in the top and a 2D bottom graphene layer separated by an F4B substrate with a dielectric constant 2.2, tan
δ = 0.003. All geometry parameters are marked in
Figure 4, and the optimized parameters are as follows:
p = 123 μm,
w = 11 μm,
h1 = 150 μm,
h2 = 0.5 μm and
h3 = 0.05 μm. The propagation phases
ϕx and
ϕy are controlled by
lx and
ly, respectively, and the geometry phase is controlled by rotating the unit cell counter clockwise
β degree.
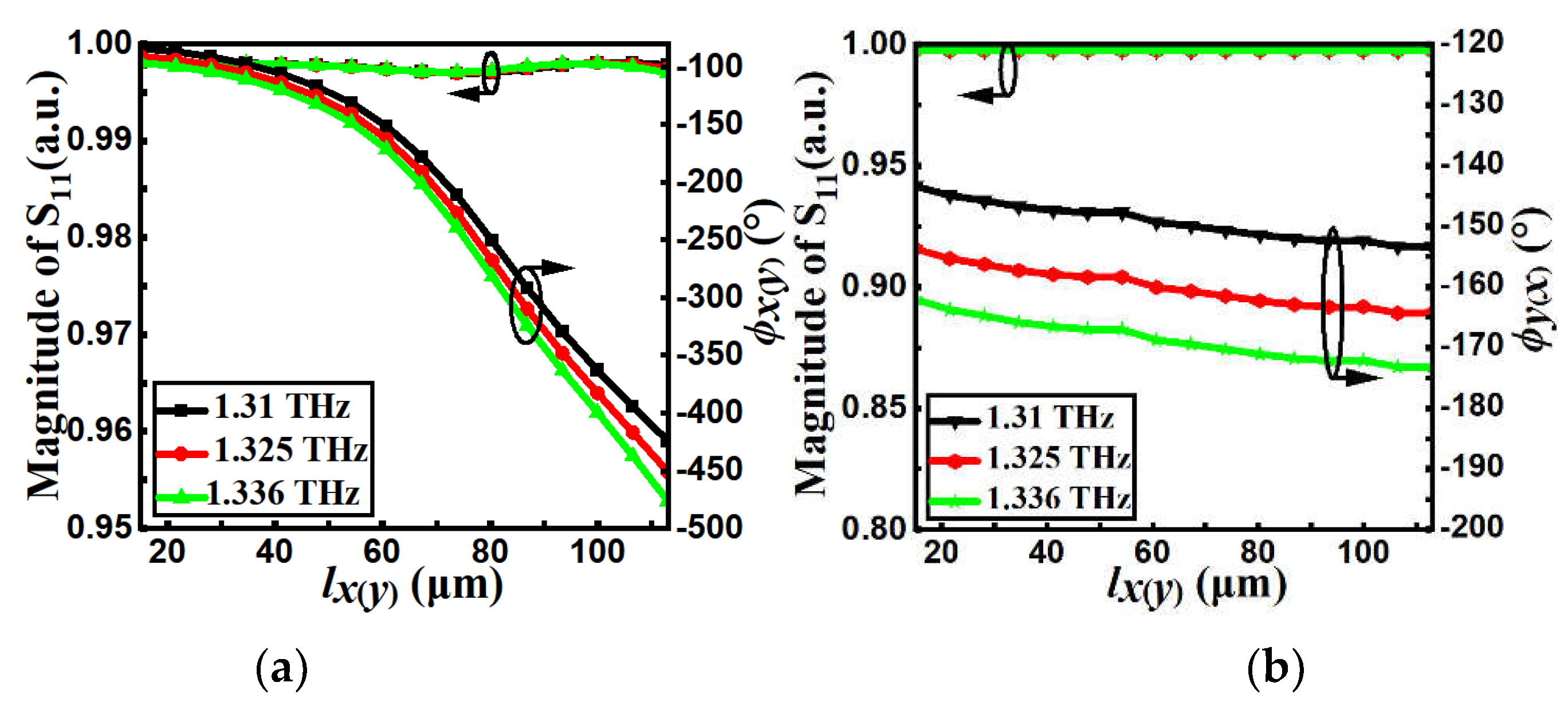
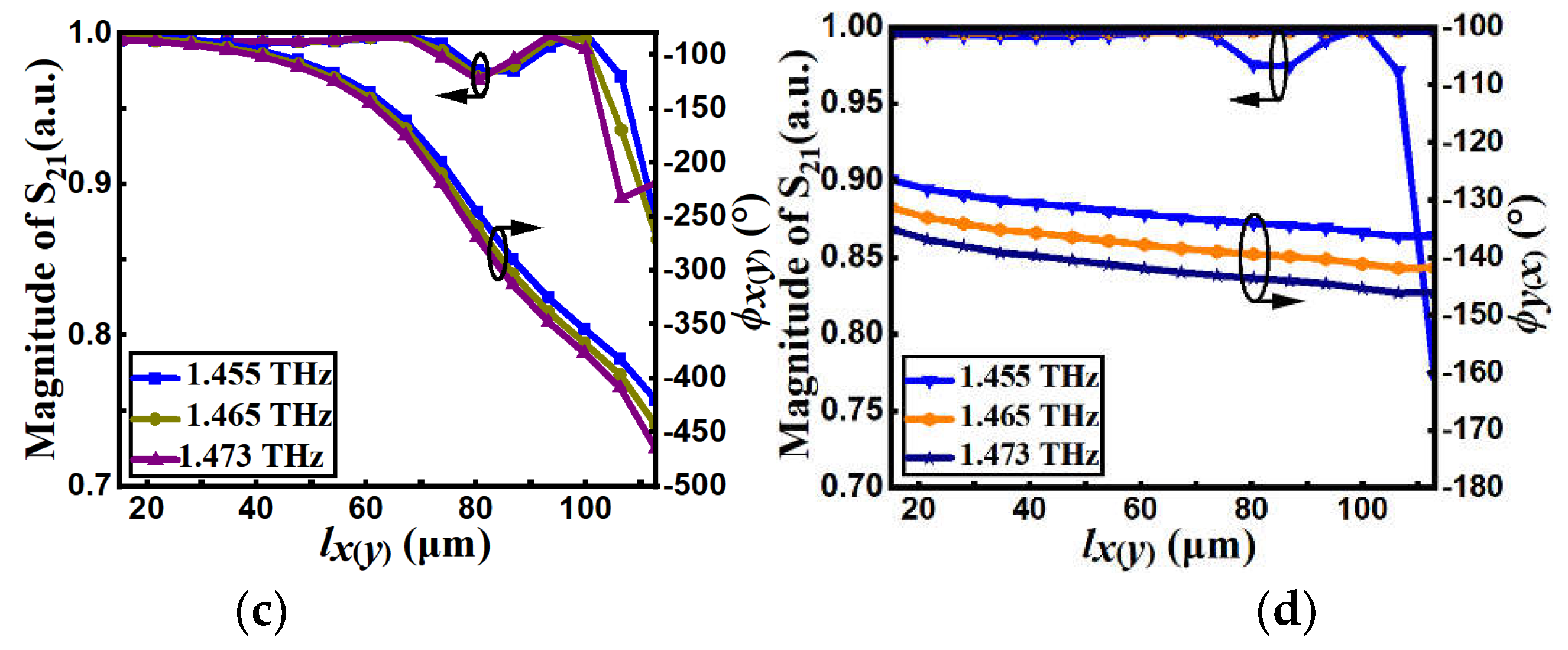
Under normal
x- (
y-) polarized incident excitation: (1) For reflection mode at 1.31THz, 1.325THz and 1.336THz,
Figure 5a shows the simulated S
11 and phase
ϕx(y) as a function of
lx(y), and
Figure 5b shows the simulated S
11 and phase
ϕy(x) as a function of
lx(
y). (2) For transmission mode at 1.455THz, 1.465THz, and 1.473 THz:
Figure 5c shows the simulated amplitude (S
21) and phase
ϕx(y) curves as function of
lx(y), and
Figure 5d is the simulated amplitude (S
21) and phase
ϕy(x) curves as function of
lx(y). For both transmission and reflection modes when
lx(y) varies from 15 μm to 113 μm: (1) The phase of the co-polarization
ϕx(y) increases from -450° to -90°, covering a 360
o phase range. (2) The phase shift of the cross-polarization
ϕy(x) remains basically unchanged, indicating that
ϕx and
ϕy can be independently adjusted by
lx and
ly, respectively. S
11 > 0.99 for reflection mode, and S
21 > 0.85 for transmission mode. The phase
ϕx(y) curves versus
lx(
y) for different frequency points (at 1.31THz, 1.325THz for reflection mode or at 1.455 THz, 1.465 THz, and 1.473 THz for transmission mode) are parallel, indicating that the metasurface can operate within a certain bandwidth. According to
Figure 5a,c, a polynomial formula for the relationship between
ϕx(
y) and
lx(
y) can be fitted as follows:
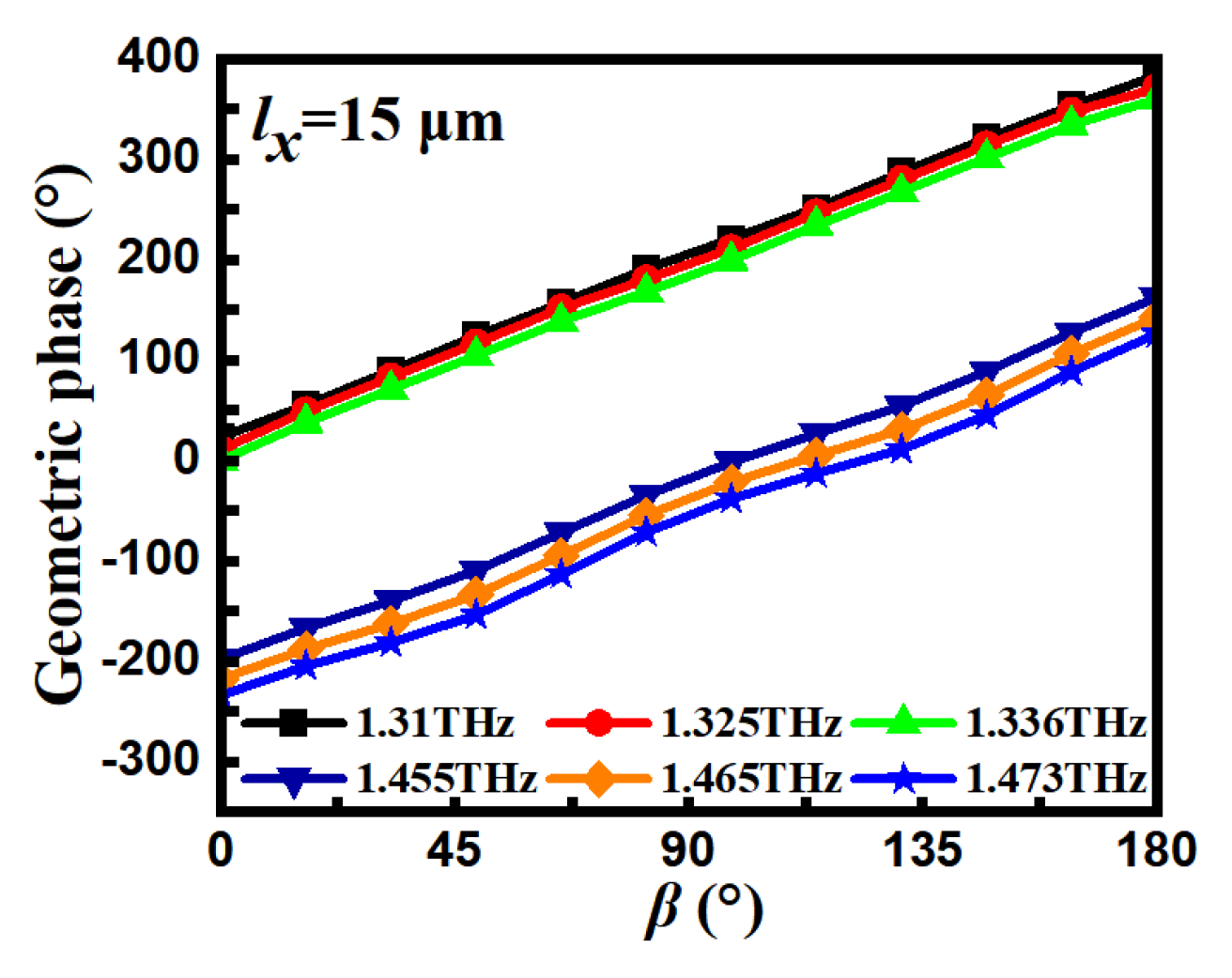
When
lx =15 μm,
Figure 6 shows the curves of the geometric phase as a function of the rotation angle
β for reflection mode when
lx=15um (at 1.31THz, 1.325THz, and 1.336 THz) and transmission mode (at 1.455THz, 1.465THz, and 1.473THz). When
β ranges from 0° to 180°, the geometric phase shift covers 360°, and the geometric phase vs
β curves at different frequency points (1.31THz, 1.325THz and 1.336THz for reflection mode or 1.455THz, 1.465THz, and 1.473 THz for transmission mode) are parallel.
2.7. Metasurface Design
The transmission-reflection reconfigurable metasurface shown in
Figure 3 is formed by the proposed 91×91 unit cells with size 11.193mm×11.193mm×0.15mm (50.4
λ0×50.4
λ0×0.68
λ0) for dual-mode reconfigurable multifunctional holographic imaging: (1) Reconfigurable cross-polarized holographic imaging in transmission mode when
Ef = 0.1eV: (a) (RCP, ‘

’, -14°, 0°), (b) (LCP, ‘

’, 17.5°, 0°), and (c) both (RCP, ‘

’, -14°, 0°) and (LCP, ‘

’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional co-polarized holographic imaging in reflection mode when
Ef = 0.9eV: (a) (RCP, ‘

’, -16°, 0°), (b) (LCP, ‘

’, 20°, 0°), (c) both (RCP, ‘

’, -16°, 0°) and (LCP, ‘

’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively.
The compensated phase distributions for
ϕx,
ϕy and 2
β according to Equation (5) are shown in
Figure 7, and then the corresponding geometry length distributions for
lx,
ly in the metasurface are obtained according to Equation (11).
4. Discussion
A comparison in operation frequency, holographic imaging channel number, operation mode number, operation bandwidth and holographic efficiency has been made between the proposed design and published holographic metasurfaces as in
Table 2. References [
9,
10,
11,
17] only work in only reflection or transmission mode. Ours works in both reflection and transmission modes, and is reconfigurable for reflection or transmission mode by switching among the RCP, LCP and LP incidence. In addition, ours has more holographic imaging channel numbers and higher holographic efficiency.
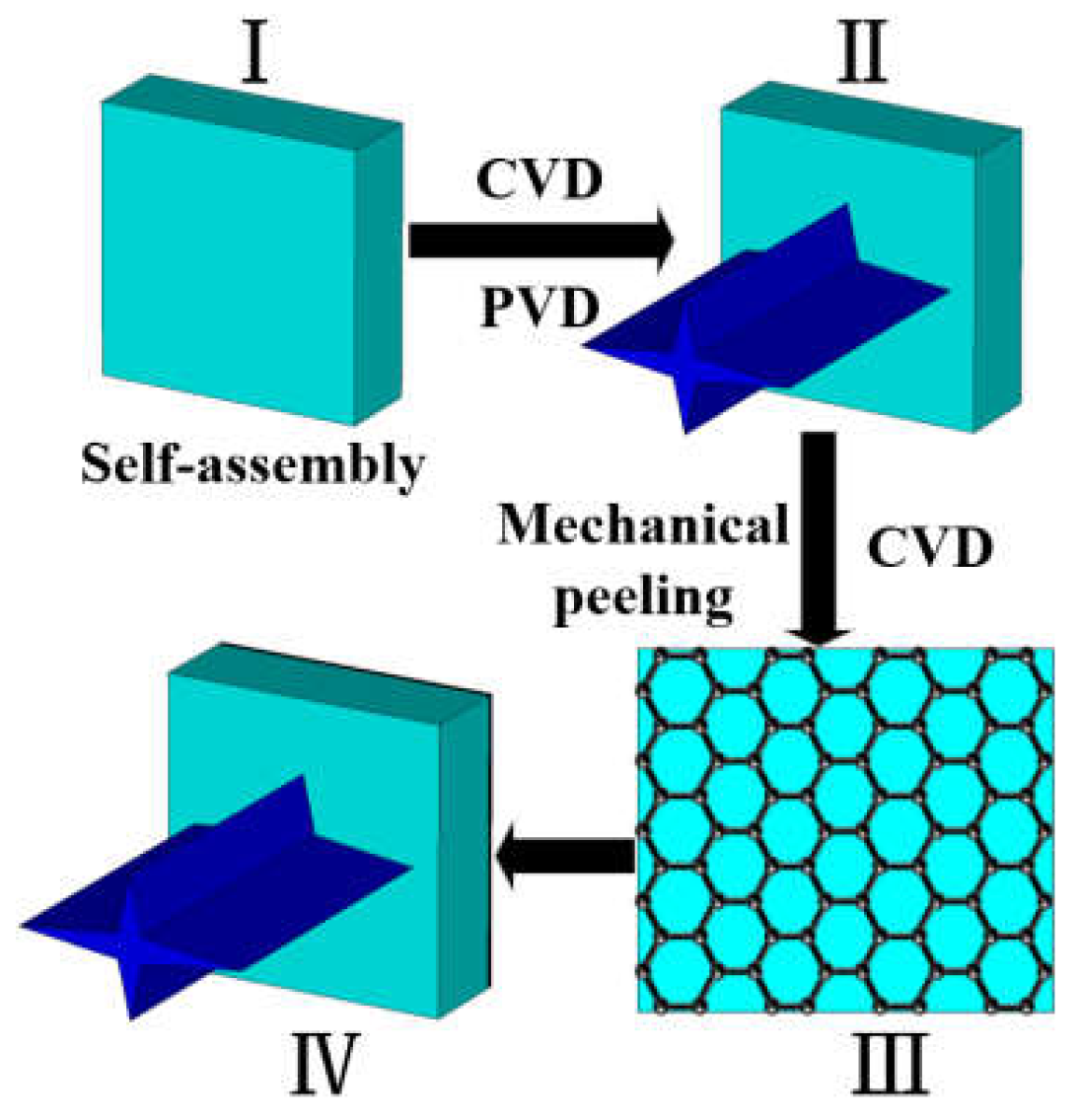
In addition, we also discuss the fabrication of the proposed metasurface. While our design theory has been validated from a simulation perspective, we still face two key challenges. The first challenge pertains to the fabrication of metasurface.
Figure 11 illustrates potential fabrication methods. Firstly, the F4B material layer can be obtained through self-assembly to form the required dielectric substrate. Secondly, there are two methods to obtain the top layer of indium telluride. One approach involves chemical vapor deposition (CVD), whereby indium telluride thin films are deposited on the F4B substrate, with control over temperature, humidity, and deposition rate to achieve the desired material thickness and quality. Another method entails utilizing physical vapor deposition (PVD), employing techniques such as sputtering or evaporation to deposit indium telluride material on the substrate, with deposition parameters controlled to achieve the desired dielectric dimensions. Finally, the bottom graphene layer can be prepared through mechanical exfoliation, as referenced in reference [
26], for transferring graphene onto the substrate. Alternatively, graphene can be grown directly on the F4B material bottom using CVD, with precise management of reaction conditions to achieve the required graphene thickness.
The second challenge pertains to the method of controlling graphene’s chemical potential. As documented in reference [
18,
20,
21,
27], the application of an electric field between the graphene layer and the upper dielectric can effectively manipulate the carrier concentration of graphene, subsequently allowing for the adjustment of the Fermi level. Moreover, techniques such as chemical doping, direct laser writing, the imposition of mechanical strain, and the utilization of piezoelectric effects can be employed to modulate the lattice structure of graphene. This, in turn, alters its electronic properties and facilitates the subsequent adjustment of the Fermi level positioning.
5. Conclusions
This paper develops a multifunctional and reconfigurable reflection-transmission dual-mode THz dielectric holographic metasurface formed by propagation - geometry composite units. The dual-mode is achieved by controlling the Fermi energy level of graphene integrated into the metasurface unit, and the proposed metasurface works in reflection and transmission modes when
Ef = 0.9 eV, 0.1eV, respectively. The reconfigurability is realized by switching incidence polarization. The metasurface is designed based on transmission mode, and the physical model switching to the reflection mode is established. For the first time, dynamic modulation reflection-transmission holographic imaging metasurface based on graphene is developed. As example, a multifunctional and reconfigurable metasurface has been developed: (1) Reconfigurable cross-polarized three-channel holographic imaging in transmission mode from 1.32THz to 1.6THz: (‘

’, RCP, θ = -14°, φ = 0°), (‘

’, LCP, θ = 17.5°, φ = 0°) and (‘

’, RCP, θ = -14°, φ = 0° and ‘

’, LCP, θ = 17.5°, φ = 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable co-polarized three-channel holographic imaging in reflection mode from 1.15THz to 1.35THz: (‘

’, RCP, θ = -16°, φ=0°), (‘

’, LCP, θ = 20°, φ = 0°), and (‘

’, RCP, θ = -16°, φ = 0° and ‘

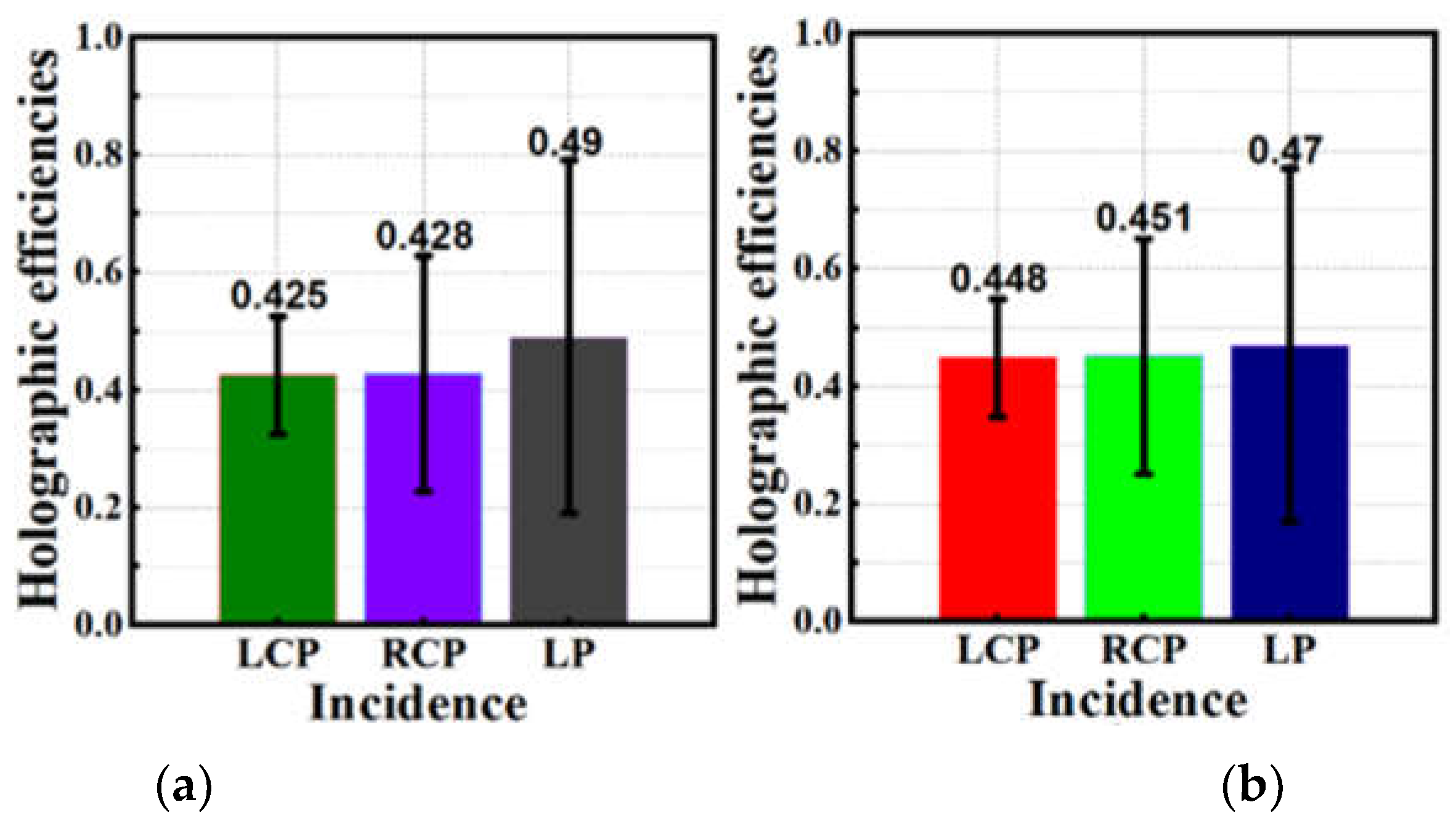
’, LCP, θ = 20°, φ = 0°) by switching the RCP, LCP and LP incidences, respectively. Compare with published holographic imaging, ours has more channel numbers (six holographic imaging channels) and higher holographic efficiency (42.5% to 49%). These characteristics make the proposed metasurface has potential applications in information encryption transmission, multi-channel imaging, and other related fields.
Author Contributions
Conceptualization, H.H. and J.W.; methodology, J.W.; software, J.W.; validation, H.H. and J.W.; formal analysis, J.W.; investigation, J.W.; resources, J.W.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, H.H.; visualization, J.W.; supervision, H.H. and J.W. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Schematic diagram for the dual-mode reconfigurable multifunctional metasurface. (a) Reconfigurable reflection mode. (b) Reconfigurable transmission mode. (c) Graphene switching sketch map: metal when Ef = 0.9 eV, insulator when Ef = 0.1eV.
Figure 1.
Schematic diagram for the dual-mode reconfigurable multifunctional metasurface. (a) Reconfigurable reflection mode. (b) Reconfigurable transmission mode. (c) Graphene switching sketch map: metal when Ef = 0.9 eV, insulator when Ef = 0.1eV.
Figure 2.
Basic flowchart of the GS algorithm.
Figure 2.
Basic flowchart of the GS algorithm.
Figure 3.
The transmission-reflection reconfigurable metasurface.
Figure 3.
The transmission-reflection reconfigurable metasurface.
Figure 4.
The proposed unit cell: (a) 3D stereogram, (b) Top view, (c) Side view.
Figure 4.
The proposed unit cell: (a) 3D stereogram, (b) Top view, (c) Side view.
Figure 5.
(a) Simulated S11 and phase shift ϕx(y) as a function of lx(y) at 1.31, 1.325, and 1.336 THz. (b) Simulated S11 and phase shift ϕy(x) as a function of lx(y) at 1.31, 1.325, and 1.336 THz. (c) Simulated S21 and phase shift ϕx(y) as a function of lx(y) at 1.455, 1.465, and 1.473 THz. (d) Simulated S21 and phase shift ϕy(x) as a function of lx(y) at 1.455, 1.465, and 1.473 THz.
Figure 5.
(a) Simulated S11 and phase shift ϕx(y) as a function of lx(y) at 1.31, 1.325, and 1.336 THz. (b) Simulated S11 and phase shift ϕy(x) as a function of lx(y) at 1.31, 1.325, and 1.336 THz. (c) Simulated S21 and phase shift ϕx(y) as a function of lx(y) at 1.455, 1.465, and 1.473 THz. (d) Simulated S21 and phase shift ϕy(x) as a function of lx(y) at 1.455, 1.465, and 1.473 THz.
Figure 6.
Simulated geometric phase versus β curves when lx = 15 μm.
Figure 6.
Simulated geometric phase versus β curves when lx = 15 μm.
Figure 7.
Phase distribution for the designed metasurface: (a) Propagation phase ϕx. (b) Propagation phase ϕy. (c) Geometric phase 2β.
Figure 7.
Phase distribution for the designed metasurface: (a) Propagation phase ϕx. (b) Propagation phase ϕy. (c) Geometric phase 2β.
Figure 8.
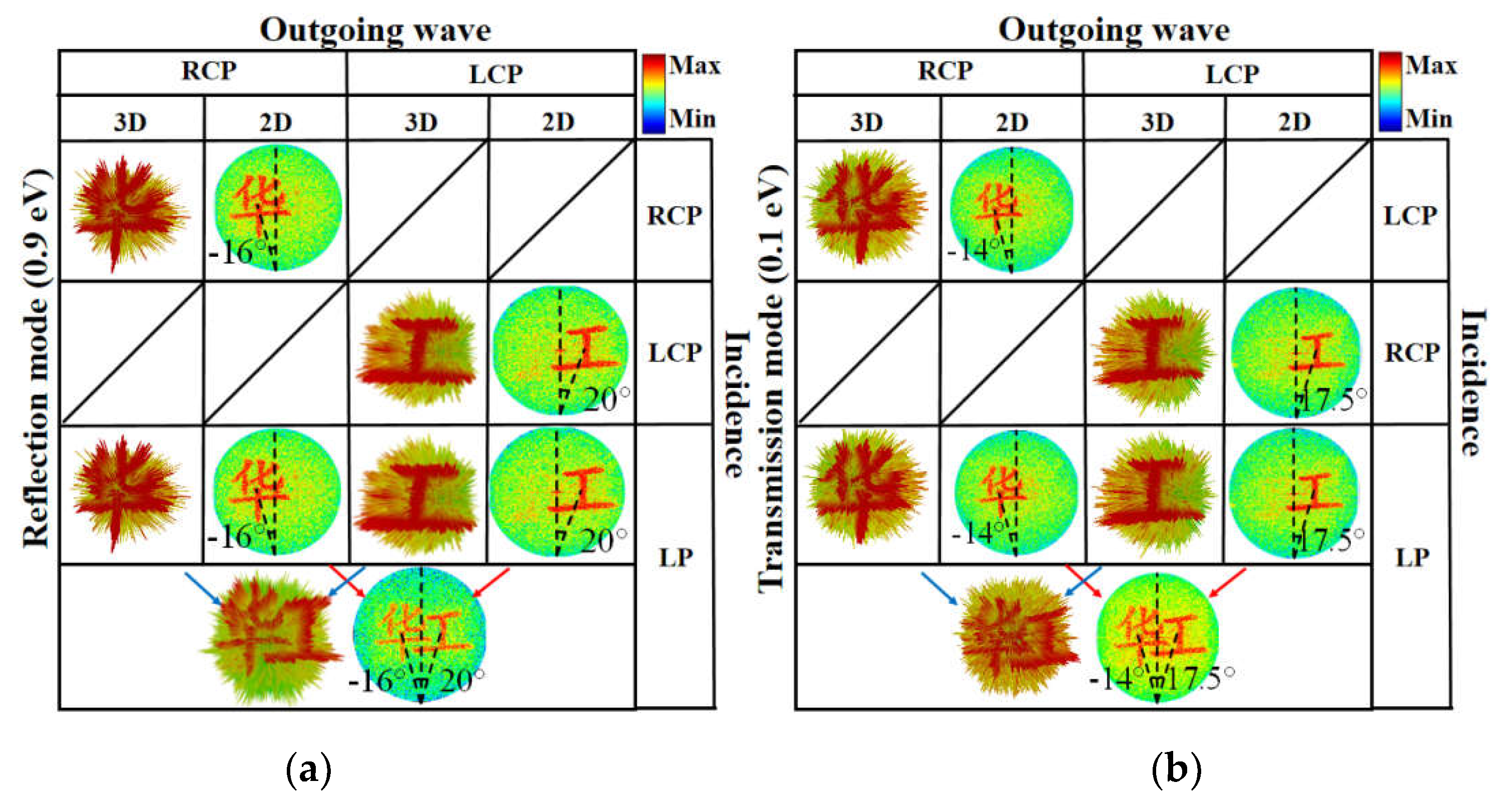
Simulated 3D and 2D far-field holographic imaging under RCP, LCP and LP incidence: for reflection mode at (a), for transmission mode (b).
Figure 8.
Simulated 3D and 2D far-field holographic imaging under RCP, LCP and LP incidence: for reflection mode at (a), for transmission mode (b).
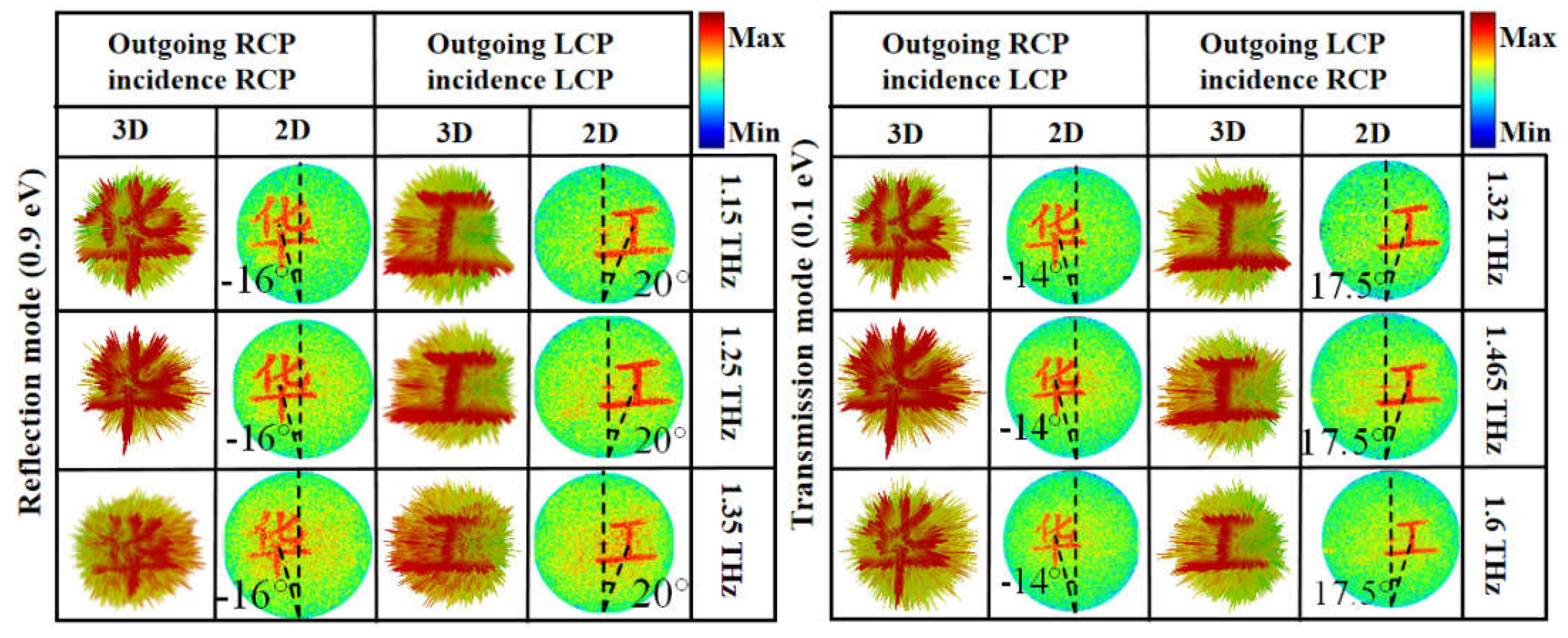
Figure 9.
Simulated 3D and 2D far-field holographic imaging under RCP and LCP incidence: (a) co-polarization in reflection mode at 1.15 THz, 1.25 THz and 1.35 THz, (b) cross- polarization in transmission mode at 1.32 THz, 1.465 THz and 1.6 THz.
Figure 9.
Simulated 3D and 2D far-field holographic imaging under RCP and LCP incidence: (a) co-polarization in reflection mode at 1.15 THz, 1.25 THz and 1.35 THz, (b) cross- polarization in transmission mode at 1.32 THz, 1.465 THz and 1.6 THz.
Figure 10.
Holographic efficiencies under LCP, RCP, and LP incidences: (a) for reflection mode at 1.25 THz, (b) for transmission mode at 1.465 THz.
Figure 10.
Holographic efficiencies under LCP, RCP, and LP incidences: (a) for reflection mode at 1.25 THz, (b) for transmission mode at 1.465 THz.
Figure 11.
Fabrication chart of the proposed metasurface.
Figure 11.
Fabrication chart of the proposed metasurface.
Table 1.
Six holographic imaging channels of proposed metasurface.
Table 1.
Six holographic imaging channels of proposed metasurface.
| Incidence |
Fermi Energy |
Frequency |
Channel |
Hologram (Polarization, Pattern, Reflection angle) |
| LCP |
0.1 eV |
f1 |
T1 1
|
RCP, ‘ ’, (θ1,0°) ’, (θ1,0°) |
| 0.9 eV |
f2 |
R1 |
LCP, ‘ ’, (θ3,0°) ’, (θ3,0°) |
| RCP |
0.1 eV |
f1 |
T2 |
LCP, ‘ ’, (θ2,0°) ’, (θ2,0°) |
| 0.9 eV |
f2 |
R2 |
RCP, ‘ ’, (θ4,0°) ’, (θ4,0°) |
| LP |
0.1 eV |
f1 |
T3 |
RCP, ‘ ’, (θ1,0°), and LCP, ‘ ’, (θ1,0°), and LCP, ‘ ’, (θ2,0°) ’, (θ2,0°) |
| 0.9 eV |
f2 |
R3 |
RCP, ‘ ’, (θ4,0°), and LCP, ‘ ’, (θ4,0°), and LCP, ‘ ’, (θ3,0°), ’, (θ3,0°), |
Table 2.
Comparison of the proposed metasurface and published holographic metasurfaces.
Table 2.
Comparison of the proposed metasurface and published holographic metasurfaces.
| Reference |
Frequency |
Number of
channels |
TS or RS |
Relative bandwidth |
Holographic efficiency |
| [9] |
375 THz |
2 |
TS |
0 |
NA1
|
| [10] |
7.5, 13 GHz |
4 |
RS |
0 |
NA |
| [11] |
7.2, 9.1, 10.9, 15.2 GHz |
4 |
TS |
0 |
NA |
| [17] |
1.1-1.6 THz |
4 |
RS |
37% |
44.2%, 45.9% |
| This work |
1.15-1.35,
1.32-1.6 THz |
6 |
TS, RS |
16%(TS),
19% (RS) |
42.5%,42.8%,49% (TS),
44.8%,45.1%,47% (RS) |
 ’, ‘
’, ‘ ’ and ‘
’ and ‘ ’are achieved by switching LCP, RCP and LP incidence, respectively. The operation frequency range is 1.15THz – 1.35THz (16%) for reflection mode, and 1.32 THz - 1.6 THz (19%) for transmission mode. The holographic imaging is co- and cross- polarization for reflection and transmission modes, respectively.
’are achieved by switching LCP, RCP and LP incidence, respectively. The operation frequency range is 1.15THz – 1.35THz (16%) for reflection mode, and 1.32 THz - 1.6 THz (19%) for transmission mode. The holographic imaging is co- and cross- polarization for reflection and transmission modes, respectively. ’, ‘
’, ‘ ’ in z axis direction are established by Computer holography technology based on MATLAB. First, painting software is used to draw the required images (including the black background and the white images). Second, the amplitude matrix A0 (m×n) in the image area is obtained by MATLAB function ‘imread’ and ‘binary’. In A0 (m×n), the intensities are “1” and “0” for points (x, y, 0) in white and black, respectively. Third, the MATLAB function ‘random’ generates a random phase matrix ΦGS0 (m×n). Apply Fourier transform to the matrices A0 and ΦGS0, and obtain amplitude and phase matrices in frequency domain A1 and ΦGS1. Then, update all the amplitude matrix values in A1 (m×n) into 1, that is, A′1(x, y) = 1. Perform inverse Fourier transform to A′1 and ΦGS1, and obtain amplitude and phase matrices in time domain A2 and ΦGS2. Repeat iterative operations of step 2 and step 3, and update the i-th iteration amplitude Ai (x, y) to A′I (x, y) = 1 until the error threshold , where . Then the phase distribution map for the Metasurface is obtained.
’ in z axis direction are established by Computer holography technology based on MATLAB. First, painting software is used to draw the required images (including the black background and the white images). Second, the amplitude matrix A0 (m×n) in the image area is obtained by MATLAB function ‘imread’ and ‘binary’. In A0 (m×n), the intensities are “1” and “0” for points (x, y, 0) in white and black, respectively. Third, the MATLAB function ‘random’ generates a random phase matrix ΦGS0 (m×n). Apply Fourier transform to the matrices A0 and ΦGS0, and obtain amplitude and phase matrices in frequency domain A1 and ΦGS1. Then, update all the amplitude matrix values in A1 (m×n) into 1, that is, A′1(x, y) = 1. Perform inverse Fourier transform to A′1 and ΦGS1, and obtain amplitude and phase matrices in time domain A2 and ΦGS2. Repeat iterative operations of step 2 and step 3, and update the i-th iteration amplitude Ai (x, y) to A′I (x, y) = 1 until the error threshold , where . Then the phase distribution map for the Metasurface is obtained. ’ is generated in direction (θ1, 0°). Under RCP incidence, a holographic imaging LCP ‘
’ is generated in direction (θ1, 0°). Under RCP incidence, a holographic imaging LCP ‘ ’ is generated in direction (θ2, 0°). The phase compensation for the metasurface obtained by GS algorithm is ΦGS, which is for the images in normal direction. An additional compensated phase is added for the desired imaging direction (θ, 0°), and the compensated phase for RCP ‘
’ is generated in direction (θ2, 0°). The phase compensation for the metasurface obtained by GS algorithm is ΦGS, which is for the images in normal direction. An additional compensated phase is added for the desired imaging direction (θ, 0°), and the compensated phase for RCP ‘ ’ or LCP ‘
’ or LCP ‘ ’ for the metasurface unit located at (x, y, 0) is as follows:
’ for the metasurface unit located at (x, y, 0) is as follows:  ’, ‘
’, ‘ ’ and ‘
’ and ‘ ’ is calculated by Equation (5) and Equation (8).
’ is calculated by Equation (5) and Equation (8). ’, θ1, 0°) and (LCP, ‘
’, θ1, 0°) and (LCP, ‘ ’, θ2, 0°) designed in transmission mode has changed into co-polarized imaging of (LCP, ‘
’, θ2, 0°) designed in transmission mode has changed into co-polarized imaging of (LCP, ‘ ’, θ3, 0°) and (RCP, ‘
’, θ3, 0°) and (RCP, ‘ ’, θ4, 0°) in reflection mode as shown in Figure 3. Though the phase distribution map of the metasurface is calculated based on transmission mode, (LCP, ‘
’, θ4, 0°) in reflection mode as shown in Figure 3. Though the phase distribution map of the metasurface is calculated based on transmission mode, (LCP, ‘ ’, θ3, 0°) and (RCP, ‘
’, θ3, 0°) and (RCP, ‘ ’, θ4, 0°) are generated under LCP and RCP incidences in reflection mode, respectively. Because the graphene permittivity is a function of its state, the operation frequency f2 and direction θ3(4) for reflection mode are different from f1 and θ1(2) in transmission mode. The direction θ3(4) is calculated as follows:
’, θ4, 0°) are generated under LCP and RCP incidences in reflection mode, respectively. Because the graphene permittivity is a function of its state, the operation frequency f2 and direction θ3(4) for reflection mode are different from f1 and θ1(2) in transmission mode. The direction θ3(4) is calculated as follows: ’, -14°, 0°), (b) (LCP, ‘
’, -14°, 0°), (b) (LCP, ‘ ’, 17.5°, 0°), and (c) both (RCP, ‘
’, 17.5°, 0°), and (c) both (RCP, ‘ ’, -14°, 0°) and (LCP, ‘
’, -14°, 0°) and (LCP, ‘ ’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional holographic imaging (Chinese characters) with co-polarized are achieved in reflection mode when Ef = 0.9 eV: (a) (RCP, ‘
’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional holographic imaging (Chinese characters) with co-polarized are achieved in reflection mode when Ef = 0.9 eV: (a) (RCP, ‘ ’, -16°, 0°), (b) (LCP, ‘
’, -16°, 0°), (b) (LCP, ‘ ’, 20°, 0°), (c) both (RCP, ‘
’, 20°, 0°), (c) both (RCP, ‘ ’, -16°, 0°) and (LCP, ‘
’, -16°, 0°) and (LCP, ‘ ’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively. All the curves and field patterns are simulated by CST Microwave Studio software.
’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively. All the curves and field patterns are simulated by CST Microwave Studio software. ’, -14°, 0°), (b) (LCP, ‘
’, -14°, 0°), (b) (LCP, ‘ ’, 17.5°, 0°), and (c) both (RCP, ‘
’, 17.5°, 0°), and (c) both (RCP, ‘ ’, -14°, 0°) and (LCP, ‘
’, -14°, 0°) and (LCP, ‘ ’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional co-polarized holographic imaging in reflection mode when Ef = 0.9eV: (a) (RCP, ‘
’, 17.5°, 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable multifunctional co-polarized holographic imaging in reflection mode when Ef = 0.9eV: (a) (RCP, ‘ ’, -16°, 0°), (b) (LCP, ‘
’, -16°, 0°), (b) (LCP, ‘ ’, 20°, 0°), (c) both (RCP, ‘
’, 20°, 0°), (c) both (RCP, ‘ ’, -16°, 0°) and (LCP, ‘
’, -16°, 0°) and (LCP, ‘ ’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively.
’, 20°, 0°) by switching the RCP, LCP and LP incidence, respectively.  ’, RCP, θ = -14°, φ = 0°), (‘
’, RCP, θ = -14°, φ = 0°), (‘ ’, LCP, θ = 17.5°, φ = 0°) and both (‘
’, LCP, θ = 17.5°, φ = 0°) and both (‘ ’, RCP, θ = -14°, φ = 0°) and (‘
’, RCP, θ = -14°, φ = 0°) and (‘ ’, LCP, θ = 17.5°, φ = 0°) by switching LCP, RCP and LP incidence, respectively. Reconfigurable multifunctional co-polarized holographic imaging is achieved at 1.325 THz in reflection mode among (‘
’, LCP, θ = 17.5°, φ = 0°) by switching LCP, RCP and LP incidence, respectively. Reconfigurable multifunctional co-polarized holographic imaging is achieved at 1.325 THz in reflection mode among (‘ ’, RCP, θ = -16°, φ = 0°), ‘
’, RCP, θ = -16°, φ = 0°), ‘ ’, LCP, θ = 20°, φ = 0°), and both (‘
’, LCP, θ = 20°, φ = 0°), and both (‘ ’, RCP, θ = -16°, φ = 0°) and (‘
’, RCP, θ = -16°, φ = 0°) and (‘ ’, LCP, θ = 20°, φ = 0°) by switching the RCP, LCP and LP incidence, respectively. The simulated and calculated holographic imaging are in good agreement. Because LP wave can be decomposed into two equal LCP and RCP waves, both the LCP and RCP excitation are done simultaneously, and the holographic imaging for LP incidence are the holographic imaging sum of LCP and RCP incidences.
’, LCP, θ = 20°, φ = 0°) by switching the RCP, LCP and LP incidence, respectively. The simulated and calculated holographic imaging are in good agreement. Because LP wave can be decomposed into two equal LCP and RCP waves, both the LCP and RCP excitation are done simultaneously, and the holographic imaging for LP incidence are the holographic imaging sum of LCP and RCP incidences. ’, RCP, θ = -14°, φ = 0°), (‘
’, RCP, θ = -14°, φ = 0°), (‘ ’, LCP, θ = 17.5°, φ = 0°) and (‘
’, LCP, θ = 17.5°, φ = 0°) and (‘ ’, RCP, θ = -14°, φ = 0° and ‘
’, RCP, θ = -14°, φ = 0° and ‘ ’, LCP, θ = 17.5°, φ = 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable co-polarized three-channel holographic imaging in reflection mode from 1.15THz to 1.35THz: (‘
’, LCP, θ = 17.5°, φ = 0°) by switching LCP, RCP and LP incidence, respectively. (2) Reconfigurable co-polarized three-channel holographic imaging in reflection mode from 1.15THz to 1.35THz: (‘ ’, RCP, θ = -16°, φ=0°), (‘
’, RCP, θ = -16°, φ=0°), (‘ ’, LCP, θ = 20°, φ = 0°), and (‘
’, LCP, θ = 20°, φ = 0°), and (‘ ’, RCP, θ = -16°, φ = 0° and ‘
’, RCP, θ = -16°, φ = 0° and ‘ ’, LCP, θ = 20°, φ = 0°) by switching the RCP, LCP and LP incidences, respectively. Compare with published holographic imaging, ours has more channel numbers (six holographic imaging channels) and higher holographic efficiency (42.5% to 49%). These characteristics make the proposed metasurface has potential applications in information encryption transmission, multi-channel imaging, and other related fields.
’, LCP, θ = 20°, φ = 0°) by switching the RCP, LCP and LP incidences, respectively. Compare with published holographic imaging, ours has more channel numbers (six holographic imaging channels) and higher holographic efficiency (42.5% to 49%). These characteristics make the proposed metasurface has potential applications in information encryption transmission, multi-channel imaging, and other related fields.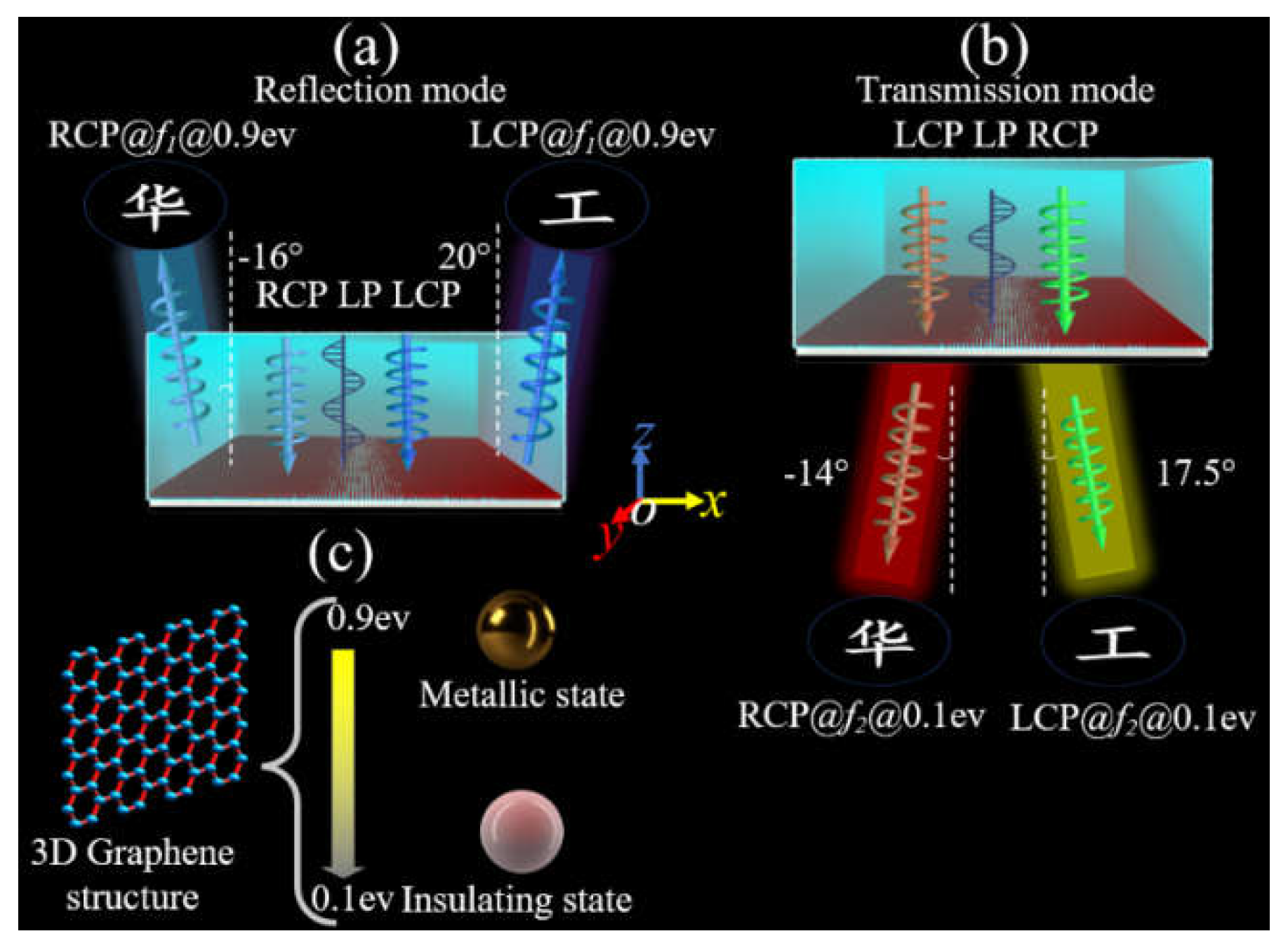

 ’, (θ1,0°)
’, (θ1,0°) ’, (θ3,0°)
’, (θ3,0°) ’, (θ2,0°)
’, (θ2,0°) ’, (θ4,0°)
’, (θ4,0°) ’, (θ1,0°), and LCP, ‘
’, (θ1,0°), and LCP, ‘ ’, (θ2,0°)
’, (θ2,0°) ’, (θ4,0°), and LCP, ‘
’, (θ4,0°), and LCP, ‘ ’, (θ3,0°),
’, (θ3,0°),



