Post-Quantum Authentication Scheme for IoT Security in Smart Cities

Preprint

Article

Post-Quantum Authentication Scheme for IoT Security in Smart Cities

Altmetrics

Downloads

297

Views

132

Comments

A peer-reviewed article of this preprint also exists.

Noman Minhas^*

This version is not peer-reviewed

This preprints belongs to the Topic

Trends and Prospects in Security, Encryption and Encoding

Submitted:

27 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts

Abstract

Internet of Things (IoT) devices are going to be the primary data source in smart cities, often generating and communicating critical, sensitive, and private data that face threats of confidentiality breaches due to the rise of quantum computers. Even though NIST has approved post-quantum cryptography (PQC) schemes that promise to protect from quantum computer threats, these schemes can not be implemented efficiently on IoT devices, which often have computational and memory constraints. Hence, due to the substantial key size requirements and computationally intensive nature of PQC schemes, their direct deployment on IoT devices within smart city architecture is impeded by inherent computational and storage limitations. Consequently, it is imperative to devise PQC-based, resource-efficient authentication protocols tailored to IoT devices operating within smart cities. In this paper, we propose an offloading scheme that uses PQ Edge Server (PQES) for the network that performs PQC-related computation and memory operations for IoT devices in the network. The suggested technique transfers all storage and processing responsibilities from IoT devices in a network to ensure their normal operation and performance without any compromise. PQES generates a distinct PQ key pair for every network device and oversees a separate stream for each device. Therefore, IoT devices in the network may function without cryptographic processes, improving their efficiency by removing the need for conventional cryptography. Our results show that the proposed scheme reduces RAM usage to 1.05 KB and CPU usage to 1.75%, with maximum CPU context switches of 92.8. The proposed scheme uses TCP, a transport layer protocol, which is applicable to lightweight end devices without application-level protocols like HTTP or MQTT. When benchmarked on a Raspberry Pi, the PQES can handle 1000 concurrent connections and use a maximum of 73.5% of RAM. In comparison, previous research used at least 5.1 MB of RAM for one concurrent connection and may use up to 552.6 MB of RAM for 1000 concurrent connections. The maximum CPU usage for our method was 1.75%, whereas the previous proposal had a utilization of 67.1%. The greatest CPU context switches for our system were 92.8, far lower than the 3449 observed for the usual approach. Hence, our proposed scheme reduces the computational, memory, and network load for IoT devices by manifolds and increases device performance while providing PQC security.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

The shift from 5G to 6G is creating a more interconnected world, making the concept of smart cities increasingly feasible. IoT devices are crucial to the concept of smart cities and serve as the main source of data creation and transmission. IoT devices are projected to produce 79.4 zettabytes of data by 2025 [1]. The data frequently includes very crucial system-critical, sensitive, personal, and financial information, making the security and privacy of this data essential components of smart cities.

A smart city is an urban environment that uses Information and Communication Technology (ICT) and other sophisticated technologies to improve city operations and increase services for people. It integrates physical, social, commercial, and ICT infrastructure to improve the city’s intelligence. The primary goal is to improve the quality of life for urban residents by addressing concerns such as energy management, transportation, healthcare, and governance. Smart cities are seen as a solution to the issues caused by urbanization, population growth, energy depletion, and environmental pollution. Organizations like ISO provide standards to ensure the quality, safety, and performance of smart city initiatives globally. Various experimental methodologies have challenges when transferring into practical applications, such as scalability, lack of user environment, mobility restrictions, and device variations [2].

Smart cities are defined by four main attributes: sustainability, quality of life, urbanization, and smartness [3]. Sustainability includes infrastructure, governance, pollution, waste, energy, climate change, social issues, economics, and health. Urbanization encompasses technical, economic, infrastructural, and governmental aspects when shifting from rural to urban settings. Smartness strives to improve the social, environmental, and economic conditions of the city and its inhabitants. Since the 1980s, sustainability has been a prominent notion in urban planning, in accordance with the triple bottom line concept. Smart communities strive to improve quality of life by introducing innovative solutions that lessen barriers to social interaction and participation. Modern city administrations establish explicit social initiatives to recognize and involve skilled inhabitants, enhancing municipal services and economic prosperity.

Smart cities use networked technologies such as embedded systems, wearable sensors, and ordinary goods to offer communication and tailored services. Yet, these devices frequently lack sufficient security protections because of hardware, software, and network constraints. Hewlett-Packard discovered that 80% of devices utilize basic passwords, 70% employ unencrypted network services, and 60% possess security weaknesses. Smart devices gather crucial data without permission, and consumers frequently need to grasp the importance of this data. Protecting physical infrastructure in smart cities is difficult because of the potential for losing control and experiencing cascade failures. Therefore, the security of this data is critical in smart cities [4].

Therefore, the implementation of smart cities also raises security concerns. The Center for Long-Term Cyber Security at UC-Berkeley released a white paper discussing the cybersecurity threats linked to smart cities technology [5]. Nation-state and Insider Threats are identified as the most dangerous actors in this research, with terrorists and cyber criminals ranking next. Emergency and Security Alert Systems, Street Video Surveillance, and Smart Traffic Lights/Signals are the most susceptible targets that might lead to human casualties and data privacy breaches. Data security issues in the storage, transmission, and computing phases take precedence over the present infrastructure.

Traditionally, Public-Key Infrastructure (PKI) is utilized to ensure data security and integrity. Quantum computers pose a threat to PKI, rendering it unusable in the foreseeable future. Quantum computing is advancing rapidly, with improvements in efficiency, stability, and accessibility while still in its early stages. IBM introduced their initial quantum processor, Tenerife, consisting of five qubits in 2016, and progressed to an Osprey processor in 2022 with 433 qubits. One year after Osprey, IBM introduced the Condor processor in 2023, which utilized 1,121 qubits. New studies and breakthrough claims emerge annually with these advancements. In August 2023, researchers reported successfully breaking RSA-2048 encryption using quantum computing methods [6]. Setting aside the plausibility of these bold assertions, quantum computers are progressing rapidly.

1.1. Introduction of Public Key Infrastructure

PKI is a crucial element of internet security that creates an encryption system to protect and authenticate digital communications based on asymmetric encryption. Contrary to symmetric encryption, where the same key is used, asymmetric encryption uses different keys for encryption and decryption. Asymmetric encryption uses a Public-Private key pair (

K_{p u b}

K_{p r v}

) where a cipher text generated by

K_{p u b}

can be converted to plain text by using

K_{p r v}

and vice-versa. This approach is used on the Internet every day to establish secure connections between servers and clients, helping in key and secret exchanges. For example, PKI is used to issue public keys, secure email messages, encrypt documents, verify user identities, develop secure communication protocols like IKE and SSL, and create mobile signatures. It also supports secure communication protocols like IKE and SSL and is used in mobile signatures and the Universal Metering Interface (UMI) for smart meters and home automation. Even though symmetric cryptography is also used in PKI, asymmetric cryptography makes use of PKI to start. The sender’s identity is authenticated by cryptographic public keys associated with a digital certificate issued by a trusted certificate authority (CA). PKI ensures secure communication between servers and users, such as websites and clients, and inside organizations to ensure that communications are available to both the sender and receiver and stay unchanged during transmission.

A PKI requires cooperation among several entities, including the certification authority (CA), registration authority (RA), deposit certificate, server recovery keys, and the end user. A CA is responsible for issuing, managing, and revoking certificates for end users to verify their validity. There are two types of websites: public and private. An RA serves as a mediator between the user and the CA, authenticating their identity and passing on the certificate request to the CA. The Resident Assistant carries out functions such as Authenticating and Authorizing new user registrations, Generating keys for end users, Approving backup and key recovery requests, and Certificate Revocation requests. After a certificate is issued, it should be stored in a centralized location. X500 deposits are commonly used as deposit certificates, and LDAP is used for managing and distributing certificates. The main function of PKI is to ensure confidence in data communication via the Internet or other electronic channels. Management protocols provide an online exchange of information between users and management within a PKI [7].

1.2. Working of Asymmetric Cryptography

RSA, derived from Rivest-Shamir-Adleman, is a widely used asymmetric encryption method in cybersecurity. It enables users to encrypt conversations using a public key that can only be decrypted with the corresponding private key, ensuring safe communication. The process of RSA can be described as follows:

Generation of Public and Private Key Pair

A user creates a public-private key pair. The public key is distributed to those required to transmit encrypted communications to the user, while the private key is confidential and solely known by the user. The public key is symbolized by a pair of integers (e, n), where n is a big integer resulting from the multiplication of two prime numbers, p and q. If p = 982451653 and q = 899809343, then n = p * q = 884019176415193979. The variable n is used in both the public and private keys; nevertheless, it is essential to safeguard the private key in order to uphold the encryption’s security. The public key is utilized for encrypting messages, while the private key is employed for decoding. These keys enable safe communication over unsecured channels by ensuring that only the designated receiver, who has the private key, may decode messages that are encrypted using the public key.

Encryption

A sender encrypts a message using the recipient’s public key before sending it. Only the person with the associated private key may decode and access the message.

Decryption

The user deciphers the encrypted communication they received using their private key. The message stays safe during transmission because only the user holds the private key.

Key Security

RSA security depends on the challenge of factoring huge numbers. The public key comprises an exponent (e) and a modulus (n), calculated as the result of multiplying two significant prime integers (p and q). The private key comprises an exponent (d) and the same modulus (n).

Potential Vulnerability

The primary weakness of RSA encryption lies in the vulnerability of being able to factor the modulus (n) into its prime factors (p and q) to calculate the private key (d). If an attacker can efficiently factorize the modulus, they can obtain the private key and decode communications meant for the user.

1.3. Introduction to Quantum Computers

1 Richard Feynman, a Nobel Laureate in Physics, explored the capability of computers to accurately replicate physics in his 1982 work titled "Simulating Physics with Computers". This marked the beginning of quantum computers. Quantum computing utilizes subatomic particles to represent application variables or information units, similar to the 0 and 1 states in conventional computing. Consider these phases as interdependent attributes of a unified entity. Quantum theory suggests that subatomic particles have a spinning motion similar to tossed coins, eventually settling into a state of either 0 or 1. You may use quantum mechanical methods to synchronize all the throws at the same time. By interconnecting the activities, you may impact their overall behavior in a distinctive manner that cannot be accomplished by treating them separately. Proficiently manipulating the movement of coins in the air enables quantum computing to exhibit the characteristic of existing in several states simultaneously, leading to the development of creative problem-solving techniques [8].

Quantum computers are extremely powerful compared to conventional computers in many cases (not in all, however). This can be explained when considering a scenario to simulate a single caffeine molecule. Caffeine is a tiny molecule composed of protons, neutrons, and electrons. The molecule’s structure is dictated by the energy configuration and bonds, requiring a significant amount of information for a detailed description. In the case of conventional computers, approximately 108 bits (≈ 11.529 petabytes) are required to store information about a single caffeine molecule [9]. This is equivalent to 1% to 10% of all atoms on Earth. However, a quantum computer of just 160 (perfect) qubits can hold approximately 1.46 × 108 bits during calculations, which is sufficient to store information about the caffeine molecule. Hence, it is impossible to represent the caffeine molecule using a conventional computer fully, and we need more powerful machines like quantum computers for more intensive computations.

2. Background

2.1. Need for Post-Quantum Cryptography

2.1.1. Shor’s Algorithm

Peter Shor, a physicist at Bell Labs, achieved a major advancement in cryptography in 1994 by developing a polynomial-time algorithm for factoring large numbers with the use of a quantum computer. Shor’s approach, a notable advancement, threatens traditional cryptographic systems that rely on the complexity of factoring large numbers for protection. The algorithm’s quick factorization of large numbers garnered attention, highlighting quantum computing’s potential impact on encryption.

It relies on the periodic nature of a mathematical function and by utilizing quantum parallelism, this approach may perform an exponential number of operations in a single step, resulting in a significant reduction in time complexity compared to classical algorithms.

This method calculates the period of the function. A quantum memory register is established, and a superposition of integers representing potential values of a is inserted into the starting segment of the register. The process calculates the result of

x^{a} mod n

for each superposition and stores it in the second part of the register.

It compresses the state into an observed value labeled as k, following the measurement of the second portion of the register. When measured, the initial component of the register collapses into a superposition of basic states that correspond to the observed value. The algorithm can determine the period and factorize n with a high likelihood by performing a discrete Fourier transform on the first segment of the register [10].

Shor’s approach was a significant advancement in quantum computing and posed a potential threat to PKI, the backbone of our digital security. Moreover, after the proposal of Shor’s algorithm, many algorithms have been proposed that either improved upon the original work of Shor or took a new approach as a whole to solve the different mathematical complexities used in conventional cryptography. With gradual improvements in quantum computers and their becoming more and more stable, the threat to PKI is becoming more serious. Hence, there is a need for alternate cryptographic algorithms that could resist attacks from quantum computers, which are now known as Post-Quantum Cryptographic (PQC) algorithms.

2.1.2. NIST’s Post-Quantum Cryptography

In light of the above discussion, NIST called for proposals of different schemes that could resist quantum attacks in 2016. NIST received 69 different “complete and proper” submissions, and after multiple rounds of evaluations, NIST identified four different algorithms in 2022 to be standardized as PQC schemes. NIST recommended implementing two main algorithms for most scenarios: CRYSTALS-KYBER for key setup and CRYSTALS-Dilithium for DigSig. FALCON and SPHINCS+ signature systems were also planned for standardization. In addition, four other key-exchange mechanism (KEM) schemes were moved to the next phase for evaluations, i.e., BIKE, Classic McEliece, HQC, SIKE [11,12].

These algorithms use different mathematical problems for cryptography purposes that can not be solved by quantum computers in practical time (at least as per the latest research). Some examples of PQC types are Code-based encryption (CBE), Lattice-based encryption (LBE), Multivariate-quadratic-equation encryption (MQEE), and Hash-based encryption (HBE). Each of these types uses a different set of mathematical problems to achieve quantum-resistant security.

CBE was first introduced by J. McEliece in 1978. It relies on the complexity of deciphering a random linear code to ensure the security of the cryptosystem and uses a generator matrix as a public key. Due to the complexity of this issue being NP-hard, CBE is considered to be quantum-resistant. These error-correcting codes are in use even today in many systems like quantum computers and satellites. In CBE, the private key consists of a linear code C that can effectively correct t errors. The public key is a transformed form of the linear code designed to obfuscate the secret code and exhibit random behavior. The owner of

C^{'}

may encrypt messages and can also introduce deliberate flaws. An attacker would only perceive a random code and would have to decode it in order to get the message. The secret code owner can effectively decode the encoded message into a codeword of C [13].

LBE creates a ciphertext polynomial by combining two secret polynomials with small coefficients. A lattice point is located in a lattice (L) to decode the ciphertext and determine the secrets. LBEs like NTRU efficiently create the public key using Euclidean techniques.

Multivariate public key cryptography uses systems of multivariate quadratic equations as the public key and as part of the private key. Thus, multivariate public key cryptosystems are multivariate quadratic public key cryptosystems. This approach consists of two different mathematical problems that are considered to be hard for quantum computers. The first problem is known as the MQ problem, where MQ stands for multivariate quadratic. The second problem is known as the Isomorphism of Polynomials problem, sometimes called the IP problem. MQ-based encryption systems rely on the difficulty of solving random instances of the MQ problem and the IP problem to ensure their security [14].

In HBE, in order to generate a key pair, users choose two random strings, x0 and x1, and the public key is derived as (h(x0), h(x1)). Merkle proposed combining 2k public keys into one, which can verify all 2k signatures. This approach reduces the public key size but requires additional information to verify signatures. Merkle’s signatures are considered prime candidates for post-quantum signatures due to their security and efficient hash function computation. XMSS systems are being adopted for Internet protocols but must never reuse a secret key, leading to stateless systems with longer signatures and signature-generation times [15].

One of the promising approaches to quantum-resistant cryptography is lattice-based cryptography. Lattice-based cryptography offers strong security guarantees against quantum attacks and is considered a viable alternative to traditional public-key cryptosystems like RSA and ECC. Additionally, PQC standards are being developed by organizations such as NIST to identify and standardize quantum-resistant algorithms, providing a roadmap for transitioning to secure cryptographic systems in the quantum era.

2.1.3. Threat of Data Harvesting

Even though quantum computers are still in their early stages, we still need to implement quantum-resistant solutions due to tackle the threat of data harvesting. Even though the data transmitted through PKI-based communication is currently secure, there is still a risk that malicious actors could intercept, harvest and store this data in order to decrypt it later when quantum computers become a reality [16]. This threat is particularly concerning for data that remains critical and sensitive for many decades, such as trade secrets and government communications.

2.2. IoT and Post-Quantum Cryptography

PQC algorithms provide a means to safeguard the PKI from potential threats posed by quantum computers but at a cost. Post-quantum schemes need more calculations and bigger key sizes than traditional methods. Dilithium has three security levels (2, 3, and 5). The public key size for its lowest security level is 1312 bytes, and the signature size is 2420 bytes, as opposed to RSA’s 256 bytes for both public key and signature size [17]. Therefore, even at the lowest security level, Dilithium has a public key size that is five times greater and a signature size that is nine times larger.

Although memory sizes may seem small, they become significant when dealing with devices such as ARM Cortex-M4. It may not be feasible to apply greater security levels such as Dilithium 5 owing to limitations in RAM capacity [18]. Several strategies and implementations have been suggested, some of which were previously mentioned, but they have a negative impact on performance. Ideally, IoT devices such as sensors are designed to provide real-time data. Implementing PQC on these devices may jeopardize their main purpose. We compare the key and signature sizes of various PQC and conventional methods in Table 1 since the size of the key or signature has a direct impact on the number of cycles needed to create the value. Therefore, the certificate size of various methods varies greatly. The table also includes a comparison of the certificate size of different methods, which were created using WolfSSL and LibOQS.

Matthias J Kannwischer et al. (2019) [19] assessed the performance of several PQC algorithms on ARM Cortex-M4 processors, as shown in Table 2 and Table 3. Stack memory needed for cryptographic processes may reach up to 70KBs when using Dilithium, posing a substantial memory demand for compact IoT devices. Sphincs provides key and signature sizes similar to traditional schemes, but the CPU operations needed for key generation, signing, and verification are much more compared to Dilithium. Falcon offers an intermediate technique but is not the most optimum option for employing PQC with IoT devices since it has the greatest key generation and verification processing needs compared to the other two stated PQC schemes.

2.3. Problem Statement

IoT devices used in smart cities exchange critically sensitive information. With the rise of quantum computers, the cryptographic schemes used in these devices will become vulnerable, and the sensitive data will be exposed to adversaries. Quantum computing poses a significant threat to traditional cryptography systems, such as RSA and ECC, due to its ability to factor in large numbers rapidly. Peter Shor’s 1994 algorithm, known as Shor’s algorithm, demonstrated quantum computers’ ability to factor large numbers rapidly, causing a need for PQC algorithms. PQC uses quantum parallelism to factor large numbers efficiently, reducing time complexity compared to conventional algorithms. NIST requested ideas for PQC algorithms in 2016, selecting four methods, including CRYSTALS-KYBER for key setup, CRYSTALS-Dilithium for DigSig, and planned standardization for FALCON and SPHINCS+ signature systems. PQC algorithms offer robust security against quantum attacks but face issues like larger key sizes and higher computational costs. Implementing PQC on resource-limited devices like IoT sensors may affect performance and require novel approaches.

Based on the above discussions, we formulate the following problem statement for our research.

“Owing to the substantial key size requirements and computationally intensive nature of PQC schemes, their direct deployment on IoT devices within smart city architecture is impeded by inherent computational and storage limitations. Consequently, it is imperative to devise PQC-based, resource-efficient authentication protocols tailored to IoT devices operating within smart cities.”

3. Literature Review

Saif E. Nouma and Attila A. Yavuz have addressed the issue of integrating PQC with IoT devices by proposing a “Hardware-Supported Efficient Signature” DigSig scheme. It was implemented and evaluated on an 8-bit AVR ATmega2560 microcontroller, and their results show that it was 271 times faster than (forward-secure) eXtended Merkle Signature Scheme and 34 times faster than (plain) Dilithium [20].

Michael Scott has conducted a very useful experiment [21] on implementation and evaluation of TLS coupled with PQC algorithms by developing an open source and custom TLS1.3 implementation. Scott used Arduino Nano RP2040 Connect with 264kb of SRAM and up to 16MB of flash memory and TinyPICO with 4MB of flash memory and up to 4MB of SRAM. This paper also suggested using Pairing-based IBE (Identity-Based encryption) in the context of TLS as an alternative to PKI.

Ajay Kaushik et al. [22] have developed a lightweight post-quantum symmetric and asymmetric scheme which, when compared with algorithms like LWE, LIZARD, and NTRU, is claimed to be 70 times faster and 6000 times less memory consuming. Similarly, Gandeva Bayu Satrya, Yosafat Marselino Agus, and Adel Ben Mnaoue [23] developed and evaluated customized implementations of RSA, NTRU, and Saber for lightweight PQC security.

Figure 1. PQC DigSig comparison by [24].

Figure 2. PQC Key-Exchange Methods comparison by [24].

Juliet Samandari and Clementine Gritti [25] Used CRYSTALS-Dilithium to provide post-quantum security to MQTT traffic and evaluated CPU, memory, and disk usage. They also evaluated a KEM approach proposed by Peter Schwabe, Douglas Stebila, and Thom Wiggers [26] for TLS and CRYSTALS-KYBER for 71% faster authentication.

Callum McLoughlin, Clementine Gritti, and Juliet Samandar [27] also implemented and evaluated using PQC schemes with DTLS in IoT. Their results on a Raspberry Pi 4B model show that PQC actually has low CPU usage yet requires an extra 800KB of memory for 100 devices, and a single connection establishment uses up to 6 times more packets. Another work [28] proposes a lightweight, strong post-quantum lattice-based hybrid encryption method for IoT devices with limited resources. The Ring-Learning with Errors (Ring-LWE) method uses Bernstein reconstruction in polynomial multiplication for the lowest computing cost. This method provides location and identity privacy indefinitely, making signature creation and verification efficient. The post-quantum hybrid code-based encryption technique uses SLDSPA and QC-LDPC Codes for minimal hardware requirements.

Another study by Malina et al. [29] explores PQC’s feasibility in small, constrained devices like mobile and IoT networks. Experimental implementations are presented and compared on different platforms. Lattice-based schemes like New Hope and NTRU are promising due to their efficiency and reasonable key lengths. These schemes can run on 32-bit architecture and Android OS mobile devices. However, the study only considers specific post-quantum cryptographic algorithms and does not consider hardware acceleration costs or software optimization.

A paper by Tasopoulos et al. [30] discusses how TLS 1.3 can be made quantum-safe by modifying its architecture to accommodate the latest PQC algorithms. It evaluates the execution time, memory, and bandwidth requirements of this post-quantum variant. The study reveals that Dil2-Hqc1 and Dil2-Bike1 consume more memory than Dil2-Kyb1, indicating potential performance differences for other embedded systems.

A study by Sikeridis, D., Kampanakis, P., & Devetsikiotis, M. evaluates [31] NIST signature algorithm candidates, examining latency on TLS 1.3 connection establishment and their impact on TLS session throughput. Two PQ signature algorithms could be viable with minimal overhead, and many NIST PQ candidates can be used for less time-sensitive applications. The study also discusses the integration of PQ authentication in encrypted tunneling protocols and its challenges, improvements, and alternatives.

Gonzalez, R., & Wiggers compared KEMTLS against TLS 1.3 in an embedded environment. They concluded that KEMTLS may decrease handshake duration by up to 38%, minimize peak memory use, and save data traffic compared to TLS 1.3. The research needs to address the security aspects of the KEMTLS and post-quantum TLS implementations. Their implementations may be susceptible to attack [32].

Campos et al. offered two versions of Commutative Supersingular Isogeny Diffie–Hellman (CSIDH) protocol [33]: one focused on strong security against physical assaults using Sublinear Vélu Quantum-resistant isogeny Action with Low Exponents (SQALE) and another designed for speed and bigger parameter values based on CTIDH (Constant Time CSIDH). dCSIDH is about twice as fast as SQALE, whereas CTIDH, without determinism, is three times faster than dCSIDH at these specific values. This research does not assess the efficacy of PQC Transport Layer Security on IoT devices.

Figure 3. PQC Schemes Memory usage comparison by [34].

A study by Paul, S. [24] introduces and assesses three innovative incorporations of PQC into the industrial communication standard Open Platform Communications Unified Architecture (OPC UA): Hybrid-KEX OPC UA, Hybrid OPC UA, and PQ OPC UA. If the ICA certificate is included, the size of the OSC Request and OSC Response message typically rises by a factor of 7.5. The lowest increase in certificate size is seen at security level 1 when adding a Falcon512 public key and signature, resulting in a 2.8-fold increase. This study only includes some of the NIST finalists in formulating the findings.

Kern et al. introduced QuantumCharge [35], a PQC extension for ISO 15118, including ideas for transition, cryptographic flexibility, provable security, and the use of PQC-enabled hardware security modules. Both versions of ISO 15118 demand an increase in the maximum certificate size for all PQC techniques, ensuring that they can all fulfill the specified time criteria. All PQC signature algorithms Dilithium, FALCON, and SPHINCS+ with fast f-parameter settings chosen by NIST for standardization are applicable in QuantumCharge.The research needs to take into account lower-powered IoT devices, and the conclusions are based on an examination of a limited selection of relatively high-powered IoT devices.

Scott, M. [21] developed and utilized a novel version of TLS1.3 to investigate the effects of transitioning to post-quantum security, suggesting a TLS implementation that incorporates identity-based encryption. They showed that the NanoRP2040 requires 584 ms for an optimized ECC full TLS handshake and 251 ms for a resumption handshake without client authentication. A Post-Quantum complete handshake requires 771 milliseconds, whereas a resumption takes 512 milliseconds. This article has developed a custom implementation of TLS1.3, making it non-standardized and unsuitable for conversion to a production environment.

Another research by Septien-Hernandez et al. focuses on analyzing post-quantum cryptosystems for compatibility with IoT devices, integrating them with existing cryptography and communication software, and evaluating their performance to provide recommendations for selecting the most suitable system for various applications on hardware with limited resources [34]. Kyber512 is the top performer with a total time of 204 ms, followed by LightSaber with 255 ms. NTRUhps2048509 outperforms NTRULPr and FrodoKEM640 in encapsulation and decapsulation. However, in overall use, both NTRULPr653 and FrodoKEM640 perform better than NTRUhps2048509. Kyber512 and LightSaber have the best performance in terms of execution time. This research does not assess all NIST finalists for computing results. It only examines a small number of IoT devices. Furthermore, the authentication process for IoT devices needs to be clearly specified.

Chung et al. assessed the efficiency of PQC algorithms on IoT devices [36]. As per their conclusion, Kyber, NTRU, NTRU Prime, and SABER are more appropriate for IoT systems since they surpass the traditional performance approach. Kyber saw a 12.3% decrease in TLS latency, NTRU saw a 5.7% drop, NTRU Prime saw a 10.1% reduction, and SABER had a 5.8% reduction. This article focuses only on time as the assessment criteria and does not address computational overhead or security-related issues.

Another research [37] presents an assessment methodology for PQC on limited devices and enhances the field by offering performance metrics of the leading algorithms on a widely used single-board low-power device. It presents a collection of five principles that may be used to assess the robustness of certain algorithms. Saber has a moderate key size and operates in less than a millisecond. On the contrary, SIKE has a decent key size but takes over 3 seconds for encapsulating or decapsulating. This article assesses the schemes on a single IoT device, which may not provide a reliable outcome. Additionally, it does not take into account the NIST PQC finalist methods.

Figure 4. PQC Algorithms comparison by [38].

Research work from Liu, Z., Choo, K. K. R., & Grossschadl, J. examines the appropriateness of lattice-based cryptosystems for devices with limited resources and presents efficient implementations for eight and 32-bit microcontrollers [39]. The encryption process on the ATmega12841 microcontroller is quicker than on the ARM Cortex-M4F microcontroller; however, the security level of the ATmega12841 implementation is worse. The key exchange mechanism on the ATmega128A1 microcontroller provides just 120 bits of security, which needs to be improved. This study does not address the authentication protocols for IoT devices and their performance on used IoT devices.

A method for task management is suggested by Karakaya, A., & Akleylek, S. [40], using a priority queue and adjusting the list of fog nodes inside the fog layer. FLAT provides authentication and data confidentiality while ensuring integrity using the SDN controller based on blockchain. The suggested algorithm’s execution time is 80.93 ms, representing a 37.5% improvement over the comparable work’s execution time of 124 ms. The suggested algorithm’s total network consumption is 385 KB, representing a 42.6% reduction compared to the comparable work’s total network usage of 647 KB. The suggested approach reduces the application loop delay time to 17.71 ms, which is a 98.4% decrease compared to the previous work’s application loop delay time of 718.92 ms. The suggested algorithm’s cloud execution cost is $4.23, representing a 67.1% reduction compared to the comparable work’s cloud execution cost. This work does not explore the implementation of PQC techniques in fog computing settings.

A proposal [41] from Roy, K. S., Deb, S., & Kalita, H. K. suggests a lightweight authentication protocol for granting access to devices. It also includes a fail-safe method in case the authenticating server fails, allowing IoT devices to self-organize and continue delivering services without human involvement. When examining several public-key cryptosystems such as NTRU, Ring-LWE, Niedderieter, RSA-1024, and ECC, it was discovered that NTRU, Ring-LWE, and Niedderieter are more efficient than RSA and ECC in terms of execution time, with Ring-LWE being the most superior among them. This article does not assess NIST PQC finalists systems for authentication. The suggested approach has yet to be tested on low-power microcontrollers.

Moreover, Seyhan et al. suggested a sensitive categorization by upgrading the limited resource classification of IETF [42]. Using the suggested classification and efficiency definition, the employment of lattice-based cryptosystems in IoT device security is investigated. The LP-LWE method is considered an efficient and usable cryptosystem in the post-quantum future for IoT. NTRUEnc is considered to be efficient for most IoT devices by using strategies that enable the time spent in the key generation to be decreased. This research does not tackle the security risks associated with IoT devices in a post-quantum era. Also, it does not assess the NIST PQC finalist candidates.

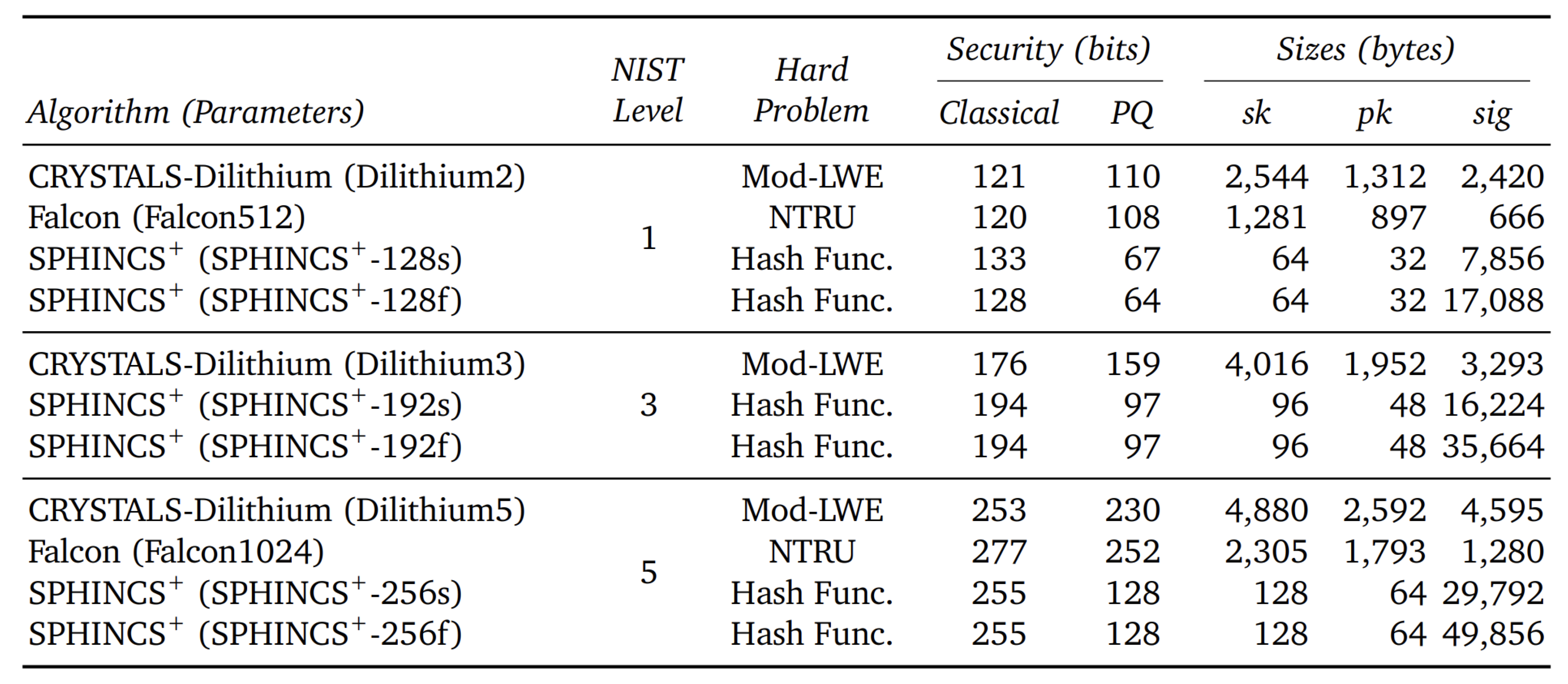
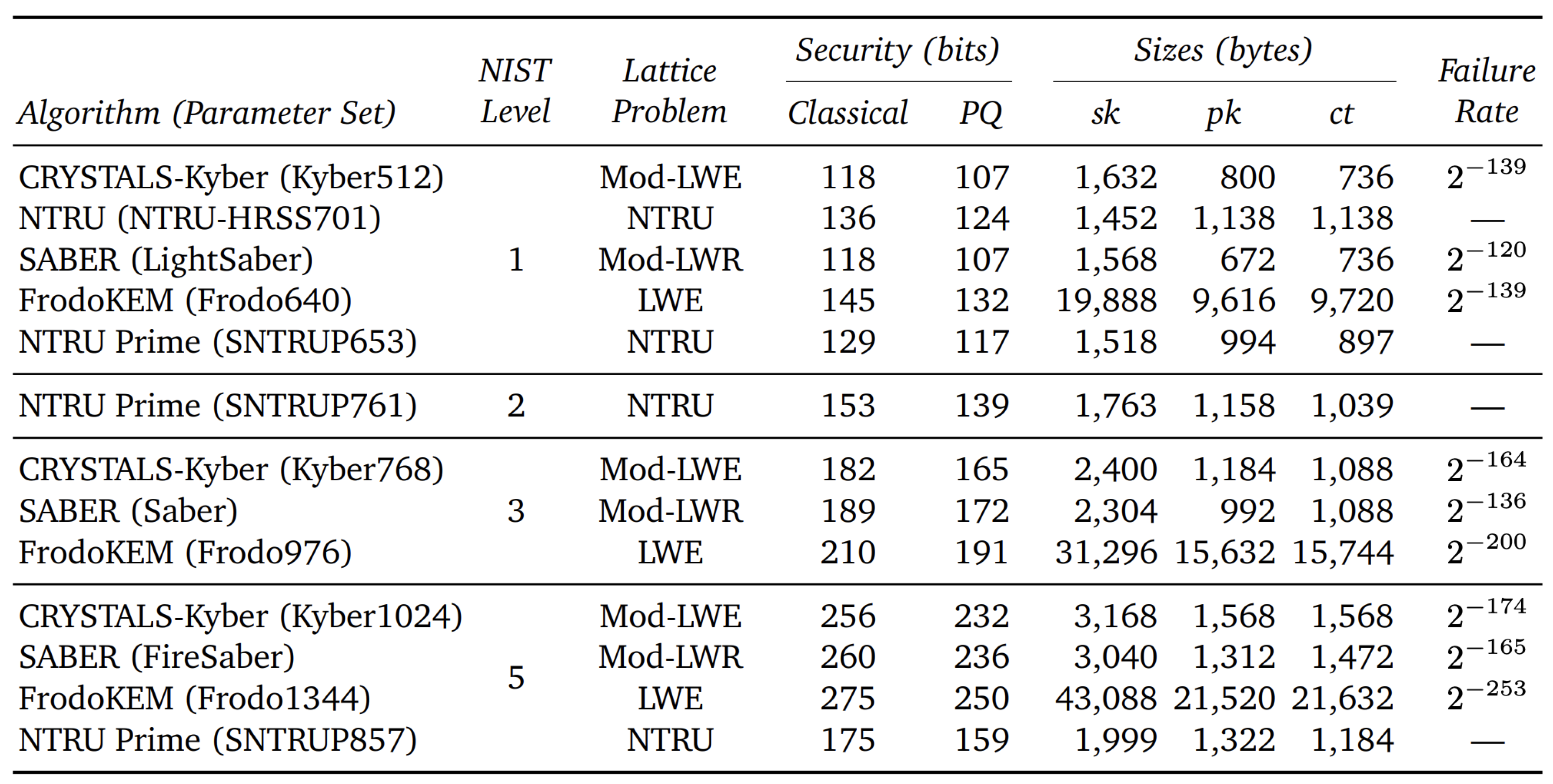
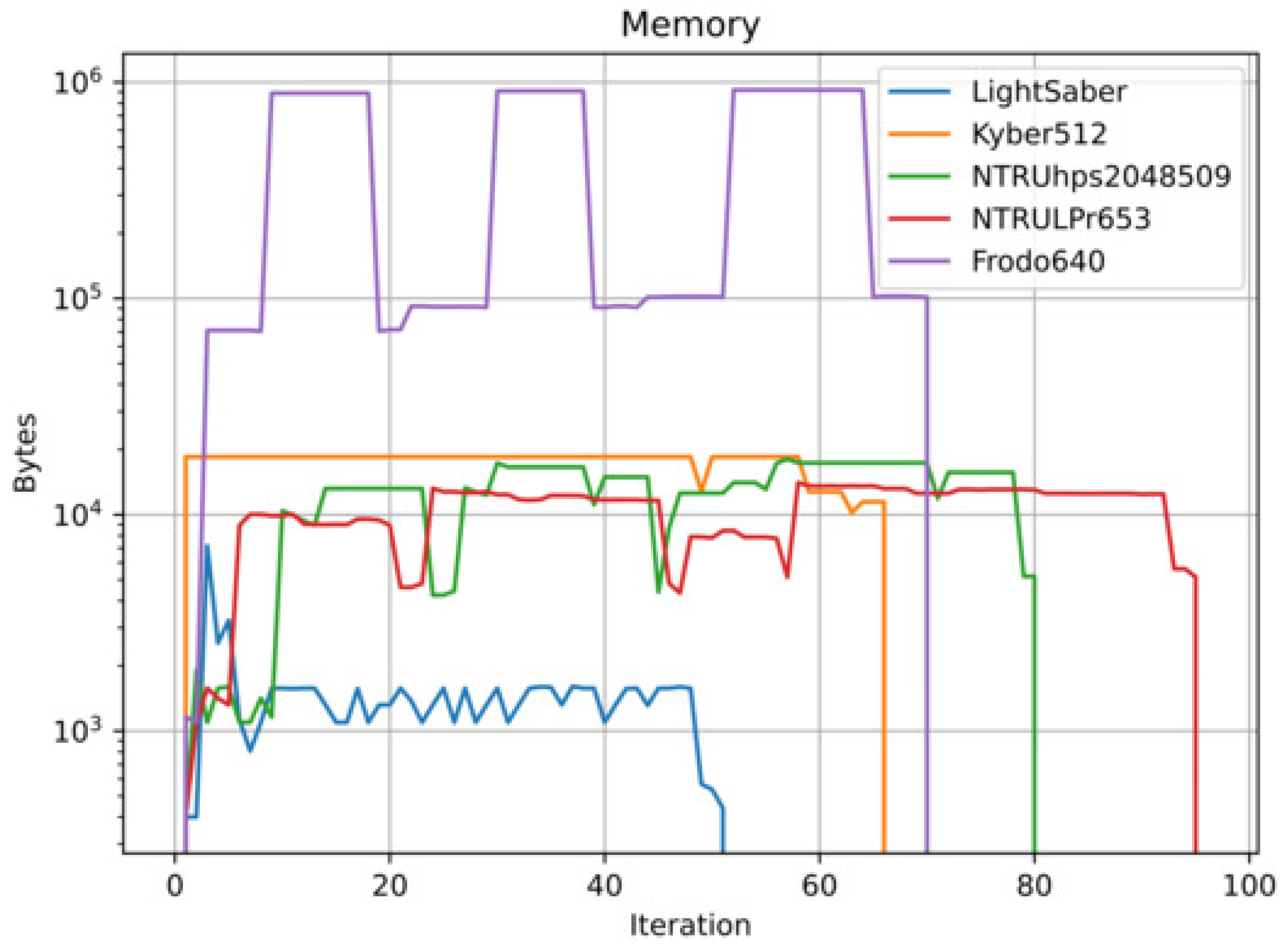
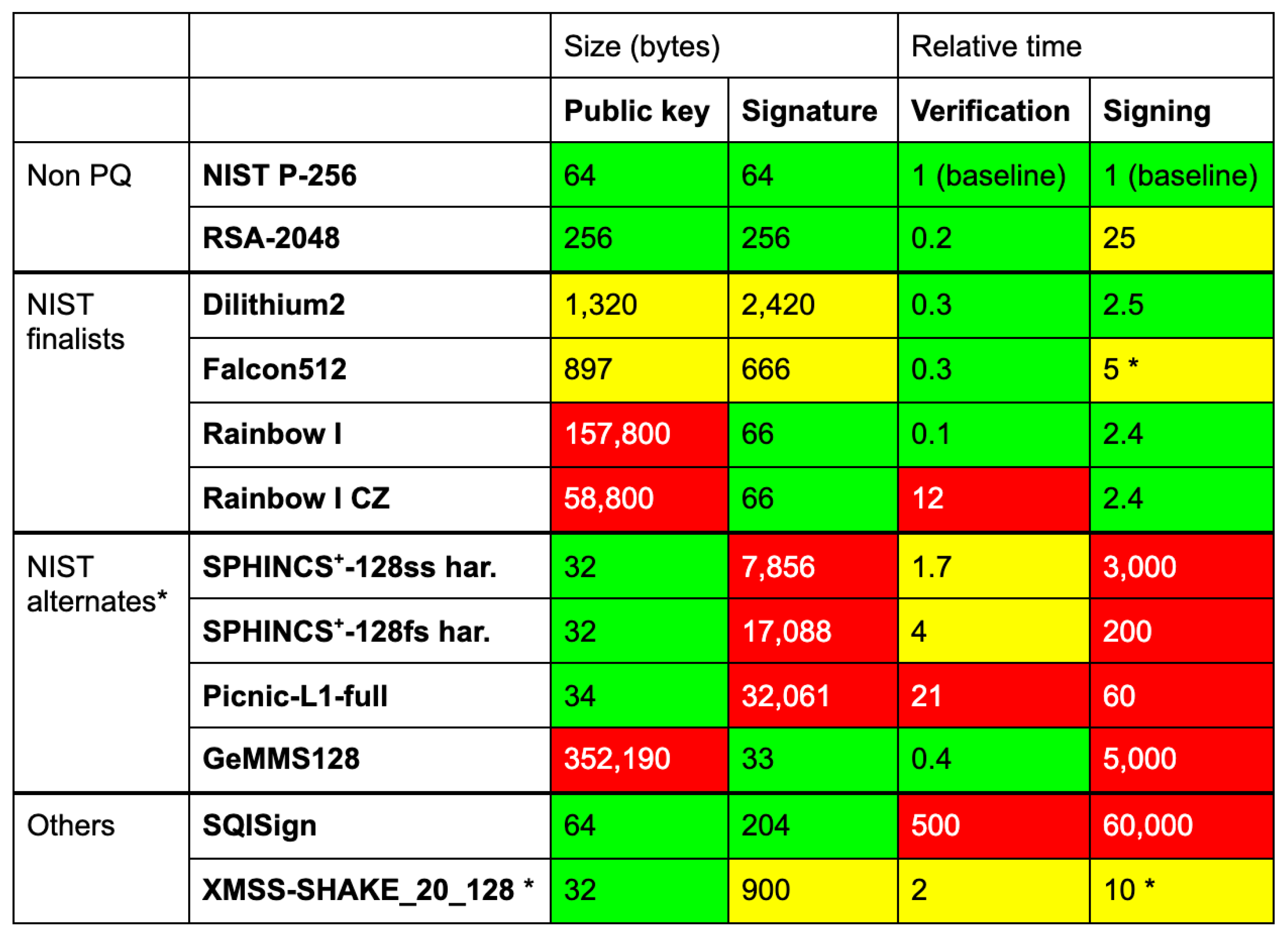
4. Proposed System

4.1. Current Smart Cities Infrastructure

Although there is no standardized architecture for smart cities, a generalized infrastructure has been described by K. Zhang et al. [43]. The smart city uses data from physical, communication, and digital realms to provide intelligent services for efficient city management. The system comprises sensor components, a varied network architecture, computing units, and control and operational components.

Sensing components use wearable devices, industrial sensors, cellphones, smart meters, and video security cameras to collect data from the physical environment and transmit it to the processing unit for analysis. Sensing components act as the bridge between the physical and information domains. Government agencies, departments, corporations, or consumers employ the sensing devices. Due to limitations in device size, battery, and processing capability, resource-constrained sensing devices often preprocess or compress real-time and detailed data before sending it to the network.

Figure 5. Conventional Smart City Architecure.

Heterogeneous networks are essential for facilitating smart cities by gathering sensory data from many devices and applications via various methods. They integrate several types of networks, including cellular networks, wireless local area networks (WLANs), wide area networks (WANs), device-to-device (D2D) communications, millimeter-wave communications, and sensor networks. They provide seamless transitions between various network types. Heterogeneous networks facilitate communication in smart cities by connecting the physical and information domains.

The processing unit uses cloud computing servers, databases, and control systems to analyze and understand sensory inputs from the physical world to make decisions. The processing unit manages data activities in a smart city. Authorized entities, including government agencies, hospitals, companies, and users, possess certain rights and permissions to access the collected data. They may set the criteria or rules for decision-making and oversight in a smart city. A smart city uses the processing unit to make optimal decisions and regulate the physical environment using components such as servo actuators or smartphones. The control and operational components improve and adjust the physical environment to increase the quality of life in a smart city. The smart city infrastructure incorporates bidirectional data transfer for sensing and control activities. His bidirectional connectivity allows him to collect data on the physical environment and monitor all equipment in a smart city to guarantee optimal and intelligent operation.

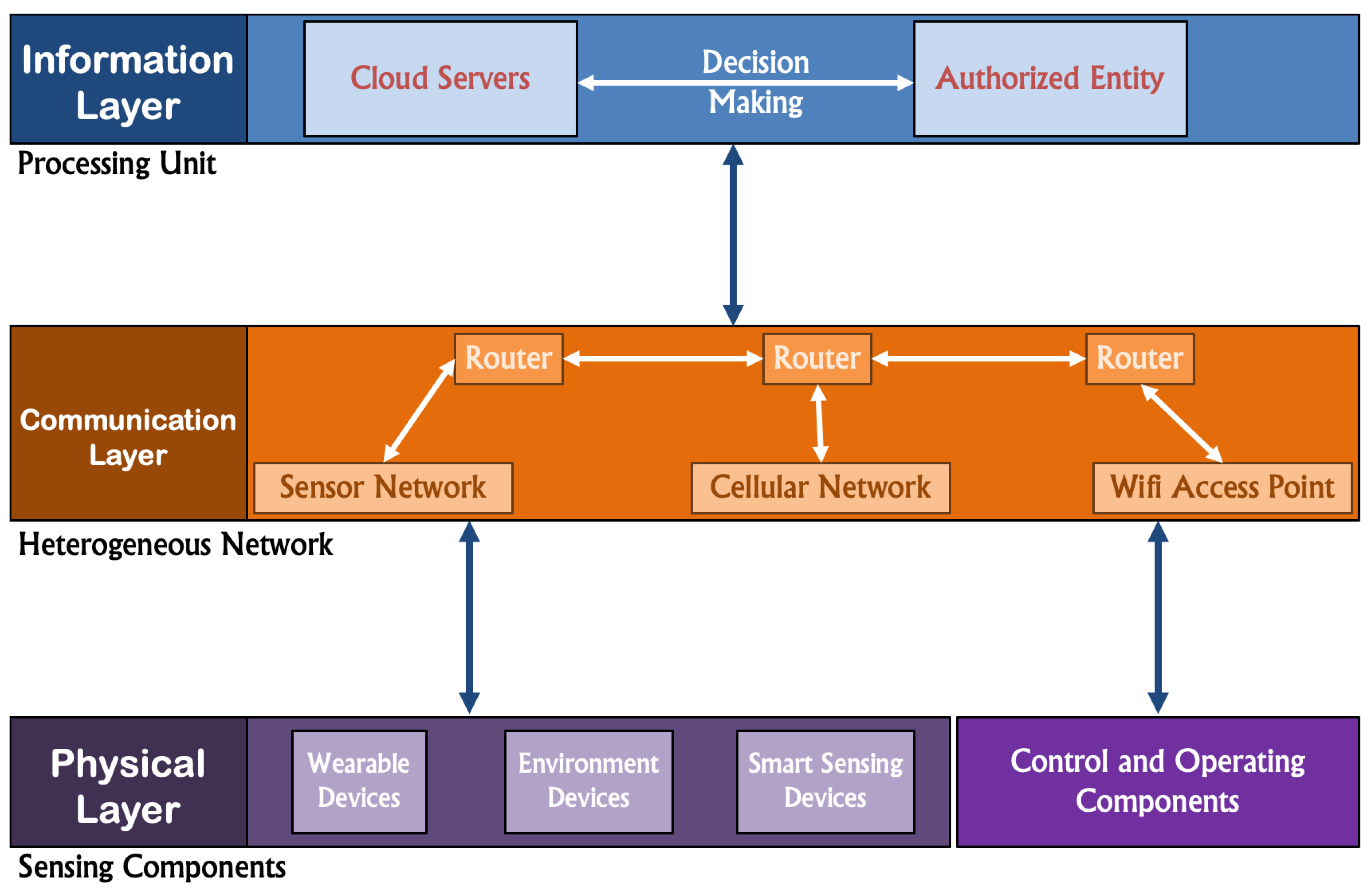
4.2. Issues with the IoT in Smart Cities

There are several vulnerabilities in a smart city infrastructure as well as the end devices, the IoT devices, that form the base of this infrastructure. For example, the IoT links RFID and sensor devices to the internet, but many need more resources and robust security measures. Inadequate encryption is another issue in smart city programs, as many IoT devices cannot maintain secure encrypted connections, making them vulnerable to attacks. Integration layer communication technologies like RFID, NFC, Bluetooth, BLE, ZigBee, 6LoWPAN, WiFi, LPWAN, 3G, and 4G mobile technologies have security weaknesses that render them vulnerable to being hijacked [44].

Cloud systems face security challenges such as outsourcing, multi-tenancy, and processing large amounts of data that require significant computational power. Outsourcing necessitates remote access, leading to less control over data and potential security vulnerabilities. Multi-tenancy allows multiple users to access and use the cloud platform, but it presents security risks due to heavy communication or computation overhead.

With the continuous progress in quantum computer research and their becoming more and more stable, these issues have become more aggravated in an already fragile security environment of IoT devices. As stated in Section 1.1, as per studies, 80% of devices utilize basic passwords, 70% employ unencrypted network services, and 60% possess security weaknesses. Even though all of these devices used encrypted network services, they are still vulnerable to quantum computers, even today, due to the threat of data harvesting attacks and PKI’s vulnerability to these computers.

Even though NIST is in the process of standardizing PQC algorithms to ensure the security of PKI against IoT devices, the algorithms can not be efficiently implemented on these devices, as discussed in Section 2.2. Hence, there is a gap between the possibilities and practicality of using PQC schemes in an IoT-based smart city infrastructure.

4.3. Proposed Solution

The reasoning above makes it evident that even when it is feasible, there are better courses of action than using PQC on IoT devices. Instead, we must take a different approach. As seen before, an IoT infrastructure typically has three layers: Physical, Communication, and Information [43]. Our research proposes a new method that utilizes edge computing architecture by including a PQ layer between the physical and communication layers. In this setup, an edge server is the main entity responsible for the cryptographic commitments for PQC activities. The proposed post-quantum edge server (PQES) acts as a middleware between the network router and other devices in the network. It translates between PQC and traditional cryptography, similar to how the router translates between private and public IP addresses via NAT.

The proposed approach offloads all storage and computing tasks from IoT devices in a network to maintain their regular functioning and performance without any compromise. PQES creates an individual PQ key pair for each network device and manages a unique stream for each device. The proposed system focuses on securing internal network traffic and does not consider internal network security, addressing data security outside the network instead. The proposed approach transfers all storage and processing responsibilities from IoT devices in a network to ensure their primary operation and optimal performance without any additional commitments. Our PQES generates a distinct PQ key pair for every network device and oversees a separate stream for each device.

Figure 6. Proposed Architecture.

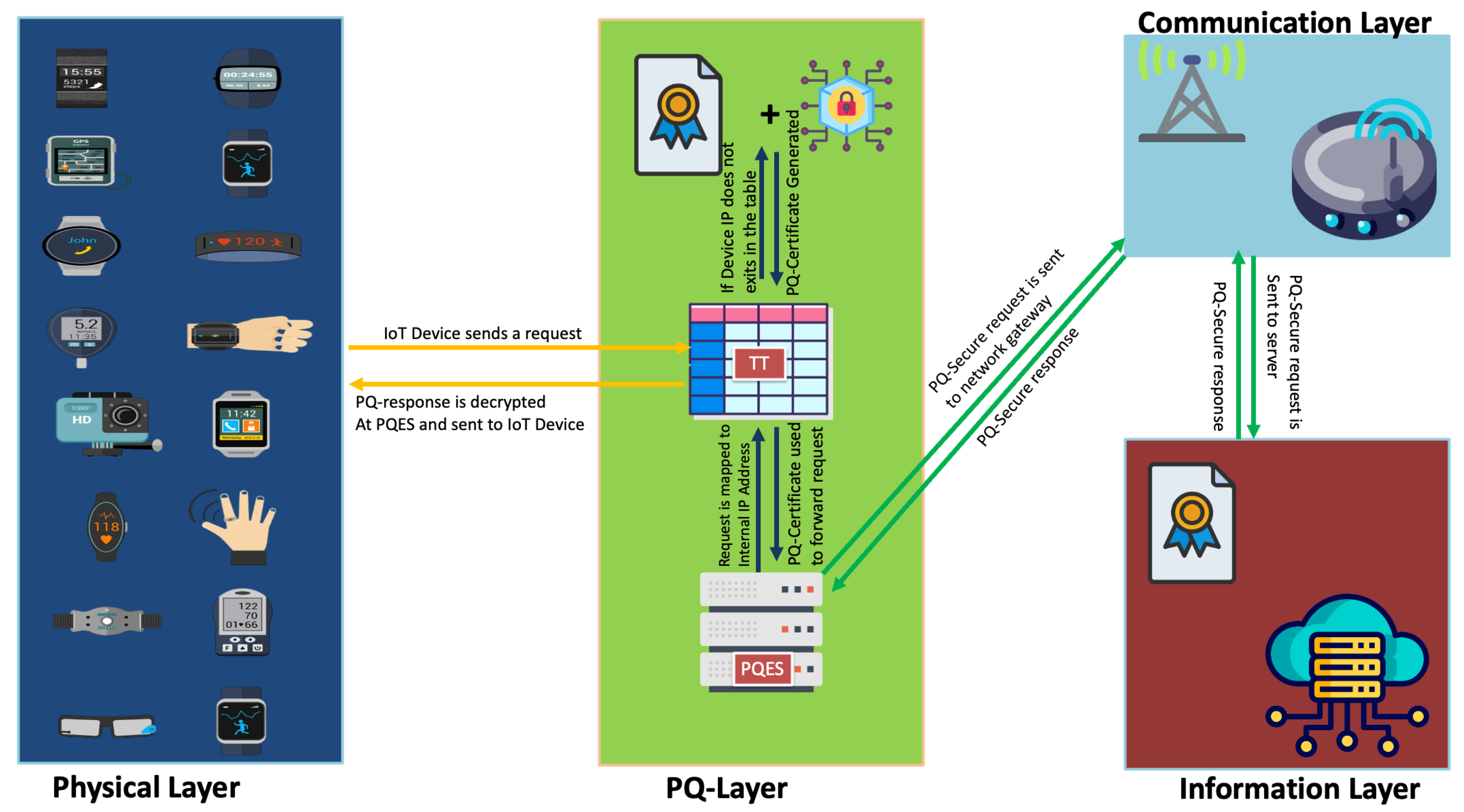
4.4. Implications of Proposed System on Smart Cities

The proposed scheme has important implications for different components of smart city architecture. The proposed solution provides quantum-resistant security for e-health data by transferring PQC procedures from sensors and devices to the PQES; hence optimizing performance of low-powered e-health devices and allowing for the implementation of PQC algorithms on devices with varying architectures and specifications.

Similarly, smart homes use networked technologies to automate operations and improve security but are susceptible to cyber-attacks. Our proposed system ensures the security and privacy of smart home data by transferring PQC-related functions to the PQES. This improves the effectiveness of smart home sensors and devices with quantum-resistant security and secures the private information exchanged between smart home devices and cloud services.

Moreover, smart grids use digital technologies to control power production, transmission, and usage, ensuring data integrity and security. This communication very critical and is often targeted by sophisticated cyber attacks and needs to be secure. In the same context, urban mobility systems rely on networked devices and data for efficient control. The proposed method improves the security and efficiency of urban transportation networks by transferring PQC-related processes to the PQES.

Hence, our proposed system has important implications for smart cities, which can be categorized as below.

4.4.1. Efficiency and Performance

Our proposed approach improves the efficiency and performance of IoT devices in smart cities. Centralizing cryptographic activities on the PQES allows these devices to function without the additional burden of conventional cryptography, resulting in enhanced responsiveness and overall performance. Real-time data processing is crucial in industries such as transportation for regulating traffic flow and enhancing public transportation networks.

4.4.2. Scalability and Interoperability

We address the challenge of implementing PQC algorithms on devices with heterogeneous architectures and specifications. The PQES offers a centralized solution that guarantees scalability and interoperability across smart city infrastructure. Efficient communication and cooperation among various IoT devices are crucial in industries such as energy management to enhance energy use and minimize wastage.

4.4.3. Security and Future-Readiness

Implementing my proposed approach could improve the security level of smart cities and help them be ready for the advancements in quantum computing. As quantum computers advance, conventional encryption techniques will be at risk. My proposed solution takes a proactive approach on security by offering quantum-resistant technologies, such as the the proposed PQES, to ensure that smart cities are ready for new attacks.

4.5. Proposed System Algorithm

My proposed algorithm (as shown in Algorithm 1) follows the preceding procedure. The first step is to establish a network-level proxy server, then setting it up with Post-Quantum algorithms and a translation table (TT). The proxy server, called PQES, then listens for incoming requests. PQES verifies whether the incoming IP (DV Ci) is present in the TT upon receiving a request. If DV Ci is not present in TT, the proposed PQES creates a new PQ certificate for the incoming IP and then adds an entry for it in TT. However, If DV Ci is already present in TT, PQES will get the corresponding PQ certificate.

The PQES establishes a connection with the destination server (DS) using the PQ certificate for DV Ci and then forwards the request to the DS. PQES decrypts the response from the DS and forwards the decrypted response to DV Ci. This approach guarantees safe communication between the client and the server by using PQ algorithms for encryption and decryption.

Initialization

Set up the proposed network-level proxy server.
Setup the proposed PQES with a TT.

Listening for Requests

The PQES listens for incoming requests.

Processing Incoming Requests

The PQES checks if the incoming IP $D V C_{i}$ exists in TT.
If $D V C_{i}$ does not exist in TT, PQES generates a new PQ certificate for incoming IP and adds an entry for the respective TT.
If $D V C_{i}$ exists in TT, then PQES reads the respective PQ certificate.

Establishing Connection

PQES creates a connection with the destination server using PQ-certificate for $D V C_{i}$ .

Forwarding Request

PQES forwards the request to the destination server.

Receiving and Decrypting Response

PQES receives the response from the destination server and decrypts the response.

Sending Decrypted Response

PQES sends the decrypted response to $D V C_{i}$ .

5. System Implementation

The proposed architecture, a significant step forward in the field of IoT and cryptography, was validated and implemented through a robust proof-of-concept (PoC) developed in Golang, SvelteJS, and C++. The PoC, a Raspberry Pi Model B with 1GB RAM and a 1.5 GHz Processor, was equipped with a TCP client written in GoLang and a front-end created using SvelteJS and Wails. It was connected to a DS18B20 body temperature sensor and a Max30100 Heart Rate and Oxygen Saturation sensor for data transmission. A PQ TCP server on WSL written in C language was set up on an Intel Core-i5 CPU with 8GB RAM. PQ certificates were created using Lib-OQS+WolfSSL.

We evaluated Dilithium DigSig level 2,3,5 with the Kyber key-exchange method level 1,3,5 by sending 1000 transactions with 1KB payload each over a TCP connection. This setup was implemented using both conventional and proposed approaches and final results were compiled and compared for both approaches.

5.1. Algorithms Evaluated

I used permuatations of different security levels, such as Dilithium for DigSig and Kyber for key exchange. I used WolfSSL and LibOQS to generate certificates for these algorithms. The following combinations were evaluated for both conventional on-device and our proposed offloading approach.

Dilithium Level 2 with Kyber Level 1.
Dilithium Level 2 with Kyber Level 3.
Dilithium Level 2 with Kyber Level 5.
Dilithium Level 3 with Kyber Level 1.
Dilithium Level 3 with Kyber Level 3.
Dilithium Level 3 with Kyber Level 5.
Dilithium Level 5 with Kyber Level 1.
Dilithium Level 5 with Kyber Level 3.
Dilithium Level 5 with Kyber Level 5.

5.2. Implementation Details

The PoC consisted of the following components.

A Raspberry-Pi Model-B with 1GB RAM and 1.5 GHz Processor to act as the end IoT device running a TCP client programmed in GoLang with a front-end developed using SvelteJS and Wails.
This Raspberry Pi is connected with a DS18B20 body temperature sensor and Max30100 Heart Rate and Oxygen Saturation sensor to generate and send data to a remote server.
Another Raspberry Pi Model-B with 1GB RAM and 1.5 GHz Processor to act the PQES.
An Intel Core-i5 2.60 GHz processor with 8GB RAM running a PQ TCP server on WSL programmed in C language.
PQES is a combination of a PQ-TCP server and a PQ-TCP client where the earlier interacts with the end IoT device and later interacts with the WSL PQ-TCP server. Both components of PQES were programmed in C language.
LibOQS+WolfSSL generated the PQ certificates generated and used in these settings.

Evaluation Metrics

In order to evaluate the results of the proposed scheme, the following metrics were used for both the conventional on-device implementation approach and the proposed PQES approach.

Percentage of CPU used by each algorithm.
Number of CPU context switches performed.
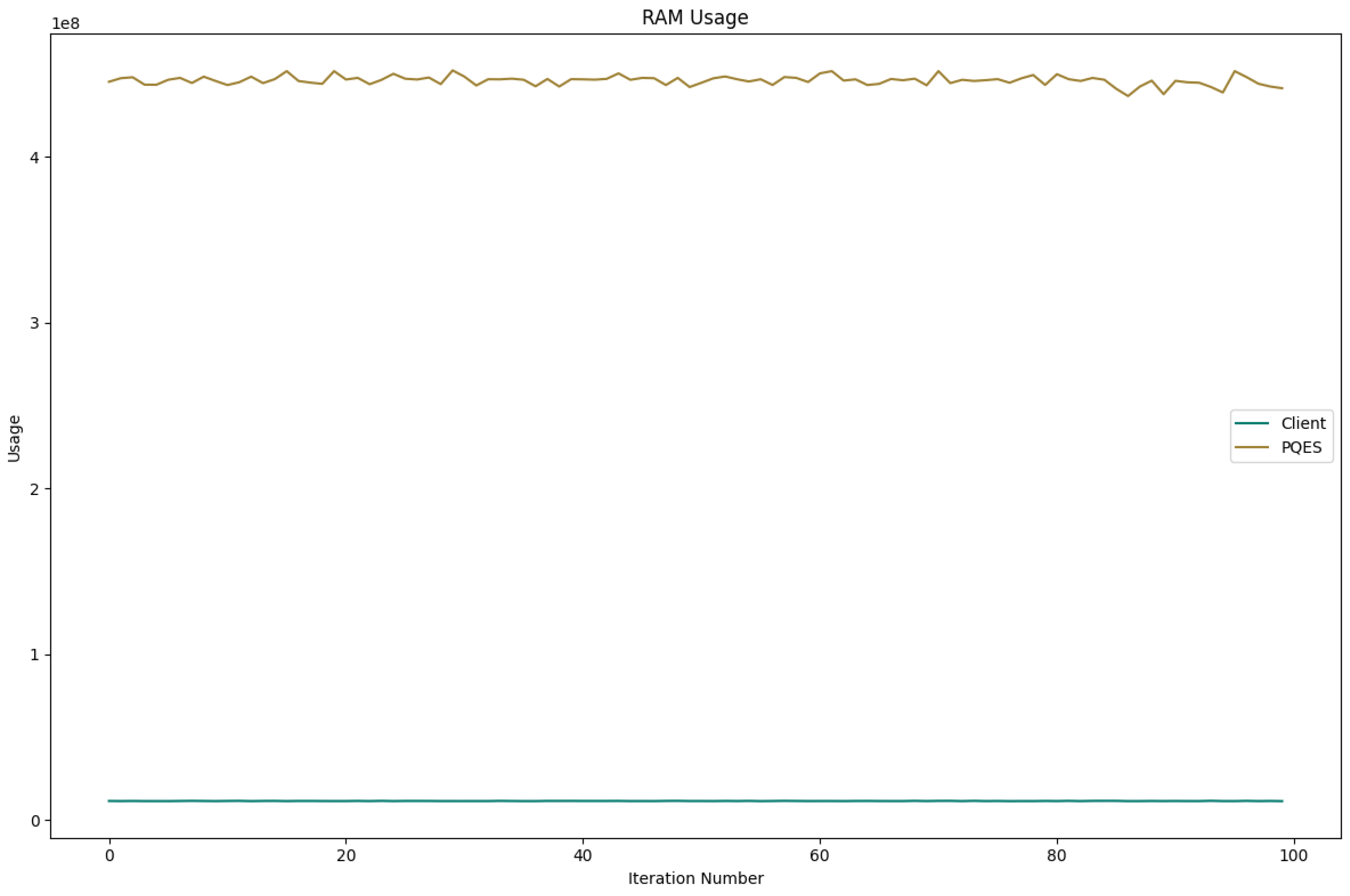
RAM (in MBs) used during each test run.
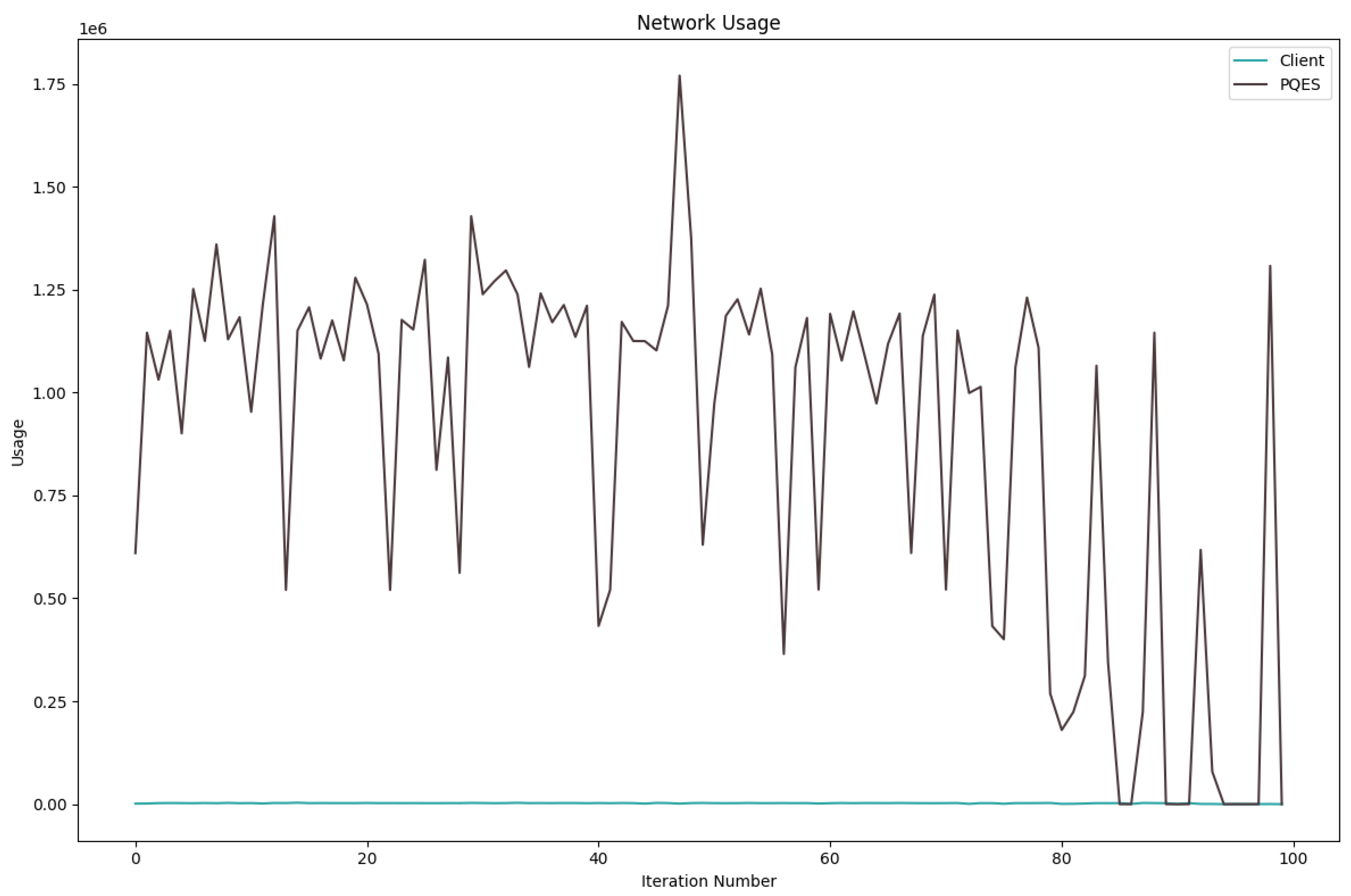
Network used (in Bytes) to perform each transaction between client-server by using the respective algorithm.

6. Results

6.1. Proposed System Results

We experimented with Dilithium as our DigSig scheme and Kyber as the KEM algorithm. We simulated establishing 1000 connections within a maximum of 5 seconds and observed the CPU, RAM, and Network usage of both implementations. Our results show that our proposed offloading scheme reduces the computational, network, and storage requirement manifolds on the end device when compared to the conventional on-device implementation approach. Our scheme reduces the RAM usage as low as 1.05 KB, with 13.4 MB being the maximum. Compared to this, the conventional implementation in this experimental setup takes a minimum of 5.1 MB RAM with just one concurrent connection. It can take up to 552.6 MB RAM with 1000 concurrent connections. Similarly, the maximum CPU usage is 1.75% for the proposed scheme as compared to 67.1%. The maximum CPU context switches for the proposed system are 92.8, while for the conventional schemes, they are 3449. Moreover, as we can see in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 where data is sorted by descending order, the computational load is somewhat consistent throughout the experiment with the proposed scheme, whereas that for the conventional scheme is increased with increase in number of connections.

Table 4. Average Matrices for PR(Proposed Offloading Architecture) vs CN (Conventional On-Device Architecture)

Algorithm	Architecture	CPU % Usage	CPU Context Switch	RAM MB Usage	Network Bytes Transferred
Dilithium2_Kyber1	CN	49.715	1858.55	435.33	600589.750
	PR	1.380	49.84	10.14	2150.78
Dilithium2_Kyber3	CN	52.738	1904.85	437.22	754461.1
	PR	1.375	45.70	10.22	1689.14
Dilithium2_Kyber5	CN	46.95	1841.8	438.96	616428.78
	PR	1.14	42.70	10.53	1254.59
Dilithium3_Kyber1	CN	52.39	1838.6	438.99	667720.73
	PR	1.31	50.54	11.55	1655.54
Dilithium3_Kyber3	CN	58.26	2131.52	440.61	962430.88
	PR	1.33	39.30	9.92	1733.32
Dilithium3_Kyber5	CN	52.63	1799.74	441.75	718451.23
	PR	1.43	51.79	10.31	1946.38
Dilithium5_Kyber1	CN	60.05	2096.56	444.79	1050030.4
	PR	1.49	52.05	11.34	2244.16
Dilithium5_Kyber3	CN	51.66	1824.91	443.31	592386.83
	PR	1.36	47.81	11.31	1592.71
Dilithium5_Kyber5	CN	57.97	2085.27	445.85	893928.28
	PR	1.50	52.29	11.38	2288.23

Moreover, the proposed scheme uses TCP, a transport layer protocol, instead of using any application-level protocol like HTTP or MQTT. Hence, any lightweight end device can be used with our scheme without having to implement any application-level protocol. The PQES can handle the application-level protocol, hence making our scheme applicable to a range of IoT devices. We benchmarked our proposed scheme by implementing the TCP client on end-device and HTTP protocol on PQES with the same parameters. Our results show that with the described setting, the PQES can handle 1000 concurrent connections while using a maximum of 73.5% of RAM on a Raspberry Pi with the specifications mentioned earlier.

6.2. Evaluation Metrics Results

In the section below, we discuss data for each evaluation metric individually by taking Dilithium 5 DigSig with Kyber 5 as KEM as an example of the outcomes. Results for the other algorithms follow the same trend, so those are not discussed separately. Figures in these sections i.e., Figure 7, Figure 8, Figure 9 and Figure 10 represent each evaluation metric individually for Dilithium 5 with Kyber 5. While Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 combines all these four metrics in a single image.

Figure 7. Percentage of CPU Used By Dilithium 5 + Kyber 5.

Figure 8. Number of CPU Context Switches Performed Dilithium 5 + Kyber 5.

Figure 9. RAM Used By Dilithium 5 + Kyber 5.

Figure 10. Network Used By Dilithium 5 + Kyber 5.

Figure 11. Dilithium2 with Kyber Level 1.

Figure 12. Dilithium2 with Kyber Level 3.

Figure 13. Dilithium2 with Kyber Level 5.

Figure 14. Dilithium3 with Kyber Level 1.

Figure 15. Dilithium3 with Kyber Level 3.

Figure 16. Dilithium3 with Kyber Level 5.

Figure 17. Dilithium5 with Kyber Level 1.

Figure 18. Dilithium5 with Kyber Level 3.

Figure 19. Dilithium5 with Kyber Level 5.

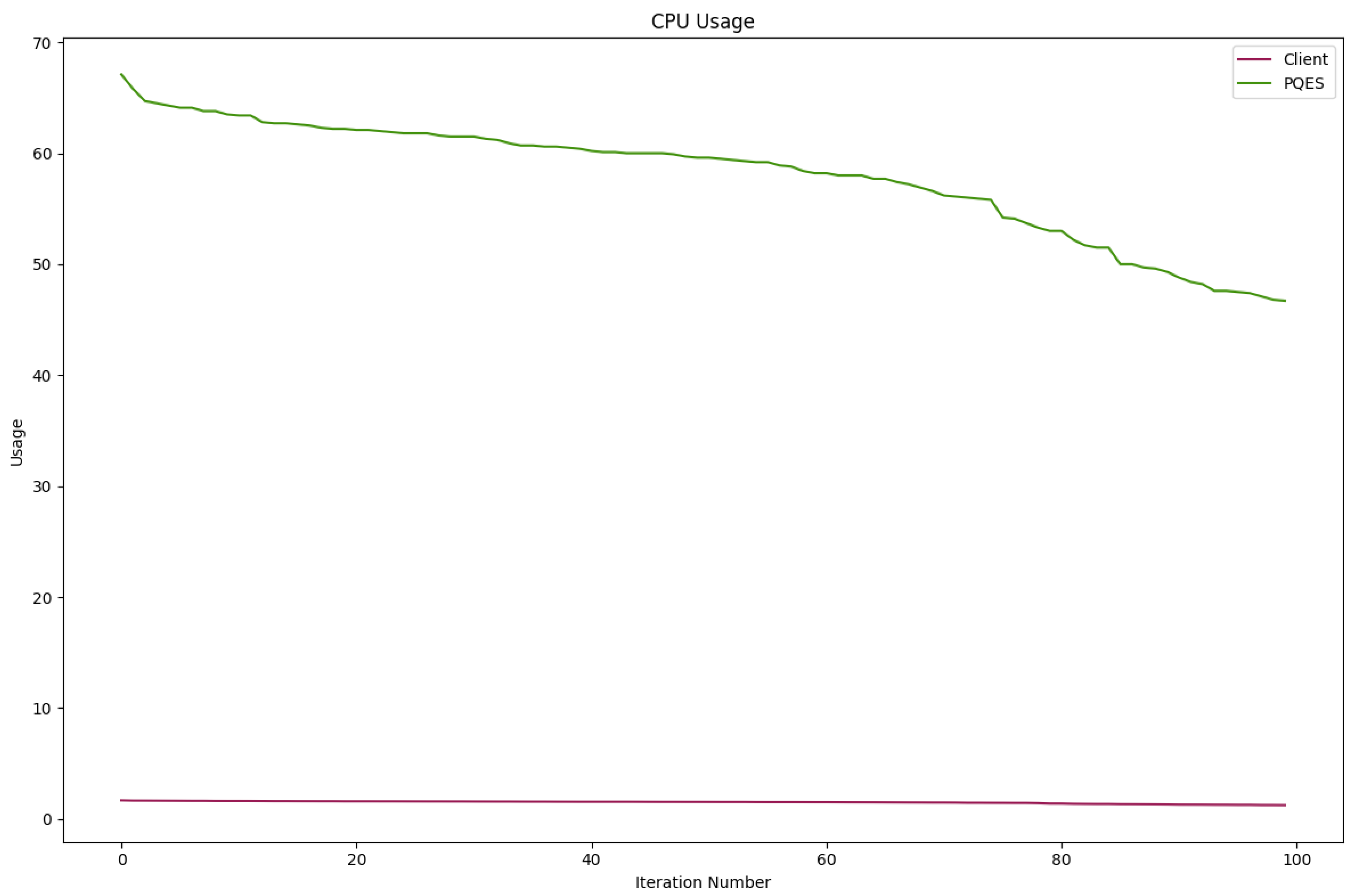
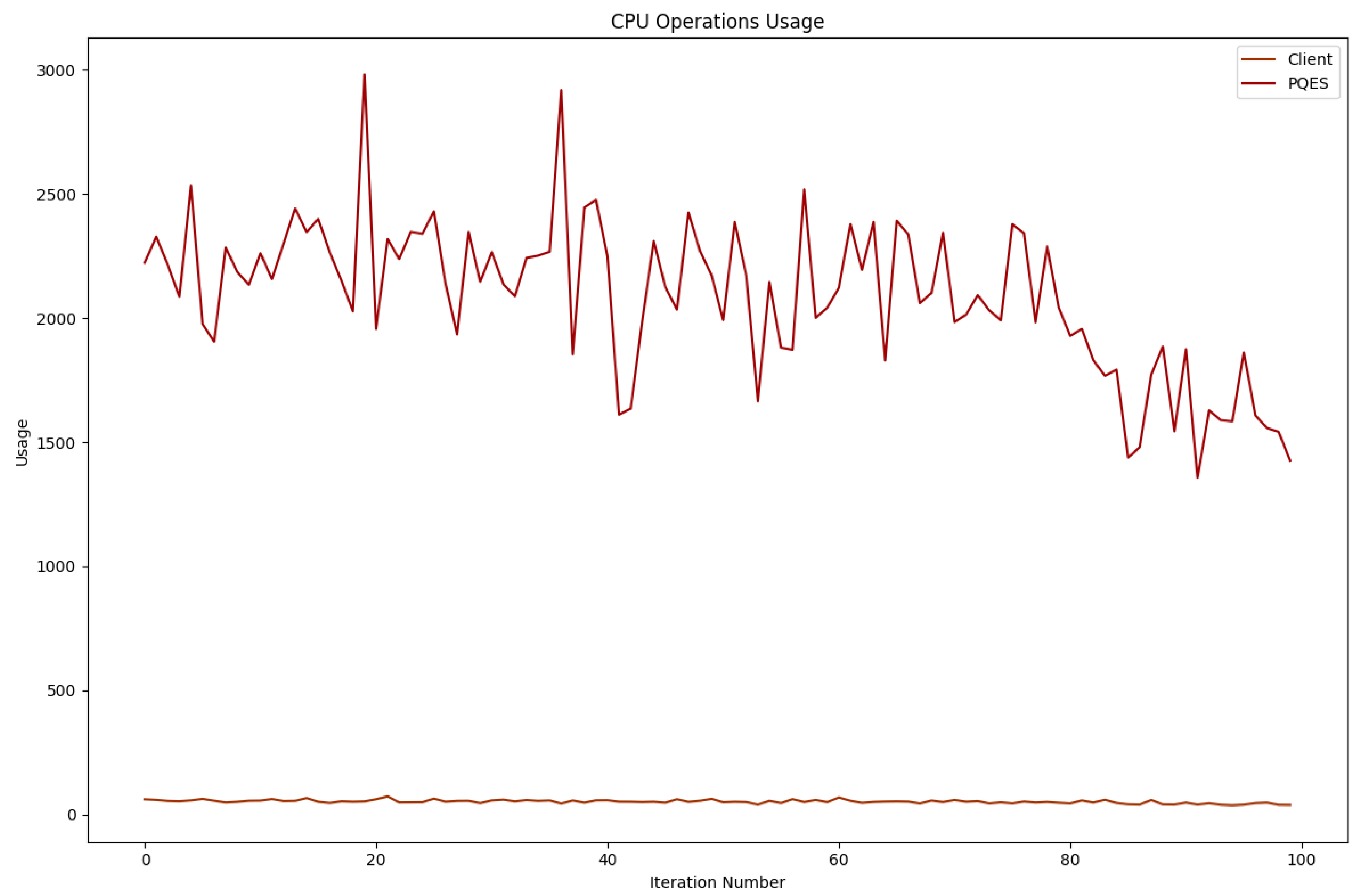
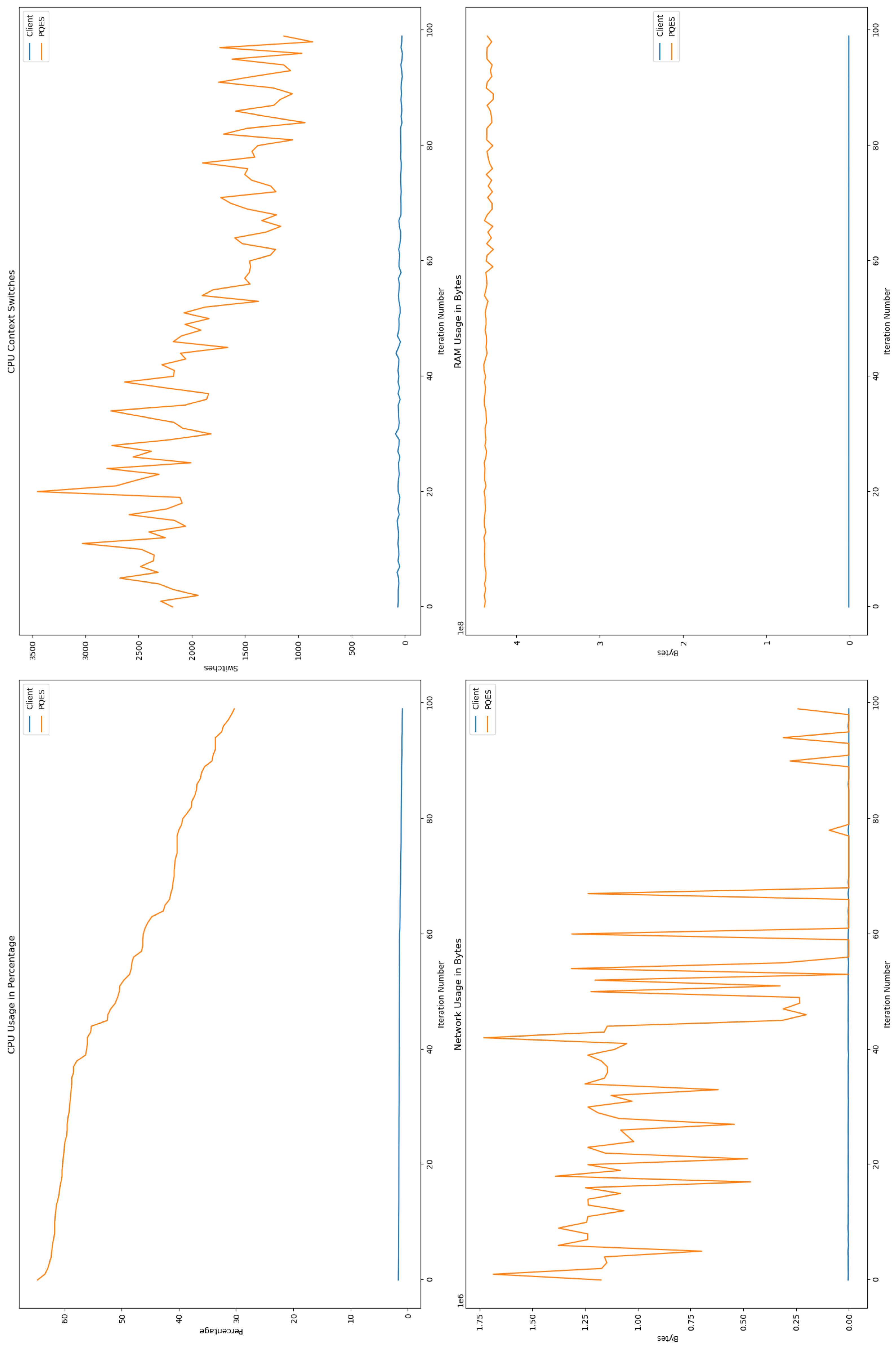
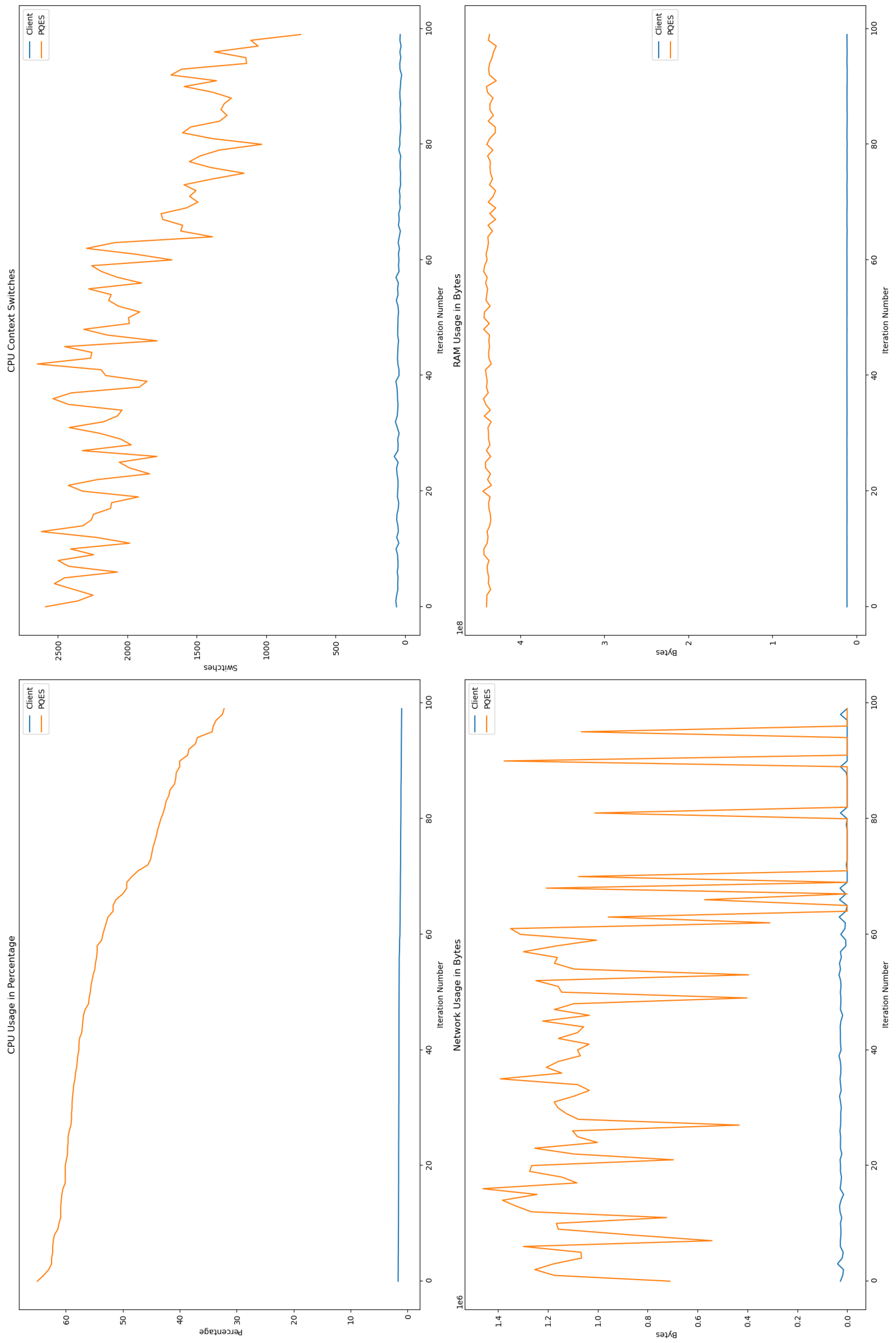
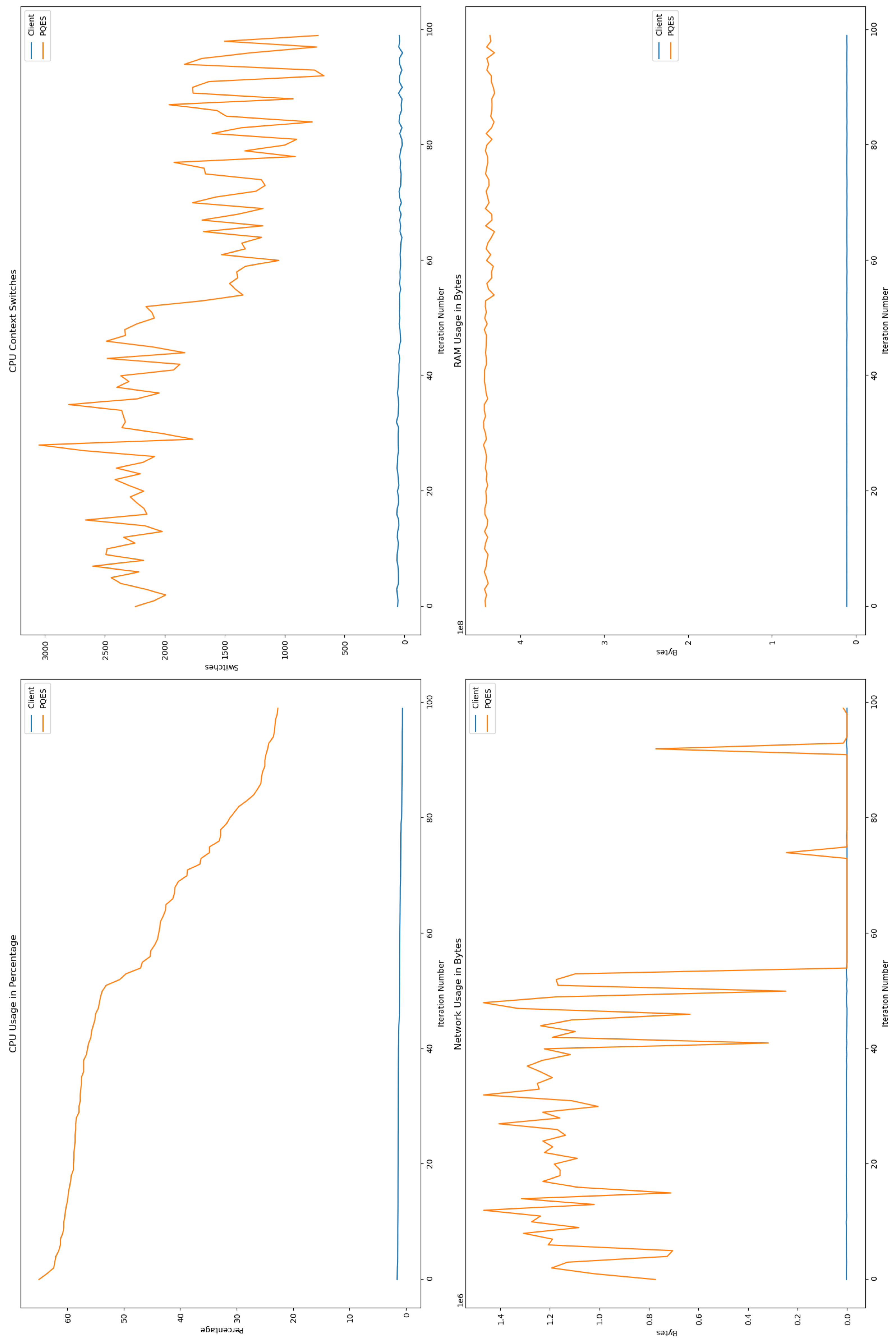
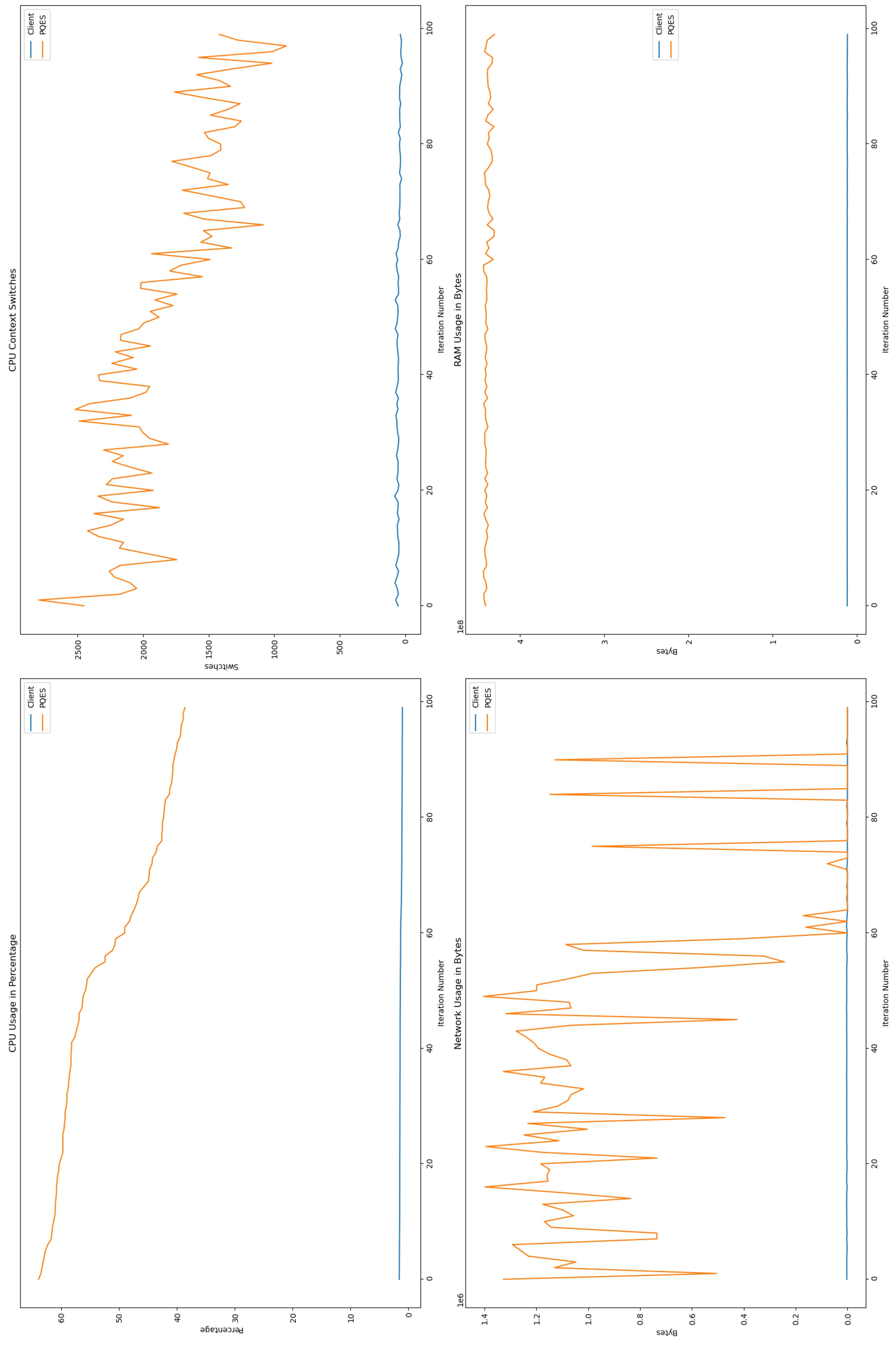
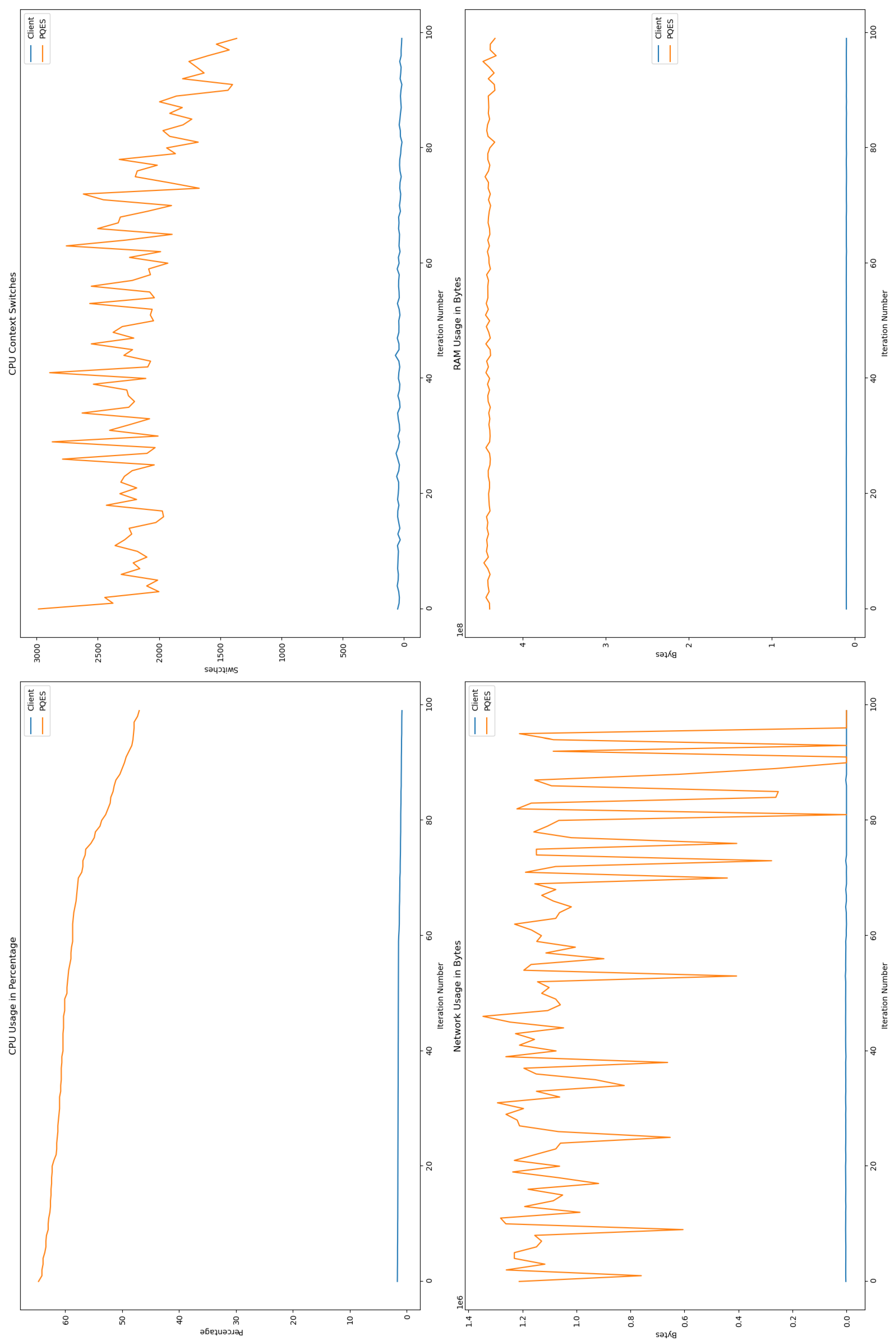
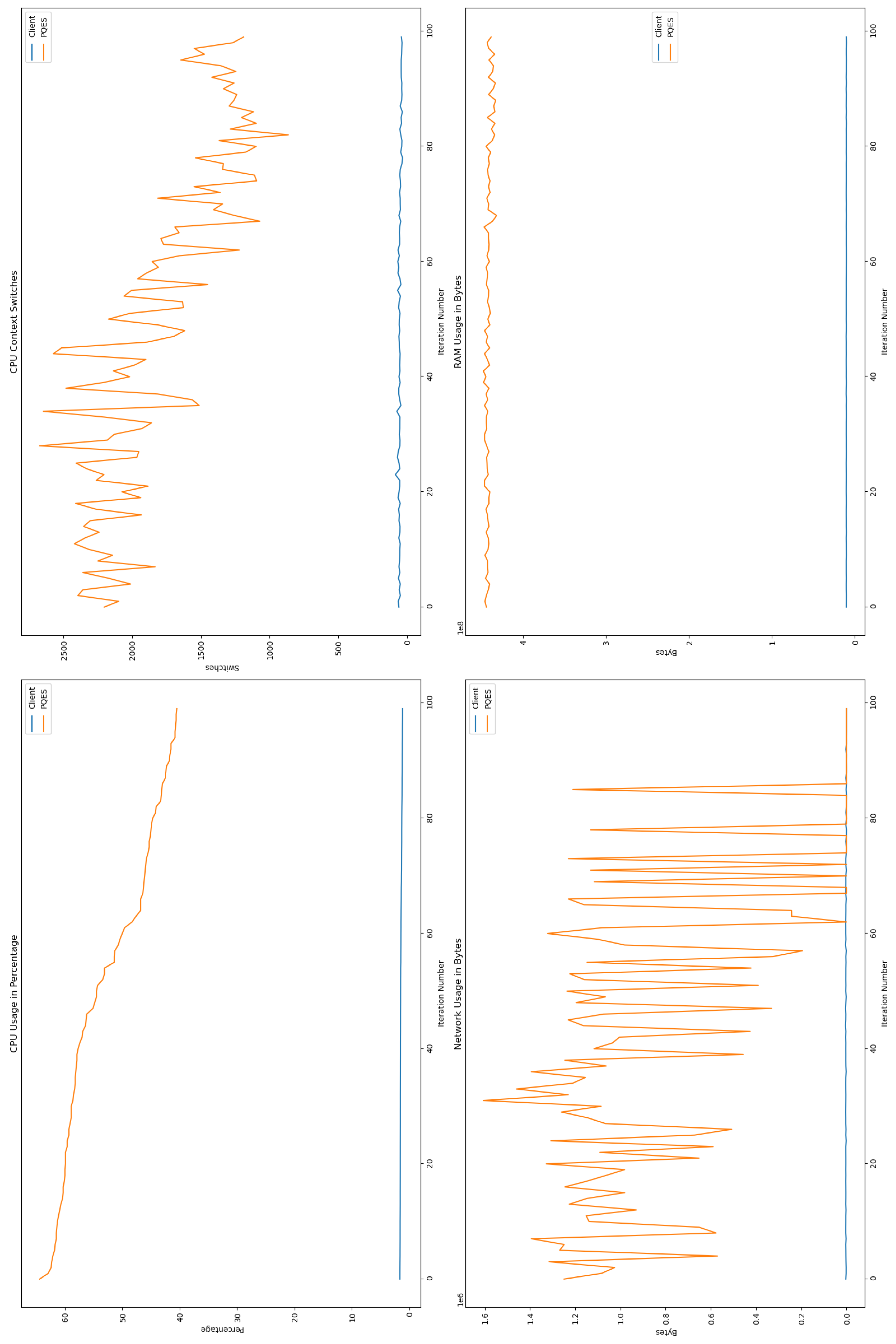
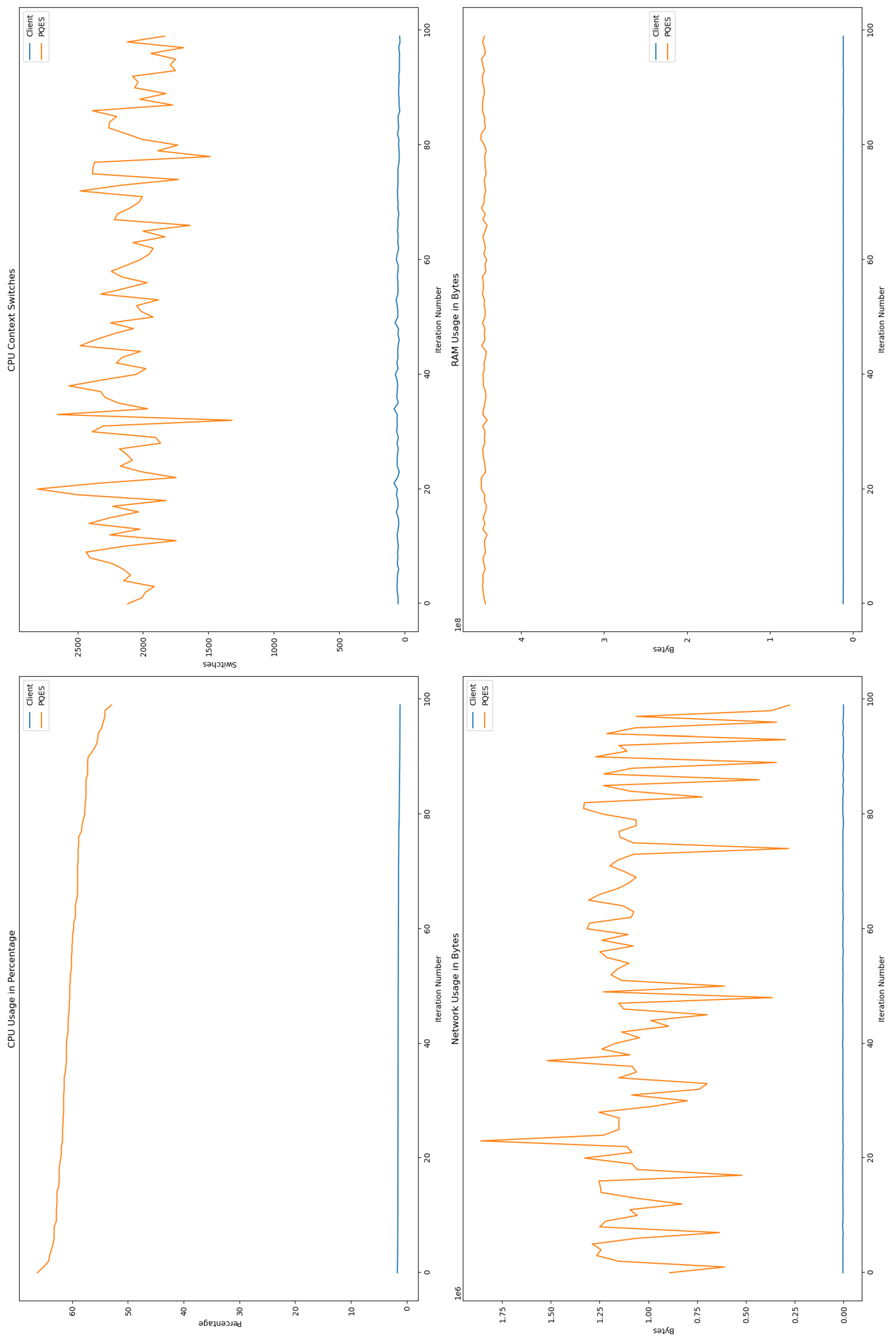
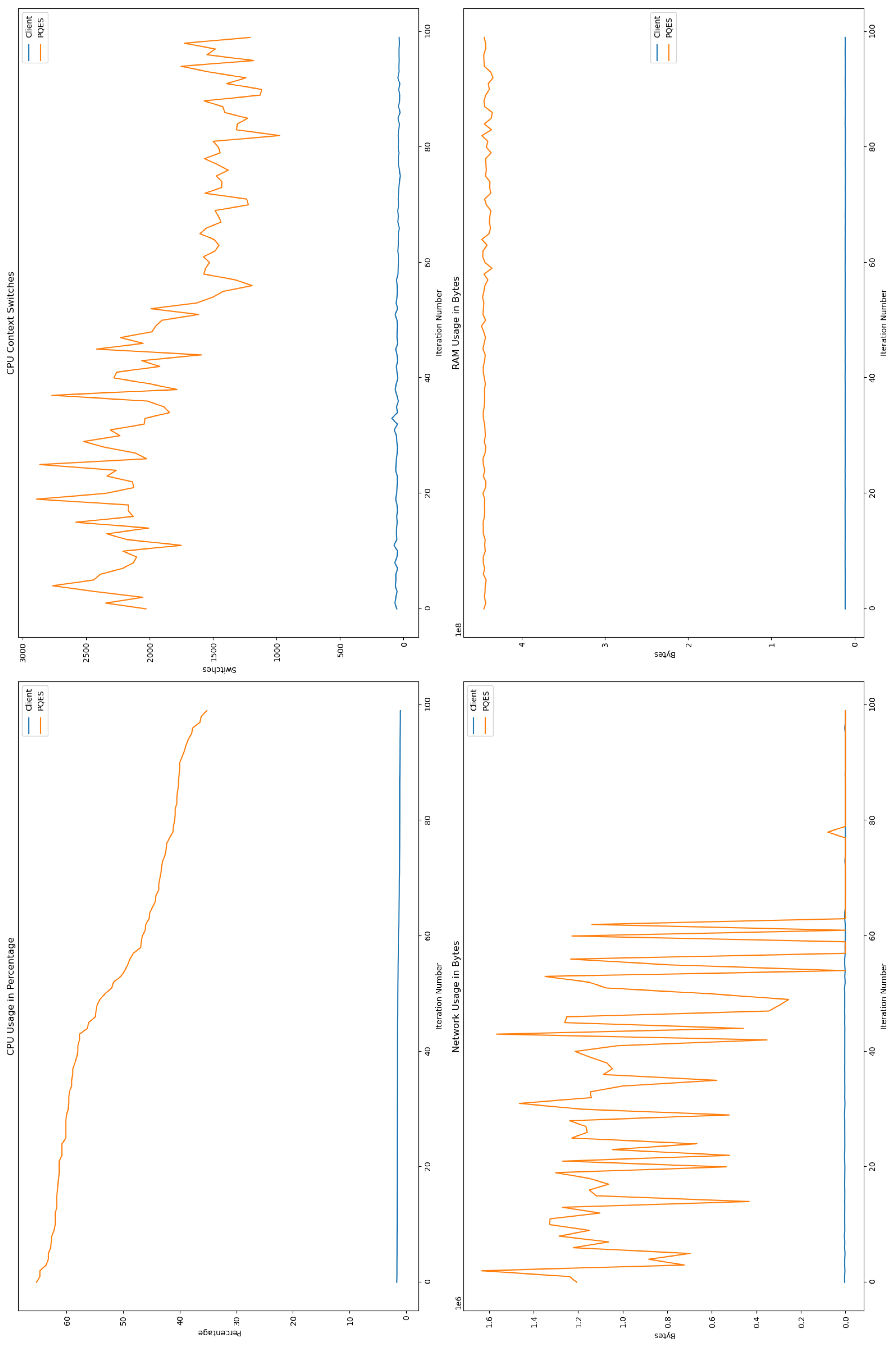
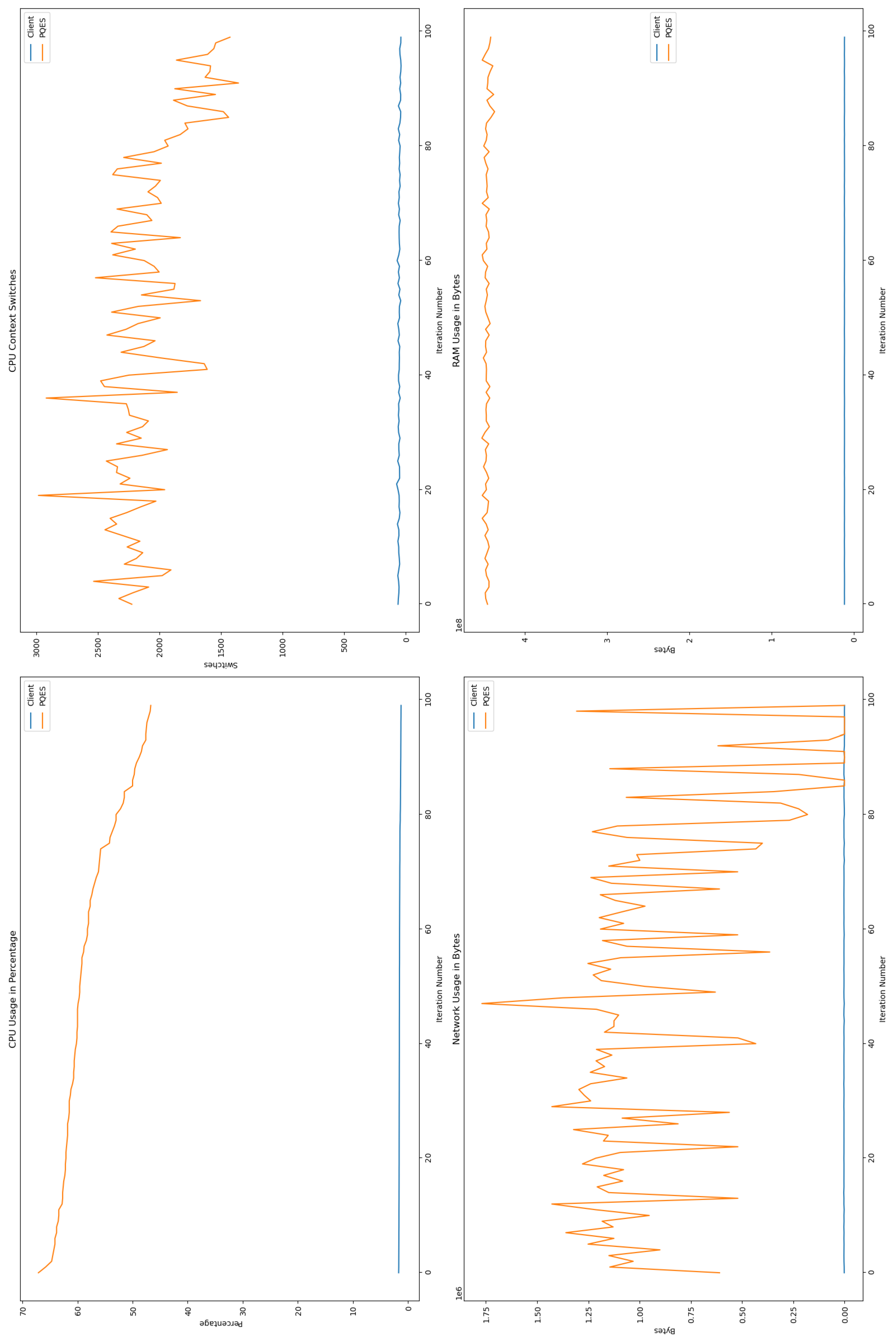
6.2.1. Percentage of CPU Used By Each Algorithm

The CPU use of the proposed approach for Dilithium 5 and Kyber 5 ranges from 1.2495% to 1.6881%, with an average of 1.5081%, indicating reliable and effective resource management. The consistent CPU consumption demonstrates that the proposed solution efficiently handles its processing requirements without encountering notable fluctuations in workload. The conventional method’s CPU utilization for Dilithium 5 and Kyber 5 fluctuates between 46.7% and 67.1%, averaging at 57.977%, suggesting inefficient resource allocation. The volatility in CPU consumption indicates that the conventional method needs help in effectively distributing resources, which might result in performance bottlenecks and variations in system responsiveness.

6.2.2. Number of CPU Context Switches Performed

My proposed solution’s shows a maximum of 73.4 CPU operations, a minimum of 37.5 operations, and an average of 52.3 operations for Dilithium 5 and Kyber 5 combination. These numbers of CPU operations show that the proposed solution can effectively handle its normal operations without having significant effect in workload due to additional PQ-related operations. On the other hand, the conventional techniques shows a range of 1357 to 2981 operations with an average of 2085.3 operations, showing inefficiency in computation management due to the additional responsibility of handling PQ cryptography operations. The larger number of CPU operations in the conventional method suggests that it has to manage more computing operations, potentially resulting in elevated CPU load and performance decline.

6.2.3. RAM Used By Each Algorithm

Similarly, my proposed architecture uses 11.5 MB (highest), 11.0 MB (minimum), and 11.4 MB (average) of RAM for Dilithium 5 and Kyber 5 configuration. This consistent RAM usage of the proposed method shows effective management of memory resources without significant overhead. The conventional approach shows increased RAM consumption, ranging from 436.1 MBs to 451.9 MBs, with an average of 445.8 MBs. This increased RAM use of the conventional on-device approach indicates that it experiences more memory demands, which might affect its efficiency and speed of response.

6.2.4. Network Used By Each Algorithm

The proposed solution for network measurements in Dilithium 5 and Kyber 5 shows a maximum of 3.6 KBs, a minimum of 1.2 KBs, and an average of 2.3 KBs. The proposed solution’s network utilization stays consistent and within a suitable range, indicating an efficient data transfer routine. The conventional approach demonstrates increased network use, ranging from 100 KBs to 1.8 MBs, with an average of 893.9 KBs. The higher network consumption of the conventional strategy suggests that it has to process a greater amount of data than the proposed approach, causing additional network congestion and performance difficulties.

6.3. Comparative Analysis

As of the date of writing, no proposed schemes have offloaded the PQC computation to an edge server. However, multiple approaches have been proposed for the efficient implementation of PQC on IoT devices. However, these schemes are much more computationally and memory intensive for the end-IoT devices than our scheme. For example, in [21], 6863 bytes are transferred during the KEM in the most efficient scenario. This means that the IoT device consumes 6863-bytes network bandwidth in addition to the size of the payload. Similarly, the scheme proposed in [25] uses 7732 bytes for key exchange. However, in the worst-case scenario of our proposed scheme, the end-IoT device uses 2288 bytes, which includes 1kb of the payload as well. Hence, it reduces the network bandwidth requirement of the end devices in a much more efficient way. Moreover, the CPU usage in [25] is lowest in Dilithium2 on 8GB on the subscriber, which is roughly 0.01% ≈ 81.92MBs. However, in our proposed approach, the end device uses 15.36MBs in the worst case while using Dilithium5.

Table 5. Comparative Results

Paper	KEM Bytes Usage	CPU MBs Usage
M. Scott [21]	6863	N/A
J. Samandari and C. Gritti [25]	7732	81.92
Our Scheme	1264	15.36

6.4. Discussion

As our results show, the proposed scheme not only provides post-quantum security to IoT devices over the internet, but it also greatly reduces the computational, memory, and network requirements. Specifically, our technique exhibited a decrease in RAM utilization to as low as 1.05 KB, with the highest RAM usage being 13.4 MB. In contrast, the typical method needed a minimum of 5.1 MB RAM for a single concurrent connection and might consume up to 552.6 MB RAM for 1000 concurrent connections. Similarly, the greatest CPU utilization for our technique was 1.75%, compared to 67.1% for the conventional approach. Additionally, the highest CPU context switches for our system were 92.8, substantially lower than the 3449 found for the standard techniques. These data illustrate the usefulness of our offloading technique in decreasing the computational and memory demands on IoT devices.

Existing methodologies for PQC implementation on IoT devices are more computationally and memory-intensive, utilizing much more network bandwidth and CPU resources. For example, previous techniques require 6863 bytes for key exchange, but our scheme utilizes just 2288 bytes in the worst-case situation, including the payload size. Similarly, the CPU utilization in previous techniques is substantially greater than that of our solution. Also, The use of transport layer protocol instead of the application layer not only enhances the flexibility of our proposed system but also reduces the protocol implementations on lightweight devices. The responsibility of implementing the application layer protocols and PQC schemes is delegated to the proposed PQES device, which can be set up for the entire network. Furthermore, our benchmarking findings demonstrate that the PQES can manage 1000 concurrent connections while utilizing a maximum of 73.5% of 1GB RAM on a Raspberry Pi, confirming the efficiency and scalability of our solution.

7. Future Work and Conclusion

7.1. Limitations

Even though our proposed scheme provides an optimal solution for implementing PQC in an IoT infrastructure, there can be certain limitations in the proposed approach. Which can be listed below:

Our scheme was evaluated by using a RaspberryPi-4B with 1GB. However, we can evaluate the proposed scheme on IoT devices on even more low-powered devices like ARM Cortex-M4 and other microprocessors. This can provide us with more authentic, realistic, and solid results to verify our approach.
Our proposed architecture implements PQC-based security for all data going out from a network; however, this does not provide data security for traffic inside the network as our scheme assumes that the traffic inside the internal network is secure. This can open up attacks on devices that do not use any encryption for their regular traffic between themselves and the router.
Even though we propose using just the transport layer protocol for data communication for these devices to avoid implementing application layer protocols, we have used HTTP as our application protocol. We can enhance this work by evaluating this scheme with other application layer protocols like MQTT and CoAP.

7.2. Future Work

Based on the limitation we have discussed above, future works might focus on completing the following tasks.

To conduct additional evaluations on IoT devices with lower power specifications, such as ARM Cortex-M4 and other microprocessors, to provide more authentic and realistic results. This will help validate the effectiveness of the proposed system over a wider range of IoT devices.
To enhance the internal network security by implementing additional security protocols to protect internal network traffic. One approach is to explore encryption techniques for internal network traffic to protect against potential attacks on devices that do not have encryption in their communication with the router.
Evaluate the proposed architecture in combination with other application layer protocols such as MQTT, CoAP and others to improve and evaluate the performance. This will provide the assessment for scheme’s compatibility and effectiveness with other protocols, providing validation on its scalability and flexibility.
Investigate other approaches to improve the effectiveness of the suggested approach, especially on low-powered IoT devices. This includes reducing computational overhead, enhancing energy efficiency, and optimizing system performance while assuring the same level of security.
Evaluate the proposed approach in IoT environments to assess its suitability, scalability, and effectiveness in practical applications. This includes collaborating with industry and testing the program in a controlled IoT environment to gather empirical data and validate its efficiency.

7.3. Conclusion

IoT devices will be the core component of smart cities, and it is imperative to ensure the confidentiality and integrity of their data. In the ever-growing threat of quantum computers against PKI, we need to provide post-quantum security to these devices without compromising their performance. Unlike other proposed solutions, our architecture takes an entirely different approach to completely offload the computation and memory-related tasks to an edge device. This ensures the post-quantum data security of the traffic outside the network without any concerns related to device-related constraints. Our results show that our solution provides a manifold lightweight solution compared to on-device implementation. Moreover, the use of the transport layer to transmit data makes it independent of application layer protocols, increasing the flexibility of our approach. There are some concerns related to data security inside network security as well as the network speed for real-time systems, which can be addressed in any future work.

Acknowledgments

I want to thank all the people who contributed to my knowledge, motivated me to pursue academia, and helped me face all the challenges in my life. I have been encouraged, sustained, inspired, and tolerated, not only by my family, but by the greatest group of friends anyone ever had. From my parents and my primary education level teachers to my thesis supervisor, I am in debt to each and every one of them for making me able to put hard work and dedication into the field of research. And lastly, I want to thank me for believing in me. I want to thank me for doing all this hard work. I want to thank me for having no days off. I want to thank me for never quitting. I want to thank me for just being me at all times. I want to mention and admire all the late nights, setbacks, and technical and academic challenges I faced during my tenure of this degree and thesis.

Abbreviations

IoT	Internet of Things
PQC	Post-Quantum Cryptography
PQES	Post-Quantum Edge Server
PKI	Public-Key Infrastructure
ICT	Information and Communication Technology
UMI	Universal Metering Interface
CA	Certificate Authority
RA	Registration Authority
KEM	Key-Exchange Mechanism

CBE	Code-Based Encryption
LBE	Lattice-Based Encryption
MQEE	Multivariate-Quadratic-Equation Encryption
HBE	Hash-Based Encryption
NIST	National Institute of Standards and Technology
DigSig	Digital Signatures
IBE	Identity-Based Encryption
LWE	Learning With Errors
CSIDH	Commutative Supersingular Isogeny Diffie–Hellman
SQALE	Sublinear Vélu Quantum-resistant isogeny Action with Low Exponents
CTIDH	Constant Time CSIDH
dCSIDH	Distributed CSIDH
OPC UA	Open Platform Communications Unified Architecture
WLAN	Wireless Local Area Networks
WAN	Wide Area Networks
D2D	Device-to-Device
TT	Translation Table
PoC	Proof-of-Concept

Appendix A. Quantum Information and Computing Primer

Appendix A.1. Introduction

Classical computers are constructed using Boolean logic gates and bits controlled by electronic transistors inside integrated circuits or chips. Quantum computers use logic gates that operate on principles of quantum mechanics. Quantum computers provide new programming possibilities by using quantum gates to handle qubits, in contrast to conventional computers that use classical bits and gates. Quantum bits have the unique characteristic of seeming to exist in a state between the two binary states, unlike normal bits, which are always in one of the two states. While spinning in the air, the coin exhibits two separate states despite seeming to be both heads and tails simultaneously. Conventional programming statements are unable to represent the capability of qubits to exist in a superposition of states while carrying out computing operations.

Since Shannon and the beginning of information theory, the bit has been the basic term in classical information. The states of a bit are either 0 or 1. In accordance with the classical concept of quantum information exists the qubit (short for quantum bit). Like for the classical bit, two states are possible,

| 0 〉

and

| 1 〉

. This special notation `

| 〉

’ is called the Dirac notation (or ket) and is the standard notation for states in quantum mechanics. The major difference to the classical bit, which accepts only 0 or 1, is that a qubit also allows states in between

| 0 〉

and

| 1 〉

, which are called superpositions. Let us denote this by

ψ = α | 0 〉 + β | 1 〉

(A1)

where

α

β

ϵ

C

. Because these factors are complex numbers, the state of a qubit can be described as a vector in a two-dimensional complex vector space

C^{2}

, also called Hilbert space. The states

| 0 〉

and

| 1 〉

form the computational basis and are orthonormal to each other.

Since a qubit state is a unit vector, meaning the length is normalized to 1, the following equation must be fulfilled by the scalars

{α, β : | α |}^{2} + {| β |}^{2} = 1

(A2)

Using this fact, we can rewrite the state of a qubit

| ψ 〉 = cos \frac{θ}{2} | 0 〉 + e^{i ψ} sin \frac{θ}{2} | 1 〉

(A3)

where

θ, ψ

are real numbers and define a point on a sphere called the Bloch sphere.

Figure A1. In quantum computing, the Bloch sphere is a possible graphical representation of the state of a quantum bit. Figure courtesy of the author.

Qubits are essential components in quantum programming. The particles are subject to quantum mechanical processes that provide the impression of oscillating between two binary states. Consequently, we may manipulate the qubits to interact with one other in ways that allow us to create decision-making logic circuits that enhance their runtime performance or encrypt data in very secure ways. To excel in designing quantum programs, it is essential to grasp the techniques for manipulating qubits. Classical bits are binary and exist in either the state of 1 or 0. Qubits have two distinct states that correspond to the conventional binary values 0 and 1. Qubits may exist in a superposition state, unlike standard binary bits, where they might be a mix of two states, similar to the analogy of a coin flip. This condition does not have an average value of 0.5. It is an idea of two states coexisting simultaneously.

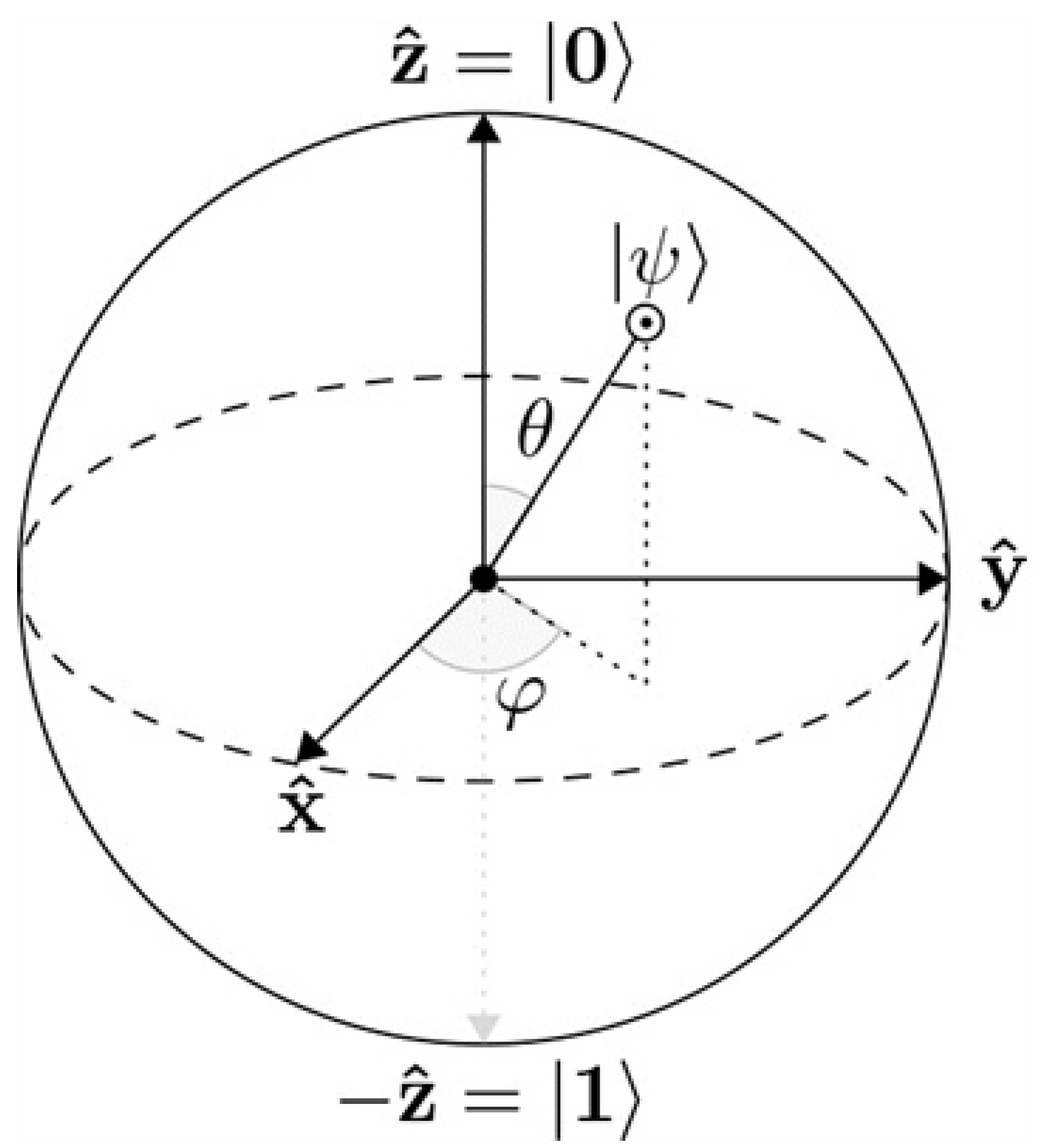
Appendix A.2. Measuring Qubits

To check the status of a classical bit during program execution on a traditional computer, we display the variable containing the bit. Observing the bit does not alter its state. In quantum computing, it is impossible to examine the quantum state of a qubit directly. The state of a qubit cannot be visually inspected since it is not transparent. To analyze the quantum state, one must randomly extract a qubelet from the cauldron. At that moment, two events occur:

The remaining qubelets in the cauldron disappear because, according to the principles of quantum physics, you cannot choose another qubelet.
The chosen qubit, either a $| 0 〉$ or a $| 1 〉$ , is designated as the state of the qubit, resulting in the collapse of the qubit. The cauldron is adjusted only to contain the chosen qubelet.

Choosing a

| 0 〉

qubit causes the qubit to collapse to the quantum state

| 0 〉

, making all other

| 0 〉

and

| 1 〉

qubits disappear from the system. When a

| 1 〉

qubit is selected from the cauldron, the qubit collapses to the idealized quantum state

| 1 〉

, causing the

| 0 〉

and other

| 1 〉

qubits to vanish. Generally, we cannot definitively anticipate which of the two idealized states the quantum state will collapse to; it may collapse to

| 0 〉

| 1 〉

. Finding a qubit in a given state after collapsing does not provide information about the relative amount of

| 0 〉

and

| 1 〉

qubelets in the quantum state before the collapse. Starting over with a qubit in an identical quantum state and collapsing does not ensure that the qubit will collapse to the same classical state as before. In quantum computing, computational tasks are carried out on qubits with uncollapsed quantum states, as explained in the next chapters. We collapse the qubits only after ensuring that they all retain the optimum or desirable states required by your algorithm.

The measurement of qubits needs to be fixed. In the special case when

α

β

is 0, the mapping to the classical bit will result in 1 or 0, respectively, as expected. But what happens if the qubit is in another superposition, i.e.,

α, β \neq 0

? Depending on the scalars, the qubit will be measured as 1 with a certain probability or as 0 with the complementary probability since the scalars fulfil Eq. A.2, the probability for a qubit to be measured as 0 is

{| α |}^{2}

, and as one, it is

{| β |}^{2}

Furthermore, in quantum mechanics, the scalars

α

and

β

are also called the amplitudes of the states

| 0 〉

and

| 1 〉

, respectively. But there exists a second term describing a qubit, the phase. Consider the state

e^{i ψ} | ψ 〉

, where

| ψ 〉

is a state vector, and

ψ

is a real number. We say that the state

e^{i ψ} | ψ 〉

is equal to

| ψ 〉

, up to the global phase factor

e^{i ψ}

Another kind of phase is the relative phase. Consider these two states

| + 〉 = \sqrt{\frac{1}{2}} (| 0 ⟩ + | 1 ⟩) and | - 〉 = \sqrt{\frac{1}{2}} (| 0 ⟩ - | 1 ⟩)

(A4)

In the state

| + 〉

, the amplitude of

| 1 〉

\sqrt{\frac{1}{2}}

. In state

| - 〉

, the amplitude has the same magnitude but a different sign. We define that two amplitudes

α_{1}

α_{2}

for some states differ by a relative phase if there is a real

ψ

such that

α_{1} = e^{i ψ} α_{2}

. In contrast to the global phase, where both amplitudes of the state are different by the factor

e^{i ψ}

, the relative phase differs only in one amplitude by the factor

e^{i ψ}

Appendix A.3. Unitary Operations

The reason quantum information is fundamentally different from classical information is that the set of allowable operations that can be performed on a quantum state is different than it is for classical information. Similar to the probabilistic setting, operations on quantum states are linear mappings — but rather than being represented by stochastic matrices as in the classical case, operations on quantum state vectors are represented by unitary matrices.

A square matrix U having complex number entries is unitary if it satisfies the equations

U^{†} U = U U^{†} = I

(A5)

Here,

I

is the identity matrix, and

U^{†}

is the conjugate transpose of U, meaning the matrix obtained by transposing U and taking the complex conjugate of each entry.

U^{†} = \bar{U^{T}}

(A6)

If either of the two equalities is true, then the other must also be true. Both equalities are equivalent to

U^{†}

being the inverse of U:

U^{- 1} = U^{†} .

(A7)

The condition that U is unitary is equivalent to the condition that multiplication by U does not change the Euclidean norm of any vector. That is, an

n \times n

matrix U is unitary if and only if

v e r t U | ψ 〉 v e r t = v e r t | ψ 〉 v e r t

for every n-dimensional column vector

ψ

with complex number entries. Thus, because the set of all quantum state vectors is the same as the set of vectors having Euclidean norm equal to 1, multiplying a unitary matrix to a quantum state vector results in another quantum state vector.

Indeed, unitary matrices are exactly the set of linear mappings that transform quantum state vectors into other quantum state vectors. Notice here a resemblance to the classical probabilistic case, where operations are associated with stochastic matrices, which are the ones that always transform probability vectors into probability vectors.

The following list describes some important unitary operations on qubits.

Appendix A.4. Pauli Operations

The four Pauli matrices are as follows:

I = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}), σ_{x} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), σ_{y} = (\begin{matrix} 0 & - i \\ i & 0 \end{matrix}), σ_{z} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}) .

(A8)

A common notation, which we will often use, is

X = σ_{x}

Y = σ_{y}

, and

Z = σ_{z}

, but we need to keep in mind that the letters X, Y, and Z are also commonly used for other purposes. The X operation is also called a bit flip or a NOT operation because it induces this action on bits:

X | 0 〉 = | 1 〉 and X | 1 〉 = | 0 〉 .

(A9)

The Z operation is also called a phase flip because it has this action:

Z | 0 〉 = | 0 〉 and Z | 1 〉 = - | 1 〉 .

(A10)

Appendix A.5. Hadamard Operation

This matrix describes the Hadamard operation:

H = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) .

(A11)

Appendix A.5.1. Phase Operations

A phase operation is one described by the matrix

P_{θ} = (\begin{matrix} 1 & 0 \\ 0 & e^{i θ} \end{matrix})

(A12)

for any choice of a real number

θ

. The operations

S = P_{π / 2} = (\begin{matrix} 1 & 0 \\ 0 & i \end{matrix}) and T = P_{π / 4} = (\begin{matrix} 1 & 0 \\ 0 & \frac{1 + i}{\sqrt{2}} \end{matrix})

(A13)

are particularly important examples. Other examples include

S = P_{0} = I

and

Z = P_{π}

All of the matrices just defined are unitary and, therefore, represent quantum operations on a single qubit.

For example, here is a calculation that verifies that H is unitary:

\begin{matrix} H^{†} H & = {(\frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}))}^{†} (\frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix})) \end{matrix}

(14)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) \end{matrix}

(15)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) \end{matrix}

(16)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 + 1 & 1 - 1 \\ 1 + 1 & 1 - 1 \end{matrix}) \end{matrix}

(17)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 2 & 0 \\ 2 & 0 \end{matrix}) \end{matrix}

(18)

\begin{matrix} = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) = I . \end{matrix}

(19)

Here’s the action of the Hadamard operation on a few commonly encountered qubit state vectors:

\begin{matrix} H | 0 〉 & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 1 \\ 0 \end{matrix}) = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ 1 \end{matrix}) = | + 〉, \end{matrix}

(20)

\begin{matrix} H | 1 〉 & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 0 \\ 1 \end{matrix}) = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ - 1 \end{matrix}) = | - 〉, \end{matrix}

(21)

\begin{matrix} H | + 〉 & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{matrix}) = (\begin{matrix} 1 \\ 0 \end{matrix}) = | 0 〉, \end{matrix}

(22)

\begin{matrix} H | - 〉 & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \end{matrix}) = (\begin{matrix} 0 \\ 1 \end{matrix}) = | 1 〉 . \end{matrix}

(23)

It’s well worth listing these four equations more succinctly:

\begin{matrix} H | 0 〉 & = | + 〉, & H | 1 〉 & = | - 〉, \end{matrix}

(24)

\begin{matrix} H | + 〉 & = | 0 〉, & H | - 〉 & = | 1 〉 . \end{matrix}

(25)

Here’s one final example of a state vector that was mentioned previously:

\begin{matrix} H (\frac{1}{\sqrt{2}} | 0 〉 + \frac{2}{\sqrt{3}} | 1 〉) & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\frac{1}{\sqrt{2}} | 0 〉 + \frac{2}{\sqrt{3}} | 1 〉) \end{matrix}

(26)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ 2 \end{matrix}) = \frac{- 1 + 2 \sqrt{3}}{2} | 0 〉 + \frac{3 + 2 \sqrt{3}}{2} | 1 〉 . \end{matrix}

(27)

It’s worth pausing to consider the fact that

H | + 〉 = | 0 〉

and

H | - 〉 = | 1 〉

. Consider a situation in which a qubit is prepared in one of the two quantum states

| + 〉

and

| - 〉

, but where it is not known to us which one it is. Measuring either state produces the same output distribution as the other: 0 and 1 both appear with equal probability

1 / 2

. So, doing

this provides no information about which of the two states

| + 〉

and

| - 〉

was originally prepared. However, if we apply a Hadamard operation and then measure, we obtain the outcome 0 with certainty if the original state was

| + 〉

and we obtain the outcome 1, again with certainty, if the original state was

| - 〉

Thus, the quantum states

| + 〉

and

| - 〉

can be discriminated perfectly. This reveals that sign changes, or more generally changes to the phases (which are also traditionally called arguments) of the complex number entries of a quantum state vector, can significantly change that state.

Here’s another example, this time of the action of a T operation on a plus state:

\begin{matrix} T | + 〉 & = T (\frac{1}{\sqrt{2}} | 0 〉 + \frac{1}{\sqrt{2}} | 1 〉) \end{matrix}

(28)

\begin{matrix} = \frac{1}{\sqrt{2}} T | 0 〉 + \frac{1}{\sqrt{2}} T | 1 〉 \end{matrix}

(29)

\begin{matrix} = \frac{1}{\sqrt{2}} | 0 〉 + \frac{1 + i}{\sqrt{2}} | 1 〉 . \end{matrix}

(30)

Notice here that we did not bother to convert to the equivalent matrix/vector forms and instead used the linearity of matrix multiplication together with the formulas

T | 0 〉 = | 0 〉 and T | 1 〉 = \frac{1 + i}{\sqrt{2}} | 1 〉 .

(A14)

Along similar lines, we may compute the result of applying a Hadamard operation to the quantum state vector just obtained:

\begin{matrix} H (\frac{1}{\sqrt{2}} | 0 〉 + \frac{1 + i}{\sqrt{2}} | 1 〉) & = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\frac{1}{\sqrt{2}} | 0 〉 + \frac{1 + i}{\sqrt{2}} | 1 〉) \end{matrix}

(32)

\begin{matrix} = \frac{1}{\sqrt{2}} (\begin{matrix} 1 \\ 1 + i \end{matrix}) \end{matrix}

(33)

\begin{matrix} = \frac{1}{\sqrt{2}} | 0 〉 + \frac{1 + i}{\sqrt{2}} | 1 〉 . \end{matrix}

(34)

The two approaches — one where we explicitly convert to matrix representations and the other where we use linearity and plug in the actions of an operation on standard basis states — are equivalent. We can use whichever one is more convenient in the case at hand.

Appendix A.6. Entangled States

Not all quantum state vectors of multiple systems are product states. For example, the quantum state vector

\frac{1}{\sqrt{2}} | 00 〉 + \frac{1}{\sqrt{2}} | 11 〉

(A15)

of two qubits is not a product state. This is because if it were so, there would exist quantum state vectors

| ϕ 〉

and

| ψ 〉

for which

| ϕ 〉 \otimes | ψ 〉 = \frac{1}{\sqrt{2}} | 00 〉 + \frac{1}{\sqrt{2}} | 11 〉 .

(A16)

But then it would necessarily be the case that.

〈 0 | ϕ 〉 〈 1 | ψ 〉 = 〈 01 | ϕ \otimes ψ 〉 = 0

(A17)

implying that

〈 0 | ϕ 〉 = 0

〈 1 | ψ 〉 = 0

(or both). That contradicts the fact that

〈 0 | ϕ 〉 〈 0 | ψ 〉 = 〈 00 | ϕ \otimes ψ 〉 = \frac{1}{\sqrt{2}}

(A18)

and

〈 1 | ϕ 〉 〈 1 | ψ 〉 = 〈 11 | ϕ \otimes ψ 〉 = \frac{1}{\sqrt{2}}

(A19)

are both nonzero.

Notice that the specific value

1 / \sqrt{2}

is not important to this argument — what is important is that this value is nonzero. Thus, for instance, the quantum state

\frac{3}{5} | 00 〉 + \frac{4}{5} | 11 〉

(A20)

is also not a product state, by the same argument.

In contrast, the quantum state vector

\frac{1}{\sqrt{2}} | 00 〉 + \frac{i}{\sqrt{2}} | 01 〉 - \frac{1}{\sqrt{2}} | 10 〉 - \frac{i}{\sqrt{2}} | 11 〉

(A21)

is an example of a product state:

\frac{1}{\sqrt{2}} | 00 〉 + \frac{i}{\sqrt{2}} | 01 〉 - \frac{1}{\sqrt{2}} | 10 〉 - \frac{i}{\sqrt{2}} | 11 〉 = (\frac{1}{\sqrt{2}} | 0 〉 - \frac{1}{\sqrt{2}} | 1 〉) \otimes (\frac{1}{\sqrt{2}} | 0 〉 + \frac{i}{\sqrt{2}} | 1 〉) .

(A22)

Hence, this state is not entangled.

Appendix A.7. Bell States

Bell States are important examples of multiple-qubit quantum states. These are the following four two-qubit states:

\begin{matrix} | Φ^{+} 〉 & = \frac{1}{\sqrt{2}} | 00 〉 + \frac{1}{\sqrt{2}} | 11 〉 \end{matrix}

(A23)

\begin{matrix} | Φ^{-} 〉 & = \frac{1}{\sqrt{2}} | 00 〉 - \frac{1}{\sqrt{2}} | 11 〉 \end{matrix}

(A24)

\begin{matrix} | Ψ^{+} 〉 & = \frac{1}{\sqrt{2}} | 01 〉 + \frac{1}{\sqrt{2}} | 10 〉 \end{matrix}

(A25)

\begin{matrix} | Ψ^{-} 〉 & = \frac{1}{\sqrt{2}} | 01 〉 - \frac{1}{\sqrt{2}} | 10 〉 \end{matrix}

(A26)

Bell states is a product state, i.e., all four of the Bell states represent entanglement between two qubits.

The collection of all four Bell states

{| Φ^{+} 〉, | Φ^{-} 〉, | Ψ^{+} 〉, | Ψ^{-} 〉}

(A27)

is known as the Bell basis; any quantum state vector of two qubits, or indeed any complex vector at all having entries corresponding to the four classical states of two bits, can be expressed as a linear combination of the four Bell states. For example,

| 00 〉 = \frac{1}{\sqrt{2}} | Φ^{+} 〉 + \frac{1}{\sqrt{2}} | Φ^{-} 〉 .

(A28)

Appendix A.7.1. GHZ and W States

These are important examples of states of three qubits.

The first state that represents a quantum of three qubits

(X, Y, Z)

is the GHZ state.

\frac{1}{\sqrt{2}} | 000 〉 + \frac{1}{\sqrt{2}} | 111 〉 .

(A29)

The second stage is the so-called W state:

\frac{1}{\sqrt{3}} | 001 〉 + \frac{1}{\sqrt{3}} | 010 〉 + \frac{1}{\sqrt{3}} | 100 〉 .

(A30)

Neither of these states is a product state, meaning that they cannot be written as a tensor product of three-qubit quantum state vectors.

Appendix A.8. Application of Entanglement

Consider below equation

| Φ^{+} 〉 = \frac{1}{2} | 00 〉 + \frac{1}{2} | 11 〉

(A31)

It is one of the four Bell states and is often viewed as the archetypal example of an entangled quantum state.

We also encountered this example of a probabilistic state of two bits:

\frac{1}{2} | 00 〉 + \frac{1}{2} | 11 〉 .

(A32)

It is, in some sense, analogous to the entangled quantum state

| Φ^{+} 〉

. It represents a probabilistic state in which two bits are correlated but it is not entangled. Entanglement is a uniquely quantum phenomenon, essentially by definition: in simplified terms, entanglement refers to any non-classical quantum correlation.

Unfortunately, defining entanglement as non-classical quantum correlation is unsatisfying at an intuitive level because it’s a definition of entanglement in terms of what it is not. It’s actually rather challenging to explain precisely what entanglement is and what makes it special in intuitive terms.

Typical explanations of entanglement often need to distinguish the two states, A.51 and A.52, in a meaningful way. For example, it is sometimes said that if one of two entangled qubits is measured, then the state of the other qubit is somehow instantaneously affected, or that the state of the two qubits together cannot be described separately, or that the two qubits somehow maintain a memory of each other. The two bits represented by this state are intimately connected: each one has a perfect memory of the other in a literal sense. But it is nevertheless not entangled.

One way to explain what makes entanglement special and what makes the quantum state A.51 very different from the probabilistic state A.52 is to explain what can be done with entanglement or what we can see happening because of entanglement that goes beyond the decisions we make about how to represent our knowledge of states using vectors. All three of the examples to be discussed in this lesson have this nature in that they illustrate things that can be done with state A.51 that cannot be done with any classically correlated state, including state A.52.

Indeed, it is typical in the study of quantum information and computation that entanglement is viewed as a resource through which different tasks can be accomplished. When this is done, state A.51 is viewed as representing one unit of entanglement, which we refer to as an e-bit. (The "e" stands for "entangled" or "entanglement." While it is true that state A.51 is a state of two qubits, the quantity of entanglement that it represents is one e-bit.)

Incidentally, we can also view the probabilistic state A.52 as a resource, which is one bit of shared randomness. It can be very useful in cryptography, for instance, to share a random bit with somebody (presuming that nobody else knows what the bit is) so that it can be used as a private key (or part of a private key) for the sake of encryption. But in this lesson, the focus is on entanglement and a few things we can do with it.

As a point of clarification regarding terminology, when we say that Alice and Bob share an e-bit, what we mean is that Alice has a qubit named A, Bob has a qubit named B, and together, the pair

(A, B)

is in the quantum state A.51. Different names could, of course, be chosen for the qubits. Still, throughout this lesson, we will stick with these names in the interest of clarity.

Appendix A.9. Teleportation

Quantum teleportation, or just teleportation for short, is a protocol where a sender (Alice) transmits a qubit to a receiver (Bob) by making use of a shared entangled quantum state (one e-bit, to be specific) along with two bits of classical communication. The name teleportation is meant to suggest the concept in science fiction, where matter is transported from one location to another by a futuristic process. Still, it must be understood that matter is not teleported in quantum teleportation — what is actually teleported is quantum information.

The setup for teleportation is as follows.

We assume that Alice and Bob share an e-bit: Alice holds a qubit A, Bob holds a qubit B, and together the pair

(A, B)

is in the state

| Φ^{+} 〉

. It could be, for instance, that Alice and Bob were in the same location in the past; they prepared the qubits A and B in the state

| Φ^{+} 〉

, and then each went their way with their qubit in hand. It could also be that a different process, such as one involving a third party or a complex distributed process, was used to establish this shared e-bit. These details are not part of the teleportation protocol itself.

Alice then comes into possession of a third qubit Q that she wishes to transmit to Bob. The state of the qubit Q is considered to be unknown to Alice and Bob, and no assumptions are made about it. For example, the qubit Q might be entangled with one or more other systems that neither Alice nor Bob can access. To say that Alice wishes to transmit the qubit Q to Bob means that Alice would like Bob to be holding a qubit that is in the same state that Q was in at the start of the protocol, having whatever correlations that Q had with other systems as if Alice had physically handed Q to Bob.

We can, of course, imagine that Alice physically sends the qubit Q to Bob, and presuming that Q reaches Bob without being altered or disturbed in transit, Alice and Bob’s task will be accomplished. In the context of teleportation, however, we assume that Alice can’t physically send Q to Bob. She may, however, send classical information to Bob.

These are reasonable assumptions in a variety of settings. For example, if Alice does not know Bob’s exact location or the distance between them is large, physically sending a qubit using today’s or the foreseeable future’s technology would be challenging, to say the least. However, as we know from everyday experiences, classical information transmission under these circumstances is quite straightforward.

At this point, one might ask whether Alice and Bob can accomplish their task without even needing to make use of a shared e-bit. In other words, is there any way to transmit a qubit using classical communication alone? The answer is no, it is not possible to transmit quantum information using classical communication alone. This is not too difficult to prove using basic quantum information theory covered in the third unit of this series — but for now, an intuitive way to rule out the possibility of transmitting qubits using classical communication alone is to think about the no-cloning theorem.

Imagine that there was a way to send quantum information using classical communication alone. Classical information can easily be copied and broadcast, which means that any classical transmission from Alice to Bob could also be received by a second receiver (Charlie, let us say). But if Charlie receives the same classical communication that Bob received, then would he not also be able to obtain a copy of the qubit Q? This would suggest that Q was cloned, which we already know is impossible from the no-cloning theorem. So, we conclude that there is no way to send quantum information using classical communication alone.

However, when the assumption that Alice and Bob share an e-bit is in place, it is possible for Alice and Bob to accomplish their task. This is precisely what the quantum teleportation protocol does.

Appendix A.10. Conclusion

Quantum computing is a revolutionary field that leverages quantum-mechanical phenomena to perform calculations exponentially faster than classical computers. Quantum bits, or qubits, are the fundamental units of quantum information, allowing quantum computers to process vast amounts of data simultaneously. Quantum operations, such as superposition and entanglement, enable qubits to exist in multiple states simultaneously and to be correlated with each other instantaneously over long distances. Quantum algorithms, like Shor’s algorithm and Grover’s algorithm, demonstrate the potential of quantum computers to solve complex problems, such as integer factorization and database searching, significantly faster than classical computers. Despite facing challenges such as decoherence and error correction, the rapid progress in quantum computing research and development indicates a promising future for this transformative technology in revolutionizing computational capabilities across various industries.

Appendix B. Proof of Concept

Figure A2. Proof of Concept Application developed by using GoLang/WailsJS and SvelteJS

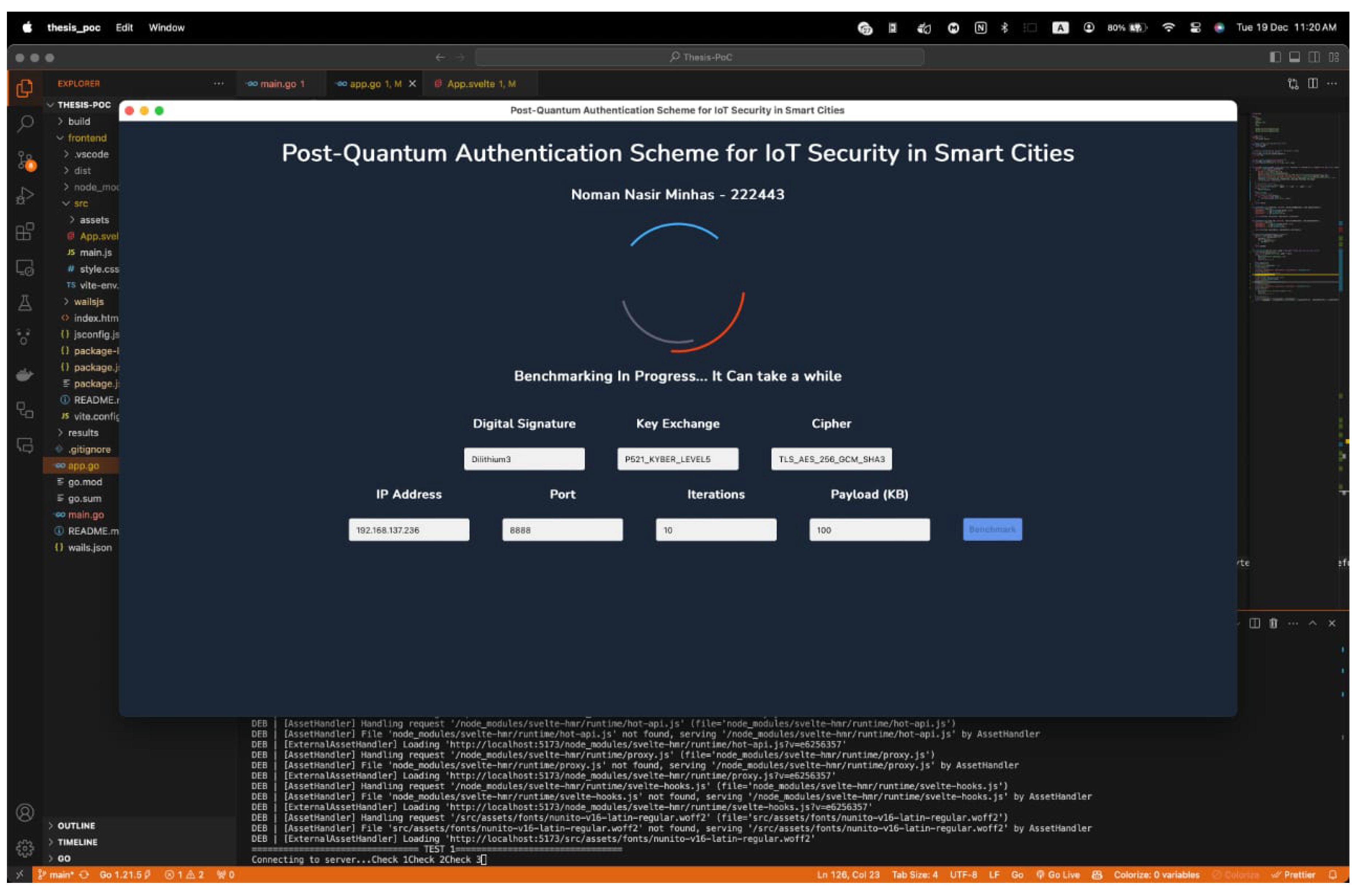
References

Taylor, P. Global IOT Connections Data Volume 2019 and 2025, 2022.
Pathak, S.; Pandey, M. Smart cities: Review of characteristics, composition, challenges and technologies. 2021 6th International Conference on Inventive Computation Technologies (ICICT). IEEE, 2021, pp. 871–876.
Silva, B.N.; Khan, M.; Han, K. Towards sustainable smart cities: A review of trends, architectures, components, and open challenges in smart cities. Sustainable cities and society 2018, 38, 697–713. [Google Scholar] [CrossRef]
Popescul, D.; Genete, L.D. Data security in smart cities: challenges and solutions. Informatica Economică 2016, 20. [Google Scholar] [CrossRef]
Frick, K.T.; Abreu, G.; Malkin, N.; Pan, A.; Post, A. The cybersecurity risks of smart city technologies: What do the experts think. White Paper, CLTC White Paper Series; UC Berkeley: Berkeley, CA, USA, 2021. [Google Scholar]
Gerck, E.; Gerck, A. QC Algorithms: Faster Calculation of Prime Numbers. published at https://www. researchgate. net/publication/373516233/. Accessed January 2024, 12.
VATRA, N. Public key infrastructure overview. Scientific Studies and Research 2009, 19. [Google Scholar]
Nihal, M. Quantum Computing: Program Next-gen Computers for Hard, Real-world Applications. Quantum Computing 2020, pp. 1–581.
Sutor, R.S. Dancing with Qubits: How quantum computing works and how it can change the world; Packt Publishing Ltd, 2019.
Hayward, M. Quantum computing and shor’s algorithm. Sydney: Macquarie University Mathematics Department 2008, 1. [Google Scholar]
Process, P.S. Announcing Four Candidates to be Standardized, Plus Fourth Round Candidates. URl: https://csrc. nist. gov/News/2022/pqc-candidates-to-be-standardized-and-round-4# newcall 2022.
Cryptography, P.Q. NIST.
Weger, V.; Gassner, N.; Rosenthal, J. A survey on code-based cryptography. arXiv 2022, arXiv:2201.07119 2022. [Google Scholar]
Feldmann, A. A survey of attacks on multivariate cryptosystems. Master’s thesis, University of Waterloo, 2005.
Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
Tan, T.G.; Zhou, J.; Sharma, V.; Mohanty, S.P. Post-Quantum Adversarial Modeling: A User’s Perspective. Computer 2023, 56, 58–67. [Google Scholar] [CrossRef]
Bai, S.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-dilithium: Algorithm specifications and supporting documentation (version 3.1). NIST Post-Quantum Cryptography Standardization Round 2021, 3.
Bos, J.W.; Renes, J.; Sprenkels, A. Dilithium for memory constrained devices. International Conference on Cryptology in Africa. Springer, 2022, pp. 217–235.
Kannwischer, M.J.; Rijneveld, J.; Schwabe, P.; Stoffelen, K. pqm4: Testing and Benchmarking NIST PQC on ARM Cortex-M4 2019.
Nouma, S.E.; Yavuz, A.A. Post-quantum forward-secure signatures with hardware-support for internet of things. ICC 2023-IEEE International Conference on Communications. IEEE, 2023, pp. 4540–4545.
Scott, M. On TLS for the Internet of Things, in a Post Quantum world. Cryptology ePrint Archive 2023. [Google Scholar]
Kaushik, A.; Vadlamani, L.S.S.; Hussain, M.M.; Sahay, M.; Singh, R.; Singh, A.K.; Indu, S.; Goswami, P.; Kousik, N.G.V. Post Quantum Public and Private Key Cryptography Optimized for IoT Security. Wireless Personal Communications 2023, 129, 893–909. [Google Scholar] [CrossRef]
Satrya, G.B.; Agus, Y.M.; Mnaouer, A.B. A Comparative Study of Post-Quantum Cryptographic Algorithm Implementations for Secure and Efficient Energy Systems Monitoring. Electronics 2023, 12, 3824. [Google Scholar] [CrossRef]
Paul, S. On the Transition to Post-Quantum Cryptography in the Industrial Internet of Things 2022.
Samandari, J.; Gritti, C. Post-quantum authentication in the MQTT protocol. Journal of Cybersecurity and Privacy 2023, 3, 416–434. [Google Scholar] [CrossRef]
Schwabe, P.; Stebila, D.; Wiggers, T. Post-quantum TLS without handshake signatures. Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, 2020, pp. 1461–1480.
McLoughlin, C.; Gritti, C.; Samandari, J. Full Post-Quantum Datagram TLS Handshake in the Internet of Things. International Conference on Codes, Cryptology, and Information Security. Springer, 2023, pp. 57–76.
Schöffel, M.; Lauer, F.; Rheinländer, C.C.; Wehn, N. Secure IoT in the era of quantum computers—where are the bottlenecks? Sensors 2022, 22, 2484. [Google Scholar] [CrossRef] [PubMed]
Malina, L.; Popelova, L.; Dzurenda, P.; Hajny, J.; Martinasek, Z. On feasibility of post-quantum cryptography on small devices. IFAC-PapersOnLine 2018, 51, 462–467. [Google Scholar] [CrossRef]
Tasopoulos, G.; Li, J.; Fournaris, A.P.; Zhao, R.K.; Sakzad, A.; Steinfeld, R. Performance evaluation of post-quantum TLS 1.3 on resource-constrained embedded systems. International Conference on Information Security Practice and Experience. Springer, 2022, pp. 432–451.
Sikeridis, D.; Kampanakis, P.; Devetsikiotis, M. Post-quantum authentication in TLS 1.3: a performance study. Cryptology ePrint Archive 2020.
Gonzalez, R.; Wiggers, T. KEMTLS vs. post-quantum TLS: Performance on embedded systems. International Conference on Security, Privacy, and Applied Cryptography Engineering. Springer, 2022, pp. 99–117.
Campos, F.; Chavez-Saab, J.; Chi-Domínguez, J.J.; Meyer, M.; Reijnders, K.; Rodríguez-Henríquez, F.; Schwabe, P.; Wiggers, T. On the practicality of post-quantum tls using large-parameter csidh. Technical report, Cryptology ePrint Archive, Paper 2023/793, 2023.
Septien-Hernandez, J.A.; Arellano-Vazquez, M.; Contreras-Cruz, M.A.; Ramirez-Paredes, J.P. A Comparative study of post-quantum cryptosystems for Internet-of-Things applications. Sensors 2022, 22, 489. [Google Scholar] [CrossRef] [PubMed]
Kern, D.; Krauß, C.; Lauser, T.; Alnahawi, N.; Wiesmaier, A.; Niederhagen, R. Quantumcharge: Post-quantum cryptography for electric vehicle charging. International Conference on Applied Cryptography and Network Security. Springer, 2023, pp. 85–111.
Chung, C.C.; Pai, C.C.; Ching, F.S.; Wang, C.; Chen, L.J. When post-quantum cryptography meets the Internet of Things: An empirical study. Proceedings of the 20th Annual International Conference on Mobile Systems, Applications and Services, 2022, pp. 525–526.
Barton, J.; Pitropakis, N.; Buchanan, W.; Sayeed, S.; Abramson, W. Post quantum cryptography analysis of TLS tunneling on a constrained device 2022.
Sizing Up Post-Quantum Signatures. https://blog.cloudflare.com/sizing-up-post-quantum-signatures. (Accessed on 04/10/2024).
Liu, Z.; Choo, K.K.R.; Grossschadl, J. Securing edge devices in the post-quantum internet of things using lattice-based cryptography. IEEE Communications Magazine 2018, 56, 158–162. [Google Scholar] [CrossRef]
Karakaya, A.; Akleylek, S. A novel IoT-based health and tactical analysis model with fog computing. PeerJ Computer Science 2021, 7, e342. [Google Scholar] [CrossRef] [PubMed]
Roy, K.S.; Deb, S.; Kalita, H.K. A novel hybrid authentication protocol utilizing lattice-based cryptography for IoT devices in fog networks. Digital Communications and Networks 2022.
Seyhan, K.; Nguyen, T.N.; Akleylek, S.; Cengiz, K. Lattice-based cryptosystems for the security of resource-constrained IoT devices in post-quantum world: a survey. Cluster Computing 2022, 25, 1729–1748. [Google Scholar] [CrossRef]
Zhang, K.; Ni, J.; Yang, K.; Liang, X.; Ren, J.; Shen, X.S. Security and privacy in smart city applications: Challenges and solutions. IEEE Communications Magazine 2017, 55, 122–129. [Google Scholar] [CrossRef]
Butt, T.A.; Afzaal, M. Security and privacy in smart cities: issues and current solutions. Smart Technologies and Innovation for a Sustainable Future: Proceedings of the 1st American University in the Emirates International Research Conference—Dubai, UAE 2017. Springer, 2019, pp. 317–323.

1	For a primer on Quantum Information and Computing, please see Appendix A.

Table 1. A comparison of Key, Signature, and Client Certificate size of Post-Quantum (PQ) and Conventional (C) Algorithms in bytes.

Algorithm	Class	Public Key	Private Key	Signature	Cert Size
Dilithium 2	PQ	1312	2528	2420	3870
Dilithium 3	PQ	1952	4000	3293	5982
Dilithium 5	PQ	2592	4864	4595	7486
Falcon 512	PQ	897	1281	690	2202
Falcon 1024	PQ	1793	2305	1330	4122
Sphincs 128f	PQ	32	64	17088	115
Sphincs 192f	PQ	48	96	35664	166
Sphincs 256f	PQ	64	128	49856	214
RSA-2048	C	256	256	256	1191
ECC 256-bit	C	64	32	256	712

Table 2. A comparison of CPU operations per second of Post-Quantum Algorithms.

Alogrithm	Key Gen.	Sign	Verify
Dilithium 2	1,400,412	6,157,001	1,461,284
Dilithium 3	2,282,485	9,289,499	2,228,898
Dilithium 5	3,097,421	8,469,805	3,173,500
Falcon 512	197,793,925	38,090,446	474,052
Falcon 1024	480,910,965	83,482,883	977,140
Sphincs 128f	16,552,135	521,963,206	20,850,719
Sphincs 192f	24,355,501	687,693,467	35,097,457
Sphincs 256f	64,184,968	1,554,168,401	36,182,488

Table 3. A comparison of stack memory size of Post-Quantum (PQ) Algorithms in bytes.

Algorithm	Key Gen.	Sign	Verify
Dilithium 2	36,424	61,312	40,664
Dilithium 3	50,752	81,792	55,000
Dilithium 5	67,136	104,408	71,472
Falcon 512	1,680	2,484	512
Falcon 1024	1,680	2,452	512
Sphincs 128f	2,192	2,248	2,544
Sphincs 192f	3,512	3,640	3,872
Sphincs 256f	5,600	5,560	5,184

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Post-Quantum Authentication Scheme for IoT Security in Smart Cities

Abstract

1. Introduction

1.1. Introduction of Public Key Infrastructure

1.2. Working of Asymmetric Cryptography

Generation of Public and Private Key Pair

Encryption

Decryption

Key Security

Potential Vulnerability

1.3. Introduction to Quantum Computers

2. Background

2.1. Need for Post-Quantum Cryptography

2.1.1. Shor’s Algorithm

2.1.2. NIST’s Post-Quantum Cryptography

2.1.3. Threat of Data Harvesting

2.2. IoT and Post-Quantum Cryptography

2.3. Problem Statement

3. Literature Review

4. Proposed System

4.1. Current Smart Cities Infrastructure

4.2. Issues with the IoT in Smart Cities

4.3. Proposed Solution

4.4. Implications of Proposed System on Smart Cities

4.4.1. Efficiency and Performance

4.4.2. Scalability and Interoperability

4.4.3. Security and Future-Readiness

4.5. Proposed System Algorithm

Initialization

Listening for Requests

Processing Incoming Requests

Establishing Connection

Forwarding Request

Receiving and Decrypting Response

Sending Decrypted Response

5. System Implementation

5.1. Algorithms Evaluated

5.2. Implementation Details

Evaluation Metrics

6. Results

6.1. Proposed System Results

6.2. Evaluation Metrics Results

6.2.1. Percentage of CPU Used By Each Algorithm

6.2.2. Number of CPU Context Switches Performed

6.2.3. RAM Used By Each Algorithm

6.2.4. Network Used By Each Algorithm

6.3. Comparative Analysis

6.4. Discussion

7. Future Work and Conclusion

7.1. Limitations

7.2. Future Work

7.3. Conclusion

Acknowledgments

Abbreviations

Appendix A. Quantum Information and Computing Primer

Appendix A.1. Introduction

Appendix A.2. Measuring Qubits

Appendix A.3. Unitary Operations

Appendix A.4. Pauli Operations

Appendix A.5. Hadamard Operation

Appendix A.5.1. Phase Operations

Appendix A.6. Entangled States

Appendix A.7. Bell States

Appendix A.7.1. GHZ and W States

Appendix A.8. Application of Entanglement

Appendix A.9. Teleportation

Appendix A.10. Conclusion

Appendix B. Proof of Concept

References

MDPI Initiatives

Important Links

Subscribe