Prerpints.org logo
Preprint
Article

Ultrasonic A-scan Signals Data Augmentation using Electromechanical System Modelling to Enhance Cataract Classification Methods

Altmetrics

Downloads

112

Views

31

Comments

0

Submitted:

29 July 2024

Posted:

29 July 2024

You are already at the latest version

Alerts
Abstract
A thorough understanding of the type and severity of cataracts is crucial for accurately estimating the optimal phacoemulsification energy. In preceding research efforts, an innovative clinical prototype known as the Eye Scan Ultrasound System (ESUS) was developed to facilitate the automated characterization of cataracts. To evaluate the effectiveness of the prototype as a medical tool, extensive data must be collected from several patients with and without cataracts. However, obtaining an adequate number of patients and data for training and testing machine learning models is challenging. To overcome this limitation, the authors implemented a simulated prototype model of the ESUS system, to augment the data. The proposed model encompasses the electric-to-acoustic signal conversion in the ultrasonic transducer, the wave propagation through the eye, and the subsequent acoustic-to-electric signal conversion. Electrical modelling of the transducer was done using a two-port network and the wave propagation was modelled by using the k-Wave MATLAB toolbox. This holistic modelling approach enabled the generation of synthetic data augmentation, presenting great similarity with real data. The synthetic data can then be employed together with real data for the purpose of cataract classification.
Keywords: 
Subject: Public Health and Healthcare  -   Public Health and Health Services

1. Introduction

Cataract is a degradation of the crystalline lens that impairs its transparency and light sensitivity, leading to deteriorated visual function and, if left untreated, eventual loss of vision [1]. According to the World Health Organization, cataract is the main cause of addressable vision impairment and blindness on a global scale. Out of the 2.2 billion individuals globally impacted by visual impairment, one billion suffer from conditions that could either be preventable or haven't yet been adequately addressed, such as cataract, a condition that affects 65.2 million people around the world [1]. Presently, surgical removal of the lens is the only effective treatment for cataracts [2]. Phacoemulsification is the most common used surgical approach for lens extraction. It employs ultrasound or laser energy to destroy the lens into fragments, which are then removed by aspiration. An artificial lens is then implanted, supported by the posterior lens capsule [3]. Phacoemulsification is a highly effective and safe technique. However, some intraoperative and postoperative complications may arise, causing delays in recovery [4]. These surgical complications are a result of different factors related to the patient, such as age and cataract density, or to the intervention itself, including phacoemulsification time, phacoemulsification energy, and surgeon experience. Common postoperative complications are corneal edema and endothelial cell loss. These problems may be minimized if the ultrasonic power and phacoemulsification time are reduced to minimum effective levels [5]. So, previous knowledge of the cataract type and severity is very important to quantitatively estimate the optimal phacoemulsification energy and plan of the surgical procedure. It also may improve the early cataract detection that by its time reduce the probability of surgical complications.
A clinical prototype has been developed and tested previously by the team [6]. To evaluate the effectiveness of the prototype as a medical tool, a big amount of data must be collected from several patients with and without cataracts. However, obtaining an adequate number of patients and data for training and testing a machine learning model will always be challenging. To overcome this limitation, the authors developed a model of the ophthalmologic transducer that generates an acoustic signal from an electrical excitation. Then, an acoustic simulation can be carried out to produce an acoustic response at the sensor surface. Finally, the same model of the ophthalmologic transducer produces an electrical echo derived from simulation results. Using this model, it is possible, through simulation, to introduce variations in the physical and acoustic parameters of the eye, thereby expanding the available data for training.
An acoustic 3D model of the eye, that comprises the propagation of the ultrasonic waves through the medium, was obtained using the MATLAB k-Wave toolbox [7]. This software package was already used to implement with success a computational tool for simulating ophthalmological applications of A-scan ultrasound, including cataract characterisation and biometry [8].
A model based on the Fourier transform and in the principle of linear superposition proposed by Fa [9] is used, to obtain the transient response of an acoustic transducer when it works as transmitter and receiver. Kinsler at al. [10], modelled a piezoelectric transducer as a two-port network that relates electrical quantities at one port to mechanical quantities at the other. There are two functions to be determined for that goal: (1) the electric-to-acoustic conversion function, given by the ratio of the pressure at the surface of the transducer, P1(s), to the applied voltage signal at the transducer electric terminals, V1(s) (H1(s)=P1(s)/V1(s)); (2) the acoustic-to-electric conversion function, determined as the ratio of the voltage signal at the transducer electric terminals, V2(s), to the acoustic pressure sensed in its surface, P2(s) (H2(s)=V2(s)/P2(s)).
Data augmentation techniques appear as a prevalent strategy to enlarge both the volume and diversity of training datasets, obviating the necessity to gather new data [11]. The task of acquiring larger datasets can often be intricate, and lead to patient discomfort arising from fatigue, limitations, or physical impairments. Notably, recent advancements in augmentation methods have materialized in specific domains within the field of biosignal processing, encompassing electroencephalography (EEG) [12,14], electromyography (EMG) [15,16,17], and electrocardiography (ECG) [18,19,20,21].
In the current study, after the comprehensive modelling of the ESUS, the generation of synthetic signals for database augmentation becomes feasible. These synthetic signals adeptly replicate cataract structures within the acoustic simulation medium. The resulting dataset, enriched with these synthetic signals, holds significant utility for training machine learning models. This approach not only addresses the challenges associated with acquiring extensive real-world data but also ensures that the model deals with a diverse scenario that faithfully represent variations in cataract structures.

2. Materials and Methods

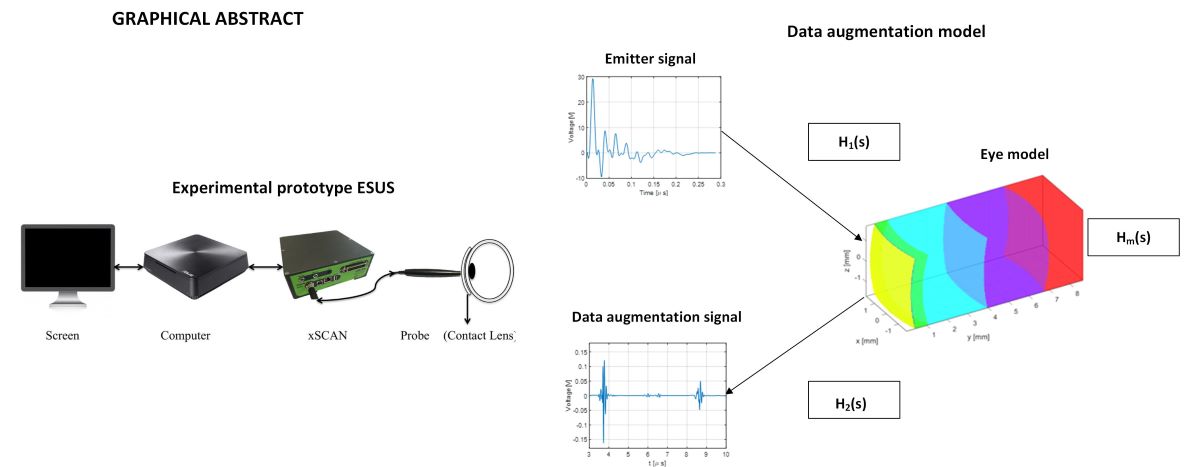
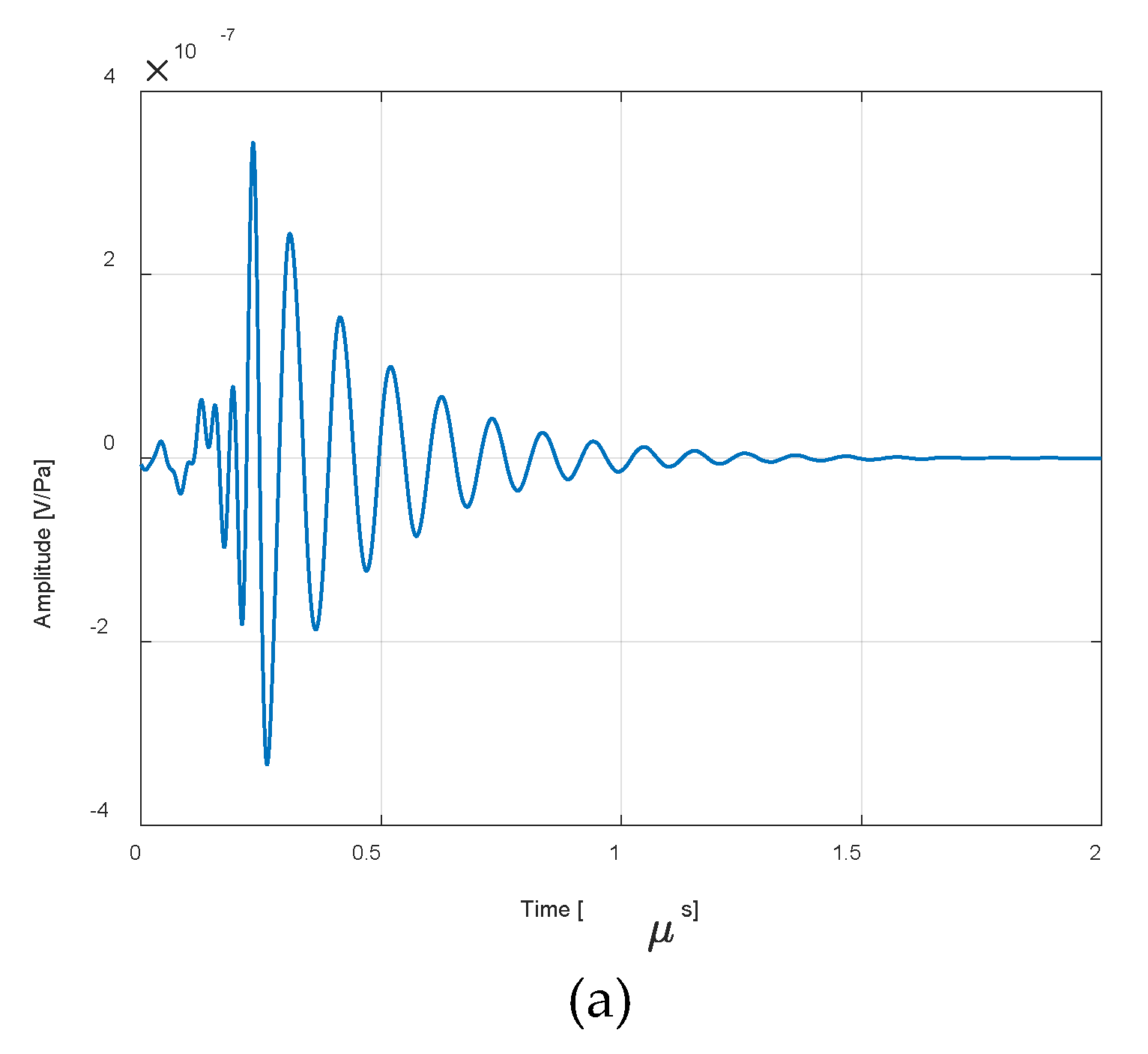
2.1. Acoustic Simulation Model

The k-Wave MATLAB toolbox is a valuable tool for simulating the propagation of ultrasound waves through the eye, as it allows time-domain simulations in 1D, 2D, and 3D. To utilize the k-Wave, it was necessary to define several parameters, such as the computational grid, excitation pulse, source and sensor transducer, and medium properties [22]. The simulated transducer is based on the ophthalmologic one used in the cataract classification prototype. It is characterized as a focused mono-element device operating in pulse-echo mode, with a 9 mm radius of curvature, a 3.2 mm diameter, an approximate focal distance of 8 mm, and a central frequency of 20 MHz. As the simulated transducer is focalized, only the central part of the eye is considered for the matrix, since the acoustic waves will not propagate to the peripheral zones. Also, once the region of interest is the crystalline lens, the matrix depth was limited to include the cornea, aqueous humour, the lens and around 1 millimetre after the lens posterior interface. This resulting matrix considerably reduces the required computational resources. The 2D and 3D computational grids used in the scope of this work are illustrated in Figure 1 (a) and (b), respectively.
A computational tool was developed to simulate the propagation of A-scan signals through various eye structures. The dimensions and acoustic properties of the different eye structures are presented in Table 1 [8].
In the simulation setup the transducer was coupled to the cornea (contact biometry). Due to the slight difference in the radii of curvature between the transducer and the cornea, water´s acoustic properties were used for the space between them.
For the simulation of cataractous lenses, the acoustic properties typical of severe nuclear cataracts were considered: velocity of 1785 m/s, density of 1200 kg/m³, and attenuation coefficient of 5.2 dB/(cm.MHz) [6].

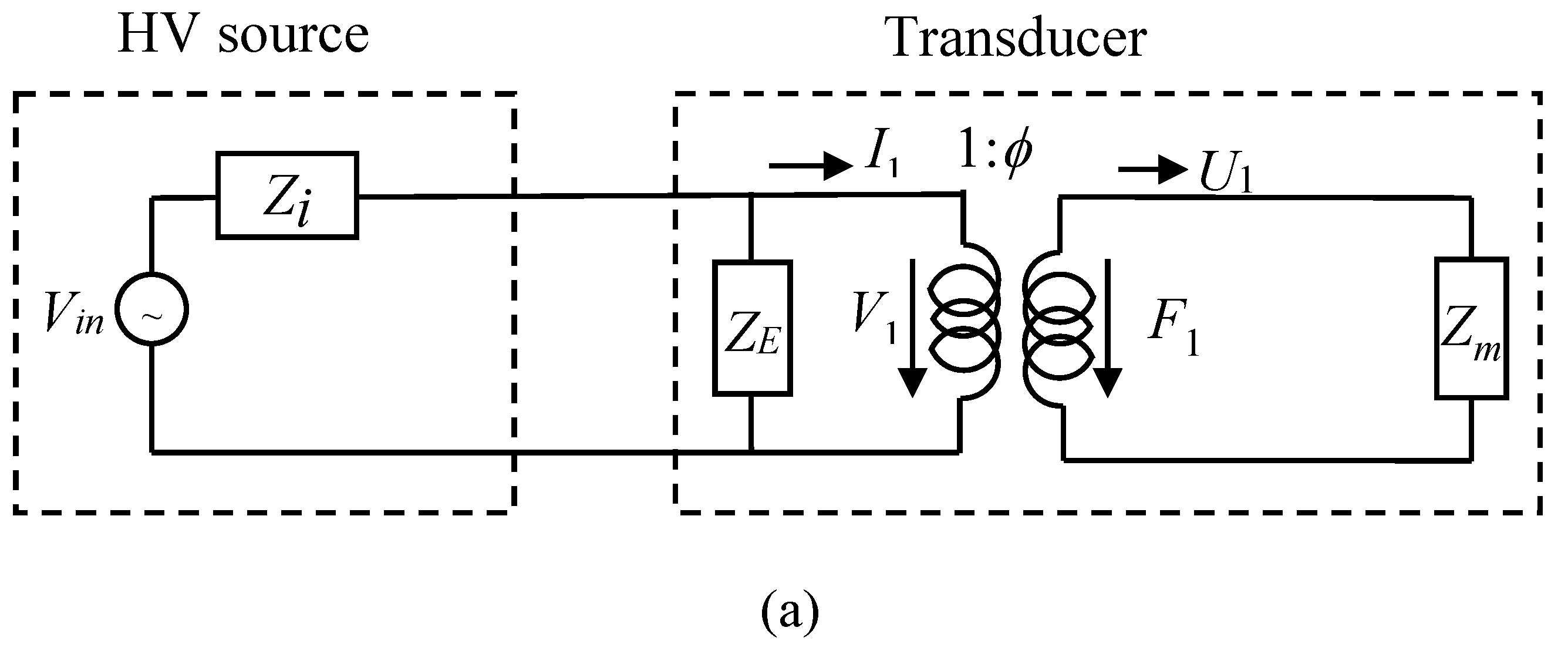
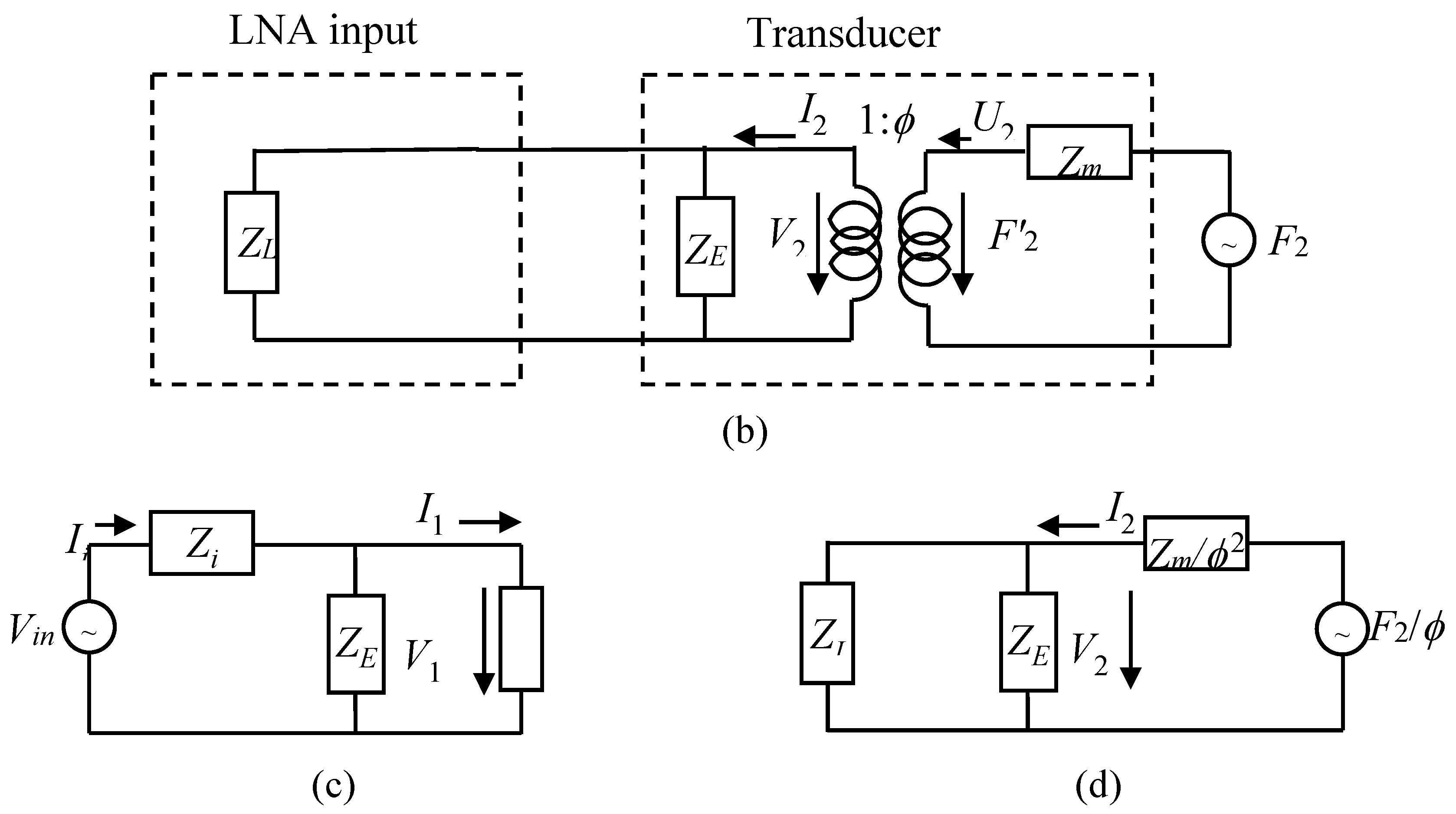
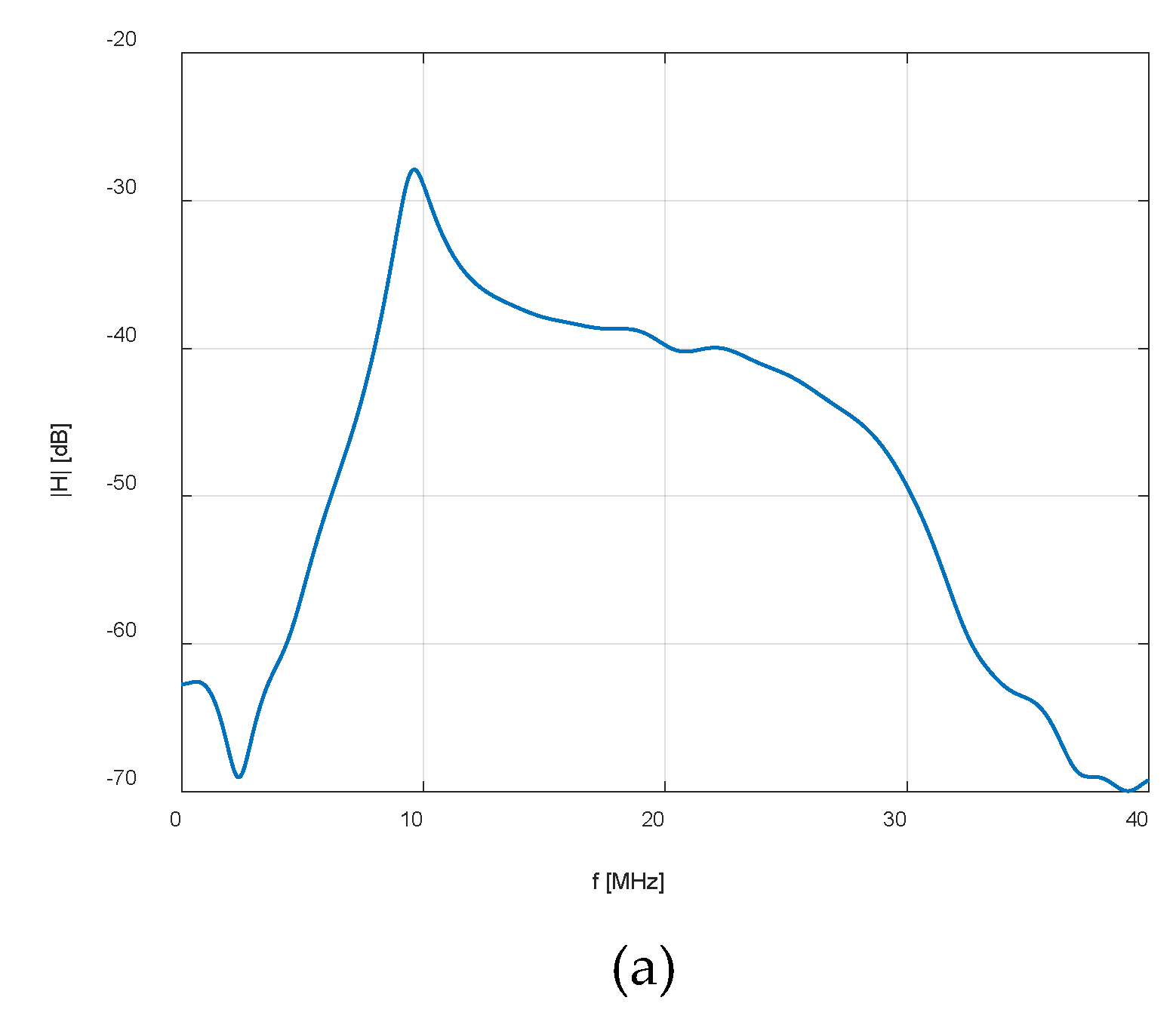
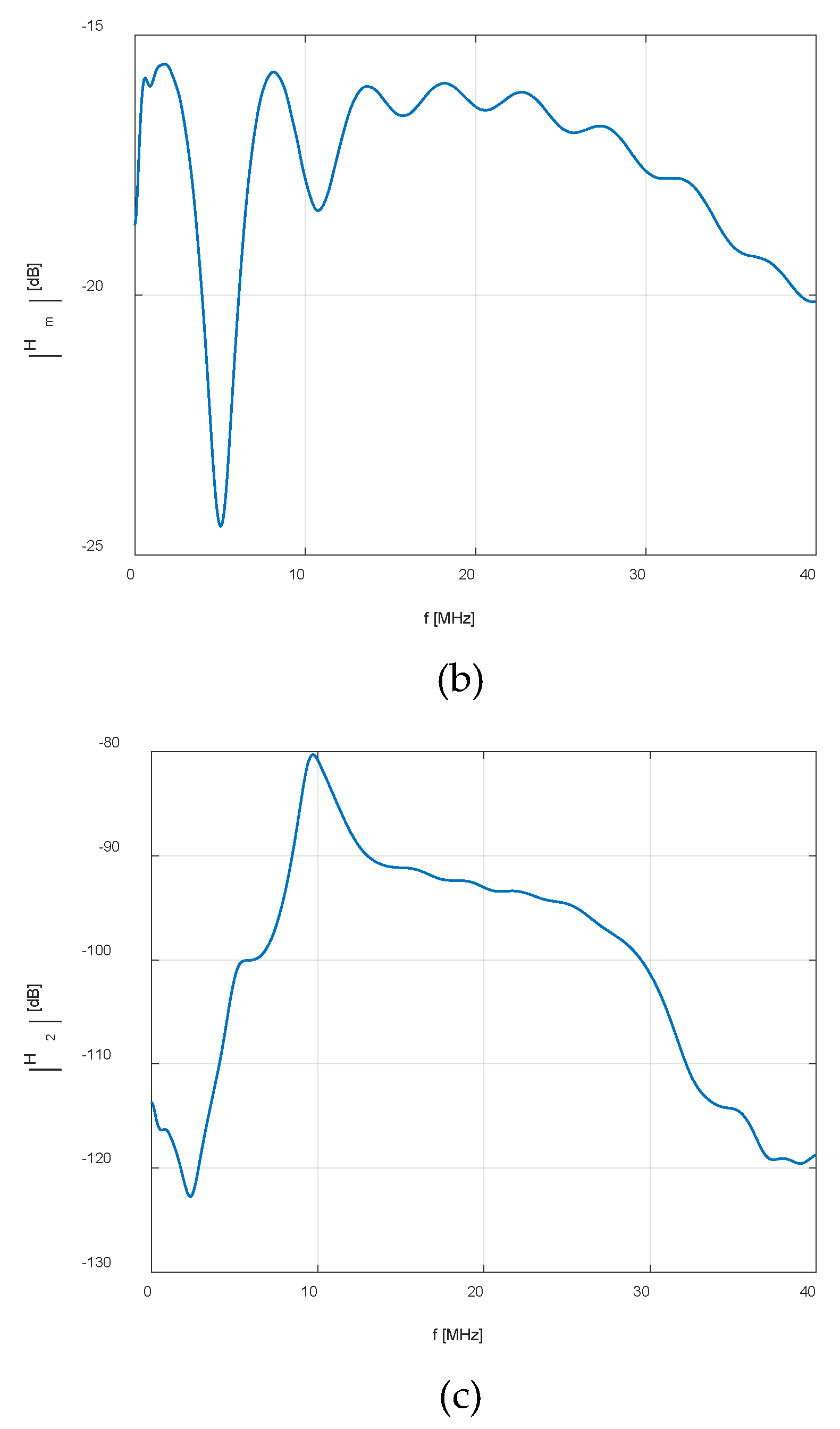
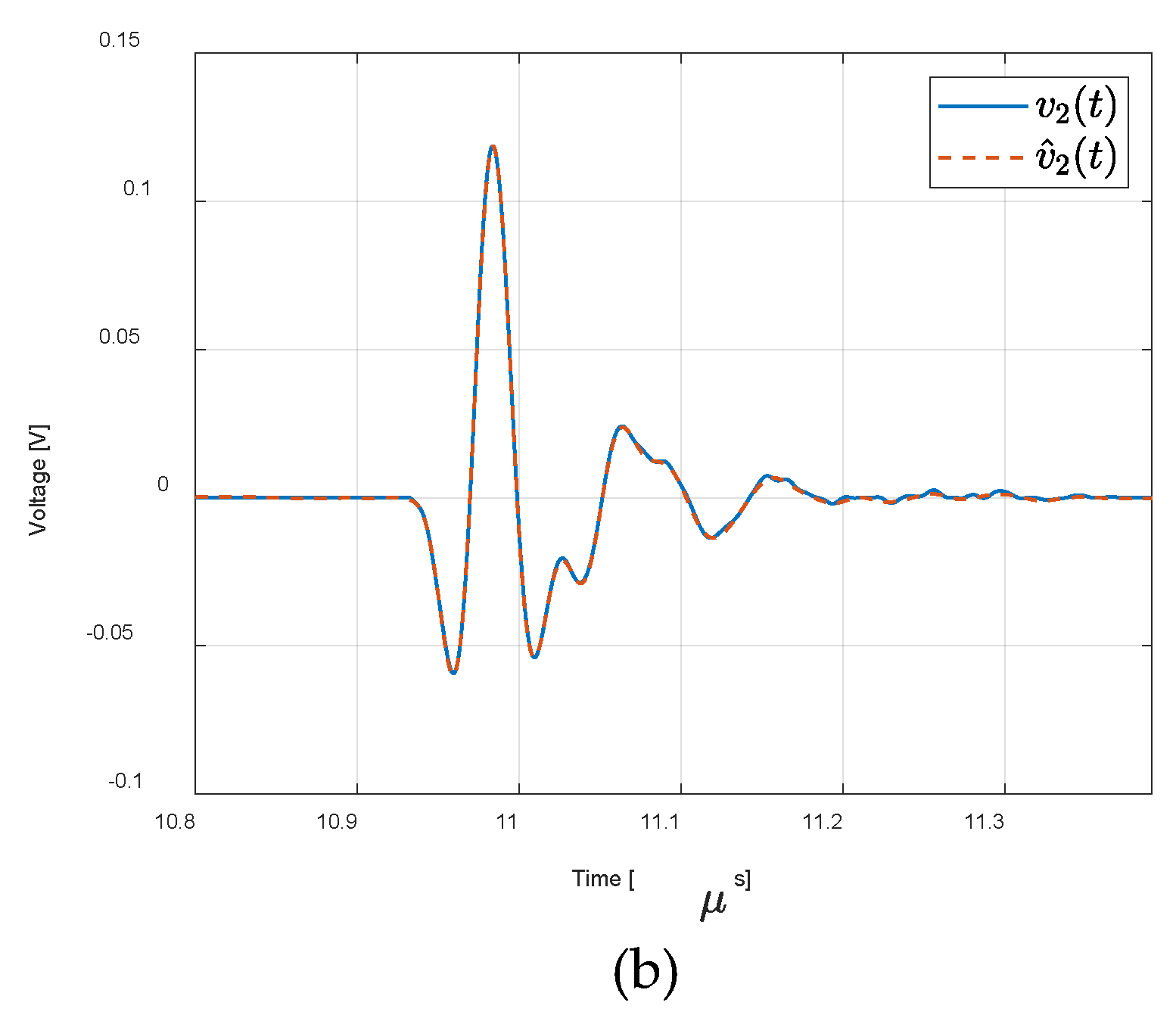
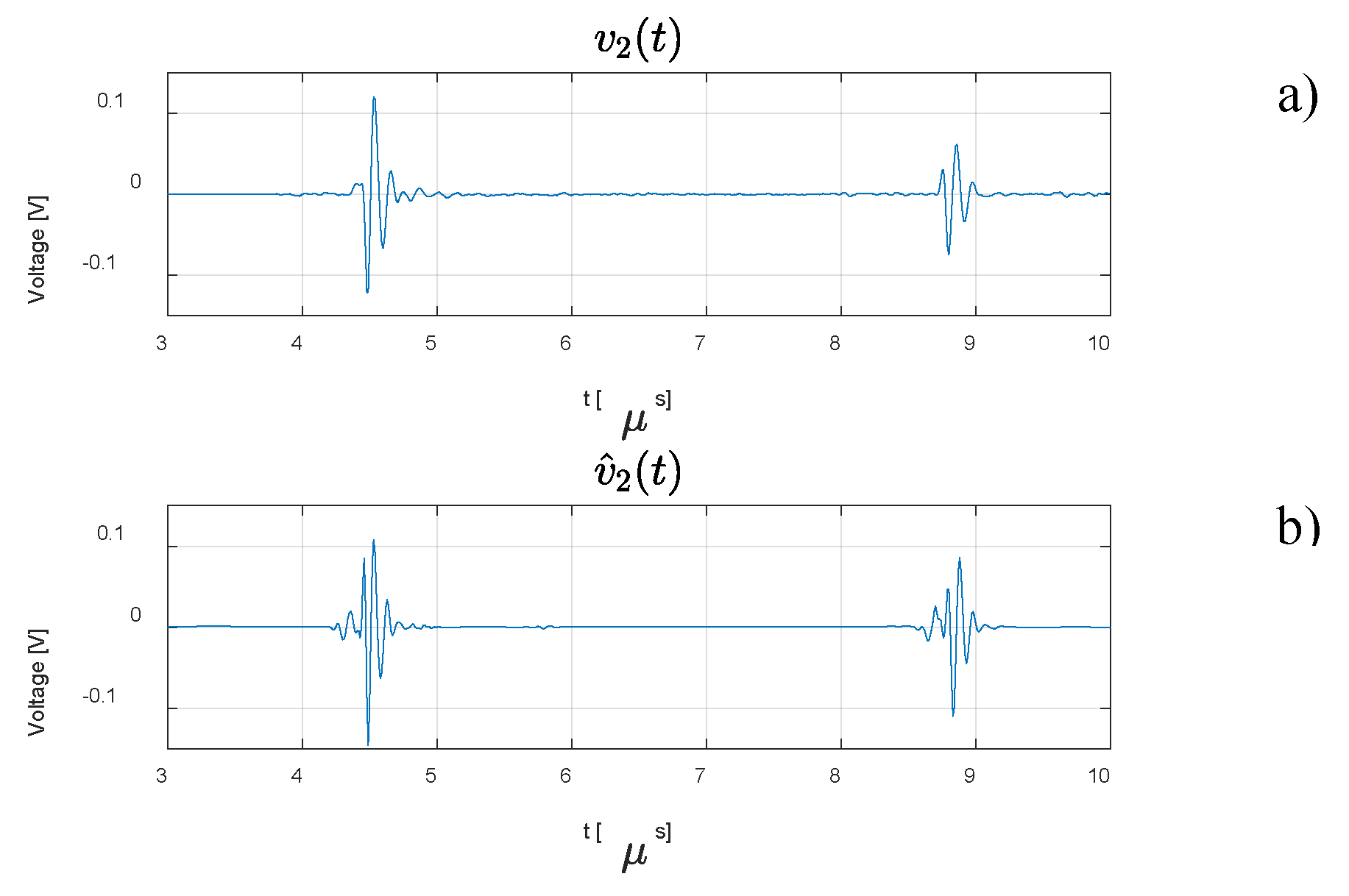
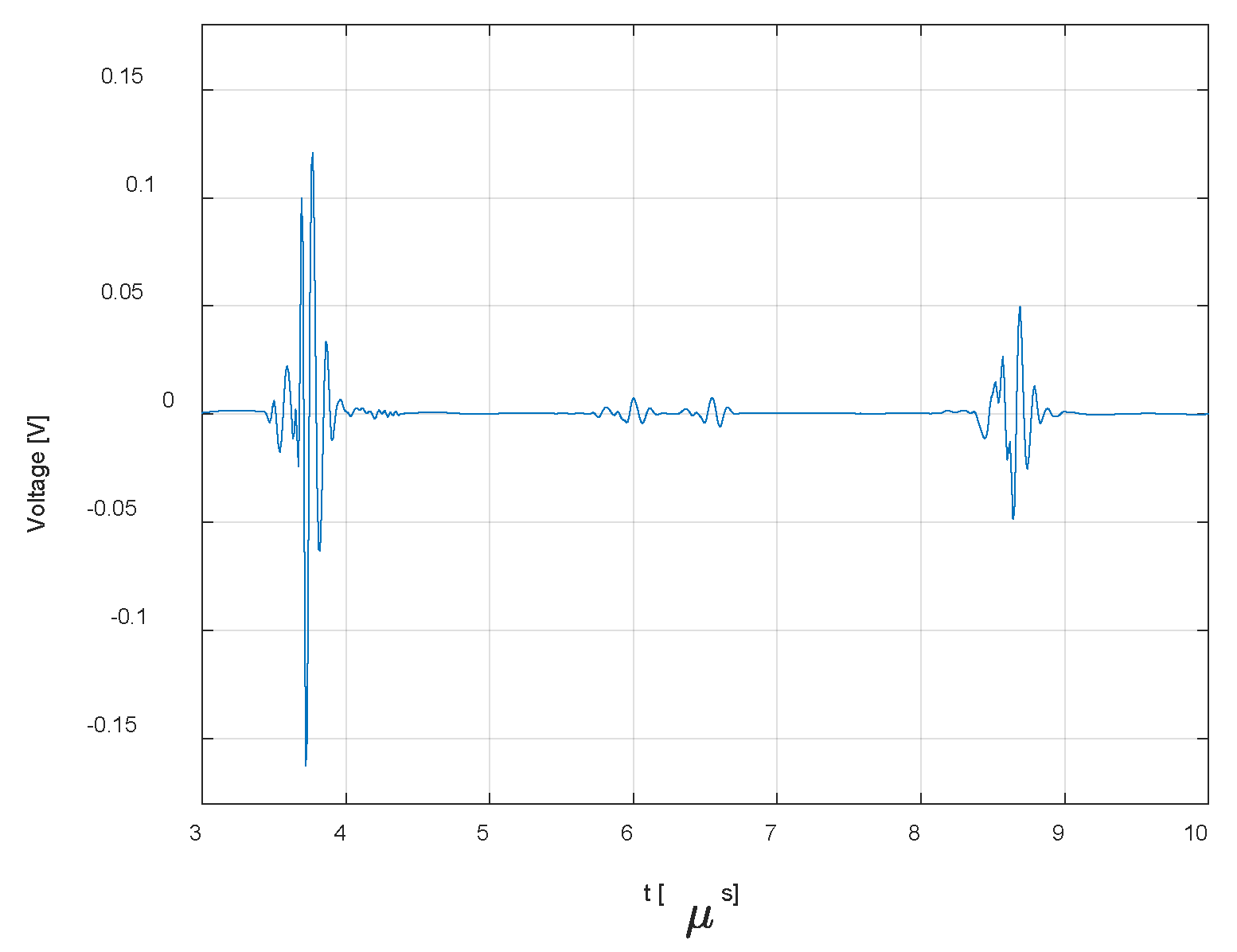
2.2. ESUS Electrical Modelling

The output y(t) of a LTI (linear and time invariant) system, with impulse response h(t), and an input x(t) is given by the convolution integral of the two continuous-time signals, as given in Eq. (1) [23].
y t = ∫ − ∞ + ∞ x τ h t − τ d τ = h t ∗ x t .
The convolution of two signals in the time domain corresponds to multiplication of their Fourier Transform (FT) in the frequency domain, given by:
y t = h t ∗ x t ↔     Y j ω = H j ω . X j ω ,
where X(jω), H(jω) and Y(jω) are the Fourier transforms of x(t), h(t) and y(t), respectively.
To represent the ESUS prototype by its impulse response, diverse system components like the signal generator, cables and connectors, transducer operating in pulse-echo mode, propagating medium, and receiver amplifier should be considered. Cables and connectors can typically be considered to have a unit frequency response.
From the approaches used by Fa [9] and Kinsler [10], two simplified circuits for the ESUS emitter and receiver stages can be obtained and are represented in Figure 2. The emitter stage is composed by the generator, which has an excitation voltage Vin and impedance Zi, and the transducer with its electric impedance ZE, mechanical impedance Zm and an ideal transformer with ratio 1:ϕ, as illustrated in Figure 2(a). The receiver stage, in echo mode, is composed by the transducer working as receiver and the low noise amplifier (LNA) with an input impedance ZL (see Figure 2(b)). Note that the impedance values for the transmitter and receiver, working in pulse-echo mode, may differ. When the transducer works as emitter (pulse mode), a high voltage source (HV) is coupled to it, while in echo mode the transducer is connected to the LNA, with probably different impedances at its terminals.
A transformer with ratio 1:ϕ, represents the electrical-to-acoustic conversion, with a voltage (V1) and a current (I1) in the electrical side, and a force (F1) and a transducer surface velocity (U1) in the acoustic side. The relation between electrical and mechanical quantities is presented in Eq. (3) [10]. The transformer is lossless, with equal power in the primary and secondary coils (V1I1=F1U1).
V 1 F 1 = U 1 I 1 = 1 ϕ   .
It is possible to reduce the circuit shown in Figure 2 (a) to the electrical side of the transformer, giving rise to the equivalent circuit shown in Figure 2 (c). Using the same methodology for the receiver stage (Figure 2 (b)), results the equivalent circuit reduced to the electrical side of the transformer, as presented in the Figure 2 (d). In this case the impedance Zm is seen in the electrical side divided by ϕ 2 and the force F2 divided by ϕ.
For data augmentation purposes, we need to know the pressure signal p1(t) to be used in the acoustic simulation as a result of an electrical excitation signal v1(t). It is also necessary to obtain the electrical signal v2(t) given a pressure signal p2(t) produced by simulation, after propagation in the eye model. This knowledge enables the derivation of the relationship between v1(t) and v2(t), in Laplace domain, as
H s = V 2 s V 1 s = P 1 s V 1 s × P 2 s P 1 s × V 2 s P 2 s = H 1 s × H m s × H 2 s ,
where H1(s) and H2(s) are the transfer functions when the system works as emitter and as receiver, respectively, and Hm(s) is the transfer function related to the propagation on the considered medium (eye structures).
From the model of the Figure 2a) and Eq. (3) the force F1 in the mechanical side of the transformer is
F 1 s = ϕ   V 1 s .
Using the relation F(s)=AP(s), where A is the transducer area, it is easy to show that the pressure signal in time domain is given by
p 1 t = ϕ A v 1 t .
So, p1(t) is proportional to v1(t), and H1(s) is a simple relationship of constants of the transducer,
H 1 s = P 1 s V 1 s = ϕ A .
The propagation medium transfer function Hm(s) is defined as the ratio between the received acoustic signal, denoted as P2(s), resulting from the reflections in the propagation medium, and the emitted acoustic signal, P1(s). Knowing the electrical excitation signal, v1(t), the emitted acoustic signal p1(t) is determined by Eq. (6) and used as the acoustic stimulus for the simulation. The pressure signal p2(t) is obtained from the simulation result presented in section 2.1. From Figure 2 d), considering a load impedance Z2 as ZL in parallel with ZE, the voltage V2(s) can easily be obtained considering a voltage divider, as:
V 2 s = ϕ Z 2 ϕ 2 Z 2 + Z m × A P 2 s ,
so, the transfer function H2(s) is given by:
H 2 s = V 2 s P 2 s = ϕ A Z 2 ϕ 2 Z 2 + Z m .
However, because V2(s) can be obtained from v2(t), the electrical echo received, and, in the same way, P2(s) can be obtained from the simulation result, p2(t), then, one can derive H2(s) without requiring the knowledge of ZL, ZE or Zm. To achieve this, an experimental echo signal, v2(t), reflected on a flat metal plate positioned perpendicularly to the beam propagation direction and at the transducer's focal point in water, was used. The acoustic pressure signal, p2(t), was obtained from the simulation, considering a plate in water, under identical conditions of the real experiment. Then, the function H2(s), which is independent of the propagation medium, can be readily obtained using these signals in the Laplace domain.
If h2(t) is the corresponding impulse response of H2(s), it is possible to estimate the electric echo signal, v ^ 2 t as
v ^ 2 t = h 2 t ∗ p 2 t ,
where (*) indicates the convolution operator and p2(t) is an estimate of the pressure echo signal.
Therefore, following the system modelling, once the simulated pressure signal for a specific medium is known, generating synthetic signals for database augmentation becomes feasible.
The impulse response h2(t) corresponds to the acoustic-to-electric transduction in the ESUS system and must be evaluated only once. Then, any electrical echo signal could be derived from the result of a simulation pressure, using Eq. (10).

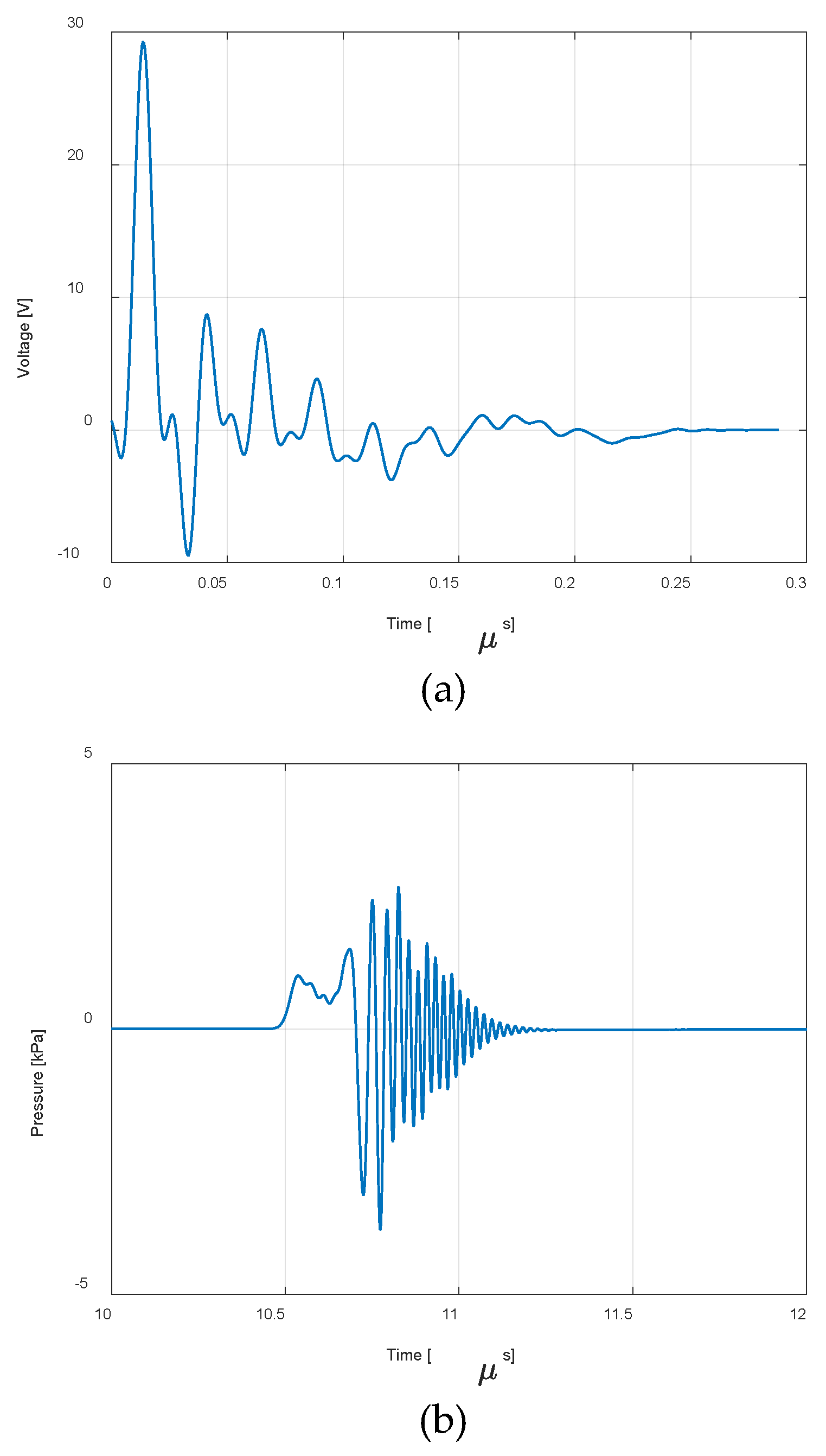
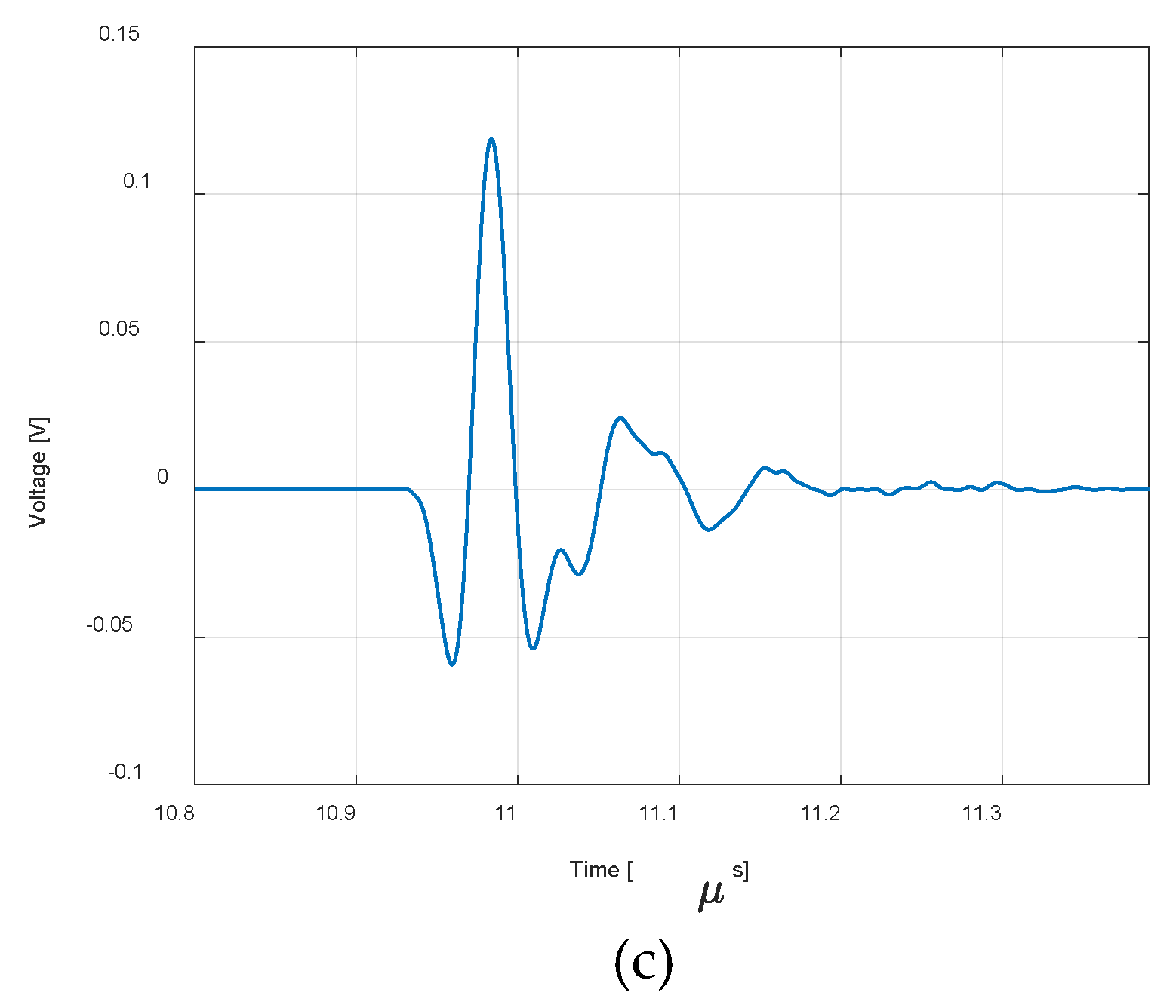
3. Results

To validate the previously proposed model, first the excitation signal v1(t), generated by the ESUS, was acquired using an oscilloscope (DPO 3054; Tektronix Inc, Beaverton, OR) at a sampling frequency of 2.5 GHz. The signal is illustrated in Figure 3(a) and is used in Eq. (6) to obtain the pressure signal p1(t).
The constant relation ϕ/A, representing the relationship between the transducer applied voltage and the pressure on its surface, was determined through experimental measurements. In a prior study [6], experimental pressure measurements at the focal point of the ophthalmic transducer were conducted for safety assessments of the proposed A-scan ultrasonic system, and the obtained maximum value was pf =1.02 MPa.
The pressure on the transducer surface when working in pulse mode can be obtained knowing the focusing gain G for the pressure amplitude [24]
G = k a 2 2 F ,
where k is the wavenumber, a the transducer radius and F the focal distance. For the presented transducer, these parameters have values of k=83.77×103 m-1, a=1.6 mm and F=8 mm, resulting in G=11.17, and the maximum value of the pressure at transducer surface is calculated as p1max=pf/G=88.1 kPa. The use of this value and the maximum voltage of v1(t) extracted from Figure 3 (a), allows deriving the transfer function H1(s)=ϕ/A=3.03 kPa/V. The pressure signal p1(t), employed as an input in the acoustic simulator, is obtained using Eq. 6. The acoustic simulation model presented in Section 2.1 was employed with p1(t) as the input to generate the echo signal p2(t), shown in the Figure 3 (b), which is the signal at the transducer surface that is reflected from a flat metal plate in water positioned at the transducer focus Figure 3 (c) presents the experimental electrical echo signal reflected from the metal plate, acquired by the oscilloscope.
Applying an inverse fast Fourier transform to H2(jω), after low-pass filtering, yields the corresponding impulse response h2(t), presented in Figure 5 (a). The estimated received signal is then obtained by applying Eq. 10. Figure 5 (b) depicts the received signal v 2 ( t ) and the estimated one v ^ 2 ( t ) . They exhibit a high degree of similarity. This observation enables us to conclude that the presented method can accurately generate signals for data augmentation purposes.
Applying the same previous procedure, the model was tested using a simulated healthy lens signal, obtained from the 3D structure presented in Figure 1 (b). From this signal, the estimate of the electrical signal is computed, based on the impulse response h2(t). The comparison with a real signal acquired using the ESUS in a previous work [25] is presented in the Figure 6. The anterior and posterior lens interfaces are clearly identified, and once again, the similarity between the estimated and the real signals is very good.
As the main goal of this work was the generation of synthetic signals for database augmentation to be used in the cataract classification process, an example of a nuclear cataract was modelled with a 1 mm diameter sphere and cataractous tissue properties presented in section 2.1. Figure 7 presents the estimated signal v ^ 2 ( t ) where it is clearly observed the echo signal from the cataract. Notice that the real dimensions and position of the eye lens can vary among people, so, the simulation in Figure 6 has different times from the one in Figure 7, meaning different propagation delays of the eye structures. Other kinds of cataracts can be modeled in the same way. In near future, an already planned clinical trial will allow acquiring real data from eyes with different cataracts that will contribute for the validation and improving of the proposed model.

4. Discussion

In the present work an electrical-acoustic model of the prototype ESUS was developed. A 3D computational model was established using the k-Wave MATLAB toolbox to simulate the propagation of ultrasonic waves through the eye. The electrical modelling considered different equivalent circuits, depending on whether the transducer is working as emitter or receiver. In the emitter mode the acoustic pressure is proportional to the excitation signal, being the electrical-to-acoustic transduction obtained by a direct relation. In the receiver mode, the transfer function depends on the transducer impedance and on the receiver LNA input impedance. However, it was shown that by using the simulated pressure echo signal, the acoustic-to-electrical transfer function can be straightforwardly obtained, avoiding the knowledge of those impedances. This transfer function was obtained with an experimental setup using a flat reflector positioned in the transducer focus. A good agreement was observed between the experimental result and the estimated one.
The model was also evaluated on signals acquired from healthy eyes and the obtained results demonstrated that the proposed approach is a valuable way to implement synthetic data augmentation, replicating real observed data. The model was also tested for a simulated signal from a nuclear cataract. The promising achieved results can lead to dataset production, which is very useful for the development of machine learning models. In future work the proposed approach can be validated in a context of a clinical trial and used in the development of machine learning models. The presented approach can be used in other ultrasonic systems working in pulse-echo mode.
The integration of real-world patient data will enhance the model's accuracy and applicability, contributing to the refinement and validation of the ESUS system for robust cataract characterization. This research is a contribution to bridge the gap between theoretical modelling and practical clinical application, and thus to enhance the precision and effectiveness of cataract diagnosis and treatment planning.

Author Contributions

Conceptualization, formal analysis, methodology M.S. and F.P.; software, L.P.; writing—original draft preparation M.S. and F.P.; validation, writing—review and editing M.S., F.P., L. P. and J.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This research is sponsored by FCT – Fundação para a Ciência e a Tecnologia under the projects UIDB/00285/2020, LA/P/0112/2020 and UIDB/00326/2020.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Michael, R.; Bron, A. The ageing lens and cataract: A model of normal and pathological ageing, Philosophical Transactions of the Royal Society B: Biological Sciences. 366, 1568 (2011) 1278–1292. [CrossRef]
  2. World Health Organization, World report on vision 2019. https://www.who.int/publications/i/item/9789241516570 (accessed 22 February 2024).
  3. Queirós, L.; Redondo, P.; França, M.; Silva, S.; Borges, P.; Melo, A.; Pereira, N.; Costa, F.; Carvalho, N.; Borges, M.; Sequeira, I.; Gonçalves, R.; Lemos, J. Implementing ICHOM standard set for cataract surgery at IPO-Porto (Portugal): clinical outcomes, quality of life and costs, BMC Ophthalmol. 21, 1, (2021). [CrossRef]
  4. Martínez, M.; Moyano, D.; González-Lezcano, R. Phacoemulsification: Proposals for improvement in its application. Healthcare. 9, 11, (2021) 1-13. [CrossRef]
  5. Abell, R.; Kerr, N.; Howie, A.; Kamal M.; Allen, P.; Vote B. Effect of femtosecond laser–assisted cataract surgery on the corneal endothelium. J Cataract Refract Surg. 40, 11, (2014) 1777-1783. [CrossRef]
  6. Petrella, L.; Fernandes, P.; Santos, M.; Caixinha, M.; Nunes, S.; Pinto, C.; Morgado, M.; Santos, J.; Perdigão, F.; Gomes, M. Safety Assessment of an A-Scan Ultrasonic System for Ophthalmic Use, Journal of Ultrasound in Medicine, 39, 11, (2020) 2143–2150. [CrossRef]
  7. Treeby, B.; Cox, B. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J Biomed Opt. 15, 2, (2010) 021314. [CrossRef]
  8. Petrella, L.; Perdigão, F.; Caixinha M.; Santos, M.; Lopes, M.; Gomes, M.; Santos, J. A-scan ultrasound in ophthalmology: A simulation tool. Med Eng Phys, 97, (2021) 18–24. [CrossRef]
  9. Fa, L.; Liu, D.; Gong, H.; Chen, W.; Zhang, Y.; Wang, Y.; Liang, R.; Wang, B.; Shi, G.; Fang, X. A Frequency-Dependent Dynamic Electric–Mechanical Network for Thin-Wafer Piezoelectric Transducers Polarized in the Thickness Direction: Physical Model and Experimental Confirmation. Micromachines. 14(8), 1641 (2023). [CrossRef]
  10. Kinsler, L.; Frey, A.; Coppens, A.; Sanders, J. Fundamentals of Acoustics, 4th edition, John Wiley & Sons, New York, 2000.
  11. Bull, D.; Zhang, F. Intelligent Image and Video Compression, Academic Press, 2021. [CrossRef]
  12. Krell, M.; Kim, S. Rotational data augmentation for electroencephalographic data, 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2017. [CrossRef]
  13. Lashgari, E.; Liang, D.; Maoz, U. Data Augmentation for Deep-Learning-Based Electroencephalography. J. Neurosci. Methods. 346, 108885 (2020) 1-25. [CrossRef]
  14. Wang, F.; Zhong, S.; Peng, J.; Jiang, J.; Liu, Y. Data Augmentation for EEG-Based Emotion Recognition with Deep Convolutional Neural Networks. MultiMedia Modeling, MMM 2018, Lecture Notes in Computer Science, 10705, (2018) 82–93. [CrossRef]
  15. Atzori, M.; Cognolato, M.; Müller, H. Deep Learning with Convolutional Neural Networks Applied to Electromyography Data: A Resource for the Classification of Movements for Prosthetic Hands. Front. Neur. 10, (2016). [CrossRef]
  16. Geng, W.; Du, Y.; Jin, W.; Wei, W.; Hu, Y.; Li, J. Gesture recognition by instantaneous surface EMG images. Sci. Rep. 6, 36571 (2016). [CrossRef]
  17. Cornelis, P.; Cornelis, J.; Jansen, B.; Skodras, A. Data Augmentation of Surface Electromyography for Hand Gesture Recognition, Sensors. 20, 17, 4892 (2020). [CrossRef]
  18. Ma, S.; Cui, J.; Chen, C.; Chen, X.; Ma, Y. An Effective Data Enhancement Method for Classification of ECG Arrhythmia. Measurement, 203, 111978. (2022) 1-13. [CrossRef]
  19. Golany, T.; Radinsky, K. PGANs: Generative adversarial networks for ECG synthesis to improve patient-specific deep ECG classification. In Proceedings of the AAAI Conference on Artificial Intelligence, 33 (2019) 557–564.
  20. Golany, T.; Radinsky, K.; Freedman, D. SimGANs: Simulator-based generative adversarial networks for ECG synthesis to improve deep ECG classification. ICML'20: Proceedings of the 37th International Conference on Machine Learning, (2020) 3597–3606.
  21. Wicaksono, P.; Philip, S.; Alam, I.; Isa, S. Dealing with Imbalanced Sleep Apnea Data Using DCGAN. Trait. Signal, 39, 5, (2022) 1527–1536. [CrossRef]
  22. Treeby, B.; Cox, B. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields, J. Biomed. Opt. 15, 2, 021314 (2010). [CrossRef]
  23. Oppenheim, A. Signals and Systems, Second edition, Willsky, A. S., Prentice-Hall, New Jersey, 1997.
  24. Bessonova, O.; Khokhlova, V.; Bailey, M.; Canney, M.; Crum, L. Focusing of high power ultrasound beams and limiting values of shock wave parameters. Acoustical physics, 55, (2009) 463–476. [CrossRef]
  25. Santos, M.; Conceição, I.; Petrella, L.; Perdigão, F.; Santos, J.; Caixinha, M.; Gomes, M.; Morgado, M. Modelling of an ultrasound-based system for cataract detection and classification, Proceedings of the 13th European Conference on Non-Destructive Testing (ECNDT), (2023). Research and Review Journal of Nondestructive Testing, 1(1). [CrossRef]
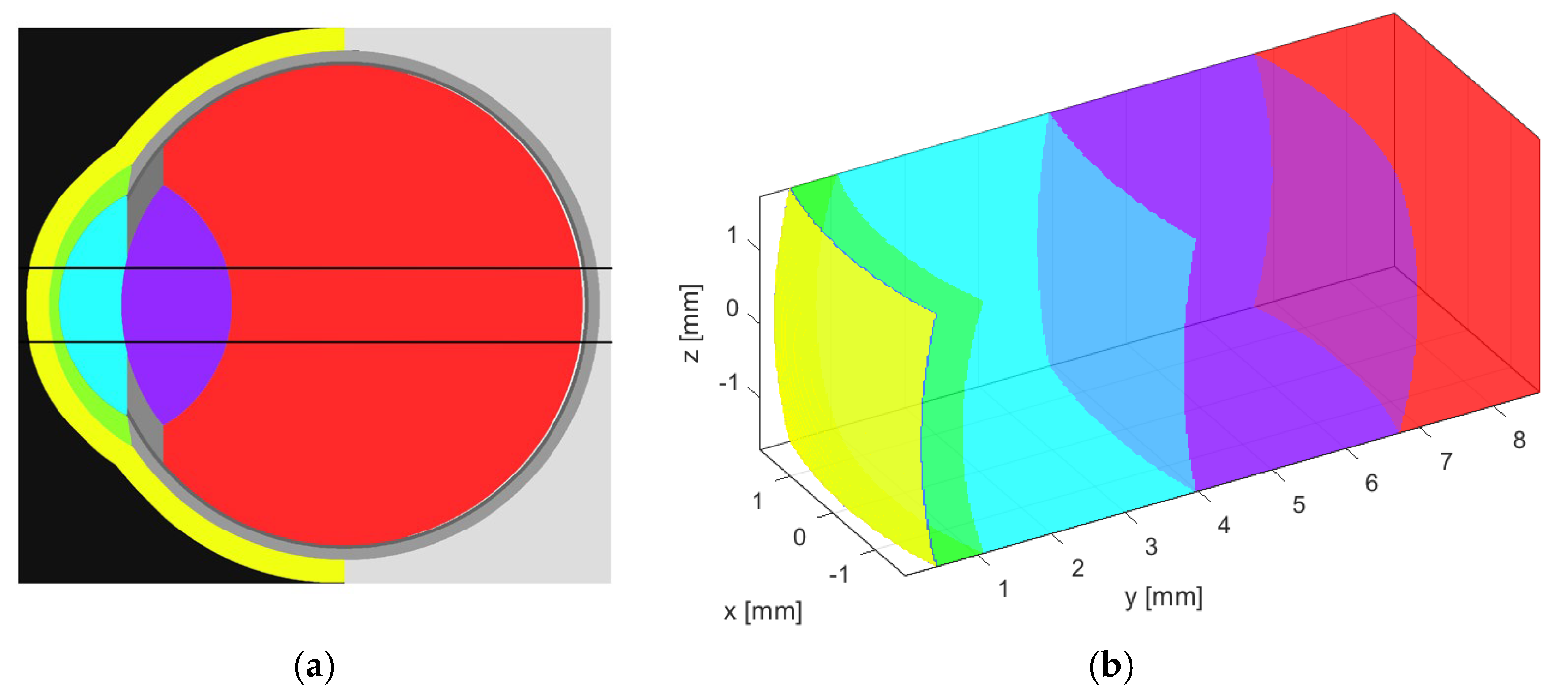
Preprints 113644 g001
Figure 1. Computational grids: 2D (a) and 3D (b). Components: cornea surface (yellow), cornea (green), aqueous humour (light blue), lens (purple), and vitreous humour (red).
Figure 1. Computational grids: 2D (a) and 3D (b). Components: cornea surface (yellow), cornea (green), aqueous humour (light blue), lens (purple), and vitreous humour (red).
Preprints 113644 g001
Preprints 113644 g002aPreprints 113644 g002b
Figure 2. Electric circuit models for the pulse-echo system. (a) Emitter stage (F=0); (b) Receiver stage (Vin=0); (c) and (d) Simplification of the equivalent circuits to the primary side of the transformer for the emitter and the receiver stages, respectively. Vin is the excitation voltage source and Zi its output impedance; ZE and Zm are the electric and mechanical impedances of the transducer; ϕ is equivalent to a transform ratio; V1 and I1 are the voltage and the current in the electrical side; F1 and U1 are the force and a transducer surface velocity in the acoustic side; ZL is the low noise amplifier (LNA) input impedance.
Figure 2. Electric circuit models for the pulse-echo system. (a) Emitter stage (F=0); (b) Receiver stage (Vin=0); (c) and (d) Simplification of the equivalent circuits to the primary side of the transformer for the emitter and the receiver stages, respectively. Vin is the excitation voltage source and Zi its output impedance; ZE and Zm are the electric and mechanical impedances of the transducer; ϕ is equivalent to a transform ratio; V1 and I1 are the voltage and the current in the electrical side; F1 and U1 are the force and a transducer surface velocity in the acoustic side; ZL is the low noise amplifier (LNA) input impedance.
Preprints 113644 g002aPreprints 113644 g002b
Preprints 113644 g003aPreprints 113644 g003b
Figure 3. Signals used to validate the implemented model: (a) Electrical excitation signal v1(t); (b) Simulated echo signal p2(t) reflected in a flat metal plate; (c) Electrical echo signal from the reflector v2(t).
Figure 3. Signals used to validate the implemented model: (a) Electrical excitation signal v1(t); (b) Simulated echo signal p2(t) reflected in a flat metal plate; (c) Electrical echo signal from the reflector v2(t).
Preprints 113644 g003aPreprints 113644 g003b
Preprints 113644 g004aPreprints 113644 g004b
Figure 4. Transfer functions obtained when a flat reflector is placed at the focus of the transducer: (a) H(s); (b) Hm(s); (c) H2(s).
Figure 4. Transfer functions obtained when a flat reflector is placed at the focus of the transducer: (a) H(s); (b) Hm(s); (c) H2(s).
Preprints 113644 g004aPreprints 113644 g004b
Preprints 113644 g005aPreprints 113644 g005b
Figure 5. (a) Impulse response h2(t); (b) Experimental and estimated received signals.
Figure 5. (a) Impulse response h2(t); (b) Experimental and estimated received signals.
Preprints 113644 g005aPreprints 113644 g005b
Preprints 113644 g006
Figure 6. a) Real signal from a healthy lens (v2(t)); b) Estimated signal from a healthy lens ( v ^ 2 ( t ) ) .
Figure 6. a) Real signal from a healthy lens (v2(t)); b) Estimated signal from a healthy lens ( v ^ 2 ( t ) ) .
Preprints 113644 g006
Preprints 113644 g007
Figure 7. Estimated signal v ^ 2 ( t ) from a cataractous lens.
Figure 7. Estimated signal v ^ 2 ( t ) from a cataractous lens.
Preprints 113644 g007
Table 1. Radius of curvature, thickness and acoustic properties of the eye structures that compose the eye matrix.
Table 1. Radius of curvature, thickness and acoustic properties of the eye structures that compose the eye matrix.
Eye structure Radius of curvature (mm) Thickness (mm) Sound speed (m/s) Density (kg/m3) Attenuation Coefficient
Water - - 1494 997 0.0022
Cornea 7.259 0.449 1553 1024 0.78
Aqueous humour 5.585 2.794 1495 1007 0.003
Lens 8.672 4.979 1649 1090 0.42
Vitreous humour 6.328 1.000 1506 1003 0.0022
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated