Prerpints.org logo
Preprint
Article

Shear and Bending Stresses in Prismatic, Non-Circular-Profile Shafts with Epitrochoidal Contours Under Shear Force Loading

Altmetrics

Downloads

70

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts
Abstract
This article deals with an analytical approach to determining the stress state in trochoidal profiles under shear bending. The transverse shear stresses cannot be neglected, especially in the case of (space-saving) shafts with a low aspect ratio (l/d). In addition to bending stresses, the transverse shear stresses are a significant component of the principal stresses. The approach is based on a formulation of the elastic behavior of a non-circular-profiled shaft using complex stress functions, according to Muskhelishvili. In order to determine the shear stresses, similar to the torsion load case, a conformal mapping must be found that can completely transform the unit circle in the model plane to the profile area in the real plane. For simple and higher epiotrochoidal profiles, an exact and complete mapping was determined from the contour equation. The method was applied to such profiles as an example. Equations were derived to determine the maximum shear and bending stresses and the bending deformations. For practical applications, additional equations for the main stresses that are decisive in dimensioning were determined. Accompanying numerical investigations were carried out and compared with the analytical results, where a very good agreement was observed.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

As a general rule, the shear stress is neglected in comparison with the bending stresses in a beam or shaft loaded with shear force. However, this is only permissible for large length ratios ( l / d ) depending on the bearing type of the shaft, where l is the length and d is the diameter of the shaft. Based on classical engineering mechanics (see, e.g., [1]), an aspect ratio limit of l / d > 6.67 for double-sided beams (Figure 1; case 1) and an aspect ratio limit of l / d > 3.34 for single-sided beams (Figure 1; case 2) can be determined for the stress ration limit of τ / σ < 5 % .
In many industrial applications in drive technology, bearing supports similar to case 1 are generally used, although the length ratios can also be in the range of 2.0 to 3.0. In such applications, the magnitude and effect of the transverse shear stresses should, therefore, be checked. The classical approach to calculating the shear stress, according to textbooks, assumes that the transverse shear stress also remains parallel to the shear force everywhere on the edge of the cross-section (see Figure 2). However, this assumption violates the boundary condition of the free lateral surface (e.g., [1]) and, depending on the shear contraction number, can lead to deviations of up to approx. 10 % for round cross-sections. Furthermore, there are no general solutions for determining the shear stresses for trochoidal profile shafts using the classical formulation.
In [2], the torsionally loaded non-circular profile cross-sections were treated in detail with the aid of conformal mapping. Suitable mapping functions were found using the successive approximation for hypotrochoidal profiles and torsional stresses, and deformations were determined on this basis.
The pure bending loads for both stationary and rotating load cases were also discussed in [3], and the corresponding solutions for the bending stresses were derived. This article, therefore, also deals with the case of bending with shear force.

2. Geometrical Description

The non-circular contours used in technical applications are often developed on the basis of general cycloids or trochoids. These curves are also referred to and classified in the technical literature as trochoids [4] and wheel lines [5]. Cycloids can be generated by rolling a circle on a path curve (usually also a circle). Depending on the rolling side, epicycloids (Fig. 1a), hypocycloids, and hybrid cycloids are produced. If the resulting curve is used as the base curve for a new trochoid, the secondary curve is referred to as a higher-level trochoid. This, in turn, can be used as a new base for further trochoids, whereby the level of the trochoid is increased accordingly.
The general representation and classification of higher-level trochoids is described in detail in [6].
Simple epicycloids
Figure 3 shows the generation of a simple epicycloid or a second-stage wheel line. Here, a circle rolls from the outside on a base circle, and point A 2 generates a simple epitrochoid with the eccentricity A 1 A 2 .
The geometry of the movement of the generating point A 2 can be described as follows:
x = r cos t + e 1 cos ⁡ n + 1 t
y = r sin t + e 1 sin ⁡ n + 1 t
Here, r denotes the nominal radius, e 1 the eccentricity, and n the periodicity (number of sides) of the cycloids. Equation (1) can be represented as follows by using the complex function:
z = r ζ + e 1 ζ n + 1
where z = x + i   y and ζ = ρ   e i t with i = − 1 . If the generation point A 2 lies on the circumference of the rolling circle K 2 , the path describes a limiting case where the curve begins to cut itself. The following applies to the eccentricity:
e = r n + 1
For an epitrochoid with a flat point (on the flank), the following applies according to ([7]):
e = r n + 1 2
The epitrochoid with a flat point with n = 3 was used for the first time in industry as a non-circular polygonal shaft–hub connection. These profiles became known as K-profiles [8] and were the basis of the later standardized P3G profiles [9].
Equation (2) can "conformally" map a unit circle to the profile cross-section. This property plays an important role in determining the stress state in a profile shaft [10].
Figure 4 shows simple epitrochoids with different numbers of drivers.
If the rolling circle K 2 is on the inside of the base circle, the so-called hypotrochoid results.
Simple epitrochoids can be produced economically as inner and outer contours using the twin-spindle turning process [11]. Figure 5 shows some examples produced by [12] using this process.
Higher epitrochoids
The higher rolling curves were systematically treated for the first time by Wunderlich in [5] with the aid of complex functions. This allows the two parameter equations to be combined into one complex equation and reduces the mathematical effort. This procedure was also used in [4] for the representation of plane curves. According to Figure 6, the higher epitrochoid K m is defined by the planetary motion of several levers with the corresponding angular velocities ω 1 ,   ω 2 , ⋅ ⋅ ⋅ ω m . The position of the creation point A m is determined by the sum of the vectors A 0 A 1 , A 1 A 2 , … A m − 1 A m and can be determined as follows.
The following conditions apply to the higher epitrochoids [3]:
Angular velocities, ω j , all act in the same direction and in the positive direction.
r > 0 ,   ω 1 = n + 1 ,   ω 1 = 2 n + 1 ,   ⋅ ⋅ ⋅   ω m = m ⋅ n + 1 ,
where n ≥ 1 is arbitrary and an integer.
The higher trochoids are described in detail in [3]. The profiles generally have the following parameter descriptions:
x = r c o s t + e 1 c o s n + 1 t + e 2 c o s 2 n + 1 t + … + e m cos ⁡ m · n + 1 t
y = r s i n t + e 1 s i n n + 1 t + e 2 s i n 2 n + 1 t + … + e m sin ⁡ m · n + 1 t
In a complex form, Equation (3) can be combined into a single equation:
z = r ⋅ e i ω 0 t + e 1 ⋅ e i ω 1 t + e 2 ⋅ e i ω 2 t + ⋅ ⋅ ⋅ = r ⋅ e i ω 0 t + ∑ j = 1 m e j ⋅ e i ω j t
If ζ = e i t and the associated ω j are inserted into Equation (6), the following equation can be obtained to describe the higher epitrochoid:
ω ζ = r ζ + e 1 ζ n + 1 + e 2 ζ 2 n + 1 + e 3 ζ 3 n + 1 + e 4 ζ 4 n + 1 ⋅ ⋅ ⋅ .
Figure 7 shows examples of a class of higher epitrochoids with four eccentricities from the generalized Equation (7) for different numbers of flanks, using the following values for nominal radii and eccentricities:
r = 20 ,   e 0 = r n + 1 2 ,
e 1 = 3 n 4 e 0 , e 2 = 1 3 e 1 , e 3 = 1 3 e 2   and   e 4 = 1 3 e 3 .
Figure 8 compares a simple epitrochoid with one eccentricity and a higher epitrochoid with four eccentricities, according to Equations (7) and (8). The figure shows that the higher epitrochoid (on the right) has a larger radius of curvature when the eccentricity e 0 is increased. This results in advantages from a manufacturing point of view, as well as a smaller shape number (stress factor) in terms of the profile when compared to a simple epitrochoid (left in Figure 8).

2.1. State of the Art

Torsional loading
A torsional function was found using a suitable mapping that transforms the area enclosed by the unit circle to conform to the profile base area, and the torsional stresses and deformations were determined based on this.
f ζ = φ ζ + i ψ ζ ,
Here, φ and ψ are conjugate to each other. The real part of the torsion function φ can be used to determine the torsional moment of inertia and the stress components. The method is discussed in detail in [2].
Pure bending load
For the case of pure bending, it is assumed that the plane cross-sections remain plane after loading (see, e.g., [13]). This means the following for the stresses:
σ z = − M b I y x , σ x = σ y = τ x y = τ z x = τ z y = 0 .
Based on this, the task is reduced to determining the bending moment of inertia, I y , of the profile cross-section. The procedure is described in detail in [3], and solutions for the M-sections were derived.
The method was used in [14], specifically and in detail, for the hypotrochoidal profiles standardized according to DIN 3689, and the so-called stress factors were determined and presented in tabular form.

2.2. Shear force Bending and Formulation

The general formulation for shear force bending is presented in [13,15] based on the elasticity behavior of the material. The method is described in more detail in [15], but a corresponding practical application is complex, as four stress functions must first be determined as a function of the profile contour. The method is, therefore, no longer suitable for practical applications. In contrast, the procedure described in [13] is presented in a more compact form. However, this also requires a complex bending stress as a function of the profile geometry. Based on the latter formulation, a general procedure was developed in the present work from a parametric profile description, according to Equations (3) and (4). The application was demonstrated in more detail using a number of test examples.
In order to analyze the transverse shear stresses, the origin of the co-ordinate is placed in the center of gravity of the profile surface, as shown in Figure 9. Force F is applied on the right side at the center of the cross-section and in the x -direction.
At any axial point at z distance from the co-ordinate origin O , the resulting bending moment M b in relation to the y -axis is as follows:
M b = F l − z ,
where l is the length of the beam. However, in the case of shear force bending, τ x z and τ y z no longer disappear, as the shear force causes a shear stress on the cross-section. The following equations are, hence, valid:
σ z = − F l − z I y x , σ x = σ y = τ x y = 0 .
If we insert these values into the equilibrium conditions, we obtain
∂ τ x z ∂ z = ∂ τ y z ∂ z = ∂ τ x z ∂ x + ∂ ∂ y ∂ τ y z + F x I y = 0
The first two parts of the equation mean that τ x z and τ y z are not dependent on z .
For the further procedure, a complex stress function for bending G z is required, which satisfies the corresponding compatibility conditions of the deformations, as well as the boundary conditions (load-free profile contour). It has the following general form:
G z = Φ 1 x , y + i Ψ 1 x , y ,
where Φ 1 x , y describes the real and Ψ 1 x , y the imaginary part of the G -function. Both functions are dependent on the contour geometry of the profile (e.g., Equations (1) and (3)). If the variable of z is transformed into ζ, Equation (5) can be presented as follows:
g ζ = φ 1 ζ + i ψ 1 ζ ,
Here, φ 1 ζ and ψ 1 ζ are conjugate to each other, i.e.,
∂ φ 1 ∂ x = ∂ ψ 1 ∂ y , ∂ φ 1 ∂ y = − ∂ ψ 1 ∂ x
φ 1 is labeled as a bending stress function. If a conformal mapping for transforming the unit circle on the cross-sectional area is available (Figure 10), a solution of φ 1 for the entire profile cross-section can be determined from the boundary condition for ψ 1 on the profile contour. The corresponding procedure is described in more detail below using an example.
The boundary condition on the profile contour, ψ 1 can be derived as follows [13]:
ψ 1 = − 1 − υ 2 y 3 3 − υ x 2 y 2 + 2 1 + υ ∫ y x d x + C 1
Due to the closed profile contour, the constant value C 1 on the right side of Equation (8) disappears. If the ψ 1 function is known, g ζ or φ 1 can be determined using Cauchy's integral formula.
Procedure for determining φ 1
If the contour geometry has been described by parametric equations with “cos” and “sin” terms (e.g., Equation (1) or (3)), the cos and sin functions are first rewritten as expressions of λ = e i t :
c o s t = 1 2 e i t + e − i t = 1 2 λ + 1 λ
s i n t = 1 2 i e i t − e − i t = 1 2 i λ − 1 λ
where e is the Euler number. If these expressions are inserted into the parametric equations, the variables x and y can be represented as functions of λ . λ is the edge of the unit circle and corresponds to the profile contour in the real plane. Based on this, Equation (8) is represented as follows:
ψ 1 λ = − 1 − υ 2 y λ 3 3 − υ x λ 2 y λ 2 + 2 1 + υ ∫ x λ y λ x ´ λ d λ + C 1
This can be used to determine g ζ or φ 1   using Cauchy's integral formula:
g ζ = 1 π i ∮ ψ 1 λ λ − ζ d λ + c o n s t  
φ 1   and ψ 1 are the real and imaginary parts of the complex bending stress function in the so-called model or ζ plane. The stress components can be determined using Equations (4) and (5) as follows:
τ x z = − F 2 1 + υ I y ∂ φ 1 ∂ x + 1 2 υ x 2 + 1 − υ 2 y 2
τ y z = − F 2 1 + υ I y ∂ φ 1 ∂ y + 2 + υ x y
σ z = − F l − z I y x
For the partial derivatives of φ 1   occurring in Equation (21), ψ 1 is also required:
∂ φ 1 ∂ x = x ˙ φ ˙ 1 + y ˙ ψ ˙ 1 x ˙ 2 + y ˙ 2 ,
∂ φ 1 ∂ y = y ˙ φ ˙ 1 − x ˙ ψ ˙ 1 x ˙ 2 + y ˙ 2
where x ˙ ,   y ˙ ,   φ ˙ 1 , and ψ ˙ 1 denote the corresponding derivatives according to parameter t .
I y is the moment of inertia around the y -axis and can be determined from the following relationship according to [3]:
I y = ∬ x 2 d x d y  
The deformations can then also be determined as follows [13]:
u x = F E I y υ 2 l − z x 2 − y 2 + 1 2 l z 2 − 1 6 z 3
u y = F E I y υ l − z x y  
u z = − F E I y x l z − 1 2 z 2 + φ 1 − x y 2
The displacement in the z-direction u z (the 3rd equation in (24)) consists of a z -dependent component, u z 1 , which represents the rotation of the cross-section (Equation (25)), and a warping, u z 2 , which is caused by the distribution of the shear stress. u z 2 is independent of z and can be determined from Equation (26):
u z 1 = − F E I y x l z − 1 2 z 2 ,  
u z 2 = − F E I y φ 1 − x y 2  
The deflection is obtained from the first equation in (24), where x and y are equal to zero:
f x = F 2 E I y l z 2 − 1 3 z 3  
In the following, the procedures are first applied to the circular cross-section as a well-known classic example, and the results are compared with the solutions known from the technical literature. Then, the epitrochoidal profile cross-sections are also investigated.

3. Applications

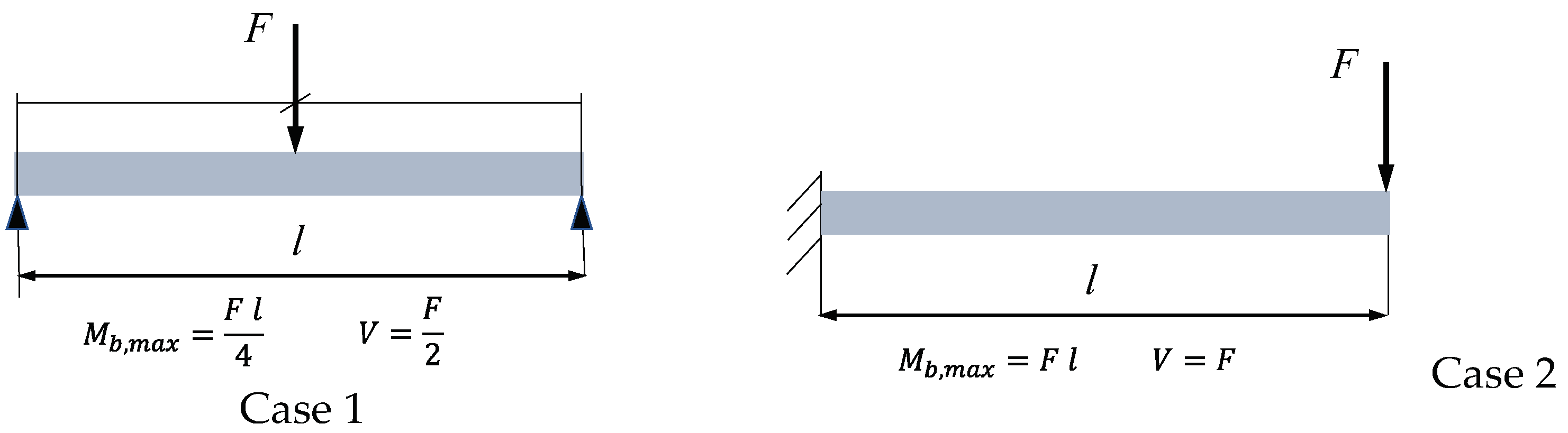
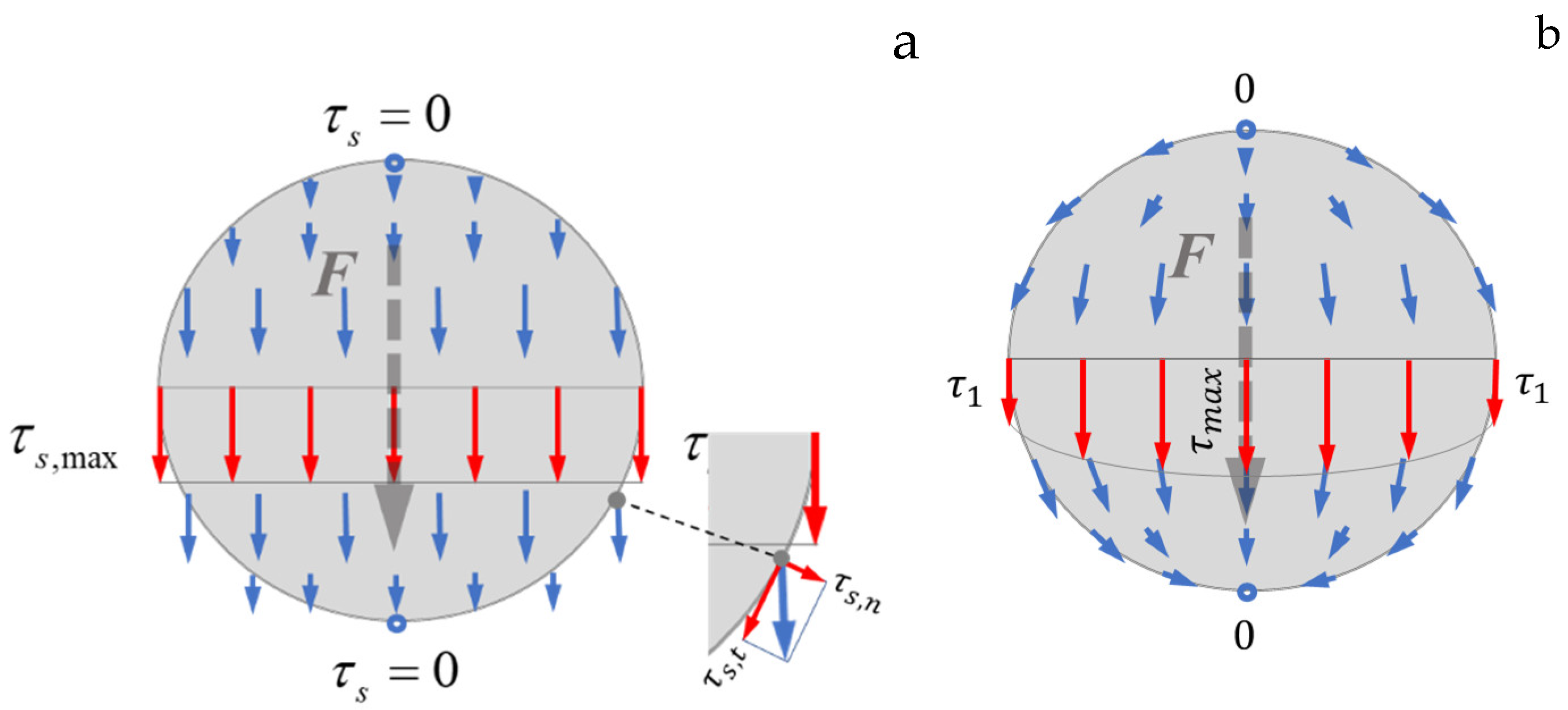
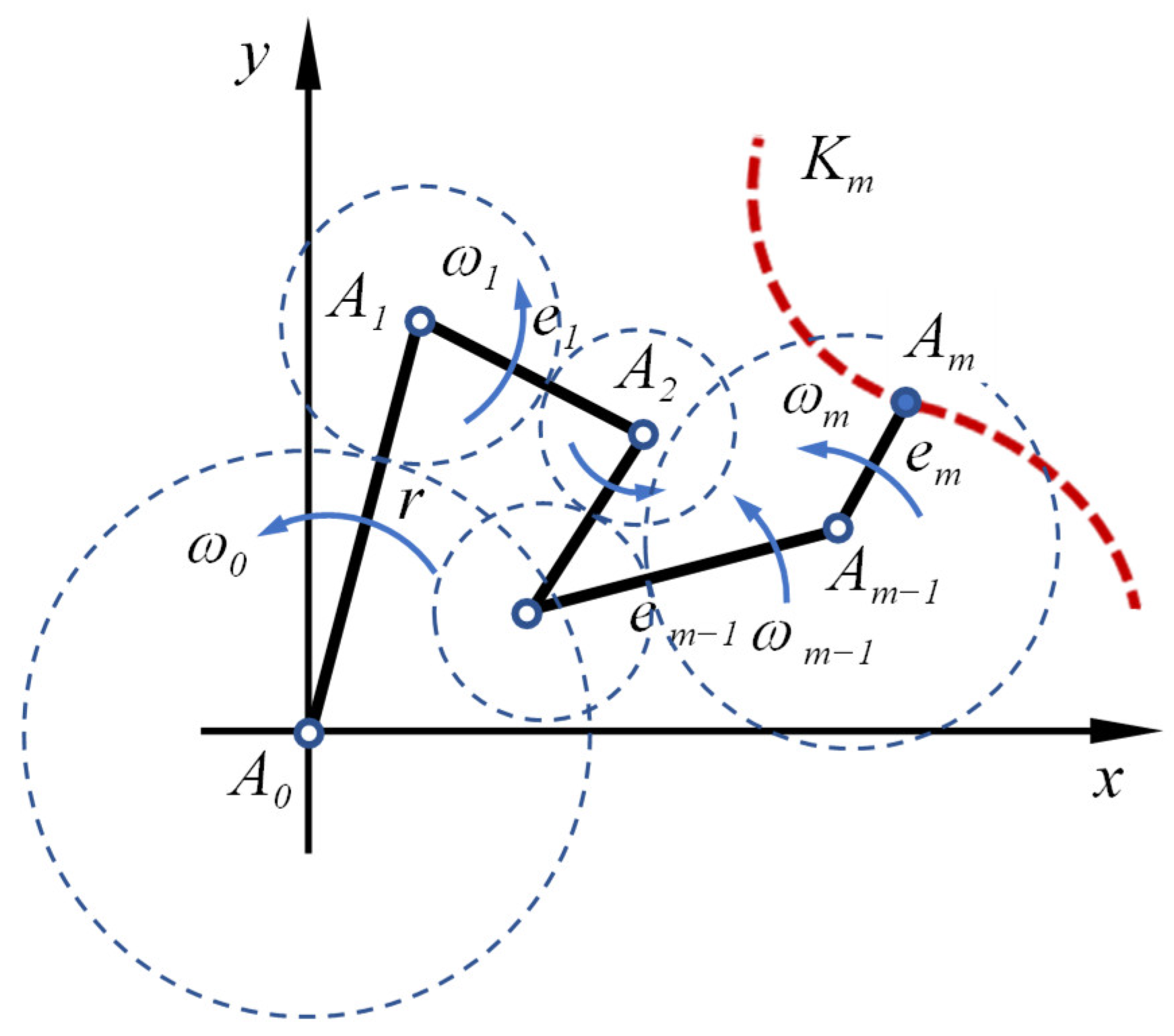
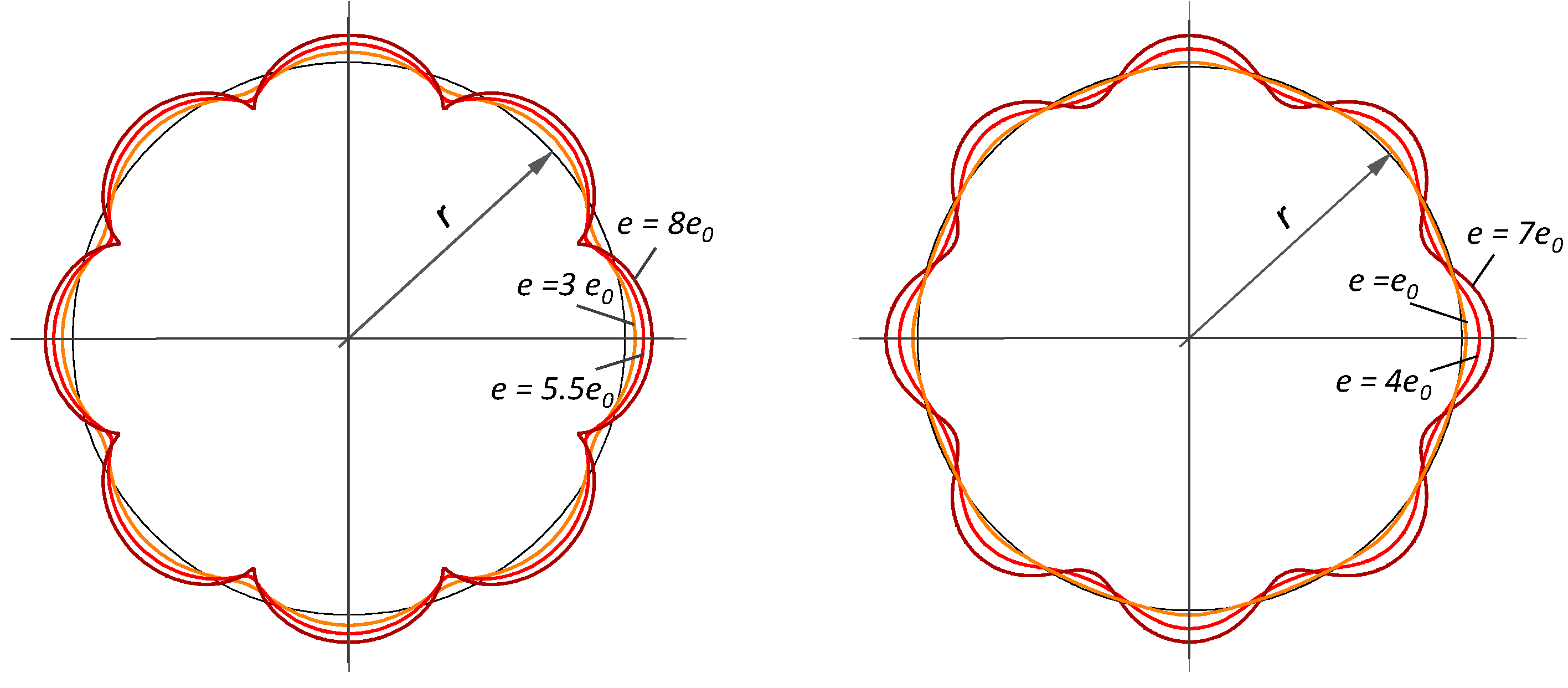
3.1. Circular Cross-Section

The following conformal mapping applies to a circular cross-section:
z ζ = r   ζ ,
This function forms the unit circle conformally and completely on the cross-section of the shaft. The contour edge can be described as parametric:
x = r c o s t
y = r s i n t
If Equation (18) is inserted into (29) and the results for x and y are inserted into Equation (19), the function ψ 1 for the contour can be obtained. Based on this, the complex stress function g ζ is determined from Equation (20). If ζ = ρ e i t is inserted into g ζ , the real part can be determined as follows:
φ 1 = 1 4 ρ r 3 cos ⁡ t − 2 ν − ρ 2 + 2 ρ 2 cos ⁡ 2 t − 3
Here, ρ assumes values between 0 and 1. Substitute φ 1 from Equation (30) into Equation (21) and replace x and y with the following relationships:
x = r ρ cos ⁡ t = r ρ 2 λ + 1 λ
y = r ρ sin ⁡ t = r ρ 2 i λ − 1 λ ,
Thus, the equations for the shear stress components are obtained:
τ x z = − F ρ 2 2 + 2 ν + 1 cos ⁡ 2 t − 2 ν − 3 2 π r 2 ν + 1
τ y z = − F 2 ν + 1 ρ 2 sin ⁡ 2 t 2 π r 2 ν + 1
The resulting shear stress can then be determined as the vectorial sum of the two components:
τ = τ x z 2 + τ y z 2
With A = π r 2 , the shear stress components can be determined as follows:
τ x z = − F A · ρ 2 2 + 2 ν + 1 cos ⁡ 2 t − 2 ν − 3 2 ν + 1
τ y z = − F A · 2 ν + 1 ρ 2 sin ⁡ 2 t 2 ν + 1
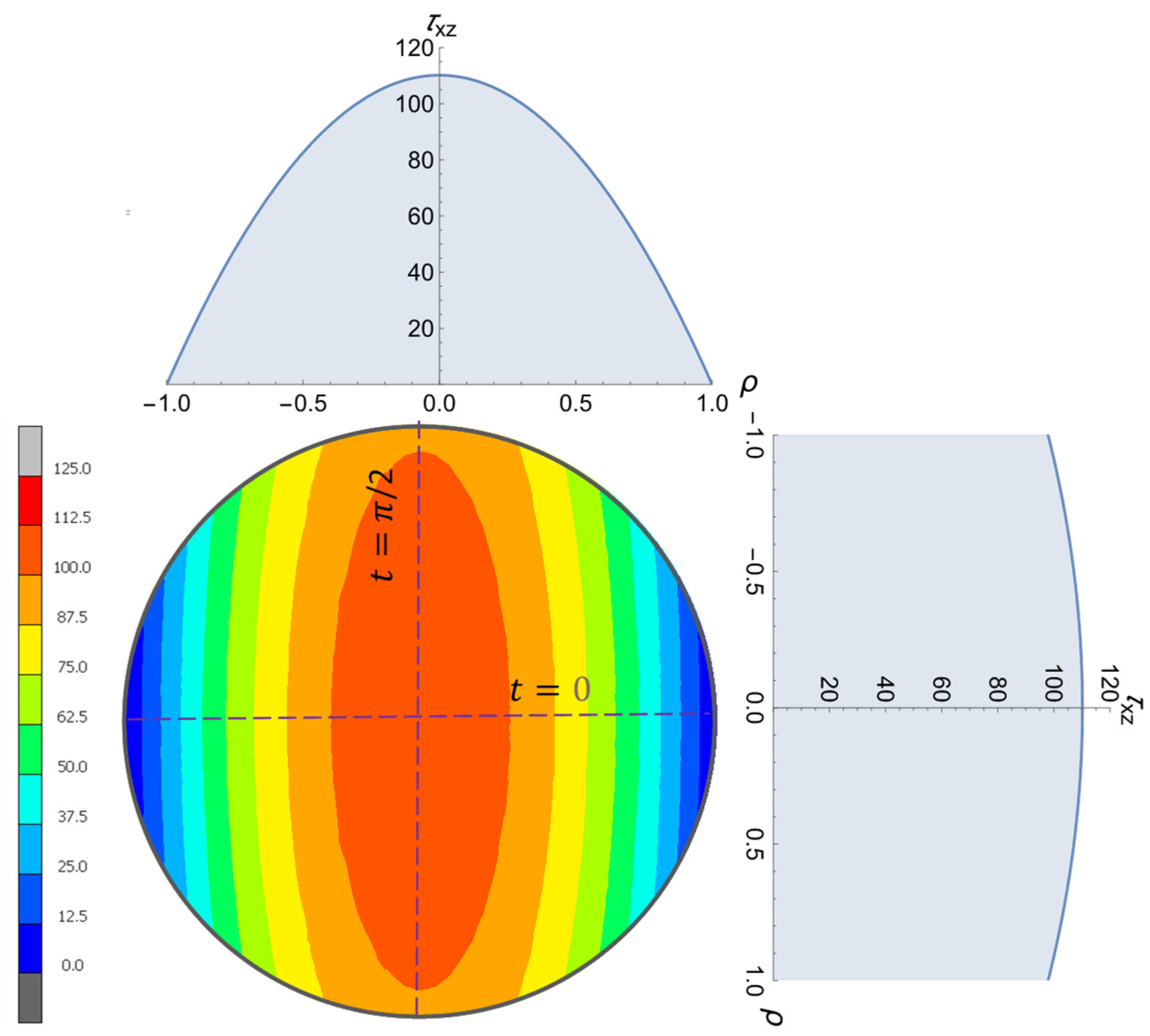
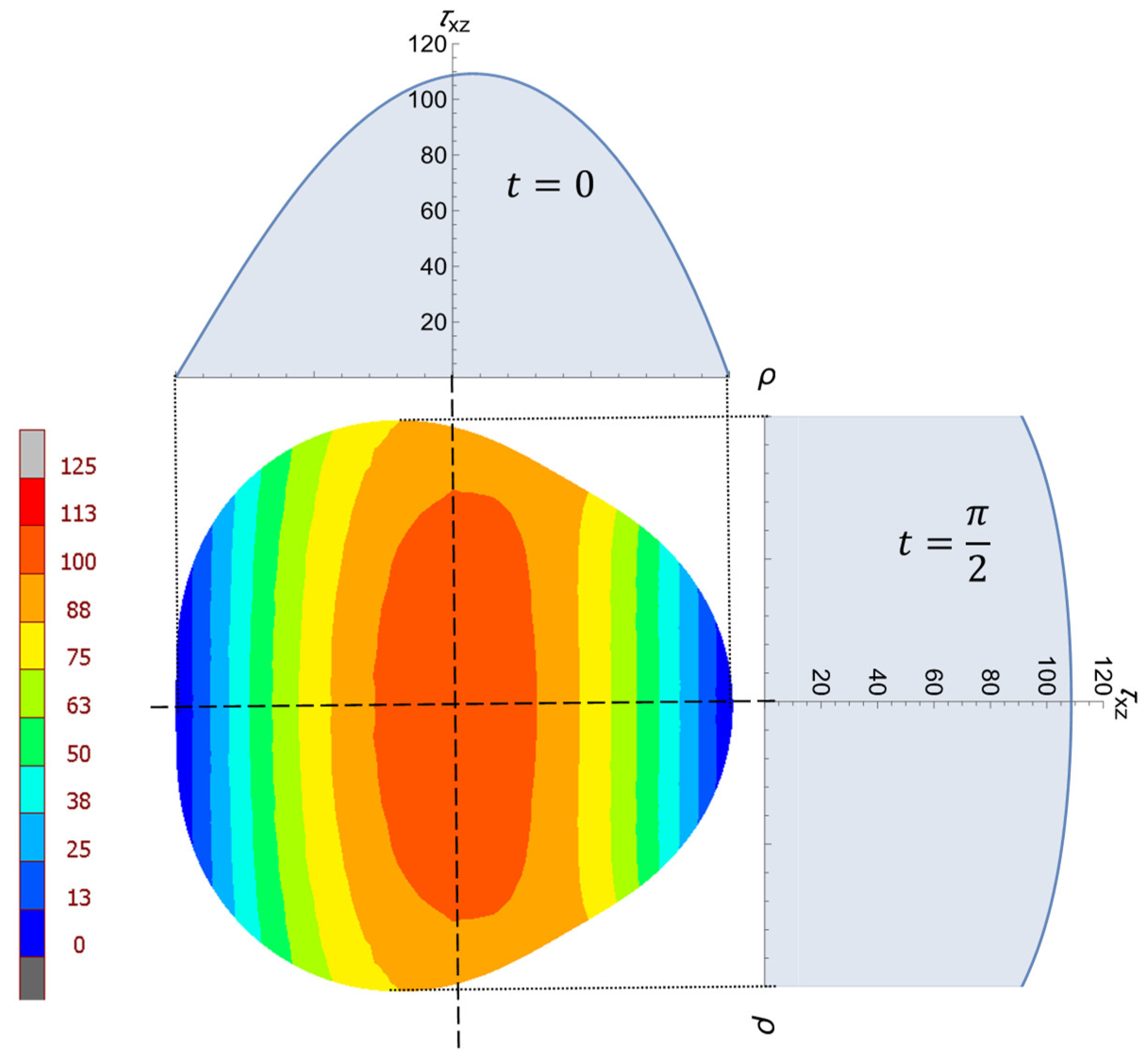
The stress distribution on the cross-section is shown in Figure 11. This is the result of the shear stress component τ x z from the numerical investigations (FEA) for a round cross-section with r = 25 mm and F = 100   k N . The material chosen for the shaft was steel with E = 210000   N / m m 2 and a Poisson’s ratio of ν = 0.3 . According to Equation (32), the analytical solutions for the two parameter angle positions t = 0 and t = π 2 are also shown, where the agreement of the results can be traced by observing the color scalar.
A more concrete comparison can be made using the stress distributions on the lateral surface, where ρ = 1 applies. If ρ = 1 is inserted into Equations (32) to (34), the following relationships are obtained:
τ x z 1 , t = F 2 ν + 1 s i n 2 t π r 2 ν + 1
τ y z 1 , t = − F 2 ν + 1 sin ⁡ t cos ⁡ t π r 2 ν + 1
The resulting shear stress can be determined from (34) as follows:
τ 1 , t = F 2 ν + 1 sin ⁡ t π r 2 1 + ν
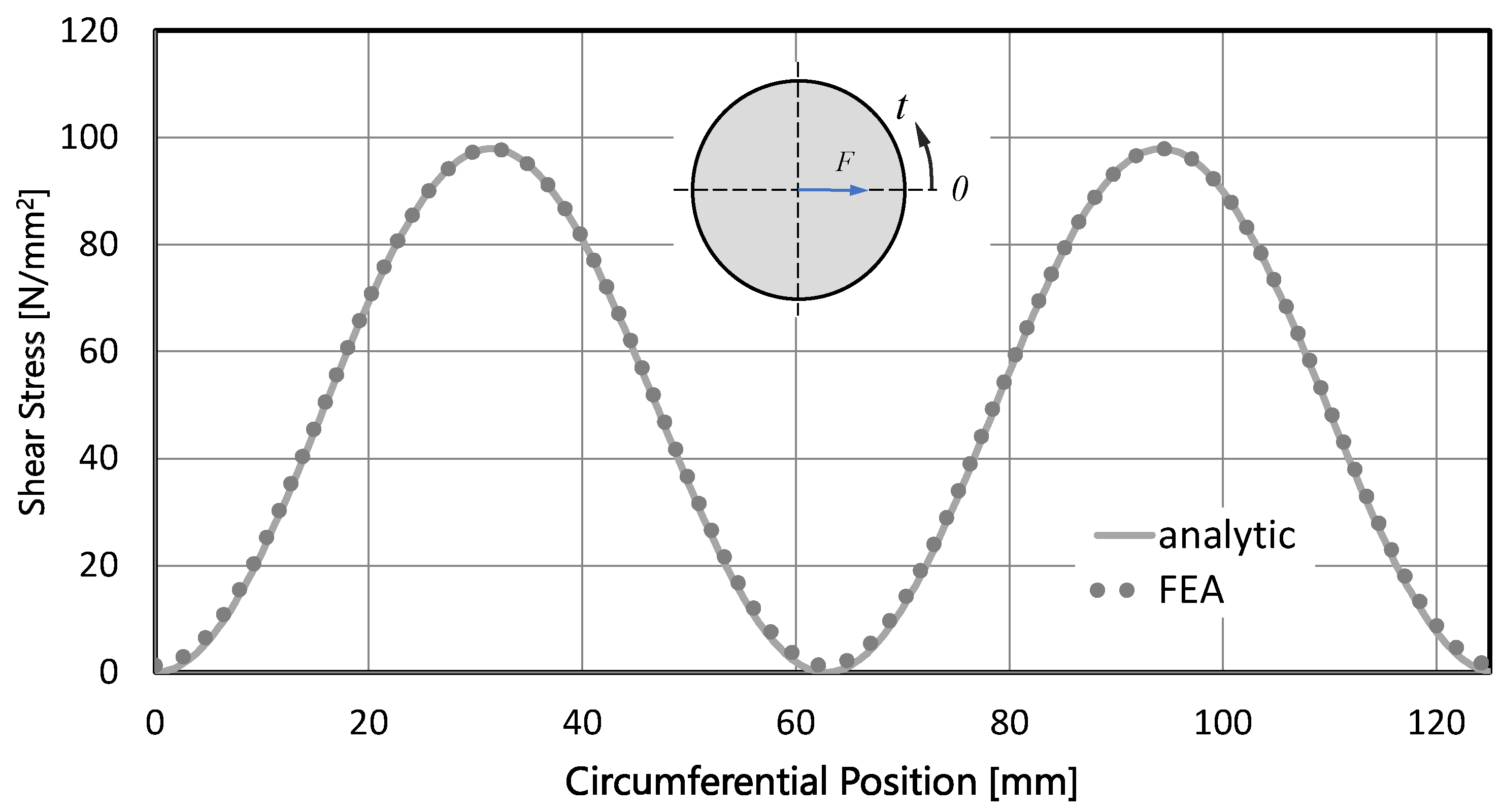
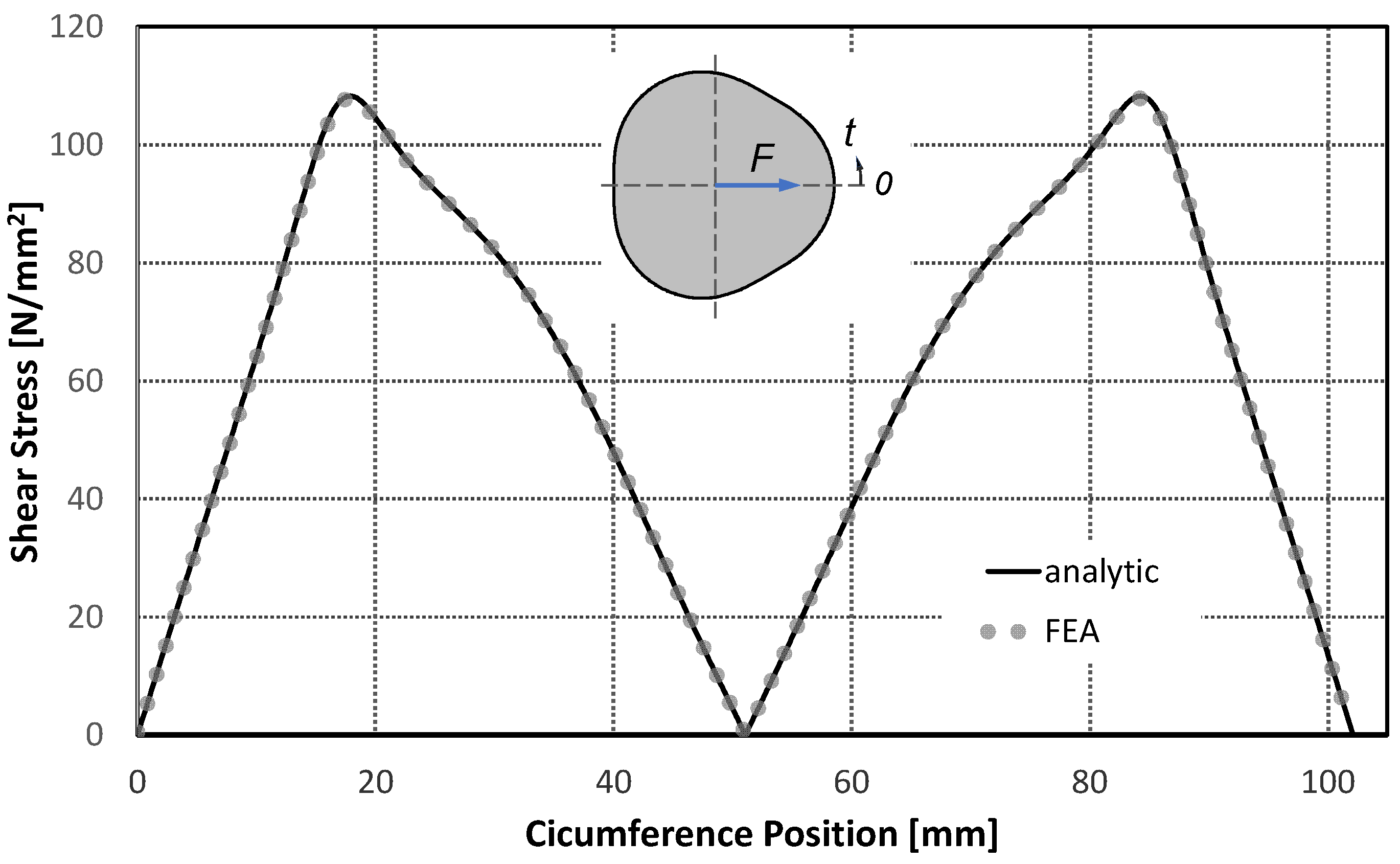
Figure 12 shows the course of τ x z on the contour of the cross-section. A very good agreement between the numerical results and the analytical solution—according to Equation (37)—can be seen from the figure.
The maximum stress τ x z , m a x   of the contour occurs at t = π 2 and can be determined according to the following equation:
τ x z , m a x = τ x z 1 , π 2 = F 2 ν + 1 π r 2 ν + 1 = F A · 2 ν + 1 ν + 1
The maximum shear stress occurs at the center of the cross-section (0,0). At ρ = 0 , τ x z is maximum and τ y z =0; therefore,
τ m a x = τ x z 0,0 = F 2 ν + 3 2 π ν + 1 r 2 = F A · 2 ν + 3 2 ν + 1
For a Poisson’s ratio of ν = 0.3 (steel), the maximum shear stress at the center point can be determined from Equation (41), and the maximum shear stress on the profile outline from Equation (40) is as follows:
τ m a x = 1.385 F A ( at the center ) ,
τ m a x = 1.231 F A ( on the profile outline ) .
Compared with existing solutions
The solution for circular cross-sections known from the literature is based on the formulation of the classical theory of elasticity, which always depends on finding a suitable real shear function. This shear function ϕ ( x , y ) should satisfy the corresponding equilibrium and compatibility conditions depending on the profile geometry. Therefore, solutions are only available for some specific profile geometries such as a circle, ellipse, or quadrilateral. Timoshenko [16] presents such a solution for the circular cross-section. Here, a real stress function is given in Cartesian co-ordinates, which leads to the same results from Equations (32) and (33):
ϕ x , y = 1 + 2 ν 8 1 + ν F I y x 2 + y 2 − r R 2 y ,  
R is here the radius of the cross-section. The same results from (40a) and (41a) are obtained in [16].

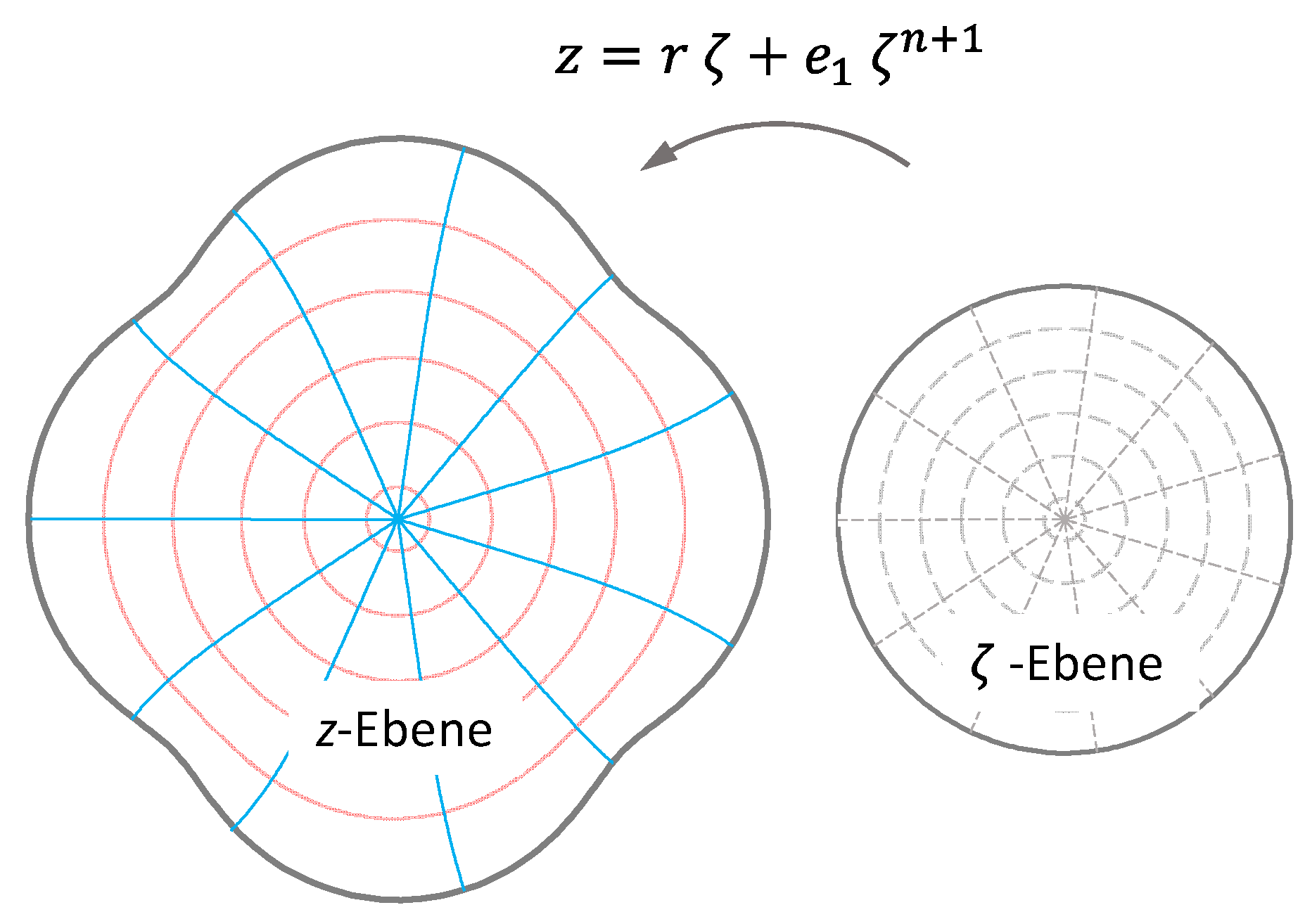
3.2. Epitrochoidal Profile Cross-Sections

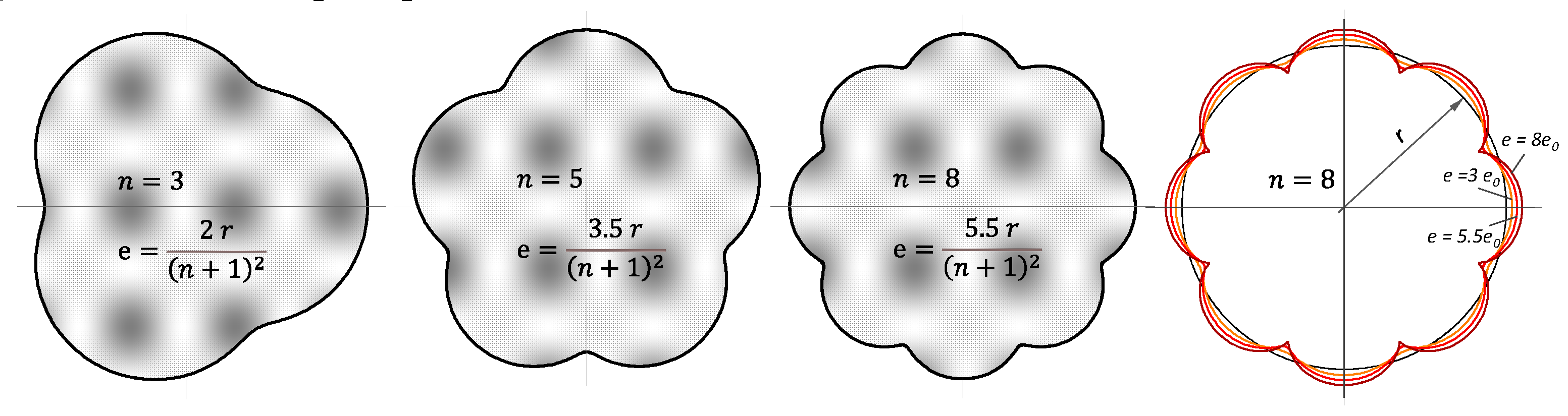
For the epitrochoidal cross-section, the conformal mapping, according to Equation (2), applies, where n is the number of sides of the profile. This function maps the unit circle conformally and completely on the profile cross-section (see Figure 10). This guarantees the solution over the entire profile cross-section according to Equation (20).
The contour in Equation (1) can be rewritten as follows:
x = r 2 λ + 1 λ + e 2 λ n + 1 + 1 λ n + 1
y = r 2 i λ − 1 λ + e 2 i λ n + 1 − 1 λ n + 1 ,  
Substituting Equation (43) into Equation (19) gives the function ψ 1 for the profile contour. Based on this, the complex stress function g ζ can be determined from Equation (20) using Cauchy's integral formula (20). If ζ = ρ e i t is inserted into g ζ , the real part of the stress function φ 1 can be determined. Substituting φ 1 into Equation (21) and replacing x   and y with the following relations for the entire profile cross-section yields
x = ρ r 2 λ + 1 λ + ρ e 2 λ n + 1 + 1 λ n + 1
y = ρ r 2 i λ − 1 λ + ρ e 2 i λ n + 1 − 1 λ n + 1 ,  
The components of the shear stresses can be determined for the entire profile cross-section. Here, ρ takes values between 0 and 1 ( 0 ≤ ρ ≤ 1 ).
Because of the size of the equation, the general solution is not shown here. This can be found in the appendix.
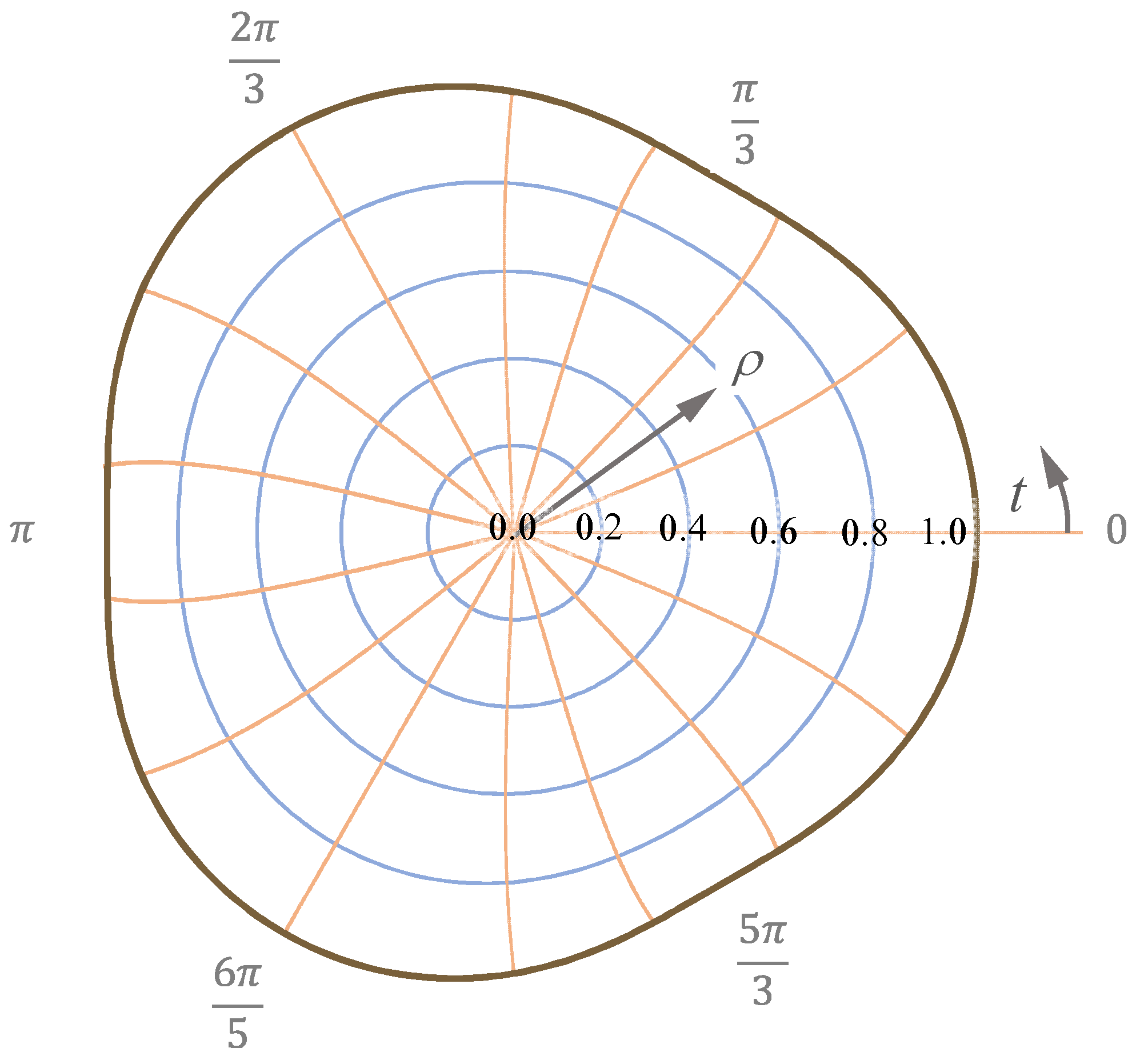
In the following, two application examples for n = 3 (Figure 5 left) and n = 5 (Figure 5 right) are presented, and the results are compared with the FE analysis.
Example 1: n = 3
with flat flanks
For an epitrochoid with three sides, the following mapping function applies, which conformally transforms the unit circle on the epitrochoid:
z ζ = r   ζ + e ζ 4
If e=r/16 is inserted into Equation (44), the epitrochoid with three flat point flanks is obtained:
z ζ = r   ζ + ζ 4 16 .
Figure 13 shows the iso-   ρ and t lines for this profile with e = r 16 .
If n = 3 and e = r 16 are inserted into Equation (A4) in the appendix, the following relationship is obtained for the stress function:
φ 1 = 1 114688 ρ ρ ρ 28672 r 3 cos ⁡ 3 t − 7 ρ 2 ν + 256 ν + 3 r 2 + 3 cos ⁡ 4 t + 16 ρ 3 r 336 r cos ⁡ 6 t − 2 ν + 9 ρ cos ⁡ 7 t + 21 ρ 3 cos ⁡ 9 t + 7 ρ 9 cos ⁡ 12 t − 1792 4 ν + 3 r 2 cos ⁡ 2 t − 224 r 8 ν + 128 2 ν + 3 r 2 + 9 cos ⁡ t
If ν = 3 10 is also used for steel, the following function for the distribution of the shear stress component τ x z ρ , t on the profile cross-section is obtained from (A6):
τ x z ρ , t = − F 221325 π r 2 ( ρ 6 + 8 ρ 3 c o s ⁡ ( 3 t ) + 16 ) 128 ( 5 ρ 14 + 2000 ρ 8 − 2121 ρ 6 + 20480 ρ 2 + 4 ρ 14 c o s ⁡ ( 8 t ) + 200 ρ 11 c o s ⁡ ( 3 t ) + 144 ρ 11 c o s ⁡ ( 5 t ) + 16 ρ 11 c o s ⁡ ( 11 t ) − 96 ρ 9 c o s ⁡ ( 3 t ) + 640 ρ 8 c o s ⁡ ( 6 t ) + 576 ρ 8 c o s ⁡ ( 8 t ) − 384 ρ 6 c o s ⁡ ( 6 t ) + 12800 ρ 5 c o s ⁡ ( 3 t ) + 6144 ρ 5 c o s ⁡ ( 5 t ) + 256 ( 16 ρ 4 − 21 ) ρ c o s ⁡ ( t ) − 17928 ρ 3 c o s ⁡ ( 3 t ) + 64 ( 24 ρ 6 − 21 ρ 2 + 256 ) ρ 2 c o s ⁡ ( 2 t ) − 37776 )
Furthermore, the following equation for the shear stress component τ y z ρ , t results from (A7):
τ y z ρ , t = − F ρ 221325 π r 2 ρ 6 + 8 ρ 3 cos ⁡ 3 t + 16 1024 sin ⁡ t 20 ρ 10 + 12 ρ 8 + 256 ρ 4 − 120 ρ 2 + ρ 13 cos ⁡ 3 t + ρ 13 cos ⁡ 5 t + ρ 13 cos ⁡ 7 t + 40 ρ 10 cos ⁡ 4 t + 4 ρ 10 cos ⁡ 6 t + 4 ρ 10 cos ⁡ 8 t + 4 ρ 10 cos ⁡ 10 t + 144 ρ 7 cos ⁡ 3 t + 144 ρ 7 cos ⁡ 5 t + 144 ρ 7 cos ⁡ 7 t + 96 ρ 5 cos ⁡ 3 t + 96 ρ 5 cos ⁡ 5 t + 1536 ρ 4 cos ⁡ 4 t + 8 5 ρ 8 + 3 ρ 6 + 192 ρ 2 − 30 ρ 2 cos ⁡ 2 t + ρ 12 + 528 ρ 6 + 96 ρ 4 − 336 ρ 2 + 4096 ρ cos ⁡ t + 672
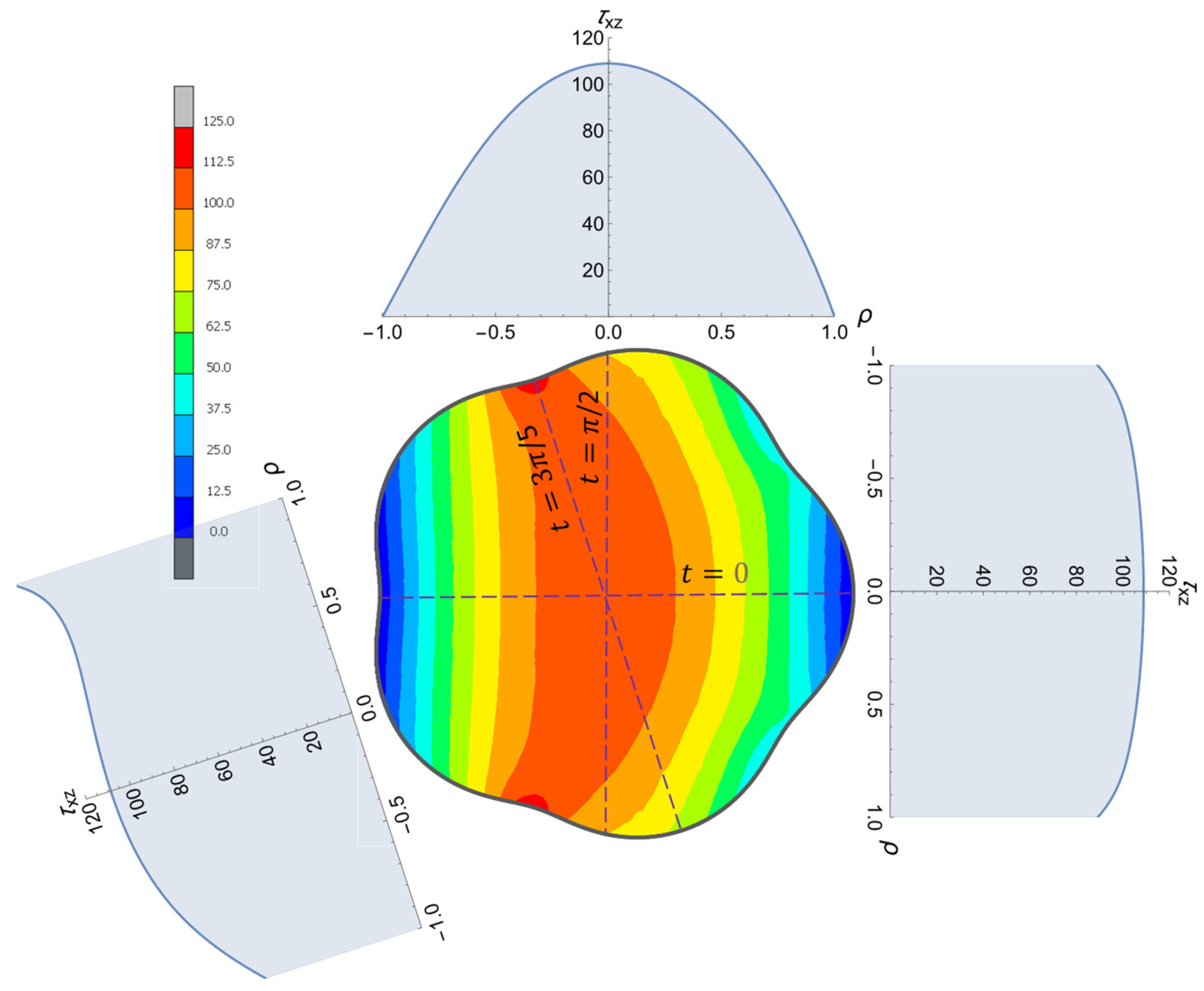
Figure 14 shows the distribution of the shear stress τ x z from the numerical FE investigations for the epitrochoidal cross-section with n = 3 , r = 16 mm, e = 1 mm, and F = 100 kN (for a load). The material chosen for the bar was steel with E = 210000   N / m m 2 and a Poisson’s ratio of ν = 3 10 . Analytical solutions according to Equation (48) for the two parameter angle positions of t = 0 and t = π 2 are also shown, where the agreement of the results can be traced by observing the color scalar.
In order to determine the resulting shear stresses on the profile outline, ρ = 1 is used in Equations (48) and (49). Equation (34) is used to obtain the following relationship for the total stress distribution on the contour of the shaft:
τ 1 , t = 1024 F 1056 sin ⁡ t + 80 sin ⁡ 2 t + 129 sin ⁡ 4 t + 4 sin ⁡ 7 t 221325 π r 2 8 cos ⁡ 3 t + 17
A comparison of Equation (50) with the numerical results is shown in Figure 15, where very good agreement can be recognized.
Maximum shear stress occurs at the center point of the cross-section ( 0,0 ) :
τ m a x = τ 0,0 = 64 88 ν + 131 5675 ν + 1 · F π r 2
Example 2: n = 5
For an epitrochoid with five sides, the following mapping function applies, which can conformally transform the unit circle on the epitrochoid area:
z ζ = r   ζ + e ζ 6
Figure 16 shows this profile for this example with e = r / 20 . The iso- t and ρ lines are shown in the figure.
If n = 5 and e = r / 20 are inserted into Equation (A4), the following relationship is obtained for the stress function:
φ 1 = 1 132 ρ 3 e ρ − 11 ρ 2 cos ⁡ 6 t e 2 6 ν + 9 + 2 ν + 4 r 2 + 33 e 2 ρ 14 cos ⁡ 18 t − 6 e ν ρ 7 r cos ⁡ 11 t + 99 e ρ 9 r cos ⁡ 13 t − 39 e ρ 7 r cos ⁡ 11 t − 33 − 33 3 ν + 2 r 2 cos ⁡ 4 t + 99 ρ 4 r 2 cos ⁡ 8 t + 33 r 3 cos ⁡ 3 t − 33 ρ r cos ⁡ t e 2 24 ν + 26 + 2 ν + 3 r 2
Furthermore, Equation (A5) yields the following relationship for ψ 1 :
ψ 1 = 1 132 ρ 3 e ρ − 11 ρ 2 sin ⁡ 6 t e 2 6 ν + 9 + 2 ν + 4 r 2 + 33 e 2 ρ 14 sin ⁡ 18 t − 6 e ν ρ 7 r sin ⁡ 11 t + 99 e ρ 9 r sin ⁡ 13 t − 39 e ρ 7 r sin ⁡ 11 t − 33 3 ν + 2 r 2 sin ⁡ 4 t + 99 ρ 4 r 2 sin ⁡ 8 t + 33 r 3 sin ⁡ 3 t − 33 ρ r sin ⁡ t e 2 24 ν + 26 + 2 ν + 3 r 2
Consequently, the following equation for the shear stress component τ x z   ( ρ , t ) on the profile cross-section can be obtained for ν = 3 / 10 (steel) from (A6):
τ x z ρ , t = F 26 I y 9 ρ 10 + 60 ρ 5 cos ⁡ 5 t + 100 − 45 ρ 22 − 24500 ρ 12 + 25881 ρ 10 − 200000 ρ 2 + 4 ρ 2 − 30 ρ 15 cos ⁡ 17 t − 9 ρ 10 + 1300 ρ 10 cos ⁡ 12 t − 500 24 ρ 4 − 29 ρ cos ⁡ 3 t − 50 96 ρ 10 − 87 ρ 6 + 800 cos ⁡ 2 t − 10 39 ρ 10 + 1600 ρ 5 cos ⁡ 7 t + 50 17 − 30 ρ 2 ρ 8 cos ⁡ 10 t + 5 − 105 ρ 12 + 51 ρ 10 − 7000 ρ 2 + 9838 ρ 3 cos ⁡ 5 t + 368300
Furthermore, the following relation follows from (A7) for τ y z ρ , t :
τ y z ρ , t = 2 F 13 I y 9 ρ 10 + 60 ρ 5 cos ⁡ 5 t + 100 ρ 2 − 30 ρ 15 sin ⁡ 17 t − 9 ρ 10 + 1300 ρ 10 sin ⁡ 12 t − 850 ρ 8 sin ⁡ 10 t + 500 24 ρ 4 − 29 ρ sin ⁡ 3 t − 50 96 ρ 10 − 87 ρ 6 + 800 sin ⁡ 2 t − 10 39 ρ 10 + 1600 ρ 5 sin ⁡ 7 t + 5 1211 − 51 ρ 10 ρ 3 sin ⁡ 5 t
Figure 17 shows the distribution of the shear stress components τ x z from the numerical FE investigations for the epitrochoidal cross-section with n = 5 , r = 20   mm, and e = 1 mm. A shear force of F = 100   k N was applied, and the chosen material was steel with E = 210000   N / m m 2 and a Poisson’s ratio of ν = 0.3 . Analytical solutions according to Equation (55) for the three parameter angle positions t = 0 , t = π / 2 , and t = 3 π / 5 are also shown, where the agreement of the results can be identified using the color scalar.
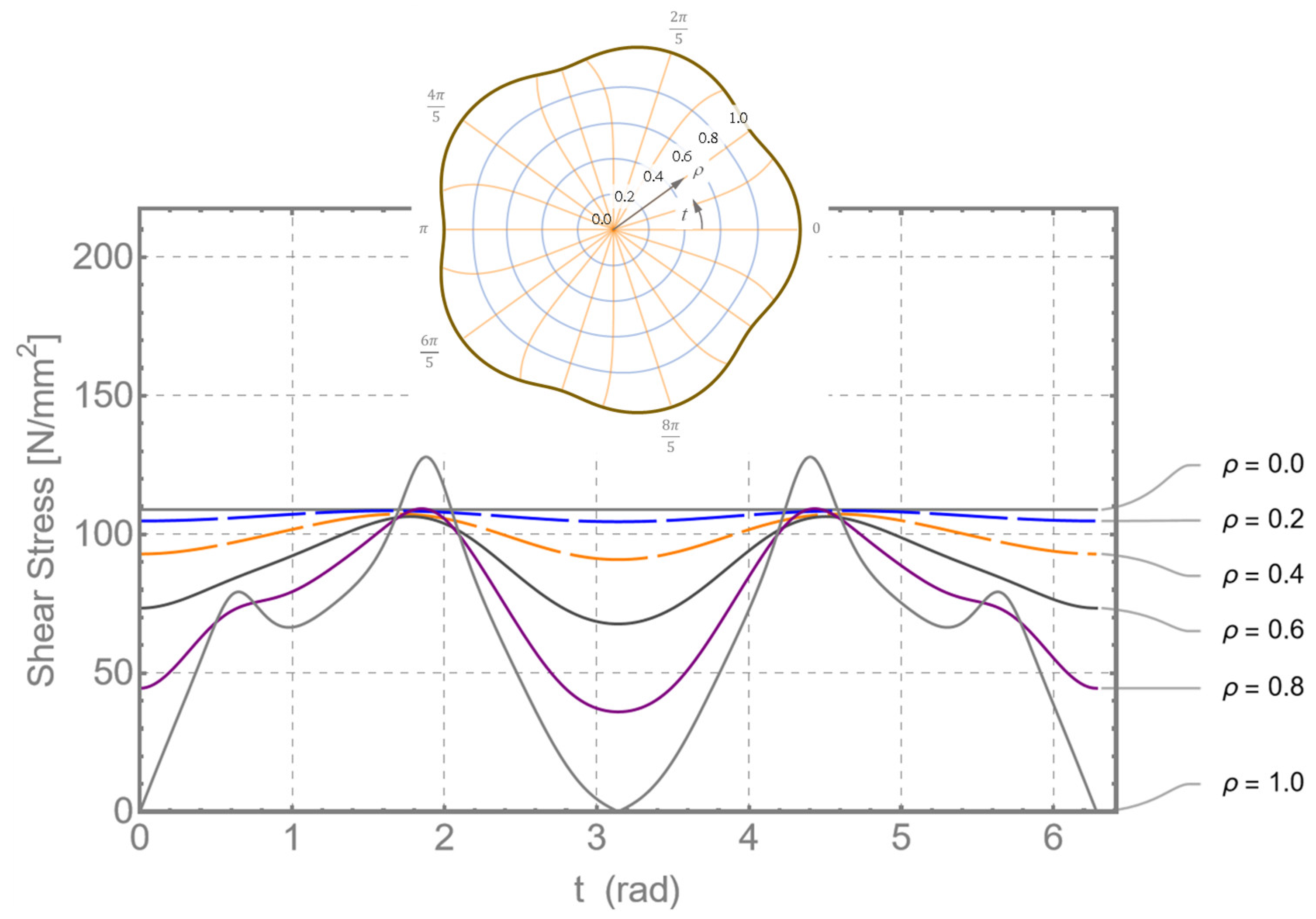
The total shear stress is the vectorial sum of the two components according to Equations (55) and (56). Figure 18 shows the distribution of the resulting shear stresses over different ρ -lines.
The shear stresses on the profile contour correspond to ρ = 1 . This fact leads to the following equation for the distribution of the shear stress on the profile contour with n = 5 :
τ 1 , t = F 2 ν + 1 r 12 e 2 + r 2 sin ⁡ t + e 2 ν + 1 2 3 e 2 + r 2 sin ⁡ 6 t + er sin ⁡ 11 t + 2 e r 2 sin ⁡ 4 t 4 I y ν + 1 36 e 2 + 12 e r cos ⁡ 5 t + r 2
The following then applies to the investigation case with r = 20 and e = 1 :
τ 1 , t = F 4120 2 ν + 1 sin ⁡ t + 2 ν + 1 403 sin ⁡ 6 t + 10 sin ⁡ 11 t + 400 sin ⁡ 4 t 4 I y ν + 1 60 cos ⁡ 5 t + 109
Equation (58) represents the curve with ρ = 1 in Figure 18.
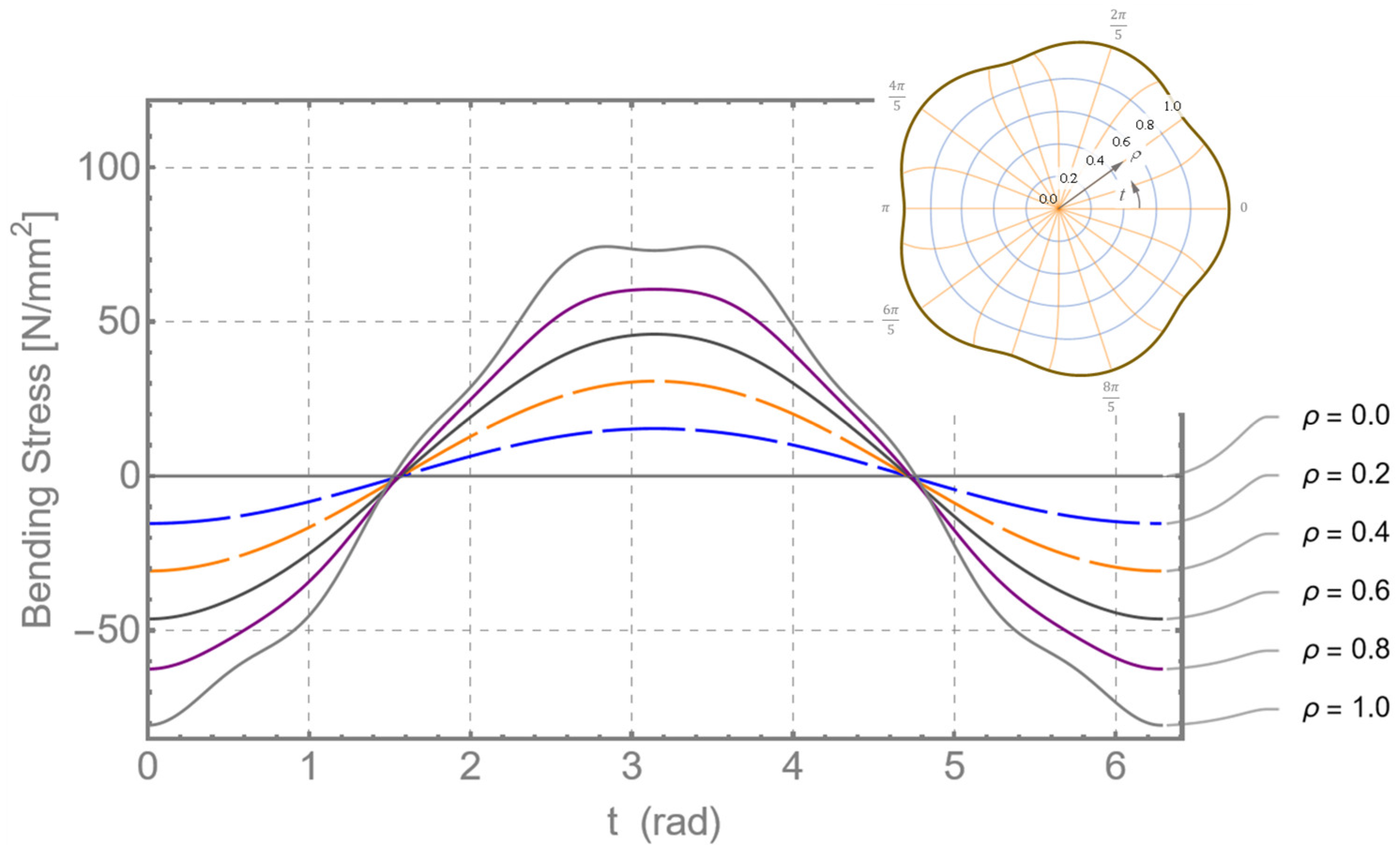
Bending stress according to [3]
For the general case of bending stress, according to [3], the following relationship can be determined for the bending stress due to a shear force:
σ z = − 4 F ρ l − z e ρ n sin ⁡ n t + t + ϕ + rsin ⁡ t + ϕ π e 4 n + 1 + 2 e 2 n + 2 r 2 + r 4
Here, ϕ denotes the angle of rotation of the shear force, F , around the z -axis. Variable ρ accepts the value 0 for the center point (neutral axis) and the value 1 for the outer profile contour. Figure 19 shows the distribution of the bending stress, according to Equation (59), for different ρ -lines.
Deformations
The deformations of the profile cross-section can be determined from (24) as functions of x and y with the known stress function φ 1 . The results for the three displacement components in curvilinear co-ordinates ( ρ , t ) are summarized in the appendix. If n = 5 is inserted into Equations (A9) to (A11), the following equations are obtained for the deformation components:
u x = F 6 E I y 3 ν ρ 2 l − z r 2 cos ⁡ 2 t + 2 ρ 5 r cos ⁡ 7 t + ρ 10 cos ⁡ 12 t + 3 l z 2 − z 3
u y = F E I y ν ρ 2 l − z r sin ⁡ t + ρ 5 sin ⁡ 6 t r cos ⁡ t + ρ 5 cos ⁡ 6 t
u z = F 132 E I y ρ 11 ρ 5 cos ⁡ 6 t 3 4 l z − 2 ν + ρ 12 − 2 z 2 − 3 − 2 r 2 ν − 3 ρ 2 + 4 − 33 r cos ⁡ t 2 z z − 2 l + 24 ν − 2 ρ 12 + r 2 2 ν − ρ 2 + 3 + 26 + 33 ρ 3 r 2 − 3 ν + ρ 4 − 2 cos ⁡ 4 t + 3 ρ 10 r − 2 ν + 11 ρ 2 − 13 cos ⁡ 11 t
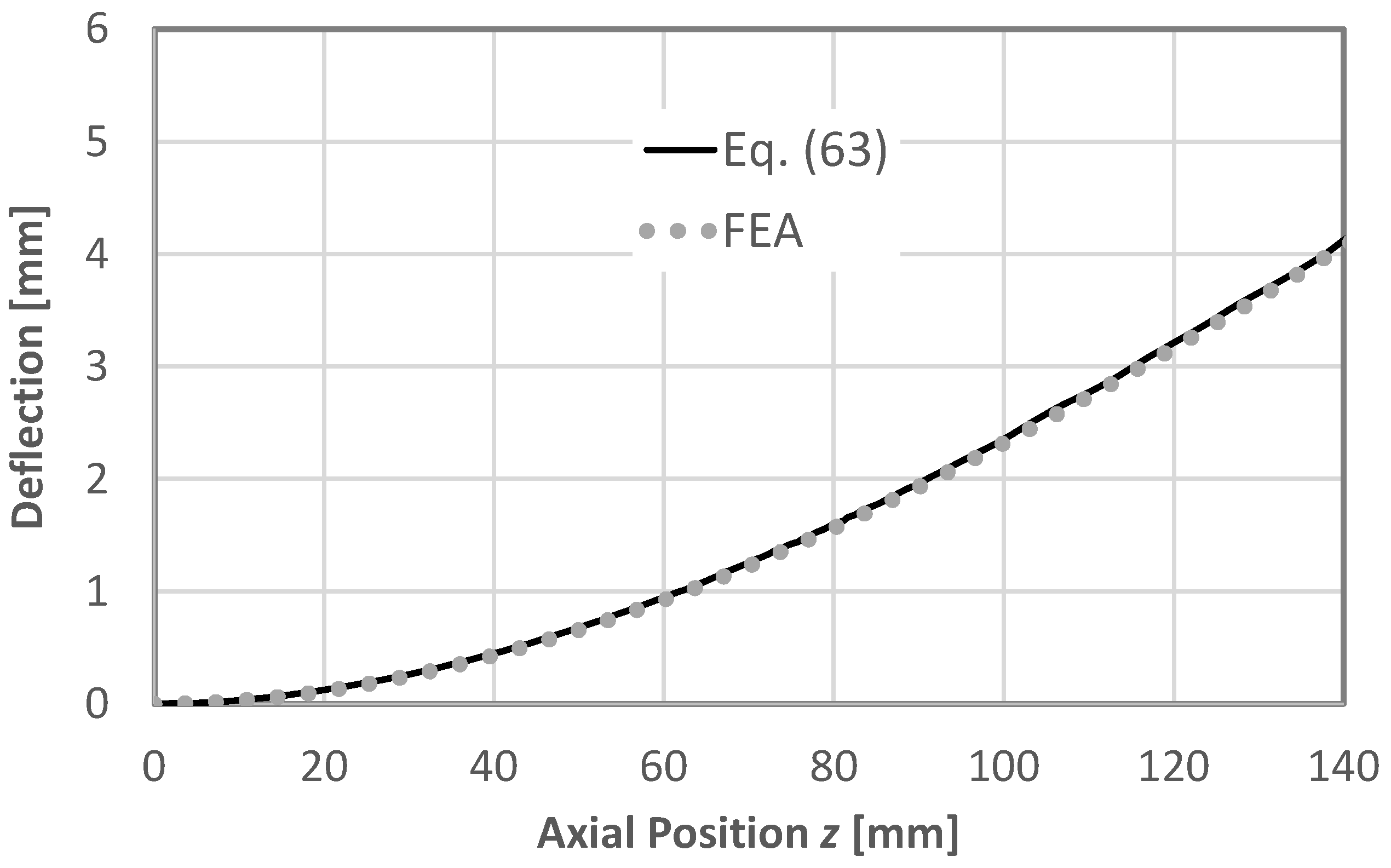
The deflection can then be determined from Equation (60) for the center of the cross-section (with ρ = 0 ) as follows:
f x = u x ρ = 0 = F 6 E I y 3 l − z z 2
Figure 20 compares Equation (63) with the results of the FEA, wherein a good match can be recognized.

4. Summary and Outlook

In this paper, first, the geometry of simple and higher epitrochoids, which are suitable for technical applications as positive shaft–hub connections, was depicted. An approach to determine the transverse shear stresses in non-circular elastic profile cross-sections was then presented. The formulation is based on the complex stress functions of Muskhelishvili [13]. The developed method was first applied to a round profile cross-section, and the results were compared to the solutions known from the literature, according to Timoshenko [16]. A complete agreement was proven. Furthermore, two epitrochoidal profiles with three and five flanks were examined. The analytical stress results show very good agreement with the numerical investigations from FEA. For the example with five flanks, the bending stresses were also determined and presented based on the approach described in Ziaei [3]. The elastic deformation components were also determined for both examples. An equation for determining the deflection was derived from u x , for which very good agreement with the FEA was also observed.
For the so-called H-profiles (hypotrochoids), no suitable mapping functions can be determined directly from parametric equations. Therefore, appropriate mappings using the method of Kantorovich [18] are to be developed and used to determine the stress function in future work. The results may be of interest for the hypotrochoidal profiles standardized in DIN 3689 [17].
In addition, the shear stresses due to a shear force can be super-imposed onto the torsional stresses in the case of combined loading. This issue is to be investigated in further study.

Appendix A

Mapping function for "simple" epitrochoids:
z ζ = r   ζ + e ζ n + 1
Surface area:
A = π e 2 1 + n + r 2
Area moment of inertia:
I y = 1 4 π e 4 n + 1 + 2 e 2 n + 2 r 2 + r 4
Real part of the stress function :
φ 1 = 1 4 n − 1 n + 1 2 n + 1 ρ e ρ n n − 1 ρ 2 n + 1 e 2 2 n + 1 ρ 2 n + 2 cos ⁡ 3 n + 1 t + r e ρ n 3 2 n + 1 ρ 2 cos ⁡ 2 n + 3 t − 2 ν + 2 n + 3 cos ⁡ 2 n t + t + 3 2 n + 1 ρ 2 rcos ⁡ n + 3 t − 2 n + 1 cos ⁡ n + 1 t e 2 2 ν + 3 n + 1 + 2 r 2 2 ν + n + 3 − 2 n 2 + 3 n + 1 r 2 2 ν + 2 ν n + n + 3 cos ⁡ n − 1 t − 2 n 3 + n 2 − 2 n − 1 ρ 2 rcos ⁡ t e 2 4 ν + 4 ν + 1 n + 6 + 2 ν + 3 r 2 + 2 n 3 + n 2 − 2 n − 1 ρ 4 r 3 cos ⁡ 3 t
Imaginary part of the stress function:
ψ 1 = 1 4 n − 1 n + 1 2 n + 1 ρ e ρ n n − 1 ρ 2 n + 1 e 2 2 n + 1 ρ 2 n + 2 sin ⁡ 3 n + 1 t + r e ρ n 3 2 n + 1 ρ 2 sin ⁡ 2 n + 3 t − 2 ν + 2 n + 3 sin ⁡ 2 n t + t + 3 2 n + 1 ρ 2 rsin ⁡ n + 3 t − 2 n + 1 sin ⁡ n + 1 t e 2 2 ν + 3 n + 1 + 2 r 2 2 ν + n + 3 − 2 n 2 + 3 n + 1 r 2 2 ν + 2 ν n + n + 3 sin ⁡ n − 1 t − 2 n 3 + n 2 − 2 n − 1 ρ 2 rsin ⁡ t e 2 4 ν + 4 ν + 1 n + 6 + 2 ν + 3 r 2 + 2 n 3 + n 2 − 2 n − 1 ρ 4 r 3 sin ⁡ 3 t
Stress component: τ x z
:
τ x z = F 4 π ν + 1 ρ 2 e 4 n + 1 + 2 e 2 n + 2 r 2 + r 4 1 e 2 n + 1 2 ρ 2 n + 2 e n + 1 r ρ n cos ⁡ n t + r 2 2 − 3 e 4 n + 1 2 ρ 4 n + 4 cos ⁡ 2 n + 1 t − e 3 n + 1 r ρ 3 n + 2 3 ρ 2 2 n + 3 cos ⁡ n + 2 t + cos ⁡ 3 n + 2 t − 2 ν + 2 n + 3 cos ⁡ n t − e 2 r 2 ρ 2 n − n + 1 cos ⁡ 2 t 2 ν + 2 ν n − 3 n + 3 ρ 4 + n + 3 − ρ 2 2 ν + 2 n + 3 cos ⁡ 2 n t + 3 2 n + 3 ρ 4 cos ⁡ 2 n + 1 t + e r ρ n ρ 2 cos ⁡ n t e 2 n + 1 6 ν + 4 ν + 1 n + 9 + r 2 2 ν n + 3 + 5 n + 9 + r 2 2 ν + 2 ν n − 3 n + 1 ρ 4 + n + 3 cos ⁡ n − 2 t − 3 n + 3 ρ 4 r 2 cos ⁡ n + 2 t + ρ 2 e 4 2 ν + 3 n + 1 2 ρ 2 n + 2 e 2 r 2 2 ν + n + 1 2 ν + n + 3 ρ 2 n + 2 ν n + 2 n + 3 + 2 ν + 3 r 4 − 3 ρ 4 r 4 cos ⁡ 2 t + 4 ν − 2 ρ 4 e ρ n sin ⁡ n t + t + rsin ⁡ t 2 − 4 ν ρ 4 e ρ n cos ⁡ n t + t + rcos ⁡ t 2
Stress component: τ y z
:
τ y z = − 2 F π ν + 1 e 4 n + 1 + 2 e 2 n + 2 r 2 + r 4 ν + 2 ρ 2 e ρ n sin ⁡ n t + t + rsin ⁡ t e ρ n cos ⁡ n t + t + rcos ⁡ t − 1 4 ρ 2 e 2 n + 1 2 ρ 2 n + 2 e n + 1 r ρ n cos ⁡ n t + r 2 3 e 4 n + 1 2 ρ 4 n + 4 sin ⁡ 2 n + 1 t + e 3 n + 1 r ρ 3 n + 2 3 ρ 2 2 n + 3 sin ⁡ n + 2 t + sin ⁡ 3 n + 2 t − 2 ν + 2 n + 3 sin ⁡ n t + e 2 r 2 ρ 2 n n + 1 sin ⁡ 2 t 2 ν + 2 ν n + 3 n + 3 ρ 4 + n + 3 − ρ 2 2 ν + 2 n + 3 sin ⁡ 2 n t + 3 2 n + 3 ρ 4 sin ⁡ 2 n + 1 t + 1 2 e r ρ n 2 ρ 2 sin ⁡ n t e 2 n + 1 2 ν + 4 ν + 1 n + 3 + r 2 2 ν n − 1 + n − 3 + r 2 4 ν n + 1 + 3 n + 1 ρ 4 + 2 n + 6 sin ⁡ 2 t − n t + 3 ρ 4 2 n + 3 sin ⁡ n + 2 t + n + 1 sin ⁡ n + 4 t − 3 ρ 4 r 3 cos ⁡ 3 t e n + 1 ρ n sin ⁡ n t + t + r sin ⁡ t + 3 2 ρ 4 r 4 sin ⁡ 2 t + sin ⁡ 4 t
Bending stress:
σ z = − 4 F ρ l − z e ρ n sin ⁡ n t + t + ϕ + rsin ⁡ t + ϕ π e 4 n + 1 + 2 e 2 n + 2 r 2 + r 4
Displacement in the x-direction:
u x = F 2 E I y l − z e 2 ν ρ 2 n + 2 cos ⁡ 2 n + 1 t + 2 e ν r ρ n + 2 cos ⁡ n + 2 t + ν ρ 2 r 2 cos ⁡ 2 t + z 2
Displacement in the y-direction:
u y = F E I y ν ρ 2 l − z e ρ n sin ⁡ n + 1 t + r sin ⁡ t e ρ n cos ⁡ n + 1 t + r cos ⁡ t
Displacement in the z-direction:
u z = F 4 E I y 1 ρ e 3 ρ 3 n + 4 cos ⁡ n t + t − e ρ n n − 1 ρ 2 cos ⁡ n t + t e 2 2 ν + 3 n + 1 + 2 n + 1 z z − 2 l + 2 r 2 2 ν − n + 1 ρ 2 + n + 3 + n + 1 r 2 2 ν + 2 ν n − n ρ 4 + n + ρ 4 + 3 cos ⁡ t − n t n 2 − 1 + ρ 2 rcos ⁡ t − 2 e 2 2 ν + 2 ν + 1 n + 3 + 4 ρ 2 e 2 ρ 2 n s i n 2 n t + t + r 2 s i n 2 t + 2 z 2 l − z − 2 ν + 3 r 2 + e 2 r ρ 2 n + 2 − 2 ν + 2 2 n + 1 ρ 2 − 2 n − 3 cos ⁡ 2 n t + t + 2 n + 1 ρ 2 cos ⁡ 2 n + 3 t 2 n + 1 + ρ 4 r 3 cos ⁡ 3 t
Deflection:
f x = u x ρ = 0 = F 6 E I y 3 l − z z 2
Formula symbols:
A mm2 Area of profile cross-section
e mm Profile eccentricity
e - Euler's number
E MPa Young’s modulus
F N Shear force
f x mm Deflection
f ζ Torsiol stress function in the polygon coordinate system
g ζ Bending stress function in the polygon coordinate system
G z Bending stress function in the Cartesian coordinate system
I y , mm4 Area moment of inertia in the Cartesian coordinate system
l mm Length of profile shaft
M b Nm Bending moment
n - Profile periodicity (number of sides)
r mm Nominal or mean radius
t - Profile parameter angle
u x ,   u y ,   u z mm Displacement components
x , y , z mm Cartesian coordinates
z ζ Complex function of polygon contour
Greek formula symbols:
ε = e / r - Relative eccentricity
ϕ Rotation angle of the coordinate system
ϕ x , y Real stress function in Cartesian coordinate system
λ = e i t - Physical plane unit circle
ν Poisson’s ratio
Φ 1 x , y Real part of stress function in Cartesian coordinate system
φ 1 Real part of stress function in polygon coordinate system
Ψ 1 x , y Imaginary part of stress function in Cartesian coordinate system
ψ 1 Imaginary part of stress function in polygon coordinate system
( ρ , t ) Curvilinear polygonal coordinates
σ z MPa Bending stress (z-component of stress vector)
τ x y ,   τ x z ,   τ y z MPa Shear sress components
τ MPa Total shear stress
ω ( ζ ) - Coformal mapping function
ζ - Complex variable in model plane

References

  1. Hibbeler, R.C. , Mechanics of Material, 8th Edition, Pearson, Prentice Hall, 2011.
  2. Ziaei, M. Torsionsspannungen in Prismatischen, Unrunden Profilwellen mit Trochoidischen Konturen, Forschung im Ingenieurwesen; Ausgabe 4/2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
  3. Ziaei, M. Bending Stresses and Deformations in Prismatic Profiled Shafts with Noncircular Contours Based on Higher Hybrid Trochoids. Appl. Mech. 2022, 3, 1063–1079. [Google Scholar] [CrossRef]
  4. Zwikker, C. The Advanced Geometry of Plane Curves and Their Applications, Dover Books on Advanced Mathematics, 1963.
  5. Wunderlich, W. : Ebene Kinematik. Mannheim: Bibl. Inst. 1968.
  6. Ziaei, M.: Optimale Welle-Nabe-Verbindung mit mehrfachzyklischen Profilen, 5. VDI-Fachtagung "Welle-Nabe-Verbindungen" in Nürtingen, 25./26. September 2012.
  7. Frank, A.; Pflanzl, M.; Mayer, R.: Vom K-Profil und Polygonprofil zu funktionsoptimierten Unrundprofilen – eine österreichische Entwicklung. Präzision im Spiegel, Herbst 1992, S. 42-48.
  8. Musyl, R.: Die kinematische Entwicklung der Polygonkurve aus dem K-Profil. Wärmewirtschaft 10 (1) 18-22, 1955.
  9. DIN 32711, Welle-Nabe-Verbindung - Polygonprofil P3G, Teil 1, Deutsches Institut für Normung e. V., Berlin 2009.
  10. Ziaei, M. : Analytische Untersuchung unrunder Profilfamilien und numerische Optimierung genormter Polygonprofile für Welle-Nabe-Verbindungen „Habilitationsschrift“, Technische Universität Chemnitz, 2002.
  11. Maximov, J.T.; Hristov, H.: Machining of Hypocycloidal Surfaces by Adding Rotations around Parallel Axes, Part I: Kinematics of the Method and Rational Field of Application. Trakya Univ J Sci, 6(1), 1-11, 2005.
  12. Iprotec GmbH, Polygonverbindungen, www.iprotec.de.
  13. Muskelishvili, N.I.: Some Basic Problems of the Mathematical Theory of Elasticity, Springer Dordrecht 1977.
  14. Ziaei, M. Bending and Torsional Stress Factors in Hypotrochoidal H-Profiled Shafts Standardised According to DIN 3689-1. Eng 2023, 4, 829–842. [Google Scholar] [CrossRef]
  15. Sokolnikoff, I.S.: Mathematical Theory of Elasticity. Robert E. Krieger Publishing Company, Malaba, Florida, 1983.
  16. Timoshenko, S.P.; Goodier, J.N.: Theory of Elasticity. McGraw-Hill Book Company, 1985.
  17. DIN 3689-1:2021-11, Shaft to collar connection - Hypotrochoidal H-profiles - Part 1: Geometry and dimensions. Beuth-Verlag, Berlin 2021-12.
  18. Kantorovich, L.V.; Krylov, V.I. Approximate Methods of Higher Analysis; Dover Publications: Dover; Translation Edition, Mineola, New York, USA: 2018.
Preprints 113540 g001
Figure 1. Effect of bearing type on maximum cross-section load.
Figure 1. Effect of bearing type on maximum cross-section load.
Preprints 113540 g001
Preprints 113540 g002
Figure 2. a): Distribution of shear stress according to the classical parallel distribution approach; b): real shear distribution.
Figure 2. a): Distribution of shear stress according to the classical parallel distribution approach; b): real shear distribution.
Preprints 113540 g002
Preprints 113540 g003
Figure 3. Generation of simple epicycloids.
Figure 3. Generation of simple epicycloids.
Preprints 113540 g003
Preprints 113540 g004
Figure 4. Epitrochoids with different numbers of sides and eccentricities.
Figure 4. Epitrochoids with different numbers of sides and eccentricities.
Preprints 113540 g004
Preprints 113540 g005
Figure 5. Epitrochoidal inner and outer contours for shaft–hub connections produced using the twin-spindle process; source: Iprotec:Guido Kochsiek [12].
Figure 5. Epitrochoidal inner and outer contours for shaft–hub connections produced using the twin-spindle process; source: Iprotec:Guido Kochsiek [12].
Preprints 113540 g005
Preprints 113540 g006
Figure 6. Generation of the higher epitrochoids.
Figure 6. Generation of the higher epitrochoids.
Preprints 113540 g006
Preprints 113540 g007
Figure 7. Examples of higher epitrochoids.
Figure 7. Examples of higher epitrochoids.
Preprints 113540 g007
Preprints 113540 g008
Figure 8. Comparison of the simple and higher epitrochoids.
Figure 8. Comparison of the simple and higher epitrochoids.
Preprints 113540 g008
Preprints 113540 g009
Figure 9. Definition of the co-ordinate system.
Figure 9. Definition of the co-ordinate system.
Preprints 113540 g009
Preprints 113540 g010
Figure 10. Illustration of the conformal mapping for transforming the unit circle ( r = 1 ) on the cross-sectional area, which is exemplary for an epitrochoid with four sides ( n = 4 ).
Figure 10. Illustration of the conformal mapping for transforming the unit circle ( r = 1 ) on the cross-sectional area, which is exemplary for an epitrochoid with four sides ( n = 4 ).
Preprints 113540 g010
Preprints 113540 g011
Figure 11. Distribution of the shear stress component τ x z on a circular cross-section from FEA and Equation (32).
Figure 11. Distribution of the shear stress component τ x z on a circular cross-section from FEA and Equation (32).
Preprints 113540 g011
Preprints 113540 g012
Figure 12. Distribution of the shear stress component τ x z on the round profile contour from FEA and Equation (37).
Figure 12. Distribution of the shear stress component τ x z on the round profile contour from FEA and Equation (37).
Preprints 113540 g012
Preprints 113540 g013
Figure 13. ρ and t -constant lines for the epitrochoid with n = 3 and e = r / 16 , according to Equation (46).
Figure 13. ρ and t -constant lines for the epitrochoid with n = 3 and e = r / 16 , according to Equation (46).
Preprints 113540 g013
Preprints 113540 g014
Figure 14. Distribution of the shear stress component τ x z on the epitrochoidal cross-section with n = 3 from FEA and Equation (48).
Figure 14. Distribution of the shear stress component τ x z on the epitrochoidal cross-section with n = 3 from FEA and Equation (48).
Preprints 113540 g014
Preprints 113540 g015
Figure 15. Distribution of the total shear stress τ on the epitrochoidal profile contour with n = 3 from FEA and Equation (50).
Figure 15. Distribution of the total shear stress τ on the epitrochoidal profile contour with n = 3 from FEA and Equation (50).
Preprints 113540 g015
Preprints 113540 g016
Figure 16. ρ - and t -constant lines for the epitrochoid with n = 5 and e = r / 20 , according to Equation (52).
Figure 16. ρ - and t -constant lines for the epitrochoid with n = 5 and e = r / 20 , according to Equation (52).
Preprints 113540 g016
Preprints 113540 g017
Figure 17. Distribution of the shear stress τ x z on a five-sided epitrochoidal cross-section from FEA and Equation (55).
Figure 17. Distribution of the shear stress τ x z on a five-sided epitrochoidal cross-section from FEA and Equation (55).
Preprints 113540 g017
Preprints 113540 g018
Figure 18. Distribution of the resulting shear stress for different ρ -lines on the epitrochoidal cross-section.
Figure 18. Distribution of the resulting shear stress for different ρ -lines on the epitrochoidal cross-section.
Preprints 113540 g018
Preprints 113540 g019
Figure 19. Distribution of the bending stress on the profile cross-section for different ρ -lines.
Figure 19. Distribution of the bending stress on the profile cross-section for different ρ -lines.
Preprints 113540 g019
Preprints 113540 g020
Figure 20. Deflection according to Equation 63 compared with the FEA results.
Figure 20. Deflection according to Equation 63 compared with the FEA results.
Preprints 113540 g020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated